Research on intelligent three-dimensional anchor position detection method for ships utilizing Traversal and Monte Carlo algorithms

As intelligent ship technology advances, the importance of intelligent anchor position detection, as one of the key technologies, can ensure the safe anchoring of ships and enhance the efficiency of port operation. At present, most of the anchor position selection and detection algorithms are mainly based on two-dimensional planes, and there is a lack of research on the intelligent detection of safe water depth for ship anchoring in three-dimensional space. It not only restricts the full utilization of anchorage resources but also affects the safety and environmental adaptability of anchoring operations. To address these issues, this study proposes a three-dimension anchor position detection method. Firstly, based on the establishment of a three-dimensional ocean model, the possible anchor positions selected by the ship are simulated using the Monte Carlo algorithm. Secondly, the simulated anchor positions are optimized using a Traversal algorithm to filter out the optimal anchoring position that meets the requirements, the safety distance between each point and the existing ship is calculated, and the anchor position is determined according to the corresponding required safety spacing. Finally, to verify the applicability and effectiveness of the method under different sea conditions and different ship types, this study conducts a series of simulation experiments with 5000 random samples. These experiments compare the demand of anchor position selection for anchoring ships with changing water depths in the case of empty and full load drafts, and visualize the impact of varying water depth parameters on the selection of anchor positions for anchoring ships in various ship types. The outcomes of the experiment indicate that the algorithm’s detection area encompasses the whole anchorage area, ensuring both the anchorage area’s usage rate and the accuracy of anchor position detection. This study demonstrates that the Traversal and Monte Carlo Algorithms effectively improve the accuracy of the selection of anchoring position of the ship, makes full use of the resources of anchorage, and further improves the safety and efficiency of the anchoring operation.

1 Introduction

1.1 Background

With the increasing importance of oceans in the 21st century, the advancement of intelligent ships has become the focus of global attention (Yan, 2016). Intelligent ships not only represent the forefront of shipping industry technology but also an important pillar of future marine transportation. On a global scale, countries have invested resources to promote the research and application of intelligent ship technology (Chen and Yang, 2019). The intelligent ship technology covers several functional modules, for example, through the integrated use of Global Positioning System (GPS) navigation, radar perception, and intelligent algorithm, they achieve autonomous path planning and obstacle avoidance operation, thus enhance the safety and efficiency of navigation (Zhang et al., 2021). At the same time, these systems can optimize the cargo handling process and improve the efficiency of port operations. With the help of accurate positioning technology and intelligent control system, intelligent ships can realize automatic berthing operation, greatly reducing the risk and error of manual operation.

Anchoring operation is the key link in the process of ship operation, including anchoring, adjusting the length of the anchor chain. Crew errors during anchoring operations can lead to accidents at sea, such as cargo pump unloading operations (Sezer et al., 2024), tanker oil handling and oil spill risks (Aydin et al., 2024b), pilot transfer operations at sea (Aydin et al., 2022), and fire and explosion incidents in bulk carrier cargo compartments and decks (Aydin et al., 2024a). Therefore, the accuracy and safety of anchoring operations are crucial to the overall operation of the ship. However, there is relatively few intelligent research and application in this field. To make up for this shortage, the application of anchoring detection technology is particularly important. Through the intelligent anchoring system, the ship can achieve more accurate positioning and safer anchoring, and further improve the autonomous operation ability. Therefore, it is necessary to further pay attention to and develop intelligent anchoring detection technology to comprehensively improve the operational performance of intelligent ships, and inject new impetus into the development of the global economy by continuously promoting the research and application of ship technology.

The precision and effectiveness of ship anchor position detection are greatly influenced by intelligent detection technology for anchor positioning, which is one of the critical technologies to guarantee ship safety and enhance port operation efficiency against the backdrop of rapidly developing intelligent ship technology. The traditional planar, two-dimensional observation method is still commonly used today when ships perform anchoring operations. This means that in real operations, the captain’s comprehensive assessment of the ship’s distribution, wind, and wave currents, and other external environments is typically used to determine the ship’s anchor position. To protect the ship during anchoring operations, an increased anchoring radius is typically used, which partially results in the waste of anchorage resources. On the other hand, there can be risks if the anchoring radius is set too short. As a result, this anchor position selection approach struggles to fulfill the demands of modern navigation practice due to its low accuracy and significant risks. However, the majority of existing anchor detection methods do not account for the relationship between the ship’s draft and the anchorage area’s depth, which could reduce the accuracy of the anchor detection model and make it more difficult for crew and shore management staff to accurately assess the anchorage area’s safety. Additionally, ships frequently encounter large ships anchored in deep water in the anchorage area during normal shipping operations. In the field of intelligent ships, a key technology that needs to be researched is an intelligent anchoring detection system that combines high efficiency with good safety performance.

1.2 Literature review

In the field of anchorage operation, the existing studies focus on anchor position allocation, anchor position detection, and intelligent anchor position selection.

In terms of anchor position assignment, Huang et al. (2011) discussed the methods and criteria for assessing anchorage capacity considering multiple and other factors, and at the same time, discussed the feasibility of utilizing technological tools such as Monte Carlo simulation to improve anchorage utilization, providing practical suggestions for anchorage management and planning. Li et al. (2020) proposed a calculation method of anchorage capacity of the anchorage based on the simulation of the Monte Carlo algorithm, which can solve the problems of improving the anchorage’s rate of use and safety under the consideration of a variety of external environmental factors, and was widely used in the fields of the anchorage planning and the safe operation and management. However, this method selected the anchored vessels under uniform ship type, which was not in line with the situation of mixed casting of multiple types of anchored vessels in the actual anchorage. Cao et al. (2022) used the Monte Carlo stochastic algorithm to simulate the target ships to be anchored under multiple ship types, which not only improved the simulation experiment by more ship samples, but also realized the ship anchorage detection in two-dimensional space on the water surface, and then put forward a new intelligent detection algorithm for Maritime Autonomous Surface Ships (MASS) single-anchor anchoring area. However, the algorithm did not fully consider the impact of the water depth factor on anchoring operation, so the applicability and stability of the existing model under the dynamic variation of the anchorage and the complex environment need to be further verified.

On the aspect of anchor position detection, Zhao et al. (2023) put forward a dynamic multi-objective berth allocation optimization model and used a genetic algorithm-based multi-objective optimization technique to solve the model and optimize the position allocation of anchored ships. The dynamic multi-target anchor allocation optimization model had high computational complexity and long optimization time when dealing with large-scale practical applications, which affected the efficiency of practical applications. However, when the existing model deals with multi-objective optimization, it lacks sufficient flexibility for the trade-offs among various objectives (such as safety, efficiency, cost, etc.), which may lead to the unsatisfactory optimization effect of some objectives. Madadi and Aksakalli (2020) used Monte Carlo simulation to study the three-objective dynamic anchorage planning, including anchorage utilization rate, ship collision risk, and fuel consumption performance, and simulated and measured the influence of different planning index combinations on the objective function. Malekipirbazari et al. (2015) improved the computational efficiency of the original algorithm by introducing a heuristic algorithm considering the uneven water depth of anchorage.

With regard to intelligent anchor position selection, Yin and Zhang (2022) proposed a method for unmanned ship single anchor anchoring position selection based on a decision tree algorithm, which combined the decision tree algorithm with raster processing technology, and initially applied water depth information and bottom mass analysis to enrich the consideration factors for intelligent ship anchorage selection. However, the current intelligent anchor selection model does not consider the variability of the actual environment, so further research and optimization of the application effect of information and substrate analysis in different environments are still needed. Meanwhile, to meet the actual needs of intelligent ships, the introduction of research on deep learning technology can undoubtedly improve the response speed and application efficiency of intelligent ships. A surface target detection algorithm for intelligent ships was presented by Liang et al. (2021). The algorithm utilized deep learning technology to effectively detect and identified water surface targets with full consideration of the complexity and variability of the water surface environment. It not only improved the accuracy and efficiency of target detection but also better met the needs of intelligent ships for rapid response to surface targets during navigation. Yasir et al. (2023) system reviewed the research conducted between 2016 and 2022, summarized the application and limitations of deep learning technology in ship inspection, and called for more attention to deep learning technology in future intelligent ship research. Er et al. (2023) re-examined the existing ship inspection technology, collected and analyzed popular data sets, unified the evaluation standards of ship inspection, and initially improved the efficiency of intelligent ship inspection. The application of deep learning technology in ship inspection is not extensive enough, there is a lack of empirical research, and the field of ship inspection lacks systematic methodology, unified evaluation standards, and widely accepted data sets. When deep learning models deal with complex scenarios in ship inspection, they still face problems of accuracy and reliability.

In summary, there is few studies on the intelligent detection of a ship’s anchor position, and the existing research results mainly focus on the safety spacing of anchor position, anchorage planning, anchorage utilization, etc., whereas the current development of ship intelligent technology needs more accurate detection methods as support. Aiming at the current status of insufficient research on 3D anchor position detection considering water depth, and to bridge the gap of research cognitive re-updating, this study proposes a 3D anchor position intelligent detection model combining with water depth Traversal algorithm on the basis of Monte Carlo algorithm (Cui et al., 2024), and simulates the ship’s anchoring area, which is different from the common 2D sea simulation calculation. The proposed intelligent detection methods are inspired by advanced machine learning models that have been effectively used in offshore operations to predict results such as carbon emissions and accident severity. Similar to advanced machine learning methods for enhancing the precision of maritime accident severity prediction (Feng et al., 2024a; Shi et al., 2024), the proposed algorithm optimizes the anchor position by considering environmental and operational factors (Feng et al., 2024b). In this study, a Monte Carlo stochastic simulation algorithm is utilized to select anchoring points on a planar surface, integrating a water depth Traversal algorithm to evaluate the water depth within the designated anchoring circle. Additionally, a constraint regarding the minimum safe water depth for ship anchoring is imposed. Consequently, a detection model for anchor positions within a three-dimensional space is established, offering a multidimensional and comprehensive detection framework that addresses existing deficiencies in the anchoring process. Meanwhile, the establishment of a unified evaluation standard and data set will correspondingly improve the efficiency and reliability of ship detection. In turn, it can enrich the considerations of intelligent anchor position selection based on existing research, and strengthen the application of three-dimensional regional anchor position detection technology in intelligent anchor position selection.

2 Materials and methods

2.1 Monte-Carlo method

The Monte-Carlo method is a computational technique grounded in probabilistic statistics that estimates the solution to a problem by generating numerous random samples. Its fundamental principle involves leveraging randomness to address complex computational challenges. The algorithm is widely used in the fields of estimation (Lashomb et al., 2024; Gucma and Schoeneich, 2008), optimization (Homem-de-Mello and Bayraksan, 2014), simulation (Mordechai, 2011; He et al., 2020), etc., and shows unique advantages in dealing with high-dimensional, non-linear, or difficult-to-model accurate problems.

The problem of detecting the anchorage area of a ship is based on the same scientific principles as solving these engineering difficulties, that is, multiple uncertainties in the anchoring area are modeled by random sampling under predefined input conditions, and the results are finally analyzed scientifically and comprehensively. In this study, random number generation is utilized to simulate multiple factors within the anchoring area, such as ship position, resulting in a variety of possible outcomes. The anchoring point can be stabilized by repeatedly running the simulation computations, and suitable anchoring locations can be accurately identified in subsequent steps. However, in intricate dynamic environments that consider the water depth factor, the inherent randomness of the Monte Carlo simulation algorithm may lead to the oversight of potential anchor points when determining the ship’s anchoring position through simulation. This, in turn leads to a reduction in the accuracy of the algorithm. In order to make the simulation more accurate, 5000 times of random simulation and the Traversal algorithm were used to optimize the Monte Carlo simulation results. The Traversal algorithm can systematically analyze the entire anchoring area to ensure that no potential suitable anchor points are missed, thus reducing the problem of missing anchor points due to randomness. This combination method not only ensures the rationality of anchoring position selection but also improves the overall accuracy and reliability of the algorithm under a complex dynamic environment.

2.2 Traversal algorithm

The Traversal algorithm is a method for accessing or searching all elements of a data structure such as an array, list, tree, or graph. The goal of such an algorithm is to access each element of a data structure once and only once to perform some operation or inspection. It is widely used in various data structures such as array or list traversal (Hong, 2001), tree data structures (Kalra and Bhatt, 1985), depth-first search algorithms and breadth-first search algorithms (Eppstein, 1996). The traversal algorithms have also been widely used and deeply explored in the research related to intelligent ships. For example, unmanned ship path planning (Lyu et al., 2019), obstacle detection and analysis (Li et al., 2022), and autonomous traversal in complex environments (Tian et al., 2004) have been developed to solve the complex problems of intelligent ships in various aspects, such as design, navigation, maintenance, and safety assessment. The algorithms can help intelligent ships systematically traverse and evaluate various scenarios to find optimal or feasible solutions.

To address the potential issue of omitting anchor point, this study innovatively proposes an intelligent anchor position detection algorithm that combines a Monte Carlo algorithm with a Traversal algorithm. This hybrid method leverages the systematic and exhaustive search capabilities of the Traversal algorithm alongside the stochastic and flexible nature of the Monte Carlo algorithm. The combination can ensure the effective retrieval of most of the points within the simulation experiment area, significantly reducing the possibility of overlooking some suitable anchor position points.

Through the systematic search strategy of the Traversal algorithm, an exhaustive and orderly traversal of the target space can effectively avoid the omission of certain nodes in the experimental process and ensure the comprehensiveness of the experiment. In this study, by setting the initial conditions and loop order, the platform will traverse the circle of anchor points drawn by anchor points that meet the two-dimensional safety spacing. Additionally, by flexibly adjusting the constraints such as step length and interval, the optimal traversal results are obtained. In this circumstance, the traversal results are calibrated with the water depth, and then the anchor points that satisfy the three-dimensional water depth restriction are fished out again. Eventually, it will make good preparation for the subsequent accurate detection of the applicable anchoring position. In addition, the concept of an optimized dataset is introduced in the screening of traversal results, which reduces the repeated calculation of anchor points in the simulation experiment and improves the computational efficiency of the Traversal algorithm. The computational results are also counted in the optimized dataset during the bathymetric validation process. The approach reduces the traversal operation rate and significantly improves the effectiveness of the bathymetric detection.

2.3 Anchor position circle radius model and safe spacing model

This study employs a simplified model for the anchorage radius, derived from the standard chain length used by Chinese anchored ships. The radius can be calculated using (Equation 1) presented below:

$\begin{array}{ll}\{\begin{array}{c}R=L+3H+90,(\text{Wind force }\le 7)\\ R=L+4H+145,(\text{Wind force >}7)\end{array}& (1)\end{array}$

where, R denotes the radius of the ship's anchor circle, L represents the overall length of the anchored ship, H stands for water depth (m).

For this reason, the safe spacing between two anchored ships of the same type should satisfy the (Equations 2, 3):

$\begin{array}{ll}\{\begin{array}{c}{D}_S\ge \sigma R_1+\tau R_2\\ R_1=L_1+3H+90\\ R_2=L_2+3H+90\end{array}\text{ (Wind force }\le \mathrm{7)}& (2)\end{array}$

$\begin{array}{ll}\{\begin{array}{c}{D}_S\ge \sigma R_1+\tau R_2\\ R_1=L_1+4H+145\\ R_2=L_2+4H+145\end{array}\text{ (Wind force }>\mathrm{7)}& (3)\end{array}$

where, $D_s$ indicates the required safe separation between ships, $L_1$, $L_2$ represents the length of the ships that will be anchored and the ones that are now anchored, respectively, $R_1$ and $R_2$ are the radius of the anchor circle of the ships that will be anchored and the ones that are now anchored (m), $\sigma$, $\tau$ represents the ship type, $\sigma ,\tau \in [1,1.2]$, if the ship is carrying general cargo, use the lower limit; if the ship is carrying oils, liquefied gas or chemicals, use the upper limit (Xie et al., 2024).

2.4 Anchoring area detection model

A Plane Rectangular Coordinate System is established on the plane of the anchorage area to assign plane coordinates to the existing ships or other obstructions that hinder the operation of the anchorage. The Euclidean metric method is employed to build the anchoring position detection model of the anchoring ship, which is used to choose the anchoring position that satisfies the safe distance between ships, as shown in (Equation 4):

$\begin{array}{ll}\{\begin{array}{c}{d}_n=\sqrt{{(x_a-x_n)}^2+{(y_a-y_n)}^2}\\ Min(d_n)\ge D_s\end{array}& (4)\end{array}$

where, $d_n$ represents the actual spacing value of the ship, $Min(d_n)$ denotes the minimum value of $d_n$, $(x_n,y_n)$ denotes the position of current ships or other obstructions impede anchoring operations within the Cartesian coordinate system where the anchorage is situated, point $(x_a,y_a)$ represents the anchoring position that satisfies the required safe separation between anchored ships.

2.5 Safe water depth model

This study determines the ship’s demand for under-keel clearance when anchoring by utilizing (Equation 5) (Hong, 2016):

$\begin{array}{ll}\{\begin{array}{c}\mathit{h}\mathbf{=}\mathit{k}\mathbf{\times }\mathit{d}\mathbf{+}{\mathit{h}}_{\mathit{w}}\\ \mathit{h}\mathbf{>}{\mathit{H}}_{\mathit{m}}\end{array}& (5)\end{array}$

where, h represents the safe anchoring depth required for the ship to be anchored, d indicates the maximum draft of the ship when anchor, k is the sheltering coefficient, which is set at 1.2 under calm conditions or with good sheltering, and 1.5 in cases of surge or poor sheltering, h_w indicates the wave under-keel clearance, generally between 2 to 3 meters, and H_m indicates the simulated draft depth of the ship to be anchored. To enhance the safety of anchorage selection, we use the upper limit of the sheltering coefficient k, which allows the simulation experiments to fully account for the safety hazards posed by unfavorable conditions such as poor clearance, ship pitch, and surge (Hong, 2016). In the initial stage, based on the recommendations from the British “Offshore Buildings”, the wave under-keel clearance is determined to be 20% of the ship’s maximum draught.

3 Experiment and simulation

3.1 Experimental procedure

In order to test the accuracy of the Monte Carlo-based anchor area detection model, simulation experiments were performed according to the following detailed steps, with the logical diagram of the model solution shown in Figure 1.

Figure 1

Figure 1. Model solving logic.

Step 1: Using MATLAB simulation software, create a three-dimensional anchorage area with a water depth of 20 to 40 meters that is 3 nautical miles by 3 nautical miles.

Step 2: Utilizing information gathering devices such as Automatic Identification System (AIS) or radar devices, find out the two-dimensional coordinates of any ships that are currently in the anchorage region as well as information about obstacles, denote the coordinates as $(x_1,y_1)$, $(x_2,y_2)$…… $(x_n,y_n)$, and the aggregate of coordinates is marked as $S_b$, and input this information to determine the anchorage radius of current ships using an optimized model for the ship anchorage radius.

Step 3: Using the two-dimensional coordinates of the anchorage obstruction in Step 2 as the center of the circle, set the restricted water area of the safe radius $R_d$, and its coordinates set is $S_d$.

Step 4: Enter pertinent data such as the length of ship and the length of anchor chain of current ships into the safety spacing model as illustrated in (Equation 2) or (Equation 3) for calculating the anchorage radius and ship safety spacing value D of current ships.

Step 5: Utilizing the Monte Carlo stochastic algorithm to produce n sets of two-dimensional coordinates $(x_1\text{'},y_1\text{'})$, $(x_2\text{'},y_2\text{'})$…… $(x_i\text{'},y_i\text{'})$…… $(x_n\text{'},y_n\text{'})$, denoted as $S_m$, to simulate the selection of anchorage points for ships awaiting anchorage.

Step 6: Employing the anchorage area detection model of the anchored ship as demonstrated in (Equation 4) to iteratively calculated the coordinate sets $S_b$ and $S_m$ to get the two-dimensional coordinates $(X_{e1},Y_{e1})$, $(X_{e2},Y_{e2})$…… $(X_{ei},Y_{ei})$…… $(X_{en},Y_{en})$ of the ship’s anchoring points to be anchored meeting the value D for the ship’s safety spacing in Step 4, with the coordinate set denoted as $S_e$.

Step 7: Construct the Traversal algorithm with the following procedure:

1. Set the initial state: take the anchor position point in the set as the circle’s center, and draw the anchor position circle with the anchoring radius.

2. Determine the loop condition: traversal operation from the origin $center\_x(1)$ to the point $center\_x(n)$, in order.

3. Simulate the operation: starting from the origin, traverse through the path from top to bottom and from left to right in steps of 1 meter interval. Record the traversal results.

Step 8: The anchor position point in the circle’s center, the radius of the anchoring as the radius of the anchor position circle, in the range of the anchor position circle, from the origin $center\_x(1)$ to the point $center\_x(n)$ of the traversal operation, starting from the starting point, in the first traversal, after the point of the depth of the water depth verification results will be added to a new data dimension, identifying the depth of the water to meet the needs. $(x_r,y_r,h_r,1)$ denotes for satisfying the safe water depth limit, $(x_r,y_r,h_r,0)$ stands for failing to satisfy the safe water depth limit, and $(x_r,y_r,h_r)$ denotes for traversing the points and incorporating the data from the water depth calibration operation into set $S_{S1}$; for the second traversal, the coordinates of the traversed points are compared with the coordinates in the set $S_{S1}$, additionally, if such a coordinate exists, the water depth calibration data is then directly used, meanwhile, for the coordinates that don’t have the data in the set $S_{S1}$ the data values are incorporated in the set after the water depth calibration $S_{S2}$; By traversing the path from top to bottom and from left to right with a certain step interval, and checking the traversal result with the draft value of the ship to be anchored to get the anchor point of the ship to be anchored that meets the requirements of two-dimensional plane and three-dimensional water depth. The set of points is noted as $S_f$, and it is judged that the points within the anchor circle drawn with the coordinate point within the set $S_f$ as the center of the circle are not within the set of points $S_d$ and the set of points that meets the requirements is noted as S_g, and its coordinates are marked as $({\phi }_1,{\lambda }_1,h_1)$, $({\phi }_2,{\lambda }_2,h_2)$,… $({\phi }_i,{\lambda }_i,h_i)$,…, $({\phi }_m,{\lambda }_m,h_m)$.

Step 9: The results obtained from the traversal are checked against the model (5) and the water depth values in Table 1. If all points traversed within this anchor position circle satisfy the water depth requirement, then this point is the anchor position point of the ship to be anchored that satisfies the 2D planar and 3D water depth requirements and is labeled with this coordinate as $(X_1,Y_1,Z_1)$, $(X_2,Y_2,Z_2)$… $(X_n,Y_n,Z_n)$. The set of coordinates is $S_E$.

Table 1

Table 1. Required safety water depth for ship anchoring (unit: m).

Step 10: The three-dimensional anchor point acquired in Step 8 that satisfies the safety spacing and meets the water depth limit is converted into the three-dimensional coordinates of the drop anchor point understood by the ship position sensor and sent to the electronic chart or other relevant equipment, and the ship to be anchored selects a suitable location for the anchor operation by the actual need.

3.2 Parameter setting

This study establishes an anchorage simulation system for evaluating and contrasting the impact of various ship types on anchorage choice. In this system, a 3D intelligent anchorage detection algorithm is utilized to identify the optimal anchoring position for a ship. This algorithm integrates the Monte Carlo random plane anchoring position detection method with a depth detection Traversal algorithm, employing both real data from ship design parameters and synthetic data generated through Monte Carlo simulation.

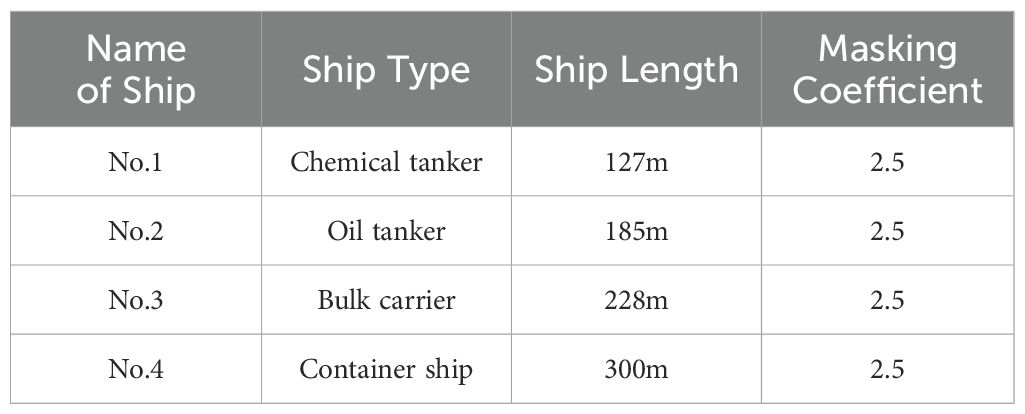
Initially, a 3D anchorage sea area measuring 3 nautical miles by 3 nautical miles is created using MATLAB. Ningbo Zhoushan Harbor features numerous anchorages with water depths ranging from 3 m to 51 m. For this study, water depths between 20 m and 40 m are selected, as they are suitable for accommodating large ships without being excessively deep, thereby meeting the requirements of most commercial ships. Consequently, this study references the water depth data from Ningbo Zhoushan Harbor to establish anchorage depths within the 3D sea area at 20-40 meters. The ship type chosen for this study is the standard type representative of common ship classifications, with relevant parameters provided in Table 2.

Table 2

Table 2. The ship parameters selected for the simulation experiment.

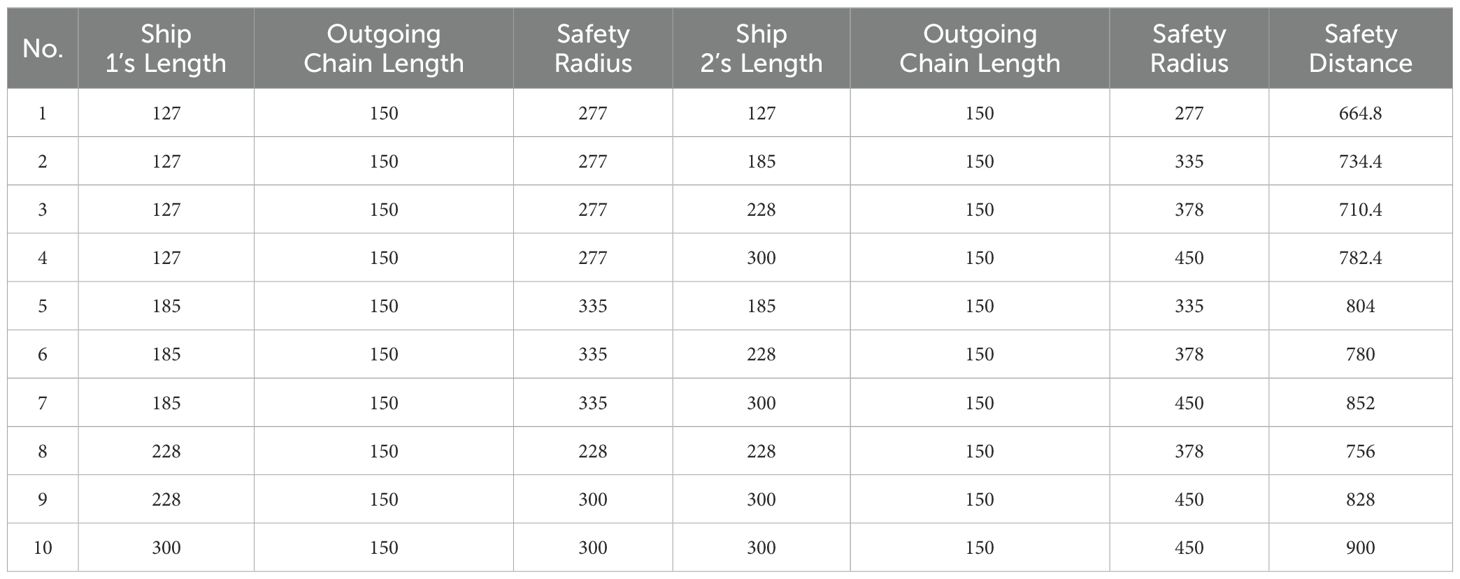
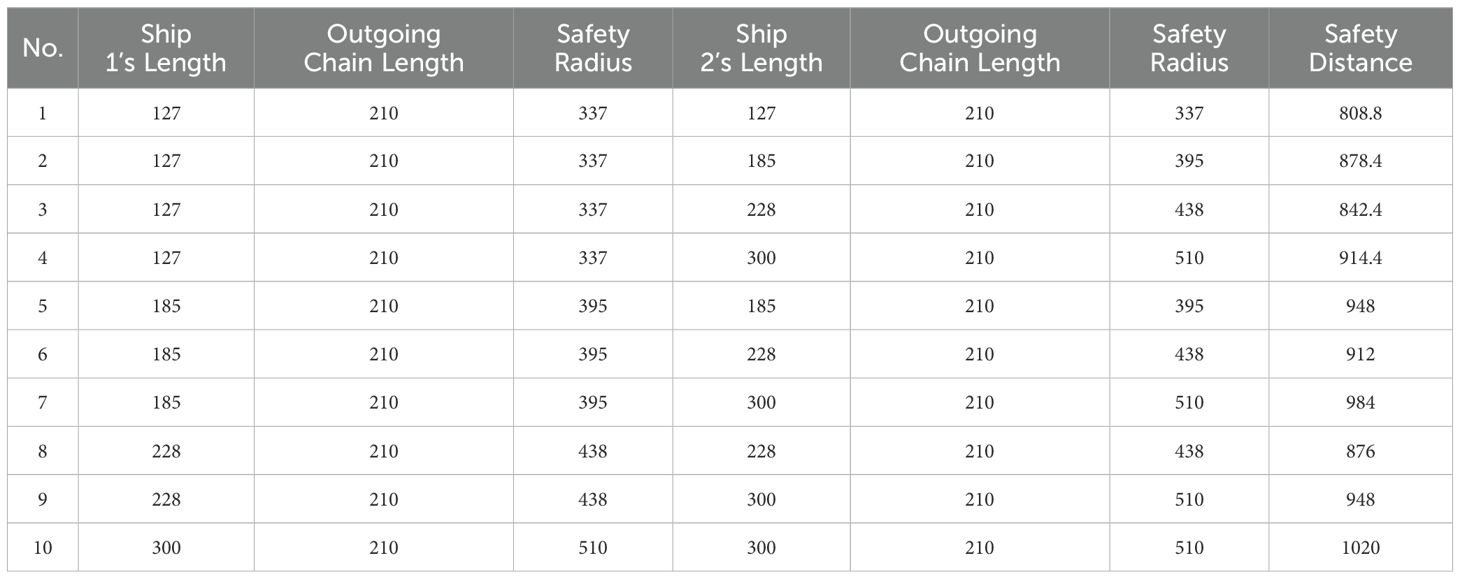
The anchorage area detection simulation was conducted using MATLAB, utilizing the ship parameters outlined in Table 2 along with the anchoring ship safety distance model. The current ships within the anchorage and those waiting to anchor are categorized into the four specified types. The spacing between current ships in the anchorage adheres to the necessary safe separation requirements for anchoring ships. Additionally, under conditions of wind force equal to or less than level 7, as well as conditions exceeding level 7, and considering two water depth scenarios of 20m and 40m, the safety spacing for the four ship classes can be established. Tables 3, 4 display two sets of anchorage detection data under wind force conditions of level 7 or lower, while Tables 5, 6 show two sets of anchorage detection data under wind force conditions exceeding level 7.

Table 3

Table 3. Safety distance data of ships with wind ≤7 (water depth 20 m) (unit: m).

Table 4

Table 4. Safety distance data of ships with wind ≤7 (water depth 40 m) (unit: m).

Table 5

Table 5. Safety distance data of ships with wind >7 (water depth 20 m) (unit: m).

Table 6

Table 6. Safety distance data of ships with wind >7 (water depth 40 m) (unit: m).

Based on maritime practices, the minimum average draft for a ship in ballast condition is typically half of its full load draft. However, during winter navigation, this figure should be increased to between 55% and 60% due to heightened wave and wind conditions. These benchmark values are derived from the practical experiences of seafarers and are referenced in maritime literature (Du and Jiang, 2011). Therefore, this study adopts a draft of 50% of the full load draft for calculations in ballast conditions. Utilizing the data from Table 2 in conjunction with the safety depth model, the required safe water depth for ship anchoring has been established, as outlined in Table 1.

4 Results and discussion

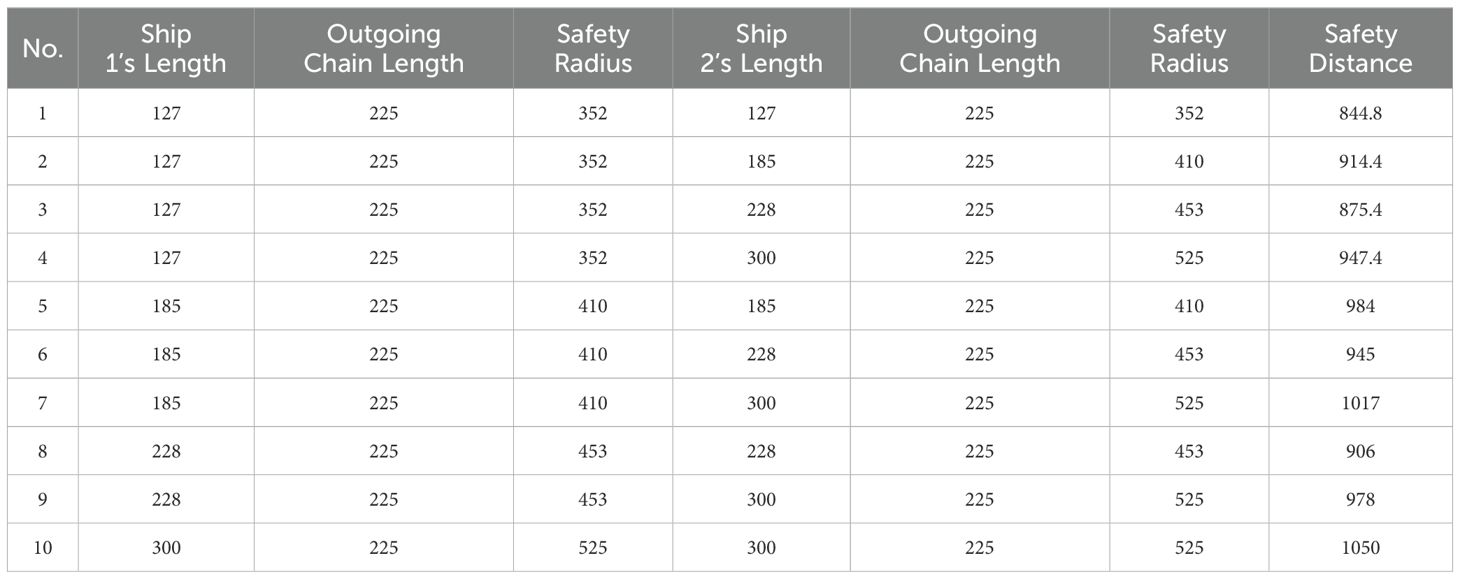
The data described above are incorporated into the MATLAB simulation environment, and the simulation experiments were conducted following the procedure described above. Through the operation of Monte Carlo random simulation algorithm and Traversal algorithm, the ship anchor points that satisfy the demands for safe anchoring spacing and safe water depth are identified, allowing for a further determination of the ship’s anchoring area. Additionally, the four sets of data can be processed to produce a total of 40 three-dimensional anchor detection images. Figures 2–5 display a selection of 8 anchor detection images that have been randomly chosen from the dataset. Among them, the red color in the figure simulates the existing ship, while the pink point represents the drop anchor point that satisfies the 2D condition and meets the water depth constraint under ballast conditions, the yellow point represents the drop anchor point that further meets the water depth constraint under full load condition based on the pink point, and the green point is the drop anchor point that meets the requirement of being generated within the circle of the anchorage position and meeting the water depth based on the yellow point at the same time.

Figure 2

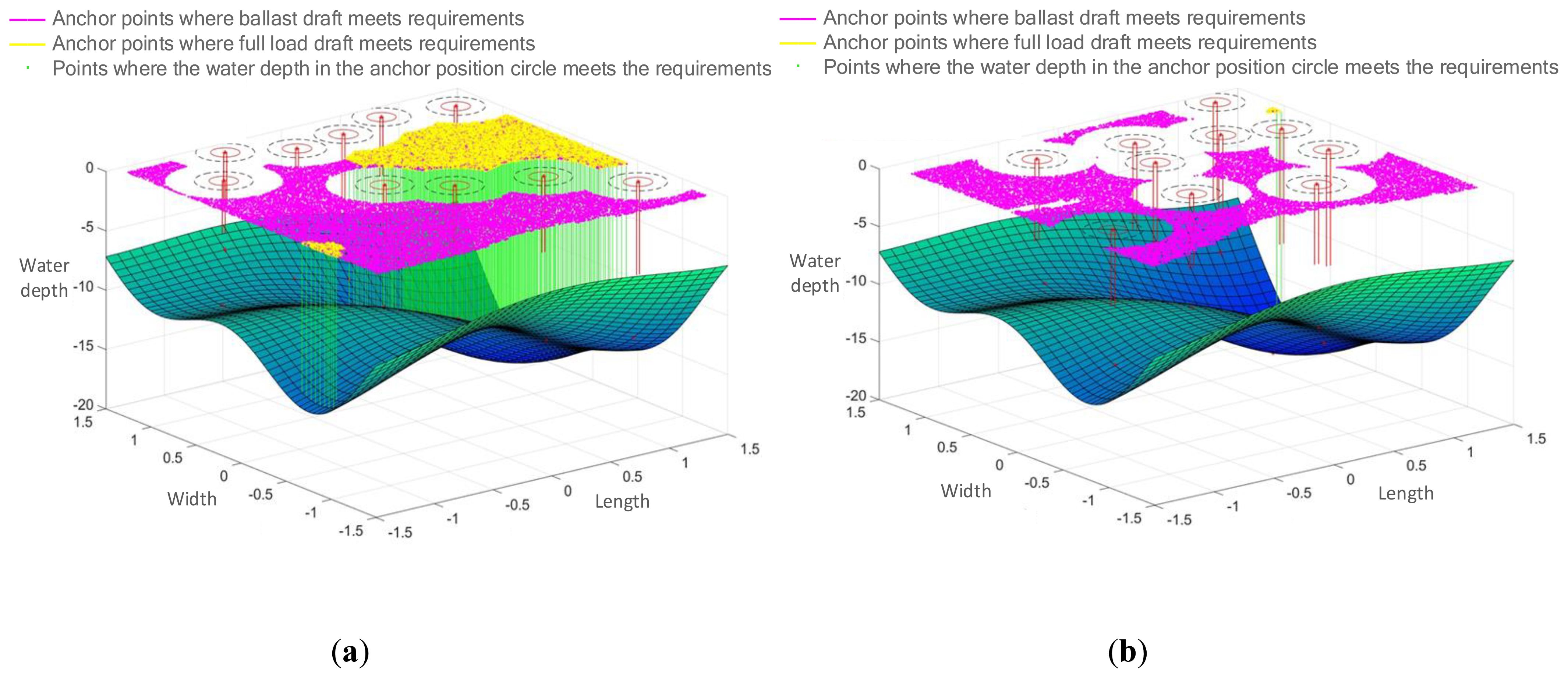
Figure 2. Detection result of anchoring area with wind force ≤7 and water depth of 20. (A) Detection of 127-meter and 185-meter ship anchoring areas. (B) Detection of 228-meter and 300-meter ship anchoring areas.

Figure 3

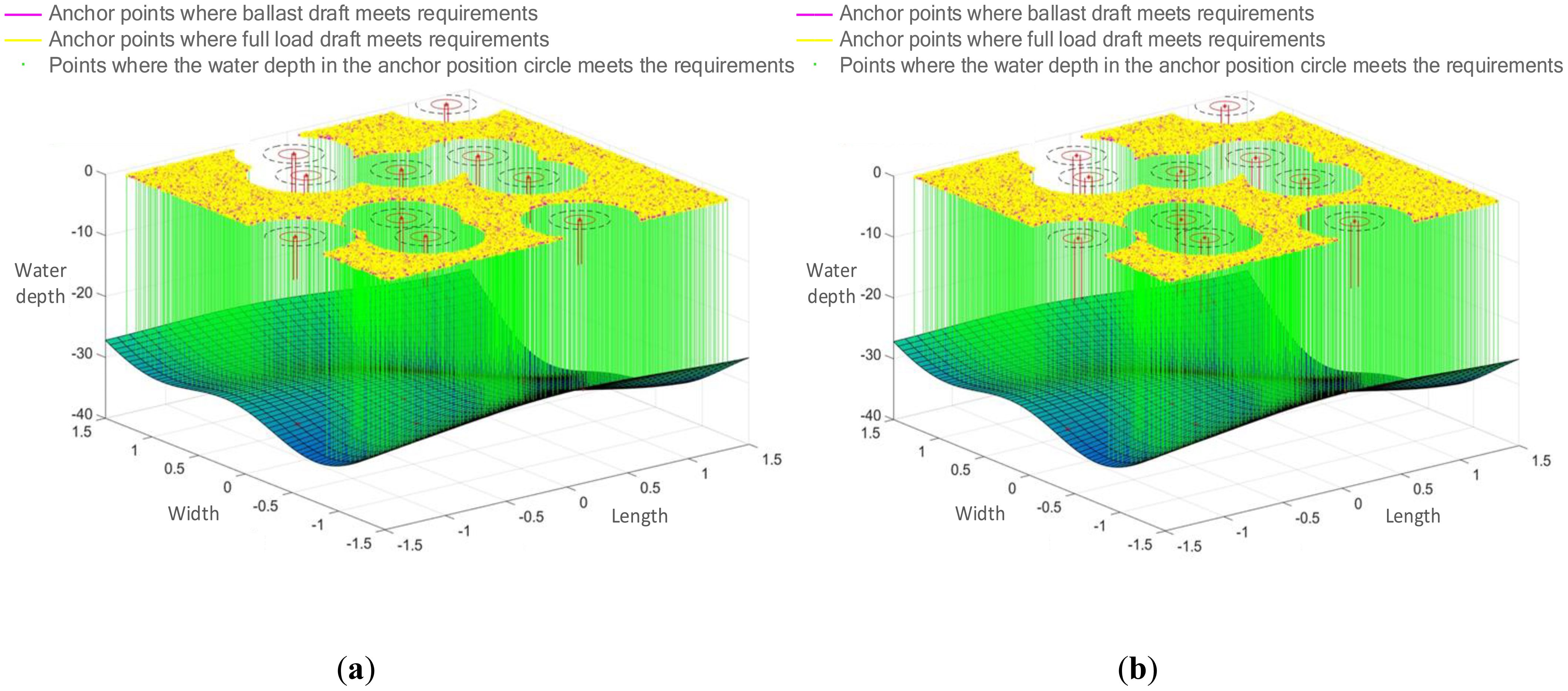
Figure 3. Detection result of anchoring area with wind force >7 and water depth of 40. (A) Detection of 127-meter and 185-meter ship anchoring areas. (B) Detection of 228-meter and 300-meter ship anchoring areas.

This series of figures demonstrates the effect of different wind magnitudes under the same water depth conditions and different water depths under the same wind conditions on the number of anchoring positions in a ship anchoring detection experiment.

The two control sets, Figures 2, 4, and Figures 3, 5, depict the effect of wind force magnitude on the number of anchoring positions of a ship under the same water depth conditions. In particular, Figures 2, 5 show the distribution of anchoring positions for winds not greater than Force 7, with those eligible for anchoring marked in yellow. Figures 3, 4, on the other hand, reflect the distribution of anchoring positions when the wind is more than level 7, and it can be clearly observed that the number of anchoring positions eligible for anchoring decreases significantly when the wind is more than level 7, which indicates that the size of the wind is an important factor affecting the selection of anchoring positions for ships.

Figure 4

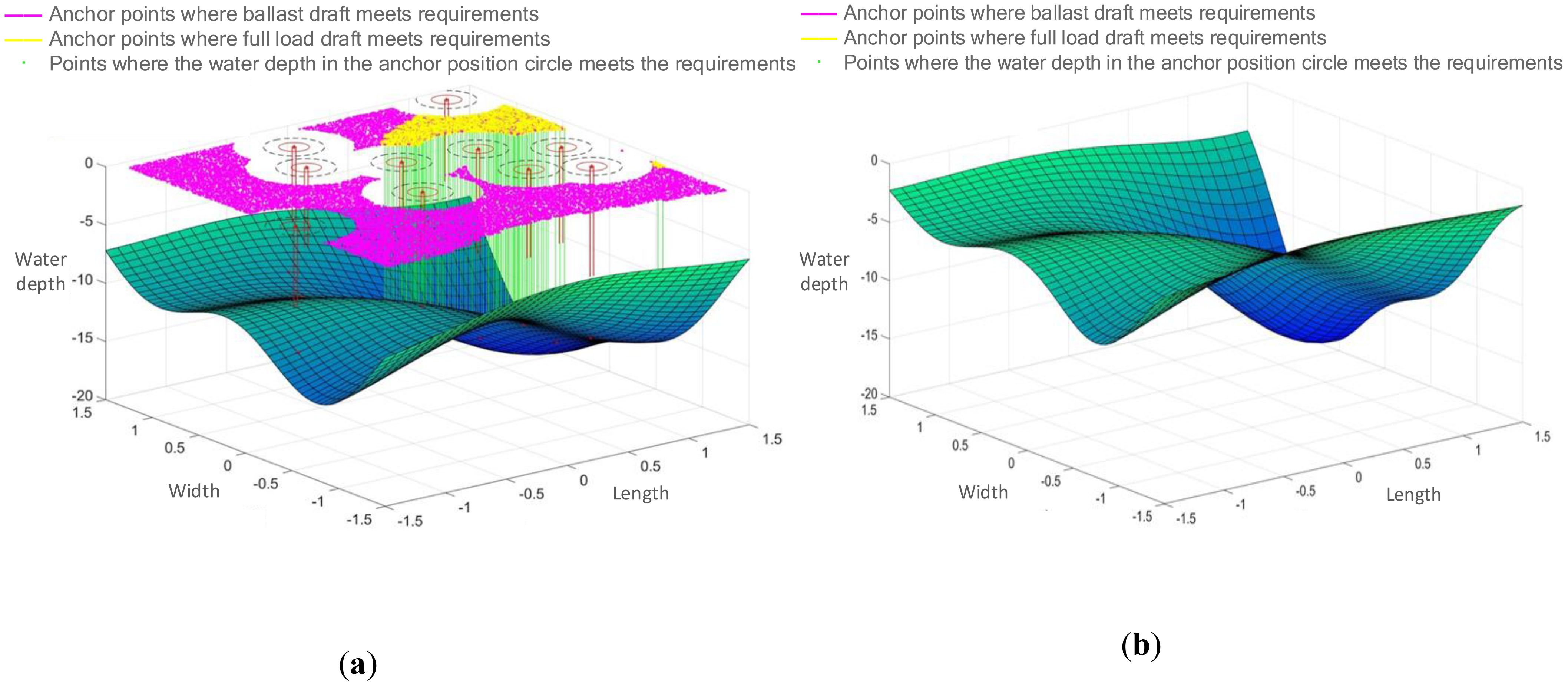
Figure 4. Detection result of anchoring area with wind force >7 and water depth of 20. (A) Detection of 127-meter and 185-meter ship anchoring areas. (B) Detection of 228-meter and 300-meter ship anchoring areas.

Figure 5

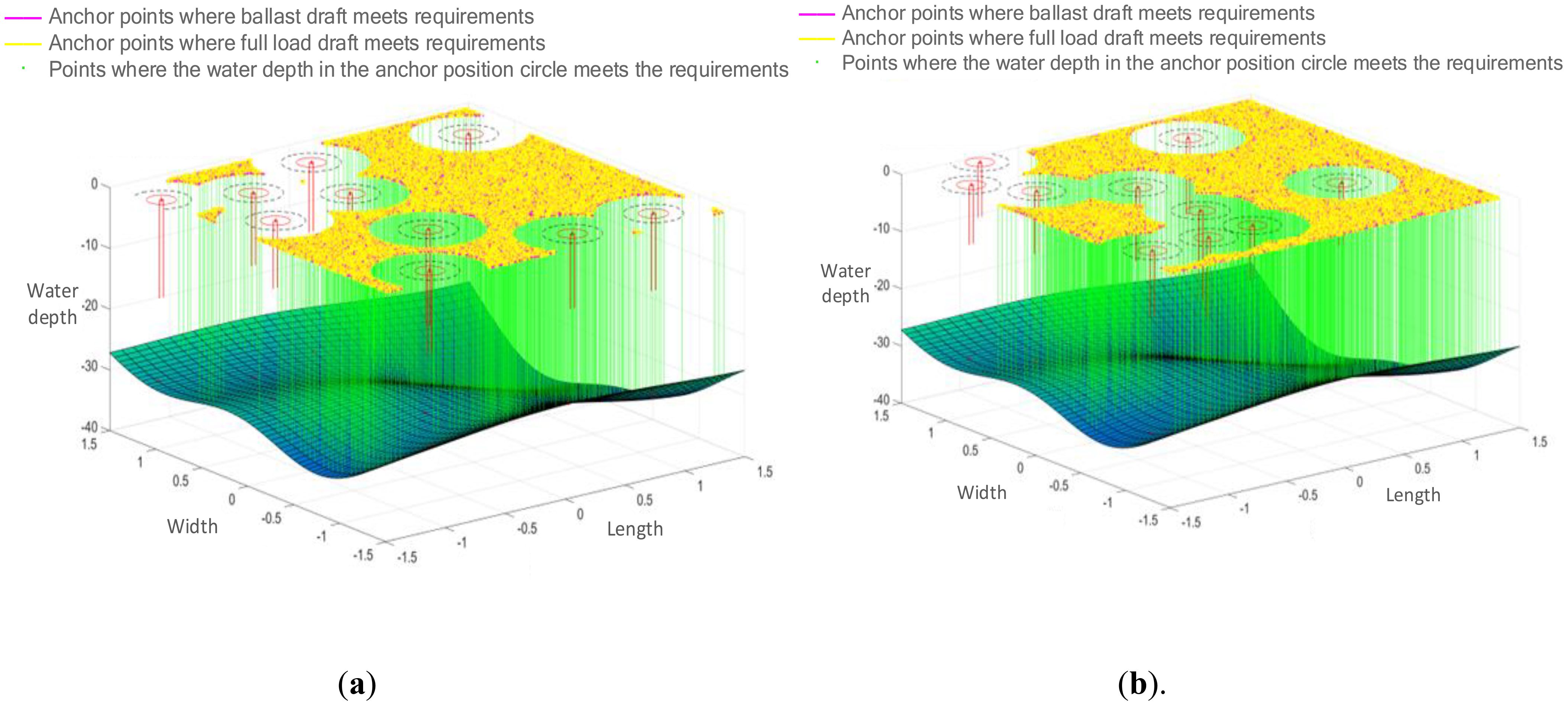
Figure 5. Detection result of anchoring area with wind force ≤7 and water depth of 40. (A) Detection of 127-meter and 185-meter ship anchoring areas. (B) Detection of 228-meter and 300-meter ship anchoring areas.

Figures 2, 5, and Figures 3, 4 show the effects of different water depths on the anchorage sites under the same wind conditions. Figures 2, 4 show the distribution of anchorages in shallower water depths, and the anchorages that meet the anchoring conditions are also marked in yellow. By comparison, it can be found that the number of yellow dots in the results increases significantly with deeper water depth, implying that the number of anchoring sites that meet the anchoring requirements is more abundant with greater water depth, further verifying the importance of water depth in the choosing of anchoring positions for ships.

In addition, “a” in Figures 2–5 represents small and medium-sized ships with lengths of 127 m and 185 m, and “b” represents ships with lengths of 228 m and 300 m. It is obvious that, both under different wind conditions and water depths It is obvious that the larger the ship type, the fewer the anchor points to meet the requirements, which means that the size of the ship type is also one of the important factors to be considered in the choice of the ship’s anchor position.

The main findings of this study include the following:

1. The intelligent anchor position detection method, which integrates the Monte Carlo simulation algorithm with the Traversal algorithm, comprehensively accounts for the impacts of ship type, safety spacing, and water depth on the selection of anchorage areas. This approach offers a more rational and safer reference for anchoring operations within the designated area.

2. To illustrate the accuracy and effectiveness of the algorithm, this study compares the water depth limits for both ship ballast and full load conditions, providing a visual representation of how various parameters associated with different ship types influence the selection of anchoring zones.

3. This experiment constructed an optimized dataset for anchor position detection by preprocessing the simulation data, which not only optimized the bathymetry detection process and reduced the redundant and repetitive calculations in the current research on anchor position detection, but also significantly improved the computational efficiency of anchor position detection in this study.

This study holds considerable practical value for real-world anchoring operations. Firstly, the intelligent anchor position detection method that combines the Monte Carlo algorithm with the Traversal algorithm can evaluate the stability and safety of the anchor position in real time, ensuring that the ship remains securely anchored in a relatively safe location. This is essential to avoid the ship moving to dangerous areas in bad weather or strong currents. Secondly, with this intelligent anchor detection technology, ships can identify suitable anchor positions more quickly, reducing waiting and searching time. This is particularly beneficial for ships that need to anchor frequently, such as cargo ships and fishing vessels, and can significantly improve operational efficiency. Moreover, this technology can reduce human errors in anchoring operations, enhancing overall safety and minimizing the risks associated with incorrect anchoring. In the long term, the integration of such intelligent systems could contribute to the development of fully autonomous ships, transforming traditional maritime practices. Future work could focus on refining the algorithm’s accuracy and robustness across various marine environments, as well as its adaptability to different ship types and sizes, further broadening its practical applications in the shipping industry.

In terms of theory application, the 3D intelligent anchor position detection method, enhanced by the additional dataset, can gather extensive data on ocean and anchor conditions. This data facilitates further analysis, optimizing future anchor position selection and navigation strategies. Furthermore, enhancing the intelligent anchor position detection method through the integration of the Monte Carlo algorithm and Traversal algorithms offers robust theoretical support for innovation in related fields. For instance, this approach can be integrated with GPS positioning, deep learning algorithms, ocean topography, and environmental big data computing, making it applicable to the field of intelligent ships. This undoubtedly presents new opportunities and challenges for development and innovation in the field of intelligent ships, fostering continuous progress.

5 Conclusions

The accuracy and efficiency of ship anchor position detection are significantly impacted by anchor position intelligent detection technology, which is one of the critical technologies to guarantee ship safety and enhance port operation efficiency against the backdrop of rapidly developing intelligent ship technology. This study centers on intelligent anchor position detection algorithms for ships in three-dimensional space. The Monte Carlo stochastic algorithm is utilized to ascertain the safe distance in the planar anchor position, while the Traversal algorithm for water depth retrieval is applied to enhance the three-dimensional intelligent anchor position detection algorithm. The ship anchor position with appropriate safe water depth in three-dimension view is obtained through simulation, and various computational simulation experiments are performed according to various ship parameters to mimic the actual ship anchoring situation. The results show that the detection algorithm is fast and accurate, and can solve the problems of low accuracy of 2D planar anchor position detection and experience-based anchoring, which is of practical significance for the efficiency and safety enhancement of anchoring position selection for large-sized and deep-water ships. However, the research presented in this study also contains the following limitations. On the one hand, there is no encrypted sampling to eliminate the abnormal anchor points of ship parameters and anchor depth, which affects the accuracy of anchoring operation. In order to solve this problem, future research can combine cryptographic sampling technology or anomaly detection algorithm based on machine learning to filter outliers more effectively, improve the accuracy of anchor selection, and thus improve the reliability of data. On the other hand, the depth detection algorithm needs to be further optimized. In future studies, multi-sensor data fusion and advanced signal processing techniques can be integrated to improve the accuracy and resolution of bathymetric measurements. In addition, using AI-driven optimization methods can help improve the algorithm’s performance under different environmental conditions, enabling more robust and adaptive water depth detection. What’s more, future studies could also explore extending the method to different Marine environments, such as areas with greater changes in seafloor morphology or more complex hydrological conditions. This will improve the applicability and reliability of the method in a wider range of scenarios.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

MZ: Writing – original draft, Conceptualization, Data curation, Software, Validation. LC: Conceptualization, Data curation, Funding acquisition, Methodology, Project administration, Supervision, Writing – review & editing. JHL: Formal analysis, Resources, Writing – original draft. ZZ: Methodology, Project administration, Supervision, Visualization, Writing – review & editing. ZL: Formal analysis, Visualization, Writing – original draft. ZC: Investigation, Writing – original draft. XZ: Investigation, Writing – original draft. JWL: Resources, Writing – review & editing. XL: Software, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by Guangdong Provincial Education Science Planning Leading Group Office, grant number 2023GXJK313; China Transportation Education Research Association, grant number 2023GXJK313; Zhanjiang Federation of Social Science Circles, grant number ZJ20YB0; Guangdong Ocean University, grant number PX-131223629, grant number PX-128223315, PX-972024013, grant number C22809 (Humanities), Undergraduate Innovation Team Project of Guangdong Ocean University (CXTD2024019).

Acknowledgments

We are sincerely grateful to the many teachers, friends, and classmates who generously shared their valuable inputs as we finalized this study. In addition, we would like to express our sincere gratitude to the university we are currently attending for encouraging us to be innovative and enterprising, and for providing us with a platform and opportunity to combine theory and practice.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aydin M., Akyuz E., Boustras G. (2024a). A holistic safety assessment for cargo holds and decks fire & Explosion risks under fuzzy Bayesian network approach. Saf. Sci. 176, 106555. doi: 10.1016/j.ssci.2024.106555

Crossref Full Text | Google Scholar

Aydin M., Kamal B., Çakır E. (2024b). Evaluation of human error in oil spill risk in tanker cargo handling operations. Environ. Sci. pollut. Res. 31, 3995–4011. doi: 10.1007/s11356-023-31402-x

PubMed Abstract | Crossref Full Text | Google Scholar

Aydin M., Uğurlu Ö., Boran M. (2022). Assessment of human error contribution to maritime pilot transfer operation under HFACS-PV and SLIM approach. Ocean Eng. 266, 112830. doi: 10.1016/j.oceaneng.2022.112830

Crossref Full Text | Google Scholar

Cao L., Wang X. J., Zhang W. J., Gao L. G., Xie S., Liu Z. J. (2022). Research on intelligent detection algorithm of the single anchored mooring area for maritime autonomous surface ships. Appl. Sci. 12, 6009. doi: 10.3390/app12126009

Crossref Full Text | Google Scholar

Chen L., Yang L. X. (2019). Development status of smart ships in the world's major shipbuilding countries. Ship Standardization Engineer 52, 10–14. doi: 10.14141/j.31-1981.2019.04.002

Crossref Full Text | Google Scholar

Cui Z., Zhang X., Chen Y., Cao L., Zhang Z., Liang Z., et al. (2024). Intelligent detection of 3D anchor position based on Monte Carlo algorithm. J. Mar. Sci. Eng. 12, 1347. doi: 10.3390/jmse12081347

Crossref Full Text | Google Scholar

Du J. L., Jiang H. (2011). Ship principle (Dalian: Dalian Maritime University Press), 75–76.

Google Scholar

Eppstein D. (1996). Breadth-first search and depth-first search (California: University of California-Irvine).

Google Scholar

Er M. J., Zhang Y., Chen J. (2023). Ship detection with deep learning: a survey. Artif. Intell. Rev. 56, 11825–11865. doi: 10.1007/s10462-023-10455-x

Crossref Full Text | Google Scholar

Feng Y., Wang X., Chen Q., Yang Z., Wang J., Li H., et al. (2024a). Prediction of the severity of marine accidents using improved machine learning. Transp. Res. Part E Logist. Transp. Rev. 188, 103647. doi: 10.1016/j.tre.2024.103647

Crossref Full Text | Google Scholar

Feng Y., Wang X., Luan J., Wang H., Li H., Liu Z., et al. (2024b). A novel method for ship carbon emissions prediction under the influence of emergency events. Transp. Res. Part C Emerg. Technol. 165, 104749. doi: 10.1016/j.trc.2024.104749

Crossref Full Text | Google Scholar

Gucma L., Schoeneich M. (2008). Monte Carlo method of ship's under keel clearance evaluation for safety of ferry approaching to ystad port determination. J. Konbin 8, 35–44. doi: 10.2478/v10040-008-0098-3

Crossref Full Text | Google Scholar

He B., Zhu X., Zhang D. (2020). Boundary encryption-based Monte Carlo learning method for workspace modeling. J. Computing. Inf. Sci. Eng. 20, 034502. doi: 10.1115/1.4046816

Crossref Full Text | Google Scholar

Homem-de-Mello T., Bayraksan G. (2014). Monte Carlo sampling-based methods for stochastic optimization. Surv. Oper. Res. Manag. Sci. 19 (1), 56–85. doi: 10.1016/J.SORMS.2014.05.001

Crossref Full Text | Google Scholar

Hong B. G. (2016). Ship handling Vol. 163 (Dalian: Dalian Maritime University Press).

Google Scholar

Hong L. (2001). Arrays-transform-traversal algorithm for solving tow-dimension balance of data. Comput. Eng. Appl. (19), 140–141+169. doi: 10.3321/j.issn:1002-8331.2001.19.048

Crossref Full Text | Google Scholar

Huang S. Y., Hsu W. J., He Y. (2011). Assessing capacity and improving utilization of anchorages. Transp. Res. E: Logist. Transp. Rev. 47, 216–227. doi: 10.1016/J.TRE.2010.09.009

Crossref Full Text | Google Scholar

Kalra N. C., Bhatt P. C. P. (1985). Parallel algorithms for tree traversals. PARALLEL Comput. 2 (2), 163–171. doi: 10.1016/0167-8191(85)90026-2

Crossref Full Text | Google Scholar

Lashomb P., Morgan R. B., Whyte T., Wilcox W. (2024). Multipolynomial Monte Carlo for trace estimation in lattice QCD. Comput. Phys. Commun. 300, 109163. doi: 10.1016/j.cpc.2024.109163

Crossref Full Text | Google Scholar

Li L. G., Guo Y. J., Li L., Hao X. F., Jin J. C., Liu D. Q., et al. (2022). Target detection of Shipborne Lidar based on variable size grid map. Laser Optoelectronics Prog. 59, 8. doi: 10.3788/LOP202259.0828002

Crossref Full Text | Google Scholar

Li W., Xu J. X., Guo X. H. (2020). Anchorage capacity calculation method based on Monte Carlo simulation. Digital Technol. Appl. 38, 108–110. doi: 10.19695/j.cnki.cn12-1369.2020.08.42

Crossref Full Text | Google Scholar

Liang Y. X., Feng H., Xu H. X. (2021). Surface small target detection algorithm for Intelligent ships. J. Dalian Univ. Technol. 61, 255–264. doi: 10.7511/dllgxb202103005

Crossref Full Text | Google Scholar

Lyu X. F., Cheng Q. Z., Li S. H., Lin Z. (2019). Unmanned surface vehicle full traversal path planning based on improved A* Algorithm. J. Unmanned Undersea Syst. 027, 695–703. doi: 10.11993/j.issn.2096-3920.2019.06.014

Crossref Full Text | Google Scholar

Madadi B., Aksakalli V. (2020). A stochastic approximation approach to spatio-temporal anchorage planning with multiple objectives. Expert Syst. Appl. 146, 113170. doi: 10.1016/j.eswa.2019.113170

Crossref Full Text | Google Scholar

Malekipirbazari M., Dindar O. Z., Aksakalli V., Alkaya A. F., Aydogdu V. (2015). Capacity planning in non-uniform depth anchorages (Cham: Springer International Publishing).

Google Scholar

Mordechai S. (2011). Applications of Monte Carlo method in science and engineering. IntechOpen Press. doi: 10.5772/1954

Crossref Full Text | Google Scholar

Sezer S. I., Elidolu G., Aydin M., Ahn S. I., Akyuz E., Kurt. R. E. (2024). Analyzing human reliability for the operation of cargo oil pump using fuzzy CREAM extended Bayesian network (BN). Ocean Eng. 299, 117345. doi: 10.1016/j.oceaneng.2024.117345

Crossref Full Text | Google Scholar

Shi J., Liu Z., Feng Y., Wang X., Zhu H., Yang Z., et al. (2024). Evolutionary model and risk analysis of ship collision accidents based on complex networks and DEMATEL. Ocean Eng. 305, 117965. doi: 10.1016/j.oceaneng.2024.117965

Crossref Full Text | Google Scholar

Tian C. Y., Liu Y., Feng S. S., Zhu S. Q. (2004). COMPLETE COVERAGE OF KNOWN SPACE——RECTANGULAR DECOMPOSITION J. J. Mechanical Eng. 40, 6. doi: 10.3901/JME.2004.10.056

Crossref Full Text | Google Scholar

Xie S., Yin J. C., Li R. H. (2024). Improvement of ship anchor position circle radius model and its based anchor position intelligent detection method (Guangdong, China: Intellectual Property Publishing House). CN116933480B.

Google Scholar

Yan X. P. (2016). Research status and development trend of intelligent ships J. Transportation and Port & Shipping 3 (01), 25–28. doi: 10.16487/j.cnki.issn2095-7491.2016.01.007

Crossref Full Text | Google Scholar

Yasir M., Jianhua W., Mingming X., et al. (2023). Ship detection based on deep learning using SAR imagery: a systematic literature review[J]. Soft Comput. 27 (1), 63–84.

Google Scholar

Yin Y., Zhang H. C. (2022). Selection of anchor position with decision tree for single anchoring of unmanned ship [J]. Navigation of China 45 (3), 5.

Google Scholar

Zhang D., Zhao Y. X., Cui Y. F., Wan C. P. (2021). Visualization analysis and development trend of intelligent ship research status J. Traffic Inf. Saf. 39, 7–16, 34. doi: 10.3963/j.jssn.1674-4861.2021.01.002

Crossref Full Text | Google Scholar

Zhao J., Zhou C., Li Y., Gan. L. (2023). Optimization of anchor position allocation considering efficiency and safety demand. Ocean Coast. Manage. 241, 106644.1–106644.13. doi: 10.1016/j.ocecoaman.2023.106644

Crossref Full Text | Google Scholar