High-resolution mapping of significant wave heights in the Northeast Pacific and Northwest Atlantic using improved multi-source satellite altimetry fusion method

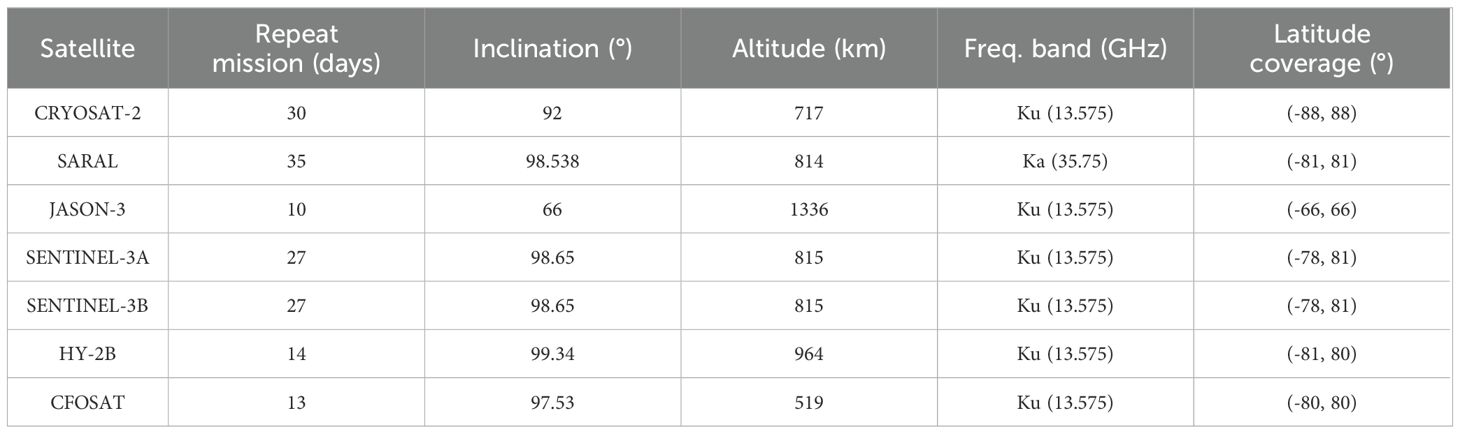
Significant wave height (SWH) is an important parameter to reflect wave state, which is of great significance in ocean engineering. However, the current wave observation methods have limitations in capturing wave field data with high spatial resolution. In this study, to generate the SWHs field over the Northeast Pacific and Northwest Atlantic, multi-source satellite altimeter data (CRYOSAT-2, SARAL, JASON-3, SENTINEL-3A, SENTINEL-3B, HY-2B and CFOSAT) are fused with a spatial resolution of 0.125° x 0.125° and a temporal resolution of 1 day. We employ the Inverse Distance Weighting (IDW) method and the IDW-based spatiotemporal (IDW-ST) method for data fusion. The fusion results exhibit a consistent spatial distribution characteristic, but the results of the IDW method display the visible trajectory. Moreover, the IDW-ST method, which incorporates time factors, shows great agreement between the fused SWH and buoy data. However, when the water depth change near the grid point has a great influence on the fusion, the complexity of bathymetric topography makes the traditional two-dimensional spatial fusion methods inadequate. Therefore, an improved method is proposed based on the IDW-ST fusion method, which introduces the water depth factor and significantly enhances fusion accuracy in regions where bathymetric variations greatly affect fusion results. The proposed method can be used to generate reliable SWH fields, especially in complex bathymetric topography conditions, and provide significant support for marine infrastructure design, ocean energy utilization and marine disaster protection.

1 Introduction

Significant Wave Height (SWH) is a crucial parameter describing the wave energy and wave state in the ocean, which plays an important role in the fields of ocean engineering, offshore shipping, and ocean energy development. Accurate SWH data are essential for ocean dynamics research, marine disaster warning systems, ocean engineering design, and ensuring the safety of offshore operations (Liang et al., 2019; Qin and Li, 2021; Yang et al., 2022; Liu et al., 2023b). However, due to the complexity of the marine environment and limitations in observation methods, the existing measured SWH data exhibit certain deficiencies in terms of spatial and temporal coverage (Shi et al., 2019).

Although traditional methods of ocean observation, including buoys, ocean platforms, and ship observations, can provide highly accurate SWH data in localized areas, these methods have limitations due to geographical constraints and technical considerations (Chai et al., 2020; Lin and Yang, 2020). As a result, achieving continuous monitoring over large-scale areas becomes challenging. The limited deployment density of buoys and platforms contributes to significant spatial inhomogeneity in the observed data (Woo and Park, 2017; Collins et al., 2024). Additionally, ship observations, being random and discontinuous, are unable to provide long-term and stable records of SWHs (Gulev et al., 2003). Furthermore, these observation methods may lead to missing or inaccurate wave data under the influence of adverse weather and sea conditions, making it difficult to obtain timely information on SWH fluctuations during tropical cyclones.

As an important means of accessing SWHs data in the global ocean, satellite altimetry has the advantages of wide coverage, long time span, and easy access to data (Young, 1994; Zieger et al., 2009; Abdalla et al., 2021). Since the launch of the first satellite altimeter (Geosat) in 1985, satellite altimeter data have been widely utilized in long-term monitoring of the global marine environment (Young et al., 2011; Woo and Park, 2017; Young and Ribal, 2019; Timmermans et al., 2020b), investigation and estimation of extreme meteorological systems (Cooper and Forristall, 1997; Wimmer et al., 2006; Vinoth and Young, 2011; Young et al., 2012; Timmermans et al., 2020a), model validation and accuracy evaluation (Li et al., 2018; Yu et al., 2018; Yurovskaya et al., 2022; Liu et al., 2023a). However, data from a single satellite altimeter often suffer from limited spatial and temporal resolution and accuracy, which can hinder their effectiveness in detailed oceanographic research and engineering applications (Appendini et al., 2014; Abdalla et al., 2021; Hamlington et al., 2023). Consequently, the fusion of SWH data from multi-mission satellite altimeters has emerged as an effective method to obtain high-resolution observation field data (Pascual et al., 2007; Yaakob et al., 2016).

Currently, many scholars have conducted research in SWH data fusion, applying various methods to improve the accuracy and reliability of SWH fields in different scales (e.g., Yang et al., 2008, 2012; Chen et al., 2009; Han and Yang, 2016; Badriana et al., 2021). One commonly used method in the spatial fusion of SWH data is the traditional Inverse Distance Weighting (IDW) method. This method is favored for its computational simplicity and ease of implementation (Lu and Wong, 2008; Maleika, 2020). Despite its widespread use, the traditional IDW method does not account for temporal variations in wave dynamics, which may limit the accuracy of fusion results, particularly in regions with rapidly changing wave conditions. To overcome this limitation, the IDW-based spatiotemporal (IDW-ST) method has been developed, incorporating temporal factors into the fusion process (Li et al., 2016). However, when the influence of water depth change near the fusion data points is significant, traditional two-dimensional spatial fusion methods are still insufficient due to the complexity of the bathymetric topography. Specifically, sharp bathymetric gradients significantly affect wave propagation characteristics and distribution. Therefore, methods that consider only spatial and temporal factors are difficult to adequately capture the true characteristics of SWH changes in these regions.

Additionally, the increasing number of satellite missions with more track data enables the fusion generation of SWH fields with high resolution and wide coverage. Thus, in this study, we use data from seven satellite altimeters launched in recent years, including CRYOSAT-2, SARAL, JASON-3, SENTINEL-3A, SENTINEL-3B, HY-2B and CFOSAT, to fuse SWH data for 2020 over the Northeast Pacific (NEP) and Northwest Atlantic (NWA). The temporal and spatial resolutions of the fused SWH fields are 1 day and 0.125 degrees, respectively. We employ both the IDW and IDW-ST methods for data fusion and conduct a comparative analysis to evaluate their performance. Based on the insights gained from this analysis, an improved fusion method, Depth-Weighted-IDW-ST (DW-IDW-ST) is proposed. This method enhances the IDW-ST approach by introducing the influence of the water depth factor, thereby improving the fusion accuracy of SWH data when the influence of water depth change near the fusion data points is significant. By integrating the effects of distance, time, and water depth on SWHs, the DW-IDW-ST method provides a more accurate and reliable representation of SWHs in these complex environments.

This paper is organized as follows: Section 2 provides an introduction to the data source with satellite altimeter and buoy, and presents the fusion algorithms and evaluation methods for the results. In Section 3, the fusion results of different algorithms are compared, and an improved method considering the depth factor is proposed and evaluated. Finally, Section 4 presents the conclusions drawn from the study.

2 Materials and methods

2.1 Satellite altimeter data

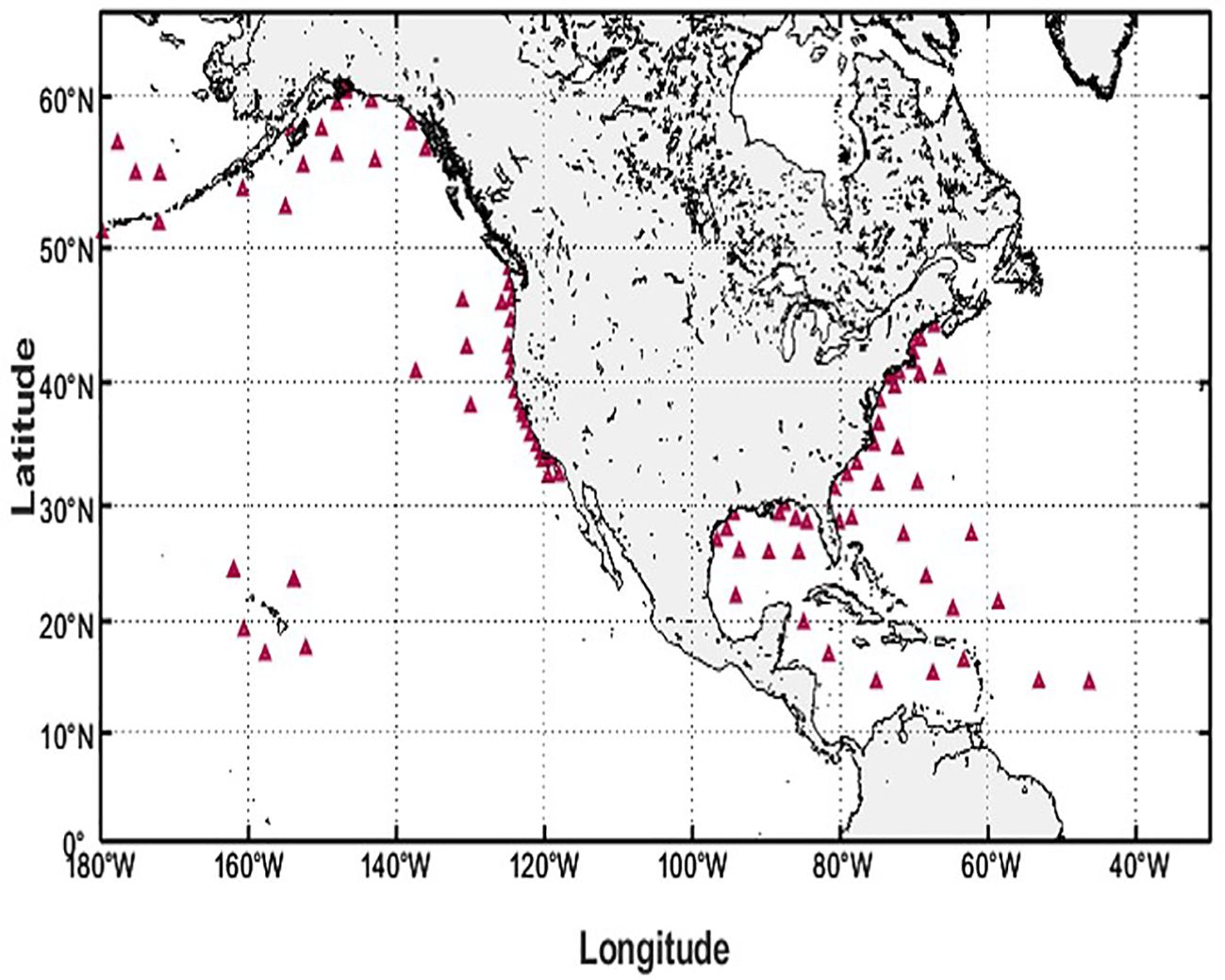
The multi-mission satellite datasets developed by Ribal and Young (2019) are widely utilized on both global and regional scales. A satellite altimeter measures the time delay between the transmission and reception of radar pulses reflected from the ocean surface, and then uses it to calculate the sea surface height and wave conditions. With this important ocean engineering observation tool, large-scale and continuous measurements of SWHs can be obtained. Figure 1 illustrates the operating years of each satellite altimeter from 1985 to the present. The corresponding altimeter data can be accessed through the Australian Ocean Data Network (AODN) at https://portal.aodn.org.au. In this paper, data from seven satellite altimeters (CRYOSAT-2, SARAL, JASON-3, SENTINEL-3A, SENTINEL-3B, HY-2B and CFOSAT) are fused to generate SWH fields in 2020. The parameter information (inclination, altitude, frequency band and latitudinal range) of these multi-mission satellites is listed in Table 1. Figure 2 displays the trajectory of each satellite altimeter in the study area over a day. All SWHs used in this study are calibrated, and anomalous data (indicated by flag 4) are systematically excluded. Flag 4 designates data points that have not passed the quality control checks and are classified as “bad” data. These data points do not meet the required quality standards and are thus omitted from the analysis to ensure the reliability of the SWHs used. For more detailed information on quality control procedures and flag definitions, see Ribal and Young (2019).

Figure 1

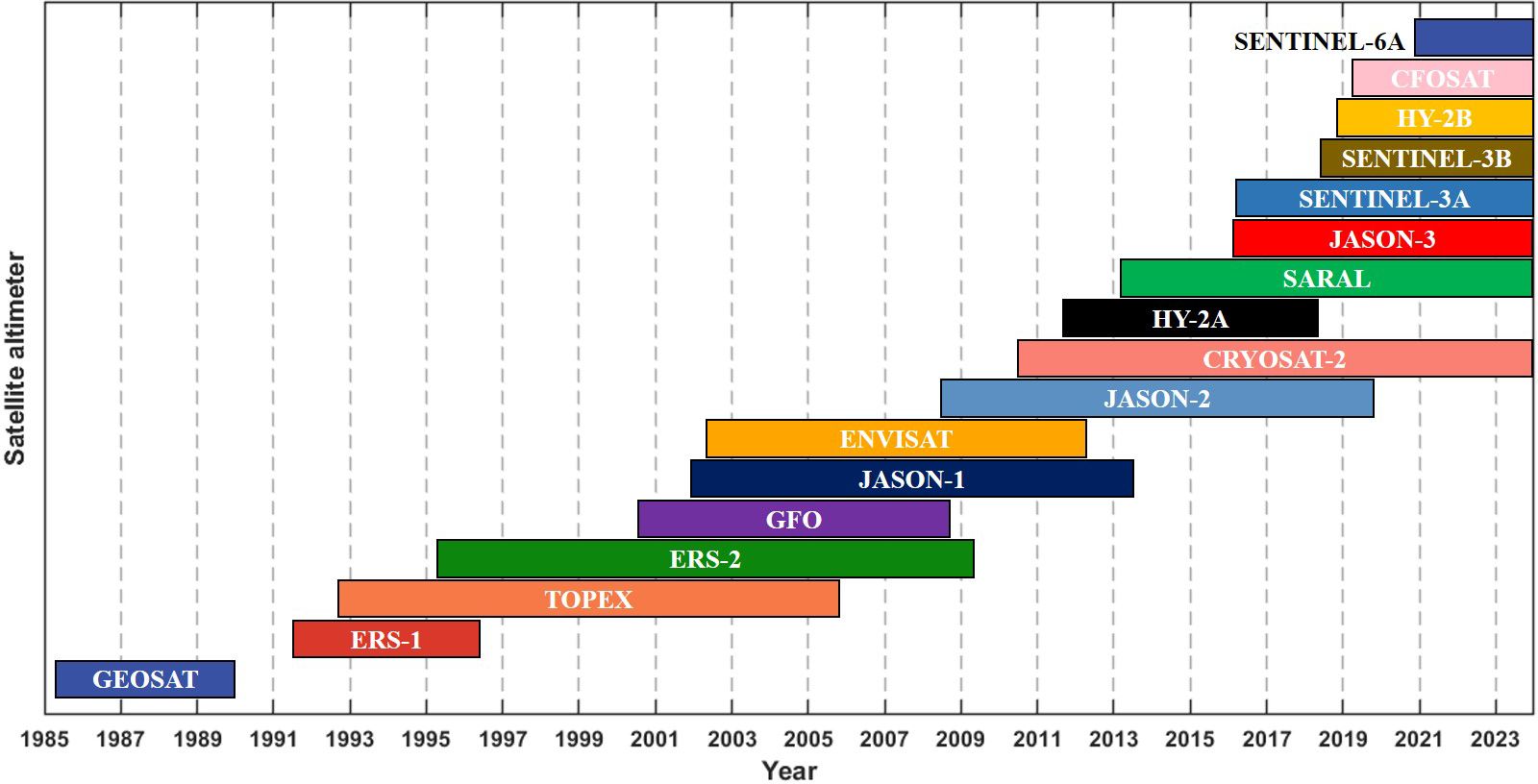
Figure 1. Duration of altimeters data in the AODN database from all the satellite missions over the period of 1985-2024.

Table 1

Table 1. Parameter information on multi-mission satellites used in the study.

Figure 2

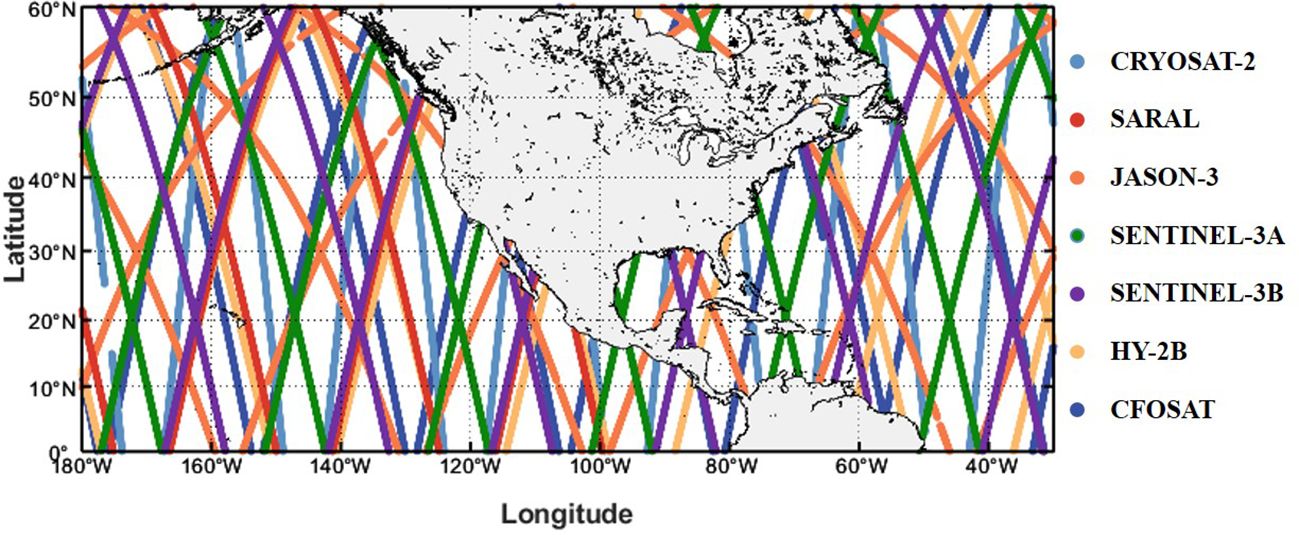
Figure 2. The track paths of the seven satellite altimeters (CRYOSAT-2, SARAL, JASON-3, SENTINEL-3A, SENTINEL-3B, HY-2B and CFOSAT) in the NEP and NWA during one day.

2.2 Buoy data

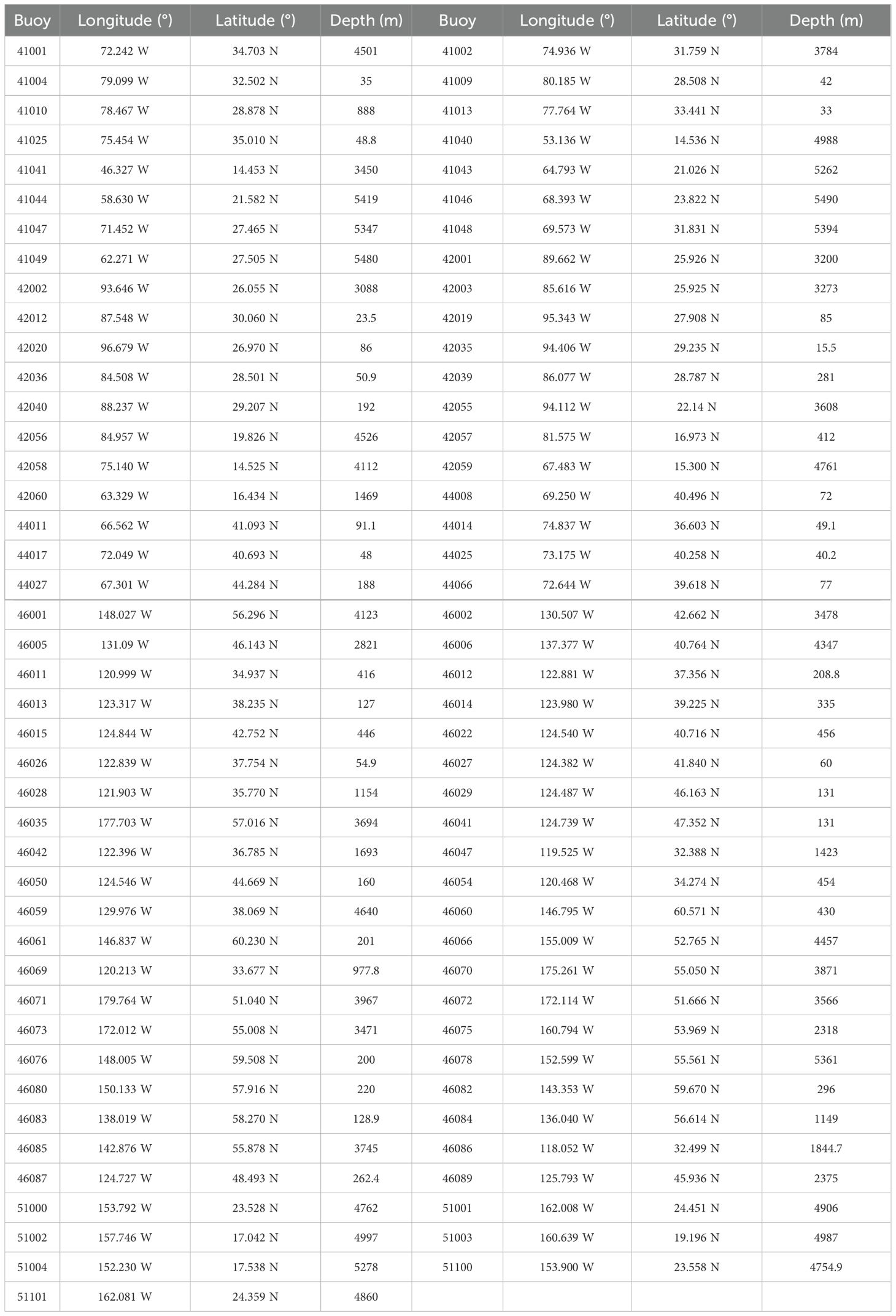
The National Data Buoy Center (NDBC), part of the National Oceanic and Atmospheric Administration, manages an extensive array of in-situ buoys that provide crucial oceanographic and meteorological data in both real-time and historical formats. These buoys measure key parameters such as wave parameters, which are widely used to validate remote sensing data, particularly satellite altimeter measurements of wave conditions. The high accuracy of buoys makes this in-site measurement an ideal reference for comparison with satellite-derived products such as SWHs, helping to refine satellite algorithms and improve data fusion methods. In this study, we utilize historical wave measurements from NDBC buoys to validate satellite altimeter-derived SWHs and fused SWHs. Specifically, buoys located greater than 50 km offshore are selected for evaluating the satellite altimeter SWH data to avoid the influence of land and ensure the accuracy of the comparison (Zhang et al., 2015; Wan et al., 2020). The widely accepted matching criterion is 50 km in spatial distance and 30 min in temporal difference (Monaldo, 1988; Queffeulou, 2004). In addition to these buoys, the buoys located within 50 km offshore are also included in the comprehensive assessment of fused SWHs. The locations of the buoys and the study area are shown in Figure 3. Table 2 presents detailed information on the buoys. The corresponding buoy data can be accessed at https://www.ndbc.noaa.gov/.

Figure 3

Figure 3. The locations of NDBC buoys (red triangles) in the NEP and NWA.

Table 2

Table 2. Information on buoys used in this study.

2.3 Fusion methods

2.3.1 IDW fusion method

The IDW fusion method is widely employed in data fusion as a commonly used spatial method due to its simplicity and efficiency (Setianto and Triandini, 2015). This method utilizes distance as the primary criterion, where the contribution of an observation point (i.e., the location where ocean wave measurements from satellites) to the fusion data output at the grid center increases as the distance to the grid center decreases. The mathematical expression associated with this approach is presented below:

$\begin{array}{ll}{Z}_{ij}=\sum _{\text{n}=1}^{n}Z(x_n)W_n/\sum _{n=1}^n{W}_n& (1)\end{array}$

$\begin{array}{ll}{W}_n={(1/d_n)}^m& (2)\end{array}$

where Z_ij represents the fusion result at the grid center point (i, j); n represents the total number of observation points in proximity to the grid; Z (x_n) represents the nth observation values of the satellite altimeters near the grid point; the weighting factor, W_n, is assigned to each altimeter observation point based on its distance, d_n, from the grid center; m is generally taken as 2.

2.3.2 IDW-ST fusion method

The IDW-ST fusion method is an extension of the IDW method that incorporates a temporal parameter to establish the spatio-temporal relationship between data points (Wang et al., 2018). This integration enables the generation of desired wave fields at specific time points. By incorporating the time parameter, the IDW-ST fusion method enhances the synthesis of spatial and temporal information, leading to more accurate and comprehensive wave field estimations. The mathematical expression representing the IDW-ST fusion method is presented as follows:

$\begin{array}{ll}Z(x,y,ct)=\sum _{i=1}^N{W}_i{Z}_i,W_i=\frac{{\left(\frac{1}{d_i}\right)}^m}{{\displaystyle \sum _{i=1}^N}{\left(\frac{1}{d_i}\right)}^m}& (3)\end{array}$

$\begin{array}{ll}{d}_i=\sqrt{{(x_i-x)}^2+{(y_i-y)}^2+c^2{(t_i-t)}^2}& (4)\end{array}$

where Z represents the result to be fused at the target grid point; Z_i represents the observation values of the satellite altimeter near the grid point at the corresponding moment; x and y represent the coordinates of the target grid point; x_i and y_i represent the coordinates of the altimeter observation point; W_i represents a weighting factor incorporates both distance and time the distance and time parameters; m represents the power exponent of the weighting function; d_i represents the distance between the grid point and the observation point taking into account the time parameter, and c is a parameter defined as a spatial unit divided by a time unit.

2.4 Evaluation method

In order to assess the precision of the satellite altimeter data and evaluate the efficacy of each fusion method, several statistical parameters are utilized in this study. These parameters include bias (BIAS), root mean square error (RMSE), scatter index (SI), and Pearson’s correlation coefficient (r). Additionally, to provide a comprehensive evaluation of the method performance, the performance score (Ps) is also employed (Hanson et al., 2009). The Ps is a normalized measure of BIAS, RMSE, and SI, defined as a combination of these parameters. The definitions of these statistical parameters are outlined below:

$\begin{array}{ll}BIAS=\frac{1}{N}\sum _{\text{i}=1}^N(Y_i-X_i)& (5)\end{array}$

$\begin{array}{ll}RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N}{(Y_i-X_i)}^2}& (6)\end{array}$

$\begin{array}{ll}SI=\frac{\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N}{[(Y_i-\overline{Y})-(X_i-\overline{X})]}^2}}{\overline{X}}& (7)\end{array}$

$\begin{array}{ll}r=\frac{{\displaystyle \sum _{i=1}^N}[(Y_i-\overline{Y})(X_i-\overline{X})]}{\sqrt{{\displaystyle \sum _{i=1}^N}[{(Y_i-\overline{Y})}^2{(X_i-\overline{X})}^2]}}& (8)\end{array}$

$\begin{array}{ll}P\text{s}=\frac{R\widehat{M}SE+B\widehat{I}AS+\widehat{S}I}{3}& (9)\end{array}$

$\begin{array}{ll}B\widehat{I}AS=\frac{\left|BIAS\right|}{Orms},R\widehat{M}SE=\frac{RMSE}{Orms},\widehat{S}I=SI& (10)\end{array}$

$\begin{array}{ll}Orms=\sqrt{\frac{{\displaystyle \sum _{i=1}^N{X}_i^2}}{N}}& (11)\end{array}$

where X_i represents the SWH of the buoy and Y_i represents the SWH of the altimeter; $\overline{X}$ represents the mean value of the SWH of the buoy and $\overline{Y}$ represents the mean value of the SWH of the altimeter; N represents the total number of data points, and Orms is the root-mean-square value of the observed data from the buoy. Ps is a non-directional index that ranges from 0 to 1, with a value of 0 indicating a perfect result.

3 Results

3.1 Altimeter data evaluation

Before the fusion of SWH fields, a thorough evaluation of the calibrated data from the AODN platform’s satellite altimeters is conducted by comparing it with the data obtained from NDBC buoys. The statistical performance of the SWHs from the seven satellite altimeters used in this study is presented in Figure 4. The results demonstrate a strong agreement between the SWHs data obtained from all satellite altimeters and the buoy data, with correlation coefficient r exceeding 0.970 and BIAS values ranging from -0.016 m to 0.017 m. Additionally, other statistical parameters, such as RMSE ranging from 0.214 to 0.279, SI consistently below 0.150, and Ps ranging from 0.071 to 0.092, further support the high quality of the altimeter data. Notably, the three satellites launched after 2018 (SENTINEL-3B, HY-2B, and CFOSAT) exhibit relatively superior data quality with excellent statistical performance, except for BIAS. Comprehensively, the Ps values for these three satellite altimeter data are consistently below 0.080, with respective scores of 0.078, 0.077, and 0.071. It is worth mentioning that the differences in operational cycles and durations of the satellites affect the amount of matched data, which could contribute to the observed variations in the accuracy of satellite data. Overall, the calibrated satellite altimeter data provided by the AODN platform demonstrate exceptional accuracy and consistency, thereby meeting the requirements for multi-source data fusion.

Figure 4

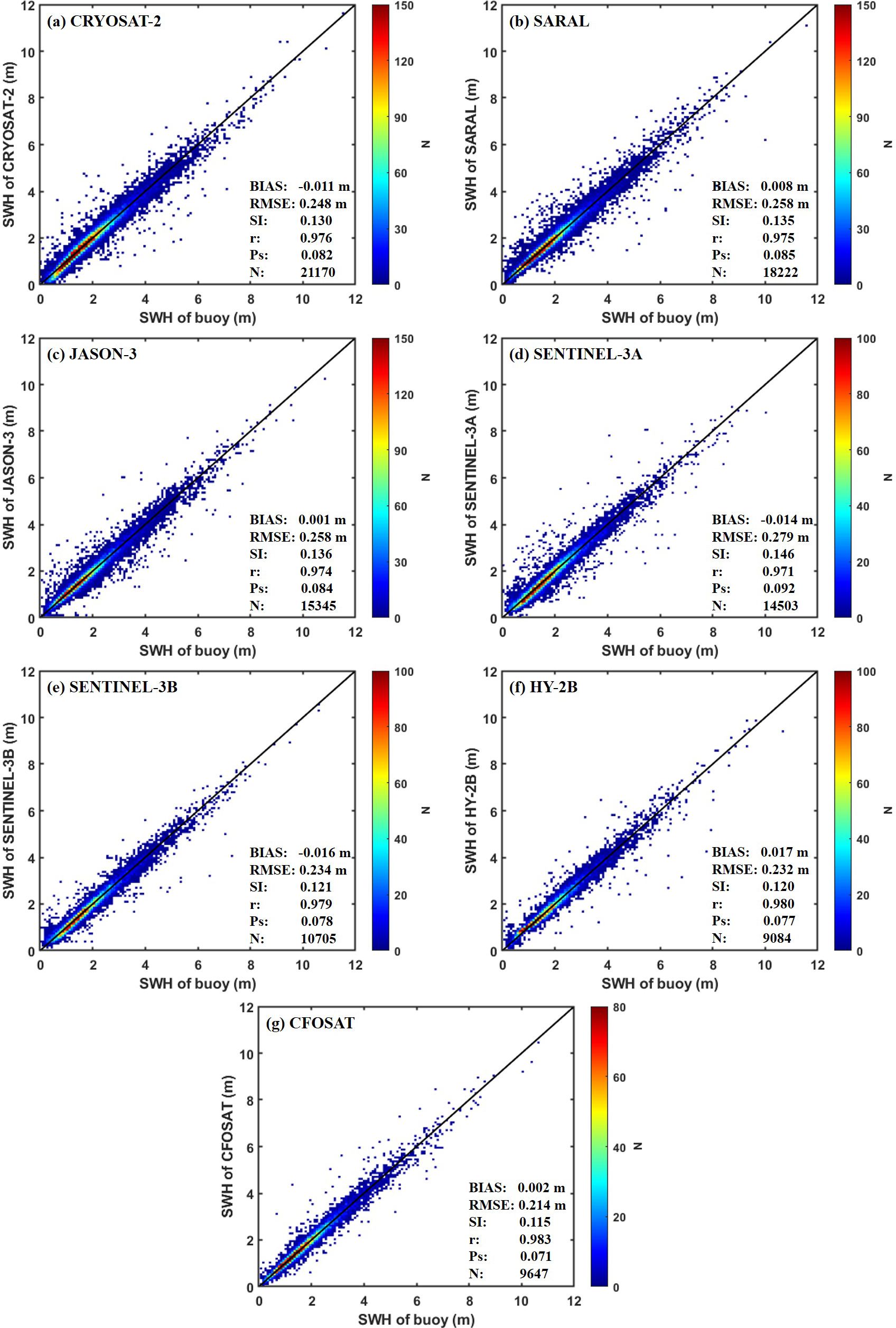
Figure 4. Scatter comparison of calibrated SWH data from 7 satellite altimeters ((A) CRYOSAT-2, (B) SARAL, (C) JASON-3, (D) SENTINEL-3A, (E) SENTINEL-3B, (F) HY-2B and (G) CFOSAT) versus NDBC buoys data.

3.2 Comparison of fusion methods

To generate the daily SWH field, we employ altimeter data from 7 satellite missions over a 3-day period, which can be used to integrate the data of the target day, the day before and after the target day. This window ensures a high time correlation of the observation, and the corresponding observation distance is reasonable. Figure 5 illustrates the fused SWH field with a spatial resolution of 0.125 degrees on August 1, 2020, along with the annual mean SWH for both the IDW and IDW-ST methods. It can be observed that the spatial distributions of the daily SWH fields generated by both methods are largely similar, with IDW demonstrating relatively higher peak wave heights. However, a notable distinction exists between the fused results of IDW-ST and IDW. The IDW-ST method yields more natural and smooth results, while the IDW method exhibits visible track traces. This discrepancy may be attributed to the fact that IDW solely considers geospatial factors. Moreover, the mean values of the fused SWH data generated by both methods in 2020 exhibit similarity, while it is evident that regions with higher latitudes experience higher SWH values.

Figure 5

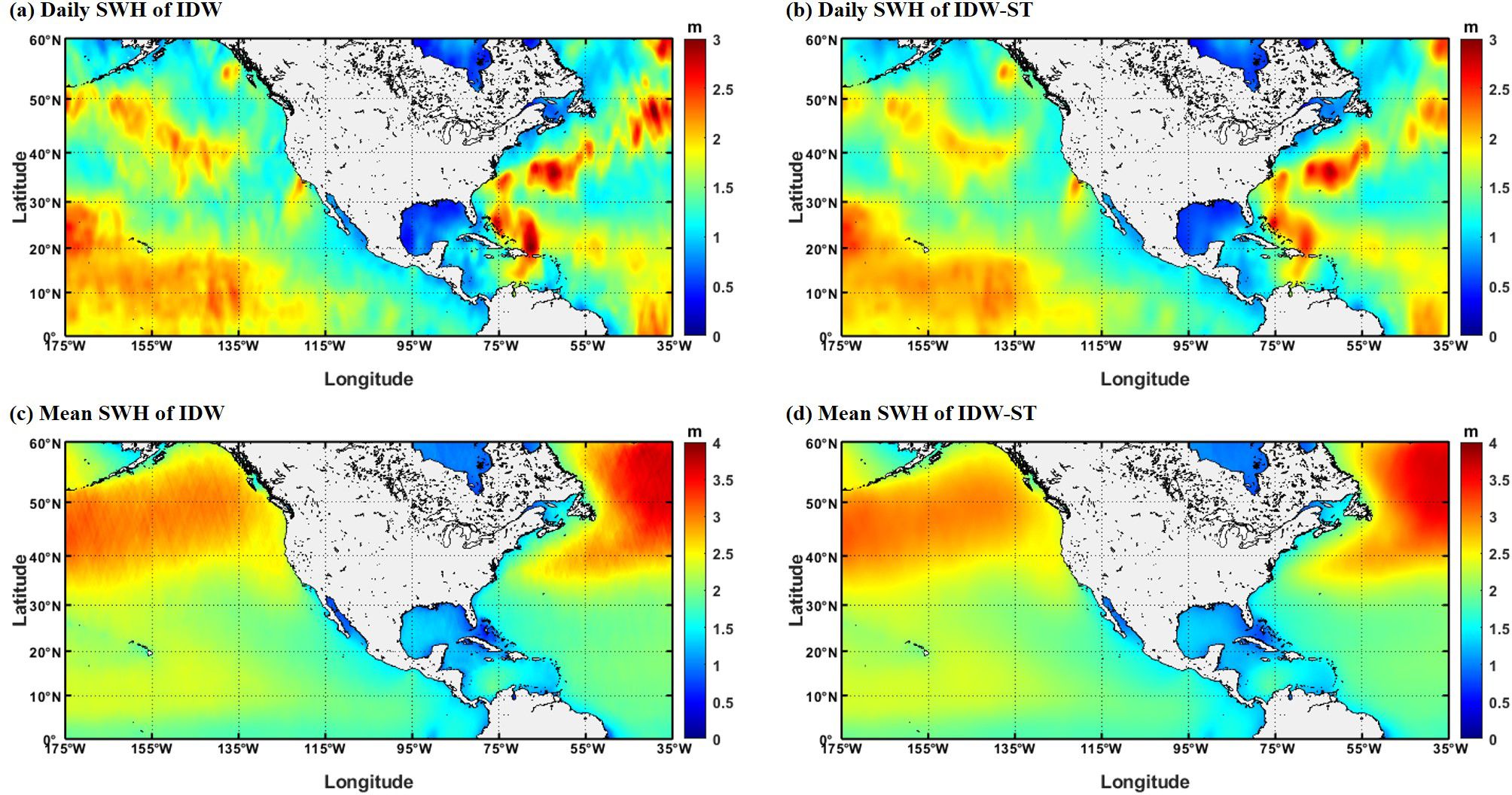
Figure 5. The daily spatial distribution on August 1, 2020, and mean spatial distribution in 2020 of SWH fields using IDW and IDW-ST methods. (A) daily SWH of IDW method, (B) daily SWH of IDW-ST method, (C) mean SWH of IDW method and (D) SWH of IDW-ST method.

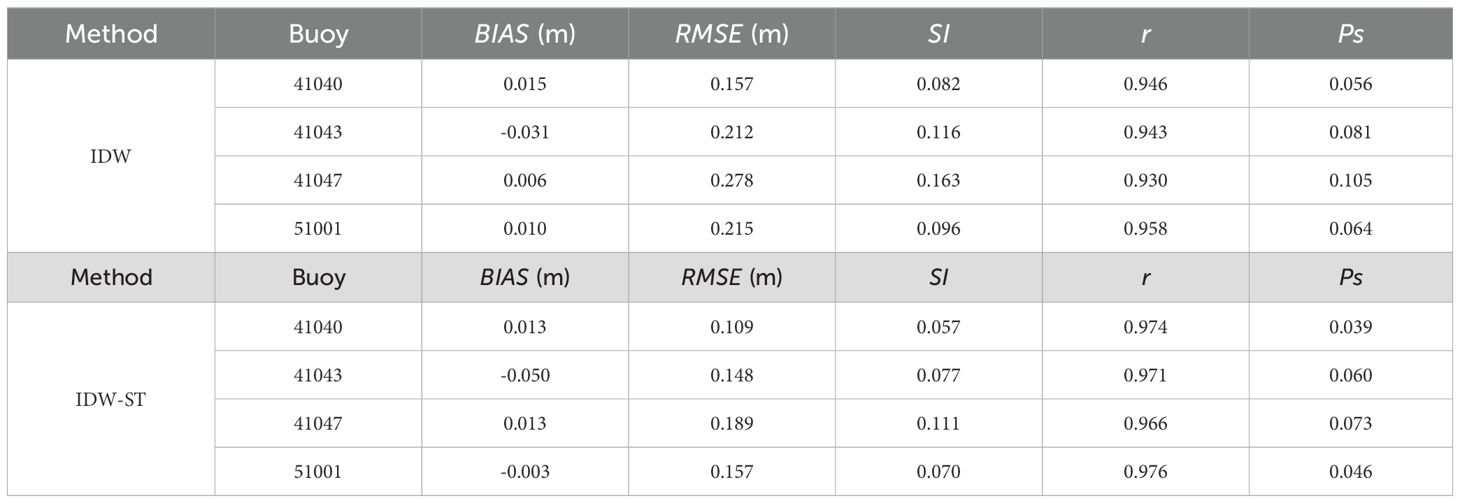
To further analyze the performance of the fusion methods, four buoy stations (41040, 41043, 41047, and 51001) are selected to conduct a time series comparison between the fused SWH and the measured data (as shown in Figure 6). The buoy data is averaged to obtain the daily average SWH, which is comparable to the fused daily SWH. Figure 6 illustrates the time series comparison of the SWHs at these sites. It is observed that the fused results and the buoy data exhibit a high degree of consistency in terms of both the trend and amplitude of the SWH changes. This consistency validates the effectiveness of the IDW and IDW-ST methods in accurately representing the actual sea state. However, when compared to the IDW-ST method, the fused SWHs generated by IDW display relatively discrete characteristics, particularly showing significant deviations at the peak values. For instance, at buoy 41043, the IDW method notably overestimates the measured data on January 16, 2020, as well as on July 30, 2020. Table 3 shows the statistical parameters of buoy measurements and fused SWHs, which are obtained by the IDW method and IDW-ST method. Compared with the IDW method, the IDW-ST method has lower RMSE, SI and Ps values, and higher correlation (r) values at each buoy station, indicating better agreement with the buoy measurement results. For example, at buoy 41043, the IDW-ST method achieves an RMSE of 0.148 m and a correlation (r) of 0.971, outperforming the IDW method (RMSE: 0.212 m, r: 0.943). This improved performance is particularly evident in the strong temporal variation of the wave field, such as under extreme wave conditions, which shows the importance of the IDW-ST method in considering the spatiotemporal variation of waves.

Figure 6

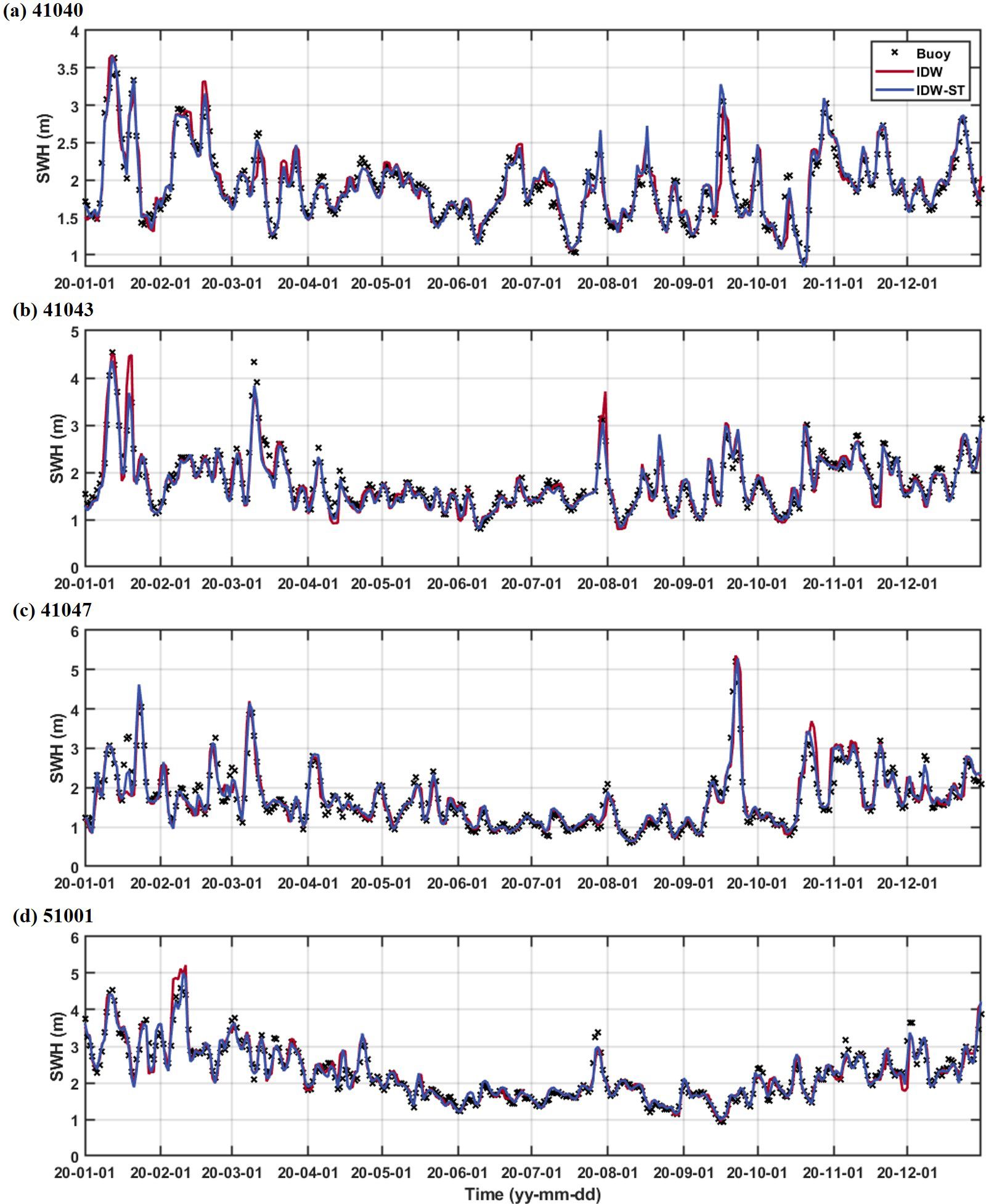
Figure 6. The time series comparison between the fused SWHs and measured data obtained from NDBC buoys (A) 41040, (B) 41043, (C) 41047, and (D) 51001 in 2020.

Table 3

Table 3. Statistical performance of time series SWH fused by IDW and IDW-ST methods at four buoys.

For a comprehensive evaluation, Figure 7 presents the scatter comparison between the fused SWH data and all buoy data. From the scatter plots, it is evident that both the IDW and IDW-ST fused data exhibit a strong correlation with the buoy data (r: 0.923 and 0.947), and the scatter distributions closely align with the ideal 45-degree diagonal line. However, the results of the IDW method present relative dispersion with relatively large values for RMSE (0.365 m), SI (0.193) and Ps (0.128). This characteristic is also reflected in the significant orbital traces observed in the fused SWH fields (Figure 5) and the deviations in the SWH time series (Figure 6) at peak values. In contrast, the IDW-ST method demonstrates a more concentrated distribution of fused data, particularly for large SWHs, resulting in smaller values for RMSE (0.300 m), SI (0.158) and Ps (0.108). The notable advantage of the IDW-ST method can be attributed to the incorporation of the time factor, which enhances the temporal correlation and assigns greater weight to the nearby altimeter SWH data on a spatiotemporal scale. This becomes particularly significant when there are substantial variations in the SWH field across these two scales, further highlighting the fusion advantage of the IDW-ST method. Overall, the IDW-ST fusion method, which generates stable and reliable fusion results, is suitable for the following research.

Figure 7

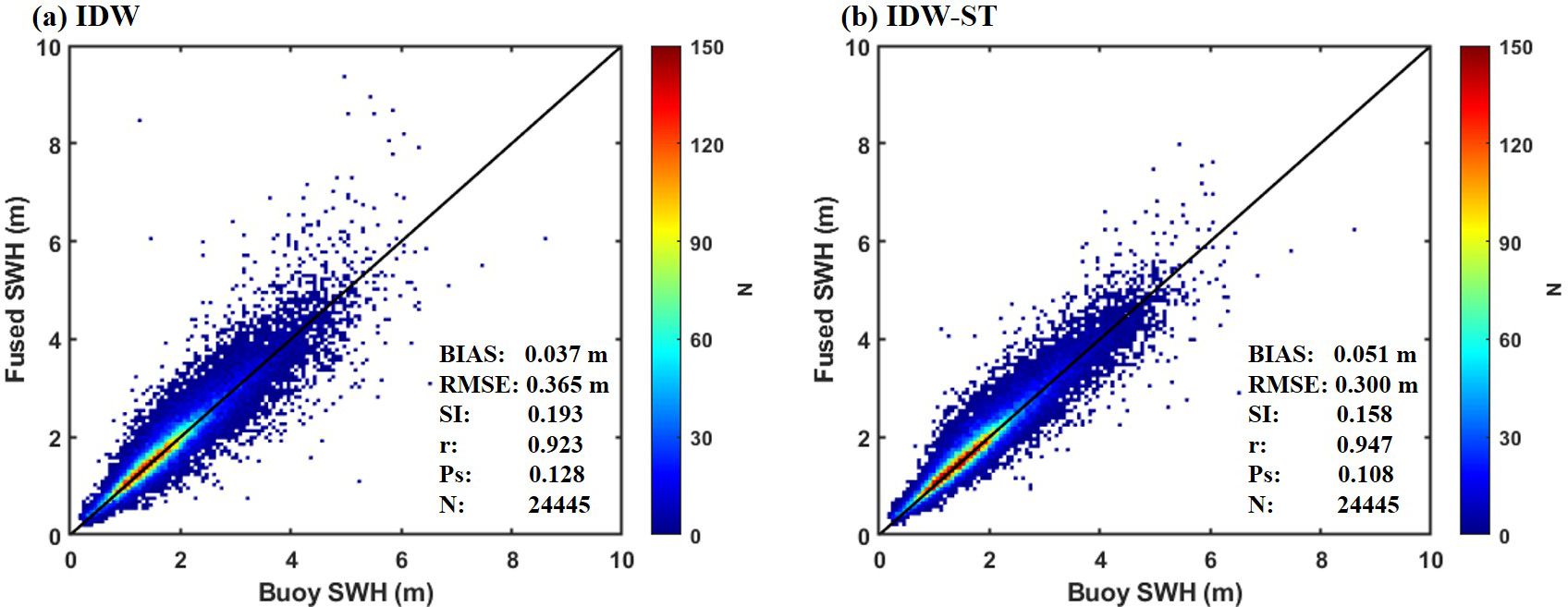
Figure 7. Scatter comparison of SWHs fused by (A) IDW method and (B) IDW-ST method with measured data from all buoy.

3.3 Improvement of IDW-ST

Although the IDW-ST method has demonstrated superior performance, significant discrepancies between fusion results and observed data have been noted at certain buoy locations, such as buoys 41013 and 41025. By investigating the environmental characteristics of these locations, it is observed that the water depth in the area surrounding the fusion points exhibits significant variations, which in turn exert a notable influence on the wave characteristics. It is worth noting that fusing satellite measurements on a spatial scale with distance as an important weight may ignore the effect of water depth on ocean waves. Specifically, the spatial distribution characteristics of SWHs considered in data fusion should not only be a two-dimensional distribution of a plane, but a three-dimensional distribution. If the water depth near the grid point where SWH is to be fused changes greatly, and this variation has a significant effect on the spatial distribution of SWHs, then water depth should also be selected as a fusion factor. Thus, we propose incorporating the depth factor, alongside the time factor and distance factor, into the satellite data fusion process. This lead to the development of the Depth Weighting-IDW-ST (DW-IDW-ST) method. The expression of this method can be defined as follows:

$\begin{array}{ll}{W}_i=\frac{{\lambda }_i{\left(\frac{\Delta D_i}{d_i}\right)}^m}{{\displaystyle \sum _{i=1}^N{\left(\frac{\Delta D_i}{d_i}\right)}^m}},{\lambda }_i=\exp (-\alpha \frac{\Delta D_i}{r-d_i})& (12)\end{array}$

where $W_i$ represents a weighting factor that combines distance, time and depth; $\Delta D_i$ represents the difference between the water depth at the grid point to be fused and the water depth at the satellite orbit position; $d_i$ represents the distance between the grid point and the observation point in Equation 4 that takes into account the time factor; ${\lambda }_i$ represents a factor that balances the depth difference and the distance, and α represents an adjustable coefficient, which is chosen to be 0.02 in this paper.

The DW-IDW-ST method, which modulates the joint influence of distance, time, and depth factors on data fusion, is utilized to generate daily SWH fields in the study area for the year 2020. These results are compared with the fusion outcomes of the IDW-ST method. The comparison focuses specifically on the buoy locations mentioned above, where significant water depth variations are identified to have a substantial impact on ocean waves. Figure 8 illustrates a comparison of the time series of SWHs between the IDW-ST and DW-IDW-ST fusion methods at buoys 41013 and 41025. The results reveal that the IDW-ST method tends to overestimate the true sea state in certain peak values when compared to the buoy measurements, such as on February 7, 2020. This discrepancy can be attributed to the fact that the IDW-ST method solely utilizes distance as the spatial fusion factor, giving significant weights to satellite orbital locations close to the grid points. However, due to large variations in water depths, the wave characteristics at these specific locations can differ significantly. Therefore, data at satellite track locations where the water depth is similar to the grid points should be assigned greater weights compared to all locations. For example, in satellite altimeter data at nearly equal distances from the grid points, some locations with significant differences in water depth compared to the grid point may exhibit large SWHs. Conversely, other locations might have similar water depths to the grid point with comparable wave characteristics. When only distance is considered as the spatial fusion factor, the weights of all these data points are treated similarly. Consequently, this leads to an overestimation of the measured values by the IDW-ST method, as depicted in Figure 8. However, by accounting for the influence of water depth, the DW-IDW-ST method demonstrates relatively good agreement with the buoy data during this period, providing a more realistic representation of the sea state. Table 4 shows the statistical parameters of buoy measurements and fused SWHs, which are obtained by the IDW-ST method and DW-IDW-ST method. For example, at buoy 41025, the DW-IDW-ST method yields lower RMSE (0.363 m) and Ps (0.139) compared to the IDW-ST method. When the significant water depth change near the grid point has a great influence on the fusion, the DW-IDW-ST method shows a strong fusion ability.

Figure 8

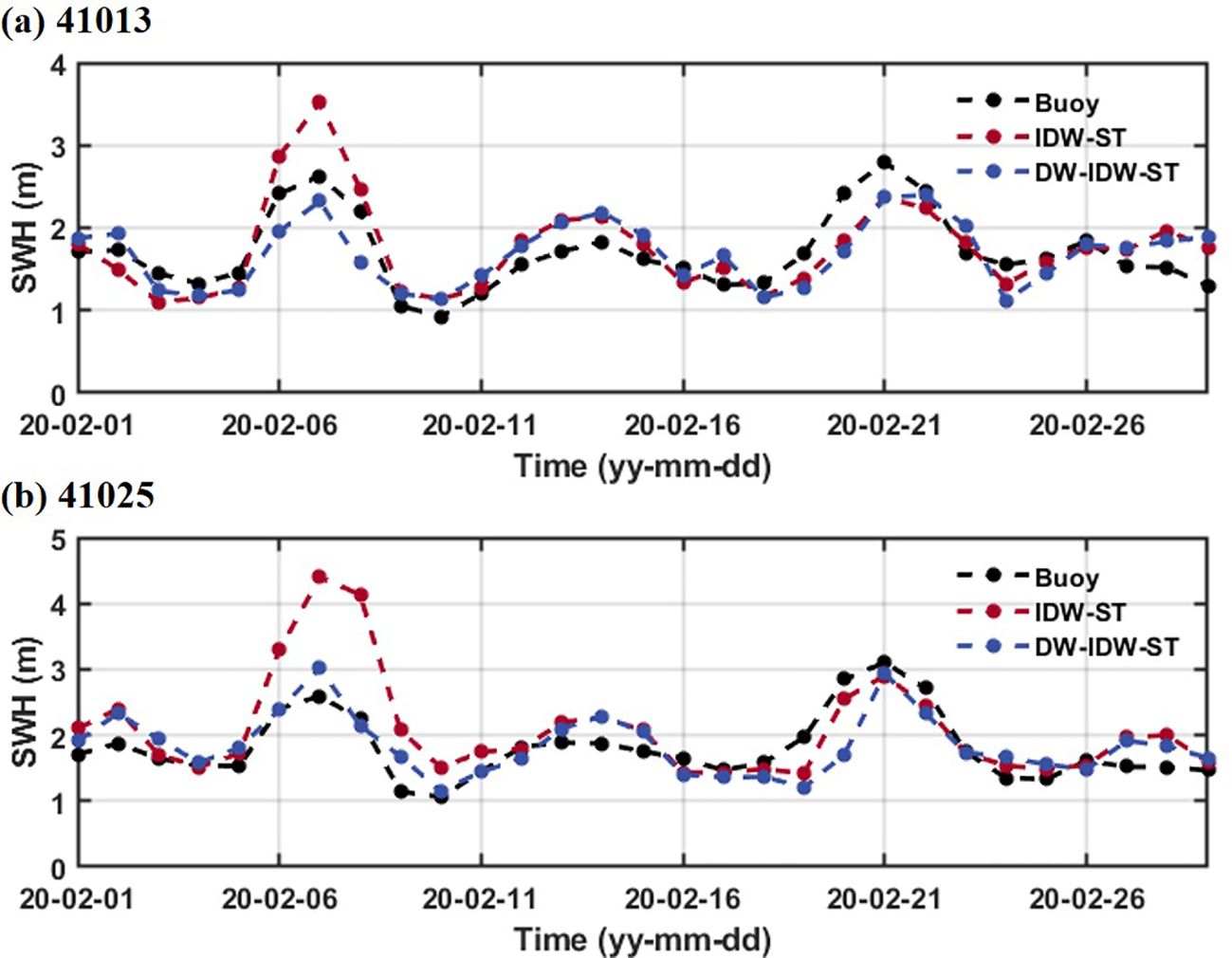
Figure 8. Time series comparison of fused SWHs derived by IDW-ST and DW-IDW-ST methods at buoys (A) 41013 and (B) 41025.

Table 4

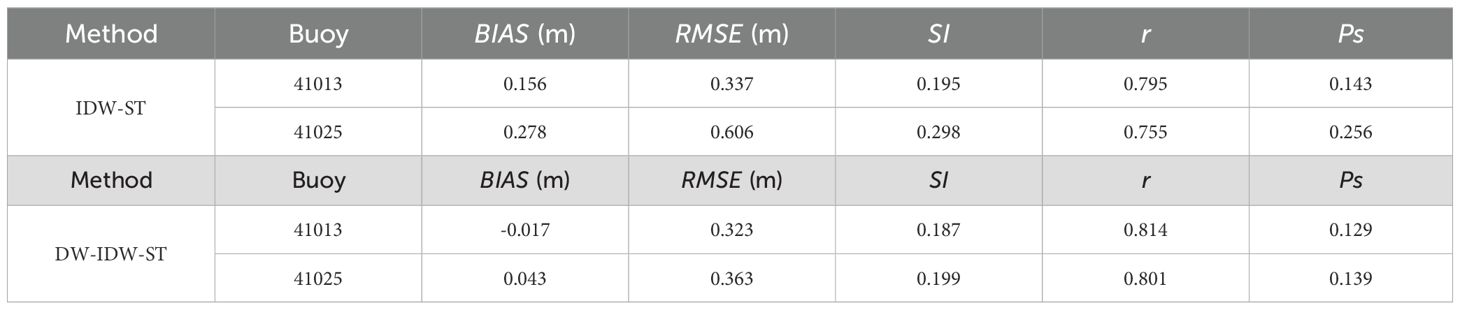
Table 4. Statistical performance of time series SWH fused by IDW-ST and DW-IDW-ST methods at two buoys.

A scatter-comparison analysis is performed to evaluate the fusion performance of the IDW-ST and the DW-IDW-ST methods in areas with significant water depth variations (as shown in Figure 9). The results indicate that the introduction of the depth factor in the DW-IDW-ST method improves the fusion accuracy and reduces the overestimation of the measured values when compared to the IDW-ST method. Specifically, the fusion results of the DW-IDW-ST method demonstrate a substantial decrease in BIAS, RMSE, and SI, indicating relatively small errors. The enhanced correlation coefficient, with the value of r increasing from 0.900 to 0.920, signifies a stronger relationship between the fusion results of the DW-IDW-ST method and the measured data. Additionally, the decrease in Ps from 0.179 to 0.160 further highlights the comprehensive advantages of the DW-IDW-ST method. Overall, these findings confirm the effectiveness and necessity of incorporating bathymetric parameters into the SWH fusion process of satellite altimeters.

Figure 9

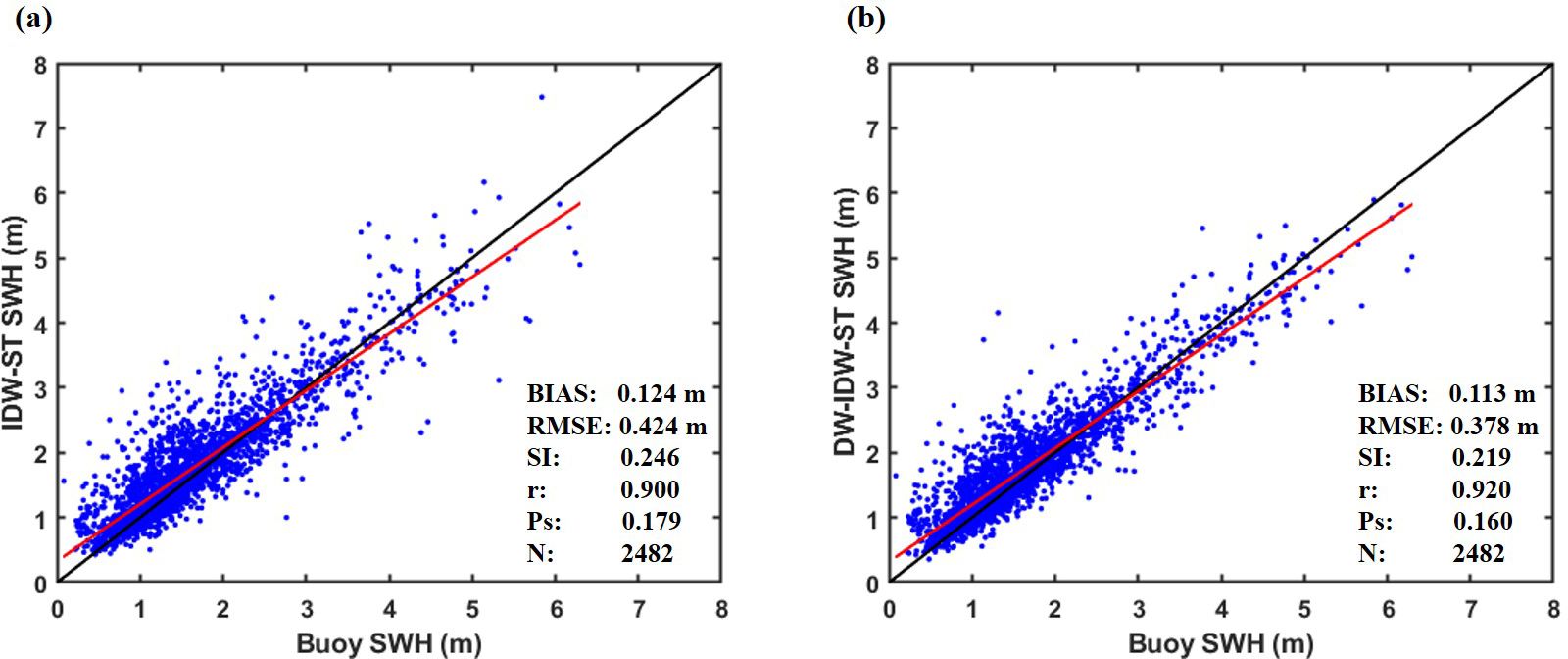
Figure 9. Scatter comparison of fusion results of (A) IDW-ST method and (B) DW-IDW-ST method with buoy data at locations with significant water depth variations. The solid black line represents the diagonal line, and the solid red line indicates the regression line.

4 Conclusion

The study of wave fields plays a vital role in ensuring safety, feasibility, and sustainability in marine meteorological forecasting, ocean engineering planning and design, marine ecological research, and marine disaster warning and protection. In this study, the calibrated data from multi-source satellite altimeters (CRYOSAT-2, SARAL, JASON-3, SENTINEL-3A, SENTINEL-3B, HY-2B and CFOSAT) using the IDW and IDW-ST methods are fused to generate SWH fields in the NEP and NWA. The spatial resolution is set at 0.125° x 0.125°, and the temporal resolution is set at 1 day. The SWH fields obtained from both fusion methods present similar spatial distributions. However, the results produced by the IDW-ST method appear more natural and smooth, while the results of the IDW method show a visible trajectory. This difference could be attributed to the fact that the IDW-ST method takes into consideration not only the spatial distance factor but also the influence of the time factor, thus reinforcing the spatio-temporal connection in the fusion of satellite altimeters data. As a result, compared to the IDW method, the IDW-ST method produces relatively stable and reliable fused SWHs data with high accuracy (Ps of 0.108) when compared to buoy data.

In the case of substantial variations in water depth near the fusion points, it is likely to have a significant impact on the fusion results. The spatial distribution characteristics of SWHs considered in data fusion should account for the three-dimensional distribution due to the effect of water depth on ocean waves. Therefore, a comprehensive approach, the DW-IDW-ST fusion method, is proposed to consider the distance factor, time factor and depth factor in data fusion. The results reveal that the fused SWHs from the DW-IDW-ST method generally match the buoy measurements, and the overestimation of SWHs is notably improved compared to the fused results of the IDW-ST method, especially for large SWHs. The DW-IDW-ST method significantly enhances the fusion accuracy when confronted with substantial variations in water depths surrounding the grid points, as these variations can influence the spatial distribution of waves. In such cases, solely relying on distance to characterize the spatial distribution of SWHs may assign excessive weight to satellite orbit positions proximate to grid points, even if the water depth conditions at these positions significantly differ from those of the grid points.

Consequently, the DW-IDW-ST method not only considers the temporal and spatial changes of waves, but also considers the influence of water depth changes on the fusion results. This method can be used to fuse SWH fields with large spatiotemporal variations, especially in regions with significant topographic variations. The fused data provide important support for marine equipment layout, route planning and disaster protection. Future research is expected to establish a multi-source fusion of cross-platform data, such as satellite data, buoy observations, radar data, drone observations and ship-based measurements. The fusion method can be further improved on the basis of machine learning and neural networks, which can handle complex nonlinear relationships between different data sources. By effectively fusing cross-platform data, high-resolution and multi-scale wave field monitoring can be achieved, which is critical for ocean engineering.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.

Author contributions

HY: Writing – original draft, Visualization, Validation, Software, Investigation, Formal analysis, Data curation, Conceptualization, Writing – review & editing, Methodology. BL: Supervision, Resources, Project administration, Funding acquisition, Writing – review & editing, Validation, Conceptualization. HG: Methodology, Data curation, Conceptualization, Writing – review & editing, Supervision, Resources, Project administration, Funding acquisition. ZS: Formal analysis, Writing – review & editing, Supervision, Resources, Project administration, Methodology, Funding acquisition, Conceptualization.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The authors gratefully acknowledge the support from the Key R&D Program of Shandong, Province, China (Grant Nos. 2022CXPT004), the National Natural Science Foundation of China (Grant Nos. 52301344, 42406249), the China Postdoctoral Science Foundation (Grant Nos. 2023M733334), the Postdoctoral Innovation Project of Shandong Province (Grant Nos. SDCX-ZG-202203083, SDCX-ZG-202203081).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdalla S., Abdeh Kolahchi A., Ablain M., Adusumilli S., Aich Bhowmick S., Alou-Font E., et al. (2021). Altimetry for the future: Building on 25 years of progress. Adv. Sp. Res. 68, 319–363. doi: 10.1016/j.asr.2021.01.022

Crossref Full Text | Google Scholar

Appendini C. M., Torres-Freyermuth A., Salles P., López-González J., Mendoza E. T. (2014). Wave climate and trends for the Gulf of Mexico: A 30-yr wave hindcast. J. Clim. 27, 1619–1632. doi: 10.1175/JCLI-D-13-00206.1

Crossref Full Text | Google Scholar

Badriana M. R., Lee H. S., Diastomo H., Avrionesti, Surya M. Y., Abdurrahman U., et al. (2021). Multi-data ensemble estimation of wave energy potential in Indonesian seas. J. Coast. Res. 114, 271–275. doi: 10.2112/JCR-SI114-055.1

Crossref Full Text | Google Scholar

Chai F., Johnson K. S., Claustre H., Xing X., Wang Y., Boss E., et al. (2020). Monitoring ocean biogeochemistry with autonomous platforms. Nat. Rev. Earth Environ. 1, 315–326. doi: 10.1038/s43017-020-0053-y

Crossref Full Text | Google Scholar

Chen X. Y., Yang J. S., Huang W. G., Zhang R., Wang J. (2009). Analysis on the temporal and spatial distribution of the wave height during Typhoon RANANIM with altimeter data. J. Mar. Sci. 27 (4), 10–16.

Google Scholar

Collins C. O., Dickhudt P., Thomson J., Paolo T., Merrifield S., Terrill E., et al. (2024). Performance of moored GPS wave buoys. Coast. Eng. J. 66, 17–43. doi: 10.1080/21664250.2023.2295105

Crossref Full Text | Google Scholar

Cooper C. K., Forristall G. Z. (1997). The use of satellite altimeter data to estimate the extreme wave climate. J. Atmos. Ocean. Technol. 14, 254–266. doi: 10.1175/1520-0426(1997)014<0254:TUOSAD>2.0.CO;2

Crossref Full Text | Google Scholar

Gulev S. K., Grigorieva V., Sterl A., Woolf D. (2003). Assessment of the reliability of wave observations from voluntary observing ships: Insights from the validation of a global wind wave climatology based on voluntary observing ship data. J. Geophys. Res. Ocean. 108, 1–21. doi: 10.1029/2002jc001437

Crossref Full Text | Google Scholar

Hamlington B. D., Willis J. K., Vinogradova N. (2023). The emerging golden age of satellite altimetry to prepare humanity for rising seas. Earth’s Futur. 11, 1–7. doi: 10.1029/2023EF003673

Crossref Full Text | Google Scholar

Han W., Yang J. (2016). Wave height possibility distribution characteristics of significant wave height in China Sea based on multi-satellite grid data. IOP Conf. Ser. Earth Environ. Sci. 46. doi: 10.1088/1755-1315/46/1/012033

Crossref Full Text | Google Scholar

Hanson J. L., Tracy B. A., Tolman H. L., Scott R. D. (2009). Pacific hindcast performance of three numerical wave models. J. Atmos. Ocean. Technol. 26, 1614–1633. doi: 10.1175/2009JTECHO650.1

Crossref Full Text | Google Scholar

Li L., Zhou X., Kalo M., Piltner R. (2016). Spatiotemporal interpolation methods for the application of estimating population exposure to fine particulate matter in the contiguous U.S. and a real-time web application. Int. J. Environ. Res. Public Health 13. doi: 10.3390/ijerph13080749

Crossref Full Text | Google Scholar

Li X., Han G., Yang J., Chen D., Zheng G., Chen N. (2018). Using satellite altimetry to calibrate the simulation of typhoon seth storm surge offSoutheast China. Remote Sens. 10, 1–15. doi: 10.3390/rs10040657

Crossref Full Text | Google Scholar

Liang B., Gao H., Shao Z. (2019). Characteristics of global waves based on the third-generation wave model SWAN. Mar. Struct. 64, 35–53. doi: 10.1016/j.marstruc.2018.10.011

Crossref Full Text | Google Scholar

Lin M., Yang C. (2020). Ocean observation technologies: A review. Chin. J. Mech. Eng. (English Ed. 33, 1–18. doi: 10.1186/s10033-020-00449-z

Crossref Full Text | Google Scholar

Liu J., Xu B., Wang J. (2023a). Ensemble-based assimilation of wave model predictions: Contrasting the impact of assimilation in nearshore and offshore forecasting at different distances from assimilated data. Appl. Ocean Res. 140, 103726. doi: 10.1016/j.apor.2023.103726

Crossref Full Text | Google Scholar

Liu Q., Young I. R., Zieger S., Ribal A., Long S. M., Dong X., et al. (2023b). On global wave height climatology and trends from multiplatform altimeter measurements and wave hindcast. Ocean Model. 186, 102264. doi: 10.1016/j.ocemod.2023.102264

Crossref Full Text | Google Scholar

Lu G. Y., Wong D. W. (2008). An adaptive inverse-distance weighting spatial interpolation technique. Comput. Geosci. 34, 1044–1055. doi: 10.1016/j.cageo.2007.07.010

Crossref Full Text | Google Scholar

Maleika W. (2020). Inverse distance weighting method optimization in the process of digital terrain model creation based on data collected from a multibeam echosounder. Appl. Geomatics 12, 397–407. doi: 10.1007/s12518-020-00307-6

Crossref Full Text | Google Scholar

Monaldo F. (1988). Expected differences between buoy and radar altimeter estimates of wind speed and significant wave height and their implications on buoy-altimeter comparisons. J. Geophys. Res. 93, 2285–2302. doi: 10.1029/JC093iC03p02285

Crossref Full Text | Google Scholar

Pascual A., Pujol M. I., Larnicol G., Le Traon P. Y., Rio M. H. (2007). Mesoscale mapping capabilities of multisatellite altimeter missions: First results with real data in the Mediterranean Sea. J. Mar. Syst. 65, 190–211. doi: 10.1016/j.jmarsys.2004.12.004

Crossref Full Text | Google Scholar

Qin L., Li Y. (2021). Significant wave height estimation using multi-satellite observations from GNSS-R. Remote Sensing 13 (23), 4806. doi: 10.3390/rs13234806

Crossref Full Text | Google Scholar

Queffeulou P. (2004). Long-term validation of wave height measurements from altimeters. Mar. Geod. 27, 495–510. doi: 10.1080/01490410490883478

Crossref Full Text | Google Scholar

Ribal A., Young I. R. (2019). 33 years of globally calibrated wave height and wind speed data based on altimeter observations. Sci. Data 6, 1–15. doi: 10.1038/s41597-019-0083-9

PubMed Abstract | Crossref Full Text | Google Scholar

Setianto A., Triandini T. (2015). Comparison of kriging and inverse distance weighted (Idw) interpolation methods in lineament extraction and analysis. J. Appl. Geol. 5, 21–29. doi: 10.22146/jag.7204

Crossref Full Text | Google Scholar

Shi J., Zheng J., Zhang C., Joly A., Zhang W., Xu P., et al. (2019). A 39-year high resolution wave hindcast for the Chinese coast: Model validation and wave climate analysis. Ocean Eng. 183, 224–235. doi: 10.1016/j.oceaneng.2019.04.084

Crossref Full Text | Google Scholar

Timmermans B., Shaw A. G. P., Gommenginger C. (2020a). Reliability of extreme significant wave height estimation from satellite altimetry and in situ measurements in the coastal zone. J. Mar. Sci. Eng. 8, 1–19. doi: 10.3390/jmse8121039

Crossref Full Text | Google Scholar

Timmermans B. W., Gommenginger C. P., Dodet G., Bidlot J. R. (2020b). Global wave height trends and variability from new multimission satellite altimeter products, reanalyses, and wave buoys. Geophys. Res. Lett. 47, 1–16. doi: 10.1029/2019GL086880

Crossref Full Text | Google Scholar

Vinoth J., Young I. R. (2011). Global estimates of extreme wind speed and wave height. J. Clim. 24, 1647–1665. doi: 10.1175/2010JCLI3680.1

Crossref Full Text | Google Scholar

Wan Y., Zhang R., Pan X., Fan C., Dai Y. (2020). Evaluation of the significant wave height data quality for the sentinel-3 synthetic aperture radar altimeter. Remote Sens. 12, 1–14. doi: 10.3390/RS12183107

Crossref Full Text | Google Scholar

Wang B., Shi L., Lu Y. (2018). A space - time Reverse distance weighted interpolation method considering elevation. Geomatics Spatial Information Technol. 41 (10), 82–85.

Google Scholar

Wimmer W., Challenor P., Retzler C. (2006). Extreme wave heights in the North Atlantic from Altimeter Data. Renew. Energy 31, 241–248. doi: 10.1016/j.renene.2005.08.019

Crossref Full Text | Google Scholar

Woo H. J., Park K. A. (2017). Long-term trend of satellite-observed significant wave height and impact on ecosystem in the East/Japan Sea. Deep. Res. Part II Top. Stud. Oceanogr. 143, 1–14. doi: 10.1016/j.dsr2.2016.09.003

Crossref Full Text | Google Scholar

Yaakob O., Hashim F. E., Mohd Omar K., Md Din A. H., Koh K. K. (2016). Satellite-based wave data and wave energy resource assessment for South China Sea. Renew. Energy 88, 359–371. doi: 10.1016/j.renene.2015.11.039

Crossref Full Text | Google Scholar

Yang H., Shao Z., Liang B., Wang Z., Lee D. (2022). Performance of different input and dissipation packages in WAVEWATCH III model during tropical cyclones. Phys. Fluids 34. doi: 10.1063/5.0120059

Crossref Full Text | Google Scholar

Yang J., Chen X., Wang J., Zhang R., Huang W. (2008). “Data fusion of significant wave height from multiple satellite altimeters,” in Microwave remote sensing of the atmosphere and environment VI (Washington, D.C., USA: SPIE), 55–59.

Google Scholar

Yang J., Xu G., Yin L., Xiao Q., Xu Y. (2012). “Data fusion of significant wave height from HY-2A and other satellite altimeters,” in Remote sensing of the ocean, sea ice, coastal waters, and large water regions 2012 (Washington, D.C., USA: SPIE), 148–154.

Google Scholar

Young I. R. (1994). Global ocean wave statistics obtained from satellite observations. Appl. Ocean Res. 16, 235–248. doi: 10.1016/0141-1187(94)90023-X

Crossref Full Text | Google Scholar

Young I. R., Ribal A. (2019). Multiplatform evaluation of global trends in wind speed and wave height. Sci. (80-.). 364, 548–552. doi: 10.1126/science.aav9527

Crossref Full Text | Google Scholar

Young I. R., Vinoth J., Zieger S., Babanin A. V. (2012). Investigation of trends in extreme value wave height and wind speed. J. Geophys. Res. Ocean. 117, 1–13. doi: 10.1029/2011JC007753

Crossref Full Text | Google Scholar

Young I. R., Zieger S., Babanin A. V. (2011). Global trends in wind speed and wave height. Sci. (80-.). 332, 451–455. doi: 10.1126/science.1197219

Crossref Full Text | Google Scholar

Yu H., Li J., Wu K., Wang Z., Yu H., Zhang S., et al. (2018). A global high-resolution ocean wave model improved by assimilating the satellite altimeter significant wave height. Int. J. Appl. Earth Obs. Geoinf. 70, 43–50. doi: 10.1016/j.jag.2018.03.012

Crossref Full Text | Google Scholar

Yurovskaya M., Kudryavtsev V., Mironov A., Mouche A., Collard F., Chapron B. (2022). Surface wave developments under tropical cyclone goni, (2020): multi-satellite observations and parametric model comparisons. Remote Sens. 14. doi: 10.3390/rs14092032

Crossref Full Text | Google Scholar

Zhang H., Wu Q., Chen G. (2015). Validation of HY-2A remotely sensed wave heights against buoy data and Jason-2 altimeter measurements. J. Atmos. Ocean. Technol. 32, 1270–1280. doi: 10.1175/JTECH-D-14-00194.1

Crossref Full Text | Google Scholar

Zieger S., Vinoth J., Young I. R. (2009). Joint calibration of multiplatform altimeter measurements of wind speed and wave height over the past 20 Years. J. Atmos. Ocean. Technol. 26, 2549–2564. doi: 10.1175/2009JTECHA1303.1

Crossref Full Text | Google Scholar