Numerical modeling of an offshore shellfish farm exposed to extreme wave conditions

Shellfish cultivation is a sustainable method of providing human food and can help remove large amounts of CO₂ from the atmosphere. Over the last two decades, longline-based structures have dominated farming systems. So far, the innovative technologies for open-ocean shellfish farming remain stagnant and need to be developed. As such, this paper preliminarily studies the operation and survivability abilities of an innovative shellfish farm under extreme wave conditions. To that end, an efficient numerical scheme with a robust implicit finite element method is established. First, the numerical modeling of a single module of the shellfish farm is conducted and the numerical results are verified against physical model tests. Then, the numerical modeling is implemented in a full-scale shellfish farm containing nine floating rafts with suspended lantern nets in a 3×3 configuration exposed to extreme wave conditions. Different angles of wave attack and shellfish rafts with and without lantern nets are fully considered, allowing an assessment of the operation and survivability abilities of the shellfish farm under extreme wave conditions in various situations. The results highlight that the angle of wave attack significantly affected the energy absorption of the mooring system. Moreover, non-linear instability such as subharmonics, which existed in the motion dynamics, can be manipulated to avoid resonant motions. This study provides insights into the evaluation of the safety design of a shellfish farm at both operational and survivability levels. The numerical method can also model other advanced offshore marine structures with multi-modules, such as floating bridges, airports, and even floating energy islands.

1 Introduction

Aquaculture continues to play a critical role in providing food and nutrition to the growing world population. In 2022, global aquaculture production reached a record of 130.9 million tonnes, with a total value of US$312.8 billion (FAO, 2024). At this time, marine shellfish or bivalve aquaculture production reached 18.9 million tonnes (US$34.4 billion), accounting for a significant fraction of the total world production of cultured seafood. China, in particular, is by far the largest producer of marine bivalves, accounting for 85% of the world’s production and responsible for the production growth (Wijsman et al., 2019).

Marine bivalves such as oysters, clams, and mussels have been cultivated to provide a rich source of human nutrition and an associated economic value for local communities. They can regulate water quality and sequester carbon and nitrogen. Despite these considerable benefits, the growth of nearshore bivalve aquaculture is increasingly constrained by space, economics, and environmental concerns (Cheney et al., 2010). In this regard, the open ocean offers tremendous potential for the expansion of shellfish farming. However, harsh high-energy environments make shellfish farming systems more challenging in open-ocean waters. Traditional nearshore shellfish culture methods are no longer suitable for offshore farming. In this circumstance, farming in fully exposed offshore waters requires a comprehensive understanding of site conditions and appropriate culture methods.

Research has been ongoing for the last decade and identified the surface/submerged longline-based structures as the dominant culture methods in open ocean waters (Langan and Horton, 2003). Within these cultural methods, mussels are a preferred species due to their rapid growth characteristics and natural attachment ability to objects in the water. So far, the longline technology has been proven to be effective for mussel production in very high-energy conditions (Cheney et al., 2010). Alongside the mussel longline, cage-based oyster/abalone cultures are also favorable in many areas of the world (Fredriksson et al., 2010; Kim et al., 2014). However, to advance the design and mechanics of these shellfish systems in the open ocean, the effect of the offshore environmental conditions, such as wave/current on the farms, and the reverse impact of the farms on the flow fields, need to be resolved. This is because structural survival and wave attenuation are highly dependent on the interactions between farms and environmental conditions. Advanced techniques such as prototype site measurements, high-fidelity numerical simulations, and physical model tests were incorporated to study the interactions between shellfish farms and environmental conditions.

Plew et al. (2005) examined the hydrodynamic implications of large offshore mussel farms in New Zealand via field observations. They focused on the effect of the farm on waves, currents, and stratification. Their results indicated that wave dissipation was a function of frequency and it reached 5% to 20% with significant wave heights less than 0.25 m. Further work was suggested to focus on the drag properties of longlines rather than individual mussel droppers. In particular, the effect of mussel dropper roughness and spacing on flow was studied by laboratory drag measurements and particle tracking velocimetry (PTV) visualization techniques (Plew, 2005). The results highlighted that high surface roughness shortened the near-wake region, increased the peak turbulent kinetic energy (TKE) behind the cylinder, and decreased the Strouhal number. Later on, most of the same group from New Zealand (see, e.g., Stevens et al., 2007) studied the hydrodynamic forcing of long-line mussel farms via field measurements. The results helped identify the dominant modes of flow-structure interaction and provide a baseline for the prediction of future structures. Furthermore, Stevens et al. (2008) systematically reviewed the physics of open-water shellfish aquaculture in New Zealand and other areas of the world. The authors summarized extensively the wave/current induced structural mechanics and forcing to facilitate the future design of shellfish farms.

The University of New Hampshire (UNH) started open ocean aquaculture research in 1999, and the overall goal was to establish commercial offshore aquaculture in New England (Goseberg et al., 2017). The numerical and physical modeling approaches were used to help determine safety factors before the aquaculture systems were deployed (Fredriksson et al., 2004; Tsukrov et al., 2003, 2000). In particular, the modeling of the shellfish systems using Aqua-FE is based on the Morison equation and has been described by DeCew et al. (2010); Tsukrov et al. (2003), and Tsukrov et al., 2005). This is because most components of the shellfish systems have small diameters compared with the wavelength. Following these pioneering studies, Dewhurst (2016) studied the dynamics of a submersible mussel raft using wave tank testing, numerical modeling, and full-scale field tests. The numerical results showed that the submerged configuration exhibited significantly less heave and pitch motion than the surfaced configuration. Recently, Knysh et al. (2020) predicted the dynamic response of the mussel longlines subjected to the typical and extreme environmental conditions of a North Atlantic mussel farm site. The numerical tool, namely Hydro-FE, is an expansion of the finite element program Aqua-FE developed at the UNH. Overall, the proposed model with the equivalent droppers provided a robust and computationally efficient tool for shellfish farm modeling.

Moreover, studies of shellfish farms exposed to open ocean waters also received considerable attention in China and other South Asia countries such as South Korea. Wang et al. (2015) numerically examined the dynamics of submersible mussel rafts in waves and currents. Both the surface and submerged rafts were modeled in the finite element program Aqua-FE. The results indicated that the submergence had a significant effect on the vertical motion of mussel rope connection points. Zhao et al. (2019) studied the hydrodynamic response of a longline aquaculture system with lantern nets in waves based on physical model tests. The results showed that the mooring tension of the longline system was affected by the wave period, the incident wave angle, and the lantern net layout. Feng et al. (2021) experimentally examined the forces and structural response of a longline aquaculture system in waves. Forces on floating buoys, droppers, and longlines were reported thoroughly. Alongside this, the effects of dropper weight, buoy pattern, and incident wave angle were also studied. Most recently, Wang et al. (2023) studied the hydrodynamic characteristics of a longline aquaculture system under current and wave conditions based on physical model tests. The drag force coefficients of the lantern nets were determined and the dependence between motions and wavelength was established. Furthermore, the co-existence of longline aquaculture and an offshore wind farm under extreme conditions was studied numerically (Boo et al., 2023). The farm line strength/fatigue, buoy tension, and displacement were obtained.

Overall, these shellfish aquaculture systems range from surface floating to semi-submerged to fully submerged systems based on local conditions. So far, submerged longlines are the most widely used method for mussel/oyster farming. More information about the cultured species and techniques can be found in Wijsman et al. (2019). Aside from this, advanced techniques such as prototype site measurements, high-fidelity numerical simulations, and physical model tests significantly advanced the design of offshore shellfish aquaculture systems. Nevertheless, there remain several issues that still need to be resolved. These include but are not limited to the following: (1) these aforementioned studies of interactions between farms and environmental conditions mainly focused on linear waves and therefore harsh conditions such as non-linear wave dynamics received little attention; (2) the dominant shellfish systems were restrained by the longline-based structures, and the innovative technologies for offshore shellfish farming remain stagnant and need to be developed; and (3) what the restraints of the shellfish farm under extreme conditions will be and how to avoid them for safety design purpose remain unclear. To address these issues, the present study first proposes an innovative shellfish farm that contains nine floating rafts with suspended lantern nets in a 3×3 configuration, as shown in Figure 1. This newly developed structure encompasses several design goals:

1. is large enough to have sufficient economic potential at the required investment cost;

2. is robust enough to survive a 5.6 m harsh wave condition;

3. can be used to grow more than one aquaculture shellfish species (i.e., oyster and scallop); and

4. is designed with a moorings concept allowing easy operation, maintenance, and harvesting.

Figure 1

Figure 1. The shellfish farm in the open ocean waters.

The potential target location of the shellfish farm is based on Nanji island in the east China sea, approximately 30 miles away from the coastline. The wave height in the typhoon condition could reach over 5 m by the measured data. Thus, the Stokes fifth-order waves (Zhao and Liu, 2022) are introduced to model the extreme conditions in the open ocean waters, so that the non-linear dynamic response of the shellfish farm can be better understood for safety design considerations. To efficiently model the full-scale shellfish farm with thousands and millions of meshes, an efficient numerical scheme with a robust implicit finite element method is proposed in this paper.

The remainder of this paper is organized as follows. First, we introduce the description of the shellfish farm in Section 2. Then, the numerical modeling of the components, such as the floating rafts, the lantern nets, the mooring system, and the buoys, are presented. In Section 3, we conduct the numerical modeling of a single module of the shellfish farm and verify the numerical results against physical model tests. Section 4 provides the numerical results of the shellfish farm. In particular, the trajectories of the moorings and the non-linear dynamic response of each module are portrayed. Section 5 provides a discussion about the operation and survivability abilities of the shellfish farm for safety design purposes. Finally, Section 6 presents the concluding remarks of this paper.

2 Materials and methods

2.1 Shellfish farm

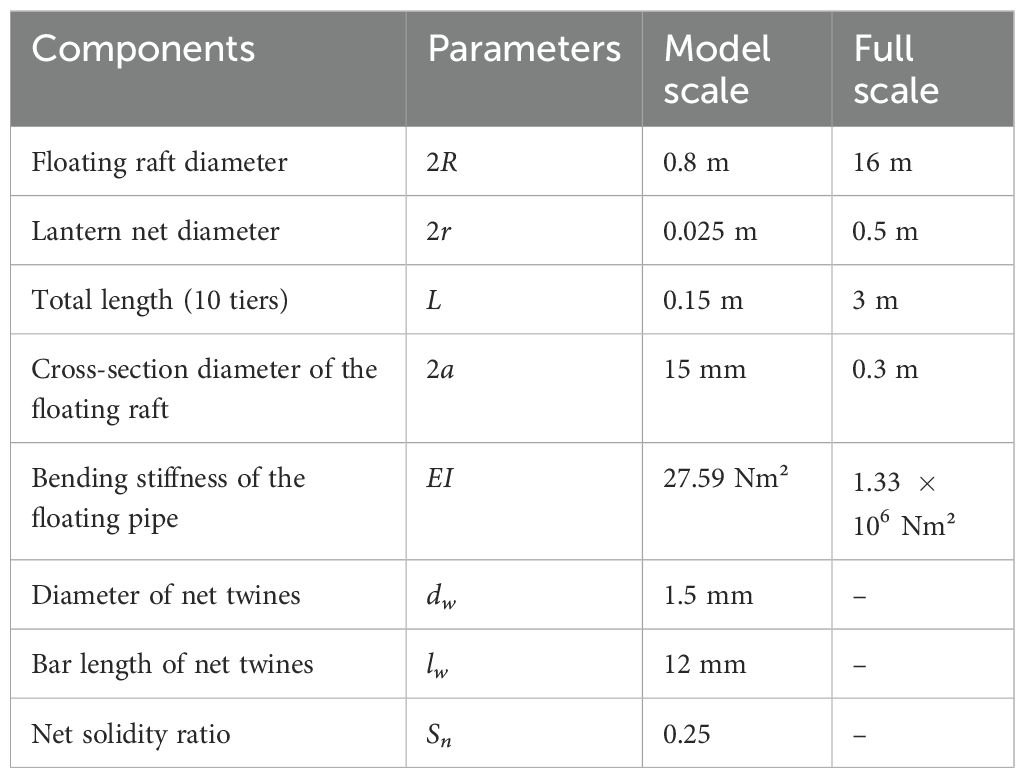
This shellfish farm contains nine floating rafts with suspended multi-tier cylindrical lantern nets in a 3×3 configuration and each has a circumference of 50 m (2R=16 m), as depicted in Figure 2. The floating raft is made of high-density polyethylene (HDPE) pipe with suspended lantern nets ($S_n=$0.2). Four sets of bridle lines connect each floating raft to the submerged grid. The mooring grid containing 16 anchor legs is located at a depth of 4 m and is supported by sixteen 1.2 m diameter spherical buoys, which are supposed to accommodate the weight of the chain for anchor legs. The anchor legs, incorporating co-polymer rope and catenary chains, extend down to the bottom beneath the buoys and the grid. The catenary chain in the anchor legs provides compliance with the system and maintains static pre-tensioning. The dimensions of the shellfish farm, as stationed by the mooring grid, are 200 m×200 m, with individual square grid dimensions of 20 m. The water depth of the target site is approximately 27 m. Specific information about the shellfish farm is listed in Table 1.

Figure 2

Figure 2. Schematic of the shellfish farm under waves.

Table 1

Table 1. Specific parameters of the shellfish system.

It is worth mentioning that the stocking density significantly affects the nutrient intake and the survival of the farmed shellfish. Hence, this critical factor has been repeatedly reported in many studies concerning different species. Stevens et al. (2008) suggested that a shellfish farm holding between 0.01 and 0.1 elements (e.g., dropper) per m². The common space between two longline droppers is at 0.5–0.9 m, as described by Gagnon and Bergeron (2017) and Plew (2005). With these recommendations, the space between two neighboring lantern nets is designated as 1 m concerning the diameter of the lantern net and the overall area of each raft.

Moreover, this paper introduces the elastic modulus of the floating raft based on previous aquaculture net cage studies (Fredriksson et al., 2007; Li et al., 2016; Shen et al., 2023). Based on these pioneering studies, the present study sets the modulus of elasticity for the floating raft to be 8.96× ${10}^8$Pa, as listed in Table 1.

2.2 Wave field

We assume that the shellfish farm is under non-linear wave attack and the wave is in a severe condition. Thus, a Stoke fifth-order wave (5.6 m height with a period of 6 s) is prescribed, as Stokes waves are frequently used as the design waves in many ocean and coastal engineering applications (Zhao and Liu, 2022). Alongside this, we also follow the latest Stokes wave solutions (Zhao and Liu, 2022) to incorporate the accuracy within the perturbation scheme. The solutions up to the fifth order are summarized into different harmonics.

Then, the horizontal and vertical velocities are given by

$\begin{array}{ll}\begin{array}{c}u=\frac{\partial \varphi }{\partial x}={\displaystyle \sum _{i=1}^{5}i\frac{\omega }{k}{\varphi }_i^{\text{'}}\cosh \left\{k(z+h)\right\}\sin \theta } \end{array}& (1)\end{array}$

$\begin{array}{ll}\begin{array}{c}w=\frac{\partial \varphi }{\partial z}={\displaystyle \sum _{i=1}^{5}i\frac{\omega }{k}{\varphi }_i^{\text{'}}\sinh \left\{k(z+h)\right\}\cos \theta }\end{array}& (2)\end{array}$

where

$\begin{array}{ll}\begin{array}{c}\{\begin{array}{c}{\varphi }_1^{\text{'}}=\lambda A_{11}+{\lambda }^3{A}_{13}+{\lambda }^5{A}_{15}\\ {\varphi }_2^{\text{'}}={\lambda }^2{A}_{22}+{\lambda }^4{A}_{24}\\ {\varphi }_3^{\text{'}}={\lambda }^3{A}_{33}+{\lambda }^5{A}_{35}\\ {\varphi }_4^{\text{'}}={\lambda }^4{A}_{44}\\ {\varphi }_5^{\text{'}}={\lambda }^5{A}_{55}\end{array}\end{array}& (3)\end{array}$

2.3 Time-domain dynamic analysis

The numerical model of the shellfish raft concerning the individual components, such as the floating raft, the lantern net, and the mooring system, are described in this subsection. All the system components are modeled based on an implicit finite element (FE) framework. The applied FE model is a displacement formulation that allows for large displacements and rotations in the 6 degrees of freedom (DOF).

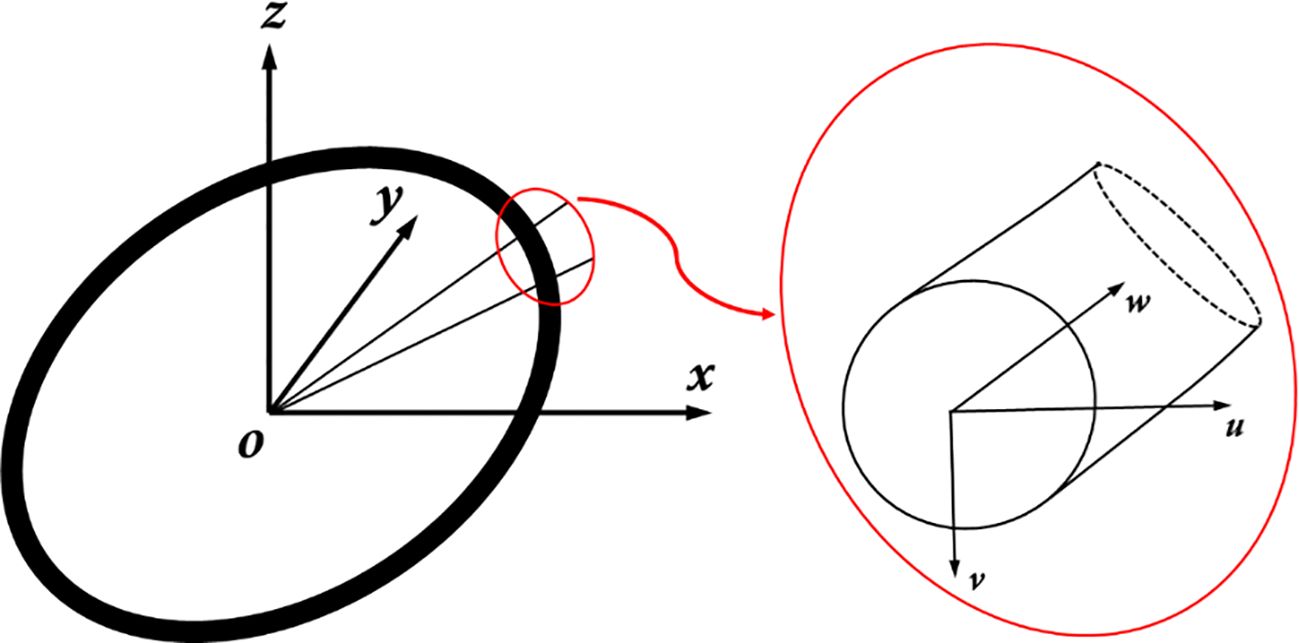
The diameter of the floating raft is much smaller than the wavelength, and as with the net twine and mooring systems, it is considered a slender structure. We examine the hydrodynamic loads exerted on the floating raft by dividing it into several mini-segments. The wave force on each mini-segment can be obtained using the Morison equation (Li et al., 2007; Xu et al., 2018).

$\begin{array}{ll}\begin{array}{c}{F}_w=\frac{1}{2}{C}_D\rho A_p\left|\mathit{u}-\mathit{U}\right|\cdot (\mathit{u}-\mathit{U})+\rho V_0\dot{\mathit{u}}+C_m\rho V_0(\dot{\mathit{u}}-\dot{\mathit{U}}) \end{array}& (4)\end{array}$

where $u$ and $U$ represent the velocity vectors of water particles and the slender body, respectively; $\dot{u}$ and $\dot{U}$ are the acceleration vectors of water particles and the slender body. $\rho$ is the water density and $A_p$is the projected area normal to the wave propagation direction. $V_0$ is the time-dependent water-displaced volume of a slender body. $C_D$ and $C_m$ represent the drag and added mass coefficients. These hydrodynamic coefficients for the mini-segment of the floating raft, are set to be $C_{Dw}=0.4$, $C_{Du}=C_{Dv}=0.6$, $C_{mu}=C_{mv}=0.2$, $C_{mw}=0$ (Li et al., 2007), as shown in Figure 3.

Figure 3

Figure 3. The local coordinate in a mini-segment of the floating collar.

Then, the 6 DOF equation for the non-linear motion of the floating raft can be written as

$\begin{array}{ll}\begin{array}{c}\mathit{M}\ddot{\mathit{d}}+\mathit{C}\dot{\mathit{d}}+\mathit{K}\mathit{d}={\mathit{F}}_{\mathit{R}}\end{array}& (5)\end{array}$

Here, $M$ is a $6\times 6$ system mass matrix, including mechanical and hydrodynamic added mass. $C$ is the $6\times 6$ damping matrix and $K$ is the $6\times 6$ stiffness matrix. $F_R$ is the $6\times 1$ total force matrix and $d$ is the $6\times 1$ displacement matrix. The numerical implementation will be presented in Section 2.4 of this paper.

The lantern net and mooring system are modeled as a series of lumped mass points interconnected with massless springs. In this paper, the interaction between the net bars is overlooked. The hydrodynamic forces on the slender body (e.g., net twine/moorings) can be obtained using the generalized Morison equation as below.

$\begin{array}{ll}\begin{array}{c}{f}_n=\frac{1}{2}{C}_{Dn}\rho D_h\left|u_n-U_n\right|\cdot (u_n-U_n)+\rho \frac{\pi D_b^2}{4}{C}_{mn}\dot{u_n}-\rho \frac{\pi D_b^2}{4}(C_{mn}-1)\dot{U_n }\end{array}& (6)\end{array}$

$\begin{array}{ll}\begin{array}{c}{f}_t=\frac{1}{2}{C}_{Dt}\rho D_h\left|u_t-U_t\right|\cdot (u_t-U_t)+\rho \frac{\pi D_b^2}{4}{C}_{mt}\dot{u_t}-\rho \frac{\pi D_b^2}{4}(C_{mt}-1)\dot{U_t }\end{array}& (7)\end{array}$

where $f_n$ and $f_t$ are forces per unit length in normal and tangential directions. $D_h$ and $D_b$ are hydrodynamic and buoyancy diameters. $u_n$ and $u_t$ are fluid velocities in normal and tangential directions, $U_n$ and $U_t$ are slender body velocities in normal and tangential directions. The hydrodynamic coefficients $C_m$ have been provided by (Li et al., 2006). Moreover, the hydrodynamic coefficients $C_D$ of a slender body (e.g., net twine/moorings) are considered a function of the Reynolds number. According to DeCew et al. (2010), the normal and tangential drag coefficients used in the present work are expressed as

$\begin{array}{ll}{C}_{Dn}=\{\begin{array}{l}\frac{8\pi }{R{e}_n\cdot s}(1-0.87s^{-2})(0<R{e}_n\le 1)\\ 1.45+8.55R{e}_n{-}^{0.90}(1<R{e}_n\le 30)\\ 1.1+4R{e}_n{-}^{0.50}(30<R{e}_n\le 2.33\times {10}^5)\\ -3.41\times {10}^{-6}(R{e}_n-5.78\times {10}^5)(2.33\times {10}^5<R{e}_n\le 4.92\times {10}^5)\\ 0.401\left(1-e^{-\frac{R{e}_n}{5.99}\times {10}^5}\right)(4.92\times {10}^5<R{e}_n\le {10}^7)\end{array}& (8)\end{array}$

$\begin{array}{ll}\begin{array}{c}{C}_{Dt}=\pi \mu \left(0.55R{e}_n{}^{\frac{1}{2}}+0.084R{e}_n{}^{\frac{2}{3}}\right)\end{array}& (9)\end{array}$

where $C_{dn}$ and $C_{dt}$ are the normal and tangential coefficients of the resistance. $\mu$ is the fluid viscosity, $s$ is the arc length between the lower-end point and a material point of cable in an unstrained state, and $s=-0.077215665+\text{ln}(8/R{e}_n)$. $R{e}_n$ is the Reynolds number based on the normal velocity.

Furthermore, to account for the wake effect generated by the upstream lantern net, two wake models are considered in the numerical simulations for flow velocity reduction. These include the twine-to-twine wake model and the net-to-net wake model, as described by Cheng et al. (2020). To incorporate the twine-to-twine wake model in the Morison-type force model, Equation 10 is prescribed to describe the flow pattern behind a cylinder (i.e., net twine).

$\begin{array}{ll}\begin{array}{c}{U}_{downstream}=U_{upstream}\left(1-1.02\sqrt{\frac{C_D}{6+\frac{x}{d_w}}}exp\left\{\frac{-{\left(\frac{y}{d_w}\right)}^2}{0.076C_D(6+\frac{x}{d_w})}\right\}\right) \end{array}& (10)\end{array}$

where $U_{downstream}$ is the velocity of the downstream cylinder.

The net-to-net wake model is used to approximate the interaction of cage arrays. This model divides an aquaculture cage into two parts, namely, the wake generation zone and the wake reacting zone. Then, a flow velocity reduction factor is defined to represent the net-to-net wake model. It is crucial to determine the flow reduction factor as it is a function of the Reynolds number, net solidity ratio, and angle of attack.

2.4 Numerical implementation

During the simulations, the floating raft, lantern net, and mooring systems are modeled in a finite-element formulation. Then, we establish the mass, damping, stiffness, and load matrices at each element. The equation of motion can be written as follows for discretization and calculation.

$\begin{array}{ll}\begin{array}{c}{\mathit{M}}^S{\ddot{\mathit{d}}}^{n+1-{\text{α}}_m^s}+{\mathit{C}}^S{\dot{\mathit{d}}}^{n+1-{\text{α}}_f^s}+{\mathit{K}}^S{\mathit{d}}^{n+1-{\text{α}}_f^s}={\mathit{ℛ}}_s{}^{n+1-{\text{α}}_f^s}\end{array}& (11)\end{array}$

where $M^S$ is the mass matrix, $C^S$ is the damping matrix, $K^S$ is the stiffness matrix, and ${ℛ}_s$ is the force vector. The responses are obtained in the time domain by integrating the non-linear equation of motion by an incremental time marching scheme called the generalized- $\text{α}$ method (Chung and Hulbert, 1993). Based on the generalized- $\text{α}$ method, these vectors are expressed by

$\begin{array}{ll}\begin{array}{c}{\ddot{\mathit{d}}}^{n+1-{\text{α}}_m^s}=(1-{\text{α}}_m^s){\ddot{\mathit{d}}}^{n+1}+{\text{α}}_m^s{\ddot{\mathit{d}}}^n\end{array}& (12)\end{array}$

$\begin{array}{ll}\begin{array}{c}{\dot{\mathit{d}}}^{n+1-{\text{α}}_f^s}=(1-{\text{α}}_f^s){\dot{\mathit{d}}}^{n+1}+{\text{α}}_f^s{\dot{\mathit{d}}}^n\end{array}& (13)\end{array}$

$\begin{array}{ll}\begin{array}{c}{\mathit{d}}^{n+1-{\text{α}}_f^s}=(1-{\text{α}}_f^s){\mathit{d}}^{n+1}+{\text{α}}_f^s{\mathit{d}}^n\end{array}& (14)\end{array}$

$\begin{array}{ll}\begin{array}{c}{\mathit{ℛ}}_s{}^{n+1-{\text{α}}_f^s}=(1-{\text{α}}_f^s){\mathit{ℛ}}_s{}^{n+1}+{\text{α}}_f^s{\mathit{ℛ}}_s{}^n\end{array}& (15)\end{array}$

We consider the implicit Newmark time integration method (Newmark, 1959) for the acceleration and velocity at $t^{n+1}$:

$\begin{array}{ll}\begin{array}{c}{\ddot{\mathit{d}}}^{n+1}=\frac{1}{\beta \text{Δ}{t}^2}({\mathit{d}}^{n+1}-{\mathit{d}}^n)-\frac{1}{\beta \text{Δ}t}{\dot{\mathit{d}}}^n-\frac{1-2\beta }{2\beta }{\ddot{\mathit{d}}}^n\end{array}& (16)\end{array}$

$\begin{array}{ll}\begin{array}{c}{\dot{\mathit{d}}}^{n+1}=\frac{\gamma }{\beta \text{Δ}t}({\mathit{d}}^{n+1}-{\mathit{d}}^n)-\frac{\gamma -\beta }{\beta }{\dot{\mathit{d}}}^n-\frac{\gamma -2\beta }{2\beta }\mathrm{\Delta }t{\ddot{\mathit{d}}}^n\end{array}& (17)\end{array}$

The acceleration and velocity vectors at the generalized midpoints are:

$\begin{array}{ll}\begin{array}{c}{\ddot{\mathit{d}}}^{n+1-{\text{α}}_m^s}=\frac{1-{\text{α}}_m^s}{\beta \text{Δ}{t}^2}({\mathit{d}}^{n+1}-{\mathit{d}}^n)-\frac{1-{\text{α}}_m^s}{\beta \text{Δ}t}{\dot{\mathit{d}}}^n-\frac{1-{\text{α}}_m^s-2\beta }{2\beta }{\ddot{\mathit{d}}}^n\end{array}& (18)\end{array}$

$\begin{array}{ll}\begin{array}{c}{\dot{\mathit{d}}}^{n+1-{\text{α}}_f^s}=\frac{\left(1-{\text{α}}_f^s\right)\gamma }{\beta \text{Δ}t}({\mathit{d}}^{n+1}-{\mathit{d}}^n)-\frac{\left(1-{\text{α}}_f^s\right)\gamma -\beta }{\beta }{\dot{\mathit{d}}}^n-\frac{\left(1-{\text{α}}_f^s\right)(\gamma -2\beta )}{2\beta }\mathrm{\Delta }t{\ddot{\mathit{d}}}^n\end{array}& (19)\end{array}$

The time integration parameters $\beta$, $\gamma$, ${\text{α}}_m^{s,}$, and ${\text{α}}_f^s$ are expressed as

$\begin{array}{ll}\begin{array}{c}\beta =\frac{1}{4}{(1-{\text{α}}_m^s+{\text{α}}_f^s)}^2, \gamma =\frac{1}{2}-{\text{α}}_m^s+{\text{α}}_f^s, {\text{α}}_m^s=\frac{2{\rho }_{\infty }^s-1}{{\rho }_{\infty }^s+1}, {\text{α}}_f^s=\frac{{\rho }_{\infty }^s}{{\rho }_{\infty }^s+1}\end{array}& (20)\end{array}$

where the spectral radius ${\rho }_{\infty }\in [0,1]$. In the present study, we set the spectral radius ${\rho }_{\infty }$ to be 0.4.

In the present study, a time step of 0.005 with a maximum iteration number of 20 is set, and the total simulation time is 150 s for non-linear dynamic simulations. To reduce the computational effort, a mesh grouping method is employed in the present work. Similar approaches such as the equivalent mesh method have already been reported by Li et al. (2006) and Tsukrov et al. (2003).

3 Experimental verifications

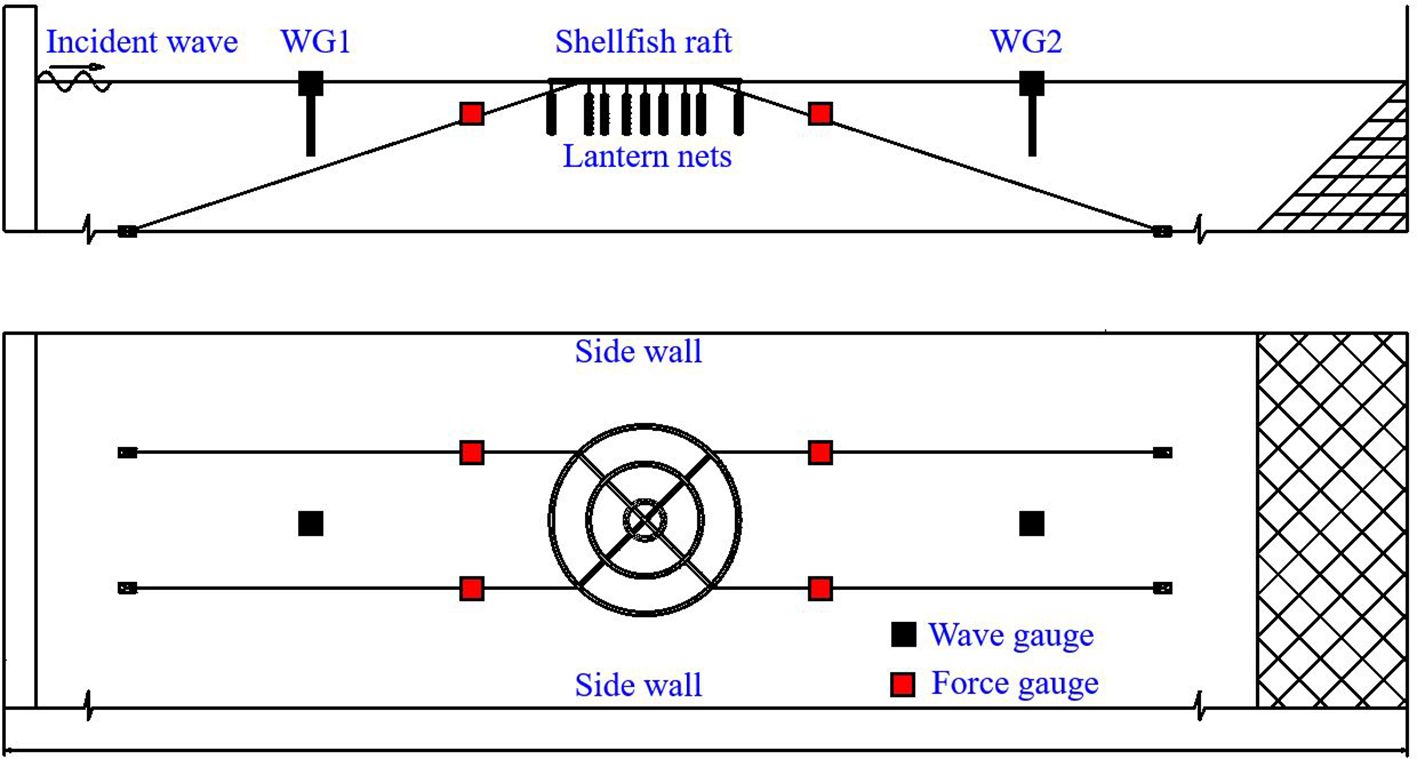
In this section, we conduct physical model tests of an individual shellfish raft to verify the present numerical model. A wave flume, with a dimension of 30 m $\times$ 2 m $\times$ 1.2 m, at the Ningbo Institute of Dalian University of Technology, Ningbo, China, is used. This flume is equipped with a piston-type wave-maker to generate prescribed wave conditions. The shellfish raft containing suspended multi-tier cylindrical lantern net models is connected by a four-line mooring system, as depicted in Figure 4.

Figure 4

Figure 4. The experimental setup of the shellfish raft model.

Considering the wall effect of the flume, the physical model of each net cage is scaled by 1:20 based on the Froude similarity except for the lantern nets. Chakrabarti (1994) mentioned that the walls should be at least 2.5 diameters from the center lines of a cylinder during experiments. Hence, we scaled the floating collar to be 0.8 m in diameter to meet the width (2 m) of the tank walls to be 2.5 diameters of the floating collar. In this manner, the wall effect can be reduced. The geometric similarity is applied to the netting so that the prototype and the model nets have the same projected area (Ma et al., 2022). The catenary mooring system is scaled based on gravity similarity. The detailed parameters of each shellfish raft model are illustrated in Table 2.

Table 2

Table 2. Parameters of each shellfish raft model.

During the experimental tests, the water surface elevations are monitored by two wave probes in the weather and lee sides of the shellfish raft. The predefined frequency of the wave probe is 50 Hz, and the accuracy of each is approximately 0.1%. One charge-coupled device (CCD) camera with a frame rate of 25 is used to record the dynamic response of the shellfish raft. The mooring tensions are measured by the force gauges (50N) connected between the mooring lines and the floating raft. Two cameras, with a frame rate of 60 fps and a resolution of 3,840 $\times$ 2,160 pixels, are used to capture the overall behavior of the shellfish raft. Each case repeats three times to ensure reproducibility. Then, the average value is obtained to minimize the error and improve the accuracy.

Regular wave tests are conducted for the physical model. Three prescribed wave steepnesses include $H/\lambda =1/37.5$, $H/\lambda =1/75,$ and $H/\lambda =1/150$ are prescribed. Here, $H$ is the wave height and $\lambda$ is the wavelength. The wave with a period of 1.9 s, and the corresponding ratio of the wavelength to the shellfish raft diameter $\lambda /D\approx 5$, representing a low-frequency long wave, is used as input at a constant water depth of 0.8 m. This wave condition is consistent with the wave used for the 3 $\times$3 shellfish raft array, both represent the low-frequency long wave and the wavelength is much greater than the diameter of the individual raft.

Furthermore, the mesh grouping method is considered in the present study to improve computational efficiency. Three representative mesh groups of the lantern nets are established to balance the numerical accuracy and computational efficiency. These include Model A, $N_H\times N_V=40\times 64$, Model B, $N_H\times N_V=20\times 64$, and Model C, $N_H\times N_V=10\times 64$. The equivalent net twines correspond to that of a physical lantern net and are proportioned by 1:4, 1:8, and 1:16, respectively. Here, $N_H$ and $N_V$ represent the equivalent net twines (number of meshes) in the horizontal and vertical directions. The numerical model of the single shellfish raft and the representative mesh groups are shown in Figure 5.

Figure 5

Figure 5. Numerical models of the single shellfish raft and the representative mesh groups.

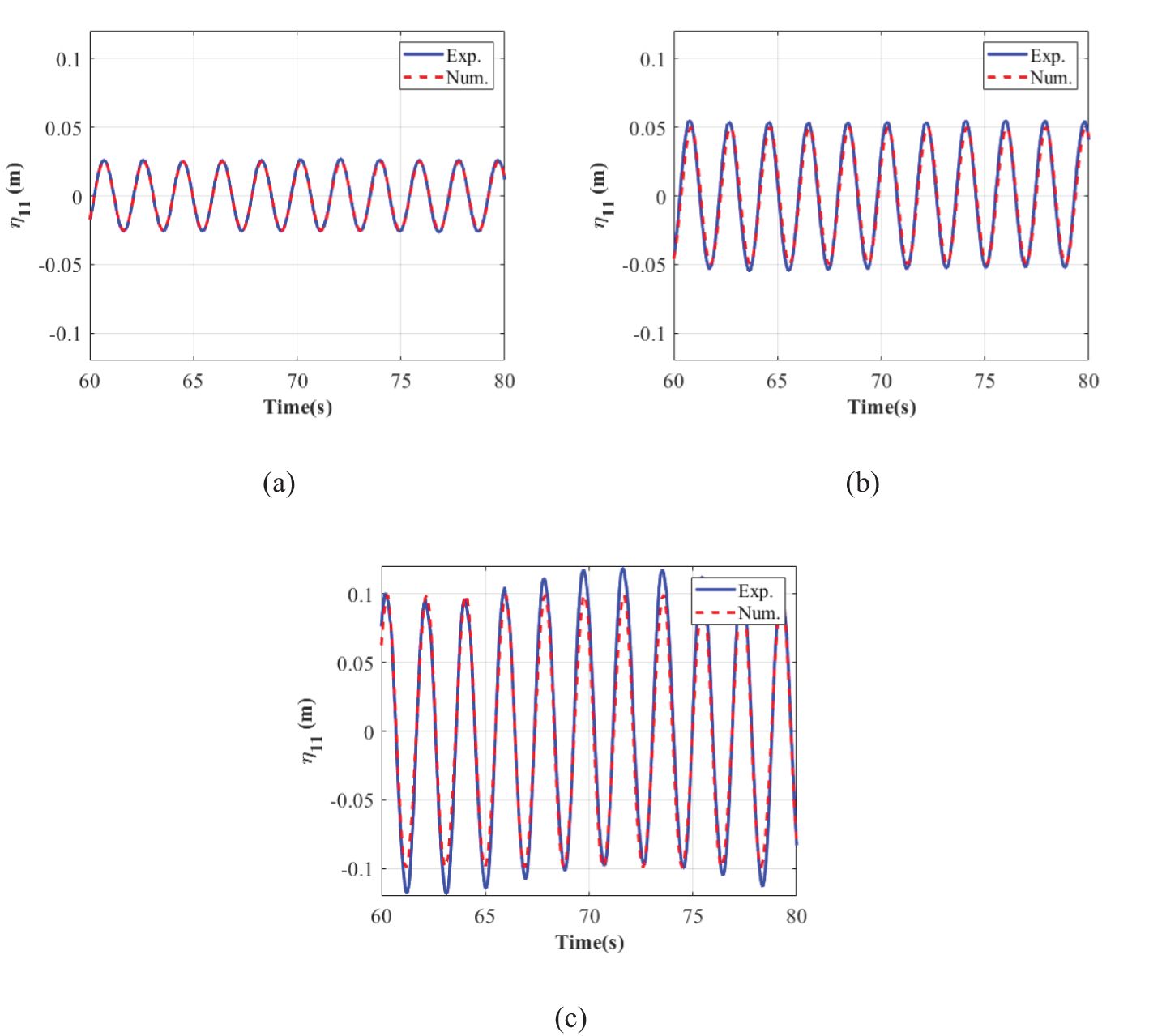
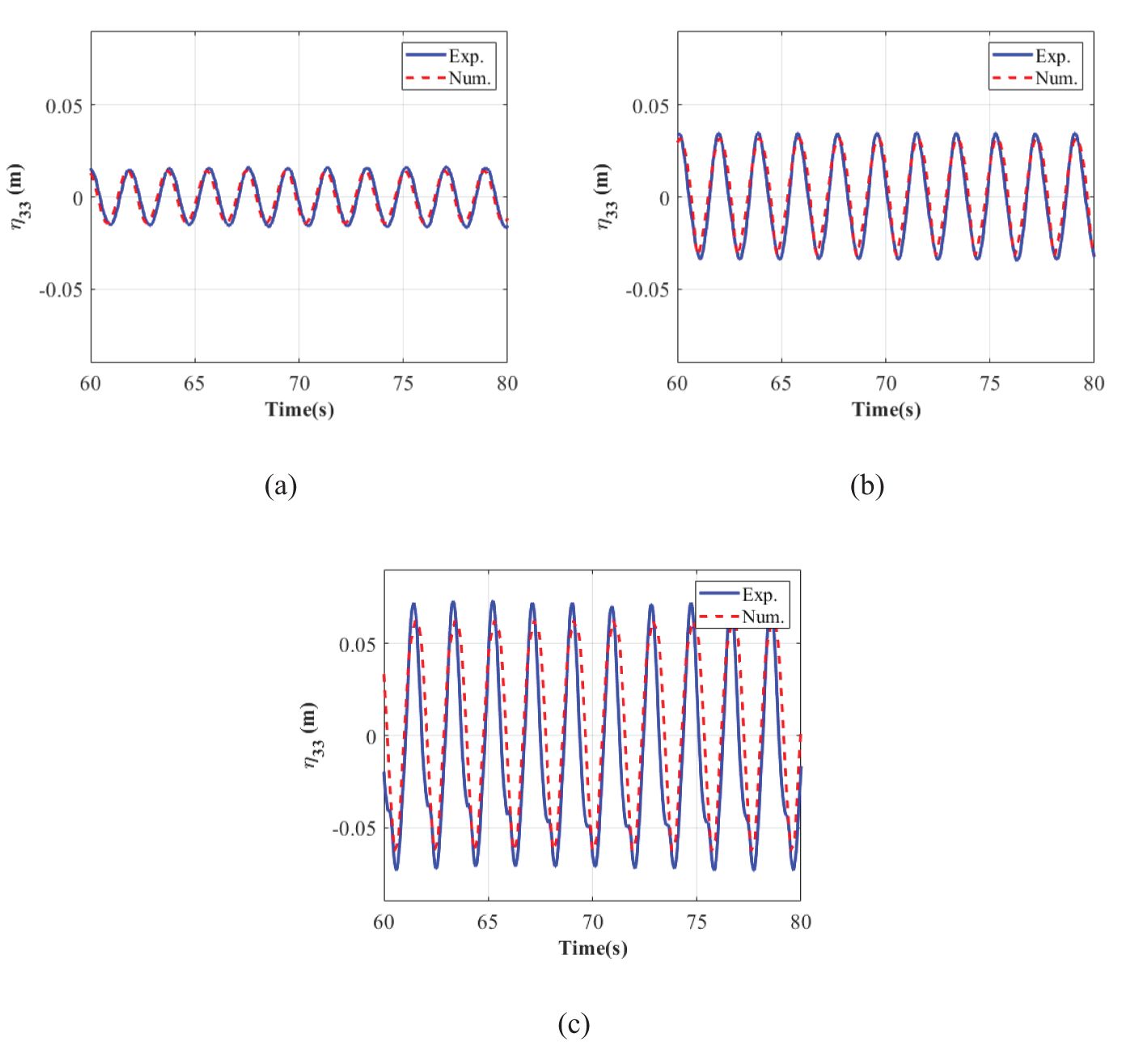
The verification has been conducted in our previous work for aquaculture cages (Shen et al., 2023). Thus, we will not repeat the verification for the mesh grouping method again but directly use the proportioned scale of 1:16 (Model C) between the equivalent and the physical net twines, assuming that the virtual and the physical nets are geometrically identical and have the same physical properties (the detailed parameters are listed in Table 3). Here, ${\lambda }_V$ and ${\lambda }_H$ represent the net bar lengths in vertical and horizontal directions. Then, the comparisons of the motion response such as surge (${\eta }_{11}$) and heave (${\eta }_{33}$) of a single shellfish raft model between experimental tests and numerical simulations are displayed in Figures 6 and 7.

Table 3

Table 3. Parameters of the representative mesh groups.

Figure 6

Figure 6. Time histories of the surge. (A–C) Represent wave steepness from $1/150$ to $1/37.5$.

Figure 7

Figure 7. Time histories of the heave. (A–C) Represent wave steepness from $1/150$ to $1/37.5$.

Figure 6 exhibits the harmonic surge response of a single shellfish raft between experimental tests and numerical simulations in the time domain, and (a)-(c) represents the wave steepness from $1/150$ to $1/37.5$. The overall surge response increases linearly alongside the wave steepness. The general trend between the experimental and the numerical almost overlaps at the smallest wave steepness. The numerical results are slightly smaller than the experimental measurements. This is attributed to the numerical model in the present study making assumptions for simplification, and the wave breaking induced by the interaction of the wave and the cage raft is not considered in the numerical model.

Regular harmonic patterns for the heave response can be observed in Figure 7. Similar to the situation in Figure 6, the numerical results are a bit smaller than the experimental results. Alongside this, the experimental heave response shows evident non-linearity at the wave steepness of $1/37.5$. This non-linearity is attributed to the damping effect of the suspended lantern nets. As we can see from the water flume tests (Figure 8), the suspended lantern nets move up and down with the floating raft, causing the damping effect, which, in turn, enhances the non-linearity in the heave response. Overall, the experimental tests show that the present numerical model is feasible for predicting the dynamic response of the shellfish raft array in waves.

Figure 8

Figure 8. Physical model test of the shellfish raft in waves. (A) $\frac{1}{4}$T. (B) $\frac{3}{4}$T.

4 Results

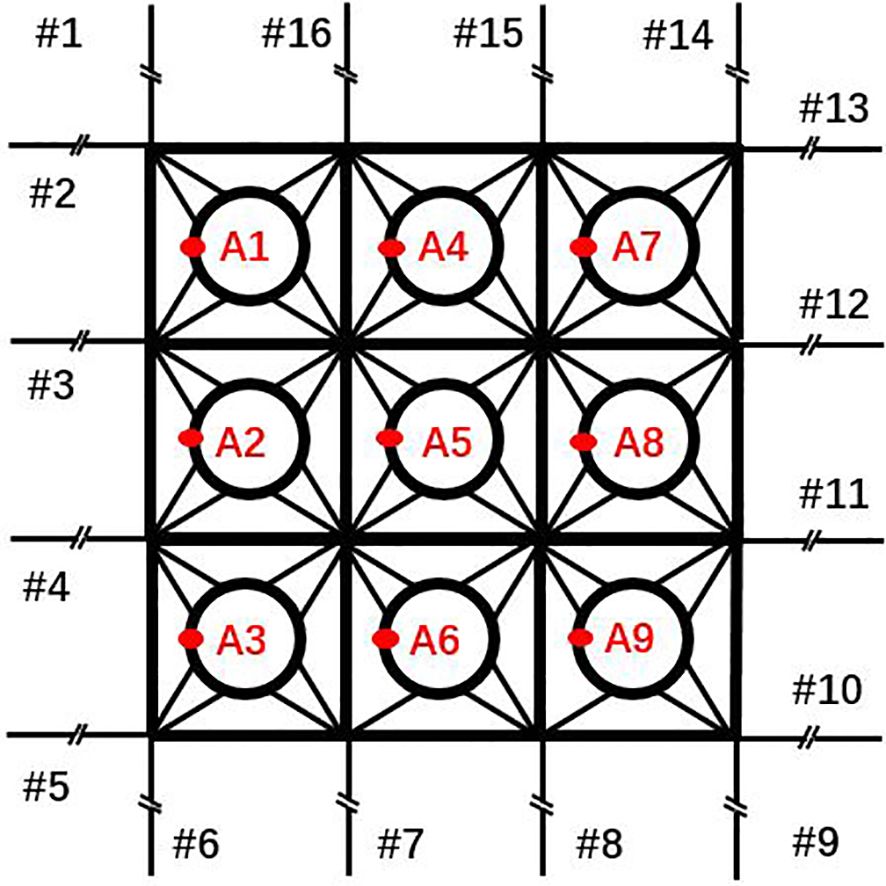
To guarantee the safety design of the mooring grid for the full-scale aquaculture shellfish system, two different angles of wave attack, namely, $0°$ and $45°$, are fully considered in this paper. The mooring dynamics are analyzed from the perspective of fairlead trajectory and energy dissipation. In this manner, the dependence of the tensions on the fairlead positions can provide a quick visual interpretation of the energy absorption induced by mooring dynamics. Alongside this, the wave-induced non-linear motion of each shellfish raft is examined in conjunction with their trajectories so that hydrodynamic forcing mechanisms can be identified. First, we define the numbering of the mooring system and markers on the floating raft in Figure 9 as below.

Figure 9

Figure 9. Numbering of the mooring lines and markers on the floating rafts.

4.1 Dynamics under different wave attacks

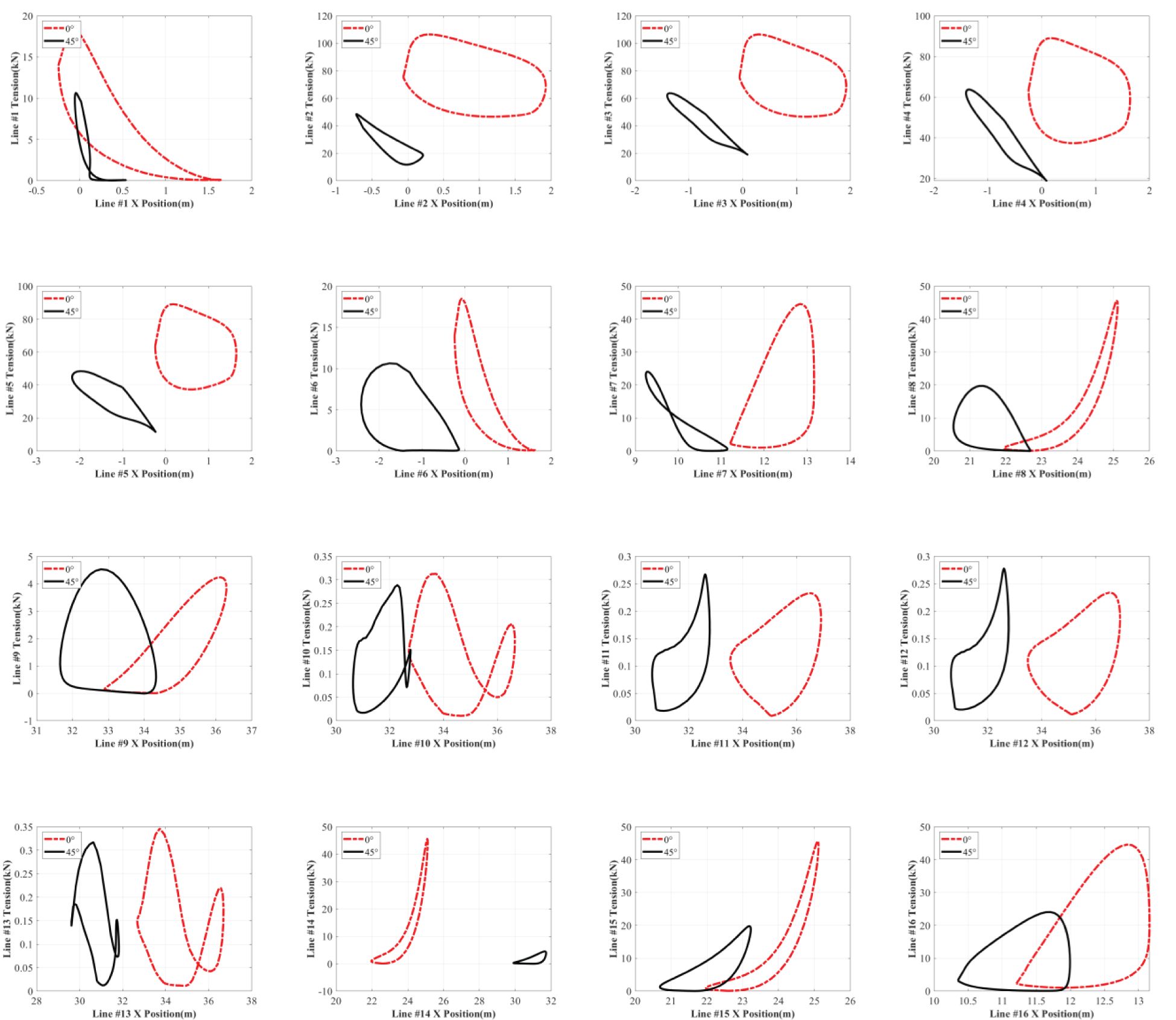
One crucial design issue when determining the performance of the shellfish farm is that the mooring system should be capable of absorbing the extreme environmental loads without failure (i.e., the survivability problem). Thus, Figure 10 exhibits the dependence of the mooring tensions on the fairlead positions under different wave attacks. All the data are collected after the dynamic simulations reach a steady state and the line configurations are in harmonic conditions. For the convenience of comparison, only one complete cycle of motion is plotted. The corresponding area in the horizontal motion-tension curve represents the energy absorption. Thus, a quick visual interpretation of the energy absorption caused by mooring dynamics can be achieved (Webster, 1995).

Figure 10

Figure 10. Dependence of the mooring tensions on the fairlead positions.

As can be seen from Figure 10, the overall horizontal motion-tension curves show that the areas under the ${45}^{°}$ incident wave are smaller than those under the $0^{°}$ incident wave. According to the description by Webster (1995), the energy absorption $E_m$, occurring at one complete cycle of motion, is given by $E_m=\underset{t}{\overset{t+T}{\int }}{T}_n(q_n)\frac{d{q}_n}{dt}dt={\oint }^{ }{T}_n(q_n)d{q}_n$, where $T_n$ is the tension component in the direction of n and $q_n$ is the instantaneous displacement in that direction. This indicates that the mooring system under a $0°$ incident wave absorbs much more energy than that under a $45°$ incident wave. Therefore, the oblique wave has a significant effect on the mooring dynamics. The maximum tension forces occur at the weather-side of the shellfish farm when the wave incident angle is $45°$. The maximum value reaches 118.68 kN for mooring line #2. In this situation, horizontal motions like surge and sway can cause very large instantaneous tensions in the taut lines, leading to mooring failure. The minimum tension forces occur at the lee side of the shellfish farm when the wave incident angle is $0°$. The average value is only 0.12 kN for mooring lines from #10, #11, #12, to #13. The tension statistics in all mooring lines are also listed in Table 4 for comparison. Overall, it is suggested to avoid oblique wave attacks concerning energy absorption and mooring tension, for safety considerations of a shellfish farm deployed in the open ocean.

Table 4

Table 4. Tension statistics in all mooring lines (kN).

It also can be observed in Figure 10 that almost all the horizontal motion-tension curves at the $45°$ incident wave do not exhibit elliptical patterns like the trajectories of water particles. This highlights that evident non-linearity appears in the mooring dynamics. Most likely, the non-linearity is caused by the wave-frequency (WF) response due to wave excitations and the low-frequency (LF) response due to wave drift. This is because the mooring tensions are closely related to the horizontal and vertical motions of the fairleads induced by wave excitations. Alongside this, mooring damping should also be responsible for the non-linear characteristics of the mooring dynamics, as the mooring-induced damping and the energy dissipation could enhance the non-linearity (Xu et al., 2023). Finally, as the shellfish raft undergoes wave excitation, lee-side mooring lines slacken and the weather sides become taut, thus providing a net non-linear restoring force to the raft. This is also a leading contributor to the non-linearity of the mooring dynamics.

Other issues that arise in the design of a shellfish farm include the following: the motions of the shellfish raft are supposed to be small enough so that equipment can be easily handled, and the horizontal/vertical excursion of the structure is contained within a certain range (i.e., the operation problem). Therefore, in the second half of this subsection, we examine the motion dynamics of the shellfish farm. Specifically, LF-induced slow-drift motions in the horizontal plane (e.g., surge) and wave-frequency excitations-induced motions in the vertical plane (e.g., heave) under different wave incident angles, together with their trajectories, are depicted in Figures 11 and 12 for comparison.

Figure 11

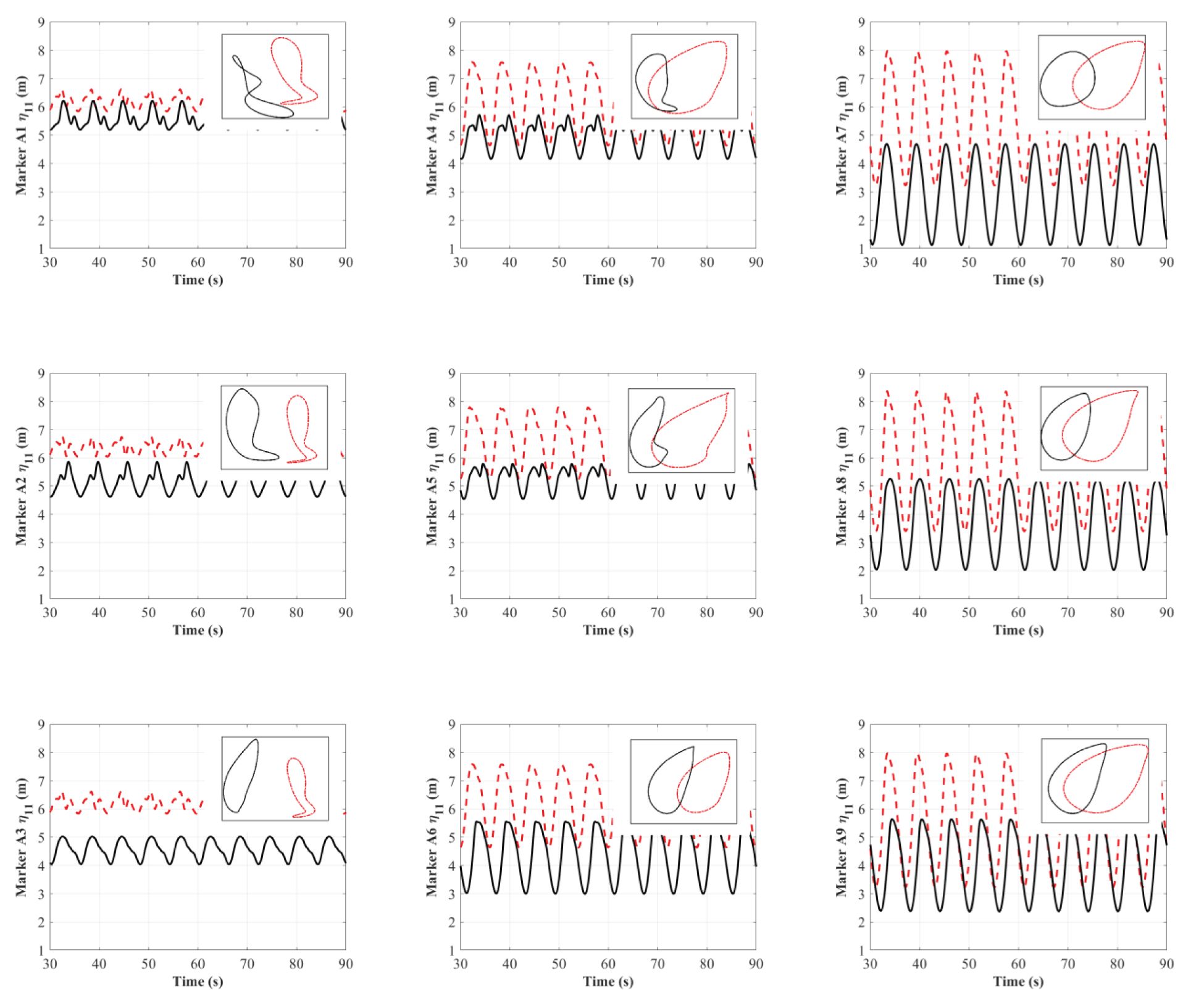
Figure 11. Time histories of the surge. Red dashed line, $45°$ incident wave; black solid line, $0°$ incident wave.

Figure 12

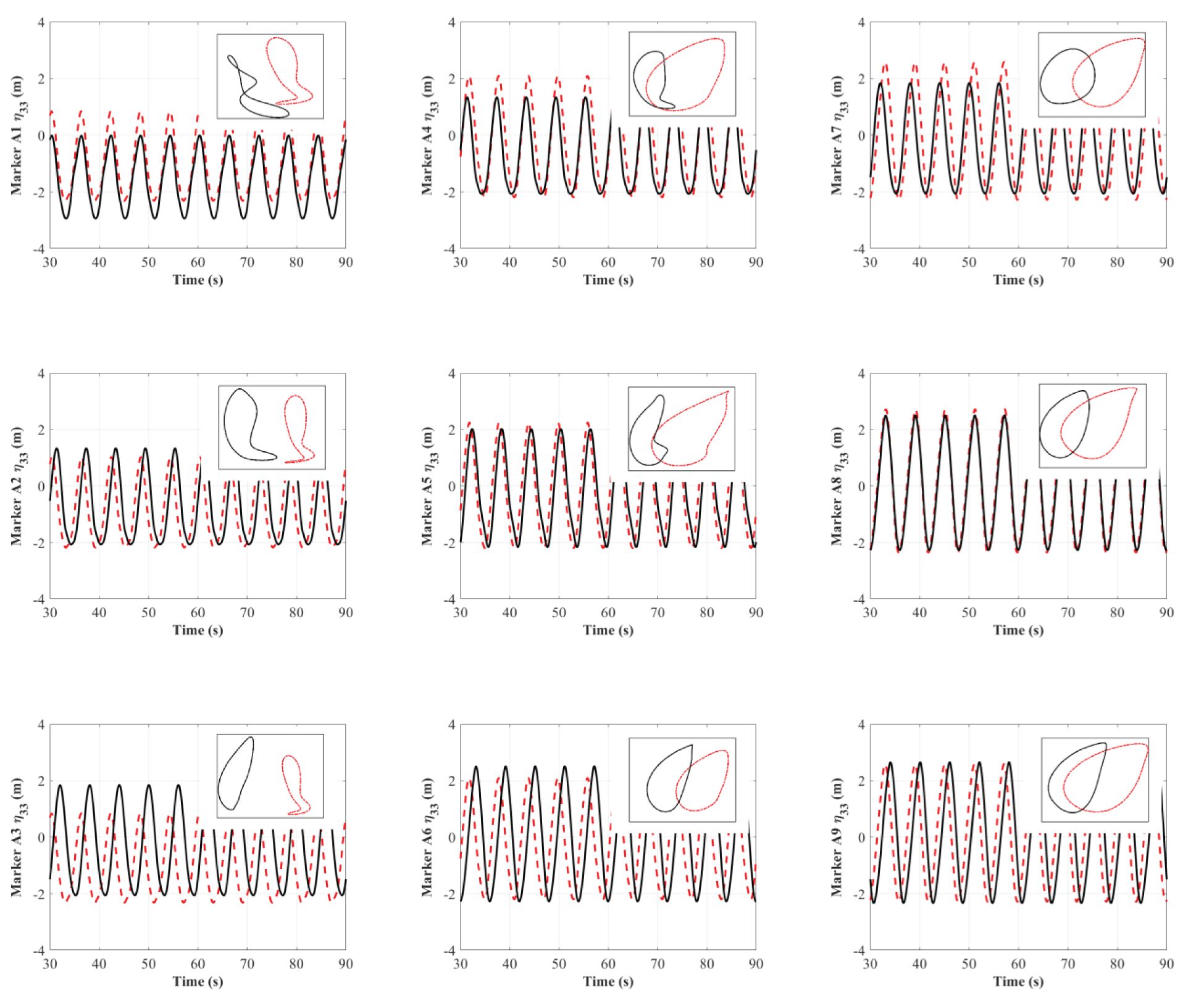
Figure 12. Time histories of the heave. Red dashed line, $45°$ incident wave; black solid line, $0°$ incident wave.

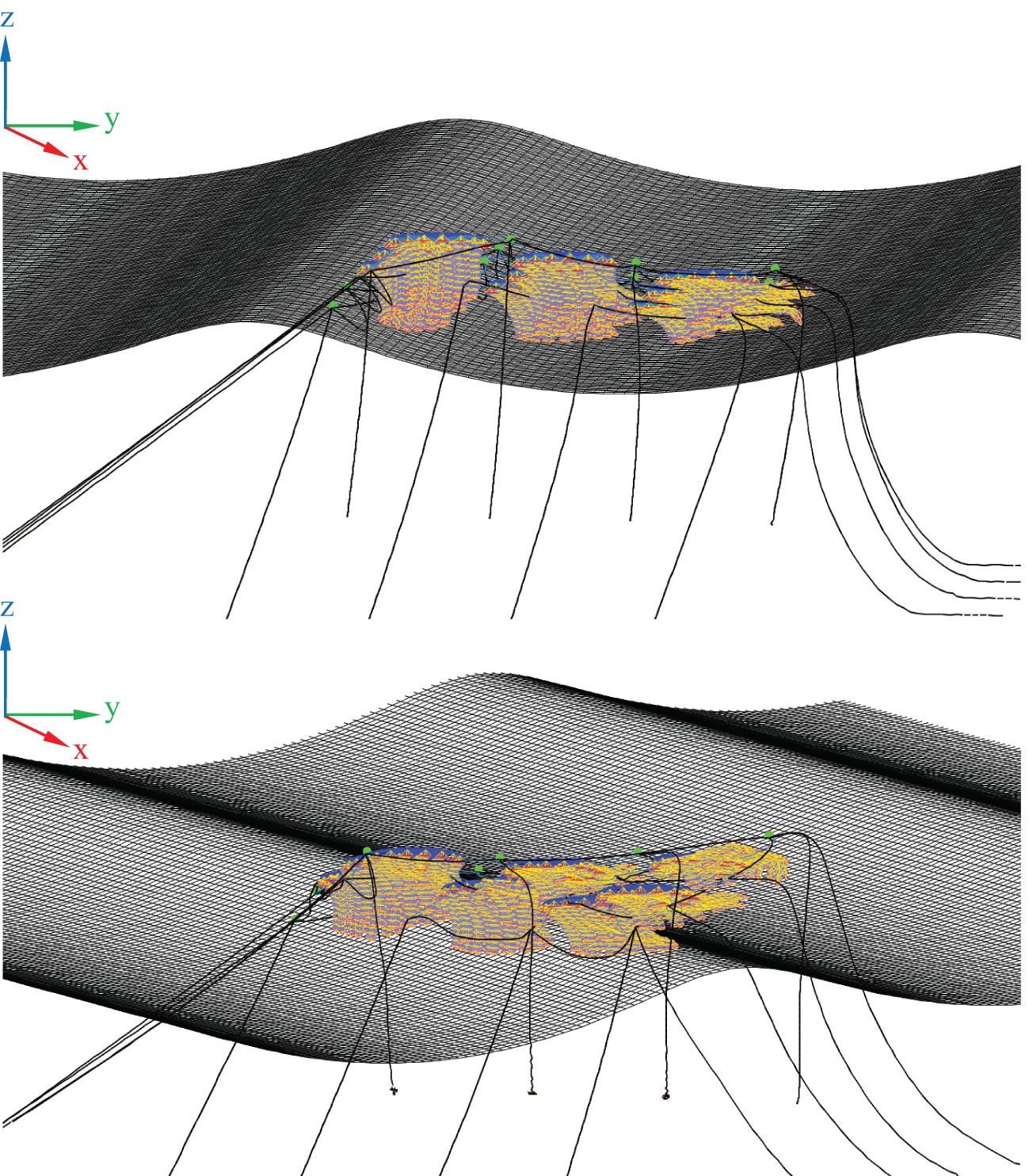
Figure 11 depicts the time histories of the surge based on the markers on the floating rafts, and the order of the figures exactly follows the arrangement in Figure 9. For instance, figures in the left column represent the surge motions of weather-side shellfish rafts, and those in the right column represent the surge motions of the lee side. The overall trend for surge motion increases from the weather side to the lee side due to the horizontal motion. If we see the configurations of the mooring lines in Figure 13, it can be observed that the weather-side mooring lines are in a taut state, whereas the lee-side mooring lines slacken concerning different wave incident angles. The taut mooring lines significantly restrain the horizontal motion of the shellfish farm on the weather side. The overall surge motions in the weather and lee sides of the shellfish farm exhibit different situations: for shellfish rafts in the weather side, the surge under $0°$ incident wave is greater than that under $45°$ incident wave; on the contrary, for shellfish rafts between the weather and lee sides, the surge under $0°$ incident wave is relatively smaller than that under $45°$; for shellfish rafts in the lee side, the surge under $0°$ incident wave is slightly smaller than that under $45°$ incident wave. Still, the horizontal excursion of the shellfish farm has been significantly affected by the oblique wave.

Figure 13

Figure 13. Numerical modeling of the shellfish farm under $0°$ (upper) and $45°$ (lower) wave attacks.

Moreover, the surge motions of weather-side shellfish rafts show evident non-linearity at both $0°$ and $45°$ wave attacks. The restoring force induced by the taut mooring on the weather side and the slack mooring on the lee side could be partially responsible for this non-linearity. But the leading contributor should be the damping induced by the moorings on the weather side. Even though all the data have been post-processed via Gaussian smoothing codes, there are still subharmonics in the time histories of the surge motion under $0°$ incident wave. One possible reason for these subharmonics is the free surface effect (Qin et al., 2020; Xu et al., 2018), as most of the floating rafts are submerged under the water surface, resulting in wave breaking and turbulence. This, in turn, increases the non-linearity in the surge motion.

From Figure 12, we see that the overall amplitude of the heave motion is slightly smaller than the wave amplitude (${\text{ζ}}_a=2.8$m). Aside from this, there is no evident non-linearity in the time histories of the heave motion. The difference in heave motion between $0°$ and $45°$ incident waves is also subtle, meaning that the wave fields have little effect on the heave motion. However, in a previous study (Qin et al., 2020), the vertical accelerations of a net cage have been decomposed into non-linear harmonics so that the non-linearity of the heave motion can be analyzed. The authors also reported that drag-driven damping from the netting significantly affected the non-linearity of the vertical motions.

4.2 Dynamics with/without lantern nets

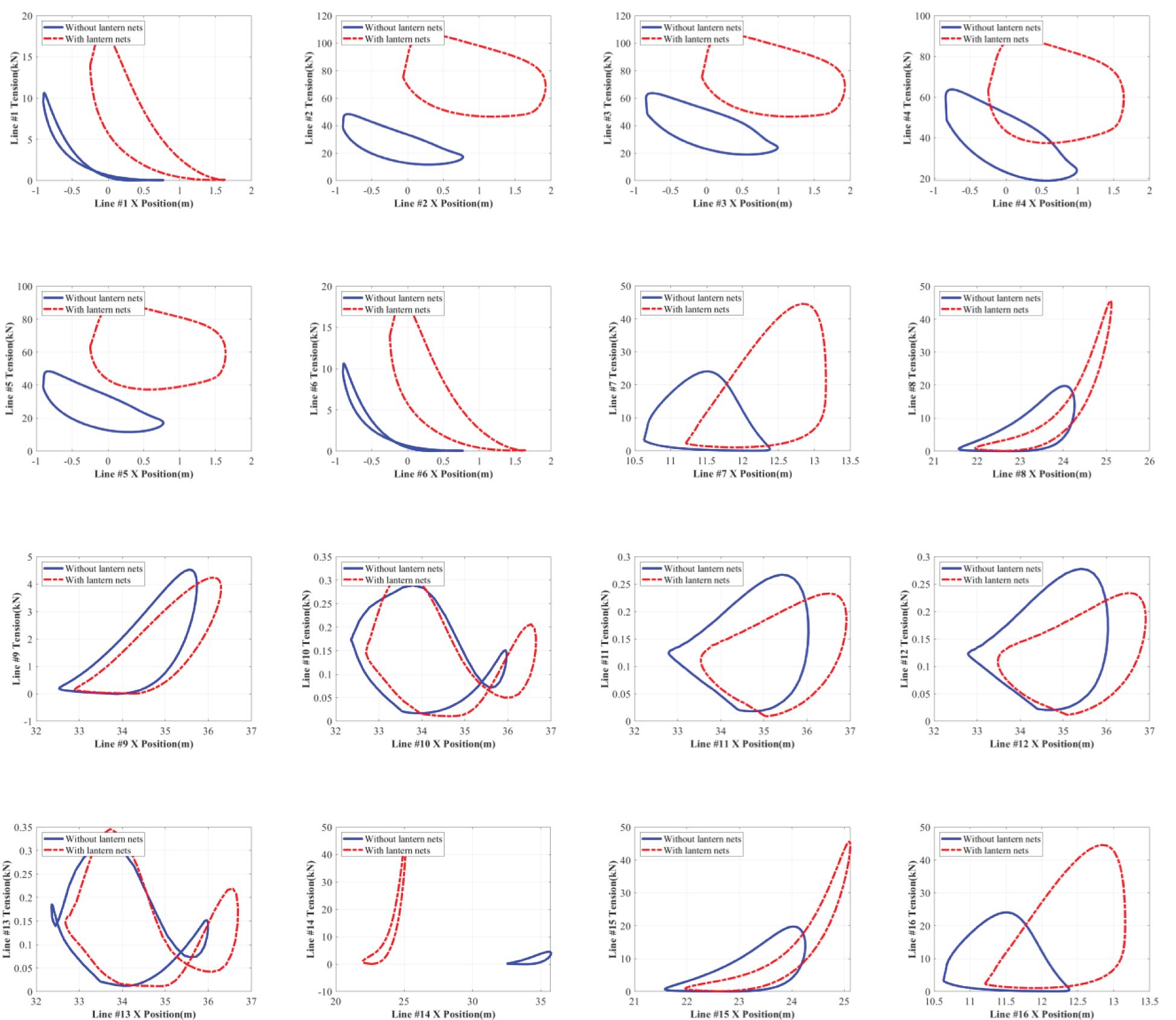
In this section, the focus will be placed on the damping effect of the lantern nets. Therefore, the damping effect on the mooring and motion dynamics can be quantitatively analyzed. All the simulations are conducted under $0°$ wave attack, and the data are collected after the dynamic simulations reach a steady state and the line configurations are in harmonic conditions. For the convenience of comparison, only one complete cycle of motion is plotted.

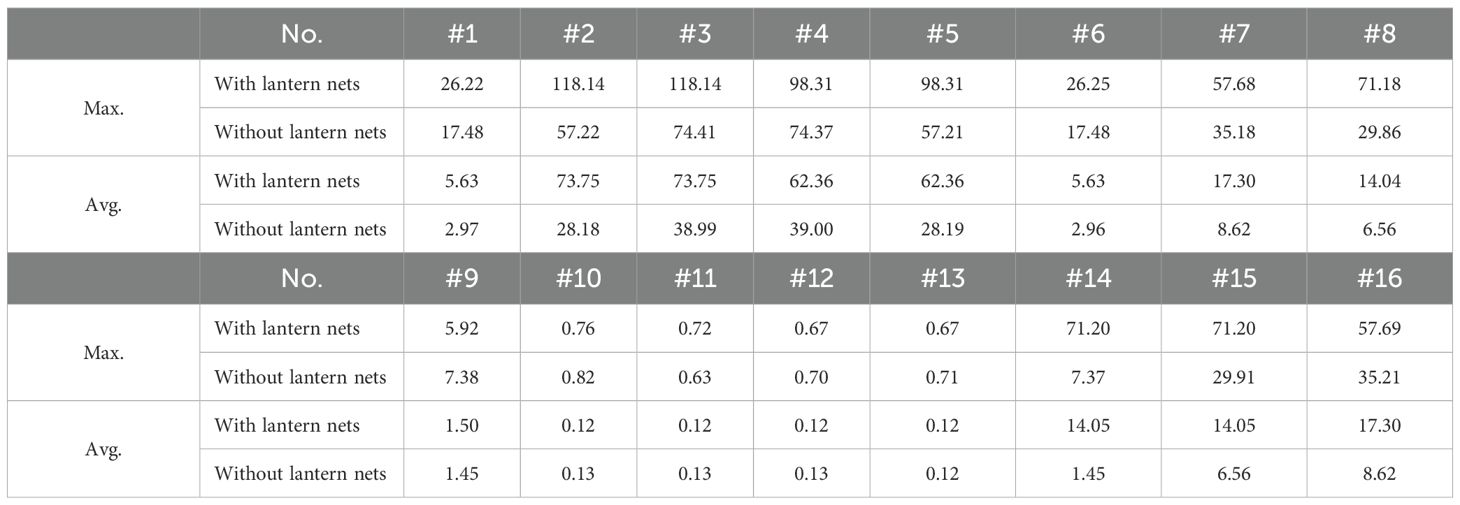
Figure 14 depicts the dependence of the mooring tensions on the fairlead positions of the shellfish raft with and without lantern nets. The overall horizontal motion-tension curves show that almost all the areas with lantern nets are greater than those without lantern nets. Therefore, it can be determined that shellfish rafts with lantern nets absorb much more wave energy than those without lantern nets. It seems that the lantern nets greatly contribute to the energy dissipation when the wave interacts with the shellfish farm. Regarding the mooring tension, the maximum tension forces occur at the weather side of the shellfish raft with lantern nets. The maximum value reaches 118.14 kN for mooring lines #2 and #3. The WF-induced horizontal motions such as surges lead to very large instantaneous tensions in the taut lines. The minimum tension forces occur at the lee side of the shellfish raft with lantern nets. The average value reaches 0.12 kN for mooring lines #10, #11, #12, and #13. The tension statistics in all mooring lines are also listed in Table 5 for comparison. Overall, the lantern nets can lead to more than two times the average tension for the shellfish raft with lantern nets on the weather side.

Figure 14

Figure 14. Dependence of the mooring tensions on the fairlead positions.

Table 5

Table 5. Tension statistics in all mooring lines (kN).

Figure 14 also shows that almost all the horizontal motion-tension curves of the shellfish rafts with and without lantern nets do not exhibit elliptical patterns such as the trajectories of water particles. Evident non-linearity appears at the mooring dynamics. Similar to the situation in Figure 10, the non-linearity is caused by the WF response due to wave excitations and the LF response due to wave drift. Since the mooring tensions are dependent on the horizontal and vertical motions of the fairleads induced by wave excitations. Moreover, Shellfish rafts with lantern nets exhibit significantly more non-linearity than those without lantern nets. If the damping from moorings and the lantern nets increase the non-linearity of the mooring dynamics for shellfish rafts with lantern nets, then the restoring force would be the leading contributor to the non-linearity of the mooring dynamics for shellfish rafts without lantern nets.

Figure 15 exhibits the time histories of the surge based on the markers on the floating rafts. Similar to the situation in Figure 11, the overall trend for surge motion increases from the weather side to the lee side due to the horizontal motion. In general, the surge motions in the weather and lee sides of the shellfish farm show different situations: on the weather side, the surge of the shellfish raft without lantern nets is greater than that with lantern nets. However, the reverse situation occurs for shellfish rafts in the lee side and those between the weather and lee sides. The surge for shellfish rafts with lantern nets is greater than that for shellfish rafts without lantern nets. One common reason is that the taut mooring lines significantly restrain the horizontal motion of the shellfish rafts with and without lantern nets on the weather side. However, because of the combined effect from the damping of lantern nets and moorings, shellfish rafts with lantern nets have a much smaller horizontal excursion (i.e., surge).

Figure 15

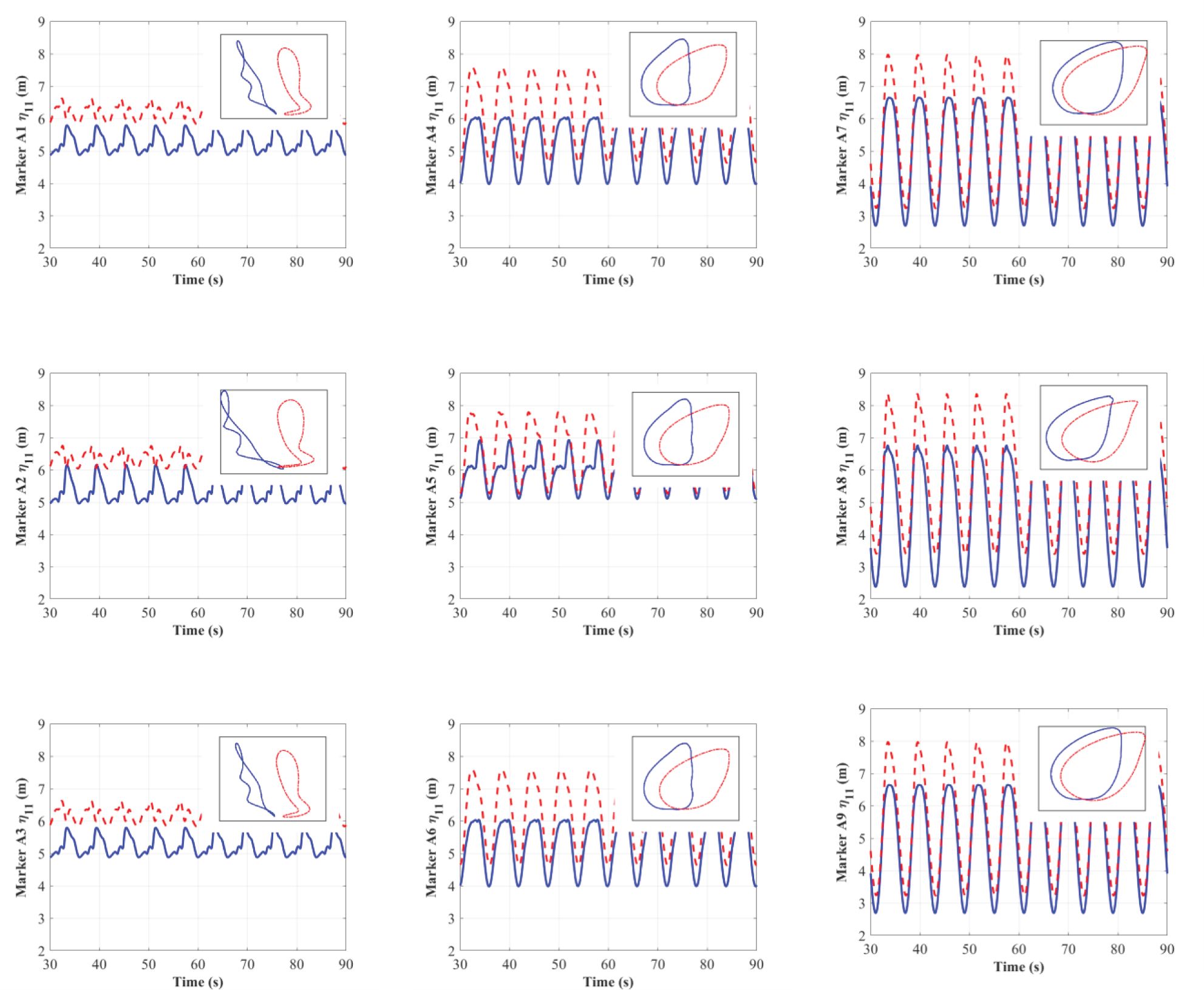
Figure 15. Time histories of the surge. Red dashed line, shellfish raft with lantern nets; blue solid line, shellfish raft without lantern nets.

In addition, the surge motions of weather-side shellfish rafts with and without lantern nets show evident non-linearity. This non-linearity is attributed to the restoring force induced by the taut mooring on the weather side and the slack mooring on the lee side. However, the damping induced by the moorings and lantern nets should be responsible for the non-linearity of the shellfish raft with lantern nets. Aside from this, there are regular subharmonics in the time histories of the surge motion on the weather side. These subharmonics are possibly caused by the free surface, as wave breaking and turbulence will happen when the wave interacts with the floating rafts of the shellfish rafts.

Figure 16 shows that the overall amplitude of the heave motion is slightly smaller than the wave amplitude (${\text{ζ}}_a=2.8$m). Similar to the situation in Figure 12, there is no evident non-linearity in the time histories of the heave motion. There is also a marginal discrepancy in heave motions for shellfish rafts with and without lantern nets. This indicates that, under wave conditions, the damping effect of the lantern nets has little effect on the heave motion. However, it is still suggested that the drag-driven damping from the netting under combined wave and current conditions should be further analyzed.

Figure 16

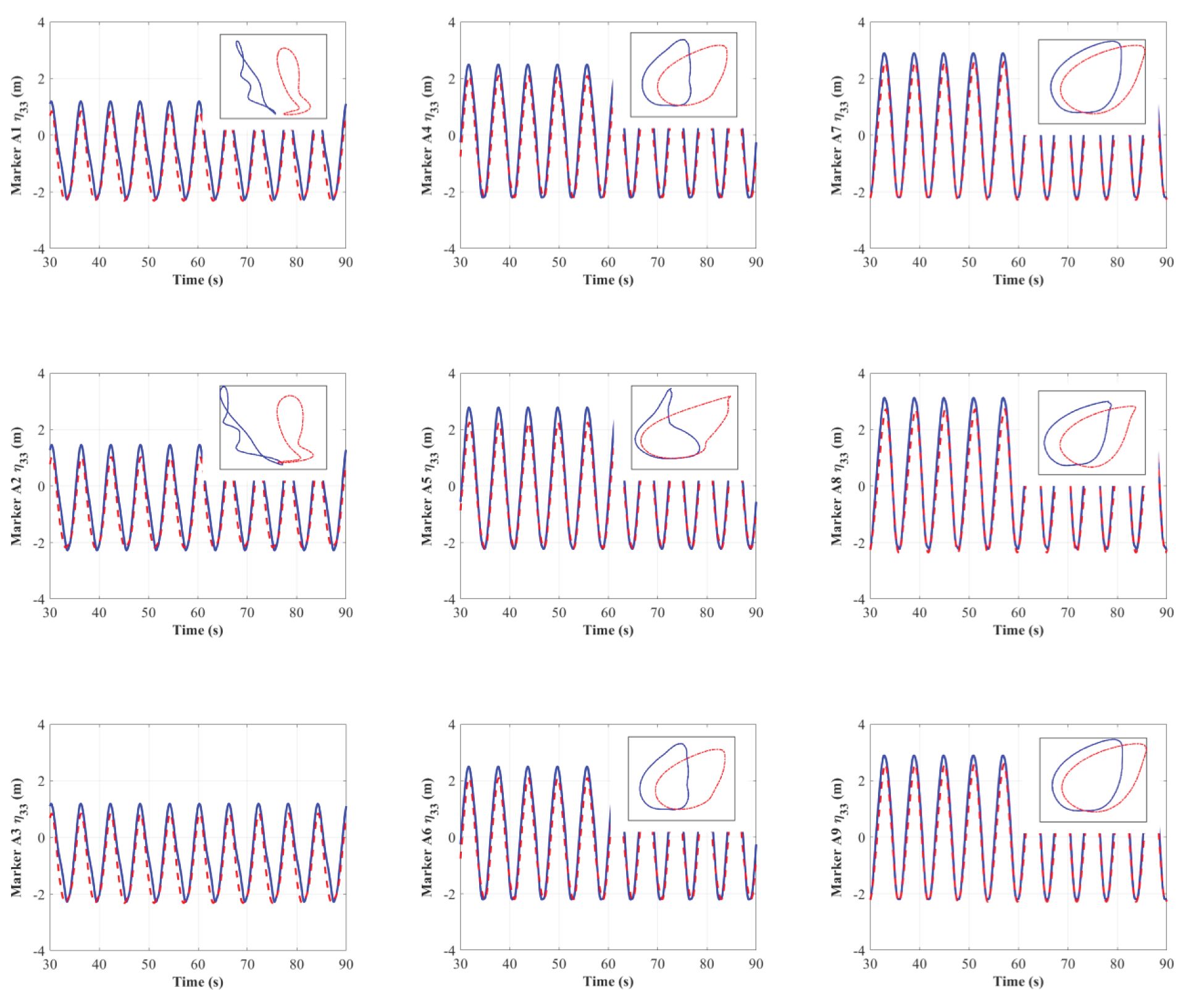
Figure 16. Time histories of the heave. Red dashed line, shellfish raft with lantern nets; blue solid line, shellfish raft without lantern nets.

5 Discussion

Previously, studies have been conducted via numerical models to understand the non-linear mooring dynamics (Fan et al., 2017; Gutiérrez-Romero et al., 2016; Liu et al., 2014; Tsukrov et al., 2005; Webster, 1995; Wu et al., 2015) and non-linear motion dynamics (Shen et al., 2023; Xu et al., 2023; Zhu et al., 2023) of the floating structures/cage array. This work focused on the mooring non-linearity with respect to material property (Tsukrov et al., 2005), tension-elongation (Liu et al., 2014), and energy absorption (Fan et al., 2017; Webster, 1995) under cyclic loads. Specifically, WF- and LF-induced tension damping and fatigue, and second non-linear forces were predicted via a non-linear FEM model for mooring dynamics (Gutiérrez-Romero et al., 2016; Wu et al., 2015). This pioneering work significantly facilitated the safety design of the mooring system for offshore floating structures.

The present study modeled an offshore shellfish farm under a Stokes wave based on an implicit finite element framework. Different angles of wave attack and the damping effect of the lantern nets were fully considered so that the mooring and motion dynamics could be studied comprehensively. In particular, the extreme excursion of the fairlead, energy absorption, and horizontal/vertical excursion of the structure were determined in this paper. Finally, novel insights have been gained for the safety design of the offshore shellfish farm.

For the safety design of the mooring system, Faltinsen (1993) suggested that the approved extreme horizontal excursion of the fairlead should be less than 10% of the water depth. In the present paper, the extreme horizontal excursion of the mooring system was less than 10% of the water depth (i.e., 2.7 m), satisfying the excursion requirement of the mooring system. Regarding energy dissipation, Webster (1995) introduced energy absorption by integrating the tension components in the direction of instantaneous displacement. This energy absorption was defined to represent a mooring-induced damping. With this interpretation, the present study verified the conclusion of (Wu et al., 2015) and found that the angle of wave attack significantly affected the energy absorption of the mooring system. Moreover, the lantern nets beneath the shellfish raft also provided additional damping, leading to more energy absorption for the mooring system.

Another key consideration in the design of the mooring system is the non-linearity induced by the coupled dynamics of the floating raft, mooring system, and lantern nets. Although the mooring system provided the restoring forces to the floating raft, the damping arising from the moorings and lantern nets was also comparable with the floating raft. Together with the wave-induced non-linearity and geometric non-linearity, all these contributed to the non-linearity of the mooring dynamics. Tsukrov et al. (2005) already examined the geometric non-linearity for moorings with different material properties. The authors suggested that the mooring system cannot be approximated by simple quasi-static springs. Instead, they introduced the non-linear material behavior into the numerical time-integration procedure. However, this paper primarily focuses on the damping-induced non-linearity. In particular, the damping effect has been interpreted by energy absorption. Similar studies on the non-linear dynamics of an aquaculture cage array have been reported by Xu et al. (2023). The authors emphasized that the LF effects on the non-linearity of the mooring were crucial. However, wave conditions and structure types should be distinguished for specific farming purposes. Alongside this, for the safety design of the mooring system, it should be conservative to suggest that both the WF and LF excitations should be incorporated when analyzing the non-linearity of the mooring dynamics.

For the safety design of the floating structure system, the horizontal/vertical excursion (e.g., surge/heave) of the structure is required to be within a certain range. Otherwise, the extreme horizontal offset could lead to the failure of marine operations and threaten the farmed bivalves. These motion responses are either induced by a WF due to wave excitations, or induced by an LF due to wave drift. In the present study, the amplitude of the surge/heave motion is smaller than the wave amplitude (${\text{ζ}}_a=2.8$m) and stays within a certain range. Thus, the dynamic response meets the design criteria for the proposed shellfish farm.

Aside from the horizontal/vertical excursion, another critical issue that needs to be addressed is the non-linear motion dynamics, since the non-linear coupling of motion significantly affects the stability and safety design of the floating structures containing multiple modules (e.g., shellfish farm). The most evident non-linear dynamics for the present shellfish farm due to the coupling motion are the subharmonics in the time history of the surge. This non-linearity is partially attributed to the damping induced by the moorings and lantern nets. Previously, subharmonics and ultra-subharmonics have received considerable attention concerning biomechanics (Wang et al., 2019), composite materials (Ma et al., 2020), and marine structures (Orszaghova et al., 2021). To improve the performance of the biosystem, Wang et al. (2019) provided a solution to eliminate the subharmonics by adjusting the structural parameters. Ma et al. (2020) suggested suppressing the subharmonics by controlling the amplitude of the external excitation. Orszaghova et al. (2021) revealed that the subharmonics were dominant by second-order difference-frequency excitations. Overall, these studies provide insights into the safety design of a shellfish farm with multi-modules.

6 Conclusions

An innovative shellfish farm that contains nine floating rafts with suspended lantern nets in a 3×3 configuration was proposed in this paper. An implicit finite element method was leveraged to model the shellfish farm under extreme wave conditions so that the safety design of the shellfish farm can be potentially guaranteed. The operation and survivability abilities of the shellfish farm under extreme wave conditions were specifically assessed. The conclusions are summarized as follows.

i. For the safety design of the mooring system, the extreme horizontal excursion of the mooring system was less than 10% of the water depth (i.e., 2.7m), satisfying the excursion requirement of the mooring system at a survivability level.

ii. This paper would suggest avoiding oblique wave attack as it significantly affected the energy absorption of the moorings of the shellfish system. Moreover, the lantern nets beneath the shellfish raft also provided additional damping, leading to more energy absorption for the mooring system.

iii. The restoring forces to the floating raft, the damping arising from the moorings and the lantern nets, the wave-induced non-linearity, and geometric nonlinearity, together contribute to the non-linearity of the mooring dynamics.

iv. For the safety design of the mooring system, it should be conservative to treat the WF and LF excitations equally when analyzing the non-linearity of the mooring dynamics.

v. The amplitude of the surge/heave motion stays within a certain range and is smaller than the wave amplitude (${\text{ζ}}_a=2.8$m). Thus, the dynamic response meets the design criteria for the proposed shellfish farm at an operation level.

vi. There is evident non-linearity in the time history of the surge, and it is increased by the damping induced by the moorings and lantern nets. Non-linear instability such as subharmonics in the motion dynamics can be manipulated to avoid resonant motions.

This study provides insights into evaluating the safety design of a shellfish farm at operation and survivability levels. The present method can also be used for modeling other advanced offshore marine structures with multi-modules, such as floating bridges, floating airports, and even floating energy islands.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

HY: Conceptualization, Data curation, Formal analysis, Methodology, Writing – original draft. YL: Data curation, Software, Validation, Writing – review & editing. JW: Data curation, Software, Validation, Writing – review & editing. YM: Funding acquisition, Investigation, Methodology, Project administration, Validation, Writing – review & editing. ZX: Conceptualization, Formal analysis, Funding acquisition, Methodology, Project administration, Supervision, Validation, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Fund of Guangdong Provincial Key Laboratory of Intelligent Equipment for South China Sea Marine Ranching (2023B1212030003); Non-found Science and Technology Research Program Project of Zhanjiang (2023B01099); and the Doctor Initiate Project of Guangdong Ocean University (060302072304 and 060302072404).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Boo S. Y., Shelley S. A., Shin S.-H., Park J., Ha Y.-J. (2023). Design and analysis of a sub-surface longline marine aquaculture farm for co-existence with offshore wind farm. J. Mar. Sci. Eng. 11, 1034. doi: 10.3390/jmse11051034

Crossref Full Text | Google Scholar

Chakrabarti S. K. (1994). Offshore Structure Modeling (Singapore: World Scientific).

Google Scholar

Cheney D., Langan R., Heasman K., Friedman B., Davis J. (2010). Shellfish culture in the open ocean: lessons learned for offshore expansion. Mar. Technol. Soc. J. 44, 55–67. doi: 10.4031/MTSJ.44.3.6

Crossref Full Text | Google Scholar

Cheng H., Li L., Aarsæther K. G., Ong M. C. (2020). Typical hydrodynamic models for aquaculture nets: A comparative study under pure current conditions. Aquacultural Eng. 90, 102070. doi: 10.1016/j.aquaeng.2020.102070

Crossref Full Text | Google Scholar

Chung J., Hulbert G. (1993). A time integration algorithm for structural dynamics with improved numerical dissipation: the generalized-α method. J. Appl. Mechanics 60, 371–375. doi: 10.1115/1.2900803

Crossref Full Text | Google Scholar

DeCew J., Tsukrov I., Risso A., Swift M., Celikkol B. (2010). Modeling of dynamic behavior of a single-point moored submersible fish cage under currents. Aquacultural Eng. 43, 38–45. doi: 10.1016/j.aquaeng.2010.05.002

Crossref Full Text | Google Scholar

Dewhurst T. (2016). Dynamics of a submersible mussel raft. University of New Hampshire, Durham, NH, United States.

Google Scholar

Faltinsen O. (1993). Sea loads on ships and offshore structures (Cambridge, England: Cambridge university press).

Google Scholar

Fan T., Qiao D., Yan J., Chen C., Ou J. (2017). An improved quasi-static model for mooring-induced damping estimation using in the truncation design of mooring system. Ocean Eng. 136, 322–329. doi: 10.1016/j.oceaneng.2016.05.042

Crossref Full Text | Google Scholar

FAO. (2024). The State of World Fisheries and Aquaculture 2024. Blue Transformation in action. Transformation in action. Rome. doi: 10.4060/cd0683en

Crossref Full Text | Google Scholar

Feng D., Meng A., Wang P., Yao Y., Gui F. (2021). Effect of design configuration on structural response of longline aquaculture in waves. Appl. Ocean Res. 107, 102489. doi: 10.1016/j.apor.2020.102489

Crossref Full Text | Google Scholar

Fredriksson D. W., DeCew J., Swift M. R., Tsukrov I., Chambers M. D., Celikkol B. (2004). The design and analysis of a four-cage grid mooring for open ocean aquaculture. Aquacultural Eng. 32, 77–94. doi: 10.1016/j.aquaeng.2004.05.001

Crossref Full Text | Google Scholar

Fredriksson D. W., DeCew J. C., Tsukrov I. (2007). Development of structural modeling techniques for evaluating HDPE plastic net pens used in marine aquaculture. Ocean Eng. 34, 2124–2137. doi: 10.1016/j.oceaneng.2007.04.007

Crossref Full Text | Google Scholar

Fredriksson D. W., Steppe C. N., Wallendorf L., Sweeney S., Kriebel D. (2010). Biological and hydrodynamic design considerations for vertically oriented oyster grow out structures. Aquacultural Eng. 42, 57–69. doi: 10.1016/j.aquaeng.2009.11.002

Crossref Full Text | Google Scholar

Gagnon M., Bergeron P. (2017). Observations of the loading and motion of a submerged mussel longline at an open ocean site. Aquacultural Eng. 78, 114–129. doi: 10.1016/j.aquaeng.2017.05.004

Crossref Full Text | Google Scholar

Goseberg N., Chambers M. D., Heasman K., Fredriksson D., Fredheim A., Schlurmann T. (2017). Technological approaches to longline-and cage-based aquaculture in open ocean environments (New York City: Springer International Publishing).

Google Scholar

Gutiérrez-Romero J. E., García-Espinosa J., Serván-Camas B., Zamora-Parra B. (2016). Non-linear dynamic analysis of the response of moored floating structures. Mar. Structures 49, 116–137. doi: 10.1016/j.marstruc.2016.05.002

Crossref Full Text | Google Scholar

Kim T., Lee J., Fredriksson D. W., DeCew J., Drach A., Moon K. (2014). Engineering analysis of a submersible abalone aquaculture cage system for deployment in exposed marine environments. Aquacultural Eng. 63, 72–88. doi: 10.1016/j.aquaeng.2014.10.006

Crossref Full Text | Google Scholar

Knysh A., Tsukrov I., Chambers M., Swift M. R., Sullivan C., Drach A. (2020). Numerical modeling of submerged mussel longlines with protective sleeves. Aquacultural Eng. 88, 102027. doi: 10.1016/j.aquaeng.2019.102027

Crossref Full Text | Google Scholar

Langan R., Horton F. (2003). Design, operation and economics of submerged longline mussel culture in the open ocean. Bull. Aquaculture Assoc. Canada 103, 11–20.

Google Scholar

Li P., Faltinsen O. M., Lugni C. (2016). Nonlinear vertical accelerations of a floating torus in regular waves. J. Fluids Structures 66, 589–608. doi: 10.1016/j.jfluidstructs.2016.08.007

Crossref Full Text | Google Scholar

Li Y., Gui F., Teng B. (2007). Hydrodynamic behavior of a straight floating pipe under wave conditions. Ocean Eng. 34, 552–559. doi: 10.1016/j.oceaneng.2006.01.012

Crossref Full Text | Google Scholar

Li Y.-C., Zhao Y.-P., Gui F.-K., Teng B. (2006). Numerical simulation of the hydrodynamic behaviour of submerged plane nets in current. Ocean Eng. 33, 2352–2368. doi: 10.1016/j.oceaneng.2005.11.013

Crossref Full Text | Google Scholar

Liu H., Huang W., Lian Y., Li L. (2014). An experimental investigation on nonlinear behaviors of synthetic fiber ropes for deepwater moorings under cyclic loading. Appl. Ocean Res. 45, 22–32. doi: 10.1016/j.apor.2013.12.003

Crossref Full Text | Google Scholar

Ma T., Song X. J., Lu S. F. (2020). Nonlinear dynamics modeling and subharmonic resonances analysis of a laminated composite plate. Shock Vibration 2020, 1–16. doi: 10.1155/2020/7913565

Crossref Full Text | Google Scholar

Ma C., Zhao Y.-P., Xu Z., Bi C.-W. (2022). Experimental investigation on the wave performance with the interference of floating aquaculture cages in single and tandem arrangements. Ocean Eng. 262, 112255. doi: 10.1016/j.oceaneng.2022.112255

Crossref Full Text | Google Scholar

Newmark N. M. (1959). A method of computation for structural dynamics. J. Eng. Mech. Div. 85, 67–94. doi: 10.1061/JMCEA3.0000098

Crossref Full Text | Google Scholar

Orszaghova J., Taylor P. H., Wolgamot H. A., Madsen F. J., Pegalajar-Jurado A. M., Bredmose H. (2021). Wave-and drag-driven subharmonic responses of a floating wind turbine. J. Fluid Mechanics 929, A32. doi: 10.1017/jfm.2021.874

Crossref Full Text | Google Scholar

Plew D. R. (2005). The hydrodynamic effects of long-line mussel farms.

Google Scholar

Plew D. R., Stevens C. L., Spigel R. H., Hartstein N. D. (2005). Hydrodynamic implications of large offshore mussel farms. IEEE J. Oceanic Eng. 30, 95–108. doi: 10.1109/JOE.2004.841387

Crossref Full Text | Google Scholar

Qin H., Xu Z., Li P., Yu S. (2020). A physical model approach to nonlinear vertical accelerations and mooring loads of an offshore aquaculture cage induced by wave-structure interactions. Ocean Eng. 197, 106904. doi: 10.1016/j.oceaneng.2019.106904

Crossref Full Text | Google Scholar

Shen H., Zhao Y.-P., Bi C.-W., Xu Z. (2023). Nonlinear dynamics of an aquaculture cage array induced by wave-structure interactions. Ocean Eng. 269, 113711. doi: 10.1016/j.oceaneng.2023.113711

Crossref Full Text | Google Scholar

Stevens C., Plew D., Hartstein N., Fredriksson D. (2008). The physics of open-water shellfish aquaculture. Aquacultural Eng. 38, 145–160. doi: 10.1016/j.aquaeng.2008.01.006

Crossref Full Text | Google Scholar

Stevens C., Plew D., Smith M., Fredriksson D. (2007). Hydrodynamic forcing of long-line mussel farms: observations. J. Waterway Port Coast. Ocean Eng. 133, 192–199. doi: 10.1061/(ASCE)0733-950X(2007)133:3(192)

Crossref Full Text | Google Scholar

Tsukrov I., Eroshkin O., Fredriksson D., Swift M. R., Celikkol B. (2003). Finite element modeling of net panels using a consistent net element. Ocean Eng. 30, 251–270. doi: 10.1016/S0029-8018(02)00021-5

Crossref Full Text | Google Scholar

Tsukrov I., Eroshkin O., Paul W., Celikkol B. (2005). Numerical modeling of nonlinear elastic components of mooring systems. IEEE J. Oceanic Eng. 30, 37–46. doi: 10.1109/JOE.2004.841396

Crossref Full Text | Google Scholar

Tsukrov I. I., Ozbay M., Swift M. R., Celikkol B., Fredriksson D. W., Baldwin K. (2000). Open ocean aquaculture engineering: numerical modeling. Mar. Technol. Soc. J. 34, 29–40. doi: 10.4031/MTSJ.34.1.4

Crossref Full Text | Google Scholar

Wang Y., Jing X., Dai H., Li F.-M. (2019). Subharmonics and ultra-subharmonics of a bio-inspired nonlinear isolation system. Int. J. Mechanical Sci. 152, 167–184. doi: 10.1016/j.ijmecsci.2018.12.054

Crossref Full Text | Google Scholar

Wang X.-x., Swift M. R., Dewhurst T., Tsukrov I., Celikkol B., Newell C. (2015). Dynamics of submersible mussel rafts in waves and current. China Ocean Eng. 29, 431–444. doi: 10.1007/s13344-015-0030-2

Crossref Full Text | Google Scholar

Wang X., Xie J., Luo Y., Wang X., Guo G., You X. (2023). Experimental investigation of the hydrodynamic characteristics of longline aquaculture facilities under current and wave conditions. Fishes 8, 204. doi: 10.3390/fishes8040204

Crossref Full Text | Google Scholar

Webster W. C. (1995). Mooring-induced damping. Ocean Eng. 22, 571–591. doi: 10.1016/0029-8018(94)00027-5

Crossref Full Text | Google Scholar

Wijsman J., Troost K., Fang J., Roncarati A. (2019), 7–26.

Google Scholar

Wu Y., Wang T., Eide Ø., Haverty K. (2015). Governing factors and locations of fatigue damage on mooring lines of floating structures. Ocean Eng. 96, 109–124. doi: 10.1016/j.oceaneng.2014.12.036

Crossref Full Text | Google Scholar

Xu Z., Bi C.-W., Ma C. (2023). Nonlinear dynamics of an aquaculture cage array under oblique wave attack. Ocean Eng. 288, 115948. doi: 10.1016/j.oceaneng.2023.115948

Crossref Full Text | Google Scholar

Xu Z., Qin H., Tsukrov I. (2018). Determination of hydrodynamic coefficients of the floating cage collar with forced oscillation experiments. Ocean Eng. 159, 175–186. doi: 10.1016/j.oceaneng.2018.04.015

Crossref Full Text | Google Scholar

Zhao K., Liu P. L.-F. (2022). On Stokes wave solutions. Proc. R. Soc. London. Ser. A: Mathematical Phys. Eng. Sci. 478, 20210732. doi: 10.1098/rspa.2021.0732

Crossref Full Text | Google Scholar

Zhao Y.-P., Yang H., Bi C.-W., Chen Q.-P., Dong G.-H., Cui Y. (2019). Hydrodynamic responses of longline aquaculture facility with lantern nets in waves. Aquacultural Eng. 86, 101996. doi: 10.1016/j.aquaeng.2019.101996

Crossref Full Text | Google Scholar

Zhu L., Cheng Y., Wang J., Zhu H., Xu Z. (2023). Time–frequency analysis of nonlinear dynamics of an aquaculture cage array in waves. J. Mar. Sci. Eng. 11, 1818. doi: 10.3390/jmse11091818

Crossref Full Text | Google Scholar