
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mar. Sci. , 15 October 2024
Sec. Physical Oceanography
Volume 11 - 2024 | https://doi.org/10.3389/fmars.2024.1445116
This article is part of the Research Topic Wave-Induced Particle Motions in the Ocean View all 10 articles
Surface waves and currents are crucial to the mass transfer in the air-sea interaction as they can drive a variety of dynamical processes. How mass can be transported by surface waves and current coupling is addressed through a study of their induced motions of fluid parcels. To this end, a weakly nonlinear wavetrain is imposed on the background flow whose direction and magnitude are permitted to vary with water depth and second-order features of this configuration are investigated. A leading-order approximation to the Stokes drift is derived, correct to the second order in wave steepness, and applicable to an arbitrarily depth-dependent background flow. The reduced forms of the approximate Stokes drift are provided in a few limiting cases such as a current with an exponential profile or propagating in an orthogonal direction to the wave propagation. Novel features related to the Stokes drift and particle trajectories have been reported for the first time as a result of the rotation induced by the wave and current coupling. A non-vanishing component of the Stokes drift velocity and net-mean displacement of fluid parcels in the span-wise direction to the wave propagation are observed in the cases where a shear current propagates obliquely to the waves direction. A non-monotonic dependence on water depth of the stream-wise component of the Stokes drift is shown, and thereby the largest mass transport induced no longer occurs on the still water surface but some depth beneath. The non-monotonic behavior occurs beyond the regime of the near-irrotational assumption of wave-induced motions. It can also lead to the change of the signs for the stream-wise Stokes drift throughout the water column, and thus an overall cancellation of the integrated mass transport by waves over the water column, indicating that the depth-integrated models can likely lead to underestimated effects of the mass transport which is non-trivial at a local depth. The results from this study have far-reaching impact. The Stokes drift profile is a direct input to the parametrization of the surface waves forcing in ocean circulations and the obliquely propagating Stokes drift can be plausibly responsible for the formation of oblique Langmuir rolls to wave propagation in the open ocean.
Surface waves are ubiquitous in the ocean. They are an essential factor driving dynamical processes near the ocean surface including the exchange of mass, momentum, and energy in the upper ocean with both the atmosphere and deeper sea. One particularly important process involves the interaction of waves with ocean currents which has been widely investigated for example in the context of ocean circulations and the occurrence of rogue waves (Kharif and Pelinovsky, 2003; Sullivan and McWilliams, 2010; Onorato et al., 2011). In the present contribution, attention is given to mass transport due to the interaction of waves with depth-dependent currents, and in particular how the wave-induced Stokes drift changes if the waves propagate on a pre-existing depth-dependent background flow.
The net forward drift of fluid particles in a steady periodic wavetrain was discovered in Stokes (1847). This celebrated result is very well known and has been famously illustrated in the collection (Van Dyke, 1982). The Stokes drift has been verified in various recent wave tank experiments (Chen et al., 2010; van den Bremer et al., 2019), but it is also well known that the result needs to be modified when dealing with finite depth due to bottom drag (Longuet-Higgins, 1953; Ursell, 1953; Monismith et al., 2007), when considering the more realistic case of wave groups (Smith, 2006; Li and Li, 2021), the influence of infragravity waves (Bjørnestad et al., 2021), mean currents and rotation (Constantin and Monismith, 2017), or random sea states (Myrhaug et al., 2014; Myrhaug, 2015). Nevertheless, Stokes drift correlates well with the transport of small objects by surface waves in field observations, for example in the case of oil spills (Yang et al., 2021). In particular when dealing with wave groups, the depth-dependent net displacement of fluid parcels in the form of a mean flow should be taken into account (Dysthe, 1979; McIntyre, 1981; Davey and Stewartson, 1974; Higgins et al., 2020; Li, 2021). In the last couple of decades, environmental concerns over plastic pollution in the oceans have led to several studies assessing the role of surface waves in the transport of plastic particles near the ocean surface, see, e.g., van den Bremer and Breivik (2018); Chamecki et al. (2019); Calvert et al. (2021); Larsen et al. (2023); Sutherland et al. (2023) among others.
While the interaction of surface waves and currents occurs naturally in the oceans at all times, there are many features which have not been investigated thoroughly, owing partially to the technical difficulties in describing various configurations analytically. On the other hand, understanding wave-current interaction better is of utmost importance in various applications. For example, wave-current interactions have been reported as a plausible mechanism for the generation of rogue waves, i.e. unexpected and abnormally large waves which pose a great risk to maritime transportation and man-made structures in coastal waters. The physical origins of such unexpected waves are indicated as linear refraction (White and Fornberg, 1998) or nonlinear effects like modulational instability and crest amplification as a result of bound waves (Shrira and Slunyaev, 2014; Pizzo et al., 2023; Zheng et al., 2023; Li and Chabchoub, 2024).
Stokes drift has been considered in a few regional ocean models in the last few decades as it is the main physical origin for various forces sometimes called Stokes forces, as has been explained in-depth by Suzuki and Fox-Kemper (2016) and Zippel et al. (2022). Craik and Leibovich (1976) have demonstrated the role of Stokes drift in triggering Langmuir circulations through the so-called Craik-Lebovich Type 2 (CL2) Instability. Based on large-eddy simulations, McWilliams et al. (1997) first showed that Stokes drift in wind-induced mean current leads to Langmuir turbulence in the ocean which represents flow structures similar to Langmuir cells but considerably more irregular in both time and space. The role of Langmuir turbulence in both vertical mixing and the horizontal transport of materials has been addressed in a variety of papers, see, e.g., Sullivan and McWilliams (2010); McWilliams (2016). Stokes velocity profiles are parameterized in the form of explicit expressions for better numerical efficiency in oceanic models, accounting for different sea states like short-crested waves, swell, or well-developed wind seas, see, e.g., Kenyon (1969); Ardhuin et al. (2009); Breivik et al. (2014); Webb and Fox-Kemper (2011), Webb and Fox-Kemper, 2015); Breivik and Christensen (2020). In contrast to the Stokes forces, there are various models which have accounted for the roles of surface waves in ocean models through radiation stress (Lane et al., 2007; Qiao et al., 2010; Mellor, 2015) and steep wave-induced turbulence (Babanin, 2006; Babanin and Chalikov, 2012; Ghantous and Babanin, 2014).
Among the works which have examined the effect of a depth-dependent flow on waves at the free surface, most have considered the special case of a linearly sheared current. This configuration induces a number of mathematical simplifications which have been exploited by many authors (see Ali and Kalisch (2013); Flamarion et al. (2023) and many others). Constant background vorticity introduces a directional asymmetry in the linear dispersion relation and rotational wave-induced motions (Peregrine, 1976; Ellingsen, 2014a), giving rise to novel features in the pattern of both ship waves and these generated by a moving oscillating body, see, e.g., Ellingsen (2014b); Li and Ellingsen (2016a); Li and Ellingsen, (2016b); Li (2018). Touboul et al. (2016) derived a mild envelope equation for waves in a water region with a slowly varying bathymetry and linearly sheared current. In accordance with Craik (1970), a second-order theory for three-dimensional waves in a linearly sheared current has been derived by Akselsen and Ellingsen (2019). Expressions for Stokes drift velocity and particle trajectories are particularly presented, which differ from Hsu (2013) by that the linearly current advection effects in the linear orbital velocity of fluid parcels have been properly considered. Thomas et al. (2012) have derived a nonlinear Schrödinger (NLS) equation for the evolution of the energy of surface waves with constant vorticity. It is especially shown that different vorticity strengths can result in various instability regions and growth rates when a Stokes wavetrain is subject to modulational instability, which is experimentally validated by Steer et al. (2020). Curtis et al. (2018) have extended the NLS equation to a higher order and additionally considered the surface tension, where a formula for the Stokes drift velocity on a still surface has also been obtained.
In contrast, studies on waves atop an arbitrarily depth-dependent flow have been scarce. A majority of the very few exceptions have placed their focus on the linear dispersive properties of surface waves, see, e.g., Stewart and Joy (1974); Skop (1987); Kirby and Chen (1989); Shrira (1993); Ellingsen and Li (2017); Li and Ellingsen (2019); Ellingsen et al. (2024). Both Quinn et al. (2017) and Li and Ellingsen (2019) lead to the linear wave action equation which in addition to the shear flow can handle non-trivial bathymetry in a consistent manner. Based on a newly derived second-order theory for narrowband waves in a depth-dependent flow, Xin et al. (2023) report that the wave-current coupling leads to much amplified loads on a bottom-fixed vertically installed slender cylinder, posing a big risk to the safety and reliability of offshore structures. Zheng et al. (2023) extended Xin et al. (2023) and Li and Ellingsen (2019) to permit broadband waves, where statistical features of surface elevation altered by a depth-dependent flow are examined, showing the important relevance of depth-dependent structure of current to extremely large wave events. In both Xin et al. (2023) and Zheng et al. (2024), considerably different wave kinematics are shown as a result of shear current-modified second-order bound waves, where a non-vanishing velocity field forced by second-harmonic deep-water waves is shown by both and the latter in addition a considerable Eulerian mean flow even in the limit of extremely narrow-banded waves.
Through laboratory observations, Pizzo et al. (2023) have, for the first time, reported how modulational instability can be suppressed by a background current whose profile is similar to the Stokes drift as a result of the Stokes wave. Using a newly derived higher-order Shear-Current Modified NLS (SC-MNLS) equation, Li and Chabchoub (2024) also lead to a similar conclusion but due to a wave-modified rotational flow whose profile is arbitrarily dependent on depth instead. Interestingly, Li and Chabchoub (2024) have led to a hypothesis that states the plausible link between the formation of rogue waves owing to modulational instability and the CL2 instability, addressing the need for resolving wave phases in ocean circulations for the test of the hypothesis. Fully nonlinear depth-integrated models for two-dimensional waves in a depth-dependent current have been developed by Yang and Liu (2022).
Despite of the aforementioned extensive literature, Stokes drift accounting for the effects of an arbitrary depth-dependent flow in both the dispersion relation and the magnitude of wave-induced orbital motions has, to the best of the authors’ knowledge, not been derived before, and thus never been physically elucidated. The main objective of this work is to fill in this gap by deriving the Stokes drift and the particle trajectories of passive fluid parcels in such a physical setting. Novel physical features are demonstrated. With the widely recognized role of Stokes drift, the results from this work can be used to assessing shear current-modified wave effects in ocean circulations, particularly in wave phase resolved oceanic models, as addressed by Li and Chabchoub (2024). We highlight that Stokes drift itself will be shown to possess a misalignment with the wave propagation, and thereby likely to trigger misaligned Langmuir rolls in realistic scenarios. Such misaligned Langmuir rolls would differ from Van Roekel et al. (2012) in the physical origin, where they are a result of wind surface stress and Stokes drift which is assumed to be aligned with the wave propagation direction.
This paper is laid out as follows. A theoretical description of the system is introduced in section 2, covering the underlying assumptions, perturbation expansion, and the solution to a linearized boundary value problem. The quadratic features of surface waves atop a depth-dependent flow have been newly derived in section 3 with a special focus on the Stokes drift and particle trajectories. Approximations to Stokes drift in a few limiting cases are particularly derived. Novel features of Stokes drift and particular trajectories are demonstrated in section 4 in which the approximations are tested. The conclusions from this paper are drawn in section 5.
Let U(z) = (Ux(z),Uy(z)) be the velocity vector of a horizontally-oriented depth-dependent flow and V(x,z,t) = [u(x,z,t),w(x,z,t)] be the flow velocity induced by surface waves in an Eulerian frame which has accounted for the modified effects by the depth-dependent flow, where u and w denote the velocity vector in the horizontal plane and the vertical velocity, respectively; x = (x,y) denotes the position vector in the horizontal plane and z is the vertical axis with z = 0 denoting a still water surface, Uxand Uyare the component of the flow velocity in the x and y direction, respectively. Assuming an incompressible flow, negligible viscosity, and Coriolis force, the fluid system of surface waves in a large-scale flow is described by the continuity and Euler momentum equations given by
where is the velocity vector due to a background depth-dependent flow; denotes the spatial gradient operator in three dimensions with the gradient operator in the horizontal plane, is the dynamic pressure, with P the total pressure, ρ the water density which is assumed constant, and g the gravitational acceleration. The system is described by the dynamic and kinematic boundary conditions at the free water surface , respectively,
and the finite-water seabed boundary condition
where h denotes the water depth. The perturbed approximate solution to the boundary value problem described by Equations 1–4 are obtained with additional assumptions detailed in the following sections.
Following the derivations by Zheng et al. (2023); Xin et al. (2023), the wave-induced velocity is expressed in an approximate form of power series in wave steepness ε which is a non-dimensional scaling parameter,
where the corrections at the third and higher orders are truncated, and the superscript ‘(j)’ denotes . The leading order approximations to the unknowns are solved in the context of a prescribed train of monochromatic waves whose perturbed elevation is given by
where c.c. denotes the complex conjugates, denotes the wave phase, a, k, and are the (real) current-modified amplitude, wave vector, and angular frequency of monochromatic waves, respectively. The prescribed linear elevation leads to the linear velocity and pressure to be solved for in the form as
where , , and are the dimensionless and depth-dependent horizontal velocity vector, vertical velocity, and pressure, respectively. These dimensionless quantities are solved for in the next sub-section.
Substituting the expression for the linear vertical velocity into the linearized boundary value problem based on Equations 1–4 gives rise to [see, e.g., Li and Ellingsen (2019)]
where ℜ the prime denotes the derivative with respect to z (e.g., and ) and subscript ‘0’ denotes the evaluation at z = 0. Following Li and Ellingsen (2019), the dispersion relation and the linearized boundary value problem are solved together for the unknown dimensionless velocity and angular velocity using the Direct Integration Method (DIM). Specifically, the dispersion relation is described by
Furthermore, the horizontal velocity vector and pressure of linear wave-induced flow in the presence of an arbitrary depth-dependent background current are given by, respectively
We remark that a current propagating in the orthogonal direction to the wave propagation, which means , , and , does not affect the dispersion relation and dimensionless vertical velocity described together by Equations 8–11. Nevertheless, the orbital velocity in the span-wise direction remains altered by the vorticity of the shear current when in Equation 12. This non-vanishing orbital velocity has far-reaching effects on the Stokes drift and particle trajectories, as elaborated in sub-section 3.2.2 and section 4.
The particle trajectories of fluid motions due to linear waves can be directly obtained by noting that the linear particle velocity
which gives rise to
where denotes the real component, denotes the linear displacement related to the position of the particle at an initial time instant . For later reference, we introduce a time-averaging operator ‘ ’ defined as
which denotes the time averaging with respect to the period of the wave phase.
Assuming infinitestimal waves where ≪ 1, the particle velocity in the second order in wave steepness can be obtained by a Taylor expansion about r(t) = r(1)(t)
where , , and , as noted, denote the Eulerian velocity vector in the horizontal plane and the vertical velocity due to second-order waves, respectively. The Stokes drift denotes the net mean transport velocity of particles correct to second order in wave steepness. It is obtained by averaging the second term on the right-hand side of Equation 17, and thus
where by definition, the continuity equation was used, both and the asterisk denote the complex conjugates. We note that the vertical velocity of the mean motion of particles vanishes (as ), and thus
Substituting (12) for into (19) gives rise to
In the absence of a shear current, i.e., , and with
the Stokes drift denoted by Equation 20 becomes
where denotes the unit vector in the direction of the wave vector k. We remark that the dimensionless vertical velocity given by Equation 21 also corresponds the vertical velocity for linear waves atop a linearly sheared current, which will be used in §3.2.1. The Stokes drift velocity given by Equation 22 agrees with the net mean horizontal displacement driven by a train of linear Stokes waves on a finite water depth and also on deep water in the limit of (Kenyon, 1969). For later reference and convenience, we introduce
corresponding to the Stokes drift velocity at a still water surface in the absence of a current.
It is worth noting that the Stokes drift velocity given by Equation 20 has a non-vanishing component as long as the profile shear of the current is non-zero in the spanwise direction, giving rise to a non-vanishing component of the vorticity of fluid parcels in the wave propagation direction.
We proceed to the explicit expression for the profiles of Stokes drift velocity in three limiting cases which are elaborated below.
A linearly sheared current whose velocity profile U = Sz is firstly assumed, where S denotes the constant vorticity vector of the shear. For a train of Stokes wave, the vertical velocity of the particles induced by linear waves are the same as these in the absence of a shear current, i.e., Equation 21 [see, e.g (Peregrine, 1976; Ellingsen, 2014a)]. Substituting both the linear shear current profile and the dimensionless vertical velocity in the form of Equation 21 into Equation 20 gives rise to
where the linear dispersion relation of waves atop a linearly shear current admits an accurate expression (Peregrine, 1976; Li and Ellingsen, 2016a)
We notice that there exists a pole at ω/(k·S) = zcfor k·S < 0 in Equation 24, where zcdenotes a critical depth which may trigger the instability of the flow system, as discussed in previous works like Shrira (1993) and Li and Ellingsen, (2019, their §4.3). From a physical point of view, it is nevertheless typical that either |zc|≫ h on a finite depth or the current projection in the wave propagation direction cannot reach the same magnitude as the phase velocity in deep water in practice. As a result, the critical depth does not bear much physical meaning in the applicability regime considered in this work.
We proceed to consider the limiting cases of a nonlinear profile of shear current propagating in the direction orthogonal to the wave propagation direction, i.e., k · U(z) = 0 is understood, leading to simplifications for the Stokes drift velocity given by Equation 20. In particular, such current profiles are unidirectionally oriented at different depths, and the Stokes drift velocity possesses a reduced form as follows
where is understood to be in the form as Equation 21 (Li and Ellingsen, 2019) and is admitted. Evidently, the Stokes drift velocity in the limiting cases where a shear current orients in the direction which is constant in the vertical direction and normal to the wave propagation has a non-vanishing component in the direction normal to wave propagation, in contrast to the cases in the absence of a shear current where the Stokes drift induced by a train of monochromatic waves always follows the direction of wave propagation.
As has been detailed in Ellingsen and Li (2017) and Shrira (1993), the near-potentiality (or irrotationality) assumption can be made when the dimensionless parameter єcis small, i.e., єc≪ 1, with єcbeing defined as
with . The dimensionless small parameter єcbears the physical meaning of the wave vector weighted, depth-integrated, and current-modified effect on the dispersion relation as a leading-order approximation to the wave dispersion relation given by (see, Ellingsen and Li (2017))
where the approximate dispersion relation (Equation 28) is correct to . The higher-order approximations to the dispersion relation of waves than Equation 28 are derived by Kirby and Chen (1989) and Ellingsen and Li (2017). Under the near-irrotationality assumption, the normalized vertical velocity ŵ is given by Equation 21, inserting which into Equation 20 gives rise to a leading-order approximation to the Stokes drift velocity with
where the approximation by Equation 28 to the angular frequency was used. We remark that Equation 29 is an approximation to the Stokes drift for any current profiles in the applicability regime while Equations 24, 26 are second-order accurate expressions of the Stokes drift velocity due to waves in a linearly sheared current and a depth-dependent current propagating in the span-wise direction, respectively.
Following Ellingsen and Li (2017), a higher-order approximation to the Stokes drift velocity can be readily obtained by inserting a higher-order approximation to the dimensionless vertical velocity and angular frequencies, respectively,
where
and
Here, the second term on the right hand side of Equation 31 corresponds to the solution of the homogeneous Laplace equation. The boundary conditions at the still water surface and seabed for the dimensionless vertical velocity are well satisfied; i.e., and
being an approximation to Vswhich is correct to 𝒪(є2єc) and with an accuracy at one higher order of magnitude in єc than the approximation given by Equation 29.
The particle trajectories in the first and second order in wave steepness are given by definition according to, respectively,
which denote the time integration of the respective particle velocities. The initial time instant t0 is set 0 without any loss of generality. A leading-order approximation to the total particle transport can thus be given by
where the definition Δrp= is introduced to denote the net mean displacement of flow parcels due to waves or wave and current interaction. This means that the mean displacement due to the current alone is not included in Δrpas it is not the focus of this work. We note that the trajectories predicted by Equations 36, 37 are leading-order approximations in contrast to the approach from a known velocity field via systems of ordinary differential equations, the latter of which has been used by a number of authors in different settings (Borluk and Kalisch, 2012; Chen et al., 2021).
In this section, the analytical and semi-analytical solutions derived in § 3 are numerically implemented for the analysis. The setup for the numerical implementations is explained in subsection 4.1, where a few current profiles are assumed. The novel features related to the Stokes drift are demonstrated in subsection 4.2 due to a background current and the approximations to Stokes drift presented in 3.2 are validated. The trajectories and the net mean displacement of fluid parcels are presented in subsection 4.3 using the expressions derived in subsection 3.3.
Three different vertically sheared current profiles are chosen for numerical implementations, including a linearly sheared, exponential, and realistic profile measured at a river mouth implemented in Li and Ellingsen (2019). The linearly and exponential profiles admit analytical expressions as follows, respectively,
where Frxand Fryare non-dimensional parameters which measure the magnitude of a profile velocity component of the background current in the x and y direction, respectively, relative to the phase velocity of deepwater waves; and the dimensionless parameters αxand αyare a measure of the shear strength of the current velocity at a still water surface in the x and y direction, respectively, compared with the decay of the magnitude of the wave-induced orbital velocity. When αx,y > 1, it denotes that the decay rate of the magnitude of the current velocity component with depth is larger than that of the wave-induced orbital velocity.
Specific values in various cases are chosen for the four dimensionless parameters, Frx, Fry, αx, and αy. We remark that, as a result of the profile variation with depth being the focus of this work, the profile velocity of both the linear and exponential current is set zero; i.e., UL(0) = 0 m/s and Uexp(0) = 0 m/s. Doing so permits the profile variation to be better assessed as the physics origin differs from the effects from a uniform current which has been extensively investigated (see, e.g., Peregrine (1976)). The neglect of current velocity on a still water surface can be physically represented as that the wave frequency considered here is intrinsic, i.e., ω – k·U0, corresponding to the difference between the absolute wave frequency and the effect of a background uniform current on the linear dispersion of waves.
The exponential profiles and velocity profile measured at a river mouth against the dimensionless water depth are shown in Figure 1, the latter of which are referred to as the river profile for later references. Moreover, the dimensionless parameter єc based on Equation 27 has been given for a specific current profile shown in Figure 1, where a larger value of єc indicates a stronger profile shear of current ‘felt’ by the chosen wave. Any current oriented in the direction orthogonal to the wave propagation admits єc = 0 as the identity of k·U′ = 0 holds.
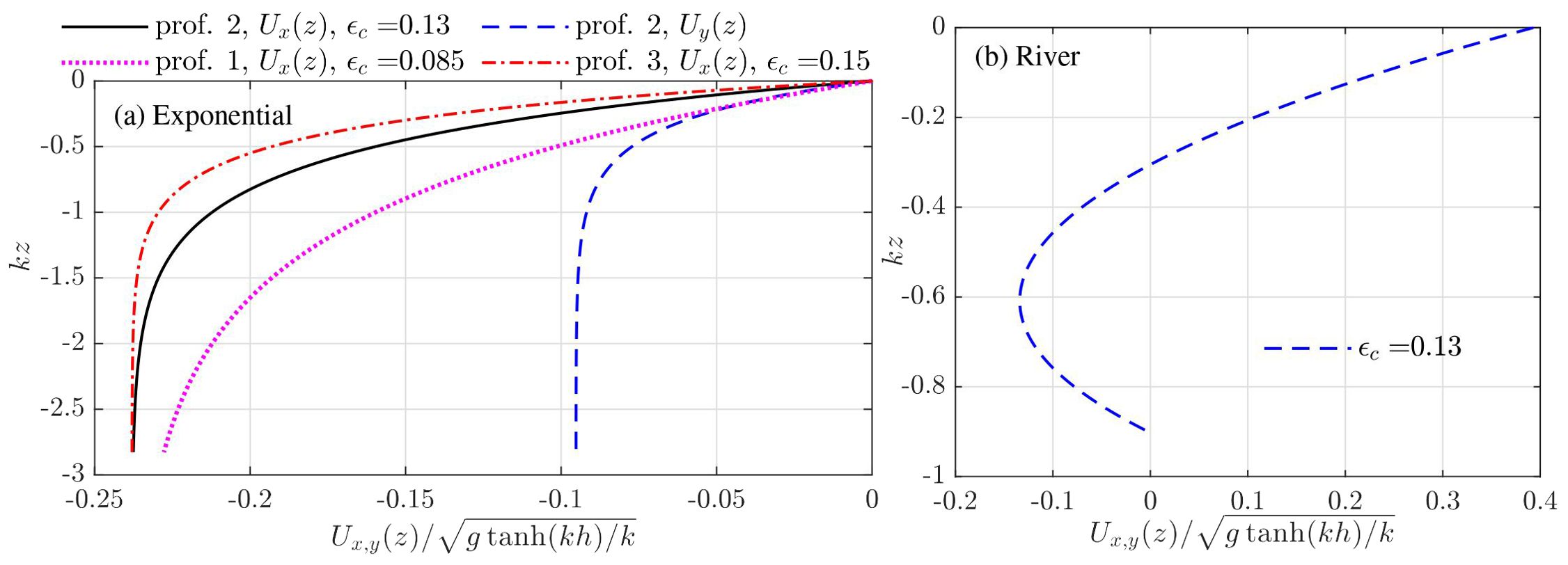
Figure 1. Current profiles used for numerical demonstrations. Panel (A) exponential profiles and (B) current profile measured at a river mouth [see, e.g., Li and Ellingsen (2019)].
The Stokes drift profiles against depth in various currents are shown in Figure 2. Three novel features are demonstrated as a result of wave and shear current interaction, compared with the classic conclusion for Stokes drift. Firstly, the Stokes drift has a non-vanishing component in the direction orthogonal to the wave propagation as a result of a non-vanishing depth-dependent component of the current in the span-wise direction, as is observed in panels (d, e, f) of Figure 2. This feature is regardless of the specific dependence of the current component Uy(z), as long as the inequality holds, being consistent with the physical interpretation of the Stokes drift expression given by Equation 20. This feature can only be demonstrated without the assumption of two-dimensional cases which have been extensively examined, see, e.g., Akselsen and Ellingsen (2019); Ellingsen (2014a). Hence, it can be expected in many realistic situations due to the three-dimensional nature of physical processes in the open ocean, although it is, for the first time, physically elucidated here. A few relevant examples of currents can be found in previous works that are expected to result in such a novel feature reported here, should it be physically resolved in the models. For example, depth-dependent wind drifts being misaligned with waves propagation as highlighted in Van Roekel et al. (2012). The Ekman currents are also typical of possessing a non-uniform directionality (McWilliams et al., 1997).
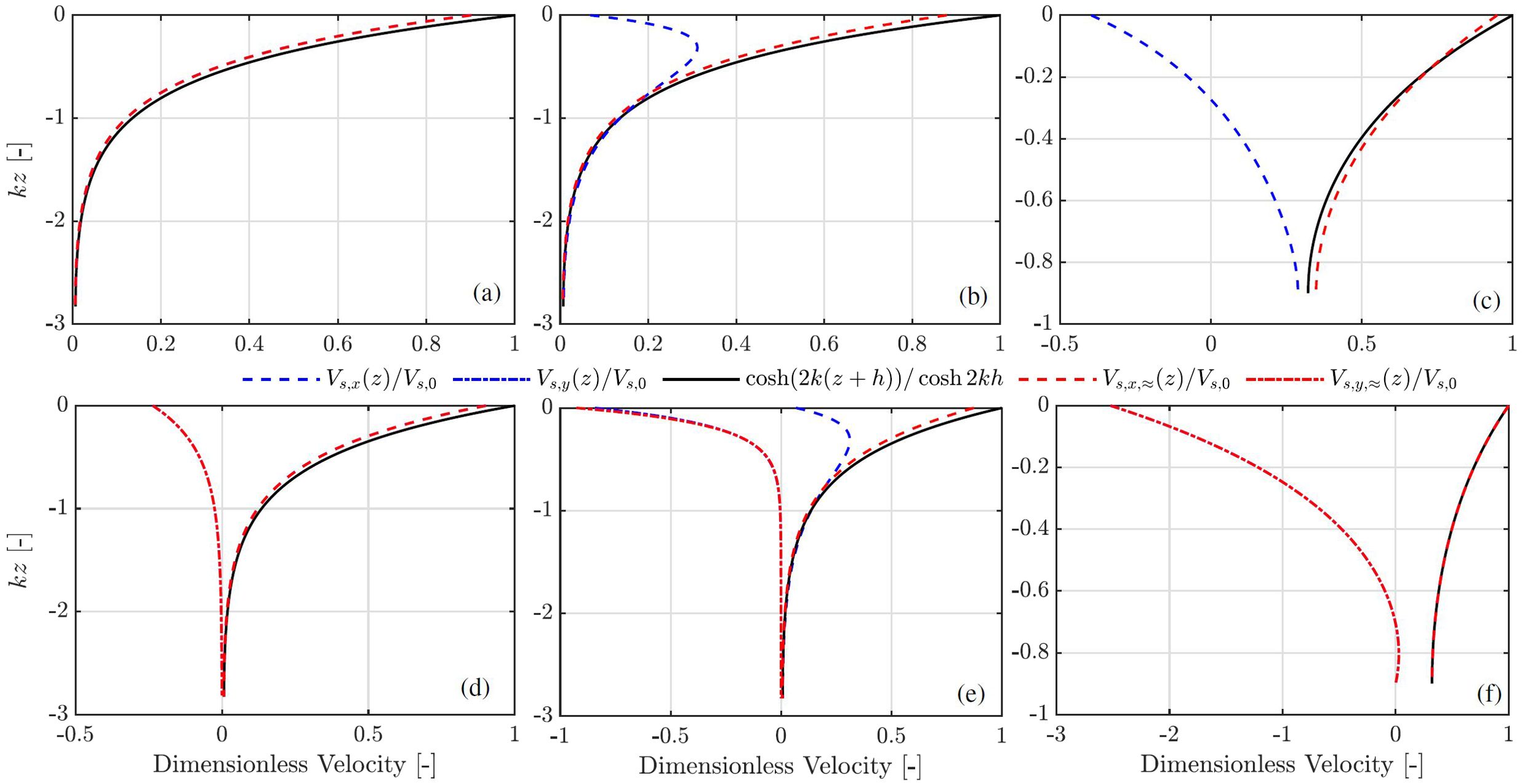
Figure 2. Stokes drift velocity profiles at various depths; two main aspects to highlight; (1) Novel physics illustrated (e.g., 2D cases and 2D versus 3D; linear versus profiles with non-vanishing curvature); (2) general and approximate results: clearly state the overlapping blue and red lines); panels (A, D) linearly sheared current and kh = π; panels (B, E) exponential currents and kh = π, where profile 2 in Figure 1A was used but Uy(z) = 0 m/s was set instead for the two dimensional case; (C, F) kh = 1 and the river profile with [Ux(z),0] and [0,Uy(z)] was chosen for the 2D and 3D case, respectively, where Ux,yis according to Figure 1B.
The second feature is demonstrated in panels (b, e) in Figure 2 which correspond to an exponentially sheared current, that the magnitude of the Stokes drift does not decrease exponentially with water depth but experiences firstly an increase in magnitude and thereafter a decrease as depth increases from the surface to a sufficiently large depth. The non-monotonically varying magnitude of the Stokes drift with depth is due to Equation 20 which consists of both the wave following and opposing terms, the latter of which relies on a non-vanishing shear and curvature of the current profile. In other words, such a non-monotonic nature mainly arises from the contribution of the shear production of current opposing to the wave propagation while noting that the cases of waves alone produce a Stokes drift which decreases exponentially with depth in the wave-propagation direction. The second feature is examined more in detail in Figure 3 where the Stokes drift is depicted against an exponential current with an increase in the shear strength from panel (a) to (c) indicated by an increasing value of єc. It is seen from panel (a) that the behavior of the Stokes drift is monotonic with depth when the shear strength of the current is small, which becomes non-monotonic as the shear strength is sufficiently large in panel (b) and remains so in panel (c).
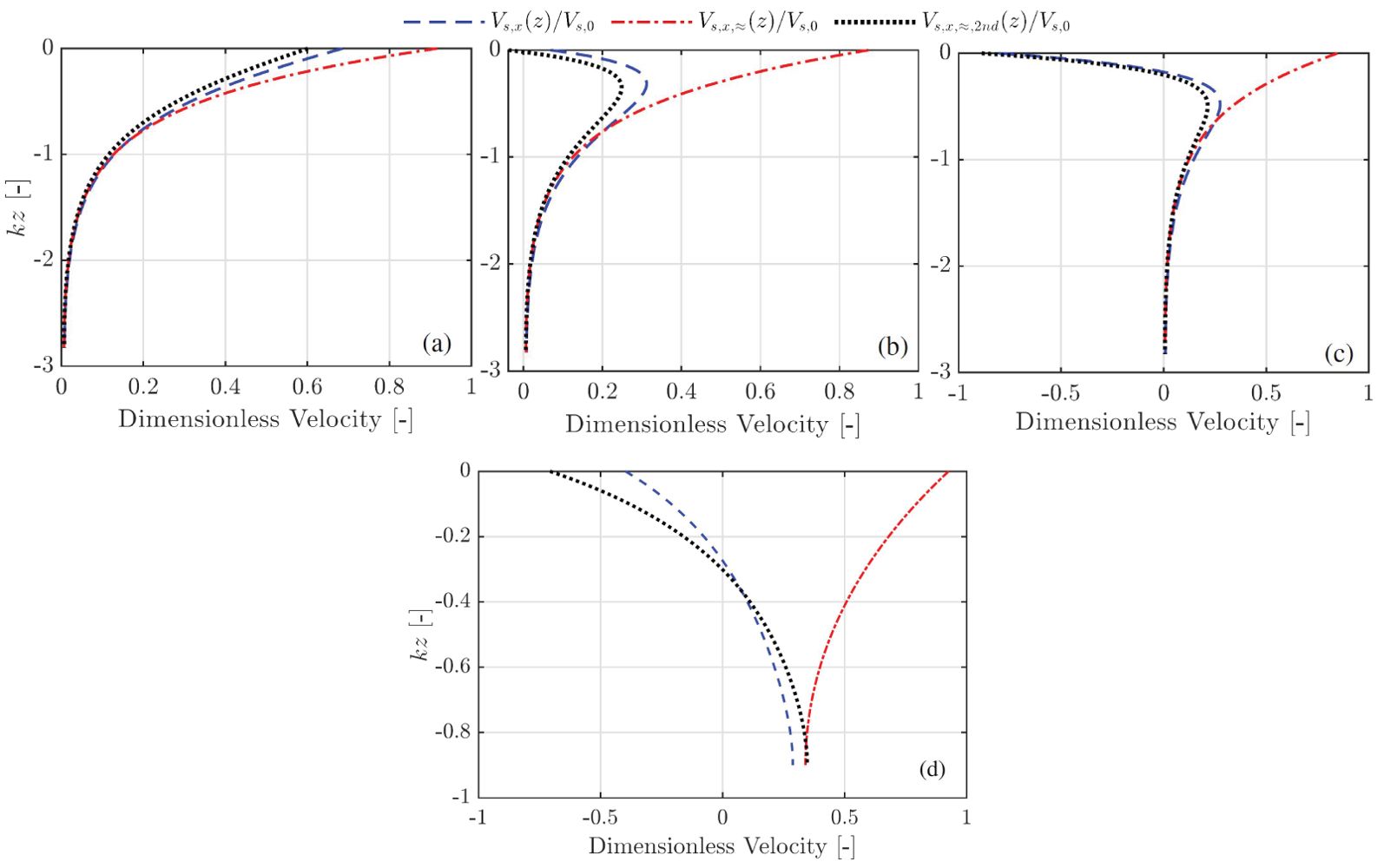
Figure 3. Comparison of the approximations to the Stokes drift and the general Stokes drift given by Equation 20, where Uy= 0 m/s was used for all cases. The first- and second-order approximations are based on Equations 29, 35, respectively. Panel (A–C) used exponential profile (1,2,3) in Figure 1B) with єc = 0.085, єc = 0.13, and єc = 0.15, respectively. Panel (D) used the river profile.
The third feature is demonstrated in panel (c) of both Figures 2 and 3 that the Stokes drift profile experiences a change of sign in the magnitude over the water column from the surface to a deeper depth. From the perspective of mass transport over an entire water column, the change of the sign indicates a cancellation in the depth integrated manner, thereby likely leading to an underestimated role of shear current on mass transport in depth-integrated models such as Yang and Liu (2022). Furthermore, different from the general understanding, the Stokes drift holds a sign opposing the wave propagation near the water surface, which again arises from the terms having a negative sign in Equation 20 being more dominant, i.e., the terms proportional to where holds a positive sign in all examples in panels (b, c) of Figures 2 and 3.
We stress that the aforementioned three features are strikingly different from the cases in the absence of the currents (or in the presence of uniform currents) which are also depicted in Figure 2, where the Stokes drifts have a magnitude that decreases exponentially with depth as ∼ cosh[2k(z + h)]/cosh(2kh), as well as a direction only aligned with the propagation direction of the ‘parent’ wave (i.e., the positive x direction). With real-life example profiles of tidal currents shown in Figure 4 where the current profiles were measured at the mouth of Columbia river by Zippel and Thomson (2017) and used in Zheng et al. (2024), the novel features of the Stokes drift in 2D cases are confirmed. The non-monotonic behavior of the Stokes drift with depth is clearly demonstrated again in Figure 4B, owing to the change of the sign of the profile shear of the opposing current and the respective moderate value measured by єc.
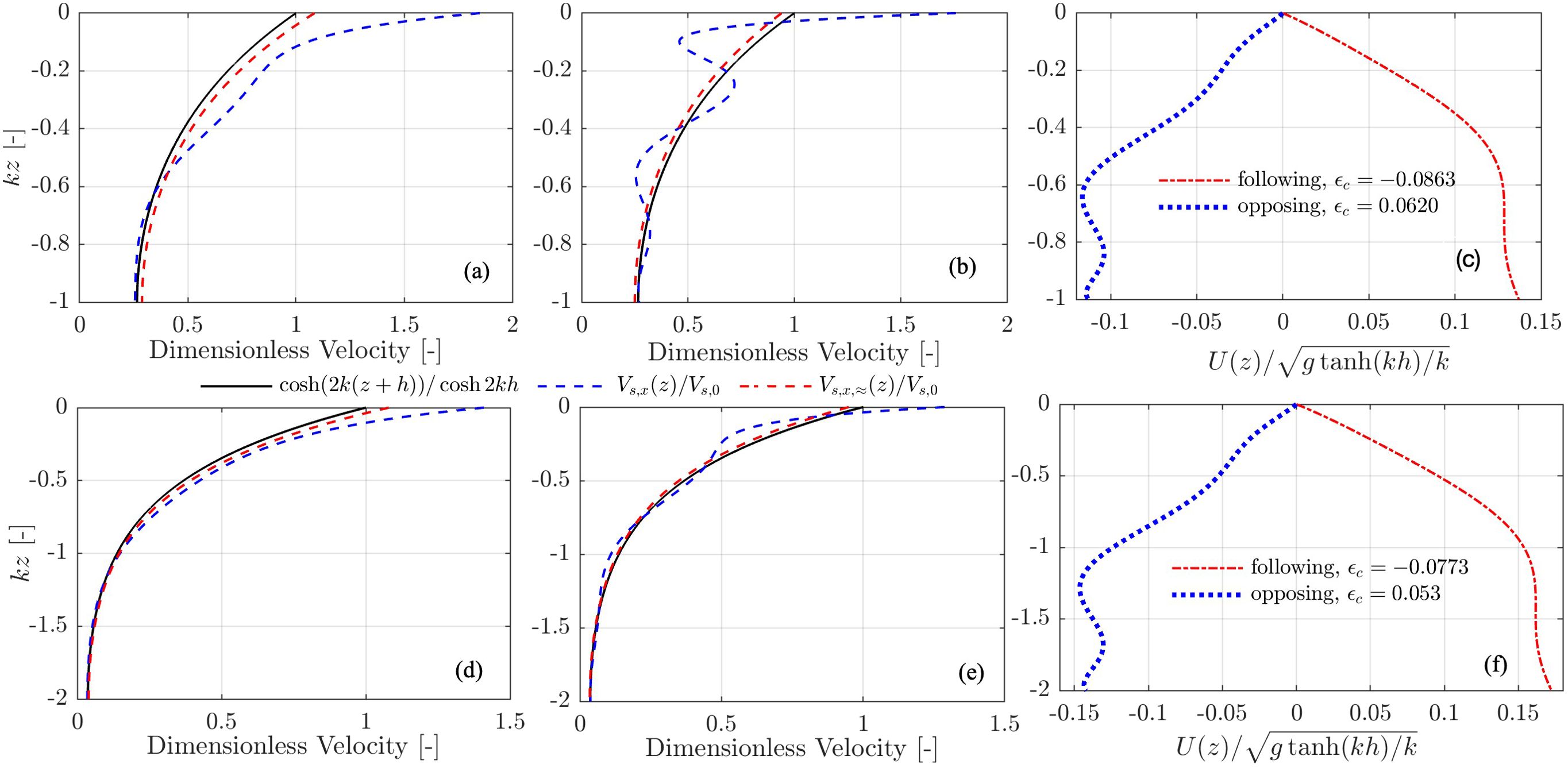
Figure 4. Stokes drift velocity profiles against the depth (panels (A, B, D, E) atop a following (panels (A, D) and opposing (panels (B, E) tidal current measured at the mouth of Columbia river (Zippel and Thomson, 2017; Zheng et al., 2024), where the water depth of 25 m was used and the dimensionless parameter єc was estimated based on Equation 27. The scaled velocity profiles of the following (with negative surface shear) and opposing (with positive surface shear) tidal currents are shown in both panel (C, F) due to two different monochromatic waves chosen in panels (A, B) and panels (D, E), where kh = 1 and kh = 2 were set for the top and lower rows, respectively.
We proceed to examine the Stokes drift profiles derived in subsection 3.2 in limiting cases through the comparisons with the expression (Equation 20) for general cases shown in both Figures 2 and 3. Figure 2 shows three example current profiles for both two and three-dimensional waves, including a linearly and exponentially sheared current and a current representing the profile measured at the mouth of a river. The Stokes drift profile (Equation 24) is analytic for the cases in the presence of a linearly sheared current and a spanwise oriented current profile, which is demonstrated by panels (a, d) and panel (f), respectively as expected. Specifically, the results from either Equations 24 or 26 and 20 are not distinguishable to the numerical extent of the thickness of the lines. When the currents propagate along the spanwise direction or are not linearly sheared, the differences between the approximate Stokes drift (Equation 29) and the general expression given by Equation 20 are noticeable. The differences are considerable in the case of an exponential current in both the two- (panel (b)) and three-dimensional (panel (e)) cases, where the non-monotonic depth-dependent structure is not well predicted by the first-order approximation using Equation 29. A similar observation is reported in panel (c) of Figure 2 where the first-order approximation represents more similar profile features as the Stokes drift in the absence of a current but far off the accurate prediction. It is worth noting that the component of the approximate Stokes drifts in the y direction which is orthogonal to the wave propagation, shows a good agreement with Equation 20 in panel (e), which corresponds to when the shear strength of the current profile is considered to be large. This good agreement may be explained by that the Stokes drift component in the span-wise direction is more shear-production dominated and less affected by shear-current modified wave dispersion properties and єc = 0 is admitted.
The wave-induced particle trajectories are shown in Figures 5 and 6 for two- and three-dimensional waves in a current modeled by 3 different depth-dependent profiles, respectively, together with the net mean displacement due to the Stokes drift given by Equation 20. Similar to the classic conclusion, it is seen from Figures 5 and 6 that the particle trajectories are not closed arising from a net mean horizontal displacement accumulated per period. In contrast, a striking difference is demonstrated in Figure 6 for three-dimensional cases in which rotational particle trajectories are observed, owing to the non-vanishing transverse y particle motions and the respective net mean displacements. Interestingly, the net mean displacement of particles at various depths shown in panels (a, b, c) behaves in a spiral manner as the depth increases in the presence of an exponentially sheared current. The largest net mean displacement in the wave-propagation direction over a fixed time interval does not appear for the particles at the surface but these below a certain depth. For the special case examined in panels (a, b, c) of Figure 6, it appears for particles at kzp,0 ≈−0.3, where zp,0 is the vertical position of a particle at rest as noted. Generally, the net displacement of particle motions in Figures 5 and 6 show consistent results with the predictions using the Stokes drift velocity as they should, which well validate the expression of Stokes drift given by Equation 20, in addition to these shown in Appendix 1.
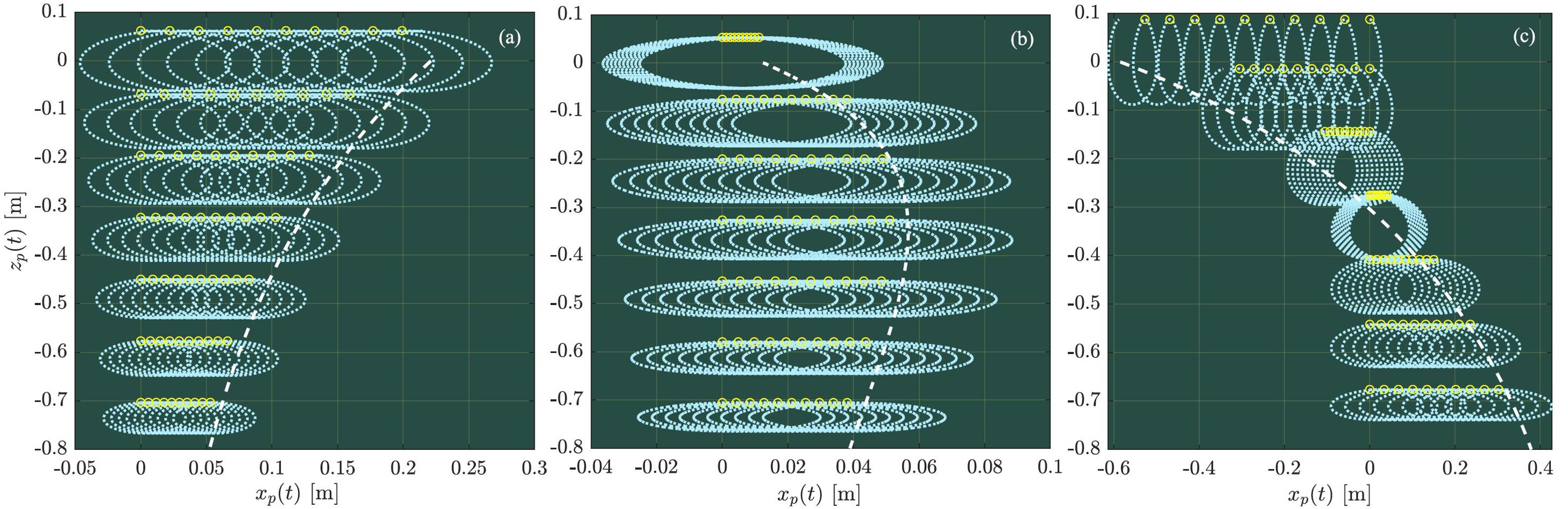
Figure 5. Wave-induced trajectories for two-dimensional waves from the initial time instant of t = 0 s to t = 10Tp, where Tpdenotes the period of waves and the net mean displacement due to current alone was not included. The net horizontal displacement is computed due to Stokes drift velocity (white dashed) based on Equation 20.
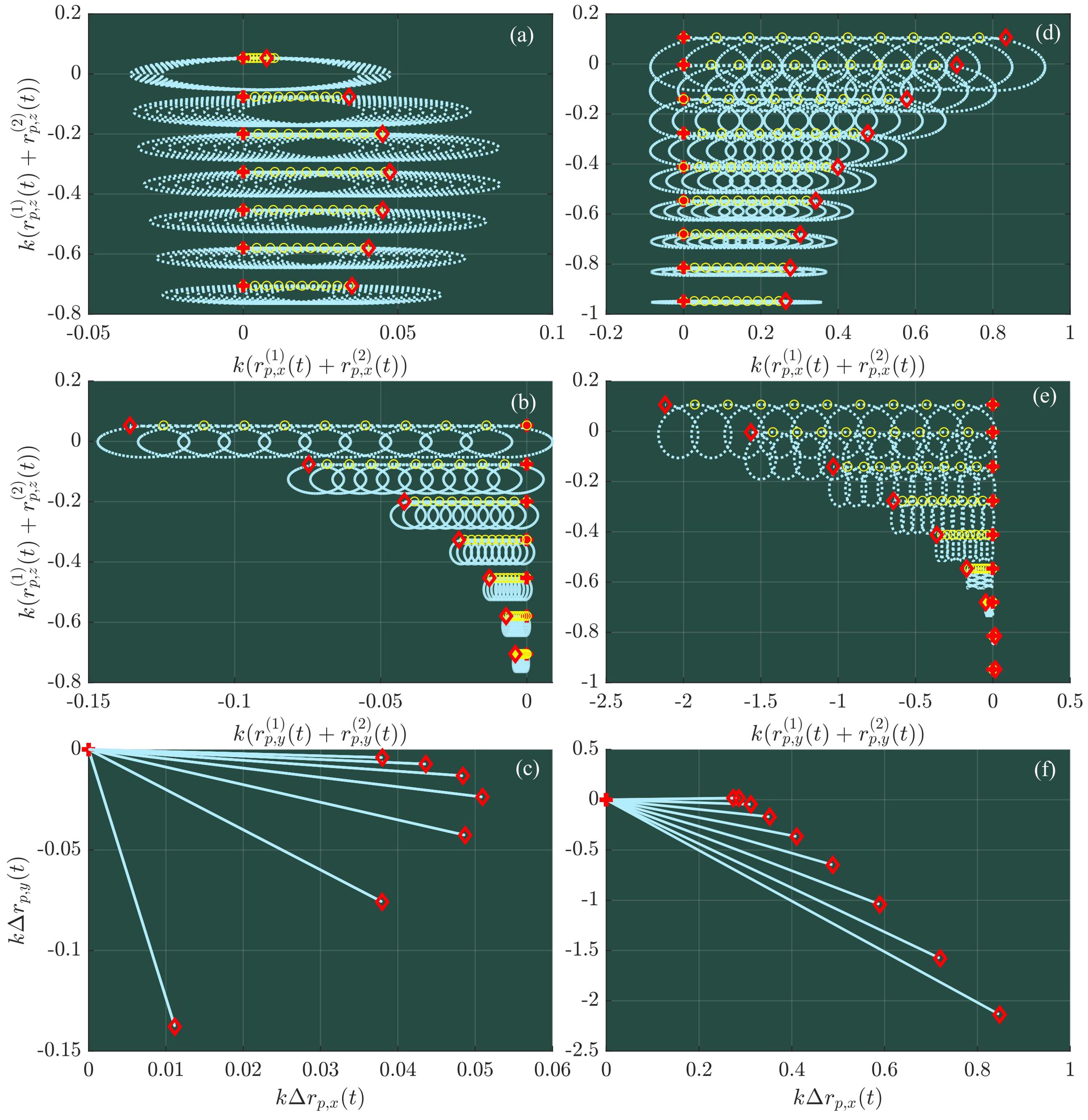
Figure 6. Wave-induced trajectories for 3D cases: The top, middle, and bottom rows show the particle trajectories in the xoz, yoz, and xoy planes, respectively.
This paper has derived explicit formulae for the Stokes drift velocity and particle trajectories by monochromatic waves in an arbitrarily depth-dependent flow, following the Direct Integration Method (DIM) proposed by Li and Ellingsen (2019) for the linear dispersion relation and orbital velocity of fluid parcels. Numerical implementation has been carried out based on the analytical results derived by this work using a few cases which involve different current profiles. Three novel features related to the Stokes drift, and thereby the particle trajectories, have been demonstrated for the first time, as a result of rotational motions of fluid parcels due to the coupling between a shear current and surface waves.
i. When the depth-dependent flow poses a non-vanishing shear in the span-wise direction, the Stokes drift velocity is no longer aligned with the direction of the wave propagation. This feature naturally introduces a misalignment to the wave propagation, being a likely cause to the misaligned Langmuir rolls which have been widely observed in nature, see, e.g., Van Roekel et al. (2012).
ii. When the depth-dependent structure of the flow velocity affects the features of surface waves in a nonweak manner, which corresponds to the wavenumber and depth weighted dimensionless parameter defined in expression (Equation 27) in the regime of єc≳ 0.1, the magnitude of the Stokes drift does not decrease with depth in a monotonic manner. We show that this leads to that the maximum of the net mean displacement of fluid parcels by waves after a fixed duration is no longer at the surface but at a depth below a still water surface. The physical implications of this feature in other physical processes in the air-sea interaction remain to be demonstrated in future works.
iii. When the surface shear is strong, i.e., єc≳ 0.1, a change of the direction (or sign) of Stokes drift velocity has been observed, and thereby a cancellation in the mass transport over a water column can develop, given that the mass transport by monochromatic waves can be estimated through integratingthe Stokes drift over the entire water column. This indicates that a depth-integrated model such as Yang and Liu (2022) can likely lead to underestimated effects of a current on the local mass transport.
Reduced forms of the approximate Stokes drift velocity have been derived under the assumption of weak irrotationality of wave-induced flow motions as explained in Shrira (1993); Ellingsen and Li (2017). The first and second-order approximations are compared with the more general formulae derived by this work. The former provides a good approximation when єc ≲ 0.05 but the second-order approximation is necessary for demonstrating the key features of the Stokes drift for єc≳ 0.1. It shall be noted that the numerical implementation of the second-order approximation demands a much larger computational cost than the direct implementation of the Stokes drift given by Equation 20 based on the DIM and thus is not recommended from a practical point of view. Nevertheless, good agreement between the second-order approximation and the predictions by Equation 20 has been consistently observed.
Although based on an asymptotic approximate model, the aforementioned three novel features enable unconventional insights into Stokes drift induced by surface waves, producing far-reaching impact on physical processes in the open oceans as well as suggesting potential directions for future studies. The results obtained from here can be directly used for a more accurate parameterization of the Stokes drift as a driving force due to surface waves in regional circulation models, see such as Breivik et al. (2014); Suzuki and Fox-Kemper (2016) for an example. This work can also be used to shed light on the question: how the misalignment between the Stokes drift velocity and waves in an obliquely oriented depth-dependent current affect the formation of Langmuir rolls to an oblique angle to the wave propagation.
The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
YL: Conceptualization, Formal analysis, Funding acquisition, Investigation, Methodology, Validation, Visualization, Writing – original draft. ZZ: Investigation, Methodology, Validation, Writing – review & editing. HK: Conceptualization, Investigation, Methodology, Writing – review & editing.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. YL acknowledges the support from the Research Council of Norway through a POS-ERC grant (project no. 342480).
The authors would like to thank Simen A. Å Ellingsen for the useful discussions which have contributed to the preparation of this work.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Akselsen A. H., Ellingsen S. (2019). Weakly nonlinear transient waves on a shear current: Ring waves and skewed Langmuir rolls. J. Fluid Mech. 863, 114–149. doi: 10.1017/jfm.2018.960
Ali A., Kalisch H. (2013). Reconstruction of the pressure in long-wave models with constant vorticity. Eur. J. Mech.-B/Fluids 37, 187–194. doi: 10.1016/j.euromechflu.2012.09.009
Ardhuin F., Marié L., Rascle N., Forget P., Roland A. (2009). Observation and estimation of Lagrangian, Stokes, and Eulerian currents induced by wind and waves at the sea surface. J. Phys. Oceanography 39, 2820–2838. doi: 10.1175/2009JPO4169.1
Babanin A. V. (2006). On a wave-induced turbulence and a wave-mixed upper ocean layer. Geophys. Res. Lett. 33, L20605. doi: 10.1029/2006GL027308
Babanin A. V., Chalikov D. (2012). Numerical investigation of turbulence generation in non-breaking potential waves. J. Geophys. Res.: Oceans 117, C06010. doi: 10.1029/2012JC007929
Bjørnestad M., Buckley M., Streßer M., Horstmann J., Cysewski M., Carrasco-Alvarez R. (2021). Lagrangian measurements of orbital velocities in the surf zone. Geophys.Res. Lett. 48, e2021GL095722. doi: 10.1029/2021GL095722
Borluk H., Kalisch H. (2012). Particle dynamics in the KdV approximation. Wave Motion 49, 691–709. doi: 10.1016/j.wavemoti.2012.04.007
Breivik Ø., Christensen K. H. (2020). A combined Stokes drift profile under swell and wind sea. J. Phys. Oceanogr. 50, 2819–2833. doi: 10.1175/JPO-D-20-0087.1
Breivik Ø., Janssen P. A., Bidlot J.-R. (2014). Approximate Stokes drift profiles in deep water. J. Phys. Oceanogr. 44, 2433–2445. doi: 10.1175/JPO-D-14-0020.1
Calvert R., McAllister M., Whittaker C., Raby A., Borthwick A., Van Den Bremer T. (2021). A mechanism for the increased wave-induced drift of floating marine litter. J. Fluid Mech. 915, A73. doi: 10.1017/jfm.2021.72
Chamecki M., Chor T., Yang D., Meneveau C. (2019). Material transport in the ocean mixed layer: recent developments enabled by large eddy simulations. Rev. Geophys. 57, 1338–1371. doi: 10.1029/2019RG000655
Chen L., Basu B., Martin C.-I. (2021). On rotational flows with discontinuous vorticity beneath steady water waves near stagnation. J. Fluid Mech. 912, A44. doi: 10.1017/jfm.2020.1057
Chen Y.-Y., Hsu H.-C., Chen G.-Y. (2010). Lagrangian experiment and solution for irrotational finite-amplitude progressive gravity waves at uniform depth. Fluid Dyn. Res. 42, 045511. doi: 10.1088/0169-5983/42/4/045511
Constantin A., Monismith S. (2017). Gerstner waves in the presence of mean currents and rotation. J. Fluid Mech. 820, 511–528. doi: 10.1017/jfm.2017.223
Craik A. D. (1970). A wave-interaction model for the generation of windrows. J. Fluid Mech. 41, 801–821. doi: 10.1017/S0022112070000939
Craik A., Leibovich S. (1976). A rational model for Langmuir circulations. J. Fluid Mech. 73, 401–426. doi: 10.1017/S0022112076001420
Curtis C., Carter J., Kalisch H. (2018). Particle paths in nonlinear Schrodinger¨ models in the presence of linear shear currents. J. Fluid Mech. 855, 322–350. doi: 10.1017/jfm.2018.623
Davey A., Stewartson K. (1974). On three-dimensional packets of surface waves. Proc. R. Soc London Ser. A. Math. Phys. Sci. 338, 101–110. doi: 10.1098/rspa.1974.0076
Dysthe K. B. (1979). Note on a modification to the nonlinear Schrodinger¨ equation for application to deep water waves. Proc. R. Soc London Ser. A. Math. Phys. Sci. 369, 105–114. doi: 10.1098/rspa.1979.0154
Ellingsen S.Å. (2014a). Initial surface disturbance on a shear current: The Cauchy-Poisson problem with a twist. Phys. Fluids 26, 082104. doi: 10.1063/1.4891640
Ellingsen S.Å. (2014b). Ship waves in the presence of uniform vorticity. J. Fluid Mech. 742, R2. doi: 10.1017/jfm.2014.28
Ellingsen S.Å., Abid M., Kharif C., Li Y. (2024). Dispersive wave focusing on a shear current: Part 1 — Linear approximations. Water waves 6, 367-411. doi: 10.1007/s42286-024-00085-3
Ellingsen S., Li Y. (2017). Approximate dispersion relations for waves on arbitrary shear flows. J. Geophys. Res.: Oceans 122, 9889–9905. doi: 10.1002/2017JC012994
Flamarion M. V., Castro E. M., Ribeiro-Jr R. (2023). Pressure anomalies beneath solitary waves with constant vorticity. Eng 4, 1306–1319. doi: 10.3390/eng4020076
Ghantous M., Babanin A. V. (2014). Ocean mixing by wave orbital motion. Acta Phys. Slovaca 64, 1–57. doi: 10.2478/apsrt-2014-0001
Higgins C., van Den Bremer T., Vanneste J. (2020). Lagrangian transport by deep-water surface gravity wavepackets: effects of directional spreading and stratification. J. Fluid Mech. 883, A42. doi: 10.1017/jfm.2019.877
Hsu H.-C. (2013). Particle trajectories for waves on a linear shear current. Nonl. Analy. Real World App. 14, 2013-2021. doi: 10.1016/j.nonrwa.2013.02.005
Kenyon K. E. (1969). Stokes drift for random gravity waves. J. Geophys. Res. 74, 6991–6994. doi: 10.1029/JC074i028p06991
Kharif C., Pelinovsky E. (2003). Physical mechanisms of the rogue wave phenomenon. Europ. J. Mech.-B/Fluids 22, 603–634. doi: 10.1016/j.euromechflu.2003.09.002
Kirby J., Chen T. (1989). Surface waves on vertically sheared flows: approximate dispersion relations. J. Geophys. Res.: Oceans 94, 1013–1027. doi: 10.1029/JC094iC01p01013
Lane E. M., Restrepo J., McWilliams J. C. (2007). Wave–current interaction: A comparison of radiation-stress and vortex-force representations. J. Phys. Oceanogr. 37, 1122–1141. doi: 10.1175/JPO3043.1
Larsen B. E., Al-Obaidi M. A. A., Guler H. G., Carstensen S., Goral K. D., Christensen E. D., et al. (2023). Experimental investigation on the nearshore transport of buoyant microplastic particles. Mar. pollut. Bull. 187, 114610. doi: 10.1016/j.marpolbul.2023.114610
Li Y. (2018). Wave-interference effects on far-field ship waves in the presence of a shear current. J. Ship Res. 62, 37–47. doi: 10.5957/JOSR.170017
Li Y., Ellingsen S. (2019). A framework for modeling linear surface waves on shear currents in slowly varying waters. J. Geophys. Res.: Oceans 124, 2527–2545. doi: 10.1029/2018JC014390
Li Y. (2021). Three-dimensional surface gravity waves of a broad bandwidth on deep water. J. Fluid Mech. 926, 1–43. doi: 10.1017/jfm.2020.1076
Li Y., Chabchoub A. (2024). How currents trigger extreme sea waves. The roles of Stokes drift, Eulerian return flow, and a background flow in the open ocean. Geophys. Res. Lett. 51, e2023GL107381. doi: 10.1029/2023GL107381
Li Y., Ellingsen S. (2016a). Multiple resonances of a moving oscillating surface disturbance on a shear current. J. Fluid Mech. 808, 668–689. doi: 10.1017/jfm.2016.637
Li Y., Ellingsen S. (2016b). Ship waves on uniform shear current at finite depth: wave resistance and critical velocity. J. Fluid Mech. 791, 539–567. doi: 10.1017/jfm.2016.20
Li Y., Li X. (2021). Weakly nonlinear broadband and multi-directional surface waves on an arbitrary depth: A framework, Stokes drift, and particle trajectories. Phys. Fluids 33, 076609. doi: 10.1063/5.0057215
Li Y., Smeltzer B. K., Ellingsen S. A. (2019). Transient wave resistance upon a real shear current. Europ. J. Mech.-B/Fluids 73, 180–192. doi: 10.1016/j.euromechflu.2017.08.012
Longuet-Higgins M. S. (1953). Mass transport in water waves. Philos. Trans. R. Soc A 245, 535–581. doi: 10.1098/rsta.1953.0006
McIntyre M. (1981). On the’wave momentum’ myth. J. Fluid Mech. 106, 331–347. doi: 10.1017/S0022112081001626
McWilliams J. C. (2016). Submesoscale currents in the ocean. P. R. Soc London. A. 472, 20160117. doi: 10.1098/rspa.2016.0117
McWilliams J. C., Sullivan P. P., Moeng C. (1997). Langmuir turbulence in the ocean. J. Fluid Mech. 334, 1–30. doi: 10.1017/S0022112096004375
Mellor G. (2015). A combined derivation of the integrated and vertically resolved, coupled wave–current equations. J. Phys. Oceanogr. 45, 1453–1463. doi: 10.1175/JPO-D-14-0112.1
Monismith S., Cowen E., Nepf H., Magnaudet J., Thais L. (2007). Laboratory observations of mean flows under surface gravity waves. J. Fluid Mech. 573, 131–147. doi: 10.1017/S0022112006003594
Myrhaug D. (2015). Stokes drift estimation based on long-term variation of wave conditions. Proc. Institution Mechanical Engineers Part M: J. Eng. Maritime Environ. 229, 141–146. doi: 10.1177/1475090213506699
Myrhaug D., Wang H., Holmedal L. E. (2014). Stokes drift estimation for deep water waves based on short-term variation of wave conditions. Coast. Eng. 88, 27–32. doi: 10.1016/j.coastaleng.2014.01.014
Onorato M., Proment D., Toffoli A. (2011). Triggering rogue waves in opposing currents. Phys. Rev. Lett. 107, 184502. doi: 10.1103/PhysRevLett.107.184502
Peregrine D. H. (1976). Interaction of water waves and currents. Adv. Appl. Mech. 16, 9–117. doi: 10.1016/S0065-2156(08)70087-5
Pizzo N., Lenain L., Rømcke O., Ellingsen S.Å., Smeltzer B. K. (2023). The role of Lagrangian drift in the geometry, kinematics and dynamics of surface waves. J. Fluid Mech. 954, R4. doi: 10.1017/jfm.2022.1036
Qiao F., Yuan Y., Ezer T., Xia C., Yang Y., Lü X., et al. (2010). A three-dimensional surface wave–ocean circulation coupled model and its initial testing. Ocean Dynamics 60, 1339–1355. doi: 10.1007/s10236-010-0326-y
Quinn B., Toledo Y., Shrira V. (2017). Explicit wave action conservation for water waves on vertically sheared flows. Ocean Model. 112, 33–47. doi: 10.1016/j.ocemod.2017.03.003
Shrira V. I. (1993). Surface waves on shear currents: solution of the boundary-value problem. J. Fluid Mech. 252, 565–584. doi: 10.1017/S002211209300388X
Shrira V., Slunyaev A. (2014). Nonlinear dynamics of trapped waves on jet currents and rogue waves. Phys. Rev. E 89, 041002. doi: 10.1103/PhysRevE.89.041002
Skop R. A. (1987). Approximate dispersion relation for wave-current interactions. J. Waterway Port Coastal Ocean Eng. 113, 187–195. doi: 10.1061/(ASCE)0733-950X(1987)113:2(187)
Smith J. A. (2006). Observed variability of ocean wave Stokes drift, and the Eulerian response to passing groups. J. Phys. Oceanogr. 36, 1381–1402. doi: 10.1175/JPO2910.1
Steer J. N., Borthwick A. G., Stagonas D., Buldakov E., van den Bremer T. S. (2020). Experimental study of dispersion and modulational instability of surface gravity waves on constant vorticity currents. J. Fluid Mech. 884, A40. doi: 10.1017/jfm.2019.951
Stewart R. H., Joy J. W. (1974). HF radio measurements of surface currents. Deep Sea Res. Oceanogr. Abstracts 21, 1039–1049. doi: 10.1016/0011-7471(74)90066-7
Sullivan P. P., McWilliams J. C. (2010). Dynamics of winds and currents coupled to surface waves. Ann. Rev. Fluid Mech. 42, 19–42. doi: 10.1146/annurev-fluid-121108-145541
Sutherland B. R., DiBenedetto M., Kaminski A., Van Den Bremer T. (2023). Fluid dynamics challenges in predicting plastic pollution transport in the ocean: A perspective. Phys. Rev. Fluids 8, 070701. doi: 10.1103/PhysRevFluids.8.070701
Suzuki N., Fox-Kemper B. (2016). Understanding Stokes forces in the wave-averaged equations. J. Geophys. Res. C: Oceans 121, 3579–3596. doi: 10.1002/2015JC011566
Thomas R., Kharif C., Manna M. (2012). A nonlinear Schrödinger equation for water waves on finite depth with constant vorticity. Phys. Fluids 24, 127102. doi: 10.1063/1.4768530
Touboul J., Charland J., Rey V., Belibassakis K. (2016). Extended mild-slope equation for surface waves interacting with a vertically sheared current. Coast. Eng. 116, 77–88. doi: 10.1016/j.coastaleng.2016.06.003
Ursell F. (1953). The long-wave paradox in the theory of gravity waves. Math. Proc. Cambridge Philos. Soc. 49, 685–694. doi: 10.1017/S0305004100028887
van den Bremer T. S., Breivik Ø. (2018). Stokes drift. Philos. Trans. R. Soc A 376, 20170104. doi: 10.1098/rsta.2017.0104
van den Bremer T., Whittaker c., Calvert R., Raby A., Taylor P. (2019). Experimental study of particle trajectories below deep-water surface gravity wave groups. J. Fluid Mech. 879, 168-186. doi: 10.1017/jfm.2019.584
Van Roekel L., Fox-Kemper B., Sullivan P., Hamlington P., Haney S. (2012). The form and orientation of langmuir cells for misaligned winds and waves. J. Geophys. Res.: Oceans 117, C05001. doi: 10.1029/2011JC007516
Webb A., Fox-Kemper B. (2011). Wave spectral moments and Stokes drift estimation. Ocean Model. 40, 273–288. doi: 10.1016/j.ocemod.2011.08.007
Webb A., Fox-Kemper B. (2015). Impacts of wave spreading and multidirectional waves on estimating Stokes drift. Ocean Modell. 96, 49–64. doi: 10.1016/j.ocemod.2014.12.007
White B. S., Fornberg B. (1998). On the chance of freak waves at sea. J. Fluid Mech. 355, 113–138. doi: 10.1017/S0022112097007751
Xin Z., Li X., Li Y. (2023). Coupled effects of wave and depth-dependent current interaction on loads on a bottom-fixed vertical slender cylinder. Coast. Eng. 183, 104304. doi: 10.1016/j.coastaleng.2023.104304
Yang Y., Li Y., Li J., Liu J., Gao Z., Guo K., et al. (2021). The influence of Stokes drift on oil spills: Sanchi oil spill case. Acta Oceanologica Sin. 40, 30–37. doi: 10.1007/s13131-021-1889-9
Yang Z., Liu P. L.-F. (2022). Depth-integrated wave–current models. part 2. current with an arbitrary profile. J. Fluid Mech. 936, A31. doi: 10.1017/jfm.2022.42
Zheng Z., Li Y., Ellingsen S.Å. (2023). Statistics of weakly nonlinear waves on currents with strong vertical shear. Phys. Rev.Fluids 8, 014801. doi: 10.1103/PhysRevFluids.8.014801
Zheng Z., Li Y., Ellingsen S.Å. (2024). Dispersive wave focusing on a shear current. part 2: nonlinear effects. Water Waves. 6, 413-449. doi: 10.1007/s42286-024-00097-z
Zippel S. F., Farrar J. T., Zappa C. J., Plueddemann A. J. (2022). Parsing the kinetic energy budget of the ocean surface mixed layer. Geophys. Res. Lett. 49, e2021GL095920. doi: 10.1029/2021GL095920
Zippel S., Thomson J. (2017). Surface wave breaking over sheared currents: Observations from the Mouth of the Columbia River. J. Geophys. Res.: Oceans 122, 3311–3328. doi: 10.1002/2016JC012498
In this section, we validate the derivations used for the results presented in section 4. Appendix 1 shows the good agreement between the Stokes drift velocity evaluated using (20) and the analytical approach for the cases without a current and with a linearly sheared current. Appendix 2 depicts that the particle trajectories predicted by (38) agree well with the net mean displacement obtained from the predictions using the Stokes drift velocity given by (20) in both the x and y direction.
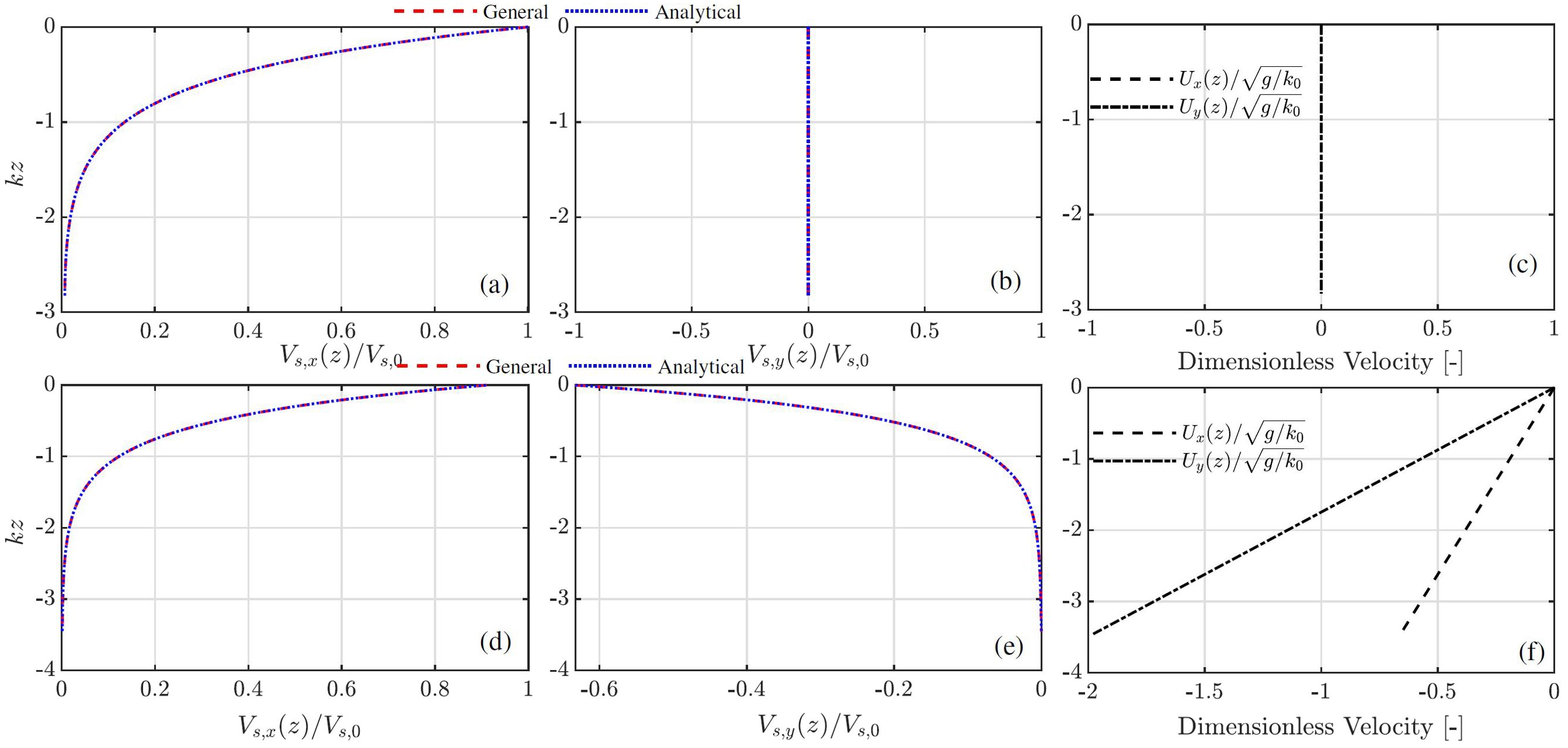
Appendix 1. Stokes drift velocity in the x and y direction for waves alone and in the presence of a linearly sheared current, where the analytical results for the case in the former and latter are based on (22) and (24), respectively.
Keywords: Stokes drift, surface waves (fluid), shear current, ocean modelling, wave-current interaction (WCI), wave forcing in the upper ocean, particle trajectories
Citation: Li Y, Zheng Z and Kalisch H (2024) Stokes drift and particle trajectories induced by surface waves atop a shear flow. Front. Mar. Sci. 11:1445116. doi: 10.3389/fmars.2024.1445116
Received: 06 June 2024; Accepted: 12 August 2024;
Published: 15 October 2024.
Edited by:
Xiaohui Xie, Ministry of Natural Resources, ChinaReviewed by:
Emilian Parau, University of East Anglia, United KingdomCopyright © 2024 Li, Zheng and Kalisch. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yan Li, eWFuLmxpQHVpYi5ubw==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.