Humpback whales (Megaptera novaeangliae) in Hervey Bay, Australia: a stopover for females early in their southern migration

In the Southern Hemisphere, humpback whales (Megaptera novaeangliae) migrate along the extended continental coastlines of Australia, South America, and South Africa. This study reports on photo-identification capture–recapture data from a long-term survey conducted in Hervey Bay, Queensland, where a substantial proportion of the population stop over early in the southern migration. Photo-identification data were collected over 10 weeks per year from 1997 to 2009. The migration through Hervey Bay is dominated and led by females with high fidelity to the site. Mature females, yearlings, and immature whales use the Bay during August, while mature lactating females with calves dominate during September and October. Complex social behaviours occur throughout the season and differ between the early and late cohorts. We argue that the composition of the two cohorts and their distinctively different behaviours indicate that Hervey Bay is not simply a resting site but an area of aggregation that serves important social and biological benefits. A multistate open robust design model was fitted to capture–recapture data to estimate the annual number of whales visiting the Bay, the permanent emigration rate, proportions of the visiting population that do not enter the Bay each year, the number present during each week, and their residency times. The number of annual visitors to the Bay increased approximately linearly from 857 in 1997 to 2175 at the end of sampling in 2009 with two-thirds migrating through during the first half of each season. The population rate of growth may have been slowing by 2009, but there was considerable uncertainty in the trajectory and little basis for projection into the future. While it is desirable to know the current status of the Hervey Bay population and what has occurred since 2009, the cost and effort required make further manual collection and matching of images unlikely. The development of AI algorithmic matching software may enable further research in future.

1 Introduction

Humpback whales, Megaptera novaeangliae (Borowski, 1781), engage in long-distance, annual migrations from low-latitude winter breeding grounds to high-latitude summer feeding areas in both the Northern Oceans (see review in Clapham, 2000) and the Southern Oceans (Dawbin, 1966, 1997; Meynecke et al., 2021). In the Northern Oceans, humpback whales generally migrate through open waters between breeding grounds and feeding areas (Calambokidis et al., 2008; Smith et al., 1999). In the Southern Oceans, however, humpback whales’ migratory pathways are constrained by the geography of the ocean basins within which they travel (e.g., Dawbin, 1966, 1997; Garrigue et al., 2015; Andrews-Goff et al., 2023). Most Southern hemisphere humpback populations migrate along extensive continental coastlines and near-shore islands of Australia, Africa, and South America before returning to widely dispersed Antarctic feeding areas (Dawbin, 1997; Barendse et al., 2010, 2013; Constantine et al., 2014; Franklin et al., 2017a & b; Andrews-Goff et al., 2023). The exceptions are whales that migrate through the open waters and island chains of the South Pacific (Garrigue et al., 2011).

Hervey Bay (25°S, 153°E) is a broad, shallow embayment (Ribbe, 2014) offering protection from the southeasterly winds prevailing off the Queensland coast (Corkeron et al., 1994). It lies just south of the humpbacks’ presumed northern overwintering grounds encompassing areas of the Great Barrier Reef, which are considered to stretch from 16°S to 23°S (Smith et al., 2012; Fariello et al., 2024). A specific subgroup of whales (the Hervey Bay subgroup) divert into Hervey Bay during their Southern migration.

Humpback migrations are segregated by age and sex (Dawbin, 1966, 1997; Franklin et al., 2018), including the migration through Hervey (Corkeron et al., 1994; Franklin et al., 2018, 2021). Using a large sample of data derived from commercial whaling, Dawbin, 1966, 1997, described the structure of the migratory procession along Southern Ocean coastlines; mature females with new-season calves are the first to leave Antarctic feeding areas followed and travelling with the immature cohort of whales (aged 1 to 6 years), mature males follow shortly after and preceding the last cohort to leave, and pregnant mature females extend their stay in Antarctica to feed prior to birthing in the Barrier Reef (Smith et al., 2012; Fariello et al., 2024). Franklin et al. (2018) reported that the classes and timing of humpback whales migrating through Hervey Bay during the southern migration did not differ from the earlier reports of Dawbin with the exception that few mature males enter Hervey Bay.

The population of humpback whales migrating off eastern Australia (E1, IWC, 2011) has increased rapidly (around 11% per annum) since the early 1990s to 2015, when the last survey to estimate abundance was conducted and abundance was estimated at 24,545 (95% confidence interval 21,631–27,851; Noad et al., 2019; see review in Harrison and Woinarski, 2018). Noad et al. (2019) reported an estimated historical K of 26,133 and pointed out that the population may be seen as essentially having recovered by 2019 at this value of K (p.206).

Recent research in Hervey Bay has reported significant differences in pod characteristics, classes of whales, and behaviour in August compared to September and October. Mature females, including early pregnant females and females not calving in the current year, use Hervey Bay during mid-July and August, socially interacting with immatures (both males and females) (Franklin et al., 2011, 2018, 2021; Franklin, 2012). During September and October, mature lactating females with new calves dominate (from 3.6% of pods per week to 92.8% of pods per week, Franklin et al., 2011) accompanied by a few escorts (Franklin et al., 2018). The sex ratio of whales in the Bay is skewed towards females (2.9:1 female to male, Franklin et al., 2018).

While this research has demonstrated that Hervey Bay is used preferentially by female humpbacks and identified the classes and timing of humpback whales using the Bay (Franklin et al., 2011, 2018), these studies used subsets of the available data consisting of whales identified by age and sex, or analysed the data at the pod level and did not quantify the total numbers of annual visitors, the numbers present throughout the season, or how long they stayed in the Bay. Here, we use all available individual data to investigate these and other related questions.

Long-term capture histories of individual humpback whales were obtained by systematic photo-identification sampling for 10 weeks each season over 13 years from 1997 to 2009. The data were analysed with program MARK (White and Burnham, 1999) and modelled using a multistate open robust design model (MSORD: Pollock, 1982; Kendall et al., 1995, 1997; Kendall and Nichols, 1995; Kendall and Bjorkland, 2001; Kendall et al., 2019). The parameters estimated by the MSORD model are formally described subsequently in Section 3.4 below.

These estimates are used to discuss the social and biological functions of the Hervey Bay stopover, and the relationship between the whales using Hervey Bay and the eastern Australian (E1) population of humpback whales.

2 Methods

2.1 Study area

Hervey Bay, formed by K’gari (formerly Fraser Island) and the Australian mainland, is located at 25°S, 153°E on the eastern coast of Queensland (Figure 1). It is a wide, shallow embayment approximately 4,000 km² in area and is generally less than 16 m deep, with a sand and mud bottom (Ribbe, 2014). K’gari is 126 km long, it lies along a northeasterly axis, and its northern end bridges the continental shelf. The most southerly islands of the Great Barrier Reef are approximately 110 km north of Hervey Bay (Figure 1).

Figure 1

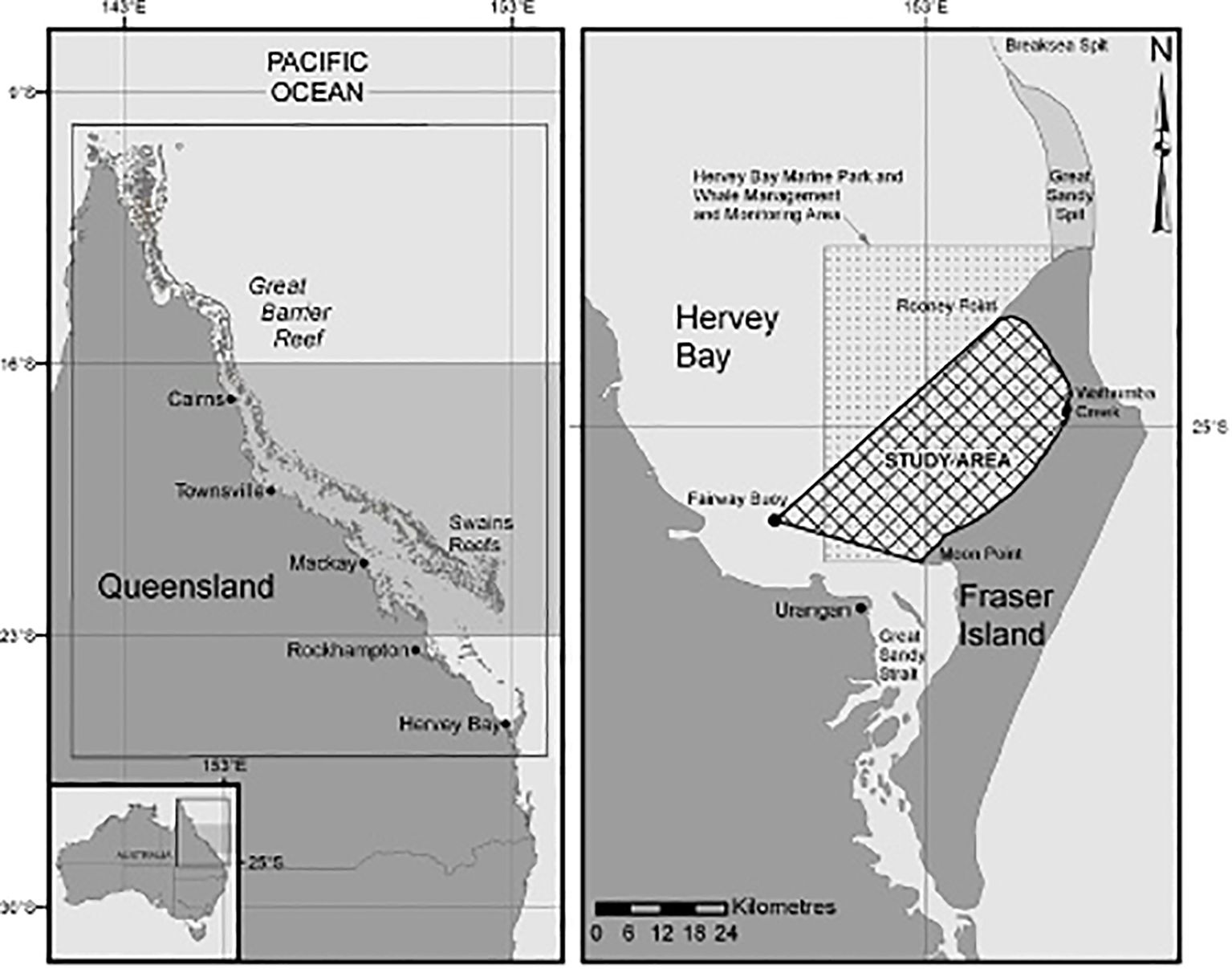
Figure 1. The location of Hervey Bay on the eastern coast of Australia and its geographic relationship to the reefs and inter-reef lagoon of the Great Barrier Reef is shown in the left-side map. The primary overwintering and breeding ground for eastern Australian humpback whales is believed to be off the Queensland coast within the Great Barrier Reef inter-reef lagoon between 16°S and 23°S (shaded). The study area and the original Hervey Bay Marine Park boundaries are shown on the eastern side of Hervey Bay in the right-side map.

2.2 Sampling, capture histories, and effort

Prior to the start of The Oceania Project’s research program in Hervey Bay, earlier work established that the southern migration of humpback whales began in late July with humpback whales using Hervey Bay in early August to mid-October (Paterson, 1991; Corkeron et al., 1994).

A vessel-based photographic identification survey was conducted for 5.25 days per week for 10 weeks per year over 13 years from 1997 to 2009 starting on the first Sunday after the 5th of August each year. The method applied took advantage of communication with commercial whale-watch vessels to travel to the nearest available pod to maximise the number sightings. A spatially random search pattern was unnecessary as it was not intended to describe the spatial distribution of pods. The mobility of both the whales and the tour boats throughout the sampling area mitigated against the possibility of selectively sampling classes of whales that may have preferred specific parts of it. This approach aimed to take a random sample of whales rather than a random sample of locations.

Photo-identification matching was undertaken using an innovative categorisation method (for a comprehensive description see, Franklin et al., 2020), and all photography selected for matching was assessed for photo-quality using established protocols (Calambokidis et al., 2008). Calves were not included in the sample as they do not display permanent distinctive natural marks. All whales in the sample were successfully identified with good-quality photography. Daily capture histories were collapsed into weeks for analysis to reduce the complexity of the model used, and to ensure that there was good coverage of the study area in each weekly sample. This yielded capture histories over 130 weeks (13 years × 10 weeks).

An effort variable was calculated for each week based on the number of full days (0700 till 1700) in each week. Saturdays, which were used for reprovisioning and crew changes, and days lost to bad weather or mechanical problems were counted as zero. Sundays were counted as 0.75 days due to a later start and Fridays as 0.5 days due to an earlier stop. This calculation yielded a value of 5.25 days for a full sampling week and resulted in an overall average of 5.20 days per week.

2.3 Robust design models

The sampling design creates a hierarchical sampling structure in which the intervals between samples occur at two scales: (1) between years (primary samples) and (2) between samples (weeks) within years (secondary samples).

Robust design models (Pollock, 1982; Kendall et al., 1995, 1997; Kendall and Nichols, 1995) were designed to take advantage of hierarchical sampling schemes where, in the classic case, the sets of secondary samples were taken over periods of time short enough for the population to be considered closed within primary samples while being open between them (Kendall et al., 1995, 1997). In the case of breeding grounds or migratory stopovers, whales may arrive and leave the sampling area in sequence creating an open population within each of the primary samples. The open robust design model (Schwarz and Stobo, 1997; Kendall and Bjorkland, 2001; Stauffer et al., 2013) was developed for this situation, and the rates of entry into the sampling area and probabilities of apparent survival between secondary samples may be estimated along with abundance within primary samples.

Only apparent survival was estimated between primary samples in early formulations of the model (Kendall et al., 1995), but subsequent development has also incorporated estimation of temporary emigration, i.e., the proportion of the population present in one primary sample that is absent from the sampling area and unavailable for capture in the next (Kendall et al., 1997). Temporary emigration may be a random process in which the previous state of an animal (present or absent) does not affect its subsequent state, or a Markovian process in which it does. An example of Markovian temporary emigration is when primary samples of females that breed every second year are taken annually on breeding grounds and the probability of presence varies by reproductive state.

Consequently, the model provides estimates of apparent survival both between and within primary samples; the between primary sample estimate describes the probability of remaining alive and maintaining fidelity to (remaining part of the population that visits) Hervey Bay (biological survival × fidelity) while the within primary sample estimate describes the probability of remaining in the sampling area between secondary samples (related to residency or length of stay, Kendall and Bjorkland, 2001).

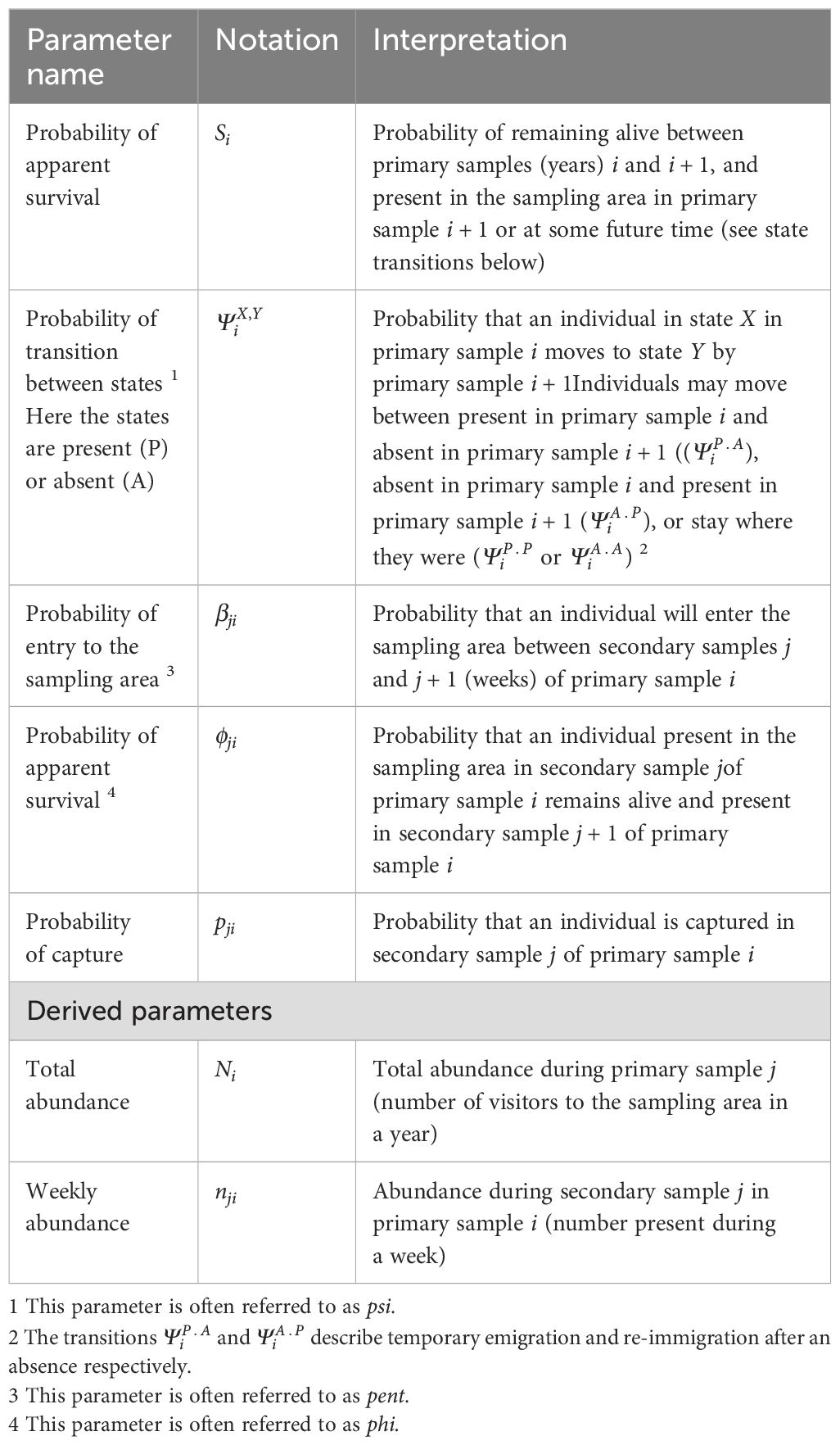
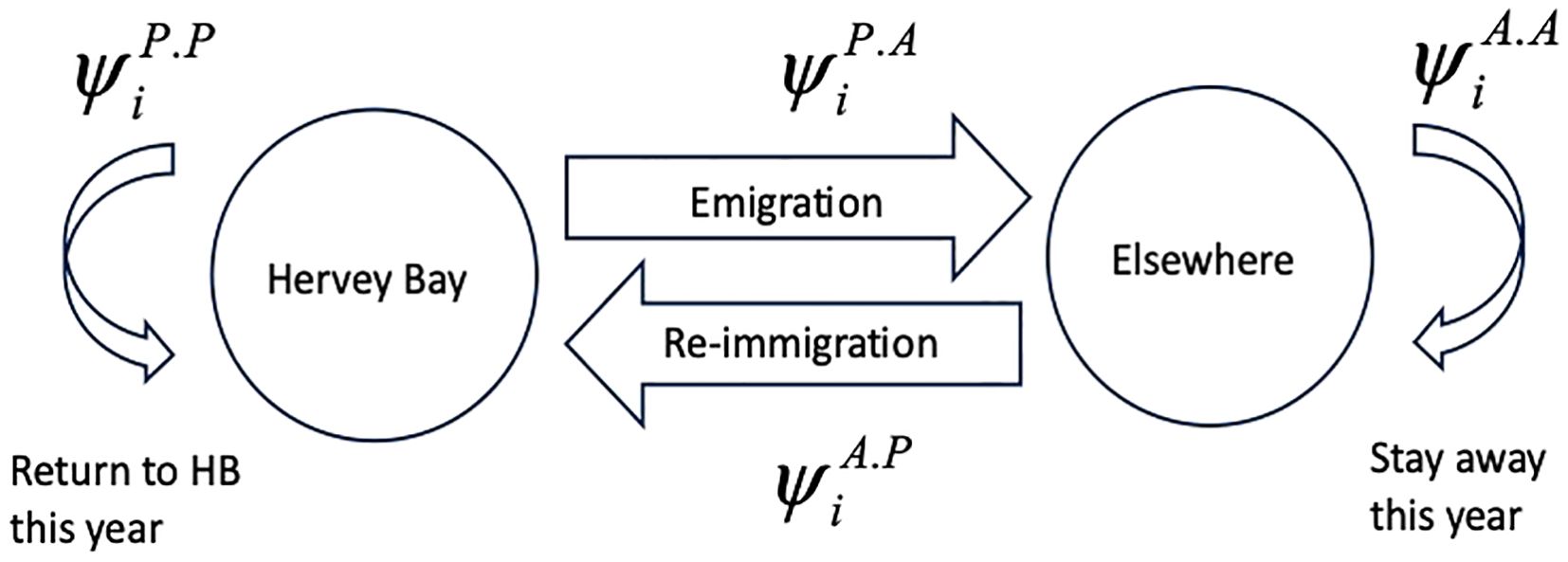
In the open robust design model, temporary emigration is modelled in terms of state transition probabilities. In the basic model, the states are present or ‘observable’ (P) and absent or ‘unobservable’ (A), and the possible transitions are present to absent (PA) and absent to present (AP). A diagram depicting temporary emigration is presented below in Section 3.4. Further states in addition to present or absent may be included in the model, such as capture locations (e.g., bay 1, bay 2, bay 3), maturity (e.g., juvenile, adult), or breeding status (e.g., with, or without neonate), and the transitions among them can be estimated (Stauffer et al., 2013). The capacity to incorporate multiple states in the open robust design has resulted in the model being described as the open robust design multistate (ORDMS) or multistate open robust design (MSORD) model. Analysis of the capture history data was undertaken with program MARK (White and Burnham, 1999).

2.4 Parameters estimated by the multistate open robust design model

Table 1 presents the parameters estimated by the MSORD model.

Table 1

Table 1. Parameters of the MSORD model.

2.4.1 Apparent survival

Capture–recapture studies typically yield an estimate of apparent survival or the probability of both remaining alive and available for recapture in the sample area. Estimates of the probability of remaining alive (biological survival) must be made by other means. If estimates of both apparent and biological survival are available, however, an estimate may be made of the probability of permanent emigration from the sample area. More formally, an estimate of the probability of permanent emigration $\widehat{E}$ may be derived as $\widehat{E}=1-\frac{\widehat{\varphi }}{\widehat{S}}$ where $\widehat{\varphi }$ is an estimate of the probability of apparent survival and $\widehat{S}$ is an estimate of the probability of biological survival. It should be noted that the notation used here, although traditional, does not refer to the parameters estimated by the MSORD where S is used to denote apparent survival at the primary sample (years) level and $\varphi$ denotes apparent survival at the secondary sample (weeks) level.

2.4.2 State transitions

The possible state transitions when there are only the two states, present in Hervey Bay or elsewhere, are illustrated in Figure 2.

Figure 2

Figure 2. Possible state transitions including temporary emigration and re-immigration.

Of the four state transition possibilities only two, ${\Psi }_i^{P.A}$and ${\Psi }_i^{A.P}$, are directly estimated. The other two are their complements, i.e., ${\Psi }_i^{P.P}=1-{\Psi }_i^{P.A}$ and ${\Psi }_i^{A.A}=1-{\Psi }_i^{A.P}$.

There are three forms that temporary emigration may take:

1. Markovian ${\Psi }_i^{P.A}$ and ${\Psi }_i^{A.P}$ are separately estimated.

2. Random ${\Psi }_i^{P.A}=1-{\Psi }_i^{A.P}={\Psi }_i^{A.A}$ such that ${\Psi }_i^{A.P}$ is the complement of ${\Psi }_i^{P.A}$.

3. Even flow ${\Psi }_i^{P.A}={\Psi }_i^{A.P}$.

Note that 1 is necessary to allow for dependency between an animal’s state at time $i$ and time $i+1$.

2.5 Model reduction—constraints on parameter estimates

The probability of apparent survival between primary samples (S) may be modelled as constant, as time varying, or as a function of covariates.

The probability of transition from present to absent (PA) may be specified as its complement PP (present to present), and AP (absent to present) may be specified as its complement AA (absent to absent). A model in which the transition probabilities PA and AA = 1-AP are separately estimated is a Markovian temporary emigration model, a model in which PA is constrained equal to AA = 1-AP is a random temporary emigration model, and a model in which PA is constrained to equal AP is an ‘even flow’ temporary emigration model (Kendall et al., 1995, 1997). The transition probabilities may be modelled as constant, as time-varying, or as a function of covariates with an additional constraint being necessary for identification of the parameter estimates when both between primary sample apparent survival (S) and the transition probabilities (psi) are estimated as time-varying. Specifically, the last transition probabilities PA and AA must be set equal to the transition probabilities PA and AA from some earlier interval.

The probabilities of entry, being the proportions of the total number of visitors to the sampling area in a primary sample that are present at the beginning of sampling and enter between the secondary samples, must sum to 1 (the total). The software employed for the analysis, program MARK (V8.1; White and Burnham, 1999), does not explicitly estimate the proportion that enter prior to the beginning of the last sample (sample k), but it may be estimated as $pen{t}_k=1-{\displaystyle \sum _{j=1}^{j=k-1}pen{t}_j}$, where $j$ indexes the secondary samples within a primary sample.

The probability of entry (pent), apparent survival (phi), and capture (p) may be modelled in terms of primary samples (constant, time-varying, or as a function of covariates), secondary samples (constant, time-varying, or as a function of covariates), or a combination of both.

2.6 Model comparisons

In Mark, the MSORD is estimated by maximum likelihood and a set of alternative models (i.e., with different structures for, or constraints on, the parameters) may be compared using an information criterion such as Akaike’s information criterion (AIC) which is adjusted for small samples for capture–recapture models (AIC_c) and may be further adjusted for overdispersion (QAICc, Burnham and Anderson, 2002). Models with smaller values of (Q)AIC_c are considered better in the sense that they balance the virtue of close fit of the model to data (smaller deviance is better) with the vice of using many parameters to fit it (models using fewer parameters are better). The ‘balance’ involved arises because similar models with more parameters generally have smaller deviances but may include separate estimates that vary little relative to their precision and be less interpretable in terms of theories about the underlying processes that generated the data (Burnham and Anderson, 2002). (Q)AIC_c weights, which describe the relative likelihoods of a set of models, may also be used in model comparison, with larger (Q)AIC_c weights indicating better models.

2.7 Goodness of fit

Goodness-of-fit tests were performed on data collapsed to years with program U-CARE (Choquet et al., 2009). Model comparison statistics and estimates were adjusted for overdispersion by adjustment of the variance inflation factor c-hat in Mark. In the event of significant overdispersion, a version of AIC_c for overdispersed data (QAIC_c; Burnham and Anderson, 2002) was employed for model comparisons. The variance inflation factor was estimated as the ratio of the overall test statistic for the model from U-CARE and the model degrees of freedom.

2.8 Estimates

When one model in a set has a clearly lower (Q)AIC_c than all others and attracts the major proportion of the (Q)AIC_c weight, the parameter estimates from this ‘best’ model may be reported; when several models have similar (Q)AIC_c values and share the (Q)AIC_c weight, model-averaging may be applied (Buckland et al., 1997) whereby weighted averages of the parameter estimates from several models are reported.

2.9 Data demands of the MSORD

With five parameter types and samples at both the primary and secondary sample levels, and the potential for all to be time-varying (with appropriate constraints on transition probabilities when required), a very large number of parameters may theoretically be estimated. In the present study, it is possible to specify but not necessarily estimate 399 parameters with additional parameters, such as abundance, derived from these. The number of parameters it is possible to estimate in any case is dependent upon there being sufficient data to support each separate estimate. The number of different models (i.e., with different structures for [constraints on] the various parameters) can be very large indeed. The MSORD is a model for which prior expectations (theories) are very important in guiding specification of constraints on the various parameters of a set of models for comparison that are estimable and meaningfully interpretable.

2.10 Prior expectations for the Hervey Bay data

There is a regular within-year pattern to the humpback whale movements through Hervey Bay, with several age-sex classes of whale entering, staying for a period, and then leaving the Bay in sequence throughout the season. The probability of capture by fluke photograph may vary among classes due to their varying propensities to make fluke-up dives. Capture probability may also vary with the number of whales in the Bay, being smaller when more whales are present. Indeed, with more whales in the Bay and a limit to the total number that can be ‘captured’ in a day, the probability of capturing any one of them may be smaller than when there are fewer whales in the Bay. The total number of visitors is very likely to have increased from year to year with growth in the size of the migrating eastern Australian population (Noad et al., 2019), while the number of humpback whales in the Bay appears to decrease within the year from a maximum early in the season to a minimum at the end.

While the different classes of whales may have different probabilities of capture, the strong correlation of their presence in the Bay with week means that, if capture probability is modelled as a function of week, the heterogeneity that may otherwise be present due to behavioural differences between classes would be largely stratified out.

These considerations led to expectations that the probability of capture may vary by both year and week within year. The probabilities of entry (pent) and within-year apparent survival (phi) are likely to vary by week but also by year with the timing of the migration relative to the timing of sampling.

With 13 years by 10 weeks per year of data, there would be 130 p, 117 pent, and 117 phi parameters if all were estimated separately (i.e., year*week). It is likely, however, given the regularity of the pattern of within-year entries and exits, that models which estimate the weekly variation within year with an overall adjustment (offset) for year (i.e., year + week) will provide reasonable estimates of the variation in these parameters and interpretable models. For these ‘additive’ models, there are 23 p, 22 pent, and 22 phi parameters. Multiplicative models (year*week) are not included among the models considered here due to their extreme complexity, with 297 fewer parameters for a model with year+week rather than year*week structures for p, pent and phi.

Both the between-year apparent survival (S) and transition parameters (psi) may vary by year, and temporary emigration may be Markovian, random, display an even flow pattern or not occur at all.

The most complex model considered had S varying by year, psi displaying a yearly variable Markovian pattern (with constraint on the last psi), and pent and phi varying additively by year and week (year+week). The effort variable was also included in the model for capture probability (year+week+effort).

As required for the MSORD model, S for the absent state is set equal to S for the present state in each year, and p (absent), pent (absent) and phi (absent) are set to zero (Kendall and Bjorkland, 2001).

2.11 Supplementary analyses

The rationale for model definition established an a priori set of models for comparison to be ranked and from which to extract parameter estimates. While the results reported here were extracted from models in the a priori set, some additional MSORD models were fitted to see whether there was any tendency for apparent survival to reduce over time that was not represented in the estimates from the better fitting [smaller AIC_c (or QAIC_c)] models. These models were not included in the a priori set but were suggested by results from models that were. The additional models included extra parameters that yielded separate estimates for apparent survival for the first eight and last four inter annual intervals, a linear trend and a quadratic trend. These models were compared with the best fitting [smallest AIC_c (or QAIC_c)] of the a priori models with likelihood ratio tests (see Buse, 1982). Estimates of annual abundance are obtained as derived parameters. Linear, exponential and quadratic regression models were fitted to the series for comparison.

3 Results

3.1 Sampling and capture data in Hervey Bay 1999 to 2007

There were 130 weeks of sampling from 1997 to 2009. Of the weekly samples, there were 113 full weeks (5.25 days, 86.9%), 8 weeks of 4.75 days (6.2%), 4 weeks of 4.5 days (3.1%), and 5 weeks of 4.25 days (3.8%).

A total of 2,708 individual humpback whales were each captured between 1 and 17 times: 2,133 once, 382 twice, 96 three times, 41 four times, 26 five times, 10 six times, 8 seven times, and 5 more than eight times. There was a total of 3,717 captures over the 13 years from 1997 to 2009. The dates of beginning sampling each year and the number of captures by week within year are summarised (Table 2). The dataset used in analyses is provided in Supplementary Material: Dataset_Supplmemtary_Information_R_File_HB9709W.inp.

Table 2

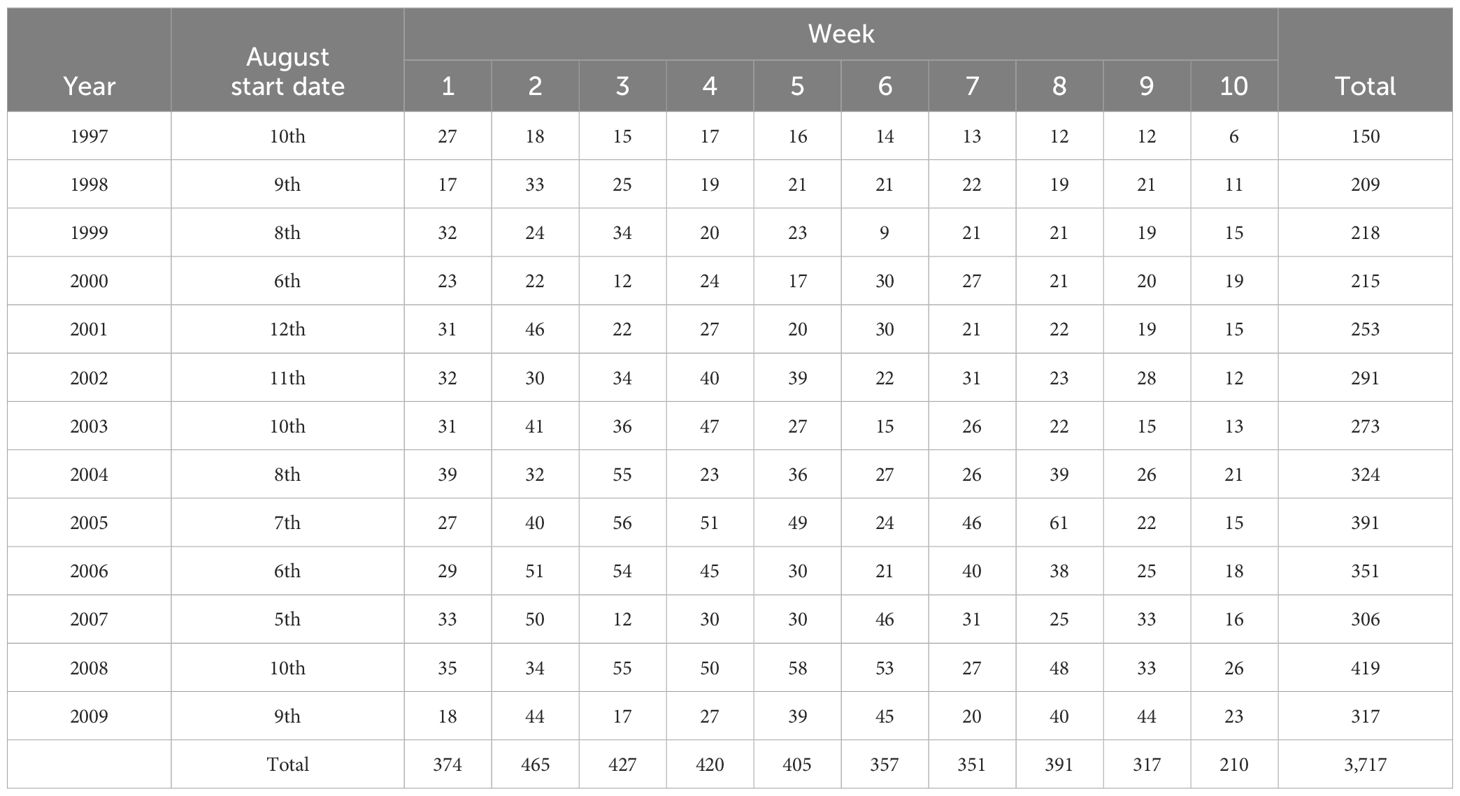
Table 2. Sampling in Hervey Bay for years 1997 to 2009, start date in August, and number of captures of individual humpback whales by week.

3.2 Models

The goodness-of-fit test indicated that the data were significantly overdispersed. The variance inflation factor was estimated at 3.11, and program Mark adjusted the variances of the estimates and the AIC_c values accordingly. QAICc (for adjusted AIC_c) was employed for model comparison.

An initial set of 23 models was fitted following the prior expectations for the patterns of visitation of whales to the Bay outlined in 3.10 above. The four models with the lowest QAICc accounted for 99.8% of the QAIC_c weight in the set, and the two with the lowest QAICc accounted for 98.4%, so we present information on only these two models. The parameter structures of the two lowest QAICc models, a description of their temporary emigration types, their QAICc values, QAICc weights, likelihoods, numbers of parameters, and deviances are presented (Tables 3A, B). Table 3A gives the model structures and descriptions of the temporary emigration types, and Table 3B gives the statistics for each model.

Table 3A

Table 3A. Model structures and description of temporary emigration type for the two lowest QAICc models.

Table 3B

Table 3B. QAICc, QAICc delta, QAICc weight, model likelihood, number of parameters, and qDeviance for the two selected models (arranged by increasing QAICc values).

Between-year apparent survival was estimated as constant over years. Models with apparent survival varying by year fitted poorly and were eliminated from the set.

Temporary emigration varied by year and largely followed an even flow pattern, although model 2 indicated some evidence of a random pattern. An even flow pattern indicates that the probability of a whale being absent in a year is equal to the probability that a previously absent whale returns and is present in that year.

The probability of entering the Bay (pent) and within-year apparent survival (phi, probability of remaining) were estimated as functions of week in both two lowest QAICc models.

3.3 Model averaged parameter and derived estimates

Model-averaged estimates from the best two (lowest QAIC_c) models are reported below.

Also see Supplementary Table 4 - MSORD model-averaged parameter estimates.

3.3.1 Capture probabilities [p(effort)]

Capture probability for a week in which there was full effort was estimated at p = 0.11 (95% CI 0.08 to 0.15, SE 0.02), and capture probability is constant over years. The estimates for weeks with less than full effort were adjusted by use of the effort (survey days) covariate.

3.3.2 Between-year apparent survival [S(constant)]

Between-year apparent survival was estimated as constant over years at S = 0.89 (95% CI, 0.85 to 0.93, SE 0.02).

A model with separate estimates for the first eight (1997–1998 to 2004–2005) and last four (2005–2006 to 2008–2009) inter annual intervals estimated a slight decrease from 0.897 to 0.873 (likelihood ratio test compared to the best-fitting model, (${\chi }_1^2=0.840,p=0.370$). A linear trend model estimated a slight decrease between the first interval (0.909) and the last interval (0.872) (likelihood ratio test compared to the best-fitting model, (${\chi }_1^2=0.501,p=0.479$). A quadratic model found no evidence of curvature in the series (likelihood ratio test compared to the best-fitting model, (${\chi }_2^2=0.159,p=0.927$). A slight decrease was estimated by all three of these models, but none fitted significantly better than the best of the a priori models by a likelihood ratio test (all $p\ge 0.370$).

Point estimates of biological survival in humpback whale populations are generally high, ranging from 0.925 to 0.984 pa (Zerbini et al., 2010). With our estimate of apparent survival of 0.890 pa, permanent emigration is estimated at about 9% pa if the higher estimate of biological survival is assumed or about 4% pa if the lower estimate is assumed. The population of humpback whales migrating off the east coast of Australia has been increasing rapidly from as few as 100–500 individuals for about four decades (Bryden et al., 1990; Noad et al., 2019; reviewed in Harrison and Woinarski, 2018). As humpback whales can live to almost a century (Chittleborough, 1965), with an exponential growth rate of approximately 11.0% pa (Noad et al., 2019) most whales have entered the population more recently and the population structure must be skewed towards younger whales, and biological survival and permanent emigration are likely to be near their upper ranges at about 0.984 pa and 9% pa, respectively.

3.3.3 Temporary emigration [even flow+random (year)]

Two sets of estimates describe temporary emigration: the probability that a whale which was present in the previous year will be absent in the present year, and the probability that a whale which was absent in the previous year returns to the Bay in the present year. Due to an even flow pattern being dominant (model 1), these estimates are very similar. There is, however, a degree of a random structure from model 2 in the estimates which account for the differences. Figure 3 shows the estimates for emigrating and returning. The point estimates of the number of temporary emigrants increased from about 17% from 1997 to 2005 to about 54% thereafter.

Figure 3

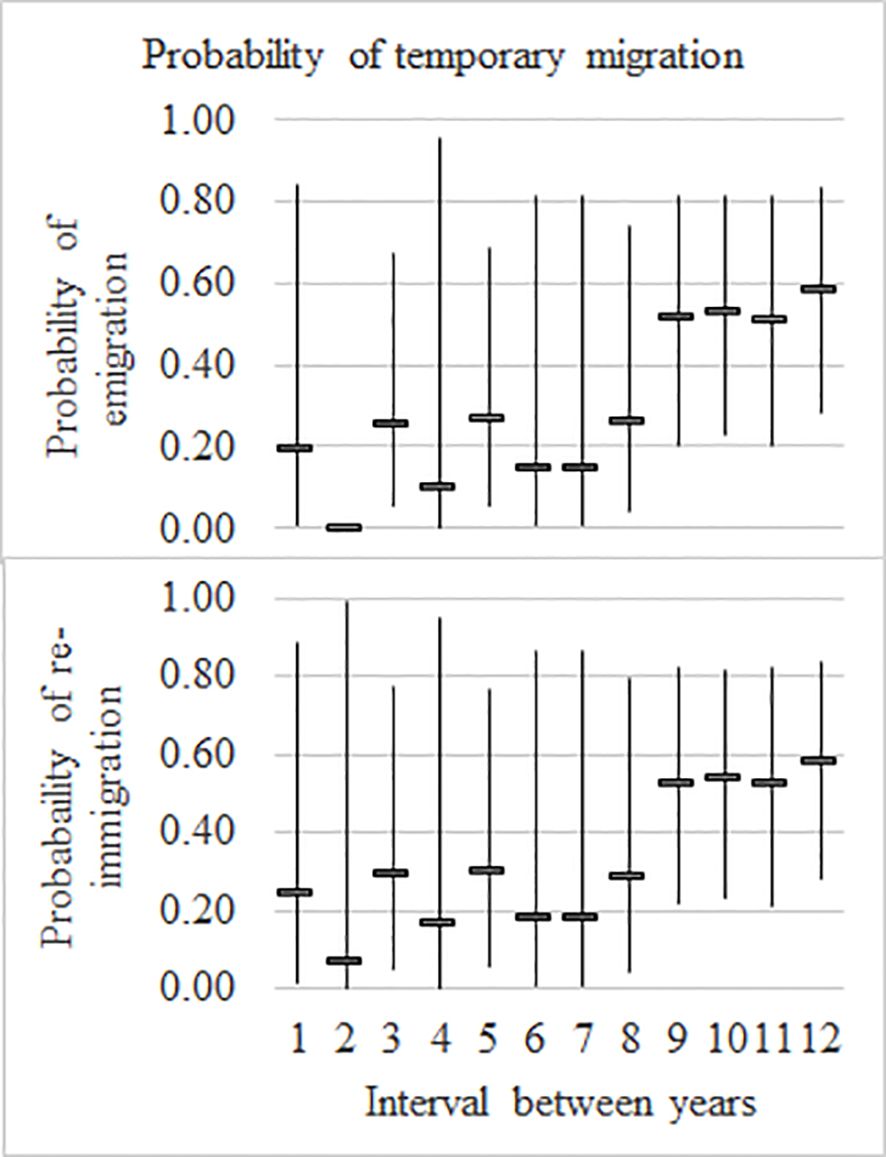
Figure 3. Temporary migration Hervey Bay: by probability of emigration (A, top panel) and probability of re-immigration (B, bottom panel) where interval 1 represents between 1997/1998, 2 represents between 1998/1999 … and 12 represents between 2006/2007, with 95% confidence intervals.

3.3.4 Proportion of visitors entering the Bay: probability of entry [pent(week)]

The proportion of visitors entering the Bay varied by week, and the weekly pattern was constant over years (Figure 4). The highest estimated proportion of visitors entering the Bay was in week 1 (0.15), which included the proportion of visitors in the sampling area prior to commencement of sampling. The estimated proportion of visitors in weeks 2 to 5 ranged from 0.11 to 0.14, decreased in week 6 (0.09), and even further in weeks 7 and 8 (0.07) before increasing slightly in week 9. Week 10 had the lowest proportion and calculated as 1-sum (weeks 1 to 9) = 0.03 with no SE.

Figure 4

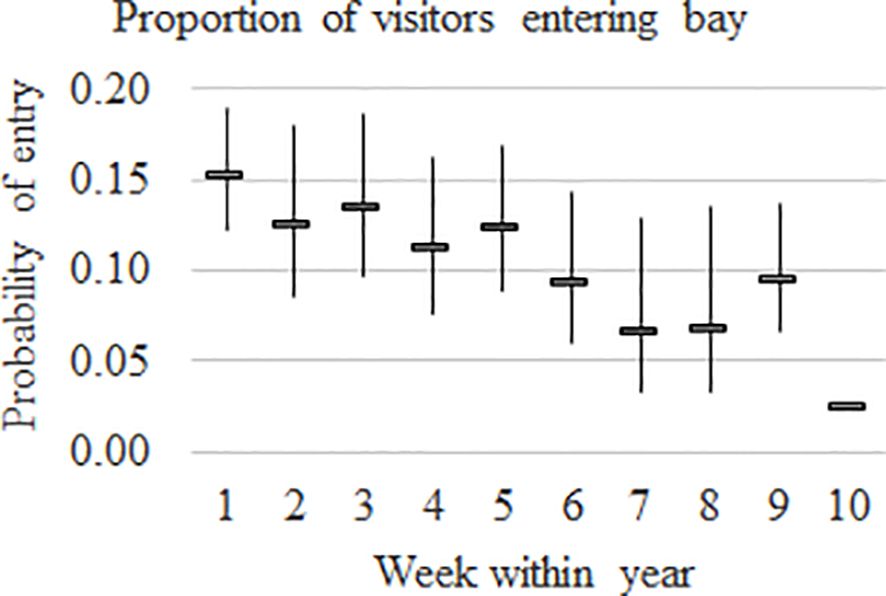
Figure 4. Proportion of visitors entering Hervey Bay by week within year with 95% confidence intervals.

3.3.5 Probability of remaining in the Bay: probability of remaining [phi(week)]

Within-year apparent survival (phi, probability of remaining) was estimated as a function of week. These estimates can be understood as the probability of whales present at the beginning of a week remaining in the Bay and being present at the end of the week.

The probability of a whale which was present at the beginning of each week remaining in the Bay until the end of the week is plotted by week in Figure 5.

Figure 5

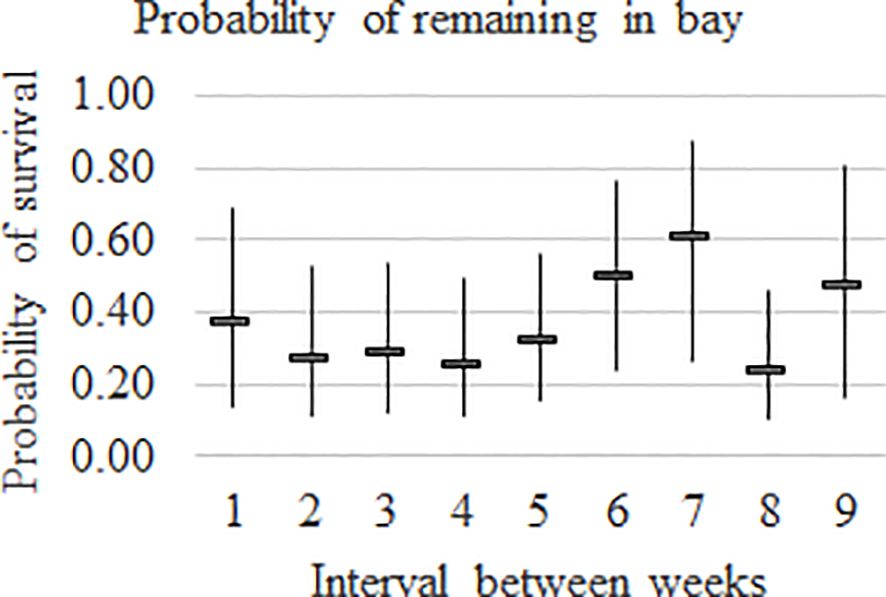
Figure 5. Probability of remaining in Hervey Bay by interval between weeks within year with 95% confidence intervals.

The probability of remaining in the Bay varies by week and the weekly pattern was constant over years (Figure 5). The probability of remaining in the Bay ranged from 0.26 to 0.38 between weeks 1 and 5. The highest proportion remaining by week was in weeks 6 and 7 (0.50 and 0.62, respectively). In week 8, the probability of remaining decreased to 0.24 and increased to 0.48 in week 9 with a probability of only 0.11 remaining in week 10.

3.3.6 Estimated mean residency time

The estimated mean residency of humpback whales in Hervey Bay was 1.53 weeks (SE = 0.22 weeks, LCI 1.09 week: UCI 1.96 weeks, see Kendall et al., 2019).

The mean residency time up to beginning of week 5 is 1.20 weeks; the mean residency time from beginning of week 5 to end of week 10 is 2.05 weeks. As such, the residency time for the cohorts that came in during weeks 5 to 10 was 171% of (71% greater than) that for the cohorts that came in prior to week 5 (2.05/1.20 = 1.71).

3.3.7 Number of visitors to the Bay each year (yearly abundance)

Yearly abundances (total number of visitors to the Bay) with 95% confidence intervals are presented in Figure 6.

Figure 6

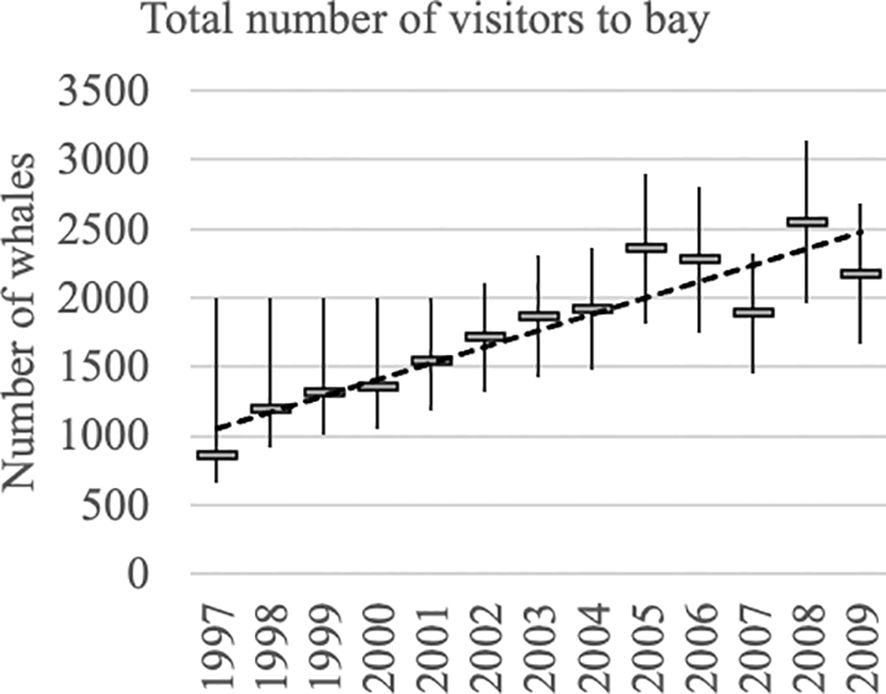
Figure 6. Yearly abundance estimates (total number of visitors to Hervey Bay) from 1997 to 2009 with 95% confidence intervals, with a fitted linear regression line.

Linear regression (growth rate = 118.3 whales per year, SE = 15.1, RSQ = 0.848) was better fitting than an alternative exponential regression function (RSQ = 0.835), which showed relatively large negative residuals towards the ends of the series and positive residuals in the middle. While from 1998 to 2004 the fit of the line to the estimates was very close, the pattern from 2005 to 2009 was more irregular. A quadratic model was fitted to assess whether there was curvature in the series. Although the quadratic coefficient was not significant (t =- 2.0, p = 0.073), there was slight tendency for the growth rate to decrease towards the ends of the series but, such curvature as there is, may be largely driven by the low estimate for 1997, and there is some uncertainty around the fit from 2005 to 2009.

3.3.8 Within-year abundance

Estimated weekly abundances in 2003 with 95% CI’s are presented in Figure 7. The within-year pattern of abundance follows a regular pattern from year to year because of the weekly structures (i.e., no effect for year) for pent and psi in the models, i.e., the pattern remained the same while the absolute abundances increased as the population grew over years.

Figure 7

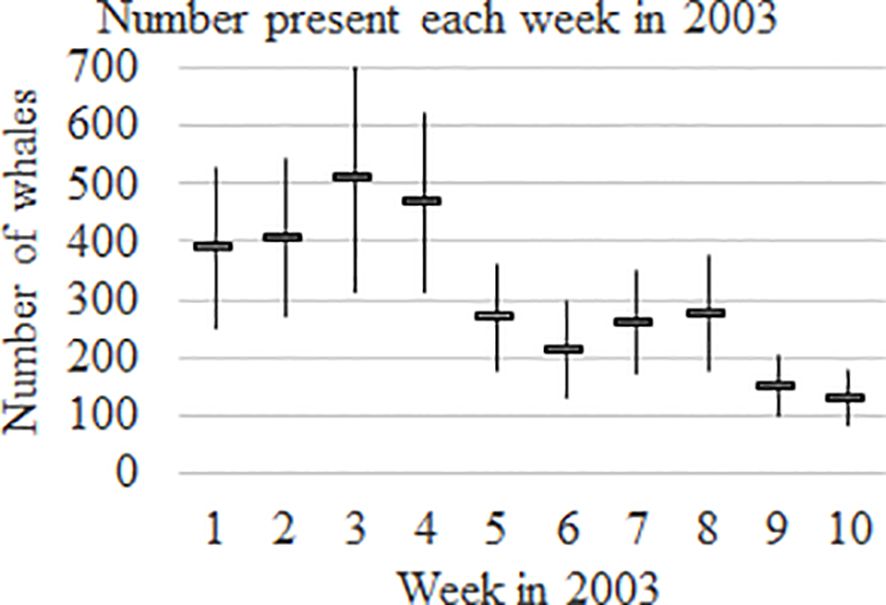
Figure 7. Weekly abundance estimates within season in Hervey Bay for 2003 (numbers present each week, n-hat) with 95% confidence intervals.

Two-thirds of the whales were estimated to be present in Hervey Bay during the first 5 weeks, and a third were estimated to be present during the last 5 weeks of the season, while only 9% were estimated to be present in the last 2 weeks.

4 Discussion

The number of whales that visited Hervey Bay on their southern migration showed a steady increase from 857 in 1997 to 2,175 at the end of sampling in 2009. The rate of increase was approximately linear with an average of 118 new whales joining the Hervey Bay group each year. The annual estimates fitted closely to the linear regression line until 2004, while those for the last 5 years from 2005 to 2009 were more irregular. The irregularity of the estimates for this period leaves considerable uncertainty about the population growth trajectory in the few years prior to 2009 and offers little support for expectations of growth after that. Although these data were taken earlier than the Eastern Australian population (E1) was judged to have reached its historical carrying capacity (Noad et al., 2019), it is possible that there may already have been a decline in the growth rate of the migration and that this may have been reflected in the number visiting Hervey Bay. However, we found no strong evidence of the population growth curve levelling off towards the end of the series, although the estimates for 2005 to 2009 are consistent with a relatively flat trajectory when considered on their own.

While the Hervey Bay group was growing approximately linearly the Eastern Australian migration was growing at an exponential rate. Noad et al. (2019) estimated the rate of growth of E1 at 11% pa by fitting an exponential curve to a series of 10-hour daily counts over 4 weeks during the peak of the annual northern migration (see their section 3.3 and Figure 5). The difference between E1 and Hervey Bay population growth rates is very likely to be due to permanent emigration from the Hervey Bay group with whales that permanently emigrate from this group ceasing to visit Hervey Bay but likely to remain part of the Eastern Australian population; substantial emigration from E1 is inconsistent with its estimated growth rate with permanent emigration estimated at 9% pa, and the expected rate of increase in Hervey Bay is a modest 2% pa (11%–9%). We found no evidence of exponential growth even at this modest rate, however, and the analyses suggest that the rate may even have begun to slow rather than continue to increase according to an exponential form.

While the proportion of the Eastern Australian migration that enters Hervey Bay will inevitably decline over time, it has been substantial. Noad et al. (2019) adjusted an early 2004 estimate to make it as consistent as possible with later estimates made using more thorough methods. The ratio of our Hervey Bay estimate (2,361 whales) to their adjusted Eastern Australian estimate (7,819 whales) shows that about 30% of the Eastern Australian migration visited Hervey Bay in 2004 just prior to the onset of irregularity in the Hervey Bay estimates.

If the Hervey Bay population trajectory were indeed levelling off, we might expect the estimated apparent survival estimates to decrease and the estimated rate of permanent emigration to increase toward the end of the series. Although not included among our a priori set, a model fitted subsequently found only a trivial and non-significant difference in the estimated apparent survival between the first eight (1997–1998 to 2004–2005) and last four (2005–2006 to 2008–2009) inter-annual intervals. Similarly, a linear model found no evidence of trend and quadratic model found no evidence of curvature. If there were a decrease underlying the irregular pattern of abundance estimates from 2005 to 2009, it seems unlikely that this is due to a decrease in apparent survival.

There may be several sources of permanent emigration including young males that cease migrating through Hervey Bay as they mature, and whales that are not part of the high-fidelity group may enter the Bay in association with a group member only once or a few times and not return, including mature males that may escort mothers and calves into the Bay. With a female-to-male ratio of 2.9:1 in Hervey Bay (Franklin et al., 2018), we estimate that about two-thirds of males recruited into the population (i.e., 4% or two-thirds of 6% = half of the 11% estimated growth rate of the Eastern Australian population plus 1% deaths) emigrate at some stage. While this may account for nearly half of the annual emigrants, it is likely that most of the remainder emigrate from the more abundant early cohort.

There was a sharp increase in the typical rates of temporary emigration and reimmigration after 2005 with a mean of 17% being absent and returning each year up to 2005 and 54% thereafter. As with permanent emigration, temporary emigration in these data is unlikely to identify a portion of E1 that do not embark on the northern migration but a portion of the Hervey Bay subgroup that remain with E1 rather than diverting through Hervey Bay on the southern migration.

We note that the change in the rate of temporary emigration corresponds to commencement of irregular annual abundance estimates from 2005. The irregularity in the abundance estimates might possibly be accounted for by rates of temporary emigration and reimmigration not being equal each year as in our models. Markovian models that might have shown this fitted poorly, however, due to the large number of parameters required to estimate them and were consequently eliminated from the final set for comparison. Whether or not the irregularity in abundance estimates from 2005 to 2009 may be due to irregularity in differences between the rates of temporary emigration and return, the average levels of these estimates were high with 54% of whales that were present in the previous year being temporarily absent in the present year and 54% of whales that were previously absent returning. Some of this cohort may be females who use the Bay when they have calves but rarely otherwise, but with less than one-third of whales that visit the Bay in any year being mothers with calves (see Section 4.3.7, see also Franklin et al., 2011); this can account for only a small portion of the absences. With most visitors migrating through the Bay in the first half of the season, most of the temporary emigration must involve the mature females, yearlings, and immature whales in the early season cohort. The even flow pattern—the probability of not returning after the presence on current visit (temporary emigration) is equal to the probability of returning after an absence (re-immigration)—suggests that a subgroup of the whales that visit Hervey Bay began ‘taking turns’ to visit or skip the visit each year: i.e., some whales may be remaining with the E1 southern migration or entering Hervey Bay in alternate years.

It is possible that whales may be opting not to enter the Bay on some occasions in response to the increased density. Alternatively, it may be that resources were becoming limited in Antarctica as the Southern Hemisphere humpback whale populations become very large and whales may be embarking on the migration with less energy reserves than previously and choosing to return to feed in the Southern Ocean as soon as possible rather than spending time in Hervey Bay.

The probabilities of entering the Bay fall and the probabilities of remaining the week increase in week 6 (see Section 4.3.5) corresponding with the transition from the presence of mature females, yearlings, and immature whales to mothers with calves (Franklin et al., 2018). Individual whales remain in the Bay for just over a week in the first half of the season, whereas in the second half, they remain for approximately 2 weeks (see Section 4.3.6). The differential probability of length of stay, depending on the time in the season when different classes of whales are present, was constant over years and consistent with a regular annual migratory structure (Dawbin, 1966, 1997; Franklin et al., 2018).

Hervey Bay is clearly an important stopover early in the southern migration for mature females, yearlings, and immature whales (Franklin et al., 2018) with a substantial proportion of the Eastern Australian population visiting the Bay for a week or more each year. Franklin et al. (2017b) argued that Eden, NSW, may be used as a meeting point prior to dispersal in several directions. We suggest that Hervey Bay similarly serves as a meeting point where the onward migration of the Hervey Bay subgroup is organised. That females with relatively young calves remain in the Bay for around 2 weeks reinforces the conclusion that Hervey Bay is also an important area for females with calves for physical and social development of new-season calves (Franklin et al., 2011, 2018, 2021; Franklin, 2012).

Both classes of whales in the earlier and later cohorts are involved in active and complex social behaviours. Franklin et al. (2021) studied the behaviour of humpback whales in Hervey Bay in terms of pod associations, competitive groups, and non-agonistic social pods. The formation of newly associated pods was observed as a greater proportion of observed pods in the first 4 weeks of the season, and non-agonistic behaviours occurred in greater proportion in the first 5 weeks, when the mature females and immature whales’ cohort was present. In contrast, competitive groups occurred most frequently in the last 5 weeks of the season and typically consisted of a mother and calf and two or more escorts. Typical interactions in non-agonistic social groups are calm with no high-energy interactions or aggressive or competitive behaviours. Such non-agonistic behaviours include head rising, spy hops, rolling over ventral side up, pectoral fin extensions, tail fluke extensions, breaching, pectoral fin slapping, lobtailing, and milling. Competitive groups display such behaviours as lunging through the surface with throat pleats distended, high-speed chases, and body strikes.

Stopover sites along Australian coastal migratory corridors including Hervey Bay have been characterised as resting areas for females with new calves (Carvalho et al., 2011; Meynecke et al., 2013; Bruce et al., 2014; Bejder et al., 2019; Stack et al., 2020). We suggest that characterisation of Hervey Bay as a ‘resting area’ is inappropriate, as active and complex social behaviours occur throughout the season (Franklin et al., 2021). Franklin et al. (2018) reported mature females use ecological niche areas as stopovers during the southern migration along the extended coastlines of Australia and Africa, both on and off the migratory corridor, for reproductive success and social development. Given the marked differences in the behaviours observed in the early and late cohorts, we suggest that characterisation of site-specific stopovers along the long coastlines of eastern Australia and other Southern Ocean continents should be based on the study of the classes of whales using the stopover, their durations of stay, and the behaviours observed during the stopover.

The task of assessing, selecting, and matching images grew greatly over the course of the study as the population grew and more years of photographs were added to the catalogue, so that by 2009, it took nearly the whole inter-season period to complete the photographic analysis (e.g., see Franklin et al., 2020). This problem is particularly acute when the population under study is growing, more images are captured, and there are more images in the catalogue to be matched to each year. There is a point at which continuing a capture–recapture study may cease to be viable without a large and increasing expenditure of time and resources. At least that was the case until the relatively recent development of algorithmic matching technology, e.g., HappyWhale.com (Franklin et al., 2020; Cheeseman et al., 2022, 2024; Patton et al., 2023). HappyWhale.com provides a platform for assembly, and accurate algorithmic matching, of very large collaborative photo-identification datasets (e.g., see Cheeseman et al., 2023). As of November 2023, the HappyWhale.com Hervey Bay accumulated a dataset consisting of 9,239 individuals and 18,020 encounters (Personal Communication, Ted Cheeseman). Availability of a very large collaborative photo-identification dataset for Hervey Bay, including systematic and ‘Citizen Scientist’ data, will be crucial for assessment of future humpback whale abundance and emigration, both permanent and temporary. With the Eastern Australian population having grown very large and difficult to study due to the geographic scale of their migratory habitat, data collected in Hervey Bay may offer an opportunity to identify responses to changing conditions in Antarctica. Indeed, informative models like the Robust Design built on Hervey Bay data may be the first opportunity to detect critical changes in response to Antarctic conditions.

With no systematic surveys having been conducted in Hervey Bay since 2009, we believe that now, with the Hervey Bay catalogue of fluke images in HappyWhale having reached a substantial size and growing, it is appropriate to extend the work we did in Hervey Bay up to the present to assess changes that may have occurred with increasing density in Hervey Bay or growth of the East Australian population past the estimated historical carrying capacity of its Antarctic feeding grounds.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Ethics statement

The animal study was approved by Southern Cross University Animal Care and Ethics Committee. The study was conducted in accordance with the local legislation and institutional requirements.

Author contributions

LB: Formal Analysis, Writing – original draft, Writing – review & editing. TF: Conceptualization, Data curation, Funding acquisition, Methodology, Project administration, Writing – review & editing, Supervision. WF: Conceptualization, Data curation, Funding acquisition, Methodology, Project administration, Writing – review & editing. PH: Writing – review & editing, Supervision. PC: Conceptualization, Writing – review & editing. KP: Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The long-term study of humpback whales in Hervey Bay conducted by TF and WF is supported by The Oceania Project and in part by an Australian Research Council Linkage grant (LP0562517) with the Southern Cross University Marine Ecology Research Centre and the International Fund for Animal Welfare (IFAW). Research undertaken in Hervey Bay was conducted under research permits issued by the Queensland Parks and Wildlife Service (permit numbers MP2006/020 and WISP03749806).

Acknowledgments

We thank Emeritus Professor Peter Baverstock of Southern Cross University and Dr Phil Clapham for their support during this study. We also thank Dr Tim Stevens for assistance in the implementation of the long-term study in Hervey Bay. We are grateful to Dr Delphine Chabanne and Dr Glenn Stauffer for their helpful reviews of the draft manuscript. Finally, we thank the participants in The Oceania Project’s Internship program, particularly Mark Cornish, for their financial contribution and assistance to the study.

Conflict of interest

Author LB was employed by the company StatPlan Consulting Pty Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2024.1426248/full#supplementary-material

References

Andrews-Goff V., Gales N., Childerhouse S. J., Laverick S. M., Polanowski A. M., Double M. C. (2023). Australia’s east coast humpback whales: Satellite tag-derived movements on breeding grounds, feeding grounds and along the northern and southern migration. ARPHA Preprints 4. doi: 10.3897/BDJ.11.e114729

PubMed Abstract | Crossref Full Text | Google Scholar

Barendse J., Best P. B., Carvalho I., Pomilla C. (2013). Mother knows best: occurrence and associations of resighted humpback whales suggest maternally derived fidelity to a Southern hemisphere coastal feeding ground. PloS One 8, e81238. doi: 10.1371/journal.pone.0081238

PubMed Abstract | Crossref Full Text | Google Scholar

Barendse J., Best P. B., Thornton M., Pomilla C., Carvalho I., Rosenbaum H. C. (2010). Migration redefined? Seasonality, movements and group composition of humpback whales Megaptera novaeangliae off the west coast of South Africa. Afr. J. Mar. Sci. 32, 1–22. doi: 10.2989/18142321003714203

Crossref Full Text | Google Scholar

Bejder L., Videsen S., Hermannsen L., Simon M., Hanf D., Madsen P. T. (2019). Low energy expenditure and resting behaviour of humpback whale mother-calf pairs highlights conservation importance of sheltered breeding areas. Sci. Rep. 9, 771. doi: 10.1038/s41598-018-36870-7

PubMed Abstract | Crossref Full Text | Google Scholar

Bruce E., Albright L., Sheehan S., Blewitt M. (2014). Distribution patterns of migrating humpback whales (Megaptera novaeangliae) in Jervis Bay, Australia: A spatial analysis using geographical citizen science data. Appl. Geogr. 54, 83–95. doi: 10.1016/j.apgeog.2014.06.014

Crossref Full Text | Google Scholar

Bryden M. M., Kirkwood G. P., Slade R. W. (Eds.) (1990). Humpback Whales, Area V. An Increase in Numbers off Australia’s East Coast (Berlin & Heidelberg: Springer-Verlag).

Google Scholar

Buckland S. T., Burnham K. P., Augustin N. H. (1997). Model selection: An integral part of inference. Biometrics 53, 603–618. doi: 10.2307/2533961

Crossref Full Text | Google Scholar

Burnham K. P., Anderson D. R. (2002). Model selection and multimodel inference: a practical information-theoretic approach. 2nd Edition (New York, New York, USA: Springer-Verlag), 488.

Google Scholar

Buse A. (1982). The likelihood ratio, wald, and lagrange multiplier tests: an expository note. Am. Statistician 36, 153–157.

Google Scholar

Calambokidis J., Falcone E. A., Quinn T. J., Burdin A. M., Clapham P. J., Ford J. K. B., et al. (2008). SPLASH: Structure of Populations, Levels of Abundance and Status of Humpback Whales in the North Pacific. Final report for Contract AB133F-03-RP-00078. Seattle, Washington: U.S. Dept of Commerce Western Administrative Center, Vol. 57.

Google Scholar

Carvalho I., Brito C., Dos Santos M. E., Rosenbaum H. C. (2011). The waters of São Tomé: a calving ground for West African humpback whales? Afr. J. Mar. Sci. 33, 91–97. doi: 10.2989/1814232X.2011.572353

Crossref Full Text | Google Scholar

Cheeseman T., Barlow J., Acebes J. M., Audley K., Bejder L., Birdsall C., et al. (2024). Bellwethers of change: population modelling of North Pacific humpback whales from 2002 through 2021 reveals shift from recovery to climate response. R. Soc. Open Sci. 11, 231462. doi: 10.1098/rsos.231462

PubMed Abstract | Crossref Full Text | Google Scholar

Cheeseman T., Southerland K., Acebes J. M., Audley K., Barlow J., Bejder L., et al. (2023). A collaborative and near-comprehensive North Pacific humpback whale photo-ID dataset. Sci. Rep. 13, 10237. doi: 10.1038/s41598-023-36928-1

PubMed Abstract | Crossref Full Text | Google Scholar

Cheeseman T., Southerland K., Park J., Olio M., Flynn K., Calambokidis J., et al. (2022). Advanced image recognition: a fully automated, high-accuracy photo-identification matching system for humpback whales. Mamm. Biol. 102, 915–929. doi: 10.1007/s42991-021-00180-9

Crossref Full Text | Google Scholar

Chittleborough R. G. (1965). Dynamics of two populations of the humpback whale, Megaptera novaeangliae (Borowski). Aust. J. Mar. Freshw. Res. 16, 33–128. doi: 10.1071/MF9650033

Crossref Full Text | Google Scholar

Choquet R., Lebreton J.-D., Gimenez O., Reboulet A. M., Pradel R. (2009). U-CARE: Utilities for performing goodness of fit tests and manipulating CApture–REcapture data. Ecography 32. doi: 10.1111/j.1600-0587.2009.05968.x

Crossref Full Text | Google Scholar

Clapham P. J. (2000). “The Humpback whale. Seasonal feeding and breeding in a baleen whale,” in Cetacean Societies, field studies of dolphins and whales (University of Chicago Press, Chicago), 173–196 2000.

Google Scholar

Constantine R., Steel D., Allen J., Anderson M., Andrews O., Baker C. S., et al. (2014). Remote Antarctic feeding ground important for east Australian humpback whales. Mar. Biol. 161, 1087–1093. doi: 10.1007/s00227-014-2401-2

Crossref Full Text | Google Scholar

Corkeron P. J., Brown M., Slade R. W., Bryden M. M. (1994). Humpback whales, megaptera novaeangliae (Cetacea: balaenopteridae), in Hervey Bay, Queensland. Wildlife Res. 21, 293–305. doi: 10.1071/WR9940293

Crossref Full Text | Google Scholar

Dawbin W. H. (1966). “The seasonal migratory cycle of humpback whales,” in Whales, Dolphins and Porpoises. Ed. Norris K. S. (University of California Press, Berkeley, California), 145–170.

Google Scholar

Dawbin W. H. (1997). Temporal segregation of humpback whales during migration in southern hemisphere waters. Memoirs Queensland Museum 42, 105–138.

Google Scholar

Fariello C. M., Meynecke J.-O., De Bie J. (2024). Defining humpback whale (Megaptera novaeangliae) potential distribution in the Great Barrier Reef Marine Park: a two-way approach. Pacific Conserv. Biol. 30. doi: 10.1071/PC23032

Crossref Full Text | Google Scholar

Franklin T. (2012). The social and ecological significance of Hervey Bay Queensland for eastern Australian humpback whales (Megaptera novaeangliae). Lismore, NSW, Australia: School of Environmental Science and Management, Southern Cross University, 245.

Google Scholar

Franklin T., Franklin W., Brooks L., Harrison P. (2018). Site-specific female-biased sex ratio of humpback whales (Megaptera novaeangliae) during a stopover early in the southern migration. Can. J. Zool. 96, 533–544. doi: 10.1139/cjz-2017-0086

Crossref Full Text | Google Scholar

Franklin T., Franklin W., Brooks L., Harrison P., Baverstock P., Clapham P. (2011). Seasonal changes in pod characteristics of eastern Australian humpback whales (Megaptera novaeangliae), Hervey Bay 1992-2005. Mar. Mammal Sci. 27, E134–E152. doi: 10.1111/j.1748-7692.2010.00430.x

Crossref Full Text | Google Scholar

Franklin T., Franklin W., Brooks L., Harrison P., Pack A. A., Clapham P. J. (2021). Social behaviour of humpback whales (Megaptera novaeangliae) in Hervey Bay, Eastern Australia, a preferential female stopover during the southern migration. Front. Mar. Sci. 8, 1761. doi: 10.3389/fmars.2021.652147

Crossref Full Text | Google Scholar

Franklin T., Franklin W., Brooks L., Harrison P. L., Burns D., Holmberg J., et al. (2020). Photo-identification of individual Southern Hemisphere humpback whales (Megaptera novaeangliae) using all available natural marks: implications for misidentification & automated algorithm matching technology. J. CETACEAN Res. MANAGE 21, 71–83. doi: 10.47536/jcrm.v21i1.186

Crossref Full Text | Google Scholar

Franklin W., Franklin T., Cerchio S., Rosenbaum H., Jenner C., Jenner M., et al. (2017a). Photo-identification comparison of humpback whale (Megaptera novaeangliae) flukes from Antarctic Area IV with fluke catalogues from East Africa, Western Australia and Eastern Australia. J. CETACEAN Res. MANAGE, 1–7.

Google Scholar

Franklin W., Franklin T., Andrews-Goff V., Paton D. A., Double M. (2017b). Movement of two Humpback whales (Megaptera novaeangliae) satellite-radio tagged off Eden, NSW and matched by photo-identification with the Hervey Bay catalogue. J. CETACEAN Res. MANAGE, 29–33. doi: 10.47536/jcrm.v17i1.429

Crossref Full Text | Google Scholar

Garrigue C., Clapham P. J., Geyer Y., Kennedy A. S., Zerbini A. N. (2015). Satellite tracking reveals novel migratory patterns and the importance of seamounts for endangered South Pacific humpback whales. R. Soc. Open Sci. 2. doi: 10.1098/rsos.150489

PubMed Abstract | Crossref Full Text | Google Scholar

Garrigue C., Constantine R., Poole M., Hauser N., Clapham P., Donoghue M., et al. (2011). Movement of individual humpback whales between wintering grounds of Oceania (South Pacific), 1999 to 2004. J. Cetacean Res. Manage. (Special Issue 3), 275–282.

Google Scholar

Harrison P. L., Woinarski J. C. Z. (2018). “Recovery of Australian subpopulations of humpback whale. Chapter 2,” in Recovering Australian Threatened Species. Eds. Garnett S., Latch P., Lindemeyer D., Woinarski J. (Melbourne: CSIRO Publishing), 5–12.

Google Scholar

IWC (2011). International Whaling Commission: Report of the Workshop on the Comprehensive Assessment of Southern Hemisphere humpback whales, 4–7 April 2006, Hobart, Tasmania. J Cetacean Res Manage. Cambridge, United Kingdom; special issue, Vol. 3. 5–50.

Google Scholar

Kendall W. L., Bjorkland R. (2001). Using open robust design models to estimate temporary emigration from capture-recapture data. Biometrics 57, 1113–1122. doi: 10.1111/j.0006-341X.2001.01113.x

PubMed Abstract | Crossref Full Text | Google Scholar

Kendall W. L., Nichols J. D. (1995). On the use of secondary capture-recapture samples to estimate temporary emigration and breeding proportions. J. Appl. Stat 22, 751–762. doi: 10.1080/02664769524595

Crossref Full Text | Google Scholar

Kendall W. L., Nichols J. D., Hines J. E. (1997). Estimating temporary emigration using capture-recapture data with Pollock’s robust design. Ecology 78, 563–578.

Google Scholar

Kendall W. L., Pollock K. H., Brownie C. (1995). A likelihood-based approach to capture-recapture estimation of demographic parameters under the robust design. Biometrics 51, 293–308. doi: 10.2307/2533335

PubMed Abstract | Crossref Full Text | Google Scholar

Kendall W. L., Stapleton S., White G. C., Richardson J. I., Pearson K. N., Mason P. (2019). A multistate open robust design: population dynamics, reproductive effort, and phenology of sea turtles from tagging data. Ecol. Monogr. 89, e01329. doi: 10.1002/ecm.1329

Crossref Full Text | Google Scholar

Meynecke J.-O., De Bie J., Barraqueta J.-L. M., Seyboth E., Dey S. P., Lee S. B., et al. (2021). The role of environmental drivers in humpback whale distribution, movement and behavior: A review. Front. Mar. Sci. 8, 1685. doi: 10.3389/fmars.2021.720774

Crossref Full Text | Google Scholar

Meynecke J.-O., Vindenes S., Teixeira D. (2013). Monitoring humpback whale (Megaptera novaeangliae) behaviour in a highly urbanised coastline: gold coast, Australia. Global Challenges Integrated Coast. Zone Management.

Google Scholar

Noad M. J., Kniest E., Dunlop R. A. (2019). Boom to bust? Implications for the continued rapid growth of the eastern Australian humpback whale population despite recovery. Popul. Ecol., 1–12. doi: 10.1002/pope.2019.61.issue-2

Crossref Full Text | Google Scholar

Paterson R. A. (1991). The migration of Humpback Whales Megaptera novaeangliae in east Australian waters. Memoirs Queensland Museum 30, 333–341.

Google Scholar

Patton P. T., Cheeseman T., Abe K., Yamaguchi T., Reade W., Southerland K., et al. (2023). A deep learning approach to photo–identification demonstrates high performance on two dozen cetacean species. Methods Ecol. Evol. doi: 10.1111/2041-210X.14167

Crossref Full Text | Google Scholar

Pollock K. H. (1982). A capture–recapture design robust to unequal probability of capture. J. Wildlife Manage. 46, 757–760. doi: 10.2307/3808568

Crossref Full Text | Google Scholar

Ribbe J. (2014). “Hervey Bay and Its Estuaries,” in Estuaries of Australia in 2050 and Beyond, Estuaries of the World, vol. 11 . Ed. Wolanski E. (Netherlands: Springer Science+Business Media Dordrecht).

Google Scholar

Schwarz C. J., Stobo W. T. (1997). Estimating temporary migration using the robust design. Biometrics 53, 178–194. doi: 10.2307/2533106

Crossref Full Text | Google Scholar

Smith T. D., Allen J., Clapham P. J., Hammond P. S., Katona S., Larsen F., et al. (1999). An ocean-basin-wide mark-recapture study of the North Atlantic humpback whale (Megaptera novaeangliae). Mar. Mammal Sci. 15, 1–32. doi: 10.1111/j.1748-7692.1999.tb00779.x

Crossref Full Text | Google Scholar

Smith J. N., Grantham H. S., Gales N., Double M. C., Noad M. J., Paton D. (2012). Identification of humpback whale breeding and calving habitat in the Great Barrier Reef. Mar. Ecol. Prog. Ser. 447, 259–272. doi: 10.3354/meps09462

Crossref Full Text | Google Scholar

Stack S. H., Currie J. J., McCordic J. A., Machernis A. F., Olson G. L. (2020). Distribution patterns of east Australian humpback whales (Megaptera novaeangliae) in Hervey Bay, Queensland: a historical perspective. Aust. Mammal. 42, 16–27. doi: 10.1071/AM18029

Crossref Full Text | Google Scholar

Stauffer G., Rotella J., Garrott R. (2013). Variability in temporary emigration rates of individually marked female Weddell seals prior to first reproduction. Oecologia 172, 129–140. doi: 10.1007/s00442-012-2472-z

PubMed Abstract | Crossref Full Text | Google Scholar

White G. C., Burnham K. P. (1999). Program MARK: survival estimation from populations of marked animals. Bird Study 46 Supplement, 120–138. doi: 10.1080/00063659909477239

Crossref Full Text | Google Scholar

Zerbini A. N., Clapham P. J., Wade P. R. (2010). Assessing plausible rates of population growth in humpback whales from life-history data. Mar. Biol. 157, 1225–1236. doi: 10.1007/s00227-010-1403-y

Crossref Full Text | Google Scholar