Simulating the near-field dynamic plume behavior of disposed fine sediments

Gundlach, Jannek; Herbst, Maximilian; Alex, Antje Svenja; Zorndt, Anna; Jordan, Christian; Visscher, Jan; Schlurmann, Torsten

doi:10.3389/fmars.2024.1416521

ORIGINAL RESEARCH article

Front. Mar. Sci., 27 August 2024

Sec. Coastal Ocean Processes

Volume 11 - 2024 | https://doi.org/10.3389/fmars.2024.1416521

Simulating the near-field dynamic plume behavior of disposed fine sediments

Anna Zorndt³

¹Leibniz University Hannover, Ludwig-Franzius-Institute for Hydraulic, Estuarine and Coastal Engineering, Hannover, Germany
²German Aerospace Center (DLR), Institute for the Protection of Maritime Infrastructures, Bremerhaven, Germany
³Federal Waterways Engineering and Research Institute (BAW), Hamburg, Germany

Projections of the effects of fine sediment disposals, relevant for managed estuaries and tidally influenced coastal areas, are typically based on numerical far-field models. For an accurate consideration of the disposal itself, near-field models are often needed. The open source near-field model, PROVER-M, simulates the relevant processes of the physics based, dynamic behavior of disposed fine sediments in coastal waters and is applied in this study. First, new small scale laboratory experiments of instantaneous disposals are presented, documenting the dynamic behavior of fine material disposed in shallow waters. Second, results of the PROVER-M model are shown for disposals in three different settings: (1) a field-scaled study complementary to the laboratory set-up, (2) a parametric study of sequentially varied model input and (3) a far-field model coupling for estimation of the PROVER-M impact. By comparing results of the laboratory experiments to the PROVER-M model, the physical behavior of PROVER-M is successfully validated. The impact of the ambient setting and dredged material parameters is evaluated by the PROVER-M simulations, where the results show non-linear, complex interdependencies of the input parameters on disposal properties in dependence of ambient site conditions and material composition. In this context, limits of the model application are assessed and critically discussed. Finally, an exemplary coupling to a far-field model based on a real set of disposals in the tidally influenced Weser estuary (Germany) illustrates the potential impact of PROVER-M for assessing far-field suspended sediment concentration (SSC), with increased maximum SSC values of up to 10%.

Introduction

Estuaries are coastal systems that are oftentimes exposed to stresses stemming from human activities, such as damming (e.g., Figueroa et al., 2020), sand mining (e.g., Jordan et al., 2019), pollution (e.g., Painting et al., 2007), or overfishing (e.g., Kennish, 2002). Since many major ports are located along estuaries, they are also subject to dredging activities and disposal operations to keep their waterways navigable. As the disposal of dredged material may have adverse effects on the marine environment, sustainable sediment management strategies are desired. Beneficial management of dredged material strives to find applications that are beneficial for humans and the natural environment, with the material itself being considered a resource (Burt, 1996; Yozzo et al., 2004; Baptist et al., 2019; CEDA, 2019). One applied approach is to keep the dredged material in the same aquatic system and relocating it without processing the yielded material on land as illustrated in Figure 1 (process a). However, transport of the relocated material back to its original dredging area is usually not desired. Consequently, an assessment of the relocation strategy is required by predicting the re-suspension and transport of the dredged material after disposal. Behind the background of future socio-economic challenges, e.g., intensified use of coastal areas and growth of maritime traffic (Nicholls, 2004; Neumann et al., 2015) and climate-induced changes, e.g., sea level rise and increasing flood dominance (Wachler et al., 2020; Jordan et al., 2021; Timmerman et al., 2021), such assessments will only become more important in any harbor or waterways management strategies. In shallow coastal zones like the UNESCO world heritage Wadden Sea, a system of tidal flats and channels, sediment management has a direct impact on its morphology and thus is a crucial part of its present-day and future challenges (Wang et al., 2012; Timmerman et al., 2021). Any proactively initiated sediment management concepts can contribute to facing such challenges. i.e., by consciously disposing sediments at specific locations to compensate shoal erosion (van der Werf et al., 2015) or to support salt marsh growth (Baptist et al., 2019). To develop a beneficial sediment disposal strategy, it is important to gain a systemic understanding of the natural morphological development (van der Wegen and Roelvink, 2012; Wang et al., 2012; Benninghoff and Winter, 2019; Gundlach et al., 2021; Elmilady et al., 2022; Huismans et al., 2022) in order to credibly evaluate the impacts and range of a disposal. A deep understanding of the relevant processes and tools for prediction are required. Here, numerical models are a key component. In regional models that simulate the far-field (scale of hundred meters to kilometers), mass or volume compensation can be carried out using integrated dredging and disposal modules. However, only the passive behavior of deposited masses/volumes as consolidated material on the ground is considered. Near-field effects, which are active processes on a smaller scale (meters), are not considered. Thus, a model for the near-field range is necessary for a more realistic and accurate representation.

Figure 1

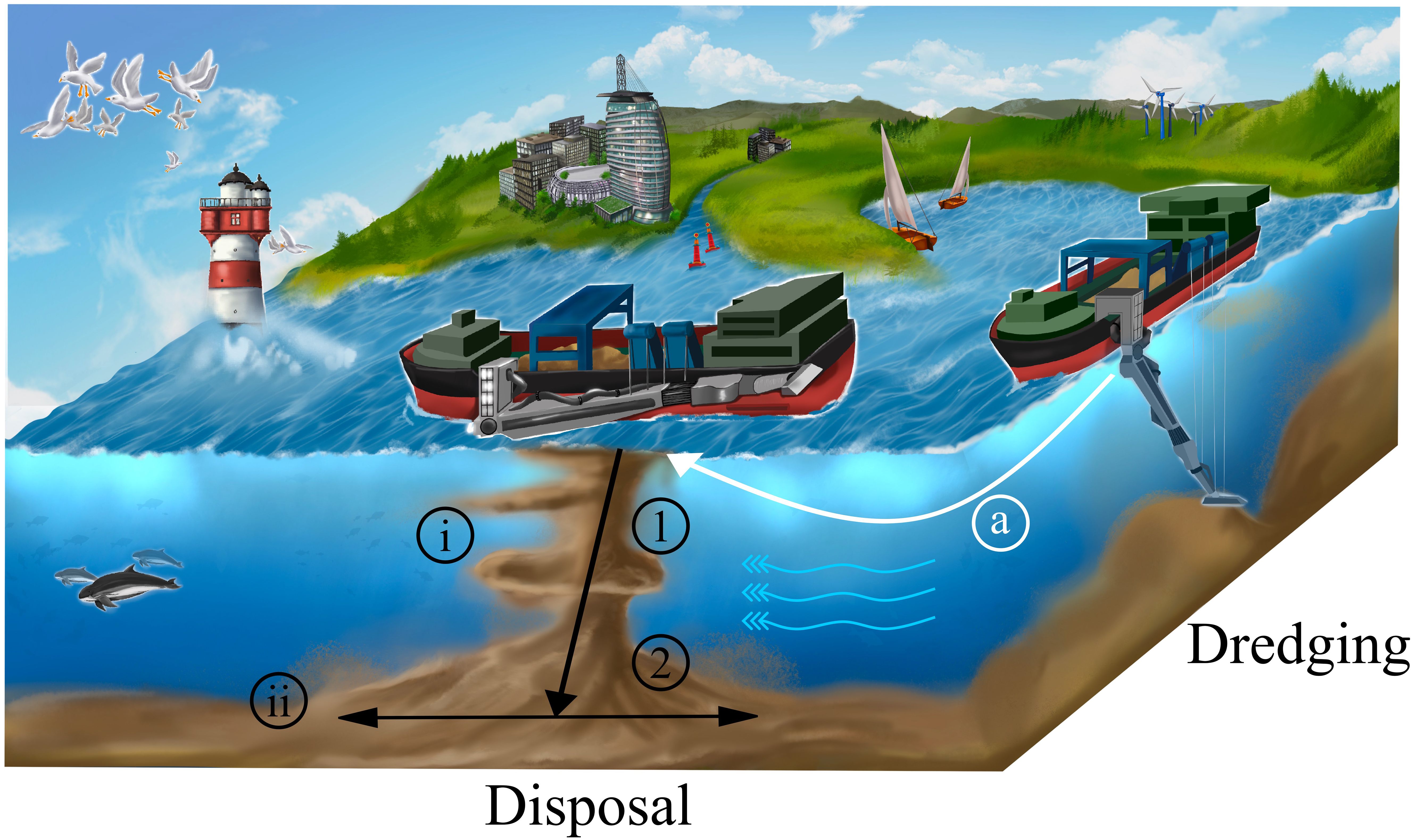
Figure 1. Sediment management strategy, where the dredged material is kept in the aquatic system by transporting dredged material to a disposal site (a). At the disposal site the material is released for convective descent (1) and the dynamic collapse starts upon impact on the ground (2). During the convective descent, material can be stripped (i) and during dynamic collapse settle (ii) while spreading on the ground.

In general, when focusing on the disposal of fine sediments, the settling and advection behavior of sediments differs depending on the sediment characteristics and water content. While coarse material and sediment loads with a low water content fall as clumps, settling of fine material with high water content is often regarded as “thermal-like” behavior (Bowers and Goldenblatt, 1978; Ruggaber, 2000). For disposals of mixed materials containing both coarse and fine sediments, descending processes of individual fractions become dominant and control the overall settling process, so that the coarse material will segregate as the individual settling velocity becomes decisive in the descending cloud (Noh and Fernando, 1993; Bush et al., 2003). While coarse material (e.g. sand) deposits locally within a limited distance from the disposal point, projecting the dynamic behavior and fate of fine material is more challenging. The disposal of fine sediment can be divided into three stages: Convective descent, dynamic collapse (Figure 1, process 1 and 2) and passive diffusion. These are described among others by Clark et al. (1971), Koh and Chang (1974), Delo et al. (1987), Truitt (1988) and Gensheimer (2010).

In the convective descent, the material descends downward as a cloud due to negative buoyancy, while ambient water gets entrained into the cloud leading to cloud growth and dilution (top part of Figure 2). Depending on the material composition, water content and disposal time, the cloud may initially behave as a dense sediment agglomeration that descends fast and transfers gradually into a negatively buoyant thermal. The physics of thermal-like behavior are described by Morton et al. (1956), Scorer (1957), Woodward (1959), and Abraham (1970) and a mathematical transcription in close analogy to sediment disposals has been initially given by Clark et al. (1971), Koh and Chang (1974), and Brandsma and Divoky (1976). Rahimipour and Wilkinson (1992) divided the decent in three phases: Initial acceleration phase, self-preserving phase and dispersive phase. This definition originates from observations in laboratory experiments, where a relatively small amount of sediment was released in a relatively large water depth. For the disposal of large volumes in shallow waters these three stages are not necessarily completed but interrupted (and superimposed) by the bottom impact of the sediments. During the convective descent, material can be stripped away from the disposed sediment cloud and remains in suspension (Figure 1, process i and Figure 2). Although the driving processes are only little understood (Wallingford, 2000), several studies indicate that the amount of material being disintegrated from the descending sediment agglomeration is in the range of $1 - 5 %$ (Gordon, 1974; Sustar et al., 1977; Bokuniewicz et al., 1978; Tavolaro, 1984; Truitt, 1986; Delo and Burt, 1987; Truitt, 1988). Field studies and laboratory experiments indicate that additional turbidity is created upon impact of the cloud on the ground (Kraus, 1991; Johnson et al., 1993). After the impact, the convective descent is terminated, and the dynamic collapse begins. During the dynamic collapse (bottom part of Figure 2), the former vertically descending sediment cloud is transformed into a merely horizontally propagating density current that spreads radially from the impact point. The physical characteristics and mathematical behavior of sediment density currents are described among others by Koh and Chang (1974), Simpson (1986) and Wells and Dorrell (2021). Bokuniewicz et al. (1978) as well as Delo and Burt (1987) provide detailed descriptions of the bottom surge of disposed sediments based on field measurements. The termination of radial spreading of the dynamic plume behavior is reached when ambient flow dynamics take control of the density plume behavior, and the third phase of passive transport begins.

Figure 2

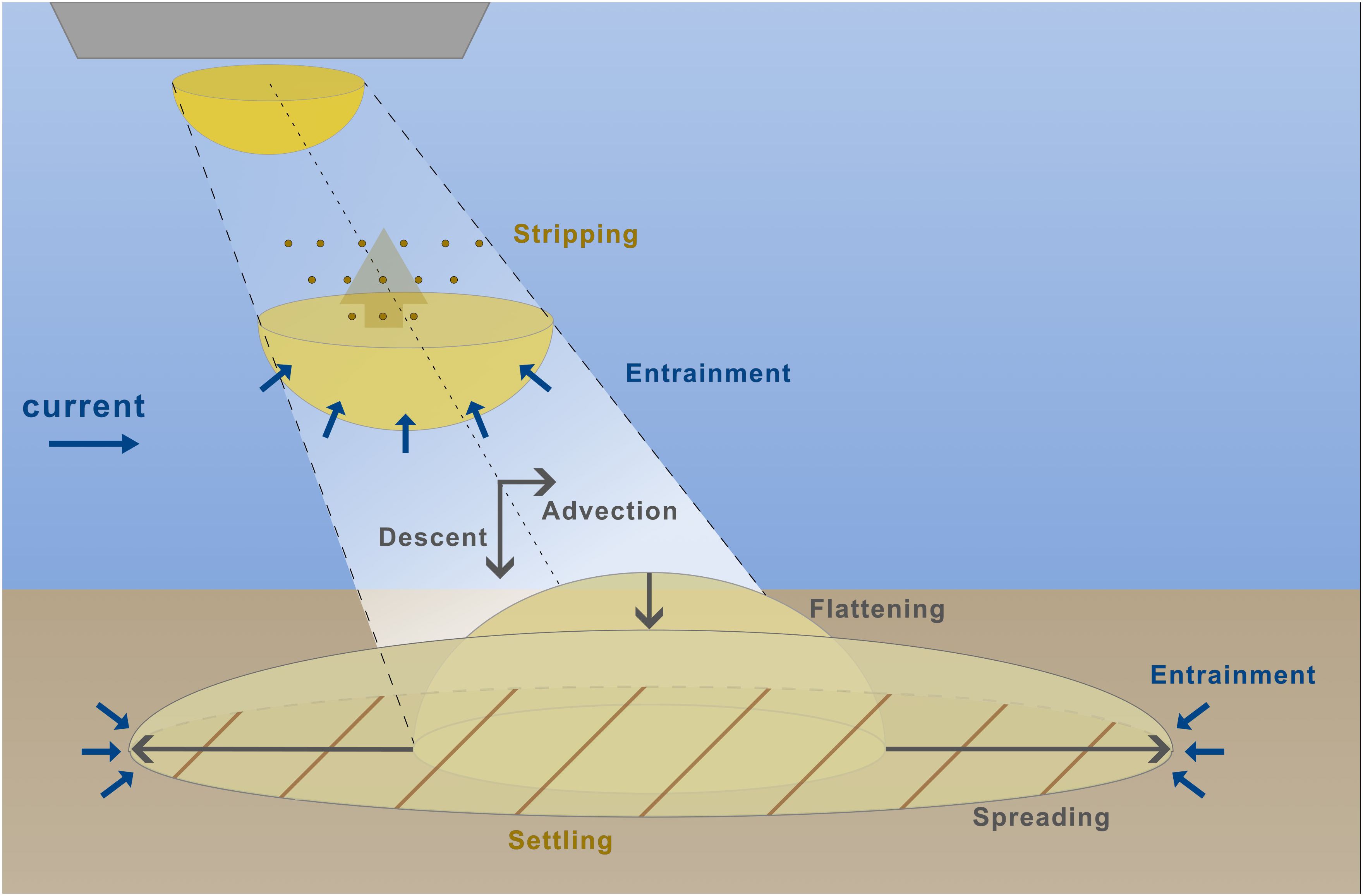
Figure 2. Sketch of the dynamic plume behavior: First, the convective descent, where the sediment cloud moves downward due to negative buoyancy. Second, the dynamic collapse on the bottom, where the material spreads radially from the disposal spot.

Due to the challenging character of detecting and attributing the drivers of the inherent processes in field measurements, a set of laboratory experiments mimicking the three phases under controlled boundary conditions are reported in literature: A small amount of sediment being disposed in water offers a more profound understanding of the previously described underlying processes, such as outfall of coarser sediments, stripping or influence of currents on the descent (Bowers and Goldenblatt, 1978; Rahimipour and Wilkinson, 1992; Noh and Fernando, 1993; Ruggaber, 2000; Bush et al., 2003; Gensheimer, 2010; Gensheimer et al., 2013). Hence, laboratory experiments are crucial to progress a better understanding of controlling and interacting drivers and pivotal processes. Even though scaling and laboratory effects hamper the observation of involved processes or could even disrupt the underlying physics as observed in the field, laboratory experiments greatly help to improve our understanding and allow to verify conceptual models.

Several such mathematical models have been developed to simulate the active behavior of disposed sediments in the near-field. The Short-Term-Fate (STFATE) model developed by the US Army Corp of Engineers (USACoE) (Schroeder et al., 2004) is one of the most prominently applied models (Er et al., 2016). STFATE is based on the conservation of mass, momentum, buoyancy, vorticity and solids (Koh and Chang, 1974; Brandsma and Divoky, 1976) for the convective descent and on the conservation of energy (Johnson and Fong, 1995) for the dynamic collapse. Other models such as Jet3D, a semi empirical model based on laboratory experiments with oil in water, have been applied for modeling near-field disposals, but are not publicly available (Abraham, 1970; Delvigne, 1979; Aarninkhof and Luijendijk, 2010). A two-phase CFD model that calculates the convective descent of particle clouds by Lai et al. (2013) focuses on the convective decent. The recently published Barged Sediment Disposal Model (BSDM), a classification scheme-based model that partly applies a similar approach as the buoyant jet assessment of CORMIX (Er et al., 2016, 2020) provides a detailed representation of the convective descent, but has been developed for the application of sand and has shortcomings in the simulation of the dynamic collapse (Gundlach et al., 2023). From the existing model approaches, the schematization of the disposal into conservation equations introduced in STFATE offers a good balance between the simplicity, process representation and far-field compatibility. Building upon this approach, the model PROVER-M has been introduced (Gundlach et al., 2023), which simplifies the physics-based processes towards a coupling to far-field models, enhances its applicability and improves model results (e.g. temporal development of a sediment cloud during the dynamic collapse).

In this study, PROVER-M was applied in three different settings to verify the physical behavior, define application limits, reveal the impact of the ambient conditions on sediment disposals and give an outlook on potential results and effects from coupling with a far-field model. For verification, novel laboratory experiments were conducted and compared with disposed cloud characteristics as simulated by PROVER-M, showcasing the model’s realistic physical behavior. Furthermore, for the first time PROVER-M was coupled to a far-field model simulating 49 sets of real disposal.

The paper is structured as follows: First, a laboratory setup for scaled new disposal experiments is presented and the scaling described. Second, a short introduction of the model concept of PROVER-M is given, including the definition of application limits. Third, disposal applications are described, starting with the model set-ups evaluating the impact of the disposal settings on the model results. Afterwards, the full scale model set-up equivalent to the scaled laboratory disposal experiments is given, followed by the settings of a coupled application with a far-field model in an estuarine environment. Fourth, the results are illustrated, starting with the results from the laboratory experiments, continuing with the model data validation based on the comparison with the laboratory results and ending with the model applications showing both the effect of varying disposal input on the PROVER-M results and the potential impact of PROVER-M on simulating sediment disposals in far-field models. Finally, the presented results of the applications are discussed regarding limitations, assumptions and insights provided.

Methods

Laboratory experiments

Using different masses of silica flour (material: Sibelco Silverbond M500,. $d_{50} = 5 μ m$ .) of 0.5 kg, 1.0 kg and 1.5 kg, three experimental settings were conducted in a laboratory wave and current basin (20 m x 40 m x 1 m, Figure 3C, see Welzel et al., 2019; Schendel et al., 2020) to yield a sound and reliable data basis for model validation. For dumping of the sediment water mixture (water content 55%), a clamshell bucket with a length of 30 cm and an opening width of 7 cm was used, operated by two gas tension springs without damping (retracted by default) (Figure 3B, construction design in Supplementary Material). At the lower edge of the bucket, its two halves were held together by a bolt when closed. The closed clamshell bucket tensioned the gas tension springs by traction, locked by the bolt. The bolt unlocked the clamshell bucket when being turned ~120° due to the recess on the bolt’s longitudinal axis (Figure 3D). Pulled from outside the basin via a cord, the bolt turned, unlocking the clamshell bucket which was immediately fully opened by the gas tension springs, releasing the sediment. By using gas springs in the opening mechanism, an instantaneous and reliable sediment release was realized. The clamshell bucket was placed a few cm inside the water, in order to ensure that the sediment was released directly in the water to minimize the clouds initial momentum (Rahimipour and Wilkinson, 1992; Ruggaber, 2000; Bush et al., 2003) and to emulate a real dumping event. The sediment fell directly into the 35 cm deep water (Figure 3A). Only a fine film of sediment remained on the inside of the bucket. To be comparable to particle sizes common to real field disposals, sediment mass and water depth were scaled by the rules described in the next section.

Figure 3

Figure 3. Laboratory set-up of the model tests: (A) set-up of the orthogonal axis between clamshell bucket and camera, (B) photography of the clamshell bucket as installed, (C) view on the 3D-wave-current basin of the Ludwig-Franzius-Institute in Hannover, Germany with the experimental set-up, including instrumental setting and (D) release mechanism of the clamshell bucket.

The experiments were recorded by three underwater cameras (GoPro Hero8 Black) being 60 cm apart from the bucket’s centerline and 15 cm over the ground, facing the released sediment cloud according to the set-up in Figures 3A, C. In contrast to the 3 dimensional, nearly radial dispersion of the cloud, the cameras can only capture the dispersion in one plane, which is here parallel to the longer side of the bucket. To capture additional information in a second, perpendicular plane, an additional camera was mounted above the water surface, which covers the radial spreading during the dynamic collapse. From all videos, binary images were generated by different image processing methods like blurring, background subtraction, contrast enhancement and thresholding according to Otsu’s method (Otsu, 1979). After applying morphological operations, the convex hull of the biggest connected region detected in the image was determined.

For the convective descent, videos and derived images were recorded by the first frontal underwater camera with a time step of 0.1 s. For analysis of the cloud’s behavior, the vertical cloud contour was detected manually in the images. After impact upon the bottom, frames with an interval of 1.0 s were extracted from the camera above the water surface for the dynamic collapse. The radial spread was estimated automatically as the equivalent radius (radius of a circle with the same area) of the convex hull.

Scaling

Scaling of experiments was done according to geometric, kinematic and dynamic similarity. In general, geometric and kinematic similarity is expressed by a length and time scaling factor ( $L_{r}, T_{r}$ ) as a function of volumina according to (Gensheimer et al., 2013; Zhao et al., 2013; Er et al., 2016).

L_{r} = \frac{L_{field}}{L_{model}} = {(\frac{V_{field}}{V_{model}})}^{\frac{1}{3}} = {(V_{r})}^{\frac{1}{3}}

T_{r} = \frac{T_{field}}{T_{model}} = {(V_{r})}^{\frac{1}{6}}

Using numerical simulations, Wang et al. (2015) showed that only geometrical scaling is not sufficient. The dynamic scaling for sediment clouds is done using the cloud number:

N_{C} = w_{s} r \sqrt{\frac{ρ_{a}}{B}}

described by Rahimipour and Wilkinson (1992) as a variation of the Froude Number. $F r = \frac{i n e r t i a l f o r c e}{g r a v i t y f o r c e} = \frac{v}{\sqrt{g L}}$ . The Cloud Number increases as the sediment cloud radius r grows. For scaling of the particle size the initial Cloud Number Nc₀ is used. The individual particle sinking velocity w_s is determined by the empirical formula from Dietrich (1982).

Furthermore, the Reynolds Number $R e = (r_{0} w_{0}) / ν$ must be identical in both systems. Since the kinematic viscosity in the field and in the model are nearly identical and the radius and velocity are each scaled, no conformity of the Reynolds Number can be reached that is known as a common conflict of modeling as reported by Soldate et al. (1992), Johnson et al. (1993), Kobus (1980), Hughes (1993), Heller (2011); White et al. (2011) and Le Mehaute (2013). However, similarity is sufficient if the Reynolds number in the model is > 1000 and the flow conditions are in the turbulent range (Johnson et al., 1993). The reference parameters for the scenario “German Bight” and the corresponding scaled model parameters are listed in Table 1.

Table 1

Table 1. Reference parameters for the field and model disposal site, i.e. length scaling factor L_r, particle diameter d₅₀, initial cloud volume V₀, sediment mass m_s, water content $\emptyset$ and water depth h.

PROVER-M model concept

The objective of the model PROVER-M, as presented in Gundlach et al. (2023), is a simplified and easily adaptable near-field model for simulating the active behavior of the disposal of fine sediments in shallow waters. It is designed for quantitatively describing the distribution of fine sediments in the water column and on the bottom as a result of the disposal. Thus, the developed analytical model focusses on the near-field processes and provides essential initial conditions and key parameters for far-field and regional models to simulate entire estuarine processes. These models, such as UNTRIM (Casulli and Walters, 2000) or Delft3D (Lesser et al., 2004) then numerically account for simulating the passive behavior of the disposed sediment. The general understanding of the governing physical processes and its subsequent modeling approach are depicted in its sequence and generic steps in Figure 4. The main conception of the model is: Initiation of cloud and ambient parameters, transition of the results between the two phases and termination of the calculations. For the convective descent and dynamic collapse phase this concept is schematized in Figure 2.

Figure 4

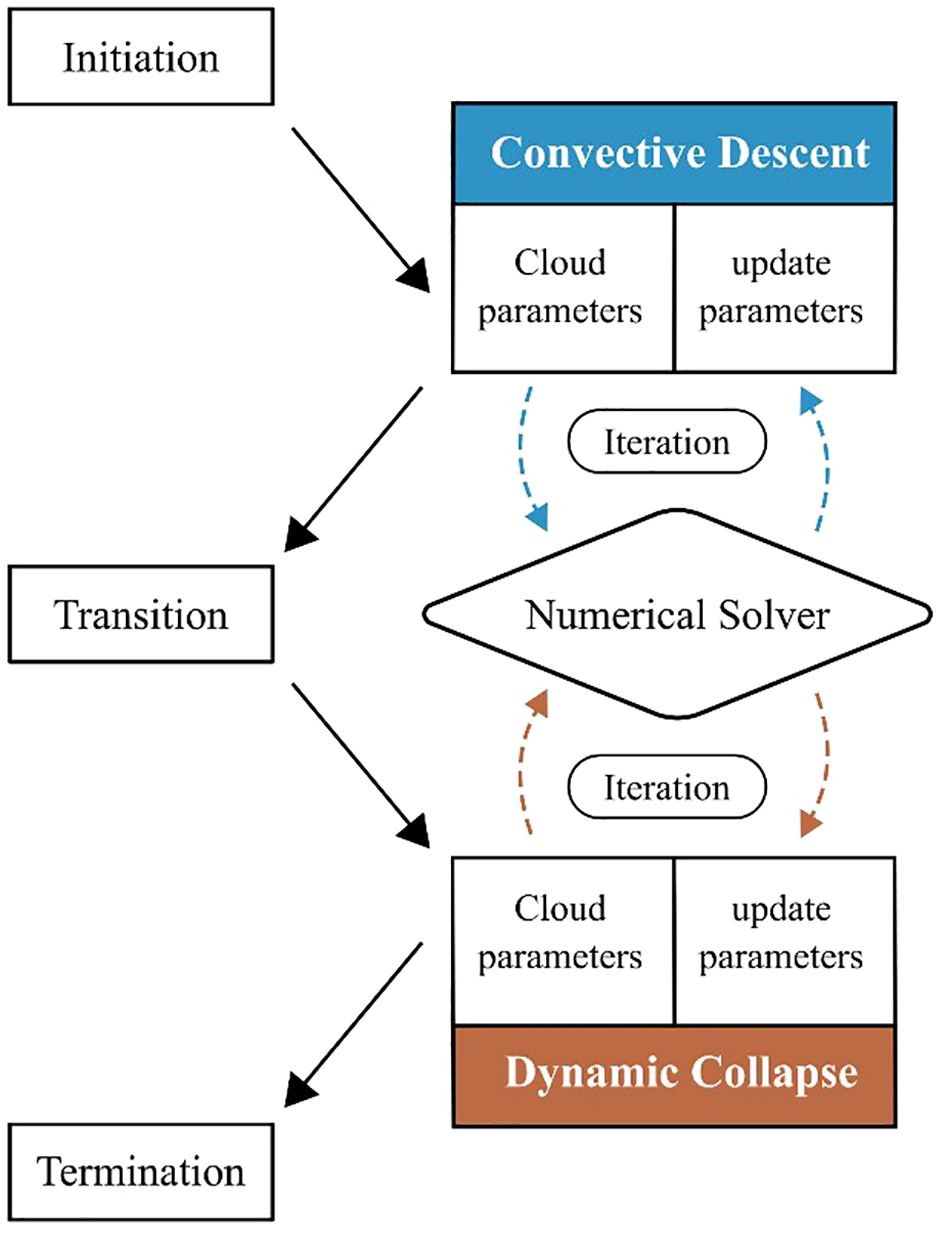
Figure 4. Schematic flow chart of the program structure. Blue labels indicate the processing during the convective descent phase, while red labels indicate the computation during the dynamic collapse phase.

The convective descent phase terminates in the very instant that the tip of the sediment cloud reaches the ground. The end of the dynamic collapse phase is reached when the movement of the cloud is overruled by the ambient conditions, either represented by the current of the surrounding water body or a priorly defined threshold for turbulence.

The consecutive phases embedded in the conceptual model rigorously follow systematic approximations for disposal geometries and material representations for the cloud’s shapes (Figure 2). Throughout the convective descent phase, the cloud is assumed to be shaped like a lower hemisphere with a specific radius. The cloud radius increases by entraining surrounding fluid and diffusion of the sediment. When the cloud impacts upon the bottom, the shape is reversed to an upper hemisphere. A transitional stage accomplishes the change in shape by an intermediate state of an ellipsoid. The second phase is characterized by a decreasing height of the cloud due to horizontal spreading and dispersion. During that dimensional change, the geometry of the cloud is represented as the upper half ellipsoid.

The PROVER-M model is based on conservation equations governing momentum and energy, for which the reader is referred to Gundlach et al. (2023). Several assumptions and boundary conditions are implied for the model. The description of the convective descent is derived from isolated liquid buoyant thermals (Scorer, 1957; Woodward, 1959). Thus, it assumes that the sediment-water mixture behaves as a dense homogeneous fluid, descending as one coherent body, that is independent of the individual material property. This applies to fine sediments and high water contents. Furthermore, it is assumed that the mathematical analogy of a negatively buoyant thermal is appropriate to account for the behavior of the disposed cloud. Additionally, the ambient boundary conditions are simplified: The ambient fluid has time-invariant horizontal flow velocity components that are depth-averaged. Furthermore, the given depth is constant and the water column is not stratified, i.e. the density is homogeneous. Mathematically, the model formulates the sediment cloud to adapt density-driven gradients that cause a vertical descent, based on approximations of fluid-fluid interaction. Utilizing a concept of energy conservation, the collapse of the cloud on the bottom is described, where the cloud radially spreads as a density current.

For a more in-depth understanding of the working principle of the model and the functional relationships of the cloud disposal, the reader is referred to Gundlach et al. (2023).

Application limits

To fulfil the assumptions of uniform density and to ensure a collapse on the bottom, a certain ratio of the disposed material (volume and mixture) over the water depth cannot be exceeded. The interaction between disposed material and ambient fluid is rather complex, so is deriving a physical and simple limiting relation. However, as a pragmatic, non-proven boundary the dimensionless relation $\frac{V * \emptyset}{d^{3} * n} > 0.025$ is to be satisfied, where V [in m³] is the disposed volume, d [in m] is the depth at the disposal site, n is the number of disposal sub-volumes V/n and. $\emptyset$ . [in %] is the amount of solids in the disposed volume. A value of 0.025 provides a good limit for avoiding neutral buoyancy as can be seen in Figure 5. Additionally, a depth of 100 m should not be exceeded with this model, due to the physical constraints of the model. If the condition is not met, the cloud could reach neutral buoyancy and fully remain in the water column, which is not the purpose of the PROVER-M model. Additionally, Figure 5 indicates that a large disposed volume in very shallow water (e.g. 10 or 15 m) will lead to a direct calculation of the second phase, as the initial radius of the cloud already reaches the ground. To prevent this from happening, the disposal can be temporally divided into n > 1 disposal increments. Within the range of these site conditions the given assumptions are valid (Ruggaber, 2000). However, different desired conditions can be easily simulated by adjusting the model input. Theoretically, the model can be adapted to simulate other situations, where highly concentrated sediment-water mixtures follow gravity-driven motion in water (e.g. highly concentrated bottom surges due to landslides), but basic assumptions (such as the shape of the cloud) and parameter settings (e.g. sediment stripping) are set for the disposal of dredged material.

Figure 5

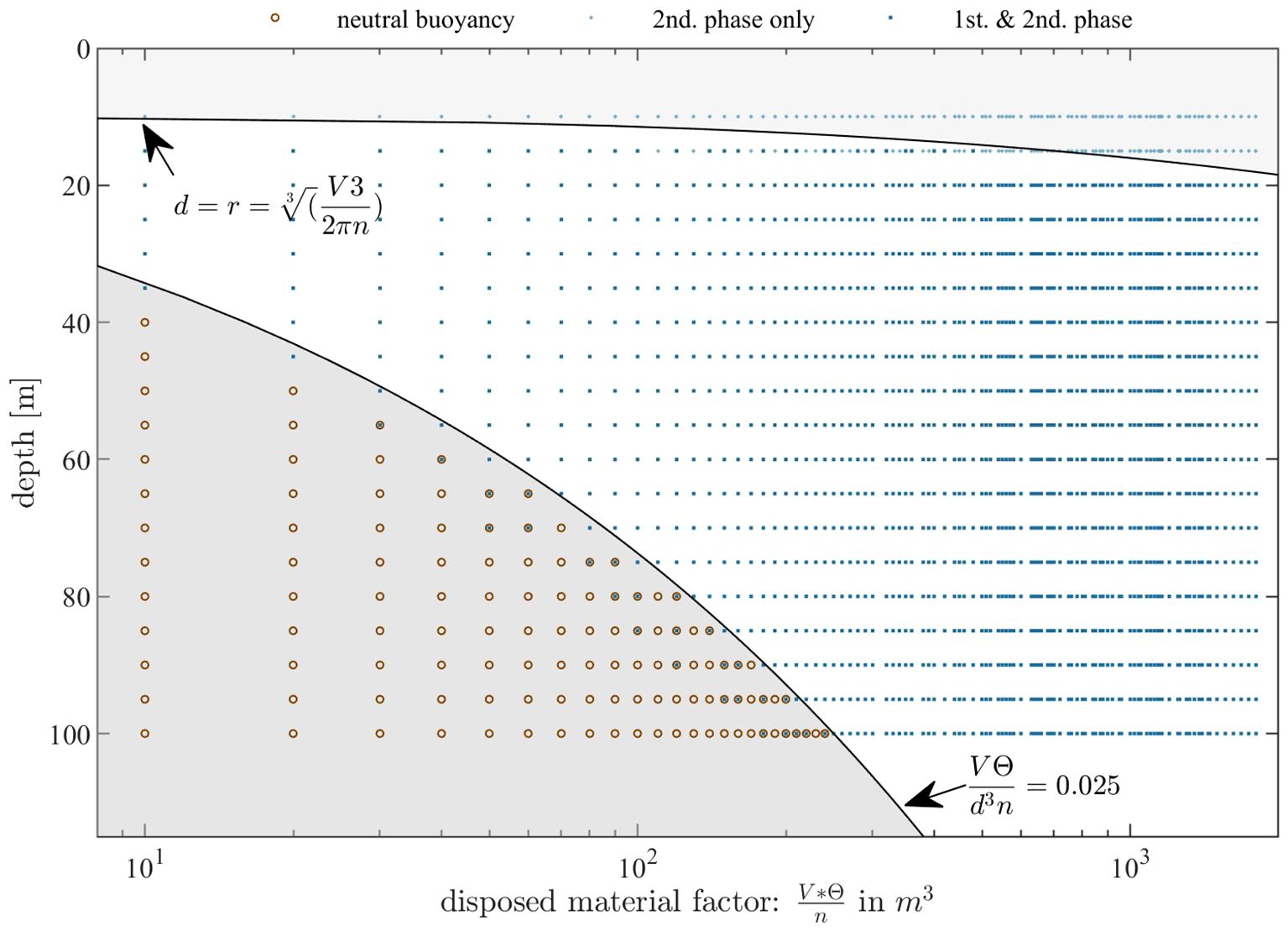
Figure 5. Validity check for PROVER-M applications based on the parameter comparison of the depth vs. the disposed volume, concentration of solids and the number of disposal cycles.

This includes a strong dependence on model parameters, such as the entrainment and drag coefficient. Especially for integrated modeling of the convective descent, this dependency has been reported (Johnson and Holliday, 1978; Johnson and Fong, 1995; Ruggaber, 2000). Both parameters affect the cloud growth and density. With a higher entrainment of ambient fluid, stronger dilution of the cloud occurs and in return affects the cloud’s motion through the water column. An increased drag limits the descending speed, leading to an increased duration of the descent and consequently an increased entrainment. Ultimately, both entrainment and drag coefficient influence the distribution of the disposed sediment. A loss of accuracy due to the implementation itself is addressed in the model verification subsection.

Disposal scenarios

In order to analyze the parameters that either control or have an influence on the disposed sediment cloud and its dimensions/characteristics at the end of the dynamic/active behavior, a range of realistic values was simulated with PROVER-M, combining the influence of water depth (20 - 30 m; 1 m interval), ambient current (0 - 1.5 m/s; 0.1 m/s interval), disposal volume (1000 - 4000 m³; 500 m³ interval) and amount of solids (10 – 40%; 5% interval) to a set of 8624 simulations. The effect of sediment stripping as well as the diameter and density of the disposed sediment cloud at the end of the dynamic behavior were then further analyzed. For the simulations made, default settings of the PROVER-M model as set in the GUI were used. For details see Gundlach et al. (2023) and the readme of the corresponding repository.

Further, PROVER-M was used in two case studies within its application range. First, to verify the physical behavior of the model, the previously introduced laboratory experiments were performed with PROVER-M on full-scale, based on conditions typical for the German Bight. Afterwards, a second case study illustrates a near-field/far-field coupling for a set of 49 recorded disposals in an estuarine environment. This provides a first assessment of the potential impact of PROVER-M on far-field results. Compared to the commonly applied simplification of simply placing all material on the ground, this already constitutes a huge improvement. However, it must be emphasized that an assessment of the quantitative accuracy is still pending due to a lack of suitable field data. While the representation of the disposal process is improved, it remains challenging to ascertain whether the model output accurately reflects reality, making the results preliminary estimates.

The case study “German Bight” considers a water depth of 40 m, as well as disposal volumes of 3605 m³ 1552.5 m³ and 5157.5 m³, each with a bulk density of 1205 kg/m³ and containing only silt and clay particles. Under the assumed conditions, the influence of tidal currents becomes less decisive (ambient currents are neglected), and the water depth is sufficiently large to reproduce process sequences during the descent and evaluate the process fidelity of the model. Here, the disposal process is considered to last long enough to divide the disposed volumes into three sub-volumes (n=3) for each of the considered volumes: 1235 m³, 618 m³ and 1853 m³. These are instantaneously disposed in a physical model test as well as in PROVER-M. The results for one sub-volume are compared, illustrating the underlying processes.

The case study “Jade-Weser”, is designed based on 49 recorded disposals in shallow water (10 – 15 m) under ambient currents ranging between 0 and 1.1 m/s. For this application disposal volumes ranged between 3000 and 5000 m³, with a bulk density of 1135 kg/m³ containing a mixture of silt and clay. This scenario uses a set of disposal operations from maintenance dredging (given in the Supplementary Materials) that are simulated with PROVER-M and coupled to an UNTRIM/SEDIMORPH model through the DredgeSim module. The results demonstrate the potential impact of coupling PROVER-M to a far-field simulation. Here, a series of disposal operations in an environment typically found in busy harbors located in estuaries (e.g. Bremerhaven, Hamburg, Antwerp) is applied to illustrate the functionality and utility of the model to potential stakeholders in similar environments.

Far-field model settings

To test the influence of PROVER-M on far-field models, simulations of recorded sediment disposals in the outer Weser estuary, Germany, were conducted. The Weser estuary has an outer part with a deep navigation channel and vast sand and mud flats at the sides, followed by a narrow channel up to the tidal weir in which the brackish water zone and the estuarine turbidity maximum are located [e. g. Koesters et al. (2014)]. The maximum tidal range is 4.2 m at the tidal weir.

The numerical simulations presented here were carried out with the 3D baroclinic model UnTRIM2 (Casulli, 2009), coupled with the modules SediMorph (BAW, 2005) for sediment transport and DredgeSim (Maerker and Malcherek, 2010) for sediment dredging and dumping. DredgeSim, in which the PROVER-M output is considered, handles time- or criteria-driven dredging and dumping events by mass changes at the bottom and volume flow into the water column.

The model domain encompasses the tidally influenced area of the Weser estuary and the Jade bay out to the German Bight. The model has ~ 72.000 elements with edge lengths of 8 m in the inner estuary to 850 m in the outer estuary. The vertical discretization is 0.5 m. For turbulence closure, the k-ϵ model was used. The buoyancy production, induced by fine sediment stratification, is included, however, rheological stresses are not included.

For sediment transport, eight sediment fractions were considered. To describe the natural sediment dynamics in the background, four bed-load fractions covering grain sizes from 63 μm to 2 mm and two suspended sediment fractions covering the cohesive material smaller than 63 μm were used. All bedload and suspended sediment fractions were initialized in a horizontally variable sediment distribution based on surface samples. To describe the disposed sediments under investigation here, two additional suspended sediment fractions were modeled. Based on available measurements (soil samples in the dredging areas, in-situ laser-diffraction (LISST) measurements), the disposed sediments were evenly divided into two fractions, one with a mean diameter of 42 μm and a settling velocity of 1.5 mm/s and one with a mean diameter of 8 μm and a settling velocity of 0.5 mm/s. The model was run for a two-month period for morphological spin-up. It was validated with a realistic hindcast of the hydrological year 2016 which showed RMSEs of 0.09 m – 0.20 m for water surface elevations (12 stations), 0.3 psu – 2.3 psu for salinities (10 stations) and 0.05 kg/m2 – 0.17 kg/m2 for suspended sediment concentrations (8 stations).

For the results presented here, all sediment disposals from April to May 2016 at the dumping site T2 were simulated in a hindcast. T2, also called “T2 Fedderwarder Fahrwasser”, is located in the mid-outer estuary east of the main channel (Figure 6A). It has a water depth of 12.5 m and maximum ebb and flood current velocities of about 1.2 m/s. Book-keeping of all maintenance dredging is available via an administration-wide database provided by the Waterways and Shipping Administration. Besides dredging and dumping areas, volumes and times, the data base also contains the portion of mud and sand. In these simulations, only the mud volume was disposed. In total, a volume of 205.000 m³ of mud was dumped in 49 vessel circulations (given in the Supplementary Material). The water level and the disposed volume of mud is shown in Figure 6B. Disposals were made mostly during the flood phase and lasted 7 minutes on average, with mean disposal volumes of 4.200 m³ ranging from 3.300 m³ to 4.900 m³.

Figure 6

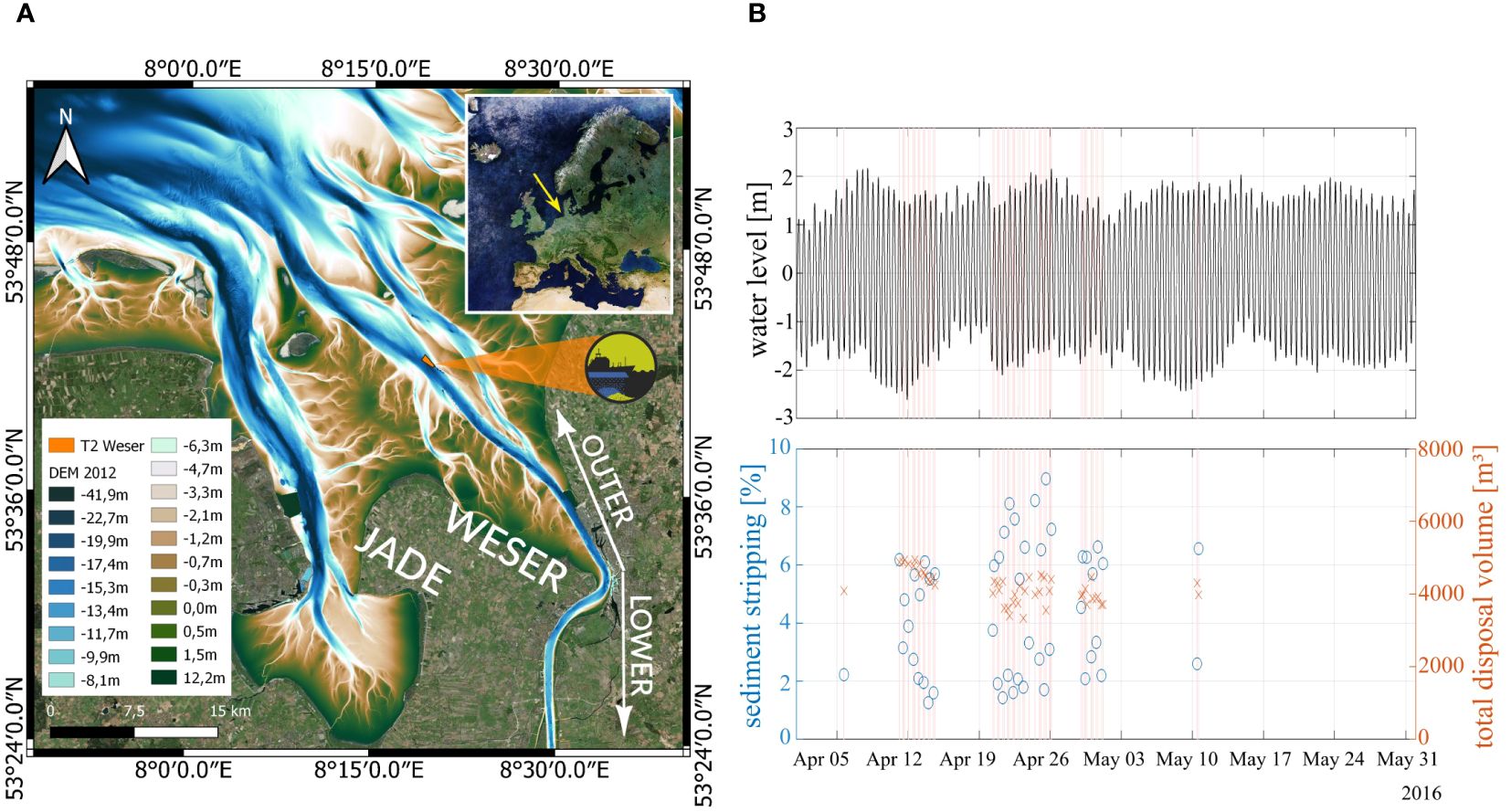
Figure 6. Results of the UnTRIM2 simulation coupled with PROVER-M. The location of the study area, the bathymetry and disposal location are displayed in (A), water level at the disposal site (upper panel) and the disposal volumes and sediment stripping (lower panel) in (B).

For the PROVER-M application, the default calibration parameters were used as no monitoring data was available for calibration. Sediment volume, composition and water content were based on the above-mentioned disposal data. The time dependent water depth, density and current velocity were calculated by the UNRTIM far-field model for each dumping event. The vessel draft reduction was assumed to be linearly dependent on the disposed volume in a range of 0.5 – 1 m. The number of sub-disposals n was estimated by choosing a time interval resulting in the highest stripping rate considering the whole set of disposals. For each disposal, the stripping of a partial disposal was considered and the sum of all individual partial disposals of the set was compared. The highest total amount of stripped material was obtained with a time interval of 20 s.

In an initial step, both models were coupled offline by running a simulation without PROVER-M for extraction of the background values that generate the input for the set of PROVER-M simulations. Subsequently, the PROVER-M simulations were subsequently conducted and the output of PROVER-M was then used in the far-field Weser estuary model recalculating the simulation period including the sediment disposal events. The resulting percentages of stripped material were added as volume flows into the water column. The remaining material was placed on the bed in the disposal area.

As a control scenario, a second simulation was carried out in which all material was placed on the bed.

Results

Laboratory experiments

The descending cloud over time for 1 kg of sediment is shown in Figure 7. The contours of the convective descent are presented in Figure 8 and the contours for the dynamic collapse are visualized in Figure 9. After the release mechanism was pulled, the material left the bucket and hit the bottom after 1.0 s. A thin film of the sediment remained in the bucket and was slowly washed out as a surface plume (see frame after 60 s in Figure 7). Also, in the water column a small amount of sediment remained after one minute. The extracted contours of the descending cloud (of 1 kg sediment) for the first two seconds are shown in Figure 8. At the cloud front, turbulence occurred and the main cloud formed. The cloud was followed by the stem, which narrowed closer to the main cloud. During the descent, entrainment of ambient water into the cloud led to a minimal growth. The time until the cloud fronts hit the bottom ranged from $t_{b o t t o m} =$ 0.9 s (1.5 kg sediment) to 1.2 s (0.5 kg sediment) (Figure 10A). During the initial acceleration phase (from 0 s to 0.5 s) a larger mass resulted in a faster descent. For a mass of 1.5 kg, a descent rate of 43.68 cm/s was reached, while half of this rate was reached for 1 kg and 0.5 kg of mass (at 0.3 s in Figure 10B). While the mass of 1.5 kg remained at 43.68 cm/s (±10%) during the self-preserving phase (0.5 s until impact), 1 kg and 0.5 kg of mass accelerated to 53.76 cm/s before impact on the ground. Generally, during the convective descent, the clouds of disposed material with a mass of 1 kg and 0.5 kg showed a relatively similar behavior compared to the experiment with a mass of 1.5 kg (Figures 10A, B). After impact, the dynamic collapse was analyzed. The contours of the 1 kg disposal event are shown in Figure 9. During the dynamic collapse, the radial spreading of the cloud on the ground differed more clearly between the masses disposed. The radial spreading of the experiments are compared in Figure 10C. Although all results show a strong increase in radius in the beginning (until 10 s after impact) and later exhibit declining growth (approaching a constant radius after 30 s), differences are visible. The time of the impact and the transition during impact differ in timing and resulting radius. Thus, at the end, a disposed mass of 1.5 kg resulted in a radius of 140 cm, while masses of 1 kg and 0.5 kg led to radii of 131.4 cm and 124.7 cm, respectively. This distinction can be found in the spreading rate (Figure 10D). The disposed mass of 1.5 kg started with a peak spreading rate of 11.4 cm/s, detected 4 s after disposal. For masses of 1 kg and 0.5 kg, the peak rate was 5.2 cm/s after 7s. After reaching these peak rates, the spreading was reduced until a rate of 1.6 cm/s was observed after 30 s for all masses disposed. Generally, the largest disposed mass had the highest spreading rate over time. Although 1 kg and 0.5 kg disposed material started with the same spreading rate, the rate decreased faster for 0.5 kg. The results are summarized in Table 2.

Figure 7

Figure 7. Descending cloud over time for a mass of 1 kg of silica powder. Images were taken in front of the disposal area, 60 cm apart from the clamshell bucket. The cloud front hit the bottom after 1.0 s. Afterward, the cloud spread over the ground during the dynamic collapse. After 60.0s only a small amount of sediment remained at the water surface and in the water column.

Figure 8

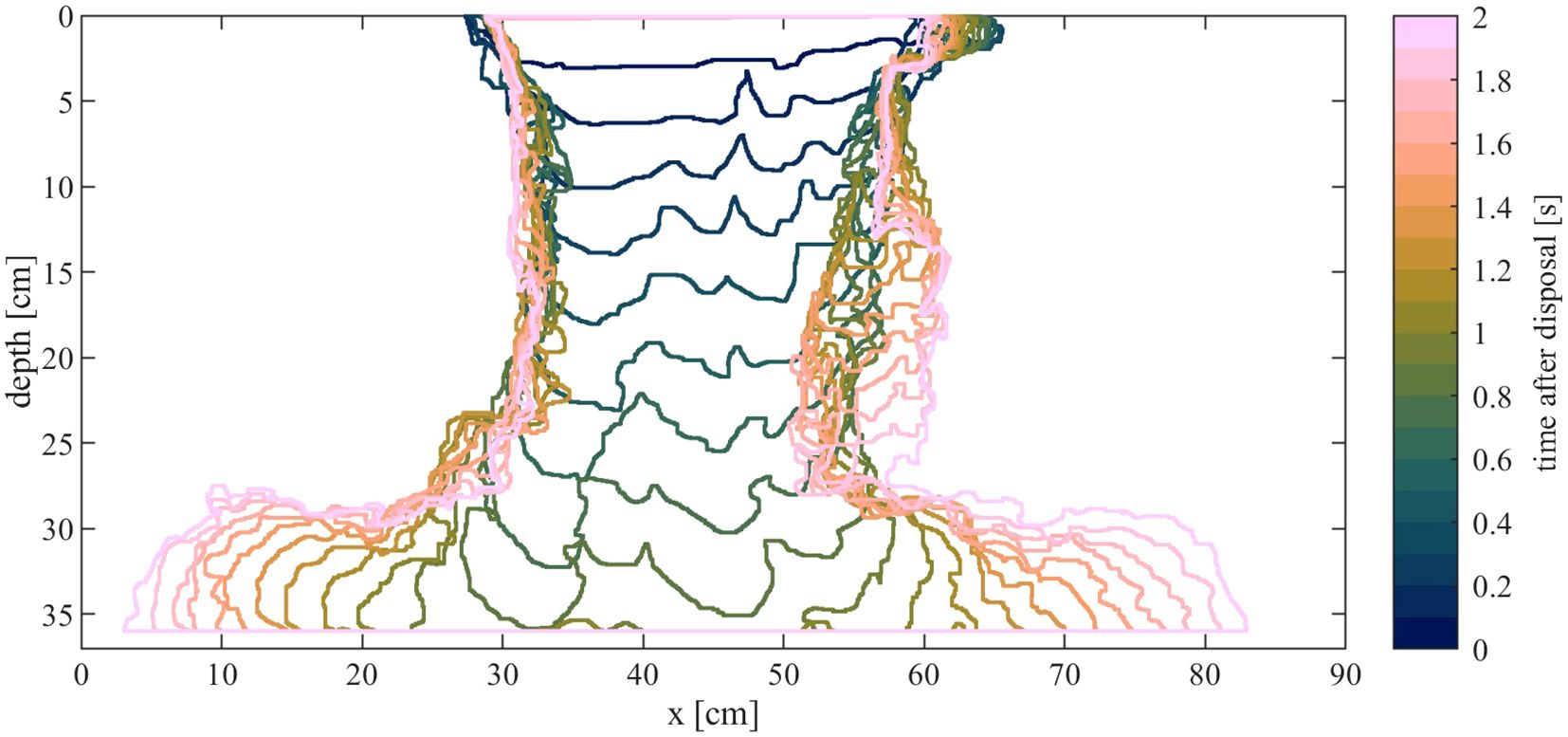
Figure 8. Contour of descending cloud in longitudinal direction over the first two seconds after sediment release. Shown here are contours for a mass of 1 kg, which were manually extracted.

Figure 9

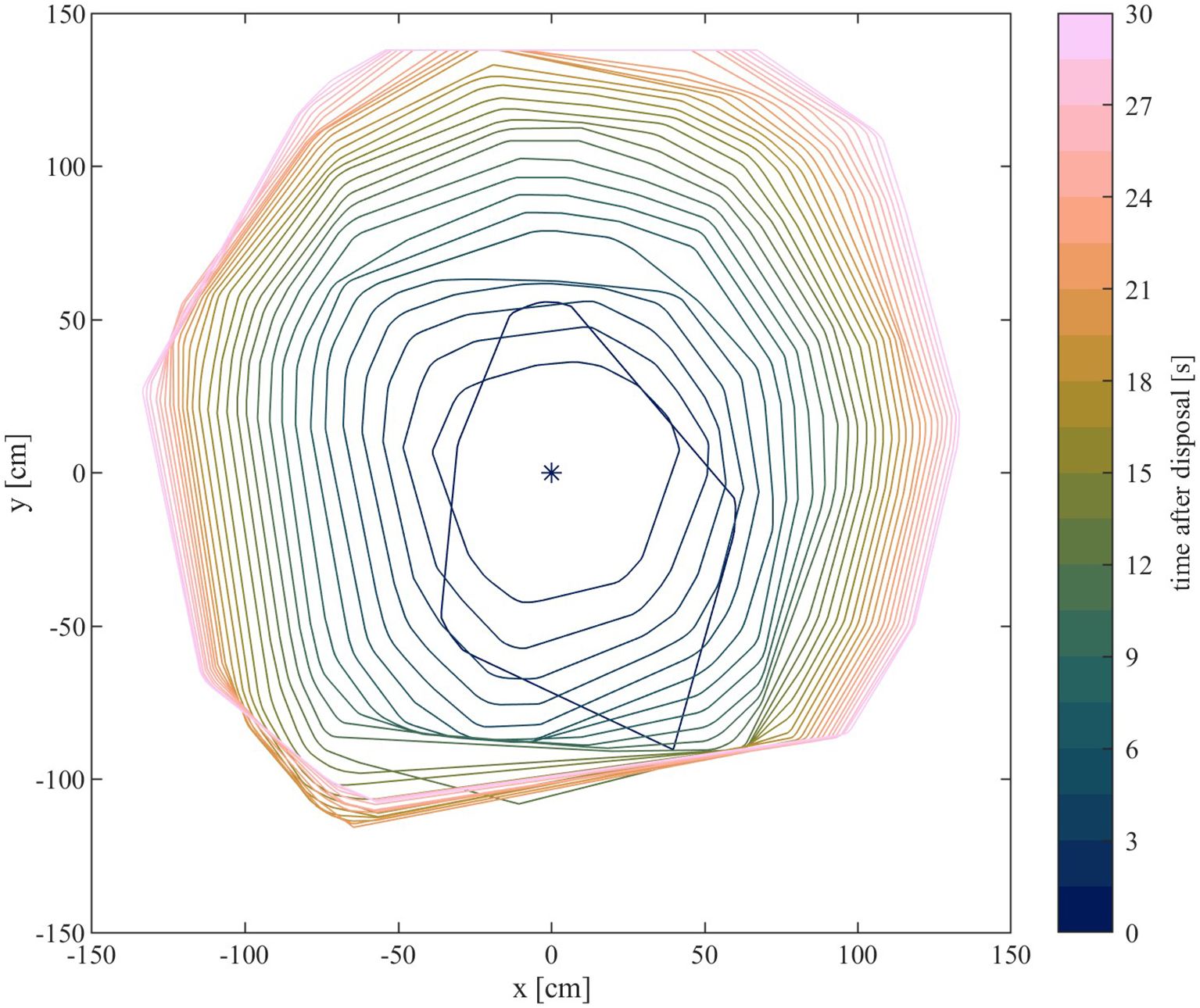
Figure 9. Convex hull of sediment spread at the bottom for a mass of 1 kg of silica powder. The convex hull is determined as the biggest connected region after applying background subtraction and different morphological operations, e.g. dilation and erosion.

Figure 10

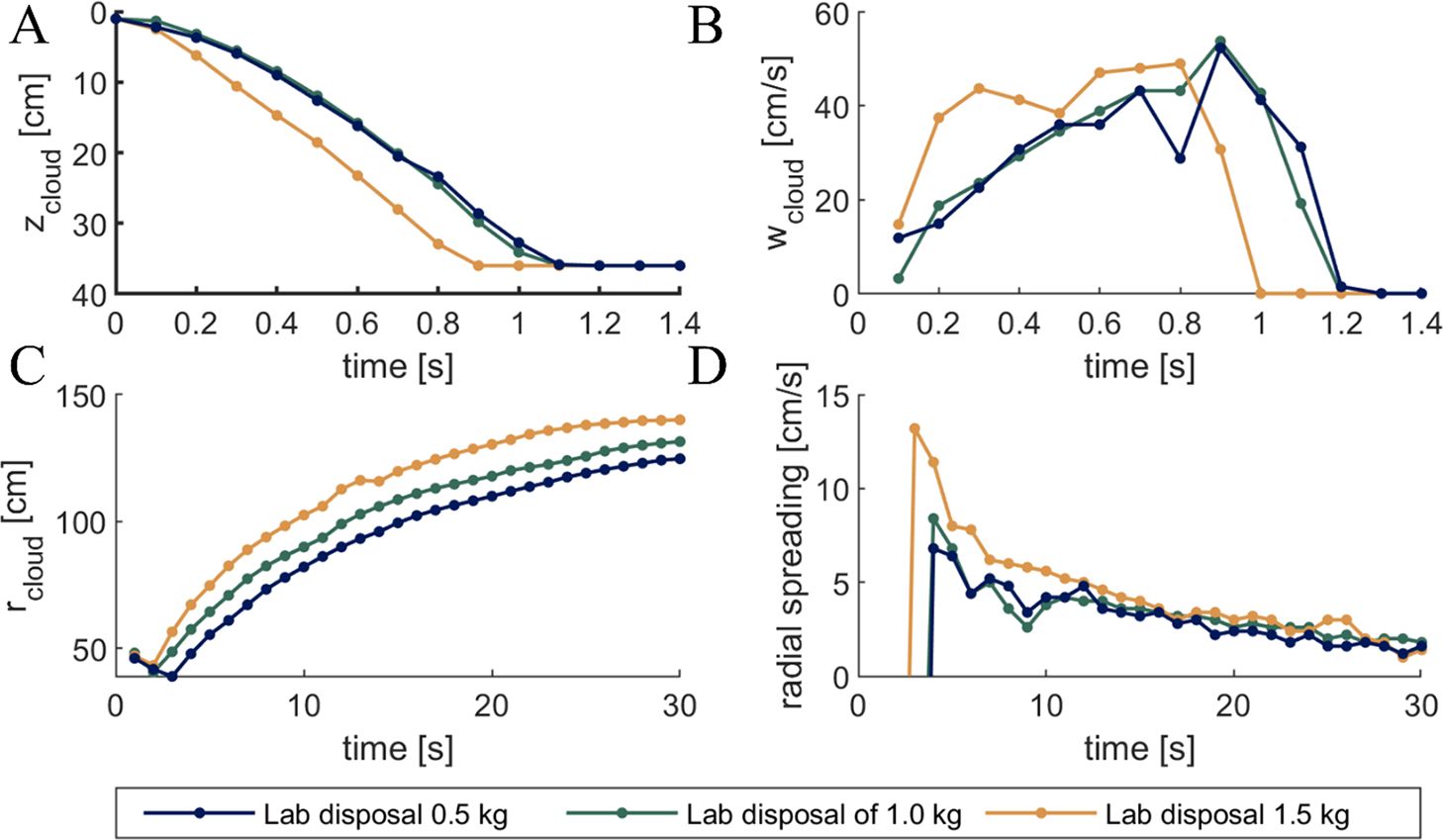
Figure 10. Results from the laboratory tests with sediment masses of 1 kg (dark green), 1.5 kg (dark yellow) and 0.5 kg (dark blue). The convective descent over time with (A) the z-position of the clouds centroid and (B) the descending speed of the clouds centroid. The dynamic collapse over time with (C) the radius of the cloud and (D) the spreading speed.

Table 2

Table 2. Summary of the laboratory results from Figure 10, including the descending speed $w_{c l o u d}$ and the radius $r_{c l o u d}$ .

Model-data validation

The model was validated against the laboratory experiments that were scaled to the field setting of the German Bight scenario. Here, the convective descent was compared by the cloud contours (Figure 11) and the dynamic collapse was compared by examining the spreading rate over the distance to the disposal point (Figure 12).

Figure 11

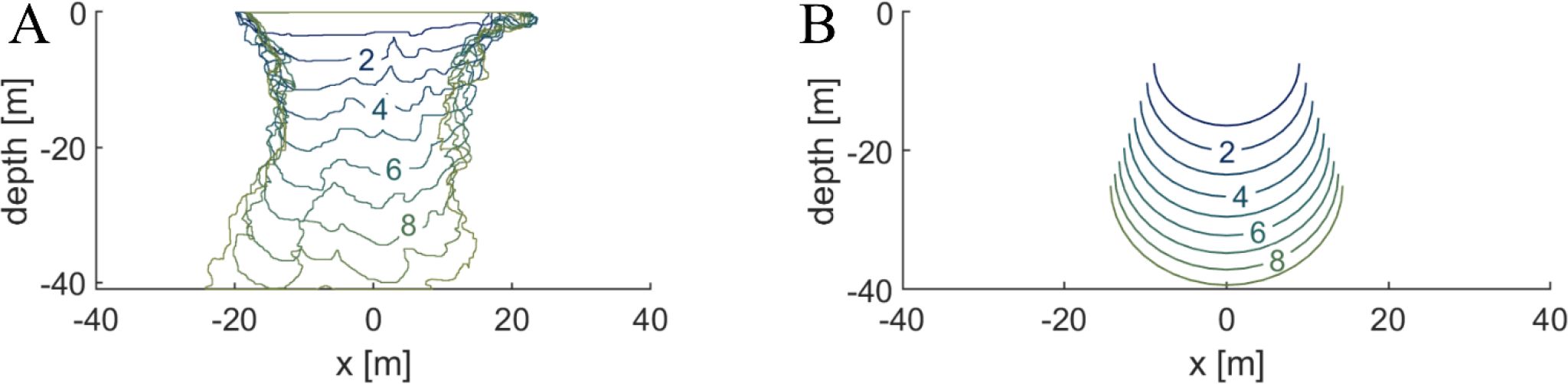
Figure 11. Cloud contours in field scale over time ranging from 1 second after disposal to 10 seconds after disposal. The cloud contours from the laboratory experiment (longitudinal axis) in (A) and the half-sphere cloud from PROVER-M in (B).

Figure 12

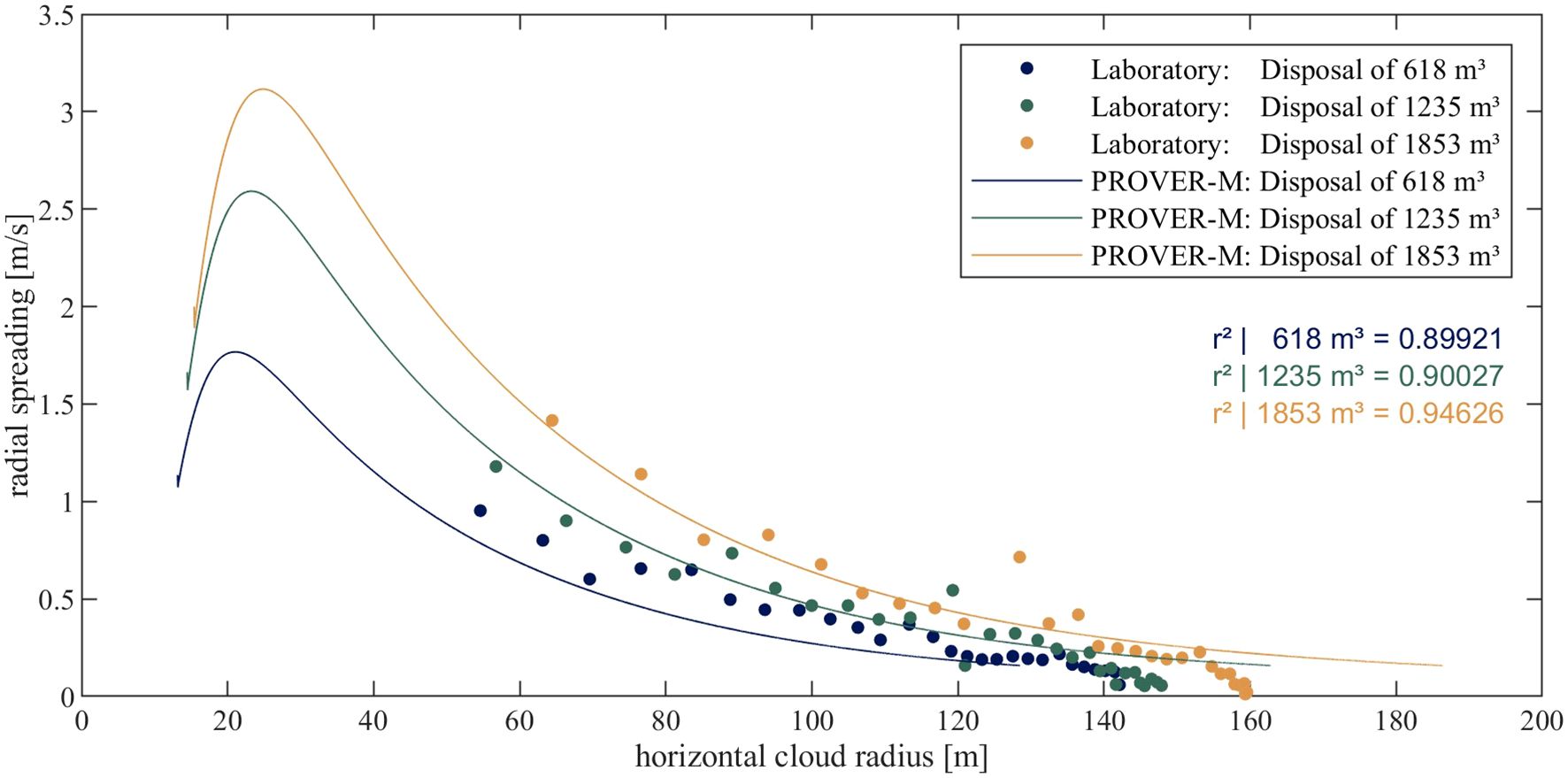
Figure 12. Validation of the dynamic collapse for disposed volumes of 618 m³ (yellow), 1235 m³ (green) and 1853 m³ (blue). The dots are measured values from the laboratory experiment, while the lines are results from the PROVER-M model.

For the convective descent, the laboratory result for this volume is plotted in Figure 11A, while the idealized model results are shown for a volume of 1235 m³ in Figure 11B. Differences between both were observed at the beginning of the descent: While for the laboratory experiments, the cloud contour was recorded starting with its release at the water surface, the PROVER-M model started with a predefined draft of the dredger vessel (here 5.5 m). Thus, the release of the cloud started some meters below the water surface. Furthermore, due to the form of the clamshell bucket, the cloud in the laboratory initially had a long and narrow shape. In contrast, the PROVER-M model started with a narrower half sphere. After 5 seconds, the laboratory cloud was tapered in its horizontal axis (max horizontal extend = 18.2 m), while the PROVER-M cloud grew continuously (r = 12.5 m at 5 s). From this point until the impact, both clouds expanded non-linearly during descent. Before impact, the laboratory cloud had a radius of around 19.75 m after 9 seconds, while the PROVER-M cloud reached a radius of 14.5 m after 9.3 seconds.

The dynamic collapse was compared by analyzing the spreading rate of the cloud in distance to the disposal point, presented in Figure 12. This parameter combination (spreading rate over distance to the disposal point) is a valid indicator for the correct projection of the physical behavior. In the PROVER-M model, all projections showed an acceleration of the spreading rate until a peak (3.11 m/s for 1853 m³, 2.59 m/s for 1235 m³ and 1.76 m/s for 618m³) was reached 20-25 m away from the disposal point. Afterwards, the spreading rate decreased non-linearly towards a spreading rate of 0.15 m/s. For the decrease in spreading rate between 50 m and 160 m, where the laboratory data was recorded, a comparison between projections and laboratory results led to coefficients of determination of 0.899, 0.9 and 0.946 for the volumes of 618 m³, 1235 m³ and 1853 m³, respectively. However, the final spreading rates differed: For these volumes, the cloud in the laboratory reached final spreading rates of 0.06 m/s, 0.05 m/s and 0.01 m/s at distances of 142 m, 147 m and 159 m, respectively. In contrast, PROVER-M terminated with a spreading rate of 0.15 m/s at distances of 128 m, 162 m and 185 m, respectively.

Model application

Parametric study of disposal site impacts

By constantly varying model input parameters within a plausible range, the model behavior and the effect of input parameters on the model output are demonstrated in Figure 13. The impact of the ambient conditions on the model results is shown in Figure 13A. An increased depth increases the amount of stripped material almost linearly. At the same time it has a small, decreasing influence on the clouds density and an even smaller effect on the clouds diameter at the end of the dynamic plume behavior. Contrary, the ambient current impacts the final cloud diameter almost linearly, while its impact on the amount of stripped sediment is quite small compared to the ambient depth. Figure 13B illustrates the impact of the disposed sediment characteristics, specifically the disposed volume and the amount of solids. The results indicate that the outcomes are influenced by both the volume of sediment disposed and the solid content. The density of the sediment cloud after the dynamic collapse shows a stronger dependence on the amount of solids. The percentage of stripped material (more dependent on the amount of solids) and the cloud diameter, on the other hand, are influenced non-linearly by both, variations in the disposed volume and the amount of solids.

Figure 13

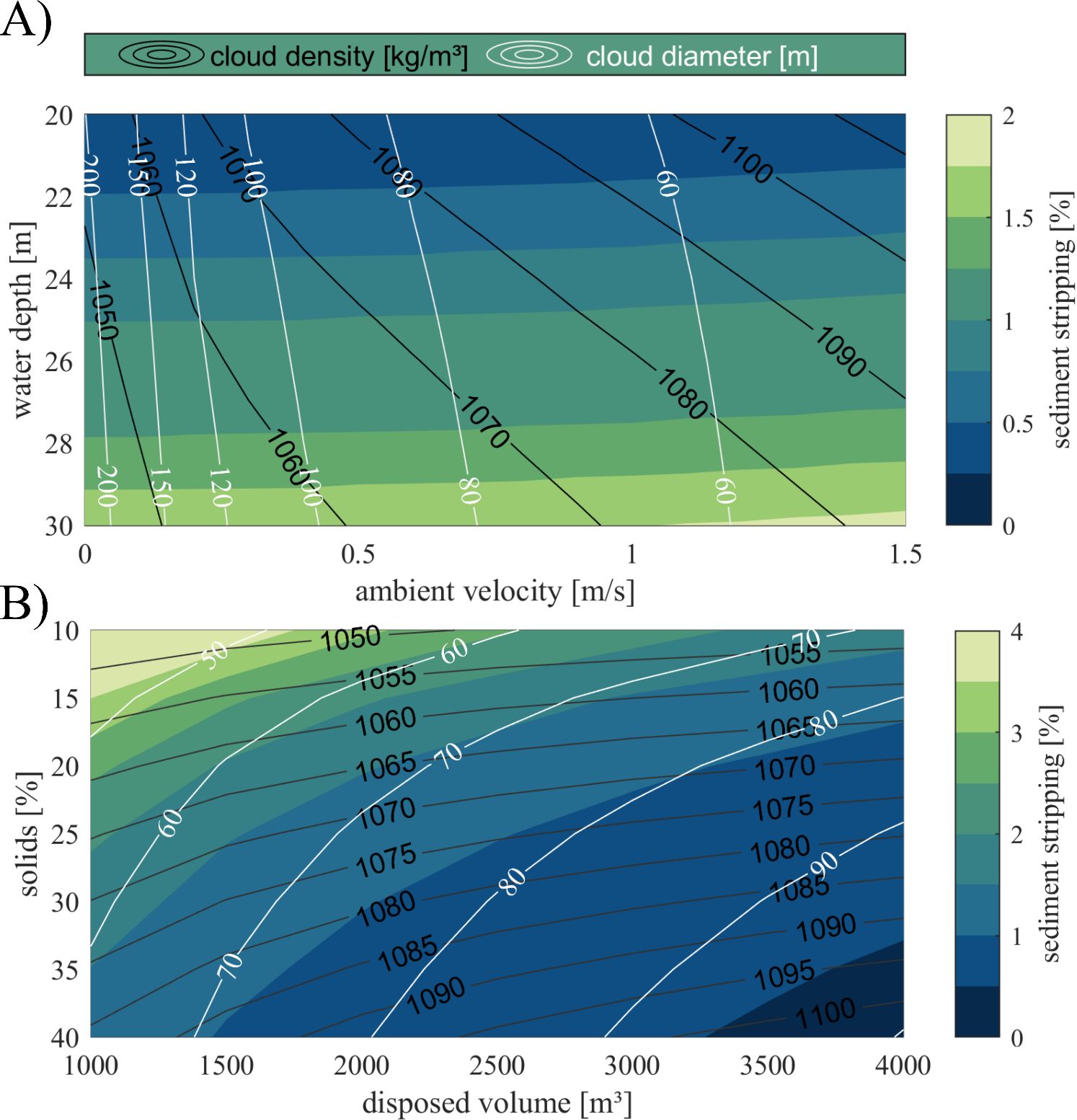
Figure 13. Simulations based on PROVER-M regarding the effects of the ambient conditions [x- and y- axis in (A)] and disposed sediment characteristics [x- and y-axis in (B)] on the amount of stripped sediments (colormap) after the convective descent, the average density of the cloud on the bottom (black contours) and the diameter of the cloud (white contours) at the end of the dynamic plume behavior. The results in (A) are shown for a disposed volume of 2500 m³ and 25% solids. In (B) a constant water depth of 25 m and ambient currents of 0.7 m/s are forming the setup.

Case study: Jade-Weser estuary

After verifying the process fidelity of PROVER-M via the previously presented experiments, we coupled PROVER-M to the UnTRIM2 model. Since quantification of the accuracy from field measurements is missing, the far-field SSC results can only be considered preliminary. Nevertheless, they illustrate the potential impact of including PROVER-M in far-field modeling when using plausible model assumptions.

For the given series of disposals, the amount of stripped material that was calculated by PROVER-M varied between 1.26% and 8.96% (Figure 6B and table in the Supplementary Material).

After a sediment disposal in the far-field model, the disposed sediments were transported away from the disposal site with the tidal currents and distributed in the study area. During slack water, the sediments settled, to be resuspended again with the next tide or by the impacts of waves. After some time, they settled permanently. Hence, disposal-induced SSC showed strong spatial and temporal variations. To illustrate the maximum disposal-induced SSC in the area, the 99^th quantile at each location was calculated.

The spatial distribution of the 99^th SSC quantile is shown in Figure 14A. The 99^th SSC quantile in the main channel of the outer estuary ranged from 35 – 45 mg/L with a peak of 81 mg/L at the disposal area. The plume extended into the inner estuary with values of 30-40 mg/L. In the side channels, 99^th SSC quantile values of 15 – 35 mg/L were calculated, while 5 – 15 mg/L were found on the adjacent tidal flats.

Figure 14

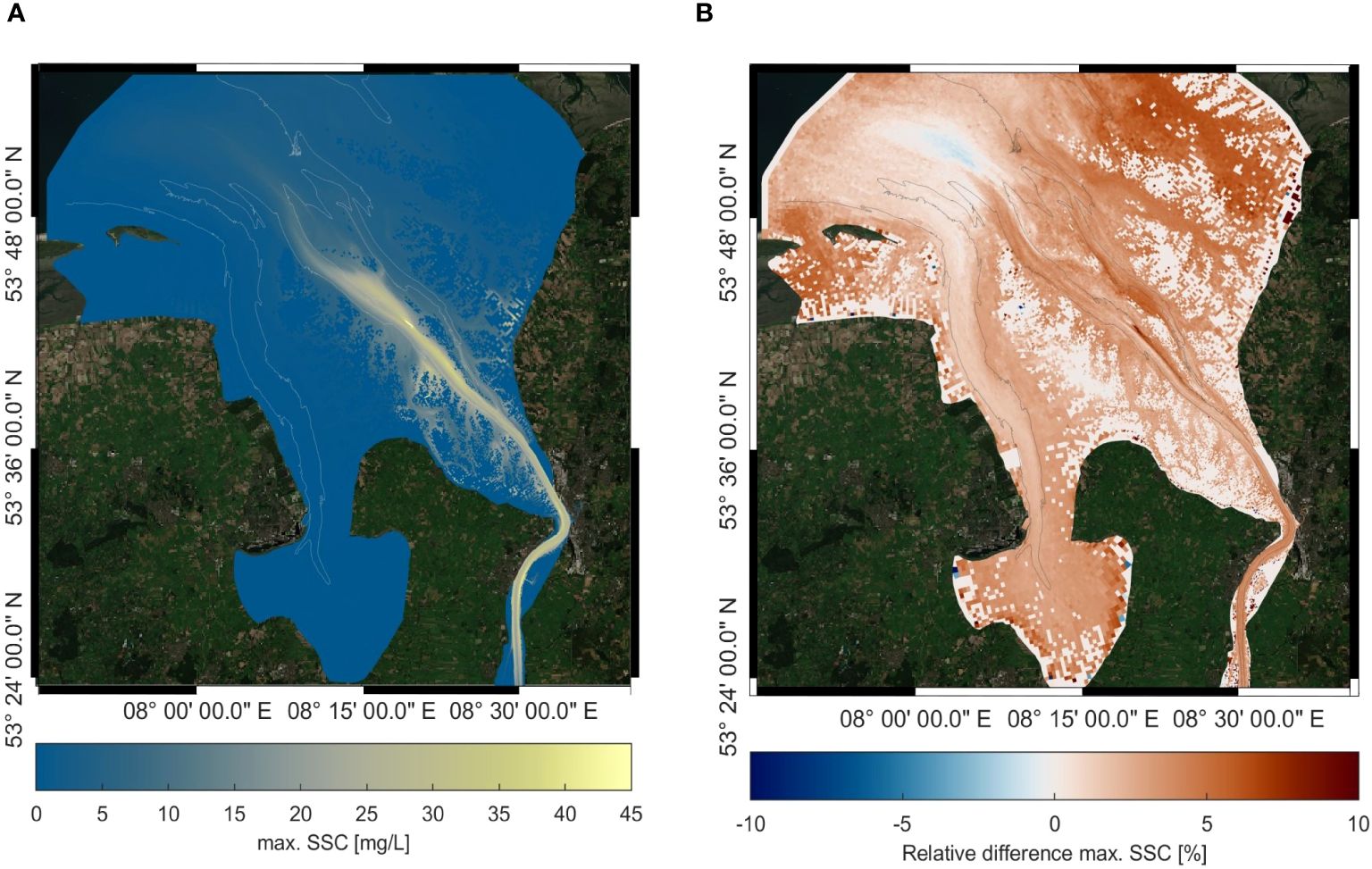
Figure 14. The resulting 99% quantile of SSCs for UnTRIM2 coupled with PROVER-M is given in (A) and the relative difference of the 99% quantile of SSCs with and without coupling with PROVER-M is presented in (B). Sattelite background maps by the European Space Agency (ESA).

In comparison to the control simulation in which all sediment was placed on the bed, the 99^th SSC quantile was increased in the model domain in order of 5%, while locally a 10% increase in peak SSC was reached (Figure 14B). Furthermore, areas with lower values were found in deeper waters (30 km offshore).

Discussion

Insights from the laboratory study

The results gained from the present laboratory study are valuable and verify the general understanding provided in literature. The vertical movement is determined according to the sediment mass. A higher mass results in less time needed until the cloud front hits the bottom (Figure 10) and thus results in a higher mean velocity of the sinking cloud $\bar{w_{c}} = \frac{d h}{d t}$ at. $t = t_{b o t t o m} - 0.1 s$ . The cloud growth during the descent can be linked to the entrainment and is independent from the sediment mass, being in line with Bush et al. (2003) and the results from Ruggaber (2000) for 3-dimensional clouds.

Scaling the sediment cloud disposal is a well described method (Rahimipour and Wilkinson, 1992; Ruggaber, 2000; Wang et al., 2015) but nevertheless has limits. Scaling fine sediments leads to very fine material in the experimental set-up. Cohesive properties, although not considered of highest priority in accurately accounting for the descending behavior, are not included. Determination of the cloud number and the therefore used dimensionless settling velocity after Dietrich (1982) is based on experiments with non-cohesive particles, and may be less accurate outside the test range (Rahimipour and Wilkinson, 1992; Ruggaber, 2000). Zhao et al. (2014) showed that for small cloud numbers (Nc< 0.03), which goes along with small particle diameters of cohesive materials, led to clumps and thus a different behavior of the cloud. By not using dry sediments but a suspension with less than 50% (by weight) solids the formation of clumps is avoided (Zhao et al., 2014) and the released cloud show “thermal-like” characteristics (Ruggaber, 2000). So to reproduce cloud characteristics for very small Nc a strict scaling may not be required (Ruggaber, 2000), but the effects need to be researched further (Lai et al., 2018). Furthermore, no scaling considerations of the water content of the material are known to the authors, but play a major role in imitating the descending behavior of a cloud (Ruggaber, 2000). For the very fine material used in the laboratory experiments, the same water content as in the field leads to a fluid-like disposal material, while dredged material in field applications with a high content of fines has a higher viscosity and lower plasticity, which may result in a different entrainment rate. Additionally, scaling of the disposal makes it challenging to provide a constant flow field of low velocity (~0.04 m/s) in shallow water for disposal investigations.

During the convective descent, the cloud contour (Figure 8) is detected manually with repercussions on the accuracy. Automatic detection of the cloud contour is very sensitive to the contrast between sediment and background and the increased water turbidity over the number of experiments. An additional point is that the sediment cloud occludes itself during propagation. The cloud spreads radially which includes the camera viewing direction. When spreading towards the camera, cloud parts closer to the camera cover a larger area of the image and thus occlude the cloud at the disposal point. During the dynamic collapse, the radial spread (Figure 9) is detected automatically and represented by an equivalent radius. This is justified given the assumption that the sediment spreads equally in all directions under no ambient currents. Despite the oval clamshell opening, following Er et al. (2016) and the laboratory results here, the cloud grows during the convective descent in such a way, that its projection is suggested to be of circular shape. Reaching the circular projection shape depends on the water depth and sinking velocity. Furthermore, the automatic generation of the equivalent radius compensates setup-based occlusion and shadowing in the image.

An important disadvantage of the scaled small-scale model tests is that an assessment of the sediment stripping during the convective descent is a challenge due to the very short disposal time (< 1 s) and the shallow water depth (35 cm). This renders it impossible to derive a physics-based stripping formula for the cloud’s descent. Additionally, measurements based on optical backscatter sensors might include inaccuracies due to the material used and scaling effects discussed above.

Assumptions and simplifications of the PROVER-M model

The applied model PROVER-M simplifies the procedure and geometry of descending sediment clouds from dredgers, by assuming one closed volume that descends as a half sphere in a defined time. For instantaneous releases this is an accurate representation, reasonably proven by the laboratory tests and other applications of the model approach in STFATE (Johnson and Fong, 1995). The disposal of a larger volume from a hopper lasting several minutes can be more accurately considered by dividing the total volume into a finite number of n fractions based on the disposal time. The time interval between the sub-disposals can be estimated conservatively (based on the criterion of maximum cumulative sediment stripping) which was 20 s for the set of disposals in the Weser estuary. A different approach was chosen by Er et al. (2016) where the emptying time is dependent on the geometrical dimensions of the vessel, the disposed material and a continuous flow of sediments. Although the approach of dividing the disposed volume into n sub-disposals appears rudimentary, it corresponds to the geometric simplifications of the model, was validated by field measurements (Delo and Burt, 1987; Gundlach et al., 2023) and was considered realistic for STFATE (Johnson and Fong, 1995). In the current version PROVER-M is limited to the instantaneous disposal of material and does not incorporate a dedicated mode for jet disposal.

Focusing on the sediment stripping, the calculation of stripped material and its distribution through the water column are purely parametric and developed by simple considerations that assume a dependency of the stripped material on the entrainment combined with a calibration parameter. Furthermore, some processes causing suspended sediment concentrations in the near field, like the cleaning of a dredger’s loading space after disposal and “reflection” of fine sediments during the impact of the sediment cloud upon the ground (Kraus, 1991; Johnson et al., 1993), are not addressed in the PROVER-M model. Nevertheless, compared to previous models, where the stripped material is based on the descending velocity, the cloud’s surface and a calibration coefficient (US Environmental Protection Agency, 1998) or is even neglected (Er et al., 2016), PROVER-M offers an improved methodology to estimate the overall sediment distribution of disposals. A more physics-based estimation of the stripped sediment is desirable but remains challenging due to the complexity of the processes involved and the lack of a validation basis from the field. Published laboratory experiments, where a small amount of sediment was disposed in large water depths (Zhao et al., 2014; Lai et al., 2018), cannot be used as calibration data for the PROVER-M application range, as they do not resemble the overall characteristics of fine materials in shallow waters. Ruggaber (2000) concluded that in real-world applications 2 -21% of the disposed material may be stripped, based on laboratory investigations under deep water conditions. Published field measurements report a sediment loss of 1-5% within 30 m of water depth (Truitt, 1988) which gives an indication for the order of magnitude. However, a high-resolution database for deriving more accurate process-based equations for the sediment stripping is missing and rather motivates sophisticated field experiments to acquire crucial data of inherent transport and deposition processes.

The process of flocculation of the disposed sediment is not included. This limitation is considered justifiable for two reasons. First, the disposed sediment is already flocculated during transportation in the dredging vessel and a higher individual settling velocity is entered accordingly in the PROVER-M material mask. Second, and more important, the temporal scale of the active disposal is too short and highly dynamic (including strongly induced physical shear) most likely preventing flocculation in the dumping phases. It is assumed that flocculation of the disposed cohesive sediment starts to be important after the active behavior ends, as soon as the sediment is transported passively. The individual settling velocity is adjusted internally when hindered settling occurs, according to the method of Johnson and Fong (1995).

PROVER-M case studies

The simulations of varying model input illustrate both model dependencies and effects of ambient conditions and disposed material composition on the distribution of sediments in coastal waters. Depending on the output/cloud parameter, a correlation to an input parameter can be seen. In the case of the ambient velocity, this relationship is based on the definition of dynamic behavior, since the cloud movement becomes passive more quickly with strong currents. The same applies to the relationship between the percentage of stripped material and the water depth. The reason for this is that the amount of stripped material is calculated by PROVER-M for each time step during the convective descent. The amount of stripping is therefore dependent on the descent time, which increases with depth. Given these mathematical implementations of the descent and spreading on the ground, the observed results in Figure 13A are plausible. For Figure 13B, none of the output parameters is solely dependent on one input value. The initial cloud density is higher when the amount of solids is increased, which has a corresponding effect on the cloud density at the end of the dynamic behavior. A higher initial cloud volume will automatically cause a larger initial radius, leading to larger cloud diameters at the end of the dynamic behavior. Both observations are consistent with the expected results. However, the effect of the both input parameters combined (Figure 13B) is more difficult to assess. Thus, non-linear variations of the clouds density, diameter and the stripped sediments shown in Figure 13 indicates, why a mathematical model is needed for accurate calculations.

Comparing the laboratory experiments to the projections of PROVER-M, the overall characteristics of the descending and collapsing cloud are in good agreement (90-95% coefficient of determination). Starting with the beginning of the convective descent phase, the differences between model results and the scaled experiments can be clearly seen, as the cloud leaves the laboratory vessel/barge geometrically distorted ( $l e n g t h \neq w i d t h$ ), while PROVER-M assumes perfect symmetry in the horizontal plain from the start. As the cloud descends and tends to become more symmetrical, this misbalance becomes less prominent. These observations are consistent for all disposed sediment volumes. Regardless of the shape, the descending behavior of the cloud is projected accurate by the model as indicated by the comparable contour lines in Figure 11. During the dynamic collapse, the accuracy of the model projection correlates to the laboratory experiments with a coefficient of determination between 90-95% (Figure 12). The larger the disposed volume, the better the statistical accuracy of the model. However, there is a deviation in the low spreading velocities at the end of the dynamic collapse. In the laboratory experiments, the observed values approached zero from 0.2 m/s within a short distance and at an earlier (for 1235 m³ and 1853 m³) cloud radius. In contrast, the spreading velocity approached zero asymptotically in PROVER-M. The difference might be caused by a limited representation of a process in the model for low spreading velocities of large sediment clouds with a high water content, which becomes increasingly relevant below a critical spreading velocity. A more prominent role of the turbulence component under the given conditions is arguable. However, a physically based correction of the relevant dissipative components in the model source code requires further experiments and investigations. For this reason, a user-defined critical velocity threshold (expert system) has been defined in PROVER-M that stops the simulation at a critical spreading velocity, until missing processes are identified and added to the model. For applications in open water under prototype conditions, it becomes less relevant, as ambient currents (higher than 0.2 m/s) will become the main driver for spreading and stop the simulation before the critical velocity threshold is reached.

As shown for the case study of the Weser estuary, the integration of PROVER-M into the UnTRIM2/SediMorph model significantly impacts the results for local and regional sediment transport processes in the far-field model. The results of PROVER-M are very sensitive to the ambient and disposal conditions. For the stripped material, the results showed a considerable range, with a minimum value of 1.26% and a maximum value that was more than seven times the minimum value (8.96%). Here, especially the water depth and ambient currents are decisive, which is in line with the conclusions of Lai et al. (2018). Apart from the ambient conditions, the stripping coefficient is an important calibration parameter, as it influences the amount of stripped material linearly. For presenting the resulting sediment distribution, the 99% quantile of the SSC was chosen due to its direct dependency on the sediment stripping and its illustrative character. Accordingly, the spatial effect of taking PROVER-M into account is clearly shown in Figures 14A, B. The increased SSC was mainly visible in the main channel of the Outer Weser but extended over the entire model domain. Even though the disposal area was located in the tidal channel, where disposed material is highly likely to be eroded and transported even if it is fully placed on the bottom, a comparison with the simulations including PROVER-M most plausibly revealed increased max. SSC values by up to 10%. Even though these results should be further validated by in-situ-measurements, this indicates the potential advantages that can be gained by coupling a far-field model with PROVER-M. Apart from the limitations linked to the sediment stripping in PROVER-M discussed before, an important limitation is the consideration of the bottom cloud in the far-field model. Far-field models often cannot horizontally and vertically resolve the disposed sediment cloud above the bed, nor are they able to simulate the high density gradients between bottom cloud and ambient water and the resulting effects on mixing and current velocities. Thus, the bottom cloud is considered as bottom material. This leads to a different consideration of the bottom cloud in the transport of disposed material over time and potentially in the spatial effect, where disposed material might be transported not as far, as it would occur in reality. An increased stripping factor could compensate this as a work around. This again underlines the necessity of calibration measurements from the field.

Currently, PROVER-M is coupled offline to a far-field model. Potentially, feedback between the two models could lead to a somewhat increased ambient density, which in turn would reduce the density difference between the deposited material and the ambient water. A reduced density difference would cause the sediment cloud to descend more slowly, resulting in a longer time until the dynamic collapse and, based on the approach used to calculate sediment stripping in PROVER-M, an increased amount of stripping. Although these differences and the increasing or decreasing parameters may be small, the effects could potentiate and become relevant for some applications. However, in the present example, both the time span between depositions and the hydrodynamic activity are large, justifying the offline coupling approach.

Perspective of PROVER-M

Applying a near-field model for the disposal of fine sediments is of advantage when considering sediment distributions and processes near-field (e.g. disposal area management, environmental assessments), or evaluating the far-field impact (i.e. sediment management strategies in estuaries, sediment “feeding” of tidal bays/salt marshes). Depending on the application, either the sediment stripping or the sediment cloud on the bottom are of interest. In contrast to previous models dedicated to simulating the disposal of fine sediments (e.g., STFATE, BSDM), PROVER-M determines and implements additional physics-based processes and is more broadly applicable (for more details, see Gundlach et al., 2023). Due to its open-source character, PROVER-M also has the advantages of being easily accessible and progressing crowd-sourced development. Yet, sophisticated, full-scale field measurements are necessary to provide a valuable basis for a process-based assessment of i.e. sediment stripping, fading of the radial spread and applied calibration parameters such as entrainment and drag, which has been recommended earlier by Johnson and Holliday (1978) and is still valid today. Since these processes are highly dynamic, the repeatability of the measurements is advantageous, hence a setup in real-world experiments with defined (controllable) conditions is recommended.

Conclusion

Findings from novel scaled laboratory experiments were presented used for validation. The open-source near-field model PROVER-M was tested and validated for three sets of disposal simulations. First, the accurate reproduction of the relevant physical processes during disposal was successfully shown by comparing the modeled data with the new laboratory experiments of scaled sediment disposals with a coefficient of determination in the range of 0.9 to 0.95. Secondly, the effects of realistic parameter ranges on the applicability and results of the model were analyzed and evaluated. The results show a strong non-linear and complex dependence of the properties of the disposed plume on the environmental conditions and the composition of the disposed material. The behavior of the dynamic plume is as expected in relation to the individual input parameter, but the combination of influences reveals interesting insights. By combining input parameters of the deposition material and the water depth, the definitions for the application limits of the model were derived. Third, the model was coupled to a far-field model to assess the potential difference and advantage of applying a dedicated near-field model. As shown by the illustrative example using a real set of sediment disposals, a large-scale increase of SSCs (up to 10% for the 99% quantile) was found. This demonstrates the relevance of near-field models for sensitive environmental considerations. The extensive application of PROVER-M in three different settings has proven its practical applicability and benefit for disposal simulations, but has also revealed shortcomings and limitations of the existing model (e.g. purely empirically based sediment detachment). It is recommended to address these limitations by performing field experiments and dedicated measurements to obtain full-scale data for a better understanding of the underlying processes and to clarify open questions in the far-field (model) consideration of disposal impacts.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

JG: Conceptualization, Data curation, Funding acquisition, Investigation, Methodology, Resources, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. MH: Methodology, Software, Visualization, Writing – original draft, Writing – review & editing. AA: Data curation, Investigation, Methodology, Visualization, Writing – original draft, Writing – review & editing. AZ: Conceptualization, Data curation, Methodology, Software, Supervision, Writing – original draft, Writing – review & editing. CJ: Software, Supervision, Writing – original draft, Writing – review & editing. JV: Conceptualization, Funding acquisition, Project administration, Supervision, Writing – review & editing. TS: Conceptualization, Funding acquisition, Project administration, Supervision, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The publication of this article was funded by the Open Access Fund of Leibniz Universität Hannover through the transformed framework agreement -a national, fully open access flat-fee deal -for Germany.

Acknowledgments

The development of the PROVER-M model was funded by the Federal Waterways Engineering and Research Institute (BAW), Germany in Hamburg (2018–2021). The authors would like to acknowledge the importance of the technical discussions we had with Frank Kösters, Holger Weilbeer and Benjamin Fricke from BAW Hamburg during the development of this project. Further, the authors would like to thank Sibelco for supporting this study with the silica flour Silverbond M500. All color maps within this publication are based on scientific color maps (Crameri et al., 2020; Crameri, 2023). Furthermore, we would like to express our thanks to Sarah Brase for the free hand drawing of Figure 1 and René Klein for designing and manufacturing the clamshell bucket of Figure 3.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2024.1416521/full#supplementary-material

References

Aarninkhof S., Luijendijk A. (2010). Safe disposal of dredged material in an environmentally sensitive environment. Port Technol. Int. 47, 39–45.

Google Scholar

Abraham G. (1970). “Round buoyant jet in cross-flow,” in 5th International Conf. Water Pollut. Res. San Francisco, USA (July-August, 1970)

Google Scholar

Baptist M. J., Gerkema T., van Prooijen B. C., van Maren D. S., van Regteren M., Schulz K., et al. (2019). Beneficial use of dredged sediment to enhance salt marsh development by applying a ‘Mud Motor’. Ecol. Eng. 127, 312–323. doi: 10.1016/j.ecoleng.2018.11.019