Ruma Chatterji
John E. Layne- Department of Biological Sciences, University of Cincinnati, Cincinnati, OH, United States
Path integration is the navigational process by which animals construct a memory of a previous location by continuously measuring and summing their movements to form a single home vector pointing to the starting location. It is intrinsically error prone, subject to random errors and, potentially, to systematic errors in either measurement or the summing algorithm. Both types of errors lead to an incorrect vector memory and thus to an error in homing. Because the errors are incurred when animals move, they are theoretically predictable from the movements. We analyzed the behavior of fiddler crabs (Leptuca pugilator) as they performed foraging excursions followed by homing with varying degrees of error. From video recordings we measured body orientations and locations and computed these spatiotemporal path characteristics: duration, distance, turns, bearing and arc sector. These were analyzed for their effect on, separately, the magnitude, and the direction, of crabs’ homing error. The magnitude of the homing error was predicted by arc sector, Δbearing and path length, and several interactions. The direction of the homing error was predicted by interactions including arc sector x Δbearing, arc sector x turns, and Δbearing x turns. Covariance among these factors results in a path that traces a large arc while maintaining body orientation toward the burrow direction and leads to an error with the same clockwise/counterclockwise sign as the arc and the body turns. These results place L. pugilator’s path integration mechanism among others with known systematic errors.
Introduction
Spatial navigation is the integration of sensory information to orient and move from one place to another (Halliday and Slater, 1983; Schone, 1984; Papi, 1992). Many animals across a wide range of taxa use a spatial navigation strategy called path integration (Mittelstaedt and Mittelstaedt, 1980; Etienne and Jeffery, 2004). First postulated by Charles Darwin, the idea was that, like sailors’ dead reckoning, animals could also use distance and direction measurements to locate home from any point on their journey (Darwin, 1873). This was later formally defined by Mittelstaedt and Mittelstaedt (1980) as path integration whereby animals construct a memory of a previously visited location by measuring body rotations and translations and storing this information in memory (Mittelstaedt and Mittelstaedt, 1980). Each new movement is added to the existing vector to create a single, continuously updated memory-stored vector, called the home vector. This allows the animal a straight return home after a sinuous trip. It is a highly useful navigation mechanism as animals can explore new terrain, not requiring previous knowledge of the landscape and, in theory, travel distances without becoming lost. Path integration appears to be universal among animals that have a spatially restricted home or central reference point, including insects (von Frisch, 1967; Wehner and Wehner, 1986; Beugnon and Campan, 1989), arachnids (Mittelstaedt, 1985), crustaceans (Altevogt and Hagen, 1964; Hoffmann, 1984; Zeil, 1998; Layne et al., 2003a, 2003b; Cheng, 2012), birds (Mittelstaedt and Mittelstaedt, 1982; von Saint Paul, 1982; Wiltschko and Wiltschko, 1982), and mammals [(Mittelstaedt and Mittelstaedt, 1980); reviewed in (Etienne and Jeffery, 2004)], including humans (Loomis et al., 1993).
While obviously useful, path integration is also inherently error prone. Errors can arise in the accuracy with which directions and distances are measured, and in the precision of the algorithm for adding new vectors to the current home vector (Etienne et al., 2004). There inevitably will be random estimation errors, but also potentially systematic errors (Benhamou et al., 1990). Because both types of errors are incurred when animals move, they are theoretically predictable from those movements. In this study, we examined the homing errors made by a well-known path integrator, the Atlantic Sand Fiddler Crab, Leptuca pugilator (Bosc, 1802). These are central-place foragers that, at low tide, leave their burrows in the sand to go on short-range excursions to perform activities such as foraging and courtship (Crane, 1975; Zeil and Layne, 2002). They appear to do this using exclusively idiothetic (self-motion) cues (Layne et al., 2003b). The shapes of the crabs’ paths during these excursions range from straight out-and-back to arcs subtending over 180° relative to the burrow. A unique aspect of these excursions is that the crabs tend to align their transverse body axis approximately with their burrow direction throughout, even if an object comes between them (Land and Layne, 1995; Zeil, 1998; Layne et al., 2003a). Though the body thus indicates a general notion of the home direction, it is often out of alignment to a significant degree. Crabs still accurately return home, so the home vector cannot be strictly identical to the body axis. Instead, the crabs know the amount by which their body is out of alignment, and monitor this angle constantly, and it is that which monitors this angle that forms the crabs’ directional reference. It has been proposed that this directional reference is provided by the optokinetic system, and that the eyes better indicate the home vector direction than does the body axis (Chatterji and Layne, 2023). According to this theory, if the eyes are well stabilized the crab will maintain a more accurate home vector than if they are not, i.e., if the eyes “drift” then the home vector will also drift. Fiddler crabs have a robust optokinetic system that stabilizes the eyes against body rotations (Nalbach and Nalbach, 1987; Layne et al., 1997; Land, 2019), and movements that tax the optokinetic system are more likely to produce drift and thus errors in homing. A major portion of these errors may not be random but, rather, directionally biased according to the demands placed on the optokinetic system by the shape of the foraging path.
To test this idea that the structure of foraging paths can predict the type of errors they produce, we analyzed the spatiotemporal structure of fiddler crabs’ foraging excursions. Specifically, we investigated the following path characteristics: length, duration, arc sector, change in crabs’ bearing relative to the burrow, and body turns. We found that, not only can the presence and magnitude of homing errors be predicted, but the shape of the paths can predict the direction in which these errors occur.
Materials and methods
Experiments were conducted on the fiddler crab Leptuca pugilator at the University of Cincinnati, from fall of 2019 through spring of 2023 using animals imported from Beaufort, NC or purchased from livebrineshrimp.com (Oak Hill, FL, USA).
Laboratory setup and experimental design
The main tank was a 1.5-meter diameter stainless steel tank filled to ~25 cm with sand from North Carolina sandflats, a natural habitat of L. pugilator. A pseudo-tidal rhythm of brackish water created with Instant Ocean salt (salinity of 25 ppt as measured by a refractometer) was pumped in and out of the arena every ~6.2 hours, and the lab temperature was maintained at 26°C. To simulate circadian rhythms, a 12:12 hour day/night ratio was implemented. Fidder crabs were fed once every other day with crushed fish flakes (Tetra Cichlid Diet).
To track foraging excursions the left and right fronto-lateral tips of the carapace were marked with white reflective paint. Two to six painted animals were placed into the experimental arena, of which only one or two actively foraged at a time, while the others were underground. The arena consisted of a four-sided box (60 cm × 40 cm × 10 cm) constructed on top of the sand in the main tank, the walls of which were made of Sintra®. Vertical black and white stripes alternating with a spatial period of ~10 cm created visual contrast in the surround. Fiddler crabs were acclimated to the experimental arena for several hours, and acclimation was considered adequate when crabs exhibited natural behaviors such as making their own burrows, participating in courtship and burrow defense, and embarking on foraging excursions. Acclimated crabs making foraging excursions at pseudo low tide were continuously recorded with a Sony HDR-HC1 camcorder during both day and night (infrared nighttime illumination was achieved using the “night-shot” mode in the camera setting). Both sexes were used indiscriminately, with the exception of gravid females, and only adult fiddler crabs (with a minimum size of 1 cm carapace width) were used in this study.
Data analysis
Foraging excursions (n=70) were digitized using custom MATLAB code (Layne, 2023). Each excursion was clicked by hand at 10-frame intervals (three times per second). On every 10th frame the painted left and right fronto-lateral points of the carapace were clicked and the x-y data thus acquired were used to compute the path characteristics used to model homing error.
The section of the path within two body lengths of the burrow was trimmed to avoid computing spuriously large angles, and because crabs are often able to see the burrow entrance from that distance making path integration superfluous. The path characteristics used to model homing error were computed using the portion of the path between this (trimmed) departure from the burrow and the point at which the crabs clearly began homing. This homing point was identified by the cessation of feeding and a more-or-less straight journey of approximately the correct distance to the burrow and ending either at the burrow or in an abrupt, large-angle change in direction, the beginning of the search for the burrow entrance.
In order to compare spatial characteristics between natural paths all of them were resampled to a uniform step length. This was done by computing the center of the crab’s carapace as the midpoint between the two clicked lateral points, and computing the cumulative distance traveled as the cumulative sum of the distances between successive center points. Plotting the body center x- and y-coordinates (ordinate) against cumulative distance traveled (abscissa), the latter of which increases monotonically, the body center x- and y-coordinates were resampled at regular distance intervals (0.05 body width) by linear interpolation. The length of the path was then recalculated from the new x-y coordinates, and this was always shorter than the original length due to the smoothing of digitizing noise. The resampling process was repeated until a new, re-calculated path length decreased less than 0.5 body width compared to path length from the previous resampling iteration.
Foraging paths were normalized to the clockwise direction. Because crabs venture away from their burrow by moving laterally, they face either clockwise or counterclockwise on a radius connecting them to their burrow entrance. Those facing counterclockwise had their paths flipped around the y-axis by multiplying their x-coordinates by -1 (with the burrow at x = 0, y = 0).
The body orientation of the crabs was computed using the original, non-resampled data, from the slope of the line connecting the two carapace points. It is an angle relative to a coordinate system established by the video frame (see Figure 1 inset). Body orientation was then subject to the same resampling procedure as body location (above). The path characteristic Turns is this vector of values differentiated (clockwise negative, counterclockwise positive) and summed.
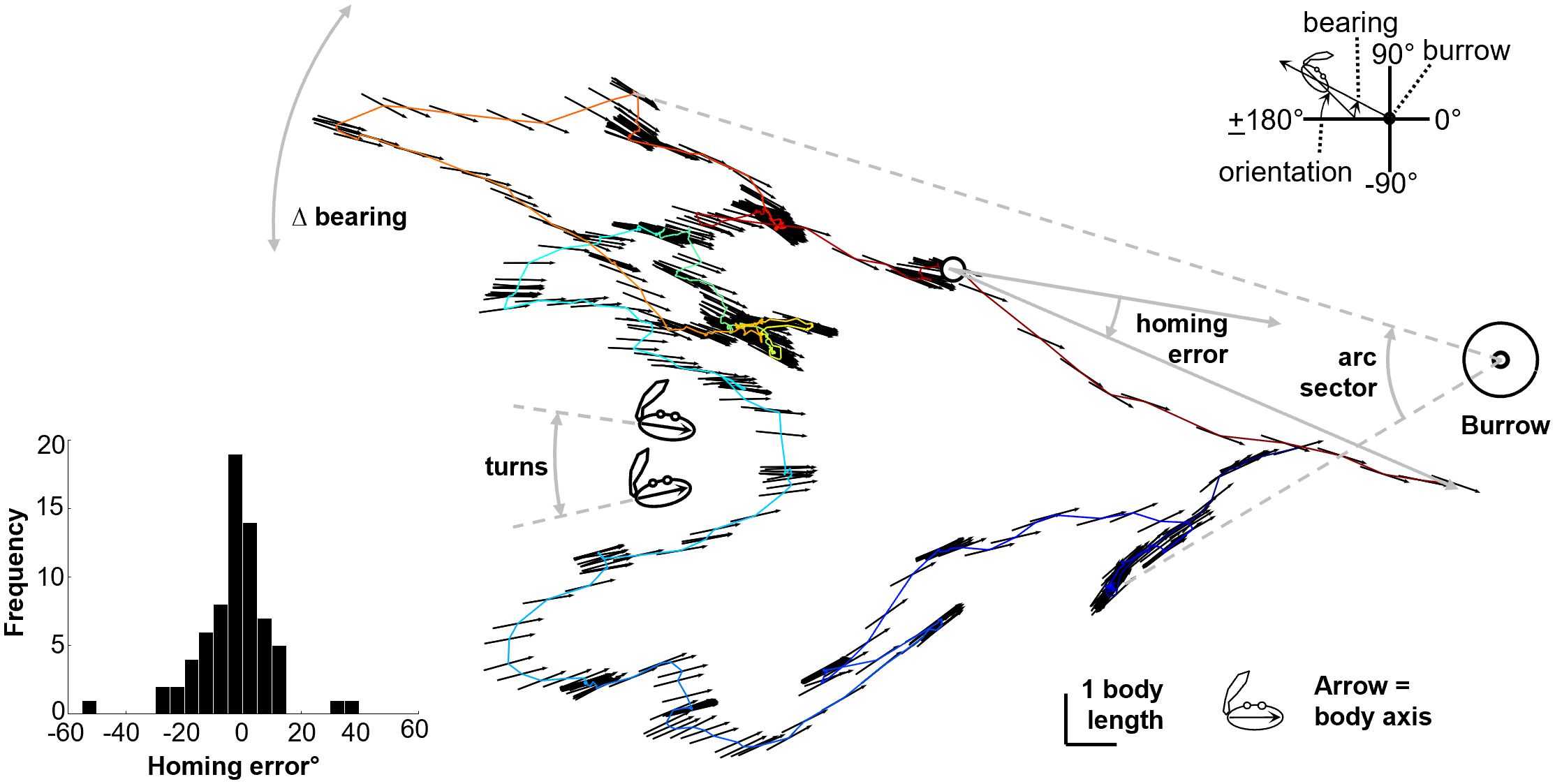
Figure 1 Example path illustrating the transverse body axis of the crab with the arrow pointing toward the ‘homeward’ side and defining the angular path characteristics. Top right inset: definition of “bearing” and “body orientation” angles. Bottom left inset: a histogram of the homing errors from the 70 foraging excursions. See Supplementary Material for video.
The bearing of the crabs was computed using the resampled body center points, from the slope of the line connecting the body center with the burrow (see Figure 1 inset); like body orientation it is an angle in frame-based coordinates. The path characteristic ΔBearing is this vector of values differentiated and summed, as with body Turns.
The path characteristic Arc sector is the angle subtending the counterclockwise-most to the clockwise-most bearing of the crabs’ path, and is assigned a direction (clockwise negative, counterclockwise positive) according to which of these occurs earlier in the foraging excursion (see Figure 1).
We conducted a stepwise multiple linear regression analysis with interactions on the relationship between homing errors and the magnitudes and directions of path characteristics. To determine the overall significance of the multiple linear regression, an ANOVA test was conducted using a significance alpha value of 0.05. Data analysis was conducted using the Data Analysis ToolPak in Excel (Version 2402).
Results
We recorded 70 foraging excursions that ended with homing error magnitudes from 0° to ~55° (Figures 1, 2). From these we computed the following spatiotemporal characteristics: arc sector, Δbearing, turns, path length and path time. We created a multiple regression model of the relationship between the absolute magnitude of these characteristics and the absolute magnitude of the crabs’ homing errors. This model showed that arc sector (p<0.0001), Δbearing (p<0.0001), and path length (p=0.0002) were all significant predictors of homing error magnitude. In addition, interactions between several characteristics had significant predictive effect: arc sector x Δbearing (p=0.005), arc sector x path time (p=0.020), Δbearing x turns (p<0.0001), Δbearing x path time (p=0.044), turns x path length (p<0.0001) (Figure 3A and Table 1).
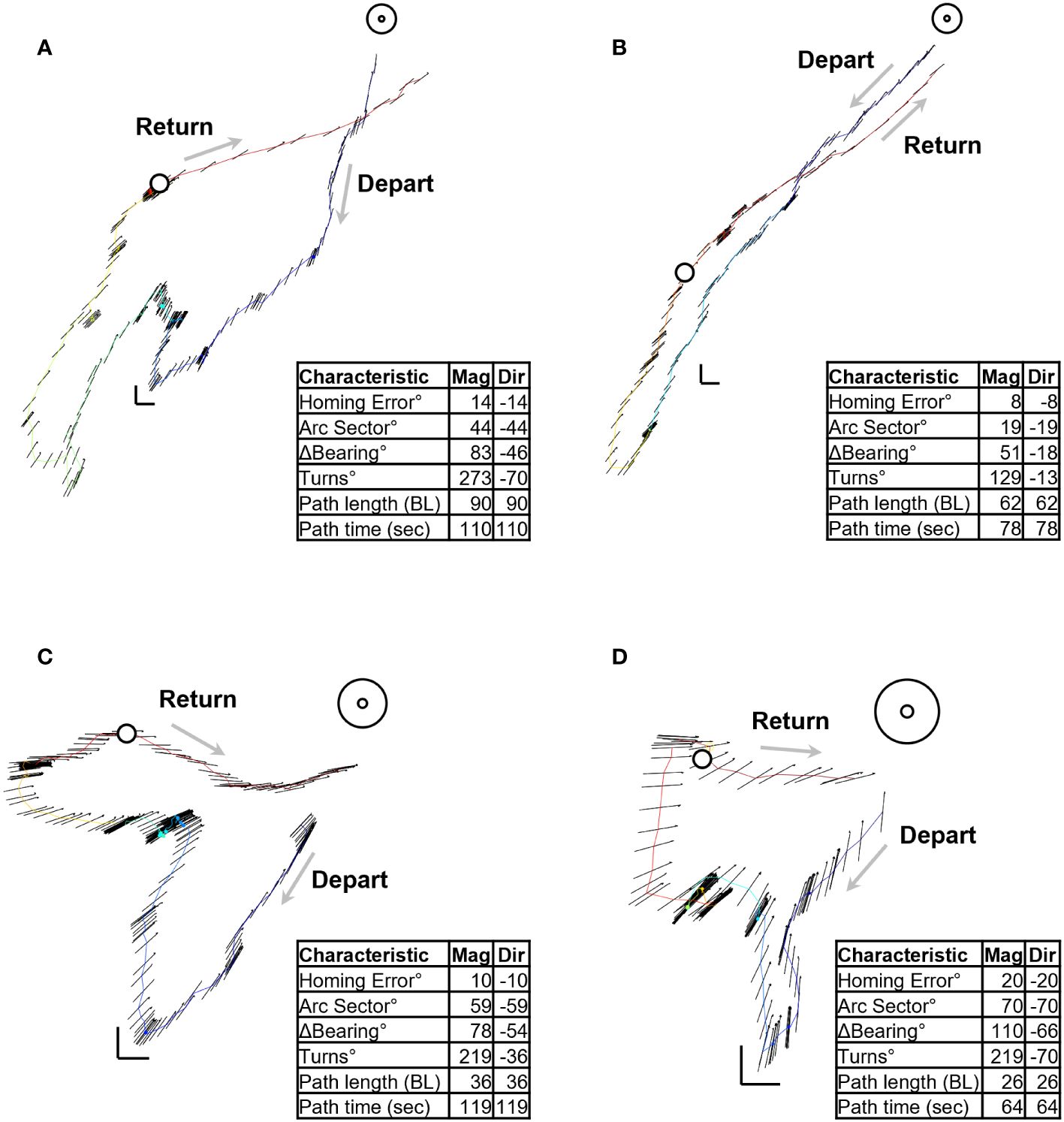
Figure 2 Four examples of digitized foraging excursions. Table in each panel (A–D) lists the magnitude and direction of the spatiotemporal characteristics. Open circle on each path indicates the beginning of the homeward journey. Color gradient indicates the direction of progress along the path, beginning with blue and ending in red.
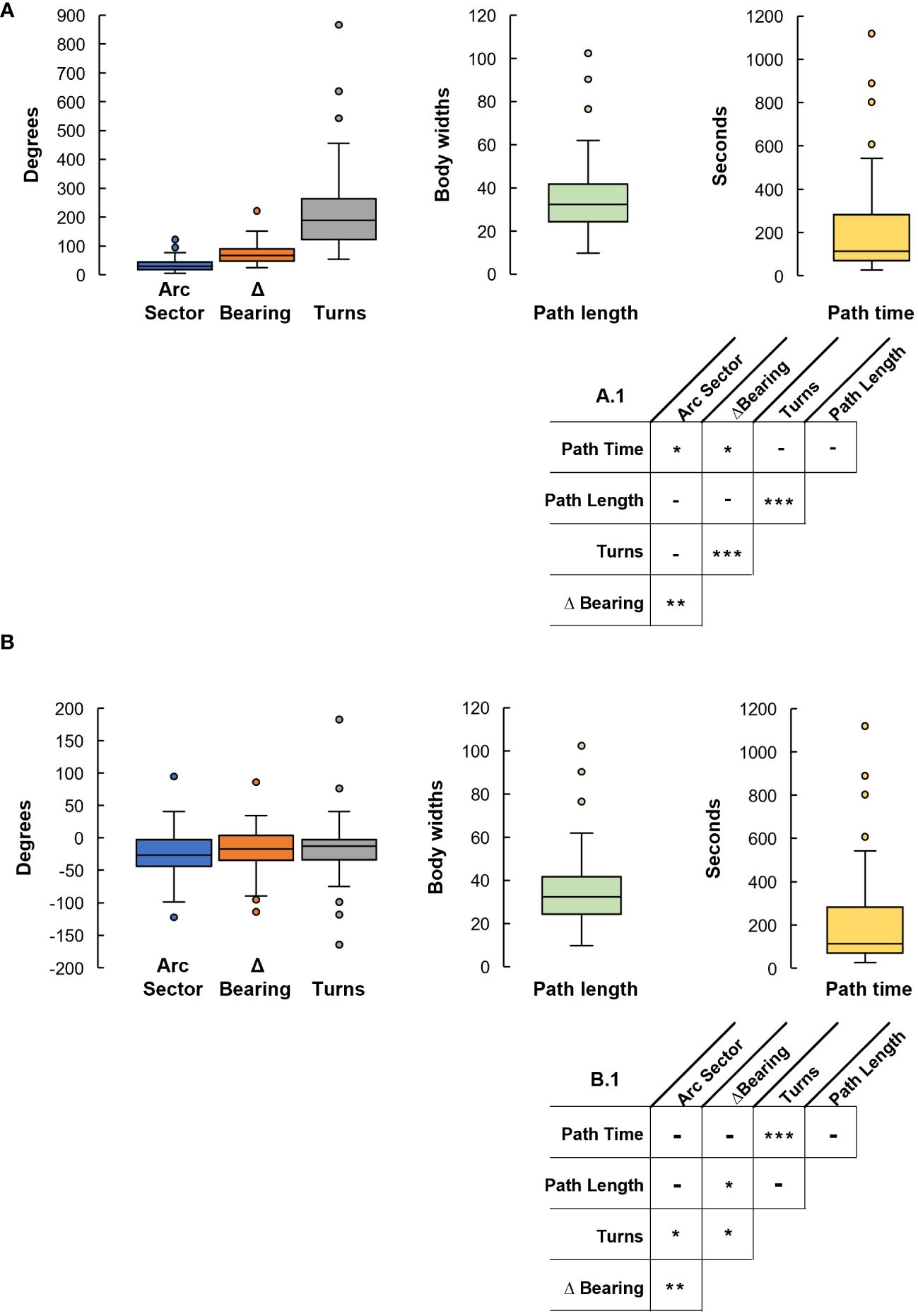
Figure 3 Results of the multiple regression analysis. (A) Box plots illustrating the magnitude of each spatiotemporal characteristic (n=70). (A.1) Interactions between the spatiotemporal magnitude characteristics. (B) Box plots of the signed spatiotemporal characteristics (n=70). (B.1) Interactions of the direction of the spatiotemporal characteristics. [* p<0.05; ** p<0.01; *** p<0.001].
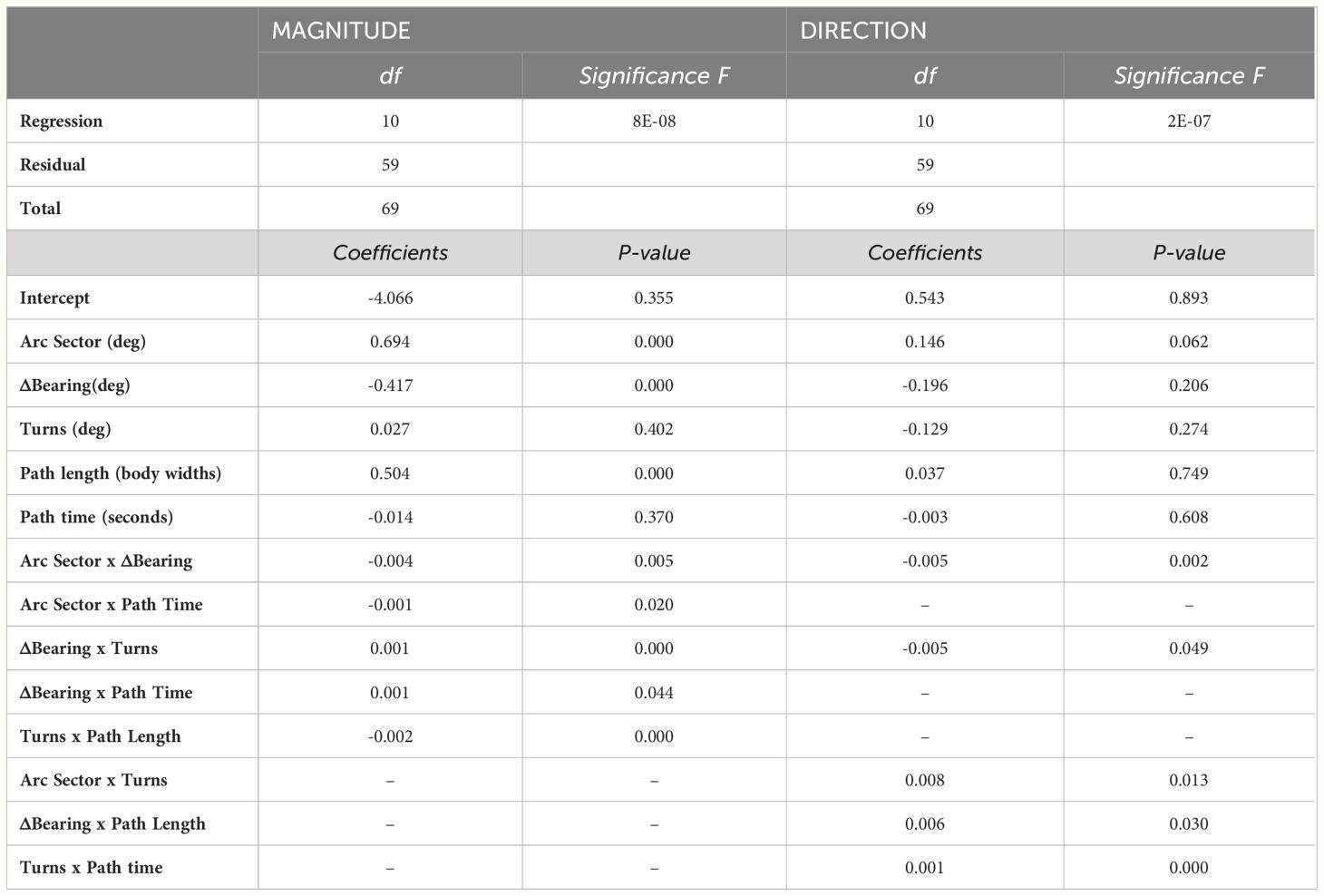
Table 1 Results of two multiple linear regression models (magnitude and direction): path characteristics as predictors of homing error.
We created a second multiple regression model to determine which (signed) spatiotemporal characteristics predicted the magnitude and direction of the crabs’ homing error. For this, the homing error and those characteristics that are angular in nature all had a clockwise = negative, counterclockwise = positive convention. We found evidence of a systematic error, in that interactions between several characteristics had significant predictive effect: arc sector x Δbearing (p=0.002), arc sector x turns (p=0.013), Δbearing x turns (p=0.049), Δbearing x path length (p=0.030), and turns x time (p<0.0001) (Figure 3B and Table 1).
Discussion
In path integration animals measure their translations and rotations and continuously sum these to form a single memory-stored home vector (Mittelstaedt and Mittelstaedt, 1980). As with any biological mechanism path integration is not perfect, and is inherently error prone, especially if the sensory information used for the measurements is idiothetic (Benhamou et al., 1990), as is the case for the study species, Leptuca pugilator (Layne et al., 2003b). These errors can be random which is demonstrated by an arbitrary scatter in homing errors (Benhamou et al., 1990; Maurer and Séguinot, 1995; Seguinot et al., 1998). The errors can also be systematic in nature and can accrue in a directional pattern. Such errors can arise where there is a consistent under or overestimation of translation or rotations and are demonstrated by consistent homing error directions (Sommer and Wehner, 2004).
In this study, we analyzed the natural foraging excursions of L. pugilator to determine the degree to which homing errors are random or systematic. Using the body locations and orientations of the crab, we analyzed a variety of path characteristics: arc sector, path length and duration, body turns and changes in the bearing of the animal relative to the burrow. These characteristics and associated body movements comprise the size and shape of the paths and they are causative of the errors that are produced. As such, the homing errors incurred can be predicted by the structure of the path.
We found evidence that homing errors incurred by L. pugilator during path integration are both random and systematic in nature. We first analyzed the relationship between the absolute magnitude of the above-mentioned path characteristics and the absolute magnitude of homing errors (which ranged from 0° to ~55°). Homing errors analyzed this way will include those arising from both random and systematic measurement errors. The results show a strong relationship between the magnitudes of the error and several path characteristics. For example, the longer the path and the larger the arc sector, the larger the homing error incurred. To determine what portion of these errors were specifically systematic we ran a second test, maintaining the signed direction of the path characteristics and homing errors, and this revealed several positive correlations. For example, there was a significant relationship between homing error and the interaction between arc sector and body turns. Thus, if the path consisted of a large, circumferential arc in the clockwise (negative, by our convention) direction, the homing error direction was also negative. Such errors generated in a direction-dependent way persist if clockwise and counterclockwise turns are not balanced (Müller and Wehner, 1988; Seguinot et al., 1993), as they are not when forming an arc.
This trend has been observed in other animals, such as in desert ants, where systematic errors generated during the outbound path resulted in a homing error that reflected the cumulative sum of the turn angles (Müller and Wehner, 1988). Systematic homing errors have also been observed from as early as 1957 in honeybees (Bisetzky, 1957) and are present in a wide range of taxa, from hamsters (Seguinot et al., 1993), spiders (Goerner, 1958), dogs and humans [ (Seguinot et al., 1998); reviewed in (Etienne and Jeffery, 2004)]. The errors indicated in all these cases are strikingly similar in that they are all “inward”, that is, they have the same sign as the cumulative turns in the path. This consistency throughout such a wide variety of taxa suggests that the algorithm for path integration has evolved in a similar manner among different groups (Etienne and Jeffery, 2004). Our results place L. pugilator among the disparate taxa exhibiting this type of systematic error, though very few of these have been examined for path-related sources of error. One exception is the desert ant (Cataglyphis bicolor), in which it has been demonstrated that cumulative turns and longer distances during foraging excursions predict error directions and wider search patterns, respectively, when returning home (Wehner and Wehner, 1986; Müller and Wehner, 1988; Merkle et al., 2006). Similarly, in humans, increasing distance (Stangl et al., 2020) and unbalanced turns account for systematic biases (Qi and Mou, 2023).
The systematic errors and their apparent path-related causes shown here are consistent with our theory of how this fiddler crab retains the direction of its home vector. While L. pugilator moves circumferentially around the burrow, the direction of home relative to its body orientation can be read out from, and is possibly maintained by, the neural-behavioral mechanism controlling eye stability, the optokinetic system (Chatterji and Layne, 2023). As this system rotates the eyes to counter body rotations, the horizontal eye-body angle becomes the basis of the crabs’ directional reference for the home vector. If the optokinetic system functions efficiently, the only eye movements are saccadic updates of their orientation as the crab moves around an arc, and these are accounted for by the path integrator. However, if the eyes “drift” then the directional reference will also drift, thereby leading to an error in homing. The crabs’ tendency to align their body with the burrow direction as they form an arc necessitates body rotations in one direction. This behavior places demands on the optokinetic system in a directionally biased way, and this can lead to directionally biased drift. One might even speculate that maintaining the eye-burrow relationship is the reason the crabs align with the burrow in the first place. Overall, our research shows that much of the error that L. pugilator incurs during path integration is systematic in nature and is consistent with the idea that their optokinetic system function ultimately determines the animals’ homing success.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding authors.
Ethics statement
The manuscript presents research on animals that do not require ethical approval for their study.
Author contributions
RC: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Validation, Visualization, Writing – original draft, Writing – review & editing. JL: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was supported by the University of Cincinnati-Wieman-Wendell-Benedict Research Award to RC.
Acknowledgments
We would like to thank Mildreth Diaz Perez, Prashanth Prabhakar, Joy Oakes, and Tyonna Mitchell for their assistance with data collection. We would also like to extend our gratitude to Matthew Hodanbosi, Stephanie Rollmann, and Dieter Vanderelst for their assistance and discussion on statistical analyses/presentation.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2024.1406753/full#supplementary-material
References
Altevogt R., Hagen H.-O. V. (1964). Über die orientierung von uca tangeri eydoux im freiland. Z. für Morphologie und Ökologie der Tiere 10, 636–656. doi: 10.1007/BF00407731
Benhamou S., Sauvé J.-P., Bovet P. (1990). Spatial memory in large scale movements: Efficiency and limitation of the egocentric coding process. J. Theor. Biol. 145, 1–12. doi: 10.1016/S0022-5193(05)80531-4
Beugnon G., Campan R. (1989). Homing in the field cricket, gryllus campestris. J. lnsect Behav. 2, 187–198. doi: 10.1007/BF01053291
Bosc L. A. G. (1802). “Histoire naturelle des crustaces,” in Histoire naturelle de buffon. Paris: R. R. Castel.
Chatterji R., Layne J. E. (2023). Eye movement reflexes indicate the homing direction in the path-integrating fiddler crab, uca pugilator. J. Mar. Sci. Eng. 11. doi: 10.3390/jmse11091719
Cheng K. (2012). ““Arthropod navigation ants, bees, crabs, spiders finding their way,”,” in The Oxford Handbook of Comparative Cognition (New York, USA: Oxford University Press). doi: 10.1093/oxfordhb/9780195392661.013.0019
Crane J. (1975). Fiddler Crabs of the World: Ocypididae: Genus Uca (Princeton, USA: Princeton University Press). doi: 10.1515/9781400867936
Etienne A. S., Jeffery K. J. (2004). Path integration in mammals. Hippocampus 14, 180–192. doi: 10.1002/hipo.10173
Etienne A. S., Maurer R., Boulens V., Levy A., Rowe T. (2004). Resetting the path integrator: A basic condition for route-based navigation. J. Exp. Biol. 207, 1491–1508. doi: 10.1242/jeb.00906
Goerner P. (1958). Die optische und kinästhetische Orientierung der Trichterspinne Agelena labyrinthica. Z. für vergleichende Physiologie 41, 111–153. doi: 10.1007/BF00345583
Halliday T. R., Slater P. J. B. (Eds.) (1983). Animal Behavior, Volume 1: Causes and Effects (New York City, USA: Blackwell Science Ltd).
Hoffmann G. (1984). Orientation behaviour of the desert woodlouse Hemilepistus reaumuri: Adaptations to ecological and physiological problems. Symposium Zoological Soc. London 53, 405–422. doi: 10.1007/BF00293211
Land M. (2019). Eye movements in man and other animals. Vision Res. 162, 1–7. doi: 10.1016/j.visres.2019.06.004
Land M., Layne J. (1995). The visual control of behaviour in fiddler crabs II. Tracking control systems in courtship and defence. J. Comp. Physiol. A 177, 91–103. doi: 10.1007/BF00243401
Layne J. E., Barnes W. J. P., Duncan L. M. J. (2003a). Mechanisms of homing in the fiddler crab Uca rapax 1. Spatial and temporal characteristics of a system of small-scale navigation. J. Exp. Biol. 206, 4413–4423. doi: 10.1242/jeb.00660
Layne J. E., Barnes W. J. P., Duncan L. M. J. (2003b). Mechanisms of homing in the fiddler crab Uca rapax 2. Information sources and frame of reference for a path integration system. J. Exp. Biol. 206, 4425–4442. doi: 10.1242/jeb.00661
Layne J. E., Wicklein M., Dodge F. A., Barlow R. B. (1997). Prediction of maximum allowable retinal slip speed in the fiddler crab, uca pugilator. Biol. Bull. 193, 202–203. doi: 10.1086/BBLv193n2p202
Loomis J. M., Klatzky R. L., Golledge R. G., Cicinelli J. G., Pellegrino J. W., Fry P. A. (1993). Nonvisual navigation by blind and sighted: Assessment of path integration ability. J. Exp. Psychol. Gen. 122, 73–91. doi: 10.1037/0096-3445.122.1.73
Maurer R., Séguinot V. (1995). What is modelling for? a critical review of the models of path integration. J. Theor. Biol. 175, 457–475. doi: 10.1006/jtbi.1995.0154
Merkle T., Knaden M., Wehner R. (2006). Uncertainty about nest position influences systematic search strategies in desert ants. J. Exp. Biol. 209, 3545–3549. doi: 10.1242/jeb.02395
Mittelstaedt H. (1985). “Analytical cybernetics of spider navigation,” in Neurobiology of Arachnids (Springer Berlin Heidelberg, Berlin, Heidelberg), 298–316. doi: 10.1007/978-3-642-70348-5_15
Mittelstaedt H., Mittelstaedt M.-L. (1982). “Homing by path integration,” in Avian navigation (Springer-Verlag, Berlin), 290–297.
Mittelstaedt M. L., Mittelstaedt H. (1980). Homing by path integration in a mammal. Naturwissenschaften 67, 566–567. doi: 10.1007/BF00450672
Müller M., Wehner R. (1988). Path integration in desert ants, cataglyphis fortis. Proc. Natl. Acad. Sci. 85, 5287–5290. doi: 10.1073/pnas.85.14.5287
Nalbach H.-O., Nalbach G. (1987). Distribution of optokinetic sensitivity over the eye of crabs: its relation to habitat and possible role in flow-field analysis. J. Comp. Physiol. A 160, 127–135. doi: 10.1007/BF00613448
Papi F. (1992). Animal Homing. Ed. Papi F. (Chapman and Hall, London, United Kingdom: Springer). doi: 10.1007/978-94-011-1588-9
Qi Y., Mou W. (2023). Sources of systematic errors in human path integration. J. Exp. Psychol. Hum. Percept. Perform. 49, 197–225. doi: 10.1037/xhp0001076
Schone H. (1984). Spatial Orientation: The Spatial Control of Behaviour in Animals and Man (Princeton, USA: Princeton University Press). doi: 10.1515/9781400856848
Seguinot V., Cattet J., Benhamou S. (1998). Path integration in dogs. Anim. Behav. 55, 787–797. doi: 10.1006/anbe.1997.0662
Seguinot V., Maurer R., Etienne A. S. (1993). Dead reckoning in a small mammal: the evaluation of distance. J. Comp. Physiol. A 173, 103–113. doi: 10.1007/BF00209622
Sommer S., Wehner R. (2004). The ant’s estimation of distance travelled: Experiments with desert ants, Cataglyphis fortis. J. Comp. Physiol. A Neuroethol Sens Neural Behav. Physiol. 190, 1–6. doi: 10.1007/s00359-003-0465-4
Stangl M., Kanitscheider I., Riemer M., Fiete I., Wolbers T. (2020). Sources of path integration error in young and aging humans. Nat. Commun. 11. doi: 10.1038/s41467-020-15805-9
von Frisch K. (1967). The Dance Language and Orientation of Bees (Cambridge, USA: Harvard University Press). doi: 10.4159/harvard.9780674418776
von Saint Paul U. I. (1982). “Do geese use path integration for walking home?,” in Avian navigation. (Berlin; Heidelberg; New York: Springer), 296–307.
Wehner R., Wehner S. (1986). Path Integration in Desert Ants. Approaching a long-standing puzzle in insect navigation. Ital. J. Zoology 20, 309–331. doi: 10.1080/00269786
Wiltschko W., Wiltschko R. (1982). “The role of outward journey information in the orientation of homing pigeons,” in Avian navigation. 239–252. doi: 10.1007/978-3-642-68616-0_24
Zeil J. (1998). Homing in fiddler crabs (Uca lactea annulipes and Uca vomeris: Ocypodidae). J. Comp. Physiol. A 183, 367–377. doi: 10.1007/s003590050263
Keywords: navigation, path integration, fiddler crab, homing errors, home vector, systematic errors
Citation: Chatterji R and Layne JE (2024) Spatiotemporal structure of foraging and path integration errors by fiddler crabs, Leptuca pugilator. Front. Mar. Sci. 11:1406753. doi: 10.3389/fmars.2024.1406753
Received: 25 March 2024; Accepted: 16 May 2024;
Published: 28 May 2024.
Edited by:
Kareen E. Schnabel, National Institute of Water and Atmospheric Research (NIWA), New ZealandReviewed by:
Jose Maria Landeira, Instituto de Oceanografía y Cambio Global (IOCAG), SpainRaül Triay-Portella, University of Las Palmas de Gran Canaria, Spain
Copyright © 2024 Chatterji and Layne. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ruma Chatterji, chattera@mail.uc.edu; John E. Layne, john.layne@uc.edu