Collaborative communication-based ocean observation research with heterogeneous unmanned surface vessels

Unmanned surface vehicles (USVs) are crucial in ensuring maritime safety and observation, attracting widespread attention and research. However, a single USV exhibits limited performance and cannot effectively observe complex marine environments. In contrast, clusters of USVs can collaborate to execute complex maritime tasks, thereby enhancing the overall operational efficiency. USVs typically form heterogeneous clusters by combining vehicles with varying maneuverabilities and communication network capabilities. This has sparked an increased interest in cooperative communication research within heterogeneous USV clusters. The heterogeneous USVs discussed in this paper share the same dynamic model; however, they differ in dynamic parameters and communication capabilities. First, this study establishes a three-degree-of-freedom motion mathematical model for an underdriven USV considering environmental interference. It estimates the dynamic parameters of four USVs and evaluates their communication abilities, laying the foundation for researching the cooperative control of heterogeneous USV clusters and their application in Ocean Observation. Next, the communication capability of the USVs is assessed by studying the communication mode and signal transmission loss within the USV clusters. This study investigates the problem of cooperative communication in USV cluster formation, starting with the communication delay of USV clusters under a directed switching topology. Finally, a coherent formation controller is designed under a switching communication topology to address the dynamic transformation of communication topologies within heterogeneous USV clusters. This verifies that heterogeneous USV clusters can seamlessly form and maintain formation shapes during communication topology transformations through formation simulation experiments involving four heterogeneous USVs was 22% higher than that of dispersed control topology structures. This study provides a solid foundation for future investigations into the cooperative control of heterogeneous USV clusters and their applications in marine observations.

1 Introduction

Unmanned surface vehicles (USVs) are pivotal tools for ocean exploration and are currently garnering global attention. In December 2018, the International Maritime Organization (IMO) Maritime Safety Committee approved a framework and methodology for a regulatory scoping exercise for autonomous surface vessels at sea during its 100th session (Schröder-Hinrichs et al., 2019). Owing to its capability to conduct autonomous navigation at sea, USVs offer advantages such as high autonomy, broad operating range, effective concealment, and substantial reductions in labour and maintenance costs. Equipped with various technologies, USVs can autonomously execute a diverse range of maritime tasks, significantly enhancing task execution efficiency (Zhang et al., 2019). Consequently, USVs are considered crucial platforms for future maritime operations. In addition, the technological advancements in this field are significant for the exploration, development, and protection of oceans.

When a USV performs autonomous navigation and operation at sea, the motion is characterised by typical underdrive, non-linearity, uncertainty, multiple constraints, unpredictable state, and limited communication (Gu et al., 2019). Furthermore, the superposition of multiple factors makes it difficult to control the USV, and the operating environment at sea is complex, with relatively severe perturbations of wind, waves, and currents, limited communication, and relatively complicated task allocation problems. The cooperative control of USV clusters under communication constraints also faces significant challenges (Wang et al., 2020).

USV clusters are connected via the communication network to form a whole, and the communication mode determines the control mode between clusters to a certain extent. The interaction of USV information can be divided into three types (Xie et al., 2021): centralised, decentralised, and distributed communications.

Centralised communication (Sun et al., 2022) is a multi-intelligence body cluster with a control centre that designs the global control protocol and communicates with all other intelligences to exchange information. Thus, the performance of centralised communication has a natural superiority, is easy to implement, and is currently the most commonly used communication method in cluster research. However, centralised communication has a high computational cost and poor robustness, is not easily scalable, and has poor responsiveness to environmental changes.

Decentralised communication (Chainho et al., 2017) means that each intelligence has a controller that can communicate directly with other intelligences, and each intelligence autonomously processes information and makes plans and decisions. This depends on local information, which reduces the computational burden and complexity; however, the lack of communication and cooperation between intelligences leads to a lower synergy efficiency and does not ensure the realisation of global goals.

Distributed communication (Lim et al., 2008) differs from centralised and decentralised communication and is a type of communication between the two. Intelligent bodies and adjacent intelligent bodies in distributed communication can realise mutual communication and coordinated action, and the information of intelligent bodies does not need to pass through the control centre. This apportions the communication pressure of the entire system to each intelligent body, improves the coordination of multi-intelligent body communication systems, and has the advantages of robustness, flexibility, and ease of expansion.

For a USV cluster adopting distributed communication, each USV interacts with the neighbouring USV with information to ensure that the state quantity or a certain variable of all USVs is eventually consistent. Moreover, it can effectively improve the efficiency of the system synergy and the robustness of the system under the premise of realising a global goal. This paper presents a method for assessing the communication capabilities of heterogeneous USVs. By comparing three communication methods among USVs clusters, stable and real-time radio communication has been chosen as the mode for information exchange between USVs clusters. A method for evaluating the communication capabilities of heterogeneous USVs based on a signal transmission loss model is proposed. The communication topology of USVs is abstracted into a graph data structure, and several important properties of Laplace matrices are provided. Based on the observation progress consistency controller, the speeds of heterogeneous USVs are adjusted through the optimization of communication topology to achieve consistent observation progress among all vessels. Finally, compared with dispersed control experiments, the optimization of communication topology based on the consistency controller has improved observation efficiency by 22%.

2 Mathematical modelling of heterogeneous USV motion

To study the motion simulation and cooperative communication problems of a USV, it is necessary to obtain its dynamic parameters. Currently, the kinetic parameters of a USV are identified through experiments, theoretical calculations, and approximate projections (Wu, 2011). Owing to the complexity and variability of the structure and working conditions of a USV (Xing, 2012), theoretical calculations and experimental measurements have certain errors and limitations. Therefore, this study adopts an integrated method to estimate the dynamic parameters of a USV using a combination of theoretical calculations and experiments. The method is based on the known parameters of the USV for theoretical calculation, and the principles of the theoretical calculation are as follows:

(1) Additional inertial mass term, $m_1\approx 1.05m$, where m is the actual mass of the USV.

(2) Additional inertial mass term, $m_2\approx m+0.5(\rho \pi D^{2}L)$, where ρ is the density of water, D is the average depth of immersion of the ship, and L is the effective length of the ship.

(3) Additional inertial mass term $m_3\approx m{L}^2/8$. This formula is applicable to paddle rudder and dual-thruster USVs, $m_3\approx (m(L^2+W^2)+0.5(0.1m{B}^2+\rho \pi D^2{L}^3))/12$ Fig, where W is the actual width of the ship and B is the distance between the two thrusters (Lim et al., 2008).

(4) The hydrodynamic damping term is $d_1\approx m_{1}g/(2u_0)$, where g is the gravitational acceleration and $u_0$ is the economical velocity of the USV.

(5) Hydrodynamic damping term $d_2\approx -0.5\rho u_0{L}^2{Y}^{\prime }v$, where $Y^{\prime }v=-5{(D/L)}^2$.

(6) Hydrodynamic damping term $d_3\approx 0.5\rho V{L}^4{N}^{\prime }r$, where $N^{\prime }r=-0.65{(D/L)}^2$.

These kinetic parameters were partially calculated using Smit’s formula. First, according to the above theoretical calculation, the calculation results are then substituted into the standard USV motion model to obtain a set of preliminary dynamic parameters Ship slewing simulation experiments are carried out on the computer, and the simulation results are compared and analysed with the measured data of the actual slewing test on the water surface to determine the differences between the two and the reasons for the differences. Moreover, according to the results of the analysis, the dynamic parameters are adjusted and optimised appropriately to ensure they are more aligned with the real situation. Finally, based on the analysis results, the dynamic parameters were adjusted and optimised to make them more consistent with the actual situation.

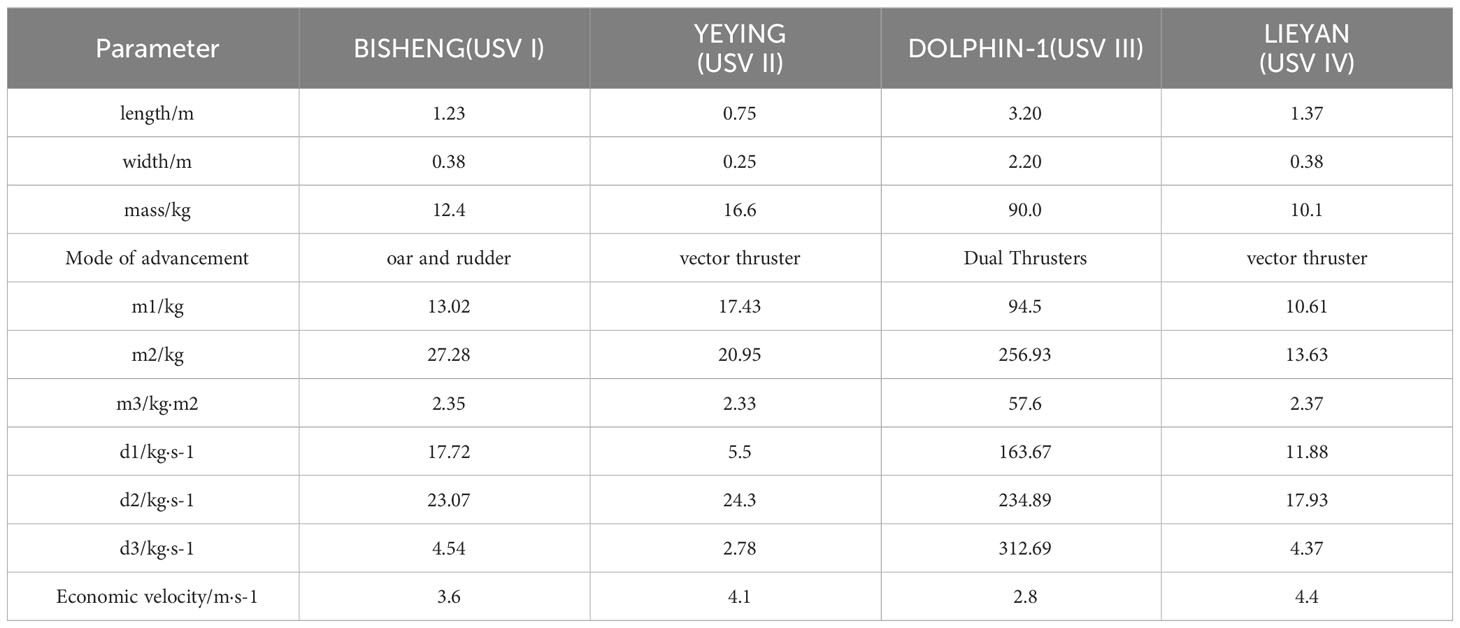
In the following, real ship data verify the abovementioned kinetic parameter identification method, and four USVs, named USV I-IV, developed by a 3I team personnel of the School of Marine Science and Technology of Tianjin University, are considered. The physical photos are shown in Figure 1.

Figure 1

Figure 1 Physical drawing of four USV. (A) USV I, (B) USV II, (C) USV III, (D) USV VI.

A comprehensive approach combining theoretical calculations and experiments, as described above, was used to confirm the kinetic parameters of the USV; Table 1 lists the parameters of each USV and the kinetic parameters determined.

Table 1

Table 1 Physical and kinetic parameters of four USV.

The accuracy of the established motion model and parameters of the USV were verified, and a constant-slewing motion simulation was performed using the USV dynamic parameters listed in Table 1. The USV sailed in the due north direction at an economical velocity with the paddle or vector thrusters turned to the right by 35° (USV III was turned off by controlling the right thrusters).

In static waters without environmental interference, the motion trajectories depicted by the centres of gravity of the four USVs are shown in Figure 2A. It is shown that the different USVs exhibit different longitudinal and transverse distances as well as different diameters of rotary gyration, reflecting the different manoeuvrability of each USV. In the presence of interference from sea winds and currents, the wind velocity $U_T=2 m/s$, wind direction ${\psi }_T=0°$, current velocity $V_c=0.15 m/s$, and current direction ${\psi }_c=\pi /4$ were set, and the motion trajectories depicted by the centres of gravity of the four USVs are shown in Figure 2B. The experimental results show that the motion of each USV tends to drift in the direction of $\pi /4$, which indicates that the sea current has a significant influence on the USV motion state.

Figure 2

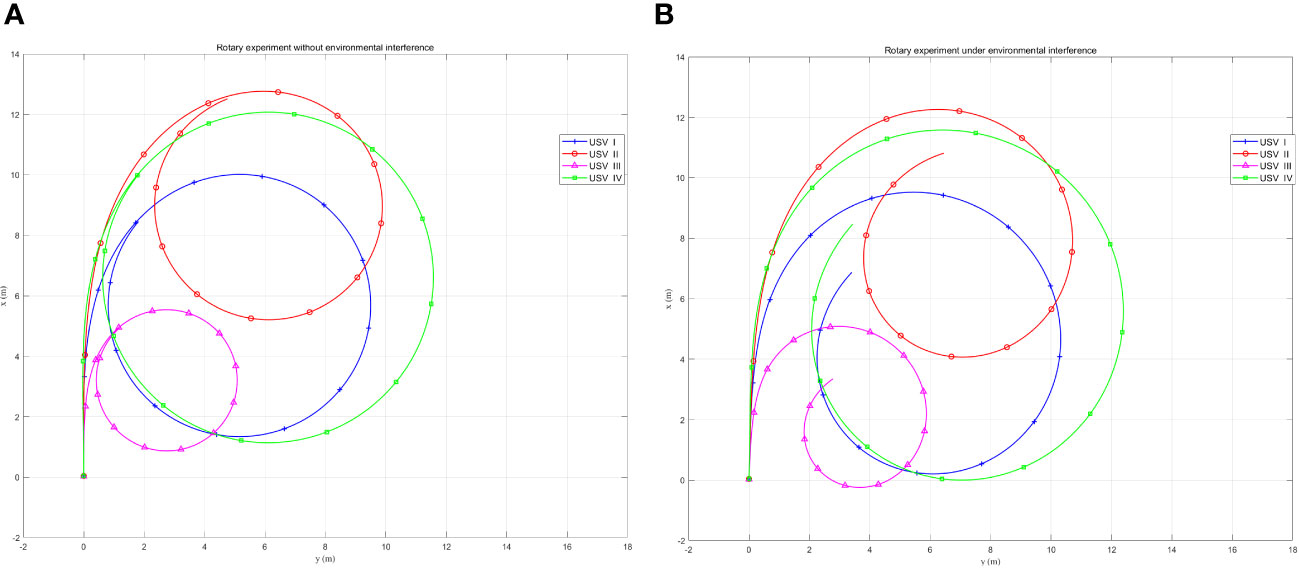
Figure 2 Steady rotation Experiment for four USVs. (A) Without environmental interference, (B) With environmental interference.

The simulation experiments show that the underdriven three-degree-of-freedom motion mathematical model established in this study can correctly describe the navigation of the USV and demonstrate the manoeuvrability of different USVs considering environmental perturbations.

3 USV cluster cooperative communications

3.1 Communication methods for USV clusters

The maritime Internet of Things (IoT) has recently emerged as a revolutionary communication paradigm where a large number of moving vessels are closely interconnected in intelligent maritime networks. To promote smart traffic services in maritime IoT, it is necessary to accurately and robustly predict the spatiotemporal vessel trajectories. It is beneficial for collision avoidance, maritime surveillance, and abnormal behaviour detection, etc. Motivated by the strong learning capacity of deep neural networks, Ryan Wen Liu et al. (Liu et al., 2022; Liang et al., 2022; Liang et al., 2024) proposed an AIS data-driven trajectory prediction framework, whose main component is a long short-term memory (LSTM) network.

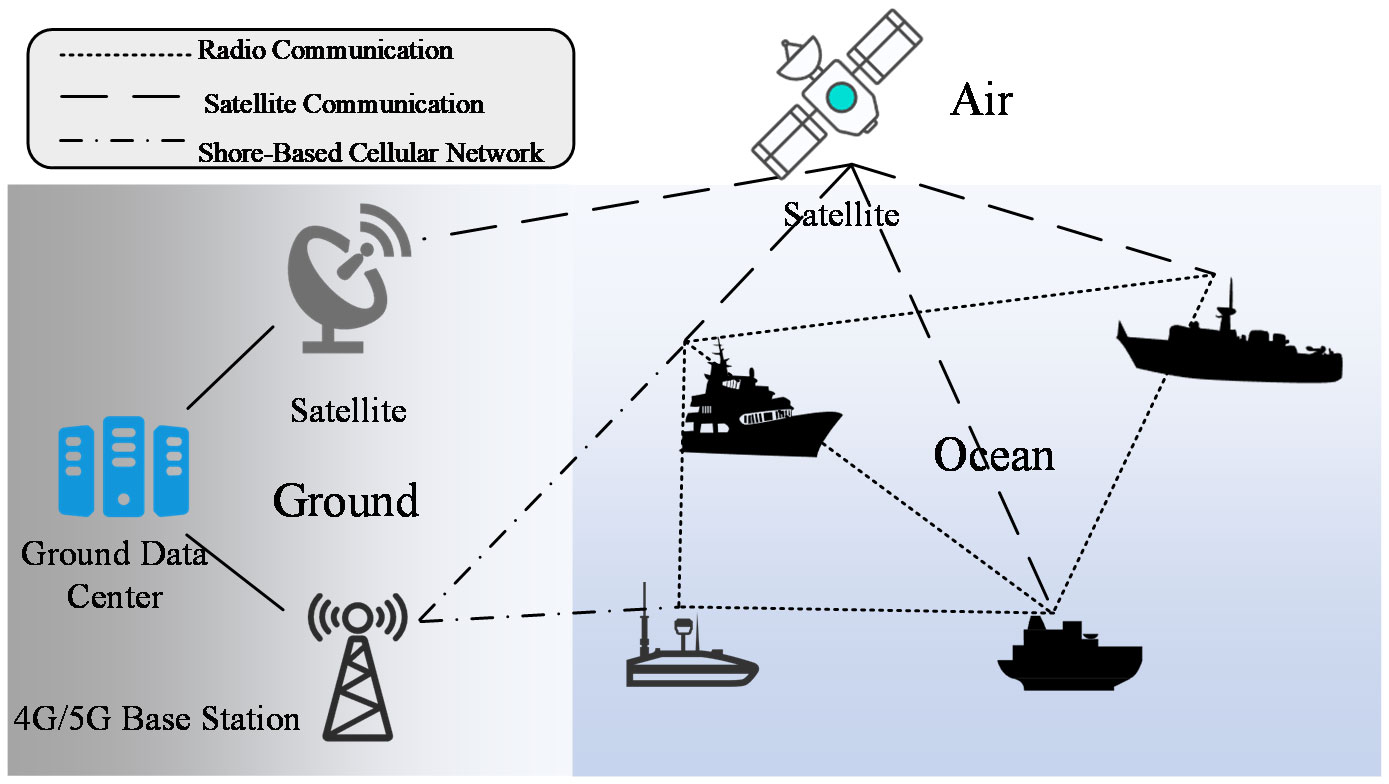
Maritime communication networks primarily include radio-, satellite-, and shore-based cellular network communication systems. All of these communication systems can be applied to USV-trunking communication. Figure 3 shows the widely used maritime communication networks.

Figure 3

Figure 3 Schematic diagram of the maritime communications network.

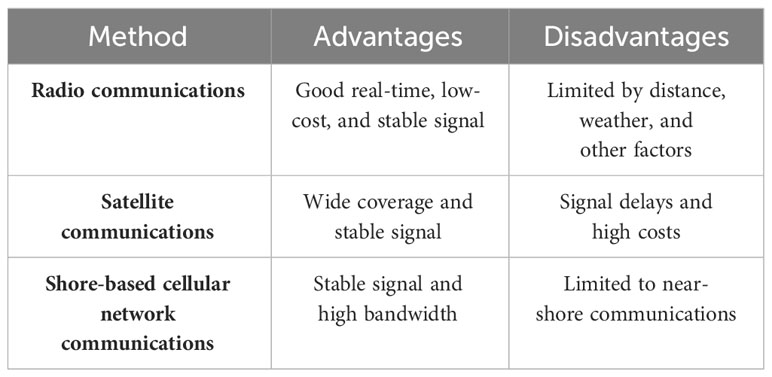
Radio communication systems (Xia et al., 2017) are widely used in marine communications and can provide near-, medium-, and long-range communication. Typical frequencies are medium frequency (MF), high frequency (HF), and very high frequency (VHF). USVs can communicate with the surrounding USVs and are generally suitable for short-range communication. The radio communication system has a stable signal, low cost, and good real-time performance; however, with increased communication distance, the data transmission rate decreases, and it cannot realise global communication coverage.

Satellite communication systems (Xia et al., 2017) play an irreplaceable role in marine communication and provide global coverage. Typical examples are the maritime satellite system (INMARSAT), the Iridium system (Iridium), and China’s Beidou satellite navigation system, which is one of the most common and reliable choices for USV communication. Moreover, USVs can communicate with ground stations or other USVs over long distances, thereby enabling remote control, data transmission, and other functions. Satellite communication systems cover a wide range of applications; however, they exhibit extremely high costs, signal delays, and information security problems.

Shore-based cellular network communication systems (Xia et al., 2017) suit offshore marine communication. USVs can use mobile communication technologies, such as 4G and 5G, to provide high-velocity and stable offshore network services. However, the range of coastal sea areas covered by shore-based cellular networks is minimal.

As shown in Table 2, Radio communication systems (Alqurashi et al., 2023) have been widely used in the field of maritime communication, offering stable signals, low costs, and good real-time capabilities for near, medium, and short-distance communication. Shore-based cellular network communication systems are an excellent choice for near-sea maritime communication, while unmanned vessels can also utilize mobile communication technologies such as 4G and 5G to provide high-speed and stable network services in coastal areas. However, the coverage range of shore-based cellular networks in maritime areas is limited. Satellite communication systems hold an irreplaceable position in maritime communication, offering global communication coverage. However, they currently suffer from high costs, significant signal latency, and potential issues related to information security. In most cases, heterogeneous USV clusters require continuous information interaction. Owing to the shortcomings of satellite communication, such as signal delay and high cost, and the limitations of cellular networks, radio communication has become the optimal communication mode for real-time control and cooperative operation of USV clusters. Stable radio communication with good real-time performance can satisfy cluster information interaction requirements.

Table 2

Table 2 Comparison of the characteristics of USV cluster communication methods.

3.2 Assessment of USV cluster communications capability

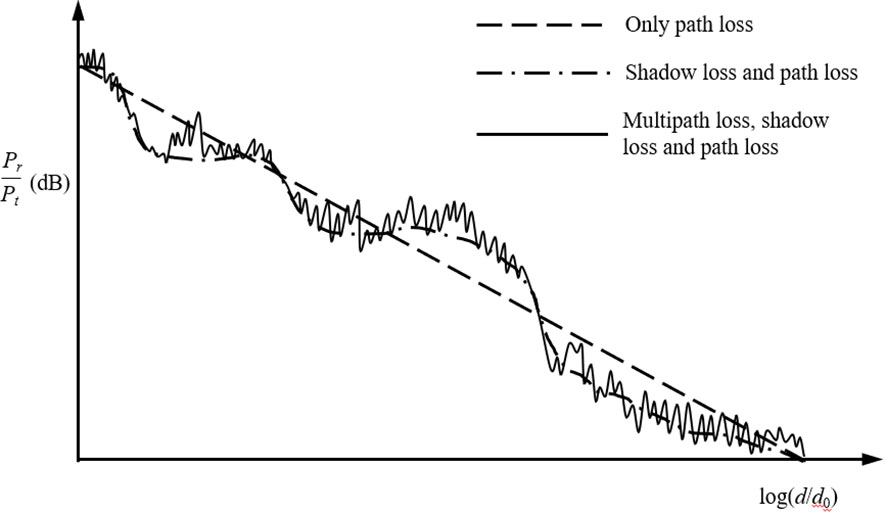
To ensure that the unmanned crafts within a cluster system communicate effectively with each other, an assessment of the communication capabilities of the unmanned craft is required to determine the communication connectivity of the cluster. The USV cluster is assumed to communicate via the HF/VHF frequency digital transmission radio, and the signals are transmitted along the line-of-sight channel. As shown in Figure 4, according to the radio transmission theory, the channel loss experienced when signals are transmitted at sea mainly consists of large-scale and small-scale fading, with large-scale fading including path transmission loss, shadow fading, and small-scale fading, including multipath fading. To confirm whether the two vessels can communicate, the performance of the communication systems of the two vessels, as well as the loss during signal transmission, can be evaluated.

Figure 4

Figure 4 Maritime communications propagation loss.

First, a signal transmission loss model is established, assuming that two USVs, A and B, in the cluster interact with each other for information. In addition, the distance between the two USVs is d (km), the frequency of the signal is f (Mhz), and the loss of the signal in the propagation process is $L_p$ (dB). According to the study (Jin, 2013), the formula is calculated as follows Equation 1:

$\begin{array}{ll}{L}_p=20{\mathit{log}}_{\mathit{10}}(f)+20{\mathit{log}}_{\mathit{10}}(d)+32.45+10\kappa {\mathit{log}}_{\mathit{10}}(\frac{d}{d_0})& (1)\end{array}$

where $\kappa$ is the path loss exponent and the specific value is determined by the communication environment factors at sea. Equation 1 considers marine environment correction compared to the signal-free space transmission model.

Second, the signal reception strength is calculated using the performance parameters of the communication systems of the two USVs and the signal transmission loss. The formula for calculating the signal reception strength of A and B USVs is as follows Equation 2:

$$RS{S}_A=P_{t,B}+G_{t,B}+G_{r,A}-L_p$$

$\begin{array}{ll}RS{S}_B=P_{t,A}+G_{t,A}+G_{r,B}-L_p& (2)\end{array}$

$RS{S}_A$ is the signal strength transmitted by USV B and received by USV A, $RS{S}_B$ is the signal strength transmitted by USV A and received by USV B, $P_{t,A}$ and $P_{t,B}$ are the signal transmitting powers of USVs A and B, respectively. $G_{t,A}$ and $G_{t,B}$ denote the transmitting antenna gains of USVs A and B, respectively. $G_{r,A}$ and $G_{r,B}$ are the receiver antenna gains for USVs A and B, respectively.

Finally, the heterogeneous USVs cluster communication capability is evaluated using the wireless signal strength to measure communication effectiveness between two USVs. It is known that the reception sensitivity of USV A is $R_{s,A}$, whereas the receiving sensitivity of USV B is $R_{s,B}$. Considering ${\Pi }_{BA}$, ${\Pi }_{AB}$ mean the success or failure status of communication from USV B to USV A and from USV A to USV B, respectively, then whether the two USVs can communicate or not can be determined using the following relationship:

(1) For communications from USVs B to A.

If $RS{S}_A-R_{s,A}\ge -83 \text{dBm}$, ${\Pi }_{BA}=1$(Communication from USVs B to A is successful).

If $RS{S}_A-R_{s,A}<-83 \text{dBm }$ or the two USVs do not communicate at the same frequency, ${\Pi }_{BA}=0$ (Communication from USVs B to A is unsuccessful).

(2) For communication from USVs A to B.

If $RS{S}_B-R_{s,B}\ge - 83\text{dBm}$, ${\Pi }_{AB}=1$(Communication from USV A to USV B is successful).

If $RS{S}_B-R_{s,B}<- 83\text{dBm}$ or the two USVs do not communicate at the same frequency, ${\Pi }_{AB}=0$ (Communication from USV A to USV B is unsuccessful).

The assessment of the communication capability of heterogeneous USVs shows that two USVs can interact with each other through the HF/VHF frequency digital transmission radios depending mainly on the frequency of the signals, the distance between the two USVs, the performance of the communication system, and the environmental interference of the communication scenario, among other factors. Furthermore, this can occur without considering the mutual communication interference between multiple USVs. Evaluating the communication capabilities of any two USVs in a cluster can determine the overall communication connectivity.

3.3 Unmanned vessel cluster communication topology

After completing the communication capability assessment of heterogeneous USV clusters, the communication topology between USVs is described using a graphical data structure (Zhou, 2011). Consider a cluster system consisting of a total of n USVs, which is represented by the graph $G=(V,E)$, where $V=\left\{v_1,v_2,\dots v_n\right\}$ is the set of vertices, and each vertex represents each USV. $E=V·V=\left\{(v_i,v_j),i,j=1\dots n\right\}$ is the set of edges, v_i is the starting point, v_j is the ending point, and E denotes whether a communication link is established between the USVs or not, and if there exists an edge from a vertex to reach v_i, the vertex is said to be a neighbour j of v_i, and the set of j is N_i. Describing the connectivity of a graph using a matrix of $A=[a_{ij}]\in R^{n\times n}$, A is the adjacency matrix, which represents the connectivity between vertices, and according to the evaluation of the communication capabilities discussed in the previous section and $a_{ij}$ is as follows Equation 3:

$\begin{array}{ll}{a}_{ij}=\{\begin{array}{c}1if {\Pi }_{ji}=1\\ 0\text{ otherwise}\end{array}& (3)\end{array}$

Consider that the USV can process its own information directly such that $a_{ii}=0,i=1,\dots ,n$, that is, the main diagonal of the adjacency matrix, is zero. If communication does not consider direction, G is an undirected graph when A is a symmetric matrix.

The degree d(v_i) of vertex v_i denotes the number of edges associated with the vertex. For directed graphs, the degree of vertex v_i is divided into the in-degree d_in(v_i) and out-degree d_out(v_i), that is, the number of directed edges from entering vertex v_i and the number of directed edges from exiting vertex v_i. Moreover, the in-degree matrix better captures the impact of neighbouring USVs on one’s ship. For an undirected graph, the degree of vertex v_i is the number of edges and is equal to the number of neighbours. $D=diag\left\{d(v_1),d(v_2),\dots ,d(v_n)\right\}$ is a degree matrix that represents the communication connectivity of a USV.

The Laplace matrix L that defines the graph is given by Equation 4.

$\begin{array}{ll}L=D-A& (4)\end{array}$

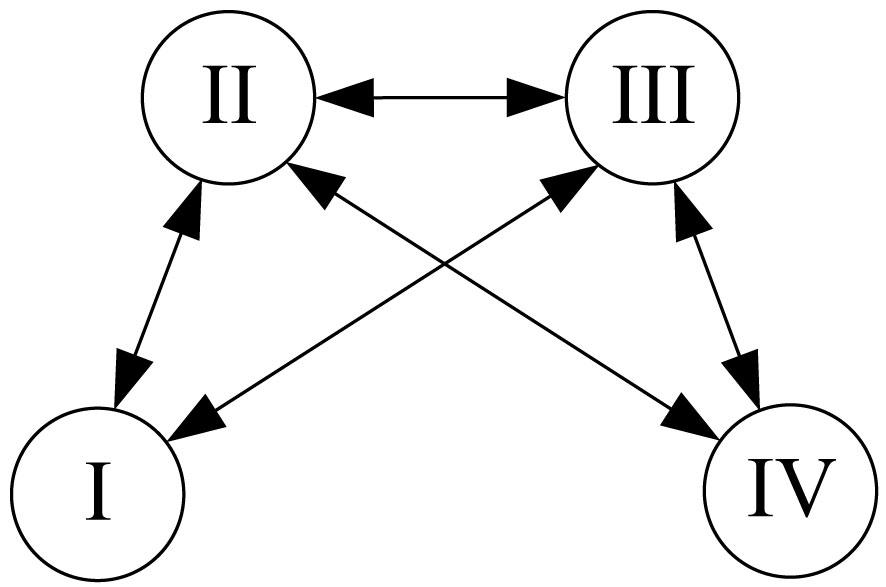
If the communication topology is a directed graph, D denotes the incidence matrix. For example, Figure 5 illustrates the communication topology of a cluster of four USVs.

Figure 5

Figure 5 Communication topology with four nodes.

The corresponding adjacency, degree, and Laplace matrices for the communication topology shown in Figure 5 are as follows:

$$\mathit{D}=\left[\begin{array}{cccc}2& 0& 0& 0\\ 0& 3& 0& 0\\ 0& 0& 3& 0\\ 0& 0& 0& 2\end{array}\right]\mathit{A}=\left[\begin{array}{cccc}0& 1& 1& 0\\ 1& 0& 1& 1\\ 1& 1& 0& 1\\ 0& 1& 1& 0\end{array}\right]\mathit{L}=\left[\begin{array}{cccc}2& -1& -1& 0\\ -1& 3& -1& -1\\ -1& -1& 3& -1\\ 0& 1& -1& 2\end{array}\right]$$

The computed Laplace matrix reflects important information regarding the communication system, and several important properties of the Laplace matrix L are described below (Liu and Huang, 2023).

(1) For undirected graphs, Laplacian matrix L is symmetric and semi-positive definite (given a real symmetric matrix A of size n × n, matrix A is a semi-positive definite matrix if there is a constant $x^{T}Ax\ge 0$for any vector x of length n).

(2) For an undirected graph, the eigenvalues of the Laplacian matrix L are ordered to satisfy λ₁≤λ₂≤…≤λ_n, where λ_{1 =} 0 and λ₂ > 0 if and only if the graph is connected.

(3) For a directed graph, a sufficient condition for containing a directed spanning tree is that L has one and only one zero eigenvalue, and all other eigenvalues have nonnegative real parts.

4 Coherent formation control of USV clusters under switching communication topology

4.1 Unmanned vessel cluster coherence control

Consistency control under a switching communication topology is a core problem in cooperative control. First, we introduce the basic concept of coherence control, analyse traditional coherence control strategies, and discuss their effects when applied to USV clusters with a single static communication topology.

The goal of consistency research is to design a consistency algorithm that relies only on the information of its neighbours to ensure that all intelligent bodies agree on a certain quantity of interest (Olfati-Saber et al., 2007). Consistency can be used to study clustered distributed architectures in which no individual of the cluster is overly dependent on any individual; therefore, the system as a whole is more robust. Designing consistency algorithms is an important aspect of consistency studies; for a first-order continuous system, it is modelled as follows Equation 5:

$\begin{array}{ll}{\dot{x}}_i(t)=u_i(t)& (5)\end{array}$

where x_i denotes the state of the ith intelligence and u_i denotes the control input of the ith intelligence. The most common continuous time consistency algorithm is shown in Equation 6:

$\begin{array}{ll}{u}_i(t)=-{\displaystyle {\sum }_{j=1}^n{a}_{ij}(t)[x_i(t)-x_j(t)]}& (6)\end{array}$

where $a_{ij}(t)$ denotes the value of the connection state between the intelligence i and neighbour j in the communication topology in a first-order system, and if $t\to \infty$ and $\left|x_i(t)-x_j(t)\right|\to 0,i,j=1,2,\dots ,n,\forall i\ne j$ exist, then the cluster of intelligences is said to have reached agreement. Suppose the communication topology graph is undirected and is connected under the control of Equation 6. In that case, the states of the individual intelligences gradually converge to those of the neighbouring intelligences until the states of all the intelligences converge to become consistent. The convergence time depends specifically on the structure of the communication topology graph, and good control must converge within the shortest possible time.

Furthermore, Equation 6 is written in matrix form as follows Equation 7:

$\begin{array}{ll}\dot{x}(t)=-{\mathit{L}}_n(t)\mathit{x}(t)& (7)\end{array}$

where $\mathit{x}(t)=[x_1(t),x_2(t),\cdots ,x_n(t)]$ is the cluster state vector and L_n(t) is the Laplace matrix of the cluster communication topology.

If x_i denotes the displacement of the ith intelligence, Equation 7 is referred to as a first-order consistency algorithm. For second-order intelligence considering displacements and velocities, the second-order multi-intelligence model is defined by Equation 8:

$\begin{array}{ll}\{\begin{array}{c}{\dot{x}}_i(t)=v_i(t)\\ {\dot{v}}_i(t)=u_i(t)\end{array},i=1,2,\dots ,n& (8)\end{array}$

where v_i denotes the velocity of the ith intelligence, and the second-order consistency algorithm is given as follows Equation 9:

$\begin{array}{ll}{u}_i(t)=-{\displaystyle {\sum }_{j=1}^n{a}_{ij}(t)[(x_i(t)-x_j(t))+\gamma (v_i(t)-v_j(t))]}& (9)\end{array}$

$\gamma$ denotes the coupling strength coefficient $\gamma >0$ in a second-order system if $t\to \infty$ or $\left|x_i(t)-x_j(t)\right|\to 0,\left|v_i(t)-v_j(t)\right|\to 0,i,j=1,2,\dots ,n,\forall i\ne j$. The cluster of intelligence is then said to have reached an agreement.

Similarly, Equation 9 can be written in matrix form as follows Equation 10:

$\begin{array}{ll}\left[\begin{array}{c}\dot{\mathit{x}}(t)\\ \dot{\mathit{v}}(t)\end{array}\right]=\left[\begin{array}{cc}{\mathbf{0}}_{n\times n}& {\mathit{I}}_n\\ -{\mathit{L}}_n(t)& -\gamma {\mathit{L}}_n(t)\end{array}\right]\left[\begin{array}{c}\mathit{x}(t)\\ \mathit{v}(t)\end{array}\right]& (10)\end{array}$

where $v(t)$ denotes the cluster velocity vector. A sufficient condition for the second-order consistency Equation 9 to achieve consistency is that the communication topology graph has a spanning tree, and the coupling strength coefficient $\gamma$ satisfies (Gao et al., 2017) Equation 11:

$\begin{array}{ll}\gamma >\underset{i=2,\cdots ,n}{max}\sqrt{\frac{2}{\left|{\lambda }_i(-\mathit{L})\right|\cos (\frac{\pi }{2}-{\tan }^{-1}\frac{-\mathrm{Re}({\lambda }_i(-\mathit{L}))}{Im({\lambda }_i(-\mathit{L}))})}}& (11)\end{array}$

where ${\lambda }_i$ denotes the characteristic root of the Laplace matrix L. It is evident that, unlike the first-order model, parameter $\gamma$ also influences whether the second-order system can achieve consistency.

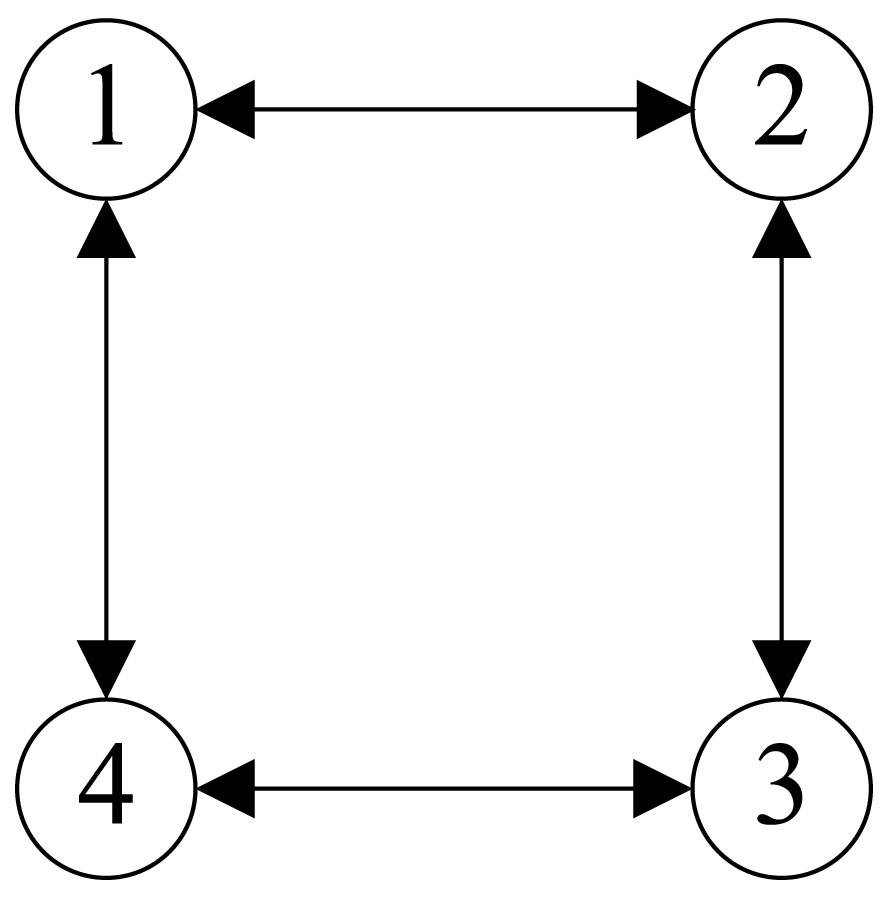
To illustrate the usefulness of the consistency algorithm, a cluster of n = 4 USVs is selected. The simplified USV model is given by Equation 8, with the cluster having the following undirected communication topology, as shown in Figure 6.

Figure 6

Figure 6 Quad-Intelligent body cluster communication topology.

The degree, adjacency, and Laplace matrices of the communication topology graph were obtained from Figure 6:

$$\mathit{D}=\left[\begin{array}{cccc}2& 0& 0& 0\\ 0& 2& 0& 0\\ 0& 0& 2& 0\\ 0& 0& 0& 2\end{array}\right]\mathit{A}=\left[\begin{array}{cccc}0& 1& 0& 1\\ 1& 0& 1& 0\\ 0& 1& 0& 1\\ 1& 0& 1& 0\end{array}\right]\mathit{L}=\left[\begin{array}{cccc}2& -1& 0& -1\\ -1& 2& -1& 0\\ 0& -1& 2& -1\\ -1& 0& -1& 2\end{array}\right]$$

Obviously this communication topology graph contains a spanning tree that sets the x(0) = [4.5, 3.0, 4.0, 5.7]^T and v(0) = [1.0, 1.5, 1.2, 1.7]^T.

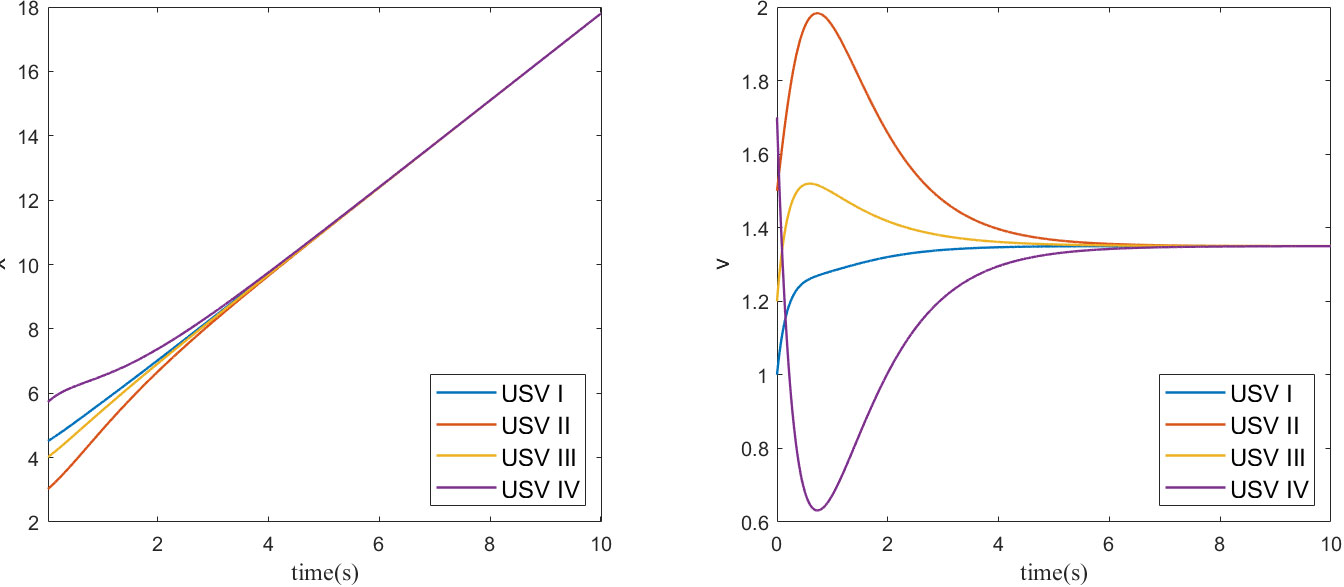
Using the second-order consistency controller (10), according to the coupling strength coefficient condition (11), it is necessary to satisfy the $\gamma >0.71$. In this study we used $\gamma =1$. The simulation was performed for 30 s, and Figure 7 depicts graphs of the positions and velocities of the four USVs under the control of a second-order consistency algorithm.

Figure 7

Figure 7 Position and velocity versus time curves of four USVs.

As shown in Figure 7, the initial positions and velocities of the four USVs are different; however, under the control of the second-order consistency algorithm, the positions of the USVs eventually converge to the same position at approximately 5 s, and later. Subsequently, the velocities of the USVs converge to the same velocity at approximately 7 s, which ultimately converge to the average value of the initial velocities. Therefore, the simulation results verify the correctness of Equation 10, and the system exhibited good convergence.

4.2 Study of coherent formation based on cooperative communication of USVs

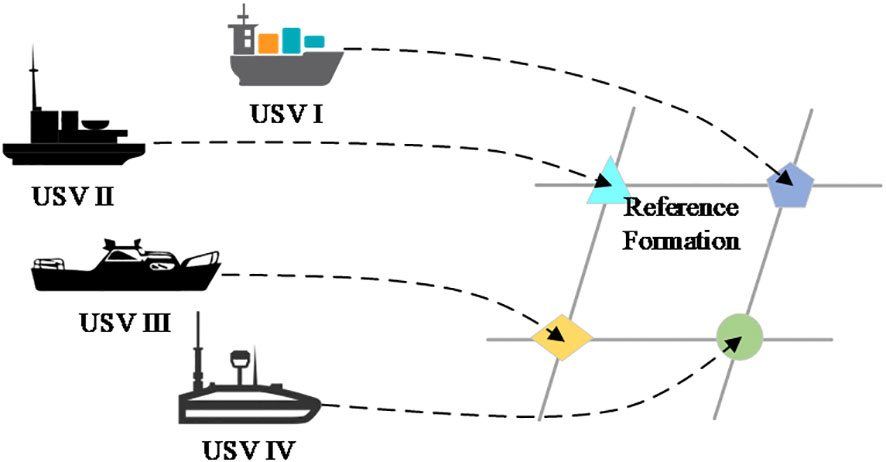
Unmanned USV clusters can cooperate with each other and adapt to the formation environment; that is, the offset is superimposed based on consistency, as shown in Figure 8. In the realisation of USV formation control, considering the communication capability of heterogeneous USV clusters, the communication distance between cluster individuals and the limitations and perturbations of the communication environment may interrupt the communication link. This results in a change in the communication topology map of the USV clusters. To ensure the consistency of the switching topology, the corresponding mechanisms and algorithms were studied to ensure that the system can adaptively deal with topology changes, maintain a high degree of reliability and stability of the cluster, and enhance the robustness and fault tolerance of the system.

Figure 8

Figure 8 Schematic diagram of USV clusters forming a formation.

Starting with the communication delay, the problem of USV cluster formation was investigated under a directed switching topology. The feedback linearisation of the USV dynamics model into a second-order integrator model considers a USV cluster system consisting of n USVs moving in a two-dimensional plane, and the motion model of the ith USV can be expressed as follows Equation 12:

$\begin{array}{ll}\{\begin{array}{c}{\dot{x}}_{xi}(t)=v_{xi}(t)\\ {\dot{v}}_{xi}(t)=u_{xi}(t)\\ {\dot{x}}_{yi}(t)=v_{yi}(t)\\ {\dot{v}}_{yi}(t)=u_{yi}(t)\end{array}& (12)\end{array}$

where x_xi, v_xi, and u_xi denote the position, velocity, and control input of the ith USV in the x-direction, respectively, and x_yi, v_yi, and u_yi denote the position, velocity, and control input of the ith USV in the y-direction, respectively.

To realise consistent control of the USV clusters, the controller of the ith USV is proposed as follows Equation 13:

$\begin{array}{ll}\begin{array}{l}{u}_i(t)=-{\partial }_1(v_i(t)-v_d(t))-\\ {\displaystyle {\sum }_{j\in N_i}{a}_{ij}(t)\left\{{\partial }_2[(x_i(t)-(x_j(t-{\tau }_t)-d_{ij}))]+{\partial }_3[(v_i(t)-v_j(t-{\tau }_t)]\right\}}\end{array}& (13)\end{array}$

where ${\tau }_t$ denotes the communication delay between individual USVs; ${\partial }_1$, ${\partial }_2$, and ${\partial }_3$ denote the control gains; $v_d(t)$ is the reference velocity for USV cluster navigation; and d_ij is the desired relative position of USV j concerning USV i.

The condition for the system to agree in a finite amount of time is the existence of $t_0\in [0,+\infty )$, then,

$\begin{array}{ll}\{\begin{array}{c}\underset{t\to t_0}{lim}\left|\right|x_i(t)-(x_j(t-{\tau }_t)-d_{ij})\left|\right|=0\\ \underset{t\to t_0}{lim}\left|\right|x_i(t)-v_j(t)\left|\right|=0\end{array}& (14)\end{array}$

This controller can prove the stability of the system by constructing Lyapunov-Krasovskii generalised functions Equation 14 (Zhang et al., 2023); eventually, the system is globally asymptotically stabilised, and controller (13) maintains the system consisting of model (12) in formation and brings the velocity to unity. Considering the USV as moving on a two-dimensional plane, the equation of motion of USV i is expressed as follows Equation 15:

$\begin{array}{ll}\{\begin{array}{l}{\dot{x}}_{xi}(t)=v_{xi}(t)\\ u_{xi}(t)=-{\partial }_1(v_{xi}(t)-v_{xd}(t))\\ -{\displaystyle {\sum }_{j\in N_i}{a}_{ij}(t)\left\{{\partial }_2[(x_{xi}(t)-(x_{xj}(t-{\tau }_t)-d_x(i,j)))]+{\partial }_3[(v_{xi}(t)-v_{xj}(t-{\tau }_t)]\right\}}\\ {\dot{x}}_{yi}(t)=v_{yi}(t)\\ u_{yi}(t)=-{\partial }_1(v_{yi}(t)-v_{yd}(t))\\ -{\displaystyle {\sum }_{j\in N_i}{a}_{ij}(t)\left\{{\partial }_2[(x_{yi}(t)-(x_{yj}(t-{\tau }_t)-d_y(i,j)))]+{\partial }_3[(v_{yi}(t)-v_{yj}(t-{\tau }_t)]\right\}}\end{array}& (15)\end{array}$

$d_x(i,j)$ and $d_y(i,j)$ are the elements in the relative position matrices d_x, and d_y in the x- and y-direction, respectively.

Consider a USV cluster system consisting of four USVs with the initial state of each USV as follows:

$$\begin{array}{l}(x_{x1},x_{y1},v_{x1},v_{y1})=(0m,0m,0\frac{m}{s},0\frac{m}{s})\\ (x_{x2},x_{y2},v_{x2},v_{y2})=(0m,100m,0\frac{m}{s},0\frac{m}{s})\\ (x_{x3},x_{y3},v_{x3},v_{y3})=(0m,200m,0\frac{m}{s},0\frac{m}{s})\\ (x_{x4},x_{y4},v_{x4},v_{y4})=(0m,300m,0\frac{m}{s},0\frac{m}{s})\end{array}$$

The communication capability is simplified to a maximum communication distance of 110 m, the parameters in the controller are set to ${\partial }_1$= 1.4, ${\partial }_2$= 1.1, and ${\partial }_3$= 1.2. Furthermore, the communication delay is set to a constant τ = 0.5 s, the desired velocity of the cluster is v_d = 2 m/s, and the setup is to form a positively oriented formation, with a relative position matrix of:

$${\mathit{d}}_x=\left[\begin{array}{cccc}0& 100& 100& 0\\ -100& 0& 0& -100\\ -100& 0& 0& -100\\ 0& 100& 100& 0\end{array}\right]{\mathit{d}}_y=\left[\begin{array}{cccc}0& 0& 100& 100\\ 0& 0& 100& 100\\ -100& -100& 0& 0\\ -100& -100& 0& 0\end{array}\right]$$

At the beginning of the formation, the USVs are lined up in a single line. The communication topology of the cluster is shown in Figure 9A, and the formation is formed after 32.8 s. The communication topologies are shown in Figure 9B, where both communication topologies contain spanning trees.

Figure 9

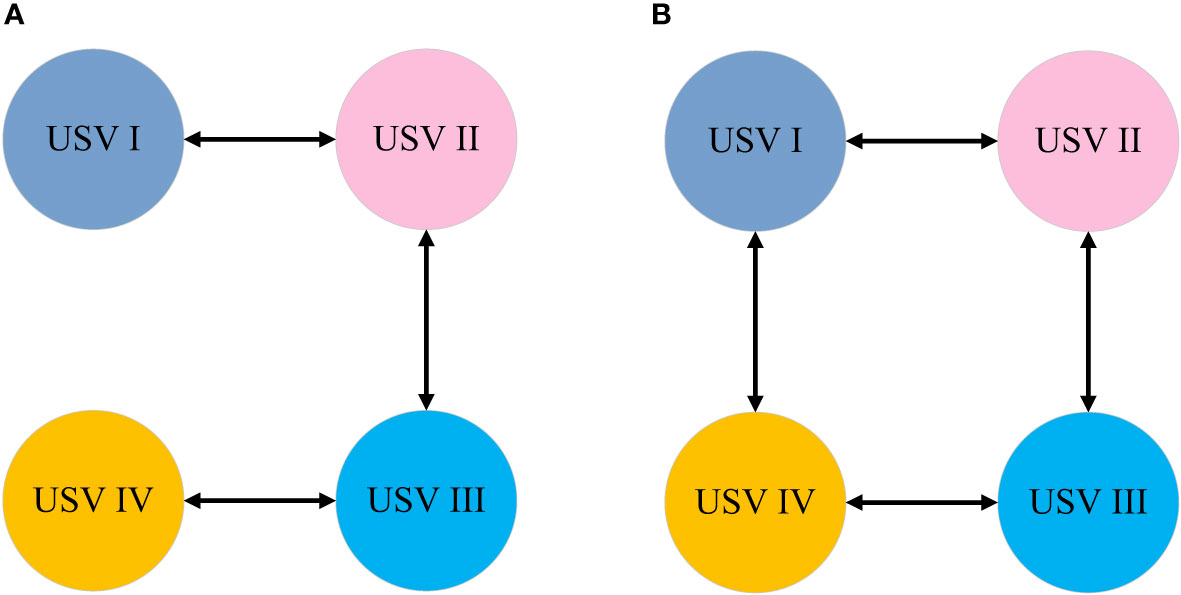
Figure 9 Communication topology before and after switchover. (A) Initial communication topology, (B) Optimized communication topology.

Figure 10 shows the position change diagram of the USV cluster that gradually formed under the control of the coherent-formation controller. In the formation process, owing to the change in the relative positions of each USV, the communication topology of the USV cluster changes accordingly. The communication topology changes from Figure 9A to Figure 9B and maintains the shape of the formation under the communication topology Figure 9B. As shown in Figure 10, at the initial position (0m), the four USVs are arranged in a line formation to begin the observation mission. As the USVs carry out different observation tasks, the relative positions of each USV change, causing the dynamic topology of the USV formation to change. Under the optimization of communication topology, the USVs cluster will restore its square formation shape at 80 meters. It can be observed that the USV cluster also forms and maintains its shape smoothly under changes in the communication topology.

Figure 10

Figure 10 Map of changes in the position of USV clusters.

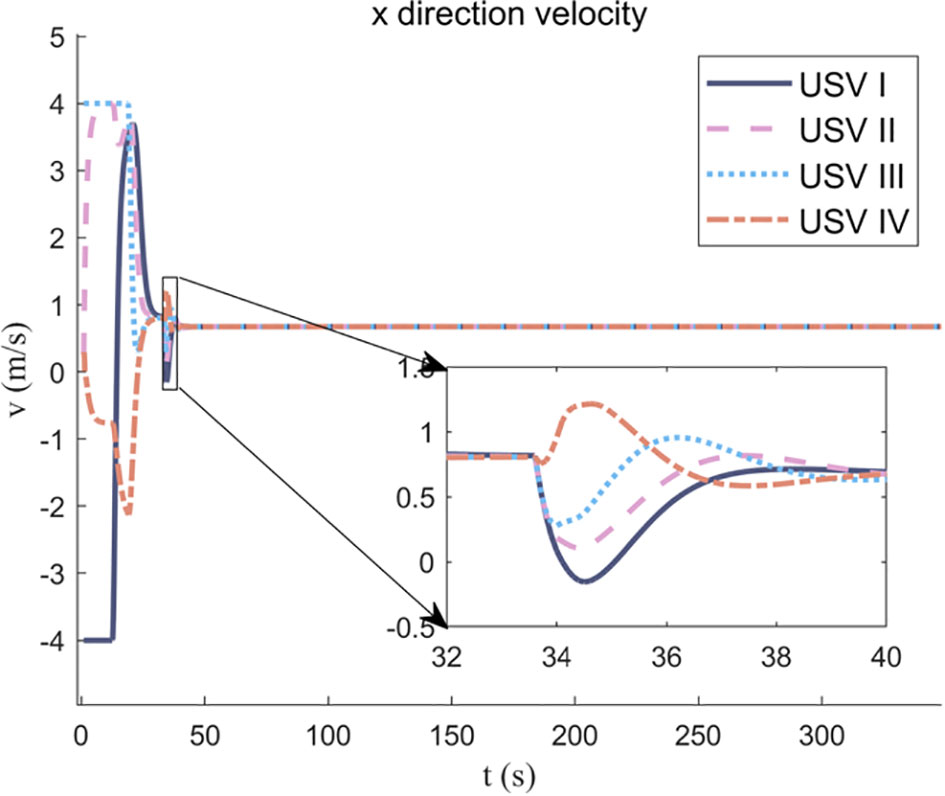
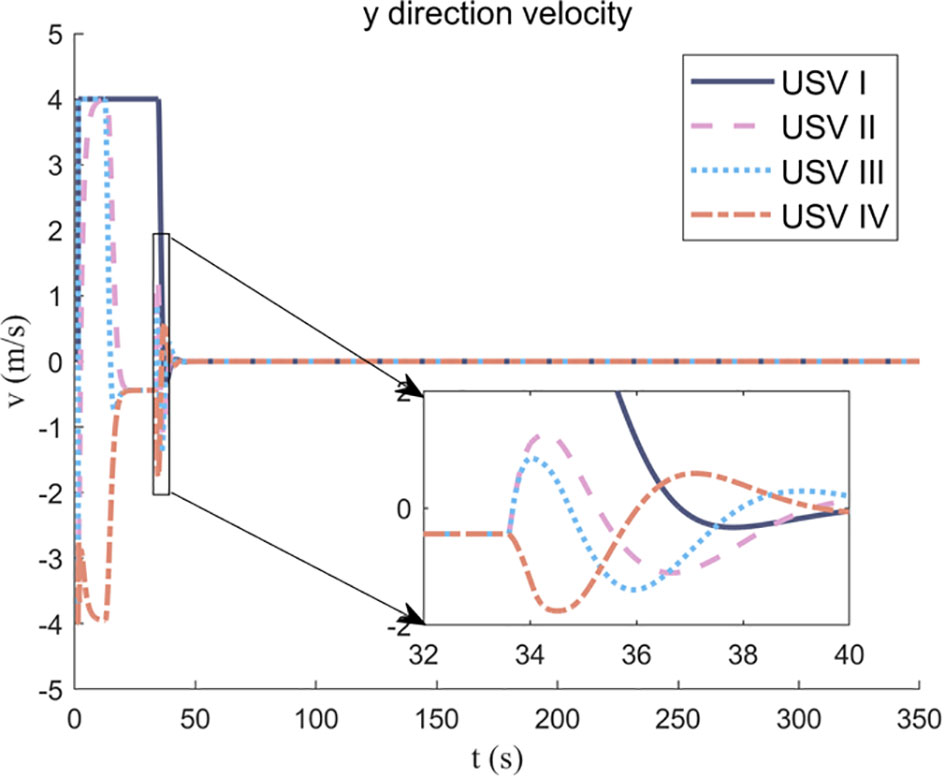
Figures 11, 12 show the velocity changes of the four USVs in the x- directions and y-directions during the communication topology switching process. It can be observed that from the initial position (0 meters) to the position at 30 meters, the velocities of the USVs change due to the variations in their relative positions. Under the transformation of communication topology, the communication topology optimization algorithm based on a consensus controller enables the velocities of the four USVs in the x and y directions to quickly converge at the position of 30 meters, maintaining the formation of the USVs cluster. This verifies the effectiveness and stability of the control algorithm.

Figure 11

Figure 11 Velocity in the x-direction of each USV under switching topology.

Figure 12

Figure 12 Velocity in the y-direction of each USV under switching topology.

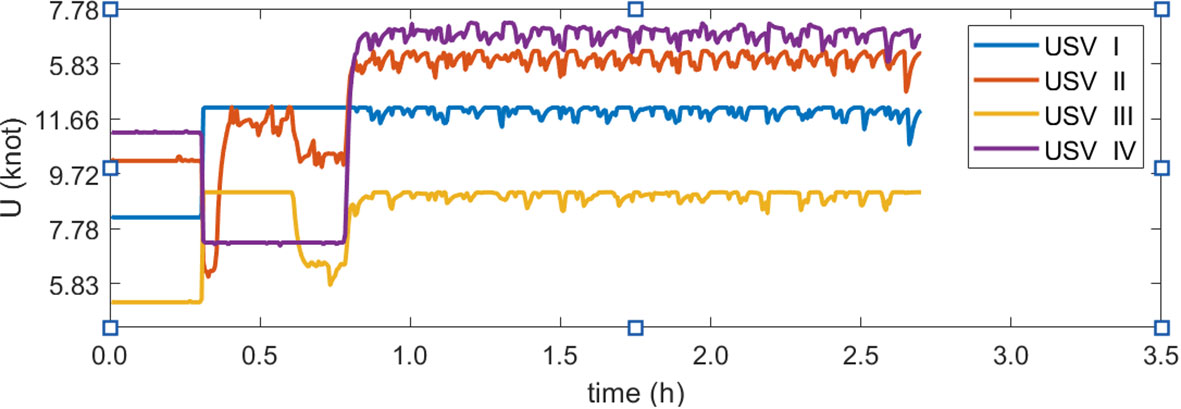
After a period under the control of the ocean observation progress consistency controller, the ocean observation progress of the four USVs gradually became consistent, synchronously completing observation tasks until the end. The variation in the velocity of each unmanned vessel, as shown in Figure 13 under the drive of the ocean observation progress consistency controller, the progress of oceanic observation based on communication topology optimization dynamically optimizes the topology structure according to the observation velocity of the USV and the ability to complete observation tasks. This ensures the completion of oceanic observation tasks while improving the efficiency of oceanic observation. From the figure, it can be seen that the slower vessels (such as: USV III) accelerate to “catch up” with the observation progress while ensuring task completion. Conversely, the faster vessel (such as: USV IV) decelerates to “slow down” the observation progress. Eventually, the progress of the final task was consistent with the constraints of the USV model.

Figure 13

Figure 13 Navigation velocity of each USV.

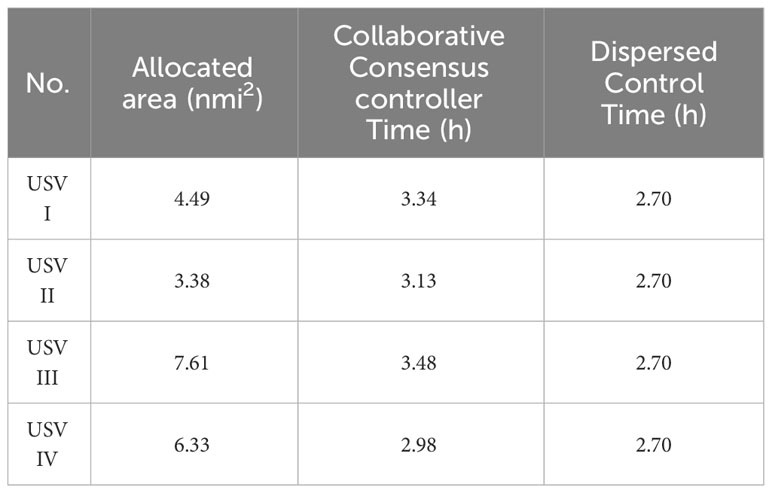
The observation coordination of the collaborative consensus controller based on communication topology optimization reduces the observation time by 22% compared to dispersed control. Because each USV initially has the same position, and dispersed control entails each USV independently completing its respective tasks based on its observation capabilities, resulting in task intersections and reduced efficiency. In contrast, the collaborative consensus controller based on communication topology optimization coordinates control according to changes in communication topology structure, as well as the velocity and observation capabilities of each USV. They complement each other’s advantages and synchronize completion until the end of the observation tasks. A comparison of test results, as shown in Table 3, demonstrates a 22% increase in search efficiency for observation progress coordination compared to dispersed control.

Table 3

Table 3 Simulation experiment results for search progress consistency.

5 Conclusion

To maintain the formation of heterogeneous USV clusters under dynamic changes in communication topology, the feedback of the heterogeneous USV model was linearised into a second-order integrator model. Starting from the communication delay, the formation generation simulation experiments with four heterogeneous USV formations verified that the communication topology transformation can smoothly form and maintain the formation shape of heterogeneous USV clusters. The efficiency of marine observation by USV clusters based on topology optimisation of consistent communication was 22% higher than that of dispersed control topology structures. This study provides a solid foundation for future investigations into the cooperative control of heterogeneous USV clusters and their applications in marine observations. Currently, the research has not considered the influence of marine environmental factors on the coordinated formation of USV clusters. The next step will involve studying factors such as wind and currents.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

ZK: Formal analysis, Methodology, Validation, Writing – original draft, Writing – review & editing. MG: Formal analysis, Resources, Writing – review & editing. AZ: Writing – review & editing, Conceptualization, Funding acquisition, Methodology, Supervision. ZL: Writing – review & editing, Validation.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was supported by the Guangdong Special Fund for Promoting Economic Development (Guangdong Natural Resources Cooperation) (Grant No. [2022119), Tianjin Research Innovation Project for Postgraduate Students (No. 2021YJSB177), and National Natural Science Foundation of China (52201414).

Acknowledgments

Special thanks go to the funding support provided for this research.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alqurashi F. S., Trichili A., Saeed N., Ooi B. S., Alouini M. S.. (2023). Maritime communications: A survey on enabling technologies, opportunities, and challenges. IEEE Internet things J. doi: 10.1109/JIOT.2022.3219674

CrossRef Full Text | Google Scholar

Chainho P., Drüsedow S., Pereira R. L., Chaves R., Portabales A. R. (2017). Decentralized communications: trustworthy interoperability in peer-to-peer networks. European Conference on Networks and Communications. IEEE. (IEEE), 1–5.

Google Scholar

Gao Y., Dai L., Xia Y., Liu Y. (2017). Decentralized communications: trustworthy interoperability in peer-to-peer networks. European Conference on Networks and Communications. IEEE, 1–5

PubMed Abstract | Google Scholar

Gu N., Wang D., Peng Z., Liu L. (2019). Distributed containment maneuvering of uncertain under-actuated USVs guided by multiple virtual leaders with a formation. Ocean Eng. 187 (Sep.1), 105996.1-105996.10. doi: 10.1016/j.oceaneng.2019.04.077

CrossRef Full Text | Google Scholar

Jin M. (2013). Analysis and research on propagation models and related algorithms in mobile communication (Beijing: Beijing University of Posts and Telecommunications).

Google Scholar

Liang M., Liu R. W., Zhan Y., Li H., Zhu F., Wang F.-Y. (2022). Fine-grained vessel traffic flow prediction with a spatio-temporal multigraph convolutional network. IEEE Trans. Intell. Transport. Syst. 23, 23694–23707. doi: 10.1109/TITS.2022.3199160

CrossRef Full Text | Google Scholar

Liang M., Weng L., Gao R., Li Y., Du L. (2024). Unsupervised maritime anomaly detection for intelligent situational awareness using AIS data. Knowledge-Based Syst. 284. doi: 10.1016/j.knosys.2023.111313

CrossRef Full Text | Google Scholar

Lim I. H., Kim Y. I., Lim H. T., Choi M., Hong S., Lee S., et al. (2008). Distributed Restoration system applying Multi-Agent in distribution automation system. doi: 10.1109/PES.2008.4596084

CrossRef Full Text | Google Scholar

Liu K., Huang Z. (2023). Research on the Hermitian Laplacian matrix of directed graphs. Comp. Sci. 50, 7.

Google Scholar

Liu R. W., Liang M., Nie J., Lim W. Y. B., Zhang Y., Guizani M. (2022). “Deep learning-powered vessel trajectory prediction for improving smart traffic services in maritime internet of things,” in IEEE Transactions on Network Science and Engineering, Vol. 9. 3080–3094.

Google Scholar

Olfati-Saber R., Fax J. A., Murray R. M. (2007). “Consensus and cooperation in networked multi-agent systems,” in Proceedings of the IEEE, Vol. 95. 215–233.

Google Scholar

Schröder-Hinrichs J. U., Song D. W., Fonseca T., Lagdami K., Loer K. (2019). Transport 2040: Automation, Technology, Employment - The Future of Work (Sverige: World Maritime University), 83–115.

Google Scholar

Sun Q., Yao Y., Yi P., Hu Y. J., Yang Z., Yang G. (2022). Learning controlled and targeted communication with the centralized critic for the multi-agent system. Appl. Intell. 53, 14819–14837. doi: 10.1007/s10489-022-04225-5

CrossRef Full Text | Google Scholar

Wang D., Fu M., Ge S. S., Li D. (2020). Velocity free platoon formation control for USVs with output constraints and model uncertainties. Appl. Sci. 10 (3), 1118. doi: 10.3390/app10031118

CrossRef Full Text | Google Scholar

Wu G. (2011). Research on maneuverability and intelligent control technology of unmanned vessels (Harbin: Harbin Engineering University).

Google Scholar

Xia M., Zhu Y., Chen E., Xing C., Yang T., Wen W. (2017). Development status and challenges of maritime communication. Sci. China: Ser. F 47, 677–695.

Google Scholar

Xie W., Tao H., Gong J., Luo W., Yin F., Liang X. (2021). Development status and research progress of key technologies for maritime unmanned systems clusters. Chin. J. Ship Res. 16, 12.

Google Scholar

Xing J. (2012). Research on parameter identification method of dynamic positioning ship motion mathematical model. Doctoral dissertation. Harbin: Harbin Eng. Univ.

Google Scholar

Zhang W., Liao Y., Jiang F., Zhao T. (2019). Review and trend analysis of unmanned surface vessel technology development. Unmanned Syst. Tech 2, 1–9.

Google Scholar

Zhang X., Zhou L., Xing W., Yao S. (2023). Consensus control of multi-autonomous underwater vehicles formation under switching topologies. J. Harbin Eng. Univ. 44, 587–593.

Google Scholar

Zhou T. (2011). Research on target detection probability in maritime observation at sea. Doctoral dissertation. Dalian: Dalian Maritime Univ.

Google Scholar