A machine learning approach for protected species bycatch estimation

Introduction: Monitoring bycatch of protected species is a fisheries management priority. In practice, protected species bycatch is difficult to precisely or accurately estimate with commonly used ratio estimators or parametric, linear model-based methods. Machine-learning algorithms have been proposed as means of overcoming some of the analytical hurdles in estimating protected species bycatch.

Methods: Using 17 years of set-specific bycatch data derived from 100% observer coverage of the Hawaii shallow-set longline fishery and 25 aligned environmental predictors, we evaluated a new approach for protected species bycatch estimation using Ensemble Random Forests (ERFs). We tested the ability of ERFs to predict interactions with five protected species with varying levels of bycatch in the fishery and methods for correcting these predictions using Type I and Type II error rates from the training data. We also assessed the amount of training data needed to inform a ERF approach by mimicking the sequential addition of new data in each subsequent fishing year.

Results: We showed that ERF bycatch estimation was most effective for species with greater than 2% interaction rates and error correction improved bycatch estimates for all species but introduced a tendency to regress estimates towards mean rates in the training data. Training data needs differed among species but those above 2% interaction rates required 7-12 years of bycatch data.

Discussion: Our machine learning approach can improve bycatch estimates for rare species but comparisons are needed to other approaches to assess which methods perform best for hyperrare species.

Introduction

Fisheries bycatch, interactions with unused or unmanaged species in commercial or recreational fisheries (Davies et al., 2009), generates negative impacts on many species, including mortality, making the reduction of bycatch a major focus in marine conservation and fisheries management (Zhou et al., 2010; Lewison et al., 2014; Komoroske and Lewison, 2015; Gray and Kennelly, 2018; Nelms et al., 2021; Pacoureau et al., 2021). The management relevance and urgency of conservation concerns are amplified when bycatch includes protected species such as marine mammals, sea turtles, sharks, and seabirds (Moore et al., 2009; Wallace et al., 2013; Lewison et al., 2014; Komoroske and Lewison, 2015; Gray and Kennelly, 2018; Clay et al., 2019). Reducing bycatch can improve the efficiency and effectiveness of commercial fishing (Richards et al., 2018; NOAA Fisheries, 2022; Senko et al., 2022) and limit risks of fishery closure as a result of high levels of protected species interactions. However, estimating the levels of bycatch in a fishery can be challenging given low interaction rates of most bycaught species and the even rarer occurrence of protected species interactions (McCracken, 2004; Amandè et al., 2012; Martin et al., 2015; Stock et al., 2019).

Fisheries management plans and regulations typically require estimating and monitoring the amount of bycatch of a given species from a given fleet. Excessive bycatch, defined differently depending on jurisdiction, can result in regulatory changes to fishing practices, changes in fishing gear, restrictions of fishing activities, or whole-fishery closures. Thus, the ability to accurately and precisely determine levels of bycatch in a fishery is an critical component of fishery management. In the United States, the Magnuson-Stevens Fishery Conservation and Management Act (MSA), Endangered Species Act (ESA), and Marine Mammal Protection Act (MMPA) apply depending on the bycatch species and fishery and require management agencies to monitor bycatch. Under the MSA (50 CFR § 600.350), bycatch is to be minimized or avoided while protected species bycatch cannot exceed the allowable take under the ESA (50 CFR 216.3) or exceed the potential biological removal level under the MMPA (16 U.S.C. 1362). Often, to achieve bycatch monitoring goals, trained fisheries observers are placed on fishing vessels to monitor for protected species interactions and document the catch and bycatch (NOAA Fisheries, 2022) since much of this information is not required to be recorded in logbooks.

These observer-collected data are used to estimate bycatch levels in the fishery through various statistical or mathematical means. In many situations, sample-based ratio estimators such as the generalized ratio estimator or Horvitz-Thompson estimator can provide unbiased estimates of bycatch (McCracken, 2000, 2019). Model-based estimates, including generalized linear models (GLMs), zero-inflated models, hurdle models, Bayesian models, and generalized additive models (GAMs) have also been implemented to account for the impact of a small number of covariates on fisheries bycatch (McCracken, 2004; Martin et al., 2015; Stock et al., 2019, 2020). Bycatch estimates from such methods then feed into the process of establishing a priori limits on bycatch of some species over a given period (typically one year) (Moore et al., 2009), as well as other downstream products and management functions such as stock assessments, authorizations of fisheries with protected species bycatch, species status reviews, and population viability analyses.

However, most existing methods of bycatch estimation struggle to accurately and precisely estimate bycatch for species with low interaction rates. Ratio-based estimators assume a constant interaction rate and the inherent linear extrapolation of such methods can result in inaccurate and imprecise estimates, especially as observer coverage decreases (Amandè et al., 2012; Martin et al., 2015; Stock et al., 2019). Model-based methods can relax the constant interaction rate assumption by establishing parametric relationships between covariates and bycatch but these relationships are nearly impossible to resolve for very rare events (McCracken, 2004; Zuur et al., 2009; Martin et al., 2015; Stock et al., 2019). This issue with existing methods is particularly acute for protected species, who almost by definition tend to rarely interact with fisheries but for whom even very low rates of interaction can be a management concern given small population sizes.

Machine-learning algorithms present an opportunity to improve upon existing model-based methods as many build nonparametric covariate relationships and can use many covariates without the risk of variance inflation due to correlated explanatory variables (Thompson et al., 2017). In particular, classification algorithms (e.g., Random Forest; Breiman, 2001) have been used to identify environmental covariates of bycatch (Eguchi et al., 2017; Hazen et al., 2018; Stock et al., 2019, 2020). These tools have been applied in dynamic management strategies to identify areas where bycatch is most likely and direct fishing vessels away from these areas through data products sent to fishers (Howell et al., 2008, 2015; Hobday et al., 2010; Hazen et al., 2018). Such models can also be used to estimate bycatch and can exhibit improved performance over other model-based estimators (Stock et al., 2020; Carretta, 2023), but also may have lower performance when predicting on new data (Becker et al., 2020). Although many of these algorithms still struggle with the rare event nature of protected species bycatch, new variants of machine-learning algorithms, such as Ensemble Random Forests (ERF), have exhibited improved performance for rare event bycatch (Siders et al., 2020). As remotely sensed environmental and oceanographic covariates have become widely available, there is an opportunity to improve upon ratio-based or linear-model based estimators by using machine learning to sift through the sea of potential covariates and create predictive models for bycatch estimation.

Modeling rare-event bycatch using fishery-dependent data does not come without costs, as fisher choices regarding where and when to fish directly influence the sampling of protected species as well as geographic and environmental space. Such environmentally-biased sampling is likely to lead to less accurate predictions (Conn et al., 2017; El-Gabbas and Dormann, 2018; Pennino et al., 2019; Karp et al., 2023), especially for rarer species in a dynamic oceanographic environment. One strategy to address these modeling challenges is to attempt to correct the model’s predictions using Type I and Type II error rates from the training data. Ascertaining when such corrections are necessary and appropriate will establish key guidance for future use of machine learning algorithms to predict bycatch.

Here, we test the ability of Ensemble Random Forests (ERFs), developed to estimate rare event bycatch (Siders et al., 2020), to estimate bycatch of protected species using data from the Hawaii shallow-set longline (SSLL) fishery. This fishery has had 100% observer coverage since 2005 allowing us to know true levels of bycatch without having to simulate a simplified version of the highly dynamic and stochastic nature of protected species bycatch in pelagic environments. Using five protected species with varying rates of bycatch, we assessed the performance of corrected and uncorrected ERF predictions across three recommended thresholds defining which sets were likely to generate a bycatch event or not. We first sought to test the ability of the ERF-based bycatch estimators to accurately predict “new” data using a leave-one-out approach to iteratively build models while holding out one year’s worth of data. We used this information to assess what rates of bycatch required error correction to achieve accurate bycatch estimation. Second, we sequentially added years of training data to understand the amount of training data necessary to develop an effective bycatch estimation framework. Finally, in order to fully understand the costs and benefits of error correction for bycatch estimation, we assessed environmental and effort-related sources of bias in the model’s predictions. Overall, our goal was to understand the benefits and drawbacks of using this new framework for bycatch estimation, particularly for species that rarely interact with fisheries.

Materials and methods

Fishery description

The Hawaii SSLL fishery is a relatively small fishery (11-28 participating vessels per year during our study period) that primarily targets swordfish (NMFS, 2004). These vessels fish in a large area of the north central Pacific Ocean (roughly 20-40°N and 180-230°E), with a large proportion of fishing activity taking place in the first quarter of the calendar year (Howell et al., 2008; Siders et al., 2023). Since 2004, NOAA Fisheries has maintained 100% observer coverage in the SSLL fishery as a result of previously high levels of bycatch of loggerhead sea turtles (NMFS, 2004). We used SSLL observer data from 2005-2021 to obtain GPS locations for longline sets and concurrent bycatch records for five protected species.

General ERF framework for bycatch estimation

Using GPS locations and dates of the SSLL set and haul activities, we matched 25 environmental variables including moon phase, bathymetry, and distance to nearest seamount, five primary remotely sensed covariates (sea surface temperature, chlorophyll-a, sea winds, ocean currents, and sea level anomaly), and 17 derived secondary remotely sensed covariates (see the Supplementary Material for more details on data sources and extraction). We combined these data with the corresponding set’s bycatch of Oceanic Whitetip Shark, Laysan Albatross, Black-footed Albatross, Loggerhead Sea Turtle (hereafter referred to as loggerheads), and Leatherback Sea Turtle (hereafter referred to as leatherbacks), representing a range of protected species bycatch rates (from higher to lower). The full dataset for the ERF-based framework consisted of all sets for which we had paired bycatch data and environmental covariates. Generally, implementing the ERF framework consisted of first training an ERF with the paired bycatch and environmental data from a set of training years, using that ERF to predict the number of sets with bycatch in a new year of data, delineating which sets had likely bycatch interactions using a threshold cutoff, applying any Type I or Type II error corrections, and, finally, multiplying by group size (Figure 1).

Figure 1

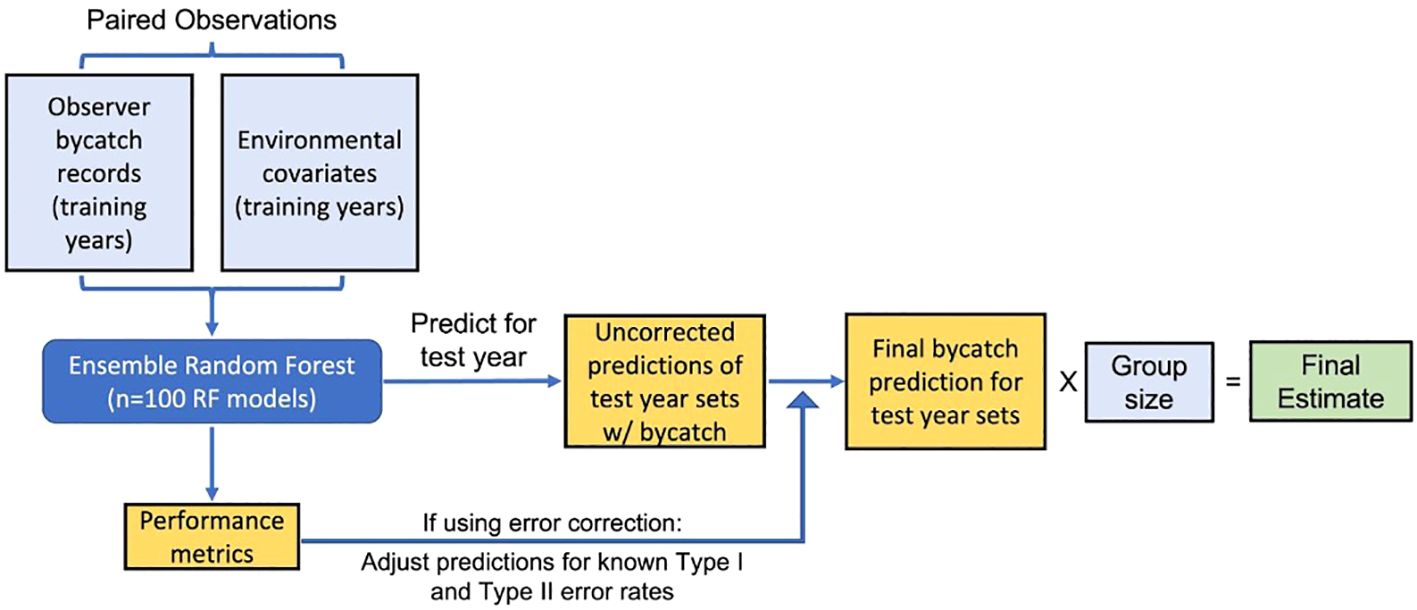
Figure 1 Flow chart depicting the general framework for deriving bycatch estimates using Ensemble Random Forests.

Training data selection

We selected training data for the ERF using two different methods. To assess which species required error correction to achieve effective bycatch estimation, we implemented a leave-one-out process that held out one year (2005-2021) from the model’s training data. This process ensured that ERFs used to predict bycatch for each year were trained using roughly equal amounts of data. However, in a real-world implementation of ERFs as bycatch estimation tools, only data from previous years would be available. To test how many years of data were necessary to maximize predictive capability, we used a sequential addition process. In this process, we trained an initial ERF on the first five years (2005–2009), predicted on the next year of data (2010 in this case), then repeated the process by sequentially adding one more year to the ERF model training data and predicting on the data for the upcoming year. We selected 2010 as a starting point for this process so that all ERFs were trained on at least five years of data, mimicking similar windows used for anticipated take limits in Hawaii longline fisheries (e.g., McCracken, 2019). We compared bycatch estimates from sequential addition results to corresponding estimates from the leave-one-out analysis with the goal of finding the year where differences were minimized between the two analyses. The amount of training data used at the year where the two estimates converge is an estimate of how much training data are necessary to maximize estimate accuracy.

Lastly, because ERFs vary in their predictions for each model run as a result of the inherent randomness of Random Forests and because the training data used can have a large impact on model predictions, we tested both of these factors simultaneously. Using loggerhead bycatch in 2021 as a test case, we used seven different versions of training data to train the ERFs: all years except for 2010, all years except for 2014, all years except for 2017, all years except for 2021, 2005-2009, 2005-2013, and 2005-2016. These are a subset of the leave-one-out and sequential addition models, with the goal of testing both changes in the content and amount of training data. We created 10 ERF replicates using each of these training data sets, and used them to conduct the bycatch estimation process for 2021 as outlined below.

Thresholds and error correction

We then used the trained ERF to predict which unobserved sets from the test year had interactions with the focal protected species. We assessed both the initial predictions on test year data, as well as error-corrected predictions, for their performance in estimating bycatch. In either case, the estimates derived from the ERF depend heavily on the probability threshold chosen to classify predictions into positives (i.e., predicted bycatch) and negatives (i.e., no predicted bycatch). We assessed three strategies for choosing a threshold: maximum sensitivity plus specificity (MSS), a common threshold used in species distribution models (Liu et al., 2013, 2016); maximum accuracy (ACC) which used the threshold that maximized the percentage of true predictions; and precision-recall break-even point (PRBE) which selected the threshold where precision (true positives/predicted positives) and recall (true positives/actual positives) were equal. We used the R package ROCR (Sing et al., 2005) to determine these metrics and their associated Type I and Type II error rates. We applied each of these thresholds to classify ERF predictions, either using the uncorrected total as our prediction or proceeding into error correction.

When correcting these predictions, we used the Type I and Type II error rates for training data as a measure of those same rates for test year data. In real-world implementation, this would be the best available measure of model performance and error rates on new data without fisheries observers. We used the positive predictive value (PPV; i.e., $P(Y=1, \widehat{Y}=1)/P(\widehat{Y}=1)$, # of true positives/# of all predicted positives) and false negative rate (FNR; i.e., $P(Y=0,\widehat{Y}=1)/P(\widehat{Y}=0)$, # of false negatives/# of all predicted negatives) of the ERF at a given threshold to develop these corrections using the following equation:

$$C=P(\widehat{Y}=1)*PPV+P(\widehat{Y}=0)*FNR$$

where C is the estimate of bycatch of a given ERF for a given species, $P(\widehat{Y}=1)$ is the threshold-delineated sets with predicted interactions, and $P(\widehat{Y}=0)$ is the threshold-delineated sets without predicted interactions. This corrected prediction was our measure of the number of sets with bycatch in the test year, which we then multiplied by the group size to get a final prediction of the number of interactions in the test year.

When assessing accuracy and bias of ERF-derived estimates over the long-term, we refer to cumulative and absolute error. Cumulative error in this context refers to the net difference over the study period between ERF estimates and the actual bycatch total; in other words, for this measure positively and negatively biased results compensate for each other. In contrast, absolute error refers to the summed absolute difference between ERF estimates and the actual bycatch total, where negatively biased and positively biased results do not compensate for one another.

Assessing ERF performance

We used three threshold-independent metrics to broadly assess ERF performance on training and test year data, all of which were calculated using the ROCR package in R (Sing et al., 2005). First, we used the area under the curve (AUC), which refers to the receiver operating curve plotting 1 - specificity against sensitivity at thresholds ranging from 0 to 1. AUC values range from 0 to 1, with values above 0.5 indicating a model performs better than random. Second, we used root mean square error (RMSE), calculated as follows:

$$RMSE=\sqrt{\frac{{\sum }_{i = 1}^n{(y_i-{\widehat{y}}_{i })}^2}{N}}$$

Where ${\widehat{y}}_{i }$ is the model prediction for a set, $y_i$ is the true value, and N is the total number of sets. Finally, we used the True Skill Statistic, the maximum of the sum of the true positive rate (TPR) and true negative rate (TNR) minus 1:

$$TSS=max(TPR+TNR-1)$$

Assessing bias in ERF bycatch estimates

For each test year, ERF predictions may be biased as a result of systematic bias in the model’s predictive capacity, spatial shifts in the fishery area reducing model performance, or methodological biases related to error correction. In order to assess what may cause bias in bycatch estimates and provide recommendations for future use of the ERF framework, we correlated environmental, spatial, and methodological covariates with estimate bias. As bycatch predictions were produced on an annual basis, we compared the annual mean of each potential covariate to the annual bias of ERF estimates (bias in this context could be positive or negative). First, we assessed the correlation of estimate bias with each of the ERF’s 25 environmental covariates (Table 1). Second, to assess effects of the SSLL fleet’s spatial distribution on our estimates, we calculated the centroid of fishing effort for each year and correlated the latitudes and longitudes of these centroids with the bias in ERF estimates. Finally, we correlated ERF estimate bias with the annual rate of bycatch (number of interactions/set) for each focal species and total sets by year to determine if bias was rooted in the methodology.

Table 1

Table 1 Mean ERF performance metrics from leave-one-out results (SD in parentheses).

Results

Summary statistics

In total, we used 18,933 Hawaii SSLL sets with arrival dates from 2005 to 2021 paired with environmental data and observer records (median = 1,172 sets per year). In total, these sets included 913 oceanic whitetip shark interactions (n = 667 sets with interaction, mean group size = 1.37, mean interactions per year = 53.7), 567 Laysan albatross interactions (n = 417 sets, group size = 1.36, interactions per year = 33.4), 411 black-footed albatross interactions (n = 354 sets, group size = 1.16, interactions per year = 24.2), 221 loggerhead sea turtles (n= 204 sets, group size = 1.08, interactions per year = 13), and 107 leatherback sea turtles (n = 105 sets, group size = 1.02, interactions per year = 6.3).

ERF performance and variable importance

The ERFs were highly successful at learning and predicting bycatch in training years for all species but showed variable success among species and years at predicting bycatch in test year data (Table 1, variable importance in Supplementary Figure 2). Overall, model performance by species correlated with overall bycatch rates for the study period, with the best threshold-independent metrics on test year data for oceanic whitetips and Laysan albatross. Notably, Laysan albatross on average exhibited better performance than oceanic whitetips despite a lower bycatch rate. Average performance when predicting black-footed albatross, loggerheads, and leatherback in test years was markedly lower. Among test years, model performance in predicting oceanic whitetip bycatch was the most variable (see SD values for test year columns in Table 1) as a result of extremely poor performance in 2006 and 2018 but very good performance otherwise (Supplementary Table 2 shows metrics by year). The other four species showed similar levels of variability in test year performance.

Leave-one-out results

Uncorrected

The accuracy of uncorrected ERF-derived estimates (Figures 2A-E) varied among species in a similar pattern to threshold-independent metrics. Threshold choice substantially altered accuracy and bias of bycatch predictions for individual years (Figure 2) and over the study period (Table 2). Over the long-term for oceanic whitetips, Laysan albatross and loggerheads, the precision-recall break-even (PRBE) threshold produced the best uncorrected results; for Laysan albatross and loggerheads, the maximum accuracy (ACC) threshold performed similarly. Black-footed albatross and leatherback estimates were most accurate over the long-term with the maximum sensitivity plus specificity (MSS) threshold. We note that there are minor differences in the best threshold choice when considering root mean square error (RMSE) of annual estimates (Supplementary Table 3).

Figure 2

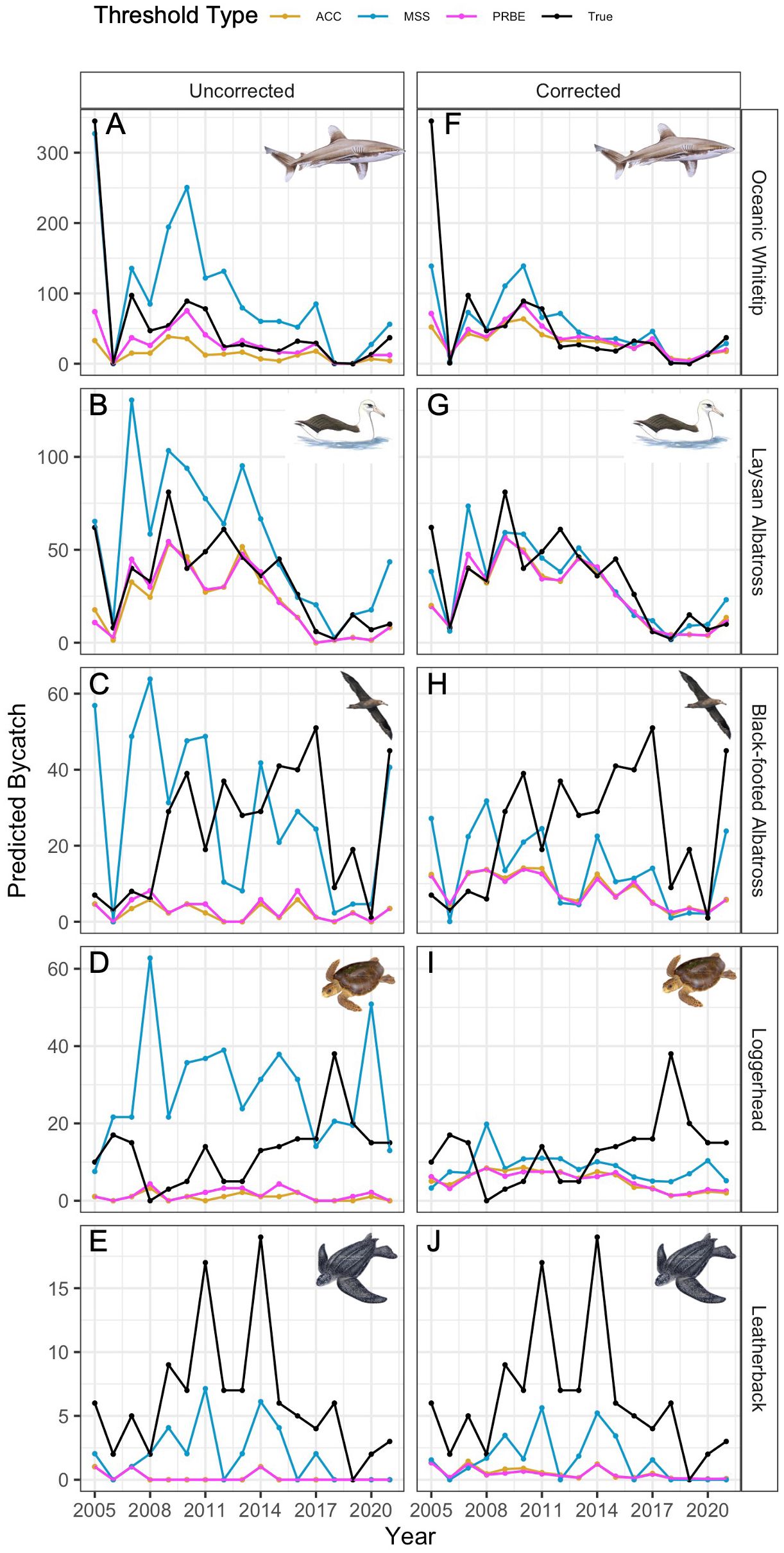
Figure 2 Leave-one-out results by species for uncorrected (left) and corrected (right) results. Species are oceanic whitetips (A, F), Laysan albatross (B, G), black-footed albatross (C, H), loggerheads (D, I), and leatherbacks (E, J). Line color indicates the threshold type applied to ERF predictions for the test year data. Note that the y-axis scale varies among species.

Table 2

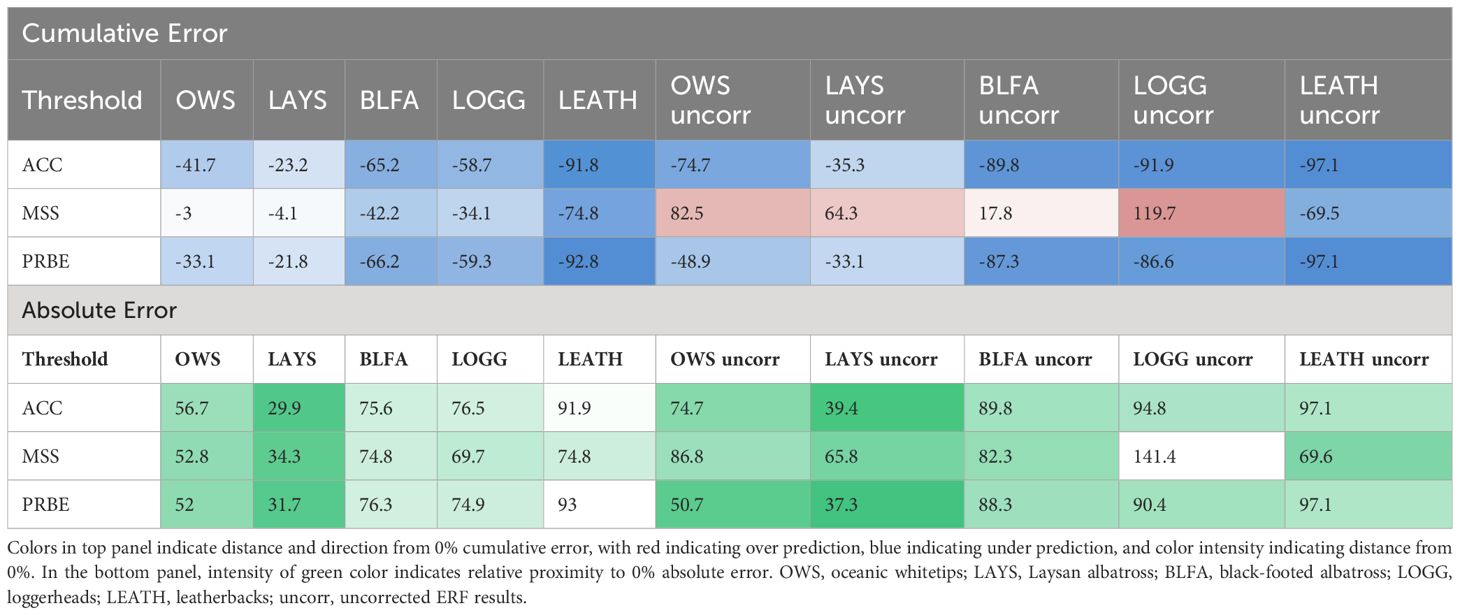
Table 2 Cumulative and absolute errors by species (columns) and threshold type (rows) across all test years in the leave-one-out analysis for both error-corrected and uncorrected results.

By cumulative error, there was a substantial decrease in accuracy between black-footed albatross (n = 411 interactions) and loggerheads (n = 224 interactions) for most thresholds, potentially indicating a sample size range where using uncorrected results becomes problematic. By absolute error, there was at least one threshold for whitetips and Laysan albatross near or below 50% error using uncorrected results, whereas minimum error for the other three species by this metric was 69%, indicating a necessary sample size somewhere between Laysan albatross (n = 567 interactions) and black-footed albatross (n = 411 interactions).

Oceanic whitetip and Laysan albatross uncorrected estimates more closely followed temporal trends over time (Figures 2A-E), an indication that accuracy of long-term estimates for these species was more influenced by the accuracy of individual test year predictions. In contrast, uncorrected estimates from the best thresholds for black-footed albatross, loggerheads, and leatherbacks showed mostly flat trends with high variation over time. For black-footed albatross, this flat trend approximated mean bycatch levels over time, but it tended to overpredict bycatch for loggerheads and underpredict bycatch for leatherbacks.

Corrected

Corrected estimates over the long-term were generally, but not always, more accurate for a given species and threshold (Figures 2F-J, Table 2). When considering cumulative error, all species except for black-footed albatross benefitted from error correction; by absolute error, all species benefited. For oceanic whitetips and Laysan albatross, the benefits of error correction were highest for the MSS threshold; for Laysan albatross, the ACC and PRBE estimates also benefited greatly. For loggerheads, estimates were improved for all thresholds. Leatherback bycatch estimates were not improved by error correction.

Notably, cumulative estimates for all species and threshold types were negatively biased (i.e., bycatch estimates were lower than actual totals), although this bias was smaller for oceanic whitetips and Laysan albatross. For oceanic whitetips, this resulted from a strong tendency to underpredict bycatch in 2005 that was not compensated for in future years. Aside from this, corrected bycatch estimates more closely tracked trends over time for whitetips and Laysan albatross than they did for other species, especially for the MSS threshold. Black-footed albatross and loggerhead corrected estimates were more accurate in earlier years, but were negatively biased from 2011 forward for black-footed albatross and from 2015 for loggerheads. The benefits of error correction were reduced or non-existent for black-footed albatross and leatherbacks.

Threshold choice had a substantial impact on estimates for individual years, as well as the long-term accuracy of the ERF estimation process. The threshold types exhibited mostly consistent trends relative to each other to produce higher or lower predictions, with MSS typically higher than ACC or PRBE for all species. However, the most accurate threshold varied among years. Using oceanic whitetips as an example, the higher predictions produced by using MSS results allowed for the most accurate whitetip bycatch estimates in 2005, but among the worst predictions in 2009 and 2010. Similarly, for loggerheads, the ACC and PRBE thresholds had the most accurate predictions before 2013, but afterwards the same thresholds had the worst predictions.

Sequential addition results

Differences between corrected leave-one-out and sequential addition ERF estimates for oceanic whitetips leveled off in 2012 and all other species aside from loggerheads leveled off in 2017. This indicates that for our highest bycatch species, seven years (roughly 10,000 sets) was an appropriate level of training data. For three other species 12 years (roughly 16,000 sets) of training data may be an appropriate amount (Figure 3). In contrast, there were small differences between corrected leave-one-out and sequential addition results for loggerheads even with minimal training data, but these continually declined over the study period for most threshold types. Uncorrected estimates showed similar temporal patterns for most species in the convergence between leave-one-out and sequential addition bycatch estimates. Loggerhead uncorrected estimates from the two analyses were initially very different when using the MSS threshold, but these differences plateaued after adding only one additional year of data.

Figure 3

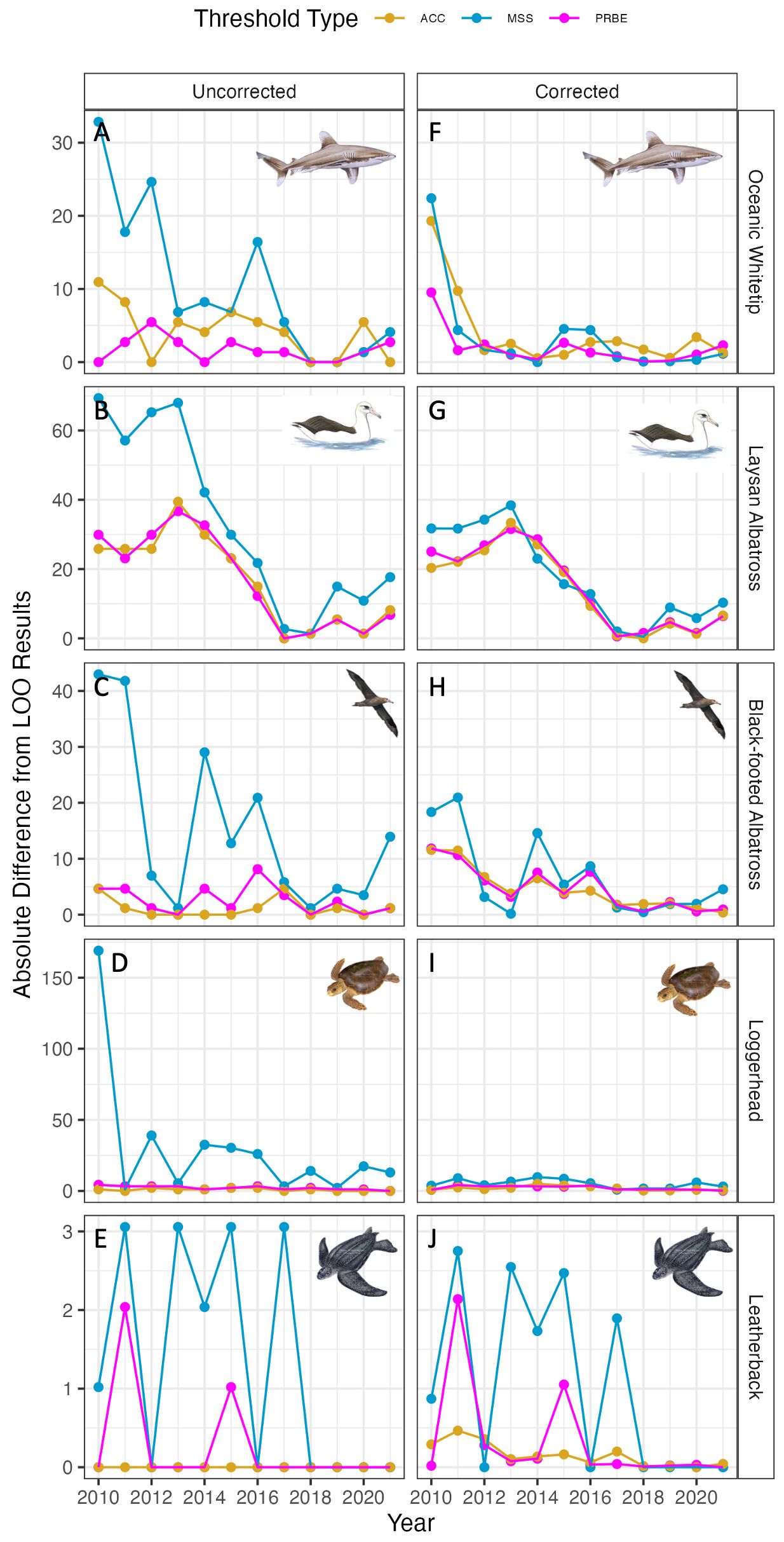
Figure 3 Absolute differences between sequential addition and leave-one-out results by species for uncorrected (left) and corrected (right) results. Species are oceanic whitetips (A, F), Laysan albatross (B, G), black-footed albatross (C, H), loggerheads (D, I), and leatherbacks (E, J). Line color indicates the threshold type applied to ERF predictions for the test year data. Note that y-axis scale varies among species.

Differences within and among training data sets

When predicting loggerhead bycatch in 2021 with different model runs using the same training data set, models showed small variation in corrected results (mean CV = 12%, Supplementary Figure 3) but high levels of variation in uncorrected results (mean CV = 58%). Among training data sets, again variation was lower in corrected results than uncorrected, but there was wide variation in predictions even for corrected results (Supplementary Figure 3). However, most of this variation was among models that did or did not include 2021 data in the training data set. This indicates that corrected estimates predicted similar levels of bycatch as long as the model had seen similar data previously in the training set.

Correlated variables with ERF estimate bias

When using error-corrected estimates, the most notable and consistent correlate of ERF estimate bias for all five species was bycatch rate in the test year (Figure 4). In four of the five species, correlation between bycatch rate and ERF estimate bias was highly negative for all threshold types (range: –0.73 - –0.98). Laysan albatross bias and bycatch rate were also negatively correlated, but to a lesser degree (mean: –0.54). This tendency is likely a result of error correction serving to regress estimates toward mean interaction rates. When using uncorrected estimates, this correlation with interaction rate was reduced for all species, but to varying degrees. For Laysan albatross and oceanic whitetips, correlation between bias and interaction rates was reduced to near 0 for the MSS threshold but this reduction was not present for the other threshold types. For black-footed albatross and loggerheads, correlation between bias and interaction rate was reduced but still less than –0.58. Using uncorrected estimates did not substantially change relationships between estimate bias and test year interaction rates for any thresholds for leatherbacks. While environmental and spatial variables were sometimes also correlated with estimated bias, the variables exhibiting correlation with bias, the magnitude of that correlation, and the consistency in the correlation among thresholds varied greatly among species.

Figure 4

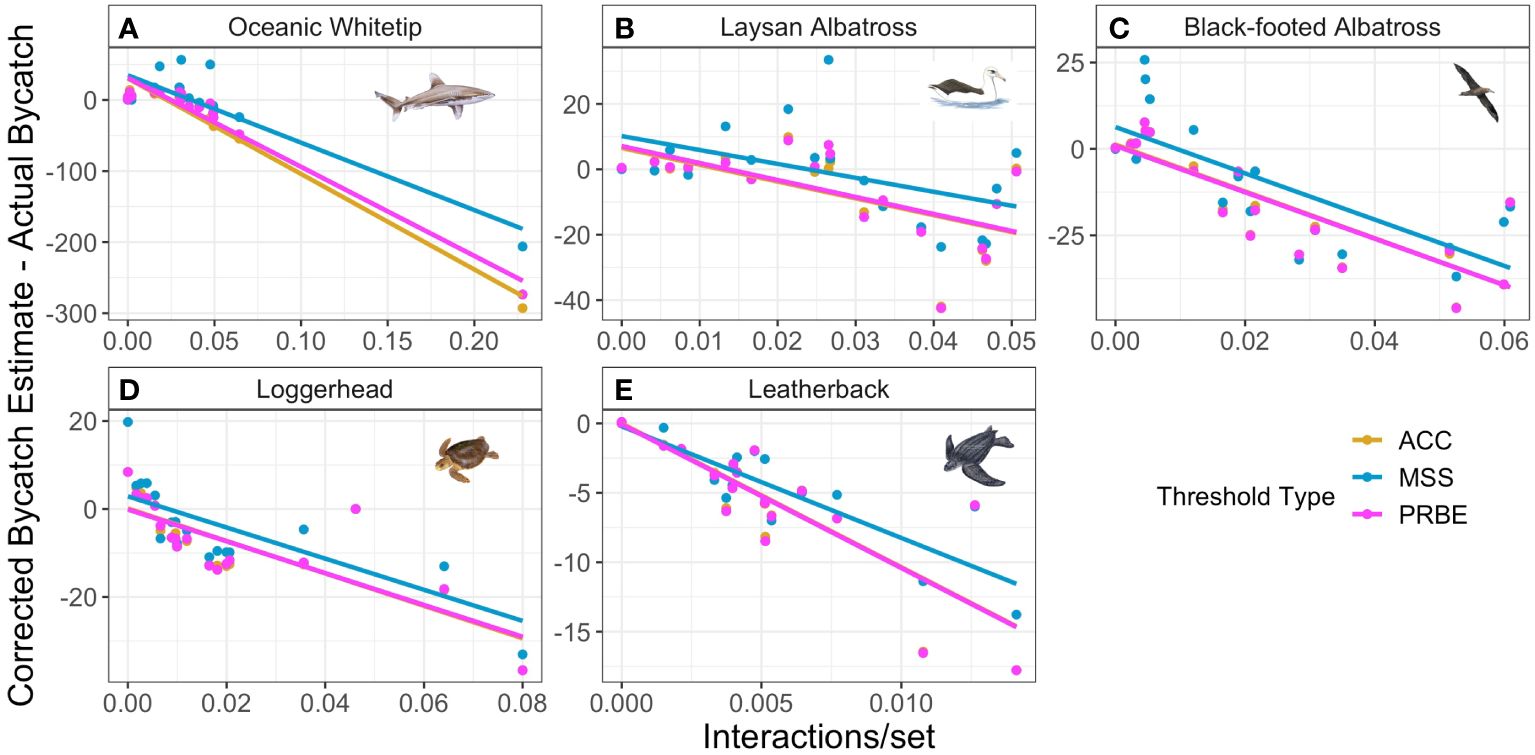
Figure 4 Relationships for each focal species (ordered A-E from highest to lowest bycatch rates) between test year interaction rate and difference between error-corrected bycatch estimate and actual bycatch in that year. Colors indicate threshold type applied to ERF predictions for test year data; note that ACC results are often obscured by the other points and lines. Axis titles are shared between all plots.

Discussion

We developed and tested a framework for protected species bycatch estimation using the predictions of Ensemble Random Forest models trained on environmental and oceanographic data. There are some general insights gained that are worth highlighting. In the leave-one-out analysis, uncorrected estimates of bycatch were relatively accurate (<50% error) in aggregate for at least one threshold for oceanic whitetips, Laysan albatross, and black-footed albatross, but no thresholds produced reliable results for loggerheads and leatherbacks (Figures 2A-E, Table 2). This suggests the number of interactions is most important for developing accurate and precise models and can limit the use of model-based estimators for hyper-rare bycatch species (Stock et al., 2019). After error correction, nearly all annual predictions were improved for all species (Figures 2F-J, Table 2); however, error correction also introduces a tendency to estimate bycatch in the test year at a rate similar to the training data (Figure 4). The threshold type and resulting Type I and Type II error corrections used were highly influential in the accuracy of predictions both for individual years and over the long-term. Approximately 12 years of training data were necessary for oceanic whitetip, Laysan albatross, and leatherback estimates to converge with leave-one-out results (Figure 3). In contrast, loggerhead estimates continually improved with more training data and black-footed albatross showed no trends in model improvements. As expected, uncorrected estimate accuracy was positively correlated with model performance and threshold choice was highly important for deriving the most accurate estimates possible. Subjectively, our results indicate that given the effort in the Hawai’i SSLL, a bycatch rate of approximately 2% is required for uncorrected estimates derived from the ERF to be relatively accurate estimators of bycatch on an annual basis.

Error correction improved estimate accuracy for nearly all species and threshold combinations. However, error correction also introduces a negative correlation between estimate bias and test year interaction rate, tending to regress estimated bycatch rates toward mean rates from the training data. For the MSS threshold, the increase in this correlation is related to overall bycatch rates; rarer species such as leatherbacks and loggerheads exhibited high bias-interaction rate correlations even without error correction. This tendency to regress towards mean bycatch rates reduces corrected estimates’ ability to account for especially high or low bycatch years occurring as a result of random variation or systematic changes in interaction rates due to changes in fisheries or bycatch species’ distribution. However, error correction is essential to producing reasonable estimates for very low bycatch rate species, and managers looking to use machine learning methods to estimate bycatch should weigh the costs and benefits of error correction.

The threshold used to classify ERF predictions at the set level altered the resulting annual-level predictions and was highly influential in determining estimated Type I and Type II error rates. In addition, the best threshold varied among species and years. In most cases, uncorrected estimates were best when using the MSS threshold whereas the threshold producing the best corrected estimates varied among species. Critically, the effectiveness of any threshold depends on the degree to which Type I and Type II error rates from training and test data correspond with one another. The correspondence of training and test error rates likely depends on sample sizes and interaction rates in both training and test data. Type I and Type II error rates, appropriate thresholds, sample sizes, interaction rates, and model performance will differ among fisheries and should be thoroughly examined if our framework is implemented in new fisheries.

Data requirements are an additional consideration for practical implementation of our framework. We showed that for oceanic whitetips (our highest bycatch species) ERF estimates derived from the leave-one-out analysis (i.e., maximum available data) converged with those from the sequential addition process around 2012, indicating that approximately seven years and 10,000 fishery sets of training data were necessary. For three other species, these values were 12 years and 16,000 sets. t is unclear whether this convergence reflects overall training sample sizes or the number of interactions but it is highly likely that species with higher rates of bycatch will require less training data in terms of years and sets. Additionally, loggerhead sequential addition analyses continually benefited from new data.Ensemble Random Forests are particularly adept at learning and predicting very rare events like protected species bycatch (Siders et al., 2020), and therefore are likely to require the least amount of training data of available algorithms. Overall, species-specific idiosyncrasies may alter data needs; in particular, spatial clustering of interactions has been shown to play a role in ERF predictive performance (Siders et al., 2020). Accurate estimation will likely be highly dependent on training data sample size, interaction rates, the stability of the interaction distributions, spatial clustering, and detection probability.

The variation in our uncorrected results among model runs highlights that very small changes in thresholds can lead to large changes in predictions. Continuous probabilities can be more informative (Vaughan and Ormerod, 2005) but for this application using a probability threshold was necessary to classify predictions and derive practical estimates for potential use by managers. Using error corrections greatly reduced this source of estimate uncertainty. Among training data sets, it was unsurprising that the training data used had large effects on model predictions. A general principle in machine learning is that the highest possible levels of similarity between training and test data are desirable, as extrapolation can result in errors due to a tendency to overfit to training data (Christin et al., 2019; Stupariu et al., 2022; Pichler and Hartig, 2023). Fluctuating rates of bycatch, changing fisher behaviors, climate change, and noisy interaction data are all challenges in this regard that may result in poor model predictions if training data are not similar to test data.

Despite their effectiveness for some of our study species, using Ensemble Random Forests or other machine learning frameworks to estimate bycatch is not a panacea, even when combined with error correction. For particularly rare species (e.g, loggerheads and leatherbacks), there simply are not enough data to effectively identify environmental correlates of bycatch and error-corrected estimates regress towards mean interaction rates that are more easily determined from ratio estimators. The spatially and environmentally-biased sampling inherent to fisheries-dependent data likely exacerbate sample size issues, reduce our ability to predict the spatial distribution of bycatch, and decrease uncorrected estimate accuracies, as has been demonstrated for many other applications of species distribution modeling (Conn et al., 2017; El-Gabbas and Dormann, 2018; Yates et al., 2018; Rufener et al., 2021; Baker et al., 2022; Karp et al., 2023). Fisheries managers looking to implement similar methods should remain mindful that our approach, like any bycatch estimator, has limitations and that there is no one-size-fits-all approach to threshold selection, necessary training data, or bycatch estimation.

There is an inherent analytical and philosophical spectrum in assessing spatial patterns of species occurrence (Merow et al., 2014) that also broadly applies to bycatch estimation, ranging between unbiased but under fitted ratio estimators (e.g., Horvitz-Thompson or generalized ratio estimators; McCracken, 2000, 2019) to potentially biased but more predictive model-based methods like those we outlined in this paper. More research is needed to compare across this spectrum (but see Stock et al., 2019 for one such comparison) and the methods we outlined here borrow from both ends of the spectrum. Similar to ratio estimators, we assume a constant group size but relax assumptions related to constant interaction rates; our estimates may be improved by implementing regression tree methods (e.g., Carretta, 2023) to explicitly estimate group size, particularly for those species with higher variation in group size among interacting sets (e.g., oceanic whitetips). Other model-based methods (e.g., zero-inflated, hurdle, Bayesian, GAMs; Mullahy, 1986; Lambert, 1992; Zuur et al., 2009; Martin et al., 2015; Stock et al., 2019; Karp et al., 2023) also relax assumptions regarding linear relationships and, in some cases, group size. However, such models may not produce effective estimates of protected species bycatch due to class imbalances (Li et al., 2019), dynamic relationships between covariates and bycatch that may limit the effectiveness of any single covariate, and interrelated covariates that either necessitate excluding correlated predictors or risk high levels of variance inflation that limit the model’s predictive ability on new data (Thompson et al., 2017). Our ERF-based approach addresses some of these concerns to develop effective bycatch estimates for species above 2% interaction rates, and error correction improved these estimates and those of loggerheads. With that said, we stress once more that no existing bycatch estimation method is a cure-all in estimating or predicting extremely rare events in a highly dynamic system.

Although we have demonstrated that the ERF framework can be effective for some species at estimating bycatch in new years of data, real-world implementation would involve observer coverage and using the ERF to predict bycatch levels for unobserved trips. A crucial consideration is how the accuracy and precision of ERF estimates compares to existing ratio-based and model-based estimators in these real-world scenarios. Given the wide variation that can occur using ratio-based methods to estimate protected species bycatch (Carretta and Moore, 2014; Martin et al., 2015) and previous findings that show machine learning-based methods to be more accurate than other model-based methods (Stock et al., 2019, 2020), we expect that the ERF estimates would be more precise and potentially more accurate, particularly at low observer coverage levels. In turn, machine learning methods may aid both managers and fishers by achieving bycatch monitoring and estimation goals while reducing observer coverage needs. It should be noted that no matter the estimation method, some level of observer coverage will always be necessary to provide information about observed levels of bycatch and environmental correlates of these interactions to inform model-based bycatch estimators; observer coverage needs are higher to achieve these bycatch detection goals for rare and/or protected species (Curtis and Carretta, 2020). In addition, although observer coverage would reduce estimate bias due to directly documenting some portion of the fleet’s bycatch, corrected estimates would retain some portion of the biases we saw in our results at the annual level. Therefore, comparing our estimates to those derived from other methods for multiple species and fisheries is key to understanding precision-bias trade-offs under different observer coverage scenarios, assessing downstream benefits and drawbacks of using ERF-derived estimates, and improving bycatch-related fisheries management.

Data availability statement

The datasets presented in this article are not readily available because the data from the Hawaii shallow-set pelagic longline fishery information used herein is confidential, protected information and cannot be disseminated. Code used to conduct data analysis are provided at 10.5281/zenodo.10819007. Requests to access the datasets should be directed to Chris Long, gator58@ufl.edu.

Ethics statement

Ethical approval was not required for the study involving animals in accordance with the local legislation and institutional requirements because the work was modeling only, with no field data collected directly.

Author contributions

CL: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Visualization, Writing – original draft. RA: Conceptualization, Funding acquisition, Methodology, Project administration, Supervision, Writing – review & editing. TJ: Writing – review & editing, Supervision, Conceptualization, Project administration, Funding acquisition. ZS: Conceptualization, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Supervision, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by NOAA PIFSC Grant NA21NMF4720548 and CL was supported in part by the National Research Council Research Associateship Program.

Acknowledgments

We would like to acknowledge the dedication of those individuals involved with the Pacific Islands Region Observer Program that worked to obtain much of the data we used.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2024.1331292/full#supplementary-material

References

Amandè M. J., Chassot E., Chavance P., Murua H., de Molina A. D., Bez N. (2012). Precision in bycatch estimates: the case of tuna purse-seine fisheries in the Indian Ocean. ICES J. Mar. Sci. 69, 1501–1510. doi: 10.1093/icesjms/fss106

CrossRef Full Text | Google Scholar

Baker D. J., Maclean I. M. D., Goodall M., Gaston K. J. (2022). Correlations between spatial sampling biases and environmental niches affect species distribution models. Glob. Ecol. Biogeogr. 31, 1038–1050. doi: 10.1111/geb.13491

CrossRef Full Text | Google Scholar

Becker E. A., Carretta J. V., Forney K. A., Barlow J., Brodie S., Hoopes R., et al. (2020). Performance evaluation of cetacean species distribution models developed using generalized additive models and boosted regression trees. Ecol. Evol. 10, 5759–5784. doi: 10.1002/ece3.6316

PubMed Abstract | CrossRef Full Text | Google Scholar

Breiman L. (2001). Random forests. Mach. Learn. 45, 5–32. doi: 10.1023/A:1010933404324

CrossRef Full Text | Google Scholar

Carretta J. V. (2023) Estimates of marine mammal, sea turtle, and seabird bycatch in the California large-mesh drift gillnet fishery: 1990-2022. Available online at: https://repository.library.noaa.gov/view/noaa/52092.

Google Scholar

Carretta J. V., Moore J. E. (2014) Recommendations for pooling annual bycatch estimates when events are rare. Available online at: https://repository.library.noaa.gov/view/noaa/4731.

Google Scholar

Christin S., Hervet É., Lecomte N. (2019). Applications for deep learning in ecology. Methods Ecol. Evol. 10, 1632–1644. doi: 10.1111/2041-210X.13256

CrossRef Full Text | Google Scholar

Clay T. A., Small C., Tuck G. N., Pardo D., Carneiro A. P. B., Wood A. G., et al. (2019). A comprehensive large-scale assessment of fisheries bycatch risk to threatened seabird populations. J. Appl. Ecol. 56, 1882–1893. doi: 10.1111/1365-2664.13407

CrossRef Full Text | Google Scholar

Conn P. B., Thorson J. T., Johnson D. S. (2017). Confronting preferential sampling when analysing population distributions: diagnosis and model-based triage. Methods Ecol. Evol. 8, 1535–1546. doi: 10.1111/2041-210X.12803

CrossRef Full Text | Google Scholar

Curtis K. A., Carretta J. V. (2020). ObsCovgTools: Assessing observer coverage needed to document and estimate rare event bycatch. Fisheries Res. 225, 105493. doi: 10.1016/j.fishres.2020.105493

CrossRef Full Text | Google Scholar

Davies R. W. D., Cripps S. J., Nickson A., Porter G.(2009). Defining and estimating globalmarine fisheries bycatch. Mar. Policy 33, 661–672. doi:10.1016/j.marpol.2009.01.003

CrossRef Full Text | Google Scholar

Eguchi T., Benson S. R., Foley D. G., Forney K. A. (2017). Predicting overlap between drift gillnet fishing and leatherback turtle habitat in the California Current Ecosystem. Fish Oceanogr. 26, 17–33. doi: 10.1111/fog.12181

CrossRef Full Text | Google Scholar

El-Gabbas A., Dormann C. F. (2018). Improved species-occurrence predictions in data-poor regions: using large-scale data and bias correction with down-weighted Poisson regression and Maxent. Ecography 41, 1161–1172. doi: 10.1111/ecog.03149

CrossRef Full Text | Google Scholar

Gray C. A., Kennelly S. J. (2018). Bycatches of endangered, threatened and protected species in marine fisheries. Rev. Fish. Biol. Fish 28, 521–541. doi: 10.1007/s11160-018-9520-7

CrossRef Full Text | Google Scholar

Hazen E. L., Scales K. L., Maxwell S. M., Briscoe D. K., Welch H., Bograd S. J., et al. (2018). A dynamic ocean management tool to reduce bycatch and support sustainable fisheries. Sci. Adv. 4, eaar3001. doi: 10.1126/SCIADV.AAR3001

PubMed Abstract | CrossRef Full Text | Google Scholar

Hobday A. J., Hartog J. R., Timmiss T., Fielding J. (2010). Dynamic spatial zoning to manage southern bluefin tuna (Thunnus maccoyii) capture in a multi-species longline fishery. Fish Oceanogr. 19, 243–253. doi: 10.1111/j.1365-2419.2010.00540.x

CrossRef Full Text | Google Scholar

Howell E. A., Hoover A., Benson S. R., Bailey H., Polovina J. J., Seminoff J. A., et al. (2015). Enhancing the TurtleWatch product for leatherback sea turtles, a dynamic habitat model for ecosystem-based management. Fish Oceanogr. 24, 57–68. doi: 10.1111/fog.12092

CrossRef Full Text | Google Scholar

Howell E. A., Kobayashi D. R., Parker D. M., Balazs G. H., Polovina J. J. (2008). TurtleWatch: a tool to aid in the bycatch reduction of loggerhead turtles Caretta caretta in the Hawaii-based pelagic longline fishery. Endanger. Species Res. 5, 267–278. doi: 10.3354/esr00096

CrossRef Full Text | Google Scholar

Karp M. A., Brodie S., Smith J. A., Richerson K., Selden R. L., Liu O. R., et al. (2023). Projecting species distributions using fishery-dependent data. Fish. Fish 24, 71–92. doi: 10.1111/faf.12711

CrossRef Full Text | Google Scholar

Komoroske L. M., Lewison R. L. (2015). Addressing fisheries bycatch in a changing world. Front. Mar. Sci. 2. doi: 10.3389/fmars.2015.00083

CrossRef Full Text | Google Scholar

Lambert D. (1992). Zero-inflated poisson regression, with an application to defects in manufacturing. Technometrics 34, 1–14. doi: 10.2307/1269547

CrossRef Full Text | Google Scholar

Lewison R. L., Crowder L. B., Wallace B. P., Moore J. E., Cox T., Zydelis R., et al. (2014). Global patterns of marine mammal, seabird, and sea turtle bycatch reveal taxa-specific and cumulative megafauna hotspots. Proc. Natl. Acad. Sci. U. S. A. 111, 5271–5276. doi: 10.1073/pnas.1318960111

PubMed Abstract | CrossRef Full Text | Google Scholar

Li Y., Bellotti T., Adams N. (2019). Issues using logistic regression with class imbalance, with a case study from credit risk modelling. Found. Data Sci. 1, 389–417. doi: 10.3934/fods.2019016

CrossRef Full Text | Google Scholar

Liu C., Newell G., White M. (2016). On the selection of thresholds for predicting species occurrence with presence-only data. Ecol. Evol. 6, 337–348. doi: 10.1002/ece3.1878

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu C., White M., Newell G. (2013). Selecting thresholds for the prediction of species occurrence with presence-only data. J. Biogeogr. 40, 778–789. doi: 10.1111/jbi.12058

CrossRef Full Text | Google Scholar

Martin S. L., Stohs S. M., Moore J. E. (2015). Bayesian inference and assessment for rare-event bycatch in marine fisheries: a drift gillnet fishery case study. Ecol. Appl. 25, 416–429. doi: 10.1890/14-0059.1

PubMed Abstract | CrossRef Full Text | Google Scholar

McCracken M. (2000). Estimation of sea turtle take and mortality in the Hawaiian longline fisheries. Washington, DC: NOAA. Available at: https://repository.library.noaa.gov/view/noaa/4441

Google Scholar

McCracken M. (2004). Modeling a very rare event to estimate sea turtle bycatch: lessons learned. Washington, DC: NOAA. Available at: https://repository.library.noaa.gov/view/noaa/3399

PubMed Abstract | Google Scholar

McCracken M. (2019). Sampling the Hawaii deep-set longline fishery and point estimators of bycatch. US Dept Commer. NOAA Technical Memorandum NOAA-TM-PIFSC-89. Washington, DC: NOAA. doi: 10.25923/2PSA-7S55

CrossRef Full Text | Google Scholar

Merow C., Smith M. J., Edwards T. C. Jr., Guisan A., McMahon S. M., Normand S., et al. (2014). What do we gain from simplicity versus complexity in species distribution models? Ecography 37, 1267–1281. doi: 10.1111/ecog.00845

CrossRef Full Text | Google Scholar

Moore J. E., Wallace B. P., Lewison R. L., Žydelis R., Cox T. M., Crowder L. B. (2009). A review of marine mammal, sea turtle and seabird bycatch in USA fisheries and the role of policy in shaping management. Mar. Policy 33, 435–451. doi: 10.1016/j.marpol.2008.09.003

CrossRef Full Text | Google Scholar

Mullahy J. (1986). Specification and testing of some modified count data models. J. Econom. 33, 341–365. doi: 10.1016/0304-4076(86)90002-3

CrossRef Full Text | Google Scholar

Nelms S. E., Alfaro-Shigueto J., Arnould J. P. Y., Avila I. C., Nash S. B., Campbell E., et al. (2021). Marine mammal conservation: over the horizon. Endanger. Species Res. 44, 291–325. doi: 10.3354/esr01115

CrossRef Full Text | Google Scholar

NMFS (2004) Fisheries Off West Coast States and in the Western Pacific; Western Pacific Pelagic Fisheries; Pelagic Longline Fishing Restrictions, Seasonal Area Closure, Limit on Swordfish Fishing Effort, Gear Restrictions, and Other Sea Turtle Take Mitigation Measures (Fed. Regist). Available online at: https://www.federalregister.gov/documents/2004/04/02/04-7526/fisheries-off-west-coast-states-and-in-the-western-pacific-western-pacific-pelagic-fisheries-pelagic (Accessed October 6, 2023).

Google Scholar

NOAA Fisheries (2022) National Bycatch Reduction Strategy (NOAA). Available online at: https://www.fisheries.noaa.gov/international/bycatch/national-bycatch-reduction-strategy (Accessed September 26, 2023).

Google Scholar

Pacoureau N., Rigby C. L., Kyne P. M., Sherley R. B., Winker H., Carlson J. K., et al. (2021). Half a century of global decline in oceanic sharks and rays. Nature 589, 567–571. doi: 10.1038/s41586-020-03173-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Pennino M. G., Paradinas I., Illian J. B., Muñoz F., Bellido J. M., López-Quílez A., et al. (2019). Accounting for preferential sampling in species distribution models. Ecol. Evol. 9, 653–663. doi: 10.1002/ece3.4789

PubMed Abstract | CrossRef Full Text | Google Scholar

Pichler M., Hartig F. (2023). Machine learning and deep learning—A review for ecologists. Methods Ecol. Evol. 14, 994–1016. doi: 10.1111/2041-210X.14061

CrossRef Full Text | Google Scholar

Richards R. J., Raoult V., Powter D. M., Gaston T. F. (2018). Permanent magnets reduce bycatch of benthic sharks in an ocean trap fishery. Fish Res. 208, 16–21. doi: 10.1016/j.fishres.2018.07.006

CrossRef Full Text | Google Scholar

Rufener M.-C., Kristensen K., Nielsen J. R., Bastardie F. (2021). Bridging the gap between commercial fisheries and survey data to model the spatiotemporal dynamics of marine species. Ecol. Appl. 31, e02453. doi: 10.1002/eap.2453

PubMed Abstract | CrossRef Full Text | Google Scholar

Senko J. F., Peckham S. H., Aguilar-Ramirez D., Wang J. H. (2022). Net illumination reduces fisheries bycatch, maintains catch value, and increases operational efficiency. Curr. Biol. 32, 911–918.e2. doi: 10.1016/j.cub.2021.12.050

PubMed Abstract | CrossRef Full Text | Google Scholar

Siders Z. A., Ahrens R. N. M., Martin S., Camp E. V., Gaos A. R., Wang J. H., et al. (2023). Evaluation of a long-term information tool reveals continued suitability for identifying bycatch hotspots but little effect on fisher location choice. Biol. Conserv. 279, 109912. doi: 10.1016/j.biocon.2023.109912

CrossRef Full Text | Google Scholar

Siders Z. A., Ducharme-Barth N. D., Carvalho F., Kobayashi D., Martin S., Raynor J., et al. (2020). Ensemble Random Forests as a tool for modeling rare occurrences. Endanger. Species Res. 43, 183–197. doi: 10.3354/esr01060

CrossRef Full Text | Google Scholar

Sing T., Sander O., Beerenwinkel N., Lengauer T. (2005). ROCR: visualizing classifier performance in R. Bioinformatics 21, 3940–3941. doi: 10.1093/bioinformatics/bti623

PubMed Abstract | CrossRef Full Text | Google Scholar

Stock B. C., Ward E. J., Eguchi T., Jannot J. E., Thorson J. T., Feist B. E., et al. (2020). Comparing predictions of fisheries bycatch using multiple spatiotemporal species distribution model frameworks. Can. J. Fish Aquat. Sci. 77, 146–163. doi: 10.1139/cjfas-2018-0281

CrossRef Full Text | Google Scholar

Stock B. C., Ward E. J., Thorson J. T., Jannot J. E., Semmens B. X. (2019). The utility of spatial model-based estimators of unobserved bycatch. ICES J. Mar. Sci. 76, 255–267. doi: 10.1093/icesjms/fsy153

CrossRef Full Text | Google Scholar

Stupariu M.-S., Cushman S. A., Pleşoianu A.-I., Pătru-Stupariu I., Fürst C. (2022). Machine learning in landscape ecological analysis: a review of recent approaches. Landsc. Ecol. 37, 1227–1250. doi: 10.1007/s10980-021-01366-9

CrossRef Full Text | Google Scholar

Thompson C. G., Kim R. S., Aloe A. M., Becker B. J. (2017). Extracting the variance inflation factor and other multicollinearity diagnostics from typical regression results. Basic Appl. Soc Psychol. 39, 81–90. doi: 10.1080/01973533.2016.1277529

CrossRef Full Text | Google Scholar

Vaughan I. P., Ormerod S. J. (2005). The continuing challenges of testing species distribution models. J. Appl. Ecol. 42, 720–730. doi: 10.1111/j.1365-2664.2005.01052.x

CrossRef Full Text | Google Scholar

Wallace B. P., Kot C. Y., Dimatteo A. D., Lee T., Crowder L. B., Lewison R. L. (2013). Impacts of fisheries bycatch on marine turtle populations worldwide: Toward conservation and research priorities. Ecosphere 4, 1–49. doi: 10.1890/ES12-00388.1

CrossRef Full Text | Google Scholar

Yates K. L., Bouchet P. J., Caley M. J., Mengersen K., Randin C. F., Parnell S., et al. (2018). Outstanding challenges in the transferability of ecological models. Trends Ecol. Evol. 33, 790–802. doi: 10.1016/j.tree.2018.08.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou S., Smith A. D. M., Punt A. E., Richardson A. J., Gibbs M., Fulton E. A., et al. (2010). Ecosystem-based fisheries management requires a change to the selective fishing philosophy. Proc. Natl. Acad. Sci. 107, 9485–9489. doi: 10.1073/pnas.0912771107

CrossRef Full Text | Google Scholar

Zuur A. F., Ieno E. N., Walker N. J., Saveliev A. A., Smith G. M. (2009). “Zero-truncated and zero-inflated models for count data,” in Mixed effects models and extensions in ecology with R Statistics for Biology and Health. Eds. Zuur A. F., Ieno E. N., Walker N., Saveliev A. A., Smith G. M. (Springer, New York, NY), 261–293. doi: 10.1007/978-0-387-87458-6_11

CrossRef Full Text | Google Scholar