
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mar. Sci., 24 January 2024
Sec. Marine Biology
Volume 10 - 2023 | https://doi.org/10.3389/fmars.2023.1292081
Introduction: Patterns of larval dispersal in the marine environment have many implications for population dynamics, biodiversity, fisheries, ecosystem function, and the effectiveness of marine protected areas. There is tremendous variation in factors that influence the direction and success of marine larval dispersal, making accurate prediction exceedingly difficult. The key physical factor is the pattern of water movement, while two key biological factors are the amount of time larvae spend drifting in the ocean (pelagic larval duration - PLD) and the time of the year at which adult populations release larvae. Here, we assess the role of these factors in the variation of predicted larval dispersal and settlement patterns from 15 locations around Aotearoa New Zealand.
Methods: The Moana Project Backbone circulation model paired with OpenDrift was used to simulate Lagrangian larval dispersal in the ocean with basic vertical control across four differing PLD groups (7, 14, 30, and 70 days) for each of twelve months.
Results: Considerable variation was observed in the pattern of particle dispersal for each major variable: release location, PLD group, and the month of release. As expected, dispersal distances increased with PLD length, but the size of this effect differed across both release location and month. Increased and directional particle dispersal matched some expectations from well-known currents, but surprisingly high self-recruitment levels were recorded in some locations.
Discussion: These predictions of larval dispersal provide, for the first time, an empirical overview of coastal larval dispersal around Aoteaora New Zealand’s main islands and highlight potential locations of “barriers” to dispersal. This dataset should prove valuable in helping predict larval connectivity across a broad range of species in this environment for diverse purposes.
For sessile species in the marine environment, dispersal of individuals is primarily conducted in their larval life history stage due to no or very limited movement as adults (Cowen et al., 2007; Cowen and Sponaugle, 2009). Dispersal plays a key role in population connectivity (Pineda et al., 2007), source and sink dynamics (Crowder et al., 2000; Coleman et al., 2017), and the spread of invasive species (Inglis et al., 2006; Levin, 2006; Le Roux and Wieczorek, 2009). Accurate measurement or prediction of larval dispersal is thus crucial to an improved understanding of each of these important processes and hence essential for adequate fisheries and conservation management of marine biodiversity through, for example, the design of marine protected areas (MPAs) and MPA networks (Harrison et al., 2012; Mertens et al., 2018). However, multiple physical and biological factors impact larval dispersal in the ocean, making accurate prediction exceedingly difficult for even one species, let alone an array or community of species, which is usually the ultimate conservation unit of interest. Here, we use biophysical modeling to predict broad-scale larval dispersal and settlement across various physical and biological parameters to provide useful insight into community-level connectivity.
Of the many factors involved, ocean currents play a prominent role in larval dispersal, varying temporally and spatially (Wang et al., 2002; Weersing and Toonen, 2009; Stevens et al., 2019). For coastal marine organisms, spatially heterogeneous currents, which vary at temporal scales ranging from hours to months, can facilitate or impede larval dispersal (Gawarkiewicz et al., 2007; White et al., 2019). Currents may entrap larvae and prevent movement back to the coastline and settlement, keep larvae close to the coast, preventing long-range settlement, or potentially drive larvae to settle very far away (Largier, 2003). Strong ocean currents may come close to the shore in some locations, creating a distinct unidirectional larval flow over considerable distances, while in other locations, a lack of strong coastal currents may lead to dominance of tidal flows, resulting in more local bidirectional larval dispersal (Gilg and Hilbish, 2003; Mitarai et al., 2009). Coastal currents can change temporally due to seasonal temperature changes, winds that vary in strength and direction, or vertical differences in temperature and salinity. These factors impact where warmer/fresher water rise and cooler/saltier water sinks, and the changing gravitational pull of the moon and sun impacting tides and tidal currents (Price et al., 1987; Le Traon and Morrow, 2001; Stevens et al., 2019).
In combination with spatial and temporal variation in ocean currents, the timing of larval release into the ocean also varies among species. Some species may continuously release their larvae, whereas others have multiple release periods throughout the year or only in one very short period (Creese and Ballantine, 1983; Dunmore and Schiel, 2000). Multiple stimuli, including water temperature and tides influence spawning time (Strathmann, 1987; Palumbi, 1994; Pineda et al., 2007; Christy, 2011). Seasonal differences in the timing of larval release modulate the effect of ocean currents on the dispersal and settlement of different species of larvae, as coastal currents can vary over time (Creese and Ballantine, 1983; Dunmore and Schiel, 2000; Shanks and Eckert, 2005; Treml and Halpin, 2012).
Another crucial factor is the time larvae spend in the ocean, as determined by their maximum pelagic larval duration (PLD) and the minimum settlement age. Larvae with a longer PLD are expected to travel and settle further away, and PLD was previously believed to be the primary factor determining larval dispersal distance (Jablonski, 1986; Siegel et al., 2003; Shanks, 2009). PLD determines how long larvae might survive in the water column, but most species can settle before the maximum duration of their PLD, determined by their minimum settlement age, and therefore reduce their dispersal (Roberts and Lapworth, 2001). However, smaller-scale oceanographic features such as eddies and tides (Botsford et al., 1994; Lundquist et al., 2000; Diehl et al., 2007) and topography and bathymetry (Cowen, 2002) are also crucial in influencing the distance traveled, and there is not necessarily a correlation between PLD and dispersal distance (Ross et al., 2009; Shanks, 2009; Faurby and Barber, 2012). An additional factor is larval swimming behavior, which can be exhibited in response to light, sound, temperature, or smell, and assists larvae in returning to the coastline or reefs (Montgomery et al., 2006; Stanley et al., 2010; Radford et al., 2011; Stanley et al., 2011; Hu et al., 2019). Swimming behavior can change through different larval stages, with earlier stages often showing upward swimming and later stages showing downward swimming as larvae prepare to settle (Grange, 1976; Cragg, 1980; Chia et al., 1984; Mann et al., 1991; Emlet, 1994; Cohen et al., 2015; Gravinese, 2018). Factors such as larval size, buoyancy, and physiological changes, including yolk sac depletion and lipid fat reserves, also influence their swimming behavior (Kelman and Emlet, 1999; Harii et al., 2007; Gravinese, 2018; Guzmán-Rivas et al., 2021).
This analysis uses the Aotearoa New Zealand region as a case study to predict broad-scale community patterns of larval dispersal. Aotearoa New Zealand is at the crossroads of various surface and sub-surface currents (Figure 1). In the North Island, the dominant current is the Tasman Front, originating from Eastern Australia and bringing warm subtropical water (Stevens et al., 2019). It meets with the northern shelf of the North Island and continues down the east coast as the East Auckland Current (Roemmich and Sutton, 1998). Near East Cape, it splits into the East Cape Eddy and the East Cape Current. The East Cape Eddy recirculates water back to the northeast, while the East Cape Current flows southward until it reaches the Chatham Rise. Additionally, the northward-flowing Wairarapa Coastal Current meets with the East Cape Current in Hawkes Bay and forms the Wairarapa Eddy (Chiswell, 2000). The west coast currents are less understood, with sparse observations suggesting high-frequency variability (Sutton and Bowen, 2011). The flows on the west coast and north of Cape Egmont are generally weak and variable but north-westerly (Heath, 1982; Sutton and Bowen, 2011). South of Cape Egmont, the d’Urville Current flows through Cook Strait and then southward, interacting with the South Island’s winds and currents (de Lange et al., 2003). On the South Island’s west coast, the variable Westland Current that flows north and south is formed from a Subtropical Front, where the northward flow becomes the d’Urville Current (Heath, 1973; Heath, 1985; Stevens et al., 2019). The Cook Strait experiences fast tidal flows and is dominated by upwellings driven by winds (Walters et al., 2010; Chiswell et al., 2017). At the bottom of the South Island, the Southland Current forms from a Subtropical Front and subantarctic water, wrapping around the bottom and traveling northward up the east coast (Sutton, 2003). These wind-driven currents around New Zealand exhibit seasonality and varying speed and direction at depth (Bell and Goring, 1998). Larval dispersal is also influenced by tidal forces, upwellings, downwellings, smaller eddies, and river inputs (Will et al., 2011).
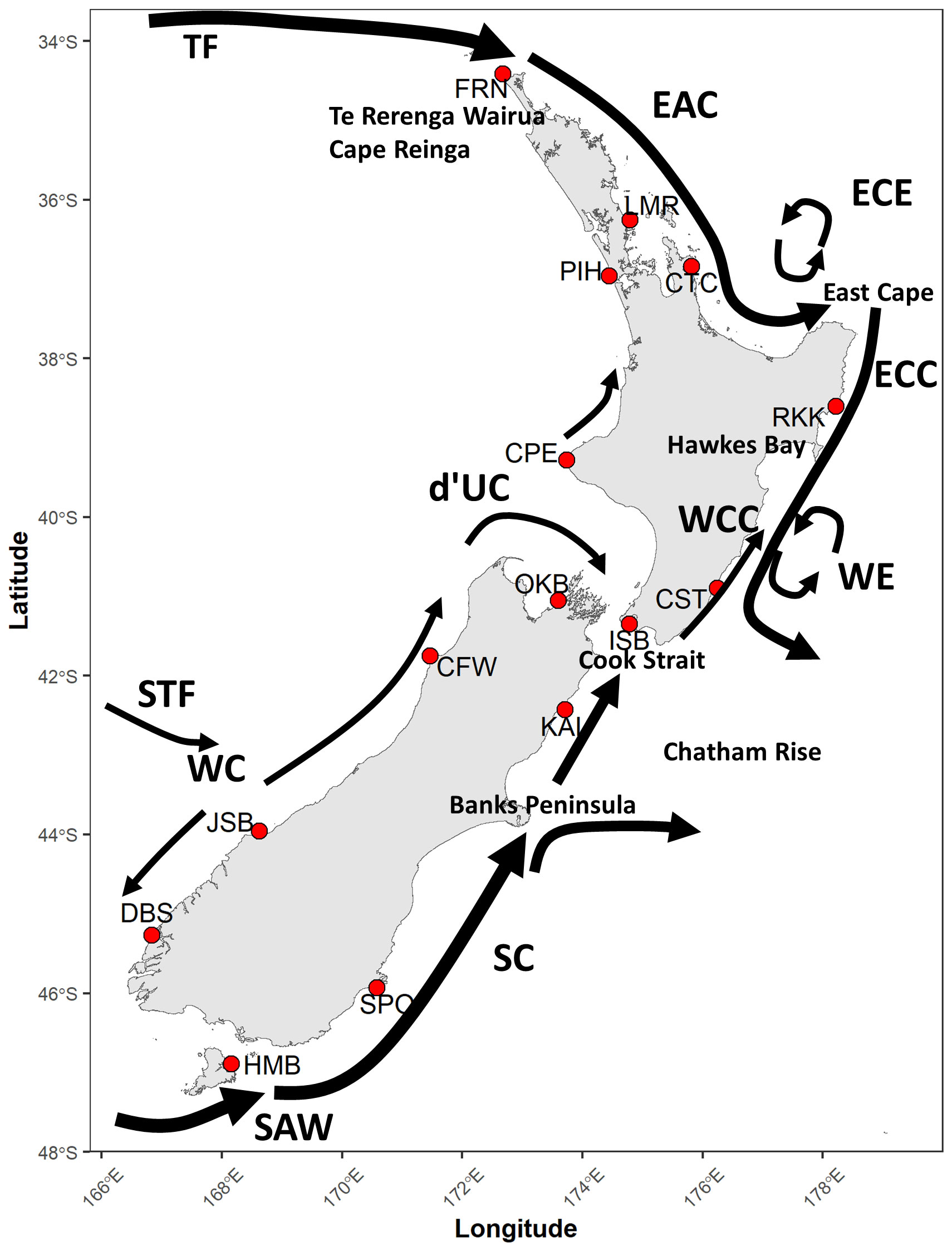
Figure 1 Map of release locations used in the biophysical simulations for this study: Leigh Marine Reserve* (LMR), Cathedral Cove* (CTC), Rongokako* (RKK), Castlepoint (CST), Island Bay* (ISB), Kaikoura* (KAI), Seal Point (SPO), Half Moon Bay* (HMB), Doubtful Sound* (DBS), Jackson Bay (JSB), Cape Foulwind (CFW), Okiwi Bay (OKB), Cape Egmont (CPE), Piha Beach (PIH), and the Far North (FRN). Locations within or adjacent to an MPA are indicated with *. Additional locations referenced in text and prevailing currents around New Zealand are shown: Tasman Front (TF), East Auckland Current (EAC), East Cape Eddy (ECE), East Cape Current (ECC), Wairarapa Eddy (WE), Wairarapa Coastal Current (WCC), Southland Current (SC), Subtropical Front (STF), Subantartic Waters (SAW), Westland Current (WC), d’Urville Current (d’UC).
Biophysical models combine essential biological features of larvae with oceanographic features from hydrodynamic data to predict the dispersal and settlement of larvae with varying biological traits across large spatial scales. These models rely on Lagrangian approaches, based on tracking the movement of individual water parcels (and the larvae within them) transported by ocean currents. Biophysical models allow the determination of larval trajectories by advecting particles across geographical locations and depths using ocean currents. Past approaches often modelled larvae as passive tracers (North et al., 2009; Swearer et al., 2019); however, including behavior can have large impacts on the outcome of simulations (Butler IV et al., 2011; Coscia et al., 2013; Leis, 2021). Biophysical models provide an opportunity to determine how the timing of release, PLD, and release location impact dispersal and settlement patterns of benthic marine invertebrates and where possible barriers to settlement are located.
Many approaches have been used to examine the larval dispersal of coastal benthic species around Aotearoa New Zealand, with special attention to species of commercial interest. Chiswell and Booth (2008) used satellite-derived currents and a model incorporating the crayfish Jasus edwardsii metamorphosis to determine sinks and sources in quota management areas. Chiswell (2009) combined satellite-derived currents and drifters from the Global Drifter Program to assess whether larval dispersal reflected mean ocean circulation for the limpet Cellana strigilis. Lundquist et al. (2009) combined particle tracking and hydrodynamic modeling with the DHI software and MIKE 21 to model the hydrodynamics of the Whangarei Harbor to show which sites can recolonize the surrounding areas by cockle Austrovenus stuchburyi. Recent efforts in Aotearoa New Zealand (e.g., Quigley et al., 2022; Chaput et al., 2023) have used the recently developed Moana Project hydrodynamic model (de Souza et al., 2022) with the open-source Lagrangian trajectory software OpenDrift (Dagestad et al., 2018) to assess the dispersal of green-lipped mussels Perna canaliculus. Few studies (e.g., Cecino and Treml, 2021) have examined the larval dispersal of multiple species, and none have undertaken this around Aotearoa New Zealand. Most studies examine a single species and determine the patterns of larval dispersal and settlement for only that species (e.g., Viard et al., 2006; Domingues et al., 2012; Norrie et al., 2020; Quigley et al., 2022). This work uses a biophysical model to predict larval dispersal and settlement patterns for differing PLDs and spawning months from representative locations around the entirety of the coastline of the main islands of Aotearoa New Zealand. It will be most applicable to coastal benthic invertebrate species that rely on planktonic larvae for their dispersal. This study examines the influence of three important physical and biological variables for dispersal: release location, PLD, and spawning time. These simulations will help identify regional communities that are highly connected or isolated, the locations of potential barriers to larval dispersal, and locations that may experience increased levels of self-recruitment.
Modeled currents and ocean circulation used in this study were provided by the Moana Project and derived from the Moana Ocean Hindcast model or the “Moana Backbone” (www.moanaproject.org; de Souza, 2022; de Souza et al., 2022), which includes 25 years (1993-2017) of hindcast-modeled oceanographic data. The Moana Backbone uses the 3D primitive equations of the Regional Ocean Modeling System (ROMS) based on the hydrostatic and Boussinesq approximations (Shchepetkin and McWilliams, 2005). The domain ranges from ≈161 to ≈185° E and ≈52 to ≈31° S with an average horizontal resolution of 5 km (4.1 km in the south, increasing to 5.8 km in the north) with 467x367 grid cells covering the ~4,600,000 km2 domain. We chose this model because it is the most recent, highest resolution (5 km) openly accessible model covering the entirety of Aotearoa New Zealand, a necessary condition for a study at the national scale. The 5 km resolution has been shown to be suitable in modeling larval dispersal along the Aotearoa New Zealand coastline (Quigley et al., 2022; Chaput et al., 2023). While higher resolution coastal models have been created for some Aotearoa New Zealand coastal regions, harbors and bays (e.g. Broekhuizen et al., 2011; Montaño et al., 2023), the Moana Backbone is the only available hydrodynamic model that includes the full national domain. The model also includes coastal tides with tidal constituents from the TPXO global tidal solution (Egbert and Erofeeva, 2002). The Moana Backbone uses bathymetry from multiple surveys and the ROMS land mask to determine the coastline. The model reliably replicates the coastal circulation and currents around Aotearoa New Zealand (de Souza et al., 2022). Further information, configuration, and validation of the Moana Backbone model are found in de Souza et al. (2022).
Particles representing larvae of marine species were released from 15 locations to determine trajectories and dispersal patterns (Figure 1; Supplementary Table 1). The locations were chosen to be representative of standard sampling sites from a range of genetic studies that have estimated genetic connectivity around the coastline (Arranz, 2017; Arranz et al., 2021a), including sufficient sites to cover the entire coastline and an appropriate number that could be analyzed in biophysical simulations within a reasonable timeframe. Several of these locations were located within or adjacent to existing Marine Protected Areas (MPAs). The exact release locations were determined after preliminary trials on the effect of distance from shore on local recruitment, and locations were chosen as close to shore as feasible that minimized immediate coastal landfall, while recognizing that the model scale was insufficient to resolve nearshore turbulent boundary dynamics, sub-mesoscale fronts and other local scale features that may either increase likelihood coastal entrainment, or alternatively may result in better understanding of features that result in offshore transport (Huret et al., 2007; Poje et al., 2010; Haza et al., 2012; Dauhajre et al., 2019). The minimum distance from the coast was 100 m within modeled grid cells. The open-source software package OpenDrift v1.8.3 (Dagestad et al., 2018) was paired with the hydrodynamic model described above and a larval model to represent several characteristics of larval behavior. OpenDrift is an offline Lagrangian trajectory model which allows many user inputs; more details can be found in Dagestad et al. (2018) and https://opendrift.github.io/.
Four maximum PLD length groups (7, 14, 30, and 70 days, which cover the range of most benthic invertebrate species in the region) were used to determine the impact of PLD on predicted dispersal patterns of a range of benthic marine species. Each group had a minimum settlement age based on the average of species within these four groups, with values of 2.7, 5, 18.2 and 34 days respectively (Table 1; Supplementary Table 2). If particles encountered the coastline or seafloor before their minimum settlement age, they did not settle and returned to their previous vertical height. Particles had a maximum settlement depth of 40 m to avoid settling in deep waters away from the coast. Although this might be deeper than where larvae would settle for some species, this depth gave the best results in sensitivity analysis to account for small offshore islands, which are not included in the ROMS land mask. Particles were categorized as non-settling for further analyses if they did not settle before their maximum PLD. Due to the large extent of the model domain, few particles reached the boundary. We did not include any boundary-specific behaviors, and particles which reached the boundary of the hydrodynamic model would remain in proximity of the boundary.
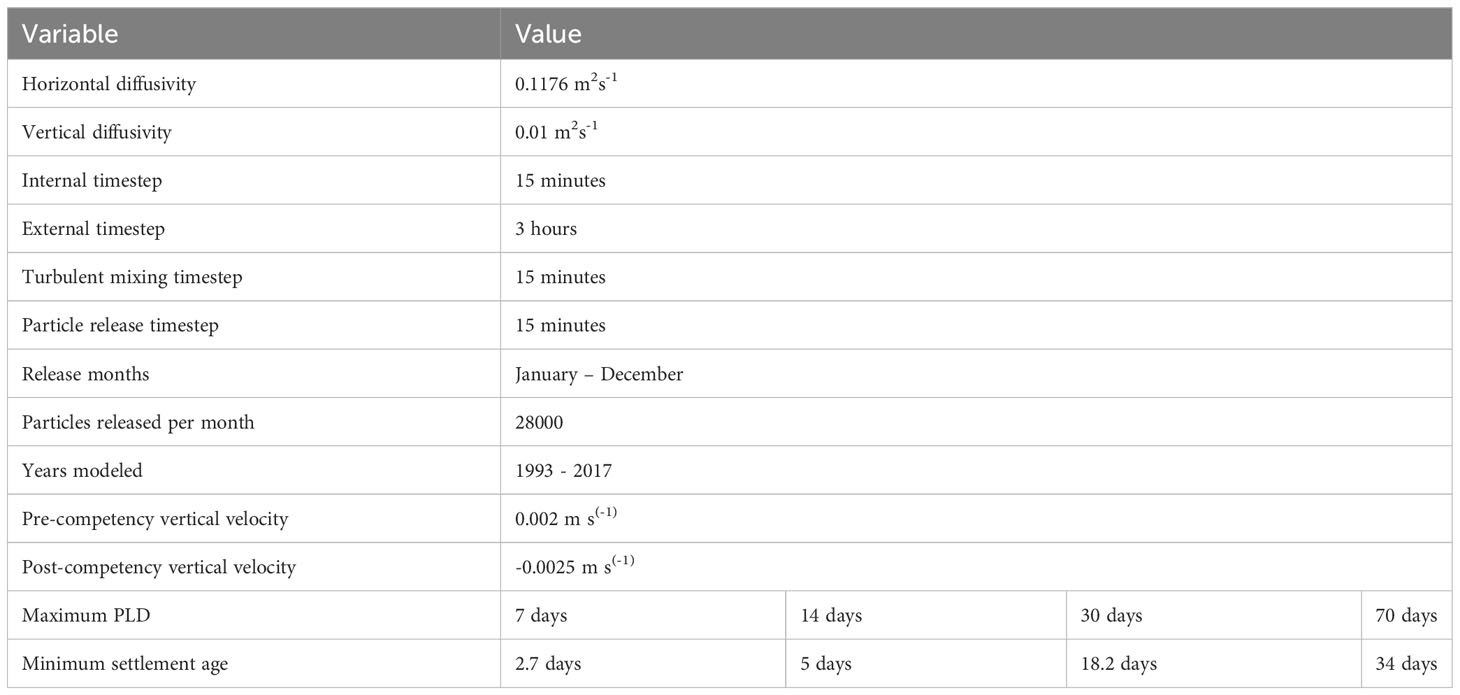
Table 1 Parameters used in the biophysical model to determine patterns of larval dispersal around Aotearoa New Zealand.
The model calculated the position of each particle with a 15-minute internal timestep based on the ocean currents and saved outputs with an external timestep of 180 minutes. The advection scheme used to simulate the Lagrangian trajectories of particles was the 4th Order Runge-Kutta algorithm, given suggestions (e.g., North et al., 2009) that it is superior to others available on OpenDrift (Euler and 2nd Order Runge-Kutta). A horizontal diffusivity coefficient of 0.1176 m2s-1 based on equations in Okubo and Ebbesmeyer (1976) and other biophysical model studies around Aotearoa New Zealand (e.g., Norrie et al., 2020) was included in the model to account for sub-grid scale diffusion. Based on similar modeling studies (e.g., Norrie et al., 2020; Quigley et al., 2022), a vertical diffusion constant of 0.01 m2s-1 was included to account for turbulence in the environment, and larvae were assumed to be vertically mixed throughout the water column (Lundquist et al., 2004).
Every 15 minutes, particles were released from within a 2 km radius of the release location, totaling 28,000 particles released over the whole month from each location each month for each PLD group. Reproductive output was assumed to be equal from all locations. Sensitivity analyses revealed that this release amount provided a satisfactory compromise between the time for simulations to run and sufficient particles to estimate dispersal, settlement, and distance traveled. Particles were released at random depths between the seafloor and the sea surface. Due to a lack of data about the mortality or survival of larvae across many species, a daily mortality rate was not included. Post-settlement mortality and other ecological processes were not included for the same reason. Particles were released for simulations representing each of the 25 years of the Moana Backbone model. For the full summary of the model parameters, see Table 1. Data from all 25 years of simulations were combined for analysis to represent where larvae can settle across multiple generations from the release locations.
Other studies have shown that benthic invertebrate larvae typically lack sufficient horizontal swimming velocity to influence horizontal dispersal, but are capable of influencing transport by vertical swimming behavior to move between surface and sub-surface currents (Gary et al., 2020; James et al., 2023). Thus, we included vertical but not horizontal movement as a representative of larval swimming behavior in the model. Before particles reached the minimum settlement age, they were given a positive vertical velocity (upward), and once they were capable of settlement, they were given a negative vertical velocity (downward). Before the minimum settlement age, the larvae are given a vertical velocity of 0.002 m s(-1) to mimic an increased frequency of upward swimming, positive buoyancy, and desire to stay closer to the surface of the water in the earlier larval stages of many species across genera (e.g., Grange, 1976; Cragg, 1980; Sulkin, 1984; Emlet, 1994; Krug and Zimmer, 2004; Tapia et al., 2010; Gravinese, 2018; Montgomery et al., 2019). After particles had surpassed their minimum settlement age, they had a vertical velocity of -0.0025 m s(-1), following the parameters used in Lundquist et al. (2009). Additionally, -0.0025 m s(-1) has been reported as a reasonable estimate of the settling velocity of larvae (Chia et al., 1984). Further, in situ larval behavior parameters (beyond estimated pelagic larval duration) are not available for the majority of species included in this study. Thus, the larval behaviors included in this study are hypothetical larval behaviors based on other studies.
Analysis of the OpenDrift simulations was performed with R v4.2.0 (R-Core-Team, 2022). Data was visualized using the package ggplot2 (Wickham, 2016). The distance traveled by particles was calculated as haversine distances between the initial release location and the end location with the ‘distGeo’ function in the R package geosphere (Hijmans et al., 2021). 1D and 2D kernel density estimations (KDEs) were calculated for each site, release month, and PLD group. 1D KDEs represent the probability density of a particle settling a certain distance from the release location, whereas 2D KDEs represent the probability density of a particle settling in a particular location. The significance between differences in maximum and median distance traveled between months, PLD groups, locations, and their interactions were examined with an ANOVA. Only particles deemed to have “settled” by the OpenDrift simulations were used in the analysis. Particle settlement included all particles that had encountered the seafloor or coastline after their minimum settlement age but did not include particles that either reached the boundary of the model grid, or did not settle before their maximum PLD.
Here, connectivity between two locations is defined as the subset of settled particles from one release location that settled within 25 km of another release location. The criterion for a successful connection was any settled particles within the 25 km radius, because even one migrant per generation impacts genetic connectivity (Lowe and Allendorf, 2010). Connectivity was calculated based on both successful dispersal to neighboring release locations from each source location and successful settlement from neighboring locations to each sink location. Probability of settlement from a source was calculated as the number of particles released from that source that settled within 25 km of each other location, divided by the total number of particles released from that source; this total includes particles that did not settle within 25 km of any release location or did not settle during the model simulation period. The probability of settlement from a source sums to one (including unsettled particles) at every source showing the probability of a released particle to end in each sink for a given source. Variance of probability was calculated as sample variance of the probability of settling from each source location over 12 months for each PLD group. The length of time each year that locations were connected by dispersal and successful settlement was measured by the number of months they were connected.
The dispersal extent of particles released over the 25-year period of the biophysical simulations varied greatly among maximum PLD groups, and the direction and distance traveled varied substantially among release locations (Figure 2). In the 7- and 14-day PLD groups, most release locations were not directly connected by any dispersal. Particles only reached the boundary of the model in the 70-day PLD group (Figure 2D) with approximately 0.15% of all particles reaching the boundary in this group.
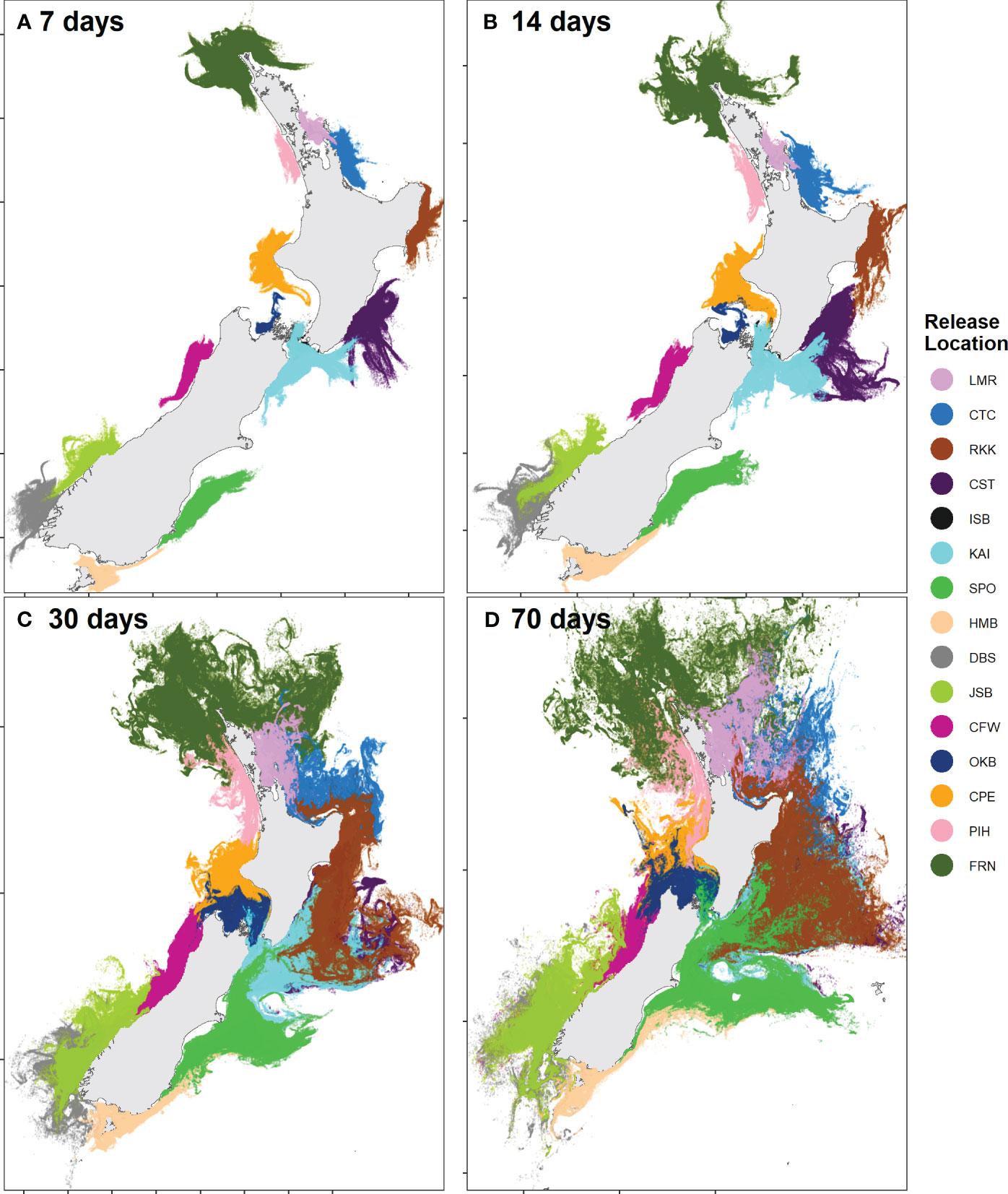
Figure 2 End locations of all particles released in March for each maximum PLD group: (A) 7 days, (B) 14 days, (C) 30 days, (D) 70 days.
Of the 126,000,000 particles released in the biophysical simulations, 51.65% had settled by the end of their competency period. Predicted settlement rates varied between locations and maximum PLD groups. Typically, the longer PLD groups had a lower predicted settlement. Across all PLD groups, ISB (93.15 – 98.66%) and PIH (80.17 – 94.4%) had the highest percentage of particles resulting in predicted settlement, while KAI (18.93 – 25.02%) and FRN (13.24 – 16.34%) had the lowest (Supplementary Figure 1). Of these settled particles, many settled very close to the release location across all locations and PLD groups. In the 7-day PLD group, more than 50% of settled particles had settled within 5 km across most locations (Figure 3A) and more than 75% within 25 km for all release locations (Figure 3B). With increasing PLD length, fewer particles settled within 5 or 25 km across all locations. However, the impact of PLD varied greatly among locations, ranging from substantial (in HMB and LMR) to minimal (ISB and PIH). Overall, ISB and PIH had the highest local recruitment, while KAI and HMB had the lowest.
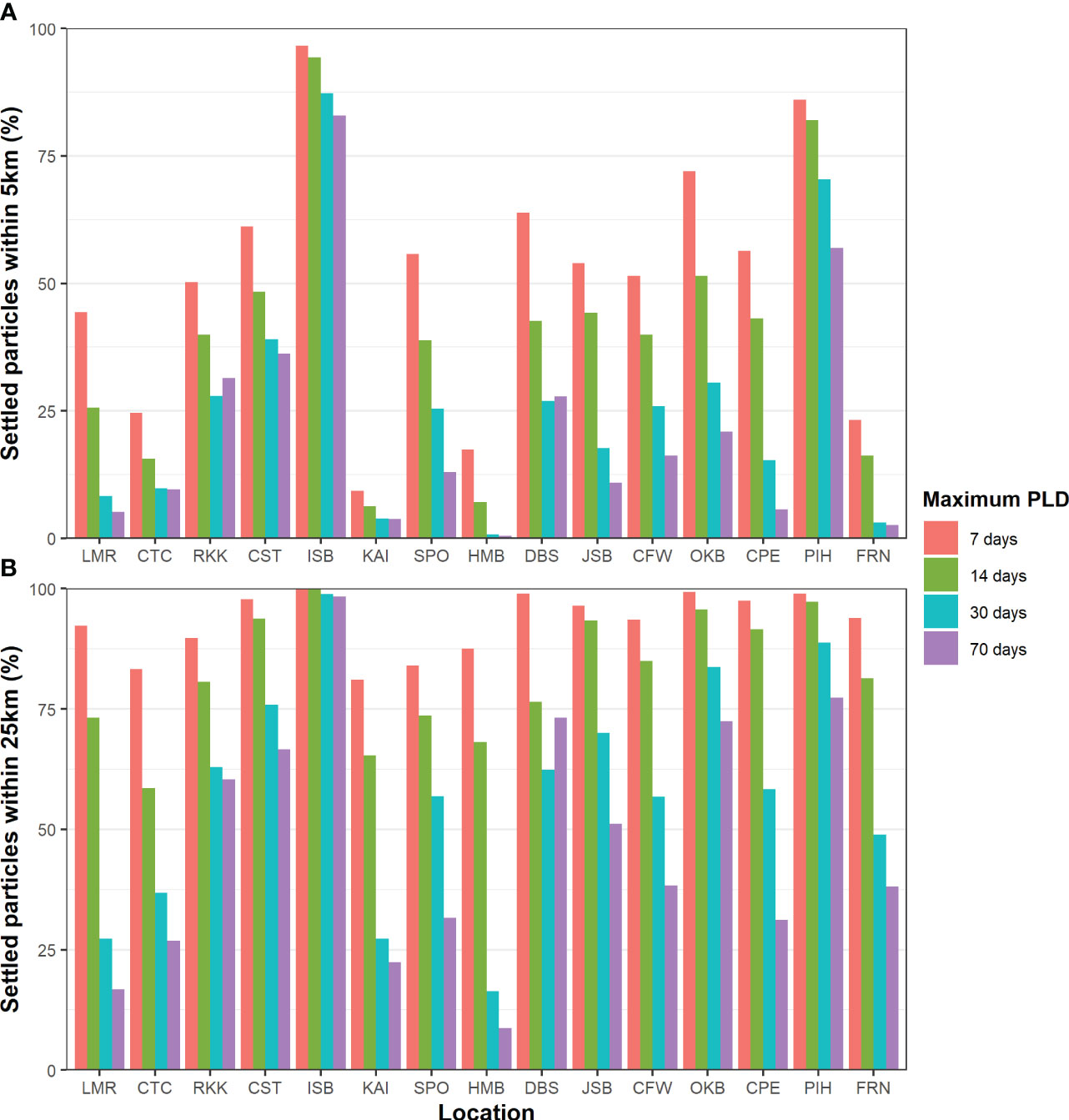
Figure 3 Percentage of settled particles within (A) 5 km and (B) 25 km of the release location across all locations and maximum PLD groups.
When pooling data across all 12 months, the categories of maximum PLD, release location, and their interaction were all highly significant for both maximum and median distance traveled to settlement (ANOVA p < 0.0001). However, the month of release did not have a statistically significant impact on the maximum and median distance traveled (ANOVA p > 0.05). Generally, the maximum (Figure 4A) and median (Figure 4B) distance traveled to settlement increased with PLD. Sites KAI, SPO, and HMB tended to have the largest dispersal distances, while ISB and PIH had the lowest distances traveled, although the patterns were not identical between maximum and median distances.
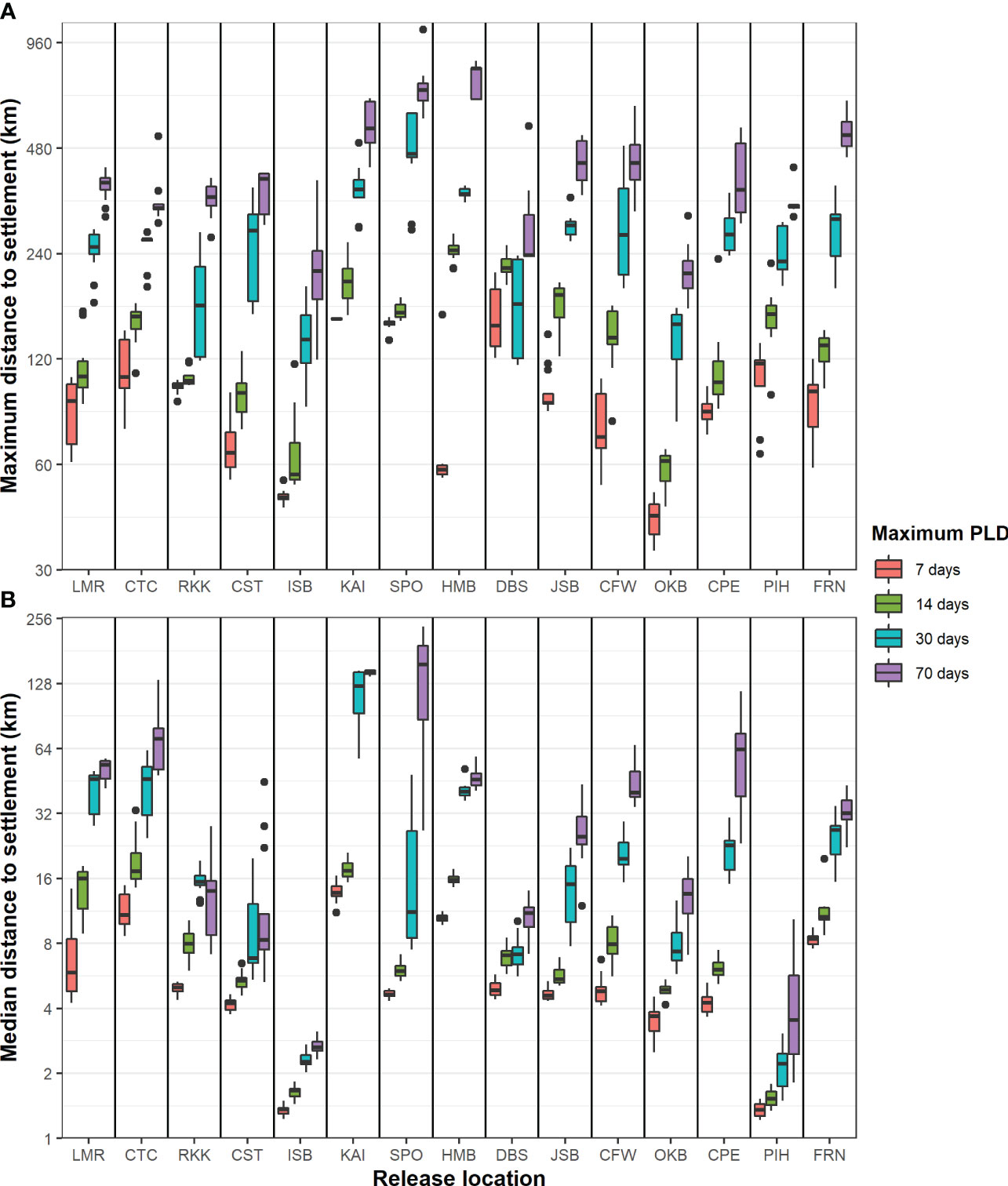
Figure 4 (A) Maximum and (B) median haversine distance travelled to settlement (km) on log scale across all maximum PLD group and release location.
The interaction of maximum PLD length and the month of release on the distance from release traveled by predicted settlement particles is reflected in 1D kernel density estimations (Supplementary Figures 2-16). For example, when released from CTC (Supplementary Figure 3), there is a difference in peaks of distance traveled. With a 14-day PLD, there are larger probability density peaks at ~50 km when released in May to October, and with a 70-day PLD, there are larger peaks at ~200 km when released in August, September, November, and December.
2D kernel density estimations show the wide variation in probability density patterns of particles settlement across locations, PLD group, and month (Supplementary Figures 17-76). Comparing across different PLD groups demonstrates that particles travel further and can settle in new locations. Separating by month of release shows monthly variation in where particles can settle. For example, when released from CFW in January and April (Figure 5), particles settled much further south of the release location toward the bottom of the South Island. While when released in January and October, particles could settle further north along the North Island and cover more of the southern coastline of Cape Egmont.
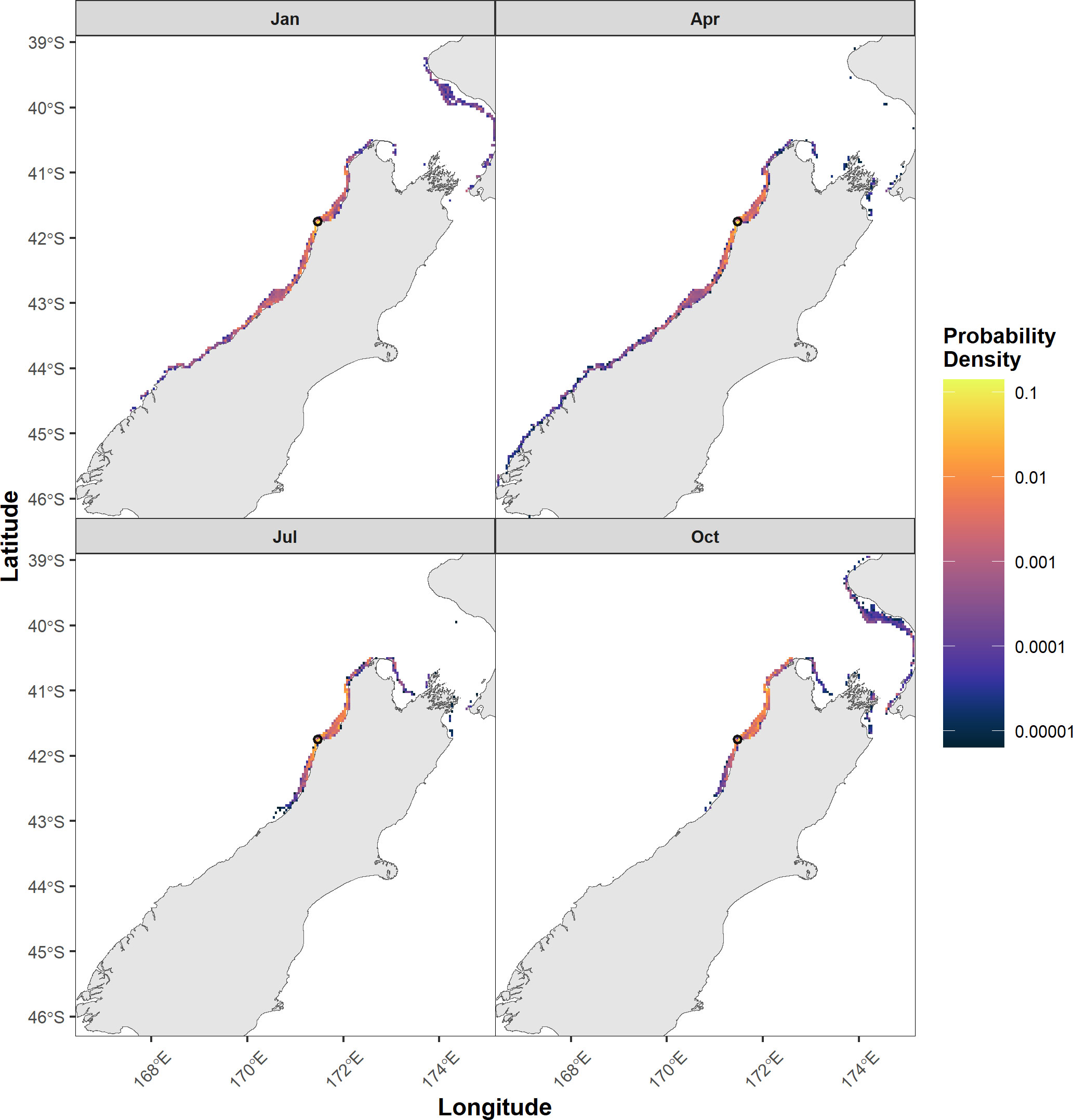
Figure 5 2D kernel density estimation of settled particles across four different months, January, April, July and October, with a maximum PLD of 70 days. The black circle is the release location. The color bar is in log scale. Example plot from Cape Foulwind (CFW). All months for each location and PLD group can be found in Supplementary Figures 17-76.
Matrices of probability of settlement to another release location (Figure 6) reveal that there is limited exchange among modeled locations for the 7- and 14-day PLD. While larval connectivity is more common in the 30- and 70-day PLD, it is much more extensive in some geographic regions than others (e.g., along the east coast of the South Island) and is often strongly biased in one direction (e.g., northward along the east coast of the South Island from HMB toward CST). In terms of probability, the most common source of particles for each location was itself; the only exception was for 70-day PLD particles from KAI, which had a higher probability of settling in ISB than in itself (Figure 6D).
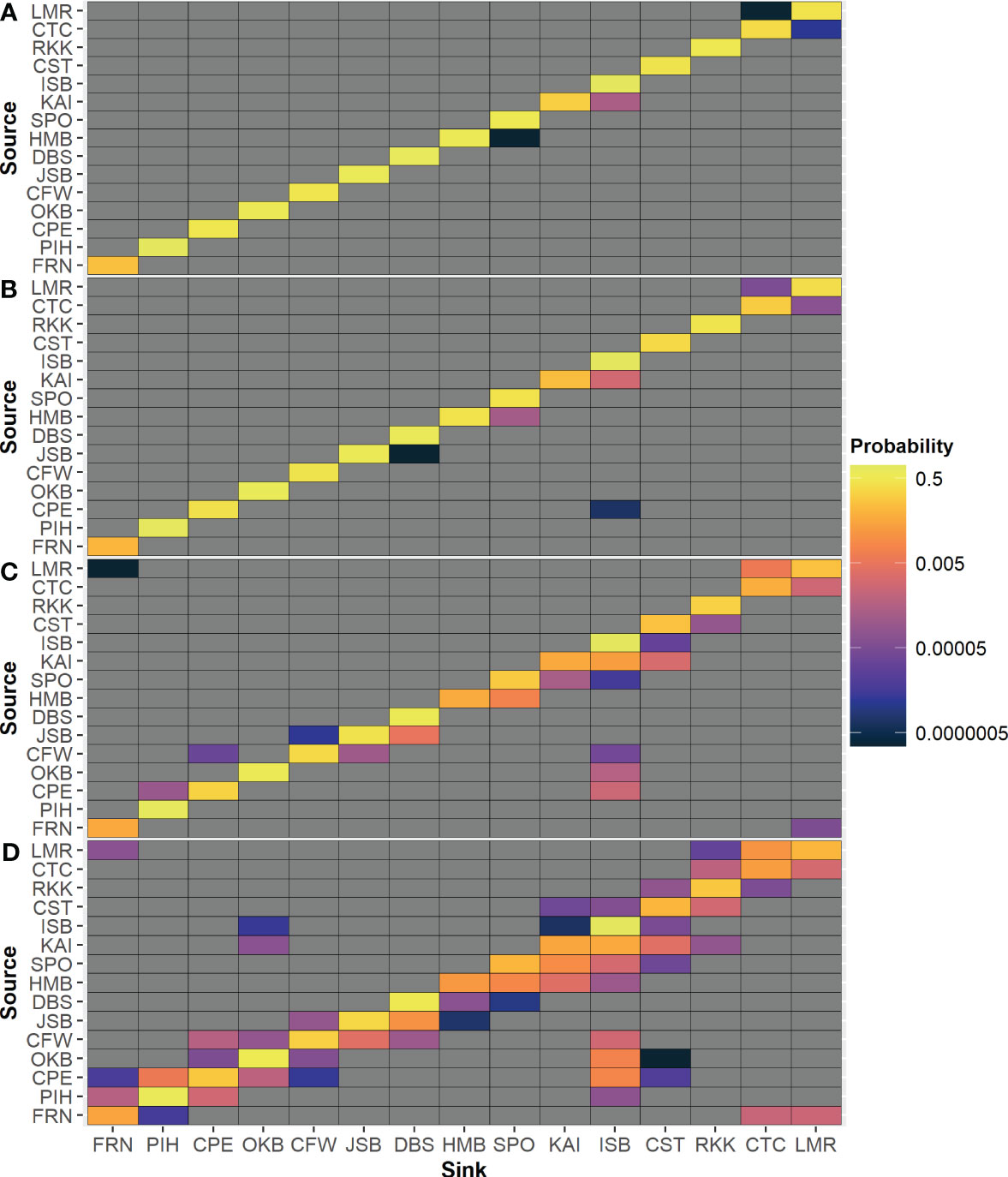
Figure 6 Probability of settlement from each source location to neighboring release locations for 12 monthly simulations for each maximum PLD group: (A) 7 days, (B) 14 days, (C) 30 days, (D) 70 days.
There was also strong variability among months in this larval connectivity. Overall, the number of months where connectivity occurred between modeled locations increased with increasing PLD (Figure 7). Biased periods of bi-directional movement were also common. For example, particles from PIH settled at FRN every month, but particles from FRN settled at PIH only three months of the year in the 70-day PLD group. Variance in the probability of settlement at each PLD demonstrates that the most variability is in self-recruitment, and there was less variance in the probability of settlement in other sink locations (Supplementary Figure 77).
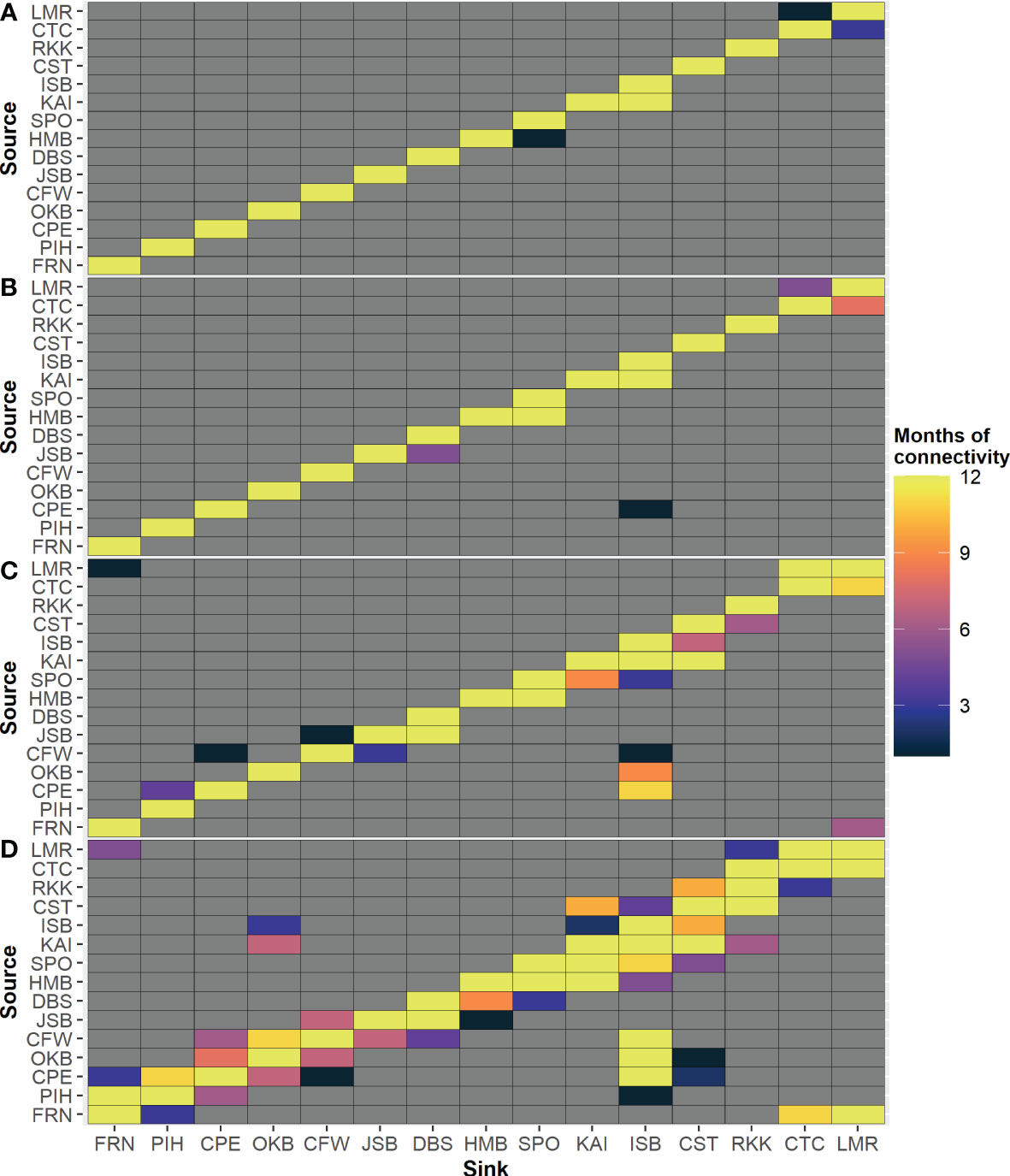
Figure 7 Months of predicted connectivity between each pair of release location for each maximum PLD group: (A) 7 days, (B) 14 days, (C) 30 days, (D) 70 days.
The patterns of dispersal and settlement from the biophysical modeling can also be summarized on maps of Aotearoa New Zealand (Figure 8), emphasizing patterns that are supported by model simulations of the 70-day PLD group, which had the most connected dispersal events between locations. This summary map highlights several regions of high and largely unidirectional connectivity (along the east coast of the South Island), as well as several regions of relatively low connectivity in both directions (e.g., the NW and SW of the South Island). Differences in connectivity between months reveal spatial variability, where some locations have large seasonal changes in connectivity, whereas others show consistent patterns throughout the year (Figure 9; Supplementary Figures 78-89). For example, along the east coast of the South Island, dispersal occurs consistently in an anti-clockwise direction. On the NE coast of the North Island, the direction and strength often changed (Figure 9).
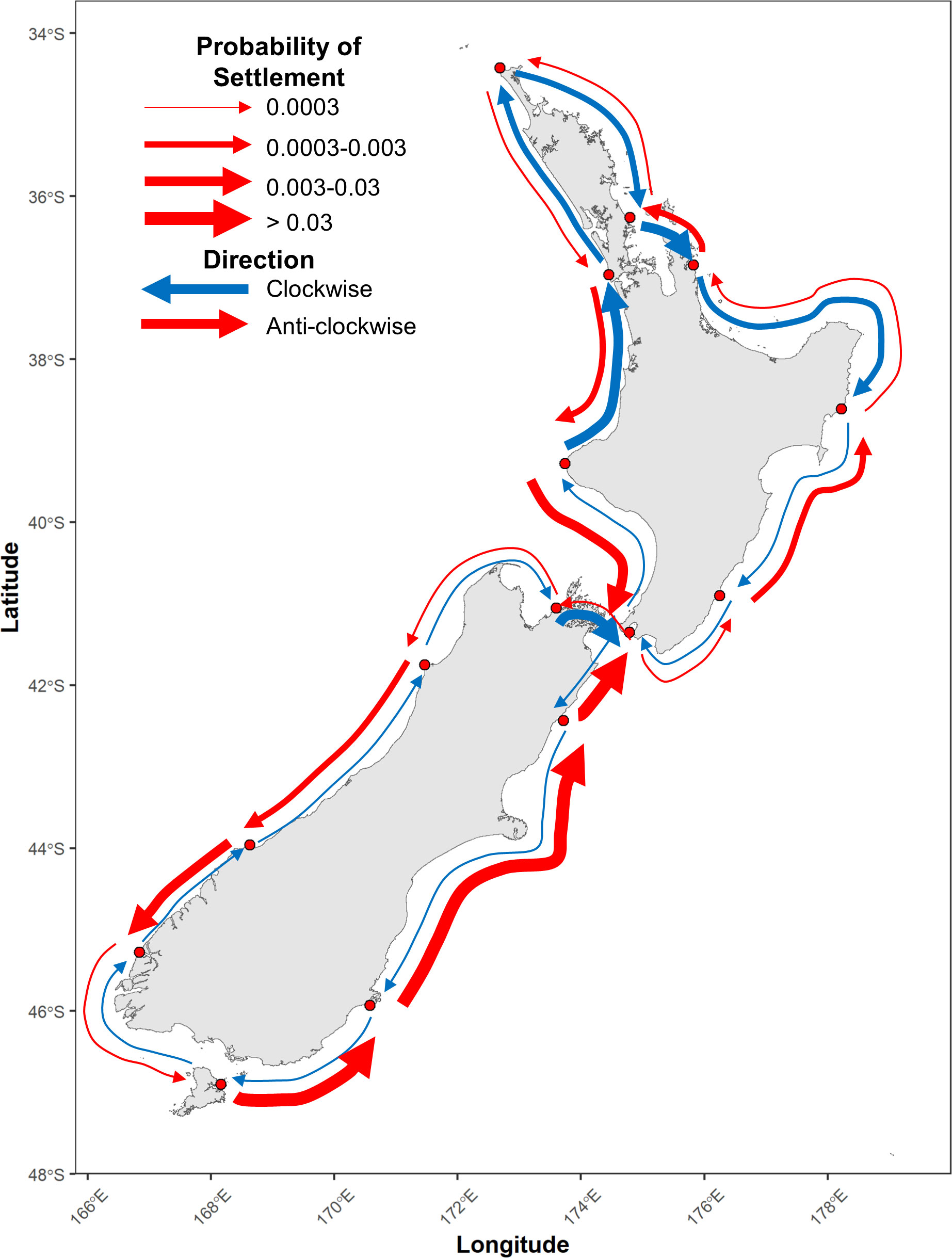
Figure 8 Probability of settlement in adjacent locations across all twelve months for particles with a maximum PLD of 70 days.
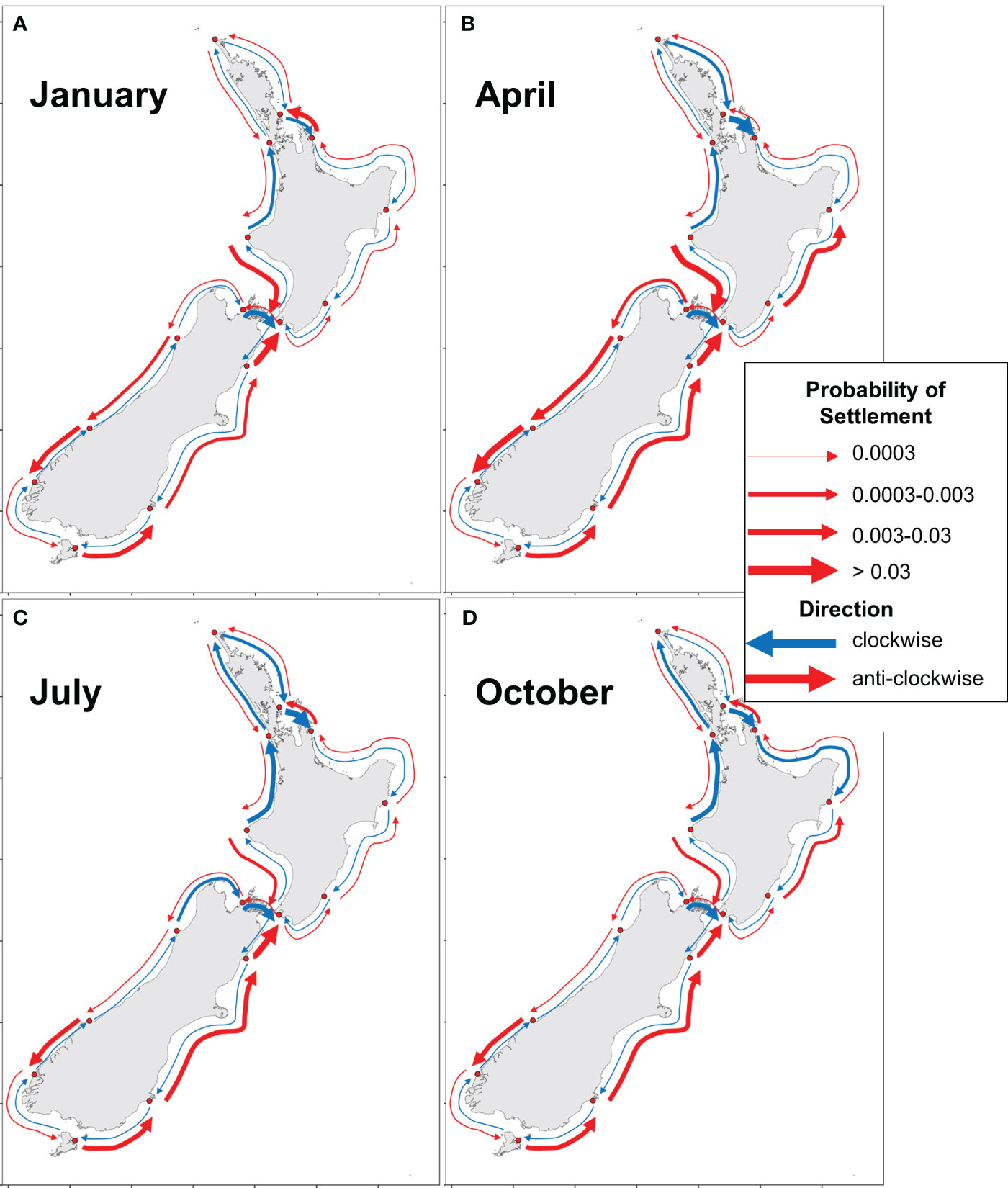
Figure 9 Probability of settlement in adjacent locations in four different months, (A) January, (B) April, (C) July, and (D) October for particles with a maximum PLD of 70 days. All months can be found in Supplementary Figures 77-88.
Differences in patterns of marine larval dispersal around Aotearoa New Zealand were assessed by biophysical modeling across three primary spatial and temporal variables: maximum pelagic larval duration (PLD), release location, and month of release. This modeling simulates the possible dispersal and settlement patterns of a range of rocky reef benthic invertebrates. Overall, the results broadly meet original expectations derived from known currents and previous studies, providing some confidence in them, but there were also unexpected results that enhance our understanding of dispersal around Aotearoa New Zealand. Most modeled particles were predicted to settle far more locally than expected if marine populations were “open” as previously assumed, even for longer PLDs, with many larvae settling close to their release location. In addition, there were surprising levels of variation in predicted dispersal across all three primary variables examined for many PLDs and release locations.
As expected, there was a clear difference in larval settlement patterns among the four maximum PLD groups. With increasing maximum PLD, there was an increase in the maximum and median distance traveled by settled particles. With shorter PLD lengths, distant populations require more generations to become connected through stepping-stone populations. However, there was far less than a proportional relationship between maximum PLD or minimum settlement age and distance traveled by settled particles; particles with a maximum PLD of 70 days did not settle ten times further away than particles with a maximum PLD of 7 days in terms of either maximum or median in most locations and varied between location and release month (Figure 4). Furthermore, there was a high level of local recruitment for all PLD groups (Figure 3), and highest probability of settlement within the source location (Figure 6).
For release location, the results were broadly in agreement with expectations from known currents and previous studies, but the degree of variation among locations was unanticipated. For example, although a general northward dispersal was expected along the east coast of the South Island, due to the Southland Current, the modeling predicted that this region had the highest dispersal and was the most connected with other locations (Figures 7, 9). In many locations, there was a strong unidirectional bias in dispersal (Figure 5). Conversely, there was unexpectedly weak connectivity along the east coast of the North Island, given the known strong currents in this region. There was also notably weak connectivity around the northwest and southwest of the South Island (Figure 9). Local recruitment reached high levels in several locations (>80% within 5 km at ISB & PIH) and was limited in other locations (<10% at KAI) (Figure 3).
The observed temporal variation at many release locations was larger than expected, with some locations showing large seasonal and even monthly differences in direction and extent of dispersal (Figures 6, 7, 9). In contrast, other locations showed reasonably consistent patterns regardless of season or month. When considering the maximum and median distance traveled by particles that reached the coastline within the competency period, the month of release had no overall significant effect, and there was no significant interaction between the month of release and the PLD group or between the month and location of release. However, the 2D density estimation plots exhibited a clear difference in the settling location of larvae between months. The temporal variation in currents around Aotearoa New Zealand is expected to cause differences in settlement patterns between months (Stanton et al., 1997; Roemmich and Sutton, 1998; Zeldis et al., 2004). The statistical tests we performed used maximum and median distances traveled but did not consider the direction of travel (i.e., clockwise or anti-clockwise around the NZ coast), which may be a factor as to why there was no significant overall effect of the month of release, despite the apparent monthly differences observed heuristically in the 2D KDE plots. Our interest was in the general dispersal patterns; however, further directional statistical tests could be used to examine directional changes in more detail.
Our models suggest that the predominant direction of dispersal changes throughout the year along the north-eastern coast of the North Island (i.e., the region around LMR and CTC, subject to the East Auckland Current; Supplementary Figure 20); larval dispersal is mainly northward in January, but this changes to predominant southward movement in April to July. This pattern is seen across many locations, especially on the west coast of the South Island near JSB and CFW (Supplementary Figure 60).
The temporal differences in settlement patterns imply species’ settlement patterns will differ depending on when they spawn. Large differences were sometimes observed at a monthly scale, highlighting the need to consider the dispersal of larvae at smaller temporal scales relevant to spawning patterns such as months or weeks. Although settlement of larvae is expected to differ across months due to the known differences in ocean currents, this study shows how large these differences can be and how these patterns differ between months of release.
The percentage of particles that successfully settled (i.e., reached the coastline or an appropriate depth by the end of their maximum PLD) varied among the release locations and PLD groups (Supplementary Figure 1). CTC, CST, KAI, and FRN had the lowest settlement percentage, which can likely be explained by the intensity of nearshore currents and their orientation concerning coastal topography. Strong nearshore currents can transport particles far from the coastline, preventing them from settling. When released from FRN, particles might be expected to travel east into the South Pacific Ocean due to the Tasman Front/East Auckland Current, while from KAI, they may become entrained in the strong currents going along the Chatham Rise (Figures 1, 2). Although this pattern sometimes occurred, particles from FRN occasionally traveled west into the Tasman Sea and north into the South Pacific, opposite to the direction of the predominant currents of the Tasman Front and East Auckland Current, most likely due to entrainment by eddies and other fine-scale circulation features. Additionally, water flow closer to the shore, where nearshore reef larvae are released, may not align with the nearby dominant surface current (Bradshaw, 1991). In other locations, particles generally followed the nearshore surface currents; for example, from SPO, particles followed the expected trajectory of the Southland Current, with particles traveling east at Banks Peninsula or continuing north, while very few traveled south. The large variation among locations in the probability of settled particles is somewhat surprising but was typically associated with areas of high variability in oceanographic conditions. ISB and PIH had the highest percentages of particles that settled, perhaps because of stronger bidirectional tidal influence in these areas compared to weaker unidirectional longshore currents (Stevens et al., 2019).
The predicted dispersal results observed here are comparable to similar studies from Aotearoa New Zealand, including other studies using the Moana Project Backbone (Quigley et al., 2022; Chaput et al., 2023). Quigley et al. (2022) released particles with a maximum PLD of 42 days and demonstrated similar dispersal to the 30- and 70-day PLD groups when released from locations near those of this study. Another biophysical simulation (Stephens et al., 2006) released particles with a maximum PLD of 9.3 days from East Cape near RKK, and was generally similar to the dispersal of our 7-day PLD group, with a maximum larval dispersal distances of ~80 km. Stephens et al. (2006) used a higher spatial resolution model (200 m), which can better account for tides and waves; thus, particles may be kept closer to the shore, explaining the slightly shorter maximum distance than the ~105 km measured here for the 7-day PLD group. Larval tracking models by Chiswell and Rickard (2011) also showed similar dispersal patterns after ten days at locations proximate to those modeled here for the 7- and 14-day PLD groups.
The percentage of particles that settled close to the release locations was high across most locations (Figure 3). The high levels of local retention were surprising in the longer PLD groups, as larvae could travel much longer before settling began due to their greater minimum settlement age. This result is consistent with the mounting evidence that local retention of larvae is more likely than previously thought and that long-distance events are uncommon even in larvae with long PLDs (Cowen et al., 2000; Cowen et al., 2003; Atalah et al., 2022; Quigley et al., 2022), and this study shows it occurs across a wide range of locations (Figures 3, 7). The distance offshore that particles were released may impact the degree of local retention. We chose realistic release locations that were close to shore but minimized immediate coastal retention. Locations further offshore are likely to lead to less local retention, but will likely be less realistic for coastal benthic invertebrates as they lack sufficient resolution to represent coastal circulation patterns, including those that result in coastal retention as well as those that result in transport out of coastal environment by winds and other coastal processes (Chiswell and Booth, 2008; Chiswell and Rickard, 2011). Local retention and self-recruitment may be higher in models with a higher spatial resolution that more closely reflect reality (Ward et al., 2023). At some sites (e.g., ISB in Cook Strait), local retention was likely driven by tides (reviewed in Cowen, 2002), which had influence even at the 5 km resolution of the Moana Backbone. Cook Strait has very strong tidal forces, which supports the concept that tides can strongly impact local larval retention (Stevens et al., 2019). For example, in the Celtic Sea, particles released in simulations without tides traveled further offshore and spent less time in the local area compared to simulations that included tides (Deschepper et al., 2020). Our simulations also simplified larval behavior and did not include complex swimming and vertical migration that also could increase local retention (Kingsford et al., 2002; Sponaugle et al., 2002; Woodson and McManus, 2007; Mertens et al., 2018; Satterthwaite et al., 2021). Others include ontogenetic behaviors that keep larvae close to the seafloor, resulting in reduced offshore transport (Drake et al., 2013).
Due to the very high level of local retention, ISB appears to be a dispersal sink, while KAI and HMB appear to be sources of dispersal, especially for the longer PLD groups. This pattern is supported by previous studies, where the crayfish management zone CRA 5 (containing the present KAI site) and CRA 8 (containing HMB) were identified as large sources of J. edwardsii (Chiswell and Booth, 2008). In addition, based on genetic data, Stewart Island populations (containing HMB) are more likely to be sources for some species (Thomas and Bell, 2013). Quigley et al. (2022) determined that for P. canaliculus, two populations on Stewart Island near HMB are likely to be sources. HMB, SPO, KAI are within the Southland Current, whereas ISB is downstream of this northward water movement. The influence on distance of strong offshore currents on larval dispersal has also been reported along the Chilean coastline (Aiken et al., 2007). Other sites that were situated adjacent to strong currents exhibited limited local retention for long PLD groups, for example, due to proximity to the East Auckland Current for LMR and CTC, and the Southland Current for KAI.
Variation in larval settlement is important when considering the location and size of MPAs and their networks (e.g., Mertens et al., 2018; Jonsson et al., 2020; Lu et al., 2023). Species with a shorter PLD likely require multiple generations through stepping-stone populations to connect populations within MPAs via larval dispersal. If the intermediate areas that act as stepping-stones are not protected and degraded, the MPA network will not be effectively connected, violating one of the MPA network goals outlined by IUCN (IUCN World Commission on Protected Areas, 2008). The patterns of larval dispersal shown here can be used to assess the adequacy of existing MPAs and whether additional sites are required to ensure effective connectivity for a range of species. For example, this study suggests that an additional MPA would be required between LMR (Cape Rodney-Okakari Point Marine Reserve) and CTC (Whanganui A Hei (Cathedral Cove) Marine Reserve) to serve as a stepping-stone; the southern coast of Aotea Great Barrier Island or the northern coast of the Coromandel could be a suitable area with model predictions of frequent settlement. This study also highlights potential source locations for seed restoration efforts. For example, a population of P. canaliculus (within the 30-day PLD group and which spawns year-round) in LMR could contribute to the restoration of populations throughout the Hauraki Gulf and other surrounding areas.
Varying settlement patterns based on PLD or month of larval release are likely to influence patterns of genetic structure (Ross et al., 2009; Arranz, 2017). The Cook Strait region (more specifically in some species, the NW and NE of the South Island, defined by Farewell Spit and Cape Campbell) has been reported as a genetic barrier for several studied species, from Sypharochiton pelliserpentis with a maximum PLD of 4 days (Veale and Lavery, 2011) to Patiriella regularis with a maximum PLD of 70 days (Waters and Roy, 2004; Ayers and Waters, 2005). However, for all 4 PLD groups across all months, some particles from KAI settled on the North Island. This settlement may imply that the observed genetic barrier may not be due to a complete lack of dispersal or population connectivity, as previously suggested (Ross et al., 2009; Veale and Lavery, 2011). On the other hand, the simulations also reveal no (or extremely limited) dispersal across Cook Strait along any other route apart from KAI to ISB. Dispersal simulations from ISB, CPE, OKB, or CFW reveal limited dispersal across this barrier for all PLD groups, and limited exchange further north between ISB and CST (Figures 7, 8).
Other coastal regions also appear to have relatively low levels of connectivity across PLD groups for all or much of the year and could potentially be considered “barriers” to settlement (Figures 7, 8). These include East Cape (between CTC and RKK) and the far southwest (between DBS and HMB). Several species, including Lunella smaragdus (maximum PLD of 4 days) have been reported to have a genetic barrier in the East Cape region (Arranz et al., 2021b), with the East Cape Eddy suggested as a possible cause through larval retention (Chiswell and Roemmich, 1998). The far southwest region has not generally been recognized as a region of very low connectivity, although the individual fjords in this region are known to be somewhat isolated (Wing and Jack, 2014).
There are several possible explanations for inconsistencies between observed genetic connectivity and predicted dispersal. One alternative for the discrepancy between the previously observed Cook Strait genetic barrier and the results of the current simulations could be that very high levels of self-recruitment and local retention in ISB contributes to this genetic barrier. Self-recruitment could prevent the successful settlement of externally sourced larvae through competition by locally adapted settlers, thus greatly reducing the effects of gene flow (e.g., Waters et al., 2013). Previous studies of P. canaliculus have observed genetic discontinuity across Cook Strait, in spite of adequate larval dispersal (Wei et al., 2013). Density-dependent processes such as competition could be included in biophysical models to account for this effect, and to determine whether they, or other processes such as historical sea level changes in Cook Strait (Goldstien et al., 2006) or environmental adaptations may be responsible for this genetic barrier.
Another potential explanation for discrepancies between the current simulations and realized connectivity (as represented by observed genetic patterns) is that the biophysical simulations neglect some key mechanisms affecting settlement. Particle tracking models can be improved through incorporation of more accurate behavioral and other biological factors (e.g., White et al., 2019; Jahnke and Jonsson, 2022). The details of coastal upwelling events are not yet well understood in Aotearoa New Zealand, and their effects could not be included in the current analyses, but clearly should be incorporated when feasible. Here, we focused on varying PLD and the timing of larval production, through analysis of monthly differences in dispersal, and included basic behaviors to represent retention in the water column during early larval stages, and seafloor seeking behaviors in later larval stages. Excluding larval vertical swimming has been shown to lead to overestimates of dispersal (James et al., 2023). However, limited information is currently available on larval behavior of Aotearoa New Zealand coastal species to parameterize particle tracking models. Model resolution can also be increased, following studies that suggest that lower resolution models predicted less offshore larval movement, perhaps resulting in unrealistically high self-recruitment and along-shore settlement (Ward et al., 2023). This may have an impact on studies using the current Moana Backbone model, although this model has been validated in other larval dispersal studies using genetic connectivity metrics (e.g. Quigley et al., 2022; Chaput et al., 2023).
It is worth considering the potential implications of the current results for future climate change scenarios. From other modeling studies (Figueiredo et al., 2022), it is expected that the greatest effect of climate change on larval dispersal will likely be reduced connectivity and increased self-recruitment due to shorter larval periods in warmer waters, particularly for short PLD species. However, some changes in speed and direction of currents may also be expected, which are likely to more strongly impact long PLD species (Bani et al., 2021). Connections which have high variability between them might be under greater threat to disruption by climate change. For example, locations KAI and ISB are consistently connected for all PLD groups in all months, suggesting a resilient connection to climate change, whereas other pathways such as PIH to ISB may be under greater threat of elimination due to more infrequent connections. It is also possible that new connections may be formed with changing currents in the future.
The results of these simulations are broadly applicable to a wide range of coastal marine species with planktonic larval dispersal, as they demonstrate how PLD length, release location, and spawning month can impact dispersal, and overall patterns of species settlement can be inferred with some caveats (Supplementary Figures 17-76). Many aspects of dispersal and settlement are simplified in this model (such as larval behavior), either because their details are unknown or because they are not common across a range of species. Also some ecologically important factors are not considered (such as predation or competition). Although particles could not escape the model’s domain, an extremely small proportion reached the domain boundaries. However, these particles remained near the boundary and likely did not influence settlement rates due to their distance from the shore. In some locations where settlement is predicted to occur, species-specific habitat requirements may prevent occupation by adults or settlement of larvae. The particular release locations selected here are rocky reefs, however nearby soft-sediment locations are likely to experience similar larval dispersal, especially for species with longer PLDs. Regardless, more detailed patterns of a single species’ larval dispersal will likely be derived from a specific modeling exercise using all available data for that species. However, this is a non-trivial exercise to perform across a broad range of larval parameters, and the results from this study can provide preliminary estimates of dispersal for many species.
The approach used in this study can be applied to other regions to determine if PLDs, locations of release, and months of release have similar influences on predicted settlement of benthic marine larvae. The prevalence of local retention, as observed in this Aotearoa New Zealand study, with many particles settling close to the release location across all maximum PLD lengths and months of release, could be tested both through models and empirical testing. Overall, this study provides a comprehensive suite of coastal larval dispersal scenarios around Aotearoa New Zealand's main islands and offers insights into a range of ongoing ecological issues, including identification of barriers to dispersal, source and sink populations, and connectivity between MPAs.
The datasets presented in this study can be found in online repositories at https://doi.org/10.5281/zenodo.8053942. An example of the larval model used can be found at https://github.com/charles-michie/Larval_model. Further inquiries can be directed to the corresponding author.
CM: Writing – original draft, Writing – review & editing, Conceptualization, Formal analysis, Data curation, Methodology. CL: Writing – review & editing, Conceptualization, Funding acquisition, Supervision, Methodology. SL: Writing – review & editing, Conceptualization, Supervision, Methodology. AD: Writing – review & editing, Conceptualization, Supervision, Methodology.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is a contribution to the Moana Project (www.moanaproject.org) funded by the New Zealand Ministry of Business Innovation and Employment, contract number METO1801. Additional funding was provided by NIWA under the Strategic Science Investment Fund, project CEME2303. This research was supported by the NIWA/University of Auckland Joint Graduate School in Coastal and Marine Science under contract number UoA 6000478.
We wish to acknowledge the use of New Zealand eScience Infrastructure (NeSI) high-performance computing facilities and consulting support as part of this research. New Zealand’s national facilities are provided by NeSI and funded jointly by NeSI’s collaborator institutions and through the Ministry of Business, Innovation & Employment’s Research Infrastructure programme. This work also relied on the Moana Project (www.moanaproject.org) hydrodynamic model, the Moana Backbone model: a 25-year hydrodynamic hindcast model of New Zealand waters by MetService licensed under CC BY-NC-SA 4.0 which was funded by the New Zealand Ministry of Business Innovation and Employment, contract number METO1801. Thank you to the development team of OpenDrift (opendrift.github.io) for creating an incredibly useful software for modeling larval trajectories. We also wish to acknowledge J.P.A. Gardner for his helpful review and feedback. The New Zealand Department of Conservation has provided long-term support for Dr Lavery’s connectivity research.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2023.1292081/full#supplementary-material
Aiken C. M., Navarrete S. A., Castillo M. I., Castilla J. C. (2007). Along-shore larval dispersal kernels in a numerical ocean model of the central Chilean coast. Mar. Ecol. Prog. Ser. 339, 13–24. doi: 10.3354/meps339013
Arranz V. (2017). Connectivity among marine communities: a multi-species approach to determining the major drivers of larval connection between populations of coastal species in New Zealand (Dissertation. Auckland, New Zealand: University of Auckland).
Arranz V., Fewster R. M., Lavery S. D. (2021a). Geographic concordance of genetic barriers in New Zealand coastal marine species. Aquat. Conservation: Mar. Freshw. Ecosyst. 31, 3607–3625. doi: 10.1002/aqc.3735
Arranz V., Thakur V., Lavery S. D. (2021b). Demographic history, not larval dispersal potential, explains differences in population structure of two New Zealand intertidal species. Mar. Biol. 168, 1–14. doi: 10.1007/s00227-021-03891-2
Atalah J., South P. M., Briscoe D. K., Vennell R. (2022). Inferring parental areas of juvenile mussels using hydrodynamic modelling. Aquaculture 555, 738227. doi: 10.1016/j.aquaculture.2022.738227
Ayers K. L., Waters J. M. (2005). Marine biogeographic disjunction in central New Zealand. Mar. Biol. 147, 1045–1052. doi: 10.1007/s00227-005-1632-7
Bani R., Marleau J., Fortin M. J., Daigle R. M., Guichard F. (2021). Dynamic larval dispersal can mediate the response of marine metapopulations to multiple climate change impacts. Oikos 130, 989–1000. doi: 10.1111/oik.07760
Bell R., Goring D. (1998). Seasonal variability of sea level and sea-surface temperature on the north-east coast of New Zealand. Estuarine Coast. Shelf Sci. 46, 307–318. doi: 10.1006/ecss.1997.0286
Botsford L., Moloney C., Hastings A., Largier J., Powell T., Higgins K., et al. (1994). The influence of spatially and temporally varying oceanographic conditions on meroplanktonic metapopulations. Deep Sea Res. Part II: Topical Stud. Oceanography 41, 107–145. doi: 10.1016/0967-0645(94)90064-7
Bradshaw B. E. (1991). Nearshore and inner shelf sedimentation on the east Coromandel coast, New Zealand (Dissertation. Hamilton, New Zealand: University of Waikato).
Broekhuizen N., Lundquist C. J., Hadfield M. G., Brown S. N. (2011). Dispersal of oyster (Ostrea Chilensis) larvae in Tasman Bay inferred using a verified particle tracking model that incorporates larval behavior. J. Shellfish Res. 30, 643–658. doi: 10.2983/035.030.0307
Butler IV M. J., Paris C. B., Goldstein J. S., Matsuda H., Cowen R. K. (2011). Behavior constrains the dispersal of long-lived spiny lobster larvae. Mar. Ecol. Prog. Ser. 422, 223–237. doi: 10.3354/meps08878
Cecino G., Treml E. A. (2021). Local connections and the larval competency strongly influence marine metapopulation persistence. Ecol. Appl. 31, e02302. doi: 10.1002/eap.2302
Chaput R., Quigley C. N., Weppe S. B., Jeffs A. G., De Souza J. M., Gardner J. P. (2023). Identifying the source populations supplying a vital economic marine species for the New Zealand aquaculture industry. Sci. Rep. 13, 9344. doi: 10.1038/s41598-023-36224-y
Chia F.-S., Buckland-Nicks J., Young C. M. (1984). Locomotion of marine invertebrate larvae: a review. Can. J. Zoology 62, 1205–1222. doi: 10.1139/z84-176
Chiswell S. M. (2000). The Wairarapa coastal current. N. Z. J. Mar. Freshw. Res. 34, 303–315. doi: 10.1080/00288330.2000.9516934
Chiswell S. M. (2009). Colonisation and connectivity by intertidal limpets among New Zealand, Chatham and Sub-Antarctic Islands. II. Oceanographic connections. Mar. Ecol. Prog. Ser. 388, 121–135. doi: 10.3354/meps08167
Chiswell S. M., Booth J. D. (2008). Sources and sinks of larval settlement in Jasus edwardsii around New Zealand: Where do larvae come from and where do they go? Mar. Ecol. Prog. Ser. 354, 201–217. doi: 10.3354/meps07217
Chiswell S. M., Rickard G. J. (2011). Larval connectivity of harbours via ocean currents: A New Zealand study. Continental Shelf Res. 31, 1057–1074. doi: 10.1016/j.csr.2011.03.012
Chiswell S. M., Roemmich D. (1998). The East Cape Current and two eddies: A mechanism for larval retention? N. Z. J. Mar. Freshw. Res. 32, 385–397. doi: 10.1080/00288330.1998.9516833
Chiswell S. M., Zeldis J. R., Hadfield M. G., Pinkerton M. H. (2017). Wind-driven upwelling and surface chlorophyll blooms in Greater Cook Strait. N. Z. J. Mar. Freshw. Res. 51, 465–489. doi: 10.1080/00288330.2016.1260606
Christy J. H. (2011). Timing of hatching and release of larvae by brachyuran crabs: patterns, adaptive significance and control. Integr. Comp. Biol. 51, 62–72. doi: 10.1093/icb/icr013
Cohen J. H., Hanson C. K., Dittel A. I., Miller D. C., Tilburg C. E. (2015). The ontogeny of larval swimming behavior in the crab Hemigrapsus sanguineus: Implications for larval transport. J. Exp. Mar. Biol. Ecol. 462, 20–28. doi: 10.1016/j.jembe.2014.10.003
Coleman M. A., Cetina-Heredia P., Roughan M., Feng M., Van Sebille E., Kelaher B. P. (2017). Anticipating changes to future connectivity within a network of marine protected areas. Global Change Biol. 23, 3533–3542. doi: 10.1111/gcb.13634
Coscia I., Robins P. E., Porter J. S., Malham S. K., Ironside J. E. (2013). Modelled larval dispersal and measured gene flow: seascape genetics of the common cockle Cerastoderma edule in the southern Irish Sea. Conserv. Genet. 14, 451–466. doi: 10.1007/s10592-012-0404-4
Cowen R. K. (2002). “Larval dispersal and retention and consequences for population connectivity,” in Coral Reef Fishes: Dynamics and Diversity in a Complex Ecosystem. Ed. Sale P. F. (San Diego, CA: Academic Press), 149–170.
Cowen R. K., Gawarkiewicz G., Pineda J., Thorrold S. R., Werner F. E. (2007). Population connectivity in marine systems an overview. Oceanography 20, 14–21. doi: 10.5670/oceanog.2007.26
Cowen R. K., Lwiza K. M. M., Sponaugle S., Paris C. B., Olson D. B. (2000). Connectivity of marine populations: open or closed? Science 287, 857–859. doi: 10.1126/science.287.5454.857
Cowen R. K., Paris C. B., Olson D. B., Fortuna J. L. (2003). The role of long distance dispersal versus local retention in replenishing marine populations. Gulf Caribb. Res. 14 (2), 129–137. doi: 10.18785/gcr.1402.10
Cowen R. K., Sponaugle S. (2009). Larval dispersal and marine population connectivity. Annu. Rev. Mar. Sci. 1, 443–466. doi: 10.1146/annurev.marine.010908.163757
Cragg S. M. (1980). Swimming behaviour of the larvae of Pecten maximus (L.)(Bivalvia). J. Mar. Biol. Assoc. United Kingdom 60, 551–564. doi: 10.1017/S002531540004025X
Creese R. G., Ballantine W. J. (1983). An assessment of breeding in the intertidal limpet, Cellana radians (Gmelin). J. Exp. Mar. Biol. Ecol. 67, 43–59. doi: 10.1016/0022-0981(83)90134-X
Crowder L. B., Lyman S., Figueira W., Priddy J. (2000). Source-sink population dynamics and the problem of siting marine reserves. Bull. Mar. Sci. 66, 799–820.
Dagestad K.-F., Röhrs J., Breivik Ø., Ådlandsvik B. (2018). OpenDrift v1.0: a generic framework for trajectory modelling. Geoscientific Model. Dev. 11, 1405–1420. doi: 10.5194/gmd-11-1405-2018
Dauhajre D. P., Mcwilliams J. C., Renault L. (2019). Nearshore Lagrangian connectivity: Submesoscale influence and resolution sensitivity. J. Geophysical Research: Oceans 124, 5180–5204. doi: 10.1029/2019JC014943
de Lange W., Bell R., Gorman R., Reid S. (2003). “Physical oceanography of New Zealand waters,” in The New Zealand Coast: Te Tai O Aotearoa. Eds. Goff J. R., Nichol S. L., Rouse H. L. (New Zealand: Dunmore Press, Palmerston North with Whitireia Publishing and Daphne Brasell Associates Ltd), 59–78.
Deschepper I., Lyons K., Lyashevska O., Brophy D. (2020). Biophysical models reveal the role of tides, wind, and larval behaviour in early transport and retention of Atlantic herring (Clupea harengus) in the Celtic Sea. Can. J. Fisheries Aquat. Sci. 77, 90–107. doi: 10.1139/cjfas-2018-0491
de Souza J., Suanda S. H., Couto P. P., Smith R. O., Kerry C., Roughan M. (2022). Moana Ocean Hindcast - a 25+ years simulation for New Zealand Waters using the ROMS v3.9 model. EGUsphere 2022, 1–34. doi: 10.5281/zenodo.5895265
Diehl J. M., Toonen R. J., Botsford L. W. (2007). Spatial variability of recruitment in the sand crab Emerita analoga throughout California in relation to wind-driven currents. Mar. Ecol. Prog. Ser. 350, 1–17. doi: 10.3354/meps07208
Domingues C. P., Nolasco R., Dubert J., Queiroga H. (2012). Model-derived dispersal pathways from multiple source populations explain variability of invertebrate larval supply. PLoS One 7, e35794. doi: 10.1371/journal.pone.0035794
Drake P. T., Edwards C. A., Morgan S. G., Dever E. P. (2013). Influence of larval behavior on transport and population connectivity in a realistic simulation of the California Current System. J. Mar. Res. 71, 317–350. doi: 10.1357/002224013808877099
Dunmore R. A., Schiel D. R. (2000). Reproduction in the intertidal limpet Cellana ornata in southern New Zealand. N. Z. J. Mar. Freshw. Res. 34, 653–660. doi: 10.1080/00288330.2000.9516966
Egbert G. D., Erofeeva S. Y. (2002). Efficient inverse modeling of barotropic ocean tides. J. Atmospheric Oceanic Technol. 19, 183–204. doi: 10.1175/1520-0426(2002)019<0183:EIMOBO>2.0.CO;2
Emlet R. B. (1994). Body form and patterns of ciliation in nonfeeding larvae of echinoderms: functional solutions to swimming in the plankton? Am. Zoologist 34, 570–585. doi: 10.1093/icb/34.4.570
Faurby S., Barber P. H. (2012). Theoretical limits to the correlation between pelagic larval duration and population genetic structure. Mol. Ecol. 21, 3419–3432. doi: 10.1111/j.1365-294X.2012.05609.x
Figueiredo J., Thomas C. J., Deleersnijder E., Lambrechts J., Baird A. H., Connolly S. R., et al. (2022). Global warming decreases connectivity among coral populations. Nat. Climate Change 12, 83–87. doi: 10.1038/s41558-021-01248-7
Gary S. F., Fox A. D., Biastoch A., Roberts J. M., Cunningham S. A. (2020). Larval behaviour, dispersal and population connectivity in the deep sea. Sci. Rep. 10, 10675. doi: 10.1038/s41598-020-67503-7
Gawarkiewicz G., Monismith S., Largier J. (2007). Observing larval transport processes affecting population connectivity: progress and challenges. Oceanography 20, 40–53. doi: 10.5670/oceanog.2007.28
Gilg M. R., Hilbish T. J. (2003). The geography of marine larval dispersal: coupling genetics with fine-scale physical oceanography. Ecology 84, 2989–2998. doi: 10.1890/02-0498
Goldstien S. J., Schiel D. R., Gemmell N. J. (2006). Comparative phylogeography of coastal limpets across a marine disjunction in New Zealand. Mol. Ecol. 15, 3259–3268. doi: 10.1111/j.1365-294X.2006.02977.x
Grange K. (1976). Larval development in Lunella smaragda (Gastropoda: Turbinidae). N. Z. J. Mar. Freshw. Res. 10, 517–525. doi: 10.1080/00288330.1976.9515634
Gravinese P. M. (2018). Vertical swimming behavior in larvae of the Florida stone crab, Menippe mercenaria. J. Plankton Res. 40, 643–654. doi: 10.1093/plankt/fby040
Guzmán-Rivas F., Quispe-Machaca M., Queirolo D., Ahumada M., Urzúa Á. (2021). Latitudinal changes in the lipid content and fatty acid profiles of juvenile female red squat lobsters (Pleuroncodes monodon) in breeding areas of the Humboldt Current System. PLoS One 16, e0253314. doi: 10.1371/journal.pone.0253314
Harii S., Nadaoka K., Yamamoto M., Iwao K. (2007). Temporal changes in settlement, lipid content and lipid composition of larvae of the spawning hermatypic coral Acropora tenuis. Mar. Ecol. Prog. Ser. 346, 89–96. doi: 10.3354/meps07114
Harrison H. B., Williamson D. H., Evans R. D., Almany G. R., Thorrold S. R., Russ G. R., et al. (2012). Larval export from marine reserves and the recruitment benefit for fish and fisheries. Curr. Biol. 22, 1023–1028. doi: 10.1016/j.cub.2012.04.008
Haza A. C., Özgökmen T. M., Griffa A., Garraffo Z. D., Piterbarg L. (2012). Parameterization of particle transport at submesoscales in the Gulf Stream region using Lagrangian subgridscale models. Ocean Model. 42, 31–49. doi: 10.1016/j.ocemod.2011.11.005
Heath R. A. (1973). Direct measurements of coastal currents around southern New Zealand. N. Z. J. Mar. Freshw. Res. 7, 331–367. doi: 10.1080/00288330.1973.9515480
Heath R. A. (1982). What drives the mean circulation on the New Zealand west coast continental shelf? N. Z. J. Mar. Freshw. Res. 16, 215–226. doi: 10.1080/00288330.1982.9515964
Heath R. A. (1985). A review of the physical oceanography of the seas around New Zealand — 1982. N. Z. J. Mar. Freshw. Res. 19, 79–124. doi: 10.1080/00288330.1985.9516077
Hijmans R. J., Karney C., Williams E., Vennes C. (2021). Package ’geosphere’. Available at: https://cran.r-project.org/web/packages/geosphere/geosphere.pdf
Hu Y., Majoris J. E., Buston P. M., Webb J. F. (2019). Potential roles of smell and taste in the orientation behaviour of coral-reef fish larvae: insights from morphology. J. fish Biol. 95, 311–323. doi: 10.1111/jfb.13793
Huret M., Runge J. A., Chen C., Cowles G., Xu Q., Pringle J. M. (2007). Dispersal modeling of fish early life stages: sensitivity with application to Atlantic cod in the western Gulf of Maine. Mar. Ecol. Prog. Ser. 347, 261–274. doi: 10.3354/meps06983
Inglis G. J., Hurren H., Oldman J., Haskew R. (2006). Using habitat suitability index and particle dispersion models for early detection of marine invaders. Ecol. Appl. 16, 1377–1390. doi: 10.1890/1051-0761(2006)016[1377:UHSIAP]2.0.CO;2
IUCN World Commission on Protected Areas (2008). Establishing Marine Protected Area Networks - Making It Happen (Washington, DC: IUCN-WCPA, National Oceanic and Atmospheric Administration and The Nature Conservancy).
Jablonski D. (1986). Larval ecology and macroevolution in marine invertebrates. Bull. Mar. Sci. 39, 565–587.
Jahnke M., Jonsson P. R. (2022). Biophysical models of dispersal contribute to seascape genetic analyses. Philos. Trans. R. Soc. B 377, 20210024. doi: 10.1098/rstb.2021.0024
James M., Polton J., Mayorga-Adame C., Howell K., Knights A. (2023). Assessing the influence of behavioural parameterisation on the dispersal of larvae in marine systems. Ecol. Model. 476, 110252. doi: 10.1016/j.ecolmodel.2022.110252
Jonsson P. R., Moksnes P. O., Corell H., Bonsdorff E., Nilsson Jacobi M. (2020). Ecological coherence of Marine Protected Areas: New tools applied to the Baltic Sea network. Aquat. Conservation: Mar. Freshw. Ecosyst. 30, 743–760. doi: 10.1002/aqc.3286
Kelman D., Emlet R. B. (1999). Swimming and buoyancy in ontogenetic stages of the cushion star Pteraster tesselatus (Echinodermata: Asteroidea) and their implications for distribution and movement. Biol. Bull. 197, 309–314. doi: 10.2307/1542784
Kingsford M. J., Leis J. M., Shanks A., Lindeman K. C., Morgan S. G., Pineda J. (2002). Sensory environments, larval abilities and local self-recruitment. Bull. Mar. Sci. 70, 309–340.
Krug P. J., Zimmer R. K. (2004). Developmental dimorphism: consequences for larval behavior and dispersal potential in a marine gastropod. Biol. Bull. 207, 233–246. doi: 10.2307/1543212
Largier J. L. (2003). Considerations in estimating larval dispersal distances from oceanographic data. Ecol. Appl. 13, 71–89. doi: 10.1890/1051-0761(2003)013[0071:CIELDD]2.0.CO;2
Leis J. M. (2021). Perspectives on larval behaviour in biophysical modelling of larval dispersal in marine, demersal fishes. Oceans 2, 1–25. doi: 10.3390/oceans2010001
Le Roux J., Wieczorek A. M. (2009). Molecular systematics and population genetics of biological invasions: towards a better understanding of invasive species management. Ann. Appl. Biol. 154, 1–17. doi: 10.1111/j.1744-7348.2008.00280.x
Le Traon P., Morrow R. (2001). “Ocean currents and eddies,” in Fu L.-L., Cazenave A. (Eds.), International Geophysics (Academic Press) 69, 171–1xi. 10.1016/S0074-6142(01)80148-0
Levin L. A. (2006). Recent progress in understanding larval dispersal: new directions and digressions. Integr. Comp. Biol. 46, 282–297. doi: 10.1093/icb/icj024
Lowe W. H., Allendorf F. W. (2010). What can genetics tell us about population connectivity? Mol. Ecol. 19, 3038–3051. doi: 10.1111/j.1365-294X.2010.04688.x
Lu J., Chen Y., Wang Z., Zhao F., Zhong Y., Zeng C., et al. (2023). Larval dispersal modeling reveals low connectivity among national marine protected areas in the yellow and east China seas. Biology 12, 396. doi: 10.3390/biology12030396
Lundquist C. J., Botsford L. W., Morgan L. E., Diehl J. M., Lee T., Lockwood D. R., et al. (2000). Effects of El Nino and La Nina on local invertebrate settlement in northern California. Rep. California Cooperative Oceanic Fisheries Investigations 41, 167–176.
Lundquist C. J., Oldman J. W., Lewis M. J. (2009). Predicting suitability of cockle Austrovenus stutchburyi restoration sites using hydrodynamic models of larval dispersal. N. Z. J. Mar. Freshw. Res. 43, 735–748. doi: 10.1080/00288330909510038
Lundquist C. J., Thrush S. F., Oldman J. W., Senior A. K. (2004). Limited transport and recolonization potential in shallow tidal estuaries. Limnology oceanography 49, 386–395. doi: 10.4319/lo.2004.49.2.0386
Mann R., Campos B. M., Luckenbach M. W. (1991). Swimming rate and responses of larvae of three mactrid bivalves to salinity discontinuities. Mar. Ecol. Prog. Ser. 68 (3), 257–269.
Mertens L. E. A., Treml E. A., Von Der Heyden S. (2018). Genetic and biophysical models help define marine conservation focus areas. Front. Mar. Sci. 5. doi: 10.3389/fmars.2018.00268
Mitarai S., Siegel D., Watson J., Dong C., Mcwilliams J. (2009). Quantifying connectivity in the coastal ocean with application to the Southern California Bight. J. Geophysical Research: Oceans 114, C10026. doi: 10.1029/2008JC005166
Montaño M. M., Suanda S. H., De Souza J. (2023). Modelled coastal circulation and Lagrangian statistics from a large coastal embayment: The case of Bay of Plenty, Aotearoa New Zealand. Estuarine Coast. Shelf Sci. 281, 108212. doi: 10.1016/j.ecss.2023.108212
Montgomery E. M., Hamel J. F., Mercier A. (2019). Larval nutritional mode and swimming behaviour in ciliated marine larvae. Mar. Biol. Assoc. United Kingdom. J. Mar. Biol. Assoc. United Kingdom 99, 1027–1032. doi: 10.1017/S0025315418001091
Montgomery J. C., Jeffs A., Simpson S. D., Meekan M., Tindle C. (2006). “Sound as an orientation cue for the pelagic larvae of reef fishes and decapod crustaceans,” in Adv. Mar. Biol. 51, 143–196.
Norrie C., Dunphy B., Roughan M., Weppe S., Lundquist C. (2020). Spill-over from aquaculture may provide a larval subsidy for the restoration of mussel reefs. Aquaculture Environ. Interact. 12, 231–249. doi: 10.3354/aei00363
North E. W., Gallego A., Petitgas P. (2009). Manual of recommended practices for modelling physical–biological interactions during fish early life. ICES Cooperative Res. Rep 295, 111.
Okubo A., Ebbesmeyer C. C. (1976). Determination of vorticity, divergence, and deformation rates from analysis of drogue observations. Deep Sea Res. Oceanographic Abstracts 23, 349–352. doi: 10.1016/0011-7471(76)90875-5
Palumbi S. R. (1994). Genetic divergence, reproductive isolation, and marine speciation. Annu. Rev. Ecol. Systematics 25, 547–572. doi: 10.1146/annurev.es.25.110194.002555
Pineda J., Hare J. A., Sponaugle S. U. (2007). Larval transport and dispersal in the coastal ocean and consequences for population connectivity. Oceanography 20, 22–39. doi: 10.5670/oceanog.2007.27
Poje A. C., Haza A. C., Özgökmen T. M., Magaldi M. G., Garraffo Z. D. (2010). Resolution dependent relative dispersion statistics in a hierarchy of ocean models. Ocean Model. 31, 36–50. doi: 10.1016/j.ocemod.2009.09.002
Price J. F., Weller R. A., Schudlich R. R. (1987). Wind-driven ocean currents and Ekman transport. Science 238, 1534–1538. doi: 10.1126/science.238.4833.1534
Quigley C. N., Roughan M., Chaput R., Jeffs A. G., Gardner J. P. A. (2022). Combined biophysical and genetic modelling approaches reveal new insights into population connectivity of New Zealand green-lipped mussels. Front. Mar. Sci. 1912. doi: 10.3389/fmars.2022.971209
Radford C., Stanley J., Simpson S., Jeffs A. (2011). Juvenile coral reef fish use sound to locate habitats. Coral Reefs 30, 295–305. doi: 10.1007/s00338-010-0710-6
R-Core-Team (2022). R: A language and environment for statistical computing (Vienna, Austria: R Foundation for Statistical Computing).
Roberts R. D., Lapworth C. (2001). Effect of delayed metamorphosis on larval competence, and post-larval survival and growth, in the abalone Haliotis iris Gmelin. J. Exp. Mar. Biol. Ecol. 258, 1–13. doi: 10.1016/S0022-0981(00)00346-4
Roemmich D., Sutton P. (1998). The mean and variability of ocean circulation past northern New Zealand: Determining the representativeness of hydrographic climatologies. J. Geophysical Research: Oceans 103, 13041–13054. doi: 10.1029/98JC00583
Ross P. M., Hogg I. D., Pilditch C. A., Lundquist C. J. (2009). Phylogeography of New Zealand's coastal benthos. N. Z. J. Mar. Freshw. Res. 43, 1009–1027. doi: 10.1080/00288330.2009.9626525
Satterthwaite E. V., Ryan J. P., Harvey J. B., Morgan S. G. (2021). Invertebrate larval distributions influenced by adult habitat distribution, larval behavior, and hydrodynamics in the retentive upwelling shadow of Monterey Bay, California, USA. Mar. Ecol. Prog. Ser. 661, 35–47. doi: 10.3354/meps13602
Shanks A. L. (2009). Pelagic larval duration and dispersal distance revisited. Biol. Bull. 216, 373–385. doi: 10.1086/BBLv216n3p373
Shanks A. L., Eckert G. L. (2005). Population persistence of California Current fishes and benthic crustaceans: a marine drift paradox. Ecol. Monogr. 75, 505–524. doi: 10.1890/05-0309
Shchepetkin A. F., McWilliams J. C. (2005). The regional oceanic modeling system (ROMS): a split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 9, 347–404. doi: 10.1016/j.ocemod.2004.08.002
Siegel D., Kinlan B., Gaylord B., Gaines S. (2003). Lagrangian descriptions of marine larval dispersion. Mar. Ecol. Prog. Ser. 260, 83–96. doi: 10.3354/meps260083
Sponaugle S., Cowen R. K., Shanks A., Morgan S. G., Leis J. M., Pineda J., et al. (2002). Predicting self-recruitment in marine populations: biophysical correlates and mechanisms. Bull. Mar. Sci. 70, 341–375.
Stanley J. A., Radford C. A., Jeffs A. G. (2010). Induction of settlement in crab megalopae by ambient underwater reef sound. Behav. Ecol. 21, 113–120. doi: 10.1093/beheco/arp159
Stanley J. A., Radford C. A., Jeffs A. G. (2011). Behavioural response thresholds in New Zealand crab megalopae to ambient underwater sound. PLoS One 6, e28572. doi: 10.1371/journal.pone.0028572
Stanton B. R., Sutton P. J., Chiswell S. M. (1997). The East Auckland current 1994–95. N. Z. J. Mar. Freshw. Res. 31, 537–549. doi: 10.1080/00288330.1997.9516787
Stephens S. A., Broekhuizen N., Macdiarmid A. B., Lundquist C. J., Mcleod L., Haskew R. (2006). Modelling transport of larval New Zealand abalone (Haliotis iris) along an open coast. Mar. Freshw. Res. 57, 519–532. doi: 10.1071/MF06020
Stevens C. L., O’callaghan J. M., Chiswell S. M., Hadfield M. G. (2019). Physical oceanography of New Zealand/Aotearoa shelf seas – a review. N. Z. J. Mar. Freshw. Res. 55, 6–45. doi: 10.1080/00288330.2019.1588746
Strathmann M. F. (1987). Reproduction and development of marine invertebrates of the northern Pacific coast: data and methods for the study of eggs, embryos, and larvae (Seattle, WA: University of Washington Press).
Sulkin S. D. (1984). Behavioral basis of depth regulation in the larvae of brachyuran crabs. Mar. Ecol. Prog. Ser. 15, 181–205. doi: 10.3354/meps015181
Sutton P. J. H. (2003). The Southland Current: A subantarctic current. N. Z. J. Mar. Freshw. Res. 37, 645–652. doi: 10.1080/00288330.2003.9517195
Sutton P. J. H., Bowen M. (2011). Currents off the west coast of Northland, New Zealand. N. Z. J. Mar. Freshw. Res. 45, 609–624. doi: 10.1080/00288330.2011.569729
Swearer S. E., Treml E. A., Shima J. S. (2019). A review of biophysical models of marine larval dispersal In: Hawkins S.J., Allcock A.L., Bates A.E., Firth L.B., Smith I.P., Swearer S.E., et al editors. Oceanography and Marine Biology: An annual review 57 (1st ed.). CRC Press. doi: 10.1201/9780429026379
Tapia F. J., Dibacco C., Jarrett J., Pineda J. (2010). Vertical distribution of barnacle larvae at a fixed nearshore station in southern California: Stage-specific and diel patterns. Estuarine Coast. Shelf Sci. 86, 265–270. doi: 10.1016/j.ecss.2009.11.003
Thomas L., Bell J. (2013). Testing the consistency of connectivity patterns for a widely dispersing marine species. Heredity 111, 345–354. doi: 10.1038/hdy.2013.58
Treml E. A., Halpin P. N. (2012). Marine population connectivity identifies ecological neighbors for conservation planning in the Coral Triangle. Conserv. Lett. 5, 441–449. doi: 10.1111/j.1755-263X.2012.00260.x
Veale A. J., Lavery S. D. (2011). Phylogeography of the snakeskin chiton Sypharochiton pelliserpentis (Mollusca: Polyplacophora) around New Zealand: are seasonal near-shore upwelling events a dynamic barrier to gene flow? Biol. J. Linn. Soc. 104, 552–563. doi: 10.1111/j.1095-8312.2011.01743.x
Viard F., Ellien C., Dupont L. (2006). Dispersal ability and invasion success of Crepidula fornicata in a single gulf: insights from genetic markers and larval-dispersal model. Helgoland Mar. Res. 60, 144–152. doi: 10.1007/s10152-006-0033-8
Walters R. A., Gillibrand P. A., Bell R. G., Lane E. M. (2010). A study of tides and currents in Cook Strait, New Zealand. Ocean dynamics 60, 1559–1580. doi: 10.1007/s10236-010-0353-8
Wang P., Ebersole B. A., Smith E. R., Johnson B. D. (2002). Temporal and spatial variations of surf-zone currents and suspended sediment concentration. Coast. Eng. 46, 175–211. doi: 10.1016/S0378-3839(02)00091-1
Ward S., Robins P., Owen A., Demmer J., Jenkins S. (2023). The importance of resolving nearshore currents in coastal dispersal models. Ocean Model. 183, 102181. doi: 10.1016/j.ocemod.2023.102181
Waters J. M., Fraser C. I., Hewitt G. M. (2013). Founder takes all: density-dependent processes structure biodiversity. Trends Ecol. Evol. 28, 78–85. doi: 10.1016/j.tree.2012.08.024
Waters J. M., Roy M. S. (2004). Phylogeography of a high-dispersal New Zealand sea-star: does upwelling block gene-flow? Mol. Ecol. 13, 2797–2806. doi: 10.1111/j.1365-294X.2004.02282.x
Weersing K., Toonen R. J. (2009). Population genetics, larval dispersal, and connectivity in marine systems. Mar. Ecol. Prog. Ser. 393, 1–12. doi: 10.3354/meps08287
Wei K., Wood A. R., Gardner J. P. A. (2013). Population genetic variation in the New Zealand greenshell mussel: locus-dependent conflicting signals of weak structure and high gene flow balanced against pronounced structure and high self-recruitment. Mar. Biol. 160, 931–949. doi: 10.1007/s00227-012-2145-9
White J. W., Carr M. H., Caselle J. E., Washburn L., Woodson C. B., Palumbi S. R., et al. (2019). Connectivity, dispersal, and recruitment. Oceanography 32, 50–59. doi: 10.5670/oceanog.2019.310
Will M., Hale M. L., Schiel D. R., Gemmell N. J. (2011). Low to moderate levels of genetic differentiation detected across the distribution of the New Zealand abalone, Haliotis iris. Mar. Biol. 158, 1417–1429. doi: 10.1007/s00227-011-1659-x
Wing S., Jack L. (2014). Fiordland: the ecological basis for ecosystem management. N. Z. J. Mar. Freshw. Res. 48, 577–593. doi: 10.1080/00288330.2014.897636
Woodson C., McManus M. (2007). Foraging behavior can influence dispersal of marine organisms. Limnology Oceanography 52, 2701–2709. doi: 10.4319/lo.2007.52.6.2701
Keywords: biophysical modeling, pelagic larval duration, OpenDrift, spawning time, predicted settlement, larval dispersal, Lagrangian
Citation: Michie C, Lundquist CJ, Lavery SD and Della Penna A (2024) Spatial and temporal variation in the predicted dispersal of marine larvae around coastal Aotearoa New Zealand. Front. Mar. Sci. 10:1292081. doi: 10.3389/fmars.2023.1292081
Received: 11 September 2023; Accepted: 28 December 2023;
Published: 24 January 2024.
Edited by:
Tomaso Fortibuoni, Istituto Superiore per la Protezione e la Ricerca Ambientale (ISPRA), ItalyReviewed by:
Donata Melaku Canu, National Institute of Oceanography and Applied Geophysics, ItalyCopyright © 2024 Michie, Lundquist, Lavery and Della Penna. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Charles Michie, Y21pYzU3MkBhdWNrbGFuZHVuaS5hYy5ueg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.