- 1College of Environment and Civil Engineering, Chengdu University of Technology, Chengdu, China
- 2Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, Chengdu, China
- 3Climate and Ecosystem Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA, United States
- 4School Emergency and Safety, University of Jinan, Jinan, China
- 5School of Water Conservancy and Environment, University of Jinan, Jinan, China
Introduction: Coastal karst aquifers face the risk of seawater intrusion due to groundwater development. Based on the conceptualization of Woodville Karst Plain (WKP), this study investigates the effect of karst conduit and pumping conditions on the aquifer vulnerability and pumping security.
Methods: According to the purposes of this study, two cases are considered: one with conduit and one without. Salinization levels are compared between two cases, considering pumping rates ranging from 50 to 200 m3/day and various pumping locations throughout the on-shore region.
Results: The results reveal that the aquifer with conduit is more susceptible to seawater intrusion at low pumping rates, whereas both scenarios experience significant salinization at high pumping rates. Specifically, in the non-conduit case, contamination is most prevalent when wells are located in the middle of the aquifer, while in the conduit case, pumping from inland areas poses high vulnerability. Moreover, conduit case and non-conduit case display different regions for pumping clean water. At low pumping rates, both cases show saline water being pumped from wells near the shore, and clean water is obtained from inland wells. At high pumping rates, the non-conduit case allows for clean water extraction from wells situated further inland, while in the conduit case, no wells within the entire aquifer are deemed safe.
Discussion: The analysis and findings of this study offer valuable insights for the management of groundwater in coastal karst aquifers, encompassing vulnerability assessment, selection of pumping locations, and determination of pumping rates.
1 Introduction
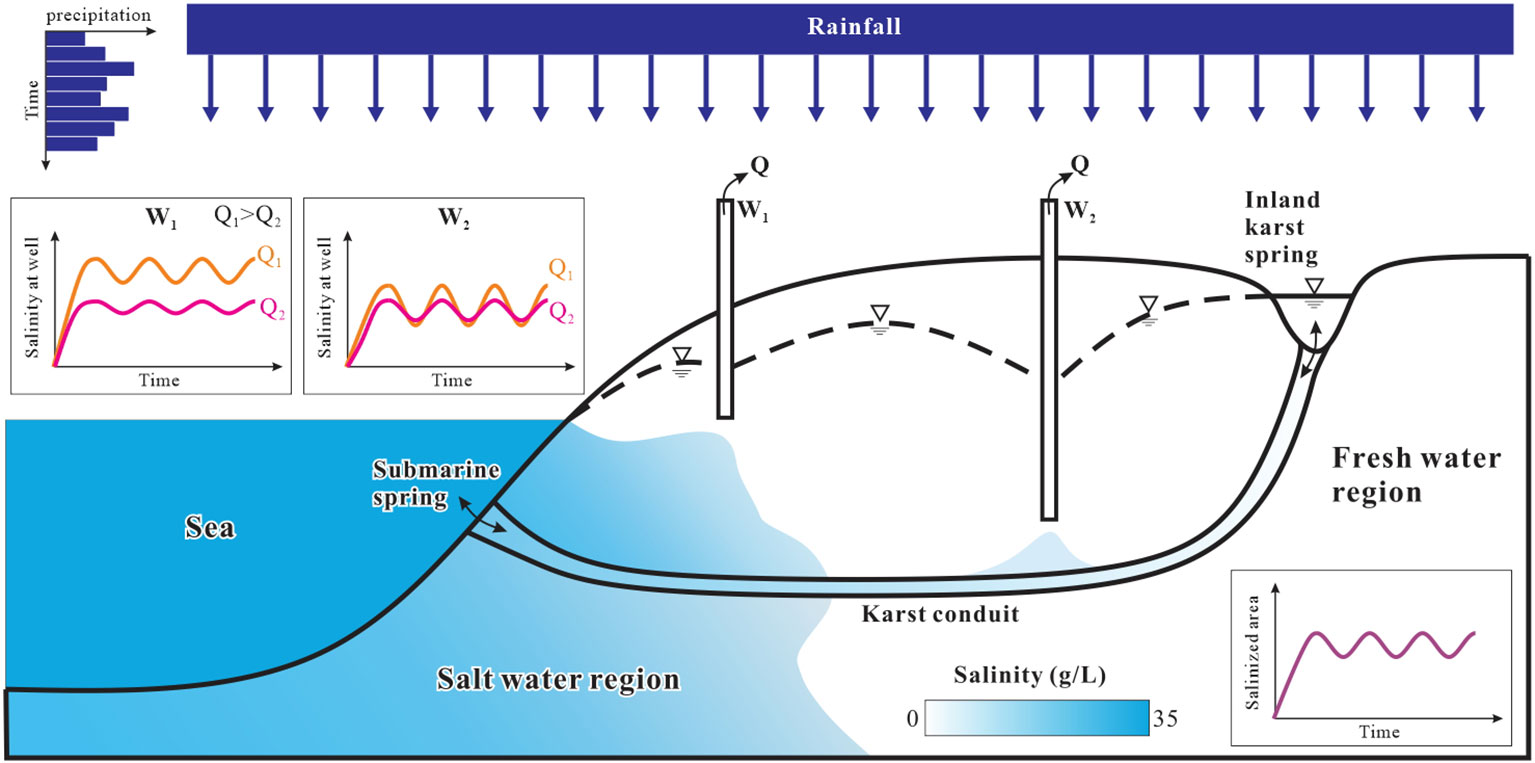
In coastal regions, interactions of seawater and freshwater bring about unique groundwater environment, numerous endeavors have investigated chemical releasing and accumulations, biological environmental problems, and different coastal carbon budgets (e.g. Luo et al., 2022; Xiao et al., 2022; Zhang et al., 2022; Wang et al., 2023). Furthermore, in coastal karst aquifers, the seawater-freshwater interactions may be amplified since the existence of interconnected conduit systems (Arthur et al., 2007; Fleury et al., 2007). Saltwater can quickly move through these conduits, extending from submarine springs to inland areas (Beddows, 2004; Fleury et al., 2007). Furthermore, water exchange between conduits and the carbonate matrix allows for the expansion of saltwater within the freshwater system (Hu, 2010). During the last decade, researchers have given significant attention to this issue (e.g., Bakalowicz, 2018; Acikel and Ekmekci, 2021; Fleury et al., 2023; Schuler et al., 2019), conducting numerous numerical simulations, lab and field experiments to understand the process of seawater-fresh water interactions, assess aquifer vulnerability, and further apply to the geochemical and nutrient investigations (e.g. Faulkner et al., 2009; Xu et al., 2015; Oehler et al., 2019; Bejannin et al., 2020; Pétré et al., 2020; Shokri et al., 2022).
Due to the large uncertainty in the karst hydrogeological investigation, numerical modeling becomes a useful tool to evaluate local water resources and quantify contaminant migration (Kalhor et al., 2019). Numerical simulations of seawater intrusion in conduit-matrix systems offer good insights into understanding the susceptibility of coastal karst aquifers. Popular conceptualizations for evaluating seepage flow and contaminant transport in karst aquifers are the dual-porosity and discrete-continuum models, such as MODFLOW-CFP (Shoemaker et al., 2008; Reimann et al., 2011). For considering the density effect in the seawater-fresh water interaction, SEAWAT (Langevin et al., 2007) was applied by ignoring the non-Darcy flow in karst conduits (Xu et al., 2019a). Xu and Hu (2017) developed the VDFST-CFP code to simulate seawater-fresh water interaction in coastal karst aquifers, which incorporates both density-driven Darcy flow in porous media and non-Darcy flow in the conduit. Xu et al. (2019b) enhanced the VDFST-CFP model by achieving simulations of double conduits and accounting for conduit wall roughness, highlighting the importance of conduit spatial distribution in evaluating seawater intrusion. Though many efforts have been made, large challenges still existed in coupling non-Darcy flow and density-driven flow in groundwater simulations, especially for a big 3D model.
The significance of connected conduits in simulating seawater intrusion has been established. Arfib et al. (2007) demonstrated the preferential flow in karst conduits influences the saline water fluctuations in the aquifer. Sebben et al. (2015) and Koohbor et al. (2019) established the influence of directions and locations of conduits/fractures on salinity distribution, emphasizing that simulating an equivalent porous medium for a conduit system is inadequate for assessing aquifer vulnerability. Kresic and Panday (2021) compared the seawater intrusion and submarine groundwater discharge in a coastal aquifer with and without a karst conduit by MODFLOW-USG simulations (Panday et al., 2013). Their findings demonstrated that conduits contribute to additional seawater intrusion, extending beyond the conduit’s physical presence. In another study, Xu et al. (2018) investigated the sensitivity of different parameters on the distribution of seawater and freshwater in 2D synthetic models using the SEAWAT code (Langevin et al., 2007). The findings highlighted that the porosity of the conduit region, effective hydraulic conductivity of karst conduits, and salinity at submarine springs play crucial roles in the process of seawater intrusion. Kreyns et al. (2020) demonstrated that the salinity distribution in connected conduit systems differs significantly from multi-Gaussian and homogeneous models. Geng and Michael (2020) highlighted that the presence of high-permeability channels, specifically lava tubes, within the aquifer can lead to significant seawater intrusion, as well as introduce large uncertainty in predicting the distribution of salinity.
The intrusion of saline water induced by coastal pumping has been a subject of study for several decades (Houben and Post, 2017). Groundwater pumping serves as a vital source of freshwater for coastal regions, and it has been a key driver to influence the vulnerability of coastal aquifers (Ferguson and Gleeson, 2012). Excessive pumping can lead to severe aquifer salinization, resulting in unsustainable aquifers and even surface water contamination (Werner et al., 2013; Michael et al., 2017; Peters et al., 2022). Many studies have investigated chemical and discharge variations in the interaction between seawater and freshwater, and the phenomenon of upcoming under pumping effects through diverse methods such as analytical models (e.g., Fahs et al., 2016; Strack et al., 2016; Shao et al., 2018), laboratory experiments (e.g. Goswami and Clement, 2007; de Franco et al., 2009), and numerical modeling (e.g. Sherif et al., 2013; de Filippis et al., 2016; Yu et al., 2022). Recent studies have revealed that geologic heterogeneity and pumping conditions strongly influence the vulnerability of onshore freshwater resources (Knight et al., 2018; Yu and Michael, 2019a) and can even contribute to the large area of land subsidence (Yu and Michael, 2019b).
Previous studies have presented significant findings regarding seawater intrusion in karst regions and the impact of coastal pumping. However, the majority of current research on the environment of coastal karst aquifers has primarily focused on investigating seawater intrusion. The compound effect of karst conduits and groundwater pumping has not been fully investigated, including pumping locations, rates, and flow behaviors in conduits. In order to explore the impact of karst conduits and different pumping scenarios on seawater intrusion, this study employs SEAWAT numerical models based on the conceptualization of the Woodville Karst Plain (WKP) in northern Florida. The recharge boundary is assigned variable values based on local precipitation data. Two cases are examined: a conduit model featuring a single karst conduit and a non-conduit model. Multiple pumping rates and locations are applied to both models.
2 Methods
To investigate the issue of seawater intrusion, a 2D synthetic SEAWAT model was constructed for this study. The governing equation and code implementation of SEAWAT are detailed illustrated in Langevin et al. (2007). This code combines the flow simulation in MODFLOW (Harbaugh, 2005) and transport simulation in MT3DMS (Zheng and Wang, 1999) to depict variable-density groundwater behavior. In this study, Darcy’s law was employed to simulate groundwater flow in either porous media or karst conduit, the possible non-Darcian flow behavior in conduit systems was simplified as Darcy flow. Similar 2D synthetic SEAWAT models were designed in previous works to investigate coastal karst contaminations, such as those by Xu et al. (2018) and Wu et al. (2022).
2.1 Model setup and discretization
The framework of this synthetic model is based on the WKP in Florida, as shown in Figure 1A (Davis et al., 2010). WKP is a research hotspot for groundwater protection in coastal karst aquifers, and previous studies have provided abundant details on this topic (e.g., Davis and Verdi, 2014; Xu et al., 2016; Xu and Hu, 2021). Researchers have confirmed the existence of a large conduit system, spanning 18 km, connecting the ocean (Gulf of Mexico) and inland karst spring (Wakulla Spring), through tracer tests as well as cave diving explorations (Kernagis et al., 2008; Kincaid and Werner, 2008). It has been observed that seawater intrusion through this karst system has affected the water quality in Wakulla Spring (Xu et al., 2016). Therefore, in this study, a 2D synthetic model was developed to represent the region between the Gulf of Mexico and the Wakulla Spring, with a single main conduit connecting the two places. The actual coastal karst plain could be a complex mixture of multiple conduits, inlets, outlets (Hendrick and Renard, 2016), a single-conduit simplification may not accurately reflect this complexity. While it is a useful tool for studying seawater intrusion behavior in a coastal karst aquifer theoretically (Xu and Hu, 2017; Xu et al., 2018), and the findings are universality and generalizability.
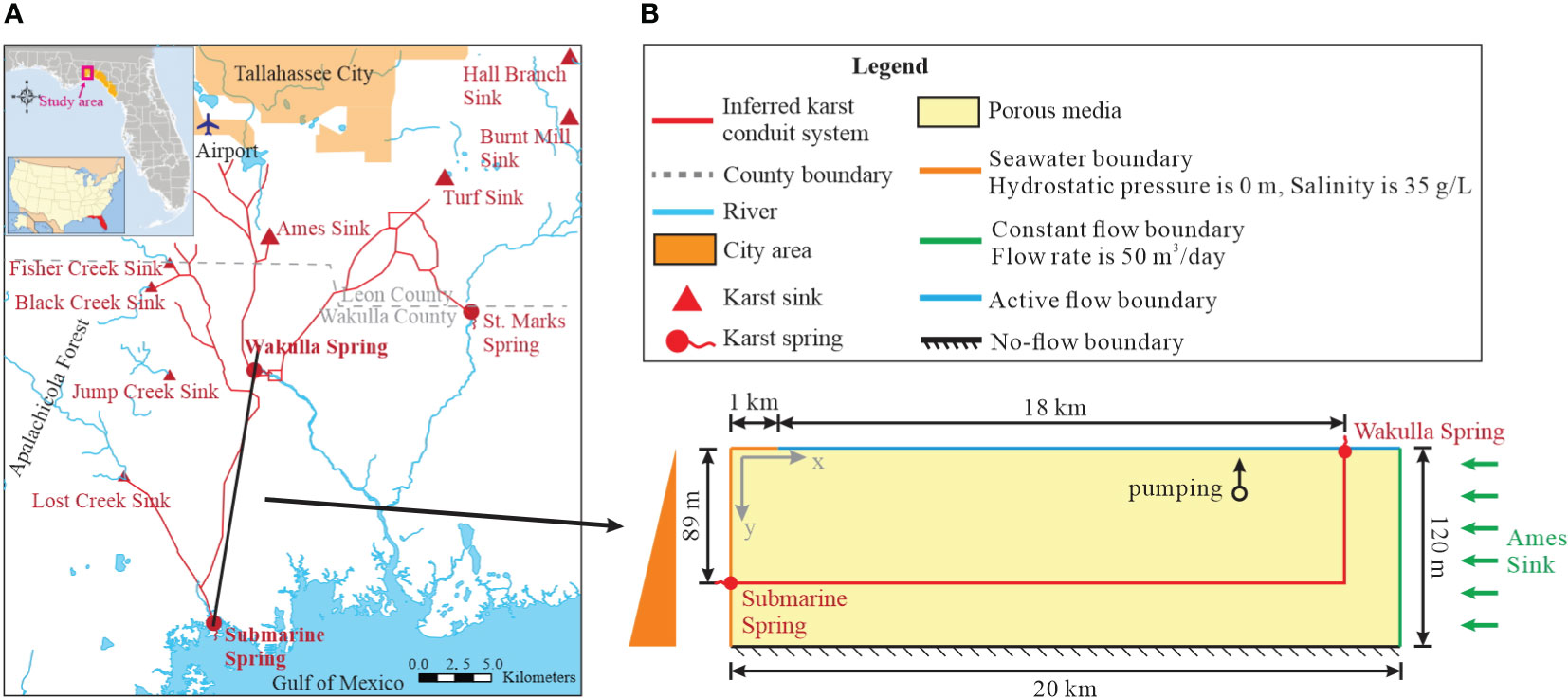
Figure 1 Study site and boundary conditions of the model. (A) The karst distribution map and surface river map of Woodville Karst Plain; (B) boundary conditions of the numerical model.
The size of the model was arranged to fit the region between Wakulla Spring and the ocean. The model has a length of 20 km, with 1 km offshore region (Figure 1B). The vertical size of the model is 120 m, representing the Upper Floridan Aquifer. We only considered one cell in the model width, which is 50 m. In the single-conduit model, the submarine spring in the ocean was located at a depth of 89 m (Davis et al., 2010; Xu et al., 2016). The conduit extended from the submarine spring 18 km inland and then vertically connected with Wakulla Spring (shown in red in Figure 1B). The size of each cell was 50 m × 50 m and 3 m in depth, which was proved to be fine enough for simulating seawater intrusion (Xu et al., 2018; Yu and Michael, 2019a). The cell size of the vertical conduit under Wakulla Spring (shown in Figure 1B) was set as 10 m in length and 3 m in depth to avoid an unacceptably large conduit. The non-conduit model has the same discretization as the single-conduit model in porous media but lacks the main karst conduit.
2.2 Aquifer parameters
The non-conduit model represents a homogeneous field, while the single-conduit model is a dual-permeability system in which the karst conduit and karst matrix (porous media) have been allocated different values (Table 1). The properties of the porous media in both models are the same. Aquifer parameters were modified from previous studies (Davis et al., 2010; Xu et al., 2018; Wu et al., 2022). The hydraulic conductivity and porosity of the porous media (shown in yellow in Figure 1B) are 86.0 m/d and 0.001, respectively, while those of the karst conduit (shown in red in Figure 1B) are 3.5e4 m/d and 0.005 (Ford and Williams, 2007). Dispersivity and specific storage in porous media were assumed to be 0.3 m and 5.0e-7, while they are 10 m and 0.05 in the conduit (Xu et al., 2018). These values have been calibrated and well-used in prior research (Davis et al., 2010; Xu et al., 2016; Wu et al., 2022).
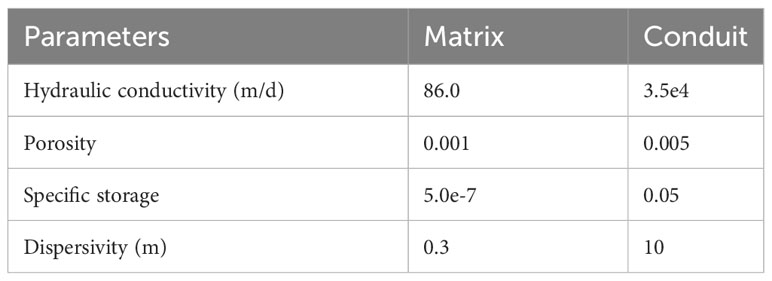
Table 1 Aquifer parameters of karst matrix and conduit (Ford and Williams, 2007; Xu et al., 2018).
2.3 Initial and boundary conditions
The model was assumed as a confined aquifer, with an impermeable boundary at the bottom that represents the low-permeability Clayton Formation (Davis et al., 2010) (Figure 1B). The top of the inland aquifer (blue in Figure 1B) is a recharge boundary with variable recharge conditions, which is detailed presented in the next section. The hydraulic head and water density of the sea boundary are constant values (orange in Figure 1B), where the head is 0.0 m and the density is 35.0 g/L. The inland boundary (green in Figure 1B) represents a constant flow boundary. The inland flow rate was calculated based on the head difference between the Wakulla Spring and Ames Sink (Figure 1A). The hydraulic head values for the Wakulla Spring and Ames Sink are 1.52 m and 2.43 m, respectively, and their distance is 11 km. Applying Darcy’s law between them with a geometric mean of hydraulic conductivity of 100.3 m/d, the calculated inland recharge is approximately 50 m3/d. The Wakulla Spring was assigned as DRAIN package which only receive water from surrounding cells (Harbaugh, 2005). The initial head and salinity distribution of the model is the steady-state simulation results under the average rainfall recharge and no-pumping conditions.
2.4 Recharge conditions
The model was subjected to variable rainfall conditions based on monthly precipitation data collected from the WKP, as shown in Figure 2. These data were gathered from monitoring sites operated by the United States Geological Survey (USGS) and National Oceanic and Atmospheric Administration (NOAA) from 2015 to 2020. Similar to the conceptual model outlined in Davis and Verdi (2014), precipitation variation can be classified into 3 periods based on rainfall intensity: the low-rainfall period, which occurs between October and March and has an average precipitation of 2.8 mm/d; the high-rainfall period, which occurs between June and August and has precipitation greater than 5.0 mm/d; April, May, and September are transition period with precipitation of 4.2 mm/d, bridging the low- and high-rainfall periods. As a result, precipitation values of 2.8, 4.2, and 7.5 mm/d were used in this modeling work for the low-rainfall, transition, and high-rainfall months, respectively (Figure 2B). The net recharge applied in the simulation was then calculated based on precipitation, evaporation, and infiltration rate in Equation (1):
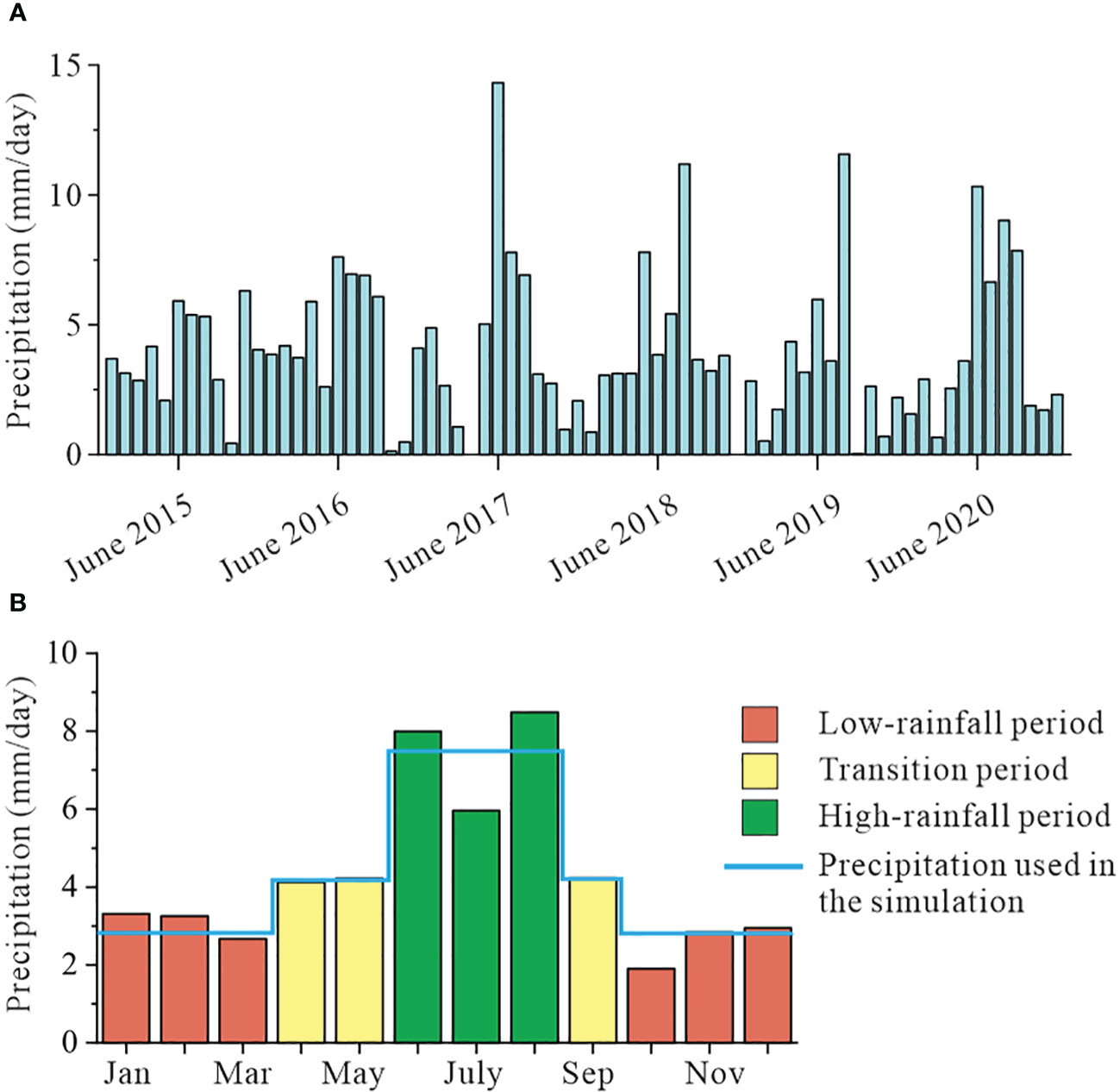
Figure 2 (A) Monthly precipitation from 2015 to 2020. (B) The average monthly precipitation was calculated from each year in (A). The blue line represents the monthly precipitation of each rainfall period that was utilized in the numerical model.
where R is the net recharge applied in the numerical simulation (LT-1); M is the monthly precipitation in Figure 2B (LT-1); Ma is the annual precipitation (LT-1), equals to ~1557 mm/year; Ta is the annual evapotranspiration (LT-1) of ~1377 mm/year (Xu et al., 2015; Xu and Hu, 2021); F is the infiltration rate of rainwater transport to the groundwater, which equals to 0.4 (Li et al., 2011).
2.5 Pumping scenarios
At the WKP, approximately 95,000 to 100,000 m3 of groundwater is extracted daily from the Upper Floridan Aquifer for domestic and industrial use, as reported by the City of Tallahassee (2016; 2017; 2018). These withdrawals are from a contributing area of roughly 800 km2 (Davis and Katz, 2007). As a result, the computed pumping rate for the model domain in Figure 1B (the area is 0.9 km2) is 105-115 m3/day. Therefore, four different pumping rates were designed in the simulation based on the above calculated pumping rate: 50 m3/day, 100 m3/day, 150 m3/day, and 200 m3/day. Additionally, the pumping location was shifted from the near-shore region to the inland boundary, specifically within the coordinates 1.5< x< 20 km and -120< y< 0 m, for each grid cell (Figure 1B). Simulations were conducted for each pumping rate and pumping location.
2.6 Seawater intrusion assessment
Five evaluation metrics were used to delineate aquifer vulnerability and pumping safety: average salinized area, variance of salinized area, throughout time at well, difference of salinized area, and difference of throughout time at pumping well. Salinized area measures the fraction of the area whose salinity is greater than 0.5 g/L EPA (2009), it is a time-dependent indicator in this study due to the rainfall variations. Therefore, we calculated the average salinized area and variance of salinized area based on simulated salinized area in the time span of 10 years. Salinity at well is another time-dependent indicator varying over 10 years, which illustrates the fluctuation in salinity at the pumping well. We calculated the throughout time at well, which is the fraction of the time span at a well pumping saline water (salinity ≥ 0.5 g/L). For emphasizing the effect of karst conduit in the seawater intrusion process, the average salinized area and throughout time at well in the single-conduit case was compared with the corresponding metrics in the non-conduit case, and the resulting differences were calculated. Difference of salinized area was calculated by the average salinized area of conduit case subtract it of non-conduit case at same locations. Similarly, difference of throughout time represent the difference of throughout time at well between two cases. All the above assessment metrics were computed for each pumping scenario (different pumping rates and locations) and then plotted at their respective pumping locations, as detailed in Section 3.
3 Results
This study aims to investigate the effect of karst conduit on seawater intrusion under dynamic recharge conditions. Examples of the simulation results and salinity distribution for conduit and non-conduit cases are displayed in Figure 3. The metrics of each pumping scenario are plotted at the pumping location in Figures 4–8.
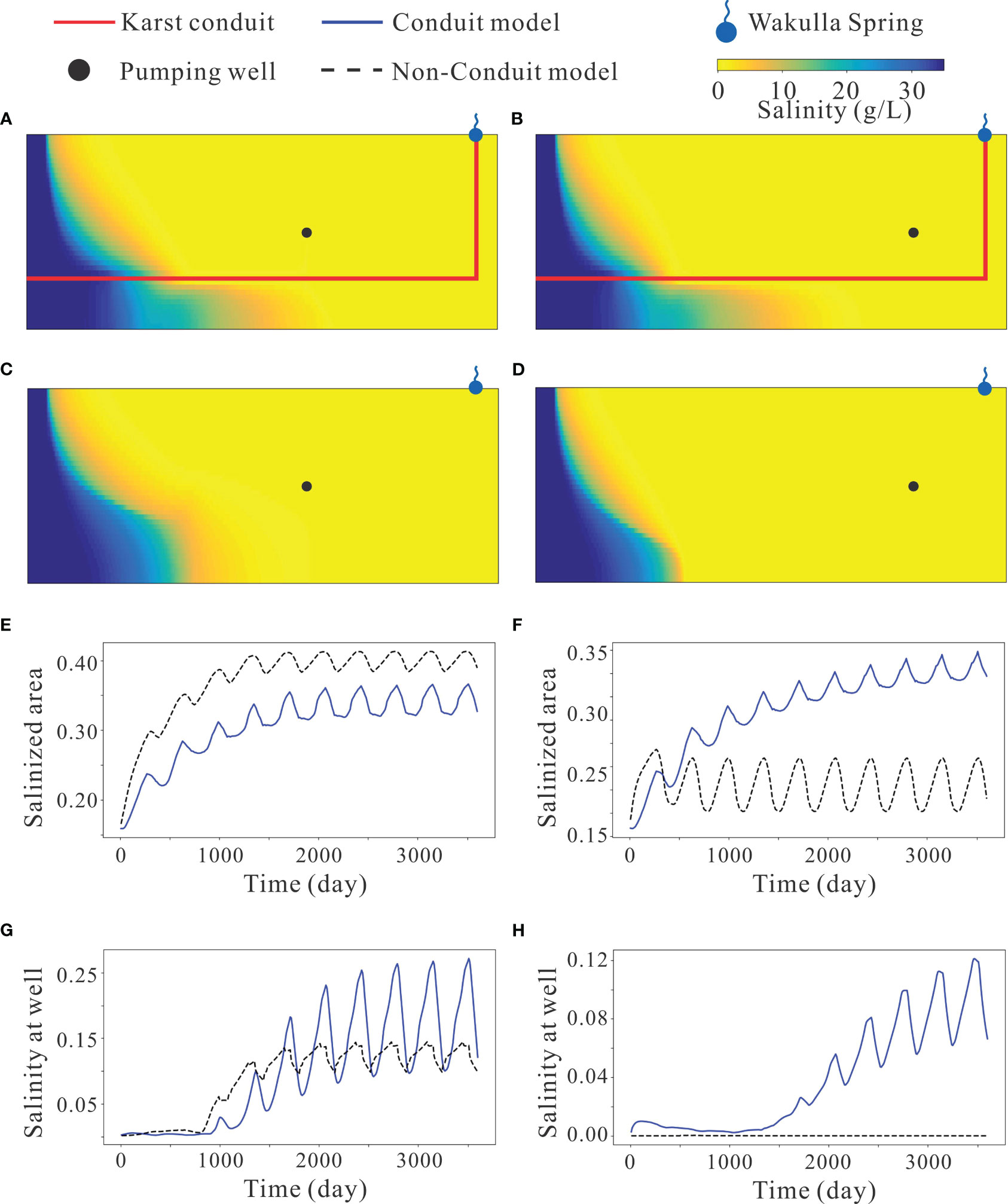
Figure 3 Examples of simulation results. (A–D) are the final salinity distribution of conduit case, final salinity distribution of non-conduit case, salinized area in 10 years, and salinity at well in 10 years, with pumping rate of 150 m3/day at 11 km onshore and 60 m depth; (E–H) are the final salinity distribution of conduit case, final salinity distribution of non-conduit case, salinized area in 10 years, and salinity at well in 10 years, with pumping rate of 150 m3/day at 15 km onshore and 60 m depth.
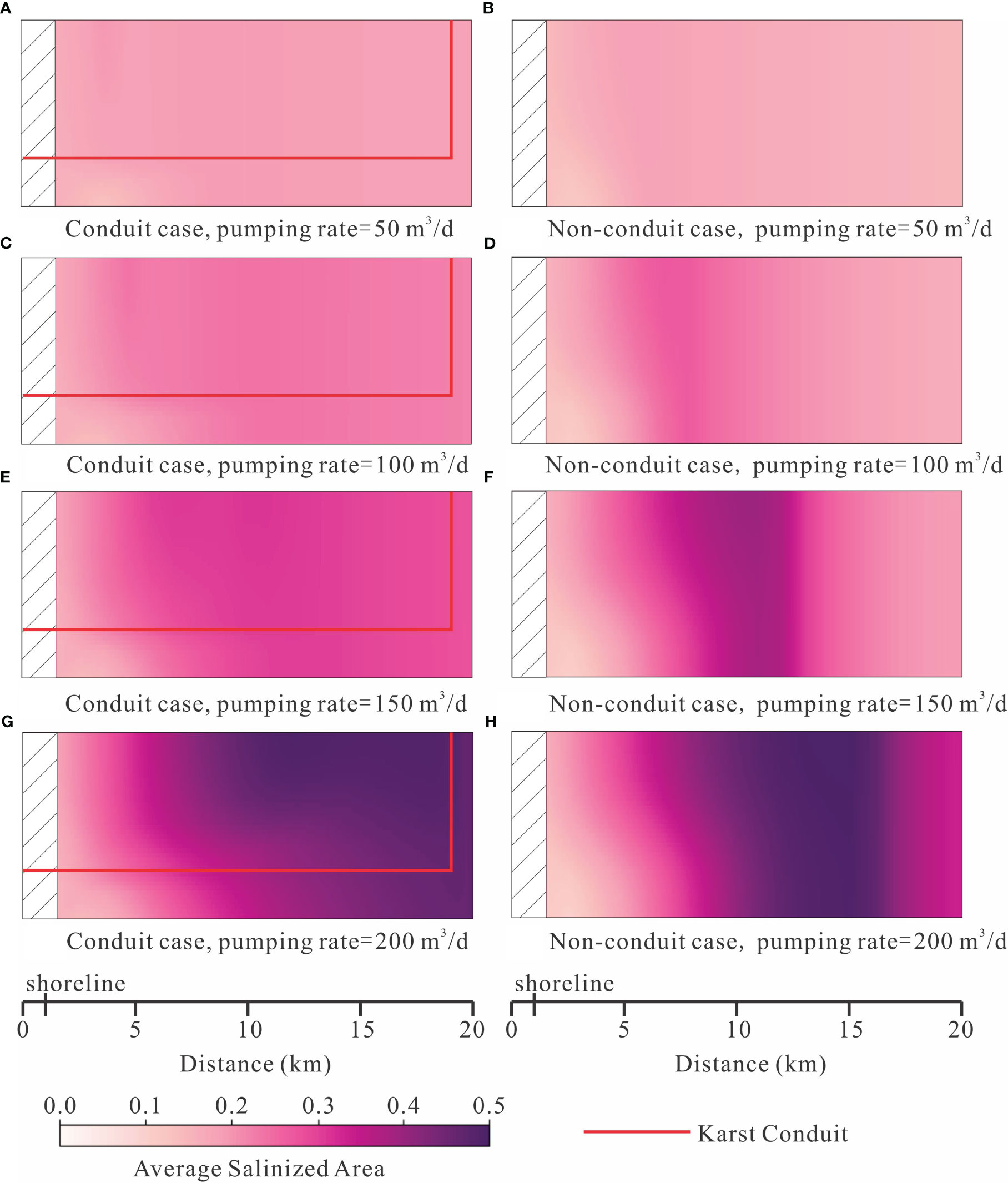
Figure 4 The average salinized area of multiple pumping scenarios under different pumping rates. The average salinized area was calculated in each pumping process and then plotted in the domain at its well location. (A) Conduit case with pumping rate 50 m3/d; (B) Non-onduit case with pumping rate 50 m3/d; (C) Conduit case with pumping rate 100 m3/d; (D) Non-conduit case with pumping rate 100 m3/d; (E) Conduit case with pumping rate 150 m3/d; (F) Non-conduit case with pumping rate 150 m3/d; (G) Conduit case with pumping rate 200 m3/d; (H) Non-conduit case with pumping rate 200 m3/d.
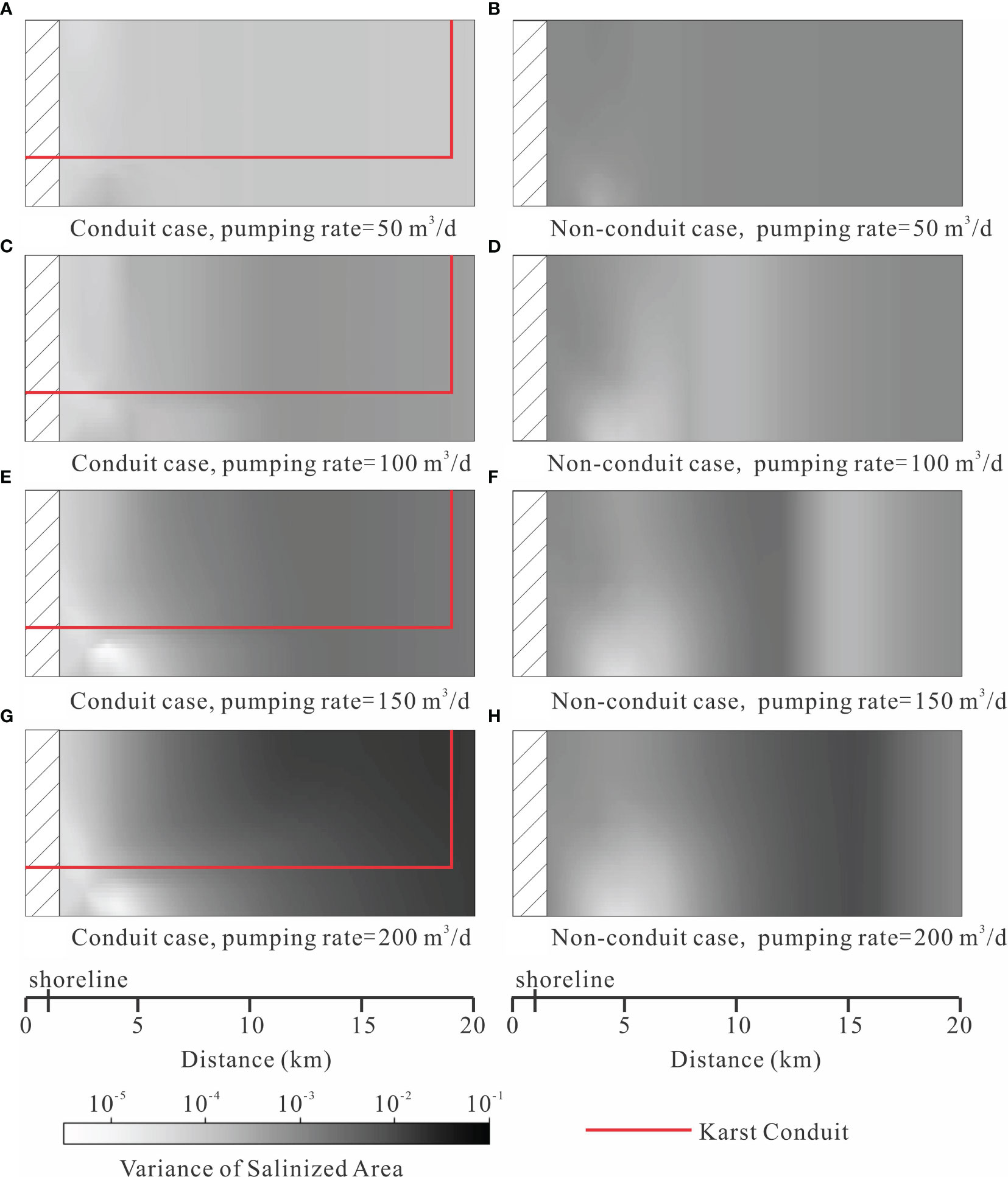
Figure 5 The variance of salinized area of multiple pumping scenarios under different pumping rates. (A) Conduit case with pumping rate 50 m3/d; (B) Non-conduit case with pumping rate 50 m3/d; (C) Conduit case with pumping rate 100 m3/d; (D) Non-conduit case with pumping rate 100 m3/d; (E) Conduit case with pumping rate 150 m3/d; (F) Non-conduit case with pumping rate 150 m3/d; (G) Conduit case with pumping rate 200 m3/d; (H) Non-conduit case with pumping rate 200 m3/d.
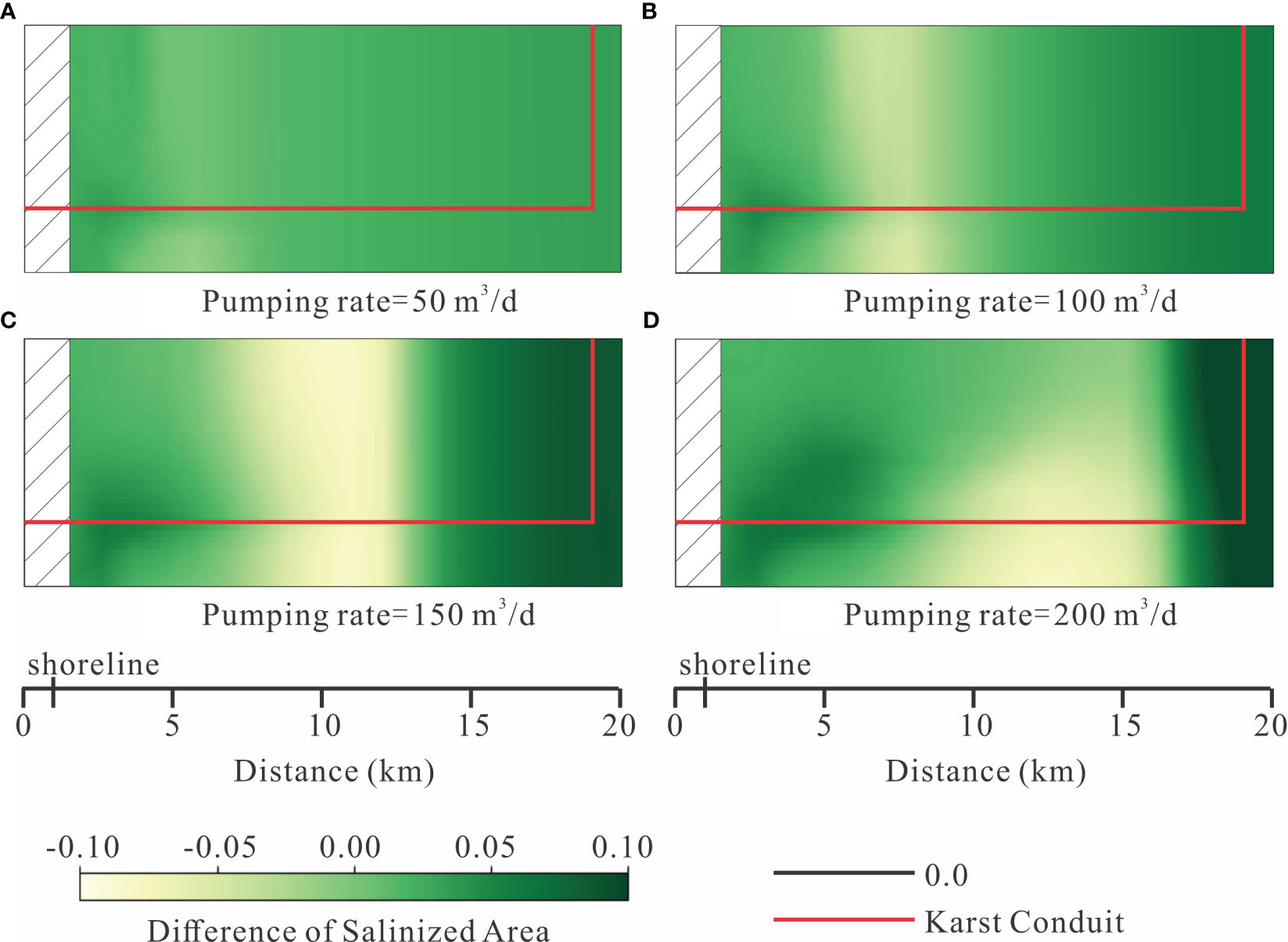
Figure 6 The difference of salinized area between conduit case and non-conduit case under different pumping rates. The value was calculated by the Average salinized area of conduit case subtracted by non-conduit case. (A) Pumping rate = 50 m3/d; (B) Pumping rate = 100 m3/d; (C) Pumping rate = 150 m3/d; (D) Pumping rate = 200 m3/d.
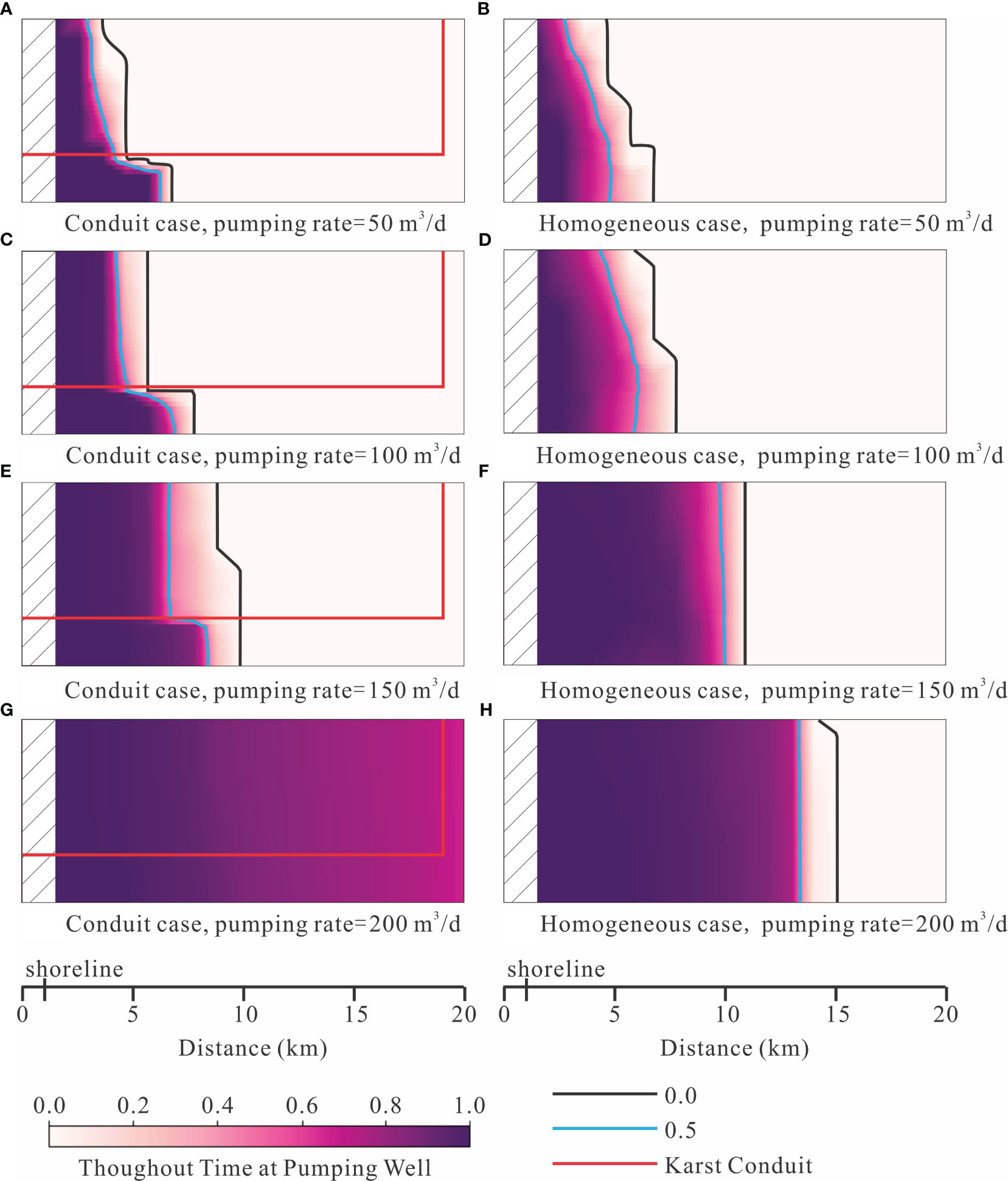
Figure 7 The throughout time at well of multiple pumping scenarios under different pumping rates. (A) Conduit case with pumping rate 50 m3/d; (B) Non-conduit case with pumping rate 50 m3/d; (C) Conduit case with pumping rate 100 m3/d; (D) Non-conduit case with pumping rate 100 m3/d; (E) Conduit case with pumping rate 150 m3/d; (F) Non-conduit case with pumping rate 150 m3/d; (G) Conduit case with pumping rate 200 m3/d; (H) Non-conduit case with pumping rate 200 m3/d.
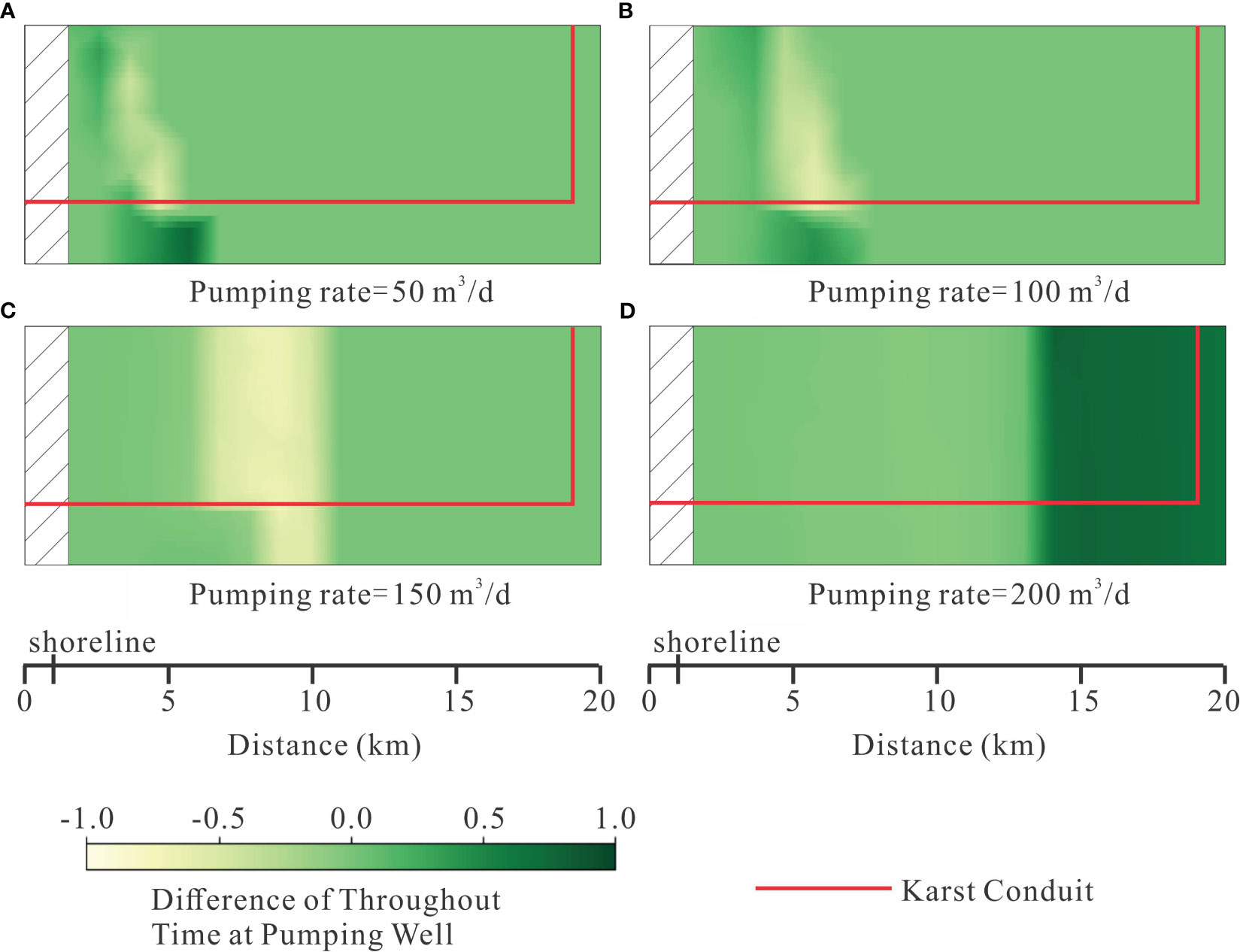
Figure 8 The difference of throughout time at well between conduit case and non-conduit case under different pumping rates. The value was calculated by the throughout time at well of conduit case subtracted by non-conduit case. (A) Pumping rate = 50 m3/d; (B) Pumping rate = 100 m3/d; (C) Pumping rate = 150 m3/d; (D) Pumping rate = 200 m3/d.
3.1 The aquifer vulnerability
The increasing pumping rates lead to more average salinized area (Figure 4) and higher variance of salinized area (Figure 5). In most pumping scenarios with low pumping rates (50-100 m3/d), the average salinized area is typically less than 0.2, and its variation is not significant across different pumping locations (Figures 4A, B, E, F). This indicates that low-rate pumping has a limited impact on the aquifer system, which the freshwater discharge to the ocean is larger than the freshwater pumping amounts. However, when higher pumping rates are employed (150-200 m3/d), the average salinized area exceeds 0.2 in most scenarios (Figures 4C, D, G, H). Notably, in the case of conduits, pumping water near the karst conduit leads to a smaller average salinized area (e.g., Figure 4D). This outcome is likely due to the fast transport of seawater through the karst conduit, allowing the salinity to reach the pumping well quickly without extensively spreading through the porous media. Furthermore, pumping scenarios further inland in the conduit case result in a higher salinized area compared to near-shore pumping scenarios (Figures 4C, D). Conversely, in non-conduit models, wells located in very inland areas exhibit a smaller average salinized area (Figures 4G, H). This observation indicates that these wells primarily extract water from the inland boundary, thus not promoting seawater intrusion.
The variance of the salinized area indicates the fluctuation of aquifer salinization over time under dynamic recharge conditions. Higher pumping rates contribute to increased variability as they facilitate the intrusion of more seawater during periods of low rainfall and its displacement during periods of high rainfall (Figure 5). The presence of a karst conduit leads to a faster movement of water during this dynamic process, resulting in a relatively higher variance of the salinized area in the conduit case compared to the non-conduit case under high pumping rates (Figures 5C, D, G, H). Furthermore, similar to the average salinized area, the effect of conduit amplifies the variability of inland pumping in the conduit case compared to the non-conduit case.
The karst conduit establishes a connection between the inland freshwater system and the submarine spring, resulting in distinct aquifer salinization patterns compared to the non-conduit case, especially for wells in the innermost areas of simulated aquifer (Figure 4). The quantitative difference of salinized area clearly demonstrates the disparity between these two cases (Figure 6). It indicates that aquifer salinization is more severe in the conduit case, whereas the non-conduit case may be more vulnerable at certain pumping wells in the middle of domain (Figures 6B–D). This illustrates that the karst conduit promotes aquifer refresh since the karst conduit increases saline water moveout in the monsoon season, especially the saline water were pumped to the middle of the aquifer. Overall, as pumping rates increase, the non-conduit case exhibits greater vulnerability relative to the conduit case, indicating stronger freshwater-saline water interchange processes due to precipitation variation are conducted by the karst conduit. Approximately 97% of pumping scenarios show higher levels of aquifer salinization in the conduit case at a pumping rate of 50 m3/d (Figure 6A). This ratio decreases to 74% at a pumping rate of 100 m3/d, with pumping wells located 5-10 km from the domain boundary exhibiting a negative difference of salinized area (Figure 6B). Under high pumping rates (150 and 200 m3/d), around 35% of pumping scenarios in the central area of the domain demonstrate a larger salinized area in the non-conduit case (Figures 6C, D).
3.2 The pumping safety
The throughout time at well serves as an indicator of pumping safety, whereas a lower throughout time signifies a higher level of water pumping security. Pumping safety increases with the distance to the shoreline and decreases with pumping rate (Figure 7). The black line in Figure 7 represents a throughout time of 0.0, indicating that wells to the right of this line consistently pump freshwater over a period of 5 years. Wells positioned between the black line and the blue line may experience seawater intrusion during approximately half of the pumping time. As pumping rates increase, these two lines gradually shift further inland. In low pumping scenarios (Figures 7A, B, E, F), they are approximately 5 km from the shoreline, but this distance extends to around 10 km at a pumping rate of 150 m3/d (Figures 7C, G). Under a pumping rate of 200 m3/d, only the most inland region in the non-conduit case can provide safe water (Figure 7H), while pumping water from the entire aquifer is unsafe in the conduit case (Figure 7D).
The impact of the karst conduit on pumping safety was measured by difference of throughout time at pumping well in different pumping locations. In Figure 8, the dark green color represents cases where the conduit model pumps saline water for a longer duration than the non-conduit model at the same pumping location. Figure 8A presents the results for pumping scenarios with a pumping rate of 50 m3/d. It shows that 9% of pumping wells in the non-conduit case pump saline water for a longer period than the corresponding wells in the conduit case. Most of these wells are located above the karst conduit. Additionally, 10% of pumping wells in the conduit case, which are situated below the karst conduit, experience a longer duration of saline water pumping. The difference of throughout time of 81% pumping wells is 0 since most area is not affected by the seawater intrusion for both cases. A similar trend is observed for a pumping rate of 100 m3/d (Figure 8B), where 13% of pumping wells in the non-conduit case and 14% in the conduit case experience a longer duration of saline water pumping. Simulations conducted at higher pumping rates demonstrate greater vulnerability in water pumping from non-conduit models. The results for a pumping rate of 150 m3/d reveal that 29% of wells in the non-conduit case experience a longer duration of saline water pumping, while only 15% of scenarios in the conduit case exhibit longer throughout times (Figure 8C). Under a pumping rate of 200 m3/d, the percentage of wells with longer salinized pumping periods is 49% for the non-conduit case and 42% for the conduit case (Figure 8D). Due to the connectivity of the karst conduit, inland wells located more than 14 km away are more vulnerable in the conduit case under a pumping rate of 200 m3/d.
4 Discussion
This study explores the impacts of the karst conduit on seawater intrusion under various pumping scenarios in dynamic precipitation conditions. We examine different pumping locations across the entire domain to provide a comprehensive evaluation of the effects of pumping location. The results reveal that the karst conduit, pumping rates and locations exert significant influence on aquifer vulnerability and pumping safety. Based on these findings, this work offers valuable perspectives on the development of groundwater in coastal karst aquifers.
Karst conduit provides a rapid pathway for seawater intrusion, while this does not necessarily mean that the aquifer in the conduit case is more vulnerable than non-conduit case due to water pumping. Under low pumping rates, the aquifer with a conduit exhibits a larger salinized area and longer throughout time at well, as the seawater intrusion process is predominantly influenced by the karst conduit. However, under high pumping rates, the volume of pumped water becomes a significant factor in controlling seawater intrusion. The aquifer without a conduit also experiences substantial contamination, with more wells exhibiting long throughout times, particularly those situated in the middle of the aquifer. The impact of the karst conduit under high pumping rates primarily manifests in the variance of seawater intrusion and the distance of intrusion. Due to the rapid water movement within the conduit, salinity changes quickly under dynamic recharge conditions in the conduit case. This leads to a significant variation in the salinized area and higher uncertainty when predicting seawater intrusion in different seasons. Additionally, the karst conduit connects the inland freshwater system and the ocean, potentially facilitating long-distance seawater intrusion if pumping occurs in the far inland regions. Therefore, groundwater managers should thoroughly investigate karst development before determining pumping rates and locations for coastal karst aquifers. In aquifers without a large and connected conduit system, managers may consider avoiding high-rate pumping in the intermediate distance to the shoreline, instead focusing on inland pumping to ensure a long-term supply of clean water. For aquifers with a connected conduit system, it is advisable to avoid large-scale pumping in the far inland regions.
In this study, we have simplified the karst aquifer by considering it as a single-conduit model, despite the fact that karst aquifers typically consist of multiple karst conduits within the system. This simplification stems from two primary reasons. Firstly, the limited availability of robust data makes it challenging to precisely identify the accurate conduits connecting between Wakulla Spring and Gulf of Mexico (Figure 1). Earlier investigations have provided valuable insights into the hydraulic connections from the ocean to the karst spring, the depth of the possible underground river, and the major orientation of karst development expansion (Davis et al., 2010; Kincaid and Werner, 2008; Xu et al., 2016). Based on the above limitation and information, we have opted to represent the aquifer as a simplified single-conduit model. Secondly, the objective of this research is to examine the typical characteristics of coastal karst aquifers under multiple pumping scenarios. Utilizing a single-conduit model simplifies the analysis and enhances the generalizability of the findings, it has also been employed in previous studies (Xu and Hu, 2017; Xu et al., 2018) to investigate the overall seawater-freshwater interactions of coastal karst aquifers. Additionally, the 2D conceptualization of the model may bring potential bias in the result evaluations. Without considering the third dimension ignores the effect of along-shore movement of groundwater, potential connectivity and preferential flow, and fully matrix-conduit water exchange (Geng and Michael, 2021). The future work may focus on the multiple conduit system and 3D conceptualization.
Conclusion
This study conducts simulations to analyze seawater intrusion in a coastal aquifer with karst conduit system under varying pumping conditions. The investigation considers aquifers both with and without a conduit to examine the influence of connected conduits on seawater intrusion. Time-dependent metrics are developed to assess aquifer vulnerability and pumping safety. The results indicate that seawater intrusion is influenced by the combined effects of pumping conditions, connected conduits, and rainfall variations. The major conclusions of this study are summarized below.
The pumping settings and the presence of a karst conduit contribute to distinct levels of aquifer vulnerability. At low pumping rates, most pumping scenarios demonstrate a larger salinized area in conduit models compared to non-conduit models. In this scenario, seawater intrusion is primarily influenced by the karst conduit. However, under high pumping rates, pumping from the central region leads to a greater salinized area in the non-conduit case compared to the conduit case. The high connectivity of the karst conduit results in substantial salinized areas, variations in salinization for inland pumping, and fast replacement of saline water by freshwater in the high-precipitation season.
Pumping safety is also influenced by pumping conditions and the presence of a karst conduit. As pumping rates increase, safe pumping regions gradually shift toward the landward direction. Eventually, under a pumping rate of 200 m3/d, all wells in the conduit case pump saline water for more than half of the time. When comparing the conduit case to the non-conduit case, the same pumping locations exhibit different throughout times. Under low pumping rates, wells below the karst conduit experience longer periods of saline water pumping in the conduit case, whereas in the non-conduit case, wells situated above the conduit have longer throughout times. However, under high pumping rates, wells located in the middle of the aquifer in the non-conduit case and wells in the inland region in the conduit case demonstrate lower pumping safety.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.
Author contributions
XW: Conceptualization, Data curation, Funding acquisition, Investigation, Visualization, Writing – original draft. ZYX: Funding acquisition, Methodology, Software, Writing – original draft. ZXX: Formal Analysis, Methodology, Validation, Writing – review & editing. BH: Supervision, Validation, Writing – review & editing.
Funding
This work was supported by the National Natural Science Foundation of China (No. 42207074) and Fundamental Research Funds for the Central Universities (No. 2682022CX036).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Acikel S., Ekmekci M. (2021). Distinction of multiple groundwater systems in a coastal karst spring zone in SW Turkey by hydrochemical and isotopic characteristics. B. Eng. Geol. Environ. 80, 5781–5795. doi: 10.1007/s10064-021-02150-4
Arfib B., de Marsily G., Ganoulis J. (2007). Locating the zone of saline intrusion in a coastal karst aquifer using spring flow data. Ground Water 45 (1), 28–35. doi: 10.1111/j.1745-6584.2006.00252.x
Arthur J. D., Wood H. A. R., Baker A. E., Cichon J. R., Raines G. L. (2007). Development and implementation of a Bayesian-based aquifer vulnerability assessment in Florida. Nat. Resour. Res. 16 (2), 93–107. doi: 10.1007/s11053-007-9038-5
Bakalowicz M. (2018). Coastal karst groundwater in the Mediterranean: a resource to be preferably exploited onshore, not from karst submarine springs. Geosciences 8 (7), 258. doi: 10.3390/geosciences8070258
Beddows P. A. (2004). Groundwater hydrology of a coastal conduit carbonate aquifer: Caribbean Coast of the Yucatán Peninsula, México (The UK: University of Bristol, Ph.D. dissertation).
Bejannin S., Tamborski J. J., van Beek P., Souhaut M., Stieglitz T., Radakovitch O., et al. (2020). Nutrient fluxes associated with submarine groundwater discharge from karstic coastal aquifers (Côte Bleue, French Mediterranean Coastline). Front. Environ. Sci. 7. doi: 10.3389/fenvs.2019.00205
Davis J. H., Katz B. G. (2007). Hydrogeologic investigation, water chemistry analysis, and model delineation of contributing areas of City of Tallahassee public-supply wells, Tallahassee, Florida (Tallahassee, Florida: US Geological Survey Scientific Investigations Report 2007-5070), 67 p. doi: 10.3133/sir20075070
Davis J. H., Katz B. G., Griffin D. W. (2010). Nitrate-N movement in groundwater from the land application of treated municipal wastewater and other sources in the Wakulla Springs Springshed, Leon and Wakulla counties, Florida, 1996-2018 (Florida: US Geological Survey Scientific Investigations Report 2010-5099), 90 p. doi: 10.3133/sir20105099
Davis J. H., Verdi R. (2014). Groundwater flow cycling between a submarine spring and an inland fresh water spring. Ground Water 52 (5), 705–716. doi: 10.1111/gwat.12125
de Filippis G., Foglia L., Giudici M., Mehl S., Margiotta S., Negri S. L. (2016). Seawater intrusion in karstic, coastal aquifers: current challenges and future scenarios in the Taranto area (southern Italy). Sci. Total Environ. 573, 1340–1351. doi: 10.1016/j.scitotenv.2016.07.005
de Franco R., Biella G., Tosi L., Teatini P., Lozej A., Chiozzotto B., et al. (2009). Monitoring the saltwater intrusion by time lapse electrical resistivity tomography: The Chioggia test site (Venice Lagoon, Italy). J. Appl. Geophys. 69 (3-4), 117–130. doi: 10.1016/j.jappgeo.2009.08.004
EPA (2009). National primary drinking water regulations, 54 total coliforms (Including fecal coliforms and E. Coli).
Fahs M., Ataie-Ashtiani B., Younes A., Simmons C. T., Ackerer P. (2016). The Henry problem: new semianalytical solution for velocity-dependent dispersion. Water Resour. Res. 52 (9), 7382–7407. doi: 10.1002/2016WR019288
Faulkner J., Hu B. X., Kish S., Hua F. (2009). Laboratory analog and numerical study of groundwater flow and solute transport in a karst aquifer with conduit and matrix domains. J. Contam. Hydrol. 110 (1–2), 34–44. doi: 10.1016/j.jconhyd.2009.08.004
Ferguson G., Gleeson T. (2012). Vulnerability of coastal aquifers to groundwater use and climate change. Nat. Clim. Change 2 (5), 342. doi: 10.1038/nclimate1413
Fleury P., Bakalowicz M., de Marsily G. (2007). Submarine springs and coastal karst aquifers: a review. J. Hydrol. 339 (1), 79–92. doi: 10.1016/j.jhydrol.2007.03.009
Fleury P., Pistre S., Bakalowicz M. (2023). Coastal karst aquifers and submarine springs: what future for their water resources? Comptes Rendus – Geosci. 355 (S1), 1–14 doi: 10.5802/crgeos.168
Ford D., Williams P. (2007). Karst hydrogeology and geomorphology (Chichester: John Wiley and Sons Ltd), 562 p.
Geng X., Michael H. A. (2020). Preferential flow enhances pumping-induced saltwater intrusion in volcanic aquifers. Water Resour. Res. 56, e2019WR026390. doi: 10.1029/2019WR026390
Geng X., Michael H. A. (2021). Along-shore movement of groundwater and its effects on seawater-groundwater interactions in heterogeneous coastal aquifers. Water Resour. Res. 57, 12. doi: 10.1029/2021WR031056
Goswami R. R., Clement T. P. (2007). Laboratory-scale investigation of saltwater intrusion dynamics. Water Resour. Res. 43, W04418. doi: 10.1029/2006WR005151
Harbaugh A. W. (2005). MODFLOW-2005, the US Geological Survey modular ground-water model: the ground-water flow process (US Geological Survey Scientific Investigations Report), 253 p. doi: 10.3133/tm6A16
Hendrick M., Renard P. (2016). Fractal dimension, walk dimension and conductivity exponent of karst networks around Tulum. Front. Phys. 4. doi: 10.3389/fphy.2016.00027
Houben G., Post V. E. A. (2017). The first field-based descriptions of pumping-induced saltwater intrusion and upconing. Hydrogeol. J. 25, 243–247. doi: 10.1007/s10040-016-1476-x
Hu B. X. (2010). Examining a coupled continuum pipe-flow model for groundwater flow and solute transport in a karst aquifer. Acta Carsol. 39 (2), 347–359. doi: 10.3986/ac.v39i2.104
Kalhor K., Ghasemizadeh R., Rajic L., Alshawabkeh A. (2019). Assessment of groundwater quality and remediation in karst aquifers: A review. Groundw. Sustain. Dev. 8, 104–121. doi: 10.1016/j.gsd.2018.10.004
Kernagis D. N., McKinlay C., Kincaid T. R. (2008). “Dive logistics of the Turner to Wakulla cave traverse,” in Diving for science. Proceedings of the American Academy of Underwater Sciences 27th Symposium (Dauphin Island, AL: AAUS).
Kincaid T. R., Werner C. L. (2008). “Conduit flow paths and conduit/matrix interactions defined by quantitative groundwater tracing in the Floridan Aquifer,” in 11th Multidisciplinary Conference on Sinkholes and the Engineering and Environmental Impacts of Karst, Tallahassee, September 2008 (ASCE).
Knight A. C., Werner A. D., Morgan L. K. (2018). The onshore influence of offshore fresh groundwater. J. Hydrol. 561, 724–736. doi: 10.1016/j.jhydrol.2018.03.028
Koohbor B., Fahs M., Ataie-Ashtiani B., Belfort B., Simmons C. T., Younes A. (2019). Uncertainty analysis for seawater intrusion in fractured coastal aquifers: effects of fracture location, aperture, density and hydrodynamic parameters. J. Hydrol. 571, 159–177. doi: 10.1016/j.jhydrol.2019.01.052
Kresic N., Panday S. (2021). Modeling of groundwater flow and transport in coastal karst aquifers. Hydrogeol. J. 29, 249–258. doi: 10.1007/s10040-020-02262-3
Kreyns P., Geng X., Michael H. A. (2020). The influence of connected heterogeneity on groundwater flow and salinity distributions in coastal volcanic aquifers. J. Hydrol. 586, 124863. doi: 10.1016/j.jhydrol.2020.124863
Langevin C. D., Thorne D. T., Dausman A. M., Sukop M. C., Guo W. (2007). SEAWAT version 4: a computer program for simulation of multi-species solute and heat transport. US Geological Survey Techniques and Methods Report, 39 p. doi: 10.3133/tm6A22
Li X., Contreras S., Sole-Benet A., Canton Y., Domingo F., Lazaro R., et al. (2011). Controls of infiltration–runoff processes in Mediterranean karst rangelands in SE Spain. Catena 86, 98–109. doi: 10.1016/j.catena.2011.03.003
Luo M., Zhang Y., Li H., Hu W., Xiao K., Yu S., et al. (2022). Pollution assessment and sources of dissolved heavy metals in coastal water of a highly urbanized coastal area: The role of groundwater discharge. Sci. Total Environ. 807 (3), 10. doi: 10.1016/j.scitotenv.2021.151070
Michael H. A., Post V. E., Wilson A. M., Werner A. D. (2017). Science, society, and the coastal groundwater squeeze. Water Resour. Res. 53, 2610–2617. doi: 10.1002/2017WR020851
Oehler T., Tamborski J., Rahman S., Moosdorf N., Ahrens J., Mori C., et al. (2019). DSi as a tracer for submarine groundwater discharge. Front. Mar. Sci. 6. doi: 10.3389/fmars.2019.00563
Panday S., Langevin C. D., Niswonger R. G., Ibaraki M., Hughes J. D. (2013). MODFLOW-USG version 1: an unstructured grid version of MODFLOW for simulating groundwater flow and tightly coupled processes using a control volume finite-difference formulation. US Geological Survey Techniques and Methods, book 6, chap A45. 66pp. Available at: https://pubs.usgs.gov/tm/06/a45
Peters C. N., Kimsal C., Frederiks R. S., Paldor A., Mcquiggan R., Michael H. A. (2022). Groundwater pumping causes salinization of coastal streams due to baseflow depletion: Analytical framework and application to Savannah River, GA. J. Hydrol. 604, 127238. doi: 10.1016/j.jhydrol.2021.127238
Pétré M. A., Ladouche B., Seidel J. L., Hemelsdaël R., de Montety V., Batiot-Guilhe C., et al. (2020). Hydraulic and geochemical impact of occasional saltwater intrusions through a submarine spring in a karst and thermal aquifer (Balaruc peninsula near Montpellier, France). Hydrol. Earth Syst. Sci. 24 (11), 5655–5672. doi: 10.5194/hess-24-5655-2020
Reimann T., Geyer T., Shoemaker W. B., Liedl R., Sauter M. (2011). Effects of dynamically variable saturation and matrix-conduit coupling of flow in karst aquifers. Water Resour. Res. 47, W11503. doi: 10.1029/2011WR010446
Schuler P., Stoekcl L., Schnegg P. A., Bunce C., Gill L. (2019). A combined-method approach to trace submarine groundwater discharge from a coastal karst aquifer in Ireland. Hydrogeol. J. 28, 561–577. doi: 10.1007/s10040-019-02082-0
Sebben M. L., Werner A. D., Graf T. (2015). Seawater intrusion in fractured coastal aquifers: a preliminary numerical investigation using a fractured Henry problem. Adv. Water Resour. 85, 93–108. doi: 10.1016/j.advwatres.2015.09.013
Shao Q., Fahs M., Hoteit H., Carrera J., Ackerer P., Younes A. (2018). A 3-D semianalytical solution for density-driven flow in porous media. Water Resour. Res. 54, 10094–10116. doi: 10.1029/2018WR023583
Sherif M., Sefelnasr A., Ebraheem A. A., Javadi A. (2013). Quantitative and qualitative assessment of seawater intrusion in Wadi Ham under different pumping scenarios. J. Hydrol. Eng. 19 (5), 855–866. doi: 10.1061/(ASCE)HE.1943-5584.0000907
Shoemaker W. B., Kuniansky E. L., Birk S., Bauer S., Swain E. D. (2008). Documentation of a conduit flow process (CFP) for MODFLOW-2005. USGS Techniques and Methods, Book 6, Chapter A24. 50 pp. doi: 10.3133/tm6A24
Shokri M., Gao Y., Kibler K. M., Wang D., Wightman M. J., Rice N. (2022). Contaminant transport from stormwater management areas to a freshwater karst spring in Florida: Results of near-surface geophysical investigations and tracer experiments. J. Hydrol.-Reg. Stud. 40, 101055. doi: 10.1016/j.ejrh.2022.101055
Strack O. D. L., Stoeckl L., Damm K., Houben G., Ausk B. K. (2016). Reduction of saltwater intrusion by modifying hydraulic conductivity. Water Resour. Res. 52, 6978–6988. doi: 10.1002/2016WR019037
U.S. Environmental Protection Agency (2009). National Primary Drinking Water Regulations, 54 Total Coliforms (Including Fecal Coliforms and E. Coli). Available at: https://www.epa.gov/sdwa/drinking-water-regulations-and-contaminants#Primary
Wang Z., Wang Q., Guo Y., Yu S., Xiao K., Zhang Y., et al. (2023). Seawater–groundwater interaction governs trace metal zonation in a coastal sandy aquifer. Water Resour. Res. 59 (9), e2022WR032828. doi: 10.1029/2022WR032828
Werner A. D., Bakker A., Post V. E. A., Vandenbohede A., Lu C., Ataie-Ashriani B., et al. (2013). Seawater intrusion processes, investigation and management: recent advances and future challenges. Adv. Water Resour. 51, 3–26. doi: 10.1016/j.advwatres.2012.03.004
Wu X., Xu Z., Xu Z., Hu B. X., Chang Q., Hu Y. (2022). The influence of seasonal recharge and groundwater pumping on the seawater intrusion in a coastal karst aquifer. J. Coast. Res. 38 (4), 785–794. doi: 10.2112/JCOASTRES-D-21-00150.1
Xiao K., Pan F., Santos I. R., Zheng Y., Zheng C., Chen N. (2022). Crab bioturbation drives coupled iron-phosphate-sulfide cycling in mangrove and salt marsh soils. Geoderma 424 15, 115990. doi: 10.1016/j.geoderma.2022.115990
Xu Z., Bassett S. W., Hu B. X., Dyer S. B. (2016). Long distance seawater intrusion through a karst conduit network in the Woodville Karst Plain, Florida. Sci. Rep. 6 (1), 1–10. doi: 10.1038/srep32235
Xu Z., Hu B. X. (2017). Development of a discrete-continuum VDFST-CFP numerical model for simulating seawater intrusion to a coastal karst aquifer with a conduit system. Water Resour. Res. 53, 688–711. doi: 10.1002/2016WR018758
Xu Z., Hu B. X. (2021). Decadal exploration of karst hydrogeology in the Woodville Karst Plain (WKP): A review of field investigation and modeling development. J. Hydrol. 594, 125937. doi: 10.1016/j.jhydrol.2020.125937
Xu Z., Hu B. X., Davis H., Kish S. (2015). Numerical study of groundwater flow cycling controlled by seawater/freshwater interaction in a coastal karst aquifer through conduit network using CFPv2. J. Contam. Hydrol. 182, 131–145. doi: 10.1016/j.jconhyd.2015.09.003
Xu Z., Hu B. X., Xu Z., Wu X. (2019a). Numerical study of groundwater flow cycling controlled by seawater/freshwater interaction in Woodville Karst Plain. J. Hydrol. 579, 123171. doi: 10.1016/j.jhydrol.2019.124171
Xu Z., Hu B. X., Xu Z., Wu X. (2019b). Simulating seawater intrusion in a complex coastal karst aquifer using an improved variable-density flow and solute transport–conduit flow process model. Hydrogeol. J. 27, 1277–1289. doi: 10.1007/s10040-018-1903-2
Xu Z., Hu B. X., Ye M. (2018). Numerical modeling and sensitivity analysis of seawater intrusion in a dual-permeability coastal karst aquifer with conduit networks. Hydrol. Earth Syst. Sci. 22, 1–19. doi: 10.5194/hess-22-221-2018
Yu X., Michael H. A. (2019a). Mechanisms, configuration typology, and vulnerability of pumping-induced seawater intrusion in heterogeneous aquifers. Adv. Water Resour. 128, 117–128. doi: 10.1016/j.advwatres.2019.04.013
Yu X., Michael H. A. (2019b). Offshore pumping impacts onshore groundwater resources and land subsidence. Geophys. Res. Lett. 46, 2553–2562. doi: 10.1029/2019GL081910
Yu X., Wu L., Yu X., Xin P. (2022). Tidal fluctuations relieve coastal seawater intrusion caused by groundwater pumping. Mar. pollut. Bull. 184, 114231. doi: 10.1016/j.marpolbul.2022.114231
Zhang Y., Zou C., Wang Z. A., Wang X., Zeng Z., Xiao K., et al. (2022). Submarine groundwater discharge in the Northern Bohai Sea, China: implications for coastal carbon budgets and buffering capacity. J. Geophys. Res-Biogeo. 127 (8), e2022JG006810. doi: 10.1029/2022JG006810
Zheng C., Wang P. P. (1999). MT3DMS: a modular three-dimensional multispecies transport model for simulation of advection, dispersion, and chemical reactions of contaminants in groundwater systems; documentation and user’s guide, DTIC Document. US Army Corps of Engineers Contract Report SERDP-99-1, 220p.
Keywords: coastal karst aquifer, seawater intrusion, groundwater development, pumping safety, conduit system
Citation: Wu X, Xu Z, Xu Z and Hu BX (2023) Impact of connected conduit on pumping-induced seawater intrusion in a coastal karst aquifer. Front. Mar. Sci. 10:1277005. doi: 10.3389/fmars.2023.1277005
Received: 13 August 2023; Accepted: 06 September 2023;
Published: 21 September 2023.
Edited by:
Kai Xiao, Southern University of Science and Technology, ChinaReviewed by:
Xiaolong Geng, University of Hawaii at Manoa, United StatesXuan Yu, Sun Yat-sen University, China
Copyright © 2023 Wu, Xu, Xu and Hu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bill X. Hu, YmlsbC54Lmh1QGdtYWlsLmNvbQ==
 Xiujie Wu
Xiujie Wu Zhongyuan Xu
Zhongyuan Xu Zexuan Xu
Zexuan Xu Bill X. Hu4,5*
Bill X. Hu4,5*