AUV planning and calibration method considering concealment in uncertain environments

Introduction: Autonomous underwater vehicles (AUVs) are required to thoroughly scan designated areas during underwater missions. They typically follow a zig-zag trajectory to achieve full coverage. However, effective coverage can be challenging in complex environments due to the accumulation and drift of navigation errors. Possible solutions include surfacing for satellite positioning or underwater acoustic positioning using transponders on other vehicles. Nevertheless, surfacing or active acoustics can compromise stealth during reconnaissance missions in hostile areas by revealing the vehicle’s location.

Methods: We propose calibration and planning strategies based on error models and acoustic positioning to address this challenge. Acoustic markers are deployed via surface ships to minimize navigation errors while maintaining stealth. And a new path planning method using a traceless Kalman filter and acoustic localization is proposed to achieve full-area coverage of AUVs. By analyzing the statistics of accumulated sensor errors, we optimize the positions of acoustic markers to communicate with AUVs and achieve better coverage. AUV trajectory concealment is achieved during detection by randomizing the USV navigation trajectory and irregularizing the locations of acoustic marker.

Results: The proposed method enables the cumulative determination of the absolute position of a target with low localization error in a side-scan sonar-based search task. Simulations based on large-scale maps demonstrate the effectiveness and robustness of the proposed algorithm.

Discussion: Solving the problem of accumulating underwater localization errors based on inertial navigation by error modeling and acoustic calibration is a typical way. In this paper, we have implemented a method to solve the localization error in a search scenario where stealth is considered.

1 Introduction

Autonomous underwater vehicles (AUVs) are widely used in marine applications like resource exploration, search and rescue, and seabed mapping (Tan et al., 2021). During search missions, AUVs must find paths to fully cover target areas while avoiding obstacles, known as the Complete Coverage Path Planning problem. However, limited underwater communication prevents AUVs from using technologies like GPS and high-frequency radio waves for precise navigation (Yan et al., 2019a). Accurate and covert navigation and control of positioning errors are critical for AUV operations.

AUVs typically navigate using inertial sensors, compasses, and acoustic positioning (Sen et al., 2014; Wang and Xie, 2015; Liu et al., 2021). For independent strap-down inertial navigation systems (SINSs), the estimation of relative velocity and position involves the integration of accelerometer and gyro sensor data, which can introduce errors and result in significant drift in the estimated position and velocity (Sahoo et al., 2019). Without feedback measurements, these errors accumulate over time and lead to positioning inaccuracies (Palomer et al., 2019). Loop closure detection using vision or sonar can address drift but is not always possible (Hong and Kim, 2019; McConnell et al., 2022). Alternatively, acoustic navigation like long baseline or ultra-short baseline methods can calibrate positioning (Zhang et al., 2018; Franchi et al., 2021).

Relying solely on ultra-short baseline (USBL) acoustic positioning for AUV navigation is imperfect due to limited communication bandwidth and latency (Font et al., 2017). Combining the new learning-based method (Bing et al., 2023b, Bing et al., 2023a) and our previous work (Wang et al., 2022a), error reduction is also enabled through planning strategies for minimum error path design. Therefore, in this paper, two solutions address trajectory drift in underwater exploration: device-based navigation algorithms and a priori error estimation for path planning. We explore Complete Coverage Path Planning (CCPP) using a priori accuracy data to minimize positioning error. To maintain convergence, the error correction under USBL communication is performed in collaboration with unmanned surface vessels (USVs). Our contributions to this paper are threefold:

1. A multi-area CCPP with known starting points is performed by applying a priori positioning device accuracy information to minimize the positioning error.

2. Regions with critical errors and in need of calibration are evaluated in terms of error margins and the operative ranges of acoustic communication. Surface vessels deploy markers at these positions along an arbitrary path.

3. An improved unscented Kalman filter (UKF) achieves precise AUV positioning through acoustic ranging and evaluates coverage capability.

The paper is structured as follows: Section 2 analyzes the relevant underwater navigation, acoustic positioning, CPP, and existing limitations. Section 3 models a cooperative system, analyzes the navigation errors, and performs non-linear optimization to execute new planning strategies. In Section 4, we propose a novel planning strategy for AUV and USV based on acoustic correction capability. Finally, Section 5 conducts simulations to analyze and validate the conclusions.

2 Related work

2.1 Underwater navigation and acoustic calibration

AUVs operate underwater where GPS is unavailable, relying on sensors like SINSs for navigation (Mu et al., 2017). However, long missions challenge position accuracy due to inertial measurement unit (IMU) errors and self-propulsion issues, with degradation over time without external reference points (Zhang et al., 2015). Doppler velocity logs (DVLs) provide self-contained velocity data without accumulating errors, enabling SINS/DVL integration for underwater navigation (Luo et al., 2019).

However, lacking external data, AUVs inevitably accumulate errors over time. Methods using acoustic communication, e.g., long baseline (LBL) and USBL, to address this. For example, global exponential stability solutions use adaptive observers and sliding mode control for single-beacon navigation with unknown exponential sensor variance (Yu et al., 2021). LBL methods apply empirical modal decomposition and maximum likelihood estimation to improve the low signal-to-noise ratio (SNR) accuracy and robustness (Yang et al., 2022). Septyanto et al. (2019) compared the accuracy errors of USBL single position calibration and quadrant calibration, demonstrating that the four-quadrant method is more accurate. Unscented Kalman filters incorporate direct and indirect measures for target localization, formulating distance measures as closed-loop control (Yan et al., 2019b). Acoustic communication co-positioning significantly improves underwater positioning accuracy and AUV applications.

Two-way travel time (TWTT) acoustic positioning enables localization but limits efficiency and users due to bandwidth. TWTT requires being active in real-time and sending signals out intermittently, which poses a risk of exposing the AUV’s position and is dangerous for warfare. In contrast, the one-way travel time (OWTT) technique only requires accurately synchronized clocks for both the vehicle and the acoustic source. OWTT methods improve accuracy, e.g., constraining INS and DVL with OWTT ranging from surface beacons (Claus et al., 2018). Passive inverted USBL uses OWTT and beamforming for passive receiver localization with direction-of-arrival azimuth resolution improvement (Wang et al., 2022b). Costanzi et al. (2017) compared the limits of AUV positioning error drift with USBL support through two different configurations of at-sea experiments and found that positioning accuracy is more affected by azimuth error. OWTT and phased-array beamforming calculate distance, azimuth, and inclination to single transmitters, providing an instantaneous estimate of the vehicle position (Rypkema et al., 2017). Importantly, the method is acoustically passive at the AUV.

Clock asynchrony commonly impacts underwater navigation, increasing delays and reducing localization accuracy. To address clock asynchrony challenges, some methods have been proposed. For example, Carroll et al. (2012) introduced on-demand algorithms that consider clock asynchrony, while Yan et al. (2020) developed an iterative least-squares estimate of water flow and enable asynchronous active/passive node localization. Another improves time-difference-of-arrival (TDoA) localization, using an AUV as a reference node at a predefined depth (Yu et al., 2019). It broadcasts/receives localization messages and calculates positions with corrections, adapting to complex environments without clock synchronization and utilizing mobile AUVs to improve coverage and accuracy.

While previous studies have focused on improving navigation accuracy, planning strategies are often neglected. New planning strategies have been designed to facilitate error reduction (Bing et al., 2022; Zhang et al., 2022) but have not been given much attention. Though acoustic-based navigation has achieved significant accuracy improvements, limitations in operating conditions could still hinder optimal outcomes. To address this issue, this paper investigates integrating planning strategies combining a priori sensor data and acoustic communication to increase mission success and accuracy.

2.2 Underwater CPP methods

Coverage algorithms typically plan online or offline based on sensor performance. For sparse, unknown targets, Zhang et al. (2023) integrated deep learning and replanning using high-dimensional data. Another approach proposed by Han et al. (2020) is the CCPP scheme for underwater gliders, which considers both the gliding angle and the relative distance to obstacles when navigating. Zacchini et al. (2022) developed a 3D probabilistic occupancy map system for sonar reconstruction with backward horizon sensor-driven coverage adaptable to environmental uncertainty.

However, the area is usually known a priori, with offline planning combining vehicle constraints and sensor capabilities. For example, a method identifies valuable subregions through expectation maximization, planning coverage within each using adaptive oval spiral coverage minimizing overlap (Yao et al., 2021). Another minimizes overlapping, turning paths for underwater mining robots based on depth-first search (Pratama et al., 2015). In another study, an improved Glasius bionic neural network (GBNN) algorithm was utilized for the CPP of AUVs, enabling discrete centralized coverage planning of multi-AUVs through collaboration and division of labor (Sun et al., 2019).

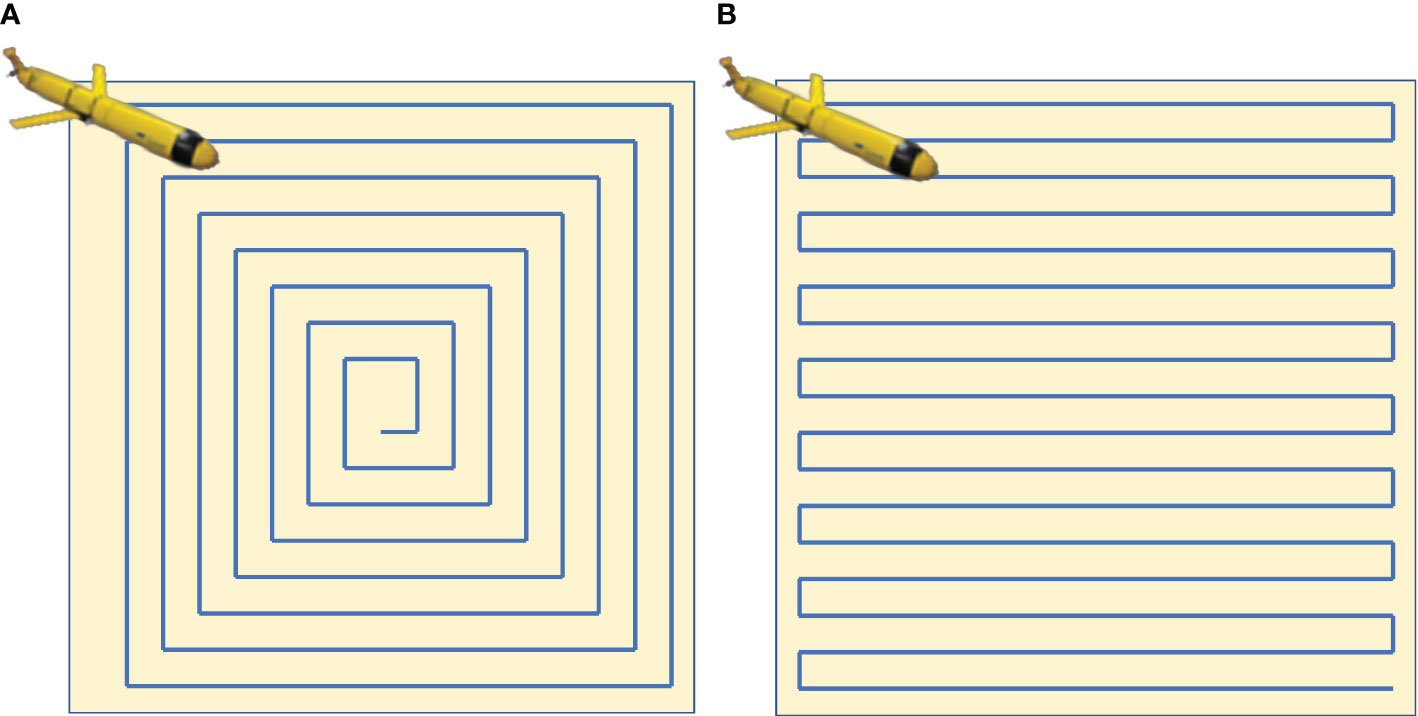
Standard coverage actions are square spirals and boustrophedon (back-and-forth), as depicted in Figure 1 (Khan et al., 2017). However, challenges such as irregular terrain and constraints on mobility lead to substantial overlapping adjacent strips in the paths of the mowers. This commonly necessitates reduced spacing between transverse strips to maximize overlap and minimize the possibility of detection failure, especially for side-scan sonar (SSS).

FIGURE 1

Figure 1 Standard actions for full coverage paths. (A) Spiral motion. (B) Boustrophedon motion.

The CPP method is efficient in covering the area; however, CPP coverage capability decreases with inaccurate positioning. To address this problem, accurate positioning needs to be prioritized, which can be costly. A potential solution is to combine positioning sensors with upgraded CPP strategies to effectively enhance coverage capability despite positioning inaccuracies. Building on this concept, we investigate the CPP strategy utilizing a priori information.

3 Principles

3.1 Problem description

This paper investigates CPP and high-precision AUV positioning challenges with localization drift and concealment constraints, including AUVs and USVs. The AUV has essential equipment: a pressure transducer for depth, IMU, electronic compass, USBL hydrophone, and DVL. Throughout the trial, AUVs are deployed outside the region of interest, while USVs release locators a priori based on requirements. The calibration and positioning of hydroacoustic communication between AUVs and USBLs within a designated area are accomplished. Refer to Figure 2 for an overview of the entire system.

FIGURE 2

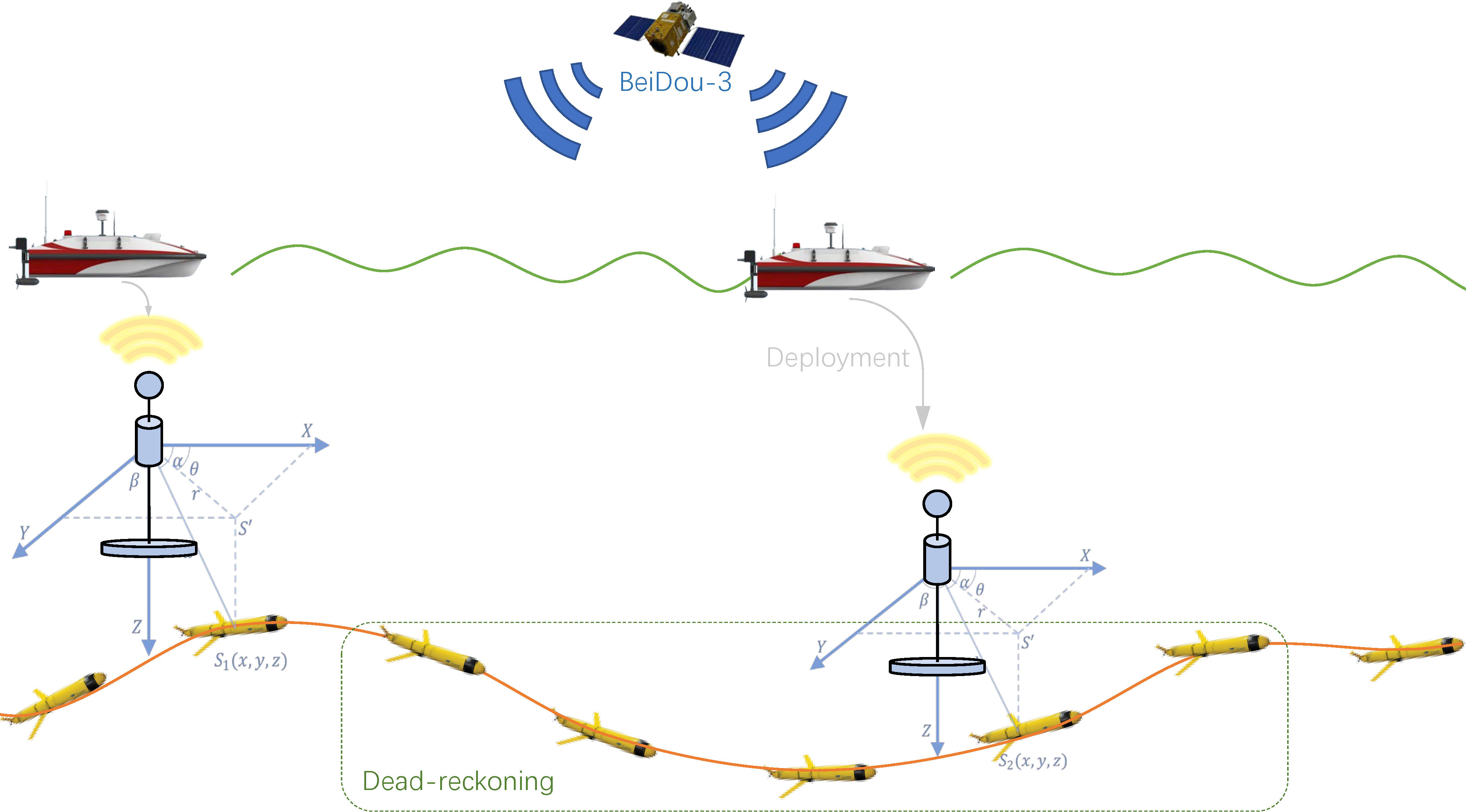
Figure 2 The AUV and USV work together in a cooperative system. The AUV uses dead reckoning for underwater positioning, calibrating via USBL when near submersible markers. The USV obtains real-time, high-accuracy positioning and deploys markers. AUV, autonomous underwater vehicle; USV, unmanned surface vessel; USBL, ultra-short baseline.

In fixed-depth detection, AUVs must consider position drift and target area coverage. Precise, synchronized cross-platform data calibrate AUV positioning errors via USBL reception within range. It is important to note that this is a one-way process to maintain confidentiality.

3.2 Model constructions

USVs are not able to maintain their location and movements as private, as they can be tracked by current satellite telemetry systems, and the deployment locations of beacons can be considered covert. Furthermore, acoustic communication poses little short-term risk of hostile eavesdropping for non-critical data. As a result, the acoustic capabilities of the submarine marker are turned on in real-time after being deployed, while the AUV is only responsible for receiving information.

The AUV can be fully defined by its six degrees of freedom (DOF). In the inertial reference system (IRS), the AUV’s position is determined by the coordinates $P_{AUV}=\left\{x,y,z\right\}$ along the X-, Y-, and Z-axes. The traverse roll, pitch, and yaw angles of the AUV are denoted by $\varphi ,\theta ,$ and $\psi$ , respectively. It is worth noting that the AUV is primarily stable in terms of traverse and pitch (Avila et al., 2012). Hence, the tracking control of traverse and pitch can be neglected, i.e., $\varphi \approx 0$ and $\psi \approx 0$.

The AUV utilizes its IMU/DVL to obtain orientation and relative velocity, allowing for heading projection. In this paper, it is assumed that the initial attitude of the AUV is known, which can be determined and calibrated by visual, initial GNSS, and other information through a loose coupling (Han et al., 2022). In particular, since the AUV is equipped with a depth sensor, the position on the Z-axis is known, while the positions on the X- and Y-axes need to be resolved.

To simplify calculations, we posit that the position of AUV is rectified contingent on gauges of velocity $V$ and angular velocity $\omega$. Conventionally, these gauges are acquired at high frequencies and amalgamated at elevated rates, yet underwater, lineal velocity is quantified at lower frequencies via DVL, while angular velocity is quantified by a high-frequency gyroscope. The visualization of the position projection over a stationary time interval is delineated in Figure 3. Furthermore, we posit that the IMU coordinate system overlaps with the conveyance coordinate system under their rigid connection and comparative fixation during mobility.

FIGURE 3

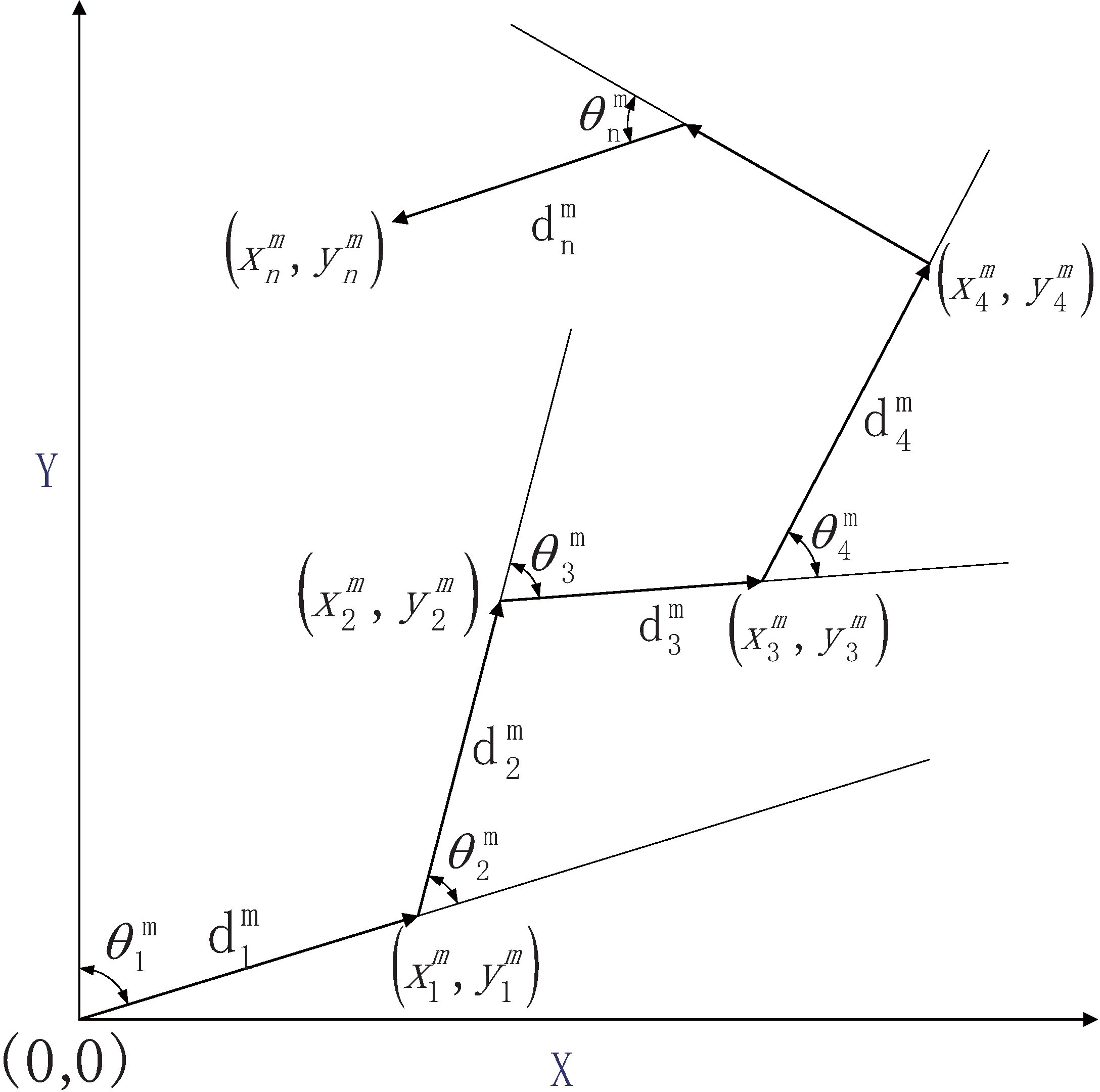
Figure 3 The AUV’s position can be estimated by measuring its velocity (i.e., distance traveled at a fixed sampling interval) and angles. AUV, autonomous underwater vehicle.

The AUV is delineated by an underactuated two-dimensional discrete-time non-linear model, where the state of the conveyance in the Northeast Celestial Reference System is denoted as ${\chi }_k={\left[x_k,y_k,{\theta }_k\right]}^T$. With a sampling interval of $△t$, the state vector is computable through the subsequent equation:

$\begin{array}{ll}{\chi }_{k+1}=f({\chi }_k,u_k)+{\omega }_k={\chi }_k+A({\chi }_k)u_k·△t+\omega ,& (1)\end{array}$

where

$A({{\displaystyle \chi }}_k)=\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & -\cos \theta & 0\\ 0& 0& 1\end{array}\right],$

$u_k={\left[v_{x,k},v_{y,k},{\omega }_k\right]}^T$ denotes the input vectors, i.e., the $x,y$ directional linear velocity measured by DVL, and the yaw rate is measured by IMU. $\omega$ is assumed to be zero-mean Gaussian process noise with covariance ${\omega }_k\sim N(0,Q)$. With the same sampling interval, the input can be simplified to

$u_k=\left[\begin{array}{cc}\cos \theta /\text{Δ}t& 0\\ \sin \theta /\text{Δ}t& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}d\\ \omega \end{array}\right]=B\eta ,$

where

$\eta =\left[\begin{array}{c}d\\ \omega \end{array}\right]$

denotes the step and heading changes based on polar coordinates.

3.3 Error representation of AUV

The per-step measurement ${\eta }^m$ of AUV is also defined as follows:

$\begin{array}{ll}{\eta }_n^m={\overline{\eta }}_n+\widetilde{{\eta }_n},& (2)\end{array}$

where $n$ is the time index and the pose measurement ${\eta }_n^m$ then consists of ground truth ${\overline{\eta }}_n$ and error $\widetilde{{\eta }_n}$ with standard deviation ${\delta }_d$ and ${\delta }_{\theta }$.

The principle of dead reckoning in the Cartesian coordinate system is as follows:

$\begin{array}{ll}{\chi }_n^m={\displaystyle {\sum }_{i=1}^n{\eta }_i^m}=\left[\begin{array}{c}{\sum }_{i=1}^n(d_i^m\cos \sum _{j=1}^i{\omega }_j^m)\\ {\sum }_{i=1}^n(d_i^m\sin \sum _{j=1}^i{\omega }_j^m)\\ {\sum }_{i=1}^n{\omega }_i^m\end{array}\right]={\sum }_{i=1}^n\left[\begin{array}{c}{d}_i^m\cos {\sum }_{j=1}^i{\omega }_j^m\\ d_i^m\sin {\sum }_{j=1}^i{\omega }_j^m\\ {\omega }_i^m\end{array}\right].& (3)\end{array}$

Noise measurements cause unbounded drift accumulation. However, multiple statistics’ error distribution characteristics enable error estimation through statistical methods.

Our previous work expresses the trajectory by the truth value. The expectations of ${\tilde{x}}_n$ and ${\tilde{y}}_n$ are formulated as follows:

$\begin{array}{ll}{\mu }_n(\overline{d},\overline{\theta })=\left[\begin{array}{c}E({\tilde{x}}_n|\overline{d},\overline{\theta })\\ E({\tilde{y}}_n|\overline{d},\overline{\theta })\end{array}\right]={\sum }_{i=1}^n\left[\begin{array}{c}{\overline{d}}_i[\sin {\sum }_{j=1}^i{\overline{\theta }}_j(\exp (-\frac{i{\delta }_{\theta }^2}{2})-1)]\\ {\overline{d}}_i[\cos {\sum }_{j=1}^i{\overline{\theta }}_j(\exp (-\frac{i{\delta }_{\theta }^2}{2})-1)]\end{array}\right].& (4)\end{array}$

For a more meticulous derivation and application, Wang et al. (2022a) furnished supplementary intelligence on computational methods requisite to ascertain the holistic cumulative error expectation. Where the trajectory is definitive, an error item is admissible to acquire a statistical delineation of the trajectory, which proffers a novel assessment metric.

3.4 UKF-based AUV positioning optimization

This paper proposes an optimization method based on unscented transformation to update the position of an AUV. The method offers excellent noise suppression and provides a smooth estimation while considering constraints on the operating environment and physical system (Wang et al., 2014). The paper focuses on the AUV’s position and heading and designs state variables:

$\begin{array}{ll}\chi ={\left[x,y,\theta \right]}^T& (5)\end{array}$

where the control input $u={[d,\omega ]}^T$ is the moving step and yaw angular velocity per unit of time.

The two-dimensional navigation state model of the AUV is correlated with the principles of mobility and is denoted as Equation 1. The real-time speed and heading angle of the AUV can be obtained by utilizing DVL and electronic compass configuration. As a result, the measurement function can be expressed as follows:

$\begin{array}{ll}z=\left[\begin{array}{c}v\\ \theta \end{array}\right]+N(0,R),& (6)\end{array}$

where it is reasonable to assume that the velocity and azimuthal measurement noise are independent; i.e., $R=diag({\sigma }_v^2,{\sigma }_{\theta }^2)$.

4 Proposed algorithm

4.1 Acoustic communication calibration

The hydroacoustic positioning system harnesses synchronized beacons for azimuth determination and localization via time differential. The time differential of the received signal at the specified frequency computes the beacon–AUV distances. It is worth noting that the scale of the surface array has an inverse relationship with localization error. Thus, using a larger scale can lead to more accurate results (Cario et al., 2019). To eschew distance ambiguity, the echo duration must not eclipse the transmission interval, or the operational distance must not transcend the CT, which is rectifiable by amplifying the locator signal transmission duration (Gemba et al., 2019).

The paper focuses on beacon–AUV acoustic interactions enabling AUV positioning/tracking alignment within communication range. Beacons furnish localization vertices and novel temporal data, whereas AUVs accept exclusively non-critical intelligence. Nonetheless, full-process communication is impossible for the sake of AUV stealth and low mission cost. Grounded on localization sensor performance, this paper investigates the relationship between localization performance and the number/location of beacons in CPP localization undertakings.

To determine the calibration areas, the paper employs a straightforward approach of evaluating if the positioning error falls outside the critical range, which is theoretically determined by the covariance. However, due to random errors, AUV positions distribute within a probability region forming a two-dimensional elliptic normal distribution. The AUV’s position is designated as follows:

$\begin{array}{ll}{P}_{AUV}=(x,y)\sim N({\sigma }_x,{\sigma }_y,{\text{Σ}}_{xy}),& (7)\end{array}$

where

$\begin{array}{ll}{\text{Σ}}_{xy}=\left[\begin{array}{c}{\delta }_{xx}{\delta }_{xy}\\ {\delta }_{yx}{\delta }_{yy}\end{array}\right].& (8)\end{array}$

Underwater communication hindrances include sound velocity fluctuations, clutter noise, and inaccurate position calibration. Similarly, USBL acoustic localization accuracy relates to oblique distance, angle between target and system coordinate axis, time delay, and phase measurement accuracy. Notably, USBL absolute positioning error increases with distance.

Furthermore, during USBL communication, AUV position calibration variance is as follows:

$\begin{array}{ll}\begin{array}{l}{\sigma }_{USBL}^2=\left[\begin{array}{c}{\sigma }_x^2\\ {\sigma }_y^2\end{array}\right]=\left[\begin{array}{c}{d}^2{(\frac{\lambda {\varphi }_{12}}{2\pi d})}^2{(2\frac{\Delta c}{c}+\frac{\Delta T}{T}+\frac{\Delta {\phi }_x}{{\phi }_x}-\frac{\Delta d}{d})}^2\\ d^2{(\frac{\lambda {\varphi }_{13}}{2\pi d})}^2{(2\frac{\Delta c}{c}+\frac{\Delta T}{T}+\frac{\Delta {\phi }_x}{{\phi }_x}-\frac{\Delta d}{d})}^2\end{array}\right]\\ =\left[\begin{array}{c}{d}^2{(\frac{\lambda {\varphi }_{12}}{2\pi d})}^2[{(2\frac{\Delta c}{c})}^2+(\frac{\Delta T}{T}{)}^2+(\frac{\Delta {\phi }_x}{{\phi }_x}{)}^2)]+{(\frac{\lambda }{2\pi d})}^2{(\text{Δ}{\varphi }_{12})}^2\\ d^2{(\frac{\lambda {\varphi }_{13}}{2\pi d})}^2[{(2\frac{\Delta c}{c})}^2+(\frac{\Delta T}{T}{)}^2+(\frac{\Delta {\phi }_x}{{\phi }_x}{)}^2)]+{(\frac{\lambda }{2\pi d})}^2{(\text{Δ}{\varphi }_{13})}^2\end{array}\right]\\ \left[\begin{array}{c}{d}^2\stackrel{2}{\cos }(\alpha ){(2\frac{\Delta c}{c}+\frac{\Delta T}{T}+\frac{\Delta {\phi }_x}{{\phi }_x})}^2\\ d^2\stackrel{2}{\cos }(\beta ){(2\frac{\Delta c}{c}+\frac{\Delta T}{T}+\frac{\Delta {\phi }_y}{{\phi }_y})}^2\end{array}\right]\end{array}& (9)\end{array}$

where $\alpha$ is the angle between the target and the base array system $x$-axis, $\beta$ is the angle between the target and the base array system y-axis, c is the speed of sound in water, $\text{Δ}c$ is the speed of sound error, T is the time delay, $\text{Δ}T$ is the time delay measurement error, ${\phi }_x,{\phi }_y$ is the phase difference of the target signal received by the corresponding axis, and $\text{Δ}{\phi }_x,\text{Δ}{\phi }_y$ is the measurement error of the phase difference of the corresponding axis. The baseline mounting error $\text{Δ}d$ is of the order of 10^-3, which is negligible. R is the measured oblique distance. The wavelength $\lambda =\frac{c}{f}$, where c and f are the speed and incident frequency of the acoustic wave propagating in the water, respectively. The phase difference between the signals is obtained by the two hydrophones $\varphi =\frac{2\pi d}{\lambda }\cos \theta$, where $\theta$is the angle of incidence of the acoustic wave.

4.2 Initial planning strategy

In this paper, the planner assumes the availability of historical records of vehicle poses and their associated uncertainties. Initially, a path is generated from the starting point to the target area, and CPP is employed to search back to the endpoint. The increment of error variance along the trajectory is then assayed subsequent to navigation. Whenever the localization error transcends V_max, the domain is documented as a beacon locus and employed to architect the USV route.

The CPP algorithm produces a path comprising straight lines and sharp turns, with the straight segments serving as the primary search path. Consequently, the vehicle trajectory in the mission area necessitates only a single entrance and exit, eliminating any Hamiltonian cycle problems that may arise. The CPP algorithm follows path boustrophedon action, and the action spacing is determined according to the detection width of the SSS.

Combining target area entrance/exit, the visual graph method is used for overall path planning in this paper. Connecting start/end points and polygon vertices separately while avoiding obstacles forms a visual view. Finally, the shortest path algorithm ascertains the optimal trajectory, which constitutes an acknowledged modus yet is not the cynosure of this treatise.

4.3 Evaluation metrics

The efficacy of the planning algorithm is contingent on the incertitude of the AUV loci and is mirrored in the CPP traverse efficiency. Nonetheless, CPP coverage cannot address AUV cumulative starting point to detect area errors accurately. In reality, it is challenging to gauge the correlation between different observations and their cumulative effects. Complex underlying math makes derivation difficult; we use Monte Carlo simulation to estimate coverage capacity suitably.

Building upon the insights from Das et al. (2011) and the more recent work of Abreu et al. (2017), the authors leverage the characteristics of the SSS to derive a probability density function (PDF) for mine detection that is only perpendicular to the AUV trajectory. As a result, the probability of achieving 1 − δ coverage for 1 − ϵ free space is as follows:

$\begin{array}{ll}P(C\ge 1-\delta )\ge 1-ϵϵ,\delta \in \left[0,1\right],& (10)\end{array}$

where C is the fraction covered.

4.4 Calibration area

The planning stratagem engenders inchoate CPP path optimized for coverage instead of length/time to account for location faults. Nonetheless, the incessant accrual of errors necessitates collaborative planning to ensure that positioning is bounded. That is, the USBL localization calibration navigates the precise positioning of the AUV and enables optimal path generation.

Once underwater, the AUV faces external information/control input challenges. Predicting possible paths and error accumulation scales using prior information is crucial. Given the system positioning sensor’s known error level, applying statistical properties through Subsection 4.2 obtains the error accumulation range and acoustic calibration area. With this, the USV traverses any designated area route. Algorithm 1 shows this approach.

Algorithm 1 delineates the location and quantity of USBLs for positioning sensor performances of different AUVs. Inter alia, the safety coefficient η intends that the errors do not transcend the proportion of the acoustical ambit to effectively enact communication interlocking. For the determined positions, locator deployment will be effectuated via USV. The AUV trajectory error correction strategy requires USV navigation with multiple position constraints. We use the cubic Bézier curve theory to generate USV trajectories based on position, moment, and velocity constraints. We assume the exact deployment positions of submarine markers, which helps to simplify the system.

5 Simulation test

5.1 Numerical simulation test

In this segment, we assess a large-scale map to validate the efficacy of the proposed collaborative localization algorithm on the coverage capability. The statistical outcomes were obtained from 500 Monte Carlo test results and are presented in a subsequent report.

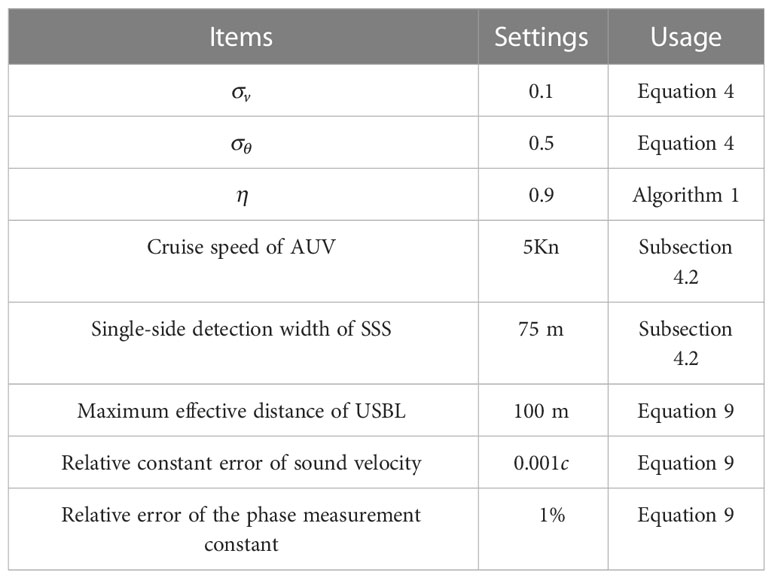
A 10 × 10 km map has obstacles and a target detection zone. The initial trajectory uses the planning strategy of Subsection 4.2. The AUV’s cruising speed is 5Kn, while its depth is maintained at 100 m, allowing it to move on a horizontal plane at a vertical distance of 100 m from the beacon. Notably, this study employs a depth gauge to measure altitude information, providing more accurate results than the altitude difference calculated between the transponder and the onboard receiver’s center.

ALGORITHM 1 DETERMINATION OF CALIBRATION AREAS, AND USV PATH PLANNING UNDER CONSTRAINTS.

Algorithm 1 Determination of calibration areas, and USV path planning under constraints..

During the USBL calibration process, the sound is assumed to propagate uniformly underwater with a velocity of 1,500 m/s and a USBL localization frequency of 1 Hz. The sound velocity is subject to a relatively constant error of $0.001c$ (where c is the true sound velocity), the measurement time has a constant error of 5×10^-4 s, and the measurement phase constant has a relative error of 1%. Additionally, the random error variance is the same as the constant error (Zhang et al., 2021). Positioning error evaluation of USBL is obtained by Equation 9.

The uncertainty of AUV localization is evaluated using Equation 4, and the fully non-linear uncertainty for each case is computed using a Monte Carlo simulation. Specifically, 500 independent Monte Carlo tests were conducted using the same statistical characterization of data errors and a priori estimation framework. The relevant parameters are presented in Table 1.

TABLE 1

Table 1 Simulation parameters of cooperative system.

In factual quantifications, detector inaccuracies and biases may induce significant drift. However, readily calibrated biases are disregarded in this study, and exclusively random errors are contemplated. Non-linear optimal localization (e.g., UKF) extends/non-linearly maps to optimize approximately Gaussian localization noise. Figure 4 shows measured/filtered trajectories under simulated electronic compass angular velocity measurement conditions.

FIGURE 4

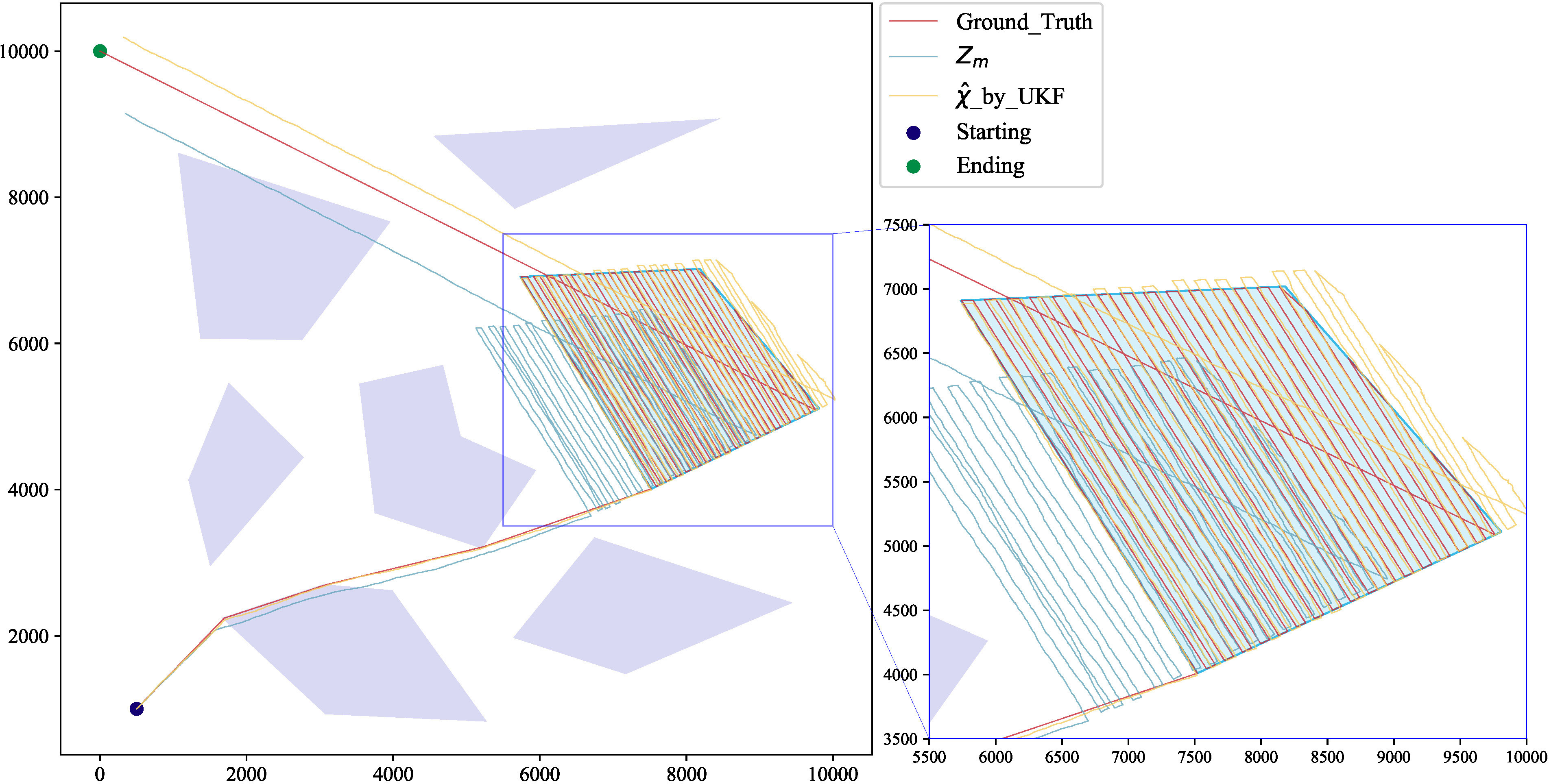
Figure 4 AUV theoretical position and unmodified optimized path based on velocity (fixed interval distance) and angle measurements. UKF processing significantly reduced error but did not satisfy the mission area coverage requirement. AUV, autonomous underwater vehicle; UKF, unscented Kalman filter.

Reducing optimized path error is crucial to avoid AUV path failure and inadequate area coverage. By leveraging the acoustic communication function of the beacons, error correction in specific areas can significantly improve coverage levels. Based on the error expectation and the performance of the beacon, the mission requires multiple corrections, which are intermittent. However, the quantity of calibrations/locators is only correlated with the predesignated parameters and the performance of the USBL. Since the surface mission does not prioritize concealment, the USV’s trajectory is not constrained, which means that the calibration position is only related to the error level of the AUV.

5.2 Results and discussion

The calibrated paths are expected to maintain good position accuracy. The innovation of this study lies in its effective concealment of trajectories and calibration under the constraint that AUV errors do not exceed the correction range. This approach significantly improves the success rate of calibration and the precision of coverage without sacrificing acoustic communication due to excessive errors. Meanwhile, the method suggested here in the situation where the error level is known but the actual trajectory is unknown proved to be effective.

The algorithm generates different calibration locations/areas for varying USBL communication distance and positioning sensor performance constraints. Figure 5 delineates the calibration locations/areas when the USBL system possesses a communicative scope of 300, 500, 1,000, and 2,000 m. The authentic trajectory of the AUV cannot be deduced from the beacon’s position; that is, the trajectory is concealed.

FIGURE 5

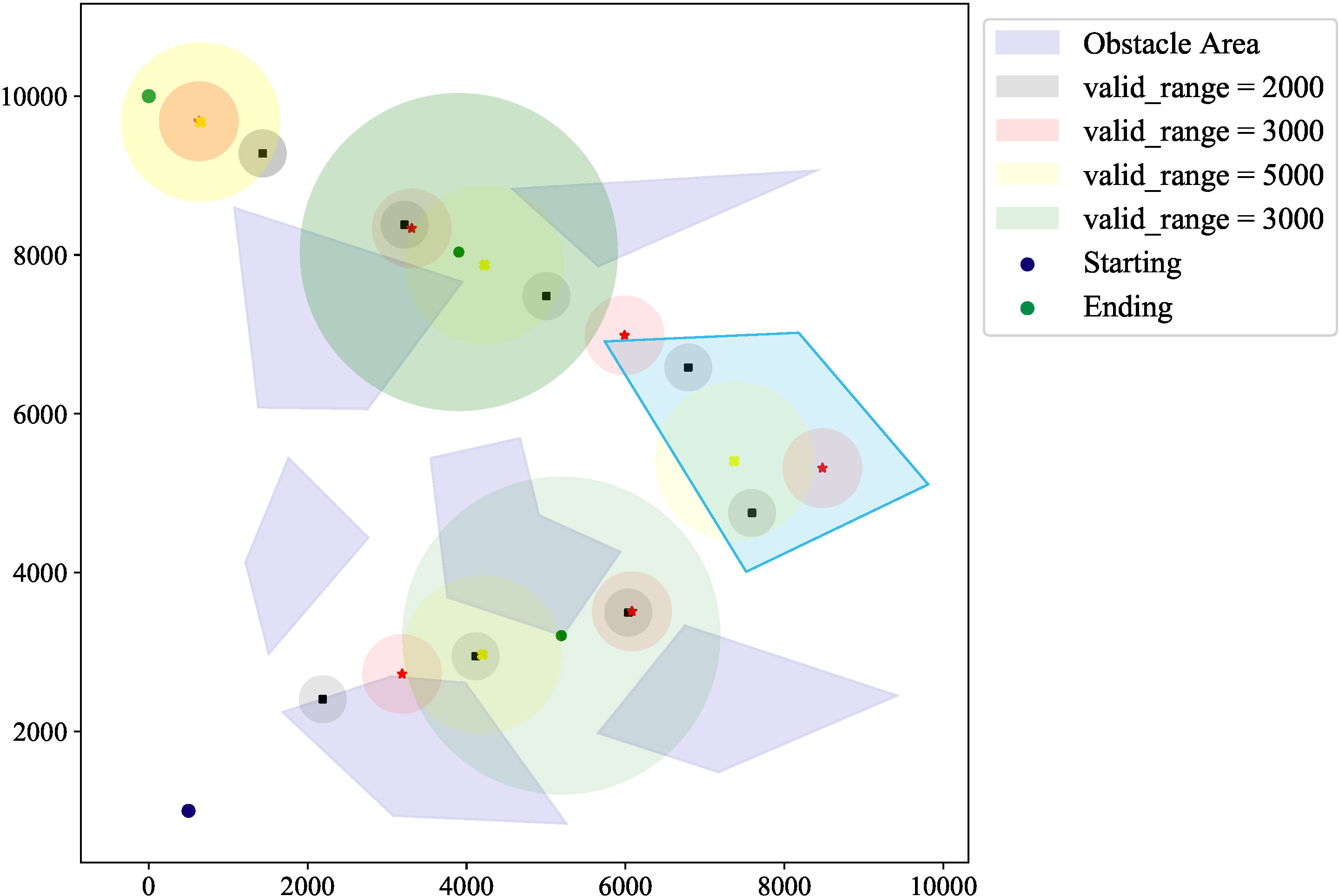
Figure 5 Location and communication range of beacons under acoustic communication distance difference. The number and position of these underwater markers depend on an AUV’s communication range and navigation precision. AUV, autonomous underwater vehicle.

The increase in positioning errors reduces detection capability and effective coverage. Our algorithm addresses invalid AUV detection overlap (Figure 6), equalizing coverage times to enhance detection. Meanwhile, denser calibration points effectively improve coverage capability, though insignificantly. This confirms that corrected paths reasonably cover the task area with excellent coverage.

FIGURE 6

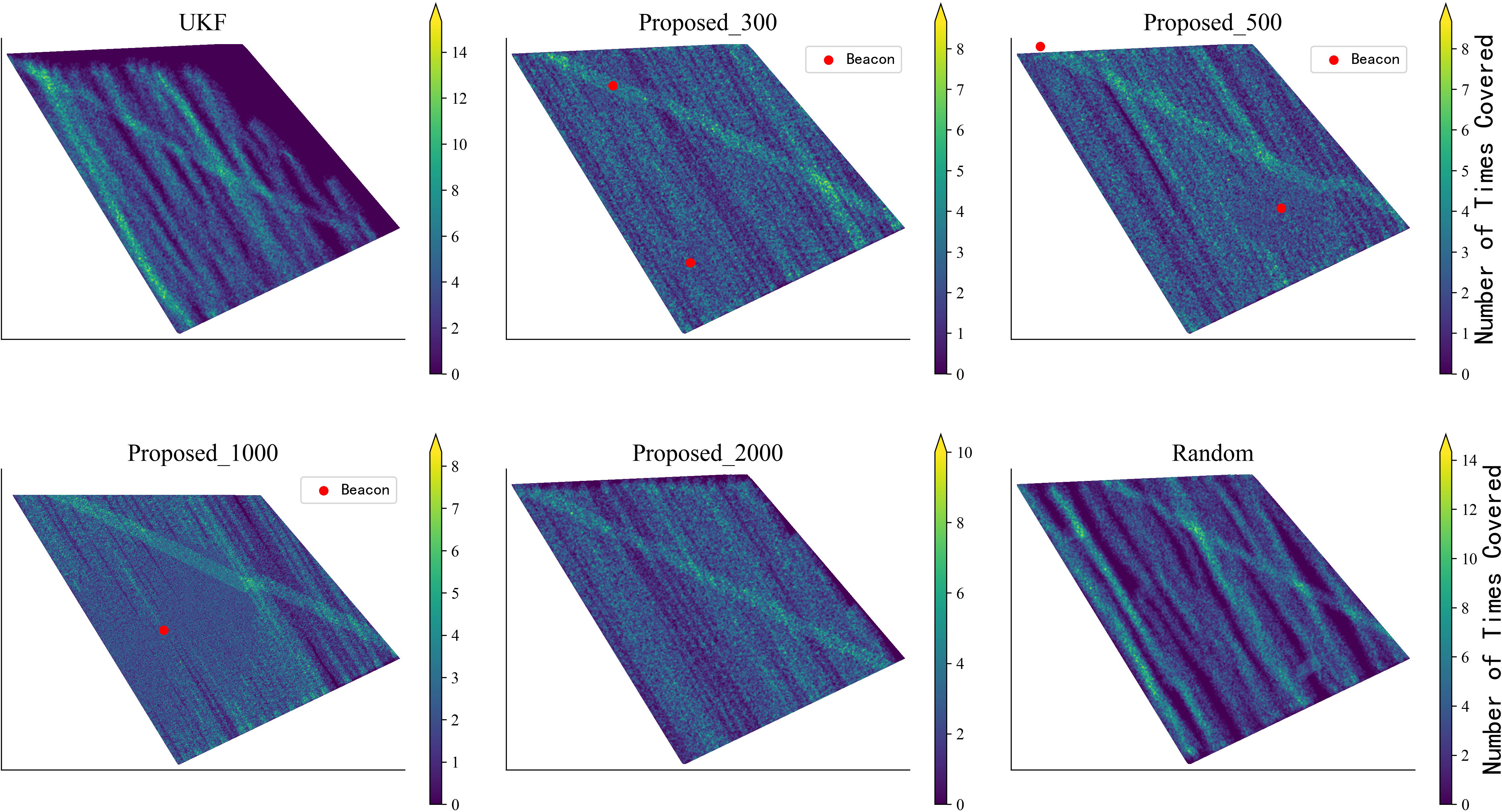
Figure 6 Compared with other algorithms, the proposed algorithm achieves superior coverage capabilities with minimal repetition and uniformity. Considerably enhanced coverage within and beyond the range of the interactions, which relies on the quantity and scope of calibration points.

Under the metric of Subsection 4.3, we evaluated optimized paths’ coverage (Figure 7). The ideal minimum/average coverage (planning parameters) is 1∼2, requiring each zone to be detected once (twice for 9 ground truth). Previously, certain regions lacked coverage, while others exhibited up to 14-fold redundant coverage. Currently, 88% of the areas are covered at minimum once, denoting a substantial decrease in detection redundancy. Furthermore, the coverage of areas is more homogeneous now, signifying a more stable mean coverage. Figure 8 compares actual/theoretical coverage, showing that the algorithm’s results have greater concentration/closeness to theory.

FIGURE 7

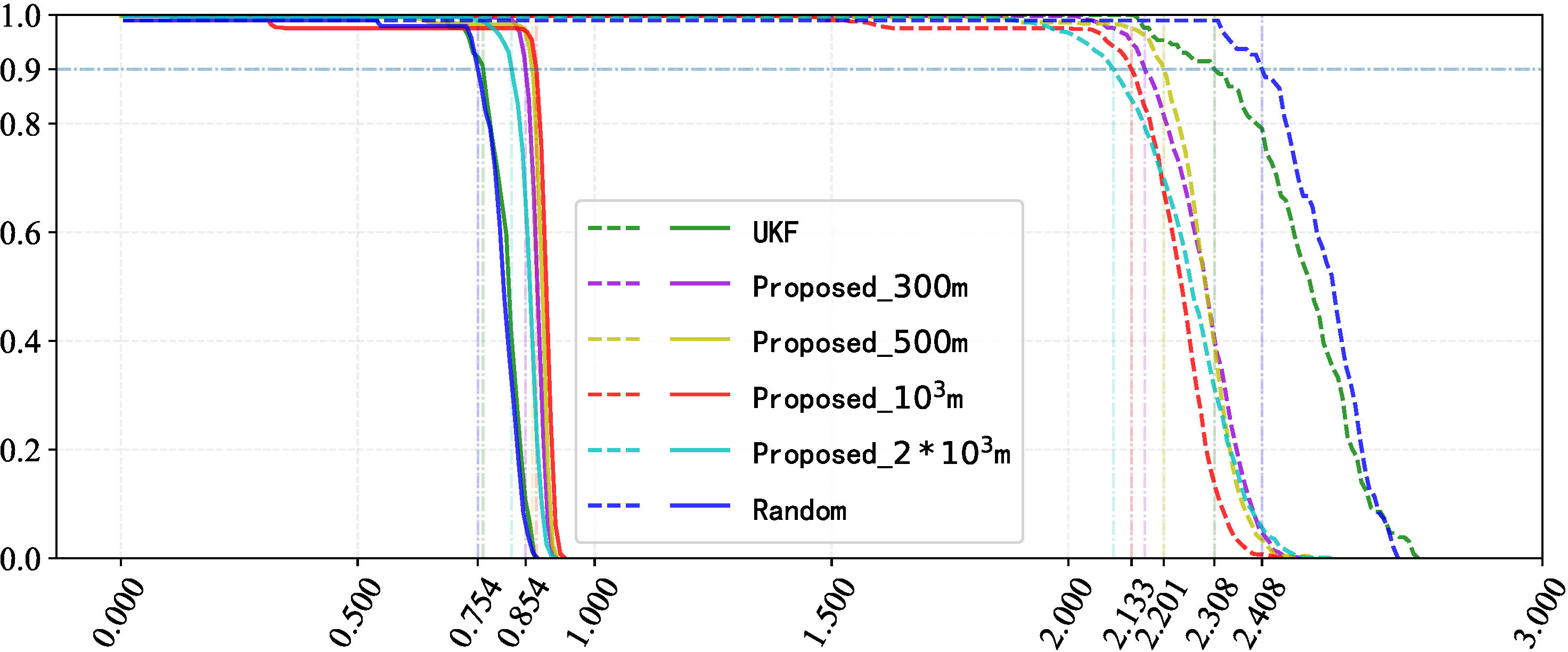
Figure 7 To achieve 90% coverage, the proposed algorithm outperforms in covering the target area uniformly and efficiently. “Minimum coverage” means covering an area at least once, while “average coverage” refers to the average number of times an area is covered.

FIGURE 8

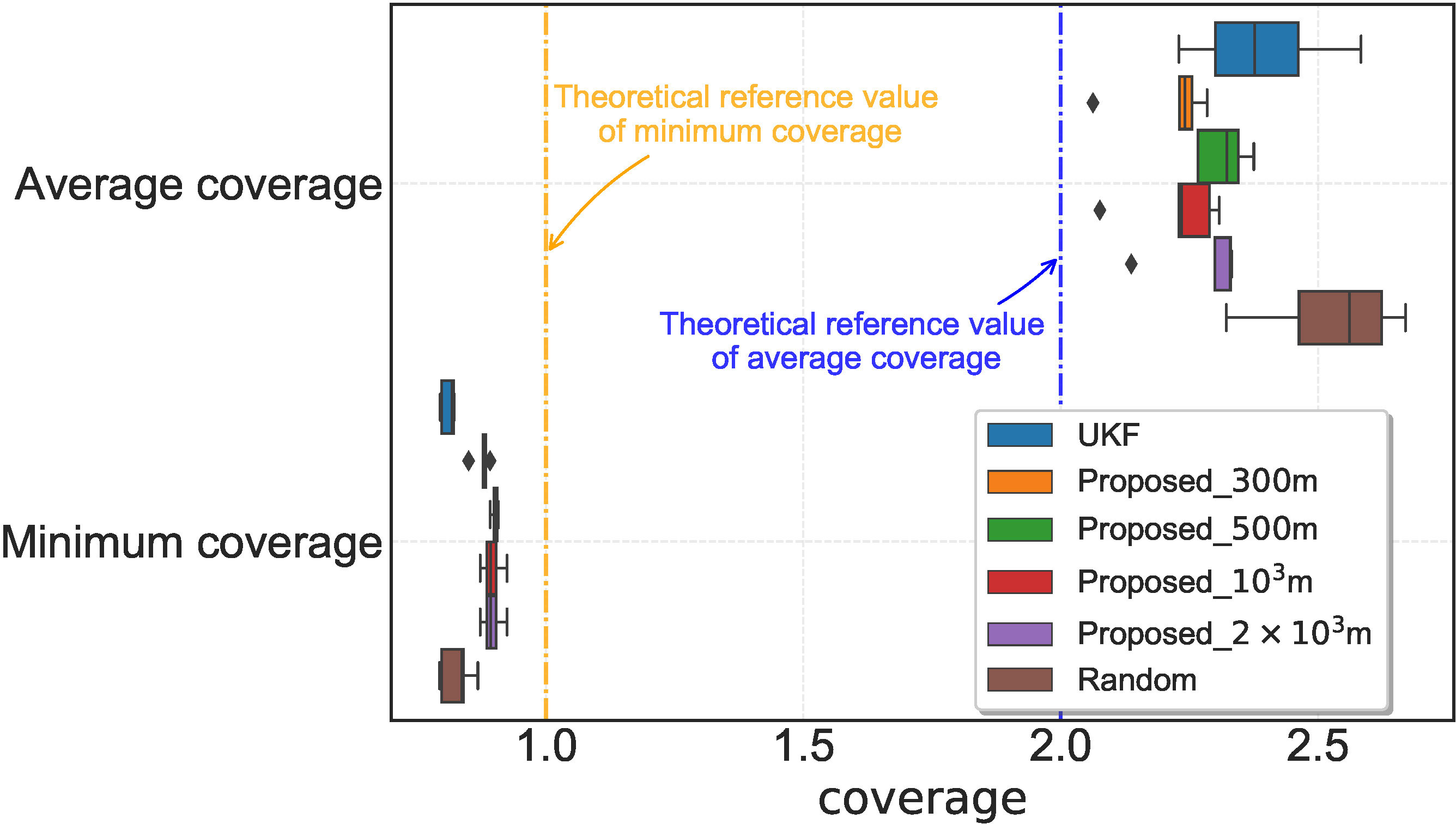
Figure 8 The bar chart depicts the coverage metric. The coverage achieved by the proposed algorithm is more concentrated and closer to the theoretical value than the other methods.

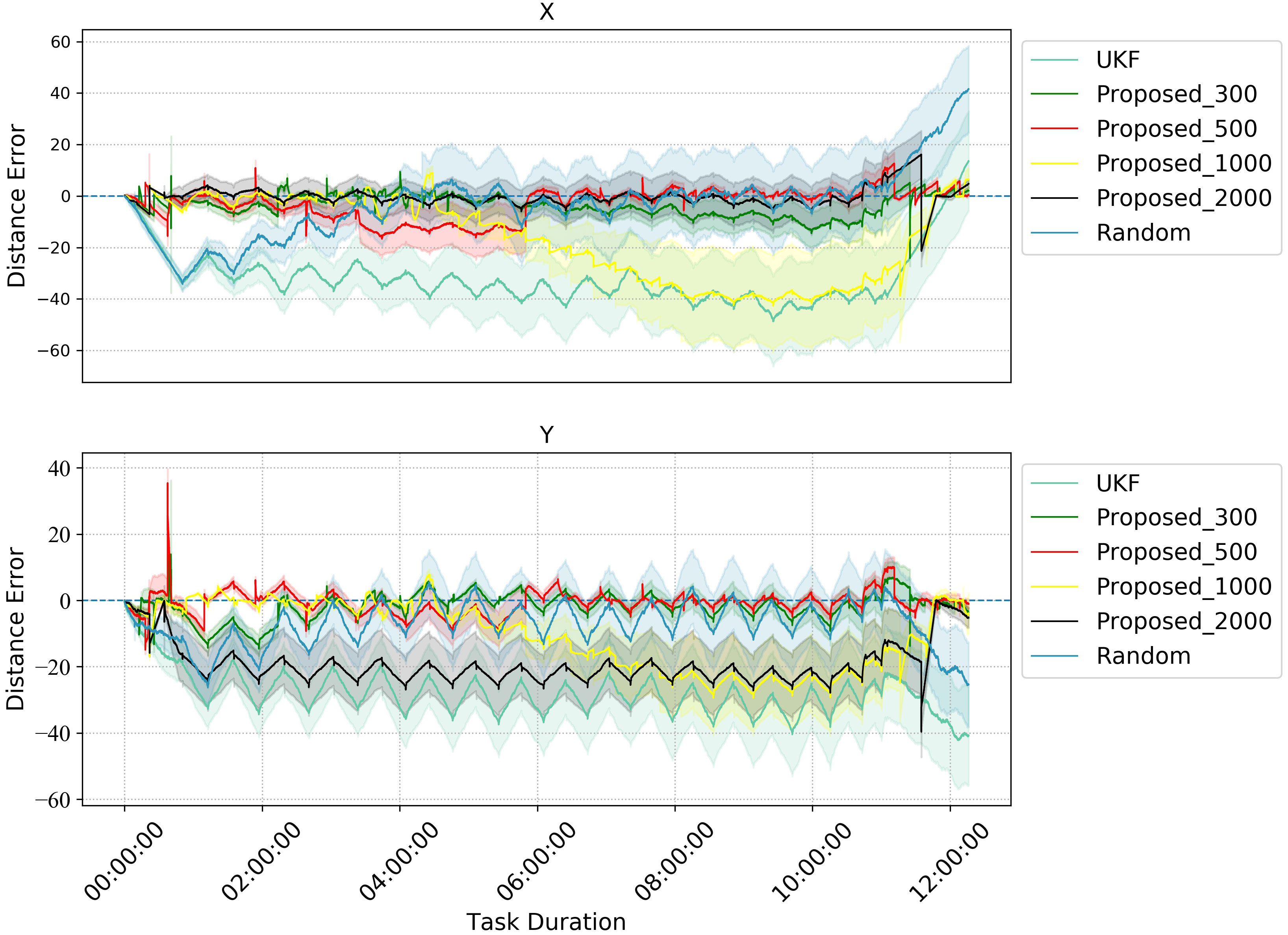
To provide quantitative insight, Figure 9 shows the x and y error mean and confidence intervals during the cruise. Results show that the proposed method significantly reduces errors vs. the UKF path. Leveraging acoustic communication and constraining position error within range, the algorithm effectively corrects near-threshold errors, ensuring overall path error fluctuation remains within range.

FIGURE 9

Figure 9 Comparison of errors of different methods of optimization.

We use the root-mean-square error (RMSE) to compare with other methods. RMSE is defined as follows:

$\begin{array}{ll}RMSE=\sqrt{\frac{{\sum }_{i=1}^n{\widehat{x_i}-x_i}^2}{n}},& (11)\end{array}$

where $\widehat{x}$ represents the real location.

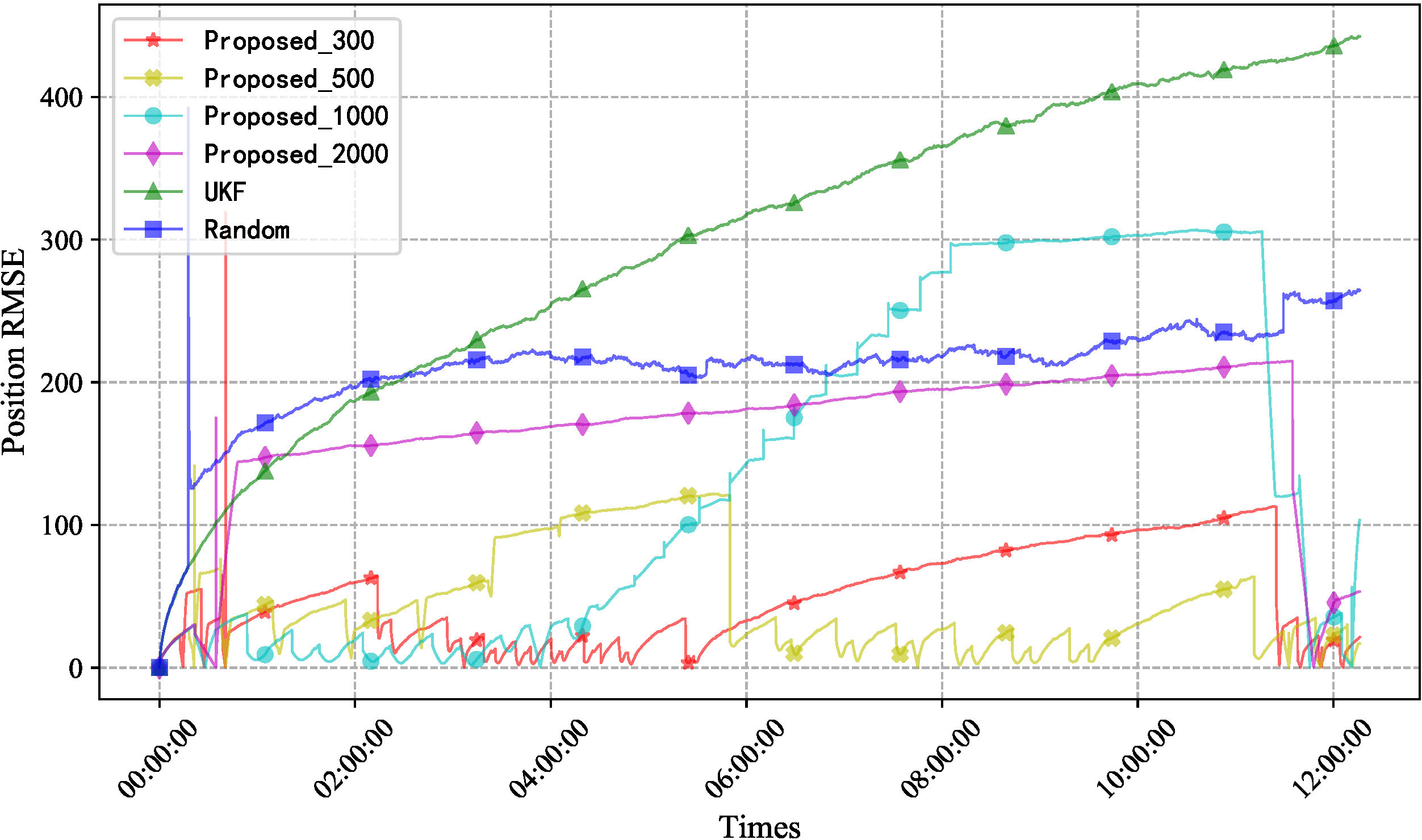
Figure 10 presents the RMSE evaluation results. The results demonstrate that the errors accumulate over duration regardless of the positioning algorithm used. Nonetheless, once an error increase to the upper threshold is permitted, the propounded algorithm disposes of beacons at the corresponding positions for error rectification, thereby retaining the error confined. This exemplifies the substantial performance superiority of the propounded algorithm over the UKF/random acoustic emendation.

FIGURE 10

Figure 10 Comparison of RMSE with different methods. RMSE, root-mean-square error.

Although the errors during cruising provide some indication of performance, they do not reflect the endpoint error, which is subject to statistical uncertainty. As delineated in Figure 11, the error distribution of the UKF procedure complies with a normal trend, while the KDE kernel density of the random method is relatively minor, which suggests that the error is more inconstant. It should be noted that more beacons allow more opportunities for communication, but the small range of communication results in suboptimal calibration. At the 1 ∗ 10³ m scenario, the high percentage of communication area leads to better coverage. The proposed method exhibits smaller errors and more stable distributions and outperforms the others, thereby demonstrating significant superiority.

FIGURE 11

Figure 11 Comparison of uncertainty for x, y, and distance.

6 Conclusion

In this paper, we propose a novel new precision positioning method for Complete Coverage Path approach that leverages a priori parameters from USBL and positioning sensors to enhance the precision of AUV navigation in GPS-deprived settings. We design a CCPP method with initial obstacle avoidance that incorporates cumulative error scaling and UKF localization. Moreover, the calibration performance is modeled and amalgamated with distance constraints to architect calibration points and hide the AUV trajectory. Finally, the UKF was applied to assess the exact coverage ability of the AUV through acoustic interaction. Simulations show that the algorithm improves localization accuracy and coverage efficiency over filtering/random methods while ensuring coverage. Critically, it enables stealth while maintaining precision, better ensuring survival in threatening areas. We will validate this approach using an experimental platform now under construction, a key move toward practical implementation.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

CW and FZ contributed to the conceptualization and design of the study. CW and CC have implemented the writing of relevant methods and programs. CW and DY completed the visualization. FZ and GP provided available resources. CW wrote the first draft of the manuscript, which has been refined by CC and DY. All authors contributed to the manuscript revision and read and approved the submitted version.

Funding

This study was supported by the National Natural Science Foundation of China (52171322), the National Key Research and Development Program (2020YFB1313200), and the Fundamental Research Funds for the Central Universities (D5000210944).

Acknowledgments

We acknowledge the facilities and technical assistance of the Key Laboratory of Unmanned Underwater Transport Technology.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abreu N., Cruz N., Matos A. (2017). “Accounting for uncertainty in search operations using auvs,” in 2017 IEEE Underwater Technology (UT) (Busan, South Korea: IEEE), 1–8. doi: 10.1109/UT.2017.7890326

CrossRef Full Text | Google Scholar

Avila J. P. J., Adamowski J. C., Maruyama N., Takase F. K., Saito M. (2012). Modeling and identification of an open-frame underwater vehicle: The yaw motion dynamics. J. Intelligent Robotic Syst. 66, 37–56. doi: 10.1007/s10846-011-9625-x

CrossRef Full Text | Google Scholar

Bing Z., Knak L., Cheng L., Morin F. O., Huang K., Knoll A. (2023a). Meta-reinforcement learning in nonstationary and nonparametric environments. IEEE Trans. Neural Networks Learn. Syst., 1–15. doi: 10.1109/TNNLS.2023.3270298

CrossRef Full Text | Google Scholar

Bing Z., Lerch D., Huang K., Knoll A. (2023b). Meta-reinforcement learning in non-stationary and dynamic environments. IEEE Trans. Pattern Anal. Mach. Intell. 45, 3476–3491. doi: 10.1109/TPAMI.2022.3185549

PubMed Abstract | CrossRef Full Text | Google Scholar

Bing Z., Sewisy A. E., Zhuang G., Walter F., Morin F. O., Huang K., et al. (2022). Toward cognitive navigation: Design and implementation of a biologically inspired head direction cell network. IEEE Trans. Neural Networks Learn. Syst. 33, 2147–2158. doi: 10.1109/TNNLS.2021.3128380

CrossRef Full Text | Google Scholar

Cario G., Casavola A., Gagliardi G., Lupia M., Severino U., Bruno F. (2019). “Analysis of error sources in underwater localization systems,” in OCEANS 2019 - Marseille (Marseille, France: IEEE), 1–6. doi: 10.1109/OCEANSE.2019.8867536

CrossRef Full Text | Google Scholar

Carroll P., Zhou S., Mahmood K., Zhou H., Xu X., Cui J.-H. (2012). “On-demand asynchronous localization for underwater sensor networks,” in 2012 Oceans (Hampton Roads, VA, USA: IEEE), 1–4. doi: 10.1109/OCEANS.2012.6404938

CrossRef Full Text | Google Scholar

Claus B., Kepper J. H. IV, Suman S., Kinsey J. C. (2018). Closed-loop one-way-travel-time navigation using low-grade odometry for autonomous underwater vehicles. J. Field Robotics 35, 421–434. doi: 10.1002/rob.21746

CrossRef Full Text | Google Scholar

Costanzi R., Monnini N., Ridolfi A., Allotta B., Caiti A. (2017). “On field experience on underwater acoustic localization through usbl modems,” in OCEANS 2017 - Aberdeen (Aberdeen, UK: IEEE), 1–5. doi: 10.1109/OCEANSE.2017.8084996

CrossRef Full Text | Google Scholar

Das C., Becker A., Bretl T. (2011). “Probably approximately correct coverage for robots with uncertainty,” in 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems (San Francisco, CA, USA: IEEE), 1160–1166. doi: 10.1109/IROS.2011.6094695

CrossRef Full Text | Google Scholar

Font E. G., Bonin-Font F., Negre P.-L., Massot M., Oliver G. (2017). “USBL Integration and Assessment in a Multisensor Navigation Approach for AUVs,” in IFAC-PapersOnLine (Durham, NC, USA: Elsevier), 50 (1), 7905–7910. doi: 10.1016/j.ifacol.2017.08.754

CrossRef Full Text | Google Scholar

Franchi M., Bucci A., Zacchini L., Ridolfi A., Bresciani M., Peralta G., et al. (2021). “Maximum a posteriori estimation for auv localization with usbl measurements_*,” in IFAC-PapersOnLine (Durham, NC, USA: Elsevier), vol. 54. , 307–313. doi: 10.1016/j.ifacol.2021.10.109

CrossRef Full Text | Google Scholar

Gemba K. L., Nannuru S., Gerstoft P. (2019). Robust ocean acoustic localization with sparse bayesian learning. IEEE J. Selected Topics Signal Process. 13, 49–60. doi: 10.1109/JSTSP.2019.2900912

CrossRef Full Text | Google Scholar

Han B., Xiao Z., Huang S., Zhang T. (2022). Multi-layer VI-GNSS global positioning framework with numerical solution aided MAP initialization. 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). (Prague, Czech Republic: IEEE), 5448–5455. doi: 10.1109/IROS51168.2021.9636871

CrossRef Full Text | Google Scholar

Han G., Zhou Z., Zhang T., Wang H., Liu L., Peng Y., et al. (2020). Ant-colony-based completecoverage path-planning algorithm for underwater gliders in ocean areas with thermoclines. IEEE Trans. Vehicular Technol. 69, 8959–8971. doi: 10.1109/TVT.2020.2998137

CrossRef Full Text | Google Scholar

Hong S., Kim J. (2019). Selective image registration for efficient visual slam on planar surface structures in underwater environment. Autonomous Robots 43, 1665–1679. doi: 10.1007/s10514-018-09824-1

CrossRef Full Text | Google Scholar

Khan A., Noreen I., Habib Z. (2017). On complete coverage path planning algorithms for nonholonomic mobile robots: Survey and challenges. J. Inf. ence Eng. 33, 101–121. Available at: https://api.semanticscholar.org/CorpusID:7278436

Google Scholar

Liu R., Liu F., Liu C., Zhang P. (2021). Modified sage-husa adaptive kalman filter-based sins/dvl integrated navigation system for auv. J. Sensors 2021, 1–8. doi: 10.1155/2021/9992041

CrossRef Full Text | Google Scholar

Luo L., Zhang Y., Fang T., Li N. (2019). A new robust kalman filter for sins/dvl integrated navigation system. IEEE Access 7, 51386–51395. doi: 10.1109/ACCESS.2019.2911110

CrossRef Full Text | Google Scholar

McConnell J., Chen F., Englot B. (2022). Overhead image factors for underwater sonar-based slam. IEEE Robotics Automation Lett. 7, 4901–4908. doi: 10.1109/LRA.2022.3154048

CrossRef Full Text | Google Scholar

Mu X., Guo J., Song Y., Sha Q., Jiang J., He B., et al. (2017). “Application of modified ekf algorithm in auv navigation system,” in OCEANS 2017 - Aberdeen (Aberdeen, UK: IEEE), 1–4. doi: 10.1109/OCEANSE.2017.8084626

CrossRef Full Text | Google Scholar

Palomer A., Ridao P., Ribas D. (2019). Inspection of an underwater structure using point-cloud slam with an auv and a laser scanner. J. Field Robotics 36, 1333–1344. doi: 10.1002/rob.21907

CrossRef Full Text | Google Scholar

Pratama P. S., Kim J.-W., Kim H.-K., Yoon S.-M., Yeu T.-K., Hong S., et al. (2015). “Path planning algorithm to minimize an overlapped path and turning number for an underwater mining robot,” in 2015 15th International Conference on Control, Automation and Systems (ICCAS) (Busan, South Korea: IEEE). 499–504. doi: 10.1109/ICCAS.2015.7364969

CrossRef Full Text | Google Scholar

Rypkema N. R., Fischell E. M., Schmidt H. (2017). “One-way travel-time inverted ultra-short baseline localization for low-cost autonomous underwater vehicles,” in 2017 IEEE International Conference on Robotics and Automation (ICRA). (Singapore: IEEE). 4920–4926. doi: 10.1109/ICRA.2017.7989570

CrossRef Full Text | Google Scholar

Sahoo A., Dwivedy S. K., Robi P. (2019). Advancements in the field of autonomous underwater vehicle. Ocean Eng. 181, 145–160. doi: 10.1016/j.oceaneng.2019.04.011

CrossRef Full Text | Google Scholar

Sen W., Chen L., Gu D., Hu H. (2014). An optimization based moving horizon estimation with application to localization of autonomous underwater vehicles. Robotics Autonomous Syst. 62, 1581–1596. doi: 10.1016/j.robot.2014.05.004

CrossRef Full Text | Google Scholar

Septyanto B., Nurdiana D., Ahmiatri Saptari S. (2019). Ultra short baseline (usbl) calibration for positioning of underwater objects. Al-Fiziya: J. Materials Science Geophysics Instrumentation Theor. Phys. 2, 73–85. doi: 10.15408/fiziya.v2i2.12524

CrossRef Full Text | Google Scholar

Sun B., Zhu D., Tian C., Luo C. (2019). Complete coverage autonomous underwater vehicles path planning based on glasius bio-inspired neural network algorithm for discrete and centralized programming. IEEE Trans. Cogn. Dev. Syst. 11, 73–84. doi: 10.1109/TCDS.2018.2810235

CrossRef Full Text | Google Scholar

Tan C. S., Mohd-Mokhtar R., Arshad M. R. (2021). A comprehensive review of coverage path planning in robotics using classical and heuristic algorithms. IEEE Access 9, 119310–119342. doi: 10.1109/ACCESS.2021.3108177

CrossRef Full Text | Google Scholar

Wang S., Chen L., Gu D., Hu H. (2014). An optimization based moving horizon estimation with application to localization of autonomous underwater vehicles. Robotics Autonomous Syst. 62, 1581–1596. doi: 10.1016/j.robot.2014.05.004

CrossRef Full Text | Google Scholar

Wang C., Cheng C., Yang D., Pan G., Zhang F. (2022a). Path planning in localization uncertaining environment based on dijkstra method. Front. Neurorobotics 16. doi: 10.3389/fnbot.2022.821991

CrossRef Full Text | Google Scholar

Wang Y., Huang S., Wang Z., Hu R., Feng M., Du P., et al. (2022b). Design and experimental results of passive iusbl for small auv navigation. Ocean Eng. 248, 110812. doi: 10.1016/j.oceaneng.2022.110812

CrossRef Full Text | Google Scholar

Wang W., Xie G. (2015). Online high-precision probabilistic localization of robotic fish using visual and inertial cues. IEEE Trans. Ind. Electron. 62, 1113–1124. doi: 10.1109/TIE.2014.2341593

CrossRef Full Text | Google Scholar

Yan J., Ban H., Luo X., Zhao H., Guan X. (2019a). Joint localization and tracking design for auv with asynchronous clocks and state disturbances. IEEE Trans. Vehicular Technol. 68, 4707–4720. doi: 10.1109/TVT.2019.2903212

CrossRef Full Text | Google Scholar

Yan J., Guo D., Luo X., Guan X. (2020). Auv-aided localization for underwater acoustic sensor networks with current field estimation. IEEE Trans. Vehicular Technol. 69, 8855–8870. doi: 10.1109/TVT.2020.2996513

CrossRef Full Text | Google Scholar

Yan J., Xu Z., Luo X., Chen C., Guan X. (2019b). Feedback-based target localization in underwater sensor networks: A multisensor fusion approach. IEEE Trans. Signal Inf. Process. over Networks 5, 168–180. doi: 10.1109/TSIPN.2018.2866335

CrossRef Full Text | Google Scholar

Yang H., Gao X., Huang H., Li B., Xiao B. (2022). An lbl positioning algorithm based on an emd–ml hybrid method. EURASIP J. Adv. Signal Process. 2022, 1–20. doi: 10.1186/s13634-022-00869-0

CrossRef Full Text | Google Scholar

Yao P., Qiu L., Qi J., Yang R. (2021). Auv path planning for coverage search of static target in ocean environment. Ocean Eng. 241, 110050. doi: 10.1016/j.oceaneng.2021.110050

CrossRef Full Text | Google Scholar

Yu K., Hao K., Li C., Du X., Wang B., Liu Y. (2019). “An improved tdoa localization algorithm based on auv for underwater acoustic sensor networks,” in Artificial Intelligence for Communications and Networks. Eds. Han S., Ye L., Meng W. (Cham: Springer International Publishing), 419–434.

Google Scholar

Yu X., Qin H.-D., Zhu Z.-B. (2021). Globally exponentially stable single beacon underwater navigation with unknown sound velocity estimation. J. Franklin Institute 358, 2515–2534. doi: 10.1016/j.jfranklin.2021.01.010

CrossRef Full Text | Google Scholar

Zacchini L., Franchi M., Ridolfi A. (2022). Sensor-driven autonomous underwater inspections: A receding-horizon rrt-based view planning solution for auvs. J. Field Robotics 39, 499–527. doi: 10.1002/rob.22061

CrossRef Full Text | Google Scholar

Zhang Q., Meng X., Zhang S., Wang Y. (2015). Singular value decomposition-based robust Cubature kalman filtering for an integrated gps/sins navigation system. J. Navigation 68, 549–562. doi: 10.1017/S0373463314000812

CrossRef Full Text | Google Scholar

Zhang J., Shi C., Sun D., Han Y. (2018). High-precision, limited-beacon-aided auv localization algorithm. Ocean Eng. 149, 106–112. doi: 10.1016/j.oceaneng.2017.12.003

CrossRef Full Text | Google Scholar

Zhang F., Wang C., Cheng C., Yang D., Pan G. (2022). Reinforcement learning path planning method with error estimation. Energies 15, 247. doi: 10.3390/en15010247

CrossRef Full Text | Google Scholar

Zhang Y., Wang Q., Shen Y., He B. (2023). An online path planning algorithm for autonomous marine geomorphological surveys based on auv. Eng. Appl. Artif. Intell. 118, 105548. doi: 10.1016/j.engappai.2022.105548

CrossRef Full Text | Google Scholar

Zhang L., Zhang T., Shin H.-S., Xu X. (2021). Efficient underwater acoustical localization method based on time difference and bearing measurements. IEEE Trans. Instrumentation Measurement 70, 1–16. doi: 10.1109/TIM.2020.3045193

CrossRef Full Text | Google Scholar