Impact of ebb-delta dynamics on shoreline evolution along inlet-interrupted coasts

Shorelines adjacent to tidal inlets are highly dynamic landforms affected by oceanic (e.g., sea-level rise) and terrestrial (e.g., fluvial sediment supply) processes. Climate change is thus expected to have substantial physical impacts on these inlet-interrupted coasts. Numerical simulation of such impacts requires a holistic approach where at least the major governing processes that affect the local sediment budget are considered. The Generalized-Scale-aggregated Model for Inlet-interrupted Coasts (i.e., G-SMIC) is such a model that is capable of holistically simulating the evolution of inlet-interrupted coasts over multi-decadal to century time periods. However, in its present form, G-SMIC does not consider the effects of ebb-delta dynamics in its computations. Here, we improve the model to include ebb-delta dynamics and pilot the improved model (G-SMIC+) at two selected case study sites in Vietnam (Thu Bon estuary) and Wales, United Kingdom (Mawddach estuary). Model hindcasts of G-SMIC+ at both case study locations show reasonable agreement with available records of shoreline variations. The evolution of the two inlet-estuary systems was assessed over the 21^st century under four of the IPCC’s sixth assessment report climate scenarios (viz., SSP1-2.6, SSP2-4.5, SSP3-7.0, and SSP5-8.5). Results show that both systems switch between sediment exporting and sediment importing systems over the study period (2031 - 2100). Moreover, while the inclusion of ebb-delta dynamics may decrease the erosion volumes of the up-drift shoreline by up to 37% and 46% at Thu Bon and Mawddach estuaries, respectively (by 2100, relative to 2030), the down-drift coast is only affected in a noticeable way at the Mawddach estuary, where the accretion volume is projected to reduce by ~50%. As a result, the ebb-delta effect decreases the up-drift shoreline retreat by up to 37% and 48% at Thu Bon and Mawddach estuaries, respectively, while it reduces shoreline progradation of the down-drift coast of Mawddach estuary by up to ~50%. These results highlight the importance of including ebb-delta dynamics in modelling efforts to assess the climate change responses of inlet-interrupted coasts worldwide.

1 Introduction

Coasts are varied and complex systems, thus, there are a number of different coastal classifications. In general, most of the world’s coastlines fall in the ‘open coast’ category, where the coastlines are exposed to the direct impacts of the ocean. These open coasts contain estuaries, cliffed and sandy coasts and gravel beaches, with heavily utilised sandy coasts (Davenport and Davenport, 2006; Elias and van der Spek, 2006; Davis, 2019; He and Silliman, 2019) comprising about one-third of the world’s coastlines (Ranasinghe, 2016; Luijendijk et al., 2018; Le Cozannet et al., 2019). Sandy coasts are considered to be one of the most complex coastal systems with respect to their geomorphological behaviour because they are continually varying due to the influences of both natural and anthropogenic drivers (Stive et al., 1990; Stive and Wang, 2003; Stive, 2004; Stive, 2006; Ranasinghe and Stive, 2009; Ranasinghe et al., 2013; Anthony, 2015; Ranasinghe, 2016; Toimil et al., 2017; Bamunawala et al., 2018; Besset et al., 2019; Bamunawala et al., 2020a; Bamunawala et al., 2020b; Bamunawala et al., 2021). A significant portion of these sandy coasts are interrupted by inlets (Aubrey and Weishar, 1988; Davis-Jr. and Fitzgerald, 2003; Woodroffe, 2003; Ranasinghe et al., 2013; FitzGerald et al., 2015; McSweeney et al., 2017; Duong et al., 2018; Duong, 2021). Although the exact number of inlets globally is somewhat ambiguous, studies suggest that approximately 8% to 13% of the global coastline (i.e., 24% to 39% of the world’s sandy coasts) is interrupted by tidal inlets (Kjerfve, 1986; Kjerfve, 1994; Stutz and Pilkey, 2001; Dürr et al., 2011; Stutz and Pilkey, 2011). Notably, the above estimates include permanently and intermittently open tidal-inlet systems, barrier island coasts, and lakes/water bodies located in the vicinity of the seas (McSweeney et al., 2017). Except for strongly wave-dominant coasts, these coastal environments may also comprise ebb-tidal deltas (Davies, 1980; Davis and Hayes, 1984; Davis, 2003; Davidson-Arnott, 2011), which increases the complexities associated with inlet-interrupted coastal systems. Here, we focus on inlet-interrupted sandy coasts with ebb-delta systems, which comprise a unique category of the world’s coastlines. Given their complex nature in geomorphological behaviour and importance to society (e.g., navigation, fishing, tourism, and recreation), it is important to understand the physical responses of these systems to plausible ranges of future environmental forcing and anthropogenic activities. Such insights on the evolution of inlet-interrupted sandy coasts may help decision-makers, planners, and managers take necessary actions to prevent/mitigate myriad damages to coastal communities, their socio-economic well-being, and coastal ecosystem services.

Tidal inlets and their associated ebb-deltas are dynamic systems that evolve in reaction to complex interactions between tides and waves (Herrling and Winter, 2018), where ebb-deltas are formed due to the interaction of tidal and wave-generated currents (Davis and Hayes, 1984; Fitzgerald, 1984). Hence, the morphological evolution of the ebb-delta systems is linked to the balance between wave-tidal energy in their vicinities (Hayes, 1975; Hayes, 1980; Davis and Hayes, 1984; Elias and van der Spek, 2006). Littoral drift brings most of the sediment inputs to the ebb-delta systems, while wave and tidal currents carry sediment through the flood channels of the inlet-estuary systems to the ebb-channels (Fitzgerald, 1984; Kraus, 2000; Elias and van der Spek, 2006). Flow regimes in the inlet channels are asymmetric, with generally more prominent ebb-tidal currents, leading to the redistribution of the deposited sediment within the inlet-estuary systems to the ebb-delta during ebb-tide. Any temporary change in such a system will lead to sediment redistribution within its components as the system thrives to maintain its dynamic equilibrium. In contrast, a large-scale perturbation (due to natural causes such as sea-level rise or anthropogenic activities such as reservoir sediment retention, river/estuarine sand mining, and breakwater construction) may result in the entire inlet-estuary-coastal systems shifting to a new (dynamic) equilibrium state (Elias and van der Spek, 2006; Syvitski et al., 2009; Garel et al., 2014).

The presence of ebb-delta systems contributes to the sediment volume exchange between inlet-estuary systems and the adjacent coastal zone on inlet-interrupted coasts, thus affecting the consequent evolution of the inlet-interrupted coastline (FitzGerald, 1988; Fenster and Dolan, 1996; Isla, 1997; Kana et al., 1999; Kraus, 1999; Kraus, 2000; Larson et al., 2007; Dissanayake et al., 2009; Dissanayake et al., 2012; Garel et al., 2014; Herrling and Winter, 2018). FitzGerald (1988) indicates that the influence of an inlet system on the adjacent shorelines may depend on the size and number of inlets and the long-term changes in the sediment budget. The number of inlets along a given open sandy coast and their sizes are controlled by the tidal prism, which is governed by the size of the estuary they are attached to and the tidal range (Fenster and Dolan, 1996; Zhang, 2016). The tidal prism also affects the size of ebb-delta systems, where larger tidal prisms support bigger ebb-delta volumes, exerting more influences on sediment volume exchange between inlet-estuary systems and the adjacent coastline (Jarrett, 1976; Walton and Adams, 1976; Nummedal and Fischer, 1978; FitzGerald, 1988). The extent to which the inlet influences extend along the up- and down-drift shorelines will depend on local conditions, where studies have indicated that the extent of inlet influence on the adjacent coast may lie somewhere between 7 km and 25 km, with larger inlet/estuary systems affecting longer extents of coastline (Fenster and Dolan, 1996; Ranasinghe et al., 2013).

Climate change impacts on inlet-interrupted coasts can be assessed by considering the sediment volume exchange between the tidal-inlet system and its adjacent coastal zone (Ranasinghe et al., 2013; Ranasinghe, 2016; Duong et al., 2018; Duong, 2021). The riverine sediment throughput and estuarine accommodation space affect the sediment volume exchange between the inlet-estuary systems and the adjacent coast. Climate-change-induced sea-level rise will increase the volume of accommodation space within the estuary. If the sediment supply from the river flow is negligible, the sediment demand caused by the increased accommodation space will have to be exclusively supplied from the adjacent coast, depleting ebb deltas and/or eroding the adjacent coast. In situations where future riverine sediment throughput is substantial, the fluvial sediment supply will fulfil part of the increased estuarine sediment demand, decreasing the sediment volume that needs to be imported to the estuary. If the future riverine sediment throughput is higher than the increased estuarine sediment demand, the resulting surplus sediment volume will be exported to the adjacent coast (Ranasinghe, 2016; Bamunawala et al., 2020a). These sediment volume exchanges between the estuary and the adjacent coastal zone are closely linked with the longshore sediment transport capacity in the vicinity of the inlet (Isla, 1997).

The potential for pronounced impacts on inlet-interrupted coastlines driven by projected climate change over the 21^st century and anthropogenic influences have led to a concerted drive to improve our understanding of these hazards and associated risks (Hallegatte et al., 2013; Woodruff et al., 2013; Brown et al., 2014; Neumann et al., 2015; Toimil et al., 2020a; Toimil et al., 2020b; Nicholls et al., 2021a; Nicholls et al., 2021b). With the increasing awareness of the global scale risks and uncertainties associated with projected climate-change-related impacts on coasts (Ranasinghe et al., 2021), the need for morphological modelling techniques capable of providing projections of multi-decadal to century-long coastline evolutions has been highlighted by many researchers (e.g., Larson et al. (2016); Ranasinghe (2020); Moore and Murray (2022)). One such approach is reduced-complexity modelling (Ranasinghe, 2016; Ranasinghe, 2020). These models usually schematize the relevant physical processes while maintaining a balance between the theoretical aspects of the processes and data-driven empirical relationships, which enables the development of computationally efficient, long-term coastline evolution models. Over the last two decades, several researchers have attempted to develop models for inlet-interrupted coasts (e.g., Jiménez & Sánchez-Arcilla (2004); Hoan et al. (2011); Larson et al. (2003); Ranasinghe et al. (2013)) that can project their long-term evolution while focusing on one or more aspects related to overall system behaviour. However, most of those studies do not consider the holistic behaviour of catchment-estuary-coastal systems and mainly focus on oceanic processes that may contribute to the evolution of coastal zones. Furthermore, all these previous models can only provide deterministic projections of shoreline evolution, thus limiting their usefulness in assessing the uncertainties associated with the model projections.

Within a reduced-complexity framework, shoreline variation along inlet-interrupted coasts on multi-decadal to century time scales can be addressed as a sediment budget-related problem. Considering such sediment balances, Ranasinghe et al. (2013) presented an initial, deterministic, reduced-complexity model to perform rapid 100-year simulations of climate-change-driven evolution of inlet-interrupted coasts (viz., Scale-aggregated Model for Inlet-interrupted Coasts (i.e., SMIC)). This model was further developed as the Generalized Scale-aggregated Model for Inlet-interrupted Coasts (i.e., G-SMIC) by Bamunawala et al. (2020a) and Bamunawala et al. (2020b). G-SMIC is a fully probabilistic, generically applicable model that simulates the evolution of inlet-interrupted coasts under climate-change impacts and anthropogenic activities. However, G-SMIC does not consider the presence of ebb-deltas in the vicinity of inlet-estuary systems. This study specifically aims to include ebb-delta dynamics in G-SMIC and assess its importance in the evolution of inlet-interrupted coasts over the 21^st century via case study applications of the improved model.

Two selected case-study sites in Vietnam (Thu Bon estuary system) and Wales, United Kingdom (Mawddach estuary system) are used in this study to pilot the enhanced G-SMIC model (hereon G-SMIC+). Here, G-SMIC+ is used to project the evolution of coastlines at the two case study sites over the 2031-2100 period under four Shared Socio-economic Pathways (SSPs) presented in IPCC’s 6^th Assessment Report (i.e., SSP1-2.6, SSP2-4.5, SSP3-7.0, and SSP5-8.5) using CMIP6 projections. The sediment volume exchange projections between the estuary and its adjacent coast were obtained (1) with the ebb-delta system and (2) without the ebb-delta system, allowing a direct comparison of the role of ebb-delta dynamics in shoreline evolutions along inlet-interrupted coasts.

2 Materials and methods

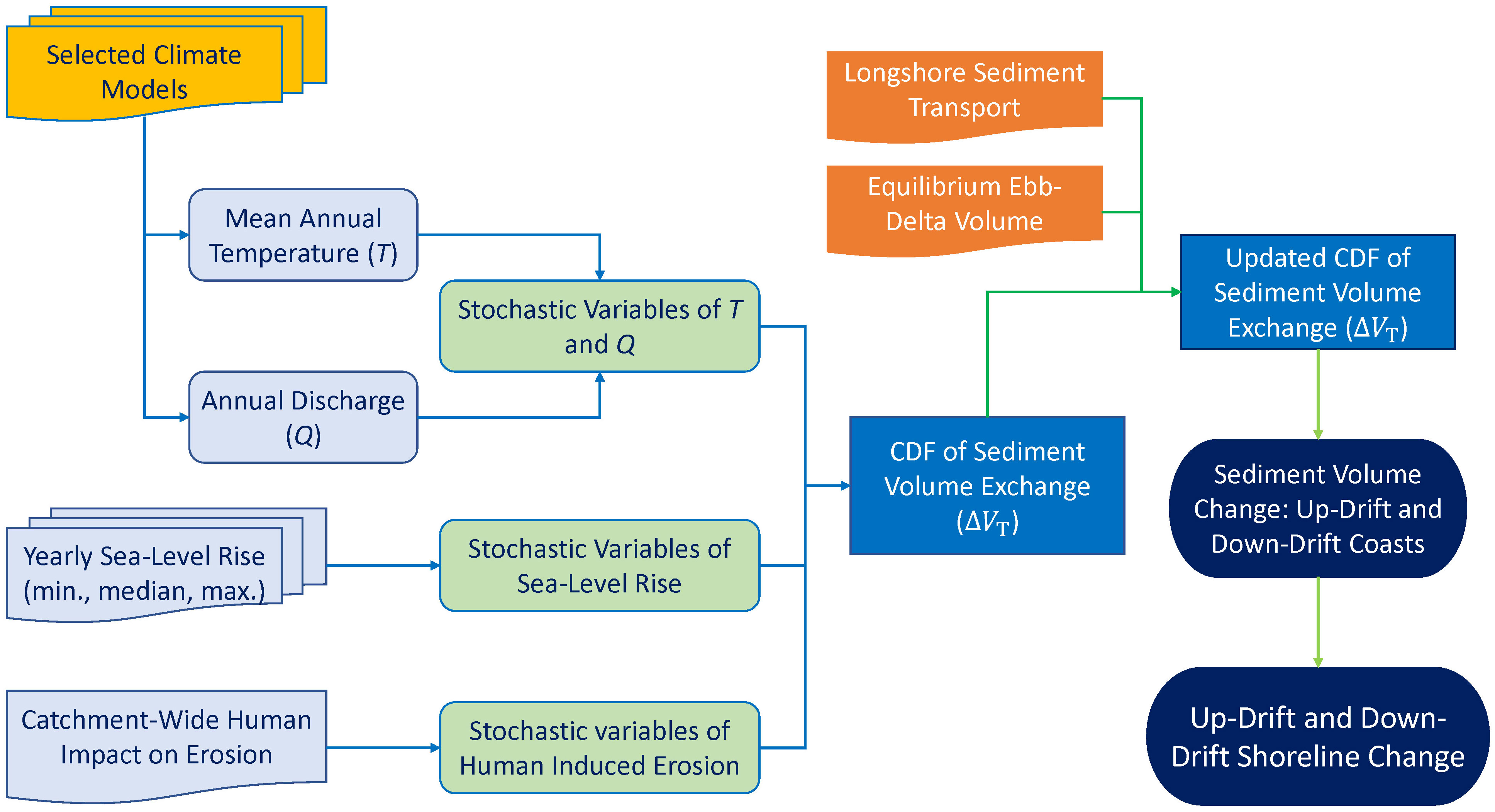
Three main sediment volume components contribute to the long-term (i.e., decadal to century periods) evolution of inlet-interrupted coasts: (1) sediment volume demand/supply by the inlet-estuary system, (2) sediment dynamics of the ebb-delta system, and (3) longshore sediment transport capacity. The modelling framework that incorporates ebb-delta dynamics to G-SMIC+ is fully described below. The sediment volume contributing to shoreline variation is calculated in two steps. First, the sediment volume exchanged between the inlet-estuary system and the coastal zone ($\Delta V_{\text{T}}$) is calculated within a probabilistic modelling framework (i.e., G-SMIC, fully described in Bamunawala et al., 2020b; Bamunawala et al., 2021). Secondly, $\Delta V_{\text{T}}$ is incorporated in ebb-delta dynamics to obtain the updated sediment volume corresponding to the shoreline variation along the up- and down-drift coasts (i.e., G-SMIC+, fully described in this manuscript). A flowchart illustrating the modelling concept is provided in Figure 1.

FIGURE 1

Figure 1 Flowchart of the overall modelling concept of G-SMIC+.

2.1 Calculation of sediment volume exchanged ($\Delta V_T$) in G-SMIC

G-SMIC assumes that the sediment volume exchanged between the inlet-estuary system and its adjacent coasts ($\Delta V_{\text{T}}$) consists of three main components [1]: (1) Basin infilling due to increases in basin accommodation space ($\Delta V_{\text{BI}}$) (driven by sea-level rise), (2) Basin volume change due to variation in river discharge ($\Delta V_{\text{BV}}$), and (3) Changes in fluvial sediment supply ($\Delta V_{\text{FS}}$) (driven by variations in temperature, discharge from river catchment, and human-induced erosion).

$\begin{array}{ll}\text{Δ}{V}_{\text{T}}=\text{Δ}{V}_{\text{BI}}+\text{Δ}{V}_{\text{BV}}+\text{Δ}{V}_{\text{FS}}& \text{[1]}\end{array}$

2.1.1 Basin infilling volume due to sea-level rise-induced increase in accommodation space

This sediment volume refers to the additional basin volume resulting from increases in sea level (ΔSL) in the vicinity of the inlet-estuary system. This sediment volume ($\text{Δ}{V}_{\text{BI}}$ ) can be computed as [2].

$\begin{array}{ll}\text{Δ}{V}_{\text{BI}}=-fac\left(A_{\text{b}}\text{Δ}SL\right)& \text{[2]}\end{array}$

where $A_{\text{b}}$ is the basin surface area (m²), ‘fac’ (0<fac<1) accounts for the morphological response lag that exists between the hydrodynamic forcing (i.e., sea-level rise) and associated morphological response from in basin (i.e., basin infilling volume ($\text{Δ}{V}_{\text{BI}}$)). Here, this ‘fac’ value is set to be 0.5 for all the simulations (adopted from Ranasinghe et al. (2013)).

2.1.2 Basin volume change due to variation in river flow

The ebb-tidal flow volume of estuaries may change due to variations in future river flow. Such a change in the ebb-flow volume induces variations in flow velocity in the estuary and inlet. In the process of striving to achieve its initial equilibrium flow velocity, an inlet-estuary system may be subjected to changes in its cross-section and bed level. Such variations in the inlet-estuary system are associated with a specific volume of sediment volume ($\Delta V_{\text{BV}}$) exchanged between the inlet-basin system and its inlet-interrupted coasts, which can be calculated as the following [3] (Ranasinghe et al., 2013).

$\begin{array}{ll}\text{Δ}{V}_{\text{BV}}=\frac{\text{Δ}{Q}_{\text{R}}{V}_{\text{B}}}{\left(P+Q_{\text{R}}\right)}& \text{[3]}\end{array}$

where $Q_{\text{R}}$ is the present river flow into the basin during ebb, $\Delta Q_{\text{R}}$ is the climate change-driven variation in river flow during ebb, $V_{\text{B}}$ is the present basin volume, and P is the mean equilibrium ebb-tidal prism, all volumes in m³.

2.1.3 Change in fluvial sediment supply

Projected changes in climate and anthropogenic activities at the catchment scale will change the annual fluvial sediment supply received by an inlet-estuary system (Vörösmarty et al., 2003; Syvitski et al., 2005; Palmer et al., 2008; Ranasinghe et al., 2019). Here, this change in fluvial sediment supply ($\Delta V_{\text{FS}}$ (m³)) is calculated using the BQART model presented by Syvitski and Milliman (2007) [4].

$\begin{array}{ll}{Q}_{\text{S}}=\text{ω}B{Q}^{0.31}{A}^{0.5}RT& \text{[4]}\end{array}$

where ω is a coefficient equal to 0.02 or 0.0006 for the annual fluvial sediment supply ($Q_{\text{S}}$) expressed in kg/s or MT/year at catchments with its mean annual temperature greater than 2 °C, Q is the annual cumulative river discharge (km³), A is the river catchment area (km²), R is the catchment relief (km), and T is the catchment-wide mean annual temperature (°C).

The term ‘B’ of the above equation represents the catchment sediment production capacity, expressed as the following equation [5].

$\begin{array}{ll}B=IL\left(1-T_{\text{E}}\right)E_{\text{h}}& \text{[5]}\end{array}$

where L is the lithology factor that represents the catchment’s soil type and erodibility, $T_{\text{E}}$ is the catchment-wide reservoir trapping efficiency factor, and $E_{\text{h}}$ is the catchment’s human-induced erosion factor.

The term I of the above equation is the glacial erosion factor, which can be calculated according to the following equation [6].

$\begin{array}{ll}I=1+\left(0.09A_{\text{g}}\right)& \text{[6]}\end{array}$

where $A_{\text{g}}$ is the ice cover percentage within the catchment area.

Studies on fluvial sediment supply from river catchments indicate that the sediment loads projected by the BQART model consist mostly of suspended sediment, which will be lost to the sea without contributing to a change in beach volume (Wright and Nittrouer, 1995). Hence, in G-SMIC+, a stochastic factor ($fac\_Q_{\text{s}}$) is used with the BQART model projections, thus, only a fraction of the sediment load is accounted for in the coastal sediment budget computations. This stochastic factor is generated via a fitted triangular distribution with minimum, peak, and maximum values of 0.10, 0.35, and 0.60, respectively. Thus, equation [4] can be updated as:

$$Q_{\text{S}}=fac\_Q_{\text{S}}.\omega B{Q}^{0.31}{A}^{0.5}RT$$

In computing the above three contributing terms [2, 3, and 4 (updated)] to $\Delta V_{\text{T}}$ stochastically [1], climatic inputs (i.e., mean annual temperature (T) and annual discharge (Q)) are obtained via suitable global climate models. These yearly values are then used to fit joint probability distributions for generating yearly T and Q stochastic variables. Corresponding yearly minimum, median, and maximum sea-level rise values (SLR) are used to fit triangular distributions that generate stochastic values of annual sea-level rise. Human FootPrint Index (HFPI) values published by NASA (Venter et al., 2016; Venter et al., 2018) are used to project future anthropogenic impacts on erosion in catchments. Stochastic values of human-induced erosion are generated via fitted triangle distributions, assuming a linear increment of present-day HFPI values till 2100 (10, 15, and 20 per cent increments by 2100 for minimum, median, and maximum HFPI).

2.1.4 Overall Monte-Carlo simulation framework used in G-SMIC

The probabilistic treatment of G-SMIC is fully described in Bamunawala et al. (2020b) and Bamunawala et al. (2021), thus not repeated and only briefly explained here. The above four model inputs (T, Q, SLR, and HFPI), and the stochastic factor (i.e., $fac\_Q_{\text{s}}$) are then used in a Monte-Carlo framework to calculate yearly sediment volume exchange ($\Delta V_{\text{T}}$) under each projection scenario considered. The dependency between T and Q are represented via the fitted joint probability distributions between those variables. The correlation between projected T and SLR is characterised within the Monte-Carlo framework by selecting SLR projections to match with the probability of occurrence of temperature in each simulation (i.e., a direct relationship between T and SLR, as suggested by Rahmstorf (2007)). Such a direct relationship between T and SLR is considered to represent the significant influence of increasing temperature on global sea-level rise, characterised by thermal expansion (i.e., steric effect) caused by warming of the oceans and increased melting of land-based ice, such as glaciers and ice sheets (Ranasinghe et al., 2021; IPCC, 2023). In G-SMIC+, 100,000 simulations are performed per year per scenario considered to derive cumulative probability distributions of $\Delta V_{\text{T}}$.

2.2 Sediment reservoir aggregated model

Here, we adopted the sediment reservoir concept for inlet sediment storage and the transfer, which was first introduced by Kraus (2000) and later used in the CASCADE model (Larson et al., 2003) to simulate longshore sediment transport and coastal evolution. The CASCADE model successfully simulated sediment transfer between the up- and down-drift barrier-islands, ebb-shoal complexes, and attachment bars (Larson et al., 2016; Palalane et al., 2016; Palalane and Larson, 2019). The same concept is adopted in this study to simulate the sediment dynamics between the ebb-delta and inlet-interrupted coasts.

Kraus (2000) presented a sediment aggregated model to determine the rate of sand leaving an ebb-shoal [7].

$\begin{array}{ll}{Q}_{\text{out}}= \left(\frac{V}{V_{eq}}\right)Q_{\text{in}}& \text{[7]}\end{array}$

where $Q_{\text{out}}$ is the rate at which sediment leaves or bypasses the ebb-shoal (${\text{m}}^3/\text{yr}$), $Q_{in}$ is taken as the longshore sediment transport rate (${\text{m}}^3/\text{yr}$), $V_{eq}$ is the equilibrium volume of the ebb-shoal (${\text{m}}^3$), and V is the volume of the ebb-shoal (${\text{m}}^3$).

The equilibrium volume of the ebb-shoal system ($V_{eq}$) can be determined based on Walton and Adams (1976), who presented three regression relationships for $V_{eq}$ (in cubic yards), at different wave exposure conditions as a function of the attached estuary system’s tidal prism (P in ft³). The level of wave exposure is categorised as highly, moderately, and mildly exposed coasts, which is determined based on the significant wave height (H_s in ft) and wave period (T in s). Walton and Adams (1976) employed $H_s^2{T}^2$ as a proxy for the energy potential of a given coast as follows:

1. (a) Highly exposed coasts: $300<H_s^2{T}^2$

2. (b) Moderately exposed coasts: $30<H_s^2{T}^2<300$

3. (c) Mildly exposed coasts: $0<H_s^2{T}^2<30$

Following Kraus (2000), the continuity equation governing the ebb-shoal volume variation can be written as [8].

$\begin{array}{ll}\frac{dV}{dt}=Q_{\text{in}}-Q_{\text{out}}& \text{[8]}\end{array}$

By substituting for $Q_{\text{out}}$ [7], above equation resolves to [9].

$\begin{array}{ll}V=V_{\text{eq}}\left(1-e^{-\alpha t}\right)& \text{[9]}\end{array}$

where $\alpha =\frac{Q_{\text{in}}}{V_{\text{eq}}}$ and t is the simulation time steps (in years).

2.3 Calculation of sediment volume exchanged ($\Delta V_T$) in G-SMIC+

In G-SMIC+, the stochastic $\Delta V_{\text{T}}$ values thus computed are used together with the sediment reservoir aggregate modelling concept presented by Kraus (2000) to include ebb-delta dynamics into $\Delta V_{\text{T}}$ and obtain the updated sediment exchange volumes that contribute to the future evolution of inlet-interrupted shorelines. To simplify the model description, here, we present the G-SMIC+ modelling concept concerning three scenarios, as described below.

2.3.1 Ebb-delta dynamics when estuary exports sediment

Here, $Q_{\text{in}}$ is defined as [10] to account for the sediment volume exported by the inlet-estuary system ($V_{\text{T}}$).

$\begin{array}{ll}{Q}_{\text{in}}=LST+V_{\text{T}}& \text{[10]}\end{array}$

With the above $Q_{\text{in}}$, the down-drift coast receives the sediment volume released from the ebb-delta system ($Q_{\text{out}}$) [7]. Under the assumption of a coastal cell with a balanced sediment budget (Komar, 1996; Komar, 1998), the down-drift coast should have a sediment load equal to LST capacity (Figure 2A). Depending on the magnitudes of LST and $Q_{\text{out}}$, the down-drift coast may prograde (if $Q_{\text{out}}>LST$) or erode (if $Q_{\text{out}}<LST$) by a volume $V_{down-drift}$, given by [11].

FIGURE 2

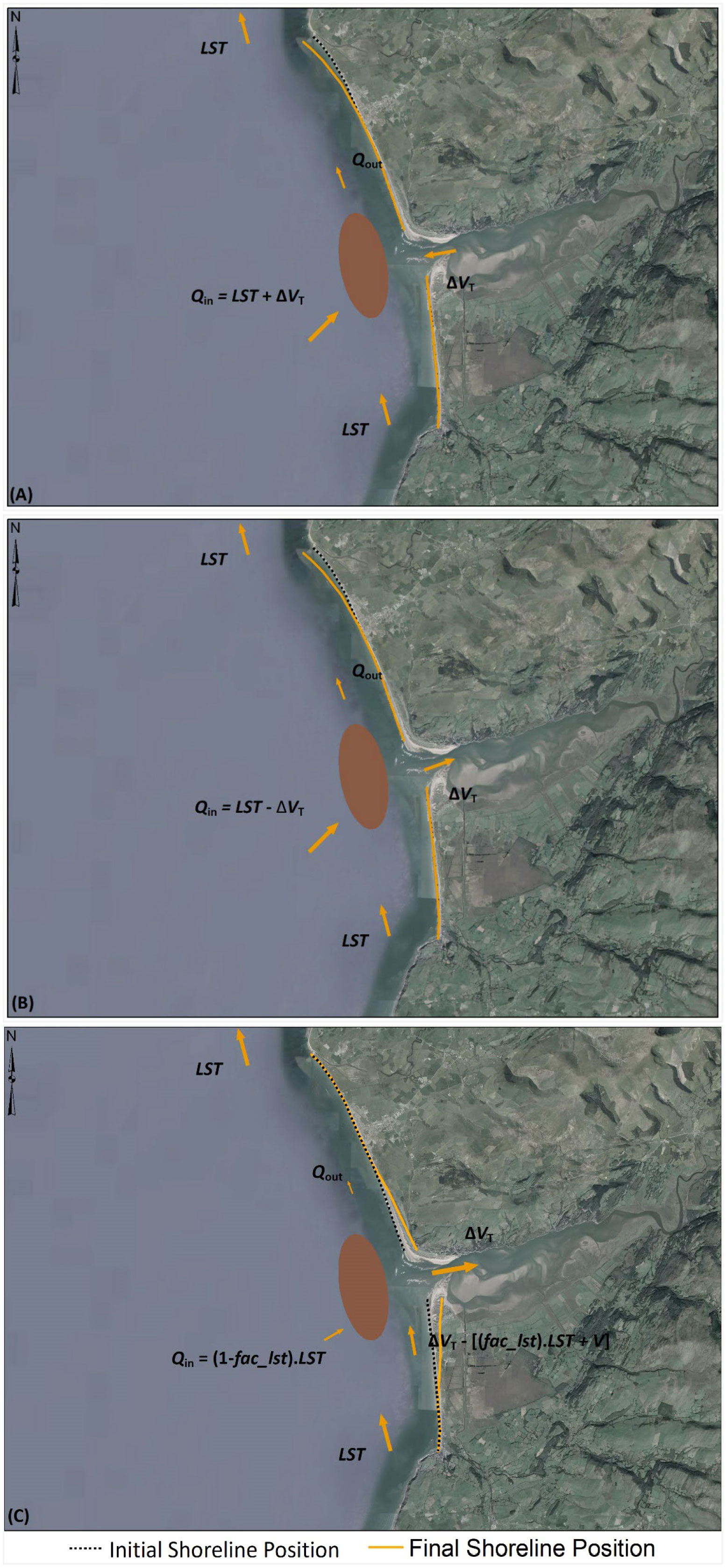
Figure 2 Schematic illustration of sediment volume components concerning ebb-delta dynamics at (A) sediment exporting estuary systems, (B) Type 1 sediment importing estuary systems (i.e., $LST>\Delta V_{\text{T}}$), and (C) Type 2 sediment importing estuary systems (i.e., $LST<\Delta V_{\text{T}}$). Note: $\Delta V_{\text{T}}$ is the sediment volume exported from/imported into the inlet-estuary system, LST is Longshore Sediment Transport, Q_in is the sediment volume received by the ebb-delta system, Q_out is the sediment volume bypassing/leaving the ebb-delta system, and V is the ebb-delta volume. The down-drift shoreline variation is illustrated in (A, B) for a situation where $Q_{\text{out}}>LST$.

$\begin{array}{ll}{V}_{\text{down}-\text{drift}}=|Q_{\text{out}}-LST|& \text{[11]}\end{array}$

Under this situation, the up-drift coast will not be affected by $\Delta V_{\text{T}}$ or ebb-delta dynamics. In addition to the above, both up- and down-drift shorelines will be subjected to retreat due to SLR alone (due to the so-called Bruun effect, Bruun (1962)). These sediment volume relationships and associated shoreline changes are illustrated conceptually in Figure 2A.

2.3.2 Ebb-delta dynamics when estuary imports sediment (Type 1)

At Type 1 sediment-importing estuary, the magnitude of the estuarine sediment demand ($V_{\text{T}}$) is less than the LST. Hence, $Q_{\text{in}}$ at this type of system is defined as [12], to account for the sediment volume imported by the inlet-estuary system ($V_{\text{T}}$).

$\begin{array}{ll}{Q}_{\text{in}}=LST-V_{\text{T}}& \text{[12]}\end{array}$

Here, the down-drift coast receives $Q_{\text{out}}$ from the ebb-delta system. However, under the assumed balanced sediment budget within the coastal cell (Komar, 1996; Komar, 1998), the down-drift coast should have a sediment load equal to LST capacity for stability (Figure 2B). Similar to ebb-delta dynamics at sediment exporting estuaries, the down-drift shoreline may prograde (if $Q_{\text{out}}>LST$) or erode (if $Q_{\text{out}}<LST$) by a volume $V_{\text{down}-\text{drift}}$[11] to maintain the sediment balance within the coastal cell.

Here too, the up-drift coast will not be affected by $\Delta V_{\text{T}}$ or ebb-delta dynamics, and both coasts will retreat an additional amount due to the SLR-driven Bruun effect. These sediment volume relationships and associated shoreline changes are illustrated conceptually in Figure 2B.

2.3.3 Ebb-delta dynamics when estuary imports sediment (Type 2)

In this type of system, LST capacity is smaller than the annual sediment demand from the estuary ($\Delta V_{\text{T}}$). As $\Delta V_{\text{T}}$ dominates the sediment budget, most of the LST may be imported into the inlet-estuary system. Here, it is assumed that a fraction of LST (i.e., $fac\_lst$) may contribute to satisfying the estuarine sediment demand ($V_{\text{T}}$), where $0.5 <fac\_lst<1$.

Hence, the remaining fraction of LST may contribute to $Q_{\text{in}}$, which can be defined as [13].

$\begin{array}{ll}{Q}_{\text{in}}=\left(1-fac\_lst\right).LST& \text{[13]}\end{array}$

Since $LST<V_{\text{T}}$, the rest of the sediment volume demand by the estuary is fulfilled by eroding the ebb-delta system. If $V_{\text{T}}$ cannot be fulfilled with the available ebb-delta volume (V), the remaining sediment requirement is supplied by eroding the up-drift coast by a volume $V_{\text{up}-\text{drift}}$ [14].

$\begin{array}{ll}{V}_{\text{up}-\text{drift}}=V_{\text{T}}-[\left(fac\_lst\right).LST+V]& \text{[14]}\end{array}$

where V is the ebb-delta volume, given by [9].

In this situation, $Q_{\text{out}}$will always be less than LST (unless there are drastic future changes in $\Delta V_{\text{T}}$ and/or LST), and the down-drift shoreline will retreat by a volume $V_{\text{down}-\text{drift}}$ [11]. In addition to the above, the up- and down-drift shorelines will also retreat due to the SLR-driven Bruun effect. These sediment volume relationships and associated shoreline changes are illustrated conceptually in Figure 2C.

Since the above-adopted fraction ($0.5 <fac\_lst<1$) will have a direct influence on the overall behaviour of the system, in this study, a series of $fac\_lst$ values (0.6, 0.7, 0.8, and 0.9) were tested at Type 2 sediment importing estuaries. This sensitivity test indicated that the ‘$fac\_lst$’ value has a minimal impact on the sediment budget projections along down-drift coasts (Supplementary Figure 1). However, the up-drift sediment budget is affected by the value of $fac\_lst$ used in computations (Supplementary Figure 2). At the Thu Bon estuary, the up-drift sediment budget projections vary between 38% to 50% by 2100. The up-drift sediment volume projection at the Mawddach estuary vary between 45% and 73% by the end of the 21^st century. Use of large $fac\_lst$ reduces the sediment needed from ebb-delta and up-drift coast, thus minimising the consequent up-drift erosion. Hence, only the results obtained with the largest factor (i.e., $fac\_lst=0.9$), representing a conservative assumption, are presented in this paper. This selection also aligns with the overall modelling concept adopted in this study, where the estuarine sediment demand is assumed to dominate the overall sediment budget exchanged at the tidal-inlet system ($\Delta V_{\text{T}}$).

2.4 Computation of shoreline change

The above-computed change in sediment volume along the up- and down-drift shorelines (i.e., $V_{\text{up}-\text{drift}}$ and $V_{\text{down}-\text{drift}}$) are used to determine the consequent sediment volume variation-driven changes along the inlet-interrupted coasts. Here, this shoreline change is computed according to the simplified method used in SMIC applications (Ranasinghe et al., 2013). In this simplified method, shoreline variation is computed by uniformly distributing the sediment volume change along potentially inlet-affected lengths of up- and down-drift coast. It assumes the sediment volume change would shift the entire active coastal profile along inlet-affected coasts, which is expressed as [15]:

$\begin{array}{ll}\text{Δ}{x}_{\text{sv}}=\frac{\text{Δ}{V}_{\text{i}}}{D{L}_{{\text{AC}}_{\text{i}}}}& \text{[15]}\end{array}$

where $\Delta x_{\text{sv}}$ is the coastline displacement in the cross-shore direction (m) due to sediment volume change along respective (i.e., up- and down-drift) coasts, $\Delta V_{\text{i}}$ is the sediment volume change (${\text{m}}^3$) along up- and down-drift shorelines, $L_{{\text{AC}}_{\text{i}}}$ is the length of potentially inlet-affected coast along up- and down-drift coasts (m), and $D$ is the depth of closure (m).

The final shoreline position is obtained by superimposing the shoreline retreat due to the Bruun effect (Bruun, 1962) on the above-computed $\Delta x_{\text{sv}}$, which provides the relative change of future shoreline position compared to present-day (or reference) conditions.

3 Case-study sites and input data

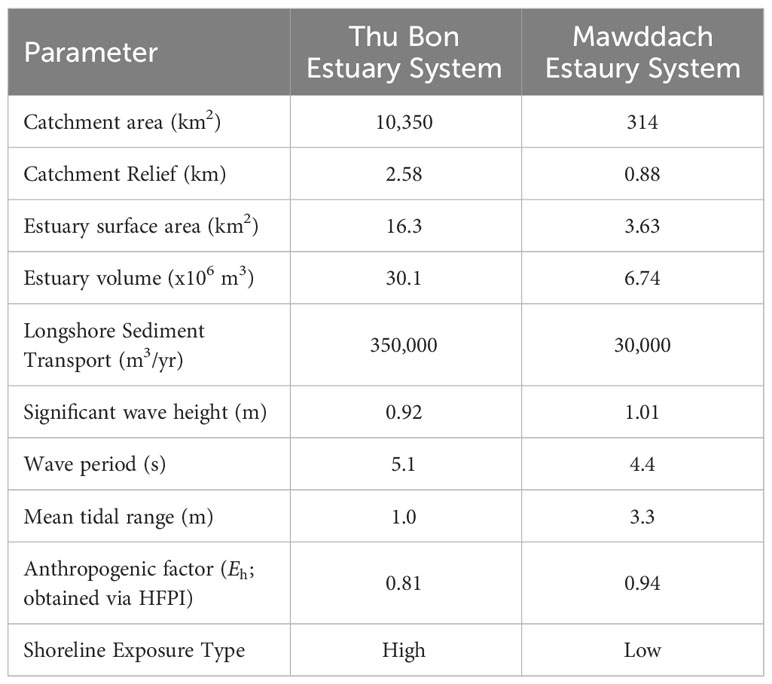
The above-introduced reduced-complexity model was applied to two selected systems with ebb-delta systems: Thu Bon estuary, Vietnam (Figure 3A) and Mawddach estuary, Wales, United Kingdom (Figure 3B). Table 1 summarises the key properties of these systems, and Figure 3 illustrates the locations of the selected case study sites and the Human FootPrint Index (HFPI) of the respective watershed areas.

FIGURE 3

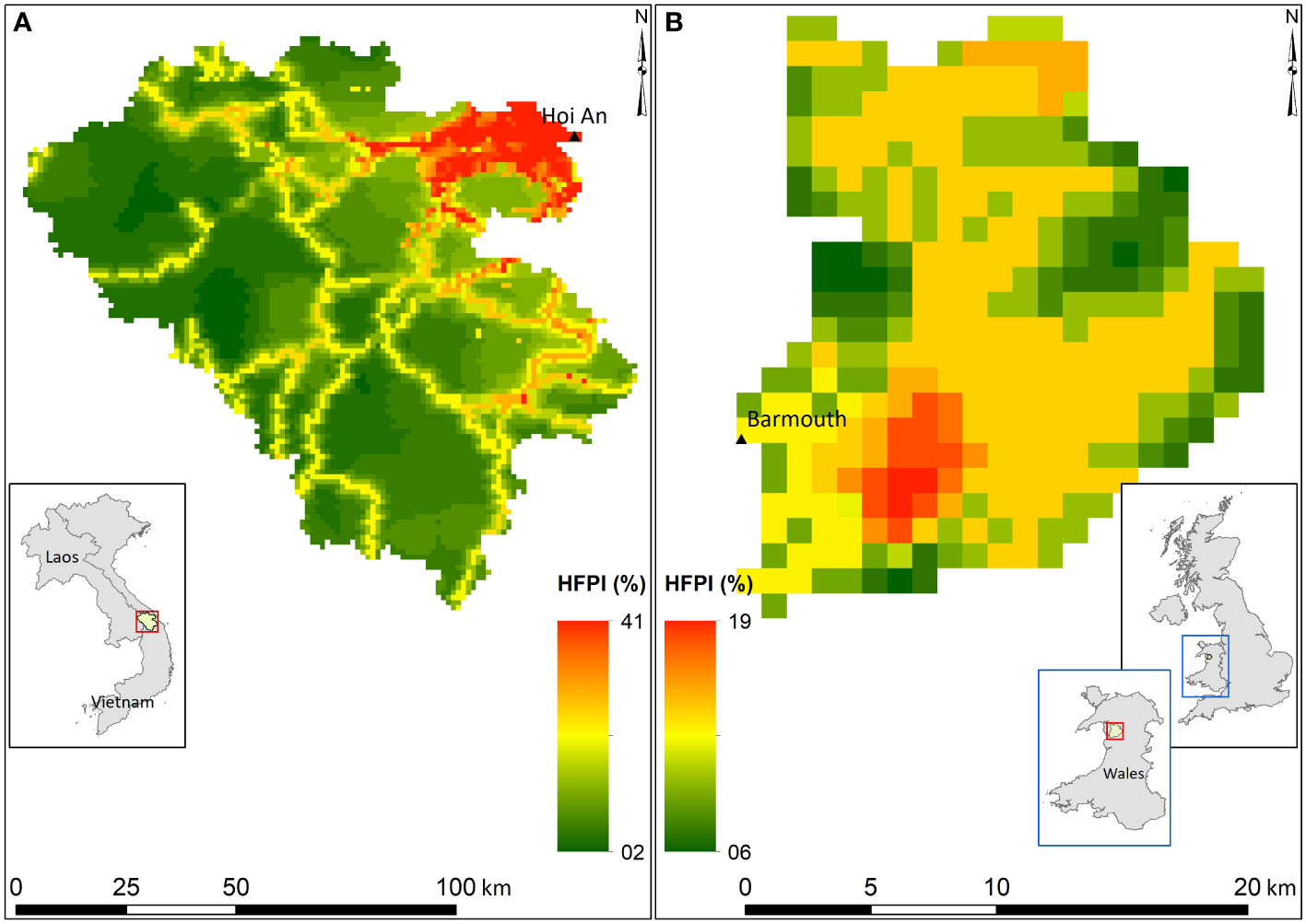
Figure 3 Human FootPrint Index, location, and watershed areas of Thu Bon Estuary System, Vietnam (A) and Mawddach Estuary System, Wales, UK (B).

TABLE 1

Table 1 Key properties of the selected Catchment-Estuary-Coastal systems.

Here, catchment relief and HFPI values were extracted from one arc-second resolution Digital Elevation Model (DEM) obtained from the USGS Earth Explorer tool (Farr et al., 2007) and Human FootPrint Index (HFPI) data presented by Venter et al. (2016), respectively. Estuary volumes were estimated via the linear regression model used in the global application of G-SMIC (Bamunawala et al., 2021). Mean tidal range values were obtained from the harmonic analysis of the TOPEX-POSEIDON global inverse solutions (Egbert and Erofeeva, 2002). Wave parameters were obtained from ERA5, and shoreline exposure was determined according to the classification given by Walton and Adams (1976). The extent of potentially inlet-affected shoreline distances ($L_{{\text{AC}}_{\text{i}}}$) at the case study sites was determined by considering the local coastline characteristics (viz., headland, tidal-inlet, rock outcrop, long groyne, or prominent change in shoreline orientation) and the suggestions given in the published literature (e.g., Fenster and Dolan (1996); Ranasinghe et al. (2013)). At the Thu Bon estuary, the maximum extent of inlet-influenced shoreline length along the up-drift is defined by the headland and change in average shoreline orientation. However, the down-drift coast of the Thu Bon estuary is relatively straight and long. Hence, the maximum extent suggested in the literature was considered as its inlet-influenced down-drift coast distance. At the Mawddach estuary, inlet-influenced shoreline lengths along up- and down-drift coasts are confined by sharp changes in average shoreline orientation.

The temperature and discharge values required by G-SMIC+ were obtained from four selected CMIP6 Global Climate Models (GCMs) (viz., BCC-CSM2-MR, CESM2, GFDL-ESM4, and IPSL-CM6A-LR). The reference climatic conditions were taken from the 2000 - 2014 period. Figures 4 and 5 show the GCM-derived projected variations of annual mean temperature (T) and the annual cumulative discharge (Q) of the Thu Bonn and Mawddach River catchments, respectively, over the three decadal periods considered (i.e., 2031 – 2040, 2061 – 2070, and 2091 – 2100).

FIGURE 4

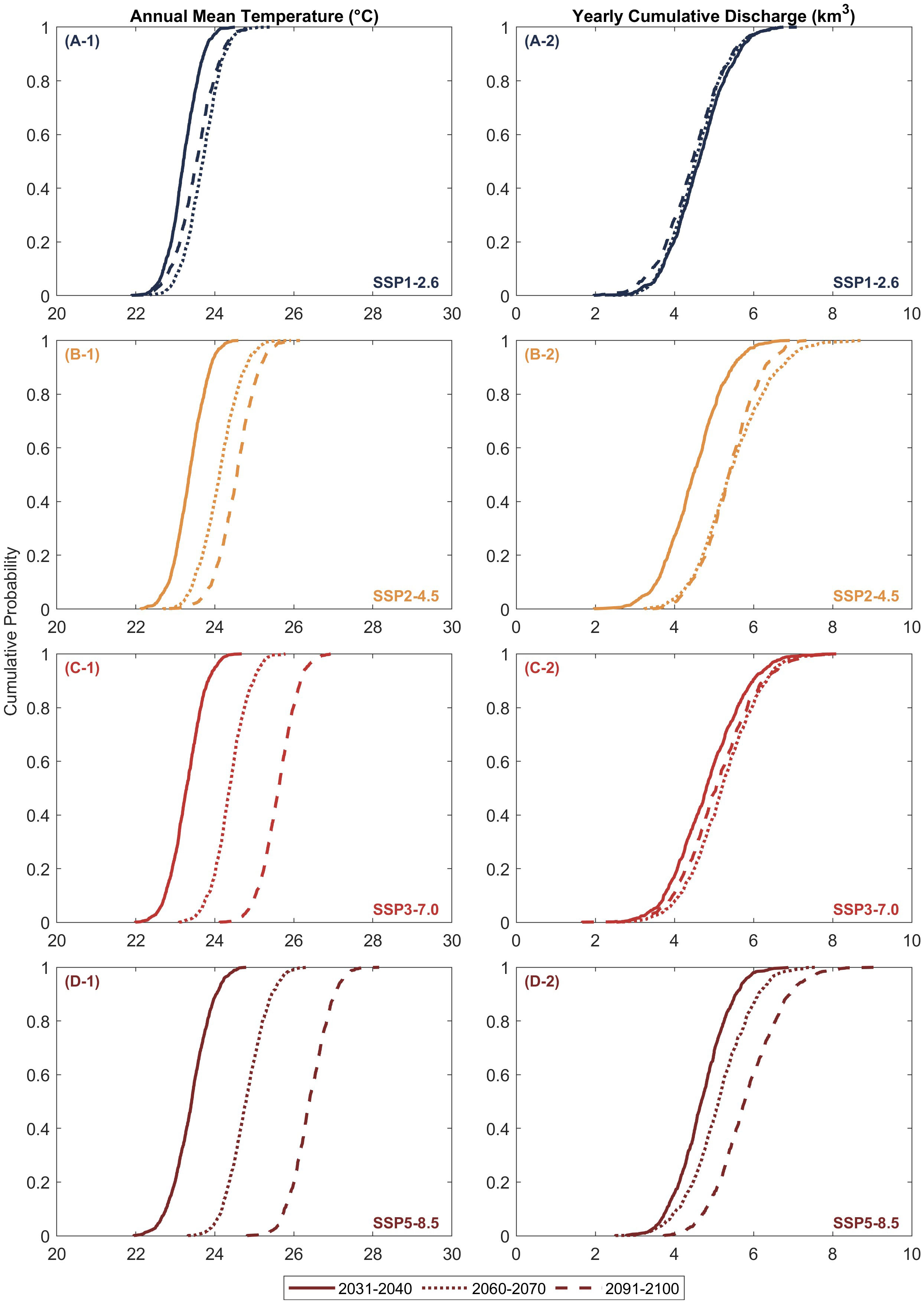
Figure 4 Empirical cumulative distributions of averaged annual mean temperature (A-1, B-1, C-1, D-1) and annual cumulative discharge (A-2, B-2, C-2, D-2) of the Thu Bon River catchment, Vietnam, over the three decadal periods considered.

FIGURE 5

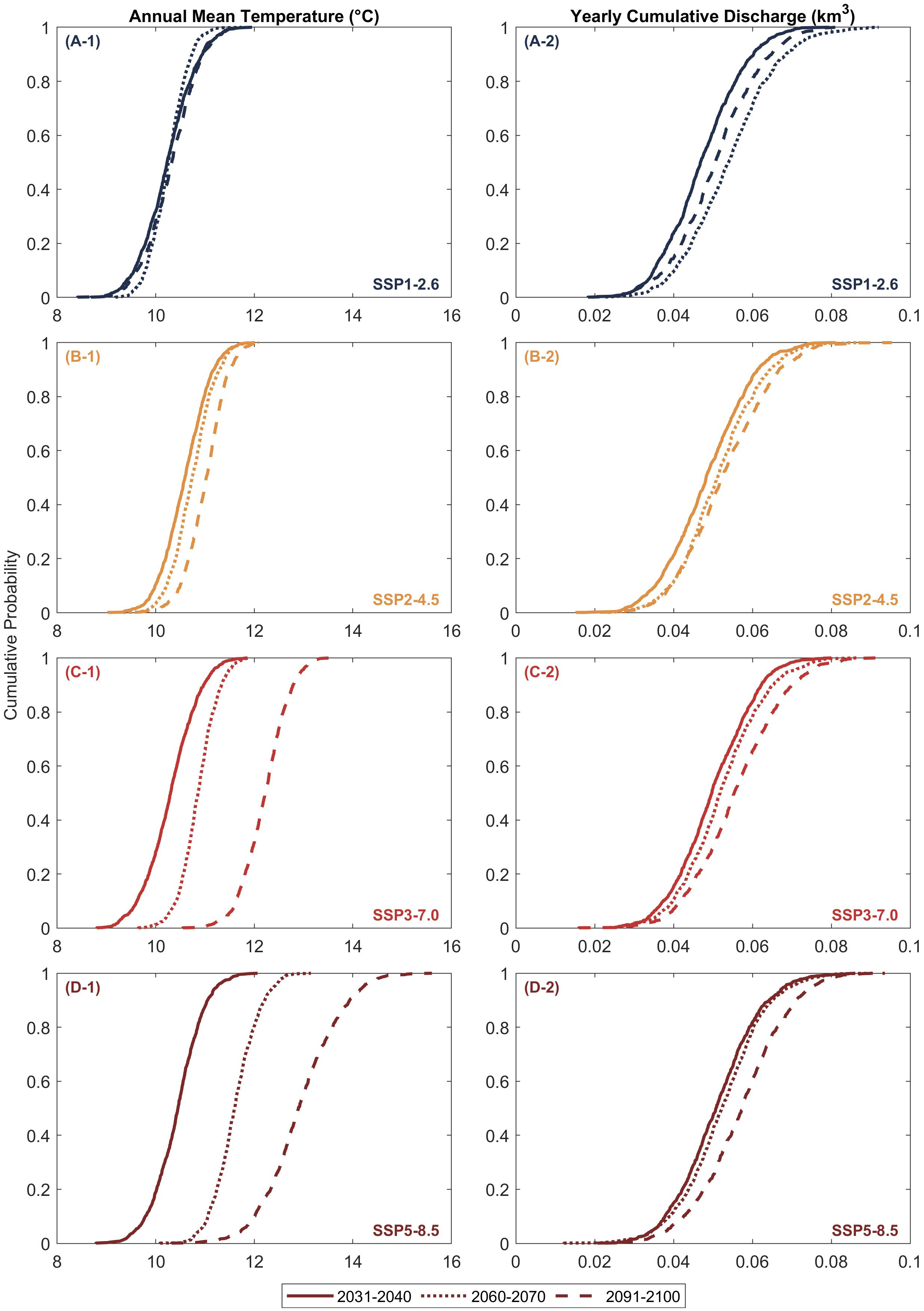
Figure 5 Empirical cumulative distributions of averaged annual mean temperature (A-1, B-1, C-1, D-1) and annual cumulative discharge (A-2, B-2, C-2, D-2) of the Mawddach River catchment, Wales, United Kingdom, over the three decadal periods considered.

Figure 4, left column, illustrates the empirical cumulative distributions of the projected mean annual temperature (T) over the Thu Bon River catchment during three decadal periods considered. The figure shows that the median annual mean temperature during the end-century period (2091 - 2100) is slightly lower than that over the mid-century period (2061 - 2070) in SSP1-2.6 projections (Figure 4 (A-1)). SSP5-8.5 projections (Figure 4 (D-1)) show the largest increment of the median temperature (~3 °C) by the 2091 - 2100 period, relative to 2031 - 2040, while ~2 °C and ~1 °C increments are observed under SSP3-7.0 (Figure 4 (C-1)) and SSP2-4.5 (Figure 4 (B-1)), respectively, over the same period.

Figure 4, right column, shows the empirical cumulative distributions of the projected annual discharge (Q) of the Thu Bon River catchment. According to the projections, the median river discharge during the 70 years may only vary marginally under SSP1-2.6 (Figure 4 (A-2)). Projected Q values under SSP5-8.5 (Figure 4 (D-2)) show the largest increment (~1.5 km³/yr) by the end of the century relative to 2031 - 2040, while an increment of only ~0.25 km³/yr is shown with SSP3-7.0 (Figure 4 (C-2)) over the same period. The median Q values are projected to increase by ~1.0 km³/yr for SSP2-4.5 over the 2031 - 2100 period, with very little change (except at low exceedance probabilities) between mid- and end-century periods (Figure 4 (B-1)).

The empirical cumulative distributions of the projected mean annual temperature over the Mawddach River catchment during three decadal periods considered are shown in Figure 5, left column. The projections indicate that the median temperature (T) values may not vary over the 21^st century under SSP1-2.6 (Figure 5 (A-1)). The median T values may only increase by ~0.5 °C by the end-century period, relative to 2031-2040, under SSP2-4.5 (Figure 5 (B-1)). The median T values are projected to increase by 2 °C and 2.5 °C under SSP3-7.0 (Figure 5 (C-1)) and SSP5-8.5 (Figure 5 (D-1)), respectively, over the same period. However, high temperatures (95^th percentile) under SSP5-8.5 are projected to increase by more than 4 °C by the end-century period, relative to 2031 - 2040 (Figure 5 (D-1)).

Figure 5, right column, shows the empirical cumulative distributions of the projected annual discharge (Q) of the Mawddach River catchment. These projections show that the median Q values may increase by the end of this century for all scenarios but SSP1-2.6. Under SSP1-2.6 (Figure 5 (A-2)), the median Q value is projected to increase by mid-century and decrease during the 2091 - 2100 period. However, compared with the Thu Bon River, the annual discharge of the Mawddach River catchment is relatively small because of its small catchment size. Hence, projected changes in discharge at this site are less than 0.01 km³/yr.

4 Results

The content of this section is structured into four sub-sections. The first sub-section presents the model hindcast results for the 1985 - 2014 period (i.e., model validation). The second sub-section presents the sediment volume exchange ($\Delta V_{\text{T}}$) projections at the case study locations for the 2031 - 2100 period, followed by differences between G-SMIC (i.e., without ebb-delta) and G-SMIC+ (i.e., with ebb-delta) projections of $\Delta V_{\text{T}}$ over the same period considered. The last sub-section presents G-SMIC+ derived shoreline variations projections over the 2091 - 2100 period.

4.1 Model hindcast for the 1985 – 2014 period

The improved modelling technique (i.e., G-SMIC+) was first applied deterministically to the 1985–2014 period to gain confidence in its capabilities. For this model hindcast, yearly values of T and Q over the historical period (1985 - 2014) were obtained from the ensemble of the selected four GCMs. The mean values of the GCM ensembles over 1970 - 1984 were taken as the reference climatic inputs (i.e., reference T and Q) for the hindcast period. The rate of sea level rise was taken as 2.1 mm/yr for the hindcast period (Oppenheimer et al., 2019). The present value of HFPI was considered to remain invariant over the hindcast period. Since there are no records of the exchange sediment volumes at the selected system, hindcasted $\Delta V_{\text{T}}$were used to compute the rate of coastline change over the same period to compare with satellite-image-derived ambient shoreline change rates presented by Luijendijk et al. (2018).

The comparison of model hindcasts shown in Table 2 indicates a reasonable agreement with the ambient shoreline change rates presented by Luijendijk et al. (2018) over the same period, providing confidence in the model’s capability to simulate the evolution of inlet-interrupted shorelines with ebb-delta dynamics.

TABLE 2

Table 2 Comparison of the model hindcasted rates of coastline change over 1985 - 2014 with the ambient shoreline change rates presented by Luijendijk et al. (2018) over the same period.

4.2 Projected total sediment volume exchange ($\Delta V_T$) at case study locations

Figures 6 and 7 show median (50^th percentile) values of the cumulative and yearly sediment volume exchanged ($\Delta V_{\text{T}}$) at Thu Bon estuary system, Vietnam and Mawddach estuary system, Wales, UK, respectively, for all four climate change scenarios considered here. These yearly $\Delta V_{\text{T}}$ values were used to compute the updated sediment volume changes by incorporating the ebb-delta dynamics.

FIGURE 6

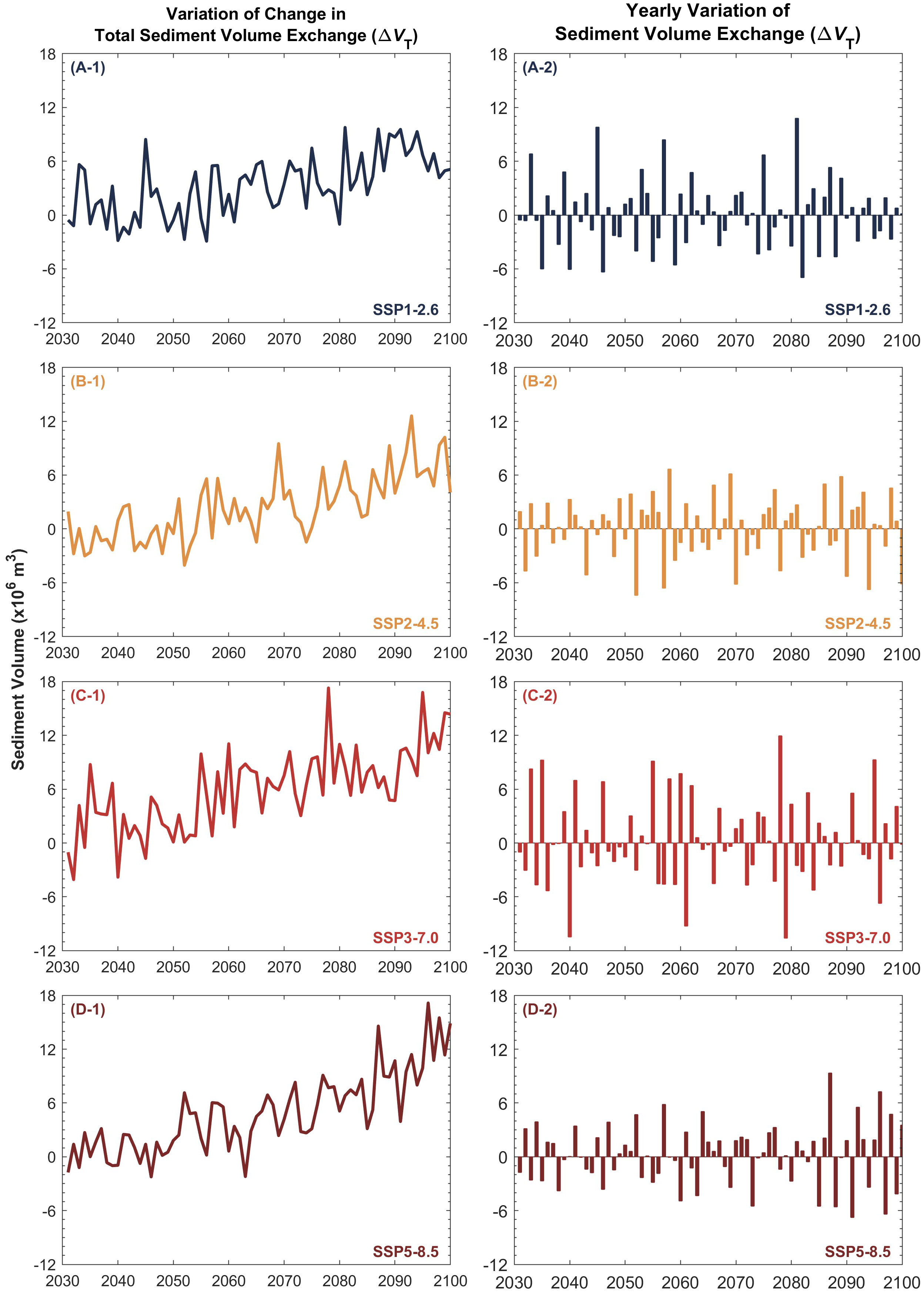
Figure 6 Projected median (50^th percentile) total sediment volume exchange ($\Delta V_{\text{T}}$ ) between the Thu Bon estuary system and the coastal zone (A-1, B-1, C-1, D-1) and the yearly variation of the median $\Delta V_{\text{T}}$ considered in ebb-delta dynamics (A-2, B-2, C-2, D-2) over the 21^st century. The negative and positive values indicate sediment export from and sediment import to the estuary, respectively.

FIGURE 7

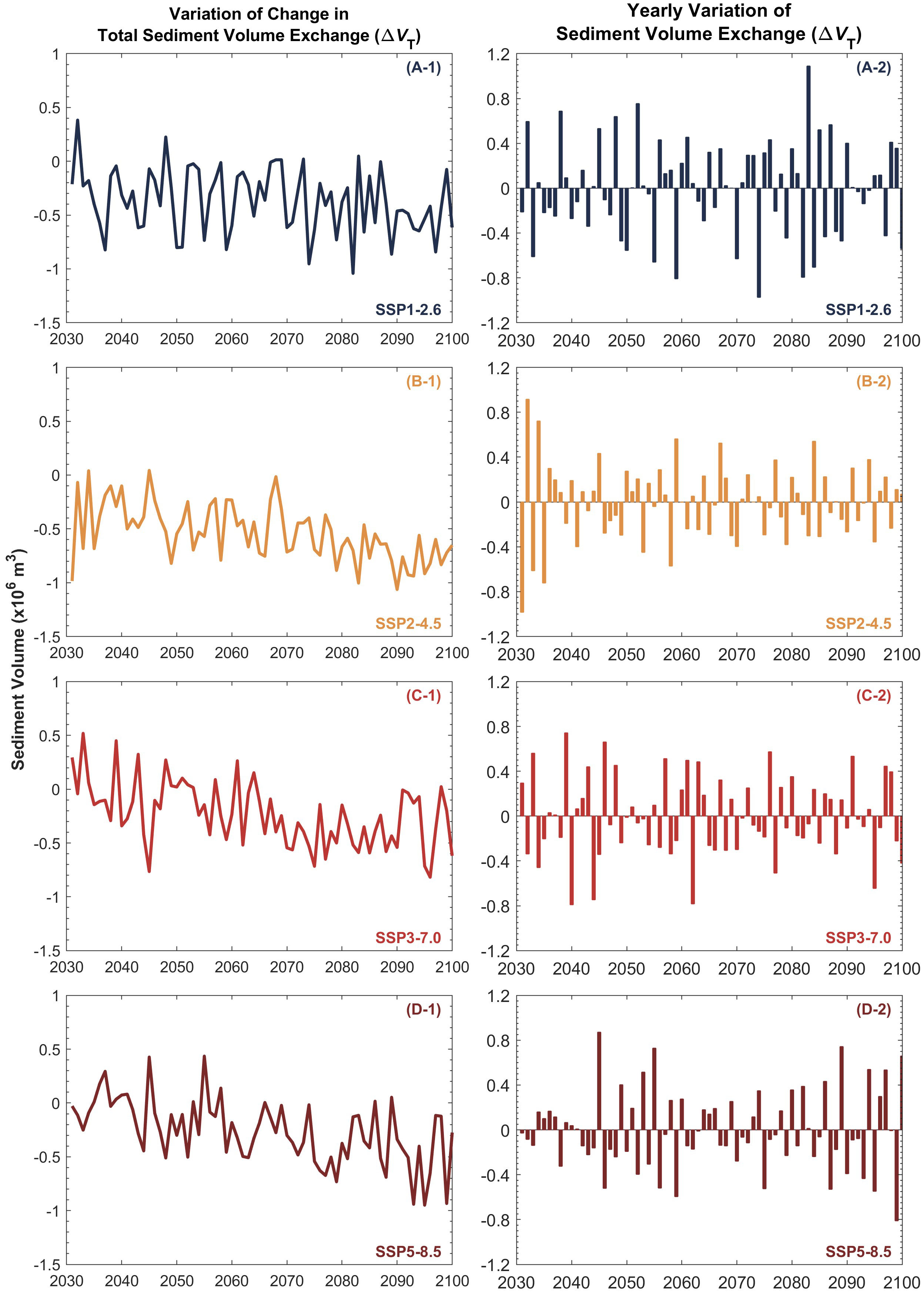
Figure 7 Projected median (50^th percentile) total sediment volume exchange ($\Delta V_T$ ) between the Mawddach estuary system and the coastal zone (A-1, B-1, C-1, D-1) and the yearly variation of the median $\Delta V_{\text{T}}$ considered in ebb-delta dynamics (A-2, B-2, C-2, D-2) over the 21^st century. The negative and positive values indicate sediment export from and sediment import to the estuary, respectively.

It is noteworthy that there are significant fluctuations in yearly $\Delta V_{\text{T}}$ at both the systems considered (Figures 6 and 7), which directly affect the projected variation of the respective shorelines. Accordingly, both systems undergo all three types of simulations considered under the G-SMIC+ modelling framework during the study period (Section 2.3.). For all four climate scenarios, despite having a positive $\Delta V_{\text{T}}$ (i.e., sediment export from the estuary) at the end of the 21^st century (Figure 6, left column), the Thu Bon estuary system imports sediment (i.e., negative $\Delta V_{\text{T}}$) during ~50% of the duration considered in this study (Figure 6, right column). Similarly, while having a negative $\Delta V_{\text{T}}$ by 2100 for all four climate scenarios considered, the Mawddach estuary system exports sediment for ~50% of the time considered in this study (Figure 7). Table 3 illustrates the details of $\Delta V_{\text{T}}$ and system behaviour type variations projected at the study locations over the 2031 - 2100 period, indicating that the two systems switch among the three system behavioural types (exporting, importing Type 1, and importing Type 2), with both systems predominantly behaving as sediment exporting or Type 2 sediment importing systems through the study period.

TABLE 3

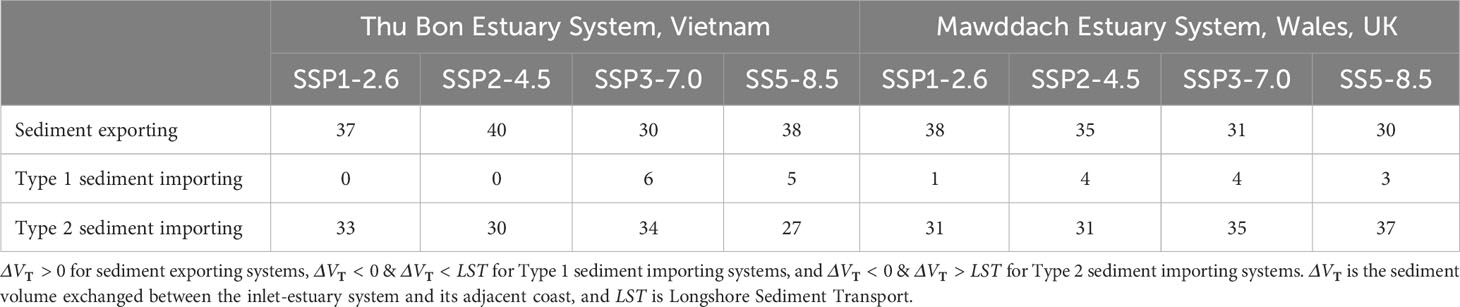
Table 3 Number of years when the selected inlet-estuary systems behave as sediment exporting and Type 1/Type 2 sediment importing systems over the 2031 - 2100 period.

4.3 Differences between G-SMIC (without ebb-delta) and G-SMIC+ (with ebb-delta) projections of sediment volume changes along up- and down-drift shorelines

In this sub-section, we discuss the differences between G-SMIC (without ebb-delta) and G-SMIC+ (with ebb-delta) projections for the two case studies. Note that, with the introduction of ebb-delta dynamics into computations, sediment volume projections of G-SMIC+ are obtained separately for up- and down-drift coasts, which results in separate assessments of subsequent shoreline variations along the respective coastlines (see Section 4.4).

Figure 8 shows the projected median cumulative sediment volume variation along the up-drift coast of Thu Bon estuary (left column) and Mawddach estuary (right column). In general, the presence of the ebb-delta decreases the sediment volume eroded from the up-drift coast to satisfy the estuary sediment demand. At the Thu Bon estuary, the largest reduction (from G-SMIC to G-SMIC+) in up-drift eroding volume over the study period (~30 MCM) is projected under SSP3-7.0, while the smallest reduction of ~25 MCM is projected under SSP5-8.5. The projections under SSP1-2.6 and SSP2-4.5 show a similar decrease in up-drift eroding volume (~30 MCM) over the 2031 - 2100 period.

FIGURE 8

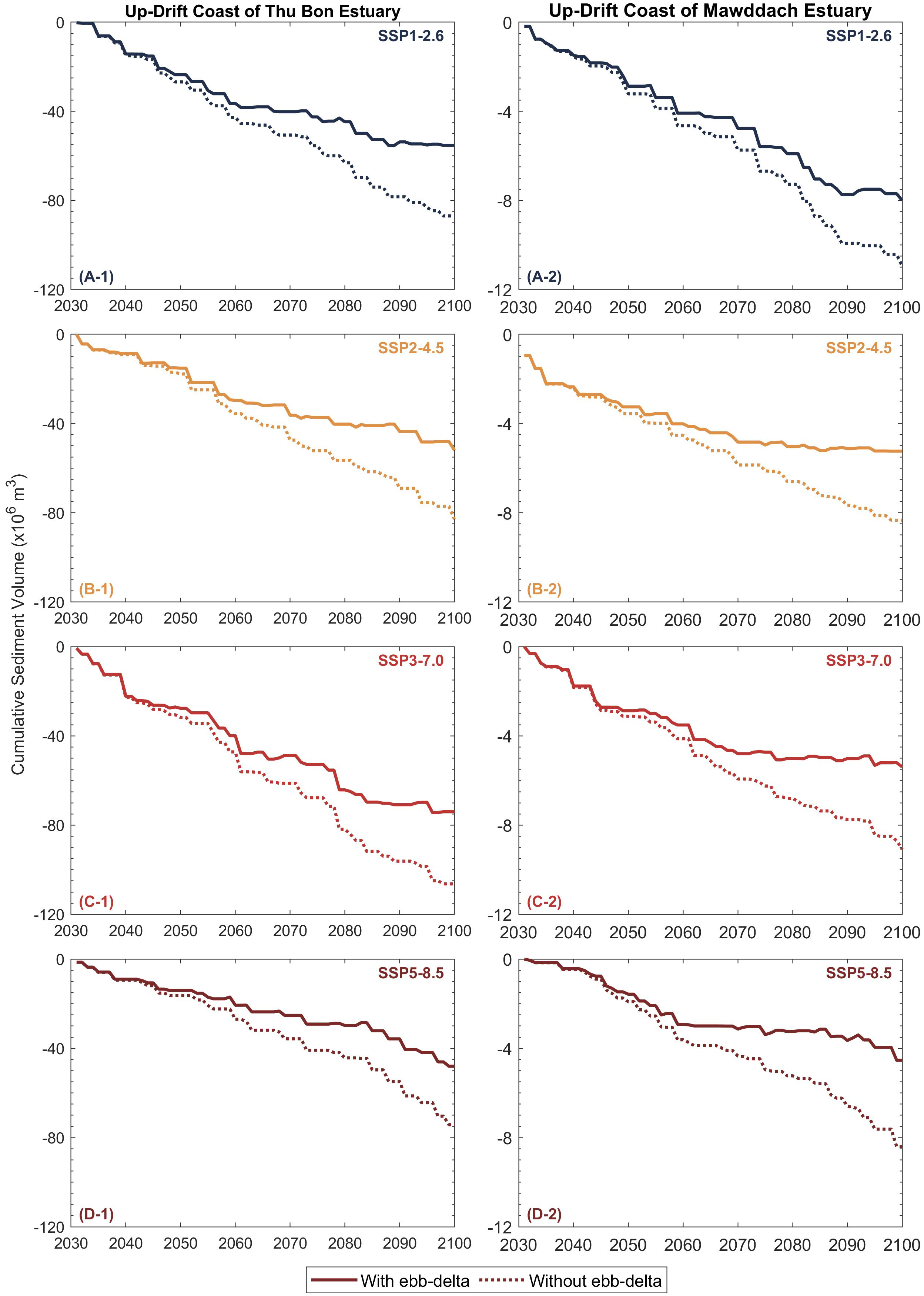
Figure 8 Projected median (50^th percentile) cumulative sediment volume change along the up-drift coast of the Thu Bon estuary (A-1, B-1, C-1, D-1) and Mawddach estuary (A-2, B-2, C-2, D-2) over the 21^st century. Negative values indicate shoreline erosion.

At the Mawddach estuary, the reductions in the up-drift eroding volume due to the inclusion of ebb-delta dynamics are much lower than at the Thu Bon estuary, with the largest reduction (~4 MCM) projected under SSP3-7.0 and SSP5-8.5 over the same period. These differences between the G-SMIC and G-SMIC+ projections are largely due to the representation of the Type 2 sediment importing behaviour (Table 3) of both systems in the latter. When $\Delta V_{\text{T}}$ > LST, in G-SMIC, all the additional sediment required to satisfy $\Delta V_{\text{T}}$ (i.e., LST - $\Delta V_{\text{T}})$ is taken from the coast, leading to shoreline retreat. However, in G-SMIC+, part of LST - $\Delta V_{\text{T}}$ is taken from the ebb-delta, and therefore, the amount of sediment eroded from the coast, and hence the resulting shoreline retreat, is less than that computed with G-SMIC.

Figure 9 illustrates the projected median cumulative sediment volume variation along the down-drift coast of Thu Bon estuary (left column) and Mawddach estuary (right column) over the 21^st century. Accordingly, the down-drift coasts of both case study sites are projected to prograde under all projection scenarios considered over the 2031 - 2100 period. Here, the Thu Bon estuary system shows hardly any differences in projected sediment volume changes obtained from both modelling frameworks (i.e., G-SMIC+ and G-SMIC), implying that the inclusion of ebb-delta sediment dynamics into the overall sediment budget has minimal impact on the behaviour of this system. The largest cumulative accretion volume change by 2100 is projected under SSP3-7.0 (~120 MCM), whereas the least (~85 MCM) is expected to occur under SSP2-4.5 and SSP5-8.5.

FIGURE 9

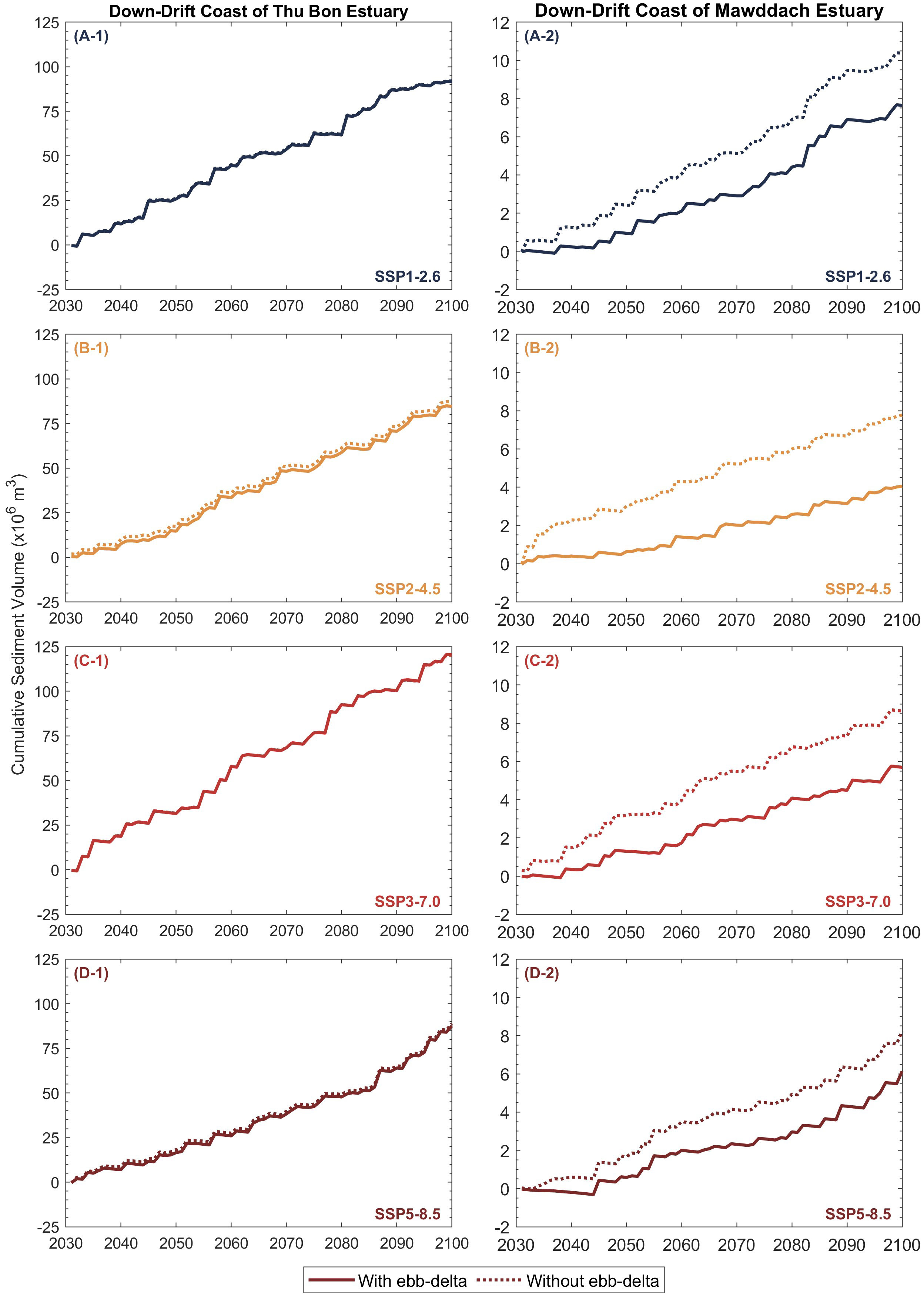
Figure 9 Projected median (50^th percentile) cumulative sediment volume change along the down-drift coast of the Thu Bon estuary (A-1, B-1, C-1, D-1) and Mawddach estuary (A-2, B-2, C-2, D-2) over the 21^st century. Positive values indicate shoreline accretion.

However, at the Mawddach estuary system, the inclusion of ebb-delta sediment dynamics into the overall sediment budget computations (i.e., G-SMIC+) has considerable implications on the down-drift coast evolution, where G-SMIC+ projections show reductions in the accretion sediment volumes under all projection scenarios over the 2031 - 2100 period (when compared with G-SMIC projections). At the Mawddach estuary, the largest reduction (from G-SMIC to G-SMIC+) in down-drift prograding volume over the study period (~4 MCM) is projected under SSP2-4.5, while the smallest reduction of ~2 MCM is projected under SSP5-8.5. The projections under SSP1-2.6 and SSP3-7.0 show a similar decrease in down-drift prograding volume (~3 MCM) over the 2031 - 2100 period.

These differences in projected down-drift sediment volume reductions from G-SMIC to G-SMIC+ at the Mawddach estuary system are due to the relatively small sediment volumes released from its ebb-delta system. When ebb-delta dynamics are not considered (i.e., in G-SMIC), the sediment volume exported from the inlet-estuary system directly contributes to the down-drift shoreline progradation. However, when ebb-delta dynamics are considered (i.e., G-SMIC+), both LST and the sediment volume exported from the inlet-estuary system contribute to the growth of the ebb-delta system (i.e., $Q_{\text{in}}$, [10], when an estuary exports sediment to its adjacent coastal zone). Under the assumptions invoked here regarding a balanced sediment budget within coastal cells, the down-drift coasts will then receive only a fraction of the sediment released from the ebb-delta system (i.e., $Q_{down-drift}$, [11]).

4.4 Projected shoreline variations at case study locations

The up-drift shoreline retreats over the 2091 - 2100 period, projected by G-SMIC and G-SMIC+ at both sites, are shown in Figure 10 and tabulated in Table 4. These results show that the presence of the ebb delta decreases up-drift shoreline retreat (by the end of the 21^st century, relative to 2030) at Thu Bon estuary and Mawddach estuary by 62 – 87 m (or 35% - 37%) and 86 – 120 m (or 25% - 48%), respectively. Moreover, the presence of the ebb-delta decreases the projected progradation of the down-drift coast at the Mawddach estuary system by 20 - 37 m (or 27% - 50%) by the end of the 21^st century, relative to 2030 (Table 4).

FIGURE 10

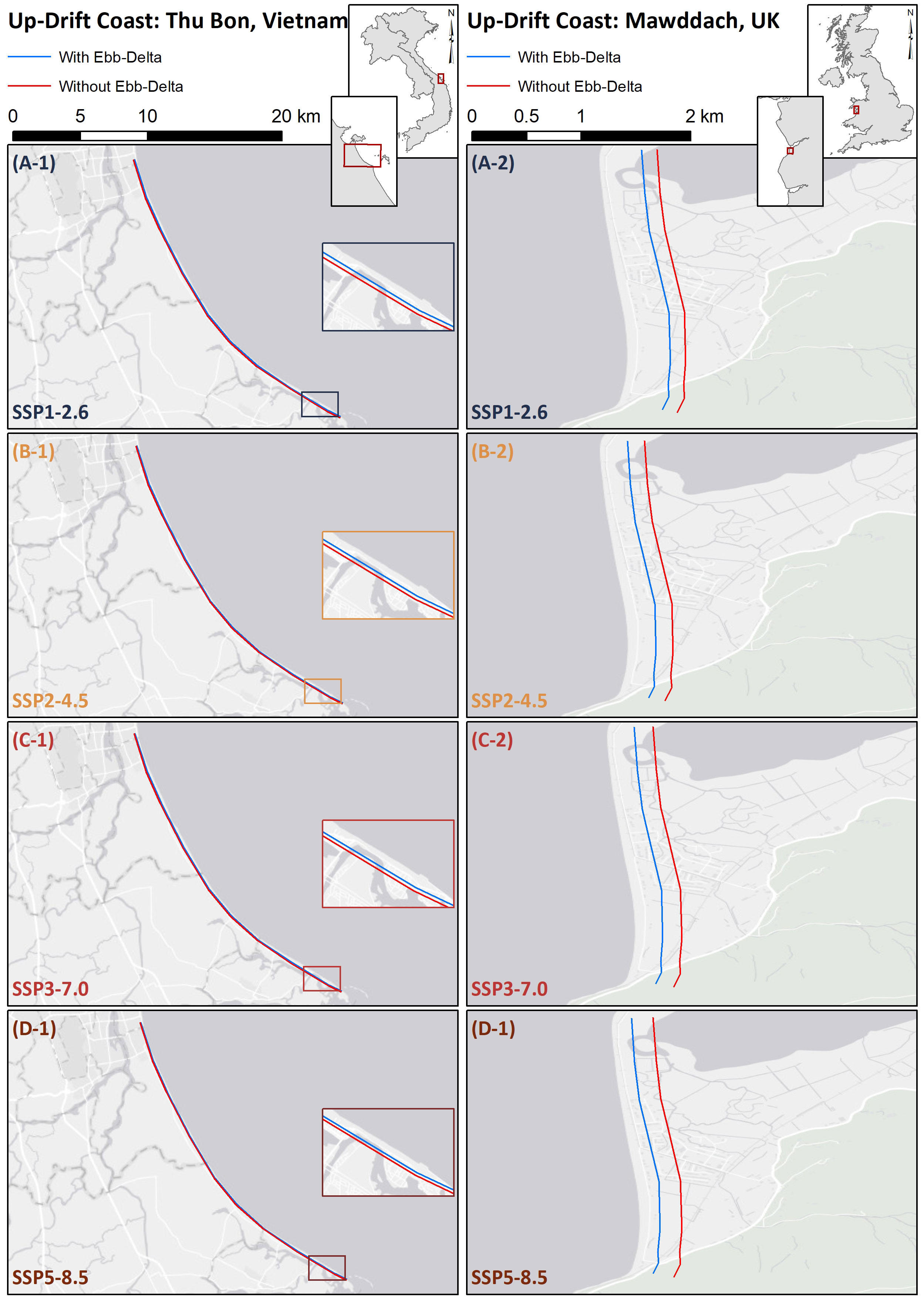
Figure 10 Projected median (50^th percentile) up-drift shoreline retreat by the end of the 21^st century period (2091 - 2100, relative to 2030) at Thu Bon estuary (A-1, B-1, C-1, D-1) and Mawddach estuary (A-2, B-2, C-2, D-2) with (i.e., G-SMIC+) and without (G-SMIC) ebb-delta dynamics.

TABLE 4

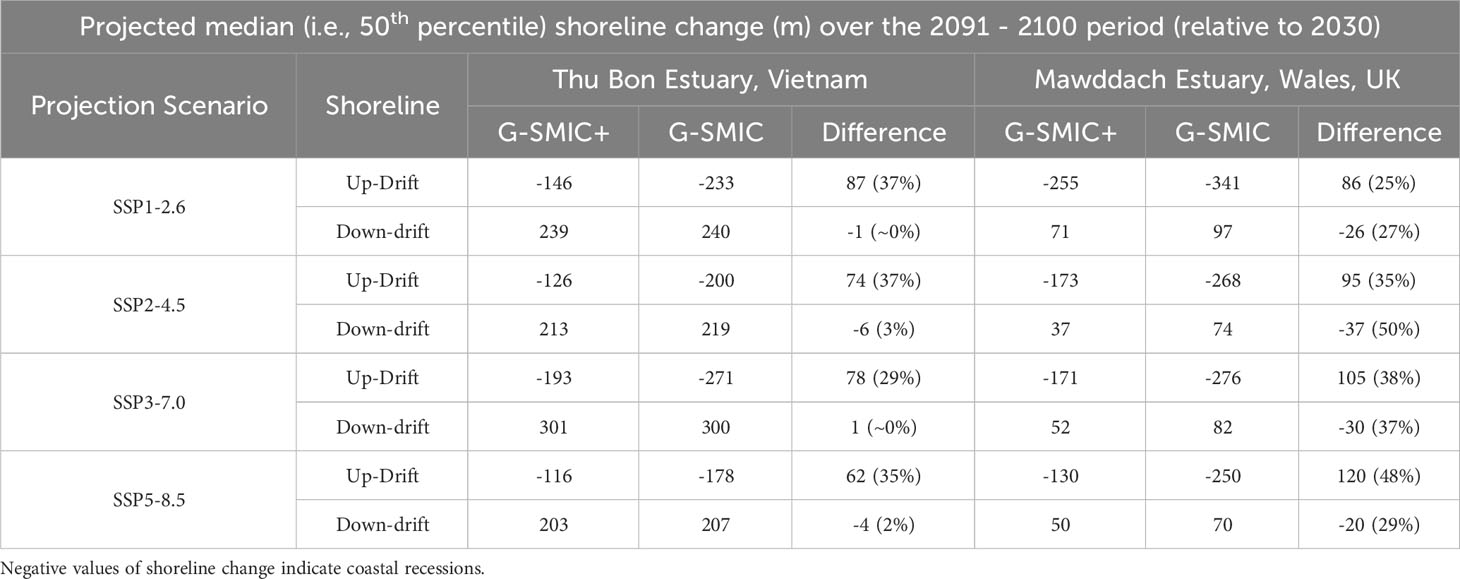
Table 4 Projected median (50^th percentile) shoreline variations for the end-century period (2091 - 2100; relative to 2030) without (i.e., G-SMIC) and with (i.e., G-SMIC+) ebb-delta dynamics at Thu Bon and Mawddach estuaries for the four climate scenarios considered.

5 Discussion

Application of the G-SMIC+ to the selected case study sites indicates that including ebb-delta sediment dynamics into the overall sediment budget significantly impacts the evolution of adjacent shorelines. The model applications also show that the impacts of ebb-delta dynamics on the behaviour of inlet-interrupted coasts may vary markedly from system to system. While the inclusion of ebb-delta dynamics may reduce the up-drift shoreline retreat, the impacts on the evolution of the down-drift shoreline may vary based on the ebb-delta system and the prevailing longshore sediment transport capacity at the vicinity.

It is noteworthy that the shoreline variation projected by G-SMIC+ are essentially future deviations of inlet-interrupted coasts from the reference (or present-day) average conditions (i.e., present-day rate of shoreline change), resulting from the perturbations of riverine sediment and flow rates and sea-level-rise rates that are greater than present conditions. Hence, the results presented in this study must always be interpreted with reference to the present-day conditions. Furthermore, shoreline changes computed here are based on the simplified method presented by Ranasinghe et al. (2013) and do not account for any possible variation in longshore sediment transport rates and gradients therein or changes to the cross-shore profile due to future changes in wave conditions. This simplified method also does not account for local variations in coastal orientation or, where applicable, the impact of any coastal structures (i.e., G-SMIC+ assumes that there are no coastal structures present in the study area). The model also does not account for any limitation in sand availability along up- and down-drift coasts. It is also worth mentioning that we only focused on the tidal-inlet systems connected to estuaries that receive substantial riverine flow/sediment. Such systems were selected to continue the larger research ambitions of enhancing the understanding of source-to-sink behaviour of catchment-estuary-coastal systems. Hence, the findings of this study cannot be directly related to systems with little or no significant riverine contributions.

Table 5 compares median (i.e., 50^th percentile) shoreline change projections at the two case study locations by 2100 with similar projections presented in two other studies (i.e., Vousdoukas et al. (2020) and Bamunawala et al. (2021)). In their global assessment of sandy coastline variations, Vousdoukas et al. (2020) did not explicitly account for estuarine and river catchment effects when computing shoreline recession. The global assessment of inlet-interrupted shorelines presented by Bamunawala et al. (2021) utilises G-SMIC, thus accounting for the holistic behaviour of catchment-estuary-coastal systems but without the ebb-delta effects added here in G-SMIC+. Thus, the projected shoreline variations presented in this study and the global assessment of inlet-interrupted coasts presented by Bamunawala et al. (2021) will, by necessity, differ from the projections of sandy shoreline variations presented by Vousdoukas et al. (2020).

TABLE 5

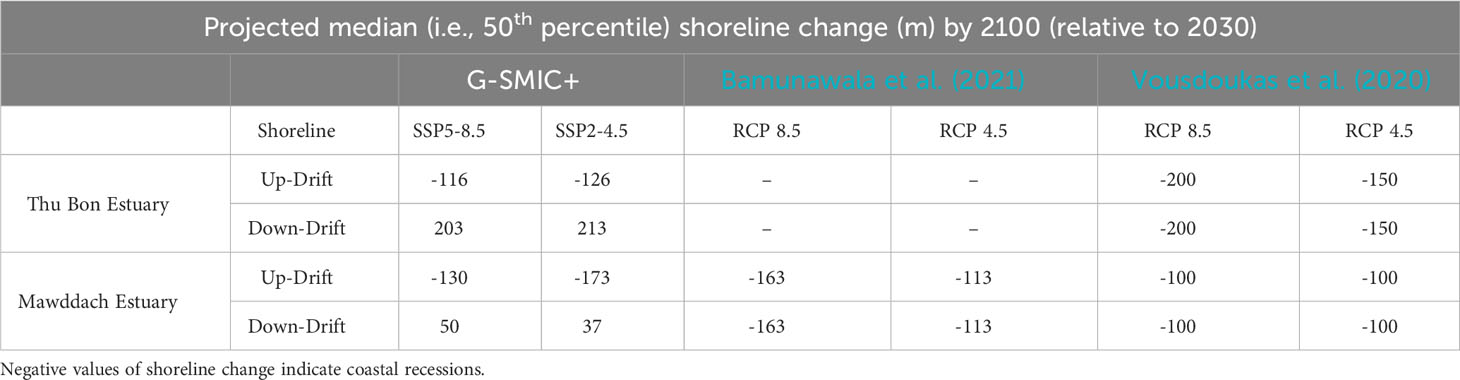
Table 5 Comparison of projected median (i.e., 50^th percentile) shoreline change at Thu Bon and Mawddach estuaries by 2100 with the shoreline variations presented in other published literature.

In comparing the results of this study with that of Bamunawala et al. (2021), it should be noted that, in G-SMIC applications, shoreline variations are projected by considering the total up- and down-drift inlet-affected shoreline distances (i.e., without treating the two shorelines separately, as done in the present study) and by distributing the cumulative change in sediment volume exchange ($\Delta V_{\text{T}}$) over that total shoreline distance. Thus, the negative sediment budget projected at the Mawddach estuary system over 2091 - 2100 results in an overall shoreline retreat in Bamunawala et al. (2021)’s projections. By introducing ebb-delta sediment dynamics into the overall sediment budget and computing the up- and down-drift sediment volumes that contribute to their shoreline evolution, G-SMIC+ has substantially improved its applicability at a broader range of inlet-interrupted coast coasts (when compared with G-SMIC).

6 Conclusions

The G-SMIC model was extended (G-SMIC+) by including ebb-delta dynamics into the modelling framework and applied at two selected case study locations (Thu Bon estuary system, Vietnam and Mawddach estuary system, Wales, UK) to assess the impact of ebb-delta dynamics on shoreline evolution over the 21^st century. G-SMIC+ can simulate the evolution of inlet-interrupted coasts and their interaction with ebb-deltas over multi-decadal/century periods. The ebb-delta system is represented in G-SMIC+ as sediment reservoirs interacting with the longshore sediment transport and estuarine sediment demand/supply, subsequently affecting the long-term evolution of inlet-interrupted coasts. Model hindcasts of G-SMIC+ at both case study locations show reasonable agreement with available records of shoreline variations, providing sufficient confidence to apply the model in projection mode.

The application of G-SMIC+ at Thu Bon estuary (Vietnam) and Mawddach estuary (UK) over the 21^st century under four of the IPCC AR6 climate scenarios (i.e., SSP1-2.6, SSP2-4.5, SSP3-7.0, and SSP5-8.5) using CMIP6 projections indicate that both systems switch between sediment exporting and sediment importing systems over the study period considered. The inclusion of ebb-delta dynamics does not affect the down-drift shoreline at the Thu Bon estuary system in a noticeable way, but it reduces the progradation of the down-drift coast of the Mawddach estuary by 27% - 50% by the end of the 21^st century (relative to 2030). The erosion volumes (by 2100, relative to 2030) of the up-drift shoreline decrease noticeably (30% - 37% and 27% - 46% decrease at Thu Bon and Mawddach estuaries, respectively) when ebb-delta dynamics are taken into account. Consequently, the inclusion of ebb-delta dynamics also decreases the up-drift shoreline retreat (by the end of the 21^st century, relative to 2030) by 29% - 37% and 25%- 48% at Thu Bon and Mawddach estuaries, respectively. These results indicate that the inclusion of ebb-delta dynamics in modelling the response of inlet-interrupted coasts to climate change is important.

Here, G-SMIC+ was piloted at only two inlet-estuary systems. Application of the model at more systems with diverse climatic and geographic conditions is necessary to gain more insights into the model’s strengths and limitations.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author contributions

JB and RR conceived and designed the study. JB developed the model, carried out all model applications, and wrote the first draft of the manuscript. TS assisted with GCM data collection and catchment delineation. All authors contributed to the article and approved the submitted version.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This study was supported by the Deltares Internal Research Programme ‘Long Term Evolution of Deltas’ and the AXA Research Fund.

Acknowledgments

Professor Magnus Larson (Lund University, Sweden) is gratefully acknowledged for providing invaluable advice and guidance on the ebb-delta dynamics-related aspects during the model development. Last of the Wild Project, Global Human Footprint, Version 3 data were developed by Venter, O., E. W. Sanderson, A. Magrach, J. R. Allan, J. Beher, K. R. Jones, H. P. Possingham, W. F. Laurance, P. Wood, B. M. Fekete, M. A. Levy, and J. E. Watson. 2018. Last of the Wild Project, Version 3 (LWP-3): 2009 Human Footprint, 2018 Release. Palisades, New York: NASA Socioeconomic Data and Applications Center (SEDAC). https://doi.org/10.7927/H46T0JQ4. Accessed 01-03-2023.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2023.1224881/full#supplementary-material

References

Anthony E. J. (2015). Wave influence in the construction, shaping and destruction of river deltas: A review. Mar. Geol 361, 53–78. doi: 10.1016/j.margeo.2014.12.004

CrossRef Full Text | Google Scholar

Aubrey D. G., Weishar L. (1988). Hydrodynamics and sediment dynamics of tidal inlets (New York, NY: Springer New York). doi: 10.1007/978-1-4757-4057-8

CrossRef Full Text | Google Scholar

Bamunawala J., Dastgheib A., Ranasinghe R., van der Spek A., Maskey S., Murray A. B., et al. (2020a). A holistic modeling approach to project the evolution of inlet-interrupted coastlines over the 21st century. Front. Mar. Sci. 7. doi: 10.3389/fmars.2020.00542

CrossRef Full Text | Google Scholar

Bamunawala J., Dastgheib A., Ranasinghe R., van der Spek A., Maskey S., Murray A. B., et al. (2020b). Probabilistic application of an integrated catchment-estuary-coastal system model to assess the evolution of inlet-interrupted coasts over the 21st century. Front. Mar. Sci. 7. doi: 10.3389/fmars.2020.579203

CrossRef Full Text | Google Scholar

Bamunawala J., Maskey S., Duong T. M., van der Spek A. (2018). Significance of fluvial sediment supply in coastline modelling at tidal inlets. J. Mar. Sci. Eng. 6, 79. doi: 10.3390/jmse6030079

CrossRef Full Text | Google Scholar

Bamunawala J., Ranasinghe R., Dastgheib A., Nicholls R. J., Murray A. B., Barnard P. L., et al. (2021). Twenty-first-century projections of shoreline change along inlet-interrupted coastlines. Sci. Rep. 11, 14038. doi: 10.1038/s41598-021-93221-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Besset M., Anthony E. J., Bouchette F. (2019). Multi-decadal variations in delta shorelines and their relationship to river sediment supply: An assessment and review. Earth Sci. Rev. 193, 199–219. doi: 10.1016/j.earscirev.2019.04.018

CrossRef Full Text | Google Scholar

Brown S., Nicholls R. J., Hanson S., Brundrit G., Dearing J. A., Dickson M. E., et al. (2014). Shifting perspectives on coastal impacts and adaptation. Nat. Clim Chang 4, 752–755. doi: 10.1038/nclimate2344

CrossRef Full Text | Google Scholar

Bruun P. M. (1962). Sea-level rise as a cause of shore erosion. Am. Soc. Civil Engineers Proceeding J. Waterways Harbors Division 88, 117–132. doi: 10.1061/JWHEAU.0000252

CrossRef Full Text | Google Scholar

Davenport J., Davenport J. L. (2006). The impact of tourism and personal leisure transport on coastal environments: A review. Estuar. Coast. Shelf Sci. 67, 280–292. doi: 10.1016/j.ecss.2005.11.026

CrossRef Full Text | Google Scholar

Davidson-Arnott R. (2011). “Wave-dominated coasts,” in Treatise on estuarine and coastal science. Eds. Wolanski E., McLusky D. (Waltham: Academic Press), 73–116. doi: 10.1016/B978-0-12-374711-2.00305-3

CrossRef Full Text | Google Scholar

Davies J. L. (1980). Geographical variation in coastal development. 2nd edition (London; New York: Longman).

Google Scholar

Davis R. A. (2003). “Coastal geology,” in Encyclopedia of physical science and technology, 3rd ed.Ed. Meyers R. A. (New York: Academic Press), 123–153doi: 10.1016/B0-12-227410-5/00113-7

CrossRef Full Text | Google Scholar

Davis R. A. (2019). “Human impact on coasts,” in Encyclopedia of coastal science. Eds. Finkl C. W., Makowski C. (Cham: Springer International Publishing), 983–991. doi: 10.1007/978-3-319-93806-6_175

CrossRef Full Text | Google Scholar

Davis R. A., Hayes M. O. (1984). What is a wave-dominated coast? Marien Geology 60, 313–329. doi: 10.1016/0025-3227(84)90155-5

CrossRef Full Text | Google Scholar

Davis-Jr. R. A., Fitzgerald D. M. (2003). Beaches and coasts (Hoboken, NJ: Wiley-Blackwell).

Google Scholar

Dissanayake D. M. P. K., Ranasinghe R., Roelvink J. A. (2012). The morphological response of large tidal inlet/basin systems to relative sea level rise. Clim Change 113, 253–276. doi: 10.1007/s10584-012-0402-z

CrossRef Full Text | Google Scholar

Dissanayake D. M. P. K., Roelvink J. A., van der Wegen M. (2009). Modelled channel patterns in a schematized tidal inlet. Coast. Eng. 56, 1069–1083. doi: 10.1016/j.coastaleng.2009.08.008

CrossRef Full Text | Google Scholar

Duong T. M. (2021). Climate change induced coastline change adjacent to small tidal inlets. Front. Mar. Sci. 8. doi: 10.3389/fmars.2021.754756

CrossRef Full Text | Google Scholar

Duong T. M. T. M., Ranasinghe R., Thatcher M., Mahanama S., Wang Z. B. Z. B. Z. B., Dissanayake P. K. P. K. P. K., et al. (2018). Assessing climate change impacts on the stability of small tidal inlets: Part 2 - Data rich environments. Mar. Geol 395, 65–81. doi: 10.1016/j.margeo.2017.09.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Dürr H. H., Laruelle G. G., van Kempen C. M., Slomp C. P., Meybeck M., Middelkoop H. (2011). Worldwide typology of nearshore coastal systems: defining the estuarine filter of river inputs to the oceans. Estuaries Coasts 34, 441–458. doi: 10.1007/s12237-011-9381-y

CrossRef Full Text | Google Scholar

Egbert G. D., Erofeeva S. Y. (2002). Efficient inverse modeling of barotropic ocean tides. J. Atmos Ocean Technol. 19, 183–204. doi: 10.1175/1520-0426(2002)019<0183:EIMOBO>2.0.CO;2

CrossRef Full Text | Google Scholar

Elias E. P. L., van der Spek A. J. F. (2006). Long-term morphodynamic evolution of Texel Inlet and its ebb-tidal delta (The Netherlands). Mar. Geol 225, 5–21. doi: 10.1016/j.margeo.2005.09.008

CrossRef Full Text | Google Scholar

Farr T. G., Rosen P. A., Caro E., Crippen R., Duren R., Hensley S., et al. (2007). The shuttle radar topography mission. Rev. Geophysics 45, RG2004. doi: 10.1029/2005RG000183

CrossRef Full Text | Google Scholar

Fenster M., Dolan R. (1996). Assessing the impact of tidal inlets on adjacent barrier island shorelines. J. Coast. Res. 12, 294–310.

Google Scholar

Fitzgerald D. M. (1984). Interactions between the ebb-tidal delta and landward shoreline: price inlet, south carolina. SEPM J. Sedimentary Res. 54. doi: 10.1306/212F85C6-2B24-11D7-8648000102C1865D

CrossRef Full Text | Google Scholar

FitzGerald D. M. (1988). “Shoreline erosional-depositional processes associated with tidal inlets,” in Hydrodynamics and sediment dynamics of tidal inlets. Eds. Aubrey L., G. D., Weishar (New York, NY: Springer New York), 186–225.

Google Scholar

FitzGerald D. M., Georgiou I., Miner M. (2015). “Estuaries and tidal inlets,” in Coastal environments and global change wiley online books. Eds. Masselink G., Gehrels R. (Chichester, UK, UK: John Wiley & Sons, Ltd). doi: 10.1002/9781119117261.ch12

CrossRef Full Text | Google Scholar

Garel E., Sousa C., Ferreira Ó., Morales J. A. (2014). Decadal morphological response of an ebb-tidal delta and down-drift beach to artificial breaching and inlet stabilisation. Geomorphology 216, 13–25. doi: 10.1016/j.geomorph.2014.03.031

CrossRef Full Text | Google Scholar

Hallegatte S., Green C., Nicholls R. J., Corfee-Morlot J. (2013). Future flood losses in major coastal cities. Nat. Clim Chang 3, 802. doi: 10.1038/nclimate1979

CrossRef Full Text | Google Scholar

Hayes M. O. (1975). “Morphology of sand accumulation in estuaries,” in Estuarine research, ed. Lewis eugene cronin (London, UK and New York: USA: Academic Press, Inc), 3–22.

Google Scholar

Hayes M. O. (1980). General morphology and sediment patterns in tidal inlets. Sediment Geol 26, 139–156. doi: 10.1016/0037-0738(80)90009-3

CrossRef Full Text | Google Scholar

He Q., Silliman B. R. (2019). Climate change, human impacts, and coastal ecosystems in the anthropocene. Curr. Biol. 29, R1021–R1035. doi: 10.1016/j.cub.2019.08.042

PubMed Abstract | CrossRef Full Text | Google Scholar

Herrling G., Winter C. (2018). Tidal inlet sediment bypassing at mixed-energy barrier islands. Coast. Eng. 140, 342–354. doi: 10.1016/j.coastaleng.2018.08.008

CrossRef Full Text | Google Scholar

Hoan L. X., Hanson H., Larson M., Kato S. (2011). A mathematical model of spit growth and barrier elongation: Application to Fire Island Inlet (USA) and Badreveln Spit (Sweden). Estuar. Coast. Shelf Sci. 93, 468–477. doi: 10.1016/j.ecss.2011.05.033

CrossRef Full Text | Google Scholar

IPCC (2023). Summary for Policymakers. In: Climate change 2023: synthesis report. contribution of working groups I, II and III to the sixth assessment report of the intergovernmental panel on climate change. [Core Writing Team, Lee H., Romero J. (eds.)]. IPCC, Geneva, Switzerland, 1–34. doi: 10.59327/IPCC/AR6-9789291691647.001

CrossRef Full Text | Google Scholar

Isla F. I. (1997). Seasonal behaviour of mar chiquita tidal inlet in relation to adjacent beaches, Argentina. J. Coast. Res. 13, 1221–1232.

Google Scholar

Jarrett J. T. (1976). “Tidal prism - inlet area relationships,” in GITI report #3. (Fort Belvoir, VA: Department of the Army Corps of Engineers).

Google Scholar

Jiménez J. A., Sánchez-Arcilla A. (2004). A long-term (decadal scale) evolution model for microtidal barrier systems. Coast. Eng. 51, 749–764. doi: 10.1016/j.coastaleng.2004.07.007

CrossRef Full Text | Google Scholar

Kana T. W., Hayter E. J., Work P. A. (1999). Mesoscale sediment transport at southeastern U.S. Tidal inlets: conceptual model applicable to mixed energy settings. J. Coast. Res. 15, 303–313.

Google Scholar

Kjerfve B. (1986). “Comparative oceanography of coastal lagoons,” in Estuarine variability. Ed. Wolfe D. A. (Newyork: Academic Press), 63–81. doi: 10.1016/B978-0-12-761890-6.50009-5

CrossRef Full Text | Google Scholar

Kjerfve B. (1994). “Chapter 1 coastal lagoons,” in Elsevier oceanography series. Ed. Kjerfve B. (Amsterdam: Elsevier), 1–8. doi: 10.1016/S0422-9894(08)70006-0

CrossRef Full Text | Google Scholar

Komar P. (1996). The budget of littoral sediments, concepts and applications. Shore Beach 64, 18–26.

Google Scholar

Komar P. D. (1998). Beach processes and sedimentation. 2nd edition (Hoboken, NJ, NJ: Prentice Hall).

Google Scholar

Kraus N. C. (1999). “Analytical model of spit evolution at inlets,” in 4th international symposium on coasting engineering and science of coastal sediment processes. Ed. McDougal W. G. (New York, USA: American Society of Civil Engineers), 1739–1754.

Google Scholar

Kraus N. C. (2000). Reservoir model of ebb-tidal shoal evolution and sand bypassing. J. Waterw Port Coast. Ocean Eng. 126, 305–313. doi: 10.1061/(ASCE)0733-950X(2000)126:6(305

CrossRef Full Text | Google Scholar

Larson M., Kraus N. C., Connell K. J. (2007). “Modeling sediment storage and transfer for simulating regional coastal evolution,” in Coastal engineering 2006. Ed. Smith J. M. (San Diego, California, USA: World Scientific Publishing Company), 3924–3936.

Google Scholar

Larson M., Kraus N. C., Hanson H. (2003). “Simulation of regional longshore sediment transport and coastal evolution - The “CASCADE” model,” in 28th international conference on coastal engineering 2002. Ed. Smith J. M. (Cardiff, Wales, UK: World Scientific Publishing Company), 2612–2624. doi: 10.1142/9789812791306_0218

CrossRef Full Text | Google Scholar

Larson M., Palalane J., Fredriksson C., Hanson H. (2016). Simulating cross-shore material exchange at decadal scale. Theory and model component validation. Coast. Eng. 116, 57–66. doi: 10.1016/j.coastaleng.2016.05.009

CrossRef Full Text | Google Scholar

Le Cozannet G., Bulteau T., Castelle B., Ranasinghe R., Wöppelmann G., Rohmer J., et al. (2019). Quantifying uncertainties of sandy shoreline change projections as sea level rises. Sci. Rep. 9, 42. doi: 10.1038/s41598-018-37017-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Luijendijk A., Hagenaars G., Ranasinghe R., Baart F., Donchyts G., Aarninkhof S. (2018). The state of the world’s beaches. Sci. Rep. 8, 6641. doi: 10.1038/s41598-018-24630-6

PubMed Abstract | CrossRef Full Text | Google Scholar

McSweeney S. L., Kennedy D. M., Rutherfurd I. D., Stout J. C. (2017). Intermittently Closed/Open Lakes and Lagoons: Their global distribution and boundary conditions. Geomorphology 292, 142–152. doi: 10.1016/j.geomorph.2017.04.022

CrossRef Full Text | Google Scholar

Moore L. J., Murray A. B. (2022). Islands on the move. Nat. Geosci 15, 602–603. doi: 10.1038/s41561-022-01000-6

CrossRef Full Text | Google Scholar

Neumann B., Vafeidis A. T., Zimmermann J., Nicholls R. J. (2015). Future coastal population growth and exposure to sea-level rise and coastal flooding - A global assessment. PloS One 10, e0118571. doi: 10.1371/journal.pone.0118571

PubMed Abstract | CrossRef Full Text | Google Scholar

Nicholls R. J., Hanson S. E., Lowe J. A., Slangen A. B. A., Wahl T., Hinkel J., et al. (2021a). Integrating new sea-level scenarios into coastal risk and adaptation assessments: An ongoing process. WIREs Climate Change 12, e706. doi: 10.1002/wcc.706

CrossRef Full Text | Google Scholar

Nicholls R. J., Lincke D., Hinkel J., Brown S., Vafeidis A. T., Meyssignac B., et al. (2021b). A global analysis of subsidence, relative sea-level change and coastal flood exposure. Nat. Clim Chang 11, 338–342. doi: 10.1038/s41558-021-00993-z

CrossRef Full Text | Google Scholar

Nummedal D., Fischer I. A. (1978). “Process-response models for depositional shorelines: the german and Georgia bights,” in Coastal engineering 1978 (New York, NY: American Society of Civil Engineers), 1215–1231. doi: 10.1061/9780872621909.072

CrossRef Full Text | Google Scholar

Oppenheimer M., Glavovic B. C., Hinkel J., van de Wal R., Magnan A. K., Abd-Elgawad A., et al (2019). “Sea level rise and implications for low-lying islands, coasts and communities” in IPCC special report on the ocean and cryosphere in a changing climate. Eds. Pörtner H. -O., Roberts D. C., Masson-Delmotte V., Zhai P., Tignor M., Poloczanska E., et al. Cambridge, UK and New York, NY, USA: Cambridge University Press, 321–445. doi: 10.1017/9781009157964.006

CrossRef Full Text | Google Scholar

Palalane J., Fredriksson C., Marinho B., Larson M., Hanson H., Coelho C. (2016). Simulating cross-shore material exchange at decadal scale. Model application. Coast. Eng. 116, 26–41. doi: 10.1016/j.coastaleng.2016.05.007

CrossRef Full Text | Google Scholar

Palalane J., Larson M. (2019). A long-term coastal evolution model with longshore and cross-shore transport. J. Coast. Res. 36, 411–423. doi: 10.2112/JCOASTRES-D-17-00020.1

CrossRef Full Text | Google Scholar

Palmer M. A., Liermann C. A. R., Nilsson C., Flörke M., Alcamo J., Lake P. S., et al. (2008). Climate change and the world’s river basins: anticipating management options. Front. Ecol. Environ. 6, 81–89.

Google Scholar

Rahmstorf S. (2007). A semi-empirical approach to projecting future sea-level rise. Science 315, 368–370. doi: 10.1126/science.1135456

PubMed Abstract | CrossRef Full Text | Google Scholar

Ranasinghe R. (2016). Assessing climate change impacts on open sandy coasts: A review. Earth Sci. Rev. 160, 320–332. doi: 10.1016/j.earscirev.2016.07.011

CrossRef Full Text | Google Scholar

Ranasinghe R. (2020). On the need for a new generation of coastal change models for the 21st century. Sci. Rep. 10, 2010. doi: 10.1038/s41598-020-58376-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Ranasinghe R., Duong T. M., Uhlenbrook S., Roelvink D., Stive M. (2013). Climate-change impact assessment for inlet-interrupted coastlines. Nat. Clim Chang 3, 83–87. doi: 10.1038/nclimate1664

CrossRef Full Text | Google Scholar

Ranasinghe R., Ruane A. C., Vautard R., Arnell N., Coppola E., Cruz F. A., et al. (2021). “Climate change information for regional impact and for risk assessment,” in Climate change 2021: the physical science basis. Contribution of working group I to the sixth assessment report of the intergovernmental panel on climate change. Eds. Masson-Delmotte V., Zhai P., Pirani A., Connors S. L., Péan C., Berger S., et al (Cambridge, United Kingdom and New York, NY, USA: Cambridge University Press), 1767–1926.

Google Scholar

Ranasinghe R., Stive M. J. F. (2009). Rising seas and retreating coastlines. Clim Change 97, 465. doi: 10.1007/s10584-009-9593-3

CrossRef Full Text | Google Scholar

Ranasinghe R., Wu C. S., Conallin J., Duong T. M., Anthony E. J. (2019). Disentangling the relative impacts of climate change and human activities on fluvial sediment supply to the coast by the world’s large rivers: Pearl River Basin, China. Sci. Rep. 9, 9236. doi: 10.1038/s41598-019-45442-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Stive M. J. F. (2004). How important is global warming for coastal erosion? Clim Change 64, 27–39. doi: 10.1023/B:CLIM.0000024785.91858.1d

CrossRef Full Text | Google Scholar

Stive M. (2006). Morphodynamics of coastal inlets and tidal lagoons. J. Coast. Res., 28–34.

Google Scholar

Stive M. J. F., Roelvink J. A., de Vriend H. J. (1990). “Large-scale coastal evolution concept,” in 22nd international conference on coastal engineering proceedings (The Netherlands: Delft), 1962–1974. doi: 10.1061/9780872627765.150

CrossRef Full Text | Google Scholar

Stive M. J. F., Wang Z. B. (2003). “Morphodynamic modeling of tidal basins and coastal inlets,” in Advances in coastal modeling. Ed. Lakhan V. C. B. T.E. O. S. (Amsterdam: Elsevier), 367–392. doi: 10.1016/S0422-9894(03)80130-7

CrossRef Full Text | Google Scholar

Stutz M. L., Pilkey O. H. (2001). A review of global barrier island distribution. J. Coast. Res., 15–22.

Google Scholar

Stutz M. L., Pilkey O. H. (2011). Open-ocean barrier islands: global influence of climatic, oceanographic, and depositional settings. J. Coast. Res. 72, 207–222. doi: 10.2112/09-1190.1

CrossRef Full Text | Google Scholar

Syvitski J. P. M., Kettner A. J., Overeem I., Hutton E. W. H., Hannon M. T., Brakenridge G. R., et al. (2009). Sinking deltas due to human activities. Nat. Geosci 2, 681–686. doi: 10.1038/ngeo629

CrossRef Full Text | Google Scholar

Syvitski J. P. M. M., Milliman J. D. (2007). Geology, geography, and humans battle for dominance over the delivery of fluvial sediment to the coastal ocean. J. Geology 115, 1–19. doi: 10.1086/509246

CrossRef Full Text | Google Scholar

Syvitski J. P. M. J. P. M., Vörösmarty C. J., Kettner, Ka. J., Green P. (2005). )Impact of humans on the flux of terrestrial sediment to the global coastal ocean. Science 308, 376–380doi: 10.1126/science.1109454

PubMed Abstract | CrossRef Full Text | Google Scholar

Toimil A., Camus P., Losada I. J., Le Cozannet G., Nicholls R. J., Idier D., et al. (2020a). Climate change-driven coastal erosion modelling in temperate sandy beaches: Methods and uncertainty treatment. Earth Sci. Rev. 202, 103110. doi: 10.1016/j.earscirev.2020.103110

CrossRef Full Text | Google Scholar

Toimil A., Losada I. J., Camus P., Díaz-Simal P. (2017). Managing coastal erosion under climate change at the regional scale. Coast. Eng. 128, 106–122. doi: 10.1016/j.coastaleng.2017.08.004

CrossRef Full Text | Google Scholar

Toimil A., Losada I. J., Nicholls R. J., Dalrymple R. A., Stive M. J. F. (2020b). Addressing the challenges of climate change risks and adaptation in coastal areas: A review. Coast. Eng. 156, 103611. doi: 10.1016/j.coastaleng.2019.103611

CrossRef Full Text | Google Scholar

Venter O., Sanderson E. W., Magrach A., Allan J. R., Beher J., Jones K. R., et al. (2016). Sixteen Years of change in the global terrestrial human footprint and implications for biodiversity conservation. Nat. Commun., 12558. doi: 10.1038/ncomms12558

PubMed Abstract | CrossRef Full Text | Google Scholar

Venter O., Sanderson E. W., Magrach A., Allan J. R., Beher J., Jones K. R., et al. (2018). Last of the wild project, version 3 (LWP-3): 2009 human footprin release (Palisades, New York: NASA Socioeconomic Data and Applications Center (SEDAC) (Accessed 01 03 2023).

Google Scholar

Vörösmarty C. J., Meybeck M., Fekete B., Sharma K., Green P., Syvitski J. P. M. (2003). Anthropogenic sediment retention: major global impact from registered river impoundments. Glob Planet Change 39, 169–190. doi: 10.1016/S0921-8181(03)00023-7

CrossRef Full Text | Google Scholar

Vousdoukas M. I., Ranasinghe R., Mentaschi L., Plomaritis T. A., Athanasiou P., Luijendijk A., et al. (2020). Sandy coastlines under threat of erosion. Nat. Clim Chang 10, 260–263. doi: 10.1038/s41558-020-0697-0

CrossRef Full Text | Google Scholar

Walton T. L., Adams W. D. (1976). “Capacity of inlet outer bars to store sand,” in Coastal engineering 1976 (New York, NY: American Society of Civil Engineers), 1919–1937. doi: 10.1061/9780872620834.112

CrossRef Full Text | Google Scholar

Woodroffe C. D. (2003). Coasts: form, process and evolution (First. Cambridge, UK: Cambridge University Press).

Google Scholar

Woodruff J. D., Irish J. L., Camargo S. J. (2013). Coastal flooding by tropical cyclones and sea-level rise. Nature 504, 44–52. doi: 10.1038/nature12855

PubMed Abstract | CrossRef Full Text | Google Scholar

Wright L. D., Nittrouer C. A. (1995). Dispersal of river sediments in coastal seas: six contrasting cases. Estuaries 18, 494–508. doi: 10.2307/1352367

CrossRef Full Text | Google Scholar

Zhang W. (2016). “Barrier island,” in Encyclopedia of estuaries. Ed. Kennish M. J. (Dordrecht: Springer Netherlands), 47–52. doi: 10.1007/978-94-017-8801-4_124

CrossRef Full Text | Google Scholar