Navigating the depths: a stratification-aware coarse-to-fine received signal strength-based localization for internet of underwater things

Underwater wireless sensor networks (UWSNs) are the primary enabling technology for the Internet of underwater things (IoUT), with which all underwater objects can interact and communicate. In UWSNs, localization is vital for military or civilized applications since data collected without location are meaningless. However, accurate localization using acoustic signals in UWSNs is challenging, especially for received signal strength (RSS)-based techniques. The adverse effect of hybrid loss (path and absorption loss) and stratified propagation may severely impact localization accuracy. Even though some schemes have been proposed in the literature, the accuracy is unsatisfactory. To this end, this study proposes a coarse-to-fine localization method (CFLM). The problem is reformed into an alternating nonnegative constrained least squares (ANCLS) framework, where a constrained ellipse adjustment (CEA) using block principal pivoting is proposed to obtain the coarse estimation. A refined step using a Taylor series expansion is then further presented, in which a corrected solution is acquired by iteration. Additionally, this study derives the Cramér-Rao lower bound (CRLB) to evaluate the proposed method. Simulation results show that the proposed CFLM improves the localization accuracy by up to 66 percent compared with weighted least squares (WLS), privacy-preserving localization (PPSL), two-step linearization localization approach (TLLA), particle swarm optimization-based (PSO) localization, and differential evolution-based (DE) localization under different scenarios.

1 Introduction

The Internet of underwater things (IoUT) is an emerging technology for ocean exploration (Pei et al., 2023). All underwater objects in IoUT enable interconnections with each other and pass on the sensing data to users of interest (Jiang et al., 2023). For instance, underwater nodes, including autonomous underwater vehicles (as targets) and stationary nodes on the seabed, sense data and forward it to buoys using wireless links. Then the data are further transmitted to satellite or coastal users, as shown in Figure 1. In what concerns IoUT, underwater wireless sensor networks (UWSNs) are the enabling technologies to ensure stable nodes’ communication and information interaction (Ahmad et al., 2021; Ahmad et al., 2022a). There are several ways for underwater communications in UWSNs, including acoustic, radio, and optical signal-based techniques (Khalil et al., 2021; Islam et al., 2022). It is worth noting that acoustic signal-based schemes are generally considered a priority in underwater communications since they can propagate long distances (Ahmad et al., 2022b; Aman et al., 2023).

FIGURE 1

Figure 1 Systematic structure of IoUT.

In UWSNs, accurate location information is essential to several applications, including military or civilized missions (Chen et al., 2022; Han et al., 2022a; Han et al., 2022b; Li et al., 2022a; Weiss et al., 2022; Chen et al., 2023). However, acquiring the target location underwater is infeasible because global positioning system (GPS) signals suffer from severe attenuation (Mei et al., 2022b). Therefore, underwater localization techniques have been extensively investigated (Zhang et al., 2019; Zhao et al., 2020; Luo et al., 2021; Mei et al., 2023; Sathish et al., 2023). Tons of localization methods have been developed, including time of arrival (TOA), time difference of arrival (TDOA), angle of arrival (AOA), and received signal strength (RSS)-based techniques (Luo et al., 2021). It should be noted that RSS-based techniques have gained substantial attention because they are cost-effective and synchronization-free compared with TOA-, TDOA-, and AOA-based approaches (Saeed et al., 2019; Mei et al., 2020b; Mei et al., 2021; Li et al., 2022c). However, obtaining accurate locations using RSS-based methods is challenging. Even though some approaches have been proposed in the literature (Mei et al., 2020a; Luo et al., 2021; Li et al., 2022b; Mei et al., 2022b), the accuracy is not satisfactory, especially when suffering from hybrid loss (path loss and absorption loss) and stratified propagation simultaneously.

Therefore, this study develops a coarse-to-fine localization method (CFLM) using RSS information. The localization problem is reshaped into an alternative nonnegative constraint least squares (ANCLS) framework, in which a compensated ray-tracing model with RSS information is established. A constrained ellipse adjustment (CEA) is proposed based on block principal pivoting, with which the potential coarse estimation is filtered and exchanged from one group to another within the constraint. In addition, a Taylor series expansion method is further proposed in the second step of CFLM, in which an iteration acquires a corrected solution.

The main contributions of the paper are as follows:

1. The study presents a novel CFLM that integrates the CEA technique and a first-order Taylor series expansion to obtain more accurate location information than existing methods.

2. An RSS-based CRLB considering hybrid loss and stratification effect is derived to serve as a benchmark for evaluating the performance of an estimator.

3. Simulations are carried out in different scenarios to demonstrate the outperformance of CFLM compared with some localization methods.

The remainder of this paper is organized as follows: In Section 2, the paper illustrates some related works of underwater localization in UWSNs. The problem with RSS measurement is formulated under the stratification effect in Section 3. Section 4 demonstrates the CFLM, while the CRLB is derived in Section 5. Section 6 discusses the comprehensive simulations and results. Finally, Section 7 concludes the study.

2 Related works

Underwater localization is a challenging task that has drawn much attention in the literature (Luo et al., 2021). It has been proved that range-based methods can obtain more accurate location information than ranged-free techniques (Mei et al., 2022b). Thus, the range-based scheme is considered the priority when localization accuracy matters in the mission. In the range-based scheme, the localization contains 1) ranging acquirement and 2) solution acquisition. The former is calculated based on the time flight, array angle, or signal intensity, while the latter is generally solved by algorithms (Wu et al., 2018).

Compared with the ranging acquirement, algorithmic performance improvement is an efficient way to upgrade localization accuracy (Chang et al., 2019). The authors (Menaka and Gauni, 2022) presented an energy-free heuristic neural network (HNN) localization approach that combines the long- and short-term memory (LSTM) methods and particle swarm optimization (PSO) with a repeated iterative technique (RFT) to achieve minimum localization error. The authors (Strumberger et al., 2019) have proposed the improved tree growth algorithm (TGA) and the elephant herding optimization (EHO) for localization, wherein a dynamic behavior and a limit control parameter were introduced in TGA and EHO, respectively. Similar metaheuristic methods have been developed for localization in the area of interest (Derrac et al., 2011; Miao et al., 2021; Bacanin et al., 2022). However, the localization accuracy is modified at the cost of tremendous particles or iterations, which may need extra computational time for calculation (Sharma and Gupta, 2020).

Analytical methods can achieve a closed-formed solution without particles than metaheuristic methods. Moreover, efficiency can significantly improve (Su et al., 2020). To mention a few, (Li et al., 2020) studied a majorization-minimization-based underwater localization using TDOA measurements, wherein the target location was determined through a three-step operation. (Jia et al., 2023) investigated the motion effect for locating a target using an AOA-based technique, wherein a computationally attractive closed-form estimator was derived. (Li et al., 2023) have proposed a novel localization framework based on the track-before-detect (TBD) theory using TOA measurements.

In contrast to TDOA, AOA, and TOA-based methods, there is no need for RSS-based techniques to address time synchronization and array equipment (Mei et al., 2022a). In this case, an upsurge of interest has been taken to the RSS-based approaches in underwater localization. To name a few, Mei et al. (2022a) investigated the optimal deployment of autonomous surface vehicles (ASVs) to minimize underwater localization errors. Pourkabirian et al. (2023) have proposed a semidefinite programming (SDP) method to mitigate errors caused by path loss. Mei et al. (2020a) studied a localization scheme with hybrid loss, including path and absorption losses. They reconstructed the localization problem as a generalized trust region subproblem and presented an absorption mitigation technique. Mahmutoglu and Turk (2019) proposed an absorption mitigation method using RSS information using a differential operation to improve localization accuracy.

As mentioned above, research has been investigated under the straight propagation assumption. Nevertheless, acoustic signal propagation may suffer from the stratification effect caused by underwater heterogeneity (Berger et al., 2008). The stratification effect has been proven to degrade localization accuracy significantly (Han et al., 2018). Poursheikhali and Zamiri-Jafarian (2021) developed an array-RSS localization method based on an iterative algorithm to mitigate the errors caused by inhomogeneous underwater media. Yan et al. (2021) investigated underwater localization using RSS information with a malicious anchor detection strategy under a stratification effect. (Zhang et al., 2016) have verified the stratified propagation impacts on localization accuracy via simulation results.

Unfortunately, these studies considered either hybrid loss or stratification effects. Hybrid loss and stratification effects were rarely considered simultaneously, posing a challenge in acquiring accurate location information. Moreover, the existing methods could not achieve satisfactory localization performance under the stratified propagation and severe path and absorption loss. The paper studies the localization algorithm under the negative factors in this case. The problem is formulated as an ANCLS framework after a linearization manipulation. Then, a block pivoting principle-based CEA is proposed to acquire the coarse estimation, in which the solution is filtered by constraints from one group to another. The study develops a refined step based on the first-order Taylor expansion series to refine the solution further. The final solution is obtained by iteration, which CRLB also validates in simulations.

3 Problem formulation

In this section, the study first investigates the measurement model by the RSS-based technique. The model is then expanded to the scenario with stratified propagation.

3.1 Received signal strength model

This study considers a three-dimensional UWSN containing $N$anchor nodes with known locations and a target whose position needs determining. Suppose that the position of the $i^{\text{th}}$ anchor node is $a_i={[a_{i1},a_{i2},a_{i3}]}^T$ , where $i=1,\cdots ,N$and the target position is

$x={[x_1,x_2,x_3]}^T$.

$T$ represents the transpose operation. This study assumes that the target can transmit an acoustic signal with RSS information to the anchors (Mei et al., 2020a).

$\begin{array}{ll}{P}_{\text{r}i}=P_0-10\alpha {\log }_{10}\frac{d_i}{d_0}-{\alpha }_f{d}_i+{\gamma }_i,& (1)\end{array}$

where $P_{\text{r}i}$ denotes the received signal power of the $i^{\text{th}}$ anchor node from the target, $P_0$ is the transmit power, $\alpha$ represents the path loss exponent, $d_i$ is the distance between the $i^{\text{th}}$ anchor and target, $d_0$ is the reference distance (1 m), ${\gamma }_i$ is the shadowing noise modeled as a Gaussian distribution with zero mean and variance ${\sigma }_i^2$ , and ${\alpha }_f$ is the absorption coefficient obtained from Thorp’s formula (Stojanovic and Preisig, 2009) according to

$\begin{array}{ll}{\alpha }_f=\frac{0.11f^2}{1+f^2}+\frac{44f^2}{4100+f^2}+2.75\times {10}^{-4}{f}^2+0.003,& (2)\end{array}$

where $f$ is the frequency.

A standard RSS-based terrestrial localization scheme is developed using ${\alpha }_f=0$ . In practice, the frequency at which the acoustic system operates in UWSNs varies from 10 kHz to 1000 kHz, where the corresponding ${\alpha }_f$ can be 0.001 dB/m to 0.32 dB/m (Stojanovic and Preisig, 2009).

3.2 Ray-tracing length under stratification effect

In contrast to terrestrial environments, acoustic signals do not propagate straightly owing to stratification. The travel length is prone to an arc, as shown in Figure 2 (Yan et al., 2021). Moreover, the localization accuracy may degrade if directly using the straight propagation line (Mei et al., 2022b). Accordingly, a compensated model using Snell’s law is used (Zhang et al., 2020) such that

FIGURE 2

Figure 2 Example of a stratification effect scheme.

$\begin{array}{ll}\frac{\cos \theta }{C(z)}=\frac{\cos {\theta }^x}{C(x_3)}=\frac{\cos {\theta }^i}{C(a_{i3})}=k,{\theta }^x,{\theta }^i\in \left[-\frac{\pi }{2},\frac{\pi }{2}\right],& (3)\end{array}$

where ${\theta }^x$ and ${\theta }^i$ are the corresponding angles to the target and $i^{\text{th}}$ anchor, respectively, $k$ is a constant, $z$represents the depth information, and

$C(·)$is the function of sound speed following the isogradient model (Su et al., 2022) such that

$\begin{array}{ll}C(z)=\vartheta z+b,& (4)\end{array}$

where $\vartheta$ is the steepness of the sound speed profile (SSP), and $b$ is the speed of sound on the ocean surface.

From Figure 2, we also have

$\begin{array}{ll}\partial r=\frac{\partial z}{\tan \theta },\partial l=\frac{\partial z}{\sin \theta },\text{ and }\partial t=\frac{\partial l}{C(z)},& (5)\end{array}$

where $r$ denotes the horizontal range following $r=r^x-r^i=\sqrt{{(x_1-a_{i1})}^2+{(x_2-a_{i2})}^2}$ , $l$ denotes the ray-tracing length, and $t$ represents the travel time.

The following expression is obtained by exploiting derivates with respect to

$z$ and

$\theta$ , i.e

$\begin{array}{ll}\partial z=-\frac{1}{\vartheta k}\sin \theta \partial \theta .& (6)\end{array}$

Taking the integral and replacing (6) with (5), the underwater ray-tracing length, considering an isogradient SSP, can be expressed as

$\begin{array}{ll}{l}_i=-(\vartheta x_3+b)\frac{{\theta }^x-{\theta }^i}{\vartheta \cos {\theta }^x},& (7)\end{array}$

where ${\theta }^x$ and ${\theta }^i$ are further expressed as ${\theta }^x={\beta }_0+{\alpha }_0$ and ${\theta }^i={\beta }_0-{\alpha }_0$ with ${\beta }_0=\arctan [\raisebox{1ex}{$(a_{i3}-x_3)$}\!\left/ \!\raisebox{-1ex}{$(r^x-r^i)$}\right.]$ and ${\beta }_0=\arctan \left[\raisebox{1ex}{$0.5\vartheta (r^x-r^i)$}\!\left/ \!\raisebox{-1ex}{$[b+0.5\vartheta (a_{i3}+x_3)]$}\right.\right]$ , respectively.

The compensated model is then derived, and the distance between the

$i^{\text{th}}$ anchor and target can be acquired using the ray-tracing length. To this end, the RSS-based measurement model in (1) is then further transformed into

$\begin{array}{ll}{P}_{\text{r}i}=P_0-10\alpha {\log }_{10}\frac{l_i}{d_0}-{\alpha }_f{d}_i+{\gamma }_i.& (8)\end{array}$

4 Proposed method

This section illustrates the proposed method, where the localization problem is transformed into an ANCLS framework first. Subsequently, a coarse estimation method based on block principal pivoting is presented. A Taylor series expansion approach is further developed using a linearization operation to refine the solution.

4.1 Alternative nonnegative constrained least squares framework

Let $c_i={\alpha }_f{l}_i$, and provide the observation vector $P={[P_{\text{r}i}]}^T$. Then the probability density function (PDF) can be expressed as

$\begin{array}{ll}p(P|x)={\displaystyle \prod _{i=1}^N\frac{1}{\sqrt{2\pi {\sigma }_i^2}}\exp \left\{\frac{P_{\text{r}i}-P_0+10\alpha {\log }_{10}\frac{l_i}{d_0}+c_i}{2{\sigma }_i^2}\right\}}& (9)\end{array}$

By maximizing the PDF, the maximum likelihood (ML) estimator can be derived as

$\begin{array}{ll}\widehat{x}=\underset{x}{\arg \min }{\displaystyle \sum _{i=1}^N\left\{\frac{P_{\text{r}i}-P_0+10\alpha {\log }_{10}\frac{l_i}{d_0}+c_i}{2{\sigma }_i^2}\right\}}& (10)\end{array}$

where $\widehat{x}$ is the estimate.

However, solving the problem in (10) accurately is challenging owing to its high nonconvexity. Thus, the problem is then transformed into an ANCLS framework.

Let ${\sigma }^i=\sigma$. By applying the transformation and linearization manipulation, the problem in (10) can be converted into

$\begin{array}{ll}\widehat{x}=\underset{x}{\arg \min }{\displaystyle \sum _{i=1}^N{\left(d_0{10}^{{\kappa }_i}-\parallel x-a_i\parallel \right)}^2},& (11)\end{array}$

where ${\kappa }_i=\frac{P_0-P_{\text{r}i}-c_i}{10\alpha }$, and $\parallel ·\parallel$is the ${\ell }_2$norm.

After squaring the range, (11) can be rewritten as

$\begin{array}{ll}\widehat{x}=\underset{x}{\arg \min }{\displaystyle \sum _{i=1}^N{\left(d_0^2{10}^{2{\kappa }_i}-\chi +2a_i^{T}x-{\parallel a_i\parallel }^2\right)}^2},& (12)\end{array}$

where $\chi ={\parallel x\parallel }^2$.

Given

$\xi ={[x_1,x_2,x_3,\chi ]}^T$as the estimated parameter, the localization problem can be transformed into

$\begin{array}{ll}\widehat{\xi }=\underset{\xi }{\arg \min }{\parallel \text{W}\xi -H\parallel }^2,& (13)\end{array}$

where

$\begin{array}{ll}W=\left[\begin{array}{c}-2a_1^T\mathrm{\hspace{1em}1}\hspace{1em}⋮\hspace{1em}⋮\\ -2a_N^T\mathrm{\hspace{1em}1}\end{array}\right]\text{and }H=\left[\begin{array}{c}{d}_0^2{10}^{2{\kappa }_1}-{\parallel a_1\parallel }^2\\ ⋮\\ d_0^2{10}^{2{\kappa }_N}-{\parallel a_N\parallel }^2\end{array}\right]& (14)\end{array}$

With the constraint of $\xi$, i.e., $\xi \ge 0$, the original problem in (10) can be reformed into the ANCLS framework, as shown in (13), with a single right-hand side (RHS) vector (Kannan et al., 2018).

4.2 Coarse estimation by CEA

Assuming that the matrix $W$ has a full column rank, the problem in (13) is strictly convex because

$W^{T}W$ is positively definite. An optimal solution is acquired when it satisfies the Karush–Kuhn–Tucker (KKT) optimality condition, expressed as

$\begin{array}{ll}y=W^{T}W\xi -W^{T}H,& (15)\end{array}$

$\begin{array}{ll}\xi ,y\ge 0,& (16)\end{array}$

$\begin{array}{ll}{\xi }_j{y}_j=0,j=1,\cdots ,M,& (17)\end{array}$

where $M$is the number of estimated variables (blocks) in $\xi$.

To obtain a feasible solution in (13), the index set $\left\{1,\cdots ,M\right\}$is split into two groups, $\mathscr{H}$and $ℂ$, such that $\mathscr{H}\cup ℂ=\left\{1,\cdots ,M\right\}$and $\mathscr{H}\cap ℂ=\varnothing$. In addition, ${\xi }_{\mathscr{H}}$, ${\xi }_{ℂ}$ , $y_{\mathscr{H}}$, and $y_{ℂ}$ are defined as subsets of variables with corresponding indices and $W_{\mathscr{H}}$ and $W_{ℂ}$ are the submatrices of $W$ with corresponding column indices.

At the initiation, let

$\mathscr{H}=\varnothing$ ,

$ℂ=\left\{1,\cdots ,M\right\}$ , and

${\xi }_{ℂ}=y_{\mathscr{H}}=0$ . Accordingly, (17) holds for any values of

${\xi }_{\mathscr{H}}$ and

$y_{ℂ}$ . A complementary basic solution

$({\xi }_{\mathscr{H}},y_{ℂ})$ that can be acquired by (18) and (19) is feasible only when

${\xi }_{\mathscr{H}}\ge 0$ and

$y_{ℂ}\ge 0$ . Otherwise,

$({\xi }_{\mathscr{H}},y_{ℂ})$ is infeasible.

$\begin{array}{ll}{\xi }_{\mathscr{H}}=\underset{{\xi }_{\mathscr{H}}}{\arg \min }{\parallel {\text{W}}_{\mathscr{H}}{\xi }_{\mathscr{H}}-H\parallel }^2.& (18)\end{array}$

$\begin{array}{ll}{y}_{ℂ}=\text{W}{ℂ}_T^{}(\text{W}{\mathscr{H}}_{}{\xi }_{\mathscr{H}}-H).& (19)\end{array}$

If

$({\xi }_{\mathscr{H}},y_{ℂ})$ is infeasible, an updated procedure must be manipulated by exchanging variables for which (16) does not hold. This study defines an index set as

$\begin{array}{ll}ℱ=\left\{j\in \mathscr{H}:{\xi }_j<0\right\}\cup \left\{j\in ℂ:y_j<0\right\}.& (20)\end{array}$

Accordingly, a variable

${\xi }_j$ with

$j\in ℱ$ is an infeasible variable. The updated rule of

$\mathscr{H}$ and

$ℂ$can be expressed as

$\begin{array}{ll}\mathscr{H}=(\mathscr{H}-ℛ)\cup (ℛ\cap ℂ),& (21)\end{array}$

$\begin{array}{ll}ℂ=(ℂ-ℛ)\cup (ℛ\cap \mathscr{H}),& (22)\end{array}$

where $ℛ$ is the nonempty subset, such that $ℛ\subset ℱ$.

Notably, a cycle or failure to find an optimal solution may occur during the updated procedure. Therefore, a backup rule should be adopted to ensure a finite termination, which can be expressed as

$\begin{array}{ll}R=\{j:j=max\{j\in F\}\}& (23)\end{array}$

In addition, this study defines variable $\Delta$ as a buffer in the updated procedure. The value of $\Delta$ is reduced by 1 if the updated round increases the number of infeasible variables. When $\Delta$ is zero, the backup rule is used, such that the number of infeasible variables is smaller than the lowest value and stored in $\beta$ . The procedure for coarse estimation is as follows: |F| denotes the number of variables at each iteration, and $\Delta =3$ is suggested by (Cimini and Bemporad, 2017) to accelerate the convergence.

4.3 Refined estimation

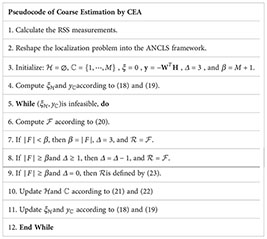
Although CEA can obtain a relatively feasible solution, it can easily drop to a local optimum owing to its nature. This section proposes a Taylor series expansion-based algorithm to refine the solution further.

Recalling the problem in (11), the equation is expanded, and the constant item is ignored.

$\begin{array}{ll}\widehat{x}=\underset{x}{\arg \min }{\displaystyle \sum _{i=1}^N\left({\parallel x-a_i\parallel }^2-2d_0{10}^{{\kappa }_i}\parallel x-a_i\parallel \right)}.& (24)\end{array}$

(24) can be further converted into a surrogate function, such that

$\begin{array}{ll}\Im (x)=\underset{f(x)}{\underbrace{{\displaystyle \sum _{i=1}^N{\parallel x-a_i\parallel }^2}}}+\underset{g(x)}{\underbrace{(-2{\displaystyle \sum _{i=1}^N{d}_0{10}^{{\kappa }_i}\parallel x-a_i\parallel })}},& (25)\end{array}$

where $f(x)$ is convex, and $g(x)$ is concave.

Theoretically, the concave function should have an upper bound based on the first-order Taylor expansion (Zhang and Zheng, 2010). Assuming that

$x^{\wp }$ is the estimate in the

${\wp }^{\text{th}}$iteration,

$\begin{array}{ll}g(x)\le g(x^{\wp })+\nabla g{(x^{\wp })}^T(x-x^{\wp }),& (26)\end{array}$

where $\nabla g(·)$ denotes the gradient.

Substituting (26) for

$g(x)$ in (25) yields

$\begin{array}{ll}\Im (x|x^{\wp })={\displaystyle \sum _{i=1}^N({\parallel x-a_i\parallel }^2-2d_0{10}^{{\kappa }_i}\parallel x-a_i\parallel )}-2{\displaystyle \sum _{i=1}^N{d}_0{10}^{{\kappa }_i}\frac{{(x^{\wp }-a_i)}^T}{\parallel x^{\wp }-a_i\parallel }(x-x^{\wp })}.& (27)\end{array}$

Notably, the surrogate function is bounded below and can converge to a limit point (Sun et al., 2017). Therefore, given the ${\wp }^{\text{th}}$location estimate, the refined solution can be obtained by an iterative operation, such that

$\begin{array}{ll}{x}^{\wp +1}=\frac{1}{N}{\displaystyle \sum _{i=1}^N\left(a_i+d_0{10}^{{\kappa }_i}\frac{{(x^{\wp }-a_i)}^T}{\parallel x^{\wp }-a_i\parallel }\right)},& (28)\end{array}$

where the initial guess is obtained through CEA; that is $x^0={\widehat{x}}_{\text{CEA}}$. The flowchart of the proposed method is depicted in Figure 3, while the pseudocode of the CFLM is summarized as follows:

FIGURE 3

Figure 3 The flowchart of the proposed method.

4.4 CRLB of RSS-based technique under the stratification effect

The CRLB using the RSS-based technique under the stratification effect was derived as a benchmark for the unbiased estimator (Sengijpta, 1993). Given the Gaussian noise assumption, such that ${\sigma }_i=\sigma$, the CRLB is expressed as

$\begin{array}{ll}CRLB=\text{Tr}(FI{M}^{-1})=\text{Tr}{\left[{(\frac{\partial P}{\partial x})}^T{\sigma }^{-2}{(\frac{\partial P}{\partial x})}^T\right]}^{-1},& (29)\end{array}$

where $\text{Tr}$ is the trace function, and $FIM$ is the Fisher information matrix.

From (1), the partial derivatives can be expressed as

$\begin{array}{ll}\frac{\partial P_{\text{r}i}}{\partial x_1}=-10\alpha \frac{1}{l_i\ln 10}\frac{\partial l_i}{\partial x_1}-{\alpha }_f\frac{\partial l_i}{\partial x_1},& (30)\end{array}$

$\begin{array}{ll}\frac{\partial P_{\text{r}i}}{\partial x_2}=-10\alpha \frac{1}{l_i\ln 10}\frac{\partial l_i}{\partial x_2}-{\alpha }_f\frac{\partial l_i}{\partial x_2},& (31)\end{array}$

$\begin{array}{ll}\frac{\partial P_{\text{r}i}}{\partial x_3}=-10\alpha \frac{1}{l_i\ln 10}\frac{\partial l_i}{\partial x_3}-{\alpha }_f\frac{\partial l_i}{\partial x_3}.& (32)\end{array}$

Inserting (6) into (5) and taking the integral operation yields

$\begin{array}{ll}\frac{x_3-a_{i3}}{r^x-r^i}=-\frac{\cos {\theta }^x-\cos {\theta }^i}{\sin {\theta }^x-\sin {\theta }^i},\text{ s.t. }{r}^x\ne r^i,& (33)\end{array}$

$\begin{array}{ll}\frac{b+\vartheta x_3}{b+\vartheta a_{i3}}=\frac{\cos {\theta }^x}{\cos {\theta }^i}.& (34)\end{array}$

The following equations are derived after obtaining the partial derivatives of (33) and (34) with respect to

$x_3$ and

$r^x$, respectively:

$\begin{array}{ll}\frac{\partial {\theta }^x}{\partial r^x}+\frac{\partial {\theta }^i}{\partial r^x}=-\frac{x_3+a_{i3}}{{(r^x-r^i)}^2}\frac{{(\sin {\theta }^x-\sin {\theta }^i)}^2}{1-\cos ({\theta }^x-{\theta }^i)},& (35)\end{array}$

$\begin{array}{ll}\frac{\partial {\theta }^x}{\partial x_3}-\frac{b+\vartheta x_3}{b+\vartheta a_{i3}}\frac{\sin {\theta }^i}{\sin {\theta }^x}\frac{\partial {\theta }^i}{\partial x_3}=-\frac{\vartheta }{b+\vartheta a_{i3}}\frac{\cos {\theta }^i}{\sin {\theta }^x},& (36)\end{array}$

$\begin{array}{ll}\frac{\partial {\theta }^x}{\partial r^x}=\frac{b+\vartheta x_3}{b+\vartheta a_{i3}}\frac{\sin {\theta }^i}{\sin {\theta }^x}\frac{\partial {\theta }^i}{\partial r^x},& (37)\end{array}$

$\begin{array}{ll}\frac{\partial {\theta }^x}{\partial x_3}+\frac{\partial {\theta }^i}{\partial x_3}=\frac{1}{r^x-r^i}\frac{{(\sin {\theta }^x-\sin {\theta }^i)}^2}{1-\cos ({\theta }^x-{\theta }^i)}.& (38)\end{array}$

According to (7), the derivatives of the ray-tracing length with respect to

$x$ are

$\begin{array}{ll}\frac{\partial l_i}{\partial x_1}=-\frac{\vartheta x_3+b}{\vartheta \cos {\theta }^x}\left\{\left(1+\left({\theta }^x-{\theta }^i\right)\tan {\theta }^x\right)\frac{\partial {\theta }^x}{\partial r^x}-\frac{\partial {\theta }^i}{\partial r^x}\right\}\frac{\partial r^x}{\partial x_1},& (39)\end{array}$

$\begin{array}{ll}\frac{\partial l_i}{\partial x_2}=-\frac{\vartheta x_3+b}{\vartheta \cos {\theta }^x}\left\{\left(1+\left({\theta }^x-{\theta }^i\right)\tan {\theta }^x\right)\frac{\partial {\theta }^x}{\partial r^x}-\frac{\partial {\theta }^i}{\partial r^x}\right\}\frac{\partial r^x}{\partial x_2},& (40)\end{array}$

$\begin{array}{ll}\frac{\partial l_i}{\partial x_3}=-\frac{\vartheta x_3+b}{\vartheta \cos {\theta }^x}\left\{\left(1+\left({\theta }^x-{\theta }^i\right)\tan {\theta }^x\right)\frac{\partial {\theta }^x}{\partial x_3}-\frac{\partial {\theta }^i}{\partial x_3}\right\}-\frac{{\theta }^x-{\theta }^i}{\cos {\theta }^x},& (41)\end{array}$

Where

$$\frac{\partial r^x}{\partial x_1}=\frac{x_1-a_{i1}}{r^x-r^i},$$

$$\frac{\partial r^x}{\partial x_2}=\frac{x_2-a_{i2}}{r^x-r^i},$$

$$\frac{\partial {\theta }^x}{\partial r^x}=-\frac{\mu \upsilon }{1-\upsilon },,$$

$$\frac{\partial {\theta }^i}{\partial r^x}=\frac{\mu }{1-\upsilon },$$

$$\frac{\partial {\theta }^x}{\partial x_3}=\frac{\eta -\upsilon \rho }{1-\upsilon }\text{, and}$$

$$\frac{\partial {\theta }^i}{\partial x_3}=\frac{\rho -\eta }{1-\upsilon }\text{, with}$$

$$\mu =-\frac{x_3+a_{i3}}{{(r^x-r^i)}^2}\frac{{(\sin {\theta }^x-\sin {\theta }^i)}^2}{1-\cos ({\theta }^x-{\theta }^i)},\text{, with}$$

$\begin{array}{ll}\upsilon =-\frac{b+\vartheta x_3}{b+\vartheta a_{i3}}\frac{\sin {\theta }^i}{\sin {\theta }^x}\frac{\partial {\theta }^i}{\partial x_3},& (42)\end{array}$

$$\rho =\frac{1}{r^x-r^i}\frac{{(\sin {\theta }^x-\sin {\theta }^i)}^2}{1-\cos ({\theta }^x-{\theta }^i)},\text{and}$$

$\begin{array}{ll}\eta =-\frac{\vartheta }{b+\vartheta a_{i3}}\frac{\cos {\theta }^i}{\sin {\theta }^x}& (43)\end{array}$

Following (30)–(43), $\frac{\partial P}{\partial x}$can be further expressed as

$\begin{array}{ll}\frac{\partial P}{\partial x}=\left(\begin{array}{}-\varpi \frac{\partial l_1}{\partial x_1}-{\alpha }_f\frac{\partial l_1}{\partial x_1}\cdots -\varpi \frac{\partial l_N}{\partial x_1}-{\alpha }_f\frac{\partial l_N}{\partial x_1}-\varpi \frac{\partial l_1}{\partial x_2}-{\alpha }_f\frac{\partial l_1}{\partial x_2}\cdots -\varpi \frac{\partial l_N}{\partial x_2}-{\alpha }_f\frac{\partial l_N}{\partial x_2}-\varpi \frac{\partial l_1}{\partial x_3}-{\alpha }_f\frac{\partial l_1}{\partial x_3}\cdots -\varpi \frac{\partial l_N}{\partial x_3}-{\alpha }_f\frac{\partial l_N}{\partial x_3}\end{array}\right),& (44)\end{array}$

where $\varpi =\frac{10\alpha }{\ln 10}$.

Let

$\begin{array}{ll}\begin{array}{l}{\Gamma }^{\text{o}}={\displaystyle \sum _{i=1}^N{\left(\varpi \frac{\partial l_i}{\partial x_1}+{\alpha }_f\frac{\partial l_i}{\partial x_1}\right)}^2},{\Upsilon }^{\text{o}}={\displaystyle \sum _{i=1}^N\left(\varpi \frac{\partial l_i}{\partial x_1}+{\alpha }_f\frac{\partial l_i}{\partial x_1}\right)·\left(\varpi \frac{\partial l_i}{\partial x_2}+{\alpha }_f\frac{\partial l_i}{\partial x_2}\right),}\\ {\Psi }^{\text{o}}={\displaystyle \sum _{i=1}^N{\left(\varpi \frac{\partial l_i}{\partial x_2}+{\alpha }_f\frac{\partial l_i}{\partial x_2}\right)}^2},{\Xi }^{\text{o}}={\displaystyle \sum _{i=1}^N\left(\varpi \frac{\partial l_i}{\partial x_1}+{\alpha }_f\frac{\partial l_i}{\partial x_1}\right)·\left(\varpi \frac{\partial l_i}{\partial x_3}+{\alpha }_f\frac{\partial l_i}{\partial x_3}\right)},\\ {\Lambda }^{\text{o}}={\displaystyle \sum _{i=1}^N{\left(\varpi \frac{\partial l_i}{\partial x_3}+{\alpha }_f\frac{\partial l_i}{\partial x_3}\right)}^2},{\Pi }^{\text{o}}={\displaystyle \sum _{i=1}^N\left(\varpi \frac{\partial l_i}{\partial x_2}+{\alpha }_f\frac{\partial l_i}{\partial x_2}\right)·\left(\varpi \frac{\partial l_i}{\partial x_3}+{\alpha }_f\frac{\partial l_i}{\partial x_3}\right)}.\end{array}& (45)\end{array}$

The CRLB using RSS-based technique under the stratification effect is expressed as

$\begin{array}{ll}CRLB=\text{Tr}(FI{M}^{-1})=\text{Tr}{\left[\begin{array}{ccc}{\Gamma }^{\text{o}}& {\Upsilon }^{\text{o}}& {\Xi }^{\text{o}}\\ {\Upsilon }^{\text{o}}& {\Psi }^{\text{o}}& {\Pi }^{\text{o}}\\ {\Xi }^{\text{o}}& {\Pi }^{\text{o}}& {\Lambda }^{\text{o}}\end{array}\right]}^{-1}.& (46)\end{array}$

5 Simulation results

This section discusses the simulations performed for different scenarios to verify the effectiveness of the proposed method. Simulations are executed on a MATLAB R2021b setup with some fixed parameters, as shown in Table 1. In addition, a random function is used to mimic a highly dynamic situation, where the positions of the anchor and target are not fixed in each Monte Carlo trial. Moreover, some approaches, including the weighted least squares (WLS) (Zhang et al., 2019), privacy-preserving localization (PPSL) (Zhao et al., 2020), two-step linearization localization approach with RSS only (TLLA-RSS) (Mei et al., 2023), CEA, CFLM, and CRLB (45), are included in the simulations. Besides, some metaheuristic approaches, including particle swarm optimization (PSO) and differential evolution (DE)-based localization proposed in (Derrac et al., 2011), are performed for comparison. The root mean square error (RMSE) is derived to evaluate the localization accuracy. $RMSE=\sqrt{{\displaystyle {\sum }_{m=1}^{MC}{\parallel \widehat{x}-x\parallel }^2}/MC}$ , where $\widehat{x}$ is the estimated location, $MC$ is the total number of Monte Carlo trials, set to 1000 in these simulations, and $m$ is the $m^{\text{th}}$ Monte Carlo trial.

TABLE 1

Table 1 Fixed parameters in simulations.

5.1 Scenario with variable anchors

Figure 4 shows the results of cumulative distribution function (CDF) when ${\sigma }_i=3\text{ dB}$, $sidelength=50\text{ m}$, and $\vartheta =0.1$. Figures 4A–D) show the schemes with $N=4$, $N=6$, $N=8$, and $N=10$, respectively. Notably, the number of available measurements increases as the anchor grows. In this case, the localization accuracy improves, as shown in Figure 4. For example, the probability of $\parallel \widehat{x}-x\parallel \le 5.43\text{ m}$reaches 95% for the CFLM in Figure 4A), where the CFLM error is 3.61 m at the same probability as in Figure 4D). The same situation is observed for WLS, PPSL, CEA, PSO, DE, and TLLA-RSS. Table 2 summarizes the corresponding errors and probabilities for Figures 4A, D). Among these methods, the CFLM performs better than the WLS, PPSL, CEA, PSO, DE, and TLLA-RSS. Its performance is close to that of CRLB, although the margin remains remarkable when $N>4$.

FIGURE 4

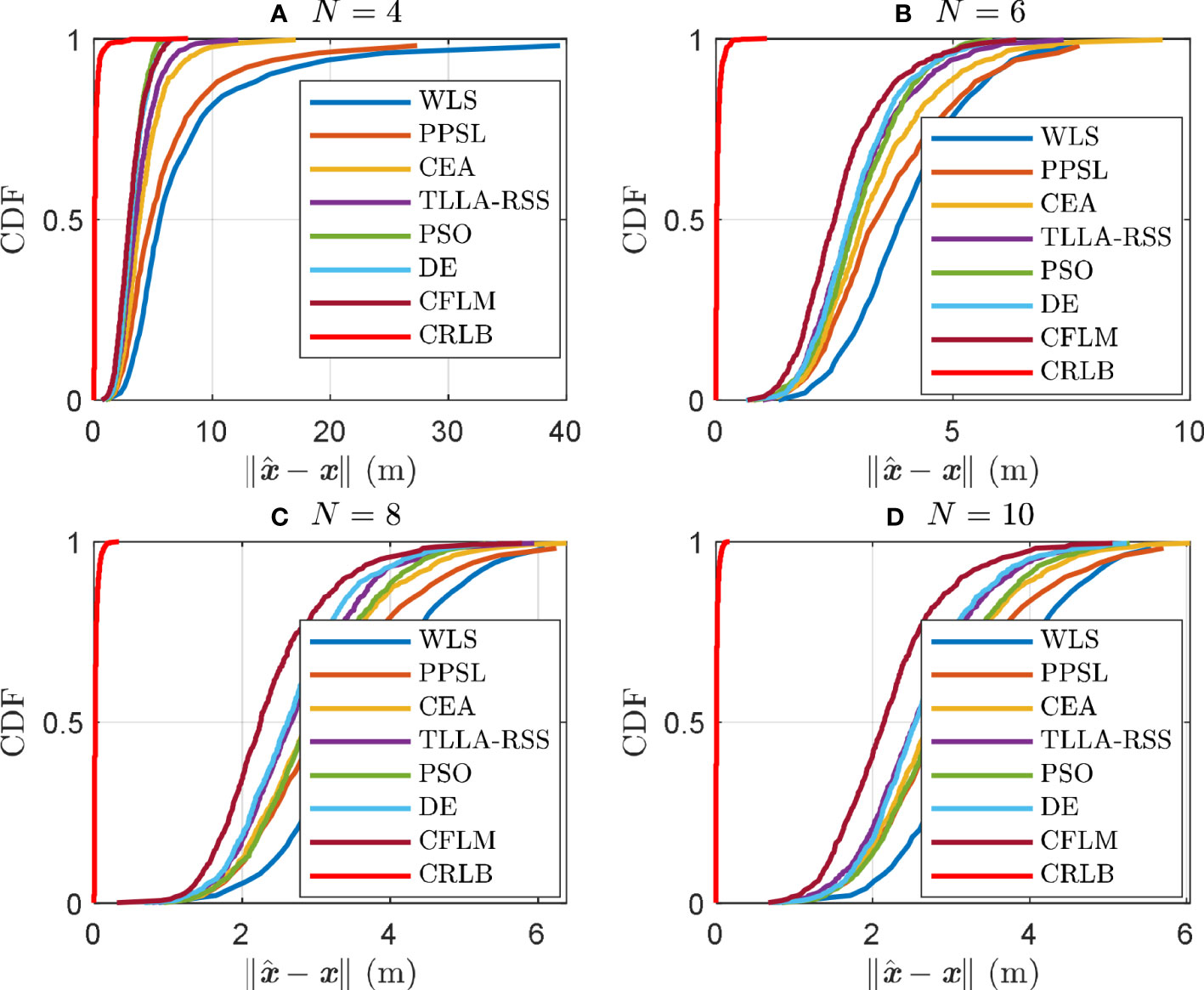
Figure 4 CDF of variable anchors when σ_i = 3 dB. sidelength = 50 m, and θ = 0.1, where A, B, C and D are scenarios with N = 4, N = 6, N = 8, and N = 10, respectively.

TABLE 2

Table 2 CDF of the methods under variable anchors.

An error analysis is performed to further evaluate the performance of each Monte Carlo trial, as shown in Figure 5. Figures 5A, B) show the scenarios with $N=6$and $N=10$, respectively. As shown in Figure 5, outliers can occur in some situations. However, the CFLM performs better than the other methods. Its third quartile, median, and first quartile errors in Figure 5A) are 3.12 m, 2.51 m, and 1.96 m, respectively. This outperformance is remarkable with $N=10$. The median errors of the CFLM, TLLA-RSS, CEA, PPSL, PSO, DE, and WLS in Figure 5B) are 2.14 m, 2.54 m, 2.71 m, 2.84 m, 2.81 m, 2.55 m, and 3.33 m, respectively. Moreover, the corresponding results show that the proposed CEA obtains a better solution than the WLS and PPSL in some situations. The refined step proposed in Section 3.3 can further improves the localization accuracy.

FIGURE 5

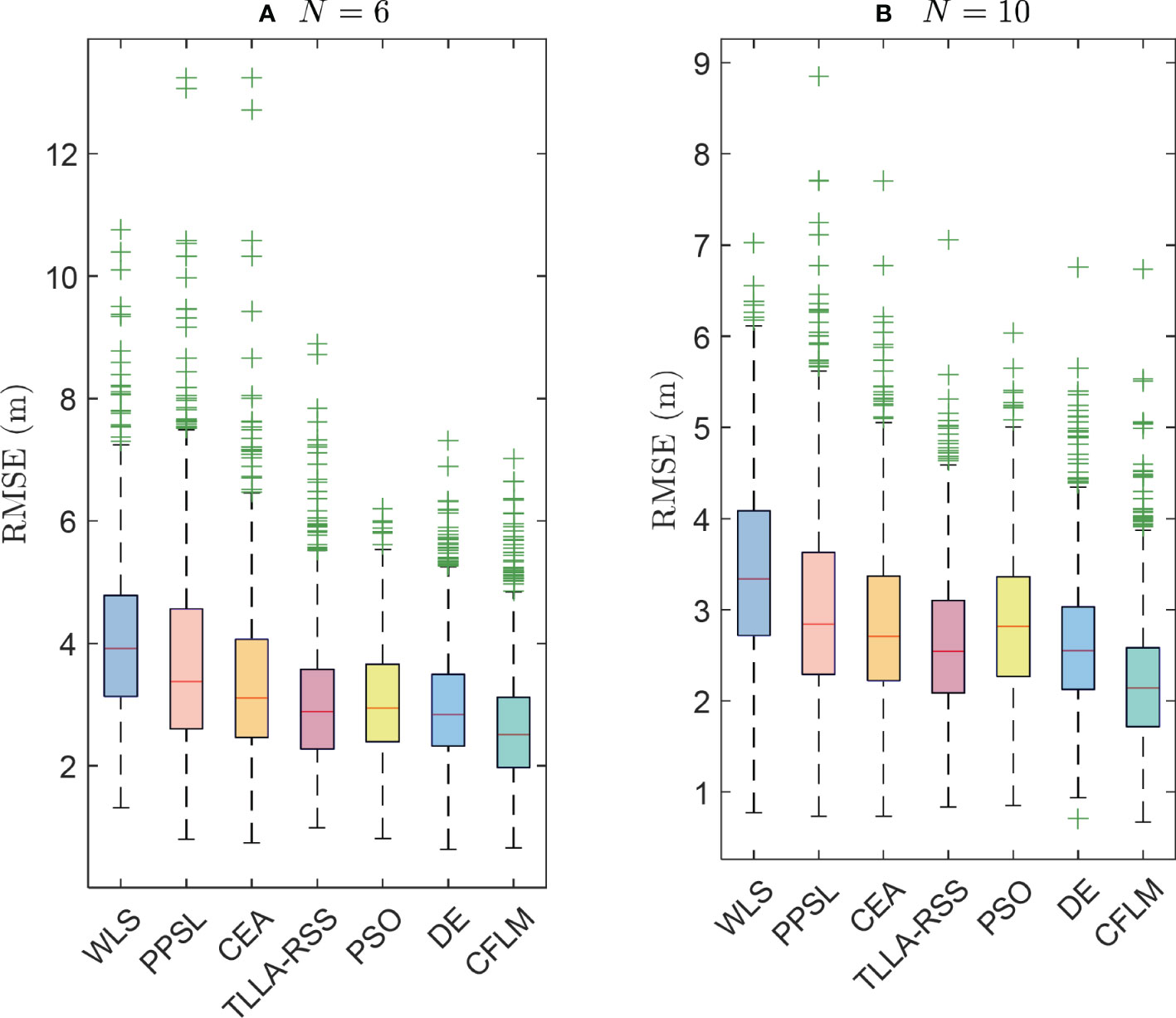
Figure 5 RMSE analysis when σi = 3 dB, sidelength = 50 m, and θ = 0.1 under variable anchors, where A and B are scenarios with N = 6 and N = 10, respectively.

5.2 Scenario with variable noises

Figure 6 shows the CDF of variable noises under $N=8$, $sidelength=50\text{ m}$, and $\vartheta =0.1$. Figures 6A–D show the schemes with ${\sigma }_i=1\text{ dB}$, ${\sigma }_i=3\text{ dB}$, ${\sigma }_i=5\text{ dB}$, and ${\sigma }_i=7\text{ dB}$, respectively. The measurement error increases with ${\sigma }_i$. Therefore, the performance degrades with increased noise. For example, the probability of $\parallel \widehat{x}-x\parallel \le 2.15\text{ m}$reaches 95% for the CFLM in Figure 6A), exhibiting a 3.86 m error at the same probability in Figure 6B). It is worth noting that the performance is close between CFLM and PSO when the noise enlarges. However, the PSO localization achieves the accuracy at cost of numerous particles, which increases the computational complexity. On the contrary, the proposed method can get a satisfactory performance at a relatively low computational complexity. Table 3 lists the results. The CFLM outperforms the other methods, which is within 3.86 m when ${\sigma }_i=3\text{ dB}$, reaching 95% compared with that of the WLS (5.47 m), PPSL (5.30 m), CEA (4.73 m), PSO (4.35 m), DE (4.16 m), and TLLA-RSS (4.35 m). However, the margin between the CFLM and CRLB remains remarkable.

FIGURE 6

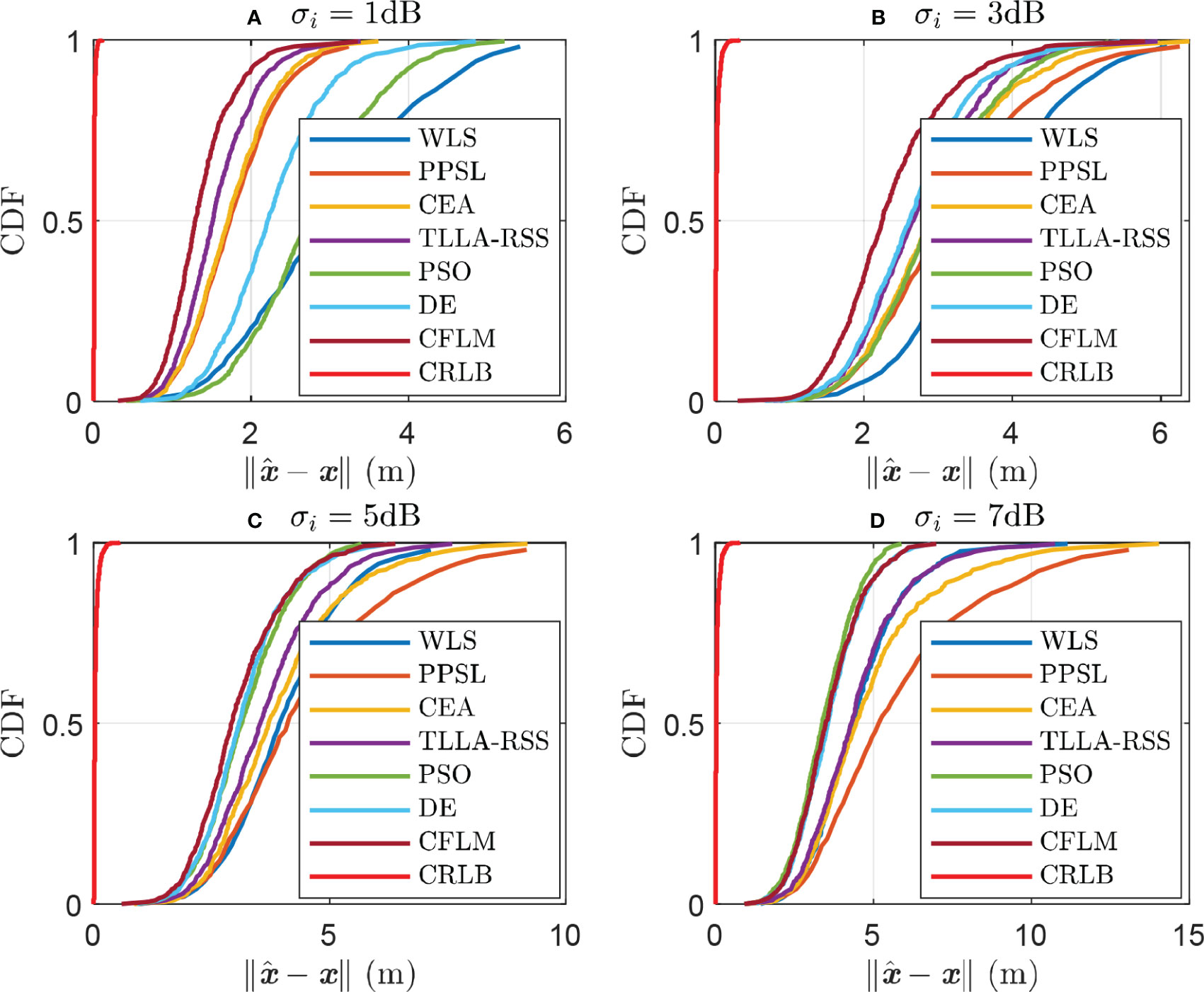
Figure 6 CDF of variable noises when N = 8, sidelength = 50 m, and θ = 0.1, where A, B, C and D are scenarios with σ_i = 1 dB, σ_i = 3 dB, σ_i = 5 dB, and σ_i = 7 dB, respectively.

TABLE 3

Table 3 CDF of the methods under variable noises.

Figures 7A, B) show the scenarios with ${\sigma }_i=3\text{ dB}$and ${\sigma }_i=7\text{ dB}$, respectively. The PPSL is sensitive to noise. Its performance fluctuates significantly compared with that of the other methods. Moreover, the outliers of the PPSL increases with noise. The median errors of the CFLM when ${\sigma }_i=3\text{ dB}$and ${\sigma }_i=7\text{ dB}$are 2.24 m and 3.49 m, respectively, better than that of the other methods.

FIGURE 7

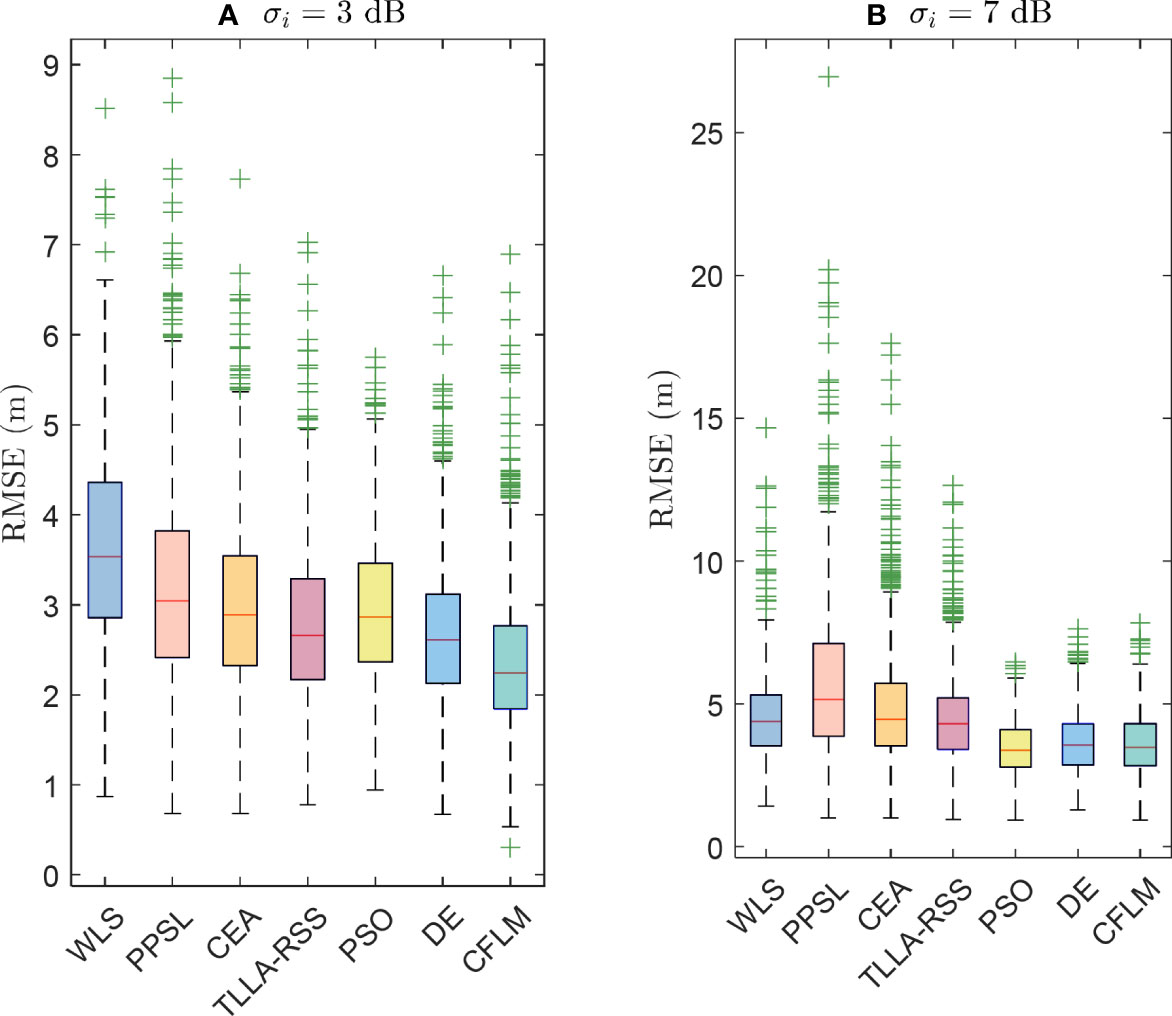
Figure 7 RMSE analysis when N = 8 sidelength = 50 m, and θ = 0.1 under variable noises, where A and B are scenarios with σi = 3 dB and σi = 7 dB, respectively.

5.3 Scenario with variable side lengths

Figure 8 shows the CDF of the variable side lengths with $N=8$, ${\sigma }_i=3\text{ dB}$, and $\vartheta =0.1$. Figures 8A–D) show the schemes with the sidelength at 25 m, 50 m, 75 m, and 100 m, respectively. Notably, the signal attenuation becomes severe with enlarged area of interest. Accordingly, the localization error increases with the sidelength. Among the evaluated methods, the CFLM reaches $\parallel \widehat{x}-x\parallel \le \mathrm{2.73 m}$and $\parallel \widehat{x}-x\parallel \le \mathrm{5.48 m}$at 95% with sidelength at 25 m and 100 m, respectively. By contrast, the other methods could not reach the same localization accuracy. Table 4 lists the performances of the methods, whereas Figure 9 shows the corresponding box plot. The results in Figure 9) further proves the superior performance of the CFLM. Its median errors are 1.58 m and 3.17 m, as shown in Figures 9A, B), respectively.

FIGURE 8

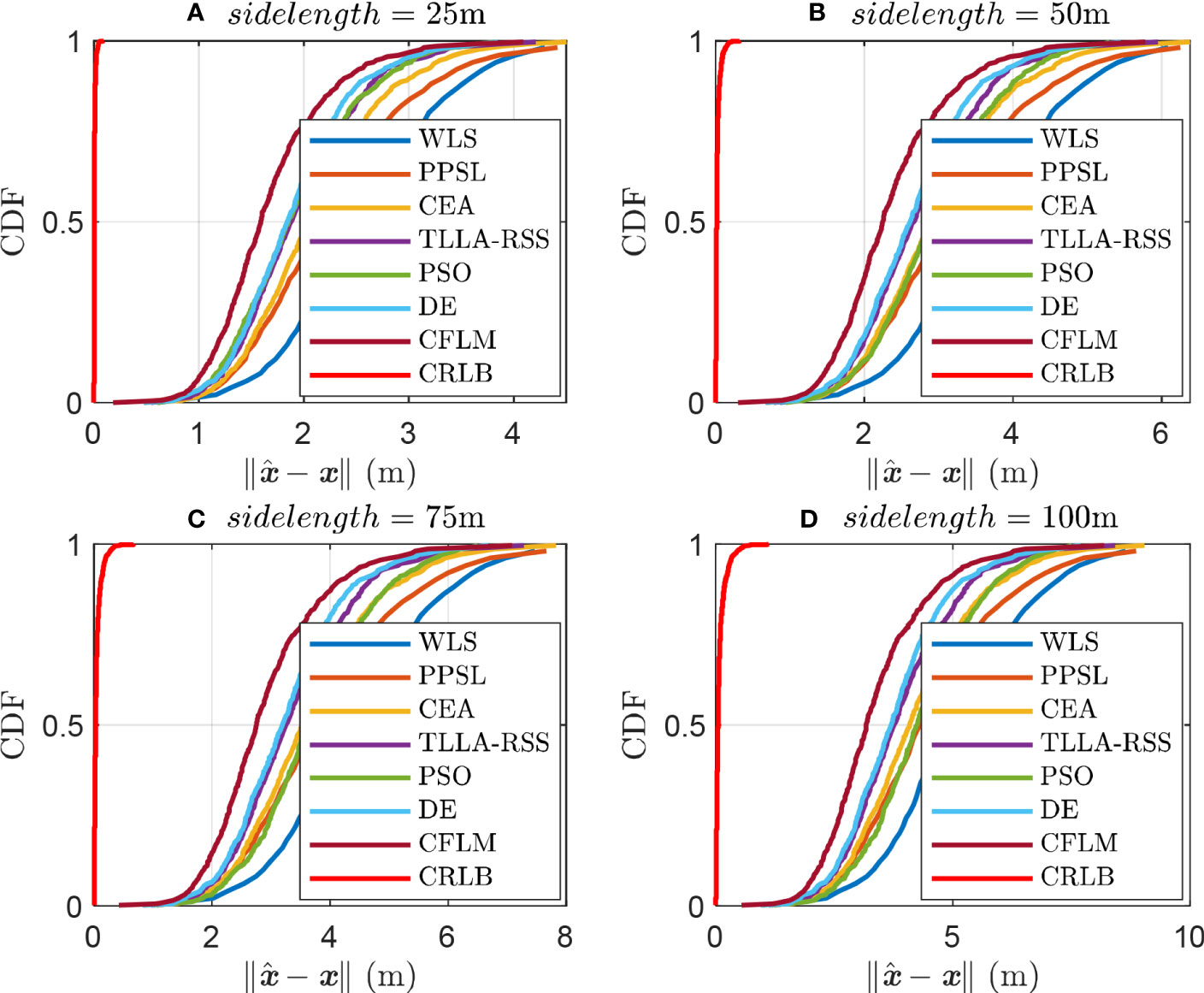
Figure 8 CDF of variable side lengths when σ_i = 3 dB, N = 8, and θ = 0.1, where A, B, C, and D are scenarios with sidelength = 25 m, sidelength = 50 m, sidelength = 75 m, and sidelength = 100 m, respectively.

TABLE 4

Table 4 CDF of the methods under variable side lengths.

FIGURE 9

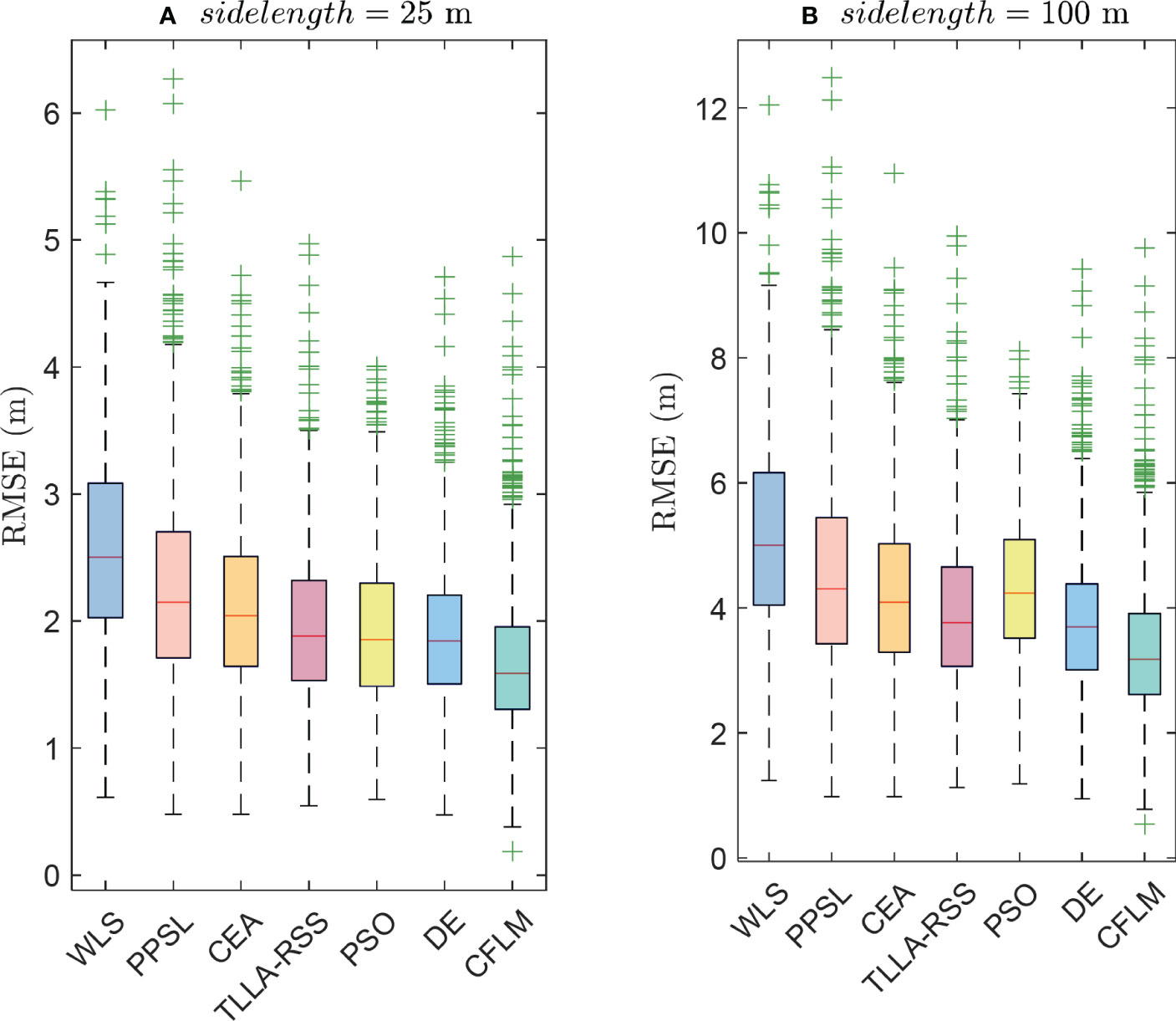
Figure 9 RMSE analysis when σi = 3 dB, N = 8, and θ = 0.1 under variable side lengths, where A and are scenarios with sidelength = 25 m and sidelength = 100 m, respectively.

5.4 Scenario with variable steepness

Steepness depends on the ocean environment characteristics, such as the temperature (Ramezani et al., 2013). Accordingly, simulations are performed to evaluate whether the proposed method still works in variable steepness. Figure 10 shows the results with $N=8$ , ${\sigma }_i=3\text{ dB}$ , and $sidelength=50\text{ m}$. The WLS, PPSL, CEA, TLLA-RSS, PSO, DE, and CFLM are robust to the steepness, as shown in Figure 10 and Table 5. Conversely, the CRLB is sensitive to the change in steepness. Its error increases with the steepness. Moreover, the CFLM performs better than the other methods, regardless of the changes in steepness. The CFLM achieves $\parallel \widehat{x}-x\parallel \le \mathrm{3.87 m}$and $\parallel \widehat{x}-x\parallel \le \mathrm{3.89 m}$ at 95% with $\vartheta =0.1$ and $\vartheta =0.7$ , respectively. The box plot of the deviation in Figure 11 also proves the superior performance of the CFLM. Its median errors are 2.24 m and 2.26 m, as shown in Figures 11A, B, respectively.

FIGURE 10

Figure 10 CDF of variable steepness.

TABLE 5

Table 5 CDF of the methods under variable steepness.

FIGURE 11

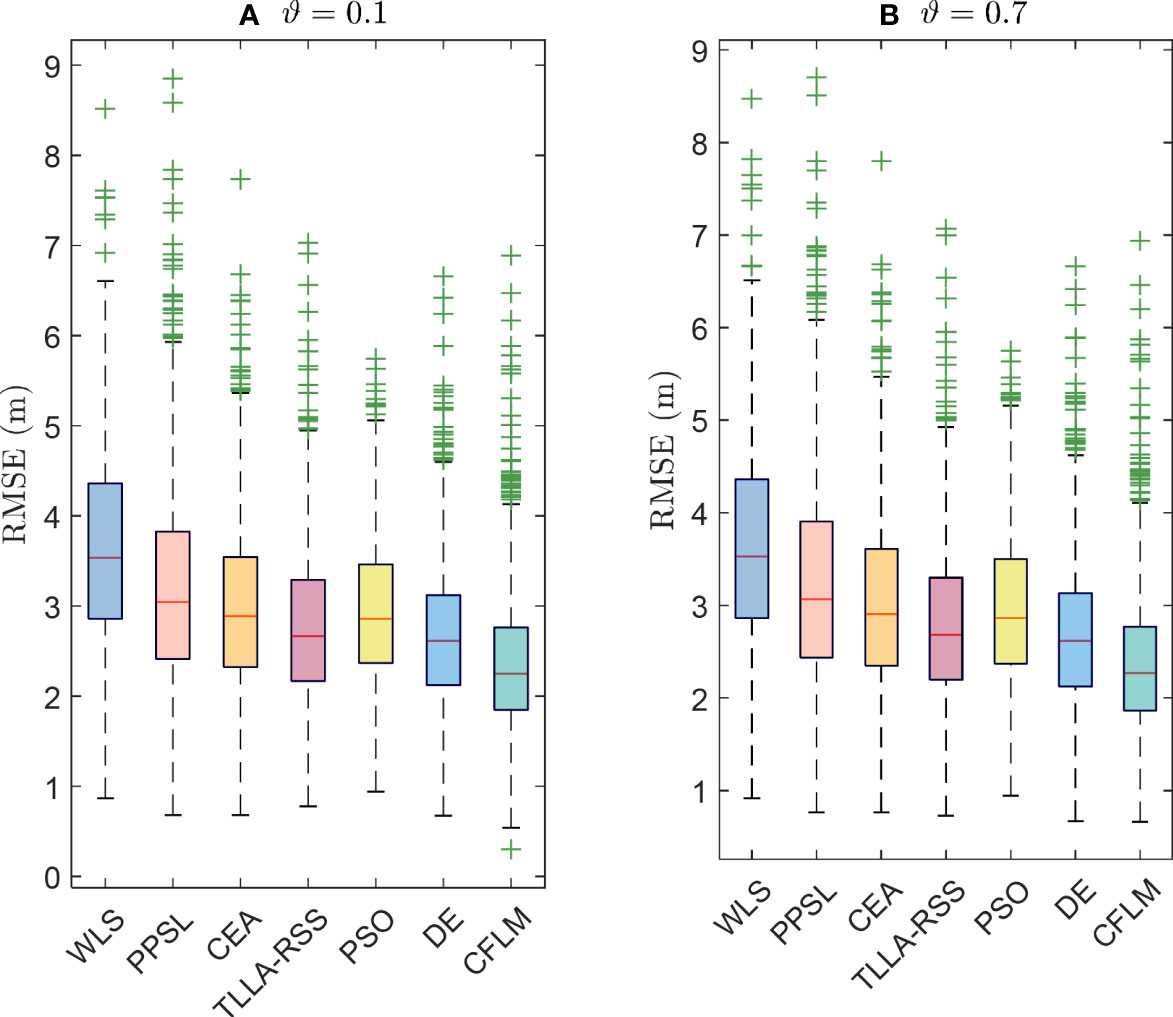
Figure 11 MSE analysis when σi = 3 dB, sidelength = 50 m, and N = 8 under variable steepness, where A and B are scenarios with θ = 0.1 and θ = 0.7, respectively.

6 Conclusion

This study develops a CFLM for UWSNs, simultaneously considering hybrid loss and stratification effects. The localization problem is solved under the ANCLS framework after linearization, in which a coarse estimation based on CEA is derived. The potential solution is filtered by the constraint from one group to another. Moreover, an approach based on a first-order Taylor series expansion is presented in the second step of CFLM to refine the solution further. In addition, the CRLB is derived for this scenario and used as a benchmark to evaluate the methods. Simulation results reveal the outperformance of the proposed method in different scenarios. The localization accuracy is improved by up to 66 percent compared with the methods, according to Section 6. Even so, the margin between the CFLM and CRLB remains remarkable. Meanwhile, the simulation environment is idealized. For instance, signal propagation may suffer from the non-line-of-sight (NLOS) noise, which may significantly impact the ranging acquirement, deteriorating localization accuracy. Unfortunately, the paper does not consider the situation. It would be interesting to take further research on localization under NLOS noise and derive a closed-form solution. Besides, it has been proved that the UWSNs may easily suffer the attack. How to achieve private communication while preserving localization accuracy is an interesting topic. In addition, the proposed method only considers schemes known to transmit power (TP) and the path loss exponent (PLE). It is worth noting that TP and PLE might be changeable according to the propagation environment and node status. Eliminating this assumption in future studies can further validate the applicability of the proposed method.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding authors.

Author contributions

XM proposed the main ideas, wrote the paper, designed the description framework, and performed the simulations. DH and HW provided guidance for the study and acquired funding. BH and NS provided guidance for the work, reviewed the paper, and collaborated in discussions on the proposed system model and localization technique. FM, XC, and JX assisted in testing the code and checking the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported in part by the National Natural Science Foundation of China (Grant Nos. 52201401, 52071200, 52201403, and 52102397), the National Key Research and Development Program (Grant No. 2021YFC2801002), the Shanghai Committee of Science and Technology, China (Grant No. 23010502000), the China Postdoctoral Science Foundation (Grant No. 2022M712027), and the Shanghai Postdoctoral Excellence Program (Grant No. 2022767).

Acknowledgments

The authors thank the reviewers for their time spent on the manuscript.

Conflict of interest

Author BH is employed by Shanghai Ship and Shipping Research Institute Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmad I., Rahman T., Khan I., Jan S., Musa S., Uddin M. I. (2022a). RACE-SM: Reliability and adaptive cooperation for efficient UWSNs using sink mobility. Front. Mar. Sci. 9. doi: 10.3389/fmars.2022.1030113

PubMed Abstract | CrossRef Full Text | Google Scholar

Ahmad I., Rahman T., Zeb A., Khan I., Othman M. T., Hamam H. (2022b). Cooperative energy-efficient routing protocol for underwater wireless sensor networks. Sensors 22 (18), 6945. doi: 10.3390/s22186945

PubMed Abstract | CrossRef Full Text | Google Scholar

Ahmad I., Rahman T., Zeb A., Khan I., Ullah I., Hamam H., et al. (2021). Analysis of security attacks and taxonomy in underwater wireless sensor networks. Wirel. Commun. Mob. Comput. 2021, 1444024. doi: 10.1155/2021/1444024

CrossRef Full Text | Google Scholar

Aman W., Al-Kuwari S., Muzzammil M., Rahman M. M. U., Kumar A. (2023). Security of underwater and air–water wireless communication: State-of-the-art, challenges and outlook. Ad Hoc Networks 142, 103114. doi: 10.1016/j.adhoc.2023.103114

CrossRef Full Text | Google Scholar

Bacanin N., Sarac M., Budimirovic N., Zivkovic M., AlZubi A. A., Bashir A. K. (2022). Smart wireless health care system using graph LSTM pollution prediction and dragonfly node localization. Sustain. Comput. Inf. Syst. 35, 100711. doi: 10.1016/j.suscom.2022.100711

CrossRef Full Text | Google Scholar

Berger C. R., Zhou S., Willett P., Liu L. (2008). Stratification effect compensation for improved underwater acoustic ranging. IEEE Trans. Signal Process. 56, 3779–3783. doi: 10.1109/TSP.2008.924801

CrossRef Full Text | Google Scholar

Chang S., Li Y., He Y., Wu Y. (2019). RSS-based target localization in underwater acoustic sensor networks via convex relaxation. Sensors 19, 2323. doi: 10.3390/s19102323

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen X., Liu S., Liu R. W., Wu H., Han B., Zhao J. (2022). Quantifying Arctic oil spilling event risk by integrating an analytic network process and a fuzzy comprehensive evaluation model. Ocean Coast. Manage. 228, 106326. doi: 10.1016/j.ocecoaman.2022.106326

CrossRef Full Text | Google Scholar

Chen X., Wang Z., Hua Q., Shang W.-L., Luo Q., Yu K. (2023). AI-empowered speed extraction via port-like videos for vehicular trajectory analysis. IEEE Trans. Intell. Transp. Syst. 24, 4541–4552. doi: 10.1109/TITS.2022.3167650

CrossRef Full Text | Google Scholar

Cimini G., Bemporad A. (2017). Exact complexity certification of active-set methods for quadratic programming. IEEE Trans. Automat. Contr. 62, 6094–6109. doi: 10.1109/TAC.2017.2696742

CrossRef Full Text | Google Scholar

Derrac J., García S., Molina D., Herrera F. (2011). A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 1, 3–18. doi: 10.1016/j.swevo.2011.02.002

CrossRef Full Text | Google Scholar

Han D., Pan N., Li K.-C. (2022a). A traceable and revocable ciphertext-policy attribute-based encryption scheme based on privacy protection. IEEE Trans. Dependable Secur. Comput. 19, 316–327. doi: 10.1109/TDSC.2020.2977646

CrossRef Full Text | Google Scholar

Han G., Shen S., Song H., Yang T., Zhang W. (2018). A stratification-based data collection scheme in underwater acoustic sensor networks. IEEE Trans. Veh. Technol. 67, 10671–10682. doi: 10.1109/TVT.2018.2867021

CrossRef Full Text | Google Scholar

Han D., Zhu Y., Li D., Liang W., Souri A., Li K.-C. (2022b). A blockchain-based auditable access control system for private data in service-centric ioT environments. IEEE Trans. Ind. Inf. 18, 3530–3540. doi: 10.1109/TII.2021.3114621

CrossRef Full Text | Google Scholar

Islam K. Y., Ahmad I., Habibi D., Waqar A. (2022). A survey on energy efficiency in underwater wireless communications. J. Netw. Comput. Appl. 198, 103295. doi: 10.1016/j.jnca.2021.103295

CrossRef Full Text | Google Scholar

Jia T., Liu H., Ho K. C., Wang H. (2023). Mitigating sensor motion effect for AOA and AOA-TOA localizations in underwater environments. IEEE Trans. Wirel. Commun. 1. doi: 10.1109/TWC.2023.3239544

CrossRef Full Text | Google Scholar

Jiang J., Han G., Lin C. (2023). A survey on opportunistic routing protocols in the Internet of Underwater Things. Comput. Networks 225, 109658. doi: 10.1016/j.comnet.2023.109658

CrossRef Full Text | Google Scholar

Kannan R., Ballard G., Park H. (2018). MPI-FAUN: an MPI-based framework for alternating-updating nonnegative matrix factorization. IEEE Trans. Knowl. Data Eng. 30, 544–558. doi: 10.1109/TKDE.2017.2767592

CrossRef Full Text | Google Scholar

Khalil R. A., Saeed N., Babar M. I., Jan T. (2021). Toward the internet of underwater things: recent developments and future challenges. IEEE Consum. Electron. Mag. 10, 32–37. doi: 10.1109/MCE.2020.2988441

CrossRef Full Text | Google Scholar

Li H., Han D., Tang M. (2022c). A privacy-preserving storage scheme for logistics data with assistance of blockchain. IEEE Internet Things J. 9, 4704–4720. doi: 10.1109/JIOT.2021.3107846

CrossRef Full Text | Google Scholar

Li D., Han D., Weng T.-H., Zheng Z., Li H., Liu H., et al. (2022a). Blockchain for federated learning toward secure distributed machine learning systems: a systemic survey. Soft Comput. 26, 4423–4440. doi: 10.1007/s00500-021-06496-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Li D., Han D., Zheng Z., Weng T.-H., Li H., Liu H., et al. (2022b). MOOCsChain: A blockchain-based secure storage and sharing scheme for MOOCs learning. Comput. Stand. Interfaces 81, 103597. doi: 10.1016/j.csi.2021.103597

CrossRef Full Text | Google Scholar

Li S., Sun H., Esmaiel H. (2020). Underwater TDOA acoustical location based on majorization-minimization optimization. Sensors 20, 4457. doi: 10.3390/s20164457

PubMed Abstract | CrossRef Full Text | Google Scholar

Li X., Wang Y., Qi B., Hao Y. (2023). Underwater acoustic localization of the long baseline based on track-before-detect. IEEE Geosci. Remote Sens. Lett. 20, 1–5. doi: 10.1109/LGRS.2023.3257990

CrossRef Full Text | Google Scholar

Luo J., Yang Y., Wang Z., Chen Y. (2021). Localization algorithm for underwater sensor network: A review. IEEE Internet Things J. 8, 13126–13144. doi: 10.1109/JIOT.2021.3081918

CrossRef Full Text | Google Scholar

Mahmutoglu Y., Turk K. (2019). Received signal strength difference based leakage localization for the underwater natural gas pipelines. Appl. Acoust. 153, 14–19. doi: 10.1016/j.apacoust.2019.04.006

CrossRef Full Text | Google Scholar

Mei X., Han D., Chen Y., Wu H., Ma T. (2023). Target localization using information fusion in WSNs-based Marine search and rescue. Alexandria Eng. J. 68, 227–238. doi: 10.1016/j.aej.2023.01.028

CrossRef Full Text | Google Scholar

Mei X., Han D., Saeed N., Wu H., Chang C.-C., Han B., et al. (2022a). Trajectory optimization of autonomous surface vehicles with outliers for underwater target localization. Remote Sens. 14, 4343. doi: 10.3390/rs14174343

CrossRef Full Text | Google Scholar

Mei X., Han D., Saeed N., Wu H., Ma T., Xian J. (2022b). Range Difference-based Target Localization under Stratification Effect and NLOS bias in UWSNs. IEEE Wirel. Commun. Lett. 11, 2080–2084. doi: 10.1109/LWC.2022.3193579

CrossRef Full Text | Google Scholar

Mei X., Wu H., Saeed N., Ma T., Xian J., Chen Y. (2020a). An absorption mitigation technique for received signal strength-based target localization in underwater wireless sensor networks. Sensors 20, 4698. doi: 10.3390/s20174698

PubMed Abstract | CrossRef Full Text | Google Scholar

Mei X., Wu H., Xian J. (2020b). Matrix Factorization based Target Localization via Range Measurements with Uncertainty in Transmit Power. IEEE Wirel. Commun. Lett. 9, 1611–1615. doi: 10.1109/LWC.2020.2998609

CrossRef Full Text | Google Scholar

Mei X., Wu H., Xian J., Chen B. (2021). RSS-based byzantine fault-tolerant localization algorithm under NLOS environment. IEEE Commun. Lett. 25, 474–478. doi: 10.1109/LCOMM.2020.3027904

CrossRef Full Text | Google Scholar

Menaka D., Gauni S. (2022). An energy efficient dead reckoning localization for mobile Underwater Acoustic Sensor Networks. Sustain. Comput. Inf. Syst. 36, 100808. doi: 10.1016/j.suscom.2022.100808

CrossRef Full Text | Google Scholar

Miao F., Yao L., Zhao X. (2021). Symbiotic organisms search algorithm using random walk and adaptive Cauchy mutation on the feature selection of sleep staging. Expert Syst. Appl. 176, 114887. doi: 10.1016/j.eswa.2021.114887

CrossRef Full Text | Google Scholar

Pei J., Liu W., Wang L., Liu C., Bashir A. K., Wang Y. (2023). Fed-ioUT: opportunities and challenges of federated learning in the internet of underwater things. IEEE Internet Things Mag. 6, 108–112. doi: 10.1109/IOTM.001.2200127

CrossRef Full Text | Google Scholar

Pourkabirian A., Kooshki F., Anisi M. H., Jindal A. (2023). An accurate RSS/AoA-based localization method for internet of underwater things. Ad Hoc Networks 145, 103177. doi: 10.1016/j.adhoc.2023.103177

CrossRef Full Text | Google Scholar

Poursheikhali S., Zamiri-Jafarian H. (2021). Source localization in inhomogeneous underwater medium using sensor arrays: Received signal strength approach. Signal Process. 183, 108047. doi: 10.1016/j.sigpro.2021.108047

CrossRef Full Text | Google Scholar

Ramezani H., JaMali-Rad H., Leus G. (2013). Target localization and tracking for an isogradient sound speed profile. IEEE Trans. Signal Process. 61, 1434–1446. doi: 10.1109/TSP.2012.2235432

CrossRef Full Text | Google Scholar

Saeed N., Celik A., Al-Naffouri T. Y., Alouini M. (2019). Localization of energy harvesting empowered underwater optical wireless sensor networks. IEEE Trans. Wirel. Commun. 18, 2652–2663. doi: 10.1109/TWC.2019.2906309

CrossRef Full Text | Google Scholar

Sathish K., Venkata R. C., Anbazhagan R., Pau G. (2023). Review of localization and clustering in USV and AUV for underwater wireless sensor networks. Telecom 4, 43–64. doi: 10.3390/telecom4010004

CrossRef Full Text | Google Scholar

Sengijpta S. K. (1993). Fundamentals of statistical signal processing: estimation theory. Technometrics 37, 465–466. doi: 10.1080/00401706.1995.10484391

CrossRef Full Text | Google Scholar

Sharma N., Gupta V. (2020). Meta-heuristic based optimization of WSNs Localisation Problem- a Survey. Proc. Comput. Sci. 173, 36–45. doi: 10.1016/j.procs.2020.06.006

CrossRef Full Text | Google Scholar

Stojanovic M., Preisig J. (2009). Underwater acoustic communication channels: Propagation models and statistical characterization. IEEE Commun. Mag. 47, 84–89. doi: 10.1109/MCOM.2009.4752682

CrossRef Full Text | Google Scholar

Strumberger I., Minovic M., Tuba M., Bacanin N. (2019). Performance of elephant herding optimization and tree growth algorithm adapted for node localization in wireless sensor networks. Sensors 19, 2515. doi: 10.3390/s19112515

PubMed Abstract | CrossRef Full Text | Google Scholar

Su J., Li Y., Ali W. (2022). Underwater passive manoeuvring target tracking with isogradient sound speed profile. IET Radar Sonar Navig. 16, 1415–1433. doi: 10.1049/rsn2.12269

CrossRef Full Text | Google Scholar

Su X., Ullah I., Liu X., Choi D. (2020). A review of underwater localization techniques, algorithms, and challenges. J. Sensors 2020, 1–25. doi: 10.1155/2020/6403161

CrossRef Full Text | Google Scholar

Sun Y., Babu P., Palomar D. P. (2017). Majorization-minimization algorithms in signal processing, communications, and machine learning. IEEE Trans. Signal Process. 65, 794–816. doi: 10.1109/TSP.2016.2601299

CrossRef Full Text | Google Scholar

Weiss A., Arikan T., Vishnu H., Deane G. B., Singer A. C., Wornell G. W. (2022). A semi-blind method for localization of underwater acoustic sources. IEEE Trans. Signal Process. 70, 3090–3106. doi: 10.1109/TSP.2022.3173731

CrossRef Full Text | Google Scholar

Wu H., Mei X., Chen X., Li J., Wang J., Mohapatra P. (2018). A novel cooperative localization algorithm using enhanced particle filter technique in maritime search and rescue wireless sensor network. ISA Trans. 78, 39–46. doi: 10.1016/j.isatra.2017.09.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Yan J., Meng Y., Luo X., Guan X. (2021). To hide private position information in localization for internet of underwater things. IEEE Internet Things J. 8, 14338–14354. doi: 10.1109/JIOT.2021.3068298

CrossRef Full Text | Google Scholar

Zhang B., Hu Y., Wang H., Zhuang Z. (2019). Sea-surface reflection-aided underwater localization with unknown sound speed. Sci. China Inf. Sci. 62, 049302. doi: 10.1007/s11432-018-9625-y

CrossRef Full Text | Google Scholar

Zhang J., Kou L., Yang Y., He F., Duan Z. (2020). Monte-Carlo-based optical wireless underwater channel modeling with oceanic turbulence. Opt. Commun. 475, 126214. doi: 10.1016/j.optcom.2020.126214

CrossRef Full Text | Google Scholar

Zhang B., Wang H., Xu T., Zheng L., Yang Q. (2016). Received signal strength-based underwater acoustic localization considering stratification effect (Shanghai, China: OCEANS 2016-Shanghai), 1–8.

Google Scholar

Zhang X., Zheng N. (2010). Geometrically convex functions and estimation of remainder terms for Taylor expansion of some functions. J. Math. Inequalities 4, 15–25. doi: 10.7153/jmi-04-03

CrossRef Full Text | Google Scholar

Zhao H., Yan J., Luo X., Gua X. (2020). Privacy preserving solution for the asynchronous localization of underwater sensor networks. IEEE/CAA J. Autom. Sin. 7, 1511–1527. doi: 10.1109/JAS.2020.1003312

CrossRef Full Text | Google Scholar