Influence of the El Niño-Southern Oscillation on upper-ocean salinity changes in the southeast Indian ocean

The interannual-decadal variability in the upper-ocean salinity of the southeast Indian Ocean (SEIO) was found to be highly correlated with the El Niño-Southern Oscillation (ENSO). Based on multisource data, this study revealed that this ENSO-like salinity variability mainly resides in the domain between 13°S-30°S and 100°E-120°E, and at depths above 150 m. This variability is principally driven by meridional geostrophic velocity (MGV), which changes with the zonal pattern of the sea surface height (SSH). Previous studies have reported that the variability in the SSH in the south Indian Ocean is principally driven by local-wind forcing and eastern-boundary forcing. Here the eastern-boundary forcing denotes the influence of SSH anomaly radiated from the western coast of Australia. A recent study emphasized the contribution of local-wind forcing in salinity variability in the SEIO, for its significant role in generation of the zonal dipole pattern of SSH anomaly in the south Indian Ocean, which was considered to be responsible for the anomalous MGV in the SEIO. While our results revealed a latitudinal difference between the domain where the SSH dipole pattern exists (north of 20°S) and the region in which the ENSO-like salinity variability is strongest (20°S-30°S), suggesting that this salinity variability cannot be attributed entirely to the SSH dipole pattern. Our further investigation shows that, the MGV in the SEIO changes with local zonal SSH gradient that principally driven by eastern-boundary forcing. In combination with the strong meridional salinity gradient, the boundary-driven MGV anomalies cause significant meridional salinity advection and eventually give rise to the observed ENSO-like salinity variability. This study revealed the leading role of eastern-boundary forcing in interannual variability of the upper-ocean salinity in the SEIO.

1 Introduction

Salinity plays an important role in ocean dynamics processes in the southeast Indian Ocean (SEIO). For example, the existence of the Eastern Gyral current (EGC) can be largely attributed to the strong meridional salinity gradient in the SEIO (Figure 1; Menezes et al., 2013). The halosteric contribution to sea level change in the SEIO is found to be more significant than the thermosteric contribution (Llovel and Lee, 2015). The significant freshening of upper-layer water in the SEIO during 2010-2011 led to a remarkable increase in Leeuwin Current (LC) transport and resulted in the subsequent strong marine heatwave near the western coast of Australia (Pearce and Feng, 2013; Feng et al., 2015), which is also known as a Ningaloo Niño named by Feng et al. (2013). Therefore, a better understanding of the variability of the upper-layer salinity in the SEIO is crucial for improving the ability to simulate and predict the regional oceanic and climate changes.

FIGURE 1

Figure 1 Mean sea surface salinity (SSS; psu) from the MOAA GPV for 2005-2020. The solid black arrows denote surface currents: the Indonesian Throughflow (ITF); South Equatorial Current (SEC); East Gyral Current (EGC) and the Leeuwin Current (LC). The dashed red arrow represents the oceanic waveguide along which the Pacific ENSO signals propagate. The blue arrows demonstrate the walker circulation.

Previous studies have reported that, the interannual-decadal variability in the SEIO upper-ocean salinity is tightly related to the ENSO signal (Phillips et al., 2005; Zhang et al., 2016; Zhang et al., 2018; Hu et al., 2019; Nie et al., 2020; Wu et al., 2021). This ENSO-like variability was mainly attributed to the variability in horizontal advection, while surface freshwater flux was found to play a secondary role. Through salinity budget analyses, researchers have further noted that variability in horizontal advection is mainly determined by anomalous meridional velocity (Zhang et al., 2016; Zhang et al., 2018; Huang et al., 2020; Wu et al., 2021). This is largely due to the strong meridional salinity gradient that exists between 15°-28°S (Figure 1), which is formed by the northern freshwater conveyed by the Indonesian throughflow (ITF) and the South Equatorial Current (SEC), and the southern high-salinity water generated by strong evaporation in the subtropical South Indian (e.g. Rochford, 1962; Wijffels et al., 2002; Nie et al., 2022). Because of this salinity front, even small meridional velocity changes could result in significant meridional salinity flux and lead to remarkable changes in salinity.

Therefore, the physical mechanism for meridional velocity changes is key to understanding the ENSO-like variability in the SEIO upper-ocean salinity. A recent study by Wu et al. (2021) attributed the anomalous meridional transport to the zonal dipole pattern of sea surface height (SSH) anomalies in the south Indian Ocean, and emphasized the role of local-wind forcing for its dominant role in variations of the SSH in the western basin (the western pole of the dipole pattern). However, based on previous studies, this zonal SSH dipole pattern is used to represent basin-wide meridional geostrophic transport in the south Indian Ocean (Lee, 2004; Lee and McPhaden, 2008; Zhuang et al., 2013; Meng et al., 2020; Nagura, 2020), rather than regional meridional transport in the SEIO. In addition, the significant contribution from local-wind forcing to the SSH anomaly is confined to lower latitudes (between 10° and 18°S; Masumoto and Meyers, 1998; Zhuang et al., 2013; Nagura and McPhaden, 2021). It becomes relatively weak at midlatitudes (between 19° and 33°S), where the eastern-boundary forcing becomes dominant (Zhuang et al., 2013; Menezes and Vianna, 2019; Nagura and McPhaden, 2021). Based on our analyses (Figure 2), the region where salinity is most strongly affected by ENSO signal covers latitudes from 13° to 30°S, with the highest correlation coefficients in the southern part of this range (20°-30°S). Clearly, there is a latitudinal difference between the region where the local-wind forcing is significant and the SSH dipole pattern exists (north of 20°S) and the region where the ENSO-like salinity variability is strongest. This suggests that the anomalous meridional velocity and the associated salinity variability in the SEIO cannot be attributed entirely to the zonal SSH dipole pattern.

FIGURE 2

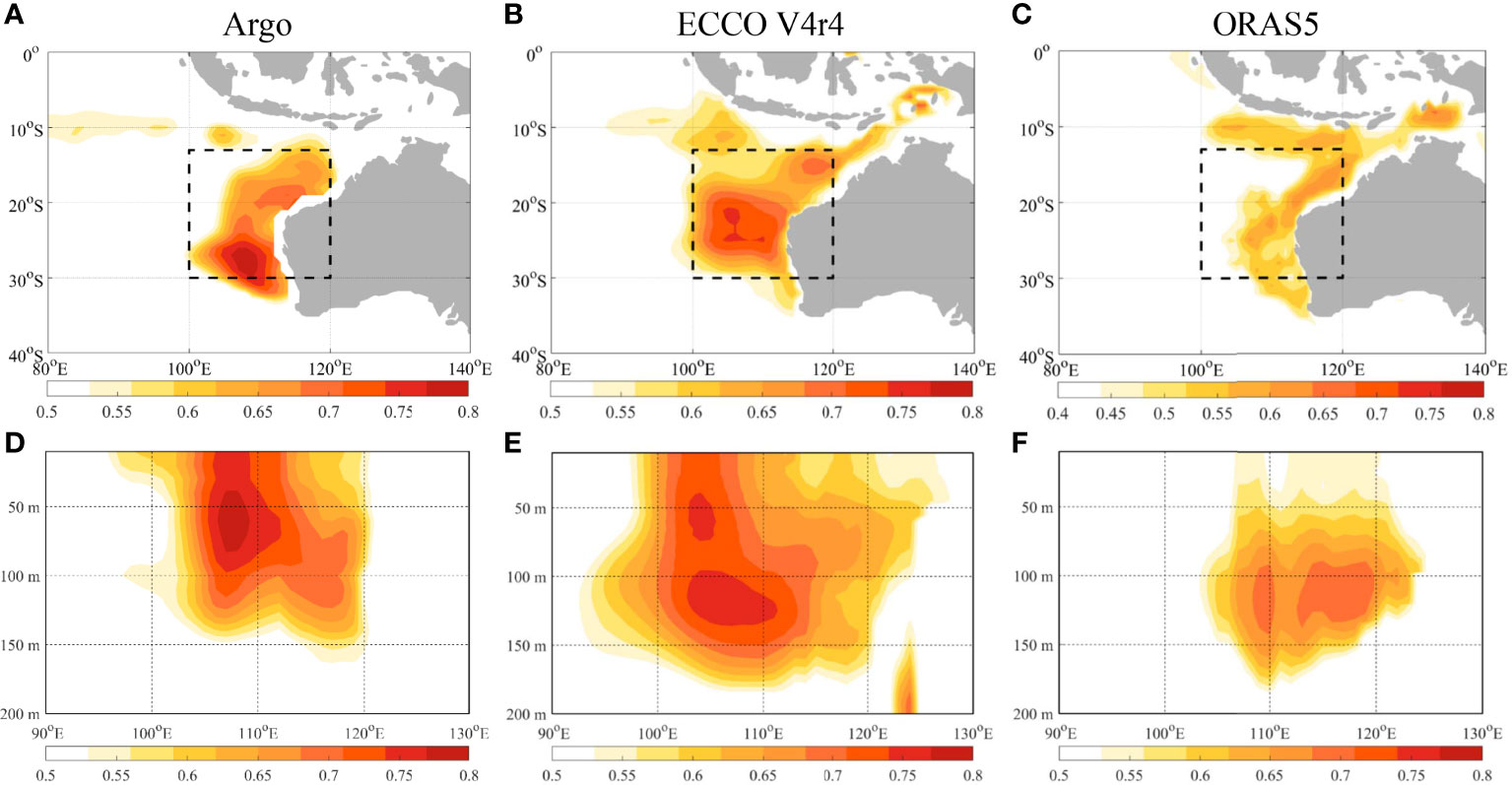
Figure 2 The correlation coefficient between the Niño 3.4 index and salinity tendency (∂S/∂t) averaged at depths above 150 m (A, C, E). The correlation coefficient between the Niño 3.4 index and salinity tendency averaged at latitudes between 13°S and 30°S (B, D, F). The results are based on salinity data from the Argo (A, B; 2005-2020), ECCO V4r4 (C, D; 1992-2017) and ORAS5 (E, F; 1979-2018). Values exceeding the 95% confidence level are shown. The black box denotes the study area, referred to as the “SEIO ENSO zone”.

The eastern-boundary forcing is significantly modified by the remote forcing from the Pacific. This includes the effects of oceanic planetary waves generated by tropical Pacific winds, which enter the south Indian Ocean through the oceanic waveguide (Figure 1) crossing the Indonesian archipelago as coastal trapped Kelvin waves, and then propagate westwards as Rossby waves from the western coast of Australia (Clarke, 1991; Clarke and Liu, 1994; Meyers, 1996; Potemra, 2001; Wijffels and Meyers, 2004; Cai et al., 2005; Feng et al., 2010; Feng et al., 2011; Menezes and Vianna, 2019; Nagura, 2020). Recently, alongshore winds at the western coast of Australia were also found to play a sizeable role in setting up the eastern boundary conditions (Kersalé et al., 2022). As a consequence, the SSH variability driven by eastern-boundary forcing is tightly linked with ENSO events. Therefore, we speculate that the meridional velocity and the ENSO-related salinity variability in the SEIO is primarily driven by eastern-boundary forcing, while the influence from the western SSH anomaly driven by local winds in the interior ocean is limited.

To fully understand the underlying dynamics of the correlation between the upper-ocean SEIO salinity and ENSO signal, this study first clarified the domain where this correlation is most significant. Then, salinity budget analyses were conducted to verify the dominant role of the meridional geostrophic velocity (MGV) in salinity variability. Next, a one-dimensional (1D), 1.5-layer long Rossby wave model was used to evaluate the relative importance of local-wind forcing and eastern-boundary forcing in the variability of the SSH in the SEIO. The contributions of these factors to MGV and upper-layer salinity changes were computed and compared. Through these analyses, we clarified the dominance of eastern-boundary forcing in determining the ENSO-like salinity variability in the SEIO. The remainder of this paper is organized as follows: Section 2 provides a brief description of the datasets and methods used. Sections 3 and 4 describe the results. The main conclusions are summarized in Section 5.

2 Data and methods

2.1 Data

Salinity data from three dataset were adopted in this study. The Monthly Objective Analysis using Argo float data (MOAA GPV) is an Argo-based gridded products from the Japan Agency for Marine-Earth Science and Technology (Hosoda et al., 2008). It provides monthly salinity data from 2001 onwards with a horizontal resolution of $1°\times 1°$ and vertical grid spacings ranging from 10 m near the sea surface to 250 m at 2000 m depth. The global ocean model product of Estimating the Circulation and Climate of the Ocean Version 4 release 4 (ECCO V4r4) is ECCO’s latest ocean state estimate (Forget et al., 2015; ECCO Consortium et al., 2021). It covers the period of 1992-2017 with a horizontal resolution that spatially varies from 22 km to 110 km, with the lowest resolution at mid latitudes and the highest resolution at high latitudes. The vertical grid intervals increase from 10 m near the surface to 457 m near the ocean bottom. The monthly data from ECCO V4r4 are also used for the salinity budget analyses in this study because they provide all the variables and enable the closure of the salinity budget equation. The ECMWF Ocean Reanalysis System 5 (ORAS5) is a global ocean ensemble reanalysis (Zuo et al., 2019) that assimilates the on-site temperature and salinity profiles from the quality-controlled EN4 dataset (Good et al., 2013). This reanalysis provides gridded monthly salinity data at 75 levels with a resolution of $0.25°\times 0.25°$ and covers the period from 1979 to the present, with a backwards extension from 1958 onwards.

To analyze the variability of geostrophic velocities and run the linear, 1D, 1.5-layer long Rossby wave model (section 2.2), monthly multi-satellite merged SSH anomalies and the corresponding geostrophic velocities from the French Archiving, Validation, and Interpolation of Satellite Oceanographic Data (AVISO) project and surface winds from the ECMWF ERA5 reanalysis were also used in this study. The gridded global AVISO SSH data are available from January 1993 to present, with a horizontal resolution of $0.25°\times 0.25°$. ERA5 is the fifth generation ECMWF reanalysis product of the global climate and weather (Hersbach, 2020). It provides gridded monthly wind speed data at 37 pressure levels with a resolution of 0.25°×0.25° and covers the period from 1959 to the present.

2.2 Methods

The salinity budget in the SEIO is evaluated following the methods of Qu et al. (2011); Gao et al. (2014) and Zhang et al. (2018):

$\begin{array}{ll}\frac{\partial [S]}{\partial t}=SEF+ADV+MIX+Res,& (1)\end{array}$

$\begin{array}{ll}[S]=\frac{{\iiint }_{V}SdV}{V},& (2)\end{array}$

$\begin{array}{ll}SEF=[S]\frac{{\iint }_A^{}(E-P)dA}{V},& (3)\end{array}$

$\begin{array}{ll}ADV=\frac{{\iiint }_V[-\nabla ·(uS,vS)]dV}{V},& (4)\end{array}$

where S is salinity, t is time, and V and A are the volume and surface area of the studying region, respectively. E and P are evaporation and precipitation, respectively, and SEF represents surface external forcing due to E‐P. MIX is the tendency due to salinity diffusive fluxes, which consists of isopycnal and diapycnal components. In ECCO V4r4, the mixing coefficients for eddies are parameterized by the Gent and Mcwilliams (1990) scheme, those for isopycnal mixing are parameterized by Redi (1982) and those for diapycnal mixing by Gaspar et al. (1990). Res denotes the residual which is induced by interpolating the budget terms from the native grid of ECCO to the specific grid of our study area. The advection term (ADV) can be further decomposed as follows:

$\begin{array}{ll}-\nabla ·(uS,vS)=-\left[\left(\overline{u}\frac{\partial \overline{S}}{\partial x}+\overline{v}\frac{\partial \overline{S}}{\partial y}\right)+\left(\overline{u}\frac{\partial S\text{'}}{\partial x}+\overline{v}\frac{\partial S\text{'}}{\partial y}+u\text{'}\frac{\partial \overline{S}}{\partial x}+v\text{'}\frac{\partial \overline{S}}{\partial y}\right)+\left(u\text{'}\frac{\partial S^{\prime }}{\partial x}+v\text{'}\frac{\partial S\text{'}}{\partial y}\right)\right],& (5)\end{array}$

In Eq. (5), the overbars represent the climatological mean and primes represent the deviation from the mean value. The first and third parts on the right-hand side of the equation, representing the mean advection terms and higher-order nonlinear terms, are not discussed in this work due to their small contributions. The first two terms (- $\overline{u}\frac{\partial S\text{'}}{\partial x}$, $-\overline{v}\frac{\partial S\text{'}}{\partial y}$) in the middle part represent the effect of the salinity anomaly that is advected by mean currents, and the last two terms ($-u\text{'}\frac{\partial \overline{S}}{\partial x}$, $-v\text{'}\frac{\partial \overline{S}}{\partial y}$) are advection terms linked with anomalous currents and the mean horizontal salinity gradient.

The SSH variability is examined using the linear, 1D, 1.5-layer long Rossby wave model (e.g. Qiu et al., 1997):

$\begin{array}{ll}\frac{\partial \eta }{t}-c_R\frac{\partial \eta }{\partial x}=-\frac{g^{\prime }}{g}{\nabla }_h\times (\frac{\tau }{{\rho }_{0}f})-\alpha \eta ,& (6)\end{array}$

where $\eta$ is the SSH, t is time, phase speed $c_R$ is computed following the methods used by Nagura and McPhaden (2021), x is longitude, $g$ and $g^{\prime }$ are the acceleration due to gravity and reduced gravity, respectively, ${\nabla }_h$ is the horizontal gradient operator, $\tau$ is the wind stress vector, f is the Coriolis parameter, ${\rho }_0=1025 kg m^{-3}$ is the mean seawater density, and ${\alpha }^{-1}=3 years$ denotes the damping coefficient.

3 Correlation between upper-ocean SEIO salinity and ENSO

The strong correlation between upper-ocean SEIO salinity and the ENSO index has been detected in both observations and reanalyzes (Phillips et al., 2005; Zhang et al., 2016; Zhang et al., 2018; Hu et al., 2019; Nie et al., 2020; Wu et al., 2021). In these studies, correlation estimation between upper-layer SEIO salinity and the ENSO index was commonly based on spatial mean salinity values. The spatial scales of the SEIO that were defined by different studies were remarkably different to achieve different research goals. For examples, Hu et al. (2019) analyzed the salinity anomaly in the domain of 100°-120°E and 12°-16°S within the upper 400 m depth, while Wu et al. (2021) defined the SEIO as the region between 90°-110°E and 12°-30°S at depths shallower than 200m. This study aimed to explore the relationship between upper-layer salinity changes and ENSO signals. Therefore, it was a precondition for us to clarify the domain where the effect of the ENSO signal is the most significant. However, we first needed to determine which variable should be studied, salinity or the salinity tendency (∂S/∂t)? Earlier studies investigated the relationship between the SEIO salinity anomalies and the ENSO signal and reported a positive correlation coefficient of roughly 0.5-0.6 (e.g., Zhang et al., 2016; Hu et al., 2019). More recent studies tended to emphasize the positive correlation between the salinity tendency and the ENSO signal (e.g. Nie et al., 2020; Wu et al., 2021) due to the higher correlation coefficient (approximately 0.7) between them. This could be attributed to the fact that the ENSO modulated ∂S/∂t more directly by influencing local advection velocities or freshwater flux, as can be referenced from Eq. (1). Therefore, this study also chose salinity tendency as the target variable.

The spatial distribution of the correlation coefficient between the Niño 3.4 index and upper-ocean salinity tendency is shown in Figure 2. We can observe that the ARGO-based results show the highest values (>0.5) along the western coast of Australia between approximately 13°S-30°S and 100°E-120°E (Figure 2A) and at depths above 150 m (Figure 2B). The ECCO-based results show a similar pattern but over a broader region (Figures 2C, D) and show the highest values at latitudes between 13°S-30°S. The highest values in the ORAS5-based results are narrowly confined to the northwestern coast of Australia at lower latitudes (13°S -20°S), but expand towards the west and cover a larger area at midlatitudes (20°S -30°S). They also vertically exist at depths shallower than 150 m, with the maxima residing at the subsurface between 80 m and 150 m. The differences between these results may result from the different lengths of their respective time periods. However, in general, a significant positive correlation can be found in the domain between 100°E -120°E and 13°S -30°S (black dashed boxes in Figure 1) and at depths above 150 m. Therefore, this should be the key region for estimating of the relationship between salinity changes and ENSO signals, and it was thus selected as the study region in this work and referred to as the “SEIO ENSO zone” hereafter. In particular, these results commonly show the strongest values at midlatitudes (20°S-30°S), where the eastern-boundary forcing play the dominant role in SSH variability. On the other hand, the ENSO-like salinity variability is relatively weak at lower latitudes (north of 20°S), where the zonal SSH gradient and basinwide meridional geostrophic transport are strongly modulated by local-wind forcing. This suggests that the contribution from local winds to variabilities in the MGV and salinity in the SEIO might be limited. For the regional mean results (Figure 3), the correlation coefficients between the salinity tendency and Niño 3.4 index for different time periods basically show positive values of approximately 0.7, demonstrating that this connection is not time dependent.

FIGURE 3

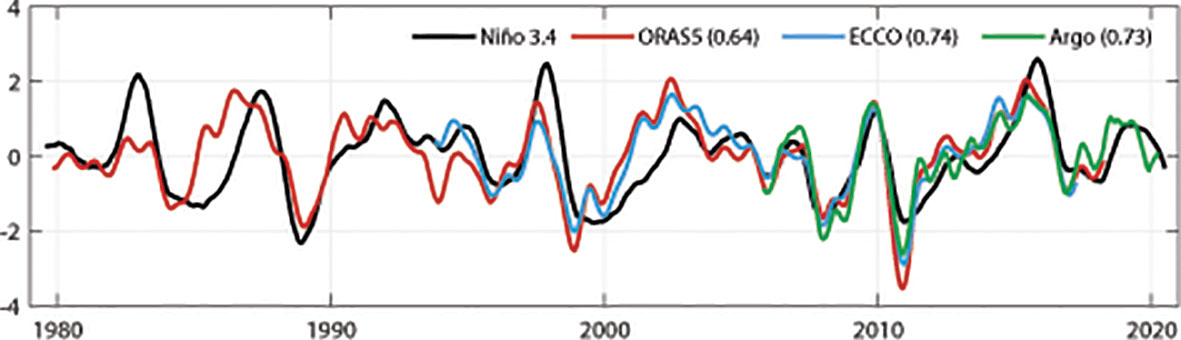
Figure 3 Normalised time series of the Niño 3.4 index (black) and the averaged salinity tendency in the “SEIO ENSO Zone” based on ORAS5 (red), ECCO (blue) and Argo (green) datasets. The numbers in parentheses denote the correlation coefficients between the Niño 3.4 index and salinity tendency.

Since both the horizontal and vertical scales of our study area were remarkably different from those of former relevant studies, we re-examined the salinity budget in the “SEIO ENSO zone” (Figure 4). The terms of salinity tendency, air-sea freshwater flux, advection, and mixing data were extracted from the ECCO V4r4 outputs (Figure 4A). The horizontal geostrophic advection term was also illustrated in this figure, which was obtained by using geostrophic velocities based on AVISO SSH anomalies and temperature/salinity from ECCO. Our results were basically in accordance with those of former studies. There were good consistencies between the salinity tendency and the advection term, as well as the geostrophic horizontal advection. However, the contributions by freshwater flux and mixing were comparably much weaker. This indicated that horizontal geostrophic advection was the main contributor to salinity variability. Further analyzation reveals that, the non-geostrophic horizontal advection term changes oppositely with the advection term and horizontal geostrophic advection term (Supplementary Figure 1). This suggests that the non-geostrophic horizontal advection offset the contributions from the geostrophic horizontal advection. The reason is probably as follows, the surface winds in the SEIO show anticyclonic (cyclonic) anomaly during El Niño (La Niña) (Supplementary Figure 2), which induce a southward (northward) Ekman transport that opposite with the meridional geostrophic transport anomaly.

FIGURE 4

Figure 4 (A) Anomalies of the salinity tendency (ST) and salinity budget terms (psu/mon) calculated in the “SEIO ENSO zone”: freshwater flux (E-P), mixing (MIX), residual (Res), advection (ADV) and its component due to effect of geostrophic flow (ADVg). (B) Same as (A) but for ADVg and its composite terms: $-(\partial \overline{S}/\partial y)v_g\text{'}$, $-(\partial \overline{S}/\partial x)u_g\text{'}$, $-(\partial S\text{'}/\partial y)\overline{v_g}$, and $-(\partial S\text{'}/\partial x)\overline{u_g}$.

Then, horizontal geostrophic advection was further decomposed into four terms according to Eq. 5 (Figure 4B). Higher-order nonlinear terms ($-u\text{'}\frac{\partial S^{\prime }}{\partial x},-v\text{'}\frac{\partial S\text{'}}{\partial y}$) are not show due to their negligible contributions, which will be further discussed in section 5. The results demonstrated that, the $-v_g\text{'}\frac{\partial \overline{S}}{\partial y}$ term, determined by anomalous MGV, was the predominant contributor to horizontal advection changes. The $-\overline{u_g}\frac{\partial S\text{'}}{\partial x}$ and $-\overline{v_g}\frac{\partial S\text{'}}{\partial y}$ terms represented advection of salinity anomalies from upstream regions and they clearly have no significant influence on geostrophic horizontal advection and salinity variability in the “SEIO ENSO zone”. The role of the $-u_g\text{'}\frac{\partial \overline{S}}{\partial x}$ term, representing the contribution of anomalous zonal geostrophic currents, was also insignificant because of the weak climatological zonal salinity gradient. This can be further observed in the composite maps of the four terms during the El Niño events and La Niña events (Figure 5). The anomalies of the $-v_g\text{'}\frac{\partial \overline{S}}{\partial y}$ term during different ENSO phases are significant in the SEIO, especially in the “SEIO ENSO Zone”. The anomalies of the other terms are comparably much weaker. Therefore, to understand the underlying dynamics between upper-ocean SEIO salinity changes and ENSO signals, we first need to clarify the role of ENSO events in the variability of the MGV.

FIGURE 5

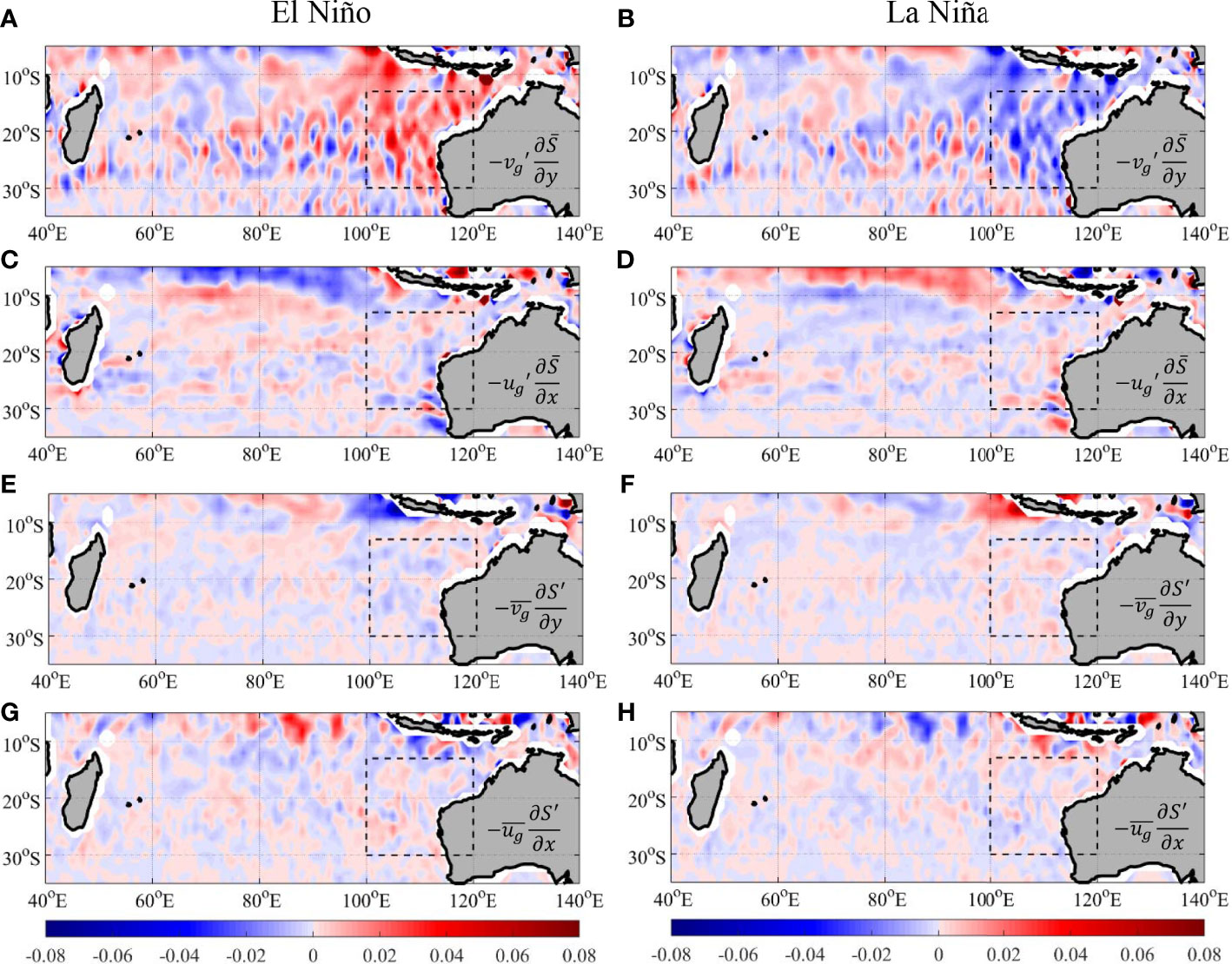
Figure 5 Composite of the advection terms (psu/mon) induced by geostrophic flow during El Niño and La Niña: (A, B) $-(\partial \overline{S}/\partial y)v_g\text{'}$, (C, D) $-(\partial \overline{S}/\partial x)u_g\text{'}$, (E, F) $-(\partial S\text{'}/\partial y)\overline{v_g}$, and (G, H) $-(\partial S\text{'}/\partial x)\overline{u_g}$.

4 The formation of MGV anomaly

To study the MGV changes in the “SEIO ENSO Zone”, we first investigated the variability in SSH and its connection with ENSO events based on observed SSH anomalies. The observed monthly SSH anomalies from January 1993 to December 2020 were obtained from satellite altimetry provided by the AVISO project. The seasonal variability of meridionally averaged SSH anomalies in the “SEIO ENSO Zone” during five typical El Niño events (1994, 1997, 2002, 2009, 2015) and five typical La Niña events (1998, 1999, 2007, 2010, 2011) are illustrated in Figures 6 and 7, respectively. During the El Niño events, the SSH gradually changed from a flat form to a pattern with higher values in the western part and lower values in the eastern part (Figure 6). The zonal SSH gradient became largest during boreal winters when ENSO events peaked in amplitude (Rasmusson and Carpenter, 1982; Trenberth, 1997). As a result, the MGV show northwards anomalies due to the geostrophic balance. In contrast, the SSH shifted to a pattern with lower values in the western part and higher values in the eastern part during La Niña events (Figure 7), and the MGV show southwards anomalies. Figures 8A, B further demonstrates that the zonal SSH difference in the “SEIO ENSO Zone” can be mostly attributed to SSH anomalies along the west coast of Australia, while the SSH anomalies near the western boundary at 100°E were comparatively small. The time series in Figure 8C demonstrates the simultaneous shift between the MGV and the local zonal SSH gradient within the “SEIO ENSO Zone”, with a correlation coefficient of -0.83, and both were closely related to the ENSO signal. Note that the variability in the zonal SSH gradient was represented by the zonal slope of the linear fitted results, as illustrated in Figures 6, 7. The above results indicated that the ENSO signal influenced the MGV in the SEIO by modulating the local SSH pattern.

FIGURE 6

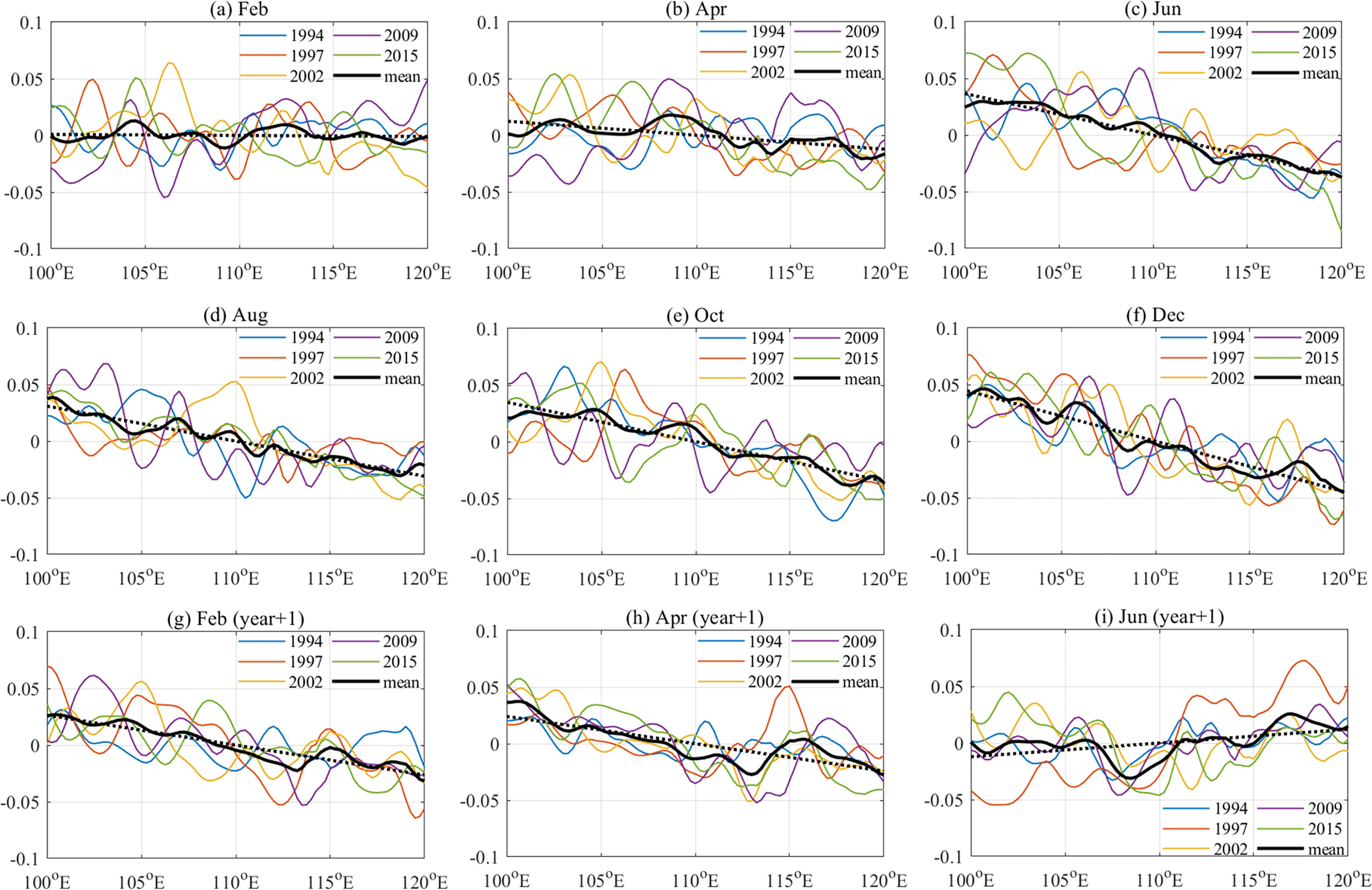
Figure 6 (A–I) Seasonal variability of the meridional mean SSH anomaly (m) between 13°S and 30°S in El Niño years (1994, 1997, 2002, 2009, and 2015; colored lines). The mean value for each month (solid black line) with a linear fit (dashed black line) is also illustrated.

FIGURE 7

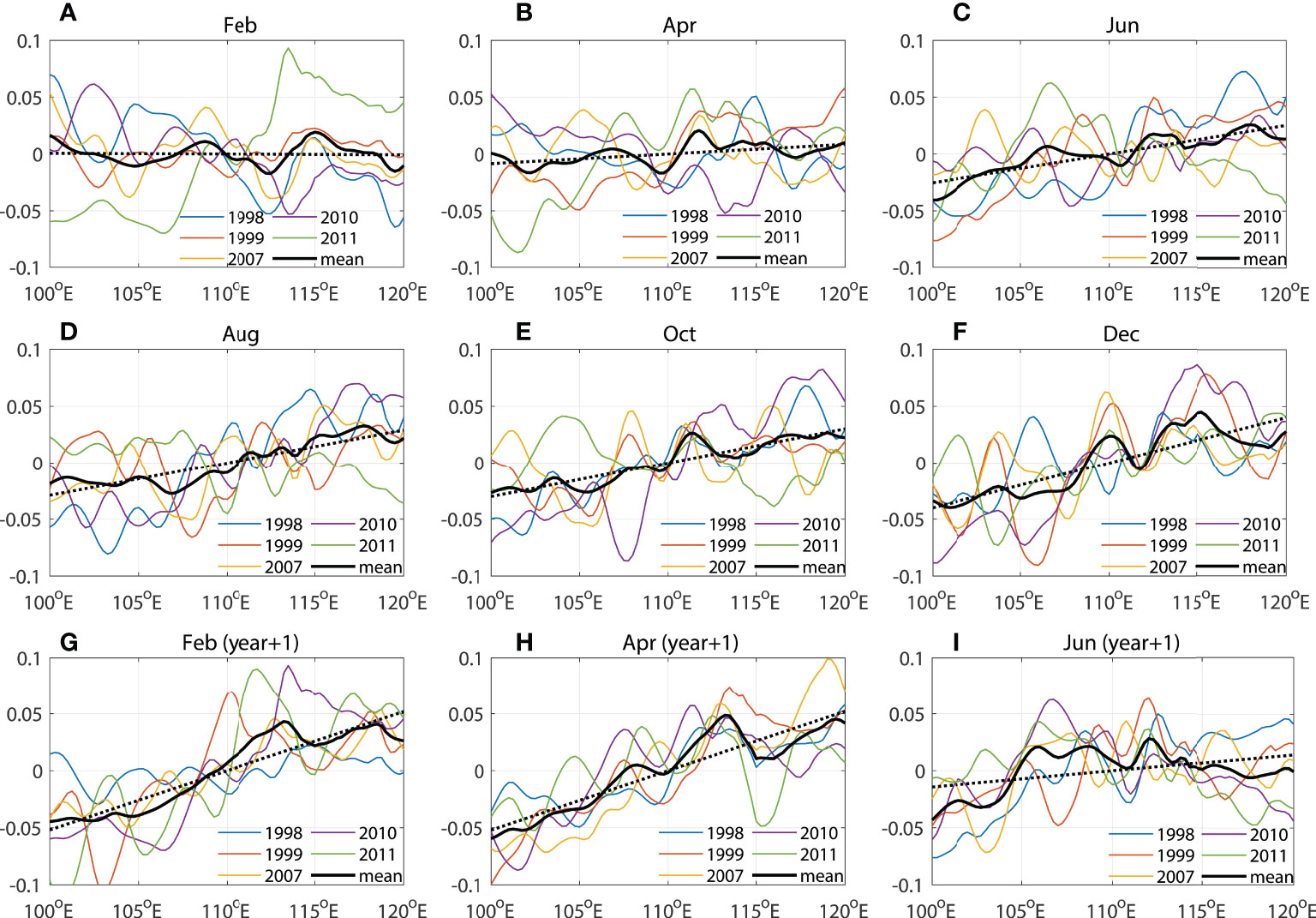
Figure 7 (A–I) Seasonal variability of the meridional mean SSH anomaly (m) between 13°S and 30°S in La Niña years (1998, 1999, 2007, 2010, and 2011; colored lines). The mean value for each month (solid black line) with a linear fit (dashed black line) is also illustrated.

FIGURE 8

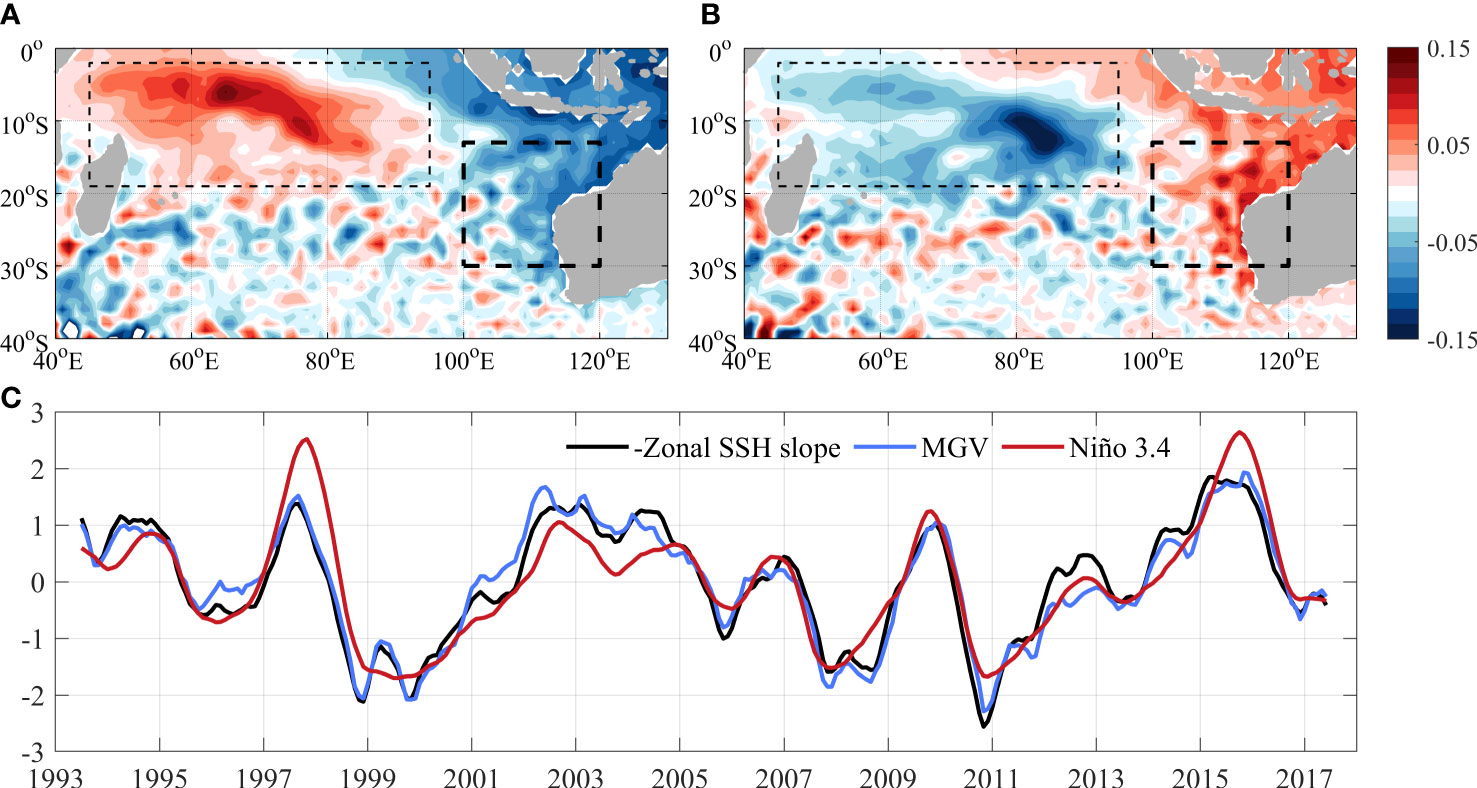
Figure 8 Composite of the SSH anomaly (m) in boreal winters of El Niño (A) and La Niña (B) years. The dashed black box on the left represents the region where the SSH shows significant opposite anomalies in compare with that in the “SEIO ENSO zone” (dashed black box on the right) in different ENSO events. (C) Normalized time series for the zonal slope of the linear fitted meridional mean SSH anomaly, meridional geostrophic velocity (MGV) in the “SEIO ENSO zone” and Niño 3.4 index. The slope is shown with an opposite sign for easier comparison.

Previous studies have noted that ENSO events interact with the Indian Ocean through both “atmospheric bridge” and oceanic routes. By zonally shifting the convective center of the Walker Circulation, local surface winds in the southern Indian Ocean are influenced by the ENSO via the atmospheric bridge (Yu et al., 2005; Volkov et al., 2020). Then, the wind-induced Ekman pumping anomalies alter the SSH in the interior region of the south Indian Ocean by generating westwards propagating Rossby waves. Through the oceanic waveguide crossing the Indonesian archipelago, oceanic planetary waves generated by tropical Pacific winds can be conveyed into the south Indian Ocean as coastally-trapped Kelvin waves and then propagate westwards as Rossby waves from the western coast of Australia influencing the SSH and geostrophic velocity in the south Indian Ocean (Clarke, 1991; Clarke and Liu, 1994; Meyers, 1996; Potemra, 2001; Wijffels and Meyers, 2004; Cai et al., 2005; Feng et al., 2010; Feng et al., 2011; Menezes and Vianna, 2019; Nagura, 2020; Nagura and McPhaden, 2021). Therefore, both local surface winds and the westwards propagating signals from the eastern boundary of the south Indian Ocean could be responsible for the ENSO-related SSH variability in the “SEIO ENSO Zone”. For simplicity, the effects of the local surface wind and signals from the eastern boundary will be referred to as local-wind forcing and eastern-boundary forcing respectively in the remainder of this paper.

To evaluate the relative role of local-wind forcing and eastern-boundary forcing in SSH variability, a linear, 1D, 1.5-layer long Rossby wave model was adopted in this study. By using this model, the SSH variability could be separated into parts that is forced by local winds and those forced by SSH anomalies radiating from the eastern boundary, thus allowing us to make comparisons and find the dominant dynamic process. Eq. (6) was integrated from 100°E to 120°E at each latitude. Surface wind stresses from ERA5 were adopted. SSH anomalies along the western coast of Australia based on satellite observations from the AVISO project, were set as the eastern-boundary condition, and the values in January 1993 were set as the initial condition. The equation was integrated from January 1993 to December 2020, during which both SSH anomalies and surface wind data were available. The first two years of the integration were considered the spin-up period, and the corresponding results were excluded. The time series of modeled SSH anomalies were compared with the observations. The components driven by the local winds and eastern boundary SSH anomalies were determined by setting the eastern boundary SSH anomalies to zero and the wind stress to zero, respectively.

The variability of the SSH at latitudes from 13°S to 30°S was simulated individually. Here, the results representing the lower (13°S), middle (19°S) and higher (28°S) latitudes of the “SEIO ENSO zone” are shown as examples (Figure 9). Modeled SSH anomalies were generally consistent with the observations despite some small discrepancies. Except for the slower westwards propagation speed of the SSH anomalies, the SSH anomalies at middle and higher latitudes were similar to those at lower latitudes. This can be explained by the fact that the observed SSH anomalies along the western coast of Australia are meridionally coherent, and the amplitude does not change much from 10° to 35°S as a result of the poleward propagation of coastal Kelvin waves (Menezes and Vianna, 2019). Generally, the total solution in the “SEIO ENSO Zone” is largely contributed by the boundary-driven part, whereas the variability of the wind-driven part is weak in this region. This indicates that the SSH variability in our study region is dominated by eastern-boundary forcing, rather than local-wind forcing.

FIGURE 9

Figure 9 SSH anomalies (m) at 13°S (A–D), 19°S (E–H) and 28°S (I–L), representing lower, middle and higher latitudes in the “SEIO ENSO zone”, for observations (A, E, I), simulated results (B, F, J), the part of the simulated solution driven by eastern-boundary forcing C, G, K), and the part of the simulated solution driven by local-wind forcing (D, H, L). The seasonal cycle was removed by using the 13-month running mean method.

Then the MGV values were computed based on boundary-driven SSH anomalies and wind-driven SSH anomalies (Figure 10A). The simulated MGV values were generally consistent with the observed results from the AVISO project. The boundary-driven part was apparently the dominant component, while the contribution by the wind-driven part was insignificant. Their contributions to upper-ocean salinity variability in the “SEIO ENSO Zone” are shown in Figure 10B, from which we can observe that the simulated $-v_g\text{'}\frac{\partial \overline{S}}{\partial y}$ term was consistent with the advection term from ECCO outputs, suggesting that the geostrophic advection induced by local SSH anomalies was the primary contributor to salinity variability in the “SEIO ENSO zone”. The variability of $-v_g\text{'}\frac{\partial \overline{S}}{\partial y}$ was principally composed of the boundary-driven part, and the contribution of the wind-driven part was minor. This demonstrates the dominant role of eastern-boundary forcing in this region.

FIGURE 10

Figure 10 (A) Anomaly of meridional geostrophic flow (m/s) based on observational SSH anomaly (solid black line) and modeled SSH anomaly (black dashed line), and its decomposition into the effects of eastern-boundary conditions (red) and local-wind forcing (blue). (B) Anomalies of the advection term for the salinity budget from ECCO (black), with $-(\partial \overline{S}/\partial y)v_g\text{'}$ (psu/mon) term generated by simulated meridional geostrophic flow (dashed black line) and its two components (colored lines).

According to previous studies, the amplitude of wind-driven SSH anomalies increases to the west and plays a dominant role in SSH variability (Volkov et al., 2020; Nagura and McPhaden, 2021). These wind-driven SSH anomalies in the western part of the south Indian Ocean, in combination with the SSH anomalies along the eastern boundary, induced the zonal SSH difference in the south Indian Ocean and resulted in variabilities in the basinwide meridional geostrophic transport (Lee, 2004; Lee and McPhaden, 2008; Zhuang et al., 2013; Nagura, 2020). However, the significance of local-wind forcing is confined to low latitudes (equatorward of 20°S), and it becomes relatively weak at midlatitudes due to the weakened wind stress (Masumoto and Meyers, 1998; Zhuang et al., 2013; Nagura and McPhaden, 2021). This can also be observed from the composite SSH anomalies in Figure 8. During different ENSO phases, the SSH anomaly in the western south Indian Ocean mainly resides in region north of 20°S (dashed box to the western side), and there was a significant latitudinal difference between this domain and the region with the strong ENSO-related variations in SSH (dashed box to the eastern side) and salinity (Figure 2). Note that the salinity shows the strongest ENSO-like variability in latitudes between 20°S and 30°S. Thus, the SSH anomaly in the western south Indian Ocean driven by local winds in the interior ocean, and the associated SSH dipole pattern is apparently insufficient to explain those variabilities in the SEIO. On the other hand, without considering the SSH anomaly in the western basin, our results based on local SSH anomaly in the SEIO explained a major component of the variations in the MGV and salinity. Therefore, we conclude that the MGV and salinity tendency in the “SEIO ENSO Zone” is the primarily driven by local SSH variations that largely determined by easter-boundary forcing.

5 Conclusions and discussion

The close relationship between the interannual-decadal variability in the SEIO upper-ocean salinity and the ENSO signal has been discussed in plenty of previous work (Phillips et al., 2005; Zhang et al., 2016; Zhang et al., 2018; Hu et al., 2019; Nie et al., 2020; Wu et al., 2021). Based on multi-sources datasets, this work clarified the domain where this ENSO-like salinity variability mainly exists for the first time. Based on our results, the correlation between the salinity variability and ENSO signal is strongest in the region between 100°E and 120°E, 13°S and 30°S, and in depths above 150 m. And this relationship is not time-dependent.

This ENSO-like variability can be largely attributed to the MGV anomalies driven by the zonal SSH gradient, as had been suggested by several former works (Zhang et al., 2016; Zhang et al., 2018; Huang et al., 2020; Wu et al., 2021). The variability in the SSH in the south Indian Ocean is influenced by both local-wind forcing and eastern-boundary forcing (e.g. Menezes and Vianna, 2019; Nagura and McPhaden, 2021). A recent study by Wu et al. (2021) attributed the MGV changes in the SEIO to the zonal SSH dipole pattern in the south Indian Ocean and emphasized the contribution from local winds for its dominant role in SSH variability in the western basin. Their analyses supported the idea that local-wind forcing plays an important role in SSH variability in the western south Indian Ocean and forming of the zonal SSH dipole pattern across the basin. But their study did not verify the causality between the SSH dipole pattern and the MGV anomalies in the SEIO. On the other hand, our results revealed a latitudinal difference between the domain where the SSH dipole pattern exists (north of 20°S) and the region in which the ENSO-like salinity variability is strongest (20°S-30°S), suggesting that this salinity variability cannot be attributed entirely to the zonal SSH dipole pattern.

To find the dominant factor that modulating the interannual MGV variability in the SEIO, this study evaluated the relative contribution from local-wind forcing and eastern-boundary forcing. Results show that both local SSH and MGV are driven primarily by eastern-boundary forcing. In combination with the strong meridional salinity gradient, the significant boundary-driven MGV anomalies cause large meridional salinity advection and eventually lead to the observed ENSO-like salinity variability. Note that, even without considering the SSH anomaly in the western basin, our results based on local SSH anomaly explained a major component of the variations in the MGV and salinity. This demonstrates that the MGV and salinity in the SEIO is primarily determined by local SSH anomaly that driven mostly by the eastern-boundary forcing, while the influence from SSH anomaly in the western basin forced by local winds in the interior ocean is limited.

The eastern-boundary forcing is determined by eastern-boundary conditions along the western coast of Australia. Based on previous studies, the eastern-boundary conditions are principally driven by oceanic planetary waves associated with ENSO signals in the tropical Pacific, which are transported into the south Indian Ocean via the oceanic waveguide crossing the Indonesian archipelago (Clarke, 1991; Clarke and Liu, 1994; Meyers, 1996; Potemra, 2001; Wijffels and Meyers, 2004; Cai et al., 2005; Feng et al., 2010; Feng et al., 2011; Menezes and Vianna, 2019; Nagura, 2020). A recent study by Kersalé et al. (2022) suggest that the alongshore wind forcing also drives SSH anomaly along the coast and play an important role in setting up the eastern boundary conditions. And the alongshore winds are also tightly related with ENSO via the Walker circulation between the Pacific and Indian Ocean. Therefore, the eastern-boundary forcing is strongly modified by the remote ENSO events through both oceanic pathways and atmospheric bridge, and this may explain the strong ENSO signal preserved in the associated variations in the MGV and salinity in the SEIO.

One important caveat is that the contribution of ocean eddies to salinity variability in the SEIO is probably underestimated by existing research, as has already been suggested by former studies (e.g. Zhang et al., 2016; Huang et al., 2020; Wu et al., 2021). This is because the research so far, including this work, are mostly based on dataset with coarse resolution. The SEIO is known for energetic eddies propagating westward from West Australia coast with strong interannual variability associated with the ENSO (Zheng et al., 2018). And eddy-induced meridional salinity flux was found to play an essential role in freshwater balance in the SEIO (Qu et al., 2019). Therefore, a better understanding for the effect of the mesoscale process still requires further investigation based on eddy-resolving model outputs.

As has been emphasized by plenty of previous studies, salinity play an essential role in ocean dynamic processes in the SEIO and therefore have potential influence on changes of regional climate and the marine ecosystem (e.g. Feng et al., 2013; Menezes et al., 2013; Pearce and Feng, 2013; Llovel and Lee, 2015; Feng et al., 2015). This work clarified the domain where the upper-ocean salinity is strongly influenced by the remote ENSO events and the underlying dynamics. And thus provide a new theoretical basis for regional ocean modelling and help to promoting marine environmental protection.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author contributions

XN and ZW conceived and led the manuscript. XN performed the data analysis and wrote the original manuscript. HL, TX, and ZW provided the input and/or improved the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work is jointly supported by the Qingdao Marine Science and Technology Center (No. LSKJ202202700), the Basic Scientific Fund for National Public Research Institutes of China (2022Q02), the National Natural Science Foundation of China (NSFC) Projects (42276030, 41806040,42076023, 42076024), the Global Change and Air-Sea Interaction II (Contact No.GASI-01-ATP-STwin).

Acknowledgments

The authors thank two reviewers for their constructive comments that led to significant improvements of this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2023.1181278/full#supplementary-material

References

Cai W., Meyers G., Shi G. (2005). Transmission of ENSO signal to the Indian ocean. Geophysical Res. Lett. 32 (5). doi: 10.1029/2004GL021736

CrossRef Full Text | Google Scholar

Clarke A. J. (1991). On the reflection and transmission of low frequency energy at the irregular western pacific ocean boundary. J. Geophys. Res. 96, 3289–3305. doi: 10.1029/90JC00985

CrossRef Full Text | Google Scholar

Clarke A. J., Liu X. (1994). Interannual sea level in the northern and eastern Indian ocean. J. Phys. Oceanography 24 (6), 1224–1235. doi: 10.1175/1520-0485(1994)024<1224:ISLITN>2.0.CO;2

CrossRef Full Text | Google Scholar

ECCO Consortium, Fukumori I., Wang O., Fenty I., Forget G., Heimbach P., et al. (2021). Synopsis of the ECCO central production global ocean and Sea-ice state estimate (Version 4 release 4). doi: 10.5281/zenodo.4533349

CrossRef Full Text | Google Scholar

Feng M., Benthuysen J., Zhang N., Slawinski D. (2015). Freshening anomalies in the Indonesian throughflow and impacts on the leeuwin current during 2010–2011. Geophys. Res. Lett. 42, 8555–8562. doi: 10.1002/2015GL065848

CrossRef Full Text | Google Scholar

Feng M., Böning C., Biastoch A., Behrens E., Weller E., Masumoto Y. (2011). The reversal of the multidecadal trends of the equatorial pacific easterly winds, and the Indonesian throughflow and leeuwin current transports. Geophys. Res. Lett. 38, L11604. doi: 10.1029/2011GL047291

CrossRef Full Text | Google Scholar

Feng M., McPhaden M. J., Lee T. (2010). Decadal variability of the pacific subtropical cells and their influence on the southeast Indian ocean. Geophysical Res. Lett. 37 (9), L09606. doi: 10.1029/2010GL042796

CrossRef Full Text | Google Scholar

Feng M., McPhaden M. J., Xie S.-P., Hafner J. (2013). La Niña forces unprecedented Leeuwin Current warming in 2011. Sci Rep 3, 1277. doi: 10.1038/srep01277

PubMed Abstract | CrossRef Full Text | Google Scholar

Forget G., Campin J.-M., Heimbach P., Hill C. N., Ponte R. M., Wunsch C. (2015). ECCO version 4: an integrated framework for non-linear inverse modeling and global ocean state estimation (Geoscientific Model Development), 8. Available at: https://www.geosci-model-dev.net/8/3071/2015/.

Google Scholar

Gao S., Qu T., Nie X. (2014). Mixed layer salinity budget in the tropical pacific ocean estimated by a global GCM. J. Geophys. Res. Oceans 119, 8410–8421. doi: 10.1002/2014JC010336

CrossRef Full Text | Google Scholar

Gaspar P., Grégoris Y., Lefevre J. M. (1990). A simple eddy kinetic energy model for simulations of the oceanic vertical mixing: tests at station papa and long-term upper ocean study site. J. Geophysical Res. 95 (C9), 16179–16193. doi: 10.1029/JC095iC09p16179

CrossRef Full Text | Google Scholar

Gent P. R., Mcwilliams J. C. (1990). Isopycnal mixing in ocean circulation models. J. Phys. Oceanography 20 (1), 150–155. doi: 10.1175/1520-0485(1990)020<0150:IMIOCM>2.0.CO;2

CrossRef Full Text | Google Scholar

Good S. A., Martin M. J., Rayner N. A. (2013). EN4: quality controlled ocean temperature and salinity profiles and monthly objective analyses with uncertainty estimates. J. Geophysical Research: Oceans 118, 6704–6716. doi: 10.1002/2013JC009067

CrossRef Full Text | Google Scholar

Hersbach H. (2020). The ERA5 global reanalysis. Quart. J. R. Meteor. Soc. 146, 1999–2049. doi: 10.1002/qj.3803

CrossRef Full Text | Google Scholar

Hosoda S., Ohira T., Nakamura T. (2008). A monthly mean dataset of global oceanic temperature and salinity derived from argo float observations. Jamstec Rep. Res. Dev. 8, 47–59. doi: 10.5918/jamstecr.8.47

CrossRef Full Text | Google Scholar

Hu S., Zhang Y., Feng M., Du Y., Sprintall J., Wang F., et al. (2019). Interannual to decadal variability of upper-ocean salinity in the southern Indian ocean and the role of the Indonesian throughflow. J. Clim. 32, 6403–6421. doi: 10.1175/JCLI-D-19-0056.1

CrossRef Full Text | Google Scholar

Huang J., Zhuang W., Yan X., Wu Z. (2020). Impacts of the upper-ocean salinity variations on the decadal sea level change in the southeast Indian ocean during the argo era. Acta Oceanologica Sin. 39 (7), 1–10. doi: 10.1007/s13131-020-1574-4

CrossRef Full Text | Google Scholar

Kersalé M., Volkov D. L., Pujiana K., Zhang H. (2022). Interannual variability of sea level in the southern Indian ocean: local vs. remote forcing mechanisms. Ocean Sci. 18, 193–212. doi: 10.5194/os-18-193-2022

CrossRef Full Text | Google Scholar

Lee T. (2004). Decadal weakening of the shallow overturning circulation in the south Indian ocean. Geophys. Res. Lett. 31, L18305. doi: 10.1029/2004GL021774

CrossRef Full Text | Google Scholar

Lee T., McPhaden M. J. (2008). Decadal phase change in large-scale sea level and winds in the indo- pacific region at the end of the 20th century. Geophysical Res. Lett. 35, L01605. doi: 10.1029/2007GL032419

CrossRef Full Text | Google Scholar

Llovel W., Lee T. (2015). Importance and origin of halosteric contribution to sea level change in the southeast Indian ocean during 2005-2013. Geophysical Res. Lett. 42 (4), 1148–1157. doi: 10.1002/2014GL062611

CrossRef Full Text | Google Scholar

Masumoto Y., Meyers G. (1998). Forced rossby waves in the southern tropical Indian ocean. J. Geophys. Res. 103, 27 589–27 602. doi: 10.1029/98JC02546

CrossRef Full Text | Google Scholar

Menezes V. V., Phillips H. E., Schiller A., Domingues C. M., Bindoff N. L. (2013). Salinity dominance on the Indian ocean Eastern gyral current, geophys. Res. Lett. 40, 5716–5721. doi: 10.1002/2013GL057887

CrossRef Full Text | Google Scholar

Menezes V. V., Vianna M. L. (2019). Quasi- biennial rossby and kelvin waves in the south Indian ocean: tropical and subtropical modes and the Indian ocean dipole. Deep-Sea Res. Part II 166, 43–63. doi: 10.1016/j.dsr2.2019.05.002

CrossRef Full Text | Google Scholar

Meng L., Zhuang W., Zhang W., Yan C., Yan X. (2020). Variability of the shallow overturning circulation in the Indian ocean. J. Geophysical Research: Oceans 125, e2019JC015651. doi: 10.1029/2019JC015651

CrossRef Full Text | Google Scholar

Meyers G. (1996). Variation of Indonesian throughflow and El niño-southern oscillation. J. Geophysical Res. 101, 12,255–12,263. doi: 10.1029/95JC03729

CrossRef Full Text | Google Scholar

Nagura M. (2020). Variability in meridional transport of the subtropical circulation in the south Indian ocean for the period from 2006 to 2017. J. Geophysical Research: Oceans 124, e2019JC015874. doi: 10.1029/2019JC015874

CrossRef Full Text | Google Scholar

Nagura M., McPhaden M. J. (2021). Interannual variability in sea surface height at southern midlatitudes of the Indian ocean. J. Phys. Oceanography 51 (5), 1595–1609. doi: 10.1175/JPO-D-20-0279.1

CrossRef Full Text | Google Scholar

Nie X., Liu H., Xu T., Wei Z. (2022). Indian Ocean subtropical underwater and the interannual variability in its annual subduction rate associated with the southern annular mode. J. Phys. Oceanography 52 (3), 383–397. doi: 10.1175/JPO-D-21-0191.1

CrossRef Full Text | Google Scholar

Nie X., Wei Z., Li Y. (2020). Decadal variability in salinity of the Indian ocean subtropical underwater during the argo period. Geophys Res Lett 47. doi: 10.1029/2020GL089104

CrossRef Full Text | Google Scholar

Pearce A., Feng M. (2013). The rise and fall of the “marine heat wave” off Western Australia during the summer of 2010/2011. J. Mar. Syst. 111–112, 139–156. doi: 10.1016/j.jmarsys.2012.10.009

CrossRef Full Text | Google Scholar

Phillips H. E., Wijffels S. E., Feng M. (2005). Interannual variability in the freshwater content of the Indonesian-Australian basin. Geophys. Res. Lett. 32, L03603. doi: 10.1029/2004GL021755

CrossRef Full Text | Google Scholar

Potemra J. T. (2001). Contribution of equatorial pacific winds to southern tropical Indian ocean rossby waves. J. Geophysical Res. 106 (C2), 2407–2422. doi: 10.1029/1999JC000031

CrossRef Full Text | Google Scholar

Qiu B., Miao W., Müller P. (1997). Propagation and decay of forced and free baroclinic rossby waves in off-equatorial oceans. J. Phys. Oceanogr. 27, 2405–2417. doi: 10.1175/1520-0485(1997)027,2405:PADOFA.2.0.CO;2

CrossRef Full Text | Google Scholar

Qu T., Gao S., Fukumori I. (2011). What governs the sea surface salinity maximum in the north Atlantic?, geophys. Res. Lett. 38, L07602. doi: 10.1029/2011GL046757

CrossRef Full Text | Google Scholar

Qu T., Lian Z., Nie X., Wei Z. (2019). Eddy-induced meridional salt flux and its impacts on the sea surface salinity maxima in the southern subtropical oceans. Geophys. Res. Lett. 46, 11 292–11 300. doi: 10.1029/2019GL084807

CrossRef Full Text | Google Scholar

Rasmusson E. M., Carpenter T. H. (1982). Variations in tropical sea surface temperature and surface wind fields associated with the southern Oscillation/El niño. Mon. Wea. Rev. 110, 354384. doi: 10.1175/1520-0493(1982)110<0354:VITSST>2.0.CO;2

CrossRef Full Text | Google Scholar

Redi M. H. (1982). Oceanic isopycnal mixing by coordinate rotation. J. Phys. Oceanography 12 (10), 1154–1158. doi: 10.1175/1520-0485(1982)012<1154:OIMBCR>2.0.CO;2

CrossRef Full Text | Google Scholar

Rochford D. J. (1962). Hydrology of the Indian ocean. II. the surface waters of the south-east Indian ocean and the arafura sea in the spring and summer, aust. J. Mar. Freshw. Res. 13 (3), 226–251. doi: 10.1071/MF9620226

CrossRef Full Text | Google Scholar

Trenberth K. E. (1997). The definition of El niño. Bull. Amer. Meteor. Soc 78, 2771–2777. doi: 10.1175/1520-0477(1997)078<2771:TDOENO>2.0.CO;2

CrossRef Full Text | Google Scholar

Volkov D. L., Lee S.-K., Gordon A. L., Rudko M. (2020). Unprecedented reduction and quick recovery of the south Indian ocean heat content and sea level in 2014-2018. Sci. Adv. 6, eabc1151. doi: 10.1126/sciadv.abc1151

PubMed Abstract | CrossRef Full Text | Google Scholar

Wijffels S., Meyers G. (2004). An intersection of oceanic waveguides: variability in the Indonesian throughflow region. J. Phys. Oceanogr. 34, 1232–1253. doi: 10.1175/1520-0485(2004)034<1232:AIOOWV>2.0.CO;2

CrossRef Full Text | Google Scholar

Wijffels S., Sprintall J., Fieux M., Bray N. (2002). The JADE and WOCE I10/IR6 throughflow sections in the southeast Indian ocean. Part 1: Water mass distribution variability Deep Sea Res. Part II 49, 1341–1362. doi: 10.1016/S0967-0645(01)00155-2

CrossRef Full Text | Google Scholar

Wu Y., Zheng X., Sun Q., Zhang Y., Du Y., Liu L. (2021). Decadal variability of the upper-ocean salinity in the southeast Indian ocean: role of local ocean–atmosphere dynamics. J. Climate 34 (19), 7927–7942. doi: 10.1175/JCLI-D-21-0122.1

CrossRef Full Text | Google Scholar

Yu W., Xiang B., Liu L., Liu N. (2005). Understanding the origins of interannual thermocline variations in the tropical Indian ocean. Geophys. Res. Lett. 32, L24706. doi: 10.1029/2005GL024327

CrossRef Full Text | Google Scholar

Zhang Y., Du Y., Feng M. (2018). Multiple time scale variability of the sea surface salinity dipole mode in the tropical Indian ocean. J. Climate 31, 283–296. doi: 10.1175/JCLI-D-17-0271.1

CrossRef Full Text | Google Scholar

Zhang N., Feng M., Du Y., Lan J., Wijffels S. E. (2016). Seasonal and interannual variations of mixed layer salinity in the southeast tropical Indian ocean. J. Geophys. Res. Oceans 121, 4716–4731. doi: 10.1002/2016JC011854

CrossRef Full Text | Google Scholar

Zheng S., Feng M., Du Y., Meng X., Yu W. (2018). Interannual variability of eddy kinetic energy in the subtropical southeast Indian ocean associated with the El niño-southern oscillation. J. Geophysical Research: Oceans 123 (2), 1048–1061. doi: 10.1002/2017JC013562

CrossRef Full Text | Google Scholar

W., Feng M., Du Y., Schiller A., Wang D. (2013). Low-frequency sea level variability in the southern Indian ocean and its impacts on the oceanic meridional transports. J. Geophys. Res. Oceans 118, 1302–1315. doi: 10.1002/jgrc.20129

CrossRef Full Text | Google Scholar

Zuo H., Balmaseda M. A., Tietsche S., Mogensen K., Mayer M. (2019). The ECMWF operational ensemble reanalysis-analysis system for ocean and sea-ice: a description of the system and assessment. Ocean Sci. Discussions 15 (3), 779–808. doi: 10.5194/os2018-154

CrossRef Full Text | Google Scholar