- 1School of Civil Engineering, Chongqing University, Chongqing, China
- 2National Joint Engineering Research Center of Geohazards Prevention in the Reservoir Areas, Chongqing University, Chongqing, China
- 3School of Geosciences, Yangtze University, Wuhan, China
- 4Chongqing Institute of Geological Environment Monitoring, Chongqing, China
Reservoir bank slopes with weak interlayers are common in the Three Gorges Reservoir area. Their stabilities are affected by multi-coupled factors (e.g., reservoir water fluctuations, rainfall, and earthquakes in the reservoir area). Meanwhile, the differences in mechanical parameters of reservoir banks make it more difficult to determine the dynamic stability of bank slopes under complex mechanical environments. In this paper, the multiple disaster-causing factors and spatial variability of the landslide were comprehensively considered to study the long-term evolution trend of the bank slopes with weak interlayers. Specifically, the limit equilibrium method combined with the random field was performed to calculate the reliability. Furthermore, the long-term effects of dry-wet cycles on reservoir bank landslides and the sensitivity analysis of the statistical parameters of the random field were discussed. The results show that the earthquake action had the most significant impact on the failure probability of the landslide. The failure probability was more significantly affected by the vertical fluctuation range of the parameters and the coefficient of variation of the internal friction angle. The increase in failure probability under the action of dry-wet cycles was mainly caused by the reduction of the parameters of the weak interlayer. The reliability evaluation method of reservoir bank slopes can be applied to predict the long-term stability of the coastal banks.
1 Introduction
Coastal engineering (e.g., the building of sea walls, dykes, and embankments) requires high manufacturing and maintenance costs (Temmerman et al., 2013; Firth et al., 2014; Malone and Newton, 2020; Wang et al., 2020). The rise and fall of sea levels can threaten the long-term operation of coastal engineering; thus, it is necessary to analyze the effect of the changing sea levels on the coastal banks. Similar to the periodically changing reservoir water levels (Bromhead and Ibsen, 2004; Zhan et al., 2019; Rui et al., 2020), the evaluation method of the stability of the reservoir bank can be applied to coastal engineering to some extent. There are many landslides in the Three Gorges Reservoir area, and the mechanical of the landslide with weak interlayer is complicated. Specifically, many factors induce landslides on reservoir banks, involving reservoir water level, rainfall, and seismic (Wang et al., 2021; Wang et al., 2023). Numerous researchers have studied the causes of landslide failures and concluded that rainwater infiltration is the most important triggering factor in the instability of landslides (e.g., Rahimi et al., 2011; Huang et al., 2016; Wang et al., 2019a; Zhang et al., 2020). The influencing factors of rainfall infiltration slope stability can be summarized as followings: the rainfall intensity, rainfall duration, rainfall before instability and the initial state of soil (Ng and Pang, 2000). Instability mechanism of slope under earthquake action is the key to evaluating and control slope stability under earthquake conditions. At present, there are many methods of slope stability analysis under earthquake conditions, such as the pseudo-static method, the Newmark slider analysis method, and the numerical simulation method (Shukha and Baker, 2008; Zhang and Cao, 2013; Yang et al., 2014; Yeznabad et al., 2021). Based on the quasi-static method, Biondi et al. (2002) put forward the calculation formula of pore water pressure and slope stability by studying the stability of non-cohesive soil slopes during and after earthquakes. The analysis method of the influencing factors of slope stability usually only considers the change of one factor. Notably, in the earthquake zone, the area of landslides induced by rainstorms is three times that of the landslides directly induced by earthquakes (Lin et al., 2006; Chai et al., 2013). It can be found that the rainfall in the strong earthquake area will induce a wider range of landslide disasters.
Slope stability analysis is a popular field of geotechnical engineering for the application of probabilistic methods (Xie et al., 2020). There are differences and correlations in the properties of rock and soil parameters in different spatial locations. Random field theory can better characterize this spatial variability (Wang et al., 2017; Hu and Huang, 2019; Wang et al., 2020). The use of spatially variable analysis has been shown to affect the calculated failure probability of the slope models. For example, it has been shown that for slope models with a mean factor of safety greater than 1, accounting for spatial variability of material properties (e.g., cohesion and unit weight) results in a lower failure probability, compared to the same analysis without using spatial variability (Griffiths and Fenton, 2004; Cho, 2010; Javankhoshdel et al., 2017). A probabilistic analysis that does not consider spatial variability has been shown to result in unrealistic and overly conservative failure probabilities.
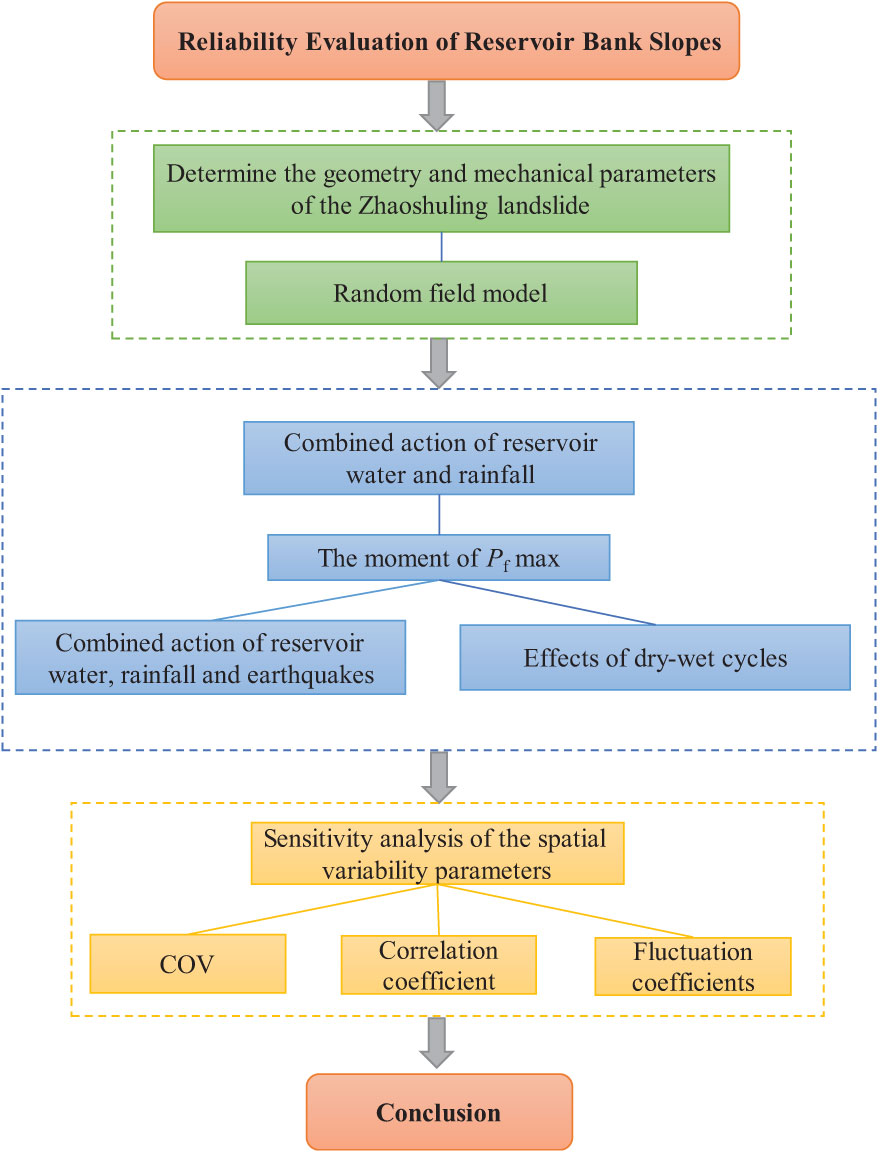
In this paper, the influence of spatial variability of geotechnical parameters on actual landslide deformation and stability cannot be considered by traditional methods (Zhang et al., 2023). Thus, the effect of spatial variability of geotechnical materials on landslide stability was studied using the random field. Then, based on the actual reservoir water level fluctuation, rainfall, and regional seismic intensity in 2017, the reliability of the Zhaoshuling landslide within one year was evaluated. Moreover, the effect of dry-wet cycles on failure probability was discussed to determine the long-term evolution trend of the Zhaoshuling landslide.
2 Study area
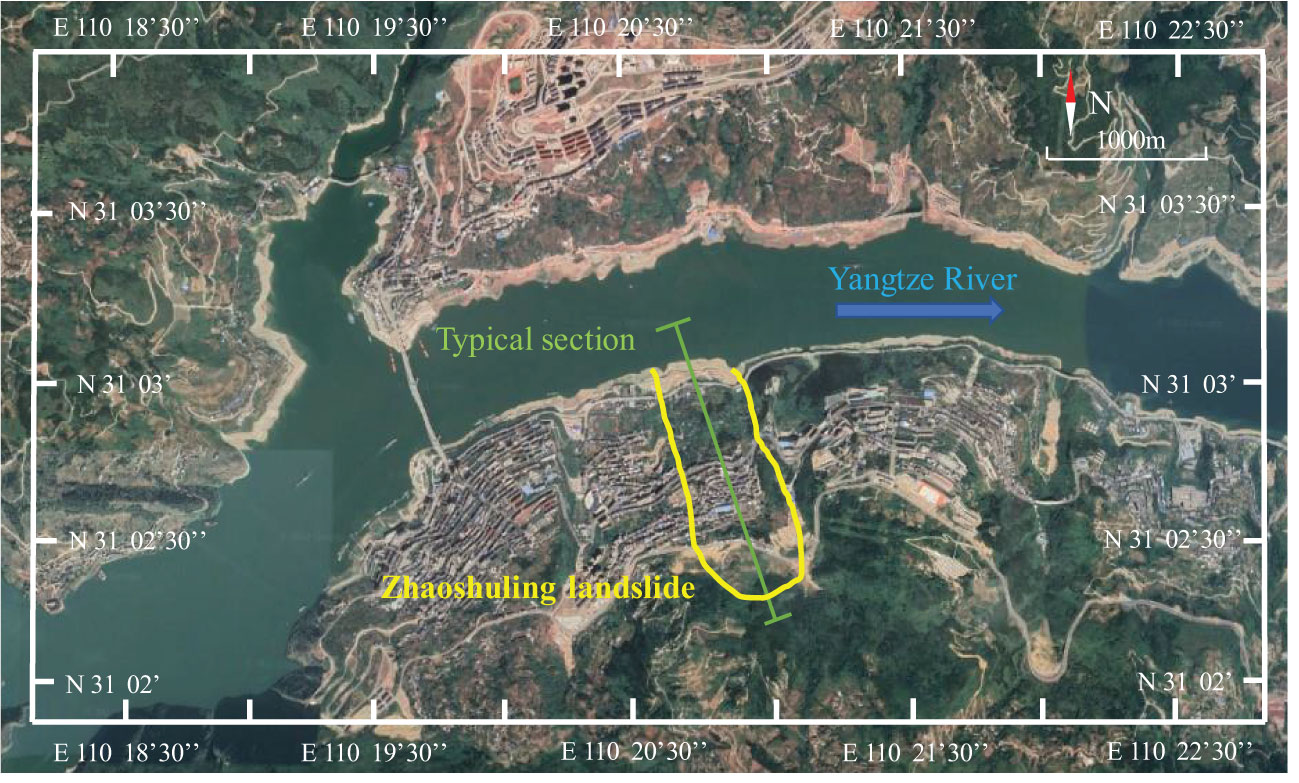
The Zhaoshuling landslide is situated in Badong County, Hubei Province, adjacent to the Yangtze River in the north and 74 km from the Three Gorges Dam in the east (Figure 1). It is a large reservoir bank bedding landslide. The trailing edge of the Zhaoshuling landslide is about 500 m, and the leading edge is about 100 m. The main strata of the landslide were the second and third sections of the Triassic Badong Formation (T2b2 and T2b3). The stratum of the Zhaoshuling landslide can be divided into three parts from top to bottom: sliding mass, sliding zone, and bedrock (Zhan et al., 2022; Zhang et al., 2022a; Yang et al., 2023). Sliding mass includes sliding rock mass, gravel soil, and the main component of the sliding zone is gravel sandy clay.
The reservoir water level fluctuated between 145~175 m every year (Figure 2A); thus, there was a dry-wet cycles area with 30 m on the bank slope. In addition, there was concentrated rainfall in Badong County (Figure 2B), and the peak acceleration of ground motion was 0.05 g.
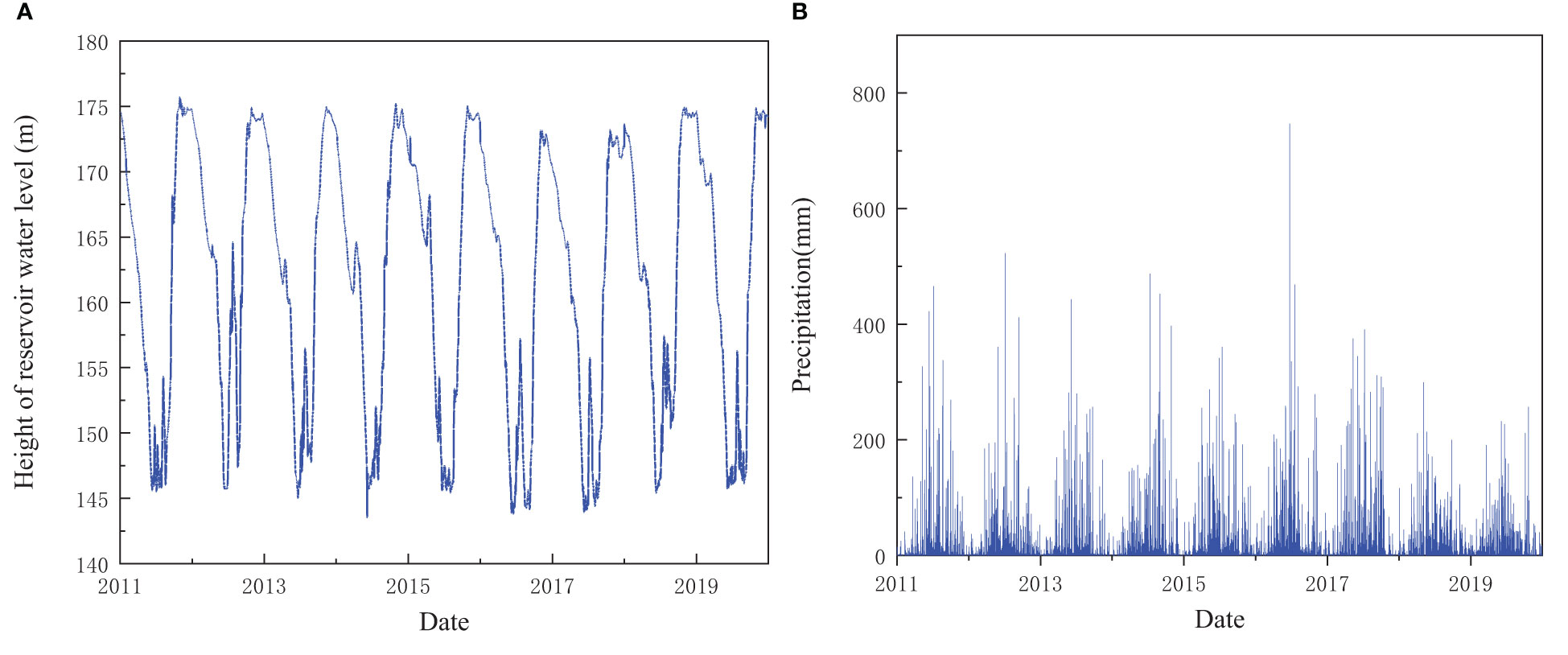
Figure 2 The factors affecting the seepage field of the bank landslide. (A) The reservoir water level of Three Gorges Reservoir; (B) Daily precipitation of Badong County.
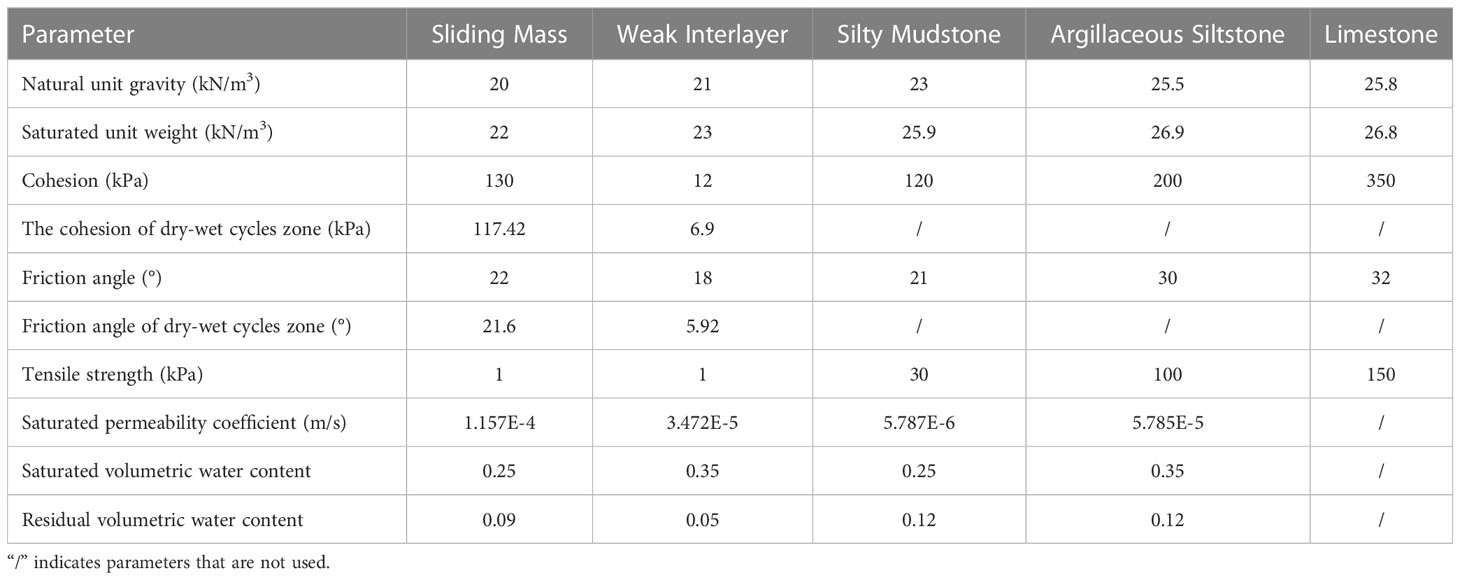
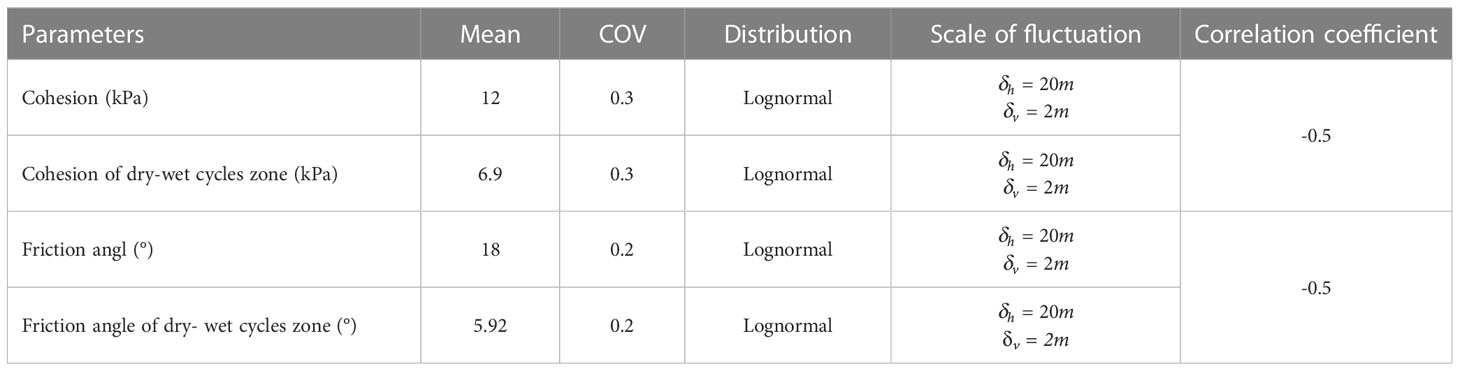
The parameters of each layer of the Zhaoshuling landslide are shown in Table 1. Notably, the dry-wet cycles area was the reduced value after 10 dry-wet cycles. And the relevant parameters were obtained from the statistics of the existing papers (Chen et al., 2011; Li et al., 2016; Salimi et al., 2021; Zhang et al., 2022a).
3 Methodology
3.1 Morgenstern-price method
Landslide stability problems are commonly analyzed by using LEMs of slices, and the approach presented here adopts the Morgenstern-Price method. The Morgenstern-Price method assumes that the relationship between the vertical force and the lateral force is , The FOS of the slip surface can be obtained by iterative calculation of the balance equation, and the expression is as follows:
Where is the coefficient of variation of the force between the soil strips; is the change function of the force between the soil strips; is the length of the soil strip on the sliding surface; is the length of the lever arm from the centroid of the soil bar to the center of the sliding surface; is the distance from the midpoint of the soil strip at the sliding surface to the corresponding normal; is the angle between the tangent of the soil strip and the horizontal plane; is the normal force of the sliding face to the soil strip.
3.2 Random field theory
The random field uses easily available and physically meaningful parameters to characterize random phenomena at different spatial scales.
A random field can be expressed as a trend component and a volatility component . The trend component is related to the absolute position in space. In addition, the trend component can be regarded as the mean value when it is considered as a constant. If the correlation of the fluctuation component is only related to the relative distance, the fluctuation component can be considered as statistically uniform.
Where represents the spatial position.
There is an autocorrelation between the parameters of the rock and soil mass in the spatial range, which needs to be described by the autocorrelation function. The mean and variance of the random field of parameter can be defined as follows:
The covariance function of can be expressed as follows:
During the random field generation using the Local Average Subdivision method, the Markovian covariance functions are used to calculate the covariance value between cells in the field.
Where represent the horizontal relative distance and vertical relative distance between any two points in space, respectively; represent the horizontal and vertical fluctuation ranges, respectively.
3.3 Monte Carlo simulation
The method is generating a random variable sample that conforms to a certain distribution by sampling. And the set of random sample can be used in the performance function. Then, the probability of failure (Pf) is obtained by counting the proportion of failure samples:
where probability density function of random variable ; failure samples;
If there are N trials in calculating FOS, and M times where FOS, the Pf can be defined as follows:
The coefficient of variation of the failure probability can be expressed as:
3.4 Latin hypercube sampling
Latin hypercube sampling will be used in Monte Carlo simulations, it is a multidimensional stratified sampling method. The random variable is divided into N groups equally, then building a matrix , its column elements are random integers between 1-N and vary. Correspondingly, building a matrix , its column elements are random rational numbers between 1-N and vary.
where represents the element in the row and column of matrix ; means the variable of the group of samples; represents the distribution function of the variable; means sample variable.
Latin hypercube sampling avoids repeated sampling by Monte Carlo method and improves computational efficiency
3.5 Computational model of the Zhaoshuling landslide
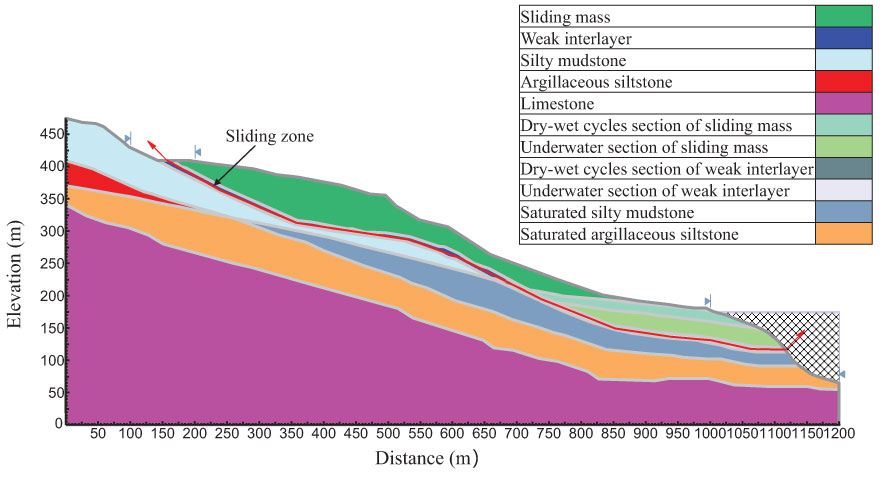
The two-dimensional saturated-unsaturated seepage slope stability model was established in SLIDE2 (Figure 3). The length of the landslide is 1200 m, and the height of the trailing edge is 475 m. Considering that the overall stability of the Zhaoshuling landslide was controlled by the weak interlayer, the weak interlayer was the sliding zone. The changing reservoir water levels are set at the leading edge, the other parts of the landslide are set as rainfall boundaries, and the bottom of the model is set as a waterproof boundary (Zhan et al., 2018; Rui et al., 2021).
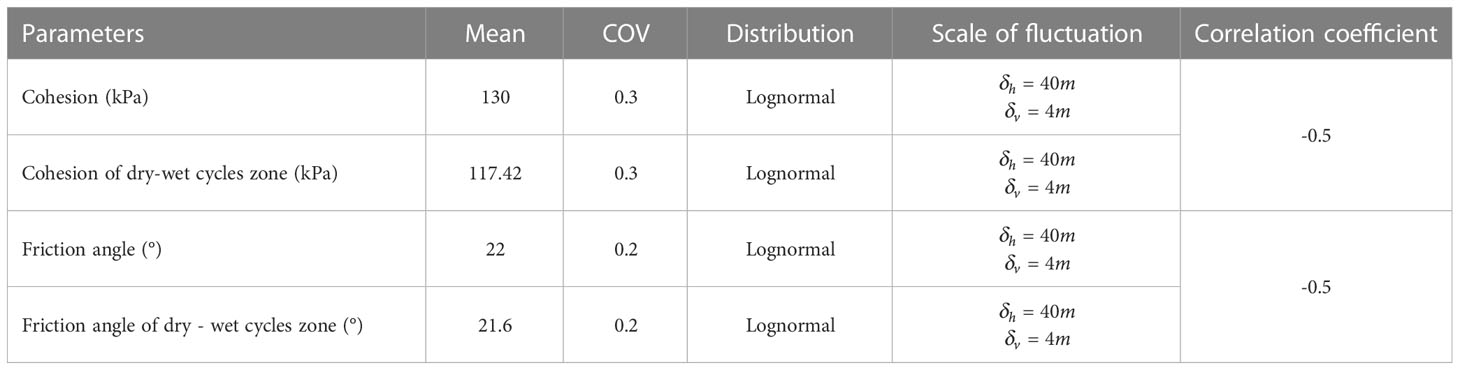
The cohesion and friction angle of the sliding mass and the weak interlayer are respectively assigned to the spatial variability, the statistical parameters are obtained with reference to literatures (Suchomel and Masin, 2010; Jiang et al., 2015; Lü et al., 2018; Hu et al., 2020), as shown in Tables 2, 3 respectively.
3.6 Operating conditions
To facilitate the understanding of the proposed multi-factor calculation, a flow chart of failure probability assessment of the Zhaoshuling landslide is shown in Figure 4.
The reliability analysis of the Zhaoshuling landslide in a one-year period considering the spatial variability of parameters would be carried out. The pseudo-static method was used to analyze the reliability of seismic landslide when the annual failure probability was the highest. In order to study the critical instability of landslides under earthquake conditions, the horizontal seismic coefficients were calculated as 0.028, 0.05, 0.1, 0.15, and 0.224, respectively. In addition, the horizontal seismic coefficient was regarded as a random variable conforming to the log-normal distribution, and the COV of the seismic coefficient was 0.3 (Zhang et al., 2021).
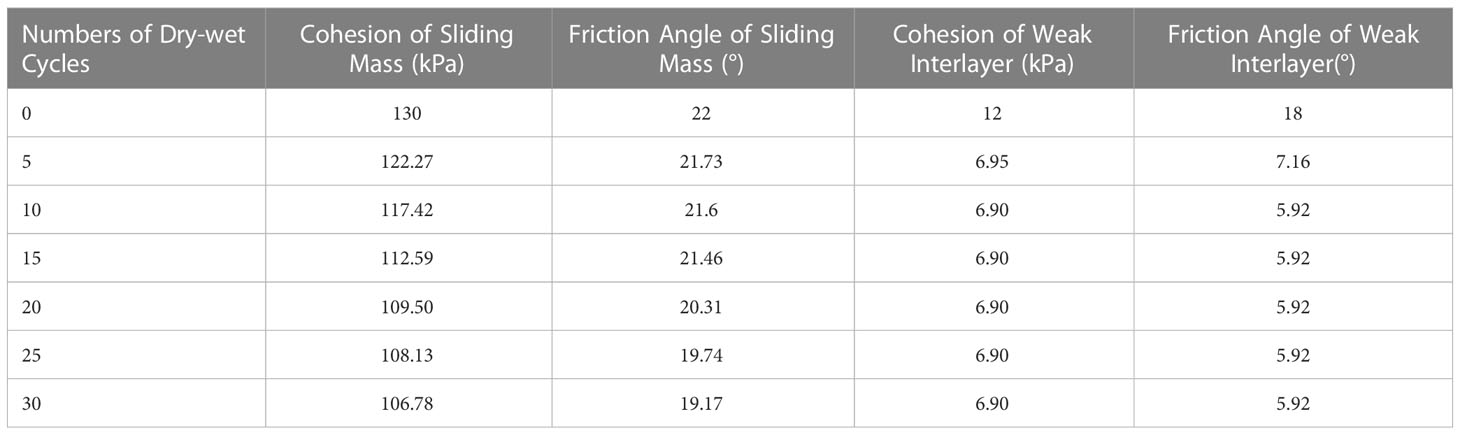
The landslide reliability calculation of 30 dry-wet cycles would be carried out when the failure probability was the highest under the combined action of reservoir water level and rainfall. At the same time, the simultaneous reduction and separate reduction of the parameters of the sliding mass and the weak interlayer in the dry-wet cycles would be considered, and the influence of the dry-wet cycles on the failure probability of the landslide could be explored. Correspondingly, the parameters of the dry-wet cycles referred to the published papers (Table 4; Wang et al., 2020; He, 2020; Zhang et al., 2022a; Zhang et al., 2022b).
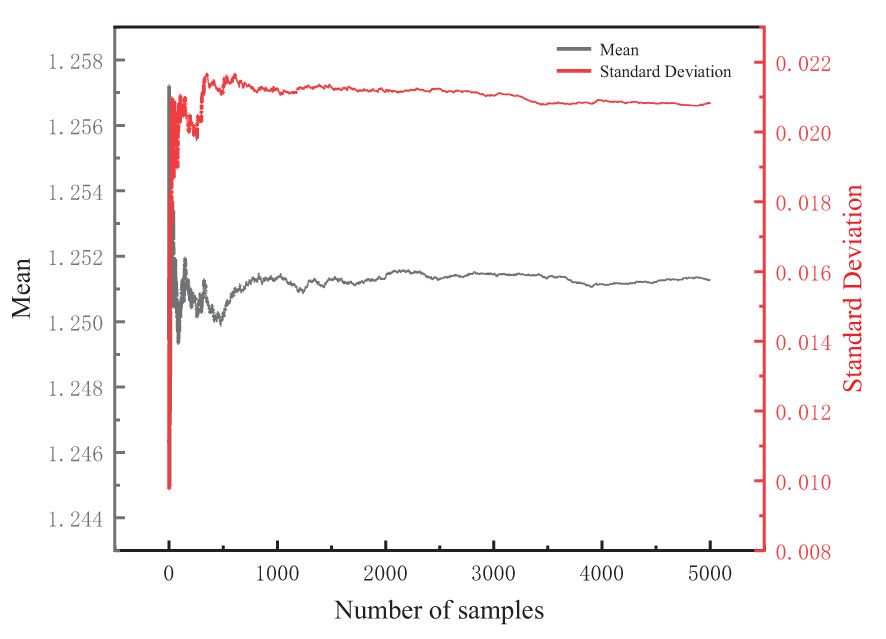
The random fields of cohesion and internal friction angle generated in one sampling are shown in Figures 5A, B. The mean and standard deviation of the FOS gradually converge with the increase of the number of simulations, when the number of simulations is 5000 times, (Liu et al., 2019), the calculation results reached convergence in all cases (Figure 6).
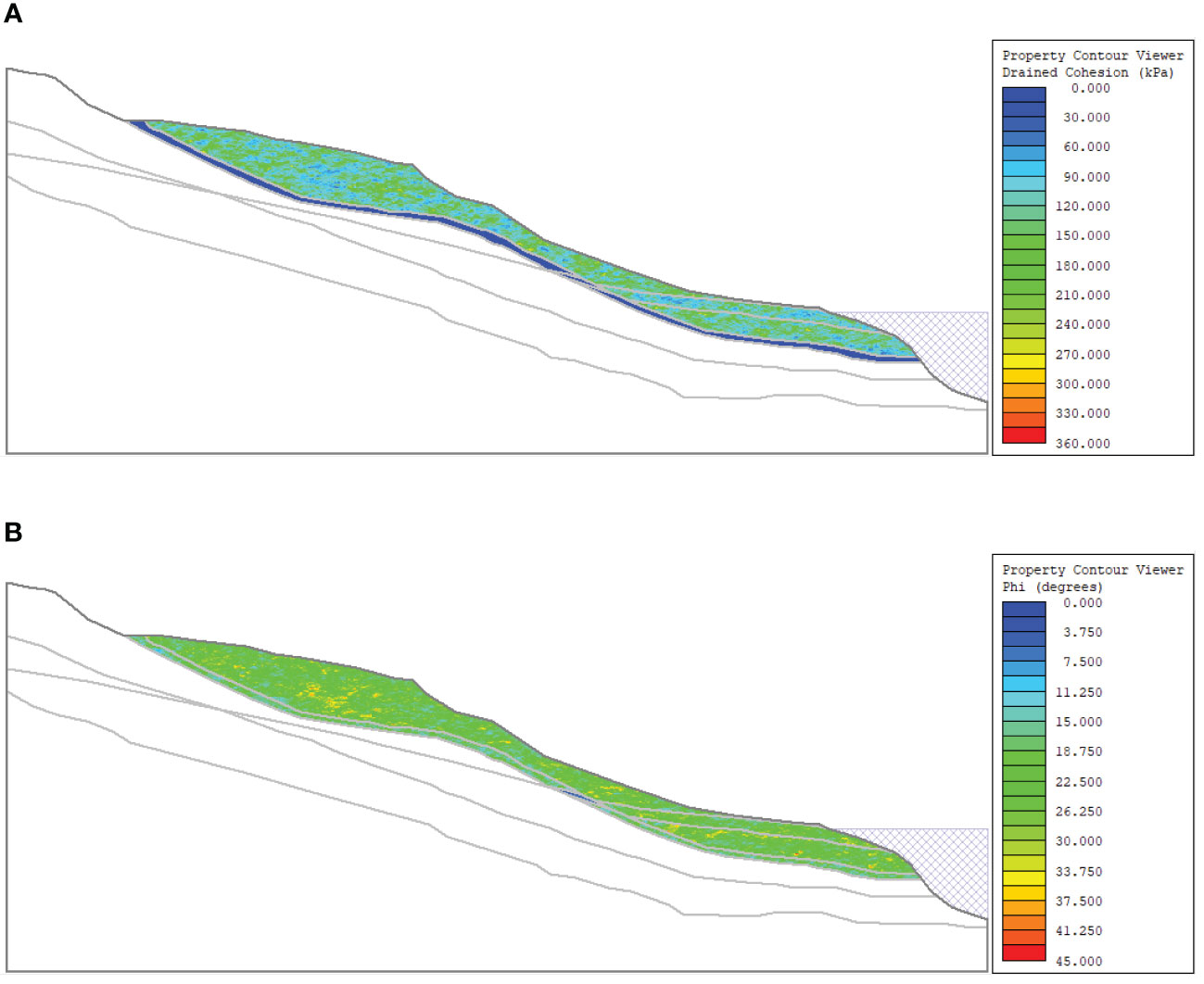
Figure 5 Random field model of Zhaoshuling landslide: (A) Random field model of cohesion; (B) Random field model of internal friction angle.
4 Result
4.1 Reliability analysis of landslide under reservoir water level and rainfall
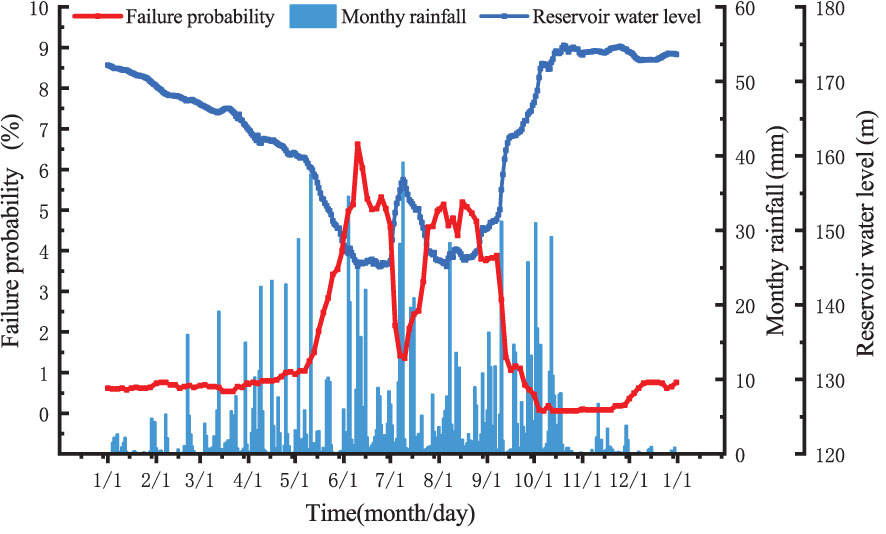
4.1.1 January 1st ~ March 20th
In the first stage, the reservoir water level dropped slowly and there was less rainfall. The landslide failure probability was the highest at 0.76% and the lowest at 0.54%, which was always kept at a low level. The seepage pressure generated by the water level difference has little effect on the stability of the landslide. Correspondingly, there is no significant change in failure probability.
4.1.2 March 21th~ June 10th
In the second stage, the failure probability increased rapidly, from 0.54% to 6.62%. The water level difference inside and outside the landslide will generate seepage pressure pointing to the outside of the landslide. In this case, the stability of the landslide will be reduced, and the failure probability will significantly increase. Theoretically, when the reservoir water level drops rapidly to the lowest point, the seepage pressure will increase to a maximum, and the stability of the landslide is the worst at this time. With the decline of the reservoir water, the landslide stability also gradually decreased. Therefore, the landslide stability was mainly affected by the change of reservoir water level.
4.1.3 June 11th ~ August 20th
The reservoir water level remained at 145 m between June 11th and July 1st. Nevertheless, the failure probability as a whole showed a downward trend, from 6.04% to 4.58%. It was speculated that the hysteresis of seepage inside the slope caused the groundwater infiltration line to still change. With the gradual decline of the groundwater level in the landslide, the seepage pressure will gradually decrease. Thus, the stability of the landslide is enhanced again, and the failure probability will be reduced. After that, the reservoir water level rose, and the failure probability dropped rapidly to 1.36%. This suggests that the rising process of the reservoir water level was conducive to the stability of the landslide.
4.1.4 August 21st ~ October 20th
The reservoir water level continued to rise, and the failure probability continued to decline, from 4.92% to 0.06%. In the follow-up, even if the slope stability was significantly enhanced, the decline in the failure probability was not large. Thus, it can be found that when the failure probability was small, the stability change of the landslide cannot be well reflected. The water level in the landslide rises slowly, and the seepage pressure will be generated towards the landslide. The stability of the landslide will be enhanced, and the failure probability will be reduced.
4.1.5 October 21st ~ December 31st
At this stage, the change trends of the failure probability curve were first stable, then rising and then stable. It can be found that although the reservoir water level and rainfall fluctuated slightly, the landslide stability decreased.
The annual failure probability with reservoir water fluctuation and rainfall changes as shown in Figure 7. The most unstable period of the landslide is in June. The probability of failure increased when the water level decreased, and decreased when the water level increased. Therefore, the failure probability and the water level were basically in the opposite trend. It can be found that the landslide stability was closely related to the fluctuation of the reservoir water level, while the influence of rainfall on the landslide stability was relatively small. In addition, the failure probability at the beginning of the year fluctuated around 0.6%, and the failure probability at the end of the year reached 0.7%. Thus, the landslide stability formed a closed loop after the annual reservoir water level and rainfall experienced a cyclical change.
4.2 Reliability analysis of landslide under combined seismic action of reservoir water level and rainfall
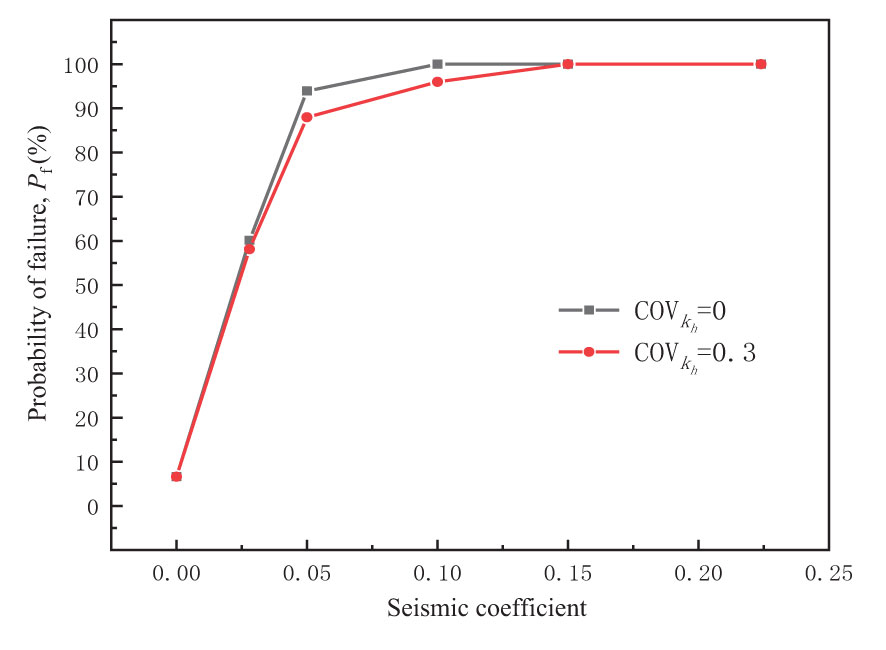
Figure 8 shows results with and without the COV of the seismic coefficient. With the increase of seismic coefficient, the failure probability of the landslide increased significantly. Obviously, the earthquake had a significant effect on the stability of the landslide. In the case of an actual seismic coefficient of 0.05, the failure probability of the landslide reaches about 90%. Notably, failure probability decreases when seismic coefficients were regarded as random variables. Thus, the failure probability of landslide will be increased when the seismic coefficients were regarded as constants.
Figure 9A shows the distribution of the FOS was relatively concentrated when the seismic coefficients were small. Conversely, when the seismic coefficient was large, the calculated FOS were more scattered. Notably, Figure 9B shows the probability of FOS less than 1.0 was 46.58% under the horizontal seismic coefficients was 0.224. Similarly, when the horizontal seismic coefficients were 0.224, it can be found that more than half of the cases where the FOS was less than 1.0 (Figure 8A). The Zhaoshuling landslide may be in an unstable state at this time.
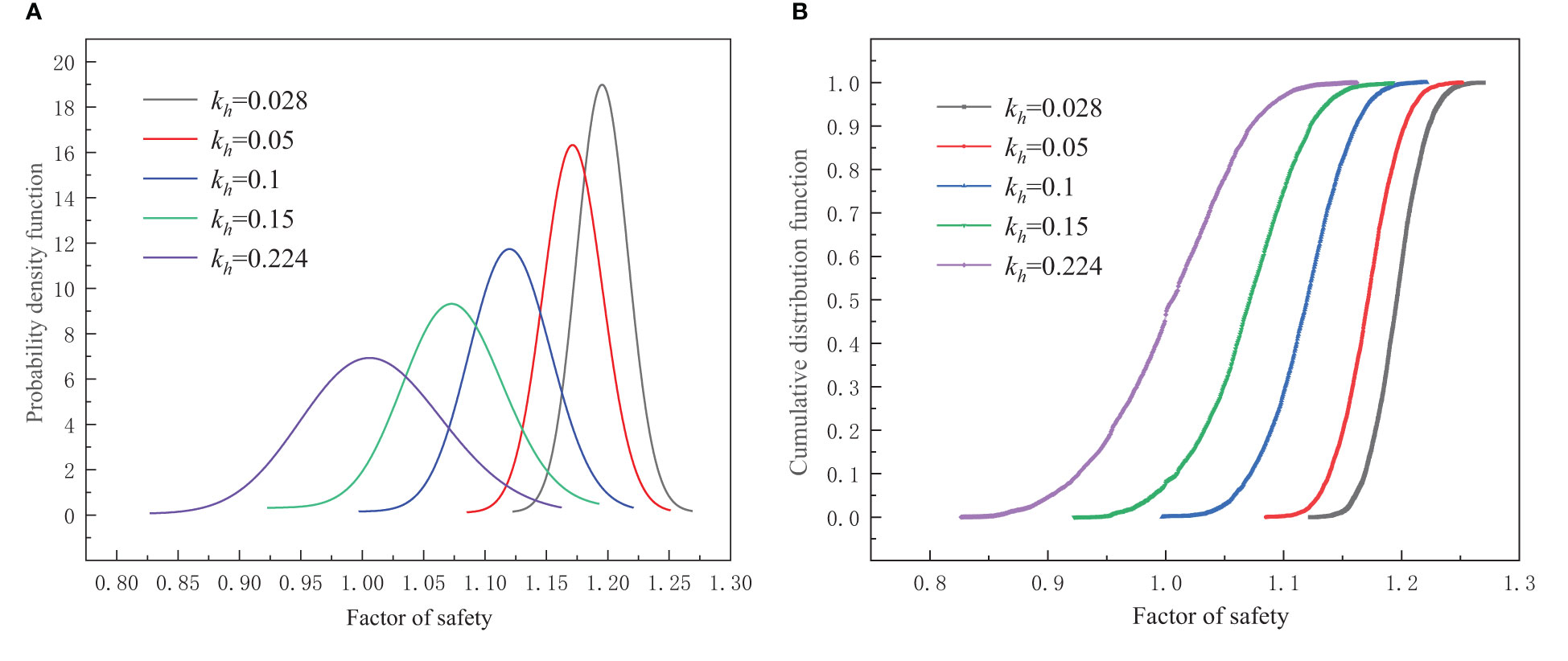
Figure 9 Probability density curve and cumulative distribution curve under different seismic coefficients: (A) probability density function; (B) cumulative distribution function.
4.3 Sensitivity analysis
4.3.1 The effect of the COV
As the COV of cohesion or friction angle increased, the failure probability of landslide increased. Therefore, it can be found the greater the variation of strength parameters, the less conducive to the stability of the landslide. And the degree of variation in the friction angle had a greater impact on the failure probability. Notably, the small mean value of cohesion led to limited variation in the range of cohesion values under the two COV. Thus, the variation degree of cohesion had little influence on the landslide stability.
Figure 10A shows the probability density functions of the FOS. The shape of the probability density function became narrower and the uncertainty in the FOS decreased when the negative value of the COV of the friction angle increased. Similarly, the probability distribution estimated also shows the same trend (Figure 10B). In addition, although when the COV was 0.5 and the FOS was 1.0, the cumulative distribution value was still 0. The landslide will not be completely unstable.
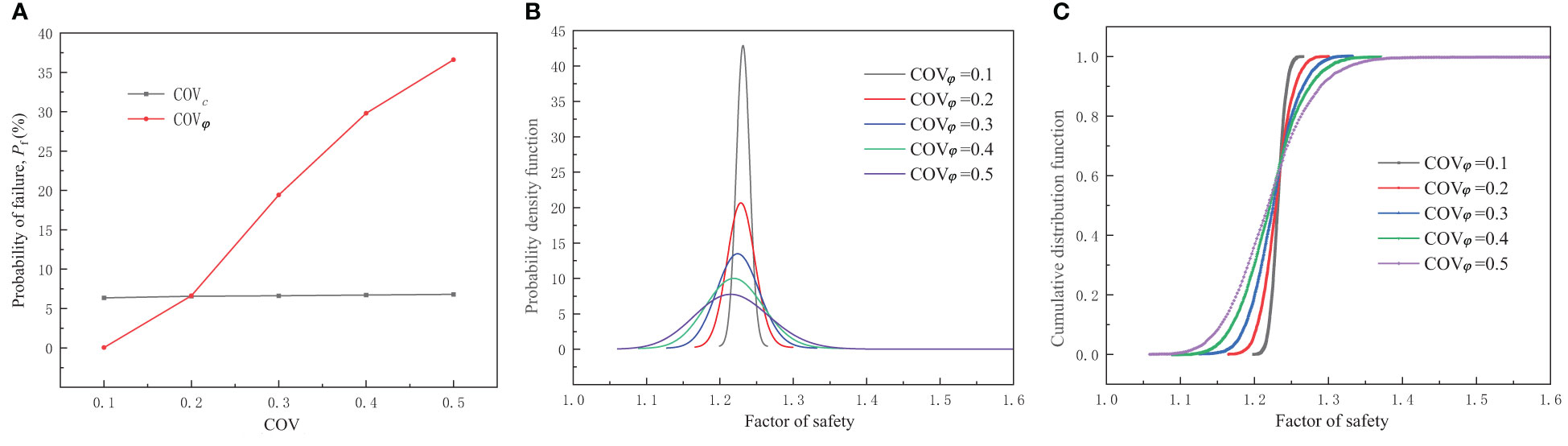
Figure 10 The effect of the COV: (A) Influence of different COV on failure probability; (B) probability density function; (C) probability distribution of the FOS.
4.3.2 The effect of the correlation coefficient
Figure 11A shows that the probability of failure increased as the correlation coefficient increased. Thus, the stronger the negative correlation between the cohesion and the friction angle, the more conducive to the stability of the slope. But the failure probability did not change much.
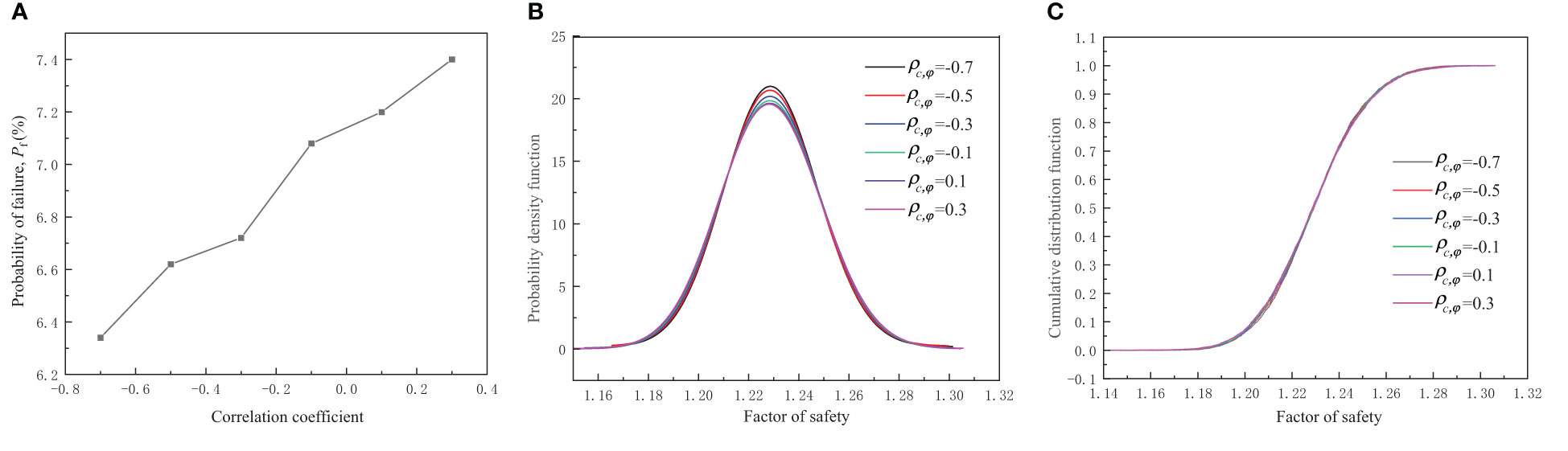
Figure 11 The effect of the correlation coefficient: (A) Influence of different correlation coefficients on failure probability; (B) probability density function; (C) probability distribution of the FOS.
Figures 11B, C show that the probability density functions and the probability distribution of the FOS determined from the five correlation coefficients were almost. The reason was that the cohesion had little effect on failure probability.
4.3.3 The effect of the fluctuation
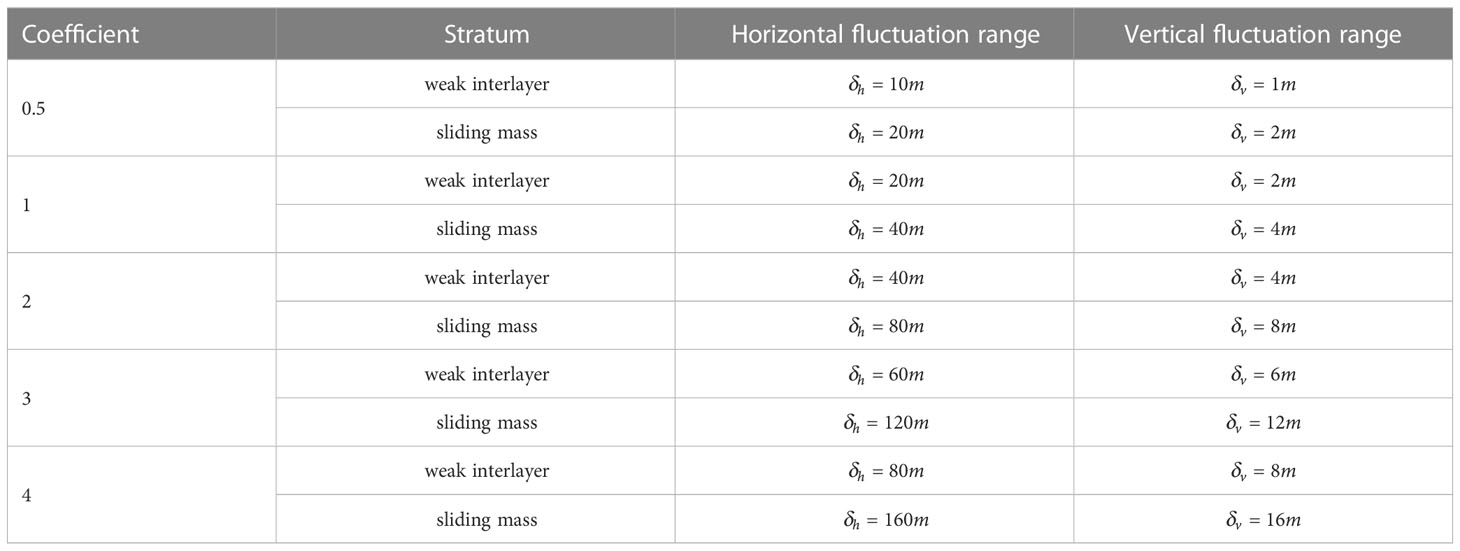
This section introduces a coefficient to represent the change in the scale of fluctuation, then the fluctuation range of the sliding mass and the weak interlayer is increased or decreased by the same multiple (Table 5). Figure 12A shows the effect of scale of fluctuation on the failure probability. Whether it was the horizontal fluctuation range or the vertical fluctuation range , as the fluctuation range increased, the failure probability of landslide increased gradually. Notably, the failure probability was more significantly affected by changes in the vertical fluctuation range.
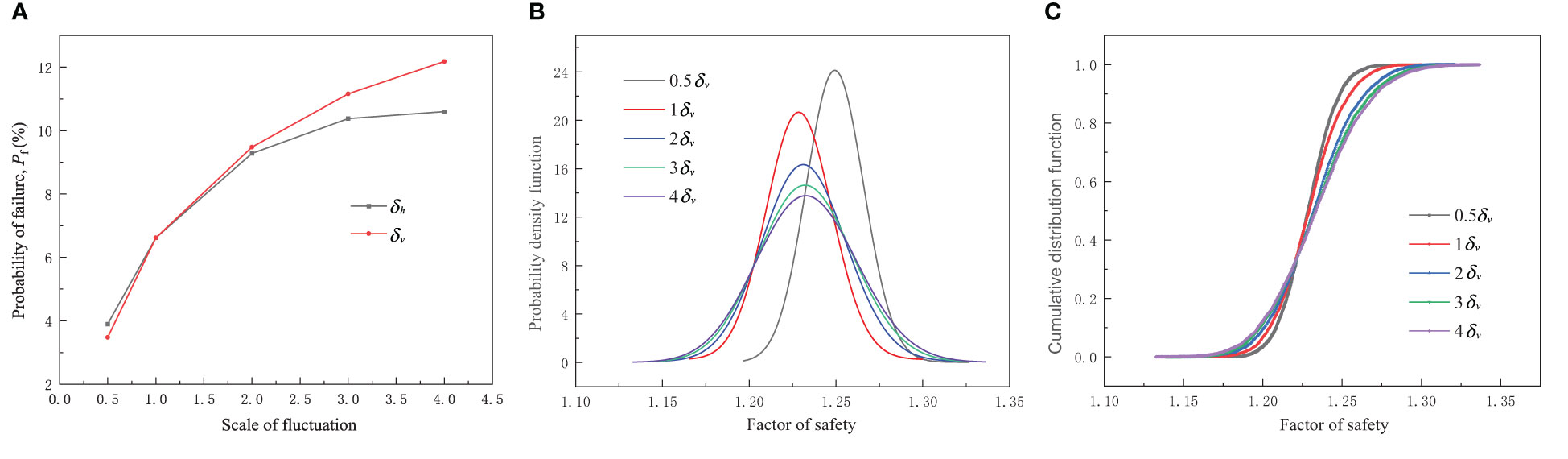
Figure 12 The effect of the fluctuation: (A) Influence of different fluctuation coefficients on failure probability; (B) probability density function; (C) probability distribution of the FOS.
Figure 12B shows that the probability density function curve had a very obvious change under different vertical fluctuation ranges. As the vertical fluctuation range increased, the peak value of the curve gradually decreased and shifted to the left. Therefore, the distribution of the FOS gradually became scattered and the mean value gradually decreased, and the landslide stability was gradually decreasing. And the curve difference was large when the vertical fluctuation range coefficient was between 0.5 and 2, the probability distribution estimated also shows the same trend (Figure 12C). It can be found that when the vertical fluctuation range exceeded a certain value, the failure probability was not sensitive to its change.
5 Discussion
More than 85% of the slope instability is inseparable from the action of water (Wang et al., 2019b; Yin et al., 2022; Zhang et al., 2022c). The dry-wet cycles effect caused by the rise and fall of the reservoir water level affects the stability of the bank landslide (Rejeb and Bruel, 2001). Lin et al. (2005) studied the microscopic mechanism of water weakening in sandstone, and used dry-wet cycles to simulate leaching effects. The result shows that after 60 dry-wet cycles, the strength loss of sandstone reached 20%, and the porosity showed a nonlinear increase. Under the repeated dry-wet cycles, the surface roughness coefficient, compressive strength and friction angle of the rock mass gradually decrease (Fang et al., 2019). Wang et al. (2019) analyzed the effect of water level rise and fall on the shear strength of sandstone-mudstone, and concluded that the decrease in shear strength was in a logarithmic relationship with the increase in the number of cycles. Therefore, the dry-wet cycles play an important role in the long-term effect of the reservoir bank landslides.
The results of the simulation are summarized in Figures 13, 14. With the increase of the number of dry-wet cycles, the strength of the rock and soil was reduced, and the failure probability of the landslide increased significantly. Obviously, the failure probability basically did not change after 10 dry-wet cycles. So the weakening of the landslide stability by the dry-wet cycle was limited. The reduction of rock and soil strength parameters was also consistent with the failure probability.
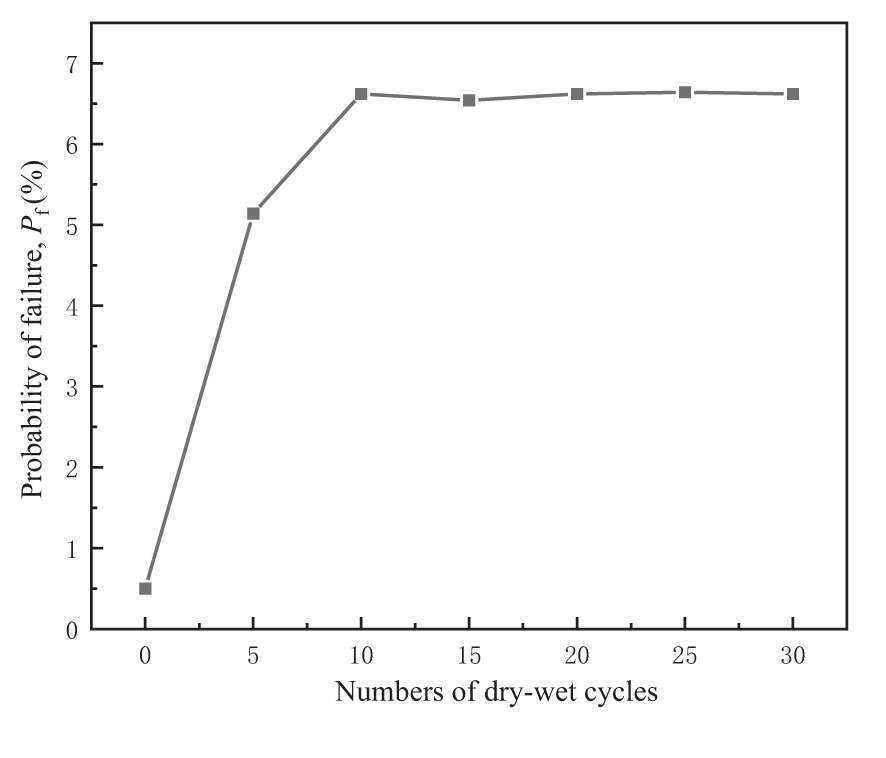
Figure 13 Influence of parameters degradation of sliding body and weak interlayer on failure probability under dry-wet cycles.
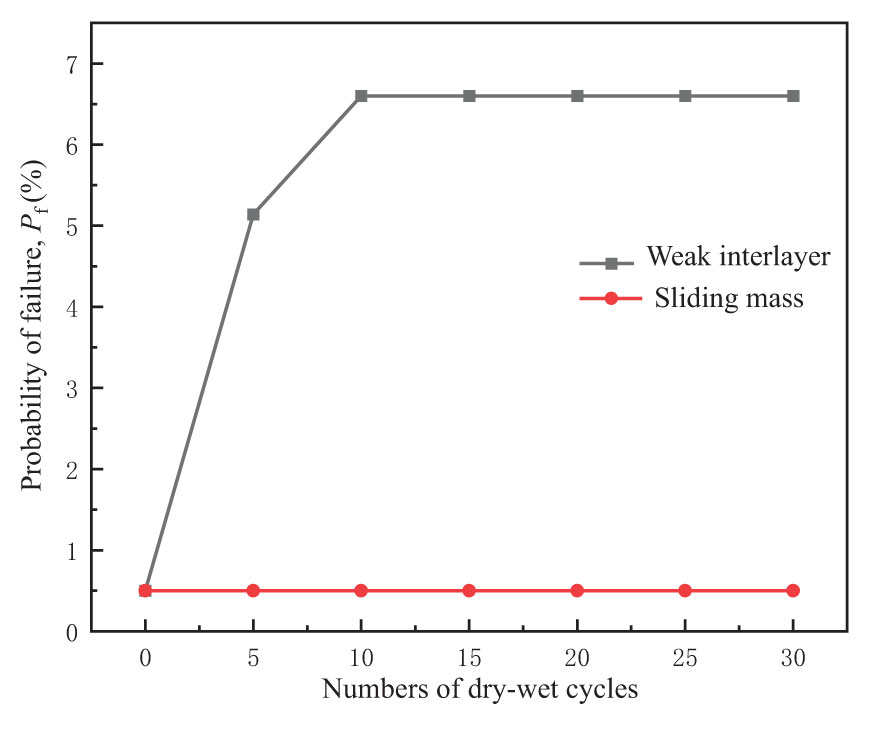
Figure 14 Influence of parameters degradation of only sliding mass or weak interlayer on failure probability under dry-wet cycles.
Figure 14 shows the change of the failure probability of the landslide was mainly affected by the reduction of the parameters of the weak interlayer. It can be concluded that the weak interlayer played a decisive role in the landslide stability.
The stability of coastal banks is affected by the changing water levels, rainfall, and earthquakes (Sassa and Takagawa, 2019; Liu et al., 2023). The reliability evaluation method of reservoir banks under various disaster-causing factors in this paper can be applied to predict the long-term safety of the coastal banks (Cavanaugh et al., 2019).
6 Conclusion
Considering the spatial variability of rock and soil parameters, this paper evaluated the reliability of the Zhaoshuling landslide within one year. Furthermore, the influence of dry-wet cycles on failure probability was discussed, and the sensitivity analysis of random field-related statistical parameters was carried out. Several conclusions can be obtained as followings:
(1) The annual failure probability of the Zhaoshuling landslide varied with reservoir water level and rainfall. When the reservoir water level decreased, the failure probability of the slope increased. Correspondingly, when the reservoir water level increased, the failure probability of the slope decreased. Meanwhile, rainfall had relatively little effect on failure probability. And the June was identified as the most unstable period of the year for the Zhaoshuling landslide.
(2) With the increase of seismic coefficient, the failure probability of landslide increased significantly. Thus, the most important external action affecting the stability of the slope was the earthquake. In addition, the resulting failure probability was slightly reduced when the seismic coefficients were treated as random variables.
(3) Due to the increase in the number of dry-wet cycles, the strength of rock and soil was gradually reduced, and the failure probability of landslide increased significantly. Moreover, the change of the failure probability of the landslide was mainly caused by the reduction of the parameters of the weak interlayer. It was proved that the weak interlayer played a decisive role in the landslide stability.
(4) The spatial variability of rock and soil parameters had a significant impact on the slope stability. The failure probability will increase with the increase of the COV, correlation coefficient, and fluctuation range, respectively. Especially, attention should be paid to the COV of the internal friction angle and the vertical fluctuation range of the parameter when evaluating the reliability of the landslide. The research results can provide important references for the analysis of the formation mechanism of wading landslides, monitoring, and emergency management.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
WZ: Supervision, writing- reviewing, and editing. LW: Data curation and writing- original draft preparation. XM and FM: Conceptualization and methodology. YW: Visualization and validation. PL: investigation. All authors contributed to the article and approved the submitted version.
Funding
This study was supported by the National Key R & D Program of China (2019YFC1509605), Cooperation projects between Chongqing University, Chinese Academy of Sciences and other institutes (HZ2021001), Sichuan Transportation Science and Technology Project (2018-ZL-01), China Postdoctoral Science Foundation funded project (2021M700608) and Natural Science Foundation of Chongqing, China (cstc2021jcyj-bsh0047).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Biondi G., Cascone E., Maugeri M. (2002). Flow and deformation failure of sandy slopes. Soil Dynamics Earthquake Eng. 22 (9-12), 1103–1114. doi: 10.1016/S0267-7261(02)00136-7
Bromhead E. N., Ibsen M. L. (2004). Bedding-controlled coastal landslides in southeast Britain between axmouth and the Thames estuary. Landslides 1, 131–141. doi: 10.1007/s10346-004-0015-3
Cavanaugh K. C., Reed D. C., Bell T. W., Castorani M. C. N., Beas-Luna R. (2019). Spatial variability in the resistance and resilience of giant kelp in southern and Baja California to a multiyear heatwave. Front. Mar. Sci. 6, 413. doi: 10.3389/fmars.2019.00413
Chai B., Yin K. L., Du J., Xiao L. L. (2013). Correlation between incompetent beds and slope deformation at badong town in the three gorges reservoir, China. Environ. Earth Sci. 69 (1), 209–223. doi: 10.1007/s12665-012-1948-9
Chen L. X., Yin K. L., Dai Y. X. (2011). Building vulnerability evaluation in landslide deformation phase. J. Mountain Sci. 8 (2), 286–295. doi: 10.1007/s11629-011-2101-z
Cho S. E. (2010). Probabilistic assessment of slope stability that considers the spatial variability of soil properties. J. Geotechnical Geoenvironmental Eng. 136 (7), 975–984. doi: 10.1061/(ASCE)GT.1943-5606.0000309
Fang J. C., Deng H. F., Qi Y., Xiao Y., Zhang H. B., Li J. L. (2019). Analysis of changes in the micromorphology of sandstone joint surface under dry-wet cycling. Adv. Materials Sci. Eng. 11, 8758203. doi: 10.1155/2019/8758203
Firth L. B., Thompson R. C., Bohn K., Abbiati M., Airoldi L., Bouma T. J., et al. (2014). Between a rock and a hard place: Environmental and engineering considerations when designing coastal defence structures. Coast. Eng. 87, 122–135. doi: 10.1016/j.coastaleng.2013.10.015
Griffiths D. V., Fenton G. A. (2004). Probabilistic slope stability analysis by finite elements. J. Geotechnical Geoenvironmental Eng. 130 (5), 507–518. doi: 10.1061/(ASCE)1090-0241(2004)130:5(507)
He Q. (2020). Effect of dry-wet cycle on landslide soil strength and landslide stability analysis in three gorges reservoir area (Wuhan, China: Wuhan Institute of Technology).
Hu H. Q., Huang Y. (2019). PDEM-based stochastic seismic response analysis of sites with spatially variable soil properties. Soil Dynamics Earthquake Eng. 125, 105736. doi: 10.1016/j.soildyn.2019.105736
Hu H. Q., Huang Y., Zhao L. Y. (2020). Probabilistic seismic-stability analysis of slopes considering the coupling effect of random ground motions and spatially-variable soil properties. Natural Hazards Rev. 21 (3), 04020028. doi: 10.1061/(ASCE)NH.1527-6996.0000402
Huang Q. X., Wang J. L., Xue X. (2016). Interpreting the influence of rainfall and reservoir infilling on a landslide. Landslides 13 (5), 1139–1149. doi: 10.1007/s10346-015-0644-8
Javankhoshdel S., Luo N., Bathurst R. J. (2017). Probabilistic analysis of simple slopes with cohesive soil strength using RLEM and RFEM. Georisk-Assessment Manage. Risk Engineered Syst. Geohazards 11 (3), 231–246. doi: 10.1080/17499518.2016.1235712
Jiang S. H., Li D. Q., Cao Z. J., Zhou C. B., Phoon K. K. (2015). Efficient system reliability analysis of slope stability in spatially variable soils using monte carlo simulation. J. Geotechnical Geoenvironmental Eng. 141 (2), 04014096. doi: 10.1061/(ASCE)GT.1943-5606.0001227
Li D. L., Liu X. R., Li X. W., Liu Y. Q. (2016). The impact of microearthquakes induced by reservoir water level rise on stability of rock slope. Shock Vibration, 7583108. doi: 10.1155/2016/7583108
Lin M. L., Jeng F. S., Tsai L. S., Huang T. H. (2005). Wetting weakening of tertiary sandstones-microscopic mechanism. Environ. Geology 48 (2), 265–275. doi: 10.1007/s00254-005-1318-y
Lin C. W., Liu S. H., Lee S. Y., Liu C. C. (2006). Impacts of the chi-chi earthquake on subsequent rainfall-induced landslides in central Taiwan. Eng. Geology 86 (2-3), 87–101. doi: 10.1016/j.enggeo.2006.02.010
Liu X., Wang Y., Li D. Q. (2019). Investigation of slope failure mode evolution during large deformation in spatially variable soils by random limit equilibrium and material point methods. Comput. Geotechnics 111, 301–312. doi: 10.1016/j.compgeo.2019.03.022
Liu S., Wang L., Zhang W., He Y., Pijush S. (2023). A comprehensive review of machine learning-based methods in landslide susceptibility mapping. Geological J. 1, 19. doi: 10.1002/gj.4666
Lü Q., Xiao Z. P., Zheng J., Shang Y. Q. (2018). Probabilistic assessment of tunnel convergence considering spatial variability in rock mass properties using interpolated autocorrelation and response surface method. Geosci. Front. 9 (6), 1619–1629. doi: 10.1016/j.gsf.2017.08.007
Malone T. C., Newton A. (2020). The globalization of cultural eutrophication in the coastal ocean: causes and consequences. Front. Mar. Sci. 7, 670. doi: 10.3389/fmars.2020.00670
Ng C. W. W., Pang Y. W. (2000). Influence of stress state on soil-water characteristics and slope stability. J. Geotechnical Geoenvironmental Eng. 126 (2), 157–166. doi: 10.1061/(ASCE)1090-0241(2000)126:2(157)
Rahimi A., Rahardjo H., Leong E. C. (2011). Effect of antecedent rainfall patterns on rainfall-induced slope failure. J. Geotechnical Geoenvironmental Eng. 137 (5), 483–491. doi: 10.1061/(ASCE)GT.1943-5606.0000451
Rejeb A., Bruel D. (2001). Hydromechanical effects of shaft sinking at the Sellafield site. Int. J. Rock Mechanics Min. Sci. 38 (1), 17–29. doi: 10.1016/S1365-1609(00)00061-7
Rui S. J., Guo Z., Si T. L., Li Y. J. (2020). Effect of particle shape on the liquefaction resistance of calcareous sands. Soil Dynamics Earthquake Eng. 137, 106302. doi: 10.1016/j.soildyn.2020.106302
Rui S. J., Wang L. Z., Guo Z., Cheng X. M., Wu B. (2021). Monotonic behavior of interface shear between carbonate sands and steel. Acta Geotechnica 16, 167–187. doi: 10.1007/s11440-020-00987-9
Salimi K., Cerato A. B., Vahedifard F., Miller G. A. (2021). General model for the uniaxial tensile strength characteristic curve of unsaturated soils. J. Geotechnical Geoenvironmental Eng. 147 (7), 04021051. doi: 10.1061/(ASCE)GT.1943-5606.0002567
Sassa S., Takagawa T. (2019). Liquefied gravity flow-induced tsunami: first evidence and comparison from the 2018 Indonesia sulawesi earthquake and tsunami disasters. Landslides 16, 195–200. doi: 10.1007/s10346-018-1114-x
Shukha R., Baker R. (2008). Design implications of the vertical pseudo-static coefficient in slope analysis. Comput. Geotechnics 35 (1), 86–96. doi: 10.1016/j.compgeo.2007.01.005
Suchomel R., Masin D. (2010). Comparison of different probabilistic methods for predicting stability of a slope in spatially variable c-phi soil. Comput. Geotechnics 37 (1-2), 132–140. doi: 10.1016/j.compgeo.2009.08.005
Temmerman S., Meire P., Bouma T., Herman P. J., Ysebaert T., De Vriend H., et al. (2013). Ecosystem-based coastal defence in the face of global change. Nature 504, 79–83. doi: 10.1038/nature12859
Wang C. F., Chen Q. S., Shen M. F., Juang H. (2017). On the spatial variability of CPT-based geotechnical parameters for regional liquefaction evaluation. Soil Dynamics Earthquake Eng. 95, 153–166. doi: 10.1016/j.soildyn.2017.02.001
Wang J. J., Liu M. N., Jian F. X., Chai H. J. (2019). Mechanical behaviors of a sandstone and mudstone under loading and unloading conditions. Environ Earth Sci 78, 30. doi: 10.1007/s12665-018-8020-3
Wang L. Z., Rui S. J., Guo Z., Gao Y. Y., Zhou W. J., Liu Z. Y. (2020). Seabed trenching near the mooring anchor: History cases and numerical studies. Ocean Eng. 218, 108233. doi: 10.1016/j.oceaneng.2020.108233
Wang L., Tang L., Wang Z., Liu H., Zhang W. (2020). Probabilistic characterization of the soil-water retention curve and hydraulic conductivity and its application to slope reliability analysis. Comput. Geotechnics 121, 103460. doi: 10.1016/j.compgeo.2020.103460
Wang L. Q., Yin Y. P., Huang B. L., Dai Z. W. (2020). Damage evolution and stability analysis of the jianchuandong dangerous rock mass in the three gorges reservoir area. Eng. Geology 265, 105439. doi: 10.1016/j.enggeo.2019.105439
Wang L. Q., Yin Y. P., Huang B. L., Zhang Z. H., Wei Y. J. (2019a). Formation and characteristics of guang'an village landslide in wuxi, chongqing, China. Landslides 16 (1), 127–138. doi: 10.1007/s10346-018-1086-x
Wang L. Q., Yin Y. P., Zhang Z. H., Huang B. L., Wei Y. J., Zhao P., et al. (2019b). Stability analysis of the xinlu village landslide (Chongqing, China) and the influence of rainfall. Landslides 16 (10), 1993–2004. doi: 10.1007/s10346-019-01240-5
Wang L., Zhang Z., Huang B., Hu M., Zhang C. (2021). Triggering mechanism and possible evolution process of the ancient qingshi landslide in the three gorges reservoir. Geomatics Natural Hazards Risk 12 (1), 3160–3174. doi: 10.1080/19475705.2021.1998230
Wang L. Q., Xiao T., Liu S. L., Zhang W. G., Yang B. B., Chen L. C. (2023). Quantification of model uncertainty and variability for landslide displacement prediction based on Monte Carlo simulation. Gondwana Res. doi: 10.1016/j.gr.2023.03.006
Xie J., Uchimura T., Wang G., Shen Q., Maqsood Z., Xie C. R., et al. (2020). A new prediction method for the occurrence of landslides based on the time history of tilting of the slope surface. Landslides 17, 301–312. doi: 10.1007/s10346-019-01283-8
Yang C. W., Zhang J. J., Fu X., Zhu C. B., Bi J. W. (2014). Improvement of pseudo-static method for slope stability analysis. J. Mountain Sci. 11 (3), 625–633. doi: 10.1007/s11629-013-2756-8
Yang H., Song K., Chen L., Qu L. (2023). Hysteresis effect and seasonal step-like creep deformation of the Jiuxianping landslide in the Three Gorges Reservoir Region. Eng. Geol. doi: 10.1016/j.enggeo.2023.107089
Yeznabad A. F., Molnar S., Naggar H. E. (2021). Probabilistic solution for the seismic sliding displacement of slopes in greater Vancouver. Soil Dynamics Earthquake Eng. 140, 106393. doi: 10.1016/j.soildyn.2020.106393
Yin Y. P., Wang L. Q., Zhang W. G., Zhang Z. H., Dai Z. W. (2022). Research on the collapse process of a thick-layer dangerous rock on the reservoir bank. Bull. Eng. Geology Environ. 81, 109. doi: 10.1007/s10064-022-02618-x
Zhan J. W., Wang Q., Zhang W., Shangguan Y., Song S., Chen J. (2019). Soil-engineering properties and failure mechanisms of shallow landslides in soft-rock materials. Catena 181, 104093. doi: 10.1016/j.catena.2019.104093
Zhan J., Yu Z., Lv Y., Peng J., Song S., Yao Z. (2022). Rockfall hazard assessment in the taihang grand canyon scenic area integrating regional-scale identification of potential rockfall sources. Remote Sens. 14 (13), 3021. doi: 10.3390/rs14133021
Zhan J., Zhang W., Chen J., Niu C., Han X., Sun X., et al. (2018). Mass movements along the rapidly uplifting river valley, southeast margin of the Tibetan plateau. Environ. Earth Sci. 77, 634. doi: 10.1007/s12665-018-7825-4
Zhang K., Cao P. (2013). Slope seismic stability analysis on kinematical element method and its application. Soil Dynamics Earthquake Eng. 50, 62–71. doi: 10.1016/j.soildyn.2013.03.002
Zhang W., He Y., Wang L., Liu S., Meng X. (2023). Landslide susceptibility mapping using random forest and extreme gradient boosting: A case study of fengjie, chongqing. Geological J. 1–16. doi: 10.1002/gj.4683
Zhang W., Li H., Tang L., Gu X., Wang L., Wang L. (2022c). Displacement prediction of jiuxianping landslide using gated recurrent unit (GRU) networks. Acta Geotechnica 17, 1367–1382. doi: 10.1007/s11440-022-01495-8
Zhang W. G., Meng F. S., Chen F. Y., Liu H. L. (2021). Effects of spatial variability of weak layer and seismic randomness on rock slope stability and reliability analysis. Soil Dynamics Earthquake Eng. 146, 106735. doi: 10.1016/j.soildyn.2021.106735
Zhang W. G., Meng X. Y., Wang L. Q., Meng F. S. (2022a). Stability analysis of the reservoir bank landslide with weak interlayer considering the influence of multiple factors. Geomatics Natural Hazards Risk 13 (1), 2911–2924. doi: 10.1080/19475705.2022.2149356
Zhang W. G., Tang L. B., Li H. R., Wang L., Cheng L. F., Zhou T. Q., et al. (2020). Probabilistic stability analysis of bazimen landslide with monitored rainfall data and water level fluctuations in three gorges reservoir, China. Front. Struct. Civil Eng. 14 (5), 1247–1261. doi: 10.1007/s11709-020-0655-y
Keywords: slope stability, random fields, failure probability, spatial variability, multiple factors
Citation: Zhang W, Meng X, Wang L, Meng F, Wang Y and Liu P (2023) Reliability evaluation of reservoir bank slopes with weak interlayers considering spatial variability. Front. Mar. Sci. 10:1161366. doi: 10.3389/fmars.2023.1161366
Received: 08 February 2023; Accepted: 07 March 2023;
Published: 20 March 2023.
Edited by:
Shengjie Rui, Norwegian Geotechnical Institute (NGI), NorwayReviewed by:
Jiewei Zhan, Chang’an University, ChinaLulu Liu, China University of Mining and Technology, China
Copyright © 2023 Zhang, Meng, Wang, Meng, Wang and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Luqi Wang, d2xxOTNAY3F1LmVkdS5jbg==
 Wengang Zhang
Wengang Zhang Xuanyu Meng1,2
Xuanyu Meng1,2 Luqi Wang
Luqi Wang Yankun Wang
Yankun Wang