Comparative analysis of four types of mesoscale eddies in the North Pacific Subtropical Countercurrent region - part II seasonal variation

The North Pacific Subtropical Countercurrent area (STCC) is high in mesoscale eddy activities. According to the rotation direction of the eddy flow field and the sign of temperature anomaly within the eddy, they can be divided into four categories: cyclonic cold-core eddy (CCE), anticyclonic warm-core eddy (AWE), cyclonic warm-core eddy (CWE) and anticyclonic cold-core eddy (ACE). CCE and AWE are called normal eddies, and CWE and ACE are named abnormal eddies. Based on the OFES data and vector geometry automatic detection method, we find that at the sea surface, the maximum monthly number of the CCE, AWE, CWE, and ACE occurs in December (765.70 ± 52.05), January (688.20 ± 82.53), August (373.40 ± 43.09) and August (533.00 ± 56.92), respectively. The number of normal eddies is more in winter and spring, and less in summer and autumn, while abnormal eddies have the opposite distribution. The maximum rotation velocity of the four types of eddies appears in June (11.71 ± 0.75 cm/s), June (12.24 ± 0.86 cm/s), May (10.63 ± 0.99 cm/s) and June (9.97 ± 0.91 cm/s), which is fast in winter and spring. The moving speed of the four types of eddies is almost similar (about 10 ~ 11 cm/s). The amplitude of normal and abnormal eddies is both high in summer and autumn, and low in winter and spring, with larger amplitudes in normal than abnormal eddies. The eccentricity (defined as the eccentricity of the ellipse obtained by fitting the eddy boundary) of the four types of eddies is also close to each other, and their variation ranges from 0.7 to 0.8, with no apparent seasonal variation. The vertical penetration depth, which has no significant seasonal difference, is 675.13 ± 67.50 m in cyclonic eddies (CCE and CWE), which is deeper than that 622.32 ± 81.85 m in anticyclonic eddies (ACE and AWE). In addition, increasing the defined temperature threshold for abnormal eddies can significantly reduce their numbers but does not change their seasonal variation trend.

1. Introduction

Satellite observations show that mesoscale eddies are almost ubiquitous in the global oceans (Chelton et al., 2007; Chelton et al., 2011; Ma and Wang, 2014; Wang et al., 2015; Chen and Han, 2019; Dong et al., 2022). The lifespan of these mesoscale eddies is from several weeks to months, and the eddy diameter is O(100 km). Mesoscale eddies are strongly nonlinear and have significant effects on physical quantities in the ocean and the atmospheric bottom boundary layer. Mesoscale eddies can transport material and energy through their horizontal movement (Dong et al., 2014), rotation (He et al., 2018) and asymmetric flow field structure (Qiu et al., 2022). Eddy-induced zonal mass transport is comparable in magnitude to the large-scale wind- and thermohaline-driven circulation (Zhang et al., 2014a). Therefore they play a crucial role in the redistribution of heat and freshwater (Chen et al., 2012; Gaube et al., 2015; Xu et al., 2016; Dong et al., 2017; Lin et al., 2019; Xu et al., 2019; Dai et al., 2020; Ding et al., 2021a).

Mesoscale eddies also affect biological productivity in the upper ocean (Xian et al., 2012; McGillicuddy, 2016; Wang et al., 2018; He et al., 2019; Patel et al., 2020; Geng et al., 2021). In the south Indian Ocean, anticyclonic eddies (AEs) can induce a positive chlorophyll anomaly within the eddy (Gaube et al., 2013). Besides, cyclonic eddies (CEs) usually cause the upper mixed layer depth to become shallow, while AEs can cause the deepening of the upper mixed layer (Sun et al., 2017; Gaube et al., 2019; Ding et al., 2021b). Using satellite data from 2006 ~ 2009 in the Kuroshio Extension region, Ma et al. (2015) demonstrated that CEs-induced (AEs-induced) surface winds speed decelerate (accelerate) and reduce (increase) latent and sensible heat fluxes, water vapor content, cloud liquid water, and rain rate.

According to the rotation direction of the eddy surface flow field, mesoscale eddies are usually divided into CEs (with a counterclockwise rotation flow field) and AEs (with a clockwise rotation flow field). Synthetic analysis of large samples found that CEs are usually associated with a cold eddy core, while the AEs usually have a warm eddy core (Qiu and Chen, 2004; Meijers et al., 2007; Wang et al., 2012; Zhang et al., 2014b; Yang et al., 2015; Amores et al., 2016; Treguier et al., 2017). Therefore, CEs are also called cyclonic cold-core eddies (CCEs), and AEs are also named anticyclonic warm-core eddies (AWEs). However, recent studies have pointed out the existence of CEs with a warm eddy core (CWEs) and AEs with a cold eddy core (ACEs) (Itoh and Yasuda, 2010; Ji et al., 2016; Ni et al., 2021; An et al., 2022; Sun et al., 2022). In order to distinguish these eddies from the traditional CCEs and AWEs, these eddies are named abnormal eddies (Sun et al., 2019).

Using different definitions and identification methods, the proportion of abnormal eddies is from about 10% (Sun et al., 2019) to 20% (Ni et al., 2021) and even as high as 1/3 (Liu et al., 2021). Sun et al. (2019) pointed out that abnormal eddies are widespread in the North Pacific Ocean and have significant regional differences. The CWEs are concentrated in the northwest and southeast of the North Pacific Ocean. At the same time, the ACEs are also widely distributed in the northeast area in addition to these above two regions. The monthly distribution of the abnormal eddy numbers shows they are more numerous in summer than in winter.

Ni et al. (2021) pointed out that CWEs account for 19% of the global CEs, and AWEs account for 22% of the total AEs. The proportion of abnormal eddies is higher in tropical and boundary current regions. Besides, they have a noticeable seasonal difference in extratropical oceans area caused by the seasonal difference in the mixed layer depth. Combining the global Archiving, Validation, and Interpretation of Satellite Oceanographic (AVISO) and Advanced Very High-Resolution Radiometer (AVHRR) data from 1996 to 2015 and an artificial intelligence identification algorithm, Liu et al. (2021) found that abnormal eddies account for one-third of the total mesoscale eddies. Abnormal eddies showed a decreasing trend year by year in the global ocean, which is consistent with the results of Sun et al. (2019) in the North Pacific Ocean. They pointed out that there is a good correlation between the change in the number of abnormal eddies and the sea surface temperature gradient induced by global warming. The correlation coefficient between the two can reach 0.68, significant at 90% confidence level.

An et al. (2022, hereafter known as Part I) discussed the spatial characteristics of the four types of eddies in the STCC region based on the OFES data from 2008 to 2017. They found that the proportion of the four eddy types is 35.60, 32.08, 12.95, and 19.37% at the sea surface, respectively. From the vertical distribution, abnormal eddies are mainly distributed in the oceanic upper layer. There is no significant difference in eddy radius (about 70 ~ 80 km) and amplitude (3 ~ 6 cm) for the four types of eddies. These mesoscale eddies generally move westward at about 3 ~ 5 km per day. Part I provides a reference to comprehensively understand the spatial characteristics of mesoscale eddies in the STCC area.

The STCC area is located in the East-Asian monsoon region, and its eddy kinetic energy (EKE) shows a prominent annual cycle (Qiu, 1999; Kang et al., 2010; Qiu and Chen, 2010; Qiu et al., 2014). Therefore, this region’s mesoscale eddies characteristics may have obvious seasonal variation. Following Part I, this study systematically explores the seasonal variation of the four mesoscale eddy types. The findings are useful for getting a more comprehensive understanding of mesoscale eddy characteristics in the STCC region.

The rest of the study is organized as follows. Section 2 introduces the OFES data, the automatic eddy detection method, and the definition of the four types of mesoscale eddies. Section 3 analyzes the seasonal variations of the four types of mesoscale eddies in detail, including eddy number, radius, rotation velocity, horizontal movement velocity, nonlinearity, amplitude, eccentricity, and penetration depth. The eddy anomaly ratio (the ratio of the abnormal eddy existence duration to that of the eddy lifespan) and the influence of different temperature thresholds value on abnormal eddy numbers are discussed in Section 4. Finally, the main conclusions of this study are summarized in Section 5.

2. Data and methods

2.1. OFES data

This study explores the seasonal variation of the mesoscale eddies in the STCC region (16°N ~ 27°N, 115°E ~ 160°W) based on the OFES data (OGCM for the Earth Simulator), which extends from January 2008 to December 2017. The horizontal resolution of this data is 1/10° × 1/10° and is vertically divided into 54 uneven layers. The minimum depth at the upper-most layer is 2.5 m, and the maximum depth is 6,300 m. The time resolution of this data is three days. It can be downloaded from the Asia-Pacific Data Research Center of the University of Hawaii (http://apdrc.soest.hawaii.edu/las_ofes).

We use 3-day snapshots of sea surface height (η), three-dimensional zonal velocity (U), meridional velocity (V), and temperature (T) in this study. The OFES data are first passed through a high-pass space filter of 3° × 3° to obtain the sea surface height (η^′ ), velocity (U^′ and V^′ ), and temperature (T^′ ) anomalies. The spatial resolution of the OFES data is higher than common satellite data (generally only 0.25° × 0.25°, such as AVISO data, Pujol et al., 2016), and it contains three-dimensional variables. Thus the OFES data is more suitable than satellite data for mesoscale eddies studies. In addition, the OFES data does not adopt an assimilation scheme. Therefore its dynamic process is self-consistent and can be used for numerical diagnosis of thermodynamic or dynamic processes. Many previous works used this data for mesoscale eddy and other mesoscale process research (Taguchi et al., 2010; Zhang et al., 2017; Ji et al., 2018; Sun et al., 2022; Wang et al., 2022). For more information about the OFES data, please refer to Sasaki et al. (2008).

2.2. Two-dimensional eddy detection method

The automatic eddy detection algorithm is essential for extensive sample analysis studies. Predecessors have proposed a variety of automatic eddy identification methods, such as the Okubo-Weiss parameter method (Okubo, 1970; Weiss, 1991), the Winding-Angle method (Sadarjoen and Post, 2000), and the Sea Surface Height Topological method (Chelton et al., 2011). Among these methods, the Okubo-Weiss parameter method is the easiest to implement, but its accuracy is relatively low. Winding-Angle method has a high accuracy of eddy identification but with low computational efficiency. The altimeter sampling ability limits the Sea Surface Height Topological method, resulting in a lower successful identification (Tang et al., 2019).

This study adopts a vector geometry automatic detection method based on the geometric characteristics of mesoscale eddies (Nencioli et al., 2010). This method has already been applied to multiple data sources and complex flow fields (Dong et al., 2009; Aguiar et al., 2013; Lin et al., 2015; Sun et al., 2018; Yang et al., 2020; Sun et al., 2021a; Sun et al., 2021b; Qiu et al., 2022). Recently research has shown that the vector geometry method has more advantages than the Sea Surface Height Topology approach in terms of correct eddy identification rate and detection efficiency (You et al., 2022). The specific operations of this method are summarized as follows:

Firstly, based on the two-dimensional flow field data and the rotation characteristics of the eddy velocity field, the eddy center point is defined as a point meeting the following four constraints.

1~2) In the east-west (north-south) direction across the eddy center, the meridional (zonal) velocity component V^′ (U^′ ) has an opposite sign on the left and right (upper and lower) sides of the eddy center, and its size gradually increases with the distance from the eddy center.

3) The velocity at the eddy center point has the minimum value among the local area around the eddy center.

4) The velocity vector rotates clockwise or counterclockwise around the eddy center, and the rotation direction remains unchanged.

After the eddy center is determined, the outermost closed streamline of the local stream function around the eddy center is extracted as the eddy boundary. The eddy radius is then calculated as the radius of a circle which gives a circle area equivalent to the polygonal area enclosed by the eddy boundary.

2.3. Two-dimensional eddy tracking algorithm

Mesoscale eddy is a “living” marine phenomenon that goes through different life stages, from formation to decay (Liu et al., 2012). This study uses a similar method following Doglioli et al. (2007) and Chaigneau et al. (2008) to track the mesoscale eddies’ trajectory. The tracking steps are as follows:

1) The search area (S₁) and extended search area (S₂) with a radius of 1.2° and 1.8° are defined, with the eddy center as the circle center. The search area’s size selection depends on the background field’s current velocity and the data’s spatiotemporal resolution. On the one hand, the center of the mesoscale eddy is required not to move out of S₁ at the next time step. On the other hand, S₁ should not be too large. Otherwise, two distinct eddies will be incorrectly identified as the same eddy. The radius of S₂ is generally set as 1.5 times that of S₁.

2) If an arbitrary eddy (the current eddy hereafter) is successfully detected at the time step t, then we search for an eddy with the same polarity as the current eddy in the search area S₁ at time step t+1. If more than one eddy meets the requirement, the eddy closest to the current eddy center is selected as the continuation of the current eddy. If no eddy is successfully identified at the time step t+1, we search again using the extended search area S₂ at the time step t+2. If still no eddy with the same polarity is found, then the current eddy is considered decayed, and its lifespan is defined as the time interval from the time step of the first successful detection to the time step t. After the automatic eddy detection and tracking, a dataset containing eddy radius, polarity, boundary, lifespan, and the moving path is obtained.

2.4. Three-dimensional eddy detection algorithm

Based on the two-dimensional eddy detection results (subsection 2.3), three-dimensional eddy detection is carried out layer by layer from the sea surface down to the bottom layer (Dong et al., 2012; Lin et al., 2015). The specific steps are summarized as follows:

According to the eddy information at the sea surface (N₁ , current layer): eddy center position P₁(x₁.y₁) , occurrence time (t₁ ), eddy radius (R₁) , and eddy polarity (cyclonic/anticyclonic), we search for the eddy center at time (t₁ ) with the same polarity within the area S₃ in the next layer (search layer). S₃ is a circular area, with P₁(x₁,y₁) as the center and 0.25R₁ as the radius. If no eddy center satisfies the conditions in the next layer, the eddy penetration depth is equal to the depth of the current layer. If only one eddy center meeting the conditions is found in the next layer, it is regarded as the vertical extension of the current eddy. The eddy central point position P₂(x₂,y₂) , radius (R₂) and other information in the second layer are extracted. Then, the second layer is used as the current layer, and the third layer is the search layer, thus continuing the search process until no eddy can be found or the search reaches the bottom boundary. If more than one eddy satisfies the conditions in the search layer, then the one with the nearest eddy center is taken as the vertical extension of the current eddy. Using this method, the eddy vertical penetration depth is slightly shallower than the realistic value. The difference depends on the interval between the two layers in the vertical direction. In this study, we consider it as a small amount and do not discuss this difference.

2.5. Eddy classification

Eddies are classified into four types according to the combination of the rotation direction (clockwise or counterclockwise) of the eddy flow fields and the signs of the temperature anomaly (warm or cold) within the eddy. They are cyclonic cold-core eddy (CCE, with a counterclockwise rotating flow field and a negative temperature anomaly); cyclonic warm-core eddy (CWE, with a counterclockwise rotating flow field and a positive temperature anomaly); anticyclonic cold-core eddy (ACE, with a clockwise rotating flow field and a negative temperature anomaly), and anticyclonic warm-core eddy (AWE, with a clockwise rotating flow field and a positive temperature anomaly). CCEs and AWEs are also known as normal eddies because they satisfied traditional mesoscale eddies definition, while CWEs and ACEs are known as abnormal eddies (Sun et al., 2019).

There are two ways to define temperature anomaly. One is the average temperature anomaly within the eddy ($T_1=\frac{1}{N}{\displaystyle \sum _{i=1}^N{T}^{\prime }}$), where T^′ is the temperature deviation from the background field and N represents the number of grid points within the eddy (Sun et al., 2022). The other one is the difference between the average temperature anomaly within the eddy (T^′ ) and the eddy background field ($T_2=\frac{1}{M}{\displaystyle \sum _{i=1}^M{T}^{\prime }}$). Where M represents the number of grid points within the eddy background field, usually defined as the annular area from the eddy boundary to 1.5 times the eddy radius (Sun et al., 2019).

The method in Part I is also used here to determine the eddy temperature anomaly. That is, the first definition method is adopted. Considering that the time scale of mesoscale eddies is several weeks to months, eddies with a lifespan shorter than 30 days are removed to increase the results’ robustness. This study focuses on eddies’ seasonal variation, concentrated in the oceanic upper layer. Therefore, although the maximum depth of the OFES data is 6,300 m, we only focus on the oceanic upper layer shallower than 1,000 m.

3. Eddy seasonal variations

The STCC region (16°N ~ 27°N, 115°E ~ 160°W) is affected by the East-Asian monsoon and has obvious seasonal variations. Part I of the study discusses the three-dimensional spatial distribution of mesoscale eddies from 2008 to 2017. The present study focuses on the seasonal variations of the eddy number, radius, rotation velocity, horizontal moving velocity, nonlinearity, amplitude, eccentricity, and vertical penetration depth.

3.1. Eddy number

Previous studies have shown that the temporal variability of sea surface temperature (SST) gradient on a seasonal scale is closely related to the number of eddies generated (Liu et al., 2012). The larger SST gradient generates more eddies in the early spring than in summer. To verify this result, Figure 1 shows the monthly distribution of multi-year average (2008 ~ 2017) eddy numbers at the sea surface (Figures 1A, B) and 1,000 m (Figures 1C, D). At the sea surface, the multi-year average monthly number of CCEs, AWEs, CWEs, and ACEs are 631.34 ± 100.11, 568.37 ± 97.90, 229.62 ± 98.36, and 343.31 ± 128.81, respectively. The largest number of the four types of eddies (hereafter, the order of the four types of eddies is CCEs, AWEs, CWEs, and ACEs) appears in December (765.70 ± 52.05), January (688.20 ± 82.53), August (373.40 ± 43.09), and August (533.00 ± 56.92). Accordingly, the four types of eddies reach the minimum number in April, April, February and February, and the corresponding values are 529.00 ± 29.92, 440.30 ± 32.28, 112.20 ± 22.51 and 151.00 ± 28.41, respectively. The result indicates that the number of normal eddies, whether average value, maximum or minimum, is far greater than abnormal eddies.

FIGURE 1

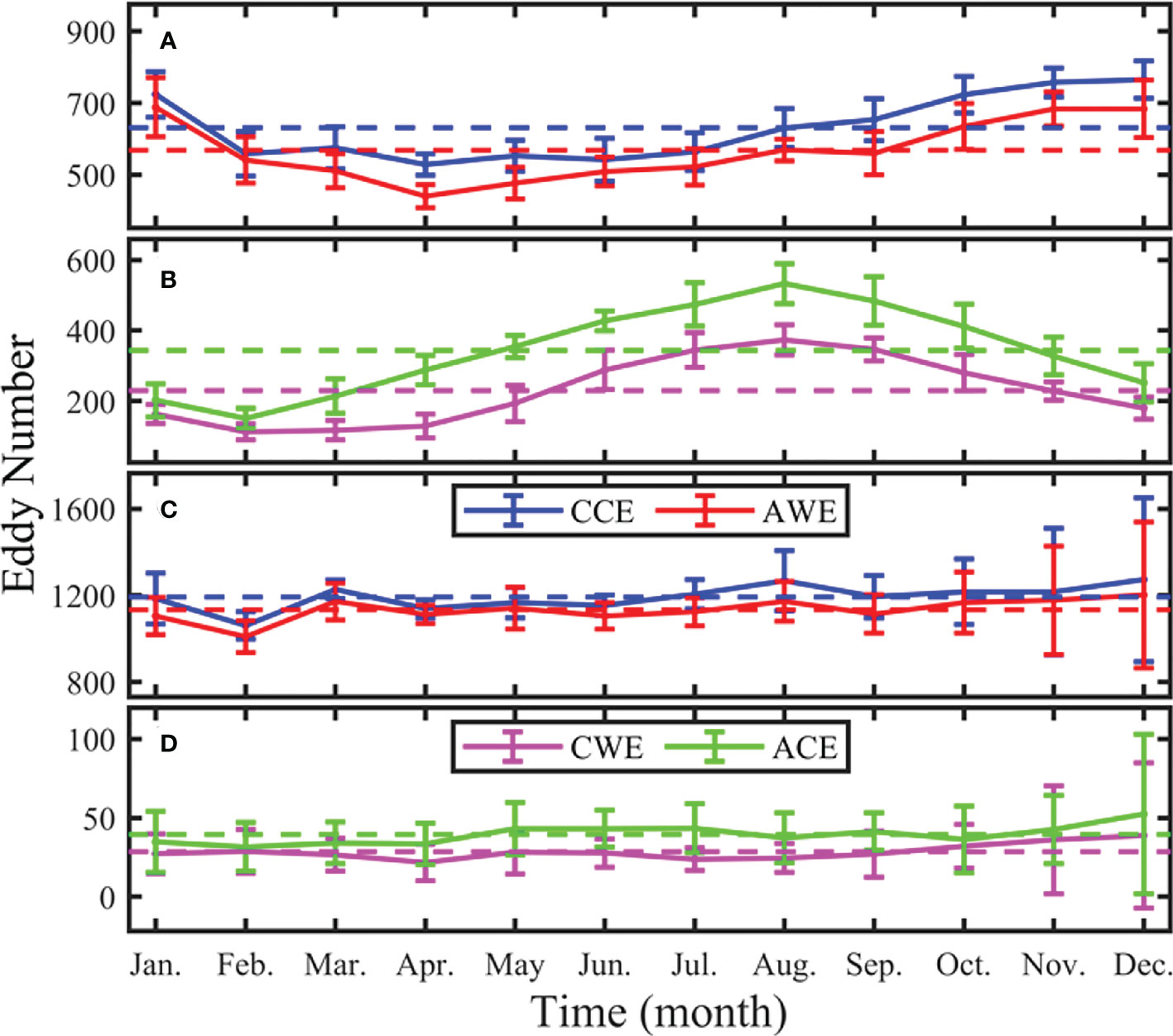
Figure 1 Monthly distribution of multi-year (2008 ~ 2017) average eddy number at the sea surface (A, B) and 1,000 m (C, D) in the STCC region. Blue, red, pink, and green curves represent cyclonic cold-core eddy, anticyclonic warm-core eddy, cyclonic warm-core eddy, and anticyclonic cold-core eddy, respectively. The bar represents the standard deviation, and the dotted line represents the multi-year average value.

Normal eddies at the sea surface are more in winter and spring, and less in summer and autumn (Figure 1A). Unlike normal eddies, the number of abnormal eddies is higher in summer and autumn, and less in spring and winter (Figure 1B). The mechanism causing this difference may be that the wind stress curl in the STCC region, pointed out by Ni et al. (2021), is stronger in winter than in summer. Therefore, the eddies generated by the wind stress curl are more normal eddies, while the abnormal eddies occur more in summer when the wind stress curl is weak. Of course, there are other mechanisms for eddy generation in the STCC region (such as flow instability and the interaction between flow field and topography), but this is beyond the scope of this paper, and we will further discuss it in future studies. In addition, CCEs are generally slightly more than AWEs, which is consistent with the result of Tang et al. (2019).

At 1,000 m, the multi-year monthly average number of CCEs, AWEs, CWEs, and ACEs are 1,192.38 ± 163.66, 1,133.62 ± 146.50, 28.50 ± 19.46 and 39.46 ± 21.14, respectively. Their maximum values all appear in December, with corresponding values of 1,272.40 ± 378.98, 1,202.10 ± 337.32, 38.80 ± 46.08, and 52.40 ± 50.52. Accordingly, the minimum is in February (1,061.40 ± 63.11), February (1,009.40 ± 73.01), April (21.60 ± 11.54), and February (31.60 ± 15.58). Comparing Figures 1C, D with Figures 1A, B, it can be concluded that eddy numbers at 1,000 m do not vary with seasons.

Whether at the sea surface or 1,000 m, the number of CCEs is generally higher than that of AWEs, while the number of ACEs is generally higher than that of CWEs, and the number of normal eddies is greater than that of abnormal eddies. Hence, the multi-year monthly average eddy number has an apparent seasonal variation at the sea surface, but there is no seasonal variation in the eddy numbers at 1,000 m.

3.2. Eddy radius

Figure 2 shows the monthly distribution of the four types of mesoscale eddies radii at the sea surface (Figures 2A, B) and 1,000 m (Figures 2C, D). At the sea surface, the multi-year average monthly radii of CCEs, AWEs, CWEs, and ACEs are 79.19 ± 2.95, 83.28 ± 3.47, 73.23 ± 4.45, and 79.37 ± 3.48 km, respectively. The maximum monthly average radii of the four eddy types occur in February, January, June, and July, and their corresponding values are 81.29 ± 1.85, 85.07 ± 3.97, 76.60 ± 3.68, and 81.48 ± 3.20 km. Accordingly, the minimum values appear in June (77.13 ± 3.46 km), June (81.45 ± 2.45 km), December (70.84 ± 2.06 km), and December (77.65 ± 4.58 km). That is, the maximum of the multi-year monthly average radius of the normal eddies (CCEs and AWEs) appears in winter (February, January), and the minimum appears in summer (June, July). However, the opposite is observed in abnormal eddies. Besides, there is no apparent difference between the multi-year monthly average radii of the four eddy types, which are all about 80 km.

FIGURE 2

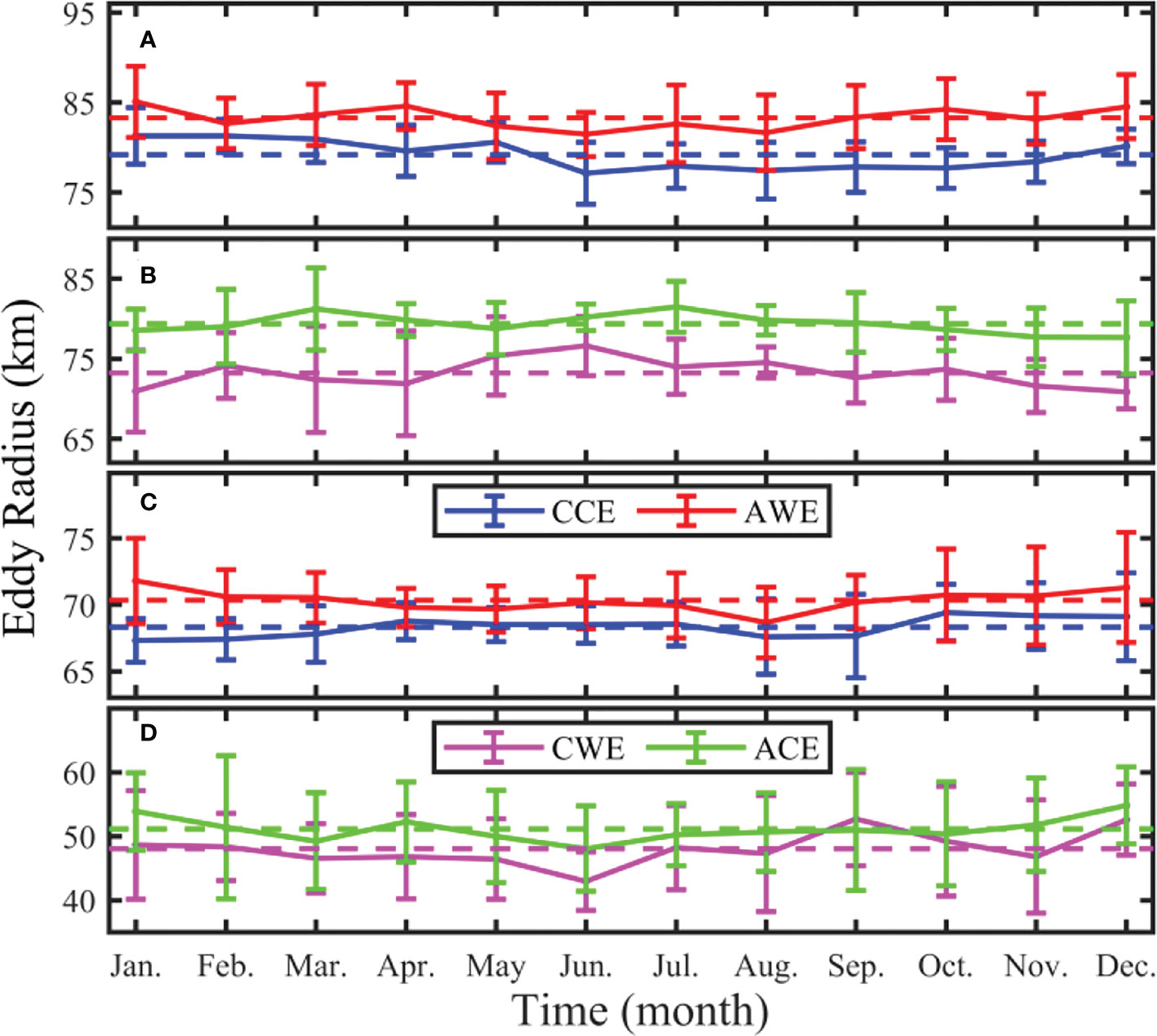
Figure 2 Monthly distribution of multi-year (2008 ~ 2017) average eddy radius at the sea surface (A, B) and 1,000 m (C, D) in the STCC area. Blue, red, pink, and green curves represent cyclonic cold-core eddy, anticyclonic warm-core eddy, cyclonic warm-core eddy, and anticyclonic cold-core eddy, respectively. The bar represents the standard deviation, and the dotted line represents the multi-year average value.

At 1,000 m, the multi-year monthly average radii of the four eddy types are 68.32 ± 2.20, 70.34 ± 2.68, 48.06 ± 7.17, and 51.14 ± 7.28 km. The maximum multi-year monthly average radii occur in October, January, September, and December, with corresponding values of 69.43 ± 2.12, 71.79 ± 3.21, 52.69 ± 7.30, and 54.81 ± 6.01 km. Accordingly, the minimum value is in January, August, June, and June, and their corresponding values are 67.31 ± 1.64, 68.67 ± 2.67, 43.00 ± 4.58, and 48.07 ± 6.67 km, respectively.

In Figure 2, the radius of the four types of eddies has no obvious variation with the month, either at the surface or at 1,000 m. This characteristic is consistent with the result of Tang et al. (2019), based on AVISO data in the STCC area. At the sea surface and 1,000 m, the average radius of AEs (ACEs and AWEs) is slightly larger than that of CEs (CWEs and CCEs), except in September (Figure 2D). By comparing Figures 2A, B with Figures 2C, D, the eddy radius at the sea surface is larger than that at 1,000 m.

3.3. Eddy rotation velocity

Eddy rotation velocity embodies its ability to encircle its internal seawater and is an important influencing factor of eddy nonlinearity. In this study, the eddy rotation velocity is defined as the average value of the flow velocity within the eddy ($U_R=\frac{1}{N}{\displaystyle \sum _{i=1}^N\sqrt{{U^{\prime }}_i^2+{V^{\prime }}_i^2}}$), where N represents the total number of grid point within the eddy. At the sea surface, the monthly distribution of the multi-year average rotation velocity of the four types of eddies shows large values in summer and small values in winter (Figures 3A, B). Their average values are 10.59 ± 1.05, 10.53 ± 1.36, 8.93 ± 1.50, 8.96 ± 1.13 cm/s, respectively. It can be seen that the normal eddy’s rotation velocity is greater than that of the abnormal eddy. The maximum eddy rotation velocity of the four types of eddies occurs in June, June, May, June, and their corresponding values are 11.71 ± 0.75, 12.24 ± 0.86, 10.63 ± 0.99, and 9.97 ± 0.91 cm/s, respectively. Accordingly, the minimum rotation velocity is 9.47 ± 0.65, 9.02 ± 0.73, 7.44 ± 0.83, and 7.84 ± 0.71 cm/s, appearing in December, December, November, and December, respectively. At the sea surface, the eddy rotation velocity in summer is significantly higher than in winter. The normal eddy rotation velocity is faster than that of the abnormal eddy.

FIGURE 3

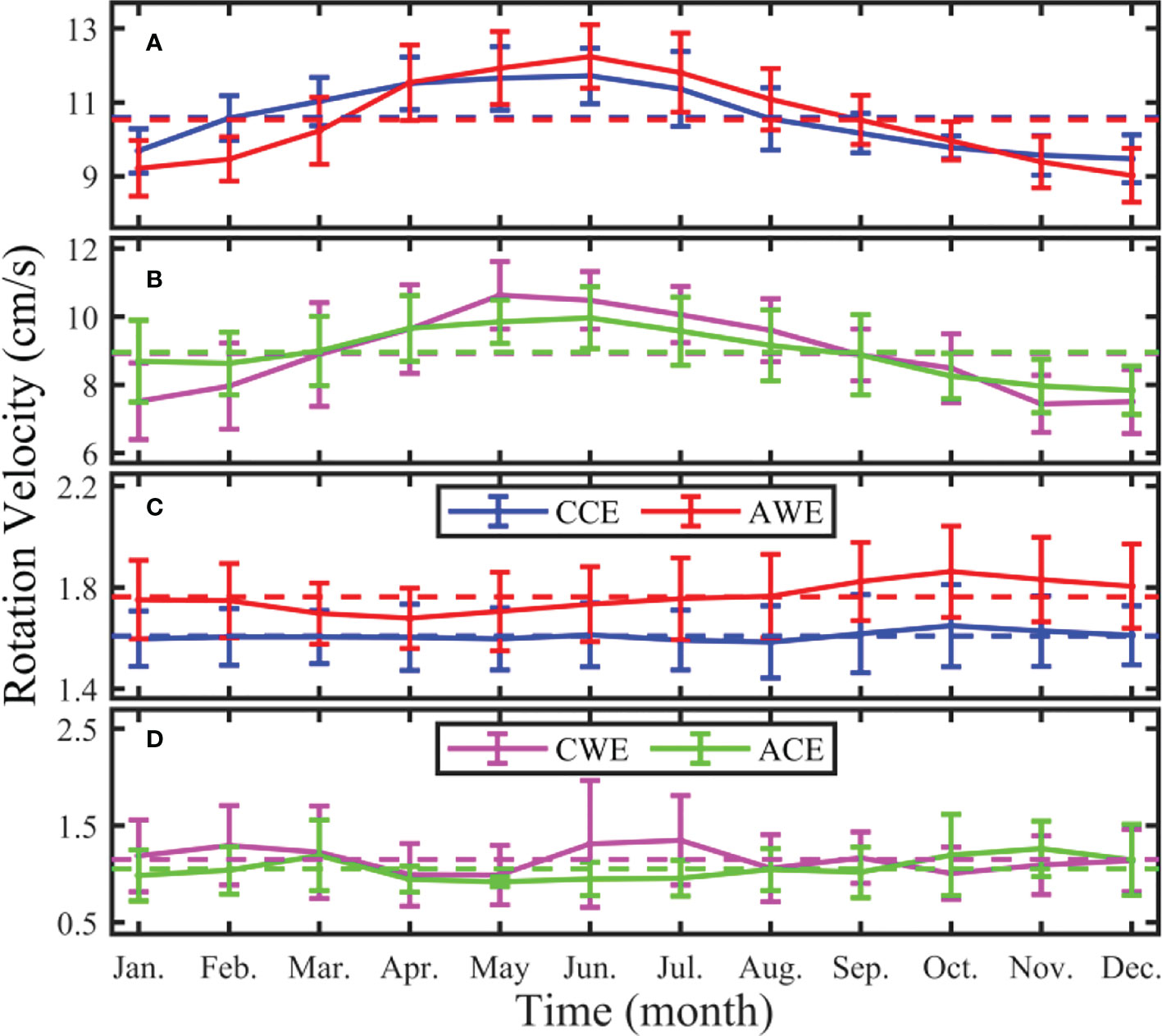
Figure 3 Monthly distribution of multi-year (2008 ~ 2017) average eddy rotation velocity at the sea surface (A, B) and 1,000 m (C, D) in the STCC area. Blue, red, pink, and green curves represent cyclonic cold-core eddy, anticyclonic warm-core eddy, cyclonic warm-core eddy, and anticyclonic cold-core eddy, respectively. The bar line represents the standard deviation, and the dotted line represents the multi-year average value.

In contrast, at 1,000 m, the multi-year monthly average rotation velocity of the four types of eddies slightly varies with time (Figures 3C, D). The rotation velocity of the four eddy types is 1.61 ± 0.12, 1.76 ± 0.16, 1.15 ± 0.39, and 1.06 ± 0.28 cm/s, respectively. Their maximum values appear in October (1.65 ± 0.64 cm/s), October (1.86 ± 0.56 cm/s), July (1.35 ± 1.59 cm/s), and November (1.26 ± 1.11 cm/s), respectively. Accordingly, it reaches its minimum in August, April, May, and May, with 1.59 ± 0.47, 1.68 ± 0.51, 0.99 ± 1.50, and 0.92 ± 1.25 cm/s. The eddy rotation velocity at the sea surface is larger by about 4 ~ 5 times than that at 1,000 m. The average rotation velocity of normal eddies is larger than that of abnormal eddies at both the surface and 1,000 m.

3.4. Eddy horizontal movement velocity

Eddy horizontal moving velocity is another crucial factor determining its heat and freshwater transport capacity. The horizontal moving velocity ($U_H=\frac{L}{\Delta t}$) is defined as the ratio of the eddy center moving distance $(L=\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2})$ to the temporal resolution of the OFES data Δt , where (x₁,y₁) and (x₂,y₂) represent the spatial position of the eddy center at two adjacent time steps. From Figure 4, the eddy horizontal moving velocity at the sea surface and 1,000 m show no noticeable seasonal variations. The eddy horizontal moving velocity at the sea surface is about 1.7 ~ 2.0 times at 1,000 m.

FIGURE 4

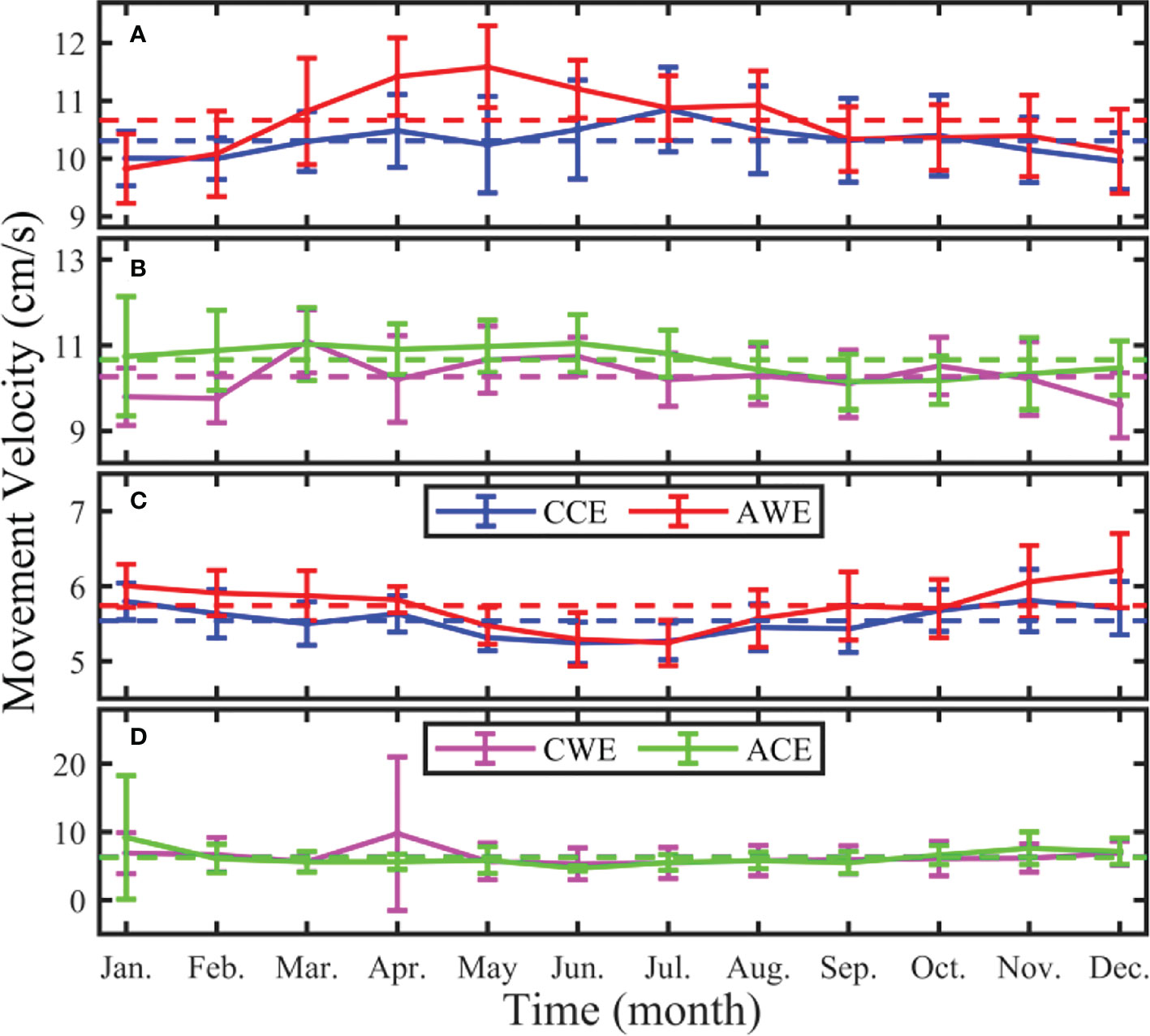
Figure 4 Monthly distribution of multi-year (2008 ~ 2017) average eddy horizontal moving velocity at the sea surface (A, B) and 1,000 m (C, D) in the STCC area. Blue, red, pink, and green curves represent cyclonic cold-core eddy, anticyclonic warm-core eddy, cyclonic warm-core eddy, and anticyclonic cold-core eddy, respectively. The bar line represents the standard deviation, and the dotted line represents the multi-year average value.

At the sea surface, the multi-year monthly average horizontal moving velocities of the four eddy types are 10.31 ± 0.67, 10.66 ± 0.83, 10.27 ± 0.81, and 10.66 ± 0.81 cm/s, respectively. The maximum horizontal moving velocity appears in July, May, March, and June, and their corresponding values are 10.85 ± 0.73, 11.59 ± 0.71, 11.09 ± 0.74, and 11.04 ± 0.67 cm/s. The minimum values are reached in December, January, December, and September, and the corresponding values are 9.96 ± 0.49, 9.82 ± 0.60, 9.60 ± 0.76, 10.15 ± 0.65 cm/s, respectively.

The eddy horizontal moving velocity (average, maximum or minimum) at 1,000 m is about half of that at the sea surface. Accordingly, at 1,000 m, the average horizontal moving velocity of four types of eddies are 5.54 ± 0.34, 5.74 ± 0.45, 6.36 ± 3.92, and 6.28 ± 3.12 cm/s, respectively. The maximum moving velocities appear in November, December, April, and January, and their corresponding values are 5.81 ± 0.41, 6.21 ± 0.49, 9.75 ± 11.28, and 9.19 ± 9.08 cm/s. The minimum values appear in June, July, June, and June with 5.25 ± 0.28, 5.25 ± 0.30, 5.33 ± 2.32, and 4.70 ± 0.40 cm/s, respectively.

3.5. Eddy nonlinearity

Following Chelton et al. (2011) and Part I, the eddy nonlinearity is defined as $R_{NL}=\frac{U_R}{U_H}$, where U_R and U_H are the eddy rotation velocity and the horizontal moving velocity, respectively. When the eddy nonlinearity is greater than 1.0, an eddy can entrap material and transport them horizontally. Figure 3 illustrates that the eddy rotation velocity at the sea surface is large in summer and autumn, and small in winter and spring. There are discernable seasonal variations at 1,000 m. Correspondingly, Figure 4 shows that the eddy horizontal moving velocity does not vary with seasons at the sea surface and 1,000 m. The eddy nonlinearity shown in Figure 5 at the sea surface is large in summer and autumn, and small in winter and spring, indicating that the eddy rotation velocity plays a dominant role in the seasonal variation of the eddy nonlinearity.

FIGURE 5

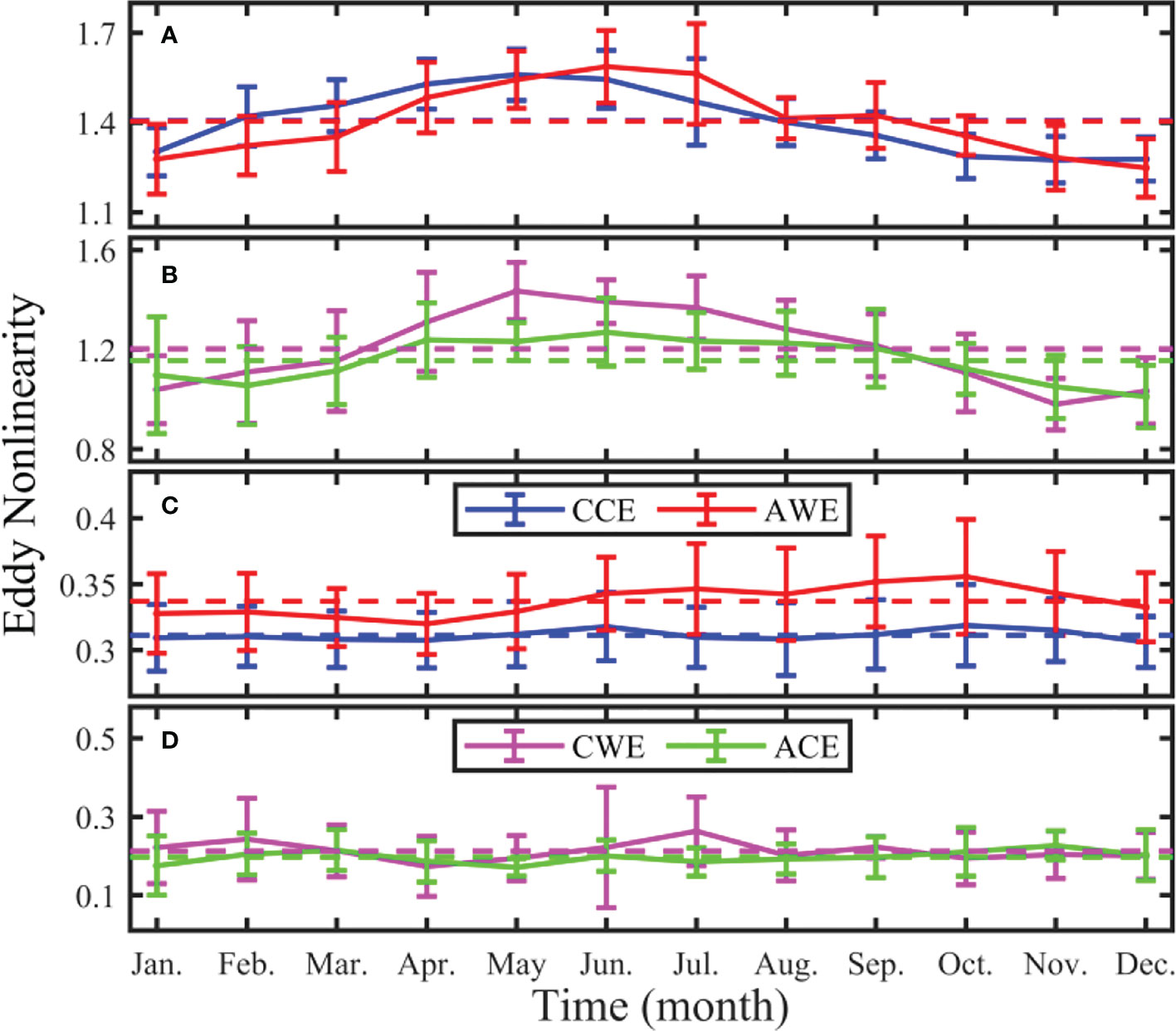
Figure 5 Monthly distribution of multi-year (2008 ~ 2017) average eddy nonlinearity at the sea surface (A, B) and 1,000 m (C, D) in the STCC area. Blue, red, pink, and green curves represent cyclonic cold-core eddy, anticyclonic warm-core eddy, cyclonic warm-core eddy, and anticyclonic cold-core eddy, respectively. The bar line represents the standard deviation, and the dotted line represents the multi-year average value.

At the sea surface layer, the average nonlinearity of CCEs, AWEs, CWEs, and ACEs are 1.41 ± 0.13, 1.40 ± 0.15, 1.20 ± 0.20, and 1.16 ± 0.16, respectively. Except for CWEs, eddy nonlinearity in November is slightly less than 1.0, while in other months, they are all greater than 1.0 (Figures 5A, B). The nonlinearity of the four eddy types reaches the maximum value in May, June, May, and June, and the corresponding values are 1.56 ± 0.09, 1.59 ± 0.12, 1.44 ± 0.127 ± 0.14, and 1.27 ± 0.14, respectively. Accordingly, it reaches the minimum in November, December, November, and December, and the corresponding values are 1.28 ± 0.08, 1.25 ± 0.10, 0.98 ± 0.10, and 1.01 ± 0.13, respectively. In a word, the eddy nonlinearity is maximum in summer and minimum in winter.

Accordingly, there is no seasonal variation in eddy nonlinearity at 1,000 m. The variation of eddy nonlinearity is small, ranging from 0.17 to 0.36 (Figures 5C, D). The average nonlinearity of the four types of eddies is 0.31 ± 0.02, 0.34 ± 0.03, 0.21 ± 0.08, 0.20 ± 0.05, which is far less than 1.0. At 1,000 m, the nonlinearity of the four types of eddies reaches the maximum in October, October, July, and November, respectively, and the corresponding values are 0.32 ± 0.13, 0.36 ± 0.13, 0.26 ± 0.13, and 0.23 ± 0.13. Accordingly, the eddy nonlinearity reaches its minimum in December, April, April, and May, with 0.31 ± 0.13, 0.32 ± 0.13, 0.17 ± 0.13, and 0.17 ± 0.13, respectively. The eddy nonlinearity at the sea surface is about 4 ~ 5 times greater than that at 1,000 m. It can be inferred that the eddy-induced heat and freshwater transports are mainly concentrated in the oceanic upper layer.

3.6. Eddy amplitude

Following Part I, the sea surface height abnormal (SSHA) data is obtained by using a high-pass filter on the OFES data. Then the absolute of the extreme SSHA value within the eddy (the minimum value for CEs and the maximum value for AEs) is taken as the eddy amplitude. Figures 6A, B show the multi-year monthly average eddy amplitude distribution for normal and abnormal eddies, respectively. The amplitude of four types of eddies are 3.73 ± 0.35, 3.62 ± 0.33, 3.33 ± 0.57, and 3.30 ± 0.42 cm, respectively. The amplitude of the CCEs is larger than that of AWEs from February to July, and is smaller in other months (Figure 6A).

FIGURE 6

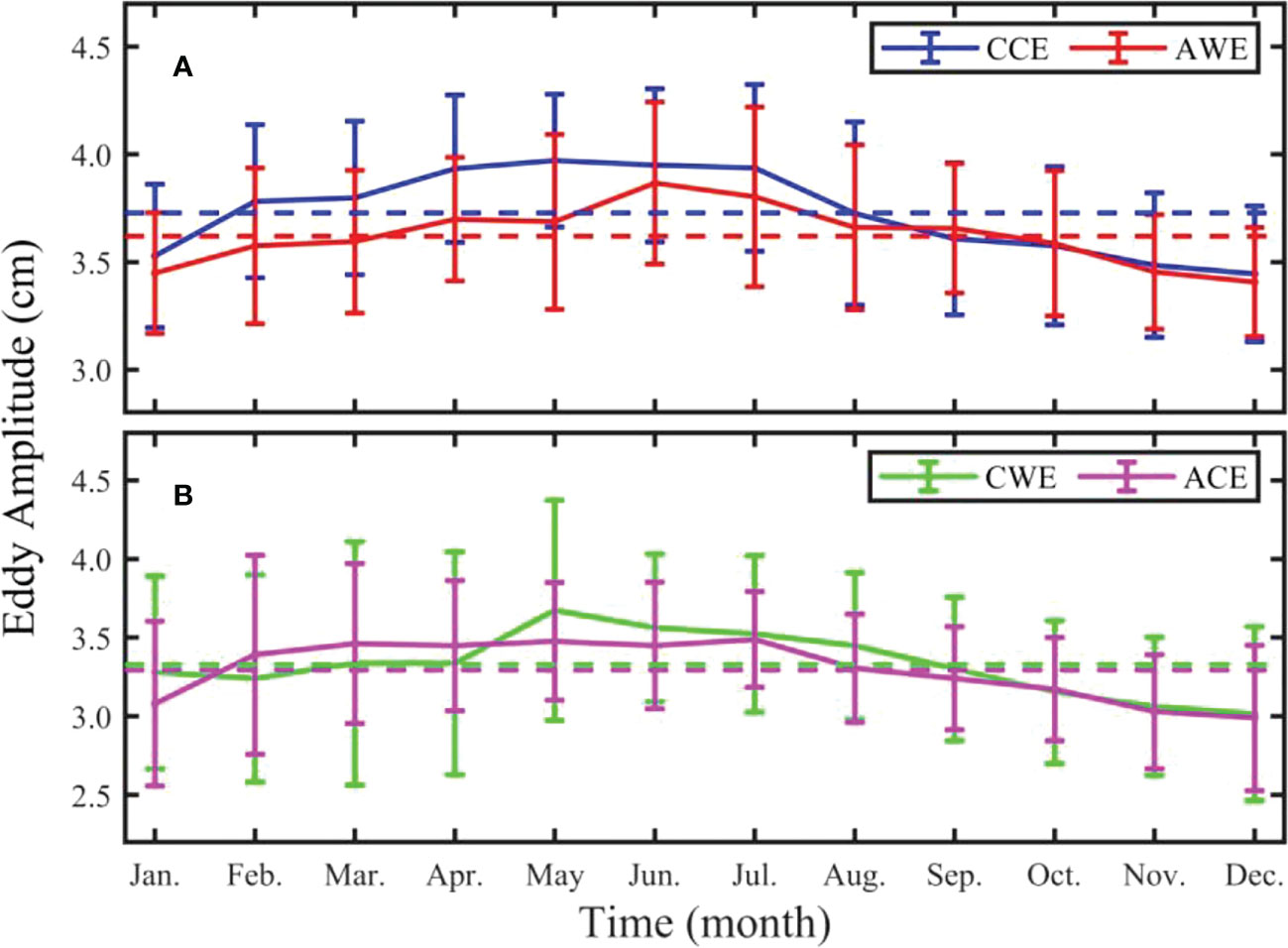
Figure 6 Monthly distribution of multi-year (2008 ~ 2017) average eddy amplitude at the sea surface (A, B) in the STCC area. Blue, red, pink, and green curves represent cyclonic cold-core eddy, anticyclonic warm-core eddy, cyclonic warm-core eddy, and anticyclonic cold-core eddy, respectively. The vertical line represents the standard deviation, and the dotted line represents the multi-year average value.

For abnormal eddies, the amplitude of CWEs is very close to that of ACEs except in May and June (Figure 6B). The maximum amplitude of the four types of eddies appear in May, June, May, and July, respectively, and the corresponding values are 3.97 ± 0.31, 3.87 ± 0.38, 3.67 ± 0.70, 3.49 ± 0.30 cm. The minimum amplitude all appear in December, and their corresponding values are 3.45 ± 0.25, 3.41 ± 0.31, 3.02 ± 0.55, and 2.99 ± 0.46 cm, respectively. By comparing Figures 6A, B, the amplitude of normal and abnormal eddies has the same change trend, but the size of the former is larger than that of the latter.

3.7. Eddy eccentricity

Using the same definition as in Part I, eddy eccentricity, which represents the flatness of the eddy shape, is obtained by fitting the eddy boundary. At the sea surface, the average eccentricity of four types of eddies are 0.79 ± 0.02, 0.78 ± 0.02, 0.78 ± 0.04, and 0.76 ± 0.03 (Figure 7A). The maximum eccentricity appear in September (0.80 ± 0.02), July (0.79 ± 0.02), May (0.79 ± 0.03), and June (0.77 ± 0.03), respectively, and the minimum in April (0.78 ± 0.02), February (0.77 ± 0.02), January (0.76 ± 0.05), and March (0.74 ± 0.04).

FIGURE 7

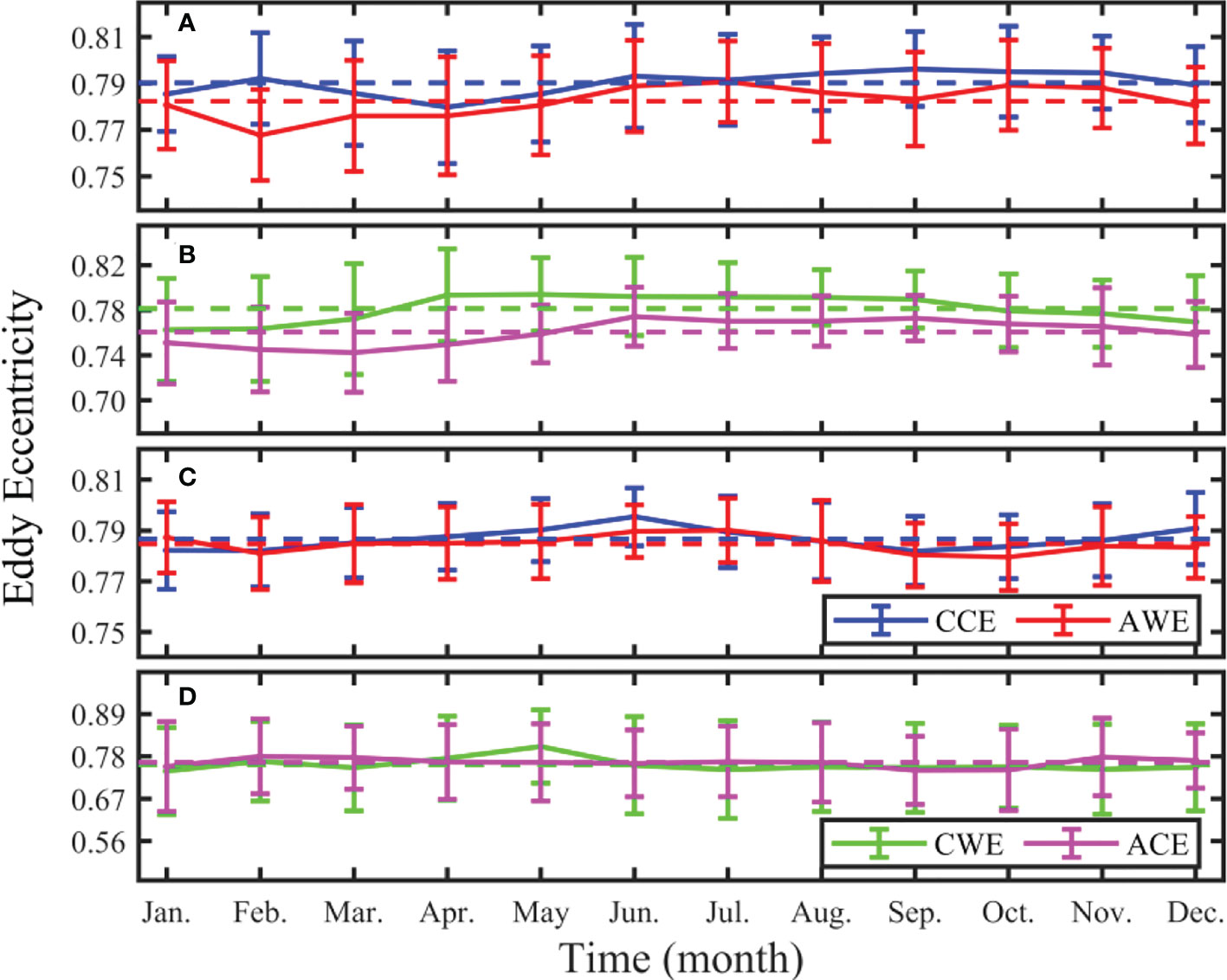
Figure 7 Monthly distribution of multi-year (2008 ~ 2017) average eddy eccentricity at the sea surface (A, B) and 1,000 m (C, D) in the STCC area. Blue, red, pink, and green curves represent cyclonic cold-core eddy, anticyclonic warm-core eddy, cyclonic warm-core eddy, and anticyclonic cold-core eddy, respectively. The vertical line represents the standard deviation, and the dotted line represents the multi-year average value.

At 1,000 m, the average eccentricity of the four types of eddy are 0.79 ± 0.01, 0.78 ± 0.01, 0.76 ± 0.11, and 0.76 ± 0.09, respectively (Figure 7B). The maximum eccentricity of the four eddy types appear in September (0.78 ± 0.01), October (0.78 ± 0.01), January (0.74 ± 0.11), and September (0.74 ± 0.09), respectively. Correspondingly, the minimum eccentricity appear in September (0.78 ± 0.01), October (0.78 ± 0.01), January (0.74 ± 0.11), and September (0.74 ± 0.09).

The eddy eccentricity of CEs (CWEs and CCEs) is greater than that of AEs (AWEs and ACEs) at the sea surface, indicating that the shape of AEs is more regular than that of CEs. The eccentricity of abnormal eddies at 1,000 m is larger than that at the sea surface. Besides, the eddy eccentricity of the normal eddies at 1,000 m is smaller than that at the sea surface. Similarly to that at the sea surface, the eddy eccentricity at 1,000 m shows no seasonal variation.

3.8. Eddy penetration depth

The eddy vertical penetration depth depends on the eddy’s energy and the stratification of ambient water. In the vertical direction, part of the eddy is normal in some layers and abnormal in other layers (Part I). Thus, the four eddy categories cannot be used when discussing the eddy penetration depth. Therefore, according to the rotation direction of the eddy flow field at the sea surface, only two types of eddies are considered: CEs and AEs.

The average penetration depth of CEs is 675.13 ± 67.50 m, with the maximum value in May (698.24 ± 55.79 m) and the minimum in July (635.86 ± 59.16 m, Figure 8A). The average penetration depth of AEs is 622.32 ± 81.85 m, with the maximum value in April (648.81 ± 67.24 m) and the minimum in August (595.25 ± 96.80 m). That is, the penetration depth of CEs is always deeper than that of AEs. There is no apparent seasonal variation in these two categories of eddies.

FIGURE 8

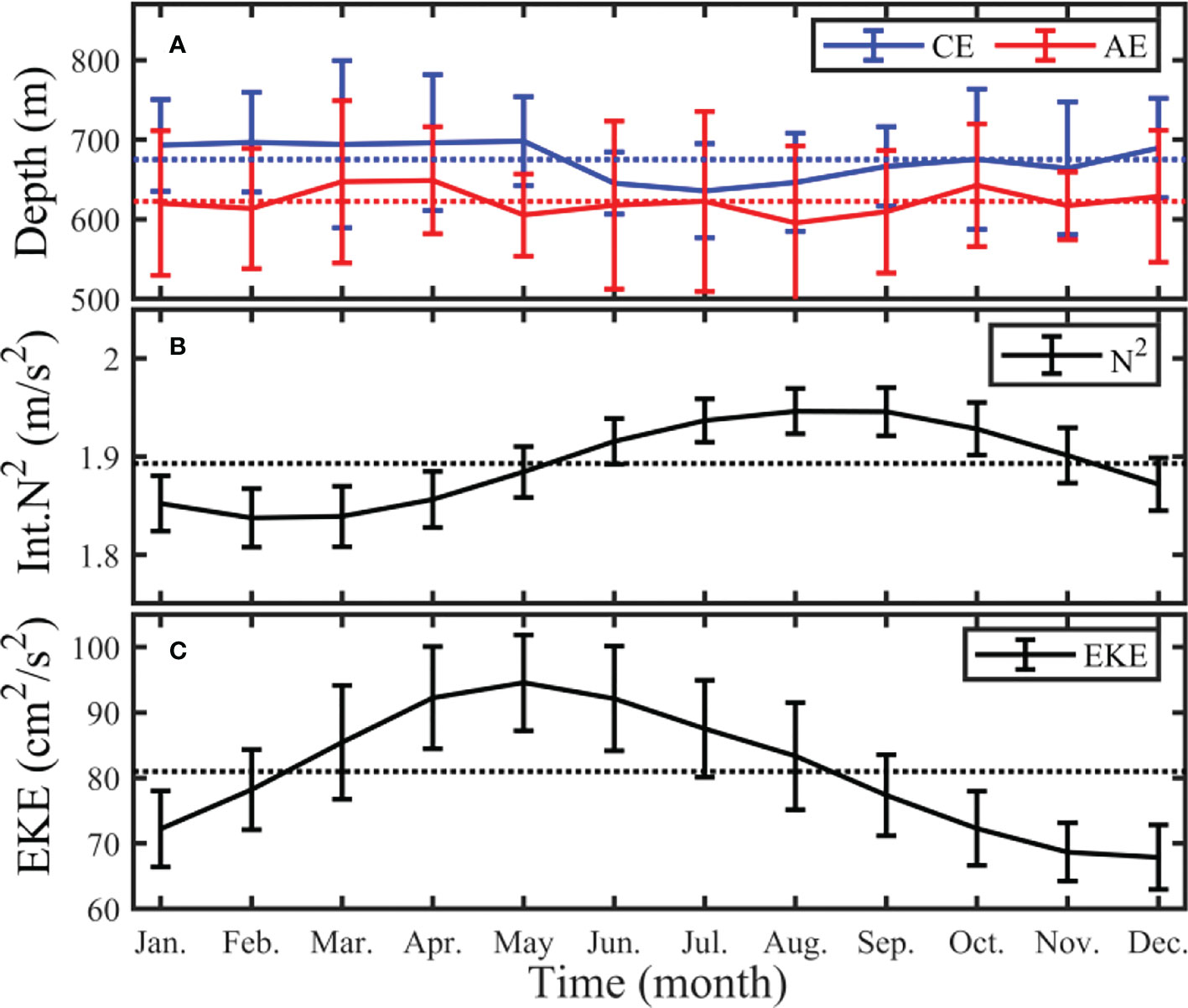
Figure 8 Monthly distribution of multi-year (2008 ~ 2017) average eddy penetration depths (A), integrated stratification (B), and eddy kinetic energy (C) in the STCC area. Blue and curves represent cyclonic eddy and anticyclonic eddy, respectively. The corresponding vertical lines on each curve represent the standard deviation, and the dotted line represents the multi-year average value.

Stratification is an important parameter to measure the vertical stability of seawater. Vertical penetration of eddy needs to overcome the blocking effect of stratification. In order to explain the monthly variation of eddy penetration depth, Figure 8B shows the monthly variation of the integrated stratification from 1,000 m to the sea surface. The integrated stratification over the upper 1,000 m has a seasonal pattern, greater in summer and autumn than in winter and spring. Its multi-year monthly average value is 1.89 ± 0.03 m/s², the maximum value appears in August (1.96 ± 0.02 m/s²), and the minimum value appears in February (1.84 ± 0.03 m/s²).

Correspondingly, the multi-year monthly average EKE is characterized by a high-value distribution in spring and summer, and low values in autumn and winter (Figure 8C), similar to the vertically-integrated stratification distribution. The multi-year monthly average EKE is 80.99 ± 0.02 cm²/s², the maximum value appears in May (94.55 ± 7.31 cm²/s²), and the minimum value appears in December (67.88 ± 4.95 cm²/s²). The integrated stratification and the EKE have a similar trend, and their combined effects show almost no seasonal variations in eddy penetration depth.

4. Discussion

4.1. Eddy anomaly ratio

During the lifespan of an eddy, some eddies can convert from one eddy type to another. At present, the known mechanisms for a normal eddy changing into an abnormal eddy include 1) at the eddy decay period, due to the instability of its structure, the radius of the normal eddy suddenly increases and wraps around the surrounding water to form an abnormal eddy; 2) through eddy-eddy interaction to form an abnormal eddy (Sun et al., 2019). Therefore, the ratio of the survival time of abnormal eddies to the overall eddy lifespan is an interesting topic. Figure 9 shows the statistical histogram (Figures 9A, C) and cumulative frequency distribution (Figures 9B, D) of the anomaly ratio γ₂ at the sea surface (Figures 9A, B) and 1,000 m (Figures 9C, D). The horizontal axis (γ₂ ) indicates the ratio of the abnormal eddy existence duration to that of the eddy lifespan. For example, suppose a CE has a lifespan of 60 days, including 12 and 15 discontinuous days as a CWE and the remaining 33 days as a CCE. In that case, the anomaly ratio is 0.2 and 0.25, respectively, located within the bins of 0.1 ~ 0.2 and 0.2 ~ 0.3 in Figure 9A. The vertical axis γ₁ (${\gamma }_1=\frac{N_1}{N_2}\times 100\%$) in Figures 9A, C means the percentage of the eddy numbers (N₁ ) in the corresponding section of the horizontal axis to the total eddy numbers (N₂ ) with the same polarity.

FIGURE 9

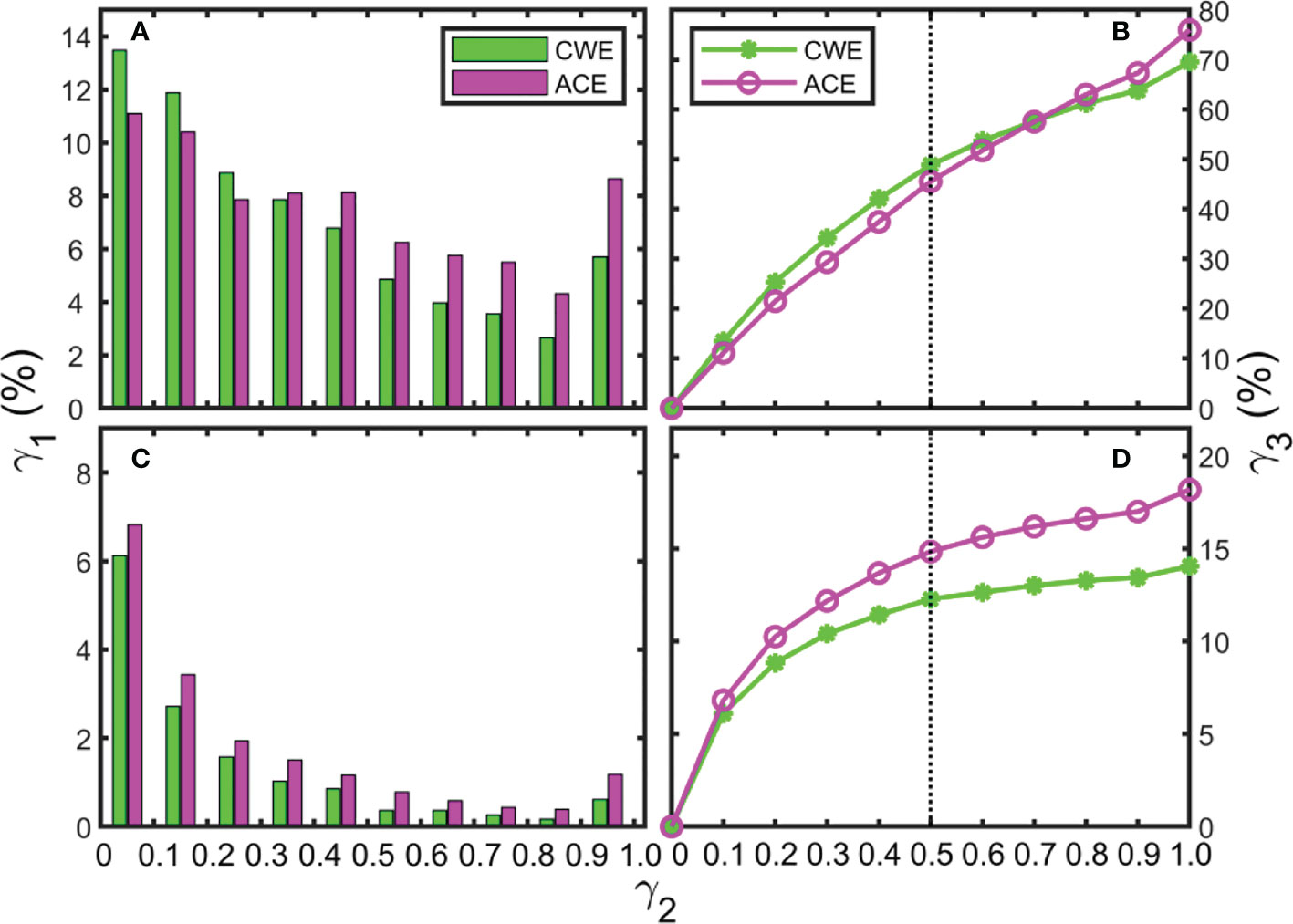
Figure 9 Statistical histogram of the anomaly ratio, which is the time length during which an eddy is abnormal to the overall eddy lifespan (A, C), and the corresponding cumulative frequency (B, D) at the sea surface layer (A, B) and 1,000 m (C, D) in the STCC area. Green and magenta indicate cyclonic cold-core eddy and anticyclonic warm-core eddy, respectively.

From Figure 9A, the number of CWEs decreases with the increase in anomaly ratio, except in the interval of 0.9 ~ 1.0. The highest ratio γ₁ of CWEs appears in the 0.0 ~ 0.1 bin, accounting for 13.47% of the total CEs. About 48.84% of the CWEs exist for less than half of the overall CEs lifespan (Figure 9B). Only 5.69% of CWEs have an anomaly ratio γ₂ that exceeds 90% of the CEs lifespan. Accordingly, the highest proportion of ACEs appears in the range of 0.0 ~ 0.1, reaching 11.09% of the total AEs. About 45.54% of the ACEs are less than half of the overall AEs lifespan. Only 8.64% of the AEs have an anomaly ratio γ₂ exceeding 90% of their lifespan.

From Figure 9B, the proportion of ACEs is always more than that of CWEs within the cumulative frequency of less than 0.7. In contrast, the proportion of CWEs within a cumulative frequency between 0.7 and 1.0 is more than that of ACEs. There are 1,393 (30.47%) CCEs and 1,099 (24.04%) AWEs, which are normal eddies throughout their lifespan (Figure 9B).

The abnormal eddies are mainly concentrated in the oceanic upper layer. The number of ACEs in each interval bin is more than that of CWEs at 1,000 m (Figure 9C). This result is more clearly shown in the cumulative frequency distribution in Figure 9D. At 1,000 m, the proportion of abnormal eddies is smaller than that at the sea surface, and the cumulative frequency of CWEs and ACEs are 14.06% and 18.19%, respectively. This feature is consistent with the results of Sun et al. (2021a) in the South China Sea.

4.2. Influence of different definitions of abnormal eddy

Abnormal eddies have several definitions. Sun et al. (2019) proposed a rigorous definition of an abnormal eddy. In addition to the conditions already used in this study, the anomalous temperature within an abnormal eddy is 0.1°C higher (for CWE) or lower (for ACE) than the surrounding background field temperature. This condition (set the temperature threshold as 0.1°C) can make the abnormal eddies more robust and eliminate some weak eddies. On the other hand, it leads to a significant reduction in abnormal eddy numbers. The research in the North Pacific Ocean pointed out that the proportion of abnormal eddies is about 10% (Sun et al., 2019), far less than the results pointed out by Ni et al. (2021), which accounted for about 20%, and that of Liu et al. (2021), which accounted for about 1/3.

Figure 10 shows the multi-year monthly average eddy number distribution under the temperature thresholds of 0.025 (solid line) and 0.05°C (dotted line). It can be seen that when the temperature threshold is set to 0.025°C (0.05°C), the number of CCEs is less in summer and autumn, and more in winter and spring. Accordingly, the multi-year monthly average CCEs is 522.39 ± 48.84 (419.06 ± 46.57), the maximum value is 684.70 ± 47.25 (591.30 ± 55.64), which appears in December (January), and the minimum value is 406.50 ± 45.92 (279.10 ± 35.90) appearing in July (July). AWEs are less in summer and autumn, and more in winter and spring. The average number of AWEs is 454.59 ± 51.26 (355.56 ± 48.85), the maximum number is 625.40 ± 80.10 (556.60 ± 75.00), which appears in January (January), and the minimum number is 368.20 ± 45.67 (240.10 ± 53.41) appearing in July (September).

FIGURE 10

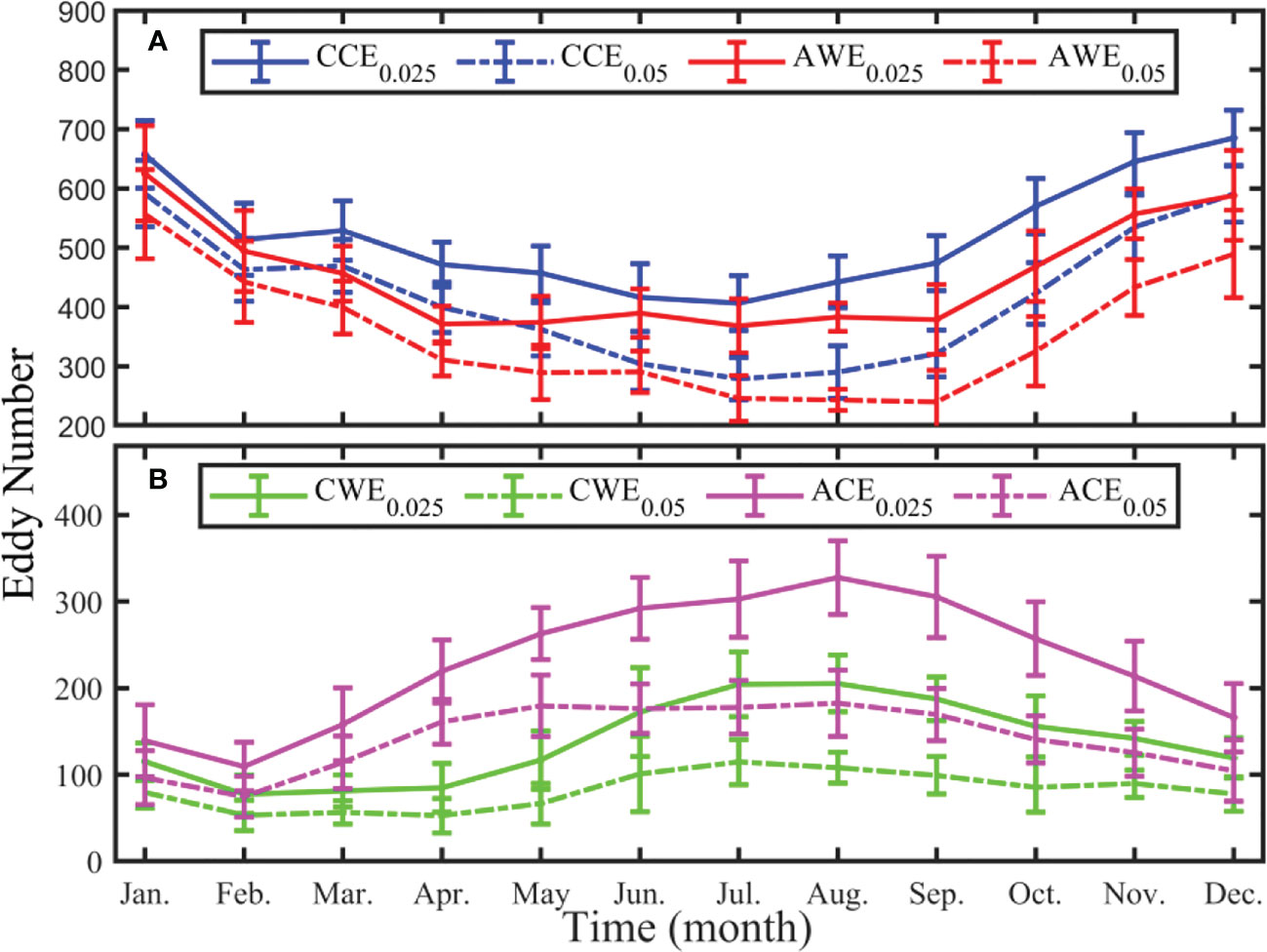
Figure 10 Monthly distribution of multi-year (2008 ~ 2017) average eddy number under different temperature threshold conditions (0.025 and 0.05°C) in the STCC area. (A) Cyclonic cold-core and anticyclonic warm-core eddy, and (B) cyclonic warm-core and anticyclonic cold-core eddy.

The average number of CWEs is 138.48 ± 29.02 (81.97 ± 22.14), the maximum is 205.40 ± 32.89 (114.60 ± 26.00) in August (July), and the minimum is 77.30 ± 22.21 (52.60 ± 19.93), which occurs in February (April) (Figure 10B). ACEs are more in summer and autumn, and less in winter and spring. The average number of ACEs is 229.47 ± 39.14 (141.95 ± 30.34), the maximum value is 327.60 ± 42.69 (182.70 ± 38.34), which appears in August (August), the minimum value is 109.50 ± 27.98 (74.70 ± 23.60), appears in February (February) (Figure 10B). From Figure 10, when the temperature threshold increases from 0.025 to 0.05°C, the number of eddies shows a decreasing trend, but the variation trend of the eddy number does not change.

The seasonal variation of normal and abnormal eddies presents opposite trends, consistent with the results in the main text. Under different temperature thresholds, the monthly average number of CCEs is always more than that of AWEs, while the CWE is always less than that of ACE. In order to verify the reliability of the results, we also use temperature thresholds of 0.075 and 0.1°C (Figures not shown). As the temperature threshold value increases, the number of the four types of eddies further decreases, but the seasonal variation trend remains unchanged.

5. Conclusions

Previous studies pointed out that the STCC area has abundant mesoscale eddy activities (Liu et al., 2012; Tang et al., 2019). Based on the OFES data and vector geometry automatic detection method, the seasonal variation of various characteristics for four types of mesoscale eddies is studied in detail. Following Part I, according to the rotation direction of the eddy flow field and the sign of anomalous temperature within the eddy, they can be divided into four categories: CCE, AWE, CWE, and ACE. We draw the following conclusions from this study:

1) At the sea surface, there are significant seasonal variations for four types of eddies number, rotation velocity, nonlinearity, and amplitude. Specifically, the normal eddies in winter and spring are more than in summer and autumn, while the abnormal eddies show the opposite distribution. The rotation velocity of the four types of eddies is faster in summer and autumn than in winter and spring, making the nonlinearity of eddies in summer and autumn stronger than in winter and spring. The amplitude of the four types of eddies is strong in summer and autumn, weak in winter and spring, and the amplitude of the normal eddy is larger than that of the abnormal eddy.

2) There is no significant seasonal difference in eddy radius, horizontal velocity, eccentricity, and vertical penetration depth of the four types of eddies at the sea surface.

3) At 1,000 m, there is no seasonal variation in each characteristic of the four types of eddies.

4) It is a common phenomenon that the abnormal eddy alternates between a normal and an abnormal eddy during its overall lifespan. Only 30.47% (24.04%) of cyclonic (anticyclonic) eddies belong to the normal eddy in the overall eddy lifespan.

5) Increasing the defined temperature threshold value of abnormal eddies can significantly reduce the eddy numbers but the seasonal trend of abnormal eddies does not change.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

WS, YL, MA, JSL and JL conceived and designed the experiments. WS, YL and MA performed the experiments. MA, JSL, and JL analyzed the data. WS, YL and MA drafted the original manuscript. WS, YL, JY, KL, WT, JJ and CD revised and edited the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This study was supported by the National Natural Science Foundation of China under contract Nos. 41906008, 42192562; the China Scholarship Council under contract No. 202008320195; the Open Fund of State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, MNR under contract No. QNHX2231; and the Innovation Group Project of Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai) under contract No. 311020004.

Acknowledgments

The OFES simulation was conducted on the Earth Simulator under the support of JAMSTEC. This data is downloaded from http://apdrc.soest.hawaii.edu/(Data doi: https://doi.org/10.17596/0002029). We thank the editor (Prof. Zhao Hui) and two reviewers for their constructive comments and helpful suggestions on an earlier manuscript version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aguiar A. C. B., Peliz Á., Carton X. (2013). A census of meddies in a long-term high-resolution simulation. Prog. Oceanogr. 116 (9), 80–94. doi: 10.1016/j.pocean.2013.06.016

CrossRef Full Text | Google Scholar

Amores A., Melnichenko O., Maximenko N. (2016). Coherent mesoscale eddies in the north Atlantic subtropical gyre: 3D structure and transport with application to the salinity maximum. J. Geophys. Res. 122, 23–41. doi: 10.1002/2016JC012256

CrossRef Full Text | Google Scholar

An M., Liu J., Liu J., Sun W., Yang J., Tan W., et al. (2022). Comparative analysis of four types of mesoscale eddies in the north pacific subtropical countercurrent region – part I spatial characteristics. Front. Mar. Sci. 9. doi: 10.3389/fmars.2022.1004300

PubMed Abstract | CrossRef Full Text | Google Scholar

Chaigneau A., Gizolme A., Grados C. (2008). Mesoscale eddies off Peru in altimeter records: Identification algorithms and eddy spatio-temporal patterns. Prog. Oceanogr. 79 (2), 106–119. doi: 10.1016/j.pocean.2008.10.013

CrossRef Full Text | Google Scholar

Chelton D. B., Schlax M. G., Samelson R. M. (2011). Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 91 (2), 167–216. doi: 10.1016/j.pocean.2011.01.002

CrossRef Full Text | Google Scholar

Chelton D. B., Schlax M. G., Samelson R. M., De Szoeke R. A. (2007). Global observations of large oceanic eddies. Geophys. Res. Lett. 34 (L15606), 87–101. doi: 10.1029/2007GL030812

CrossRef Full Text | Google Scholar

Chen G., Gan J., Xie Q., Chu X., Wang D., Hou Y. (2012). Eddy heat and salt transports in the south China Sea and their seasonal modulations. J. Geophys. Res. 117 (C05021), 78–91. doi: 10.1029/2011JC007724

CrossRef Full Text | Google Scholar

Chen G., Han G. (2019). Contrasting short-lived with long-lived mesoscale eddies in the global ocean. J. Geophys. Res. 124 (5), 3149–3167. doi: 10.1029/2019JC014983

CrossRef Full Text | Google Scholar

Dai J., Wang H., Zhang W., An Y., Zhang R. (2020). Observed spatiotemporal variation of three-dimensional structure and heat/salt transport of anticyclonic mesoscale eddy in Northwest pacific. J. Oceanol. Limnol. 38 (6), 1654–1675. doi: 10.1007/s00343-019-9148-z

CrossRef Full Text | Google Scholar

Ding R., Xuan J., Zhang T., Zhou L., Zhou F., Meng Q., et al. (2021a). Eddy-induced heat transport in the south China Sea. J. Phys. Oceanogr. 51, 2327–2348. doi: 10.1175/JPO-D-20-0206.1

CrossRef Full Text | Google Scholar

Ding Y., Xu L., Zhang Y. (2021b). Impact of anticyclonic eddies under stormy weather on the mixed layer variability in april south of the kuroshio extension. J. Geophys. Res. 126, e2020JC016739. doi: 10.1029/2020JC016739

CrossRef Full Text | Google Scholar

Doglioli A. M., Blanke B., Speich S., Lapeyre G. (2007). Tracking coherent structures in a regional ocean model with wavelet analysis: Application to cape basin eddies. J. Geophys. Res. 112, C5043. doi: 10.1029/2006JC003952

CrossRef Full Text | Google Scholar

Dong C., Lin X., Liu Y., Nencioli F., Chao Y., Guan Y., et al. (2012). Three-dimensional oceanic eddy analysis in the southern California bight from a numerical product. J. Geophys. Res. 117, C00H14, 92–99. doi: 10.1029/2011JC007354

CrossRef Full Text | Google Scholar

Dong C., Liu L., Nencioli F., Bethel B. J., Liu Y., Xu G., et al. (2022). The near-global ocean mesoscale eddy atmospheric-oceanic-biological interaction observational dataset. Sci. Data. 9 (1). doi: 10.1038/s41597-022-01550-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Dong C., Mcwilliams J. C., Liu Y., Chen D. (2014). Global heat and salt transports by eddy movement. Nat. Commun. 5 (2), 1–6. doi: 10.1038/ncomms4294

CrossRef Full Text | Google Scholar

Dong D., Peter B., Chang P., Florian S., Yang X., Yan J., et al. (2017). Mesoscale eddies in the northwestern pacific ocean: Three-dimensional eddy structures and heat/salt transports. J. Geophys. Res. 122, 9795–9813. doi: 10.1002/2017JC013303

CrossRef Full Text | Google Scholar

Dong C., Timothy M., Francesco N., Jiang S., Yusuke U., Mcwilliams J. C., et al. (2009). An oceanic cyclonic eddy on the lee side of Lanai island, Hawaii. J. Geophys. Res. 114, C10008. doi: 10.1029/2009JC005346

CrossRef Full Text | Google Scholar

Gaube P., Chelton D. B., Samelson R. M., Schlax M. G., O Neill L. W. (2015). Satellite observations of mesoscale eddy-induced ekman pumping. J. Phys. Oceanogr. 45 (1), 104–132. doi: 10.1175/JPO-D-14-0032.1

CrossRef Full Text | Google Scholar

Gaube P., Chelton D. B., Strutton P. G., Behrenfeld M. J. (2013). Satellite observations of chlorophyll, phytoplankton biomass, and ekman pumping in nonlinear mesoscale eddies. J. Geophys. Res. 118 (12), 6349–6370. doi: 10.1002/2013JC009027

CrossRef Full Text | Google Scholar

Gaube P., J. M. D., Moulin A. J. (2019). Mesoscale eddies modulate mixed layer depth globally. Geophys. Res. Lett. 46 (3), 1505–1512. doi: 10.1029/2018GL080006

CrossRef Full Text | Google Scholar

Geng B., Xiu P., Liu N., He X., Chai F. (2021). Biological response to the interaction of a mesoscale eddy and the river plume in the northern south China Sea. J. Geophys. Res. 126 (9), e2021J–e17244J. doi: 10.1029/2021JC017244

CrossRef Full Text | Google Scholar

He Q., Zhan H., Cai S., He Y., Huang G., Zhan W. (2018). A new assessment of mesoscale eddies in the south China Sea: Surface features, three-dimensional structures, and thermohaline transports. J. Geophys. Res. 123, 4906–4929. doi: 10.1029/2018JC014054

CrossRef Full Text | Google Scholar

He Q., Zhan H., Xu J., Cai S., Zhan W., Zhou L., et al. (2019). Eddy-induced chlorophyll anomalies in the western south China Sea. J. Geophys. Res. 124 (12), 9487–9506. doi: 10.1029/2019JC015371

CrossRef Full Text | Google Scholar

Itoh S., Yasuda I. (2010). Water mass structure of warm and cold anticyclonic eddies in the western boundary region of the subarctic north pacific. J. Phys. Oceanogr. 40 (12), 2624–2642. doi: 10.1175/2010JPO4475.1

CrossRef Full Text | Google Scholar

Ji J., Dong C., Zhang B., Liu Y. (2016). Oceanic eddy statistical comparison using multiple observational data in the kuroshio extension region. Acta Oceanol. Sin. 36 (3), 1–7. doi: 10.1007/s13131-016-0882-1

CrossRef Full Text | Google Scholar

Ji J., Dong C., Zhang B., Liu Y., Zou B., Gregory P. K., et al. (2018). An oceanic eddy characteristics and generation mechanisms in the kuroshio extension region. J. Geophys. Res. 123, 2018J–2123J. doi: 10.1029/2018JC014196

CrossRef Full Text | Google Scholar

Kang L., Wang F., Chen Y. L. (2010). Eddy generation and evolution in the north pacific subtropical countercurrent (NPSC) zone. Chin. J. Oceanology Limnol. 28 (5), 968–973. doi: 10.1007/s00343-010-9010-9

CrossRef Full Text | Google Scholar

Lin X., Dong C., Chen D., Liu Y., Yang J., Zou B., et al. (2015). Three-dimensional properties of mesoscale eddies in the south China Sea based on eddy-resolving model output. Deep Sea Res. 99, 46–64. doi: 10.1016/j.dsr.2015.01.007

CrossRef Full Text | Google Scholar

Lin X., Qiu Y., Sun D. (2019). Thermohaline structures and heat/freshwater transports of mesoscale eddies in the bay of Bengal observed by argo and satellite data. Remote Sens. 11 (24) 2989. doi: 10.3390/rs11242989

CrossRef Full Text | Google Scholar

Liu Y., Dong C., Guan Y., Chen D., Mcwilliams J., Nencioli F. (2012). Eddy analysis in the subtropical zonal band of the north pacific ocean. Deep Sea Res. 68 (5), 54–67. doi: 10.1016/j.dsr.2012.06.001

CrossRef Full Text | Google Scholar

Liu Y., Zheng Q., Li X. (2021). Characteristics of global ocean abnormal mesoscale eddies derived from the fusion of sea surface height and temperature data by deep learning. Geophys. Res. Lett. 48 (17), e2021GL094772. doi: 10.1029/2021GL094772

CrossRef Full Text | Google Scholar

Ma L., Wang Q. (2014). Mean properties of mesoscale eddies in the kuroshio recirculation region. Chin. J. Oceanol. Limn. 32 (3), 681–702. doi: 10.1007/s00343-014-3029-2

CrossRef Full Text | Google Scholar

Ma J., Xu H., Dong C., Lin P., Liu Y. (2015). Atmospheric responses to oceanic eddies in the kuroshio extension based on composite analyses. J. Geophys. Res. 120 (13), 6313–6330. doi: 10.1002/2014JD022930

CrossRef Full Text | Google Scholar

McGillicuddy D. J. Jr. (2016). Mechanisms of physical-biological-biogeochemical interaction at the oceanic mesoscale. Ann. Rev. Mar. Sci. 8 (1), 125. doi: 10.1146/annurev-marine-010814-015606

PubMed Abstract | CrossRef Full Text | Google Scholar

Meijers A. J., Bindoff N. L., Roberts J. L. (2007). On the total, mean, and eddy heat and freshwater transports in the southern hemisphere of a global ocean model. J. Phys. Oceanogr. 37 (2), 277–295. doi: 10.1175/JPO3012.1

CrossRef Full Text | Google Scholar

Nencioli F., Dong C., Dickey T., Washburn L., Mcwilliams J. C. (2010). A vector geometry-based eddy detection algorithm and its application to a high-resolution numerical model product and high-frequency radar surface velocities in the southern California bight. J. Atmos. Oceanic Technol. 27 (27), 564–579. doi: 10.1175/2009JTECHO725.1

CrossRef Full Text | Google Scholar

Ni Q., Zhai X., Jiang X., Chen D. (2021). Abundant cold anticyclonic eddies and warm cyclonic eddies in the global ocean. J. Phys. Oceanogr. 51 (9), 2793–2806. doi: 10.1175/JPO-D-21-0010.1

CrossRef Full Text | Google Scholar

Okubo A. (1970). Horizontal dispersion of floatable particles in the vicinity of velocity singularities such as convergences. Deep Sea Res. 17, 445–454. doi: 10.1016/0011-7471(70)90059-8

CrossRef Full Text | Google Scholar

Patel R. S., Llort J., Strutton P. G., Phillips H. E., Moreau S., Conde Pardo P., et al. (2020). The biogeochemical structure of southern ocean mesoscale eddies. J. Geophys. Res. 125 (8). doi: 10.1029/2020JC016115

CrossRef Full Text | Google Scholar

Pujol M. I., Faugère Y., Taburet G., Dupuy S., Pelloquin C., Ablain M., et al. (2016). DUACS DT2014: The new multi-mission altimeter dataset reprocessed over 20 years. Ocean Sci. Discuss. 6 (1), 1–48. doi: 10.5194/os-2015-110

CrossRef Full Text | Google Scholar

Qiu B. (1999). Seasonal eddy field modulation of the north pacific subtropical countercurrent: TOPEX/Poseidon observations and theory. J. Phys. Oceanogr. 29 (10), 2471–2486. doi: 10.1175/1520-0485(1999)029<2471:SEFMOT>2.0.CO;2

CrossRef Full Text | Google Scholar

Qiu B., Chen S. (2004). Eddy-induced heat transport in the subtropical north pacific from argo, TMI, and altimetry measurements. J. Phys. Oceanogr. 35 (4), 458–473. doi: 10.1175/JPO2696.1

CrossRef Full Text | Google Scholar

Qiu B., Chen S. (2010). Interannual variability of the north pacific subtropical countercurrent and its associated mesoscale eddy field. J. Phys. Oceanogr. 40, 213–225. doi: 10.1175/2009JPO4285.1

CrossRef Full Text | Google Scholar

Qiu B., Chen S., Klein P., Sasaki H., Sasai Y. (2014). Seasonal mesoscale and submesoscale eddy variability along the north pacific subtropical countercurrent. J. Phys. Oceanogr. 44 (12), 3079–3098. doi: 10.1175/JPO-D-14-0071.1

CrossRef Full Text | Google Scholar

Qiu C., Yi Z., Su D., Wu Z., Liu H., Lin P., et al. (2022). Cross-slope heat and salt transport induced by slope intrusion eddy’s horizontal asymmetry in the northern south China Sea. J. Geophys. Res. 127 (9). doi: 10.1029/2022JC018406

CrossRef Full Text | Google Scholar

Sadarjoen I. A., Post F. H. (2000). Detection, quantification, and tracking of vortices using streamline geometry. Comput. Graphics. 24 (3), 333–341. doi: 10.1016/S0097-8493(00)00029-7

CrossRef Full Text | Google Scholar

Sasaki H., Nonaka M., Masumoto Y., Sasai Y., Uehara H., Sakuma H. (2008). “An eddy-resolving hind cast simulation of the quasi-global ocean from 1950 to 2003 on the earth simulator,” in High resolution numerical modelling of the atmosphere and ocean. Eds. Hamilton K., Ohfuchi W. (New York: Springer), 157–185.

Google Scholar

Sun W., An M., Liu J., Liu J., Yang J., Tan W., et al. (2022). Comparative analysis of four types of mesoscale eddies in the kuroshio-oyashio extension region. Front. Mar. Sci. 9. doi: 10.3389/fmars.2022.984244

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun W., Dong C., Tan W., He Y. (2019). Statistical characteristics of cyclonic warm-core eddies and anticyclonic cold-core eddies in the north pacific based on remote sensing data. Remote Sens. 11 (2), 208. doi: 10.3390/rs11020208

CrossRef Full Text | Google Scholar

Sun W., Dong C., Tan W., Liu Y., He Y., Wang J. (2018). Vertical structure anomalies of oceanic eddies and eddy-induced transports in the south China Sea. Remote Sens. 10, 795. doi: 10.3390/rs10050795

CrossRef Full Text | Google Scholar

Sun W., Dong C., Wang R., Liu Y., Yu K. (2017). Vertical structure anomalies of oceanic eddies in the kuroshio extension region. J. Geophys. Res. 122 (2), 1476–1496. doi: 10.1002/2016JC012226

CrossRef Full Text | Google Scholar

Sun W., Liu Y., Chen G., Tan W., Lin X., Guan Y., et al. (2021a). Three-dimensional properties of mesoscale cyclonic warm-core and anticyclonic cold-core eddies in the south China Sea. Acta Oceanol. Sin. 40 (10), 17–29. doi: 10.1007/s13131-021-1770-x

CrossRef Full Text | Google Scholar

Sun W., Yang J., Tan W., Liu Y., Zhao B., He Y., et al. (2021b). Eddy diffusivity and coherent mesoscale eddy analysis in the southern ocean. Acta Oceanol. Sin. 40 (10), 1–16. doi: 10.1007/s13131-021-1881-4

CrossRef Full Text | Google Scholar

Taguchi B., Qiu B., Nonaka M., Sasaki H., Xie S., Schneider N. (2010). Decadal variability of the kuroshio extension: Mesoscale eddies and recirculations. Ocean Dynam. 60 (3), 673–691. doi: 10.1007/s10236-010-0295-1

CrossRef Full Text | Google Scholar

Tang B., Hou Y., Yin Y., Po H. (2019). Statistical characteristics of mesoscale eddies and the distribution in the north pacific subtropical countercurrent (in Chinese). Oceanol. Limnol. Sin. 50 (5), 937–947. doi: 10.11693/hyhz20190300050

CrossRef Full Text | Google Scholar

Treguier A. M., Lique C., Deshayes J., Molines J. M. (2017). The north Atlantic eddy heat transport and its relation with the vertical tilting of the gulf stream axis. J. Phys. Oceanogr. 47 (6), 1281–1289. doi: 10.1175/JPO-D-16-0172.1

CrossRef Full Text | Google Scholar

Wang X., Li W., Qi Y., Han G. (2012). Heat, salt and volume transports by eddies in the vicinity of the Luzon strait. Deep Sea Res. 61, 21–33. doi: 10.1016/j.dsr.2011.11.006

CrossRef Full Text | Google Scholar

Wang Z., Li Q., Sun L., Li S., Yang Y., Liu S. (2015). The most typical shape of oceanic mesoscale eddies from global satellite sea level observations. Front. Earth Sci. 9 (2), 202–208. doi: 10.1007/s11707-014-0478-z

CrossRef Full Text | Google Scholar

Wang Y., Zhang H., Chai F., Yuan Y. (2018). Impact of mesoscale eddies on chlorophyll variability off the coast of Chile. PloS One 13 (9), e203598. doi: 10.1371/journal.pone.0203598

CrossRef Full Text | Google Scholar

Wang Q., Zhang B., Zeng L., He Y., Wu Z., Chen J. (2022). Properties and drivers of marine heat waves in the northern south China Sea. J. Phys. Oceanogr. 52 (5), 917–927. doi: 10.1175/JPO-D-21-0236.1

CrossRef Full Text | Google Scholar

Weiss J. (1991). The dynamics of enstrophy transfer in two-dimensional hydrodynamics. Physica D. 48, 273–294. doi: 10.1016/0167-2789(91)90088-Q

CrossRef Full Text | Google Scholar

Xian T., Sun L., Yang Y., Fu Y. (2012). Monsoon and eddy forcing of chlorophyll-a variation in the northeast south China Sea. Int. J. Remote Sens. 33 (23), 7431–7443. doi: 10.1080/01431161.2012.685970

CrossRef Full Text | Google Scholar

Xu G., Dong C., Liu Y., Gaube P., Yang J. (2019). Chlorophyll rings around ocean eddies in the north pacific. Sci. Rep. 9 2019. doi: 10.1038/s41598-018-38457-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu L., Li P., Xie S. P., Liu Q., Liu C., Gao W. (2016). Observing mesoscale eddy effects on mode-water subduction and transport in the north pacific. Nat. Commun. 7, 10505. doi: 10.1038/ncomms10505

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang X., Xu G., Liu Y., Sun W., Xia C., Dong C. (2020). Multi-source data analysis of mesoscale eddies and their effects on surface chlorophyll in the bay of Bengal. Remote Sens. 12 (21) 3485. doi: 10.3390/rs12213485

CrossRef Full Text | Google Scholar

Yang G., Yu W., Yuan Y., Zhao X., Wang F., Chen G., et al. (2015). Characteristics, vertical structures, and heat/salt transports of mesoscale eddies in the southeastern tropical Indian ocean. J. Geophys. Res. 120 (10), 6733–6750. doi: 10.1002/2015JC011130

CrossRef Full Text | Google Scholar

You Z., Liu L., Bethel B. J., Dong C. (2022). Feature comparison of two mesoscale eddy datasets based on satellite altimeter data. Remote Sens. 14 (1), 116. doi: 10.3390/rs14010116

CrossRef Full Text | Google Scholar

Zhang Z., Wang W., Qiu B. (2014a). Oceanic mass transport by mesoscale eddies. Science 345 (6194), 322–324. doi: 10.1126/science.1252418

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang Z., Zhao W., Qiu B., Tian J. (2017). Anticyclonic eddy sheddings from kuroshio loop and the accompanying cyclonic eddy in the northeastern south China Sea. J. Phys. Oceanogr. 47 (6), 1243–1259. doi: 10.1175/JPO-D-16-0185.1

CrossRef Full Text | Google Scholar

Zhang Z., Zhong Y., Tian J., Yang Q., Zhao W. (2014b). Estimation of eddy heat transport in the global ocean from argo data. Acta Oceanol. Sin. 33 (1), 42–47. doi: 10.1007/s13131-014-0421-x

CrossRef Full Text | Google Scholar