Generation of macro-vortices in estuarine compound channels

We report the results of a numerical investigation of the flow structure and mechanism of macro-vortex generation in estuarine compound channels. The Finite-Volume Coastal Ocean Model (FVCOM) was implemented to simulate tidal currents in compound channels, e.g., the Lantau Channel, which lies in the middle of the Pearl River Estuary (PRE). Results showed that the velocity magnitude in channels was significantly larger than that of floodplains during the ebb and flood phases, resulting in a high-velocity gradient at the depth discontinuity. Vorticity and Q-criterion were used to analyze the macro-vortex distribution inside the PRE. Massive macro-vortices were generated along the compound channels where high vorticity was also detected. The across-estuary sections with single and multiple channels were selected as representatives to analyze velocity distribution during ebb and flood tides. To characterize the channel flow, the ratio of the main channel depth of the Lantau Channel to floodplain depth (R_h) was calculated using the topography information and surface elevation of sections. It was found that there existed a channel segment where the flow periodically changed between shallow flow (R_h > 3) and intermediate flow (2< R_h< 3). This dynamic change in R_h greatly influenced the generation of macro-vortices. Transverse dispersive stresses were calculated to evaluate the longitudinal momentum transfer in the lateral direction. We found that the dispersive stresses could play an important role in the redistribution of momentum in addition to barotropic and baroclinic transport. This paper revealed the mechanism of the dynamic generation of macro-vortices in the estuarine compound channel, serving as a valuable example in understanding natural compound channel flows.

1 Introduction

Natural channels are usually classified as compound channels, which are featured by cross-stream sections containing a deep main channel and shallow floodplains. There existed strong lateral momentum and mass exchange due to the shear layer caused by the velocity gradient between the main channel and floodplains, i.e., the transition area (Xie et al., 2013). Thus, the flow patterns and turbulence features in compound channels are of vital importance when considering sediment transport, morphological change, and pollutant transport.

In the last decades, researchers have conducted laboratory experiments and numerical modeling (Myers, 1978; Shiono and Knight, 1991; Lin and Shiono, 1995) based on compound channels with rectangular or trapezoidal cross-sectional shapes. Great efforts have been made to explore how the dynamics of uniform and non-uniform flows evolved in compound channels in order to better understand the fundamental processes. The overall flow is, in general, a complicated 3D turbulent flow. However, the main agents of transport of momentum and mass between the main channel and the floodplains were found to be the quasi-2D macro-vortices (with vertical axes) generated at the transition region, where there is an intense generation of vorticity owing to the flow depth jump (Soldini et al., 2004). Secondary flows are, usually, disregarded since they have a major effect in a confined region, close to the bottom, of the main channel. For this reason, many authors have chosen to apply a two-dimensional analysis based on the shallow-water approximation (Shiono and Knight, 1991; Nezu et al., 1999; van Prooijen and Uijttewaal, 2002). The “shallow flow” assumption is applied not only to compound channel flows but also to a variety of other flows that are globally shallow but still retain local vertical gradients as described in Jirka (2001); Socolofksy and Jirka (2004); Nikora et al. (2007). The presence of strong flow depth gradients could trigger the generation of vertical vorticity. This mechanism has been previously studied in a shallow-water framework (Schär and Durran, 1997; Brocchini and Colombini, 2004; Soldini et al., 2004). The vorticity and enstrophy budgets were rigorously derived, and new peculiar terms appeared in the equation, which formally demonstrated a production term in the equation related to the flow depth gradients. These terms can explain why natural compound geometries are found to locally generate vorticity, and macro-vortices, at the flow depth jump (Brocchini and Colombini, 2004; Soldini et al., 2004). Various Eulerian flow patterns have been reported based on the analysis of macro-vortices. Wang et al. (2021) studied the turbulence structures and momentum exchange in compound channel flows with shore ice on the floodplains where a strong shear layer was created near the edge of the ice-covered floodplain. Stocchino and Brocchini (2010) reported the properties of quasi-2D macro-vortices in compound channel experiments and showed how, differently from a free mixing layer, the macro-vortex dimensions scale with the size of the transition zone where the depth varies and, most importantly, the typical size remains unchanged as they are convected by the mean flow.

The ratio of main channel depth to floodplain depth (R_h) assumed great importance in discriminating different hydrodynamic regimes where macro-vortices could be observed in compound channel flows. Following [20], compound channel flows were classified into three categories considering the values of R_h, namely, shallow flows (R_h > 3), intermediate flows (2< R_h > 3), and deep flows (R_h > 2), among which shallow flows were dominated by strong shearing and large macro-vortices populated the transition region between the main channel and the floodplains, whereas for the latter two cases, shear and macro-vortices decreased (Stocchino and Brocchini, 2010).

Moreover, Lagrangian-based methods were also used to identify the coherent structures and particle trajectories in compound channels (Stocchino et al., 2011; Enrile et al., 2018). Except for laboratory scale, numerical methods, such as the Reynolds-averaged Navier–Stokes (RANS) model (Naik et al., 2018) and Large-eddy simulation (Kara et al., 2012; Xie et al., 2013), were also implemented. Combining ANSYS-Fluent and Artificial Neural Network, Naik et al. (2018) succeeded in predicting turbulent flow in an ideal convergent compound channel.

Although several methods have been used to study compound channel flows from both theoretical and experimental points of view, few works focused on the exploration of natural compound channels due to the irregular topography and unsteady flow (Carling et al., 2002; Pan et al., 2020). Carling et al. (2002) found a vertically two-layer structure around the main channel–floodplain interface based on field measurements in the River Severn, England from 1999 to 2001. These analyses provided valuable information, which considered comprehensive conditions in the natural environment, disregarding; however, the role of the transverse bathymetric changes, and the peculiarity of the compound channel flows. Much fewer studies compared to riverine environments have been dedicated to estuarine compound channels where periodical tidal currents greatly influence the flow direction, not to mention the velocity magnitude. Deep channels in estuaries are quite common and often excavated for navigation purposes, where the mean flow depth is too shallow (Yang et al., 2019).

The Pearl River Estuary (PRE) is a great example of this. The PRE has a funnel-like shape and contains two longitudinal channels inside, namely, Lantau Channel and Urmston Road. River discharge and tidal currents meet in the PRE, generating a periodical flow in channels flashing back and forth. The coastal circulation made compound channel flows far more complex when considering buoyancy, surface mixing brought by wind stress, and vertical stratification. Many papers have reported the hydrodynamics in PRE and its impacts, such as the role of tides and wind on estuarine circulation (Mao et al., 2004; Zu and Gan, 2015), sediment transport (Zhang et al., 2021; Zhu et al., 2021), and the relationship between vortex formation and pollutant transport (Li et al., 2020). Very few papers mentioned the role of compound channels in PRE and its impact on flow patterns and the generation of macro-vortices. Pan et al. (2020) analyzed the convergence and divergence of lateral velocity in channels of the PRE, but they did not consider the generation and distribution of macro-vortices.

Relevant to the present study is the strong morphological evolution of the sea floor that occurred in the last decades in the PRE. Recently, satellite remote sensing images and bathymetric data have been used to analyze the decadal morphological evolution of the Pearl River Estuary. The impact factors such as the change in river discharge and sediment discharge and human activities were used to explain morphological evolution. For example, a group of researchers used 100 years of navigational and bathymetric data, together with more than 50 years of fluvial discharge data, to examine the impact of human activities on the Pearl River Delta and its estuary at Lingding Bay, China (Wu et al., 2014; Wu et al., 2016; Wu et al., 2018). The authors found that the continuous economic expansion in the Pearl River Delta led to a shrinking in both the area and water volume of Lingding Bay. Wu et al. (2016) addressed the impact of human activities on the morphodynamic evolution of Lingding Bay. They reported that reclamation, dredging, and navigation channel projects all play important roles in affecting the sediment in Lingding Bay, and these activities have increased recently. Tan et al. (2019), using the multi-source digital elevation model data from 1994 to 2020, investigated the morphological change in the estuary mouth bar of the Modaomen Estuary, which is located in the Pearl River Delta. It is found that the mouth bar has gradually moved toward the sea. Yang et al. (2019), combining bathymetric data and satellite images, studied the morphological response of Lingding Bay to human intervention in recent decades. They found that the evolution of Lingding Bay switched from siltation to erosion after the 1980s, and the morphology of Lingding Bay was narrowed and deepened since the 1990s. Moreover, a well-documented effect of the changes that the LE underwent is the strong decrease of the sediment supply from the rivers and the strong modification of the sediment grain size distribution (Yuan et al., 2019). Therefore, the new sediment supply and nature of sediments represent a new constraint on the estuary evolution.

What appears clearly from the cited literature is that the main channels in the PRE developed due to intense anthropogenic interventions, and their configuration is a result of years of continuous dredging works. One of the aims of the present study is to understand the consequences on the local hydrodynamics caused by the presence of a compound geometry.

In this paper, our focus is to explore the flow patterns in the natural estuarine compound channels, along with revealing the role of deep channels in the generation of macro-vortices and lateral momentum transfer. The Finite-Volume Coastal Ocean Model (FVCOM) was implemented to simulate estuarine circulation in PRE, which possessed two longitudinal compound channels as well as bridge channels. Tidal elevation, wind stress, river discharge, and air pressure were considered as main external forcing. The remainder of this paper is organized as follows. Section 2 describes the model setup, including a brief introduction to PRE. Section 3 shows the results of FVCOM containing the analysis of velocity field, vorticity, and Q-criterion. Section 4 is a detailed discussion explaining the mechanism of macro-vortex generation and evaluation of transverse shear stresses, followed by conclusions in Section 5.

2 Methods

2.1 Study area

The Pearl River is the second largest river in China in terms of river discharge and delivers 2.86 × 10¹¹ m³ of freshwater annually into the South China Sea (SCS) through eight outlets, namely, Modaomen, Humen, Hongqimen, Jiaomen, Jitimen, Hengmen, Yamen, and Hutiaomen (Zhang et al., 2021). As shown in Figure 1A, the PRE is surrounded by four river outlets of the Pearl River and several highly developed cities, such as Hong Kong and Shenzhen. Two deep longitudinal waterways were dredged for transportation inside the PRE, acting as a bridge between the Pearl River Delta and the SCS (Wu et al., 2018). The west channel labeled as Lantau Channel lies in the middle of the PRE and runs to the south of Hong Kong, as presented in Figure 1A. The east channel named Urmston Road is closer to the coastlines and passes through Hong Kong. Outside the PRE, the water depth is shown in isobaths (Figure 1A), which are larger than 20 m in general, whereas inside the PRE, the water is relatively shallow with a depth ranging from 2 to 10 m except for those two deep waterways whose depth can reach 15 to 25 m. In this study, we mainly focus on the area of the PRE and those two interesting compound channels.

FIGURE 1

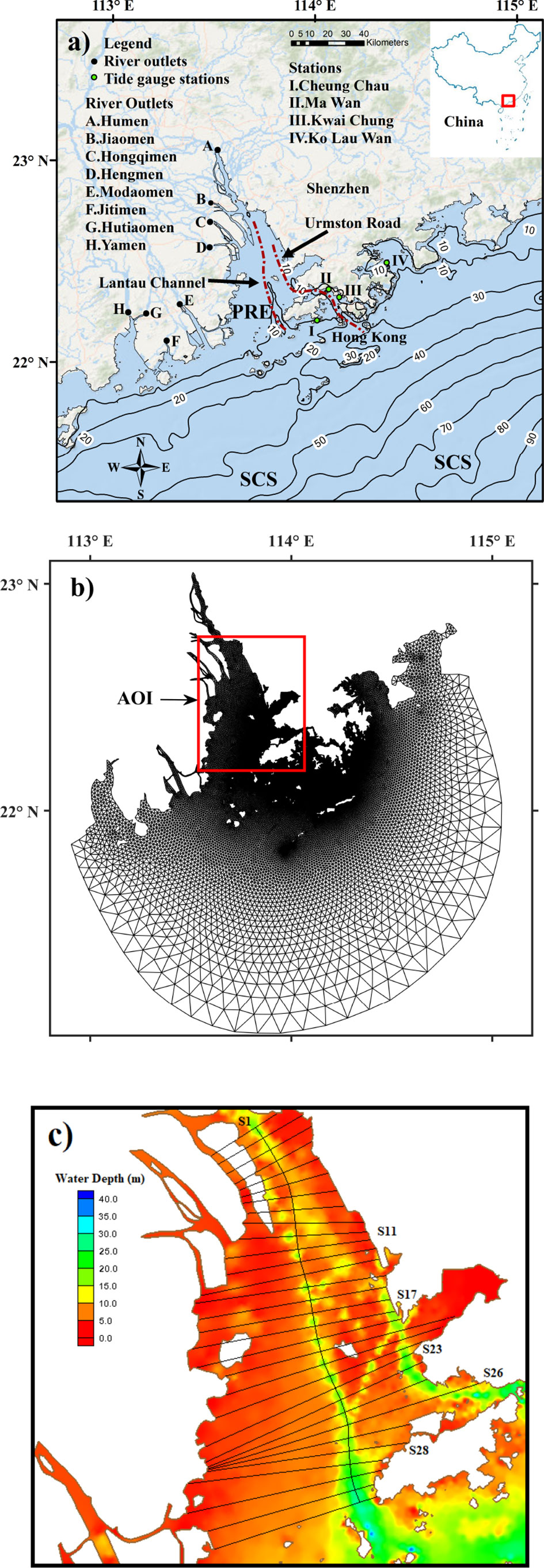
Figure 1 (A) Map of the Pearl River Estuary (PRE) with topographic features and isobaths (in meters), including northern part of the South China Sea. (B) Horizontal grids of Finite-Volume Coastal Ocean Model (FVCOM) model showing area of interest (AOI). (C) Water depth inside the PRE and the distribution of the PRE sections, among which S1 shows the approximate shape of the Lantau Channel, whereas the other sections are normal to S1 and are named in an increasing sequence from north to south.

The Pearl River has an average river discharge of 10,000 m³/s, and half of the river runoff passes through the PRE (Pan et al., 2020). The maximum river discharge happens in the summer reason with approximately 20,000 m³/s of freshwater rushing into the SCS and decreases to 4,000 m³/s during the winter season (Gong et al., 2018). The PRE area experiences monsoon winds with gentle southwest winds prevailing during the wet summer season whereas stronger northeast winds during the dry winter season. The periodical tides from the SCS can be another important force modulating flow patterns inside the PRE. The tide regimes of the PRE area are microtidal and mixed semi-diurnal, and M₂ is the dominant tidal constituent, followed by K₁, O₁, and S₂ [16]. The spring–neap tide cycles and estuary convergence affect the tide’s elevation, with tidal ranges varying from 1.0 to 1.7 m [16].

2.2 Model configuration

The FVCOM was implemented with an unstructured grid, finite volume, free-surface, and three-dimensional primitive equation model (Chen et al., 2003). FVCOM has been widely used in the studies of coastal simulations, such as the PRE [22], Changjiang Estuary (Ge et al., 2015), and Chesapeake Bay (Jiang and Xia, 2016). The horizontal grids were centered around the PRE with a longitude from 113°E to 115°E and a latitude from 21°N to 23°N. The triangular mesh contained 103,690 cells and 55,525 nodes with an open boundary in the SCS, displayed in Figure 1B. The PRE was selected as the area of interest (AOI) whose spatial resolution varied from 200 to 500 m, gradually increasing to 10 km on the open boundary. Ten uniform sigma layers were used in the vertical direction. The wet/dry treatment was applied to deal with the event that the nearshore area was occasionally dry and inundated, especially near the upstream coastal area. The mode-splitting solver was adopted with 1 s for the external mode and 5 s for the internal mode. The Smagorinsky eddy parameterization method (Smagorinsky, 1963) and the k-omega model (Menter, 1993) were implemented to calculate the horizontal diffusion coefficients and the vertical eddy viscosity, respectively. The simulation started on 1 January and run for the whole year of 2017 after obtaining a stable output of the spin-up test.

Tidal elevation was applied to the open boundary generated by the TPXO Tide Models (Egbert and Erofeeva, 2002) using eight tidal constituents, namely, M₂, K₂, K₁, O₁, S₂, N₂, P₁, and Q₁. Wind speed and air pressure data, obtained from the National Oceanic and Atmospheric Administration Physical Sciences Laboratory (NOAA PSL, https://psl.noaa.gov/), were six-hourly based and were implemented on the surface layer of the model domain. Temperature and salinity, which were also provided by NOAA PSL, were applied to a series of specific water depths as initial conditions in the whole domain. Monthly-averaged Pearl River discharge for eight outlets was obtained from the Water Resources Department of Guangdong Province (http://slt.gd.gov.cn/), as well as the Ministry of Water Resources, China (http://www.mwr.gov.cn/).

For further analysis of lateral circulation and momentum transfer in the compound channel, we settled 31 cross sections inside the PRE, which were normal to the thalweg of the Lantau Channel, as shown in Figure 1C. Section S1 followed the deepest depth of the Lantau Channel, starting from the intersection of the Humen branch and Jiaomen branch to the southwest of Hong Kong. The other 31 sections were perpendicular to the S1 and were distributed at intervals of 2 km on the S1.

Detailed information on model validation was shown by He et al. (2022). This model has been validated against both observed sea surface elevation and velocity series. Observation data from four tidal gauge stations around Hong Kong waters were obtained from the Hong Kong Hydrographic Office (https://www.hydro.gov.hk/eng/index.php). Velocity fields were compared using two datasets with corresponding simulation periods, by adjusting the bottom roughness length scale (z₀). One was observed in the cruise velocity data of transect D in May 2014 (Pan et al., 2020), and the other was velocity data in the time series of four velocity gauge stations in August 2007 (Zhu et al., 2021).

3 Results

3.1 Circulation pattern

The PRE has a funnel-like shape, whose width increases from 4 km near Humen to 54 km between Hong Kong and Zhuhai at the southern end (section S26 in Figure 1C). The length of the PRE is approximately 54 km if considering Humen and S26 as two ends. Periodical tidal currents from the SCS are shaped by this convergent geometry, and different flow patterns could be generated during ebb or flood tide, like lateral convergence or divergence (Pan et al., 2020). Among all the months in 2017, the largest river discharge of the Pearl River occurred in July. Thus, more significant velocity could be obtained during ebb tide accordingly. Therefore, the ebb and flood tide phases in July were chosen to present model results and further calculations, such as velocity field and vorticity.

Figure 2 shows examples of the velocity field on the surface layer during three phases of tidal cycles in July 2017, and the corresponding bathymetry of the PRE is presented in Figure 2A. The majority of the PRE was shallow with water depth below 10 m, except the Lantau Channel and the Urmston Road, whose depth reached 30 m at the southern end. The floodplain on the left side of the Lantau Channel was smooth, whereas on the right side, the bottom became more irregular, as shown in Figure 2A. Figures 2B, D display the velocity field during the ebb and flood tide, respectively. Intense velocity was detected in the main channels in both the ebb and flood tide phases, compared to the velocity in the floodplain area. During ebb tide, the flow run toward the south in the main body of the PRE and turned east at the end of the estuary due to the prevailing southeast wind in July, whereas the velocity direction reversed during flood tide. It is interesting to notice that low-velocity areas showed up in the lee of the islands, especially at the southern end of the PRE. The velocity arrows in Figure 2C indicate that this phase was the start of the flood tide. The flow on the floodplain went north and started the flood phase, whereas the flow in the main channel just ended the ebb phase. There existed a phase lag between the main channel and the floodplain during the change of flow direction, resulting in higher velocity in the floodplain.

FIGURE 2

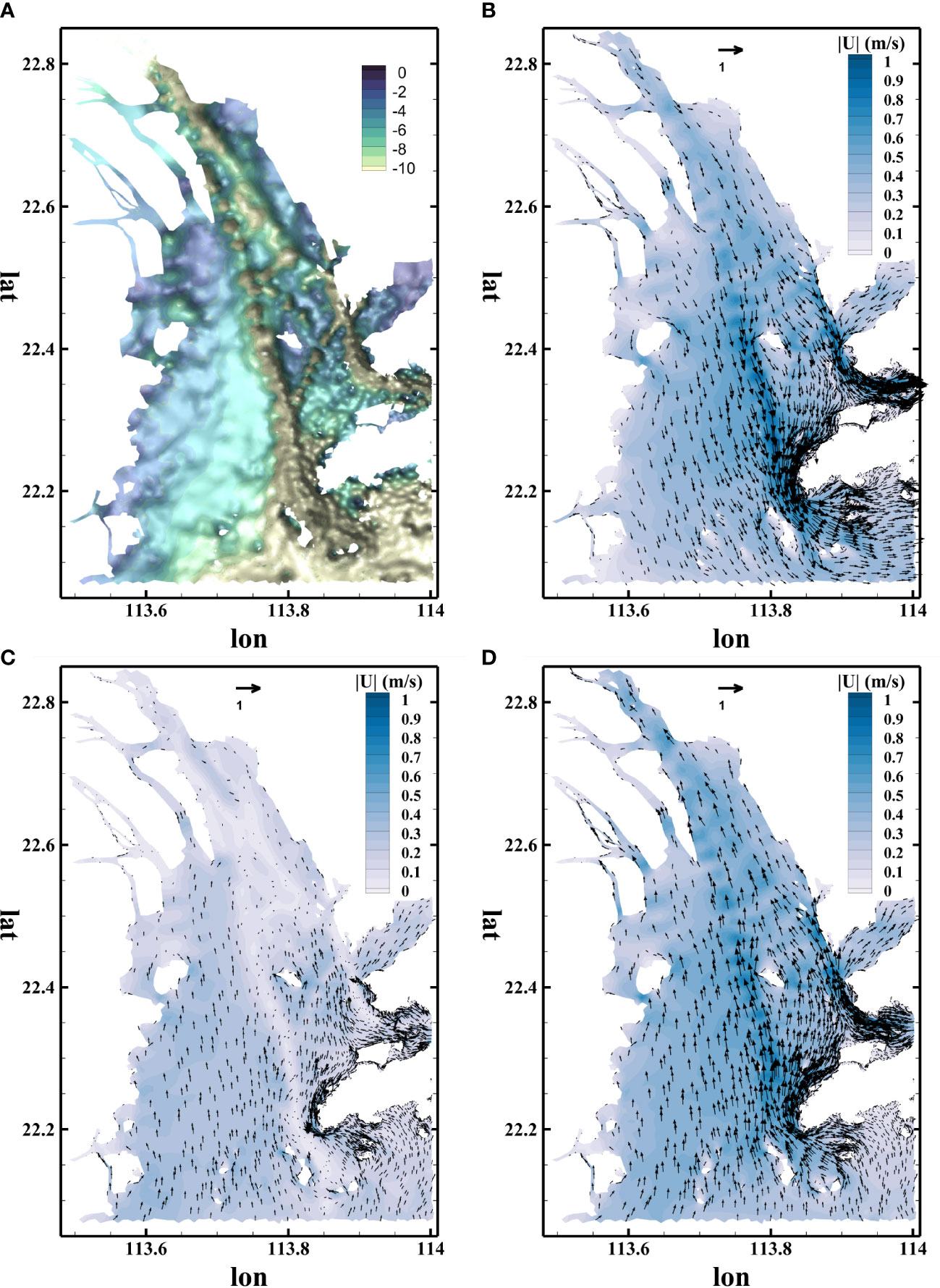
Figure 2 Examples of velocity field during different phases of tidal cycles. Bathymetry in the Pearl River Estuary (PRE) (A) and the contour indicating the water depth. Velocity field of surface layer during ebb tide (B), surface elevation equaling zero (C), and flood tide (D). Arrows represent velocity magnitude and direction of specific nodes, and contour represents absolute velocity magnitude.

3.2 Vortices along compound channels

As discussed above, velocity fields inside the PRE were significantly affected by periodical tides, and a strong velocity gradient was found between the thalweg of channels and floodplains. This strong velocity gradient may result in intense vorticity and, possibly, coherent vortices. To further investigate the flow structure inside the PRE, we computed vorticity fields, defined as Ω = ∇ × u, and used the Q-criterion as a vortex measure [10], with the aim to analyze the generation and distribution of macro-vortices. The Q-criterion was calculated as follows:

$\begin{array}{ll}Q=\frac{1}{2}\left(\left|\left|\text{Ω}\right|{|}^2-\right|\left|\mathit{\text{S}}\right|{|}^2\right)& (1)\end{array}$

where Ω is the 3D vorticity vector, S is the strain, and ||·|| denotes the Euclidean norm of a tensor. Q-criterion considers a connected region to be a vortex if the second invariant is positive, i.e., Q > 0. Regions where Q< 0 are dominated by the shear strain S (Jeong and Hussain, 1995).

Figure 3 presents the vorticity and Q-criterion during ebb tide and flood tide. During ebb tide, tides together with river discharge run toward the south, generating strong vorticity around the channels, capes, and islands, as shown in Figure 3A. Particularly, negative vorticity was observed on the west side of channels, whereas positive vorticity was detected on the east side. From west to east, the velocity magnitude increased from the floodplain to the main channel and then decreased from the main channel to the floodplain, resulting in a reverse of velocity gradient and vorticity on two sides of the main channel. Figure 3B displays the map of the Q-criterion during ebb tide. The red color indicates the location of vortices, whereas the blue color represents the area dominated by strain. It could be found that strong strain appeared where bathymetry was discontinuous and irregular, especially inside the channels. Accompanied by shear stress, vortices were identified inside the channels and in the lee of the capes and islands. During flood tide, tides run toward the north and collided with the Pearl river discharge, resulting in a decrease in velocity gradient and vorticity around the channels, as displayed in Figure 3C. Figure 3D shows the distribution of vortices inside the PRE during flood tide. Vortices were spotted around the channels during ebb tide. It is interesting to point out that the islands at the south end of the PRE could also generate vortices in the lee of islands with respect to the velocity direction. This phenomenon could be understood as the periodical shedding of vortices around the island.

FIGURE 3

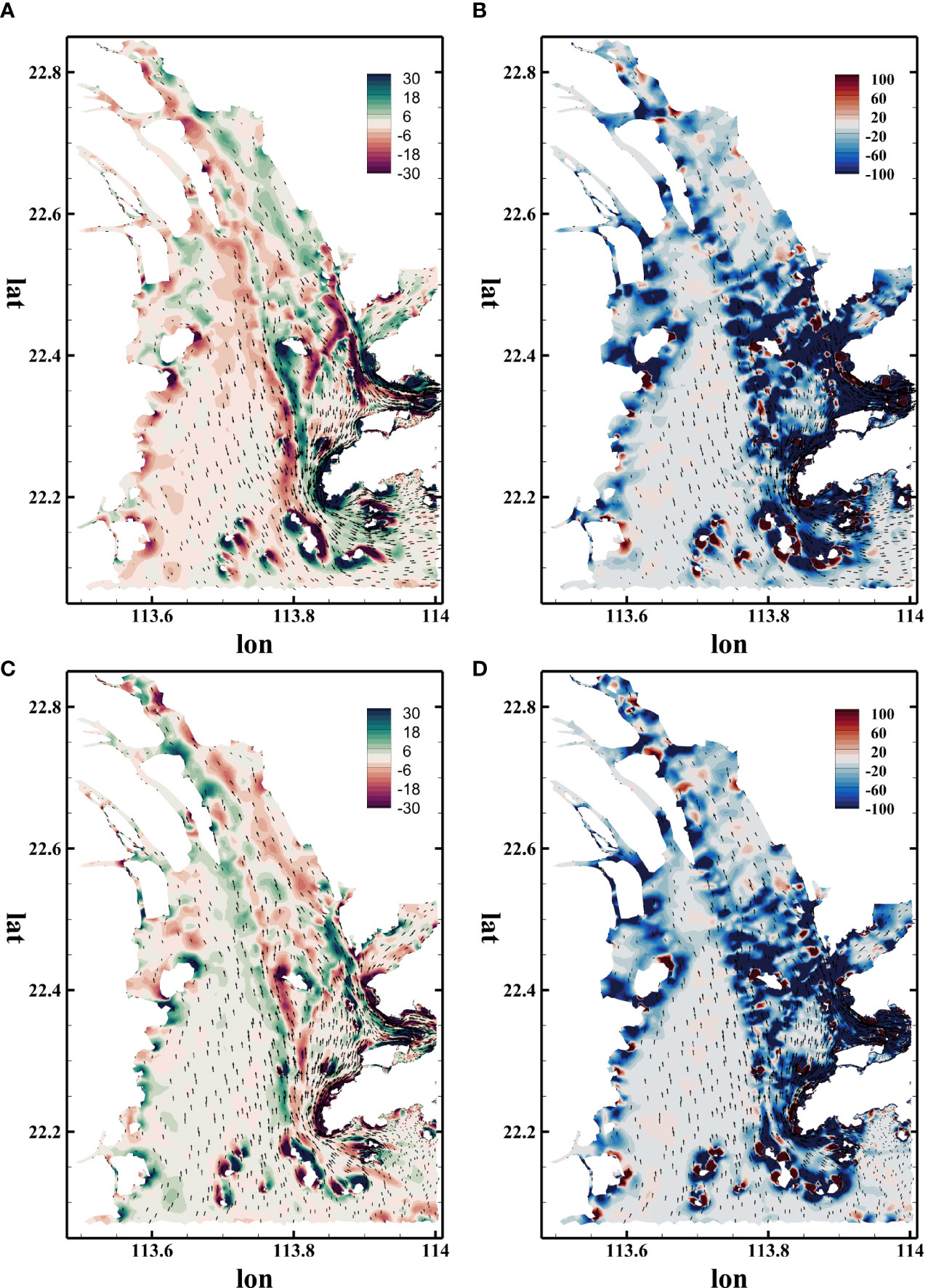
Figure 3 Maps of vortices on surface layer using different extraction methods during ebb tide and flood tide: vorticity (A) and Q-criterion maps (B) during ebb tide; (vorticity (C) and Q-criterion maps (D) during flood tide.

In Figure 4A, we report the same time snapshot shown in 3 (Figure 4A) together with three cross-estuary sections placed in the north end (Figure 4B), middle (Figure 4C), and south end (Figure 4D) of the PRE to present the vorticity along the vertical direction. Figure 4A reports vorticity on the surface layer, whereas Figures 4B–D present the vorticity in the vertical direction during ebb tide. The section in the north had a maximum water depth in the main channel of approximately 14 m, and its floodplain was blocked by islands and peninsulas. The section in the middle was continuous and had two gentle depth peaks and one sharper channel. The section in the south had three stinging channels with a maximum depth reaching 20 m. For those sharper channels, vorticity changed its direction at the maximum depth of the channel. During ebb tide with flow running toward the south, vorticity was negative on the west side of those sharper channels and positive on the east side. In addition, vorticity showed higher magnitude with deeper channel depth, particularly the east channel of Figure 4D, i.e., the Urmston Road. For the mild channel shown in Figure 4C, vorticity remained in the same direction. Moreover, the most intense vorticity patches are found in the correspondence of the highest bottom gradients. The vertical distribution is almost constant, as expected in compound channel flows (Shiono and Knight, 1991; Stocchino and Brocchini, 2010).

FIGURE 4

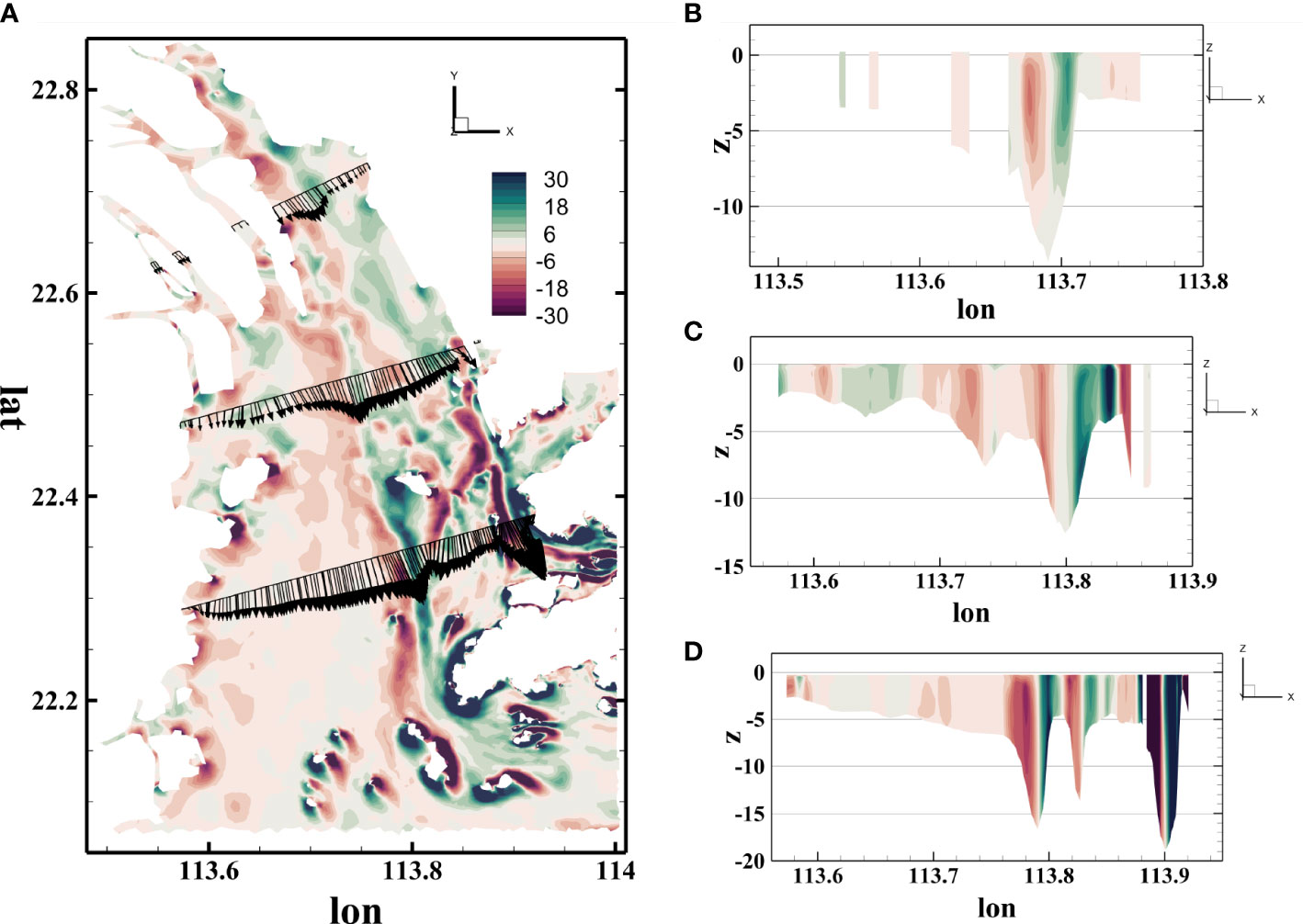
Figure 4 Vorticity map on the surface layer during ebb tide (A) and vorticity in the vertical direction of three cross-estuary sections (B, north; C, middle; D, south).

In a recent contribution, He et al. (2022) analyzed in detail the interaction among the numerous islands and headlands in the PRE and the Hong Kong waters and presented a statistical analysis of the typical macro-vortex dimensions and geometry using the eccentricity parameter (є) of the vortices, defined as the ratio between the minor and major axes of the vortex, which is a measure of the vortex symmetry. One important conclusion regarded the generating mechanisms of the vortices, distinguishing between tidal and wind-wake generated vortices. For the present analysis and, in particular, regarding the identified macro-vortices, we can confirm that the principal hydrodynamic forcing is the tide, rather than wind circulation interacting with islands. Indeed, the position of the vortices is forced by the bathymetry and, in particular, by the presence of deeper channels. Ebb and flood tides generated periodically the vortices and the consequent current in the PRE and, then, advects them, always closely following the deep channels. A second interesting aspect was the shape of the vortices analyzed by He et al. (2022). The pdf of the observed eccentricity parameter presented multiple peaks in the range 0.6< є< 0.8, implying that, statistically, the vortices tended to be more elliptical than circular. Also in the present case, the vortices are observed to be far from a symmetrical shape (i.e., circular), and this feature was already reported in previous experiments on macro-vortices in regular compound channels (Stocchino and Brocchini, 2010). The shape of the vortices is important and linked to their stability and evolution. Elliptical vortices are the most unstable and tend to become circular if the flow conditions are favorable (Tabeling, 2002). The compound channel geometry is responsible for the generation of the macro-vortices and imposes a typical size of them of the order of the transition region (the length over which we assist the change of flow depth). However, this process could be interpreted as a geometrical forcing on the vorticity generation process, and it results also in forcing the shape of the vortices (Stocchino and Brocchini, 2010). Differently from the uniform or quasi-uniform conditions of rivers, the periodic nature of the flow, governed by tides, interferes with the vortex generation due to a time variation of the depth and of the velocities, which reverse every half cycle. In the next section, we further discuss these aspects.

3.3 Cross-section velocity distribution in single and multiple channels

The PRE exhibits a complex seafloor bathymetry, also due to the important anthropogenic interventions of the last decades (Wu et al., 2014; Wu et al., 2016; Wu et al., 2018). Relevant to the present analysis is the modification of the bathymetry of the main channels from the original morphology to the current shape. As mentioned above, deeper and sharper channels resulted in a higher magnitude of vorticity together with the change of vorticity direction. This indicated that the velocity gradient is particularly intense along the channel sides, and in the present sections, we show an example of velocity distributions helpful to quantify these effects.

The longitudinal section S1 in Figure 1C is the thalweg of the Lantau Channel, which lies in the middle of the PRE. The other 31 cross-estuary sections (labeled from S2 to S32) were extracted along the longitudinal profile S1 and perpendicular to it with a spacing equal to 2 km. Depth-averaged velocities were used to calculate the velocity normal to each cross-section. Among all cross-sections, sections S28 and section S23 are chosen as representatives to report the velocity distribution under single-channel and multi-channel conditions. Figures SI–3 shows the bathymetry of section S28 (panel a) and section S23 (panel b). The period investigated started from neap tide to spring tide, which was approximately one-fourth of July 2017.

Figure 5 presents the depth-averaged velocity normal to cross-estuary sections, namely, section S28 (panels (a)–(c)) and section S23 (panels (d)–(f)).

FIGURE 5

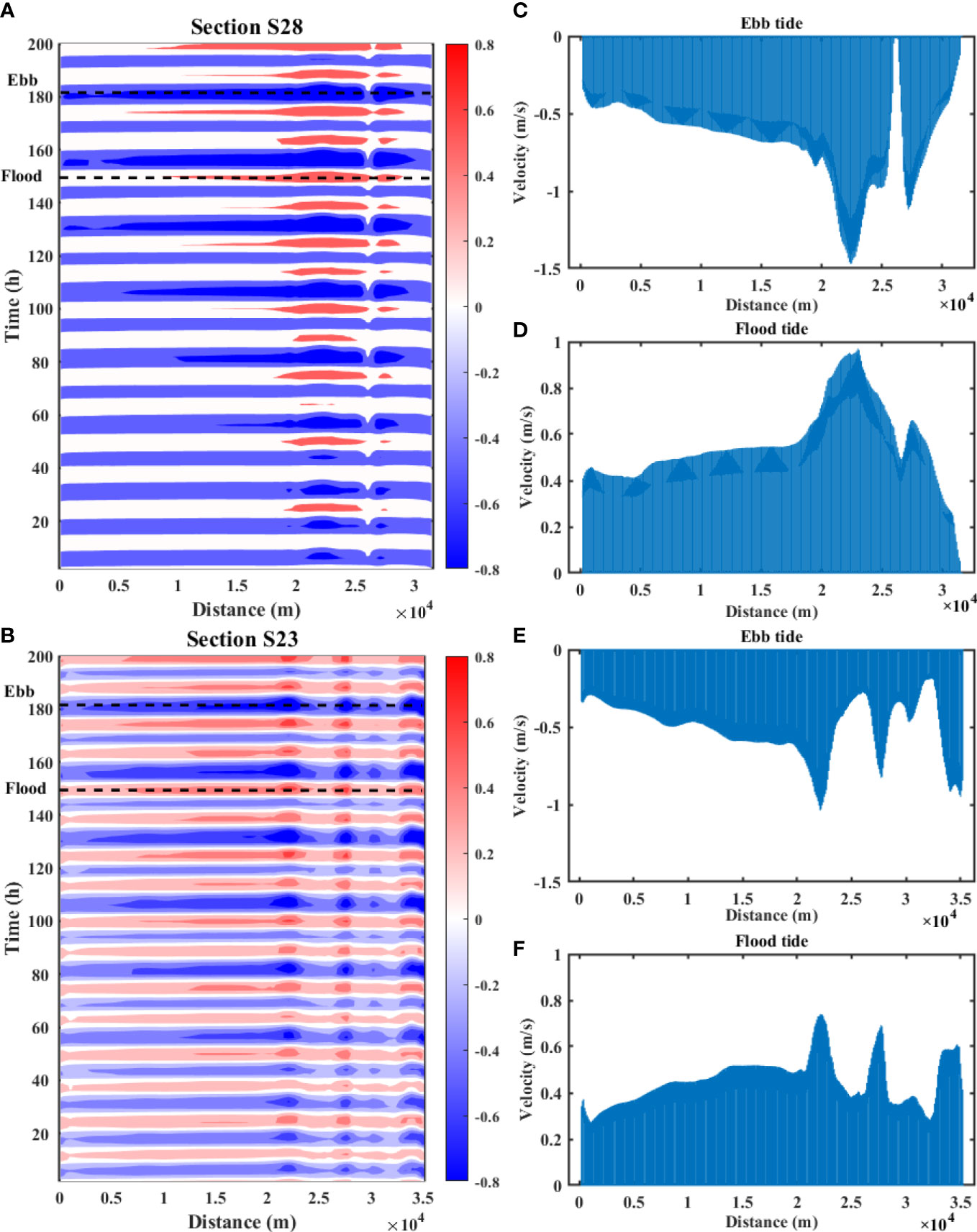
Figure 5 Depth-averaged velocity normal to the sections. Contours showing the change of section velocity of S28 (A) and S23 (D) with the tidal cycles. Section velocity of S28 at ebb tide (B) and flood tide (C) whose time points are indicated in panel A, whereas time points of section velocity of S23 at ebb tide (E) and flood tide (F) were are in (D).

Section S28 contained one main channel, the depth of which was above 16 m occurring at x = 22,400 m. Figure 5A reports the contours of the velocity of S28 varying with time. Northward (positive value) and southward velocities (negative value) alternated with time, following the tidal cycle. It could be identified that the highest velocity also appeared approximately x = 22,400 m, and at this location, the magnitude of velocity gradually grew from the neap tidal cycles to spring tidal cycles. Another interesting location of S28 was at x = 26,200 m. Figures SI–3A presents that in S28, there existed a flat platform on the east side of the Lantau Channel, followed by a large-scale bedform of approximately x = 26,200 m and a trough at x = 28,000 m. A secondary velocity peak appeared at x = 28,000 m, which resulted in a local minimum velocity between two velocity peaks at x = 26,200 m. For instance, Figures 5B, C show the velocity distribution on S28 at two instances, namely, t = 201 and 219 h, which corresponded to the maximum flood and ebb phases, respectively; see the dashed lines in Figure 5A. Velocity at x = 26,200 m was significantly smaller than that at two peaks in both the ebb tide and flood tide phases, which caused a velocity gradient exhibiting opposite directions on the two sides of x = 26,200 m.

Section S23 had a far more complex bathymetry with three main channels whose depths were 12.3, 12.1, and 21.3 m listing from west to east. As shown in Figure 5D, three columns of hot spots were lined up according to the locations of the main channels. Figures 5E, F report the velocity of S23 at the ebb and flood tide phases, respectively. Velocities in three channels had comparable magnitudes during both ebb tide and flood tide, although the velocity peak on the east side corresponded to the deepest channel, i.e., the Urmston Road. The west and middle channels had commensurate depths, but the velocity peak of the middle channel was sharper than that of the west channel. This is mainly because the west channel connected with long and flat floodplains, whereas the middle channel was clipped by two steep hillsides. It is apparent that the velocity gradient of S23 frequently changed its direction once coming across with main channels.

It can be concluded that the velocity in the main channel had a larger magnitude than that of the floodplain at both the ebb and flood phases. The rugged bottom could affect the velocity gradient to some extent. With a short floodplain, the velocity peak could be narrow and sharp, whereas velocity changed gently on the long and flat floodplain. The velocity gradient around the transition area between the main channel and floodplain was higher compared with that of the floodplain, where the bottom was flat with little velocity gradient in the lateral direction. To a certain extent, the shape of the cross-section velocity distribution is quite similar to that of several other cases of experimental measurements in compound channels; see van Prooijen et al. (2005), among others.

4 Discussion

4.1 The role of the depth ratio parameter R_h on the mechanism of macro-vortex generation

It has been widely reported that the ratio of main channel depth to floodplain depth (R_h) had a significant role in generating macro-vortices in compound channel flows (Stocchino and Brocchini, 2010; Stocchino et al., 2011; Kara et al., 2012; Xie et al., 2013).

Based on the results of numerical simulations, we calculated the depth ratio parameter R_h and its variability depending on the tidal phase. In fact, differently from the cases of compound channels in rivers, in this case, the periodicity of the main hydrodynamic forcing, naturally, induces a variability of the flow depth and, in return, a time dependence of R_h. Moreover, care must be taken in our application since the natural geometry of the estuary is far from regular. In fact, before calculating the temporal and spatial variations of R_h, it is necessary to properly define the main channel and floodplains in a compound channel flow. The main channel was characterized as the location with the deepest depth, defining the locus of the deepest depth as thalweg. Thus, in our case, longitudinal section S1, which followed the thalweg of the Lantau Channel, was the main channel, as shown in Figure 1C. Then, the temporal variation of the main channel depth equaled the bathymetry of the main channel plus the surface elevation. Unlike the floodplains in the laboratory, the bottom of the PRE exhibited highly irregular features, which significantly complicated the evaluation of the floodplain depth. Velocity gradients along the cross-sections were chosen to evaluate the starting and ending point of floodplains. Velocity in the main channel was significantly higher than that of floodplains, whereas velocity magnitudes of floodplains were comparable, as shown in Figure 5. Therefore, there existed inflection points when calculating the velocity gradient along the sections. These inflection points were featured as the boundary of floodplains for every section. Then, the floodplain depth used to calculate R_h was the average depth of the bounded segment. As in the section velocity analysis, the time period started from neap tide to spring tide in July 2017.

Figure 6 presents the temporal and spatial variation of R_h. Figure 6A shows the contours of R_h of the whole Lantau Channel varying with time (approximately 200 h of simulation). The red color in the contour indicates R_h > 3, suggesting that the flow regime could be described as shallow when the macro-vortices were observed at the corresponding time and location. The blue color implies the time and location where R_h< 3; i.e., the flow conditions were in the intermediate or deep, when R_h< 2. By inspecting Figure 6A, several observations can be deduced. First, starting from the northernmost point of the estuary at the exit of the Humen river (see Figure 1A) and following the Lantau Channel, there are several transitions around the values R_h = 3. We remind that this value is commonly used to discriminate the flow regime where the highest production of vorticity around the vertical axis is expected, corresponding to the generation of quasi-two-dimensional macro-vortices. A second important observation regards the persistence of similar values of the depth ratio parameter depending on the longitudinal position along the Lantau Channel. In fact, in most locations, the values of R_h consistently remain above 3 (red vertical stripes) or below it (blue vertical stripes) during the entire tidal cycle. Few sections show an alternate behavior, e.g., approximately x = 2.2 × 10⁴ m, where we observe a change in colors. The time-averaged values are reported in Figure 6B, together with the elevation of the thalweg and the indication of the threshold values for R_h, namely, 2 and 3. The mean value reported as a black solid line is surrounded by a colored band indicating the range of variation. One important piece of information is that on average, the PRE shows that during a neap and spring cycle, the flow regime can be defined as shallow or intermediate. Thus, we may expect that the generation of macro-vortices triggered by the gradients of the bathymetry is always sustained. In very few exceptions, the flow consistently remains in deep regime, approximately x ≈ 1 × 10⁴ m and x ≈ 3 × 10⁴ m. As examples of the behavior at some sections, we identified four sections, namely, S11, S17, S23, and S28 (see dotted lines in Figure 6A), to further investigate the time dependence of the depth ratio parameter.

FIGURE 6

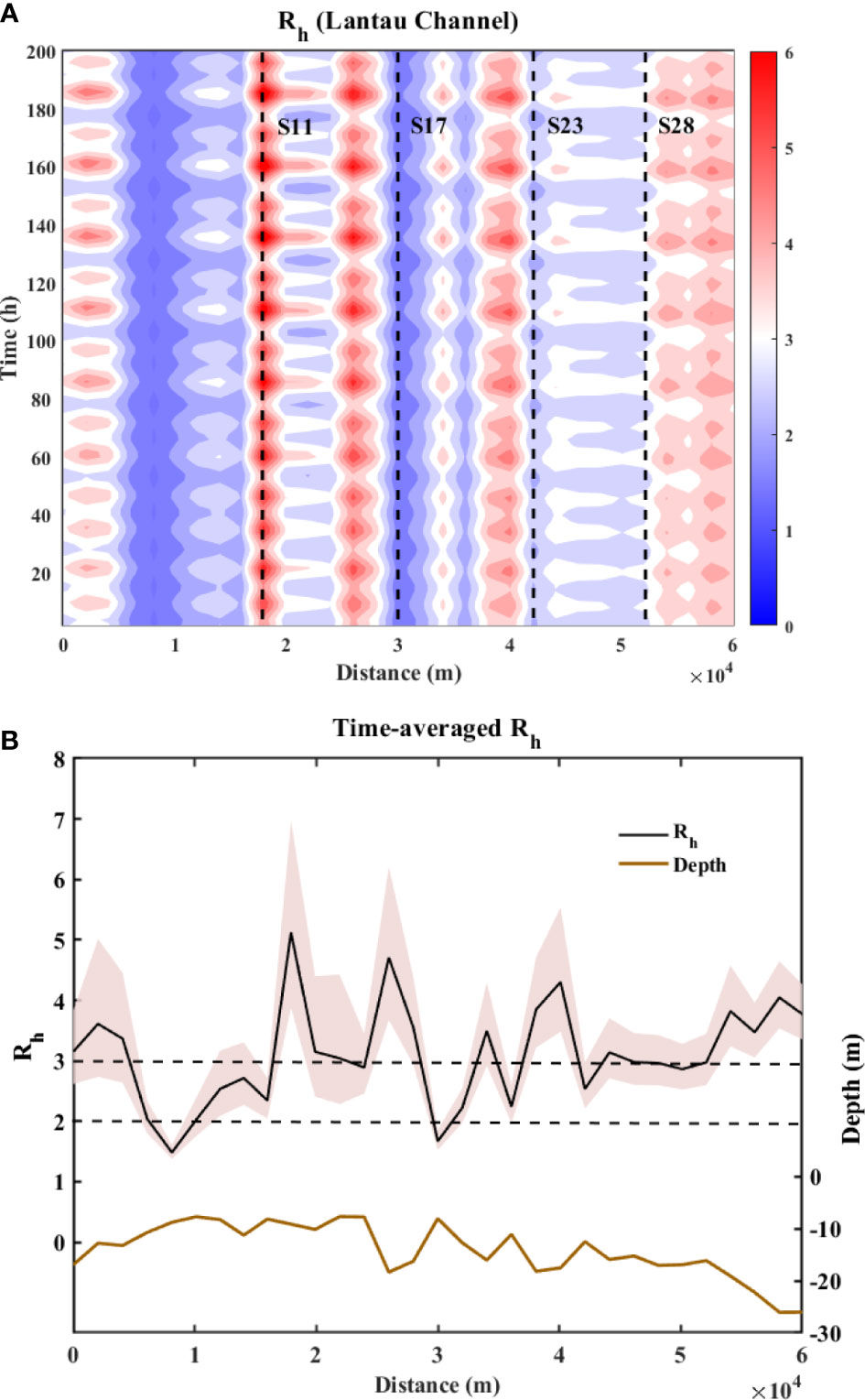
Figure 6 (A) Temporal and spatial variations of R_h, i.e., ratio of main channel depth to averaged floodplain depth. Contour presenting the shift of R_h with the tidal cycles in the Lantau Channel. Distance equaling zero represents the north end of the Lantau Channel. The counting of distance followed the thalweg of the Lantau Channel (section S1) and ended at the south end of the Pearl River Estuary (PRE). The relative location of S11, S17, S23, and S28 are indicated in dash lines. (B) The dashed line shows time-averaged variations of R_h along the Lantau Channel. The solid line shows the bathymetry of the Lantau Channel from the north to the south end. The red area represents the area between the maximum and minimum R_h calculated by main channel depth divided by averaged floodplain depth.

The extracted values of R_h versus time along the four cross-sections are displayed in Figure 7. The plot has been prepared similarly to Figure 6B, where the black line indicates the mean value of R_h surrounded by a colored band representing the range of values (from minimum to maximum) and the dotted lines represent the threshold values of R_h= 2, 3.

FIGURE 7

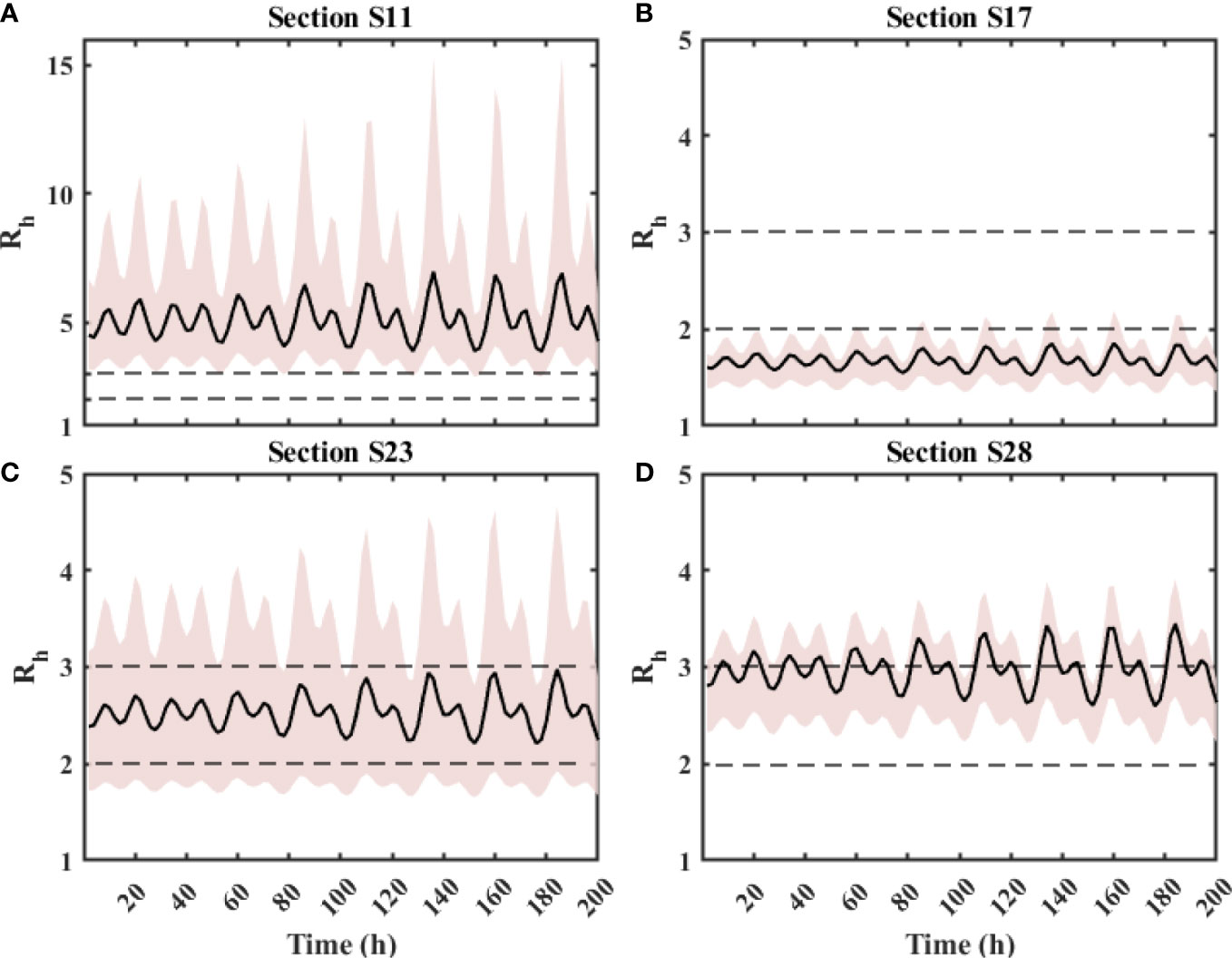
Figure 7 R_h in time series of different sections: (A) S11, (B) S17, (C) S23, and (D) S28. The black lines in (B, C) stand for the R_h calculated by average depth of floodplain. The red areas were bounded by the maximum and minimum R_h calculated by minimum and maximum depths of the floodplains, respectively.

Figure 7A corresponds to the results obtained along section S11, which is the place in the north part of the estuary downstream of the Humen and Jiaomen river mouths; see Figure 1A. This section is representative of situations where there is only a deep channel, namely, the beginning of the Lantau channel, and very shallow later tidal flats; see Figure 1B for the bathymetry. In this case, for the entire duration of the simulation, the values of the depth ratio parameter oscillate around a value equal to 5, in a range with minimum values never less than 3. Moreover, the oscillations of the mean value tend to increase, driven by the increasing maximum values, with time, i.e., following tide spring tide cycle. The strong shallow flow character suggests that around this section, a strong vorticity production is expected, and as we will discuss in the next section, we expect intense dispersive stress gradients.

On the contrary, section S17 shown in panel (b), placed in the middle of the estuary longitudinal direction, seems to be always in deep flow regime. In fact, the values of R_h are persistently less than 2. We expect that in this case vorticity generation is dumped by the presence of much less intense transverse velocity gradients.

Section S23, in panel (c), represents an interesting example where the mean value of the depth ratio remains always bounded between 2 and 3, maintaining, on average, the character of the flow as intermediate. However, the colored band indicates that R_h can exceed 3, especially during the spring cycle. We must note that for natural conditions such as the present one, the intermediate regime might be less significant compared to a river channel with a finite width. In fact, this regime is associated with both the generation of macro-vortices at the transition region of the main channel and the ones generated by the interaction with the lateral banks (Nezu et al., 1999; Stocchino and Brocchini, 2010). In this case, the cross-section is too wide, and, in particular, the lateral tidal flats are so wide to not allow any interaction with the lateral coastlines.

Finally, panel (d) displays the trend of R_h of section S28, placed at the southernmost end of the PRE. In this case, the values of R_h fluctuated by approximately 3, particularly, strong shearing dominated in the transition area during ebb tide, whereas shear decreased and the wall boundary layer increased during flood tide. As the tidal range grows from neap tide to spring tide, the range of R_h also increased. The maximum of R_h occurred in ebb tide during the spring period, reaching a magnitude of 3.78. Again, we expect that for most of the tidal cycles, the flow depth jump can strongly influence the flow.

It is reported by Proust et al. (2017) and Proust and Nikora (2020) that the dimensionless shear parameter λ=(U₂−U₁)/(U₂+U₁) higher than 0.3 was found to be a necessary condition for the emergence and development of the Kelvin–Helmholtz-type coherent structures, where U₁ and U₂ represent streamwise velocities outside the shear layer on the low-speed side and high-speed side, respectively. Proust et al. (2022) also studied the shallow mixing layers in a tilted rectangular open channel flow. Although the shear parameter λ works perfectly in mixing layer problems, it is recommended that we could not treat compound channel flow as purely a mixing layer problem, especially in an estuarine environment. Tidal forcing makes compound channel flow periodical. It is hard to evaluate λ under periodical changing of U₁ and U₂. Moreover, as discussed by Stocchino and Brocchini (2010), compound channels should not be described in terms of free mixing layers. In fact, the main source of vertical vorticity is linked to the sharp depth gradient located at the transition region. The main difference compared to the free mixing layers is the constant size of the transition region and the generated macro-vortices. If the mixing layer theory would be the correct support for the description of the flow, the typical lateral dimensions of the transition regions and the macro-vortices would linearly increase along the longitudinal development of the flow. However, this is not the case with compound channels. The main reason is that a compound channel flow is not a free turbulence problem but a forced turbulent flow, where the forcing is a geometrical constraint.

To fully understand how the flow depth jump across the tidal flats and the main channel can trigger the generation of intense vertical vorticity, it is useful to refer to previous studies dedicated to the analysis of the vorticity and enstrophy budget for shallow-water flows (Schär and Durran, 1997; Brocchini and Colombini, 2004; Soldini et al., 2004). In the above contributions, the vorticity and enstrophy budgets were studied in the framework of shallow-water flows with both the inviscid and dissipative formulation. The final equations derived by Schär and Durran (1997) and Brocchini and Colombini (2004) are particularly relevant to explain the mechanisms observed in the present study. Although the two formulations slightly differ, both clearly showed how two new production terms appeared in the vorticity equation. Recall the equation by Schär and Durran (1997), as follows:

$\begin{array}{ll}\frac{\partial \omega }{\partial t}+\nabla ·\left(v\omega \right)=\nu {\nabla }^2\omega +\nu \frac{\nabla D}{D}·\nabla \omega +\nu k\left(\frac{\nabla D}{D}\times \nabla \left(\nabla ·v\right)\right),& (2)\end{array}$

where ω indicates the vertical vorticity, D denotes the local flow depth, v is in this case an effective viscosity, and k is the vertical unit vector. The last two terms of the right-hand side of the equation are two production terms that depend on the presence of flow depth gradients and the alignment of the latter with the vorticity gradient (the first) and divergence (the second). It is clear that the compound geometry of the PRE is prone to generate gradients of flow depth and vorticity that lead to a concentrated production of vertical vortical at the boundaries of the deep channels. The parameter R_h is exactly expressing the intensity of the gradients, and as shown in Figure 7, the periodicity of the tidal forcing is dominant in the time evolution of the gradients.

4.2 The contribution to the longitudinal momentum transfer

In this final section, we are interested in evaluating the role of the compound geometry on the overall momentum balance in the direction of the main flow. In fact, the importance of the transverse exchange of momentum is well known owing to the generation of additional stresses along a cross-section with variable depth. In uniform and steady flows, such as those in compound river flows, the transverse momentum exchange is enhanced by two main effects: the appearance of non-negligible dispersive stresses owing to the difference between the vertical profile of the longitudinal velocity and its depth-averaged value, and the increment in the turbulent stresses owing to the generation of intense vertical vorticity at the depth discontinuity along a compound cross-section (van Prooijen et al., 2005; Stocchino and Brocchini, 2010). In the previous section, we have shown that the presence of the two deep channels in the PRE is the cause for the generation of transitional macro-vortices closely following the mechanisms observed in uniform flows. It is now interesting to understand whether this mechanism could enhance the momentum exchange and then be linked to the observation of the estuarine front discussed by Pan et al. (2020).

In order to study this process, we base our analysis on the depth-averaged non-linear shallow water equations (NLSWEs), similar to those of Soldini et al. (2004); van Prooijen et al. (2005); Stocchino and Brocchini (2010), among many others, since in this framework the contribution to the longitudinal momentum appears extremely clear.

Starting from the 3D NLSWEs and taking the average overflow depth, we are left with the following equation along the longitudinal direction (in this case, the along-estuary direction):

$\begin{array}{ll}\frac{\partial \overline{U}}{\partial t}+\overline{U}\frac{\partial \overline{U}}{\partial x}+\overline{V}\frac{\partial \overline{U}}{\partial y}+f\overline{U}=-g\frac{\partial h}{\partial x}+\frac{{\tau }_x^w+{\tau }_x^b}{\rho D}+\frac{1}{\rho D}\frac{\partial D{\overline{T}}_{xx}}{\partial x}+\frac{1}{\rho D}\frac{\partial D{\overline{T}}_{xy}}{\partial y}& (3)\end{array}$

where the overline indicates depth-averaged quantities; ${\tau }_x^w$ and ${\tau }_x^b$ indicate the shear stresses acting at the free surface and the bottom, respectively; ${\overline{T}}_{xx}$ and ${\overline{T}}_{xy}$ are the depth-averaged total stresses. D is the local flow depth, whereas h is the water level above the sea level. For the present discussion, the term that we are mostly interested in is the transverse stress ${\overline{T}}_{xy}$ and its derivative. The stress ${\overline{T}}_{xy}$ can be rigorously computed, and it is composed of two parts, namely, the depth-averaged turbulent stress ${\overline{T}}_{xy}^T$ and the so-called dispersive stress ${\overline{T}}_{xy}^D$. The first one is simply the average along the vertical of the turbulent stress and, assuming a Boussinesq closure, can be written as follows:

$\begin{array}{ll}{\overline{T}}_{xy}^T=\frac{1}{D}{\int }_D-\rho \langle uv\rangle dz\simeq {\overline{\nu }}_t\frac{\partial \overline{U}}{\partial y},& (4)\end{array}$

where ${\overline{\nu }}_t$ is the depth-averaged eddy viscosity. The dispersive stress arises from the difference between the vertical profile of the longitudinal velocities U and V and their depth-averaged values $\overline{U}$ and $\overline{V}$, as follows:

$\begin{array}{ll}{\overline{T}}_{xy}^D=-\frac{1}{D}{\int }_D\rho \left(U-\overline{U}\right)\left(V-\overline{V}\right)dz.& (5)\end{array}$

By definition, the dispersive stress ${\overline{T}}_{xy}^D$ is more intense in the regions where the difference between the actual velocities and their averages is more intense. The last two terms of Equation (3) represent the exchange of streamwise momentum along the transverse direction, and it has been recognized as an important contribution when the flow depth varies along the cross-stream direction as occurs in a compound geometry, where the flow depth varies between the deep main channels and the shallow lateral expansion areas (Soldini et al., 2004; van Prooijen et al., 2005; Stocchino and Brocchini, 2010; Proust et al., 2017; Proust and Nikora, 2020).

Starting from our simulations, we have evaluated the contribution of the fluxes of ${\overline{T}}_{xy}$, considering both contributions and compared to the barotropic and Coriolis terms. A similar analysis has been performed by Pan et al. (2020) disregarding, however, the possible contributions from the dispersive stresses. First, we interpolated the output from FVCOM onto a regular grid with a resolution of 200 m, using an inverse distance algorithm, and then, we computed separately each term and the corresponding fluxes.

Figure 8 shows the results obtained during July. In particular, Figure 8A shows a map of the flux $1/\left(\rho D\right)\left(\partial D{\overline{T}}_{xy}\right)/\left(\partial y\right)$ during the high flood, and Figure 8B shows the map taken during peak ebb.

FIGURE 8

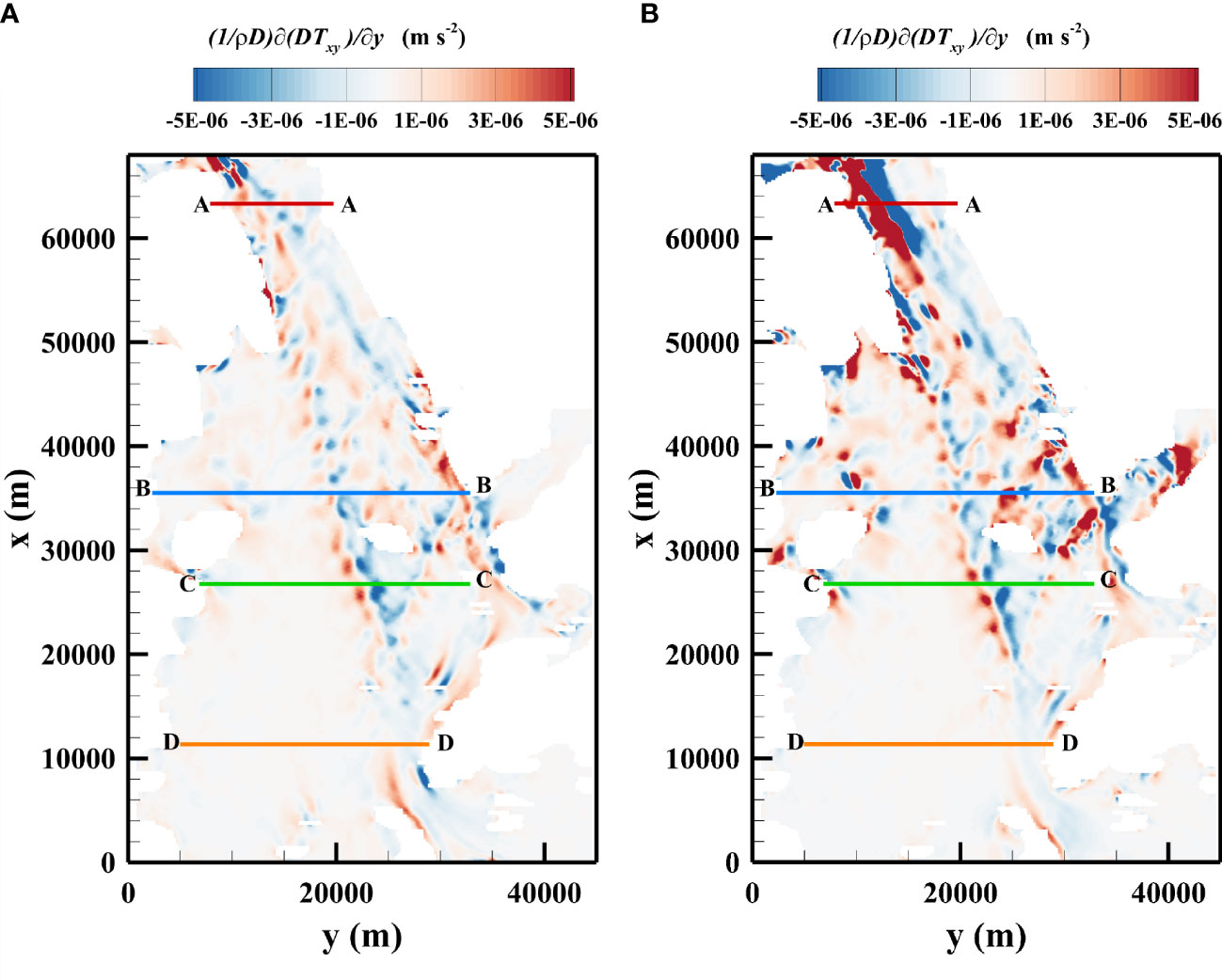
Figure 8 (A) Map of the transverse shear stress $1/\left(\rho D\right)\left(\partial D{\overline{T}}_{xy}\right)/\left(\partial y\right)$ taken during peak flood. (B) Map of the transverse shear stress $1/\left(\rho D\right)\left(\partial D{\overline{T}}_{xy}\right)/\left(\partial y\right)$ taken during peak ebb.

The distribution of the transverse flux of ${\overline{T}}_{xy}$ was clearly affected by the PRE geometry and presented strong peaks along the channel banks, whereas it was extremely low in the lateral flatland aside from the channels. The along-estuary distribution is influenced by the bathymetry and follows closely the behavior of the depth ratio parameter R_h previously discussed. A stronger transverse gradient of the flow depth was associated with higher dispersive stresses and higher fluxes. The most intense values were, not surprisingly, at the peaks of the flood and ebb tidal phases. In the Supplementary Material, we have uploaded a movie of the time evolution of the transverse flux of ${\overline{T}}_{xy}$ for the entire month of July 2017. Different from the studies performed on uniform straight flows, more pertinent for riverine environments, the periodicity of the tidal forcing influenced the intensity of this term, as already discussed in the previous sections.

In Figure 8, four cross-sections are indicated with labels AA, BB, CC, and DD. The lateral distribution of the transverse flux of ${\overline{T}}_{xy}$ along the selected cross-sections (AA, BB, CC, and DD) on an hourly basis are shown in Figures 9A–D. The maximum values were observed in the northernmost cross-section where the compound geometry effect was further enhanced by the river output; see Figure 7A and relative discussion. In all cases, the values of this term were $\mathcal{O}\left(\left|1/\left(\rho D\right)\left(\partial D{\overline{T}}_{xy}\right)/\left(\partial y\right)\right|\right)\sim 5\times {10}^{-6}÷8\times {10}^{-5}$ m · s^-2. The contribution due to the depth-averaged turbulent stresses $ne{T}_{xy}^T$ was much smaller compared to the one due to the dispersive stresses ${\overline{T}}_{xy}^D$.

FIGURE 9

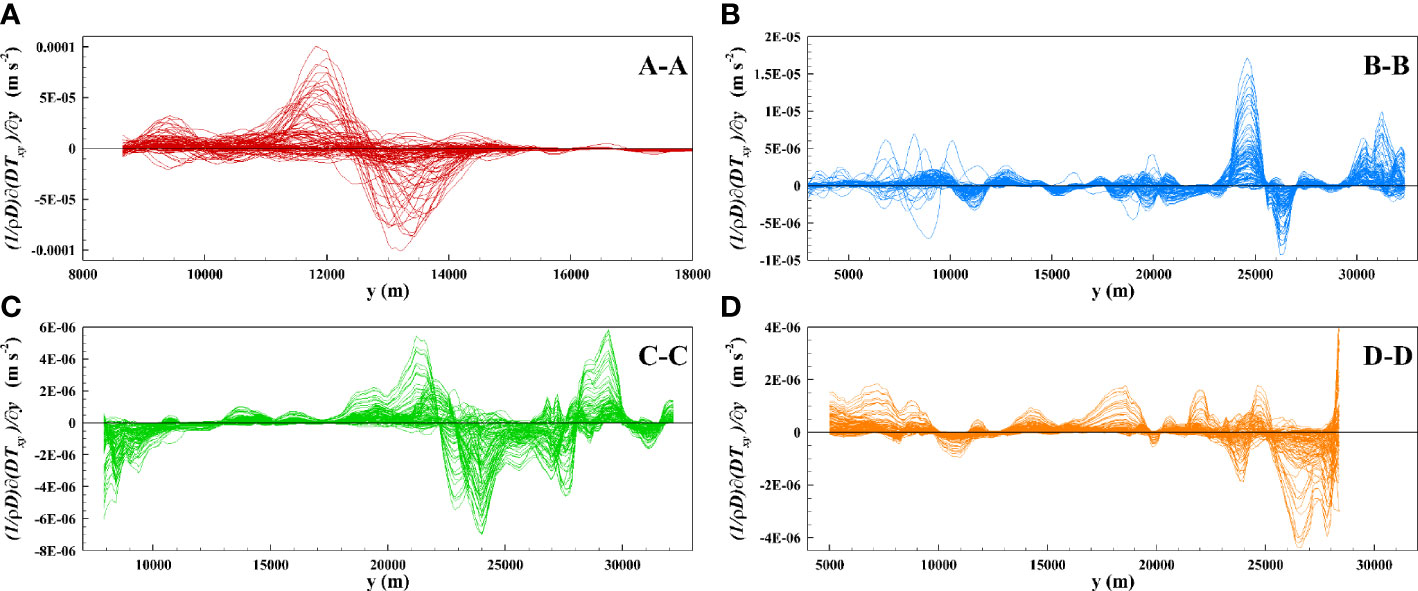
Figure 9 Four panels showing the distribution of the transverse shear stress $1/\left(\rho D\right)\left(\partial D{\overline{T}}_{xy}\right)/\left(\partial y\right)$ with time: (A) section AA, (B) section BB, (C) section CC, and (D) section DD.

It is now interesting to compare the contribution of the flux of ${\overline{T}}_{xy}$ to the terms of the momentum equation (3). The leading term is the barotropic term −g(∂h)/(∂x) , which presented values with order of magnitude O(|−g(∂h)/(∂x)|)∼5×10⁻⁴m·s⁻², as also estimated by Pan et al. (2020). The Coriolis term was, on the contrary, much smaller compared to both contributions with order of magnitude O(|−fv|)∼5×10⁻⁷m·s⁻². This implies that the contribution to the exchange of longitudinal momentum owing to the appearance of the dispersive stress was less than one order of magnitude smaller than the driving barotropic term and much higher than the Coriolis term, compare also to the data reported by Pan et al. (2020). This effect is naturally confined in a narrow region around the deep channels, where the depth lateral gradients are more intense. However, this could be an important term to be considered when estuarine fronts were observed as in the present study in the PRE.

5 Conclusion

In the present study, we have numerically investigated the role of the deep channels that characterize the bathymetry of the Pearl River Estuary on the generation of intense vorticity streets and macro-vortices at the boundaries of the channels. The main mechanism of the formation of the macro-vortices was explained in terms of vorticity production related to strong gradients of the flow depth. Owing to the periodicity of the tidally induced circulations, the depth ratio parameter was monitored in time, showing that different tidal phases were characterized by oscillatory values that, however, most of the time were typical of shallow-water conditions. Moreover, the presence of sharp depth gradients favored the generation of intense transverse dispersive stresses. Using a depth-averaged shallow-water framework, it was observed that the transverse gradients of the dispersive stresses contributed to the transport of longitudinal momentum. Depending on the tidal phase, this contribution was found to be only one order of magnitude less than the leading order term, i.e., the barotropic term. The described mechanism could be an important factor in explaining the observed estuarine fronts along the Pearl River Estuary and, in general, should be considered whenever an estuary is characterized by a compound-like geometry. Finally, the presence and persistence of coherent vortices along the channel boundary could also strongly affect the mass transport processes in analogy with what has been studied in the context of uniform flows in compound channels (Stocchino et al., 2011; Besio et al., 2012; Enrile et al., 2018). The present study deeply discussed the dynamic generation of macro-vortices in natural estuarine compound channels, providing valuable experience in understanding the natural compound channel flow. Further research will be dedicated to this important aspect and its impact on the transport of biogeochemicals and nutrients.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://zenodo.org/record/6619142/#.Y85_LHbLddi10.5281/zenodo.6619142.

Author contributions

CH: investigation, data curation, and writing—original draft. AS: conceptualization, methodology, data curation, and writing—review and editing. Z-YY: writing—review and editing, methodology, and resources. OW: methodology and writing—review and editing. All authors contributed to the article and approved the submitted version.

Funding

This work is supported by the Research Impact Fund of the Research Grants Council of Hong Kong (grant no. RGC R5037-18).

Acknowledgments

The observed sea level data of tide gauge stations are provided by the Hydrographic Office of the Hong Kong Marine Department. The FVCOM source code was obtained from the Marine Ecosystem Dynamics Modeling Laboratory (http://fvcom.smast.umassd.edu/).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2023.1082506/full#supplementary-material

References

Besio G., Stocchino A., Angiolani S., Brocchini M. (2012). Transversal and longitudinal mixing in compound channels. Water Resour. Res. 48:1–15. doi: 10.1029/2012WR012316

CrossRef Full Text | Google Scholar

Brocchini M., Colombini M. (2004). A note on the decay of vorticity in shallow flow calculations. Phys. Fluids 16, 2469–2475. doi: 10.1063/1.1756551

CrossRef Full Text | Google Scholar

Carling P. A., Cao Z., Holland M., Ervine D., Babaeyan-Koopaei K. (2002). Turbulent flow across a natural compound channel. Water Resour. Res. 38, 6–1. doi: 10.1029/2001WR000902

CrossRef Full Text | Google Scholar

Chen C., Liu H., Beardsley R. C. (2003). An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: Application to coastal ocean and estuaries. J. atmospheric oceanic Technol. 20, 159–186. doi: 10.1175/1520-0426(2003)020<0159:AUGFVT>2.0.CO;2

CrossRef Full Text | Google Scholar

Egbert G. D., Erofeeva S. Y. (2002). Efficient inverse modeling of barotropic ocean tides. J. Atmospheric Oceanic Technol. 19, 183–204. doi: 10.1175/1520-0426(2002)019<0183:EIMOBO>2.0.CO;2

CrossRef Full Text | Google Scholar

Enrile F., Besio G., Stocchino A. (2018). Shear and shearless lagrangian structures in compound channels. Adv. Water Resour. 113, 141–154. doi: 10.1016/j.advwatres.2018.01.006

CrossRef Full Text | Google Scholar

Ge J., Shen F., Guo W., Chen C., Ding P. (2015). Estimation of critical shear stress for erosion in the c hangjiang e stuary: A synergy research of observation, goci sensing and modeling. J. Geophysical Research: Oceans 120, 8439–8465. doi: 10.1002/2015JC010992

CrossRef Full Text | Google Scholar

Gong W., Lin Z., Chen Y., Chen Z., Zhang H. (2018). Effect of winds and waves on salt intrusion in the pearl river estuary. Ocean Sci. 14, 139–159. doi: 10.5194/os-14-139-2018

CrossRef Full Text | Google Scholar

He C., Yin Z.-Y., Stocchino A., Wai O. W. H., Li S. (2022). The coastal macro-vortices dynamics in hong kong waters and its impact on water quality. Ocean Model., (175):102034. doi: 10.1016/j.ocemod.2022.102034

CrossRef Full Text | Google Scholar

Jeong J., Hussain F. (1995). On the identification of a vortex. J. fluid mechanics 285, 69–94. doi: 10.1017/S0022112095000462

CrossRef Full Text | Google Scholar

Jiang L., Xia M. (2016). Dynamics of the chesapeake bay outflow plume: Realistic plume simulation and its seasonal and interannual variability. J. Geophysical Research: Oceans 121, 1424–1445. doi: 10.1002/2015JC011191

CrossRef Full Text | Google Scholar

Jirka G. (2001). Large Scale flow structures and mixing processes in shallow flows. J. Hydr. Res. 39, 567–573. doi: 10.1080/00221686.2001.9628285

CrossRef Full Text | Google Scholar

Kara S., Stoesser T., Sturm T. W. (2012). Turbulence statistics in compound channels with deep and shallow overbank flows. J. Hydraulic Res. 50, 482–493. doi: 10.1080/00221686.2012.724194

CrossRef Full Text | Google Scholar

Li D., Gan J., Hui R., Liu Z., Yu L., Lu Z., et al. (2020). Vortex and biogeochemical dynamics for the hypoxia formation within the coastal transition zone off the pearl river estuary. J. Geophysical Research: Oceans 125, e2020JC016178. doi: 10.1029/2020JC016178

CrossRef Full Text | Google Scholar

Lin B., Shiono K. (1995). Numerical modelling of solute transport in compound channel flows. J. Hydraulic Res. 33, 773–788. doi: 10.1080/00221689509498551

CrossRef Full Text | Google Scholar

Mao Q., Shi P., Yin K., Gan J., Qi Y. (2004). Tides and tidal currents in the pearl river estuary. Continental Shelf Res. 24, 1797–1808. doi: 10.1016/j.csr.2004.06.008

CrossRef Full Text | Google Scholar

Menter F. (1993). “Zonal two equation kw turbulence models for aerodynamic flows,”AIAA 24th Fluid Dynamics Conference., July 6-9, 1993, Orlando, Florida.

Google Scholar

Myers W. (1978). Momentum transfer in a compound channel. J. Hydraulic Res. 16, 139–150. doi: 10.1080/00221687809499626

CrossRef Full Text | Google Scholar

Naik B., Khatua K., Wright N., Sleigh A., Singh P. (2018). Numerical modeling of converging compound channel flow. ISH J. Hydraulic Eng. 24, 285–297. doi: 10.1080/09715010.2017.1369180

CrossRef Full Text | Google Scholar

Nezu I., Onitsuka K., Iketani K. (1999). “Coherent horizontal vortices in compound open-channel flows,” in Hydraulic modeling. Eds. Singh V. P., Seo I. W., Sonu J. H. (Water Resources Pub), 17–32 Seoul National University, Seoul, Korea.

Google Scholar

Nikora V., Nokes R., Veale W., Davidson M., Jirka G. (2007). Large-Scale turbulent structure of uniform shallow free-surface flows. Environ. Fluid Mech. 7, 159–172. doi: 10.1007/s10652-007-9021-z

CrossRef Full Text | Google Scholar

Pan J., Lai W., Devlin A. T. (2020). Channel-trapped convergence and divergence of lateral velocity in the pearl river estuary: Influence of along-estuary variations of channel depth and width. J. Geophysical Research: Oceans 125, e2019JC015369. doi: 10.1029/2019JC015369

CrossRef Full Text | Google Scholar

Proust S., Berni C., Nikora V. I. (2022). Shallow mixing layers over hydraulically smooth bottom in a tilted open channel. J. Fluid Mechanics 951, A17. doi: 10.1017/jfm.2022.818

CrossRef Full Text | Google Scholar

Proust S., Fernandes J. N., Leal J. B., Rivière N., Peltier Y. (2017). Mixing layer and coherent structures in compound channel flows: Effects of transverse flow, velocity ratio, and vertical confinement. Water Resour. Res. 53, 3387–3406. doi: 10.1002/2016WR019873

CrossRef Full Text | Google Scholar

Proust S., Nikora V. I. (2020). Compound open-channel flows: effects of transverse currents on the flow structure. J. Fluid Mechanics, (885):885. doi: 10.1017/jfm.2019.973

CrossRef Full Text | Google Scholar

Schär C., Durran D. R. (1997). Vortex formation and vortex shedding in continuously stratified flows past isolated topography. J. atmospheric Sci. 54, 534–554. doi: 10.1175/1520-0469(1997)054<0534:VFAVSI>2.0.CO;2

CrossRef Full Text | Google Scholar

Shiono K., Knight D. (1991). Turbulent open-channel flows with variable depth across the channel. J. Fluid Mech. 222, 617–646. doi: 10.1017/S0022112091001246

CrossRef Full Text | Google Scholar

Smagorinsky J. (1963). General circulation experiments with the primitive equations: I. @ the basic experiment. Monthly weather Rev. 91, 99–164. doi: 10.1175/1520-0493(1963)091<0099:GCEWTP>2.3.CO;2

CrossRef Full Text | Google Scholar

Socolofksy S., Jirka G. (2004). Large-Scale flow structures and stability in shallow flows. J. Environ. Eng.Sci. 3, 451–462. doi: 10.1139/s04-032

CrossRef Full Text | Google Scholar

Soldini L., Piattella A., Mancinelli A., Bernetti R., Brocchini M. (2004). Macrovortices-induced horizontal mixing in compound channels. Ocean Dynamics 54, 333–339. doi: 10.1007/s10236-003-0057-4

CrossRef Full Text | Google Scholar

Stocchino A., Besio G., Angiolani S., Brocchini M. (2011). Lagrangian Mixing in straight compound channels. J. Fluid Mechanics 675, 168. doi: 10.1017/S0022112011000127

CrossRef Full Text | Google Scholar

Stocchino A., Brocchini M. (2010). Horizontal mixing of quasi-uniform, straight, compound channel flows. J. Fluid Mech. 643, 425–435. doi: 10.1017/S0022112009992680

CrossRef Full Text | Google Scholar

Tabeling P. (2002). Two-dimensional turbulence: a physicist approach. Phys. Rep. 362, 1–62. doi: 10.1016/S0370-1573(01)00064-3

CrossRef Full Text | Google Scholar

Tan C., Huang B., Liu F., Huang G., Qiu J., Chen H., et al. (2019). Recent morphological changes of the mouth bar in the modaomen estuary of the pearl river delta: Causes and environmental implications. Ocean Coast. Manage. 181, 104896. doi: 10.1016/j.ocecoaman.2019.104896

CrossRef Full Text | Google Scholar

van Prooijen B., Battjes J., Uijttewaal W. (2005). Momentum exchange in straight uniform compound channel flow. J. Hydr. Engng 131, 175–183. doi: 10.1061/(ASCE)0733-9429(2005)131:3(175)

CrossRef Full Text | Google Scholar

van Prooijen B., Uijttewaal W. (2002). A linear approach for the evolution of coherent structures in shallow mixing layers. Phys. Fluids 14, 4105–4114. doi: 10.1063/1.1514660

CrossRef Full Text | Google Scholar

Wang F., Huai W., Guo Y., Liu M. (2021). Turbulence structure and momentum exchange in compound channel flows with shore ice covered on the floodplains. Water Resour. Res. 57, e2020WR028621. doi: 10.1029/2020WR028621

CrossRef Full Text | Google Scholar

Wu Z., Milliman J. D., Zhao D., Cao Z., Zhou J., Zhou C. (2018). Geomorphologic changes in the lower pearl river delta 1850–2015, largely due to human activity. Geomorphology 314, 42–54. doi: 10.1016/j.geomorph.2018.05.001

CrossRef Full Text | Google Scholar

Wu Z., Milliman J. D., Zhao D., Zhou J., Yao C. (2014). Recent geomorphic change in lingding bay, china, in response to economic and urban growth on the pearl river delta, southern china. Global Planetary Change 123, 1–12. doi: 10.1016/j.gloplacha.2014.10.009

CrossRef Full Text | Google Scholar

Wu Z., Saito Y., Zhao D., Zhou J., Cao Z., Li S., et al. (2016). Impact of human activities on subaqueous topographic change in lingding bay of the pearl river estuary, china, during 1955–2013. Sci. Rep. 6, 1–10. doi: 10.1038/srep37742

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie Z., Lin B., Falconer R. A. (2013). Large-Eddy simulation of the turbulent structure in compound open-channel flows. Adv. Water Resour. 53, 66–75. doi: 10.1016/j.advwatres.2012.10.009

CrossRef Full Text | Google Scholar

Yang L., Liu F., Gong W., Cai H., Yu F., Pan H. (2019). Morphological response of lingding bay in the pearl river estuary to human intervention in recent decades. Ocean Coast. Manage. 176, 1–10. doi: 10.1016/j.ocecoaman.2019.04.011

CrossRef Full Text | Google Scholar

Yuan X., Yang Q., Luo X., Yu F., Liu F., Li J., et al. (2019). Distribution of grain size and organic elemental composition of the surficial sediments in lingding bay in the pearl river delta, china: A record of recent human activity. Ocean Coast. Manage. 178, 104849. doi: 10.1016/j.ocecoaman.2019.104849

CrossRef Full Text | Google Scholar

Zhang G., Chen Y., Cheng W., Zhang H., Gong W. (2021). Wave effects on sediment transport and entrapment in a channel-shoal estuary: The pearl river estuary in the dry winter season. J. Geophysical Research: Oceans 126, e2020JC016905.

Google Scholar

Zhu L., Zhang H., Guo L., Huang W., Gong W. (2021). Estimation of riverine sediment fate and transport timescales in a wide estuary with multiple sources. J. Mar. Syst. 214, 103488. doi: 10.1016/j.jmarsys.2020.103488

CrossRef Full Text | Google Scholar

Zu T., Gan J. (2015). A numerical study of coupled estuary–shelf circulation around the pearl river estuary during summer: Responses to variable winds, tides and river discharge. Deep Sea Res. Part II: Topical Stud. Oceanography 117, 53–64. doi: 10.1016/j.dsr2.2013.12.010

CrossRef Full Text | Google Scholar