
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mar. Sci. , 12 April 2023
Sec. Physical Oceanography
Volume 10 - 2023 | https://doi.org/10.3389/fmars.2023.1027704
This article is part of the Research Topic Meridional Exchanges of the Southern Ocean View all 6 articles
 Fabio Boeira Dias1,2,3*
Fabio Boeira Dias1,2,3* Stephen R. Rintoul4,5
Stephen R. Rintoul4,5 Ole Richter6
Ole Richter6 Benjamin Keith Galton-Fenzi5,7,8
Benjamin Keith Galton-Fenzi5,7,8 Jan D. Zika3,9
Jan D. Zika3,9 Violaine Pellichero4,10
Violaine Pellichero4,10 Petteri Uotila1
Petteri Uotila1Water mass transformation (WMT) around the Antarctic margin controls Antarctica Bottom Water formation and the abyssal limb of the global meridional overturning circulation, besides mediating ocean-ice shelf exchange, ice sheet stability and its contribution to sea level rise. However, the mechanisms controlling the rate of WMT in the Antarctic shelf are poorly understood due to the lack of observations and the inability of climate models to simulate those mechanisms, in particular beneath the floating ice shelves. We used a circum-Antarctic ocean-ice shelf model to assess the contribution of surface fluxes, mixing, and ocean-ice shelf interaction to the WMT on the continental shelf. The salt budget dominates the WMT rates, with only a secondary contribution from the heat budget. Basal melt of ice shelves drives buoyancy gain at lighter density classes (27.2<σθ< 27.6 kg m-3), while salt input associated with sea-ice growth in coastal polynyas drives buoyancy loss at heavier densities (σθ> 27.6). We found a large sensitivity of the WMT rates to model horizontal resolution, tides and topography within the Filchner-Ronne, East and West Antarctica ice shelf cavities. In the Filchner-Ronne Ice Shelf, an anticyclonic circulation in front of the Ronne Depression regulates the rates of basal melting/refreezing and WMT and is substantially affected by tides and model resolution. Model resolution is also found to affect the Antarctic Slope Current in both East and West Antarctica, impacting the on-shelf heat delivery, basal melt and WMT. Moreover, the representation of the ice shelf draft associated with model resolution impacts the freezing temperature and thus basal melt and WMT rates in the East Antarctica. These results highlight the importance of resolving small-scale features of the flow and topography, and to include the effects of tidal forcing, to adequately represent water mass transformations on the shelf that directly influence the abyssal global overturning circulation.
Antarctic Bottom Water (AABW) is the densest water mass of the global ocean and redistribute heat and salt through the lower limb of the global meridional overturning circulation (MOC). AABW forms on the Antarctic continental shelf, sinks down the continental slope and partially fills the ocean’s abyss, accounting for about 36% of the global ocean’s volume (Johnson, 2008) and representing a primary ventilation pathway of the deep ocean (Purkey and Johnson, 2013; Newsom et al., 2016). AABW has become warmer and fresher in recent decades (Rintoul, 2007; Jacobs and Giulivi, 2010; Schmidtko et al., 2014; van Wijk and Rintoul, 2014), therefore contracting in volume and contributing to sea-level changes (Church et al., 2011; Purkey and Johnson, 2013). However, the mechanisms driving change in AABW are not yet fully understood (Silvano, 2020).
Processes on the Antarctic shelf influence present and future climate largely through water mass transformations occurring on the continental shelf and under the ice shelves. Dense Shelf Water (DSW) forms in coastal polynyas (Orsi et al., 1999; Tamura et al., 2011), where strong buoyancy loss (due to cooling and brine rejection during sea-ice formation) produces the dense water that ultimately is exported from the shelf to form AABW. Circumpolar Deep Water (CDW), a relatively warm and salty water with origins in the subpolar North Atlantic, upwells around the Antarctic continent and in some locations reaches ice shelf cavities; being relatively warm, CDW drives strong ice shelf basal melting and mass loss (Jacobs et al., 1992; Pritchard et al., 2012; Schmidtko et al., 2014; Rignot et al., 2019).
Observations on the Antarctic continental shelf are sparse and biased towards summer months (Heywood et al., 2014). Observations of water mass transformation processes in winter (Garabato et al., 2016) and under ice shelves are particularly sparse. Modelling of Antarctic shelf processes, such as coastal polynyas, Dense Shelf Water (DSW) formation, ocean-ice shelf interaction, and eddy transports, is also challenging, requiring higher resolution than that available in current climate models (Dias et al., 2021; Heuzé, 2021). Ocean-ice shelf models have generally been applied to particular regions of the Antarctic margin (Dinniman et al., 2016).
Given the importance of water mass transformations on the Antarctic shelf, and the challenges in both observing and simulating them, we adopt an alternative approach to investigating these interactions. We use the water mass transformation (WMT) framework (Abernathey et al., 2016; Groeskamp et al., 2019) to quantify the contribution of individual physical processes to WMT on the Antarctic continental shelf. We apply the method to output from a high resolution (up to 2 km) circum-Antarctic regional ocean-ice shelf model (Richter et al., 2022a). By combining observation-based estimates of the salt fluxes produced by sea-ice formation in coastal polynyas and by ocean-ice shelf interaction, this study takes a major step towards improving scientific understanding of water mass interactions on the Antarctic shelf.
This study aims to quantify the rates of water mass transformation over the whole Antarctic shelf and understand the contribution from processes acting on the continental shelf and in the ice shelf cavities. While other studies have highlighted WMT driven by freshwater fluxes in the open Southern Ocean (Abernathey et al., 2016; Pellichero et al., 2018), our model results show that sub-ice shelf processes also drive strong WMT. We found that WMT is particularly sensitive to changes in model resolution (including topography) as well as to tides; which impacts the ocean circulation within and/or nearby the ice shelf cavities, causing temperature changes that affects ocean-ice shelf fluxes (i.e., basal melting and refreezing) and the transformation rates. This sensitivity is largest underneath the Filchner-Ronne Ice Shelf (FRIS) and in parts of the East and West Antarctica sectors; therefore our analyses explore the processes driving WMT these particular regions.
Details of the ocean-ice shelf model and the WMT framework are described in Section 2. The experimental design and validation are shown in Section 3.1. Analyses of the circumpolar WMT on the Antarctic shelf is presented in Section 3.2 and model sensitivity to tidal forcing and bathymetric resolution is investigated in Section 3.3. Plausible mechanisms of regional WMT in the FRIS, East and West Antarctica regions are explored in Section 3.4. Discussion and conclusions are summarized in Section 4.
The Whole Antarctica Ocean Model (WAOM) was developed at the University of Tasmania and builds on extensive experience in ocean-ice shelf modelling (e.g. Galton-Fenzi et al., 2012; Cougnon et al., 2013; Gwyther et al., 2016) to create a circum-Antarctic domain (Richter et al., 2022a). WAOM is based on the Regional Ocean Modelling System (ROMS 3.6), a primitive-equation, finite-difference model with terrain-following vertical coordinate (Haidvogel et al., 2008; Shchepetkin and McWilliams, 2009). WAOM is configured with a curvilinear coordinate grid (south polar projection) in a circum-Antarctic domain that extends roughly to 60°S (see model domain in Figure 1) and contains 31 vertical layers. We run the model in three configurations with different horizontal resolution (10, 4 and 2 km), all including tidal forcing (Makinson et al., 2011; Arzeno et al., 2014). The 2 km setup is capable of resolving the internal Rossby radius of deformation (Hallberg, 2013) at most regions and details of the bathymetry and ice shelf. The focus of WAOM is on resolving ocean-ice shelf interactions and it does not include a sea-ice model; instead, the model is forced with air-sea fluxes from sea-ice estimates derived from satellite imagery (Tamura et al., 2011) - see Section 2.1.
The main details of the model configuration are described below; for more information see Richter et al. (2022a). WAOM is implemented using a 4th-order Akima advection scheme for horizontal and vertical tracers and harmonic horizontal mixing along epineutral (isopycnal) surfaces for tracers with coefficients varying accordingly to horizontal resolution (50, 20 and 10 m2s-1 for 10, 4 and 2 km, respectively). For momentum, WAOM used harmonic horizontal viscosity (coefficients of 500, 200, 100 m2s-1, respectively) along sigma surfaces. Vertical mixing of tracers followed the K-Profile Parameterisation (KPP, Large et al., 1994). The ice sheet-ocean thermodynamics followed the 3-equation melt parameterization (Holland and Jenkins, 1999) as implemented by Galton-Fenzi et al. (2012) and described in Gwyther et al. (2016).
WAOM simulates the year 2007 following a Repeat Year Forcing (RYF) approach, where surface fluxes and wind stress for this specific year are non-anomalous for the period between 1992 and 2011 (Richter et al., 2022a). The spin-up approach involves different lengths for each resolution: 20-years for the 10 km setup (WAOM10), 10 years for the 4 km (WAOM4), and 5-years for the 2 km (WAOM2), where the high-resolution simulations are initiated from the restart of the next coarser experiment (Figure 2). All the analyses presented are based on the last year of each simulation. In addition to the 10, 4 and 2 km experiments, two decade-long sensitivity experiments were conducted with the 4 km resolution: a non-tidal simulation (only deactivating tidal forcing - hereafter referred as WAOM4-NOTIDE) and an experiment with coarse-resolution topography (10 km topography interpolated by nearest neighbor to 4 km grid, WAOM4-COARSE).
The bottom topography and ice draft are derived from Bedmap2 (south of 60°S) (Fretwell et al., 2013) and RTopo-2 (north of 60°S) (Schaffer et al (2016). The model topography was smoothed using the Mellor-Ezer-Oey method Mellor et al., (1998) to constrain the slope factor r=|(hi−hi+1)|/(hi+hi+1) , h, is the water column thickness) below or equal to 0.3. This criteria was imposed in all experiments.
Lateral conditions on the WAOM open boundaries are a combination of a global reanalysis and tidal forcing. The model domain extends roughly to 60°S (Figure 1), where at the northern open boundary the model is forced with sea surface height (ssh), barotropic and baroclinic currents, temperature and salinity from monthly outputs from the ECCO2 reanalysis (Menemenlis et al., 2008). The relaxation time scale is 3 (ssh and momentum) and 365 (tracers) days, with an outflow/inflow nudging factor of 30 (i.e., stronger nudging on the inflow than on outflow; Marchesiello et al., 2001). Tidal forcing is derived from the global tidal solution TPXO7.2 (Egbert and Erofeeva, 2002), comprising 13 tidal constituents (M2, S2, N2, K2, K1, O1, P1, Q1, MF, MM, M4, MS4, MN4), forced at the open boundaries through sea surface height and barotropic currents (added to the ECCO2 conditions). The initial ocean temperature and salinity are also from ECCO2, obtained from January 2007; values from the ice front are extrapolated to under the ice shelves. A spin-up of 20 years should be long enough to flux the cavities (Holland, 2017) and achieving an equilibrate state (Richter et al., 2022b). There is no river runoff (from sub-glacial hydrology) applied in WAOM.
WAOM does not include a sea-ice model; instead, the surface buoyancy fluxes are estimated from satellite based sea-ice data (Tamura et al., 2011). Daily surface buoyancy fluxes are estimated via bulk formulae (Dee et al., 2011) using the sea-ice thickness calculated through the Tamura et al. (2007) algorithm, ERA Interim atmospheric state, and sea surface temperature (SST) from the optimum interpolation climate-scale in situ and satellite SST (OISST; weekly average) dataset for ice-free areas; SST is defined as the surface freezing temperature in sea ice-covered areas (Tamura et al., 2011). The surface salinity is relaxed towards the Southern Ocean State Estimate, which is based on global ECCO but focused on Southern high-latitudes (Mazloff et al., 2010), with a timescale of one month. Prescribed surface buoyancy fluxes are more likely to represent the strength and position of coastal polynyas than sea-ice models (Tamura et al., 2008; Tamura et al., 2011; Ohshima et al., 2016; Tamura et al., 2016), as the current generation of sea-ice models does not capture the small-scale effects of (katabatic) winds and icebergs well (Richter et al., 2022a), important processes regulating activity and extend of coastal polynyas (Kusahara et al., 2010; Mathiot et al., 2010). This approach helps to simulate the ocean heat loss and brine rejection fluxes that contribute to High-Salinity Shelf Water formation - see Section 3.2. The Tamura et al. (2007) fluxes include an estimate of freshwater input by sea-ice melt, as well as brine released during sea-ice formation.
The WAOM configuration in this study differs slightly from Richter et al. (2022a) with regards to the model domain and the treatment of surface fluxes. The domain has been extended north in the Ross Sea sector, which results in more realistic circulation patterns and reduced SST biases (not shown). The treatment for the surface fluxes has also been modified. Downward (positive) surface heat flux (i.e., during summer months) has been reduced by 25% of the original value - sensitivity tests have shown that this helps to further to reduce SST warm biases (Richter et al. (2022a) used 50% reduction). In contrast to the treatment of surface salt fluxes in Richter et al. (2022a), where salt input (i.e., brine rejection) was suppressed if the water temperature was not at the freezing point, here we did not modify the salt fluxes from Tamura et al. (2011). While this modification may seem less realistic, as brine rejection does not occur if water temperature is above the surface freezing point, this ensures that the salt input to the ocean remains close to the observation-based product, even if the model temperature in WAOM has positive temperature biases. Ultimately, this considerably increases continental shelf bottom salinity in comparison with Richter et al. (2022a) (see their Figure 9 versus Figure 1) and makes it more realistic. Surface cooling is still suppressed if SST is at freezing point to avoid supercooling. Surface relaxation towards the SOSE was maintained for salinity, but it was disabled for temperature as the configuration changes described above decreased SST biases to an acceptable level.
To quantify the mechanisms contributing to water mass transformation on the Antarctic shelf, we implemented the WMT framework (Walin, 1982; Abernathey et al., 2016; Groeskamp et al., 2019) to the last year of WAOM simulations. The WMT framework quantifies the transformation rates of water masses toward denser (positive transformation) or lighter (negative transformation) densities. The WMT calculations in WAOM (ROMS) are based on the temperature (Eqn. 1) and salinity (Eqn. 2) equations:
where θ is the potential temperature (hereafter just temperature) and S is the salinity, and are the material derivative of temperature and salinity given by the sum of the time tendencies ( and ) and advective terms ( and ), Kθ and Ks are the vertical eddy diffusivities, and Dθ and DS are the horizontal diffusive terms. We saved heat and salt budget diagnostics as 5-day averages, which include the terms of Eqns. 1 and 2 decomposed into net tendency, horizontal advection, vertical advection, horizontal diffusion, and vertical diffusion.
The vertical boundary condition for the vertical diffusion is zero at the bottom and equal to the surface heat and salt fluxes at the ocean surface. This means that the vertical integral (between the free surface elevation ζ and the ocean bottom -h) of the vertical diffusion terms (Kθ ∂θ/∂z and KS ∂S/∂z ) equal to the surface fluxes:
where Q is the surface heat flux, ρ0 is a reference density (1025 kg m-3), Cp is the specific heat of seawater (3985 J kg-1 °C-1), SSS is the sea surface salinity, F is the surface freshwater flux (kg m-2 s-1) and Δzk=1 is the surface layer thickness. While the surface fluxes – which includes both the Tamura et al. (2011) fluxes outside of the ice shelf cavities and the exchanges at the base of the ice shelf – is embedded in the vertical diffusion term in equations 1 and 2; the effect from the surface fluxes is separated from the diffusion terms for the WMT analyses (Section 3.2) by subtracting the surface fluxes from the vertical diffusion in order to distinguish WMT caused by internal mixing from WMT induced by the surface fluxes.
The contribution of the heat (Eqn. 1) and salt (Eqn. 2) budgets to changes in water masses are combined via the potential density (σθ) equation:
where ∂σθ/∂θ and ∂σθ/∂S are the thermal expansion and salinity contraction coefficients, respectively, calculated from the annual averaged 2-D potential temperature, absolute salinity and pressure model fields using the Gibbs-SeaWater toolbox (McDougall and Barker, 2011) that follows TEOS-10.
To evaluate the transformation rates (Ω), we follow previous work (e.g. Abernathey et al., 2016; Pellichero et al., 2018) and discretize potential density into 40 evenly spaced bins (Δσθ= 0.05 kg m-3). For each density bin, the terms in the potential density equations are integrated vertically through the water column (h) and horizontally:
where Ac is the horizontal area of the grid cell, Nx and Ny are the grid horizontal coordinates, Δzk is the thickness of vertical layers, and δ(σθ−σθ′) is the delta function that defines the density bins in relation to an outcrop density σ′θ
In addition to interpretation of the transformation rates in density space (Section 3.2), we also explored the regional variability in the annual mean transformation processes (Section 3.4). Transformation m s-1 are produced by evaluating Eqn. 6 without the grid cell area (Ac) and without the summations over the horizontal coordinates (Nx and Ny; Brambilla et al., 2008; Maze et al., 2009; Abernathey et al., 2016).
The spin-up approach of our WAOM simulations is summarized in Figure 1. As the model is forced with repeat year forcing, changes in ocean properties at timescales longer than annual are only expected as a result of the model adjustment to its preferred state. The evolution of the ocean heat content (OHC) anomalies (relative to the first year) integrated throughout the continental shelf (defined as regions shallower than 2000 m) is shown in Figure 1A. The WAOM10 evolves to a warmer state (∼0.41-43 GJ) during the first 9 years, reaching an equilibrium after that. The WAOM4 is initiated from the year 10 of the WAOM10 and it drifts toward colder shelf waters (∼0.2 GJ during 10 simulated years) - a substantially smaller drift than WAOM10. Similarly, the WAOM2 is initialized from year 5 of the WAOM4 and drifts ∼0.2 GJ, mostly in the first year. The evolution of salt content shows that the salinity drift of shelf waters in WAOM10 experiences a freshening in the first 9 years, stabilizing afterwards, while the WAOM4 and WAOM2 experience salinity increasing throughout the simulations (Figure 1B). These two experiments have enhanced HSSW formation in comparison with WAOM10 (see Section 3.2 and Figures 2F, H) and this contributes to the salt content drift. This drift reflects the contribution of the Ross Sea and East Antarctica sectors, while other regions (see Figure 2C for sectors’ limits) have relatively small salinity drifts (not shown). Despite the moderate drift in ocean temperatures and salinity, mean kinetic energy (MKE, Figure 1C) decreases after model initialization in all experiments, showing stabilization of the ocean circulation after the first 8 years of the simulation. Experiments with higher horizontal resolution seem to achieve a lower energetic state faster than the coarse resolution one. The model has been initialized from a reasonable state from ECCO2 (except for sub-ice shelf cavities). The purpose of the spin-up is to get the model over its initial shock (e.g. flush the cavities, for which 20 years is enough time, Holland, 2017). Remaining model drift is considered to be acceptable for the purpose of this study, which focuses on transformation rates and not ocean states. In particular, the substantial salt drift in WAOM4 and WAOM2 does not affect qualitatively the WMT results shown in the Section 3.2 (Figure S1).
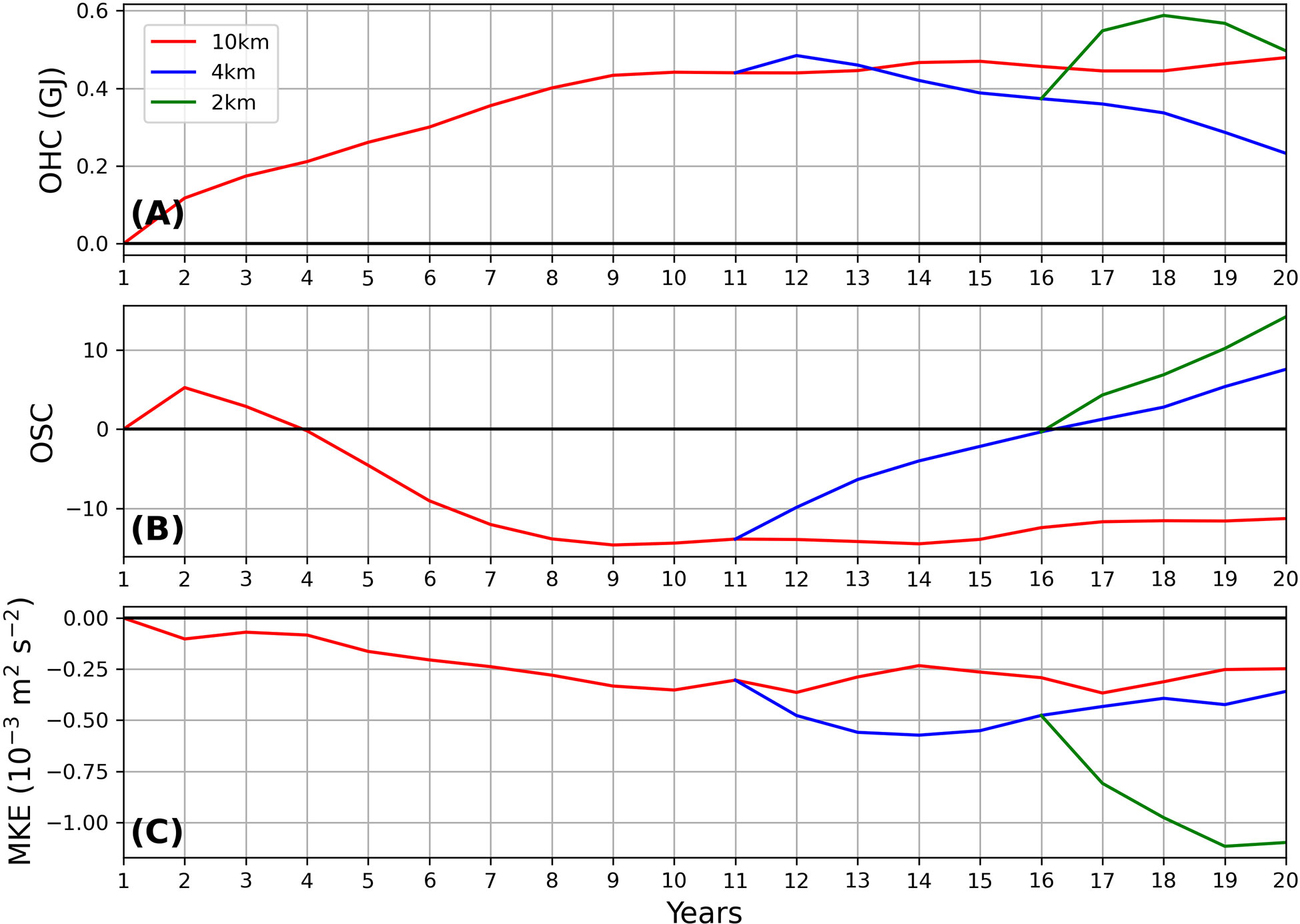
Figure 1 Time evolution of the annual mean, horizontally-integrated anomalies with respect to the first model year average of (A) ocean heat content (10 Joules = GJ) and (B) ocean salt content on the continental shelf (depths shallower than 2000 m); (C) mean kinetic energy (m s) averaged through the entire domain, for the WAOM10 (red), WAOM4 (blue), and WAOM2 (green) experiments.
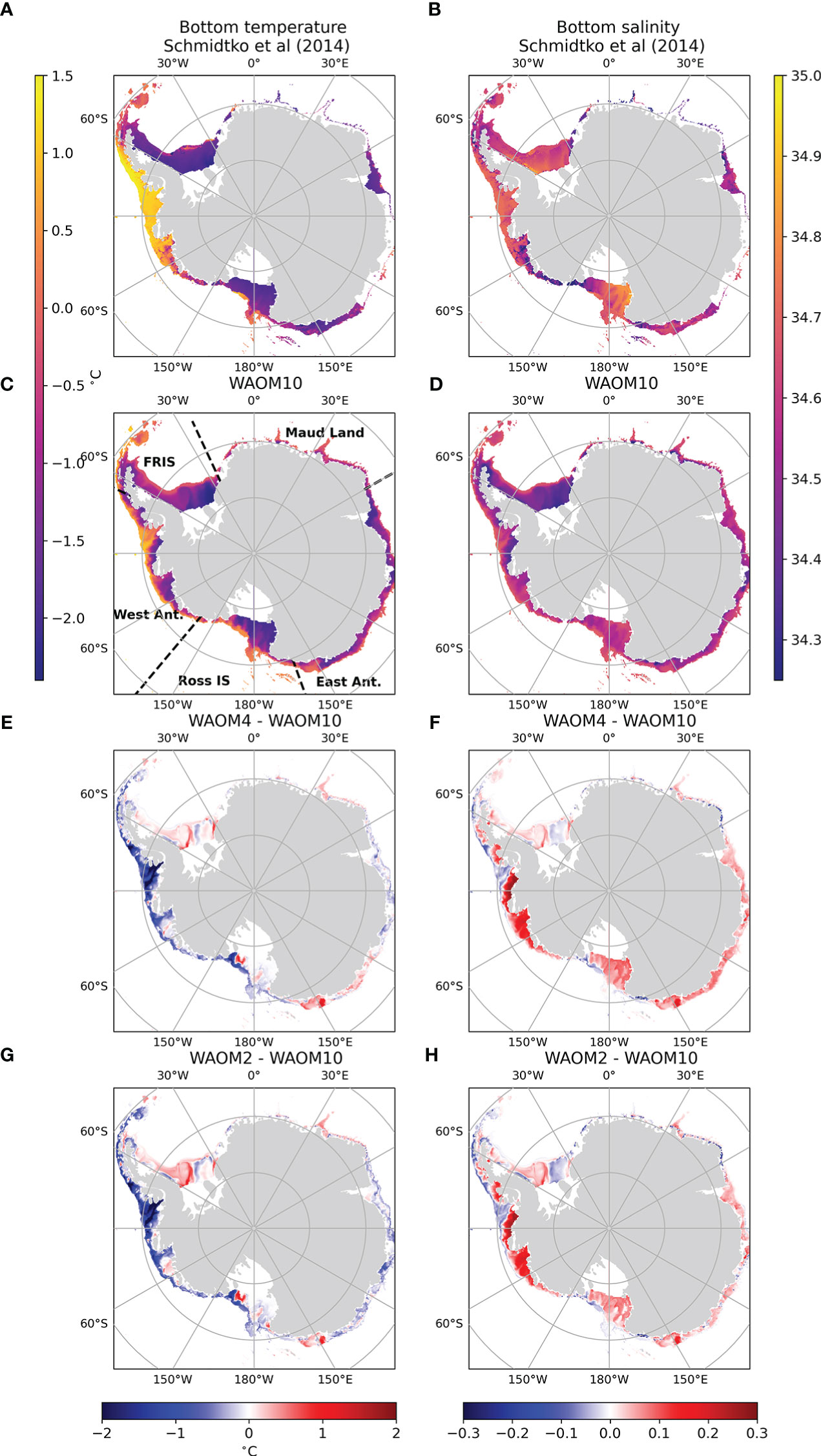
Figure 2 Annual average bottom potential temperature (°C, left column) and salinity (right column) from Schmidtko et al. (2014) (A, B) and for the last year of WAOM10 (C, D); and bottom potential temperature and salinity anomalies for (E, F) WAOM4 (WAOM4 - WAOM10) and (G, H) WAOM2 (WAOM2 - WAOM10). Ice shelf cavities and regions deeper than 2000 m are masked to allow a direct comparison with [942014Schmidtko et al.Schmidtko, Heywood, Thompson, and Aoki].
The bottom temperature and salinity properties on the continental shelf (excluding the ice shelf cavities) are presented in Figure 2. Our baseline for comparison between modelled and observed bottom temperature and salinity is from Schmidtko et al. (2014), shown in Figures 2A, B, which gathered observations for the 1975–2012 period from six different sources, including the World Ocean Database, Argo floats, and others. Even though the lack of observations over the Antarctic shelf is striking (see Schmidtko et al., 2014, Figure S1), some biases in the WAOM simulations are evident: (a) the Bellingshausen and Amundsen Seas are colder than observational estimates, especially in the WAOM4 and WAOM2, and fresher in the WAOM10 experiments, (b) the Weddell Sea is too fresh in all experiments, and (c) the Cosmonaut Sea and the shelf between Ross and Amundsen seas are too salty (Figure 2).
An evaluation of the modelled spatial patterns and magnitude of the ocean-driven basal melting of the Antarctica Ice Shelf is shown in Figure 3. The simulated basal melt rates represents similarities with the observation estimates in many regions, although some discrepancies are also evident (Richter et al., 2022b). In the Filchner-Ronne Ice Shelf, the simulated pattern of melting near both the ice front and the grounding line, and refreezing in the central cavity, resembles those estimated from satellites (Adusumilli et al., 2020), although the refreezing rates are underestimated by the model (enhancement of refreezing occurs with increased model resolution, Section 3.4.1). The Maud Land region (30°W-45°E) and East Antarctica sector both overestimate the melt rates at WAOM10 (linked with warm bias, Figure 2), whereas lower rates are seen at higher resolution. The West Antarctica, despite the cold bias in WAOM10, have fairly close melt rate distribution to observational estimates; enhancement of this cold bias at high resolution (WAOM4/WAOM2) result in underestimated melt rates. Lastly, beneath the Ross Ice Shelf, modelled melt rates are smaller than those from observations, except in WAOM10 where high melt rates are seen in the east side near the ice front (due to warm water intrusion, Figures 2A, C). A more comprehensive assessment of the melt rates in WAOM is presented in Richter et al. (2022b).
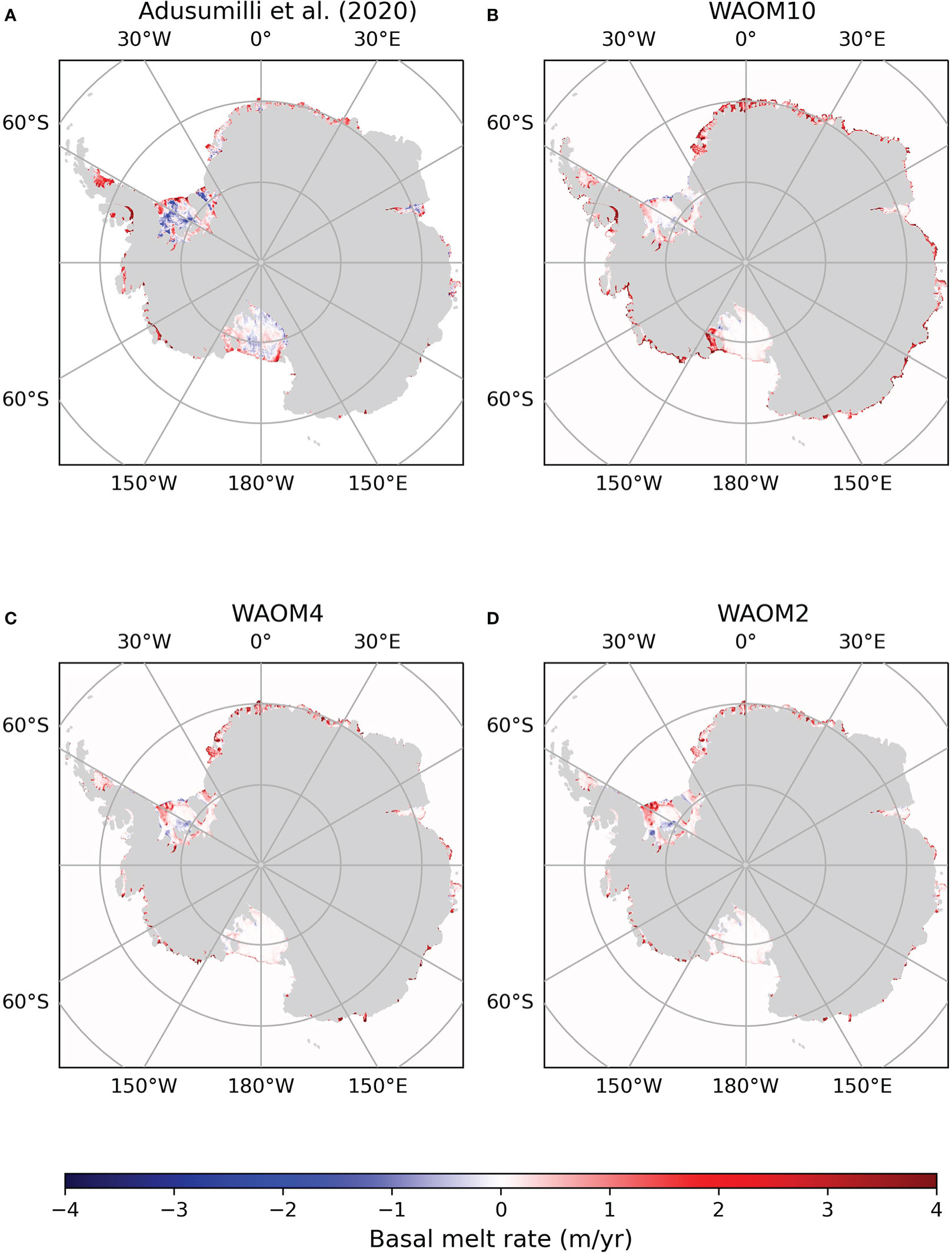
Figure 3 Maps of annual averaged basal melt rates (m yr-1) for (A) the observational estimate from Adusumilli et al. (2020) and WAOM experiments: (B) WAOM10, (C) WAOM4, and (D) WAOM2. Positive melt rates mean basal melting of the ice shelf and negative rates represent refreezing.
Differences between modelled and observed states can occur due to several factors: variations in time period (e.g., simulated year 2007 versus observations from a 37-year average in the case of Schmidtko et al., 2014), the spatial and temporal sparseness of observations (e.g., measurement bias towards summer months), and uncertainties in the surface fluxes (either in the Tamura et al., 2011 dataset and in WAOM due to the lack of a sea-ice model). The cold biases in West Antarctica at higher resolutions (2 and 4 km) are caused by the lack of warm, salty waters (i.e., CDW). Previous studies indicate that CDW transport to the shelf is enhanced with increased model resolution (Nakayama et al., 2014; Dinniman et al., 2016), but the opposite is observed in our set of WAOM simulations, as shown in Richter et al. (2022a; their Figure 5A). A stronger Antarctic Slope Current (ASC) in the shelf break between the Bellingshausen and Amundsen Seas at higher resolutions (Section 3.4.3) inhibits the CDW transport to the shelf. Low salinity in the Weddell Sea is associated with the surface forcing (Tamura et al., 2011), where there exists a lower salt input in this region as compared to other coastal polynyas; basal melting also contributes to low salinity (Figure 3 and Section 3.4.1). Reasons for salty biases in the Cosmonaut Sea are not clear, as the ice shelves and associated ice melting in this region are generally small (Rignot et al., 2013). In contrast, the section between Amundsen and Ross seas has a fair amount of basal melting in all WAOM experiments (e.g., Richter et al., 2022a, Figure 11), although bottom salinity is higher than observed (Schmidtko et al., 2014). This might be a case where apparent model biases may in part reflect sparse observations; Figure S1 in Schmidtko et al. (2014) shows that this shelf region has only been observed once in the 1990s.
The water mass transformation rates due to individual processes are presented in Figure 4. The transformation rates are calculated over the Antarctic shelf (depths < 2000 m) for each potential density class (Δσθ = 0.05), following Eqn. 6. The contribution from the surface heat and salt fluxes to WMT accounts for the fluxes from [1072011 Tamura et al. (2011) Tamura, Ohshima, Nihashi, and Hasumi] and the fluxes due to ocean-ice shelf interaction (magenta lines in Figure 4). Positive transformation indicates waters are becoming denser (reducing buoyancy) whereas negative transformation indicates waters are becoming lighter (increasing buoyancy). The surface heat flux makes waters heavier as a response to surface heat loss through a large range of densities (27.3< σ θ < 27.7 kg m-3), peaking at ∼2 Sv at 27.7 kg m-3 (Figures 4A, C, E). The surface salt fluxes decrease buoyancy at σθlarger than ∼27.5 kg m-3 (up to 6 Sv at 27.7 kg m-3) and increase buoyancy at σθsmaller than ∼27.5 kg m-3 (Figures 4B, D, F). Density increase due to salt fluxes results from brine rejection in coastal polynyas, whereas density reduction is associated with freshwater input from basal melting of the ice shelves (Sections 3.4). (Buoyancy gain driven by sea-ice melt makes a small contribution on the Antarctic shelf.) The distribution of WMT driven by surface heat fluxes is mostly similar across WAOM experiments; however, the model experiments show differences in WMT due to surface salt fluxes: stronger buoyancy gain occurs in WAOM10 (∼5 Sv) than WAOM4/WAOM2 (around 2 Sv) and buoyancy loss slightly increases with higher model resolution.
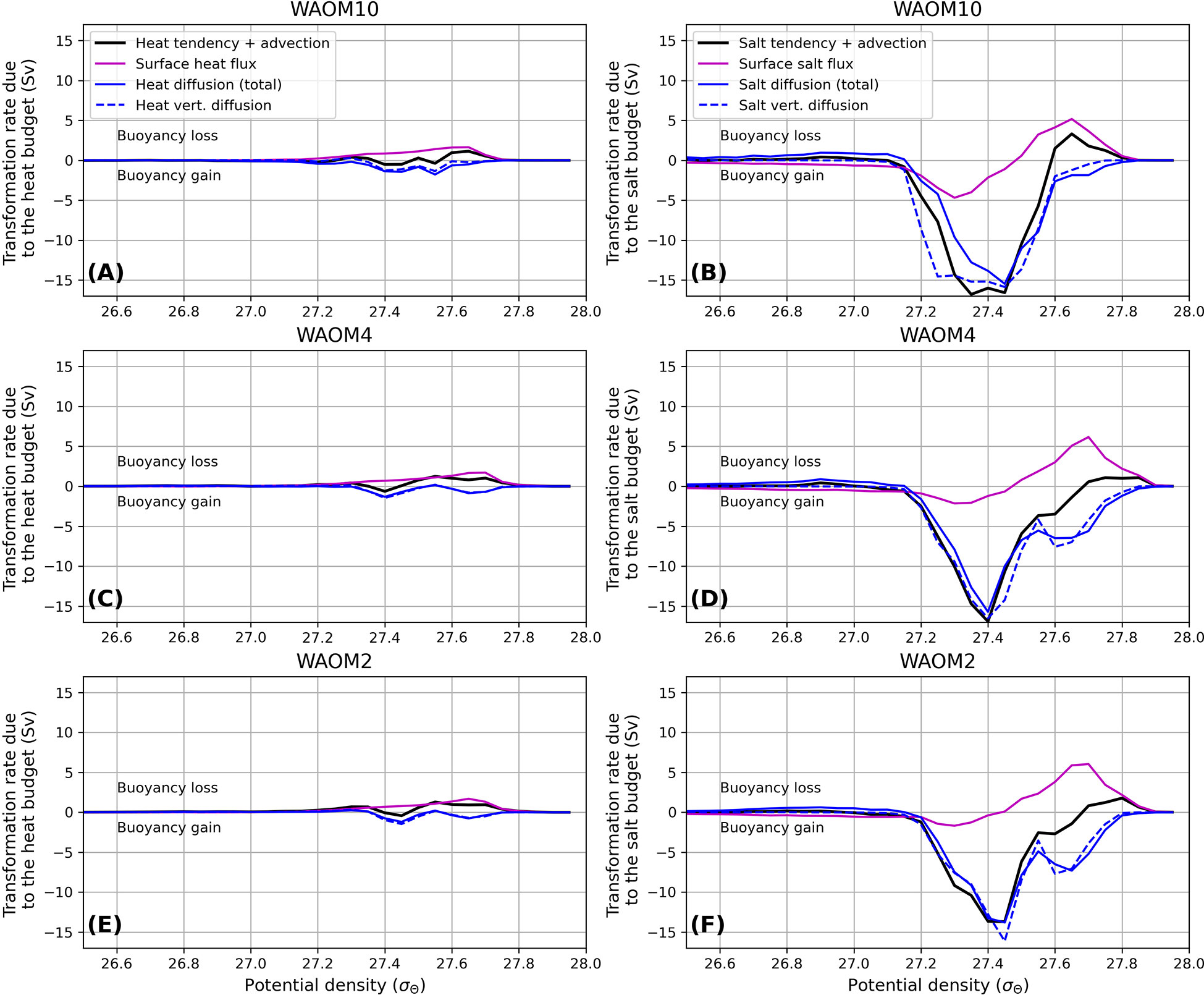
Figure 4 Water Mass Transformation rates over the Antarctic shelf (depth less than 2000 m, in Sv), calculated following Eqn. 6, for the WAOM10 (A, B), WAOM4 (C, D) and WAOM2 (E, F) experiments. WMT due to the heat (left column) and salt (right column) budgets are broken down into the contribution from the surface fluxes (magenta) and total internal diapycnal diffusion (horizontal plus vertical, blue; vertical diffusion only is shown as dashed blue lines), and the total WMT (material derivatives in LHS of Eqns. 1 and 2, black). Positive (negative) WMT rates denote buoyancy loss (gain).
The total WMT at a specific density class is given by the sum of the surface fluxes effect and the internal diapycnal mixing (Eqns. 1-4). Buoyancy loss is induced by the surface heat flux (peak at σθ = 27.7 kg -3), which is weakly compensated by buoyancy gain due to internal mixing of heat, resulting small WMT at order of ∼1-2 Sv (black lines in Figures 4A, C, E). The combined WMT (due to both heat and salt diapycnal fluxes) is largely dominated by the salt contribution, with WMT reaching up to -16 Sv at ∼27.4 kg m-3 (black lines at Figures 4B, D, F). This increase in buoyancy is driven by internal mixing of salt/freshwater (blue lines, with a secondary contribution from the surface salt fluxes), mostly due to the vertical diffusion component (blue dashed line), and occurs between 27.2 to 27.6 kg m-3; increased model resolution reduces the buoyancy gain. At densities larger than 27.6 kg m-3, the total WMT due to the salt fluxes is a balance between positive effect from the surface salt fluxes (i.e., brine rejection at coastal polynyas) and negative effect from internal mixing. Increased resolution enhances this negative effect from internal mixing, resulting in smaller total buoyancy loss (black line) in WAOM4/WAOM2 than WAOM10, although this occurs at higher densities in the high-resolution simulations (Figures 4D, F). Given the dominance of salt budget to WMT, the remainder of the paper will focus on WMT due to salt fluxes.
The WMT rates shown in Figure 4 are the results of transformation occurring at different areas of the Antarctic shelf. We decomposed the circum-Antarctic WMT on the continental shelf into regions within the ice shelf cavities (i.e., under the ice shelves) and the remaining portion of the continental shelf (i.e., the continental shelf excluding the ice shelf cavities). In addition, we defined five different sectors: Filchner-Ronne Ice Shelf (90°-25°W), Maud Land (25°W-60°E), East Antarctica (60°-160°E), Ross Ice Shelf (160°E-140°W), and West Antarctica (90°-160°W); black dashed boundaries in Figure 2C show the horizontal integration boundaries (Eqn. 6) used to explore contributions from different Antarctic sectors.
Considering water mass transformation in ice shelf cavities and on the continental shelf separately gives some insights on the drivers of net buoyancy loss and gain observed in Figure 4. Buoyancy gain occurs mostly under the ice shelves (Figure 5, left column). The Filchner-Ronne, Maud Land, East and West Antarctica sectors are primarily responsible for negative transformation rates. While buoyancy gain in Maud Land seems less sensitive to model resolution, the other sectors show important differences between simulations with different resolution. In the Filchner-Ronne Ice Shelf (FRIS), buoyancy gain (∼27.4 kg m-3) is enhanced in the high-resolution experiments (WAOM4/WAOM2). In the East and West Antarctica sectors, increased model resolution reduces buoyancy gain at lower densities (σ θ < 27.5 kg m-3) and enhances buoyancy gain at higher densities σθ < 27.6 kg m-3 (i.e., shifts the negative WMT driven by basal melt towards higher densities). In contrast to ice shelf cavities, on the continental shelf north of the ice fronts, buoyancy loss occurs over a large range of densities (27.2 - 27.8 kg m-3); East Antarctica is the main contributor, followed by the Ross Sea and West Antarctica sectors, to the positive WMT in the circum-Antarctic domain. Positive WMT is slightly stronger and occurs at higher densities in the high-resolution experiments (WAOM4/WAOM2) when compared with WAOM10, explained by enhanced buoyancy loss in the Ross Sea and West Antarctica sectors. Over the circum-Antarctic domain, increased buoyancy loss on the continental shelf in the high-resolution experiments is partially compensated by increased buoyancy gain within the ice shelf cavities (27.6 - 27.8 kg m-3; Figure 5). This suggests that ocean-ice shelf interactions have a large influence on the overall WMT around the Antarctic margin and thus on the abyssal limb of the meridional overturning circulation.
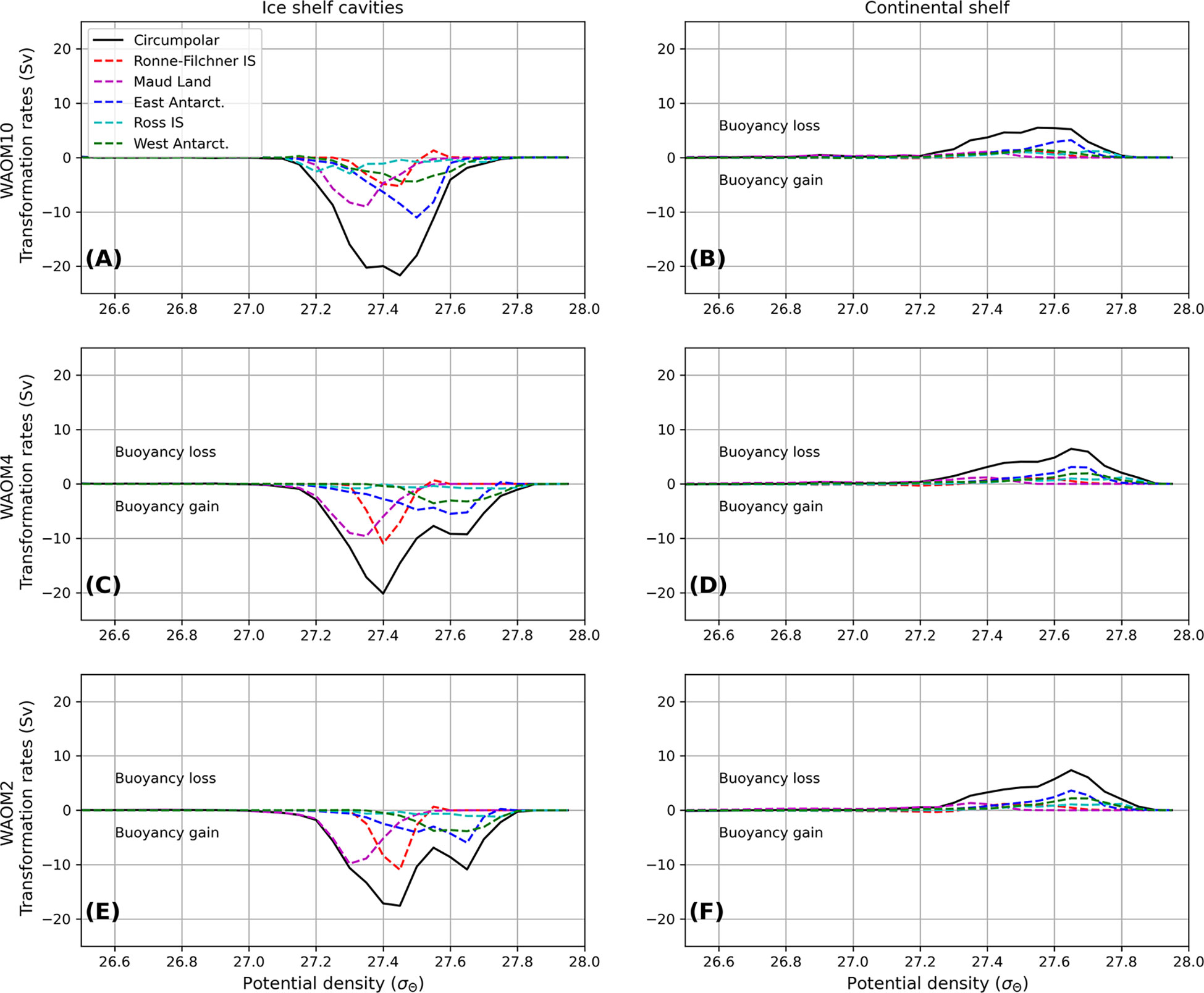
Figure 5 Total Water Mass Transformation rates (Sv) due to the salt budget for the WAOM10 (A, B), WAOM4 (C, D) and WAOM2 (E, F) experiments for the ice shelf cavities (left column) and continental shelf regions (right column, depths shallower than 2000 m excluding ice shelf cavities). The circum-Antarctic WMT (black line) is decomposed into the subregions showed in Figure 2: Filchner-Ronne Ice Shelf (dashed red), Maud Land (dashed magenta), East Antarctica (dashed blue), Ross Ice Shelf (dashed cyan), and West Antarctica (dashed green).
Isolating the contributions of the continental shelf and the ice shelf cavity supports the interpretation of the surface salt flux effects (Figures 4B, D, F): at lower densities (σ θ < ~ 27.6 kg m-3), buoyancy gain occurs due to basal melting of the ice shelves; at higher densities (σθ > ~27.6 kg m-3), buoyancy loss results from brine rejection due to sea-ice formation in coastal polynyas. The circum-Antarctic WMT suggests that the FRIS, East and West Antarctica are the most sensitive regions to model horizontal resolution. In the next section, we explore the influence of tidal forcing and bathymetric resolution on the circum-Antarctic WMT through sensitivity experiments using the WAOM4 setup (WAOM4-NOTIDE and WAOM4-COARSE).
Based on the WAOM4 setup, we conduct two sensitivity experiments: (1) deactivating the tidal forcing (WAOM4-NOTIDE) and (2) using a coarse resolution topography (10 km topography gridded via nearest interpolation, see Section 2.1 for details). Differences between the WAOM4 and WAOM4-NOTIDE experiments can be attributed exclusively to the tidal forcing. The WAOM4-COARSE experiment aims to separate the effects of mesoscale eddies (present in both WAOM4 and WAOM4-COARSE) from the effects of small-scale bathymetric features like channels, ridges and steep slopes (present in WAOM4 and smoothed in WAOM4-COARSE).
Figure 6 shows the circum-Antarctic WMT beneath the ice shelves and the decomposition into sectors (horizontal limits shown in Figure 2C) for WAOM4, WAOM4-NOTIDE and WAOM4-COARSE. When tides are not included, buoyancy gain under the ice shelves is decreased (peak at 27.4 kg m-3 reduces from -20 to -10 Sv, Figure 6B). The decrease of buoyancy gain in the simulation without tides largely reflects changes at the FRIS (with a secondary contribution from the Maud Land sector). The mechanisms of buoyancy gain under FRIS are investigated in detail in Section 3.4.1; this reveals a tidally-forced anticyclonic circulation north of the Ronne Ice Shelf that brings warm waters towards the cavity and affects basal melt rates. This circulation is sensitive to model resolution (stronger at higher resolution experiments), which results in buoyancy gain differences under FRIS across the WAOM simulations (Figures 5A, C, E).
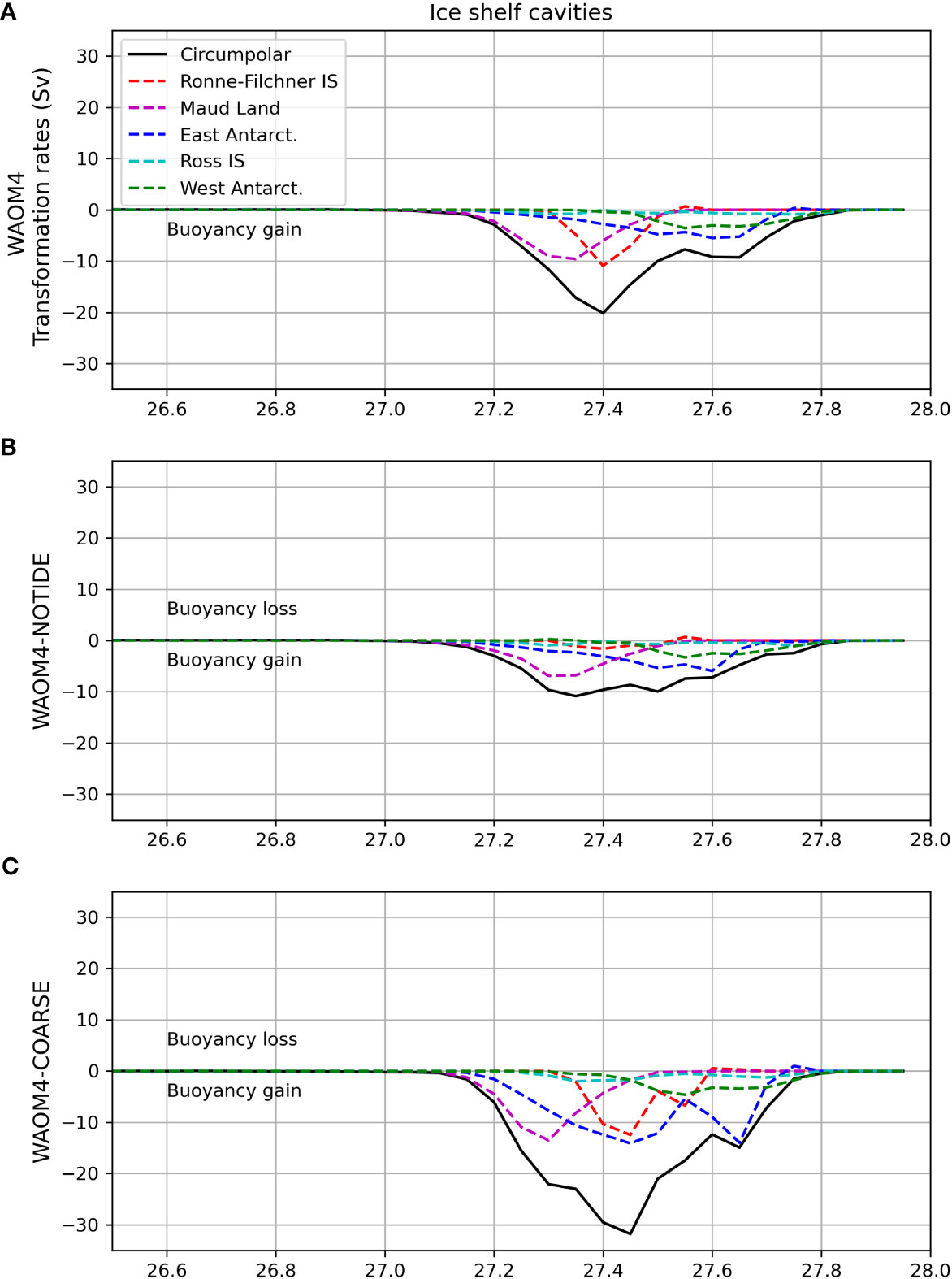
Figure 6 Total Water Mass Transformation rates (Sv) for the (A) WAOM4, (B) WAOM4-NOTIDE and (C) WAOM4-COARSE experiments integrated for the circum-Antarctic ice shelf cavities (solid lines) and regional sectors: FRIS (red dashed line), Maud Land (magenta dashed line), East Antarctica (blue dashed line), Ross (cyan dashed line) and West Antarctica (green dashed line). Positive (negative) WMT rates denote buoyancy loss (gain).
The experiment using coarse topography has increased buoyancy gain (up to -30 Sv at ∼27.45 kg m-3, Figure 8C), particularly beneath ice shelves in the East Antarctica sector, with smaller but significative contributions from FRIS and Maud Land. The East Antarctica changes occur across a large range of densities (27.3 to 27.7 kg m-3); these changes result from differences in melting rates near the grounding line (due to differences in the depth of the ice shelf base across experiments) and in cross-shelf heat transport (Section 3.4.2). The Maud Land sector experience a mild increase in buoyancy gain (from -10 to -13 Sv at 27.3 kg m-3. Underneath FRIS, an enhancement of the buoyancy gain between 27.4 and 27.55 m-3 is associated with a deeper Filchner Trough in WAOM4-COARSE than in WAOM4, which transports warm anomalies towards the Filchner Ice Shelf and increases melting near the ice front (not shown). The changes in the trough topography likely enhances the Antarctic Slope Current and eddy interaction (Klinck et al., 2010), resulting in stronger onshelf heat transport.
The circum-Antarctic WMT analyses show that regions beneath the ice shelves are the most sensitive to changes in model horizontal resolution, tidal forcing and topography. Regional decomposition indicates that WMT under the Filchner-Ronne, East and West Antarctica ice shelves are particularly sensitive. In this section, we evaluate the mechanisms driving WMT in each of these regions. Figure 7 shows the contribution of individual terms in Eqn. 2 (total WMT, salt tendency plus advection; internal diapycnal mixing, and surface salt flux) to the net WMT in the five model simulations (WAOM10, WAOM4, WAOM2, WAOM4-NOTIDE and WAOM4-COARSE). The total WMT integrated over the water column under the ice shelves is dominated by the contribution from internal mixing (Figures 7B, E, H), with secondary (but non-negligible) contribution from the surface salt fluxes (Figures 7C, F, I; note the different y-axis limits). The integrated WMT highlights the main factors contributing to the sensitivity of WMT in each of these regions: Filchner-Ronne depends on tidal forcing and model horizontal resolution; East Antarctica depends on model horizontal resolution and topography; West Antarctica depends on model horizontal resolution.
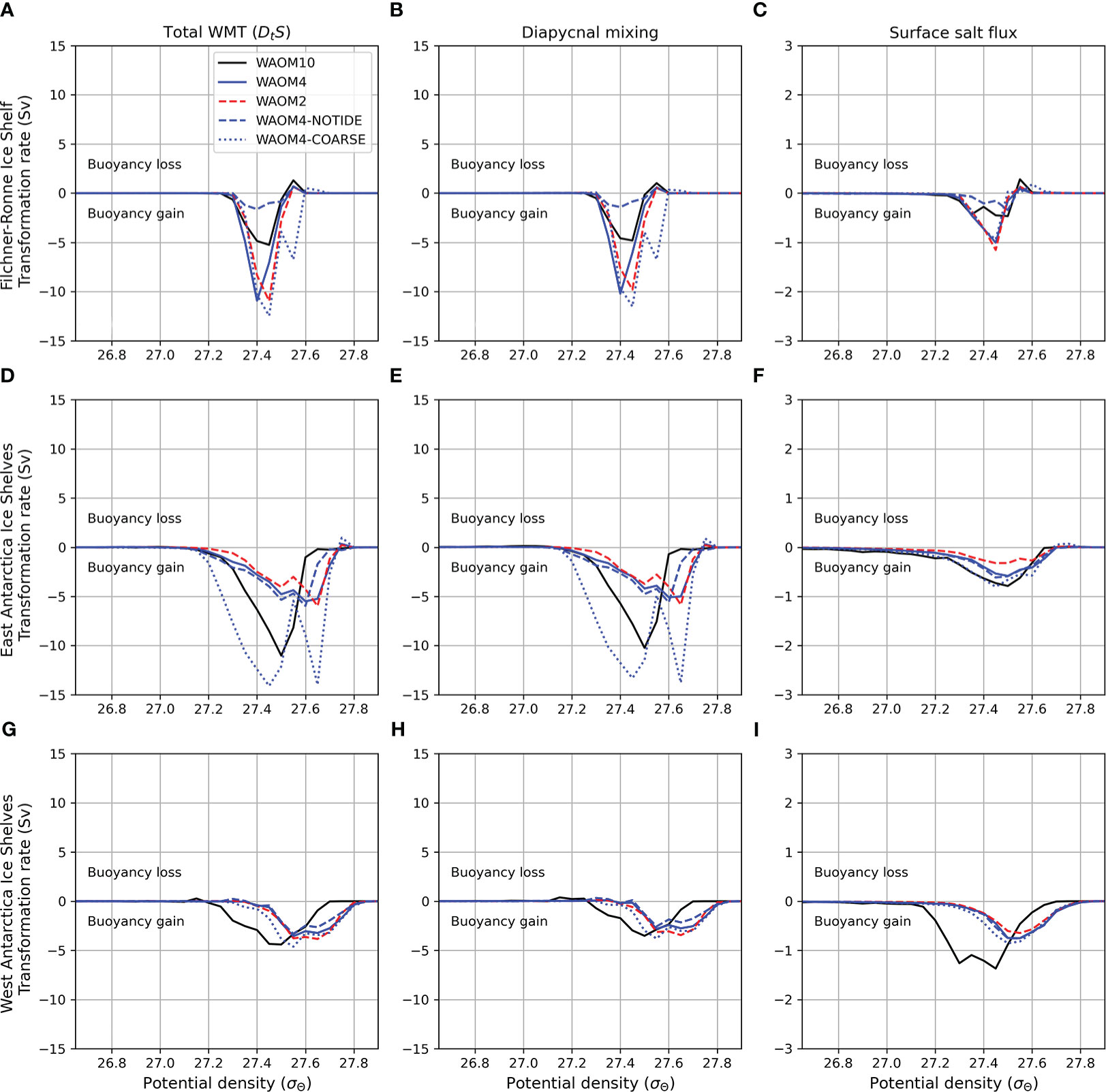
Figure 7 Water Mass Transformation rates (Sv) decomposition into total WMT (tendency - advection; panels A, D, G), interior diapycnal mixing (panels B, E, H) and surface salt flux (panels C, F, I; note that the y-limits are five times smaller than for total WMT and diapycnal mixing), integrated over subregions: Filchner-Ronne Ice Shelf (panels A–C), East Antarctica Ice Shelves (panels D–F) and West Antarctica Ice Shelves (panels G–I). Experiments are shown in: WAOM10 (black line), WAOM4 (blue line), WAOM2 (dashed red line), WAOM4-NOTIDE (dashed blue line), WAOM4-COARSE (dotted blue line). Positive (negative) WMT rates denote buoyancy loss (gain).
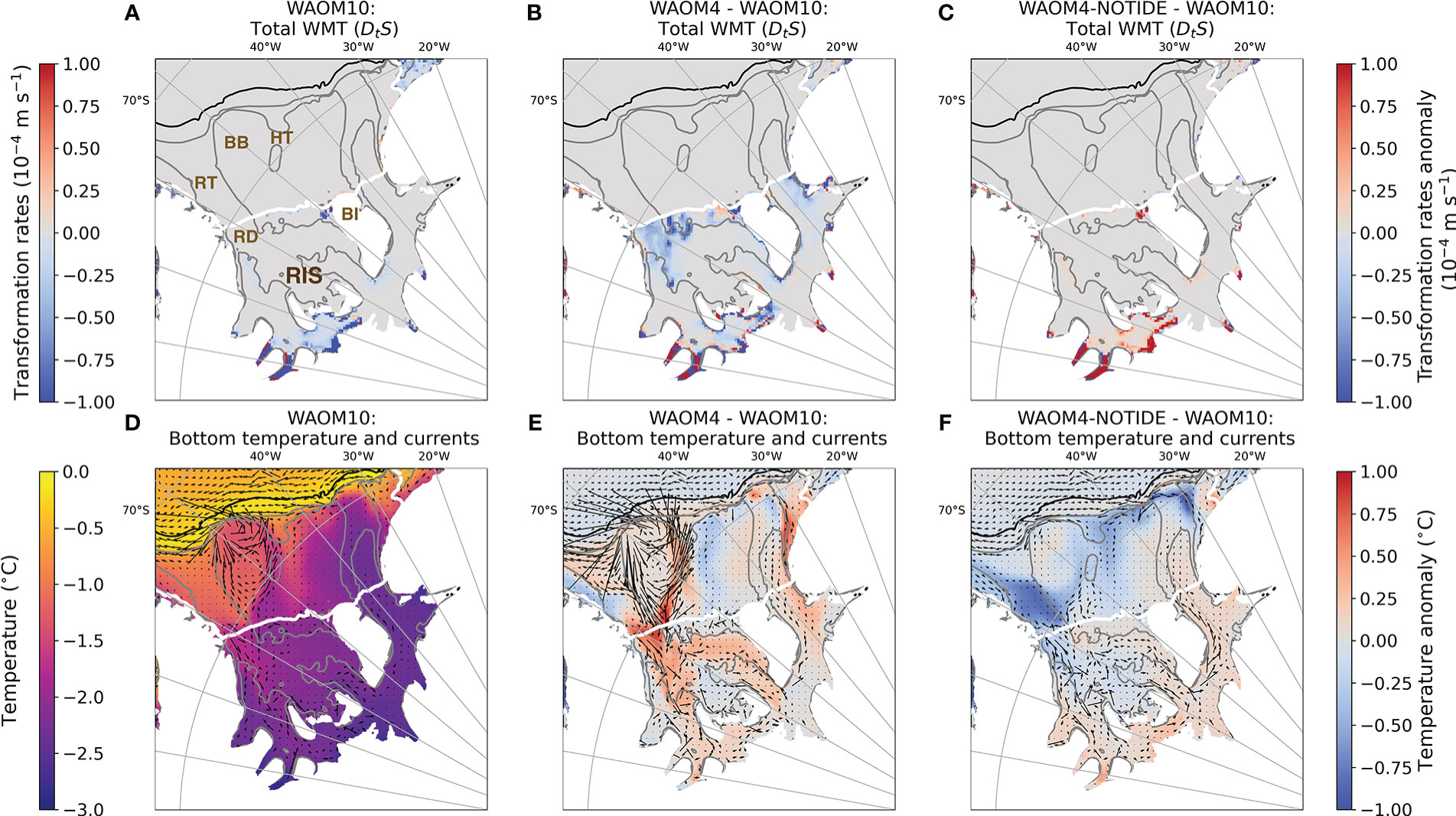
Figure 8 Filchner-Ronne Ice Shelf region annual transformation rates maps (ms-1, upper row), integrated from σθ = 27.3 to 27.5 kg m-3, due to the salt tendency (LHS of Eqn. 2, DtS), for the (A) WAOM10, (B) WAOM4 (anomalies referent to WAOM10) and (C) WAOM4-NOTIDE anomalies referent to WAOM10) experiments; annual bottom temperature and temperature anomalies (lower row, °C) for the (D) WAOM10, (E) WAOM4 (minus WAOM10) and (F) WAOM4-NOTIDE (minus WAOM10) experiments. Annual bottom currents (absolute values) are shown overlayed the temperature plots (bottom row). Black dashed lines show the 2000 m isobath and white dashed lines show the ice shelf front. Grey contours show isobaths of 200, 400, 600, and 800 m. Positive WMT means buoyancy loss (associated with salt convergence) and negative WMT means buoyancy gain (salt divergence). Main locations are identified in the panel (A): Ronne Trough (RT), Belgrano Bank (BB), Hughes Trough (HT), Ronne Depression (RD), Berkner Island (BI), Ronne Ice Shelf (RIS).
In the next sections, we investigate the mechanisms of WMT in each of these regions by examining the spatial patterns of buoyancy gain and/or loss.
To evaluate the geographical distribution of the transformation rates beneath FRIS, transformation maps are shown in Figure 8 (upper row). The maps show transformation integrated over the density interval between 27.3 and 27.5 kg m-3 (based on the peak of buoyancy gain in Figure 7A). These maps show that buoyancy gain in the WAOM10 experiment occurs near the grounding line (especially at the Ronne Ice Shelf) and west of Berkner Island. Major differences in the regional buoyancy gain, relative to the WAOM10 experiment, occurs (1) near the ice shelf front in WAOM4 and (2) near the grounding line in WAOM4-NOTIDE. Integrated over the FRIS region, increased horizontal resolution (from 10 km to either 4 or 2 km) results in a two-fold increase in buoyancy gain (from 5 to 10 Sv at ∼27.4 kg m-3, Figure 7A), whereas without tides the buoyancy gain falls to less than 2 Sv in the same density class.
The sensitivity of WMT under FRIS to model resolution largely reflects changes in an anticyclonic circulation just north of the Ronne Depression (Figures 8D, E). This circulation is located over the topographic high between the Ronne and Hughes Troughs. Southward flow in the western boundary of the gyre transports water towards the Ronne Ice Shelf (RIS) cavity, in agreement with previous studies suggesting inflow on the western flank of RIS from observations (Nicholls et al., 2001; Nicholls, 2004; Janout et al., 2021) and modelling (Makinson et al., 2011; Timmermann et al., 2012; Daae et al., 2020; Bull et al., 2021). Relatively warm shelf waters flow under the cavity and enhance melting near the grounding line (Figures 8A, D). At higher resolution (WAOM4, Figures 8B, E and WAOM2, not shown), the anticyclonic circulation intensifies and enhances the basal melting near the ice shelf front (see also Figure 3 and Figure S2). The bottom temperature anomalies show warm water entering the cavity in the west and splitting into southward and eastward branches beneath the ice shelf, consistent with the known circulation under FRIS (Jenkins et al., (2004); Nicholls 2004; Nicholls et al., 2009). In addition to driving basal melting near the ice front and the grounding line, these circulation pathways drive refreezing in the central area of the cavity (Figure 3) due to the convergence of meltwater plumes (Holland et al., 2007) associated with the ice-pump mechanism (Gerdes et al., 1999). The melting/refreezing pattern under FRIS resembles that obtained by past observations and modelling studies (Gerdes et al., 1999; Joughin and Padman, 2003; Rignot et al., 2013; Timmermann and Goeller, 2017; Adusumilli et al., 2020).
The model runs with and without tides show that the anticyclonic circulation in front of FRIS is primarily driven by tides. In the WAOM4-NOTIDE experiment, the circulation does not develop, which results in cold anomalies at the Ronne Trough and Ronne Depression (Figure 8F). The reduction in warm water inflow decreases the basal melting and the resulting buoyancy gain (Figure 8C). Previous studies have linked basal melting near the Ronne ice front to tidal residual currents and mixing (Makinson and Nicholls, 1999), and shown the link between tides and patterns of melting/refreezing under FRIS (Makinson et al., 2011; Hausmann et al., 2020; Stewart, 2021). Our results show that changes in temperature distribution beneath FRIS associated with the tidally-driven anticyclonic circulation are primarily responsible for the sensitivity in WMT. A similar circulation was reached by Makinson and Nicholls (1999), who also showed that this feature is sensitive to the depth of the Belgrano Bank (between Ronne and Hughes troughs), which is not well-constrained in the Bedmap2 dataset. A comparison with the BedMachine Antarctica dataset revealed a deeper Belgrano Bank and Hughes Trough, and a shallower Ronne Trough in the BedMachine dataset when compared against Bedmap2 (not shown).
MCDW intrusions have been observed on the East Antarctic continental slope (Bindoff et al., 2000; Foppert et al., 2019) and several parts of the continental shelf, including in the surroundings of the Totten Glacier (Williams et al., 2011; Rintoul et al., 2016; Silvano et al., 2017), the Denman Glacier (van Wijk et al., 2022), and the Amery Ice Shelf (Herraiz-Borreguero et al., 2015; Guo et al., 2022). Bottom temperatures simulated by WAOM (Figures 9D–F) are generally within the observed range, indicating MCDW intrusion in many locations of the East Antarctica sector. The transformation maps for the East Antarctica region (Figures 9A–C) show that buoyancy gain occurs beneath most of the large ice shelves in this sector: West Ice Shelf, Shackleton Ice Shelf, Totten Glacier, Moscow University Ice Shelf, and Mertz Glacier. In WAOM10, a continuous narrow band of buoyancy gain occurs along the grounding line in this sector (Figure 9A). The warmest bottom temperature on the continental shelf surrounding those ice shelves reaches -0.5°C, indicating modified Circumpolar Deep Water (MCDW) reaches the ice shelf cavities where it can drive basal melt.
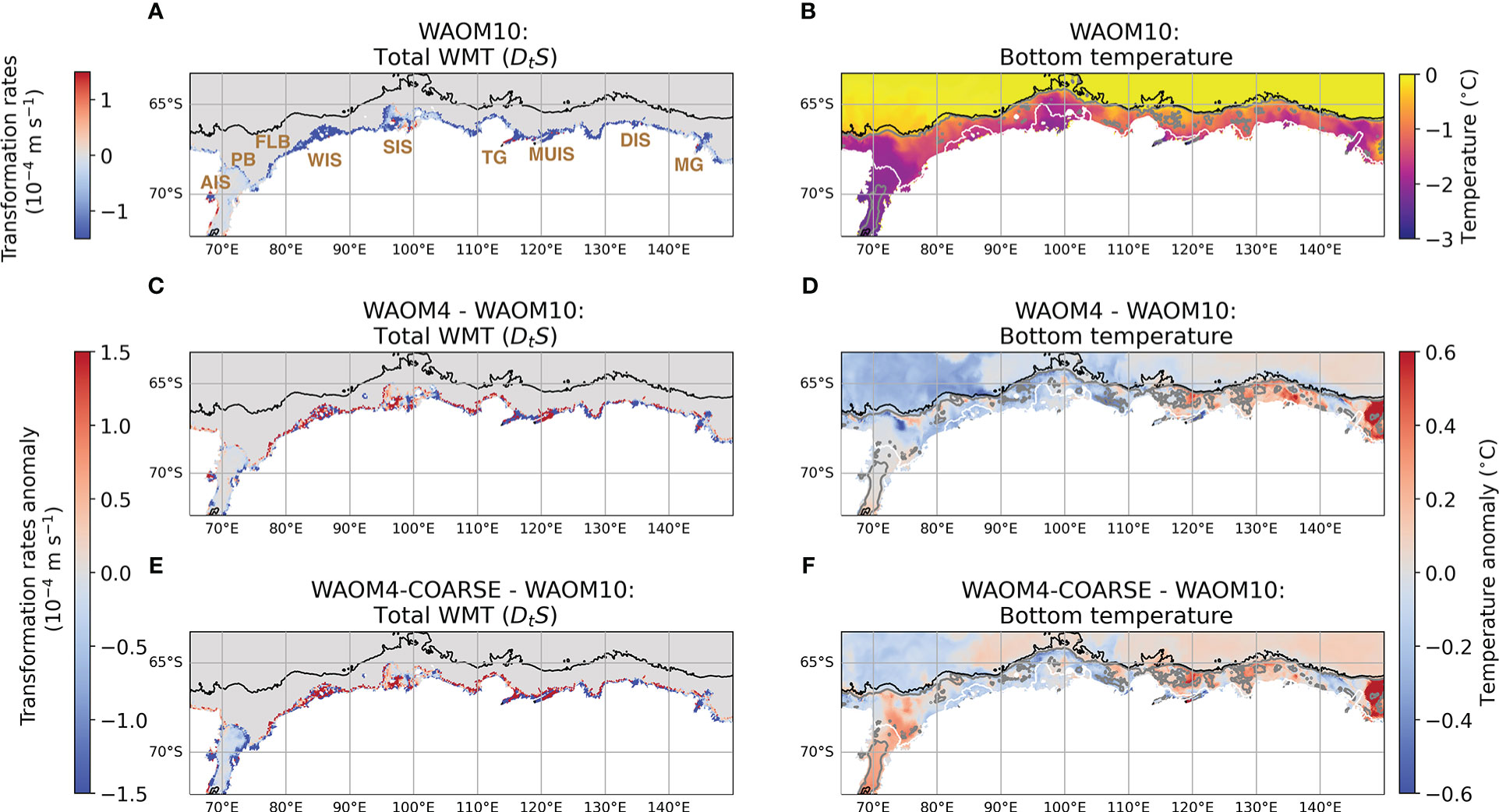
Figure 9 East Antarctica region annual transformation rates maps (ms-1, left column), integrated from σθ = 27.2 to 27.8 kg m-3, due to the salt tendency (LHS of Eqn. 2, DtS), for the (A) WAOM10, (C) WAOM4 (anomalies referent to WAOM10) and (E) WAOM4-COARSE anomalies referent to WAOM10) experiments; annual bottom temperature and temperature anomalies (right column, °C) for the (B) WAOM10, (D) WAOM4 (minus WAOM10) and (F) WAOM4-COARSE (minus WAOM10) experiments. Black line shows the 2000 m isobath and white dashed lines show the ice shelf front. Positive WMT means buoyancy loss (associated with salt convergence) and negative WMT means buoyancy gain (salt divergence). Main locations are identified in the panel (A): Prydz Bay (PB), Amery Ice Shelf (AIS), Four Ladies Bank (FLB), West Ice Shelf (WIS), Shackleton Ice Shelf (SIS), Totten Glacier (TG), Moscow University Ice Shelf (MUIS), Dibble Ice Shelf (DIS), Mertz Glacier (MG).
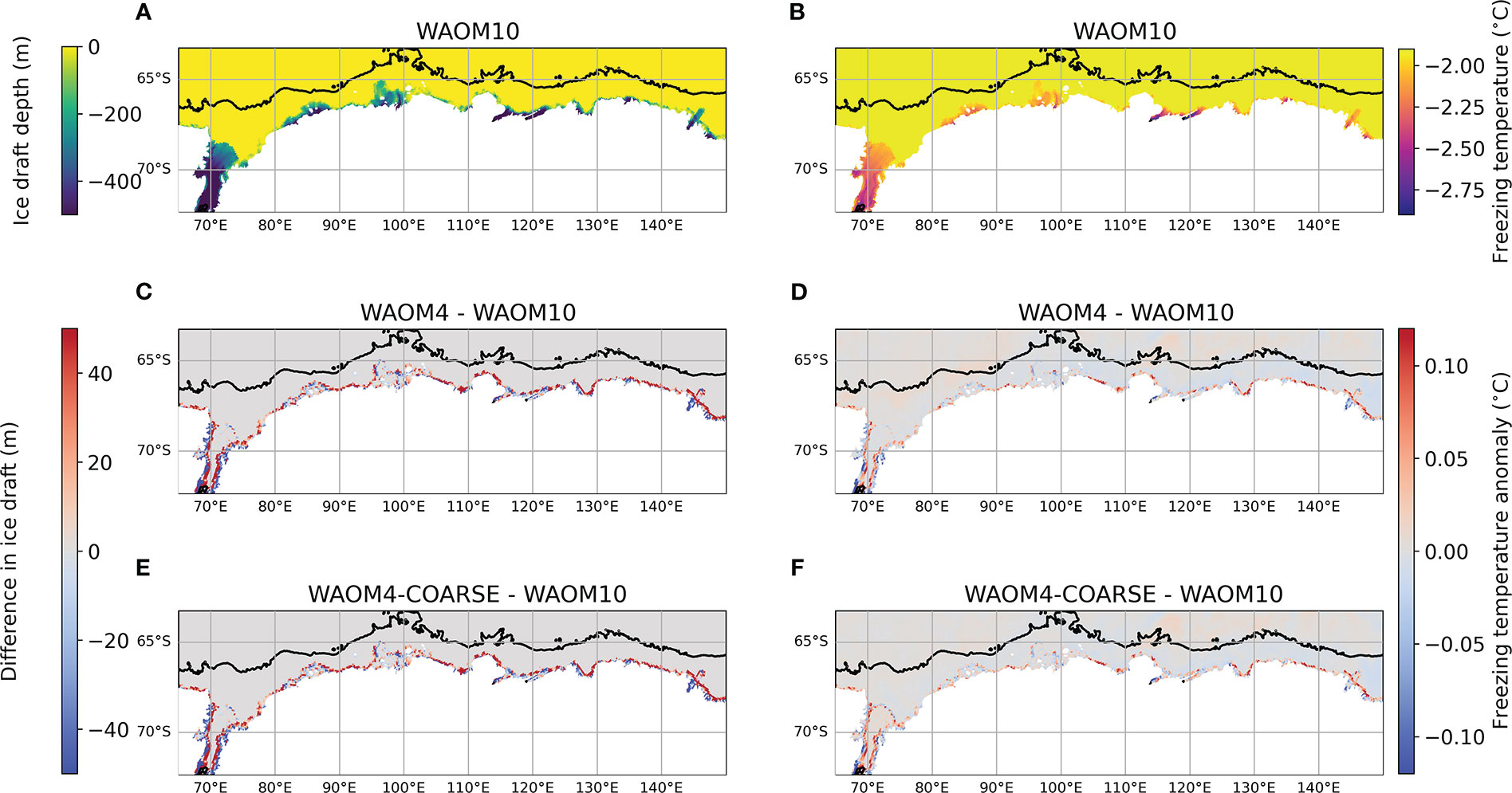
Figure 10 East Antarctica (left panels) ice shelf draft (A, WAOM10) and ice shelf draft differences (C, WAOM4 minus WAOM10; B, WAOM4-COARSE minus WAOM10. Positive (negative) differences means the base of the ice shelf is deeper (shallower) in WAOM10. Freezing temperature (Tf, right panels)) for the upper model layer (B, WAOM10) and differences in Tf (D, WAOM4 minus WAOM10; F, WAOM4-COARSE minus WAOM10). Positive (negative) differences means Tf is lower (higher) in WAOM10. Black line shows the 2000 m isobath.
WMT towards lighter densities (buoyancy gain) beneath East Antarctica ice shelves is sensitive to both model horizontal resolution, including the resolution of topography (Figure 7D). The change in model resolution from 10 to 4 km causes the peak of buoyancy gain to reduce by half (from 10 to 5 Sv) and to shift to heavier density classes. The shift of buoyancy gain to higher density classes coincides with a shift to denser waters produced by stronger buoyancy loss in the higher resolution experiments (Figures 5B, D). This suggests that in these runs denser shelf water is produced in coastal polynyas, which then spreads to the ice shelf cavity to drive basal melt, resulting in buoyancy gain (negative WMT) that peaks at higher density than in the coarse resolution run. The shift to melt driven by denser shelf water has a substantial impact on circum-Antarctic WMT (Figures 5A, C, E). The maps of transformation anomalies in WAOM4 (Figure 9C) show that some ice shelves have higher buoyancy gain (such as Totten, Dibble, and Mertz) in WAOM4, but most of the larger ice shelves experience a reduction of buoyancy gain (West, Shackleton and Moscow University). Moreover, the narrow band of buoyancy gain along the grounding line (seen in WAOM10) is largely reduced in WAOM4. Changes along the grounding line and in the West, Shackleton and Moscow University ice shelves drive an overall reduction in buoyancy gain in the East Antarctica sector (Figure 7D).
Changes in model resolution affect WMT in two ways: (a) by changing the depth of the grounding line and (b) by altering how much MCDW reaches the continental shelf and ice shelf cavities. The narrow band of buoyancy gain along most of the grounding line (and also parts of the West and Shackleton ice shelves) in WAOM10 is due to lower resolution of the ice shelf draft, which artificially makes the base of the ice shelf deeper than at higher resolution (Figure 10C). A deeper ice shelf base decreases the freezing point (Tf) due to the pressure effect (Figures 10C, E), facilitating basal melt to occur at WAOM10 (Figure 3B). The effect on Tf is seen at all σ layers, which are displaced downward in WAOM10 in comparison with WAOM4, indicating extra melting occurs at several model layers. Similar ice draft and Tf anomalies are seen in WAOM4 and WAOM4-COARSE (Figures 10C–F), which retains the same ice shelf draft as WAOM4 despite the 10 km topography. These results indicate that the resolution of the ice draft can have a non-negligible impact on the simulated WMT in the East Antarctica sector by affecting Tf and the basal melt rates.
The intrusion of MCDW onto the continental shelf shows distinct patterns in the coarse (WAOM10) and high-resolution (WAOM4/WAOM4-COARSE) experiments. The region between 80°-110°E (near the West and Shackleton Ice Shelves) has warmer bottom waters in WAOM10 (bottom temperatures between -0.5 and -1°C, Figure 9B) than in WAOM4 and WAOM4-COARSE experiments (cold anomalies in Figures 9D, F). The reduction of MCDW intrusion in the high-resolution experiments (including WAOM2, not shown) decreases basal melt (Figure 3) and buoyancy gain in comparison with WAOM10 at these ice shelf cavities (Figures 9A, C, E). The bottom-intensified Antarctic Slope Current (ASC) in this region is stronger in the high-resolution experiments (as seen in the Mean Kinetic Energy/MKE calculated from bottom currents, Figures 11A, C, E), especially between 105°-112°E and 80°-94°E, which inhibits MCDW reaching the shelf (Nakayama et al., 2021). Further east in the East Antarctica sector (between 115° and 140°E), bottom temperature anomalies of opposite sign are seen between WAOM10 and WAOM4/WAOM4-COARSE experiment, with warm anomalies on the shelf in the high-resolution experiments (Figures 9D, F). However, these anomalies do not reach the Totten and Moscow University cavities, resulting in a variable pattern of changes in buoyancy gain associated with basal melt (Figures 9C, E). The sector between 115°-140°E has lower MKE (weaker ASC at the bottom of the shelf break) in the higher resolution experiments (Figures 11A, C, E), while the Eddy Kinect Energy (EKE) is also stronger in both WAOM4 and WAOM4-COARSE than WAOM10 between 131°-140cE and 118°-126° (Figures 11B, D, F), locations where warm anomalies are observed (Figures 9E, F).
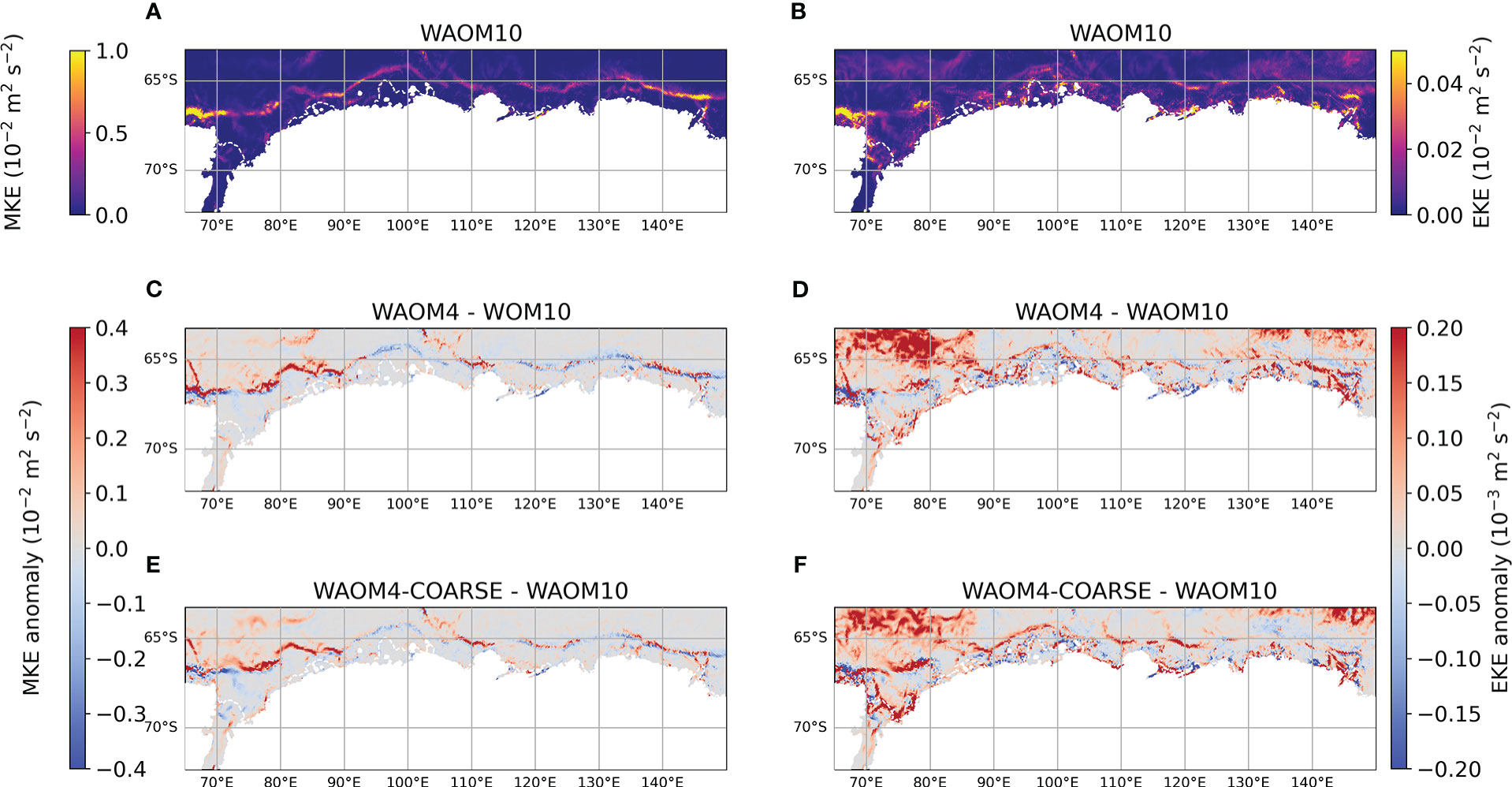
Figure 11 Annual mean Mean Kinect Energy (MKE, left panels) and Eddy Kinect Energy (EKE, right panels) for (A, B) WAOM10, and MKE and EKE anomalies (referent to WAOM10) for (C, D) WAOM4 and (E, F) WAOM4-COARSE. White dashed lines show the ice shelf front.
In summary, higher resolution impacts the cross-shelf heat transport in different ways at different parts of the East Antarctic shelf: (a) intrusions of MCDW are enhanced between 115°-140°E, and (b) reduced between 80°-110°E. In (a), the sector between Mertz and Totten glaciers, the ASC weakens and eddy transport (i.e., EKE) is enhanced at high resolution, both acting to facilitate the transport of MCDW to the shelf (Stewart and Thompson, 2015; Stewart et al., 2018; Foppert et al., 2019). In (b), a stronger ASC blocks MCDW intrusion (Nakayama et al., 2021), reducing basal melt and WMT rates. These results show that the interaction of both mean and eddy flow of the ASC with topographic features is sensitive to horizontal and topography resolution, impacting directly on the slope current and heat transport towards the ice shelf cavities (Klinck and Dinniman, 2010; St-Laurent et al., 2013; Stewart and Thompson, 2015; Silvano et al., 2019).
The sensitivity of WMT to topography resolution is further illustrated by comparison between the WAOM4-COARSE and WAOM4 experiments. Larger buoyancy gain occurs in WAOM4-COARSE, increasing the peak in WMT at lower densities (around 27.4-27.5 kg m-3) from 10 to 14 Sv, and with a second peak of 14 Sv at 27.65 kg m-3 (Figure 7D). The transformation maps (Figure 9C) show that the differences are largest under the Amery Ice Shelf (AIS) – besides the changes already discussed between WAOM10 and WAOM4. At AIS, buoyancy gain occurs both near the grounding line and at the ice front. The bottom temperature anomalies (relative to WAOM10) show that the Prydz Bay region has warmer bottom temperatures in WAOM4-COARSE than in WAOM10, which increases basal melt and WMT. A southward coastal current on the east side of Prydz Bay brings warm anomalies from the continental shelf towards the AIS cavity. This current is called Prydz Bay Eastern Coastal Current (PBECC) and has been previously identified in models (Liu et al., 2017) and observations (Herraiz-Borreguero et al., 2015). The PBECC originates through interaction of the ASC with small submarine troughs perpendicular to the shelf break (between 82° and 90°E), then flows southwest on the eastern side of the Four Ladies Bank (Liu et al., 2017). The PBECC is intensified in WAOM4-COARSE because the channel is artificially deep in the smoothed topography used in this experiment (not shown). In addition, high horizontal resolution is needed for the PBECC to develop, as it is associated with baroclinic instabilities arising from interaction of the ASC with the submarine troughs (Klinck and Dinniman, 2010; St-Laurent et al., 2013; Stewart and Thompson, 2015). These instabilities are enhanced in the higher resolution runs, as seen in the EKE anomalies (Figures 11E, F).
WMT under the West Antarctica Ice Shelves is most sensitive to model horizontal resolution - especially in the transition from 10 to 4 km (Figure 7G). While peak in negative WMT reduces by only about 1 Sv (from ∼5 to 4 Sv), WMT shifts to higher density in the higher resolution experiments. The transformation maps for the WAOM10 experiment (Figure 12A) shows that buoyancy gain occurs beneath many West Antarctic ice shelves, including George VI, Abbott, Cosgrove, Pine Island, Thwaites, Crosson, Dotson, and Getz. Although WAOM10 is biased cold relative to observations (Figures 2A, C), bottom water on the shelf reaches values as high as 0.5°C (Figure 12D). Onshore bottom currents transport modified Circumpolar Deep Waters (MCDW) mainly towards George VI, Pine Island and Thwaites ice shelves. Given the cold biases in the model, the basal melting (Figure 3) and WMT (Figure 12) towards lighter waters in the real ocean should be even larger than simulated by WAOM10.
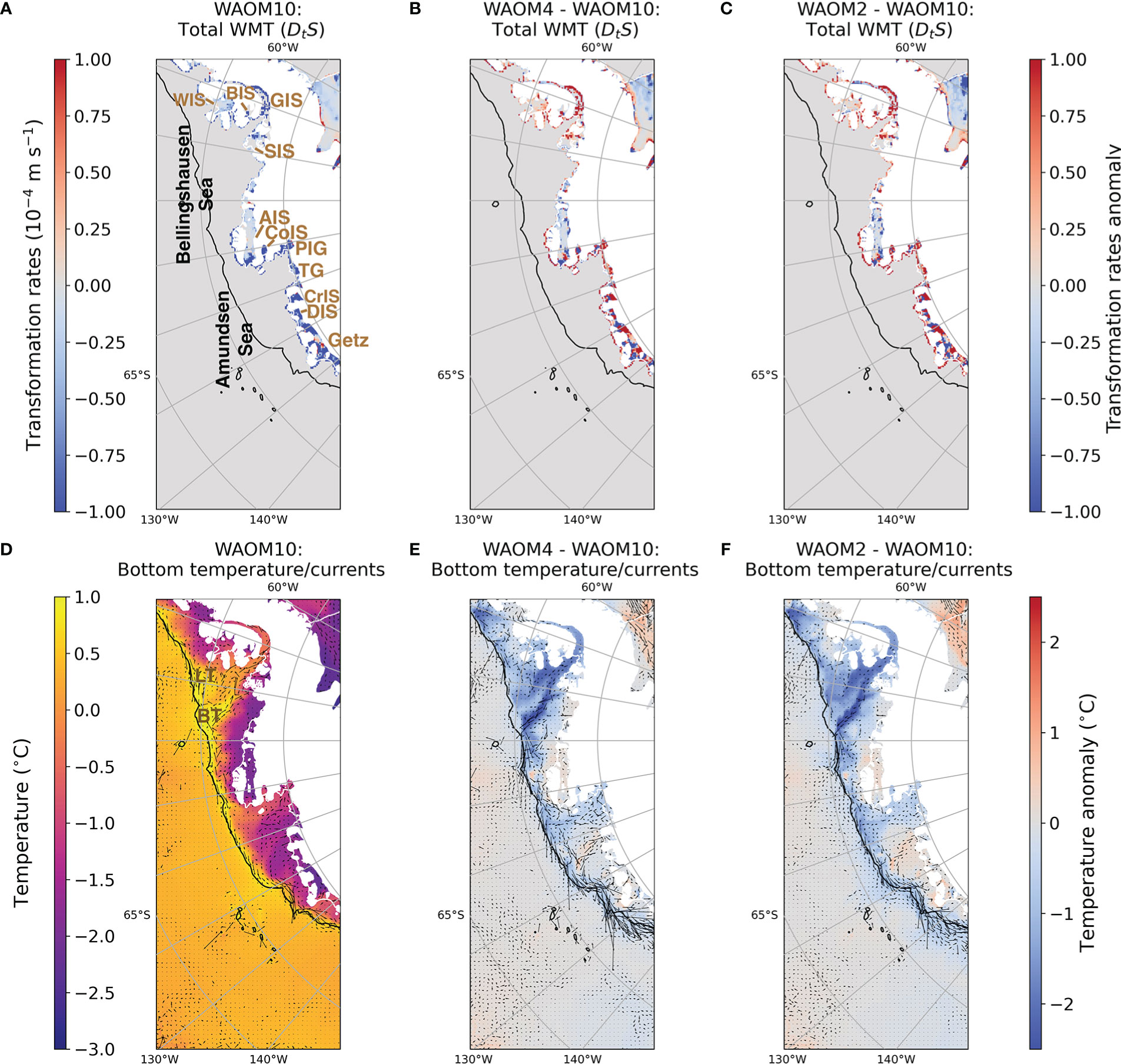
Figure 12 West Antarctica region annual transformation rates maps (ms-1, upper row), integrated from σθ = 27.3 to 27.5 kg m-3, due to the salt tendency (LHS of Eqn. 2, DtS), for the (A) WAOM10, (B) WAOM4 (anomalies referent to WAOM10) and (C) WAOM2 anomalies referent to WAOM10) experiments; annual bottom temperature and temperature anomalies (lower row, °C) for the (D) WAOM10, (E) WAOM4 (minus WAOM10) and (F) WAOM2 (minus WAOM10) experiments. Annual bottom currents (absolute values) are shown overlayed the temperature plots (bottom row). Black line shows the 2000 m isobath and white dashed lines show the ice shelf front. Positive WMT means buoyancy loss (associated with salt convergence) and negative WMT means buoyancy gain (salt divergence). Main locations are identified in the panel (A): Wilkins Ice Shelf (WIS), Bach Ice Shelf (BIS), George VI Ice Shelf (GIS), Stange Ice Shelf (SIS), Abbott Ice Shelf (AIS), Cosgrove Ice Shelf (CoIS), Pine Island Glacier (PIG), Thwaites Glacier (TG), Crosson Ice Shelf (CoIS), Dotson Ice Shelf (DIS), Getz Ice Shelf (Getz). The Belgica Trough (BT) and Latady Trough (LT) are referenced in the panel (D).
Increasing model resolution from 10 to 4 km impacts the buoyancy gain beneath different ice shelves in different ways (Figure 12B). The George VI, Pine Island and Thwaites ice shelves have a reduction of buoyancy gain (positive anomalies), whereas Abbott, Crosson, Dotson and Getz ice shelves show a mixed response. In WAOM2, the integrated WMT and transformation maps are similar to WAOM4 in this region (Figures 7G and 12B, C). Reduced melt and WMT are explained by a large reduction in on-shelf transport of MCDW in the high-resolution experiments (Figures 12E, F). Particularly large cold anomalies are observed in the Bellinghausen and Amundsen Seas.
Currents in the Bellingshausen and Amundsen Seas are sensitive to model resolution and this influences how much MCDW reaches the shelf. In the Belligshausen Sea, the annual averaged bottom currents in the Belgica Trough are mostly onshore in WAOM10, whereas they are offshore in WAOM4/WAOM2 (Figures 12D–F and Figure 13). The cyclonic circulation at the Belgica Trough suggested by Zhang et al. (2016) is observed in all model experiments at surface (not shown), but it is not clearly identified at the bottom (where it could efficiently transport MCDW towards the ice shelves). The bottom currents at the Belgica Trough seem to be linked to the shelf break current. Near the shelf break, all model experiments simulate an eastward flow at the surface (not shown) associated with the Southern Antarctica Circumpolar Current Front (SACCF, Orsi et al., 1995). Near the bottom, the high-resolution experiments simulate an undercurrent flowing westward that is stronger and forms further east than seen in WAOM10 (Figures 12D–F). This westward undercurrent, considered to be the source of the Antarctic Slope Current (Thompson et al., 2020), originates around 100°W in WAOM10 and around 90°W in WAOM4/WAOM2. In the high-resolution experiments, offshore flow at depth in the Belgica Trough feeds the ASC flowing westward at the shelf break. At coarse resolution (WAOM10), the onshore flow at the Belgica Trough does not connect with the shelf break current, shifting the origin of the ASC westward into the Amundsen Sea.
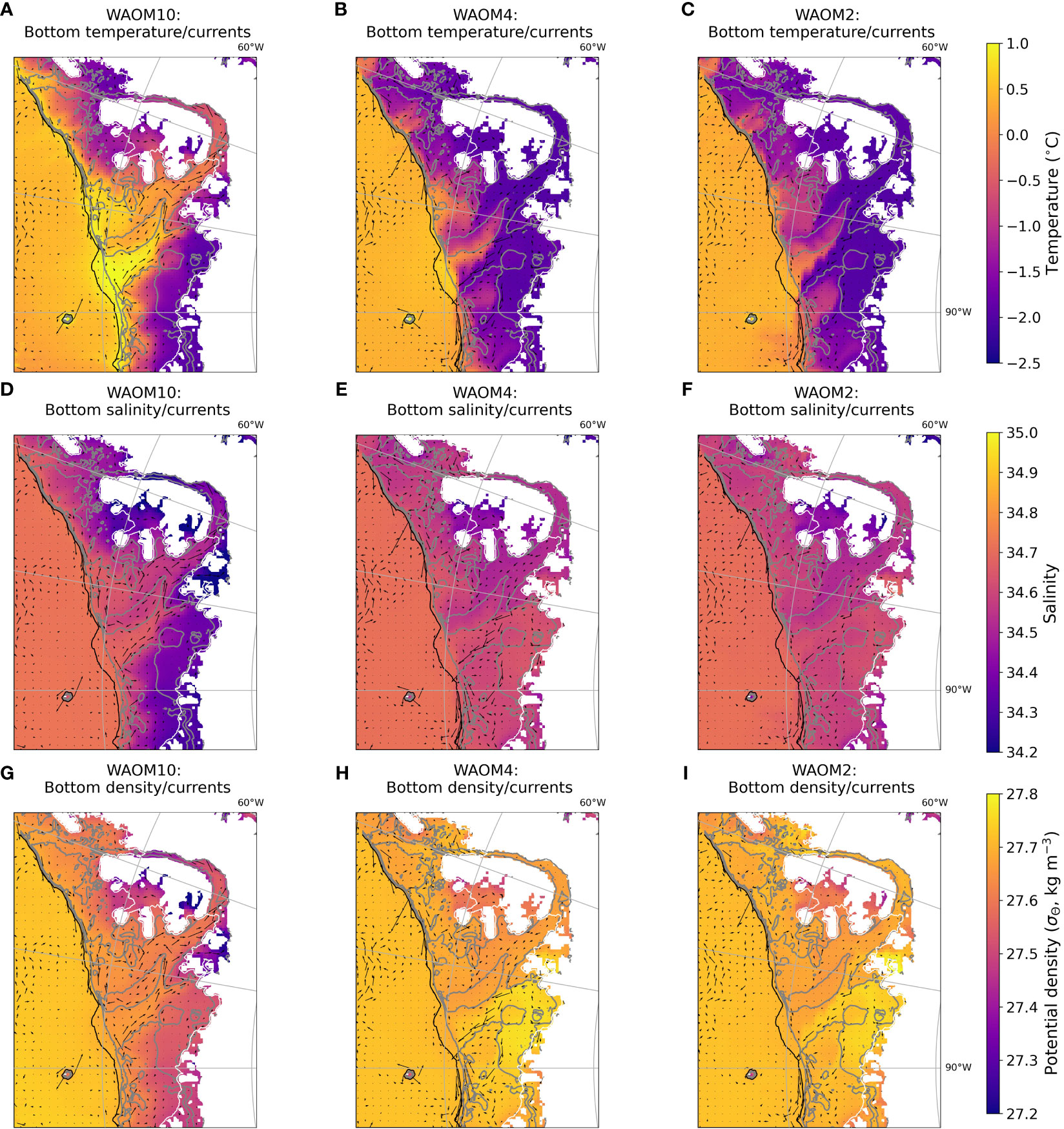
Figure 13 Maps of annual averaged bottom temperature (°C, panels A–C), salinity (panels D–F) and potential density (σθ, panels G–I) focused on the Bellinghausen Sea; model experiments are shown in different columns: WAOM10 in the left column (panels A, D, G), WAOM4 in the middle column (B, E, H), and WAOM2 in the right column (C, F, I). Black vectors show the annual averaged bottom currents. Black line shows the 2000 m isobath, grey contours show isobaths of 500 m, and white dashed lines show the ice shelf front.
The maps of bottom temperature, salinity and potential density provide some insights into the mechanisms that cause differences in the bottom currents at the Bellingshausen Sea (Figure 13). Although relatively warm waters penetrate the continental shelf in WAOM4 and WAOM2 in the Bellingshausen Sea (Figures 13B, C), they do not extend as far onshore as in WAOM10 (Figure 13A). In WAOM10, there is onshore flow at both the Belgica Trough and the Latady Trough; these currents have a strong barotropic component (as they flow in the same direction as the surface currents, not shown) and are therefore strongly influenced by topography. The large amount of heat delivered to George VI, Wilkins, Bach and Stange ice shelves in WAOM10 causes rapid basal melting, with the resulting meltwater input decreasing the salinity (between 34.2-34.5) not only in those cavities, but also westward along the coast (Nakayama et al., 2014). In contrast, the WAOM4 and WAOM2 experiments have higher salinity in those regions (varying from 34.5 to 34.7), reflecting the reduced melting. The larger surface salinity in WAOM4/WAOM2 also affects the surface salt flux; while the surface freshwater flux from Tamura et al. (2008) is the same for all WAOM experiments, the conversion from freshwater to salt flux taking into account the surface salinity (i.e., higher surface salinity ∼ stronger surface salt flux). Because the salinity is higher in the Bellingshausen Sea at high-resolution experiments (Figures 2F, H), salt input over the Bellingshausen coastal polynya is also enhanced in WAOM4/WAOM2 experiments (not shown). Ultimately, these salty (and cold, < 2°C), hence dense (σθ >27.7 kg m-3, Figures 13H, I) waters flow offshore via the Belgica Trough. In contrast to WAOM10, the flow in the Belgica Trough is baroclinic with strong vertical shear (onshore surface currents and offshore bottom currents). This offshore flow at the bottom of the Belgica Trough is linked with the origin of the baroclinic structure of the ASC in the western Bellingshausen Sea (Thompson et al., 2020).
In summary, we observed a positive feedback between cross-shelf CDW transport and the strength of the ASC in our model suite. When the flow of CDW is strongly onshore at both Belgica and Latady Troughs, the ocean heat transport drives high basal melt beneath the ice shelves of the Bellingshausen Sea (as seen in WAOM10 and likely in the real ocean), and the ASC is weaker and originates further west, which allows more CDW transport towards the Amundsen Sea shelf. In contrast, with less CDW flow towards the coast in the Bellingshausen Sea (as seen in WAOM4/WAOM2), the reduced basal melting (Figure 3) and increased salinity/density of coastal waters drives an offshore bottom flow at the Belgica Trough, which initiates a stronger ASC just west of the trough. The stronger ASC further reduces CDW transport towards the Amundsen Sea shelf (impacting basal melting and buoyancy gain at Pine Island and Thwaites glaciers, Figures 12B, C). A positive feedback between CDW transport and CDW-driven ice shelf melt (Moorman et al., 2020) and the ASC (Beadling et al., 2022) has been observed in model simulations; Beadling et al. (2022) also identified a connection (model-dependent) between the ASC and onshore transport of CDW. While the mechanisms driving the generation of the ASC have similarities with observational studies (Zhang et al., 2016; Thompson et al., 2020), our results suggest the strength and origin of the ASC depend on water mass properties on the Bellingshausen Sea shelf.
We investigated the processes driving Water Mass Transformation over the Antarctic continental shelf using a set of high-resolution Circum-Antarctic ocean-ice shelf simulations. We found that the WMT rates around Antarctica (1) are dominated by the contribution from salt fluxes, (2) reflect buoyancy gain under the ice shelves and buoyancy loss over the continental shelf (north of the ice shelf front), and (3) are highly sensitive to model horizontal resolution, topographic resolution, and tidal forcing. These three factors were evaluated for the most sensitive regions: the Filchner-Ronne Ice Shelf (FRIS), East Antarctica and West Antarctica. In the FRIS, tidal forcing and model resolution are the most influential factors; in East Antarctica, model and topographic resolution have the largest effect on WMT; while in West Antarctica, model resolution is the most important.
Surface fluxes of both heat and salt induce buoyancy loss of water masses with density (σθ) larger than ∼27.5 kg m-3, in agreement with previous studies computing WMT from surface fluxes in the open Southern Ocean (Abernathey et al., 2016; Newsom et al., 2016; Pellichero et al., 2018). However, the contribution from surface heat fluxes is mostly balanced by internal diapycnal mixing processes when WMT is integrated over the full water depth, resulting in only a small net WMT by surface heat fluxes (Figure 4). For the salt budget, internal mixing partially offsets the contribution from the surface salt flux, but the net effect results in substantial WMT. Transformation towards light waters (bouyancy gain) peaks around 15 Sv at σ θ between 27.3 to 27.6 kg m-3, whereas transformation towards heavier waters (buoyancy loss) occurs at densities larger than 27.6 kg m-3. High-resolution experiments (WAOM4 and WAOM2) experience less buoyancy gain at lower densities than WAOM10, while the buoyancy loss occurs at heavier densities but with smaller transformation rates.
Our analyses demonstrated that most of the buoyancy gain (at all model resolutions) is associated with the surface freshwater fluxes occurring within the ice shelf cavities (i.e., basal melt), while the buoyancy loss takes place on the continental shelf north of the ice front (for all experiments, Figure 5). The latter is closely associated with the model forcing provided from Tamura et al. (2011), where several coastal polynyas around Antarctica supply salt input during wintertime to form HSSW. The buoyancy gain under the ice shelves is linked to basal melting, with the thermal forcing enhanced by the pressure effect on lowering the freezing point (Jacobs et al., 1992). It is important to note that our simulations do not take into account the effect from sub-glacial rivers (Dow et al., 2022), which can affect the rates of buoyancy gain beneath the ice shelves. The interaction between water masses gaining and losing buoyancy over the Antarctic shelf, which occurs primarily via internal mixing (Figures 4B, D, F), ultimately determines the net production of Dense Shelf Water (i.e., the densest water mass in Figure 4). Dense Shelf Water exported across the shelf break feeds the Antarctic Bottom Water layer which forms the abyssal branch of the meridional overturning circulation. The high-resolution experiments (WAOM4 and WAOM2) form around ∼1 Sv of DSW σθ > 27.8 kg m-3), while the WMT rates at this density in WAOM10 is nearly zero.
Beneath the Filchner-Ronne Ice Shelf (FRIS), tides and model resolution are the main factors influencing the sensitivity of WMT (Figure 7A). This sensitivity is associated with a tidally-driven anticyclonic circulation in the Ronne Depression vicinity, which intensifies (weakens) with increased (decreased) model horizontal resolution (Section 3.4.1). This circulation controls the transport from the continental shelf towards the cavity via the Ronne Depression (Nicholls et al., 2001; Nicholls, 2004; Makinson et al., 2011; Timmermann et al., 2012; Daae et al., 2020; Bull et al., 2021; Janout et al., 2021), which enhances basal melting near the ice front and the grounding line, and refreezing in the central part of FRIS (Holland et al., 2007; Makinson et al., 2011; Hausmann et al., 2020; Stewart, 2021), resulting in a pattern of basal melting and refreezing similar to that obtained from models and observations (Gerdes et al., 1999; Joughin and Padman, 2003; Rignot et al., 2013; Timmermann and Goeller, 2017; Adusumilli et al., 2020). Rates of basal melting and refreezing are sensitive to the water mass properties in the ice shelf cavity (Jacobs et al., 1992); WAOM simulates somewhat too fresh continental shelf waters in the Weddell Sea (Figure 2), indicating lack of High Salinity Shelf Water. This could be related to the use of surface salt fluxes from a particular year (2007) to force the model (Tamura et al., 2011), to overly mixed conditions on the continental shelf, or to a mismatch between modelled ocean properties and the surface fluxes (Richter et al., 2022a). Moreover, the anticyclonic circulation has only been observed in modelling studies so far (Makinson and Nicholls, 1999; Richter et al., 2022b) and therefore needs to be confirmed with in-situ measurements. The simulated circulation might be sensitive to the depth of the Belgrano Bank (located between the Ronne and Hughes Troughs) and to the lack of a sea-ice model, which impacts the air-sea ice-ocean momentum transfer (Jendersie et al., 2018).
The WMT sensitivity in the East Antarctica sector is related to the model topography and horizontal resolution. The horizontal resolution impacts the representation of the ice draft; results show that the coarse experiment artificially deepens the base of the ice shelf near the grounding line, which impact the freezing temperature (Tf) and the basal melt rates (Section 3.4.2). Moreover, the transport of modified Circumpolar Deep Water (MCDW) is also affected by the model resolution. With enhanced model resolution (from 10 to 4 km), MCDW intrusions are weakened where the averaged bottom-intensified Antarctica Slope Current (ASC) strengthens (such as near the West and Shackleton Ice Shelves). In other regions (such as the shelf off the Wilkes Land), weakening of the ASC and intensification of the mesoscale eddy activity results in more MCDW on the shelf (Stewart and Thompson, 2015; Nakayama et al., 2021). The topographic resolution mostly impacts the Amery Ice Shelf, where the simulation run with 4 km horizontal resolution and 10 km topography artificially (as this does not occur in either WAOM10 or WAOM4) enhances the Prydz Bay Eastern Coastal Current (Herraiz-Borreguero et al., 2015; Liu et al., 2015), which transports warm anomalies to the cavity and increases basal melting and transformation towards light waters. The influence of eddy fluxes (Nøst et al., 2011; Thompson et al., 2014; Stewart and Thompson, 2015; Palóczy et al., 2018; Stewart et al., 2018; Foppert et al., 2019) and the mean slope current (Rintoul, 2018; Silvano et al., 2019) on on-shelf heat transport has been highlighted before; both the eddy and mean currents interact with topographic features to modulate the localized on-shelf transport in many sectors of the Antarctic margin (Klinck, 1996; Williams et al., 2008; St-Laurent et al., 2013; Stewart and Thompson, 2015; Jenkins et al., 2016; Dinniman et al., 2018). Our results show how model resolution and topography in the East Antarctica sector modulate the mean ASC and eddy fluxes, with consequences for ice shelf basal melting and WMT.
The West Antarctica WMT is sensitive to model resolution, which mainly impacts the amount of MCDW intrusion reaching the shelf. While the coarse resolution experiment (WAOM10) is already biased cold relative to observations (Schmidtko et al., 2014), the intrusion of warm MCDW is further reduced in the high-resolution experiments (WAOM4/WAOM2). This impact of model resolution is contrary to that suggested by previous work (Dinniman et al., 2016). The reduction of shelf bottom temperatures and hence buoyancy gain in our experiments is related to the representation of currents over the continental shelf and slope (Section 3.4.3). In particular, the amount of MCDW reaching the shelf is tightly linked to the coastal currents in the Bellingshausen Sea and the origin of the Antarctic Slope Current. The increased basal melting due to MCDW intrusion has a positive feedback on the MCDW transport (Moorman et al., 2020) via changes in the origin and strength of the ASC (Beadling et al., 2022); changes in basal melt affect water mass properties and hence currents on the shelf in the Bellingshausen Sea and the strength and location of the ASC origin (Thompson et al., 2020).
This study demonstrates the impact of tidal forcing, model horizontal and topographic resolution on the transformation of water masses over the Antarctic shelf. The sensitivity of water mass transformations is largest under the ice shelves, where currents (tides, mean flow, and eddy field) interact with the topography to regulate the transport of heat towards the ice shelf cavities, impacting basal melt and refreezing and therefore the transformation rate towards lighter waters. Lightening of water masses in ice shelf cavities and densification in coastal polynyas results in a net WMT that is linked to the formation of AABW and its sinking to the ocean abyss as part of the global meridional overturning circulation. Given the limitations of the current generation of climate models (Heuzé, 2021; Mohrmann et al., 2021), reanalyzes (Azaneu et al., 2014; Abernathey et al., 2016; Aguiar et al., 2017) and observations (Pellichero et al., 2018) in representing AABW processes and ocean-ice shelf interaction, our model setup brings novel insights into how ocean-ice shelf interaction impacts circum-Antarctic water mass transformation. Specifically, we show that the processes contributing to WMT around the Antarctic margin are highly sensitive to model resolution, topography and tidal processes, with substantial impact on the total transformation towards Dense Shelf Water (i.e., heavier density classes, σθ larger than 27.6 kg m-3) and thus AABW. An important finding is that merely including ocean-ice shelf interactions explicitly in future generations of ocean and coupled atmosphere-ocean general circulation models (OGCMs and AOGCMs) is not sufficient to simulate the impacts of ocean-ice shelf interaction on water mass formation and the MOC; the models must also have sufficient resolution to represent shelf circulation and its interaction with topography, as well as tidal forcing, to capture the sensitivity of sub-ice shelf processes to changes in forcing.
While these results are representative of present-day conditions, they indicate that WMT around Antarctica will be sensitive to future changes in the ice shelves (e.g. thinning and basal mass loss, Rignot et al., 2019). In the Weddell Sea region, previous studies showed that thinning and grounding line retreat of FRIS are affected by the inflow of warm water in future scenarios (Hellmer et al., 2012; Timmermann and Goeller, 2017; Daae et al., 2020; Naughten et al., 2021). The sensitivity of cross-shelf heat transport to the characteristics of the ASC in both West and East Antartica suggests that the response of the ASC to future wind changes (Spence et al., 2014) is also likely to influence basal melt and WMT in ice shelf cavities. Intensification of ocean-driven melt would, in turn, accelerate the retreat of ice shelf grounding lines and glacial mass loss, as has already been observed at the Pine Island (Favier et al., 2014), Thwaites (Milillo et al., 2019), Denman (Brancato et al., 2020), and Totten (Li et al., 2015) glaciers (Rignot et al., 2013), and may also increase the mass loss via calving (Liu et al., 2015). These changes will not only have a large impact on the global sea level (Pan et al., 2021), but will also affect the stability of the global MOC as the Weddell Sea and East Antarctica contribute a large fraction of the total formation of AABW (Jullion et al., 2014; Vernet et al., 2019; Foppert et al., 2021; Mensah et al., 2021; Portela et al., 2022).
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
FB has performed the analyses and wrote the manuscript. SR assisted with the results interpretations and manuscript editing. OR, BG-F, and PU assisted with the model development, results interpretations and manuscript editing. VP and JZ assisted with the Water Mass Transformation analyses implementation and interpretation, and manuscript editing. All authors contributed to the article and approved the submitted version.
This work was supported by the Academy of Finland (Project 322432). PU was supported the European Union’s Horizon 2020 research and innovation framework programme under Grant agreement no. 101003590 (PolarRES project). This research was supported by the Australian Research Council Special Research Initiative, Australian Centre for Excellence in Antarctic Science (Project Number SR200100008).
We appreciate the constructive comments from the reviewers that greatly helped to improve the manuscript.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2023.1027704/full#supplementary-material
Supplementary Figure 1 | Annual mean water mass transformation due to the salt budget over the Antarctic shelf (depth less than 2000 m, in Sv), calculated following Eqn. 6, for the WAOM4 (upper panels) and WAOM2 (botom panels) at distinct years: (A) WAOM4 year 10 (same as Figure 4D), (B) WAOM4 year 20, (C) WAOM2 year 1, (D) WAOM2 year 5 (same as Figure 4F). WMT due to the salt budget is broken down into the contribution from the surface fluxes (magenta) and total internal diapycnal diffusion (horizontal plus vertical, blue; vertical diffusion only is shown as dashed blue lines), and the total WMT (material derivatives in LHS of Eqns. 1 and 2, black). Positive (negative) WMT rates denote buoyancy loss (gain).
Supplementary Figure 2 | Annual mean temperature and salinity fields for the WAOM10 (panels A, D, G, J), WAOM4 (minus WAOM10, panels B, E, H, K) and WAOM4-NOTIDE (minus WAOM10, panels C, F, I, L) experiments. Surface (bottom) temperature are shown in the first (second row). Surface (bottom) salinity are shown in the third (fourth row). Black dashed lines show the 2000 m isobath and white dashed lines show the ice shelf front. Grey contours show isobaths of 200, 400, 600, and 800 m.
Abernathey R. P., Cerovecki I., Holland P. R., Newsom E., Mazloff M., Talley L. D. (2016). Water-mass transformation by sea ice in the upper branch of the southern ocean overturning. Nat. Geosci. 9, 596–601. doi: 10.1038/ngeo2749
Adusumilli S., Fricker H. A., Medley B., Padman L., Siegfried M. R. (2020). Interannual variations in meltwater input to the southern ocean from antarctic ice shelves. Nat. Geosci. 13, 616–620. doi: 10.1038/s41561-020-0616-z
Aguiar W., Mata M. M., Kerr R. (2017). On deep convection events and antarctic bottom water formation in ocean reanalysis products. Ocean Sci. 13, 851–872. doi: 10.5194/os-13-851-2017
Arzeno I. B., Beardsley R. C., Limeburner R., Owens B., Padman L., Springer S. R., et al. (2014). Ocean variability contributing to basal melt rate near the ice front of ross ice shelf, antarctica. J. Geophys. Res.: Oceans 119, 4214–4233. doi: 10.1002/2014JC009792
Azaneu M., Kerr R., Mata M. M. (2014). Assessment of the representation of antarctic bottom water properties in the ecco2 reanalysis. Ocean Sci. 10, 923–946. doi: 10.5194/os-10-923-2014
Beadling R. L., Krasting J. P., Griffies S. M., Hurlin W. J., Bronselaer B., Russell J. L., et al. (2022). Importance of the antarctic slope current in the southern ocean response to ice sheet melt and wind stress change. J. Geophys. Res.: Oceans 127. doi: 10.1029/2021JC017608
Bindoff N. L., Rosenberg M. A., Warner M. J. (2000). On the circulation and water masses over the antarctic continental slope and rise between 80 and 150°e. Deep-Sea Res. Part II: Topical Stud. Oceanogr. 47, 2299–2326. doi: 10.1016/S0967-0645(00)00038-2
Brambilla E., Talley L. D., Robbins P. E. (2008). Subpolar mode water in the northeastern atlantic: 2. origin and transformation. J. Geophys. Res.: Oceans 113, 1–16. doi: 10.1029/2006JC004063
Brancato V., Rignot E., Milillo P., Morlighem M., Mouginot J., An L., et al. (2020). Grounding line retreat of denman glacier, east antarctica, measured with cosmo-skymed radar interferometry data. Geophys. Res. Lett. 47, 1–10. doi: 10.1029/2019GL086291
Bull C. Y., Jenkins A., Jourdain N. C., Vaňková I., Holland P. R., Mathiot P., et al. (2021). Remote control of filchner-ronne ice shelf melt rates by the antarctic slope current. J. Geophys. Res.: Oceans 126. doi: 10.1029/2020JC016550
Church J. A., White N. J., Konikow L. F., Domingues C. M., Cogley J. G., Rignot E., et al. (2011). Revisiting the earth’s sea-level and energy budgets from 1961 to 2008. Geophys. Res. Lett. 38, 1–8. doi: 10.1029/2011GL048794
Cougnon E. A., Galton-Fenzi B. K., Meijers A. J., Legrésy B. (2013). Modeling interannual dense shelf water export in the region of the mertz glacier tongue, (1992-2007). J. Geophys. Res.: Oceans 118, 5858–5872. doi: 10.1002/2013JC008790
Daae K., Hattermann T., Darelius E., Mueller R. D., Naughten K. A., Timmermann R., et al. (2020). Necessary conditions for warm inflow toward the filchner ice shelf, weddell sea. Geophys. Res. Lett. 47. doi: 10.1029/2020GL089237
Dee D. P., Uppala S. M., Simmons A. J., Berrisford P., Poli P., Kobayashi S., et al. (2011). The era-interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 137, 553–597. doi: 10.1002/qj.828
Dias F. B., Domingues C. M., Marsland S. J., Rintoul S. R., Uotila P., Fiedler R., et al. (2021). Subpolar southern ocean response to changes in the surface momentum, heat, and freshwater fluxes under 2xco2. J. Climate 34, 8755–8775. doi: 10.1175/jcli-d-21-0161.1
Dinniman M. S., Asay-Davis X. S., Galton-Fenzi B. K., Holland P. R., Jenkins A., Timmermann R. (2016). Modeling ice shelf/ocean interaction in antarctica: A review. Oceanography 29, 144–153. doi: 10.5670/oceanog.2016.106
Dinniman M. S., Klinck J. M., Hofmann E. E., Smith W. O. (2018). Effects of projected changes in wind, atmospheric temperature, and freshwater inflow on the ross sea. J. Climate 31, 1619–1635. doi: 10.1175/JCLI-D-17-0351.1
Dow C. F., Ross N., Jeofry H., Siu K., Siegert M. J. (2022). Antarctic Basal environment shaped by high-pressure flow through a subglacial river system. Nat. Geosci. 15, 892–898. doi: 10.1038/s41561-022-01059-1
Egbert G. D., Erofeeva S. Y. (2002). Efficient inverse modeling of barotropic ocean tides. J. Atmos. Oceanic Technol. 19, 183–204. doi: 10.1175/1520-0426(2002)019<0183:EIMOBO>2.0.CO;2
Favier L., Durand G., Cornford S. L., Gudmundsson G. H., Gagliardini O., Gillet-Chaulet F., et al. (2014). Retreat of pine island glacier controlled by marine ice-sheet instability. Nat. Climate Change 4, 117–121. doi: 10.1038/nclimate2094
Foppert A., Rintoul S. R., England M. H. (2019). Along-slope variability of cross-slope eddy transport in east antarctica. Geophys. Res. Lett. 46, 8224–8233. doi: 10.1029/2019GL082999
Foppert A., Rintoul S. R., Purkey S. G., Zilberman N., Kobayashi T., Sallée ,. J. B., et al. (2021). Deep argo reveals bottom water properties and pathways in the australian-antarctic basin. J. Geophys. Res.: Oceans 126, 1–18. doi: 10.1029/2021JC017935
Fretwell P., Pritchard H. D., Vaughan D. G., Bamber J. L., Barrand N. E., Bell R., et al. (2013). Bedmap2: improved ice bed, surface and thickness datasets for antarctica. Cryosphere 7, 375–393. doi: 10.5194/tc-7-375-2013
Galton-Fenzi B. K., Hunter J. R., Coleman R., Marsland S. J., Warner R. C. (2012). Modeling the basal melting and marine ice accretion of the amery ice shelf. J. Geophys. Res.: Oceans 117, 1–19. doi: 10.1029/2012JC008214
Garabato A. C. N., Zika J. D., Jullion L., Brown P. J., Holland P. R., Meredith M. P., et al. (2016). The thermodynamic balance of the weddell gyre. Geophys. Res. Lett. 43, 317–325. doi: 10.1002/2015GL066658
Gerdes R., Determann J., Grosfeld K. (1999). Ocean circulation beneath filchner-ronne ice shelf from three-dimensional model results. J. Geophys. Res.: Oceans 104, 15827–15842. doi: 10.1029/1999JC900053
Groeskamp S., Griffies S. M., Iudicone D., Marsh R., Nurser A. J., Zika J. D. (2019). The water mass transformation framework for ocean physics and biogeochemistry. Annu. Rev. Mar. Sci. 11, 271–305. doi: 10.1146/annurev-marine-010318-095421
Guo G., Gao L., Shi J., Zu Y. (2022). Wind-driven seasonal intrusion of modified circumpolar deep water onto the continental shelf in prydz bay, east antarctica. J. Geophys. Res.: Oceans 127, e2022JC018741. doi: 10.1029/2022JC018741
Gwyther D. E., Cougnon E. A., Galton-Fenzi B. K., Roberts J. L., Hunter J. R., Dinniman M. S. (2016). Modelling the response of ice shelf basal melting to different ocean cavity environmental regimes. Ann. Glaciol. 57, 131–141. doi: 10.1017/aog.2016.31
Haidvogel D., Arango H., Budgell W., Cornuelle B., Curchitser E., Dilorenzo E., et al. (2008). Ocean forecasting in terrain-following coordinates: Formulation and skill assessment of the regional ocean modeling system. J. Comput. Phys. 227, 3595–3624. doi: 10.1016/j.jcp.2007.06.016
Hallberg R. (2013). Using a resolution function to regulate parameterizations of oceanic mesoscale eddy effects. Ocean Model. 72, 92–103. doi: 10.1016/j.ocemod.2013.08.007
Hausmann U., Sallée J. B., Jourdain N. C., Mathiot P., Rousset C., Madec G., et al. (2020). The role of tides in ocean-ice shelf interactions in the southwestern weddell sea. J. Geophys. Res.: Oceans 125, 1–29. doi: 10.1029/2019JC015847
Hellmer H. H., Kauker F., Timmermann R., Determann J., Rae J. (2012). Twenty-first-century warming of a large antarctic ice-shelf cavity by a redirected coastal current. Nature 485, 225–228. doi: 10.1038/nature11064
Herraiz-Borreguero L., Coleman R., Allison I., Rintoul S. R., Craven M., Williams G. D. (2015). Circulation of modified circumpolar deep water and basal melt beneath the amery ice shelf, east antarctica. J. Geophys. Res.: Oceans 120, 3098–3112. doi: 10.1002/2015JC010697
Heuzé C. (2021). Antarctic Bottom water and north atlantic deep water in cmip6 models. Ocean Sci. 17, 59–90. doi: 10.5194/os-17-59-2021
Heywood K. J., Schmidtko S., Heuzé C., Kaiser J., Jickells T. D., Queste B. Y., et al. (2014). Ocean processes at the antarctic continental slope. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 372. doi: 10.1098/rsta.2013.0047
Holland P. R. (2017). The transient response of ice shelf melting to ocean change. J. Phys. Oceanogr. 47, 2101–2114. doi: 10.1175/JPO-D-17-0071.1
Holland P. R., Feltham D. L., Jenkins A. (2007). Ice shelf water plume flow beneath filchner-ronne ice shelf, antarctica. J. Geophys. Res.: Oceans 112, 1–12. doi: 10.1029/2006JC003915
Holland D. M., Jenkins A. (1999). Modeling thermodynamic ice-ocean interactions at the base of an ice shelf. J. Phys. Oceanogr. 29, 1787–1800. doi: 10.1175/1520-0485(1999)029<1787:mtioia>2.0.co;2
Jacobs S. S., Giulivi C. F. (2010). Large Multidecadal salinity trends near the pacific-antarctic continental margin. J. Climate 23, 4508–4524. doi: 10.1175/2010JCLI3284.1
Jacobs S. S., Helmer H. H., Doake C. S., Jenkins A., Frolich R. M. (1992). Melting of ice shelves and the mass balance of antarctica. J. Glaciol. 38, 375–387. doi: 10.1017/S0022143000002252
Janout M. A., Hellmer H. H., Hattermann T., Huhn O., Sültenfuss J., Østerhus S., et al. (2021). Fris revisited in 2018: On the circulation and water masses at the filchner and ronne ice shelves in the southern weddell sea. J. Geophys. Res.: Oceans 126, 1–19. doi: 10.1029/2021JC017269
Jendersie S., Williams M. J., Langhorne P. J., Robertson R. (2018). The density-driven winter intensification of the ross sea circulation. J. Geophys. Res.: Oceans 123, 7702–7724. doi: 10.1029/2018JC013965
Jenkins A., Dutrieux P., Jacobs S., Steig E. J., Gudmundsson G. H., Smith J., et al. (2016). Decadal ocean forcing and antarctic ice sheet response: Lessons from the amundsen sea. Oceanography 29, 106–117. doi: 10.5670/oceanog.2016.103
Jenkins A., Holland D. M., Nicholls K. W., Schröder M., Østerhus S. (2004). Seasonal ventilation of the cavity beneath filchner-ronne ice shelf simulated with an isopycnic coordinate ocean model. J. Geophys. Res.: Oceans 109, 1–12. doi: 10.1029/2001jc001086
Johnson G. C. (2008). Quantifying antarctic bottom water and north atlantic deep water volumes. J. Geophys. Res.: Oceans 113, 1–13. doi: 10.1029/2007JC004477
Joughin I., Padman L. (2003). Melting and freezing beneath filchner-ronne ice shelf, antarctica. Geophys. Res. Lett. 30. doi: 10.1029/2003GL016941
Jullion L., Garabato A. C. N., Bacon S., Meredith M. P., Brown P. J., Torres-Valdés S., et al. (2014). The contribution of the weddell gyre to the lower limb of the global overturning circulation. J. Geophys. Res.: Oceans 119, 3357–3377. doi: 10.1002/2013JC009725
Klinck J. M. (1996). Circulation near submarine canyons: A modeling study. J. Geophys. Res.: Oceans 101, 1211–1223. doi: 10.1029/95JC02901
Klinck J. M., Dinniman M. S. (2010). Exchange across the shelf break at high southern latitudes. Ocean Sci. 6, 513–524. doi: 10.5194/os-6-513-2010
Kusahara K., Hasumi H., Tamura T. (2010). Modeling sea ice production and dense shelf water formation in coastal polynyas around east antarctica. J. Geophys. Res.: Oceans 115, 1–10. doi: 10.1029/2010JC006133
Large W. G., McWilliams J. C., Doney S. C. (1994). Oceanic vertical mixing: A review and a model with a nonlocal boundary layer parameterization. Rev. Geophys. 32, 363–403. doi: 10.1029/94RG01872
Li X., Rignot E., Morlighem M., Mouginot J., Scheuchl B. (2015). Grounding line retreat of totten glacier, east antarctica 1996 to 2013. Geophys. Res. Lett. 42, 8049–8056. doi: 10.1002/2015GL065701
Liu Y., Moore J. C., Cheng X., Gladstone R. M., Bassis J. N., Liu H., et al. (2015). Ocean-driven thinning enhances iceberg calving and retreat of antarctic ice shelves. Proc. Natl. Acad. Sci. United States America 112, 3263–3268. doi: 10.1073/pnas.1415137112
Liu C., Wang Z., Cheng C., Xia R., Li B., Xie Z. (2017). Modeling modified circumpolar deep water intrusions onto the prydz bay continental shelf, east antarctica. J. Geophys. Res.: Oceans 122, 5198–5217. doi: 10.1002/2016JC012336
Makinson K., Holland P. R., Jenkins A., Nicholls K. W., Holland D. M. (2011). Influence of tides on melting and freezing beneath filchner-ronne ice shelf, antarctica. Geophys. Res. Lett. 38, 4–9. doi: 10.1029/2010GL046462
Makinson K., Nicholls K. W. (1999). Modeling tidal currents beneath filchner-ronne ice shelf and on the adjacent continental shelf: Their effect on mixing and transport. J. Geophys. Res.: Oceans 104, 13449–13465. doi: 10.1029/1999jc900008
Marchesiello P., McWilliams J. C., Shchepetkin A. (2001). Open boundary conditions for long-term integration of regional oceanic models. Ocean Model. 3, 1–20. doi: 10.1016/S1463-5003(00)00013-5
Mathiot P., Barnier B., Gallée H., Molines J. M., Sommer J. L., Juza M., et al. (2010). Introducing katabatic winds in global era40 fields to simulate their impacts on the southern ocean and sea-ice. Ocean Model. 35, 146–160. doi: 10.1016/j.ocemod.2010.07.001
Maze G., Forget G., Buckley M., Marshall J., Cerovecki I. (2009). Using transformation and formation maps to study the role of air-sea heat fluxes in north atlantic eighteen degree water formation. J. Phys. Oceanogr. 39, 1818–1835. doi: 10.1175/2009JPO3985.1
Mazloff M. R., Heimbach P., Wunsch C. (2010). An eddy-permitting southern ocean state estimate. J. Phys. Oceanogr. 40, 880–899. doi: 10.1175/2009JPO4236.1
McDougall T. J., Barker P. M. (2011). Getting started with TEOS-10 and the Gibbs Seawater (GSW) Oceanographic Toolbox. 28pp., SCOR/IAPSO WG127, ISBN 978‑0-646‑55621‐5.
Mellor G. L., Oey L. Y., Ezer T. (1998). Sigma coordinate pressure gradient errors and the seamount problem. J. Atmos. Oceanic Technol. 15, 1122–1131. doi: 10.1175/1520-0426(1998)015<1122:SCPGEA>2.0.CO;2
Menemenlis D., Campin J., Heimbach P., Hill C., Lee T., Nguyen A., et al (2008). ECCO2: High resolution global ocean and sea ice data synthesis. In American Geophysical Union, Fall Meeting 2008, abstract id. OS31C-1292.
Mensah V., Nakayama Y., Fujii M., Nogi Y., Ohshima K. I. (2021). Dense water downslope flow and aabw production in a numerical model: Sensitivity to horizontal and vertical resolution in the region off cape darnley polynya. Ocean Model. 165, 101843. doi: 10.1016/j.ocemod.2021.101843
Milillo P., Rignot E., Rizzoli P., Scheuchl B., Mouginot J., Bueso-Bello J., et al. (2019). Heterogeneous retreat and ice melt of thwaites glacier, west antarctica. Sci. Adv. 5, 1–9. doi: 10.1126/sciadv.aau3433
Mohrmann M., Heuzé C., Swart S. (2021). Southern ocean polynyas in cmip6 models. Cryosphere 15, 4281–4313. doi: 10.5194/tc-15-4281-2021
Moorman R., Morrison A. K., Hogg A. M. C. (2020). Thermal responses to antarctic ice shelf melt in an eddy-rich global ocean-sea ice model. J. Climate 33, 6599–6620. doi: 10.1175/JCLI-D-19-0846.1
Nøst O. A., Biuw M., Tverberg V., Lydersen C., Hattermann T., Zhou Q., et al. (2011). Eddy overturning of the antarctic slope front controls glacial melting in the eastern weddell sea. J. Geophys. Res.: Oceans 116, 1–17. doi: 10.1029/2011JC006965
Nakayama Y., Greene C. A., Paolo F. S., Mensah V., Zhang H., Kashiwase H., et al. (2021). Antarctic Slope current modulates ocean heat intrusions towards totten glacier. Geophys. Res. Lett. 48. doi: 10.1029/2021GL094149
Nakayama Y., Timmermann R., Schröder M., Hellmer H. H. (2014). On the difficulty of modeling circumpolar deep water intrusions onto the amundsen sea continental shelf. Ocean Model. 84, 26–34. doi: 10.1016/j.ocemod.2014.09.007
Naughten K. A., Rydt J. D., Rosier S. H., Jenkins A., Holland P. R., Ridley J. K. (2021). Two-timescale response of a large antarctic ice shelf to climate change. Nat. Commun. 12, 1–10. doi: 10.1038/s41467-021-22259-0
Newsom E. R., Bitz C. M., Bryan F. O., Abernathey R., Gent P. R. (2016). Southern ocean deep circulation and heat uptake in a high-resolution climate model. J. Climate 29, 2597–2619. doi: 10.1175/JCLI-D-15-0513.1
Nicholls K. W., Østerhus S., Makinson K., Gammelsrød T., Fahrbach E. (2009). Ice-ocean processes over the continental shelf of the southern weddell sea, antarctica: A review. Rev. Geophys. 47, 1–23. doi: 10.1029/2007RG000250
Nicholls K. W., Østerhus S., Makinson K., Johnson M. R. (2001). Oceanographic conditions south of berkner island, beneath filchner-ronne ice shelf, antarctica. J. Geophys. Res.: Oceans 106, 11481–11492. doi: 10.1029/2000jc000350
Nicholls K. W. (2004). Interannual variability and ventilation timescales in the ocean cavity beneath filchner-ronne ice shelf, antarctica. J. Geophys. Res. 109, C04014. doi: 10.1029/2003JC002149
Ohshima K. I., Nihashi S., Iwamoto K. (2016). Global view of sea-ice production in polynyas and its linkage to dense/bottom water formation. Geosci. Lett. 3. doi: 10.1186/s40562-016-0045-4
Orsi A. H., Johnson G. C., Bullister J. L. (1999). Circulation,mixing and production of antarctic bottom water. Prog. Oceanogr. 43, 55–109. doi: 10.1016/S0079-6611(99)00004-X
Orsi A. H., Whitworth T., Nowlin W. D. (1995). On the meridional extent and fronts of the antarctic circumpolar current. Deep-Sea Res. Part I 42, 641–673. doi: 10.1016/0967-0637(95)00021-W
Palóczy A., Gille S. T., McClean J. L. (2018). Oceanic heat delivery to the antarctic continental shelf: Large-scale, low-frequency variability. J. Geophys. Res.: Oceans 123, 7678–7701. doi: 10.1029/2018JC014345
Pan L., Powell E. M., Latychev K., Mitrovica J. X., Creveling J. R., Gomez N., et al. (2021). Rapid postglacial rebound amplifies global sea level rise following west antarctic ice sheet collapse. Sci. Adv. 7, 1–10. doi: 10.1126/sciadv.abf7787
Pellichero V., Sallée J. B., Chapman C. C., Downes S. M. (2018). The southern ocean meridional overturning in the sea-ice sector is driven by freshwater fluxes. Nat. Commun. 9, 1–9. doi: 10.1038/s41467-018-04101-2
Portela E., Rintoul S. R., Herraiz-Borreguero L., Roquet F., Bestley S., van Wijk E., et al. (2022). Controls on dense shelf water formation in four east antarctic polynyas. J. Geophys. Res.: Oceans 127, 1–21. doi: 10.1029/2022JC018804
Pritchard H. D., Ligtenberg S. R., Fricker H. A., Vaughan D. G., Broeke M. R. V. D., Padman L. (2012). Antarctic Ice-sheet loss driven by basal melting of ice shelves. Nature 484, 502–505. doi: 10.1038/nature10968
Purkey S. G., Johnson G. C. (2013). Antarctic Bottom water warming and freshening: Contributions to sea level rise, ocean freshwater budgets, and global heat gain. J. Climate 26, 6105–6122. doi: 10.1175/JCLI-D-12-00834.1
Richter O., Gwyther D. E., Galton-Fenzi B. K., Naughten K. A. (2022a). The whole antarctic ocean model (waom v1.0): Development and evaluation. Geosci. Model. Dev. 15, 617–647. doi: 10.5194/gmd-15-617-2022
Richter O., Gwyther D. E., King M. A., Galton-Fenzi B. K. (2022b). The impact of tides on antarctic ice shelf melting. Cryosphere 16, 1409–1429. doi: 10.5194/tc-16-1409-2022
Rignot E., Jacobs S., Mouginot J., Scheuchl B. (2013). Ice-shelf melting around antarctica. Science 341, 266–270. doi: 10.1126/science.1235798
Rignot E., Mouginot J., Scheuchl B., Broeke M. V. D., Wessem M. J. V., Morlighem M. (2019). Four decades of antarctic ice sheet mass balance from 1979—2017. Proc. Natl. Acad. Sci. United States America 116, 1095–1103. doi: 10.1073/pnas.1812883116
Rintoul S. R. (2007). Rapid freshening of antarctic bottom water formed in the indian and pacific oceans. Geophys. Res. Lett. 34, 1–5. doi: 10.1029/2006GL028550
Rintoul S. R. (2018). The global influence of localized dynamics in the southern ocean. Nature 558, 209–218. doi: 10.1038/s41586-018-0182-3
Rintoul S. R., Silvano A., Pena-Molino B., Wijk E. V., Rosenberg M., Greenbaum J. S., et al. (2016). Ocean heat drives rapid basal melt of the totten ice shelf. Sci. Adv. 2, 1–6. doi: 10.1126/sciadv.1601610
Schaffer J., Timmermann R., Arndt J. E., Kristensen S. S., Mayer C., Morlighem M., et al. (2016). A global, high-resolution data set of ice sheet topography, cavity geometry, and ocean bathymetry. Earth Syst. Sci. Data 8, 543–557. doi: 10.5194/essd-8-543-2016
Schmidtko S., Heywood K. J., Thompson A. F., Aoki S. (2014). Multidecadal warming of antarctic waters. Science 346, 1227–1231. doi: 10.1126/science.1256117
Shchepetkin A. F., McWilliams J. C. (2009). Correction and commentary for "ocean forecasting in terrain-following coordinates: Formulation and skill assessment of the regional ocean modeling system" by haidvogel et al., j. comp. phys. 227, pp. 3595-3624. J. Comput. Phys. 228, 8985–9000. doi: 10.1016/j.jcp.2009.09.002
Silvano A. (2020). Changes in the southern ocean. Nat. Geosci. 13, 4–5. doi: 10.1038/s41561-019-0516-2
Silvano A., Rintoul S. R., Kusahara K., Peña-Molino B., van Wijk E., Gwyther D. E., et al. (2019). Seasonality of warm water intrusions onto the continental shelf near the totten glacier. J. Geophys. Res.: Oceans 124, 4272–4289. doi: 10.1029/2018JC014634
Silvano A., Rintoul S. R., Peña-Molino B., Williams G. D. (2017). Distribution of water masses and meltwater on the continental shelf near the totten and moscow university ice shelves. J. Geophys. Res.: Oceans 122, 2050–2068. doi: 10.1002/2016JC012115
Spence P., Griffies S. M., England M. H., Hogg A. M., Saenko O. A., Jourdain N. C. (2014). Rapid subsurface warming and circulation changes of antarctic coastal waters by poleward shifting winds. Geophys. Res. Lett. 41, 4601–4610. doi: 10.1002/2014GL060613
Stewart A. L. (2021). Mesoscale, tidal and seasonal/interannual drivers of the weddell sea overturning circulation. J. Phys. Oceanogr. 51. doi: 10.1175/JPO-D-20-0320.1
Stewart A. L., Klocker A., Menemenlis D. (2018). Circum - antarctic shoreward heat transport derived from an eddy- and tide- resolving simulation. Geophys. Res. Lett. 45, 834–845. doi: 10.1002/2017GL075677
Stewart A. L., Thompson A. F. (2015). Eddy-mediated transport of warm circumpolar deep water across the antarctic shelf break. Geophys. Res. Lett. 42, 432–440. doi: 10.1002/2014GL062281
St-Laurent P., Klinck J. M., Dinniman M. S. (2013). On the role of coastal troughs in the circulation of warm circumpolar deep water on antarctic shelves. J. Phys. Oceanogr. 43, 51–64. doi: 10.1175/JPO-D-11-0237.1
Tamura T., Ohshima K. I., Fraser A. D., Williams G. D. (2016). Sea Ice production variability in antarctic coastal polynyas. J. Geophys. Res.: Oceans 121, 2967–2979. doi: 10.1002/2015JC011537
Tamura T., Ohshima K. I., Markus T., Cavalieri D. J., Nihashi S., Hirasawa N. (2007). Estimation of thin ice thickness and detection of fast ice from ssm/i data in the antarctic ocean. J. Atmos. Oceanic Technol. 24, 1757–1772. doi: 10.1175/JTECH2113.1
Tamura T., Ohshima K. I., Nihashi S. (2008). Mapping of sea ice production for antarctic coastal polynyas. Geophys. Res. Lett. 35, 1–5. doi: 10.1029/2007GL032903
Tamura T., Ohshima K. I., Nihashi S., Hasumi H. (2011). Estimation of surface heat/salt fluxes associated with sea ice growth/melt in the southern ocean. SOLA 7, 17–20. doi: 10.2151/sola.2011-005
Thompson A. F., Heywood K. J., Schmidtko S., Stewart A. L. (2014). Eddy transport as a key component of the antarctic overturning circulation. Nat. Geosci. 7, 879–884. doi: 10.1038/ngeo2289
Thompson A. F., Speer K. G., Chretien L. M. S. (2020). Genesis of the antarctic slope current in west antarctica. Geophys. Res. Lett. 47. doi: 10.1029/2020GL087802
Timmermann R., Goeller S. (2017). Response to filchner-ronne ice shelf cavity warming in a coupled ocean-ice sheet model - part 1: The ocean perspective. Ocean Sci. 13, 765–776. doi: 10.5194/os-13-765-2017
Timmermann R., Wang Q., Hellmer H. H. (2012). Ice-shelf basal melting in a global finite-element sea-ice/ice-shelf/ocean model. Ann. Glaciol. 53, 303–314. doi: 10.3189/2012AoG60A156
van Wijk E. M., Rintoul S. R. (2014). Freshening drives contraction of antarctic bottom water in the australian antarctic basin. Geophys. Res. Lett. 41, 1657–1664. doi: 10.1002/2013GL058921
van Wijk E. M., Rintoul S. R., Wallace L. O., Ribeiro N., Herraiz-Borreguero L. (2022). Vulnerability of denman glacier to ocean heat flux revealed by profiling float observations. Geophys. Res. Lett. 49. doi: 10.1029/2022GL100460
Vernet M., Geibert W., Hoppema M., Brown P. J., Haas C., Hellmer H. H., et al. (2019). The weddell gyre, southern ocean: Present knowledge and future challenges. Rev. Geophys. 57, 623–708. doi: 10.1029/2018RG000604
Walin G. (1982). On the relation between sea-surface heat flow and thermal circulation in the ocean. Tellus 34, 187–195. doi: 10.3402/tellusa.v34i2.10801
Williams G. D., Bindoff N. L., Marsland S. J., Rintoul S. R. (2008). Formation and export of dense shelf water from the adélie depression, east antarctica. J. Geophys. Res.: Oceans 113, 1–12. doi: 10.1029/2007JC004346
Williams G. D., Meijers A. J., Poole A., Mathiot P., Tamura T., Klocker A. (2011). Late winter oceanography off the sabrina and banzare coast (117-128°e), east antarctica. Deep-Sea Res. Part II: Topical Stud. Oceanogr. 58, 1194–1210. doi: 10.1016/j.dsr2.2010.10.035
Keywords: Southern Ocean, Antarctic shelf, water mass transformation, high salinity shelf water (HSSW), ice shelf water (ISW), coastal polynyas, ice shelf cavities, ocean-ice shelf interaction
Citation: Boeira Dias F, Rintoul SR, Richter O, Galton-Fenzi BK, Zika JD, Pellichero V and Uotila P (2023) Sensitivity of simulated water mass transformation on the Antarctic shelf to tides, topography and model resolution. Front. Mar. Sci. 10:1027704. doi: 10.3389/fmars.2023.1027704
Received: 25 August 2022; Accepted: 06 February 2023;
Published: 12 April 2023.
Edited by:
Arthur J. Miller, University of California, San Diego, United StatesReviewed by:
Tyler Pelle, University of California, San Diego, United StatesCopyright © 2023 Boeira Dias, Rintoul, Richter, Galton-Fenzi, Zika, Pellichero and Uotila. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fabio Boeira Dias, Zi5ib2VpcmFfZGlhc0B1bnN3LmVkdS5hdQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.