Numerical and experimental investigation on hydrodynamic performance of the stick-held dip net in Pacific saury fishery

Stick-held dip (SHD) net is an effective fishing gear target for catching the Pacific saury. In this study, the hydrodynamic performance of an SHD net in current was investigated by means of numerical simulation and experimental test, and a mathematical model based on the lumped-mass method and principle of rigid body kinematics was developed to predict the net shape and tension of the cable. A series of physical model tests based on Tauti’s law and full-scale measurements at sea were conducted to evaluate the applicability of the numerical model. The results showed that the prediction performance of the numerical model was good, with a mean relative error of approximately 20% among the numerical, experimental, and field measured data. The dynamic shooting behavior of the SHD net at different current velocities and the effects of the length of the hauling rope and the mesh size on the net shape and tension of the cable were analyzed using the numerical simulation approach. When the current velocity increased from 0.12 to 0.46 m/s, the enclosed volume of the SHD net decreased by 62.9%. The height of net opening increased by 9.29% to 13.53% for every 10% increase in the length of the hauling rope from 0.96 to 1.44 m. With the increase in mesh size from 24 to 30 and 35 mm, the sinking depth and speed of the net increased, and the tension force of the cables decreased by 9.02% and 12.10%, respectively. The results suggested that (1) the numerical model could realistically represent the hydrodynamic characteristics of the SHD net; (2) the suitable operation current velocity is below 0.60 m/s; (3) the reasonable length of the hauling rope is about 30 m; and (4) the mesh size of the main netting could be increased to 30 mm.

Introduction

The Pacific saury (Cololabis saira, hereafter saury) is an important pelagic fish widely distributed in the North Pacific Ocean and was recognized as a priority species by the North Pacific Fisheries Commission in 2015 (NPFC, 2015). The saury typically inhabits depths of 15–20 m (Ueno et al., 2004; Prants et al., 2021) and experiences complicated oceanographic conditions as it migrates through the Oyashio and Kuroshio waters (Huang et al., 2007; Prants et al., 2021). During its seasonal migration, the saury is primarily exploited by countries and regions such as Japan, China, Chinese Taipei, Russia, South Korea, and Vanuatu. The annual commercial fishery for saury in China, with fishing vessels operating on the high seas, begins in June and ends in November (Hua et al., 2020).

The stick-held dip (SHD) net is one of the many types of lift nets employed to catch pelagic fishes such as saury, squid, sardine, and mackerel (Yamazaki, 1981; Semedi et al., 2002). The SHD net system consists mainly of nets (main netting and selvedge), cables, and bamboo poles that keep the headline floating on the water surface (hereafter float pole). In the fishing operation, the netting and float pole are first laid into the water from one side of the vessel while using the equipped overwater fishing lamps to attract the fish (Li F. et al., 2021), and finally the saury is caught by quickly lifting the net. Because of its simple structure, convenient fishing method, and high selectivity, the SHD net has become the most popular fishing gear in the Pacific saury fishery, except for a small number of gillnet catches in the exclusive economic zones of Japan and Russia (NPFC).

Over the last decades, relatively few studies have been carried out to understand the fishing behavior and working performance of SHD net. Yamazaki and Chuenchitpong (1981) investigated the gear construction and fishing methods of SHD net for squid off the coast of Thailand. Xu et al. (2005) described the fishing operation techniques of SHD net on the basis of field investigation. Hasegawa and Suzuki (2005) summarized the production processes of the catching activity of SHD net and compared it with the fishery characteristics of drift gillnet in Japanese blue sprat. Zhang et al. (2006) proposed an optimal design of SHD net system in terms of netting material, mesh size, buoyancy and sinking force by combining field surveys and theoretical analysis. In recent years, an experimental research conducted by Shi et al. (2016) who evaluated the tension force of cables of SHD net at different lifting speeds during the pursing phase. Furthermore, the sinking and lifting characteristics of this fishing gear were explored by field trials (Shi et al., 2018). Currently, it has been about 90 years since the invention of SHD net in Japan and 20 years since the introduction of this fishing gear in China. There is still an urgent need for improvements in engineering analysis and technical operation, which are mostly set based on personal experience. Therefore, detailed information about the behavior response of this gear in current becomes important to understand the hydrodynamic performance of the SHD net.

Common methods for studying the hydrodynamic performance of fishing gear include numerical simulation, physical model test, and full-scale field measurement (Fredriksson et al., 2003; Takagi et al., 2004; Guan et al., 2022). Each of these approaches has its advantages and limitations, and Nguyen et al. (2015) pointed out that the use of two or three methods should be encouraged as the ideal process for design, modification, and performance evaluation of fishing gear development. A modified tuna purse seine was described in Hosseini’s study, in which the sinking performance of gear with a large-mesh panel and heavier net material was analyzed numerically (Hosseini et al., 2011). Song et al. (2019) studied the dynamic retrieval procedure of longline gear using numerical simulation established by the lumped mass method and discussed the shape, tension, hydrodynamic force, and impact of catch on fishing operation. Wan et al. (2020) analyzed the hydrodynamic performance of a set net in current by numerical simulation and physical model test and concluded that the current where the net was placed should not exceed 0.7 kn by comparing the tension of mooring lines and net shapes at different flow velocities. To date, considerable efforts have been dedicated to explore the hydrodynamic behavior and optimize the catch performance of fishing gear such as trawls (Priour, 2009), seines (Kim et al., 2007), longlines (Song et al., 2019), gillnets (Takagi et al., 2003), and net cages (Huang et al., 2008); however, to our knowledge, there is little information on the published studies or reports on the hydrodynamic characteristics of SHD net are available. In this study, we aimed to investigate the dynamic response of the SHD net in current and analyze the effects of current velocity, hauling rope length and mesh size on the hydrodynamic performance of the SHD net with numerical simulation and experimental test.

Materials and methods

Physical model test

Model net specifications

A prototype SHD net of 38.3 m×41.7 m (headline × side rope) was studied in this work. A 1:25 scale (λ=25) model of the gear was fabricated based on Tauti’s law with the small-scale ratio λ′=3. The schematic diagram of the SHD model net is shown in Figure 1. As the main component of buoyancy, the float pole is a complex structure, commonly consisting of inner fiberglass tubes and outer layer of bamboos. In recent years, some fishermen have replaced bamboo with polyvinyl chloride (PVC). As a result, the float pole was simplified to a straight pipe and the PVC material was used in physical model test. The floats attached to both ends of the float pole are used for the purpose of preventing collisions with fishing vessel during operation, and rings on the net are utilized to thread the purse line inside and pull the sides of the net up immediately to prevent fish from escaping. The main netting is made of polyester (PES) material of braided knotless netting, and the selvedges are braided knotted netting made of PES material. Since the mesh count of the selvedge is much smaller than that of the main netting (approximately 1:300), the selvedge parts were neglected when making the model net. The detailed dimensions and specifications of the model net are tabulated in Table 1.

FIGURE 1

Figure 1 Schematic of the structure of the SHD net.

TABLE 1

Table 1 Specifications of the model net used for experiments.

Experimental setup

Experiments on the geometrical shape and the tension force of cables of the model net were performed in a flume tank at Shanghai Ocean University, China. The observation window of the flume tank is 15 m long, 3.5 m wide, and 2.3 m deep, delivering a maximum current velocity of 1.5 m/s.

The setup of the experiment is shown in Figure 2. Two bridle lines and three hauling ropes (e.g., left hauling rope, LHR; middle hauling rope, MHR; right hauling rope, RHR) of the SHD net were attached to three vertical fixed bars, each bridle line and hauling rope having a length of 1.44 and 1.2 m. The height from the attachment point on the bar to the water surface was 26 and 20 cm for the two types of cables, respectively, and each end of the cable was connected with a load cell with a capacity of 100 N and an accuracy of 0.01% N. The average sinking weight of 0.31 kg/m was attached to the lead line. Three LED diodes were fixed to the left side rope of the model net for motion analysis and recorded by a charge-coupled device (CCD) camera through an observation window. The shape of the net and tension force of the cables were measured at incoming current velocities of 0.12, 0.23, 0.35, 0.46, and 0.58 m/s. The load cells were calibrated and zeroed at both the beginning and end of the experiment, and the sinking characteristics of the diodes were obtained from the pictures by means of GetData software.

FIGURE 2

Figure 2 Schematic diagram of the flume tank test.

Numerical modeling

Modeling of the SHD net

The SHD net is composed of flexible parts (netting and cables) and rigid parts (float pole and sinker), and the system can be modeled by connecting the main components of the fishing gear. The lumped-mass method is applied to establish the mathematical model of netting and cable, which divides them into finite elements of mass points and springs. For the main netting, the knots of the mesh are regarded as mass points, and the bars of the mesh are considered as massless springs that connect these points together (Figure 3). The principle of rigid body kinematics is used to build the motion equation of the float pole. To calculate the external forces on the float pole, it is divided into a series of microsegments, and the forces on the float pole can be obtained by summing the forces on each microsegment (Figure 4).

FIGURE 3

Figure 3 Schematic of the connection pattern of the topology structure for netting.

FIGURE 4

Figure 4 Schematic of the microsegment of the float pole.

Motion equations

(1) For the flexible part, the schematic view of the major forces acting on the mass point i is depicted in Figure 5. According to Newton’s second law, the motion equation for each mass point is written as:

$\begin{array}{ll}\left(m_i+\Delta m_i\right)a_i=\stackrel{\rightharpoonup }{F}+\stackrel{\rightharpoonup }{T}+\stackrel{\rightharpoonup }{B}+\stackrel{\rightharpoonup }{G}& (1)\end{array}$

FIGURE 5

Figure 5 Mechanical analysis acting on the mass point.

Where m_i and Δm_i are the mass and added mass, respectively; a_i is the acceleration vector; $\stackrel{\rightharpoonup }{F}$ is the hydrodynamic force; $\stackrel{\rightharpoonup }{T}$ is the tension force; $\stackrel{\rightharpoonup }{B}$ is the buoyancy; and $\stackrel{\rightharpoonup }{G}$ is the force of gravity.

The added mass Δm_i is given by (Lee et al., 2008):

$\begin{array}{ll}\Delta m_i={\rho }_w{V}_1{C}_{m1}+{\rho }_w{V}_2{C}_{m2}& (2)\end{array}$

where ρ_w is the density of the water; V₁ is the volume of the knot, the diameter of the knot for the knotless mesh is taken to be 1.5 times as large as the diameter of the mesh bar (Fredheim and Faltinsen, 2003); C_m1 is the added mass coefficient of knot, which is 1.5 as it is regarded to be a sphere (Zhou and Xu, 2018); V₂ is the volume of the mesh bar; and C_m2 is the added mass coefficient of mesh bars and is expressed as (Hosseini et al., 2011):

$\begin{array}{ll}{C}_{m2}=1+\sin \alpha & (3)\end{array}$

where α is the angle of attack.

The hydrodynamic force $\stackrel{\rightharpoonup }{F}$, including the drag force $\stackrel{\rightharpoonup }{F_D}$ and lift force $\stackrel{\rightharpoonup }{F_L}$, can be calculated by the Morison formular:

$\begin{array}{ll}\stackrel{\rightharpoonup }{F_D}=\frac{1}{2}{C}_D{\rho }_{w}S\left|\stackrel{\rightharpoonup }{u}-\stackrel{\rightharpoonup }{U}\right|\left(\stackrel{\rightharpoonup }{u}-\stackrel{\rightharpoonup }{U}\right)& (4)\end{array}$

$\begin{array}{ll}\stackrel{\rightharpoonup }{F_L}=\frac{1}{2}{C}_L{\rho }_{w}S\left|\stackrel{\rightharpoonup }{u}-\stackrel{\rightharpoonup }{U}\right|\left(\stackrel{\rightharpoonup }{u}-\stackrel{\rightharpoonup }{U}\right)& (5)\end{array}$

Where C_D is the drag coefficient; C_L is the lift coefficient; S is the projected area of the mass point; and $\stackrel{\rightharpoonup }{u}$ and $\stackrel{\rightharpoonup }{U}$ are the velocity of the water particle and the mass point, respectively.

The drag coefficient C_D and lift coefficient C_L are estimated by (Zhou et al., 2015; Zhou and Xu, 2018):

$\begin{array}{ll}{C}_D=si{n}^3\alpha C_{N90}+\pi C_f& (6)\end{array}$

$\begin{array}{ll}{C}_L=si{n}^2\alpha \cos \alpha C_{N90}& (7)\end{array}$

Where C_N90 is the hydrodynamic coefficient at an attack angle of 90˚ (C_{N90 =} 1.1); and C_f is the friction coefficient, πC_f=0.02 (Hoernor, 1965).

The relationship between the tension $\stackrel{\rightharpoonup }{T}$ and elongation of a bar element is given by (Suzuki et al., 2003):

$\begin{array}{ll}\stackrel{\rightharpoonup }{T_{ij}}=\frac{ES\text{'}}{L_{ij}}\left(L_{ij}-L_0\right)& (8)\end{array}$

where E is the Young modulus of the material; S' is the cross-section area of the element; L_ij is the deformed length (j=1, 2, 3, 4); and L₀ is the original length.

The buoyancy $\stackrel{\rightharpoonup }{B}$ and gravity $\stackrel{\rightharpoonup }{G}$ can be written as follows:

$\begin{array}{ll}\stackrel{\rightharpoonup }{B}+\stackrel{\rightharpoonup }{G}=\left({\rho }_i-{\rho }_w\right)\forall g& (9)\end{array}$

where ρ_i is the density of the material; ∀ is the volume of the element; and g is the gravity acceleration.

The second-order derivative of the spatial displacement of node i (x_i, y_i, z_i) is the accelerated velocities in the x, y, and, z-axes. The differential equations for the acceleration are implicit and high-order ordinary differential equations which can then be converted to first-order differential equations.

The mesh grouping method is used to reduce the number of calculations. A given number of actual meshes are modeled by a fictitious equivalent mesh, which has the same physical features as the actual meshes (Lee et al., 2005). In this study, 24×24 actual meshes were modeled as a fictitious equivalent mesh. Similarly, the cables (bridle line and hauling rope) were divided into finite elements, each consisting of a finite number of mass points connected by springs with the same properties as described above.

(2) For the motion of the float pole, two sets of coordinate systems are defined: the fixed-coordinate system O-xyz and the body-coordinate system G-τnυ (Figure 4). In the fixed-coordinate system, the origin O is located on the water surface and the current propagates along the positive direction of the x-axis. In the body-coordinate system, G is the center of mass of the float pole, which can follow its movement, and τ, n, and υ are the inertial principal axes along the tangent, normal and vertical directions of the float pole. In the initial state, the x-y-z axes of the fixed-coordinate system are parallel to the τ-n-υ axes of the body-coordinate system.

The equation of motion of each microsegment is established as:

$\begin{array}{ll}\left(m+\Delta m\right)a=\stackrel{\rightharpoonup }{F_m}+\stackrel{\rightharpoonup }{T_m} +\stackrel{\rightharpoonup }{B_m}+\stackrel{\rightharpoonup }{G_m}+\stackrel{\rightharpoonup }{f}+\stackrel{\rightharpoonup }{Q}& (10)\end{array}$

where m and Δm are the mass and added mass of the microsegment; a is the acceleration vector; $\stackrel{\rightharpoonup }{F_m}$ is the fluid force; $\stackrel{\rightharpoonup }{T_m}$ is the pulling force of the cable; $\stackrel{\rightharpoonup }{B_m}$ is the buoyancy; $\stackrel{\rightharpoonup }{G_m}$ is the force of gravity; $\stackrel{\rightharpoonup }{f}$ is the tension of the mesh bar of the adjacent net below; and $\stackrel{\rightharpoonup }{Q}$ is the wind force acting on the part of the microsegment above the water surface.

The fluid force $\stackrel{\rightharpoonup }{F_m}$ and the added mass on the microsegment can be expressed as (Zhao et al., 2007):

$\begin{array}{ll}\stackrel{\rightharpoonup }{F_m}=\frac{1}{2}{C}_d{\rho }_{w}A\left|\stackrel{\rightharpoonup }{u}-\stackrel{\rightharpoonup }{U}\right|\left(\stackrel{\rightharpoonup }{u}-\stackrel{\rightharpoonup }{U}\right)+{\rho }_w{\left(C_{m3}+1\right)\forall }^{\text{'}}{a}_w-{\rho }_w{C}_{m3}a\text{'}& (11)\end{array}$

Where C_d is the drag coefficient; A is the projected area of the microsegment perpendicular to the current direction; $\stackrel{\rightharpoonup }{u}$ and $\stackrel{\rightharpoonup }{U}$ are the velocity vectors of the water particle and the microsegment; C_m3 and a’ are the added mass coefficient and acceleration vector of the microsegment; ∀' is the volume of the microsegment; and a_w is the acceleration vector of the water particle.

Under the condition of uniform current, the acceleration vector of water particle is zero (a_w=0). Thus, for a moving body, the fluid forces on the microsegment of the τ component is given by:

$\begin{array}{ll}\stackrel{\rightharpoonup }{F_{m\tau }}=\frac{1}{2}{C}_{d\tau }{\rho }_w{A}_{\tau }\left|\stackrel{\rightharpoonup }{u_{\tau }}-\stackrel{\rightharpoonup }{U_{\tau }}\right|\left(\stackrel{\rightharpoonup }{u_{\tau }}-\stackrel{\rightharpoonup }{U_{\tau }}\right)-{\rho }_w{C}_{m3\_\tau }a{\prime }_{\tau }& (12)\end{array}$

where C_dτ, A_τ, $\stackrel{\rightharpoonup }{u_{\tau }}$, $\stackrel{\rightharpoonup }{U_{\tau }}$, C_{m3_τ}, and $a_{\tau }^{\text{'}}$ are the corresponding physical quantities of the τ component. And, the fluid forces in the n and υ directions can be expressed in the same manner.

For a cylinder floated at the water surface, the drag coefficient of the microsegment can be taken as a constant (Li et al., 2007). With reference to previous studies, the drag coefficient of a circular cylinder in current can be set as C_dτ=0.1, C_dn=C_dV=1.2, and the added masses coefficients C_{m3_τ}=0.0, C_{m3_n}=C_{m3_V}=1.0 (Théret, 1993; Zhao et al., 2007).

As shown in Figure 6, G (x_i, y_i, z_i) is the central point of the microsegment, and the submerged depth of the microsegment d_n is written as:

$\begin{array}{ll}{d}_n=r\left(1-\cos \frac{{\phi }_i}{2}\right)& (13)\end{array}$

FIGURE 6

Figure 6 Schematic of the model float pole for calculating.

where r is the radius of the float pole; and φ_i is the central angle of the submerged part of the microsegment.

The projected chord length d_v is expressed as:

$\begin{array}{ll}{d}_v=2r\sin \frac{{\phi }_i}{2}& (14)\end{array}$

The effective projected area A_n, A_τ, and A_v of the underwater part of the microsegment is calculated as follows:

$\begin{array}{ll}{A}_n=d_n·dl=r\left(1-\cos \frac{{\phi }_i}{2}\right)dl& (15)\end{array}$

$\begin{array}{ll}{A}_{\tau }=\frac{r^2}{2}\left({\phi }_i-\text{sin} {\phi }_i\right)& (16)\end{array}$

$\begin{array}{ll}{A}_{\nu }=d_v·dl=2r\sin \frac{{\phi }_i}{2}{d}_l& (17)\end{array}$

where d_l is the length of the microsegment.

The effective projected area along the tangent direction τ of the microsegment, which is used as the product of the diameter and length. With the float pole on the surface of water, the tangential force of the microsegment is related to the arc area r·φ_i·d_l . When the float pole is completely submerged in water, the projected area is taken as the ratio of the water arc area to π. For the vertical projected area, d_n is taken as 2r when d_n >r.

The translation of the motion of the microsegment between the fixed-coordinate system and body-coordinate system is expressed as:

$\begin{array}{ll}\stackrel{\rightharpoonup }{F_x}=\stackrel{\rightharpoonup }{F_{m\tau }}\text{cos}\delta -\stackrel{\rightharpoonup }{F_{mv}}\text{sin}\delta & (18)\end{array}$

$\begin{array}{ll}\stackrel{\rightharpoonup }{F_z}=\stackrel{\rightharpoonup }{F_{m\tau }}\text{sin}\delta +\stackrel{\rightharpoonup }{F_{mv}}\text{cos}\delta & (19)\end{array}$

where δ is angle between the positive direction of the τ and x-axis.

The pulling force $\stackrel{\rightharpoonup }{T_m}$ of the bridle line can be expressed as:

$\begin{array}{ll}\stackrel{\rightharpoonup }{T_m}=A\prime C_1{\left(\frac{l-l_0}{l_0}\right)}^{C_2}& (20)\end{array}$

where A’ is the cross-sectional area of the cable; l₀ is the initial length of the cable; l is the length of the cable after deformation; and C₁ and C₂ are the elastic coefficients of the cable.

The buoyancy $\stackrel{\rightharpoonup }{B_m}$ of the microsegment is calculated as:

$\begin{array}{ll}\stackrel{\rightharpoonup }{B_m}={\rho }_{w}g\frac{r^2}{2}\left({\phi }_i-sin{\phi }_i\right)dl& (21)\end{array}$

The gravity $$\stackrel{\rightharpoonup }{G_m}$$ of each microsegment is:

$\begin{array}{ll}\stackrel{\rightharpoonup }{G_m}=\frac{M_G}{N}& (22)\end{array}$

where M_G is the gravity of the float pole; and N is the number of the microsegments.

The tension $\stackrel{\rightharpoonup }{f}$ can be calculated by the mesh bar of the adjacent netting. The wind force $\stackrel{\rightharpoonup }{Q}$ acting on the microsegment is expressed as (Song and Li, 2022):

$\begin{array}{ll}\stackrel{\rightharpoonup }{Q}=\frac{1}{2}{S}_m{\rho }_a{V}_w^2& (23)\end{array}$

where S_m is the projected area of the microsegment in the direction of wind; ρ_a is the density of the air; and V_w is the wind speed.

Due to the pull of the heavy nettings below, it is important to note that the motion of the float pole in the current in this work includes only surge–sway–heave translation. According to Newton’s second law, the motion equations of the microsegment of the float pole in the body coordinate system are given by:

$\begin{array}{ll}\begin{array}{l}X\prime {\prime }_G=\frac{1}{M_G}{\displaystyle {\sum }_{i=1}^N{F}_{xi}}\hfill \\ Y\prime {\prime }_G=\frac{1}{M_G}{\displaystyle {\sum }_{i=1}^N{F}_{yi}}\hfill \\ Z\prime {\prime }_G=\frac{1}{M_G}{\displaystyle {\sum }_{i=1}^N{F}_{zi}}\hfill \end{array}& (24)\end{array}$

where $X_G^{\prime \prime }$, $Y_G^{\prime \prime }$, and $Z_G^{\prime \prime }$ are the accelerations of the center of mass of the float pole; and F_xi, F_yi, and F_zi are the components of the external forces on the float pole in the x, y, and z directions.

To obtain the dynamic response of the entire SHD net system, the virtual fishing gear was assembled by connecting the mass points of the netting, the cables (two bridle lines and three hauling ropes), and the end nodes of the float pole. The motion behavior of the SHD net was described in nonlinear and stiff equations, and a fifth-order Runge–Kutta method (Lee et al., 2008; Xu et al., 2013) was applied to solve the differential equation with the given initial conditions. A time step of 0.0005 s was taken in the numerical computation.

Field experiment

The trial experimental data were collected from two typical Chinese saury fishing vessels in the high seas of the Northwest Pacific Ocean during July-October 2015 and July-September 2021. The specifications of the porotype SHD net and a total of 10 net fishing operations, current, wind speed data and operational parameters were recorded. The sinking characteristics (sinking depth and speed) of the foot line were measured by DRs (TDR-2050, RBR Co., Ottawa, Canada) with a measurement range of 10-740 m and an accuracy of 0.05% of full scale. Three DRs were attached to the corners and midpoint of the foot line of the fishing gear and were set to record data per second. Current data were collected using a ship-borne Doppler tidal current meter (JLN-628, Japan Radio Co., Ltd.) in the water layer from 0 to 50 m. Wind data were collected using a hand-held digital anemometer (Cima AS8336) with a range of 0.3-45 m/s and a resolution of 0.001 m/s.

Determination of the mesh size

The SHD net is designed to prevent the saury from penetrating or stabbing the mesh of the main netting. According to the theory of gillnet (Xu, 2004), the relationship between mesh size and the body length of fish can be expressed as:

$\begin{array}{ll}a\le a_1& (25)\end{array}$

$\begin{array}{ll}{a}_1=KL& (26)\end{array}$

where a and a₁ are the lengths of the mesh bar of SHD net and gillnet, respectively; K, a dimensionless coefficient, is the fish body shape coefficient and is related to the fish species; and L is the body length of the fish.

The saury has a “spindle-shaped” body with K ranging from 0.08 to 0.10 (Zhang et al., 2006). In this study, we assumed that the allowable catch-size of saury in the high seas is 200 to 300 mm (Li W. J. et al., 2021), and the theoretical mesh size (a’) of the main netting of the SHD net should be 32-60 mm calculated by the Equation (26). Furthermore, the target fish species should be considered especially their behavioral responses to the gear such as the dash towards the netting. Thus, the mesh size can be further modified with reference to the bunt part of the seine net, i.e., 0.5 a’ to 0.6 a’, corresponding to a mesh size of 16-36 mm. Consequently, the hydrodynamic performances of the prototype SHD net with mesh sizes of 24, 30, and 35 mm were explored.

Results

Validation of the numerical model

The equilibrium shapes of SHD net at different current velocities were obtained from the physical model test (Figure 7) and calculated by numerical simulation (Figure 8). As can be seen, both experimental and numerical results showed that the shape of SHD net varied with the current velocity. The height of net opening decreased and the foot line moved upward with increasing current velocity, and the netting is seriously deformed when the velocity was greater than 0.46 m/s. The configurations of SHD net obtained by numerical simulations were consistent with those obtained by CCD camera. Variations of the sinking depth of the midpoint of the foot line are displayed in Figure 8F, the sinking depth increased firstly and then decreased (0.35, 0.46, and 0.58 m/s) or stabilized (0.12 and 0.23 m/s) with time. The sinking depths of the foot line in the model test converted to the full-scale SHD net were 24.77, 22.16, 15.32, 9.19, and 4.66 m at different velocities, with attenuation rates ranging from 11.82% to 97.30%. Additionally, there were significant differences among the different sinking depths of the foot line (P< 0.05, ANOVA).

FIGURE 7

Figure 7 Equilibrium shape of SHD net from the model test at different current velocities of 0.12, 0.23, 0.35, 0.46, and 0.58 m/s.

FIGURE 8

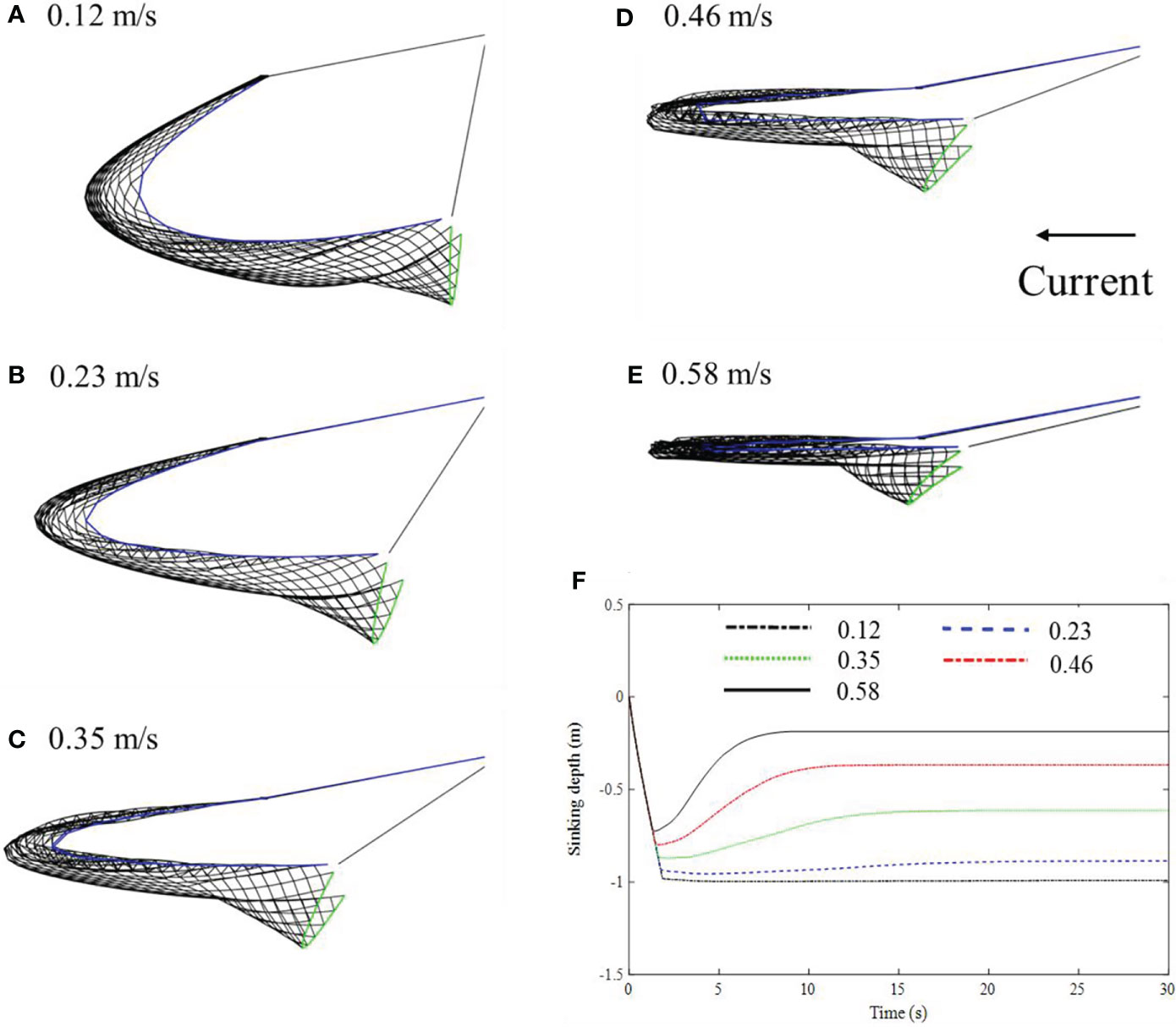
Figure 8 Equilibrium shape of SHD net from numerical simulation at different current velocities of 0.12, 0.23, 0.35, 0.46, and 0.58 m/s. (A) 0.12 m/s; (B) 0.23 m/s; (C) 0.35 m/s; (D) 0.46 m/s; (E) 0.58 m/s; (F) sinking depth of the midpoint of the foot line.

Figure 9 shows the simulated and experimental sinking depths of the midpoint of the foot line from model test and numerical simulation at different current velocities. Both the calculated and measured results indicated that the sinking depth decreased with the increase of current velocity. The simulated sinking depths at lower velocities were overestimated compared to those of the flume tank test, and the average relative error between the simulated and experimental values was 20.18%. Analysis of variance demonstrated that there was no significant difference between the simulated and observed sinking depths (P=0.90, ANOVA).

FIGURE 9

Figure 9 Sinking depth of the midpoint of the foot line at different current velocities.

The tension forces of the bridle line derived from the physical model tests and numerical simulations are compared in Figure 10. Both simulated and measured tensions gradually increased with increasing velocity. At each velocity, the tension values obtained in the experiment showed good agreement with the results calculated from the numerical simulation, with an average relative error of 20.57%. No significant differences in the tension force of the bridle line were found between the model tests and numerical simulations at different velocities (P=0.94, ANOVA).

FIGURE 10

Figure 10 Tension of the bridle line at different current velocities.

The sinking depths of the midpoint of the foot line of the full-scale SHD net obtained from the field experiments and numerical simulations are shown in Figure 11. For most of the elapsed time, the simulated sinking depths were slightly greater than those of the sea trial. The simulated depth increased in a relatively linear manner with time until the maximum sinking depth was reached, and the measured depth was closely tracked. In general, the sinking depths obtained from the numerical simulation were basically consistent with the measured results, with an average relative error of about 17.43% (P=0.32, ANOVA).

FIGURE 11

Figure 11 Sinking depth of the foot line in field experiment and numerical simulation.

Shooting operation of SHD net

The dynamic shooting process of the SHD net in a three-dimensional (3-D) side view at a current velocity of 0.12 m/s is given in Figure 12. The netting deformed and spread before reaching equilibrium. In the early stage, the foot line sank rapidly and the headline with the adjacent netting was blown downstream and formed a bow shape under the water fluid. After approximately 23 s of elapsed time, the SHD net reached an equilibrium state and eventually formed a dustpan like shape as a result of its weight, hydrodynamics and the tension force of the cables. Figure 13 presents the visualization of the SHD net from different views, the foot line (green color) was W-shaped due to being pulled by the three hauling ropes.

FIGURE 12

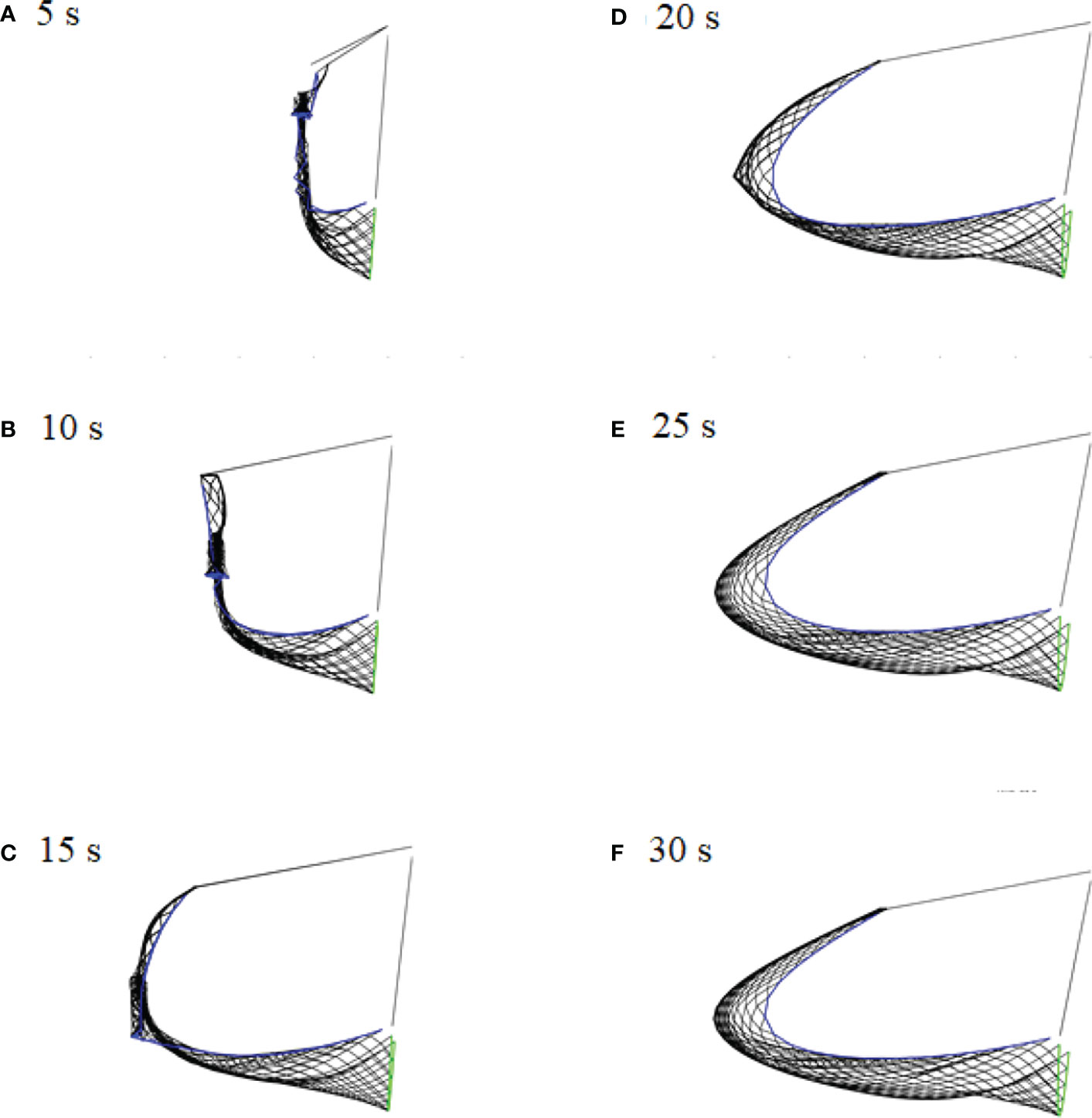
Figure 12 The dynamic shooting process of SHD net at a velocity of 0.12 m/s. (A) 5s; (B) 10 s; (C) 15s; (D) 20 s; (E) 25s; (F) 30 s

FIGURE 13

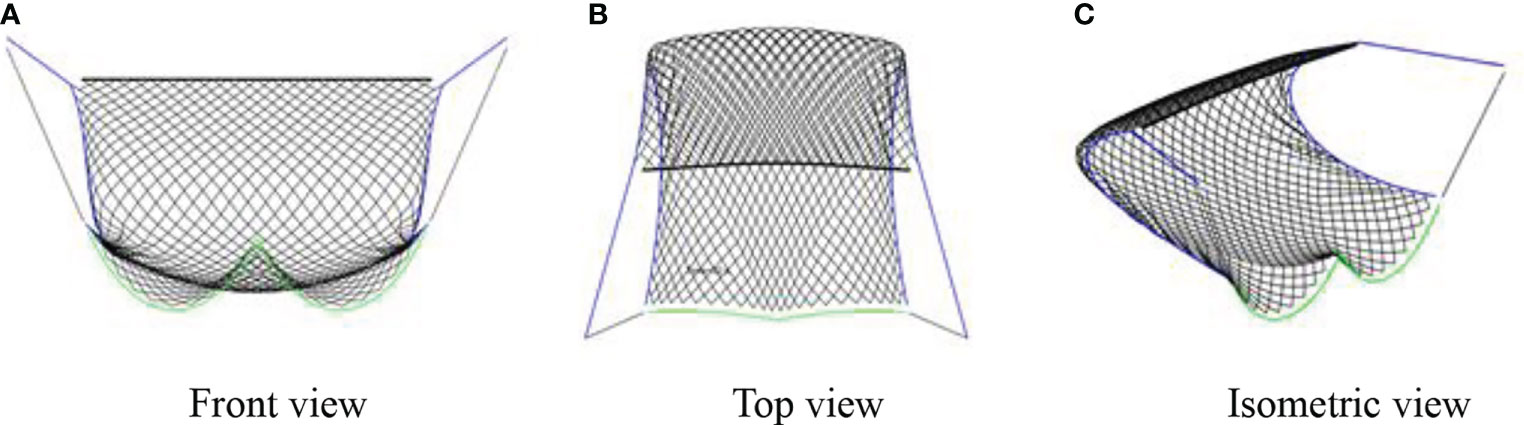
Figure 13 Different views of the equilibrium shape of shooting of SHD net. (A) front view; (B) top view; (C) isometric view.

Length of hauling rope of SHD net

The effects of hauling rope length on the hydrodynamic performance of the SHD net, including geometrical shape and tension force of cables, were evaluated using the verified mathematical model. The shapes of the net were simulated for different lengths of hauling rope (Figure 14, dotted lines denote the same height or width). It was observed that the length of the hauling rope could influence the sinking depth of the foot line, the height of the net opening and the spread of the netting. Figure 15 depicts the sinking depth of the midpoint of the foot line for each length, where the sinking depth increased with increasing hauling rope length. Moreover, the sinking depth of the model net converted to that of the prototype net was 16.89, 19.54, 22.16, 24.71, and 27.24 m respectively when the hauling rope length increased from 0.96 to 1.44 m, with an increasing rate ranged from 13.53% to 9.29%. The sinking depths of the net with longer hauling rope increased significantly compared to those with shorter lengths (P<0.05, ANOVA), indicating that the length of the hauling rope had a greater influence on the sinking depth of SHD net. In addition, each curve in Figure 15 had the same slope until the maximum sinking depth was reached, which meant that the change in hauling rope length did not affect the sinking speed of the foot line during the shooting process.

FIGURE 14

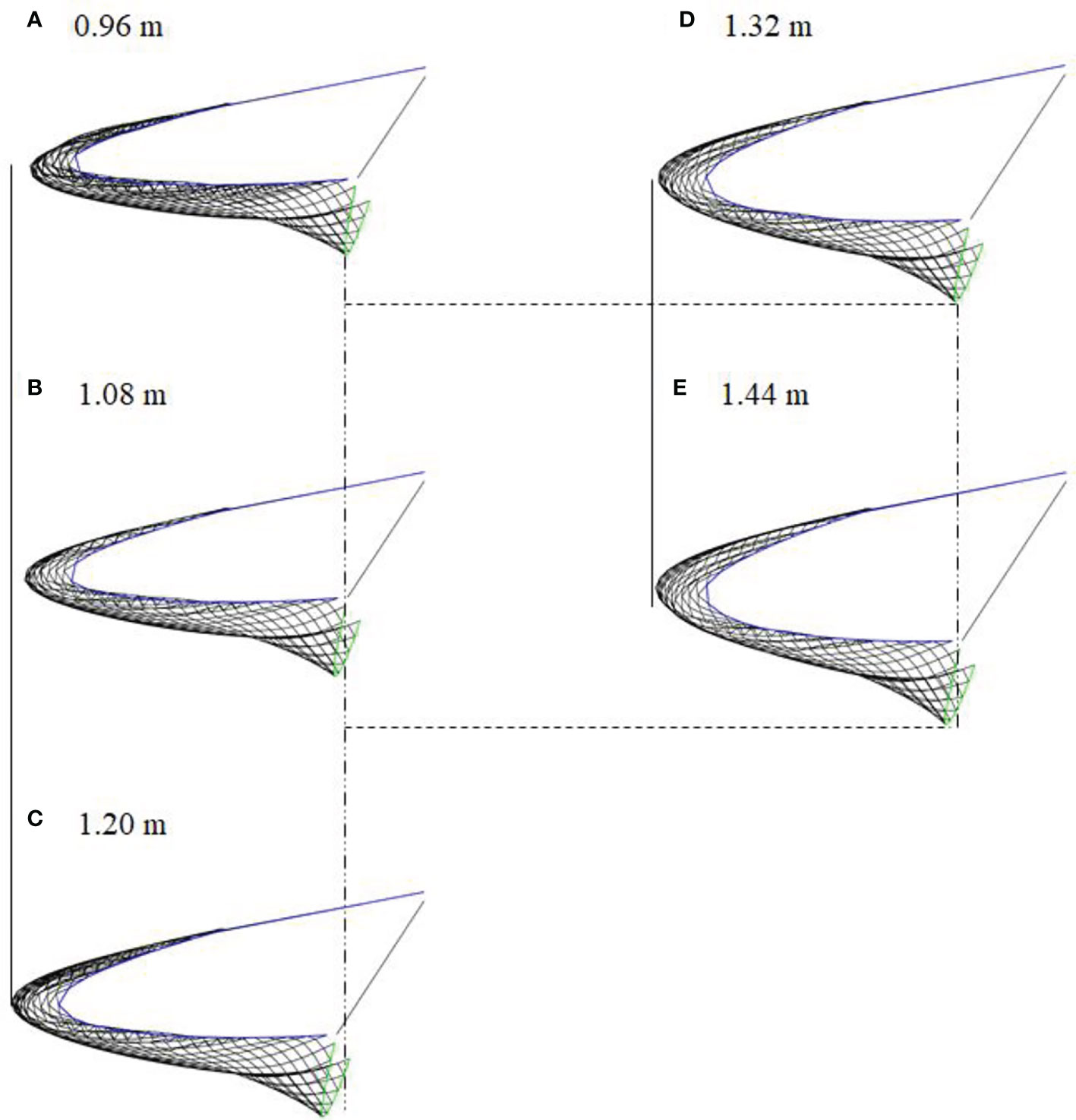
Figure 14 Simulated shape of SHD net with different lengths of the hauling rope. (A) 0.96 m; (B) 1.08 m; (C) 1.20 m; (D) 1.32 m; (E) 1.44 m.

FIGURE 15

Figure 15 Sinking depth of the foot line of SHD net with different lengths of the hauling rope.

The tension force of the hauling rope and bridle line of the SHD net with different lengths of the hauling rope are shown in Figure 16. As seen from (a), the tension force of the hauling rope was much greater than that of the bridle line, and the tension of the hauling ropes decreased slightly, while the bridle line increased as the length of the hauling rope increased. The tension of the middle hauling rope (MHR) was larger than that of the left and right hauling ropes (LHR and RHR). When the length of the hauling rope was increased from 0.96 m to 1.44 m, the sum of the tension force of all cables varied between -0.03% and 1.64%.

FIGURE 16

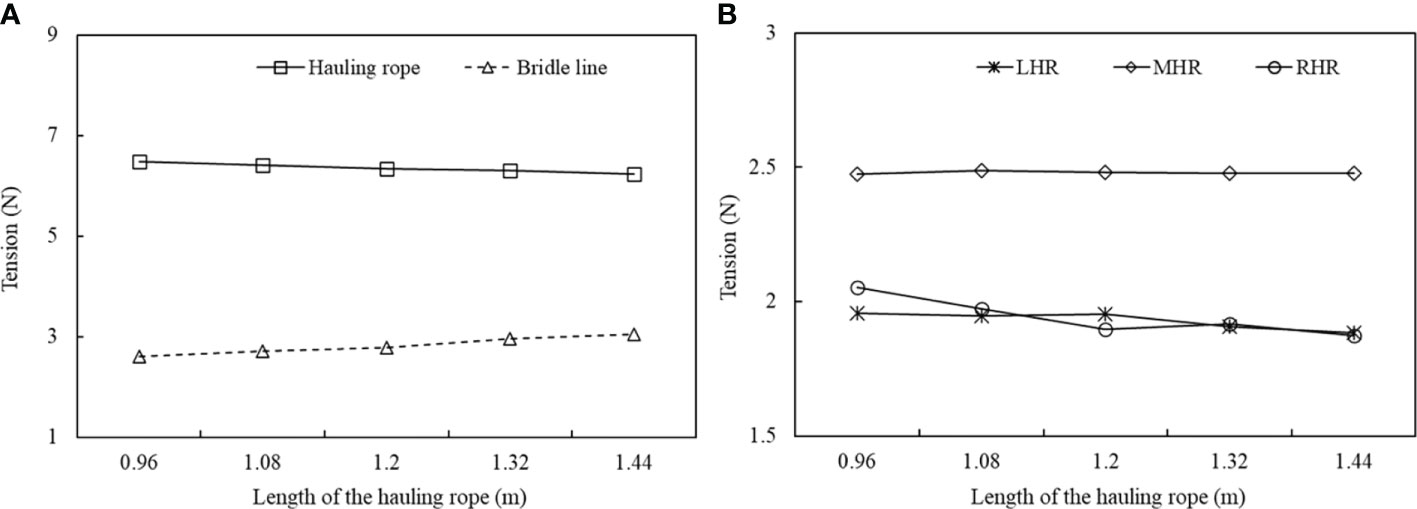
Figure 16 Tension of cables of the SHD net with different lengths of the hauling rope. (A) hauling rope and bridle line; (B) left, middle, and right hauling ropes.

Mesh size of SHD net

Figure 17 illustrates the simulated shapes of the SHD net at three kinds of mesh sizes. There were differences in the net opening and the stretch of the netting. The sinking depth of the midpoint of the foot line is shown in Figure 18. By comparison, the net made of a large mesh size sank deeper, and the sinking speed of the foot line increased. The sinking depths of the foot line with the mesh size of 24, 30, and 35 mm converted to that of the full-scale SHD net were 22.26, 23.07, and 23.28 m, with increase rates of 3.98% and 0.90%., respectively. Variance analysis showed that there was a significant difference in the sinking depth of different mesh sizes (P<0.05, ANOVA). In addition, the sinking speed of the foot line of the net with the mesh size of 30 mm and 35 mm was greater than that of 24 mm.

FIGURE 17

Figure 17 Simulated shape of SHD net at different mesh sizes. (A) 24 mm; (B) 30 mm; (C) 35 mm.

FIGURE 18

Figure 18 Sinking depth of the foot line of SHD net at different mesh sizes.

The result of comparing the tension force of the hauling rope and bridle line of the SHD net among different mesh sizes is given in Figure 19. Similarly, the tension force of the hauling rope was greater than that of the bridle line. With the increase in mesh size from 24 to 30 and 35 mm, the tension forces of the hauling rope and bridle line decreased slightly, with the sum of the tension of them decreasing by approximately 9.02% and 12.10%, respectively.

FIGURE 19

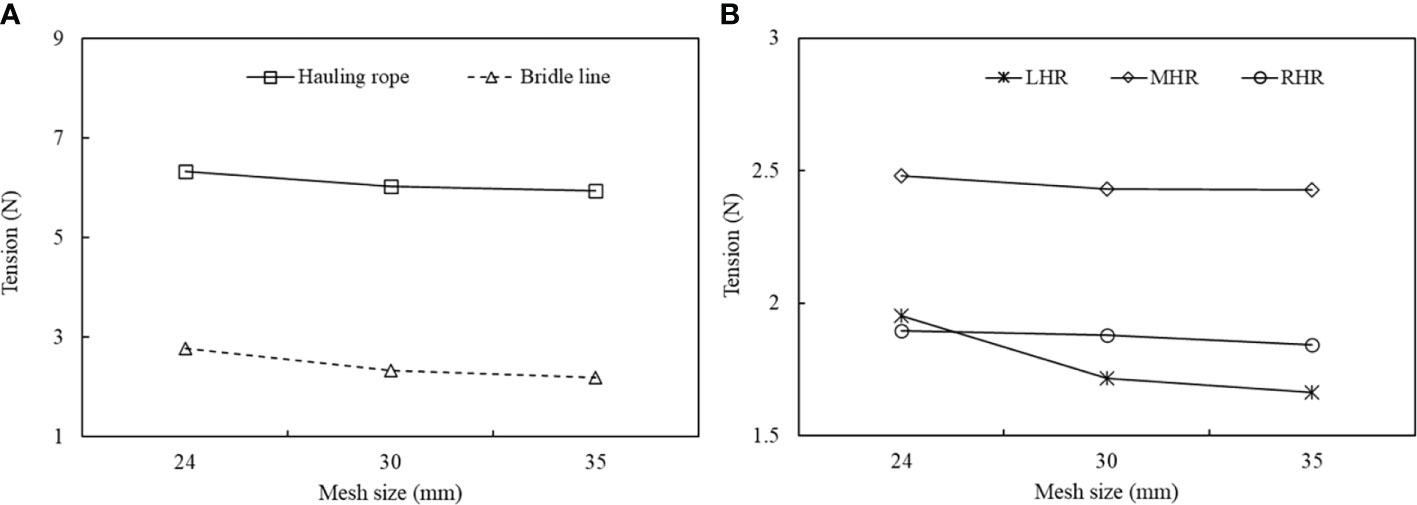
Figure 19 Tension of cables of SHD net at different mesh sizes. (A) hauling rope and bridle line; (B) left, middle, and right hauling ropes.

Discussion

Performance evaluation of the numerical model

The numerical model had good predictive performance and could realistically represent the hydrodynamic characteristics of the SHD net. The mean relative error between simulated and experimental values (sinking depth and tension force) were about 20%, which was highly related to the structure and fishing method of the gear. The SHD net has a small hanging ratio, implying that several meshes were gathered and then assembled with a cable. Additionally, the foot line of the net was pulled by the hauling ropes, making the netting like a “dustpan” after the SHD net is stabilized. The above two reasons lead to many folds and bulges on the net body during fishing, especially at lower velocities, as observed in the flume tank experiment. In contrast, the simulated shooting behavior did not consider these situations and the numerical netting is smooth, resulting in a relatively large bias that was observed. Furthermore, the mesh size of the SHD net is small, and the mesh grouping method used a large grouped mesh (24×24 meshes), which could also result in differences between the measured and calculated results (Huang et al., 2019). When the fishing gear is stored on the side board of the vessel the netting often stacks and tangles with cables, thus the sinking speed of the foot line may be limited once shooting begins. In addition, the complexity of flows and environmental factors cannot be accurately predicted during actual fishing operations (Kim et al., 2007). Compared to the net shape obtained from the model test, the shape of the numerical simulation at the same velocity was consistent, but there were slightly differences in the net opening, which may be due to the heavier sinker, the simplified structure of the net before modeling and assumptions, i.e., the flow is uniform, constant and does not change with depth. Based on the field-measured sinking data of the SHD net, Shi et al. (2019) used the bootstrap method to calculate the mean distribution of the sinking depth of the foot line range from 20.37 m to 29.54 m, which is consistent with the results of this work. Overall, our findings showed good agreement, with no significant discrepancies between the simulated and measured sinking depths or tensions of the cable in the different simulation scenarios.

Analysis of shooting operation of SHD net

Clear understanding of the dynamic shooting behaviors, including the shape and cable tension force, would help to reveal the hydrodynamic performance of SHD net and contribute to optimization of the operational strategies in the Pacific saury fishery. The fishing activity of the SHD net operates on one side of the vessel, while the saury is attracted by the fishing lamps on the other side. Consequently, the sinking performance and drag force of the SHD net are largely related to fishing efficiency. During the shooting operation, it was found that the sinking speed of the foot line tended to decrease with time, which resulted from the increase in the drag of the net with the extension of the netting.

The water fluid plays an important role in the shooting behaviors of fishing gear, and the results indicate that the current velocity significantly affects the net shape and sinking performance of the SHD net. During the fishing process, the float pole always floats on the water surface, and the horizontal distance from the vessel to the float pole generally remains constant. In other words, the sinking depth of the foot line can represent the enclosed volume of the SHD net to some extent. A small sinking depth indicates a limited volume to surround the fish and high probabilities of impacting the fish shoals. Therefore, the current status was closely correlated to the enclosed volume of the net and could be applied as a key indicator for predicting the underwater states of the SHD net, providing scientific fishing operations in advance. With the increase in velocity, the foot line was floating upward, and the lower part of the netting deformed seriously before the net reached stability. Analysis showed that the sinking depth of the net at a velocity of 0.46 m/s sharply decreased by about 62.9% compared to that at a velocity of 0.12 m/s. Previous experimental trial has showed that the velocity at a depth of 30 m had the greatest influence on the sinking depth of the SHD net (Shi et al., 2018). Combining the shape of the SHD net at different current velocities obtained from the physical model test and numerical simulation, we recommended that the suitable operation current velocity was lower than 0.35 m/s (0.60 m/s at sea). Optionally, if the current velocity was larger or in the months of poor sea conditions (usually October and November), the operating requirements could be met by increasing the sinker of the gear or lengthening the length of the hauling rope.

Effects of length of hauling rope on performance of SHD net

The hauling rope is an important factor that directly affects the sinking performance and enclosed volume of the SHD net, and the fishing operation can be adjusted by controlling its length. To quantify the effects of changing hauling rope length on the hydrodynamic characteristics of the SHD net, the sinking depth and tension of the cables in the virtual net with different lengths of hauling rope were performed by the numerical simulation approach. Variance analysis results revealed that the hauling rope length significantly affects the sinking depth of the SHD net but does not affect its sinking speed. An increase in the maximum sinking depth of the foot line was observed as well as in the height of net opening when the length of the hauling rope changed from 0.96 m to 1.44 m. This highlights the importance of considering the length of the hauling rope when planning an SHD fishing. Shi et al. (2018) stated that the length of the hauling rope was one of the important factors affecting the maximum sinking depth of the SHD net based on the generalized additive model (GAM), which was consistent with our conclusion. In contrast, for the tension force of cables, the effect of changes in the length of the hauling rope was small. The tensions of the hauling rope were larger than those of the bridle line, because the bridle lines were connected to the float pole, which floats on the water surface, while the hauling ropes were attached to the foot line of the SHD net. Thus, the hauling ropes afford a large proportion of the hydrodynamic force and gravity of the net, which may be one of the reasons that the actual fishing gear assembled more foot lines.

During the saury individuals concentrated under the fishing lamp, the fish shoals were mostly distributed from the surface to a maximum depth of approximately 20 m underwater. Setting large hauling rope length for SHD net increases the horizontal distance between the foot line and the vessel (Figure 14), which is detrimental to fishing gear operations and wastes more pursing time. Therefore, it is not useful to set large sinking depth of with too long hauling rope. Considering the sinking depths of the foot line obtained from mode test, numerical simulation and field trial, we proposed that the reasonable length of the hauling rope is about 30 m (corresponding to a length of 1.2 m in the flume tank test). Particularly, the length of the hauling rope can be increased in the cases of high current velocity and when catching for deep-water saury.

Effects of mesh size on performance of SHD net

The mesh, a fundamental element of the netting panel, has profound influences on the hydrodynamic performance and selectivity of fishing gear (Vincent et al., 2022). The effects of mesh size on the geometrical shape as well as the sinking properties of the SHD net were studied using numerical simulation. The results indicated that an SHD net made of larger mesh size (30 or 35 mm) netting showed better performance than one made with netting of small mesh size (24 mm) in terms of sinking depth, sinking speed, and drag force, which is largely associated with the reduction of the shielding effect of the main netting. Studies on purse seine have shown that the change to larger meshed panels and the change in netting material from PA to PES increased the net sinking speed and reduced the tension force of the bridle line, and the optimized net was proven to prevent the fish from escaping (Hosseini et al., 2011; Widagdo et al., 2015).

According to our field investigations, the mesh size of the selvedge (31.6 mm) of the SHD net is larger than that of the main netting (24 mm). In some cases, several saury individuals were found hanging on the upper selvedge after the net was pursed. To avoid stab or damage to the main netting by the catch, reduce the drag force and catch of juveniles, we suggest the mesh size of the main netting should be increased to 30 mm. In addition, the netting close to the foot line is first put down when the net is shot and retrieved first when the net is pursed, indicating that this part of the net is not involved in harvesting fish. Therefore, a new design of net with a larger mesh size (35 mm) in the lower part of the SHD net could be further tested to improve the speeds of sinking and pursing and to reduce the operational time.

Conclusion

The hydrodynamic performance of the SHD net and its relationship with the environmental conditions, fishing technique, and net structure in current was numerically and experimentally investigated. The main conclusions of this study included the following: (1) the integrated mathematical model could effectively predict the net shape, the tension of cables, and the sinking characteristics of the SHD net; (2) the SHD net could operate well at current velocity below 0.60 m/s; (3) the reasonable length of the hauling rope is about 30 m; (4) the mesh size of the main netting should be increased to 30 mm. Admittedly, there are some limitations in the present work. Firstly, only the current and wind were involved in the construction of the numerical model; future researches are recommended to consider other factors, such as wave and fish behavior. Secondly, the mesh sizes we studied in this work were extracted in a theoretical way, and the biological features of catches and the mesh deformability could be considered to explore the mechanism of selectivity. Investigating the hydrodynamic performance of the SHD net and exploring its relationships with fishing gear and method can provide a scientific reference for the modification and optimization of the fishing gear to make it more selective, efficient, and energy saving.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

FL: conceptualization, investigation, methodology, data curation, writing original draft and revision. LS: conceptualization, supervision and revision. CH: conceptualization and supervision. QZ: conceptualization and funding. All authors contributed to the article and approved the submitted version.

Funding

This research was supported by the National Key R&D Program of China (Grant No. 2019YFD0901503), the National Natural Science Foundation of China (Project No. 32273185).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Fredheim A., Faltinsen O. M. (2003). “Hydroelastic analysis of a fishing net in steady inflow conditions,” in Proceedings of the Third International Conference on Hydroelasticity in Marine Technology, Oxford, United Kingdom, September 2003.

Google Scholar

Fredriksson D. W., Swift M. R., Irish J. D., Tsukrov I., Celikkol B. (2003). Fish cage and mooring system dynamics using physical and numerical models with field measurements. Aquacult. Eng. 27 (2), 117–146. doi: 10.1016/S0144-8609(02)00043-2

CrossRef Full Text | Google Scholar

Guan Q. L., Zhu W. B., Zhou A. Z., Wang Y. J., Tang W. Y., Wan R. (2022). Numerical and experimental investigations on hydrodynamic performance of a newly designed deep bottom trawl. Front. Mar. Sci. 9. doi: 10.3389/fmars.2022.891046

PubMed Abstract | CrossRef Full Text | Google Scholar

Hasegawa K., Suzuki S. (2005). Fisheries characteristics of stick-held dip net and drift gill net for blue sprat spratelloides gracilis catch. Fish. Eng. 42 (1), 79–86. doi: 10.18903/fisheng.42.1_79

CrossRef Full Text | Google Scholar

Hoernor S. F. (1965). Fluid dynamic drag (Bakersfield CA: Hoerner Fluid Dynamics).

Google Scholar

Hosseini S. A., Lee C. W., Kim H. S., Lee J., Lee G. H. (2011). The sinking performance of the tuna purse seine gear with large-meshed panels using numerical method. Fish. Sci. 77, 503–520. doi: 10.1007/s12562-011-0371-6

CrossRef Full Text | Google Scholar

Hua C. X., Li F., Zhu Q. C., Zhu G. P., Meng L. W. (2020). Habitat suitability of pacific saury (Cololabis saira) based on a yield-density model and weighted analysis. Fish. Res. 221, 105408. doi: 10.1016/j.fishres.2019.105408

CrossRef Full Text | Google Scholar

Huang L. Y., Li Y. Y., Ni Y., Cheng H., Wang X. X., Wang G., et al. (2019). “Study on the influence of mesh grouping on numerical simulation results of fish cages,” in Proceedings of the ASME 2019 38th International Conference on Ocean, Offshore and Arctic Engineering, Glasgow, Scotland, UK, June 2019. doi: 10.1115/OMAE2019-95706

CrossRef Full Text | Google Scholar

Huang W. B., Lo N., Chiu T. S., Chen C. S. (2007). Geographical distribution and abundance of pacific saury, Cololabis saira (Brevoort) (Scomberesocidae), fishing stocks in the northwestern pacific in relation to sea temperatures. Zool. Stud. 46 (6), 705–716. Available at: https://zoolstud.sinica.edu.tw/Journals/46.6/705.html

Google Scholar

Huang C. C., Tang H. J., Liu J. Y. (2008). Effects of waves and currents on gravity-type cages in the open sea. Aquacult. Eng. 38 (2), 105–116. doi: 10.1016/j.aquaeng.2008.01.003

CrossRef Full Text | Google Scholar

Kim H. Y., Lee C. W., Shin J. K., Kim H. S., Cha B. J., Lee G. H. (2007). Dynamic simulation of the behavior of purse seine gear and sea-trial verification. Fish. Res. 88, 109–119. doi: 10.1016/j.fishres.2007.08.007

CrossRef Full Text | Google Scholar

Lee C. W., Kim Y. B., Lee G. H., Choe M. Y., Lee M. K., Koo K. Y. (2008). Dynamic simulation of a fish cage system subjected to currents and waves. Ocean. Eng. 35 (14-15), 1521–1532. doi: 10.1016/j.oceaneng.2008.06.009

CrossRef Full Text | Google Scholar

Lee C. W., Lee J. H., Cha B. J., Kim H. Y., Lee J. H. (2005). Physical modeling for underwater flexible systems dynamic simulation. Ocean. Eng. 32 (3-4), 331–347. doi: 10.1016/j.oceaneng.2004.08.007

CrossRef Full Text | Google Scholar

Li L., Fu S. X., Xu Y. W., Wang J. G., Yang J. M. (2013). Dynamic responses of floating fish cage in waves and current. Ocean. Eng. 72, 297–303. doi: 10.1016/j.oceaneng.2013.07.004

CrossRef Full Text | Google Scholar

Li Y. C., Gui F. K., Teng B. (2007). Hydrodynamic behavior of a straight floating pipe under wave conditions. Ocean. Eng. 34, 552–559. doi: 10.1016/j.oceaneng.2006.01.012

CrossRef Full Text | Google Scholar

Li F., Hua C. X., Zhu Q. C., Song L. M. (2021). Optimization of LED fishing lamp allocation based on numerical modeling in pacific saury fishery. Fish. Sci. 87), 283–296. doi: 10.1007/s12562-021-01513-w

CrossRef Full Text | Google Scholar

Li W. J., Zhang C., Tian Y. J., Liu Y., Liu S. G., Tian H., et al. (2021). Otolith shape analysis as a tool to identify two pacific Saury(Cololabis saira) groups from a mixed stock in the high-seas fishing ground. J. Ocean. Univ. China 20 (2), 402–408. doi: 10.1007/s11802-021-4541-6

CrossRef Full Text | Google Scholar

Nguyen T. X., Winger P. D., Orr D., Legge G., Delouche H., Gardner A. (2015). Computer simulation and flume tank testing of scale engineering models: How well do these techniques predict full-scale at-sea performance of bottom trawls? Fish. Res. 161, 217–225. doi: 10.1016/j.fishres.2014.08.007

CrossRef Full Text | Google Scholar

North Pacific Fisheries Commission (NPFC) (2022). Available at: https://www.npfc.int/ (Accessed May 10, 2022).

Google Scholar

Prants S. V., Budyansky M. V., Uleysky M. Y., Kulik V. V. (2021). Lagrangian Fronts and saury catch locations in the northwestern pacific in 2004-2019. J. Mar. Syst. 222 (103605), 1–16. doi: 10.1016/j.jmarsys.2021.103605

CrossRef Full Text | Google Scholar

Priour D. (2009). Numerical optimisation of trawls design to improve their energy efficiency. Fish. Res. 98, 40–50. doi: 10.1016/j.fishres.2009.03.015

CrossRef Full Text | Google Scholar

Semedi B., Saitoh S. I., Saitoh K., Yoneta K. (2002). Application of multi-sensor satellite remote sensing for determining distribution and movement of pacific saury Cololabis saira. Fish. Sci. 68, 1781–1784. doi: 10.2331/FISHSCI.68.SUP2_1781

CrossRef Full Text | Google Scholar

Shi Y. C., Zhu Q. C., Hua C. X., Zhang Y. D. (2018). Sinking and rising performance of saury stick-held based on field measurements. Mar. Sci. Bull. 37 (4), 459–467. doi: 10.11840/j.issn.1001-6392.2018.04.012

CrossRef Full Text | Google Scholar

Shi Y. C., Zhu Q. C., Hua C. X., Zhang Y. D. (2019). Evaluation of saury stick-held net performance between model test and on-sea measuremet. Haiyang Xuebao. 41 (2), 123–133. doi: 10.3969/j.issn.0253-4193.2019.02.012

CrossRef Full Text | Google Scholar

Shi Y. C., Zhu Q. C., Zhang Y. D., Hua C. X., Zhou W. B. (2016). Factors influencing the rope tension of saury stick-held lift nets. J. Fish. Sci. China 23 (3), 704–712. doi: 10.3724/SP.J.1118.2016.15304

CrossRef Full Text | Google Scholar

Song L. M., Li Y. T. (2022). Dynamic numerical simulation of the pelagic longline settlement process based on the runge-kutta method. J. Fish. Sci. China 29 (1), 157–169. doi: 10.12264/JFSC2021-0076

CrossRef Full Text | Google Scholar

Song L. M., Qi Y. K., Li J., Shen Z. B., Zhang X. F., Shen X. (2019). Dynamic simulation of pelagic longline retrieval. J. Ocean. Univ. China 18 (2), 255–266. doi: 10.1007/s11802-019-3990-7

CrossRef Full Text | Google Scholar

Suzuki K., Takagi T., Shimizu T., Hiraishi T., Yamamoto K., Nashimoto K. (2003). Validity and visualization of a numerical model used to determine dynamic configurations of fishing nets. Fish. Sci. 69 (4), 695–705. doi: 10.1046/j.1444-2906.2003.00676.x

CrossRef Full Text | Google Scholar

Takagi T., Shimizu T., Suzuki K., Hiraishi T., Matsushita Y., Watanabe T. (2003). Performance of “NaLA”: a fishing net shape simulator. J. Fish. Eng. 40 (2), 125–134. doi: 10.18903/fisheng.40.2_125

CrossRef Full Text | Google Scholar

Takagi T., Shimizu T., Suzuki K., Hiraishi T., Yamamoto K. (2004). Validity and layout of “NaLA”: A net configuration and loading analysis system. Fish. Res. 66, 235–243. doi: 10.1016/S0165-7836(03)00204-2

CrossRef Full Text | Google Scholar

Théret F. (1993). Étude de l’équilibre des surfaces réticulées placées dans un courant uniforme: application aux chaluts (Nantes, France; Université de Nantes).

Google Scholar

Ueno Y., Suyama S., Kurita Y., Kumazawa T. (2004). Design and operation methods of a mid-water trawl for quantitative sampling of a surface pelagic fish, pacific saury (Cololabis saira). Fish. Res. 66, 3–17. doi: 10.1016/S0165-7836(03)00178-4

CrossRef Full Text | Google Scholar

Vincent B., Robert M., Simon J., Vacherot J. P., Faillettaz R. (2022). Exploring the mechanics of fish escape attempts through mesh. Fish. Res. 248, 106195. doi: 10.1016/j.fishres.2021.106195

CrossRef Full Text | Google Scholar

Wan R., Guan Q. L., Li Z. G., Hu F. X., Dong S. C., You X. X. (2020). Study on hydrodynamic performance of a set-net in current based on numerical simulation and physical model test. Ocean. Eng. 195, 1–9. doi: 10.1016/j.oceaneng.2019.106660

CrossRef Full Text | Google Scholar

Widagdo A., Lee C. W., Lee J. (2015). Calculating and measuring the sinking performance of small-scale purse seine gear in Java, Indonesia, to improve the gear. Fish. Aquat. Sci. 18 (2), 221–227. doi: 10.5657/FAS.2015.0221

CrossRef Full Text | Google Scholar

Xu L. X. (2004). Theory and design of fishing gear (Beijing: China Agriculture Press). doi: CNKI:SUN:JOKE.0.2005-10-033

Google Scholar

Xu T. J., Zhao Y. P., Dong G. H., Gui F. K. (2013). Analysis of hydrodynamic behavior of a submersible net cage and mooring system in waves and current. Appl. Ocean. Res. 42, 155–167. doi: 10.1016/j.apor.2013.05.007

CrossRef Full Text | Google Scholar

Xu W., Zhu Q. C., Zhang X. C., Qian W. G., Zhu G. P., Xia H. (2005). Bouke net fishing technology of pacific saury in the northwestern pacific. Shandong. Fish. 22 (10), 43–45.

Google Scholar

Yamazaki T. (1981). Stick-held dip net (Thailand: Training Department, Southeast Asian Fisheries Development Center).

Google Scholar

Yamazaki T., Chuenchitpong M. (1981). Survey report on squid stick-held dip net at banphe district (Japan: Training Department, Southeast Asian Fisheries Development Center).

Google Scholar

Zhang X., Yu Y. F., Huang H. L., Xu B. S., Wang M. Y. (2006). The study on designing method of stick- held net for Cololabis saira. J. Zhejiang. Ocean. Univ. 25 (1), 40–45. doi: 10.3969/j.issn.1008-830X.2006.01.008

CrossRef Full Text | Google Scholar

Zhao Y. P., Li Y. C., Dong G. H., Gui F. K., Teng B. (2007). Numerical simulation of the effects of structure size ratio and mesh type on three-dimensional deformation of the fishing-net gravity cage in current. Aquacult. Eng. 36, 285–301. doi: 10.1016/j.aquaeng.2007.01.003

CrossRef Full Text | Google Scholar

Zhou Y. Q., Xu L. X. (2018). Mechanics of fishing gear (Beijing: Science Press).

Google Scholar

Zhou C., Xu L. X., Zhang X. F., Ye X. C. (2015). Application of numerical simulation for analysis of sinking characteristics of purse seine. J. Ocean. Univ. China 14 (1), 135–142. doi: 10.1007/s11802-015-2384-8

CrossRef Full Text | Google Scholar