- 1School of Marine Engineering and Technology, Sun Yat-sen University, Zhuhai, China
- 2Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai), Zhuhai, China
- 3School of Marine Sciences, Sun Yat-sen University, Zhuhai, China
- 4Zhuhai UM Science and Technology Research Institute, Zhuhai, China
Tidal asymmetry is one of the main factors for generating net transport for waterborne materials in tidal estuaries, and thus, this phenomenon has significant influences on controlling morphological development and the ecological environment. Tidal propagation is sensitive to changes in the coastline and geometry of estuarine regions. Moreover, tidal waveforms vary with various factors, such as coastline changes and bathymetry evolution due to local anthropogenic activities. The topography of Lingding Bay (LDB) of the Pearl River Estuary (PRE) has greatly changed since the 1960s because of human interventions, but the response of tidal duration asymmetry (TDA) to morphological changes is still poorly understood. Utilizing the two-dimensional Delft-3D flexible mesh numerical model, the spatial pattern of TDA and its primary contributors in LDB of the PRE were reproduced for 1964, 1989, and 2016, accounting for the changes in both shoreline and bathymetry owing to human interventions. The results reveal that as the tidal wave propagates upstream, the tidal skewness increases from negative values to positive values longitudinally, indicating the transition from a shorter ebb-duration state to a shorter flood-duration state. Additionally, a prominent shift in TDA and its primary contributors takes place approximately in the period of 1989. In 1964-1989, the tidal skewness increased by at least 0.1 throughout the LDB, indicating that the flood duration of the entire bay was shortened significantly. However, in 1989-2016, the tidal skewness decreased by at most 0.15 throughout the LDB, representing a longer flood duration in the entire LDB. The scenario simulations reveal that reclamation-induced shoreline changes control the increase in TDA and its primary contributors by enhancing width convergence of estuary in the period of 1964-1989. Conversely, the increase in water depth plays a vital role in the decrease of TDA in the period of 1989-2016. The results obtained from this study are particularly useful for understanding the controlled factors contributing to net sediment transport and the associated long-term morphological evolution in estuaries heavily impacted by human interventions.
1 Introduction
Estuaries, found in transitional areas between rivers and the open seas, are vital to the life cycles of numerous species for their feeding and breeding functions (Savenije, 2005; Shi et al., 2021), vast economies, valuable ecosystems, and ability to sustain large populations (Murray et al., 2014). Owing to economic development, many estuaries have been intensely modified by anthropogenic activities worldwide (e.g., land reclamation, channel dredging, and sand excavations), causing irreversible and remarkable changes in estuarine morphology (Guo et al., 2021). The morphological changes caused by human activities can drastically change the processes of tidal propagation and distortion in estuaries, leading to modifications in tidal properties such as tidal amplitudes and phases, wave celerity, tidal attenuation/amplification, and tidal asymmetry (Wang et al., 2020; Zhu et al., 2021; Zhang et al., 2021a). These modifications of tidal properties, especially tidal asymmetry, impact large-scale morphological evolution and water quality in tide-dominated estuaries because of their important role in the import-export process of sediments and waterborne pollutants (Hoitink et al., 2003; Chernetsky et al., 2010; Winterwerp, 2011; Maren and Gerritsen, 2012; Guo et al., 2018). Therefore, we sought to evaluate changes in tidal asymmetry in response to morphological changes caused by human activities, as this information is crucial in developing sustainable coastal management and healthy ecological environments.
The waveform of astronomical tides can be strongly distorted when propagating into shallow estuaries, manifesting as a duration difference between falling and rising tides (LeBlond, 1978; Pugh, 1987; van de Kreeke and Robaczewska, 1993; Lanzoni and Seminara, 1998), known as tidal duration asymmetry (TDA). The main sources of tidal asymmetry are closely related to tidal regimes. For example, TDA in a semidiurnal tidal regime (tidal form number ) is primarily subject to the interactions between the M2 tide and its first-order harmonic tide M4. Typically, the direction and degree of tidal asymmetry in semidiurnal tidal regimes are determined by the tidal amplitude ratio (aM4/aM2 ) and relative phase lags (2θM2−θM4 ), respectively (Speer and Aubrey, 1985; Friedrichs and Aubrey, 1988). Additionally, the interactions between the semidiurnal tide, M2, S2, and its compound shallow-water tide MS4 also strongly influence TDA in the semidiurnal tidal regime (Byun and Cho, 2006). Moreover, for diurnal or mixed-semidiurnal tidal regimes, the interactions among astronomical tides must also be considered (Hoitink et al., 2003; Woodworth et al, 2005). Nidzieko (2010) introduced the sampling skewness of tidal elevation time derivatives to quantify tidal asymmetry for the first time, deriving a tidal metric that includes both the tidal amplitude ratio and relative tidal phase. Regardless of how many constituents are significant in the time series, only combinations of two or three constituents, of which a few meet the frequency conditions 2ω1=ω2 or ω1+ω2=ω3 , can contribute to TDA on a long-term time scale (Song et al., 2011). Using the general framework proposed by Song et al. (2011), the contribution of each interaction between the tidal constituents responsible for TDA could be identified and quantified further. In addition, based on a global model of ocean tides and observed water levels from several hundreds of tidal gauges distributed along the coasts worldwide, Song et al. (2011) and P. Núñez et al. (2020) revealed the spatial distribution of TDA. However, for estuaries, this approach is not applicable to TDA analyses due to the coarse resolution of the global tidal model, which is urgently needed more studies.
The TDA can vary with morphological changes under the impacts of anthropogenic activities. Previous studies (e.g., Zhou et al., 2018) have noted that TDA in the estuary is sensitive to two-dimensional hydraulic parameters, including the ratio between tidal amplitude and mean water depth (a/h ) and the ratio of intertidal water storage to channel volume (Vs/Vc ). Generally, human activities have significant impacts on the vertical and lateral dimensions of estuarine morphology, causing variability in the above two factors, and therefore, an adjustment of the TDA. Specifically, reclamation in lateral intertidal areas can decrease the channel width and shrink intertidal storage, which favors the evolution of TDA towards flood dominance (Song et al., 2013; Winterwerp and Wang, 2013; Gao et al., 2014; Xu et al., 2014; Li et al., 2018; Guo et al., 2021; Chu et al., 2021). By contrast, channel dredging and sand mining can increase water depth and channel volume, quicken tidal celerity, reduce effective friction, and strengthen tidal hydrodynamics, leading to weakening variability in tidal asymmetry (Bolle et al., 2010). Although the singular effects of shoreline or water depth changes on the TDA have been studied, the intertwined impacts of shoreline and bathymetric changes on the TDA are still lack of investigation.
The Lingding Bay (LDB) of Pearl River Estuary (PRE), located at the core of the Guangdong-Hong Kong-Macao Greater Bay Area, is one of the most densely urbanized regions in the world. Many studies have shown that with the rapid development of cities around the PRE, many tidal flats have been reclaimed, and the widths of estuaries have decreased as shorelines have extended offshore (Wu et al., 2014; Zhang et al., 2015). Moreover, owing to channel dredging and sand mining, together with a sharp decrease in the amount of sediment debouching into estuaries, the underwater geomorphology of estuaries has also changed significantly (Wu et al., 2014; Wu et al., 2016; Yang et al., 2019; Chen et al., 2020). Previous studies have revealed the impacts of human-intervened topographic changes on estuarine hydrodynamics by observations or numerical modeling, including tidal dynamics (Zhang et al., 2010; Cai et al., 2018a; Lin et al., 2021; Chu et al., 2022), water level dynamics (Zhang et al., 2017; Cai et al., 2018b; Cao et al., 2020; Luo et al., 2020; Yang et al., 2020), and the main astronomical tides and tidal regime shifts (Wang et al., 2020; Zhang et al., 2021a; Zhang et al., 2021b). Few studies have focused on the TDA in the PRE, even though it is strongly linked to large-scale morphological evolution. For instance, 2018; Zhang et al. (2010) have found increasing trends in flood-tide duration and unraveled the main causes of TDA evolutions in the Pearl River networks, but they did not mention the variability of TDA in the PRE. Gong et al. (2016) investigated tidal asymmetry variability in the Huangmaohai estuary of the Pearl River Delta by conducting sensitivity numerical experiments on the effects of width convergence and complexity of underwater topography. Therefore, the aim of this paper is to study how the TDA in PRE responds to morphological changes due to human interventions for decades.
In this study, we attempt to address the above questions by studying the changes in TDA from 1964 to 2016 in LDB, a microtidal, convergent estuary with lateral multi-outlets, using a two-dimensional barotropic model (Delft3D Flexible Mesh). The remainder of the paper is structured as follows. Section 2 introduces the study area and its morphological evolution. Section 3 shows the adopted tidal skewness method and numerical model. Section 4 presents the model results of the changes in TDA and its primary contributors owing to morphological changes. In section 5, diagnostic analyses are used to detail the effects of the changes in shorelines and bathymetry. Finally, the conclusions are made in section 6.
2 Study area
LDB is a funnel-shaped estuarine bay system of PRE in the Pearl River Delta, south of China (Figure 1A), with an approximate area of 2110 km2 and an approximate length of 72 km. The width of the bay near the Humen outlet is approximately 5 km and increases to 60 km in the mouth, with a length of approximately 63 km between the two ends. LDB collects 50-55% of river discharges and approximately 40% of the sediment load from the Pearl River through four outlets, namely, Humen, Jiaomen, Hongqili, and Hengmen (Liu et al., 2014). The Humen outlet is dominated by tidal dynamics, whereas the others are dominated by river runoff (Dai et al., 2008; Zhang et al., 2010). The underwater geomorphology of the bay features a complex shoal-channel pattern that comprises two channels and three shoals: the West Channel and the East Channel, the West Shoal, the Middle Shoal, and the East Shoal. Several islands such as Longxue Island, Qiao Island, Neilingding Island, and Lantau Island are scattered in the bay (Figure 1B).

Figure 1 Location and bathymetry of the Pearl River Delta (A) and Lingding Bay (B). The four red triangles in panel (B) represent tidal gauging stations: Chiwan (CW), Hengmen (HM), Wanqingshaxi (WQSX), and Nansha (Nansha). Lingding Bay can be divided into the inner bay and the outer bay in panel (B). SZB indicates Shenzhen Bay. The four outlets are Humen, Jiaomen, Hongqili, and Hengmen. There are two channels and three shoals: The West Channel (WC), the East Channel (EC), the West Shoal (WS), the Middle Shoal (MS), and the East Shoal (ES). Bathymetry and shorelines of LDB in the year 1964 (C), 1989 (D), and 2014 (E). Morphological evolution in LDB during the period of 1964-1989 (F), 1989-2014 (G), and 1964-2014 (H). The reclaimed areas are shown with the green diagonal cross.
A subtropical monsoon climate prevails in the LDB, with high precipitation during the wet season (from May to September). During the wet season, the annual freshwater discharge of the Pearl River reaches as high as 8000 m3 s-1, which is four times as much as the discharge rate during the dry season (Luo et al., 2007). The tides in the LDB propagate from the western Pacific Ocean through the Luzon Strait and are dominated by an irregularly mixed semidiurnal regime, where the semidiurnal M2 tide is the most significant constituent, followed by the K1, O1, and S2 tides (Mao et al., 2004). The average tidal range is between approximately 1.0 m (Lantau Island) and 1.7 m (Humen outlet) (Zhang et al., 2019), indicating a microtidal character in LDB. As the tidal wave propagates upstream, the tidal energies converge owing to the effect of the convergent funnel-shaped shorelines overwhelming the frictional dissipation, which amplifies the tidal ranges (Wang et al., 2020; Zhang et al., 2021a).
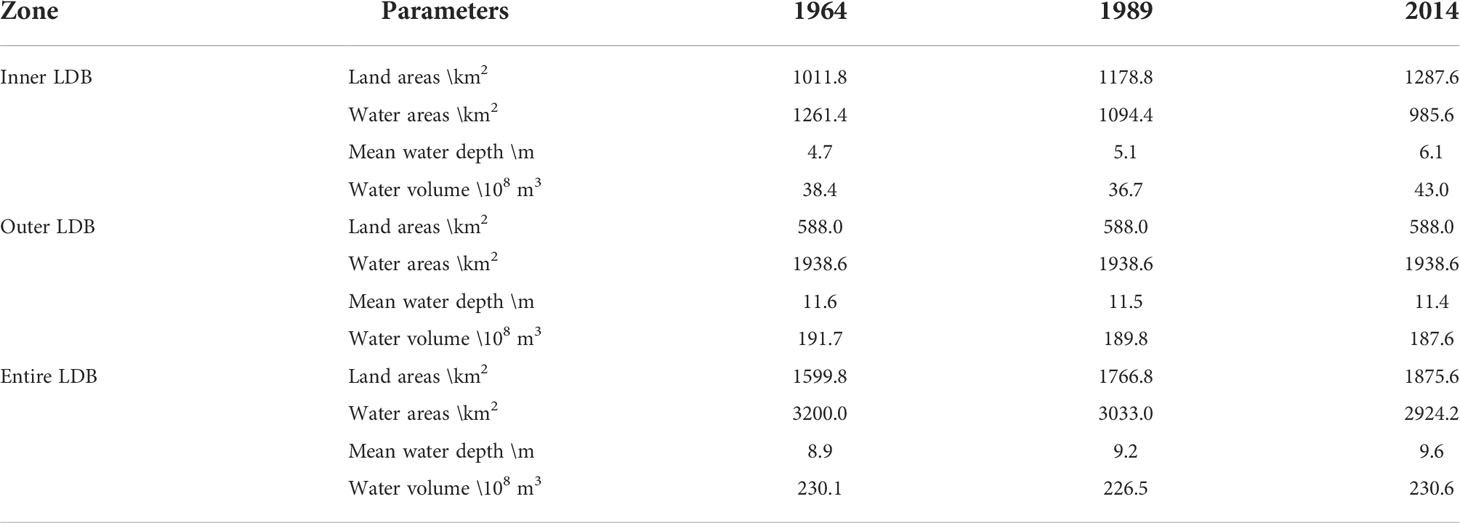
With the development of the local economy and the boosting of urbanization during the past 50 years, the LDB has been significantly altered from its natural state by human interventions. The shorelines and bathymetry of LDB in different years are shown in Figures 1C–E, suggesting that the shoal-channel pattern does not shift, while the width and the mean water depth are getting narrower and deeper (see Table 1), respectively, due to human interventions (e.g., land reclamation, channel dredging, and sand excavation). The water area and West Shoal in LDB have shrunk, while the West Channel and East Channel have been deepened. Consequently, the funnel-shaped geometry of LDB converted to a bell shape during the 1964-2014 period. Figures 1F–H represents the siltation and deposition pattern in LDB for the period 1964-1989, 1989-2014, and 1964-2014, respectively. Specifically, during the 1964-1989 period, the west coastlines (see Figure S1 in the Supporting Information) of LDB have extended seawards drastically due to large-scale land reclamation on the West Shoal, leading to a sharp increase in the new land (~275.8 km2), hence, a decrease in the surface water area, while the spatially averaged water depth has changed a little (only increased by approximately 0.3 m for the entire bay). Since the land was mainly reclaimed in the inner LDB, thus the water volume decreased by 1.7×108 m3 in relation to the substantial reduction in surface water area. During the 1989-2014 period, the mean water depth in the inner LDB increased by 1 m, while the outer LDB decreased by 0.1 m, indicating the depocenters transferred south (Chen et al., 2020). As a result, the water volume substantially increased by 6.3×108 m3 in the inner LDB, while it continued to decrease by 2.2×108 m3 in the outer LDB. Therefore, the inner LDB is getting narrower and deeper, while the outer LDB is getting shallower.
3 Methodology
3.1 Analysis of TDA
Tidal asymmetry can be approximated using amplitudes and phases of tidal constituents. In general, water levels can be considered as a result of a linear superposition of N cosine harmonic waves with residual water levels (Foreman and Henry, 1989; Pan et al., 2018):
where t is the time, η(t) is the time series of the water levels, ai is the amplitude, ωi is the frequency, φi is the phase, s0 is the residual water level, and i denotes the i-th tidal constituent. Therefore, the time derivative of the temporal water level in tidal-dominated estuaries can be written as follows:
Moreover, Nidzieko (2010) proposed that the statistical skewness of the water-level time derivative can be used to quantify the TDA:
where μ3 is the third moment about the mean, σ is the standard deviation, and the averaged time derivative of the temporal water levels. If τ is an integer multiple of the period of diurnal (24.8h, usually 25h) or long enough (e.g., one month), and then Equation (3) can be approximated:
If γ1>0, the periods of flood tides are shorter than those of ebb tides, and conversely, if γ1<0, the periods of ebb tides are shorter than those of flood tides. Furthermore, to quantify the contribution of different combinations of tidal constituents to TDA, Song et al. (2011) derived a general framework for evaluating TDA by substituting Equation (2) into Equation (4), which is expressed as (Feng and Feng, 2021):
The sets of Equation (5) demonstrate that TDA can be generated or canceled only by interactions between two harmonic constituents with a frequency relationship 2ω1=ω2 or among three constituents with a frequency relationship ω1+ω2=ω3. Moreover, introducing β as the weight of TDA from the skewness caused by a specific pair or triplet of tidal constituents, the total TDA is equal to the cumulative effects of β (Feng and Feng, 2021):
Similarly, if β>0, the interactions between two or three constituents can result in a shorter flood tide duration. Otherwise, if β<0, the interactions of two or three constituents can favor a shorter ebb tide duration.
Before calculating the TDA and its main contributors, tidal harmonic analysis was implemented using the T_TIDE MATLAB toolbox (Pawlowicz et al., 2002). The tides in LDB are dominated by a mixed semidiurnal tidal regime, where the amplitudes of the semi-diurnal tides are comparable to those of the diurnal tides (Zhang et al., 2021a), so the nonlinear interaction between K1, O1, and M2 tides is the dominant source of TDA. The M4 tide is the first harmonic of the M2 tide and dominates the non-linear processes of many estuaries; therefore, the interaction between the M2 and M4 tides may represent another major source contributing to TDA (Guo et al., 2019). Moreover, the shallow-water tide MK3 is significant in LDB, and the interaction between the K1, M2, and MK3 tides may play an important role in quantifying TDA. Finally, according to Gong et al. (2016) and Zhang et al. (2018), the interactions between the M2, S2, and MS4 tides represent one of the main contributors to tidal asymmetry in the Pearl River Delta. In conclusion, the tidal asymmetry of LDB can be calculated using the following four tidal constituent combinations:
3.2 Numerical model
To investigate the impacts of physical alteration on the TDA in LDB, the two-dimensional Delft3D-Flexible Mesh model was utilized to simulate the tidal dynamics, inherited from the unstructured domain system used by Chu et al. (2022) for tidal simulations. The large-scale domain covering the entire northern parts of the South China Sea spans across the ocean between the Taiwan (north of Fujian Province) and Qiongzhou Straits (south of Hainan Province), with latitudes ranging from 18.67°N to 24.66°N and longitudes ranging from 110.19°E to 120.45°E. The computational domain has varying horizontal scales, with the finest cells in the Pearl River networks having dimensions of 20×30 m and the coarsest cells on the open sea having approximate dimensions of 7000×7000 m. Within the LDB, the grid size is approximately 200×300 m, which allows the domain to be discretized with optimized flexible grids close to the complex shorelines to improve computational accuracy. Grids of different sizes were connected using triangular cells, and the computational grids contained approximately 150,000 nodes. The bed elevation spans from –3000 m to 5 m, as collected from multiple sources, including measured data of the river networks, Huangmaohai Estuary, and Modaomen Estuary in 2010, nautical charts of LDB published by the Maritime Safety Administration of the P. R. of China, and GEBCO datasets for the continental shelf regions (Intergovernmental Oceanographic Commission et al., 2003).
The model was driven by the predicted tidal levels obtained from TPXO7.2 (http://volkov.oce.orst.edu/tides/global.html) on the open boundary and the observed hourly discharges at six hydrological stations at the upstream boundary. We chose 13 tidal constituents (M2, S2, N2, K2, K1, O1, P1, Q1, MF, MM, M4, MN4, and MS4) to forecast tidal levels, considering 18.6-year nodal variability. Additionally, two long-period tidal constituents (Sa and Ssa) were included to accurately predict total water levels, as suggested by Twigt et al. (2009). The wetting-drying mode was used in the modeling system. When the transient water depth was less than 0.1 m, the grid cell was treated as dry cells with a zero-flow rate. The effect of hydraulic drag was expressed in terms of the Manning coefficient n (s m-1/3), which was converted from the Nikuradse roughness length ks and the mean water depth h (e.g., Zhu et al., 2021):
To simplify the factors associated with the uncertainties in estimating the evolution of TDA owing to bathymetric and topographic influences, meteorological forcing and oceanic currents were not included in the model (e.g., Feng and Feng, 2021). The numerical model was run from November 10, 2016, to March 1, 2017, owing to low-stratified water columns and the weakest river discharges in the dry season.
The model results were compared with measured data, including the simulated tidal levels, major tidal harmonics, and cross-sectional discharges. The computed water levels were validated against data from 30 November to December 7, 2016, whereas the discharge was compared with data in two separate spring-neap tidal cycles. Besides, the modeled tidal skewness was calculated every 25-hour to validate against gauged data in LDB (Figure 1B). We used statistical metrics (e.g., model efficiency and percentage bias) to assess model performance in water level simulation (e.g., Chu et al., 2022). The model efficiency (ME) is calculated by (Nash and Sutcliffe, 1970):
where Xobs is an observed sampling, Xobs is a prediction by the model, and is the mean of observations. Allen et al. (2007) proposed four levels to assess the model performance, which are defined as excellent (ME≥0.65 ), very good (0.4≤ME<0.65 ), good (0.2≤ME<0.4 ), and poor (ME<0.2 ). The percentage bias (PB) is calculated as:
Using the absolute value of PB, the performance levels are categorized as (Allen et al., 2007): Excellent (|PB|≤10% ), very good (10%<|PB|≤20% ), good (20%<|PB|≤40% ), and poor (|PB|>40% ).
The model results showed an acceptable performance for the LDB domain. The MEs of the water levels between the computed and observed data were all larger than 0.95, while the |PB|s were all less than 10% in the LDB, indicating that the water level simulation is excellent (Figure 2 and Table 2). However, differences were occasionally large for weak tidal constituents, whose amplitudes are small. Slightly larger differences occurred in the phases of the overtides and compound tides. This may be caused by a lack of detailed bathymetry of the nearshore region for the LDB domain. However, since the signs and magnitudes of the TDA mainly depend on the phase lags or amplitude ratios between the tidal constituents of the tidal interactions, the bias of a given harmonic constituent can be offset by those of another. Detailed calibration and validation instructions for constructing a realistic modeling system can also be found in the Supplemental Information of Chu et al. (2022), and thus are mentioned here for brevity. Following the model evaluation, the predicted water levels from the last month at an interval of 1 h in the LDB domain were extracted to quantify and diagnose the spatial variation in TDA. With a timeseries spanning 31 days, a list of 29 tidal constituents were extracted making use of the commonly used T_TIDE software. We then calculated the monthly averaged γN via the sets of Equation (5-7), using the seven significant tidal constituents. Comparing the computed γN with γ1 (the statistical skewness of the water-level time derivative) over the LDB domain, the feasibility of the sets of Equations (5-7) was verified (Figure 3).
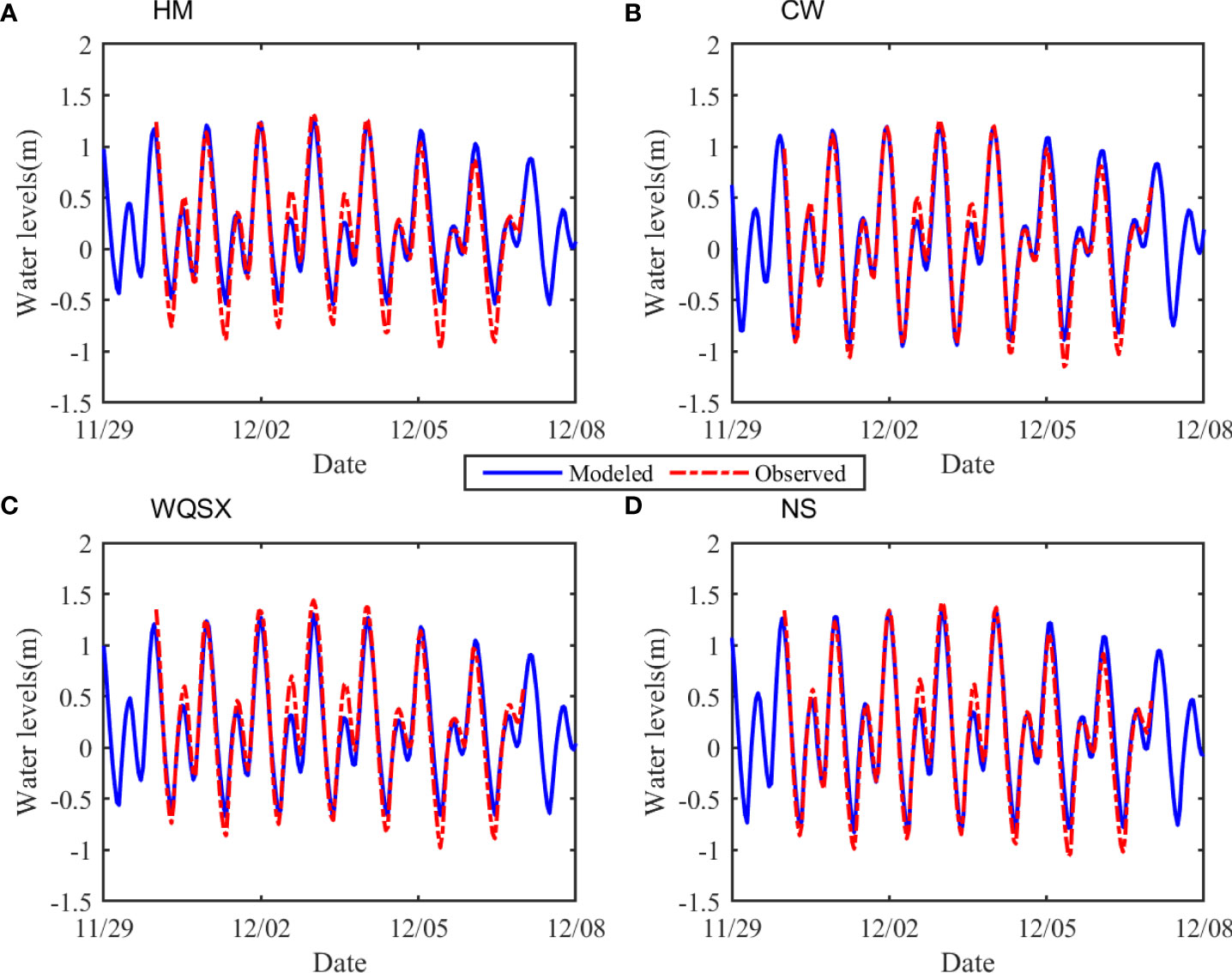
Figure 2 Model Calibration for water levels at tidal gauging station HM (A), CW (B), WQSX (C), and NS (D), where the blue lines represent modeled water levels and the red dashed lines represent the observations.

Table 2 Statistical metrics of error analysis between modelled and observed water levels at four tidal gauging stations in LDB.

Figure 3 Comparison between the statistical skewness of the water-level time derivative (blue bar) and the total tidal skewness estimated by tidal constituents (red bar) for HM, CW, WQSX, and NS tidal gauging stations in LDB.
3.3 Design of numerical experiments
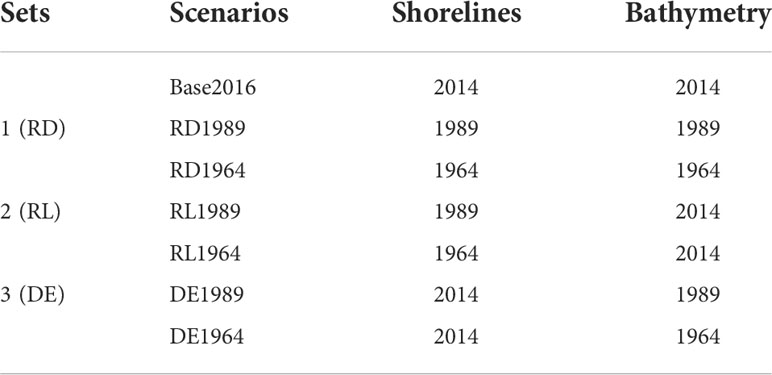
Three sets of scenario experiments (Table 3) were designed to study the response of TDA to historical morphological changes in LDB. First, having been compared with the thoroughly calibrated model named “Base2016,” the two scenarios in Set 1 named with “RD” were deployed to investigate the combined effects of shoreline and bathymetry variation on the TDA. Second, to assess the impacts of shoreline changes on the TDA, the next two scenarios in Set 2 named with “RL” were configured with shorelines in the years 1964 and 1989, respectively, as well as the underwater topography and the Manning coefficients in accordance with the base model “RD2016”. Chu et al. (2022) discussed tidal dynamics in response to successive land reclamation using a similar configuration. Finally, the last two scenarios in Set 3 named with “DE” were configured with complex bathymetry in the years 1964 and 1989, respectively, using the same coastlines and the Manning coefficients with the base model “Base2016.” This approach allowed us to study the effects of bathymetry variation induced by channel dredging and sand mining on tidal propagation and distortion. By analyzing all the numerical experiments listed in Table 3, the impacts of the shoreline and bathymetric changes caused by different types of human activities on the TDA were assessed.
4 Results
4.1 Spatial pattern of TDA and its variation caused by morphological changes
To investigate the spatial pattern of TDA in LDB, the tidal skewness γN was calculated based on the results of the numerical model named “Base2016” (Figure 4C). The results show that the tidal skewness is negative (γN > -0.5) in large areas of LDB, indicating a shorter duration of ebb tide and favoring ebb dominance. Meanwhile, the tidal skewness increases to positive values (γN< 0.1) in the northern head of LDB as the tidal wave propagates upstream, indicating a transitional zone where the tidal skewness trends towards zero and the phenomenon of distortion disappears. The tidal skewness in the river-dominant Jiaomen, Hongqili, and Hengmen outlets was larger than that in the tide-dominant Humen outlet, thereby indicating that river discharges can enhance tidal skewness and strengthen TDA by squeezing the durations of flood tides.
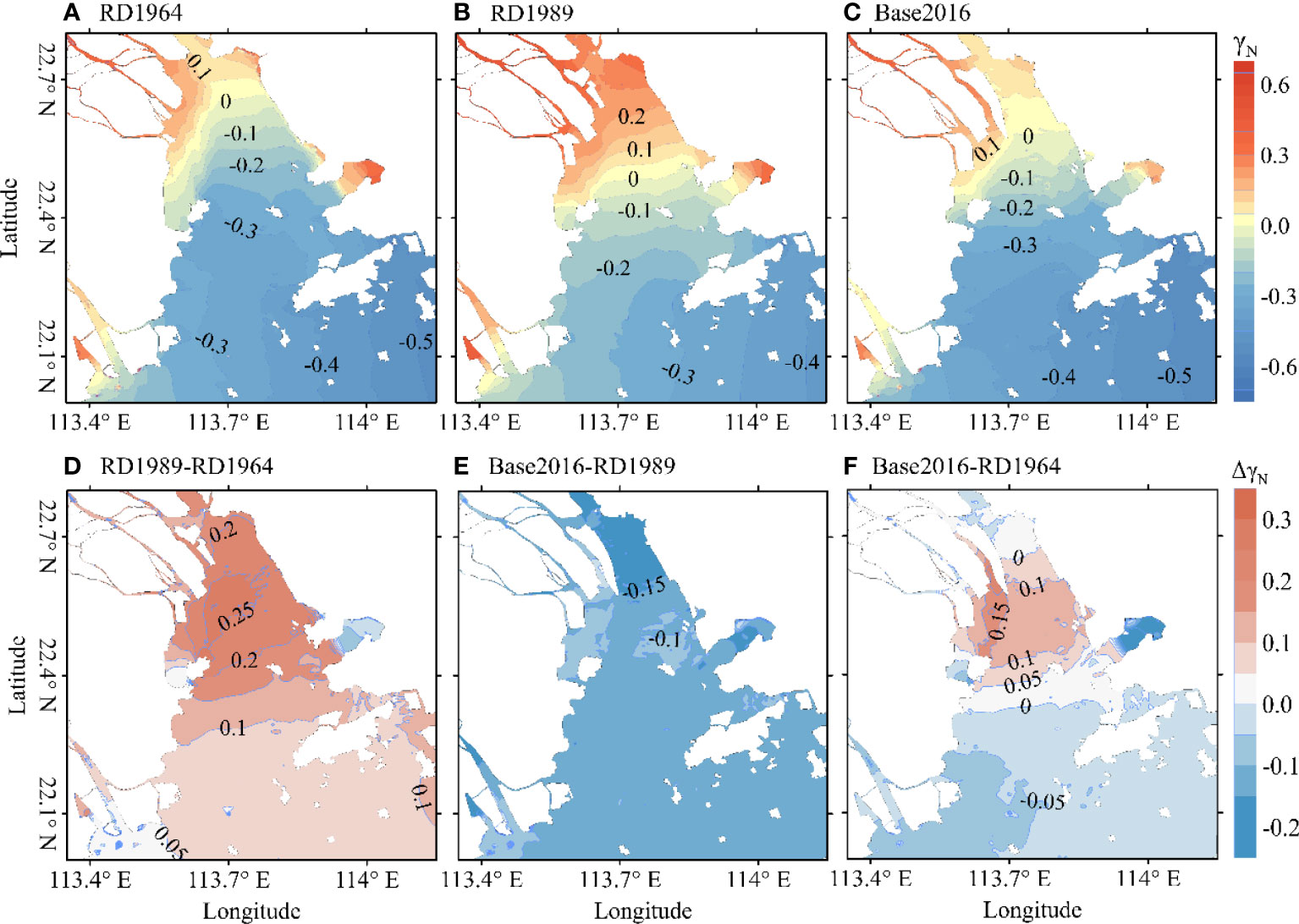
Figure 4 Contour map of tidal skewness for the different scenarios; (A–C) denotes the case of RD1964, RD1989, and Base2016, respectively. Contour map of the difference between two scenarios, including RD1989-RD1964 (D), Base2016-RD1989 (E), and Base2016-RD1964 (F). Panels (D) and (E) show the stepwise changes of tidal skewness in response to morphological evolutions, whereas panel (F) shows the cumulative effect of morphological change between 1964 and 2014 on tidal skewness.
The calculated tidal skewness in the scenario “RD1964” and “RD1989” is shown in Figures 4A–B, respectively. The spatial patterns of the TDA in the two cases were similar to those of the base model, with some differences in the magnitude of the TDA. The contour line of the zero value was close to the head of the bay in 1964 while moving southward in 1989, indicating a larger area of ebb-dominant TDA in 1964 and flood-dominant TDA in 1989. The densely distributed contours of tidal skewness on the western shoals in the inner bay indicate that the tidal waves are strongly distorted owing to significant river runoffs and shallow water effects. Compared with the base model, tidal skewness was lower in 1964 and larger in 1989, showing a regime shift in the TDA in the latter year.
The differences in tidal skewness between two period are shown in Figures 4D–F. In 1964-1989, the tidal skewness increased by at least 0.1 throughout the LDB, indicating that the flood duration of the entire bay was shortened significantly. However, in 1989-2016, the tidal skewness decreased by at most 0.15 throughout the LDB, representing a longer flood duration in the entire LDB. Overall, during 1964-2016, the tidal skewness decreased slightly (not larger than 0.1) in the outer and the head of the bay, whereas it increased significantly (larger than 0.1) in the middle parts owing to the cumulative effects of morphological changes.
4.2 Variations of tidal constituents determining the changing TDA
4.2.1 Tidal amplitudes
Tidal amplitudes, which are sensitive to changes in estuarine topography, are important factors that affect tidal asymmetry. According to Equation (7), the tidal asymmetry of LDB is mainly determined by seven harmonic constituents, including four major astronomical tides (K1, O1, M2, and S2) and three shallow-water tides (MK3, M4, and MS4). Constituents in the same tidal band generally have similar propagation properties (Guo et al., 2015). Because K1/O1, M2/S2, and M4/MS4 belong to the diurnal D1, semidiurnal D2, and 1/4 diurnal D4 tidal bands (Chu et al., 2022), respectively, variations of the K1, M2, MK3, and M4 tidal amplitudes in different periods were chosen for further evaluation, while the spatial distribution of other three tidal constituents can be seen in Figure S2 in the Supporting Information.
The amplitude differences in tidal constituents between two typical years (1964-1989 and 1989-2016) and the cumulative changes over the study period (1964-2016) were quantified (Figure 5). In 1964-1989 (Figure 5A1), the amplitudes of the K1 tide became larger in the middle of the bay but smaller in the western outlets (Jiaomen, Hongqili, and Hengmen) and outside of the bay. However, this variation pattern changed during– 1989-2016 (Figure 5A2), where the K1 amplitude differences were positive in the upper parts of the LDB and river networks and negative in the middle. The cumulative effect of topographic evolution on the K1 tidal amplitudes is shown in Figure 5A3. The K1 amplitudes increased maximally by 0.03 m in the bay but remained nearly unchanged, specifically at the outer LDB.
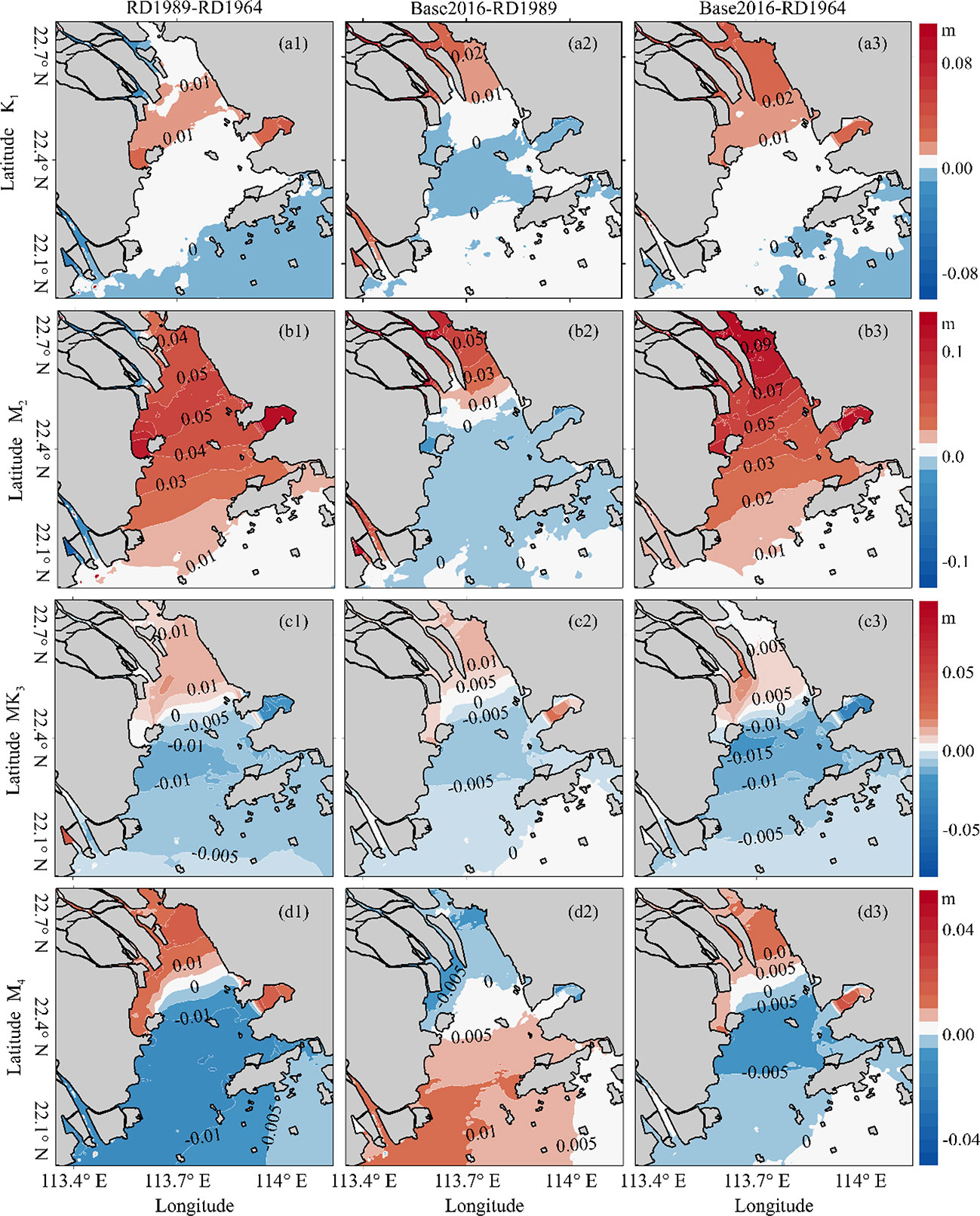
Figure 5 Contour map of the changes in K1 (A1–A3), M2 (B1–B3), MK3 (C1–C3), and M4 (D1–D3) amplitudes, where the numbers (1, 2, 3) represent the periods of 1964-1989, 1989-2016, 1964-2016, respectively.
The variation pattern of the M2 amplitudes was more or less the same as that of the K1 amplitudes, with a larger magnitude. In 1964-1989 (Figure 5B1), the M2 tidal amplitude increased throughout the bay, whereas it decreased slightly in the river networks. However, in 1989-2016 (Figure 5B2), the M2 tidal amplitude continued to increase in the upper LDB and river networks but decreased slightly in the lower LDB. Overall, the M2 tidal amplitude increased significantly in LDB (Figure 5B3). The amplitude increments are positively correlated with proximity to the top of the bay.
The variation patterns of the MK3 amplitudes in different periods were nearly unchanged (Figures 5C1–C3). For example, the amplitude differences of MK3 tides were positive in the upper LDB and negative in the lower LDB, ranging from -0.005 m to 0.1 m. The M4 tide is a shallow water constituent derived from the semidiurnal M2 tides. Although its amplitude is relatively small, interactions between the M4 and M2 tides are one of the main sources contributing to tidal asymmetry. In the first period (Figure 5D1), the M4 tidal amplitude increased at the top of the estuary bay and in the river networks, whereas it decreased in the middle and lower parts of the bay. This variation pattern of the amplitude change was reversed in the second period (Figure 5D2), where the M4 tidal amplitudes increased in the outer LDB and decreased in the inner LDB. For 1964-2016 (Figure 5D3), the cumulative change in the M4 tidal amplitude shows that the increasing area is located at the top of the bay, and the decreasing area is located in the middle and lower parts of the bay.
4.2.2 Tidal phases
The tidal phase characterizes tidal wave celerity and is another important factor contributing to the TDA. Figure 6 shows the co-phase charts of the K1, M2, MK3, and M4 tides for different periods, and the spatial distribution of other three tidal constituents can be seen in Figure S3 in the Supporting Information. The phase isolines are perpendicular to the central axis of the LDB, showing the northward propagating direction of the four tides. The contour distributions of the four tidal constituents become intensive, implying that tidal wave celerity decreased. Compared with the phase pattern in 1964, the phase isolines of the two astronomical tides (K1 and M2) moved upstream, whereas the phase isolines of the two shallow-water tides (MK3 and M4) shifted downstream in 1989. During 1989-2016, the tidal phases increased at the same locations, and the increments in the phases in the outer bay were larger than those in the inner bay. Overall, between 1964 and 2016, the co-phase lines did not change significantly in the outer bay, whereas they decreased for the K1, M2, and M4 tides and increased for the MK3 tide in the inner bay. The tidal phase variations are inconsistent among the tidal constituents in response to the morphological changes caused by human interventions, thus indicating that the relative phase lags for pairs or triplets of tidal constituents have also changed, which can lead to the variability in TDA.
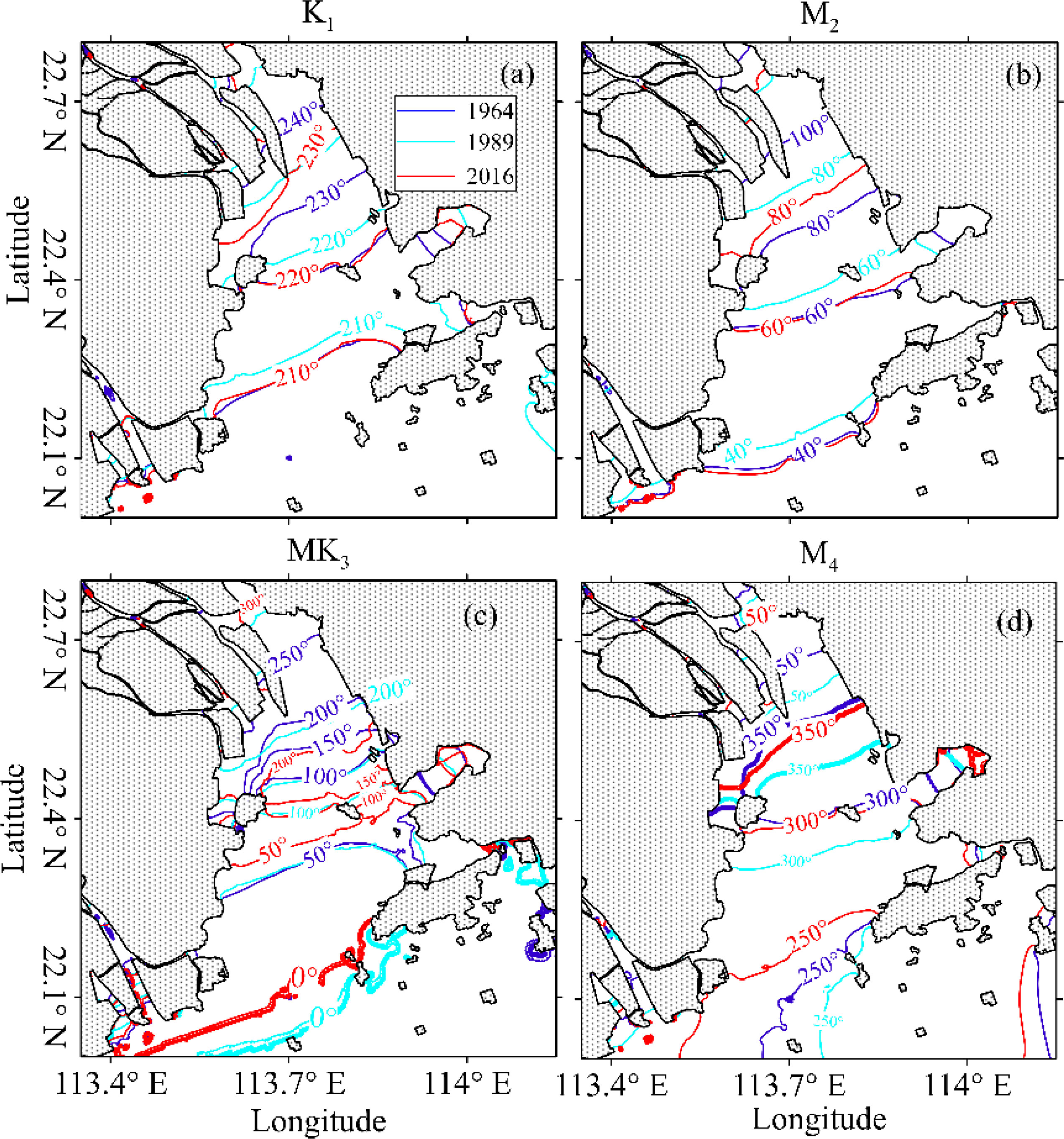
Figure 6 Contour map of K1 (A), M2 (B), MK3 (C), and M4 (D) phases. The blue lines represent phase isolines in 1964, the dashed cyan lines represent phase isolines in 1989, and the red lines represent phase isolines in 2016.
4.3 Changes in the primary contributors of TDA
The primary contributors to TDA in LDB are βK1/O1/M2 , βK1/M2/MK3 , βM2/S2/MS4 , and βM2/M4 , so the changes in total TDA are the sums of the changes in the four contributors (Figure 7). During the first period (1964-1989), the morphological changes caused all four contributors to increase, among which the changes in βM2/M4 and βM2/S2/MS4 were the most significant, followed by βK1/M2/MK3 and βK1/O1/M2 . However, the trends of the four contributors reversed to a decrease with the development of the shoreline and bathymetry in LDB, except for βK1/M2/MK3 in the middle of LDB. The overall changes from 1964 to 2016 in the four contributors shared the same pattern in LDB, with an increasing trend in the middle of the LDB and a decreasing trend in the upper and lower LDB.
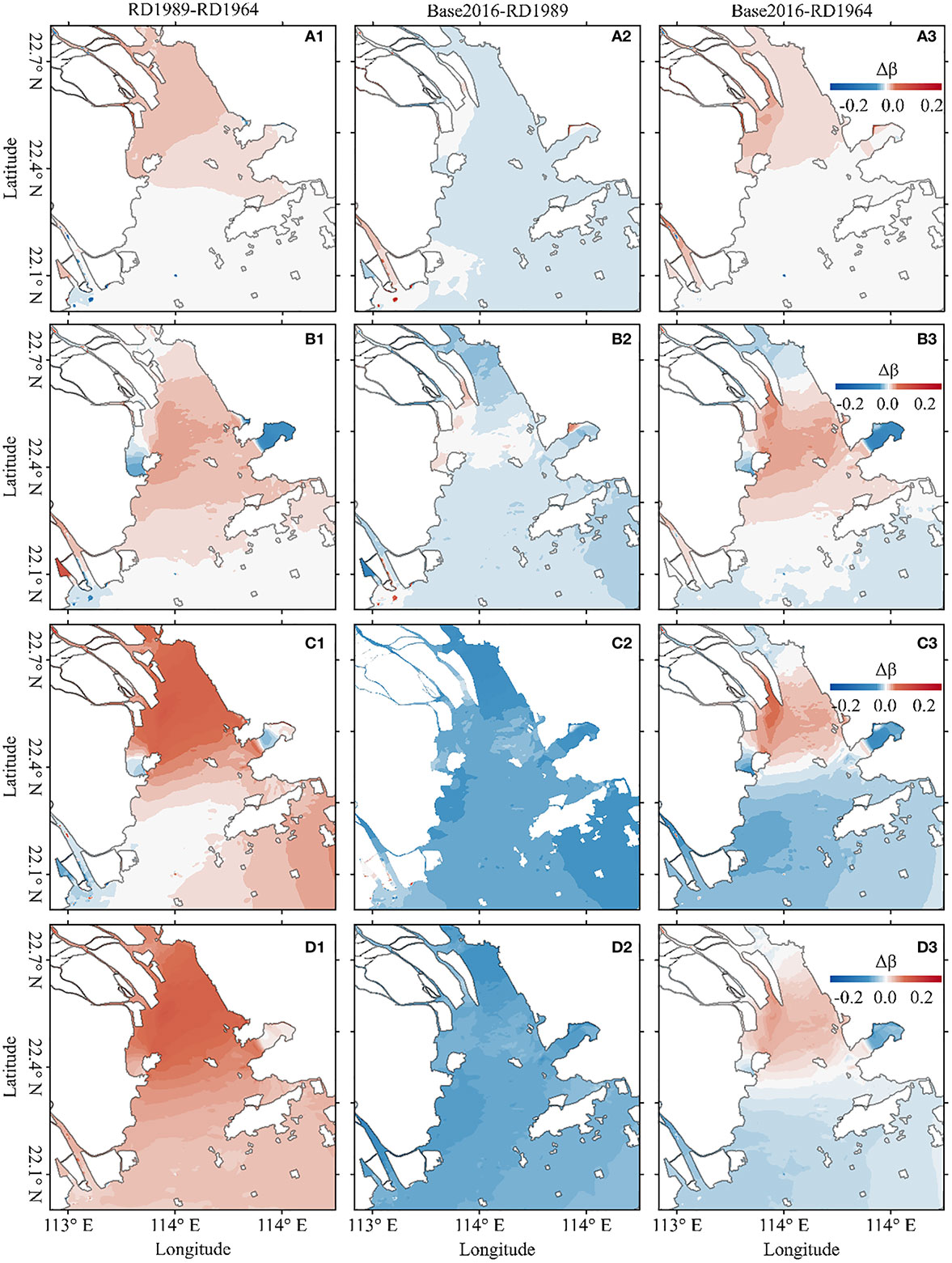
Figure 7 Contour map of the changes in primary contributors of tidal skewness, including βK1/O1/M2 (A1–A3), βK1/M2/MK3 (B1–B3), βM2/S2/MS4 (C1–C3), and βM2/M4 (D1–D3); number 1, 2, 3 represent 1964-1989, 1989-2016, and 1964-2016, respectively.
5 Discussion
5.1 Impacts of changes in shorelines on the TDA
To explore the impacts of reclamation-induced shoreline changes on the TDA and its primary contributors, two numerical models configured by the shoreline in different years and the same bathymetry in the year 2014 (named as “RL1964” and “RL1989”) were used. The impacts of shoreline changes on the total tidal skewness are shown in Figures 8A1–A3. The TDA first increased with the shoreline extending to the sea, showing an enhanced width convergence of the tidal propagation at the bay scale. However, as the shoreline changes continued, the changes in TDA slightly decreased in the areas of the upper bay and the open seas but increased in the middle of the bay. Therefore, the cumulative land reclamation for the past 50 years caused the TDA to increase by at most 0.3 in the middle of the bay, favoring a shorter flood duration and a stronger flood-dominant regime. In addition, the changes in the primary contributors to TDA in response to shoreline changes differed. The changes in βK1/O1/M2 were positive and increased under all three circumstances (Figures 8B1–B3), promoting a larger tidal skewness. The βK1/M2/MK3 ratio decreased in the upper bay but decreased in the middle and lower bays (Figures 8C1–C3), leading to a shorter ebb duration in the upper bay and a shorter flood duration in the middle and lower bays. βM2/S2/MS4 increased significantly in the inner bay but decreased in the outer bay (Figure 8D1) between RL1964 and RL1989. However, with the coastline of Longxue Island extending southward, the changes in βM2/S2/MS4 became negative (Figure 8D2). The overall changes in βM2/S2/MS4 were largely enhanced in the inner bay and slightly decreased in the outer bay (Figure 8D3). Finally, βM2/M4 was the main factor influencing the variations in TDA, as shown in Figures 8E1–E3. The changes in βM2/M4 were positive, indicating that TDA increased between RL1964 and RL1989. By comparison, the changes in βM2/M4 were negative, indicating that TDA decreased between RL1989 and Base2016. The overall changes in βM2/M4 were positive in most areas of the bay, except in the open seas, leading to an shortened flood duration.

Figure 8 Contour map of the variations of the tidal skewness and its primary contributors caused by shoreline changes, including βK1/O1/M2 (B1–B3), βK1/M2/MK3 (C1–C3), βM2/S2/MS4 (D1–D3), and βM2/M4 (E1–E3). Number 1, 2, 3 represent RL1989-RL1964, Base2016-RL1989, and Base2016-RL1964, respectively.
This is consistent with the theoretical frameworks for reclamation-induced TDA changes formulated by Guo et al. (2021), which shows that the effect of reclamation of tidal flats tends to enhance flood asymmetry and hence increases sediment import. The underlying mechanism can be primarily attributed to the increased width convergence, which intensifies the tidal distortion together with generating a larger tidal current and wavelength (Friedrichs and Aubrey, 1994). However, the actual direction of either flood or ebb dominance depends on whether an evolving tidal system is approaching a morphologically stable state (e.g., Lanzoni and Seminara, 2002; Guo et al., 2014; Zhou et al., 2018), since morphological equilibrium is characterized with a minimum tidal asymmetry (e.g., Toffolon and Lanzoni, 2010; van der Wegen, 2013; Zhou et al., 2018).
5.2 Impacts of bathymetric alterations on the TDA
To explore the impacts of bathymetry changes on the TDA and its primary contributors owing to channel dredging and sand mining, another two numerical models configured by the underwater morphology in different years with the same shoreline of 2014 (named “DE1964” and “DE 1989”) were used. The impacts of bathymetry changes on the total tidal skewness are shown in Figures 9A1–A3. The TDA first increased with decreasing mean water depth in the inner bay. Moreover, the changes in the primary contributors to TDA in response to bathymetric changes were similar. The changes in βK1/O1/M2 were negative in all the three circumstances (Figures 9B1–B3), promoting a smaller tidal skewness. The βK1/M2/MK3 increased throughout the entire bay (Figure 9C1) between DE1964 and DE1989, leading to a shorter flood duration. However, the βK1/M2/MK3 decreased throughout the entire bay (Figure 9C2) between the cases of DE1989 and Base2016, leading to a shorter ebb duration. The overall impacts of bathymetric changes on the βK1/M2/MK3 were negative, favoring a smaller tidal skewness and shorter ebb-duration (Figure 9C3). The changes in both βM2/S2/MS4 and βM2/M4 were positive in the inner bay, but became negative in the outer bay with a small magnitude. However, the changes in βM2/S2/MS4 and βM2/M4 were negative, indicating that the TDA decreased between RL1989 and Base2016. The overall changes in βM2/S2/MS4 and βM2/M4 were negative over the entire study area.
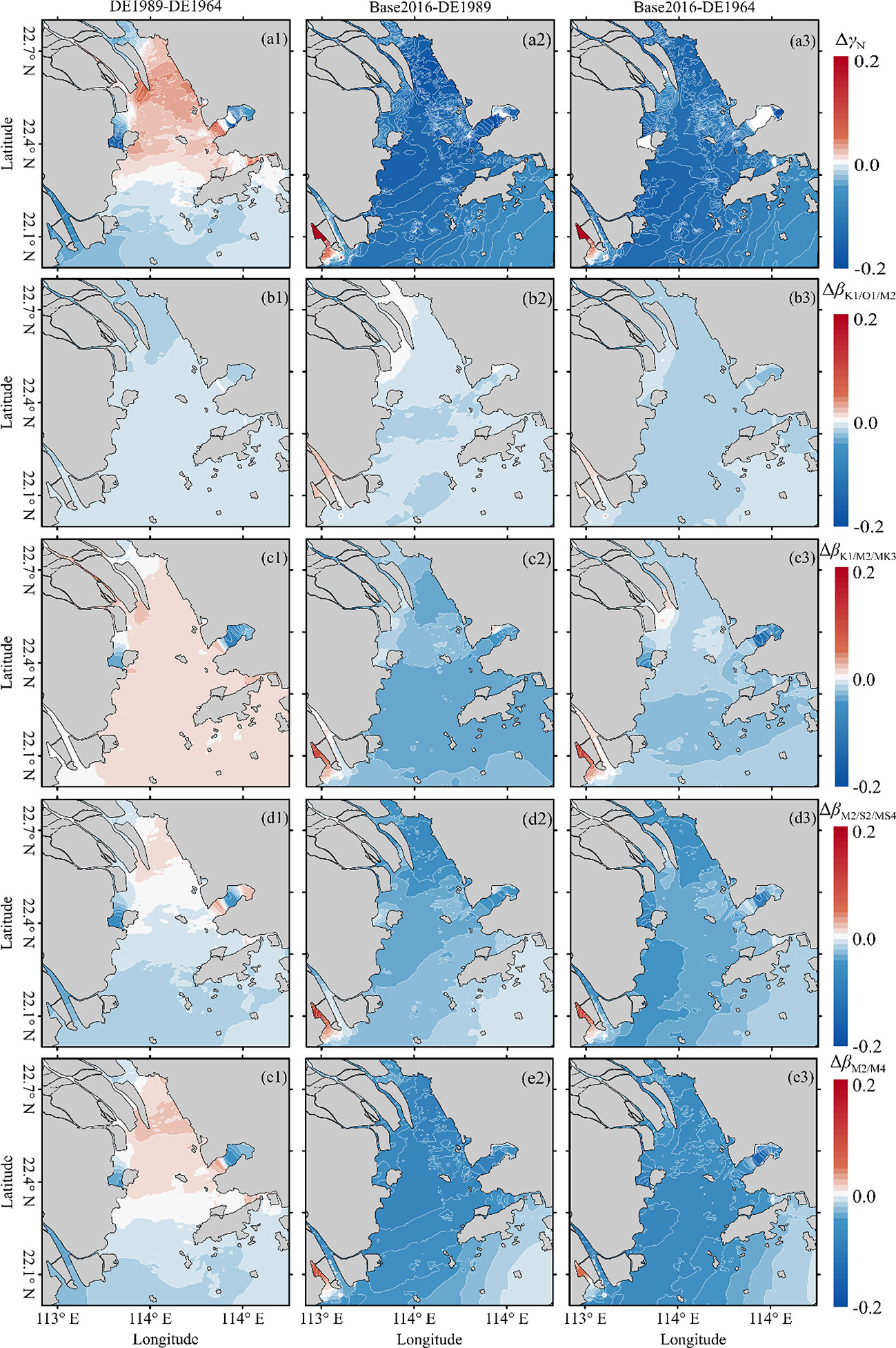
Figure 9 Contour map of the variations of the tidal skewness and its primary contributors owing to bathymetric alterations, including the total tidal skewness γN (A1–A3) βK1/O1/M2 (B1–B3), βK1/M2/MK3 (C1–C3), βM2/S2/MS4 (D1–D3), and βM2/M4 (E1–E3). Number 1, 2, 3 represent DE1989-DE1964, Base2016-DE1989, and Base2016-DE1964, respectively.
Therefore, the cumulative bathymetry evolution for the past 50 years caused the TDA to decrease by approximately 0.2 throughout the entire system, favoring a shorter ebb duration and a stronger ebb-dominant regime, which is consistent with previous studies on the TDA implying that deep channels with an absence of large intertidal flats favor ebb dominance (e.g., Dronkers, 1986; Wang et al., 2002; Guo et al., 2022). The case is rather different from several European estuaries as presented by Winterwerp et al. (2013), which is due to the stronger effect of tidal amplification on the TDA (resulting in an increase of the TDA) than that of the larger water depth.
5.3 Contribution of shoreline and bathymetric changes to changes of TDA
The half-centennial morphological evolution of LDB features channel narrowing and deepening owing to human activities. Between 1964 and 1989, large areas of tidal flats were reclaimed and the shoreline extended southward, resulting in a further enhanced convergent funnel shape. In contrast, the mean water depth decreased. Tides were strongly amplified and became the primary forcing condition forcing sediment trapping with increasing TDA, thus implying a flood-dominated regime. However, during the–1989-2016, the rates of land reclamation slowed. However, channel-dredging and sand mining have become increasingly frequent, which has spurred a decrease in sediment supply since the 2000s. This has resulted in significant estuarine scouring and an increase in mean and maximum water depth. During this period, the effects of bathymetric changes on the TDA dominated the effects of coastline changes, showing a significant decreasing trend in the entire bay. Overall, the relative role of the effects of shoreline and bathymetric changes on the TDA can vary spatially (Figure 4F), with an increasing trend in the middle but an insignificant decreasing trend in the upper and lower bays, respectively. This indicates that shoreline changes were dominant in the middle parts of the bay, whereas the changes in TDA in the rest of the bay were dominated by bathymetric changes.
5.4 Implication for sustainable management
River discharges generally reduce the tidal asymmetry in the upper reaches of tidal systems (Hoitink et al., 2017; Zhang et al., 2018; Yu et al., 2020), which has to do with the different responses of TDA generated by the combinations of two or three constituents (e.g., K1-O1-M2, M2-M4, M2-S2-MS2) to river discharge. However, for an estuary with active morphological evolutions, the flood dominance may considerably increase during the high flow periods owing to the substantial river-bed erosion and larger tidal range than in the low flow periods (Xie and Wang, 2021; Xie et al., 2022). It is highly recommended to further investigate the effects of river discharge on spatiotemporal dynamics of TDA and the related long-term morphological changes.
Morphological changes and associated tidal asymmetry evolutions have been detected in several tidal basins and estuaries worldwide (e.g., Hoitink et al., 2017; Zhang et al., 2018; Guo et al., 2021), and are beneficial for water resources and ecological management given regional sediment starvation and sea level rise. For instance, a historic review of the sediment export-import shift in the North Branch of the Yangtze River estuary indicated that human-initiated tidal flat embankments, together with a reduced river inflow, foster positive feedback between tidal asymmetry and land reclamation (Guo et al., 2021). An analytical model was developed to study the man-induced regime shifts in small, narrow, and converging estuaries in Europe, arguing that upon the loss of intertidal areas, floods become dominant, upon which fine sediments are pumped into rivers, reducing their effective hydraulic drag (Winterwerp and Wang, 2013). The more tidal flats reclaimed, the stronger the flood dominance, resulting in sediment trapping and deposition, fast channel aggradation, and loss of channel volume, which counteracts the inundation impacts of sea level increases (Wang et al., 2018; Guo et al., 2022). However, channel deepening owing to waterway dredging and sand mining may bring the positive feedback between tidal asymmetry and land reclamation to an equilibrium state.
While flood dominance and the associated sediment import caused by large-scale reclamation of intertidal flats are beneficial for estuaries to counteract the drowning impact of mean sea level rise and worldwide sediment deficiency in general, it raises an essential water resources management concern regarding increased flood risk in coastal areas, especially considering significant amplification of tidal wave together with the occurring of storm surge events. To increase the tidal system’s long-term stability and resilience to coastal floods, restoring waterfront tidal flats as well as salt marshes or mangroves is considered as a more effective measure than the traditional hard engineering projects, for example, dikes or seawalls (Temmerman et al., 2013). Consequently, from perspectives of coastal and ecosystem protection, it is suggested to allow tidal flats to accrete and expand under sediment import, rather than progressively reclaiming them, until the tidal system leads toward a new hydro-morphodynamic equilibrium after intensive human interventions.
6 Conclusions
In this study, we revisited the half-centennial morphological changes in LDB and their impact on the TDA using an analysis of bathymetric data and a series of numerical modeling scenarios. The topography of LDB gradually narrowed and deepened. During the first stage between 1964 and 1989, the morphological evolution featured narrowing and shallowing trends as a combined result of natural evolution and land reclamation, and the TDA and its main primary contributors all increased from the mouth to the end of the bay. However, between 1989 and 2016, the morphological evolution featured narrowing and deepening as a combined result of natural evolution, channel dredging, sand mining, and land reclamation; the TDA and its main primary contributors all decreased throughout the entire bay. During the whole period between 1964 and 2016, the tidal skewness was reduced slightly in the outer and the head of the bay, whereas it increased significantly in the middle parts owing to the cumulative effects of morphological changes.
Shoreline variations caused by land reclamation can cause the TDA to change, depending on the convergence of the bay. The stronger the convergence of the bay, the larger the TDA and the tendency toward flood-dominance. Bathymetric alterations caused by the combined effects of channel dredging, reduced sediment supply, and sand mining can induce a significant decrease throughout the entire bay. The role of bathymetric alteration was more important than that of shoreline variations in the TDA. Channel deepening can mitigate the effects of channel narrowing on the TDA, leading to a possible equilibrium state between tidal asymmetry and estuarine morphology. Further studies are highly recommended to understand the potential impacts of river discharge on the TDA and the associated long-term morphological changes as well as the increased coastal flood risks.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding authors
Author contributions
QY, HC, and FL, supervision, review, funding acquisition. SH, formal analysis, figure drawing, and writing (original draft). NC, LF, and PZ, software and data checking. All authors contributed to the article and approved the submitted version.
Funding
The research reported herein is funded by the National Key R&D of China (Grant No. 2016YFC0402600), and the Guangzhou Science and Technology Program of China (Grant No. 202102020450).
Acknowledgments
The authors thank Dr. Lixia Niu, Heng Wang, and Suying Ou for their advices and supervision on this study. Finally, we are really grateful to the two reviewers for their constructive comments.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2022.983182/full#supplementary-material
References
Allen J. I., Somerfield P. J., Gilbert F. J. (2007). Quantifying uncertainty in high resolution coupled hydrodynamic-ecosystem models. J. Mar. Syst. 64, 3–14. doi: 10.1016/j.jmarsys.2006.02.010
Bolle A., Wang Z. B., Amos C., De Ronde J. (2010). The influence of changes in tidal asymmetry on residual sediment transport in the Western scheldt. Cont. Shelf Res. 30 (8), 871–882. doi: 10.1016/0022-1694(79)90130-6
Byun D., Cho Y. (2006). Double peak-flood current asymmetry in a shallow-water-consituent dominated embayment with a macro-tidal flat. Geophys. Res. Lett. 33, (16). doi: 10.1029/2006GL026967
Cai H., Huang J., Niu L., Ren L., Liu F., Ou S., et al. (2018a). Decadal variability of tidal dynamics in the pearl river delta: Spatial patterns, causes, and implications for estuarine water management. Hydrol. Process. 32 (25), 3805–3819. doi: 10.1002/hyp.13291
Cai H., Yang H., Liu J., Niu L., Ren L., Liu F., et al. (2018b). Quantifying the impacts of human interventions on relative mean sea level change in the pearl river delta, China. Ocean Coast. Manage. 173, 52–64. doi: 10.1016/j.ocecoaman.2019.02.007
Cao Y., Zhang W., Zhu Y., Ji X., Xu Y., Wu Y., et al. (2020). Impact of trends in river discharge and ocean tides on water level dynamics in the pearl river delta. Coast. Eng. 157, 103634. doi: 10.1016/j.coastaleng.2020.103634
Chen K., Dong H., Jia L., He Z. (2020). Depocentre transfer in the lingdingyang estuary: Interferences from natural and anthropogenic forcings. Ocean Coast. Manage. 185, 105064. doi: 10.1016/j.ocecoaman.2019.105064
Chernetsky S. A., Schuttelaars M. H., Talke A. S. (2010). The effect of tidal asymmetry and temporal settling lag on sediment trapping in tidal estuaries. Ocean Dyn. 60, 1219–1241. doi: 10.1007/s10236-010-0329-8
Chu D., Niu H., Wang Y., Cao A., Li L., Du Y., et al. (2021). Numerical study on tidal duration asymmetry and shallow-water tides within multiple islands: An example of the zhoushan archipelago. Estuar. Coast. Shelf Sci. 262, 107576. doi: 10.1016/j.ecss.2021.107576
Chu N., Yao P., Ou S., Wang H., Yang H., Yang Q. (2022). Response of tidal dynamics to successive land reclamation in the lingding bay over the last century. Coast. Eng. 173, 104095. doi: 10.1016/j.coastaleng.2022.104095
Dai M., Wang L., Guo X., Zhai W., Li Q., He B., et al. (2008). Nitrification and inorganic nitrogen distribution in a large perturbed river/estuarine system: the pearl river estuary, China. Biogeosciences 5 (5), 1227–1244. doi: 10.5194/bg-5-1227-2008
Dronkers J. (1986). Tidal asymmetry and estuarine morphology. Neth. J. Sea Res. 20 (2-3), 117–131. doi: 10.1016/0077-7579(86)90036-0
Feng X., Feng H. (2021). On the role of anthropogenic activity and Sea-level-rise in tidal distortion on the open coast of the yellow Sea shelf. J. Geophys. Res. Oceans 2021, 126(3). doi: 10.1029/2020JC016583
Foreman M. G. G., Henry R. F. (1989). The harmonic analysis of tidal model time series. Adv. Water Resour. 12 (3), 109–120. doi: 10.1016/0309-1708(89)90017-1
Friedrichs C. T., Aubrey D. G. (1988). Non-linear tidal distortion in shallow well-mixed estuaries: a synthesis. Estuar. Coast. Shelf Sci. 27 (5), 521–545. doi: 10.1016/0272-7714(88)90082-0
Friedrichs T. C., Aubrey G. D. (1994). Tidal propagation in strongly convergent channels. J. Geophys. Res. 99 (C2), 3321–3336. doi: 10.1029/93JC03219
Gao G. D., Wang X. H., Bao X. W. (2014). Land reclamation and its impact on tidal dynamics in jiaozhou bay, qingdao, China. Estuar. Coast. Shelf Sci. 151, 285–294. doi: 10.1016/j.ecss.2014.07.017
Gong W., Schuttelaars H., Zhang H. (2016). Tidal asymmetry in a funnel-shaped estuary with mixed semidiurnal tides. Ocean Dyn. 66 (5), 637–658. doi: 10.1007/s10236-016-0943-1
Guo L., Brand M., Sanders B. F., Foufoula-Georgiou E., Stein E. D. (2018). Tidal asymmetry and residual sediment transport in a short tidal basin under sea level rise. Adv. Water Resour. 121, 1–8. doi: 10.1016/j.advwatres.2018.07.012
Guo L., van der Wegen M., Roelvink J. A., He Q. (2014). The role of river flow and tidal asymmetry on 1-D estuarine morphodynamics. J. Geophys. Res. Earth Surf. 119, 2315–2334. doi: 10.1002/2014JF003110
Guo L., van der Wegen M., Jay D. A., Matte P., Wang Z.B., Roelvink D. (2015). River-tide dynamics: Exploration of nonstationary and nolinear tidal behavior in the Yangtze River Estuary. J. Geophys. Res. Oceans 120, 3499–3521. doi: 10.1002/2014JC010491
Guo L., Wang Z., Townend I., He Q. (2019). Quantification of tidal asymmetry and its nonstationary variations. J. Geophys. Res. Oceans 124 (1), 773–787. doi: 10.1029/2018JC014372
Guo L., Xie W., Xu F., Wang X., Zhu C., Meng Y., et al. (2021). A historical review of sediment export-import shift in the north branch of changjiang estuary. Earth Surf. Process. Landforms. 47 (1), 5–16. doi: 10.1002/esp.5084
Guo L., Zhu C., Xie W., Xu F., Wu H., Wan Y., et al. (2021). Changjiang delta in the anthropocene: Multi-scale hydro-morphodynamics and management challenges. Earth Sci. Rev. 223, 103850. doi: 10.1016/j.earscirev.2021.103850
Guo L., Zhu C., Xu F., Xie W., van der Wegen M., Townend I., et al. (2022). Reclamation of tidal flats within tidal basins alters centennial morphodynamic adaptation to sea-level rise. J. Geophys. Res. Earth Surf. 127 (6), e2021JF006556. doi: 10.1029/2021JF006556
Hoitink A., Hoekstra P., Van Maren D. S. (2003). Flow asymmetry associated with astronomical tides: implications for the residual transport of sediment. J. Geophys. Res.: Oceans 108 (C10), 207–215. doi: 10.1029/2002JC001539
Hoitink A. J. F., Wang Z. B., Vermeulen B., Huismans Y., Kastner K. (2017). Tidal controls on river delta morphology. Nat. Geosci. 10, 637–645. doi: 10.1038/NGEO3000
Intergovernmental Oceanographic Commission, International Hydrographic Organization, British Oceanographic Data Centre (2003). “Centenary edition of the GEBCO digital atlas,” in British Oceanographic data centre, Liverpool(UK:British Oceanographic Data Centre (BODC)).
Lanzoni S., Seminara G. (1998). On tide propagation in convergent estuaries. J. Geophys. Res. Oceans 103 (C13), 30793–30812. doi: 10.1029/1998JC900015
Lanzoni S., Seminara G. (2002). Long-term evolution and morphodynamic equilibrium of tidal channels. J. Geophys. Res. 107(C1), 3001. doi: 10.1029/2000JC000468
LeBlond P. H. (1978). On tidal propagation in shallow rivers. J. Geophys. Res. Oceans 83 (C9), 4717–4721. doi: 10.1029/JC083iC09p04717
Li L., Guan W., Hu J., Cheng P., Wang X. H. (2018). Responses of water environment to tidal flat reduction in xiangshan bay: Part I hydrodynamics. Estuar. Coast. Shelf Sci. 206, 14–26. doi: 10.1016/j.ecss.2017.11.003
Lin S., Liu G., Niu J., Wei X., Cai S. (2021). Responses of hydrodynamics to changes in shoreline and bathymetry in the pearl river estuary, China. Cont. Shelf Res. 229, 104556. doi: 10.1016/j.csr.2021.104556
Liu F., Yuan L., Yang Q., Ou S., Xie L., Cui X. (2014). Hydrological responses to the combined influence of diverse human activities in the pearl river delta, China. Catena 113, 41–55. doi: 10.1016/j.catena.2013.09.003
Luo X., Zeng E., Ji R., Wang C. (2007). Effects of in-channel sand excavation on the hydrology of the pearl river delta. Hydrol. 343, 230–239. doi: 10.1016/j.jhydrol.2007.06.019
Luo X., Zhang W., Chen S., Feng X., Ji X., Xu Y. (2020). Evolution of reversal of the lowest low waters in a tidal river network. J. Hydrol. 585, 124701. doi: 10.1016/j.jhydrol.2020.124701
Mao Q., Shi P., Yin K., Gan J., Qi Y. (2004). Tides and tidal currents in the pearl river estuary. Cont. Shelf Res. 24 (16), 1797–1808. doi: 10.1016/j.csr.2004.06.008
Maren D. S., Gerritsen H. (2012). Residual flow and tidal asymmetry in the Singapore strait, with implications for resuspension and residual transport of sediment. J. Geophys. Res. Oceans 117 (C4), C04021. doi: 10.1029/2011JC007615
Murray J. N., Clemens S. R., Phinn R. S., Possingham P. H., Fuller A. R. (2014). Tracking the rapid loss of tidal wetlands in the yellow Sea. Front. Ecol. Environ. 12 (5), 267–272. doi: 10.1890/130260
Nash J. E., Sutcliffe J. V. (1970). River flow forecasting through conceptual models part I - a discussion of principles. J. Hydrol. 10, 282–290. doi: 10.1016/0022-1694(70)90255-6
Nidzieko N. J. (2010). Tidal asymmetry in estuaries with mixed semidiurnal/diurnal tides. J. Geophys. Res.: Oceans 115 (C8), 488–507. doi: 10.1029/2009JC005864
Núñez P., Castanedo S., Medina R. (2020). A global classification of astronomical tide asymmetry and periodicity using statistical and cluster analysis. J. Geophys. Res. Oceans 125, (8). doi: 10.1029/2020JC016143
Pan H., Lv X., Wang Y., Matte P., Chen H., Jin G. (2018). Exploration of tidal-fluvial interaction in the Columbia river estuary using S_Tide. J. Geophys. Res. Oceans 123 (9), 6598–6619. doi: 10.1029/2018JC014146
Pawlowicz R., Beardsley B., Lentz S. (2002). Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Comput. Geosci. 28 (8), 929–937. doi: 10.1016/S0098-3004(02)00013-4
Pugh D. T. (1987). Tides, surges and mean Sea-level. J. Wiley. Available at: https://www.osti.gov/biblio/5061261
Savenije H. (2005). Salinity and tides in alluvial estuaries (Amsterdam: Elsevier Science Ltd.). doi: 10.1016/B978-044452107-1/50000-9
Shi B., Yang S., Temmerman S., Bouma T., Ysebaert T., Wang S., et al. (2021). Effect of typhoon-induced intertidal-flat erosion on dominant macrobenthic species (Meretrix meretix). Limnol. Oceanogr. 66, 4197–4209. doi: 10.1002/lno.11953
Song D., Wang X. H., Kiss A. E., Bao X. (2011). The contribution to tidal asymmetry by different combinations of tidal constituents. J. Geophys. Res. Oceans 116 (C12), 338–348. doi: 10.1029/2011JC007270
Song D., Wang X. H., Zhu X., Bao X. (2013). Modeling studies of the far-field effects of tidal flat reclamation on tidal dynamics in the East China seas. Estuar. Coast. Shelf Sci. 133, 147–160. doi: 10.1016/j.ecss.2013.08.023
Speer P. E., Aubrey D. G. (1985). A study of non-linear tidal propagation in shallow inlet/estuarine systems part II: theory. Estuar. Coast. Shelf Sci. 21 (2), 207–224. doi: 10.1016/0272-7714(85)90097-6
Temmerman S., Bouma J. T., Herman M. P., Ysebaert T., De Veriend J. H. (2013). Ecosystem-based coastal defence in the face of global change. Nature 504, 79–83. doi: 10.1038/nature12859
Toffolon M., Lanzoni S. (2010). Morphological equilibrium of short channels dissecting the tidal flats of coastal lagoons. J. Geophys. Res. 115, F04036. doi: 10.1029/2010JF001673
Twigt D. J., Goede E. D. D., Zijl F., Schwanenberg D., Chiu A. Y. W. (2009). Coupled 1D-3D hydrodynamic modelling, with application to the pearl river delta. Ocean Dyn. 59, 1077–1093. doi: 10.1007/s10236-009-0229-y
Van de Kreeke J., Robaczewska K. (1993). Tide-induced residual transport of coarse sediment: Application to the ems estuary. J. Sea Res. 31 (3), 209–220. doi: 10.1016/0077-7579(93)90022-K
Van der Wegen M. (2013). Numerical modelling of the impact of sea level rise on tidal basin morphodynamics. J. Geophys. Res. Earth Surf. 118 (2), 447–460. doi: 10.1002/jgrf.20034
Wang Z. B., Elias E., van der Spek A., Lodder Q. (2018). Sediment budget and morphological development of the Dutch wadden Sea: Impact of accelerated sea-level rise and subsidence until 2100. Neth. J. Geosci. 97 (3), 183–214. doi: 10.1017/njg.2018.8
Wang Z. B., Jeuken M. C. J. L., Gerritsen H., de Vriend H. J., Kornman B. A. (2002). Morphology and asymmetry of the vertical tide in the westerschelde estuary. Cont. Shelf Res. 22, 2599–2609. doi: 10.1016/S0278-4343(02)00134-6
Wang H., Zhang P., Hu S., Cai H., Liu F., Yang Q. (2020). Tidal regime shift in lingding bay, the pearl river delta: An identification and assessment of driving factors. Hydrol. Process. 34 (13), 2878–2894. doi: 10.1002/hyp.13773
Winterwerp C. J. (2011). Fine sediment transport by tidal asymmetry in the high-concentrated ems river: indications for a regime shift in response to channel deepening. Ocean Dyn. 61, 203–215. doi: 10.1007/s10236-010-0332-0
Winterwerp C. J., Wang Z. B. (2013). Man-induced regime shifts in small estuaries–I: theory. Ocean Dyn. 63, 1279–1292. doi: 10.1007/s10236-013-0662-9
Winterwerp C. J., Wang Z. B., Braeckel A., Holland G., Kösters F. (2013). Man-induced regime shifts in small estuaries–II: a comparison of rivers. Ocean Dyn. 63, 1293–1306. doi: 10.1007/s10236-013-0663-8
Woodworth P. L., Blackman D. L., Pugh D. T., Vassie J. M. (2005). On the role of diurnal tides in contributing to asymmetries in tidal probability distribution functions in areas of predominantly semi-diurnal tide. Estuar. Coast. Shelf Sci. 64 (2), 235–240. doi: 10.1016/j.ecss.2005.02.014
Wu Z., Milliman J. D., Zhao D., Zhou J., Yao C. (2014). Recent geomorphic change in LingDing bay, China, in response to economic and urban growth on the pearl river delta, southern China. Global Planet. Change 123, 1–12. doi: 10.1016/j.gloplacha.2014.10.009
Wu Z., Saito Y., Zhao D. N., Zhou J. Q., Cao Z. Y., Li S. J., et al. (2016). Impact of human activities on subaqueous topographic change in lingding bay of the pearl river estuary, China, during 1955-2013. Sci. Rep. 6, 37742. doi: 10.1038/srep37742
Xie D., Wang Z. B. (2021). Seasonal tidal dynamics in the qiantang estuary: The importance of morphological evolution. Front. Earth Sci. 9, 782640. doi: 10.3389/feart.2021.782640
Xie D., Wang Z. B., Huang J., Zeng J. (2022). River, tide and morphology interaction in a macro-tidal estuary with active morphological evolutions. Catena 212, 106131. doi: 10.1016/j.catena.2022.106131
Xu P., Mao X., Jiang W., Zhou L. (2014). A numerical study of tidal asymmetry: preferable asymmetry of nonlinear mechanisms in xiangshan bay, East China sea. J. Ocean Univ. China 13 (5), 733–741. doi: 10.1007/s11802-014-2251-z
Yang L., Liu F., Gong W., Cai H., Yu F., Pan H. (2019). Morphological response of lingding bay in the pearl river estuary to human intervention in recent decades. Ocean Coast. Manage. 176, 1–10. doi: 10.1016/j.ocecoaman.2019.04.011
Yang H., Zhang X., Cai H., Hu Q., Liu F., Yang Q, et al (2020). Seasonal changes in river-tide dynamics in a highly human-modified estuary: Modaomen Estuary case study. Mar. Geo. 427, 106273. doi: 10.1016/j.margeo.2020.106273
Yu X., Zhang W., Hoitink A. J. F. (2020). Impact of river discharge seasonality change on tidal duration asymmetry in the Yangtze river estuary. Sci. Rep. 10 (1), 1–17. doi: 10.1038/s41598-020-62432-x
Zhang W., Cao Y., Zhu Y., Zheng J., Ji X., Xu Y., et al. (2018). Unravelling the causes of tidal asymmetry in deltas. J. Hydrol. 564, 588–604. doi: 10.1016/j.jhydrol.2018.07.023
Zhang G., Cheng W., Chen L., Zhang H., Gong W. (2019). Transport of riverine sediment from different outlets in the pearl river estuary during the wet season. Mar. Geol. 415, 105957. doi: 10.1016/j.margeo.2019.06.002
Zhang W., Ruan X., Zheng J., Zhu Y., Wu H. (2010). Long-term change in tidal dynamics and its cause in the pearl river delta, China. Geomorphology 120 (3), 209–223. doi: 10.1016/j.geomorph.2010.03.031
Zhang W., Xu Y., Hoitink A. J. F., Sassi M. G., Zheng J., Chen X., et al. (2015). Morphological change in the pearl river delta, China. Mar. Geol. 363, 202–219. doi: 10.1016/j.margeo.2015.02.012
Zhang W., Cao Y., Zhu Y., Wu Y., Ji X., He Y., et al. (2017). Flood frequency analysis for alterations of extreme maximum water levels in the Pearl River Delta. Ocean Eng. 129, 117–132. doi: 10.1016/j.oceaneng.2016.11.013
Zhang P., Yang Q., Pan H., Wang H., Xie M., Cai H., et al. (2021b). Impacts of human interventions on the seasonal and nodal dynamics of the M2 and K1 tides in lingdingyang bay of the zhujiang river delta, China. Acta Oceanol. Sin. 40 (11), 1–16. doi: 10.1007/s13131-021-0000-00
Zhang P., Yang Q., Wang H., Cai H., Liu F., Zhao T., et al. (2021a). Stepwise alterations in tidal hydrodynamics in a highly human-modified estuary: The roles of channel deepening and narrowing. J. Hydrol. 597, 126153. doi: 10.1016/j.jhydrol.2021.126153
Zhou Z., Coco G., Townend I., Gong Z., Wang Z., Zhang C. (2018). On the stability relationships between tidal asymmetry and morphologies of tidal basins and estuaries. Earth Surf. Proc. Land. 43, 1943–1959. doi: 10.1002/esp.4366
Keywords: tidal duration asymmetry, land reclamation, channel deepening, tidal amplitude, tidal phase
Citation: Yang Q, Hu S, Fu L, Zhang P, Chu N, Liu F and Cai H (2022) Responses of tidal duration asymmetry to morphological changes in Lingding Bay of the Pearl River Estuary. Front. Mar. Sci. 9:983182. doi: 10.3389/fmars.2022.983182
Received: 30 June 2022; Accepted: 10 August 2022;
Published: 02 September 2022.
Edited by:
Yang Yang, Nanjing Normal University, ChinaReviewed by:
Dongfeng Xie, Zhejiang Institute of Hydraulics and Estuary, ChinaBenwei Shi, East China Normal University, China
Copyright © 2022 Yang, Hu, Fu, Zhang, Chu, Liu and Cai. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Feng Liu, bGl1ZjUzQG1haWwuc3lzdS5lZHUuY24=; Huayang Cai, Y2FpaHk3QG1haWwuc3lzdS5lZHUuY24=
 Qingshu Yang1,2
Qingshu Yang1,2 Shuai Hu
Shuai Hu Feng Liu
Feng Liu Huayang Cai
Huayang Cai