- 1College of Geomatics and Geoinformation, Guilin University of Technology, Guilin, China
- 2Department of Natural Resources Science, University of Rhode Island, Kingston, RI, United States
The high-precision estimation of mangrove leaf area index (LAI) using a deep learning regression algorithm (DLR) always requires a large amount of training sample data. However, it is difficult for LAI field measurements to collect a sufficient amount of sample data in mangrove wetlands. To tackle this challenge, this paper proposed an approach for expanding training samples and quantitatively evaluated the performance of estimating LAI for mangrove communities using Deep Neural Networks (DNN) and Transformer algorithms. This study also explored the effects of unmanned aerial vehicle (UAV) and Sentinel-2A multispectral, orbital hyper spectral (OHS), and GF-3 SAR images on LAI estimation of different mangrove communities. Finally, this paper evaluated the LAI estimation ability of mangrove communities using ensemble learning regression (ELR) and DLR algorithms. The results showed that: (1) the UAV images achieved the better LAI estimation of different mangrove communities (R2 = 0.5974–0.6186), and GF-3 SAR images were better for LAI estimation of Avicennia marina with high coverage (R2 = 0.567). The optimal spectral range for estimating LAI for mangroves in the optical images was between 650–680 nm. (2) The ELR model outperformed single base model, and produced the high-accuracy LAI estimation (R2 = 0.5266–0.713) for different mangrove communities. (3) The average accuracy (R2) of the ELR model was higher by 0.0019–0.149 than the DLR models, which demonstrated that the ELR model had a better capability (R2 = 0.5865–0.6416) in LAI estimation. The Transformer-based LAI estimation of A. marina (R2 = 0.6355) was better than the DNN model, while the DNN model produced higher accuracy for Kandelia candel (KC) (R2 = 0.5577). (4) With the increase in the expansion ratio of the training sample (10–50%), the LAI estimation accuracy (R2) of DNN and Transformer models for different mangrove communities increased by 0.1166–0.2037 and 0.1037–0.1644, respectively. Under the same estimation accuracy, the sample enhancement method in this paper could reduce the number of filed measurements by 20–40%.
1 Introduction
Mangroves are one of the most prolific and productive ecosystems on earth (Borges, 2003; Behrouz-Rad, 2014). It not only nurtures abundant aquatic life, but also plays an irreplaceable role in sequestering and storing carbon and maintaining sustainable development (Wang et al., 2003). The Leaf Area Index (LAI) can reflect the leaf sparsity and canopy structure characteristics and is a key indicator for monitoring the health of vegetation (Giri et al., 2007; Heumann, 2011; Tian et al., 2017). Due to high plant density, intertwined roots and branches, and tidal fluctuations, traditional in situ observations are difficult to accomplish in large-scale LAI measurements. Recently, remote sensing technology has been an effective way to estimate the LAI of mangroves (Guo et al., 2021).
The vegetation index has been used to estimate LAI (Green et al., 1997). Studies have employed the original spectral bands (e.g., Blue, NIR) and vegetation index (e.g., EVI, NDVI) to construct the LAI estimation model (Kamal et al., 2016; Wang et al., 2019). For example, Kamal et al. (2021) used WorldView-2 imagery and NDVI to achieve a high-precision (R2 = 0.98) estimation of LAI for mangroves. However, the influence of different spectral band combinations on the LAI estimation of mangrove communities had rarely been considered, so the spectral information was not fully utilized. Therefore, this paper calculated combined features with vegetation indices and original spectral bands to construct a high-dimensional mangrove LAI dataset. However, different band combinations caused information redundancy, which affected the computational efficiency and accuracy of the model. Data dimensionality reduction can eliminate data redundancy and improve model estimation accuracy (Liang et al., 2020; Lou et al., 2020). Active and passive remote sensing images in different spatial resolutions have also been used to estimate different vegetation biophysical parameters (Jia et al., 2019; Zhu et al., 2020). UAVs can provide a wide range of cost-effective image data based on their flexible imaging cycles (Hardin and Jensen, 2011; Knoth et al., 2013; Bhardwaj et al., 2016). Tian et al. (2021) achieved high precision estimation accuracy of above-ground biomass of mangroves (R2 = 0.8319, RMSE = 22.7638 Mg/ha) using UAV imagery. Hyperspectral images may provide rich spectral information. Studies have demonstrated the potential of hyperspectral imagery in estimating the LAI of mangroves (Neukermans et al., 2008; Liang et al., 2015; Yang et al., 2022). Chen et al. (2020) achieved a high accuracy (R2 = 0.834, RMSE = 0.824) estimation of the LAI of mangroves using GF-5 hyperspectral imagery and a machine learning regression model. However, the sensitivity of certain spectral bands to LAI is influenced by the canopy structure. (Zhu et al., 2017). The reflectance of bare soil under optical imaging and the spectral saturation effect under high cover can also reduce the accuracy of LAI estimation in mangrove communities (Dong et al., 2019). Meanwhile, optical sensors mainly obtain information on the top of the vegetation canopy, and it is difficult to obtain information on the vertical structure of the vegetation (Lu, 2006; Chang and Shoshany, 2016). Synthetic Aperture Radar (SAR) images have canopy penetration capability and can better obtain vertical structure information (Lucas et al., 2004; Omar et al., 2017; Ke Huang et al., 2022). There is a lack of research to compare and evaluate the differences in the accuracy of LAI estimation of mangrove communities from multispectral, hyperspectral, and SAR images.
There are two main types of remote sensing estimates of LAI: physical models based on radiative transfer theory and biophysical processes; and empirical models based on the relationship between measured data and image spectral bands (Kovacs et al., 2005; Bocca and Rodrigues, 2016; Tian et al., 2017). Although the physical models enable us to accurately reflect the physiological process of vegetation growth, such methods require a large number of biophysical parameters (Zhu et al., 2017), and the model adjustment and calibration require complex processes, making it difficult to apply to the estimation of vegetation physical parameters in a large range (Sun et al., 2019). Empirical models have been successfully used to estimate various vegetation biophysical parameters (Kovacs et al., 2005; Tian et al., 2017). Shallow machine learning regression models explain the relationship between biophysical parameters and model parameters (Zhu et al., 2017). For example, Liang et al. (2020) obtained good estimation accuracy (R2 = 0.939, NRMSE = 6.474%) for crop LAI using a shallow machine learning regression model. But the shallow machine learning regression algorithm is prone to overfitting (Chlingaryan et al., 2018), and the single regression model has poor stability and low prediction accuracy, which requires frequent trade-offs between the balance and accuracy of the model (Christensen, 2003). The ensemble learning algorithm integrates the advantages of each algorithm, makes up for the shortcomings of a single algorithm, and improves the model stability and prediction accuracy. For example, Yan et al. (2021) proposed and used EIM for estimating water, carbon, and ecological footprints. Compared to traditional methods, EIM achieves similar predictive performance but with 80% less data than a single machine learning regression algorithm that improves estimation accuracy by more than 20%. Stacking models integrate the advantages of multiple base regression models to generate stable estimation results and provide better generalization ability for regression predictions (Dietterich, 2000; Ghosh et al., 2021). However, the ability of the ensemble learning algorithm to estimate the LAI of different mangrove communities remains to be verified. Deep learning (DL) algorithms are regarded as a breakthrough technology in machine learning and remote sensing data mining (Zhu et al., 2017). DL algorithms have been used for vegetation parameter and crop yield estimation (Sun et al., 2019; Khaki and Wang, 2019). Tamiminia et al. (2021) achieved high estimation accuracy (RMSE = 2.69 Mg/ha and R2 = 0.89) for shrub willow biomass using a DL (Convolutional Neural Networks, CNN) model. The traditional DL algorithm requires a large amount of computation and complex model training, while the Tansformer algorithm proposed by the Google AI team (Vaswani et al., 2017) realizes the “self-attention” mechanism, which reduces the complexity of the architecture and enables the achievement of very fast computation, and reduced training time. At present, the applicability of the Tansformer algorithm for LAI estimation of different mangrove communities has not been verified. Few studies have evaluated the ability of ELR and DLR models (Tansformer and DNN) to estimate the LAI of different mangrove communities.
Quantitative remote sensing research has high requirements for measured data and requires a large amount of measured data for model training and verification (Kamal et al., 2016). The number of training samples was also critical for the high-accuracy estimation of the DLR model (LeCun et al., 2015). For example, Kamal et al. (2016) validated the accuracy of LAI estimation for mangroves in different regions using 63 and 37 independent samples, respectively, and obtained better results (R2 = 0.83 and R2 = 0.82). Huang et al. (2020) found that insufficient training data can lead to severe overfitting problems in the DLR model and reduce model accuracy. However, for most of the natural vegetation with a more complex growth environment, such as mangroves growing mainly in the coastal intertidal zone, it is difficult to obtain sufficient actual measurement data. To solve this problem, a training sample expansion method based on UAV multispectral images and the ELR model was proposed in this paper. At the same time, this paper quantitatively analyzes the effects of different training sample expansion ratios on the accuracy of mangrove LAI estimation by Tansformer and DNN models, and argumentative sample expansion addresses the problem of insufficient training samples for Tansformer and DNN models.
To fill the research gaps, this paper takes the mangrove nature reserve in Beibu Gulf, China as the study area, and estimates the LAI of different mangrove communities using the ELR and DLR algorithms with multispectral, hyperspectral, and SAR images. The main objectives of this study include: (1) exploring the differences in LAI estimation of different mangrove communities between optical and SAR images; (2) comparative analysis of the stability and accuracy of LAI estimation between ELR and a single base model; (3) quantitatively evaluating the ability of ELR and DLR models to estimate LAI of mangroves and determining the optimal LAI estimation model for each mangrove community; (4) examining the effectiveness of the sample enhancement method proposed in this study for LAI estimation; and quantifying the effect of different expansion ratios of the training sample on the accuracy of LAI estimation using Transformer and DNN models.
2 Study Area and Data Source
2.1 Study Area
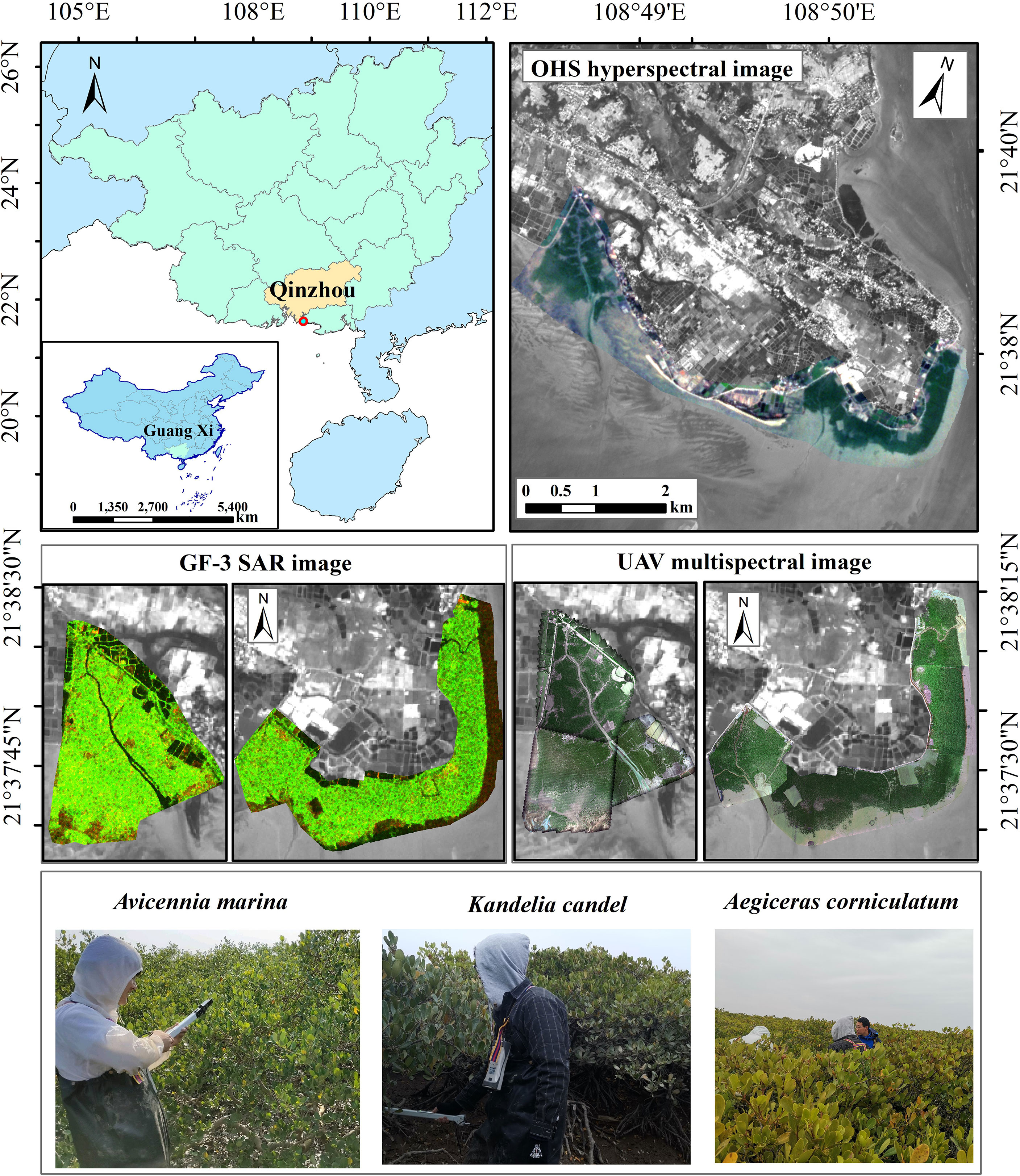
The total area of mangroves in Guangxi Province reaches 9,330.34 hectares, accounting for 32.7% of the country, ranking second in the country, with the largest area of Avicennia marin natural growing place. The experimental research area is located in the coastal mangrove nature reserve in Qinzhou City, Beibu Gulf, China. The geographical location is 108°48′50″E-108°52′17″E, 21°37′02″N-21°38′21″N (Figure 1). The region is mainly in subtropical to tropical transitional marine monsoon climate. The annual average sunshine is 1,782.9 hours, and the precipitation is 2,104.2 mm. However, because of the influence of natural and human factors, mangroves have been degraded on a large scale. The large-scale, high-precision estimation of LAI for mangroves can effectively monitor the growth of mangroves and provide data support for the protection and restoration of mangroves.
2.2 Data Sources
2.2.1 UAV Images Acquisition and Processing
This study uses a DJI Matrice 210 (DJI M210) UAV equipped with a Micasense Red Edge-MX sensor from 10:30 to 15:30 (UTC+08:00) every day from 4 to 25 April 2021, and the resolution of the research area was obtained as a 0.07 m multispectral image. The flight altitude was 100 m. Both the side-to-side overlap rate and the heading overlap rate were set to 80%. Timed shots were taken for 3 s and 45 sorties were flown. Before each flight, radiometric calibration was performed using a calibration plate provided by Micasense. The sensors and calibration parameters are shown in Table 1. Before each sortie, six ground control points were laid out for UAV image processing by using Hi-Target V90 RTK ( ± 0.25 cm).
Multispectral data processing: In this paper, Pix4D mapper 4.7 software was used to process the acquired UAV images, including image quality check, image matching, aerial triangulation solution, dense point cloud generation, 3D modeling, and finally, multispectral images with a spatial resolution of 0.07 m were generated for the study area, and the projection coordinate system was set to WGS 1984 UTM Zone 49N.
The Sentinel-2A multispectral image (S2), Zhuhai No. 1 Orbita Hyper Spectral (OHS) hyperspectral image, and C-band VV/VH polarized Gaofen-3 (GF-3) SAR image were selected. The specific information and imaging times are shown in Supplementary Table 1.
OHS is China’s commercial satellite with hyperspectral data acquisition capability. Equipped with a CMOSMSS sensor, the image has a spatial resolution of 10 m and a spectral resolution of 2.5 nm in 32 bands. Launched on 10 August 2016, the GF-3 SAR image has 12 imaging modes with a 1 m spatial resolution. In this paper, the SAR images are processed by dual polarization in fine strip map 1 (FSI) mode. The specific imaging parameters of the four images are shown in Supplementary Table 1.
For Sentinel-2A image processing, we used the Sen2cor 2.5.5 model written in Python code to process L1C-level image data into L2A-level products. We also used SNAP software to resample the L2A-level data to 10 m resolution by nearest neighbor to be consistent with the field measurement sample (10 × 10 m).
For GF-3 (SAR) image processing, the backscattering coefficient image (sigma0) with a projected coordinate system was generated by VV/VH dual-polarization processing, radiometric correction, multi-view processing, filtering processing (Lee), and geocoding in GF-3 SAR image data.
For OHS image processing, we used the ENVI 5.4 software for radiometric calibration, atmospheric correction, and orthorectification. We generated the reflectance image data with accurate geometric positioning.
In this study, the six ground control points collected by GNSS RTK were used to georeference and subset the UAV and satellite images in the ENVI 5.6 software. The georeferenced errors were less than one pixel. The final projection coordinate system for UAV and satellite images of the study area was unified as the WGS-84 data and the Universal Transverse Mercator (UTM) Zone 49 North coordinate system.
2.2.2 Multiscale LAI Field Measurements
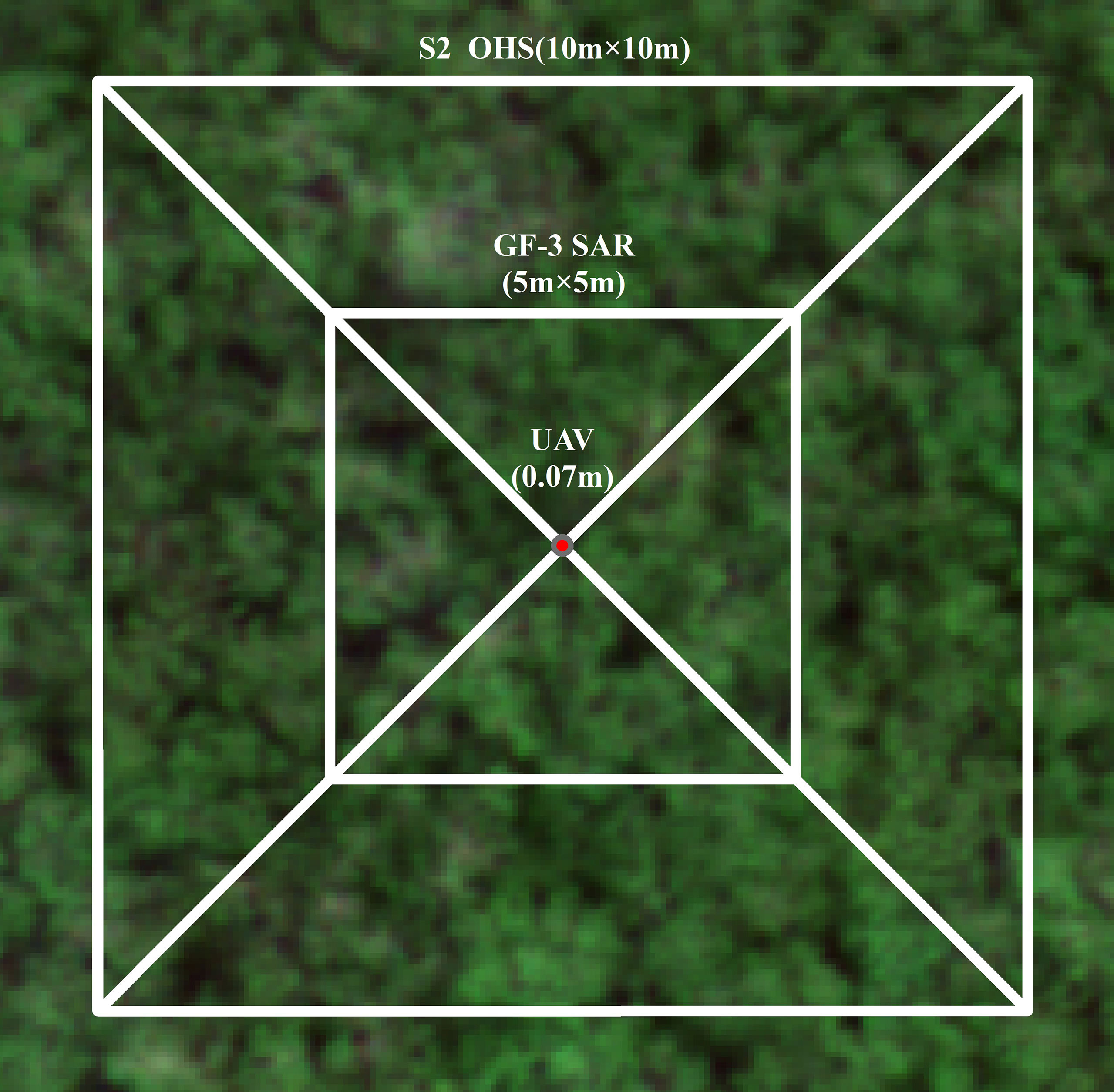
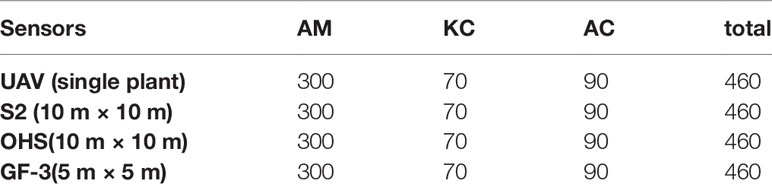
We used the hand-held LAI-2200C leaf area index meter to measure the leaf area index of different communities of mangroves in the study area. The in-situ measurements were conducted from 4 to 25 April 2021. To ensure data accuracy, the measurements were taken between 6:30–9:00 and 16:30–19:00 Beijing time every day when the sky was cloud free and there was no direct sunlight. We measured single plants at 5 m × 5 m and 10 m × 10 m (Figure 2) to obtain the LAI data.
The specific protocol of measurements includes: (1) for a single plant LAI: independent and representative plants were selected, and a leaf area index meter was used to measure once above four times the height of the leaf above the canopy in each direction of the plant to record the A value. The bottom of the crown was measured from the root and stem of the plant to the outside in turn, and the average of four times was recorded as the B value. Each plant was measured in four directions. (2) For 10 m × 10 m (OHS and S2) plots LAI: On each 10 m × 10 m plot, 10–15 plants were evenly measured with LAI-2200 leaf area index meter. The position of the center point of the plot was recorded with Hi-Target V90RTK ( ± 0.25 cm + 1 ppm). The LAI value of the plants was averaged as the LAI value of the center point of the plot. (3) For 5 m × 5 m (GF-3 SAR) plot LAI: a 5 m × 5 m plot was set up in the center of each 10 m × 10 m plot, and 6–8 plants were evenly measured using LAI-2200 leaf area indexer. The position of the center point of the plot was recorded with Hi-Target V90RTK ( ± 0.25 cm + 1 ppm). The LAI value of the plants measured in the plot was averaged as the LAI value of the center point of the plot. The field measurement methods of mangrove LAI are shown in Table 2.
3 Methods
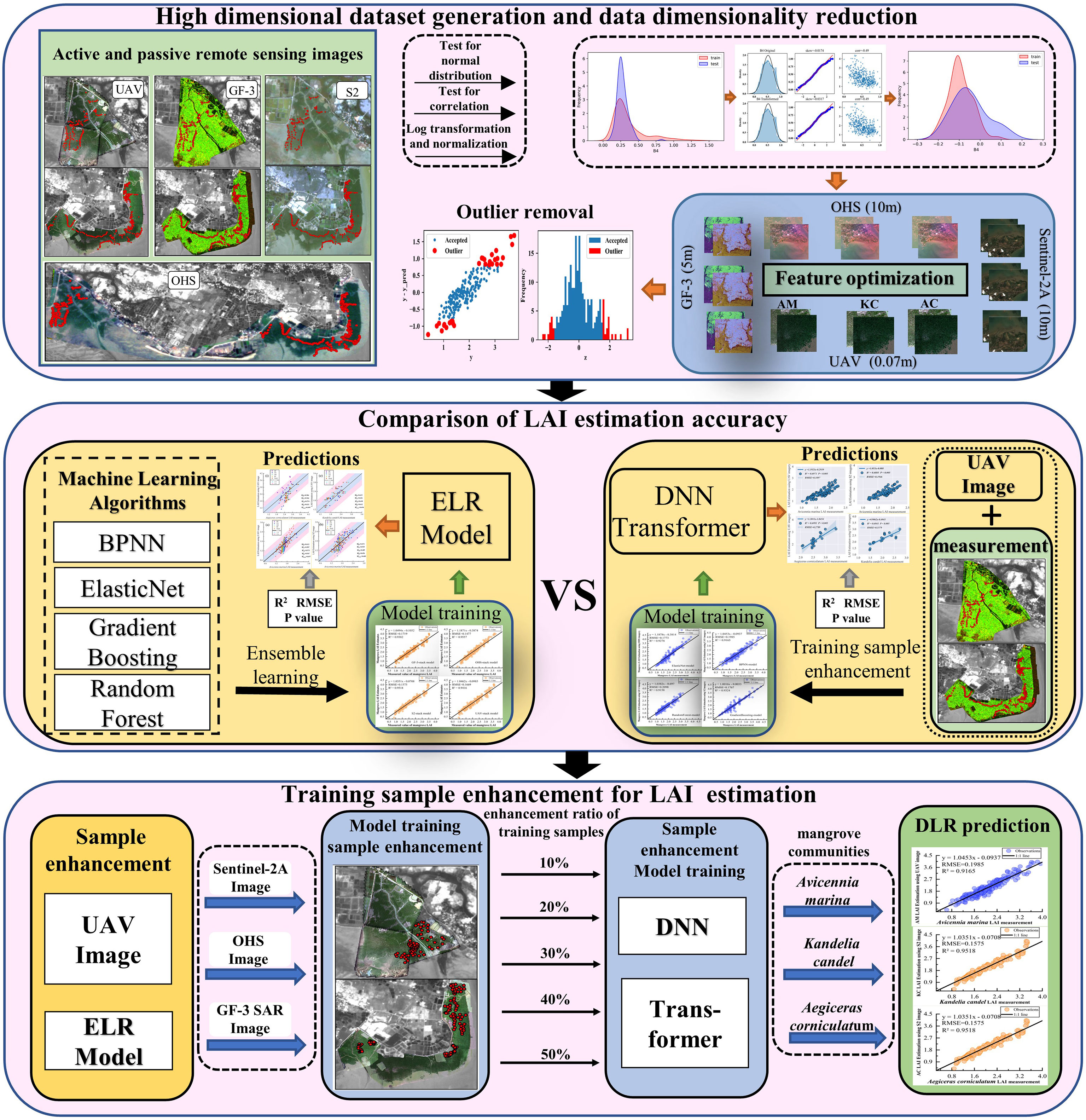
The technical route includes four parts, as illustrated in Figure 3. (1) The vegetation index and combined features were calculated using active and passive remote sensing images to create a high-dimensional data set, and data dimensionality reduction was used for feature optimization. (2) ensemble BPNN, Elastic Net, Gradient Boosting and Random Forest algorithms to build an ensemble learning model, Comparing the estimation accuracy of ELR and DLR models (DNN and Transformer) for the LAI of different communities; (3) The effects of optical and SAR images on the LAI estimation accuracy of different mangrove communities were analyzed; (4) The method of extending the training samples of DLR algorithm based on UAV images and ELR model is proposed to solve the problem of insufficient training samples of DLR model.
3.1 High Dimensional Datasets and Dimensionality Reduction
3.1.1 High Dimensional Dataset Generation
This study integrates the original band, vegetation index, combined features, or polarized backscatter coefficient combined features. A high-dimensional dataset of LAI estimation for different mangrove communities was constructed, as shown in Table 3. Seventeen vegetation indices (see Appendix Table A1 for details) and 168 to 2,169 combined features were calculated under optical remote sensing images (UAV, S2, and OHS). For GF-3 SAR images, 43 combined polarized backscatter coefficient features were calculated. The specific calculations of the combined features and polarized backscattering coefficient combination features are shown in formulas (1)–(4).
Where bi and bjare any two bands or different polarizations of the UAV, S2, OHS images, and GF-3 SAR data, respectively, ρbi, ρbj are the mangrove canopy reflectance values or the backscattering coefficients (sigma0) of VV and VH polarization for the two bands corresponding to bi, bj, respectively.
3.1.2 Data Dimensionality Reduction
High Correlation filter and Backward Feature Elimination were used to reduce dimensionality and eliminate redundant data on the mangrove LAI high-dimensional dataset of UAV, S2, OHS, and GF-3 SAR observations.
(1) The vegetation index calculation and band combination were performed to construct the LAI high-dimensional dataset for optical and SAR images. The normal distribution test was used to generate the normal distribution trend and kernel density maps of each spectral band and combined feature (Figures 4A, B), and the combined features without conforming to a normal distribution were normalized and log-transformed (Figures 4C–E).
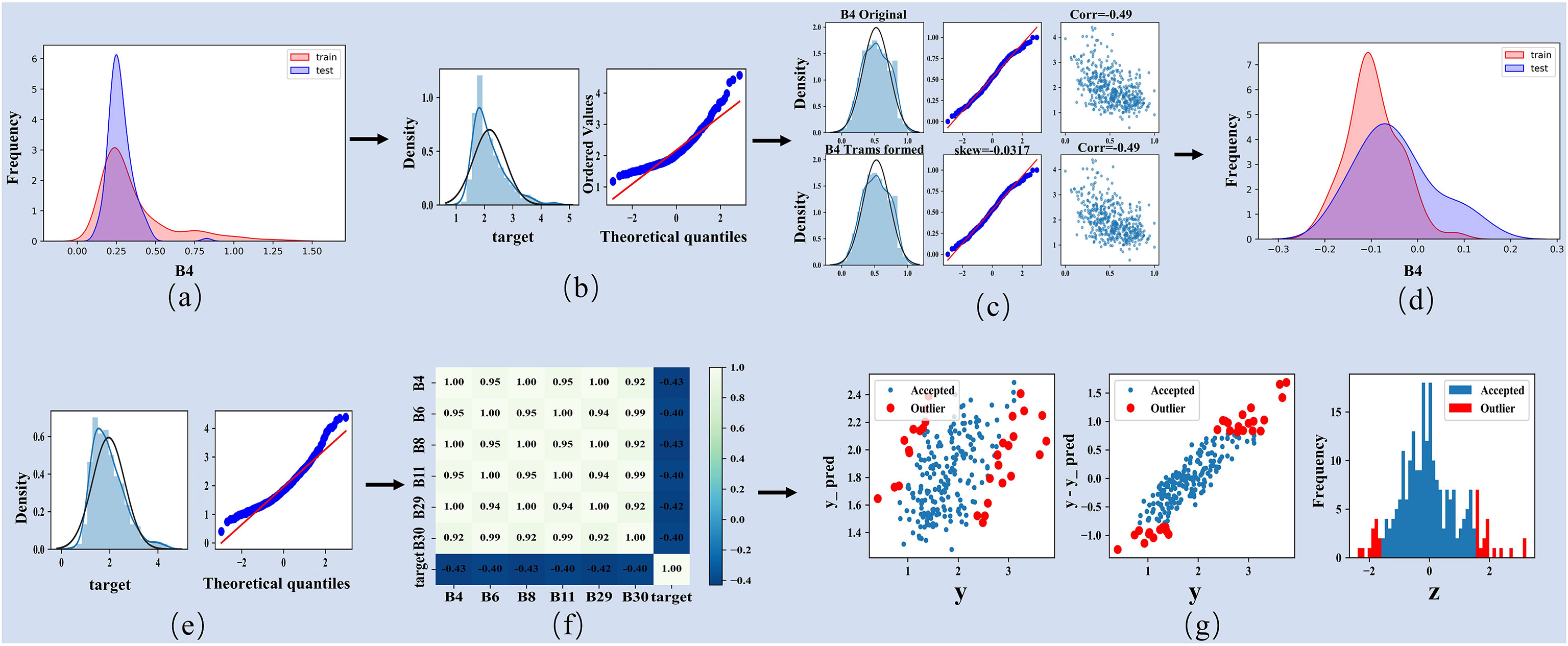
Figure 4 Processing process of four kinds of high-dimensional image datasets. (A, B) Normal distribution map and kernel density map representing unprocessed feature bands. (C) Indicates standardization and logarithmic transformation of feature bands that do not conform to the normal distribution. (D, E) Indicates the normal distribution map and kernel density map of the processed feature bands. (F) Represents a graph of correlation coefficients between bands and between bands and target values (LAI). (G) represents the removal of outliers.
(2) Correlation analysis was performed on the transformed high-dimensional dataset and the field-based measurement LAI values using the mcorr package in Python, and removed the combined features with low correlation (R<0.5) in the high-dimensional dataset (Figure 4F).
(3) Model iterative training was performed until achieving high prediction accuracy (R2 >0.85) and no performance improvement was achieved using the remaining combined features. In the iterative training procedure, redundant features with a high correlation were further removed according to the model training accuracy. (4) According to the difference in LAI values between remote sensing estimation and field-based measurement, the abnormal field-measured sample points are automatically removed to improve the estimation accuracy of the model (Figure 4G). The final measured sample points were selected and used to estimate the LAI of mangrove communities (Table 4). The calculation formula is shown in Supplementary Table 2.
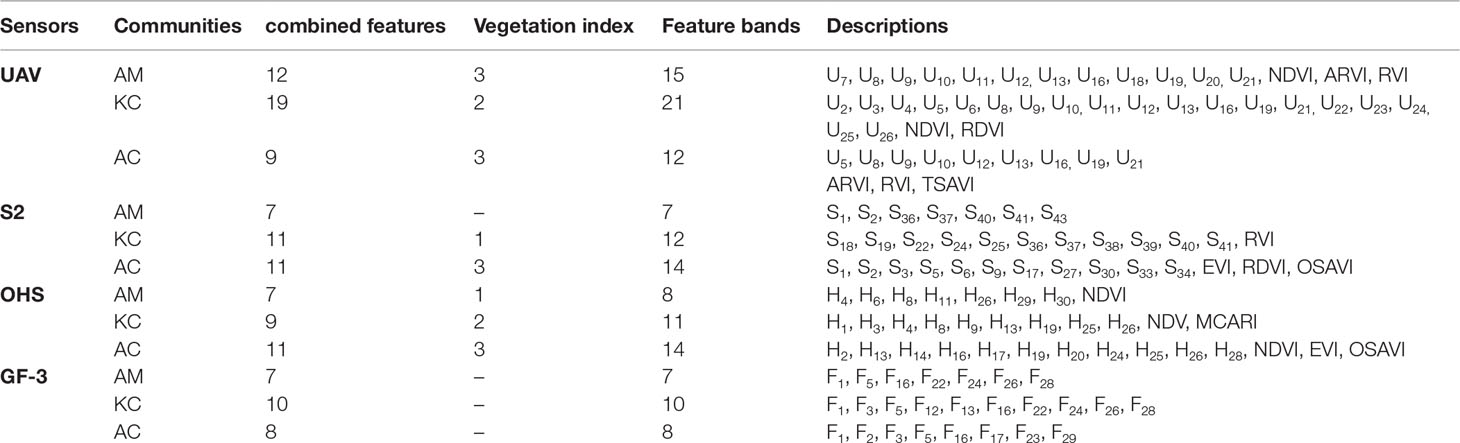
Table 4 Preferred feature variables for mangrove LAI estimation from UAV, S2, OHS, and GF-3 SAR images.
3.2 Ensemble Learning Regression (ELR) Model
Stacking is a technique that integrates multiple compatible learning algorithms or models to perform a single task and obtains better estimation results by integrating the advantages of multiple base models. This paper stacked four base models (BPNN, Elastic Net, Gradient Boosting, and Random Forest algorithms) for an ELR model to estimate LAI with feature variables. The specific process is as follows:
(1) The datasets combining feature variables with the LAI of different mangrove communities were randomly divided into 70% for training and 30% for testing, and the training sets were equally divided into train1, train2, train3, train4, and train5.(2) One dataset from train1 to train5 was selected as the validation set for different base models in turn, and the remaining 4 datasets are the training set. Each training model was performed with 5-fold cross-validation, and achieved five copies of prediction data, which were stacked and divided into training (A1–A4) and prediction (B1–B4) data.(3) An ELR model was built and trained using the A1–A4 dataset, and the final prediction results were obtained using the B1–B4 dataset. The ELR model structure is shown in Supplementary Figure 1.
3.3 Deep Learning Regression (DLR) Models
3.3.1 DNN Algorithm
The DNN (Hinton and Salakhutdinov, 2006) network consists of several inputs and outputs with multiple implicit layers (Hidden Layer) of perceptrons (as shown in Supplementary Figure 2), and the multilayer perceptron solves the defects of the previous inability to simulate or logic and enhances the model expression capability.
3.3.2 Transformer Algorithm
A Transformer (Vaswani et al., 2017) network includes multiple identical encoders and decoders stacked together to form a stack encoder and decoder with the same number of units. The encoder has a layer of multi-head attention and a layer of a feedforward neural network. The decoder has an additional multi-head attention mask. The network structure is shown in Supplementary Figure 3.
3.4 Model Parameters Optimization
In order to achieve high accuracy estimation of LAI for different mangrove communities, this paper optimized the parameters for building mangrove LAI estimation models based on ELR and DLR algorithms (Transformer and DNN). The specific optimization parameters are shown in Supplementary Table 3.
The maximum number of iterations, the depth of the decision tree, the minimum number of samples required for segmentation, and the learning rate are set by n_estimators, max_depth, min_samples_split, and learning_rate for optical and SAR image data respectively to prevent overfitting of the model and to tune the parameters to improve the estimation accuracy of the ELR model for different mangrove communities LAI under optical and SAR image data.
The model optimizer was set to Adam (Diederik and Jimmy, 2015), and the input layer was set to X (X: number of mangrove communities variables under different images). DNN model: the initial learning rate was set to 0.0001, the iterative number (epochs) was set to 1,500; the loss function was set to mean_squared_error. Transformer model: the encoder and decoder were set to 6 layers, and the initial learning rate was set to 0.0001. The iterative number was set to 8. The loss function was set to mean_squared_error.
3.5 Mangrove LAI Estimation Using Training Sample Enhancement
In this paper, we propose a training sample expansion method based on an ELR model and UAV multispectral images, which is then used in the DLR algorithm for high-accuracy estimation of LAI of mangrove communities. We tested five training sample expansion schemes with an expansion ratio of 10 to 50%. The ability of the Transformer and DNN models to improve the LAI estimation accuracy of mangrove communities under different expansion ratios was explored. To ensure the reliability of the experimental results, this paper only increased the number of training samples for the DLR model, and the verification samples of the LAI estimation model under each expansion scheme use the ground-measured LAI data. The specific process is as follows:
① The expanded sample points of three mangrove communities were selected from the UAV images using the random sampling method. The type of mangrove community one by one was determined by field measurements and visual interpretation of UAV images (0.07 m). The spectral reflectance of each sample point was extracted and input into the ELR model trained with high precision to estimate its corresponding LAI value, as the real LAI value of the extended training sample in the DLR model under 4 kinds of images (UAV, S2, OHS, and GF-3). The specific calculation formula is as in formula (5). The proportion of the extended training sample data of various mangrove communities in the measured data ranges from 0 to 50%.
Where LAIUAV represents the LAI values of mangroves at different extended sample points estimated based on the high-precision training ELR model and UAV multispectral images, x is the number of mangrove communities LAI measured data points, i is the proportion of extended sample data to the measured data (0–50%).
②; Extract the spectral reflectance or backscattering coefficient values of the expanded sample points from the optical (UAV, S2, and OHS) and GF-3 SAR images, respectively, and use the LAI value estimated by formula (5) as the true value of the LAI of the extended sample points in the four types of images to generate the extended training data of the DLR model under different images. We used extended training data and measured data to build high-dimensional data sets and perform data dimensionality reduction and feature optimization. Finally, the optimal feature variables are input into the Transformer and DNN models, respectively, to estimate the LAI value of the mangrove communities. After training samples expand under different images, the calculation formula is as in formula (6).
In the formula represents the mangrove LAI value estimated by the DLR model under different expansion ratios in each image, D represents DNN and Transformer models, j represents UAV, S2, OHS, and GF-3 remote sensing images, x is the number of LAI measured data points of mangrove communities, and i Indicates the proportion of the extended sample data to the measured data (0–50%).
3.6 Accuracy Assessment
Accuracy validation is the process of evaluating the accuracy of model estimates using independent validation data. The uncertainty of field LAI measurements was caused by the spatial structure of the canopy, sampling methods, instrument errors, and measurement environment (Waske et al., 2009). In this paper, the coefficient of determination (R2) and root mean square error (RMSE) were used to verify the model prediction accuracy, and 30% of the ground-measured LAI values (single plant and sample scale) were used as independent validation data to evaluate the model estimation accuracythe calculation formulas are as in formula(7)-(8).
Where yi is the mangrove LAI value measured in the field, is the estimated value of mangrove LAI, wi is the weight, wi >0 usually set to 1, represents the mean value of mangrove LAI, and m represents the number of mangrove samples.
4 Results Analysis
4.1 Assessing the Effect of Optical and SAR Images on LAI Estimation of Mangrove Communities
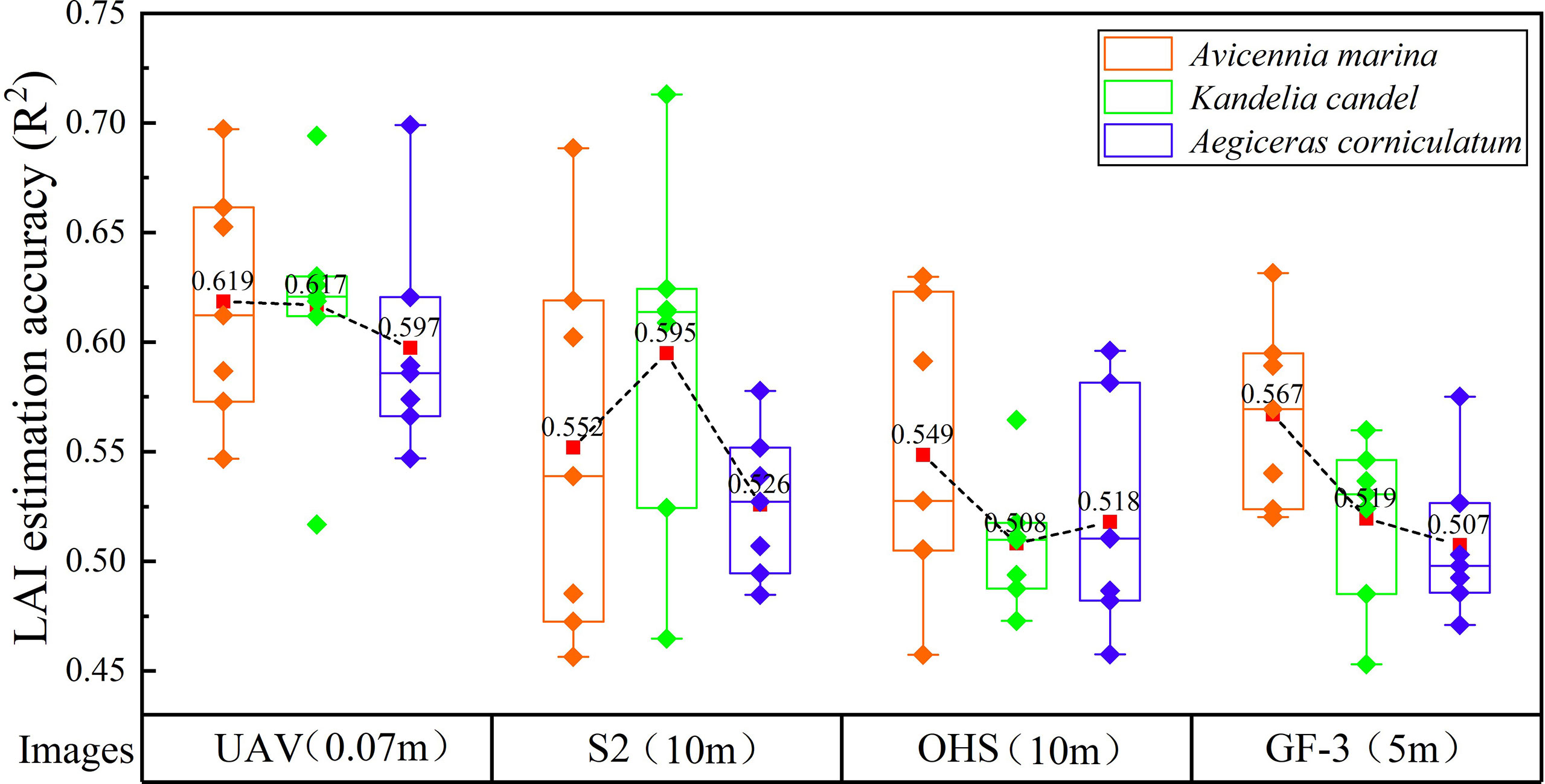
In order to explore the difference in the accuracy of LAI estimation of different mangrove communities under optical and SAR image data. In this paper, seven mangrove LAI estimation models were constructed using shallow machine learning, ELR, and DLR algorithms. The accuracy of LAI estimation for the three dominant communities in mangroves under different image data is shown in Figure 5.
Figure 5 shows that the spatial resolution, spectral reflectance, and radar backscatter coefficient have a certain effect on the estimation accuracy of mangrove LAI. The average LAI estimation accuracy of mangrove communities by different models under UAV multispectral images was the highest (R2 = 0.597–0.619), which was 0.052–0.109 higher than that by OHS hyperspectral images, respectively. Compared with GF-3 SAR images, the mean LAI estimation accuracy (R2) of different mangrove communities was improved by 0.052–0.098 from UAV images, and the LAI estimation accuracy (R2) of Kandelia candel was the most affected. The average LAI estimation accuracy of different images for K. candel was UAV> GF-3> OHS. The reasons are as follows: (1) Compared with 5 × 5 m and 10 × 10 m sample plots, the ultra-high spatial resolution (0.07 m) of UAV images and individual tree measurement method of mangrove LAI reduced the influence of bare soil, thus improving the accuracy of LAI estimation by images; (2) There were inevitably other communities in 10 m × 10 m plots, leading to errors in the spectral reflectance extraction.
The UAV image produced the highest average LAI estimation accuracy (R2) of three mangrove communities using different models, followed by the S2 and OHS images. S2 and OHS images both obtained good accuracy for LAI estimation of different mangrove communities (R2 = 0.508–0.598). There are 26 feature variables extracted by dimensionality reduction in the S2 multi-spectral image (Table 3 and Supplementary Table 2), among which 20 feature variables are calculated using the original bands B4 (Red) and B8 (NIR) of the image. The results showed that the Red Edge (650–680 nm) and NIR (785–900 nm) bands were sensitive to mangrove LAI. Additionally, 20 feature variables were extracted from OHS hyperspectral image data after dimensional-reduction. The calculation of 19 feature variables included the original band B12 (637–642 nm) and B17 (713–718 nm). Meanwhile, 15 of the 21 feature bands selected from the UAV images are calculated by the B4 (Red Edge) and B5 (NIR) bands, indicating that the Red Edge (707–727 nm) and NIR (800–880 nm) are more sensitive to mangrove LAI. The reflectance range of different spectral bands also has a certain influence on the LAI estimation of mangrove communities. The optimal spectral reflectance range of optical images for LAI estimation of mangroves was 650–900 nm.
In Figure 5, the average LAI estimation accuracy (R2) of A. marina under different images is in the following order: GF-3 >S2 >OHS. Comparing S2 multispectral and OHS hyperspectral images, the mean estimation accuracy (R2 = 0.567) of GF-3 for LAI for A. marina was improved by 0.015 and 0.018, respectively. The reasons for this are as follows: 1) optical images cannot penetrate the vegetation canopy, making it difficult to obtain vegetation structure information; and 2) the problem of spectral saturation of surface reflectance and vegetation index under high coverage, while SAR images can penetrate the canopy to obtain vegetation structure information.
4.2 Evaluating LAI Estimation Accuracy Between ELR and Single Base Models
To make LAI estimates more comparable, this study selected four machine learning algorithms (BPNN, Elastic Net, Gradient Boosting, and Random Forest) with different regression criteria to construct an ELR model and explored the differences in the accuracy and stability of LAI estimates for mangrove communities between ELR and single-base models. This paper estimated the LAI of three mangrove communities using ELR and single base models, respectively. The specific estimation accuracy is shown in Supplementary Table 4.
In Figure 6, the ELR model has higher accuracy in estimating LAI for different mangrove communities under optical and SAR image data, and the R2 was mainly concentrated between 0.5266 and 0.713. The estimation accuracy (R2) of the ELR model for the LAI of A. marina was improved by 0.0197–0.1497 compared to the single base model; the best estimation accuracy of LAI for K. candel (R2 = 0.713) was improved by 0.0126–0.0887 over the single base model; the estimation accuracy (R2) of LAI for Aegiceras corniculatum (AC) was improved by 0.0117–0.0785, and the RMSE was reduced by 0.0253–0.0262. The estimates of LAI of different mangrove communities from the ELR model were mainly concentrated within one standard deviation of the measured values than the single-base model, indicating that the ELR model has better generalizability and stability for LAI estimation of different mangrove communities under optical and SAR images.
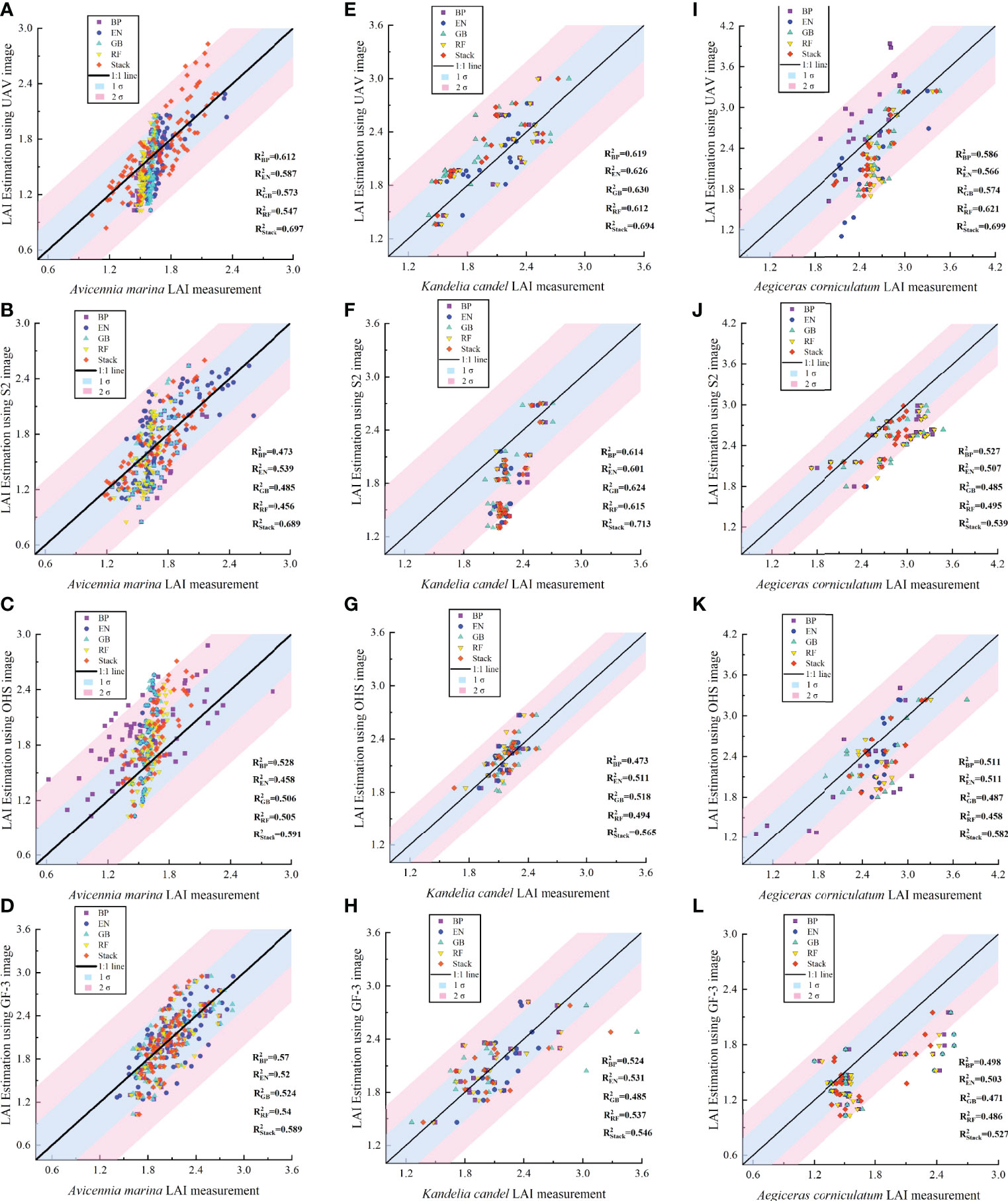
Figure 6 Statistical analysis of the LAI estimation accuracy of different mangrove communities using the ELR model. The shaded area represents the standard deviation (σ) between the estimated and measured LAI value of mangrove communities. (A–L) Respectively represent the LAI estimation accuracy (R2) of 'Avicennia marina', 'Kandelia candel' and 'Aegiceras corniculatum' using 5 algorithms under 4 image data.
The estimation of LAI for mangrove communities also differed between different base models under optical and SAR image data. The accuracy of the BP model for LAI estimation of A. marina (R2 = 0.5276 to 0.6123) improved by 0.0256 to 0.0656 and RMSE decreased by 0.0074 to 0.0381 compared with the other three algorithms. The accuracy of the GB model for LAI estimation of K. candel (R2 = 0.5175–0.63) improved by 0.0039–0.0182 in R2 and was reduced by 0.0049–0.0234 in RMSE compared to the other three algorithms; the LAI estimation accuracy of the RF model for A. corniculatum (R2 = 0.6206, RMSE = 0.3042) improved by 0.0348–0.0543 and RMSE decreased by 0.0227–0.0873 compared with the other three algorithms. The EN model showed better accuracy in LAI estimation of A. corniculatum under OHS and GF-3 image data (R2 = 0.5108, 0.5031).
4.3 Comparative Analysis of LAI Estimation Ability of ELR and DLR Algorithms
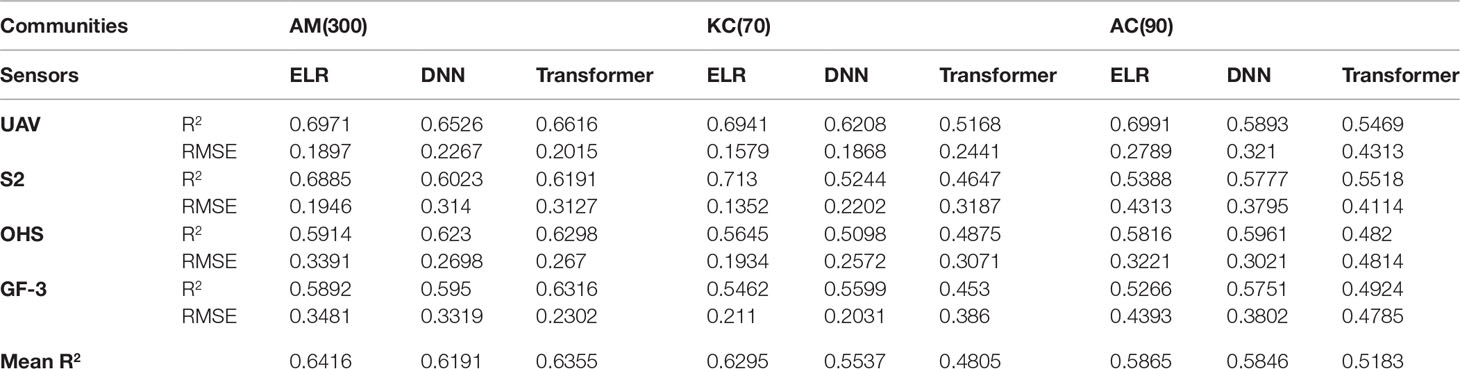
This study explores the ability of ELR and DLR models to estimate the LAI of mangrove communities. This study quantitatively analyzes the estimation accuracy of the ELR and DLR models for the LAI of different communities. It can be seen from Table 5 that the average estimation accuracy (R2) of the ELR model for the LAI of different mangrove communities under optical and SAR images was improved by 0.001–0.149 compared with the DLR model (Transformer and DNN).
From Table 5, it can be seen that the average estimation accuracy (R2) of the ELR model for the LAI of mangrove communities under different images improved by 0.0019–0.149 compared with the Transformer and DNN models, and the estimation accuracy of the ELR model for the LAI of different mangrove communities was relatively stable. DLR algorithms, especially the Transformer model, in optical and SAR images gradually decreases with the average estimation accuracy of the estimation models for the LAI from A. marina to K. candel. The average estimation accuracy of the LAI for A. marina (R2 = 0.6355) was only 0.006 lower than the ELR model (R2 = 0.6416), and the average estimation accuracy (R2) of the Transformer model for the LAI of K. candel was 0.149 lower than that of the ELR model. The reason for the analysis may be that A. marina has 300 measured LAI data points and K. candel has only 70, which reduces the training accuracy of the DLR model and leads to lower accuracy of LAI estimation.
Figure 7 showed that under UAV and S2 images, the accuracy of the ELR model for LAI estimation of A. marin (R2 = 0.6971, RMSE = 0.1897, and P<0.005) increased by 0.0355–0.0445 compared with the DNN and Transformer models; under OHS and GF-3 images, the accuracy of the LAI estimation of the Transformer model for A. marin (R2 = 0.6316, RMSE = 0.2302, and P<0.005) increased by 0.0424 and 0.0366, and RMSE decreased by 0.1179 and 0.1017 compared with the ELR and DNN models.
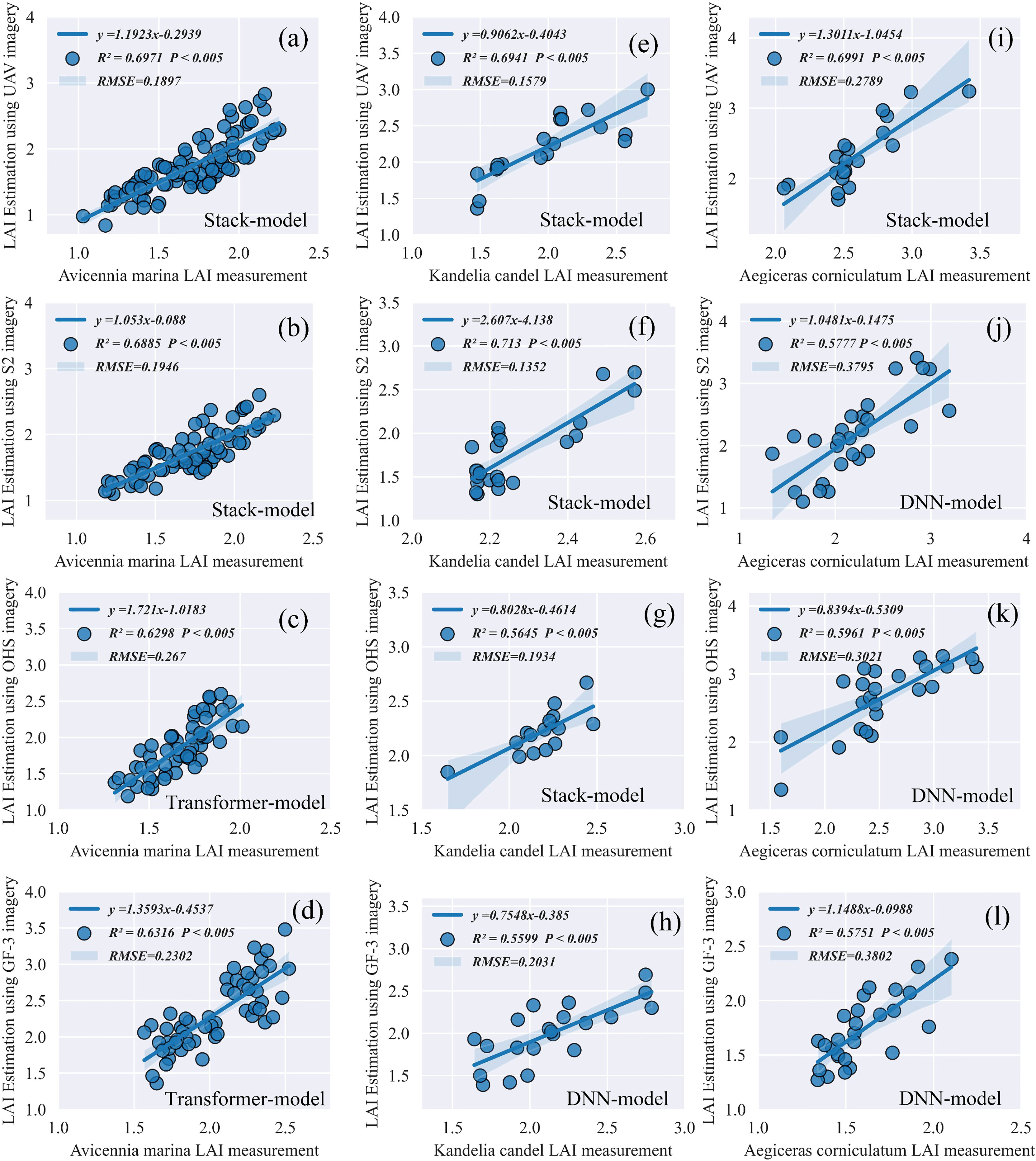
Figure 7 Comparative analysis of estimation accuracy of the LAI for mangrove communities between the ELR and DLR models. The P-value represents the significant difference between the estimated and measured LAI values of mangrove communities. (A–L) Represent the LAI estimation accuracy (R2 and RMSE) of the optimal model for 'Avicennia marina', 'Kandelia candel' and 'Aegiceras corniculatum' under the 4 image data, respectively.
At 95% confidence interval, the LAI estimation accuracy (R2) of the ELR model for K. candel was better than that of the Transformer model, which was 0.1886–0.2483 higher than that of the DNN and Transformer models, and RMSE decreased by 0.085–0.1835. Under the GF-3 radar image, the LAI estimation accuracy of the DNN model for K. candel (R2 = 0.5599, RMSE = 0.2031) was 0.014 and 0.107 higher than that of the ELR and Transformer models, and RMSE was reduced by 0.008 and 0.1829, respectively.
The LAI estimation accuracy of the DNN model for A. corniculatum (R2 = 0.5961, RMSE = 0.3021) was 0.015–0.1141 higher than that of the ELR and Transformer models using the S2, OHS, and GF-3 images, while the ELR model with the UAV image produced better accuracy for the LAI estimation of A. corniculatum (R2 = 0.6991, RMSE = 0.2789).
4.4 The Effect of Training Sample Enhancement on LAI Estimation Using DLR Models
In this study, a method of combining the ELR and DLR models of UAV images to train sample expansion was proposed. Five sample expansion schemes were carried out, with the proportion of extended training samples accounting for 10–50% of ground measured data, to verify the ability of the Transformer and DNN models to improve the accuracy of mangrove community LAI estimation under different schemes.
4.4.1 The Effect of Training Sample Expansion for Estimating the LAI of Mangrove Communities Using the DNN Model
In this paper, mangrove communities with the lowest LAI estimation accuracy were selected from under 4 images, and training sample expansion was carried out for the DNN model according to 5 sample expansion schemes. The improvement of the LAI estimation accuracy of different mangrove communities by training sample expansion is shown in Table 6.
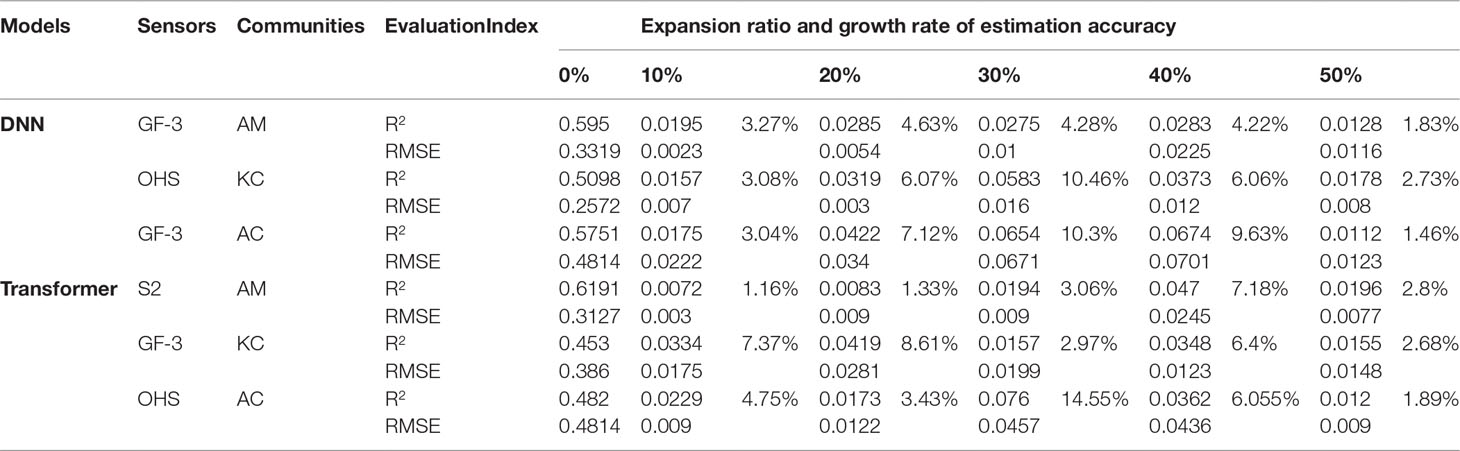
Table 6 The LAI estimation accuracy of mangrove communities for the DNN and Transformer models with training sample extension.
Figure 8 shows the changes in LAI estimation accuracy of different mangrove communities by the DNN model under five expansion schemes. The improvement of the LAI estimation accuracy of A. corniculatum by training sample expansion is the largest, as shown in Figures 8A–F. Under GF-3 SAR images, as the number of A. corniculatum samples increased from 90 to 135, the LAI estimation accuracy (R2) of the DNN model for A. corniculatum increased from 0.5751 to 0.7788, an increase of 0.2037. The RMSE decreased from 0.4814 to 0.2757. When the number of extended training samples accounted for 40% of the measured data, the LAI estimation accuracy (R2) of A. corniculatum by the DNN model improved the most (0.0674), with an improvement of 9.63%. However, when the number of training samples accounted for 30% of actual data, the DNN model had the greatest influence on the LAI estimation accuracy (R2) of A. corniculatum (10.3%).
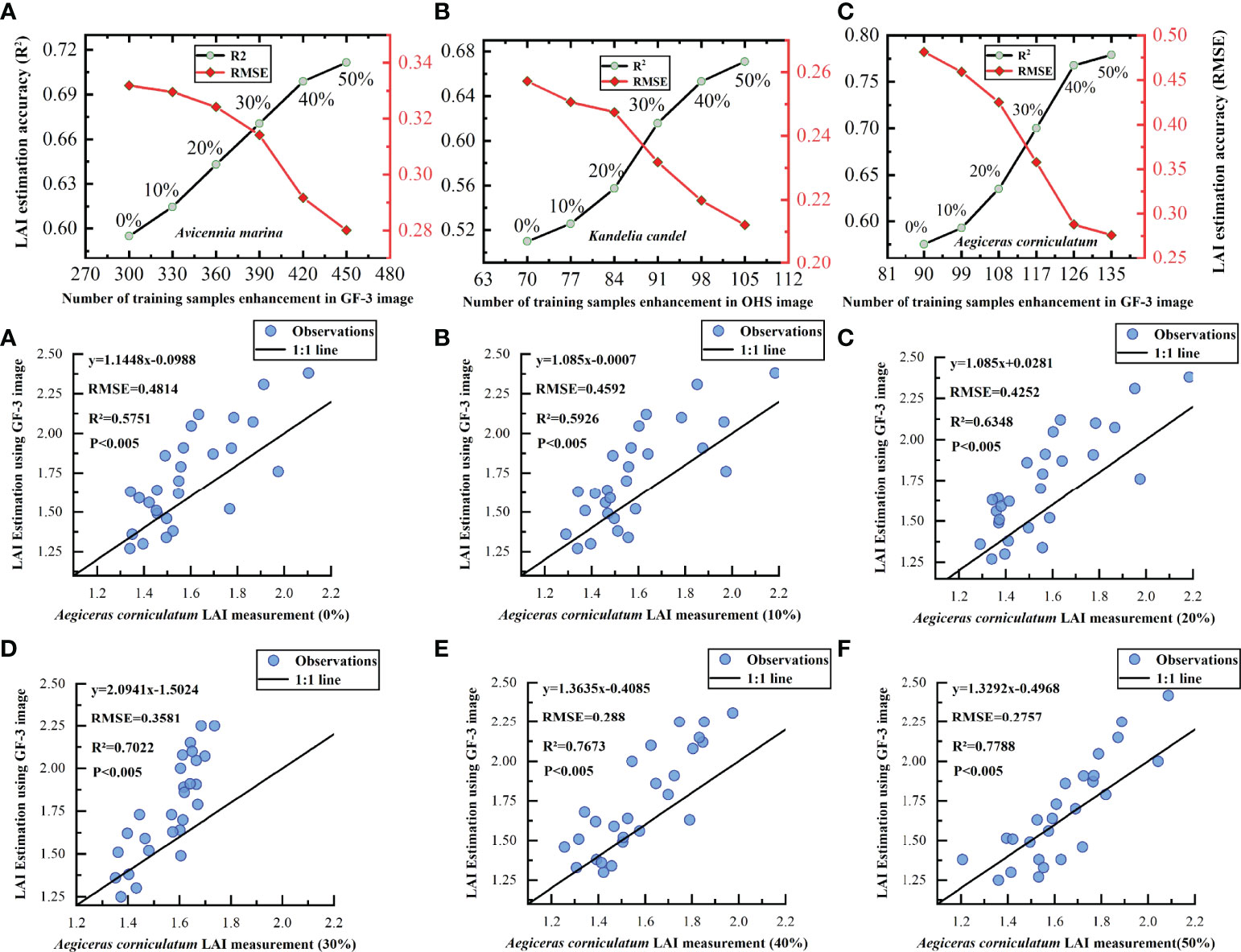
Figure 8 Estimating mangrove LAI based on the DNN model under different sample expansion ratios. (A–C) Represents the variation trend of the estimation accuracy of the DNN model for the LAI of 'Avicennia marina', 'Kandelia candel' and 'Aegiceras corniculatum' under OHS and GF-3 image data with the enhancement of training sample data. (A–F) Indicates the variation trend of the estimation accuracy of the DNN model for the LAI of 'Aegiceras corniculatum' under the GF-3 image data, with the increase of the training sample expansion ratio (0%-50%).
The expansion of training samples had relatively little influence on the accuracy of the LAI estimation of A. marina. Under GF-3 images, as the number of samples of A. marina increased from 300 to 450, the LAI estimation accuracy (R2) of A. marina by the DNN model increased from 0.595 to 0.7116, increasing by 0.1166, and RMSE decreased from 0.3319 to 0.2801. When the number of extended training samples accounted for 20% of the measured data, the LAI estimation accuracy of A. marina was improved the most by the extension of training samples (4.63%). The LAI estimation accuracy (R2) of A. marina was improved by 0.0285, and RMSE decreased by 0.005.
Under OHS hyperspectral images, as the number of K. candel samples expanded from 70 to 105, the LAI estimation accuracy (R2) of the DNN model for K. candel increased from 0.5098 to 0.6708, increasing by 0.161. When the number of extended training samples accounted for 30% of the measured data, the LAI estimation accuracy of K. candel of the DNN model improved the most (10.46%), the LAI estimation accuracy (R2) of K. candel of the DNN model increased by 0.0583, and RMSE decreased by 0.016.
4.4.2 The Effect of Training Sample Expansion for Estimating the LAI of Mangrove Communities Using the Transformer Model
Mangrove communities with the lowest LAI estimation accuracy were selected under different image data and the Transformer model was trained for sample expansion according to five sample expansion schemes. The improvement of the LAI estimation accuracy of different mangrove communities is shown in Table 6.
Figure 9 shows the changes in the LAI estimation accuracy of the Transformer model for different mangrove communities under different training sample expansion ratios (10–50%). The LAI estimation accuracy of A. corniculatum improved the most by training sample expansion, as shown in Figures 9A–F. With the increase in the number of extended training samples, the accuracy of the LAI estimation of different mangrove communities by the Transformer model increased by 0.1015–0.1644.
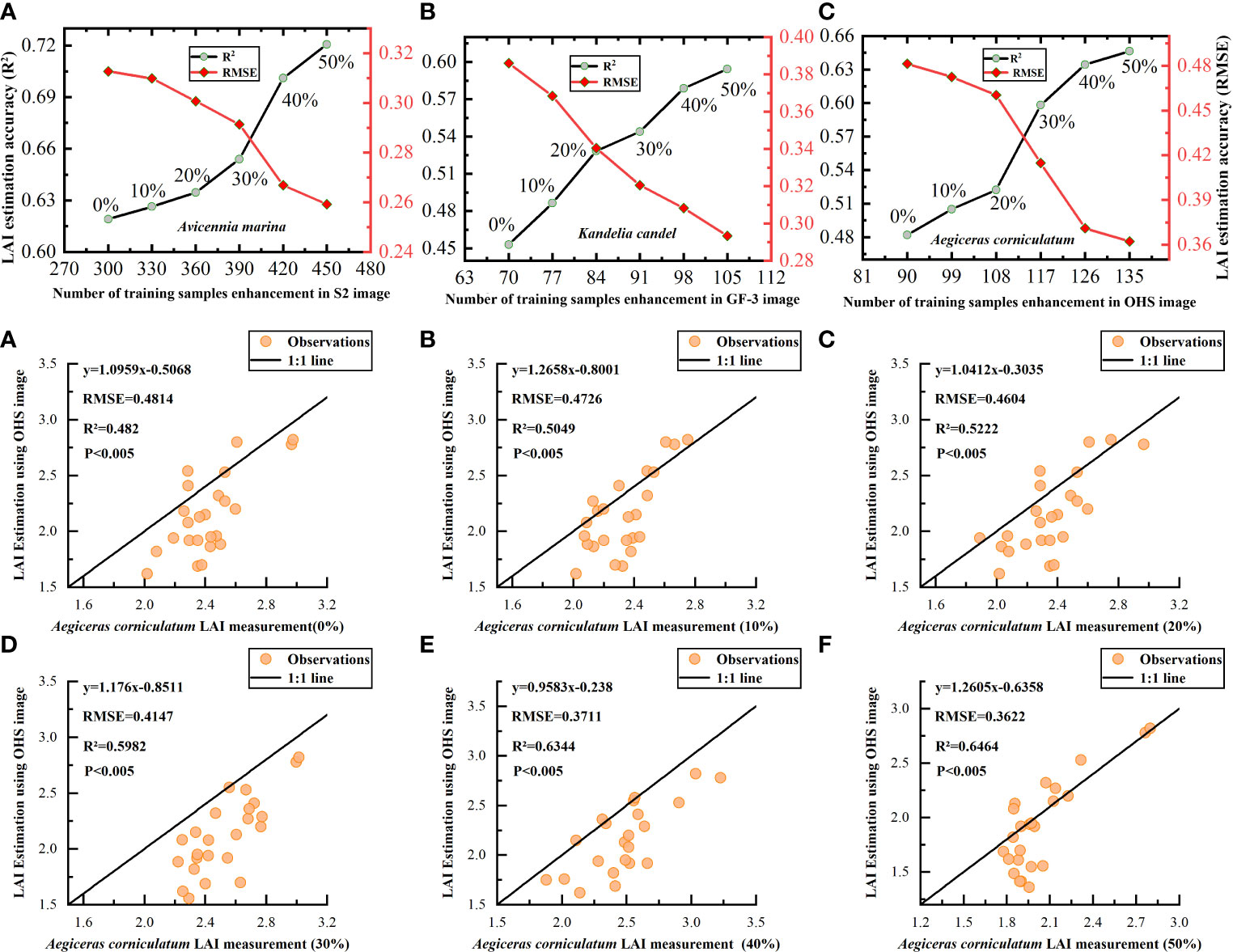
Figure 9 Estimating mangrove LAI using the Transformer model under different sample expansion ratios. (A–C) Represents the variation trend of the estimation accuracy of the Transformer model for the LAI of 'Avicennia marina', 'Kandelia candel' and 'Aegiceras corniculatum' under S2,GF-3 and OHS image data with the enhancement of training sample data. (A–F) Indicates the variation trend of the estimation accuracy of the Transformer model for the LAI of 'Aegiceras corniculatum' under the OHS image data, with the increase of the training sample expansion ratio (0%-50%).
Compared with the DNN model, the influence of training sample expansion on the Transformer model was relatively small, but the LAI estimation accuracy (R2) of the Transformer model for different communities was also improved by 0.1015–0.1644. The optimal training expansion ratio of the Transformer model for the LAI estimation of three mangrove communities was 40% (AM), 20% (KC), and 30% (AC). Under the optimal expansion ratio, the amplitude of the LAI estimation accuracy of different communities increased by 7.18–15.55%, and R2 increased by 0.0419–0.076. The optimal expansion ratio of training samples for estimating the LAI of A. marina, K. candel, and A. corniculatum using the DNN model was 20, 30, and 40%, respectively. The LAI estimation accuracy (R2) of three communities increased by 0.0285–0.0674. With the sample expansion ratio reaching 50% of three mangrove communities, the training time of the DNN model for the LAI of A. marina, K. candel, and A. corniculatum increased by 6.28, 2.059, and 2.112 s, respectively. The training time of the Transformer model for A. marina, K. candel, and A. corniculatum increased by 17.361, 3.945, and 5.431 s, respectively.
As shown in Figures 8, 9, with the increase in the number of training samples of the DLR model, the LAI estimation accuracy (R2) of different mangrove communities by the DNN and Transformer models showed an upward trend, while RMSE gradually decreased. However, when the number of extended training samples reached 40% of the measured data, the improvement range of the LAI estimation accuracy of different mangrove communities began to slow down significantly (Table 6). By training sample expansion, the LAI estimation accuracy (R2) of A. corniculatum was improved by 0.2631 and 0.1415 under GF-3 SAR and OHS images, respectively. Under GF-3 SAR and S2 images, the LAI estimation accuracy (R2) of A. marina increased by 0.1166 and 0.1015, respectively. The influence of training sample expansion on the LAI estimation accuracy (R2) of different communities was A. corniculatum > K. candel > A. marina.
5 Discussion
This study found that after data dimension reduction, the number of combined VEGETATION indices used for LAI estimation of different mangrove communities was more than that of vegetation indices (Table 3), and high estimation accuracy was obtained (R2 = 0.6971~0.713, RMSE=0.1352~0.1897). This was because the spectral similarity of mangrove communities and the vegetation index only uses limited spectral bands, which cannot make full use of effective information of spectral bands. The combined features were used to arrange and combine all band information of multispectral image, which can estimate the characteristics of different communities more accurately. It was the same conclusion as that of Zhu et al. (2017); Feng et al. (2019) and Curran et al. (1992). In this study, under UAV images, the average LAI estimation accuracy of different communities (R2 = 0.5865~0.6416) was superior to other images; This indicated that UAV images had better applicability for LAI estimation of mangroves. but it was different from the conclusion of Guo et al. (2021). They found that the LAI model constructed by using the combined features under UAV images was not suitable for LAI estimation of mangrove communities. This may be because bare soil in 10m×10m plots under high-resolution UAV images has a more prominent impact on LAI estimation of different mangroves (Tian et al., 2017). However, in this study, single mangrove communities were measured one by one under UAV images, so that UAV images completely corresponded to each ground measured point, reducing the impact of bare soil on vegetation index. This study found that the reflectance range of different spectral bands also had certain influence on LAI estimation of mangrove communities, and the optimal spectral reflectance range for LAI estimation of mangroves by optical images was 650nm~900nm. This was consistent with the results of Zhen et al. (2021), who calculated the combinations of five types of vegetation indices in the spectral range of 400~1000 nm to estimate the mangrove SPAD and obtained good estimation results (R2 = 0.792, RMSE=3.578).
Compared with the single base model, the estimation accuracy (R2) of the ELR model for LAI of different mangrove communities was improved by 0.009~0.232 under optical and SAR images; This study found that ensemble learning algorithm can integrate the advantages of different algorithms, make up for the shortcomings of single algorithm, produce more robust estimation results, and can provide better generalization ability in regression prediction, This was consistent with the findings of (Dietterich, 2000). Ghosh et al. (2021) used multi-temporal image stack data set to estimate aboveground biomass of mangrove forests (RMSE 74.493t/ha), which was better than single data set (RMSE=151.149t/ha). The accuracy of AGB inversion using stack algorithm was further improved (RMSE was 72.864t/ha). After data dimension reduction, the LAI estimation accuracy (R2) of DNN and Transformer models for mangrove communities could reach up to 0.6619, and the LAI estimation accuracy of Avicennia marina could reach above 0.61. It was found in this study that data dimension reduction was suitable for mangrove LAI estimation of DLR model, and data dimension reduction can eliminate redundant data caused by spectral information combination and improve the calculation efficiency and accuracy of estimation model. This was the same as the findings of Pyo et al. (2020). They combined convolutional autoencoders and CNN reflectance spectroscopy for data dimensionality reduction to estimate As, Cu, and Pb and obtained good estimation results (R2 = 0.86, 0.72 and 0.82).
This study found that insufficient training data would lead to overfitting of the model and reduced the accuracy of model estimation. The average LAI estimation accuracy of the Transformer model for Avicennia marina (R2 = 0.6355) was only 0.006 lower than that of the ELR model (R2 = 0.6416). However, the mean LAI estimation accuracy (R2) of Transformer model for Kandelia candel was 0.149 lower than that of ELR model. It was also found that training sample expansion can reduce the measured data required for DLR model training and effectively improve the LAI estimation accuracy of the model. In this paper, the accuracy (R2) of LAI estimation of mangrove communities by DNN and Transformer models increased by 0.1166~0.2037 and 0.1015~0.1644, respectively, after the extension of training samples. This obtained the same conclusion as Huang et al. (2020). At the same time, this study found that with the increase of the expansion proportion of training samples, the LAI estimation accuracy (R2) of different mangrove communities by DNN and Transformer models was rapidly improved, When the expansion data amount reached 40% of the measured data, the growth trend of estimation accuracy would slow down. Therefore, we set the maximum expansion ratio of training samples estimated by LAI of mangroves as 40%, which was the identical to the findings of Chen et al. (2017).
6 Conclusion
This study proposed a novel approach for estimating mangrove LAI by combining training sample expansion with the DLR algorithm to resolve the problem of insufficient field measurement and quantitatively evaluated the ability of the ELR and DLR algorithms to estimate the LAI of different mangrove communities using multispectral, hyperspectral, and SAR images. The UAV images produced the highest LAI estimation accuracy of different mangrove communities (R2 = 0.597–0.619). GF-3 SAR images have high estimation accuracy (R2 = 0.567) for the LAI of A. marina with high coverage. The ELR algorithm outperformed the DLR algorithm in mangrove LAI retrieval, which has better stability and higher estimation accuracy (R2 = 0.5266–0.713), and was the optimal model for mapping mangrove LAI. The Transformer model produced a better LAI estimation (R2 = 0.6355) for A. marina, which was 0.007–0.037 higher than the DNN model. The DNN model achieved a better LAI estimation for K. candel (R2 = 0.5577). Training sample expansion improved the performance of the DLR models for LAI retrieval. When the expansion ratio of training samples increased from 10 to 50%, the estimation accuracy (R2) of the DNN and Transformer models for mangrove LAI increased by 0.1166–0.2037 and 0.1037–0.1644, respectively. The effect of training sample expansion on the LAI estimation of different communities was in the order of A. corniculatum > K. candel > A. marina. With the same LAI estimation accuracy, the sample enhancement method presented in this paper could reduce the number of field measurements by 20–40%.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
BF planned the study, collected, and analyzed the data, and wrote the manuscript. JS wrote the manuscript, and research model, and analyzed the data. YW, HH, and LL directed work and supervision. WY, LH, DF, and EG collected, and analyzed the data. BF and JS did the main manuscript revision and editing. All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported by the National Natural Science Foundation of China (Grant number 41801071), the Natural Science Foundation of Guangxi Province (CN) (Grant number 2018GXNSFBA281015), the ‘Ba Gui Scholars’ program of the provincial government of Guangxi, and the Guangxi Science & Technology Program (Grant number GuikeAD20159037), the Innovation Project of Guangxi Graduate Education (Grant number YCSW2022328), and the Youth Innovation Promotion Association of Chinese Academy of Sciences (2021227).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We appreciate the anonymous reviewers for their comments and suggestions, which helped to improve the quality of this manuscript. We appreciate Zhuhai Orbita Aerospace Science & Technology Co. Ltd. for providing the Zhuhai No. 1 Orbita Hyper Spectral (OHS) hyperspectral image of mangrove forests in the Qinzhou City, Beibu Gulf, China.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2022.944454/full#supplementary-material
References
Behrouz-Rad B. (2014). Population Dynamic and Species Diversity of Wintering Waterbirds in Mangroves Wetland (Persian Gulf) in 1983 and 2013. Int. J. Mar. Sci. 4(63), 1−7. doi: 10.5376/ijms.2014.04.63
Bhardwaj A., Sam L., Akanksha, Martín-Torres F. J., Kumar R., , (2016). UAVs as Remote Sensing Platform in Glaciology: Present Applications and Future Prospects. Remote Sens. Environ. 175, 196–204. doi: 10.1016/j.rse.2015.12.029
Bocca F. F., Rodrigues L. H. A. (2016). The Effect of Tuning, Feature Engineering, and Feature Selection in Data Mining Applied to Rainfed Sugarcane Yield Modelling. Comput. Electron. Agric. 128, 67–76. doi: 10.1016/j.compag.2016.08.015
Borges A. V. (2003). Atmospheric CO2flux From Mangrove Surrounding Waters. Geophysical Res. Lett. 30(11). doi: 10.1029/2003gl017143
Chang J., Shoshany M. (2016). “Mediterranean Shrublands Biomass Estimation Using Sentinel-1 and Sentinel-2,” in 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). 300−5303.
Chen Z., Jia K., Xiao C., Wei D., Zhao X., Lan J., et al. (2020). Leaf Area Index Estimation Algorithm for GF-5 Hyperspectral Data Based on Different Feature Selection and Machine Learning Methods. Remote Sens. 12, 2110. doi: 10.3390/rs12132110
Chen H., Xiong F., Wu D., Zheng L., Peng A., Hong X., et al. (2017). “Assessing Impacts of Data Volume and Data Set Balance in Using Deep Learning Approach to Human Activity Recognition,” in 2017 IEEE International Conference on Bioinformatics and Biomedicine (BIBM). 1160−1165
Chlingaryan A., Sukkarieh S., Whelan B. (2018). Machine Learning Approaches for Crop Yield Prediction and Nitrogen Status Estimation in Precision Agriculture: A Review. Comput. Electron. Agric. 151, 61–69. doi: 10.1016/j.compag.2018.05.012
Christensen S. W. (2003). Ensemble Construction via Designed Output Distortion, in: Multiple Classifier Systems (Berlin, Heidelberg: Springer Berlin Heidelberg), 286–295.
Curran P. J., Dungan J. L., Gholz H. L. (1992). Seasonal LAI in Slash Pine Estimated With Landsat TM. Remote Sens. Environ. 39, 3–13. doi: 10.1016/0034-4257(92)90136-8
Diederik Kingma, Jimmy Ba, (2015). Adam: A Method for Stochastic Optimization. Published as a conference paper at ICLR.
Dietterich T. G. (2000). Ensemble Methods in Machine Learning, in: Multiple Classifier Systems (Berlin, Heidelberg: Springer Berlin Heidelberg), 1–15.
Dong T., Liu J., Shang J., Qian B., Ma B., Kovacs J. M., et al. (2019). Assessment of Red-Edge Vegetation Indices for Crop Leaf Area Index Estimation. Remote Sens. Environ. 222, 133–143. doi: 10.1016/j.rse.2018.12.032
Feng H., Yang F., Yang G., Pei H. (2019). “Hyperspectral Estimation of Leaf Area Index of Winter Wheat Based on Akaike’s Information Criterion,” in Computer and Computing Technologies in Agriculture X (Cham: Springer International Publishing), 528–537.
Ghosh S. M., Behera M. D., Jagadish B., Das A. K., Mishra D. R. (2021). A Novel Approach for Estimation of Aboveground Biomass of a Carbon-Rich Mangrove Site in India. J. Environ. Manage. 292, 112816. doi: 10.1016/j.jenvman.2021.112816
Giri C., Pengra B., Zhu Z., Singh A., Tieszen L. L. (2007). Monitoring Mangrove Forest Dynamics of the Sundarbans in Bangladesh and India Using Multi-Temporal Satellite Data From 1973 to 2000. Estuarine Coast. Shelf Sci. 73, 91–100. doi: 10.1016/j.ecss.2006.12.019
Green E. P., Mumby P. J., Edwards A. J., Clark C. D., Ellis A. C. (1997). Estimating Leaf Area Index of Mangroves From Satellite Data. Aquat. Bot. 58, 11–19. doi: 10.1016/s0304-3770(97)00013-2
Guo X., Wang M., Jia M., Wang W. (2021). Estimating Mangrove Leaf Area Index Based on Red-Edge Vegetation Indices: A Comparison Among UAV, WorldView-2 and Sentinel-2 Imagery. Int. J. Appl. Earth Observation Geoinformation 103, 102493. doi: 10.1016/j.jag.2021.102493
Hardin P. J., Jensen R. R. (2011). Small-Scale Unmanned Aerial Vehicles in Environmental Remote Sensing: Challenges and Opportunities. GIScience Remote Sens. 48, 99–111. doi: 10.2747/1548-1603.48.1.99
Heumann B. W. (2011). Satellite Remote Sensing of Mangrove Forests: Recent Advances and Future Opportunities. Prog. Phys. Geography: Earth Environ. 35, 87–108. doi: 10.1177/0309133310385371
Hinton G. E., Salakhutdinov R. R. (2006). Reducing the Dimensionality of Data With Neural Networks. Science 313, 504–507. doi: 10.1126/science.1127647
Huang L., Pan W., Zhang Y., Qian L., Gao N., Wu Y. (2020). Data Augmentation for Deep Learning-Based Radio Modulation Classification. IEEE Access 8, 1498–1506. doi: 10.1109/access.2019.2960775
Jia W., Wang, Mao, Zhang, , , (2019). A New Vegetation Index to Detect Periodically Submerged Mangrove Forest Using Single-Tide Sentinel-2 Imagery. Remote Sens. 11, 2043. doi: 10.3390/rs11172043
Kamal M., Phinn S., Johansen K. (2016). Assessment of Multi-Resolution Image Data for Mangrove Leaf Area Index Mapping. Remote Sens. Environ. 176, 242–254. doi: 10.1016/j.rse.2016.02.013
Kamal M., Sidik F., Prananda A. R. A., Mahardhika S. A. (2021). Mapping Leaf Area Index of Restored Mangroves Using WorldView-2 Imagery in Perancak Estuary, Bali, Indonesia. Remote Sens. Applications: Soc. Environ. 23, 100567. doi: 10.1016/j.rsase.2021.100567
Ke Huang Y., Yuan Y., Sun W., Meng X., Ge Y. (2022). Optical and SAR Images Combined Mangrove Index Based on Multi-Feature Fusion. Sci. Remote Sens. 5, 100040. doi: 10.1016/j.srs.2022.100040
Khaki S., Wang L. (2019). Crop Yield Prediction Using Deep Neural Networks. Front. Plant Sci. 10, 621. doi: 10.3389/fpls.2019.00621
Knoth C., Klein B., Prinz T., Kleinebecker T. (2013). Unmanned Aerial Vehicles as Innovative Remote Sensing Platforms for High-Resolution Infrared Imagery to Support Restoration Monitoring in Cut-Over Bogs. Appl. Vegetation Sci. 16, 509–517. doi: 10.1111/avsc.12024
Kovacs J. M., Wang J., Flores-Verdugo F. (2005). Mapping Mangrove Leaf Area Index at the Species Level Using IKONOS and LAI-2000 Sensors for the Agua Brava Lagoon, Mexican Pacific. Estuarine Coast. Shelf Sci. 62, 377–384. doi: 10.1016/j.ecss.2004.09.027
Liang L., Di L., Zhang L., Deng M., Qin Z., Zhao S., et al. (2015). Estimation of Crop LAI Using Hyperspectral Vegetation Indices and a Hybrid Inversion Method. Remote Sens. Environ. 165, 123–134. doi: 10.1016/j.rse.2015.04.032
Liang L., Geng D., Yan J., Qiu S., Di L., Wang S., et al. (2020). Estimating Crop LAI Using Spectral Feature Extraction and the Hybrid Inversion Method. Remote Sens. 12, 3534. doi: 10.3390/rs12213534
Lou P., Fu B., He H., Li Y., Tang T., Lin X., et al. (2020). An Optimized Object-Based Random Forest Algorithm for Marsh Vegetation Mapping Using High-Spatial-Resolution GF-1 and ZY-3 Data. Remote Sens. 12, 1270. doi: 10.3390/rs12081270
Lu D. (2006). The Potential and Challenge of Remote Sensing-Based Biomass Estimation. Int. J. Remote Sens. 27, 1297–1328. doi: 10.1080/01431160500486732
Lucas R. M., Moghaddam M., Cronin N. (2004). Microwave Scattering From Mixed-Species Forests, Queensland, Australia. IEEE Trans. Geosci. Remote Sens. 42, 2142–2159. doi: 10.1109/tgrs.2004.834633
Neukermans G., Dahdouh-Guebas F., Kairo J. G., Koedam N. (2008). Mangrove Species and Stand Mapping in Gazi Bay (Kenya) Using Quickbird Satellite Imagery. J. Spatial Sci. 53, 75–86. doi: 10.1080/14498596.2008.9635137
Omar H., Misman M., Kassim A. (2017). Synergetic of PALSAR-2 and Sentinel-1a SAR Polarimetry for Retrieving Aboveground Biomass in Dipterocarp Forest of Malaysia. Appl. Sci. 7, 675. doi: 10.3390/app7070675
Pyo J., Hong S. M., Kwon Y. S., Kim M. S., Cho K. H. (2020). Estimation of Heavy Metals Using Deep Neural Network With Visible and Infrared Spectroscopy of Soil. Sci. Total Environ. 741, 140162. doi: 10.1016/j.scitotenv.2020.140162
Sun J., Di L., Sun Z., Shen Y., Lai Z. (2019). County-Level Soybean Yield Prediction Using Deep CNN-LSTM Model. Sensors 19, 4363. doi: 10.3390/s19204363
Tamiminia H., Salehi B., Mahdianpari M., Beier C. M., Klimkowski D. J., Volk T. A. (2021). Comparison of Machine and Deep Learning Methods to Estimate Shrub Willow Biomass From UAS Imagery. Can. J. Remote Sens. 47, 209–227. doi: 10.1080/07038992.2021.1926952
Tian Y., Huang H., Zhou G., Zhang Q., Tao J., Zhang Y., et al. (2021). Aboveground Mangrove Biomass Estimation in Beibu Gulf Using Machine Learning and UAV Remote Sensing. Sci. Total Environ. 781, 146816. doi: 10.1016/j.scitotenv.2021.146816
Tian J., Wang L., Li X., Gong H., Shi C., Zhong R., et al. (2017). Comparison of UAV and WorldView-2 Imagery for Mapping Leaf Area Index of Mangrove Forest. Int. J. Appl. Earth Observation Geoinformation 61, 22–31. doi: 10.1016/j.jag.2017.05.002
Vaswani A., Shazeer N., Parmar N. (2017). Attention is All You Need. Adv. Neural Inf. Process. Syst. 30, 5998−6008.
Wang Y., Ngusaru A., Tobey J., Makota V., Bonynge G., Nugranad J., et al. (2003). Remote Sensing of Mangrove Change Along the Tanzania Coast. Mar. Geodesy 26 (1-2), 35–48. doi: 10.1080/01490410306708
Wang J., Xiao X., Bajgain R., Starks P., Steiner J., Doughty R. B., et al. (2019). Estimating Leaf Area Index and Aboveground Biomass of Grazing Pastures Using Sentinel-1, Sentinel-2 and Landsat Images. ISPRS J. Photogrammetry Remote Sens. 154, 189–201. doi: 10.1016/j.isprsjprs.2019.06.007
Waske B., Benediktsson J. A., Arnason K., Sveinsson J. R., (2009). Mapping of Hyperspectral AVIRIS Data Using Machine-Learning Algorithms. Canadian Journal of Remote Sensing 35, S106−S116. doi: 10.5589/m09-018
Yang G., Huang K., Sun W., Meng X., Mao D., Ge Y. (2022). Enhanced Mangrove Vegetation Index Based on Hyperspectral Images for Mapping Mangrove. ISPRS J. Photogrammetry Remote Sens. 189, 236–254. doi: 10.1016/j.isprsjprs.2022.05.003
Yan P., Lu H., Chen Y., Li Z., Li H. (2021). A Stack-Based Set Inversion Model for Smart Water, Carbon and Ecological Assessment in Urban Agglomerations. J. Cleaner Production 319, 128665. doi: 10.1016/j.jclepro.2021.128665
Zhen J., Jiang X., Xu Y., Miao J., Zhao D., Wang J., et al. (2021). Mapping Leaf Chlorophyll Content of Mangrove Forests With Sentinel-2 Images of Four Periods. Int. J. Appl. Earth Observation Geoinformation 102, 102387. doi: 10.1016/j.jag.2021.102387
Zhu Y., Liu K., Liu L., Myint S., Wang S., Liu H., et al. (2017). Exploring the Potential of WorldView-2 Red-Edge Band-Based Vegetation Indices for Estimation of Mangrove Leaf Area Index With Machine Learning Algorithms. Remote Sens. 9, 1060. doi: 10.3390/rs9101060
Keywords: mangrove communities, LAI estimation, ensemble learning regression and deep learning regression algorithms, sample enhancement, optical and SAR images
Citation: Fu B, Sun J, Wang Y, Yang W, He H, Liu L, Huang L, Fan D and Gao E (2022) Evaluation of LAI Estimation of Mangrove Communities Using DLR and ELR Algorithms With UAV, Hyperspectral, and SAR Images. Front. Mar. Sci. 9:944454. doi: 10.3389/fmars.2022.944454
Received: 15 May 2022; Accepted: 09 June 2022;
Published: 22 July 2022.
Edited by:
Mingming Jia, Chinese Academy of Sciences (CAS), ChinaReviewed by:
Xiangchao Meng, Ningbo University, ChinaQing Xia, Changsha University of Science and Technology, China
Copyright © 2022 Fu, Sun, Wang, Yang, He, Liu, Huang, Fan and Gao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bolin Fu, ZnVib2xpbkBnbHV0LmVkdS5jbg==
†These authors contributed equally to this work
 Bolin Fu
Bolin Fu Jun Sun1†
Jun Sun1† Yeqiao Wang
Yeqiao Wang Hongchang He
Hongchang He Donglin Fan
Donglin Fan