On an adaptation of the Reynolds number, applicable to body-caudal-fin aquatic locomotion

The Reynolds number, which describes the relative importance of viscous and inertial contributions is commonly used to analyze forces on fish and other aquatic animals. However, this number is based on steady, time-independent conditions, while all swimming motions have a periodic component. Here we apply periodic flow conditions to define a new non-dimensional group, which we name the “Periodic Swimming Number, P”, which rectifies this lacuna. This new non-dimensional number embodies the periodic motion and eliminates the arbitrariness of choosing a length scale in the Reynolds number for Body –Caudal-Fin (BCF) swimming. We show that the new number has the advantage of compressing known data on fish swimming to two orders of magnitude, vs. over six required when using the existing Reynolds number and can point to a new comparison of swimming effectiveness for swimming modes.

Introduction

One of the most important advances in fluid dynamics (and physical science in general) was the introduction of non-dimensional groups that enabled compressed experimental data and parametrized flow problems (Batchelor, 1967). This allows for generalizations and understanding of the relative importance of various factors and mechanisms associated with a given physical phenomenon. The choice of non-dimensional numbers is not arbitrary. The choice of these numbers depends on the physical phenomena, the boundary and initial conditions within the investigated control volume, the environment and so on.

The Reynolds number (Re), which shows the relative importance between inertial and viscous forces, is among the most influential for animal locomotion in a fluid medium such as water or air (Shadwick and Lauder, 2006; Shyy et al., 2007). In the case of the Reynolds number, the choice of length scale in seen to determine the flow regime. Common classifications are laminar and turbulent flows, where for specific flow geometries, i.e.: pipe, flat plate or bluff body, a critical Reynolds number exists (Schlichting and Gerstel, 2000) where the flow conditions transit from laminar to turbulence. However, there are two ambiguities associated with this number, which have been largely neglected: 1) the unsteadiness of the flow and, 2) the essentially arbitrary choice of the characteristic length. For aquatic locomotion; the motions are commonly periodic or indicial (Daniel, 1984; Sfakiotakis et al., 1999; Triantafyllou et al., 2000; Fish and Lauder, 2006; Costa et al., 2020); However, using the Reynolds number for characterization of the flow regime, implicitly assumes that the motion has constant velocity. This is a good approximation in many cases as the periodic component can be much smaller that the speed of the center of mass, but it misses the essential non-steady motion that causes locomotion (Lighthill, 1969; Webb and Weihs, 2015), as illustrated in Figure 1 where L and D correspond to the normal force (i.e.: lift) and streamwise force (i.e.: drag) as functions of the tail motion, decomposed to four quadrants of motion (resulting from differences in the tail angle of attack as it moves right and left). Furthermore, using the Reynolds number introduces an arbitrary length coordinate and leads to the discussion of laminar vs. turbulent flow conditions, which under natural aquatic conditions is irrelevant as the real aqueous environment is almost exclusively turbulent due to wind, currents, and previous disturbances (Thorpe, 2007).

FIGURE 1

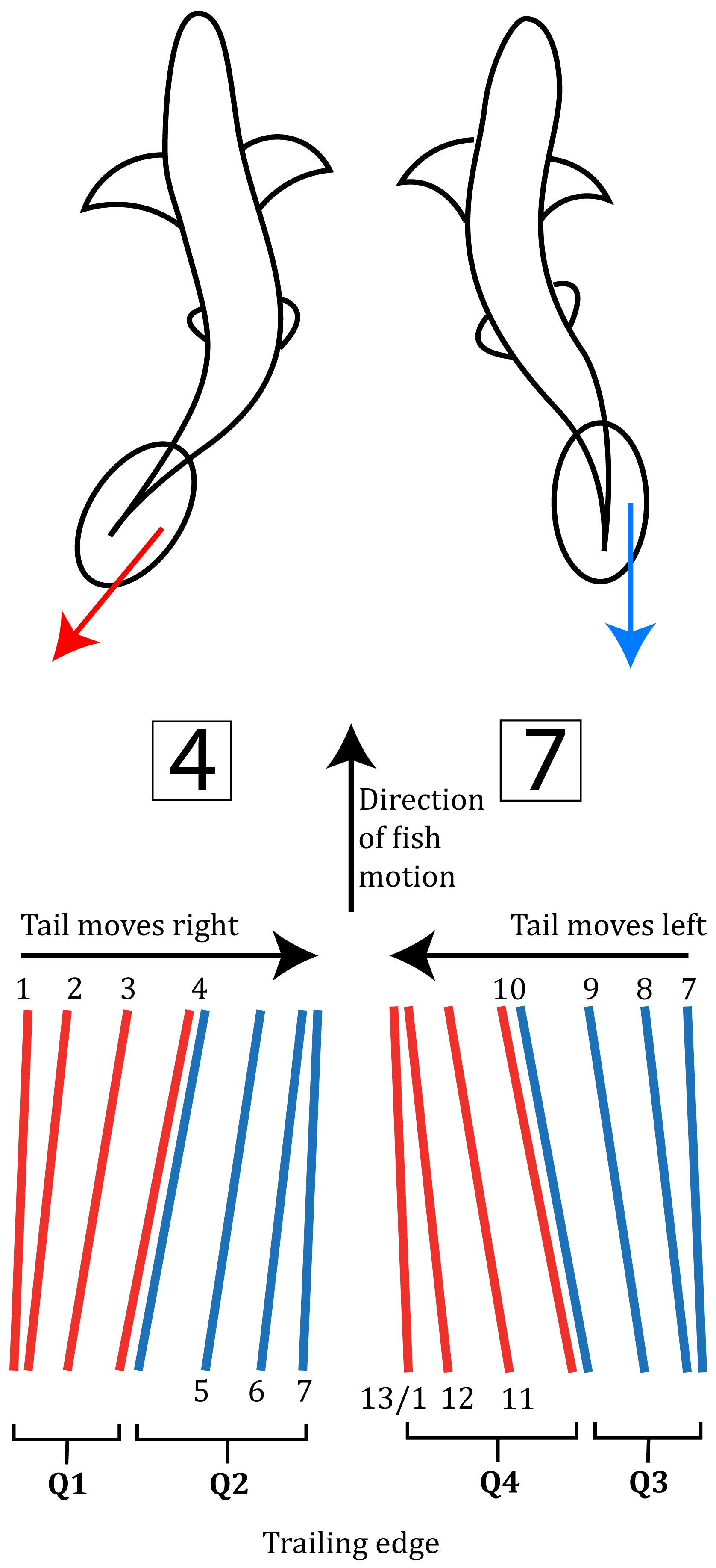
Figure 1 Schematic illustration of the fin motion in respect to the fish during locomotion. The bottom figure represents the oscillatory phases, adapted from refs (Lighthill, M. J. (1969). L indicates the force normal to the direction of tail motion (equivalent to lift in airfoils), and D is the force acting in the direction of motion (i.e.: drag). Q_i (i = 1 - 4) indicates quadrants of the motion as function of angle of attack; during Q₁: the tail’s angle of attack increases while the tail moves to the right, Q₂: the tail’s angle of attack decreases whilst the tail keeps moving right and Q₃ and Q₄ are similar during the tail motion moving to the left (back to complete the cycle).

Some other groupings are useful such as the Strouhal number (St), which defines the ratio between frequency and speed in inviscid flow, and also includes a characteristic length. There, the length scale is obtained from the wavelength of the oscillatory motion or some characteristic related to it (i.e.: rate) (Taylor and Nudds RL Thomas, 2003; Lagopoulos et al., 2019). Saadat et al. (2017) showed that the Strouhal number is narrowly bounded for many aquatic organisms. Yet, Strouhal number relates inertia to unsteadiness, therefore, it does not account for drag losses during motion. Similarly, the Roshko number (Roshko, 1952) which is a combination of Re and St connecting time dependent, to viscous forces, bypassing the need to define the velocity, assumes an arbitrary characteristic length. Here we add a new non-dimensional combination to represent periodic motion of animals in viscous flow. At this stage, the analysis is for Body Caudal Fin (BCF) locomotion only, with generalization to other types of locomotion to be presented in the future.

The choice of length scale is important to parametrize the flow problem. Commonly, in studying the locomotion of aquatic organisms, the body length or fin length are used. Yet as mentioned, the choice of length when applying the Reynolds number to periodic motions is arbitrary. Within this group, the scale mainly depends on their size as the medium is water. Thus, the length essentially determines the flow regime, when characterized using the Reynolds number (Webb, 1988). This can be misleading, especially for small animals, which are assumed to move in laminar flow (Schlichting and Gerstel, 2000). More so, the representative length can be chosen to be fin chord, fork length etc.; each choice yielding a different result with significant implications. During cruising (i.e.: swimming over long distances relative to the fish size), most fish locomotory motions have a periodic component, with velocity changes small relative to the average speed. Here we suggest a definite length factor for periodic fish swimming motions, which has several advantages in analyzing fish swimming.

Length scale based on time dependent motion

The motivation of choosing a different, time periodic length scale is to enable a more realistic non-dimensional number which fits aquatic organisms that move by undulating motion of the whole body (Anguilliform), portion of the body (Carangiform), or the caudal fin (Thunniform), all BCF type motions first described by Breder (1926). The propulsion is done by the body portion that moves in an oscillatory fashion (commonly harmonic). For these types of motions, the average angle of each force producing segment with the direction of motion is relatively small (Lighthill, 1960; Yates, 1983). Thus, each body section experiences fully developed viscous flow influenced by periodic flow conditions. We apply a case of periodic flow that is a solution of the full Navier-Stokes equations for periodic viscous flows (Stokes, 1851), so that the ambiguities due to scale choice do not occur.

Stokes solved the flow above an infinite flat plate experiencing linear harmonic oscillatory motion parallel to the plate, known as ‘Stokes second problem’ (Stokes, 1851). This can be compared to fin motions, as fins move at small angles of attack to avoid flow separation. Therefore, these motions can be approximately viewed as a plate moving along its plane. Next, subtracting the forward speed, the remaining motion produces an oscillating motion with zero average speed (see Figure 1). The resultant velocity profile at the vicinity of the plate takes the form of a damped harmonic oscillation function. Stokes named the region where the flow velocity experiences these oscillations as the ‘depth of penetration of the viscous wave’ (Schlichting and Gerstel (2000); p. 129). From the solution to Stokes second problem, we observe that 99% of the viscous effects due this motion are confined within a nondimensional distance of η = 5 (Schlichting and Gerstel, 2000) for all frequencies and amplitudes. So, η = 5 is the end of the layer from the oscillating plate where the effects of viscosity are measurable and, as mentioned, is obtained from a full solution to the Navier Stokes equations; thus, more general than a boundary layer solution, which uses some approximations. The non-dimensional distance is defined as:

$\begin{array}{ll}\eta =y\sqrt{\frac{\omega }{2\nu }}& (1)\end{array}$

and ω is the plate frequency (assuming harmonic oscillations), ν is the fluid kinematic viscosity and y is the normal coordinates indicating the distance of the fluid for a given η from the plate perpendicular to it. This non-dimensional distance assumes a rigid smooth surface at each section (Lighthill, 1960). Surface characteristics of fish such as varying stiffness, roughness etc. are not considered here as these are secondary effects, and add complications that mask the main issue considered here, of time dependent effects. In the future, it may be interesting to compare surface textures of different fish species coupled with the flow mechanisms described above.

We can re-write equation (1) as:

$\begin{array}{ll}y=\frac{\eta }{\sqrt{\frac{\omega }{2\nu }}} => T=\frac{5}{\sqrt{\frac{\omega }{2\nu }}}=\sqrt{\frac{50\nu }{\omega }}=10\sqrt{\frac{\nu }{2\omega }}& (2)\end{array}$

We now use equation (2) to define the effective thickness of the viscous layer, T. T is used as a length scale that incorporates both viscosity and frequency and can be applied to the definition of a nondimensional group that enables adapting the Reynolds number to account for the periodic motion. We call this group the “periodic swimming number”, P (see equation (3))

$\begin{array}{ll}P=\frac{UT}{\nu }=\frac{U}{\nu }10\sqrt{\frac{\nu }{2\omega }}=\frac{10U}{\sqrt{2\omega \nu }}& (3)\end{array}$

where U is the fish speed in still water or separately can be applied as the speed relative to the water column when swimming in a current (Breder, 1926). We assume a constant average velocity. Commonly, this speed is related to the fish length and its tail-beat frequency (Weihs, 1973). However, these relations depend on the swimming mode of locomotion, the range of frequencies and the tail-beat amplitudes (Bainbridge, 1958).

The present nondimensional representation of swimming motions has several advantages over using the classical Reynolds number for BCF swimming. First, it embodies the periodic motion; second, it eliminates the arbitrariness of choosing a length scale (fish length, fin chord, etc. are chosen in different papers); and third, it reduces the bandwidth of results from six orders of magnitude using the Reynolds number to two. As shown in the next section, experimental data from numerous sources for different fish species demonstrate the advantage discussed above on swimming effectiveness of the various BCF modes of locomotion, when applying the Periodic number, P, that accounts for the unsteadiness mechanism coupled with intertie and viscosity.

Experimental data

In order to show how this scaling parameter, which combines the viscous and time dependent effects can be used, we bring examples of experimental data from the literature. Having checked over numerous references found through keywords in several search engines, we found about 30 that had details enough to obtain the values of the scaling parameter, P. These are detailed in Table S1 and S2 in the Supplementary Material. We stress that these are just examples applied here and we expect further insights once researchers use this factor. We calculated the periodic swimming number, P for 40 aquatic species moving at different speeds and modes of BCF locomotion (herein: Carangiform, Sub-carangiform and Thunniform) using data from the literature. The data extracted herein is based on published material that contained full available information such as: characteristic range of fish lengths, speeds and tail-bait frequencies conditioned that the data was gathered from a relatively large sample size of the fish species or alternatively a large set of species that can be compared (see Table S2). Table S1 (enclosed in the Supplementary Material) provides the basic parameters used to define and calculate the new number: species name, size, speed, frequency of the body/fin oscillation, the classical Reynolds number and the new Periodic number. We applied data from the literature for a vast range of species considering large ranges of size, speeds and mode of locomotion resulting with 40 species. Table S1 is also divided into several sub-groups, based on the form of their undulatory motion. For the whole range of species, the periodic swimming number spans only 2 orders of magnitude compared to the classical Reynolds number which spans over 6 orders of magnitude (Gazzola et al., 2014). In instances where the oscillation frequency was not provided, we used the empirical relation proposed by Webb et al. (1984) to estimate the oscillation frequency based on the length and speed, using the present definitions: ω= 3.19L^-1/3 + 1.29U/L, where ω is the body/fin/tailbeat frequency, L is the total body length and U is the swimming speed. The estimated frequencies were compared with former empirical correlations to estimate the frequency by Hunter (1971) and Bainbridge (1958) and provided the same values for the selected species used here.

The formulation of the swimming Periodic number couples the inertia, viscosity and time dependent forces. Therefore, the Periodic number depends on both fish speed and tail/body beat frequencies in non-linear fashion (see Figure S2). The periodic number increases in an exponential fashion and depends strongly on the swimming speed (Figure S2A) whilst we could not observe any coherent trend with the tail/body beat frequency. However, since the swimming velocity is also a function of the frequency, the P dependency on the frequency is two-fold.

The periodic swimming number ranges between 100 - 10,000. The range narrowing as compared to the classical Reynolds number (based on the fish length) range suggests that the flow phenomena observed during fish locomotion at cruising speeds over range of species are well described by the P number (see Figure 2). Furthermore, this range suggests that that fish-fluid interaction is dominated by three mechanisms: inertia, viscous and unsteadiness. The latter is ignored when using Reynolds number for the flow characterization over a large range of species. Given the narrow range, we cannot ignore the unsteadiness; thus, all three mechanisms should be considered when researching fish locomotion. In Figure 2 we see an empirical exponential connection between P and Re, which quantifies the compression of data from over several decades.

FIGURE 2

Figure 2 Periodic swimming number vs. Reynolds number.

We separate the data into four swimming modes following Breder (1926): Anguilliform, Sub-carangiform, Carangiform and Thunniform. We show that, when plotted versus swimming speed (Figure 3) the fish using different modes are separated. We have performed linear curve-fitting for three of the modes of locomotion whilst for the Anguillform swimmers, we had only 3 species which is not sufficient to justify curve fitting. R² for the three swimming modes is above 0.85 where the slopes change with the locomotion mode. Based on these, we see that the curve fitting of the data is more accurate in the case of sub-carangiform locomotion, as compared with the one for Thunniform locomotion. This is presumably because Thunnifirm locomotion strongly depends on the forward velocity of the tail, which is subtracted here, while the other modes of locomotion are more added-mass based and less on the forward velocity. Thus, for high-speed locomotion the periodic component is less clear, explaining why the analyses in the literature using Reynolds numbers gave relatively good results. While the actual values of the slope are arbitrary, the speed is dimensional and we chose to use a scale of mm/sec, the difference in slope is real. It seems that clustering the fish into various modes of locomotion, provides a coherent relation between speed, locomotion and the periodic swimming number; which presumably encapsulates both the average and transient forces acting on the fish during forward swimming.

FIGURE 3

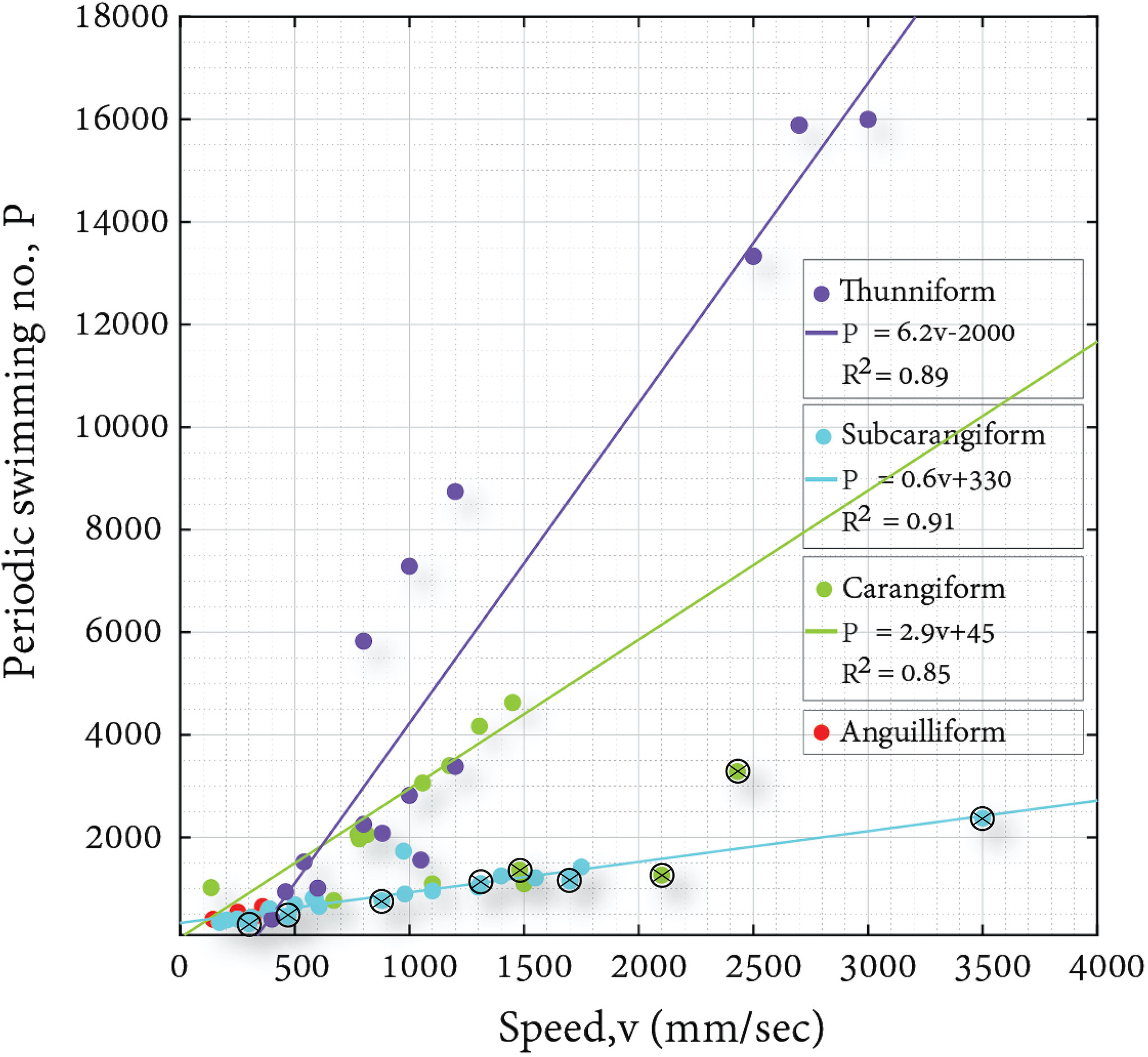
Figure 3 Periodic swimming number vs. speed (top) cluster based on mode of locomotion. Straight lines represent linear fit for the different points. Open black circles with an internal cross correspond to data points where the oscillation frequency was estimated based on speed and length correlation provided by Webb et al. (1984).

Discussion

The main difference between the Reynolds and the Periodic Swimming Number, beyond the basic assumption of steady flow, is associated with the choice of length scale. Whilst such a nondimensional grouping is essential to characterize fluid-fish interaction, the use of the classical Reynolds number introduces an arbitrariness: body or caudal fin lengths, among others. Here, using a length scale, characteristic of the interaction between the body and the fluid based on a full Navier-Stokes’s solution, we obtain a more rigorous description, which also results in a compact range of numbers by applying the so-called (Schlichting and Gerstel, 2000) Stokes second problem. The new non-dimensional number couples inertia effects (swim speed), viscous effects and unsteadiness (frequency). This number bundles Reynolds and Strouhal non-dimensional groupings through a proper choice of length scale that can be associated with both numbers. Furthermore, applying the Periodic swimming number to a range of species yielded a compact range of values.

We show that this number is better suited to characterize fish locomotion during cruising than the Reynolds number as it accounts for the unsteadiness component of propulsive motions (Daniel, 1984; Sfakiotakis et al., 1999; Triantafyllou et al., 2000; Fish and Lauder, 2006). This allows an insight into swimming effectiveness, as the higher slope indicates a lower oscillation frequency for the same speed. This in turn can be interpreted as requiring less effort per distance crossed (lower cost of transport) thus, a lower rate of energy consumption or potentially enabling travelling longer distances with fixed energy. Other locomotion features such as burst and coast swimming (Weihs, 1974), turning etc. could be treated by adding additional scaling factors, but are beyond the scope of the present paper.

This non-dimensional grouping avoids the ambiguity of defining the state of the flow in rivers or oceans as laminar or turbulent as suggested by (Gazzola et al., 2014), because large bodies of water have multiple forces acting simultaneously in time and space. Therefore, even if the flow locally is not fully turbulent, it is unsteady, three dimensional with strong mixing generally, which is sometimes referred to as fossil turbulence (Thorpe, 2007).

The results obtained using the Periodic swimming number P, which concentrate the data cover only two decades, suggest that the fluid-fish interaction is better described by P. In addition, the observation that using P separates the fish species based on their locomotion modes, supports the utility of using this number. This shows the importance of considering not only inertia and viscous forces but also the time-dependent contribution to the forces. Furthermore, most of the current work in the literature uses the Reynolds number (Sfakiotakis et al., 1999; Gazzola et al., 2014) to scale fish locomotion, yet do not address the unsteadiness effects; this aspect is critically important when comparing species’ swimming performance in different environment as well as in performing numerical simulations associated with fluid-fish interaction where typically the flow simulations are applied in a non-dimensional manner; this can cause a bias in the results when not accounting for the unsteadiness contribution. We hope that this note will encourage experimental and computational studies of swimming speed of additional species, so as to enable finding more generalizations and understanding.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Ethics statement

Ethical review and approval was not required for the animal study because this is a theoretical study on fish locomotion.

Author contributions

RG and DW: Concept and theoretical approach analysis and editing. RG, AN and DW: Methodology, data collection, writing. All authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2022.914214/full#supplementary-material

References

Bainbridge R. (1958). The speed of swimming of fish as related to size and to the frequency and amplitude of the tail beat. J. Exp. Biol. 35 (1), 109–133. doi: 10.1242/jeb.35.1.109

CrossRef Full Text | Google Scholar

Batchelor G. K. (1967). An introduction to fluid dynamics (Cambridge, UK: Cambridge University Press).

Google Scholar

Breder C. M. Jr (1926). The locomotion of fishes. Zoologica 4, 159–291. doi: 10.5962/p.203769

CrossRef Full Text | Google Scholar

Costa D., Palmieri G., Palpacelli M. C., Scaradozzi D., Callegari M. (2020). Design of a carangiform swimming robot through a multiphysics simulation environment. Biomimetics 5 (4):46. doi: 10.3390/biomimetics5040046

CrossRef Full Text | Google Scholar

Daniel T. L. (1984). Unsteady aspects of aquatic locomotion. Am. Zoologist 24 (1), 121–134. doi: 10.1093/icb/24.1.121

CrossRef Full Text | Google Scholar

Fish F., Lauder G. V. (2006). Passive and active flow control by swimming fishes and mammals. Annu. Rev. Fluid Mechanics 38, 193–224. doi: 10.1146/annurev.fluid.38.050304.092201

CrossRef Full Text | Google Scholar

Gazzola M., Argentina M., Mahadevan L. (2014). Scaling macroscopic aquatic locomotion. Nat. Phys. 10 (10), 758–761. doi: 10.1038/nphys3078

CrossRef Full Text | Google Scholar

Hunter J. R. (1971). Swimming speed, tail beat frequency, tail beat amplitude and size in jack mackerel, trachurus symmetricus, and other fishes. Fishery Bulletins 69, 253–266.

Google Scholar

Lagopoulos N. S., Weymouth G. D., Ganapathisubramani B. (2019). Universal scaling law for drag-to-thrust wake transition in flapping foils. J. Fluid Mechanics 872, R1. doi: 10.1017/jfm.2019.361

CrossRef Full Text | Google Scholar

Lighthill M. J. (1960). Note on the swimming of slender fish. J. Fluid Mechanics 9 (2), 305–317. doi: 10.1017/S0022112060001110

CrossRef Full Text | Google Scholar

Lighthill M. J. (1969). Hydromechanics of aquatic animal propulsion. Annu. Rev. Fluid Mechanics 1 (1), 413–446. doi: 10.1146/annurev.fl.01.010169.002213

CrossRef Full Text | Google Scholar

Roshko A. (1952). On the development of turbulent wakes from vortex streets, Ph.D (Caltech, US: Dissertation).

Google Scholar

Saadat M., Fish F. E., Domel A. G., Di Santo V., Lauder G. V., Haj-Hariri H. (2017). On the rules for aquatic locomotion. Phys. Rev. Fluids 2 (8), 083102. doi: 10.1103/PhysRevFluids.2.083102

CrossRef Full Text | Google Scholar

Schlichting H., Gerstel K. (2000). Boundary layer theory. 8th ed (Berlin: Springer).

Google Scholar

Sfakiotakis M., Lane D. M., Davies J. B. C. (1999). Review of fish swimming modes for aquatic locomotion. IEEE J. oceanic Eng. 24 (2), 237–252. doi: 10.1109/48.757275

CrossRef Full Text | Google Scholar

Shadwick R. E., Lauder G. V. (Eds.) (2006). “Fish physiology,” in Fish biomechanics. (San-Diego, CA, USA: Elsevier), vol. 23.

Google Scholar

Shyy W., Lian Y., Tang J., Viieru D., Liu H. (2007). Aerodynamics of low reynolds number flyers (vol. 22) (Cambridge: Cambridge University Press).

Google Scholar

Stokes G. G. (1851). On the effect of the internal friction of fluids on the motion of pendulums. Trans. Cambridge Philos. Soc. 9, 8–106.

Google Scholar

Taylor G. K., Nudds RL Thomas A. L. (2003). Flying and swimming animals cruise at a strouhal number tuned for high power efficiency. Nature 425 (6959), 707–711.

PubMed Abstract | Google Scholar

Thorpe S. A. (2007). An introduction to ocean turbulence. (Cambridge: Cambridge University Press), vol. 10.

Google Scholar

Triantafyllou M. S., Triantafyllou G. S., Yue D. K. P. (2000). Hydrodynamics of fishlike swimming. Annu. Rev. fluid mechanics. 32 (1), 33–53. doi: 10.1146/annurev.fluid.32.1.33

CrossRef Full Text | Google Scholar

Webb P. W. (1988). Simple physical principles and vertebrate aquatic locomotion. Am. Zoologist 28 (2), 709–725. doi: 10.1093/icb/28.2.709

CrossRef Full Text | Google Scholar

Webb P. W., Kostecki P. T., Stevens E. D. (1984). The effect of size and swimming speed on locomotor kinematics of rainbow trout. J. Exp. Biol. 109 (1), 77–95. doi: 10.1242/jeb.109.1.77

CrossRef Full Text | Google Scholar

Webb P. W., Weihs D. (2015). Stability versus maneuvering: challenges for stability during swimming by fishes. Integr. Comp. Biol. 55 (4), 753–764. doi: 10.1093/icb/icv053

PubMed Abstract | CrossRef Full Text | Google Scholar

Weihs D. (1973). Optimal fish cruising speed. Nature 245 (5419), 48–50.

Google Scholar

Weihs D. (1974). Energetic advantages of burst swimming of fish. J. Theor. Biol. 48 (1), 215–229. doi: 10.1016/0022-5193(74)90192-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Yates G. T. (1983). “Hydrodynamics of body and caudal fin propulsion,” in Fish biomechanics. Eds. Webb P. W., Weihs D. (New York: Praeger Scientific), 177–213.

Google Scholar