Uncertainty and Consistency Assessment in Multiple Microplastic Observation Datasets in the Baltic Sea

This paper aims to quantify data uncertainties in marine microplastic measurements, including spatiotemporal sampling error and sample volume estimation error, identify impacts of varying mesh sizes, sampling and analysis methods, and evaluate consistency in multiple microplastic observation datasets. Twenty-seven datasets on surface marine microplastics with particle size >100 µm in the Baltic Sea are compiled. Results show that the trawl datasets have a spatiotemporal sampling error of 25% for microlitter concentration, 36% for microplastic fiber concentrations and 40-56% for microplastic particle concentration. By taking surface currents and wave-induced Stokes drift into account, the sample volume of the trawl measurements is corrected, leading to a mean microplastic concentration correction of 12%. The differences of microplastic concentration between datasets with varying mesh sizes from 100 – 500 µm are not statistically significant. Analysis methods, however, can lead to significant differences in microplastic datasets. The dataset consistency is further examined among the three dataset categories using trawl, pump and bulk sampling techniques. It is found that an individual dataset is often self-consistent. Most of the datasets within one monitoring category are more consistent than those from different categories. More than 70% of the datasets within individual categories are consistent, which have mean microplastic concentration significantly smaller than the rest of the datasets. Significant inconsistencies are identified between different data categories. Six out of eight highest relative standard deviations are found in the pump and bulk datasets. The median value of the mean microplastic concentration from the 10 pump datasets is about 4.5 times as much as that of the 14 trawl datasets, both for fiber and non-fiber particles. Significant differences are also identified on microplastic fiber fraction in different dataset categories. Two thirds of the 13 bulk and pump datasets have a microplastic fiber fraction >85% while the 14 trawl datasets show much lower microplastic fiber fractions between 45-70%. In addition, the particle collection efficiency, potential leakage of particles with irregular shapes, clogging, the false zero samples and related lower limit of the detectable microplastic concentration for given sampling methods and water environment, are also discussed.

1 Introduction

“Micro-litter” refers to a diverse group of particulate materials originating from human activities. The Marine Strategy Framework Directive (EC, 2008) defines microlitters (ML) as objects with the largest measurement below a limit of 5 mm (Hanke, 2013). Part of ML is made of microplastics (MP), released from e.g., laundry, wearing of tyres and use of personal care and cosmetic products. The shapes of MP particles involve filaments (fibres), beads, fragments etc. In this paper, the MP particles are categorized into two types: the MP filament hereafter being referred as MP fiber (MPF) and the rest of the non-fiber microplastics, referred as MP particles (MPP).

The Baltic Sea is a semi-enclosed sea, carrying pollutants emitted from the Baltic Sea catchment with a population of more than 80 million people. Due to a water renewal period of about 30 years (Leppäranta and Myrberg, 2009), the pollutants in the Baltic Sea have a relatively long residence time which worsens the marine environment. Marine microplastics have received much public and scientific attention over the past decade due to its possible consequences on marine ecosystems (Ajith et al., 2020). Monitoring of the MP litter in the sea is an important area of research as it provides a basis for environment assessment and protection.

The MP litter in the sea can be measured by filtering water samples from the sea using a net with a certain mesh size and then analyzing, categorizing and counting the collected particles in the laboratories. Although, in the Baltic Sea, microplastic litter has been widely monitored in coastal, estuary and open waters (Norén, 2007; Magnusson and Norén, 2011; Norén et al., 2015; Setälä et al., 2016; Bagaev et al., 2017; Tamminga et al., 2018; Beer et al., 2018; Zobkov et al., 2019; Schönlau et al., 2020; Aigars et al., 2021), common technological standards, both on sampling and analysis methods, are still under development. Existing research have shown large discrepancies between different datasets. For example, most of the trawl samples showed a MP concentration of 10^-2-10⁰ particles per cubic meter (pcs/m³) (Magnusson and Norén, 2011; Norén et al., 2015; Setälä et al., 2016; Tamminga et al., 2018; Karlsson et al., 2020; Schönlau et al., 2020; Aigars et al., 2021; Mishra et al., 2022), while some pump and bulk samples measured up to 10^2-3 pcs/m³ (Bagaev et al., 2017; Tamminga et al., 2018; Schönlau et al., 2020). In addition, pump datasets often have many samples with false-zero concentrations (Setälä et al., 2016; Schönlau et al., 2020). Even replicate samples from the trawl and pump sampling can have big differences (Schönlau et al., 2020). In an effort to analyze spatial distribution of the microplastic particle concentration using a basin scale sampling in the Baltic Sea, Schönlau et al. (2020) found that spatial distribution derived from the pump data is not consistent with the trawl data. Although the differences in the multiple datasets can be caused by sampling locations, field surveys with replicated pump and trawl samples (Setälä et al., 2016; Schönlau et al., 2020) suggested that such significant differences in the datasets are mainly caused by the sampling methods. However, existing research on the data consistency are mainly based on individual datasets, a systematic study on the data consistency using multiple datasets is needed to quantify both the significant differences and synergy between different datasets.

The uncertainties in MP litter measurements from the sea can be caused by three major error sources: sampling error, instrument error and laboratorial analysis error. Some error sources are common to all monitoring methods thus, can be quantified in a common way such as net contamination and spatiotemporal sampling error. However, there are also a few error sources related to analyzing methods, such as uncertainties in particle collection, sample water volume and sample size. Below we will streamline the existing studies and knowledge on the MP litter measurement according to the three error types (sampling, instrument and analysis error) and analyzing methods.

Sampling error - it is a measure of repetitiveness or randomness of data when sampling from a stochastic spatiotemporal field, which can be estimated as the difference between the estimated sample mean value from observations and the real mean. The sampling error depends not only on the probability distribution of MP concentration but also on the sample size or the number of MP particles per collected sample. To ensure that the sample represents the local mean condition of MP (i.e., with small standard deviation), a recommendation of a minimum of 26 particles in one sample was made based on an assumption of Gaussian distribution of the MP concentration with particle size > 300 µm (Karlsson et al., 2020). A lower number of particles will increase the randomness of the measurements. The spatiotemporal randomness in the sampling also affects the sampling error. The real value of this uncertainty cannot be obtained at a given spatiotemporal position since only one measurement can be made. However, the spatiotemporal sampling error can be approximated by using variance in a small spatiotemporal box which can be estimated by using multiple measurements in the box. The spatiotemporal MP sampling error has rarely been quantified in previous studies.

Instrument error - the second category of observation error, i.e. the instrument error, is attributed to uncertainties from using different sampling instruments during the sampling. This can be described instrument-wise. The trawl method uses a net, e.g., a manta trawl or bongo net, tailored to a ship. When the ship is moving, water flows through the net and marine litter in the surface layer is collected, where the sampling layer thickness depends on the height of the manta, often 20-70 cm. Since the ship can move a long distance, sufficient amounts of MP particles can be collected to avoid false zero samples and reach a statistically stable result (Karlsson et al., 2020). For relatively low concentration of 10^-2 – 10⁰ pcs/m³, an effective sampling to catch a minimum of 26 particles needs to sample a water volume of 10² cubic meters. Thus, trawl method represents a good choice: towing a manta net with a ship speed of 2 knots for 15-60 minutes can normally meet the requirements.

The main instrument error of the trawl method includes several sources, e.g., atmospheric contamination which mainly affects fiber data, uncertainties in the sample water volume estimation and particle collection efficiency. The sample water volume is calculated from the ship’s moving distance and the area of the trawl mouth. In most of the cases, a flow meter is not used. Several potential error sources for sample water volume estimation should be considered. As pointed out by Karlsson et al. (2019), the net may not always be submerged in the water, especially in high seas, thus a few percentage underestimation of the sample volume may be made. Another error source is the neglect of the impacts of flow velocity in the water volume calculation in the trawl sampling, including surface currents, wave-induced Stokes drift and maybe turbulence flow in the wake area of the moving ship. This error source has not been well quantified in previous studies. The particle collection efficiency is another source of error, caused by leaking of particles with irregular shapes, clogging due to biomass accumulation etc.

The pump method has been developed to provide more accurate sample volume estimation with a flow meter (Magnusson and Norén, 2011; Setälä et al., 2016), and also the capacity to measure the smaller particles between 10-100 µm (Norén et al., 2015; Schönlau et al., 2020). This smaller fraction is the major part of the MP particles from sources such as wastewater treatment plants (WWTPs), as shown by Lassen et al. (2015). The water is pumped through a filter to collect MP litter. This can be made on board either in a moving or standby ship. The main weakness of the pump method is its small sample volume, normally 10^-3-10⁰ m³ depending on the mesh size. For large particles (> 100 µm), the pumping method gives more false-zero values than the trawl method, especially for the MPPs. For example, the pump samples from Setälä et al. (2016) only gave 13% of the samples with non-zero MPP concentration. It should also be noted that the pump method does not permit sampling from a microlayer of the surface layer where the highest MP concentration is found (Song et al., 2014), and the maximum sampling depth is also limited to several meters because of the submersible pump’s water resistance rating. Zobkov et al. (2019) further improved the pumping method so that it can be used to measure microplastic concentration for the entire water column.

In addition, a bulk method has also been frequently used where water samples are directly taken from a given depth using a water container, such as Niskin bottles. The volume of water is generally low (between 10⁰-10¹ liters) compared to the trawl methods. Such an amount of water is sufficient for detecting smaller particles, e.g., with a size ranging from 10-50 µm, but it can be insufficient for particles larger than 100 µm with a relatively low concentration. The low water volume used in the bulk method may lead to large statistical errors in low concentration waters and end up with very high concentrations, for example, 10^1-3 pcs/m³ with minimum sizes of 80-300 µm were reported by using this method (Norén, 2007; Gorokhova, 2015, Bagaev et. al., 2017) in the Baltic Sea.

Another major source of instrument error in MP monitoring is the “efficiency of particle collection”, as mentioned above. The MP shape involves beads, fragments, fibres and films. The MP monitoring collects MP particles using a filter with a certain mesh size l (µm), then only particles with a size between l-4999 µm are considered as valid. Here, the “size” means the length in the largest dimension of the particle. Such a practice is perfect for spherical particles, but will lead to potential leakage of valid particles with irregular shapes. Microplastic fibres (MPFs) are a typical example. The average diameter of MPFs released from a washing machine is 12-18 µm (Napper and Thompson, 2016) while their length is often much longer than 300 µm. Therefore, they can be either collected or leaked from the filter with a mesh size > 100 µm, depending on the situation of the litter collected in the net and water flow. In principle, particle leakage can happen in different monitoring methods. The trawl methods, due to its long sampling time and large size of the trawl net, may be mostly affected by this factor. The bulk and pump methods, on the other hand, may be less affected compared to the trawl method. Especially, when a filter with fine mesh (e.g. 20 µm) is used, the efficiency of collecting large MP particles will be high. However, there is still a lack of studies on the quantitative impact of the particle leaking.

Another issue related to the efficiency of particle collection is the potential clogging of the mesh. For the trawl method, the mesh size of the net should not be too small as this can lead to frequent clogging. Due to these reasons, the trawl method is mainly used with a mesh size > 100 µm, most often 300 or 330 µm. In general, the sampling should also avoid periods of microbiota and/or gelatinous plankton bloom which can quickly clog the filter.

Analysis error - After the samples are taken to laboratories, the filters are rinsed and/or digested with oxidizing agent to remove organic matter and microbiota, then microlitter is sorted out from the sample, categorized and counted (GESAMP, 2019), using either FTIR and/or visual counting under a microscope together with hot needle test. The visual counting together with the hot needle test allows the quantification of fibres. FTIR analysis, instead, enables plastic polymers identification avoiding bias from other materials, such as natural particles. However, FTIR may not be so efficient and accurate in identifying MPFs, and a specific algorithm will be needed for MPF detection (Primpke et al., 2019). Furthermore, the analysis error of the visual counting method is also analyst-dependent. An experienced analyst may generate more consistent observations with lower uncertainties. However, the analysis error of these two kinds of analysis methods has rarely been quantitatively documented.

As a summary, there is still a lack of study on the quantification of the different kinds of MP data uncertainties, and consistency between different datasets. The lack of knowledge on these two issues has hampered creation of common technological standards for microplastic monitoring and integrated use of multiple MP datasets for spatiotemporal pattern analysis and for model calibration and validation. The purpose of this research is two-folded: the first is to quantitatively assess a few kinds of measurement errors in the MP data which have not been well examined before, including spatiotemporal sampling error, sample volume error in the trawl data due to neglecting surface water flow; the second is to investigate consistency of MP data in multiple datasets, related to both sampling and analysis methods. In section 2, methods and data used in the study are described. The results on the uncertainty estimation and consistency between different datasets are given in section 3. Based on the findings, discussions are made on some technical issues and recommendations are given for using multiple observation datasets for large scale MP observation studies in section 4. Conclusions are given in section 5.

2 Methods and Materials

2.1 Spatiotemporal Sampling Error Analysis

Spatiotemporal sampling error is the uncertainty raised when using a local observation to present the mean value of a spatiotemporal sampling box. It reflects the level of small scale variability of the measured parameter and representativeness of the observation. For a given spatiotemporal sampling box, the relative sampling error 𝞮 can be defined as

$\begin{array}{ll}ϵ=SD/Mean& (1)\end{array}$

Where “SD” is the standard deviation and “Mean” is the mean value of the measured parameter in the box.

The sampling error can be estimated by using high density and frequency observations, such as satellite measurements for sea surface temperature (She and Nakamoto, 1996; She et al., 2007). In this study, the spatiotemporal box is defined as 15km by 15km in space and 24hours in time. First, we search available observations in the defined sampling box. If multiple observations are available in the same box, they can be used for estimating the sampling error.

Datasets from TalTech cruises, EU H2020 CLAIM (Cleaning Litter by developing and Applying Innovative Methods in European seas) project and Schönlau et al. (2020) have replicated trawl samples or spatially close samples which are suited for the local sampling error calculation. Sampling locations of the three datasets are shown in Figure 1.

FIGURE 1

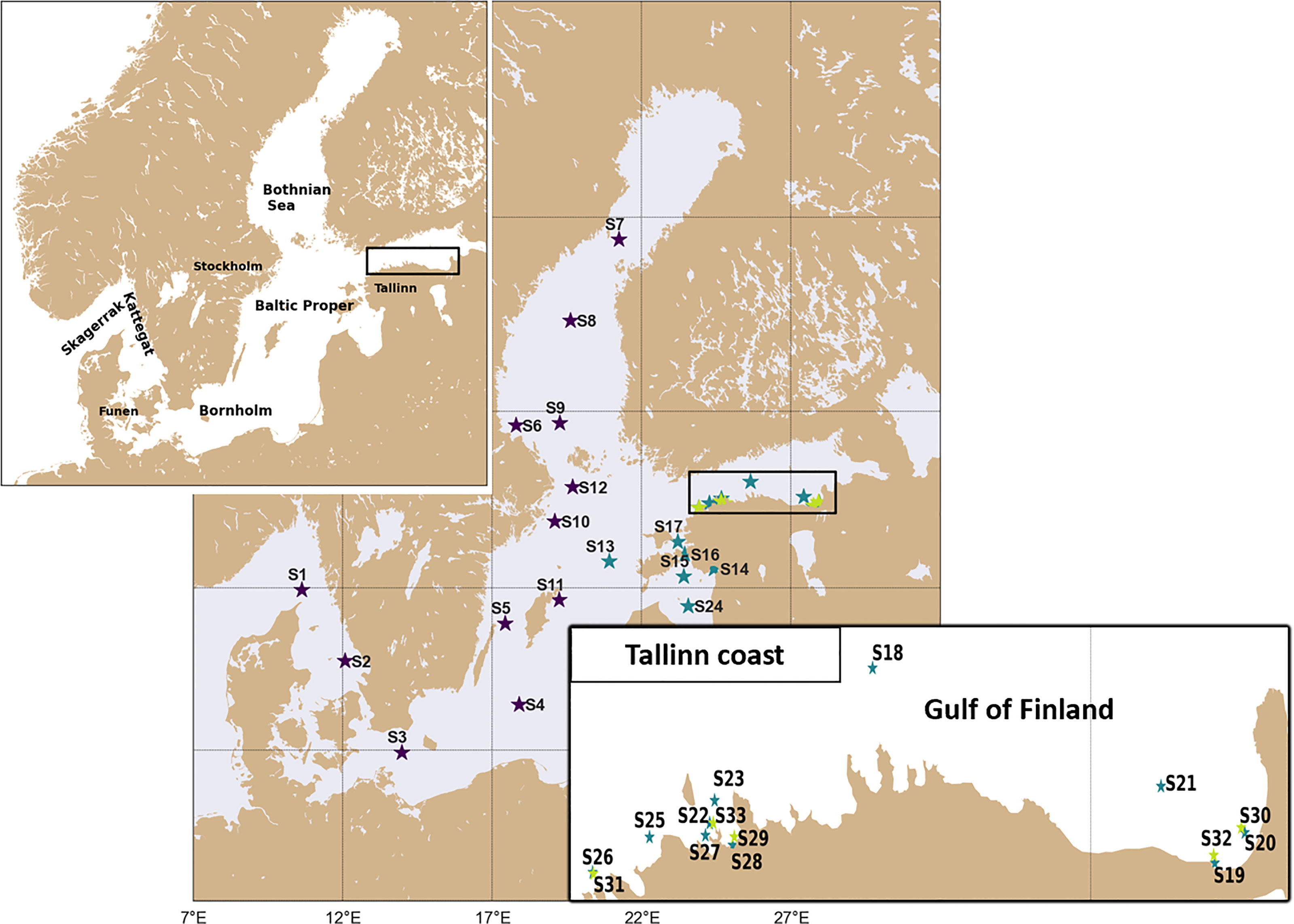
Figure 1 Station locations and IDs from three microplastic datasets: CLAIM dataset - green; Data from Schönlau et al. (2020) - black and TalTech dataset - blue. Locations and station names are given in Table S1 in Supplementary Material.

The TalTech microlitter monitoring data were collected in 2016-2020, mainly during April – October. Microlitter monitoring was carried out using a research vessel Salme with a manta trawl with mesh size of 330 µm, in the eastern Baltic Sea in a geographical area (20.9-28.0°E, 57.6-59.9°N). Microlitter samples were collected at 16 stations (Figure 1). In total 122 data points were collected. A detailed introduction to the TalTech dataset can be found in Mishra et al. (2022). In total, 42 sampling boxes are identified with two data per box from the Taltech dataset (Table 1). Some locations have three replicated data, in such a case, three data pairs are obtained by blending different data.

TABLE 1

Table 1 Microplastic datasets used in sampling error calculation.

In the CLAIM project, two field campaigns were carried out in the Gulf of Finland with a manta trawl: one in 24/9/2018 and the other in 17/4/2019. During each cruise, two replicate samples were taken at each of the five stations (Figure 1), among which four of them overlapped with TalTech stations. The samples were collected with a manta trawl with varying mesh sizes from 100 to 330 µm. When using these data to estimate the spatiotemporal sampling error, the differences due to particle size were also included. Data from Schönlau et al. (2020) consist of MPP and MPF concentrations in the Baltic Sea scale with replicates at 12 stations (Figure 1). The datasets used in sampling error calculation are summarized in Table 1.

2.2 Uncertainty in Volume Estimation in Trawl Method

One major error in the trawl method is the uncertainty in measuring and calculating the water volume through the net. In practice, the water volume V is calculated from

$\begin{array}{ll}V=L\ast S_{net}& \text{(2a)}\end{array}$

Where L is the towing distance and S_net the open area in the mouth of the manta trawl. The formula assumes that the manta trawl is always below the water surface. In many cases, there is no flowmeter attached to the manta trawl, thus, the surface water movement from currents and Stokes drift is neglected. In such a case, missing water flow will affect the final results of the water volume calculation and then estimated MP concentration. Karlsson et al. (2020) observed that concentrations of microlitter in the trawl samples were sensitive to the trawl direction, i.e., the samples that were sampled in the same direction had similar concentration values. This may reflect the impact of water flow. In this study, simulated hourly surface currents and wave-induced Stokes drift are used to calculate the impact. First, for a given sample, the surface currents and Stokes drift are projected on the ship transection. Then a corrected sample volume can be calculated:

$\begin{array}{ll}{V}_c=\left[W_{ship}+ W_c\ast cos {\theta }_1+ W_s*cos {\theta }_2\right]\ast S_{net}\ast T& \text{(2b)}\end{array}$

Where V_c is the corrected sample volume, W_ship is the ship speed, T the towing time, W_c the surface current speed, W_s the Stokes drift, θ₁ and θ₂ the angles between ship direction and surface currents and Stokes drift, respectively. In practice the hourly surface currents data are obtained from an operational three-dimensional ocean forecast which are provided by Danish Meteorological Institute, and the hourly Stokes drift data are extracted from Copernicus Marine Environment Monitoring Service (CMEMS) wave forecast product (Lindgren et al., 2020). With this information, we can make corresponding corrections on sample volume estimation and also the final estimation of the MP concentration.

The flow correction is applied to the TalTech dataset in 2016-2020 to estimate its impact on the volume and concentration estimation.

2.3 Uncertainty Related to the Analysis Methods

The uncertainty in the analysis can be studied either by estimating different types of analysis error in an individual dataset, e.g., MPP or MPF counting errors in the trawl method or intercompare analysis results from using different analysis methods on the same samples. During the two cruises in September 2018 and April 2019, the TalTech and CLAIM datasets are sampled closely in space and time and locations but analyzed with different methods. The TalTech data was derived from visual counting together with the hot needle test. The CLAIM data was derived by using the visual counting coupled with the FTIR analysis. Both datasets applied blank sample calibration but with different standards. TalTech blank sample is used as a reference and it was found that only a few percentage uncertainties were attributed to the filter contamination. CLAIM partners, however, applied a very strict blank sample test. If one color of MPF was found in the blank sample, MPF with this color was counted as zero. Due to this reason, MPF data in CLAIM are not used in the analysis. The data are displayed in the supplementary materials (Table S2). One can find that, at each location, there is one observation using visual counting together with hot needle test and two observations with different mesh size using visual/FTIR method. The two datasets are inter-compared and potential reasons for their differences, such as spatiotemporal sampling uncertainties, mesh size, local singularities and the analysis methods, are analyzed.

2.4 Consistency in Data and Datasets

In this part, several issues, including self-consistency of data in individual dataset, consistency between multiple datasets with same monitoring method and with different monitoring methods, are investigated. Mean or median, relative standard deviation (RSD), i.e., standard deviation (SD) divided by mean as well as outlier data are estimated and analyzed both within individual dataset and between multiple datasets. Considering the significant leaking effect of MPFs, MP litter is divided into two groups: MPFs and MPP. In addition to mean and RSD, consistency of MPF fraction, i.e., percentage of MPF in total amount of MP litter, is also investigated.

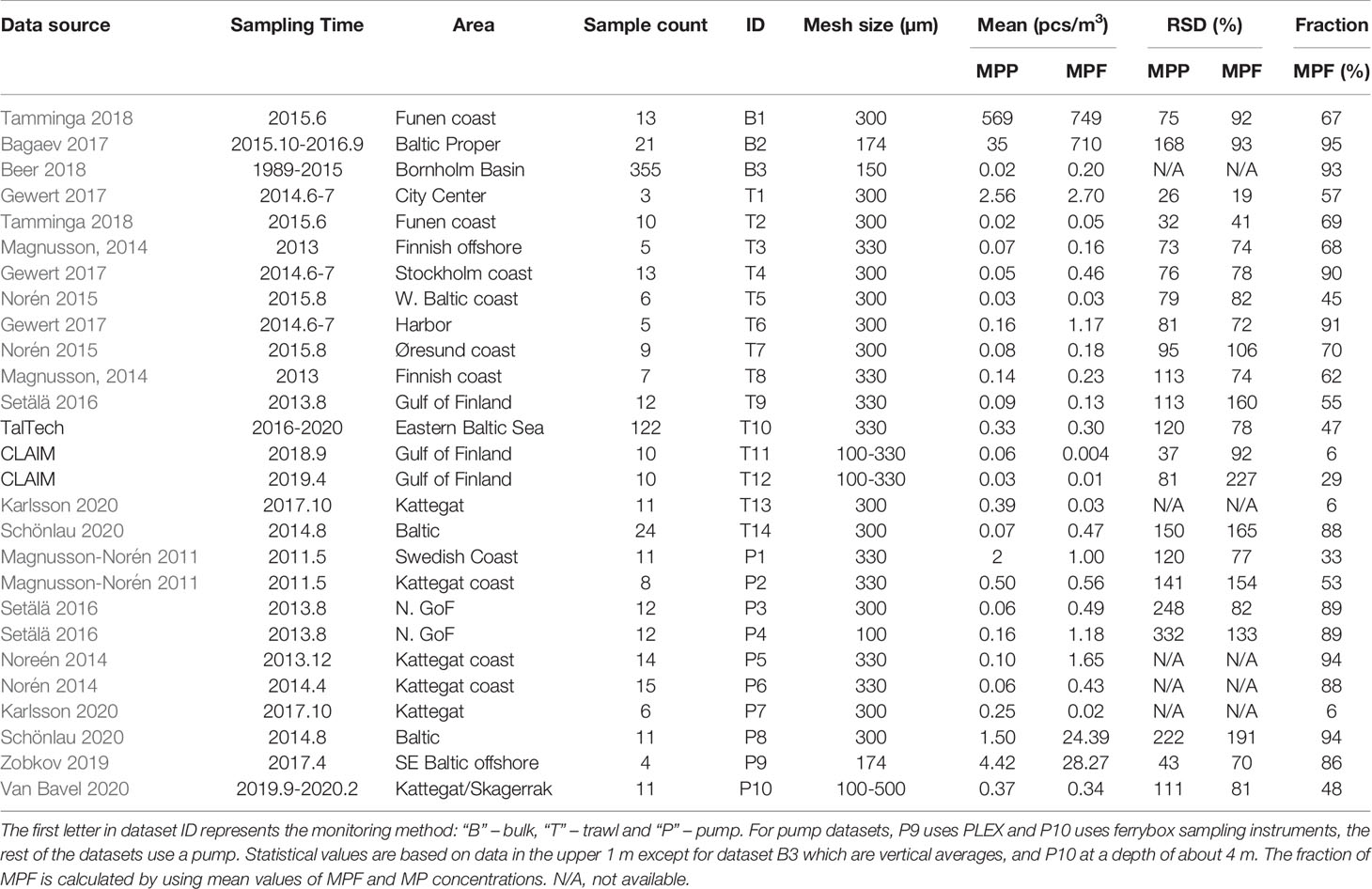
To quantitatively analyze consistency in multiple datasets, in addition to TalTech, CLAIM and Schönlau et al. (2020) datasets, more than 20 other research datasets were also collected from existing publications and used (Table 2), among which 14 datasets use trawl method, 10 use pumping and 3 use bulk method. For some datasets, raw data are not available, thus only mean value and MPF fraction are cited. Only observations from upper 1 m with mesh sizes >100 µm are considered in the present study.

TABLE 2

Table 2 Multiple microplastic datasets and statistics.

3 Results

3.1 Spatiotemporal Sampling Error Analysis

The sampling error is estimated using 64 data pairs sampled in spatiotemporal boxes of a few kms by hours. With 42 data pairs from the TalTech dataset, the sampling error is calculated for concentrations of MPP, MPF, MP and ML. It is found that ML has the least mean sampling error that is 25%, MPP has the largest which is 40% and MP and MPF with 36% in between. This is true for each of the five years (Figure 2). The standard deviation of the sampling error also shows a similar feature as the mean sampling error: 19% for ML, 23% for MP, 27% for MPF and 30% for MPP (Table S3). Considering that MP is retrieved from ML, and MPP/MPF are retrieved from MP, the escalated mean sampling error from ML to MPP reflects that sampling uncertainties increase with the amount of particles per sample. There is an interannual variability of the sampling error: 2020 has the smallest sampling error and 2018 has the largest, which is true for all four types of litter except that the highest MPF sampling error is found in 2019 (Figure 2). Reasons for this variability are not yet known. It is noted that the number of data pairs and the size of the boxes where the data were sampled are also different. Half of the data pairs are replicated samples in 2017 while other years have less data pairs and larger box size for sampling error estimation (Table 1). It is also found that sampling errors of MPP and MPF are not correlated although MPP concentration is correlated with MPF concentration (correlation coefficient = 0.55, p-value <0.0001). The uncorrelated spatiotemporal sampling error between MPP and MPF indicates that their spatiotemporal variability is independent on a small scale.

FIGURE 2

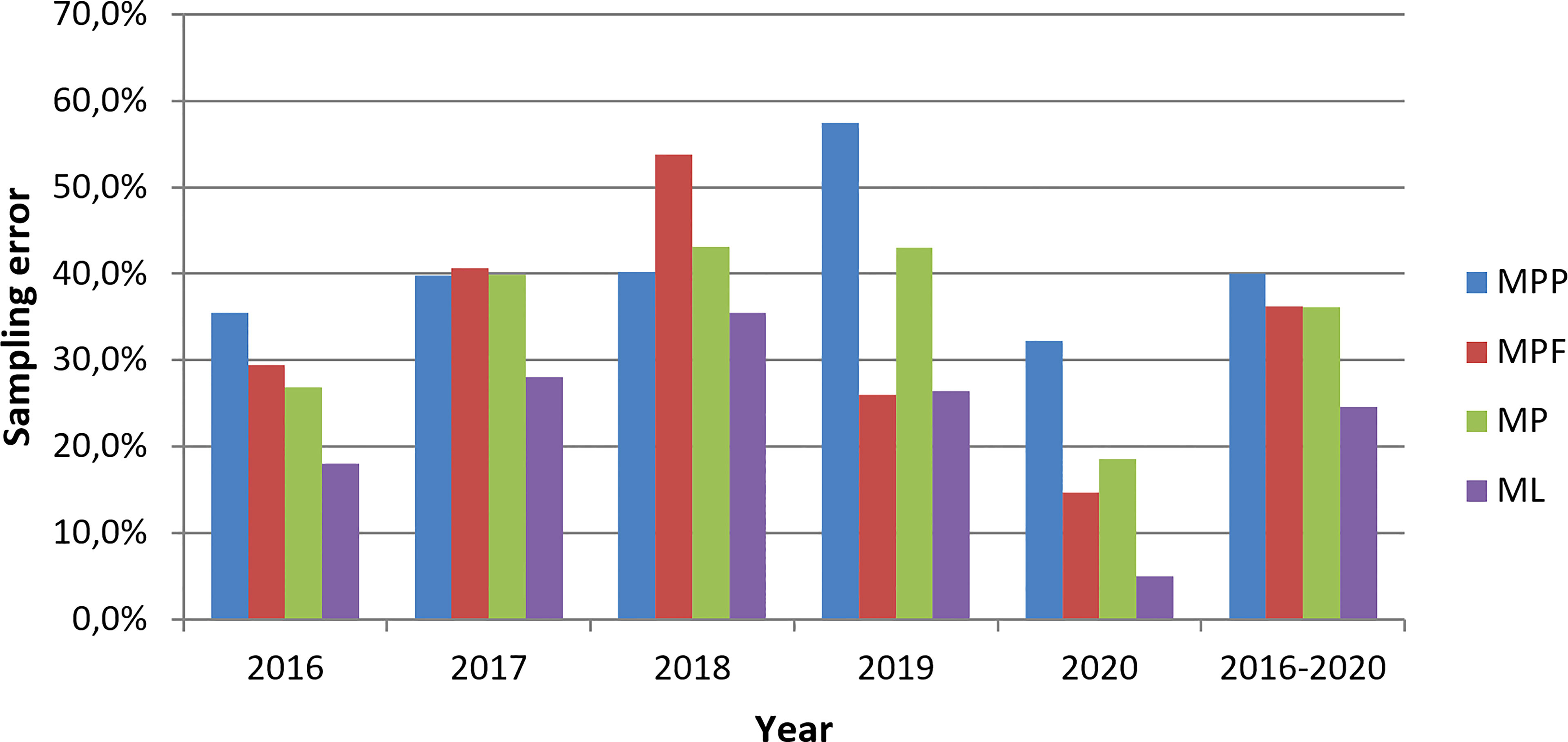
Figure 2 Yearly spatiotemporal sampling error estimated from TalTech data during 2016 – 2020 for ML (microlitter), MP (microplastics), MPF (microplastic fiber) and MPP (non-fiber microplastic) concentrations.

The frequency distribution of the sampling error from the TalTech data is shown in Figure 3, which gives richer information on the frequency of the sampling error in 0.1 sampling error intervals. It shows that more sampling error values are found in the lower end: about 75% of the samples have a sampling error smaller than 40%. However, since the sampling error is calculated as a percentage of concentration differences between the sample pairs to the mean concentration, the sampling error can be sensitive to very small concentration values which may lead to high values of the sampling error. There are indeed a few sampling error values found in the high end (Figure 3). This is also reflected by the fact that the annual medium sampling error is 10-16% lower than the mean value (Table S3).

FIGURE 3

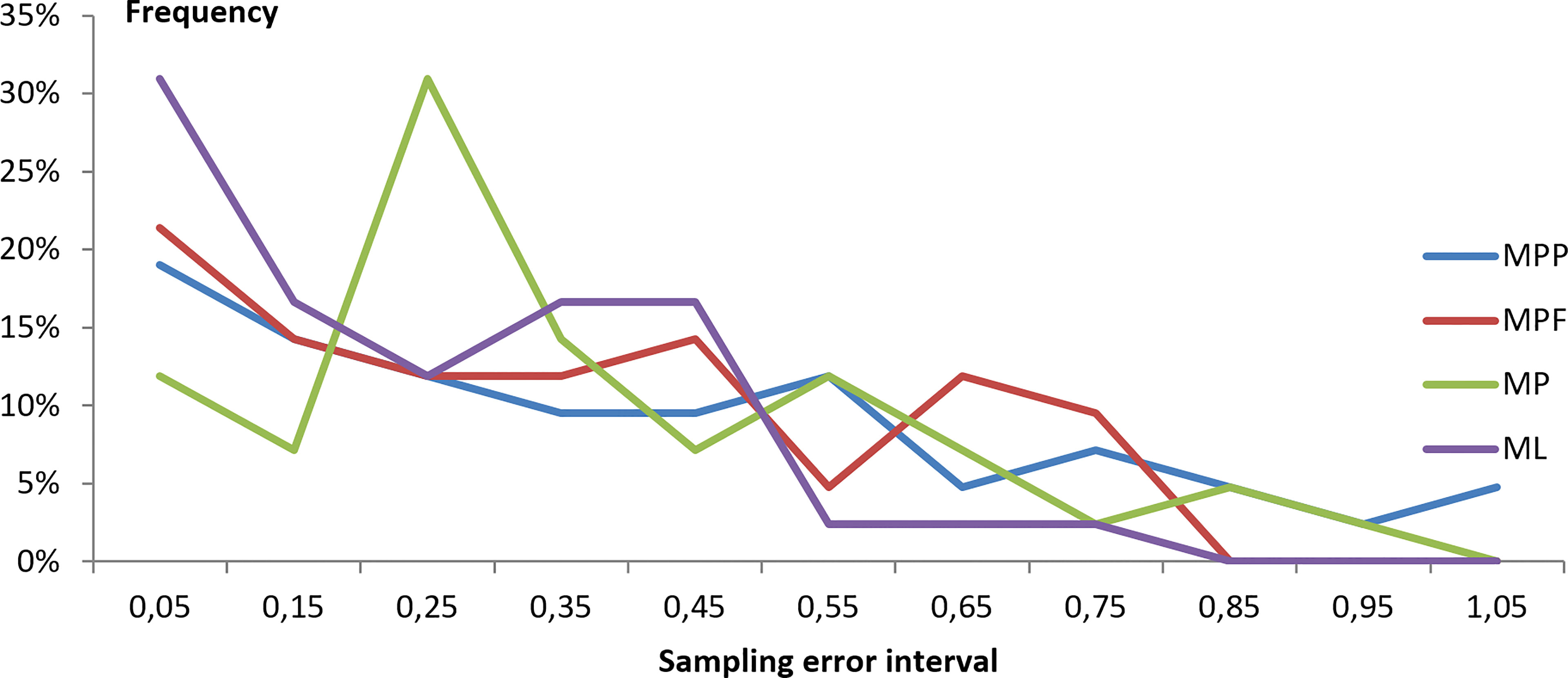
Figure 3 Frequency distribution of sampling error in the sampling boxes of a few kilometers by a few hours from TalTech data. The frequency is calculated for a sampling error bin of 0.1 interval.

With the CLAIM dataset, the MPP sampling error is estimated for samples obtained from 2018 and 2019 cruises. The CLAIM data gives a MPP sample error of 33.8% and 77.0% for 2018 and 2019, respectively, which is comparable to the ones obtained from the TalTech data, i.e., 47.2% and 50.5% (Table S2). Such a difference is understandable as TalTech samples use the same mesh size of 330 µm while CLAIM samples use three different mesh sizes: 100 µm, 200 µm and 330 µm.

In addition, sampling error is also estimated by using MP measurements in Schönlau et al. (2020). The data cover Swedish waters in Baltic Sea, Kattegat and Skagerrak in August 2014 (Figure 1). The sampling error estimated from the trawl dataset is 54% for MPP concentration which is at a similar level as obtained from CLAIM and TalTech datasets in 2018 and 2019 (Table S3). For MPF concentration, data from Schönlau et al. (2020) gives a mean sampling error of 52%, which is comparable to the highest yearly mean sampling error in TalTech data, i.e. 53.8% in 2018 (Table S3).

3.2 Impact of Water Flow on MP Concentration Estimation

The impact of the water flow on the MP concentration estimation is determined by the amplitude and direction of surface currents, Stokes drift and ship movement. The water volume and MP concentration of the TalTech dataset was re-calculated by using hourly surface currents and Stokes drift from the ocean and wave models. The mean relative correction of the MP concentration is 12.1% ± 12.2% and the individual correction varies between -0.55 – 0.58 pcs/m³, with a mean of -0.0046 pcs/m³. Occasionally, in rough conditions with high surface current speed and wave-induced Stokes drift, the correction can be 40% high of the measured concentrations. The linear correlation between the original and corrected MP concentration is 0.97, thus the correction does not change the statistical features e.g., temporal variability of the dataset, as shown in Figure 4.

FIGURE 4

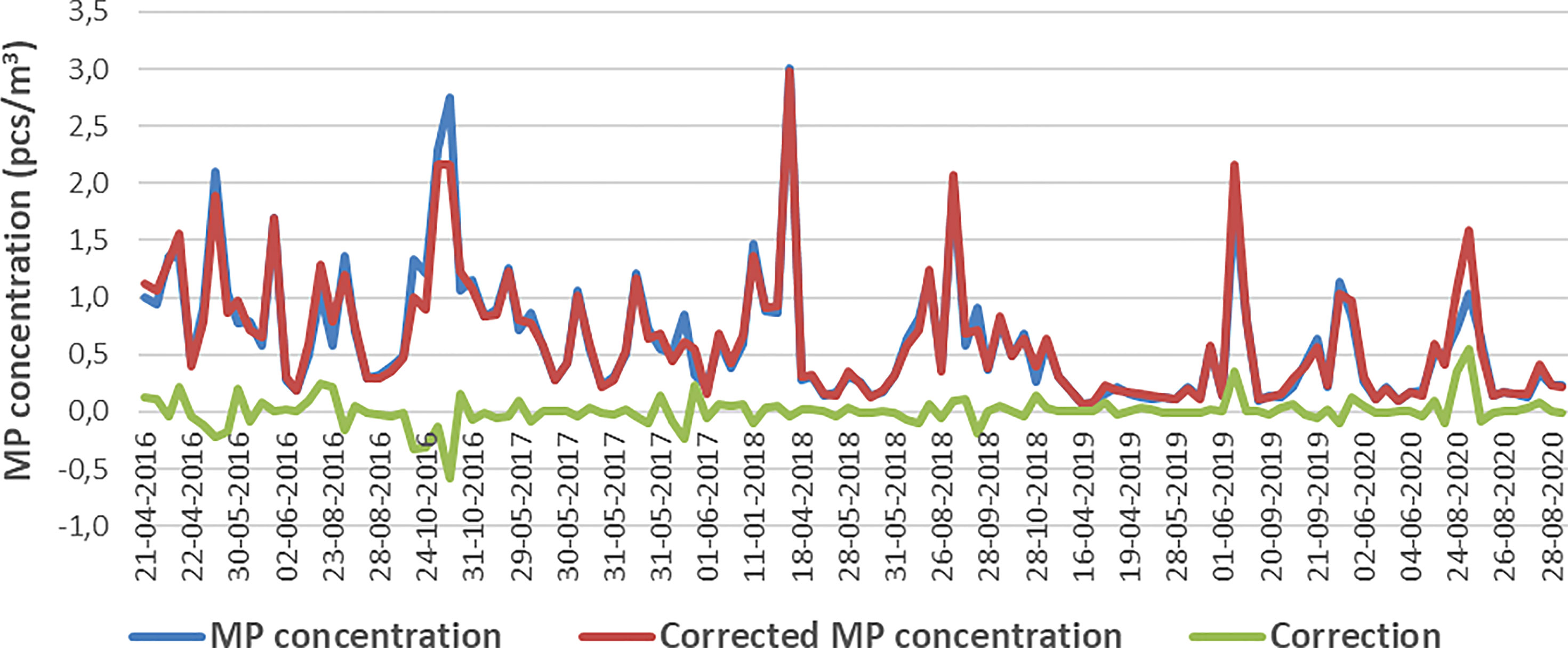
Figure 4 MP concentrations from TalTech dataset during 2016-2020: blue – original estimation by using ship distance; red: corrected estimation by considering the surface currents and Stokes drift; green: the corrections.

3.3 Uncertainties Related to Analysis Method

Here we focused on the difference between visual counting method and visual/FTIR analysis method by comparing the sample pairs from TalTech and CLAIM datasets. The samples were collected at almost the same time and location but analyzed with visual counting with hot needle test for TalTech samples and visual/FTIR method for CLAIM samples. Using TalTech-CLAIM data pairs in Table S2, it is found that, for MPP concentration, the mean value of TalTech data is 7.4 times higher than CLAIM data in 2018 and only 60% higher in 2019, based on data in Table S2. The higher MPP concentration in TalTech data cannot be explained by differences in mesh size as CLAIM samples were measured with smaller meshes than TalTech. Can this difference be explained by spatiotemporal sampling error? As shown in Table S3, the sampling errors of MPP concentration are 34-40% in 2018 and 58-77% in 2019, thus the difference of MPP concentration between the two datasets in 2019 (i.e., 60%) is within the range of the sampling error. It is therefore to suggest that the MPP concentration difference caused by the analysis methods in 2019 may be small, compared to the sampling error. However, the difference in 2018 is well beyond the range of sampling error thus cannot be explained by the sampling error. The largest differences for 2018 data is found between station Prita (1.463 pcs/m³) and 57a (0.073m³). Pirita sample was taken exactly from the river mouth to estimate the microplastic inflow from Pirita river and yacht harbor. Station 57a, also close to station Prita, is in the inner bay. Considering that the pollution transport in this area largely depends on the highly variable currents in the river mouth, the difference between the CLAIM and TalTech data in 2018 may be partly explained by the local variability.

3.4 Differences in Data Measured With Multiple Mesh Sizes

The lower limit of the particle size selected in this study is set as 100 µm since this will widen the data coverage. In the 27 datasets compiled, seven of them have a size lower limit below 300 µm. We have combined these datasets in the analysis. A natural question to ask is how much differences will be caused by using different mesh sizes above 100 µm? With the CLAIM data, we found that the differences between data using different meshes are not statistically significant. In total, the CLAIM datasets (T11 and T12 in Table 2) have 20 data samples at five stations measured from two cruises. At each station, two replicate samples were collected, but with different mesh sizes. The data can be divided into two groups. In Group I, the samples used 200 µm and 300 µm meshes while in Group II, 100µm and 200µm mesh sizes were used. The two-sample t-test (Snedecor and Cochran, 1989) is used to determine if two population means are equal. It is found that the difference of mean MPP concentration between data groups with different mesh sizes is not significant (p values >>0.05), in both data groups (Table 3).

TABLE 3

Table 3 Inter-comparison of microplastic datasets using nets with different mesh sizes.

This issue can also be investigated by using the pump data. The pump data from Setälä et al. (2016) were measured with mesh size of 100 and 300 um, each with 12 samples (datasets P3 and P4, Table 3). This allows a similar analysis to the CLAIM data. It is found that differences between the two datasets are much larger than those obtained in the CLAIM datasets. However, due to high standard deviation in the data samples, such a difference is not statistically significant (p value >> 0.05). Similar analysis can also be made for ferrybox data from NIVA Denmark (data ID – P10, Van Bavel et al., 2020) but with 100 µm and 500 µm mesh sizes. For 11 samples, the total number of collected MP particles are 20 for the 100 µm mesh size and 18 for 500 µm mesh size. Again, the difference of the two dataset is not statistically significant (p value >> 0.05).

3.5 Variability in MPF Measurements

3.5.1 MPF Concentration

Existing research (Setälä et al., 2016; Tamminga et al., 2018; Schönlau et al., 2020) has shown that the trawl method measured significantly less MPF concentration than the pump and bulk methods. This is further confirmed as a general feature by comparing the 14 trawl datasets and 10 pump datasets. The median MPF concentration in the 10 pump datasets is 4.6 times as much as that from the 14 trawl datasets (Figure 6); among 10 datasets with the highest MPF concentrations, only two use the trawl method, suggesting that the latter may leak more MPFs than the non-trawl methods.

More detailed features on MPFs can be revealed from the TalTech dataset during 2016-2020. It is found that MPF concentration is actually less variable than MPP concentration. The relative standard deviation during 2016-2020 is 120% for MPP concentration and 78% for MPF concentration, respectively. In addition, ML concentration is linearly correlated with MPF concentration (Figure S1). This means that when more ML particles are collected in a sample, there is a tendency to collect more MPFs. However, this is only partly true for MPP (Figure S2). When MPP concentration is <0.5 pcs/m³, part of the samples can have quite high ML concentration (> 2 pcs/m³) and MPF concentration.

3.5.2 MPF Fraction

The MPF fraction represents the relative amount of MPFs detected in the total amount of MP particles. It shows a large variability ranging 6 – 95% in the 27 datasets used in Table 2, which can be categorized into three groups: five datasets have MPF fraction below 35% and 11 datasets in 45-70% and the other 11 datasets in 85-95%. On average, the MP fraction is 64% ± 29%. Among the five datasets with less than 40% of MPF fraction, the low MPF fraction in two CLAIM datasets (T11 and T12) is caused by the counting methods used, which removed the fibres with colors occurring in the blank sample. The P1 dataset from Magnusson and Norén (2011) measured extraordinarily high MPP concentration, hence the MPF fraction is low. The additional two low MPF fractions are from Karlsson et al. (2020), in which the MPF concentrations were quite low (0.017 – 0.026 pcs/m³). The 11 datasets with MPF fraction > 70% can be divided into two categories: the first category measured very high MPF concentrations (24.4-710 pcs/m³), containing 3 datasets B2, P1 and P10; the second category has MPF concentrations in an ordinary range (0.195-1.175 pcs/m³), containing eight datasets (Table 2).

The pump and bulk datasets measure much higher MPF fraction than the trawl datasets. If only considering the 24 datasets with MPFs >10%, two thirds of the bulk and pump datasets have a high MPF fraction between 85-95% but only one fourth of the trawl datasets fall in this range.

Details of MPF fraction can be investigated with a more homogeneous, long-term dataset from TalTech in 2016-2020. The 122 samples give a mean MPF fraction of 47%. It is found that MPF fraction differs greatly in samples with extremely high or low MP concentration. For 10 samples with the highest MP concentrations, the mean MPF fraction is 34%; while for the 10 samples with the lowest MP concentrations, the MPF fraction is 72%. This suggests that the observed MPF distribution is more homogeneous than the MPP in the collected microplastics: when measured MP concentration is very high, the majority of the microplastics detected is particles (fragments); when measured MP concentration is very low; the majority of the measured microplastics is fibres (figures not shown).

3.6 Consistency in Multiple Datasets

3.6.1 Self-Consistency of Data in an Individual Dataset

Although a single dataset is often regarded as self-consistent since the same monitoring method and standards are applied, however, due to differences in natural variability, sampling errors, instrument errors and analysis errors in the samples, there can be outliers on the individual dataset. It is also expected that some datasets are less consistent than others are.

Outliers in a single dataset can be identified using a Grubbs’ test (Grubbs, 1969) if the population of the dataset is regarded as valid. They are often valid observations but just significantly differ from the majority of observations. For example, Magnusson and Norén (2011) measured MP concentrations in the Swedish coastal waters with a pump and filter mesh size of 300 µm. Among 21 valid samples, one sample shows a high MPP concentration of 13 pcs/m³ while the rest of the samples have a mean MPP concentration of 1.37 ± 2 pcs/m³. The particles in the outlier are identical, yellowish-white and oval, approx. 500 μm * 300 μm in size. These were found nowhere else and no explanation for their origin was given. In another occasion, Norén et al. (2015) measured 7.97 and 35.03 pcs/m³ for MPP and MPF concentrations, respectively at a station near a pollution source while the rest of the 15 stations showing 0.059 ± 0.068 pcs/m³ for MPP concentration and 0.116 ± 0.168 pcs/m³ for MPF concentration. In observation analysis, the outliers in an individual dataset can significantly change the statistical features of the dataset, so they should not be jointly used with the other data.

RSD is one of the measures of self-consistency in individual datasets. Lower RSD may suggest a high self-consistency in the data. Figure 5 displays RSD of MPP concentration from 22 datasets, including 13 trawl datasets, 7 pump datasets and 2 bulk datasets. Half of the 22 datasets have RSD < 100%. The other half of the datasets has an RSD ranging 111-332%.

FIGURE 5

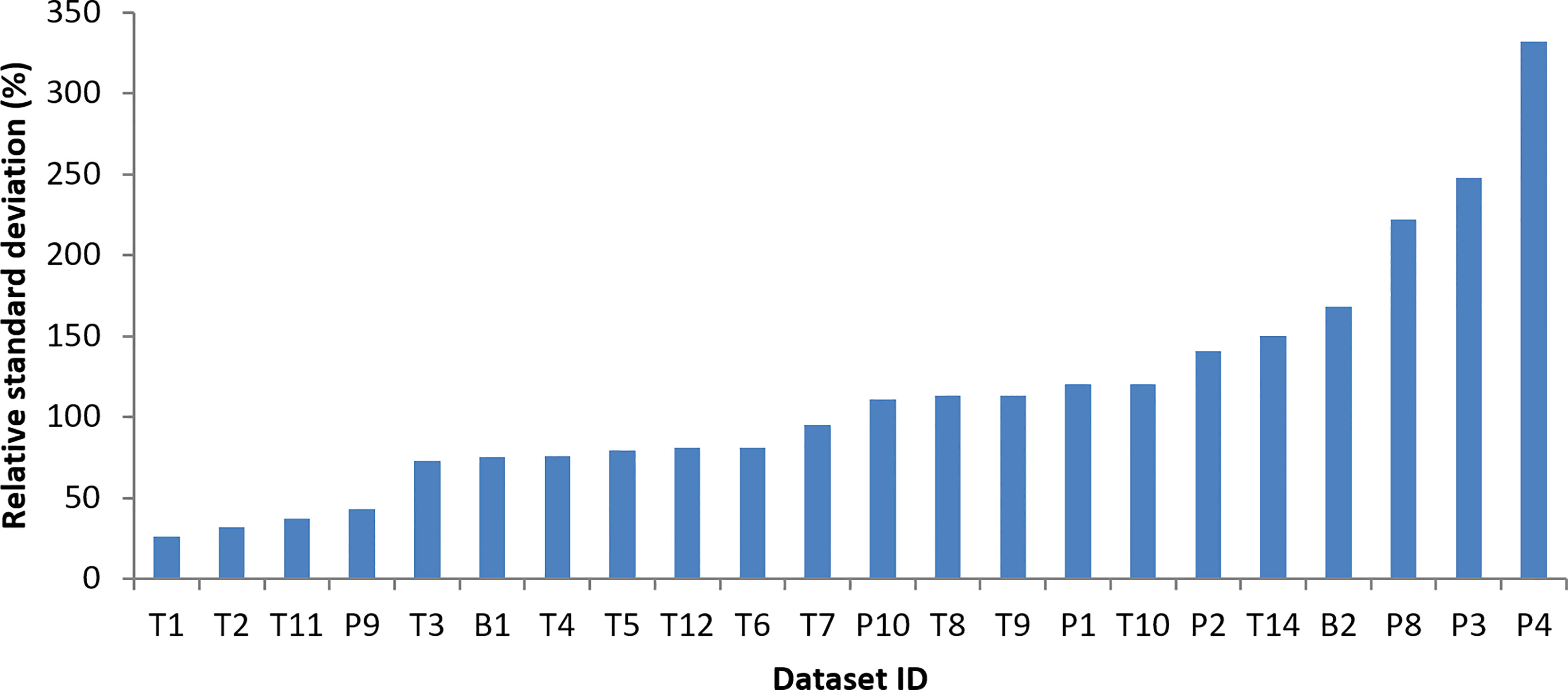
Figure 5 Relative standard deviation of microplastic particle concentration derived from 22 microplastic datasets.

It was found that, among the eight highest RSD values, only two of them are derived from trawl datasets (T10 and T14): one is TalTech (T10) and the other is from Schönlau et al. (2020). Their high RSD values can be attributed to their highest spatial and/or temporal coverage of the dataset: T10, TalTech data, covers a 5-year period in Gulf of Finland, Gulf of Riga and Northern Baltic Proper and T14, from Schönlau et al. (2020), covers a wide area from Skagerrak to Bothnian Sea. When a sub-dataset in a smaller geographic area and less number of years is used, e.g., for a sub-dataset of TalTech data on a cruise in the Gulf of Finland, it is found that RSD can be reduced significantly to 60-70% (results not shown).

High RSD values in the pumping and bulk datasets indicate that these datasets are of more randomness than the trawl datasets. Due to small sampling volume, normally a few cubic meters of water, pump samples have more false zero measurements than the trawl samples, which can be an important reason for the high RSD values in the pump datasets.

3.6.2 Multi-Dataset Consistency

The first step is to divide multiple datasets with the same monitoring method into multiple populations or categories so that datasets in one population are consistent and inter-comparable, i.e., the mean value difference between different populations is maximized and variance within one population is minimized. Then the populations from trawl and pump datasets can be compared.

3.6.2.1 Trawl Datasets

14 trawl datasets can be divided into two populations: one with larger mean value and the other with smaller mean value. For MPP concentration, the population with large mean contains only dataset T1, with a mean value of 2.56 pcs/m³. Samples in dataset T1 were collected in Stockholm city center waters (Gewert et al., 2017), which are not representative of coastal and open sea water conditions. The population with small mean contains the remaining 13 datasets with a mean ± SD of 0.12 ± 0.12 pcs/m³ and a range of 0.02 - 0.39 pcs/m³. This population represents MPP conditions in the Baltic Sea measured by trawl method.

For MPF concentration, due to different counting methods for MPFs, the two CLAIM datasets (T11 and T12) should not be used in the consistency analysis. Similarly, the rest 12 datasets can be divided into two populations: datasets T1 and T6, measured in Stockholm city center and harbor waters (Gewert et al, 2017) constitute the population with large mean 1.94 pcs/m³; the rest 10 datasets fall in a population with smaller mean ± SD 0.20 ± 0.16 pcs/m³, representing MPF condition measured by trawl method in Baltic Sea.

3.6.2.2 Pumping Method

10 datasets use pumping method, including one using PLEX (P9) and another using Ferrybox (P10). The 10 datasets can also be divided into two populations, one with a smaller mean and one with a larger mean. For MPP concentration, datasets P1, P8 and P9 form a large-mean population with a mean ± SD of 2.64 ± 1.562 pcs/m³ and a range of 1.5 – 4.42 pcs/m³, and the remaining 7 datasets form a small-mean population with 0.21 ± 0.17 pcs/m³ and a range of 0.06 – 0.5 pcs/m³.

For MPF concentration, P8 and P9 form a large-mean population with a mean ± SD of 26.33 ± 2.74 pcs/m³, and the remaining 7 datasets form a small-mean population with 0.71 ± 0.53 pcs/m³ and a range of 0.02 – 1.65 pcs/m³.

3.6.2.3 Bulk Method

The three bulk datasets have quite different mean values. Dataset B3 contains vertical averaged MPP and MPF concentrations from a long-term sampling in 28 years in Bornholm Basin (Beer et al., 2018). It shows similar mean values of MPP and MPF concentrations as the trawl datasets (Table 2). The other two datasets, one sampled in Danish Strait and another in the Baltic Proper, give very large numbers: 35-569 pcs/m³ for MPP concentration and more than 700 pcs/m³ for MPF concentration.

3.6.2.4 Differences Between Pump and Trawl Data

Several studies have collected the trawl and pump data at the same time and location and conducted intercomparison between the two methods, including T9 and P3 collected by Setälä et al. (2016) in northern Gulf of Finland, T13 and P7 collected by Karlsson et al. (2020) at a station in Kattegat and T14 and P8 collected by Schönlau et al. (2020) in 12 stations in Skagerrak, Kattegat and open Baltic Sea. The three intercomparison studies show controversial results. Setälä et al. (2016) showed that MPF concentration from the pump data is four times as much as the trawl data but the MPP concentration of the pump data is just half of the trawl data. The pump data from Schönlau et al. (2020) resulted in notably higher concentrations than the trawl in four locations: Skagerrak, Kattegat, the Southern Baltic Proper and the Bothnian Sea. Overall, the MPP concentration was higher in pump samples than trawl samples in ten out of eleven sampling sites. MPF concentration from pump data is also 7 times higher than the trawl data. In another study, however, Karlsson et al. (2020) found that the trawl data have a bit higher concentration of MPP than the pump data.

Considering controversial results from the above intercomparison studies, it is useful to compare the multiple pump and trawl datasets. Small-mean populations represent 10-13 trawl datasets and 7-8 pump datasets. It is worthy to note that the pump datasets show higher values in mean, median and standard deviation of MP concentration than the trawl datasets (Figure 6). For MPP concentration, the pump small-mean population is 1.8 and 2.3 times as much as the trawl small-mean population for the mean and median, respectively. For MPF concentration, the pump small-mean population is 3.5 and 3.1 times as much as the trawl data for the mean and median, respectively. It should also be noted that some pump datasets could have much higher concentrations: the pump large-mean population has a mean value that is 21.9 and 132 times as much as that of trawl small-mean population, for MPP and MPF concentrations.

FIGURE 6

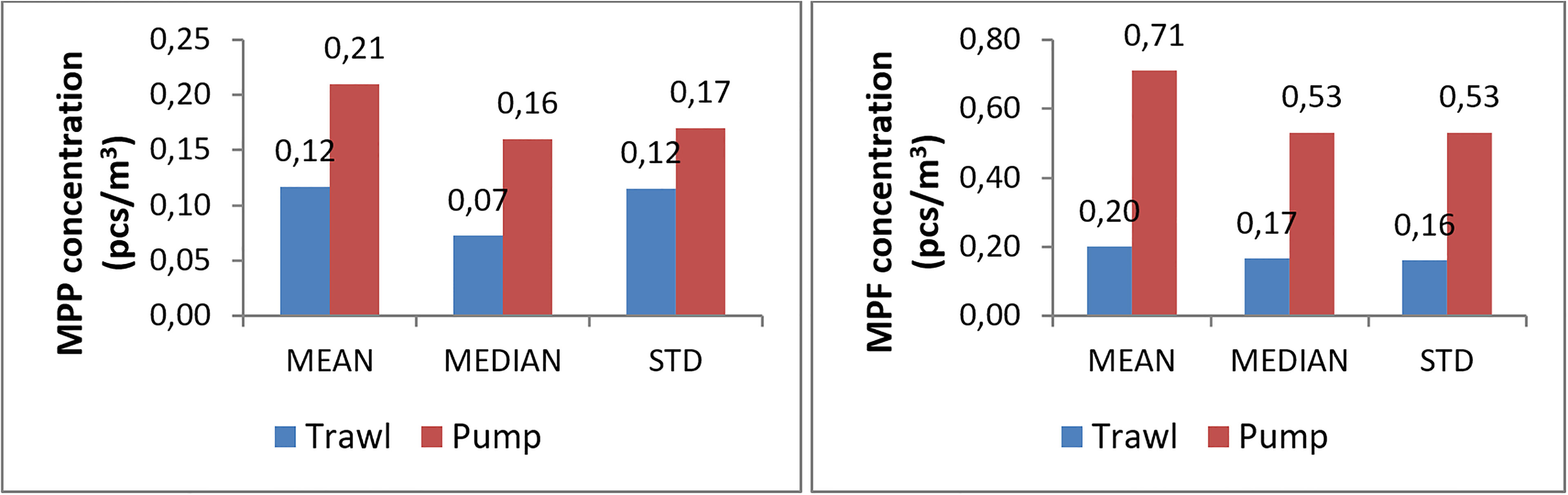
Figure 6 Mean, median and standard deviation (SD) of the multiple microplastic datasets. Left panel: MPP, right panel: MPF. Blue: trawl small-mean population, red: pump small-mean population.

4 Discussions

4.1 Compilation and Use of Multiple Datasets

In this study 27 datasets from existing research and databases are compiled and used for the consistency study, including 25 published datasets and 2 unpublished ones (CLAIM data). The datasets cover a period of 10 years (2011-2020). The seasonal distribution of the existing datasets are rather uneven: most of the datasets were measured during summer (June-September), however, few observations were collected in winter seasons (November-March). The spatial coverage of the datasets is rather wide: a basin scale survey using both trawl and pump sampling was analyzed in Schönlau et al. (2020); sub-basin scale data were collected in Setälä et al. (2016); Bagaev et al. (2017); Beer et al. (2018), TalTech (2016-2020), CLAIM (2018-2019), Zobkov et al. (2019) and Van Bavel et al. (2020); while data in harbor, estuarial and coastal waters are collected in Norén et al. (2014); Norén et al. (2015); Gewert et al. (2017); Tamminga et al. (2018) and Magnusson and Norén (2011). Data from Magnusson (2014) and Karlsson et al. (2020) are mainly local offshore observations. Among the 27 datasets, three are sampled with bulk method, 10 with pump method (including PLEX profiler by Zobkov et al., 2019 and ferrybox by Van Bavel et al., 2020) and 14 with the trawl method. It is noted that not all published data are included, e.g., trawl observations in eastern Baltic Sea and southern Gulf of Riga (Aigars et al., 2021). Adding more observations would certainly enrich the results but we do not think it will change the major outcomes of the study.

4.2 Spatiotemporal Sampling Error

The error is estimated by using observation pairs sampled in small spatial and temporal intervals by assuming that all other measurement errors (e.g., instrument and analysis errors for the individual observation pairs) are equal. Sampling error is the lowest in ML concentration (25%) and highest in MPP concentration (40-56%), reflecting impacts of the number of litter particles per sample on the sampling error. Even for replicating data pairs from CLAIM and Schönlau et al. (2020), the sampling error is in the similar level as from TalTech data. This means that such a level of randomness exists in individual MP observations, which should be taken into account when the observations are used for model validation or spatiotemporal analysis. The replicate observations include valuable information. However, there is a lack of sampling error estimation for the pump data, it is important to make such an estimation via replicate samples considering large variability in the pump data.

4.3 Impact of Different Analysis Methods

Impact of different analysis methods is estimated by comparing two datasets sampled at the similar time and locations but analyzed with different approaches: one uses visual analysis with hot needle test (i.e., TalTech dataset) and the other uses visual and FTIR analysis (i.e., CLAIM dataset). The results can be quite different when different analysis methods are used, as was found in the year 2018 cruise: the visual counting resulted in 7.4 times higher MPP concentration than the FTIR method. While in the year 2019 cruise, the difference between the two datasets is within the range of the sampling error. The differences between the two datasets consist of not only analysis error, but also spatiotemporal sampling error and differences caused by different mesh size. CLAIM data has a mixed mesh size from 100-330 µm while TalTech data has a single mesh size of 300 µm. It should be noted that this study is just a rough estimation. More strict investigation should use exactly the same samples but then analyzed by using different methods, as done by Song et al. (2015).

4.4 Consistency in Individual Dataset and Between Different Datasets

This is an important issue when using multiple MP observation datasets, e.g., for model validation or spatiotemporal pattern analysis. By using the 27 datasets, the data consistency is examined at three levels: data, individual dataset and categorized dataset for different monitoring methods. In data level, it is not so exceptional to find outliers, which can be valid data but indicate a high local MP concentration. Some outliers may not be regarded as valid data if they are below the lower limit of the detectable concentration. In the observation analysis, outliers should be treated separately as they can largely change the statistical feature of the entire dataset. For the consistency at dataset level, results show that 6 out of 8 datasets with the highest relative standard deviation are from pump and bulk methods. When using multiple datasets for joint observation analysis, it is important to use consistent datasets. Therefore both the pump and trawl datasets are divided into different populations with small and large mean values. An encouraging outcome is that, for datasets using the trawl or pump method, 10-13 trawl datasets and 7-8 pump datasets fall in small-mean populations, which can be regarded as consistent datasets. The difference of mean value of the small-mean and large-mean population are more than 10 times. By comparing the small-mean pump and trawl populations, it is found that MPP concentration of pump data is about 2 times as much as the trawl data while for MPF concentration it is more than 3 times. The large-mean pump population gives much higher differences with the small-mean trawl population.

Reasons for the significant differences between the trawl and pump datasets have been attributed mainly to the different sampling volume that leads to low representability and more false-zero samples in the pump data. However this cannot explain the systematically higher MP concentration obtained by the pump sampling. It is suggested that future research may further investigate differences on particle collection efficiency between different sampling methods.

4.5 Data Measured With Different Mesh Sizes

In this study, most of the datasets used a net with mesh size of 300 or 330 µm. However, seven datasets use mesh sizes smaller than 300 µm and the ferrybox dataset (Van Bavel et al., 2020) used both 100 and 500 µm. The results of the inter-comparison study show that the differences between datasets with different meshes are not statistically significant (p value >> 0.05). This suggests that the differences made by varying particle sizes from 100 – 500 µm are not significantly larger than other error sources such as the sampling error.

4.6 MPF Fraction

The MPF data show a large fraction of presence in the MP litter data, however, depending on the sampling methods used. Two thirds of the 13 bulk and pump datasets measured MPF fraction >85%. However, the 14 trawl datasets show much lower MPF fractions, with a majority between 45-70%. In addition, multi-datasets analysis also show that the measured MPF concentration is much more variable than the microplastic particles, ranging from 0.20 ± 0.16 pcs/m³ in the 10 trawl datasets, to 0.71 ± 0.53 pcs/m³ in the 8 pump datasets, 26 pcs/m³ in the 2 pump datasets and above 700 pcs/m³ in the two bulk datasets. The differences are so large between the three monitoring methods which cannot be explained by sampling and analysis error, or spatiotemporal variability. Potential leakage of MP litter with irregular shape may provide an explanation. With a width much smaller than the mesh size 100 µm, MPFs are typical ones which can leak from the meshes. Our results support the hypothesis that trawl sampling can lead to more leakage than the pump and bulk sampling. The leakage of MPFs presence is dependent on several factors such as clogging and entanglement which are related to mesh size and presence of biolitter etc. The leakage of MPFs may be reduced in a high microlitter concentration environment, as is shown in Figures S1, S2 where high ML concentration is positively correlated with high MPF concentration but may not with high MPP concentration.

Due to the potential leakage of MPFs in MP monitoring, MPFs may not be properly measured especially in the trawl data. It is recommended not to use existing MPF data for model validation and spatial pattern studies.

4.7 Measurement Precision and Representativeness

Measurement precision and representativeness is less addressed in this paper but a general analysis can be given for particle size > 100 µm. As pointed out by Karlsson et al. (2020), in order to be statistically representative, a sample should contain a sufficient number of MP particles which was 26 in their case. For trawl monitoring with a set of typical parameters, e.g., ship speed of 2 knots, towing time of 15 - 60 minutes and a net opening size of 60 cm by 17 cm, a minimum MP concentration of 0.07 - 0.28 pcs/m³ has to be reached. For pump samples, with the water volume of 2 – 10 m³, the number of particles collected by pump method is lower than 26 per sample. A more straightforward measure for the measurement precision is the lower limit of the detectable MP concentration. If MP concentration is below this limit, the sample will contain zero particles. With the typical monitoring setup mentioned above, the lower limit of the detectable MP concentration is 0.003 – 0.012 pcs/m³. When the pump method is used, the lower limit of the detectable MP concentration is 0.1 – 0.5 pcs/m³ corresponding to a sample water volume of 2 – 10 m³. For the bulk method, normally 10 liters of water is sampled. This corresponds to a lower limit of the detectable MP concentration of 100 pcs/m³. This is also why, in general, for microplastic particles, the pump data have much more false zero samples than the trawl data and bulk data have even more false zero samples than the pump data. In principle, if the real MP concentration is lower than the lower limit of the detectable MP concentration, the sample should not be regarded as a valid one for representing the condition in the sampling time and location. However, the sample can be used to generate valid mean values with other samples.

It is recommended that future microplastic monitoring in the sea should further improve and harmonize the monitoring and analysis standards so that data from the pump and trawl methods are comparable and wide particle size spectrum should be resolved so that the leakage of pliable and irregular shape microplastic litter is no more a major issue.

5 Conclusions

With 27 MP observation datasets compiled from existing publications and projects in the Baltic Sea, uncertainties and consistency in surface MP measurements with particle size > 100 µm are investigated by using multiple observational datasets. Specific issues related to sampling error, instrument error, analysis error, variability in MPF measurements, and data consistency within individual dataset and between different datasets, are explored.

Spatiotemporal sampling error reflects randomness of data due to small errors in sampling location and time. Based on 64 data pairs from the trawl datasets of TalTech, CLAIM and Schönlau et al. (2020), it is found that the sampling error is the least for ML concentration (25%), increase to 36% for MPF and MP concentrations and 40-56% for MPP concentration.

The surface currents and wave-induced Stokes drift have an impact on the sample volume estimation, which has not been taken into account in previous studies. The error in the sample volume in the trawl monitoring due to neglecting water flow impacts is estimated by using operational model data and the five-year TalTech dataset. This leads to a correction on MP concentration of about 12% in the calm weather conditions. In the high sea, the flow correction can be up to 40% or more.

Variability of MP concentration due to changing mesh sizes from 100 – 500 µm is also examined using multiple datasets. The results showed that the differences between datasets with different mesh sizes are not statistically significant.

The multiple datasets show both consistency and inconsistency in MP concentrations. The data from an individual dataset are often self-consistent. Within one data category, i.e., using the same sampling method, more than 70% of the datasets can be regarded as statistically consistent, with relatively small mean MP concentration. Up to 30% of the datasets may be regarded as statistically inconsistent, with mean MP concentration 10 times larger than the consistent datasets. In addition, datasets between different categories are significantly inconsistent, reflected in MP, MPF and MPP concentrations, and MPF fraction. This inconsistency is mainly caused by different sampling methods, e.g., trawl and pump sampling. The dataset inconsistency can also be caused by using different analysis methods, e.g., visual and FTIR methods, as shown in the inter-comparison of two datasets sampled at the similar time and locations but analyzed with different approaches: one uses visual analysis with hot needle test (i.e., TalTech dataset) and the other uses visual and FTIR analysis (i.e., CLAIM dataset). However, the reasons are still unknown for the occurrence of this analysis method-related difference.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

JS developed the underlying framework, data analysis methods and first draft of the manuscript, collected data and conducted multi-datasets preprocessing, sampling error analysis, uncertainty and consistency analysis. AMi estimated water flow impact. NB, KL, and IL contributed to TalTech data collection, method description and analysis. EC, CG, AMo, MF, and FG contributed to CLAIM data collection, method description and analysis. VK contributed to multi-dataset collection and preprocessing. All authors contributed to the article and approved the submitted version.

Funding

The research leading to these results has received funding from the Horizon 2020 project “Cleaning Litter by developing and Applying Innovative Methods in European seas” under Grant Agreement ID 774586. Also from the projects financed by Ministry of Environment of Estonia: Monitoring of marine litter in Estonian sea area, contract 4-2/16/32, Monitoring of microlitter in the sea surface of Estonian waters, contract 4-1/17/137, Study on microlitter on the sea surface layer and in sediments in 2018, contract 4-1/18/87; and projects financed by Environment Agency of Estonia: Microlitter monitoring in 2019, contract nr. 4-1/19/13, Study on microlitter on the sea surface layer and in sediments in 2020, contract 4-3/20/33.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2022.886357/full#supplementary-material

References

Aigars J., Barone M., Suhareva N., Putna-Nimane I., Dimante-Deimantovica I. (2021). Occurrence and Spatial Distribution of Microplastics in the Surface Waters of the Baltic Sea and the Gulf of Riga. Mar. Pollut. Bull. 172, 112860. doi: 10.1016/j.marpolbul.2021.112860

PubMed Abstract | CrossRef Full Text | Google Scholar

Ajith N., Arumugam S., Parthasarathy S., Manupoori S., Janakiraman S. (2020). Global Distribution of Microplastics and Its Impact on Marine Environment—a Review. Environ. Sci. Pollu. Res. 27(21), 25970–25986.

Google Scholar

Bagaev A., Khatmullina L., Chubarenko I. (2017). Anthropogenic Microlitter in the Baltic Sea Water Column. Mar. Pollut. Bull. 129 (2), 918–923. doi: 10.1016/j.marpolbul.2017.10.049

PubMed Abstract | CrossRef Full Text | Google Scholar

Beer S., Garm A., Huwer B., Dierking J., Nielsen T. G. (2018). No Increase in Marine Microplastic Concentration Over the Last Three Decades - a Case Study From the Baltic Sea. Sci. Tot. Environ. 621, 1272–1279. doi: 10.1016/j.scitotenv.2017.10.101

CrossRef Full Text | Google Scholar

European Commission (2008). Directive 2008/56/EC of the European Parliament and of the Council 17 June 2008, Establishing a Framework for Community Action in the Field of Marine Environmental Policy (Marine Strategy Framework Directive). Off. J. Eur. Union. L164, 19–40.

Google Scholar

GESAMP (2019). Guidelines for the Monitoring and Assessment of Plastic Litter in the Ocean. J. Ser. GESAMP. Rep. Stud. 2019-99, 123.

Google Scholar

Gewert B., Ogonowskia M., Barth A., MacLeoda M. (2017). Abundance and Composition of Near Surface Microplastics and Plastic Debris in the Stockholm Archipelago, Baltic Sea. Mar. Pollut. Bull. 120, 292–302. doi: 10.1016/j.marpolbul.2017.04.062

PubMed Abstract | CrossRef Full Text | Google Scholar

Gorokhova E. (2015). Screening for Microplastic Particles in Plankton Samples: How to Integrate Marine Litter Assessment Into Existing Monitoring Programs? Mar. Pollut. Bull. 99, 271–275. doi: 10.1016/j.marpolbul.2015.07.056

PubMed Abstract | CrossRef Full Text | Google Scholar

Grubbs F. (1969). Procedures for Detecting Outlying Observations in Samples. Technometrics 11 (1), 1–21.

Google Scholar

Hanke G. (20132009). “Guidance on Monitoring of Marine Litter in European Seas,” in A Guidance Document Within the Common Implementation Strategy for the Marine Strategy Framework Directive. J.R.C. MSDF Technical Subgroup on Marine Litter, Report no. EUR 26113 EN, 128 (Cheshire, A.C.: UNEP/IOC), pag. 27.

Google Scholar

Karlsson T. M., Kärrman A., Rotander A., Hassellöv M. (2020). Comparison Between Manta Trawl and in Situ Pump Filtration Methods, and Guidance for Visual Identification of Microplastics in Surface Waters. Environ. Sci. Pollut. Res. 27, 5559–5571. doi: 10.1007/s11356-019-07274-5

CrossRef Full Text | Google Scholar

Lassen C., Hansen S. F., Magnusson K., Hartmann N. B., Rehne Jensen P., Nielsen T. G., et al. (2015). Microplastics: Occurrence, Effects and Sources of Releases to the Environment in Denmark (Copenhagen K: Danish Environmental Protection Agency).

Google Scholar

Leppäranta M., Myrberg K. (2009). Physical Oceanography of the Baltic Sea (Berlin Heidelberg: Springer).

Google Scholar

Lindgren E., Tuomi L., Huess V. (2020) Quality information document (QUID): Baltic Sea Production Centre BALTICSEA_REANALYSIS_WAV_003_015. Available at: https://catalogue.marine.copernicus.eu/documents/QUID/CMEMS-BAL-QUID-003-015.pdf.

Google Scholar

Magnusson K. (2014). Micro-Litter and Other Microscopic Anthropogenic Particles in the Sea Area Off Rauma at Turku, Finland (Stockholm: Environmental Research Institute), 18pp.

Google Scholar

Magnusson K., Norén F. (2011). “Mikroskopiskt Skräp I Havet Metodutveckling För Miljöövervakning”, in Naturvårdsverket Report, Stockholm.

Google Scholar

Mishra A., Buhhalko N., Lind K., Lips I., Liblik T., Väli G., et al. (2022). Spatiotemporal Variability of Microplastics in the Eastern Baltic Sea. Front. Mar. Sci.

Google Scholar

Napper I. E., Thompson R. C. (2016). Release of Synthetic Microplastic Plastic Fibres From Domestic Washing Machines: Effects of Fabric Type and Washing Conditions. Mar. Pollut. Bull. 112 (1–2), 39–45. doi: 10.1016/j.marpolbul.2016.09.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Norén F. (2007). Small Plastic Particles in Coastal Swedish Waters. Gothenburg: KIMO Report. pp11.

Google Scholar

Norén K., Haikonen K., Norén F. (2015). Marint Mikroskopiskt Skräp Längs Skånes Kust (IVL IVL Svenska Miljöinstitutet Report C-139), pp47.

Google Scholar

Norén F., Magnusson K., Norén K. (2014). Marint Mikroskopiskt Skräp Undersökning Längs Svenska Västkusten 2013 Och 2014 (Stockholm: Länsstyrelsen Rapporter 2014-52), pp24.

Google Scholar

Primpke S., Dias P., Gerdts G. (2019). Automated Identification and Quantification of Microfibres and Microplastics. Anal. Methods 11:2138–2147. doi: 10.1039/C9AY00126C

CrossRef Full Text | Google Scholar

Schönlau C., Karlsson T. M., Rotander A., Nilsson H., Engwall M., van Bavel B., et al. (2020). Microplastics in Sea-Surface Waters Surrounding Sweden Sampled by Manta Trawl and In-situ Pump. Mar. Pollu. Bull. 153, 111019.

Google Scholar

Setälä O., Magnusson K., Lehtiniemi M., Norén F. (2016). Distribution and Abundance of Surface Water Microlitter in the Baltic Sea: A Comparison of Two Sampling Methods. Mar. Pollut. Bull. 110, 177–183. doi: 10.1016/j.marpolbul.2016.06.065

PubMed Abstract | CrossRef Full Text | Google Scholar

She J., Høyer J. L., Larsen J. (2007). Assessment of Sea Surface Temperature Observational Networks in the Baltic Sea and North Sea. J. Mar. Syst. 65 (1-4), 314–335.

Google Scholar

She J., Nakamoto S. (1996). Spatial Sampling Study for the Tropical Pacific With Observed Sea Surface Temperature Fields. J. Atmosph. Ocean. Technol. 13 (6), 1189–1201.

Google Scholar

Snedecor G. W., Cochran W. G. (1989). Statistical Methods. 8th Edition (Ames: Iowa State University Press). 1989. xix + 491 pp

Google Scholar

Song Y. K., Hong S. H., Jang M., Han G. M., Rani M., Lee J., et al. (2015). A Comparison of Microscopic and Spectroscopic Identification Methods for Analysis of Microplastics in Environmental Samples. Mar. Pollut. Bull. 93 (1), 202–209. doi: 10.1016/j.marpolbul.2015.01.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Song Y. K., Hong S. H., Jang M., Kang J. H., Kwon O. Y., Han G. M., et al. (2014). Large Accumulation of Micro-Sized Synthetic Polymer Particles in the Sea Surface Microlayer. Environ. Sci. Technol. 48 (16), 9014–9021. doi: 10.1021/es501757s

PubMed Abstract | CrossRef Full Text | Google Scholar

Tamminga M., Hengstmann E., Fischer E. K. (2018). Microplastic Analysis in the South Funen Archipelago, Baltic Sea, Implementing Manta Trawling and Bulk Sampling. Mar. Pollut. Bull. 128, 601–608. doi: 10.1016/j.marpolbul.2

PubMed Abstract | CrossRef Full Text | Google Scholar

Van Bavel B., Lusher A. L., Jaccard P. F., Pakhomova S., Singdahl-Larsen C., Andersen J. L., et al. (2020). Monitoring of Microplastics in Danish Marine Waters Using the Oslo-Kiel Ferry as a Ship-of-Opportunity. Copenhagen: NIVA-Denmark Report Serial number 7524-2020. pp35.

Google Scholar

Zobkov M. B., Esiukova E. E., Zyubin A. Y., Samusev I. G. (2019). Microplastic Content Variation in Water Column: The Observations Employing a Novel Sampling Tool in Stratified Baltic Sea. Mar. Pollut. Bull. 138, 193–205. doi: 10.1016/j.marpolbul.2018.11.047

PubMed Abstract | CrossRef Full Text | Google Scholar