Intra-Annual Sea Level Fluctuations and Variability of Mesoscale Processes in the Northern Japan/East Sea From Satellite Altimetry Data

Intra-annual sea level fluctuations and variability of mesoscale processes based on eddy kinetic energy (EKE) were studied in the northern (northward of 41 N) Japan/East Sea (JES) using data from satellite altimetry for 1993–2020. Decomposition to empirical orthogonal functions (EOF) was performed of the high-pass filtered, with the cut-off period of 250 days, sea level anomalies. The leading mode accounting for the major fraction of the variance yielded sea level fluctuations which were simultaneous in the entire sea and occurred in the range from 70 to 250 days without any preferable timescale. EKE in the northern sea was also expanded to EOF and yielded the leading mode capturing mesoscale variability within the Primorye (Liman) Current and the Tsushima Warm Current. The seasonal signal was found in the simultaneous intra-annual sea level fluctuations, which matches that of EKE, and, as found in the earlier studies, of the mean currents. The sea level rises, the mean currents intensify and EKE increases in summer and fall and the opposite changes occur in winter and spring, with the seasonal extremes in October/November and March/April, respectively. This is in line with the EKE generation by instability of the mean currents. The intra-annual sea level fluctuations and EKE manifest rich variability on quasi-biennial, interannual and decadal timescales. However, in contrast with the seasonal signal, the low-frequency variability does not match, implying different kinds of forcing, probably by local wind in the northern JES and by the transport variations in the Korea – Tsushima Strait (KTS) in the southern JES. Intra-annual simultaneous SLA reveal changing relationship with Pacific Decadal Oscillation (PDO): both were in-phase in 1993–1994 and from late 2007 to 2013 and out-of-phase from 1997 to 2002, while there was no specific relationship in other times. However, the relationship of these SLA with the interannual KTS transport variation seems inconclusive.

Introduction

The sea level is an important indicator of dynamic processes in the ocean and an essential climate variable. Therefore, a lot of attention has been paid to sea level variability, in particular, in the Japan/East Sea (JES), first from tide gauge data and since 1990s from satellite altimetry. In the first place, the seasonal variation was studied and the sea level rise in the warm season and decline in the cold season was detected and attributed to the steric effects due to thermal forcing (see original results and review by Oh et al., 1993). As revealed from satellite altimetry, the sea level in the JES is, on average, the highest in October and the lowest in March (Choi et al., 2004; Trusenkova and Kaplunenko, 2013). Warm water enters the JES in the south through the Korea/Tsushima Strait (KTS) and the excess water leaves the sea through the Tsugaru and La Perouse (Soya) Straits in the northeast (Figure 1A), therefore, the imbalance in the straits can be another mechanism of sea level variations. On timescales longer than one year, quasi-biennial (QB) fluctuations were revealed in the southern JES (Hirose and Ostrovskii, 2000; Choi et al., 2004) and later in the entire sea (Trusenkova and Kaplunenko, 2013). Sea level trends were estimated several times from the extending record and were eventually found to be close to the global mean trends (Kang et al., 2005; Marcos et al., 2012; Trusenkova, 2018). Decadal signal was also detected, with the sea level rising in 1995–2000 and 2008–2013 and declining in 2001–2007 simultaneously in the entire JES (Trusenkova, 2018). Low-frequency variability was examined and the relationship with Pacific Decadal Oscillation (PDO) was found in the JES, with higher or lower sea level during the negative or positive PDO phases, respectively (Gordon and Giulivi, 2004).

FIGURE 1

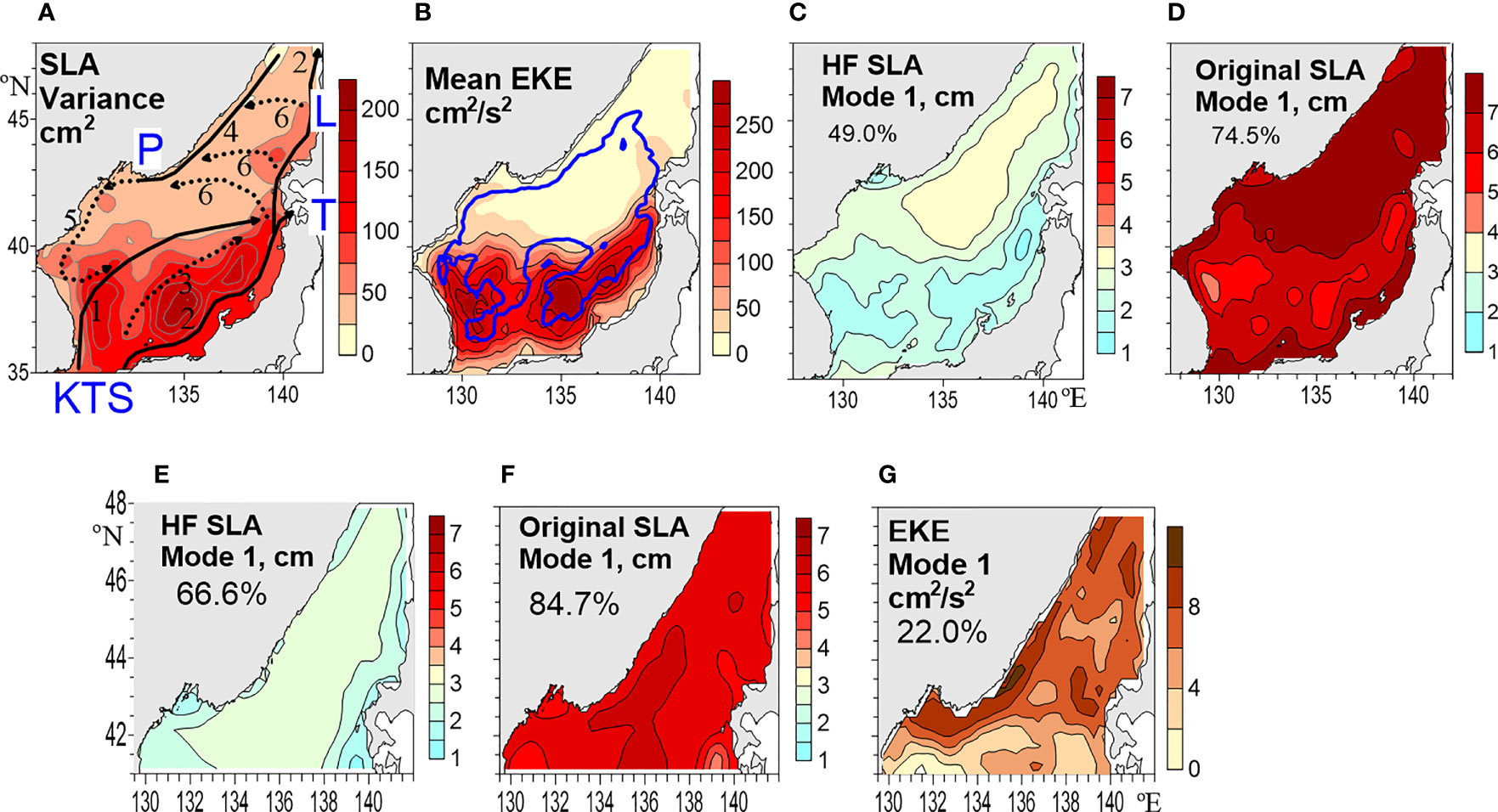
Figure 1 (A) Sea level variance (cm²). Currents are schematically shown by arrows and labeled by numbers: the East Korea Warm Current (EKWC) and its continuation off the coast by 1, the Tsushima Warm Current (TWC) by 2, the East Sea Current by 3, the Primorye (Liman) Current by 4, the North Korea Cold Current (NKCC) by 5, the western branches of the TWC by 6; the intermittent currents are shown by the dotted lines. Peter the Great Bay is marked by the letter P, the KTS, Tsugaru and La Perouse (Soya) Straits are marked as KTS, T, and L, respectively. (B) Time-averaged EKE from the satellite altimetry data (cm²/s²); 2000-m isobath is shown by the blue contour. EOF 1 (cm) from the (C, E) high-frequency (HF) and (D, F) original SLA for the (C, E) entire and (D, F) northern JES. (G) EOF 1 (cm²/s²) from EKE in the northern JES. Contours are shown for every 25 cm² in (A), 25 cm²/s² in (B), 0.5 cm in (C, E, F), 1 cm in (D), and 2 cm²/s² in (G).

The JES features the complex circulation system including both cold currents in the northern part and warm currents in the southern part, divided by the Subarctic Front at 40–41 N° (see review by Danchenkov et al., 2006). The former are the Primorye (Liman) Current and North Korea Cold Current (NKCC) and the latter are the East Korea Warm Current (EKWC), East Sea Current (Lee and Niiler, 2005), Tsushima Warm Current (TWC) and TWC western branches (Figure 1A). Using altimetry data, it was found that the mean currents in the JES intensify in the warm season and slacken in the cold season (Morimoto and Yanagi, 2001). More exactly, the seasonal variation in the sea level gradient across the Subarctic Front and in the strength of the mean currents matches that in the simultaneous sea level fluctuations, with the seasonal extremes in October and March, respectively, due to differential surface cooling and the thermal forcing from the KTS (Trusenkova and Kaplunenko, 2013).

Mesoscale eddies are abundant in the JES (Danchenkov et al., 2006) and their frequent locations were detected from infrared satellite imagery (analysis of A. Nikitin, published in Trusenkova et al., 2009) and from satellite altimetry (Lee et al., 2019). However, the resolution of altimetry data is probably enough for detecting individual eddies in the southern JES (see, for instance, Lee and Niiler, 2010) but not for the northern JES. In particular, only few areas of the increased sea level variance (Morimoto et al., 2000) and of frequent eddy locations (Lee et al., 2019) were found northward of 41° N, namely, along the Hokkaido Island and off Peter the Great Bay, while the central northern JES seems to be an ‘eddy desert’. However, mesoscale eddies were frequently found northward of the Subarctic Front (Takematsu et al., 1999; Lobanov et al., 2007) and in the entire area of 40–42° N, 133–135° E from infrared satellite imagery (Trusenkova et al., 2009), while these eddies are not always captured by satellite altimetry due to their smaller sizes (less than 100 km).

Intra-annual sea level fluctuations can be related to eddy formation; however, the fluctuations on the 70–150-day timescales were found to be simultaneous in the entire JES, which was attributed to the transport imbalance in the straits (Choi et al., 2004; Trusenkova and Kaplunenko, 2013). The physical mechanism was suggested as fast barotropic waves traveling from the KTS towards the Tsugaru and La Perouse Straits and generated by high-frequency transport variations in the KTS, with the latter being forced by wind and sea level differences outside the JES (Choi et al., 2004; Lyu and Kim, 2005). Accordingly, the 64-day Fourier spectral peak (Ostrovskii et al., 2009) and variability on even shorter timescales (3–50 days; Kang et al., 2014) were found in the KTS transport and these variations can be as strong as the seasonal ones. The intra-annual sea level fluctuations were also found in tide gauge records, being in-phase along the Korea and Japanese coasts (Choi et al., 2004) but not always in-phase along the Russian coast (Trusenkova et al., 2021).

Mesoscale processes can be quantified by eddy kinetic energy (EKE) based on velocities computed from altimetry SLA or from drifter data. Time-averaged EKE is an order of magnitude less in the northern JES than in the southern JES, as was estimated from both altimetry data (Figure 1B) and surface drifters (Lee and Niiler, 2005). Mean EKE based on buoys is increased within the Primorye Current zone, compared to the adjacent area, although this feature does not appear in the altimetric EKE; however, anticyclonic slope eddies were frequently detected between the Primorye Current and the coast (from infrared satellite imagery; Ponomarev et al., 2011). Still, statistics of mesoscale processes and high-frequency sea level variability are still poorly known in the northern JES. Therefore, the purpose of this study is to clarify the variability of the sea level and mesoscale processes in the northern JES.

Data and Methods

The Copernicus Marine Service (CMEMS) daily gridded sea level anomalies (SLA) from January 1, 1993, through December 31, 2020, were used in this study. Data cover the area between 35° and 48° N and 127.5° and 141.5° E, with the 0.25° spatial resolution. We use the dataset based on sea level data from two satellite systems which were maintained throughout the record, namely, T/P – Jason and ERS – Envisat – Saral; this dataset is suitable for the long-term analysis. The data were gridded by optimal interpolation and SLA were computed by subtracting the 20-year mean for 1993–2012 in every bin (Mertz et al., 2017). As the data record covers 1993–2020, time-averaged SLA for the entire 1993–2020 period are not zero and vary between 3 and 6 cm over the JES. The CMEMS products include errors for the interpolated data, which, on average, are between 1 and 2.5 cm in the northern JES and between 1.5 and 3.5 cm in the southern JES.

To analyze mesoscale processes, eddy kinetic energy (EKE) was computed as (u´²+v´²)/2 where u´ and v´ are the geostrophic velocity anomalies. We computed these velocities as u´ = -(ξ/f) ∂ξ/y and v´ = (g/f) ∂ξ/x, where ξ is SLA, g is the constant acceleration due to gravity, f is the Coriolis parameter, x and y are the Cartesian coordinates in the directions from west to east and from south to north, respectively. To exclude the effect of non-zero mean SLA on EKE, mean values were subtracted from SLA prior to the EKE computation. The spatially averaged EKE was used for the analysis and during its computation EKE in every bin was weighted by the latitude cosine in order to account for the bin changes with latitude.

For our analysis we expanded SLA and EKE into empirical orthogonal functions (EOFs) computed as eigenvectors of the symmetrical correlation matrix rather than from conventional covariances, thus enabling the detection of patterns in areas of weaker signals. Note that the correlation computation involves the subtraction of temporal mean values, eliminating any effect of non-zero mean SLA. The expansion to EOFs provides a kind of averaging, thus reducing data errors by (N*)^-1/2 where N* is the number of degrees of freedom (Preisendorfer, 1988). Derived modes are considered significant if SLA related to them exceed data errors. The considered modes are summarized in Table 1.

TABLE 1

Table 1 The analyzed modes.

To identify timescales of non-stationary timeseries, wavelet transform (WT) was used, with the DOG-9 mother wavelet, which is the 9th order derivative of the Gaussian distribution (Torrence and Compo, 1998). It features good resolution in the time domain and reasonable resolution in the frequency domain, thus providing informative spectra. The statistical significance of the spectra was estimated with respect to the red noise at the 90% confidence level. The cone of influence (COI) of edge effects (Torrence and Compo, 1998) is shown in the spectra; everything within COI should not be considered. Note that calculating spectra by squaring the WT based on DOG-9 mother wavelet generates two maxima per period.

Data filtering was performed by timeseries reconstruction based on the inverse WT (Torrence and Compo, 1998). SLA were high-pass filtered with the cut-off period of 250 days which separates the seasonal and longer scale variability from the intra-seasonal variability (see below). EKE was low-pass filtered, with the cut-off period of 15 weeks, in order to remove noise resulted from the differentiation when computing velocities from SLA.

Computations were performed with the use of the modified Torrence and Compo, 1998 procedure.

Results and Discussion

Intra-annual Fluctuations of Sea Level

To analyze intra-annual fluctuations, high-pass filtered SLA were expanded to EOFs; for comparison, the original SLA were also expanded to EOFs. The decompositions were performed for the entire and northern JES (Table 1). The leading modes from all samples account for the major fraction of the total variance (49% – 84%; Table 1), while every next mode accounts for less than 5% of the variance and cannot be considered as significant. Thus, only the leading mode is further analyzed for every sample.

As for the entire JES, the spatial patterns of both high-frequency and original leading modes are of the same sign everywhere, i.e. they capture the simultaneous sea level fluctuations. Their loadings are the largest northward of 40–41° N, although the loadings are somewhat decreased in the narrow zone along the northeastern sea boundary (Figures 1C, D). If the EOF decompositions were based on covariances in data, the largest loadings would be in areas of the largest variance and the spatial EOF patterns would resemble that of the variance (Figure 1A), as in (Trusenkova, 2018). In contrast, the modes based on correlations analyzed in this study highlight the areas of maybe weaker signals but stronger variability.

The modes for the northern JES are the counterparts of those for the entire sea, as they have the matching spatial patterns (compare Figures 1C, D with Figures 1E, F, respectively) and the temporal functions (principal components; PCs) are practically the same, with the correlations between the corresponding timeseries of about 0.98. Thus, the leading mode for the northern JES captures fluctuations which are simultaneous in the entire JES, for both the original and high-pass filtered SLA, which was not evident beforehand. Note that the modes for the northern JES account for the larger fractions of the variance than those for the entire JES (Table 1) and the loadings are larger in the northern area. The PC timeseries and their WT spectra for the high-frequency and original leading modes in the northern JES are shown in Figures 2, 3, respectively.

FIGURE 2

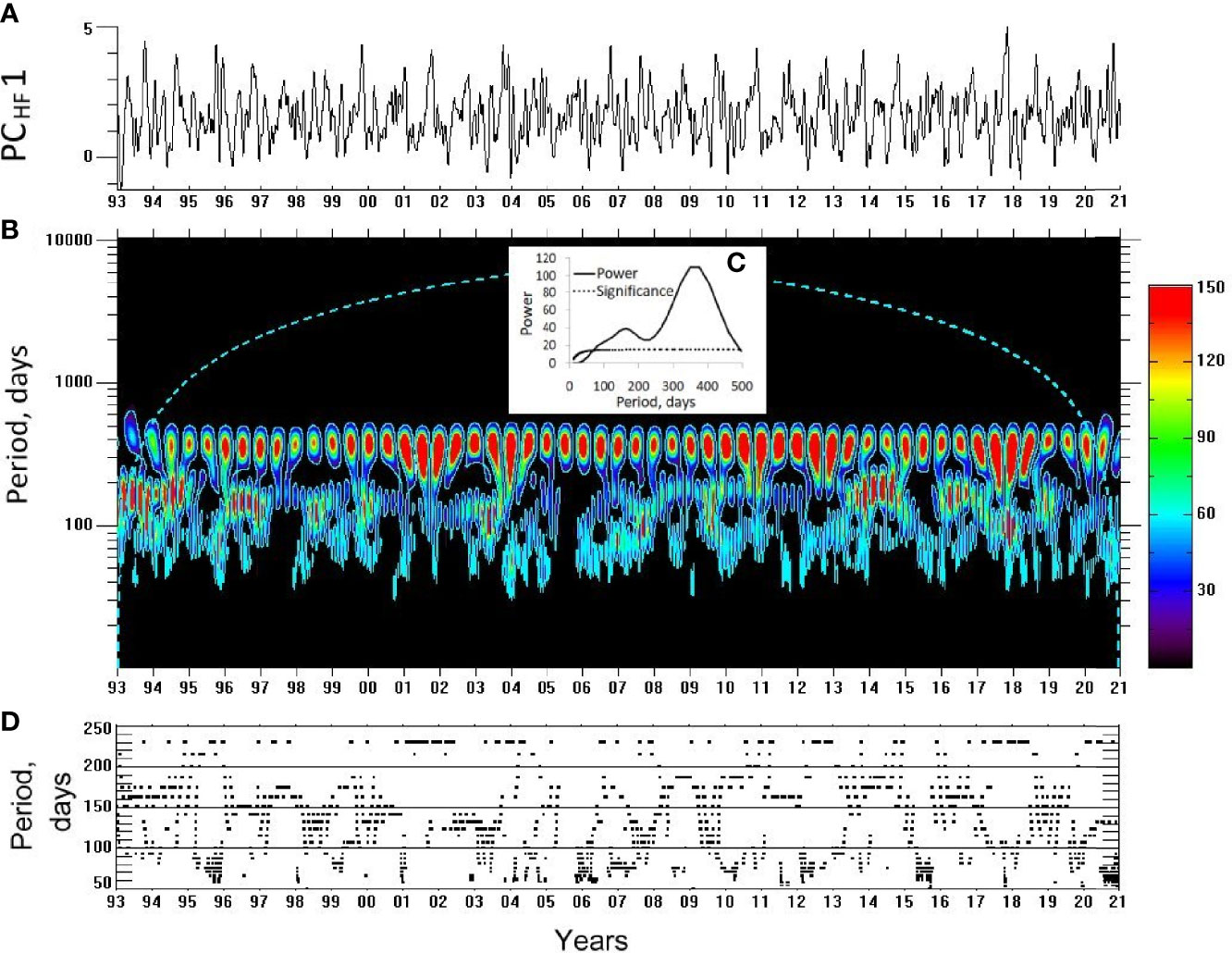
Figure 2 (A) The principal component PC_HF 1 (dimensionless) for the northern JES, (B) its WT spectrum, (C) its time-averaged WT spectrum, and (D) the periods (days) of maximum power in the range between 50 and 250 days. In (B) and hereafter the 90% confidence levels are shown by solid cyan contours and COIs by dashed cyan lines.

FIGURE 3

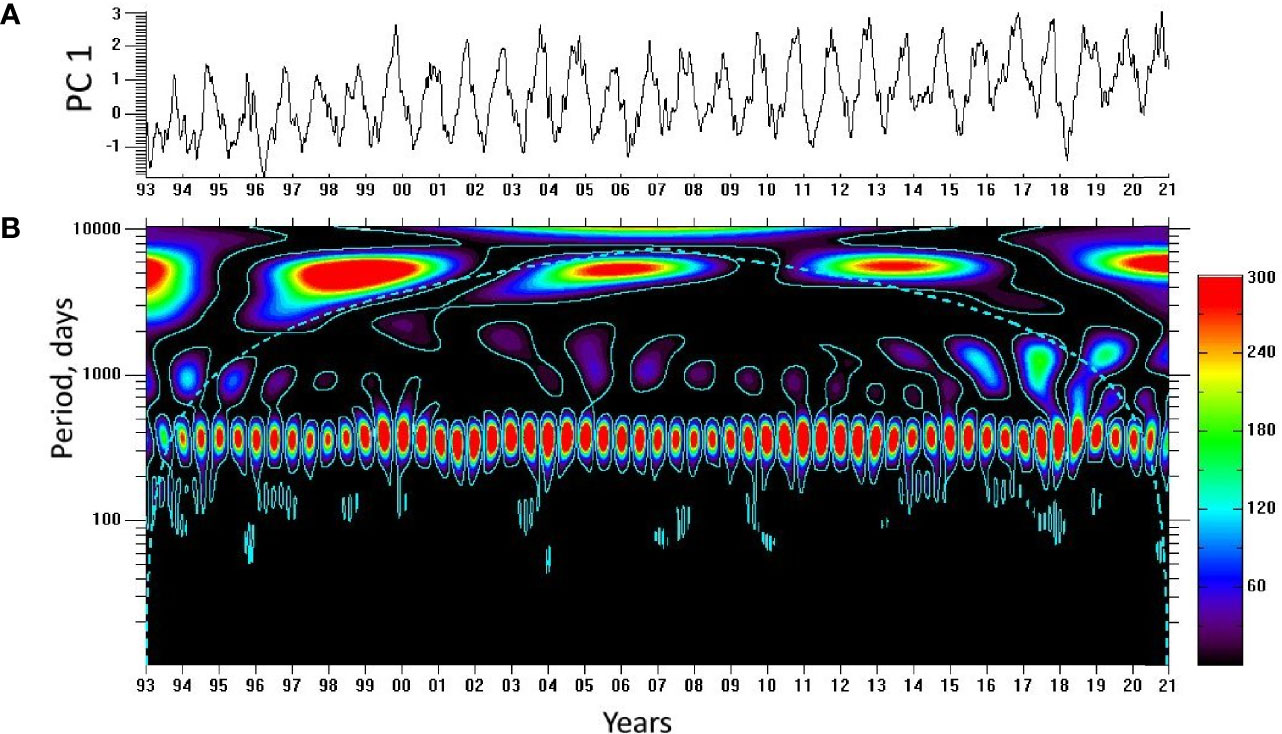
Figure 3 (A) The principal component PC 1 (dimensionless) for the northern JES and (B) its WT spectrum.

In the northern JES, loadings in the spatial maxima of the leading high-frequency and original modes are equal to 2.2–2.6 cm and 5.5–7.5 cm, respectively (Figures 1C–F). As the PC absolute values mostly exceed 0.5 (Figures 2A, 3A), the absolute values of SLA related to these modes mostly exceed 1.1–1.3 cm and 2.7–3.7 cm, respectively. The numbers of degrees of freedom for PC_HF 1 and PC 1 are estimated as N* = 93 and N* = 27, respectively; therefore, data errors are reduced, due to EOF, by (N*)^-1/2 (Preisendorfer, 1988) and they are equal to 0.3 and 0.5 cm, respectively. This means that SLA related to the considered modes exceed the data errors in the northern JES.

The PCs of the high-frequency mode for both entire and northern JES (PC_HF 1; Figure 2A for the northern JES) feature fluctuations in the range between 30–50 and 250 days, with the strong variability, as seen in the WT spectrum (Figure 2B for the northern JES). This is in line with the earlier findings of the intra-annual fluctuations simultaneous in the entire JES (Trusenkova and Kaplunenko, 2013). However, an unexpected feature is a seasonal signal found throughout the record in these fluctuations, which is rather obscured in the PC_HF 1 timeseries (Figure 2A) but is clearly seen in both original and time-averaged WT spectra (Figures 2B, C).

The seasonal signal in PC_HF 1 needs explanation, as the data were preliminary high-pass filtered, with the cut-off period of 250 days, i.e. the annual variation is supposed to be excluded. To clarify this, temporal variation of the original, non-filtered mode is considered (see PC 1 for the northern JES and its WT spectrum in Figures 3A, B, respectively). As expected, PC 1 of the original mode features the well known strong seasonal cycle, with the sea level rise from spring to fall and decline from fall to spring and the seasonal extremes in October/November and March/April, respectively. Note that WT with the DOG mother wavelet provides good resolution in the time domain and not so good resolution in the frequency domain (Torrence and Compo, 1998). The statistically significant maxima cover periods between 270 and 400 days in Figures 2B, 3B; the corresponding maximum lies at the 350–375-day period in the time-average spectra, which corresponds to the annual timescale. This kind of the annual variation was earlier found for sea level averaged in the entire JES (Choi et al., 2004) and as the leading EOF mode for the shorter record (Trusenkova and Kaplunenko, 2013). It was explained by the steric effects due to the thermal forcing on the sea surface and from the transport of warm water in the KTS. One can see in Figure 2A that PC_HF 1 is higher in summer and fall and lower in winter and spring.

For comparison, the seasonal cycles were extracted from both PC 1 and PC_HF 1 by the band-pass filtrations, with the cut-off periods of 275 and 445 days; the corresponding timeseries are shown in Figure 4. To check statistical significance, estimated are an average seasonal range of PC_HF 1 as 0.3 (Figure 4) and spatial loadings of the high-frequency mode as 2.2–2.6 cm (Figures 1C, E); therefore, the seasonal range of the intra-annual sea level fluctuations is equal to 0.6–0.7 cm, i.e. small but still above the data errors. It turned out that the seasonal cycle is the same for both PC 1 and PC_HF 1, with the statistically significant correlation of 0.47 for the original timeseries shown in Figures 2A and 3A and the correlation of 0.95 for the band-pass filtered timeseries shown in Figure 4. The sea level is higher in summer and fall and it is lower in winter and spring, affecting high-frequency fluctuations.This matching means that the seasonal signal in PC_HF 1 should be attributed to the thermal steric effects, modulating high-frequency fluctuations.

FIGURE 4

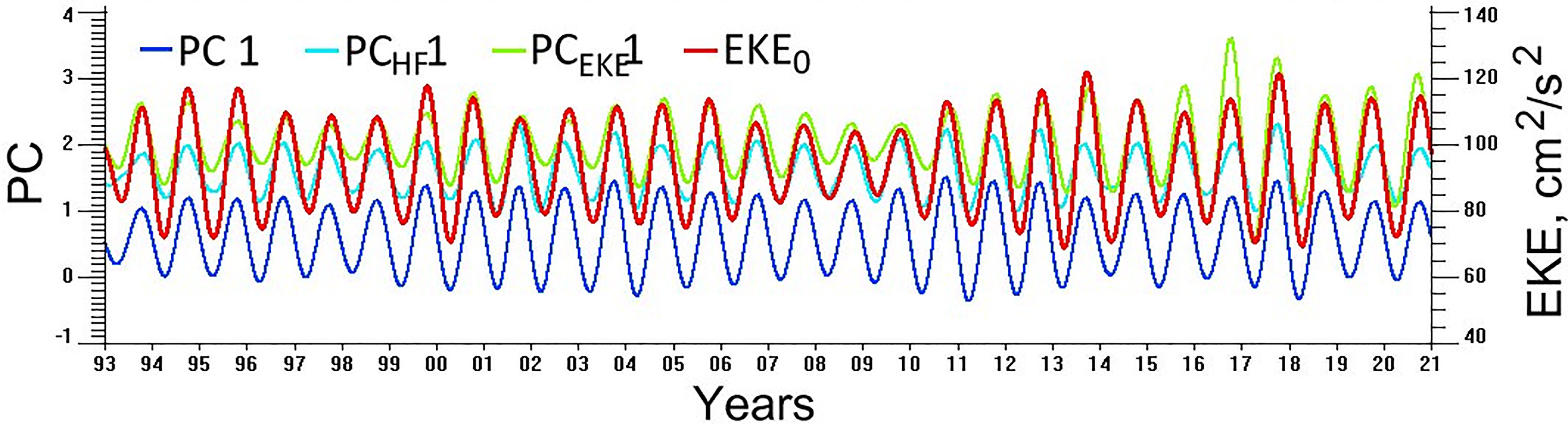
Figure 4 The annual cycles of (blue line) PC 1, (cyan line) PC_HF 1 and (green line) PC_EKE 1 (dimensionless; left-hand side y axis) and that of (red line) EKE averaged in the entire JES (EKE₀; cm²/s²; right-hand side y axis). The timeseries are band-pass filtered, with the cut-off periods of 275 and 445 days.

The WT spectrum of PC 1 (Figure 3B) also features weak long-term fluctuations, mostly on the QB timescale, and the strong decadal variability which was discussed by Trusenkova (2018).

The intra-annual sea level fluctuations represented by PC_HF 1 are subjected to the strong interannual variability (Figure 2B). To emphasize this variability, periods were estimated for which the instantaneous power was the largest (Figure 2D). The periods of maximum intensity were frequently longer than 150 days, which happened in 1993–1994, late 1997, mid 1999, late 2008, 2014, and 2016. In other years the most intense fluctuations were more frequent on the timescales shorter than 150 days, such as in 1995, 2001–2006, 2010–2012, and 2015. There were also times when the maximum intensity shifted throughout the range from the shorter to longer periods or vice versa, which happened in 1997, 1998, early 2008, and 2009 (Figure 2D). In the time-averaged spectrum there is a broad statistically significant maximum between 70 and 200 days, with the largest power at the periods from 150 to 160 days (Figure 2C). However, Figures 2B, D do not show any preferable timescale in the intra-annual range, so the peak in the mean WT spectrum is a result of averaging. This kind of variability makes the Fourier spectra unsuitable for the analysis. Note that this is different from sea level variability in the coastal zone within the Primorye Current where the preferable timescales of 70–80 and 120–130 days were detected from tide gauge data (Trusenkova et al., 2021).

To further analyze interannual changes of intra-annual sea level fluctuations, the WT spectrum of PC_HF 1 was integrated in the 70–250-day range and averaged (P_70–250). Note that CMEMS provides daily SLA but the satellite repeat periods are about 10 days for the rarely spaced T/P – Jason tracks and 35 days for the denser spaced ERS – Envisat – Saral tracks (https://www.aviso.altimetry.fr/en/missions.html). This is why the Nyquist period was accepted as 70 days and was taken as the lower bound of the range. The P_70–250 timeseries is shown in Figure 5A and its WT spectrum in Figure 5B.

FIGURE 5

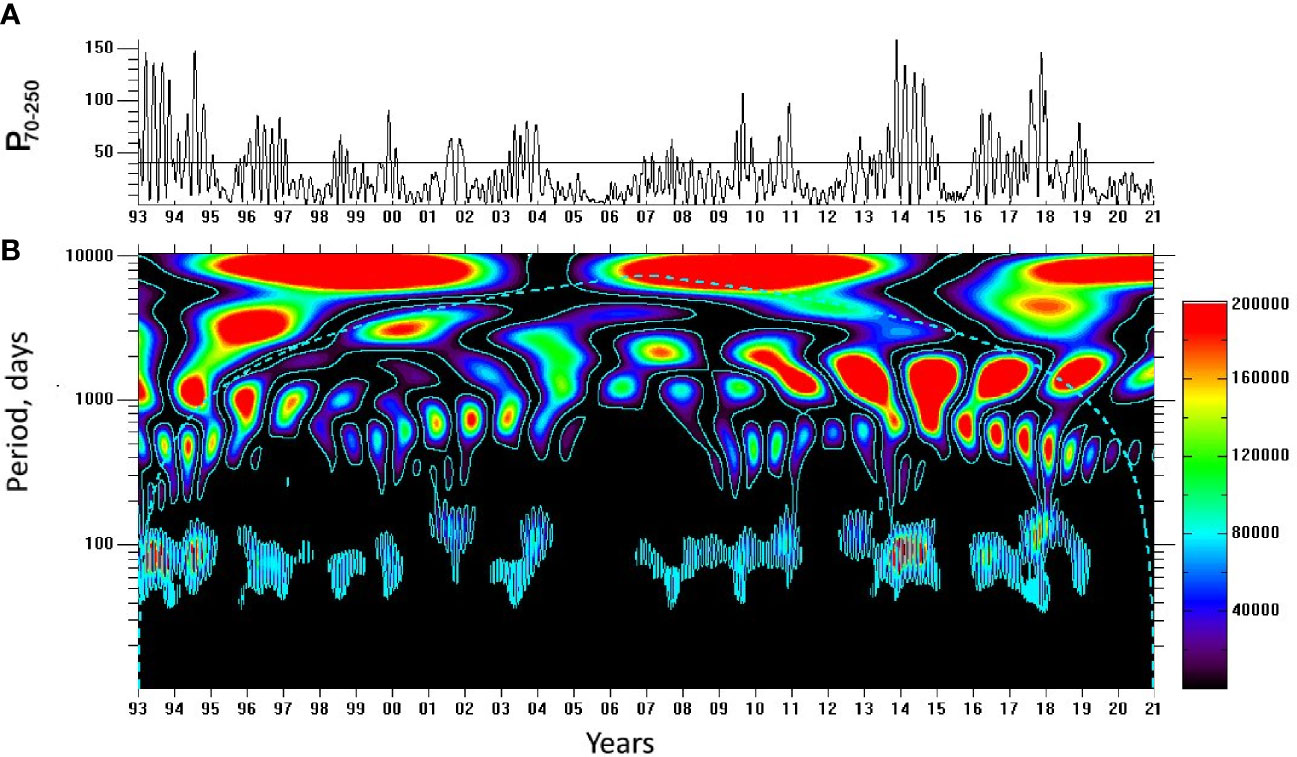
Figure 5 (A) The band-averaged power of the PC_HF 1 (dimensionless) and (B) its WT spectrum. In (A) the horizontal line corresponds to the sum of median and mean deviation.

The power on the annual timescale is very small in the P_70–250 spectrum in contrast with the PC_HF 1 spectrum (comp. Figures 5B and 2B). Therefore, the intensity (differences between the highs and lows) of the intra-annual sea level fluctuations does not reveal any seasonal variation, confirming that the seasonal signal found in the PC_HF 1 should be related to the steric effects. The strong maxima of P_70–250, exceeding the sum of median (20.9) and mean deviation (20.0) shown in Figure 5A, were detected in 1993–1994, 1996, early 1997, mid 1998, late 1999, mid 2003, late 2007, mid 2009, late 2010, 2014, 2016, 2017, and early 2019 (Figure 5A). Accordingly, the WT spectrum of P_70–250 reveals QB fluctuations, which were the strongest in 1995–1999 and 2013–2015, and the interannual variability on the timescales between 4 and 6 years (Figure 5B). The decadal variability seems also strong but the power on these timescales lies within COI and can only be considered later when the longer record is available.

One can expect that the high frequency KTS transport variations and, therefore, the intra-annual sea level fluctuations intensify in times when the transport itself is large and vice versa. In particular, P_70–250 was low in 2004–2006 (Figure 5A) and the transport was extremely low in 2005 but it was just moderate in 2004 and 2006 (Fukudome et al., 2010; Yoon et al., 2016). In contrast, the transport was extremely large throughout 1999, while P_70–250 was large in late 1999 only. No marked relationship between the transport and P_70–250 was otherwise detected in 1997–2006, the period of the reported data (Fukudome et al., 2010; Yoon et al., 2016).

In order to put the long-term changes of the intra-annual SLA fluctuations in context of climate variability, several climate indices acting in the region around the JES are applied. They are the Southern Oscillation Index (SOI) representing the most intense climate cycle acting in the tropical Pacific (see the recent review by Wang et al., 2016) and also having the strong global impact (Serykh et al., 2019); the Arctic Oscillation Index (AOI), capturing switches between mid-latitude zonal and meridional atmospheric circulation (Thompson and Wallace, 2001); the Pacific Decadal Oscillation (PDO), an El Niño-like pattern with the strongest impact in the extratropical region (Mantua and Hare, 2002); the North Pacific Index (NPI) accounting for the intensity of the Aleutian Low (Trenberth and Hurrell, 1994); the Western Pacific Index (WPI) capturing variations in the Pacific (East Asian) jet steam (Wallace and Gutzler, 1981; Barnston and Livezey, 1987).

No clear linkages between P_70–250 and SOI, AOI, NPI, or WPI were found. However, a relationship with PDO was detected and estimated qualitatively; to this end, the PDO index and P_70–250 were low-pass filtered, with the cut-off period of 1.5 year. As seen from Figure 6 representing both timeseries, they were in-phase in 1993–1994 and from late 2007 to 2013 and out-of-phase from 1997 to 2002, while there was no specific relationship in other times. (These periods were short and the numbers of degrees of freedom were small, preventing from deriving statistically significant quantitative estimates.) Gordon and Giulivi (2004) found that the sea level in the JES rose during the negative PDO phases and declined during the positive phases; they explained this by the changes in Kuroshio intensity south of Japan and in its portion entering the JES through the KTS. However, the relationship of the intra-annual sea level fluctuations and KTS transport is inconclusive, as discussed above, and it is yet unclear how to explain their changing linkages with PDO.

FIGURE 6

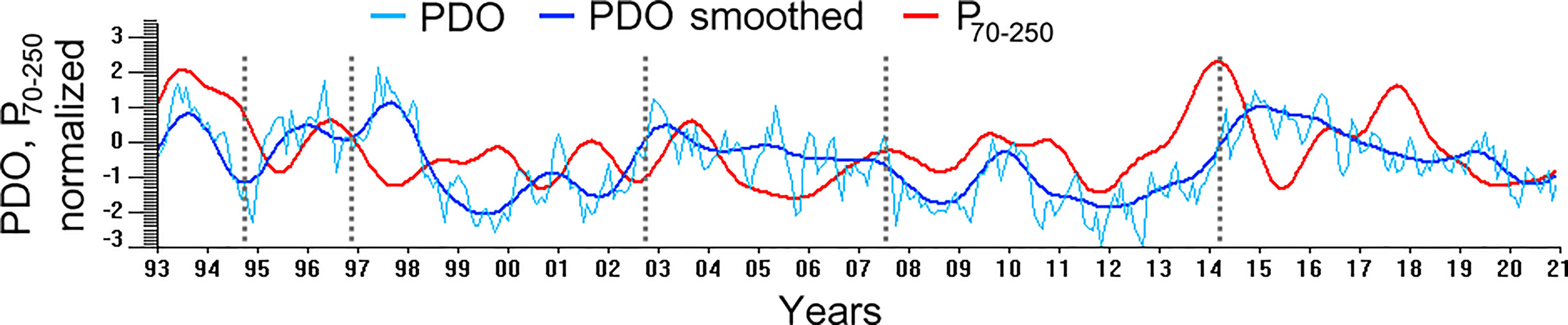
Figure 6 The low-pass filtered, with the cut-off period of 1.5 year, timeseries of (red line) P_70–250 and (blue line) PDO index; the original PDO index is shown for comparison by light-blue line. The vertical grey dashed lines separate the times with different character of the relationship between PDO and P_70–250.

Variability of Eddy Kinetic Energy

To analyze mesoscale processes in the northern JES, EKE northward of 41° N was expanded to EOFs. High-frequency signals were removed from EKE by filtering (see above); however, the satellite altimetry cannot resolve small and short-lived eddies which are frequent in the northern JES, while the decreased noise made it possible to derive a reasonable leading EKE mode, although accounting for merely a moderate fraction of the variance (20.5%; Table 1). The lower modes turned out to be undistinguishable and not interpretable.

The spatial pattern of the leading EKE mode shown in Figure 1G features the largest loadings along the northwestern and northeastern JES boundaries, i.e. within the Primorye Current and TWC, respectively. The loadings are also increased off Hokkaido within the path of the TWC western branch marked in Figure 1A. In contrast, the loadings are low in the central area to the south of 42–43° N, corresponding to the ‘eddy desert’ reported by Lee et al. (2019). However, numerous eddies were detected in this area from infrared satellite imagery (Takematsu et al., 1999; Lobanov et al., 2007; Trusenkova et al., 2009), which are too small to be captured by the altimetry data. The leading mode represents well temporal EKE variability in the northern JES, as demonstrated by the principal component (PC_EKE 1) and EKE averaged in the northern JES (EKE_N) which are shown in Figure 7A. The correlation between two timeseries is equal to 0.86 and it increases to 0.92 if EKE_N is low-pass filtered, with the cut-off period of 15 weeks. This kind of temporal variability and the consistent spatial pattern justify this mode despite the moderate variance fraction accounted for.

FIGURE 7

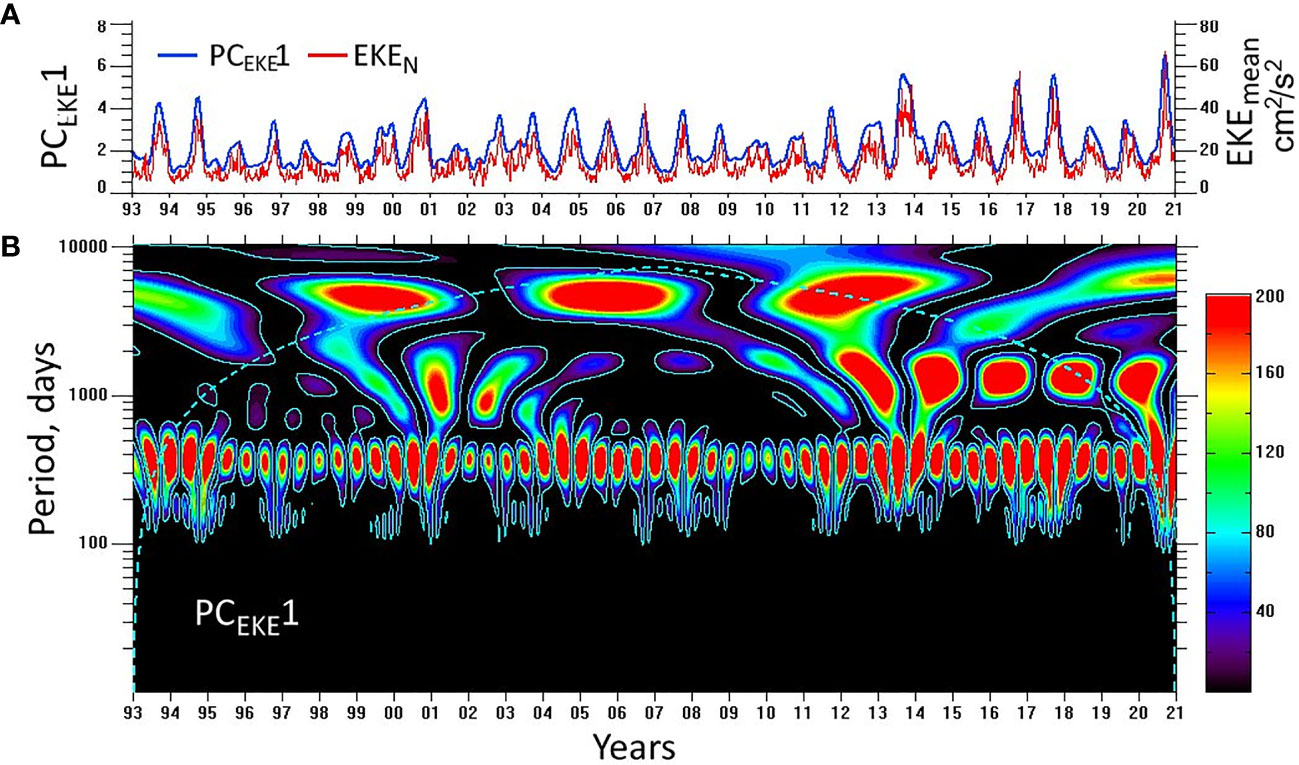
Figure 7 (A) (blue line) The principal component PC_EKE 1 (dimensionless; left-hand side y axis) and (red line) EKE averaged in the northern JES (EKE_N; cm²/s²; right-hand side y axis) and (B) WT spectrum of PC_EKE 1.

EKE in the northern JES reveals a clear seasonal signal, although its amplitude considerably varies throughout the record, as demonstrated by the PC_EKE 1 timeseries (Figure 7A). The WT spectrum of PC_EKE 1 is shown in Figure 7B and it features statistically significant maxima between 300 and 450 days, corresponding to the annual timescale, keeping in mind that the DOG mother wavelet provides only moderate resolution in the frequency domain. As the range of the PC_EKE 1 seasonal variation is equal to 1.5–2 and the spatial loadings within the mode maxima are equal to 8–12 cm²/s², the seasonal signal related to the first mode can be estimated as 12–24 cm²/s², which is close to that of EKE_N (Figure 7A). The same seasonal signal is typical of EKE averaged in the entire JES (EKE₀) shown in Figure 8A. EKE increases in summer and fall and decreases in winter and spring, with the seasonal extremes in October/November and March/April, respectively. The correlation between EKE₀ and EKE_N is equal to 0.66 and to 0.88 for the timeseries band-pass filtered around the annual timescale; the latter are shown in Figure 4. The matching EKE in the northern and entire JES is not a priori evident, as the latter is an order of magnitude larger than the former (Figure 1B) and, therefore, actually represents EKE in the southern JES (EKE_S; Figure 8A), with the correlation of 0.99 between EKE₀ and EKE_S.

FIGURE 8

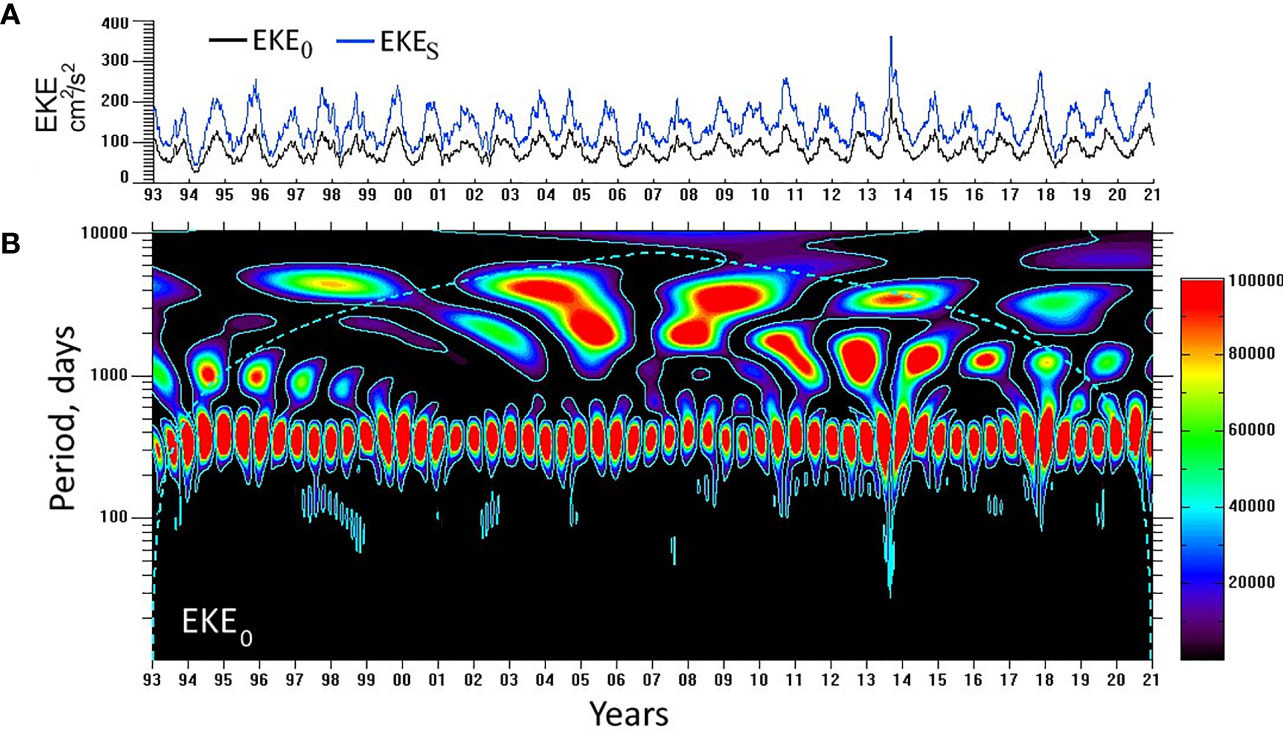
Figure 8 (A) (black line) EKE (cm²/s²) averaged in the entire JES (EKE₀) and (blue line) in the southern JES (EKE₀) and (B) WT spectrum of EKE₀ (cm⁴/s⁴).

Thus, the seasonal cycles of PC_HF 1, PC 1, PC_EKE 1 and EKE₀ match each other, with the pair correlations between the band-bass filtered timeseries of 0.89–0.95 (Figure 4). Moreover, they match the seasonal variation of the mean currents in the JES, strengthening in summer and fall and slackening in winter and spring, with the seasonal extremes in October and March, respectively (Trusenkova and Kaplunenko, 2013). Therefore, the spatial pattern and annual cycle of the leading EKE mode indicate that mesoscale processes are generated by instability of the mean currents.

In contrast to the annual cycle, the longer scale variability differs for EKE in the northern and entire (southern) JES; this is clearly seen in the WT spectra shown in Figures 7B, 8B, respectively. PC_EKE 1 features variability on the 3–5-year timescale from 1997 through 2005 and from 2010 through 2017 (out of COI), while the interannual variability was low from 2006 through 2009 when the seasonal signal was also weak. Accordingly, decadal variability manifests itself in the WT spectrum, being out of COI from 2001 through 2011 (Figure 7B). EKE₀ mostly representing the southern JES reveals QB variability from 1995 through 1998, 5–8-year variability from 2002 through 2009, and 3–5-year variability from 2010 through 2016 (out of COI; Figure 8B). This is also quite different of interannual variability of the intra-seasonal sea level fluctuations (P_70–250). A remarkable exception is late 2013 when both EKE_N and EKE_S showed very strong maxima. An attempt to look for linkages with the climate indices, such as and SOI, AOI, NPI, WPI and PDO index, turned out ineffective.

Conclusion

Intra-annual sea level fluctuations and variability of mesoscale processes were studied in the northern JES (northward of 41° N), using data from satellite altimetry for 1993–2020. Decomposition to EOFs was performed of both high-pass filtered, with the cut-off period of 250 days, and original SLA. In both cases, the leading modes capture fluctuations which are simultaneous in the entire sea. The leading SLA modes for both high-pass filtered and original SLA in the northern JES are the counterparts to those in the entire sea, with the matching spatial patterns and temporal variability. Actually, simultaneous sea level fluctuations were already found, with the prevailing periods of 80, 100 and 150 days (Choi et al., 2004) and on variety of timescales from the intra-annual to decadal ones (Trusenkova and Kaplunenko, 2013; Trusenkova, 2018). However, the present analysis made it possible to reveal new features, as summarized below.

It is newly found that the simultaneous intra-annual SLA occur in the entire range from 50 to 250 days, without any preferable timescale. The seasonal signal is newly found in the intra-annual SLA, which matches that in the original SLA. Note that that the sea level in the JES rises or declines from spring to fall or from fall to spring, respectively, with the seasonal extremes in October/November and March/April, respectively, due to the steric effects caused by the thermal forcing at the sea surface and from the warm water inflow in the KTS (Choi et al., 2004; Trusenkova and Kaplunenko, 2013). The seasonal variation is the same for the simultaneous intra-annual fluctuations, with the short-term SLA larger in summer and fall and smaller in winter and spring. However, the intensity of these fluctuations (differences between the highs and lows) is not subjected to any seasonal variation.

As the leading SLA mode covering the major fraction of the variance captures the simultaneous fluctuations, an analysis of mesoscale processes in the northern JES is based on EKE computed from the altimetry data and expanded to EOFs. The leading EKE mode captures mesoscale variability within the Primorye Current in the northwestern JES and TWC in the northeastern JES. Although this mode accounts for only a moderate fraction of the total variance, it is justified by the consistent spatial pattern and by the temporal variability matching that of EKE averaged over the northern JES. The seasonal EKE signal in the northern JES matches that of EKE in the entire JES which actually represents EKE in the southern JES where it is an order of magnitude larger than in the northern sea. The seasonal EKE signal also matches that of sea level fluctuations which are simultaneous in the entire JES and that of the circulation intensity, the latter being in line with the EKE generation due to current instability.

Both intra-annual simultaneous SLA and EKE representing mesoscale processes manifest rich variability on QB, interannual and decadal timescales. However, in contrast with the seasonal signal, the low-frequency SLA variability does not match that of EKE in the northern or southern JES. However, it is remarkable that in 2013 EKE was extremely large in both northern and southern JES. This implies different forcings on the low-frequency timescales. The low-frequency EKE variability can be forced either by local winds or indirectly by winds from outside the JES through their impact on the KTS transport affecting eddy generation in the southern sea. Accordingly, the long-term wind variability can differ in different areas, resulting in the mismatching low-frequency variations of sea level and mesoscale processes in the northern and southern JES. As can be judged from the published data (Fukudome et al., 2010; Yoon et al., 2016), the relationship of intra-annual simultaneous SLA with the KTS transport interannual variation is inconclusive. The intra-annual simultaneous SLA reveal changing relationship with Pacific Decadal Oscillation (PDO): both were in-phase in 1993–1994 and from late 2007 to 2013 and out-of-phase from 1997 to 2002, while there was no specific relationship in other times.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://resources.marine.copernicus.eu/product-download/SEALEVEL_GLO_PHY_L4_MY_008_047. The climatic indices used in this study can be found here: https://www.ncdc.noaa.gov/climate-monitoring/#wx-patterns and https://www.cpc.ncep.noaa.gov/data/teledoc/wp.shtml.

Author Contributions

OT designed the study, analyzed the data and wrote the manuscript and DK prepared the data. All authors contributed to the article and approved the submitted version.

Funding

The study was carried out as a part of the State Task No. 121021700346-7 for V.I. Il’ichev Pacific Oceanological Institute, Far-Eastern Branch of Russian Academy of Sciences.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Barnston A. G., Livezey R. E. (1987). Classifications, Seasonality, and Persistence of Low-Frequency Atmospheric Circulation Patterns. Month. Weath. Rev. 115, 1083–1126. doi: 10.1175/1520-0493(1987)115<1083:CSAPOL>2.0.CO;2

CrossRef Full Text | Google Scholar

Choi B.-J., Haidvogel D. B., Cho Y.-K. (2004). Nonseasonal Sea Level Variations in the Japan/East Sea From Satellite Altimeter Data. J. Geophys. Res. 109 (12), C12028, 1–12. doi: 10.1029/2004JC002387

CrossRef Full Text | Google Scholar

Danchenkov М.А., Lobanov V. B., Riser S. C., Kim K., Takematsu M., Yoon J.-H. (2006). A History of Physical Oceanographic Research in the Japan/East Sea. Oceanography 19 (3), 18–31. doi: 10.5670/oceanog.2006.41

CrossRef Full Text | Google Scholar

Fukudome K. I., Yoon J. H., Ostrovskii A. G., Takikawa T., Han I.-S. (2010). Seasonal Variation of the Tsushima Warm Current Through the Tsushima Strait From 10 Years ADCP Observation. J. Oceanogr. 66 (4), 539–551. doi: 10.1007/s10872-010-0045-5

CrossRef Full Text | Google Scholar

Hirose N., Ostrovskii A. G. (2000). Quasi-Biennial Variability in the Japan Sea. J. Geophys. Res. 105 (6), 14011–14027. doi: 10.1029/2000JC900046

CrossRef Full Text | Google Scholar

Gordon A. L., Giulivi C. F. (2004). Pacific Decadal Oscillation and Sea Level in the Japan/East Sea. Deep. Sea. Res. Part I 51, 653–663. doi: 10.1016/j.dsr.2004.02.005

CrossRef Full Text | Google Scholar

Kang S. K., Cherniawsky J. Y., Foreman G. G., Min H. S., Kim C.-H., Kang H.-W. (2005). Patterns of Recent Sea Level Rise in the East/Japan Sea From Satellite Altimetry and in Situ Data. J. Geophys. Res. 110 (C07), C07002, 1-10. doi: 10.1029/2004JC002565

CrossRef Full Text | Google Scholar

Kang D., Hirose N., Fukudome K. (2014). Transport Variability in the Korea/Tsushima Strait: Characteristics and Relationship to Synoptic Atmospheric Forcing. Cont. Shelf. Res. 81, 55–66. doi: 10.1016/j.csr.2014.03.010

CrossRef Full Text | Google Scholar

Lee K., Nam S., Kim Y.-G. (2019). Statistical Characteristics of East Sea Mesoscale Eddies Detected, Tracked, and Grouped Using Satellite Altimeter Data From 1993 to 2017. J. Kor. Soc. Oceanogr. 24 (2), 267–281. doi: 10.7850/JKSO.2019.24.2.267

CrossRef Full Text | Google Scholar

Lee D.-K., Niiler P. P. (2005). The Energetic Surface Circulation Patterns of the Japan/East Sea. Deep. Sea. Res. Part II. 52 (11-13), 1547–1563. doi: 10.1016/j.dsr2.2003.08.008

CrossRef Full Text | Google Scholar

Lee D.-K., Niiler P. (2010). Eddies in the Southwestern Japan/East Sea. Deep-Sea. Res. I. 57 (10), 1233–1242. doi: 10.1016/j.dsr.2010.06.002

CrossRef Full Text | Google Scholar

Lobanov V. B., Ponomarev V. I., Salyuk A. N., Tishchenko P., Talley L. D. (2007). “Struktura I Dinamika Sinopticheskikh Vikhrei Severnoi Chasti Yaponskogo Morya (Structure and Dynamics of Mesoscale Eddies in the Northwestern Japan Sea),” in Dal’nevostochnye Morya Rossii, Kniga 1, Okeanologicheskie Issledovaniya (Far Eastern Seas of Russia, Book 1, Oceanological Research) (Moscow: Nauka), 450–473.

Google Scholar

Lyu S. J., Kim K. (2005). Subinertial to Interannual Transport Variations in the Korea Strait and Their Possible Mechanisms. J. Geophys. Res. 110, C12016. doi: 10.1029/2004JC002651

CrossRef Full Text | Google Scholar

Mantua N. J., Hare R. (2002). The Pacific Decadal Oscillation. J. Oceanogr. 58, 35–44. doi: 10.1023/A:1015820616384

CrossRef Full Text | Google Scholar

Marcos M., Tsimplis M. N., Calafat F. M. (2012). Inter-Annual and Decadal Sea Level Variations in the North-Western Pacific Marginal Seas. Progr. Oceanogr. 105, 4–21. doi: 10.1016/j.pocean.2012.04.010

CrossRef Full Text | Google Scholar

Mertz F., Rosmorduc V., Maheu C., Faugére Ya. (2017). Product User Manual for Sea Level SLA Products, 51 (Paris: EU Copernicus Marine Service).

Google Scholar

Morimoto A., Yanagi T. (2001). Variability of Sea Surface Circulation in the Japan Sea. J. Oceanogr. 57 (1), 1–13. doi: 10.1023/A:1011149401735

CrossRef Full Text | Google Scholar

Morimoto A., Yanagi T., Kaneko A. (2000). Eddy Field in the Japan Sea Derived From Satellite Altimetric Data. J. Oceanogr. 56 (4), 449–462. doi: 10.1023/A:1011184523983

CrossRef Full Text | Google Scholar

Oh I. S., Rabinovich A. B., Park M. S., Mansurov R. N. (1993). Seasonal Sea Level Oscillations in the East Sea (Sea of Japan). J. Kor. Soc. Oceanogr. 28, 1–16.

Google Scholar

Ostrovskii A. G., Fukudome K., Yoon J. H., Takikawa T. (2009). Variability of the Volume Transport Through the Korea/Tsushima Strait as Inferred From the Shipborne Acoustic Doppler Current Profiler Observations in 1997–2007. Oceanology 49 (3), 338–349. doi: 10.1134/S0001437009030060

CrossRef Full Text | Google Scholar

Ponomarev V. I., Faiman P. A., Dubina V. A., Ladychenko S., Lobanov V. B. (2011). Sinopticheskaya Vikhrevaya Dinamika Nad Severo-Zapadnym Materikovym Sklonom I Shel'fom Yaponskogo Morya (Modelirovanie I Rezul'taty Distantsionnykh Nablyudenii) (Mesoscale Eddy Dynamics Over Northwestern Japan Sea Continental Slope and Shelf (Simulation and Remote Sensing Results)). Sovrem. Probl. Distantsionnog. Zondirovan. Zemli. Kosm. (Curr. Probl. Remote Sens. Earth Spac.) 8 (2), 100–104.

Google Scholar

Preisendorfer R. W. (1988). Principal Component Analyses in Meteorology and Oceanography (Amsterdam: Elsevier), 425.

Google Scholar

Serykh I. V., Sonechkin D. M., Byshev V. I., Neiman V. G., Romanov Y. (2019). Global Atmospheric Oscillation: An Integrity of ENSO and Extratropical Teleconnections. Pure. Appl. Geophys. 176, 3737–3755. doi: 10.1007/s00024-019-02182-8

CrossRef Full Text | Google Scholar

Takematsu M., Ostrovskii A. G., Nagano Z. (1999). Observations of Eddies in the Japan Basin Interior. J. Oceanogr. 55 (2), 237–246. doi: 10.1023/A:1007846114165

CrossRef Full Text | Google Scholar

Thompson D. W. J., Wallace J. M. (2001). Regional Climate Impacts of the Northern Hemisphere Annular Mode. Science 293, 85–89. doi: 10.1126/science.1058958

PubMed Abstract | CrossRef Full Text | Google Scholar

Torrence C., Compo G. P. (1998). A Practical Guide to Wavelet Analysis. Bull. Amer. Meteorol. Soc. 79 (1), 61–78. doi: 10.1175/1520-0477(1998)079<0061:APGTWA>2.0.CO;2

CrossRef Full Text | Google Scholar

Trenberth K. E., Hurrell J. W. (1994). Decadal Atmosphere-Ocean Variations in the Pacific. Climate Dynam. 9, 303–319. doi: 10.1007/BF00204745

CrossRef Full Text | Google Scholar

Trusenkova O. O. (2018). Long-Term Variation in the Level of the Sea of Japan Based on Satellite Altimetry Measurements. Izvest. Atmos. Ocean. Phys. 54 (9), 1023–1030. doi: 10.1134/S0001433818090396

CrossRef Full Text | Google Scholar

Trusenkova O. O., Kaplunenko D. D. (2013). Variability Modes of Sea Level in the Sea of Japan. Oceanology 53 (3), 308–316. doi: 10.1134/S000143701302015X

CrossRef Full Text | Google Scholar

Trusenkova O. O., Lobanov V. B., Primachev E. V. (2021). Sea Level Intra-Annual Variability in the Coastal Northwestern Part of the Sea of Japan. Fundament. I. Prikladn. Gidrofiz. 14 (1), 54–62. doi: 10.7868/S2073667321010056

CrossRef Full Text | Google Scholar

Trusenkova O. O., Nikitin A. A., Lobanov V. B. (2009). Circulation Features in the Japan/East Sea Related to Statistically Obtained Wind Patterns in the Warm Season. J. Mar. Sys. 78 (2), 214–225. doi: 10.1016/j.jmarsys.2009.02.019

CrossRef Full Text | Google Scholar

Wallace J. M., Gutzler D. S. (1981). Teleconnections in the Geopotential Height Field During the Northern Hemisphere Winter. Month. Weath. Rev. 109, 784–812. doi: 10.1175/1520-0493(1981)109<0784:TITGHF>2.0.CO;2

CrossRef Full Text | Google Scholar

Wang C., Deser C., DiNezio J.-Y., Yu P., Clement A. (2016). “El Niño-Southern Oscillation (ENSO): A Review,” in Coral Reefs of the Eastern Pacific. Eds. Glymn P., Manzello D., Enochs I. (Springer Science Publisher), 85–106.

Google Scholar

Yoon S.-T., Chang K.-I., Na H., Minobe S. (2016). An East-West Contrast of Upper Ocean Heat Content Variation South of the Subpolar Front in the East/Japan Sea. J. Geophys. Res. C121 (8), 6418–6443. doi: 10.1002/2016JC011891

CrossRef Full Text | Google Scholar