
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mar. Sci., 14 March 2022
Sec. Marine Biogeochemistry
Volume 9 - 2022 | https://doi.org/10.3389/fmars.2022.857413
This article is part of the Research TopicChemical and Biogeochemical Processes at Methane and Other Cold SeepsView all 15 articles
The lack of the quantification of deep dissolved methane flux prevents us from accurately understanding hydrate accumulation and distribution at a given geologic setting where vertically upward methane advection dominates the hydrate system. The upward deep methane flux was usually applied as an assumed value in many previous studies. Considering the deep methane flux changes the methane concentration in the pore water and further affects the phase transfer between the gas and aqueous phases depending on the in situ methane concentration, we link gas bubbles distribution to deep dissolved methane flux. Here, we constructed a numerical model to quantify the dissolved methane flux from depth based on the parameters related to gas bubble distribution, including the residual gas saturation in sediments and the free gas zone (FGZ) thickness. We then applied our model to ODP Site 995 at the Blake Ridge where methane was sourced from deep layers. Our model results predict an upward deep methane flux of 0.0231 mol/m2/a and the occurrence of another gas interval in deeper sediments, which are consistent with seismic data. We further explored the influence of upward methane flux on hydrate accumulation and found that the thin hydrate occurrence zone at nearby Site 994 likely resulted from a small deep methane flux. Combined with the previous conclusion of high deep methane flux at Site 997, we showed that along the Blake Ridge drilling transect the estimated deep methane fluxes decrease with increasing distance from the crest of the ridge. This approach for quantifying deep methane flux is complementary to the current hydrate accumulation model and provides new insights into the regional methane flux estimation at the Blake Ridge.
Natural gas hydrates precipitate in submarine sediments under suitable thermodynamic conditions of low temperature and high pressure (Kvenvolden, 1993; Sloan and Koh, 2008). These factors restrict a maximum suitable interval for hydrate stability, which is called the gas hydrate stability zone (GHSZ) (Xu and Ruppel, 1999). However, the amount of methane in the GHSZ limits the methane hydrate occurrence to a finite region below the seafloor, often referred to as the actual hydrate occurrence zone (GHOZ) (Zatsepina and Buffett, 1997; Bhatnagar et al., 2007; Malinverno, 2010; Malinverno and Goldberg, 2015. Methane can be generated by such as in situ methanogenesis, or supplied by upward advection of methane-bearing fluids and free gas flow (Chen and Cathles, 2003, 2005; Cao et al., 2013; Vanderbeek and Rempel, 2018; Dhakal and Gupta, 2021). The mode of methane supply by the advection of methane-bearing fluids has been demonstrated in various hydrate deposits globally, such as the Blake Ridge (Hyndman and Davis, 1992; Liu and Flemings, 2007; Malinverno et al., 2008; You et al., 2019). This deep methane source is produced in the deep subsurface sediments and subsequently migrated into the GHSZ by upward fluid flow. Numerous studies confirmed the existence of an external dissolved methane source at the Blake Ridge through porosity and capillary pressure analyses as well as the calculation of in situ methane production and geochemical data simulations (Davie and Buffett, 2003a,b; Flemings et al., 2003; Wallmann et al., 2006). In addition, the age of the pore fluids dated via radioisotope 129I was significantly older than the surrounding sediments. The older age and the elevated bromide and iodide concentrations also suggest a deep fluid source at the Blake Ridge (Egeberg and Dickens, 1999; Fehn et al., 2000).
The effect of these deep methane-bearing fluids on hydrate formation depends on the flow velocity and the methane concentration in rising fluids. The velocity of the fluid flow can be estimated by investigating the measured pore water chloride profiles (Davie and Buffett, 2003a,b; Torres et al., 2004; Bhatnagar et al., 2008, 2011). However, the composition of this deep methane source is not well constrained. For simplification, numerous quantitative studies assumed the methane solubility at the BHSZ (base of the GHSZ) or a certain value inferred from gas distribution characteristics as the methane concentration in the rising fluids (Davie and Buffett, 2003b; Torres et al., 2004; Garg et al., 2008; Haacke et al., 2008). The model developed by Bhatnagar et al. (2007) has emphasized the significance of an accurate methane flux value for quantifying methane hydrate accumulation. Results suggest that a certain minimum methane flux is required to form hydrates in a hydrate system which is dominated by a deep methane source (Xu and Ruppel, 1999; Bhatnagar et al., 2007). If methane supplied from depth exceeds this minimum value, methane hydrate would extend to the BHSZ at a steady state due to the sedimentation (Burwicz and Haeckel, 2020). But more time is required to achieve this steady state if the methane concentration in the rising fluids is low. Therefore, the evolution of the methane hydrate deposits can be observed only if an accurate deep-sourced methane flux is obtained.
In addition to its influence on hydrate accumulation and distribution, this deep methane source significantly affects the formation and properties of the free-gas zone (FGZ) beneath the BHSZ (Pecher et al., 2001; Haacke et al., 2008). Haacke et al. (2007, 2008) adopted an methane concentration of the rising fluid that is approximately equivalent to the half the equilibrium solubility at the BHSZ to model the evolution of FGZ in the west Svalbard and suggested that the deep dissolved methane flux was a primary factor in controlling the gaseous methane occurrence and distribution in the FGZ (Haacke et al., 2007, 2008). Upward methane flux from depth toward the BHSZ affects pore-water methane concentration and resulting inter-conversion between the gaseous methane and dissolved methane as it moves upwards. Therefore, the deep dissolved methane flux is closely linked to gas bubbles distribution in the FGZ.
Here, a numerical model was constructed to quantify the upward methane flux based on methane mass conservation in the FGZ. This model was then applied to ODP Site 995 at the Blake Ridge where methane sourced from depth dominates the hydrate accumulation. Unlike previous work, our model established a relationship between the deep dissolved methane flux and gas bubbles saturation (gas volume fraction) and provides an approach for calculating the flux of deep methane. We subsequently combined our results at Site 995 with previous results about methane flux at nearby sites and yielded an integrated picture of regional methane flux patterns along the Blake Ridge drilling transect. This model for quantifying deep methane flux is complementary to the current hydrate accumulation model.
In porous media of the GHSZ, methane can be present in aqueous, gaseous and hydrate phases (You et al., 2019). A Bottom Simulating Reflector (BSR) often marks the boundary between the base of the GHSZ and the underlying FGZ (Stoll et al., 1971; Shipley et al., 1979; Wood and Ruppel, 2000; Westbrook and Thatcher, 2009). The model domain in this study extended from the BHSZ to a few hundred meters below the BHSZ. Two spatial domains below the BHSZ were defined: the free gas domain (Domain 1) and the methane undersaturated domain (Domain 2). This conceptual model was illustrated in Figure 1. Domain 1 extended from the BHSZ to the base of the FGZ (BFGZ), and Domain 2 represented the section below the BFGZ (Figure 1). In Domain 1 where gas bubbles existed, gas and water were in equilibrium. The methane concentration in Domain 1 was equal to the gas-liquid solubility, which was regulated by local thermodynamic conditions (Duan et al., 1992; Davie et al., 2004). In contrast, in Domain 2, the dissolved methane concentration in pore water is less than its solubility. Therefore, only dissolved methane was expected (Figure 1).
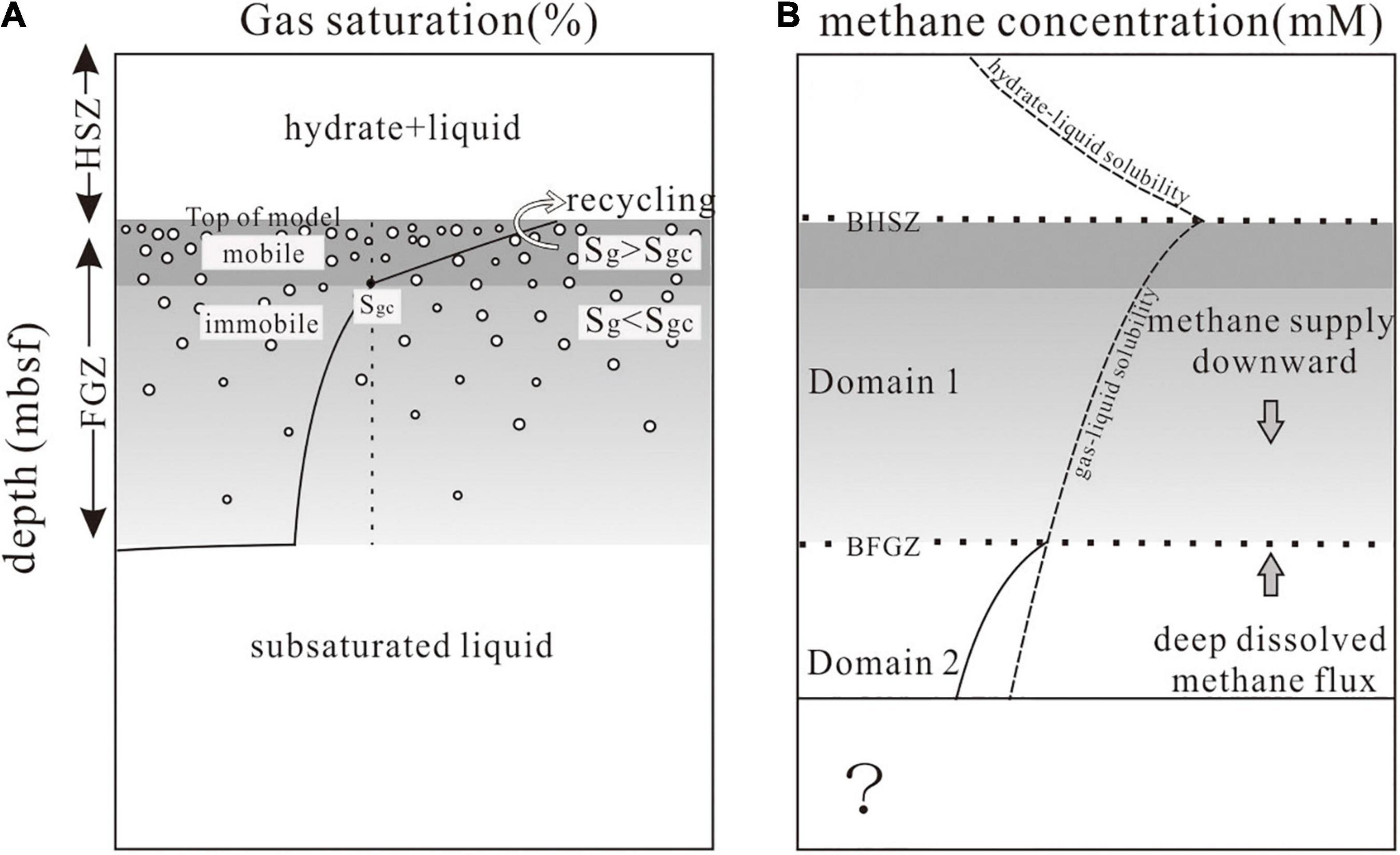
Figure 1. Conceptual illustration of the free gas system below the BHSZ. (A) The region below the top of model (BHSZ) is divided into two domains. The mobile free gas shown in shaded dark gray was produced through hydrate dissociation, accumulated at the BHSZ or moved upward due to the buoyancy and left a certain gas which equals to the residual gas saturation (Sgc). These mobile gas bubbles occupy an extremely thin layer compared with the large gas distribution zone that controlled by the sedimentation and shown in shaded light gray. This model neglects the upward gas bubbles. (B) Dotted lines represent the BHSZ and BFGZ. Dashed lines represent hydrate-liquid and gas-liquid solubility curves. The downward gaseous methane and diffused methane and the upward flow of unsaturated fluid collectively affect the amount of methane in pore water, which results in inter-conversion between the gaseous methane and dissolved methane. The gas bubbles no longer exist below the BFGZ because gaseous methane at the BFGZ compensates the deep unsaturated dissolved methane. The methane concentration profile represented by black solid line in Domain 2 is plotted according to the deep methane flux. The question mark represents the possibility of the gas bubble occurrence beneath Domain 2 since the gas-liquid solubility tends to decrease with depth. The gas bubbles would exist if the methane concentration exceeds the gas-liquid solubility.
The methane hydrate tended to dissociate and produce free gas and water when being buried out of the GHSZ (Xu, 2004; Figure 1). The hydrate burial may result in a thin region with three-phase coexisting beneath the BHSZ (Liu and Flemings, 2011). A fraction of the gas bubbles moved upwards due to buoyancy. They were recycled into the GHSZ through overcoming the capillary forces or accumulated below the BHSZ as a thin horizon (Haacke et al., 2008; Figure 1). We did not take into account these migrating gas bubbles toward the BHSZ since they appeared to be only important in hydrate accumulation which was dominated by gaseous methane recycling (Mogollon et al., 2009). Besides these mobile gas, there are some gases trapped in sediments which are unable to migrate freely. In fact, these residual gas bubbles exerted a significant control on the characteristics of the FGZ (Haacke et al., 2008). We focused on these residual gas bubbles that moved downward with sedimentation and their behavior within the sediment column which was influenced by the deep methane flux (Minshull and White, 1989; Haacke et al., 2008; Figure 1). As gas bubbles move downward via sedimentation, the mass transfer between gas and aqueous phases occurred. Because the methane concentration in the pore water is affected by the advection of methane-carrying pore fluids and diffusion of dissolved methane. This methane phase transfer is dependent on the in situ methane concentration: if unsaturated, gas bubbles represent a methane source for the aqueous phase; and if oversaturated, gas bubbles represents a methane sink (Mogollon et al., 2009). Therefore, the deep methane-carrying fluids controls the methane concentration in the pore water and further affects gas dissolution and formation (Su and Chen, 2007; Archer et al., 2012). The characteristics of gas bubbles distribution can be visualized through seismic imaging. Hence, the relationship between the gas bubbles distribution and the deep methane-carrying fluids enables the calculation of the deep methane flux as a function of gas bubble saturation and the depth of BFGZ.
The gaseous methane profile was controlled by physical processes including advection of methane-carrying pore fluids, diffusion of dissolved methane, and burial of the gas bubbles. We derived the gas control equation in the FGZ based on conservation of methane mass and obtained the gas distribution characteristics (Figure 1). Under the steady-state condition, the gaseous methane at the BFGZ exactly compensates the upward unsaturated dissolved methane, rendering the absence of gas below the BFGZ. Therefore, the mass balance of methane at the BFGZ can be used to calculate the deep methane flux. Furthermore, we established the methane mass balance equation to generate the dissolved methane profile in Domain 2 using the computed dissolved methane flux from depth. The curvature of the methane concentration profile in Domain 2 could reflect the flux of this deep methane.
Before introducing the numerical representations, several assumptions need to be made to build the mass balance equations: (1) the residual gas bubbles are trapped at the BHSZ and transported downwards with sediment burial (Davie and Buffett, 2003b); (2) the immobile gas is assumed to be distributed in a homogeneous mixture of water and gas, and (3) in-situ methanogenesis is neglected considering its extremely low contribution where FGZ develops (Haacke et al., 2008); (4) the salinity remains constant (3.5% seawater value), and its influence on solubility is neglected (Davie and Buffett, 2001); (5) the sediment-grain density and porosity are assumed to be constant (Wallmann et al., 2006).
In Domain 1, the governing equation of the free gas is constructed. Fluid advection and diffusion are two mechanisms of dissolved methane transport through the liquid phase, which are represented by two terms on the right-hand side of Equation 1. This aqueous transport controls the gas bubble distribution in Domain 1 as discussed before. Simultaneously, the formed gas bubbles are transported by sedimentation, which is represented by the second term in Equation 1 (Xu and Ruppel, 1999; Davie and Buffett, 2001). The phase transfer occurs during this process. The volume fraction of methane gas becomes the primary dependent variable across Domain 1. The two-phase mass balance equation for gas bubbles in Domain 1 is as follows:
where t is time; z (mbsf) is the depth below the seafloor defined as positive downwards;ρw (kg/m3) (1,030 kg/m3) and ρg (kg/m3) are the densities of pore water and methane in the immobile gaseous phase, respectively; Sg denotes gaseous methane saturation (volume fraction of pore space); Dm(m2/a) (0.028 m2/a) is the diffusion coefficient of methane in free water; ϕ is porosity; θ is tortuosity, which can be calculated using Archie’s law: θ2 = ϕ−1(Torres et al., 2004); (mol/kg) is the concentration of aqueous methane; Mg is the relative molecular mass of methane (16 g/mol); qw is the mass flux of pore water; and us (m/a) is the burial rate of gas bubbles with sediments, given in terms of u0 (sedimentation rate at the seafloor) by Equation (2) (Davie and Buffett, 2001):
where ϕ0 is the porosity of the seafloor. The sedimentation rate in Domains 1 and 2 remains constant, considering assumption (6). The influence of this simplification on the results will be assessed in the “Discussion” section.
The density of gaseous methane is calculated using Duan et al. (1992) and can be written as:
where P and T are the pressure and temperature at depth z, R is the universal gas constant (8.314 J/mol/k), and Z is the compressibility factor, which can be calculated using Duan et al. (1992).
Equation (1) can be rearranged to:
where represents the gas mass growth rate of a specific layer and is marked as Ag (kg/m3/a). Integrating Equation (4) yields
where is the initial gaseous methane mass of a specific layer at the initial depth z0 (BHSZ) and the initial time t0. is the residual gas beneath the BHSZ that transported downwards with sediments, and its saturation is a boundary condition in this model (Firoozabadi et al., 1992; Haacke et al., 2008). represents the change in gaseous methane mass in the pore media of a specific layer from t0 (initial time) to 0 (present time), that is, from z0 (initial depth) toz (present depth), ϕρgSg is the present mass of methane gas in a specific layer. Rearranging Equation (5), the gas saturation profile in Domain 1 is obtained as follows:
where
In the steady state, the flux value of the unsaturated dissolved methane migrating to the BFGZ from below can be calculated through the methane flux above the BFGZ. The downward gas bubbles at the BFGZ is compensated exactly by the deep unsaturated methane-bearing fluid. Therefore, methane mass conservation is carried out in two vanishingly thin volumes above and below the BFGZ, respectively. These two flux values are equal in these two volumes. The methane flux in the upper thin volume includes contributions from advection of methane in the fluid, the diffusion of methane through the pore fluid, and the gaseous phases. For a unit surface area, the flux from the upper volume is:
where is the methane flux in the upper volume (positive downward) and denotes the methane concentration in the pore water at the BFGZ. is the gas volume fraction of the pore space at the BFGZ which can be calculated through Equation (6).
Simultaneously, the value of methane flux in the lower volume that is transported toward the BFGZ is:
where is the flux value of methane bearing fluid that migrating upward to the BFGZ. For a vanishingly thin volume, is equal to. Of note, the methane concentration in pore water is equal to the value of . So far, the deep methane flux has been obtained.
was performed using the above analysis. No free gas exists in Domain 2. The dissolved methane profile in the steady state here can be calculated according to the (Equation 9). Therefore, the dissolved methane profiles in Domain 2 could reflect the value of the . If the methane fluxes from depth () were different, the methane profiles in Domain 2 would also be different. As only dissolved methane exists here, the transport of dissolved methane by the advection-dispersion equation can be described:
The dissolved methane curve in Domain 2 in the steady state is obtained by assuming the time derivative of Equation (10) to zero and proceeding with the boundary conditions (the deep methane flux) obtained above.
The Blake Ridge, located offshore in the southeast United States, contains abundant methane and gas hydrate (Paull et al., 1996; Dickens et al., 1997). The Ocean Drilling Program (ODP) Leg 164 drilled at the Blake Ridge has greatly enhanced our understanding of the effect of deep methane sources on methane hydrate accumulation (Bhatnagar et al., 2007; Frederick and Buffett, 2011; Burwicz and Rüpke, 2019). Three sites were drilled along the Blake Ridge transect with distinct BSR characteristics: the edge flank site without a BSR (Site 994), the flank site with a BSR (Site 995), and the site located on the crest of the drift deposit with a well-developed BSR (Site 997) (Figure 2a; Paull et al., 1996, 2000). The gas saturation at Site 995 is smaller than 1%, which is close to that of the residual gas bubbles in sediments (Paull et al., 1996, 2000; Holbrook, 2001; Reagan and Moridis, 2007). The occurrence of thick gas layer with low gas saturation made Site 995 appropriate for our model application because the gas bubble distribution here is obviously not affected by migrating gas bubbles formed by rapid hydrate dissociation. In addition, Site 995 is characterized by two gas-bearing zones that are detected by seismic profiles and downhole logging data (Figure 2b; Paull et al., 1996, 2000; Holbrook, 2001). The results computed from the upper gas interval could be verified through the lower gas interval. This is because that the second gas interval would be reproduced if the methane concentration beneath the BFGZ deriving from Equation 10 is reliable (Figure 1; Xu and Ruppel, 1999). Therefore, applying to Site 995 made the model convenient to be verified.
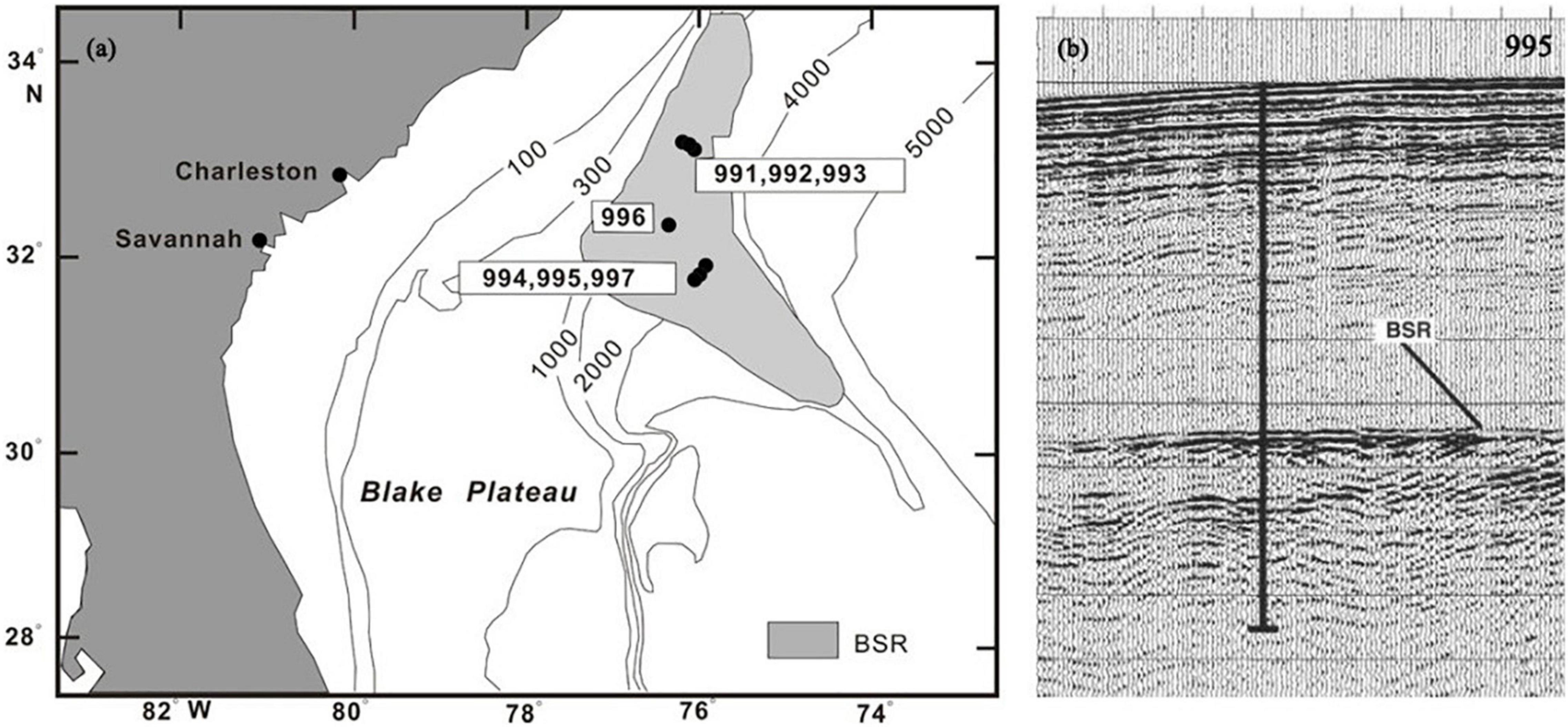
Figure 2. (a) Map showing the location of the ODP Leg 164 and the BSR area in gray. (b) Seismic reflection profile across Site 995 showing the location of BSR (Paull et al., 1996).
The basic parameters used in this model have been listed in Table 1. Some site-specific parameters needed to be stated before application to Site 995 include the fluid flow rate, the porosity, the sedimentation rate and the density of the gas bubbles. The rate of upward fluid flow was predicted by fitting the computed chloride profiles to the chloride measurements at ODP Site 995 (Paull et al., 1996; Dickens, 2001; Zheng et al., 2020). Accordingly, the value of the flow rate was determined to be 0.125 kg/m2/a, which was described as the mass flux. This result is roughly consistent with the interstitial fluid velocity at the nearby Site 997 which was obtained by Davie and Buffett (2003b). The porosity profile (ϕ) as a function of depth was determined by fitting an empirical exponential function to the measurement data (Zheng et al., 2020). Finally, the porosity exhibits a limited variation in Domains 1 and 2, which represents a nearly complete compaction below BHSZ. Therefore, we assume a constant porosity value beneath the BHSZ (Table 1). Another parameter of particular importance is the sedimentation rate. Nannofossil biostratigraphy at Site 995 indicated that the recovered sequence was mainly continuous. An average sedimentation rate of 60 m/Ma at the seafloor was documented using log and core data (Paull et al., 1996). Combing with the assumption of a constant porosity, the burial velocity of the gas bubbles beneath the BHSZ was calculated as 28 m/Ma by Equation 2. The density of the gas bubbles (ρg) was calculated using Equation 3 on the basis of parameters in Table 1 and finally it showed few changes in Domains 1 and 2. Meanwhile, the minor influence of the density value on gas saturation results has been mentioned before (Haacke et al., 2007, 2008; Mogollon et al., 2009). Therefore, the bubble density in this study was assumed to be constant (Table 1).
The numerical model relates the deep dissolved methane flux to the residual methane gas distribution characteristics in the FGZ. The residual gas saturation and the depth of BFGZ are another two important gas distribution related parameters. Below, we opted to discuss their effects on the deep methane flux. With the exception of these two values, all model parameters required for the simulation are listed in Table 1.
For the results that will be presented, the depth of BSR is assumed as where the top of the free gas interval occurs (Paull et al., 1996, 2000). And the influence of two parameters describing the free gas properties on results have been explored. Three BFGZ depths of 470, 480, and 490 mbsf were simulated to explore their effects on the model results (Figure 3A). The residual gas saturation is defined as 0.5%, given the local amount of gas bubbles. The gas is transported downwards with sediments and ceases at the BFGZ where the deep unsaturated methane compensates, as discussed in the Conceptual Model. The results show that a shallower BFGZ depth corresponds to more gas bubbles being buried (higher gas saturation) at the BFGZ, as well as a more unsaturated methane-bearing fluid migrating upward from the deep source (Figures 3A,B). The computed upward methane fluxes were 0.0229, 0.0230, and 0.0231 mol/m2/a in these three scenarios. These unequal dissolved methane fluxes from deep can be distinguished by three methane concentration profiles with different gradients in Domain 2 (Equation 10) (Figure 3A).
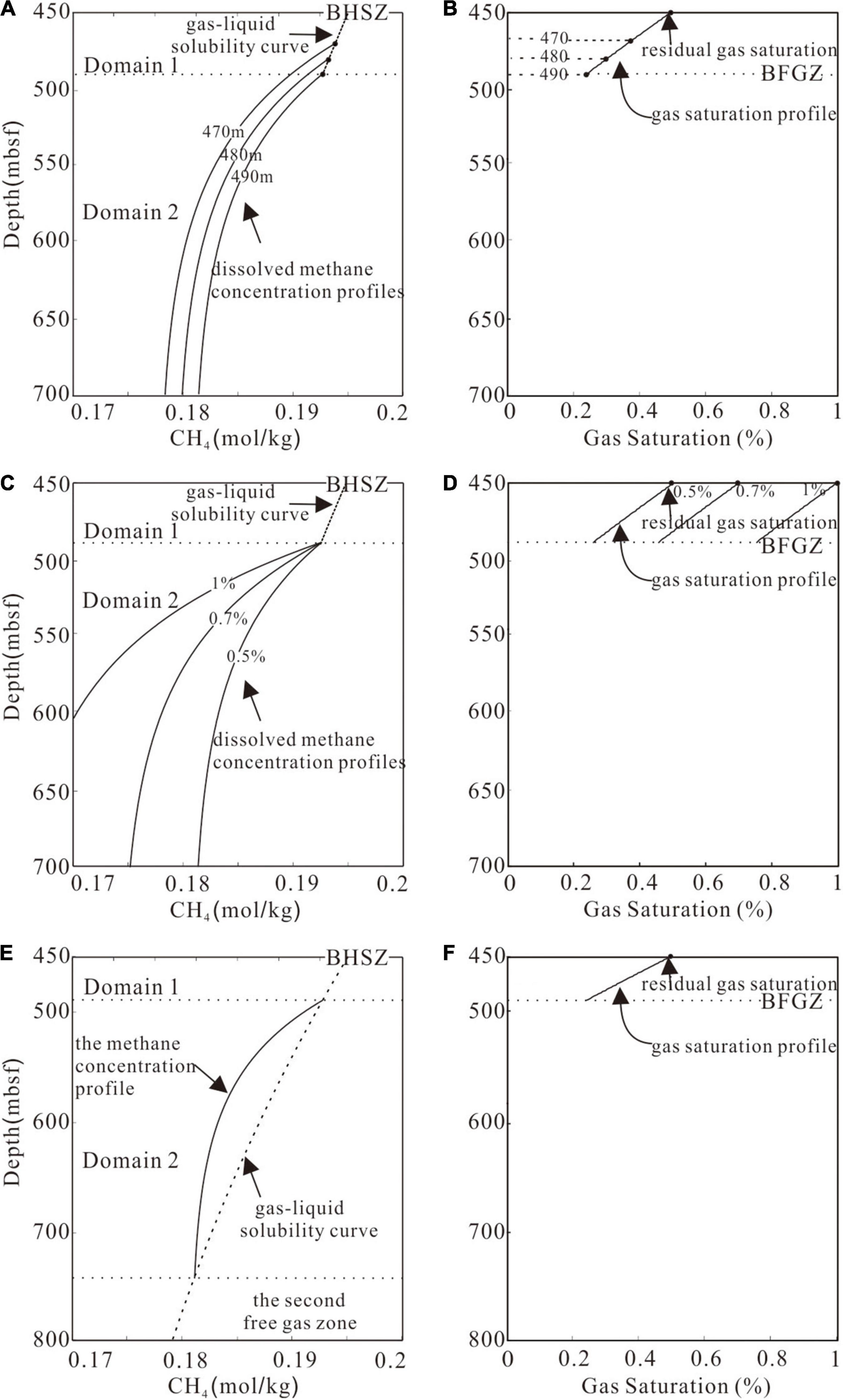
Figure 3. (A) Black solid dots in Domain 1 correspond to BFGZ depth of 470, 480, and 490 mbsf, respectively. Dashed line in Domain 1 depicts the methane gas–liquid solubility curve. Three different FGZ thicknesses correspond to three methane concentration profiles, which indicate different values of methane fluxes from depth. (B) Methane gas saturation profiles according to the same residual gas saturation but different BFGZ depths. (C) Different dissolved methane fluxes from deep are represented by three lines with different slopes in Domain 2, corresponding to three distinct residual gas saturations of 0.5, 0.7, and 1%, respectively. (D) Three gas bubble profiles based on different residual gas saturations but the same BFGZ depth. (E) The dissolved methane concentration in Domain 2 is computed through the deep dissolved methane flux at Site 995 (Equation 10). The methane concentration is lower than the gas-liquid solubility in Domain 2. The deep methane flux satisfies a second gas interval occurs, which begins at approximately 740 mbsf. (F) Gas bubbles saturation profile at Blake Ridge Site 995.
We next considered the impact of the residual gas saturation in sediments on the calculation results, with BFGZ assumed to be 490 mbsf. Unequal residual gas bubbles beneath the BHSZ are transported downwards with sediments and are trapped at the BFGZ with different amounts of gas bubbles. A larger residual gas saturation at the top of model corresponds to more gas bubbles (higher gas saturation) at the BFGZ (Figures 3C,D). The computed upward methane fluxes were 0.0231, 0.0227, and 0.0221 mol/m2/a when the residual gas saturations were defined as 0.5, 0.7, and 1%, respectively.
The above analysis show that the amount of gas bubbles in the sediments could reflect the flux of deep dissolved methane. The gas bubble distribution at Site 995 need to be constrained first to quantify the deep dissolved methane flux here. In this study, the average gas hydrate saturation at the BHSZ at Site 995 was estimated to be 5% of the pore volume (Holbrook et al., 1996; Paull et al., 1996). The methane hydrate in this saturation would produce a maximum amount of gaseous methane in approximately 2.7% of the pore volume if it is completely dissociated (Haacke et al., 2008; Daigle et al., 2020). However, any gas in excess of the residual gas saturation tends to migrate upward into the GHSZ (Claypool and Kvenvolden, 1983; Haacke et al., 2008). In other words, the residual gas that moves with sediments from the BHSZ is estimated to be less than 2.7% (Daigle et al., 2020). The values of the residual volume fraction of methane gas are often assumed to be about 1% in modeling studies (Firoozabadi et al., 1992; Reagan and Moridis, 2007; Archer et al., 2012). For example, Haacke et al. (2007, 2008) assumed a value of 0.4% as the residual gas volume in sediments to investigate the free gas evolution in the west Svalbard. Consequently, we assumed a low residual gas saturation of 0.5% in this model, which is in agreement with drilling data and previous investigations (Holbrook et al., 1996; Paull et al., 1996; Holbrook, 2001). Furthermore, the layer occupied by recycling gas bubbles with a high gas saturation has not been observed neither by downhole log-inferred nor seismic analysis (Paull et al., 1996; Holbrook, 2001). Therefore, it can be concluded that the recycling gas bubbles occupy a thin region comparing with the immobile free gas beneath the GHSZ at Site 995. The influence of the recycling gas thickness on the entire free gas thickness has been neglected. Analyses of seismic studies by Holbrook (2001) and downhole log inference by Paull et al. (2000) suggest that the depth of BFGZ at ODP Site 995 is approximately 490 mbsf. Therefore, 490 mbsf was adopted as the BFGZ depth, which was another parameter that characterizes gas distribution.
The obtained dissolved methane flux from deep at Site 995 was 0.0231 mol/m2/a (Figures 3E,F), which resulted in a second free-gas interval that occurs at approximately 740 mbsf. This depth is in agreement with those reported by Paull et al. (1996, 2000) and Holbrook (2001). The occurrence of second gas layer at 740 mbsf predicted by our model confirmed the reliability of the estimated deep methane flux.
The sedimentation rate was assumed to be constant in Domains 1 and 2 (Table 1). Therefore, we opted to discuss the influence of this assumption. The second term on the left of Equation (1) () can be divided into two parts and expressed as . In the conversion from Equations (1) to (4), the latter phase () was ignored because of the assumption of a constant sedimentation rate. Hence, we should compare the values of and . The magnitude of is computed using the porosity function (Equation 2) and the parameters listed in Table 1. However, the value of should be computed indirectly. The variation in the usϕρgSg value through Domain 1 is equivalent to the methane flux variation between the top and bottom of Domain 1, which can be calculated using Equation 8. Eventually, the value of is proven to be several orders of magnitude greater than that of . Therefore, the change in the sedimentation rate has only a minor influence on the simulation results.
Previously, the methane concentration in deep rising fluids was commonly assumed to be the methane concentration at BHSZ. In fact, the methane concentration in the deep fluid is lower than this value; otherwise, the pores of the sediments below BHSZ would all be occupied by gas bubbles as methane solubility decreases with depth beneath the BHSZ. Therefore, we first quantified the deep dissolved methane flux and applied the model at Site 995. We also explored the influence of a low deep methane flux on hydrate accumulation. A minimum methane flux from depth is required for hydrate formation in hydrate systems with deep methane sources (Xu and Ruppel, 1999; Bhatnagar et al., 2007). A larger deep methane flux causes the hydrate system to reach steady-state more rapidly. However, we applied a lower upward methane flux (0.015 mol/m2/a) comparing with that at Site 995 on hydrate accumulation and found that the methane hydrate occurrence was extremely difficult to extend to the BHSZ, despite the evolution time is long enough. The detailed model system for hydrate accumulation is described by Zheng et al. (2020). Finally, the actual hydrate occurrence thickness was thinner than that of the GHSZ. Site 994, a hydrate system with a thin zone of hydrate occurrence, might be attributed to the low methane flux from deep. This finding explains the discrepancy in hydrate distribution between Sites 994 and 995. Meanwhile, ODP Site 997 is located on the topographic crest of the Blake Ridge, 6.7 km northeast of Site 995. Numerous studies have shown that the methane hydrate deposit at Site 997 may be attributed to methane bubble migration along the fractured regions, suggesting a large deep methane flux (Flemings et al., 2003; Wallmann et al., 2006; Bhaumik and Gupta, 2007). Comparisons among Sites 994, 995, and 997 demonstrate that the deep methane flux is likely to increase along this drilling transect. Notably, the drilling report has also indicated that the hydrate occurrence discrepancy may be caused by variations in fluid composition (Paull et al., 1996). Therefore, we showed that along the Blake Ridge drilling transect the estimated deep methane fluxes decrease with increasing distance from the crest of the ridge (Figure 4). Previous studies have shown that a strong BSR is linked to elevated methane flux in deep layers (Pecher et al., 2001). Therefore, the regularly variable BSR characteristics at the Blake Ridge correspond well with our speculation.
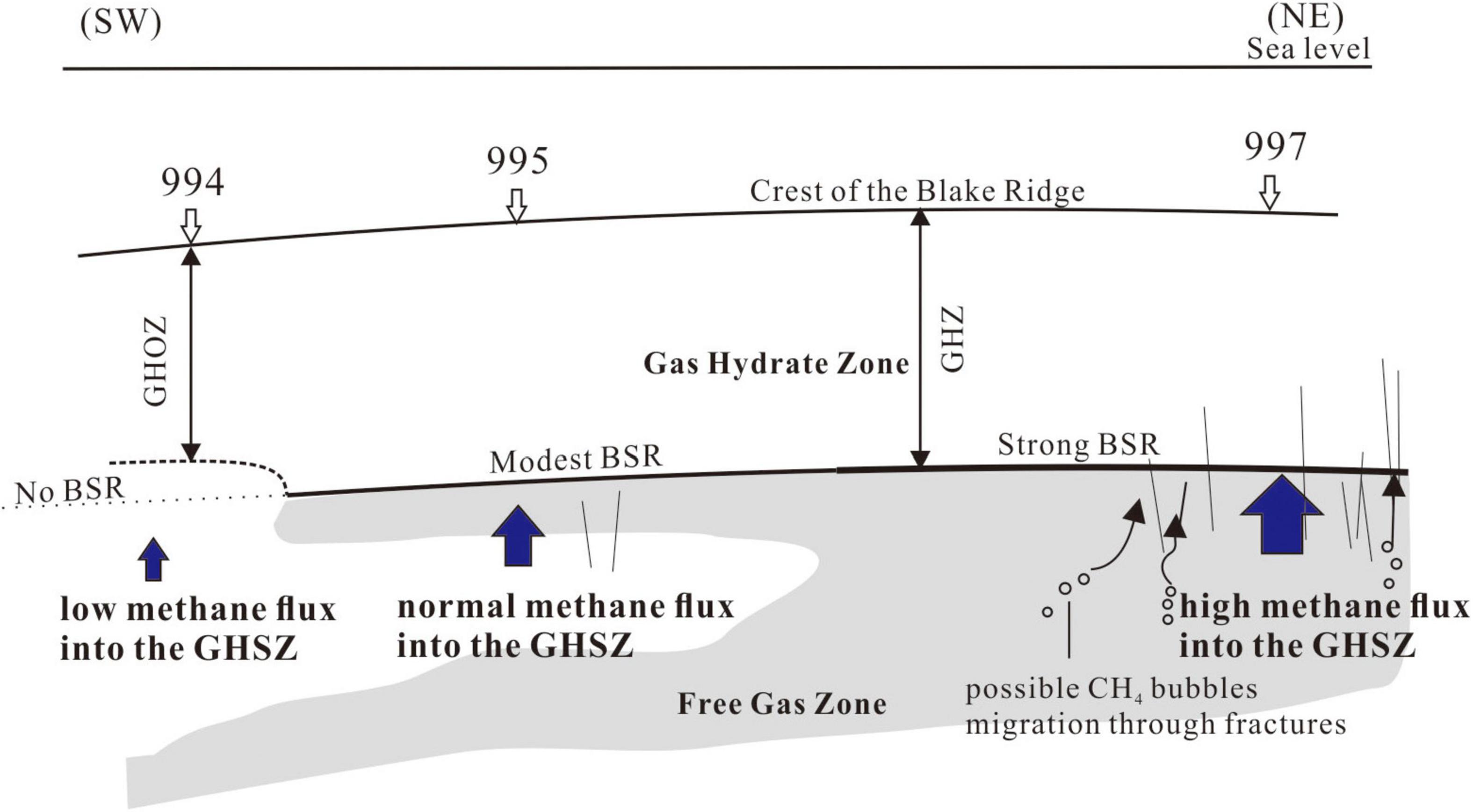
Figure 4. Conceptual representation of the methane hydrate reservoir system at the Blake Ridge. From flank Site 994 to flank Site 995 and finally to crest Site 997, the deep methane flux (dark blue arrow) is changeable from low to high, corresponding to no BSR to strong BSR occurrence. FGZ (light gray) is beneath the BSRs. The methane hydrate-bearing zone at Site 994 (GHOZ) does not extend to the BSRs depth. However, thicker hydrate occurrences (GHZ) appear at Sites 995 and 997, which both extend to the BSRs.
In general, our numerical model provides a simple tool for estimating the value of deep methane flux. However, some caveats must be noted before the application. Our new approach is applicable to the system where the residual gas saturation has been determined or a low gas saturation is detected below the BHSZ. In such cases, methane gas originating from hydrate dissociation does not interfere with the FGZ.
With the aim of determining the deep dissolved methane flux transported into the GHSZ, we developed a numerical model based on the one-dimensional mass balance for methane to relate the characteristics of gas bubble distribution to the deep upward unsaturated methane-bearing fluid. Our calculations show that the methane flux in deep-sourced systems could be reflected by the volume fraction of residual methane gas in sediments and the FGZ thickness.
To the best of our knowledge, this is the first study that quantified the deep dissolved methane flux in a gas hydrate system with well-characterized FGZ beneath the BGHZ. The model-derived upward methane flux at Site 995 was 0.0231 mol/m2/a. This result indicates the existence of a second free-gas interval at approximately 740 mbsf, which is consistent with the seismic data and further verifies our results. The hydrate occurrence is extremely difficult to extend to the BHSZ in a low methane flux scenario, such as Blake Ridge Site 994. Therefore, by combining these results and previous estimation of high deep methane flux at nearby Site 997, we showed that along the Blake Ridge drilling transect the estimated deep methane fluxes decrease with increasing distance from the crest of the ridge.
Publicly available datasets were analyzed in this study. This data can be found here: http://www-odp.tamu.edu/publications/pubs.htm.
ZZ: conceptualization, methodology, data analysis, and writing-original manuscript. YC: conceptualization, methodology, funding acquisition, writing-review and editing. WX: methodology and writing-review. DC: writing-review and funding acquisition. All authors contributed to manuscript preparation.
This work was supported by the National Key Research and Development Program of China (No. 2018YFC0310001), the NSF of China (Nos. 41776050, 91858208, and 41730528), and the China Geological Survey Project (No. DD20190230).
WX was employed by the Independent Consultant.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Archer, D. E., Buffett, B. A., and Mcguire, P. C. (2012). A two-dimensional model of the passive coastal margin deep sedimentary carbon and methane cycles. Biogeosciences 9, 2921–2966. doi: 10.5194/bg-9-2859-2012
Bhatnagar, G., Chatterjee, S., Chapman, W. G., Dugan, B., Dickens, G., and Hirasaki, G. J. (2011). Analytical theory relating the depth of the sulfate-methane transition to gas hydrate distribution and saturation. Geochem. Geophys. Geosys. 12:Q03003. doi: 10.1029/2010GC003397
Bhatnagar, G., Chapman, W. G., Dickens, G. R., Dugan, B., and Hirasaki, G. J. (2007). Generalization of gas hydrate distribution and saturation in marine sediments by scaling of thermodynamic and transport processes. Am. J. Sci. 307, 861–900. doi: 10.2475/06.2007.01
Bhatnagar, G., Chapman, W. G., Dickens, G. R., Dugan, B., and Hirasaki, G. J. (2008). Sulfate-methane transition as a proxy for average methane hydrate saturation in marine sediments. Geophys. Res. Lett. 35:L03611. doi: 10.1029/2007gl032500
Bhaumik, A. K., and Gupta, A. K. (2007). Evidence of methane release from blake ridge ODP hole 997A during the plio-pleistocene: benthic foraminifer fauna and total organic carbon. Curr. Sci. 92, 192–199. doi: 10.1126/science.1135926
Burwicz, E., and Rüpke, L. (2019). Thermal state of the blake ridge gas hydrate stability zone (GHSZ)—insights on gas hydrate dynamics from a new multi-phase numerical model. Energies 12:3403. doi: 10.3390/en12173403
Burwicz, E., and Haeckel, M. (2020). Basin-scale estimates on petroleum components generation in the western black sea basin based on 3-D numerical modelling. Mar. Pet. Geol. 113:104122. doi: 10.1016/j.marpetgeo.2019.104122
Cao, Y., Chen, D. F., and Cathles, L. M. (2013). A kinetic model for the methane hydrate precipitated from venting gas at cold seep sites at hydrate ridge, cascadia margin, oregon J. Geophys. Res. Solid Earth 118, 1–13. doi: 10.1007/s11430-012-4553-6
Chen, D. F., and Cathles, L. M. (2003). A kinetic model for the pattern and amounts of hydrate precipitated from a gas stream: application to the bush hill vent site, green canyon block 185, Gulf of Mexico. J. Geophys. Res. Solid Earth 108:2058. doi: 10.1029/2001jb001597
Chen, D. F., and Cathles, L. M. (2005). On the thermal impact of gas venting and hydrate crystallization. J. Geophys. Res. Solid Earth 110:204. doi: 10.1029/2004JB003533
Claypool, G., and Kvenvolden, K. A. (1983). Methane and other hydrocarbon gases in marine sediment. Ann. Rev. Earth Planet. Sci. 11, 299–327. doi: 10.1146/annurev.ea.11.050183.001503
Daigle, H., Cook, A., Fang, Y., Bihani, A., Song, W., and Flemings, P. B. (2020). Gas-driven tensile fracturing in shallow marine sediments. J. Geophys. Res. Solid Earth 125, 1–19. doi: 10.1029/2020JB020835
Davie, M. K., and Buffett, B. A. (2001). A numerical model for the formation of gas hydrate below the seafloor. J. Geophys. Res. Solid Earth 106, 497–513. doi: 10.1029/2000jb900363
Davie, M. K., and Buffett, B. A. (2003a). Sources of methane for marine gas hydrate: inferences from a comparison of observations and numerical models. Earth Planet. Sci. Lett. 206, 51–63. doi: 10.1016/s0012-821x(02)01064-6
Davie, M. K., and Buffett, B. A. (2003b). A steady state model for marine hydrate formation: constraints on methane supply from pore water sulfate profiles. J. Geophys. Res. Solid Earth 108:2495. doi: 10.1029/2002jb002300
Davie, M. K., Zatsepina, O. Y., and Buffett, B. A. (2004). Methane solubility in marine hydrate environments. Mar. geol. 203, 177–184. doi: 10.1016/S0025-3227(03)00331-1
Dhakal, S., and Gupta, I. (2021). Simulating gas hydrate formation in the southern hydrate ridge. cascadia margin. J. Nat. Gas Sci. Eng. 88:103845. doi: 10.1016/j.jngse.2021.103845
Dickens, G. R., Paull, C. K., and Wallace, P. (1997). Direct measurement of in situ methane quantities in a large gas-hydrate reservoir. Nature 385, 426–428. doi: 10.1038/385426a0
Dickens, G. R. (2001). Sulfate profiles and barium fronts in sediment on the blake ridge: present and past methane fluxes through a large gas hydrate reservoir. Geochim. Cosmochim. Acta. 65, 529–543. doi: 10.1016/S0016-7037(00)00556-1
Duan, Z., Moller, N., Greenberg, J., and Weare, J. H. (1992). The prediction of methane solubility in natural waters to high ionic strength: from 0 to 250? and from 0 to 1600 bar. Geochim. Cosmochim. Acta. 56, 1451–1460. doi: 10.1016/0016-7037(92)90215-5
Egeberg, P. K., and Dickens, G. R. (1999). Thermodynamic and pore water halogen constraints on gas hydrate distribution at ODP Site 997 (Blake Ridge). Chem. Geol. 153, 53–79. doi: 10.1016/S0009-2541(98)00152-1
Fehn, U., Snyder, G., and Egeberg, P. K. (2000). Dating of pore waters with 129I: relevance for the origin of marine gas hydrates. Science 289, 2332–2335. doi: 10.1126/science.289.5488.2332
Firoozabadi, A., Ottesen, B., and Mikkelsen, M. (1992). Measurements of supersaturation and critical gas saturation. SPE Form. Eval. 7, 337–344. doi: 10.2118/19694-PA
Flemings, P. B., Liu, X., and Winters, W. J. (2003). Critical pressure and multiphase flow in Blake Ridge gas hydrates. Geology 31, 1057–1060. doi: 10.1130/g19863.1
Frederick, J. M., and Buffett, B. A. (2011). Topography and fracture-driven fluid focusing in layered ocean sediments. Geophys. Res. Lett. 38:L08614. doi: 10.1029/2010GL0460272011
Garg, S. K., Pritchett, J. W., Katoh, A., Baba, K., and Fujii, T. (2008). A mathematical model for the formation and dissociation of methane hydrates in the marine environment. J. Geophys. Res. 113:B01201. doi: 10.1029/2006JB004768
Haacke, R., Westbrook, G. K., and Hyndman, R. D. (2007). Gas hydrate, fluid flow and free gas: formation of the bottom-simulating reflector. Earth Planet. Sci. Lett. 261, 407–420. doi: 10.1016/j.epsl.2007.07.008
Haacke, R. R., Westbrook, G. K., and Riley, M. S. (2008). Controls on the formation and stability of gas hydrate-related bottom-simulating reflectors (BSRs): a case study from the west Svalbard continental slope. J. Geophys. Res. 113:B05104. doi: 10.1029/2007JB005200
Holbrook, W. S., Hoskins, H., and Wood, W. T. (1996). Methane hydrate and free gas on the Blake Ridge from vertical seismic profiling. Science 273, 1840–1843. doi: 10.1126/science.273.5283.1840
Holbrook, W. S. (2001). “Seismic studies of the blake ridge: implications for hydrate distribution, methane expulsion and free gas studies,” in Natural Gas hydrates: Occurrence, Distribution and Detection, eds K. P. Charles and P. D. William (Washington, D.C: American Geophysical Union).
Hyndman, R. D., and Davis, E. E. (1992). A mechanism for the formation of methane hydrate and sea floor bottom-simulated reflectors by vertical fluid expulsion. J. Geophy. Res. 97, 7025–7041. doi: 10.1029/91JB03061
Kvenvolden, K. A. (1993). Gas hydrates: geological perspective and global change. Rev. Geophy. 31, 173–187. doi: 10.1029/93rg00268
Liu, X., and Flemings, P. B. (2007). Dynamic multiphase flow model of hydrate formation in marine sediments. J. Geophys. Res. 112:B03101. doi: 10.1029/2005jb004227
Liu, X., and Flemings, P. B. (2011). Capillary effects on hydrate stability in marine sediments. J. Geophys. Res. 116:B07102. doi: 10.1029/2010JB008143
Malinverno, A., Kastner, M., Torres, M. E., and Wortmann, U. G. (2008). Gas hydrate occurrence from pore water chlorinity and downhole logs in a transect across the northern cascadia margin (integrated ocean drilling program expedition 311). J. Geophys. Res. 113:B8. doi: 10.1029/2008JB005702
Malinverno, A. (2010). Marine gas hydrates in thin sand layers that soak up microbial methane. Earth Planet. Sci. Lett. 292, 399–408. doi: 10.1016/j.epsl.2010.02.008
Malinverno, A., and Goldberg, D. S. (2015). Testing short-range migration of microbial methane as a hydrate formation mechanism: results from andaman sea and kumano basin drill sites and global implications. Earth Planet. Sci. Lett. 422, 105–114. doi: 10.1016/j.epsl.2015.04.019
Minshull, T., and White, R. (1989). Sediment compaction and fluid migration in the Makran accretionary prism. J. Geophys. Res. 94, 7387–7402. doi: 10.1029/JB094iB06p07387
Mogollon, J. M., Heureux, I. L., Dale, A. W., and Regnier, P. (2009). Methane gas-phase dynamics in marine sediments: a model study. Am. J. Sci. 309, 189–220. doi: 10.2475/03.2009.01
Paull, C. K., Matsumoto, R., and Wallace, P. J. (1996). Proceedings of the Ocean Drilling Program, Initial Reports, 164.
Paull, C. K., Matsumoto, R., and Wallace, P. J. (2000). Proceedings of the Ocean Drilling Program, Scientific Results, 164.
Pecher, I. A., Kukowski, N., Huebscher, C., Greinert, J., and Bialas, J. (2001). The link between bottom-simulating reflections and methane flux into the gas hydrate stability zone – new evidence from lima basin. Peru Margin. Earth Planet. Sci. Lett. 185, 343–354. doi: 10.1016/S0012-821X(00)00376-9
Reagan, M. T., and Moridis, G. J. (2007). Oceanic gas hydrate instability and dissociation under climate change scenarios. Geophys. Res. Lett. 34:L22709. doi: 10.1029/2007GL031671
Shipley, T. H., Houston, M. H., Buffler, R. T., Shaub, F. J., McMillen, K. J., Ladd, J. W., et al. (1979). Seismic reflection evidence for the widespread occurrence of possible gas hydrate horizons on continental slopes and rises. Am. Assoc. Pet. Geol. Bul. 63, 2204–2213. doi: 10.1306/2f91890a-16ce-11d7-8645000102c1865d
Sloan, D. E., and Koh, C. A. (2008). Clathrate Hydrates of Natural Gases, 3rd Edn. New York, NY: CRC Press.
Stoll, R. D., Ewing, J., and Bryan, G. M. (1971). Anomalous wave velocities in sediments containing gas hydrates. J. Geophys. Res. 76, 2090–2094. doi: 10.1029/jb076i008p02090
Su, Z., and Chen, D. F. (2007). Calculation of methane hydrate solubility in marine environment and its constraints on gas hydrate occurrence. Chin. J. Geophys. 50, 1518–1526. doi: 10.1002/cjg2.1152
Torres, M. E., Wallmann, K., Tre´hu, A. M., Bohrmann, G., Borowski, W. S., and Tomaru, H. (2004). Gas hydrate growth, methane transport, and chloride enrichment at the southern summit of hydrate ridge, cascadia margin off oregon. Earth Planet. Sci. Lett. 226, 225–241. doi: 10.1016/j.epsl.2004.07.029
Vanderbeek, B. P., and Rempel, A. W. (2018). On the importance of advective versus diffusive transport in controlling the distribution of methane hydrate in heterogeneous marine sediments. J. Geophys. Res. Solid Earth 123, 5394–5411. doi: 10.1029/2017JB015298
Wallmann, K., Aloisi, G., and Haeckel, M. (2006). Kinetics of organic matter degradation, microbial methane generation, and gas hydrate formation in anoxic marine sediments. Geochim. Cosmochim. Acta. 70, 3905–3927. doi: 10.1016/j.gca.2006.06.003
Westbrook, G. K., and Thatcher, K. E. (2009). Escape of methane gas from the seabed along the West Spitsbergen continental margin. Geophys. Res. Lett. 36:L15608. doi: 10.1029/2009GL039191
Wood, W. T., and Ruppel, C. (2000). Seismic and thermal investigation of the Blake Ridge gas hydrate area: a synthesis. Proc. Ocean. Drill. Prog. Sci. Results 164, 253–264.
Xu, W., and Ruppel, C. (1999). Predicting the occurrence, distribution, and evolution of methane gas hydrate in porous marine sediments. J. Geol. Res. 104, 5081–5095. doi: 10.1029/1998JB900092
Xu, W. (2004). Modeling dynamic marine gas hydrate systems. Am. Mineral. 89, 1271–1279. doi: 10.2138/am-2004-8-916
You, K., Flemings, P. B., Malinverno, A., Collett, T. S., and Darnell, K. (2019). Mechanisms of methane hydrate formation in geological systems. Rev. Geophys. 57, 1–51. doi: 10.1029/2018RG000638
Zatsepina, O. Y., and Buffett, B. A. (1997). Phase equilibrium of gas hydrate: implications for the formation of hydrate in the deep sea floor. Geophys. Res. Lett. 24, 1567–1570. doi: 10.1029/97gl01599
Zheng, Z. H., Cao, Y. C., Xu, W. Y., and Chen, D. F. (2020). A numerical model to estimate the effects of variable sedimentation rates on methane hydrate formation-application to the ODP Site 997 on blake ridge, southeastern North American continental margin. J. Geol. Res. Solid Earth 125, 1–17. doi: 10.1029/2019jb018851
Keywords: methane flux, numerical simulation, methane gas, gas hydrate, Blake Ridge
Citation: Zheng Z, Cao Y, Xu W and Chen D (2022) A Numerical Model for Determining Deep Methane Flux Linked to the Free Gas Zone: Application to the Ocean Drilling Program Site 995 and Implications for Regional Deep Methane Flux at the Blake Ridge. Front. Mar. Sci. 9:857413. doi: 10.3389/fmars.2022.857413
Received: 18 January 2022; Accepted: 22 February 2022;
Published: 14 March 2022.
Edited by:
Davide Oppo, University of Louisiana at Lafayette, United StatesReviewed by:
Ewa Burwicz-Galerne, University of Bremen, GermanyCopyright © 2022 Zheng, Cao, Xu and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yuncheng Cao, eWNjYW9Ac2hvdS5lZHUuY24=; Duofu Chen, ZGZjaGVuQHNob3UuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.