Climate Change Will Fragment Florida Stone Crab Communities

Many marine species have been shown to be threatened by both ocean acidification and ocean warming which are reducing survival, altering behavior, and posing limits on physiology, especially during earlier life stages. The commercially important Florida stone crab, Menippe mercenaria, is one species that is affected by reduced seawater pH and elevated seawater temperatures. In this study, we determined the impacts of reduced pH and elevated temperature on the distribution of the stone crab larvae along the West Florida Shelf. To understand the dispersion of the larvae, we coupled the multi-scale ocean model SLIM with a larval dispersal model. We then conducted a connectivity study and evaluated the impacts of climate stressors by looking at four different scenarios which included models that represented the dispersion of stone crab larvae under: 1) present day conditions as modelled by SLIM for the temperature and NEMO-PISCES for the pH, 2) SSP1-2.6 scenario (-0.037 reduction in pH and +0.5°C compared to present-day conditions), 3) SSP2-4.5 scenario(-0.15 reduction in pH and +1.5°C) and 4) SSP5-8.5 scenario (-0.375 reduction in pH and +3.5°C). Our results show a clear impact of these climate change stressors on larval dispersal and on the subsequent stone crab distribution. Our results indicate that future climate change could result in stone crabs moving north or into deeper waters. We also observed an increase in the number of larvae settling in deeper waters (defined as the non-fishing zone in this study with depths exceeding 30 m) that are not typically part of the commercial fishing zone. The distance travelled by larvae, however, is likely to decrease, resulting in an increase of self-recruitment and decrease of the size of the sub-populations. A shift of the spawning period, to earlier in the spring, is also likely to occur. Our results suggest that habitats in the non-fishing zone cannot serve as a significant source of larvae for the habitats in the fishing zone (defined as water depth< 30 m) since there is very little exchange (< 5% of all exchanges) between the two zones. These results indicate that the stone crab populations in Florida may be susceptible to community fragmentation and that the management of the fishery should consider the potential impacts of future climate change scenarios.

1 Introduction

Anthropogenic inputs, like excess atmospheric CO₂, is resulting in a warmer, more acidic ocean. At the current rate, the ocean’s temperature could increase by 1-3.5°C by 2100, while the pH could decrease by 0.14-0.43 unit (Hoegh-Guldberg et al., 2014; Fox-Kemper et al., 2021). These global effects are compounded by localized inputs in many coastal habitats, such as increasing organic nutrient loads into coastal zones, that further reduce seawater pH through remineralization. Coastal areas are also more threatened by the increase in seawater temperature as they warm faster than open ocean (Hoegh-Guldberg et al., 2014; Fox-Kemper et al., 2021). The reductions in seawater pH and increases in seawater temperature can have deleterious effects on many coastal species, especially during earlier life-stages, which are often more sensitive than adult conspecifics (Kurihara, 2008; Ceballos-Osuna et al., 2013; Bednaršek et al., 2021). Crustaceans are especially sensitive to those changes. Higher temperatures can lead to an acceleration in their metabolism and destabilize the proteins (Young and Hazlett, 1978). For some species, exposure to combined stressors of reduced pH and elevated temperature can lead to shorter larval stages, a higher mortality rate and smaller individuals (Kuhn, 2017). Additionally, synergistic effects between acidification and warmer water have been observed for several crustacean species, resulting in high mortality, hypercapnia and reduction in oxygen circulation (Metzger et al., 2007; Dissanayake and Ishimatsu, 2011; Gravinese et al., 2018).

The stone crab (Menippe mercenaria) is an economically important species in Florida, where its commercial value is about $25-30 million annually. The fishery season ranges between the 15^th of October and the 1^st of May (Florida Fish And Wildlife Conservation Commission, 2020). The landings (i.e. only the claws) peaked in the 2000-01 fishing season with a total of 3.5 million pounds of claws statewide and has since declined by ~30%. The fishing of crabs mostly occurs between 6 and 15 meters depth due to the cost associated with going far from the coast, although some fishermen work in water up until 30 m depth (Muller et al., 2011).

Recent studies have shown that the stone crab is sensitive to rising ocean temperature and acidification (Gravinese, 2018b; Gravinese et al., 2018; Gravinese et al., 2019). Elevated temperature significantly reduces larval survivorship (Brown et al., 1992; Gravinese et al., 2018), while reductions in seawater pH have been shown to slow embryonic development rate (and hence increase the time to hatching), reduce hatching success (Gravinese, 2018b) and change the larval vertical swimming behavior (Gravinese et al., 2019). Like all brachyuran crabs, M. mercenaria has a complex life cycle, made of four main stages: the larval stage, which is composed of five zoeal stages, the post-larval or megalopal stage, the juvenile stage and the adult stage (Sulkin, 1984; Gulf Shores Marine Fisheries Commission, 2001). Each zoeal stage lasts between about 3 to 6 days (Porter, 1960), but these durations can drastically change with temperature (Brown et al., 1992). Stone crab larvae require warm water and high salinity, with the highest survival rate observed in laboratory studies at 30°C and a salinity of 30 (Porter, 1960; Lindberg and Marshall, 1984; Brown et al., 1992). Stone crab larvae also elicit vertical swimming behaviors in response to changes in light and hydrostatic pressure. For example, stage 1 and 3 larvae exhibit negative geotaxis, hence positioning themselves at shallower depths. This is however counterbalanced by a negative phototactic response that makes them migrate deeper in the water column during the day and then return near to the surface at night (Gravinese, 2018b). The sensitivity to gravity, light, and pressure changes in stage 5 larvae, which exhibit a positive geotaxis resulting in positioning deeper in the water column to more easily find settlement habitats. All larval stages exhibit an upward movement when exposed to increasing hydrostatic pressure and a downward movement when exposed to decreasing hydrostatic pressure (Gravinese, 2018b).

The defined larval vertical swimming behaviors provide a feedback mechanism for regulating their relative depth distribution (Gravinese, 2018b). Understanding the vertical swimming behavior of stone crab larvae can help describe the dispersion, recruitment patterns, and the larval exchanges between the different stone crab habitats, which could help to further improve the sustainable management of the stone crab fishery. This can be done through biophysical modeling and genetic studies (Pineda et al., 2007; Baeza et al., 2019; Seyoum et al., 2021). While genetic studies can identify if genetical material has been exchanged between habitats, they cannot provide the timing and the importance of those exchanges (Cowen and Sponaugle, 2009). Biophysical dispersal models can provide a more accurate picture of larval dispersal and exchanges between separated habitats over temporal scales. Such an approach has been used to model other brachyuran crabs dispersion, such as the European green crab (Carcinus maenas) and the blue crab (Callinectes sapidus) (Peliz et al., 2007; Banas et al., 2009; Criales et al., 2019).

Here, we used a multi-scale biophysical model to evaluate the potential impacts of climate change on the dispersion of the stone crab larvae along the West Florida Shelf (WFS). We used the 3D version of the Second-generation Louvain-la-Neuve Ice-Ocean Model to simulate the hydrodynamics over the WFS and coupled it with a larval dispersal model that represents the biological swimming traits of the different stages of stone crab larvae. Our objective was to (1) assess how stone crab larval dispersal and connectivity will be modified under different climate change scenarios (i.e., reduced pH and elevated temperature) and (2) estimate the potential for non-fishing areas (defined as depths > 30m) to repopulate habitats that occur in the predominate fishing areas (defined as depths< 30 m).

2 Data and Methods

2.1 Stone Crab Habitats

The predominate stone crab fishery occurs along the WFS which is in the eastern part of the Gulf of Mexico and stretches from Apalachicola Bay to the Florida Keys. The WFS is a broad continental shelf, reaching about 250 km offshore and has a maximum depth of about 110 m (Figure 1A). The circulation on the WFS is mainly driven by local winds but is also forced by tides, buoyancy fluxes and by the Loop Current (Weisberg et al., 2001). The WFS is also subject to seasonal changes in circulation. The circulation is predominantly downwelling-favorable during summer months and upwelling-favorable during the winter months. The amplitude and direction of the horizontal currents also present a seasonal dynamic due to the seasonal wind variability. On the inner shelf, where the bathymetry is shallower, the monthly mean current amplitude ranges from 2-12 cm/s from fall to spring and decreases to 0-6cm/s during summer months. The direction of the currents tends to be southeastward between October and April, and northwestward between June and September. The seasonal variability is less pronounced below 50m depth (Liu and Weisberg, 2012). On the outer shelf, seasonal variations are drowned out by the influence of water circulation from the rest of the Gulf. In our study, the hydrodynamic model outputs were validated with respect to velocity and temperature observations from the NOAA stations 42013, 42022 and 42023. Station locations are shown in Figure 1A.

FIGURE 1

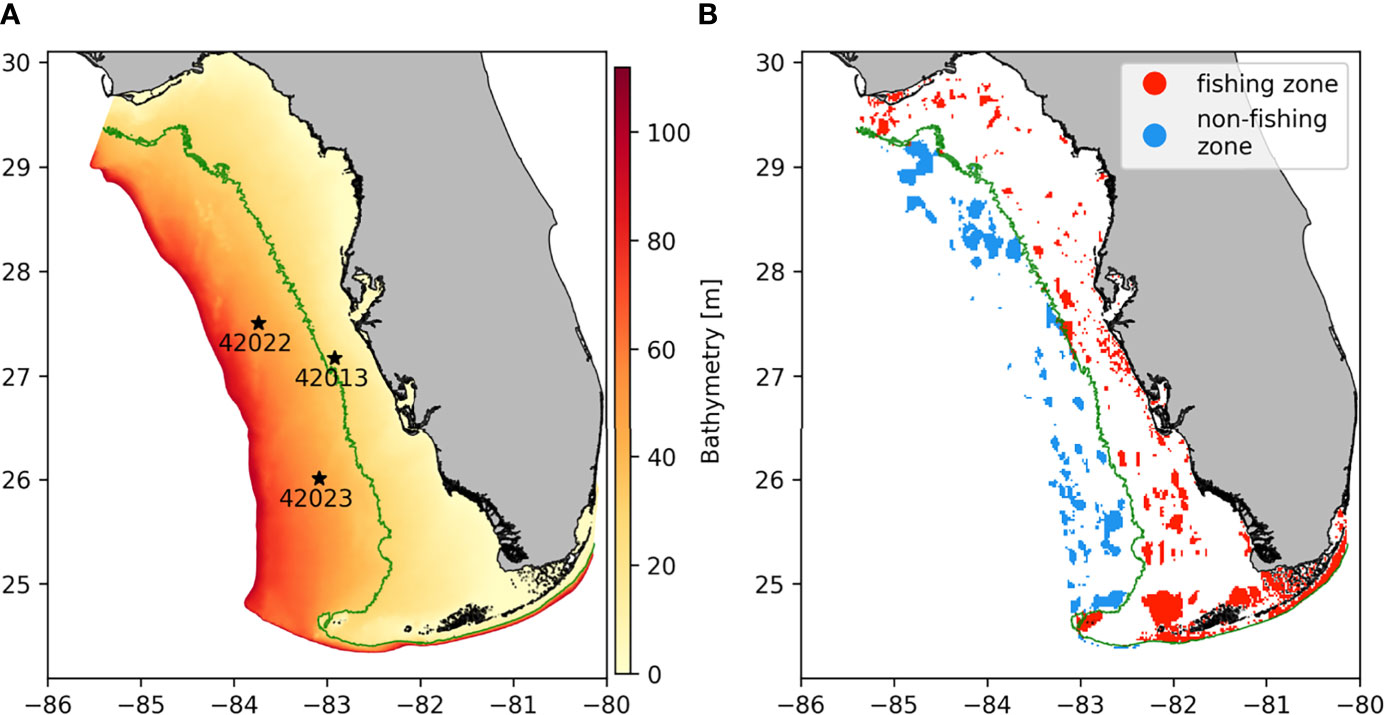
Figure 1 Model computational domain with (A) the bathymetry and location of validation stations for the hydrodynamics (black stars) and (B) the stone crabs’ habitats and their distribution between fishing and non-fishing zone. The green line represents the 30m isobath.

Since there are no stone crab habitat maps for the WFS, we used a seafloor substrate map and assumed that all rocky, muddy or gravely substrates shallower than 60 m could be suitable stone crab habitats (Bert et al., 1978; Beck, 1995; Krimsky and Epifanio, 2008). The seafloor substrate map we used was made by the Institute of Arctic and Alpine research of the University of California and has a resolution of 4km² (Jenkins 2011). The selection of benthic habitats was validated by looking at punctual observations reported on the Global Biodiversity Information Facility (GBIF) between 2011 and 2021 (GBIF Backbone Taxonomy, 2019). As a result, our study considered 3858 habitat patches of 4 km² (Figure 1B). Among these habitats, we further distinguish between habitats that are fished vs. habitats that are normally not fished (hereon characterized as habitats of the non-fishing zone). The former corresponds to habitats shallower than 30 m as we assumed that fishing is not economically viable at greater depths (Muller et al., 2011). There is therefore a clear separation between fishing and non-fishing habitats, which corresponds to the 30m isobath (Figure 1B).

2.2 Habitat Connectivity Model

2.2.1 Hydrodynamic Model

We simulate the three-dimensional ocean circulation over the WFS with the multi-scale ocean model SLIM. SLIM solves the 3D hydrostatic governing equations under the Boussinesq approximation (Vallaeys et al., 2018; Vallaeys et al., 2021; Duquesne et al., 2021). The outputs of SLIM’s model are the speed of the currents but also the temperature and salinity. The model equations are discretized with the discontinuous Galerkin finite element method on a 3D mesh made of triangular prisms. The 3D mesh is obtained by extruding an unstructured 2D mesh made of triangles in the vertical. The horizontal resolution can be locally increased to better represent small-scale circulation features driven by the topography or by the bathymetry. The horizontal mesh resolution depends on the distance to the coast, the distance to stone crabs’ habitats, the bathymetry and the bathymetry gradient. The horizontal resolution reaches 400 m along the coast and about 10 km offshore (Figure 2A). The vertical dimension is discretized with 20 terrain-following sigma layers that are clustered near the surface such that there are at least 5 layers in the top 11 meters.

FIGURE 2

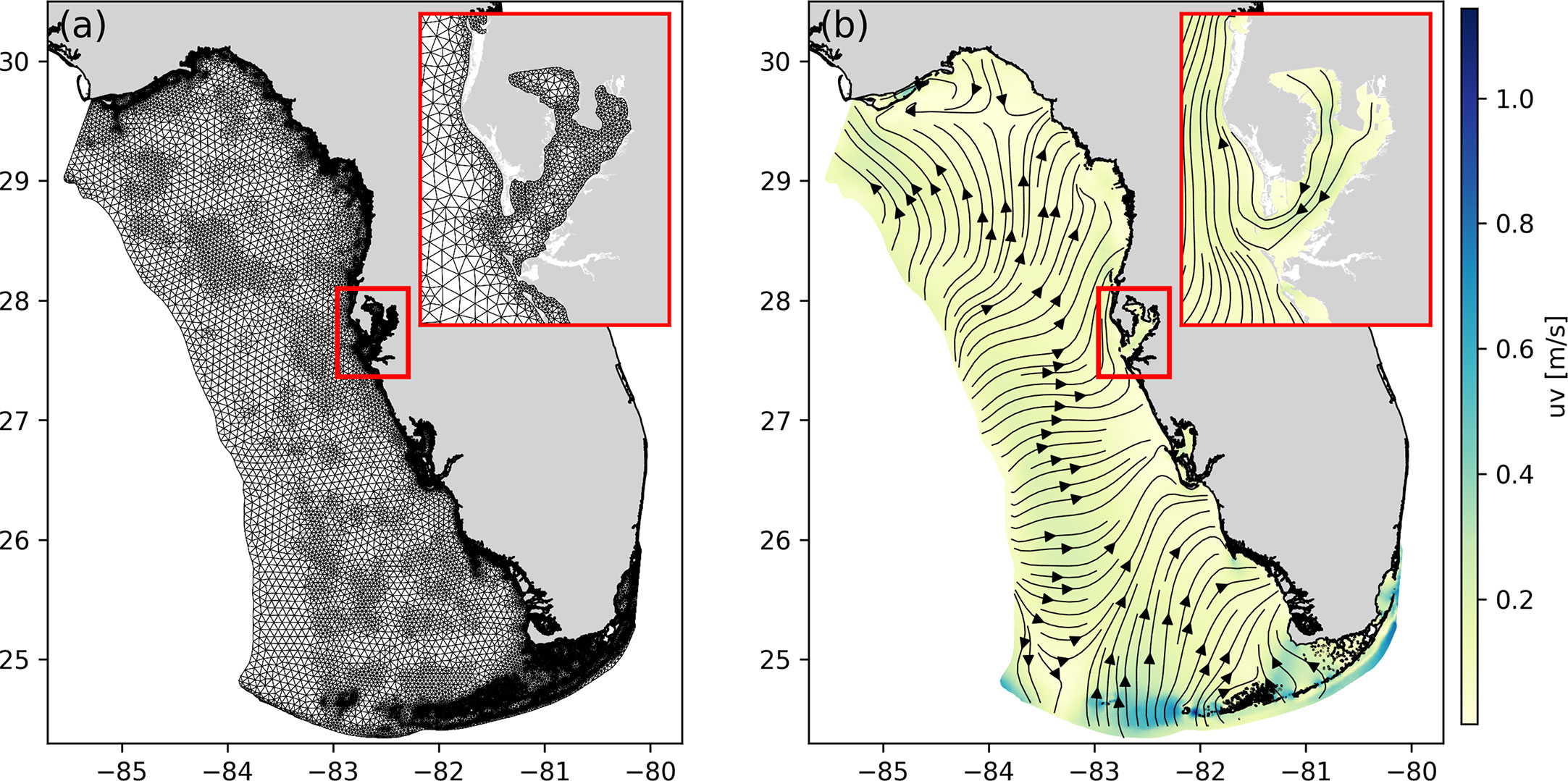
Figure 2 Model computational domain with a close-up view on Tampa Bay showing (A) the horizontal unstructured mesh whose resolution ranges between 400m and 10km and (B) a snapshot of the surface circulation as modelled by SLIM on the 15^th of July, 2019 at 00:00, with uv as the horizontal water speed.

The model bathymetry is extracted from the Coastal Relief Model, which offers a representation of the US coast with a resolution of 3 arc-seconds, or roughly 90 m (NOAA National Geophysical Data Center, 2001). The model dynamics are forced on the boundaries by wind, tides, surface heat, salinity fluxes and the large-scale circulation from the Gulf of Mexico, from the ERA5 model (Hersbach et al., 2018), the OSU TOPEX/Poseidon Global Inverse Solution dataset TPXO9 (Egbert and Erofeeva, 2002) and the operational Navy HYbrid Coordinate Ocean Model (HYCOM) product GOMl0.04,2 (Chassignet et al., 2007). The resulting circulation correctly reproduces the large-scale flow features over the WFS as well as smaller-scale flow features driven by the topography (Figure 2B). We provide additional details on the model formulation and its validation with respect to NOAA stations data in the Supplementary Materials.

2.2.2 Larval Transport Model

The simulated currents are then used to model the transport of virtual crab larvae by using a Lagrangian biophysical model. This Lagrangian tracker, coupled with the 2D-version of SLIM, has been repeatedly used to model the dispersal of different drifting materials, such as coral larvae (Frys et al., 2020; Figueiredo et al., 2022), plastics (Critchell and Lambrechts, 2016; Li et al., 2018), SCTLD agents (Dobbelaere et al., 2020) or seagrass propagules (Grech et al., 2016; Grech et al., 2018). This method has several advantages, the main one being that it is object-based, meaning that each particle has its own characteristics and behavior. The advection velocity of each larvae is the sum of its vertical swimming velocity and the currents’ 3D velocity. Larval advection velocity is integrated with a 4th order Runge-Kutta scheme. The model also includes a stochastic diffusion term represented as a Wiener process with a diffusivity calculated using Okubo (1971)’s formula. Below we describe the choices we made in setting up the larval transport model. The equations governing the movement of the larvae and other additional details are provided in the supplementary materials.

Stone crabs’ spawning peaks in the summer, from May to August. The eggs remain attached to the female until hatching, after which the larvae are going to exhibit a planktonic behavior (Lindberg and Marshall, 1984). Females can extrude secondary egg masses (or more) in one reproductive season. The extrusion of an additional egg mass is generally separated by 17 to 21 days (Binford, 1913; Porter, 1960). Larval spawning usually begins in early afternoon and can last for several hours, the median time being 20 hours (Krimsky et al., 2009). In this model, we simulate larval dispersal following 7 spawning events, separated by 21 days and starting on May 1st, 2019, at 14:00. Each spawning event lasts for 20 hours, with a release rate of 4 particle per km² and per hour. Each particle represents a large number of real larvae and is characterized by an initial mass that exponentially decreases with time to represent larval mortality. Larvae are released 1 m above the stone crabs’ habitats as defined in (Figure 1).

Biological processes representing larval life history traits include the duration of each larval stage, the survival rate and the vertical swimming behaviour. The duration of each larval stage varies according to temperature as observed by Brown et al. (1992). We used their data for larvae that hatched from eggs developed at sea to build a general multivariate regression model that gives the duration of each larval stage as a function of temperature. The resulting regression has an adjusted R² value of 0.95 and the F-test gave a significant result (F = 64.16; P< 0.0001). We used the temperature at the beginning of each larval stage to determine the duration of that stage. The survival rate for each larval stage is based on observations from Brown et al. (1992) and Gravinese et al. (2018). We derived equations describing the survival rate of each stage, according to temperature (and salinity for the first larval stage) by using a general linear model. The proportion of surviving larvae is calculated at the end of each stage. Seawater pH also impacts the hatching success rate in stone crabs, as observed by (Gravinese, 2018a). We made a general linear model based on these results to obtain an equation describing the hatching success rate as a function of pH. The resulting hatching rate was used to multiply a posteriori the number of larvae that settle.

We modeled the larval vertical swimming behaviors according to their known responses to light, hydrostatic pressure and pH as measured by Gravinese (2018b); Gravinese et al. (2018) and Gravinese et al. (2019). Since the different stages react differently to those external factors, we defined the vertical velocity of each stage separately. Larvae’s response to light was defined by using the time of the day. Larval stages 1 to 3 were characterized with an upward swimming behaviour during the night (between 18:00 and 06:00) and a downward swimming behaviour during the day (between 06:00 and 18:00). Similar approaches have been used in other studies that take daily migration of crabs’ larvae into account (Peliz et al., 2007; Banas et al., 2009; Pires et al., 2020). However, unlike those studies, we chose not to have fixed velocities during the day/night, but instead used a smooth sinusoidal function for larval velocity with a period of 24 hours. This allowed us not to have larvae that react in a binary way to light, but rather to have velocities that smoothly mimic the response to changes in light intensity. The maximal amplitude of the velocities was modeled after observations made by Gravinese (2018b). Our model assumes that larval stages 4 and 5 are less sensitive to light resulting in constant downward vertical velocities.

The vertical velocity in response to pH was defined based on observations made by Gravinese et al. (2019). They observed that stage 3 larval swimming behaviour reverses with reduced seawater pH, while swimming behaviour of stage 5 larvae was unaffected (i.e., still a downward response). We therefore impose an identical pH-dependent vertical velocity for stages 1 to 3, and a vertical velocity that does not depend on pH for stages 4 and 5. As ocean pH is naturally variable both in space and time (NOAA National Geophysical Data Center, 2001; Byrne et al., 2010) because of a number of biological, chemical and physical factors (Hendriks et al., 2015), we used the NEMO-PISCES model (Mercator-Ocean, 2019) to determine the behavior of the larvae. This model presents monthly means of pH with a spatial resolution of 0.25° on 75 vertical layers.

Finally, all larval stages respond to changes in pressure (Gravinese, 2018b). At a rate of 0.1 mbar/sec, stages 1, 3 and 5 larvae need to experience a pressure increase of 80 mbar, 60 mbar and 100 mbar, respectively before a corrective change in vertical swimming behavior modifies swimming direction. At the same rate, stages 1 and 3 react to a 60 mbar and 100 mbar decrease, respectively. That pressure effect results in a decrease of the vertical velocity of the larvae. We have therefore represented the effect of changes in hydrostatic pressure by multiplying the larval vertical velocity by a stage-dependent damping factor.

To avoid that all larvae behave in the same way, we added stochasticity to the biological behaviors elicited by the larvae. For biological processes that are described by a regression (like stage duration or survival rate), we added to the parameters of the regression the residual standard error of the estimate multiplied by a random number following a standard normal distribution. For biological parameters that are solely based on experiments (like the upward and downward vertical velocities used in larvae’s response to light), we used a similar technique, except that the residual standard error is replaced by the standard deviation of the observations reported in Gravinese (2018b).

Larvae become sensitive to cues from suitable settlement habitats in their final development stage, called the megalopal stage. No information was available concerning the vertical velocity of this stage. We therefore defined its vertical velocity as being equal to the reported mean downward swimming velocity of stage-5 larvae (Gravinese, 2018b). The duration of this stage is set to 13 days, as this was the longest duration observed for this stage by Brown et al. (1992). If the megalopa finds itself one meter or less above a habitat during that time, it will settle in that habitat. If the megalopa has not settled on any suitable habitat after 13 days, it dies and is removed from the simulation. Larvae that exit the domain before settling are removed from the simulation, as we don’t know what happens to them outside the domain.

2.3 Connectivity Indicators

The larval transport model yields a potential connectivity matrix C_ij whose entries correspond to the number of virtual larvae produced on habitat i that settled on habitat j. Since we consider 3858 separated crab habitats, the connectivity matrix has ~1.5x10⁷ entries. The connectivity matrix is usually normalized by dividing all the entries of a given row by the number of larvae seeded on the corresponding source reef. The resulting matrix ${\tilde{C}}_{ij}$ then represents the probability of connection between habitats. While most of the connectivity matrix entries are empty, it remains challenging to analyse such a large matrix. One way to make the task easier is to interpret the connectivity matrix as a large graph whose nodes are the crab habitats, and the edges correspond to the non-zero entries in the connectivity matrix. The strength of an edge directed from node i to node j simply corresponds to ${\tilde{C}}_{ij}$.

Many graph-theory indicators are available to extract useful information from the connectivity graph (see for instance Minor and Urban, 2007; Rayfield et al., 2011; Kool et al., 2013; Dubois et al., 2016). Here, we only consider indicators that best highlight the connectivity differences resulting from climate change. First, we consider a source index that identifies habitats that export many larvae to many different habitats. This can be obtained by combining the habitat out-degree (i.e. the number of outgoing connections) and the number of larvae exported from that habitat to other habitats:

$\begin{array}{ll}\begin{array}{c}S{I}_i = N_i^{out}·{\displaystyle {\sum }_j{\tilde{C}}_{ij},} \end{array}& (1)\end{array}$

where $N_i^{out}$is the out-degree of habitat i (Figueiredo et al., 2022). We also consider self-recruitment, which identifies isolated habitats by looking at the fraction of settlers that were locally produced:

$\begin{array}{ll}\begin{array}{c}S{R}_i = \frac{{\tilde{C}}_{ij}}{{\sum }_j\text{\hspace{0.17em}\hspace{0.17em}}{\tilde{C}}_{ij}}.\end{array}& (2)\end{array}$

A large self-recruitment (i.e., close to 1) means that the habitat is mostly isolated as it receives almost exclusively produced on the same habitat. It is therefore not resilient to disturbances (Botsford et al., 2009). Finally, the average distance travelled by larvae originating from a given habitat can be computed with the weighted connectivity length:

$\begin{array}{ll}\begin{array}{c}WC{L}_i = \frac{{\sum }_j\left(d_{ij}·{\tilde{C}}_{ij}\right)}{{\sum }_j{\tilde{C}}_{ij}}, \end{array}& (3)\end{array}$

where d_ij is the distance between habitats i and j (Dobbelaere et al., 2020).

We also applied the strongly connected components (SCC) algorithm to the crab habitat connectivity graph to identify clusters of strongly connected habitats. The SCC method groups together habitats that are linked through bi-directional connections (Tarjan, 1972; Nuutila and Soisalon-Soininen, 1994). The communities created through this method do not depend on the strength of the connections but just on the existence of bi-directional connectivity pathways that connect any two habitats within the SCC, possibly through multistep connections. All the habitats within a SCC will thus have higher genetic mixing among them than with habitats in separate SCCs. The existence of closed-loop multi-generational connectivity pathways is a key factor that fosters population persistence (Hastings and Botsford, 2006)

2.4 Climate Change Scenarios

To evaluate the impacts of climate change, we run the larval dispersal model for four different scenarios. The first one corresponds to present-day conditions, with the water temperature simulated by SLIM (with the atmospheric conditions of 2019 as provided by the forcing models) and a pH distribution coming from the NEMO-PISCES model for the same period. The second scenario includes the effect of climate change by assuming a uniform water temperature increase of 0.5°C as compared to present-day conditions and a uniform decrease of seawater pH of —0.037. This scenario corresponds to global estimates for 2100 under the IPCC Shared Socioeconomic Pathway (SSP) 1-2.6 scenario for drastic emission reduction (Fox-Kemper et al., 2021). The third scenario represents the effect of climate change by assuming a water temperature increase of 1.5°C and a pH decrease of -0.15, which would correspond to global estimates for 2100 under the SSP2-4.5 scenario for moderate emission reduction. The last scenario represents the effect of an climate change by assuming a water temperature increase of 3.5°C and a pH decrease of -0.375, which would correspond to global estimates for 2100 under the SSP5-8.5 scenario for no emission reduction.

To better understand the impact of the different scenarios on the larvae, we simulate for each of them the vertical position of a crab larva in an idealized environment with constant temperature, constant pH and no currents. The movements of the larvae are therefore only due to its biological response to the fixed temperature, the fixed pH, the pressure and the light. We assume that the larva is spawned at a depth of 60 m and the present-day conditions are a temperature of 27°C and a pH of 8.075 (National Oceanic and Atmospheric Administration, 2021).

Our model assumes that the effects of climate change, through water temperature increase and pH decrease, are only impacting crab larvae swimming activity and mortality. We did not consider the effect of climate change on the large-scale atmospheric and oceanic circulations, which could also influence larval dispersal in the region of interest. This simplification is due to the lack of precise information on projected changes in the wind regime over the Gulf of Mexico and the Loop Current dynamics. In a similar study on the effect of climate change on coral connectivity in the Great Barrier Reef, (Figueiredo et al., 2022) have shown that projected changes in ocean currents had a limited effect on larval dispersal.

3 Results

The movement of the larvae without the hydrodynamics show that climate change will have two major effects on crab larvae’s dispersion by: 1) reducing the duration of the larval stages, and 2) changing their vertical larval distribution in the water column (i.e., deeper distribution). The former effect is due to increasing temperature and the latter is due to decreasing pH. In present-day conditions, the larva quickly reaches the surface and stays within about 10 meters from the surface until stage 4 when the individual moves towards the seabed (Figure 3A). In the SSP1-2.6 scenario, the impact of pH on vertical position is almost not visible. The main impact of this scenario on larval dispersal is therefore through the increase in temperature, that leads to a decrease of 6% (almost 1.5 day) in the duration of the whole larval stage (Figure 3B). The SSP2-4.5 climate change scenario is strong enough to modify the larva’s ability to swim near the surface. In this scenario, the larva moves back and forth through the water column daily, thus positioning itself deeper on average. The overall duration of the larval cycle is about 13% shorter (Figure 3C). In the case of extreme climate change, the larva barely leaves the sea bottom throughout the entire larval stage. The duration of that cycle is further reduced, with a decrease of about 25% compared to present-day conditions (Figure 3D).

FIGURE 3

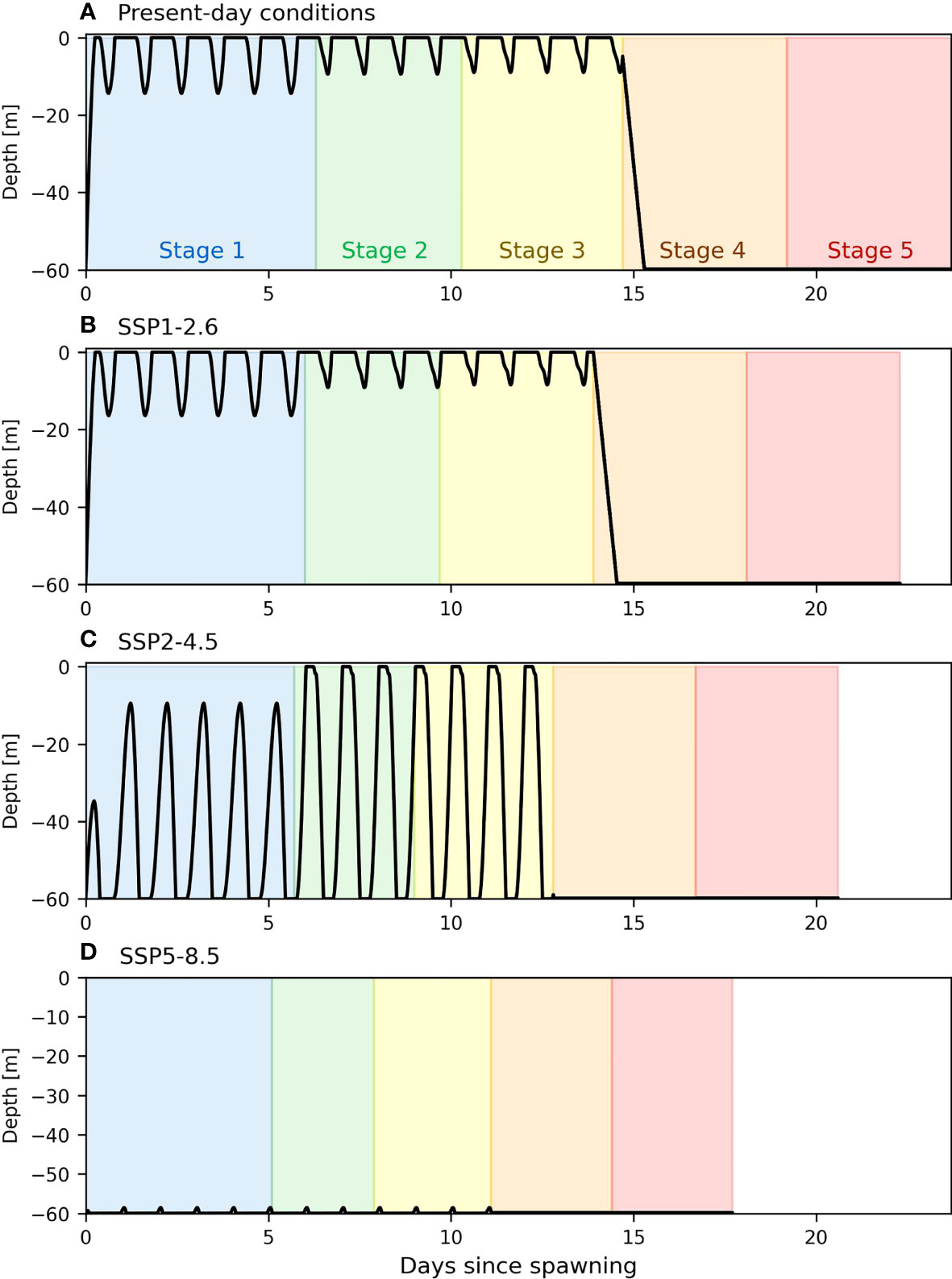
Figure 3 Theoretical vertical movements (black line) of a stone crab larva spawned at a depth of 60m through the five larval stages (each represented by a different colour).

When taking hydrodynamics into account, the combined effect of temperature and pH changes increases the dispersal distance of crab larvae on average by 0.4% for the SSP1-2.6 climate change scenario (but with a standard deviation of 62% and a median change of -4%). In more extreme climate change, the dispersal distance decreases on average by 6% (SD = 46%, median change = -10%) for SSP2-4.5 scenario and by 14% (SD = 90%, median change = -21%) for the SSP5-8.5 scenario. Unpaired t-test were performed to compare all the averages WCL of the different scenarios two by two, and all scenarios are significantly different from one another for WCL (maximal p-value of 0.004). These projected changes are however not spatially uniform as some habitats will experience much larger reductions in the distance at which larvae are dispersed (Figure 4A). An increase of WCL can be seen in some very localized parts of the domain, but the trend remains downward, with 58%, 68% and 74% of habitats experiencing a decrease in the distance traveled by the larvae they send for scenarios SSP1-2.6, SSP2-4.5 and SSP5-8.5 respectively.

FIGURE 4

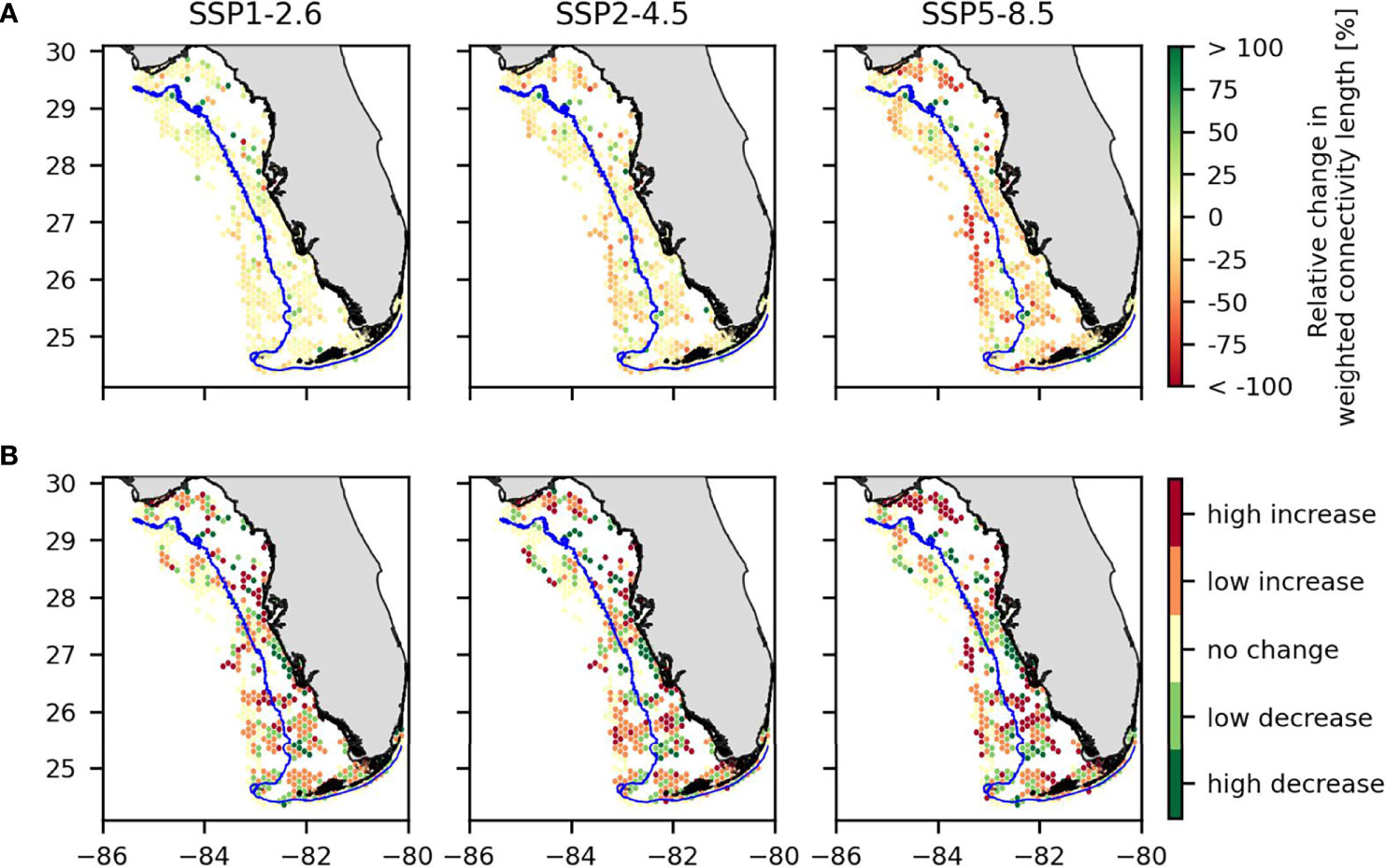
Figure 4 (A) Relative change in weighted connectivity length and (B) absolute change in self-recruitment for the three climate change scenarios. The blue line represents the 30m-depth isobath separating the fishing and non-fishing zones.

Since larvae remain in their planktonic phase for about a month, many habitats experience a self-recruitment (SR) equal to 0, especially in the present-day scenario (65% of the habitats have a SR of 0) where the larvae tend to travel farther away from their source habitat. This suggests that self-recruitment is not suitable to compute relative variations, as we would have to divide by 0 for most than half of the habitats. We therefore assessed the absolute change of SR for both climate change scenarios. In the SSP1-2.6 climate change scenario, there is an increase of self-recruitment for 25% of the habitats, a decrease for 20% of the habitats, and no observable change in 53% of the habitats. During the SSP2-4.5 climate change simulations, these percentages change to 28%, 20%, and 50% for the increase, decrease and no change in self-recruitment, respectively. In the most extreme scenario, the SR percentages were 30%, 19% and 47%, for the increase, decrease and no change in self-recruitment, respectively. The average SR is significantly different from one scenario to the other (p-value always< 0.04) except between the SSP1-2.6 and SSP2-4.5 scenarios (p-value = 0.35).

Again, these changes are not spatially uniform as there is a large inter-habitat variability, meaning that some habitats will fare considerably worse than suggested by the average changes, and a small proportion of habitats will see an increase in recruitment (Figure 4B). Most of the changes occur in the fishing zone, as 70-78% of the habitats in the non-fishing zone experience no changes, regardless of the scenario. In the fishing area, the trend is towards an increase, with 35%, 37% and 41% of the habitats showing an increase in SR in scenarios SSP1-2.6, SSP2-4.5 and SSP5-8.5 respectively.

The proportion of larvae that settle, the number of out-going connections (e.g., number of habitats to which each habitat send larvae), and the source index all behave similarly: an increase in the mean value that does not represent a significant difference (p-value > 0.05) when comparing the present-day case with scenarios SSP1-2.6 or SSP2-4.5; and a significant decrease in the mean value when comparing the present-day and SSP5-8.5 scenarios (p-value< 10^-11). We also observe that all three indicators tended to increase in the non-fishing zone and decrease in the fishing zone (Figure 5). This phenomenon is more marked for the source index and the number of larvae that settle (Figures 5A, C). For both of these indicators, the proportion of habitats of the non-fishing zone that showed an increase was ~70%, regardless of the climate scenario. In the fishing area, we observed an equal distribution of habitats that experienced an increase and a decrease under scenario SSP1-2.6 (close to a 50%-50% distribution). This result in the fishing zone changed to more than 75% of habitats experiencing a decrease in these indicators for scenario SSP5-8.5. At least 55% of the habitats in the non-fishing zone experienced an increase in the number of out-going connections (Figure 5B), regardless of the scenario. In the fishing zone, we also observed more habitats experiencing a decrease in the number of out-going connections with worsening climate change. In the SSP1-2.6 scenario, the repartition of habitats between those experiencing decreasing and increasing number of out-going connections is 48%-42%. In the SSP5-8.5 scenario, the proportion of habitats showing a decrease in the number of out-going connections is 66%.

FIGURE 5

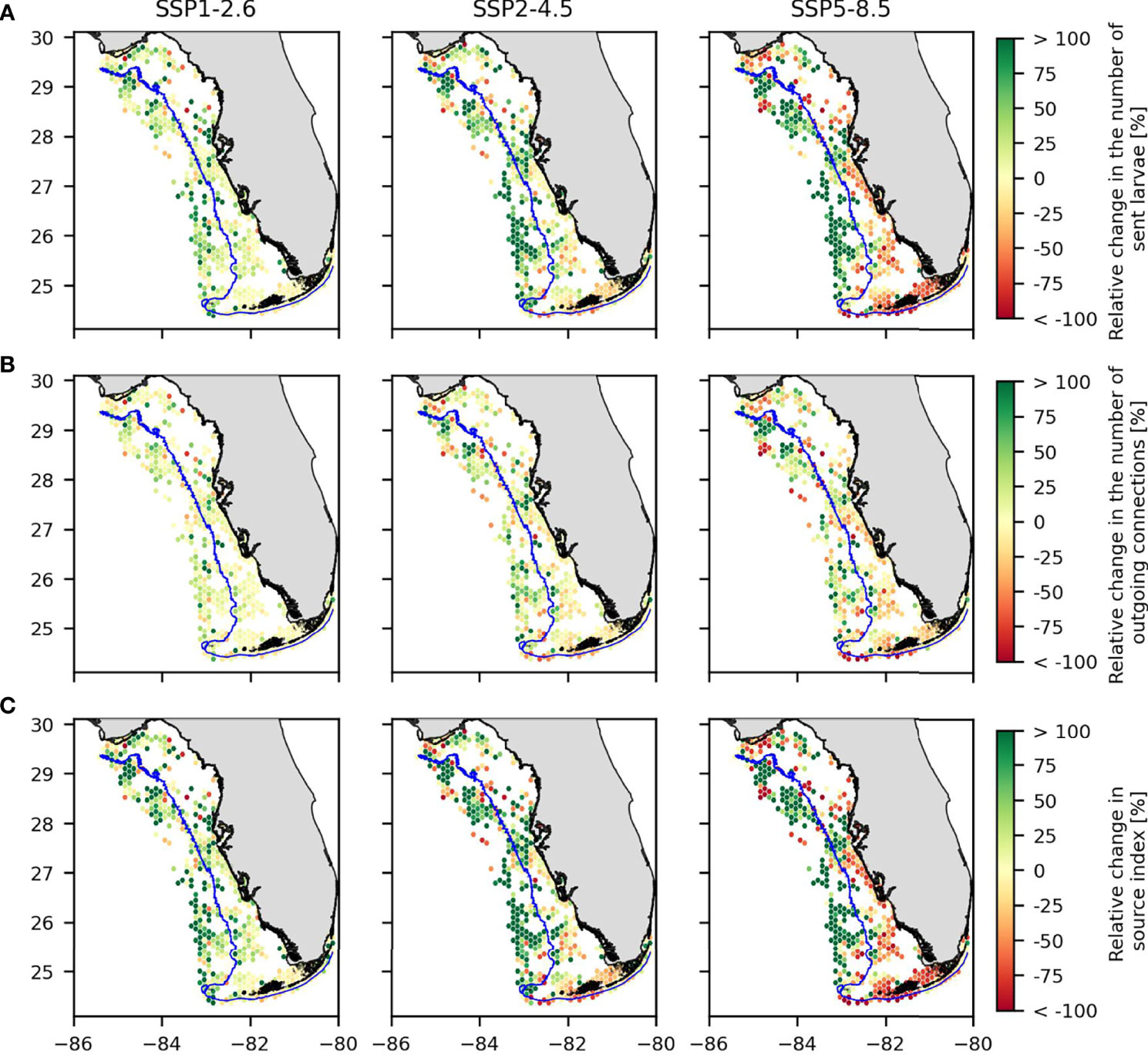
Figure 5 Relative change in (A) the number of larvae sent away that settle, (B) the number of outgoing connections with sink habitats and (C) the source index for the three climate change scenarios compared to present-day values. The blue line represents the limit between the fishing and non-fishing zones.

The community structure obtained with the SCC algorithm confirms an overall increase in the number of isolated habitats. The number of SCCs increases from 26 in present-day conditions to 27, 31 and 52 for SSP1-2.6, SSP2-4.5 and SSP5-8.5 scenarios, respectively (Figure 6). As a result, the average number of habitats per community decreases by 4% for SSP1-2.6, by 17% for SSP2-4.5 and by 55% in the SSP5-8.5 case. In the present-day scenario, there is one large community that covers most of the shelf. In SSP1-2.6 and SSP2-4.5 scenarios, the increase in the number of communities observed is mostly due to the appearance of isolated communities within this large community. In SSP5-8.5 scenario, the large community becomes fragmented.

FIGURE 6

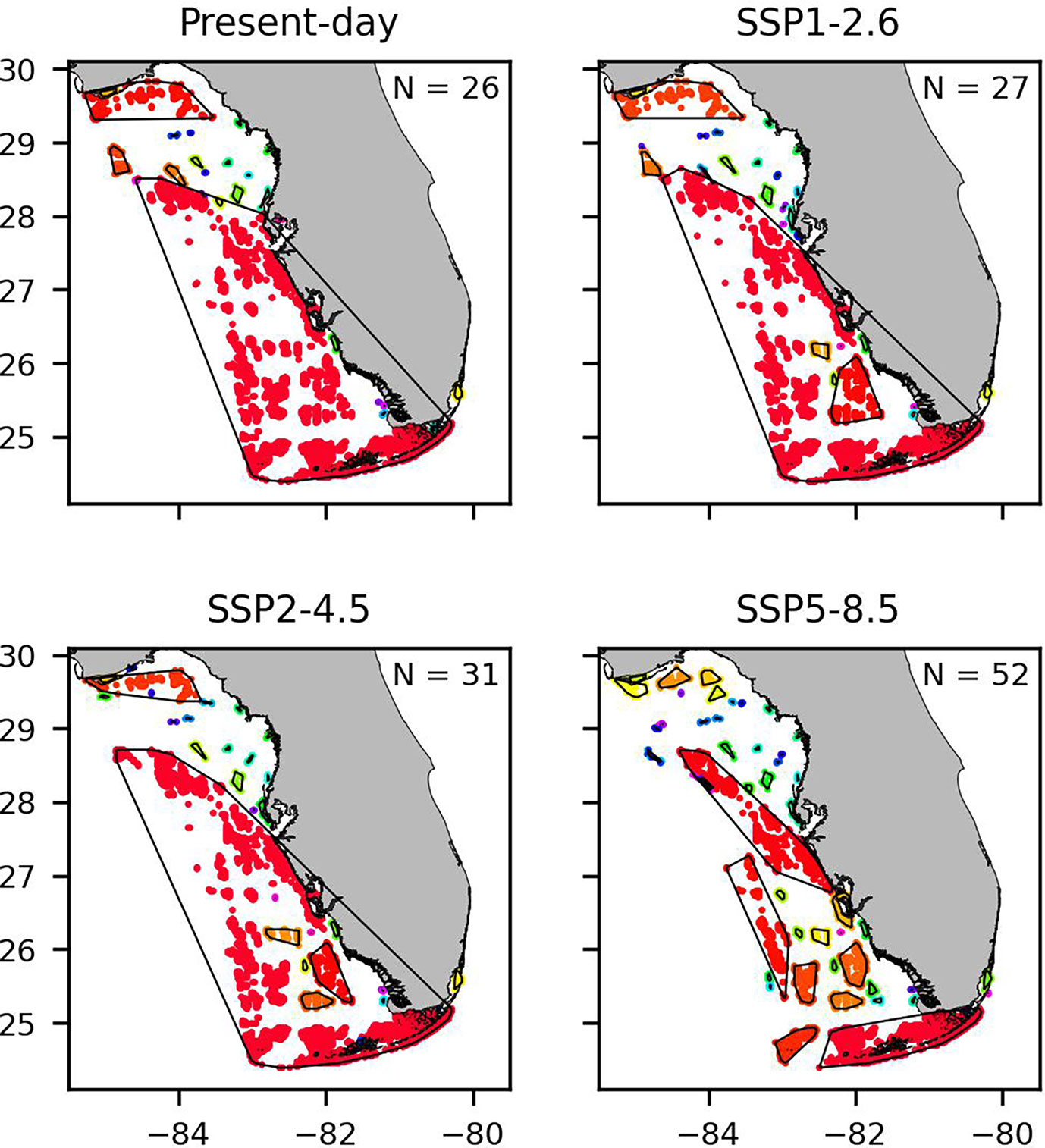
Figure 6 Map of the communities obtained with the SCC method for each climate change scenario. Each community is coloured in a different colour and is circled by a black line.

The proportion of all larvae produced that eventually settle increases in the SSP1-2.6 scenario for aggressive emissions reduction, but then decreases with the intensity of climate change (Table 1). The fishing zone and non-fishing zone show opposite behaviour. The proportion of larvae seeded in the fishing zone that settle there decreases with the intensity of climate change (-40% from present-day to SSP5-8.5) while it increases for larvae that stay in the non-fishing zone (+36% from present-day to SSP5-8.5). Very few larvae go from one zone to the other: cumulated, they never represent more than 6% of all the exchanges.

TABLE 1

Table 1 Percentage of larvae produced in the fishing (F) or non-fishing (NF) zones that settled in the fishing or non-fishing zones.

4 Discussion and Conclusions

Climate change will undoubtedly increase the ocean temperature and decrease the seawater pH. Our results confirm that those two effects will impact the dispersal and connectivity of stone crab larvae in four different ways. First, a small increase in seawater temperatures will reduce larval mortality. In more extreme climate change scenarios however, the ocean temperature will exceed larvae’s optimum temperature, increasing larval mortality. Second, increases in seawater temperatures will also reduce larval stage durations by up to 25%. Third, the decrease in seawater pH will reduce the hatching success, therefore decreasing the number of larvae that will settle. Finally, decreasing seawater pH will impact larval stone crab’s relative position in the water column by resulting in an overall deeper depth distribution The combination of these four consequences of climate change will lead to an increase in the number of larvae that settle on some habitats but also reduce the distance larvae can disperse. As a result, self-recruitment will increase, and habitat communities will become more fragmented along the WFS and throughout the Florida Keys. The spatial distribution of the Florida stone crab is also expected to change as southern and shallow habitats will be more impacted by increasing ocean temperature than northern and deeper habitats. This potential spatial shift in the stone crab distribution could impact the fishery, especially those in the southern part of the WFS such as in the Florida Keys, since the number of larvae settling in the fishing zone is expected to decrease.

Our model shows that stone crab larvae are expected to stay closer to the benthos and experience shorter larval stages during future climate scenarios. Both are known to reduce larval dispersion of several marine species (Shanks et al., 2003; North et al., 2008; Sundelöf and Jonsson, 2012). Since ocean currents weaken with greater depths (He and Weisberg, 2002; He and Weisberg, 2003; National Oceanic and Atmospheric Administration, 2021), crab larvae will therefore be transported over shorter distances and will have a higher probability of settling within their natal habitat. Self-recruitment will thus increase and the size of habitat clusters that are connected through larval exchanges will decrease. The resulting smaller communities are therefore likely to be less resilient to external disturbances or additional environmental stressors. Species that have high dispersal capabilities and form large communities are indeed less vulnerable to sudden changes in external conditions and diseases due to higher genetic diversity and the potential of local recovery through larval transport (Hastings and Botsford, 2003; Jones et al., 2007).

Our model shows that stone crab spatial distribution and abundance will also change. Temperature is a major factor influencing the proportion of larvae that successfully settle, as the mortality rate is function of the temperature. In our model of the present-day scenario, the number of settlers is higher in southern and shallow areas, because water in northerner and deeper areas is too cold to allow high settlement during the first spawning events. With a small change in temperature (+0.5°C), such as the increase modeled in the SSP1-2.6 scenario, the proportion of larvae that settle increases throughout the entire WFS. However, for more extreme temperature increases, as could be observed by the end of the century in SSP5-8.5 scenario, water temperature in shallow areas exceeds the larvae optimal temperature, leading to an increase in larval mortality. As a result, we expect that the stone crab larvae in the fishing zone will not benefit from the increase in temperature, and could instead see its population decline if the increase in temperature is too high. On the contrary, larvae produced in the non-fishing zone will likely benefit from the increase in water temperature, even in the case of the SSP5-8.5 scenario. This suggests that climate change could lead to a shift in the stone crab abundance and distribution, with an increase of the number of larvae settling in deeper and northerner water, while the number of larvae settling in the shallower and southern area will likely decrease. A shift to deeper or higher latitude water due to climate change has been observed for several marine species (Mieszkowska et al., 2006; Fujiwara et al., 2019) as well as other brachyuran crabs (Murphy, 2020). According to our model, the number of larvae settling in the fishing zone will however remain larger than the number of larvae settling in the non-fishing zone.

This shift in spatial abundance of the stone crab population is especially troublesome for the fishing industry because we observed very little exchanges between the fishing and non-fishing zone (less than 5% of exchanges from the non-fishing zone to the fishing zone), regardless of the scenario. This suggests that the non-fishing zone cannot serve as a source of larvae for the habitats within the fishing zone. As a result, the fishing industry should expect a reduction in the number of crabs in the current fishing area (<30m depth) and more fragile populations due to population fragmentation. In this context, the persistence of interconnected stone crab subpopulations is important for population survival and could be achieved with more targeted management measures for ovigerous females and sublegal crabs within the regions that show subpopulation persistence. For example, management protection of the reproductive stocks and recruitment habitats could increase resiliency of stone crab populations (Crowley et al., 2019). Studies have shown that the removal of stone crab claws done during harvest and the subsequent regeneration of a claw is a significant energy investment that takes several molts (Duermit et al., 2015; Gandy et al., 2016). Furthermore, removal of claws reduces feeding, especially during warmer temperatures which can increase stone crabs’prey mortality. A decrease in prey consumption (50% decrease in bivalves consumed with claw removal) in stone crabs was estimated to result in an annual decrease of energy intake equivalent to the energy contained within ~70 million eggs (the annual fecundity of a median legal-sized stone crab of 102 mm carapace width is around 2 million eggs (Ros et al., 1981; Hogan and Griffen, 2014)). Crowley et al. (2019) supports the claim that reproductive output is reduced with claw removal and showed that crab fecundity is 39% lower for crabs with no claws. Management efforts could also target preservation of locations on the West Florida Shelf where fecundity and recruitment are observed to be elevated. For example, fecundity was 1.35 and 1.39 times higher in Pavilion Key and Tampa Bay, FL relative to Cedar Key (Crowley et al., 2019), where waters offshore of the Florida Everglades, Cedar Key, Tampa Bay, and Steinhatchee represents 75% of the state’s stone crab recruitment over the last several decades (Bert et al., 2021). Due to the possible future habitat fragmentation the habitats located just west of Tampa bay would be good candidates for management or protection, as our model shows these habitats were always included in one of the largest stone crab communities and show increases in source index, regardless of the climate scenario.

As for every model study, this work was based on different assumptions. Due to lack of more accurate data, we could not completely represent all the processes driving the vertical larval dynamics for the 5 different larval stages of the stone crab. This could be improved by conducting vertically stratified plankton surveys to estimate vertical velocities according to larval depth distribution, like in Peliz et al. (2007). Furthermore, there is also some uncertainty on the location of crab habitats. For lack of better data, we assumed that all rocky, muddy or gravely substrates shallower than 60 m would be suitable for stone crabs. This is probably an overestimation of the actual crab habitats. Habitat maps could be refined by following the approach of Criales et al. (2019) who backtracked larvae from locations where crabs have been observed to identify their source habitat. Another limitation is that we did not take the spatial heterogeneity of pH decreases and temperature increases into account. In the climate change scenarios, we decreased (resp. increased) the water pH (resp. temperature) by a constant over the entire domain, while these changes are probably not going to be spatially homogeneous. We also assumed that the oceanic and atmospheric circulation would remain the same for the different climate change scenarios. This assumption is supported by the study of Figueiredo et al. (2022) on coral connectivity changes in the Great Barrier Reef due to climate change. They found that changes in the hydrodynamics have a much weaker effect than changes in larval biology on connectivity. Finally, while we considered several spawning events, we did not consider multiple years to explicitly take interannual variability into account. This is mostly due to the heavy computational cost for running high-resolution three-dimensional simulations over the entire WFS.

Despite these limitations, our model brings unprecedented perspectives on the impact climate change will have on the stone crab population along the WFS and within the Florida Keys. As the first model to evaluate the current and future dispersion of M. mercenaria, this work could help local authorities to understand the mechanisms underlying stone crab distribution and population connectivity which is beneficial if fisheries management is to prepare for future changes in climate. Our work could also serve as a reference for other studies aiming to model the dispersion of brachyuran crabs. Brachyuran crabs are found all around the world, in almost all coastal habitats, with many species being commercially important (Azra et al., 2020). In this work we introduced several new elements compared to other dispersal models of brachyuran crabs, like the sinusoidal response to light (more realistic than a binary up and down vertical swimming behavior) or the pH-dependent vertical velocity component that allowed to evaluate the impacts of ocean acidification on the stone crabs distribution. Since all brachyuran crabs respond to external stimuli like hydrostatic pressure and light (Epifanio and Cohen, 2016), our approach could be used to estimate their dispersion patterns.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

LA developed the model, ran the simulations, and analyzed the results. EH conceptualized the study and designed the modeling experiments. PG collected and analyzed the biological data. TD developed the model. All authors contributed to the writing of the manuscript. All authors contributed to the article and approved the submitted version.

Funding

Gravinese’s research is supported by an U.S. National Science Foundation Biological Oceanography Grant (award number OCE-2049047). Computational resources were provided by the Consortium des Équipements de Calcul Intensif (CÉCI), funded by the F.R.S.-FNRS under Grant No. 2.5020.11. LA is a Ph.D. student supported by the Fund for Research Training in Industry and Agriculture (FRIA/FNRS).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2022.839767/full#supplementary-material

References

Azra M. N., Aaqillah-Amr M. A., Ikhwanuddin M., Ma H., Waiho K., Ostrensky A., et al. (2020). Effects of Climate-Induced Water Temperature Changes on the Life History of Brachyuran Crabs. Rev. Aquac. 12, 1211–1216. doi: 10.1111/raq.12380

CrossRef Full Text | Google Scholar

Baeza J., Holstein D., Umaña-Castro R., Mejía-Ortíz L. (2019). Population Genetics and Biophysical Modeling Inform Metapopulation Connectivity of the Caribbean King Crab Maguimithrax Spinosissimus. Mar. Ecol. Prog. Ser. 610, 83–97. doi: 10.3354/meps12842

CrossRef Full Text | Google Scholar

Banas N. S., McDonald P. S., Armstrong D. A. (2009). Green Crab Larval Retention in Willapa Bay, Washington: An Intensive Lagrangian Modeling Approach. Estuaries. Coasts 32, 893–905. doi: 10.1007/s12237-009-9175-7

CrossRef Full Text | Google Scholar

Beck M. W. (1995). Size-Specific Shelter Limitation in Stone Crabs: A Test of The Demographic Bottleneck Hypothesis. Ecology 76, 968–980. doi: 10.2307/1939360

CrossRef Full Text | Google Scholar

Bednaršek N., Ambrose R., Calosi P., Childers R. K., Feely R. A., Litvin S. Y., et al. (2021). Synthesis of Thresholds of Ocean Acidification Impacts on Decapods. Front. Mar. Sci. 8. doi: 10.3389/fmars.2021.651102

PubMed Abstract | CrossRef Full Text | Google Scholar

Bert T. M., Crawford C., Shea C. (2021). Young-Of-The-Year Stone Crab (Genus Menippe) Recruitment in the Gulf of Mexico Off Florida: Key Shallow-Water Hotspots. J. Shellfish Res. 40, 339–398. doi: 10.2983/035.040.0211

CrossRef Full Text | Google Scholar

Bert T. M., Warner R. E., Kessler L. D. (1978) The Biology and Florida Fishery of the Stone Crab, Menippe Mercenaria (Say), With Emphasis on Southwest Florida. Available at: https://ufdc.ufl.edu/UF00072275/00001/1j.

Google Scholar

Binford R. (1913). The Germ-Cells and the Process of Fertilization in the Crab, Menippe Mercenaria. J. Morphol. 24, 147–201. doi: 10.1002/jmor.1050240202

CrossRef Full Text | Google Scholar

Botsford L. W., White J. W., Coffroth M.-A., Paris C. B., Planes S., Shearer T. L., et al. (2009). Connectivity and Resilience of Coral Reef Metapopulations in Marine Protected Areas: Matching Empirical Efforts to Predictive Needs. Coral Reefs 28, 327–337. doi: 10.1007/s00338-009-0466-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Brown S. D., Bert T. M., Tweedale W. A., Torres J. J., Lindberg W. J. (1992). The Effects of Temperature and Salinity on Survival and Development of Early Life Stage Florida Stone Crabs Menippe Mercenaria (Say). J. Exp. Mar. Biol. Ecol. 157, 115–136. doi: 10.1016/0022-0981(92)90078-O

CrossRef Full Text | Google Scholar

Byrne R. H., Mecking S., Feely R. A., Liu X. (2010). Direct Observations of Basin-Wide Acidification of the North Pacific Ocean. Geophys. Res. Lett. 37, L02601. doi: 10.1029/2009GL040999

CrossRef Full Text | Google Scholar

Ceballos-Osuna L., Carter H. A., Miller N. A., Stillman J. H. (2013). Effects of Ocean Acidification on Early Life-History Stages of the Intertidal Porcelain Crab Petrolisthes Cinctipes. J. Exp. Biol. 216, 1405–1411. doi: 10.1242/jeb.078154

PubMed Abstract | CrossRef Full Text | Google Scholar

Chassignet E. P., Hurlburt H. E., Smedstad O. M., Halliwell G. R., Hogan P. J., Wallcraft A. J., et al. (2007). The HYCOM (HYbrid Coordinate Ocean Model) Data Assimilative System. J. Mar. Syst. 65, 60–83. doi: 10.1016/j.jmarsys.2005.09.016

CrossRef Full Text | Google Scholar

Cowen R. K., Sponaugle S. (2009). Larval Dispersal and Marine Population Connectivity. Annu. Rev. Mar. Sci. 1, 443–466. doi: 10.1146/annurev.marine.010908.163757

CrossRef Full Text | Google Scholar

Criales M. M., Cherubin L., Gandy R., Garavelli L., Ghannami M., Crowley C. (2019). Blue Crab Larval Dispersal Highlights Population Connectivity and Implications for Fishery Management. Mar. Ecol. Prog. Ser. 625, 57–70. doi: 10.3354/meps13049

CrossRef Full Text | Google Scholar

Critchell K., Lambrechts J. (2016). Modelling Accumulation of Marine Plastics in the Coastal Zone; What are the Dominant Physical Processes? Estuar. Coast. Shelf. Sci. 171, 111–122. doi: 10.1016/j.ecss.2016.01.036

CrossRef Full Text | Google Scholar

Crowley C. E., Shea C. P., Gandy R. L., Daly K. L. (2019). Fecundity Assessment of Stone Crabs in the Eastern Gulf of Mexico. Mar. Coast. Fish. 11, 32–47. doi: 10.1002/mcf2.10059

CrossRef Full Text | Google Scholar

Dissanayake A., Ishimatsu A. (2011). Synergistic Effects of Elevated CO2 and Temperature on the Metabolic Scope and Activity in a Shallow-Water Coastal Decapod (Metapenaeus Joyneri; Crustacea: Penaeidae). ICES. J. Mar. Sci. 68, 1147–1154. doi: 10.1093/icesjms/fsq188

CrossRef Full Text | Google Scholar

Dobbelaere T., Muller E. M., Gramer L. J., Holstein D. M., Hanert E. (2020). Coupled Epidemio-Hydrodynamic Modeling to Understand the Spread of a Deadly Coral Disease in Florida. Front. Mar. Sci. 7. doi: 10.3389/fmars.2020.591881/full

CrossRef Full Text | Google Scholar

Dubois M., Rossi V., Ser-Giacomi E., Arnaud-Haond S., López C., Hernández-García E. (2016). Linking Basin-Scale Connectivity, Oceanography and Population Dynamics for the Conservation and Management of Marine Ecosystems. Glob. Ecol. Biogeogr. 25, 503–515. doi: 10.1111/geb.12431

CrossRef Full Text | Google Scholar

Duermit E., Kingsley-Smith P. R., Wilber D. H. (2015). The Consequences of Claw Removal on Stone Crabs Menippe Spp. And the Ecological and Fishery Implications. North Am. J. Fish. Manage. 35, 895–905. doi: 10.1080/02755947.2015.1064836

CrossRef Full Text | Google Scholar

Duquesne F., Vallaeys V., Vidaurre P. J., Hanert E. (2021). A Coupled Ecohydrodynamic Model to Predict Algal Blooms in Lake Titicaca. Ecol. Model. 440, 109418. doi: 10.1016/j.ecolmodel.2020.109418

CrossRef Full Text | Google Scholar

Egbert G., Erofeeva S. (2002). Efficient Inverse Modeling of Barotropic Ocean Tides. J. Atmospheric. Ocean. Technol. 19, 183–204. doi: 10.1175/1520-0426(2002)019<0183:EIMOBO>2.0.CO;2

CrossRef Full Text | Google Scholar

Epifanio C. E., Cohen J. H. (2016). Behavioral Adaptations in Larvae of Brachyuran Crabs: A Review. J. Exp. Mar. Biol. Ecol. 482, 85–105. doi: 10.1016/j.jembe.2016.05.006

CrossRef Full Text | Google Scholar

Figueiredo J., Thomas C. J., Deleersnijder E., Lambrechts J., Baird A. H., Connolly S. R., et al. (2022). Global Warming Decreases Connectivity Among Coral Populations. Nat. Clim. Change 12, 83–87. doi: 10.1038/s41558-021-01248-7

CrossRef Full Text | Google Scholar

Florida Fish and Wildlife Conservation Commission. (1998). Public Fisheries-Dependent Monitoring: Commercial Fisheries Landings Summaries. Available at: https://public.myfwc.com/FWRI/PFDM/ReportCreator.aspx (Accessed August 5, 2021).

Google Scholar

Florida Fish And Wildlife Conservation Commission. (2020). Stone Crab Season Starts Oct. 15 With Regulation Changes in Place. Fla. Fish Wildl. Conserv. Comm. Available at: http://myfwc.com/news/all-news/stone-crab-1020/ (Accessed May 24, 2021).

Google Scholar

Fox-Kemper B., Hewitt H. T., Xiao C., Aðalgeirsdóttir G., Drijfhout S. S., Edwards T. L., et al. (2021). ““Ocean, Cryosphere and Sea Level Change,”,” in Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Chang IPCC. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA. Available at: https://www.ipcc.ch/report/ar6/wg1/#FullReport.

Google Scholar

Frys C., Saint-Amand A., Le Hénaff M., Figueiredo J., Kuba A., Walker B., et al. (2020). Fine-Scale Coral Connectivity Pathways in the Florida Reef Tract: Implications for Conservation and Restoration. Front. Mar. Sci. 7. doi: 10.3389/fmars.2020.00312

CrossRef Full Text | Google Scholar

Fujiwara M., Martinez-Andrade F., Wells R. J. D., Fisher M., Pawluk M., Livernois M. C. (2019). Climate-Related Factors Cause Changes in the Diversity of Fish and Invertebrates in Subtropical Coast of the Gulf of Mexico. Commun. Biol. 2, 1–9. doi: 10.1038/s42003-019-0650-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Gandy R., Crowley C., Chagaris D., Crawford C. (2016). The Effect of Temperature on Release Mortality of Declawed <I>Menippe Mercenaria</I> in the Florida Stone Crab Fishery. Bull. Mar. Sci. 92, 1–15. doi: 10.5343/bms.2015.1036

CrossRef Full Text | Google Scholar

GBIF Backbone Taxonomy. (2019). Menippe Mercenaria (Say 1818). Available at: https://www.gbif.org/species/5178757 (Accessed March 13, 2021). GBIF Secr.

Google Scholar

Gravinese P. (2018a). Ocean Acidification Impacts the Embryonic Development and Hatching Success of the Florida Stone Crab, Menippe Mercenaria. J. Exp. Mar. Biol. Ecol. 500, 140–146. doi: 10.1016/j.jembe.2017.09.001

CrossRef Full Text | Google Scholar

Gravinese P. M. (2018b). Vertical Swimming Behavior in Larvae of the Florida Stone Crab, Menippe Mercenaria. J. Plankton. Res. 40, 643–654. doi: 10.1093/plankt/fby040

CrossRef Full Text | Google Scholar

Gravinese P. M., Enochs I. C., Manzello D. P., van Woesik R. (2018). Warming and Pco2 Effects on Florida Stone Crab Larvae. Estuar. Coast. Shelf. Sci. 204, 193–201. doi: 10.1016/j.ecss.2018.02.021

CrossRef Full Text | Google Scholar

Gravinese P. M., Enochs I. C., Manzello D. P., van Woesik R. (2019). Ocean Acidification Changes the Vertical Movement of Stone Crab Larvae. Biol. Lett. 15, 1–7. doi: 10.1098/rsbl.2019.0414

CrossRef Full Text | Google Scholar

Grech A., Hanert E., McKenzie L., Rasheed M., Thomas C., Tol S., et al. (2018). Predicting the Cumulative Effect of Multiple Disturbances on Seagrass Connectivity. Glob. Change Biol. 24, 3093–3104. doi: 10.1111/gcb.14127

CrossRef Full Text | Google Scholar

Grech A., Wolter J., Coles R., McKenzie L., Rasheed M., Thomas C., et al. (2016). Spatial Patterns of Seagrass Dispersal and Settlement. Divers. Distrib. 22, 1150–1162. doi: 10.1111/ddi.12479

CrossRef Full Text | Google Scholar

Gulf Shores Marine Fisheries Commission. (2001). Summary Table of the Stone Crab, *Menippe Mercenaria*,: Life History for the Gulf of Mexico (Mississipi, USA: Gulf Shores Marine Fisheries Commission). Available at: http://www.gsmfc.org/pubs/habitat/tables/stonecrab.pdf.

Google Scholar

Hastings A., Botsford L. (2003). Comparing Designs of Marine Reserves for Fisheries and for Biodiversity. Ecol. Appl. - Ecol. Appl. 13, 65–70. doi: 10.1890/1051-0761(2003)013[0065:CDOMRF]2.0.CO;2

CrossRef Full Text | Google Scholar

Hastings A., Botsford L. W. (2006). Persistence of Spatial Populations Depends on Returning Home. Proc. Natl. Acad. Sci. 103, 6067–6072. doi: 10.1073/pnas.0506651103

CrossRef Full Text | Google Scholar

Hendriks I. E., Duarte C. M., Olsen Y. S., Steckbauer A., Ramajo L., Moore T. S., et al. (2015). Biological Mechanisms Supporting Adaptation to Ocean Acidification in Coastal Ecosystems. Estuar. Coast. Shelf. Sci. 152, A1–A8. doi: 10.1016/j.ecss.2014.07.019

CrossRef Full Text | Google Scholar

Hersbach H., Bell B., Berrisford P., Biavati G., Horányi A., Muños Sabater J., et al. (2018)ERA5 Hourly Data on Single Levels From 1979 to Present. In: Copernic. Clim. Change Serv. Available at: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=overview (Accessed March 10, 2021).

Google Scholar

He R., Weisberg R. H. (2002). West Florida Shelf Circulation and Temperature Budgetfor the 1999 Spring Transition. Cont. Shelf. Res. 22, 719–748. doi: 10.1016/S0278-4343(01)00085-1

CrossRef Full Text | Google Scholar

He R., Weisberg R. H. (2003). West Florida Shelf Circulation and Temperature Budget for the 1998 Fall Transition. Cont. Shelf. Res. 23, 777–800. doi: 10.1016/S0278-4343(03)00028-1

CrossRef Full Text | Google Scholar

Hoegh-Guldberg O., Cai R., Poloczanska E. S., Brewer P. G., Sundby S., Hilmi K., et al. (2014). “The Ocean,” (Cambridge, United Kingdom and New York, NY, USA: Cambridge University Press), 1655–1731.

Google Scholar

Hogan J. M., Griffen B. D. (2014). The Dietary and Reproductive Consequences of Fishery-Related Claw Removal for the Stone Crab Menippe Spp. J. Shellfish. Res. 33, 795–804. doi: 10.2983/035.033.0314

CrossRef Full Text | Google Scholar

Jenkins C. (2011). Seafloor Substrates Griddings, Gulf of Mexico, U. @ of C.

Google Scholar

Jones G., Srinivasan M., Almany G. (2007). Population Connectivity and Conservation of Marine Biodiversity. Oceanogr. INSTAAR University of Colorado, USA. Wash. DC 20, 100–111. doi: 10.5670/oceanog.2007.33

CrossRef Full Text | Google Scholar

Kool J. T., Moilanen A., Treml E. A. (2013). Population Connectivity: Recent Advances and New Perspectives. Landsc. Ecol. 28, 165–185. doi: 10.1007/s10980-012-9819-z

CrossRef Full Text | Google Scholar

Krimsky L. S., Epifanio C. E. (2008). Multiple Cues From Multiple Habitats : Effect of Metamorphosis of the Florida Ston Crab, Menippe Mercenaria. J. Exp. Mar. Biol. Ecol. 358, 178–184. doi: 10.1016/j.jembe.2008.02.010

CrossRef Full Text | Google Scholar

Krimsky L. S., Gravinese P. M., Tankersley R. A., Epifanio C. E. (2009). Patterns of Larval Release in the Florida Stone Crab, Menippe Mercenaria. J. Exp. Mar. Biol. Ecol. 373, 96–101. doi: 10.1016/j.jembe.2009.03.013

CrossRef Full Text | Google Scholar

Kuhn A. A. (2017) Effects of Temperature on Growth and Molting in Blue Crabs Effects of Temperature on Growth and Molting in Blue Crabs (Callinectes Sapidus) and Lesser Blue Crabs ((Callinectes Sapidus) and Lesser Blue Crabs (Callinectes Similiscallinectes Similis) ). Available at: https://aquila.usm.edu/cgi/viewcontent.cgi?article=1361&context=masters_theses.

Google Scholar

Kurihara H. (2008). Effects of CO2-Driven Ocean Acidification on the Early Developmental Stages of Invertebrates. Mar. Ecol. Prog. Ser. 373, 275–284. doi: 10.3354/meps07802

CrossRef Full Text | Google Scholar

Lindberg W. J., Marshall M. J. (1984). Species Profiles: Life Histories and Environmental Requirements of Coastal Fishes and Invertebrates (South Atlantic): Stone Crab (Washington (D.C: Florida Gulf Coast University). Available at: https://fgcu.digital.flvc.org/islandora/object/fgcu%3A27184.

Google Scholar

Liu Y., Weisberg R. H. (2012). Seasonal Variability on the West Florida Shelf. Prog. Oceanogr. 104, 80–98. doi: 10.1016/j.pocean.2012.06.001

CrossRef Full Text | Google Scholar

Li Y., Wolanski E., Dai Z., Lambrechts J., Tang C., Zhang H. (2018). Trapping of Plastics in Semi-Enclosed Seas: Insights From the Bohai Sea, China. Mar. Pollut. Bull. 137, 509–517. doi: 10.1016/j.marpolbul.2018.10.038

PubMed Abstract | CrossRef Full Text | Google Scholar

Mercator-Ocean. (2019). Global Ocean Biogeochemistry Hindcast. Available at: doi: 10.48670/moi-00019.

CrossRef Full Text | Google Scholar

Metzger R., Sartoris F. J., Langenbuch M., Pörtner H. O. (2007). Influence of Elevated CO2 Concentrations on Thermal Tolerance of the Edible Crab Cancer Pagurus. J. Therm. Biol. 32, 144–151. doi: 10.1016/j.jtherbio.2007.01.010

CrossRef Full Text | Google Scholar

Mieszkowska N., Kendall M. A., Hawkins S. J., Leaper R., Williamson P., Hardman-Mountford N. J., et al. (2006). ““Changes in the Range of Some Common Rocky Shore Species In Britain — A Response To Climate Change?,”,” in Marine Biodiversity: Patterns and Processes, Assessment, Threats, Management and Conservation Developments in Hydrobiology. Eds. Martens K., Queiroga H., Cunha M. R., Cunha A., Moreira M. H., Quintino V. (Dordrecht: Springer Netherlands), 241–251. doi: 10.1007/1-4020-4697-9_20

CrossRef Full Text | Google Scholar

Minor E. S., Urban D. L. (2007). Graph Theory as a Proxy for Spatially Explicit Population Models in Conservation Planning. Ecol. Appl. 17, 1771–1782. doi: 10.1890/06-1073.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Muller R. G., Chagaris D., Bert T. M., Crawford C., Gandy R. (2011) The 2011 Stock Assessment Update for the Stone Crab, Menippe Spp., Fishery in Florida (St. Petersburg, Florida: Fish and Wildlife Research Institute, Florida Fish And Wildlife Conservation Commission). Available at: http://myfwc.com/research/saltwater/crustaceans/stone-crabs/stock-assessments/ (Accessed April 21, 2021).

Google Scholar

Murphy J. T. (2020). Climate Change, Interspecific Competition, and Poleward vs. Depth Distribution Shifts: Spatial Analyses of the Eastern Bering Sea Snow and Tanner Crab (Chionoecetes Opilio and C. Bairdi). Fish. Res. 223, 105417. doi: 10.1016/j.fishres.2019.105417

CrossRef Full Text | Google Scholar

National Oceanic and Atmospheric Administration. (2021). (USA: National Data Buoy Center). Available at: https://www.ndbc.noaa.gov/ (Accessed October 15, 2020).

Google Scholar

NOAA National Geophysical Data Center. (2001). U.S. Coastal Relief Model Vol.3 - Florida and East Gulf of Mexico.

Google Scholar

North E., Schlag Z., Hood R., Li M., Zhong L., Gross T., et al. (2008). Vertical Swimming Behavior Influences the Dispersal of Simulated Oyster Larvae in a Coupled Particle-Tracking and Hydrodynamic Model of Chesapeake Bay. Mar. Ecol.-Prog. Ser. 359, 99–115. doi: 10.3354/meps07317

CrossRef Full Text | Google Scholar

Nuutila E., Soisalon-Soininen E. (1994). On Finding the Strongly Connected Components in a Directed Graph. Inf. Process. Lett. 49, 9–14. doi: 10.1016/0020-0190(94)90047-7

CrossRef Full Text | Google Scholar

Okubo A. (1971). Oceanic Diffusion Diagrams. Deep. Sea. Res. Oceanogr. Abstr. 18, 789–802. doi: 10.1016/0011-7471(71)90046-5

CrossRef Full Text | Google Scholar

Peliz A., Marchesiello P., Dubert J., Marta-Almeida M., Roy C., Queiroga H. (2007). A Study of Crab Larvae Dispersal on the Western Iberian Shelf: Physical Processes. J. Mar. Syst. 68, 215–236. doi: 10.1016/j.jmarsys.2006.11.007

CrossRef Full Text | Google Scholar

Pineda J., Hare J. A., Sponaugle S. (2007). Larval Transport and Dispersal in the Coastal Ocean and Consequences for Population Connectivity. Oceanography 20, 22–39. doi: 10.5670/oceanog.2007.27

CrossRef Full Text | Google Scholar

Pires R. F. T., Peliz Á., Pan M., dos Santos A. (2020). “There and Back Again” – How Decapod Megalopae Find the Way Home: A Modelling Exercise for Pachygrapsus Marmoratus. Prog. Oceanogr. 184, 102331. doi: 10.1016/j.pocean.2020.102331

CrossRef Full Text | Google Scholar

Porter H. J. (1960). Zoeal Stages of the Stone Crab, Menippe Mercenaria Say. Chesap. Sci. 1, 168. doi: 10.2307/1350394

CrossRef Full Text | Google Scholar

Rayfield B., Fortin M.-J., Fall A. (2011). Connectivity for Conservation: A Framework to Classify Network Measures. Ecology 92, 847–858. doi: 10.1890/09-2190.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Ros R. M., Perez D., Menocal R. (1981). Fecundidad En El Cangrejo Moro Menippe Mercenaria (Say 1818) [Fecundity in the Stone Crab Menippe Mercenaria]. Revisita. Investig. Mar. 2, 73–91.

Google Scholar

Seyoum S., Gandy R. L., Crowley C. E., Puchulutegui C. (2021). A Novel Interpretation of Speciation, Hybridization, and Genetic Population Structure of the Stone Crabs Menippe Mercenaria (Say 1817–1818) and M. Adina Williams & Felder 1986 (Decapoda: Brachyura: Menippidae). J. Crustac. Biol. 41, 1–14. doi: 10.1093/jcbiol/ruab018

CrossRef Full Text | Google Scholar

Shanks A. L., Grantham B. A., Carr M. H. (2003). Propagule Dispersal Distance and the Size and Spacing of Marine Reserves. Ecol. Appl. 13, 159–169. doi: 10.1890/1051-0761(2003)013[0159:PDDATS]2.0.CO;2

CrossRef Full Text | Google Scholar

Smagorinsky J. (1963). General Circulation Experiments With the Primitive Equations : I. The Basic Experiment. Mon. Weather. Rev. 91, 99–164. doi: 10.1175/1520-0493(1963)091<0099:GCEWTP>2.3.CO;2

CrossRef Full Text | Google Scholar

Smith S. D., Banke E. G. (1975). Variation of the Sea Surface Drag Coefficient With Wind Speed. Q. J. R. Meteorol. Soc 101, 665–673. doi: 10.1002/qj.49710142920

CrossRef Full Text | Google Scholar

Sulkin S. D. (1984). Behavioral Basis of Depth Regulation in the Larvae of Brachyuran Cra. Mar. Ecol. Prog. Ser. 15, 181–205. doi: 10.3354/meps015181

CrossRef Full Text | Google Scholar

Sundelöf A., Jonsson P. R. (2012). Larval Dispersal and Vertical Migration Behaviour – a Simulation Study for Short Dispersal Times. Mar. Ecol. 33, 183–193. doi: 10.1111/j.1439-0485.2011.00485.x

CrossRef Full Text | Google Scholar

Tarjan R. (1972). Depth-First Search and Linear Graph Algorithms. SIAM. J. Comput. 1, 146–160. doi: 10.1137/0201010

CrossRef Full Text | Google Scholar

Vallaeys V., Kärnä T., Delandmeter P., Lambrechts J., Baptista A. M., Deleersnijder E., et al. (2018). Discontinuous Galerkin Modeling of the Columbia River’s Coupled Estuary-Plume Dynamics. Ocean. Model. 124, 111–124. doi: 10.1016/j.ocemod.2018.02.004

CrossRef Full Text | Google Scholar

Vallaeys V., Lambrechts J., Delandmeter P., Pätsch J., Spitzy A., Hanert E., et al. (2021). Understanding the Circulation in the Deep, Micro-Tidal and Strongly Stratified Congo River Estuary. Ocean. Model. 167, 101890. doi: 10.1016/j.ocemod.2021.101890

CrossRef Full Text | Google Scholar

Weisberg R. H., Li Z., Muller-Karger F. (2001). West Florida Shelf Response to Local Wind Forcing: April 1998. J. Geophys. Res. Oceans. 106, 31239–31262. doi: 10.1029/2000JC000529

CrossRef Full Text | Google Scholar

Young A. M., Hazlett T. L. (1978). The Effect of Salinity and Temperature on the Larval Development of Clibanarius Vittatus (Bosc) (Crustacea: Decapoda: Diogenidae). J. Exp. Mar. Biol. Ecol. 34, 131–141. doi: 10.1016/0022-0981(78)90036-9

CrossRef Full Text | Google Scholar