- 1Ocean Engineering Program – COPPE, Universidade Federal do Rio de Janeiro, Rio de Janeiro, Brazil
- 2Ocean Predictions and Applications Division, Centro Euro-Mediterraneo sui Cambiamenti Climatici, Lecce, Italy
- 3Department of Oceanography, Universidade Federal do Espírito Santo, Vitória, Brazil
A methodology that combines a 24-year long (January 1993 to December 2016) global dataset of eddy trajectories, derived from altimetry, with vertical temperature and salinity profiles from the EN4.2.0 database, derived from XBTs/MBTs, CTDs and Argo floats, was used to reconstruct the mean vertical structure of North Brazil Current (NBC) rings, and to calculate some of their properties. The number of NBC rings formed each year varied from 2 to 8, with an annual-mean formation of 5.3 ± 1.5. During the analyzed period, 112 rings were sampled at least once, at various distances from the center of the rings, leading to a total of 1323 (604) temperature (salinity) profiles available to compute the mean NBC ring, depicting a large, surface intensified, and relatively shallow ring, with intense temperature and salinity anomalies. The meridional volume transport was estimated in 1.3 Sv (1Sv = 106 m3s-1) per ring, leading to an annualized transport of ~7 ± 2 Sv. The amount of South Atlantic Water (SAW) within the mean ring was estimated in ~40 to 60% of the ring volume. According to these estimates, NBC rings may be responsible in different years for approximately 20 to 80% of the northward volume transport associated with the upper limb of the Atlantic Meridional Overturning Circulation (AMOC), and approximately 15 to 55% of the meridional heat transport in the tropical Atlantic.
1 Introduction
The North Brazil Current (NBC) is an intense western boundary current which crosses the equator and retroflects around 6° to 8°N, feeding the North Equatorial Counter Current - NECC (Schott et al., 1998). Throughout the year, the NBC retroflection sheds isolated warm-core rings that can reach more than 450 km in overall diameter (Johns et al., 1990; Richardson et al., 1994; Fratantoni et al., 1995; Johns et al., 2003). These large features propagate northwestward along the South American coast (Ffield, 2005) and represent a major contribution to the transport of South Atlantic water that crosses the equator into the North Atlantic Subtropical Gyre (Jonhs et al., 1990; Didden & Schott, 1993; Richardson et al., 1994). Such upper-ocean transport is required, as part of the Atlantic Meridional Overturning Circulation (AMOC), in order to compensate for the southward export of North Atlantic Deep Water (NADW) in the deep ocean. The remainder of the AMOC upper-ocean flow in this region is transported by shallow coastal currents along the South American shelf (Halliwell et al., 2003) and by Ekman transport in the ocean interior (Candela et al., 1992). The NBC rings may also present a significant contribution to the total meridional heat transport at low latitudes (Garzoli et al., 2003).
After being shed at the retroflection the NBC rings translate for three to four months until they reach the Lesser Antilles, experiencing significant depth variations of the water column (from approximately 500 to 4000m, in particular at their southwestern border) along their trajectories. Interaction with the complex bottom topography may have an impact on the rings’ pathway, and in some cases on their shape, dynamics, and vertical structure (Fratantoni et al., 1995; Fratantoni and Glickson, 2002). Different vertical structures may also reflect different conditions at the retroflection, leading to shallow surface-intensified rings, deep-reaching surface-intensified rings, and subsurface intensified rings (Wilson et al., 2002). Surface intensified rings are associated with positive sea level anomaly (SLA), which can be tracked with satellite altimetry data, while subsurface intensified rings have little or no surface signal (Johns et al., 2003).
Estimates on the number of NBC rings formed per year vary from 2 to 9 in the literature, since they were first identified by Johns et al. (1990) using color scanner imagery, as more data from in situ and satellite observations have become available. Didden and Schott (1993) were able to track 5 rings, from their formation at the retroflection until 60°W, in approximately two and a half years of Geosat sea level anomaly (SLA) data. Shortly after, Richardson et al. (1994) followed 6 different rings along their trajectory, from 1989 to 1992, using surface and subsurface drifters. Goni and Johns (2001) provided the first satellite-based census of NBC rings, based on Topex/Poseidon data from 1992 to 1998, and found 2 to 7 rings forming each year. From a total of 34 rings identified during the 6-year long period of available observations, 24 originated at the retroflection and 10 possibly so, resulting in an average of 4 to almost 6 NBC rings per year. Latter, Goni and Johns (2003) updated these estimates with a longer (10 years) period of altimetry data, finding 3 to 7 rings formed at different years. Their average of 5-6 rings per year is close to the 6 NBC rings identified each year from September 1997 to September 2000 by Fratantoni and Glickson (2002), using ocean color data. Johns et al. (2003) raised these estimates to 8-9 NBC rings per year, based on 20 months of direct measurements taken on cruise surveys and moored current meters. Sharma et al., 2009 using drifting buoys, ADCP and satellite data identified during 8 years the formation of 5 to 8 rings over the period of 1 year. More recently, long period studies such as Jochumsen et al. 2010, which used 15 years of modeling data, estimated an averaged shedding of 6.8 rings per year. Mélice and Arnault (2017) provided an updated census based on almost 23 years of altimeter data and found from 2 to 7 NBC rings formed at different years, with an average of 5 rings per year. Recently, Aroucha et al. (2020) applied an eddy detection algorithm based on dynamical and geometrical constraints in the NBC region for 24 years of altimetry data found an averaged shedding rate of 5 rings per year.
Estimates on the volume transport per ring have been more consistent throughout the literature, and most authors agree with the average value of roughly 1Sv first proposed by Johns et al. (1990). If one considers the large range of values reported for the number of rings formed each year, such estimates lead to annualized transports as low as 2Sv or as high as 9Sv. These figures correspond to 15% up to 70% of the canonical 13Sv required to close the AMOC transport at low latitudes (Schmitz Jr. and McCartney, 1993). More recent estimates performed by Johns et al. (2003), based on in situ observations of a large number of NBC rings, indicate a transport of 1.1Sv per ring, corresponding solely to that portion of water with origin in the South Atlantic ocean.
The contribution of NBC rings to the meridional heat transport has been estimated considering their volume transport, and the difference between the temperature within the ring and that of the deep portions of the AMOC. Fratantoni et al. (1995) evaluated 5 rings sampled during one year by a fixed mooring line, finding a total transport of 0.18PW, with an average of 0.036PW per ring. Garzoli et al. (2003) computed the volume transport for 11 NBC rings sampled for 18 months and assumed a fixed temperature difference of 15°C, finding a mean annualized transport of 0.54PW, with an averaged 0.07PW per ring. These two estimates place the contribution of NBC rings to the meridional heat transport at low latitudes (~1PW, according to Ganachaud and Wunsch, 2000) as something between 20% and 50% of the total transport.
The large variation on the estimates provided by previous studies leads to uncertainties regarding the real contribution of NBC rings to the total meridional volume and heat transports of the AMOC. In order to improve on these estimates, the present study makes use of two extensive and continuous series of surface and subsurface data. Ring shedding and translation are identified from the 24-year long Mesoscale Eddy Trajectory Atlas – META product (Schlax and Chelton, 2016) derived from satellite altimetry data. Historical temperature and salinity profiles compiled by the Met Office Hadley Center (EN4.2.0) are used to analyze the vertical structure of the rings. By combining both products, the vertical structure of the mean NBC ring is reconstructed, its heat and salt anomalies are evaluated, and the associated annual volume and heat transports are estimated.
This paper is organized as follows. The automatic eddy detection global dataset and the historical compilation of vertical temperature and salinity profiles are described in section 2, together with the methodology used to reconstruct the mean NBC ring. In section 3, results are presented detailing the NBC ring formation during the 24 years of analysis, the vertical structure of the mean NBC ring, and the annualized volume, and heat transports. Two individual rings that were intensely sampled, one by Eulerian methods (hydrographical profiles) and one by Lagrangian methods (ARGO floats) are also analyzed, and their structure is compared to that of the mean ring. A general discussion on the contribution of the NBC rings to the total volume and heat transports of the AMOC, and the main conclusions are then presented in section 4.
2 Datasets and Methods
2.1 The Data
META2.0 DT is an altimetry-based global dataset of eddy trajectories and properties, from January 1993 to December 2016, distributed by Archiving Validation and Interpretation of Satellite Data in Oceanography (AVISO – https://www.aviso.altimetry.fr/en/data/products/). The methodology of Schlax and Chelton (2016), which is a modified version of Chelton et al. (2011), employs an automatic detection and tracking algorithm applied to daily high-pass filtered grid fields of Sea Level Anomaly (SLA), which contains only mesoscale variability. Anticyclonic (cyclonic) eddies are identified and tracked as coherent structures surrounding local SLA maximum (minimum) values. On each local maximum or minimum, the algorithm searches the points around it to extend the area detected as an eddy, following some rules, such as: the tested area must be equal or smaller in amplitude than the area already defined; the distance between the two remotest points must be less than 700km for latitudes lower than +/-25° of latitude; the maximum area must not exceed 2000 pixels; and no-holes are not allowed on the edges and within the interior of the area. If the tested area is not already included in the detection region of another eddy, an eddy is considered as detected. Any further detection on this area is stopped. Only eddy trajectories longer than (or equal to) 4 weeks are retained. For each eddy detected, the following properties are defined: (i) amplitude, which is the difference between the maximum (minimum) sea surface high (SSH) value and the averaged SSH over the edge pixels that define the outer perimeter of the eddy; (ii) radius of maximum velocity; and (iii) rotational velocity, which is the average of geostrophic speed over the radius of maximum velocity. This same methodology has been successful applied by other authors, such as Arur et al. (2014) in their study of eddies in the Indian Ocean, Jufaili and Piontkovski (2020) for eddies in the western Arabian Sea, and Brokaw et al. (2020) for eddies generated by the Loop Current in the eastern Gulf of Mexico. A newer version of mesoscale eddy trajectory atlas product META3.1 DT was made available recently and uses a different algorithm based on py-eddy-tracker to detect eddies. According to Pegliasco et al. (2022) the major differences between both dataset comes from the detection algorithm and the newest version contains smaller eddies and shorter trajectories, aspects that are not mandatory for the objective of this study, since small eddies of shorter lifetime are poorly sampled.
The temperature (T) and salinity (S) profiles from the EN4.2.0 dataset (https://www.metoffice.gov.uk/hadobs/en4/), used to compute the mean vertical structure of the NBC rings, combine data from WOD09 (World Ocean Database), GTSPP (Global Temperature and Salinity Profile Program), and Argo Global Data Assembly Centers (GDACs), and is available from 1900 to the present. This data has undergone quality control, as described by Good et al. (2013). However, bad data were still identified between 1993 and 2016 in our study area, and based on Pegliasco et al. (2015) a more restrictive criterion has been applied in which the depth difference between two consecutive data does not exceed the following threshold: 25 m for the 0–150 m layer, 50 m for the 150–300 m layer, 75 m for the 300–500 m layer and 100 m below 500 m depth. Only profiles that extend beyond 500m, and with data within three standard deviations from the local average were retained.
2.2 Identification and Tracking of the NBC Rings
The NBC rings were identified as those anticyclonic eddies in the META product that originated between 3°N and 10°N, and 44°W and 55°W (Figure 1). The ring formation area was defined considering: (a) the mean position of the NBC retroflection, between latitudes 6°N and 8°N, and longitudes 49°W and 50°W (Didden and Schott, 1993; Richardson et al., 1994); (b) its reported seasonal variability, oscillating between 45°W and 55°W (Flagg et al., 1986; Schott et al., 1998; Garzoli et al., 2004; Goes et al., 2005); and (c) previous identification in the literature of NBC rings up to 10°N (Richardson et al., 1994; Goni and Johns, 2001; Fratantoni and Glickson, 2002; Garzoli et al., 2003). Rings originating from other regions that crossed the ring formation area were not classified as NBC rings and were disregarded in the following analysis, which take into account only the anticyclonic rings that had their first and unique appearance within the established area. NBC rings were then followed along their northwestward trajectories until reaching 12°N or 60°W. These end-limits were imposed in order to eliminate from the analysis the rings after they interact with the bathymetric obstacles established by the Lesser Antilles Arc System, which significantly deform their shape, and possibly their vertical structure.
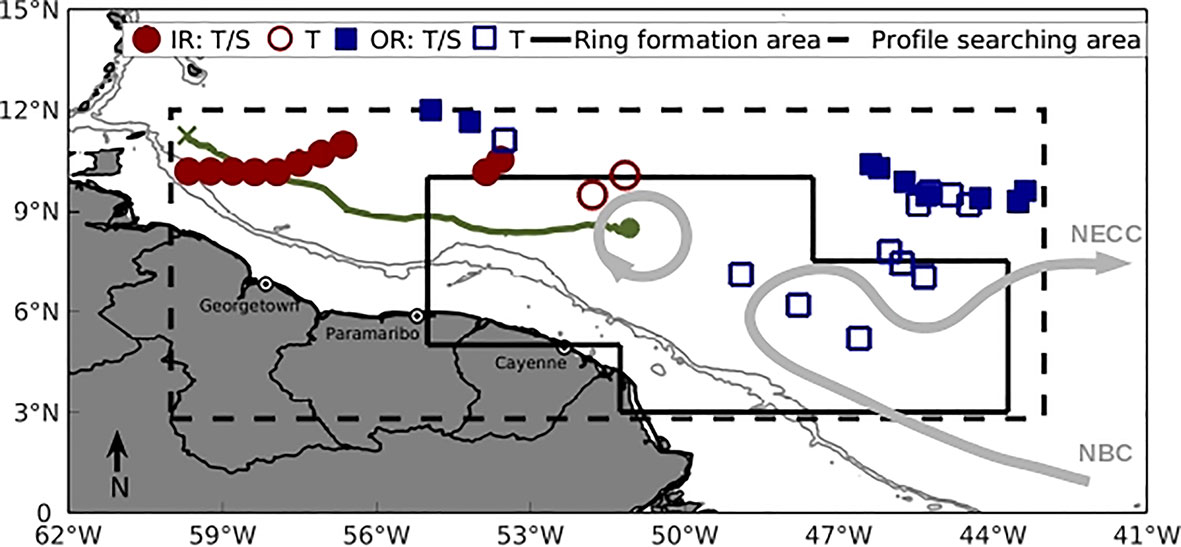
Figure 1 Searching area (dashed lines) for T and S profiles and for ring trajectories originated at the NBC retroflection (ring formation area, defined by solid lines). See text for details. The green line indicates the trajectory of one NBC ring, originated near 51°W and 8°N, illustrating the selection of T and S profiles as IR (circles) or OR (squares). Filled markers indicate that T and S profiles were available (from CTD casts or ARGO floats), while empty markers indicate that only T profiles were available (from MBTs or XBTs). The ring, the NBC and NECC are illustrated schematically by the thick gray lines, for reference. The thin gray lines are the 200 and 1000 m isobaths.
2.3 Reconstructing the Mean Ring
After identification and tracking, META and EN4.2.0 datasets were combined by selecting and classifying, within the study area, those T and S profiles that were taken either inside or outside a ring. Inside ring profiles were used to reconstruct the mean vertical structure of the NBC ring. The mean ring volume transport and its T and S anomalies compared to the outside environment (evaluated from the outside ring profiles) were then calculated. Considering the total number of rings formed each year (as provided by META) it was then possible to estimate the total contribution of NBC rings to the meridional volume and heat transports.
The area inside a NBC ring was assumed as that within 2R from the ring center, in which R is the radius of maximum speed provided by the META product. Once defined the limits of the ring influence, the T and S profiles were classified into two categories depending on their distances from the center of the ring, considering all profiles within the searching area (dashed rectangle in Figure 1) and the ring location for a given date during its trajectory. The profiles captured by the rings, or those located within a maximum distance of 2R from the center, were classified as Inside-Ring (IR) profiles. IR profiles were used to reconstruct the mean NBC ring. The profiles located at distances larger than 2.5R from the center, and limited by the searching area were classified as Outside-Ring (OR) profiles. OR profiles were used to estimate the mean state of the area of occurrence of NBC rings, and to evaluate the rings T and S anomalies. Profiles located between 2R and 2.5R were not considered in the analysis, to avoid uncertainties regarding the real extent of the influence of each ring.
This methodology is illustrated in Figure 1 for one single NBC ring, the trajectory of which is shown as the green line originating near 51°W and 8°N. From a total of 32 profiles that were taken from the time this ring was first identified within the ring formation area (solid lines in the figure) until it left the searching area (dashed lines), 10 T/S profiles and 2 T-only profiles (filled and empty circles, respectively) where located within 2R from the center of the ring and were classified as IR, while 9 T/S profiles and 10 T-only profiles (filled and empty squares, respectively) where beyond 2.5R and were classified as OR. Care was taken in order not to duplicate OR profiles when two or more rings were observed simultaneously within the searching area. This was possible since each profile in the EN4.2.0 dataset has a unique code, allowing for duplicated profiles to be excluded at the end of the profile selection. From the total number of profiles originally identified within the searching area in the EN4.2.0 dataset, 70% of the T profiles (or 5772) and 60% of the S profiles (or 2746) remained after the quality control procedure. A total of 1323 T and 604 S profiles were classified as IR, and 4449 T and 2142 S profiles as OR (Table 1 and Figure 2). Circa 50% of the temperature data were profiled by XBTs/MBTs, which explains why the number of T profiles is larger than the number of S profiles (originated from CTD casts and ARGO floats). The OR ARGO and XBT profiles are homogeneously distributed within the profile searching area, while IR profiles are concentrated along the path of the NBC rings, as expected (see Figure 2). The OR CTD casts are somewhat more concentrated at the NBC retroflection region, with only four sections (64 T and 65 S profiles) sampling NBC rings. More than half of OR and IR and ARGO and CTD profiles reach 2000m depth, while XBTs are somewhat well distributed among 1000, 12000 and 2000m. Considering all the NBC rings identified and followed along their trajectories, about 88% were sampled by T and/or S profiles at least once.
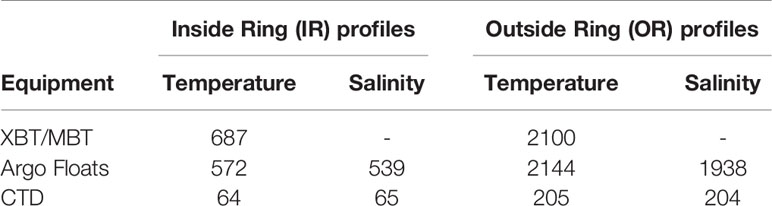
Table 1 Number of temperature and salinity profiles from the EN4.2.0 dataset remaining after quality control.
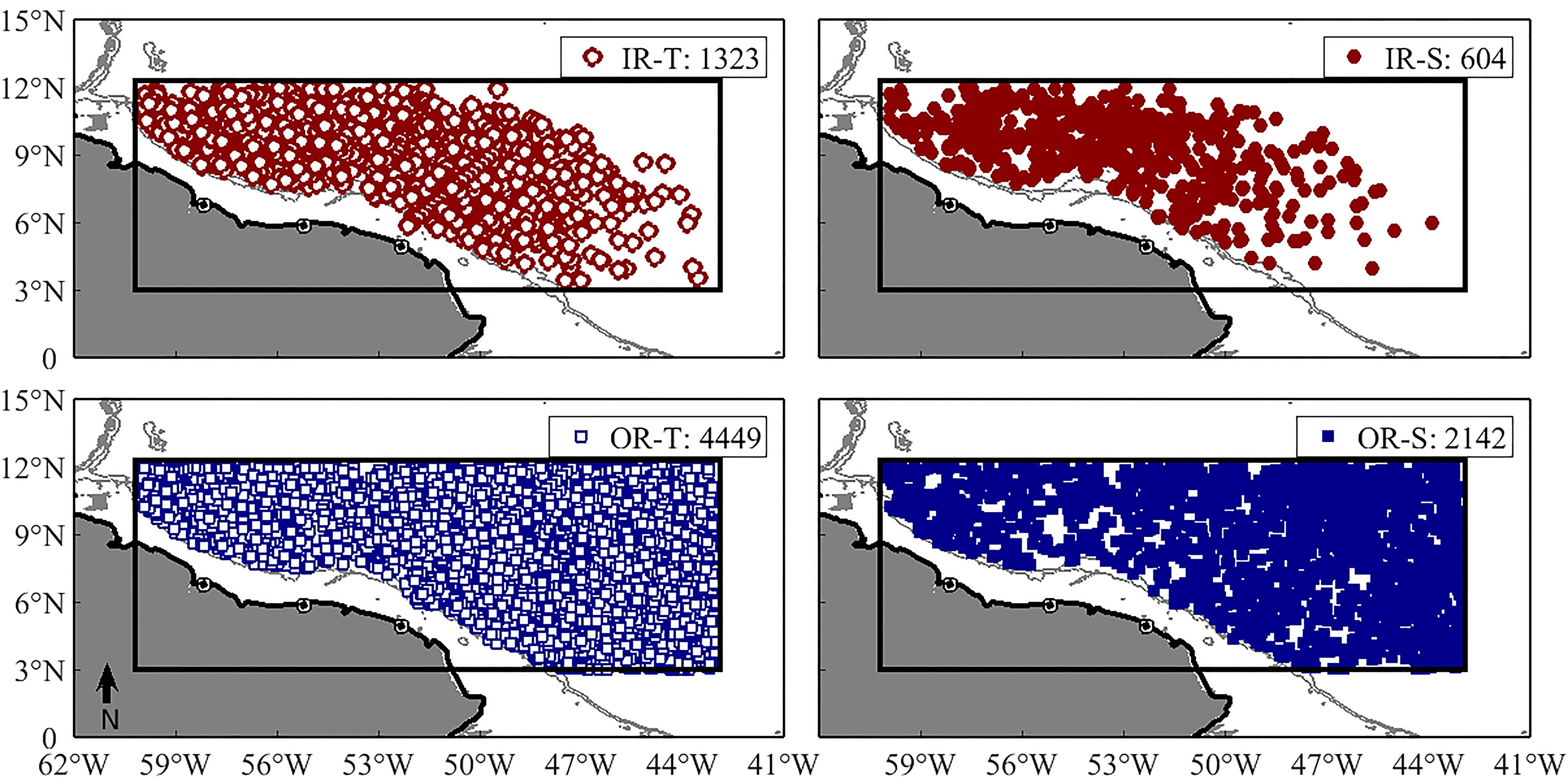
Figure 2 Spatial distribution of the Inside Ring (IR) profiles (upper panels) and Outside Ring (OR) profiles (lower panels) within the searching area from 1993 to 2016, from the EN4.2.0 dataset. Empty markers (left panels) indicate T profiles, while filled markers (right panels) indicate S profiles. The rectangle defined by solid lines delineates the searching area (see text and Figure 1 for details). The gray lines are the 200 and 1000 m isobaths.
In order to obtain the three-dimensional structure of the mean NBC ring, the T and S IR profiles were interpolated following Yang et al. (2013). First, the location of all profiles was transformed into a normalized ring-coordinate space (Figure 3), according to:
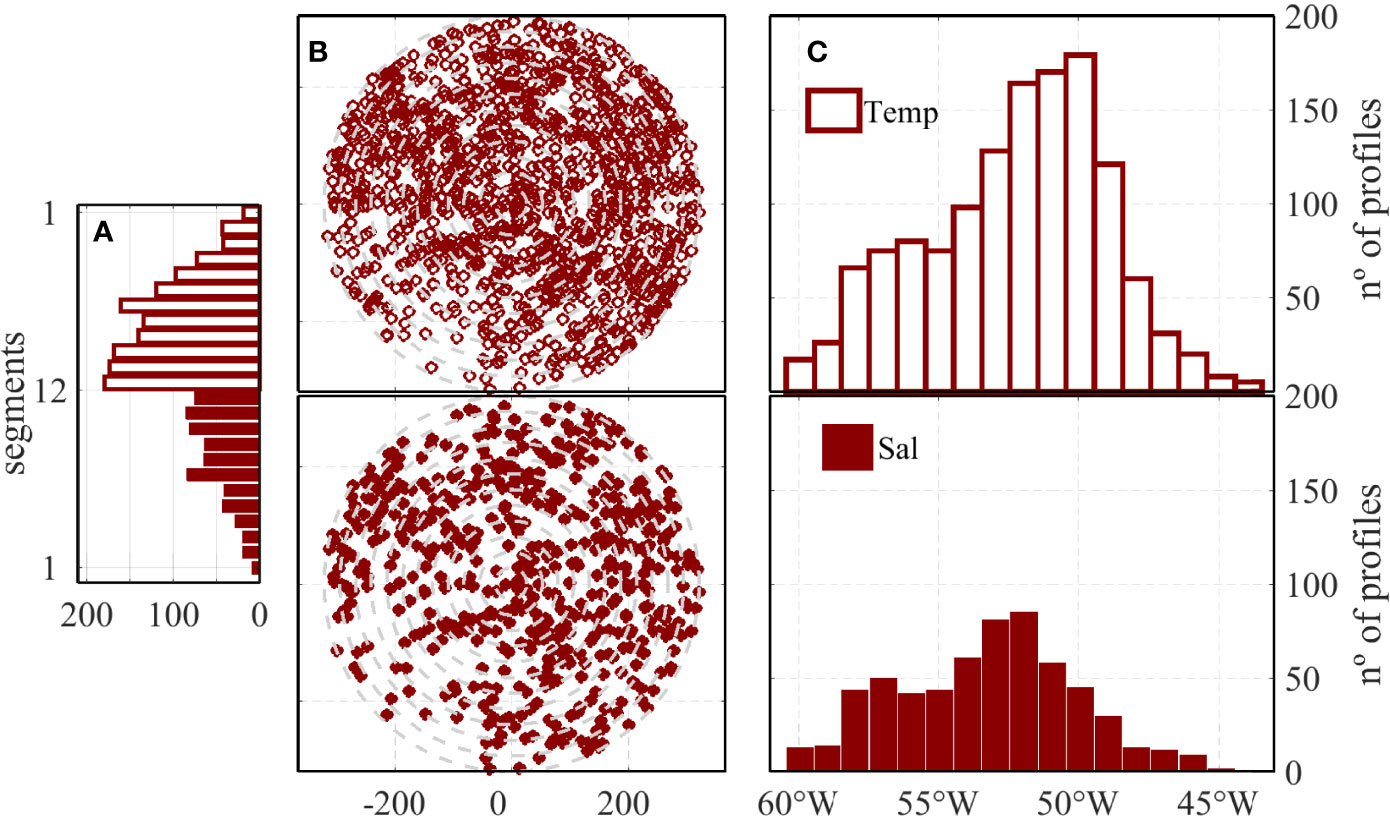
Figure 3 Distribution of the selected IR profiles: (A) number of T (upper) and S (lower) profiles in 12 equally spaced intervals along the radius of the mean ring, after normalization according to equation 1; (B) spatial distribution of all selected T (upper) and S (lower) profiles, after normalization; and (C) number of T (upper) and S (lower) profiles for different longitudinal bands.
in which DMR is the profile equivalent distance from the ring center for the reconstructed mean ring, DR is the instantaneous distance from each profile to the observed ring center (considering the geographical locations given by EN4.2.0 and META datasets), RR is the instantaneous radius of maximum speed for each ring, taken from META at the same time as the profile observations, and RMR is the average radius for all rings (also from META). Assuming circular rings (as implicit in Eq. 1) may not be perfectly true (see, for instance, Fratantoni and Glickson, 2002), in particular in latter stages of their life cycle in which interaction with topography may have deformed somewhat their shape. It is, however, a limitation of the META dataset in which the ring radius is taken as that of a circle which better represents, on an average sense, the region of maximum swirl velocities.
The resulting distribution of T and S profiles is relatively uniform over the composite ring area (Figure 3B), providing adequate data for deriving the mean NBC ring structure. Less data is observed at the southwest quadrant, possibly reflecting the interaction of the rings with topography along the continental margin. The longitudinal distributions of T and S profiles (Figure 3C), however, show that more than half (about 77% for T and 71% for S profiles) are distributed eastward of 54°W, indicating that most profiles sampled newly formed rings, which have been little influenced or modified by the interaction with topography. The mean NBC ring T and S cross-sections were calculated assuming symmetry in all directions, projecting all profiles into one side of the ring’s radial axis, and mirroring them to the opposite side. This approach is also not perfectly true, but ensures more confidence in the analysis, and leads to a more robust estimate of the mean ring.
Following Souza et al. (2011), a 7th degree Lagrange polynomial was used to fit the T and S data at each depth. This polynomial captures the approximate Gaussian shape of the anomaly distribution corresponding to anticyclonic rings. Both normalization and fitting are essential to obtain the vertical structure of the mean ring. The corresponding NBC mean ring T and S anomaly sections were then calculated, by removing the mean state of the searching area calculated with all the OR profiles. A similar procedure (see details in Analysis Along Isopycnals) was then carried out along isopycnals (instead of depth levels) taking into consideration only IR profiles for which T/S pairs were available (so that density could be calculated for each profile). This approach was applied to allow for an estimation of the percentage contribution of South Atlantic waters to the total transport of the mean ring.
3 Results
3.1 Ring Census
A total of 128 NBC rings were identified in the META dataset, originating at the NBC retroflection between January 1993 and December 2016, leading to a mean formation of 5.3 ± 1.5 rings per year. Significant inter-annual variability was observed during these 24 years, with minimum formation of 2 (in 2006 and 2009) and maximum formation of 8 (in 1999) rings per year (Figure 4A). Apart from 2006 and 2009, at least four rings were formed each year for the entire period, while 7 or more rings were formed only in 7 different years. Maximum ring formation can be distinctly observed in the boreal summer, with 35 rings (27% of the total) formed in June or July, but large values also occur in the Winter and early Spring months (Figure 4B). The lowest formation occurs both in May and from September to November, with no more than 7 rings formed in each month for the entire period of observations. While a semiannual cycle is apparent, with maximum formation both in summer and winter, and minimum in spring and autumn, no clear seasonal cycle could be established for the NBC ring formation based on the META dataset, in accordance with previous studies (Fratantoni et al., 1995; Pauluhn and Chao, 1999; Goni and Johns, 2001; Fratantoni and Glickson, 2002; Goni and Johns, 2003; Johns et al., 2003).
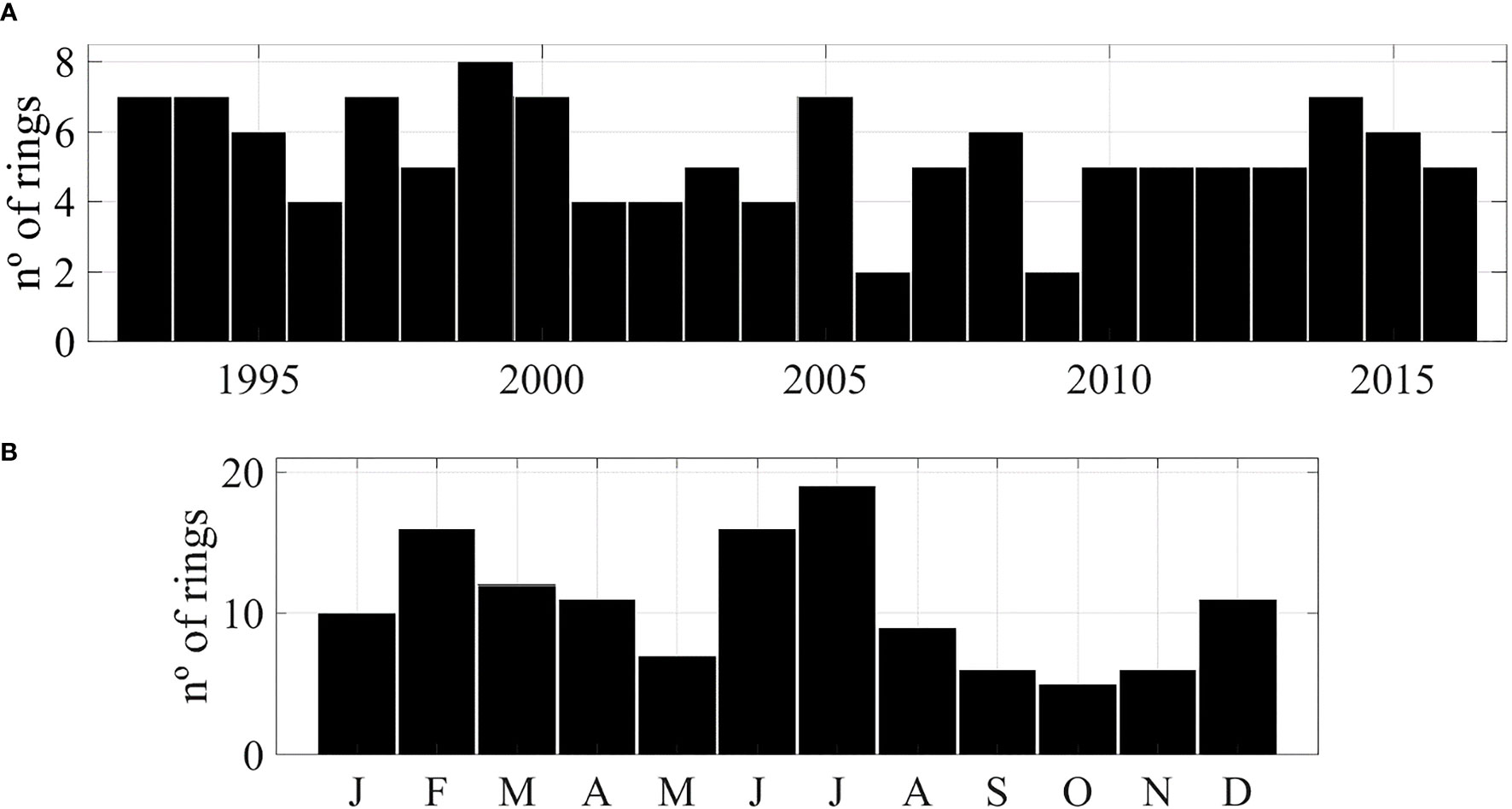
Figure 4 Total number of NBC rings identified in the META dataset: (A) for each year, from 1993 to 2016; and (B) for each month, for the entire 24-year period. The annual and monthly values were calculated based on the date when each ring was identified for the first time within the ring formation area.
After formation, most rings follow a relatively well-defined path towards the Caribbean (Figure 5). In their journey along the South American continental margin, the NBC rings travel on average 840 ± 320 km, with a lifetime of 80 ± 50 days. The large standard deviations reflect the fact that the SSH signal is lost for several rings before reaching the Lesser Antilles. It is not clear, however, if that indicates the demise of such rings or just that the signal has fallen below a detection threshold. About half of the total (68 rings) reach the Antilles, with 2 rings passing through the Caribbean.
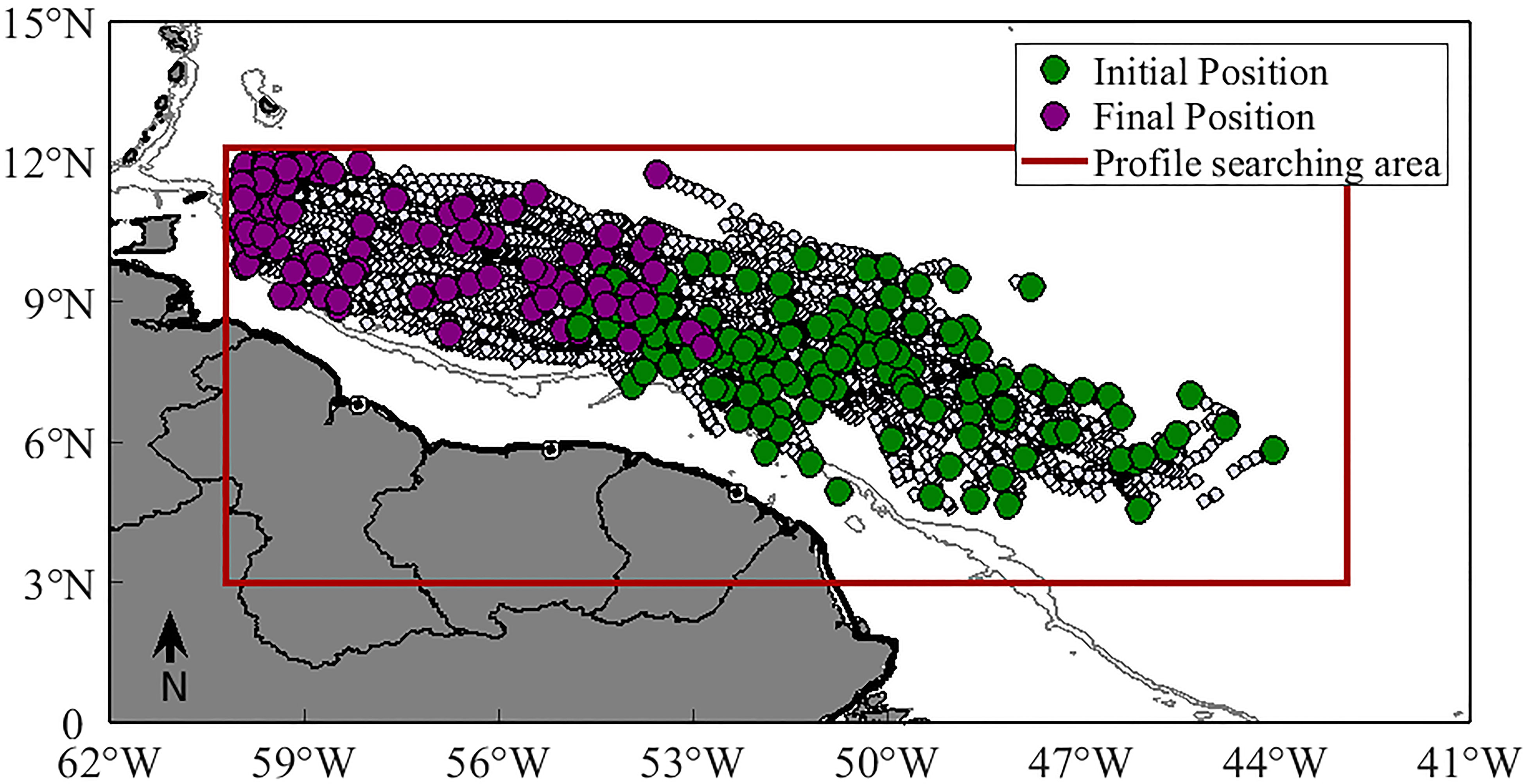
Figure 5 The trajectory of the 128 NBC rings identified in the META dataset (white dots), between 1993 and 2016. Green dots indicate their initial position, and purple dots their final position within the searching area (defined by the red retangle). The gray lines are the 200 and 1000 m isobaths.
Table 2 presents the mean properties of the 128 NBC rings, taken from the META dataset, which are within the range of previously estimated values, such as Johns et al., 1990; Didden and Schott, 1993; Richardson et al., 1994; Fratantoni et al., 1995; Pauluhn and Chao, 1999; Goni and Johns, 2001; Fratantoni and Glickson, 2002; Wilson et al., 2002; Garzoli et al., 2003; Goni and Johns, 2003; Johns et al., 2003 (Table 3). Also shown in Table 2 are the same properties computed only for those 112 rings that were sampled at least once by T and/or S profiles, and that were used to reconstruct the mean NBC ring. Most significant differences are observed for the ring radius (138 ± 43 km for the former, and 160 ± 41 km for the latter), albeit not beyond the reach of the standard deviations, pointing to the fact that the present estimate of the rings mean vertical structure may favor somewhat larger rings. It is interesting to note that the ratio between the azimuthal velocity and the translation speed is larger than one for the mean ring (and also for most individual rings considering their standard deviation), indicating that NBC rings are fairly non-linear and trap water in their interior (Chelton et al., 2011).

Table 2 Mean NBC ring properties derived from the META dataset: radius of maximum surface geostrophic velocities (km), amplitude (10-2m), maximum surface velocity and translation speed (ms-1), estimated for all 128 rings identified in the META dataset, and for the 112 rings that were sampled at least once by T and/or S profiles.
3.2 The Mean NBC Ring
3.2.1 Analysis Along Constant Levels
The mean NBC ring, computed for constant levels with the IR profiles according to the methodology presented in section 2, is better visualized as vertical sections of T and S anomalies with respect to the mean OR profile (Figures 6A, B). These sections depict a moderately shallow ring, with positive anomalies penetrating down to approximately 500m. Geostrophic velocities referred to 500db (Figure 6C) also depict a shallow, surface intensified mean NBC ring. Swirl velocities above 0.1 m/s are observed in the upper 150 to 200 m, while the maximum geostrophic velocity reaches 0.36 m/s, at a distance of ~160km from the center of the mean ring. The 500m depth level corresponds to the approximate depth of the 27.1 kgm-3 isopycnal within the mean ring (also shown in Figure 6), which marks the transition between Antarctic Intermediate Waters - AAIW and South Atlantic Central Waters – SACW in the tropics (Stramma and England, 1999). This correspondence indicates that the mean ring transports primarily thermocline waters, or more specifically surface tropical and subsurface central water masses.
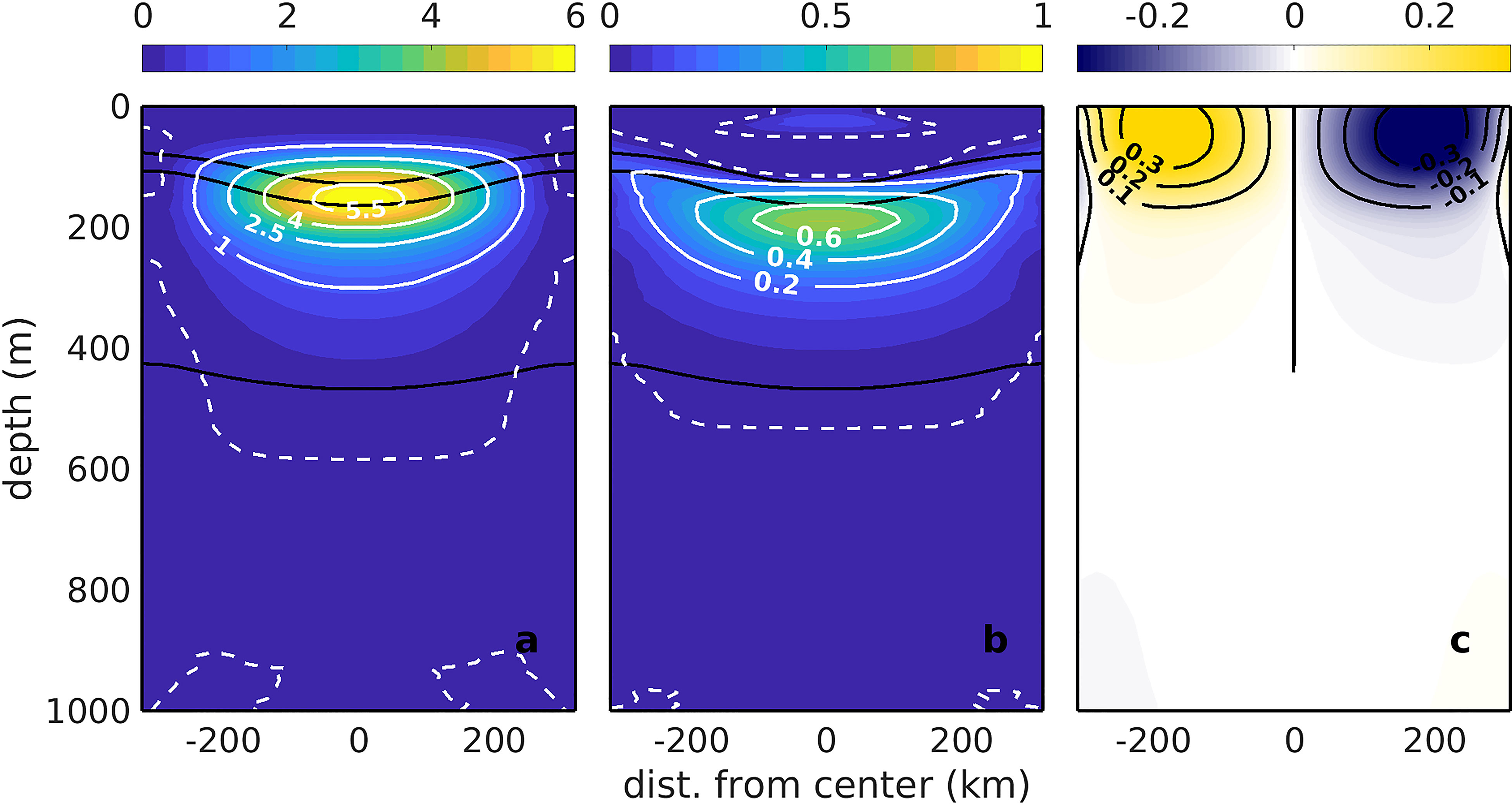
Figure 6 Vertical sections across the mean NBC ring. In (A, B) the T and S anomalies, respectively, calculated by subtracting the T and S of all IR profiles from the mean T and S of all OR profiles. The white dashed lines represent the zero anomaly isolines, and the black lines are (from top to bottom) the 24.5, 25.5 and 27.1 kgm-³ isopycnals. In (C) the anticyclonic geostrophic velocities (in ms-1) of the mean NBC ring, referred to 500db and computed for the Coriolis parameter corresponding to a mean latitude of 8.7°N.
The anticyclonic mean ring is, as expected, warmer and saltier than the environment (Figures 6A, B). Maximum T and S anomalies at the ring core reach 5.9°C at ~150m depth, and 0.7 at 180m depth, respectively. On the one hand, these are intense anomalies, when contrasted to those reported for anticyclonic mean rings in different regions of the world, and computed with similar methodology, as for example T (S) anomalies of ~2.0°C (0.1) for the Kuroshio region (Yang et al., 2013); ~2°C (0.2 - 0.3) for the southeastern Indian ocean (Yang et al., 2015); ~0.5 to 1.0°C (0.1) for eastern boundary current regions (Pegliasco et al., 2015); and ~2.5°C for Agulhas rings (Souza et al., 2011). On the other hand, the mean NBC ring T and S anomalies compare well with those computed with in situ data for three individual NBC rings by Fratantoni and Glickson (2002), which varied from approximately 3 to 6°C, and 0.5 to 1.0, respectively, in the depth range from 100 to 200m. Also in agreement with observations, the surface signature of the NBC mean ring is significantly reduced within the shallow surface mixed layer, due to intense mixing associated with heat and mass exchanges with the atmosphere.
Calculating the outside ring average T and S profiles is an important step to compute the mean NBC ring anomalies. In order to evaluate these profiles estimated based on the OR data from EN4.2.0, the T and S anomalies were compared to those calculated with respect to the WOA13 climatology (World Ocean Atlas 2013, available at www.nodc.noaa.gov/OC5/woa13/). This comparison is illustrated in Figure 7, which shows the total T and S anomalies obtained by subtracting the mean IR profile from both the mean OR profile and the WOA13 mean profile for the searching area (defined in Figure 1). T and S maximum anomalies (~1.7°C at ~160m, and ~0.3 at ~170m, respectively) are lower than those presented in Figure 6 as expected, since these estimates take into account the total mean profile for the entire ring, but are very similar for both the EN4.2.0 and the WOA13 cases. Within the mean ring core, S anomalies show no significant difference, while T anomalies computed with respect to the OR profiles are somewhat warmer (by ~0.3°C) than those computed with the WOA13 climatology. This possibly reflects the fact that the climatological profile was computed with all information within the searching area, without distinguishing the inside and outside ring data. Larger differences are observed near the surface, associated with the large T and S spatial variability in the tropical region.
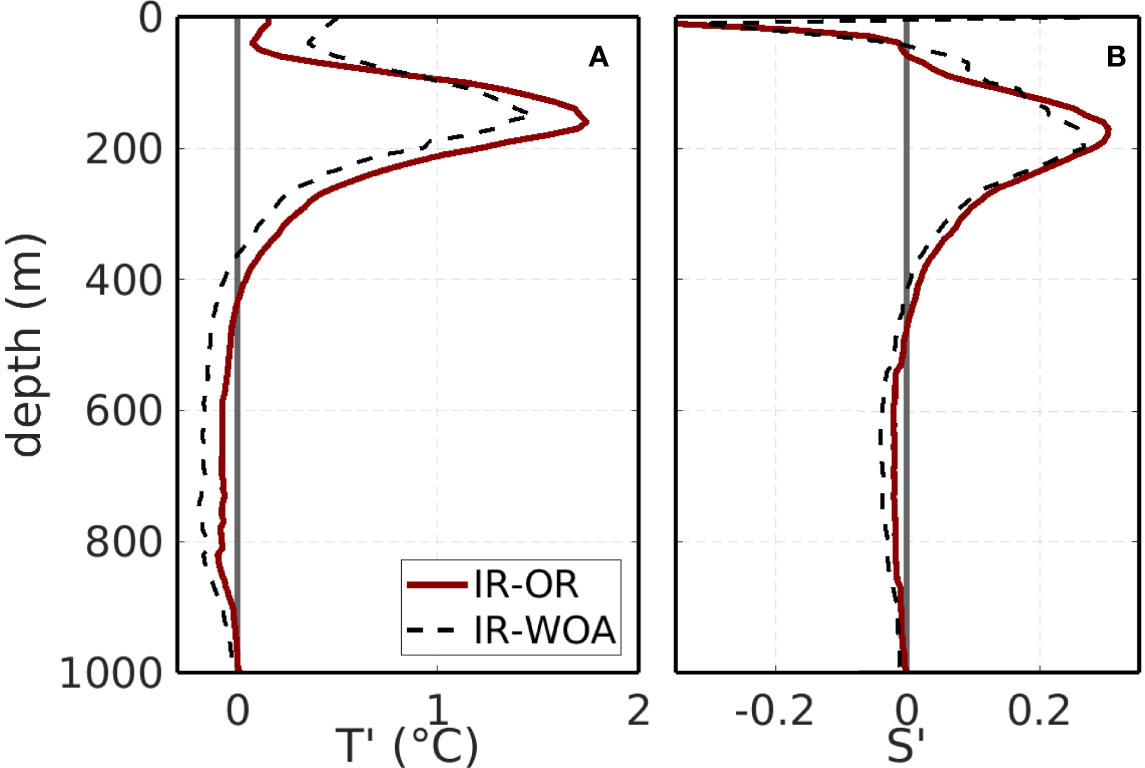
Figure 7 Total mean T (A) and S (B) NBC ring anomalies with respect to the OR mean profile from EN4.2.0 (solid red line) and to the WOA13 climatology (dashed black lines).
The mean NBC ring was assumed to have a Gaussian shape and to carry the volume of a cylinder, V = πR2h, where R is the radius of maximum velocity and h is the vertical extension. Thus, the volume of the mean NBC ring was estimated in 4x1013m3, based on a radius of the maximum velocity of 160km and a vertical extension of 500m, leading to an annualized volume transport of ~1.3Sv per ring by dividing its volume by the number of seconds in one year (following Johns et al., 1990 and Didden and Schott, 1993; Fratantoni and Glickson, 2002; Johns et al., 2003). This value is on the same order, but somewhat larger than the canonical 1Sv, generally assumed in the literature since Johns et al. (1990), but is within the range of previous estimates for individual rings, based on satellite or in situ data (see, for instance, Didden and Schott, 1993; Johns et al., 2003). The contribution of the mean NBC ring to the heat transport in the tropics can be estimated using ρVcpΔT, in which ρ is a reference density, V is volume transport, cp is the specific heat and ΔT is the difference between the mean temperature of the ring and that of a reference level, divided by the number of seconds in one year. A similar computation can be done for the freshwater transport, estimated as ρV(1-ΔS/1000), in which ΔS is the difference between the mean salinity of the ring and that at the same reference level. Using the composite structures of T and S, the average temperature of the mean ring was estimated at 16°C and the average salinity was 35.5. Assuming that the water carried by the NBC rings is compensated by the opposite flow of NADW (Garzoli et al., 2003), with mean T~3°C (Broecker, 1991) and mean S~34.9 (Reid and Lynn, 1971), the heat and freshwater transports of the mean NBC ring were estimated in 0.07PW and 0.45x106kgs−1. On the one hand, such an estimate for the heat transport of the mean NBC ring is higher than the averaged transport per ring of 0.036PW, which can be inferred from the results presented by Fratantoni et al. (1995) for five individual rings sampled from 1987 to 1988, of variable size and temperature (which varied from 0.010 ± 0.008 to 0.066 ± 0.019 PW). On the other hand, it is numerically the same average transport computed by Garzoli et al. (2003), from the analysis of eleven individual rings (ranging from 0.06 to 0.10PW) sampled from 1998 to 2000.
3.2.2 Analysis Along Isopycnals
In order to estimate the contribution of waters originating in the South Atlantic to the total volume transport of the mean ring, the previous analysis was also conducted along constant potential densities. In this case, however, only profiles containing both T and S values were considered, corresponding to 1653 OR profiles, 463 profiles within 2R, and 95 profiles within 1R from the ring center. The ratio of South Atlantic Waters - SAW within the mean ring was computed following Johns et al. (2003), considering the salinity values (S) of the mean ring relative to the expected salinity for South (SS) and North (SN) Atlantic waters, at each density, given by:
In equation 2, SS and SN are evaluated as the average of the 10% minimum and maximum salinity values, respectively, for all the available profiles within the study area. As in Johns et al. (2003), such estimates do not differ much from climatological values for SS, and are slightly saltier for SN. The curves for S, SS and SN are shown in the S-σθ diagram in Figure 8A.
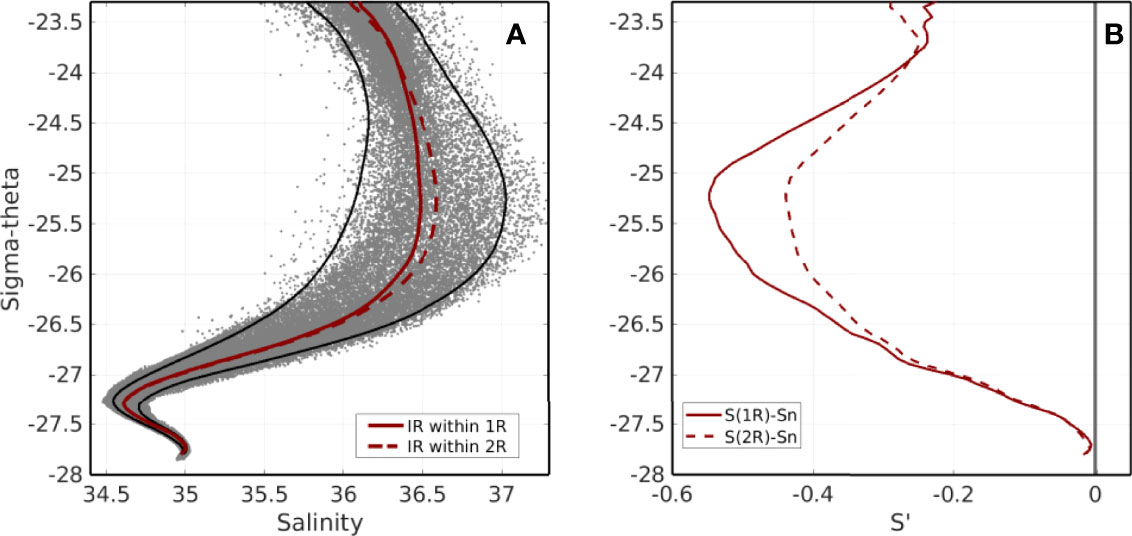
Figure 8 (A) S-σθ diagram for all IR + OR profiles within the searching area (gray dots), from the subset containing observations with both T and S values. The black lines are the SS (left) and SN (right) curves, respectively. The red lines are the average salinity (S) for the mean ring, computed with all IR profiles located within 1R (solid) and 2R (dashed) from the ring center. One standard deviation (not shown) is about 0.5 for σθ = 25.5 kgm-3, decreasing for lower and higher densities. (B) Salinity anomaly, in density space, of the mean ring with respect to the expected salinity of North Atlantic waters (SN), for the IR profiles located within 1R (solid) and 2R (dashed) from the ring center.
The mean NBC ring is fresher (negative anomalies, for S-SN) then North Atlantic waters in density space, from the surface to the lower limits of SACW (σθ ~ 27.1kgm-3), indicating northward transport of waters with a distinct South Atlantic signature (e.g., Emery and Dewar, 1982). This picture is in contrast with the positive anomalies computed in depth levels (see Figure 7) due to the heaving effect of isopycnals, characteristic of anticyclonic eddies. Maximum anomalies (absolute values of ~0.55) are observed for densities around 25 to 26 kgm-3 (Figure 8B), corresponding to thermocline levels located roughly from 150 to 200m deep, decreasing towards lower (upper) and higher (deeper) densities (levels). Negative anomalies (absolute values of ~0.02) are also observed within the AAIW domain (σθ ~ 27.25kgm-3), decreasing to zero for densities within the North Atlantic Deep Water – NADW. Anomalies computed with all profiles within 2R from the ring center are somewhat lower, but close to those computed only with profiles within 1R from the ring center.
The percentage of SAW in the water column (derived from eq. 2) is shown in density space in Figure 9, from the surface down to intermediate levels. Percentages vary from 40 to 60% for the entire density range (average of ~50%) with two local maxima at upper SACW or thermocline levels (σθ ~ 24 to 25 kgm-3) and at lower SACW and AAIW levels (σθ ~ 27.0 to 27.25 kgm-3). Percentages are somewhat lower (average of ~45%) when the anomalies are computed for a mean profile considering the IR profiles within 2R of the ring center, as expected. Considering, as before, a mean ring with geometrical volume of 4x1013m3, computed for a radius of 160 km (corresponding to the maximum geostrophic velocities) and total depth of 500m, and integrating the SAW ratio from the surface to σθ = 27.1 kgm-3, the annualized transport by the mean NBC rings is reduced by approximately 50%, from 1.3Sv to 0.66Sv. This new estimate would represent, in fact, the annualized transport of SAW by the mean NBC ring (see Discussion and Conclusions for a discussion on these estimates). Johns et al. (2003) suggest that the anomalies and percentages calculated for σθ below 24.5 kgm-3 are not reliable, since there is no clear definition of the water mass sources near the surface, and assume a constant percentage value from this isopycnal to the surface. This approach is sensible, but does not change the previous calculations by more than 3%.
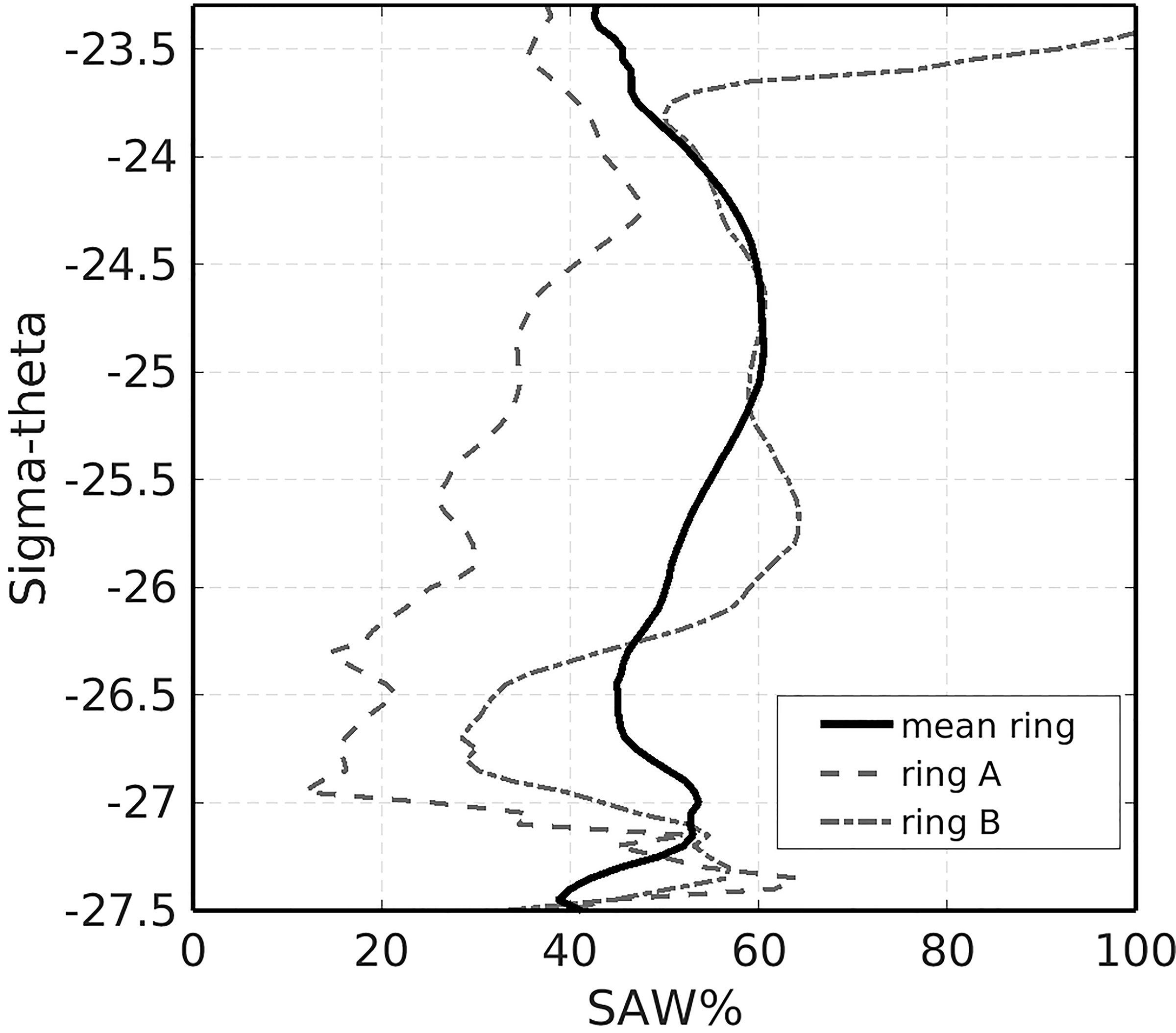
Figure 9 Percentage of South Atlantic Water (SAW) estimated according to Eq. 2 for the mean NBC ring (solid line), ring A (dashed line) and for ring B (dotted-dashed line), considering only profiles located within 1R from the ring center.
3.3 Sampling Two Individual NBC Rings
Two NBC rings, among the 128 identified in this study (or 112 with T and/or S profiles), were more intensely sampled during their lifetime, allowing for a detailed view of their vertical structure. One ring (hereafter ring A) was sampled by a CTD section midway between the retroflection and the Antilles, providing a synoptic view across the center of the ring (Figure 10). A second ring (hereafter ring B), was sampled by an ARGO float during 64 days, for circa 800 km, providing a Lagrangian view for a significant part of its lifetime (Figure 11). Sections of T and S anomalies, with respect to the OR profiles, and geostrophic velocities (for ring A) were built, and the percentages of SAW transported by each ring were calculated, helping to evaluate how representative the mean NBC ring is.
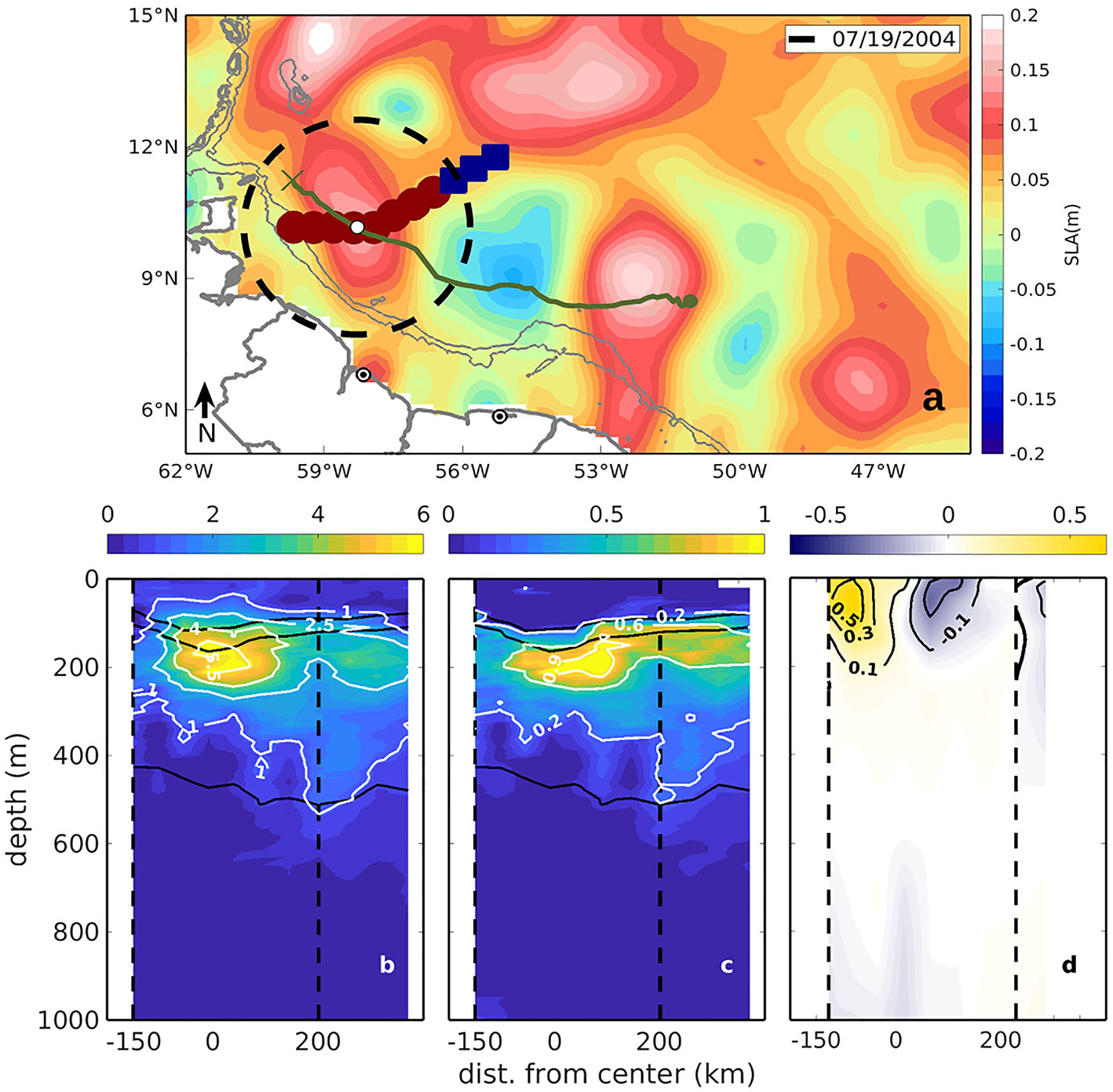
Figure 10 Ring A seen as a positive sea level anomaly near 59°W in (A). The green line is the ring trajectory from the META dataset; the dashed circle corresponds to twice the ring radius (2R), and the brown and blue markers are the positions of the IR and OR profiles, respectively. The T and S anomalies with respect to the ring exterior (the OR profiles) are presented in panels (B, C) together with the 24.5, 25.5 and 27.1 kgm-³ isopycnals (black lines, from top to bottom); and the geostrophic velocities referred to 550db in panel (D). The vertical dashed lines indicate the limits for the IR profiles. No smoothing was applied to the CTD data.
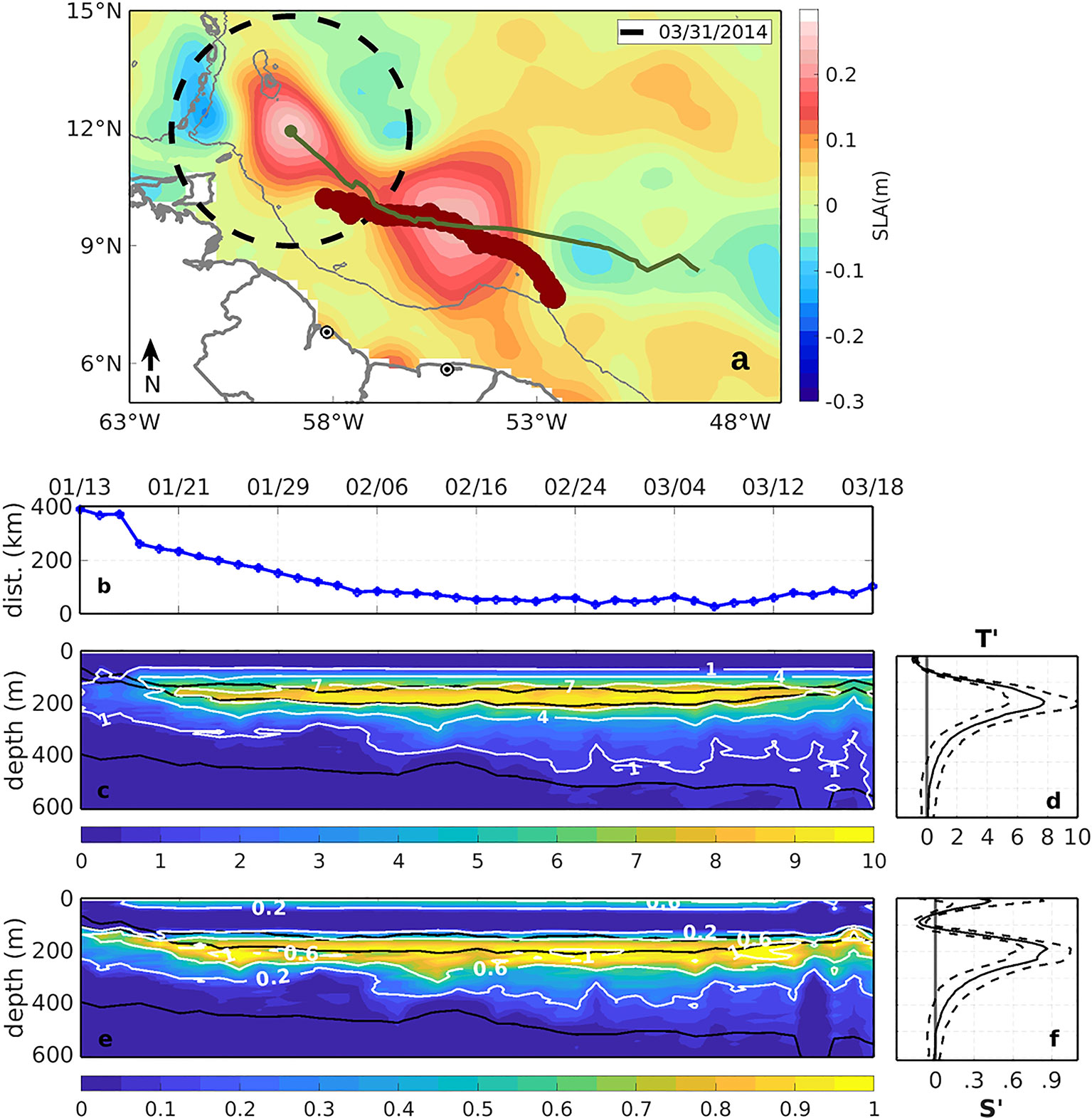
Figure 11 Ring B seen as a positive sea level anomaly at the end of its recorded trajectory in the META dataset in (A). The green line is the ring trajectory, the dashed circle corresponds to twice the ring radius (2R), and the brown markers are the locations of the IR profiles from ARGO. The distances from the ring center to the ARGO profiles is shown in panel (B). The T and S anomalies with respect to the ring exterior (OR profiles) are presented in panels (C, E) together with the 24.5, 25.5 and 27.1 kgm-³ isopycnals (black lines, from top to bottom); and their time average (plus and minus one standard deviation) in panels (D, F). No smoothing was applied to the ARGO data.
Ring A was first observed in the META dataset on May 30th, 2004, near 8.5°N and 51°W, traveling for approximately two months before its signal was lost near 10°N and 60°W. The CTD section sampled the ring around July 19th, leading to 8 IR profiles and 3 OR profiles, spaced on average by 53 km (Figure 10A). The samples were taken down to 2600 m, with the closest profile located approximately 8km from the ring center. The mean radius of Ring A (~134 km) was below average considering the 112 rings sampled by T and S profiles, and average sized considering the 128 tracked in the altimeter data (see Table 2). Maximum T anomalies reached ~5.5°C, centered around 150 to 200m depth, similar to the mean ring (compare Figures 6A, 10B). Maximum S anomalies reached ~0.9, about 30% larger than the mean ring, also centered around 150 to 200 m depth (same depth of the maximum T anomaly, unlike the mean ring which presented a somewhat deeper S anomaly core). Both T and S anomaly fields suggest an approximately symmetric ring, somewhat deeper at the offshore side. Geostrophic velocities indicate a surface intensified ring, with significant velocities above 0.1 m/s concentrated in the upper 200m. The inshore side of the ring is more intense than its offshore side, with northwestward (southwestward) velocities reaching 0.5 m/s (0.3 m/s), possibly reflecting the interaction with the continental margin, which tends to squeeze the inshore side of the ring. The velocity structure of Ring A is similar to those of the surface intensified rings classified by Fratantoni et al. (1995) and Wilson et al. (2002) based on in situ data.
The volume of the ring A was estimated in 3.1x10¹³m³ based on its radius of maximum velocity of 134km and a vertical extension of 550m, leading to an annualized volume transport of 0.98Sv, about 75% of the volume transport of the mean ring. The percentage of SAW transported by ring A (considering profiles located within 1R from the ring center) is shown in Figure 9. The maximum percentage (~43%) occurs at shallower levels than the mean ring, decreasing to less than 20% in the lower thermocline. The average percentage of ~30%, computed within the depth range of ring A, is significantly lower than that of the mean ring, leading to an annualized transport of SAW of ~0.3Sv. It is unclear from the data if these differences reflect different conditions during the ring formation or, otherwise, result from the erosion of the SAW composition due to mixing. It is noteworthy that ring A was sampled near the end of its life cycle, suggesting that the latter may be true. Using the composite structures of T and S, its average temperature was 15.5°C and average salinity 35.5, leading to a heat transport of 0.05PW and freshwater transport of 0.4x106kgs−1. These figures are about 30% and 20% lower than the corresponding ones for the mean ring, and are associated primarily with the smaller radius, and therefore smaller volume of Ring A.
Ring B was first identified in the altimeter dataset on January 8th, 2014, near 8°N and 49°W, and traveled for three months until it crossed the 12°N threshold and left the searching area near 60°W (Figure 11A). The ARGO float was captured by the ring just after its separation from the retroflection. The float traveled within the ring for 64 days, and over 800km, maintaining an average distance of ~60km from the rings center for at least 30 days. The mean ring radius of 157km was close to the average size for the 112 rings sampled by T and/or S profiles (see Table 2). The average T anomaly at the ring core is ~7.5°C (larger than the T anomaly of the mean ring) with maximum observed anomalies reaching 10°C (Figures 11C, E). The average S anomaly at the ring core is ~0.7 (similar to the S anomaly of the mean ring) with maximum observed anomalies reaching 0.9 (Figures 11D, F). The S anomaly core is located around the depth of 200m, somewhat deeper than the T anomaly core, similar to the mean ring.
The volume of ring B was estimated at 3.8x10¹³m³, based on its radius of maximum velocity of 157km and vertical extension of 500m, leading to an annualized volume transport of 1.2Sv, close to the volume transport of the mean ring. The percentage of SAW transported by ring B (considering profiles located within 1R from the ring center) is shown in Figure 9. The maximum percentage (~62%) is somewhat larger and occurs at lower levels and higher densities (σθ ~ 25.7kgm-3) when compared to the mean ring. The percentage of SAW is lower than that of the mean ring for higher densities, and similar to that of the mean ring for lower densities (until σθ ~23.8kgm-3). Near the surface, for σθ < 23.8kgm-3, anomalies with respect to SN increase significantly, with the percentage of SAW reaching 100% at the surface. Following Johns et al. (2003), as discussed above, these near surface anomalies are disregarded and an average of 54% is estimated within the depth range of ring B, similar to the mean ring, leading to an annualized transport of ~0.66Sv of SAW. The heat transport of Ring B is 0.07PW, similar to the mean NBC ring, and its fresh water transport 0.26x106kgs-1 (about 42% lower).
Rings A and B are surface intensified rings, with anomalous T and S vertical structures similar to that of the mean ring, both in terms of vertical extension and core location. Ring A, however, is significantly saltier and has a somewhat deeper T core, while Ring B presents both saltier and warmer cores. The relatively oversampling of these two rings may raise some concerns that the estimation of the mean ring might be somewhat biased towards these two well sampled events. In order to address this issue, the mean ring was recomputed, eliminating all the IR profiles that sampled rings A and B. The resulting mean NBC ring is virtually indistinguishable from the previous estimate shown in Figure 6, giving confidence in the representativeness of the mean NBC ring.
4 Discussion and Conclusions
The vertical structure of the mean NBC ring was reconstructed from a combined analysis of two global datasets, spanning 24 years (1993 to 2016) of freely distributed altimetry products and hydrographic data. The mean NBC ring depicts a large, moderately intense and relatively shallow feature, with radius of ~160km, surface velocities reaching ~0.36ms-1, and significant temperature and salt anomalies present in the upper 500m of the water column. Maximum T and S anomalies (5.9°C and 0.7, respectively) are found at subsurface levels, near 150 to 200m deep. A mean NBC ring formation of 5.3 ± 1.5 rings per year was estimated from the altimetry data. This value agrees with previous estimates based on satellite data, but is derived from a much longer dataset comprising 24 years of altimetry data, as opposed to the 6 and 10 years analyzed by Goni and Johns (2001 and 2003, respectively). More recent studies (Mélice and Arnault, 2017, and Aroucha et al., 2020), also based on longer time series of satellite data, find average formation rates similar to that of the present study.
A high variability in the number of NBC rings formed each year was found in the present study, with a minimum of 2 and a maximum of 8 rings. This is an interesting and important aspect, which should be taken with care since it will lead to a large inter-annual variability in the contribution of NBC rings to volume and heat transport in the tropics. Such a variability was also found by previous authors, such as the early studies of (Goni and Johns 2001; 2003) who found from 2 to 7 rings per year, and in more recent estimates based on longer time series of data, such as Mélice and Arnault (2017), who found 2 to 7 rings per year, and Aroucha et al. (2020), who found 3 to 8 NBC rings per year.
No clear correlation could be established between the annual formation of NBC rings and the Northern Tropical Atlantic Index, as previously speculated by Goni and Johns (2003). Very weak correlation was also found when comparing the number of NBC rings shed per year and the maximum SSH anomaly identified with the Oceanic Niño Index (ONI), similar to what was obtained by Aroucha et al. (2020). These authors actually attempted to correlate several Atlantic climate indexes with NBC parameter anomalies, but could not find significant correlations. Their higher value was only 0.34, obtained for SSH anomalies and the Atlantic Multidecadal Oscillation - AMO (a value of 0.26 was found in the present study in this case). Other studies (e.g., Fonseca et al., 2004; Hormann et al., 2012) have associated the ring formation with the position of the retroflection, the northward displacement of the NECC, and the wind stress curl over the tropical Atlantic. Sharma et al. (2009), on the other hand, indicated that ITCZ migration and forcing by trade winds are not the main factors influencing the shed of NBC rings during the year. To further investigate the causes of the observed inter-annual variability is beyond the scope of the present study, in which such variability is relevant insofar as it affects the estimates of NBC volume and heat transport.
An annualized transport of ~1.3Sv was computed for the mean NBC ring in the present study. Combined with the mean formation of 5.3 ± 1.5 rings per year, the total contribution of NBC rings to the meridional volume transport reaches approximately 7 ± 2Sv. Considering the canonical 13Sv of newly formed North Atlantic Deep Water that flows southward in the deep ocean (Schmitz Jr. and McCartney, 1993), these estimates amount to rough estimates of 40 to 70%, with an average of circa 50% of the upper ocean transport required to close the Atlantic Meridional Overturning Cell (AMOC) at low latitudes. The heat transport by the mean NBC ring was estimated at 0.07PW. Compared to a total heat transport of 1PW, according to Ganachaud and Wunsch (2000), and taking into consideration the average number of rings formed per year, the NBC rings may account for approximately 25 to 50% of the meridional heat transport in the tropical Atlantic, highlighting their important role for the earth’s climate. This estimate is consistent and reinforces those made by Fratantoni et al. (1995) and Garzoli et al. (2003), who placed the contribution of NBC rings to the meridional heat transport at low latitudes as something between 20% and 50% of the total transport.
These estimates, despite being derived from a large amount of altimetry and hydrographic data, should be evaluated with care. A major issue is to determine how much of the total volume transports actually correspond to waters with South Atlantic origin. This aspect will be tackled in the following discussion, but first some uncertainties in calculating the mean ring volume, from which the annualized transport is derived, must be taken into consideration. The mean NBC ring volume was estimated at 4x1013m3 for a radius of maximum geostrophic velocities of ~160km and maximum penetration depth of 500m. A first, and possibly minor issue, is the estimated penetration depth of the mean ring. As long as the in situ data, sampling 112 different rings, may be considered as representative of a large variety of rings with different vertical penetration, which has been observed to occur in the observations of individual rings (e.g, Johns et al., 2003) this should not be a major concern. The 500m seems to be a robust value, determined both from the average depth of zero T and S anomalies, and from the depth of the σθ = 27.1kgm-3 isopycnal (the limit between SACW and AAIW, as discussed below), but a reasonable uncertainty of ~50m for this estimated penetration depth should lead per se to a 10% variation in the volume transport of the mean ring.
A second issue is related to the radius of maximum geostrophic velocity. The value of 160km was calculated from the individual observations of the 112 rings for which T and/or S profiles were available. This favors somewhat larger rings, when compared to the average radius of 138km calculated from the individual observations of the 128 rings detected by altimetry. The question of why there is less hydrographic information for smaller rings (despite ring A discussed in Section 3.3) is beyond the scope of the present investigation. But if one assumes that the average anomalies computed for the mean NBC ring could be extended to all the rings presented in the altimetry dataset, different values of volume and transport could be estimated. Such a transport, for a radius of 138km, would drop to 0.95Sv (closer to previous estimates reported in the literature) and the total contribution of NBC rings to the AMOC would vary accordingly. A related issue is that the average radius in the altimetry data set seems to decrease from east to west, suggesting that larger rings are more representative of their conditions at the formation region, and shorter rings reflect a general decay during their lifetime. It is unclear whether these two factors compensate each other or not.
With these assumptions regarding the ring volume taken into account, there remains the issue that the value of 1.3Sv for the annualized transport by the mean ring is somewhat larger than the canonical 1Sv, generally assumed in the literature since Johns et al. (1990). This agreement in the literature between different estimates of the volume transport per ring, however, is possibly somewhat fortuitous since they have been made based on several simplified, and sometimes contradictory assumptions. Johns et al. (1990), for instance, obtained a transport of 0.8Sv computing the volume of a cylinder with a diameter of 400km, corresponding to the outer edge under the rings influence (based on the available satellite images) and 200m height, or the thickness of the upper-layer South Atlantic water. Didden and Schott (1993) considered the same diameter, but estimated the volume for a scale height of 350m, or the average depth of the 10°C isotherm in the equatorial region, obtaining a volume transport of ~1.4Sv (closer to the present estimate). Shortly after, Richardson et al. (1994) observed that the signature of the NBC rings in the subsurface drifters reached more than 900m in the water column and that the diameter of the rings was reduced by ~50% at these depths. Their estimated 0.9Sv of volume transport was only possible because they assumed a lower surface diameter of 250km, much lower than the two previous estimates, corresponding to the radial distance of maximum swirl velocity. Fratantoni and Glickson (2002) tracked 12 rings using SeaWiFS chlorophyll-a signature and assumed their shape as elliptical cylinders, with an average major (minor) axis of 304 (213) km, and vertical height of 600m based on the oxygen signature from three sampled rings, obtaining a volume transport of 1.0 ± 0.4Sv. The large range of values obtained for individual rings by these authors, from 0.55Sv and 1.73Sv, points also to a large variability around these estimated values of transport per ring.
In order to compute the amount of SAW transported by the mean NBC ring, anomalous salinity in density space within the ring could not be computed with respect to the average salinity of the OR profiles, as done for the analysis at constant depth levels. Such anomalies, otherwise, were evaluated with respect to “endpoint” salinities (SN), or the average of the highest 10% salinities for each density in the S-σθ diagram. This points to the fact that significant percentages of SAW are present outside NBC rings in the tropical western Atlantic, and SAW is also sampled by the OR profiles. This is observed to occur at all density levels from intermediate to subsurface and surface waters, and is illustrated in Figure 12 for σθ = 25.5 kgm-3. Higher percentages, above 40%, are observed in the eastern domain, within the region of the NBC retroflection, and along the general trajectory of NBC rings in the western domain. Westward from 55°W, lower percentages are observed both to the south and to the north of the average ring trajectory, indicating transport by the NBC rings. High percentages of SAW for OR profiles in the eastern domain may indicate both transport by the NBC and NECC, and mixing within the retroflection. Otherwise, high percentages for OR profiles and low percentages for IR profiles in the western domain possibly indicates mixing of SAW transported by NBC rings with the surrounding waters. The general pattern seen in Figure 12 is similar for all density levels within the range of SACW, and to some extent in the upper part (lower densities) of AAIW. At intermediate levels in the eastern domain, however, a larger meridional variability is observed and values above 40% are rare north of 9°N.
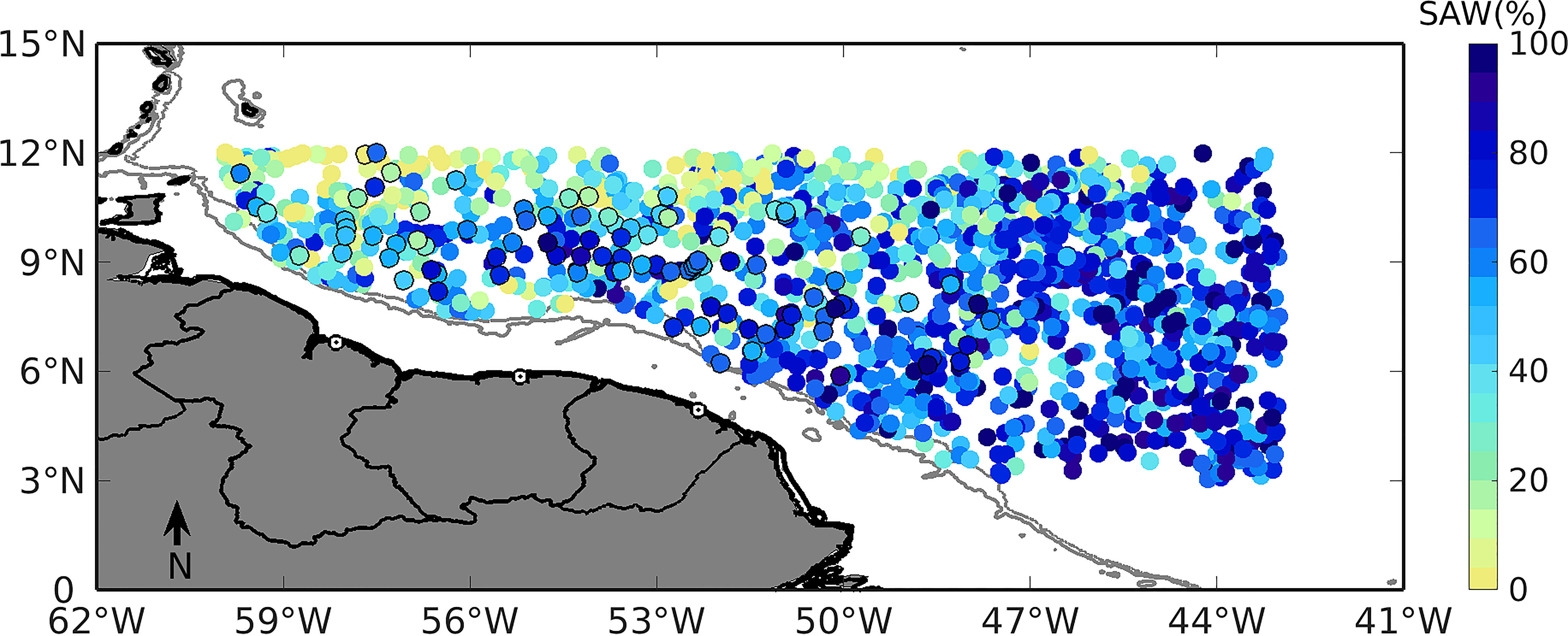
Figure 12 Percentage of SAW for the σθ = 25.5 kgm-3 density level, for all IR and OR profiles containing T/S pairs, within the sampling region. Each dot is one individual profile, and dots with highlighted perimeter represent the IR profiles.
Computing the percentage of SAW transported by the NBC rings, and by the mean ring, is relatively easy when the averages are done in density space (see Eq. 2), but actually depends on some different and possibly controversial approaches. Considering the salinity anomalies for density surfaces below σθ = 27.1kgm-3 leads to, on average, approximately 50% of SAW (circa 0.66Sv) being transported by the mean ring. This should reduce the contribution of NBC rings to the AMOC to about 20 to 35%, but should not influence their contribution to the meridional heat transport. Such an estimate was done considering salinity anomalies and ring volumes calculated for profiles located within 1R from the ring center. Johns et al. (2003), however, suggests that such a calculation (for individual rings, in their case) should be performed not within 1R (R being the radius of maximum geostrophic velocities) but within the ring outer edge. This is defined in their work as the radial distance in which the swirl velocity drops below ~15cms-1, and is justified by the authors with respect to Flierl (1981) ideas on the water trapping within rings, and penetration depths in which the swirl velocity drops below 10cms-1, a rather arbitrary value. Such approach is sensible and, applied to the mean ring would lead to radial distances close to 2R in the present case, although it is arguable whether it makes sense considering average instead of instantaneous velocities. Taking all profiles within 2R, and penetration depth of 200m (see Figure 6 for the average depth in which the velocities of the mean ring are ~10cms-1), the SAW transport by the mean NBC ring is raised by approximately 40%, from 0.66 to 0.92Sv. This estimate is close to the average SAW transport of 1.1Sv, and within the range from 0.2 to 2.3Sv in individual rings, estimated by Johns et al. (2003).
The estimates of SAW by Johns et al. (2003) also include a portion of intermediate waters. These are not considered in the present study, since waters with densities above σθ = 27.1kgm-3 are located below the penetration depth of the mean NBC ring. It is certain that some intermediate waters are carried by NBC rings, since observations have shown that some individual rings reach depth levels below 1000m, with densities in the range of AAIW. What percentage of AAIW is transported by NBC rings, or otherwise by the mean flow, can not be asserted in the present study. At the same time, subsurface intensified rings, with little or no surface SSH signal, also considered by Johns et al. (2003), are probably absent, or under-sampled (since some degree of coupling may exist between surface and subsurface rings) in the present analysis. Fratantoni and Richardson (2006) verified that more intense surface-intensified rings which translate relatively quickly are able to overtake smaller and slower subsurface rings. At the same time, the lowest observed value of SSH anomaly by the tracking method was 1.0 cm, similar to the minimum values observed by Aroucha et al. (2020), who used a hybrid algorithm of eddy detection based on geostrophic velocity at 50m. Of the total of 128 rings identified in the entire period of analysis, 7 of them were first identified with the minimum SSH anomaly value of 1cm and that might indicate the META dataset is able to identify rings with small surface signals, such as the subsurface ones. Whether the mean NBC ring, and the associated meridional transports are representative of the full set of NBC rings or only of those shallow and surface-intensified is still to be determined. Numerical studies, such as that performed by Garrafo et al. (2003), in which surface and subsurface intensified rings are generated, may help to shed some light as to the degree of coupling between such rings, and whether subsurface rings may be detected but their surface signal.
The present study, despite the limitations inherent to the data, is an attempt to improve on the estimates of volume and heat transport by NBC rings, proposing an assemblage of a large amount of data, from different but complementary observational approaches. The geometric volume, associated heat transport, and percentage of SAW within the mean NBC ring appear to be robust estimates. To infer the annualized meridional volume transport by the rings and the percentage contribution by SAW, however, depends on several assumptions on the limits for integrating the ring anomalies, and the uncertainties may be higher. This limitation is not restricted to the present study. Taking also into account the large variability on the number of rings formed at individual years, from a minimum of 2 to a maximum of 8 rings, the total contribution of NBC rings to the upper limb of the AMOC may be considered to vary within a large range, from ~20 to 80% in different years.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: The META dataset is made available at https://www.aviso.altimetry.fr/en/data/products/, and The EN4.2.0 dataset is made available at https://www.metoffice.gov.uk/hadobs/en4/.
Author Contributions
LB developed this work during a master program under the supervision of AP, VC, and GM. All authors contributed to the writing of the manuscript. All authors contributed to the article and approved the submitted version.
Funding
The first author was funded with a fellowship by the Brazilian National Council for Scientific and Technological Development (CNPq).
Conflict of Interest
Author VC, despite being currently employed by Fugro GeoConsulting, was an exclusive part of the university’s research group at the time of the development of this research.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors would like to thank the SSALTO/DUACS team for running and distributing the “Mesoscale Eddy Trajectory Atlas” product, which was developed and validated in collaboration with D.Chelton and M. Schlax at Oregon State University. The EN4.2.0 dataset is made freely available by the Met Office Hadley Centre observations datasets, who join all types of ocean profiling instruments that provide temperature and (if available) salinity information.
References
Aroucha L. C., Veleda D., Lopes F. S., Tyaquiçã P., Lefèvre N., Araujo M. (2020). Intra- and Inter-Annual Variability of North Brazil Current Rings Using Angular Momentum Eddy Detection and Tracking Algorithm: Observations From 1993 to 2016. J. Geophys. Res.: Ocean. 125, e2019JC015921. doi: 10.1029/2019JC015921
Arur A., Krishnan P., George G., Goutham Bharathi M. P., Kaliyamoorthy M., Hareef Baba Shaeb K., et al. (2014). The Influence of Mesoscale Eddies on a Commercial Fishery in the Coastal Waters of the Andaman and Nicobar Islands, India. Int. J. Remote Sens. 35 (17), 6418–6443. doi: 10.1080/01431161.2014.958246
Broecker W. S. (1991). The Great Ocean Conveyor. Oceanography 4 (2), 79–89. doi: 10.5670/oceanog.1991.07
Brokaw R. J., Subrahmanyam B., Trott C. B., Chaigneau A. (2020). Eddy Surface Characteristics and Vertical Structure in the Gulf of Mexico From Satellite Observations and Model Simulations. J. Geophys. Res.: Ocean. 125 (2), e2019JC015538. doi: 10.1029/2019JC015538
Candela J., Beardsley R. C., Limeburner R. (1992). Separation of Tidal and Subtidal Currents in Ship-Mounted Acoustic Doppler Current Profiler Observations. J. Geophys. Res. 97, 769–788. doi: 10.1029/91JC02569
Chelton D. B., Schlax M. G., Samelson R. M. (2011). Global Observations of Nonlinear Mesoscale Eddies. Prog. Oceanogr. 91 (2), 167–216. doi: 10.1016/j.pocean.2011.01.002
Didden N., Schott F. (1993). Eddies in the North Brazil Current retroflection region observed by Geosat altimetry. J. Geophys. Res.: Ocean. 98 (C11), 20121–20131. doi: 10.1029/93JC01184
Emery W. J., Dewar J. S. (1982). Mean Temperature-Salinity, Salinity-Depth and Temperature-Depth Curves for the North Atlantic and the North Pacific. Prog. Oceanogr. 11 (3), 219–305. doi: 10.1016/0079-6611(82)90015-5
Ffield A. (2005). North Brazil Current Rings Viewed by TRMM Microwave Imager SST and the Influence of the Amazon Plume. Deep-Sea. Res. Part I.: Oceanogr. Res. Pap. 52 (1), 137–160. doi: 10.1016/j.dsr.2004.05.013
Flagg C. N., Gordon R. L., McDowell S. (1986). Hydrographic and Current Observations on the Continental Slope and Shelf of the Western Equatorial Atlantic. J. Phys. Oceanogr. 16 (8), 1412–1429. doi: 10.1175/1520-0485(1986)016<1412:HACOOT>2.0.CO;2
Flierl G. R. (1981). Particle Motions in Large-Amplitude Wave Fields. Geophys. Astrophys. Flui. Dyn. 18 (1-2), 39–74. doi: 10.1080/03091928108208773
Fonseca C. A., Goni G. J., Johns W. E., Campos J. D. (2004). Investigation of the North Brazil Current Retroflection and North Equatorial Countercurrent Variability. Geophys. Res. Lett. 31, L21304. doi: 10.1029/2004GL020054
Fratantoni D. M., Glickson D. A. (2002). North Brazil Current Ring Generation and Evolution Observed With SeaWiFS. J. Phys. Oceanogr. 32 (3), 1058–1074. doi: 10.1175/1520-0485(2002)032<1058:NBCRGA>2.0.CO;2
Fratantoni D. M., Johns W. E., Townsend T. L. (1995). Rings of the North Brazil Current: Their Structure and Behavior Inferred From Observations and a Numerical Simulation. J. Geophys. Res.: Ocean. 100 (C6), 10633–10654. doi: 10.1029/95JC00925
Fratantoni D. M., Richardson P. L. (2006). The Evolution and Demise of North Brazil Current Rings. J. Phys. Oceanogr. 36 (7), 1241–1264. doi: 10.1175/JPO2907.1
Ganachaud A., Wunsch C. (2000). Improved Estimates of Global Ocean Circulation, Heat Transport and Mixing From Hydrographic Data. Nature 408 (6811), 453–457. doi: 10.1038/35044048
Garraffo Z. D., Johns W. E., Chassignet E. P., Goni G. J.. (2003). “North Brazil Current rings and transport of southern waters in a high resolution numerical simulation of the North Atlantic,” In: Elsevier Oceanography Series Eds. Goni G. J., Malanotte-Rizzoli P. (Amsterdam: Elsevier). vol. 68, 375–409.
Garzoli S. L., Ffield A., Johns W. E., Yao Q. (2004). North Brazil Current Retroflection and Transports. J. Geophys. Res.: Ocean. 109 (C1), 1–14. doi: 10.1029/2003JC001775
Garzoli S. L., Ffield A., Yao Q. (2003). “North Brazil Current Rings and the Variability in the Latitude of Retroflection,” in Elsevier Oceanography Series 68. Elsevier Science), 357–373. doi: 10.1016/S0422-9894(03)80154-X
Goes M., Molinari R., da Silveira I., Wainer I. (2005). Retroflections of the North Brazil Current During February 2002. Deep-Sea. Res. Part I.: Oceanogr. Res. Pap. 52 (4), 647–667. doi: 10.1016/j.dsr.2004.10.010
Goni G. J., Johns W. E. (2001). A Census of North Brazil Current Rings Observed From TOPEX/POSEIDON Altimetry: 1992–1998. Geophys. Res. Lett. 28 (1), 1–4. doi: 10.1029/2000GL011717
Goni G. J., Johns W. E. (2003). “Synoptic Study of Warm Rings in the North Brazil Current Retroflection Region Using Satellite Altimetry,” in Elsevier Oceanography Series, Vol. 68. (Elsevier Science), 335–356. doi: 10.1016/S0422-9894(03)80153-8
Good S. A., Martin M. J., Rayner N. A. (2013). EN4: Quality Controlled Ocean Temperature and Salinity Profiles and Monthly Objective Analyses With Uncertainty Estimates. J. Geophys. Res.: Ocean. 118 (12), 6704–6716. doi: 10.1002/2013JC009067
Halliwell G. R. Jr., Weisberg R. H., Mayer D. A. (2003). “A Synthetic Float Analysis of Upper-Limb Meridional Overturning Circulation Interior Ocean Pathways in the Tropical/Subtropical Atlantic,” in Interhemispheric Water Exchange in the Atlantic Ocean, vol. Vol. 68 . Eds. Goni G. J., Malanotte-Rizzoli P. (Elsevier Science).
Hormann V., Lumpkin R., Foltz G. R. (2012). Interannual North Equatorial Countercurrent Variability and its Relation to Tropical Atlantic Climate Modes. J. Geophys. Res. 117, C04035. doi: 10.1029/2011JC007697
Jochumsen K., Rhein M., Hüttl-Kabus S., Böning C. W.. (2010). “On the Propagation and Decay of North Brazil Current Rings. J. Geophys. Res.: Oceans 115, C10004. doi: 10.1029/2009JC006042
Johns W. E., Lee T. N., Schott F. A., Zantopp R. J., Evans R. H. (1990). The North Brazil Current Retroflection: Seasonal Structure and Eddy Variability. J. Geophys. Res.: Ocean. 95 (C12), 22103–22120. doi: 10.1029/JC095iC12p22103
Johns W. E., Zantopp R. J., Goni G. J. (2003). “Cross-Gyre Transport by North Brazil Current Rings,” in Elsevier Oceanography Series, (Elsevier Oceanography: Elsevier Science) 68, 411–441. doi: 10.1016/S0422-9894(03)80156-3
Jufaili S. M. A., Piontkovski S. A. (2020). Seasonal and Interannual Variations of Sardine Catches Along the Omani Coast. Int. J. Ocean. Oceanogr. 14 (1), 77–99. doi: 10.37622/IJOO/14.1.2020.77-99
Mélice J. L., Arnault S. (2017). Investigation of the Intra-Annual Variability of the North Equatorial Countercurrent/North Brazil Current Eddies and of the Instability Waves of the North Tropical Atlantic Ocean Using Satellite Altimetry and Empirical Mode Decomposition. J. Atmosph. Ocean. Technol. 34 (10), 2295–2310. doi: 10.1175/JTECH-D-17-0032.1
Pauluhn A., Chao Y. (1999). Tracking Eddies in the Subtropical North-Western Atlantic Ocean. Phys. Chem. Earth. Part A.: Solid. Earth Geodes. 24 (4), 415–421. doi: 10.1016/S1464-1895(99)00052-6
Pegliasco C., Chaigneau A., Morrow R. (2015). Main Eddy Vertical Structures Observed in the Four Major Eastern Boundary Upwelling Systems. J. Geophys. Res.: Ocean. 120 (9), 6008–6033. doi: 10.1002/2015JC010950
Pegliasco C., Delepoulle A., Mason E., Morrow R., Faugère Y., Dibarboure G. (2022). META3.1exp: A New Global Mesoscale Eddy Trajectory Atlas Derived From Altimetry. Earth Syst. Sci. Data 14, 1087–1107. doi: 10.5194/essd-14-1087-2022
Reid J. L., Lynn R. J. (1971). “On the Influence of the Norwegian-Greenland and Weddell Seas Upon the Bottom Waters of the Indian and Pacific Oceans,” in Deep-Sea Research and Oceanographic Abstracts Oceans, Vol. 18. (Elsevier), 1063–1088. doi: 10.1016/0011-7471(71)90094-5
Richardson P. L., Hufford G. E., Limeburner R., Brown W. S. (1994). North Brazil Current Retroflection Eddies. J. Geophys. Res.: Ocean. 99 (C3), 5081–5093. doi: 10.1029/93JC03486
Schlax M. G., Chelton D. B. (2016). “The “Growing Method” of Eddy Identification and Tracking in Two and Three Dimensions,” in College of Earth, Ocean and Atmospheric Sciences, vol. 8. (Corvallis, Oregon: Oregon State University).
Schmitz W. J. Jr., McCartney M. S. (1993). On the North Atlantic Circulation. Rev. Geophys. 31 (1), 29–49. doi: 10.1029/92RG02583
Schott F. A., Fischer J., Stramma L. (1998). Transports and Pathways of the Upper-Layer Circulation in the Western Tropical Atlantic. J. Phys. Oceanogr. 28 (10), 1904–1928. doi: 10.1175/1520-0485(1998)028<1904:TAPOTU>2.0.CO;2
Sharma N., Anderson S. P., Brickley P., Nobre C., Cadwallader M. L. (2009). “Quantifying the Seasonal and Inter-Annual Variability of the Formation and Migration Pattern of North Brazil Current Rings. Oceans, 1–7. doi: 10.23919/OCEANS.2009.5422142
Souza J. M. A. C., de Boyer Montégut C., Cabanes C., Klein P. (2011). Estimation of the Agulhas Ring Impacts on Meridional Heat Fluxes and Transport Using ARGO Floats and Satellite Data. Geophys. Res. Lett. 38 (21), 1–5. doi: 10.1029/2011GL049359
Stramma L., England M. (1999). On the Water Masses and Mean Circulation of the South Atlantic Ocean. J. Geophys. Res. 104 (C9), 20863–20883. doi: 10.1029/1999JC900139
Wilson W. D., Johns W. E., Garzoli S. L. (2002). Velocity Structure of North Brazil Current Rings. Geophys. Res. Lett. 29 (8), 114–111. doi: 10.1029/2001GL013869
Yang G., Wang F., Li Y., Lin P. (2013). Mesoscale Eddies in the Northwestern Subtropical Pacific Ocean: Statistical Characteristics and Three-Dimensional Structures. J. Geophys. Res.: Ocean. 118 (4), 1906–1925. doi: 10.1002/jgrc.20164
Keywords: inter-hemispheric exchange, AMOC, South Atlantic Water transport, NBC ring variability, NBC mean ring
Citation: Bueno LF, Costa VS, Mill GN and Paiva AM (2022) Volume and Heat Transports by North Brazil Current Rings. Front. Mar. Sci. 9:831098. doi: 10.3389/fmars.2022.831098
Received: 08 December 2021; Accepted: 25 May 2022;
Published: 11 July 2022.
Edited by:
Ronald Buss de Souza, National Institute of Space Research (INPE), BrazilReviewed by:
Rafael Cervantes, Instituto Politécnico Nacional (IPN), MexicoMark Jury, University of Puerto Rico at Mayagüez, Puerto Rico
Copyright © 2022 Bueno, Costa, Mill and Paiva. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Luana F. Bueno, bHVmZXJyYXowNkBob3RtYWlsLmNvbQ==
 Luana F. Bueno
Luana F. Bueno Vladimir S. Costa1,2
Vladimir S. Costa1,2 Guilherme N. Mill
Guilherme N. Mill Afonso M. Paiva
Afonso M. Paiva