
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mar. Sci., 21 November 2022
Sec. Physical Oceanography
Volume 9 - 2022 | https://doi.org/10.3389/fmars.2022.1053964
This article is part of the Research TopicMulti-Scale Fluid Physics in Oceanic Flows: New Insights from Laboratory Experiments and Numerical SimulationsView all 16 articles
According to recent studies, the large-scale effect of bottom topography on the ocean overturning circulation can be considered as a result of bottom enhancement of turbulent mixing in the abyssal ocean. Here we show, using laboratory experiments of rotating horizontal convection, that even without spatial variation of mixing intensity, oceanic meridional ridges can strongly impact both the strength and the pattern of the overturning in some fundamental ways. For example, as suggested by experimental results, the existence of the mid-Atlantic ridge can lead to the formation of another deep jet, like the deep western boundary current (DWBC), along the ridge’s eastern edge as a pathway for southward export of newly formed deep water. In response to this interior (mid-basin) jet and the associated isopycnal displacement, adiabatic flow structures may occur in upper and lower layers, including two opposing jets located respectively above and below the interior DWBC. Though unable to contribute to the overturning, they can probably affect transport along isopycnals. In the latitudinal band of the Antarctic Circumpolar Current without side boundary but with multiple ridges lying over the bottom, multiple interior DWBCs may develop preferentially along higher ridges, carrying the Antarctic Bottom Water into the northern latitudes. Moreover, the overturning cell or the strong jets can migrate vertically with the grow or decay of the ridge. Therefore, presumably strong variations of both ocean circulation and stratification may have occurred more than once during the past millions of years, as consequences of plate tectonic evolution, and have caused substantial changes of earth climate.
The overturning circulation plays an important role in transporting and storing heat, freshwater, and carbon in the global ocean. Understanding what determines the structure and strength of this circulation is key to assessing the ocean’s ability in regulating climate change. Over the past few decades, the influence of bottom topography on the overturning has been gaining increasing interest, but most studies on the topic centers around the small-scale turbulent process and its topographic enhancement. In the current paper, we extend the discussion to the large-scale effects of topography. Our laboratory experiments of rotating horizontal convection suggest that even without spatial variation of mixing intensity meridional ridges alone can strongly affect both the strength and the three-dimensional structure of the overturning. Horizontal convection (hereinafter HC) is the name for flow resulting from buoyancy variation imposed along a horizontal boundary of a fluid (Stern, 1975). According to Sandström’s theorem (Sandström, 1908), the persistent large-scale circulation of HC cannot exist without intense turbulent mixing in the deep ocean. Over a long period of time, this theorem was widely accepted until Rossby for the first time demonstrated a steady large-scale circulation in a rectangular non-rotating tank subject to differential heating applied along the bottom (Rossby, 1965). Since then, HC has been regarded as a simple model to study the overturning. Effects of various factors including earth rotation were investigated for a better match to the reality (Miller, 1968; Beardsley and Festa, 1972; Hignett et al., 1981; Rossby, 1998; Park and Whitehead, 1999; Coman et al., 2006; Hughes and Griffiths, 2008; Whitehead and Wang, 2008; Tailleux and Rouleau, 2010; Ilicak and Vallis, 2012; Stewart, 2012; Barkan et al., 2013; Wang et al., 2016). Nevertheless, considering apparent discrepancies between the reality and the idealized model, it remains a question of to what extent physical understanding achieved from HC studies can be applied to the real ocean.
Part of the answer lies in a recent paper by Zhang et al. (2016) about new laboratory experiments of rotating HC in a zonally closed annular gap that can be viewed as a 360°-wide basin. High-resolution three-dimensional measurements of both temperature and velocity field make possible an accurate analysis of the dynamical balance. Although some non-dimensional parameters are quite different from their oceanic values, experimental results show remarkable similarities to the real ocean including a strong deep western boundary current (DWBC) exporting newly formed water mass from the convecting region and weak zonal flow directed away from the western boundary. More importantly, the flow adjusts itself in such a way that in the deep ocean contours of large-scale potential vorticity (PV hereinafter), as mostly determined by stratification of the fluid, are meridionally aligned near the western boundary. The DWBC is therefore allowed to flow along PV contours with little dynamical constraint. According to the existing knowledge about the ocean circulation, the planetary β effect dominates the PV distribution and causes the formation of the western boundary jets, being viscous and flowing across PV contours. Compared with this classical view, the along-PV feature of the experimental DWBC is, at the first glance, surprising and doubtful. However, it is confirmed to be indeed the case for the North Atlantic basin by observational evidence. Although currently a satisfactory theory explaining the similarity between the experiments and the ocean is not available, the similarity itself gives us confidence in the applicability of the former.
We are thus motivated to further investigate issues of the overturning using lab experiments. Ocean topography is of particular interest because of topographic enhancement of abyssal turbulent mixing as suggested by increasingly-convincing observational evidence in the past few decades (Wunsch and Ferrari, 2004; Garrett and Kunze, 2007; Polzin et al., 1997; St. Laurent et al., 2012; Waterman et al., 2013; Waterhouse et al., 2014). More recently, a new paradigm has been proposed and suggests that the cross-density upwelling, by which the overturning cell is closed, occurs predominantly in the boundary layer along the bottom slope (Ferrari et al., 2016; McDougall and Ferrari, 2017; de Lavergne et al., 2017). Furthermore, knowledge about the impact of topography can help us understand how topographic changes induced by plate tectonic evolution have changed the ocean circulation and climate through the geological history.
Using lab experiments in an annular gap with partial-depth ridges, we gain new insights into the overturning and its relation to ocean ridges. Despite uniform distribution of intensity of diapycnal mixing, ocean ridges can affect the overturning in three main ways. First of all, the DWBC develops not only along the eastern side of the side boundary, but also along eastern sides of meridional ridges, thus leading to an interior pathway for deep or bottom water transport. Secondly, both above and below DWBCs (both along the side boundary and ridges), a meridional jet develops, flowing opposite to that in the middle. Both jets are adiabatic and geostrophic, with little contribution to the overturning but probably large impacts on isopycnal transport. Thirdly, following the grow or decay of ridges as occurred in the past millions of years, the overturning cell and DWBCs migrate in the vertical direction, causing substantial changes not only in the flow field but in the stratification of the deep ocean.
Several parameters are commonly considered relevant for HC and rotating HC (Hignett et al., 1981),
Here B is the maximum buoyancy contrast imposed on the base of the annular gap, L is the characteristic horizontal length scale.
Keeping these parameters in mind, we begin with the linear Boussinesq equations for a rotating system at the steady state:
where b denotes buoyancy, f=2Ω is the Coriolis parameter of the system with the rotating axes pointing upward, and only vertical friction is considered. In the thin boundary layer along the bottom where the differential buoyancy forcing is applied, the gradient of buoyancy is dominated by its vertical component, hence the buoyancy equation can be simplified as
Cross differentiating horizontal momentum equations leads to great simplification of the above array of equations:
where ∇h is the del in horizontal. Dimensionalizing the system with the horizontal length scale, L, vertical length scale, δ, buoyancy scale, b, we obtain the scaling for w:
Applying this scaling in non-dimensionalizing Eq.4 leads to
where w, z, and b are non-dimensional. Apparently in this equation describing the flow vorticity in the boundary layer, relative roles of stretching of the water column and the buoyancy forcing are measured respectively by two non-dimensional parameters in brackets. Equating the second parameter with one yields the well-known scaling law for the boundary layer thickness,
The first parameter is related to the ratio of two thickness,
where is the scaling of the Ekman layer thickness. Equation (9) is often written as the square of Q, a parameter widely considered by many to govern the rotating convection system (Hignett et al., 1981; Park and Whitehead, 1999; Barkan et al., 2013; Hussam et al., 2014; Sheard et al., 2016). We admit that regarding Eq. 7 the increase of Q from zero to finite or large value demonstrates the strengthening of rotation. However, its utility is limited by the fact that Eq. 7 as a differential equation itself does not encompass many other effects such as boundaries, which sometimes can be essential (Zhang et al., 2016), and topography, as will be discussed in the present study. It is actually the PV that is more essential in disclosing basic physics of the circulation, and according to Ertel’s formula PV is defined as
where ω+2Ω is the absolute vorticity with ω being the relative vorticity. By definition, the overturning stream function, ψ(r,z) , is the zonally as well as vertically integrated quantity of the meridional velocity,
where is the zonally integrated meridional velocity. How the existence of a side boundary changes the overturning strength can be understood from Eq. 2, the momentum equation for the zonal velocity. Integrating Eq. 2 along a given latitude of a zonally periodic domain, the term of pressure gradient force makes no contribution, and all the meridional component of the flow cannot exist without friction. Nevertheless, in the presence of a meridional wall, a net pressure difference remains after zonal integration, balancing the Coriolis force to support a geostrophic component of the flow, and therefore enhancing the strength of the overturning circulation.
We applied the differential buoyancy forcing at the bottom of an annular gap by maintaining a radially varying distribution of temperature. The annular gap, bounded by two coaxial Plexiglas cylinders with heights of 154 mm, was filled with ethylene glycol to a depth of H = 120 mm (Figure 1A). At 20°C, it has density ρ0=1115 kg/m3, thermal expansion coefficient α=5.7×10−4 K-1, kinematic viscosity υ=14.4 × 10−6 m2/s, thermal diffusivity κ=0.9 ×10−7 m2/s, thermal conductivity κc=0.258 W/m/K, and heat capacity Cp=2.49×103 J/kg/K (see Table 1). The inner cylinder is a clear one with the outer radius a = 15 mm. The outer cylinder has inner radius b = 180 mm and thickness 2 mm. Both cylinders were secured to a d = 10 mm thick copper plate, which was heated at the centre and cooled near its outer edge by recirculating water through two circular channels cut inward of the copper plate from below. Water circulating in the central channel was pumped out of a hot circulator bath with the target temperature Th ; while that in the outer channel was from a cold bath with temperature Tc . The two circulators used were Thermo Scientific EZ COOL 80, powerful enough to maintain temperature to the target value with an accuracy of ±0.1 K. Thermal conduction through the metal plate established a smooth conductive transition between the heating and cooling regions, leading to a radial temperature profile. Similar methods of maintaining a temperature distribution along the boundary have been adopted by many laboratory studies (Hignett et al., 1981; Pedlosky et al., 1997; Whitehead and Pedlosky, 2000; Mullarney et al., 2004). In our experiments, the heat flux through the copper base is much greater than that through the fluid, so the base temperature, Tb , was able to be decoupled from the fluid motion, remaining axisymmetric in space as well as stable in time with small perturbations on the order of O(10−2) K in the equilibrium state. It also decreases logarithmically with r at the lowest order because of the near constancy of the radial heat flux through the base. With axisymmetric base temperatures, none of our experiments showed vulnerability to instabilities, which, as suggested by several recent studies, can be potentially incited with zonal perturbations of boundary conditions (Winters and Barkan, 2013; Barkan et al., 2013; Sheard et al., 2016).
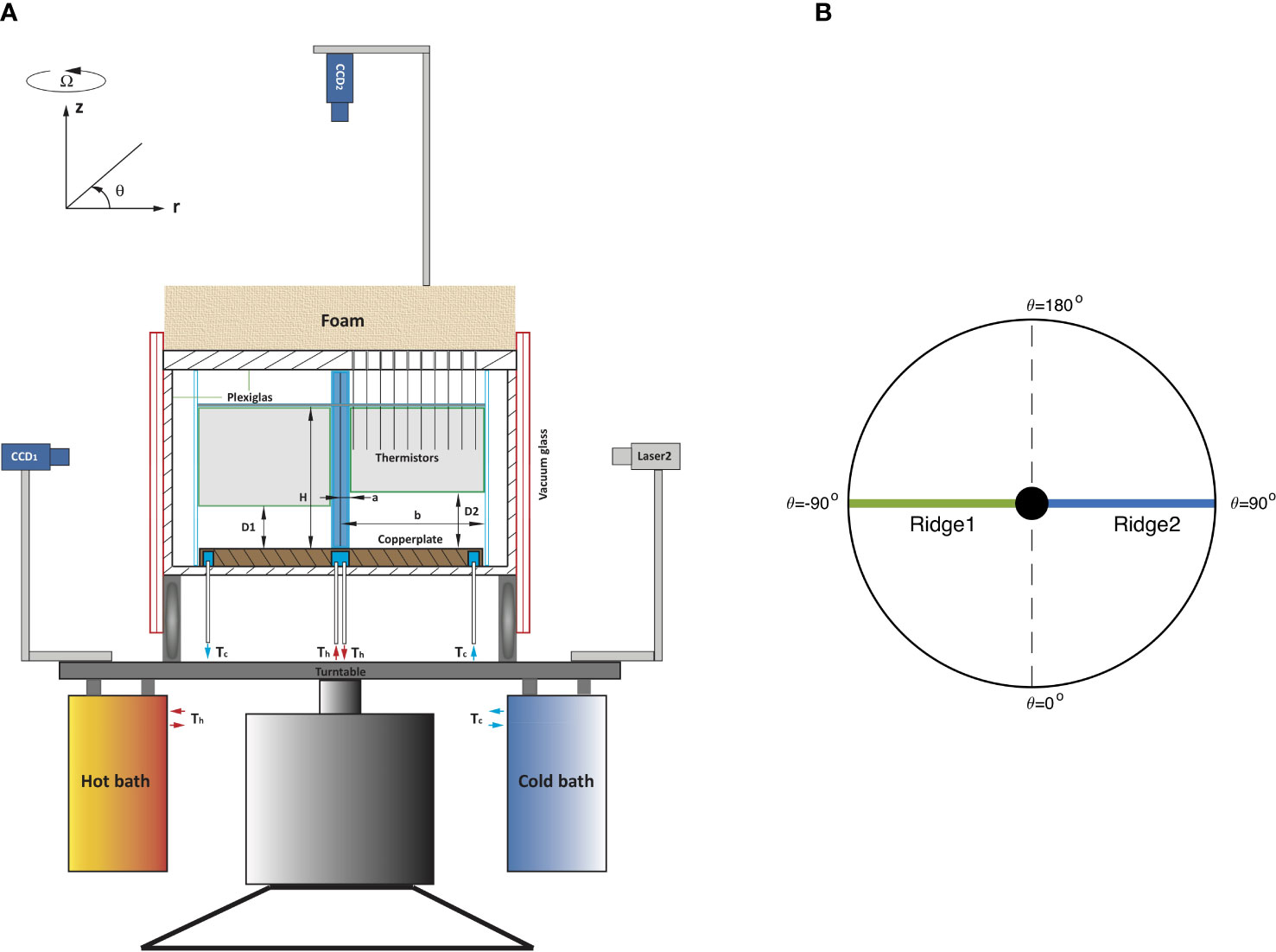
Figure 1 (A) A schematic view of the experimental apparatus. The working fluid was contained in the open region bounded by two thin-walled cylindrical tubes. The fluid was heated and cooled at its lower boundary by two baths as described in the text. (B) A schematic top view of the annulus with two ridges.
The lid of the tank was made of 25 mm thick Plexiglas, rested on the four sidewalls and in no direct contact with the fluid below. An inner lid made of 2 mm thick Plexiglas was placed on the top of the fluid, providing the solid top boundary condition mimicking that of the ocean bottom.
To reduce as much as possible the heat exchange with the environment, the cylinders with the copper base was snugly contained in a tank made of Plexiglas with a thickness of 15 mm. Immediately adjacent to its four sidewalls, the tank was further encased with double-walled glass. A high vacuum of 2×10−7 bar was maintained in the small gap with a thickness of 0.25 mm between its inner and outer walls. In addition, the tank was further covered with 60 mm thick rubber foam. All these measures helped to keep good insulation of the apparatus; the heat loss through the enclosure boundaries is negligible compared with that through the fluid.
On the lids and along different rays passing through the axial central line of the inner cylinder, there were arrays of holes that had a diameter of 3 mm and were separated 10 mm apart. Through these holes, thermistor probes were traversed vertically, measuring temperature with an accuracy of about ±0.01 K. The upper ends of the probes were attached to a horizontal rack, which could be not only moved vertically but also turned azimuthally to measure temperatures at different depths and along different radial directions.
Velocities of the fluid were measured with two sets of PIV (particle image velocimetry) systems, one for velocity measurement on the horizontal plane (Laser2 and CCD2 in Figure 1A) and the other for the vertical plane (CCD1 and Laser1 which was not shown in Figure 1A). Each PIV set consisted of a semiconductor laser with a power of 2 W at a wavelength of 532 nm and a digital CCD camera with a spatial resolution of 3296 × 2472 pixels for horizontal and 1920 × 1080 pixels for vertical respectively. Lasers with necessary optical components were used to produce a green light sheet with a thickness of 3 mm. The working fluid was seeded with silver-coated hollow glass spheres with a diameter of 0.01 mm. These particles that traverse the light sheet are nearly neutrally buoyant and could suspend in the fluid for over 200 hr. CCD cameras were used to acquire images, following which each pair of images could be translated into a velocity vector field. Motorized linear stages were used to traverse both lasers and cameras so that the velocity fields on horizontal/vertical planes could be measured as desired.
The tank containing the working fluid was levelled and centred on a 110 cm×110 cm turntable, whose rotation rate Ω could be changed smoothly between 3 and 30 rpm with an accuracy of 0.05%. Also mounted on the table were equipment for temperature and velocity measurements including the thermistor rack and the PIV system.
Since the main focus of the current study is the effects of meridional ridges with rotation, we decided to have experiments with the same parameter settings (Ω = 10 rpm, ΔT = 6°C), but different geometries. Under such configurations, those non-dimensional parameters discussed in Section 2.1 have constant values: Ra=1.2×108 , Pr = 160, and Q ≈ 2.3. As listed in Table 2, the experiments performed and investigated are divided into two sets, a single-ridged set and a two-ridged set. In the first set, a partial-depth meridional ridge with various vertical lengths was attached to the inner cylinder extending downward from the top lid with distance to the bottom denoted as D1 (Figure 1A for side view and Figure 1B for top view). In the second set, two meridional ridges (180° apart, with distances to the bottom denoted respectively as D1 and D2 were installed.
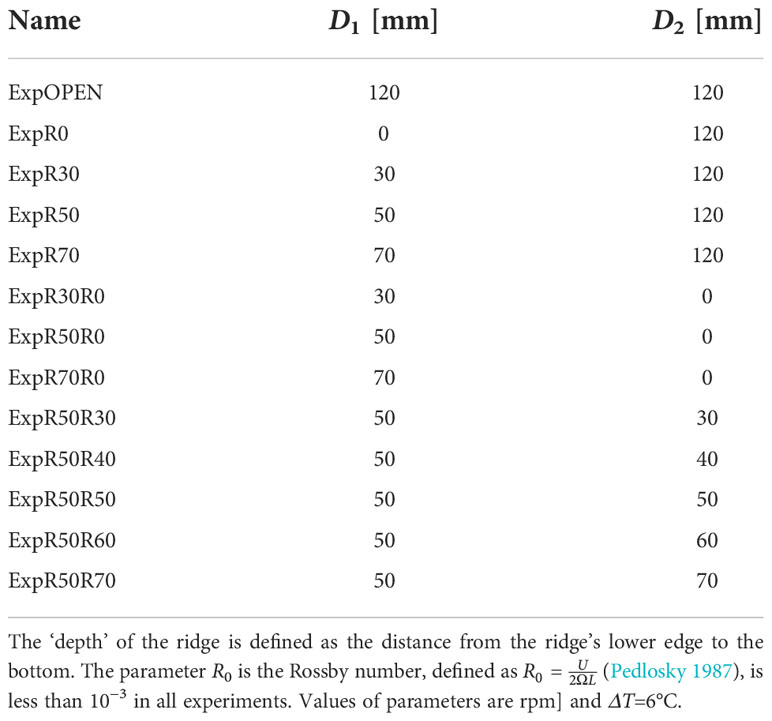
Table 2 Experimental data and computed values for the non-dimensional parameters. D1 and D2 denote respectively the depth of the first (RidgeL) and the second ridge (RidgeR), as illustrated in Figure 2.
A cylindrical polar coordinate system (r,θ,z) was used in analyzing results. The system has the origin located at the centre of the copper plate, the radial direction directed outwards from the origin, the azimuthal direction directed anti-clockwise when viewed from above and the polar axis directed upward from the base. For convenience, we sometimes used “zonal” and “meridional” to refer to azimuthal and radial directions.
Three-dimensional distribution of horizontal velocity and temperature were measured for all experiments. For velocity measurement, the horizontal light sheet created by Laser2 was traversed downward from the top to the bottom of the fluid and stopped every 2.5 mm for a period of 5 minutes. During this period, 1201 images were taken by CCD2 at a sampling rate of 4 Hz, yielding 1200 instantaneous velocity fields.
For temperature measurements, 36 radial sections were taken sequentially in 10° increments of the polar angle. For each section, thermistor probes were traversed downward through holes in the lid, and stopped every 2.5 mm. At each depth, temperatures were measured at 16 equally spaced radial locations between r = 25 mm and r = 175 mm in a period of 20 seconds and at a sampling rate of 0.5 Hz.
All experiments were carried out for long enough time to ensure that the quasi-equilibrium state had been achieved, after which measurements were made for analysis.
Under the current configuration where a radially-decreasing temperature field is prescribed along the lower boundary, the tank can be viewed as an upside-down ocean with its “abyss” being close to the top lid and the “surface” adjacent to the bottom of the tank (copper plate). The “north-pole” of the experimental ocean, where strong convection takes place nearby, is at the centre of the annulus. The clockwise direction (top view) around the annulus is also referred to as “west” in following discussions. The isothermal surfaces of the experimental ocean are parallel with isopycnal surfaces since the fluid density is only dependent on temperature that is variable.
For a no-ridge case (ExpOPEN), the overturning cell is characterized by a northward (inward) flow in the bottom boundary layer feeding deep convection (the near bottom part of the thick green line with negative value in Figure 2) and an interior (outward) flow away from the deep convection region towards the cooling end. An important result of Zhang et al. (2016) is the existence of two distinct types of the interior flow in association with two contrasting potential vorticity (PV) distributions in presence of different geometries. In a zonally open annular gap, like the flat bottomed Antarctic Circumpolar Current (ACC) region, the absence of meridional boundaries makes impossible the existence of geostrophic meridional flow, and induces axisymmetric distribution of both temperature (density) and PV that vary only in the meridional (radial) direction. As constrained by the law of PV conservation, the meridional component of the flow, axisymmetric as well, can only be supported by non-conservative processes. However, when the annular gap was changed into a closed 360°-wide basin with a full-depth radial ridge acting as side boundaries (ExpR0), the flow field adjusts itself by sloping isothermal (isopycnal) surfaces against the ridge and hence aligning PV contours along the “western” boundary. A relatively strong, geostrophic jet is therefore allowed by the law of PV; it transports newly-formed water away from the inner cylinder (outward or southward), and the strength of the MOC is much greater than that in the no-ridge case. Being analogous to the oceanic deep western boundary current (DWBC), this experimental interior jet is also referred to as DWBC in following discussions.
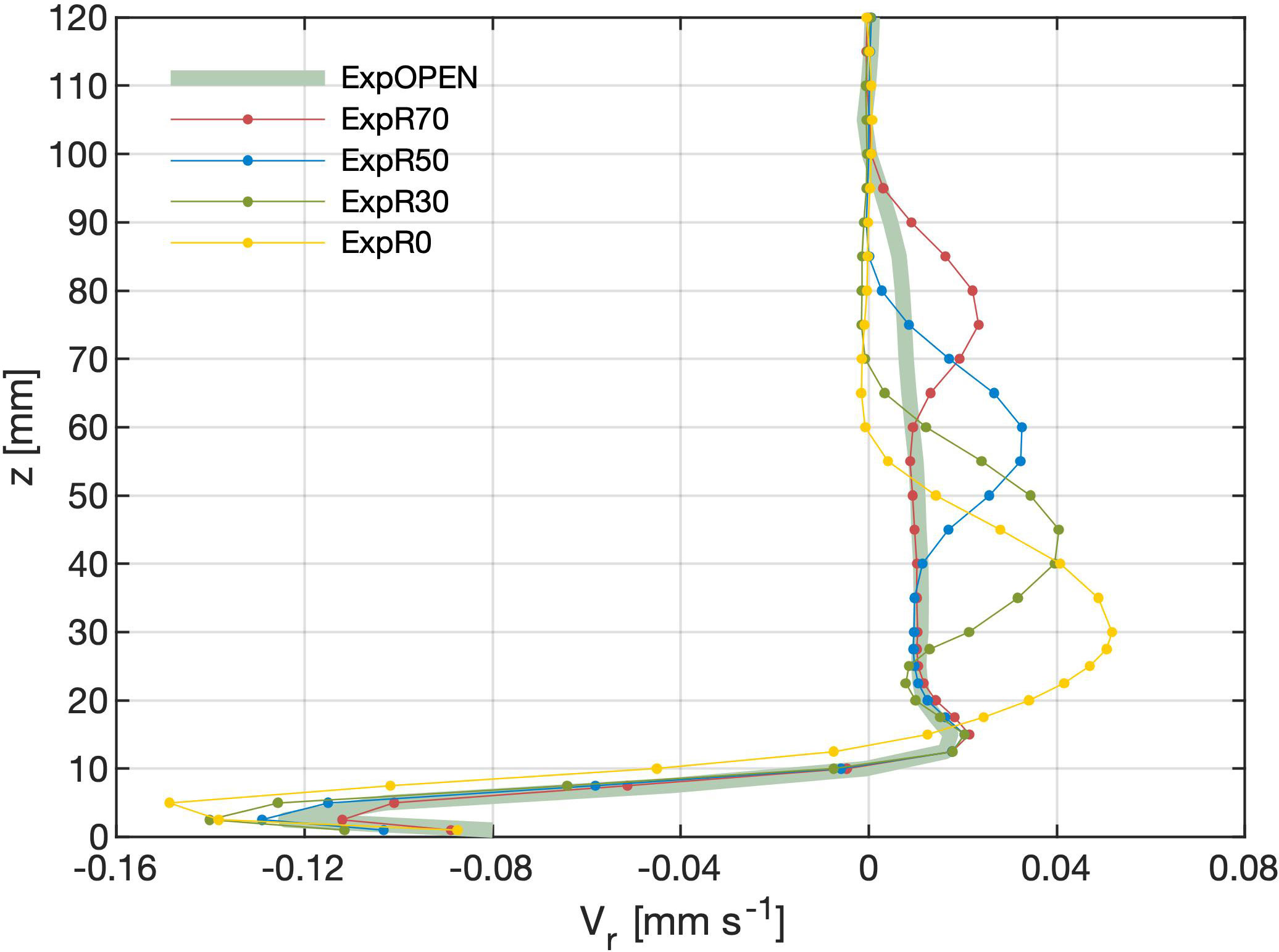
Figure 2 Vertical distribution of the zonally-averaged meridional velocity [mm/s] at r = 60 mm in single-ridged cases with various depth D1.
The above result revealed the significance of PV and meanwhile drew attention to the question of what eternally determines its distribution, since PV is not an independent variable known a prior but a consequence of intrinsic physics. Besides geometry, we speculate that topography, particularly meridional ridges may also be capable of exerting strong impacts at the large scale, as once suggested by an idealized modelling study of the meridional overturning circulation (MOC) (Toggweiler and Bjornsson, 2000). To verify this conjecture, we used partial-depth ridges that were attached to the top lid with a gap from the bottom to mimic ocean ridges, and carried out a series of rotating HC experiments.
For a meridional ridge with non-zero depth D1, defined as the distance from the ridge to the bottom of the tank, the whole domain is divided in the vertical into two sub-regions: a zonally open one below the ridge and a zonally closed one above. The lower region is geometrically similar to an open channel like ACC, whereas the upper region is a basin.
In all single partial-ridge cases, the zonally integrated meridional flow, especially that in the interior above the bottom boundary layer, shows similarly contrasting features in the two sub-regions. In the open region, the meridional flow is ageostrophic, weak and spanning a wide vertical range, as in the axisymmetric, no-ridge case (ExpOPEN in Figure 2). In the closed region, the partial-depth ridge still acts as side boundaries, though only for the upper part of the water column. By supporting zonal pressure difference across the basin, it enables a concentrated jet structure like DWBC in the full-depth ridge case (ExpR0 in Figure 2).
As the ridge has its depth increased from zero (ExpR0) to leave a larger gap below, the vertical expanse of the open region is enlarged whereas that of the closed region is decreased. Correspondingly, the ageostrophic meridional flow expands in the vertical while the geostrophic jet migrates upward with the ridge and meanwhile diminishes in both vertical range and the strength. Taking ExpOPEN and ExpR0 as the two limiting cases, results of partial-ridge cases reveal a smooth transition in between. The MOC cell is at the lowest level with the largest strength in the full-depth ridge case (ExpR0), and declines linearly with D1 (Figure 3).
The tendency of the MOC cell, particularly the DWBC, to “seek” the ridge has strong implications for the real ocean. First of all, we expect the existence of DWBC not only along the western boundary, but also along the mid-ocean ridges. Secondly, through the entire geological history characterized by complicated seafloor evolution, the DWBC probably has migrated up- or downward following the grow or decay of ocean ridges, which presumably has contributed to substantial changes in both ocean and climate.
The outward DWBC is remarkable on the curve of the zonally integrated meridional transport or the MOC (Figure 2), but it is not the only prominent feature in the three-dimensional flow field. In the case of a full-depth ridge (ExpR0), there is another reversing jet, though much weaker compared with the DWBC, along the western boundary above the DWBC (Figure 4A). Apparently this second jet transfers water inward but does not have remarkable effects on the overturning (thin green line in Figure 2). This fact suggests that the jet is part of a horizontal gyre that is dominantly adiabatic: what is transported inward within the thin jet along the boundary is almost all returned along the same isopycnal surface by much weaker and broader outward flow away from the boundary. The explanation for this jet is as follows. In association with the DWBC, the isopycnal surfaces above and below are slanted respectively up- and downward, forming a bulge-like structure along the boundary where PV is particularly low (Figure 5). This is a structure co-generated by the thermal forcing and the ridge. It in turn pushes isopycnals further up or down in the water column in opposite directions, and the weak jet above the DWBC is a consequence of slanting isopycnals at that level. Hence, this reversing jet is not independent but an accompanying feature of isopycnal structures related to DWBC, and is adiabatic in nature. By the same token, the isopycnals below the DWBC are pushed downward, leading to another reversing jet which, though embedded within the bottom boundary layer, is still noticeable in Figure 4A.
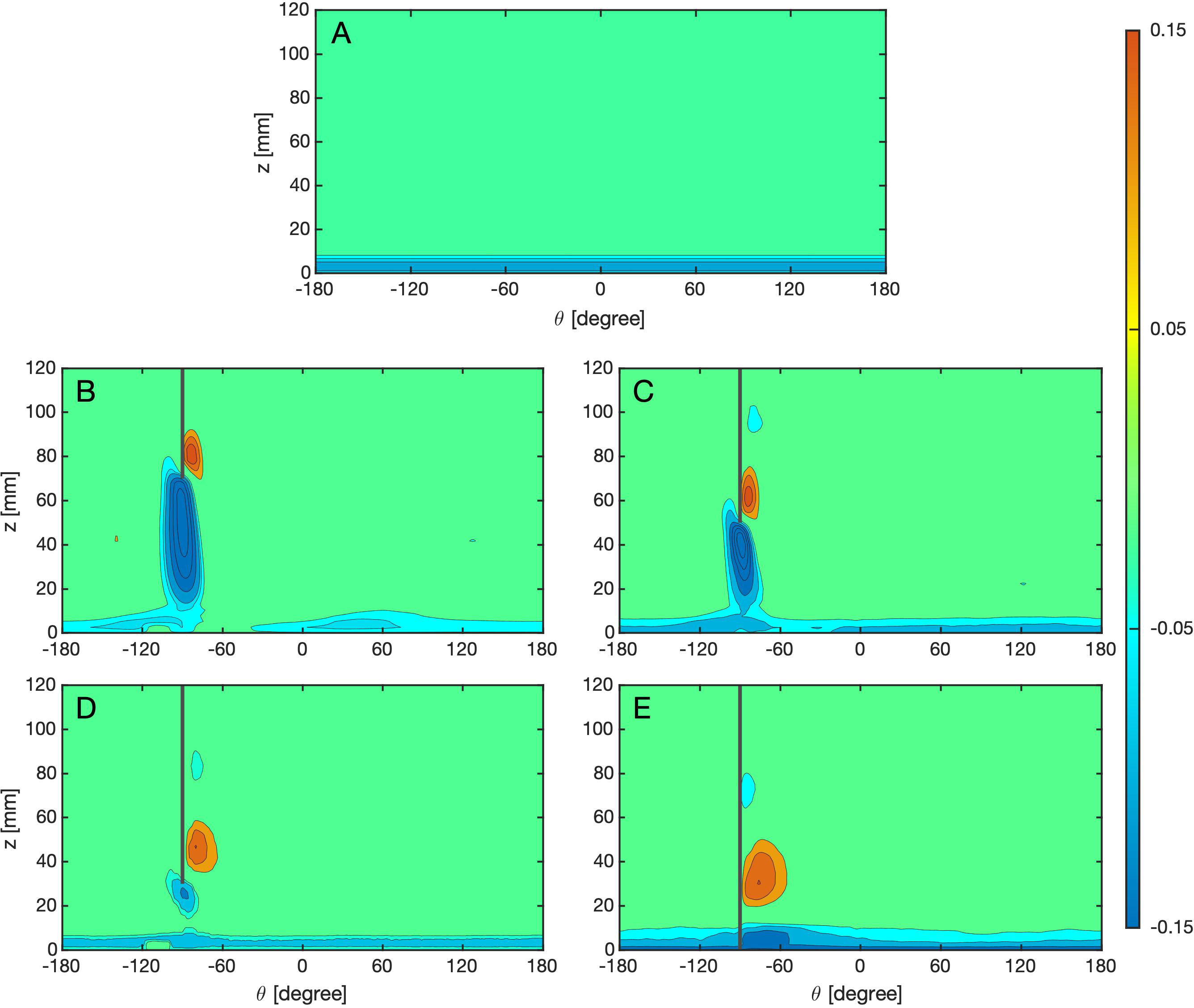
Figure 4 θ − z distribution of the meridional velocity [mm/s] at r = 120 mm in cases with a partial-depth ridge with different D1 (A) no-ridge case (ExpOPEN), (B) 70 mm (ExpR70) (C) 50 mm (ExpR50) (D) 30 mm (ExpR30) (E) 0 mm (ExpR0). The outward (southward) flow is indicated by red, while the northward flow in blue.
When the ridge is lifted upward well above the bottom boundary layer, the reversing jet above the DWBC remains more or less the same as that in the full-depth ridge case. However, the one below the DWBC, is enlarged substantially in both size and magnitude, extending all the way from the lower edge of the ridge to the bottom boundary layer (Figure 4B). At the first glance, this strong reversing jet is puzzling since it appears in the open region. However, considering the mechanism behind the reversing jet above the DWBC, the formation of this lower one can be understood in the similar way.
This three-jet structure consisting of the DWBC sandwiched between two reversing adiabatic jets can be seen more clearly in the vector plots of ExpR50 (Figure 6).
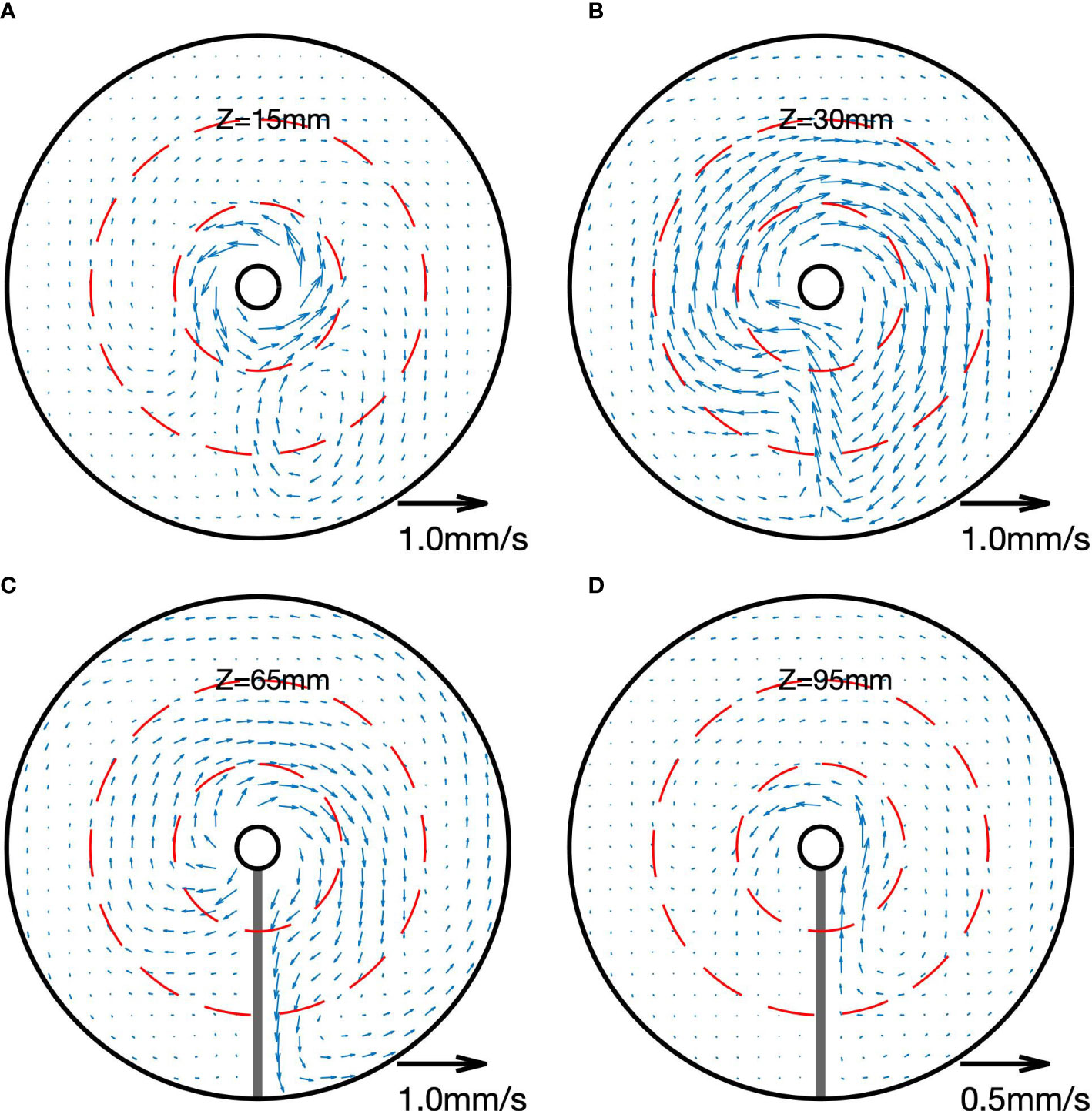
Figure 6 Horizontal velocity vectors of ExpR50 at (A) z = 15 mm, (B) z = 30 mm, (C) z = 65 mm and (D) z=95 mm above the bottom. The circles at r = 60 mm and r = 120 mm are denoted by red dashed lines.
At z = 65 mm (Figure 6C) where the domain is closed, the horizontal circulation is anti-clockwise (top view) within the basin. From the “northeastern” corner, the newly formed water flows westward around the inner cylinder, southward along the ridge as the DWBC, and then turns eastward along the exterior rim. The flow magnitude progressively weakens, indicating the existence of a strong diapycnal or diabatic component.
Above the DWBC at z =95 mm (Figure 6D), the domain is also closed and the basin-wide circulation is in the opposite direction to that below, characterized with another noticeable inward jet along the ridge that also can be seen in Figure 4B.
Below the ridge at z = 30 mm where the domain is open (Figure 6B), water parcels flow clockwise around the inner cylinder; as it approaches the longitudes of the partial-depth ridge, it first slowly turns to the south and then makes a sharp turn back to the north right below the ridge, corresponding to the lower reversing jet in Figure 4B. Along the streamlines, the amplitude of the horizontal flow does not change very much, consistent with the adiabatic nature of the flow at this level.
Further down to the upper edge of the bottom boundary layer at z =15 mm (Figure 6A), the flow becomes anti-clockwise around the inner cylinder, same as that in the boundary layer. A local clockwise eddying flow appears with its west edge under the ridge.
As what have been described, the exclusive feature of the partial-depth ridge is the existence of the jet structure along the longitude of the ridge in the ‘open’ region. In other words, though the ridge is partial in depth, the along-ridge jet structure exists through the water column, with alternating flowing directions. It is a systematic and baroclinic response to the ridge. Taking the isopycnal variations in association with the DWBC as a “topography”, the other two jets and the associated isopycnal variations can be understood as for a baroclinic Taylor column.
It becomes clear that DWBCs can develop along both full- and partial-depth ridges. Then a question arises as to what will happen if more than one ridge exists, like the co-existence of the side boundary and the mid-ocean ridge in the Atlantic basin, or the distribution of multiple partial-depth ridges in the ACC region.
As shown in Figure 7, adding a partial-depth ridge to a closed basin does not do much to affect the original overturning cell in association with the western boundary. However, a second DWBC would develop along the eastern edge of the ridge. Consequently, the total strength of the overturning is to some extent enhanced, but the strength of this second MOC cell is dependent on the ridge’s depth. It is weak as the ridge’s depth is increased, and finally disappears when the ridge is too high above. For example, a DWBC is supported along a single partial-depth ridge with D1=70 mm (Figure 2), but is hardly seen along the same ridge within a closed basin (Figure 7C). This is because as shown in the single-ridge cases the DWBC supported by the “western boundary” (a full-depth ridge) is significantly stronger than that along any partial-depth ridges, so are the related isopycnal variations. In a closed basin the existence of a primary DWBC along the western boundary makes the isopycnals above slope upward and those below downward against the boundary, acting as a large-scale background condition. With the addition of a partial-depth ridge, its DWBC, if exists, resides at a level higher than the primary DWBC and also tries to prop up isopycnals locally. This means isopycnals at levels between the two DWBCs receive two opposite impacts: a tendency of being raised upward by the primary DWBC and a tendency of being pressed down by the second DWBC. As a result of the competition between the two tendencies, the second DWBC will not appear when the related isopycnal variations are too small.
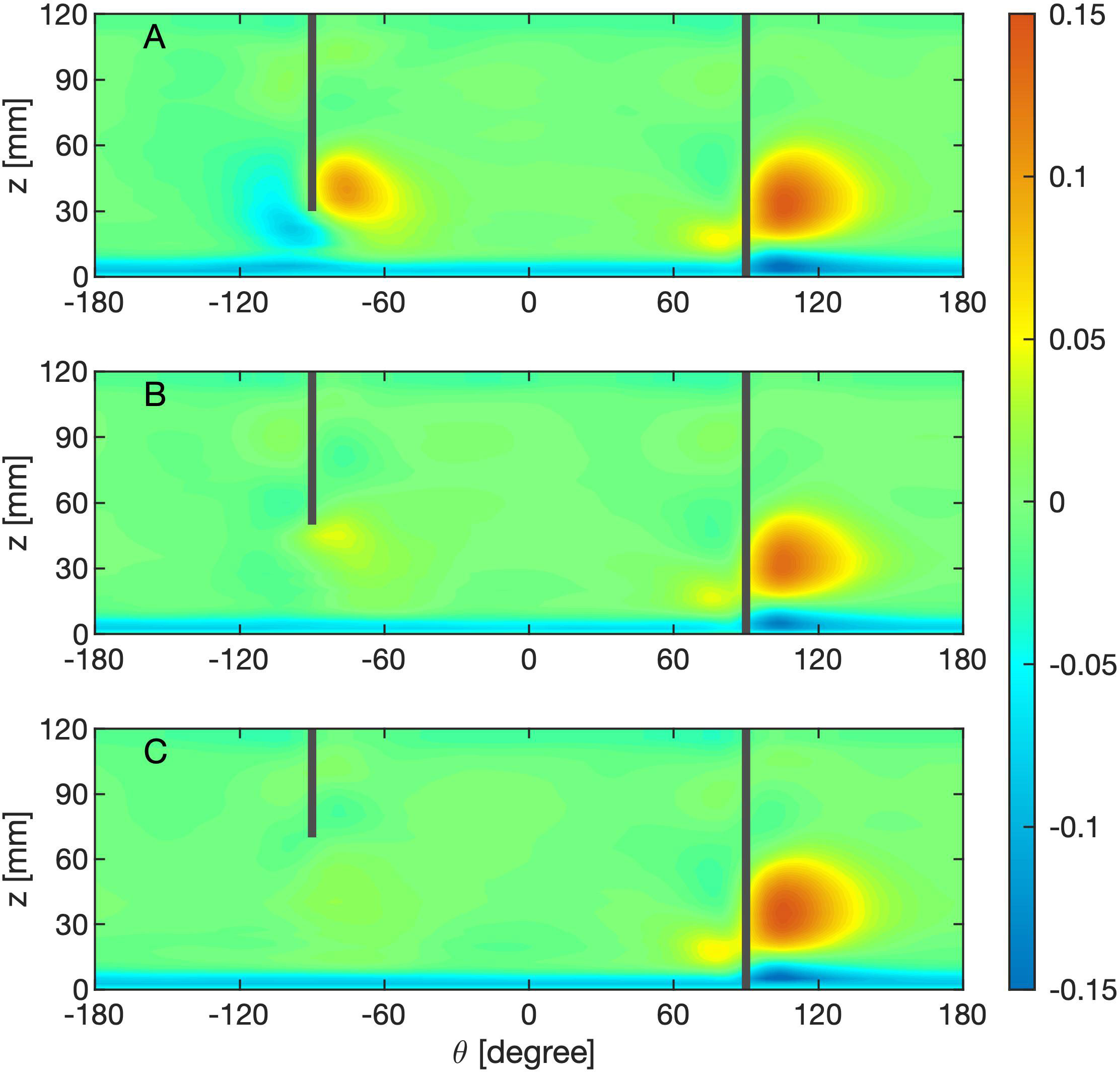
Figure 7 θ − z distribution of the meridional velocity [mm/s] at r = 120 mm in cases with a full radial barrier and a partial ridge with D1 equal to (A) 30 mm, (B) 50 mm, and (C) 70 mm.
What this implies is that in the North Atlantic basin, whether the dense water can be exported along the ridge’s eastern edge depends on its relative depth to that of the primary DWBC along the western boundary. If the mid-Atlantic ridge is lowered down, there probably would be no interior path anymore.
Therefore, we would naturally expect that in presence of multiple partial-depth ridges in a zonally open channel like the latitudinal band of ACC, the resulting flow filed regarding the MOC is determined by the relation among different ridges. This conjecture is confirmed by a series of two-ridge experiments. As shown in Figure 8, the ridge closest to the lower boundary has the strongest DWBC and the two ridges have exactly the same overturning when they have the same height. These are two features that can be easily understood. Interestingly, with two different ridges, the bigger the difference of their heights, the larger the difference of their overturning strengths. This again means the flow as well as the associated isopycnal variations along the shorter ridge with bigger D1 is dominated by those along the ridge with smaller D1. When the shorter ridge is too high above the lower DWBC along the other ridge, it can hardly support a second outward jet.
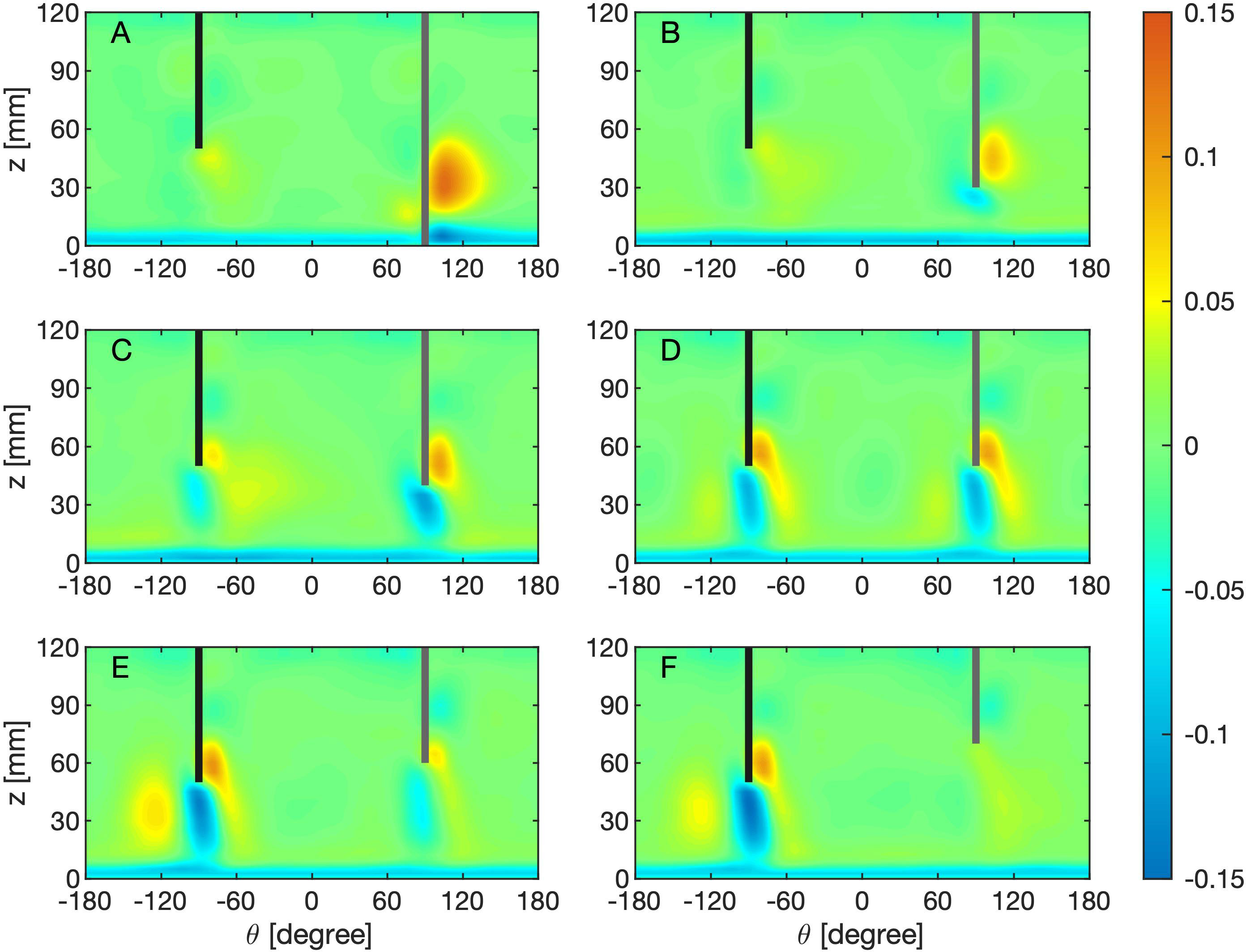
Figure 8 θ − z distribution of the meridional velocity [mm/s] at r = 120 mm with two ridges that have D1 = 50 mm and variable D2. (A) D2 = 0 mm; (B) D2 = 30 mm; (C) D2 = 40 mm; (D) D2 = 50 mm; (E) D2 = 60 mm; (F) D2 = 70 mm.
The overall strength of the overturning circulation, as indicated by the stream function at r=120 mm in Figure 9, generally declines with the increasing depth of the ridge, consistent with above results for single-ridge cases. Whether this result is applicable to the real ocean awaits more direct observational evidence in the future.
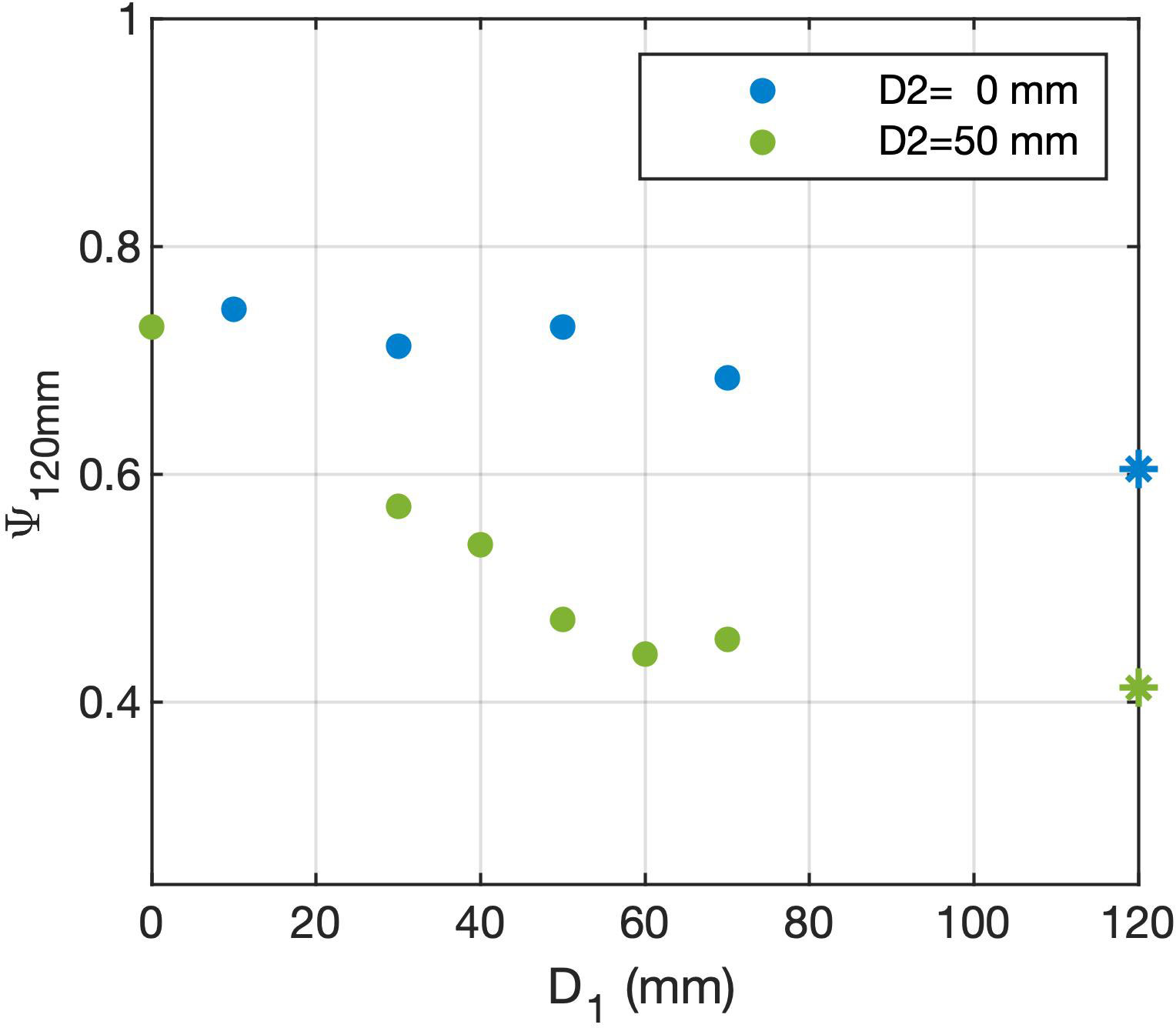
Figure 9 The MOC strength at r = 120 mm for two-ridge cases with variable D1 for D2 = 0 mm (blue dots) and D2 = 50 mm (green dots). The cases denoted by stars are actually single-ridge cases since the full depth of the working fluid is 120 mm.
One remarkable feature of bottom topography, as realized over the past few decades, is the local and substantial enhancement of turbulent mixing (Polzin et al., 1997; Waterman et al., 2013; Waterhouse et al., 2014). According to a recent argument and as a result of this topographic strengthening, the overturning is deeply affected at the large scale: the abyssal upwelling occurs predominantly within a thin boundary layer along the bottom slope, whereas the interior region nearby is characterized by downwelling; the two are comparable in magnitude with a residual balancing that is generated and sinks from the surface (Ferrari et al., 2016; McDougall and Ferrari, 2017; de Lavergne et al., 2017). This is an example of how topography matters for the large-scale baroclinic flow, but it is probably not the only way. As reported in the paper, without spatial variation of diapycnal mixing, ocean ridges can still have impacts on both strength and pattern of the overturning, some of which are fundamental.
Applying experimental results to the real ocean, following features could be presumed. In the North Atlantic Basin, due to the existence of the mid-Atlantic ridge, deep water could be transported southward, in addition to the route along the western boundary, via an interior path along the ridge’s eastern edge. The depth of this interior jet may migrate vertically, upward with increasing strength following the grow of the ridge or downward with decreasing strength following the decay of the ridge. Meanwhile, the formation of this second overturning cell can lead to adiabatic responses in the upper and lower layer, including a local horizontal meander above the ridge, and another opposing jet below the middle jet in the abyss.
However, in the latitudinal band of the Antarctic Circumpolar Current where the ocean bottom is characterized by complex topographic features including multiple meridionally oriented ridges, the transporting path of the Antarctic Bottom Water would be preferentially along higher ridges. With the grow of ridges as induced by plate tectonic evolution in the geological history, the overturning in association with the bottom water would be strengthened, accompanied by changes of stratification in the abyssal ocean which may then have strong impacts on the earth climate (Zachos et al., 2001; Scher and Martin, 2006).
All these conjectures gained from laboratory experiments, some of which are already found consistent with oceanic situation, are valuable in guiding future research in observational or modelling studies of the overturning circulation. The current results also raise some new questions, such as how, compared with ridges (or side boundary), the bottom slope can influence the circulation. Answers to these issues will finally lead us to a more comprehensive understanding of the nature of the ocean overturning.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
YZ and WW conceived the project, carried out experiments, and analyzed the data. YZ wrote the manuscript. ZZ reviewed and edited the manuscript. All authors contributed to the article and approved the submitted version.
This work was supported by the National Natural Science Foundation through Grants 42288101 and 41876007.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Barkan R., Winters K. B., Smith S. G. L. (2013). Rotating horizontal convection. J. Fluid Mech. 723, 556–586. doi: 10.1017/jfm.2013.136
Beardsley R. C., Festa J. F. (1972). A numerical model of convection driven by a surface stress and non-uniform horizontal heating. J. Phys. Oceanogr. 2, 444–455. doi: 10.1175/1520-0485(1972)002<0444:ANMOCD>2.0.CO;2
Coman M. A., Griffiths R. W., Hughes G. O. (2006). Sandström’s experiments revisited. J. Mar. Res. 64, 783–796. doi: 10.1357/002224006779698413
de Lavergne C., Madec G., Roquet F., Holmes R. M., McDougall T. J. (2017). Abyssal ocean overturning shaped by seafloor distribution. Nature 9, 181–186. doi: 10.1029/2012GL052952
Ferrari R., Mashayek A., McDougall T. J., Nikurashin M., Campin J.-M. (2016). Turning ocean mixing upside down. J. Phys. Oceanogr. 46 (7), 2239–2261. doi: 10.1175/JPO-D-15-0244.1
Garrett C., Kunze E. (2007). Internal tide generation in the deep ocean. Annu. Rev. Fluid Mech. 39, 57–58. doi: 10.1146/annurev.fluid.39.050905.110227
Hignett P., Ibbetson A., Killworth P. D. (1981). On rotating thermal convection driven by non-uniform heating from below. J. Fluid Mech. 109, 161–187. doi: 10.1017/S0022112081000992
Hughes G. O., Griffiths R. W. (2008). Horizontal convection. Annu. Rev. Fluid Mech. 40, 185–208. doi: 10.1146/annurev.fluid.40.111406.102148
Hussam W. K., Tsai T. K., Sheard G. J. (2014). The effect of rotation on radial horizontal convection and nusselt number scaling in a cylindrical container. Int. J. Heat Mass Transf. 77, 46–59. doi: 10.1016/j.ijheatmasstransfer.2014.05.007
Ilicak M., Vallis G. K. (2012). Simulations and scaling of horizontal convection. Tellus A 64, 118377. doi: 10.3402/tellusa.v64i0.18377
McDougall T. J., Ferrari R. (2017). Abyssal upwelling and downwelling driven by near-boundary mixing. J. Phys. Oceanogr. 47 (2), 261–283. doi: 10.1175/JPO-D-16-0082.1
Miller R. C. (1968). A thermally convecting fluid heated nununiformly from below (Cambridge: Mass. Inst. Technol.).
Mullarney J. C., Griffiths R. W., Hughes G. O. (2004). Convection driven by differential heating at a horizontal boundary. J. Fluid Mech. 516, 181–209. doi: 10.1017/S0022112004000485
Park Y. G., Whitehead J. A. (1999). Rotating convection driven by differential bottom heating. J. Phys. Oceanogr. 29, 1208–1220. doi: 10.1175/1520-0485(1999)029<1208:RCDBDB>2.0.CO;2
Pedlosky J., Whitehead J. A., Veitch G. (1997). Thermally driven motions in a rotating stratified fluid: theory and experiment. J. Fluid Mech. 339, 391–411. doi: 10.1017/S0022112097005168
Polzin K. L., Toole J. M., Ledwell J. R., Schmitt R. W. (1997). Spatial variability of turbulent mixing in the abyssal ocean. Science 276, 93–96. doi: 10.1126/science.276.5309.93
Rossby T. (1965). On thermal convection driven by non-uniform heating from below: an experimental study. Deep-Sea Res. 12, 9–16. doi: 10.1016/0011-7471(65)91336-7
Rossby T. (1998). Numerical experiments with a fluid heated non-uniformly from below. Tellus 50 (2), 242–257. doi: 10.3402/tellusa.v50i2.14523
Sandström J. W. (1908). Dynamishce versuche mit merrwasser. Ann. Hydrogr. Marit. Meteorol. 36, 6–23.
Scher H. D., Martin E. E. (2006). Timing and climatic consequences of the opening of drake passage. Science 312, 428–430. doi: 10.1126/science.1120044
Sheard G. J., Hussam W. K., Tsai T. (2016). Linear stability and energetics of rotating radial horizontal convection. J. Fluid Mech. 795, 1–35. doi: 10.1017/jfm.2016.193
Stewart K. D. (2012). The effect of sills and mixing on the meridional overturning circulation (Canberra: Australian National University).
St. Laurent L. C., Garabato A. C. N., Ledwell J. R., Thurnherr A. M., Toole J. M., Watson A. J. (2012). Turbulence and diapycnal mixing in drake passage. J. Phys. Oceanogr. 42, 2143–2125. doi: 10.1175/JPO-D-12-027.1
Tailleux R., Rouleau L. (2010). The effect of mechanical stirring on horizontal convection. Tellus 62 (2), 138–153. doi: 10.1111/j.1600-0870.2009.00426.x
Toggweiler J. R., Bjornsson H. (2000). Drake passage and paleoclimate. J. Quat. Sci. 15, 319–328. doi: 10.1002/1099-1417(200005)15:4<319::AID-JQS545>3.0.CO;2-C
Wang F., Huang S.-D., Zhou S.-Q., Xia K.-Q. (2016). Laboratory simulation of the geothermal heating effects on ocean overturning circulation. J. Geophys. Res.: Ocean. 121, 7589–7598. doi: 10.1002/2016JC012068
Waterhouse A. F., MacKinnon J. A., Nash J. D., Alford M. H., Kunze E., Simmons H. L., et al. (2014). Clobal pattern of diapycnal mixing from measurement of the turbulent dissipation rate. J. Phys. Oceanogr. 44, 1854–1872. doi: 10.1175/JPO-D-13-0104.1
Waterman S., Garabato A. C. N., Polzin K. L. (2013). Internal waves and turbulence in the Antarctic circumpolar current. J. Phys. Oceanogr. 43, 259–282. doi: 10.1175/JPO-D-11-0194.1
Whitehead J. A., Pedlosky J. (2000). Circulation and boundary layers in differentially heated rotating stratified fluid. Dynam. Atmos. Ocean. 31, 1–21. doi: 10.1016/S0377-0265(99)00026-3
Whitehead J. A., Wang W. (2008). A laboratory model of vertical ocean circulation driven by mixing. J. Phys. Oceanogr. 38, 1091–1106. doi: 10.1175/2007JPO3805.1
Winters K. B., Barkan R. (2013). Available potential energy density for boussinesq fluid flow. J. Fluid Mech. 714, 476–488. doi: 10.1017/jfm.2012.493
Wunsch C., Ferrari R. (2004). Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech. 36, 281–314. doi: 10.1146/annurev.fluid.36.050802.122121
Zachos J., Pagani M., Sloan L., Thomas E., Billips K. (2001). Trends, rhythms, and aberrations in global climate 65 ma to present. Science 292, 686–693. doi: 10.1126/science.1059412
Keywords: rotating, horizontal convection, meridional overturning circulation, meridional ridge, deep western boundary current
Citation: Zhang Y, Zhang Z and Wang W (2022) Rotating horizontal convection with meridional ridges. Front. Mar. Sci. 9:1053964. doi: 10.3389/fmars.2022.1053964
Received: 26 September 2022; Accepted: 07 November 2022;
Published: 21 November 2022.
Edited by:
Shengqi Zhou, South China Sea Institute of Oceanology (CAS), ChinaReviewed by:
Lei Zhou, Shanghai Jiao Tong University, ChinaCopyright © 2022 Zhang, Zhang and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wei Wang, d2VpQG91Yy5lZHUuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.