Using geostatistical analysis for simultaneous estimation of isoscapes and ontogenetic shifts in isotope ratios of highly migratory marine fish

Tracking migration of highly migratory marine fish using isotope analysis (iso-logging) has become a promising tool in recent years. However, application of this method is often hampered by the lack of essential information such as spatial variations in isotope ratios across habitats (isoscapes) and ontogenetic shifts of isotope ratios of target animals. Here, we test the utility of geostatistical analysis to generate isoscapes of δ¹³C and δ¹⁵N in the western Pacific and estimate the ontogenetic shifts in δ¹³C and δ¹⁵N values of a target species. We first measured δ¹³C and δ¹⁵N in the white muscle of juvenile (n = 210) and adult (n = 884) skipjack tuna Katsuwonus pelamis sampled across the northwest Pacific. Next we fitted a geostatistical model to account for the observed spatial variations in δ¹³C and δ¹⁵N of skipjack by fork length and other environmental variables with spatial random effects. We then used the best-fit models to predict the isoscapes of δ¹³C and δ¹⁵N in 2021. Furthermore, we measured δ¹⁵N of amino acids (δ¹⁵N_AAs) of skipjack (n = 5) to determine whether the observed spatial variation of isotope ratios resulted from baseline shifts or differences in trophic position. The geostatistical model reasonably estimated both isoscapes and ontogenetic shifts from isotope ratios of skipjack, and the isoscapes showed that δ¹³C and δ¹⁵N can clearly distinguish the latitudinal migration of skipjack in the western Pacific. The δ¹⁵N_AAs supported the results of the geostatistical model, that is, observed variations in skipjack δ¹⁵N were largely derived from a baseline shift rather than regional differences in trophic position. Thus, we showed that geostatistical analysis can provide essential basic information required for iso-logging without compound-specific isotope analysis.

Introduction

Shared fish stocks, namely fish resources with high migration ability that cross exclusive economic zone (EEZ) boundaries, are more prone to overexploitation than other stocks (e.g. McWhinnie, 2009; Kraska et al., 2015; Popova et al., 2019). Therefore, cooperative stock management among stakeholders is a necessary prerequisite for achieving sustainable fisheries of these species (e.g. Caddy, 1997; Miller and Munro, 2004). Appropriate understanding of migration routes and their individual and temporal variation is crucial for better cooperative management of shared fish stocks. Knowledge of a migration route is also essential for determining which countries share fishery resources from the same stock, as well as for assessing the effect of changes in the migration routes on the stock and fishing conditions in each country (Miller and Munro, 2004; Vatsov, 2016). Recently developed models (e.g. Carvalho et al., 2015; Sippel et al., 2015) can make use of migration data for stock assessment, thus demonstrating the benefits of understanding the migration routes of these fish.

In fishery science, one of the main approaches for studying fish migration is dynamic tracking using electronic technologies such as telemetry, radio, and computer networks (e.g. Priede et al., 1988; Thorstad et al., 2013). Although these methods have excellent spatial and temporal resolution, there are several intrinsic drawbacks, such as the high cost of bio-logging equipment (Hebblewhite and Haydon, 2010; Graves and Horodysky, 2015), the large effort required for capturing and tagging the fish, and body-size limitations for tagged fish: conventionally, the recommended tag weight is less than 3% of the fish body mass (e.g. Winter, 1983; Jepsen et al., 2002; Cooke et al., 2011). Stock assessment models are generally based on population-level data, but bio-logging methods only yield individual-level inferences, making them difficult to incorporate into overall stock condition assessments. In addition, equipment attached to a target fish can change its behavior, potentially resulting in biased migration data, although the effect is highly context-dependent and species-specific (Jepsen et al., 2015).

To overcome these drawbacks of bio-logging and make use of migration data for stock assessment of shared fish stocks, other approaches with lower cost and less effort are warranted. Recently, migration tracking techniques using isotope analysis of incremental-growth tissues such as otoliths, eye lenses, and vertebral bones (Matsubayashi et al., 2017; Sakamoto et al., 2019; Matsubayashi et al., 2020; Vecchio and Peebles, 2020) have proven promising for inferring the migration routes of individual fish. The isotopic composition of local environment and an animal’s tissue can be used as a natural tag to track its movements through isotopically distinct habitats (Graham et al., 2010), and we call this technique “iso-logging”. The major advantages of iso-logging over bio-logging are lower cost and effort, longer period of tracking (Vecchio and Peebles, 2020), and no influence on the behavior of target fish before death, although the temporal resolution and accuracy of estimated ranges are not equal to those from bio-logging.

In the case of marine fish, the ¹⁸O:¹⁶O ratio (δ¹⁸O) in otoliths is the most frequently used isotope ratio for iso-logging (e.g. Trueman et al., 2012; Hsieh et al., 2019; Sakamoto et al., 2019). δ¹⁸O can be retrospectively measured from otoliths and reflects the ambient temperature experienced by the fish. However, δ¹⁸O is not effective for iso-logging of fish that 1) migrate in oceans with similar thermal gradients, 2) have a stable body temperature, like tuna (Thunnus spp.; Carey and Teal, 1969), or 3) often dive deep, crossing the thermocline. Skipjack tuna Katsuwonus pelamis comprises one of the most commercially important shared fish stocks inhabiting warm and temperate waters. Skipjack in western Pacific populations prefer sea-surface temperatures ranging from 20.5 to 26.0°C (Mugo et al., 2010) and can maintain its body temperature higher than that of ambient water (Barrett and Hester, 1964; Stevens et al., 1974), which hampers the use of otolith δ¹⁸O for migration tracking. For this reason, it is necessary to test the applicability of other isotope ratios for tracking skipjack migration. Recent studies have suggested that stable carbon and nitrogen isotope ratios (δ¹³C and δ¹⁵N) can be excellent indicators for the migration histories of marine animals in some areas (Trueman et al., 2017; Matsubayashi et al., 2020), and these isotopes may be also applicable for tracking skipjack in the western Pacific (Coletto et al., 2021).

To use δ¹³C and δ¹⁵N for iso-logging of marine fish, at least three types of information are required: 1) the isoscapes across the habitat, 2) any ontogenetic shifts of isotope ratios of target fish, and 3) isotopic offsets between isoscapes and target fish. Unfortunately, it is generally difficult to obtain all of this information for δ¹³C and δ¹⁵N. The generation of isoscapes requires thorough field sampling of proxy organisms with low swimming ability (Trueman et al., 2017; Matsubayashi et al., 2020). Understanding isotopic offsets between isoscape and target animal requires feeding experiments over several months (e.g. Matsubayashi et al., 2019; Canseco et al., 2021). Furthermore, in the case of highly migratory piscivorous species, understanding the ontogenetic shifts of δ¹³C and δ¹⁵N is particularly difficult because isoscapes and ontogenetic dietary shifts have mutual interactions. To overcome these difficulties in iso-logging, we conceived of using a geostatistical model to simultaneously estimate isoscapes and ontogenetic shifts of isotope ratios using the fish targeted for migration tracking as a proxy organism for isoscapes. With this approach, isotopic offsets between isoscapes and target fish can be ignored. Although such modeling was technically difficult up until a few years ago, recent advances in geostatistical analysis (e.g. Rue et al., 2009; Thorson, 2019; Anderson et al., 2022) allow us to account for these factors in a single model with a user-friendly interface.

Here, we test the utility of geostatistical analysis for generating isoscapes using δ¹³C and δ¹⁵N of skipjack in the western Pacific, considering ontogenetic shifts in isotope ratios of this species. In this region, skipjack is mainly distributed from 20°S to 40°N and from 110°E to 180°E (Bartoo, 1987; Kiyofuji and Ochi, 2016), and some individuals exhibit dynamic northward migration from the subtropics into waters off the Pacific coast of Japan (Kiyofuji et al., 2019a). The water temperature range preferred by skipjack is from 18.8°C to 28.1°C and the 18.0 isotherm is the lowest thermal limit of skipjack tuna distribution (Kiyofuji et al., 2019a). We sampled the muscle tissue of skipjack of various body sizes and determined the δ¹³C and δ¹⁵N values of bulk tissue (δ¹³C_Bulk and δ¹⁵N_Bulk). We then applied a geostatistical model to account for variations in the δ¹³C and δ¹⁵N of skipjack muscle with fork length, several environmental variables, and a spatial random field. Furthermore, we performed compound-specific nitrogen isotope analysis of amino acids (δ¹⁵N_AAs) for five samples with different δ¹⁵N_Bulk values to evaluate whether the differences in bulk values resulted from a baseline shift in isotope ratios or from trophic differences (see Matsubayashi et al., 2020). On the basis of these data, we discuss the applicability of δ¹³C_Bulk and δ¹⁵N_Bulk for assessing the migration of skipjack in the western Pacific.

Materials and methods

Sample collection and preparation

Samples of juvenile skipjack (n = 210) were collected during 1995–2019 from multiple sampling stations in the western Pacific by mid-water trawl (mesh size: 16mm) during several research cruises of the Fisheries Resources Institute, Japan Fisheries Research and Education Agency. Juvenile fish from the EEZs of countries other than Japan were collected under formal agreement with each country. The 20 cm fork length is the threshold that distinguishes juvenile from adults, and it takes about 3 months for skipjack to reach this length (Kiyofuji et al., 2019b). Dorsal white muscle sampled from juvenile fish was rinsed in distilled water for at least six hours, because the samples were preserved in ethanol, and then the samples were freeze-dried. Most samples of adult skipjack (n = 884) were purchased from commercial fisheries, and some were caught by research vessel surveys. None of them were from the EEZ of countries other than Japan (Figure 1). Dorsal white muscle was sampled from each fish and kept frozen until isotopic analysis. The sampling stations for skipjack ranged from 5.0°S to 40.9°N and from 123.0°E to 164.9°E (Figure 1). The muscle samples were ground into fine powder and defatted using a methanol:chloroform mixture (1:2, v:v) and then used for bulk and compound-specific isotopic analyses.

FIGURE 1

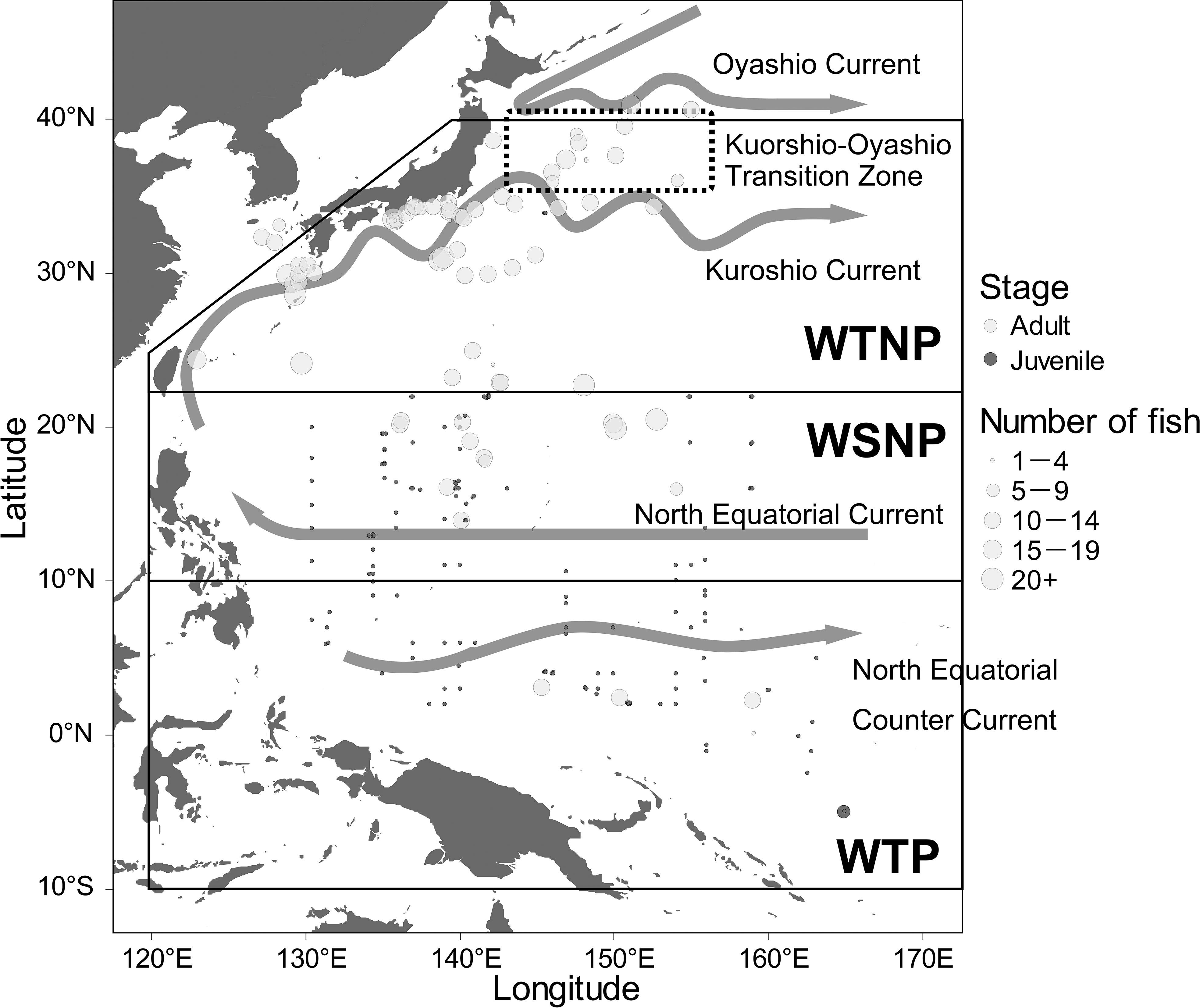
Figure 1 Sampling points and sample sizes of juvenile and adult skipjack tuna (Katsuwonus pelamis), boundaries of the western tropical Pacific (WTP), western subtropical North Pacific (WSNP), western temperate North Pacific (WTNP), and schematic diagram of the major currents in the western Pacific Ocean. The Kuroshio-Oyashio Transition Zone is known to have high net primary productivity (Nishikawa et al., 2020).

Measurement of δ¹³C_Bulk and δ¹⁵N_Bulk

The δ¹³C_Bulk and δ¹⁵N_Bulk values were measured using continuous-flow elemental analyzer (EA)/isotope-ratio mass spectrometry (IRMS) systems. Stable isotope ratios are expressed in conventional δ notation in accordance with the international standard scale, based on the following equation:

$$\delta X(‰) = (R_{sample}/R_{standard}- 1) \times 10^3$$

where X is ¹³C or ¹⁵N, R_sample is the ¹³C:¹²C or ¹⁵N:¹⁴N ratio of the sample, and R_standard is that of Vienna Pee Dee Belemnite (VPDB) or atmospheric nitrogen (AIR), respectively. Elemental concentrations and isotope ratios of carbon and nitrogen were calibrated against those of alanine, glycine, and histidine laboratory standards, which are traceable back to international standards. The analytical errors (SDs) of δ¹³C and δ¹⁵N were smaller than 0.18‰ and 0.16‰, respectively.

Measurement of δ¹⁵N_AAs

The δ¹³C_Bulk and δ¹⁵N_Bulk values allow the study area to be isotopically divided into at least three regions: the western tropical Pacific (WTP), western subtropical North Pacific (WSNP), and western temperate North Pacific (WTNP). We chose a total of five skipjack samples representing the δ¹³C_Bulk and δ¹⁵N_Bulk values in each region for δ¹⁵N_AAs analysis. Samples for δ¹⁵N_AAs were prepared using a method based on the amino-acid derivatization procedures described in Chikaraishi et al. (2015) as follows. Samples were initially hydrolyzed with 12 M HCl at 110°C overnight (>12 h) and then washed with n-hexane:dichloromethane (3:2, v:v) to remove any hydrophobic constituents. After hydrolysis, samples were derivatized using thionyl chloride:2-propanol (1:4, v:v) at 110°C for 2 h and then pivaloyl chloride:dichloromethane (1:4, v:v) at 110°C for 2 h. The amino-acid derivatives were then extracted with n-hexane:dichloromethane (3:2, v:v). The δ¹⁵N value of each amino acid was determined by gas chromatography/combustion/isotope-ratio mass spectrometry (GC/C/IRMS) using a 6890N GC instrument (Agilent Technologies, Palo Alto, CA, USA) coupled to a Delta plus XP IRMS via GC-combustion III interface (Thermo Finnigan, Bremen, Germany) at the Japan Agency for Marine-Earth Science and Technology. Reference mixtures of nine amino acids (alanine, glycine, leucine, norleucine, aspartic acid, methionine, glutamic acid, phenylalanine, and hydroxyproline) with known δ¹⁵N values (ranging from −26.4‰ to +45.6‰; Indiana University, Bloomington, IN, USA, and SI Science Co., Sugito-machi, Japan) were analyzed every four to six sample runs. The average SD of the standards was 0.7‰ (n = 16).

Estimation of trophic position

The trophic positions (TPs) of the fish sampled for δ¹⁵N_AAs (n = 5) were estimated from differences between the δ¹⁵N values of glutamic acid and phenylalanine as follows (Chikaraishi et al., 2009):

$$T{P}_{Glu-Phe}=\left({\delta }^{15}{N}_{Glu}–{\delta }^{15}{N}_{Phe}–\beta \right)/TD{F}_{Glu-Phe}+1$$

where δ¹⁵N_Glu is the δ¹⁵N of glutamic acid, δ¹⁵N_Phe is the δ¹⁵N of phenylalanine, β is the difference between δ¹⁵N_Glu and δ¹⁵N_Phe in primary producers, and TDF_Glu-Phe is the trophic discrimination factor for δ¹⁵N of glutamic acid relative to phenylalanine. We used a value of 3.4 for β and 7.6‰ for TDF_Glu-Phe (Chikaraishi et al., 2009).

Environmental variables

Data for the following environmental variables in the euphotic zone (depth < 100 m) of the western Pacific were obtained from Copernicus Marine Environment Monitoring Service (CMEMS, https://marine.copernicus.eu/): potential temperature, salinity, concentrations of chlorophyll a, dissolved oxygen, nitrate, phosphate, and iron, and surface partial pressure of carbon dioxide (spCO2). These data have at most four dimensions: latitude, longitude, date (year and month), and depth. Among these, latitude and longitude were set to the same as the skipjack sampling points; however, it was necessary to assume an interval for data aggregation of date and depth prior to allocating the environmental variables for each data point.

To determine the aggregation interval for the environmental information for each data point, we estimated the isotopic turnover rate (i.e., the rate at which the elements comprising a tissue are replaced) of muscle for adult and juvenile skipjack. Although there are no empirical studies estimating species-specific turnover times for skipjack, Coletto et al. (2021) suggested that adult skipjack has a shorter turnover time than Thunnus species, considering the faster growth rates of this species, and assumed a turnover time similar to those estimated for juvenile yellowfin tuna (around 2–4 months; Graham et al., 2007). For this reason, we used the average values of the environmental variables at each sampling point over the four months leading up to and including the sampled month for adult fish with fork length greater than 200 mm. Because juvenile fish with fork length<200 mm seem to have shorter turnover times than adult fish, given their higher growth rate (Hoyle et al., 2011), we used monthly mean values of environmental variables at each sampling point for the sampled year and month for juvenile skipjack.

As the representative depth for aggregating the environmental variables, we selected the depth at which the concentration of phytoplankton was highest by using data for phytoplankton concentration from CMEMS, assuming that δ¹³C and δ¹⁵N of phytoplankton at that depth were the main influences on the values in skipjack muscle. We then extracted and allocated the environmental variables at the location, period and depth corresponding to each data point (Supplementary Table 1).

Statistical analysis

To estimate spatial distributions of δ¹³C_Bulk and δ¹⁵N_Bulk values in the western Pacific, we used the R package “sdmTMB” ver. 0.0.26.9001 (Anderson et al., 2022), which accounts for independent region-specific noise via the stochastic partial differential equations (SPDE) approach. In sdmTMB, the spatial random effect is assumed to form continuous Gaussian Markov random fields (GMRF) and is approximated by creating a Delaunay triangularized mesh over the study area (Lindgren et al., 2011). sdmTMB makes use of the integrated nested Laplace approximation (INLA; Rue et al., 2009) to create the triangularized meshes. We set the number of nodes to 200 and determined the optimal cutoff value for the number of nodes via the “cutoff_search” option in sdmTMB (Anderson et al., 2022). Meshes on land were transformed into barrier meshes (meshes with correlation barriers) using the “add_barrier_mesh” function of sdmTMB (Anderson et al., 2022).

To maximize the prediction ability of the model, we implemented thin plate regression splines (Wood, 2003) for all covariates. We used smoothers with specified basis dimensions (k values), which were 3 for fork length and 5 for the other covariates. A smaller basis dimension (k = 3) was assumed for fork length because the relationships between fork length and δ¹³C_Bulk and δ¹⁵N_Bulk are expected to be either positive linear or positive asymptotic relationships (Fry and Sherr, 1984; Minagawa and Wada, 1984). The relationships between δ¹³C_Bulk or δ¹⁵N_Bulk and the other parameters were unknown, hence we assigned these a larger basis dimension (k = 5). We did not implement temporal random effects because there is a large bias in the year the samples were taken. The response variables were modelled using the Gaussian family with identity link function.

From this, the model can be specified as: y_i = α₀ + X_iβ + W_i where y_i is the δ¹³C_Bulk or δ¹⁵N_Bulk value of skipjack muscle at sampling location i (i = 1, …, n; n = 1094), α₀ is the intercept, β is the vector of regression parameters, X_i is the matrix of the explanatory covariates (fork length and environmental variables) at location i, and W_i represents the spatially structured random effect at location i. We searched for the best combinations of the covariates (X_i) for prediction of δ¹³C_Bulk and δ¹⁵N_Bulk values of skipjack muscle by model selection based on the Akaike information criterion (AIC). We tested three options for each covariate—the variable with smoothing, the variable without smoothing, and without the variable at all—and then calculated the AIC for models with all combinations of these three options for nine covariates. Due to computational time limitations for model selection, we could not incorporate additional explanatory variables such as the effect of season. St John Glew et al. (2021) incorporated the effect of season as explanatory variables, which improved the model predictions. However, we believe that seasonal effects are not an important variable in our model, because the CMEMS environmental data are themselves highly seasonally variable, and their effects are incorporated into the model with smoothing splines. Finally, models with the smallest AIC were chosen as best-fit models for the prediction of δ¹³C_Bulk and δ¹⁵N_Bulk values of skipjack muscle.

For the best fit models, sanity checks on the items listed below were performed by the “sanity” function of sdmTMB; the non-linear minimizer suggests successful convergence, the Hessian matrix is positive definite, no extreme or very small eigen values are detected, no gradients with respect to fixed effects are greater than 0.001, no fixed-effect standard errors are not applicable (N/A), no fixed-effect standard errors look unreasonably large, no sigma parameters are less than 0.001, and the range parameter does not look unreasonably large. All statistical analysis was conducted using R (R Core Team, 2021).

Generation of isoscapes

To generate isoscapes of δ¹³C and δ¹⁵N in the western Pacific, we obtained monthly mean values of the environmental variables within the triangularized meshes of sdmTMB from January to December 2021 from CMEMS. The environmental variables were then fitted with the best-fit models of δ¹³C and δ¹⁵N to generate isoscapes for 2021, while fork length was set to 0. The uncertainties (standard deviations) of spatial prediction were estimated via simulation from the fitted model (n = 500). Predictions with uncertainty >2 for δ¹⁵N and >1 for δ¹³C were excluded from the isoscapes to avoid excessive extrapolation.

Results

Size and distribution of sampled fish

The fork length of skipjack sampled ranged from 11 to 834 mm (384 ± 186 mm), and that of juveniles and adults were from 11 to 170 mm (36 ± 26 mm) and from 25 to 83 mm (466 ± 85 mm), respectively. Juveniles were distributed from 130.4°E to 164.9°E (mean 146.0°E) and from 5.0°S to 33.9°N (10.0°N) Adults were found from 123.0°E to 159.0°E (140.1°E) and from 2.3°S to 40.9°N (28.8°N) (Figure 1). The sample sizes at each sampling station were generally small for juvenile fish (1.3 ± 0.7) but large for adult fish (11.5 ± 7.7).

δ¹³C_Bulk and δ¹⁵N_Bulk values

The observed δ¹³C_Bulk and δ¹⁵N_Bulk values of skipjack ranged from –20.0‰ to –15.7‰ (mean ± SD, –17.8‰ ± 0.8‰) and from 3.1‰ to 18.9‰ (9.7‰ ± 2.4‰), respectively. Skipjack in the WTP had high δ¹⁵N_Bulk values and those in the WSNP and WTNP had low and intermediate values, respectively (Figure 2). The spatial variation in δ¹³C_Bulk of skipjack muscle is characterized by lower values in the WTNP than in the WSNP and WTP (Figure 2).

FIGURE 2

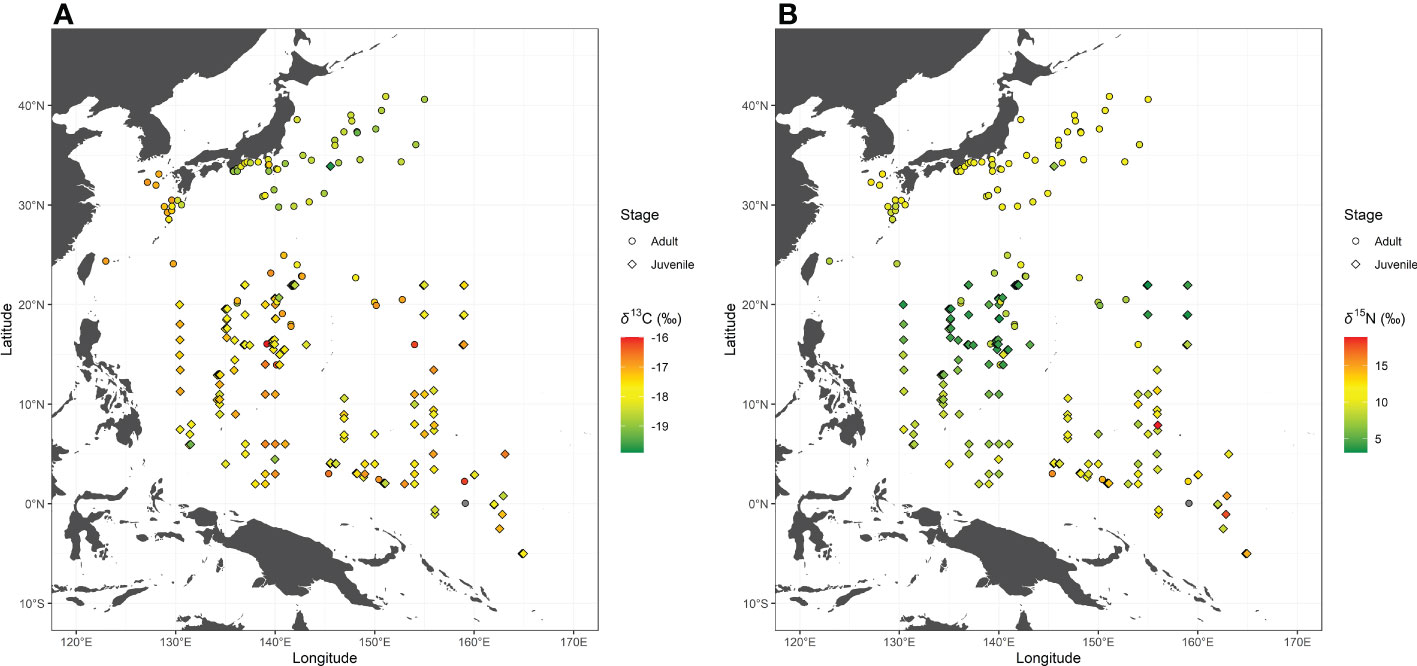
Figure 2 Bulk tissue carbon (δ¹³C_Bulk: A) and nitrogen (δ¹⁵N_Bulk: B) stable isotope ratios of skipjack tuna (Katsuwonus pelamis) in the western Pacific. Isotope ratios of skipjack of the same stage collected at the same location are averaged.

Model fit and selection

The best-fit model for δ¹⁵N included salinity, temperature, phosphate, and nitrate concentrations without smoothing, and fork length and iron concentration with smoothing (Supplementary Figures 1 and 2, Table 1). All sanity checks were positive for the best-fit model. The ΔAIC (the difference between the AIC for a model and the best-fit model) of the model with the second lowest AIC (ΔAIC_{2nd – Best}) was 0.986, and the best-fit model accounted for 86.9% of the variation in observed δ¹⁵N values of skipjack muscle.

TABLE 1

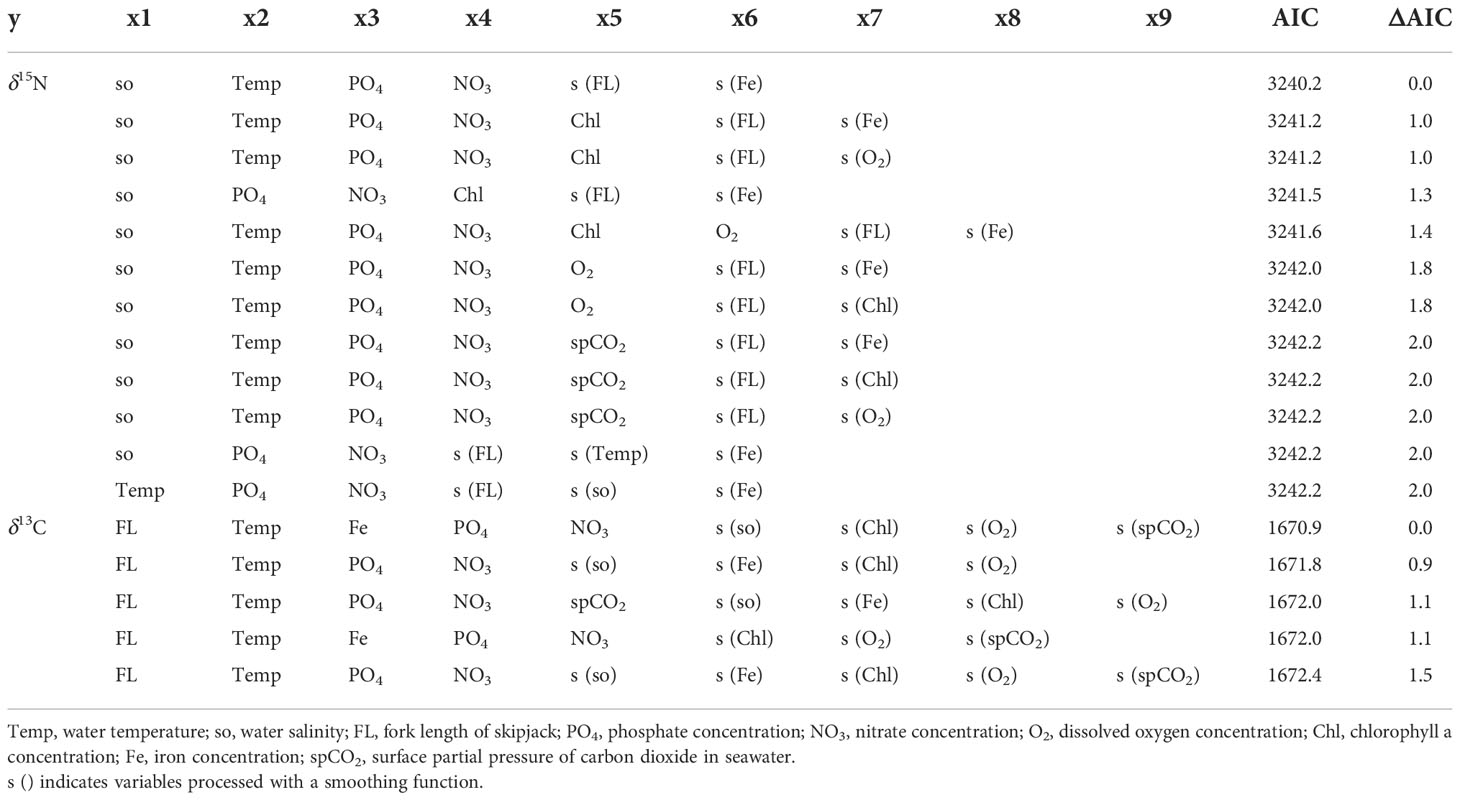
Table 1 Results of model selection based on the Akaike information criterion (AIC). Models with ΔAIC ≤ 2 are shown.

The best-fit model for δ¹³C included fork length, temperature, phosphate, nitrate, and iron concentrations without smoothing, and salinity, concentrations of chlorophyll a and dissolved oxygen, and the surface partial pressure of carbon dioxide with smoothing (Table 1). All sanity checks were positive for the best-fit model. The ΔAIC_{2nd – Best} was 0.942, and the best-fit model accounted for 72.1% of the variation in observed δ¹³C values of skipjack muscle.

The δ¹⁵N and fork length of skipjack show a positive asymptotic relationship (Figure 3A), with a largely monotonous increase until fork length reaches 400 mm (0.01265‰/mm), approaching an asymptotic value at 600 mm (Δδ¹⁵N_600mm–0mm = 5.84‰). Fork length with smoothing was included in all models with ΔAIC smaller than 2 for δ¹⁵N. The δ¹³C and fork length of skipjack showed a positive linear relationship (Supplementary Figure 2) with a small coefficient (0.00077‰/mm). Fork length without smoothing was included in all models with ΔAIC smaller than 2 for δ¹³C.

FIGURE 3

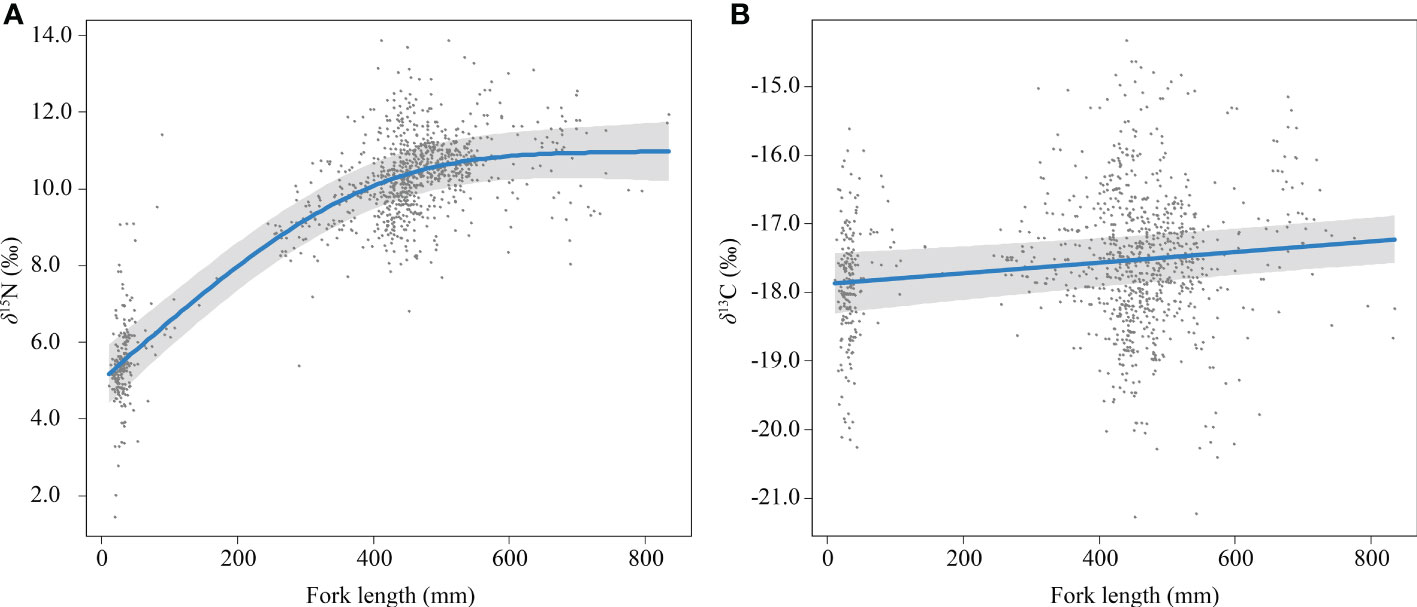
Figure 3 Relationship between fork length and δ¹⁵N_Bulk (A) and δ¹³C_Bulk (B) of skipjack tuna (Katsuwonus pelamis) in the western Pacific (blue lines) with randomized quantile partial residuals (gray areas) from the best-fit models. Each data point represents residuals from each data.

Isoscapes in the western Pacific

The western Pacific δ¹⁵N isoscape showed a clear latitudinal trend, with values in the WTP (from 10°S to 10–15°N) higher than in other northern regions (Figure 4). Overall, the uncertainty profile of δ¹⁵N was low around the sampling points, but high in the marginal region of our study area. On the other hand, δ¹³C was low in the WTNP (north of 20°N) and around the equator (from 2°S to 4°N) compared with the other regions. The uncertainty of estimated δ¹³C was low around the sampling points north of 4°N, but high in the marginal regions of the study area and south of 4°N regardless of the spatial density of sampling points.

FIGURE 4

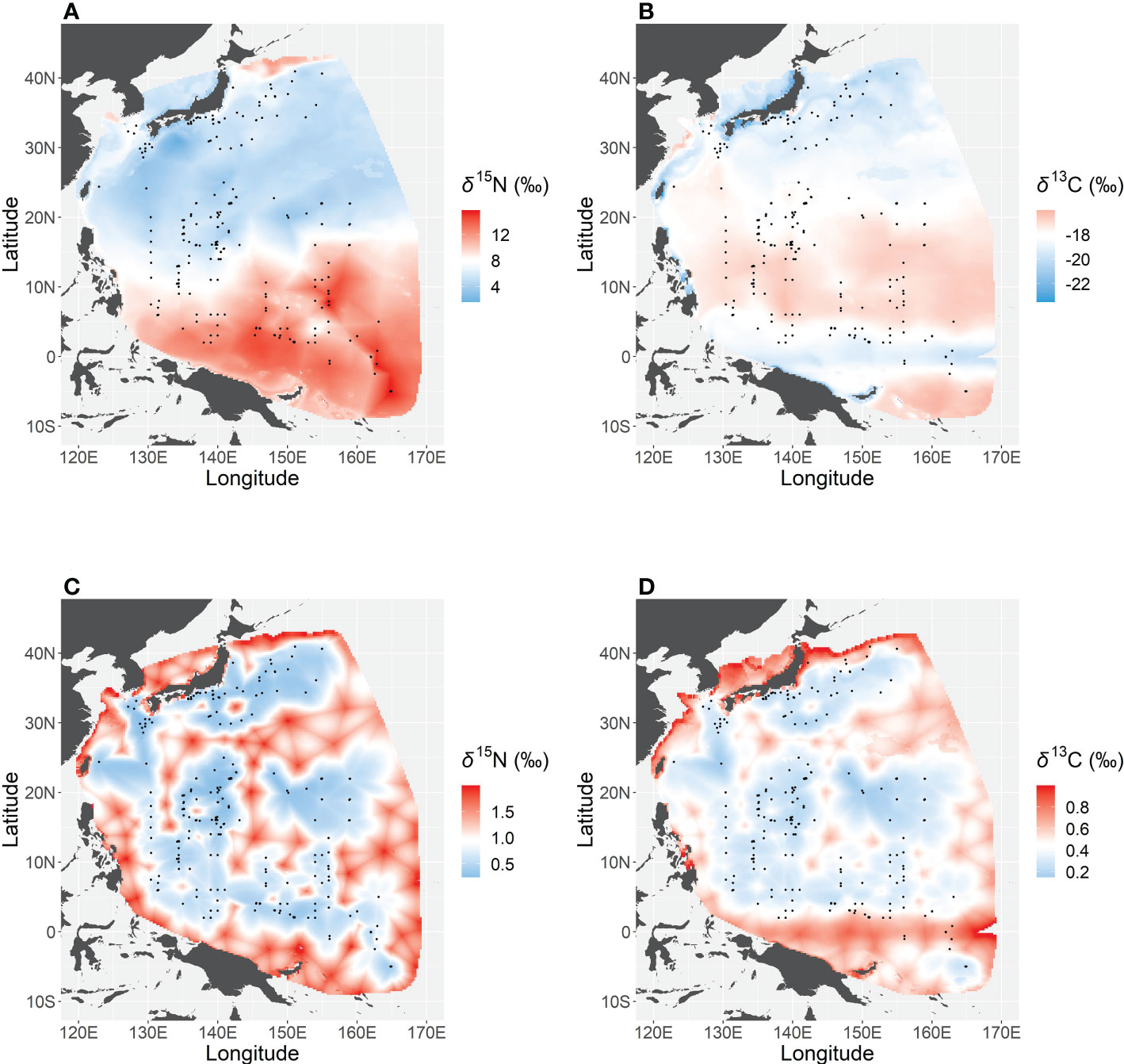
Figure 4 Isoscapes of nitrogen (A) and carbon (B) stable isotope ratios in the western Pacific, and the uncertainty (standard deviation) of predicted nitrogen (C) and carbon (D) isotope ratios estimated by simulation from the best-fit models (n = 500).

Measurement of δ¹⁵N_AAs

The results of compound-specific δ¹⁵N analysis for five skipjack samples representing the main regions (WTP, WSNP, and WTNP) with typical bulk-tissue isotope ratios are shown in Table 2. In summary, regional mean δ¹⁵N_Bulk was highest for WTP, followed by WTNP and WSNP, while TP_Glu–Phe was highest for WTNP followed by WSNP and WTP. Thus, the trend in the regional variability of δ¹⁵N_Bulk was not consistent with that of TPGlu–Phe (Figure 5).

TABLE 2

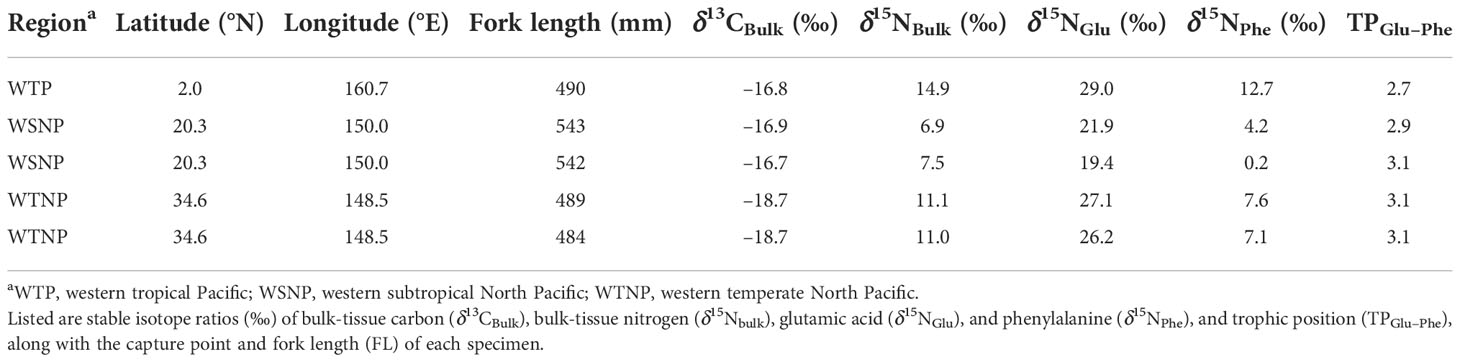
Table 2 Detailed sample information for five skipjack tuna (Katsuwonus pelamis) specimens used for compound-specific isotope analysis.

FIGURE 5

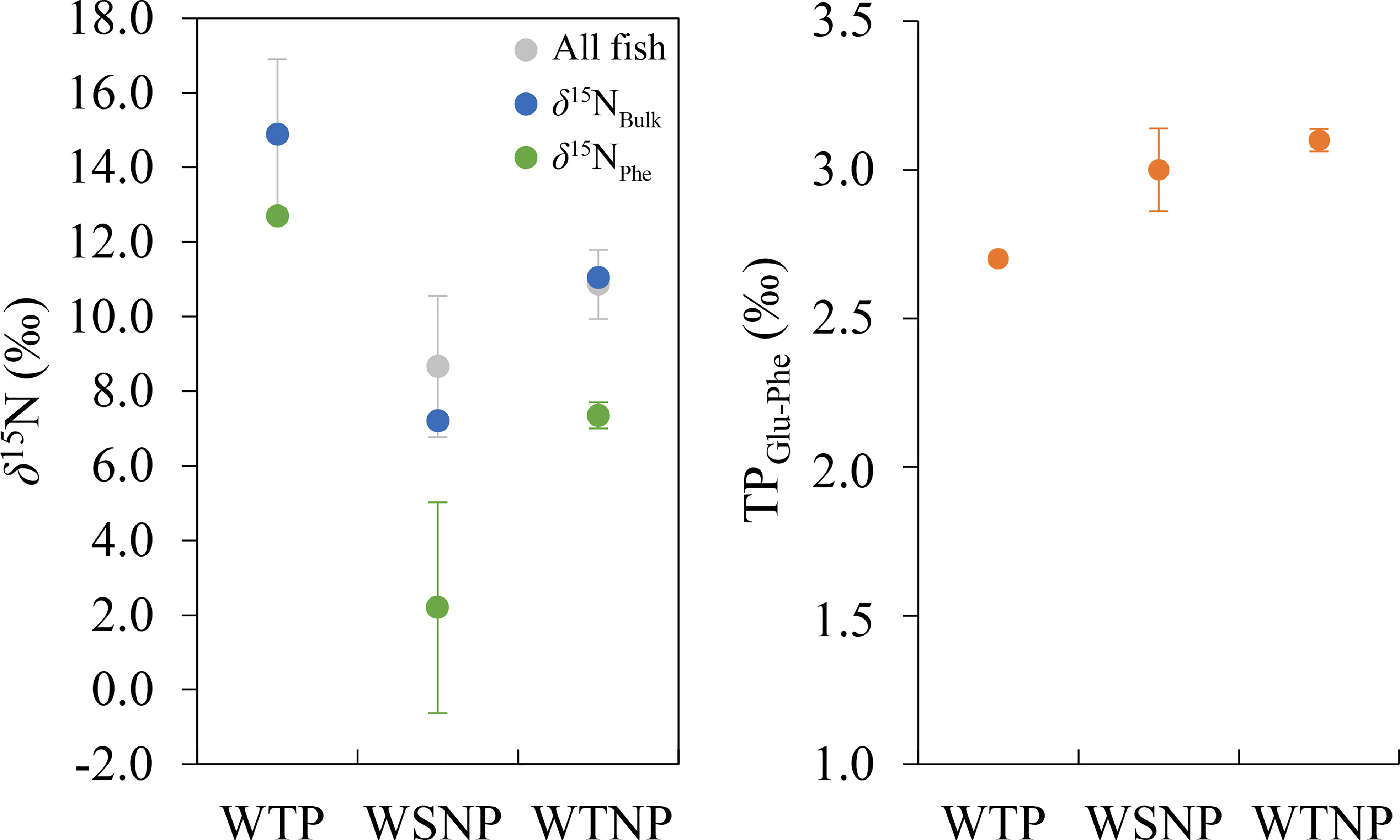
Figure 5 Mean δ¹⁵N_Bulk and δ¹⁵N_Phe (left), and TP_Glu–Phe (right) of skipjack tuna (Katsuwonus pelamis) in the western tropical Pacific (WTP), western subtropical North Pacific (WSNP), and western temperate North Pacific (WTNP). Gray, blue and green datapoints in the left panel indicate the mean (±SD) δ¹⁵N_Bulk of all skipjack samples, δ¹⁵N_Bulk and δ¹⁵N_Phe of skipjack used for δ¹⁵N_AAs, respectively. Orange datapoints in the right panel are the TP_Glu–Phe of skipjack used for determining δ¹⁵N_AAs.

Discussion

For generation of isoscapes, previous studies have used species with lower mobility like jellyfish and copepods as proxy organisms (Trueman et al., 2017; Matsubayashi et al., 2020). The advantage of using other species with low swimming ability to create isoscape is that location-specific isotope ratios can be detected with high representativeness. On the other hand, the ontogenetic shift of isotope ratios in target fish and the offset of isotope ratios between target fish and isoscapes should be estimated separately in this method. This study used a target fish as a proxy organism for isoscapes, and successfully estimated both isoscapes (Figure 4) and the ontogenetic shifts of isotope ratios (Figure 3) of skipjack without compound-specific isotope analysis, through the use of geostatistical models. Furthermore, we can apply iso-logging of skipjack without considering the isotopic offset between isoscapes and target organism, because the isoscapes were generated based on the isotope ratios of the skipjack. Thus, our approach can be a useful alternative to the previous method, although our method has one drawback in that the uncertainty of isoscapes will increase with the number of fish captured that had migrated across regions with different isoscapes in the several months before they were caught. We addressed this issue by increasing the number of adult fish at each sampling point and period (Figure 1), and this may have contributed somewhat to decreasing the uncertainty of isoscapes given the high prediction ability of our models. Another solution would be to use juvenile fish only for generating isoscapes and then to construct another model to account for the ontogenetic shift of isotope ratios. However, this is not applicable when the distribution of juvenile and adult fish does not completely overlap, as with skipjack in the western Pacific where juvenile fish are scarce in the northern area (Lehodey et al., 2013). To minimize the uncertainty associated with a high migration ability of proxy organisms, it is important to use tissues with a high turnover rate. As of now, the fish tissue with the shortest stable isotope turnover time is epidermal mucus (Winter and Britton, 2021), but this is difficult to sample from juvenile fish smaller than 100 mm. Therefore, it is important to further explore turnover rates in other tissues to discover better ways to sample proxy organisms for generation of isoscapes.

Together with the results of the geostatistical models, our δ¹⁵N_AAs data also show that the variation in isotope ratios of skipjack in the western Pacific was generally derived from the baseline shift of the isoscape and not from differences in prey items. Adult skipjack in the western Pacific are mainly piscivorous and occasionally consume cephalopods, with low selectivity for their prey (Iizuka et al., 1989). Therefore, regional shifts in prey abundance can cause regional differences in δ¹⁵N_Bulk. If the observed fluctuations of δ¹³C_Bulk and δ¹⁵N_Bulk in skipjack muscle resulted from differences in trophic position, the regional trend of δ¹⁵N_Bulk should be similar to that of TP_Glu–Phe (Figure 5). However, our δ¹⁵N_AAs data show that skipjack in the western Pacific have small individual variation in TP_Glu–Phe (maximum difference: 0.4). Assuming that δ¹⁵N_Bulk increases 3.4‰ with trophic level (Minagawa and Wada, 1984), differences in TP_Glu–Phe can only explain 1.4‰ of the observed variation of δ¹⁵N_Bulk out of 10.2‰ (Table 2, Figure 5). Given that the δ¹⁵N_Phe, which generally has a small trophic discrimination factor (about 0.4%; Chikaraishi et al., 2009), was more correlated with δ¹⁵N_Bulk of skipjack muscle than TP_Glu–Phe, individual differences in δ¹⁵N_Bulk of adult skipjack largely reflect the variation of δ¹⁵N at the base of the food web.

TP_Glu–Phe of skipjack estimated by commonly used TDF_Glu-Phe (7.6 ‰) were somewhat lower (2.7–3.1) than the trophic position estimated by stomach-content analysis (TP_SCA = 3.8; Bradley et al., 2015). Although the optimal TDF_Glu–Phe to use for estimating the trophic position of skipjack remains controversial (e.g., Bradley et al., 2015; McMahon and McCarthy, 2016; Ohkouchi et al., 2017; Coletto et al., 2022), differences in TP_Glu–Phe of skipjack do not affect intraspecific variation in TDF_Glu–Phe, and thus would not affect our conclusion that regional variation in TDF_Glu–Phe are unlikely to explain δ¹⁵N_Bulk differences among regions.

Regional differences in δ¹⁵N of skipjack in the western Pacific were largely consistent with the δ¹⁵N distribution of nitrate in this region (Rafter et al., 2019). Low δ¹⁵N around 10°N to 35°N (Figure 4) is related to extensive N₂ fixation in this region (Gruber, 2016), because N₂ fixers typically exhibit lower δ¹⁵N values than non-N₂ fixers (McClelland et al., 2003). On the other hand, our isoscape suggests that the low-δ¹⁵N area extends as far as 40°N, which is not consistent with known distributions of N₂ fixers or low nitrate δ¹⁵N (Gruber, 2016; Rafter et al., 2019). Presumably, this inconsistency is attributable to the relatively longer turnover time of skipjack muscle. The area around 35–40°N is the northern limit of skipjack migration and they can stay there at most four months a year (from June to September; Mugo et al., 2011; Kiyofuji et al., 2019a). Given that the turnover time of adult skipjack white muscle is about four months, isotope ratios of the muscle of skipjack captured around 35–40°N are likely to reflect the low δ¹⁵N values south of 35°N, and thus our isoscape shows low δ¹⁵N up to 40°N. On the other hand, the high δ¹⁵N south of 10–15°N can be explained by high nitrate utilization and limited N₂ fixation. In the surface layer of the tropical Pacific Ocean, a strong halocline above the thermocline generates a barrier layer, which impedes vertical mixing and nutrient supply from subsurface to surface waters (Sprintall & Tomczak, 1992). The limited nutrient influx results in high nitrate utilization (i.e. low nitrate concentration)—the ratio of nitrate assimilation by phytoplankton to nitrate supply in the euphotic layer—and nitrate δ¹⁵N increases with nitrate depletion (Yoshikawa et al., 2018). Furthermore, N₂ fixation is limited in this region (Gruber, 2016; Tanita et al., 2021) mainly due to the depleted dissolved iron concentration (Tanita et al., 2021). Such biogeochemical factors result in a clear latitudinal trend in δ¹⁵N, rendering it useful for segregating the habitat use of skipjack in the western Pacific.

Interpretation of spatial variation in δ¹³C is much more difficult than that of δ¹⁵N. The spatial variations in δ¹³C of skipjack muscle should be ultimately determined by that of phytoplankton (δ¹³C_phy), which is strongly influenced by the δ¹³C of dissolved inorganic carbon (DIC) and the isotopic fractionation associated with carbon uptake (Tuerena et al., 2019). In the case of the western Pacific, there are no clear latitudinal differences in δ¹³C of DIC (Quay et al., 2003), and therefore the spatial variation in the δ¹³C isoscape would be driven by the uptake fractionation by phytoplankton. Until the early 1990s, the δ¹³C of phytoplankton was thought to be determined by the DIC concentration in the ambient water (Sackett et al., 1965; Rau et al., 1991). Our geostatistical model also predicted an inverse relationship between DIC and δ¹³C (Supplementary Figure 2), and the belt-shaped low-δ¹³C zone around the equator (Figure 4) may be mainly due to the high spCO₂ in this region (Supplementary Figure 3). However, there is a large uncertainty associated with the equatorial low-δ¹³C zone and further sampling in this region would provide important clarification (Figure 4). On the other hand, the clear δ¹³C gradient around 20°N is not likely explained by spatial variation in spCO₂. Recent studies have shown that local differences in phytoplankton species composition can be important controls on δ¹³C_phy (e.g. Francois et al., 1993; Bidigare et al., 1997; Popp et al., 1998; Tuerena et al., 2019) as well as the DIC concentration, specifically in regions where the DIC is not high and is less variable, as in the western Pacific (Supplementary Figure 3). Thus, we presume that local differences in environmental variables altered the phytoplankton species composition, and ultimately generated spatial variation in δ¹³C of skipjack muscle in this region. It is worth noting that anthropogenic CO₂ emission can be another factor influencing the spatial variation in δ¹³C_phy (Tuerena et al., 2019).

In this study, we demonstrated that δ¹³C and δ¹⁵N measurements of skipjack in the western Pacific can help to identify their latitudinal migration. Because the dorsal muscle, which is a major tissue used for isotope analysis of fishes, only represents isotope ratios at a specific point in time, the utility of isoscapes will be maximized when they are used along with the isotopic analysis of incremental growth tissues such as eye lenses and vertebral bone (e.g. Quaeck-Davies et al., 2018; Matsubayashi et al., 2019). Iso-logging using such incremental growth tissue would allow us to understand how skipjack in this region utilize different habitats though their lifetime without using electronic tags. For example, if time series isotopic data for eye lens are available, the migration pattern can be tracked by the following steps: i) calculate the fork length when each layer is formed from the equation relating lens diameter to fork length, ii) using the equation relating fork length to isotopic ratios (Figure 3), correct the isotope ratios of eye lens so that the fork length is at zero; iii) subtract Δδ¹⁵N_{muscle - eye lens} from the value obtained in ii), iv) corrected lens isotope ratios can then be compared to the isoscape (Figure 4). We also suggest that the isoscapes generated in this study can be applied to other fish species that migrate in the western Pacific Ocean, such as albacore Thunnus alalunga (Nikolic et al., 2017), Pacific bluefin tuna Thunnus orientalis (Fujioka et al., 2018), and Japanese eel Anguilla japonica (Aoyama et al., 2014). For these other target species, however, it will be necessary to apply an appropriate correction to the trophic discrimination factor for differences between skipjack muscle and specific tissues of these other species. By using this method, we can better understand the immigration/emigration rates and connectivity in each region, which is crucial for cooperative management of shared fish stocks like skipjack. Further studies to generate precise isoscapes of δ¹³C and δ¹⁵N based on ocean models hold promise for improving the spatiotemporal resolution of isotope tracking and, together with the results of this study, will facilitate its use.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author contributions

JM and HM conceived this study. HM and YT provided skipjack samples and contextual information. HM, YC, NO, KK, NFI, and NOO performed bulk and compound-specific stable isotope analyses. JM performed statistical analyses and wrote the first draft of the paper. All authors contributed to the article and approved the submitted version.

Funding

This study was partially supported by the Foundation for the Japan Society for the Promotion of Science (JSPS) KAKENHI Grants 19H04247, 21H03579, 21H04784, and 22H05028 to JM, and 20H00208 to NO, and the Research and Assessment Program for Fisheries Resources of the Fisheries Agency of Japan.

Acknowledgments

This study was conducted with the support of the Joint Research Grant for the Environmental Isotope Study of the Research Institute for Humanity and Nature. We thank H. Ashida, S. Ohashi, F. Tanaka, and H. Kiyofuji at the Fisheries Resources Institute, Japan Fisheries Research and Education Agency, for their help with sample collection. We thank C. Yoshikawa at the Japan Agency for Marine-Earth Science and Technology for her helpful comments on a draft of this manuscript. We also thank the reviewers for their prompt and careful review of our draft and for their helpful comments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2022.1049056/full#supplementary-material

References

Anderson S. C., Ward E. J., English P. A., Barnett L. A. K. (2022). sdmTMB: An r package for fast, flexible, and user-friendly generalized linear mixed effects models with spatial and spatiotemporal random fields. bioRxiv 2022.03.24.485545. doi: 10.1101/2022.03.24.485545

CrossRef Full Text | Google Scholar

Aoyama J., Watanabe S., Miller M. J., Mochioka N., Otake T., Yoshinaga T., et al. (2014). Spawning sites of the Japanese eel in relation to oceanographic structure and the West Mariana ridge. PloS One 9, e88759. doi: 10.1371/journal.pone.0088759

PubMed Abstract | CrossRef Full Text | Google Scholar

Barrett I., Hester F. J. (1964). Body temperature of yellowfin and skipjack tunas in relation to sea surface temperature. Nature 203, 96–97. doi: 10.1038/203096b0

PubMed Abstract | CrossRef Full Text | Google Scholar

Bartoo N. W. (1987). “Tuna and billfish summaries of major stocks,” in Administrative report LJ-87-26 (La Jolla: National Marine Fisheries Service).

Google Scholar

Bidigare R. R., Fluegge A., Freeman K. H., Hanson K. L., Hayes J. M., Hollander D., et al. (1997). Consistent fractionation of c-13 in nature and in the laboratory: Growth-rate effects in some haptophyte algae. Global Biogeochem. Cy. 11, 279–292. doi: 10.1029/96gb03939

CrossRef Full Text | Google Scholar

Bradley C. J., Wallsgrove N. J., Choy C. A., Drazen J. C., Hetherington E. D., Hoen D. K., et al. (2015). Trophic position estimates of marine teleosts using amino acid compound specific isotopic analysis. Limnol. Oceanogr. Meth. 13, 476–493. doi: 10.1002/lom3.10041

CrossRef Full Text | Google Scholar

Caddy J. F. (1997). “Establishing a consultative mechanism or arrangement for managing shared stocks within the jurisdiction of contiguous states,” in Taking stock: Defining and managing shared resources, Australian society for fish biology and aquatic resource management association of Australasia joint workshop proceedings, vol. 15 . Ed. Hancock D. A. (Sydney: Australian Society for Fish Biology), 81–123.

Google Scholar

Canseco J. A., Niklitschek E. J., Harrod C. (2021). Variability in δ¹³C and δ¹⁵N trophic discrimination factors for teleost fishes: A meta-analysis of temperature and dietary effects. Rev. Fish. Biol. Fish. 32, 313–329. doi: 10.1007/s11160-021-09689-1

CrossRef Full Text | Google Scholar

Carey F. G., Teal J. M. (1969). Regulation of body temperature by the bluefin tuna. Comp. Biochem. Physiol. 28, 205–213. doi: 10.1016/0010-406X(69)91336-X

CrossRef Full Text | Google Scholar

Carvalho F., Ahrens R., Murie D., Bigelow K., Aires-Da-Silva A., Maunder M. N., et al. (2015). Using pop-up satellite archival tags to inform selectivity in fisheries stock assessment models: A case study for the blue shark in the south Atlantic ocean. ICES. J. Mar. Sci. 72, 1715–1730. doi: 10.1093/icesjms/fsv026

CrossRef Full Text | Google Scholar

Chikaraishi Y., Ogawa N. O., Kashiyama Y., Takano Y., Suga H., Tomitani A., et al. (2009). Determination of aquatic food-web structure based on compound-specific nitrogen isotopic composition of amino acids. Limnol. Oceanogr. Meth. 7, 740–750. doi: 10.4319/lom.2009.7.740

CrossRef Full Text | Google Scholar

Chikaraishi Y., Steffan S. A., Takano Y., Ohkouchi N. (2015). Diet quality influences isotopic discrimination among amino acids in an aquatic vertebrate. Ecol. Evol. 5, 2048–2059. doi: 10.1002/ece3.1491

CrossRef Full Text | Google Scholar

Coletto J. L., Besser A. C., Botta S., Madureira L. A. S. P., Newsome S. D. (2022). Multi-proxy approach for studying the foraging habitat and trophic position of a migratory marine consumer in the southwestern Atlantic ocean. Mar. Ecol. Prog. Ser. 690, 147–163. doi: 10.3354/meps14036

CrossRef Full Text | Google Scholar

Coletto J. L., Botta S., Fischer L. G., Newsome S. D., Madureira L. S. (2021). Isotope-based inferences of skipjack tuna feeding ecology and movement in the southwestern Atlantic ocean. Mar. Environ. Res. 165, 105246. doi: 10.1016/j.marenvres.2020.105246

CrossRef Full Text | Google Scholar

Cooke S. J., Woodley C. M., Eppard M. B., Brown R. S., Nielsen J. L. (2011). Advancing the surgical implantation of electronic tags in fish: A gap analysis and research agenda based on a review of trends in intracoelomic tagging effects studies. Rev. Fish. Biol. Fish. 21, 127–151. doi: 10.1007/s11160-010-9193-3

CrossRef Full Text | Google Scholar

Francois R., Altabet M. A., Goericke R., McCorkle D. C., Brunet C., Poisson A. (1993). Changes in the delta c-13 of surface water particulate organic matter across the subtropical convergence in the SW Indian ocean. Global Biogeochem. Cy. 7, 627–644. doi: 10.1029/93GB01277

CrossRef Full Text | Google Scholar

Fry B., Sherr E. (1984). δ¹³C measurements as indicators of carbon flow in marine and freshwater ecosystems. Contrib. Mar. Sci. 27, 49–63. doi: 10.1007/978-1-4612-3498-2_12

CrossRef Full Text | Google Scholar

Fujioka K., Fukuda H., Tei Y., Okamoto S., Kiyofuji H., Furukawa S., et al. (2018). Spatial and temporal variability in the trans-pacific migration of pacific bluefin tuna (Thunnus orientalis) revealed by archival tags. Prog. Oceanogr. 162, 52–65. doi: 10.1016/j.pocean.2018.02.010

CrossRef Full Text | Google Scholar

Graham B. S., Koch P. L., Newsome S. D., McMahon K. W., Aurioles D. (2010). “Using isoscapes to trace the movements and foraging behavior of top predators in oceanic ecosystems,” in Isoscapes. Eds. West J., Bowen G., Dawson T., Tu K. (Dordrecht: Springer), 299–318.

Google Scholar

Graham B. S., Grubbs D., Holland K., Popp B. N. (2007). A rapid ontogenetic shift in the diet of juvenile yellowfin tuna from Hawaii. Mar. Biol. 150, 647–658. doi: 10.1007/s00227-006-0360-y

CrossRef Full Text | Google Scholar

Graves J. E., Horodysky A. Z. (2015). Challenges of estimating post-release mortality of istiophorid billfishes caught in the recreational fishery: A review. Fish. Res. 166, 163–168. doi: 10.1016/j.fishres.2014.10.014

CrossRef Full Text | Google Scholar

Gruber N. (2016). Elusive marine nitrogen fixation. Proc. Natl. Acad. Sci. U.S.A. 113, 4246–4248. doi: 10.1073/pnas.1603646113

CrossRef Full Text | Google Scholar

Hebblewhite M., Haydon D. T. (2010). Distinguishing technology from biology: A critical review of the use of GPS telemetry data in ecology. Philos. Trans. R. Soc B. 365, 2303–2312. doi: 10.1098/rstb.2010.0087

CrossRef Full Text | Google Scholar

Hoyle S., Kleiber P., Davies N., Langley A., Hampton J. (2011). “Stock assessment of skipjack tuna in the Western and central pacific ocean,” in WCPFC-SC7-2011/SA-WP-04 (Pohnpei, Federated States of Micronesia: Western and Central Pacific Fisheries Commission, Seventh Regular Session).

Google Scholar

Hsieh Y., Shiao J. C., Lin S. W., Iizuka Y. (2019). Quantitative reconstruction of salinity history by otolith oxygen stable isotopes: An example of a euryhaline fish Lateolabrax japonicus. Rapid Commun. Mass. Spectrom. 33, 1344–1354. doi: 10.1002/rcm.8476

CrossRef Full Text | Google Scholar

Iizuka K., Asano M., Naganuma A. (1989). Feeding habits of skipjack tuna (Katsuwonus pelamis Linnaeus) caught by pole and line and the state of young skipjack tuna distribution in the tropical seas of the Western pacific ocean. Bull. Tohoku. Reg. Fish. Res. Lab. 51, 107–116.

Google Scholar

Jepsen N., Koed A., Thorstad E., Baras E. (2002). Surgical implantation of transmitters in fish: How much have we learned? Hydrobiologia 483, 239–248. doi: 10.1007/978-94-017-0771-8_28

CrossRef Full Text | Google Scholar

Jepsen N., Thorstad E. B., Havn T., Lucas M. C. (2015). The use of external electronic tags on fish: an evaluation of tag retention and tagging effects. Anim. Biotelem. 3, 49. doi: 10.1186/s40317-015-0086-z

CrossRef Full Text | Google Scholar

Kiyofuji H., Aoki Y., Kinoshita J., Ohashi S., Fujioka K. (2019b). “A conceptual model of skipjack tuna in the western and central pacific ocean (WCPO) for the spatial structure configuration,” in WCPFC-SC15-2019/SA-WP-11 (Pohnpei, Federated States of Micronesia: Western and Central Pacific Fisheries Commission), 2019, 23.

Google Scholar

Kiyofuji H., Aoki Y., Kinoshita J., Okamoto S., Masujima M., Matsumoto T., et al. (2019a). Northward migration dynamics of skipjack tuna (Katsuwonus pelamis) associated with the lower thermal limit in the western pacific ocean. Prog. Oceanogr. 175, 55–67. doi: 10.1016/j.pocean.2019.03.006

CrossRef Full Text | Google Scholar

Kiyofuji H., Ochi D. (2016). Proposal of alternative spatial structure for skipjack stock assessment in the WCPO. Twelfth. Session. Sci. Committee., 3–11.

Google Scholar

Kraska J., Crespo G. O., Johnston D. W. (2015). Bio-logging of marine migratory species in the law of the sea. Mar. Policy 51, 394–400. doi: 10.1016/j.marpol.2014.08.016

CrossRef Full Text | Google Scholar

Lehodey P., Senina I., Calmettes B., Hampton J., Nicol S. (2013). Modelling the impact of climate change on pacific skipjack tuna population and fisheries. Clim. Change 119, 95–109. doi: 10.1007/s10584-012-0595-1

CrossRef Full Text | Google Scholar

Lindgren F., Rue H., Lindström J. (2011). An explicit link between Gaussian fields and Gaussian Markov random fields: The stochastic partial differential equation approach. J. R. Stat. Soc Ser. A. Stat. Soc 73, 423–498. doi: 10.1111/j.1467-9868.2011.00777.x

CrossRef Full Text | Google Scholar

Matsubayashi J., Osada Y., Tadokoro K., Abe Y., Yamaguchi A., Shirai K., et al. (2020). Tracking long-distance migration of marine fishes using compound-specific stable isotope analysis of amino acids. Ecol. Lett. 23, 881–890. doi: 10.1111/ele.13496

CrossRef Full Text | Google Scholar

Matsubayashi J., Saitoh Y., Osada Y., Uehara Y., Habu J., Sasaki T., et al. (2017). Incremental analysis of vertebral centra can reconstruct the stable isotope chronology of teleost fishes. Methods Ecol. Evol. 8, 1755–1763. doi: 10.1111/2041-210X.12834

CrossRef Full Text | Google Scholar

Matsubayashi J., Umezawa Y., Matsuyama M., Kawabe R., Mei W., Wan X., et al. (2019). Using segmental isotope analysis of teleost fish vertebrae to estimate trophic discrimination factors of bone collagen. Limnol. Oceanogr. Meth. 17, 87–96. doi: 10.1002/lom3.10298

CrossRef Full Text | Google Scholar

McClelland J. W., Holl C. M., Montoya J. P. (2003). Relating low δ¹⁵N values of zooplankton to N₂-fixation in the tropical north Atlantic: Insights provided by stable isotope ratios of amino acids. Deep. Sea. Res. Part I. Oceanogr. Res. Papers. 50, 849–861. doi: 10.1016/S0967-0637(03)00073-6

CrossRef Full Text | Google Scholar

McMahon K. W., McCarthy M. D. (2016). Embracing variability in amino acid δ15N fractionation: Mechanisms, implications, and applications for trophic ecology. Ecosphere 7, e01511. doi: 10.1002/ecs2.1511

CrossRef Full Text | Google Scholar

McWhinnie S. F. (2009). The tragedy of the commons in international fisheries: An empirical examination. J. Environ. Econ. Manage. 57, 321–333. doi: 10.1016/j.jeem.2008.07.008

CrossRef Full Text | Google Scholar

Miller K. A., Munro G. R. (2004). Climate and cooperation: A new perspective on the management of shared fish stocks. Mar. Res. Econ. 19, 367–393. doi: 10.1086/mre.19.3.42629440

CrossRef Full Text | Google Scholar

Minagawa M., Wada E. (1984). Stepwise enrichment of ¹⁵N along food chains: Further evidence and the relation between δ¹⁵N and animal age. Geochim. Cosmochim. Acta 48, 1135–1140. doi: 10.1016/0016-7037(84)90204-7

CrossRef Full Text | Google Scholar

Mugo R., Saitoh S. I., Nihira A., Kuroyama T. (2010). Habitat characteristics of skipjack tuna (Katsuwonus pelamis) in the western north pacific: A remote sensing perspective. Fish. Oceanogr. 19, 382–396. doi: 10.1111/j.1365-2419.2010.00552.x

CrossRef Full Text | Google Scholar

Mugo R., Saitoh S., Nihira A., Kuroyama T. (2011). “Application of multi-sensor satellite and fishery data, statistical models and marine GIS to detect habitat preferences of skipjack tuna,” in Handbook of satellite remote sensing image interpretation: Applications for marine living resources conservation and management. Eds. Morales J., Stuart V., Platt T., Sathyendranath S. (Dartmouth, Canada: EU PRESPO and IOCCG), 166–185.

Google Scholar

Nikolic N., Morandeau G., Hoarau L., West W., Arrizabalaga H., Hoyle S., et al. (2017). Review of albacore tuna, Thunnus alalunga, biology, fisheries and management. Rev. Fish. Biol. Fish. 27, 775–810. doi: 10.1007/s11160-016-9453-y

CrossRef Full Text | Google Scholar

Nishikawa H., Nishikawa S., Ishizaki H., Wakamatsu T., Ishikawa Y. (2020). Detection of the oyashio and kuroshio fronts under the projected climate change in the 21st century. Prog. Earth Planet. Sci. 7, 29. doi: 10.1186/s40645-020-00342-2

CrossRef Full Text | Google Scholar

Ohkouchi N., Chikaraishi Y., Close H. G., Fry B., Larsen T., Madigan D. J., et al. (2017). Advances in the application of amino acid nitrogen isotopic analysis in ecological and biogeochemical studies. Org. Geochem. 113, 150–174. doi: 10.1016/j.orggeochem.2017.07.009

CrossRef Full Text | Google Scholar

Popova E., Vousden D., Sauer W. H., Mohammed E. Y., Allain V., Downey-Breedt N., et al. (2019). Ecological connectivity between the areas beyond national jurisdiction and coastal waters: Safeguarding interests of coastal communities in developing countries. Mar. Policy 104, 90–102. doi: 10.1016/j.marpol.2019.02.050

CrossRef Full Text | Google Scholar

Popp B. N., Laws E. A., Bidigare R. R., Dore J. E., Hanson K. L., Wakeham S. G. (1998). Effect of phytoplankton cell geometry on carbon isotopic fractionation. Geochim. Cosmochim. Acta 62, 69–77. doi: 10.1016/S0016-7037(97)00333-5

CrossRef Full Text | Google Scholar

Priede I. G., Solbé J. D. L., Nott J. E., O'Grady K. T., Cragg-Hine D. (1988). Behaviour of adult Atlantic salmon, Salmo salar l., in the estuary of the river ribble in relation to variations in dissolved oxygen and tidal flow. J. Fish. Biol. 33, 133–139. doi: 10.1111/j.1095-8649.1988.tb05567.x

CrossRef Full Text | Google Scholar

Quaeck-Davies K., Bendall V. A., MacKenzie K. M., Hetherington S., Newton J., Trueman C. N. (2018). Teleost and elasmobranch eye lenses as a target for life-history stable isotope analyses. PeerJ 6, e4883. doi: 10.7717/peerj.4883

CrossRef Full Text | Google Scholar

Quay P., Sonnerup R., Westby T., Stutsman J., McNichol A. (2003). Changes in the ¹³C/¹²C of dissolved inorganic carbon in the ocean as a tracer of anthropogenic CO2 uptake. Global Biogeochem. Cy. 17, 1004. doi: 10.1029/2001GB001817

CrossRef Full Text | Google Scholar

Rafter P. A., Bagnell A., Marconi D., DeVries T. (2019). Global trends in marine nitrate n isotopes from observations and a neural network-based climatology. Biogeosciences 16, 2617–2633. doi: 10.5194/bg-16-2617-2019

CrossRef Full Text | Google Scholar

Rau G. H., Froelich P. N., Takahashi T., Des Marais D. J. (1991). Does sedimentary organic d¹³C record variations in quaternary ocean [CO₂(aq)]? Paleoceanography 6, 335–347. doi: 10.1029/91pa00321

CrossRef Full Text | Google Scholar

R Core Team (2021). R: A language and environment for statistical computing (Vienna, Austria: R Foundation for Statistical Computing). Available at: https://www.R-project.org/.

Google Scholar

Rue H., Martino S., Chopin N. (2009). Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc Ser. B. 71, 319–392. doi: 10.1111/j.1467-9868.2008.00700.x

CrossRef Full Text | Google Scholar

Sackett W. M., Eckelmann W. R., Bender M. L., Be A. W. H. (1965). Temperature dependence of carbon isotope composition in marine plankton and sediments. Science 148, 235–237. doi: 10.1126/science.148.3667.23

CrossRef Full Text | Google Scholar

Sakamoto T., Komatsu K., Shirai K., Higuchi T., Ishimura T., Setou T., et al. (2019). Combining microvolume isotope analysis and numerical simulation to reproduce fish migration history. Methods Ecol. Evol. 10, 59–69. doi: 10.1111/2041-210X.13098

CrossRef Full Text | Google Scholar

Sippel T., Eveson J. P., Galuardi B., Lam C., Hoyle S., Maunder M., et al. (2015). Using movement data from electronic tags in fisheries stock assessment: A review of models, technology and experimental design. Fish. Res. 163, 152–160. doi: 10.1016/j.fishres.2014.04.006

CrossRef Full Text | Google Scholar

Sprintall J., Tomczak M. (1992). Evidence of the barrier layer in the surface layer of the tropics. J. Geophys. Res. Oceans. 97, 7305–7316. doi: 10.1029/92JC00407

CrossRef Full Text | Google Scholar

St John Glew K., Espinasse B., Hunt B.P., Pakhomov E.A., Bury S.J., Pinkerton M., et al. (2021). Isoscape models of the Southern Ocean: Predicting spatial and temporal variability in carbon and nitrogen isotope compositions of particulate organic matter. Glob. Biogeochem. Cycles35, e2020GB006901. doi: 10.1029/2020GB006901

CrossRef Full Text | Google Scholar

Stevens E. D., Lam H. M., Kendall J. (1974). Vascular anatomy of the counter-current heat exchanger of skipjack tuna. J. Exp. Biol. 61, 145–153. doi: 10.1242/jeb.61.1.145

CrossRef Full Text | Google Scholar

Tanita I., Shiozaki T., Kodama T., Hashihama F., Sato M., Takahashi K., et al. (2021). Regionally variable responses of nitrogen fixation to iron and phosphorus enrichment in the pacific ocean. J. Geophys. Res. Biogeosci. 126, e2021JG006542. doi: 10.1029/2021JG006542

CrossRef Full Text | Google Scholar

Thorson J. T. (2019). Guidance for decisions using the vector autoregressive spatio-temporal (VAST) package in stock, ecosystem, habitat and climate assessments. Fish. Res. 210, 143–161. doi: 10.1016/j.fishres.2018.10.013

CrossRef Full Text | Google Scholar

Thorstad E. B., Rikardsen A. H., Alp A., Økland F. (2013). The use of electronic tags in fish research–an overview of fish telemetry methods. Turk. J. Fish. Aquat. Sci. 13, 881–896. doi: 10.4194/1303-2712-v13_5_13

CrossRef Full Text | Google Scholar

Trueman C. N., MacKenzie K. M., Palmer M. R. (2012). Identifying migrations in marine fishes through stable-isotope analysis. J. Fish. Biol. 81, 826–847. doi: 10.1111/j.1095-8649.2012.03361.x

CrossRef Full Text | Google Scholar

Trueman C. N., MacKenzie K. M., St. John Glew K. (2017). Stable isotope-based location in a shelf sea setting: Accuracy and precision are comparable to light-based location methods. Methods Ecol. Evol. 8, 232–240. doi: 10.1111/2041-210X.12651

CrossRef Full Text | Google Scholar

Tuerena R. E., Ganeshram R. S., Humphreys M. P., Browning T. J., Bouman H., Piotrowski A. P. (2019). Isotopic fractionation of carbon during uptake by phytoplankton across the south Atlantic subtropical convergence. Biogeosciences 16, 3621–3635. doi: 10.5194/bg-16-3621-2019

CrossRef Full Text | Google Scholar

Vatsov M. (2016). Changes in the geographical distribution of shared fish stocks and the mackerel war: Confronting the cooperation maze. Scottish. Centre. Int. Law. Working. Paper. Ser. 13. doi: 10.2139/ssrn.2863853

CrossRef Full Text | Google Scholar

Vecchio J. L., Peebles E. B. (2020). Spawning origins and ontogenetic movements for demersal fishes: An approach using eye-lens stable isotopes. Estuar. Coast. Shelf. Sci. 246, 107047. doi: 10.1016/j.ecss.2020.107047

CrossRef Full Text | Google Scholar

Winter J. D. (1983). “Underwater biotelemetry,” in Fisheries techniques. Eds. Nielsen L. A., Johnson D. L. (Bethesda, Maryland: American Fisheries Society), 371–395.

Google Scholar

Winter E. R., Britton J. R. (2021). Individual variability in stable isotope turnover rates of epidermal mucus according to body size in an omnivorous fish. Hydrobiologia 848, 363–370. doi: 10.1007/s10750-020-04444-2

CrossRef Full Text | Google Scholar

Wood S. N. (2003). Thin plate regression splines. J. R. Stat. Soc Ser. B. Stat. Meth. 65, 95–114. doi: 10.1111/1467-9868.00374

CrossRef Full Text | Google Scholar

Yoshikawa C., Makabe A., Matsui Y., Nunoura T., Ohkouchi N. (2018). Nitrate isotope distribution in the subarctic and subtropical north pacific. geochem. Geophys. Geosyst. 19, 2212–2224. doi: 10.1029/2018GC007528

CrossRef Full Text | Google Scholar