The DIC carbon isotope evolutions during CO2 bubbling: Implications for ocean acidification laboratory culture

Ocean acidification increases pCO₂ and decreases pH of seawater and its impact on marine organisms has emerged as a key research focus. In addition to directly measured variables such as growth or calcification rate, stable isotopic tracers such as carbon isotopes have also been used to more completely understand the physiological processes contributing to the response of organisms to ocean acidification. To simulate ocean acidification in laboratory cultures, direct bubbling of seawater with CO₂ has been a preferred method because it adjusts pCO₂ and pH without altering total alkalinity. Unfortunately, the carbon isotope equilibrium between seawater and CO₂ gas has been largely ignored so far. Frequently, the dissolved inorganic carbon (DIC) in the initial seawater culture has a distinct ¹³C/¹²C ratio which is far from the equilibrium expected with the isotopic composition of the bubbled CO_2. To evaluate the consequences of this type of experiment for isotopic work, we measured the carbon isotope evolutions in two chemostats during CO₂ bubbling and composed a numerical model to simulate this process. The isotopic model can predict well the carbon isotope ratio of dissolved inorganic carbon evolutions during bubbling. With help of this model, the carbon isotope evolution during a batch and continuous culture can be traced dynamically improving the accuracy of fractionation results from laboratory culture. Our simulations show that, if not properly accounted for in experimental or sampling design, many typical culture configurations involving CO₂ bubbling can lead to large errors in estimated carbon isotope fractionation between seawater and biomass or biominerals, consequently affecting interpretations and hampering comparisons among different experiments. Therefore, we describe the best practices on future studies working with isotope fingerprinting in the ocean acidification background.

1. Introduction

The ocean acidification problem is becoming more and more serious with the continuous increase of atmospheric CO₂ from fossil fuel burning. Ocean acidification can be defined as the increase of dissolved CO₂ (CO₂(aq)) and consequent decrease of pH in seawater, with increases of dissolved inorganic carbon (DIC) but little variations in total alkalinity (Gattuso and Hansson, 2011). In the last two decades, thousands of studies have been carried out to study the ocean acidification effects on different marine organisms which have been reviewed and synthesized (e.g., Hoegh-Guldberg et al., 2007; Riebesell and Tortell, 2011; Meyer and Riebesell, 2015; Lemasson et al., 2017). These studies have shown that ocean acidification has complex effects on marine calcifiers (Figuerola et al., 2021), non-calcifying marine life (Hurd et al., 2019), and therefore profound impact on marine ecosystems and ocean carbon cycles (Mostofa et al., 2016). Over the past decade, more studies have employed isotopic methods in laboratory cultures to trace the ratio of stable isotopes. The variations of stable isotopes could reveal important physiological responses to ocean acidification beyond, for instance, growth rate, cell size, or elemental stoichiometry. Moreover, predicting these isotopic variations is crucial to calibrate new proxies for reconstructing the atmospheric CO₂ concentration in geological history (Hopkinson et al., 2011; Wilkes et al., 2017; Nishida et al., 2020; Phelps et al., 2021; Remize et al., 2021).

Laboratory culture is a key method to study the physiological effect of ocean acidification on different marine life. There are multiple methods to achieve the target culture media CO₂(aq) and carbonate chemistry depending on the objectives of the study. The principal methods are (1) manipulating pH by adding acid/base, (2) manipulating DIC through addition of HCO₃^- or CO₃^2- and (3) bubbling (or aeration) a gas of desired pCO₂ concentration (Gattuso et al., 2010). The method of bubbling cultures with CO₂ requires gas mixing to obtain the desired CO₂ level and humidification to prevent evaporation from culture media. Adding acid/base removes the mechanical stress upon cells from bubbles and benefits from relatively easy operations; however, it could cause shifts of alkalinity and does not reproduce the actual mechanism by which DIC concentration increases in the ongoing Ocean Acidification. Both bubbling and acid-base manipulation can well simulate the CO₂ increase and pH decrease effects in laboratory culture, but the CO₂ bubbling method has been preferred by some studies because it alone can perfectly replicate the current ocean acidification caused by anthropogenic CO₂ without changing the seawater total alkalinity.

For the CO₂ bubbling method, the guidebook by Riebesell et al. (2011), covering the methods of laboratory culture for ocean acidification research, highlighted the importance of pre-equilibrating the culture media to the required CO₂ concentration by aerating it ‘for a few days’. Considering the wide range of culture vessel shapes and volumes among experiments, our question is how long culture media should be bubbled in order to reach an ordinary chemical and isotopic balance. Some published works mentioned the pre-bubbling durations, for example, the seawater was pre-bubbled for 2 days (Iglesias-Rodriguez et al., 2008), while most publications did not fully describe their methods. Moreover, the isotopic equilibration times are usually much longer than the ordinary chemical equilibration times, because, to reach isotopic equilibrium, each ion and molecule should be fully exchanged and come to equilibrium with other ions and molecules (Mills and Urey, 1940). For the works focusing on organic or carbonate carbon isotope fractionations under different CO₂ levels, culture media with out of equilibrium or dynamic carbon isotope ratio of DIC could complicate or even preclude the interpretation of stable isotope fractionation signatures.

In this study, we provide a thorough characterization of the isotopic equilibration process in CO₂ bubbling experiments and the factors that influence the carbon isotopic equilibration time, in order to clearly document the approaches needed to accurately infer carbon isotopic fractionations in experiments with bubbling. First, we compose numerical models to simulate chemical and isotopic equilibration during bubbling processes in two different systems and present the effects of seawater volume, gas exchange rate, and difference between the isotopic composition of the bubbled CO₂ and that of the media’s DIC on the equilibration time. Secondly, we complete a series of bubbling experiments in a photobioreactor to test the performance of the model simulation. Finally, we evaluate the expected consequences of equilibration time in typical experimental bubbling setups for which carbon isotopic ratios of cultured biomass or biominerals have been reported. With the guide of this study, future works can trace the isotopic fingerprint of ocean acidification on marine biomass better.

2. Experimental setup for determination of equilibration time

We have conducted experiments in commercial photobioreactors of 1 L and 3 L (PBR FMT 150, Photon Systems International) designed for continuous culture. The aeration system allowed gas to first enter the bottom of a bottle with fresh media (‘bottle’ in Figure 1A), where gas humidification and the first exchange of gases occurred. The gas subsequently flowed out towards the photobioreactor where a sparging tube dispersed the bubbles, exchanging gases a second time. Finally, gas flowed to the waste bottle, and from there out of the system (Figure 1A). The photobioreactor compartments were monitored without inoculated cells in batch mode in order to assess the dynamics of the bubbling process itself. The two different photobioreactor sizes and CO₂ concentrations employed in this study can be found in Table 1.

FIGURE 1

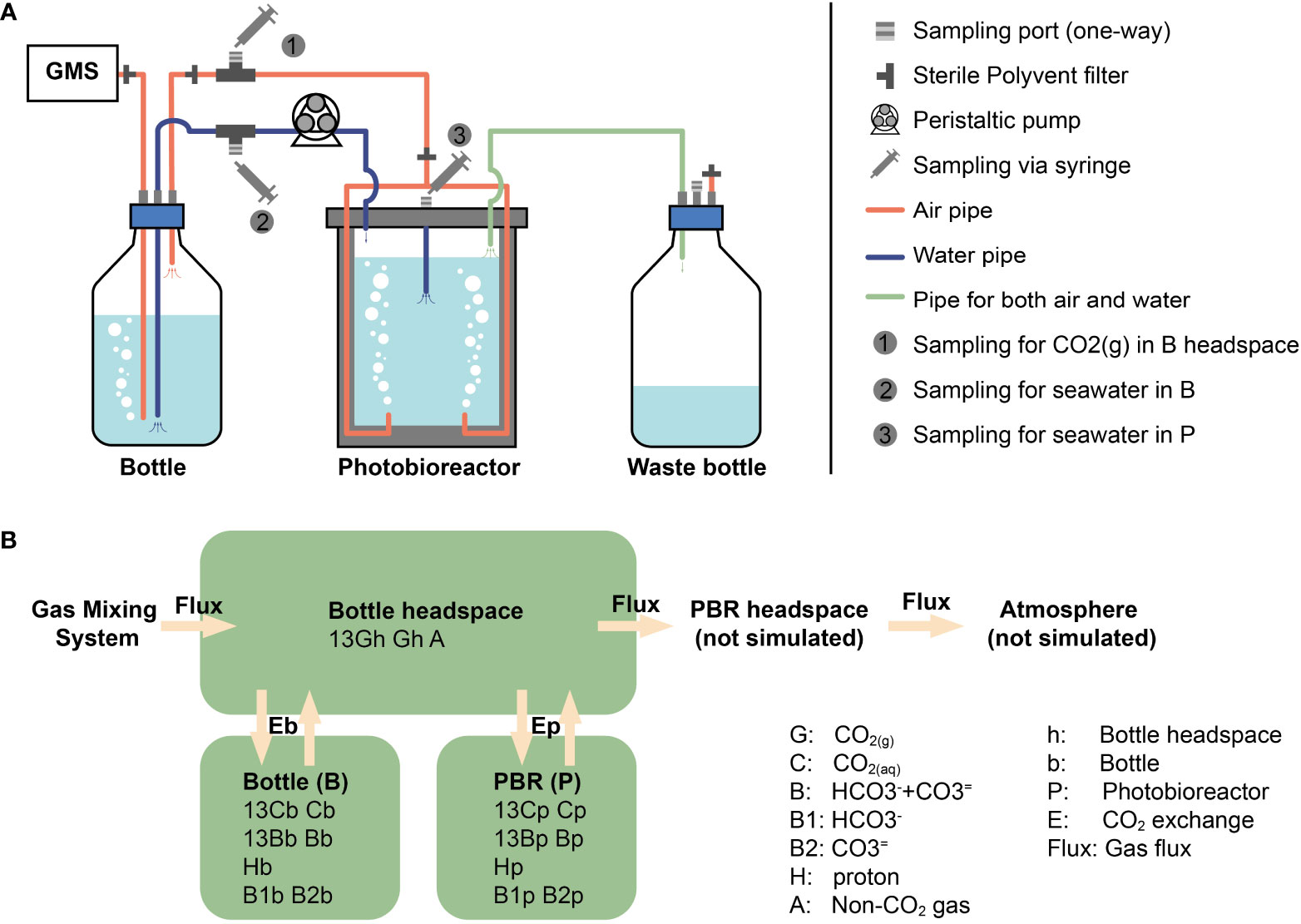
Figure 1 The photobioreactor system with CO₂ bubbling and model structure. (A) The photobioreactor system in Climate Geology laboratory, ETH Zurich. GMS means Gas Mixing System. (B) Our model consists of three compartments: bottle headspace, bottle media and photobioreactor media (words in bold). PBR is the photobioreactor. The other terms are simulated amount/concentration of substance, in which capital letters represent substance and subscript letters are abbreviation for compartments.

TABLE 1

Table 1 Parameters for photobioreactor systems.

For the different CO₂ concentration treatments, two compressed gases, pure CO₂ with a δ¹³C of -2.8‰ (Vienna Pee Dee Belemnite, VPDB) and CO₂-free synthetic air (Air Liquide), were mixed with a Gas Mixing System (GMS-150, Photon Systems Instruments). GMS output flow and pCO₂ composition were further verified with a flowmeter and a cavity ringdown spectrometer isotopic and gas concentration analyzer (G2131-i, Picarro, Inc. USA). Measurements of the Picarro CO₂ analyzer were corrected with CO₂ mixtures with certified concentrations and isotopic composition (Air Liquide).

Photobioreactors and bottles were filled with K/2 media without Tris buffer which was made by artificial seawater (ASW) with nutrient and trace metals (Keller et al., 1987). For the convenience of description, the terms of media, ASW and seawater will be treated equally to the K/2 media in the following without specific mention. The detailed recipe is described in Appendix A. Prior to filtration, 10 L artificial seawater (ASW) was supplemented with 20.48 mL 2M Na₂CO₃ and 2.90 ml 37% HCl to raise alkalinity above 4 mmol kg^-1 seawater. This operation of increasing alkalinity is specialized to maintain the growth pH in high CO₂ treatment. The salinity of ASW would increase slightly from 34.97 to 35.53 g kg^-1 and this increment in salinity could be ignored during the carbon system calculations.

Concentration of DIC in seawater and concentration and carbon isotope ratio of CO₂ in headspace were monitored with an Apollo SciTech DIC-C13 Analyzer coupled to the Picarro CO₂ analyzer using in-house NaHCO₃ standards dissolved in deionized water at different known concentrations and δ¹³C values from -4.66 to -7.94‰. δ¹³C-DIC in media were measured with a Gas Bench II with an autosampler (CTC Analytics AG, Switzerland) coupled to ConFlow IV Interface and a Delta V Plus mass spectrometer (Thermo Fischer Scientific). The system and abovementioned in-house standards were calibrated using international standards NBS 18 (-5.014‰) and NBS 19 (+1.95‰). The analytical error for CO₂(g) concentration is <20 ppm and that for DIC concentration and δ¹³C is <10 μM and 0.1‰, respectively.

Our initial δ¹³C of un-bubbled DIC (at t₀) is -6.1 ± 0.2‰. Before and after the start of bubbling at a flow of 200 ± 20 mL min^-1, both headspace and seawater media of the upstream bottle and the photobioreactor were sampled by a 50-mL syringe through one-way sampling ports. The sampling time in each experiment can be found in Tables 2, 3. To measure headspace CO₂(g) that had been humidified and exchanged with bottle media, gas flow was directed into a syringe and 50 mL of gas were injected into the Picarro CO₂ analyzer.

TABLE 2

Table 2 DIC and CO₂(g) in headspace measurements during small system bubbling.

TABLE 3

Table 3 DIC and CO₂(g) in headspace measurements during large system bubbling.

To measure seawater DIC, pH and δ¹³C_DIC, 35 mL seawater were syringed out as depicted in Figure 1A. The first 5-10 mL out of 35 mL were routinely discarded to avoid mixing effects with dead volumes in the tubing. One mL was injected into He-flushed glass vials containing H₃PO₄ for the carbon isotope ratios measurements in Gas Bench. About 12 mL were injected into the glass vials without headspace, for DIC concentration measurements using Apollo analyzer, and 3.5 mL was consumed in each duplicate. There was no gas exchange between air and samples during the sampling of DIC and CO₂. The remaining seawater in syringe (~15-20 mL) was then injected into a 50 mL centrifuge tube for pH measurement. The tube was covered with Parafilm M sealing film to reduce the CO₂ exchanging between seawater and air. The pH of seawater was measured by a Mettler Toledo LE410 pH-probe calibrated with NBS standards (Mettler Toledo) resulting in an accuracy of ±0.01. Here it should be noted that high ionic strength calibration standards, such as standards in total scale, would be optimal for pH measurement in seawater (Kadis and Leito, 2010).

3. Approach for simulating the gas bubbling process in a numerical model

There are three important processes in DIC carbon isotope evolution simulations, (1) CO₂ exchanging between gas (CO₂(g)) and seawater (CO₂(aq)), (2) DIC inter-reactions and (3) isotopic fractionation during the DIC reactions, which will be introduced separately in the following sections. Beside these three main processes, the sampling of DIC and gas in headspace can also play a minor role in DIC isotope evolution by decreasing the total amount of DIC and accelerating isotopic equilibrium. Thus, the decreasing of DIC volume and the loses of CO₂(g) in headspace during sampling are also considered in our model. As described in the last section, the CO₂ coming from the Gas Mixing System first goes into the bubbling in bottle, exchanging with DIC in bottle. Then CO₂(g) goes out of the seawater in bottle into the bottle headspace. After that, CO₂(g) goes into bubbles in photobioreactor exchanging with DIC in photobioreactor. However, in our model, bubbles in bottle and photobioreactor are combined with bottle headspace to reduce the calculation amount. Thereby, in practice, the simulated CO₂(g) goes into headspace directly after flowing out of Gas Mixing System, and exchanges with DIC in bottle and photobioreactor together (Figure 1B). With these simplifications, there are only two degrees of freedom in our model: CO₂ exchange rate constants (k_E) in bottle and photobioreactor. Using a given combination of k_E, the forward model runs ordinary differential equations (ODEs) toward steady state using the Matlab function ‘ode15s’, with seawater and CO₂(g) composition in bottle, photobioreactor and bottle headspace as initial conditions. The notations and equations of the model are described in detail in the Appendix B, C, respectively. Fitting processes were carried out to estimate the exchange rate constants and gas flux. These processes were achieved by minimizing the difference between simulated carbon isotope ratios and measured values via the Matlab function ‘fmincon’.

3.1. Exchanging between CO₂(g) and CO₂(aq)

The equilibrium between CO₂(g) in headspace and CO₂(aq) in seawater follows Henry’s law (Carroll et al., 1991). The net exchange rate (ER) between seawater and headspace follows the Fick’s diffusion law.

$\begin{array}{ll}\begin{array}{c}\text{ER}= D_{CO2} \times A \times \frac{d\left[C{O}_2\right]}{dx}\end{array}& (1)\end{array}$

where the D_CO2 is the diffusion coefficient which depends on temperature and pressure, A is the surface area and $\frac{d\left[C{O}_2\right]}{dx}$ is the CO₂ concentration gradient between seawater and headspace. In a bubbling system, the surface area depends on the number and size of bubbles, which are difficult to estimate (e.g. Martínez and Casas, 2012). Here, to simply our model, we define an exchange rate constant into the Equation 1, which is a function of bubble surface area, temperature and pressure. If the exchange flux from gas phase into seawater is defined as positive, then net CO₂ exchange rate between gas and seawater can be described by k_E (with a unit of mol s^-1 atm^-1 in this case) and the CO₂ concentration difference between headspace and seawater by the following equation:

$\begin{array}{ll}\begin{array}{c}\text{ER}=k_E\times \left(\left[pC{O}_{2h}\right]-\left[C{O}_{2aq}\right]/k_H\right)\end{array}& (2)\end{array}$

where the k_H is the Henry’s Law constant, which depends on temperature and is 0.035 mol L^-1 atm^-1 at T =291.15K for this work. The pCO_2h is the CO₂ concentration in headspace, with a unit of atm. The CO₂(aq) is the CO₂ concentration in seawater, with a unit of mol L^-1. Since the k_E is difficult to calculate directly, we can estimate it by tracing the DIC carbon isotope evolution during bubbling, which will be described in Section 4.

3.2. DICs inter-reactions

The DICs inter-reactions in the seawater include:

$\begin{array}{ll}\begin{array}{c}C{O}_{2\left(aq\right)}+ H_{2}O \stackrel{k_{+1}/k_{-1}}{\iff } H^{+}+ HC{O}_3^{-}\end{array}& (3)\end{array}$

$\begin{array}{ll}\begin{array}{c}C{O}_{2\left(aq\right)}+ O{H}^{-} \stackrel{k_{+4}/k_{-4}}{\iff } HC{O}_3^{-}\end{array}& (4)\end{array}$

$\begin{array}{ll}\begin{array}{c}C{O}_3^{2-}+ H^{+}\stackrel{k_{+5}^H/k_{-5}^H}{\iff } HC{O}_3^{-}\end{array}& (5)\end{array}$

$\begin{array}{ll}\begin{array}{c}C{O}_3^{2-}+H_{2}O \stackrel{k_{+5}^{OH}/k_{-5}^{OH}}{\iff } HC{O}_3^{-}+ O{H}^{-}\end{array}& (6)\end{array}$

The reaction rate constants follow definitions in Zeebe and Wolf-Gladrow (2001), where k₊₁ and k_-1 are constants for hydration and dehydration reactions, k₊₄ and k_-4 are for hydroxylation and dehydroxylation reactions and k₊₅ and k_-5 are for CO₃^2- and HCO₃^- exchanging. To increase the simulation efficiency, the conversions between HCO₃^- and CO₃^2- are assumed to be instantaneous since they are about 8-9 orders of magnitudes higher than the reactions rate between CO₂(aq) and HCO₃^- (Zeebe and Wolf-Gladrow, 2001). The hydrolysis reactions (Equation 6) are not simulated in our model in order to increase the simulation efficiency, but the protolysis reactions (Equation 5) are simulated to calculate H⁺ concentration and thereby simulate the dynamic seawater pH during CO₂ bubbling.

3.3. Carbon isotope fractionations

The carbon isotope ratios of DIC and CO₂(g) were shown as the relative abundance of ¹³C/¹²C in substance X (¹³R_x) compared with the ratio of ¹³C/¹²C in standard carbonate (¹³R_std, VPDB in this study):

$\begin{array}{ll}\begin{array}{c}\delta {}_{}{}^{13}C{}_X= \left(\frac{{}_{}{}^{13}R{}_X}{{}_{}{}^{13}R{}_{std}}-1\right)\times 1000 \end{array}& (7)\end{array}$

The main processes causing isotopic fractionation in our simulations are: (1) CO₂(aq)-HCO₃^- inter-reactions and (2) CO₂ diffusion in air and CO₂ diffusion from gas phase into liquid phase. In our model, beside the concentrations of CO₂(g), CO₂(aq), HCO₃^- and CO₃^2-, the concentrations of ¹³CO₂(g), ¹³CO₂(aq), H¹³CO₃^- and ¹³CO₃^2- are also calculated. Isotopic fractionations are simulated by using larger or smaller reaction rate constants following Zeebe and Wolf-Gladrow (2001). A summary of reaction rate constants and fractionation factors can be found in Appendix Table B1. The reaction rates of DIC and CO₂(g) with heavy carbon atoms are listed in Equation C1-C10.

In this work, the δ¹³C_CO2(g) is about -2.8‰. The carbon isotope fractionation between CO₂(g) and CO₂(aq) is about 1.2‰ (CO₂(g) is less enriched of ¹³C than CO₂(aq)). The fractionation between CO₂(aq) and HCO₃^- is about -9.8‰ at 291.15K (CO₂(aq) is more depleted in ¹³C than HCO₃^-). The three DIC components vary with pH: the proportion of CO₂(aq) decreases with increase of pH, while CO₃^2- increases with the concomitant increase of pH. Since the HCO₃^- is the dominant component in seawater DIC, the value of carbon isotope fractionation between CO₂(aq) and HCO₃^- is close to the one between CO₂(aq) and total DIC (~0.3‰ difference when pH is around 8, Figure 2). In conclusion, ignoring the fractionation in CO₂(g) diffusion, the carbon isotope ratios of DIC should be about 8.3‰ more positive than that of CO₂(g), when they are in equilibrium, at our culture temperature and pH. In other words, the DIC carbon isotope ratio should be around 5.5‰ after equilibrium with CO₂(g) given a temperature of 291.15K and δ¹³C_CO2(g)= -2.8‰ for this work.

FIGURE 2

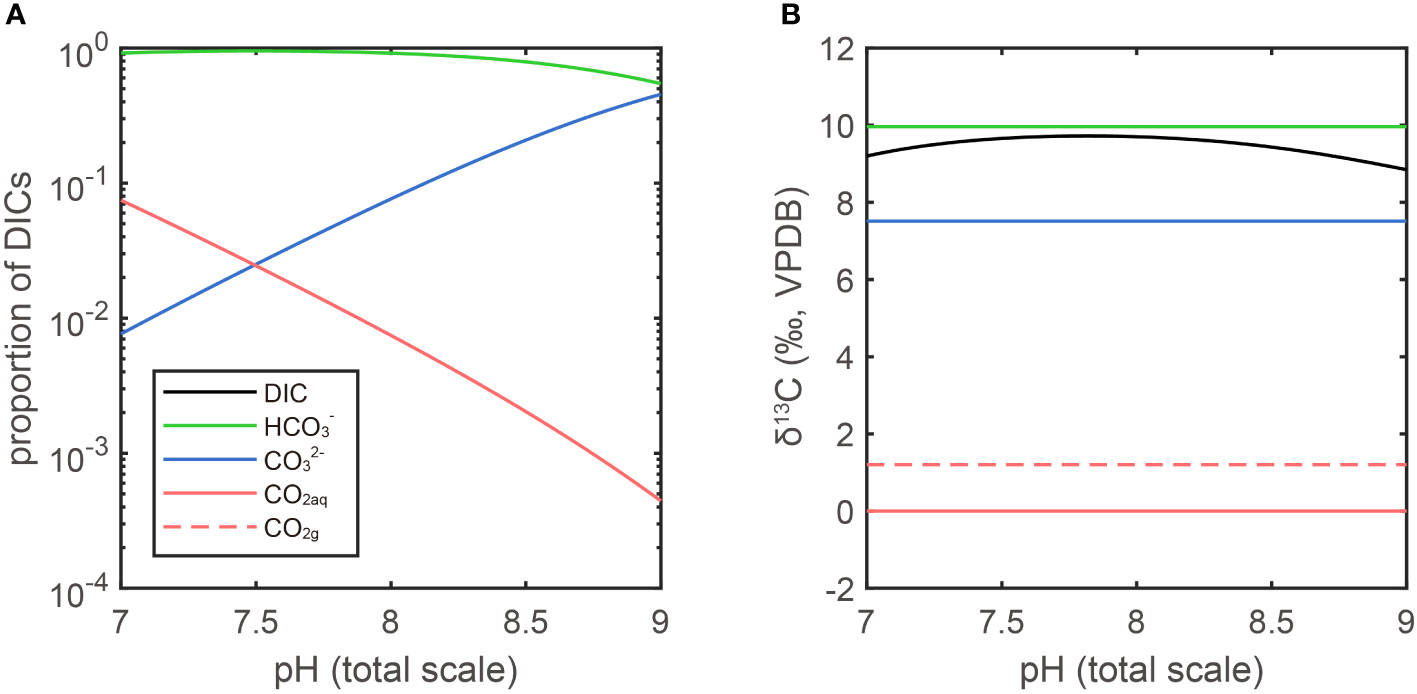
Figure 2 DIC proportion and isotope fractionation in different pH. (A) The ratio of the three components of DIC are plotted on a log scale in function of pH for a seawater at T = 291.15K and Salinity = 35‰. (B) The isotopic fractionations are calculated by the parameters in Table A1. The δ¹³C_VPDB of CO₂(aq) is arbitrarily set as 0‰ (red line). In isotopic equilibrium, the CO₂(g) is heavier than CO₂(aq) by 1.2‰, the HCO₃^- is heavier than CO₂(aq) by 9.8‰ and CO₃^2- is heavier than CO₂(aq) by 7.4‰ (Zhang et al., 1995). The fractionation between total DIC and CO₂(aq) is a function of pH as it determines the proportion of each DIC.

4. Results of simulations of the DIC evolution in bubbling

In this study, we carried out two experiments to estimate the CO₂ exchange rate constants between gas and seawater. The fitting results of CO₂ exchange rate constant (k_E) are 8.71×10^-5, 4.57×10^-5, 5.32×10^-5 and 3.36×10^-5 mol s^-1 atm^-1 for large system bottle, large system photobioreactor, small system bottle and small system photobioreactor, respectively.

The δ¹³C_DIC before bubbling are around -6.1‰ (-6.54~-5.65‰). With the onset of bubbling, δ¹³C_DIC responded logarithmically, increasing fastest during the first hours and slowing the rate of increase in the following days. The δ¹³C_DIC in both experiments did not increase further after reaching values around 5.5 ‰, about 8.3 ‰ higher than the CO₂(g), which well fitted our prediction in the last section. The δ¹³C_DIC reached equilibrium with CO₂(g) at 6 days in low CO₂ experiment with pCO₂ = 470 ppm, while in the other experiment, the isotopic equilibrium was achieved at 5 days after bubbling. In our simulations, the carbon exchange rate between CO₂(aq) and HCO₃^- is more than two orders of magnitude higher than the rate between CO₂(g) and CO₂(aq). Therefore, carbon isotope ratios of CO₂(aq) (δ¹³C_CO2(aq)) are almost parallel with δ¹³C_DIC (dashed lines in Figure 3).

FIGURE 3

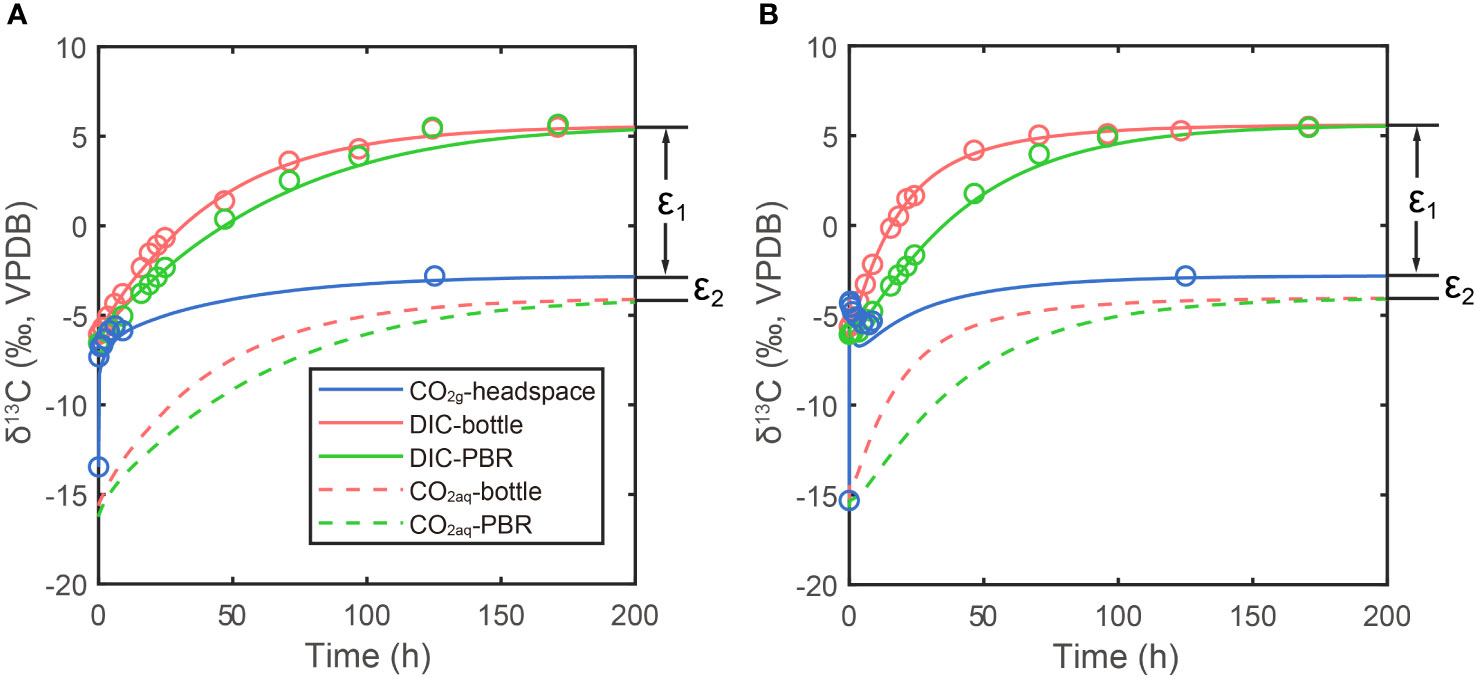
Figure 3 Measurements and simulations in two bubbling experiments: (A) lower CO₂ experiment in small photobioreactor system; (B) higher CO₂ experiment in large photobioreactor system. Lines are simulation results and dots are measured. Blue lines and dots are carbon isotope ratio of CO₂(g) in headspace, red lines and dots are DIC carbon isotope in bottle and green lines and dots are DIC carbon isotope in photobioreactor (PBR in legend). Red and green dashed lines are simulated CO₂(aq) carbon isotope ratios in bottle and photobioreactor, respectively. The ϵ₁ and ϵ₂ are carbon isotope fractionations between DIC and CO₂(g) and CO₂(g) and CO₂(aq), respectively.

Compared to the continually increasing δ¹³C_DIC and δ¹³C_CO2(aq), the carbon isotope ratio of CO₂ gas (δ¹³C_CO2(g)) in bottle headspace interestingly showed more variations (blue dots in Figure 3). The initial value of δ¹³C_CO2(g) was around -15‰, which is the atmosphere CO₂ carbon isotope ratio in the poorly ventilated laboratory. There were sharp increases in δ¹³C_CO2(g) from -15‰ to around -6‰, immediately after bubbling (-4.31‰ in high pCO₂ experiment and -7.32‰ in low pCO₂ experiment, only five minutes after bubbling). This was caused by the CO₂ in bottle headspace being rapidly replaced by the new CO₂ coming from the Gas Mixing System, which has a carbon isotope fingerprint of -2.8‰. With a fixed gas flux, this kind of rapid increase in δ¹³C_CO2(g) was more significant in high CO₂ concentration experiment (Figure 3B). The rapid increase of δ¹³C_CO2(g) was then followed by a decrease of δ¹³C_CO2(g), which was caused by CO₂ exchanging between gas in headspace and DIC in seawater. In the large system, the CO₂ exchange rate is about 640% higher than the rate in small system, due to the higher pCO₂ and higher k_E. Therefore, the ¹³C in CO₂(g) went into DIC in seawater faster in the larger system, resulting in an about 1.2‰ decline in δ¹³C_CO2(g) and also faster increases in δ¹³C_DIC (Figure 3B). This complex pattern of δ¹³C_CO2(g) was well simulated in our model (blue lines in Figure 3), though the simulation results are a bit lower value than measurements in high CO₂ experiment. This could be caused by the combination of the bubbles in bottle and photobioreactor with the headspace in our model, resulting in a more significant decline in δ¹³C_CO2(g) when CO₂(g) begins to exchange with DIC.

5. Implications for experimental setup and interpretation

5.1. Factors controlling equilibration time

To study the potential influence of experimental settings on equilibration time, a series of sensitivity tests are carried out by simulating the DIC evolution during bubbling. Here we define the ‘99% ordinary equilibration time’ as the time when [CO₂(aq)] reach [CO₂(aq) _t=0] + 0.99([CO₂(aq) _t=∞] – [CO₂(aq) _t=0]). Similarly, the ‘99% carbon isotopic equilibration time’ is defined as the time when the DIC carbon isotope ratio reaches δ¹³C_{DIC t=0} + 0.99(δ¹³C_{DIC t=∞} - δ¹³C_{DIC t=0}).

The first sensitivity test is the effect of CO₂ gas exchange rate constant (k_E) on equilibration time. Given a DIC concentration of 2200 μM and in a media volume of 1 L, and the initial carbon isotope difference between CO₂(g) and DIC of 5‰ (δ¹³C_CO2(g) - δ¹³C_{DIC t=0} = 5‰), both ordinary and isotopic equilibration time increase with a decreasing CO₂ exchange rate constant (Figure 4A). Hence, we suggest that the CO₂ exchange rate between gas and seawater is the first-order limitation of isotopic equilibration time.

FIGURE 4

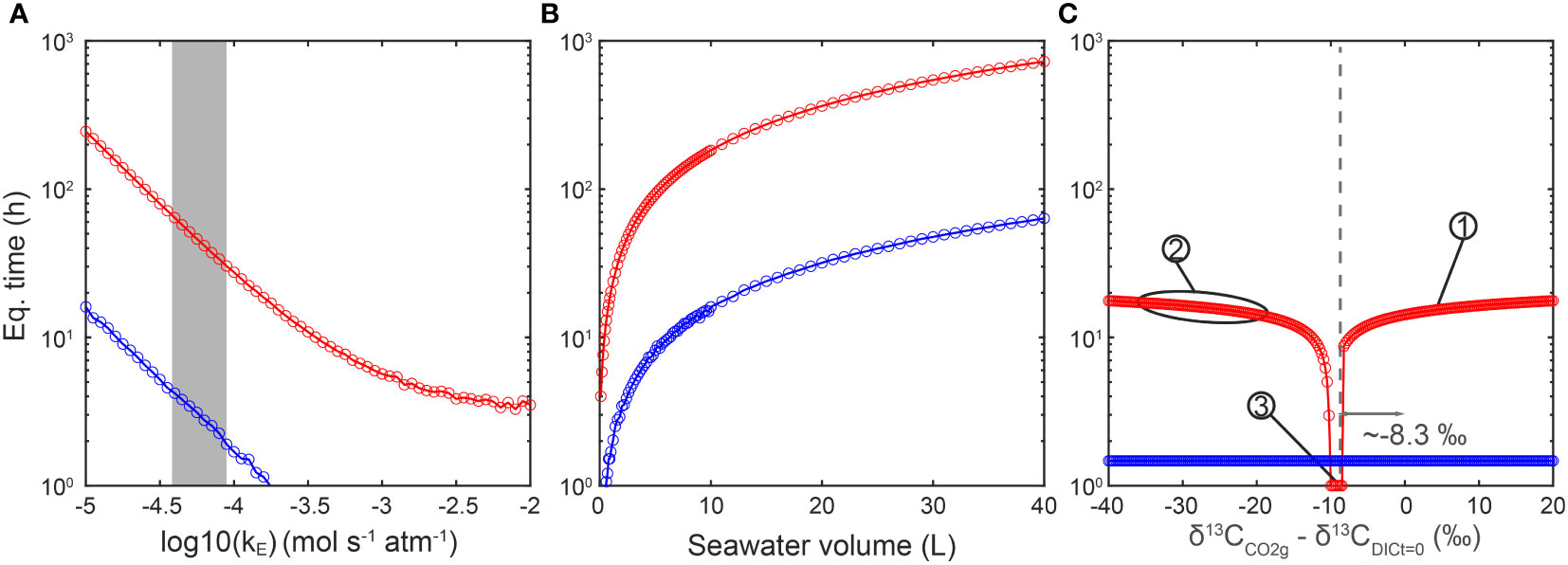
Figure 4 Sensitivity tests of different parameters effects on equilibration time. (A) Both isotopic (red) and chemical (blue) equilibration times decrease with the increase of gas exchange rate constant. The grey shaded area represents the estimated gas exchange rate constants in this work, ranging from 10^-4.4 to 10^-4.1 mol s^-1 atm^-1. (B) Both isotopic (red) and ordinary (blue) equilibration times increase with the increase of seawater volume. (C) The DIC carbon isotope reaches equilibrium faster when the carbon isotope ratio difference between DIC and CO₂(g) is around 8.3‰ (same as the ϵ₁ in Figure 3), which is the equilibrium fractionation between DIC and CO₂(g) at 291.15K. The carbon isotope difference does influence equilibration time especially when the difference is between -20‰ and -8.3‰. Numbering illustrates isotopic ratio differences in representative experiments here and in published works: No. 1 marks a Δ_t=0 = 1.7‰ in k_E measurement experiments in this study. No. 2 marks Δ_t=0 ranging from about -37 to -17‰ in several other works (e.g., Liu et al., 2018; Phelps et al., 2021). No. 3 marks a Δ_t=0 around -9‰ (Tchernov et al., 2014).

In the second simulation, the effect of culture media volume (or total DIC amount) was tested. Given a DIC concentration of 2200 μM, an initial carbon isotope difference between CO₂(g) and DIC (Δ_t=0) as 5‰ (δ¹³C_CO2(g) - δ¹³C_{DIC t=0} = 5‰) and a k_E of 10^-4 mol s^-1 atm^-1, both of ordinary and isotopic equilibration time show a linear increase with the seawater volume (Figure 4B). These simulations fit the expectation that, when the total DIC amount is higher, it will take longer to reach equilibrium in the system.

Finally, we evaluate the effect of initial carbon isotope difference between CO₂(g) and DIC on equilibration time. The carbon isotope of CO₂(g) was fixed in all simulations, but the initial carbon isotope ratio of DIC was varied, with initial carbon isotope difference ranging from -40 to 20‰. The DIC concentration was set as 2200 μM and the volume of media at 1 L. The simulation results in Figure 4C show that when the Δ_t=0 is ~-8.3‰, which is the equilibrium fractionation between CO₂(g) and DIC at T = 291.15K, the DIC reaches isotopic equilibrium with CO₂(g) even faster than the ordinary chemistry equilibrium. When the absolute isotopic difference (|Δ_t=0|) is larger, for example from -8.3 to -20‰, the isotopic equilibration time would increase exponentially. Another interesting observation is that, when the isotopic difference between CO₂(g) and DIC is large enough, the time to reach isotopic equilibrium will not increase with the |Δ_t=0|. We suggest that this is the time cost for all carbon atoms in the DIC to fully exchange with carbon atoms in CO₂(g). In contrast with the isotopic feature of seawater, the initial concentration of DIC and pH only have minor impacts on the equilibrium time, especially the isotopic equilibrium (Appendix E Figure E1).

5.2. Potential equilibration time effects in typical experimental setups

In recent years, more laboratory culture works have focused on carbon isotope variations in biogenic carbonate or bulk/special organic carbon under ocean acidification scenarios. We consider the expected behavior of carbon chemistry equilibration in three types of published experimental setups, and implications for the estimation of carbon isotope fractionation between DIC and biomass or biominerals.

5.2.1. Aeration of the gas surface without bubbling

The longest equilibration time would be expected for systems in which CO₂ is not bubbled directly but instead CO₂(g) was pumped into the bottle headspace, such as described in a recent published laboratory culture study on coccolithophores (Phelps et al., 2021). In their 2.5 L volume vessels of 1 L approximately 2000 μM DIC, the isotopic difference between CO₂ tank and the natural seawater media was not reported. Given natural seawater, the carbon isotope of DIC was likely in the range of 1 to 1.6‰ (Bidigare et al., 1997). Typical standard commercial CO₂ gas cylinders produced from fossil fuel combustion around -37‰. The range of carbon isotope difference would be ~38‰ and the expected equilibrium δ¹³C_DIC value after bubbling would be about -29‰. Measurement of δ¹³C_DIC at the start and end of the 5 day duration of experiment showed the least negative values (-7 to -9‰) in the 200 ppm CO₂ treatment and the most negative values (-15 to -17‰) in the 1000 ppm treatment (see Figure S8 in Phelps et al. (2021)). As the gas exchange rate constant should be the same between treatments, the gas exchange rate increases with the CO₂ concentration (see the Equation 2 in Section 3). This would lead to the DIC carbon isotope value in the 1000 ppm treatment being closer to equilibrium (more negative) than that in the 200 ppm CO₂ experiment. In this study, in order to minimize the impact of evolving δ¹³C_DIC, the isotopic fractionation was calculated using the final DIC carbon isotope ratio of each experiment, as representative of the DIC in which most of the harvested culture biomass was produced. Therefore, in this case, even if the DIC carbon isotope ratios did not reach equilibrium with the CO₂ gas, the fractionation results are still robust with help of DIC measurements. However, the disequilibrium between DIC and CO₂(g) could add additional errors in ϵ_p calculations, because of the gradual negative shift of DIC carbon isotope over the course of the culture. Additionally, the carbon isotope exchange rate would be faster when there is more disequilibrium with CO₂(g), resulting in a larger potential error in ϵ_p estimations (Figure 5A). In conclusion, even if the DIC carbon isotope ratios are measured carefully, it is still more optimal to ensure isotopic equilibrium in DIC for a stable δ¹³C_DIC to reduce the potential error.

FIGURE 5

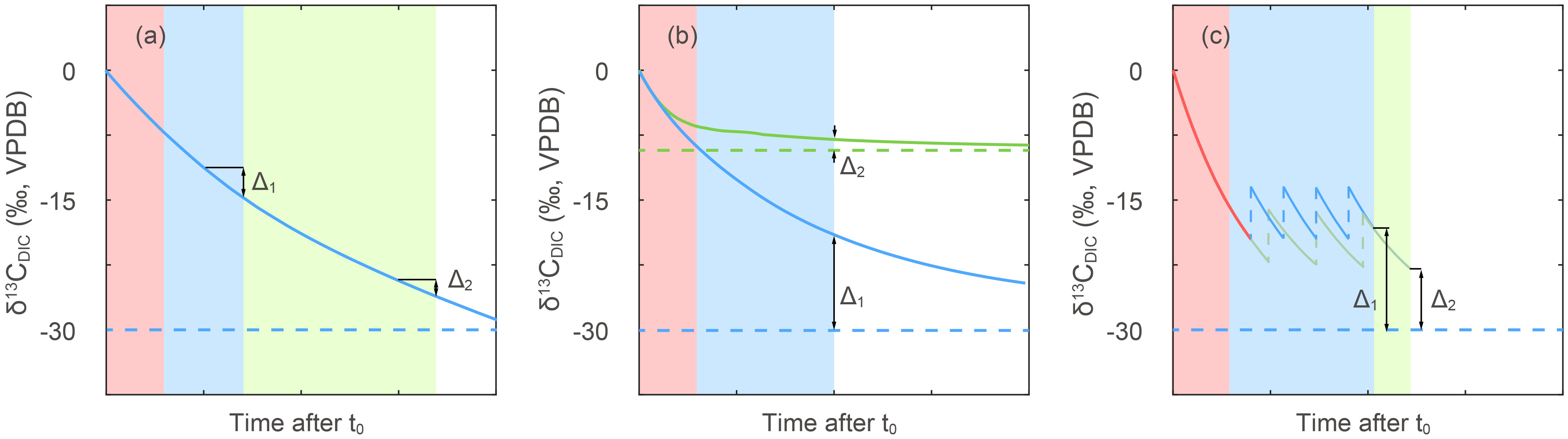
Figure 5 Concept model of isotopic disequilibrium effects in different experimental setups. Time advances from left to right in unspecified units since actual equilibration timescales depend on vessel dimensions and bubbling rate and surface area. Red shading areas represent the period in which media was bubbled before addition of cells. Blue and green shaded areas represent culture duration with bubbling. Horizontal dashed lines represent the δ¹³C_DIC after reaching equilibrium with CO₂(g), while solid lines give the time varying δ¹³C_DIC for different scenarios detailed below. Blue lines are shown for the common situation of bubbling a media of initial δ¹³C_DIC close to surface seawater (~0‰) with CO₂(g) of ~-38 ‰. The Δ₁ and Δ₂ are used to illustrate potential errors in estimation of δ¹³C_DIC, as detailed below. (A) Potential effect of the timing of sampling on the uncertainty in the δ¹³C_DIC. Because cells are produced not only the last day, but also a period of time before harvest, if the δ¹³C_DIC at time of cell harvest time was employed in fractionation calculation, the more rapid δ¹³C_DIC evolution early in the experiment could lead to a larger error as (Δ₁ vs Δ₂). Different CO₂ concentration treatments with different rates of reaching equilibrium, or different culture durations can cause differences in error as well as bias the estimation of δ¹³C_DIC corresponding to period of cell production. (B) Comparison of the effect of δ¹³C_CO2(g) of -38‰ (blue lines) vs ~-17‰ (green lines) on estimation of δ¹³C_DIC. The DIC carbon isotope would reach equilibrium faster with a CO₂(g) to DIC isotopic difference of around -8.3‰ leading to a smaller disequilibrium. This effect could be more serious when the DIC carbon isotope ratios are not measured. (C) The effect of dilution frequency on DIC carbon isotope evolution in continuous culturing set-ups. Blue and green lines present two different dilution treatments and red line represents δ¹³C_DIC evolution before first dilution. The vertical dashed lines represent positive shifts in carbon isotope caused by dilutions with un-bubbled seawater. Higher dilution rate would lead to a larger disequilibrium as Δ₁, if the seawater reservoir is not pre-bubbled to equilibrium with CO₂(g), which could also increase the error of fractionations in continuous culture set-ups.

5.2.2. Active bubbling of batch cultures

Shorter equilibration times would be expected in the cultures which are actively bubbled compared to cultures with only gas surface aeration. Remize et al. (2021) actively bubbled 2 L culture vessels of natural seawater of initially 750 μM DIC with an intensity of 5 bubbles per second. The isotopic difference between the CO₂ tank (-37.7‰) and natural seawater media (5‰) would be 42‰ and the expected equilibrium value after bubbling would be ~-30.5‰ at T_k = 292K. Measurement of δ¹³C_DIC every 4 days reveals δ¹³C_DIC attained -31‰, the expected equilibrium value after around 20 days. The equilibration likely required >10 days due to a slow gas exchange rate resulting from low-intensity bubbling and low CO₂ concentration. The δ¹³C of biomass sampled every 4 days throughout the experiment also evolves by 40‰ in parallel with the evolution of the δ¹³C_DIC.

Another example using bubbling method is Liu et al. (2018), who studied the carbon isotopic fractionation of a coastal coccolithophore, Ochrosphaera neapolitana. However, instead of measuring DIC carbon isotope ratios directly, they calculated expected DIC carbon isotope ratios assuming equilibrium with CO₂(g). Their carbon isotope fractionation results, in both calcite and organic carbon, were higher than other coccolithophores laboratory culture results (Rickaby et al., 2010; Hermoso et al., 2016; Stoll et al., 2019) by ~5–10‰. Moreover, they bubbled the DIC in three different CO_2- groups by gas with three different carbon isotope ratios ranging from -15‰ to -37‰. This could cause differences in the extent of isotopic disequilibrium among the experiments, as shown in Figures 4C, 5B.

5.2.3. Bubbling in continuous culture setups

More complex situations arise with continuous culturing set-ups. An example would be bubbling of the culture vessel but not the inflow bottle, from which new media are pumped into the culture for (semi-)continuous dilution (Wilkes et al., 2017; Wilkes et al., 2018). In this system, the CO₂ added was -38.6‰ for all cultures, and natural seawater (assumed to be about 1 to 1.6‰ as Bidigare et al. (1997)), in a 4 L culture vessel. The expected equilibrium δ¹³C_DIC would be -30‰. Different dilution rates were employed to control algae growth rate. In such a system the DIC carbon isotope could be closer to equilibrium when the dilution rate is lower. From the observations, it appears that the DIC in high CO₂ and low dilution rate treatments get closest to equilibrium (from the Table 1 in Wilkes et al. (2017)), while the faster dilution rate and lower CO₂ are furthest from equilibrium (Figure 5C). Previous authors (Wilkes et al., 2017) suggested that differences in the bubbling regimen may have contributed to the very different results from continuous cultures of Hoins et al. (2016). In Hoins et al. (2016), the biomass carbon isotope fractionation shows a much narrower range, only from 9 to 12‰, compared to the 14 to 26 ‰ in Wilkes et al. (2017), even though the CO₂ settings and cell growth rates in these two studies are similar. However, insufficient details are provided in the method of Hoins et al. (2016) to evaluate the role that isotopic equilibrium may have played in these divergent results, while the DIC carbon isotope ratios in Wilkes et al. (2017) were measured making the fractionation results more reliable.

Continuous cultures with faster equilibration are expected to result from using gas and media with a CO₂(g) to DIC isotopic difference around -9 to -8‰ (varying with temperature), as discussed in Section 5.1. Tchernov et al. (2014) described a culture in which natural seawater in Gulf of Maine, ~1.2‰ at nearest station in GLODAP V2 (Olsen et al., 2016), was bubbled with atmospheric CO₂ (~ -8.5‰), with expected equilibrium ranging from -7.6‰ at 26°C and -9.6‰ at 8°C (more equilibrium fractionations in different temperature can be found in Appendix D). The CO₂(g) and DIC were close to reach isotopic equilibrium in this study. Therefore, although only the culture vessel not the media reservoir was bubbled, the equilibration time would have been very short (as seen in Figure 4C).

5.3. Suggestions for future studies

As discussed in the previous section, isotopic disequilibrium is likely to have happened widely in current carbon isotopic studies involving bubbling of cultures. Most ocean acidification studies did check the ordinary chemistry equilibrium carefully by monitoring the seawater pH or DIC concentration during bubbling. But the carbon isotopic equilibrium has often been ignored so far, which could be much slower than the ordinary equilibrium. Here we suggest that for all laboratory culture works on carbon isotope fractionation, measuring the DIC carbon isotope ratio directly is always very necessary, at least once at the beginning and again the end of culture, in case the DIC is in disequilibrium with CO₂(g). We can estimate the isotope ratio at equilibrium quickly by δ¹³C_CO2(g) – Δ_eq, where Δ_eq is the equilibrium carbon isotope fractionation between CO₂(g) and DIC (defined as δ¹³C_CO2(g)- δ¹³C_DICeq, ~-8.3 when the temperature is about 291.15K and pH is around 7.8-8.2 in this study). The Δ_eq for different temperature and pH combinations have been listed in Table D1. If regular DIC carbon isotope measurements are not available, a safe solution could be pre-bubbling seawater for more than one week before carrying out any culture experiments. Even with measurements of DIC carbon isotope ratios, we still recommend that the DIC carbon isotope should reach (or be close to) isotopic equilibrium with CO₂(g), to minimize the error in carbon isotope fractionation calculations. For continuous cultures, the media reservoir used for dilution should also be pre-bubbled to avoid huge carbon isotopic shifts during culture, which can also reduce the error. We also suggest that it is necessary to report, as detailed as possible, the culture methods, including the CO₂(g) carbon isotope ratio, initial DIC carbon isotope ratio, pre-bubbling duration and dilution percentage, for the benefits of data comparison in future works.

For a chemostat system similar to the photobioreactor system employed in this work, both the ordinary and isotopic equilibriums are primarily limited by the CO₂ exchange rate between the gas phase and liquid phase. As discussed in the sensitivity test results, increasing the k_E can significantly accelerate the equilibration process. Firstly, exchange rate can be accelerated by increasing the gas flux. However, some large or fragile phytoplankton species, such as Trichodesmium erythraeum and dinoflagellate species, might be affected by the turbulence caused by bubbling (Hurd et al., 2009). Therefore, most studies employed a ‘gentle bubbling’, with a gas flux ranging from 100 mL min^-1 to 300 mL min^-1 for culture flasks in a few liters (e.g., Li et al., 2012; Gordillo et al., 2015). Additionally, it was also recommended to stop bubbling for the first day of incubation as the algae get acclimated (Shi et al., 2009). In conclusion, we should avoid increasing the gas exchange rate by increasing the gas flux, especially for algal cultures. Another way to accelerate equilibrium is using a gas-diffuser (also known as an air-stone), which could divide gas bubbles into a larger number of smaller bubbles significantly increasing the surface area between gas phase and seawater phase. Gas diffusers of plastic or glass are likely to provide the best option for gas diffusion in culture.

For studies evaluating vital effects in the oxygen isotope ratios of carbonate shells, such as coccoliths, the shells of foraminifera and bivalve, the oxygen isotope equilibrium between CO₂(g) and water should be also considered. In theory, the oxygen isotope equilibrium should take longer to reach equilibrium than that of the carbon isotopes. This is because in a closed system the equilibration time for carbon isotopes is only 10² seconds, but the equilibration time for oxygen isotopes is about a few hours (Zeebe and Wolf-Gladrow, 2001). Previously, the oxygen isotope issue was ignored because the oxygen atom from water is dominant in a DIC-H₂O system. For example, in 1 L seawater with [DIC] = 2.3 mM and pH = 8.2, there are only about 4.6×10^-3 mol oxygen atoms derived from DIC but about 55 mol oxygen atoms from H₂O. However, continuous CO₂ bubbling will bring more oxygen atoms from CO₂(g) into media. This will alter the seawater oxygen isotope ratio if the oxygen isotope in CO₂(g) is not naturally equilibrium with the oxygen isotope ratio of H₂O. Therefore, when biogenic carbonate oxygen isotope fractionation experiments are carried out using CO₂ bubbling, cautions are advised that the water oxygen isotope results could be influenced by disequilibrium among CO₂(g)-DIC-H₂O.

During culturing, the biomass consumes DIC and nutrients continually, modifying the culture media chemical and isotopic composition. Historically, previous work had to employ dilute batch cultures to avoid large shifts in both DIC concentration and isotopic composition. Chemostat systems were designed to keep a stable cell growth environment with help of numerical models (e.g., Ajbar and Alhumaizi, 2011). With cell density, growth rate, PIC and POC per cell, it would be possible to simulate how cell growth influences the DIC concentrations and isotope ratios evolution in continuous cultures, and very low cell density may no longer be the only way to achieve an accurate estimation of isotopic fractionation and stable carbonate system. Carbon isotope fractionation results in batch culture can also be re-calculated more accurately by employing an isotopic model to simulate a dynamic DIC carbon isotope ratio, than simply using the DIC carbon isotope ratio at the end of culture.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author contributions

IT-R and HZ carried out the bubbling experiments. IT-R and PA measured carbon isotope with help from MJ in data calibration. HZ developed the numerical model. HZ and HS wrote the paper with input from other authors. All authors contributed to the article and approved the submitted version.

Funding

This study was supported by the Swiss National Science Foundation (Award 200021_182070 to HMS) and ETH Zurich (ETH03- 19-1 to HMS). “STATEMENT”. Statement: Open access funding provided by ETH Zurich.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2022.1045634/full#supplementary-material

References

Ajbar A., Alhumaizi K. (2011). Dynamics of the chemostat: A bifurcation theory approach (CRC Press). doi: 10.1201/b11073-6

CrossRef Full Text | Google Scholar

Bidigare R. R., Fluegge A., Freeman K. H., Hanson K. L., Hayes J. M., Hollander D., et al. (1997). Consistent fractionation of 13C in nature and in the laboratory: Growth-rate effects in some haptophyte algae. Global Biogeochemical Cycles 11, 279–292. doi: 10.1029/96GB03939

PubMed Abstract | CrossRef Full Text | Google Scholar

Carroll J. J., Slupsky J. D., Mather A. E. (1991). The solubility of carbon dioxide in water at low pressure. J. Phys. Chem. Reference Data 20, 1201–1209. doi: 10.1063/1.555900

CrossRef Full Text | Google Scholar

Figuerola B., Hancock A. M., Bax N., Cummings V. J., Downey R., Griffiths H. J., et al. (2021). A review and meta-analysis of potential impacts of ocean acidification on marine calcifiers from the southern ocean. Front. Mar. Sci. 8, 24. doi: 10.3389/fmars.2021.584445

CrossRef Full Text | Google Scholar

Gattuso J.-P., Hansson L. (2011). Ocean acidification (Oxford University Press) doi: 10.1093/oso/9780199591091.001.0001.

CrossRef Full Text | Google Scholar

Gattuso J.-P., Lee K., Rost B., Schulz K. (2010). Approaches and tools to manipulate the carbonate chemistry (Publications Office of the European Union) doi: 10013/epic.35259.d001.

Google Scholar

Gordillo F. J., Aguilera J., Wiencke C., Jiménez C. (2015). Ocean acidification modulates the response of two Arctic kelps to ultraviolet radiation. J. Plant Physiol. 173, 41–50. doi: 10.1016/j.jplph.2014.09.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Hermoso M., Chan I. Z. X., McClelland H. L. O., Heureux A. M. C., Rickaby R. E. M. (2016). Vanishing coccolith vital effects with alleviated carbon limitation. Biogeosciences 13, 301–312. doi: 10.5194/bg-13-301-2016

CrossRef Full Text | Google Scholar

Hoegh-Guldberg O., Mumby P. J., Hooten A. J., Steneck R. S., Greenfield P., Gomez E., et al. (2007). Coral reefs under rapid climate change and ocean acidification. Science 318, 1737–1742. doi: 10.1126/science.1152509

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoins M., Eberlein T., Grobetamann C. H., Brandenburg K., Reichart G. J., Rost B., et al. (2016). Combined effects of ocean acidification and light or nitrogen availabilities on 13C fractionation in marine dinoflagellates. PloS One 11, e0154370. doi: 10.1371/journal.pone.0154370

PubMed Abstract | CrossRef Full Text | Google Scholar

Hopkinson B. M., Dupont C. L., Allen A. E., Morel F. M. M. (2011). Efficiency of the CO2-concentrating mechanism of diatoms. Proc. Natl. Acad. Sci. 108, 3830–3837. doi: 10.1073/pnas.1018062108

CrossRef Full Text | Google Scholar

Hurd C. L., Beardall J., Comeau S., Cornwall C. E., Havenhand J. N., Munday P. L., et al. (2019). Ocean acidification as a multiple driver: How interactions between changing seawater carbonate parameters affect marine life. Mar. Freshw. Res. 71, 263–274. doi: 10.1071/MF19267

CrossRef Full Text | Google Scholar

Hurd C. L., Hepburn C. D., Currie K. I., Raven J. A., Hunter K. A. (2009). Testing the effects of ocean acidification on algal metabolism: Considerations for experimental designs 1. J. Phycology 45, 1236–1251. doi: 10.1111/j.1529-8817.2009.00768.x

CrossRef Full Text | Google Scholar

Iglesias-Rodriguez M. D., Halloran P. R., Rickaby R. E., Hall I. R., Colmenero-Hidalgo E., Gittins J. R., et al. (2008). Phytoplankton calcification in a high-CO2 world. science 320, 336–340. doi: 10.1126/science.1154122

PubMed Abstract | CrossRef Full Text | Google Scholar

Kadis R., Leito I. (2010). Evaluation of the residual liquid junction potential contribution to the uncertainty in pH measurement: A case study on low ionic strength natural waters. Analytica chimica Acta 664, 129–135. doi: 10.1016/j.aca.2010.02.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Keller M. D., Selvin R. C., Claus W., Guillard R. R. (1987). Media for the culture of oceanic ultraphytoplankton 1, 2. J. Phycology 23, 633–638. doi: 10.1111/j.1529-8817.1987.tb04217.x

CrossRef Full Text | Google Scholar

Lemasson A. J., Fletcher S., Hall-Spencer J. M., Knights A. M. (2017). Linking the biological impacts of ocean acidification on oysters to changes in ecosystem services: A review. J. Exp. Mar. Biol. Ecol. 492, 49–62. doi: 10.1016/j.jembe.2017.01.019

CrossRef Full Text | Google Scholar

Li W., Gao K., Beardall J. (2012). Interactive effects of ocean acidification and nitrogen-limitation on the diatom phaeodactylum tricornutum. PloS One 7, e51590. doi: 10.1371/journal.pone.0051590

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu Y. W., Eagle R. A., Aciego S. M., Gilmore R. E., Ries J. B. (2018). A coastal coccolithophore maintains pH homeostasis and switches carbon sources in response to ocean acidification. Nat. Commun. 9, 2857. doi: 10.1038/s41467-018-04463-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Martínez I., Casas P. (2012). Simple model for CO2 absorption in a bubbling water column. Braz. J. Chem. Eng. 29, 107–111. doi: 10.1590/S0104-66322012000100012

CrossRef Full Text | Google Scholar

Meyer J., Riebesell U. (2015). Reviews and syntheses: Responses of coccolithophores to ocean acidification: A meta-analysis. Biogeosciences 12, 1671–1682. doi: 10.5194/bg-12-1671-2015

CrossRef Full Text | Google Scholar

Mills G. A., Urey H. C. (1940). The kinetics of isotopic exchange between carbon dioxide, bicarbonate ion, carbonate ion and water1. J. Am. Chem. Soc. 62, 1019–1026. doi: 10.1021/ja01862a010

CrossRef Full Text | Google Scholar

Mostofa K. M., Liu C.-Q., Zhai W., Minella M., Vione D., Gao K., et al. (2016). Reviews and syntheses: Ocean acidification and its potential impacts on marine ecosystems. Biogeosciences 13, 1767–1786. doi: 10.5194/bg-13-1767-2016

CrossRef Full Text | Google Scholar

Nishida K., Chew Y. C., Miyairi Y., Hirabayashi S., Suzuki A., Hayashi M., et al. (2020). Novel reverse radioisotope labelling experiment reveals carbon assimilation of marine calcifiers under ocean acidification conditions. Methods Ecol. Evol. 11, 739–750. doi: 10.1111/2041-210X.13396

CrossRef Full Text | Google Scholar

O'Leary M. H. (1988). Carbon isotopes in photosynthesis. BioScience 38, 328–336. doi: 10.2307/1310735

CrossRef Full Text | Google Scholar

Olsen A., Key R. M., Van Heuven S., Lauvset S. K., Velo A., Lin X., et al. (2016). The global ocean data analysis project version 2 (GLODAPv2)–an internally consistent data product for the world ocean. Earth System Sci. Data 8, 297–323. doi: 10.5194/essd-8-297-2016

CrossRef Full Text | Google Scholar

Phelps S. R., Hennon G. M. M., Dyhrman S. T., Hernández-Limón M. D., Williamson O. M., Polissar P. J. (2021). “Carbon isotope fractionation in noelaerhabdaceae algae in culture and a critical evaluation of the alkenone paleobarometer,” Geochem. Geophysics Geosystems. 22(7): e2021GC009657. doi: 10.1029/2021GC009657

CrossRef Full Text | Google Scholar

Remize M., Planchon F., Loh A. N., Le Grand F., Mathieu-Resuge M., Bideau A., et al. (2021). Fatty acid isotopic fractionation in the diatom chaetoceros muelleri. Algal Res. 54, 102164. doi: 10.1016/j.algal.2020.102164

CrossRef Full Text | Google Scholar

Rickaby R. E. M., Henderiks J., Young J. N. (2010). Perturbing phytoplankton: response and isotopic fractionation with changing carbonate chemistry in two coccolithophore species. Clim. Past 6, 771–785. doi: 10.5194/cp-6-771-2010

CrossRef Full Text | Google Scholar

Riebesell U., Fabry V. J., Hansson L., Gattuso J.-P. (2011). Guide to best practices for ocean acidification research and data reporting (Office for Official Publications of the European Communities). doi: 10.1093/oso/9780199591091.003.0011

CrossRef Full Text | Google Scholar

Riebesell U., Tortell P. D. (2011). “Effects of ocean acidification on pelagic organisms and ecosystems,” in Ocean acidification, 99–121. doi: 10.2777/66906

CrossRef Full Text | Google Scholar

Shi D., Xu Y., Morel F. M. M. (2009). Effects of the pH/pCO2 control method on medium chemistry and phytoplankton growth. Biogeosciences 6, 1199–1207. doi: 10.5194/bg-6-1199-2009

CrossRef Full Text | Google Scholar

Stoll H. M., Guitian J., Hernandez-Almeida I., Mejia L. M., Phelps S., Polissar P., et al. (2019). Upregulation of phytoplankton carbon concentrating mechanisms during low CO2 glacial periods and implications for the phytoplankton pCO2 proxy. Quaternary Sci. Rev. 208, 1–20. doi: 10.1016/j.quascirev.2019.01.012

CrossRef Full Text | Google Scholar

Tchernov D., Gruber D. F., Irwin A. (2014). Isotopic fractionation of carbon in the coccolithophorid emiliania huxleyi. Mar. Ecol. Prog. Ser. 508, 53–66. doi: 10.3354/meps10840

CrossRef Full Text | Google Scholar

Wilkes E. B., Carter S. J., Pearson A. (2017). CO2-dependent carbon isotope fractionation in the dinoflagellate alexandrium tamarense. Geochimica Cosmochimica Acta 212, 48–61. doi: 10.1016/j.gca.2017.05.037

CrossRef Full Text | Google Scholar

Wilkes E. B., Lee R. B. Y., McClelland H. L. O., Rickaby R. E. M., Pearson A. (2018). “Carbon isotope ratios of coccolith–associated polysaccharides of emiliania huxleyi as a function of growth rate and CO 2 concentration,” in Organic Geochemistry 119(2018):1–10. doi: 10.1016/j.orggeochem.2018.02.006

CrossRef Full Text | Google Scholar

Zeebe R. E., Wolf-Gladrow D. (2001). CO2 in seawater: equilibrium, kinetics, isotopes (Gulf Professional Publishing) doi: 10.1016/s0422-9894(01)x8001-x.

CrossRef Full Text | Google Scholar

Zhang J., Quay P. D., Wilbur D. O. (1995). Carbon isotope fractionation during gas-water exchange and dissolution of CO2. Geochimica Cosmochimica Acta 59, 107–114. doi: 10.1016/0016-7037(95)91550-D

CrossRef Full Text | Google Scholar