Digging Deeper: Bioturbation increases the preserved sulfur isotope fractionation

Bioturbation enhances mixing between the seafloor and overlying ocean due to changes the redox state of the sediment and influences the biogeochemical cycling of redox-sensitive elements such as sulfur. Before the widespread appearance of burrowing fauna over the Proterozoic-Phanerozoic transition, marine sediments were largely undisturbed and transport of material across the sediment-water interface was diffusion-dominated. Through both a microcosm experiment and numerical model, we show that the effect of bioturbation on marine sediments is to enhance the drawdown of sulfate from the water column into the sediment and thus “open-up” the sedimentary system. The key finding is that bioturbation increases the difference between the isotopic signature of seawater sulfate and pore water sulfide, the latter of which is preserved in sedimentary sulfide minerals. Our study empirically demonstrates a long-held assumption and helps identify the isotopic impact of bioturbation in the geological record and its environmental effects in modern marine systems.

1. Introduction

Throughout Earth history, the evolution and radiation of living organisms has shaped global ocean chemistry (e.g. Ridgwell and Zeebe, 2005; Butterfield, 2011; Lyons et al., 2014). The appearance of burrowing animals over the Ediacaran-Cambrian transition is recognized as the start of sedimentary bioturbation (Bottjer et al., 2000; Bottjer, 2010; Tarhan et al., 2020), which would have had a major effect on seafloor and ocean biogeochemistry (Canfield and Farquhar, 2009; Boyle et al., 2014; Schiffbauer et al., 2016; van de Velde et al., 2018). Bioturbation refers to a wide range of physical and chemical processes that occur when organisms burrow through sediments, flushing their burrows with overlying seawater and mixing sediment particles (Meysman et al., 2006; Kristensen et al., 2012). Two end-member processes of bioturbation are bioirrigation, which refers to the solute transport that occurs when organisms flush their burrows with seawater, and biomixing, which refers to the particle mixing which occurs as organisms create their burrows and defecate (Kristensen et al., 2012). Bioturbation causes an increased movement of particles and solutes from the typically-oxic upper sediment layers to the typically-anoxic lower sediment layers, and vice versa. This impacts redox-sensitive elements such as iron and sulfur (Thamdrup et al., 1994; van de Velde and Meysman, 2016). Recent studies have shown that taken separately, the effects of bioirrigation and biomixing are more complex than what the net effect that we measure shows (van de Velde and Meysman, 2016). For example, van de Velde and Meysman (2016) show using a model that bioirrigation and biomixing have very distinct, and even opposing, effects on iron and sulfur cycling in sediments. Biomixing enhances the transport of solid precipitates between the oxic and anoxic zones in sediments, thereby oxidizing reduced species (such as iron sulfides) and reducing oxidized species (such as iron oxy-hydroxides). On the other hand, bioirrigation removes reduced solutes such as sulfide and ferrous iron from the sediment pore water, where they are oxidized in the water column and not returned to the sediment (van de Velde and Meysman, 2016). In this sense, biomixing enhances the recycling of iron and sulfur in the sediment whereas bioirrigation decreases recycling. There is a marked increase in the difference between the sulfur isotopic composition of sulfate and sulfide minerals recorded with the onset of bioturbation in the geological record (Canfield and Farquhar, 2009), suggesting that bioturbation may have influenced the sedimentary sulfur cycle. Here we use microcosms and a numerical model to demonstrate empirically that bioturbation increases the difference in the sulfur isotopic composition between pore fluid sulfate and sulfide, providing a strong correlation for the coincidence of the onset of bioturbation and the increase in the difference between the sulfur isotopic composition of sulfate and sulfide minerals.

It has been previously suggested that bioturbation influences the sedimentary sulfur cycle (Canfield and Farquhar, 2009; Tarhan et al., 2015; Saitoh et al., 2017). In sedimentary environments, microbial sulfate reduction (MSR) is a key microbial metabolism, through which dissolved sulfate is reduced to dissolved sulfide. The lighter isotope (³²S) of sulfur is consumed more quickly by sulfate reducing microorganisms, resulting in the product sulfide being enriched in the light isotope of sulfur while the remaining sulfate becomes enriched in the heavier isotopes of sulfur (³³S, ³⁴S, etc.). The preferential partitioning of the light sulfur isotope during MSR into the reduced sulfur fraction is shown to be between 0 and 72‰. The magnitude of this sulfur isotope fractionation is controlled by physiological factors (Goldhaber and Kaplan, 1980; Wortmann et al., 2001; Brunner and Bernasconi, 2005; Sim et al., 2011; Leavitt et al., 2013; Wing and Halevy, 2014; Bradley et al., 2016) but also local (physico-environmental) factors that influence the reversibility of MSR (Reese, 1973; Brunner and Bernasconi, 2005; Wing and Halevy, 2014). At the sediment level, the measured difference in the sulfur isotope composition between seawater sulfate and porewater sulfide (Δ³⁴S_{SO4_sw-H2S_pw}), and further in sedimentary minerals, is also controlled by the concentration of seawater sulfate, the availability of reactive iron, and the degree of connectivity, or ‘openness’, of the sediment with the overlying water which will influence the isotopic mass balance among sulfur species (Habicht et al., 2002; Canfield and Farquhar, 2009; Gomes and Hurtgen, 2015; Sim, 2019). The burrowing activity of benthic fauna enhances the connection of seawater with the sediment, resulting in increased supply of sulfate to the sediment as well as the oxidation of reduced sulfur compounds originating from MSR (Thamdrup et al., 1994; Canfield and Farquhar, 2009; van de Velde and Meysman, 2016; Blonder et al., 2017). In marine sediments, sulfide oxidation does not impart a significant sulfur isotope fractionation (Zerkle et al., 2009), but can increase the apparent isotope fractionation (Δ³⁴S) between sulfate and sulfide by reoxidizing sulfide to intermediate sulfur compounds such as elemental sulfur, which promotes the subsequent disproportionation of these sulfur intermediates. This results in the formation of more ³⁴S-depleted sulfide and ³⁴S-enriched sulfate, which can increase Δ³⁴S to values larger than those produced by MSR alone (Canfield and Thamdrup, 1994; Pellerin et al., 2015). Thus, bioturbation may enhance sedimentary dissolved sulfide oxidation and thereby increase Δ³⁴S_{SO4_sw-H2S_pw}.

Over Earth history, the difference between the sulfur isotopic composition of sulfate and sulfide minerals in the rock record increased due to a chain of events including higher atmospheric oxygen concentrations (Great Oxidation Event) and a subsequent increase in seawater sulfate concentrations (Cameron, 1982; Canfield et al., 2000). The difference between the sulfur isotopic composition of sulfate minerals and sulfide minerals in the rock record also increased in a marked way near the Precambrian-Cambrian boundary. Specific mechanisms for this increase in Δ³⁴S_{SO4_sw-H2S_pw} are still debated, though it is suspected that the increasing oxygenation of Earth’s surface reservoirs in the Neoproterozoic may have played a role (Canfield and Teske, 1996; Fike et al., 2006; Krause et al., 2018). Although there is an increase in Δ³⁴S_{SO4_sw-H2S_pw} during the Shuram CIE (Fike et al., 2006), and geological evidence points towards increasing marine sulfate concentrations around this time (Cui et al., 2022), the Shuram CIE was a transient event that occurred tens of millions of years before the Ediacaran-Cambrian boundary (Rooney et al., 2020). Fike et al. (2006) interpret the increase as being due to successive oxygenation events, the last stage of which ended before the Ediacaran-Cambrian boundary. Therefore, any mechanism causing an increase in the apparent isotope fractionation of sulfur during the transient Shuram CIE of the Ediacaran is not necessarily the same mechanism that caused an increase in the apparent isotope fractionation of sulfur across the Ediacaran-Cambrian boundary. Because bioturbation can oxidize sediment porewaters and transport reduced sulfur compounds to oxidized surface sediments (Berner and Westrich, 1985; van de Velde and Meysman, 2016), the onset of bioturbation has been invoked as a mechanism to increase the oxidative cycling of elements such as sulfur (McIlroy and Logan, 1999). Importantly, bioturbation had a large impact on the seafloor during the Precambrian-Cambrian transition (Boyle et al., 2018; Hantsoo et al., 2018; van de Velde et al., 2018; Cribb et al., 2019). Previous studies have studied the effect of bioturbation on the evolution of the sulfur cycle throughout Earth history (Canfield and Farquhar, 2009; Tarhan et al., 2015; Saitoh et al., 2017; Hantsoo et al., 2018). Yet to date, a combined experimental and modelling approach to explore the effect of bioturbation on Δ³⁴S_{SO4_sw-H2S_pw} is lacking. We therefore performed a bioturbation microcosm experiment and applied two different numerical models to demonstrate how bioturbation affects Δ³⁴S_{SO4_sw-H2S_pw}. Both experimental and theoretical results demonstrate that bioturbation increases Δ³⁴S_{SO4_sw-H2S_pw} by enhancing mixing between porewater sulfate and overlying sulfate, changing the flux balance relative to MSR.

2. Materials and methods

2.1. Experimental setup

To recreate the sedimentary environments where bioturbation-performing organisms live, we added seawater and sulfide-rich sediment from the Blakeney salt marsh in the north Norfolk coast, UK to 35 cm tall cylindrical plastic containers, and added worms as our “agents of bioturbation”. The Blakeney salt marsh sediment is characterized by high TOC content (5-10%) and high sulfide concentrations (mM-level) and devoid of any living fauna (Antler et al., 2019; Hutchings et al., 2019).The organisms used were annelid polychaete worms (Nereis spp.), collected from an iron-rich sediment from the Blakeney salt marsh on the north Norfolk coast, UK. The paleontological record provides justification for this choice of burrowing organism: annelid worms were probably present as early as the late Ediacaran (Schiffbauer et al., 2020; Yang et al., 2020), and polychaete worms were already present in the early Cambrian (Vinther et al., 2011).The sediment was homogenized before distribution to the two containers. Sediment was homogenized in large plastic bags under a stream of nitrogen gas. After 0.3 L of sediment was distributed to each container, the overlying water was added carefully to avoid sediment resuspension. After all the suspended sediment settled (overnight), the overlying water was bubbled continuously with an air pump. The sediment was settled for one month before starting of the experiment. After one month of settling, Rhizon samplers were added at a depth of 3 cm below the sediment-water interface. To put this depth into context, the worms were between 3-5 cm in length, and in the field they dig down to 15 cm. They build their burrows relatively fast (within one day) and only later ventilate their burrows. A photograph of our experimental setup in shown in Figure 1. The two experimental containers were arranged as follows: a control experiment with no worms, and an experiment with two worms added. An initial sample of the stratified, non-bioturbated sediment and overlying water was taken before the addition of the worms. The worms were subsequently added and the geochemistry was monitored for two weeks. The concentrations and sulfur isotope composition of sulfate and dissolved sulfide in the water and sediment were measured at four different time points alongside the control experiment without worms. Because high-resolution sampling at more frequent time points itself could alter the pore water, we reduced the sampling resolution to these four time points.

FIGURE 1

Figure 1 Photograph of experimental setup showing sulfidic sediment with oxidized worm burrows. Rhizon sampler for taking sediment pore water samples also shown.

2.2. Dissolved sulfate and sulfide measurements

To measure the dissolved sulfate concentration, 1 ml of porewater was vigorously bubbled with humidified N₂/CO₂ (80:20) gas mixture to remove sulfide, and was stored at 4°C until analysis. Sulfate concentrations were measured by ion chromatography (IC, Dionex DX-500, University of Cambridge) with an error of 2% between duplicates. Dissolved sulfide concentrations were measured spectrophotometrically using the methylene blue method with an error of 2% and a detection limit of 1 μM (Cline, 1969).

2.3. Sulfur isotope measurements

An additional aliquot of sediment porewater for sulfate and sulfide isotope analysis was collected subsequently to the porewater retrieved for geochemical analysis. 2 mL of porewater was added to 400 uL of 5% zinc acetate. The sample was then centrifuged. To measure the sulfur isotopic composition of sulfate, the supernatant was filtered (0.22um disk filter) to remove suspended ZnS and was separated into vials, and a saturated barium chloride solution was added, precipitating barite (BaSO₄). The barite was cleaned using 10% HCl, triple washed with MilliQ water, and dried. To measure the sulfur isotopic composition of dissolved sulfide, the precipitate was taken and cleaned three times using MilliQ water. Sulfur isotope analysis was done at the University of Cambridge using continuous flow gas source-isotope ratio mass spectrometry (GS-IRMS) (Thermo, Delta V Plus) equipped with an element analyzer (EA). Measurements of δ³⁴S were corrected to NBS 127, IAEA-SO-6, IAEA-SO-5, and IAEA-S-3 (21.1%, -34.1%, 0.5%, and -32.4%, respectively) and are reported with respect to Vienna Canyon Diablo Troilite (VCDT).

2.4. Model of bioturbation experiments

The experiments were interpreted with a two-box model that allowed us to determine the parameters which changed between the experiments with and without bioturbation, where the two boxes are the sediment and the overlying water. The model focuses on the sedimentary sulfur cycle and looks specifically at how the concentrations of sulfate and sulfide and their sulfur isotopic composition change over time in the porewater and overlying water once bioturbation begins. The model assumes that there is no MSR or dissolved sulfide in the overlying water, and that the fluxes into and out of the sediment are equal because the flux due to bioturbation is larger than any diffusive fluxes. Bioturbation is incorporated into the model by increasing the flux of the components into and out of the sediment. In the overlying water, the change in the sulfate concentration over time is equal to the amount of sulfate entering the overlying water from the sediment minus the amount of sulfate from the water column entering the sediment:

$\begin{array}{ll}\frac{{\text{dSO}}_{4_{\text{ow}}}}{\text{dt}}\text{ = -}{\varphi }_{\text{in}}·{\text{ SO}}_{4_{\text{OW}}}\left(\text{t}\right) \text{+ }{\varphi }_{\text{out}}·{\text{ SO}}_{4_{\text{PW}}}\left(\text{t}\right) & (1)\end{array}$

where, ϕ_in and ϕ_out are the fluxes of dissolved sulfate and sulfide from the water to the sediment, and from the sediment to the water, respectively, and SO_4OW and SO_4PW are the dissolved sulfate concentration in the overlying water and sediment porewater as a function of time, respectively. The sulfate concentration in the sediment porewater over time is given by:

$\begin{array}{ll}\frac{{\text{dSO}}_{4_{\text{pw}}}}{\text{dt}}\text{ = -}{\varphi }_{\text{out}}·{\text{ SO}}_{4_{\text{PW}}}\left(\text{t}\right) \text{+ }{\varphi }_{\text{in}}·{\text{ SO}}_{4_{\text{OW}}}\left(\text{t}\right) - SRR + Ox & (2)\end{array}$

where SRR is the microbial sulfate reduction rate, and Ox is the rate of sedimentary sulfide (i.e. pyrite) oxidation defined by:

$\begin{array}{ll}\text{Ox = }{\varphi }_{\text{in}}·{\text{O}}_2·\frac{8}{15}·{\text{f}}_{\left(\mathrm{0-1}\right) } & (3)\end{array}$

where O₂ is the concentration of oxygen in seawater (which we assume to be 0.2 mM), 8/15 (15 oxygen atoms are used for the production of 8 sulfate molecules) is a stoichiometric coefficient for pyrite oxidation, and f_(0-1) is a fraction from zero to one which represents the fraction of pyrite oxidized. The rate of pyrite oxidation is also a function of the flux of seawater into the sediment (ϕ_in ) because seawater carries oxygen into the sediment, and hence there will be more or less oxygen delivered to the sediment as the flux increases or decreases. Next, we modelled dissolved sulfide (H₂S) concentrations in a bioturbated system. In this model, we assumed that any dissolved sulfide entering the overlying water from the sediment will not influence the mass balance of sulfate in the ocean. This assumption is reasonable because the amount of sulfate in the overlying water is large relative to the amount of sulfide recycled from the sediment. Therefore, the only reduced sulfur component to model is the dissolved sulfide concentration in the sediment over time, which is equal to the amount of sulfide produced during MSR minus the amount of sulfide escaping from the sediment and entering the overlying water. Pyrite and iron-monosulfide production in the sediment is small and is neglected in the mass balance (Rickard, 2012). We further assume that the term for the flux of dissolved sulfide out of the sediment includes sulfide oxidation, and therefore we do not include a term for sulfide oxidation:

$\begin{array}{ll}\frac{{\text{dH}}_2\text{S}}{\text{dt}}\text{= -}{\varphi }_{\text{out}}·{\text{H}}_2\text{S}\left(\text{t}\right)\text{ + SRR }& (4)\end{array}$

After formulating equations for the sulfate and sulfide concentrations, we derived differential equations for the sulfur isotope compositions of sulfate in the overlying water, sediment porewater, and dissolved sulfide. To model the sulfur isotopic composition over time during bioturbation we developed equations based on the mixing of two reservoirs with different δ³⁴S_SO4. For the mixing of two reservoirs, the general equation is:

$\begin{array}{ll}{\text{R}}_3·{\text{δX}}_{\mathrm{3 }}{\text{= R}}_1·{\text{δX}}_1{\text{ + R}}_2·{\text{δX}}_2 & (5)\end{array}$

where R is the flux of dissolved sulfate or sulfide into or out of the respective box, and δX is the sulfur isotope composition of sulfate or sulfide. For the sulfur isotope composition of sulfate in the overlying water, the differential equation is:

$\begin{array}{ll}\frac{{\text{dSO}}_{4_{\text{OW}}}·{\text{δSO}}_{4_{\text{OW}}}}{\text{dt}}\text{ = }{\varphi }_{\text{out}}·{\text{SO}}_{4_{\text{PW}}}\left(\text{t}\right)·{\text{δ}}^{34}{\text{S}}_{{\mathrm{SO4}}_{\text{PW}} }\text{- }{\varphi }_{\text{in}}·{\text{SO}}_{4_{\text{OW}}}\left(\text{t}\right)·{\text{δ}}^{34}{\text{S}}_{{\mathrm{SO4}}_{\text{OW}}} & (6)\end{array}$

Expanding the left side of equation 9 using the chain rule and isolating the differential leaves the final equation:

$\begin{array}{ll}\frac{{\text{dδSO}}_{4_{\text{OW}}}}{\text{dt}}\text{ = }\frac{{\varphi }_{\text{out}}·{\text{SO}}_{4_{\text{PW}}}}{{\text{SO}}_{4_{\text{sw}}}}·\left({\text{δ}}^{34}{\text{S}}_{{\mathrm{SO4}}_{\text{PW}} }{\text{- δ}}^{34}{\text{S}}_{{\mathrm{SO4}}_{\text{Ow}}}\right) & (7)\end{array}$

For the sulfur isotope composition of the sulfate in the sediment porewater, the basic equation is the same as for sulfate in the overlying water, except there is an added term for MSR. Because MSR is associated with an isotope fractionation (ϵ), a term considering the rate of MSR and isotope fractionation was derived:

$\begin{array}{ll}\text{SRR}·\left({\text{dδ}}^{34}{\text{S}}_{{\mathrm{SO4}}_{\text{sed}}} \text{- ϵ}\right) & (8)\end{array}$

Therefore, for mixing two reservoirs the general equation for the sulfur isotope composition of porewater sulfate is:

$\begin{array}{ll}\frac{{\text{dSO}}_{4_{\text{OW}}}·{\text{δSO}}_{4_{\text{OW}}}}{\text{dt}}\text{ = }{\varphi }_{\text{in}}·{\text{SO}}_{4_{\text{OW}}}\left(\text{t}\right)·{\text{δ}}^{34}{\text{S}}_{{\mathrm{SO4}}_{\text{OW}} }\text{- }{\varphi }_{\text{out}}·{\text{SO}}_{4_{\text{PW}}}\left(\text{t}\right)·{\text{δ}}^{34}{\text{S}}_{{\mathrm{SO4}}_{\text{PW}}} \text{- SRR}·\left({\text{δ}}^{34}{\text{S}}_{{\mathrm{SO4}}_{\text{PW}}} \text{- ϵ}\right) & (9)\end{array}$

Expanding the left side of this equation using the chain rule and isolating the differential leaves us with the final equation for the sulfur isotope composition of sulfate in the sediment. Here there is also a term (-10· Ox) added which represents the oxidation of sedimentary sulfide with an average isotopic composition of -10‰. Although pyrite δ³⁴S values are highly variable in both modern and ancient sediments, we used a pyrite δ³⁴S value of -10‰ which is generally taken to be the higher estimated average δ³⁴S of pyrite in modern marine sediments (Strauss, 1997):

$\begin{array}{ll}\frac{{\text{dδSO}}_{4_{\text{PW}}}}{\text{dt}}\text{ = }\frac{{\varphi }_{\text{in}}·{\text{SO}}_{4_{\text{OW}}}·\left({\text{δ}}^{34}{\text{S}}_{{\mathrm{SO4}}_{\text{OW}}} {\text{- δ}}^{34}{\text{S}}_{{\mathrm{SO4}}_{\text{PW}}}\right) \text{- SRR}·\left({\text{δ}}^{34}{\text{S}}_{{\mathrm{SO4}}_{\text{PW}}} \text{- }Є\right)\text{ + }\left(-10·\text{Ox}\right)}{{\text{SO}}_{4_{\text{PW}}}}& (10)\end{array}$

Next, we modeled the sulfur isotope composition of dissolved sulfide over time. We start with the general differential equation that considers the production of sulfide during MSR, accompanied by a sulfur isotope fractionation, and the removal of sulfide from the sediment to the overlying water:

$\begin{array}{ll}\frac{{\text{dH}}_2\text{S}·{\text{δ}}^{34}{\text{S}}_{{\text{H}}_2\text{S}}}{\text{dt}}\text{ = -}{\varphi }_{\text{out}}·{\text{δ}}^{34}{\text{S}}_{{\text{H}}_2\text{S}}·{\text{H}}_2\text{S + SRR} & (11)\end{array}$

Expanding the left side of equation 11 using the chain rule and isolating the differential leaves the final equation for the sulfur isotope composition of dissolved sulfide with time:

$\begin{array}{ll}\frac{{\text{dδ}}^{34}{\text{S}}_{{\text{H}}_2\text{S}}}{\text{dt}}\text{ = }\frac{\text{SRR}·\left({\text{δ}}^{34}{\text{S}}_{{\mathrm{SO4}}_{\text{sed}}} \text{- ϵ}\right) \text{- }{\varphi }_{\text{out}}·{\text{δ}}^{34}{\text{S}}_{{\text{H}}_2\text{S}}·{\text{H}}_2\text{S}}{{\text{H}}_2\text{S}} & (12)\end{array}$

These systems of differential equations were solved numerically. To do so, we used the following approximation:

$\begin{array}{ll}\frac{\text{dY}}{\text{dt}}\text{ = }\frac{\text{ΔY}}{\text{Δt}}\text{ = }\frac{{\text{Y}}_{\text{n}} {\text{- Y}}_{\mathrm{n-1}}}{{\text{t}}_{\text{n}} {\text{- t}}_{\mathrm{n-1}}} & (13)\end{array}$

where Y represents any of the components we modelled. We set Δt = 1 minute. To solve all six of the differential equations (equations 1, 2, 4, 7, 10, and 12), Y_n was added to the right side of each of the above equations. An initial value for each component is taken from the bioturbation experiment at t=0 days (see Table S1). Afterwards, each new value for the component for a given time point was calculated iteratively in a computer program, using the values for all the components in the equation that were determined in the previous calculation.

2.5. Bioturbation model at steady-state

To better simulate the effect of bioturbation on the global ocean on geological time scales, we derived a two-box model that evaluates the model in section 2.4 at steady-state. The goal was to describe how sediments respond to bioturbation over time scales much longer than the experiment. The equations are solved without a time dependence. Instead, the dependence of Δ³⁴S_{SO4_sw-H2S_pw} on the advective flux caused by bioturbation is tested for three scenarios: (1) no dissolved sulfide oxidation, (2) dissolved sulfide oxidation, and (3) sulfur disproportionation. For these models, we use an MSR rate of 1 mol cm^-2 day^-1 and assume that the sulfide oxidation and sulfur disproportion rates are half the rate of MSR. We vary the MSR rate from 0-10 mol cm^-2 day^-1 and the sulfide oxidation and sulfur disproportion rates from 0-1 mol cm^-2 day^-1. These ranges were chosen to evaluate how the model behaves at extreme end-member rates. See Supplementary Information for the full derivation of the model and the final equations.

3. Results and discussion

3.1. Experimental results and model of experiment

We start our discussion with the bioturbation-free sediments of our control experiment. Typically, in bioturbation-free sediments rich in organic matter, the sulfate consumption by MSR is greater than diffusion can supply from the overlying water. The result is an enrichment in the heavy isotope of sulfur in the remaining porewater sulfate pool (Goldhaber and Kaplan, 1980). The control experiment without bioturbation agrees with this prediction, where the δ³⁴S of porewater sulfate at the beginning of the experiment is 37‰ higher than that of seawater sulfate and 41‰ higher than that of dissolved sulfide in the porewater (Figure 2B). Additionally, at the beginning of the experiment, the concentration of porewater sulfate is 22 mM lower than the concentration of sulfate in the overlying water and 18 mM lower than the concentration of porewater dissolved sulfide (Figure 2A). The fact that the porewater sulfate concentration is 18 mM lower than the concentration of porewater dissolved sulfide is indicative of active MSR and limited resupply of sulfate to the sediment from the overlying water. Throughout the duration of the experiment, the concentration and δ³⁴S of porewater sulfate and sulfide remained approximately constant (Figures 2A, B), indicating that the system is in steady state. In this case, sulfate may be resupplied to the sediment through a diffusive flux, yet this can be balanced by MSR which keeps the initial concentrations and δ³⁴S values constant over time. A two-box model we used to estimate the flux exchange between the overlying water and sediment in our experiments considers the flux of sulfate and sulfide across the sediment-water interface, the MSR rate, and amount of sulfide oxidation. The purpose of the model is to assess the role of bioturbation in changing the exchange fluxes between the water column and the sediment. Therefore, the specific dynamics of diffusion are not considered in our model, but its overall impact in limiting the exchanges between the two boxes is evident in the Δ³⁴S_{SO4_sw-H2S_pw} results (Figure 3). The model results show that the flux of sulfate and sulfide across the sediment-water interface in the control is 7x10^-3 mM cm^-2 day^-1 (Table 1).

FIGURE 2

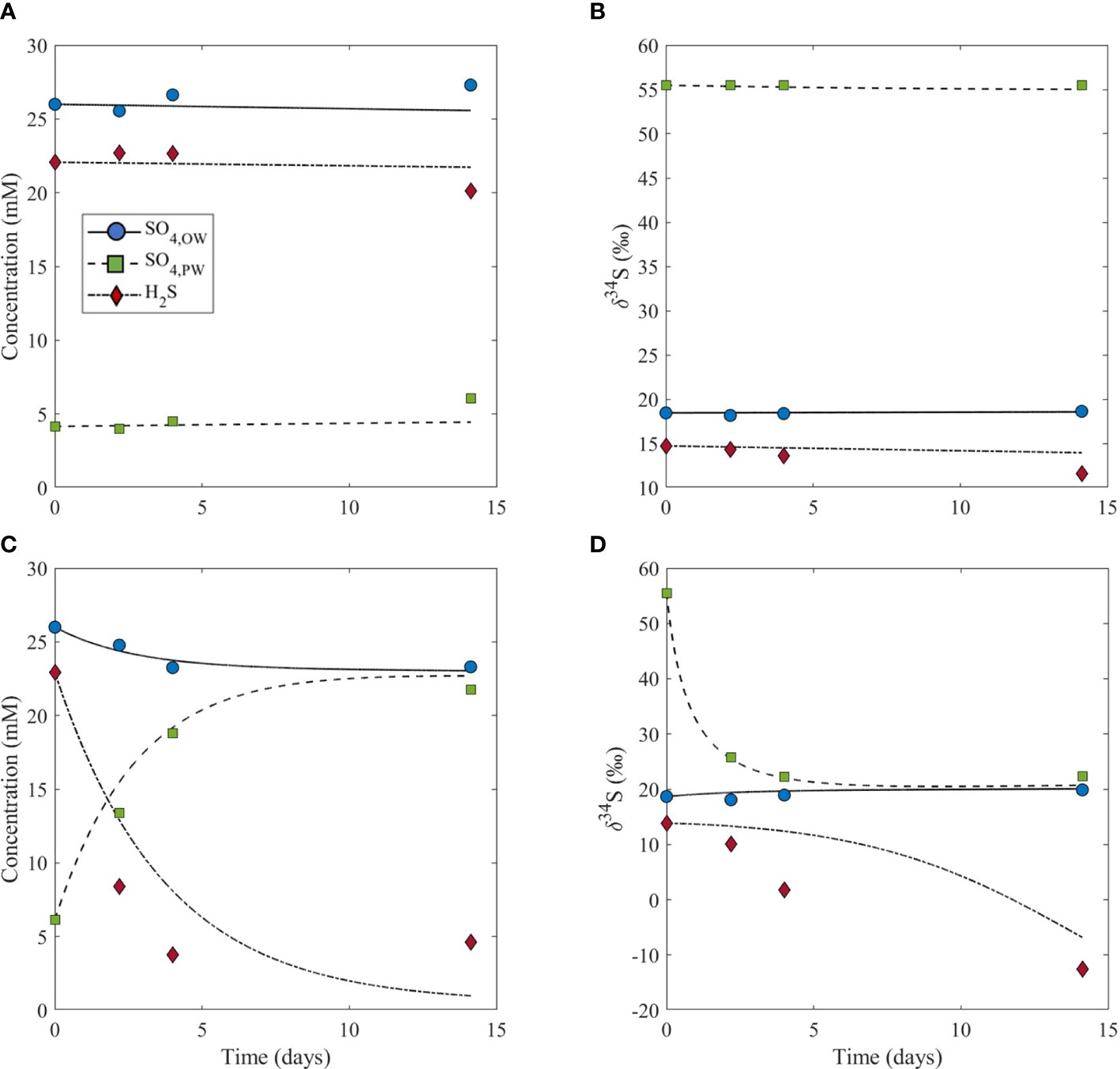
Figure 2 Model output (lines) and experiment results (symbols) for the concentrations of sulfate in the overlying water (SO4,OW), sulfate in the pore water (SO4,PW), dissolved sulfide in the pore water (H2S), and the sulfur isotope composition of these species. Plots show results for the control experiment (no bioturbation, A, B), and for the experiment with bioturbation (C, B). Note that the pore water initial values start from the same value in both experiments, and that the signals in both concentrations and isotope values are significant relative to normal variability in natural systems.

FIGURE 3

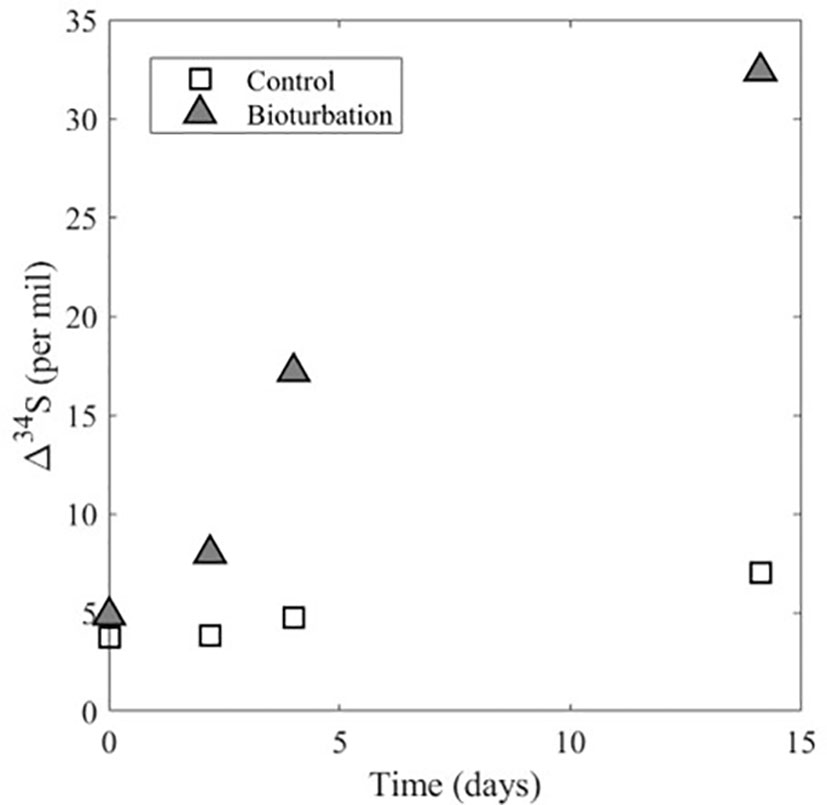
Figure 3 Experimental data for Δ³⁴S_{SO4_sw-H2S_pw} for the control experiment and the experiment with bioturbation. Δ³⁴S_{SO4_sw-H2S_pw} represents the difference in δ34S of sulfate in the overlying water and dissolved sulfide in the sediment pore water. The plot shows that in both experiments Δ³⁴S_{SO4_sw-H2S_pw} is increasing with time, but there is a larger increase in the experiment with bioturbation.

TABLE 1

Table 1 Model parameters for control experiment and experiment with bioturbation.

In the treatment experiment with bioturbation, the sulfate concentration in the sediment porewater increases from ~6 to 22 mM over the course of the experiment and the porewater sulfide concentration decreases from ~23 to 5 mM (Figure 2C). Additionally, there is a decrease of about 33‰ in the δ³⁴S of porewater sulfate over time, as well as a decrease of about 27‰ in the δ³⁴S of porewater sulfide (Figure 2D). This decrease in the δ³⁴S of porewater sulfate and sulfide over time with bioturbation also leads to a marked increase in Δ³⁴S_{SO4_sw-H2S_pw} (Figure 3). The model results show that the flux of sulfate and sulfide across the sediment-water interface is 0.24 mM cm^-2 day^-1, which is nearly two orders of magnitude higher than in the control (Table 1). The result that the flux of sulfate and sulfide across the sediment-water interface is higher in the treatment experiment with bioturbation than in the control can explain the experimental results presented above. Because the flux of sulfate in and out of the sediment is higher with bioturbation, porewater sulfate concentrations can increase due to the combined effect of sulfide reoxidation from the oxygenated overlying water, and the delivery of sulfate from the overlying water to the sediment. The decrease in sulfide concentrations in the experiment can also be explained by an increased flux of sulfate and sulfide across the sediment-water interface, as bioturbation can flush sulfide out of the sediment and bring oxygen into the sediment, which re-oxidizes sulfide back to sulfate. An increased flux due to bioturbation given by our model also explains the decrease in δ³⁴S of porewater sulfate despite ongoing MSR. The increased flux would deliver isotopically light sulfate from the overlying water (~20‰) to the sediment, decreasing δ³⁴S of porewater sulfate. This decrease in δ³⁴S of porewater sulfate to values close to that of the overlying water then allows for lower δ³⁴S of sulfide than without bioturbation (Figures 1B, D), which ultimately drives an increase in Δ³⁴S_{SO4_sw-H2S_pw} (Figure 3).

As opposed to the control experiment where concentrations and δ³⁴S values of sulfate and sulfide in the porewater change minimally with time (Figures 2A, B), the treatment experiment with bioturbation shows drastic changes in these parameters from the beginning to the end of the experiment (Figures 2C, D). The potential reasons for these differences can be explained by our model, where the model results show that the flux of sulfate and sulfide across the sediment-water interface is almost two orders of magnitude lower in the control (7x10^-3 mM cm^-2 day^-1) than in the experiment with bioturbation (0.24 mM cm^-2 day^-1) (Table 1). This higher flux physically removes sulfide from the sediment and delivers oxygen and isotopically-light sulfate to the sediment. The result is that Δ³⁴S_{SO4_sw-H2S_pw} in the treatment with bioturbation is ~25‰ higher than in the control. The enhanced supply of sulfate to the sediment enables Δ³⁴S_{SO4_sw-H2S_pw} to express a closer value to the empirical maximum sulfur isotopic fractionation (ϵ=72‰) of MSR (e.g., Wortmann et al., 2001). The experiments in this study are the first empirical evidence to demonstrate this effect of bioturbation (Figure 3). During the Precambrian-Cambrian transition, an enhanced supply of sulfate to sediments due to mixing and bioirrigation changed the seafloor system from semi-closed, where transport was diffusion-dominated (Bailey et al., 2006; Meysman et al., 2006) to open, where dissolved sulfide could become more ³⁴S-depleted relative to coeval sulfate. While iron sulfide formation can continue below the bioturbation zone, maximum pyrite formation occurs in and just below the bioturbated zone, while below it, the decreasing reactivity of iron oxides results in less accumulation (Fisher, 1986; Ferreira, 2010).

3.2. Analysis of steady-state bioturbation model

Because the experiments only show the effect of bioturbation on short time scales, three model scenarios for the sulfur cycle were developed to forward the concepts demonstrated by our experiments to the global record of the δ³⁴S in pyrite (Figures 3, 4). The scenarios take into account important parameters in the marine sulfur cycle which also influence Δ³⁴S_{SO4_sw-H2S_pw}; rate of MSR, sulfide oxidation, and sulfur disproportionation (Figures 3, 4). We assume steady-state with a global seawater sulfate reservoir that is infinite, with sulfate constant concentration and δ³⁴S of 28 mM and 21‰, respectively. These three scenarios are used to analyze how the heightened advective flux of sulfate into the sediment by bioturbation that was observed in our experiments influences Δ³⁴S_{SO4_sw-H2S_pw}, and how this contributes to an ‘open’ or ‘closed’ system in the sediment. In this case, an ‘open’ system refers to a sediment where there is an infinite supply of sulfate from an external source (the overlying water), whereas a ‘closed’ system refers to a sediment where the supply of sulfate is limited. In our model, the mechanism to increase the ‘openness’ of the system is porewater exchange due to burrowing, which in essence changes the ratio of the MSR rate to the pore water exchange rate. When the ratio is low the system is more open, and the advective flux of sulfate into the sediment outpaces its consumption by MSR, allowing Δ³⁴S_{SO4_sw-H2S_pw} to reach its highest possible value. In Figure 4, bioturbation is simulated by an advective flux of sulfate and sulfide in and out of the sediment. Our model assumes that these fluxes are equal, and as a result, the model breaks down at low fluxes since the assumption that the fluxes in and out of the sediment are equal is only relevant at high fluxes (Figure 4). If this advective flux is taken as a direct proxy for the amount of bioturbation, then our model shows that increasing levels of bioturbation increase the Δ³⁴S_{SO4_sw-H2S_pw} that can potentially be preserved in the rock record (Figure 4). In the first scenario, we assume there is no dissolved sulfide oxidation occurring and we evaluate how Δ³⁴S_{SO4_sw-H2S_pw} changes with varying advective flux and rate of MSR. For a given advective flux of sulfate from the seawater to the sediment, the Δ³⁴S_{SO4_sw-H2S_pw} increases as the rate of MSR decreases. However, at high advective fluxes of sulfate due to bioturbation, the Δ³⁴S_{SO4_sw-H2S_pw} values across all rates of MSR converge to the same value. This shows that at low advective fluxes but high rates of MSR, the system acts ‘closed’ as MSR is occurring fast relative to the resupply of sulfate. At higher advective fluxes, even with high rates of MSR, large values of Δ³⁴S_{SO4_sw-H2S_pw} can be obtained because of the increased resupply of sulfate to the sediment (Figure 5A). The ratio of the rate of MSR to the advective flux determines how open or closed the sediment is, and therefore how much sulfate is resupplied to the sediment (See Supplementary Information Eq. 1). When the ratio is high, the advective flux of sulfate into the sediment cannot resupply sulfate quickly enough to increase Δ³⁴S_{SO4_sw-H2S_pw}. When the ratio is low, the advective flux of sulfate into the sediment outpaces its consumption by MSR, allowing Δ³⁴S_{SO4_sw-H2S_pw} to reach its highest possible value.

FIGURE 4

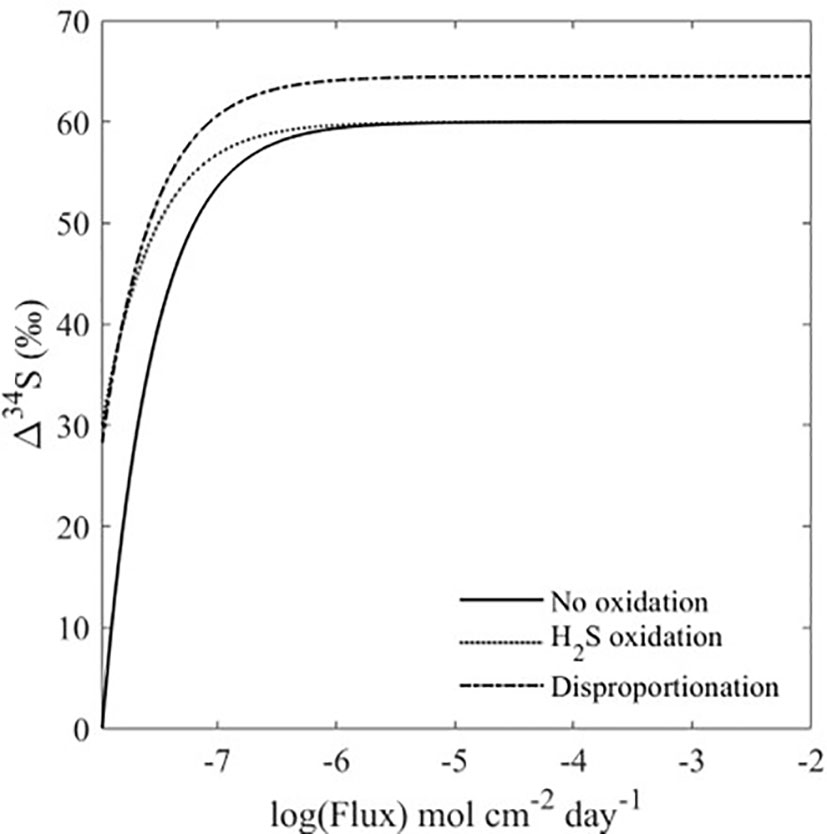
Figure 4 Δ³⁴S_{SO4_sw-H2S_pw} vs. advective flux for the global steady-state bioturbation models. The microbial sulfate reduction rate used for each model is 1 mol cm^-2 day^-1. The sulfide oxidation and disproportionation rates are half the sulfate reduction rate. All three models show that Δ³⁴S_{SO4_sw-H2S_pw} increases with an increasing advective flux, where the flux is a proxy for the amount of bioturbation.

FIGURE 5

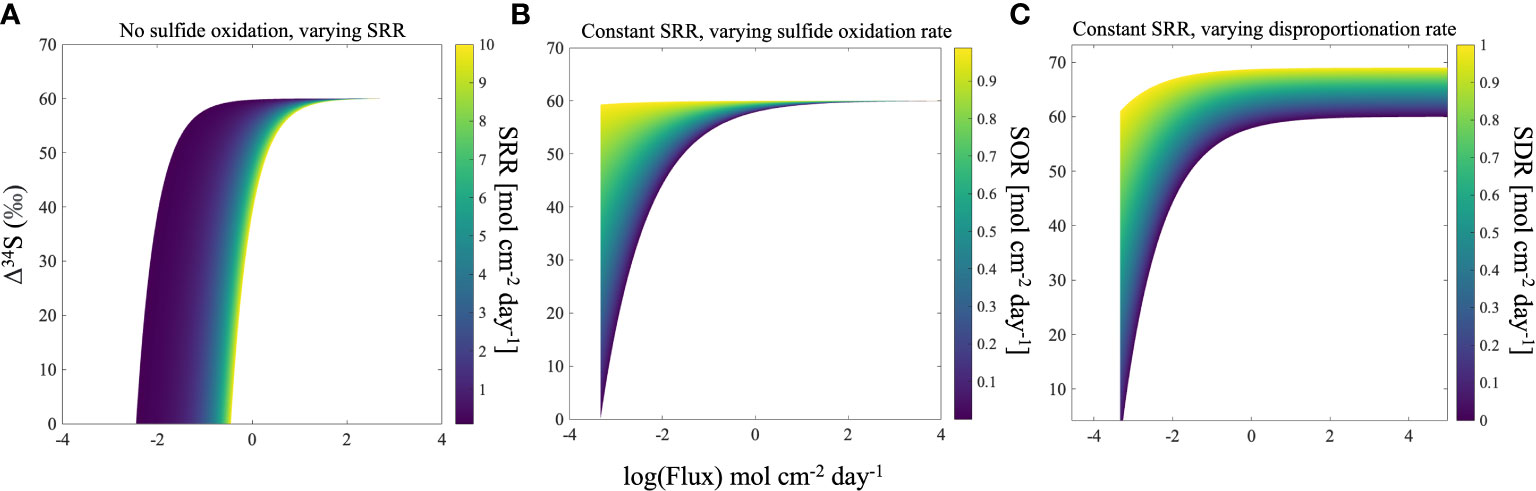
Figure 5 Model for Δ³⁴S_{SO4_sw-H2S_pw} vs. flux at steady state for three different scenarios: no hydrogen sulfide oxidation in the sediment for different sulfate reduction rates (A), dissolved sulfide oxidation for different oxidation rates (B), and sulfur disproportionation for different disproportionation rates (C). All models show that Δ³⁴S_{SO4_sw-H2S_pw} is higher at greater fluxes. SRR=microbial sulfate reduction rate, SOR=hydrogen sulfide oxidation rate, SDR=sulfur disproportionation rate.

In the second modeled scenario, we assume that porewater dissolved sulfide is oxidized, and we explore the Δ³⁴S_{SO4_sw-H2S_pw} as a function of the advective flux of sulfate into the sediment due to bioturbation and the rate of dissolved sulfide oxidation, with a fixed rate of MSR. Like the scenario with no sulfide oxidation, in this scenario for a given advective flux with varying rate of dissolved sulfide oxidation and fixed rates of MSR, the Δ³⁴S_{SO4_sw-H2S_pw} for both high and low rates of dissolved sulfide oxidation converge, and we observe that the overall Δ³⁴S_{SO4_sw-H2S_pw} increases for higher advective fluxes (Figure 5B). This further demonstrates the control of the advective flux of solutes between the seawater and sediment due to bioturbation on shaping Δ³⁴S_{SO4_sw-H2S_pw}. In the third scenario, we assume that sulfur disproportionation occurs (due to the oxidation of reduced sulfur induced by bioturbation)-and observe the influence of increasing rates of disproportionation on Δ³⁴S_{SO4_sw-H2S_pw}. The same phenomenon occurs in this scenario as in the second scenario. However, unlike in the previous two scenarios, the values for Δ³⁴S_{SO4_sw-H2S_pw} do not converge at high advective fluxes (Figure 5C). This is because there is a sulfur isotope fractionation associated with disproportionation, where higher rates of disproportionation will lead to higher sulfur isotope fractionations (Canfield and Thamdrup, 1994; Böttcher et al., 2001; Pellerin et al., 2015; Pellerin et al., 2019). Figure 4 also shows that Δ³⁴S_{SO4_sw-H2S_pw} is higher in the presence of sulfur disproportionation, even when large advective fluxes are considered. At the lowest advective fluxes, disproportionation and dissolved sulfide oxidation also result in higher Δ³⁴S_{SO4_sw-H2S_pw} (Figure 4). This shows that the oxidative part of the sulfur cycle leads to an increase in Δ³⁴S_{SO4_sw-H2S_pw}, which is promoted by bioturbation (Aller, 1994a; Aller, 1994b; Peterson et al., 1996). As biomixing is the end-member process of bioturbation that enhances oxidative sulfur cycling (van de Velde and Meysman, 2016), biomixing best describes the process occurring in our system. Furthermore, in all modeled scenarios, the δ³⁴S of porewater sulfate reaches the seawater value of 21‰, (Figures 4; S4-6), supporting the notion that bioturbation changes the system from closed to open, and reflects exchange with the overlying water. In general, regardless of the rate of MSR or sulfide oxidation, a higher advective flux of solutes between the sediment and seawater due to bioturbation changes the sedimentary system from diffusion-dominated to advection-dominated, resulting in an increased Δ³⁴S_{SO4_sw-H2S_pw} (Figure 4). Work on marine sediment cores from more recent age intervals also lend credence to our hypothesis. Chang et al. (2022) suggest that lack of bioturbation leads to heavy pyrite formation in their cores from the East China Sea, while another study shows that the presence of epifaunal foraminifera increases sediment porosity, enhancing communication between sediment pore water and seawater and resulting in lower pyrite sulfur isotope values during interglacial times (Pasquier et al., 2017).

4. Conclusion

Overall, the increased delivery of sulfate to the sediment due to bioturbation results in an increased Δ³⁴S_{SO4_sw-H2S_pw}. This Δ³⁴S_{SO4_sw-H2S_pw}, increased by bioturbation, can be preserved in the geological record. The experiments and model in this study show that the concurrent increase in Δ³⁴S observed at the Precambrian-Cambrian transition can be at least partially caused by the onset of bioturbation which turbo-charged the connection of the seafloor to the pool of seawater sulfate. Therefore, bioturbation likely had a significant effect on the sulfur cycle and seafloor biogeochemistry at its onset that left its signature in the sedimentary sulfur isotope record.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author contributions

GA contributed to the conception and design of this study. GA and AVT conducted the experiment and provided the chemical analysis. SR, GA and AP designed and implemented the model. SR wrote the manuscript with input and help from all co-authors. All authors contributed to the article and approved the submitted version.

Funding

The work was supported by ISF (2361/19) to GA and ERC 307582 StG (CARBON-SINK) to AVT.

Acknowledgments

We would like to thank our three reviewers for their thoughtful comments and feedback, which improved this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2022.1039193/full#supplementary-material

References

Aller R. C. (1994a). Bioturbation and remineralization of sedimentary organic matter: effects of redox oscillation. Chem. Geology 114, 331–345. doi: 10.1016/0009-2541(94)90062-0

CrossRef Full Text | Google Scholar

Aller R. C. (1994b). The sedimentary Mn cycle in long island sound: Its role as intermediate oxidant and the influence of bioturbation, O2, and corg flux on diagenetic reaction balances. J. Mar. Res. 52, 259–295. doi: 10.1357/0022240943077091

CrossRef Full Text | Google Scholar

Antler G., Mills J. V., Hutchings A. M., Redeker K. R., Turchyn A. V. (2019). The sedimentary carbon-Iron-Sulfur interplay – a lesson from East anglian salt marsh sediments. Front. Earth Sci. 7, 140. doi: 10.3389/feart.2019.00140

CrossRef Full Text | Google Scholar

Bailey J. V., Corsetti F. A., Bottjer D. J., Marenco K. N. (2006). Microbially-mediated environmental influences on metazoan colonization of matground ecosystems: Evidence from the lower Cambrian harkless formation. Palaios 21, 215–226. doi: 10.2110/palo.2005-p05-51e

CrossRef Full Text | Google Scholar

Berner R. A., Westrich J. T. (1985). Bioturbation and the early diagenesis of carbon and sulfur. Am. J. Sci. (United States) 285, 193–206. doi: 10.2475/ajs.285.3.193

CrossRef Full Text | Google Scholar

Blonder B, Valeria B, Alexandra T, Gilad A, Uriel S, Nadav K, Alexey K (2017). Impact of aeolian dry deposition of reactive iron minerals on sulfur cycling in sediments of the Gulf of Aqaba>." Frontiers in Microbiology 8: 1131

PubMed Abstract | Google Scholar

Böttcher M. E., Thamdrup B., Vennemann T. W. (2001). Oxygen and sulfur isotope fractionation during anaerobic bacterial disproportionation of elemental sulfur. Geochimica Cosmochimica Acta 65, 1601–1609. doi: 10.1016/S0016-7037(00)00628-1

CrossRef Full Text | Google Scholar

Bottjer D. J. (2010). The Cambrian substrate revolution and early evolution of the phyla. J. Earth Sci. 21, 21–24. doi: 10.1007/s12583-010-0160-7

CrossRef Full Text | Google Scholar

Bottjer D. J., Hagadorn J. W., Dornbos S. Q. (2000). The Cambrian substrate revolution. GSA Today 10, 1–7.

Google Scholar

Boyle R. A., Dahl T. W., Bjerrum C. J., Canfield D. E. (2018). Bioturbation and directionality in earth's carbon isotope record across the neoproterozoic–Cambrian transition. Geobiology 16, 252–278. doi: 10.1111/gbi.12277

PubMed Abstract | CrossRef Full Text | Google Scholar

Boyle R. A., Dahl T. W., Dale A. W., Shields-Zhou G. A., Zhu M. Y., Brasier M. D., et al. (2014). Stabilization of the coupled oxygen and phosphorus cycles by the evolution of bioturbation. Nat. Geosci. 7, 671–676. doi: 10.1038/ngeo2213

CrossRef Full Text | Google Scholar

Bradley A. S., Leavitt W. D., Schmidt M., Knoll A. H., Girguis P. R., Johnston D. T. (2016). Patterns of sulfur isotope fractionation during microbial sulfate reduction. Geobiology 14, 91–101. doi: 10.1111/gbi.12149

PubMed Abstract | CrossRef Full Text | Google Scholar

Brunner B., Bernasconi S. M. (2005). A revised isotope fractionation model for dissimilatory sulfate reduction in sulfate reducing bacteria. Geochimica Cosmochimica Acta 69, 4759–4771. doi: 10.1016/j.gca.2005.04.015

CrossRef Full Text | Google Scholar

Butterfield N. J. (2011). Animals and the invention of the phanerozoic earth system. Trends Ecol. Evol. 26, 81–87. doi: 10.1016/j.tree.2010.11.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Cameron E. M. (1982). Sulphate and sulphate reduction in early precambrian oceans. Nature 296, 145–148. doi: 10.1038/296145a0

CrossRef Full Text | Google Scholar

Canfield D. E., Farquhar J. (2009). Animal evolution, bioturbation, and the sulfate concentration of the oceans. Proc. Natl. Acad. Sci. 106, 8123–8127. doi: 10.1073/pnas.0902037106

CrossRef Full Text | Google Scholar

Canfield D. E., Habicht K. S., Thamdrup B. O. (2000). The archean sulfur cycle and the early history of atmospheric oxygen. Science 288, 658–661. doi: 10.1126/science.288.5466.658

PubMed Abstract | CrossRef Full Text | Google Scholar

Canfield D. E., Teske A. (1996). Late proterozoic rise in atmospheric oxygen concentration inferred from phylogenetic and sulphur-isotope studies. Nature 382, 127–132. doi: 10.1038/382127a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Canfield D. E., Thamdrup B. (1994). The production of 34S-depleted sulfide during bacterial disproportionation of elemental sulfur. Science 266, 1973–1975. doi: 10.1126/science.11540246

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang X., Liu X., Wang H., Zhuang G., Ma Z., Yu J., et al. (2022). Depositional control on the sulfur content and isotope of sedimentary pyrite from the southeast coast of China since MIS5. Front. Mar. Sci. 9. doi: 10.3389/fmars.2022.1005663

PubMed Abstract | CrossRef Full Text | Google Scholar

Cline J. D. (1969). Spectrophotometric determination of hydrogen sulfide in natural waters. Limnology Oceanography 14, 454–458. doi: 10.4319/lo.1969.14.3.0454

CrossRef Full Text | Google Scholar

Cribb A. T., Kenchington C. G., Koester B., Gibson B. M., Boag T. H., Racicot R. A., et al. (2019). Increase in metazoan ecosystem engineering prior to the ediacaran–Cambrian boundary in the nama group, Namibia. R. Soc. Open Sci. 6, 190548. doi: 10.1098/rsos.190548

PubMed Abstract | CrossRef Full Text | Google Scholar

Cui H., Kaufman A. J., Xiao S., Zhou C., Zhu M., Cao M., et al. (2022). Dynamic interplay of biogeochemical c, s, and ba cycles in response to the shuram oxygenation event. J. Geological Soc. 179 (2), jgs2021–081. doi: 10.1144/jgs2021-081

CrossRef Full Text | Google Scholar

Ferreira T. O. (2010). “Bioturbation and its role in iron and sulfur geochemistry in mangrove soils,” in Biogeochemistry and pedogenetic process in saltmarsh and mangrove systems, vol. 2010). (New York: Nova Science), 183–205.

Google Scholar

Fike D. A., Grotzinger J. P., Pratt L. M., Summons R. E. (2006). Oxidation of the ediacaran ocean. Nature 444, 744–747. doi: 10.1038/nature05345

PubMed Abstract | CrossRef Full Text | Google Scholar

Fisher I. S. J. (1986). Pyrite formation in bioturbated clays from the Jurassic of Britain. Geochimica Cosmochimica Acta 50, 517–523. doi: 10.1016/0016-7037(86)90101-8

CrossRef Full Text | Google Scholar

Goldhaber M. B., Kaplan I. R. (1980). Mechanisms of sulfur incorporation and isotope fractionation during early diagenesis in sediments of the gulf of California. Mar. Chem. 9, 95–143. doi: 10.1016/0304-4203(80)90063-8

CrossRef Full Text | Google Scholar

Gomes M. L., Hurtgen M. T. (2015). Sulfur isotope fractionation in modern euxinic systems: Implications for paleoenvironmental reconstructions of paired sulfate–sulfide isotope records. Geochimica Cosmochimica Acta 157, 39–55. doi: 10.1016/j.gca.2015.02.031

CrossRef Full Text | Google Scholar

Habicht K. S., Gade M., Thamdrup B., Berg P., Canfield D. E. (2002). Calibration of sulfate levels in the archean ocean. Science 298, 2372–2374. doi: 10.1126/science.1078265

PubMed Abstract | CrossRef Full Text | Google Scholar

Hantsoo K. G., Kaufman A. J., Huan C., Plummer R. E., Narbonne G. M. (2018). Effects of bioturbation on carbon and sulfur cycling across the ediacaran–Cambrian transition at the GSSP in Newfoundland, Canada. Can. J. Earth Sci. 55, 1240–1252. doi: 10.1139/cjes-2017-0274

CrossRef Full Text | Google Scholar

Hutchings A, Antler G, Wilkening J, Basu A, Bradbury H, Clegg J, Gorka M, et al (2019). Creek dynamics determine pond subsurface geochemical heterogeneity in East Anglian (UK) salt marshes>." Frontiers in Earth Science 7:41

Google Scholar

Krause A. J., Mills B. J. W., Zhang S., Planavsky N. J., Lenton T. M., Poulton S. W. (2018). Stepwise oxygenation of the Paleozoic atmosphere. Nat. Commun. 9, 4081. doi: 10.1038/s41467-018-06383-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Kristensen E., Penha-Lopes G., Delefosse M., Valdemarsen T., Quintana C. O., Banta G. T. (2012). What is bioturbation? The need for a precise definition for fauna in aquatic sciences. Mar. Ecol. Prog. Ser. 446, 285–302. doi: 10.3354/meps09506

CrossRef Full Text | Google Scholar

Leavitt W. D., Halevy I., Bradley A. S., Johnston D. T. (2013). Influence of sulfate reduction rates on the phanerozoic sulfur isotope record. Proc. Natl. Acad. Sci. 110, 11244–11249. doi: 10.1073/pnas.1218874110

CrossRef Full Text | Google Scholar

Lyons T. W., Reinhard C. T., Planavsky N. J. (2014). The rise of oxygen in earth’s early ocean and atmosphere. Nature 506, 307–315. doi: 10.1038/nature13068

PubMed Abstract | CrossRef Full Text | Google Scholar

McIlroy D., Logan G. A. (1999). The impact of bioturbation on infaunal ecology and evolution during the proterozoic-Cambrian transition. Palaios 14, 58–72. doi: 10.2307/3515361

CrossRef Full Text | Google Scholar

Meysman F. J. R., Middelburg J. J., Heip C. H. R. (2006). Bioturbation: A fresh look at darwin's last idea. Trends Ecol. Evol. 21, 688–695. doi: 10.1016/j.tree.2006.08.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Pasquier V., Sansjofre P., Rabineau M., Revillon S., Houghton J., Fike D. A. (2017). Pyrite sulfur isotopes reveal glacial– interglacial environmental changes. Proc. Natl. Acad. Sci. 114, 5941–5945. doi: 10.1073/pnas.1618245114

CrossRef Full Text | Google Scholar

Pellerin A., Bui T. H., Rough M., Mucci A., Canfield D. E., Wing B. A. (2015). Mass-dependent sulfur isotope fractionation during reoxidative sulfur cycling: A case study from mangrove lake, Bermuda. Geochimica Cosmochimica Acta 149, 152–164. doi: 10.1016/j.gca.2014.11.007

CrossRef Full Text | Google Scholar

Pellerin A., Antler G., Agner Holm S., Findlay A., Crockford P., Turchyn A., et al. (2019). Large sulfur isotope fractionation by bacterial sulfide oxidation Science Advances 57:eaaw1480

PubMed Abstract | Google Scholar

Peterson G. S., Ankley G. T., Leonard E. N. (1996). Effect of bioturbation on metal-sulfide oxidation in surficial freshwater sediments. Environ. Toxicol. Chem. 15, 2147–2155. doi: 10.1002/etc.5620151210

CrossRef Full Text | Google Scholar

Rees C. E. (1973). A steady-state model for sulphur isotope fractionation in bacterial reduction processes. Geochimica et Cosmochimica Acta 37 (5), 1141–1162.

Google Scholar

Rickard D. (2012). Sulfidic sediments and sedimentary rocks (Developments in Sedimentology: Newnes).

Google Scholar

Ridgwell A., Zeebe R. E. (2005). The role of the global carbonate cycle in the regulation and evolution of the earth system. Earth Planetary Sci. Lett. 234, 299–315. doi: 10.1016/j.epsl.2005.03.006

CrossRef Full Text | Google Scholar

Rooney A. D., Cantine M. D., Bergmann K. D., Gómez-Pérez I., Al Baloushi B., Boag T. H., et al. (2020). Calibrating the coevolution of ediacaran life and environment. Proc. Natl. Acad. Sci. 117 (29), 16824–16830. doi: 10.1073/pnas.200291811

CrossRef Full Text | Google Scholar

Saitoh M., Ueno Y., Matsu'ura F., Kawamura T., Isozaki Y., Yao J., et al. (2017). Multiple sulfur isotope records at the end-guadalupian (Permian) at chaotian, China: Implications for a role of bioturbation in the phanerozoic sulfur cycle. J. Asian Earth Sci. 135, 70–79. doi: 10.1016/j.jseaes.2016.12.009

CrossRef Full Text | Google Scholar

Schiffbauer J. D., Huntley J. W., O’Neil G. R., Darroch S. A., Laflamme M., Cai Y. (2016). The latest ediacaran wormworld fauna: Setting the ecological stage for the Cambrian explosion. GSA Today 26, 4–11. doi: 10.1130/GSATG265A.1

CrossRef Full Text | Google Scholar

Schiffbauer J. D., Selly T., Jacquet S. M., Merz R. A., Nelson L. L., Strange M. A., et al. (2020). Discovery of bilaterian-type through-guts in cloudinomorphs from the terminal ediacaran period. Nat. Commun. 11, 1–12. doi: 10.1038/s41467-019-13882-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Sim M. S. (2019). Effect of sulfate limitation on sulfur isotope fractionation in batch cultures of sulfate reducing bacteria. Geosciences J. 23, 687–694. doi: 10.1007/s12303-019-0015-x

CrossRef Full Text | Google Scholar

Sim M. S., Ono S., Donovan K., Templer S. P., Bosak T. (2011). Effect of electron donors on the fractionation of sulfur isotopes by a marine desulfovibrio sp. Geochimica Cosmochimica Acta 75, 4244–4259. doi: 10.1016/j.gca.2011.05.021

CrossRef Full Text | Google Scholar

Strauss H. (1997). The isotopic composition of sedimentary sulfur through time. Palaeogeography Palaeoclimatology Palaeoecol. 132, 97–118. doi: 10.1016/S0031-0182(97)00067-9

CrossRef Full Text | Google Scholar

Tarhan L. G., Droser M. L., Planavsky N. J., Johnston D. T. (2015). Protracted development of bioturbation through the early Palaeozoic era. Nat. Geosci. 8, 865–869. doi: 10.1038/ngeo2537

CrossRef Full Text | Google Scholar

Tarhan L. G., Myrow P. M., Smith E. F., Nelson L. L., Sadler P. M. (2020). Infaunal augurs of the Cambrian explosion: An ediacaran trace fossil assemblage from Nevada, USA. Geobiology 18, 486–496. doi: 10.1111/gbi.12387

PubMed Abstract | CrossRef Full Text | Google Scholar

Thamdrup B., Fossing H., Jørgensen B. B. (1994). Manganese, iron and sulfur cycling in a coastal marine sediment, Aarhus bay, Denmark. Geochimica Cosmochimica Acta 58, 5115–5129. doi: 10.1016/0016-7037(94)90298-4

CrossRef Full Text | Google Scholar

van de Velde S., Meysman F. J. (2016). The influence of bioturbation on iron and sulphur cycling in marine sediments: A model analysis. Aquat. geochemistry 22, 469–504. doi: 10.1007/s10498-016-9301-7

CrossRef Full Text | Google Scholar

van de Velde S., Mills B. J., Meysman F. J., Lenton T. M., Poulton S. W. (2018). Early Palaeozoic ocean anoxia and global warming driven by the evolution of shallow burrowing. Nat. Commun. 9, 2554. doi: 10.1038/s41467-018-04973-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Vinther J., Eibye-Jacobsen D., Harper D. A. (2011). An early Cambrian stem polychaete with pygidial cirri. Biol. Lett. 7, 929–932. doi: 10.1098/rsbl.2011.0592

PubMed Abstract | CrossRef Full Text | Google Scholar

Wing B. A., Halevy I. (2014). Intracellular metabolite levels shape sulfur isotope fractionation during microbial sulfate respiration. Proc. Natl. Acad. Sci. 111, 18116–18125. doi: 10.1073/pnas.1407502111

CrossRef Full Text | Google Scholar

Wortmann U. G., Bernasconi S. M., Boüttcher M. E. (2001). Hypersulfidic deep biosphere indicates extreme sulfur isotope fractionation during single-step microbial sulfate reduction. Geology 29, 647–650. doi: 10.1130/0091-7613(2001)029<0647:HDBIES>2.0.CO;2

CrossRef Full Text | Google Scholar

Yang B., Steiner M., Schiffbauer J. D., Selly T., Wu X., Zhang C., et al. (2020). Ultrastructure of ediacaran cloudinids suggests diverse taphonomic histories and affinities with non-biomineralized annelids. Sci. Rep. 10, 1–12. doi: 10.1038/s41598-019-56317-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Zerkle A. L., Farquhar J., Johnston D. T., Cox R. P., Canfield D. E. (2009). Fractionation of multiple sulfur isotopes during phototrophic oxidation of sulfide and elemental sulfur by a green sulfur bacterium. Geochimica Cosmochimica Acta 73, 291–306. doi: 10.1016/j.gca.2008.10.027

CrossRef Full Text | Google Scholar