Numerical Flow Modeling of Artificial Ocean Upwelling

Artificial Upwelling (AU) of nutrient-rich Deep Ocean Water (DOW) to the ocean's sunlit surface layer has recently been put forward as a means of increasing marine CO₂ sequestration and fish production. AU and its possible benefits have been studied in the context of climate change mitigation as well as food security for a growing human population. However, extensive research still needs to be done into the feasibility, effectiveness and potential risks, and side effects associated with AU to be able to better predict its potential. Fluid dynamic modeling of the AU process and the corresponding inorganic nutrient transport can provide necessary information for a better quantification of the environmental impacts of specific AU devices and represents a valuable tool for their optimization. Yet, appropriate capture of all flow phenomena relevant to the AU process remains a challenging task that only few models are able to accomplish. In this paper, simulation results obtained with a newly developed numerical solution method are presented. The method is based on the open-source modeling environment OpenFOAM. It solves the unsteady Reynolds-Averaged Navier-Stokes (RANS) equations with additional transport equations for energy, salinity, and inorganic nutrients. The method aims to be widely applicable to oceanic flow problems including temperature- and salinity-induced density stratification and passive scalar transport. The studies presented in this paper concentrate on the direct effects of the AU process on nutrient spread and concentration in the ocean's mixed surface layer. Expected flow phenomena are found to be captured well by the new method. While it is a known problem that cold DOW that is upwelled to the surface tends to sink down again due to its high density, the simulations presented in this paper show that the upwelled DOW settles at the lower boundary of the oceans mixed surface layer, thus keeping a considerable portion of the upwelled nutrients available for primary production. Comparative studies of several design variants, with the aim of maximizing the amount of nutrients that is retained inside the mixed surface layer, are also presented and analyzed.

1. Introduction

In view of a continuing growth in human population, compliance with planetary boundaries is increasingly becoming the central challenge of our time. Past human resource consumption has lead to a state, where marine fish stocks are largely overexploited (FAO, 2018) and mere reduction of greenhouse gas emissions is no longer sufficient to meet international climate goals (Lawrence et al., 2018). In the search for ways to mitigate these consequences of resource overconsumption, Artificial Upwelling (AU) of nutrient-rich Deep Ocean Water (DOW) to the ocean's sunlit surface layer has recently been proposed (Kirke, 2003; Lovelock and Rapley, 2007).

By bringing DOW to the ocean's surface, AU aims to replicate processes that occur in natural upwelling systems. Here, the supply of inorganic nutrients stimulates a high primary production, thereby providing the basis for highly efficient food chains, which make natural upwelling systems some of the world's richest fishing grounds (Roels et al., 1977). So far, it has not been shown whether AU can effectively replicate important features of natural upwelling systems. Nevertheless, AU is seen as a possible way of increasing fishery yields in less productive oceanic regions. As such, AU could promote food security for a growing human population (Kirke, 2003) and reduce pressure on natural fish stocks. Further, it has been pointed out that an increased primary production induced by AU could act as a driver for the biologic carbon pump, a process that naturally extracts CO₂ from the atmosphere (Lovelock and Rapley, 2007). This has led to a discussion on whether AU can contribute to future climate change mitigation efforts (Lovelock and Rapley, 2007; Oschlies et al., 2010; Williamson et al., 2012; Bauman et al., 2014; Pan et al., 2015; GESAMP, 2019). Despite its potential, a wide range of ecological responses and biogeochemical consequences of AU remain largely unstudied to date. Responsible use of AU on a large scale demands thorough understanding and accurate quantification of all environmental and ecological impacts associated with this process.

Numerical modeling of the involved fluid dynamic processes plays an important role in this context. Numerical models provide information for the technical design and optimization of AU systems. Additionally, the detailed information on the associated spread and concentration levels of nutrient-rich DOW can be used as a basis for biological model calculations and thus contribute to the quantification of environmental and ecological impacts of specific AU devices. Numerical methods based on the Reynolds-Averaged Navier-Stokes (RANS) equations are capable of accurately predicting both small-scale flow phenomena inside the AU device and large-scale far-field phenomena. They thus represent a valuable tool for assessing the AU processes with high accuracy.

A number of hydrodynamic studies on AU are reported in literature. Several publications deal with artificial upwelling by utilizing the energy of ocean waves. A first overview of the topic was given by Kirke (2003). Beyond pointing out the potential of the use of DOW for increasing fish stocks, Kirke also mentions the problem that the cold DOW, when artificially upwelled, generally tends to sink back down due to its high density and thus does not remain available for primary production. Liu and Jin (1995) apply a simple mathematical model to calculate upwelling volumes of a wave-driven device. They find that a flow rate of 0.95 [m³/s] could be obtained with their device in a typical sea state off the Hawaiian islands. Similar calculations are presented by Soloviev (2016), who additionally applied a numerical model that is not specified in detail. Both of these studies do not model nutrient transport.

The air lift method proposed by Liang and Peng (2005) has also been studied. Here, artificial upwelling is achieved by pumping air into the ocean at a certain depth. Thereby a flow of air bubbles is created which transports DOW to the surface. A RANS-based numerical model for this type of upwelling was presented by Meng et al. (2013). Here, it is found that the applied, simplified model was able to accurately predict the dispersed flow and achieve a satisfactory agreement with experimental data. Some authors have reported results of sea trials with air lift AU systems (Fan et al., 2013; Pan et al., 2019).

Other publications deal with a device referred to as perpetual salt fountain, which was initially proposed by Stommel et al. (1956). Here, the opposing effect which a decrease in temperature and salinity with depth (i.e., a typical open ocean depth profile) has on water density are used to drive a self-sustaining upwelling process in a long ocean pipe. Once the pipe is filled with DOW, temperature differences between the pipe- and surrounding water diminish over time while salinity differences remain and account for a positive buoyancy of the DOW in the pipe. Results of sea trials with this device are reported in Maruyama et al. (2004) and Tsubaki et al. (2007). Maruyama et al. (2004) also apply a RANS-based numerical model to predict the flow inside their device. However, they do not apply any turbulence model but use turbulent diffusion data from their experiment in the calculations. Williamson et al. (2009) extend this work to studies of near-field mixing in crossflow at the device outlet, using a commercial RANS code. Williamson et al. find that the flow can be characterized into a region with high turbulent diffusion local to the pipe outlet and a second region further downstream with very little diffusion. They further point out the problem of turbulence anisotropy in buoyancy-affected flows, which also plays a role in the present paper. Finally, Williamson et al. find that, given the small observed diffusion, the outlet depth of their device is too large for the pumped DOW to be mixed into the ocean's surface layer.

Fan et al. (2015) propose a simple mathematical model for the optimization of forced upwelling in a pipe. To maintain high nutrient concentrations for mariculture inside a confined DOW plume, Fan et al. aim to minimize dilution of the plume. They find that the plume trajectory and the DOW concentration inside the plume are highly dependent on several technical parameters, like flow rate, pipe diameter, and outlet depth as well as environmental influences, like current speed and stratification strength. A validation of their mathematical model against steady-state RANS CFD data is also provided in Fan et al. (2015) along with some validation of the CFD model.

The present paper reports of AU simulations with a new RANS solution method. The development of the new method is based on Computational Fluid Dynamics (CFD) methods available within the open-source framework OpenFOAM, namely the buoyantPimpleFoam solver and the thermophysical and turbulence modeling libraries. A transport equation for salinity is added to the buoyantPimpleFoam solver, the thermophysical modeling library is extended to correctly reproduce the physical properties of seawater, and a simple modification is introduced into the k-ωSST turbulence model to better capture turbulence effects for buoyancy-affected flows. Thus, a numerical method for small-scale oceanic flow is created which, due to its open-source basis, allows for flexible adjustment and extension to specific modeling problems, like AU. For the simulations presented in this paper the method is further extended with a transport equation for nutrient concentration, which enables a direct quantification of the nutrient transport introduced by the AU device.

The remainder of this paper is structured as follows. First, the applied method and the underlying equations will be described. Then, the results of some studies carried out with the new method will be presented and discussed. Finally, conclusions from the presented work will be drawn before finishing with recommendations for necessary future extensions.

2. Numerical Method

The method presented in this paper solves the RANS modeling problem for buoyancy-affected oceanic flow. The mathematical model and its numerical solution will be outlined briefly in this section.

At present, the method incorporates a single-phase (i.e., water) only and does not model influences of deformation of the water surface. This approach was chosen because early studies indicated that the influences of the water surface on the general flow were very small, while accurate modeling of free surface motion would have been associated with high computational cost. Also, this approach enabled a more direct control over the heat transfer processes at the surface than a multiphase simulation using the volume of fluid method.

2.1. Momentum and Mass Equations

A flow of a Newtonian fluid in an Eulerian reference frame is considered. To account for density fluctuations, Favre averaging is used instead of the more common Reynolds averaging. In the following, Favre-averaged quantities are marked by an overtilde, while Reynolds averaging is indicated by an overscore. The conservation equations for momentum and mass, in their conservative form, can thus be written as

$\begin{array}{c}\frac{\partial (\overline{\rho }\tilde{u})}{\partial t}+\nabla ·(\overline{\rho }\tilde{u}\tilde{u})=\nabla ·\left(2{\mu }_e\tilde{S}-\frac{2}{3}{\mu }_e(\nabla ·\tilde{u})I\right)\\ -\frac{2}{3}\nabla (\overline{\rho }k)-\nabla \overline{p}+\overline{\rho }g& (1)\end{array}$

and

$\begin{array}{ll}\frac{\partial \overline{\rho }}{\partial t}+\nabla ·(\overline{\rho }\tilde{u})=0\text{.}& (2)\end{array}$

In Equations (1) and (2), $\tilde{u}$ is the Favre-averaged velocity, $\overline{p}$ is Reynolds-averaged pressure and $\overline{\rho }$, μ_e and g are Reynolds-averaged density, effective dynamic viscosity and the gravitational acceleration vector, respectively. The tensor I represents the unit matrix, and $\tilde{S}$ is the mean strain rate tensor, which is defined as

$\begin{array}{ll}\tilde{S}=\frac{1}{2}\left(\nabla \tilde{u}+{(\nabla \tilde{u})}^T\right)\text{.}& (3)\end{array}$

Boussinesq's linear eddy viscosity theory is applied in Equation (1) to model the effect of turbulence. The effective dynamic viscosity consist of the molecular and eddy viscosities as follows

$\begin{array}{ll}{\mu }_e=\mu +{\mu }_t\text{.}& (4)\end{array}$

The eddy viscosity μ_t and the turbulent kinetic energy k have to be modeled by turbulence closure models as discussed in section 2.4. For convenience, a modified pressure ${\overline{p}}^{*}=\overline{p}+\frac{2}{3}\overline{\rho }k$ is introduced. Also, in Equation (1) the main hydrostatic impact is subtracted from ${\overline{p}}^{*}$ yielding

$\begin{array}{ll}{\overline{p}}_{rgh}^{*}={\overline{p}}^{*}-\overline{\rho }g·r,& (5)\end{array}$

where r is the position vector with respect to a reference position. The pressure and buoyancy terms in Equation (1) can then be restructured as follows

$\begin{array}{ll}-\nabla {\overline{p}}^{*}+\overline{\rho }g=-\nabla {\overline{p}}_{rgh}^{*}-(g·r)\nabla \overline{\rho }\text{.}& (6)\end{array}$

With these changes, the implemented momentum equation reads

$\begin{array}{c}\frac{\partial (\overline{\rho }\tilde{u})}{\partial t}+\nabla ·(\overline{\rho }\tilde{u}\tilde{u})=\nabla ·\left(2{\mu }_e\tilde{S}-\frac{2}{3}{\mu }_e(\nabla ·\tilde{u})I\right)\\ -\nabla {\overline{p}}_{rgh}^{*}-(g·r)\nabla \overline{\rho }\text{.}& (7)\end{array}$

2.2. Energy Equation

A conservation equation for energy needs to be solved to account for buoyancy effects. Here, potential enthalpy, i.e., the enthalpy that a parcel of water would have if adiabatically and without salt exchange raised to the sea surface, is used as energy variable. As pointed out by McDougall (2003), a simple conservation equation for potential enthalpy is, to a high degree of accuracy, equivalent to the first law of thermodynamics in the ocean. The conservation equation for potential enthalpy per unit mass $\tilde{h}$ reads

$\begin{array}{ll}\frac{\partial \left(\overline{\rho }\tilde{h}\right)}{\partial t}+\nabla ·\left(\overline{\rho }\tilde{u}\tilde{h}\right)=\nabla ·\left({\alpha }_e\nabla \tilde{h}\right)\text{.}& (8)\end{array}$

Here, α_e is the effective thermal diffusivity

$\begin{array}{ll}{\alpha }_e=\frac{{\mu }_t}{P{r}_t}+\frac{\mu }{Pr}=\frac{{\mu }_t}{P{r}_t}+\frac{\kappa }{c_p}\text{.}& (9)\end{array}$

As for the momentum equation, the turbulent fluctuations are modeled as additional diffusion by applying the gradient diffusion hypothesis. In Equation (9) κ is thermal conductivity, c_p is specific heat capacity and Pr and Pr_t are Prandtl number and turbulent Prandtl number, respectively. Throughout this study a value of 1 was used for Pr_t. For c_p a constant value of 3991.867 957 119 63 [J/kgK] was used, as suggested by IOC et al. (2010). κ is calculated from the thermophysical model (see section 2.4).

2.3. Scalar Transport Equation

Scalar transport equations have to be solved for salinity and nutrient concentration. By again applying the gradient diffusion hypothesis, the conservation equation for these quantities reads

$\begin{array}{ll}\frac{\partial \left(\overline{\rho }\tilde{\varphi }\right)}{\partial t}+\nabla ·\left(\overline{\rho }\tilde{u}\tilde{\varphi }\right)=\nabla ·\left(\overline{\rho }{D}_e\nabla \tilde{\varphi }\right),& (10)\end{array}$

where $\tilde{\varphi }$ is salinity or nutrient concentration. The effective diffusion coefficient D_e is defined as

$\begin{array}{ll}{D}_e=\frac{{\mu }_t}{\overline{\rho }S{n}_t}+D,& (11)\end{array}$

where D is the molecular diffusivity in [m²/s] and Sn_t is the turbulent Schmidt number. For Sn_t, a value of 1 was used throughout this study. D was set to 1 × 10⁻⁹ [m²/s] for both, salinity and nutrients. This represents a typical value for mass diffusion in water (see e.g., Zhang et al., 2004; Thorpe, 2007).

2.4. Thermophysical Model for Seawater

The flow behavior of any fluid is tightly coupled to its physical properties, which in turn depend on the state of the fluid and its composition. In the OpenFOAM framework this relation is replicated by a thermophysical model. In its standard version, the thermophysical model calculates fluid properties based on pressure and temperature. This functionality was extended here, to include the influence of salinity. For the present study, the modeled fluid properties are:

• Viscosity μ

• Thermal conductivity κ

• Density ρ.

To model ρ based on temperature, salinity, and pressure, the 75term polynomial of McDougall et al. (2003) was used. This is part of the widely used TEOS-10 (IOC et al., 2010) standard. By including pressure dependence in the calculation, the full compressibility is captured in the system of equations. Since the time steps for the applications considered here are small (about 1 × 10⁻¹ [s]), acoustic modes do not need to be filtered from the system, as often done in ocean models (Griffies and Adcroft, 2008). For μ and κ, the pressure-independent polynomials of Sharqawy et al. (2010) and Nayar et al. (2016) were implemented.

2.5. Turbulence Model for Buoyancy-Affected Flow

In Equations (7), (8), and (10) the turbulent fluxes are expressed in terms of the turbulent viscosity μ_t, by means of the eddy viscosity and gradient diffusion hypotheses. Eddy viscosity turbulence models are concerned with determining μ_t. This is usually achieved by solving one or more transport equations for different turbulence variables. Numerous approaches have been presented in the past, of which the standard k-ϵ model (Launder and Spalding, 1974) and the k-ωSST model (Menter, 1994) are the ones most widely used for industrial applications. For the present study, the k-ωSST model was chosen with a simple modification. This model is known to provide a more realistic approximation of the turbulence level in stagnation regions. Within this study, it also proved preferable for cases where a jet of DOW meets the water surface. The k-ωSST model and its application for buoyancy-affected flow will be presented here briefly.

The k-ωSST model describes μ_t as a function of turbulent kinetic energy k and its specific dissipation rate ω. The transport equations for these two quantities, as implemented in OpenFOAM, read

$\begin{array}{c}\frac{\partial \overline{\rho }k}{\partial t}+\nabla ·(\overline{\rho }\tilde{u}k)-\nabla ·((\mu +{\sigma }_k{\mu }_t)\nabla k)\\ =P_k-\overline{\rho }{\beta }^{*}k\omega & (12)\end{array}$

and

$\begin{array}{c}\frac{\partial \overline{\rho }\omega }{\partial t}+\nabla ·(\overline{\rho }\tilde{u}\omega )-\nabla ·((\mu +{\sigma }_{\omega }{\mu }_t)\nabla \omega )\\ =\overline{\rho }\gamma \frac{P_k}{{\mu }_t}-\overline{\rho }\beta {\omega }^2+2(1-F_1)\overline{\rho }\frac{{\sigma }_{\omega 2}}{\omega }(\nabla k·\nabla \omega )\text{.}& (13)\end{array}$

Here, P_k is the shear production term, β^* is a model constant, and σ_k, σ_ω, β and γ are blended between values reproducing k-ω (Wilcox, 1988) (subscript 1) and k-ϵ (Launder and Spalding, 1974) (subscript 2) model behavior, using the wall distance dependent blending factor F₁. The turbulent dynamic viscosity is calculated by

$\begin{array}{ll}{\mu }_t=\frac{\overline{\rho }{a}_{1}k}{max(a_1\omega ,\sqrt{S_2}{F}_2)},& (14)\end{array}$

where a₁ is a model constant, $\sqrt{S_2}$ is the vorticity magnitude and F₂ is an additional blending function based on the wall distance.

Within the present study a considerable overprediction of vertical diffusion was observed for the standard OpenFOAM implementation of the k-ωSST model. This problem can be accounted to the inadequate representation of buoyancy effects on turbulence and is often treated by adding additional terms to Equations (12) and (13) (Van Maele and Merci, 2006). A simple approach was recently presented by Devolder et al. (2017) following the work of Van Maele and Merci (2006). This approach was adopted for the present work. The formulation of the buoyancy term, which is added to Equation (12), reads

$\begin{array}{ll}-\frac{{\mu }_t}{\overline{\rho }S{n}_t}g·(\nabla \overline{\rho })\text{.}& (15)\end{array}$

Here, the turbulent Schmidt number Sn_t is set to 0.85, to be in line with Van Maele and Merci (2006) and Devolder et al. (2017).

As stated by Van Maele and Merci (2006), the simple approach implemented here cannot be expected to provide a fully realistic capture of turbulence effects in buoyancy-affected flow. Namely, an overprediction of vertical turbulent diffusion in stably stratified flow must still be expected as shown by several authors (Stankov et al., 2001; Worthy et al., 2001; Van Maele and Merci, 2006). However, the implemented approach was seen to provide a much-needed improvement over the standard OpenFOAM implementation of the k-ωSST model. Since the implementation of a more sophisticated buoyancy treatment method was outside the scope of this study, the shortcomings of the present approach were accepted.

2.6. Solution Method

The set of equations described above has to be solved by a numerical solution method. To do so, the partial differential equations have to be approximated by algebraic equations at a finite number of locations in space and time. The flow domain (i.e., the fluid volume for which the equations are to be solved) is discretized by a large number of small volumes (cells) and the equations are solved for each of these volumes. Using Gauss's theorem, the divergence in the conservation equations can be calculated by considering the flux across the boundaries of each volume. This discretization method is known as the finite volume method. By further applying suitable discretization methods for the remaining differentials and integrals, a system of algebraic equations, containing the contributions from all cells, is created for each of the governing equations. These algebraic systems of equations are still both coupled and non-linear. For example, the momentum (Equation 7) contains the unknown eddy viscosity, pressure, and density. By taking these values from a previous solution (e.g., a previous iteration or a previous time step) and treating non-linearities in a similar manner, the coupled system of non-linear equations can be solved by iteratively solving linear systems of equations until the difference between the current and previous solution becomes small, and with it the error of the previously explained approximation.

Here, OpenFOAMs PIMPLE algorithm is employed for the iterative solution process. The PIMPLE algorithm represents a combination of the well-known SIMPLE (Patankar and Spalding, 1972) and PISO (Issa, 1986) algorithms. A pressure equation is formulated based on the continuity equation (Equation 2)¹. Including the necessary additional equations for salinity and nutrients, the implemented PIMPLE algorithm can be summarized by the following steps:

The steps of the PIMPLE loop (1–6) are repeated for a set number of times, or until a converged solution for the time step is reached. Also, one or two additional PISO loops (Steps 5 and 6) are usually included.

The following schemes are used for the discretization of the equation system. Linear interpolation is used to obtain cell face values from the cell centered data. Likewise, all gradients occurring in the equations are calculated by linear interpolation. For the divergence terms, the limittedLinear scheme is applied, which generally uses linear interpolation but limits toward upwind interpolation in regions with strong gradient changes. For the temporal derivative, the second-order backward scheme is used for all equations except for the nutrient and salinity transport equations, where the implicit Euler scheme is used to ensure boundedness.

3. Results

3.1. AU Application

The simulations presented in this paper concentrate on forced upwelling in a pipe, powered by a large propeller at the pipe inlet. Prior to the present project, the main dimensions of a prototype system had been optimized in a dedicated study. It was found that a large-diameter pipe in combination with a single propeller ensures a maximum energy efficiency of the system. A diameter of 10 [m] was recommended as a compromise between efficiency and technical feasibility. The prototype simulated in this paper is designed for field studies in the center of the Guinea Dome region, close to 10°N, 22°W. In this region, with a water depth of 4,000–5,000 [m], nutrient-rich DOW naturally rises to depths above 100 [m]. A depth of 75 [m] is thus sufficient for the DOW inlet of this specific device. The device is intended to be deployed free-floating and powered by a renewable energy source, providing 500 [kW] of electric power. The estimated volume flow rate is 155 [m³/s]. Since the pipe will be made from an elastic material, a positive pressure inside the pipe is desirable to prevent it from collapsing. Thus, the propeller is installed at the device inlet. A schematic of the device is shown in Figure 1 along with its main dimensions. With larger inlet depths the same type of device can be deployed in other ocean regions, however, in this paper, the results concentrate solely on the Guinea Dome region.

FIGURE 1

Figure 1. AU system concept and main dimensions.

Figure 2 shows depth profiles of in situ temperature, absolute salinity, PO₄-P and NO₃-N for the deployment region. The data was taken from Krahmann (2016). As can be seen in Figure 2, high nutrient concentrations are already found at depths smaller than 100 [m] in the example region. The water column in this region is stably stratified due to large temperature and salinity-induced changes in water density. The mixed layer depth (MLD) is 21.8 [m]². Figure 3 depicts the counteracting effects of salinity and temperature on density in the modeled region. Here, profiles of the absolute density change Δρ introduced by temperature and salinity are shown for depths up to 200 [m]. Δρ is calculated with respect to a standard potential density of 1026.49 [kg/m³]. It can be seen from Figure 3 that, especially in the surface region, temperature has a much stronger influence on density than salinity.

FIGURE 2

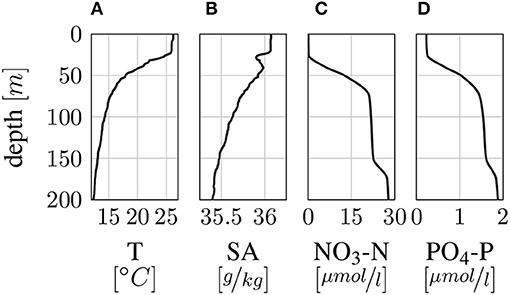
Figure 2. Depth profiles for in situ temperature (A), absolute salinity (B), NO₃-N (C) and PO₄-P (D) in the deployment region. Data taken from Krahmann (2016).

FIGURE 3

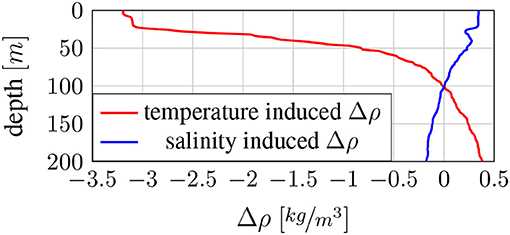
Figure 3. Density change Δρ introduced by the temperature (red) and salinity (blue) profiles in Figure 2.

Expected Flow Phenomena

The vertical density gradient has important impacts on the general flow field created by the AU device. Stratified flow exhibits the tendency to return to a stable stratification once disturbed. This will generally dampen out vertical velocities that are not driven by buoyancy forces. Thus, when artificially pumped to the surface, the cold DOW, after having dissipated its upwards directed momentum, starts sinking downwards again due to its high density. Williamson et al. therefore characterize the flow as a weak fountain (Williamson et al., 2009). During the process, the density difference between the pumped DOW and the surrounding surface water is decreased by mixing as well as water surface heat transfer. Thus, the DOW does not sink to its original depth but creates a layer in the upper region of the water column, which spreads horizontally as more water is pumped up by the AU system. Consequently, the flow close to the AU system can be characterized as buoyant flow (i.e., the main flow direction is aligned with the direction of gravity) with forced convection, while in the far field the flow fulfills the characteristics of stratified flow (i.e., the main flow direction is normal to the direction of gravity).

Simulation Setup

The geometry of the AU system is idealized to a cylindrical shape for the simulations. All structural elements or construction details are thereby neglected, which is appropriate considering the early development stage of the system. A cylindrical shape was also chosen for the flow domain (i.e., the water volume which is modeled in the simulations). Use was made of the symmetry effects in the sense that only a quarter of the cylindrical flow domain was modeled. This allows for a significant reduction of the overall count of computational cells without compromising the three-dimensional resolution of the flow. The necessary radius of the cylindrical flow domain was actively studied. Since the influence of the AU system spreads over time, the size of the flow domain critically influences how long the simulation can run before an unwanted interaction of the flow with the outer boundary can occur. Eventually, a radius of 480 [m] was chosen, which kept the computational burden acceptable and enabled simulated times of 10,000 [s] with no visible outer-boundary effects. Equally, a depth of 200 [m] was chosen for the flow domain. A heat transfer boundary condition is used at the top boundary of the flow domain to model sensible heat flux through the water surface. The air temperature is assumed to be the same as the initial water temperature at the water surface. A sensible heat transfer coefficient of 13.5 [W/m²K] was derived from work of Komori et al. (2011). The propeller, which is driving the AU device, is modeled as a momentum source inside the lower part of the pipe. Here, the desired flow velocity of 1.969 [m/s] is uniformly prescribed. It has to be noted that this approach does not realistically model the complex flow field behind a propeller. However, since full modeling of the propeller and its influences was not feasible within this study, it was decided that this approach was most general and sufficiently accurate to not have an influence on the general behavior of the AU system. All simulations were started from an initial state of zero velocity with temperature and salinity profiles as depicted in Figure 2. To represent the nutrient concentration, a Nutrient Index (NI) was defined. Its initial value is calculated based on the NO₃-N profile (see Figure 2) divided by its value at the device inlet depth (i.e., 75 [m]). The initial NI value (i.e., before the start of the AU operation) is thus close to zero at the water surface and reaches one at 75 [m] depth³. The simulation setup is depicted in Figure 4 along with the applied boundary conditions and the computational mesh.

FIGURE 4

Figure 4. Schematic of the simulation setup with Boundary Conditions (BC) and mesh details.

Discretization

The flow domain was discretized using an unstructured, polyhedral mesh. The mesh was gradually refined toward the water surface region as well as the pipe inlet and outlet. The boundary layer region inside the pipe was refined with prism layers to maintain a dimensionless wall distance (y⁺) between 30 and 100. An average grid edge size⁴ of about 1.5 [m] and a time step size of 0.125 [s] were used for all studies presented in this paper. The described geometry is thus discretized by 9.3 million cells. This discretization was chosen based on experience and sensitivity studies carried out for similar problems. On a dedicated cluster⁵ about 100 [s] of Computation Time (CT) were needed per second of Simulated Time (ST).

3.2. Basic Study

The aim of this first study is to establish whether the described numerical method is able to plausibly capture and quantify the expected flow effects corresponding to the AU process and the mixing of DOW and surface waters. This is studied here, using the previously described case setup. Figure 5 shows typical, graphical results for NI on a vertical slice through the flow domain after 5,000 [s] of simulated time (i.e., 1.39 [hrs]).

FIGURE 5

Figure 5. NI on a vertical slice through the flow domain after 5.000 [s] (ST).

The expected fountain-like flow close to the pipe outlet can be observed in Figure 5. The jet of DOW spreads on the free surface to a patch of about 130 [m] diameter before the cold DOW starts to sink due to its high density. Once the DOW has sunk to its depth of neutral buoyancy, the flow becomes almost purely horizontal and a layer with increased NI values is created, which can also be observed in Figure 5. Since the fountain-like flow feature close to the device is comparably small, changes in the NI-depth profiles need to be analyzed to be able to quantify the large-scale effect of the AU device. For this analysis a region of study between a 150 and 330 [m] radius around the AU system is defined, thus excluding the fountain-like flow feature local to the device as well as the outer part of the domain, where the nutrient-rich layer does not fully develop within the simulated time span. Figure 6 shows average NI depth profiles for this region of study. Depth profiles for multiple points in time, after the start of the AU process, are depicted. The previously described layer creation process can be observed in Figure 6. The strongest changes in the depth profile due to the AU operation take place within a confined depth range of 10–40 [m]. In this region, the nutrient concentration is increased due to the influence of the nutrient-rich layer, which is initially created at a depth of about 30 [m] and expands in height over time. Between 40 and 70 [m] depth the initial nutricline is lowered slightly due to the extraction of the DOW below. After 7500 [s] the depth profile becomes temporally stable, indicating that by this point the nutrient-rich layer is fully developed throughout the region of study.

FIGURE 6

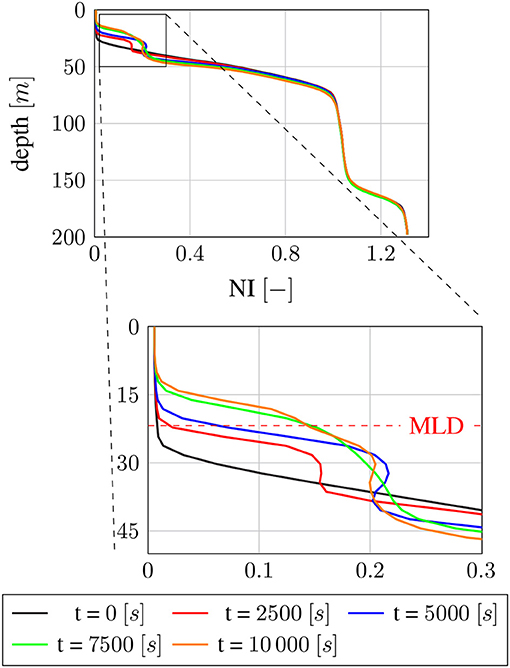
Figure 6. NI depth profiles for different points in time (ST). Profiles are averaged over a radius of 150–330 [m] around the AU system.

It is not within the scope of this study to establish to which extent the upwelled nutrients in the nutrient-rich layer can be utilized for primary production. The change of the average NI value inside the mixed layer of the studied region is thus taken as measure for the upwelling efficiency of the AU device. From the depth profiles shown in Figure 6 it can be calculated that the average NI inside the mixed surface layer is raised from an initial value of 0.0064 to 0.0402 after 10 000 [s]. This corresponds to NO₃-N values of 0.14 and 0.85 [μmol/l], respectively.

3.3. Variant Studies

Having shown the general ability of the described model to capture and quantify the flow effects relevant to the AU process, comparative studies between device variations are possible. In a first study, three design variants were chosen, which were expected to exhibit different flow characteristics at the outlet of the AU system. The investigated variants are depicted in Figure 7. The first variant, referred to as Cylinder, represents the basic cylindrical geometry as described in the previous sections. Here the flow at the outlet of the AU system is characterized by its impingement on the surface. The second variant, referred to as Funnel, features a funnel-shaped outlet with a maximum diameter of 30 [m]. Also, a body (gray shaded area in Figure 7) is installed inside the Funnel to make sure the flow follows the funnel surface (i.e., avoid flow separation). The flow for this variant is characterized by the horizontal decay of the momentum introduced by the AU system. The third variant, referred to as Slotted, represents a pipe that is closed at the top, such that the outflow occurs through multiple horizontal slots on the upper part of the pipe. Five slots are arranged over the top 10 [m] of the pipe. A width of 0.125 [m] was chosen for the slots such that the total area of all slots equals ¼ of the pipes cross-sectional area. The outflow for this variant is characterized by five planar jets. For all three variants a flow velocity of 1.969 [m/s] inside the pipe was specified.

FIGURE 7

Figure 7. Tested design variants for the AU system.

Figure 8 shows the results of the variant study after 10 000 [s] (ST). Averaged NI depth profiles are shown in Figure 8A. Again only the region between a radius of 150 and 330 [m] around the AU system is analyzed. As can be seen from this figure, a similar nutrient-rich layer is created by all device variants. It can further be seen from Figure 8A that, between 20 and 40 [m] depth, the Funnel variant reaches higher NI values than the other variants, while inside the mixed surface layer (i.e., above the MLD) the Cylinder variant reaches slightly higher values. For the Slotted variant, the nutrient-rich layer seems to be slightly narrower, which leads to smaller NI values inside the mixed surface layer.

FIGURE 8

Figure 8. Results of first variant study after 10 000 [s] (ST): (A) NI depth profiles averaged over a radius of 150–330 [m] around the AU system. The upper 50 [m] of the water column are shown. (B) Radial profiles of eddy viscosity ratio ν_t/ν averaged over the mixed layer. The inner 150 [m] of the domain are shown. (C) Average mixed layer NI values based on depth profiles in (A).

Again, the increase of the Average NI inside the mixed layer of the studied region is taken as measure for upwelling efficiency. Figure 8C shows the average mixed layer NI in the analyzed region for all device variants. Here, the superiority of the Cylinder variant becomes clearly visible.

To understand the origin of the different performances of the device variants, the amount of turbulent mixing created by these variants must be considered. Figure 8B shows the Average mixed layer eddy viscosity ratio ν_t/ν over the radial distance from the device center. This figure shows that turbulence is created near the device outlet and decays with larger distances to the device. The strongest turbulent mixing is found at some distance from the device outlet, where the DOW starts to sink down due to its high density. It becomes evident from Figure 8B that, while the Slotted variant reaches the highest eddy viscosity ratios, the Cylinder variant creates overall more turbulence, by maintaining higher values at greater radii. The Funnel variant produces generally lower eddy viscosity ratios, when compared to the Cylinder and Slotted variants, but maintains its maximum values over a relatively large range of radii.

For the Cylinder variant, the widest spread of DOW along the surface is achieved before the sinking occurs. This is reflected in Figure 8B in high eddy viscosity ratios further away from the AU system. For the Slotted variant, the horizontal momentum decays close to the device due to the high turbulence levels. Here, the sinking of the DOW occurs over a smaller region, close to the device. Finally, the Funnel variant produces a more confined jet of DOW with an intermediate spread along the water surface. Here, the peak in the eddy viscosity ratio at the maximum spreading radius along the free surface is less pronounced.

In a second variant study, different depths of the device outlet were tested for the Cylinder shape, and the influences on the DOW layer formation and nutrient enrichment in the mixed surface layer were studied. In addition to the standard version, with an outlet depth of 5 [m], two versions with outlet depths of 2.5 and 7.5 [m] were studied. Again, depth profiles and mixed surface layer average values after 10 000 [s] (ST) are analyzed to establish the influence of the device outlet depth on the nutrient-rich layer.

In Figure 9, the differences between the studied versions, in terms of nutrient enrichment, are much smaller than the ones observed in the previous variant study. As can be seen from Figure 9A, slightly higher NI values in the mixed surface layer are reached by the 2.5 [m] outlet depth variant. This is reflected in higher average values in Figure 9C, respectively. Figure 9B again shows the radial profile of the average mixed layer eddy viscosity ratio ν_t/ν. Here, much larger differences than for the NI depth profiles (Figure 9A) are observed. When compared to the other variants, the 2.5 [m] outlet depth variant reaches a slightly greater spreading radius of the DOW along the water surface and much larger eddy viscosity ratios during the sinking phase of the upwelled DOW. The 7.5 [m] outlet depth variant shows the lowest eddy viscosity ratios.

FIGURE 9

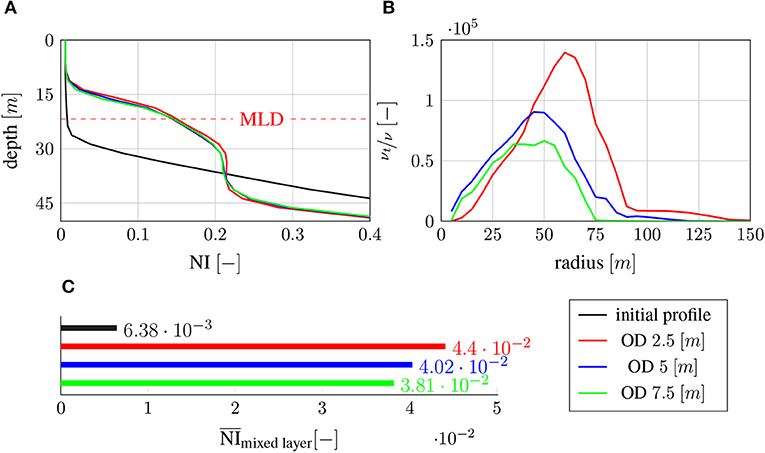
Figure 9. Results of second variant study after 10.000 [s] (ST): (A) NI depth profiles averaged over a radius of 150–330 [m] around the AU system. The upper 50 [m] of the water column are shown. (B) Radial profiles of eddy viscosity ratio ν_t/ν averaged over the mixed layer. The inner 150 [m] of the domain are shown. (C) Average mixed layer NI values based on depth profiles in (A).

4. Discussion

The results presented in this paper show that RANS-based flow simulations with the newly developed numerical method provide valuable insight into the AU process. The numerical method has been successfully applied to studies of an AU device, including general flow phenomena and the relative performance of several design variants.

4.1. Basic Study

The expected flow behavior can clearly be observed in the results of the first study. In the device near field, the flow that Williamson et al. (2009) describe as a weak fountain is reproduced. At larger distances from the device, the flow becomes purely horizontal and a distinct layer containing the upwelled DOW is created. This was expected based on the stable stratification of the water column and has been described by Fan et al. (2015), who conducted flow simulations for a similar device in crossflow. The fact that, in all cases presented here, the nutrient-rich layer extended into the mixed surface layer can be seen as an unexpected result of this study. While Kirke (2003) states that DOW, when pumped to the surface, tends to sink below the mixed layer and thus becomes unavailable for primary production, the results of this study suggest that the horizontal spreading of the nutrient-rich layer still leads to a considerable increase in the mixed layer nutrient concentration despite the initial re-sinking of the DOW. In fact, the horizontal spreading of the nutrient-rich layer appears to be the main process by which the mixed layer is fertilized through the proposed AU system. Since the horizontal spreading process is associated with very little vertical mixing, it can be assumed that the nutrient-rich layer can spread over large horizontal distances.

Within the region where the nutrient rich layer fully developed during the simulated time (i.e., between a radius of 150 and 330 [m] around the AU system) the average mixed layer NO₃-N concentration was increased ba a factor of 6.3, from an initial value of 0.14 to 0.85 [μmol/l]. These values in the same order of magnitude as those observed in natural eastern boundary upwelling regions (Chavez and Messié, 2009). The results thus seem encouraging enough to motivate further research on the concept of forced upwelling.

4.2. Variant Studies

The presented variant studies show the effect of different device outlet configurations on the local and global flow characteristics and the intended mixed layer nutrient enrichment. Generally, the importance of turbulent mixing for nutrient enrichment in the mixed surface layer is highlighted by the results. All variants show the same general flow features which have already been described for the basic study. It was expected that strong turbulence introduced by the device as high up in the water column as possible would enhance mixing between the upwelled DOW and surface waters, and thus lead to a higher efficiency of the AU system. However, the strongest turbulent mixing was generally observed at some distance to the device, during the sinking phase, which follows the initial upwelling and spreading of the DOW along the water surface. This suggests that shear-based turbulence production at the device outlet is less important than expected. The results of both variant studies show that a greater spread of the DOW jet along the surface leads to more effective mixing during the sinking phase. High turbulence levels near the device outlet, on the other hand, decrease the spread of the DOW jet, and thus the device efficiency, as observed for the Slotted variant. While the importance of turbulent mixing is confirmed by these results, they reveal that the design should be optimized for convective spreading of the nutrients along the water surface rather than for shear-based turbulent mixing local to the device outlet.

Throughout the studies presented here, the standard Cylinder variant with an outlet depth of 2.5 [m] achieved the strongest mixed layer nutrient enrichment with about 7 times the initial nutrient concentration.

It is noteworthy that the idea to maximize the dilution of the upwelled DOW contrasts with the approach of Fan et al. (2015), who aim to minimize dilution and thus maximize the nutrient concentration in the DOW plume. This is explained by the fact that Fan et al. aim to increase nutrient concentrations only local to a mariculture project within the DOW plume, whereas here the intention is to fertilize the mixed surface layer over a large area.

4.3. Limitations

While the results presented in this paper show the applicability of the newly developed method for AU simulations as well as its ability to provide insight into function principles and the effectiveness of AU devices, the significance of the results, in absolute terms, is still limited by simplifications made during both model development and experiment design.

It has to be noted that the eddy viscosity ratios observed in Figures 8B, 9B are significantly higher than the values typically obtained in engineering simulations. The high values mainly result from the coexistence of shear- and buoyancy-based turbulence production in the sinking region. While strong turbulence is a typical feature of the Raleigh-Taylor instability observed in this region, it yet has to be established whether the magnitude of the effect is realistically captured by the turbulence model.

Based on the second variant study, it may be assumed that a variant with an even smaller outlet depth than the ones studied here might perform even more desirable. It has to be noted, however, that the water surface is fixed in the simulations presented here. Thus, any water surface deformation due to the operation of the AU system is neglected. This simplification is expected to have an increasing influence as the outlet depth of the device decreases. It may thus impair the validity of simulations with very shallow outlet depths.

It also has to be noted that, since the same flow rate was taken for all variant studies, these studies do not consider the implications of the different variants on the necessary propeller shaft power to obtain the specified flow rate, which would be the limiting factor for upwelling volume in a realistic setting. This was chosen with the intention to first obtain an understanding of the implications of local design changes on the flow, before optimizing the AU system as a whole.

The results presented in this paper rely on a single set of depth profile data for a very specific ocean region. Since the efficiency in bringing nutrients to the ocean's mixed layer might depend strongly on the stratification in the deployment region, the presented results can not be generalized.

Further, in this paper the amount of permanent nutrient enrichment in the mixed surface layer was estimated by calculating the mean NI value above the initial MLD inside a region where the nutrient-rich layer was fully established within the simulated time (i.e., between a radius of 150 [m] to 330 [m] from the device center). It has to be noted that this method of estimating the amount of permanent mixed surface layer nutrient enrichment is based on simplification. It is assumed that all nutrients which permanently settle above the initial MLD can be further spread throughout the mixed surface layer by natural processes and thus remain available for primary production, while all nutrients which settle below the MLD are lost. While this assumption enables a simple comparison of device variants, it does not adequately reflect the physical processes in the ocean's surface region. In particular, this calculation method does not take into account any changes to the MLD due to AU. These changes cannot be evaluated without considering natural forcing effects which balance the perturbation in the water column caused by the AU device over time.

Finally, the total spatial extend and timescales of the device influence are not captured by the simulations presented here due to the limited availability of computational resources.

4.4. Conclusions

Flow simulations of AU have been carried out with a newly developed numerical method. The method is based on numerous modifications to the open-source framework OpenFOAM, which have been described in this paper. The capabilities of the new model have been demonstrated in several studies. The newly developed numerical method was able to reproduce expected flow phenomena and allow a first quantification of the local nutrient enrichment potential in the affected region, as well as comparative studies for device optimization. The spreading of the nutrient-rich layer, which is created by the device, was identified as the main large-scale nutrient enrichment effect. The results suggest that device variants should be optimized for a large convective spread of the DOW jet along the water surface to achieve more permanent mixed layer nutrient enrichment. With a growing interest in ocean-based solutions to the emerging challenges of our time, the role of efficient modeling of these solutions is becoming increasingly important. The presented results should provide the reasoning for continued modeling efforts to improve the understanding of AU.

4.5. Future Work

To be able to obtain more general results from the proposed numerical method, some improvements have to be made:

1. The implemented buoyancy modification for the k-ωSST turbulence marks a simplified turbulence modeling approach for the AU flow problem. A separate study should be carried out on the applicability of different turbulence modeling approaches to stratified, oceanic flow. Different formulations of the buoyancy terms for the k-ωSST turbulence model and other approaches should be taken into account.

2. The simulations presented in this paper were stopped after 10 000 [s] (ST) to avoid boundary effects due to the spatial limitation of the flow domain. A boundary condition that allows free in- and outflow through the boundary would enable longer simulated times with spatially confined flow domains and should therefore be implemented.

3. Throughout this study, a value of 1 was invariably used for the turbulent Prandtl and Schmidt numbers. The use of the gradient diffusion hypothesis with global constant Pr_t and Sn_t values is generally criticized by Combest et al. (2011). Different constant values and other alternatives should be evaluated and compared against data.

4. The numerical model should further be extended with realistic modeling approaches for natural mixing in the mixed surface layer to be able to model the effect of these processes on mixed surface layer nutrient enrichment.

Finally, after careful verification and validation of the improved numerical method, studies on greater spatial and temporal scales should be undertaken to fully determine the influence of the proposed AU device on its environment. In particular, the horizontal extent of the nutrient-rich layer and its spreading rate should be studied, along with the question what fraction of the nutrients in the nutrient-rich layer can eventually be utilized for primary production.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

JK developed and implemented the numerical method, performed the calculations, and analyzed the results under the scientific and technical supervision of UR and KG. JK wrote the manuscript with input from all authors.

Funding

This study was funded by an Advanced Grant of the European Research Council (ERC) in the framework of the Ocean Artificial Upwelling project (Ocean artUp, No. 695094). Additional support was obtained by the Test-ArtUp project, which is funded by the German Federal Ministry of Education and Research (Bundesministerium für Bildung und Forschung, BMBF) as part of the CDRmare research mission of the German Marine Research Alliance (Deutsche Allianz Meeresforschung, DAM) under Grant Agreement No. 03F0897B. The publication was financially supported by Land Schleswig-Holstein within the funding programme Open Access Publikationsfonds.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^The derivation of the pressure equation is not discussed here for brevity. For more information please refer to standard literature (e.g., Ferziger et al., 2020).

2. ^The MLD was established using a 0.03 [kg/m³] potential density criterion with a reference depth of 10 [m].

3. ^Since the nutrient concentration is still increasing with depth below the device inlet, NI values greater than one are common at depths greater than 75 [m], indicating that the nutrient concentration here is higher than the initial concentration at the device inlet.

4. ^The basic grid edge size is calculated as $\sqrt[3]{\frac{TotalVolume}{CellCount}}$.

5. ^Two dual CPU nodes were used for most of the studies presented. The nodes were based on AMD EPYC 7302, 16 Core Processors. FDR InfiniBand was used for distributed computations.

References

Bauman, S., Costa, M., Fong, M., House, B., Perez, E., Tan, M., et al. (2014). Augmenting the biological pump: the shortcomings of geoengineered upwelling. Oceanography 27, 17–23. doi: 10.5670/oceanog.2014.79

CrossRef Full Text | Google Scholar

Chavez, F. P., and Messié, M. (2009). A comparison of eastern boundary upwelling ecosystems. Prog. Oceanogr. 83, 80–96. doi: 10.1016/j.pocean.2009.07.032

CrossRef Full Text | Google Scholar

Combest, D. P., Ramachandran, P. A., and Dudukovic, M. P. (2011). On the gradient diffusion hypothesis and passive scalar transport in turbulent flows. Ind. Eng. Chem. Res. 50, 8817–8823. doi: 10.1021/ie200055s

CrossRef Full Text | Google Scholar

Devolder, B., Rauwoens, P., and Troch, P. (2017). Application of a buoyancy-modified k-ω SST turbulence model to simulate wave run-up around a monopile subjected to regular waves using OpenFOAM ^®. Coastal Eng. 125, 81–94. doi: 10.1016/j.coastaleng.2017.04.004

CrossRef Full Text | Google Scholar

Fan, W., Chen, J., Pan, Y., Huang, H., Chen, C.-T. A., and Chen, Y. (2013). Experimental study on the performance of an air-lift pump for artificial upwelling. Ocean Eng. 59, 47–57. doi: 10.1016/j.oceaneng.2012.11.014

CrossRef Full Text | Google Scholar

Fan, W., Pan, Y., Liu, C. C., Wiltshire, J. C., Chen-Tung, A. C., and Chen, Y. (2015). Hydrodynamic design of deep ocean water discharge for the creation of a nutrient-rich plume in the south china sea. Ocean Eng. 108, 356–368. doi: 10.1016/j.oceaneng.2015.08.006

CrossRef Full Text | Google Scholar

FAO (2018). The State of World Fisheries and Aquaculture 2018 - Meeting the Sustainable Development Goals. Rome. Licence: CC BY-NC-SA 3.0 IGO.

Ferziger, J. H., Perić, M., and Street, R. L. (2020). Computational Methods for Fluid Dynamics. Cham: Springer International Publishing.

Google Scholar

GESAMP (2019). “High level review of a wide range of proposed marine geoengineering techniques,” in Rep. Stud. GESAMP No. 98, (IMO/FAO/UNESCO-IOC/UNIDO/WMO/IAEA/UN/UN Environment/ UNDP/ISA Joint Group of Experts on the Scientific Aspects of Marine Environmental Protection), eds P. W. Boyd and C. M. G. Vivian (London: International Maritime Organization), 144p.

Google Scholar

Griffies, S. M., and Adcroft, A. J. (2008). Formulating the equations of ocean models. Ocean Model. Eddying Regime 177, 281–317. doi: 10.1029/177GM18

CrossRef Full Text | Google Scholar

IOC SCOR, and IAPSO. (2010). The International Thermodynamic Equation of Seawater-2010: Calculation and Use of Thermodynamic Properties. Paris: Intergovernmental Oceanographic Commission, Manuals and Guides.

Google Scholar

Issa, R. (1986). Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 62, 40–65. doi: 10.1016/0021-9991(86)90099-9

CrossRef Full Text | Google Scholar

Kirke, B. (2003). Enhancing fish stocks with wave-powered artificial upwelling. Ocean Coastal Manag. 46, 901–915. doi: 10.1016/S0964-5691(03)00067-X

CrossRef Full Text | Google Scholar

Komori, S., Kurose, R., Takagaki, N., Ohtsubo, S., Iwano, K., Handa, K., et al. (2011). Gas Transfer at Water Surfaces, Chapter Sensible and Latent Heat Transfer Across the Air-Water Interface in Wind-Driven Turbulence. Kyoto: Kyoto University Press.

Google Scholar

Krahmann, G. (2016). Property changes of deep and bottom waters in the western tropical atlantic. Deep Sea Res. I Oceanogr. Res. Pap. 124, 103–125. doi: 10.1016/j.dsr.2017.04.007

CrossRef Full Text | Google Scholar

Launder, B., and Spalding, D. (1974). The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 3, 269–289. doi: 10.1016/0045-7825(74)90029-2

CrossRef Full Text | Google Scholar

Lawrence, M. G., Schäfer, S., Muri, H., Scott, V., Oschlies, A., Vaughan, N. E., et al. (2018). Evaluating climate geoengineering proposals in the context of the paris agreement temperature goals. Nat. Commun. 9:3734. doi: 10.1038/s41467-018-05938-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, N.-K., and Peng, H.-K. (2005). A study of air-lift artificial upwelling. Ocean Eng. 32, 731–745. doi: 10.1016/j.oceaneng.2004.10.011

CrossRef Full Text | Google Scholar

Liu, C. C., and Jin, Q. (1995). Artificial upwelling in regular and random waves. Ocean Eng. 22, 337–350. doi: 10.1016/0029-8018(94)00019-4

CrossRef Full Text | Google Scholar

Lovelock, J. E., and Rapley, C. G. (2007). Ocean pipes could help the earth to cure itself. Nature 449, 403–403. doi: 10.1038/449403a

PubMed Abstract | CrossRef Full Text | Google Scholar

Maruyama, S., Tsubaki, K., Taira, K., and Sakai, S. (2004). Artificial upwelling of deep seawater using the perpetual salt fountain for cultivation of ocean desert. J. Oceanogr. 60, 563–568. doi: 10.1023/B:JOCE.0000038349.56399.09

CrossRef Full Text | Google Scholar

McDougall, T. J. (2003). Potential enthalpy: a conservative oceanic variable for evaluating heat content and heat fluxes. J. Phys. Oceanogr. 33, 945–963. doi: 10.1175/1520-0485(2003)033<0945:PEACOV>2.0.CO;2

CrossRef Full Text | Google Scholar

McDougall, T. J., Jackett, D. R., Wright, D. G., and Feistel, R. (2003). Accurate and computationally efficient algorithms for potential temperature and density of seawater. J. Atmos. Oceanic Technol. 20, 730–741. doi: 10.1175/1520-0426(2003)20<730:AACEAF>2.0.CO;2

CrossRef Full Text | Google Scholar

Meng, Q., Wang, C., Chen, Y., and Chen, J. (2013). A simplified CFD model for air-lift artificial upwelling. Ocean Eng. 72, 267–276. doi: 10.1016/j.oceaneng.2013.07.006

CrossRef Full Text | Google Scholar

Menter, F. R. (1994). Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 32, 1598–1605. doi: 10.2514/3.12149

PubMed Abstract | CrossRef Full Text | Google Scholar

Nayar, K. G., Sharqawy, M. H., Banchik, L. D., and Lienhard, V. J. H. (2016). Thermophysical properties of seawater: a review and new correlations that include pressure dependence. Desalination 387, 1–24. doi: 10.1016/j.desal.2016.02.024

CrossRef Full Text | Google Scholar

Oschlies, A., Pahlow, M., Yool, A., and Matear, R. J. (2010). Climate engineering by artificial ocean upwelling: channelling the sorcerer's apprentice. Geophys. Res. Lett. 37:L04701. doi: 10.1029/2009GL041961

CrossRef Full Text | Google Scholar

Pan, Y., Fan, W., Huang, T.-H., Wang, S.-L., and Chen, C.-T. A. (2015). Evaluation of the sinks and sources of atmospheric CO₂ by artificial upwelling. Sci. Total Environ. 511, 692–702. doi: 10.1016/j.scitotenv.2014.11.060

PubMed Abstract | CrossRef Full Text | Google Scholar

Pan, Y., Li, Y., Fan, W., Zhang, D., Qiang, Y., Jiang, Z.-P., et al. (2019). A sea trial of air-lift concept artificial upwelling in the east china sea. J. Atmos. Oceanic Technol. 36, 2191–2204. doi: 10.1175/JTECH-D-18-0238.1

CrossRef Full Text | Google Scholar

Patankar, S., and Spalding, D. (1972). A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass. Transf. 15, 1787–1806. doi: 10.1016/0017-9310(72)90054-3

CrossRef Full Text | Google Scholar

Roels, O. A., Laurence, S., Farmer, M. W., and Hemelryck, L. V. (1977). “Organic production potential of artificial upwelling marine culture,” in Microbial Energy Conversion (Pergamon: Elsevier), 69–81.

Google Scholar

Sharqawy, M. H., Lienhard, V. J. H, and Zubair, S. M. (2010). Thermophysical properties of seawater: a review of existing correlations and data. Desalination Water Treat. 16, 354–380. doi: 10.5004/dwt.2010.1079

CrossRef Full Text | Google Scholar

Soloviev, A. V. (2016). “Ocean upwelling system utilizing energy of surface waves,” in Proceedings of the 2016 Techno-Ocean Conefrence (Kobe: IEEE), 221–224.

Google Scholar

Stankov, P., Denev, J., Barták, M. M., Drkal, F., Lain, M. M., Schwarzer, J., et al. (2001). “Experimental and numerical investigation of temperature distribution in room with displacement ventilation,” in Proceedings of the 7th World Congress Clima 2000 (Naples).

Google Scholar

Stommel, H., Arons, A. B., and Blanchard, D. (1956). An oceanographical curiosity: the perpetual salt fountain. Deep Sea Res. 3, 152–153. doi: 10.1016/0146-6313(56)90095-8

CrossRef Full Text | Google Scholar

Thorpe, S. A. (2007). An Introduction to Ocean Turbulence. Cambridge: Cambridge University Press.

Google Scholar

Tsubaki, K., Maruyama, S., Komiya, A., and Mitsugashira, H. (2007). Continuous measurement of an artificial upwelling of deep sea water induced by the perpetual salt fountain. Deep Sea Res. I Oceanogr. Res. Pap. 54, 75–84. doi: 10.1016/j.dsr.2006.10.002

CrossRef Full Text | Google Scholar

Van Maele, K., and Merci, B. (2006). Application of two buoyancy-modified –turbulence models to different types of buoyant plumes. Fire Safety J. 41, 122–138. doi: 10.1016/j.firesaf.2005.11.003

CrossRef Full Text | Google Scholar

Wilcox, D. C. (1988). Reassessment of the scale-determining equation for advanced turbulence models. AIAA J. 26, 1299–1310. doi: 10.2514/3.10041

CrossRef Full Text | Google Scholar

Williamson, N., Komiya, A., Maruyama, S., Behnia, M., and Armfield, S. W. (2009). Nutrient transport from an artificial upwelling of deep sea water. J. Oceanogr. 65, 349–359. doi: 10.1007/s10872-009-0032-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Williamson, P., Wallace, D. W., Law, C. S., Boyd, P. W., Collos, Y., Croot, P., et al. (2012). Ocean fertilization for geoengineering: a review of effectiveness, environmental impacts and emerging governance. Process Safety Environ. Protect. 90, 475–488. doi: 10.1016/j.psep.2012.10.007

CrossRef Full Text | Google Scholar

Worthy, J., Sanderson, V., and Rubini, P. (2001). A comparison of modified k-ϵ turbulence models for and buoyant plumes. Numer. Heat Transfer B 39, 151–165. doi: 10.1080/10407790150503486

CrossRef Full Text | Google Scholar

Zhang, X., Maruyama, S., Sakai, S., Tsubaki, K., and Behnia, M. (2004). Flow prediction in upwelling deep seawater—the perpetual salt fountain. Deep Sea Res. I Oceanogr. Res. Pap. 51, 1145–1157. doi: 10.1016/j.dsr.2004.03.010

CrossRef Full Text | Google Scholar