- 1College of Engineering, Mathematics and Physical Sciences, University of Exeter, Exeter, United Kingdom
- 2Department of Civil Engineering and Applied Mechanics, McGill University, Montreal, QC, Canada
- 3Guangxi Laboratory on the Study of Coral Reefs in the South China Sea, School of Marine Sciences, Guangxi University, Nanning, China
The west coast of Canada is strongly affected by the extreme precipitation events triggered by frequent atmospheric river (AR) activities over the eastern North Pacific. Across the region, assessing the probable maximum precipitation (PMP), can provide valuable information for resilience building of the coastal communities that are vulnerable to hydrological risks. In this study, a 3-km convection-permitting regional climate model is used to physically estimate the PMP in Vancouver. This technique maximizes the effect of AR-related water vapor transport by spatially adjusting the lateral boundary conditions (LBCs) of the model simulations for the selected AR-related extreme precipitation events. The PMP in Vancouver is identified among the simulations driven by the spatially adjusted LBCs that are corresponding with the AR-induced “worst-case scenario,” i.e., landfalling ARs hit Vancouver with optimal landfalling location and transport direction. Results suggest that the PMP in Vancouver, in terms of the maxima of the regionally averaged 72-h total precipitation for the historical extreme precipitation events, is up to 790 mm, which is 130% greater than the historical peak precipitation for the period 1980∼2017. On average, all the PMP simulations shows an overall increase by 81% in precipitation by relative to historical simulations. In addition, the PMP simulations suggested an overall decrease in snowfall by 12% due to the warmer near-surface air temperature; however, a pronounced increase in freezing rain is seen. The precipitation increase for the estimated PMP relative to the historical extreme precipitation is closely associated with the increased atmospheric moisture transport and the changes in the atmospheric dynamic factors when the AR effects are maximized. These include the enhanced low-tropospheric ascent and moisture transport convergence, which can induce stronger depletion of atmospheric moistures as indicated by the increased precipitation efficiency.
Introduction
Extreme precipitation events can result in great economic losses in North America (Changnon and Hewings, 2001; Kunkel et al., 2013; Dottori et al., 2018; Davenport et al., 2021). These extreme events are usually associated with atmospheric rivers (ARs) featured by long and narrow bulks of intense water vapor transport driven by severe storm systems (Ralph et al., 2006; Halverson and Rabenhorst, 2010; Mahoney et al., 2016; Konrad and Dettinger, 2017; Picard and Mass, 2017). The close connections between ARs and precipitation extremes have been highlighted in the west coast of Canada according to the study based on satellite observations (Neiman et al., 2008). Curry and Zwiers (2018) suggested that the precipitation extremes associated with ARs can trigger extreme surface runoff, which can lead to peak annual floods in the Fraser River Basin, the largest Pacific watershed in western Canada. These have been highlighted by the landfalling AR events inducing widespread floods over Metro Vancouver and the Lower Fraser Valley during 26–28 January 2016 and 16–18 January 2017, which left five casualties (Mo et al., 2019). For the Pacific coast of North America, Khouakhi and Villarini (2016) observed that ARs are associated with 15–50% of the annual seawater level maxima (with the effect of tidal oscillations excluded) across 15 tide gauge stations along the west coast of the United States. They also suggested that ARs can generate storm surges and lead to widespread floods when AR landfalling events coincide with high tides and waves. Therefore, accurate estimations of the full potential of ARs to trigger precipitation extremes and their related hydrological events are of importance for mitigating regional hydrological risks, especially for the coastal urban communities that are highly exposed and vulnerable to the hazard of extreme floods (Clark et al., 1998; Kaźmierczak and Cavan, 2011) over the west coast of Canada.
To study the full potential of hydrological extremes, one of the most suitable approaches is to apply the concept and estimation of probable maximum precipitation (PMP), i.e., the greatest precipitation that is meteorologically possible over a designated region (WMO, 2009). PMP estimation has been performed for the design and management of hydraulic infrastructures in order to minimize the risk of disaster, such as dams (e.g., Cluckie and Pessoa, 1991; Svensson and Rakhecha, 1998; Stratz and Hossain, 2014) and soil/water conservation structures (Durbude, 2008). One of the commonly used methods for PMP estimation is based on the generalized extreme value (GEV) analysis proposed by Hershfield and Kohler (1960). This method has been used to assess regional PMP patterns (e.g., Rakhecha and Soman, 1994; Casas et al., 2008) and its simulation using regional climate model (Ben Alaya et al., 2018). However, there are several known issues in this method. For example, due to the lack of consideration of the physical processes associated with precipitation, the PMP value estimated by GEV analysis is difficult to be viewed as the physical upper limit of precipitation (Koutsoyiannis, 1999). The GEV analysis is also sensitive to the outliers in the precipitation data, which can lead to misestimated PMP values (Nobilis et al., 1991).
To address the disadvantages of statistical PMP estimation previous studies such as Corrigan et al. (1999) and Kulkarni et al. (2010) have attempted to use a linearized model for moisture maximization to physically estimate PMP. This method first maximized the precipitable water by prescribing the total column relative humidity to 100%. Then, PMP is calculated by the actual precipitation multiplied by the ratio of the maximum precipitable water to its actual value (WMO, 2009). Surface dew point temperature has also been used to maximize precipitable water if the vertical sounding data is not available (WMO, 2009). Beauchamp et al. (2013) used this method to study PMP in the context of climate change based on regional climate model simulations. The research found an increase (by 0.5–6%) of PMP in the Manic-5 watershed of Canada by the end of the 21st century relative to the end of the 20th century under a greenhouse gas emission scenario. Rousseau et al. (2014) and Rouhani and Leconte (2018) used similar methods and found that PMP is projected to increase significantly by up to 11% across eastern Canada under climate change. However, there is still a lack of investigation of the physical mechanism behind the potential occurrence of PMP in reality. In addition, the environmental features and the changes to the different types of precipitation associated with the potential occurrence of PMP are still not adequately understood.
Using limited area numerical weather model simulations, the study of Ohara et al. (2011) attempted to simulate precipitation with physically adjusted lateral boundary conditions (LBCs) in order to estimate PMP over a targeted watershed. This method first adjusts the LBCs of the model to simulate precipitation with varying physical processes. Then, PMP is identified when the optimal case of physical processes is captured by the model. One of the approaches to adjust LBCs is to ideally maximize the relative humidity value to 100% in the LBCs for selected severe storm events (Ishida et al., 2015a). Using this method, Ishida et al. (2015a) found that the estimated PMP indicate up to 74% increase of precipitation relative to the historical peak precipitation for the case of Northern California. Another approach to estimating PMP with adjusted LBCs is to spatially adjust LBCs in latitude and longitude to make ARs hit the targeted watersheds with the optimal landfall locations and maximized moisture transport so that the contribution of ARs to precipitation is maximized (Ohara et al., 2011; Ishida et al., 2015b; Ødemark et al., 2020). Although previous studies have found that the PMP values estimated by the simulations with spatial adjusted LBCs (Ishida et al., 2015b) are generally smaller than those estimated by the forcing of the ideally maximized relative humidity (Ishida et al., 2015a), it can be considered as a more realistic approach as the estimation process takes the possible locations and motions of the observed ARs into account. The recent study of Ødemark et al. (2020) has demonstrated a strong ability of a high-resolution regional climate model driven by spatial adjusted LBCs to capture the PMP in mountainous regions, while the internal mechanisms behind the occurrence of PMP remain unclear. Thus, further investigation is required to examine the physically plausible mechanisms and the changes in the different types of precipitation associated with the occurrence of PMP in a mountainous coastal region affected by hydrological extremes triggered by ARs.
Both GIS-based and survey-based vulnerability assessments have reported pronounced residential vulnerabilities to hazards of flood over Metro Vancouver (Oulahen et al., 2015a,b). One of the important agents of flood over this region is the frequent and intense AR activity during late autumn to early spring (Radić et al., 2015) due to the high density of winter storm tracks (Mesquita et al., 2010). This can be highlighted by the extreme AR event that occurred on January 18–19, 2005, which hit Vancouver and led to extreme flooding and mudslide for a week, leaving massive closure of roads and public transportation (Septer, 2006). The extreme precipitation during AR seasons can also result in severe debris flow in the north of Metro Vancouver (Jakob et al., 2012). Radić et al. (2015) also suggested future increases in the water vapor transport by ARs near Metro Vancouver based on the present and future climate simulations from CMIP5 under the Representative Concentration Pathway 4.5 and 8.5 scenarios, implying a greater contribution of ARs on extreme precipitation and floods under climate change. In this study, a high-resolution regional climate model based on the 4.8.12 version of Environment Canada’s Global Environment Multiscale in CLImate Model (GEMCLIM) is used to simulate the PMP values for the AR-related extreme precipitation events in Metro Vancouver. In addition, winter-time weather extremes over this urban region such as freezing rain and extreme snowfall can result in high risks of major disruption to public transport and significant property damage, which has been highlighted by the cold air outbreak event during the fall and winter seasons of 2016/17 (Odon et al., 2017). Therefore, the PMP simulations performed are also used to explore the mechanism associated with the occurrence of PMP and the changes to two different hazardous types of precipitation, i.e., snowfall and freezing rain, in Vancouver.
Data and Methods
Regional Climate Version of the Global Environmental Multiscale
GEMCLIM is a modelling platform developed for operational numerical weather prediction at Environment and Climate Change Canada (Côté et al., 1998; Yeh et al., 2002). The dynamical core of the model uses a semi-Lagrangian and semi-implicit two-time-level scheme (Côté et al., 1998). The LBCs are provided every 300 s. The prognostic variables are gradually relaxed to the LBCs through a sponge zone with a width of ten grid points. An additional lateral boundary zone with a width of ten grid points is used for semi-Lagrangian interpolation. The physical parametrizations used in the model include the boundary layer (Benoit et al., 1989; Delage, 1997), radiation (Li and Barker, 2005), sub-grid orographic gravity wave drag (McFarlane, 1987), deep convection (Kain and Fritsch, 1990), shallow convection (Bélair et al., 2005), cloud and large-scale condensation (Sundqvist et al., 1989). The land surface component applies the Canadian Land Surface Scheme, version 3.5 (Verseghy, 2000; Langlois et al., 2014). The model also uses a one-dimensional column lake model (Martynov et al., 2013) to simulate the interaction between the atmosphere and lakes. GEMCLIM also applies the Town Energy Balance model (Masson et al., 2002; Roberge and Sushama, 2018) to simulate the energy and water balance between urban areas and the atmosphere. The GEMCLIM simulations for the Metro Vancouver region are performed in two nested domains. As shown in Figure 1, the external domain is at a resolution of 0.11° × 0.11° (∼10 km for simulating the large-scale urban ambient environment) and the internal domain uses a typical convection-permitting horizontal grid spacing of ∼3 km (0.03° × 0.03°, at urban-scale). Both the external and internal domains excluding the sponge zones consist of 101 × 101 grid points.
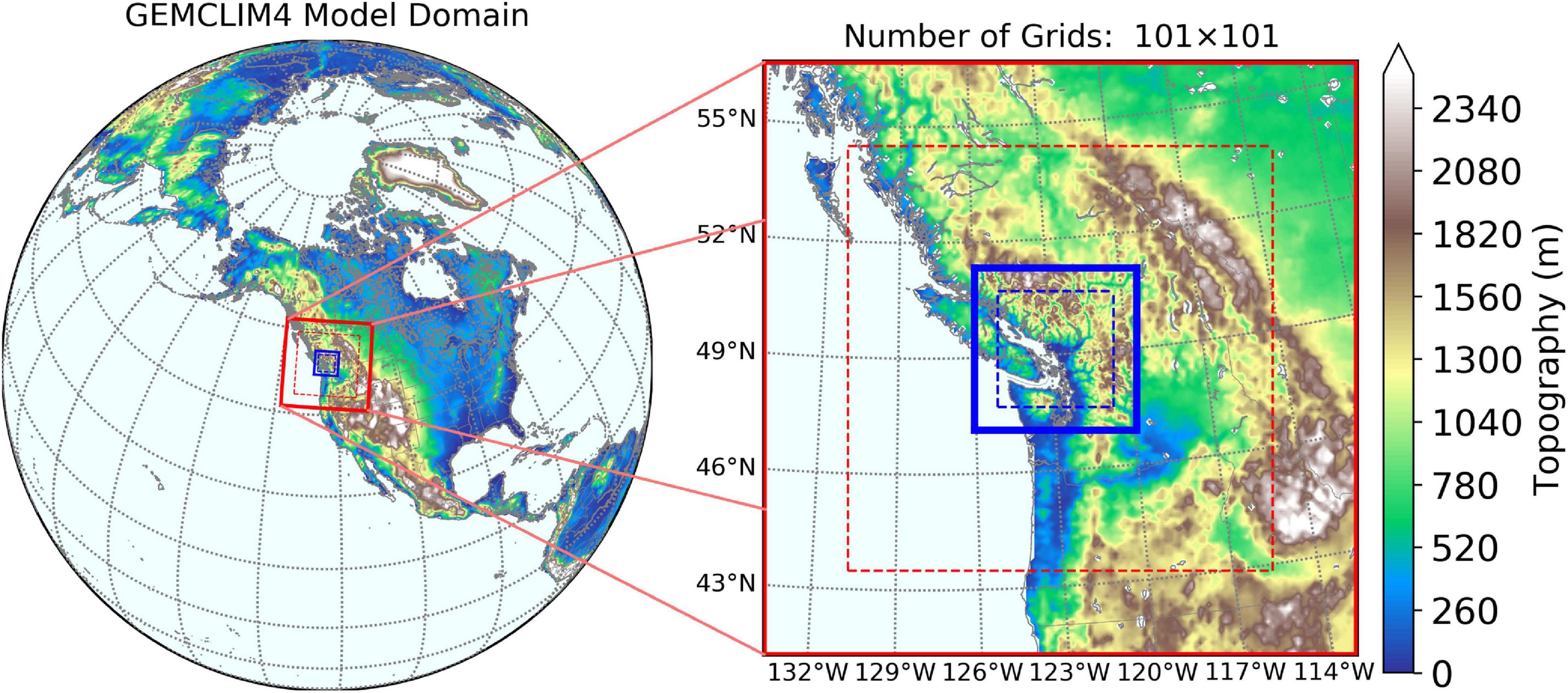
Figure 1. Nested domains of the GEMCLIM model runs for Metro Vancouver at the 10-km (red) and 3-km (blue) resolutions. Areas between the solid and dash lines depict the lateral boundary zone of the model for boundary relaxation and semi-Lagrangian interpolation. Topography data is from the SRTM v3.0 dataset (Farr et al., 2007).
The geophysical fields required for the GEMCLIM simulations are provided by the Climate Change Initiative Land Cover (Poulter et al., 2015) database for land-mask and vegetation, NASA Shuttle Radar Topography Mission (SRTM) v3.0 datasets for topography (Farr et al., 2007), Global Soil Dataset for Earth System Modeling for soil characteristics (Shangguan et al., 2014) and Canadian Vector Data v.9.0 dataset for urban properties.
Physical Maximization of Precipitation
To physically estimate PMP in Vancouver, the GEMCLIM experiments driven by spatially adjusted LBCs from the ERA-Interim reanalysis (Dee et al., 2011) are used to simulate selected extreme precipitation events in Metro Vancouver. PMP values (defined by the greatest regional-average 72-h total precipitation) are analyzed among the GEMCLIM simulations for each extreme precipitation event. The LBCs from ERA-Interim are spatially shifting in both longitude and latitude to drive GEMCLIM in order to capture the PMP with maximized AR intensities (in terms of IVT) hitting Vancouver with the optimal direction. The LBCs are meridionally shifted from 4.5° southward to 7.5° northward with a shifting interval of 0.75°. In the zonal direction, the LBCs are shifted from 6° westward to 10° eastward with a shifting interval of 1.0°. Thus, each event is simulated by 17 × 17 model runs corresponding with different spatial shifting of LBCs. We limit the range of LBC shifting because a large spatial shifting can mistakenly introduce non-AR systems outside the storm track regions to the simulation domain (Ishida et al., 2015b). The simulation for each event is initialized by a spin-up simulation of one year prior to the event. The simulations of the events driven by the spatially adjusted LBCs start seven days prior to the peak of regionally averaged 72-h total precipitation of the event and last for fourteen days.
Using the Daily Surface Weather and Climatological Summaries (Daymet, Thornton et al., 2017) at 1-km resolution, we select 30 most intense (in terms of 72-h total precipitation) extreme precipitation events associated with ARs for the period 1980∼2017 in Metro Vancouver to be simulated. Daymet is based on a local regression interpolation method to produce gridded estimates of daily meteorological variables using weather station data (Thornton et al., 1997). This dataset has been widely used for analyzing regional precipitation (Newman et al., 2020) and validating precipitation simulation (Diaconescu et al., 2016; Krebs et al., 2018; Huang et al., 2020) over Canada. Information of the selected events using Daymet, including the date of occurrence and intensity in terms of the regionally averaged 72-h total precipitation, is shown in Table 1. Daymet is also used to validate the GEMCLIM simulation of precipitation for the selected historical extreme precipitation events. To show how the physical PMP estimation performs differently from the statistical estimation, the GEV analysis based on the Fisher-Tippett distribution (Hershfield and Kohler, 1960; Nobilis et al., 1991; Kotowski and Kaźmierczak, 2013) fitted to the precipitation data by the Gumbel method is used to statistically estimate the PMP using Daymet and compared with the result of the physical method.
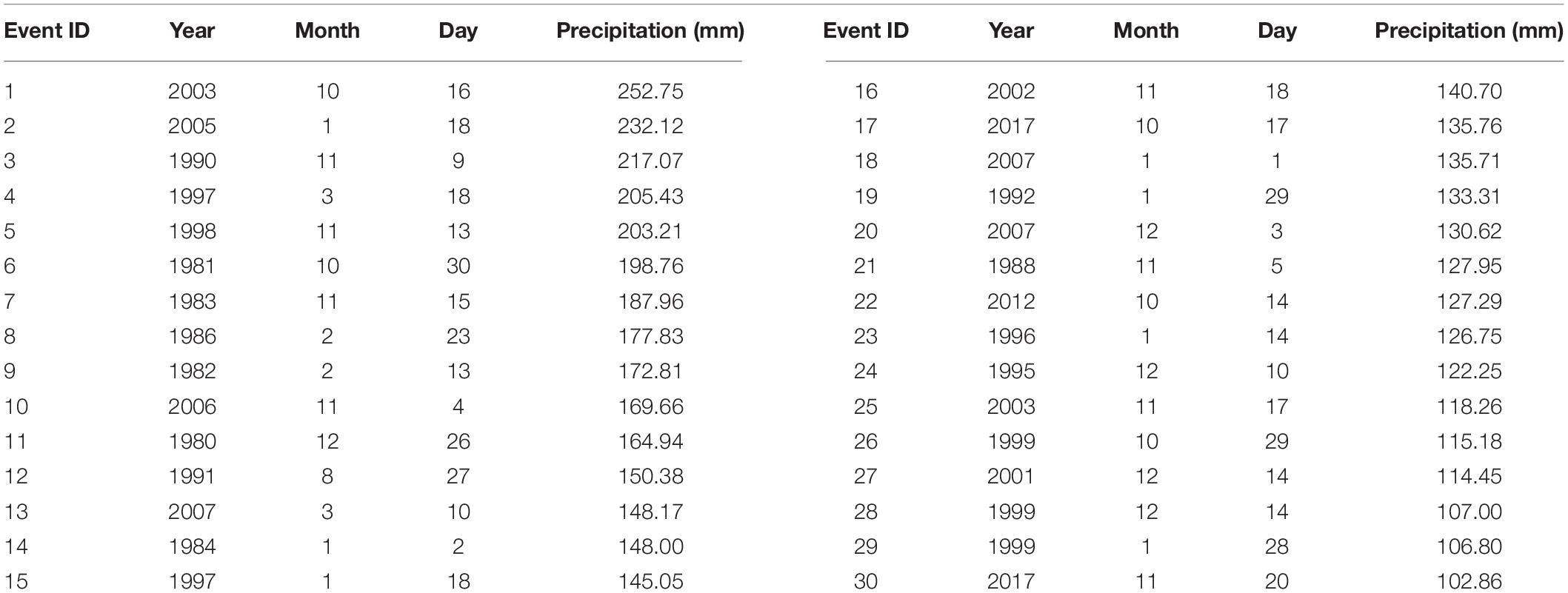
Table 1. Date and regional average of 72-h total precipitation for the 30 most intense extreme precipitation events associated with ARs affecting Metro Vancouver based on the Daymet dataset.
To investigate the mechanisms involved in the occurrence of PMP, the environmental variables associated with precipitation are analyzed. As suggested by Guan et al. (2010), Ralph and Dettinger (2012) and Liang and Sushama (2019), the large-scale environments, featured by vertically integrated water vapor transport (IVT), vertically integrated water vapor (IWV) and low-level air temperature are important characteristics of ARs responsible for different types of precipitation, hence these features are displayed for the simulated historical events and PMP estimations using the GEMCLIM simulations at 10-km resolution. To locally examine the dynamical precipitation processes in Vancouver, the changes in the dynamical factors, including the low-level vertical velocity and moisture transport convergence are analyzed using the 3-km simulations. We also calculate the large-scale precipitation efficiency, defined by the ratio of total precipitation to IWV during a certain period of time, to indicate how effective are the atmospheric dynamical processes in converting the available total column moisture to precipitation (Tuller, 1973; Ye et al., 2014).
Results
Probable Maximum Precipitation Estimates
To understand how the LBC shifting generates PMP in Metro Vancouver, we first analyze the GEMCLIM simulations for the most intense extreme precipitation event (occurring in October 2003) over Metro Vancouver for the period 1980∼2017 (event ID 1 in Table 1). Figure 2A shows that the PMP value (corresponding with the greatest precipitation in the matrix) is identified with LBCs shifted northward by 3.75° and eastward by 4°. During the historical event, Vancouver was affected by a landfalling AR with northeastward IVT of up to above 1100 kg m–1s–1 offshore Washington (state) of the United States (Figure 2B). The GEMCLIM simulation shows that the maximum 72-h precipitation reached up to 600 mm across the north of Metro Vancouver (Figure 2C). For the PMP simulation of the event, the maximum IVT within the AR plume increases by about 100 kg m–1s–1 and becomes more concentrated as affected by the spatially adjusted LBCs (Figure 2D). The PMP simulation shows that the maximum 72-h precipitation reached above 1000 mm in North Vancouver, implying an increase by about 67% relative to the historical simulation (Figure 2E).
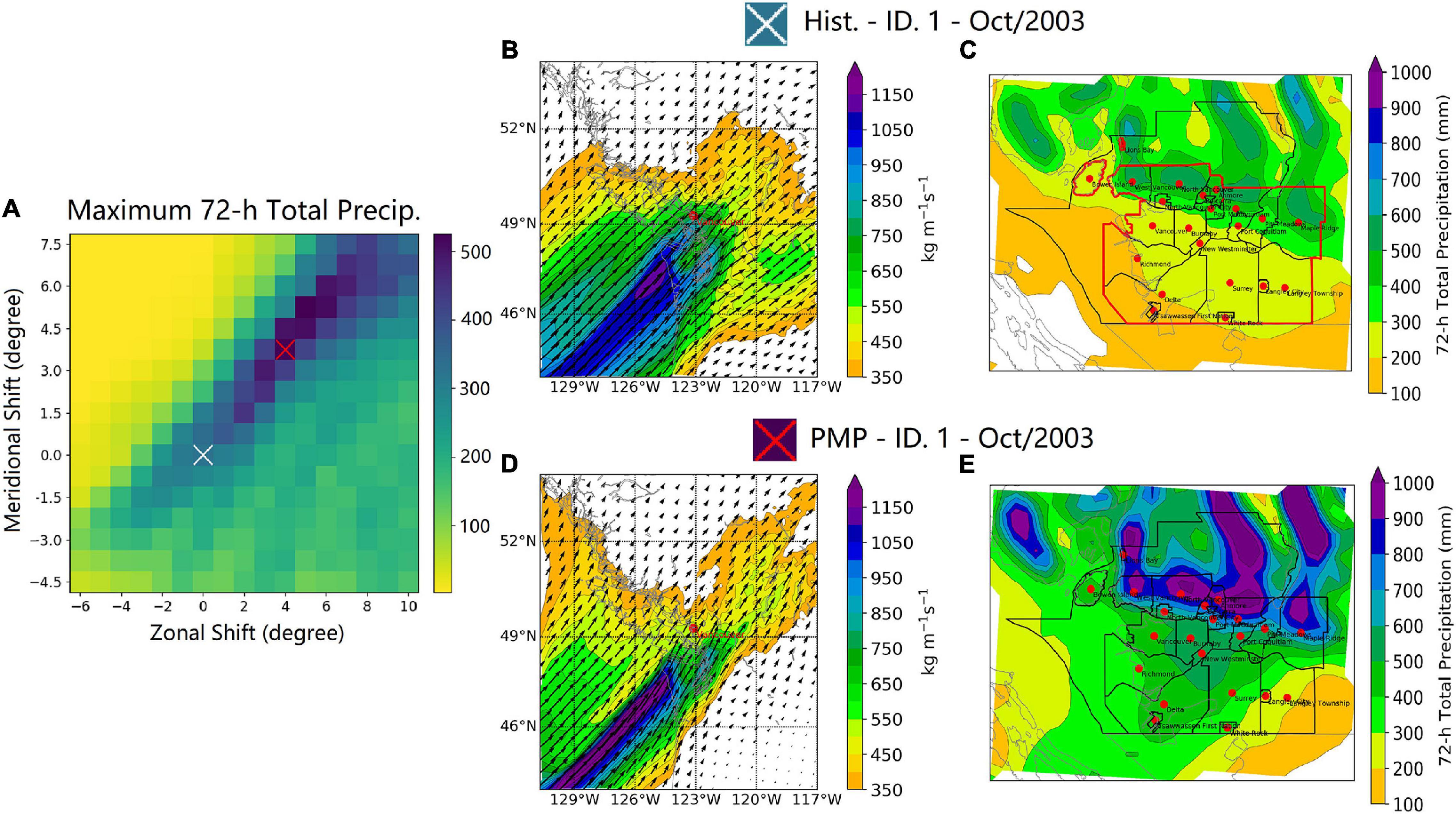
Figure 2. The GEMCLIM simulations for the most intense extreme precipitation event over Metro Vancouver (occurring in October 2003) for the period 1980∼2017: (A) The distribution of regionally averaged maximum 72-h precipitation across different spatial shifts of LBCs; (B) the simulated historical IVT field (10-km simulation) when the maximum 72-h precipitation occurred during the event; (C) the simulated historical distribution of the maximum 72-h total precipitation (3-km simulation) during the event; (D) and (E) are as (B) and (C) but for the identified PMP simulation. For (A), the white cross indicates the historical simulation (no LBC shifts) and the red cross indicates the LBC shifts corresponding with the PMP simulation.
In view of all the GEMCLIM simulations for the 30 selected historical extreme precipitation events, the PMP values (corresponding with the greatest precipitation increase relative to the historical precipitation values) are identified with LBCs shifted northward by 3.75° and eastward by 7° on average (Figure 3). In general, the regional average of 72-h precipitation over Vancouver is increased by northeastward shiftings of LBCs. Decreased precipitation is found when the LBCs are shifted southward and westward. If the LBCs are shifted only in the meridional (zonal) direction, the greatest precipitation increase is found when LBCs are shifted 0.75° northward (1° eastward), while the magnitudes of increase are much smaller than those generated by LBCs shifted in both directions. It is noticed that the direction of spatial shift corresponding with the PMP values is different from those presented by Ohara et al. (2011) and Ishida et al. (2015b), which suggested a southward shift (approximately 5∼6° southward) of the LBCs for capturing PMP. This is mainly due to the difference in the targeted area as these studies focused on the south of the main active region of ARs over the western North America.
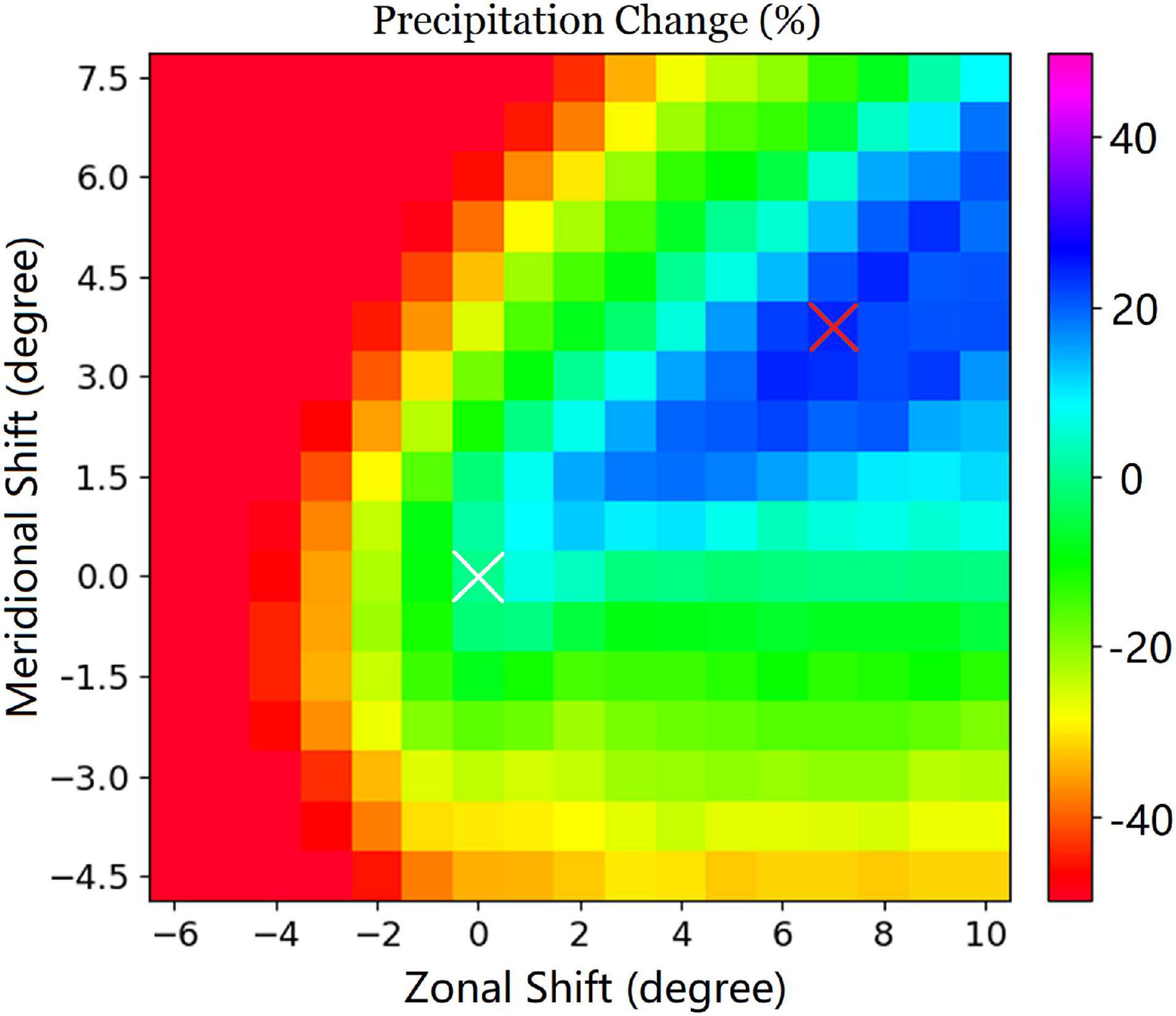
Figure 3. Mean relative changes in the regionally averaged maximum 72-h precipitation during the selected extreme precipitation events over Metro Vancouver for the simulations with different LBC shifting relative to the historical simulations. White cross indicates the historical simulations (no LBC shifts) and red cross indicates the mean LBC shifts corresponding with the maximum precipitation increase.
Figure 4 shows the PMP values, in terms of the maximum regional average of 72-h total precipitation, over Metro Vancouver for the 30 selected extreme precipitation events with respect to the observed and simulated historical precipitation values. Compared to the observations, GEMCLIM successfully represents the most intense precipitation event that occurred on October 16th, 2003 (Event ID 1) and the second most intense event on January 18th, 2005 (Event ID 2). Although GEMCLIM shows overestimation (by 37%) of precipitation in general and the model overestimates the precipitation of the two most intense events by 34% and 45%, respectively, compared to the observations, the historical simulations are well correlated with the observation with a correlation coefficient of 0.6, which is statistically significant (p-value < 0.001). The greatest PMP value (783.35 mm) is found in the simulation of the third most intense precipitation event in history (November 9th, 1999, Event ID 3), which indicates precipitation increase by a factor of 2.7 relative to the corresponding historical precipitation. Also, the greatest PMP value is 1.3 times larger than the precipitation maximum during the most intense historical event (October 16th, 2003). On average, PMP values for all the events show a precipitation increase by 81% relative to the mean precipitation of historical simulations.

Figure 4. Maximum of regional-averaged 72-h precipitation over Metro Vancouver for the 30 selected extreme precipitation events.
The spatial distributions of different types of precipitation for the historical extreme precipitation events and PMP estimates are presented in Figures 5, 6. The PMP estimated by the statistical method [i.e., 50-year return period of precipitation, following Clavet-Gaumont et al. (2017) and Afzali-Gorouh et al. (2018)] indicates up to 2 fold increases in precipitation (Figures 5B,C), particularly in the northern part of Vancouver’s downtown (i.e., the West Vancouver and North Vancouver District). The GEMCLIM simulations of historical events (Figure 5D) show relatively intense precipitation over the north of Metro Vancouver, which is generally in agreement with the precipitation pattern from Daymet (Figure 5A). The PMP simulations from GEMCLIM driven by the spatially adjusted LBCs (Figures 5E,F) generally resembles the pattern of PMP estimated by the statistical method, though a smaller magnitude of precipitation increase is found. Also, the PMP simulated by GEMCLIM shows larger precipitation increases (approximately 300 mm) in the southern part of Vancouver.
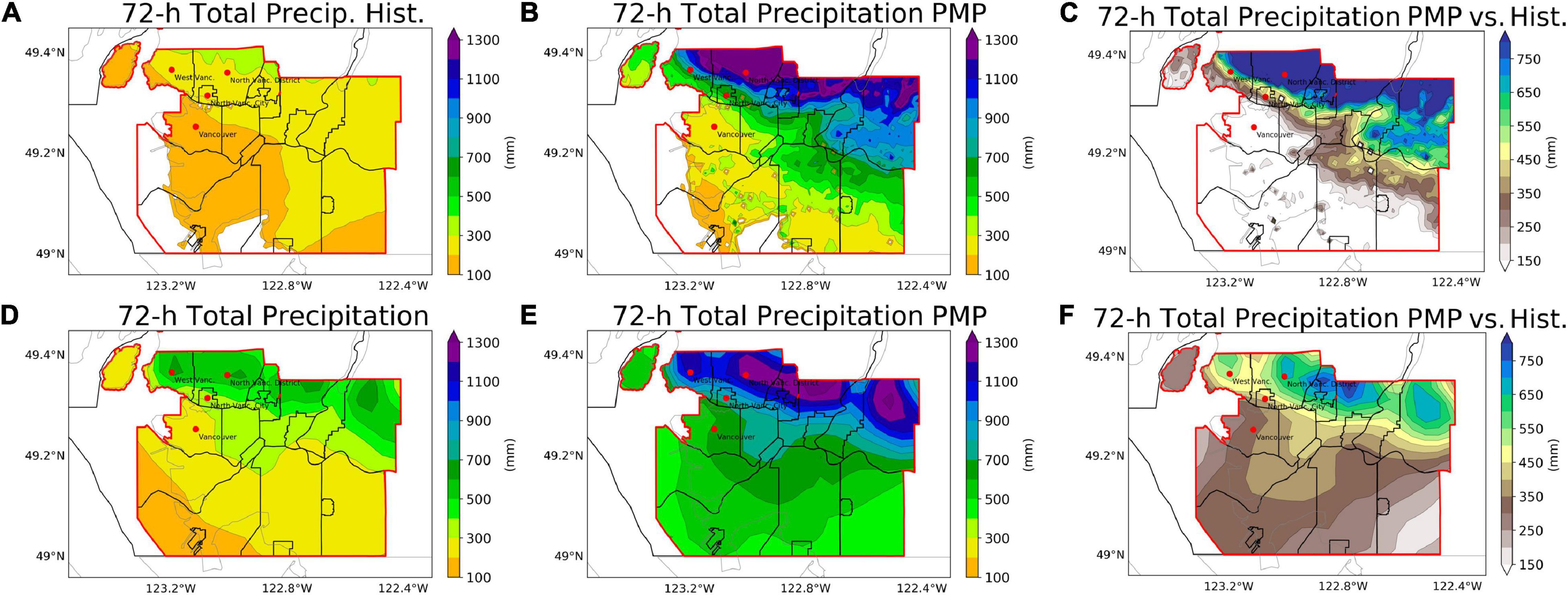
Figure 5. Precipitation and PMP estimation from the GEV analysis based on Daymet (A–C) and simulations of GEMCLIM driven by spatially adjusted LBCs (D–F) for the 30 historical extreme precipitation events in Metro Vancouver during 1980∼2017: (A,D) the maximum 72-h total precipitation in the historical events; (B,E) PMP estimates; (C,F) precipitation increase for PMP relative to the historical events. Areas marked with red stippling illustrate Vancouver’s downtown districts.

Figure 6. Simulations of the maximum 72-h total snowfall (A–C) and freezing rain (D–F) for the 30 historical extreme precipitation events in Metro Vancouver during 1980∼2017, including the simulations of the historical events (A,D), PMP (B,E) and the absolute changes for PMP relative to the historical simulations (C,F).
For the changes in the solid type precipitation, although the PMP simulations suggest an overall decrease in snowfall (by 12% on average) relative to the historical events (especially over most of the mid-south of Vancouver), a significant increase (>22.5 mm) in snowfall is displayed over the pre-slope downtown districts of Vancouver (Figure 6C). Moreover, the PMP simulations suggest an obvious increase (by up to 3 mm) and southward extension of freezing rain (Figure 6F), posing a greater hazardous impact on the transportation and electricity infrastructure of the city (Odon et al., 2017, 2019). The more widespread freezing rain implies a more pronounced thermal stratification in the lower troposphere. These can be explained by the maximized effects of ARs, including the concentrated warm advection and positive differential vorticity advection near the leading edges of AR plumes as discussed by the study of Liang and Sushama (2019).
To further understand the local hydrological response to the occurrence of PMP, the changes in the 72-h cumulative surface runoff for PMP relative to the historical events are analyzed (Figure 7). Over the northwest of Metro Vancouver, the surface runoff is approximately tripled by the occurrences of PMP (Figure 7B compared to A). Moreover, a pronounced extension of the overland flow is displayed over the east of the region during the occurrences of PMP (Figure 7B). These changes possibly indicate a dramatic increase in the intensity of runoff-induced hydrological extremes such as flood (Costa, 1987; Segond et al., 2007; Konrad and Dettinger, 2017), soil erosion (Nearing et al., 2005; Zuazo and Pleguezuelo, 2009) and debris flows (Coe et al., 2008; Kean et al., 2013).
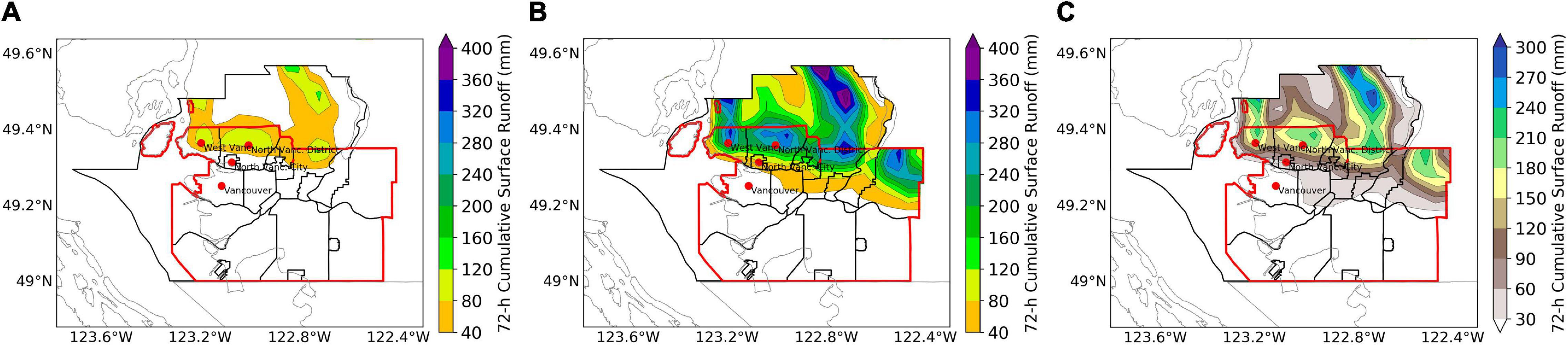
Figure 7. The simulated 72-h cumulative surface runoff (mm) when the maximum 72-h precipitation occurred during the simulated events for the historical simulation (A), PMP simulation (B) and the absolute changes for PMP relative to the historical simulations (C).
The Large-Scale Environment Associated With Probable Maximum Precipitation
Figure 8 displays the changes to the large-scale environments related to precipitation with maximized AR impacts. The simulated AR intensity (in terms of IVT) for the selected extreme precipitation events displayed more intense and concentrated IVT affecting Vancouver for the PMP simulations (Figures 8B,C) compared with the historical simulations (Figure 8A). The AR axes (shown by red lines in Figures 8A,B) also penetrate deeper toward inland when PMP occurs, which can greatly enhance heavy rainfall and flooding (Mahoney et al., 2016). Meanwhile, the IWV across the passage of ARs is approximately doubled by the maximized AR intensity, which partially explained the increase of precipitation as shown in Figures 5E,F. For the changes in the thermal environment, a warmer lower-troposphere (by about 2.1°C in terms of the vertically averaged temperature between 850 and 1000 hPa) is found near Vancouver (Figure 8I). This is possible due to the overlapped warm sectors of AR-related storms (Lavers et al., 2011) when the AR-related IVTs are shifted toward the vicinity of Vancouver. Although warmer air temperatures are favorable for the increase of IWV and precipitation, increases in the low-level temperature may result in shifts from snowfall to rainfall during AR events (Guan et al., 2010). This partly explains the overall reduction of snowfall over the mid-south of Vancouver (Figures 6B,C).
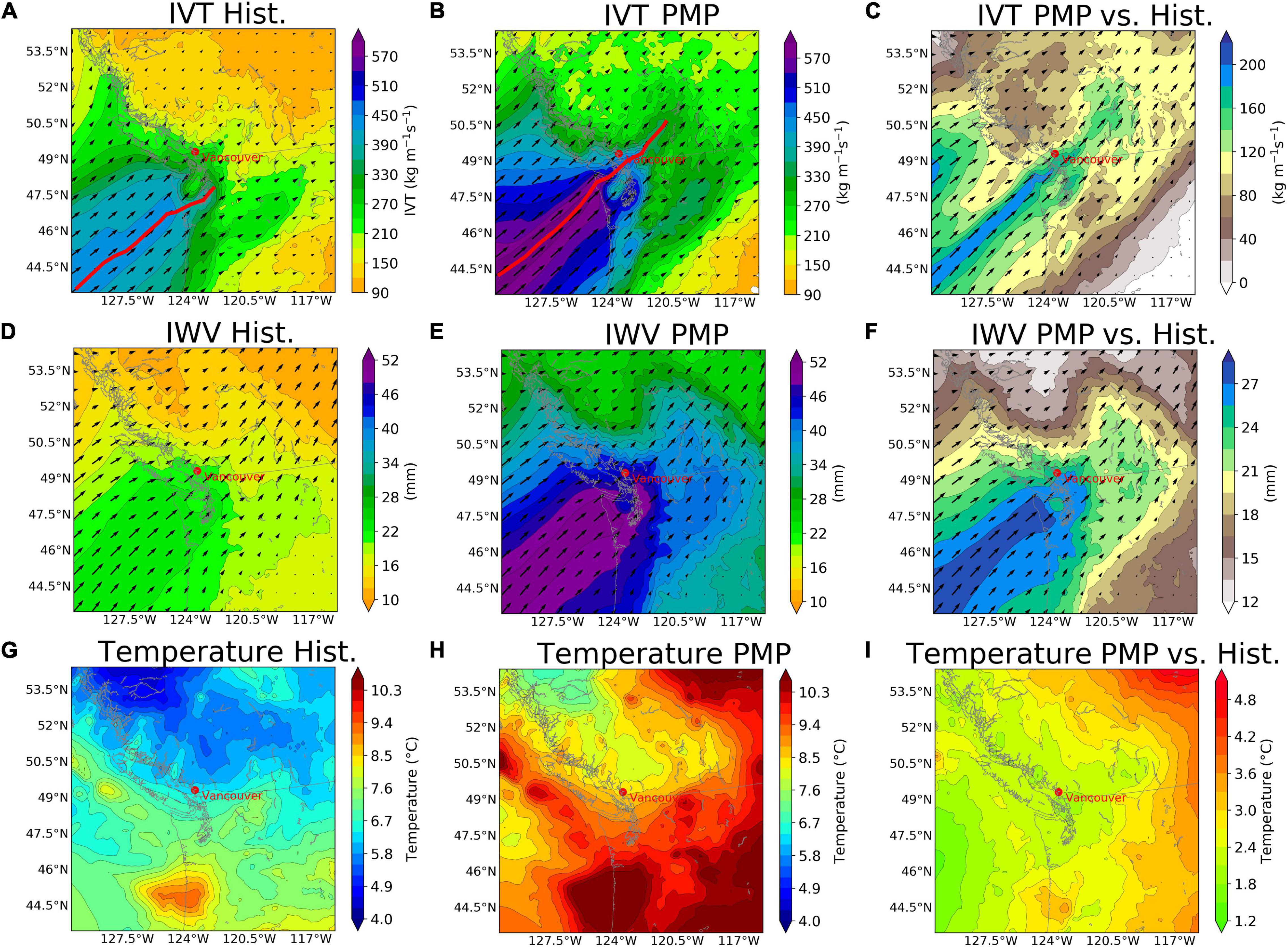
Figure 8. The simulated large-scale environmental fields when the maximum 72-h precipitation occurred during the simulated events, including IVT (A–C), IWV (D–F) and the pressure-weighted vertically averaged temperature between 850 and 1000 hPa (G–I) from the 10-km simulations, including the simulated historical events (A,D,G), PMP (B,E,H) and the absolute changes for PMP relative to the historical simulations (C,F,I). Red lines in (A,B) show the approximate mean location of AR axes.
Simulations of the urban-scale dynamical factors for the historical extreme precipitation events and their PMP estimations are shown in Figure 9. When PMP occurred, we found approximately doubled magnitudes of vertical ascent between 850 and 1000-hPa levels over Vancouver (Figures 9B,C), especially in the pre-slope districts in the north of the city. Moreover, the low-level IVT associated with PMP (Figures 9E,F) tends to exhibit more pre-slope convergence (by 2∼6 mm/h). These imply a more favorable dynamical environment for generating precipitation. To further analyze how can the more favorable dynamical environments lead to increases to precipitation, the precipitation efficiency is calculated and presented in Figures 9G–I. Compared to the simulated historical events, the PMP simulations show increases in precipitation efficiency (by around 39%) in the pre-slope districts of Vancouver. This indicates that the occurrences of PMP are associated with the maximized IWV conditions from ARs as well as the stronger ability of the dynamical factors to deplete atmospheric moistures.
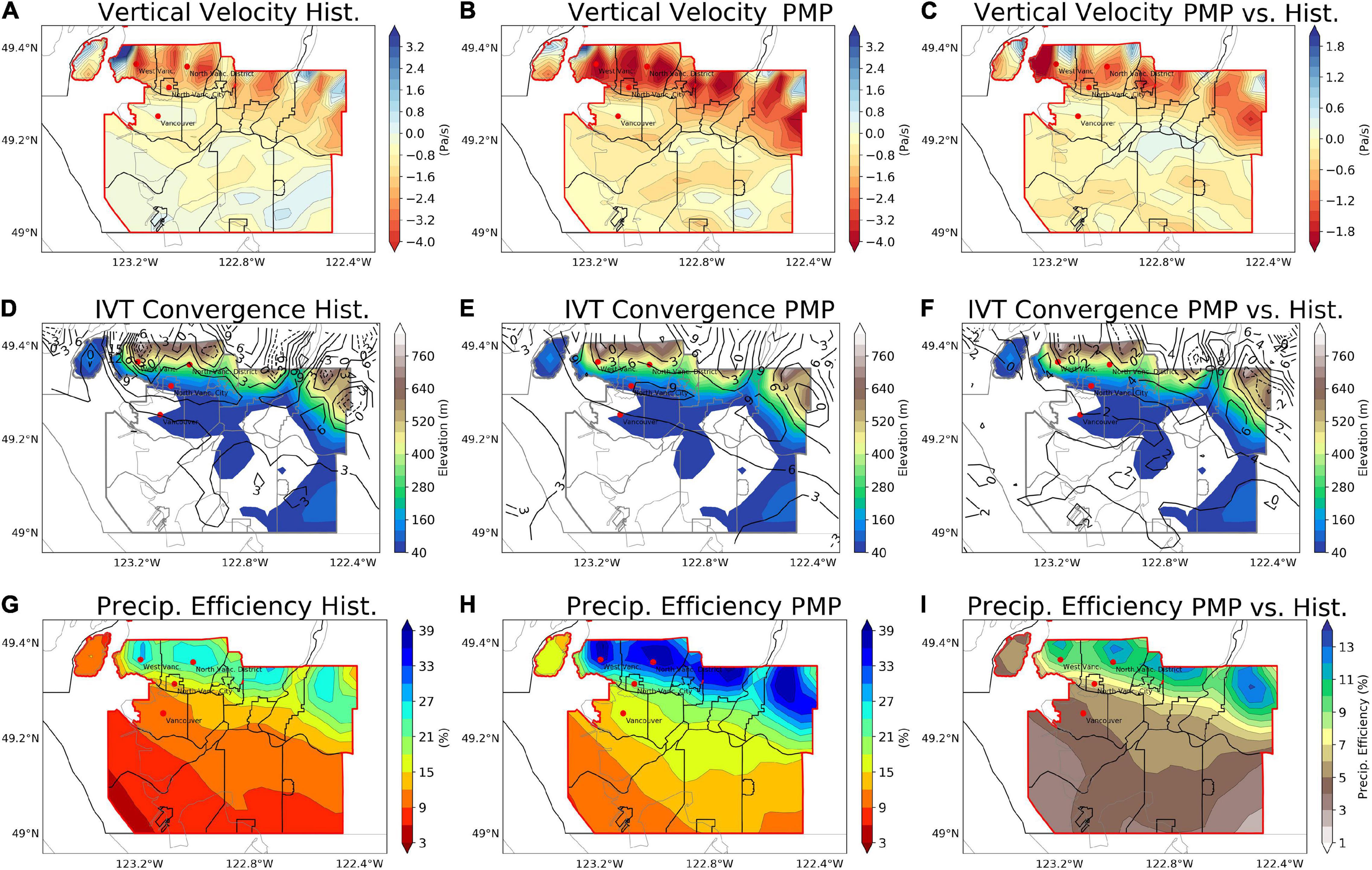
Figure 9. Dynamical environmental fields when the maximum 72-h precipitation occurred for the simulated historical extreme precipitation events, including the pressure-weighted vertically averaged vertical velocity between 850 and 1000-hPa (A–C), IVT convergence (black contours, unit: mm/h) and elevation (D–F) and precipitation efficiency (G–I): (A,D,G) the historical events; (B,E,H) PMP; (C,F,I) the absolute changes for PMP relative to the historical events.
Summary and Discussion
Physically based estimations of PMP are performed for the Metro Vancouver region and the PMP-associated environmental mechanisms are analyzed based on the GEMCLIM simulations driven by spatially adjusted LBCs. Through maximization of the influence of ARs, PMP simulations for the historical extreme precipitation events show an increase in the 72-h regional average of precipitation over Metro Vancouver by 81% on average compared with the historical simulations of the events. The precipitation maxima in the PMP simulations show an increase in precipitation by about 130% relative to the historical peak precipitation for the period 1980∼2017. We also found an overall decrease in snowfall by 12% due to the influence of concentrated warm sectors of AR-related storm systems. PMP simulations also show increased freezing rain intensity in Vancouver. The enhanced precipitation presented by the PMP simulations is found to be the result of both the increased atmospheric moisture and the increased precipitation efficiency induced by the more favorable atmospheric dynamical factors when AR intensities are maximized. These responses are observed mainly across the pre-slope coastal regions. The analyses of PMP and associated mechanisms presented in this study provide a case study of the physically plausible upper limit of precipitation, which can be further used in the other coastal regions affected by concentrated water vapor transport. This helps to develop a PMP estimation approach for the purpose of operational services in contrast to the “theoretical” PMP (WMO, 2009).
The magnitude of the increased precipitation (by 81% on average) indicated by the PMP simulations is greater than those (by 36∼74%) found in the studies using similar methods for PMP estimation (Ohara et al., 2011; Ishida et al., 2015b), though this is dependent on the selection of targeted area and extreme precipitation events to be simulated. The enhanced precipitation by PMP over the north of Metro Vancouver presented in this study is helpful to assess the maximum impacts of flooding and its secondary hazards such as soil erosions (Nearing et al., 2005; Zuazo and Pleguezuelo, 2009) and debris flows (Coe et al., 2008; Kean et al., 2013). In addition, we found that the physically estimated PMP and the associated precipitation increase is lower than that estimated by the GEV analysis based on observed precipitation. The dynamical features presented by the physically estimated PMP provide more physically plausible information, which helps to achieve better practices of management of hydrological risks and more reasonable designs of hydraulic infrastructures. However, the physically estimated PMP still has limitations in reliabilities, thus its comparison with the statistically estimated PMP will still be helpful to reliably approximate the plausible upper limit of precipitation. The limitation in the reliability of the physically estimated PMP can be linked to the uncertainties in the RCM configuration (including dynamical core and physical parameterizations) and the reanalysis dataset used as the LBC of the RCM. Therefore, the results presented in this paper should be interpreted with cautions and future work should further apply the PMP estimation method in this study to assess these uncertainties.
Another limitation of the study is that the presented dynamical features of PMP are simulated only under the present-day climate forcing based on a historical climate reanalysis dataset; hence, the experiments do not consider the responses of these features to future changes in climate forcing. A possible global increase in statistically estimated PMP due to the general moistening of the atmosphere under global warming has been reported by climate projection studies (Kunkel et al., 2013; Rousseau et al., 2014; Rouhani and Leconte, 2018), while the projected changes in the physically estimated PMP still remains unknown. One of the solutions to this issue is to use the PMP estimation method of this study to physically estimate the PMP of a targeted region driven by the LBCs from global climate simulations for both the historical climate and future climate under scenarios of greenhouse gas emissions so that the changes in the physically estimated PMP under the possible future changes in climate forcing can be quantified. Moreover, future study is required to understand the economic losses associated with the PMP triggered by ARs based on integrated assessment methods (Dominguez et al., 2018). Systematic impact assessment of urban floods is also worth being applied together with the physically estimated PMP presented in this paper to understand the resilience of coastal cities to PMP-related floods (Hammond et al., 2015). These works will help enhance our knowledge of the vulnerability and adaptive capacity of the coastal urban communities to hydrological extremes.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
JL: conceptualization, methodology, visualization, software, and writing – original draft. YY: formal analysis and writing – review and editing. Both authors contributed to the article and approved the submitted version.
Funding
Publication of this study was supported by the Natural Science Foundation of Guangxi Province (Grant Number: 2016GXNSFBA380242).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The GEMCLIM experiments applied in this study were performed using the high-performance computational facilities of Compute Canada and Calcul Québec.
References
Afzali-Gorouh, Z., Bakhtiari, B., and Qaderi, K. (2018). Probable maximum precipitation estimation in a humid climate. Nat. Hazards Earth Syst. Sci. 18, 3109–3119. doi: 10.5194/nhess-18-3109-2018
Beauchamp, J., Leconte, R., Trudel, M., and Brissette, F. (2013). Estimation of the summer-fall PMP and PMF of a northern watershed under a changed climate. Water Resour. Res. 49, 3852–3862. doi: 10.1002/wrcr.20336
Bélair, S., Mailhot, J., Girard, C., and Vaillancourt, P. (2005). Boundary layer and shallow cumulus clouds in a medium-range forecast of a large-scale weather system. Mon. Weather Rev. 13, 1938–1960. doi: 10.1175/MWR2958.1
Ben Alaya, M. A., Zwiers, F., and Zhang, X. (2018). Probable maximum precipitation: its estimation and uncertainty quantification using bivariate extreme value analysis. J. Hydrometeorol. 19, 679–694. doi: 10.1175/jhm-d-17-0110.1
Benoit, R., Côté, J., and Mailhot, J. (1989). Inclusion of a TKE boundary layer parameterization in the Canadian regional finite-element model. Mon. Weather Rev 117, 1726–1750. doi: 10.1175/1520-04931989117<1726:IOATBL<2.0.CO;2
Casas, M. C., Rodríguez, R., Nieto, R., and Redaño, A. (2008). The estimation of probable maximum precipitation: the case of catalonia. Ann. N. Y. Acad. Sci. 1146, 291–302. doi: 10.1196/annals.1446.003
Changnon, S. A., and Hewings, G. J. D. (2001). Losses from weather extremes in the United States. Nat. Hazards Rev. 2, 113–123. doi: 10.1061/(asce)1527-698820012:3(113)
Clark, G. E., Moser, S. C., Ratick, S. J., Dow, K., Meyer, W. B., Emani, S., et al. (1998). Assessing the vulnerability of coastal communities to extreme storms: the case of reverse. MA., USA. Mitig. Adapt. Strateg. Glob. Chang. 3, 59–82. doi: 10.1023/A:1009609710795
Clavet-Gaumont, J., Huard, D., Frigon, A., Koenig, K., Slota, P., Rousseau, A., et al. (2017). Probable maximum flood in a changing climate: an overview for Canadian basins. J. Hydrol. Reg. Stud. 13, 11–25. doi: 10.1016/j.ejrh.2017.07.003
Cluckie, I. D., and Pessoa, M. L. (1991). Dam safety: an evaluation of some procedures for design flood estimation. Hydrol. Sci. J. 35, 547–569. doi: 10.1080/02626669109492534
Coe, J. A., Kinner, D. A., and Godt, J. W. (2008). Initiation conditions for debris flows generated by runoff at Chalk Cliffs, central Colorado. Geomorphology 96, 270–297. doi: 10.1016/j.geomorph.2007.03.017
Corrigan, P., Fenn, D. D., Kluck, D. R., and Vogel, J. L. (1999). Probable Maximum Precipitation For California. Washington, DC: NOAA.
Costa, J. E. (1987). A comparison of the largest rainfall-runoff floods in the United States with those of the People’s Republic of China and the world. J. Hydrol. 96, 101–115. doi: 10.1016/0022-1694(87)90146-6
Côté, J., Desmarais, J.-G., Gravel, S., Méthot, A., Patoine, A., Roch, M., et al. (1998). The operational CMC–MRB Global Environmental Multiscale (GEM) model. Part II: results. Mon. Weather Rev. 126, 1397–1418. doi: 10.1175/1520-04931998126<1397:TOCMGE<2.0.CO;2
Curry, C. L., and Zwiers, F. W. (2018). Examining controls on peak annual streamflow and floods in the Fraser River Basin of British Columbia. Hydrol. Earth Syst. Sci. 22, 2285–2309. doi: 10.5194/hess-22-2285-2018
Davenport, F. V., Burke, M., and Diffenbaugh, N. S. (2021). Contribution of historical precipitation change to US flood damages. Proc. Natl. Acad. Sci. U.S.A. 118, 1–7. doi: 10.1073/pnas.2017524118
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., et al. (2011). The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 137, 553–597. doi: 10.1002/qj.828
Delage, Y. (1997). Parameterising sub-grid scale vertical transport in atmospheric models under statically stable conditions. Boundary Layer Meteorol. 82, 23–48. doi: 10.1023/A:1000132524077
Diaconescu, E. P., Gachon, P., Laprise, R., and Scinocca, J. F. (2016). Evaluation of precipitation indices over North America from various configurations of regional climate models. Atmos. Ocean 54, 418–439. doi: 10.1080/07055900.2016.1185005
Dominguez, F., Dall’erba, S., Huang, S., Avelino, A., Mehran, A., Hu, H., et al. (2018). Tracking an atmospheric river in a warmer climate: from water vapor to economic impacts. Earth Syst. Dynam. 9, 249–266. doi: 10.5194/esd-9-249-2018
Dottori, F., Szewczyk, W., Ciscar, J. C., Zhao, F., Alfieri, L., Hirabayashi, Y., et al. (2018). Increased human and economic losses from river flooding with anthropogenic warming. Nat. Clim. Change 8, 781–786. doi: 10.1038/s41558-018-0257-z
Durbude, D. (2008). Estimation of probable maximum precipitation soil and water conservation structures. J. Soil Water Conserv. 7, 31–35.
Farr, T. G., Rosen, P. A., Caro, E., Crippen, R., Duren, R., Hensley, S., et al. (2007). The Shuttle Radar Topography Mission. Rev. Geophys. 45:RG2004. doi: 10.1029/2005RG000183
Guan, B., Molotch, N. P., Waliser, D. E., Fetzer, E. J., and Neiman, P. J. (2010). Extreme snowfall events linked to atmospheric rivers and surface air temperature via satellite measurements. Geophys. Res. Lett. 37, 1–6. doi: 10.1029/2010GL044696
Halverson, J. B., and Rabenhorst, T. D. (2010). Mega-snow in the megalopolis: the mid-atlantic’s blockbuster winter of 2009–2010. Weatherwise 63, 16–23. doi: 10.1080/00431672.2010.490164
Hammond, M. J., Chen, A. S., Djordjević, S., Butler, D., and Mark, O. (2015). Urban flood impact assessment: a state-of-the-art review. Urban Water J. 12, 14–29. doi: 10.1080/1573062X.2013.857421
Hershfield, D. M., and Kohler, M. A. (1960). An empirical appraisal of the Gumbel extreme-value procedure. J. Geophys. Res. 65, 1737–1746. doi: 10.1029/jz065i006p01737
Huang, H., Winter, J. M., Osterberg, E. C., Hanrahan, J., Bruyère, C. L., Clemins, P., et al. (2020). Simulating precipitation and temperature in the Lake Champlain basin using a regional climate model: limitations and uncertainties. Clim. Dynam. 54, 69–84. doi: 10.1007/s00382-019-04987-8
Ishida, K., Kavvas, M. L., Jang, S., Chen, Z. Q., Ohara, N., and Anderson, M. L. (2015a). Physically based estimation of maximum precipitation over three watersheds in northern california: relative humidity maximization method. J. Hydrol. Eng. 20:04015014. doi: 10.1061/(ASCE)HE.1943-5584.0001175
Ishida, K., Kavvas, M. L., Jang, S., Chen, Z. Q., Ohara, N., and Anderson, M. L. (2015b). Physically based estimation of maximum precipitation over three watersheds in northern california: atmospheric boundary condition shifting. J. Hydrol. Eng. 20:04014052. doi: 10.1061/(ASCE)HE.1943-5584.0001026
Jakob, M., Owen, T., and Simpson, T. (2012). A regional real-time debris-flow warning system for the District of North Vancouver, Canada. Landslides 9, 165–178. doi: 10.1007/s10346-011-0282-8
Kain, J. S., and Fritsch, J. M. (1990). A one-dimensional entraining/detraining plume model and its application in convective parameterization. J. Atmos. Sci. 47, 2784–2802. doi: 10.1175/1520-04691990047<2784:AODEPM<2.0.CO;2
Kaźmierczak, A., and Cavan, G. (2011). Surface water flooding risk to urban communities: analysis of vulnerability, hazard and exposure. Landsc. Urban Plan. 103, 185–197. doi: 10.1016/j.landurbplan.2011.07.008
Kean, J. W., McCoy, S. W., Tucker, G. E., Staley, D. M., and Coe, J. A. (2013). Runoff-generated debris flows: observations and modeling of surge initiation, magnitude, and frequency. J. Geophys. Res. Earth Surf. 118, 2190–2207. doi: 10.1002/jgrf.20148
Khouakhi, A., and Villarini, G. (2016). On the relationship between atmospheric rivers and high sea water levels along the US West Coast. Geophys. Res. Lett. 43, 8815–8822. doi: 10.1002/2016gl070086
Konrad, C. P., and Dettinger, M. D. (2017). Flood runoff in relation to water vapor transport by atmospheric rivers over the western United States, 1949–2015. Geophys. Res. Lett. 11:462. doi: 10.1002/2017GL075399
Kotowski, A., and Kaźmierczak, B. (2013). Probabilistic models of maximum precipitation for designing sewerage. J. Hydrometeorol. 14, 1958–1965. doi: 10.1175/JHM-D-13-01.1
Koutsoyiannis, D. (1999). A probabilistic view of Hershfield’s method for estimating probable maximum precipitation. Water Resour. Res. 35, 1313–1322. doi: 10.1029/1999WR900002
Krebs, C. J., Henry, J. D., Kenney, A. J., and Hofer, E. J. (2018). Empirical test of the ClimateWNA model for local accuracy in the Kluane Lake area of the southern Yukon, Canada. Clim. Res. 75, 111–115. doi: 10.3354/CR01511
Kulkarni, B. D., Nandargi, S., and Mulye, S. S. (2010). Zonal estimation of probable maximum precipitation rain depths over the Krishna basin in peninsular India. Hydrol. Sci. J. 55, 93–103. doi: 10.1080/02626660903529015
Kunkel, K. E., Karl, T. R., Easterling, D. R., Redmond, K., Young, J., Yin, X., et al. (2013). Probable maximum precipitation and climate change. Geophys. Res. Lett. 40, 1402–1408. doi: 10.1002/grl.50334
Langlois, A., Bergeron, J., Brown, R., Royer, A., Harvey, R., Roy, A., et al. (2014). Evaluation of CLASS 2.7 and 3.5 Simulations of Snow Properties from the Canadian Regional Climate Model (CRCM4) over Québec, Canada. J. Hydrometeorol. 15, 1325–1343. doi: 10.1175/jhm-d-13-055.1
Lavers, D. A., Allan, R. P., Wood, E. F., Villarini, G., Brayshaw, D. J., and Wade, A. J. (2011). Winter floods in Britain are connected to atmospheric rivers. Geophys. Res. Lett. 38, 1–8. doi: 10.1029/2011GL049783
Li, J., and Barker, H. (2005). A radiation algorithm with correlated- k distribution. Part I: local thermal equilibrium. J. Atmos. Sci. 62, 286–309. doi: 10.1175/JAS-3396.1
Liang, J., and Sushama, L. (2019). Freezing rain events related to atmospheric rivers and associated mechanisms for western North America. Geophys. Res. Lett. 46, 10541–10550. doi: 10.1029/2019GL084647
Mahoney, K. M., Jackson, D. L., Neiman, P., Hughes, M., Darby, L., Wick, G., et al. (2016). Understanding the role of atmospheric rivers in heavy precipitation in the southeast United States. Mon. Weather Rev. 144, 1617–1632. doi: 10.1175/MWR-D-15-0279.1
Martynov, A., Laprise, R., Sushama, L., Winger, K., Šeparović, L., and Dugas, B. (2013). Reanalysis-driven climate simulation over CORDEX North America domain using the Canadian Regional Climate Model, version 5: model performance evaluation. Clim. Dynam. 41, 2973–3005. doi: 10.1007/s00382-013-1778-9
Masson, V., Grimmond, C. S. B., and Oke, T. R. (2002). Evaluation of the Town Energy Balance (TEB) scheme with direct measurements from dry districts in two cities. J. Appl. Meteorol. 41, 1011–1026. doi: 10.1175/1520-04502002041<1011:EOTTEB<2.0.CO;2
McFarlane, N. A. (1987). The effect of orographically excited gravity wave drag on the general circulation of the lower stratosphere and troposphere. J. Atmos. Sci. 44, 1775–1800. doi: 10.1175/1520-04691987044<1775:TEOOEG<2.0.CO;2
Mesquita, M. D. S., Atkinson, D. E., and Hodges, K. I. (2010). Characteristics and variability of storm tracks in the North Pacific. Bering Sea, and Alaska. J. Clim. 23, 294–311. doi: 10.1175/2009JCLI3019.1
Mo, R., Brugman, M. M., Milbrandt, J. A., Goosen, J., Geng, Q., Emond, C., et al. (2019). Impacts of hydrometeor drift on orographic precipitation: two case studies of landfalling atmospheric rivers in British Columbia, Canada. Weather Forecast. 34, 1211–1237. doi: 10.1175/WAF-D-18-0176.1
Nearing, M. A., Jetten, V., Baffaut, C., Cerdan, O., Couturier, A., Hernandez, M., et al. (2005). Modeling response of soil erosion and runoff to changes in precipitation and cover. Catena 61, 131–154. doi: 10.1016/j.catena.2005.03.007
Neiman, P. J., Ralph, F. M., Wick, G. A., Dettinger, M. D., and Lundquist, J. D. (2008). Meteorological characteristics and overland precipitation impacts of atmospheric rivers affecting the west coast of North America based on eight years of SSM/I satellite observations. J. Hydrometeorol. 9, 22–47. doi: 10.1175/2007jhm855.1
Newman, A. J., Clark, M. P., Wood, A. W., and Arnold, J. R. (2020). Probabilistic spatial meteorological estimates for Alaska and the Yukon. J. Geophys. Res. Atmos. 125:e2020JD032696. doi: 10.1029/2020JD032696
Nobilis, F., Haiden, T., and Kerschbaum, M. (1991). Statistical considerations concerning probable maximum precipitation (pmp) in the alpine country of Austria. Theor. Appl. Climatol. 44, 89–94. doi: 10.1007/BF00867996
Ødemark, K., Müller, M., and Tveito, O. E. (2020). Changing lateral boundary conditions for probable maximum precipitation studies: a physically consistent approach. J. Hydrometeorol. 22, 113–123. doi: 10.1175/JHM-D-20-0070.1
Odon, P., West, G., and Stull, R. (2017). Vancouver winter 2016/17, how bad was it? CMOS Bull. SCMO 45, 9–12.
Odon, P., West, G., and Stull, R. (2019). Evaluation of reanalyses over British Columbia. Part II: daily and extreme precipitation. J. Appl. Meteorol. Climatol. 58, 291–315. doi: 10.1175/JAMC-D-18-0188.1
Ohara, N., Kavvas, M. L., Kure, S., Chen, Z., Jang, S., and Tan, E. (2011). Physically based estimation of maximum precipitation over American River Watershed, California. J. Hydrol. Eng. 16, 351–361. doi: 10.1061/(ASCE)HE.1943-5584.0000324
Oulahen, G., Mortsch, L., Tang, K., and Harford, D. (2015a). Unequal vulnerability to flood hazards: “Ground truthing” a social vulnerability index of five municipalities in metro vancouver, Canada. Ann. Assoc. Am. Geogr. 105, 473–495. doi: 10.1080/00045608.2015.1012634
Oulahen, G., Shrubsole, D., and McBean, G. (2015b). Determinants of residential vulnerability to flood hazards in metro vancouver, Canada. Nat. Hazards 78, 939–956. doi: 10.1007/s11069-015-1751-5
Picard, L., and Mass, C. (2017). The sensitivity of orographic precipitation to flow direction: an idealized modeling approach. J. Hydrometeorol. 18, 1673–1688. doi: 10.1175/JHM-D-16-0209.1
Poulter, B., MacBean, N., Hartley, A., Khlystova, I., Arino, O., Betts, R., et al. (2015). Plant functional type classification for earth system models: results from the european space agency’s land cover climate change initiative. Geosci. Model Dev. 8, 2315–2328. doi: 10.5194/gmd-8-2315-2015
Radić, V., Cannon, A. J., Menounos, B., and Gi, N. (2015). Future changes in autumn atmospheric river events in British Columbia, Canada, as projected by CMIP5 global climate models. J. Geophys. Res. 120, 9279–9302. doi: 10.1002/2015JD023279
Rakhecha, P. R., and Soman, M. K. (1994). Estimation of probable maximum precipitation for a 2-day duration: part 2 - north Indian region. Theor. Appl. Climatol. 49, 77–84. doi: 10.1007/BF00868192
Ralph, F. M., and Dettinger, M. D. (2012). Historical and national perspectives on extreme west coast precipitation associated with atmospheric rivers during december 2010. Bull. Am. Meteorol. Soc. 93, 783–790. doi: 10.1175/BAMS-D-11-00188.1
Ralph, F. M., Neiman, P. J., Wick, G. A., Gutman, S. I., Dettinger, M. D., Cayan, D. R., et al. (2006). Flooding on California’s russian river: role of atmospheric rivers. Geophys. Res. Lett. 33, 1–5. doi: 10.1029/2006GL026689
Roberge, F., and Sushama, L. (2018). Urban heat island in current and future climates for the island of Montreal. Sustain. Cities Soc. 40, 501–512. doi: 10.1016/j.scs.2018.04.033
Rouhani, H., and Leconte, R. (2018). A methodological framework to assess PMP and PMF in snow-dominated watersheds under changing climate conditions-A case study of three watersheds in Québec (Canada). J. Hydrol. 561, 796–809. doi: 10.1016/j.jhydrol.2018.04.047
Rousseau, A. N., Klein, I. M., Freudiger, D., Gagnon, P., Frigon, A., and Ratté-Fortin, C. (2014). Development of a methodology to evaluate probable maximum precipitation (PMP) under changing climate conditions: application to southern Quebec, Canada. ZJ. Hydrol. 519, 3094–3109. doi: 10.1016/j.jhydrol.2014.10.053
Segond, M.-L., Wheater, H. S., and Onof, C. (2007). The significance of spatial rainfall representation for flood runoff estimation: a numerical evaluation based on the Lee catchment. U.K. J. Hydrol. 347, 116–131. doi: 10.1016/J.JHYDROL.2007.09.040
Septer, D. (2006). Flooding and Landslide Events Northern British Columbia. British Columbia, BC: Ministry of Environment, 1820–2006.
Shangguan, W., Dai, Y., Duan, Q., Liu, B., and Yuan, H. (2014). A global soil data set for earth system modeling. J. Adv. Model. Earth Syst. 6, 249–263. doi: 10.1002/2013MS000293
Stratz, S. A., and Hossain, F. (2014). Probable maximum precipitation in a changing climate: implications for dam design. J. Hydrol. Eng. 19:06014006. doi: 10.1061/(ASCE)HE.1943-5584.0001021
Sundqvist, H., Berge, E., and Kristjánsson, J. E. (1989). Condensation and cloud parameterization studies with a mesoscale numerical weather prediction model. Mon. Weather Rev. 117, 1641–1657. doi: 10.1175/1520-04931989117<1641:CACPSW<2.0.CO;2
Svensson, C., and Rakhecha, P. R. (1998). Estimation of probable maximum precipitation for dams in the Hongru River catchment, China. Theor. Appl. Climatol. 59, 79–91. doi: 10.1007/s007040050014
Thornton, P. E., Running, S. W., and White, M. A. (1997). Generating surfaces of daily meteorological variables over large regions of complex terrain. J. Hydrol. 190, 214–251. doi: 10.1016/S0022-1694(96)03128-9
Thornton, P. E., Thornton, M. M., Mayer, B. W., Wei, Y., Devarakonda, R., Vose, R. S., et al. (2017). Daymet: Daily Surface Weather Data On A 1-Km Grid For North America, Version 3 [WWW Document]. Oak Ridge, Ten: ORNL DAAC.
Tuller, S. E. (1973). Seasonal and annual precipitation efficiency in canada. Atmosphere (Basel). 11, 52–66. doi: 10.1080/00046973.1973.9648348
Verseghy, D. L. (2000). The Canadian land surface scheme (CLASS): its history and future. Atmos. Ocean 38, 1–13. doi: 10.1080/07055900.2000.9649637
WMO (2009). Manual on Estimation of Probable Maximum Precipitation (PMP), World Meteorological Organization (WMO), WMO. Geneva: WMO.
Ye, H., Fetzer, E. J., Wong, S., Behrangi, A., Olsen, E. T., Cohen, J., et al. (2014). Impact of increased water vapor on precipitation efficiency over northern Eurasia. Geophys. Res. Lett. 41, 2941–2947. doi: 10.1002/2014GL059830
Yeh, K. S., Cote, J., Gravel, S., Methot, A., Patoine, A., Roch, M., et al. (2002). The CMC–MRB Global Environmental Multiscale (GEM) model. part III: nonhydrostatic formulation. Mon. Weather Rev. 130, 339–356.
Keywords: probable maximum precipitation, regional climate model, atmospheric river, coastal urban area, Vancouver
Citation: Liang J and Yong Y (2022) Dynamics of Probable Maximum Precipitation Within Coastal Urban Areas in a Convection-Permitting Regional Climate Model. Front. Mar. Sci. 8:747083. doi: 10.3389/fmars.2021.747083
Received: 25 July 2021; Accepted: 31 December 2021;
Published: 08 February 2022.
Edited by:
Edmo J. D. Campos, American University of Sharjah, United Arab EmiratesReviewed by:
Ze-Nan Zhu, Ministry of Natural Resources, ChinaYueyue Yu, Nanjing University of Information Science and Technology, China
Rafaela Gomes Ferrari, Federal University of Rio de Janeiro, Brazil
Copyright © 2022 Liang and Yong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yangyang Yong, eW9uZ3l5QGd4dS5lZHUuY24=
 Ju Liang
Ju Liang Yangyang Yong
Yangyang Yong