
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
METHODS article
Front. Mar. Sci. , 14 October 2021
Sec. Marine Pollution
Volume 8 - 2021 | https://doi.org/10.3389/fmars.2021.739683
This article is part of the Research Topic Plastic Pollution in the Bay Areas View all 14 articles
Microplastics (MPs) have become the widespread contaminants, which raises concerns on their ecological hazards. In-situ detection of MP in water bodies is essential for clear assessment of the ecological risks of MPs. The present study proposes a method based on polarized light scattering which measures the polarization parameters of the scattered light at 120° to detect MP in water. This method takes the advantage of in-situ measurement of the individual particles and the experimental setup in principle is used. By use of the measured polarization parameters equipped by machine learning, the standard polystyrene (PS) spheres, natural water sample, and lab-cultured microalgae are explicitly discriminated, and MP with different physical and chemical properties can be differentiated. It can also characterize the weathering of different MP and identify the specific type from multiple types of MP. This study explores the capability of the proposed method to detect the physical and chemical properties, weathering state and concentration of MP in water which promises the future application in water quality sensing and monitoring.
Microplastics (MPs) are defined as plastic particles with size <5 mm (Amaral-Zettler et al., 2020), widely distribute in water environments including oceans (Saeed et al., 2020), lakes (Yu et al., 2020), and rivers (Auta et al., 2017). Once inside the body, microplastics can release toxins, additives, and monomers which have been found to trigger carcinogenic behavior. Moreover, the human intake of microplastics can cause lung damage and liver function changes. Thus, microplastics pollution should be understood and controlled to uphold human, animal, and aquatic health (Golwala et al., 2021). In order to assess the effects of MPs on aquatic ecosystem, the detection method of MPs in water has attracted the attention of researchers (Sadri and Thompson, 2014; Amaral-Zettler et al., 2020).
The current detection methods for MPs mainly include visual method (including naked eye visual method and microscope visual method), Fourier infrared spectroscopy, Raman spectroscopy, and thermal pyrolysis analysis (Mai et al., 2018). The analysis of MPs in water usually includes sampling, filtering, cleaning, identification, and other steps (Song et al., 2015). The difficulty of MPs identification lies in the identification of MPs from many impurity particles. Visual method is widely used due to convenience and cheapness, and it can give the physical properties of MPs, such as size, color, and shape (Eriksen et al., 2013; Vianello et al., 2013). However, the visual method is low accuracy and subjected to the subjective influence, and often makes an overestimate of the abundance of MPs in samples (Lenz et al., 2015). Spectroscopic methods, including Fourier infrared spectroscopy and Raman spectroscopy, can determine the chemical composition of the sample, and the accuracy is relatively high, and the size resolution can approach 1 micron (Kappler et al., 2016). However, there is seldom reported about the in-situ detection of MPs using spectroscopic methods. The thermal pyrolysis analysis, such as Pyrolysis-GC/MS and TGA-MS have been used for the microplastic analysis. Samples are firstly thermally degraded and the resultant products are subsequently sent to the mass spectrometer for analysis. The collected data are compared with reference to obtain such sample information as identity and concentration. However, the method is less applicable for mixtures with high concentration of impurities (Zhang et al., 2019). Due to the needed sampling, these methods are not suitable to in-situ detect MPs in water. Nowadays, an in-situ detection method with high speed, convenience, non-destruction, and acceptable accuracy is still desired (Yin et al., 2021).
Polarization is a fundamental property of light. The polarization state is more sensitive to microstructure and can provide more information than conventional optical intensity (Sun et al., 2014). Polarized light scattering methods have been successfully used to characterize and classify biological tissues (Ghosh and Vitkin, 2011), marine microalgae (Chami, 2007), and nanoplastics (Yu et al., 2021). Measurement sensors based on polarized light scattering methods have been successfully integrated into in-situ underwater instruments (Liao et al., 2019).
The polarization state of light is usually represented by the Stokes vector S as shown in Eq. 1. I represents the light intensity; Q and U represent the linearly residual polarization of light; Q is the intensity difference between the horizontal and vertical components, and U is intensity difference between 45° and −45° linear components; V is the circularly residual polarization of light, and equals to the intensity difference between the right-hand and left-hand components. Usually, the Stokes vector is normalized as Eq. 2 to obtain the three polarization parameters of q, u, and v.
In this paper, we propose a polarized light scattering method to in-situ detect the MPs in water. This method takes the advantage of the different responses of the MPs and other particles in water to the incident polarized light. We record the polarization parameters (q, u, v) of the light scattered by the individual particles at 120° scattering angle, and then use machine learning algorithms, such as linear discrimination analysis (LDA) and support vector machine (SVM) to analyze the data. The samples consist of the mixture of the natural water, the microalgae, and the MPs with different size, shape and materials. Experiments have found that microplastic (MP) can be well-discriminated from the mixtures. We also did the experiments to discriminate the weathered MP from the natural water even for the complex compositions of MPs samples, and the results are encouraging. Additionally, we found that polarization parameters can be used to characterize MP size decreasing after weathering. The concentration calibration shows a linear relationship between the measured pulse number per unit time and the concentration of MP. The results promised the present method suitable in-situ detecting those suspended MPs from complex water environment, with no weathering disturbance while a lower detectable concentration limit of MPs (0.01 mg/L).
The experimental setup designed by our lab is a backward 120° polarized light scattering measurement system for suspended particles. Its working principle and optical path design are similar with the previous work (Wang et al., 2018), and its reliability has been verified (Liao et al., 2019). Our previous works demonstrate that the polarization parameters at the 120° scattering angle can effectively characterize the microstructures of particles (Wang et al., 2018). The scattered intensity of the bulk water volume at 120° is almost not sensitive to the size distribution of particles (Boss and Pegau, 2001). Such that, we continue to use the 120° scattering angle in this work. The light source (S) emits vertically polarized light. The polarization state generator (PSG) changes the light into any polarization state we want, and in this work, PSG generate and fix at the 135° linearly polarized light. And the diaphragm (D) limits the size of the incident light spot. Lens 1 (L1) focuses the light beam to a small spot to illuminate the individual particles. The aquatic suspension is contained in a round beaker. During the experiment, the particles in the aquatic suspension are stirred to keep suspended by a magnetic stirrer at the speed of 100 rounds per minute. In the setup, the round beaker is embedded in a dodecagon pool with the central coaxial. The beaker is marked by a red arrow in Figure 1A. The distilled water is filled between the beaker and the dodecagon pool for the refractive index matching. The parallel beam is normally incident on a flat surface of dodecagon and the scattered light is received through the other flat surface at the 120° scattering angle. The flat surfaces and the distilled water are used to effectively reduce the light deformation when passing through the surfaces. The 120° backward scattered light is received by lens 2 (L2), filtered by pinhole (P), and changed by lens 3 (L3) to the parallel light and finally analyzed by the polarization state analyzer (PSA).
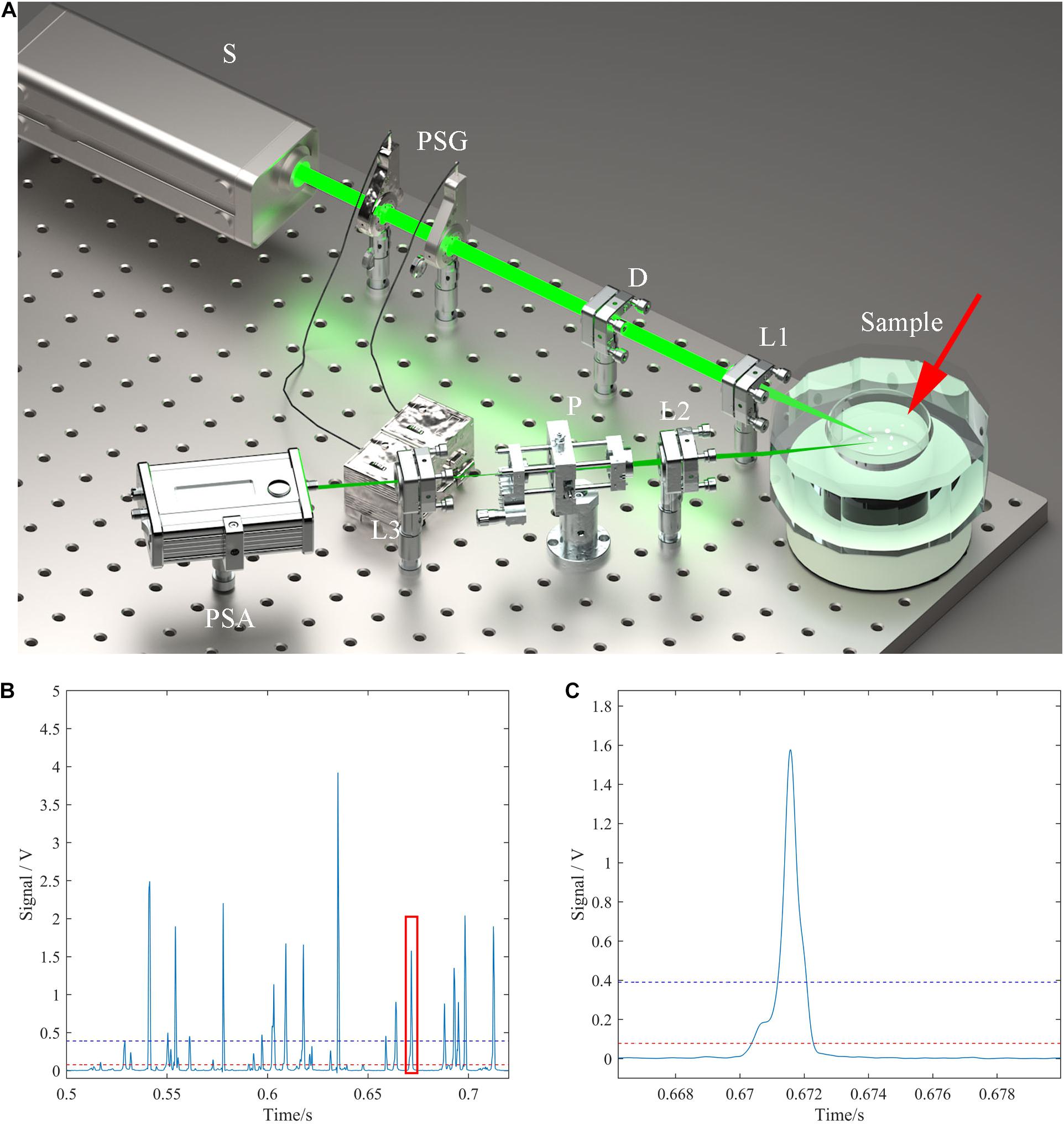
Figure 1. (A) Backward 120° suspended particle measurement system based on polarized light scattering. S, light source; PSG, polarization state generator; D, diaphragm; L, lens; P, pinhole; PSA, polarization state analysis. (B) Received signals of the setup. (C) The magnification of the temporal pulse. Red line: the background noise; blue line: threshold voltage.
In Figure 1, the detection volume containing the particle and the pinhole is the object-image relationship by L2. Since the conjugate relation, the detected volume in water and its size is determined by the location of L2 in the optical path and the size of the pinhole. The pinhole size is 100 microns in the setup. The scattering volume is the conjunction volume of the light spot and the detected volume. Finally, we can limit the scattering volume to be <0.01 micro liter (L). If the volume concentration of the particles is <105 per milliliter, in statistics there is one particle at most in the scattering volume and only its scattered light is received each time. Such that the received signals of the setup are a series of temporal pulses, as shown in Figure 1B, which demonstrates the measurement of the individual particles. Figure 1C shows one of the temporal pulse, and one can see that the temporal duration of the pulse is around 1 ms.
PSA consists of non-polarization beam splitters to split the parallel light after L3 into four parts. Passing through a 135°-oriented quarter-wave plate with 90° polarizers, a single 0° polarizers, a single 90° polarizers and a single 45° polarizers respectively, the resulting four components of the polarized light are obtained to, respectively, get the left-handed circularly polarized component, horizontal component, vertical component, and 45° linearly polarized component. They are converted by photoelectric converters to voltages, simultaneously recorded by a data acquisition card working at 300,000 samplings per second and then calculated to the Stokes vector. And finally, the polarization parameters (q, u, v) of the light scattered by the individual particles are obtained. And for each sample, more than 3,000 pulses are recorded, and that is, more than 3,000 particles are measured.
The samples in this work include the river water, 10-micron spherical Polystyrene (PS), microalgae, and 300-mesh MP. The sampling point of the river water was in the Dasha River, University Town, Shenzhen, Guangdong Province, China. The sampling time was January 13, 2021, with a 0-meter water layer. The 10-micron spherical PS was purchased from Suzhou Nanomicro Technology Co., Ltd., with a diameter of 10 microns. The microalgae include Scenedesmus Obliquus (SO), Prymnesium Parvum (PP), Haematococcus Pluvialis (HP), Scrippsiella Trochoidea (ST), Phaeodactylum Tricornutum (PT), Chlorella Vulgaris (CV), and Cyanobacteria (CB). The culture conditions are 2,000 lux light, light-dark cycle 12 h:12 h, medium BG11. 300-mesh MP are industrial plastic raw materials, granular, whose average size is <50 μm. There are six specific types, Polystyrene (PS), Polyethylene (PE), Polyethylene Eerephthalate (PET), Polypropylene (PP), Nylon (PA), and Polyvinyl Chloride (PVC). All of them are purchased from Guangdong Dongguan Huachuang Plastic Chemical Co., Ltd. Note that these types of MP are the most reported in literatures and the most common types in aquatic environments.
In this work, there are three types of samples used, namely microalgae, river water, and microplastics. All samples are stored in a constant temperature environment of 20 ± 2°C. The microalgae are stored in a closed test tube with 2,000 lux light. Each time the river water is sampled from the Dasha river and stored in glass tubes for <1 h before the measurements, the dry microplastics are stored in sealed glass cups and their aquatic suspensions are prepared and then are measured within 1 h. The preservation time of microalgae is around 4 h, the preservation time of river water is around 4 h, and the preservation time of microplastics is 2 days.
We firstly add the raw data of the four channels together to get the total temporal signals. And then we use the median filter to get rid of the random noise, and then get the histogram of the total temporal signals and consider the voltage where the peak value locates as the background. The dark noises of the detectors, the environmental light, scattering of the water, etc., may contribute to the background. We use a threshold which is 10 times of the background. Then we get the pulses whose temporal values are all larger than the threshold, such that the signal-noise-ratio of the pulse is larger than 10. Here each pulse is sampled for multiple times whose number is determined by the pulse’s time interval. Till now, we get a series of pulses and then go to find the according data of the four channels. For each pulse in each channel, we average the multiple samplings in the pulse and get the mean value. And then we can use four mean values from the four channels to calculate the Stokes vector.
Linear discrimination analysis is widely used in the field of pattern recognition, such as facial recognition, ship recognition, and other graphics and image recognition (Li and Yuan, 2005). LDA is a dimensionality reduction technology of supervised learning. It projects data to one dimension, so that the projection points of the same type of data are as close as possible, and the distance between the projection center points of different types of data is as large as possible. For the two types of polarization data, the LDA algorithm will calculate an optimal projection function f, to project the three-dimensional polarization data [q, u, v] to the one-dimensional projection parameter X, as shown in Eq. 3.
Discriminant degree, D, is defined as Eq. 4:
where and are the peak locations of the distribution 1 and distribution 2, respectively; FWHM1 and FWHM2, respectively are the full width at the half maximum (FWHM) of the distribution 1 and distribution 2. D represents the effect of discrimination. The larger is the D, the better is the discrimination effect. Generally, when D = 2, there is significant discrimination between these two distributions; when 1 = D < 2, there is good discrimination between the two distributions; and when D = 1, these two distributions cannot be discriminated.
Support vector machine is a classification technique of supervised learning (Shan et al., 2019). The goal of SVM is to find a segmentation surface that can discriminate the two sets of data, while keeping the maximum distance from the sample points of the two sets of data that are closest to the segmentation surface.
Experiments were performed on the river water and 10-micron spherical PS separately, and the experimental data of the two were processed by LDA. The projection parameter with the best discrimination between river water and 10-micron spherical PS data is X = 0.41q−0.56u−0.71v, and this projection parameter is used for LDA processing of other samples and 10-micron spherical PS unless otherwise specified below. As shown in Figure 2A, the river water is marked as RW, and the distribution of the river water is located on the left of the figure while that of the 10-micron spherical PS is located on the right, and both are normalized to the maxima of themselves. From Figure 2A, one can see that the discrimination is significant between RW and PS where D = 3.1.
Figure 2. Distribution of river water and 10-micron spherical polystyrene (PS). (A) Mixing experiment of river water and different concentrations of 10-micron spherical PS. (B) Individual experimental data. (C) Quantitative graph of PS with increasing concentration.
Then the suspension of the 10-micron spherical PS was added gradually into the river water for mixing experiments, and then the different PS concentration in the mixture were got and each mixture was measured by the setup. The experimental results are shown in Figure 2B. All the distributions of X for mixtures are bimodal and each distribution is normalized to its left peak value. According to Figure 2A, the left peak of the distributions in Figure 2B represents the river water, and the right peak represents the spherical PS. The peak values represent the relative number of particles measured in each mixture. From Figure 2B one can see that the right peak value increases with the PS concentration, which is shown in Figure 2C. The linearity can be found in Figure 2C. These results show that the current method can effectively recognize the special PS (as a specific MP) and retrieve its concentration in the river water (as a type of the natural water body).
Microalgae are one of the main compositions of suspended particles in water, and play the key role in the aquatic ecosystem. Recently, the interaction between the microalgae and MPs is an extensively discussed topic in current scientific community. In this work, to investigate the discrimination between microalgae and MP, experiments with the single composition samples and mixture were performed on SO and 10-micron spherical PS. The used projection parameter provided by LDA is same with that of river water and 10-micron spherical PS, and the results with the single composition samples are shown in Figure 3A. D equals to 2.8 which means the discrimination is still significant, and SO is distributed on the left of the figure, while the 10-micron spherical PS is distributed on the right.
Figure 3. Polarized linear discrimination analysis (LDA) distribution of microalgae and 10-micron spherical polystyrene (PS). (A) Separate experiment of Scenedesmus Obliquus (SO) and PS. (B) Mixed experiment of SO and different concentrations of PS. (C) Quantitative graph of PS with increasing concentration. (D) Adding SO, Prymnesium Parvum (PP), Haematococcus Pluvialis (HP), Scrippsiella Trochoidea (ST), Phaeodactylum Tricornutum (PT), Chlorella Vulgaris (CV), and Cyanobacteria (CB) in sequence to 1 mg/L PS.
Then the suspension of the 10-micron spherical PS was added gradually to SO suspension for mixing experiments as different PS concentrations. The experimental results are shown in Figure 3B. And the similar bimodal structure with those in Figure 2B can be found, and each distribution is normalized to its left peak value. From Figure 3A, the left peak of the distributions in Figure 3B represents SO, while the right peak represents the 10-micron spherical PS. The value of the right peak increases with the increase of the 10-micron spherical PS concentration which is shown in Figure 3C. And also, one can find the linearity relationship between the PS concentration with the relative amount of the PS in the mixtures. These experiments demonstrate that the current method can detect PS (as a specific MP) in suspended mixtures of microalgae and MP.
To test the discrimination of the microalgae with PS, we conducted more experiments with seven different species of microalgae. And the cultured suspension of each species of the microalgae was successionally added into the 10-micron spherical PS suspension with a concentration of 1 mg/L, and the order of addition was SO, PP, HP, ST, PT, CV, and CB. Distributions of the experimental results are shown in Figure 3D, and they are also bimodal. According to Figures 3A,B, the left peak of each distribution represents microalgae, the right peak represents 10-micron spherical PS, and each distribution is normalized to its right peak value. From Figure 3D, one can find that the seven microalgal species are all significantly discriminated from PS. And the values of the left peaks increase with the continuous addition of microalgae. Note that the location of the left peaks shifts which is quite different from that in Figures 3A,B. Since the polarization properties of the seven species are inherently different among them, the polarization parameters of the mixed microalgal group become diverse and the distributions correspondingly change. But still the difference of them with PS is dominant in the mixtures. These results show that our detection method can detect MP in complex scenes including a variety of microalgae.
Due to the diverse types of MP in water, MP with different size, shape, and material are also investigated in this work. The 10-micron spherical PS and industrial PS plastic raw materials were tested separately. And still using the previous projection parameter, X, the experimental results are shown in Figure 4A and normalized to their own maxima. We found that the difference between 10-micron spherical PS and 300-mesh (around 45-micron) granular PS is significant, with D = 2.4. Because of the irregular shape of the 300-mesh PS, the distribution is relatively divergent while the curve is relatively wide. On the contrary, the distribution of 10-micron spherical PS is uniform while the curve is relatively narrow.
Figure 4. Normalized distributions of different MP. (A) 10-micron spherical polystyrene (PS) and 300-mesh PS. (B) 300-mesh Prymnesium Parvum (PP) and 300-mesh PS. (C) 300-mesh PP and 300-mesh Polyethylene Eerephthalate (PET).
Then the suspension of MP with different materials were measured separately. Figure 4B shows the normalized distributions of 300-mesh PS and 300-mesh PP, with the different projection parameter X, as Figure 4A. And then, we compare the normalized distributions of PP and PET with the same sizes, as shown in Figure 4C. This time, the projection parameter is recalculated using LDA since the old one cannot work, which implies that the projection parameter in Figure 4A may be exclusively effective for MP with PS material. From Figure 4C, the 300-mesh granular PP and PET have a good discrimination, with D = 1.6. It shows that our method has the ability to characterize the shape, particle size, material and other properties of MP.
Microplastic will weather in the natural environment due to the ultra-violet radiation, physical force, chemical erosion and biological fouling (Wei et al., 2021). To detect the diverse types of MP in water, we mixed 6 kinds of 300-mesh MP of PS, PE, PET, PP, PA, PVC together as the mixed MP. We measured the river water (RW1) and the mixed MP separately. And then we soaked the mixed MP in river water for three months to simulate the weathering of MP in the natural environment. Three months later, experiments were performed on the suspension consisting of river water (RW2) and the environmental MP (E-MP). The experimental results are shown in Figure 5A, and each distribution is normalized to its own maximum. It can be found that the distribution of the final suspension (RW2 + E-MP) has a bimodal structure. The position of the left peak is close to the original river water data (RW1), and the position of the right peak is close to the mixed MP data. Based on this, the left peak can be considered as the suspended particulate matter contained in the river water itself while the right peak represents MP.
Figure 5. (A) Distribution of Microplastic (MP) in the environment water, the mixed MP, river water (RW), and environmental MP (E-MP). (B) Distribution of PS before and after weathering, original polystyrene (PS), environmental PS (E-PS). (C) 300-mesh PS before weathering. (D) 300-mesh PS after weathering.
Note that there is difference between the river waters in Figure 5A due to the time interval of 3 months. But the difference between the river water and MP is dominant, and the changes of river waters are relatively trivial. This experiment shows that even if the composition of MP in natural water is complex and weathering may occur, our method can still effectively identify MP. After weathering in the natural environment, the composition of MP is complex and may be compounded with each other. The matching degree of the spectrum of Fourier infrared spectroscopy will be reduced, which lowers the detection accuracy (Shim et al., 2017), but our method is not affected by weathering.
More weathering experiments were conducted to investigate the polarization effects of the size changes of MP. And this time, we filtered the natural water by 0.45 μm filter membrane to remove the particulate matter, and then soaked 300-mesh PS into the water in reagent bottles, and illuminated them by the ultraviolet light. At the same time, we used a magnetic stirrer to stir the suspension with 150 rounds per minute to simulate weathering in the natural environment. Six months later, the environmental PS (E-PS) suspension was obtained, and the experiment of the weathered PS suspension was carried out. And the results are shown in Figure 5B and each distribution is normalized to its own maximum. Distributions of both the original PS and E-PS data show the bimodal structures, which indicates the multiple compositions in the samples. After 6 months of weathering, the left peak of the original PS decreases, but the right peak rises, which implies some physical properties of the MP (such as size, shape, etc.) have changed.
A scanning electron microscope was used to observe the PS before and after the weathering and the results are shown in Figures 5C,D, respectively. It is observed that in statistics, the particle size of the weathered MP is reduced and it seems that the physical breaking is majority in this kind of weathering (Duan et al., 2021). Based on this, it can be inferred that the left peak in Figure 5B represents the PS with large particle sizes, and the right peak represents the PS with small particle sizes. The particle size decreases after weathering corresponding to the decrease in the height of the left peak in Figure 5B and the increase in the height of the right peak in Figure 5B. It shows that our method can characterize the weathering process of MP or provide relevant information about the degree of weathering.
As a common type of MP, we also study the polarization changes during the weathering of PE. The original suspension of the 300-mesh PE particles was measured first. And then it has been soaked in water for six months. After that, experiments were performed on the weathered PE in aquatic environment (E-PE). The results are shown in Figure 6. The projection parameter distribution of the original PE is relatively narrower than those of E-PE, which means that the particle size, shape, and surface texture of the original PE are more uniform than those of E-PE. Note that the distribution of E-PE has 2 peaks. The peak near Xn = 0 basically overlap with the original PE, indicating that the physical form of some PE remains unchanged or changes little. The two peaks around Xn equal to 0.5 and -0.7 are obviously not the original PE, which implies that these two types of particles are newly generated by the weathering. Notably the type of particles whose distribution is peaked around Xn = 0.5 is the majority in E-PE, which means the original PE is weathering toward this type of particles. Recalling the weathering of PS in Figure 5, PS is weathering toward reducing the sizes. The projection parameters in Figures 5B, 6 are different, since the polarization properties of PS and PE are quite different, and in the other wards, polarization parameters have the exclusively discriminant ability to different types of MP.
The concentration of MPs in water is one of the most concerned information. To explore the ability of our method to retrieve the concentration of MP in water, we performed experiments on suspensions containing different concentrations of 10-micron spherical PS. For each concentration, we measured the samples for some time (larger than 10 min) which consisted of the succeeding time intervals, to evaluate the detected signals of MP per unit time. The so-called “unit time” is the fixed and minimal time interval in the data acquisition, and in this work, it’s 10 s. The relationship between the number of detected pulses per unit time and MP concentration was are got and shown in Figure 7.
Figure 7. The relationship between the concentration of 10-micron spherical polystyrene (PS) and the pulse number per unit time. (A) The pulse number per unit time when the concentration is in the range of 1–10 μg/L. (B) The pulse number per unit time when the concentration is in the range of 0.01–0.1 mg/L. (C) The pulse number per unit time when the concentration is in the range of 0.1–8 mg/L.
It can be found from Figure 7A that when the concentration is in the range of 1−10μg/L, the pulse number per unit time does not obviously change with the increase of the PS concentration. However, when the concentration is in the range of 0.01–8 mg/L, as shown in Figures 7B,C, the pulse number per unit time increases with the increase of the PS concentration. There is a linear relationship between the pulse number per unit time with the PS concentration. A linear regression algorithm is used to fit the data in Figures 7B,C. When the PS concentration is in the range of 0.01–0.1 mg/L, the determination coefficient is 0.87. When the concentration is in the range of 0.1–10 mg/L, the determination coefficient is larger than 0.99. This linear relationship between the pulse number per unit time with the PS concentration is the PS concentration calibration relationship, shown as the dashed line in Figures 7B,C.
Recalling that the proposed method in this work measures the individual suspended particles, each particle passing through the scattering volume will generate a corresponding scattering pulse. Therefore, the pulse number per unit time should increase with the particle concentration. However, the linearity indicates the more direct and deep relationship between them than the expectation, which implies the possibility to retrieve the PS concentration by measuring the pulse number per unit time. At the same time, from the error bar of Figure 7C, we can find that the relative error of each measurement is small, and the data measurement is relatively stable.
These results show that our method can effectively detect the concentration of MP. The pulse number per unit time has a linear relationship with the concentration of MP, and the lower limit of detection concentration is about 0.01 mg/L.
To further testify the ability of our method to detect the concentration of MP in natural water, we investigate the data in Figures 2B, 3B. Since LDA can give the optimal projection of the multiple dimensions data to one dimension, it is used to visually present the difference of the physical features between two samples in above results. However, SVM is more convenient to build the classifier to classify the specific particles from the suspensions. Firstly, the SVM processing is used to build a classifier to classify the river water and 10-micron spherical PS. The dataset is the experimental data of separate experiments of them. Seventy percentage of the dataset is used for the classifier training, and thirty percentage of the dataset is used for the classifier testing. The accuracy obtained by the test is 98.55%, which indicates the classifier is accurate and effective. Secondly, we use this classifier to classify the experimental data of the quantitative mixing experiment of river water and 10-micron spherical PS to get the PS number, and then we divide the PS number by time duration to obtain the PS number per unit time. The relationship between the PS number per unit time and PS concentration is shown in Figure 8A. It can be found that there is a linear relationship between them, and the determination coefficient is larger than 0.99.
Figure 8. The relationship between the polystyrene (PS) concentration and the pulse number per unit time in panel (A) the data of the mixtures of the river water and different concentrations of PS, and in panel (B) the data of the mixtures of Scenedesmus Obliquus (SO) and different concentrations of PS. (C) The PS concentration calibration relationship and the experimental data in panels (A,B).
We repeat the above operation for the experimental data of SO and spherical PS, the accuracy of the testing is 98.74%, and finally the new SVM classifier works excellently. The PS pulse number per unit time and the PS concentration are shown in Figure 8B, which also has a linear relationship between them and the determination coefficient is larger than 0.99. It showed that the proposed method can not only detect the presence of PS but also the concentration of PS in the suspension with complex compositions. However, we note that the linear relationship in Figures 8A,B are slightly different, and both of them are different from the PS concentration calibration relationship. It is necessary to investigate the generalization of the linear relationship between the PS number per unit time and the PS concentration. So, we merge the data of Figures 8A,B together and draw them with the PS concentration calibration relationship in Figure 8C. It can be found that the PS number per unit time vs. the PS concentration, in two experimental data of the mixed samples are distributed near the PS concentration calibration relationship. The determination coefficient is 0.89 for the data of mixtures of river water and PS, and the determination coefficient is 0.98 for the data of mixtures of microalgae and PS. Figure 8C demonstrates that the PS concentration calibration relationship has good generalization in predicting the PS concentration in suspensions with the complex compositions.
Since PP and PET are two of the most reported MP in related literatures (Li et al., 2019), we explore the ability of the proposed method to identify them from the mixture of multiple types of MP. We firstly adjust the polarization state of the incident light to the right-handed circular polarization state. And then we do experiments on 6 types of 300-mesh MP (i.e., PS, PET, PP, PE, PVC, PA). Comparing the measured polarization parameters of PP with the other 5 MP by LDA, the result is shown in Figure 9A. D = 1.38, which is a good discrimination. If we transform the incident polarization state to the vertically linear polarization. The experimental result of PET and the other five types of MP is shown in Figure 9B. D = 1.01, which is also a good discrimination. Note that there are some fluctuations in the distributions in Figure 9. Considering the number of the measured particles are at least 3,000 which is enough for the analysis, then these fluctuations may originate from the multiple compositions in the mixed MP samples.
Figure 9. (A) Prymnesium Parvum (PP) and other five types of microplastics (MPs). (B) Polyethylene Eerephthalate (PET) and other five types of MPs.
Figure 9 tells that the polarization parameters can identify PP and PET from the set of multiple types of MP. However, the incident polarization state changes for the identification of the different MP. Note that the measured polarization parameters are originated from the Stokes vector, and only include the partial polarization properties of the particles. This means that under the illumination of the incident light with the different polarization states, we measure the different parts of the polarization properties, and some of them can be effective to discriminate PP or PET from the multiple types of MP. This makes it possible that we just need to illuminate the sample with the specified polarized light and measure the polarization parameters, and then we can identify the concerned type of MP.
Polarization theory says that the scattering of the individual particle changes the polarization state of the incident light, Sin, to the polarization state of the scattered light Sout, which carries the physical polarization property of the particle. Traditionally, the relationship between the polarization states of the incident light and the scattered light is Mueller matrix, M, which is a 4 × 4 matrix to describe the polarization property of the particle, as shown in Eqs. 5, 6.
In this work, since the incident light is 135° linearly polarized, Sin = [1,0,−1,0]T. Then from Eqs. 5, 6, we get,
So, the polarization parameters, q, u, v calculated from Eqs. 1, 2, and their derivatives are determined by the element differences of the first and third columns of Mueller matrix.
Basically, LDA gives the optimal linear combination of q, u, v, that is, X = a*q + b*u + c*v, under which the distributions of the two samples differ each other most. The coefficients, a, b, c, are just the weight of q, u, v, and are also the weight of the elements of Sout in Eq. 7. In principle, the different X in Figures 2–6 are selected to enhance the difference between the two samples and suppress the similar parts by adjusting a, b, c.
Alternatively, we can also find the way to discriminate the two samples by changing the incident polarization Sin and fixing a, b, c. In this case, we require PSG can generate the wanted polarization state of light, which needs the sophisticated design of PSG but has the advantage of the fixed X. According to Eq. 6, this way is basically different from the above one and it optimally combines the different elements of Mueller matrix to select out X.
Here we know that the difference between the samples is originated from their Mueller matrix which is fundamentally determined by the physical polarization properties, such as size, shape, structures, materials, etc. Previous researchers have reported some findings about the Mueller matrix elements and their combination which can effectively characterize the physical properties of the particles. For example, Volten et al. (1998) have shown m12/m11 is sensitive to the material and gas vacuole structure. Van De Merwe et al. (2004) find m34/m11 can determine a large size parameter range for spherical or randomly oriented rod-shaped particles. The m22/m11 is always related to the sphericity of the particles (Ossikovski and Arteaga, 2019). Svensen et al. (2011) have found that the combined elements, m12m11, m33m44 have noticeable differences between different algae species, because of their different inner structures and refractive indices. Li et al. (2021) recently have reported the combined elements of Mueller matrix are able to discriminate the particles with the different materials and microstructures.
These results and analysis encourage us that if we measure the Mueller matrix of the polarization properties of MP, we can much easily to achieve the discrimination of the different types of MP. Generally, Mueller matrix polarimetry needs multiple measurements with different incident polarization states. For the suspended MP particles in water, they are instantaneously changing and passing through the scattering volume in very short time interval. So, it’s still challenging to the community to measure the Mueller matrix of the suspended MP but it deserves to be considered in future.
In this work, we firstly use the 10-micro spherical PS to show the excellent discrimination between it with the river water and the microalgae by using our method. And then we present the ability of the method to discriminate the MPs (including PS) with different size and materials, and to characterize the MP changes originated from the weathering in the environments. Also, during the concentration calibration, we use the PS samples. However, the PS particles is just used as the standard MP to show the ability and feasibility of the proposed method to in-situ detect them in water. The potential of the method should not be limited to PS particles. It should be noted that by using the polarization parameters, the mixed MP can effectively be discriminated from the river water before and after the environmental weathering, and especially the compositions of PE sample can be also characterized during the weathering. Indeed, it is challenging to identify all types of MP in water by the current method, but the effort and expectation are still deserved to pay for its realization in future by some sophisticated methods or Mueller matrix polarimetry.
An in-situ method based on polarized light scattering is proposed to detect the microplastics (MP) in water. The scattered polarization parameters of individual particles are in-situ measured in aquatic suspensions. The illumination polarization state of the incident light can be adjusted to achieve the best discrimination of the different MPs. The polarization parameters of microalgae, natural water bodies and 10-micron spherical PS have a significant discrimination. MP in the mixture of a variety of microalgae and natural water samples therefor can be effectively identified. Moreover, the present method could be used in distinguishing MP samples with different size, shape and material. For example, 300-mesh granular PS obtained by grinding has a remarkable discrimination from the 10-micron spherical PS; and the 300-mesh granular PP has a good discrimination from PET. It is interesting that the weathering of MP is observed and the polarization parameters can still detect MP from the river water after several months’ soaking. The different compositions of the weathered MP can be characterized by the polarization parameters which is confirmed by PS and PP samples. Finally, we successfully identify the PP and PET from the multiple types of MP, which is encouraging to identify the specific MP with well-designed illumination polarization state of light. The concentration is calibrated by the 10-micron spherical PS samples. The low limit of the detected concentration can lower to 0.01 mg/L. The linear relationship of the concentration with the pulse number per unit time is well-generalized and works effectively for the former experiments. These results demonstrate the capability of the proposed method to in-situ detect the MP in water, which promises the application in water quality sensing and monitoring.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
RL conceived the project aim. TL, SY, and RL designed the methodology. YH collected and obtained the samples. TL and SY carried out the sample processing work and the analysis. TL led the manuscript writing. XZ, RL, and HM revised the analyses and manuscript. All the authors contributed critically to the drafts and gave final approval for publication.
This work was supported by the Key-Area Research and Development Program of Guangdong Province (2020B1111040001), the National Key Project of Research and Development Program of China (2018YFC1406600), the National Natural Science Foundation of China (NSFC) (41527901 and 61975088), and the Science and Technology Project of Shenzhen Grant (JCYJ20160818143050110).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
We thank the staff at the Guangdong Research Center of Polarization Imaging and Measurement Engineering Technology as well as Yihan Shi, Jincai Dai, and Yong Wang for excellent assistance during the work.
Amaral-Zettler, L. A., Zettler, E. R., and Mincer, T. J. (2020). Ecology of the plastisphere. Nat. Rev. Microbiol. 18, 139–151. doi: 10.1038/s41579-019-0308-0
Auta, H. S., Emenike, C. U., and Fauziah, S. H. (2017). Distribution and importance of microplastics in the marine environment: a review of the sources, fate, effects, and potential solutions. Environ. Int. 102, 165–176. doi: 10.1016/j.envint.2017.02.013
Boss, E., and Pegau, W. S. (2001). Relationship of light scattering at an angle in the backward direction to the backscattering coefficient. Appl. Opt. 40, 5503–5507. doi: 10.1364/AO.40.005503
Chami, M. (2007). Importance of the polarization in the retrieval of oceanic constituents from the remote sensing reflectance. J. Geophys. Res. 112:C05026. doi: 10.1029/2006JC003843
Duan, J., Bolan, N., Li, Y., Ding, S., Atugoda, T., Vithanage, M., et al. (2021). Weathering of microplastics and interaction with other coexisting constituents in terrestrial and aquatic environments. Water Res. 196:117011. doi: 10.1016/j.watres.2021.117011
Eriksen, M., Mason, S., Wilson, S., Box, C., Zellers, A., Edwards, W., et al. (2013). Microplastic pollution in the surface waters of the Laurentian Great Lakes. Mar. Pollut. Bull. 77, 177–182. doi: 10.1016/j.marpolbul.2013.10.007
Ghosh, N., and Vitkin, I. A. (2011). Tissue polarimetry: concepts, challenges, applications, and outlook. J. Biomed. Opt. 16:110801. doi: 10.1117/1.3652896
Golwala, H., Zhang, X., Iskander, S. M., and Smith, A. L. (2021). Solid waste: an overlooked source of microplastics to the environment. Sci. Total Environ. 769, 144581. doi: 10.1016/j.scitotenv.2020.144581
Kappler, A., Fischer, D., Oberbeckmann, S., Schernewski, G., Labrenz, M., Eichhorn, K. J., et al. (2016). Analysis of environmental microplastics by vibrational microspectroscopy: FTIR, Raman or both? Anal. Bioanal. Chem. 408, 8377–8391. doi: 10.1007/s00216-016-9956-3
Lenz, R., Enders, K., Stedmon, C. A., Mackenzie, D. M. A., and Nielsen, T. G. (2015). A critical assessment of visual identification of marine microplastic using Raman spectroscopy for analysis improvement. Mar. Pollut. Bull. 100, 82–91. doi: 10.1016/j.marpolbul.2015.09.026
Li, J., Lusher, A. L., Rotchell, J. M., Deudero, S., Turra, A. I, Brate, L. N., et al. (2019). Using mussel as a global bioindicator of coastal microplastic pollution. Environ. Pollut. 244, 522–533. doi: 10.1016/j.envpol.2018.10.032
Li, J. J., Wang, H. J., Liao, R., Wang, Y., Liu, Z. D., Zhuo, Z. P., et al. (2021). Statistical Mueller matrix driven discrimination of suspended particles. Opt. Lett. 46, 3645–3648. doi: 10.1364/OL.433870
Li, M., and Yuan, B. (2005). 2D-LDA: a statistical linear discriminant analysis for image matrix. Pattern Recognit. Lett. 26, 527–532. doi: 10.1016/j.patrec.2004.09.007
Liao, R., Li, Q., and Mao, X. (2019). “A prototype for detection of particles in sea water by using polarize-light scattering,” in Proccedings of the OCEANS 2019–Marseille, (Marseill), 1–4. doi: 10.1109/OCEANSE.2019.8867414
Mai, L., Bao, L. J., Shi, L., Wong, C. S., and Zeng, E. Y. (2018). A review of methods for measuring microplastics in aquatic environments. Environ. Sci. Pollut. Res. Int. 25, 11319–11332. doi: 10.1007/s11356-018-1692-0
Ossikovski, R., and Arteaga, O. (2019). Complete Mueller matrix from a partial polarimetry experiment: the nine-element case. J. Opt. Soc. Am.Opt. Image Sci. Vision 36, 403–415. doi: 10.1364/JOSAA.36.000403
Sadri, S. S., and Thompson, R. C. (2014). On the quantity and composition of floating plastic debris entering and leaving the Tamar Estuary. South. Engl. Mar. Pollut. Bull. 81, 55–60. doi: 10.1016/j.marpolbul.2014.02.020
Saeed, T., Al-Jandal, N., Al-Mutairi, A., and Taqi, H. (2020). Microplastics in Kuwait marine environment: results of first survey. Mar. Pollut. Bull. 152:110880. doi: 10.1016/j.marpolbul.2019.110880
Shan, J., Zhao, J., Zhang, Y., Liu, L., Wu, F., and Wang, X. (2019). Simple and rapid detection of microplastics in seawater using hyperspectral imaging technology. Anal. Chim. Acta 1050, 161–168. doi: 10.1016/j.aca.2018.11.008
Shim, W. J., Hong, S. H., and Eo, S. E. (2017). Identification methods in microplastic analysis: a review. Anal. Methods 9, 1384–1391. doi: 10.1039/C6AY02558G
Song, Y. K., Hong, S. H., Jang, M., Han, G. M., Rani, M., Lee, J., et al. (2015). A comparison of microscopic and spectroscopic identification methods for analysis of microplastics in environmental samples. Mar. Pollut. Bull. 93, 202–209. doi: 10.1016/j.marpolbul.2015.01.015
Sun, M., He, H., Zeng, N., Du, E., Guo, Y., Liu, S., et al. (2014). Characterizing the microstructures of biological tissues using Mueller matrix and transformed polarization parameters. Biomed. Opt. Express 5, 4223–4234. doi: 10.1364/BOE.5.004223
Svensen, O., Stamnes, J. J., Kildemo, M., Aas, L. M. S., Erga, S. R., and Frette, O. (2011). Mueller matrix measurements of algae with different shape and size distributions. Appl. Opt. 50, 5149–5157. doi: 10.1364/AO.50.005149
Van De Merwe, W. P., Czégé, J., Milham, M. E., and Bronk, B. V. (2004). Rapid optically based measurements of diameter and length for spherical or rod-shaped bacteria in vivo. Appl. Opt. 43, 5295–5302. doi: 10.1364/AO.43.005295
Vianello, A., Boldrin, A., Guerriero, P., Moschino, V., Rella, R., Sturaro, A., et al. (2013). Microplastic particles in sediments of Lagoon of Venice, Italy: first observations on occurrence, spatial patterns and identification. Estuar. Coast. Shelf Sci. 130, 54–61. doi: 10.1016/j.ecss.2013.03.022
Volten, H., De Haan, J., Hovenier, J. W., Schreurs, R., Vassen, W., Dekker, A. G., et al. (1998). Laboratory measurements of angular distributions of light scattered by phytoplankton and silt. Limnol. Oceanogr. 43, 1180–1197. doi: 10.4319/lo.1998.43.6.1180
Wang, Y., Liao, R., Dai, J., Liu, Z., Xiong, Z., Zhang, T., et al. (2018). Differentiation of suspended particles by polarized light scattering at 120 degrees. Opt. Express 26, 22419–22431. doi: 10.1364/OE.26.022419
Wei, X. F., Bohlen, M., Lindblad, C., Hedenqvist, M., and Hakonen, A. (2021). Microplastics generated from a biodegradable plastic in freshwater and seawater. Water Res. 198:117123. doi: 10.1016/j.watres.2021.117123
Yin, K., Wang, D., Zhao, H., Wang, Y., Guo, M., Liu, Y., et al. (2021). Microplastics pollution and risk assessment in water bodies of two nature reserves in Jilin Province: correlation analysis with the degree of human activity. Sci. Total Environ. 799:149390. doi: 10.1016/j.scitotenv.2021.149390
Yu, Q., Hu, X., Yang, B., Zhang, G., Wang, J., and Ling, W. (2020). Distribution, abundance and risks of microplastics in the environment. Chemosphere 249:126059. doi: 10.1016/j.chemosphere.2020.126059
Yu, S., Dai, J., Liao, R., Chen, L., Zhong, W., Wang, H., et al. (2021). Probing the nanoplastics adsorbed by microalgae in water using polarized light scattering. Optik 231:166407. doi: 10.1016/j.ijleo.2021.166407
Keywords: in-situ detection, microplastics, polarization, scattering light, classification, machine learning
Citation: Liu T, Yu S, Zhu X, Liao R, Zhuo Z, He Y and Ma H (2021) In-situ Detection Method for Microplastics in Water by Polarized Light Scattering. Front. Mar. Sci. 8:739683. doi: 10.3389/fmars.2021.739683
Received: 11 July 2021; Accepted: 21 September 2021;
Published: 14 October 2021.
Edited by:
Youji Wang, Shanghai Ocean University, ChinaCopyright © 2021 Liu, Yu, Zhu, Liao, Zhuo, He and Ma. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ran Liao, bGlhby5yYW5Ac3oudHNpbmdodWEuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.