
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mar. Sci. , 12 October 2021
Sec. Marine Pollution
Volume 8 - 2021 | https://doi.org/10.3389/fmars.2021.729954
This article is part of the Research Topic Marine Pollution - Emerging Issues and Challenges View all 13 articles
 Sang-Soo Baek1
Sang-Soo Baek1 JongCheol Pyo2
JongCheol Pyo2 Yong Sung Kwon3
Yong Sung Kwon3 Seong-Jun Chun4
Seong-Jun Chun4 Seung Ho Baek5
Seung Ho Baek5 Chi-Yong Ahn6
Chi-Yong Ahn6 Hee-Mock Oh6
Hee-Mock Oh6 Young Ok Kim7*
Young Ok Kim7* Kyung Hwa Cho1*
Kyung Hwa Cho1*In several countries, the public health and fishery industries have suffered from harmful algal blooms (HABs) that have escalated to become a global issue. Though computational modeling offers an effective means to understand and mitigate the adverse effects of HABs, it is challenging to design models that adequately reflect the complexity of HAB dynamics. This paper presents a method involving the application of deep learning to an ocean model for simulating blooms of Alexandrium catenella. The classification and regression convolutional neural network (CNN) models are used for simulating the blooms. The classification CNN determines the bloom initiation while the regression CNN estimates the bloom density. GoogleNet and Resnet 101 are identified as the best structures for the classification and regression CNNs, respectively. The corresponding accuracy and root means square error values are determined as 96.8% and 1.20 [log(cells L–1)], respectively. The results obtained in this study reveal the simulated distribution to follow the Alexandrium catenella bloom. Moreover, Grad-CAM identifies that the salinity and temperature contributed to the initiation of the bloom whereas NH4-N influenced the growth of the bloom.
The occurrence, period, and frequency of harmful algal blooms (HABs) have increased in recent years, thereby posing a serious threat to the aquatic ecosystem (Weiher and Sen, 2006; Gobler et al., 2017). The United States spends $22 million annually on public-health damages and suffers an annual loss of $75 million due to HABs (Hoagland et al., 2002; Weiher and Sen, 2006; Anderson et al., 2012). In South Korea, the economic loss incurred due to HAB over the past three decades was $121 million (Park et al., 2013). China and Japan have similarly incurred enormous economic losses in northeast Asia (Wang and Wu, 2009; Itakura and Imai, 2014). These damages can be attributed to the changes in the aquatic environmental conditions due to climate change and/or nutrient enrichment caused by such human activities as agriculture, industrialization, tourism, and urbanization (Heisler et al., 2008; Gobler et al., 2017). Accordingly, HABs have escalated to become a global concern. Anthropogenic global warming is visible in the northward expansion of the warm pool to the northwestern Pacific. The Korean Peninsula, which is closed on the marginal sea of the northwestern Pacific, has been reported as a vulnerable region in the new normal climate. Accordingly, there exists the threat of HAB expansion into the Korean coastal waters owing to changes in HAB dynamics due to global warming. Outbreaks of PSP in Korean coastal waters have been perceived as spring events since the first record in 1986 (Chang et al., 1987). Recurrent PSP events in the spring of Korea have been linked to the spring blooms of Alexandrium catenella (A. catenella) (previously reported as A. tamarense). The spring blooms of the toxic dinoflagellate population are regular in the coastal waters of marginal sea connected to the northwestern Pacific (Han et al., 1992; Ishikawa et al., 2014).
Prior research concerning HABs has mainly focused on increasing awareness and improving monitoring techniques (Kim et al., 2002; Wang et al., 2008). Since the 1970s, a significant amount of infrastructure, labor, and time has been required for HAB field monitoring. However, the extent of this requirement has differed based on the properties of HAB. Moreover, given the need for HAB monitoring and relevant analyses, computational modeling has been considered to be an alternative approach to understand and mitigate the effects of HABs (Yoshioka and Yaegashi, 2018; Pyo et al., 2019). Pinto et al. (2016) simulated the abundance of HAB species using a particle-tracking model. Likewise, He et al. (2008) developed a mathematical model for simulating A. catenella (former A. fundyense) bloom in the western Gulf of Maine. Although these efforts have contributed toward the improvement of the simulation performance of algal blooms, overcoming the limitations of these models remains a major challenge owing to the complexity of HAB dynamics that are dependent on the multiple effects from physical, chemical, and biological systems (McGillicuddy, 2010).
A data-driven deep-learning model can push the frontiers of the aforementioned models further. Deep learning has been proposed as a promising technique owing to its big-data handling capabilities (Szegedy et al., 2015). Deep learning has been adopted in several fields, including speech recognition, image analysis, and biological mechanisms (Chen and Manning, 2014; Young et al., 2018). Shen et al. (2019) estimated cyanobacteria blooms in river waters using a support vector machine. Additionally, Pyo et al. (2020) simulated algal blooms in freshwater systems using a convolutional neural network (CNN). However, these studies focused on HABs in inland waters, which further access is necessary to undergo more dynamic and complex hydrological and ecological cycles in seawater. Recently, Baek et al. (2021) suggested a method for identifying factors that influence A. catenella bloom using decision tree and hydrodynamic models. They revealed that water temperature and nutrients affected the growth of A. catenella. However, this approach is not suitable for continuous A. catenella bloom simulation because it can only generate four bloom levels based on cell density.
This study evaluates the applicability of deep learning for HAB simulation with the ocean model to generate the temporal–spatial distribution of physical, chemical, and biological variables. Using these variables and CNNs, we simulated the temporal distribution of A. catenella, a notorious dinoflagellate species causing paralytic shellfish poisoning (PSP). Convolutional neural network-based deep learning models can extract the features of multi-dimensional data using convolutional filters (Deng et al., 2009). Additionally, using gradient-weighted class activation mapping (Grad-CAM), we identified the factors that influence the simulation of A. catenella (Selvaraju et al., 2017).
We conducted spatial–temporal monitoring to investigate the occurrence of A. catenella. The monitoring site is located on the southeastern coast near Namhae, Geoje Island, and Busan, South Korea (Figure 1), opened toward off sea, causing fresh and oceanic water intrusion (Kang et al., 2012). In particular, the eastern coast of Geoje Island has frequently occurring PSP initiation (National Fisheries Research and Development Institute, 2020). PSP outbreaks provoked by A. catenella bloom in our study area have been reported (Chang et al., 1987; Kim et al., 2015). Water surface elevation, wind, and wind velocity data were measured by the Korea Ocean Observing and Forecasting System and used to set up the model. Two observations at stations 1 and 2 were used to calibrate the water level, temperature, and salinity. Another three observations at stations 3, 4, and 5 were used to calibrate NH4-N and PO4-P (Figure 1).
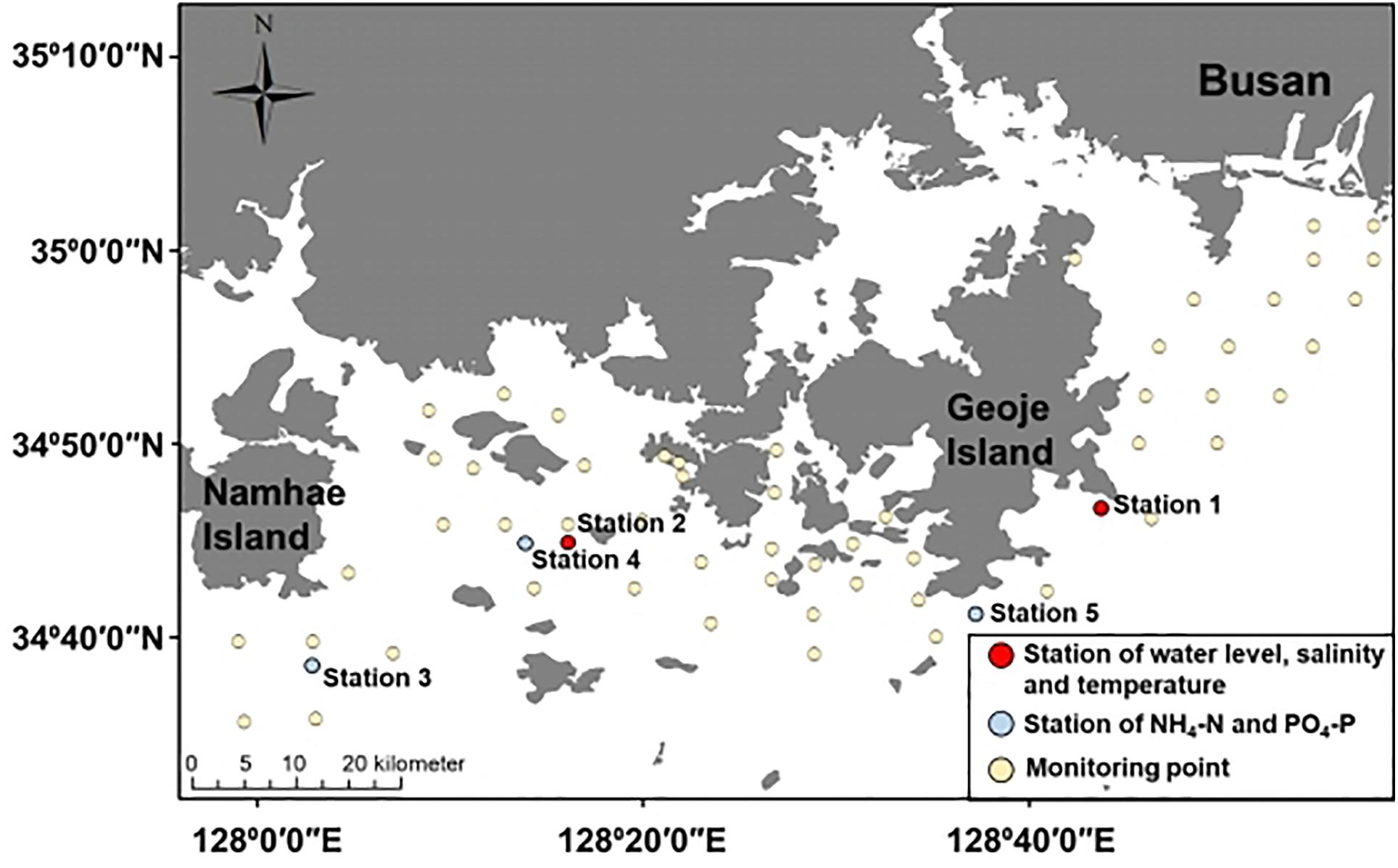
Figure 1. Study site—red dots indicate the observation station for water elevation, salinity, and temperature; blue dots indicate the observation point for NH4-N and PO4-P; yellow circles indicates the monitoring point for A. catenella.
One-thousand one-hundred and seventy-five samples were collected from the water surface at the sampling sites, which had water depths of 12 to 59 m. The monitoring period was from January 2017 to December 2019. Water samples were acquired with a Van Dorn bottle and fixed with Lugol solution (final conc., 2%) from 9:00 AM to 4:00 PM. The fixed seawater was concentrated to 5–50 mL aliquots by overnight sedimentation. Alexandrium catenella cells were enumerated using a Sedgwick–Rafter counting slide at a 200× magnification with a light microscope (Zeiss Axioscope 2). To identify the species based on morphological and molecular analyses, the cells were processed as described by Kim et al. (2020). Cysts of A. catenella were isolated from sediment samples collected using a core sampler and incubated at bottom temperatures on the sampling dates. The germination ratio of the cysts was estimated by the percentage of cysts germinating within one month. Growth experiments of A. catenella were conducted under several temperature and salinity conditions, reflecting the sampling site environments. The measurements of germination ratio and growth rate were described in detail by Kim et al. (2020).
The input data in this study consisted of two parts: (1) ocean physical data (e.g., water velocity, water temperature, water elevation, and retention time) and chemical data (e.g., salinity, PO4-P, and NH4-N) and (2) ocean biological data [e.g., germination ratio, growth rate, and operational taxonomic unit (OTU)]. This study applied the environmental fluid dynamics code (EFDC) model, adopted for simulating ocean and coastal waters (Dai et al., 2011; Du and Shen, 2016) to generate the ocean physical and chemical data. The EFDC model is a fluid simulation model that includes three-dimensional flow and biochemical transport in the ocean, estuaries, and lakes. EFDC can solve free surface, vertical hydrostatic, and turbulent equations for fluids with different densities. The governing equation was derived using the vertical hydrostatic boundary with turbulent equations and consists of the momentum [Eq. (S1, S2)], vertical hydrostatic pressure (Eq. S3), and continuity equations [Eq. (S4, S5)] (Jeong et al., 2010). The ocean physical and chemical data included the temporal and spatial distributions of water velocity, water temperature, water elevation, retention time, salinity, PO4-P, and NH4-N. These data have been verified as variables that influence the life cycle of A. catenella (Itakura and Yamaguchi, 2001; Kim and Yoo, 2007; Armi et al., 2011; Kim et al., 2020). The ocean physical and chemical distributions were calculated by the EFDC model. Ocean biological data included the temporal and spatial distributions of the germination ratio of A. catenella cysts, growth rate of vegetative cells of the species, and OTU of bacteria. The cyst germination and growth rates are critical elements in recurrent outbreaks of A. catenella blooms in situ, although dormant populations are significantly affected by environmental variables. Hence, we adopted these rates as the input data to simulate A. catenella. The data pertaining to cyst germination and growth rate were obtained by Kim et al. (2020). The microbial community data in this area, including the OTU data, were extracted from the previous study (Cui et al., 2020). operational taxonomic units were analyzed at a distance of 0.01 using the mothur v1.39.3 pipeline with SILVA database, release 132 (Schloss et al., 2009; Kozich et al., 2013). Three representative OTUs (OTU1, OTU2, and OTU3), which were identified as A. catenella-related OTUs based on ecological network analysis in the previous study (Cui et al., 2020), were selected for further analysis in this study. Taxonomically, OTU1, OTU2, and OTU3 were assigned to genera Fluviicola (family Crocinitomicaceae), Ascidiaceihabitans (family Rhodobacteraceae), Candidatus Actinomarina (family Candidatus Actinomarinaceae), respectively. Supplementary Figure 1 presents the process used to generate the temporal and spatial distribution of biological data. A linear model was adopted to generate the variation of biological data by changing the environmental variables. The linear regressions of the germination ratio and growth rate were calculated using temperature and salinity from in vivo experiments (Supplementary Figure 1A), whereas that of the OTU distribution was generated using the temperature, salinity, PO4-P, and NH4-N values from monitoring (Supplementary Figure 1B). A linear regression model explains the relationship between one response variable and multiple explanatory variables (Montgomery et al., 2021); therefore, these linear models used the simulated water temperature, salinity, PO4-P, and NH4-N from EFDC to determine the temporal and spatial distribution of biological data (Supplementary Figure 1C). The simulation period was from January 2017 to December 2019. These ocean physical, chemical, and biological data were validated using observational data. The EFDC grid was a Cartesian grid with a cell size of 200 m × 400 m. Observations of wind direction, velocity and water surface elevation were used to set up the EFDC model. More details of the experiments on germination ratio, growth rate, and OTU are presented in the Supplementary Information.
Figure 2 shows the two-step process of generating input data to apply CNN for simulating the bloom of A. catenella: (1) extracting the spatial–temporal distribution of the physical, chemical, and biological information at the study site (Figures 2A,B) and (2) converting the input data to two-dimensional data (Figure 2C). These physical, chemical, and biological data have three dimensions, m × m × (n + 1), and the simulation point of A. catenella is located in the center. Here, m is the size (i.e., height × width) of the input window that includes the simulation point, and n is the lookback, which indicates the number of time steps included based on the current simulation time. For example, when m = 3 and n = 5, the data size is 3 × 3 × (5 + 1). Because the CNN approach was developed focusing on two-dimensional data (length × height) or RGB data (length × height × 3), we converted these inputs into two-dimensional data before applying the CNN (Shin et al., 2016; Koundinya et al., 2018).
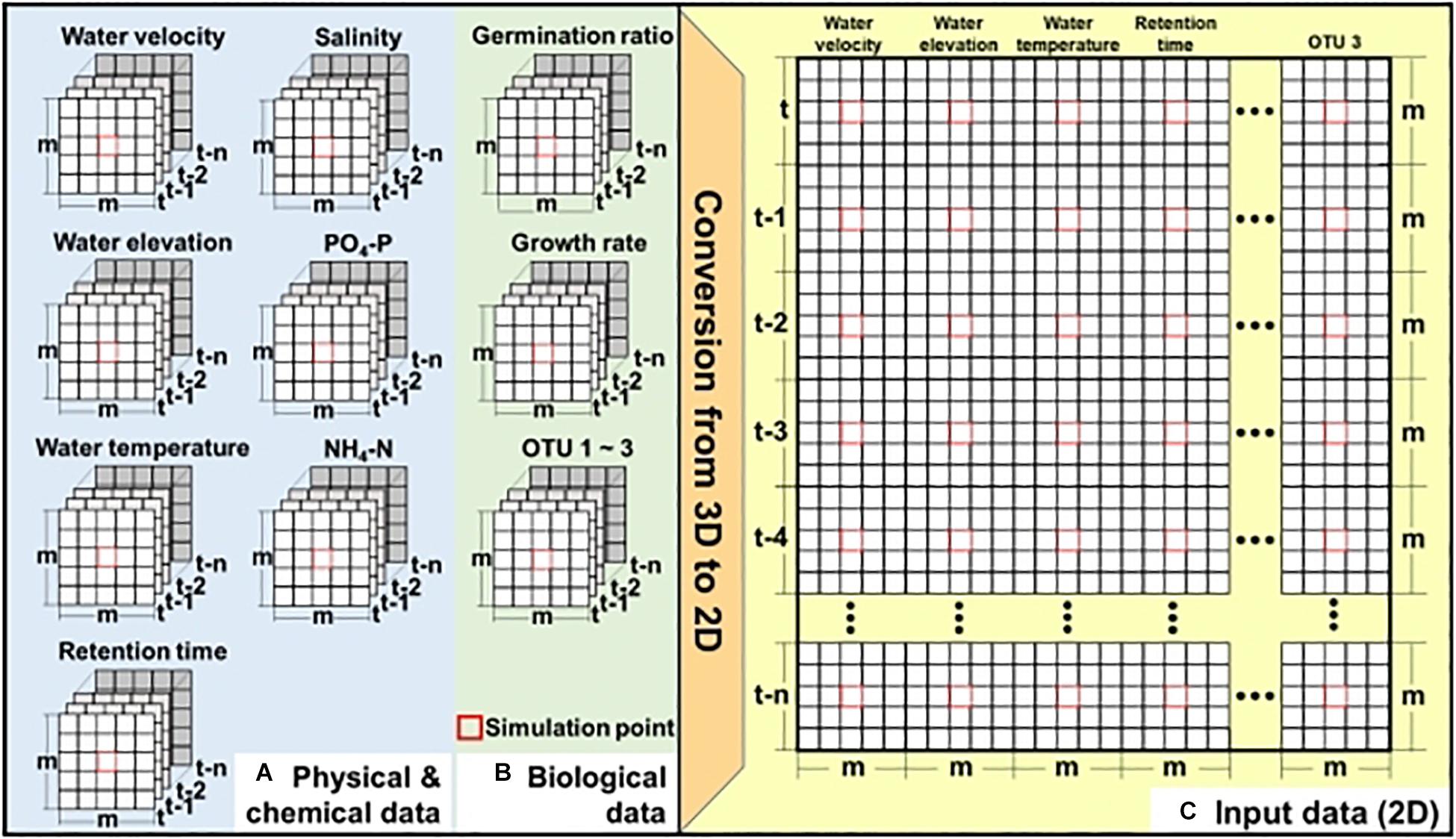
Figure 2. Preparation of input data for CNN—(A) physical and chemical data obtained using EFDC, (B) biological data obtained using EFDC and linear equation, and (C) two-dimensional input data. Here, m denotes the input window (i.e., height × width), including the simulation point located at the center of input window while n denotes the lookback size. Red boxes indicate the simulation point.
The simulation layout of A. catenella is presented in Figure 3. The simulation comprises of the following three steps: (1) optimizing the input and CNN structures, (2) simulating the bloom of A. catenella based on the optimal input and CNN structures, and (3) identifying A. catenella bloom factors based on Grad-CAM. Because these CNN structures (e.g., Resnet, GoogLeNet, and Inception) were developed using data of size 299 × 299, the input data had to be converted (Szegedy et al., 2016; Akiba et al., 2017). Subsequently, the converted data are fed to the classification and regression CNN models; the classification CNN model decided the initiation of A. catenella, while the regression CNN model generated the density after A. catenella was initiated. The initiation and the density indicated the occurrence and the number of A. catenella cells, respectively. The use of two CNNs with different roles can prevent bias in model training, as most of our monitoring data were zero, indicating that A. catenella did not occur. In addition, we optimized the input window (m), lookback (n), and CNN structures (Figure 3A) to generate the spatial–temporal distribution of A. catenella (Figure 3B). Using the optimal parameter values and CNN structures, we analyzed the performance of A. catenella forecasting with increasing forecast lead times (days) of up to seven days. Model training was performed using Intel ® Xeon CPU E-52687W v4 @ 3.00 GHz, 128 GB RAM, and NVIDIA GTX 1080 Ti. CNN was implemented with the machine and deep learning toolboxes in MATLAB. Accuracy was used for evaluating the classification CNN model, while RMSE and R2 were used for the regression CNN model. Relevant explanations can be found in the Supplementary Information.
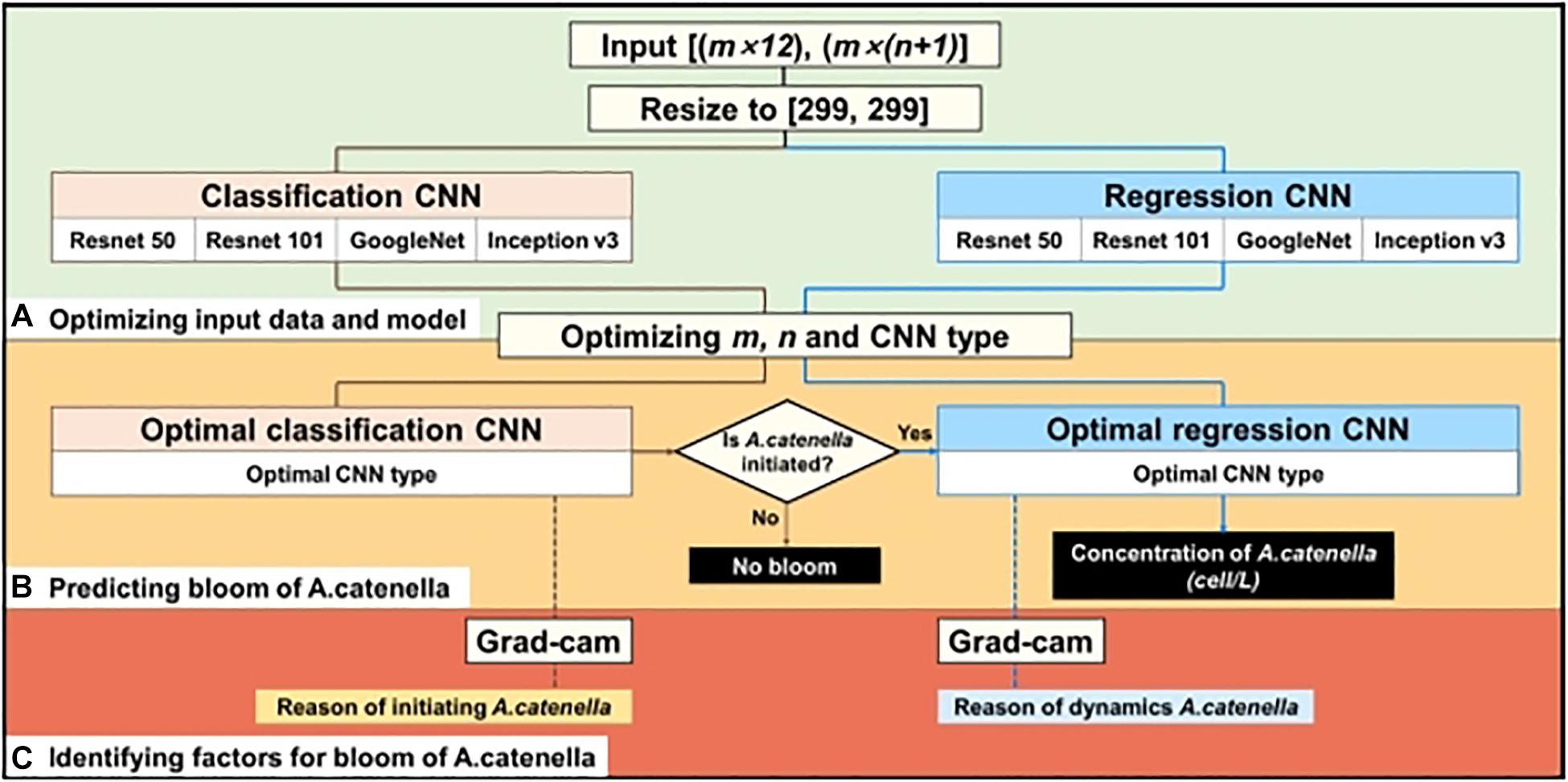
Figure 3. Procedure of simulating A. catenella using CNN—(A) optimizing input data and CNN structures, (B) predicting bloom of A. catenella based on optimal input and structures, and (C) identifying factors for bloom of A. catenella using Grad-CAM. Brown and blue lines indicate the processes of classification and regression CNN models, respectively.
Convolutional Neural Network (CNN) is a popular deep learning model that extracts data features using convolving filters (Deng et al., 2009). A typical CNN architecture consists of convolutional, pooling, ReLU, batch normalization, concatenation, normalized, and fully connected layers (LeCun et al., 2015). Each layer has a specialized role in the architecture: convolutional and pooling layers are used for feature extraction. ReLU and normalization layers are used for a linear and normalization calculation, respectively (LeCun et al., 2015). These layers can be combined to enhance model performance (Szegedy et al., 2016; Khan et al., 2019). Details concerning the CNN layers can be found in the Supplementary Materials document. Supplementary Figure 2 shows the CNN structures employed in this study. GoogleNet and Inception v3 models adopt parallel CNN layers (Szegedy et al., 2016). ResNet 50 and ResNet 101 have skip connections, i.e., the information of the output layer is transferred into the next layer, and into the earlier layer (Szegedy et al., 2016). This structure can increase model performance by reducing overfitting and vanishing gradient problems (He et al., 2016a). In our study, the softmax and mean squared error (MSE) (see Supplementary Information for more details) were used as the loss function for classification and regression CNN, respectively. The loss functions were applied for calculating the error between simulation and observation during model training. For model training, the CNN used hyperparameters, including epoch number, batch size, and learning rate (Loussaief and Abdelkrim, 2018). Epoch is the number of times the learning worked in the entire dataset, whereas batch size is the number of samples used for training (Robert, 2014). The learning rate controls the step size at each iteration to minimize the loss function (Robert, 2014). The CNN comprised 500 epochs with a mini-batch size of 32; the applied learning rates equaled 0.001 and 0.0001 for the first 200 and remaining 300 epochs, respectively. Each epoch generated a corresponding model, and the final model was selected to produce the lowest validation accuracy and MSE. Our study adopted random sampling to divide A. catenella observations into training and validation sets. A uniform distribution was used for the random sampling. Previous studies have also used random sampling with a uniform distribution to divide the data into training and validation sets (Brion et al., 2002; Caruana and Niculescu-Mizil, 2006).
The deep-learning model used in this study applied Grad-CAM for identifying factors contributing to A. catenella bloom (Figure 3C). The Grad-CAM localization map describes the simulation results by highlighting the important regions (Selvaraju et al., 2017). The model interpretability technique is proposed as a strategy that enables the input-based understanding of the results obtained because neural networks are incapable of explaining model results (Selvaraju et al., 2017). Several prior studies have verified the use of Grad-CAM in the visualization of model features (Selvaraju et al., 2017; Chen et al., 2020). This method is based on class activation mapping (CAM) that can extract the significant features by emphasizing the input data region. However, the use of CAM is restricted to CNN structures that comprise a global average pooling layer (Selvaraju et al., 2016). Grad-CAM overcomes this limitation using gradient information from the final convolutional layer for visualizing the important input data regions (Selvaraju et al., 2017). A detailed description of Grad-CAM is presented by Selvaraju et al. (2017).
We compared the simulated and observed water elevation, salinity, water temperature, NH4-N, and PO4-P results. The physical and chemical simulations are illustrated in Supplementary Figures 3, 4. The coefficient of determination (R2) of water temperature and elevation was above 0.90 at stations 1 and 2, while salinity was 0.26 and 0.65 at stations 1 and 2, respectively. The average root-mean-squared errors (RMSEs) of water temperature, elevation, and salinity were 0.82°C, 0.07 m, and 1.12, respectively. Compared to water temperature and elevation simulations, the salinity simulation had a larger error than observation. The average coefficient of determination (R2) of NH4-N and PO4-P were 0.67 and 0.30, and the average RMSE values were 0.09 and 0.01 mg L–1, respectively. Although both NH4-N and PO4-P simulations follow the observation trend, their values were underestimated at the peak point. The linear regression equations of growth rate, germination rate, and OTU are presented in Supplementary Figure 5. The growth and germination rates were more strongly influenced by temperature and salinity, respectively, whereas the OTUs related to A. catenella were affected by salinity and PO4-P.
Figures 4(A.1-4,B.1-4) shows the performance of classification and regression CNN, respectively, with respect to input window size (m) and lookback (n). Here, m denotes the input window size (e.g., height × width), including the simulation point that was located at the center of the input window, and n is the number of time steps. For example, if the input window size is three and lookback is five, the model considers a spatial distribution with 3 × 3 grid cells and temporal information from the previous five days to the current simulation time. In the classification model, except GoogleNet, there existed multiple optimal designs (m, n) in each structure; GoogleNet had an optimal design structure of (3, 30). The model performance of other structures deteriorated when m was above five and n was below fifteen (days). In the regression model, Resnet 50 and Resnet 101 had a similar optimal design of (1, 29), while GoogleNet and Inception v3 required different (m, n) designs; the optimal design of GoogleNet was (1, 2) and that of Inception v3 was (1, 27).
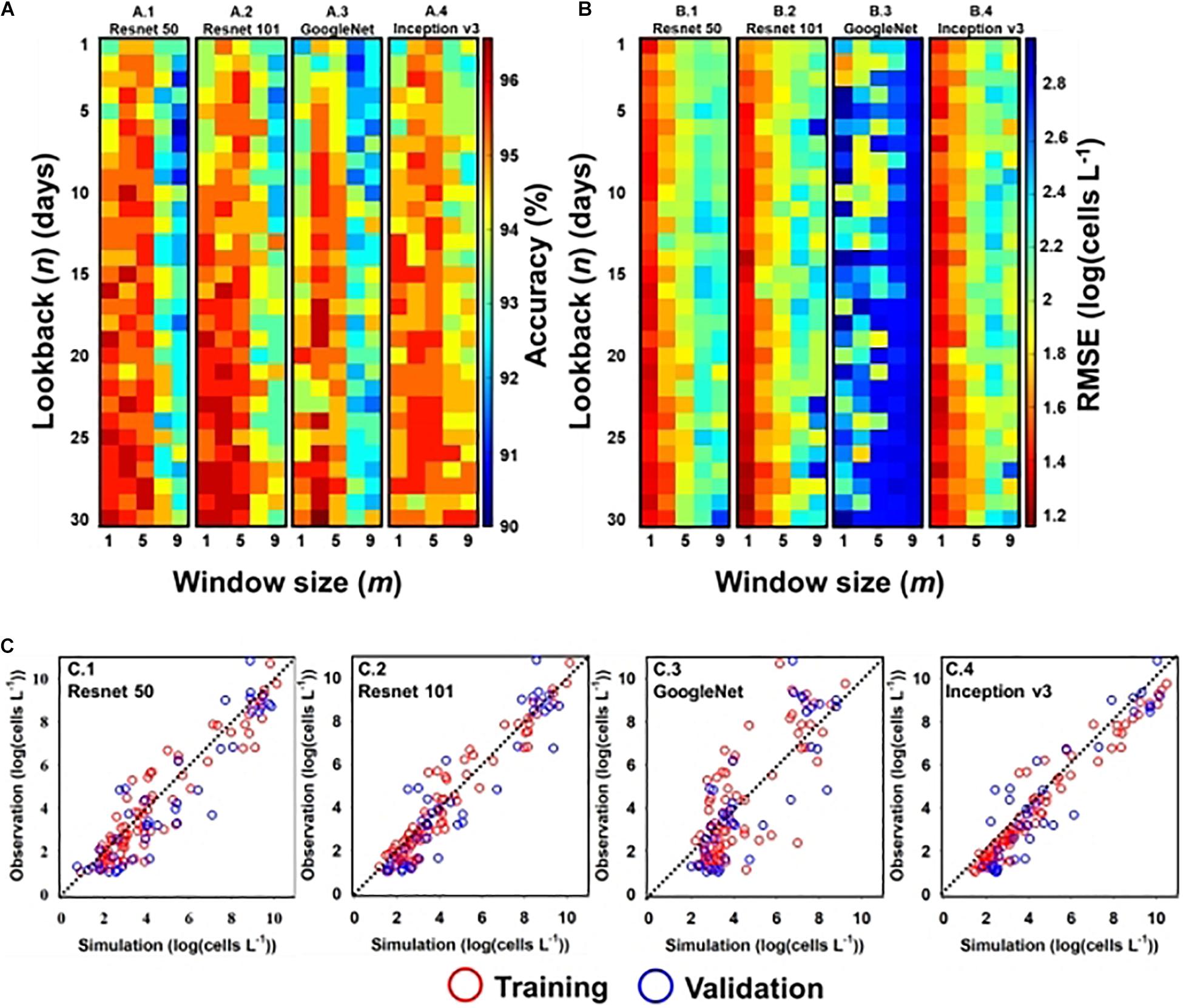
Figure 4. Optimal input and simulation results of A. catenella—(A) optimal input (m and n) of classification CNN structures: (A.1) Resnet 50, (A.2) Resnet 101, (A.3) GoogleNet, and (A.4) Inception v3; (B) optimal input (m and n) of regression CNN structures: (B.1) Resnet 50, (B.2) Resnet 101, (B.3) GoogleNet, and (B.4) Inception v3; (C) simulated and observed densities of A. catenella with regression CNN structures [e.g., (C.1) Resnet 50, (C.2) Resnet 101, (C.3) GoogleNet, and (C.4) Inception v3] with optimal input. In (A) and (B), m and n denote the input window (i.e., height × width) and lookback sizes, respectively, whereas the color range indicates the accuracy from the lowest (blue) to the highest (red) values. In (C), the red and blue circles indicate the training and validation sets, respectively. The observed line has a slope of 1:1.
The model performance with optimal input design is summarized in Table 1. Among them, GoogleNet and Resnet 101 offer the best classification performance with an accuracy of 96.83% and RMSE of 1.20 [log(cells L–1)], respectively. The model performance of Resnet 50 was similar to Resnet 101 with accuracy and RMSE of 96.29% and 1.29 [log(cells L–1)], respectively. Inception v3 (accuracy of 95.76%) and GoogleNet [RMSE of 1.66 log(cells L–1)] presented the worst performance in classification (with 95.76% accuracy) and regression models, respectively.
The results of the regression CNN model are plotted against observed A. catenella in Figures 4C.1-4. In Resnet 101, the simulated A. catenella showed good agreement with observations. GoogleNet showed that the simulated A. catenella was overestimated in the low-density cells and underestimated in the high-density cells. The temporal-spatial distribution of A. catenella is presented with observation using GoogleNet and ResNet 101 because these structures showed the best performance in classification and regression CNN (Figure 5A). The simulated distribution substantially followed actual A. catenella blooms. On December 17, 2016, and May 23, 2017, most areas did not provoke A. catenella bloom in both simulated and observed distribution, indicating that our model can simulate this phenomenon. On March 27, 2018, A. catenella blooms were observed in the coastal water. During this period, the simulated distribution of blooms can describe the actual spatial features; the eastern coast presented a relatively higher density than the western one. The data on March 28 and April 25 of 2017 shows increasing A. catenella spring bloom in the study area. The simulated distribution in both periods was in line with the actual distribution; the model generated high-density cells in the eastern coast and non-bloom near Geoje Island of the west coast. On August 19, 2019, the model determined the non-bloom and substantially low density on the western coast. Mismatched results of the spatial distributions are revealed in three spaces without observed data; the channel connected to the northern enclosed bay on May 23, 2017, the western off sea on March 28, 2017, and the enclosed bay on August 19, 2019. Figure 5B shows the performance of A. catenella forecasting with various lead times. All forecast results were found to be worse than those of nowcasting. The average accuracy of the classification model was 95.85% for a lead of up to five days, decreasing sharply thereafter. The average RMSE of the regression model was 1.36 [log(cells L–1)] until five forecast lead (days) and increased sharply thereafter.
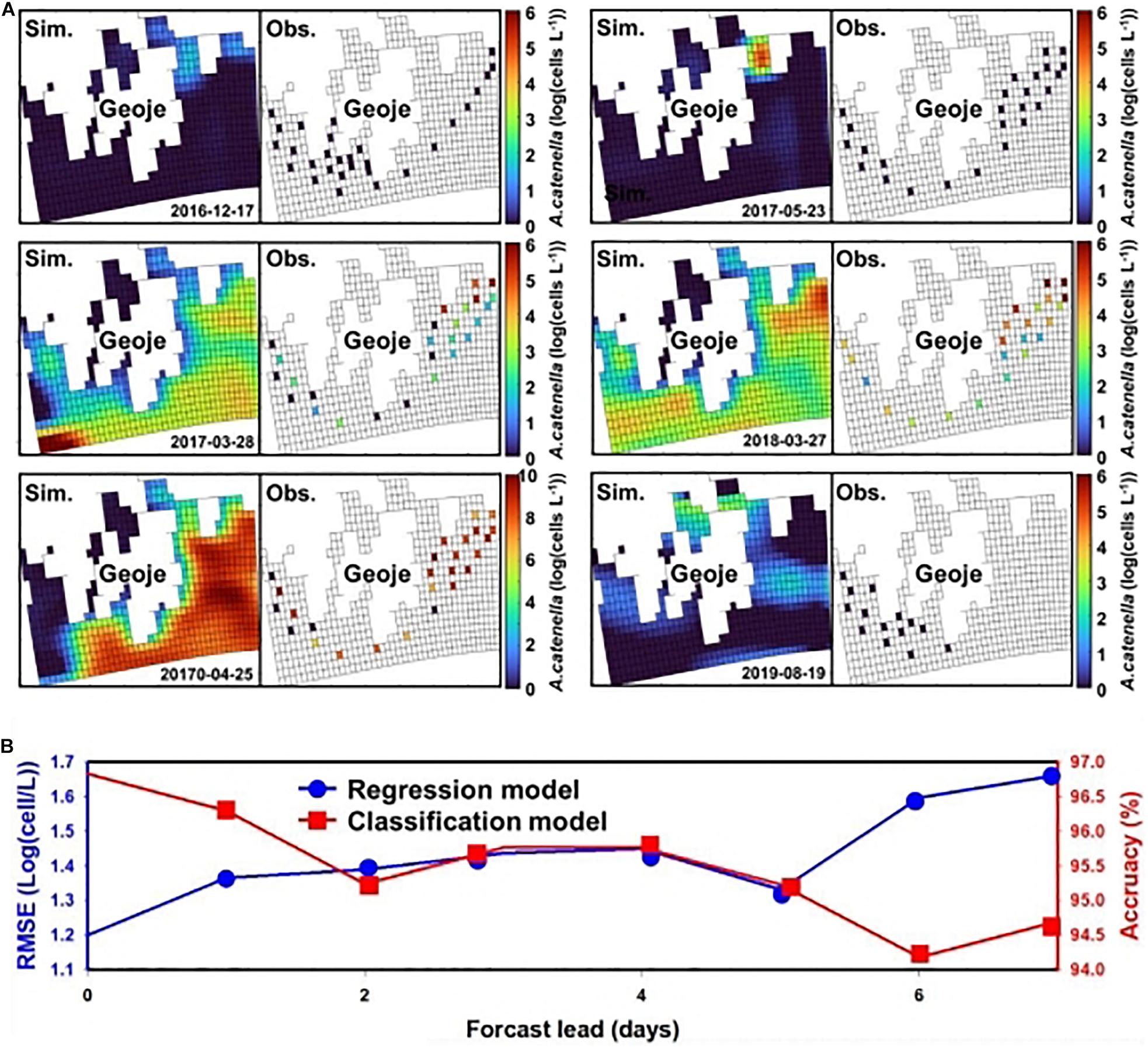
Figure 5. Spatial distribution of A. catenella and forecast performance with lead time—(A) spatial distribution of A. catenella on December 17, 2016, March 28, 2017, April 25, 2017, May 23, 2017, March 27, 2018, and August 19, 2019; (B) A. catenella forecast performance with lead time. In (A), the left and right figures indicate the simulated and observed distributions of A. catenella, respectively. The color range indicates the density variation in A. catenella from the lowest (blue) to the highest (red) value. The spatial distributions were generated using GoogleNet and ResNet 101. In (B), the blue and red curves indicate the performance of regression and classification CNN models, respectively. The x and y (left and right) axes denote the forecast lead time (days), root-mean-square error (RMSE) of the regression model, and accuracy of the classification model, respectively. The model with lower RMSE is considered for regression while that with higher accuracy is selected for classification.
Gradient-weighted class activation mapping (Grad-CAM) shows the feature maps of classification and regression CNN models with GoogleNet and Resnet 101 structures, respectively (Figure 6). These maps were generated depending on the outbreak of A. catenella blooms (e.g., bloom and non-bloom) and density level (e.g., 5–25th percentile, 25–50th percentile, 50–75th percentile, and 75–95th percentile). The regions with high values are regarded as important features in the map. In the classification model, the important features are affiliated with salinity, temperature, water elevation, latitude-velocity of water, and NH4-N from 20 to 28 days of lookback when the bloom is not provoked (Figure 6(A.1)). Among these variables, temperature and salinity are the most influenced variables, as evident from the high feature map values. In contrast, the important bloom features highlighted the variables from 3 to 12 days (Figure 6(A.2)). In the regression CNN model, the 5–25th percentile density show salinity, temperature, water elevation, and NH4-N from 5 to 30 days of lookback as important variables (Figure 6(B.1)). The important variables in the 25–50th percentile were similar to the 5–25th percentile density (Figure 6(B.2)). In the 50–75th percentile, the lookback from 6 to 27 days is highlighted in the model, while that in the 75–95th percentiles ranged from 4 to 22 days (Figures 6(B.3), (B.4)) respectively).
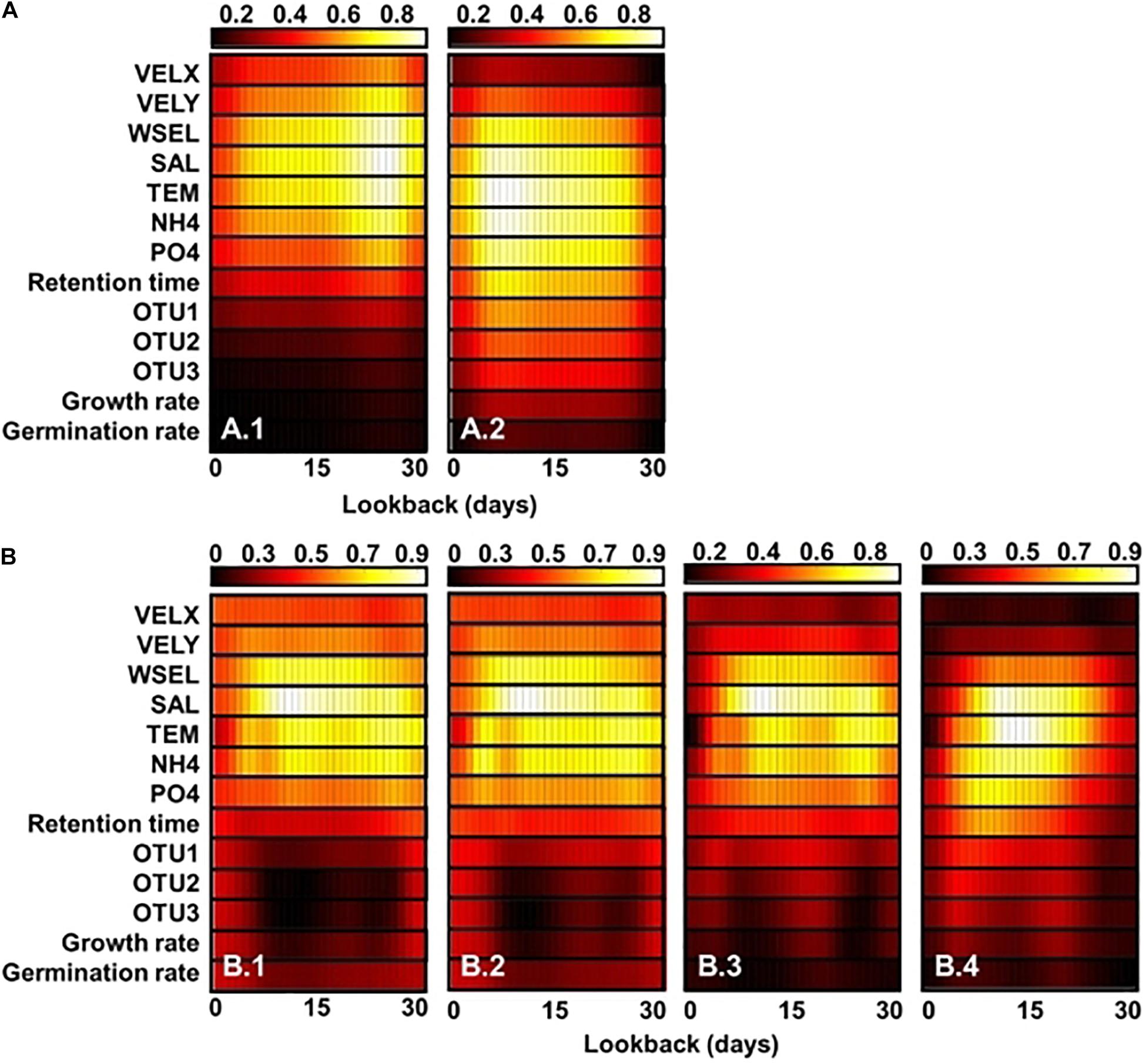
Figure 6. Feature heat maps of classification (A) and regression (B) CNN models obtained using Grad-CAM for the (A.1) bloom and (A.2) no-bloom conditions as well as cases wherein the A. catenella density lies in the (B.1) 5–25, (B.2) 25–50, (B.3) 50–75, and (B.4) 75–90 percentile ranges. The x and y axes represent the lookback and variables values, respectively. The color indicates the degree importance from the lowest (black) to the highest (white). The larger the variable value in a given cell, the greater is its importance. VELX, VELY, WSEL, SAL, TEM, OTU1, OUT2, and OUT3 denote the longitudinal velocity, latitudinal velocity, water-surface elevation, salinity, water temperature, microparticle-associated bacteria, nanoparticle-associated (NP) bacteria, and free-living (FL) bacteria, respectively.
The physical and chemical simulation results showed good agreement with the observation results (Supplementary Figures 3, 4, respectively). However, the salinity simulation was worse than that of water temperature and elevation. Previous studies have also shown that salinity cannot improve model accuracy (Hjøllo et al., 2009; Martyr-Koller et al., 2017) because it is vulnerable to external sources (e.g., rainfall and freshwater), increasing simulation uncertainty (Arfib and Charlier, 2016). The simulated water temperature at station 1 was overestimated during winter (December to February), while station 2 provided reliable outcomes in this season. This is because the model was limited to tracking water temperature at two different points if the difference between them was more than 5 °C. Moreover, the NH4-N simulation followed the observed trends, whereas the PO4-P simulation was less accurate. Specifically, the simulated NH4-N was underestimated at the peak point of observation and the simulated PO4-P was only able to follow the variation in observation. This demonstrated that the simulation of PO4-P and NH4-N could not improve model accuracy because these nutrients were observed in low concentrations, making the model sensitive to external sources. Eilola et al. (2009) and Feng et al. (2015) demonstrated that the simulated PO4-P was underestimated when compared with the observed values, and the simulated nitrogen encountered limitations when following the peak concentration. Additionally, the validation of these simulations is still limited by the lack of observed data. In further research, we will collect more data from additional sites.
In general, the optimal inputs of both the models yielded a small window size below five and long lookback of more than 19 days (Figures 4A,B). Therefore, spatial information below 5 5 grids was sufficient for simulating A. catenella, and temporal information from past 30 days was adequate for improving the simulation performance. The suitable range of grid sizes for the spatial distribution reflected the behavioral characteristics of the species. For the models with window sizes of seven and nine, the simulation performances decreased sharply, indicating that superfluous information might deteriorate the model accuracy. Previous studies have demonstrated that needless data could restrict the effectiveness of model training (Chulkov et al., 2019; Cova and Pais, 2019; Xu et al., 2019). In contrast, in the classification model, the optimal size (m, n) of the input varied depending on the structure based on whether the CNN structures adopted a skip connection or a parallel CNN layer (He et al., 2016b; Szegedy et al., 2016). This demonstrated that the model performance was affected by the structure and the properties of the input data. In addition, a simpler structure, such as GoogLeNet, was appropriate for classifying both bloom and non-bloom (Figure 4(A.3)). In the regression model, Resnet 50 and 101 had similar optimal input properties, whereas GoogleNet and Inception v3 showed lower performances than Resnet. Among the structures, Resnet 101 was the best regression model. This demonstrates that skip connection is appropriate for estimating the density of A. catenella as it can directly connect information from a previous layer to the next layer using skipped layers (Khan et al., 2019). On the contrary, GoogleNet and Inception v3 applied parallel CNN layers having 1 × 1, 3 × 3, and 5 × 5 filter sizes. Hence, the optimization process is important to improve how the input data and model structures affect model training.
ResNet 101 offered the best performance in terms of simulating the cell density of A. catenella that followed the observation distribution, whereas GoogLeNet showed limited performance in simulating A. catenella in low and high densities (Figure 4C). Specifically, the simulated A. catenella from GoogLeNet was overestimated in the case of low density and underestimated in the case of high density, indicating that this model was trained with a narrower range of cell density than that of the other models. The performance discrepancy between ResNet 101 and GoogLeNet may be attributed to the number of layers; ResNet 101 had more layers than GoogLeNet. This demonstrates that the number of layers could affect a model’s performance. According to previous studies concerning CNNs (Khan et al., 2019; Baek et al., 2020), the performance of deep learning models can be influenced by the number of layers. However, a higher number of layers can increase model complexity, leading to the overfitting problem, i.e., the simulated results will correspond too closely to the training data, thereby failing to fit the validation data and predict future simulated results in a reliable manner (Cortes et al., 2017). In contrast, GoogLeNet demonstrated the attainment of a superior validation accuracy (96.83%) as compared to other structures. This confirms that a complex structure is not necessary to identify bloom occurrence and that sufficiently accurate results can be obtained via cell estimation. The simulated distribution substantially followed the feature of actual A. catenella blooms (Figure 5A). Depending on bloom and non-bloom, the model generated similar spatial patterns of density with observation: on December 17, 2016, May 23, 2017, and August 19, 2019, there were no bloom outbreaks in both simulated and observed distributions; on March 27, 2018, the A. catenella blooms were observed in both the distributions; on March 28, 2017, and April 25, 2017, both distributions showed the bloom and non-bloom area in the coast. However, on March 28, 2017, the simulated distribution was determined as blooms in most areas, while there was no bloom of the observed distribution in the western sea. The high uncertainty in population dynamics could be due to in situ environmental and biological variables heterogeneously influencing the initiation, development, and ultimate demise of HABs (McGillicuddy et al., 2015; Brandenburg et al., 2017). The model generated a notable density in the specific spaces without observed data; the simulation of May 23, 2017, and August 19, 2019, presented a higher density in the channel connected to the northern enclosed bay and the enclosed bay, respectively. The mismatch results between simulation and observation also increase the model uncertainty by limiting the quantification of the exact spatial distribution of HABs. Remote sensing can solve this by improving model performance with the spatial distribution of physical, chemical, biological, and atmospheric factors (Shen et al., 2020). Forecast simulation showed lower performance than nowcasting. The performance of the classification and regression model decreased with increasing lead time and deteriorated sharply at a specific date (Figure 5B). These simulation results showed that the model performance would degrade with increasing forecast lead time (days) because the input data might correspond poorly with the future ocean physical and biological processes affecting A. catenella. Prior studies have reported a decline in model performance with increasing lead time. Chattopadhyay et al. (2020) reported a decrease in the model performance from 73 to 47% while predicting a cold-spell class as the lead time changed from 1 to 5 days. Pyo et al. (2020) observed the validation accuracy to decrease with increasing lead time when simulating Microcystis—a causative algal taxon of freshwater HAB. As reported by Miao et al. (2019), an increase in the forecast lead time causes an increase in model uncertainty and imperfect representation of the extracted features. This deteriorated model training and reduced the forecast accuracy. Therefore, this study demonstrated the robust short-term A. catenella forecasting ability of the DL model.
Temperature and salinity are factors with the greatest influence on the classification and regression models, as confirmed by the high values observed in the feature map (Figures 6A,B). Temperature and salinity affect cyst germination and A. catenella growth, thereby causing the proliferation of A. catenella cells (Itakura and Yamaguchi, 2001; Nagai et al., 2004). Ichimi et al. (2001) reported that temperature plays a critical role in cyst germination and algal bloom. Parkhill and Cembella (1999) demonstrated that salinity influences A. catenella growth. NH4-N and water elevation were also highlighted. A. catenella uses a nitrogen source for growth and prefers ammonium uptake (Siu et al., 1997). Collos et al. (2006) observed that the growth of A. catenella is limited by ammonium uptake and accumulation. Moreover, an increase in water elevation tends to weaken and accelerate the advection and dispersion of algal blooms, respectively (Wu and Kong, 2009). Additionally, Giddings et al. (2014) demonstrated that the physical factors of oceans influence HAB development. The regression CNN model identifies fewer important features that increase the density of A. catenella. In particular, factors, such as the salinity, temperature, and NH4-N concentration over a 5–30-day lookback period were highlighted in the 5–25th percentile while higher densities were simulated considering variables over 6–22-day lookback period. The results can be related to the initiation for bloom development of a given inoculum size at a suitable time. The Grad-CAM result reveals that the proposed model generates cell density by changing the highlighted variables. This is because the variables of influence differ depending on the life cycle A. catenella. The water temperature and salinity initiate the development of A. catenella while the nutrient and retention time accelerate its growth (Itakura and Yamaguchi, 2001; Nagai et al., 2004; Armi et al., 2011). Previous studies have reported the transitions in the highlighted region as change input. Panwar et al. (2020) adopted Grad-CAM to identify important areas of COVID-19 detection and demonstrated the change in the highlighted area as an input image. Cheng et al. (2019) extracted hip-fracture features using Grad-CAM and X-ray images. This study estimates the spatiotemporal distribution of A. catenella using CNN and determines the cause of bloom using Grad-CAM. Most previously reported algal simulations have focused on inland water species, such as cyanobacteria, green algae, and diatom. However, only few studies have addressed HAB modeling in seawater and only analyzed limited species (e.g., A. fundyense). HAB modeling in marine ecosystems should consider several environmental factors, such as the temperature, salinity, and velocity of water as well as symbiosis among different species. The paucity of relevant research in this domain could be attributed to the need for the use of complex modeling techniques and availability of limited observations (Ralston and Moore, 2020). This study overcomes this limitation via successful application of deep learning for simulating A. catenella HAB using an ocean model. Further research can be performed considering other species (e.g., Cochlodinium and Karenia) with additional monitoring. The findings of this research are expected to improve the applicability, expendability, and accuracy of HAB modeling using the deep learning models. Therefore, the proposed approach can be considered useful in establishing HAB management in marine environments.
This study applied regression and classification using CNN models for simulating spring blooms of A. catenella. The classification was used to analyze the initiation of A. catenella, while the regression generated the density of the genera. GoogLeNet and Resnet 101 were identified as the best deep learning structures for classification and regression using CNNs, yielding an accuracy and RMSE of 96.8% and 1.20 [log(cells L–1)], respectively. Using Grad-CAM, the salinity, temperature, and NH4-N were found to be significant variables that influence the bloom of A. catenella. In particular, factors such as the salinity, temperature, and NH4-N concentration over a 5–30-day lookback period were highlighted in the 5–25th percentile, while higher densities were simulated considering variables over the 6–22 day lookback period. The results can be related to the initiation for bloom development of a given inoculum size at a suitable time. As per the authors, the study makes a significant contribution to the literature because understanding and mitigating harmful algal blooms (HABs) are important for reducing economic losses and public health damages. In contrast to modeling methods that can only measure simulation performance, the proposed model can simulate the initiation and growth of HABs based on influencing factors. However, to establish an AI-based HAB modeling system, the following challenges remain: (1) additional monitoring that includes environmental variables (NH4-N and PO4-P) and target species (A. catenella) is required, and (2) models should be trained using observations from various sites to improve model adaptability. Further research can improve the models via continuous data acquisition. Hence, the suggested models could be useful in establishing HAB management systems for aquatic environments.
All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Material. Additional data related to this paper may be requested from the authors.
S-SB, YOK, and KHC conceptualized the proposed research. S-SB was responsible for preparing the methodology, data visualization, and preparing the original draft of the manuscript. YSK and JCP performed the data curation. SHB, C-YA, and H-MO performed the data validation. YOK and KHC handled funding acquisition. All authors reviewed and edited the manuscript, subsequent to the first draft.
This study was supported by the Ministry of Science, ICT & Future Planning (grant NRF-2016M1A5A1027457) and Korean Institute of Ocean Science and Technology (PE99912).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2021.729954/full#supplementary-material
Akiba, T., Suzuki, S., and Fukuda, K. (2017). Extremely large minibatch sgd: training resnet-50 on imagenet in 15 minutes. arXiv [Preprint] arXiv:1711.04325,
Anderson, D. M., Cembella, A. D., and Hallegraeff, G. M. (2012). Progress in understanding harmful algal blooms: paradigm shifts and new technologies for research, monitoring, and management. Annu. Rev. Mar. Sci. 4, 143–176. doi: 10.1146/annurev-marine-120308-081121
Arfib, B., and Charlier, J.-B. (2016). Insights into saline intrusion and freshwater resources in coastal karstic aquifers using a lumped rainfall–discharge–salinity model (the Port-Miou brackish spring, SE France). J. Hydrol. 540, 148–161. doi: 10.1016/j.jhydrol.2016.06.010
Armi, Z., Milandri, A., Turki, S., and Hajjem, B. (2011). Alexandrium catenella and Alexandrium tamarense in the North Lake of Tunis: bloom characteristics and the occurrence of paralytic shellfish toxin. Afr. J. Aquat. Sci. 36, 47–56. doi: 10.2989/16085914.2011.559688
Baek, S. S., Choi, Y., Jeon, J., Pyo, J., Park, J., and Cho, K. H. (2020). Replacing the internal standard to estimate micropollutants using deep and machine learning. Water Res. 188:116535. doi: 10.1016/j.watres.2020.116535
Baek, S. S., Kwon, Y. S., Pyo, J., Choi, J., Kim, Y. O., and Cho, K. H. (2021). Identification of influencing factors of A. catenella bloom using machine learning and numerical simulation. Harmful Algae 103:102007. doi: 10.1016/j.hal.2021.102007
Brandenburg, K. M., de Senerpont Domis, L. N., Wohlrab, S., Krock, B., John, U., van Scheppingen, Y., et al. (2017). Combined physical, chemical and biological factors shape Alexandrium ostenfeldii blooms in the Netherlands. Harmful Algae 63, 146–153. doi: 10.1016/j.hal.2017.02.004
Brion, G. M., Neelakantan, T., and Lingireddy, S. (2002). A neural-network-based classification scheme for sorting sources and ages of fecal contamination in water. Water Res. 36, 3765–3774. doi: 10.1016/s0043-1354(02)00091-x
Caruana, R., and Niculescu-Mizil, A. (2006). “An empirical comparison of supervised learning algorithms,” in Proceedings of the 23rd International Conference on Machine Learning, (New York, NY), 161–168.
Chang, D. S., Shin, I. S., Pyeun, J. H., and Park, Y. H. (1987). A study on paralytic shellfish poison of sea mussel, Mytilus edulis-food poisoning accident in Gamchun Bay, Pusan, Korea, 1986. Kor. J. Fish. Aquat. Sci. 20, 293–299.
Chattopadhyay, A., Nabizadeh, E., and Hassanzadeh, P. (2020). Analog forecasting of extreme-causing weather patterns using deep learning. J. Adv. Model. Earth Syst. 12:e2019MS001958.
Chen, D., and Manning, C. D. (2014). “A fast and accurate dependency parser using neural networks,” in Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), (Doha), 740–750.
Chen, L., Chen, J., Hajimirsadeghi, H., and Mori, G. (2020). “Adapting grad-CAM for embedding networks,” in Proceedings of the IEEE Winter Conference on Applications of Computer Vision, (Snowmass, CO), 2794–2803.
Cheng, C. T., Ho, T. Y., Lee, T. Y., Chang, C. C., Chou, C. C., Chen, C. C., et al. (2019). Application of a deep learning algorithm for detection and visualization of hip fractures on plain pelvic radiographs. Eur. Radiol. 29, 5469–5477. doi: 10.1007/s00330-019-06167-y
Chulkov, A. O., Nesteruk, D. A., Vavilov, V. P., Moskovchenko, A. I., Saeed, N., and Omar, M. (2019). Optimizing input data for training an artificial neural network used for evaluating defect depth in infrared thermographic nondestructive testing. Infrared Phys. Technol. 102:103047. doi: 10.1016/j.infrared.2019.103047
Collos, Y., Lespilette, M., Vaquer, A., Laabir, M., and Pastoureaud, A. (2006). Uptake and accumulation of ammonium by Alexandrium catenella during nutrient pulses. Afr. J. Mar. Sci. 28, 313–318. doi: 10.2989/18142320609504169
Cortes, C., Gonzalvo, X., Kuznetsov, V., Mohri, M., and Yang, S. (2017). “Adanet: adaptive structural learning of artificial neural networks,” in Proceedings of the 34 th International Conference on Machine Learning (PMLR, 2017), (Sydney), 874–883.
Cova, T. F., and Pais, A. A. (2019). Deep learning for deep chemistry: optimizing the prediction of chemical patterns. Front. Chem. 7:809.
Cui, Y., Chun, S. J., Baek, S. S., Baek, S. H., Kim, P. J., Son, M., et al. (2020). Unique microbial module regulates the harmful algal bloom (Cochlodinium polykrikoides) and shifts the microbial community along the Southern Coast of Korea. Sci. Total Environ. 721:137725. doi: 10.1016/j.scitotenv.2020.137725
Dai, Z., Chu, A., Stive, M., Zhang, X., and Yan, H. (2011). Unusual salinity conditions in the Yangtze Estuary in 2006: Impacts of an extreme drought or of the Three Gorges Dam? Ambio 40, 496–505. doi: 10.1007/s13280-011-0148-2
Deng, J., Dong, W., Socher, R., Li, L. J., Li, K., and Fei-Fei, L. (2009). “Imagenet: a large-scale hierarchical image database,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, (Miami, FL), 248–255.
Du, J., and Shen, J. (2016). Water residence time in Chesapeake Bay for 1980–2012. J. Mar. Syst. 164, 101–111. doi: 10.1016/j.jmarsys.2016.08.011
Eilola, K., Meier, H. M., and Almroth, E. (2009). On the dynamics of oxygen, phosphorus and cyanobacteria in the Baltic Sea; a model study. J. Mar. Syst. 75, 163–184. doi: 10.1016/j.jmarsys.2008.08.009
Feng, Y., Friedrichs, M. A., Wilkin, J., Tian, H., Yang, Q., Hofmann, E. E., et al. (2015). Chesapeake Bay nitrogen fluxes derived from a land-estuarine ocean biogeochemical modeling system: Model description, evaluation, and nitrogen budgets. J. Geophys. Res. Biogeosci. 120, 1666–1695. doi: 10.1002/2015jg002931
Giddings, S. N., MacCready, P., Hickey, B. M., Banas, N. S., Davis, K. A., Siedlecki, S. A., et al. (2014). Hindcasts of potential harmful algal bloom transport pathways on the Pacific Northwest coast. J. Geophys. Res. Oceans 119, 2439–2461. doi: 10.1002/2013jc009622
Gobler, C. J., Doherty, O. M., Hattenrath-Lehmann, T. K., Griffith, A. W., Kang, Y., and Litaker, R. W. (2017). Ocean warming since 1982 has expanded the niche of toxic algal blooms in the North Atlantic and North Pacific oceans. Proc. Natl. Acad. Sci. U.S.A. 114, 4975–4980. doi: 10.1073/pnas.1619575114
Han, M. S., Jeon, J. K., and Kim, Y. O. (1992). Occurrence of dinoflagellate Alexandrium tamarense, a causative organism of paralytic shellfish poisoning in Chinhae Bay. Korea. J. Plankton Res. 14, 1581–1592. doi: 10.1093/plankt/14.11.1581
He, K., Zhang, X., Ren, S., and Sun, J. (2016a). “Deep residual learning for image recognition,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, (Las Vegas, NV), 770–778.
He, K., Zhang, X., Ren, S., and Sun, J. (2016b). “Identity mappings in deep residual networks,” in European Conference on Computer Vision, eds B. Leibe, J. Matas, N. Sebe, and M. Welling (Cham: Springer), 630–645. doi: 10.1007/978-3-319-46493-0_38
He, R., McGillicuddy, D. J. Jr., Keafer, B. A., and Anderson, D. M. (2008). Historic 2005 toxic bloom of Alexandrium fundyense in the western Gulf of Maine: 2. Coupled biophysical numerical modeling. J. Geophys. Res. Oceans 113, C07040.
Heisler, J., Glibert, P. M., Burkholder, J. M., Anderson, D. M., Cochlan, W., Dennison, W. C., et al. (2008). Eutrophication and harmful algal blooms: a scientific consensus. Harmful Algae 8, 3–13. doi: 10.1016/j.hal.2008.08.006
Hjøllo, S. S., Skogen, M. D., and Svendsen, E. (2009). Exploring currents and heat within the North Sea using a numerical model. J. Mar. Syst. 78, 180–192. doi: 10.1016/j.jmarsys.2009.06.001
Hoagland, P. A. D. M., Anderson, D. M., Kaoru, Y., and White, A. W. (2002). The economic effects of harmful algal blooms in the United States: estimates, assessment issues, and information needs. Estuaries. 25, 819–837. doi: 10.1007/bf02804908
Ichimi, K., Yamasaki, M., Okumura, Y., and Suzuki, T. (2001). The growth and cyst formation of a toxic dinoflagellate, Alexandrium tamarense, at low water temperatures in northeastern Japan. J. Exp. Mar. Biol. Ecol. 261, 17–29. doi: 10.1016/s0022-0981(01)00256-8
Ishikawa, A., Hattori, M., Ishii, K. I., Kulis, D. M., Anderson, D. M., and Imai, I. (2014). In situ dynamics of cyst and vegetative cell populations of the toxic dinoflagellate Alexandrium catenella in Ago Bay, central Japan. J. Plankton Res. 36, 1333–1343. doi: 10.1093/plankt/fbu048
Itakura, S., and Imai, I. (2014). Economic impacts of harmful algal blooms on fisheries and aquaculture in western Japan-An overview of interannual variability and interspecies comparison. PICES Sci. Rep. 47, 17.
Itakura, S., and Yamaguchi, M. (2001). Germination characteristics of naturally occurring cysts of Alexandrium tamarense (Dinophyceae) in Hiroshima Bay, Inland Sea of Japan. Phycologia 40, 263–267. doi: 10.2216/i0031-8884-40-3-263.1
Jeong, S., Yeon, K., Hur, Y., and Oh, K. (2010). Salinity intrusion characteristics analysis using EFDC model in the downstream of Geum River. J. Environ. Sci. 22, 934–939. doi: 10.1016/s1001-0742(09)60201-1
Kang, E.-J., Yang, H., Lee, H.-H., Kim, K.-S., and Kim, C.-H. (2012). Characteristics of fish fauna collected from near estuaries bank and fish-way on the bank of Naktong river. Kor. J. Ichthyol. 24, 201–219.
Khan, R. U., Zhang, X., and Kumar, R. (2019). Analysis of ResNet and GoogleNet models for malware detection. J. Comp. Virol. Hacking Tech. 15, 29–37. doi: 10.1007/s11416-018-0324-z
Kim, H.-C., and Yoo, S. (2007). Relationship between phytoplankton bloom and wind stress in the sub-polar frontal area of the Japan/East Sea. J. Mar. Syst. 67, 205–216. doi: 10.1016/j.jmarsys.2006.05.016
Kim, Y. O., Choi, J., Baek, S. H., Lee, M., and Oh, H.-M. (2020). Tracking Alexandrium catenella from seed-bed to bloom on the southern coast of Korea. Harmful Algae 99:101922. doi: 10.1016/j.hal.2020.101922
Kim, Y.-O., Park, M.-H., and Han, M.-S. (2002). Role of cyst germination in the bloom initiation of Alexandrium tamarense (Dinophyceae) in Masan Bay, Korea. Aquat. Microb. Ecol. 29, 279–286. doi: 10.3354/ame029279
Kim, Y. S., Son, H.-J., and Jeong, S.-Y. (2015). Isolation of an algicide from a marine bacterium and its effects against the toxic dinoflagellate Alexandrium catenella and other harmful algal bloom species. J. Microbiol. 53, 511–517. doi: 10.1007/s12275-015-5303-1
Koundinya, S., Sharma, H., Sharma, M., Upadhyay, A., Manekar, R., Mukhopadhyay, R., et al. (2018). “2d-3d CNN based architectures for spectral reconstruction from RGB images,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, (Salt Lake City, UT), 844–851.
Kozich, J. J., Westcott, S. L., Baxter, N. T., Highlander, S. K., and Schloss, P. D. (2013). Development of a dual-index sequencing strategy and curation pipeline for analyzing amplicon sequence data on the MiSeq Illumina sequencing platform. Appl. Environ. Microbiol. 79, 5112–5120. doi: 10.1128/AEM.01043-13
Loussaief, S., and Abdelkrim, A. (2018). Convolutional neural network hyper-parameters optimization based on genetic algorithms. Int. J. Adv. Comp. Scie. Appl. 9, 252–266.
Martyr-Koller, R. C., Kernkamp, H. W. J., Van Dam, A., van der Wegen, M., Lucas, L. V., Knowles, N., et al. (2017). Application of an unstructured 3D finite volume numerical model to flows and salinity dynamics in the San Francisco Bay-Delta. Estuar. Coast. Shelf Sci. 192, 86–107. doi: 10.1016/j.ecss.2017.04.024
McGillicuddy, D. J. Jr. (2010). Models of harmful algal blooms: conceptual, empirical, and numerical approaches. J. Mar. Syst. 83:105. doi: 10.1016/j.jmarsys.2010.06.008
McGillicuddy, D. J. Jr., Sedwick, P. N., Dinniman, M. S., Arrigo, K. R., Bibby, T. S., Greenan, B. J. W., et al. (2015). Iron supply and demand in an Antarctic shelf ecosystem. Geophys. Res. Lett. 42, 8088–8097. doi: 10.1002/2015GL065727
Miao, Q., Pan, B., Wang, H., Hsu, K., and Sorooshian, S. (2019). Improving monsoon precipitation prediction using combined convolutional and long short term memory neural network. Water 11:977. doi: 10.3390/w11050977
Montgomery, D. C., Peck, E. A., and Vining, G. G. (2021). Introduction to Linear Regression Analysis. Hoboken, NJ: John Wiley & Sons.
Nagai, S., Matsuyama, Y., Oh, S.-J., and Itakura, S. (2004). Effect of nutrients and temperature on encystment of the toxic dinoflagellate Alexandrium tamarense (Dinophyceae). Plankton Biol. Ecol. 51, 103–109.
National Fisheries Research and Development Institute (NFRDI) (2020). Paralytic Shellfish Poisoning Report. Available online at: https://www.nifs.go.kr/page?id=kr_index (accessed June 13, 2021).
Panwar, H., Gupta, P. K., Siddiqui, M. K., Morales-Menendez, R., Bhardwaj, P., and Singh, V. (2020). A deep learning and grad-CAM based color visualization approach for fast detection of COVID-19 cases using chest X-ray and CT-Scan images. Chaos Solitons Fractals 140:110190. doi: 10.1016/j.chaos.2020.110190
Park, T. G., Lim, W. A., Park, Y. T., Lee, C. K., and Jeong, H. J. (2013). Economic impact, management and mitigation of red tides in Korea. Harmful Algae 30, S131–S143.
Parkhill, J.-P., and Cembella, A. D. (1999). Effects of salinity, light and inorganic nitrogen on growth and toxigenicity of the marine dinoflagellate Alexandrium Tamarense from Northeastern Canada. J. Plankton Res. 21, 939–955. doi: 10.1093/plankt/21.5.939
Pinto, L., Mateus, M., and Silva, A. (2016). Modeling the transport pathways of harmful algal blooms in the Iberian coast. Harmful Algae 53, 8–16. doi: 10.1016/j.hal.2015.12.001
Pyo, J., Duan, H., Baek, S., Kim, M. S., Jeon, T., Kwon, Y. S., et al. (2019). A convolutional neural network regression for quantifying cyanobacteria using hyperspectral imagery. Remote Sens. Environ. 233:111350. doi: 10.1016/j.rse.2019.111350
Pyo, J., Park, L. J., Pachepsky, Y., Baek, S. S., Kim, K., and Cho, K. H. (2020). Using convolutional neural network for predicting cyanobacteria concentrations in river water. Water Res. 186:116349. doi: 10.1016/j.watres.2020.116349
Ralston, D. K., and Moore, S. K. (2020). Modeling harmful algal blooms in a changing climate. Harmful Algae 91:101729. doi: 10.1016/j.hal.2019.101729
Schloss, P. D., Westcott, S. L., Ryabin, T., Hall, J. R., Hartmann, M., Hollister, E. B., et al. (2009). Introducing mothur: open-source, platform-independent, community-supported software for describing and comparing microbial communities. Appl. Environ. Microbiol. 75, 7537–7541. doi: 10.1128/AEM.01541-09
Selvaraju, R. R., Cogswell, M., Das, A., Vedantam, R., Parikh, D., and Batra, D. (2017). “Grad-cam: visual explanations from deep networks via gradient-based localization,” in Proceedings of the IEEE International Conference on Computer Vision, (Venice), 618–626.
Selvaraju, R. R., Das, A., Vedantam, R., Cogswell, M., Parikh, D., and Batra, D. (2016). Grad-CAM: Why did you say that? arXiv [preprint] arXiv:1611.07450,
Shen, J., Qin, Q., Wang, Y., and Sisson, M. (2019). A data-driven modeling approach for simulating algal blooms in the tidal freshwater of James River in response to riverine nutrient loading. Ecol. Modell. 398, 44–54. doi: 10.1016/j.ecolmodel.2019.02.005
Shen, M., Duan, H., Cao, Z., Xue, K., Qi, T., Ma, J., et al. (2020). Sentinel-3 OLCI observations of water clarity in large lakes in eastern China: implications for SDG 6.3. 2 evaluation. Remote Sens. Environ. 247:111950. doi: 10.1016/j.rse.2020.111950
Shin, H. C., Roth, H. R., Gao, M., Lu, L., Xu, Z., Nogues, I., et al. (2016). Deep convolutional neural networks for computer-aided detection: CNN architectures, dataset characteristics and transfer learning. IEEE Trans. Med. Imaging 35, 1285–1298. doi: 10.1109/tmi.2016.2528162
Siu, G. K., Young, M. L., and Chan, D. (1997). Asia-Pacific Conference on Science and Management of Coastal Environment. Cham: Springer, 117–140.
Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., et al. (2015). “Going deeper with convolutions,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, (Boston, MA), 1–9.
Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., and Wojna, Z. (2016). “Rethinking the inception architecture for computer vision,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, (Las Vegas, NV), 2818–2826.
Wang, J., and Wu, J. (2009). Occurrence and potential risks of harmful algal blooms in the East China Sea. Sci. Total Environ. 407, 4012–4021. doi: 10.1016/j.scitotenv.2009.02.040
Wang, S., Tang, D., He, F., Fukuyo, Y., and Azanza, R. V. (2008). Occurrences of harmful algal blooms (HABs) associated with ocean environments in the South China Sea. Hydrobiologia 596, 79–93. doi: 10.1007/s10750-007-9059-4
Weiher, R., and Sen, A. (2006). Economic Statistics for NOAA, 4edn Edn. Silver Spring, MD: National Oceanic and Atmospheric Sciences Administration, 1–67.
Wu, X., and Kong, F. (2009). Effects of light and wind speed on the vertical distribution of Microcystis aeruginosa colonies of different sizes during a summer bloom. Int. Rev. Hydrobiol. 94, 258–266. doi: 10.1002/iroh.200811141
Xu, Y., Lin, K., Wang, S., Wang, L., Cai, C., Song, C., et al. (2019). Deep learning for molecular generation. Future Med. Chem. 11, 567–597.
Yoshioka, H., and Yaegashi, Y. (2018). Robust stochastic control modeling of dam discharge to suppress overgrowth of downstream harmful algae. Appl. Stochastic Model. Bus. Ind. 34, 338–354. doi: 10.1002/asmb.2301
Keywords: harmful algal blooms, deep learning, convolutional neural network, classification, regression
Citation: Baek S-S, Pyo J, Kwon YS, Chun S-J, Baek SH, Ahn C-Y, Oh H-M, Kim YO and Cho KH (2021) Deep Learning for Simulating Harmful Algal Blooms Using Ocean Numerical Model. Front. Mar. Sci. 8:729954. doi: 10.3389/fmars.2021.729954
Received: 24 June 2021; Accepted: 15 September 2021;
Published: 12 October 2021.
Edited by:
Kenneth Mei Yee Leung, City University of Hong Kong, Hong Kong SAR, ChinaReviewed by:
Yongquan Yuan, Institute of Oceanology, Chinese Academy of Sciences (CAS), ChinaCopyright © 2021 Baek, Pyo, Kwon, Chun, Baek, Ahn, Oh, Kim and Cho. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kyung Hwa Cho, a2hjaG9AdW5pc3QuYWMua3I=; Young Ok Kim, eW9raW1Aa2lvc3QuYWMua3I=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.