River Jets Versus Wave-Driven Longshore Currents at River Mouths

At river mouths, fluvial jets and longshore currents (LSCs) generated by waves interact hydrodynamically. This idealized numerical modeling study simulates a large number of hydro-morphodynamic conditions (650) to explore the emergent hydrodynamics determined by different mouth bar volumes and geometries, river discharge, wave heights, and directions and their potential stress on river-mouth development. We find that in the absence of a river-mouth bar (RMB), interactions are driven by momentum balances, expressed either as the balance of wave momentum flux (Mw) and jet momentum flux (Mj), or the balance of river jet discharge (Q_Jet) and longshore current discharge (Q_LSC). When a RMB is present, the topography modifies the structure of the jet by spreading it, and we quantify this mechanism through the lateral jet transfer rate (LJT). Secondly, topography generates complex longshore wave-driven circulation as a result of the protruding shoreface which serves as a platform on which counter LSCs develop. The balance in Q_Jet/Q_LSC may be used as an indication of the type of circulation. High and oblique waves favor longshore circulation and RMB bypass, whereas low waves and normal-to-coast angles generate diverging LSCs on the mouth bar crest which interrupts the longshore circulation. A quantification of the dynamic diversion is proposed in the form of the non-dimensional Dynamic diversion index (DyD), which scales with the product of Mj and Mw, and can account for the absolute strength of hydrodynamic interactions occurring at river mouths. RMB morphology can affect DyD in multiple ways by strengthening or by weakening the interactions. The DyD effect seems to increase with increasing RMB size, indicating that the RMB scale regulates the interplay of the wave-driven circulation and the river jet which further controls the adjacent topography changes.

Introduction

River mouths are a focal point of interaction for jet currents originating from fluvial discharge, longshore currents (LSCs) generated by waves as well as circulation driven by wind, tides and density effects. Additionally, the circulation and interactions at river mouths are modulated by the presence of features derived from sediment accumulations fronting river mouths: river mouth bars (RMBs).

The dynamics of jet outflows has been intensely researched in laboratory and numerical studies. River jets display a Gaussian horizontal velocity profile that spreads and decays downstream (Rowland et al., 2009; Falcini and Jerolmack, 2010). High potential vorticity causes the preservation of a coherent jet structure over large distances (Falcini and Jerolmack, 2010). River effluents may be seen as bounded jets (Dracos et al., 1992; Canestrelli et al., 2014), and jet spreading and deceleration for these river-mouth jets occurs more rapidly than for unbounded jets, without any constriction surfaces (Özsoy and Ünlüata, 1982; Fagherazzi et al., 2015; Kundu et al., 2016). Processes such as bed friction, lateral mixing, and expansion at the outlet, jet and plume detachment, act to diverge jets from their idealized shape (Wright, 1977; Edmonds and Slingerland, 2007; Fagherazzi et al., 2015). Receiving basin depth and slope control jet hydrodynamics (Wright et al., 1974; Özsoy and Ünlüata, 1982; Leonardi et al., 2013; Fagherazzi et al., 2015; Jiménez-Robles et al., 2016), and the presence of RMBs may explain the difference between inertia-dominated effluents and friction-dominated, as defined by Wright (1977), determining patterns of jet expansion. The importance of interaction with the coastal bathymetry was shown during an experiment wherein the RMB altered flow patterns and removed the jet-like flow structure that was originally observed (Shaw et al., 2018), due to the appearance of significant pressure gradients (Olabarrieta et al., 2014). Research into frontal wave influence on jet spreading by Ismail and Wiegel (1983) indicated that the balance between the wave momentum and jet momentum can be used to predict the observed processes. Wind waves cause jet deflection and spreading (Nardin and Fagherazzi, 2012), as do tides (Leonardi et al., 2013) and salinity differences. It seems that apart from potential vorticity which acts to conserve the jet structure, all other element act against this conservation, resulting in the multitude of coastal jet and plume structures that occur in nature.

The LSC, on the other hand, is parallel to the coast and driven by the radiation stress divergence, a relatively well-known generation mechanism (Longuet-Higgins and Stewart, 1962; Longuet-Higgins, 1970). Through their protrusion, RMBs are a focal point for wave-energy focusing and induce longshore accelerations which form the LSC (Olabarrieta et al., 2011). The effects of the RMB on nearshore hydrodynamics seem to be remarkably similar to those noted for headlands (e.g., George et al., 2019), which were masterfully synthesized by van Rijn (2013). Thus, similar to headlands, RMBs may act as obstructions or behave as semi-permeable boundaries to LSCs and drift, generate nearshore re-circulation zones, form locations where seaward-directed rip currents are generated as well as sites of spit and shoal formation. River mouths, in contrast to headlands, receive the added influence of river flow which is a supplier of both liquid (Q) and solid discharge (Qs), which creates a dynamic landform. This results in more complex hydrodynamic interactions and in changing states for these particular interactions during floods and storms (Zăinescu et al., 2019).

In this article, a distinction is made between the “direct” type of wave-current interaction and the interaction between wave-driven LSCs and the river-jet current. Direct current-wave interactions produce current refraction, wave dissipation, and wave blocking when waves penetrate into strong opposing currents (Lai et al., 1989; Chawla and Kirby, 2002; Suastika, 2012). Currents affect wave propagation through the Doppler Effect, where wave period decreases, whereas wave height increases when encountering a fluvial jet (Rusu, 2010; Nardin et al., 2013; Olabarrieta et al., 2014). Waves propagating into stronger opposing currents experience a frequency spectrum downshift, due to the blocking of higher frequency components (Chawla and Kirby, 2002), effectively making river mouths a low-pass filter which removes shorter-period wind waves and lets longer waves pass (Brocchini, 2019). When the opposing river current is strong enough, waves steepen to the point of breaking and even complete blocking can occur (Brocchini, 2019), and even if waves do not get blocked, they may still lose a considerable amount of energy due to enhanced wave breaking caused by currents (Chawla and Kirby, 2002).

A noteworthy point in jet-wave interaction at river mouths is that wave breaking is usually more influenced by the RMB topography than by the direct-wave current interactions (Smith and Smith, 2001; Kang and Di Iorio, 2006; Olabarrieta et al., 2014; Zăinescu et al., 2019), and this makes the morphology a first-order determinant factor in the interaction. This observation was one of the drivers of this study, and it seems that interactions of waves with flow fields have received more attention than the indirect hydrodynamic interactions between the jet and wave-driven LSCs. Considering that storm waves break on the offshore edge of the RMB, where the jet is already spread and as such, the opposing jet-derived currents have much lower velocities, it is thus sensible to think that direct wave-current interactions may not be of first order significance in most conditions.

Because river jets often debouch in the surf zone, significant interaction with the wave-driven circulation is expected. Todd (1968) terms the interaction of LSC with effluents of inlets or river mouths as the “dynamic diversion” (DyD). The effect has been linked from a process point of view to deposition of sediments both updrift and downdrift of river mouths, such as the formation of shoal areas and the existence of chenier plains (Todd, 1968). Taylor et al. (1996) even stresses that shoreline evolution is determined by the strength of the dynamic diversion, with beach-ridge progradation taking place when DyD is strong. This was observed in the experimental modeling of Komar (1973), which was the first to propose the term “groin effect.” Later, field studies confirmed the importance of DyD: Dominguez (1996) found that sediments transported by LSC are retained at the updrift side of a delta; an inlet channel was observed to create a hydraulic obstacle to the longshore drift (Bertin et al., 2004); Giosan (2007) invoked hydrodynamic interactions at the Sfântu Gheorghe river mouth, Danube delta, to explain the development of the RMB; Sabatier et al. (2009) mentions the existence of a hydraulic effect which occurs at the Rhône river mouth, and Anthony et al. (2013) at large river mouths on the Amazon-influenced coast of South America where this effect prevents the formation of mud capes that divert the smaller river mouths. Dodet et al. (2013) and Anthony (2015) note that the “groin effect” is responsible for the disorganization of wave-driven longshore circulation, causing bedload immobilization which is related to the formation of the RMB, and, therefore, a stronger “groin effect” should result in larger deltaic growth (Anthony, 2015). Although initially “dynamic diversion” and then the “hydraulic groin effect” refer to what seems to be the same process, we use here the initial appellation of the effect, dynamic diversion (DyD), because it seems to describe better the hydrodynamic interactions between the Jet and the LSC. The DyD effect thus appears in all the cases where jets intersect LSCs at either tidal or river outlets (Todd, 1968; Anthony, 2015). Notably, the DyD manifests itself as a zone of decreased current velocity and in the diversion of both the river Jet and the LSC.

We explore, by an idealized modeling approach, the morpho-hydrodynamic interactions at river mouths. Our efforts started with the observation that there is a lack of understanding of key processes occurring at river mouths: (i) interaction of river jets with the mouth bar and depth-induced jet spreading; (ii) LSC interaction with river jets with and without mouth bars; (iii) occurrence of the DyD, as a flow interaction mechanism, despite the adoption of this concept in recent research. Taking advantage of a large number of simulations, we quantify each of these processes and provide predictions based on the forcings involved. The RMBs analyzed here share many resemblances with ebb-tidal deltas (Hansen et al., 2013), and as such, the model simulations presented here may apply to tidal inlets in ebb conditions.

Materials and Methods

Numerical Model Description

The Mike 21/3 model proposed by the Danish Hydraulic Institute (DHI) was applied to gain insight into the hydrodynamics at river mouths over a full range of conditions with different idealized river mouth bathymetries. The Mike 21/3 package used in this study comprises the following modules: Mike 3 FM (Flow module), Mike 21 SW (Spectral waves), with the capability of running in coupled mode. Mike 3 FM is based on the three-dimensional incompressible Reynolds-averaged Navier–Stokes equations with the assumptions of Boussinesq and hydrostatic pressure. It consists of continuity, momentum, temperature, salinity, and density equations with multiple models for turbulence (DHI, 2017a).

Mike 21 SW is capable of simulating wave growth due to wind action, propagation in deep and nearshore waters, breaking, dissipation, refraction, diffraction and shoaling, non-linear wave-wave interactions, wave-current interactions (refraction and whitecapping), dissipation due to whitecapping, bottom friction, and depth-induced wave breaking (DHI, 2017b). The full spectral formulation is based on the wave action conservation equation as described by Komen et al. (1994). Non-linear wave-wave interaction may be included, such as quadruplet-wave interactions which are important offshore, whereas in shallow water triad-wave interaction becomes important. Triad-wave interaction is modeled using the simplified approach proposed by Eldeberky and Battjes (1995).

The Mike 21/3 Coupled Model FM enables simulation of the mutual interaction between waves and currents using dynamic coupling between the hydrodynamic module and the spectral wave module by including the radiation stress field that drives currents in the hydrodynamic module, and that is yielded by the spectral wave simulation. Also, water levels and current field variations from the hydrodynamic module are included in the wave simulation. Current velocity has to be taken into consideration in calculating wave propagation speed (DHI, 2017a) as it generates current-induced refraction. Like the SWAN (Simulating Waves Nearshore) model, when waves get too steep, the wave energy dissipates based on the whitecapping expression of Komen et al. (1994).

Numerical aspects and a complete description of the model, with scientific documentation for each module, are available at the Mike website: http://manuals.mikepoweredbydhi.help/2017/MIKE_21.htm#MIKE_21/3_Documentation.

Model Set-Up

This numerical exercise was conceived in order to explore hydrodynamics at constructed idealized river-mouth configurations, some of which resemble the Sfântu Gheorghe (Danube) and the Grand Rhône river mouths. A full range of conditions of discharge (Q, m³/s), significant wave height (Hs, m), and wave directions (°) were included. In total, this produced 25 simulations of only river jet conditions, 125 conditions of only Hs and direction and 500 conditions of combined jet and waves for a total of 650 conditions (Table 1). Percentiles associated with these thresholds can be found in Zăinescu et al. (2019) and a previous model validation with the Mike model can be seen in the same paper.

TABLE 1

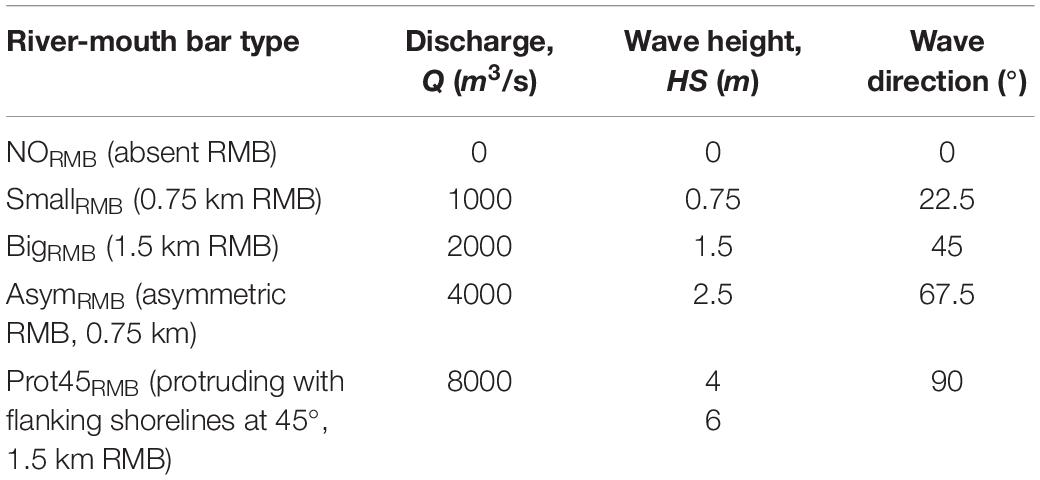
Table 1. A synthesis of the conditions for the numerical simulations (each RMB type has been modeled using each combination of Q and wave conditions).

Bathymetry Construction

Idealized bathymetries were constructed in Global Mapper by drawing lines with prescribed depths at every 2-m isobath in order to recreate observed shoreface slopes (Figure 1). Shoreface slopes near the Sfântu Gheorghe river mouth (updrift) and the Rhône are quasi-linear, different from those predicted by a concave-upward Dean equilibrium profile (Dean, 1991) and are related to sediment transport and redistribution from river mouths in these areas, an indication that the shoreface is not in equilibrium. The updrift Sfântu Gheorghe mouth shoreface has a slope of 170 m/m, whereas the Rhône has around 120 m/m, so an intermediate value of 150 m/m was chosen. The first idealized RMB type (No_RMB) uses only the constant shoreface slope of 150 m/m, and the river channel is 7 m deep at the maximum with around 5 m depth at the outlet where it merges with the shoreface (Figure 1). Mouth bars have steeper slopes on their seaward side than neighboring shorefaces, with a prescribed maximum slope of 50 m/m. Symmetric RMBs have a circular shape and smoothly join the shoreface at both updrift and downdrift sides. The Small_RMB type displays a small symmetric bar in front of the river mouth, with a distance from the river mouth centerline to the offshore edge of the mouth bar of about 750 m. In the Big_RMB type, this distance is increased to 1500 m. A case with no RMB present (No_RMB) is provided to compare the results with conditions where the RMB is present, and this type is expected to be found where sediment dredging is active. The first special type, the Asym_RMB, resembles the asymmetric and deflected Sfântu Gheorghe river mouth configuration and has the river channel oriented 45° downdrift, a shoreline that is recessed 500 m and a shoreface that is flatter downdrift (250 m/m slope down to −4 m), while maintaining similar characteristics with the Small_RMB type for the updrift side. The Prot45_RMB type is similar to the protruding Grand Rhône (the main mouth of the Rhône) RMB, having flanking shorelines that are angled at 45°, while the RMB configuration keeps the characteristics of the Big_RMB type (Figure 1). Using these bathymetries, we maintain a low number of simulation cases, with RMBs that are largely representative for the river mouths of most wave-influenced deltas. Some mesoscale RMB morphology is excluded in the model such as larger bedforms or river cut channels. These are continuously evolving and may form during particular regimes of wave height and discharge and could not be included in the prescribed meshes.

FIGURE 1

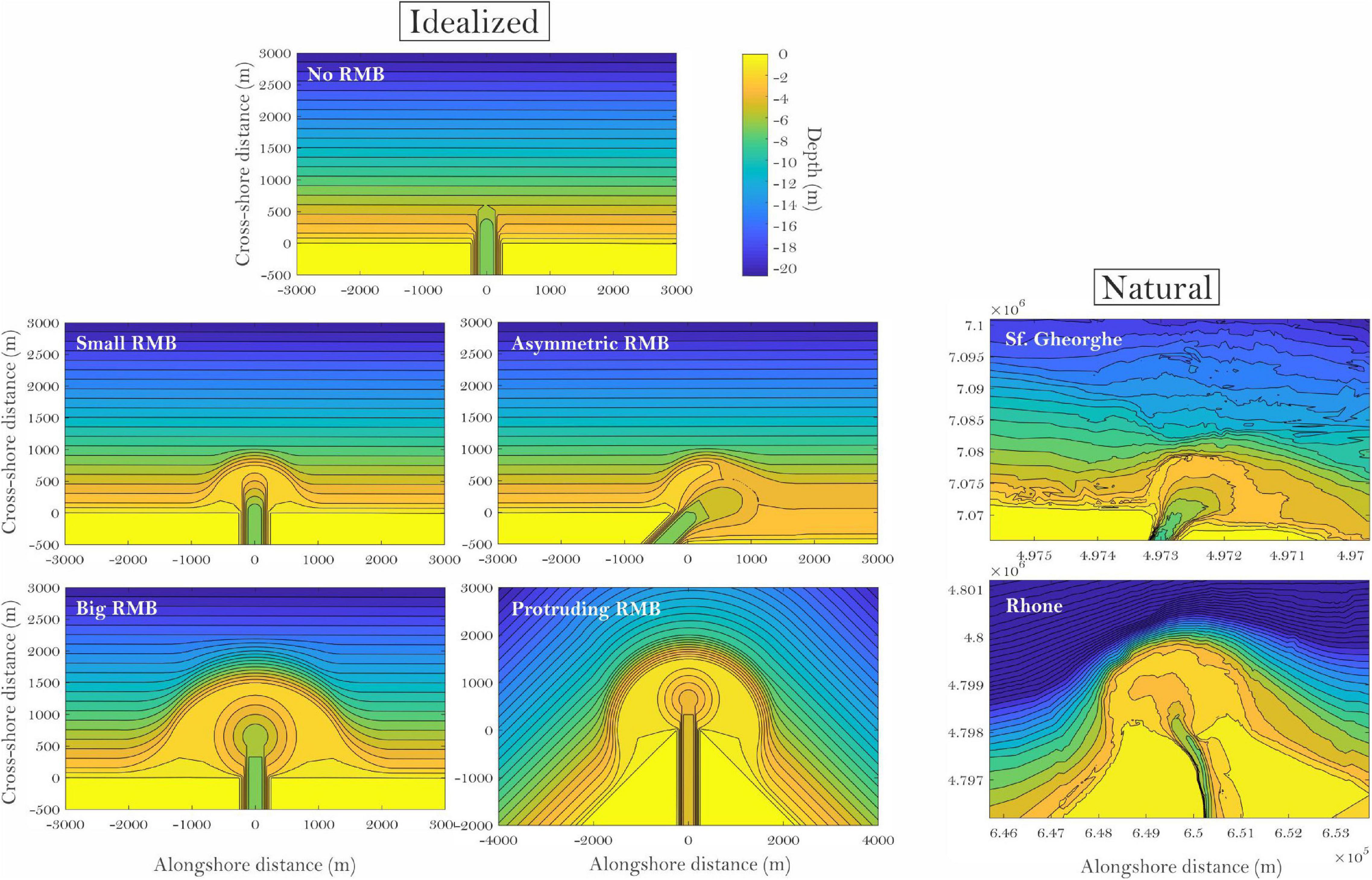
Figure 1. The idealized river mouth bar (RMB) bathymetries used in the present study, and their natural counterparts (right).

The whole domain stretches 12 km updrift, 5 km downdrift, and 8 km offshore (Supplementary Figure 1). The meshes comprise 12,000 elements and are constructed at three levels of detail (L), with L3 (close to the river mouth) having a triangular element side of about 40 m and an area of ∼700 m², L2 a triangle area of ∼14,000 m², and L1 (offshore) a triangle area of 200,000 m². The river channel mesh is quadrangular with elements of 30 m width and 100 m length. The simulations with only the river jet have an L3 extending farther offshore and Prot45_RMB is larger because the mesh extends to cover the space created by the angled shoreface.

Model Parametrization

Bed resistance was specified in the HD module as a constant roughness height of 0.05 m, with no Coriolis forcing. Eddy viscosity, which is the transfer of momentum by turbulent eddies, was specified by using a k-epsilon formulation. For this turbulence model, the eddy viscosity is determined as a function of the turbulent kinetic energy and the dissipation of the turbulent kinetic energy. For SW, fully spectral and non-stationary formulations were used, with a logarithmic frequency discretization in 24 bins, and a 15° directional resolution, a constant Nikuradse roughness for bottom friction of 0.04 m, and default coefficients for whitecapping (Cdis 4.5; DELTAdis 0.5). A constant value of the background roughness Charnock parameter of 0.01 (default) was used in SW. In the “coupled” formulation, the momentum transfer from the wind to the waves depends not only on the wind but also on the waves according to the formulation of Komen et al. (1984), DHI (2017b). Triad wave interactions are included. Wave breaking is based on the formulation of Battjes and Janssen (1978), and the gamma value which controls the wave steepness based on the functional form of Ruessink et al. (2003). This gamma parameter is determined as a function of the product of the local wave number and the water depth and it showed improved prediction of wave heights in the breaking zone (DHI, 2017b). In the case of breaking waves, energy is extracted from the organized wave motion and is converted into turbulence, where the total production of turbulent energy equals the dissipation energy. The eddy viscosity due to wave breaking is calculated from the transport equation for turbulent kinetic energy (e.g., Deigaard et al., 1986; DHI, 2017b).

Boundary conditions were specified either as wave parameters for offshore, or as land (with zero velocity). Water discharge was prescribed at the boundary of the river channel. For open boundaries, the Flather condition (Flather, 1976) was used, which is an efficient condition (DHI, 2017a). Peak period (Tp) for each wave height was determined based on ERA5 data at the Sfântu Gheorghe river mouth and is representative for wind-wave conditions. Directional standard deviation (DSD) which is a measure of wave direction variation is a fixed value of 30, as determined during storm conditions for ERA5 data, and Ws (wind speed) was based on a relation with wind speed at the Sulina meteorological station in the Danube Delta (Figure 1) and ERA5 wave data. Wind speed was used only in the SW module to drive generation and maintenance of waves, and attention was paid to the wave heights just offshore of the river mouth so that they would correspond with the values prescribed at the boundaries, but wind effects on the circulation were excluded to maintain the clear structure of LSCs.

The large number of simulations necessitated some optimizations for achieving computation in a reasonable time. First, some parametrizations were preferred and sensitivity tests were performed for comparison. These are: a low-order solution technique for space and time discretization of both HD and SW modules (no significant change in results), no Flood and Dry (not needed), no density effects (barotropic mode), no diffraction for SW simulation because the effects were only limited to inside the river channel (not the main focus of the study). These optimizations decreased the computational effort. Nevertheless, the simulation maintains conditions such as 3D hydrodynamics with 15 vertical sigma layers, high-level k-epsilon turbulence model, and although this increased computational times significantly, the maximum level of transport for waves was kept at 4 to improve model stability in high wave conditions.

Secondly, the way conditions are introduced in the model domain and at boundaries had to be efficient. Wave height increases from 0.75 up to 6 m and each particular wave height is maintained for 8 h (found to be optimal after sensitivity tests), with only one fixed direction. This resembles somehow the increase in wave height during storms and permits simulating higher waves in less time because nearshore hydrodynamics are already wave driven when a new wave height condition sets in. At the end of the 6 m Hs condition, there is a pause of 12 h to avoid residual circulation and for the hydrodynamics to become stationary. Then, direction changes with a 22.5° increment (from 0° to 22.5° for example) and the increase in wave height starts again. This produced a 11.5-day simulation (for all Hs and directions) that was run for each discharge (Q0 to Q8000 m³/s) and for each RMB type, in total for about 300 in-model days. The simulations were completed in about 3 months on a 3.5 Ghz, 4 core Intel Xeon E3 1245 v5 CPU with a Nvidia GTX 1060 graphics card, the latter used only for the HD module. Hydrodynamic computations could be run efficiently on the GPU, while the computations for the SW module were running on the CPU. Switching to 2D mode would not result in any computational advantage with our current set-up. Three-dimensional mode for hydrodynamics was preferred because it could better represent the jet structure and spreading especially in deeper areas.

The resulting simulations were imported in Matlab through the DHI MATLAB Toolbox, which allows the reading of all the proprietary.dfs file types that the Mike model outputs https://github.com/DHI/DHI-MATLAB-Toolbox.

Wave and River Discharge Data

For the Sfântu Gheorghe and Grand Rhône river mouth comparison, we used ERA5 wave data a state-of-the-art climate reanalysis (Hersbach et al., 2020) made available by the European Centre for Medium-Range Weather Forecasts (ECMWF), retrieved in front of each river mouth. More information on the ERA5 dataset can be found at https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era5. Daily river discharge was provided by the Global Runoff Data Centre https://www.bafg.de/GRDC/EN/Home/homepage_node.html.

Results

We investigate jet- and wave-driven longshore circulation and their interaction at river mouths by using a numerical simulation which represents a full range of conditions expected in wave-influenced river-mouth environments. The approach may be considered as reductionist, where we aim for an understanding of the components by firstly separating wave-driven and jet-driven circulation. Then, the more emergent circulation is analyzed to understand the interactions under steady-state flow. The hydrodynamic model is run in 3D, but all the current fields presented here are depth-averaged.

River-Mouth Jet and Wave-Driven Hydrodynamics

The hydrodynamics discussed in this chapter lay out the basic conditions found at river mouths. First, we investigate the model experiments performed on the idealized river-mouth type with no mouth bar (No_RMB case) to show how a situation with only jet-driven circulation compares to one with only wave-driven circulation. The river-mouth jet and the LSC reach a steady state with a sufficiently organized structure at the end of the simulation period for these particular conditions. In this case, the river jet is an effect of the initial outlet flow momentum, and is perpendicular to the coast, whereas the LSC can be described by the radiation stress theory (Longuet-Higgins and Stewart, 1962; Longuet-Higgins, 1970), and is shore-parallel.

The surface velocity fields indicate that the jet structure is maintained even 3 km offshore, which suggests that there is a low topography-induced friction in the No_RMB case. The candle-light bulge shape in the nearshore is related to some increased friction at the river-mouth outlet where the river channel connects to the shoreface (Figure 2). Initially, jet centerline maximum velocities start at about 0.5 m/s for Q1000 and 3.7 m/s for Q8000 and drop to about 0.23 and 1.66 m/s at 2000 m offshore distance. This is a relatively low cross-shore decrease in velocity compared to the high alongshore decrease in velocity which cause the jet to lose 90% of initial velocity in just one river-mouth width. Thus, the jet shows low lateral spreading. Three-dimensional fields reveal that it is also spreading vertically, suggesting higher vertical momentum exchange. It is noteworthy to add that in natural conditions where density differences are present, buoyancy forces will dampen this strong jet structure, advecting the jet vertically and spreading it laterally.

FIGURE 2

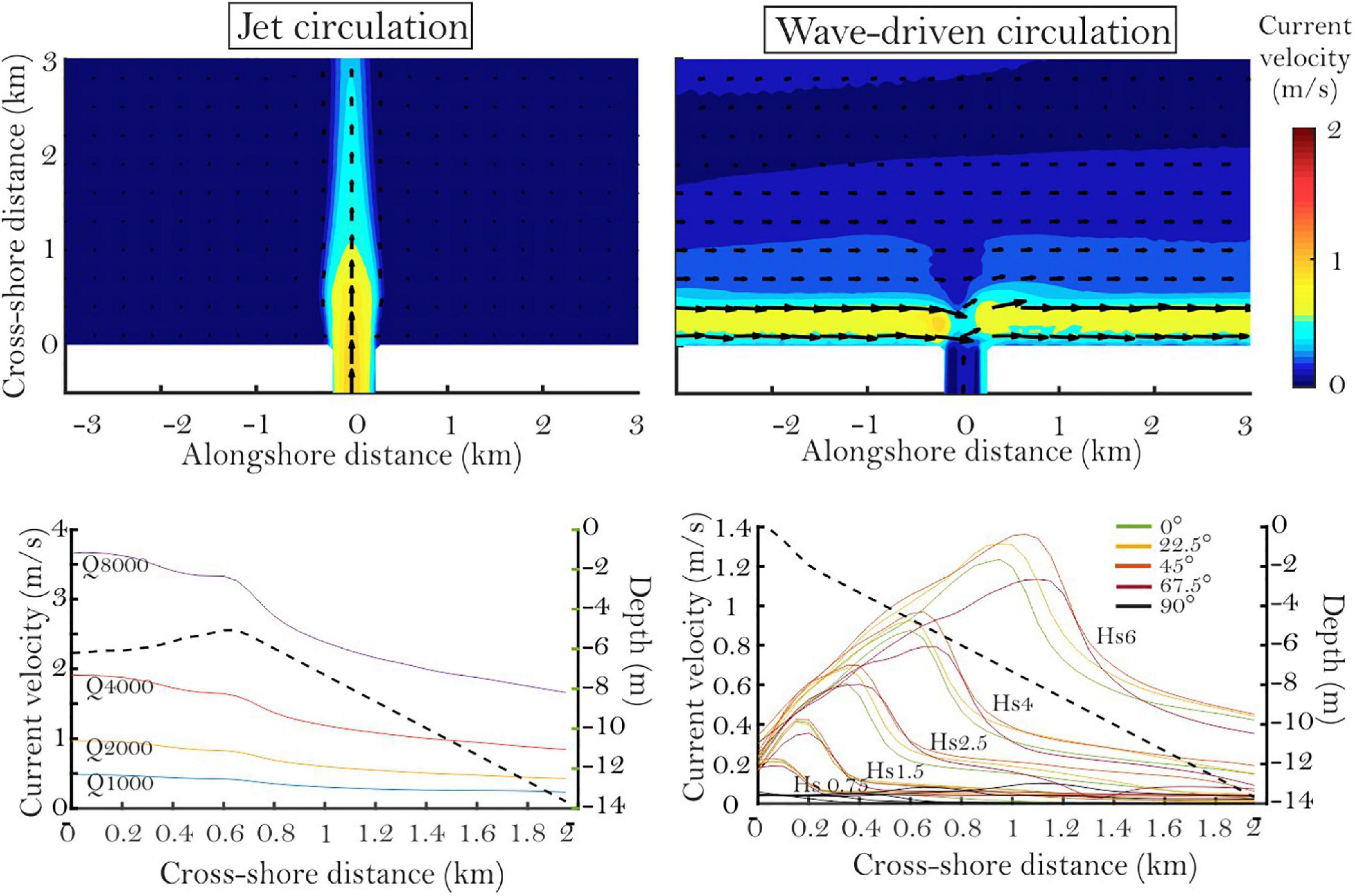
Figure 2. Jet (left) and wave-driven (right) circulation types with no RMB. Top plots show a jet at Q = 2000 m³/s and LSC conditions at Hs 2.5 m and 45° incidence. For the bottom plots, jet velocities are taken on the jet centerline, whereas LSC velocities are taken on a profile at –1.5 km alongshore. Dotted lines show the profile bathymetry.

Maximum LSC velocity increases linearly with wave height, from around 0.2 m/s at Hs_0.75 to 1.4 m/s at Hs₆. Concomitantly, the LSC offshore extension, identified as the place where the offshore velocity decrease starts to slow down, as a delimiter of the LSC that is driven by wave breaking, extends offshore linearly from 0.2 km for Hs_0.75 to 1.4 km for Hs₆. Offshore wave direction seems to be of second order in determining circulation between 0° and 67.5°, with 45° having the highest velocity, while 0° and 67.5° have comparatively the lowest values by a difference of −20%. Between 67.5° and 90°, the LSC drops to 0 because the alongshore component of the radiation stress (Sxy) also drops to 0; this case may be rare in nature, where variations in surfzone topography will generate some LSC (albeit lower). A slight decrease in the LSC can be observed just in front of the RMB where the shoreface is absent. Also, the maximum velocity in the LSC in the cross-shore dimension seems to occur at a depth of ∼1.3 Hs, indicating that wave-breaking drives the maximum velocities in these locations. Whereas velocities are saturated closer to the shoreline, remaining largely unchanged with increasing Hs, the offshore extension of LSC occurs in the surfzone (Figure 2).

Jet-RMB Interactions: Jet Spreading and Deflection

By acting as bathymetric obstacles in front of the river jet, river-mouth bars cause lateral momentum spreading and inhibit vertical spreading. Figure 3A shows the 0.2 m/s jet velocity contours at Q = 2000 m³/s overlapped on the 2 m depth bathymetric contours. The jet structure is maintained even for increasing Q. For the Asym_RMB case, the jet is both deflected and spread because of the channel orientation with the presence of the mouth bar attached to the updrift coast versus the more recessed downdrift flank. For increasing RMB dimensions, the jet takes first a more circular-elongated shape in the case of the Small_RMB, but is increasingly wedge-shaped in the case of Big_RMB, indicative of high spreading.

FIGURE 3

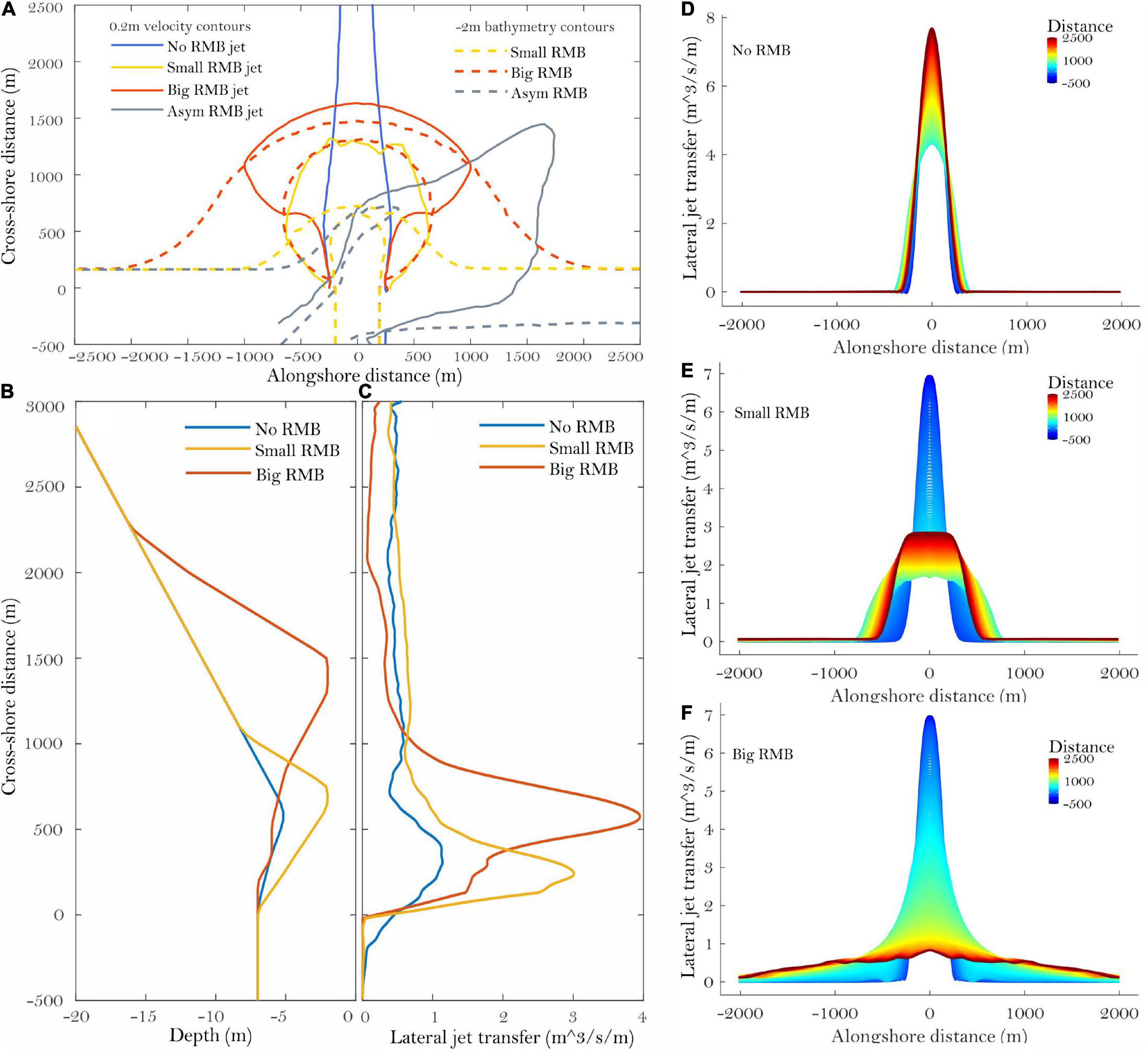
Figure 3. Influence of RMB types on jet spreading. (A) shows the contours of 0.2 m/s velocities plotted for the different jets. (B) and (C) show the bathymetric profiles on jet centerline and the lateral jet transfer rate (LJT). (D–F) illustrate the change in jet structure evidenced by the discharge (m³/s) in relation with the three types of RMB; colors represent increasing cross-shore distance (m); the river outlet located at 0. Prot45_RMB is not shown because spreading is similar to Big_RMB.

The lateral jet transfer rate (LJT) (Figure 3B) measures the discharge (m³/s/m) advected laterally from the jet structure. This discharge is calculated by integrating the cross-shore oriented component of discharge that is changing in the cross-shore dimension over each unit of distance (here, 1 m). It can be regarded as the amount of discharge that is lost from the cross-shore direction and transferred alongshore. For example, a LJT of 1 m³/s/m indicates that 1 m³/s is transferred laterally each meter in the cross-shore dimension.

$$\text{LJT}\left(\text{y}\right)=\text{∑QJet}\left(\text{y}\right)-\sum \text{QJet}\left(\text{y}+1\right)(1)$$

where Q_Jet is the discharge value (m³/s) and y is the location in the cross-shore dimension (m).

In the case of the No_RMB, the LJT has maximum values of 1 m³/s/m at the outlet and then stabilizes at around 0.5 m³/s/m. Also, Figures 3C,D shows that the jet structure is maintained with increasing distance from the river mouth. The Small_RMB forces the jet to spread more laterally, reaching 3 m³/s/m, immediately before the RMB crest, and to maintain a similar spread of 0.5 m³/s/m after the RMB crest Figure 3E. A high increase in LJT occurs in the Big_RMB case which has a RMB crest situated at double the distance of the Small_RMB crest, and a much greater volume. Maximum LJT values are 4 m³/s/m, but rates between 1 and 3 m³/s/m are maintained longer than in the Small_RMB case, thus leading to an almost complete spread of the jet by the time it leaves the RMB. This is also evidenced by the lowest offshore values of LJT which occur in the Big_RMB case (0.2 m³/s/m), indicating a jet that has already been spread (Figures 3B,F).

These results show that the RMB, through frictional effects, may profoundly change an idealized jet structure, from diverting it in the case of Asym_RMB, up to the point of completely spreading it laterally as in the case of Big_RMB.

Wave-RMB Interactions and Circulation Types

Wave-driven circulation in the presence of a RMB deviates from the continuous LSC obtained for a constant alongshore shoreface slope. With varying Hs and direction, several wave-driven circulation types were identified which we illustrate on the Big_RMB type: (i) Low waves: Updrift discharge of LSC into the RM, LSC generation on the downdrift side of the RMB crest. In this situation, there is a lack of wave-driven circulation on the mouth bar crest because wave breaking does not occur there (Figure 4A1), the depth being greater than two times the wave height. (ii) Complete bypass during high waves and high incidence angles (Figure 4A2): the LSC is somewhat diverted by the RMB, but most of its alongshore discharge remains continuous. An intensification of flow may be observed on the downdrift bar crest (D_barLSC). Although there is some flow on the flanking bar crests, most of the discharge occupies the space offshore of the −2 m bathymetric contour; (iii) LSC deflection, rip-current and eddy generation on the updrift flank (Figure 4A3). When waves approach more normal to the coast, longshore divergence points appear at the focal locations of waves on the RMB crest, which occur where the refracted waves have an orientation normal to the shoreface. The opposing LSC (compared to the offshore wave direction), named here the counter-longshore current (C_LSC), interacts with the LSC which normally flows on the straight updrift beach (Up_LSC), generating either offshore-directed jets (rip currents) or eddy circulation when the C_LSC remains at shallow depths and the Up_LSC bypasses it on the offshore flank. (iv) Diverging LSCs (C_LSC and the downdrift LSC, D_barLSC) which occur in the case of normally incident waves (Figure 4A4). When waves approach directly from 90°, the result is a generation of two LSCs, equal in magnitude, diverging from the apex of the RMB. The jet-dominated circulation type for the same Big_RMB case is shown in comparison with the wave circulation types (Figure 4B).

FIGURE 4

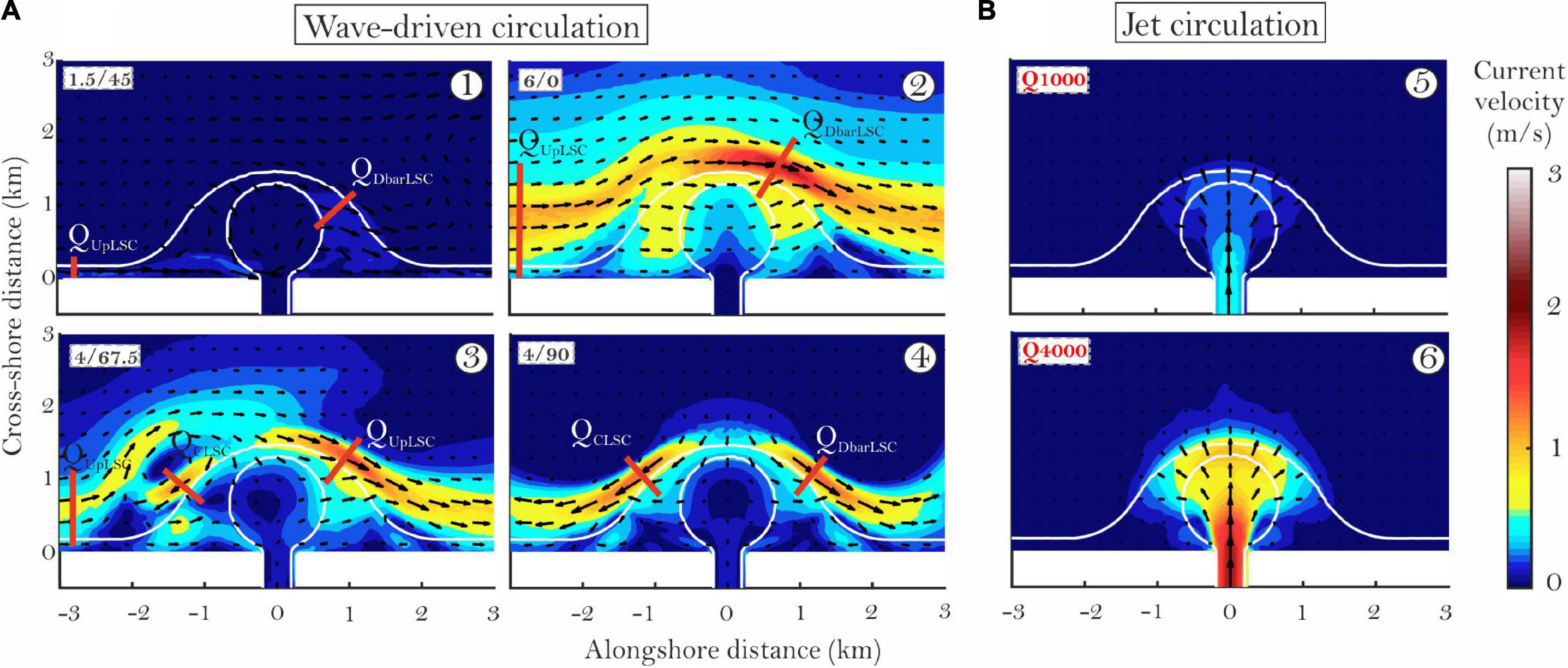
Figure 4. Wave-driven (A) and jet (B) circulation for the Big_RMB case. The red lines on the wave-driven circulation types represent the sections through which either discharges (Q) of Up_LSC, C_LSC, or DbarLSC were measured. Conditions for each simulation are shown in the upper left corner of each panel (1.5/45 denotes 1.5 m Hs, 45° direction; and Q1000 is 1000 m³/s discharge). White lines are the –2 m isobath.

LSC and JET Interactions in the No_RMB Case

First, we direct our attention to the simplest Jet-LSC interactions occurring in the No_RMB case. Either a straight jet, continuous LSC circulation, complete jet deflection or various degrees of jet deflection have been identified (Figure 5). In certain conditions, the straight Sulina mouth river jet from the Danube Delta (Figure 6) resembles quite well the modeled straight jet cases. Jet deflection is defined as the degree of deviation of the jet structure and is measured as the angle between the centerline of a straight jet and the centerline of the deflected jet. To relate jet deflection to the characteristics of waves, we use the balance of the jet momentum flux (Mj) relative to the alongshore component of wave momentum flux (Mw) which has been previously hypothesized to control momentum interactions and deflection at river mouths (Nienhuis et al., 2016):

FIGURE 5

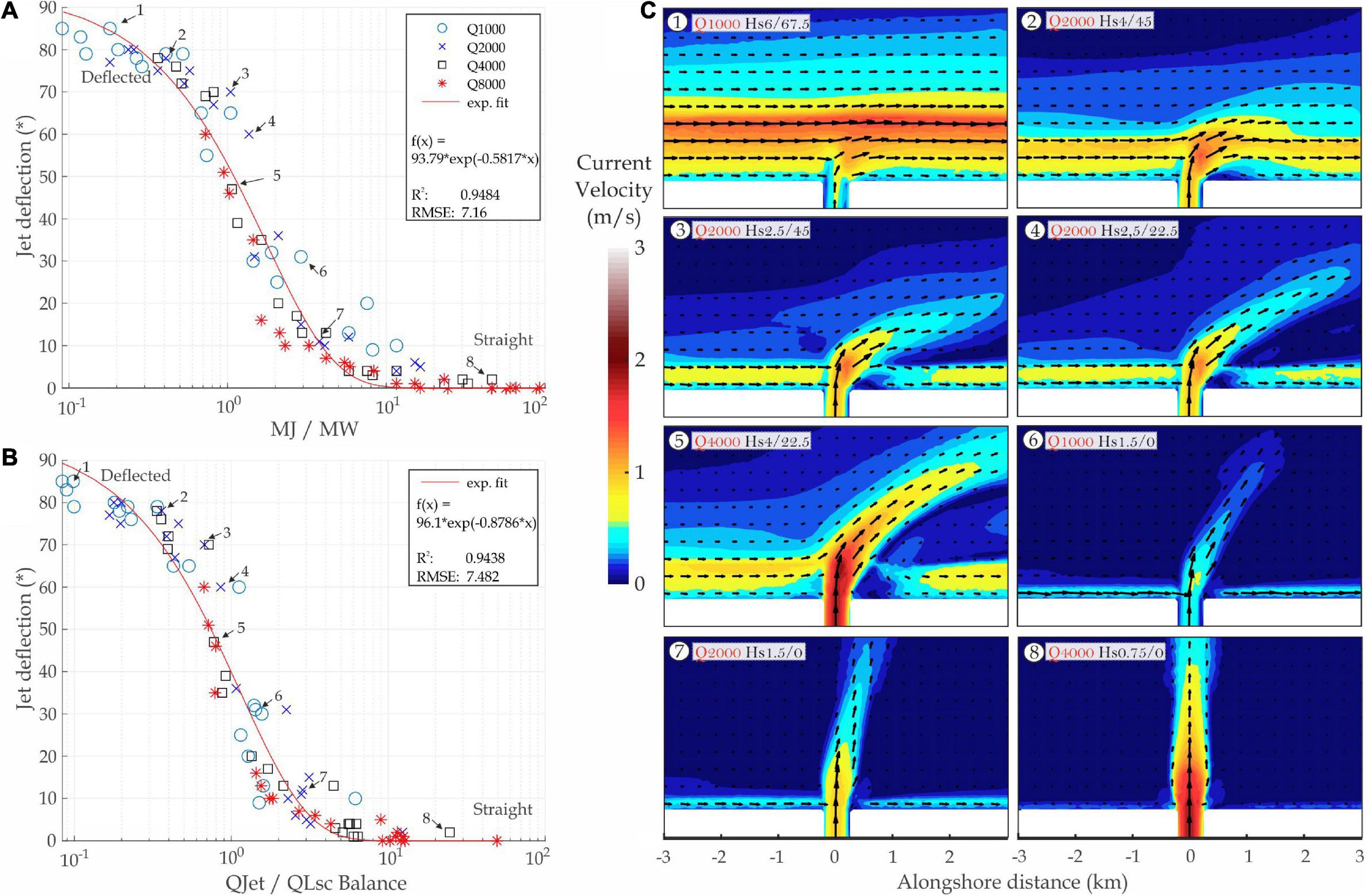
Figure 5. River jet and wave-driven LSC interactions in the No_RMB case. The jet deflection angle is plotted against the momentum of jet to the momentum of waves ratio (MJ/MW) (A), or against the balance of jet discharge (Q_Jet) and LSC discharge (Q_LSC) (B). A selection of river jets is shown in (C) which illustrate the change in jet orientation from deflected to straight. A total of 90° directions are excluded because these produce only jet spreading. Conditions for each simulation are shown in the upper left corner of each panel (Q1000 is 1000 m³/s discharge and 1.5/45 denotes 1.5 m Hs, 45° direction).

FIGURE 6

Figure 6. Straight jet of Sulina (Danube) river mouth (channelized by jetties), used to show similarities with modeled straight jets. Satellite image from Google Earth.

$$\frac{Mj}{Mw}=\frac{\mathrm{\rho }\times \text{A}\times \text{u}}{Sxy\times \text{W}}=\frac{\mathrm{\rho }\times \text{Q}}{E\times \text{n}\left(\text{cos}\times \text{sin}\right)\times \text{W}}(2)$$

where ρ is the water density, A the cross-sectional area of the river mouth outlet, u the average river velocity, Sxy the alongshore-directed component of the radiation stress (computed for the general orientation of the straight coast), W the width of the river mouth (m), E the wave energy density which equals $\frac{1}{16}gH{s}^2$ (Airy, 1841), g the gravitational vertical acceleration, Hs the significant wave height (m), n the ratio of the group velocity to phase velocity of the incoming waves, considered 2 for deepwater, and θ the incoming wave angle.

The Mj/Mw is similar to the previously proposed “discharge effectiveness index” of Wright et al. (1974) which is the ratio of the discharge per unit width of river mouth to the nearshore wave power per unit width of wave crest. Note that a value of 10° has been used for wave simulations at 0° because there is obviously some refraction in the shoreface that transfers alongshore momentum, whereas the deep-wave formulation would predict 0.

The Mj/Mw provides excellent approximations of the magnitude by which a jet will be deflected under idealized conditions (Figure 5A). Alternatively, we compute a balance based on the discharge of the jet (Q_Jet) to the discharge of the LSC (Q_LSC) obtained from numerical modeling (Figure 5B). The modeled river jet experiences less than 10° deflection at Mj/Mw and Q_Jet/Q_LSC >2, but larger than 60° of complete deflection when Q_Jet/Q_LSC <0.5. Jet deflection may not occur completely due to shoreface constraints. When Mj/Mw and Q_Jet/Q_LSC are close to 1, the jet is deflected around 40° to 45° (Figure 5C5). This means that when the jet momentum balances the alongshore wave-driven momentum, the jet is deflected half-way. Also, the relationship between Mj/Mw and Q_Jet/Q_LST with the deflection angle describes a sigmoid shape which reveals that rapid jet deflection occurs when momentum balances are close to 1 (Figures 5A,B). The above results are valid for a river jet and a LSC interacting at a 90° angle, and show a rather simple relationship with stationary conditions. Nevertheless, this may be complicated by different LSC and Jet structures and different angles of impact. Moreover, scaling effects from Q₁₀₀₀ to Q₈₀₀₀ and Hs_0.75 to Hs₆ are low, which indicates that the interaction illustrated by the model is applicable to Jet-LSC interactions over a wide range of Q_Jet and Q_LSC conditions.

Average Q_LSC for a certain wave height increases at an accelerated rate compared to Hs, because wave energy depends on Hs². Also, the discharges used for the river jet seem to be comparable to those of Hs; Q₁₀₀₀ with Hs_1.5, up to Q₈₀₀₀ with Hs₆, which indicates that the modeled thresholds of wave heights and discharge were well chosen (Supplementary Table 1).

Jet flow deflection resulting from wave effects has been observed in the field (Olabarrieta et al., 2011; Akan et al., 2017), and has been hypothesized to occur in relation to the relative intensities between the jet and coastal current (Antia, 1995). In precise and constrained conditions such as an absence of a RMB and no effects from stratification, LSC-Jet interactions seem predictable. Nevertheless, many strongly dredged and engineered river mouths that do not have a frontal RMB are bounded by jetties, which limit LSC-Jet interactions. Nevertheless, even there, the buoyant lifted jet may be deflected by wind-driven coastal currents. As such, when river mouths are disconnected from the shorelines through extended jetties, wind stress acting on a buoyant effluent may have the first-order effect, and these interactions should still be governed by a balance of momentum. This tentative extension remains to be tested with field data and further numerical investigation.

LSC and River-Jet Interaction With Different RMB Configurations

When a RMB is present, it changes both the jet effluent patterns by increasing spreading, and the LSC circulation by drift alteration on the updrift side of the bar and wave breaking-induced acceleration on the RMB crest. The Mj/Mw or Q_Jet/Q_LSC is also used here as an indication of the type of circulation. As such, circulation is wave-dominated when these ratios are <0.5; jet-dominated when >2, and strong wave-jet interactions are occurring at Mj/Mw and Q_Jet/Q_LSC approaching 1. We decided to quantify and discuss the LSC interaction on the basis of just the discharge (Q_LSC and QC_LSC) due to the difficulty of computing a value of Mw for the C_LSC on a circular subaqueous shoreface as the RMB.

Firstly, high and oblique waves favor longshore circulation and RMB bypass, whereas low waves and normal-to-coast angles generate diverging LSC on the mouth bar crest which interrupts the longshore circulation. Figure 7 shows that the transition from alongshore-dominated to divergent flow may be defined by the balance between the discharge of the counter-longshore current (QC_LSC; Figure 4A3) and the updrift longshore current (QUp_LSC). Values approaching 0 are indicative of alongshore circulation, whereas increasing values determine the appearance of a rotating eddy updrift of the RMB, and ultimately, with increasing values, an offshore-directed rip current. Smaller RMB cases (Small_RMB and Asym_RMB) are less favorable to C_LSC generation due to their less protruding shape, and less focusing effects on waves (Figure 8). As such, wave breaking-induced accelerations that form the C_LSC are lower and the circulation is more alongshore-dominated. The protruding RMB case (Prot45_RMB) seems to be the most favorable for C_LSC generation. Because the updrift coast is oriented 45°, only the wave cases of 0° and 22.5° can generate an Up_LSC, while C_LSC is generated in all cases (Figure 9). The strength and the length of the C_LSC are higher and as such, interactions with Up_LSC and rip-current generation occur farther away from the river mouth.

FIGURE 7

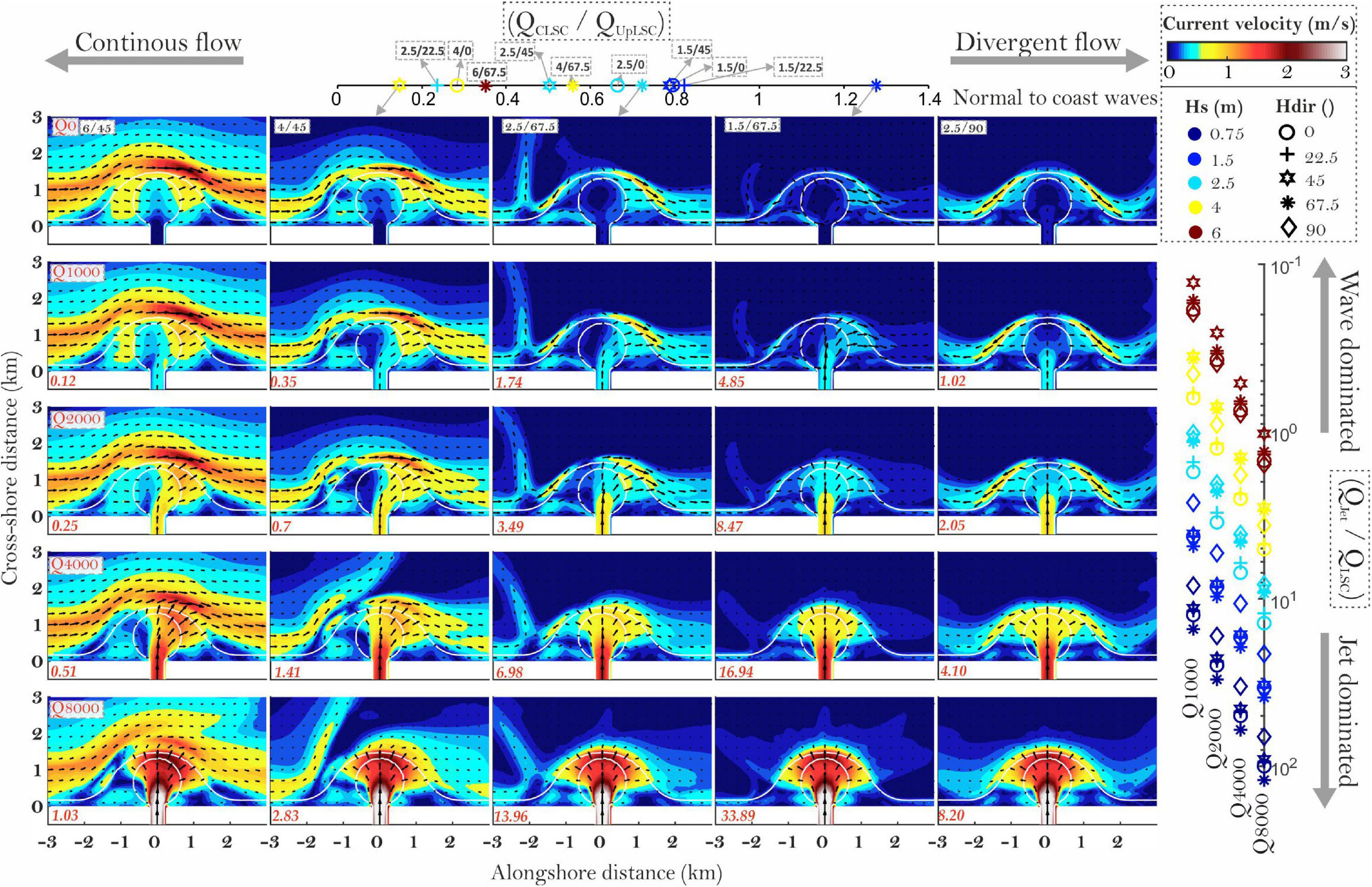
Figure 7. Circulation patterns for the Big_RMB case with a selection of wave heights, directions, and river discharges. Values in left bottom corner of each plot show the Q_Jet/Q_LSC ratio.

FIGURE 8

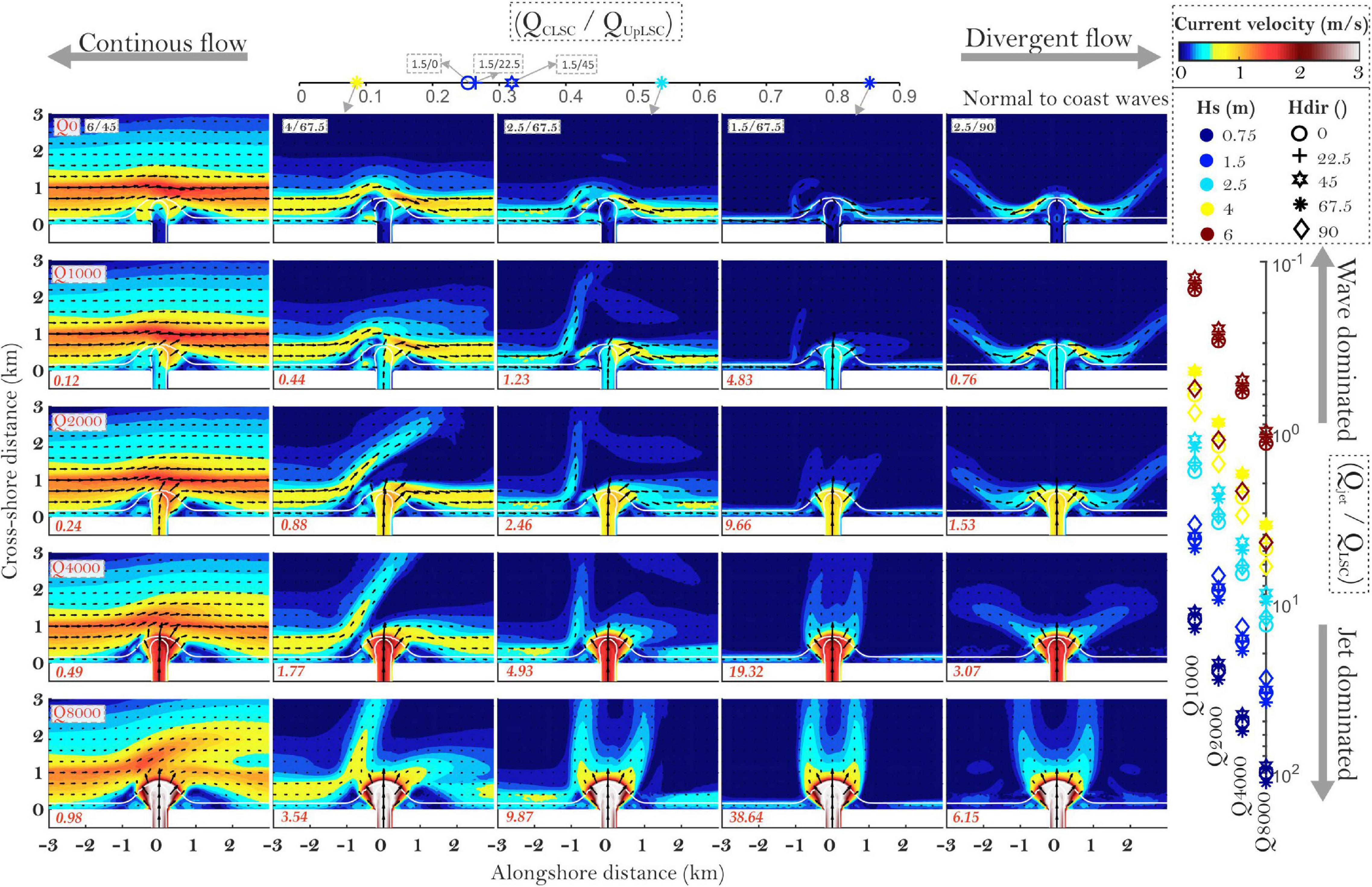
Figure 8. Circulation patterns for the Small_RMB case with a selection of wave heights, directions, and river discharges. Values in left bottom corner of each plot show the Q_Jet/Q_LSC ratio.

FIGURE 9

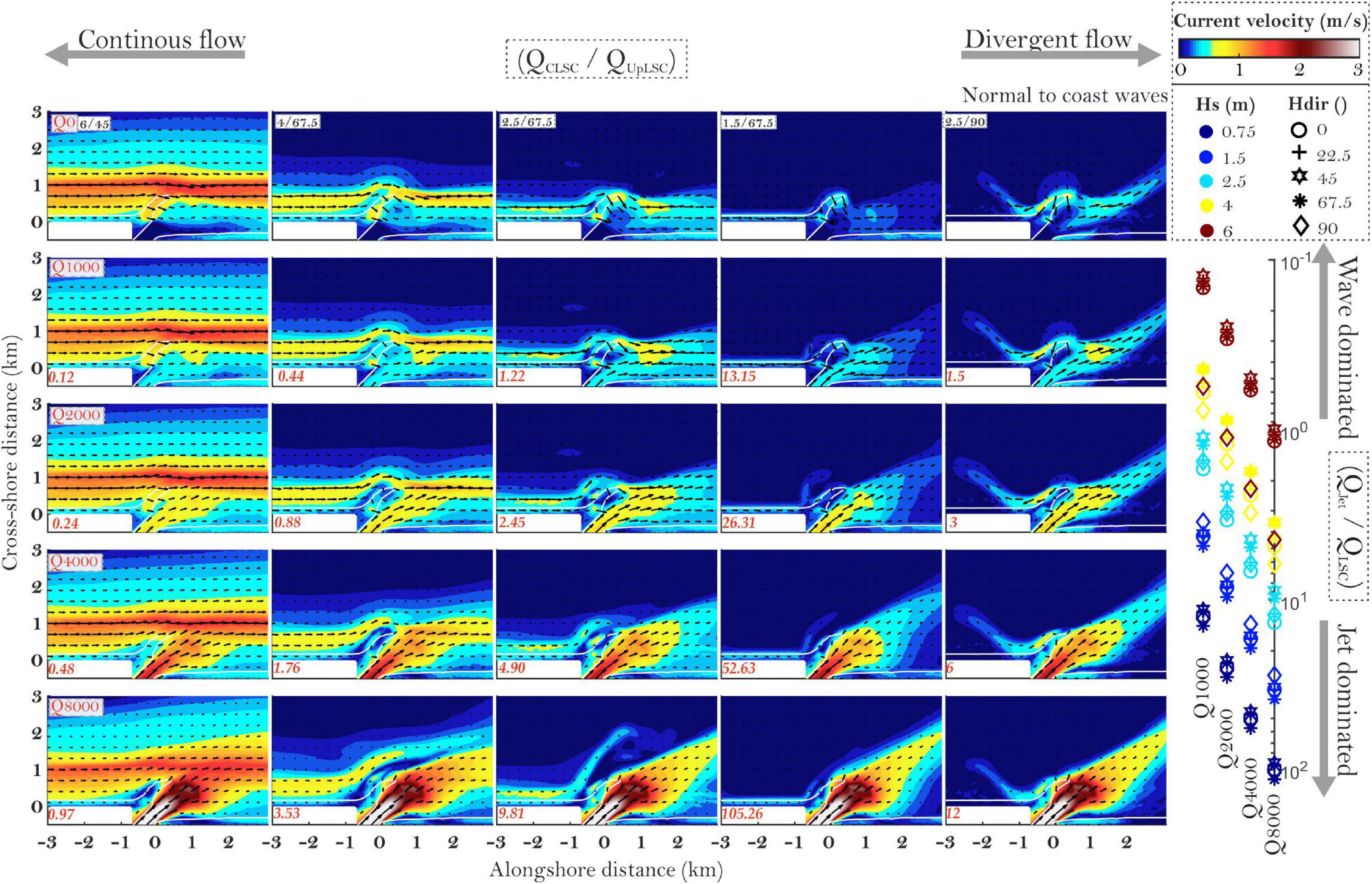
Figure 9. Circulation patterns for the Assym_RMB case with a selection of wave heights, directions, and river discharges. Values in left bottom corner of each plot show the Q_Jet/Q_LSC ratio.

The addition of the jet momentum to the wave-driven circulation may cause significant change in the flow fields when the jet is sufficiently strong. Initially, the jet seems to inhibit alongshore circulation and to strengthen C_LSC flows. Then, when the jet is sufficiently strong, the circulation can become almost completely jet-dominated on the RMB (at Q_Jet/Q_LSC >10). Also, equally valid, higher waves are clearly able to deflect the river jet even in the Big_RMB case, but compared to the No_RMB case, the jet seems to be less deflected because of the physical constrains imposed by the RMB.

The Small_RMB case, for the same C_LSC and Q_LSC, may favor a more jet-dominated circulation because of the lower jet spreading and lower C_LSC velocities, and thus lower wave focusing (Figure 8). The special case of Asym_RMB (Figure 9) is one that favors additional frictional and channelization effects which cause downdrift jet deflection that is less able to interact with the incoming wave field and the LSCs. As such, this case is the most prone to alongshore-dominated circulation. It can be also envisaged that the more wave-deflected the RMB is, the more the morphology reinforces jet deflection in a positive feedback until a new equilibrium is reached. On the other hand, the Prot45_RMB case (Figure 10) experienced only divergent circulation even in the case of offshore Hs with 0° direction.

FIGURE 10

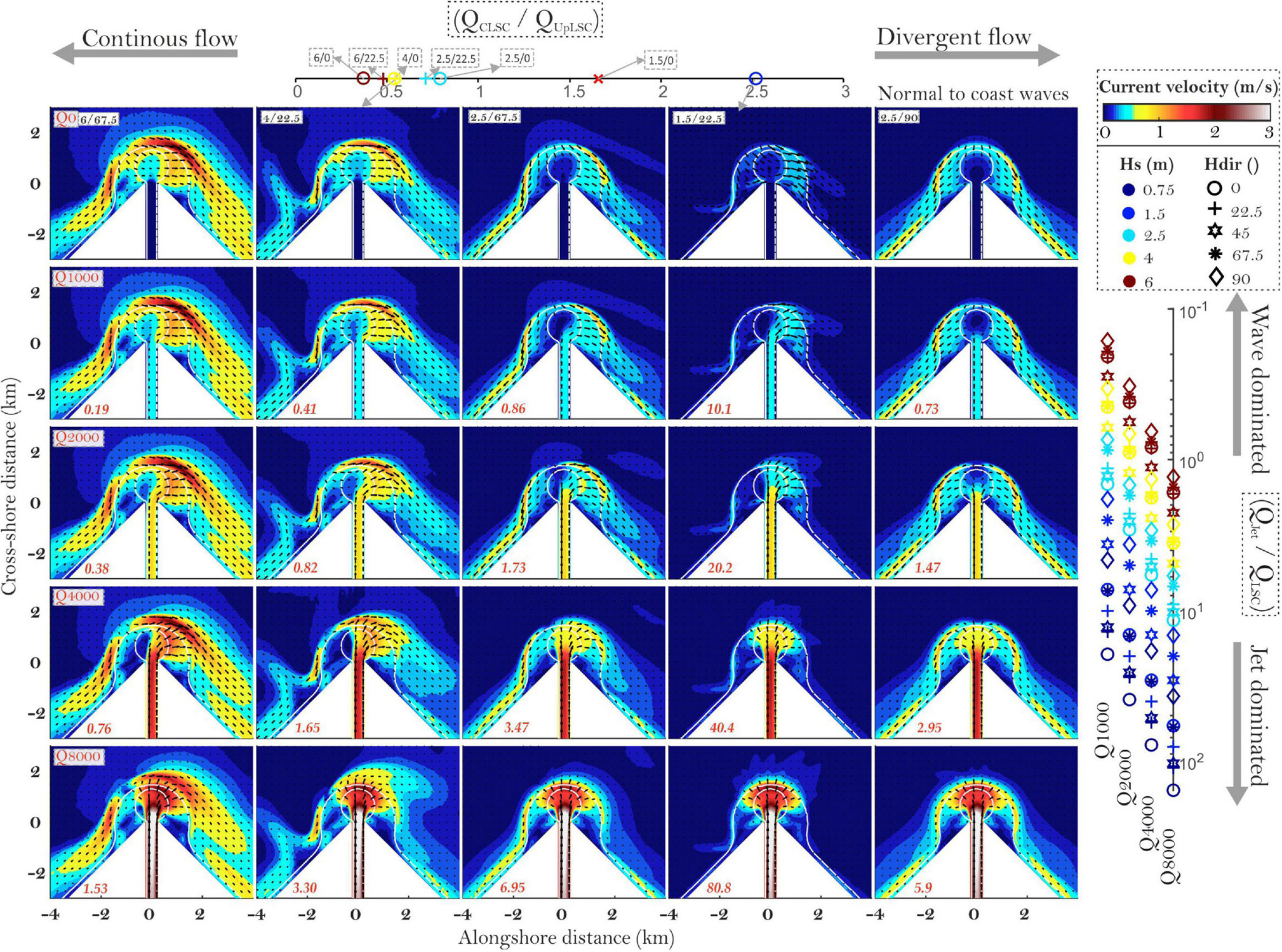
Figure 10. Circulation patterns for the Prot45_RMB case with a selection of wave heights, directions, and river discharges. Values in left bottom corner of each plot show the Q_Jet/Q_LSC ratio.

River-mouth morphologies are already the resultant of the long-term relative jet and wave conditions occurring at river mouths. It seems that for the Asym_RMB case, the morphology strengthens the alongshore domination because of a weaker jet effect, whereas increasingly large and protruding river mouths start to block alongshore circulation first by the generation of C_LSC on the updrift RMB crest, and then by the large-scale morphology which inhibits LSC generation in the direction of the approaching waves, and favors more divergent circulation in the case of Prot_RMB. Moreover, the comparison between the Big_RMB case and the Small_RMB case points out the fact that a smaller RMB means a more direct Jet–LSC interaction, and thus lower wave-driven alongshore circulation at the river mouth, whereas for a big RMB, if the same jet Q is kept, wave-driven circulation is better developed.

Quantifying the Dynamic Diversion

In order to understand the magnitude of the interactions occurring between the LSC and the river jet, a non-dimensional Dynamic diversion index (DyD) is proposed in order to compare only jet or only wave simulations (termed here c1, θ₁ – initial current and direction fields), with combined jet and wave simulations (c2, θ₂ – second current and direction fields). The localized DyD for a particular grid point location (DyD_loc) can be computed as:

$$Dy{D}_{loc}=\left(c_1-c_2\right)\times {\left(\frac{\cos (\mathrm{\theta }{}_1-\mathrm{\theta }{}_2)}{2}\right)}^2+\left(c_1+c_2\right)\times {\left(\frac{\sin (\mathrm{\theta }{}_1-\mathrm{\theta }{}_2)}{2}\right)}^2(3)$$

Condition: If c₂ > c₁, then c₂ = c₁, where c₁ is the initial velocity field, c₂ the second velocity field, θ₁ the first directional field, θ₂ the second directional field.

DyD can be applied in two situations, either to quantify the role of waves in diverting the jet fields (DyDJ) or to quantify the role of the jet in diverting the wave fields (DyDW), where c₁ and θ₁ in DyDJ are the jet-only velocity and directional fields and c₁ and θ₁ in DyDW are the wave-only velocity and directional fields, whereas c₂ and θ₂ are the combined jet and wave velocity and directional fields.

The total or combined DyD, which accounts for diversional effects on both wave and jet fields is obtained by summing the values of DyDW and DyDJ:

$$DyD=DyDJ+DyDW(4)$$

The quantification of the DyD is in line with the same momentum balance reasoning present in the article, but applied to the flow fields of either the jet-only or wave-only simulations compared to combined jet and wave simulations. For example, given a certain wave-driven-only velocity and direction field (c₁), as the jet momentum force starts acting upon the longshore flow during combined wave-driven and jet-driven circulation (c₂), it creates a negative acceleration in the nearshore water mass when the current directions are opposed, thus reducing the flow velocity. If the directional field remains the same over a particular area (θ₁–θ₂ = 0°), then DyD is the simple difference between c₁ and c₂; for example at a particular location, c₁ = 2 m/s and c₂ = 1 m/s, then DyD = 1 (Figure 11). On the other hand, if c₁ and c₂ now have opposite directions (θ₁–θ₂ = 180°), then this is indicative of a reversed circulation. As such, first an equal momentum is needed to balance the first velocity of c₁ (which was 2 m/s), and then extra momentum is needed to increase c₂ to 1 m/s, and in this case DyD = 3. In order to account for directional changes between flow fields, sine and cosine functions are used to create smooth transitions (Figure 11).

FIGURE 11

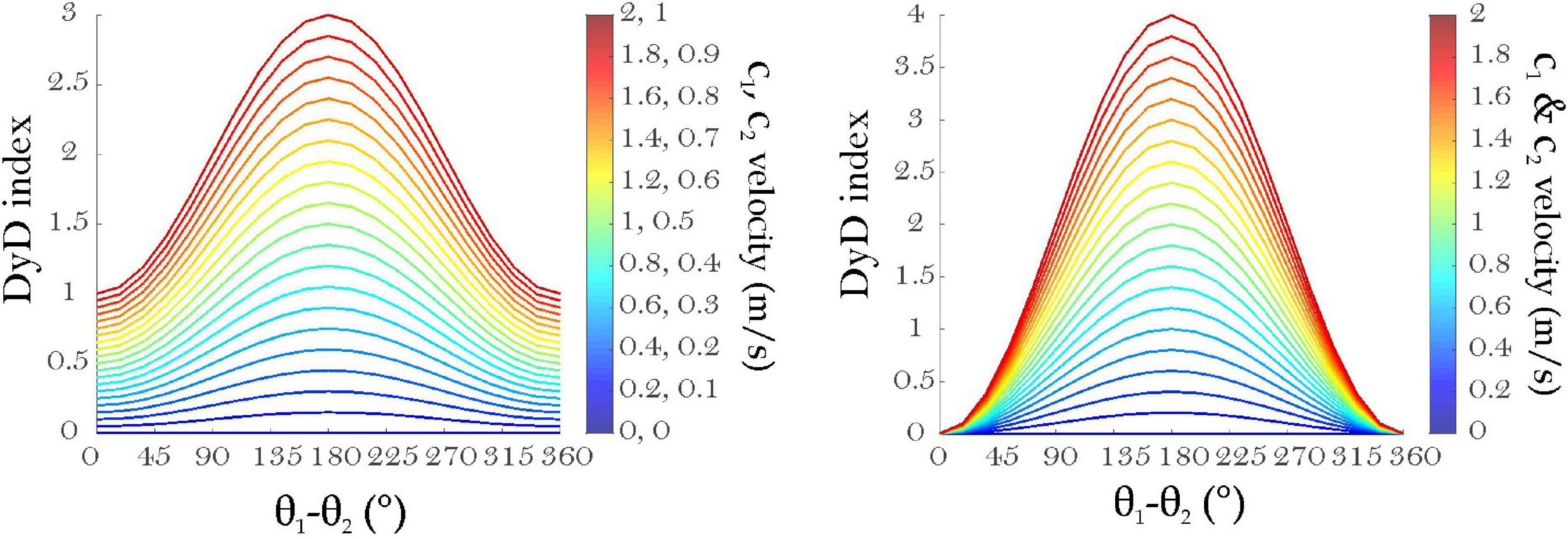
Figure 11. Examples of Dynamic diversion index (DyD) for different values of c₁ and c₂ where θ₁ > θ₂ and c₂ = ½ c₁, plotted over a full range of directions (left), and the DyD where c₁ = c₂ (right).

Overall, the DyD is an account of the force needed to decrease and divert the current flow field for both wave-driven and jet circulation types. High DyD zones are thus areas of higher pressure and lower velocities, which are maintained due to pressure gradients acting outward and balancing both the jet and wave momentum, keeping both the LSC and the jet away from each other in situations with strong interactions.

To illustrate the relation of the DyD with the flow fields, Figure 12 presents a situation of a jet-only of Q₂₀₀₀, a flow field resulting from Hs 2.5 m and 45° direction, and a combined jet and wave field. Simple differences of the simulations, between the combined jet and wave field with only the jet field, then the only the wave field, and then a hypothetical difference with both jet-only and wave-only, shows the areas and magnitudes of flow diversion and of flow acceleration (Figure 12). It seems, thus, that the DyD corresponds to, and quantifies, the areas of flow diversion.

FIGURE 12

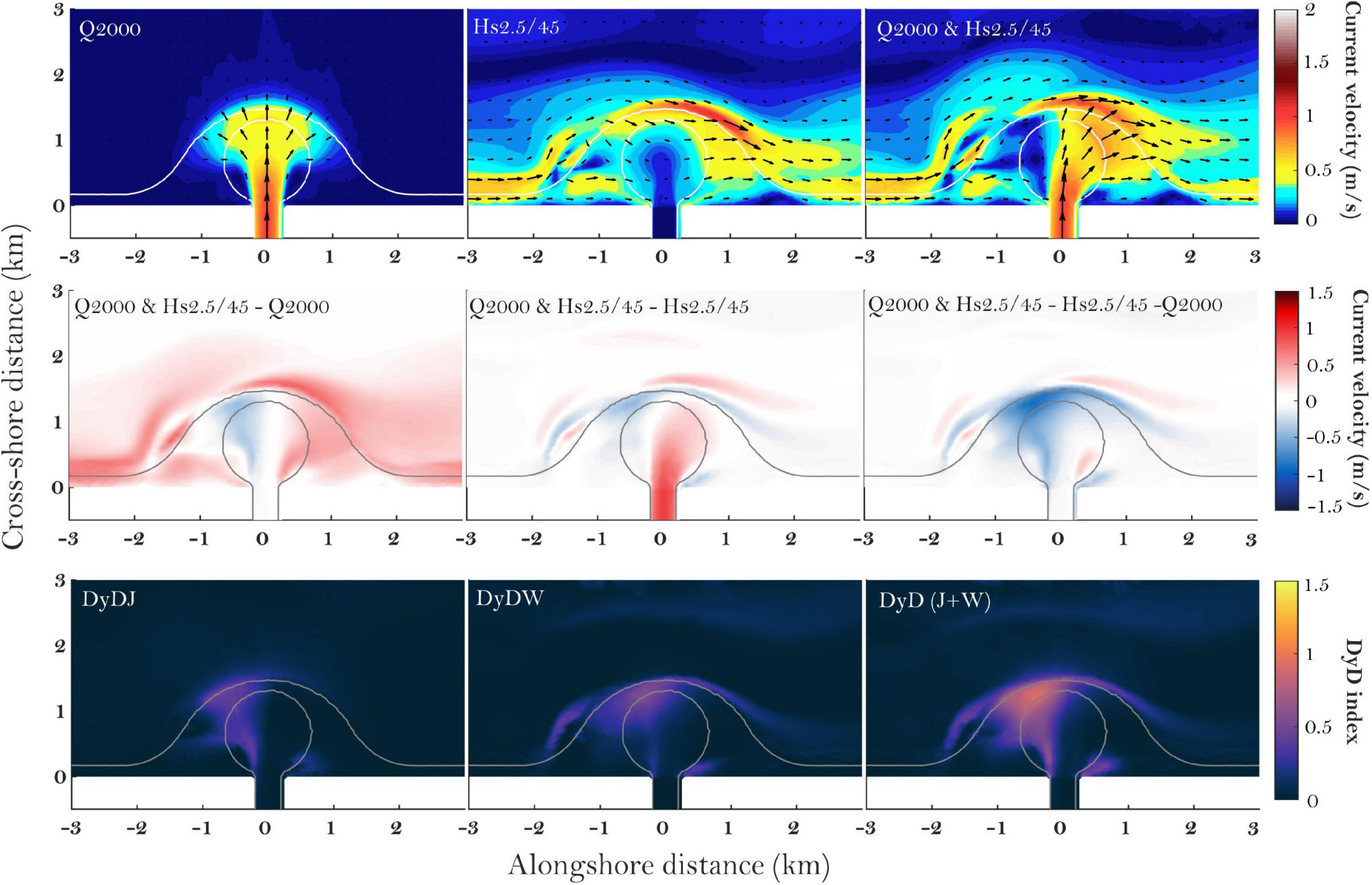
Figure 12. Relation of the DyD (bottom) to current velocities (top), and differences between current velocity fields (middle) for the Big_RMB case.

In order to compare the magnitudes of the DyD between different simulations, an average DyD was considered on an area stretching 2 km offshore and 2 km both updrift and downdrift of the river mouth. Maximum values of DyD occur on the RMB, either on the updrift side with oblique waves, or directly on the frontal crest for normally approaching waves. The surface of the DyD effect seems to increase with increasing RMB size, indicating that the RMB is a focal point of interaction and regulates the interplay of the wave-driven circulation and the river jet. The No_RMB case presents a small surface with a high intensity of DyD updrift, signifying that the effect on the LSC is only limited to the vicinity of the river mouth, whereas downdrift, the deflection of the LSC is extensive. At the same time, the jet is deflected by the waves as seen offshore. DyD intensity seems to be related to the product of Mj × Mw and describes a power law fit with the data. The higher the Mj and Mw, the progressively higher DyD becomes (Figure 13). A plateau occurs for increasing DyD for the same Q, when, irrespective of the increase in Hs, according to the power law fit of which the DyD should increase, the DyD actually seems to maintain constant values. This is indicative of a circulation that is already completely wave-dominated and the jet is comparatively weak and deflected at a maximum. DyD remains the same, but is able to increase when the Q_Jet is sufficiently high. DyD remains at values close to those of Hs_2.5 for Q₂₀₀₀, even for increasing Hs (Supplementary Figure 2), suggesting that it appears when Mj/Mw is around 1, or when the momentum of waves and jet is balanced.

FIGURE 13

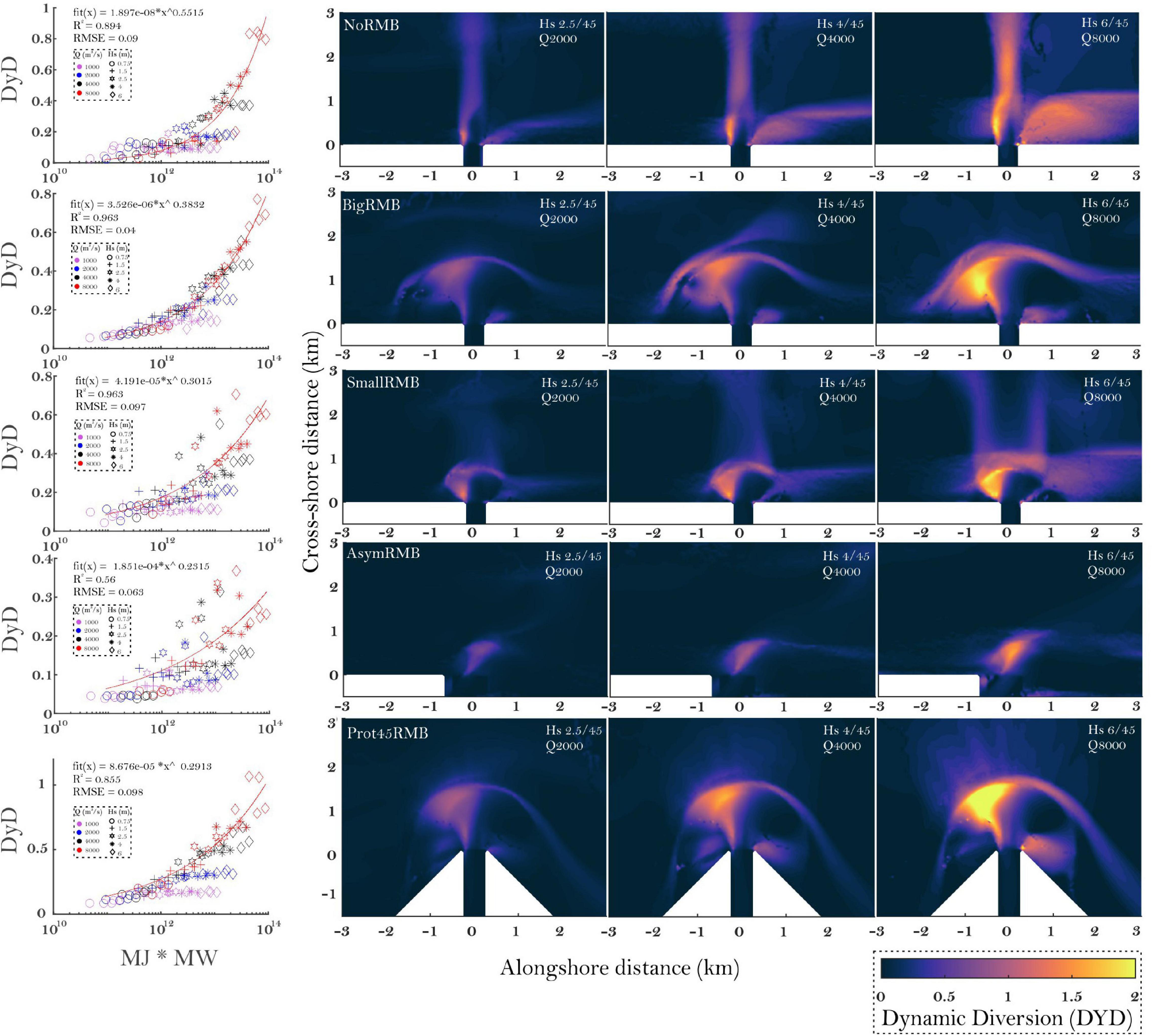
Figure 13. A selection of the Combined Dynamic diversion index (DyD) for the five types of RMB with both increasing Hs and discharge (Q). Scatter plots on the left show the relation of the average DyD with all the numerical simulations for each RMB type.

The Prot45_RMB case seems capable of generating the highest DyD values (Figure 14). This may be attributed to the dynamics of both wave and jet fields which have more space in the cross-shore dimension that they can diverge to. In contrast, the Asym_RMB seems to engender the lowest values of the DyD, because the jet flow is already topographically diverted and constrained to the coast. In all cases with a RMB, the DyDJ is lower than the DyDW, suggesting that the RMB may provide a protective role, causing less diversion of the river jet with regards to the wave-driven circulation (Figure 14).

FIGURE 14

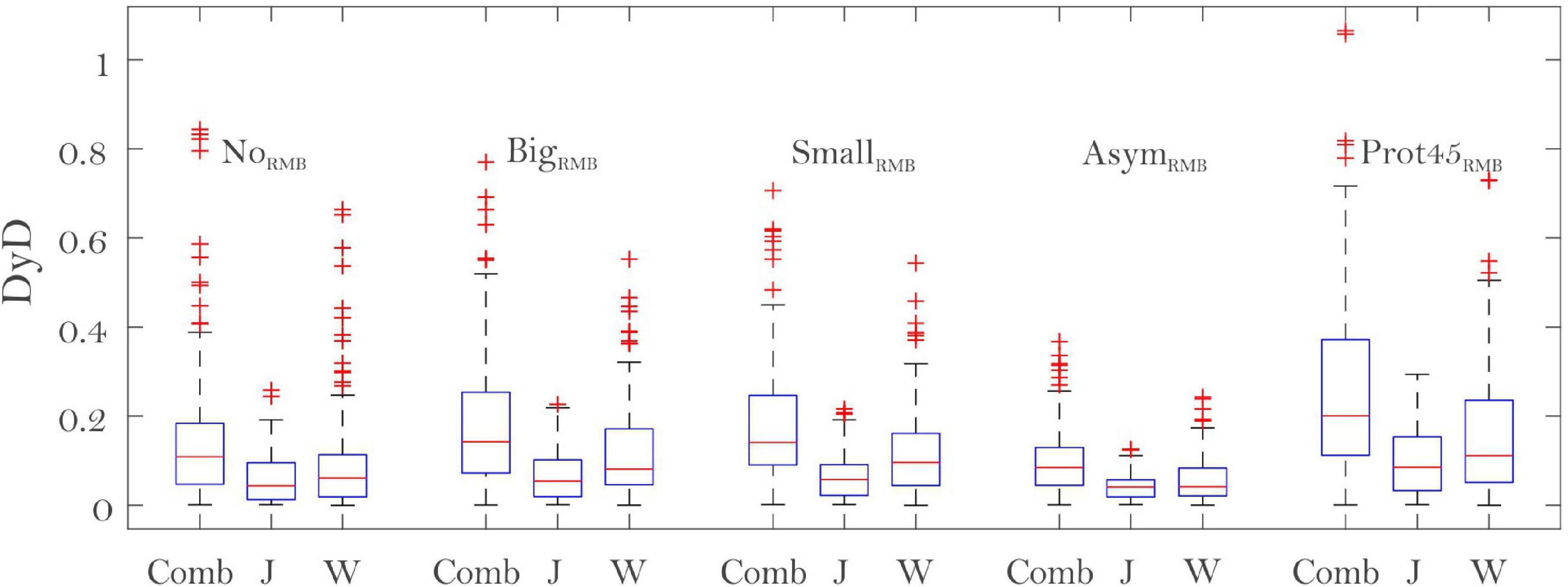
Figure 14. Box plots with average DyD using all numerical simulations for the five RMB configurations. Comb is Combined DyD; J is DyDJ; W is DyDW.

Discussion

Jet Momentum (Mj) and Wave Momentum (Mw) at River Mouths

Wave momentum flux (Mw) was described as a compelling wave property in the nearshore region, and which could link waves to the response of coastal structures (Hughes, 2004), or to wave run-up on beaches (Archetti and Brocchini, 2002). In river-mouth environments, Mw was found to influence jet spreading (Ismail and Wiegel, 1983), whereas a balance of the Mj and Mw can predict sediment bypassing during certain conditions (Nienhuis et al., 2016). Also, from the results presented above, this metric (Mj/Mw) appears to be appropriate for describing other effects occurring at river mouths such as jet deflection and the relative dominance of either alongshore wave-driven circulation or cross-shore jet circulation. Also, a new metric is proposed, the product of jet momentum and wave momentum (Mj × Mw), that can account for the absolute strength of hydrodynamic interactions occurring at river mouths. This adds to the increasing body of knowledge on different measures to quantify jet/wave/tide effects at river mouths, which converge in showing that deltaic river mouths are shaped by the relative balances of the momentum forces acting on them.

Flood–Storm Interactions at Natural River Mouths

The probability of interaction of flood jets and storm waves is analyzed at two natural river mouths. Daily discharge data for rivers is scarce, and at the moment only a comparison between the Danube (Sfântu Gheorghe mouth) and Rhône rivers is possible (Supplementary Figure 3). Also, whereas the river discharge is measured, the Hs data are derived from Era5 which has lower wave heights, especially near the coast, compared to wave buoys (around 20% lower for storms). Era5 shows wave heights that are generally higher for the Rhône river mouth, but the proportion of waves directed onshore, into the river mouth, is lower. Although the Rhône was hypothesized to have strong flood-storm interactions (Boudet et al., 2017), it seems to be not much different from the Sfântu Gheorghe river mouth. Highest simultaneous storms and floods at the Grand Rhône occur at 4 m Hs with Q4000, whereas for the Sfântu Gheorghe the 4 m Hs goes with Q3000. This is because for the Rhône, although peaks in floods can reach 10,000 m³/s, much higher than the Sfântu Gheorghe, peaks above 4000 m³/s are quite short-lasting. The Sfântu Gheorghe on the other hand has floods that can last for weeks to months at around 3000 m³/s. Rivers draining smaller basins at active continental margins where weather disturbances may affect both the coastal domain and the hydrographic basin may be more predisposed to higher jet-wave interactions. Tidal inlets on the other hand may have higher discharge during ebb for a far longer period/year than rivers, and tidal jet–wave interaction in these environments may be more important, a hypothesis which remains to be tested.

Implications for Sediment Sequestering and Bypassing

The process of constructing a protruding subaqueous river mouth and changing the LSC system, generating counter-longshore currents and weakening updrift longshore currents, is fundamental in beach-ridge plain development and ultimately in wave-influenced deltaic construction. It is long known that river mouths are places where sediment is sequestered; sediment swept around the zone of interaction is trapped in current reversal and deposited (Todd, 1968). For tidal inlets, FitzGerald (1982) identified the mechanisms involved in sediment bypass. The first type, by stable inlet processes, involves migration and attachment of large bar complexes to the downdrift inlet shoreline, whereas the second type, involves deflection of the inlet channel and breaking of the ebb-shoal or the spit that is developing and deflecting. Recently, Porcile et al. (2020) found that tropical cyclones induce mega-rip currents, similar to the rip structures modeled in this article, that flush water and sediment toward submarine canyons, and are associated with shoreline curvature induced by river mouths.

Highly protruding, big river mouths change the orientations of the nearby coastlines, and are expected to completely block bypass even during storm conditions and acute angles. Prograding deltas with comparatively high Qs have higher protruding RMs, and as such Prot45_RMB may be highly prevalent in natural deltas. In these situations, bypass becomes close to 0.

Sediment retention or bypass in deltaic river mouths should be envisaged taking into account factors such as updrift shoreline orientation and configuration, subaqueous RMB volume, and the change in external forcing strength (Hs and direction, river discharge), as well as the change in sediment grain-size composition. A more challenging full morphodynamic modeling is needed.

Limitations of the Present Approach

Although most processes are accounted for, there are intrinsic limitations in the numerical model implementation that are described below.

Dodet et al. (2013) note that wave heights can be overestimated when opposing strong currents occur as a result of incomplete dissipation. This was overcome by van der Westhuysen (2012) who implemented an enhanced dissipation term for waves, but Mike 21 SW does not benefit from this. Also, increasingly non-linear waves approaching strong currents should be modeled with a more appropriate third-order Stokes dispersion relation (Chawla and Kirby, 2002; Dodet et al., 2013), which is not implemented in Mike 21 SW. In Mike 21 SW, when opposing currents are too strong for the waves to exist wave action density is set to zero (DHI, 2017c). This is done when the following condition is satisfied:

$$(Cg+(u\times \text{cos}(\mathrm{\theta })+v\times \text{sin}(\mathrm{\theta })))/\mathit{Cg}<f(5)$$

where Cg is the group velocity, (u, v) the velocity components, θ the direction of wave propagation and f the blocking factor with a value of 0.1. In our simulations, this condition seems to be satisfied only at the immediate vicinity of the river mouth outlet and only using the highest discharges (Q4000 and Q8000). Most of the strong current jet will be spread over the mouth bar crests before this condition would apply, also indicating that direct wave-current interactions may be secondary to LSC–jet interactions in our investigated settings.

Although wave-breaking-induced accelerations were identified as the main term in determining current velocities in the inlet area, an important feature is that of wave enhancement of the apparent bed roughness, which has the effect of reducing the LSC while intensifying the currents in some areas located in the outer part of an inlet (Olabarrieta et al., 2011). We ran our simulations without the effect of waves on the apparent bed roughness as done in Olabarrieta et al. (2014). We stress the possibility that the inclusion of wind (not included as a forcing in the HD module), should compensate for some of the decrease in current speeds observed when wave-induced bed roughness is enhanced.

Melito et al. (2018) used the wave-resolving model of Brocchini et al. (2001) to test the results at an idealized inlet geometry as used in Olabarrieta et al. (2014). Our results on the LSC are similar to those of Melito et al. (2018), with maximum LSC velocities of 0.5–0.6 m/s for a Hs of 1.5 m, whereas the current velocities shown in Olabarrieta et al. (2014) seem to be slightly higher. Also, the approach of Melito et al. (2018) results in the appearance of a number of large-scale eddies which contribute to mixing at the river mouth, and which may better represent natural conditions. Nevertheless, the application of this kind of wave-resolving model on such a large number of simulations would require a much greater computational effort.

Conclusion

This numerical exercise was conceived in order to explore hydrodynamics at five constructed idealized river mouths resembling natural configurations. Our conclusions are the following:

1. The RMB morphology has a large impact on the jet structure and spreading; we measure this using the lateral jet transfer rate (LJT), which quantifies the topographically induced modifications in the jet structure and show that big and shallow RMBs can completely spread a river jet.

2. The interactions between the river jet and the LSC in the simple case of no RMB (No_RMB) can be predicted by either the balance of the jet momentum flux to the alongshore component of wave momentum flux (Mj/Mw) or by using the balances of discharges of the river jet and the LSC (Q_Jet/Q_LSC) to explain the jet deflection with different discharges relative to the angle and height of waves.

3. The presence of a RMB modifies the LSC circulation by drift alteration on the updrift side of the bar through the emergence of a counter-longshore current (C_LSC) and wave breaking-induced accelerations on the RMB crest. The Q_Jet/Q_LSC is also used here as an indication of the type of circulation. As such, the circulation is wave-dominated when Q_Jet/Q_LSC << 1; and jet-dominated when Q_Jet/Q_LSC >> 1, and strong wave-jet interactions occur at Q_Jet/Q_LSC approaching 1. High and oblique waves favor longshore circulation and RMB bypass, whereas low waves and normal-to-coast angles generate diverging LSCs on the mouth bar crest which interrupts the longshore circulation.

4. A first quantification of the Dynamic diversion is proposed in the form of the non-dimensional DyD, which scales with the product of Mj and Mw and can account for the absolute strength of hydrodynamic interactions occurring at river mouths. RMB morphology can affect DyD in multiple ways, either by strengthening or lessening the interactions. The DyD seems to increase with increasing RMB size, indicating that the RMB is a focal point of interaction and regulates the interplay of the wave-driven circulation and the river jet.

Data Availability Statement

The model outputs are available at https://zenodo.org/record/5111621. ERA5 wave data and GRDC river discharge data are available from their respective owners.

Author Contributions

FZ, EA, and AV-S devised the model scenarios. FZ set up and ran the model. All authors contributed to writing the article and approved the submitted version.

Funding

FZ benefitted from the support of the Romanian Young Academy funded by Stiftung Mercator and the Alexander von Humboldt Foundation for the period 2020–2022. This research received funding from the Norway Grants 2014–2021, under project code RO-NO-2019-0415/contract no. 30/2020, the response of climate-sensitive environments to global warming, sea-level rise and increasing extremes: the Carpathians and Danube Delta.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

FZ undertook part of the work at Aix-Marseille University under a “Bourse du Gouvernement Français” Ph.D. cotutelle thesis awarded by the Institut Français de Roumanie and was supported by the MIKE Powered by the DHI thesis program which allowed the user to use the Mike numerical model free of charge. We would like to thank François Sabatier for providing the Rhône river mouth bathymetry. Ben Mitch is thanked for creating the Panel Toolbox which made possible the creation of tight plots (https://www.mathworks.com/matlabcentral/fileexchange/20003-panel). We would also like to thank the two reviewers and the editor AS for handling the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2021.708258/full#supplementary-material

Supplementary Figure 1 | Model mesh at three levels showing the decreasing size of triangular grids (left); zoom on the river mouth (right). The elevation scatter on the basis of which the bathymetries have been interpolated is also shown.

Supplementary Figure 2 | The “plateau effect”: Upper plots show increasing Hs with Q8000 resulting in a progressive increase in DyD. Bottom plots show increasing Hs with Q2000 with a limited increase in DyD due to the higher diversion of the jet in front of the RMB before maximum Hs thresholds.

Supplementary Figure 3 | Storm and flood simultaneous occurrences in front of the Sfântu Gheorghe (A) and Grand Rhône river mouths (B). (A1,B1) wave roses based on ERA5 data; (A2,B2) daily discharge data; (A3,B3) hourly Hs based on ERA5; (A4,B4) heat plot showing the number of simultaneous occurrences of Hs and Q conditions; (A5,B5) histogram of Q; (A6,B6) histogram of Hs.

References

Airy, G. B. (1841). Tides and Waves From the Encycl. Metropolitana, Vol. 5, London.

Google Scholar

Akan, Ç, Moghimi, S., Özkan-Haller, H. T., Osborne, J., and Kurapov, A. (2017). On the dynamics of the mouth of the Columbia river: results from a three-dimensional fully coupled wave-current interaction model. J. Geophys. Res. Oceans 122, 5218–5236. doi: 10.1002/2016JC012307

CrossRef Full Text | Google Scholar

Anthony, E. J. (2015). Wave influence in the construction, shaping and destruction of river deltas: a review. Mar. Geol. 361, 53–78. doi: 10.1016/j.margeo.2014.12.004

CrossRef Full Text | Google Scholar

Anthony, E. J., Gardel, A., Proisy, C., Fromard, F., Gensac, E., Peron, C., et al. (2013). The role of fluvial sediment supply and river-mouth hydrology in the dynamics of the muddy, Amazon-dominated Amapá-Guianas coast, South America: a three-point research agenda. J. South Am. Earth Sci. 44, 18–24. doi: 10.1016/j.jsames.2012.06.005

CrossRef Full Text | Google Scholar

Antia, E. E. (1995). Sedimentary deposits related to inlet-shoreface storm flow interaction in the German bight. Estuar. Coast Shelf. Sci. 40, 699–712. doi: 10.1006/ecss.1995.0047

CrossRef Full Text | Google Scholar

Archetti, R., and Brocchini, M. (2002). An integral swash zone model with friction: an experimental and numerical investigation. Coast. Eng. 45, 89–110. doi: 10.1016/S0378-3839(02)00038-8

CrossRef Full Text | Google Scholar

Battjes, J. A., and Janssen, J. P. F. M. (1978). Energy loss and set-up due to breaking random waves. Coast. Eng. Proc. 16, 32–32. doi: 10.9753/icce.v16.32

CrossRef Full Text | Google Scholar

Bertin, X., Chaumillon, E., Weber, N., and Tesson, M. (2004). Morphological evolution and time-varying bedrock control of main channel at a mixed energy tidal inlet: Maumusson Inlet, France. Mar. Geol. 204, 187–202. doi: 10.1016/S0025-3227(03)00353-0

CrossRef Full Text | Google Scholar

Boudet, L., Sabatier, F., and Radakovitch, O. (2017). Modelling of sediment transport pattern in the mouth of the Rhône delta: role of storm and flood events. Estuar. Coast Shelf. Sci. 198, 568–582. doi: 10.1016/j.ecss.2016.10.004

CrossRef Full Text | Google Scholar

Brocchini, M. (2019). Wave-forced dynamics in the nearshore river mouths, and swash zones. Earth Surf. Process. Landf. 45, 75–95. doi: 10.1002/esp.4699

CrossRef Full Text | Google Scholar

Brocchini, M., Bernetti, R., Mancinelli, A., and Albertini, G. (2001). An efficient solver for nearshore flows based on the WAF method. Coast. Eng. 43, 105–129. doi: 10.1016/S0378-3839(01)00009-6

CrossRef Full Text | Google Scholar

Canestrelli, A., Nardin, W., Edmonds, D., Fagherazzi, S., and Slingerland, R. (2014). Importance of frictional effects and jet instability on the morphodynamics of river mouth bars and levees: friction and jet instability. J. Geophys. Res. Oceans 119, 509–522. doi: 10.1002/2013JC009312

CrossRef Full Text | Google Scholar

Chawla, A., and Kirby, J. T. (2002). Monochromatic and random wave breaking at blocking points. J. Geophys. Res. 107:3067. doi: 10.1029/2001JC001042

CrossRef Full Text | Google Scholar

Dean, R. G. (1991). Equilibrium beach profiles: characteristics and applications. J. Coast. Res. 7, 53–84.

Google Scholar

Deigaard, R., Fredsøe, J., and Hedegaard, I. B. (1986). Suspended sediment in the surf zone. J. Waterw. Port Coast. Ocean Eng. 112, 115–128. doi: 10.1061/(ASCE)0733-950X1986112:1(115)

CrossRef Full Text | Google Scholar

DHI (2017a). MIKE 21 & MIKE 3 Flow Model FM - Hydrodynamic and Transport Module, Scientific Documentation, Hørsholm, DHI, 64.

Google Scholar

DHI (2017b). MIKE 21—Spectral Wave Module, Scientific Documentation, Hørsholm, DHI, 56.

Google Scholar

DHI (2017c). MIKE 21—Spectral Wave Module, User Guide, Hørsholm, DHI, 56.

Google Scholar

Dodet, G., Bertin, X., Bruneau, N., Fortunato, A. B., Nahon, A., and Roland, A. (2013). Wave-current interactions in a wave-dominated tidal inlet: wave-current interactions in tidal inlet. J. Geophys. Res. Oceans 118, 1587–1605. doi: 10.1002/jgrc.20146

CrossRef Full Text | Google Scholar

Dominguez, J. M. L. (1996). “The Sao Francisco strandplain: a paradigm for wave-dominated deltas?,” in Geology of Siliciclastic Shelf Seas, eds M. De Batist and P. Jacobs (London: Geological Society of London, Special Publication), 15.

Google Scholar

Dracos, T., Giger, M., and Jirka, G. H. (1992). Plane turbulent jets in a bounded fluid layer. J. Fluid Mech. 241, 587–614. doi: 10.1017/S0022112092002167

CrossRef Full Text | Google Scholar

Edmonds, D. A., and Slingerland, R. L. (2007). Mechanics of river mouth bar formation: implications for the morphodynamics of delta distributary networks. J. Geophys. Res. 112:F02034. doi: 10.1029/2006JF000574

CrossRef Full Text | Google Scholar

Eldeberky, Y., and Battjes, J. A. (1995). “Parameterization of triad interaction in wave energy model,” in Proceedings of the. Coastal Dynamics Conference 1995, Poland.

Google Scholar

Fagherazzi, S., Edmonds, D. A., Nardin, W., Leonardi, N., Canestrelli, A., Falcini, F., et al. (2015). Dynamics of river mouth deposits. Rev. Geophys. 53, 642–672. doi: 10.1002/2014RG000451

CrossRef Full Text | Google Scholar

Falcini, F., and Jerolmack, D. J. (2010). A potential vorticity theory for the formation of elongate channels in river deltas and lakes. J. Geophys. Res. 115:F04038. doi: 10.1029/2010JF001802

CrossRef Full Text | Google Scholar

FitzGerald, D. M. (1982). Sediment bypassing at mixed energy tidal inlets. Coast. Eng. Proc. 1:68.

Google Scholar

Flather, R. A. (1976). A tidal model of the north-west European continental shelf. Memoires Societe Royale Des Sciences de Liege 10, 141–164.

Google Scholar

George, D. A., Largier, J. L., Pasternack, G. B., Barnard, P. L., Storlazzi, C. D., and Erikson, L. H. (2019). Modeling sediment bypassing around idealized rocky headlands. J. Mar. Sci. Eng. 7:40. doi: 10.3390/jmse7020040

CrossRef Full Text | Google Scholar

Giosan, L. (2007). Morphodynamic feedbacks on deltaic coasts: lessons from the wave-dominated Danube delta. Coast. Sediments 07, 828–841. doi: 10.1061/40926(239)63

CrossRef Full Text | Google Scholar

Hansen, J. E., Elias, E., and Barnard, P. L. (2013). Changes in surfzone morphodynamics driven by multi-decadal contraction of a large ebb-tidal delta. Mar. Geol. 345, 221–234. doi: 10.1016/j.margeo.2013.07.005

CrossRef Full Text | Google Scholar

Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horányi, A., Muñoz-Sabater, J., et al. (2020). The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 146, 1999–2049. doi: 10.1002/qj.3803

CrossRef Full Text | Google Scholar

Hughes, S. A. (2004). Wave momentum flux parameter: a descriptor for nearshore waves. Coast. Eng. 51, 1067–1084. doi: 10.1016/j.coastaleng.2004.07.025

CrossRef Full Text | Google Scholar

Ismail, N. M., and Wiegel, R. L. (1983). Opposing wave effect on momentum jets spreading rate. J. Waterw. Port Coast. Ocean Eng. 109, 465–483. doi: 10.1061/(ASCE)0733-950X1983109:4(465)

CrossRef Full Text | Google Scholar

Jiménez-Robles, A. M., Ortega-Sánchez, M., and Losada, M. A. (2016). Effects of basin bottom slope on jet hydrodynamics and river mouth bar formation: effect of bottom slope on jet dynamics. J. Geophys. Res. Earth Surf. 121, 1110–1133. doi: 10.1002/2016JF003871

CrossRef Full Text | Google Scholar

Kang, K., and Di Iorio, D. (2006). Depth- and current-induced effects on wave propagation into the Altamaha river Estuary, Georgia. Estuar. Coast. Shelf Sci. 66, 395–408. doi: 10.1016/j.ecss.2005.09.008

CrossRef Full Text | Google Scholar

Komar, P. D. (1973). Computer models of delta growth due to sediment input from rivers and longshore transport. GSA Bull. 84, 2217–2226.

Google Scholar

Komen, G., Hasselmann, S., and Hasselmann, K. (1984). On the existence of a fully developed wind-sea spectrum. J. Phys. Oceanogr. 14, 1271–1285.

Google Scholar

Komen, G. J., Cavaleri, L., Donelan, M., Hasselmann, K., Hasselmann, S., and Janssen, P. A. E. M. (1994). Dynamics and Modelling of Ocean Waves. Cambridge, MA: Cambridge University Press. doi: 10.1017/CBO9780511628955

CrossRef Full Text | Google Scholar

Kundu, P. K., Cohen, I. M., Dowling, D. R., and Tryggvason, G. (2016). Fluid Mechanics, 6th Edn. Cambridge, MA: Elsevier.

Google Scholar

Lai, R. J., Long, S. R., and Huang, N. E. (1989). Laboratory studies of wave-current interaction: kinematics of the strong interaction. J. Geophys. Res. Oceans 94, 16201–16214. doi: 10.1029/JC094iC11p16201

CrossRef Full Text | Google Scholar

Leonardi, N., Canestrelli, A., Sun, T., and Fagherazzi, S. (2013). Effect of tides on mouth bar morphology and hydrodynamics: effect of tides on mouth bar. J. Geophys. Res. Oceans 118, 4169–4183. doi: 10.1002/jgrc.20302

CrossRef Full Text | Google Scholar

Longuet-Higgins, M. S., and Stewart, R. W. (1962). Radiation stress and mass transport in gravity waves, with application to ‘surf beats’. J. Fluid Mech. 13, 481–504. doi: 10.1017/S0022112062000877

CrossRef Full Text | Google Scholar

Longuet-Higgins, M. S. (1970). Longshore currents generated by obliquely incident sea waves: 1. J. Geophys. Res. 75, 6778–6789. doi: 10.1029/JC075i033p06778

CrossRef Full Text | Google Scholar

Melito, L., Postacchini, M., Darvini, G., and Brocchini, M. (2018). Waves and Currents at a River Mouth: The Role of Macrovortices, Sub-Grid Turbulence and Seabed Friction. Water 10:550. doi: 10.3390/w10050550

CrossRef Full Text | Google Scholar

Nardin, W., and Fagherazzi, S. (2012). The effect of wind waves on the development of river mouth bars: effect of wind waves on river mouth bars. Geophys. Res. Lett. 39:12607. doi: 10.1029/2012GL051788

CrossRef Full Text | Google Scholar

Nardin, W., Mariotti, G., Edmonds, D. A., Guercio, R., and Fagherazzi, S. (2013). Growth of river mouth bars in sheltered bays in the presence of frontal waves: growth and evolution of river mouth bars. J. Geophys. Res. Earth Surf. 118, 872–886. doi: 10.1002/jgrf.20057

CrossRef Full Text | Google Scholar

Nienhuis, J. H., Ashton, A. D., Nardin, W., Fagherazzi, S., and Giosan, L. (2016). Alongshore sediment bypassing as a control on river mouth morphodynamics: littoral bypassing. J. Geophys. Res. Earth Surf. 121, 664–683. doi: 10.1002/2015JF003780

CrossRef Full Text | Google Scholar

Olabarrieta, M., Geyer, W. R., and Kumar, N. (2014). The role of morphology and wave-current interaction at tidal inlets: an idealized modeling analysis. J. Geophys. Res. Oceans 119, 8818–8837. doi: 10.1002/2014JC010191

CrossRef Full Text | Google Scholar

Olabarrieta, M., Warner, J. C., and Kumar, N. (2011). Wave-current interaction in Willapa Bay. J. Geophys. Res. 116:C12014. doi: 10.1029/2011JC007387

CrossRef Full Text | Google Scholar

Özsoy, E., and Ünlüata, Ü (1982). Ebb-tidal flow characteristics near inlets. Estuar. Coast. Shelf Sci. 14, 251–263, IN1–IN3. doi: 10.1016/S0302-3524(82)80015-7

CrossRef Full Text | Google Scholar

Porcile, G., Bolla Pittaluga, M., Frascati, A., and Sequeiros, O. E. (2020). Typhoon-induced megarips as triggers of turbidity currents offshore tropical river deltas. Commun. Earth Environ. 1, 1–13. doi: 10.1038/s43247-020-0002-1

CrossRef Full Text | Google Scholar

Rowland, J. C., Stacey, M. T., and Dietrich, W. E. (2009). Turbulent characteristics of a shallow wall-bounded plane jet: experimental implications for river mouth hydrodynamics. J. Fluid Mech. 627, 423–449. doi: 10.1017/S0022112009006107

CrossRef Full Text | Google Scholar

Ruessink, B. G., Walstra, D. J. R., and Southgate, H. N. (2003). Calibration and verification of a parametric wave model on barred beaches. Coast. Eng. 48, 139–149. doi: 10.1016/S0378-3839(03)00023-1

CrossRef Full Text | Google Scholar

Rusu, E. (2010). Modelling of wave–current interactions at the mouths of the Danube. J. Mar. Sci. Technol. 15, 143–159. doi: 10.1007/s00773-009-0078-x

CrossRef Full Text | Google Scholar

Sabatier, F., Samat, O., Ullmann, A., and Suanez, S. (2009). Connecting large-scale coastal behaviour with coastal management of the Rhône delta. Geomorphology 107, 79–89. doi: 10.1016/j.geomorph.2006.09.026

CrossRef Full Text | Google Scholar

Shaw, J. B., Miller, K., and McElroy, B. (2018). Island formation resulting from radially symmetric flow expansion. J. Geophys. Res. Earth Surf. 123, 363–383. doi: 10.1002/2017JF004464

CrossRef Full Text | Google Scholar

Smith, S. J., and Smith, J. M. (2001). Numerical Modeling of waves at Ponce de Leon Inlet, Florida. J. Waterw. Port Coast. Ocean Eng. 127, 176–184. doi: 10.1061/(ASCE)0733-950X2001127:3(176)

CrossRef Full Text | Google Scholar

Suastika, I. K. (2012). A spectral model for blocking of random waves. Coast. Eng. J. 54, 1250013–1250029. doi: 10.1142/S0578563412500131

CrossRef Full Text | Google Scholar

Taylor, M. J., Byrnes, M. R., and McBride, R. A. (1996). Form/process relationships and geomorphic evolution of the southwestern Louisiana Chenier plain. Trans. Gulf Coast Assoc. Geol. Soc. 46, 413A–422A.

Google Scholar

Todd, T. W. (1968). Dynamic diversion: influence of longshore currenttidal flow interaction on chenier and barrier island plains. J. Sediment. Petrol. 38, 734–746. doi: 10.1306/74D71A5A-2B21-11D7-8648000102C1865D

CrossRef Full Text | Google Scholar

van der Westhuysen, A. J. (2012). Spectral modeling of wave dissipation on negative current gradients. Coast. Eng. 68, 17–30. doi: 10.1016/j.coastaleng.2012.05.001

CrossRef Full Text | Google Scholar

van Rijn, L. C. (2013). Coastal Erosion Control Based on the Concept of Sediment Cells. Conscience Project Final Report. Avaliable online at: https://www.leovanrijn-sediment.com/papers/Coastalerosion2012.pdf (accessed January 5, 2021).

Google Scholar

Wright, L. D. (1977). Sediment transport and deposition at river mouths: a synthesis. Geol. Soc. Am. Bull. 88, 857–868.

Google Scholar

Wright, L. D., Coleman, J. M., and Erickson, M. W. (1974). Analysis of Major River Systems and their Deltas: Morphologic and Process Comparisons, Technical Report 156. Baton Rouge, LA: Coastal Studies Institute, Louisiana State University. 125.

Google Scholar

Zăinescu, F., Vespremeanu-Stroe, A., Anthony, E., Tãtui, F., Preoteasa, L., and Mateescu, R. (2019). Flood deposition and storm removal of sediments in front of a deltaic wave-influenced river mouth. Mar. Geol. 417:106015. doi: 10.1016/j.margeo.2019.106015

CrossRef Full Text | Google Scholar