A Non-destructive Method to Create a Time Series of Surface Area for Coral Using 3D Photogrammetry

The wax dip method typically used to determine the surface area of corals for data normalization is destructive, rendering the collection of time series for such data impossible. With recent advancements in photogrammetric technology, it is now possible to collect these data in a non-destructive manner at very high levels of accuracy. This photogrammetric method using Agisoft’s Metashape is compared to the standard wax-dip method using both objects of known surface area and objects of unknown surface area. Objects of known surface area (i.e., objects that have surface areas that can be calculated using geometrical formulas) were estimated with a similar degree of accuracy with the Photogrammetry (PG) method (R² = 0.9922, slope = 0.9835) as with the wax-dip method (R² = 0.9872, slope = 1). A single factor ANOVA confirmed that there was no significant difference between measurements from the three methods of geometrical calculation, wax dipping, or photogrammetry for objects of known surface area. This paper describes the methods for rapidly collecting surface area data of small to moderately sized coral nubbins in a laboratory setting and characterizes the relationship between buoyant weight and surface area over time for the coral species Stylophora pistillata. Finally, two predictive models are proposed to estimate surface area from weight in air measurements.

Introduction

Surface area (SA) is an extremely important parameter in benthic coral ecology (Dahl, 1973), and it is commonly used as a metric to normalize oxygen production and consumption measurements, and other biomass-dependent data. This is due to photosynthesis and respiration occurring in the surface tissues of the coral. The higher the SA of a coral the more potential it has to perform photosynthesis and respire (Hoegh-Guldberg, 1988; Jones et al., 2008; Holmes et al., 2008; Laforsch et al., 2008; Naumann et al., 2009; Veal et al., 2010). Most hermatypic corals have a thin layer of tissue that closely corresponds to the shape of the coral’s skeleton (Veal et al., 2010). For these reasons, SA is a better normalizing parameter than one like buoyant weight (BW_t) (Dodge et al., 1984). BW_t is measured by suspending the coral nubbin in a basket in seawater of a known density to estimate the weight of the calcium carbonate without the coral tissue as the BW_t method operates on the assumption that tissue and mucus are neutrally buoyant (Jokiel and Maragos, 1978). While BW_t is a good parameter for estimating health, growth, and calcification, due to the complex growth forms and differences in density exhibited by many corals, BW_t may not be indicative of the SA and thus is not the preferred normalizing parameter (Dodge et al., 1984).

There have been many methods used to estimate the SA of corals, each with its specific pros and cons. In 1962, Harrod and Hall were of the first to consider the implications of measuring actual SA. They attempted to glean the SA of leaves by precisely measuring the difference in weight of Hydrangea leaves before and after being submerged in water (Harrod and Hall, 1962). One of the first ways SA was estimated for corals was by simply taking the planar area of the corals projected from 2D images taken from the normal of the coral surface (Kanwisher and Wainwright, 1967). This method is not sufficient for most growth forms of corals as it does not consider the three-dimensionality of coral structures and would therefore grossly underestimate the SA (Hoegh-Guldberg, 1988). For this reason, a method like this would only be applicable in cases where there is virtually zero rugosity to the growth form of the coral.

More recently, prior to 1991, the most common way of collecting coral SA was the foil method (Hoegh-Guldberg, 1988). This method was used in many studies including Davies (1980); Szmant-Froelich and Pilson (1980); Hawkins and Lewis (1982); Burris et al. (1983); Muscatine et al. (1984), as well as several others. The coral samples are either covered in pieces of foil of known SA and tallied, or the coral is covered in foil, then the foil is removed and measured. Another method performed by Meyer and Schultz (1985) used a liquid latex rubber to coat the skeleton after being sealed in paraffin wax. The latex was removed after it dried and placed between plates of glass and traced on a transparent film. This film was then digitized to estimate the SA. While these methods were relatively easy to perform and produced reasonably accurate results, they were only appropriate for corals with simple growth forms or individual branches of more complex growth forms.

In 1988, Hoegh-Guldberg developed a new method to estimate the SA of more complex growth forms particularly that of Pocillopora damicornis. The corals were coated in up to 5 layers of “Verathane” plastic varnish with a thickness range of 0.03–0.05 mm then the corals were dipped in an aqueous Methylene Blue dye/detergent solution. The SA was directly proportional to the amount of dye that clung to the coral specimens and was easily estimated using this technique. While this method was successful in estimating the SA of P. damicornis, it was noted that this method consistently underestimated the SA of objects with known geometries, so this was most likely occurring with the corals as well. Also, due to the added thickness of the varnish, this method was not attempting to estimate the absolute SA, the SA of the naked skeleton of the corals, but the “primary” SA of the corals, defined as the SA occupied by the coral polyps while extended (Hoegh-Guldberg, 1988). It is critical to know what space your selected method of measurement is measuring. Due to the thickness of the Verathane, it was impossible to get a true measurement of the skeleton itself. This concept is also important to take into account when measuring corals with or without living tissue intact.

In 1991, Stimson and Kinzie developed a new method where corals were double dipped in Paraffin wax and the weight of the added wax was used as a proxy for SA. In 2010, Veil et al. further refined this method to make it more practical and more accurate using a single dip method. The wax dip method has proven to be extremely robust and has become a standard method to estimate the SA of corals in the lab and the field. All the methods described above share a common negative, being that they are all destructive and cannot be performed in vivo. Here “destructive” is defined as an action or procedure that kills the coral and not merely stresses the coral. To calculate the change in SA over time, a non-destructive method must be used to collect the data.

In the past decade, computer-aided tools have been used to estimate the SA of corals in vivo. In 2008, Jones et al. used a simple freeware 3D animation program called GMAX to create simple wire-frames that were very accurate at estimating the SA of objects with a known SA and small simple coral branches compared to the wax dip method. Others have used medical-grade X-ray computed tomography scan (CT) to measure coral SA with extremely high accuracy (Laforsch et al., 2008; Naumann et al., 2009; House et al., 2018). Unfortunately, CT scanners are expensive to operate and one would need access to special facilities to make the measurements needed, which adds another layer of difficulty to measuring the corals’ SA.

Photogrammetry (PG) is the creation of 3D models from an array of 2D images and can be used to estimate SA without sacrificing the corals. The PG method allows for the creation of a time series for SA, as well as a more accurately normalized time series for SA dependant measurements. Ferrari et al. (2017) used the PG method in the field to measure coral growth and contraction with PG-derived SA estimates for the first time, but with only two time points. Since then, House et al. (2018), compared the PG method directly to CT by measuring the same objects or corals with both methods and analyzing them for differences. While they found that PG was reasonably accurate when compared to the CT method with best fit models with adjusted R² ranging from 0.70 to 0.97, they also found that PG-derived SA was significantly different from the CT-derived SA (p = 0.008) (House et al., 2018). It is notable, however, that House et al. (2018) used a relatively small number of photos (only 39 for their smallest specimens) for the size of their specimens. PG is highly dependant on the number of photos and view angles that are input into the system to construct the 3D models. The larger and more complex a specimen is, the more images and angles are needed to accurately construct the 3D model. In the House et al.’s (2018) study, they relied more on varying the camera view angle and did not take as many images. This potential under-sampling of camera views would lead to a reduced accuracy for the models created by reducing the amount of overlap for each image. In this study due to the simple morphology of the nubbins, we will rely on saturation of photo overlaps and use a single camera angle to streamline photo collection and minimize the time in air for the coral nubbins.

The goal of this study is to use one of the latest software platforms, Agisoft Metashape, to create many 3D models of the same corals over time to create a time series of growth based on SA instead of BW_t. Agisoft Metashape was chosen because it allows for the end-to-end creation of 3D models from 2D images with little to no specialized knowledge and thus is extremely easy to allow even the most novice operators to build these models after a short tutorial. Other studies, like House et al. (2018), that use the PG method use an array of open-source software that would take some time to master. The creation of this time series will allow for new questions about SA to be asked. For example, “is SA growth linear over time?” and “how does SA change with BW_t over time?” With the previous methodologies, these types of questions were out of reach. This software provides a simple method of creating time series for the growth of coral based on SA. Also, a strict and consistent imaging protocol that oversamples the specimen to ensure saturation of camera views makes it possible to increase the accuracy of the 3D models produced. Due to the very small size and lack of complexity of the specimens used in this study, we rely on an oversampling of a single camera view angle.

Methods

Coral Acquisition and Preparation

Corals were sourced from Aqua SD, a local online coral distributor in San Diego, CA. A single head of Stylophora pistillata (approximately 30 cm in diameter) was purchased, fragmented, and grown at an average temperature of 27°C under the light of 150 μE/s/m² on average, with a 12 h/12 h day-night schedule. Each newly fragmented coral was attached to a pure aragonite coral plug that was 20 mm in diameter (Ocean Wonders, United States). The corals were attached to the plugs using Reef Glue (Ocean Wonders, United States). The seawater system was a pass-through system receiving new water pumped in from the ocean at the end of Scripps Pier (La Jolla Shores, La Jolla, CA). The water was passed through a four-stage sand filter system and heated to the temperature of 27°C. After fragmentation, the corals were acclimated for 4 weeks before any measurements were taken. Eighty nubbins were selected and tagged. The corals were then randomly subdivided into two groups of 40. Corals 1–40 (group 1) were measured weekly on a specific day, while corals 41–80 (group 2) were measured weekly on a different day.

Buoyant Weight Data Collection

The BW_t of 80 coral nubbins were collected weekly over 14 weeks using a Mettler Toledo scale (Mettler Toledo, United States) with a hanging basket attachment accurate to 0.001 g. The basket was placed into a 9.46 L tank with a 50-watt titanium tube water heater (Finnex, United States). The water temperature was controlled within a range of 25.5–27.5°C. The salinity was measured using a refractometer accurate to 1 ppt (ADE Advanced Optics, United States). The salinity and temperature data for each BW_t measurement were used to calculate the density of the water at the time of each measurement. The density of the water was then calculated using the water density formulas provided by UNESCO (Massel, 2015). The air weight (W_a) of the coral nubbins were calculated using the equation from Jokiel and Maragos (1978):

$${\text{W}}_{\text{a}}=\frac{{\text{W}}_{\text{w}}}{1-\left(\frac{{\text{D}}_{\text{w}}}{{\text{D}}_{\text{a}}}\right)}(1)$$

Where W_w is the measured BW_t, D_w is the density of the water the nubbin is weighed in, and D_a is the density of the nubbin. For this study D_a (the average density of Stylophora pistillata) is assumed to be 2.5 g/cm³ as measured by Ferrier-Pagès et al. (2003).

Wax Dipping Data Collection

Wax dip-derived SA data can only be collected from a coral that has been sacrificed (Stimson and Kinzie, 1991). Before data can be collected from corals, a calibration curve must be constructed from a series of objects with SAs that can be calculated. These SAs must be calculated using basic geometric equations. Wooden cylindrical rods of varying diameters and heights were used to create this calibration curve (Figure 1A). Where SA is the SA of the side and the top excluding the bottom of the rod using the equation:

FIGURE 1

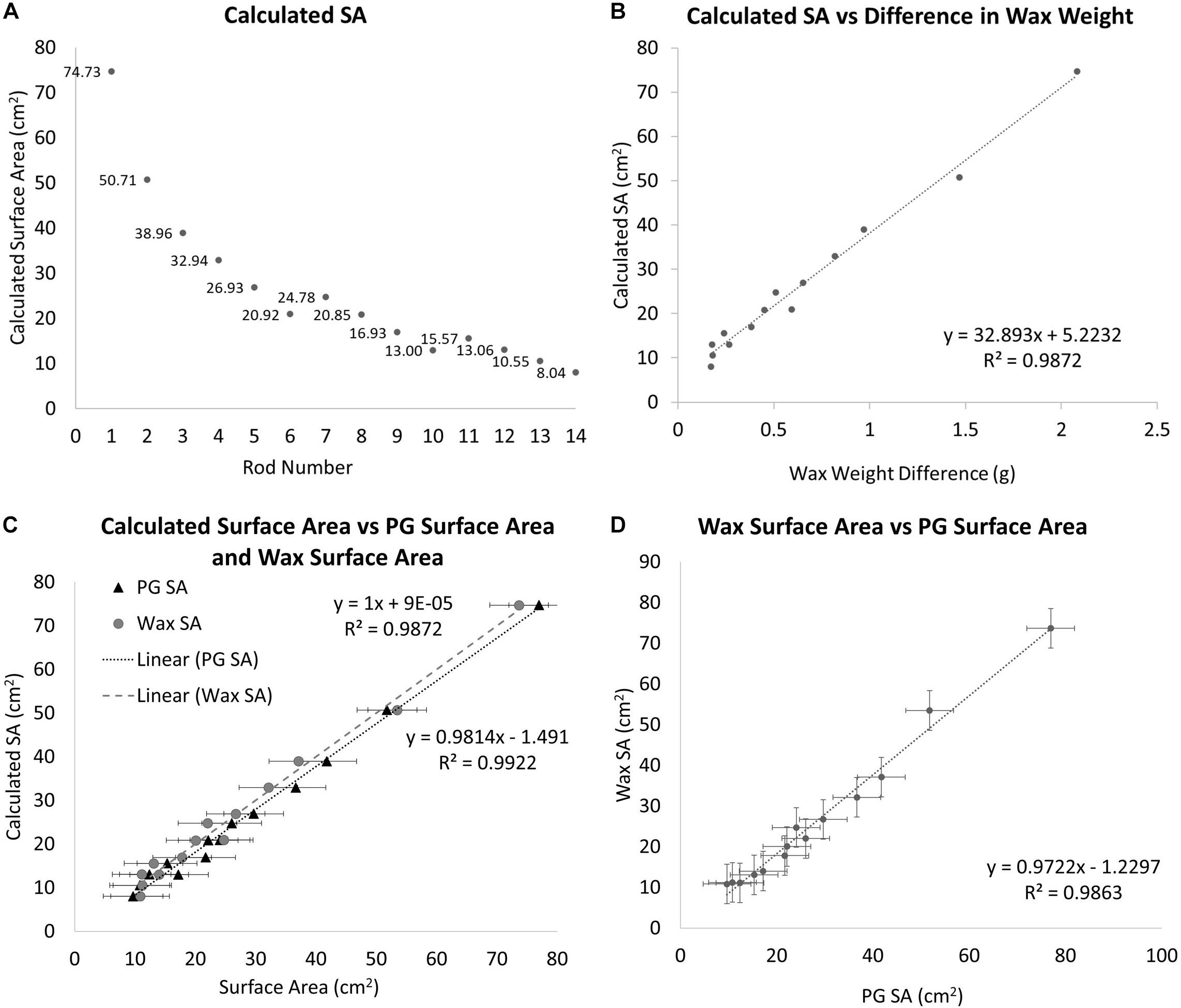
Figure 1. (A) The geometrically calculated SAs of the standards. The standards are a series of doweling rods of different diameters and lengths. SA is the SA of the side and the top excluding the bottom using the equation SA = (πr2)+ (hπD). (B) The geometrically calculated SA of the standard rods vs. the difference in pre and post-wax dipped standard rods. A best-fit line is fit to the data points with the equation y = 32.893x+ 5.2232. (C) A comparison between the geometrically calculated SA and the wax-dip derived SA, gray circles (R² = 0.9872, Slope = 1) and the PG derived SA, black triangles (R² = 0.9814, Slope = 0.9922). (D) A comparison of wax dip derived SA and PG derived SA (R² = 0.9863, Slope = 0.9722).

$$\mathrm{SA}=\left(\mathrm{\pi }\mathrm{r2}\right)+\left(\text{h}\mathrm{\pi }\text{D}\right)(2)$$

Diameters and lengths of the rods were measured using a pair of Husky digital calipers accurate to 0.01 mm (Husky, United States). After the SAs have been calculated, each standard is weighed using a Mettler Toledo scale (Mettler Toledo, United States; accurate to 0.001 g), and their masses are recorded. Each standard is then dipped in paraffin wax using the single dip method as in Veal et al. (2010), at a wax temperature of 70°C. The wax temperature was maintained using a Fisher scientific hotplate with a built-in magnetic stirrer and measured with a Fisher Scientific digital thermometer accurate to 0.1°C (Thermo Fisher Scientific, United States). A two-inch stir bar was used at the lowest setting to keep the wax at a homogeneous temperature. The stir bar was turned off while dipping and on between treatments. All specimens were at room temperature (25°C) at the time of dipping. The standards were dipped for 3 s and then pulled out and twisted back and forth for 10 s to ensure an even coating of the wax. The wax-dipped standards were set aside to dry for no less than 15 min after which time they were weighed and their masses were recorded again. The difference between the pre and post-wax weights was calculated and compared to the calculated dimensions of the rods (Figure 1B). From this comparison a best-fit line is placed giving us the following equation:

$$y=32.893x+5.2232(3)$$

Where y is the estimated SA of the unknown object and x is the difference in weight between the unknown object before and after being dipped in wax. From this equation, it is possible to estimate any objects’ SA when dipped into the same wax at the same temperature. Corals skeletons from group 1 were wax-dipped using the same method outlined above at the end of the experiment for comparison to PG-derived SA.

Photogrammetric Surface Area Data Collection

SA was measured by taking an average of 60 photos of each nubbin in air from a single camera view angle (approximately 25–30 degrees) using a custom-built motorized turntable and a Canon T3i DSLR Camera with an 18MP CMOS sensor capturing images with a resolution of 5184 × 3456 pixels (Canon, JP). The camera was operated with an infrared remote control to eliminate having to physically touch the camera after it was positioned. The motorized turntable had a wired button that turned the platform approximately 6 degrees for every press of the button. The corals were placed on a scaling disc with an arbitrary pattern of lines and geometric shapes as well as 4 scale bars. This disc allows for manual scaling of the models after the full render is completed, and also gives the computer software the necessary geometric reference patterns to properly align the photos. The nubbins were photographed in front of a contrasting blank backdrop in the ambient light condition of the lab. For live corals, a white backdrop was used and a black backdrop was used for coral skeletons.

Each set of images were then imported to the program (AgiSoft Metashape Professional, 2020). The program aligns the images, creates tie points, builds a sparse point cloud and depth maps for each image, builds the dense point cloud, builds mesh, builds texture. The model then is scaled using the aforementioned scale bars and trimmed so that only the coral remains in the model. Finally, SA is estimated using the Mesh Tool in the drop down menu entitled “tools”. In between each step, it is necessary to perform minor adjustments of the models to ensure the most accurate final model. For example, after photos are aligned, the model range, the 3D space in which the model is constructed, may not be properly set. If this is ignored, it would lead to portions of the coral not being incorporated into the final model creating holes in the model. Also, once the dense point cloud is created it is usually necessary to remove any points allocated from the background of the images. If this step is ignored, it is possible to get non-coral incorporated into the final model and it would have to be rerendered. Once a clean dense point cloud was created, the last two steps were run using a script that automatically created the mesh and texture. The average passive processing time (not including any active steps in between computer processing steps) to create one completed model was approximately 10 min. Table 1 shows each step with the relevant setting parameters to create a singe coral nubbin model.

TABLE 1

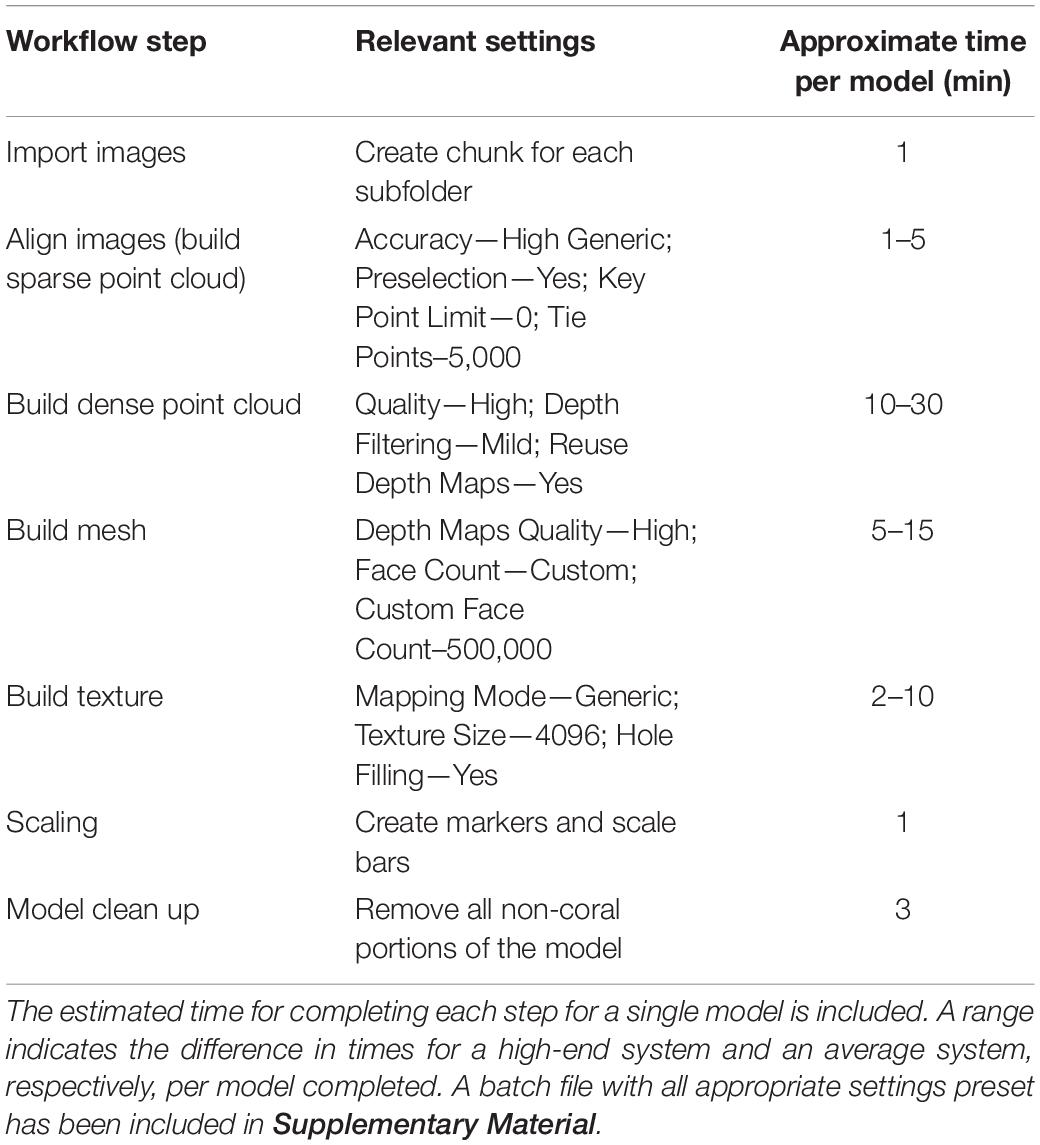
Table 1. This table shows all the steps in the workflow and the relevant settings needed to create a single model.

A custom-built computer running a Threadripper 2990wx 32 core 64 thread processor with 128 GB of RAM and two Radeon VII graphics cards with 60 compute units each was used to process the models in Windows 10 Pro. The processing time for models will vary depending on the specifications of the computer used and the number of photos per model. For 40 corals with 60 photos each, the total passive processing time was just under 12 h for this system. A lower-powered system would take significantly longer to perform these tasks. For example, a system running a Threadripper 1950 × 12 core 24 thread processor with 32 GB of RAM and a single Radeon VEGA 56 graphics card with 56 compute units would have a total passive processing time (for 40 models with 60 photos each) of approximately 33 h. It is possible to complete this entire workflow on a computer system that does not have a graphics card, but again the process would take an extremely long time comparatively. This would only be practical for a project with relatively few models that needed to be constructed. An example comparison between a photo, solid model, wireframe mesh, and a finished model with the scaling disk and a close-up of the wireframe can be seen in Figure 2. During preliminary investigations of this method, it was determined that one angle and 60 photos produced models with the same surface area as 2 angles and 120 photos. For this reason, only 60 photos and one angle were used as this practice takes half the time and limits the corals’ “in air” time. If corals with more complex growth forms, are used, more camera angles and photos would be necessary to created accurate models.

FIGURE 2

Figure 2. (A) A photo of coral nubbin 4–01 from week 3 on the motorized turntable with the scaling disk. (B) An example of a fully rendered 3D model for the coral in A with reference disc and scale bar. (C) A close-up photo of coral 4–08 from week 8. (D) Close up of the wireframe mesh for the coral in C, the yellow line represents 0.353 mm. (E) Close up of the solid mesh of the coral in C, the yellow line represents 0.353 mm. (F) Close up of the final render of the coral in (C).

Statistical Methods

Standard t-tests were used to compare the difference between geometrically calculated, wax-derived, and PG-derived SA estimates of standards. Regression analyses were used to determine the R² and slope of the wax and PG-derived SA’s relationship to the geometrically calculated SA of the standards. To determine if there was a significant difference between the results of the 3 methods on the standards an ANOVA analysis was conducted. A single factor ANOVA compared the difference between wax derived another regression analysis compared the growth rates produced by W_a and SA measurements. Additionally, to establish whether the initial size of the coral affected its growth rate a regression analysis was conducted comparing the growth rates for both methods to their respective initial measurements. A single factor ANOVA was conducted to determine the difference between both methods of calculating growth rates. To determine if there was a significant difference between the SA “simple” and “complex” prediction models and the PG-derived SA data, a regression analysis and single-factor ANOVA were conducted. Power rule models were applied to the data to create the predictive models reported here. All statistics and modeling were performed using Microsoft Excel (Microsoft, United States).

Results

Wax Dipping Comparison

A one-to-one relationship was observed between the geometrically calculated and the wax-derived SAs with an R²-value of 0.9872 (Slope = 1) (Figure 1C). The wax dip method overestimates SA when compared to the geometrically calculated SA, especially for smaller objects. On average, this method overestimated the SA of standard objects by approximately 1.61% when compared to the calculated values.

The SAs for all standards also were estimated using PG in Metashape. When the estimates were compared to the calculated values, a 1:1 relationship was observed with an R² of 0.9922 (Slope = 0.9814) (Figure 1C). The relationship between the PG method of estimating SA and the calculated SA was slightly stronger but was not significantly different from the wax-derived method (Paired t-test, p = 0.5000).

When the wax-dipped SAs were compared directly to the PG SAs, a marginally weaker relationship is observed with an R²-value of 0.9869 (Slope = 0.9746) (Figure 1D). When the results were compared for the measurements of the standards, the PG method had higher overall values. However, the results of a single factor ANOVA showed no significant difference between geometrically calculated, wax-dipped, and PG measurements [F(2, 39) = 0.056, p = 0.945]. Figure 3 shows the box plots for the percent difference from the geometrically calculated SA for both the wax dip method and the PG method.

FIGURE 3

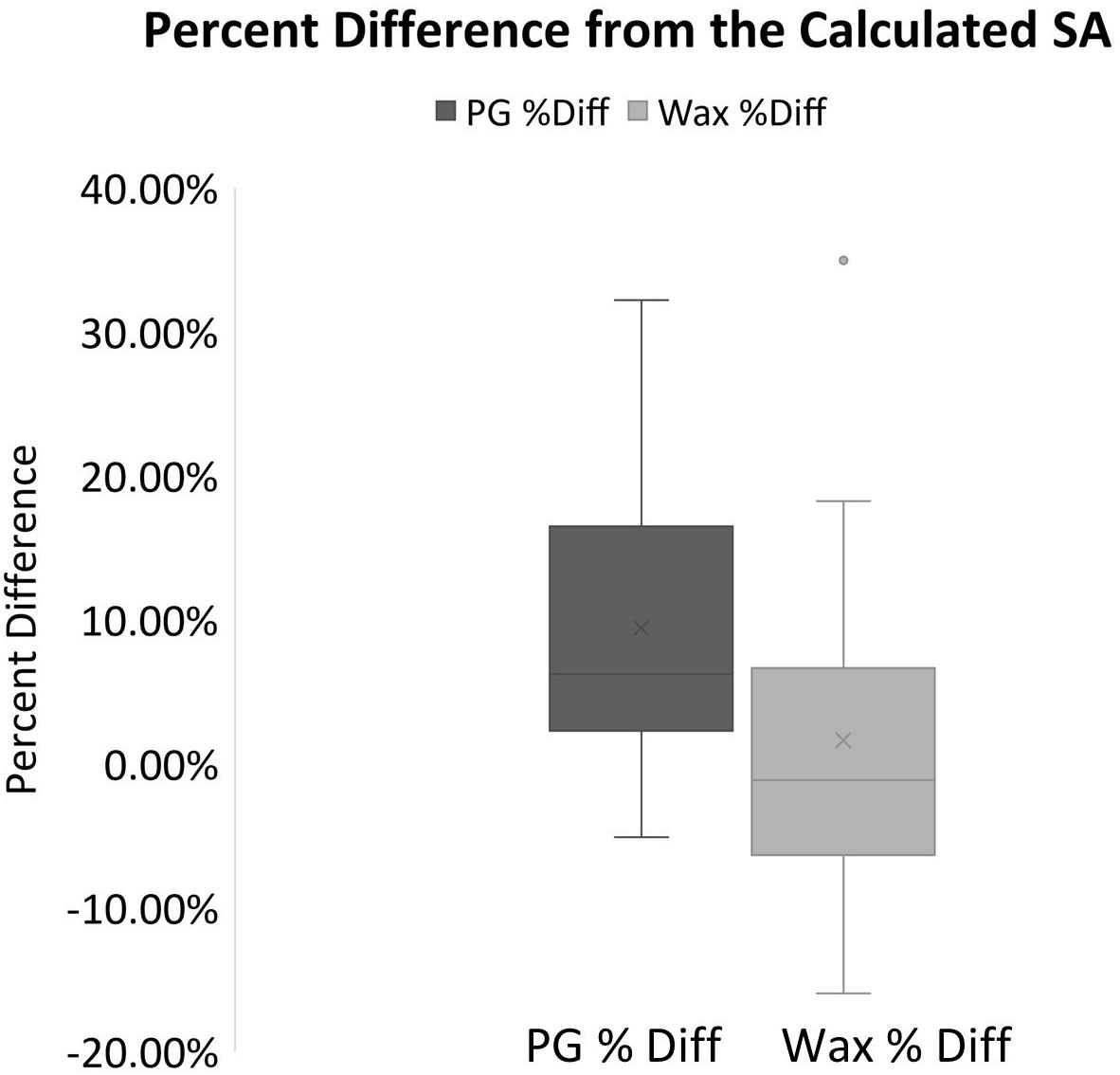
Figure 3. Box plots for the percent difference from the geometrically calculated SA for both the PG and the wax derived SA measurements. The mean is indicated x and the median is represented by the line bisecting each plot. The dark gray plot represents the PG percent difference data, and the light gray represents the data for the Wax percent difference. Dots outside the plot represent outliers in the data.

When these methods were applied to corals, a significantly different result was observed. The wax-dipped method of measuring SA of coral nubbins yielded significantly higher results than did the PG method. On average the wax dip method estimated SA 58.9% higher than did the PG method for the same coral (Figure 4). A single factor ANOVA showed a very significant difference between the two groups of wax dipped and PG measurements [F(1, 78) = 252.53, p ≤ 0.001].

FIGURE 4

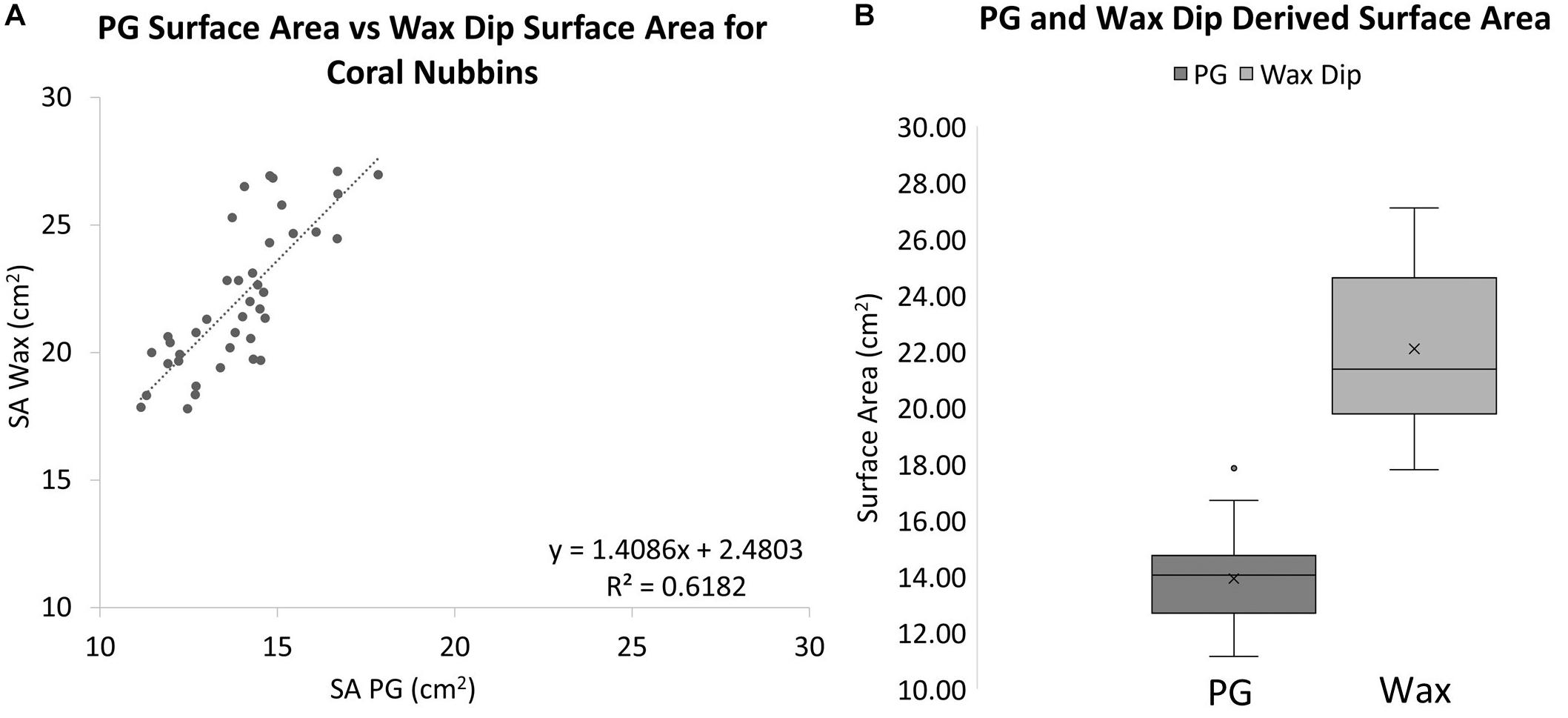
Figure 4. (A) A comparison of wax dip-derived SA and PG-derived SA for coral nubbins (R² = 0.6182, Slope = 1.4086). (B) Box plots for PG and wax dip-derived SA measurements of coral nubbins. The wax-dip method was on average 58.9% higher than the PG method. The mean is indicated x and the median is represented by the line bisecting each plot. Dots outside the plot represent outliers in the data.

Surface Area’s Relationship to Buoyant Weight

The two methods of determining growth rates also were significantly different with SA on average growing 0.69% per day for a total of 49.55% between August 19th, 2019 and October 30th, 2019, and W_a on average growing 0.21% per day for a total of 19.93% between July 29th, 2019, and October 30th, 2019. On average, measuring the growth rate with SA would yield a growth rate that was 69.8% higher than if the corals used. Figure 5 shows that while both SA and W_a increase over time, the slope of the best fit line for SA is 2.82 times steeper than the line for W_a. When compared directly, a similar relationship is observed with the average slope of the best fit lines for each week’s cluster of coral measurements being 2.57 (Figure 6A). When the W_a-derived growth rate was compared to the initial W_a weight, no correlation was observed, R² = 0.001 (Slope = 0.000) (Figure 7A). When the SA-derived growth rate was compared to the initial SA, a slight negative correlation was observed, R² = 0.3902 (Slope = –0.0008) (Figure 7B). When both growth rates are directly compared, we find that there is no relationship between the two methods, R² = 0.0715 (Slope = 0.043) (Figure 7C). A single factor ANOVA showed a very significant difference between the growth rates estimated with the two methods [F(1, 78) = 272.92, P = 0.001]. The box plots in Figure 7D illustrate that there is a much larger range in values for PG-derived growth rate when compared to W_a-derived growth rate.

FIGURE 5

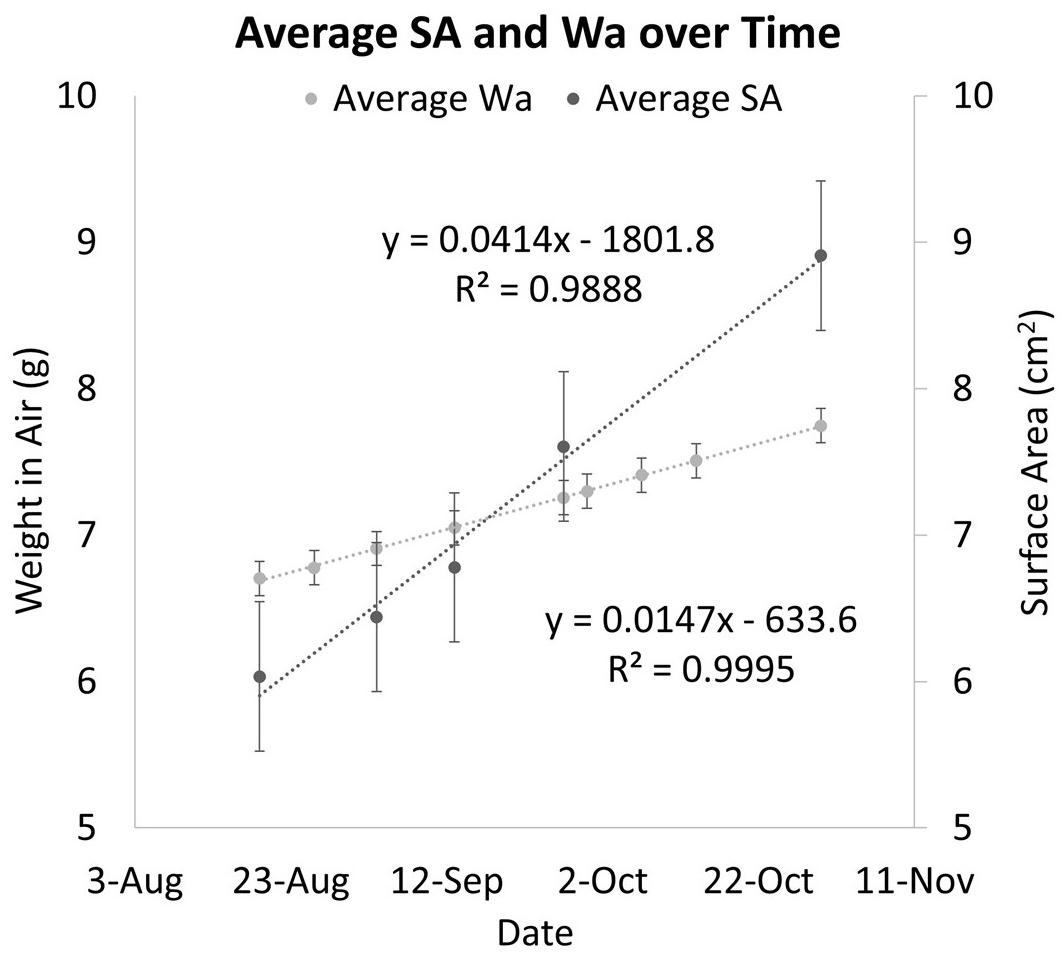
Figure 5. A comparison of W_a over time and SA over time for the same corals. Dark circles represent the average change in PG SA over time. Light circles represent the change in W_a over time. The error bars represent the standard error.

FIGURE 6

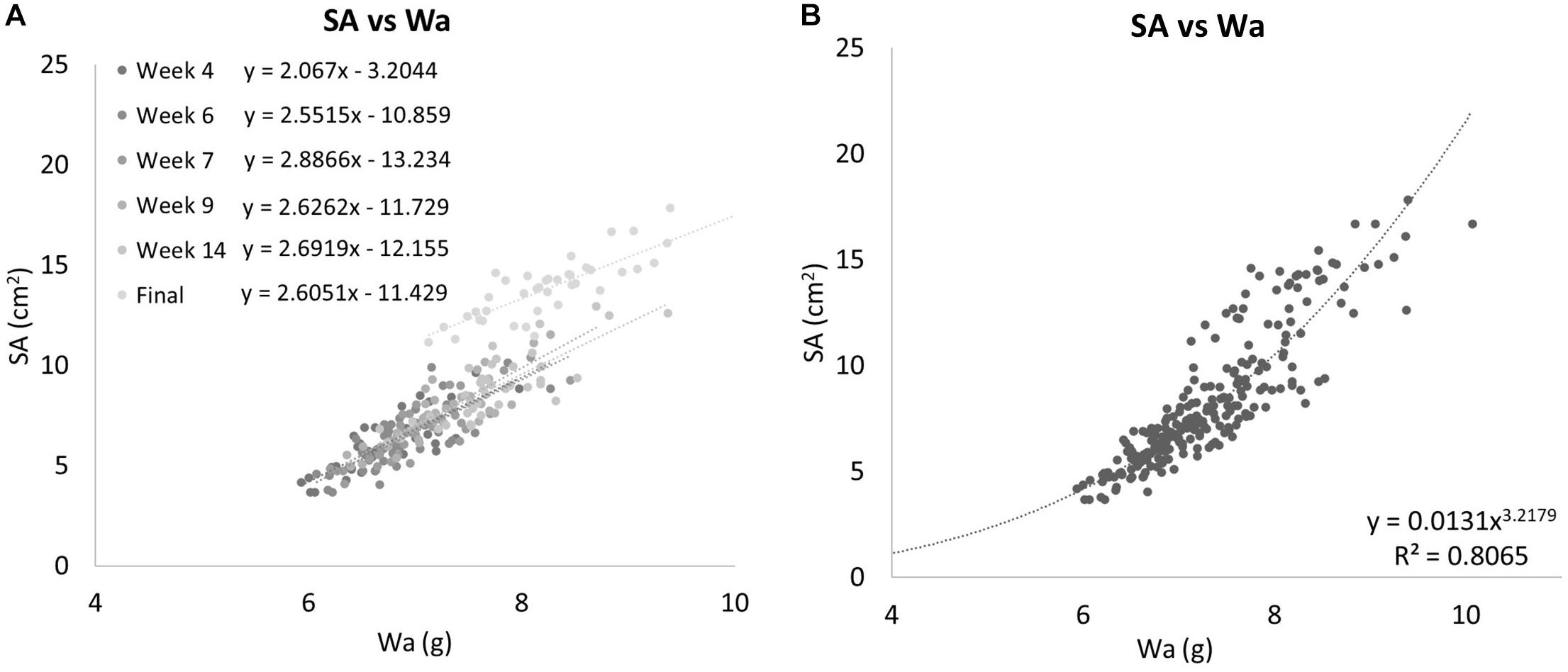
Figure 6. (A) Surface area campared to W_a for all Group 1 corals separated into individual weeks. The equations for the best fit lines of each weeks data can be found in the legend. Each time point’s data exhibit linear relationships on their own. (B) All Group 1 coral data are treated as a single group. When all data is compared together, a nonlinear relationship emerges. SA is related to W_a by the equation y = 0.0131x^3.170,R² = 0.8065.

FIGURE 7

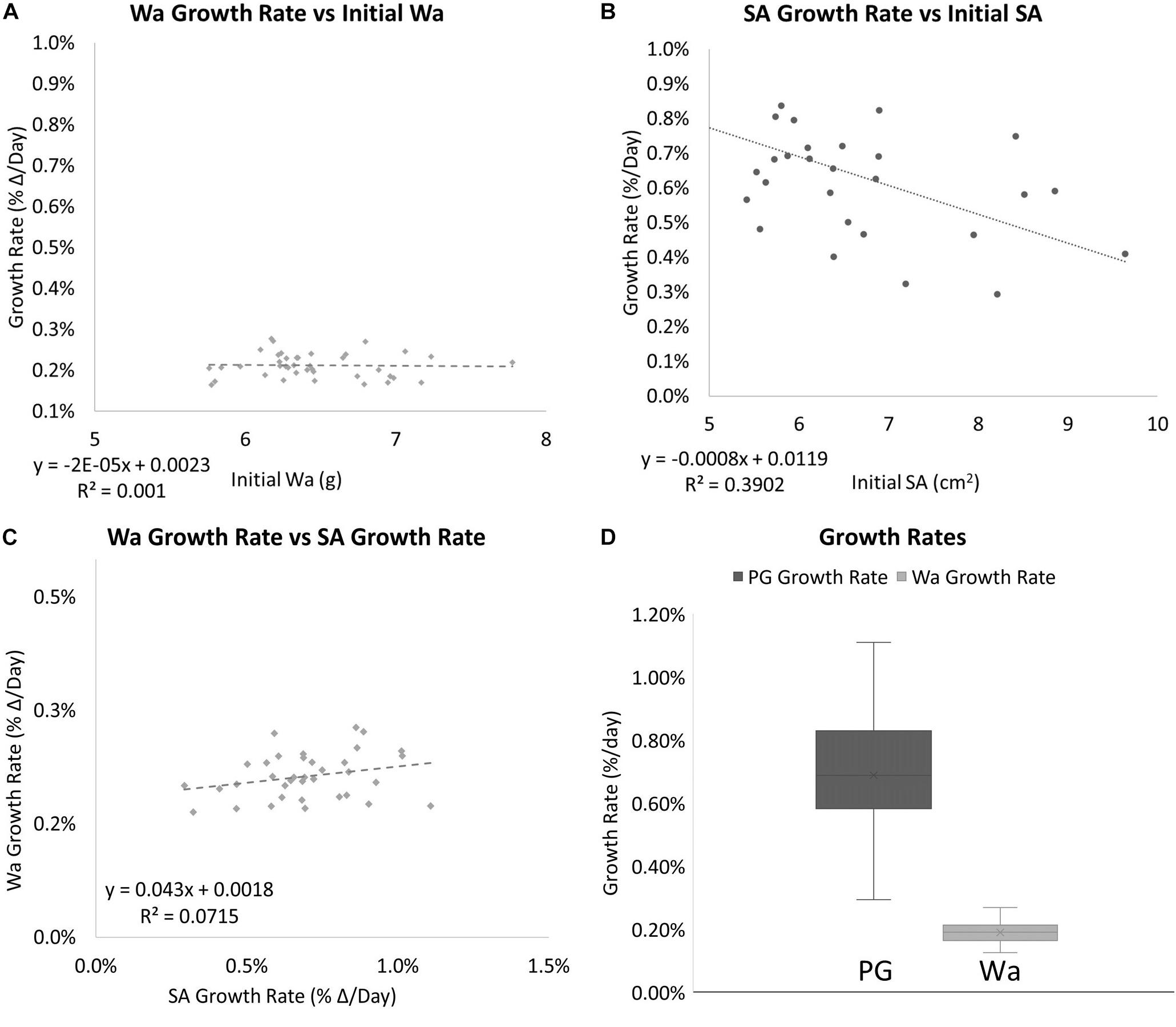
Figure 7. (A) The relationship between the initial W_a and the growth rate of individual nubbins. No correlation was observed. (B) The relationship between the initial SA vs. and the growth rate of individual nubbins. A slight negative correlation was observed (C) The relationship between the growth rate (percent Δ/Day) of W_a and the growth rate (percent Δ/Day) of SA. No correlation was observed between the two factors with an R² = 0.0715 and Slope = 0.043. (D) Box plots for the growth rates for corals based on different methods of measurement. Dark gray is the growth rate as measured by SA and light gray is the growth rate as measured by W_a. The mean is indicated x and the median is represented by the line bisecting each plot. Dots outside the plot represent outliers in the data.

The ratio between W_a and SA is shown to decrease over time as the coral grows (Figure 8). When this ratio is compared to W_a, there is a negative correlation that begins to asymptote in the 0.5–0.6 range (Figures 9A,C). This relationship is made much clearer when this ratio is compared to SA. The same asymptote can be observed in the same range as the previous example (Figures 9B,D).

FIGURE 8

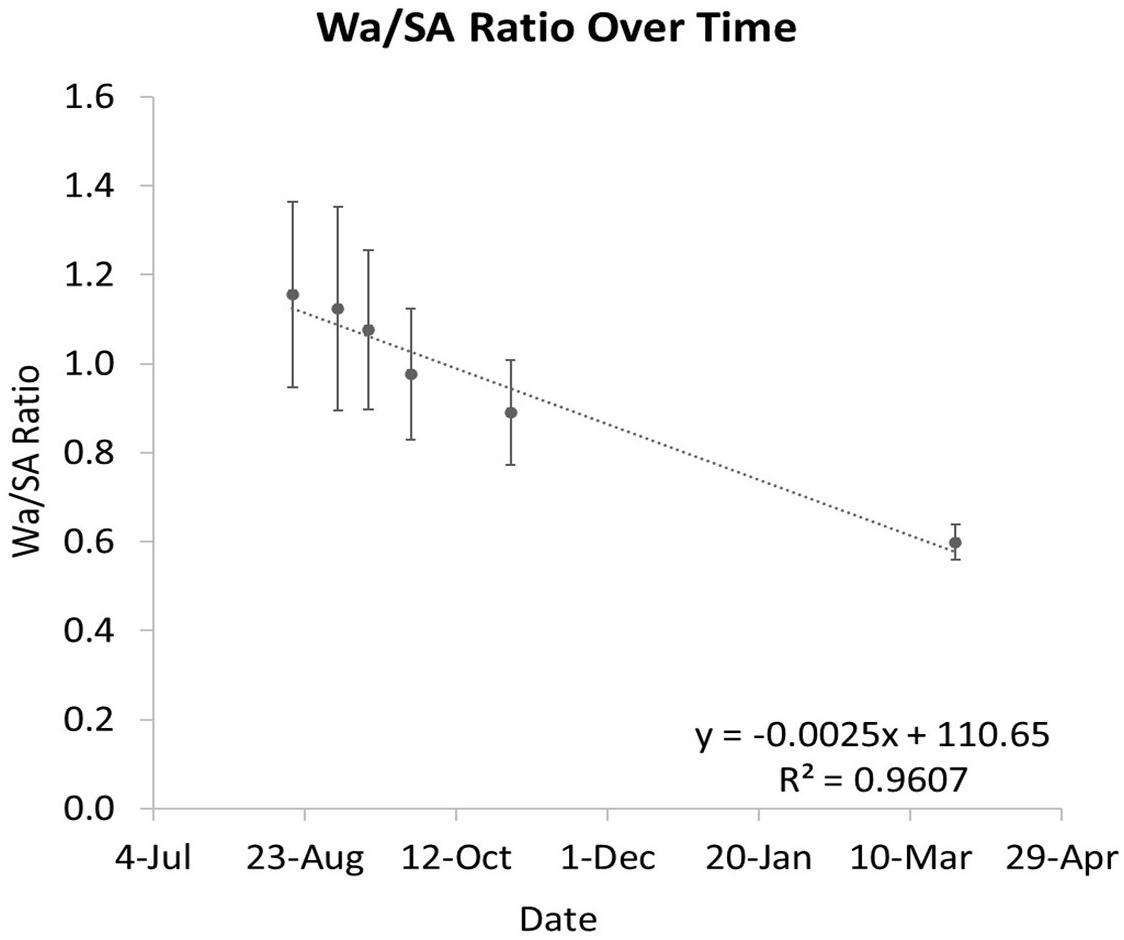
Figure 8. The ratio of W_a to SA over time. As the coral grows, this ratio decreases. The error bars represent one standard deviation from the mean on any given date.

FIGURE 9

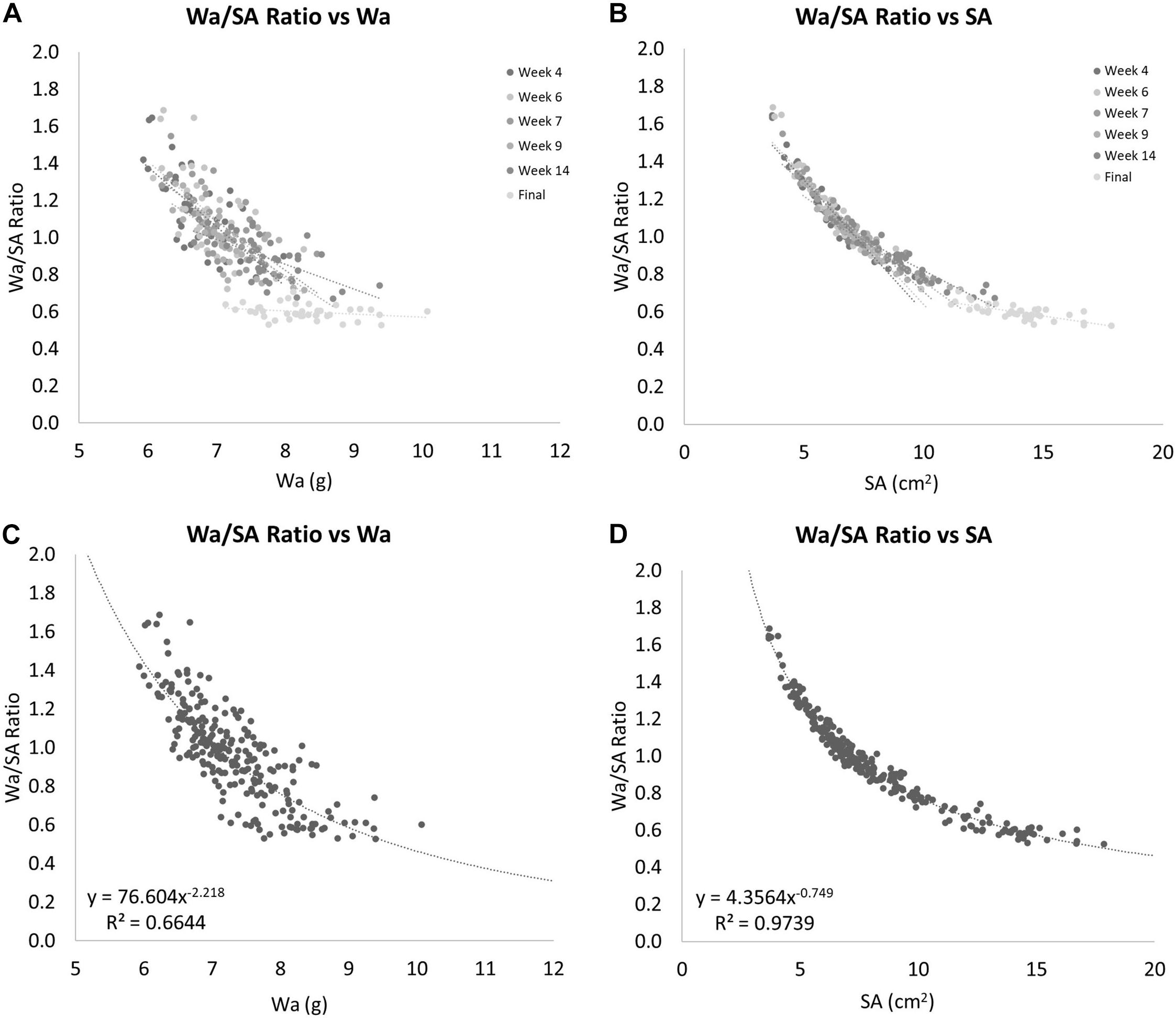
Figure 9. (A) The ratio of W_a to SA compared to W_a. This shows that as the W_a increases this ratio decreases, but seems to have a limit as this ratio never drops below 0.5. (B) The ratio of W_a to SA compared to SA. This shows that as the SA increases this ratio decreases. This example shows a clear nonlinearity to this relationship. (C) Gives the equation for the relationship between the ratio of W_a to SA vs. W_a for nubbins of S. pistillata between 6 and 10 grams in weight. (D) Gives the equation for the relationship between the ratio of W_a to SA vs. SA for nubbins of S. pistillata between 4 and 18 cm² in size.

When the SA data was directly compared to the W_a data for all dates, a nonlinear relationship was observed. This is because the SA of the corals grew much faster than the W_a (Figure 6B). If we apply a power rule model to this data, we get the equation:

$$y=0.0131x^{3.2179}(4)$$

This simple equation gives the SA for any S. pistillata W_a within the range of this data set, R² = 0.8065. It can be rewritten as:

$$SA=0.0131W_a{}^{3.2179}(5)$$

Comparing SA to W_a/BW_t of the same corals over time showed that the nubbins of S. pistillata on average grew significantly faster if measured by SA instead of by W_a with 0.69% per day and 0.21% per day average growth, respectively. This relationship provides another non-linear relationship that can be calculated when the ratio of the W_a and SA is compared to the W_a. If a power-law model is applied to these data, we get Figure 9C and the equation:

$$y=76.604x^{-2.218}(6)$$

This equation estimates the W_a/SA ratio for any S. pistillata W_a measurements within the range of our data or approximately from 6 to 10 grams, R² = 0.6644. To determine the relationship outside this range would require additional data. Now that we can estimate the W_a/SA ratio from a given W_a with the equation:

$$\frac{W_a}{SA}=76.604W_a{}^{-2.218}(7)$$

We can simply solve for SA yielding the equation:

$$SA=\frac{W_a}{76.604W_a{}^{-2.218}}(8)$$

Again, these equations can only be used within the range of the data that we have available. Now we have two equations for estimating SA from W_a. A “simple” model, Eq. 5, and a more “complex” model, Eq. 8. If we apply these two equations to the real W_a data and compare the results to the PG SA data, it produces SA data that are almost identical to each other and very close to the PG measured SA data (Figure 10). The best fit lines for both data sets are almost identical with the simple model estimating 0.33% more SA than the complex model for every data point. When compared to the actual SA data, the simple model on average overestimated the SA by 1.55%, while the complex model on average overestimated the SA by only 1.22%. A single factor ANOVA showed that there was no significant difference between the two models and the PG measured SA data [F(2, 705) = 0.5492, P = 0.93897]. A regression analysis for the complex model and the PG SA indicated a very strong relationship between the two data sets [F(1, 235) = 786.836, R² = 0.7708. p ≤ 0.001].

FIGURE 10

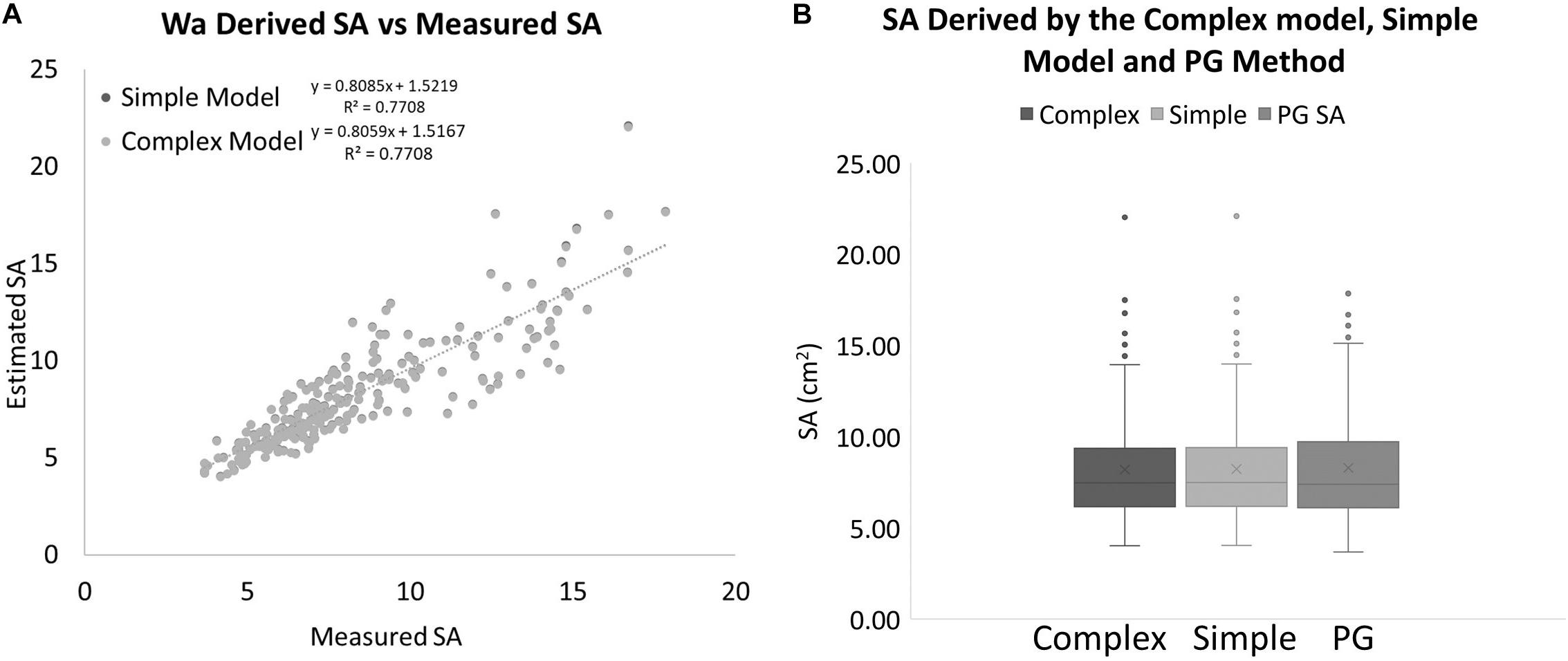
Figure 10. (A) SA values estimated with two different models using only a measurement of W_a compared to SA values that were measured with the PG method for the same coral nubbins. (B) Box plots showing the range and averages for the complex model, simple model, and PG measured SA of corals. The mean is indicated by x and the median is represented by the line bisecting each plot. Dots outside the plot represent outliers in the data.

Discussion

It has been shown that various techniques for determining SA can result in significantly different measurements in SA for the same coral (Naumann et al., 2009). In this study, the single wax-dip method was shown to significantly overestimate the value of SA for coral skeletons while relatively accurately estimating the SA of wooden objects of a known dimension. This indicates that the coral skeleton holds the wax differently enough to produce discrepancies upwards of 58.9%. This is similar to what Naumann et al. (2009) found. The wax dip estimates of branching corals similar to the ones in this study were only 57% accurate compared to the CT method (Naumann et al., 2009). An important next step would be to compare the PG technique to other techniques that use optics to estimate SA, like the CT method. If the PG method is sufficiently accurate to a highly precise method like CT scanning, it would lend credence to this method. The use of optics is advantageous here because there is no reliance on how a fluid adheres or does not adhere to various objects and substrates. If the fluid being used only adheres well to standard objects but not to corals, or has a higher adherence to corals than it does to standards, this will create discrepancies in data that can lead to gross under and overestimations of SA. The fact that there was no significant difference between the three estimations of SA for the standards means that the 59% difference seen in the wax data is most likely an overestimation. When Naumann et al. (2009) compared surface areas for various species of coral derived with different methods, the wax dip method did not compare favorably with the CT method, which was assumed to produce the true value (Naumann et al., 2009). This further suggests that the differences in how the wax is held by different coral species are most likely the reason there are discrepancies between wax-derived SA, and PG and CT-derived SA. Another consideration is the fact that the wax dipping is taking an absolute SA measurement, as mentioned before, and the practical application of this method is for live corals. While camera resolution limitations prevented the collection of fine-scale information on a live coral, this information would already be obscured by the coral tissue itself.

The wax dip method has been shown to over or underestimate the actual SA due to a variety of factors (Naumann et al., 2009). In this study, wax dipping overestimated the SA by 58.9% on average when compared to the PG method detailed here. Now with the complex model developed here, we can estimate SA from W_a measurements within approximately 1.22% of a measured value for an accuracy of 101.22% on average when compared to the PG method. This approximation is a reasonable estimate if we are comparing it to 77.3% accuracy for the branching corals in Naumann et al.’s (2009) study. Further work needs to be done to further tune the equations. For example, in this study, the D_a of 2.5 g/cm³ was used as an estimation of the density of Stylophora pistillata. While this is a reasonable assumption, it is possible that small variations in the density of various specimen accounted for some of the error seen in the models and correlations. A longer time series study may clear up any uncertainty that is found outside of the range of the current data. Also, the PG photos to construct 3D models were all taken in air which may introduce artifacts into the models like light shimmer that may lower the overall accuracy of the models. Taking the photos in water to create the 3D models could improve the accuracy of this metric. Estimates of the SA of corals with polyps extended and contracted also could be attempted. Throughout all of the data, it can be seen that as the corals become larger, more noise is apparent in the data. Even with the estimation models, it is apparent that at smaller weights the models are more accurate with the average percent difference from the PG SA for the complex model being only 4.92% for corals with a PG SA under 9 cm² and −7.21% for corals with a PG SA over 9 cm².

Any accuracy estimates in this study are in reference to another form of measurement, so they are only relative to that measurement. Therefore, if a more accurate reference measurement is selected, for example, X-ray CT scanning, it would only allow for more accurate estimation models to be created and honed. Thus far, there has only been a few studies that directly compare surface area methods to the CT method (Naumann et al., 2009; House et al., 2018), but these studies are missing either the PG method or the wax dip method. For this reason, a study comparing the latest PG methods outlined here and in Ferrari et al., 2017 and the wax dip method to X-ray CT scanning data would help confirm the accuracy of this very effective method of determining SA and its direct comparison to the wax dip method with the CT method serving as a highly accurate reference. More research is needed to increase the efficacy of this very promising emerging method of estimating coral SA of live coral specimens.

Data Availability Statement

The original contributions presented in the study are publicly available. This data can be found here: https://zenodo.org/record/5126449#.YPpd9ehKiUk.

Author Contributions

DC designed and implemented all protocols for this study and performed all analysis and authored the manuscript. EH collected and assisted in the collection of all the data necessary to perform the study, performed data management tasks to keep all the data organized and available for use. Both authors contributed to the article and approved the submitted version.

Funding

This study was funded in part by a grant provided by the UC San Diego Academic Senate grant number BG079912 at Scripps Institution of Oceanography. The grant provided funds for the computer system necessary to conduct this study in a timely fashion.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to acknowledge B. Greg Mitchell for his advising support on this project. We would also like to acknowledge the Smith/Sandin Laboratory at Scripps Institution of Oceanography for the use of wet lab and general lab space during this study. This study was funded in part by the UC San Diego Academic Senate that provided funds for the computer equipment necessary to conduct this study in a timely fashion. We would also like to acknowledge Aqua SD for providing us with the coral specimens necessary to conduct this study.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2021.660846/full#supplementary-material

References

AgiSoft Metashape Professional (2020). AgiSoft Metashape Professional (Version 1.6.2) (Software). Available online at: http://www.agisoft.com/downloads/installer/ (accessed March 01, 2020)

Google Scholar

Burris, J. E., Porter, J. W., and Laing, W. A. (1983). Effects of carbon dioxide concentration on coral photosynthesis. Mari. Biol. 75.2-3, 113–116. doi: 10.1007/bf00405992

CrossRef Full Text | Google Scholar

Dahl, A. L. (1973). Surface area in ecological analysis: quantification of benthic coral-reef algae. Mari. Biol. 23.4, 239–249. doi: 10.1007/bf00389331

CrossRef Full Text | Google Scholar

Davies, P. S. (1980). Respiration in some Atlantic reef corals in relation to vertical distribution and growth form. Biol. Bull. 158.2, 187–194. doi: 10.2307/1540930

CrossRef Full Text | Google Scholar

Dodge, R. E., Wyers, S. C., Frith, H. R., Knap, A. H., and Smith, S. R. (1984). “Coral calcification rates by the buoyant weight technique: effects of alizarin staining”. J. Exp. Mari. Biol. Ecol. 75, 3, 217–232. doi: 10.1016/0022-0981(84)90167-9

CrossRef Full Text | Google Scholar

Ferrari, R., Figueira, W. F., Pratchett, M. S., Boube, T., Adam, A., et al. (2017). 3D photogrammetry quantifies growth and external erosion of individual coral colonies and skeletons. Sci. Rep. 7.1, 1–9.

Google Scholar

Ferrier-Pagès, C., Witting, J., Tambutte, E., and Sebens, K. P. (2003). Effect of natural zooplankton feeding on the tissue and skeletal growth of the scleractinian coral Stylophora pistillata. Coral Reefs 22.3, 229–240. doi: 10.1007/s00338-003-0312-7

CrossRef Full Text | Google Scholar

Harrod, J. J., and Hall, R. E. (1962). A method for determining the surface areas of various aquatic plants. Hydrobiologia 20.2, 173–178. doi: 10.1007/bf00046315

CrossRef Full Text | Google Scholar

Hawkins, C. M., and Lewis, J. B. (1982). Benthic primary production on a fringing coral reef in Barbados, West Indies. Aquat. Bot. 12, 355–363. doi: 10.1016/0304-3770(82)90027-4

CrossRef Full Text | Google Scholar

Hoegh-Guldberg, O. (1988). A method for determining the surface area of corals. Coral Reefs 7.3, 113–116. doi: 10.1007/bf00300970

CrossRef Full Text | Google Scholar

Holmes, G., Ortiz, J., Kaniewska, P., and Johnstone, R. W. (2008). Using three-dimensional surface area to compare the growth of two Pocilloporid coral species. Mari. Biol. 155.4, 421–427. doi: 10.1007/s00227-008-1040-x

CrossRef Full Text | Google Scholar

House, J. E., Brambilla, V., Bidaut, L. M., Christie, A. P., Pizarro, O., Madin, J. S., et al. (2018). Moving to 3D: relationships between coral planar area, surface area and volume. PeerJ 6:e4280. doi: 10.7717/peerj.4280

PubMed Abstract | CrossRef Full Text | Google Scholar

Jokiel, P. L., and Maragos, J. E. (1978). Coral growth: buoyant weight technique. Coralreefs Res. Methods 41, 529–541.

Google Scholar

Jones, A. M., Berkelmans, R., Cantin, N. E., Negri, A. P., and Sinclair, W. (2008). A 3D modeling method to calculate the surface areas of coral branches. Coral Reefs 27.3, 521–526. doi: 10.1007/s00338-008-0354-y

CrossRef Full Text | Google Scholar

Kanwisher, J. W., and Wainwright, S. A. (1967). Oxygen balance in some reef corals. Biol. Bull. 133.2, 378–390. doi: 10.2307/1539833

CrossRef Full Text | Google Scholar

Laforsch, C., Christoph, E., Glaser, C., Naumann, M., Wild, C., and Niggl, W. (2008). A precise and non-destructive method to calculate the surface area in living scleractinian corals using X-ray computed tomography and 3D modeling. Coral Reefs 27.4, 811–820. doi: 10.1007/s00338-008-0405-4

CrossRef Full Text | Google Scholar

Massel, S. R. (2015). Internal Gravity Waves in the Shallow Seas. Poland: Springer International Publishing.

Google Scholar

Meyer, J. L., and Schultz, E. T. (1985). Tissue condition and growth rate of corals associated with schooling fish 1. Limnol. Oceanogr. 30.1, 157–166. doi: 10.4319/lo.1985.30.1.0157

CrossRef Full Text | Google Scholar

Muscatine, L., Falkowski, P., Porter, W. J., and Dubinsky, Z. (1984). Fate of photosynthetic fixed carbon in light-and shade-adapted colonies of the symbiotic coral Stylophora pistillata. Proc. R. Soc. London Series B. Biol. Sci. 222.1227, 181–202. doi: 10.1098/rspb.1984.0058

CrossRef Full Text | Google Scholar

Naumann, M. S., Niggl, W., Laforsch, C., Glaser, C., and Wild, C. (2009). Coral surface area quantification–evaluation of established techniques by comparison with computer tomography. Coral Reefs 28.1, 109–117. doi: 10.1007/s00338-008-0459-3

CrossRef Full Text | Google Scholar

Stimson, J., and Kinzie, R. A. III (1991). The temporal pattern and rate of release of zooxanthellae from the reef coral Pocillopora damicornis (Linnaeus) under nitrogen-enrichment and control conditions. J. Exp. Mari. Biol. Ecol. 153.1, 63–74. doi: 10.1016/s0022-0981(05)80006-1

CrossRef Full Text | Google Scholar

Szmant-Froelich, A., and Pilson, M. E. (1980). The effects of feeding frequency and symbiosis with zooxanthellae on the biochemical composition of Astrangia danae Milne Edwards & Haime 1849. J. Exp. Mar. Biol. Ecol. 48, 85–97. doi: 10.1016/0022-0981(80)90009-X

CrossRef Full Text | Google Scholar

Veal, C. J., Carmi, M., Fine, M., and Hoegh-Guldberg, O. (2010). Increasing the accuracy of surface area estimation using single wax dipping of coral fragments. Coral Reefs 29, 893–897. doi: 10.1007/s00338-010-0647-9

CrossRef Full Text | Google Scholar