Optimisation of Parameters in a German Bight Circulation Model by 4DVAR Assimilation of Current and Water Level Observations

Uncertain parameters in a 3D barotropic circulation model of the German Bight are estimated with a variational optimisation approach. Surface current measurements from a high frequency (HF) radar are used in combination with acoustic Doppler current profiler (ADCP) and tide gauge observations as input for a 4DVAR assimilation scheme. The required cost function gradients are estimated using an adjoint model code. The focus of the study is on systematic errors of the model with the control vector including parameters of the bathymetry, bottom roughness, open boundary forcing, meteorological forcing as well as the turbulence model. The model uses the same bathymetry, open boundary forcing, and metereological forcing as the operational model run at the Federal Maritime and Hydrographic Agency (BSH). The baroclinic BSH model is used as a reference to put the performance of the optimised model into perspective. It is shown that the optimised model has better agreement with HF radar data and tide gauge observations both within the fortnight training period and the test period 1 month later. Current profile measurements taken at two platforms indicate that both models have comparable error magnitudes at those locations. The optimised model was also compared with independent drifter data. In this case, drifter simulations based on the BSH model and the respective operational drift model including some surface wave effects were used as a reference. Again, these comparison showed very similar results overall, with some larger errors of the tuned model in very shallow areas, where no observations were used for the tuning and surface wave effects, which are only explicitly considered in the BSH model, play a more important role. The tuned model seems to be slightly more dissipative than the BSH model with more energy entering through the western boundary and less energy leaving toward the north. It also became evident that the 4DVAR cost function minimisation process is complicated by momentum advection, which leads to non-differentiable dependencies of the model with respect to the control vector. It turned out that the omission of momentum advection in the adjoint code still leads to robust estimates of descent directions.

1. Introduction

Although the fundamental processes of ocean dynamics are quite well-understood for most coastal regions, accurate, and reliable predictions of variables relevant for practical applications are still challenging. The situation near the coast is often complex because of the spatial heterogeneity, the dependence on open boundary forcing and the usually short time scales. For example, in shallow, tidal dominated areas like the German Bight numerical models require high resolution information about parameters related to bathymetry or bottom friction, which are hard to measure and therefore often lack accuracy.

Coastal ocean models are affected by both systematic and stochastic error components. For systems with short memory the reduction of systematic errors is of particular interest, because an improvement can be expected on all time scales. The treatment of stochastic errors, e.g., related to atmospheric forcing, can have significant impacts on shorter time scales, and makes sense as a second step, in particular as part of an operational forecast system.

Most uncertain parameters in coastal models, like bottom roughness or momentum diffusion coefficients related to turbulence are very hard to measure directly. These parameters are therefore usually estimated in an indirect way through the measurement of standard prognostic model variables like water levels or current velocities, which are dynamically connected to the uncertain quantities. This results in inversion problems with often strong non-linearities, which require a larger variety of different observations to obtain robust estimates. The relationship between model variables and observed quantities is often not straightforward as well. This is in particular true for surface currents, which are affected by various atmospheric and oceanic processes.

In this study the focus is on the three-dimensional (3-D) circulation of the German Bight and the reduction of systematic errors in a respective numerical model. The German Bight circulation is dominated by tides and is strongly influenced by the bathymetry and bottom friction processes. Overview maps and isobaths are shown in Figure 1. Impacted by wind, waves, and tides, the water masses at the coasts are periodically mixed with the open North Sea waters (during flood) and are partially exported back (during ebb). Westerly winds typically prevail in the North Sea resulting in a mean current pattern with water entering the German Bight from the west and leaving to the North. However, these mean transport directions can actually be reversed in strong easterly wind situations (Stanev E. et al., 2019). Strong tidal currents in tidal inlets connect the near coastal Wadden Sea areas, which are falling dry during ebb, with the open water. The resulting circulation dynamics is characterised by strong non-linearities and high sensitivity to small scale bathymetry features (Sündermann et al., 1999; Stanev et al., 2009). As sediment transport processes are significant in the area, the tracking of bathymetry changes through observations is very challenging and numerical models are affected by respective errors.

FIGURE 1

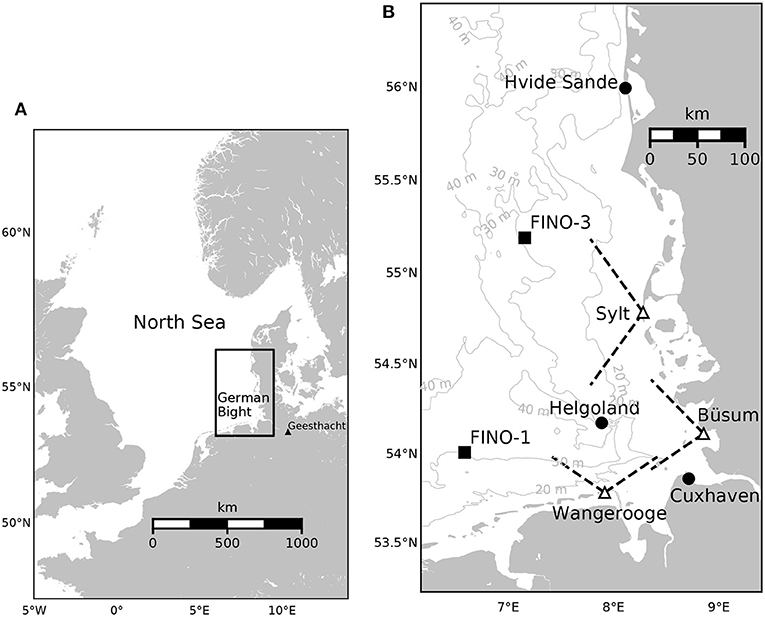
Figure 1. (A) Map of the North Sea with the German Bight and the model domain indicated by a black rectangle. (B) Detailed map of the area considered in this study with information on the used observation systems. Black dots indicate tide gauges, triangles mark positions of HF radar stations and black squares refer to fixed platforms with ADCP measurements. The dashed black line indicate the approximate look directions of the radar systems and the grey lines in the background refer to the 20, 30, and 40 m isobath.

Another process that needs some consideration is the potential impact of wind driven surface waves on the circulation. For the North Sea, the importance of wave induced processes for the ocean circulation and sea-level predictions was demonstrated in previous studies (Staneva et al., 2016, 2017; Schloen et al., 2017). Staneva et al. (2016) and Schloen et al. (2017) studied the impact of the ocean-wave coupling in the near-coastal German Bight region and showed the predictive skills of ocean circulation and sea-level could be significantly enhanced by considering wave-induced processes. In extreme storm surge conditions over the North Sea, due to strong non-linearity of wave-ocean-tidal interaction, the wave-ocean coupling is considered to be significant for correct model predictions (Cavaleri et al., 2018).

The German Bight is a very busy area with a lot of shipping and offshore activities. In particular, the offshore windfarm sector has grown rapidly over the last decade with about 1,000 turbines installed in coastal German waters. For this reason, there is high demand for reliable information on ocean parameters like currents, which are required for applications such as search and rescue (SAR), modelling of sediment transport processes, or ship operations related to building and maintenance of offshore constructions. Marine litter and transport of pollutants is of growing concern as well. Different types of model simulations are required including short term forecasts for operational applications, scenario simulations for optimised long term planning and process studies.

In the present study uncertain model parameters in a German Bight model are estimated using a combination of HF radar (HFR) surface current data, current profiles measured by Acoustic Doppler Profiler (ADCP) and tide gauge water level measurements. These data are used as input for a variational optimisation scheme (4DVAR), which takes into account nonlinearities of the model and finds optimal solutions using a gradient based iteration scheme. The required gradients are computed using an adjoint model. The approach to use HF radar data in combination with tide gauge data was motivated by the fact that surface current measurements do not necessarily correlate well with vertically integrated volume transports. As the divergence of these transports control water level changes, the sole assimilation of surface current observations can easily deteriorate water level estimates, which are one of the key variables for the German Bight. The simultaneous use of water level measurements, which are available on a routinely basis in most coastal areas, adds independent information on transports in the analysis and helps to avoid this problem.

A variety of previous studies have investigated approaches to combine HF radar measurements with model data to improve state estimates. The proposed methods include optimal interpolation (Gandin, 1963; Breivik and Saetra, 2001), more sophisticated statistical approaches (Oke et al., 2002; Barth et al., 2008, 2011; Shulman and Paduan, 2009), variational methods (Scott et al., 2000; Kurapov et al., 2003; Li et al., 2008; Yaremchuk and Sentchev, 2009; Zhang et al., 2010; Ngodock et al., 2015; Vandenbulcke et al., 2017) and ad hoc approaches (Lewis et al., 1998). Data driven empirical methods were proposed as well (Wahle and Stanev, 2011; Frolov et al., 2012).

HFR data acquired in the German Bight have already been used in previous studies for data assimilation as well as for comparisons with models (Port et al., 2011; Baschek et al., 2016). An ensemble based approach to optimise the open boundary forcing was presented in Barth et al. (2010). A similar technique was applied in a subsequent study (Barth et al., 2011) to optimise the wind forcing for a German Bight circulation model. A statistical based approach to improve short term surface current forecast was presented in Stanev et al. (2015). As with most other studies on HF radar assimilation cited above, it is often not easy to put the results into perspective because comparisons with established systems (e.g., operational systems run at forecast centres) are rarely found.

In this study a 4DVAR variational approach is applied for the assimilation of current observations in the German Bight for the first time. The main objectives of the study are as follows:

• Reduce systematic model errors based on observations in order to improved estimates of currents and water levels.

• Use a combination of surface current measurements as well as current profile and water level observations to provide information on the 3D structure of water transports.

• Demonstrate improved model performance based on independent observations

• Compare results to a well-established operational reference model

To achieve these goals, a 3D numerical coastal circulation model and the respective adjoint were implemented. This implementation will be referred to as IMCO (invertible model for the coastal ocean) in the following. To demonstrate the model improvement, a data set of surface drifter trajectories was used, which was acquired in the month following the 14 day period used for the model tuning. As a reference for the analysis, the operational model run at the Federal Maritime and Hydrographic Agency (BSH) was chosen. The BSH model could not be used for the 4DVAR assimilation directly, because there is no adjoint model code available. The decision to use a variational method is based on our experience that the improvement of models, which are already showing good performance, is hard to achieve with methods that contain a lot of implicit uncertainty and require assumptions about linearity, like the majority of existing ensemble methods. To our knowledge, the present study is the first attempt to apply a 4DVAR approach to a barotropic coastal system with Wadden Sea areas and extremely shallow water. The strong nonlinearities associated with bottom friction are particularly challenging for the resulting minimisation problem.

It is important to say that the 4DVAR setup used in this study is not meant to be run in an operational environment. The treatment of systematic model errors can be done based on a single minimisation exercise using a longer analysis window. This is in contrast to operational assimilation schemes, which try to deal with stochastic model errors repeatedly (typically every 12 or 24 h) and which have to be optimised accordingly. Because of the usually short correlation times of stochastic model errors on coastal scales, the treatment of these errors is a big challenge and it makes sense to put a focus on systematic errors in the first step.

The present study is of more general interest, because the focus on systematic model errors has some general consequences for observation data requirements. In general one can say that the temporal frequency of observation data is less critical for model tuning compared to operational data assimilation. This is of particular relevance for the assessment of current and future satellite data, which often lack temporal resolution, but which can still be of high value for model optimisation. This is in particular the case for coastal regions where high resolution information from satellites can help to treat model errors associated with insufficient representation of spatial heterogeneities (Sanchez-Arcilla et al., 2021).

The paper is structured as follows. In section 2, the model used for the 4DVAR tuning as well as the respective adjoint is introduced. The observations and the BSH model data are described in section 3. Results obtained with the tuning method are presented in section 4 and conclusions are given in section 5.

2. Numerical Model

In the following a brief description is given of the model that is used as a basis for the parameter optimisation exercise. Although the model follows the standard theory, it is important to explain the used parameterisations. In addition, the use of an adjoint model requires that the original model has certain smoothness and stability properties, which not all models have, e.g., concerning the wetting and drying scheme. More details on the numerical treatment of the model equations can be found in Appendix A.

The model used in this study to simulate the 3D circulation in the German Bight is barotropic, i.e., density variations due to temperature or salinity gradients are not treated in a prognostic way. Although the circulation in the German Bight is dominated by tidal and wind forcing as well as the bathymetry (Becker et al., 1992), this is certainly an approximation. Due to river runoff there is stratification in the Weser, Ems, and Elbe estuaries with impacts on the 3D circulation (Stanev E. V. et al., 2019), but these relatively small regions are not the focus of this study. Temperature stratification can occur in the interior of the German Bight during summer as well. However, the possible impact of stratification on the circulation by conditioning of the internal friction is to some extent taken into account in the model tuning process described below by inclusion of a spatially varying background momentum diffusivity and mixing length profiles.

The model is based on the standard Reynolds averaged Navier Stokes equations using the hydrostatic and Boussinesq approximations

$\begin{array}{ll}\frac{\partial u}{\partial t}=u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+fv-g\frac{\partial \eta }{\partial x}-\nabla ·{\nu }_h{\nabla }_{h}u-\frac{1}{\partial z}{\nu }_v\frac{\partial u}{\partial z}& (1)\end{array}$

$\begin{array}{ll}\frac{\partial v}{\partial t}=u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}-fu-g\frac{\partial \eta }{\partial y}-\nabla ·{\nu }_h{\nabla }_{h}v-\frac{1}{\partial z}{\nu }_v\frac{\partial v}{\partial z}& (2)\end{array}$

with the horizontal current components u, v, the surface elevation η, the Coriolis parameter f, the gravitational acceleration g, and the horizontal and vertical momentum diffusion parameters ν_h and ν_v, respectively.

Assuming incompressibility, the current field and the water elevations are connected by the continuity equation given as

$\begin{array}{ll}\frac{\partial \eta }{\partial t}=-\nabla ·U,& (3)\end{array}$

where U is the two-dimensional (2D) vector of vertically integrated horizontal currents.

The vertical current vector component w can be obtained from

$\begin{array}{ll}w(x,y,z)=-{\displaystyle {\int }_0^z}\nabla ·\text{u}(x,y,z^{\prime })d{z}^{\prime },& (4)\end{array}$

where the sea floor is at z = 0. As the vertical current component is three to four orders of magnitude smaller than the typical horizontal current speeds in the considered area, vertical momentum advection was neglected and the explicit computation of w as a prognostic variable was not required in the simulation.

2.1. Surface, Bottom, and Open Boundary Conditions

As stated before, bottom friction and wind forcing are important factors in the German Bight circulation. In the following we give a brief summary how these processes are parameterised in the model in the form of boundary conditions.

The bottom friction is modelled using a standard log-profile boundary layer approach, where the friction velocity $u_b^{*}$ is related to the current velocity u(z) at some distance z from the bottom by

$\begin{array}{ll}{u}_b^{*}=\frac{\kappa u(z)}{log(\frac{z+z_0}{z_0})}& (5)\end{array}$

with Karman constant κ and bottom roughness length scale z₀. For a given current velocity and bottom roughness the normalised friction force is then computed as ${\tau }_b={(u_b^{*})}^2$. The bottom roughness z₀ is used as a tuning parameter in the model optimisation.

For the sea surface, the momentum flux from the atmosphere to the ocean is given using a bulk formula of the form

$\begin{array}{ll}({(u_x^{*})}^2,{(u_y^{*})}^2)={\lambda }_{met}(U_{10},V_{10})\left|{\text{U}}_{10}\right|& (6)\end{array}$

with wind drag coefficient λ_met (Backhaus, 1976), which is used as a tuning parameter in the model optimisation.

For the open boundaries on the western and northern side of the model domain (see Figure 1B) water levels are prescribed using standard clamped conditions.

2.2. Vertical and Horizontal Momentum Diffusion

The used turbulence model is quite simple and based on a parameterised shape of the mixing length profile. The vertical momentum diffusion is then controlled by current shear and an additional background momentum diffusion.

A cubic shape of the vertical mixing length profile was used similar to parameterisations discussed in Umlauf et al. (2005).

$\begin{array}{ll}l(z)=d_s{d}_b\frac{d_b{\kappa }_s+d_s{\kappa }_b}{H^2},& (7)\end{array}$

where d_s and d_b are the distances from the surface and the bottom, respectively. The parameters κ_b and κ_s control the behaviour of the mixing length near the bottom and surface boundary layers and are part of the tuning vector. If the sea floor was an idealised wall one should get κ_b = κ with the Karman constant κ ≈ 0.4 according to the law of the wall. With the mixing length given by Equation (7) the vertical momentum diffusion coefficient is estimated as

$\begin{array}{ll}{\nu }_v=l^2(z)\sqrt{{\left(\frac{\partial u}{\partial z}\right)}^2+{\left(\frac{\partial v}{\partial z}\right)}^2}+\frac{{\beta }_{BG}}{H}.& (8)\end{array}$

The second term in Equation (8) is supposed to represent additional sources or sinks of turbulence associated with, e.g., the density stratification of the water column or ocean wave breaking. Experiments with both constant and spatially varying β were performed. Even with constant β the formulation in Equation (8) leads to an increase in background momentum diffusion with decreasing water depth.

For the horizontal momentum diffusion ν_h a constant value was assumed. A large range for this parameter can be found in literature. For the open ocean, the reported order of magnitude is between 10² and 10⁵ m²/s (Apel, 1987). The simulation results turned out to be relatively insensitive to this parameter.

2.3. 4DVAR and Adjoint Model

Given a vector of control variables α = (α₁, …, α_Nc), which are to be optimised, the following cost function is minimised in the 4DVAR approach

$\begin{array}{l}J(\alpha )=\frac{1}{2}{\displaystyle \sum _{i=1}^{N_T}}{\displaystyle \sum _{j=1}^{N_{obs}^i}}\frac{1}{{\sigma }_j^2}{\left(y_j^i-H_j{x}^i(\alpha )\right)}^2+\frac{1}{2}{\displaystyle \sum _{k=1}^{N_c}}\frac{1}{{\overline{\sigma }}_k^2}{\left({\alpha }_k-{\alpha }_k^{prior}\right)}^2.\end{array}$

Here, xⁱ and yⁱ are the model state vector and the observation vector at time step i, H is the observation operator and $\sigma ,\overline{\sigma }$ are error standard deviations assumed for the observations and the control vector respectively. This is a nonlinear minimisation problem, which is commonly solved using gradient based iteration methods. Because of the usually high dimensions of the vector α, it is in general not feasible to estimate gradients using straightforward finite differences, as this would require at least N_c forward runs with the full nonlinear ocean model for a single step of the optimiser.

To briefly explain the idea of an adjoint model, we just consider one time step in the observation dependent part of the cost function with σ = 1 and we assume that the control vector α is simply the initial state x₀ used for the model run. We then have

$\begin{array}{ll}\frac{dJ}{d{x}_0}={(H{x}^i(x_0)-y^i)}^{T}H\frac{d{x}^i}{d{x}_0}.& (9)\end{array}$

Denoting the model operations required to transform the initial state x₀ into the model state at time step i as

$\begin{array}{ll}{x}^i=M_i{M}_{i-1}\dots M_1{x}_0& (10)\end{array}$

the gradient can be re-written as

$\begin{array}{ll}{\frac{dJ}{d{x}_0}}^T={\tilde{M}}_1^T{\tilde{M}}_2^T\dots {\tilde{M}}_i^T{H}^T(H{x}^i(x_0)-y^i)& (11)\end{array}$

where ${\tilde{M}}_1,\dots ,{\tilde{M}}_i$ are the linearised model operators. Hence, the gradient can be computed by applying the adjoint model defined as $\tilde{M}={\tilde{M}}_1{\tilde{M}}_2\dots {\tilde{M}}_i$ to the innovation, i.e., the difference between the model and the observations. It is important to note that in this simplified setup the numerical model itself is assumed as error-free, i.e., all potential errors in the model state variables are due to uncertainties in the initial fields. This is usually not realistic and additional uncertain parameters in the model can be added to the state vector with some adjustments of the scheme described above (Ngodock et al., 2017).

In practice, this means that the entire forward model code has to be linearised, transposed and put in reverse order. One additional complication arises from the fact that for every nonlinear term in the forward model, information about the model trajectory is required in the adjoint model. One practical approach is to store the forward model trajectory in a direct access file and then to read this file during execution of the adjoint code in reverse order.

The adjoint model is parallelised using the same domain decomposition as the IMCO forward model, i.e., using a grid of 12 × 12 subdomains.

2.3.1. Treatment of Advection Term

The treatment of the momentum advection term is a challenge, because standard advection schemes like the first order upwind scheme used in this study given as

$\begin{array}{ll}{u}_i\nabla u_i=\{\begin{array}{c}{u}_i(u_{i+1}-u_i)/\Delta x{u}_i<0\\ u_i(u_i-u_{i-1})/\Delta x{u}_i\ge 0\end{array}& (12)\end{array}$

are not differentiable around u = 0. This problem was already discussed in previous studies (Thuburn and Haine, 2001; Liu and Sandu, 2008). Because the analysis window considered in this study contains many tidal cycles, sign changes of currents happen frequently leading to significant noise and instabilities in the adjoint of the advection scheme. The approach taken in this study is to neglect momentum advection in the adjoint code altogether and to include it only in the forward model. Because advection is at least not a dominating term in the momentum balance of the German Bight, this approach still lead to reliable estimates of descent directions for the minimisation method.

2.4. Observation Operators

For the parameter optimisation process model variables have to be related to measured quantities, which is not trivial for HF radar surface current observations. These measurements are simulated from the model by a weighted average over the top layers according to

$\begin{array}{ll}{u}_{sim}^{HFR}={\displaystyle {\int }_{z=-H}^{z=\eta }}u(z)w(z)dz& (13)\end{array}$

with a weighting function w defined as

$\begin{array}{ll}w(z)=\{\begin{array}{ll}\frac{3}{{\xi }^3}{(z+\xi )}^2& z>\xi \\ 0,& \text{otherwise}\end{array}& (14)\end{array}$

The function w has a maximum at the surface and decreases to zero at water depth ξ. For the depth parameter ξ a value of 2 m+$\sqrt{2}$ m was used for the simulations. According to Stewart and Joy (1974), the HFR measurements are representative for the upper layer with thickness ${(2k_B)}^{-1}$, where k_B is the Bragg wavenumber. For the radar frequencies used in this study the Bragg wavelength is around 13 m and the resulting observed surface layer has about 1 m thickness. For the chosen value of ξ the weighting function Equation (14) drops to half the maximum value at 1 m depths.

2.5. Control Vector

In the following the control vector used for the optimisation of the IMCO model is described. The selection of control variables is a critical step, because it reflects assumptions made about the source of model errors. If a significant model error is not explicitely represented in the control vector, this error will either not be corrected at all, or, even worse, other control variables may try to compensate this deficit by un-physical adjustments. The control vector to be optimised in our analysis contains the following components:

• The bottom roughness length scale z₀ (see Equation 5). To account for a possible anisotropic behaviour of the bottom friction, separate roughness values $z_0^x,z_0^y$ are considered for the zonal and meridional direction. Both constant and spatially varying maps for these parameters were used.

• There are two additional parameters H_z0, L₁ explained in more detail below, which are supposed to control a possible increase of bottom roughness with decreasing water depth.

• The background diffusion parameter β in Equation (8). Setups with constant and spatially varying parameters were considered.

• The water depth H was scaled with a correction factor γ_H. Setups with constant and spatially varying corrections were investigated.

• The turbulence length scale parameters κ_s, κ_b in Equation (7). These parameters were assumed to be constant in space.

• The horizontal diffusion coefficient ν_h in Equations (1) and (2). This parameter was assumed to be constant over space.

• The wind drag coefficient λ_met in Equation (6); this parameter is assumed as constant over space as well.

• Amplitude and phase corrections of the open boundary forcing both with regard to the tidal and surge component.

The amplitude and phase corrections of the open boundary forcing are allowed to vary along the boundary. To ensure a smooth correction, a quadratic 1D spline representation with 5 knots was used (Schumaker, 2007). For the tidal part separate adjustments of the M2, K1, O1, S2, and M4 components were performed. The remaining water level component consisting of surge and other tidal constituents was corrected in terms of time lag and amplitude.

The spatial variations of the bottom roughness length, background turbulence and bathymetry corrections were implemented by tensor products of quadratic 1D spline functions with 6 × 10 knots (Schumaker, 2007). In addition, the roughness length scales were multiplyed by a depth dependent function

$\begin{array}{ll}{f}_{z_0}(H)=1+L_{4}R(\frac{H_{z_0}}{H}-1)& (15)\end{array}$

with the function R defined in Equation (22). This results in a growth of z₀ below water depths of H_z0 until a maximum amplification by a factor of 1 + L₄ is applied at water depth of H_z0/2 and below.

2.6. Minimisation Procedure

The dimension of the control vector considered in this study is small enough (~ 10³) to allow storage of the Hessian matrix of the cost function. Because a direct estimation of second order derivatives is not feasible, a quasi-Newton method was applied, which uses the sequence of gradients provided by the adjoint model to iteratively improve estimates of the Hessian. The Broyden-Fletcher-Goldfarb-Shanno (BFGS) technique used in this study is a classical method, which is discussed in great detail in various publications (e.g., Fletcher, 1986). In addition, the minimisation procedure requires a line search method, which determines how far to proceeds in the search direction to select the next state vector in the iteration. The method applied here uses the Armijo condition to decide whether a step size is acceptable (Wolfe, 1969).

We are aware that other numerical approaches exist to minimise the cost function. Variants of the Gauss-Newton method have been discussed in the context of 4DVAR methods in previous work (e.g., Gürol et al., 2014). These methods are specifically designed for least-squares problems and require the tangent linear model in addition to the adjoint model. The approach typically consists of two nested iteration loops, where variants of the Lanczos or conjugate gradient method are used to find approximate solutions of a big linear system in the inner loop. The result is then used as a search direction in the outer loop. These methods provide some interesting capabilities concerning analysis diagnostics (Moore et al., 2018) and are certainly preferable for applications, where storage of the Hessian is prohibitive. This is usually the case in the classical situation, where the initial model fields are part of the control vector. In the dynamical system discussed here the memory is so short that it is not worth to adjust the initial fields. The tidal wave passes through the domain within about 4 h, i.e., after that the system has forgotten about the initial state. To account for this effect observations are not used within the first 6 h of the analysis period.

In general one can say that, due to the strong non-linearities of the model, which are in particular due to the shallow water and the strong influence of bottom friction, the resulting minimisation is a challenge. This is not surprising, because all minimisation approaches mentioned above rely on linear approximations of the cost function, which become less accurate with increasing non-linearity. As a consequence, convergence rates can suffer and stronger dependencies on the initial control vector estimate can be observed. In practice this means that some trial and error is required to find initial estimates, which lead to cost function values as low as possible.

3. Observations and Reference Model Data

3.1. HF Radar Observations

HFR surface current data were acquired by three radar stations in the German Bight (see Figure 1B). The radar is part of the COSYNA system described in more detail in Baschek et al. (2016). The radar systems make use of linear antenna arrays installed near the shoreline with the exact locations summarised in Table 1. The Wellen Radar (WERA)-type radars (Gurgel et al., 1999) operate at frequencies of 10.8-MHz (Büsum and Sylt) and 12.1-MHz (Wangerooge), respectively.

TABLE 1

Table 1. Locations of observation instruments used for the model tuning.

Ocean surface currents advecting Bragg resonant surface waves cause a Doppler shift (Barrick, 1978), which can be converted to the underlying current speed toward or away from the radar. More details on the required processing can be found in Gurgel and Schlick (2009). For the considered system the spatial radar resolution is 1.5 km in range and 3° in azimuth. The working range of the WERAs mainly depends on salinity, sea state, working frequency, and electromagnetic noise. For a table of typical working ranges, see Gurgel and Schlick (2008). The system used here can reach out to about 120 km off the coast in favorable conditions.

The radar system provides measurements with a 9 min averaging window every 20 min. The observations are interpolated to a 2 km cartesian grid. Through a combination of the radial components from the different antenna stations meridional and zonal current components can be derived, however the original radial components were used for the subsequent data assimilation procedure. One advantage of this approach is that information is available for a larger area. Furthermore, the observation error characterisation is easier in this case. Further details of the system can be found in Stanev et al. (2015).

3.2. Tide Gauges

Tide gauge data were accessed via the web-interface provided by the Copernicus Marine Environment Monitoring Service (CMEMS). The observation were taken from the respective in situ products for the NorthWest Shelf area (https://marine.copernicus.eu/). These are near real-time (NRT) in situ quality controlled observations, which are hourly updated and distributed within about 24–48 h after acquisition. The data are available as netcdf files and have 10 min temporal resolution. The locations of the three tide gauges are given in Table 1.

3.3. Acoustic Doppler Profiler (ADCP)

ADCP current profile measurements taken at the platforms FINO-1 and FINO-3 were used for the study (see Figure 1B). The bottom mounted instruments are operated by the German Federal Maritime and Hydrographic Agency (Herklotz, 2007) and the data were accessed via the web-interface provided at http://fino.bsh.de/. Current speeds and directions are available at different water depths with 2 m spacing. The water depth at the FINO-1 platform is about 30 m and about 22 m at the FINO-3 location. The locations of both platforms are given in Table 1.

3.4. Surface Drifters

Nine drifters were deployed at different locations in the German Bight during the FS Heincke cruise HE 445 in May 2015. The raw data are freely accessible (Carrasco and Horstmann, 2017) and are described in more detail in Callies et al. (2017). The drifter positions were estimated via onboard Global Positioning System (GPS) devices and transferred to land via the satellite communication network Iridium. The sampling rate was initially 15 min and later on reduced to 30 min. The trajectories of six drifters used in this study are shown in Figure 2. In this case only the period 29.5–30.6.2015 was considered and the respective initial positions are marked with solid triangles.

FIGURE 2

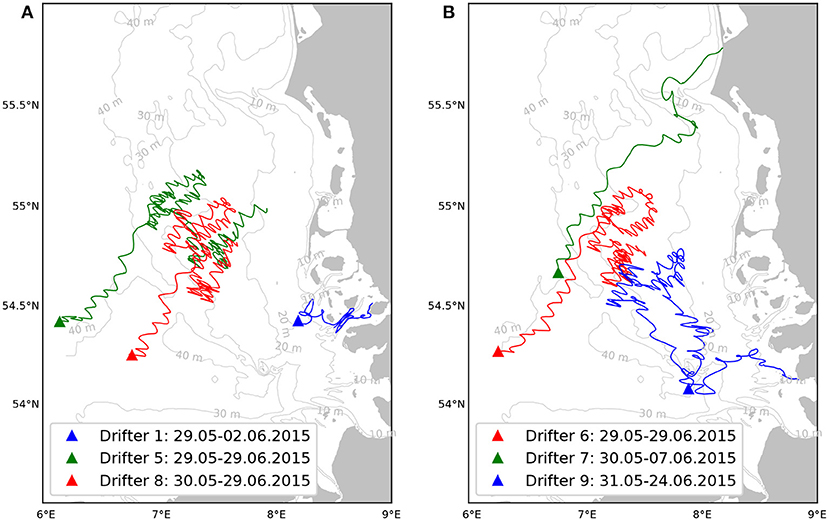
Figure 2. Trajectories of six surface drifters released in the German Bight in May/June 2015 with drifters 1, 5, 8 shown in (A) and drifters 6, 7, and 9 shown in (B).

3.5. Model Data From the Federal Maritime and Hydrographic Agency (BSH)

Apart from measurements, data from the operational model BSHcmod run at BSH were included in the analysis (Dick et al., 2001). These data were used for the open boundary forcing and the wind fields contained in the products were used as meteo forcing. The wind fields originate from the atmospheric COSMO-EU (Consortium for Small-Scale Modelling) model, which is run at the German Meteorological Service (DWD) with a spatial resolution of 7 km. The spatial resolution of the BSHcmod model is about 900 km for the German Bight area and the temporal resolution of the standard output is 15 min (Dick and Kleine, 2007). The available BSH surface current data represent approximately the upper 5 m of the water column except for the Wadden Sea areas, where the top layer thickness is reduced.

Furthermore, the bathymetry information provided with the BSH product was used as a basis for the model runs presented in this study.

4. Results

4.1. Model Tuning With HFR, Tide Gauge, and ADCP Data

The 4DVAR method was applied to data from the fortnight period May 15–May 29, 2015. The idea was to cover at least one neap spring tide cycle in the model tuning process, which is necessary to separate the M2 and S2 tidal components. Wind speeds in zonal and meridional direction for that period are shown in Figure 3. This plot also includes the period May 29–June 29, which is later on used for testing of the tuned model.

FIGURE 3

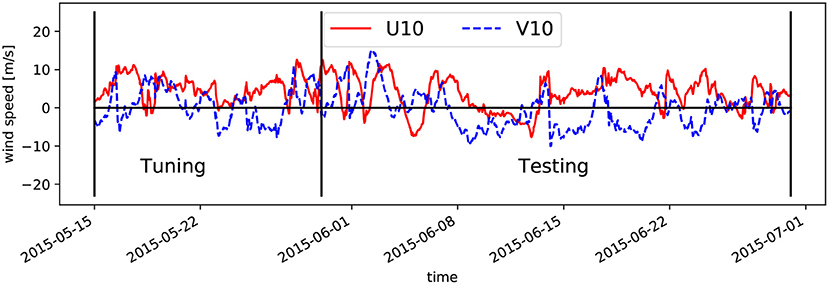
Figure 3. Zonal and meridional wind speed components in 10 height near the island Helgoland. Respective 2D windmaps were used as metereological forcing for the considered circulation models.

The optimisation was carried out with two basic setups of the control vector:

• Experiment IMCO_CONS: bottom roughness, background momentum diffusivity, and bathymetry correction are assumed as constant over space.

• Experiment IMCO_VAR: smooth spatial variations of bottom roughness, background momentum diffusivity, and bathymetry correction are permitted.

For the experiment IMCO_CONS the control vector dimension is N_c = 88 and for experiment IMCO_VAR it is N_c = 376. The total number of components in the observation vector is N_obs = 3, 522, 036, i.e., about four orders of magnitude more than the size of the control vector. This refers to the number of observed values, which are actually used within the fortnight period, i.e., excluding missing values.

The adjoint model was applied for the estimation of gradients that resulted in descent directions for the BFGS method. The iteration of the minimisation procedure was terminated when no further cost function reductions of practical value could be achieved. The resulting cost function values were J = 10.94 for experiment IMCO_CONS and J = 10.40 for experiment IMCO_VAR. Significant reductions of the gradient norm could be observed in the initial phase of the iteration, but a convergence to zero is not achieved. One important factor in this behaviour is the not-differentiable momentum advection described in section 2.3.1. Using the obtained control vector from experiment IMCO_CONS for another model run with momentum advection switched off resulted in a cost function value of 16.67. This indicates that momentum advection is not negligible in the circulation dynamics of the German Bight.

In the present configuration the IMCO setup is not optimised for execution speed and the forward model requires about 7 min for 1 day of simulation using 144 processors. The adjoint model is slower by approximately a factor of two using the same number of processors. There is some potential for speedup concerning the writing and reading of the model trajectory to disk, which is required for the gradient computation and which is done in 10 s time steps in the present setup. A coarser sampling of the trajectory would introduce some errors into the estimated gradient, but the resulting perturbations in the minimisation procedure maybe acceptable. The present study is about the reduction of systematic model errors, which ideally only has to be done once. For the application of the proposed methodology in an operational framework with the respective treatment of stochastic errors, e.g., related to atmospheric forcing, further optimisation steps concerning execution speed are desirable and will be presented in subsequent studies.

Results for the water levels at the tide gauges HvideSandeKyst, Helgoland, and Cuxhaven are shown in Figure 4. Red crosses correspond to measurements, and the green solid and blue dashed lines refer to the BSH model and the 4DVAR results, respectively. For the Cuxhaven and Helgoland tide gauge observations were missing for some periods. The tidal signal at HvideSandeKyst is interesting, because it has an almost triangle wave shape, which indicates a significant contribution of higher harmonics to the tide. In fact, for an idealised triangle signal with M2 base frequency f_M2, the spectrum of the elevation η is given as

$\begin{array}{ll}\eta (t)~{\displaystyle \sum _{i=0}^{\infty }}{(-1)}^i{n}^{-2}sin(2\pi n{f}_{M2}t)& (16)\end{array}$

i.e., in theory there is an infinite number of higher harmonics involved.

FIGURE 4

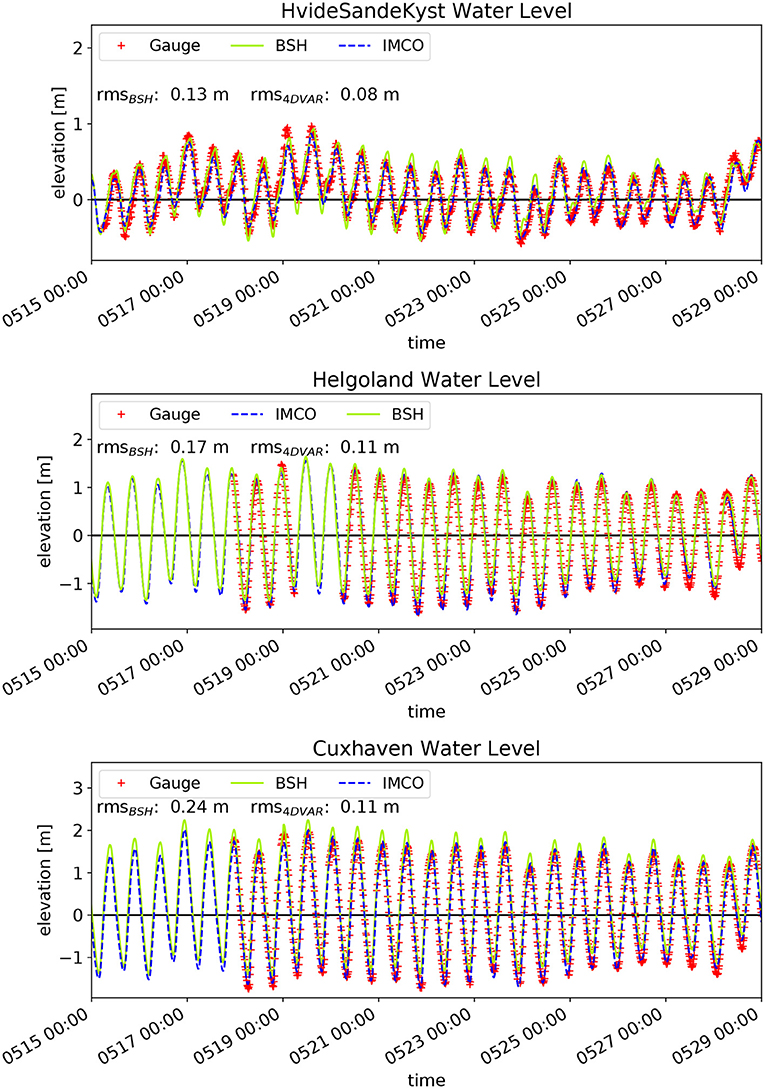
Figure 4. Comparisons of water levels at the tide gauge stations HvideSandeKyst (top), Helgoland (middle), and Cuxhaven (bottom) for the period May 15–May 29, 2015. Red crosses indicate measurements and green and blue curves correspond to the BSH model and the 4DVAR results, respectively.

Furthermore, some correlation can be found between the water levels at HvideSandeKyst and the meridional component of the wind speed in Figure 3. One can see that both the BSH model and the tuned IMCO model are able to reproduce the tidal shape quite well. The root mean square (RMS) difference with regard to the observations is 0.08 m for the tuned model and hence slightly lower than the respective value of 0.13 m for the BSH model. Again, both models reproduce the observations fairly well. The BSH model has a tendency to overestimate the low tides, which is not seen in the IMCO model. This is the main reason, why the tuned model shows a smaller RMS value of 0.11 m compared to 0.17 m of the BSH model. A similar behaviour is seen at the tide gauge Cuxhaven, but here the BSH model is also slightly overestimating the high tide. This results in RMS value of 0.24 m compared to 0.11 m for the tuned model.

Comparisons with the ADCP measurements at FINO-1 and FINO-3 are shown in Figure 5. The measured zonal and meridional current components are given as black and red crosses, respectively. The corresponding results from the 4DVAR analysis are indicated by blue and green lines. In this case the curves for the BSH model are not shown, but the respective RMS values are added in the plot. For FINO-1 comparisons can be found for 24 m depth (a) and 8 m depth (b). For this location the meridional current component is significantly smaller than the zonal component and at the same time shows a stronger influence of higher harmonics. Overall the IMCO model is able to reproduce the observed current velocities quite well with RMS differences between 0.11 and 0.15 m/s. It appears that the meridional component closer to the surface is a challenge in particular during the second week, where the wind was more northerly and thus pushing water toward the coast. For FINO-1 the BSH model shows overall slightly better results than the tuned model with RMS values around 0.01 m/s smaller than the tuned model. For FINO-3 the zonal and meridional current components displayed in Figure 5 show a much more isotropic behaviour with amplitudes of the same magnitude and a phase shift of ~180°. The RMS errors for the tuned model are between 0.08 and 0.13 m/s and thus smaller compared to the situation at FINO-1. The BSH model and the IMCO model show a very similar performance with maximum deviations of 0.01 m/s in terms of RMS errors.

FIGURE 5

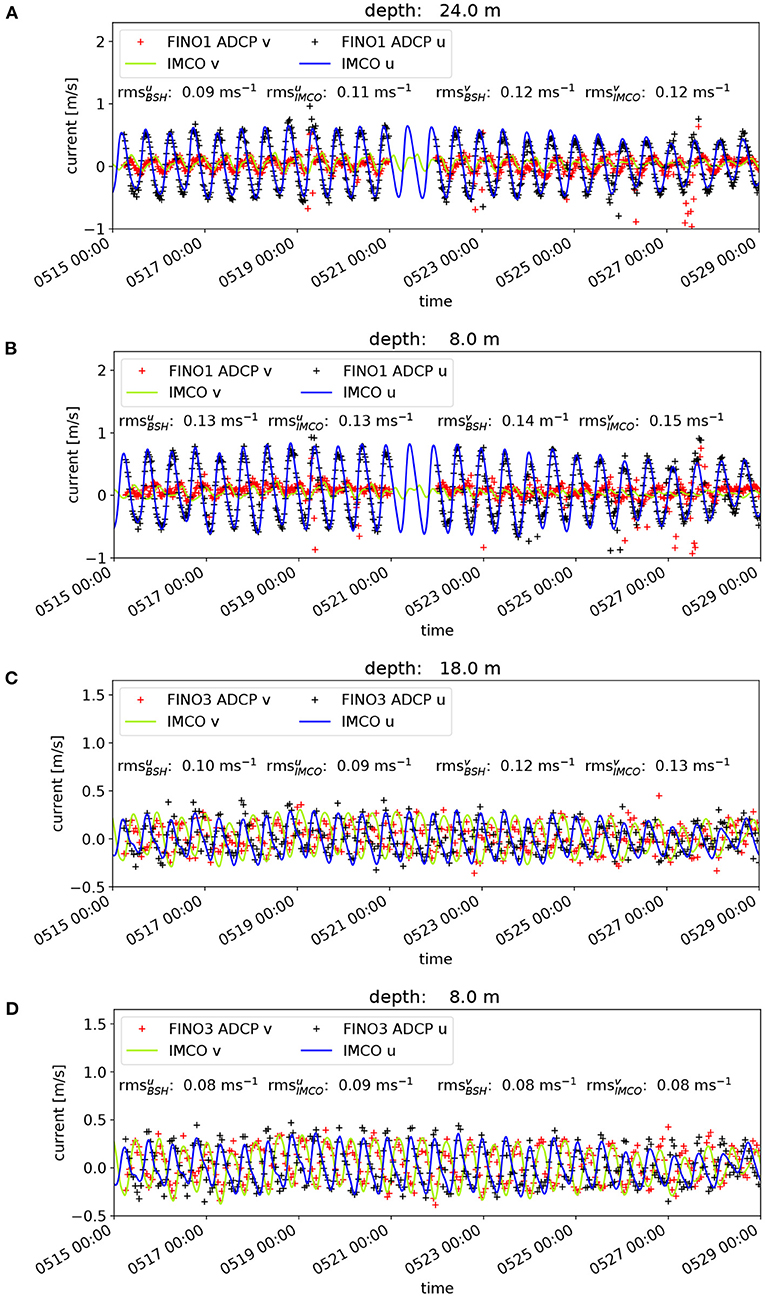
Figure 5. Comparison of FINO-1 (A,B) and FINO-3 (C,D) ADCP current measurements at two depths with 4DVAR analysis results for the period May 15–May 29, 2015. Measurements at 8 and 24 m are shown for FINO-1 whereas FINO-3 observation were taken at 8 and 18 m. Black and red crosses indicate zonal and meridional components of the measurements while the blue and green curved correspond to the zonal and meridional components of the 4DVAR analysis. RMS values are given for the comparisons with BSH model data as well.

Comparisons of model runs with radial surface current components measured by the Sylt, Büsum, and Wangerooge station are shown in Figure 6. The colours refer to RMS differences computed from the fortnight period used for tuning of the model. The 10, 30, and 4 m isobath are superimposed. Results for the BSH model are shown in the left column and the respective results for the tuned model in the right column. One can see considerable heterogeneities in the spatial distribution of errors for all radar stations. For the Sylt station the errors are the smallest with an average RMS value 0.082 m/s for the BSH model and 0.071 m/s for the tuned model. The strongest improvement is achieved in an area northwest of the island Helgoland. The same area also stands out in the comparisons with the Wangerooge measurements. Also in that case an improvement is achieved by the 4DVAR analysis. The overall biggest correction by the model tuning is found for the Büsum station with an average RMS value of 0.128 m/s reduced to 0.097 m/s. In this case an improvement can be seen for almost the entire area covered by the radar station. For the Wangerooge station the situation is a little bit more complex, because significant errors remain in an area south east of Helgoland as well as in the shallow areas along the 10 m isobath near the Elbe and Weser entances and along the North Frisian islands. Nevertheless, the mean RMS errors is reduced from 0.103 to 0.091 m/s.

FIGURE 6

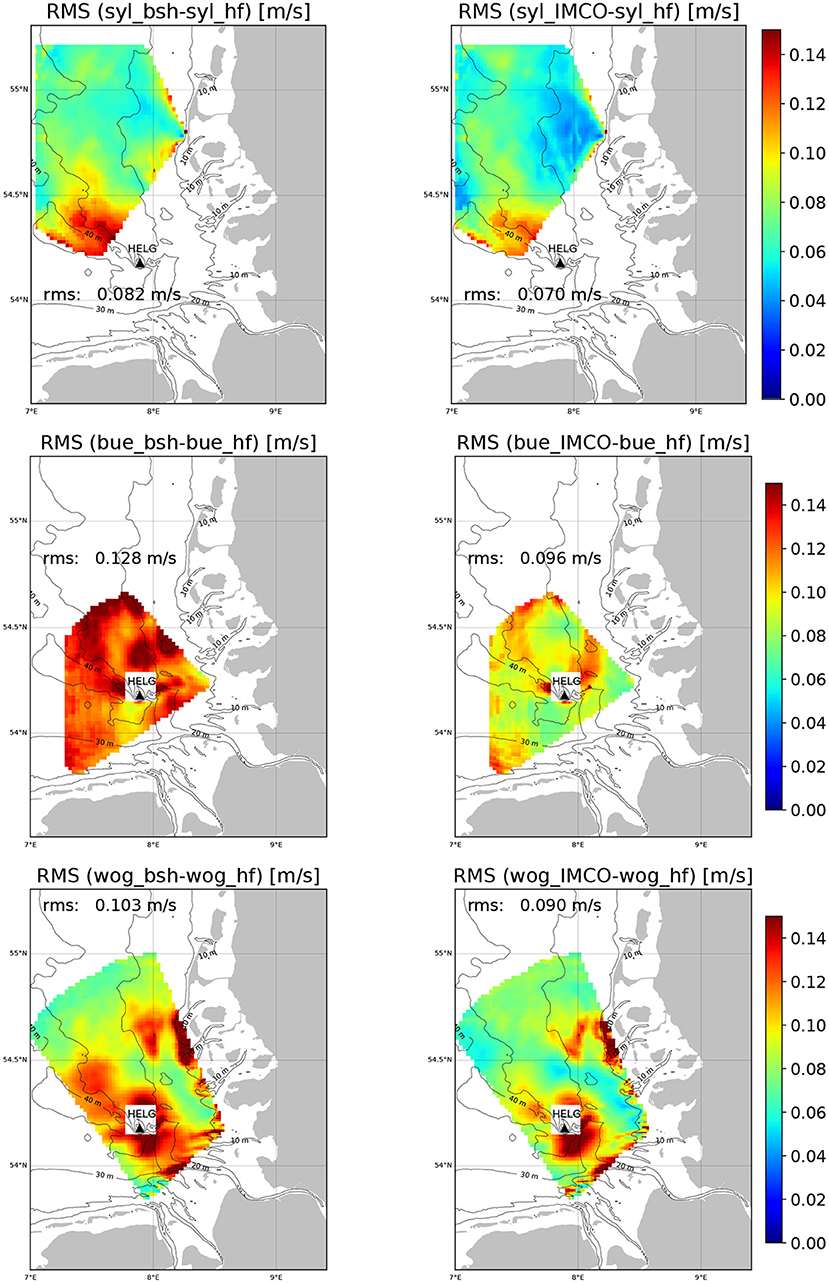
Figure 6. Comparison of tuned 4DVAR results and BSH model data with HFR measurements for the radial components acquired by the Sylt (top), Büsum (middle), and Wangerooge stations (bottom). The RMS values refer to the period May 15–May 29, 2015. The black triangle marks the position of the island Helgoland.

An overview of the achieved percentage error reduction for the different radial components is given in Figure 7. Rainbow colours indicate an improvement and grey values correspond to a deterioration. These plots confirm the quite heterogeneous distribution of improvements. The best overall improvement is achieved for the Büsum station with large areas showing at least 30% RMS reduction. For the areas in the northern part above 54.5° latitude where the tuned IMCO model shows slightly higher RMS values than the BSH model, one has to consider that these are regions where the BSH model performs very well with RMS values well below 0.1 m/s and the tuned model is still below that value. This is different for the area south of Helgoland where the BSH model shows higher RMS errors and the 4DVAR is not able to correct these and even shows 5–10% higher errors.

FIGURE 7

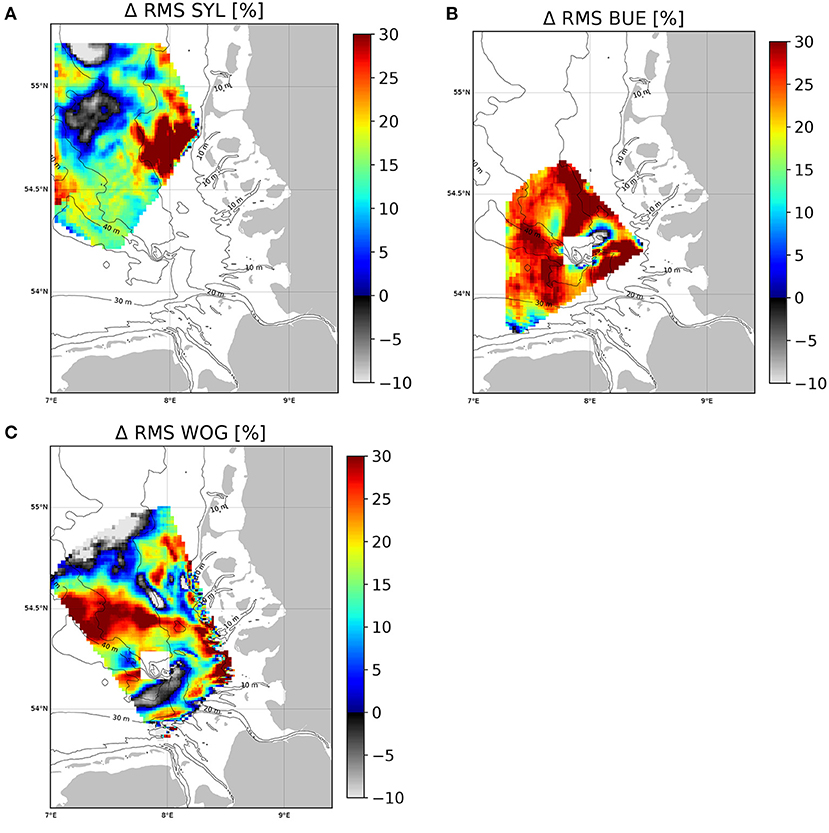
Figure 7. Relative improvements of the radial surface current components achieved with the 4DVAR analysis compared to the BSH model. The percentage values refer to the period May 15–May 29, 2015 and are given for the observations from the Sylt station (A), the Büsum station (B), and the Wangerooge station (C).

4.2. Testing of Tuned Model

4.2.1. Comparison With Independent HF Radar and Tide Gauge Data

To check whether the 4DVAR scheme is in fact able to correct systematic errors, which exist beyond the tuning period, the tuned IMCO model was compared with tide gauge and HF radar data acquired in June 2015, i.e., the month following the optimisation period. It cannot be excluded alltogether, that the optimisation procedure makes control vector adjustments due to processes, which are of a more stochastic nature, in particular the metereological forcing and density stratification. The comparison with independent data from a different period can give indications whether this is a significant factor, because these stochastic factors are changing over time. As there was a data gap in the HF radar data in the first half of June 2015, the comparisons were done for the period June 15–June 29, 2015, i.e., exactly 1 month after the tuning period and covering a fortnight period as well. One can see from Figure 3 that the wind conditions during this test period are different compared to the tuning phase showing longer periods with northerly wind directions.

The respective comparison results for the tide gauges and HF radar radial components are summarised in Table 2. The table also contains the respective numbers for the tuning period. One can see that overall the picture in the tuning and testing period is very similar. In all cases the RMS values of the tuned IMCO model are smaller than the respective values of the BSH model. The RMS values are slightly different in the tuning and testing period, but the relative improvement is still of the same order in most cases. The only notable change is seen in the Büsum radial component, where the improvement of about 30% in the tuning period is reduced to about 20% in the testing period.

TABLE 2

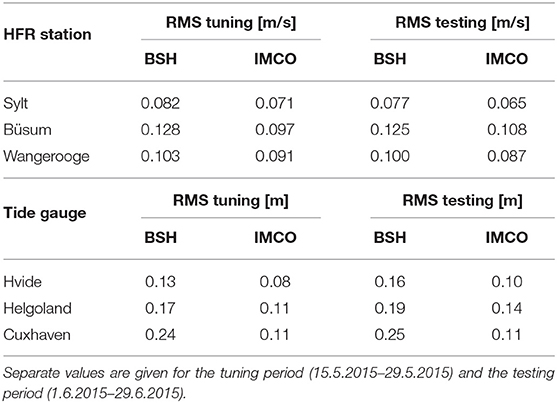
Table 2. RMS differences between observed HFR radial components and respective simulations from the BSH model and IMCO model.

These results indicate that the optimisation procedure is indeed able to reduce systematic errors in the model, which are independent of stochastic error sources like the metereological forcing. As the wind conditions in the tuning and testing period cover a larger variety of wind directions and speeds, one can also conclude that the optimisation is of more general applicability and not only useful for specific wind situations. However, it is also true that neither tuning nor testing period contain storm events where stronger nonlinear effects (e.g., related to surface waves) may become more significant and should be investigated in a separate study.

It is also important to mention that there is a quite significant difference in sea surface temperatures between the tuning and testing period. According to model data from the German weather service, the temperature at location 8.00°E54.25°N increased from 283.9 to 287.8 K between May 15 and June 15, 2015 (midnight temperatures), i.e., by about 4°. This means that the situation with regard to temperature stratification and stability of the water column is most likely not the same in both periods and hence the obtained estimate of the control vector is applicable to a certain range of stability conditions.

4.2.2. Comparison With Independent Surface Drifter Data

The tuned IMCO model for experiments IMCO_CONS and IMCO_VAR was run for the period May 29 to June 29, 2015 and compared to independent surface drifter data acquired during that period. The time series of drifter positions was used to estimate the zonal and meridional surface current components and these were co-located with the respective model simulations. Concerning the BSH system it is important to say that operational drift forecasts at BSH are not based on the BSHcmod model alone, but current speeds in the upper layer are used as input for a drift model, which takes into account a number of additional factors like Stokes drift. After noticing that a direct comparison of BSHcmod surface velocities with drifter velocities does not achieve the same level of agreement as the IMCO model, output from the BSH drift model was used instead. For the tuned model a weighted average of the upper sigma layers was computed such that the top 1 m is most relevant for the simulated drift velocity. As the drift model output was available in 3 hourly times steps, all comparisons were performed using this sampling frequency.

Respective scatter plot resulting from the IMCO simulations are shown in Figures 8A,B for drifter 8, which was sending data between May 30 and June 27, 2015. The colour coding refers to water depth and separate plots are given for the meridional (a) and zonal component (b). The dashed line is the linear regression line. Because of the used sigma coordinates this means that the weights for the sigma layers vary both in time and space. The RMS values of 0.078 and 0.093 m/s indicate a very good match, which is of similar order as the agreement achieved between the tuned model and HF radar surface currents during the tuning period. The RMS value is dominated by the standard deviation and the bias plays a significantly smaller role. Nonetheless, the slope of the regression line indicates that there is a slight relative underestimation of current magnitudes by the IMCO model. Drifter 8 was moving in areas with water depths between about 20 and 40 m and there is no pronounced dependence of the errors on water depth visible. The only effect, that is worth mentioning is a slightly stronger magnitude underestimation of the zonal component for northward currents in deeper water. Figures 8C,D show a respective comparison for the BSH model if the surface velocities are estimated from the top layer of the model. As mentioned before, the thickness of this layer is 5 m for most of the considered area and it does not make sense to consider weighted averages of different layers as done for the IMCO model. One can see that the RMS differences are significantly higher in this case. As before, these errors are mainly due to standard deviation and to a lesser extend caused by bias. Because of the very coarse resolution of the upper boundary layer in the BSH model, the relatively large deviations may not come as a surprise and this is also the reason why operational BSH drift forecasts include a second step, where the above surface currents are used as input for a drift model, which adds additional effects, e.g., Stokes drift associated with surface waves. The respective results from the BSH drift model calculations are shown in Figures 8E,F. One can see that this leads to a significant improvement, with errors, which are very close to the results obtained with the tuned IMCO model. It is interesting to see that a slight underestimation of current magnitudes indicated by the slope of the regression line is present, which is very similar to the behaviour of the IMCO model discussed before. Another similarity is that this effect also seems to be more significant for the zonal component in deeper water.

FIGURE 8

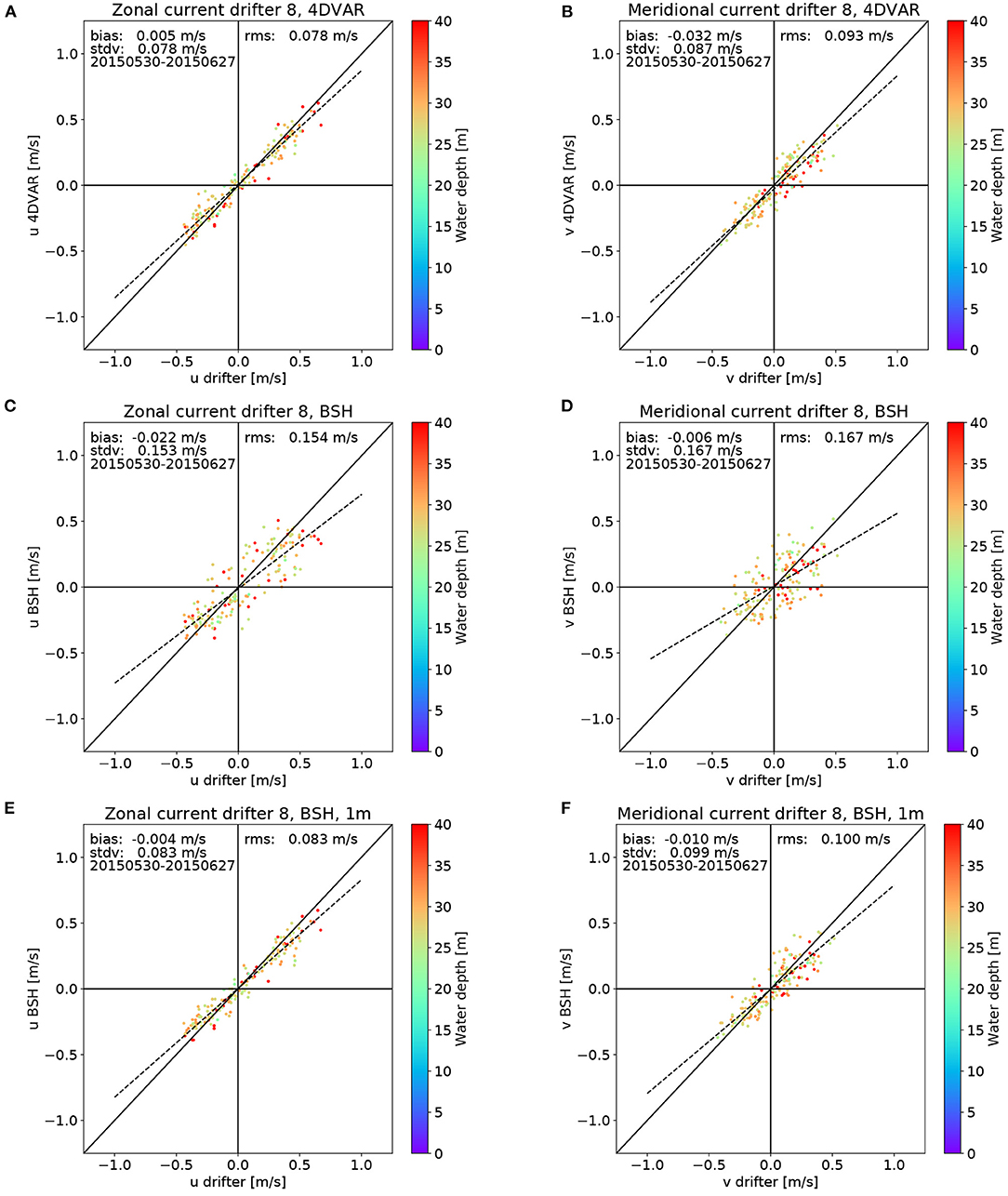
Figure 8. Comparison of surface current speeds derived from drifter 8 (see Figure 2) with co-located estimates from the tuned IMCO model surface currents (A,B), the BSH model surface currents (C,D), and the BSH drift model (E,F). Meridional components are shown on the left and zonal components on the right. The colour coding refers to water depth and dashed lines were obtained via linear regression.

A summary of the respective RMS differences between BSH drift model and the IMCO_CONS und IMCO_VAR runs are given in Table 3 for all drifters shown in Figure 2. One can see that drifter 8 gives the best performance of the tuned model compared to the BSH drift model. Depending on the drifter and the current component the BSH drifter model gives better results in several cases. In particular, for drifter 1 the IMCO simulations are definitely worse. As seen in Figure 2 drifter 1 was moving around the North Frisian island in very shallow water close to Wadden Sea areas over the entire period. This result indicates that the tuning process in these regions should be further improved. Firstly, more measurements are required in these regions to improve estimates of bottom roughness and turbulence. Secondly, a further stabilisation of the minimisation procedure close to drying is desirable, to avoid the 2 m deepening of the bathymetry applied in this study.

TABLE 3

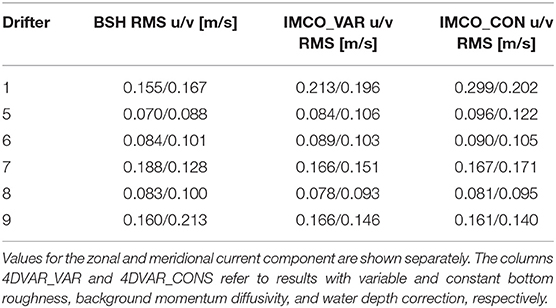
Table 3. RMS differences between drifter derived surface velocities and drift model data from BSH as well as the 4DVAR results.

Table 3 furthermore shows that the improvements achieved by spatially variable corrections of bathymetry, bottom roughness, and background diffusion are only moderate. In fact, for some cases the constant corrections of the experiment IMCO_CONS even give slightly better results in the drifter comparisons.

It is also interesting to note that drifter 8, which showed the best agreement with the IMCO simulations was moving in an area with relatively good coverage of all three antenna stations (see Figure 1B). The fact that a considerable amount of observation information was used for the tuning of the model in this area could be an important factor for the good agreement with the drifter 8 data. The good simulation of the drifter velocities by the tuned model in this areas is furthermore a strong indication that HF radar and drifter velocities are very consistent at least for the considered data set. This was also confirmed by direct comparisons of drifter and HF radar data (not shown here).

The general question whether the considered surface current data sets are consistent is of course an important point to be considered. Looking at this problem one has to consider at least the following points:

• There is so far no real consensus about the role that Stokes drift plays in HF radar measurements (Chavanne, 2018).

• The BSHcmod model output has an extremely coarse resolution of the upper boundary layer

• The consideration of Stokes drift in the BSH drift model is simplified, because it is so far not based on a numerical spectral wave model, but parametric models for the wave spectrum.

Röhrs et al. (2015) showed that the HF radar currents are usually interpreted as Eulerian currents (i.e., not including the Stokes drift), some studies (e.g., Graber et al., 1997) assume that they include the full Stokes drift. Ardhuin et al. (2008) demonstrated that the HF radar velocity partially includes the Stokes drift and compared the HF radar measurements with altered Stokes drift. Comparisons of HF radar velocity measurements with drifter observations were done by Ohlmann et al. (2007) suggesting that the HF measurements are Eulerian, however the study was inconclusive concerning possible nonlinear perturbations of the wave phase speed measured by the radar. Röhrs et al. (2015) concluded that HF radar essentially measures the Eulerian current and not the Lagrangian current that includes the Stokes drift.

The observation that the tuned IMCO model is able to replicate and in some cases supersede the results of the BSH drift model could be an indication that the simplified Stokes correction in the drift model is in fact to some extend compensating deficits associated with the coarse resolution of the BSHcmod boundary layer. Because the situation with regard to Stokes contributions in the HF radar data is not clear as well, this issue requires a more detailed investigation including analysis of 2D wave spectra from a numerical wave model, which is beyond the scope of this study. However, one can say that parameter optimisation based on a variety of different measurements, like presented here, can give valuable hints concerning the role of physical processes and their numerical treatment. In particular the inversion method allows to assess, which physical processes can explain certain features of the observations. One has to emphasise however, that the ability of a model to replicate certain observations is not a proof that the model contains all relevant physical processes. For example, it was shown previously that Stokes drift can definitely play a significant role in drift forecasts (Staneva et al., 2017). The fact that the IMCO model gives good agreement with the drifter data, although it does not include Stokes drift, suggests that wave effects were to some degree integrated into the parameterisations for the upper ocean layer by the 4DVAR optimisation process. Of particular relevance in this context are parameters for the momentum diffusion near the surface and the atmospheric drag coefficient. As pointed out before, a quantification of such effects requires the application of additional tools and data and is not feasible within the present study.

4.3. Estimated Control Vector Components

In the first experiment IMCO_CONS a simplified optimisation run was performed, where the roughness length scale $z_0^x,z_0^y$, the background diffusion ν_BG and the bathymetry correction factor γ_H were assumed constant over space. The resulting values are summarised in Table 4. With this simplified setup the cost function values are increasing by about 5% from J = 10.40 to J = 10.94.

TABLE 4

Table 4. Control parameters estimated with the 4DVAR scheme.

It is interesting, that the parameter κ_b describing the mixing length gradient near the sea floor (see Equation 7) is in fact quite close to the theoretical value of 0.4 to be expected for an idealised wall. The respective value for the sea surface κ_S is significantly smaller. The fact that the two values differ is not surprising, because the moving sea surface boundary with additional impacts of ocean surface waves is of a very different nature compared to the stationary sea floor.

The derived estimates for the bottom roughness lengths $z_0^x,z_0^y$ are on a millimeter scale and thus consistent with values reported in previous literature (Ke et al., 1994). Both values are at least of the same order and thus the anisotropy of the bottom friction is not very pronounced. The atmospheric drag coefficient is also of a magnitude similar to values reported in previous studies (Backhaus, 1976). Finally, the bathymetry correction factor γ_H indicates an about 5% increase of the mean water depth applied in the optimisation process.

The derived corrections for the open boundary forcing are shown in Figure 9. The amplitude correction factors for the five considered tidal components are given in Figure 9A with the left part, up to index number 370, belonging to the western boundary and the remaining part referring to the northern boundary. The indices are ordered from south to north (indices 1–370) and then from west to east (indices 371–523). One can see, that there is an increase of the dominating M2 amplitude (red line) along most of the western boundary up to index 300 and a decrease along the northern boundary. The remaining tidal corrections show a similar qualitative behaviour with amplifications or small reductions along the western boundary and stronger reductions along the northern boundary. Overall, these corrections are consistent with an increased dissipation of tidal energy inside the model domain compared to the BSH model, because the tidal wave passes through the model domain entering from the west and leaving to the north. The amplitude adjustment of the remaining part of the signal comprising both the left over tidal constituents and the surge component are displayed in Figure 9C. One can see that this signal is amplified along most of the open boundary except a small region south of the north-west corner of the model domain. The respective phase corrections and time lags are shown in Figures 9B,D. For the M2 component (red line) the maximum corrections occur around the north west corner of the model grid and are of the order of 30° which corresponds to a time lag of about 1 h. A positive phase indicates a delay of the tidal wave. For the remaining signal the timing corrections (Figure 9D) are applied around the north/west corner of the grid as well with maximum time lags of about 3 h. Here, positive time lags indicate delayed signals as before.

FIGURE 9

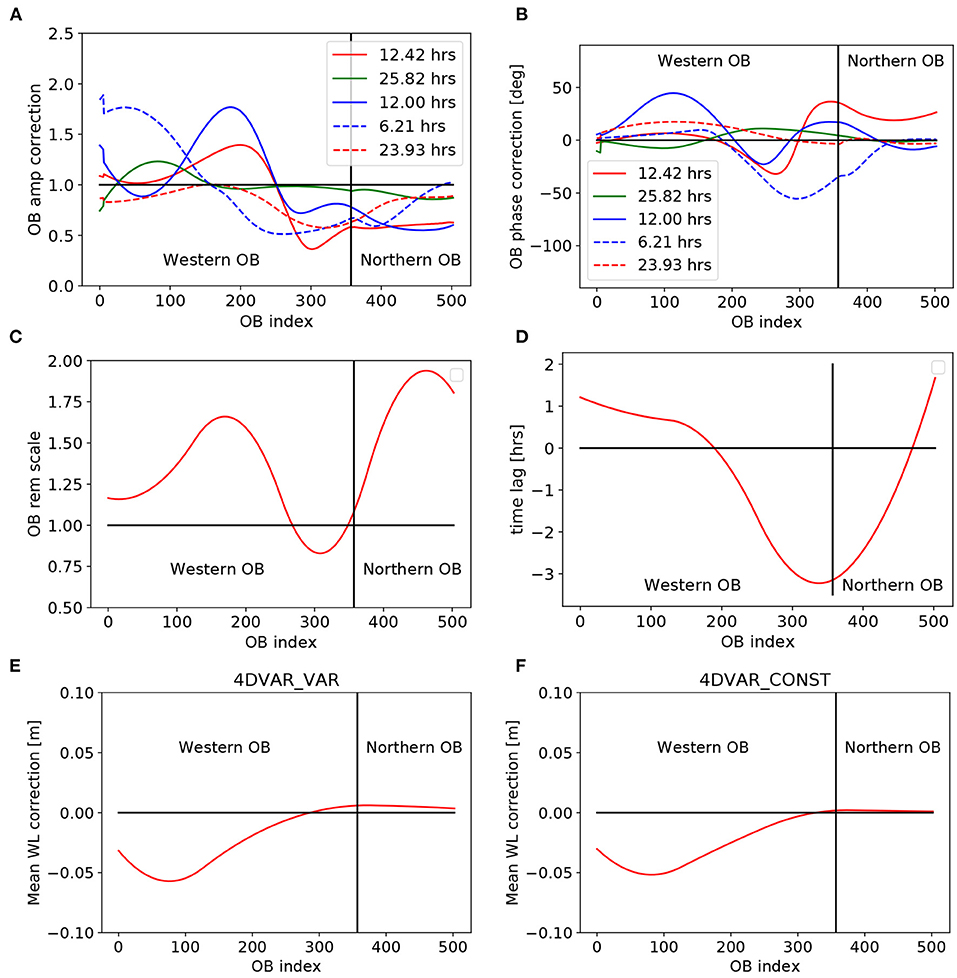
Figure 9. Amplitude (A) and phase (B) corrections of 5 tidal components along the open boundary estimated by the 4DVAR scheme. (C,D) Scaling (C) and time shift (D) of the remaining signal along the open boundary. (E,F) Corrections of mean water elevation along the open boundary for experiment IMCO_VAR (E) and IMCO_CONS (F).

Corrections of the mean surface elevation are shown in Figures 9E,F for experiment IMCO_VAR and IMCO_CONS respectively. In both cases one can see a lowering of the water level along the western boundary and very small adjustments along the northern boundary. This means that the optimisation procedure modifies pressure gradients on a spatial scale of the German Bight, which are in balance with the mean atmospheric forcing, and mean coriolis and frictional forces inside the model domain.

It seems that the tidal wave is accelerated by the deepening of the bathymetry according to the shallow water phase speed

$\begin{array}{ll}{c}_{ph}=\sqrt{gH}& (17)\end{array}$

and that the boundary forcing is adjusted accordingly. For the remaining elevation signal we see a delay near the coast and an acceleration in the deeper water.

Maps of the spatially varying control vector components of experiment IMCO_VAR are shown in Figure 10. The bathymetry corrections indicate increased water depth by between 1.5 and 3.5%. The largest corrections are found in the North Frisian Wadden Sea area and between 55 and 55.5°N latitude. The smallest corrections are applied in the central German Bight north west of the island Helgoland. It is interesting that the region with strong meridional gradient of the bathymetry coincides with a region where the meridional roughness component (Figure 10D) shows a stronger decrease from south to north. Both corrections are favorable for transports toward the north in that region. The estimated roughness components for the zonal and meridional direction in Figures 10C,D, respectively vary between ~1 and 2.5 mm. Both roughness lengths show dipol structures with characteristic length scales between 50 and 100 km. It is interesting that the spatial distributions of $z_0^x$ and $z_0^y$ are significantly different and that areas of high or low values of one component often coincide with areas of larger gradients of the other component.

FIGURE 10

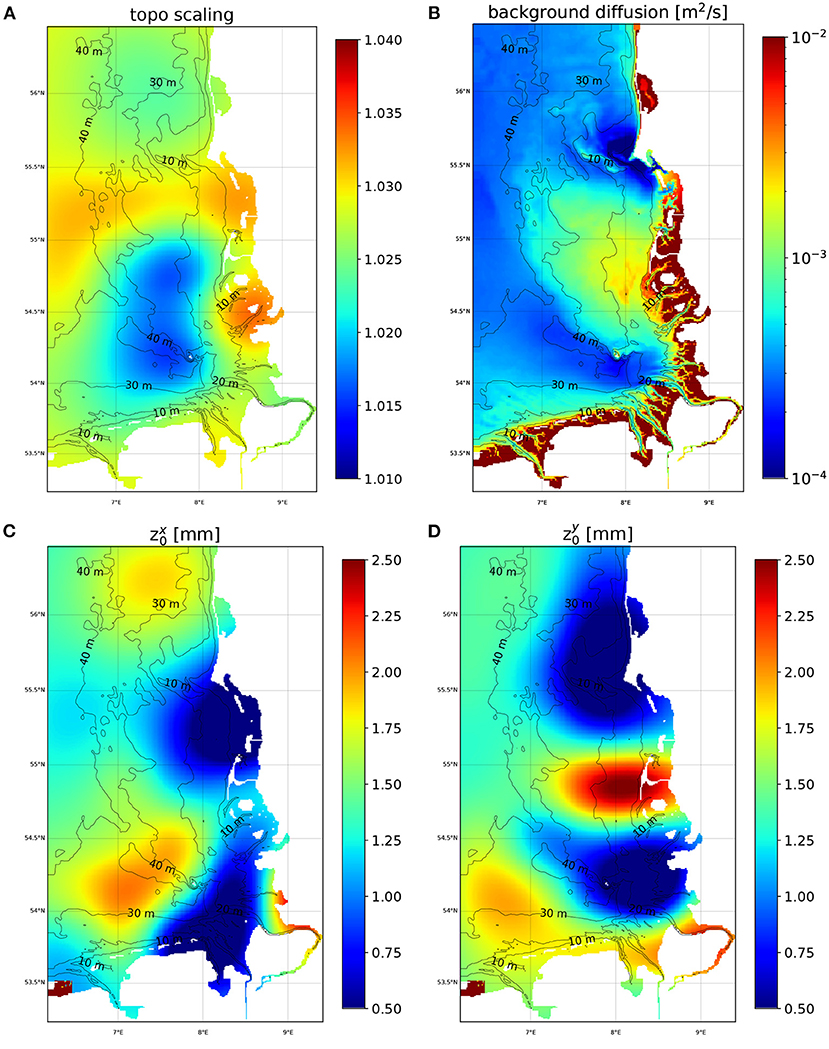
Figure 10. (A) Correction of water depth by the 4DVAR scheme. (B) Background vertical momentum diffusion map estimated by the 4DVAR scheme. (C,D) Maps of zonal (C) and meriodional (D) components of bottom roughness estimated with the 4DVAR scheme.

In Figure 10D there is a small area with high roughness (>2.5 mm) visible in the south western corner of the model domain at the Dutch coast. This location is characterised by very shallow water and by the presence of the open boundary forcing next to it. Obviously the optimisation required a strong dampening of the incoming wave at this location.

As pointed out before, the fact that the tuned model is in good agreement with the observations is not a proof that the parameterisations are physically consistent and meaningful. Concerning the roughness length maps it is definitely possible that the roughness patterns compensate errors, which are actually coming from the open boundary forcing and which are not included in the respective error parameterisation. As the length scale of the roughness patterns is considerably smaller than the length scale of the dominating M2 tide, these corrections could, for example, be related to errors of higher order overtides in the open boundary forcing. The fact that such overtides are present became apparent in the analysis of the Hvide tide gauge data close to the northern open boundary.

The possible ambiguities in the error parameterisations can also give a hint toward requirements concerning the observation system. In our case it is obvious that additional measurements along the open boundary would help to separate possible error sources. In this context it is important to point out that such measurements are of value even if data are only available for a limited time (e.g., as part of dedicated measurement campaigns) or if the temporal sampling is coarse, which is true for many satellite systems.

5. Conclusions

A 4DVAR scheme was used to estimate uncertain parameters in a 3D circulation model of the German Bight. The focus of the study was on systematic errors of the model, e.g., bottom roughness, water depth or turbulence parameterisations. A combination of measurements from HF radar, ADCP, and tide gauges was used within a fortnight tuning period. The optimised model was then tested using independent observations acquired within the following month, including a surface drifter data set. To put the results into perspective, the tuned model was compared with model data from the operational system run at BSH. For this purpose the tuned model uses the same model grid, as well as open boundary forcing and meteo forcing as the operational model.

It was discussed that the procedure is able to reduce systematic errors in the observed quantities, however there is no guarantee that the estimated model parameters are actually closer to their “truth” values. The main problem is that the majority of model parameters is very hard to verify directly and one has to rely on observations, which are connected to the considered parameters in a complicated way. In particular, this means it is possible that there are ambiguities, where the simulation of an observed quantity maybe improved in different ways, i.e., by different combinations of uncertain model parameter adjustments and it is not immediately clear, which of these should be used or disregarded. This situation can be improved by extending the variety of observations in order to reduce the ambiguities in the mapping of model parameters to observed quantities.

It was shown that the optimisation process lead to an overall improved agreement with HF radar and tide gauge measurements both for the tuning period and the test period. For the ADCP observations only minor improvements or even slight deteriorations were found. A direct comparison of drifter data with surface velocities from the BSHcmod showed significantly higher errors compared to the tuned IMCO model. However, very comparable results are achieved, if the BSH drift model is used as a postprocessing step to estimate the surface velocities. Possible reasons for this behaviour were discussed and it seems that the coarse resolution of the upper boundary layer in the BSH model is one important factor. Concerning the role of Stokes drift it was not possible to draw a definite conclusion. It appears that the IMCO parameterisation of the boundary layer can to some extend mimic stoke drift effects, but further investigations are certainly necessary to achieve a better understanding of this issue.

The optimisation lead to an increase of water depth by about 5%. The open boundary forcing was adjusted by the 3DVAR scheme in a way consistent with a slightly increased speed of the tidal wave propagation. The adjustments of the tidal amplitudes along the open boundary indicated a higher tidal dissipation in the tuned model compared to the BSH model.

The study has shown that the use of variational methods for the optimisation of coastal numerical models has big potential if suitable observation data are available. In the presented work a combination of suitable observations and an adequate optimisation procedure lead to simulation improvements with respect to an established operational model, which already showed good performance. For a dynamical consistent correction of the 3D circulation the use of profile information, e.g., from ADCP has a high value, because these data provide information on internal friction processes. It became evident as well, that there are potential ambiguities with respect to error parameterisations, for example with regard to errors in the model interior and errors in the open boundary forcing. The benefit of observational data along the open boundary was emphasised, even in case that such data have limitations with regard to time span or temporal sampling. Furthermore, it appeared that certain ambiguities in the inversion process require the additional use of a numerical wave model, ideally two-way coupled to the circulation model.

The study is of more general interest, because the focus on systematic model errors has general consequences for observation data requirements. The presented analysis has demonstrated that such errors can still be a significant factor in existing operational models and that work on further optimisation is worthwhile. The frequency of observation data is less critical for model tuning compared to operational data assimilation. This is of particular relevance for the assessment of existing and future satellite data, which often lack temporal resolution, but which can still be of high value for model optimisation. The strong spatial heterogeneity of model errors found in this study call for observations with high spatial resolutions, which are also likely to become more accessible through new monitoring systems in the future. The presented study is of particular interest in the context of the ongoing developments of new satellite based surface current measurement techniques. Using spaceborne data the methodology presented in this study could potentially be applied in a larger number of coastal regions around the world (Gommenginger et al., 2019; Rulent et al., 2020).

Data Availability Statement

The HF radar data are available from the server of the Coastal Observing System for Northern and Arctic Seas (COSYNA) via www.cosyna.de. The drifter data are available via PANGAEA (Carrasco and Horstmann, 2017).

Author Contributions

JS-S has contributed to the development and implementation of the 4DVAR system. SF contributed to the presentation and discussion of output from the operational CMOD model and the associated drift module. JH contributed to the presentation and discussion of HF radar observation data. JS contributed to the discussion of the results, in particular concerning aspects of the surface wave impact. All authors contributed to the article and approved the submitted version.

Funding

The presented work has received funding from the Federal Ministry of Education and Research (BMBF) within the Project OceanCurrents (Nr. 03F0822A) as well as from the European Union's Horizon 2020 research and innovation programme within the projects JERICO-S3 (Grant agreement ID: 871153) and IMMERSE (Grant agreement ID: 821926).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank the European Commission for supporting this work in the framework of grant agreement no. H2020-EO-2016-730030-CEASELESS. In addition, the work described in this article was supported by the project Advanced Earth System Modelling Capacity (ESM), financed through the Initiative and Networking Fund of the Helmholtz Association.

References

Apel, J. R. (1987). Principles of Ocean Physics. London: Academic Press.

Google Scholar

Ardhuin, F., Marié, L., Rascle, N., Forget, P., and Roland, A. (2008). Observation and estimation of Lagrangian, Stokes and Eulerian currents induced by wind and waves at the sea surface. arXiv preprint arXiv:0810.3537. doi: 10.1175/2009JPO4169.1

CrossRef Full Text | Google Scholar

Backhaus, J. (1976). Zur Hydrodynamik im flachwassergebiet. Ein numerisches Modell. Deutsch. Hydrogr. Zeitsch. 6, 222–238. doi: 10.1007/BF02226256

CrossRef Full Text | Google Scholar

Barrick, D. (1978). HF radio oceanography - a review. Bound. Layer Metereol. 13, 23–43. doi: 10.1007/BF00913860

CrossRef Full Text | Google Scholar

Barth, A., Alvera-Azcárate, A., Beckers, J. M., Staneva, J., Stanev, E. V., and Schulz-Stellenfleth, J. (2011). Correcting surface winds by assimilating high-frequency radar surface currents in the German Bight. Ocean Dyn. 61, 599–610. doi: 10.1007/s10236-010-0369-0

CrossRef Full Text | Google Scholar

Barth, A., Alvera-Azcárate, A., Gurgel, K.-W., Staneva, J., Port, A., Beckers, J.-M., and Stanev, E. (2010). Ensemble perturbation smoother for optimizing tidal boundary conditions by assimilation of High-Frequency radar surface currents - application to the German Bight. Ocean Sci. 6, 161–178. doi: 10.5194/os-6-161-2010

CrossRef Full Text | Google Scholar

Barth, A., Alvera-Azcárate, A., and Weisberg, R. (2008). Assimilation of high-frequency radar currents in a nested model of the West Florida Shelf. J. Geophys. Res. 113, C08033:1-15. doi: 10.1029/2007JC004585

CrossRef Full Text | Google Scholar

Baschek, B., Schroeder, F., Brix, H., Riethmüller, R., Badewien, T., Breitbach, G., et al. (2016). The coastal observing system for northern and arctic seas (COSYNA). Ocean Sci. Discuss. 1–73. doi: 10.5194/os-2016-31

CrossRef Full Text | Google Scholar

Becker, G. A., Dick, S., and Dippner, J. W. (1992). Hydrography of the German bight. Mar. Ecol. Prog. Ser. 91, 9–18. doi: 10.3354/meps091009

CrossRef Full Text | Google Scholar

Breivik, O., and Saetra, O. (2001). Real time assimilation of HF radar currents into a coastal ocean model. J. Mar. Syst. 28, 161–182. doi: 10.1016/S0924-7963(01)00002-1

CrossRef Full Text | Google Scholar

Burchard, H., and Bolding, K. (2002). GETM - a General Estuarine Transport Model. Technical report, European Comission, No EUR 20253 EN.

Google Scholar

Callies, U., Gaslikova, L., Kapitza, H., and Scharfe, M. (2017). German Bight residual current variability on a daily basis: principal components of multi-decadal barotropic simulations. Geo-Mar. Lett. 37, 151–162. doi: 10.1007/s00367-016-0466-2

CrossRef Full Text | Google Scholar

Carrasco, R., and Horstmann, J. (2017). German Bight surface drifter data from Heincke cruise HE 445, 2015. PANGAEA. doi: 10.1594/PANGAEA.874511

CrossRef Full Text | Google Scholar

Cavaleri, L., Abdalla, S., Benetazzo, A., Bertotti, L., Bidlot, J.-R., Breivik, O., et al. (2018). Wave modelling in coastal and inner seas. Prog. Oceanogr. 167, 164–233. doi: 10.1016/j.pocean.2018.03.010

CrossRef Full Text | Google Scholar

Chavanne, C. (2018). Do high-frequency radars measure the wave-induced Stokes drift? J. Atmos. Ocean. Technol. 35, 1023–1031. doi: 10.1175/JTECH-D-17-0099.1

CrossRef Full Text | Google Scholar

Dick, S., and Kleine, E. (2007). The BSH new operational circulation model using general vertical co-ordinates. Environ. Res. Eng. Manag. 3, 18–24. doi: 10.1109/BALTIC.2006.7266135

CrossRef Full Text | Google Scholar

Dick, S., Kleine, E., Müller-Navarra, K., and Klein, S. (2001). The Operational Circulation Model of BSH (BSHcmod) Model Description and Validation. BSH Report, Bundesamt für Seeschifffahrt und Hydrographie (BSH), Hamburg.

Google Scholar

Fletcher, R. (1986). Practical Methods of Optimization: Unconstrained Optimization, Vol. 1. New York, NY: John Wiley & Sons.

Google Scholar

Frolov, S., Paduan, J., Cook, M., and Bellingham, J. (2012). Improved statistical prediction of surface currents based on historic HF-radar observations. Ocean Dyn. 62, 1111–1122. doi: 10.1007/s10236-012-0553-5

CrossRef Full Text | Google Scholar

Gandin, L. S. (1963). Objective Analysis of Meteorological Fields. St. Petersburg: Gridromet.

Google Scholar

Gommenginger, C., Chapron, B., Hogg, A., Buckingham, C., Fox-Kemper, B., Eriksson, L., et al. (2019). SEASTAR: a mission to study ocean submesoscale dynamics and small-scale atmosphere-ocean processes in coastal, shelf and polar seas. Front. Mar. Sci. 6:457. doi: 10.3389/fmars.2019.00457

CrossRef Full Text | Google Scholar

Graber, H. C., Haus, B. K., Chapman, R. D., and Shay, L. K. (1997). HF radar comparisons with moored estimates of current speed and direction: expected differences and implications. J. Geophys. Res. 102, 18749–18766. doi: 10.1029/97JC01190

CrossRef Full Text | Google Scholar

Gurgel, K.-W., Essen, H.-H., and Kingsley, S. P. (1999). HF radars: physical limitations and recent developments. Coast. Eng. 37, 201–218. doi: 10.1016/S0378-3839(99)00026-5

CrossRef Full Text | Google Scholar

Gurgel, K.-W., and Schlick, T. (2008). “Land-based over-the-horizon radar techniques for monitoring the north-east Atlantic coastal zone,” in Remote Sensing of the European Seas, ed V. Barale (Dordrecht: Springer), 447–460. doi: 10.1007/978-1-4020-6772-3_34

CrossRef Full Text | Google Scholar

Gurgel, K.-W., and Schlick, T. (2009). “Remarks on signal processing in HF radars using FMCW modulation,” in International Radar Symposium IRS (Hamburg), 63–67.

Google Scholar

Gürol, S., Weaver, A. T., Moore, A. M., Piacentini, A., Arango, H. G., and Gratton, S. (2014). Bpreconditioned minimization algorithms for variational data assimilation with the dual formulation. Q. J. R. Meteorol. Soc. 140, 539–556. doi: 10.1002/qj.2150

CrossRef Full Text | Google Scholar

Herklotz, K. (2007). Oceanographic results of two years operation of the first offshore wind research platform in the German Bight-FINO1. DEWI Mag. 30, 47–51.

Google Scholar

Ke, X., Collins, M., and Poulos, S. (1994). Velocity structure and sea bed roughness associated with intertidal (sand and mud) flats and saltmarshes of the Wash, UK. J. Coast. Res. 702–715.

Google Scholar

Kurapov, A., Egbert, G., Allen, J., Miller, R., Erofeeva, S., and Kosro, P. (2003). The M2 internal tide off oregon: inferences from data assimilation. J. Phys. Oceanogr. 33, 1733–1757. doi: 10.1175/2397.1

CrossRef Full Text | Google Scholar

Lewis, J., Shulman, I., and Blumberg, A. (1998). Assimilation of Doppler radar current data into numerical ocean models. Contin. Shelf Res. 18, 541–559. doi: 10.1016/S0278-4343(98)00006-5

CrossRef Full Text | Google Scholar

Li, Z., Chao, Y., McWilliams, C., and Ide, K. (2008). A three -dimensional variational data assimilation scheme for the Regional Ocean Modelling system: implementation and basic experiments. J. Geophys. Res. 113, 1–19. doi: 10.1029/2006JC004042

CrossRef Full Text | Google Scholar

Liu, Z., and Sandu, A. (2008). On the properties of discrete adjoints of numerical methods for the advection equation. Int. J. Numer. Methods Fluids 56, 769–803. doi: 10.1002/fld.1547

CrossRef Full Text | Google Scholar

Moore, A. M., Arango, H. G., and Edwards, C. A. (2018). Reduced-rank array modes of the California current observing system. J. Geophys. Res. 123, 452–465. doi: 10.1002/2017JC013172

CrossRef Full Text | Google Scholar

Ngodock, H., Carrier, M., Smith, S., and Souopgui, I. (2017). Weak and strong constraints variational data assimilation with the NCOM-4DVAR in the agulhas region using the representer method. Monthly Weath. Rev. 145, 1755–1764. doi: 10.1175/MWR-D-16-0264.1

CrossRef Full Text | Google Scholar

Ngodock, H., Muscarella, P., Carrier, M., Souopgui, I., and Smith, S. (2015). “Assimilation of HF radar observations in the Chesapeake–Delaware Bay region using the Navy Coastal Ocean Model (NCOM) and the Four-Dimensional Variational (4DVAR) method,” in Coastal Ocean Observing Systems eds Liu, Y., Kerkering, H., and Weisberg, R. H. (London: Elsevier), 373–391. doi: 10.1016/B978-0-12-802022-7.00020-1

CrossRef Full Text | Google Scholar

Ohlmann, C., White, P., Washburn, L., Emery, B., Terrill, E., and Otero, M. (2007). Interpretation of coastal HF radar–derived surface currents with high-resolution drifter data. J. Atmos. Ocean. Technol. 24, 666–680. doi: 10.1175/JTECH1998.1

CrossRef Full Text | Google Scholar

Oke, P., Allen, J., Miller, R., Egbert, G., and Kosro, P. (2002). Assimilation of surface velocity data into a primitive equation coastal ocean model. J. Geophys. Res. 107, 1–25. doi: 10.1029/2000JC000511

CrossRef Full Text | Google Scholar

Port, A., Gurgel, K., Staneva, J., Schulz-Stellenfleth, J., and Stanev, E. (2011). Tidal and wind-driven surface currents in the German Bight: HFR observations versus model simulations. Ocean Dyn. 61, 1–19. doi: 10.1007/s10236-011-0412-9

CrossRef Full Text | Google Scholar

Röhrs, J., Sperrevik, A. K., Christensen, K. H., Broström, G., and Breivik, y. (2015). Comparison of HF radar measurements with Eulerian and Lagrangian surface currents. Ocean Dyn. 65, 679–690. doi: 10.1007/s10236-015-0828-8

CrossRef Full Text | Google Scholar

Rulent, J., Mir Calafat, F., Banks, C. J., Bricheno, L., Gommenginger, C., Green, M., et al. (2020). Comparing water level estimation in coastal and shelf seas from satellite altimetry and numerical models. Front. Mar. Sci. 7:919. doi: 10.3389/fmars.2020.549467

CrossRef Full Text | Google Scholar

Sanchez-Arcilla, A., Staneva, J., Cavaleri, L., Badger, M., Bidlot, J., Sorensen, J. T., et al. (2021). CMEMSBased coastal analyses: conditioning, coupling and limits for applications. Front. Mar. Sci. 8:180. doi: 10.3389/fmars.2021.604741

CrossRef Full Text | Google Scholar

Schloen, J., Stanev, E. V., and Grashorn, S. (2017). Wave-current interactions in the southern North Sea: the impact on salinity. Ocean Model. 111, 19–37. doi: 10.1016/j.ocemod.2017.01.003

CrossRef Full Text | Google Scholar

Schumaker, L. (2007). Spline Functions: Basic Theory. Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511618994

CrossRef Full Text | Google Scholar

Scott, R., Allen, J., Egbert, G., and Miller, R. (2000). Assimilation of surface current measurements in a coastal ocean model. J. Phys. Oceanogr. 30, 2359–2378. doi: 10.1175/1520-0485(2000)030<2359:AOSCMI>2.0.CO;2

CrossRef Full Text | Google Scholar

Shulman, I., and Paduan, J. D. (2009). Assimilation of HF radar-derived radials and total currents in the Monterey Bay area. Deep Sea Res. Part II 56, 149–160. doi: 10.1016/j.dsr2.2008.08.004

CrossRef Full Text | Google Scholar

Stanev, E., Badewien, T., Freund, H., Grayek, S., Hahner, F., Meyerjürgens, J., et al. (2019). Extreme westward surface drift in the North Sea: public reports of stranded drifters and Lagrangian tracking. Contin. Shelf Res. 177, 24–32. doi: 10.1016/j.csr.2019.03.003

CrossRef Full Text | Google Scholar

Stanev, E., Ziemer, F., Schulz-Stellenfleth, J., Seemann, J., Staneva, J., and Gurgel, K.-W. (2015). Blending surface currents from HF radar observations and numerical modelling: tidal hindcasts and forecasts. J. Atmos. Ocean. Technol. 32, 256–281. doi: 10.1175/JTECH-D-13-00164.1

CrossRef Full Text | Google Scholar

Stanev, E. V., Dobrynin, M., Pleskachevsky, A., Grayek, S., and Günther, H. (2009). Bed shear stress in the southern North Sea as an important driver for suspended sediment dynamics. Ocean Dyn. 59, 183–194. doi: 10.1007/s10236-008-0171-4

CrossRef Full Text | Google Scholar

Stanev, E. V., Jacob, B., and Pein, J. (2019b). German Bight estuaries: An inter-comparison on the basis of numerical modeling. Contin. Shelf Res. 174, 48–65. doi: 10.1016/j.csr.2019.01.001

CrossRef Full Text | Google Scholar

Staneva, J., Alari, V., Breivik, O., Bidlot, J.-R., and Mogensen, K. (2017). Effects of wave-induced forcing on a circulation model of the North Sea. Ocean Dyn. 67, 81–101. doi: 10.1007/s10236-016-1009-0

CrossRef Full Text | Google Scholar

Staneva, J., Wahle, K., Günther, H., and Stanev, E. (2016). Coupling of wave and circulation models in coastal?ocean predicting systems: a case study for the German Bight. Ocean Sci. 12, 797–806. doi: 10.5194/os-12-797-2016

CrossRef Full Text | Google Scholar

Stewart, R., and Joy, J. (1974). HF radio measurements of surface currents. Deep-Sea Res. 21, 1039–1049. doi: 10.1016/0011-7471(74)90066-7

CrossRef Full Text | Google Scholar

Sündermann, J., Hesse, K.-J., and Beddig, S. (1999). Coastal mass and energy fluxes in the southeastern North Sea. Deutsche Hydrogr. Zeitsch. 51, 113–132. doi: 10.1007/BF02764171

CrossRef Full Text | Google Scholar

Thuburn, J., and Haine, T. W. (2001). Adjoints of nonoscillatory advection schemes. J. Comput. Phys. 171, 616–631. doi: 10.1006/jcph.2001.6799

CrossRef Full Text | Google Scholar

Umlauf, L., Burchard, H., and Bolding, K. (2005). GOTM - Scientific Documentation. Marine Science Reports 63. Warnemünde: Leibnitz-Institute for Baltic Sea Research.

Google Scholar

Vandenbulcke, L., Beckers, J.-M., and Barth, A. (2017). Correction of inertial oscillations by assimilation of HF radar data in a model of the Ligurian Sea. Ocean Dyn. 67, 117–135. doi: 10.1007/s10236-016-1012-5

CrossRef Full Text | Google Scholar

Wahle, K., and Stanev, E. (2011). Consistency and complementarity of different coastal ocean observations, a neural network-based analysis for the German bight. Geophys. Res. Lett. 38, 1–4. doi: 10.1029/2011GL047070

CrossRef Full Text | Google Scholar

Wolfe, P. (1969). Convergence conditions for ascent methods. SIAM Rev. 11, 226–235. doi: 10.1137/1011036

CrossRef Full Text | Google Scholar

Yaremchuk, M., and Sentchev, A. (2009). Mapping radar-derived sea surface currents with a variational method. Contin. Shelf Res. 29, 1711–1722. doi: 10.1016/j.csr.2009.05.016

CrossRef Full Text | Google Scholar

Zhang, W. G., Wilkin, J. L., and Arango, H. G. (2010). Towards an integrated observation and modeling system in the New York Bight using variational methods. Part I: 4DVAR data assimilation. Ocean Model. 35, 119–133. doi: 10.1016/j.ocemod.2010.08.003

CrossRef Full Text | Google Scholar

Appendix A

For the numerical treatment of the model described in section 2 a standard Arakawa C grid is used for the horizontal dimension and σ-coordinates for the vertical. The layer integrated transports are then defined as

$\begin{array}{ll}{U}_i=H_i{\displaystyle {\int }_{{\sigma }_i}^{{\sigma }_{i+1}}}u(x,y,z(x,y,\sigma ))d\sigma i=1,\dots ,n_z,& (18)\end{array}$

where H_i = z(x, y, σ₂) − z(x, y, σ₂) is the layer thickness of layer number i and z(x, y, σ) is the z-coordinate of the σ-layer at position x, y parameterised by σ ∈ [−1, 0]. The sigma layers are given by

$\begin{array}{ll}z(x,y,t)=\widehat{\sigma }(H(x,y)+\eta (x,y,t)),& (19)\end{array}$

where H is water depth, η is water elevation, and $\widehat{\sigma }$ is given by

$\begin{array}{ll}\widehat{\sigma }(\sigma )=\{\begin{array}{cc}-\frac{{\zeta }_B}{2}(cos(\pi (\sigma +1))+1)+(1-{\zeta }_B)\sigma & 0\le \sigma <-0.5\\ -\frac{{\zeta }_S}{2}(cos(\pi (\sigma +1))+1)+(1-{\zeta }_S)\sigma & -0.5\le \sigma \le 1.\end{array}& (20)\end{array}$

Here, ζ_B, ζ_S ∈ [0, 1] are zooming parameters, which control the concentration of vertical layers near the bottom and the surface respectively. For ζ_B = ζ_S = 0 one gets the standard equidistant σ coordinates. In this study we used ζ_B = 0.5 and ζ_S = 0.75.

The model is parallelised using domain decomposition. For the German Bight setup a grid of 12 × 12 domains was used. To meet the Courant-Friedrichs-Lewy (CFL) condition, a time step of 10 s was chosen.

A.1 Semi-implicit Scheme

In order to perform a 4DVAR parameter optimisation, the forward model has to be very stable, such that it provides meaningful results for a wider range of model parameters. One approach to increase stability is the inclusion of implicit components in the numerical scheme as explained in the following.

A 1D semi-implicit scheme is used for the momentum balance in each bin. To estimate the frictional forces between the vertical layers, the vertical shear is computed considering velocities of the present as well as the next time, i.e.,

$\begin{array}{l}{u}_i^{(k+1)}-u_i^{(k)}=\Delta t({\tau }_R^{(k)}+\frac{v_v^{(k)}}{2}(u_{i+1}^{(k)}+u_{i+1}^{(k+1)}-u_i^{(k)}-u_i^{(k+1)})\hfill \\ -\frac{v_v^{(k)}}{2}(u_i^{(k)}+u_i^{(k+1)}-u_{i-1}^{(k)}-u_{i-1}^{(k+1)}))\hfill & (21)\end{array}$

for i = 2, …, n_z. This results in a coupled tri-diagonal linear system for $u_i^{k+1},i=2,\dots ,n_z$. The term τ_R contains all the remaining forcing terms, which are estimated from u^(k) and hence they are treated as constants in this equation system. The velocity $u_1^{(k+1)}$ is treated as a known constant in the numerical treatment as well, i.e., one has n_z − 1 unknowns. This implicit approach was found necessary to deal with instabilities, which occurred for very low water levels, if a pure explicit scheme is used.

A.2 Wetting and Drying

The wetting and drying scheme has to be differentiable to allow implementation in the adjoint model. To obtain a smooth behaviour, the function

$\begin{array}{ll}R(\tau )=\{\begin{array}{ll}1& \tau >1\\ {\tau }^2(3-2\tau )& 0<\tau \le 1\\ 0& \tau \le 0\end{array}& (22)\end{array}$

is used, which gives a differentiable transition from zero to one within the interval [0,1]. Using the function R, the drying parameter α_dry is defined similar to the approach described in Burchard and Bolding (2002) as

$\begin{array}{ll}{\alpha }_{dry}=R({\xi }_{dry})& (23)\end{array}$

with

$\begin{array}{ll}{\xi }_{dry}=\frac{H+\eta -H_{min}}{H_{crit}-H_{min}}.& (24)\end{array}$

The values of α_dry hence go from one to zero with the water depth decreasing from H_crit to H_min. We chose 1 m for H_crit and 0.5 m for H_min.

To avoid negative water depth toward the end of the drying process, the current velocities are multiplied by the factor α_dry. This is equivalent to the introduction of additional frictional forces, which bring the remaining water to a complete hold.

To further stabilise the model optimisation process water depths below 2 m in the original BSH bathymetry were set to 2 m. This is not necessary for the IMCO forward model, but the estimation of cost function gradients with the adjoint, as discussed in section 2.3, becomes more challenging if smaller water depths are allowed.