How Can Information Contribute to Management? Value of Information (VOI) Analysis on Indian Ocean Striped Marlin (Kajikia audax)

Fisheries researchers have focused on the value of information (VOI) in fisheries management and trade-offs since scientists and managers realized that information from different resources has different contribution in the management process. We picked seven indicators, which are log-normal annual catch observation error (Cobs), annual catch observation bias (Cbias), log-normal annual index observation error (Iobs), maximum length observation bias (Linfbias), observed natural mortality rate bias (Mbias), observed von Bertalanffy growth parameter K bias (Kbias), and catch-at-age sample size (CAA_nsamp), and built operating models (OMs) to simulate fisheries dynamics, and then applied management strategy evaluation (MSE). Relative yield is chosen as the result to evaluate the contribution of the seven indicators. Within the parameter range, there was not much information value reflected from fisheries-dependent parameters including Cobs, Cbias, and Iobs. On the other hand, for fisheries-independent parameters such as Kbias, Mbias, and Linfbias, similar tendency of the information value was showed in the results, in which the relative yield goes down from the upper bound to the lower bound of the interval. CAA_nsamp had no impact on the yield after over 134 individuals. The VOI analysis contributes to the trade-offs in the decision-making process. Information with more value is more worthy to collect in case of waste of time and money so that we could make the best use of scientific effort. But we still need to improve the simulation process such as enhancing the diversity and predictability in an OM. More parameters are on the way to be tested in order to collect optimum information for management and decision-making.

Introduction

Uncertainty is pervasive in natural systems and manifests itself in many forms (Morgan and Henrion, 1990; Regan et al., 2002). The role of science in conservation and management of natural resources is generally to reduce uncertainty (Halpern et al., 2006). In fisheries, managing fisheries quantitatively eventually becomes a popular tendency with adaptive management (Hilborn and Walters, 1992). The promise of adaptive management is that learning in the short term will improve management in the long term, which is best kept if the focus of learning is on those uncertainties that impede the most the achievement of management objectives (Runge et al., 2011).

Fisheries management falls into the category of decision-making under uncertainty due to the growth of adapted management. Inherent in such a task is the problem of investing in new information (Mantyniemi et al., 2009). Information comes with a cost, basically; as a result, we should find an optimum amount of valuable information in the decision-making process. The cost savings from reduced information collecting may outweigh the small potential loss in the decision accuracy of the results (Walters and Pearse, 1996; de Bruin and Hunter, 2003; Ling et al., 2006).

Fisheries management is plagued with various kinds of uncertainties, but not all uncertainties are equally important to resolve. Nevertheless, we still need a massive amount of information to conduct our conservation and management work. Experts in resource management continue to advocate for more resources for information collecting to support science-based decision-making (NOAA, 2001). This should facilitate the consideration of trade-offs that exist between resources allocated to information collecting and those allocated to other management activities. Information collecting in natural resource management can include fundamental research, monitoring, and the analytical processing of data gathered from these tasks (Hansen and Jones, 2008).

Unfortunately, experience with commercial fisheries worldwide during recent decades suggests that allocating considerable resources to data collection and stock assessments has not prevented overexploitation and collapse (Walters and Maguire, 1996; Pauly et al., 2002; Myers and Worm, 2003).

So we ask ourselves, is the data collecting extent not wide enough? Is the direction of our collecting correct? Or are the data we collected really helping with the analysis? Therefore, the problem of the value of information (VOI) has been recognized and discussed in basic fisheries stock assessment textbooks (Hilborn and Walters, 1992) and journal papers (e.g., Hansen and Jones, 2008), but examples where the VOI has been explicitly quantified in a fisheries context are scarce (Hansen and Jones, 2008; Mantyniemi et al., 2009).

In the language of classical decision theory, there is a high expected VOI reflected from important uncertainty. The value of new information is the difference between the expected value of an optimal action after the new information has been collected and the value before the new information has been collected. Therefore, Raiffa and Schlaifer (1961) described the central concept through the expected value of perfect information (EVPI):

$$EVPI=E_s[ma{x}_{a}U(a,s)]-ma{x}_a{E}_s[U(a,s)]$$

where U is a utility function that we want to maximize by implementing some action a in the presence of system uncertainty s.

Many researchers have examined the value of reducing uncertainty or the value of increased surveys in commercial fisheries using operating models (OMs) designed to maximize given objectives (e.g., McAllister et al., 1999; Punt and Smith, 1999; Moxnes, 2003) by using techniques including Monte Carlo simulations (e.g., Bergh and Butterworth, 1987; Powers and Restrepo, 1993; Punt et al., 2002) and Bayesian approaches (McAllister and Pikitch, 1997; McDonald and Smith, 1997). Punt and Smith (1999) also evaluated the VOI but neglected the parameter uncertainty and relative credibility of alternative model structures. Quantifying the VOI is more common in the fields of decision-making under uncertainty other than fisheries. The concept of the VOI belongs naturally to the theory of information economics, a branch of microeconomic theory (Quirk, 1976). Basically, the value is understood as a measure of the economic VOI, but there is no need to be so restrictive; any quantitative measure of utility can be used, such as the number of fish landed or a perception of happiness on a scale of 0–100 (Mantyniemi et al., 2009).

Ignoring the opportunity costs of information collecting can lead to overly optimistic predictions of the value of increased assessment effort, which occurs at the expense of various management activities. The value of an assessment program should be measured not by the precision of the estimates it generates but rather in how well fishery management objectives are met in a broader sense (Hansen and Jones, 2008). This requires our models to approach the situation that is happening under water as efficiently as possible. Hence, the most valuable information should be provided in order to improve the model fit and also make the best use of grants and funding.

As mentioned above, we conducted a study on the VOI analysis using Indian Ocean striped marlin (Kajikia audax) as a case study in the purpose of detecting information contribution in management strategy evaluation (MSE) process. MSE process was conducted within a simulation test. Meanwhile, relative yield was used to mature the contribution of information. Striped marlin is a common bycatch species in distant water fisheries such as tuna longline fishery (Dai and Xu, 2007). Management of bycatch species especially data-limited species is fairly necessary, and information value will provide valuable guidance to data collection for researchers and managers of these bycatch species.

Materials and Methods

Simulation of fishery dynamics was carried out using state-space age-structured OMs included in DLMtool (Carruthers and Hordyk, 2018) and MSEtool (Carruthers et al., 2018), an open-source package developed within the R environment for efficient closed-loop evaluation of fishery management procedures. MSE closed-loop testing is presented here basically following the guidelines of Punt et al. (2016).

Operating Model (OM)

A state-space age-structured model is used in the OM (Carruthers et al., 2018). This model is fitted to an index of biomass and catch-at-age composition data (for details on how these data are simulated in closed-loop testing, see Carruthers and Hordyk, 2018) and estimates time-invariant selectivity and process error in the form of recruitment deviations.

Operating model is set up based on the stock assessment materials from 2017 IOTC 15th Working Party on Billfish (WPB15) (Wang, 2017). All errors from the original assessment are moved to make a “clean” base case OM and we assume that this situation is the best case that we can achieve in the real world.

Life history and fishing parameters were based on the maximum-likelihood estimates from the stock assessments, with modifications to provide greater generality in the interpretation of results. Where values were estimated for both sexes, the female parameters were used.

Catch and index information is the most common input as the fisheries-independent data in fisheries study; hence, we set up the OM with modified catch and index error and bias, which are as follows: log-normal annual catch observation error σ_C (Cobs), log-normal annual index observation error σ_I (Iobs), and bias factor for annual catch observations b_C (Cbias). We also chose the bias factor for the observed natural mortality rate b_M (Mbias), the bias factor in the observed von Bertalanffy growth parameter K b_K (Kbias), and the bias factor in the observed maximum length b_Linf (Linfbias) as representing fisheries-dependent data in the study. The sample size of catch-at-age observation (CAA_samp) is also chosen to be tested as it is informative on stock structure and could provide special information in MSE.

Where we focus on in this study is

$${\widehat{C}}_{i,y}=b_{C,i}{\mathrm{\epsilon }}_{C,i,y}{C}_{i,y}$$

$${\mathrm{\epsilon }}_C\sim rlnorm(1,{\mathrm{\sigma }}_C)$$

$${\widehat{I}}_{i,y}=b_{I,i}{\mathrm{\epsilon }}_{I,i,y}{I}_{i,y}$$

$${\mathrm{\epsilon }}_I\sim rlnorm(1,{\mathrm{\sigma }}_I)$$

where ${\widehat{C}}_{i,y}$ and C_i,y are the observed and simulated catch of simulation i in year y, respectively. b_C is the bias factor in the catch, and ε_C,i,y is a log-normal distributed catch observation error of simulation i in year y. ${\widehat{I}}_{i,y}$ and I_i,y are the observed and simulated catch of simulation i in year y, respectively. b_I is the bias factor in the index, and ε_I,i,y is a log-normal distributed index observation error of simulation i in year y.

For natural mortality M, maximum body length Linf, and growth parameter K, biases were just implemented as a factor similar to b_C, simulated as follows:

$${\widehat{M}}_i=b_M{M}_i$$

$${\widehat{K}}_i=b_K{K}_i$$

$${\widehat{C}}_i=b_C{C}_i$$

$${\widehat{Linf}}_i=b_{Linf}Lin{f}_i$$

where M_i, K_i, C_i, and Linf_i are the simulated natural mortality, the von Bertalanffy growth parameter K, the annual catch, and the maximum length in simulation i, and ${\widehat{M}}_i$, ${\widehat{K}}_i$, ${\widehat{C}}_i$, and ${\widehat{Linf}}_i$ are the corresponding observations. Bias b is a factor (Figure 1B), and the error is a log-normal error term with mean 1 and coefficient of variation (CV) determined by M, K, C, and Linf.

FIGURE 1

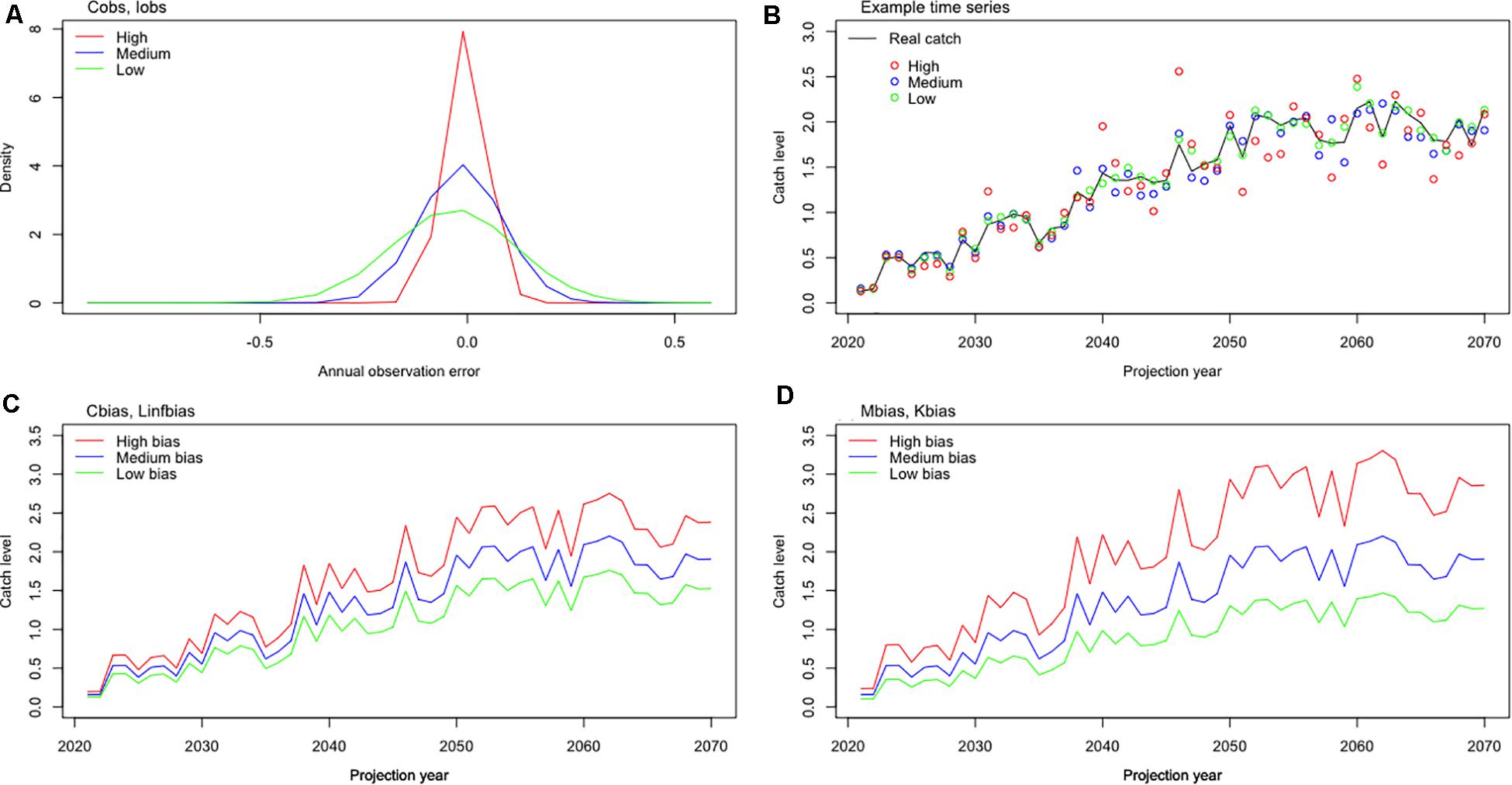
Figure 1. Parameter performance with time-series data. (A) Annual catch/index observation error distribution in low (0.05), medium (0.1), and high (0.15) level. (B) Simulated real catch with low (0.05), medium (0.1), and high (0.15) level observation error. (C) Catch level with low (4/5), medium (1), and high (5/4) level bias in Cbias and Linfbias. (D) Catch level with low (2/3), medium (1), and high (3/2) level bias in Mbias and Kbias.

Parameter Settings

Seven parameters are tested for the VOI in this case study including Cobs, Iobs, Cbias, Mbias, Kbias, Linfbias, and CAA_nsamp. All parameters are expressed with their lower and upper bounds (Table 1).

TABLE 1

Table 1. Parameter settings in striped marlin case study.

(0.05, 0.15) is applied to σ_C and σ_I, (4/5, 5/4) is applied to b_C and b_Linf, and (2/3, 3/2) is applied to b_M and b_K. (10, 1000) is applied to CAA_nsamp. Low error/bias represents the lower bound of the parameters, while high error/bias represents the upper bound of the parameters. Real catch is a stochastic time-series catch with a rising trend. Yields with errors or biases applied are shown in Figure 1.

Parameters are tested independently, which means there is only one changing variable in each MSE run without other errors in the simulation system so that VOI results are generated in a “clean” environment.

Management Strategy Evaluation (MSE)

For VOI testing, management procedures SCA_MSY, SCA_75MSY, and SCA_4010 were applied to run the MSE in this study. These three data-rich management procedures are based on statistical catch-at-age (SCA) stock assessment with MSY, 75%MSY, and 40–10 harvest control rules, respectively (Carruthers et al., 2018), in which catch = MSY, catch = 75%MSY, and 40–10 HCRs are used in fisheries management. These assessment-based MPs were chosen from nine data-rich MPs based on SCA, delay difference, and surplus production methods as catch-at-age data generated from the observation model were used when running SCA-based MPs. Nine iterations of parameter values between lower and upper bounds were applied with 128 simulations when running the MSE. Long-term yield was calculated under a 50-year projection. The average yield was rescaled as the relative yield using the yield in the last 10 years. The mean trend of each simulation for every individual MP was calculated, and the trend of each simulation was also calculated in terms of the three MPs.

Results

Different observations could be seen when MSE runs were performed with different parameter settings associated with the three data-rich MPs.

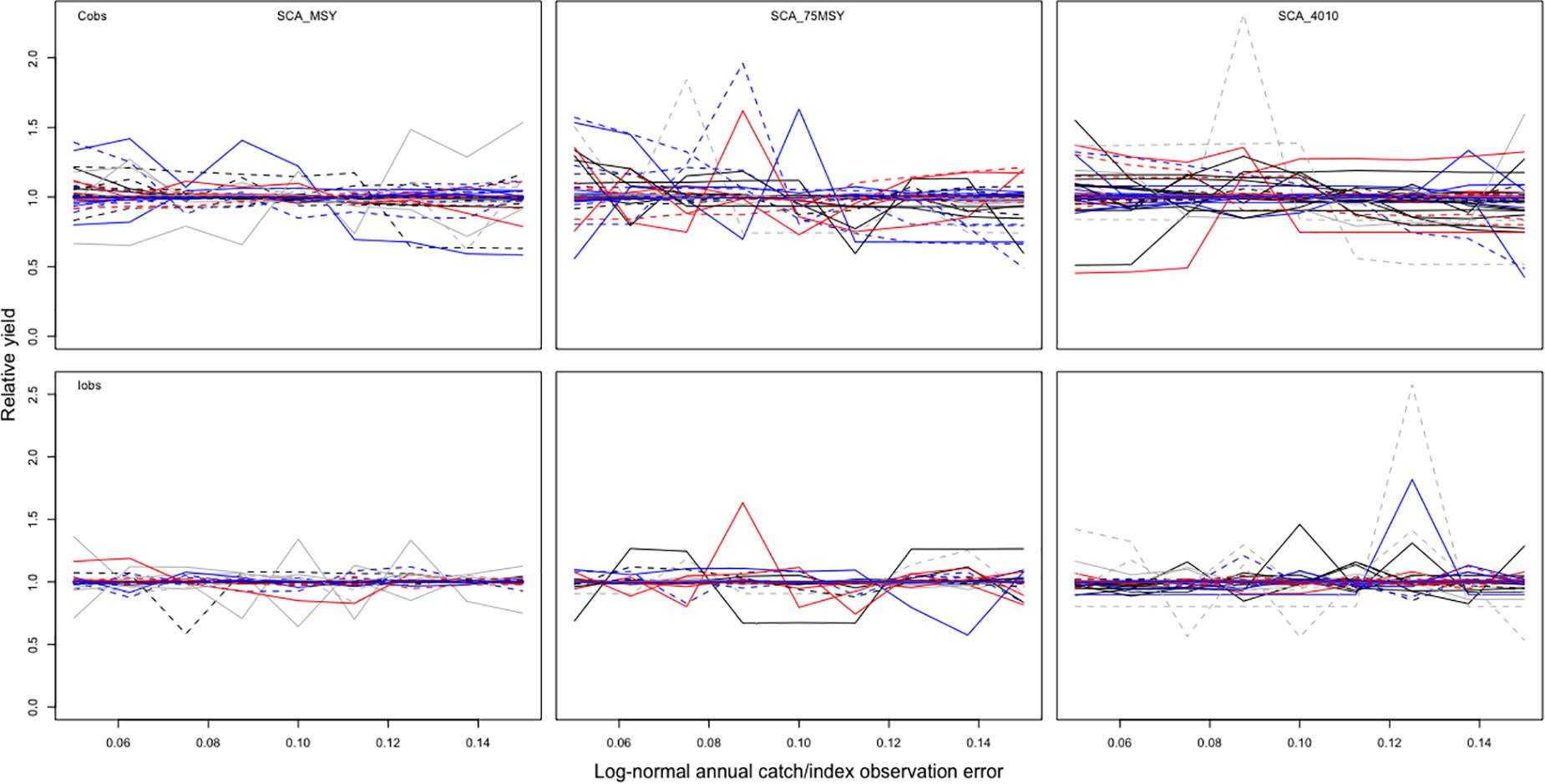
Cobs and Iobs

Simulation tests of Cobs and Iobs converged well, and the patterns showed that not much information value was necessary. When the parameter Cobs was tested, the majority of simulations with all three MPs were concentrated around the line representing a relative yield equal to 1 with only a few noise bumps mostly between 0.5 and 1.5 (Figure 2, upper row). Compared with Cobs, there were even less noises when parameter Iobs was run; almost all 128 simulations converged toward yield equal to 1 (Figure 2, lower panel). Above all, simulations in testing of parameters Cobs and Iobs are stationary and concentrated and hence had no influence on the final relative yield. We could barely get any useful VOI from Cobs and Iobs since the relative yield did not change a lot within the parameter range.

FIGURE 2

Figure 2. Results of 128 simulations of the parameters Cobs and Iobs with three MPs.

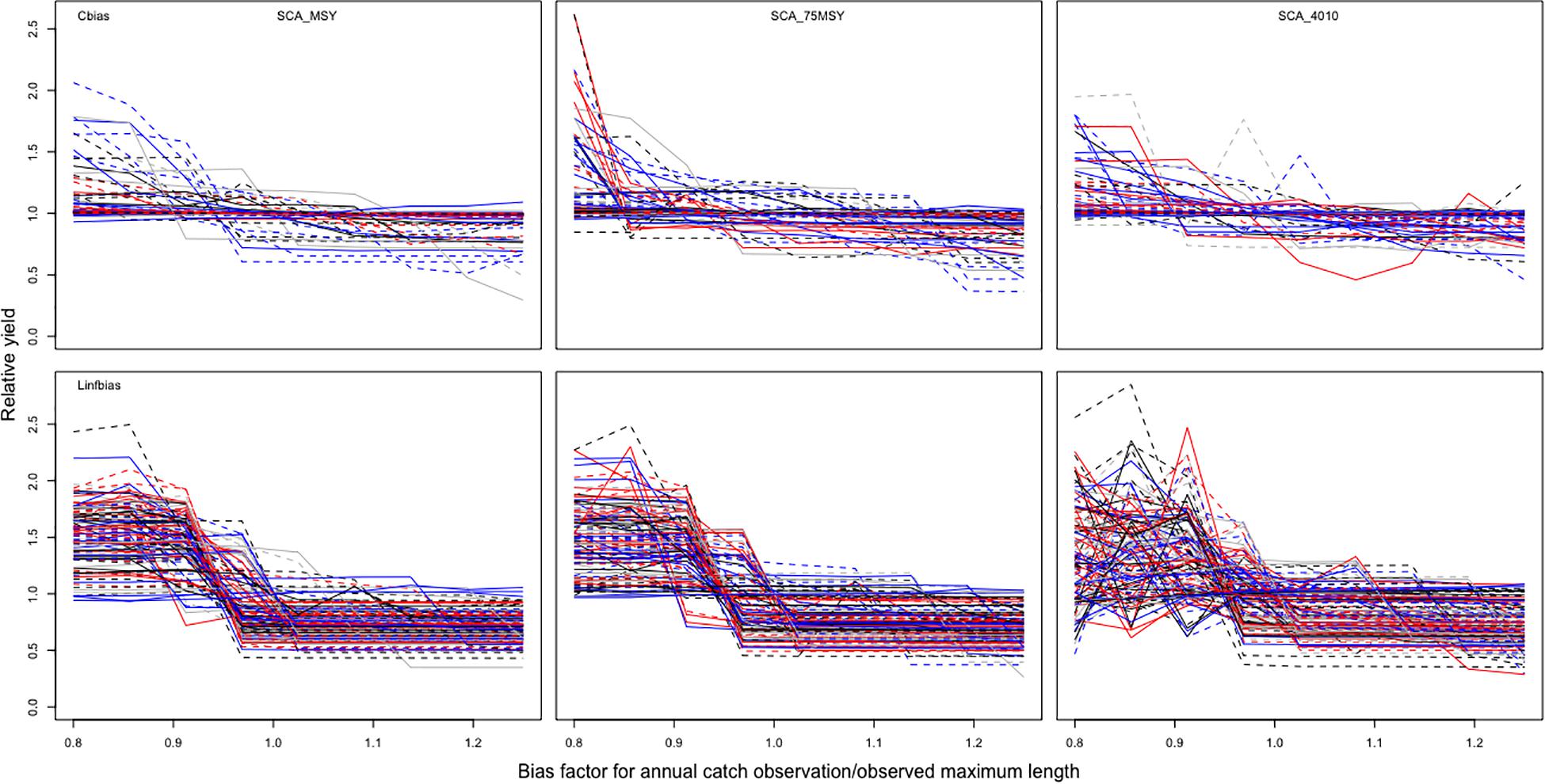
Cbias and Linfbias

Contrary to the parameters Cobs and Iobs that had tendency to converge toward yield equal to 1 after simulation runs, Cbias and Linfbias apparently had a broader distribution range diverging in most simulation cases from yield equal to 1. In fact, parameter Cbias had higher values of relative yield for lower bias factors (<0.9), in most simulations, then gradually converging toward the yield range (0.6–1) for bias factors greater than 0.9 (Figure 3, upper row). Regarding the parameter Linfbias, simulation runs showed fluctuating changes in the relative yield; very high yields were seen at lower bias values for most simulations and for all three MPs, then dropping drastically and staying constant to yield ranges between 0.5 and 1, for bias values superior to 0.95. The three MPs looked alike for most cases except for the noises observed at the beginning of SCA_4010 representing the lower bias values. For both parameters, we observed the necessity of more information value for higher relative yields when parameter values are low.

FIGURE 3

Figure 3. Results of 128 simulations of the parameters Cbias and Linfbias with three MPs.

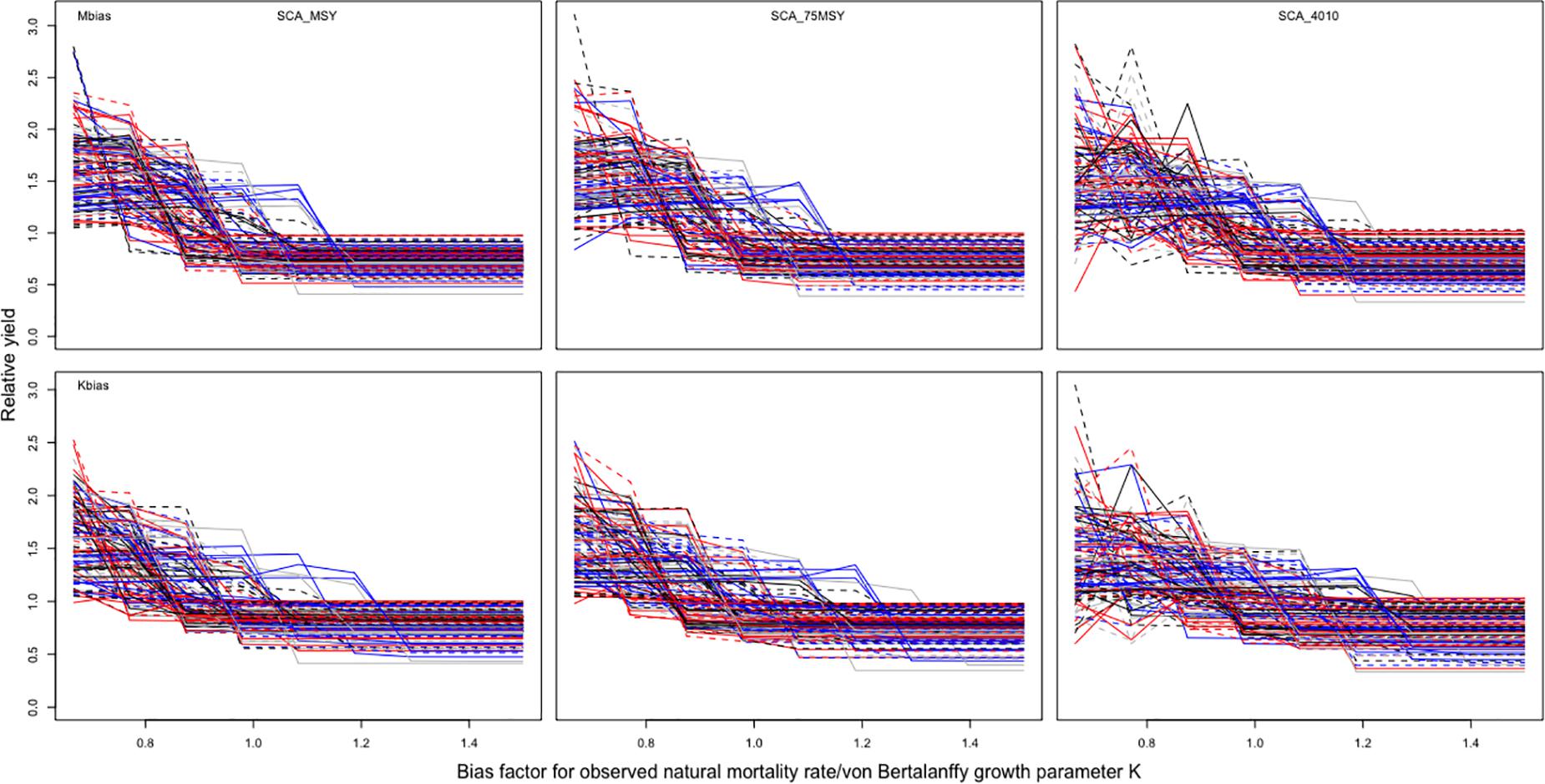
Mbias and Kbias

The results of these two bias factors, Mbias and Kbias, were quite similar with that of Linfbias. With a similar high relative yield at the beginning, it gradually drops to a relative yield equal to 1 then below 1 and constant in the range between 0.5 and 1 for both parameters Mibas and Kbias (Figure 4). Looking into details, simulations with the three MPs in Mbias are nearly exactly the same as that in Kbias.

FIGURE 4

Figure 4. Results of 128 simulations of the parameters Mbias and Kbias with three MPs.

CAA_nsamp

The parameter of the catch-at-age sample size was a bit different from the other parameters tested in this study. It is not controlled throughout a bias nor error but directly by the number of the catch-at-age sample. The result shows that the relative yield was very sensitive to CAA_nsamp at the first iteration, especially at the very beginning of the interval (Figure 5). Then the relative yield goes back to 1 and stays stationary at 1 until the end of the interval. It converged well after the first interval at a relative yield equal to 1.

FIGURE 5

Figure 5. Results of 128 simulations of the parameter CAA_nsamp with three MPs.

Mean Trend

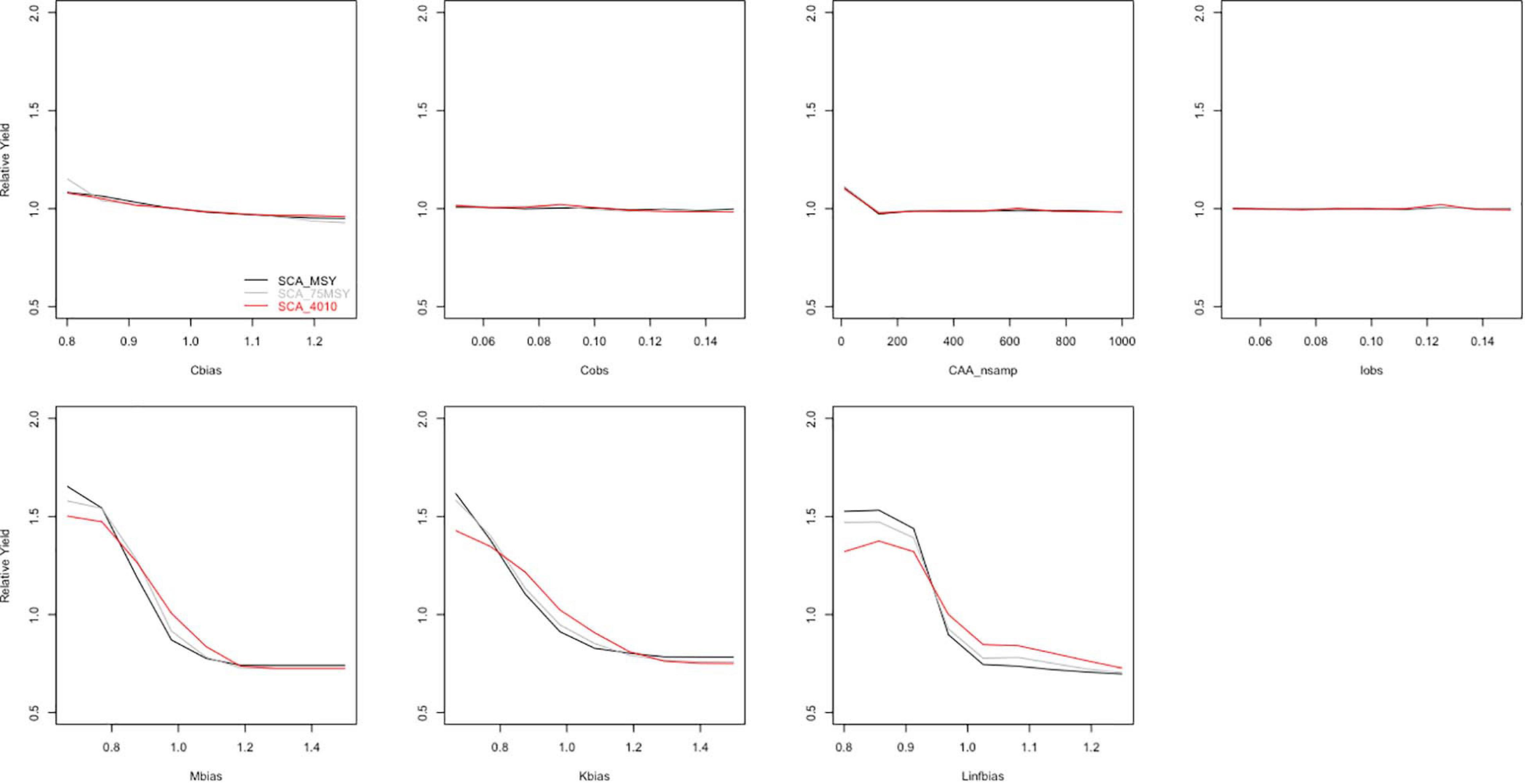
The mean trends of the seven parameters over MPs SCA_MSY, SCA_75MSY, and SCA_4010 are summarized in Figure 6.

FIGURE 6

Figure 6. Mean trend of all parameters conducted with three MPs.

Generally, the mean trend of Cbias, Cobs, CAA_nsamp, and Iobs looks similar, whereas Linfbias, Mbias, and Kbias share a similar shape. These three parameters (Linfbias, Mbias, and Kbias) as observed in Figure 6 simply show their impact on the final relative yield, since they cause the yield to drop from their expected values to lower values (relative yield < 1). For Cbias, Cobs, CAA_nsamp, and Iobs, the mean trend goes flat and smoothly within the interval. Especially, an obvious drop was observed at the beginning of CAA_nsamp, and we also noticed that this drop started slightly above 1 in Cbias and stayed constantly smooth throughout as from 1.2. Similar to what it shows in simulation-specific plots, the mean trends of Cobs and Iobs were quite flat and followed the line of a relative yield equal to 1.

It is not surprising that the relative yield results of parameters Mbias and Kbias were very close; both parameters started around 1.5 and then dropped slowly and converged around 0.75. Especially, there is a platform at the beginning of Linfbias in contrast to the rapid drop at the start interval of Mbias and Kbias.

Discussion

We notice that catch- and index-related parameters, including Cbias, Cobs, and Iobs, provide a few information values as the relative yield does not have distinct change within the parameter interval. Similarly, but slightly different, there is a significant but small signal in the first iteration, which reflects a strong information value as the relative yield goes completely flat in the following iterations. In the other three biases, Mbias, Kbias, and Linfbias, it is clear that a great information value was reflected as we can see in the mean trend plot (Figure 6). Consequently, fisheries-dependent parameters, including Cobs, Cbias, CAA_nsamp, and Iobs, tend to a flat trend of the relative yield under the three MPs. Thus, there is a special interval in CAA_nsamp that indicates a relatively huge information value at the beginning. We also found a significant information value in fisheries-independent parameters, such as Mbias, Kbias, and Linfbias. Interestingly, with almost the same tendency from the lower bound to the upper bound, the parameter value pulls the relative yield from the very top at around 1.5 and then drops rapidly and goes flat to the bottom.

Base-Case OM Settings

The base-case OM was set to represent the “best” data available situation that we can achieve in reality. Simulation studies conducted on a non-noised parameter will indicate the impact of the changing variable. However, there could always be debates on the ideal base-case OM. Questions may arise including the following: Is it really the “best” available situation? How far is it from our reality? What else can be the noise in our study based on this model structure? There are lots of questions for us to answer.

In our base-case OM, natural mortality (M) was set to 0.45 and steepness (h) to 0.86. In the stock assessment performed by Wang (2017), sensitivity analysis of M and h was conducted with M values of 0.35 and 0.55, and h values of 0.75 and 0.95. However, another stock assessment on striped marlin was performed by Wang (2018) using the Stock Synthesis package in the Indian Ocean; the author conducted a sensitivity analysis based on h values of 0.4 and 0.5 and M values of 0.25, and an age-specific M (controlled by the average M value).

In other studies, for instance, Parker et al. (2018) conducted a stock assessment of striped marlin in IOTC-WPB16 using the Bayesian State-Space Surplus Production Model software, JABBA. In their study, the reference steepness used was 0.5 with a sensitivity analysis of lower value 0.4 and higher value 0.86, while admitting reasonable uncertainty about the natural mortality M.

In the present study, for simulation test progress, individual values of information of each parameter were tested under the environment denoted “clean” and “perfect” operation models. So the results obtained are based on the assumption that the OM settings are constantly perfect. As a result, we only tested a single parameter at one time without any noises from other parameters, which is obviously non-existent in real fisheries. Nevertheless, in this preliminary study, we are still using the single-parameter testing system, as what we actually focus on is the impact of a single parameter rather than the synergistic effect. And we clearly got the valuable result that individual fisheries-independent parameters and the catch-at-age sample size are more informative than fisheries-dependent information. This could be the fundamental theory in VOI study in fisheries, and more studies on the information from other aspects could be done based on our research.

As we all know, uncertainties are glued together and always appear at the same time. Thus, future works should be geared toward multi-impact parameter simulation tests to detect interactions within uncertainties.

Impacts of Information Values

The importance of the quantity of fisheries data has been increasingly realized in fisheries stock assessments and MSEs (Restrepo and Powers, 1999). As an analysis on VOI for management, we focused mostly on the most effective information contributing to the management process. The parameters in our simulation tests, which provided large efforts in management, could also be important in stock assessment works, especially fisheries-independent parameters such as Mbias, Kbias, and Linfbias. The information brought from these parameters would be helpful in life history, growth, and species movement studies. A study by Johnson et al. (2015) suggested that in order to design better studies using simulation tests, accurate estimates of sample sizes would be more helpful than conventional power analysis and be reasonably straightforward to use so as to justify the extra time and effort required for the simulation.

Obviously, an optimum sample size is necessarily important in management case studies. Using an appropriate sample size will effectively save effort put in data collection, such as money and time. In the perspective of fisheries management, we suggest that more effort should be put on data reporting and information collection for a fisheries-independent sampling approach. Apparently, Mbias, Kbias, and Linfbias are relatively more important derivers on yield compared with Cobs, Cbias, Iobs, and CAA_nsamp. Therefore, some actions should be done in the current data collecting system, for instance, cut down the number of catch-at-age data and set a lower bound of 134 individuals due to the inflection point in the study (Figure 5). We found that Mbias, Kbias, and Linfbias derived yields in exactly the same way, that is, a half higher yield with low bias and, on the other hand, a quarter lower yield with high bias (Figure 6).

Chen et al. (2003) evaluated the impact of data quantity to fisheries and reported that the lack of sufficient data may lead to relatively higher steepness with higher uncertainty (wider distribution). According to Chen et al. (2003), a difference index of parameter mean reached +40.5% and a difference index of standard deviation reached extremely high values of +778.5%, which could definitely bring the yield to a completely different level, such as hyperdepletion or hyperstability. However, in Chen et al. (2003), natural mortality estimation was also driven by data quality, which, in turn, fluctuated the mean value (from -18 to +50%) with a wide standard deviation distribution (+3.3 to 112.0%). From the perspective of yield-expected management, this variance would drop the yield by 50% from the highest estimation to the lowest.

Regarding the use of abundance index data, Schnute (1985) and Maunder and Punt (2004) raised debates as to what type of data is appropriate to use; questions such as whether to use fisheries-independent data such as surveys or to use fisheries-dependent data such as information from commercial or recreational fisheries were raised. From our point of view, we observed that catch or abundance index data did not cause yield results to fluctuate. Therefore, we suggest that both fisheries-independent and -dependent data may be used for stock assessment and management, and that these data types may not bring severe impact on yield results. However, our study showed that bias in catch and index data were not the main drivers of yield fluctuations; it could probably also depend on the fisheries type and MPs.

The number of catch-at-age samples is always a huge challenge for bycatch species (Pelletier and Gros, 1991). The final result, i.e., the yield, is emphasized, rather than the intermediate VPA result, i.e., the fishing mortality, as stressed in a previous study by Pelletier and Gros (1991); the yield per recruit is less sensitive to catch than the VPA result. Hence, the CV of fishing mortality is approximately equal to those of catch estimators, whereas the yield variance is lower than the input catch-at-age error. Consequently, the uncertainty due to catch is moderate, and the CVs of the yield range are between 8 and 15%.

Fournier and Archibald (1982) suggested that catch-at-age data should not be produced without considering the final use to which they will be put. If the final use is an age-structured model, then aging a large number of older fish accurately may not only be a waste of money and effort but could also degrade the quality of the estimates obtained from the age-structured model. Similarly, in our study, age-structured catch data are necessary but only in a relatively low level. Too much effort put on catch-at-age data collection could be a waste of both money and time, as mentioned by Fournier and Archibald (1982).

In our base-case OM, the number of catch-at-age samples was set between 500 and 600 with the aim to remove the impact of the lacking age-structured catch data. On the other hand, in Wang’s stock assessment (Wang, 2017), the catch-at-age number was set between 100 and 200, which is quite close to the result we got at 134. Consequently, a large sample size of catch-at-age data is determined to be a waste of time and effort. However, this could also depend on age-based selectivity and vulnerability of the stock (Linton and Bence, 2011).

Future Data Collection

As computer-intensive technology and statistical methods evolve, an increase in attention is now being paid on the quality of the data collected for fisheries analyses. There are huge efforts put on global marine fisheries catch reconstruction. Pauly and Zeller (2016) described the source of catch into three contents: foreign fishing, industrially catch, and small-scale fisheries and suggested to put more effort on small-scale fisheries data collection. Based on the VOI analysis results obtained in this study, Cbias and Cobs show that the huge effort put on data collection could possibly have tiny contribution to our management. Nevertheless, Pauly and Zeller (2016) also found that reconstructed global catches between 1950 and 2010 were 50% higher than the FAO dataset and are declining rapidly since catches peaked in the 1990s, which also indicates that data collecting is still necessary in the perspective of global fishing status analysis.

The quantity of fisheries data can have a profound impact on the quality of stock assessment (Chen et al., 2003). Realistically, information has various availabilities in terms of data type or even fisheries status. A valuable fishery tends to have fisheries-independent and -dependent information collected for many fisheries variables with long time series, while a less valuable fishery, however, often has limited information collected. The optimum data size for the two fisheries could be very different, so we should implement this VOI analysis on more different types of fishery to find the best guidance of fishery-specific data collection.

Data collected from commercial fishery represent different characteristics of the stock than data collected by scientific surveys. Data collected from a well-defined fisheries-independent survey tend to be unbiased and representative of the targeted fish stock and are thus considered more reliable than the data collected from commercial fisheries (Hilborn and Walters, 1992). It is thus important to improve data quantity and collect fisheries-independent data, which often are more reliable than data collected from commercial fisheries. In our case study, fisheries-independent data such as Kbias, Mbias, Linfbias, etc., bring more impact on yield than fisheries-dependent information including Cbias, Cobs, and Iobs, which support the point of view above.

More complex cost models of observation processes are needed by managers to account for overhead costs of certain operations (survey boats, launches, and crew) and then account for prorated data collection costs (e.g., survey days at sea).

Data Availability Statement

The data analyzed in this study are subject to the following licenses/restrictions: The dataset is correlated to the conference document “Stock assessment of Striped marlin (Tetrapturus audax) in the Indian Ocean using the Stock Synthesis” in Indian Ocean Tuna Commission 15th Working Party on Billfish and is provided by the author directly. Requests to access these datasets should be directed to Shengping Wang, d3NwQG1haWwubnRvdS5lZHUudHc=.

Ethics Statement

Ethical review and approval was not required for the animal study because only simulation and computing work was done on the species.

Author Contributions

MX and TC conceived of the presented idea. MX, TC, and RK developed the theory and performed the computations. XD verified the analytical methods. MX, TC, RK, and LD designed the model and the computational framework and analyzed the data. MX, LD, and ZG carried out the implementation. MX, TC, RK, and FW wrote the manuscript with input from all authors. XD and FW provided funding for the research and study. All authors discussed the results and contributed to the final manuscript.

Funding

This study was supported by the National Observer Program from the Ministry of Agriculture and Rural Affairs of the People’s Republic of China.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We sincere thanks to researchers from the Institute for Oceans and Fisheries in the University of British Columbia and from the College of Marine Sciences in Shanghai Ocean University, which greatly facilitated this study. We also thank Observer Program from Ministry of Agriculture and Rural Affairs (MARA) to provide funding and support this study. We also thank Rémi Letestu, Sylvain Le Jeune, and Amélie Beaugrand for their collaboration.

References

Bergh, M. O., and Butterworth, D. S. (1987). Towards rational harvesting of the South African anchovy considering survey imprecision and recruitment variability. S. Afr. J. Mar. Sci. 5, 937–951. doi: 10.2989/025776187784522702

PubMed Abstract | CrossRef Full Text | Google Scholar

Carruthers, T. R., and Hordyk, A. R. (2018). The Data-Limited Methods Toolkit (DLM tool): an R package for informing management of data-limited populations. Methods Ecol. Evol. 9, 2388–2395. doi: 10.1111/2041-210x.13081

CrossRef Full Text | Google Scholar

Carruthers, T. R., Huynh, Q., and Hordyk, A. H. (2018). Management Strategy Evaluation toolkit (MSEtool): an R Package for Rapid MSE Testing of Data-Rich Management Procedures.

Google Scholar

Chen, Y., Chen, L., and Stergiou, K. I. (2003). Impacts of data quantity on fisheries stock assessment. Aquat. Sci. 65, 92–98. doi: 10.1007/s000270300008

CrossRef Full Text | Google Scholar

Dai, X. J., and Xu, L. X. (2007). A Color Atlas of Global Tuna Fishery Catch. Beijing: China Ocean Press.

Google Scholar

de Bruin, S., and Hunter, G. J. (2003). Making the trade-off between decision quality and information cost. Photogram. Eng. Rem. Sens. 69, 91–98. doi: 10.14358/pers.69.1.91

CrossRef Full Text | Google Scholar

Fournier, D., and Archibald, C. P. (1982). A general theory for analyzing catch at age data. Can. J. Fish. Aquat. Sci. 39, 1195–1207. doi: 10.1139/f82-157

CrossRef Full Text | Google Scholar

Halpern, B. S., Regan, H M., Possingham, H. P., and McCarthy, M. A. (2006). Accounting for uncertainty in marine reserve design. Ecol. Lett. 9, 2–11. doi: 10.1111/j.1461-0248.2005.00827.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Hansen, G. J., and Jones, M. L. (2008). The value of information in fishery management. Fisheries 33, 340–348. doi: 10.1577/1548-8446-33.7.340

CrossRef Full Text | Google Scholar

Hilborn, R., and Walters, C. (1992). Quantitative Fisheries Stock Assessment: Choice, Dynamics and Uncertainty. London: Chapman and Hall.

Google Scholar

Johnson, P. C., Barry, S. J., Ferguson, H. M., and Müller, P. (2015). Power analysis for generalized linear mixed models in ecology and evolution. Methods Ecol. Evol. 6, 133–142.

Google Scholar

Ling, J. M., Aughenbaugh, J. M., and Paredis, C. J. J. (2006). Managing the collection of information under uncertainty using information economics. Trans. Am. Soc. Mech. Eng. 128, 980–990. doi: 10.1115/1.2205878

CrossRef Full Text | Google Scholar

Linton, B. C., and Bence, J. R. (2011). Catch-at-age assessment in the face of time-varying selectivity. ICES J. Mar. Sci. 68, 611–625. doi: 10.1093/icesjms/fsq173

CrossRef Full Text | Google Scholar

Mantyniemi, S., Kuikka, S., Rahikainen, M., Kell, L. T., and Kaitala, V. (2009). The value of information in fisheries management: north Sea herring as an example. ICES J. Mar. Sci. 66, 2278–2283. doi: 10.1093/icesjms/fsp206

CrossRef Full Text | Google Scholar

Maunder, M. N., and Punt, A. E. (2004). Standardizing catch and effort data: a review of recent approaches. Fish. Res. 70, 141–159. doi: 10.1016/j.fishres.2004.08.002

CrossRef Full Text | Google Scholar

McAllister, M. K., and Pikitch, E. K. (1997). A Bayesian approach to choosing a design for surveying fishery resources: application to the eastern Bering Sea trawl survey. Can. J. Fish. Aquat. Sci. 54, 301–311. doi: 10.1139/f96-286

CrossRef Full Text | Google Scholar

McAllister, M. K., Starr, P. J., Restrepo, V. R., and Kirkwood, G. P. (1999). Formulating quantitative methods to evaluate fishery-management systems: what fishery processes should be modelled and what trade-offs should be made? ICES J. Mar. Sci. 56, 900–916. doi: 10.1006/jmsc.1999.0547

CrossRef Full Text | Google Scholar

McDonald, A. D., and Smith, A. D. M. (1997). A tutorial on evaluating expected returns from research for fishery management using Bayes’ theorem. Nat. Resour. Model. 10, 185–216. doi: 10.1111/j.1939-7445.1997.tb00106.x

CrossRef Full Text | Google Scholar

Morgan, G., and Henrion, M. (1990). Uncertainty: A Guide to Dealing with Uncertainty in Quantitative Risk and Policy Analysis. Cambridge: Cambridge University Press.

Google Scholar

Moxnes, E. (2003). Uncertain measurements of renewable resources: approximations, harvesting policies and value of accuracy. J. Environ. Econ. Manag. 45, 85–108. doi: 10.1016/s0095-0696(02)00011-6

CrossRef Full Text | Google Scholar

Myers, R. A, and Worm, B. (2003). Rapid worldwide depletion of predatory fish communities. Nature 423, 280–283. doi: 10.1038/nature01610

PubMed Abstract | CrossRef Full Text | Google Scholar

NOAA (2001). Marine Fisheries Stock Assessment Improvement Plan. Report of the National Marine Fisheries Service National Task Force for Improving Fish Stock Assessments. Washington, DC: U.S. Department of Commerce.

Google Scholar

Parker, D., Winker, H., da Silva, C., and Kerwath, S. E. (2018). Bayesian State-Space Surplus Production Model JABBA Assessment of Indian Ocean Striped Marlin (Tetrapturus audax), IOTC-2018-WPB16-16_-_MLS_JABBA_Final. Available online at: https://iotc.org/documents/WPB/16/16-MLS_JABBA (accessed August 27, 2018).

Google Scholar

Pauly, D., Christensen, V., Guenette, S., Pitcher, T. J., Sumaila, U. R., Walters, C. J., et al. (2002). Towards sustainability in world fisheries. Nature 418, 689–695. doi: 10.1038/nature01017

PubMed Abstract | CrossRef Full Text | Google Scholar

Pauly, D., and Zeller, D. (2016). Catch reconstructions reveal that global marine fisheries catches are higher than reported and declining. Nat. Commun. 7:10244.

Google Scholar

Pelletier, D., and Gros, P. (1991). Assessing the impact of sampling error on model-based management advice: comparison of equilibrium yield per recruit variance estimators. Can. J. Fish. Aquat. Sci. 48, 2129–2139. doi: 10.1139/f91-252

CrossRef Full Text | Google Scholar

Powers, J. E., and Restrepo, V. R. (1993). Evaluation of stock assessment research for Gulf of Mexico king mackerel: benefits and costs to management. North Am. J. Fish. Manag. 13, 15–26. doi: 10.1577/1548-8675(1993)013<0015:eosarf>2.3.co;2

CrossRef Full Text | Google Scholar

Punt, A. E., Butterworth, D. S., de Moor, C. L., De Oliveira, J. A. A., and Haddon, M. (2016). Management strategy evaluation: best practices. Fish Fish. 17, 303–334.

Google Scholar

Punt, A. E., and Smith, A. D. M. (1999). Harvest strategy evaluation for the eastern stock of gemfish (Rexea solandri). ICES J. Mar. Sci. 56, 860–875. doi: 10.1006/jmsc.1999.0538

CrossRef Full Text | Google Scholar

Punt, AE, Walker, T I., and Prince, J. D. (2002). Assessing the management-related benefits of fixed-station fishery-independent surveys in Australia’s southern shark fishery. Fish. Res. 55, 281–295. doi: 10.1016/s0165-7836(01)00276-4

CrossRef Full Text | Google Scholar

Quirk, J. P. (1976). Intermediate Microeconomics. Chicago, IL: Science Research Associates, 359.

Google Scholar

Raiffa, H., and Schlaifer, R. O. (1961). Applied Statistical Decision Theory. Cambridge, MA: Harvard University.

Google Scholar

Regan, HM, Colyvan, M., and Burgman, M. A. (2002). A taxonomy and treatment of uncertainty for ecology and conservation biology. Ecol. Appl. 12, 618–628. doi: 10.1890/1051-0761(2002)012[0618:atatou]2.0.co;2

CrossRef Full Text | Google Scholar

Restrepo, V. R., and Powers, J. E. (1999). Precautionary control rules in US fisheries management: specification and performance. ICES J. Mar. Sci. 56, 846–852. doi: 10.1006/jmsc.1999.0546

PubMed Abstract | CrossRef Full Text | Google Scholar

Runge, M. C., Converse, S. J., and Lyons, J. E. (2011). Which uncertainty? Using expert elicitation and expected value of information to design an adaptive program. Biol. Conserv. 144, 1214–1223. doi: 10.1016/j.biocon.2010.12.020

CrossRef Full Text | Google Scholar

Schnute, J. (1985). A general theory for analysis of catch and effort data. Can. J. Fish. Aquat. Sci. 42, 414–429. doi: 10.1139/f85-057

CrossRef Full Text | Google Scholar

Walters, C., and Maguire, J. J. (1996). Lessons for stock assessment from the northern cod collapse. Rev. Fish Biol. Fish. 6, 125–137.

Google Scholar

Walters, C., and Pearse, P. H. (1996). Stock information requirements for quota management systems in commercial fisheries. Rev. Fish Biol. Fish. 6, 21–42. doi: 10.1007/bf00058518

CrossRef Full Text | Google Scholar

Wang, S. P. (2017). Stock Assessment of Striped marlin (Tetrapturus audax) in the Indian Ocean using the Stock Synthesis, IOTC-2017-WPB15-32_Rev1. Available online at: https://iotc.org/documents/stock-assessment-striped-marlin-tetrapturus-audax-indian-ocean-using-stock-synthesis (accessed August 31, 2017).

Google Scholar

Wang, S. P. (2018). Stock assessment of Striped marlin (Tetrapturus audax) in the Indian Ocean using the Stock Synthesis, IOTC-2018-WPB16-19-TWN_SA_MLS_rev1. Available online at: https://iotc.org/documents/WPB/16/19-MLS_SS3 (accessed August 30, 2018).

Google Scholar