Bioenergetic Model Sensitivity to Diet Diversity Across Space, Time and Ontogeny

Consumption is the primary trophic interaction in ecosystems and its accurate estimation is required for reliable ecosystem modeling. When estimating consumption, species’ diets are commonly assumed to be the average of those that occur among habitats, seasons, and life stages which introduces uncertainty and error into consumption rate estimates. We present a case study of a teleost (Yellowfin Bream Acanthopagrus australis) that quantifies the potential error in consumption (in mass) and growth rate estimates when using diet data from different regions and times and ignoring ontogenetic variability. Ontogenetic diet trends were examined through gut content analysis (n = 1,130 fish) and incorporated into a bioenergetic model (the “primary” model) that included diet variability (n = 144 prey sources) and ontogenetic changes in metabolism (1–7 year) to estimate lifetime consumption. We quantified error by building nine model scenarios that each incorporated different spatiotemporal diet data of four published studies. The model scenarios produced individual lifetime consumption estimates that were between 25% lower and 15% higher than the primary model (maximum difference was 53%, range 11.7–17.8 kg). When consumption (in mass) was held constant, differences in diet quality among models caused a several-fold range in growth rate (0.04–1.07 g day^–1). Our findings showcase the large uncertainty in consumption rate estimates due to diet diversity, and illustrate that caution is required when considering bioenergetic results among locations, times, and ontogeny.

Introduction

Reliable consumption and growth rate estimates are needed for trophodynamic and ecosystem models, which quantify the flow of energy through ecosystems (Pauly et al., 1990; Christensen et al., 2005; Dawson et al., 2019; Leaf and Oshima, 2019). Such models are used to inform fisheries management and restocking programs (Fulton et al., 2011), estimate biodiversity loss in the Anthropocene (Pereira et al., 2010), predict ecosystem shifts (Heithaus et al., 2008) and manage ecosystem services (Christensen et al., 2005; Daily and Matson, 2008). Consumption rates are commonly estimated using energy-balance models such as bioenergetic models (Kitchell et al., 1977; Lawson et al., 2019). This is done by quantifying energy expenditure of an animal, such as that required for growth, metabolism, reproduction, digestion, and excretion/egestion, and assumes that consumption rate is at least equal to the rate of energy expenditure (Kitchell et al., 1977). Such models further consider that consumption rate is dependent on the energy density (ED) of prey items (Kleiber, 1961). For example, predators must consume more low-ED prey compared to high-ED prey to ingest equal calories. The ED of prey species may vary substantially for a generalist predator with a diverse diet (Lawson et al., 1998). Thus diet composition and prey ED are important considerations when quantifying consumption rate estimates using bioenergetic modeling (Luecke and Brandt, 1993; Surma et al., 2018).

Biological models should be reliable approximations of reality but are rarely completely precise. Such models enable an understanding of populations and ecosystems based on physiological processes, relying on regularities that emerge despite individual and interspecific variability (Pérez-Ruzafa et al., 2018). By quantifying sources of variability in predictive models, we can increase their precision. Diet studies, which inform models, can employ gut content analysis (GCA) from deceased animals or sample from live animals with lavage, scat, stable isotope, and fatty acid analyses (Fryxell et al., 2014; Hazen et al., 2019). These methods are often invasive, difficult or costly due to the need to sample large numbers of individual animals to detect diet trends (Fryxell et al., 2014). As a result, fine resolution diet data are lacking for many species and regions. Differences in food environment can lead to altered consumption rates (e.g., Lefcheck et al., 2021) and accounting for these differences may be important for effective management (e.g., Pfeiffer and Anderson, 2021). Despite these limitations of diet data, models that estimate consumption rate or trophodynamics will, by necessity, use what diet data are available, even if the dietary information is collected from different locations or with small sample sizes. This relies on the assumption that a species would occupy a similar trophic niche among regions, which may be suitable for studying a species’ basic ecology but may not hold for other applications such as ecosystem models. This is particularly true for opportunistic species that can have a region- and habitat-specific diet. There will be differences between the assumed diet and actual diet specific to a location or habitat, and these differences may impact estimates of consumption rate and other energy-dependent parameters, such as growth rate. While earlier work has shown the importance of using multiple prey items in bioenergetics models to estimate consumption (Lawson et al., 2018), there are no studies to the author’s knowledge that use detailed diet data (i.e., multiple prey items) to quantify the uncertainty of consumption and growth estimates introduced by supplementing diet information from different spatiotemporal regions.

The objective of this study was to quantify the uncertainty of individual consumption and growth rate estimates when using diet data from different locations, seasons and collection methods. This was achieved by creating a bioenergetic model using highly detailed diet information, including previously unavailable ontogenetic diet changes and consumption rates, and comparing the resulting consumption estimates with those derived from region- or habitat-specific diet information (using nine other datasets). We used Yellowfin Bream (Acanthopagrus australis, hereafter “Bream”) as a study species and describe its diet and consumption rate. Bream is a well-studied species in terms of both energetics and diet, and hence represents an ideal species to assess limited input data for bioenergetic models. Further, Bream has a diverse diet including bivalves, polychaetes, decapods and terrestrial invertebrates, as well as algae and other teleosts (Bell et al., 1984; Morton et al., 1987; Hadwen et al., 2007; Sheaves et al., 2014). However, each study of Bream diet showed differences in prey composition depending on study location, habitat type, season, sampling method, fish life stage, and sample size (Bell et al., 1984; Morton et al., 1987; Hadwen et al., 2007; Sheaves et al., 2014). This variability in the described diet composition implies different ED values of prey, and in turn different food consumption or growth rate estimates of individual predators, depending on which diet data are used.

Materials and Methods

Primary Model Diet

The primary diet data set (compared later with other studies) was measured in Bream collected during a large survey in Botany Bay and Georges River system, New South Wales, Australia (Pease et al., 1981). Fish (n = 1,130, 1.1–40.5 cm total length) were sampled using a variety of commercial fishing methods [gill net (various sizes), beach seine, and beam trawl] across the entire estuary between February 1978 and October 1979. Biometric information [total length (mm), weight (g)] was collected prior to fish dissection, and then fish stomachs were removed and prey contents sorted. Prey species were identified to the highest taxonomic level possible, were blotted and weighed, and expressed as the proportion-by-biomass of the total stomach contents for each individual, which was then averaged across all non-empty stomachs. Energy density per wet mass (kJ g^–1) of prey types were taken from published sources (Supplementary Table 1).

Respirometry

The routine metabolic rate (RMR; Chabot et al., 2016) of Bream was estimated using respirometry experiments. Mass-specific RMR to be used in a bioenergetic model was determined as:

$${\mathbf{\text{R}}}_{\mathbf{T}}={\mathbf{\text{R}}}_{\mathbf{a}}{\mathbf{\text{W}}}^{{\mathbf{R}}_{\mathbf{b}}}$$

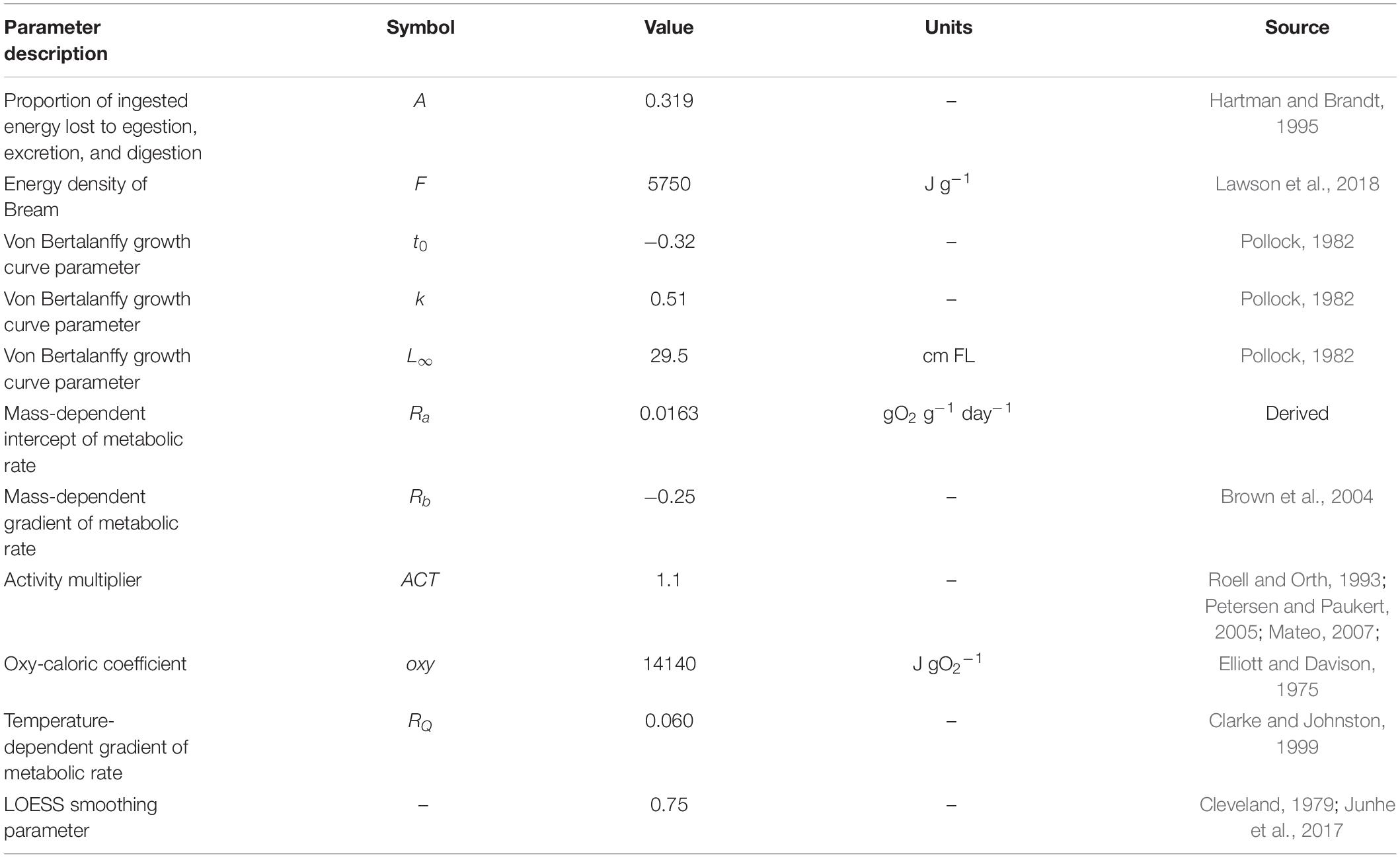
Where R_T is RMR (g O₂ g^–1 h^–1) at temperature T (°C), W is body weight (g), and R_a and R_b are constants (Table 1). R_a (gO₂ g^–1 day^–1) was derived in respirometry experiments (0.0163) and R_b was taken from the literature as a mass-specific universal allometric scaling exponent (−0.25; Brown et al., 2004) because there was limited variation in Bream size in the respirometry experiments, and available evidence suggests -0.25 is approximately a median exponent value for fish (Clarke and Johnston, 1999; Payne et al., 2015).

TABLE 1

Table 1. Summary of parameter mean values used in the bioenergetic model.

Respirometry trials of smaller Bream (n = 12, 0.015–0.08 kg) were performed at a different time and location to large Bream (n = 5, 0.411–0.738 kg). Smaller fish were caught by hook and line in Sydney Harbour, Australia, and transported to the Sydney Institute of Marine Science (33° 50′ 31.6″ S; 151° 14′ 51.18″ E) where they were kept in captivity throughout the respirometry trials (during Autumn 2016). Bream were held in a 1000-L seawater flow-through holding tank that was maintained at 24°C (approximately ambient water temperature at time of capture) using aquarium bar heaters and provided natural light. Fish were fed daily a diet of frozen fish and invertebrates, and held for one week before respirometry trials began. The RMR of fish was measured individually at 24°C in an insulated and darkened 8-L rectangular custom-built respirometry chamber. Individuals were fasted for 24 h prior to the respirometry to prevent any increased oxygen consumption associated with digestion, based on the gastric evacuation rates of other species and temperature used for the trials here (Plaut, 2000; Chang et al., 2005; Das et al., 2018). After a 3-ho acclimation period inside the chamber, the chamber was isolated from atmospheric air, and oxygen content of the water measured (Hach HQ40d, Loveland, CO, United States). Each respirometry trial ran until dissolved oxygen in the chamber reached 80%. All respirometry trials were performed in the morning to minimize diurnal changes in metabolic rate or activity (Clark et al., 2013). A background respirometry trial was performed without any fish, to account for any microbial respiration, which was subtracted from the oxygen consumption measured for each individual fish. Respirometry trials of larger Bream used the same protocol and equipment as the smaller bream, but were undertaken in August 2012 at the Cronulla Fisheries Research Centre (34° 04′ 21″ S, 151° 08′ 56″ E), and on animals that had been captured in the nearby Port Hacking estuary and subsequently held in large (10 m × 5 m × 2 m) flow-through mesocosms for several years prior to experimentation. These Bream were captured by netting and transferred to 1,000-L flow-through tanks one week prior to respirometry trials, in which they were held under the same conditions as the small Bream. They were then fasted for 24 h and individual Bream transferred to a darkened 91-L respirometer. The respirometer was continuously flushed with fresh seawater for the 3-h acclimation period, then sealed while RMR was measured at 24°C for 20–30 min per fish (sufficient time to see large, linear declines in dissolved oxygen concentration). Background respiration trials were run daily as per small Bream experiments.

For all fish, the mass-dependent intercept of RMR (R_a) was estimated using linear regression of log-transformed RMR values with mass-specific slope (R_b) forced at −0.25 (Brown et al., 2004). All statistical models were done using R statistical computing (v3.3.1; R Core Development Team, 2016). Experiments were conducted under approval of the University of New South Wales Animal Care and Ethics Committee (No. 15/152B), and all experiments were performed in accordance with relevant guidelines and regulations of this ethics approval as well as the Guide for the Care and Use of Laboratory Animals (8th edition, National Academies Press).

Consumption Rate

Consumption rate estimates for Bream were estimated using a bioenergetic model, based on the format of Kitchell et al. (1977) and modified as in Lawson et al. (2018):

$${\mathbf{\text{C}}}_{\mathbf{J}}=\frac{{\mathbf{\text{R}}}_{\mathbf{J}}\mathbf{\text{ACT}}+\mathbf{\text{G}}}{\mathbf{1}-\mathbf{\text{A}}}$$

Where C_J is consumption rate (J day^–1), R_J is metabolic rate (J day^–1), ACT is a multiplier of metabolic rate to account for costs of activity, G is energy required for growth (J day^–1), and A is the proportion of ingested energy lost to assimilation costs (Table 1). Assimilation was assumed constant and taken from the literature (Table 1; Hartman and Brandt, 1995). A generalized metabolic rate R_J (J day^–1) was determined, using R_T estimated in the respirometry experiments, by:

$${\mathbf{\text{R}}}_{\mathbf{J}}=\mathbf{24}{\mathbf{\text{R}}}_{\mathbf{T}}\mathbf{\text{W}}{\mathbf{\text{e}}}^{{\mathbf{R}}_{\mathbf{q}}\left(\mathbf{T}-{\mathbf{T}}_{\mathbf{r}}\right)}\mathbf{\text{oxy}}$$

Where R_q is the slope of the temperature-dependent function of RMR (Clarke and Johnston, 1999), T is ambient water temperature (°C; variable, see below), T_r (°C) is the temperature at which respirometry trials were performed to derive R_T, and oxy is the caloric-coefficient of oxygen used to convert metabolic rate from oxygen consumption (g O₂) to energy requirement (J) (Table 1). R_T was multiplied by 24 to determine daily metabolic rate. Energy cost of growth G (J day^–1), at body weight W, was determined by:

$$\mathbf{\text{G}}(\mathbf{W})=\mathbf{\Delta }\mathbf{\text{WF}}$$

Where ΔW is the growth rate (g day^–1) at body weight W (g), and F is the energy density of Bream tissue (J g^–1; Table 1). Growth rate was taken as the slope at W of a published von Bertalanffy growth function for Bream (Pollock, 1982; Table 1) and converted from fork length (FL, cm) as in Steffe et al. (1996):

$$\mathbf{\text{W}}=\mathbf{0.020}{\mathbf{\text{FL}}}^{\mathbf{3.0045}}$$

To convert an energy requirement (in joules) accurately to a food requirement (in grams), information on the ED of prey consumed is required. Based on the diet reported here and associated prey ED values found in the literature (Supplementary Table 1), a linear LOESS regression function (smoothing parameter = 0.75; Cleveland, 1979) was fitted to determine the relationship between prey energy density and Bream length (Lawson et al., 2018). This indicates the mean prey energy density (ED, J g^–1) throughout ontogeny of Bream. Prey energy density was used to convert energy consumed (C_J; J day^–1) to consumption rate of prey C (g day^–1):

$$\mathbf{\text{C}}=\frac{{\mathbf{\text{C}}}_{\mathbf{J}}}{\mathbf{\text{ED}}}$$

Consumption: biomass ratio (Q:B) is a metric often used to compare annual consumption rates of populations (Polovina, 1984). Q:B (g g^–1 year^–1), at body weight W, was calculated:

$$\mathbf{\text{Q}}:\mathbf{\text{B}}(\mathbf{W})=\frac{\mathbf{\text{C}}}{\mathbf{\text{W}}}\mathbf{365}$$

Where 365 is a multiplier to calculate annual Q:B. Bream lifespan (7 years), growth rate and maximum size parameters for the bioenergetic model were taken from Pollock (1982). Q:B was calculated across the life-span of a fish by calculating weight-dependent growth, consumption, and size-dependent prey energy density at each age based on the above relationships. Temperature was also varied according to a seasonal cycle, assuming a birth date of 1 September (start of Spring; Pollock, 1982). Daily temperature was measured at the inlet to the aquarium at the Sydney Institute of Marine Science in Sydney Harbour (33° 50′ 31.6″ S; 151° 14′ 51.18″ E) over 3 years (2013–2016) to generate a sine function (range 15.6–22.1°C) that provided seasonal variation in T. The bioenergetic model using the diet data found in the current study (n = 1,130) will hereafter be referred to as the “primary model scenario.”

Comparing Model Scenarios Using Different Diet Information

To compare consumption and growth rates using different sources of diet data, we produced nine comparative model scenarios based on four published studies on Bream diet (Bell et al., 1984; Morton et al., 1987; Hadwen et al., 2007; Sheaves et al., 2014). Each study provided diet as percent composition of major prey types (Supplementary Table 2), but variability among methods meant we were able to build in multiple comparative model scenarios from two studies. Two scenarios were created using diet data from Hadwen et al. (2007); the first using GCA and the second using stable isotope analysis (SIA). Five scenarios were created from Morton et al. (1987) GCA; Autumn (day and night combined), Spring (day and night combined), day (Spring, Summer, Autumn combined), night (Autumn, Winter, Spring combined), and mean (using all data). One scenario was created from Sheaves et al. (2014) using gut contents analysis, and one scenario was created from Bell et al. (1984) using gut contents analysis. Each comparative model scenario was compared against the primary scenario described above, to test the effect of using different sources of diet data on consumption and growth rate estimates.

A weighted mean ED of prey was calculated for each comparative scenario based on the proportion (by volume) of each prey item and its ED (Supplementary Tables 1, 2). This weighted mean ED was used as a constant prey ED for each comparative scenario to produce estimates of consumption rate. Unlike the primary model dataset, there was insufficient data to produce ontogeny-specific prey ED values in comparative scenarios. The lifetime and daily consumption rate produced by each comparative scenario were then compared with the primary scenario presented here. All parameters except ED were identical in all scenarios. Temperature of Sydney Harbour was used in all scenarios, despite some scenarios using dietary data from different regions, to isolate the effect of dietary composition. ED values for identical prey groups used the same values in the comparative scenarios as the primary scenario, with ED values for new prey items taken from the literature (Supplementary Table 1).

Differences in diet may not always reflect proportional change in consumption, and energy budgets can be dynamic, such that an increase in energy content of the diet may not represent a decrease in consumption rate—instead, consumption may remain the same, but the consumer is able to invest more energy into growth (Kitchell et al., 1977). We explored this in additional scenarios; we examined the effect of diet composition on potential growth rate if consumption rate (in mass) was held constant. Differences in growth rate based on the diet quality of the comparative scenarios were estimated when Bream were 100 g (∼1.4 year), 250 g (∼2.7 year), and 400 g (∼4.5 year; representing fast, moderate, and slow instantaneous growth rates, respectively). Growth was estimated by keeping consumption rate constant, based on the mean percentage of body mass consumed daily of the primary and all comparative scenarios (described above) at each of the three chosen masses. The total ingested energy, and therefore energy allocated for growth, differed between the scenarios depending on the prey composition. Energy allocated for growth (J day^–1) was calculated as:

$$\mathbf{\text{G}}=\left(\mathbf{1}-\mathbf{\text{A}}\right){\mathbf{\text{C}}}_{\mathbf{B}}{}^{*}\mathbf{\text{W}}{}^{*}\mathbf{\text{ED}}_{\mathbf{m}}-{\mathbf{\text{R}}}_{\mathbf{J}}{}^{*}\mathbf{\text{ACT}}$$

Where C_B is percent body mass consumed daily (%) estimated as the mean consumption rate of all scenarios above at each weight (100, 250, and 400 g) and ED_mis the weighted mean prey energy density of each respective scenario (J g^–1). Growth rate (ΔW, g day^–1) was calculated as:

$$\mathbf{\Delta }\mathbf{\text{W}}=\frac{\mathbf{\text{G}}}{\mathbf{\text{F}}}$$

Results

Diet

Gut content analysis of Bream using the primary diet data (n = 1,130; Pease et al., 1981) showed a diverse diet with ontogeny, with prey items from at least 34 orders and 13 phyla (Table 2). Actual prey diversity was likely higher, as some prey items were only identified to phylum or class (e.g., many polychaetes). The most common prey groups were crustaceans (found in 70.1% of guts), polychaetes (50.3%), and bivalves (26.4%; Table 2). Of the crustaceans, amphipods (31.6%) and decapods (18.9%) were the most prevalent (Table 2). Invertebrates made up at least 80% of the diet by volume at all ages (Figure 1).

TABLE 2

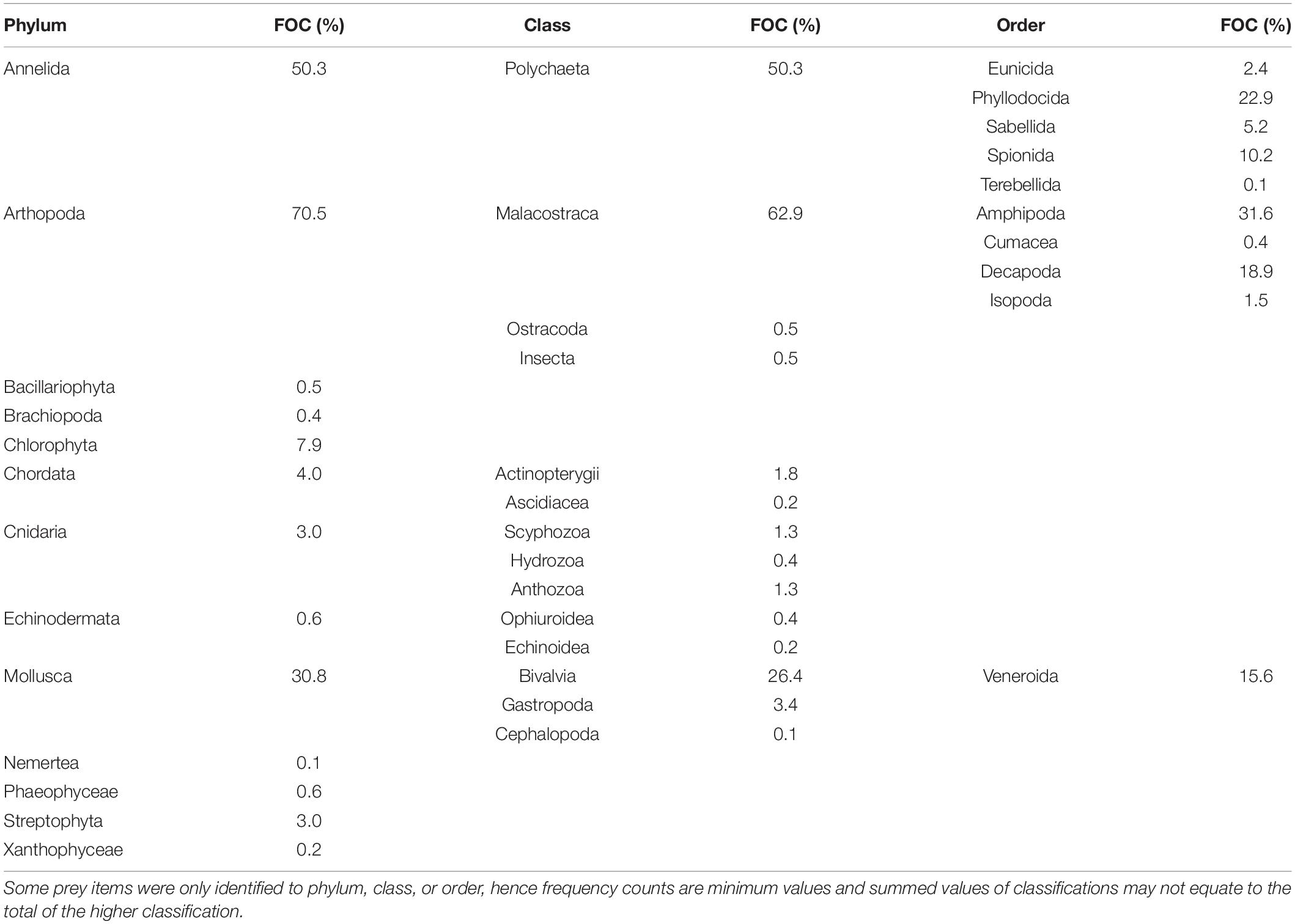
Table 2. Frequency of occurrence (FOC) of prey groups in gut contents of Yellowfin Bream in primary diet data (Pease et al., 1981).

FIGURE 1

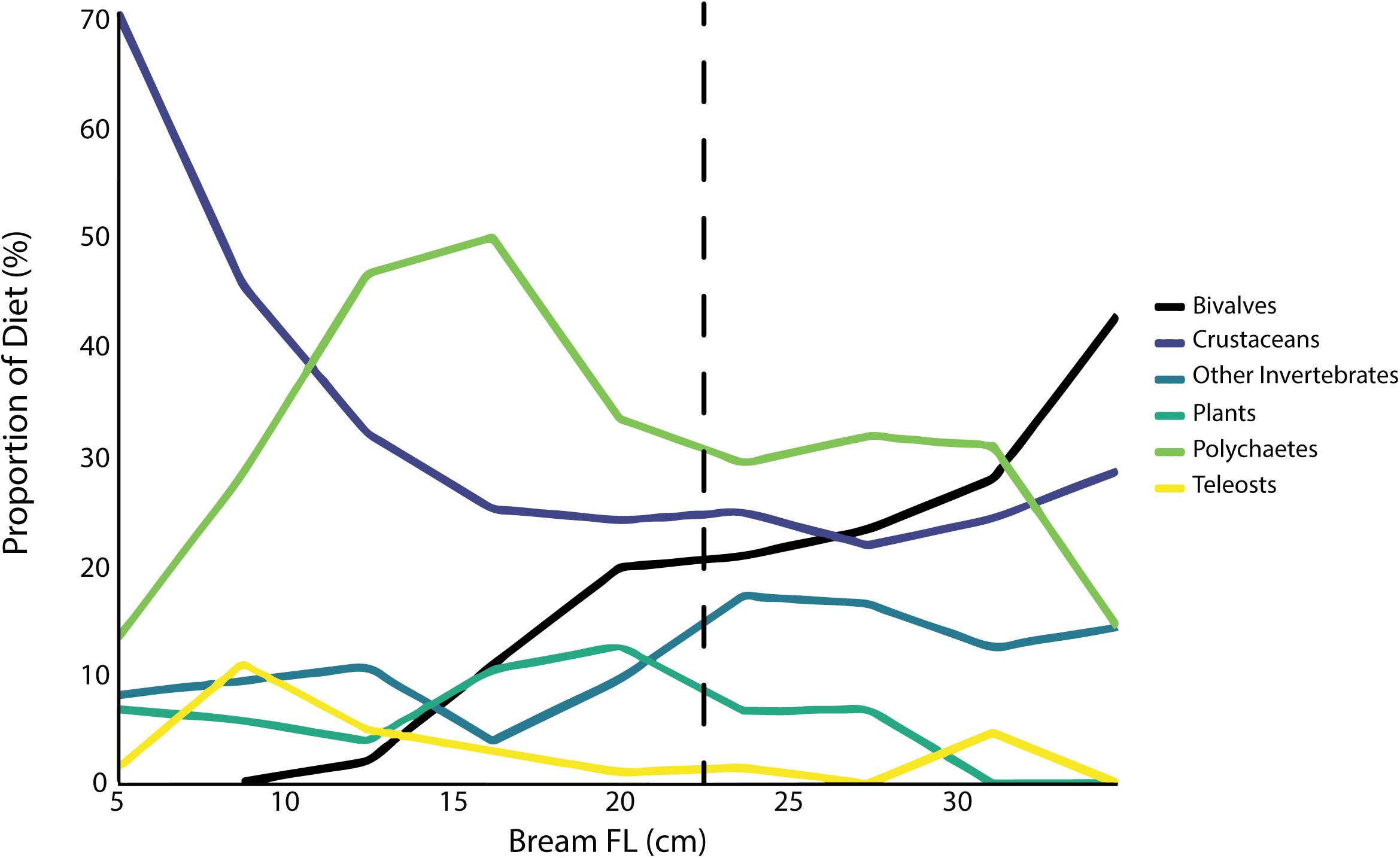
Figure 1. Proportion of diet of major prey types by volume with Yellowfin Bream length. The dashed vertical line at 22 cm indicates length at maturity.

Some ontogenetic diet changes were observed, namely crustaceans (primarily amphipods and copepods) constituting up to 70% of diet by volume for Bream under 5 cm, but then the contribution of crustaceans generally decreased with size, and bivalves increased for Bream >10 cm. However, ontogenetic diet change had only a small influence on mean prey ED (Figure 2).

FIGURE 2

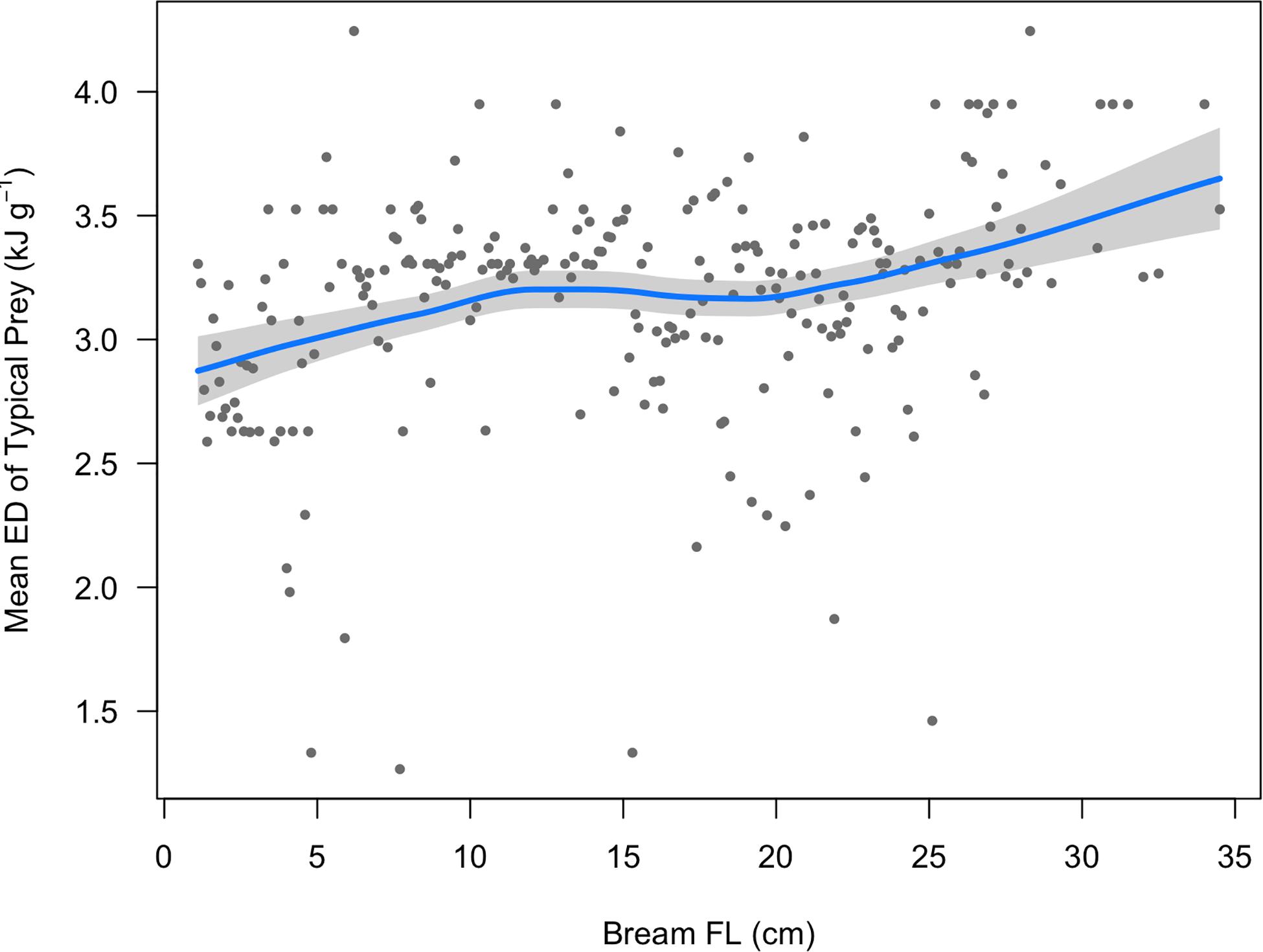
Figure 2. The mean energy density of prey typically consumed by Yellowfin Bream (ED, n = 1,130 bream stomach contents) of sizes sampled in this study, in 1 mm bins. The solid blue line is the fitted LOESS curve (smoothing parameter = 0.75). The shaded area depicts the 95% confidence band.

Respirometry and Energetics

The bioenergetic model showed mass-specific consumption rate was higher in younger individuals. A one-year old individual (14.5 cm FL) consumed 3.90% of its body weight daily, with a Q:B of 14.25, whereas a seven-year old adult (28.8 cm FL) consumed 1.42–2.12% (mean 1.79%) of its body weight daily, with a Q:B of 5.21–7.75 (mean 6.52; Figure 3). Oscillations in predicted consumption rate estimates were caused by seasonal fluctuations in water temperature and its subsequent impact on RMR (Figure 3).

FIGURE 3

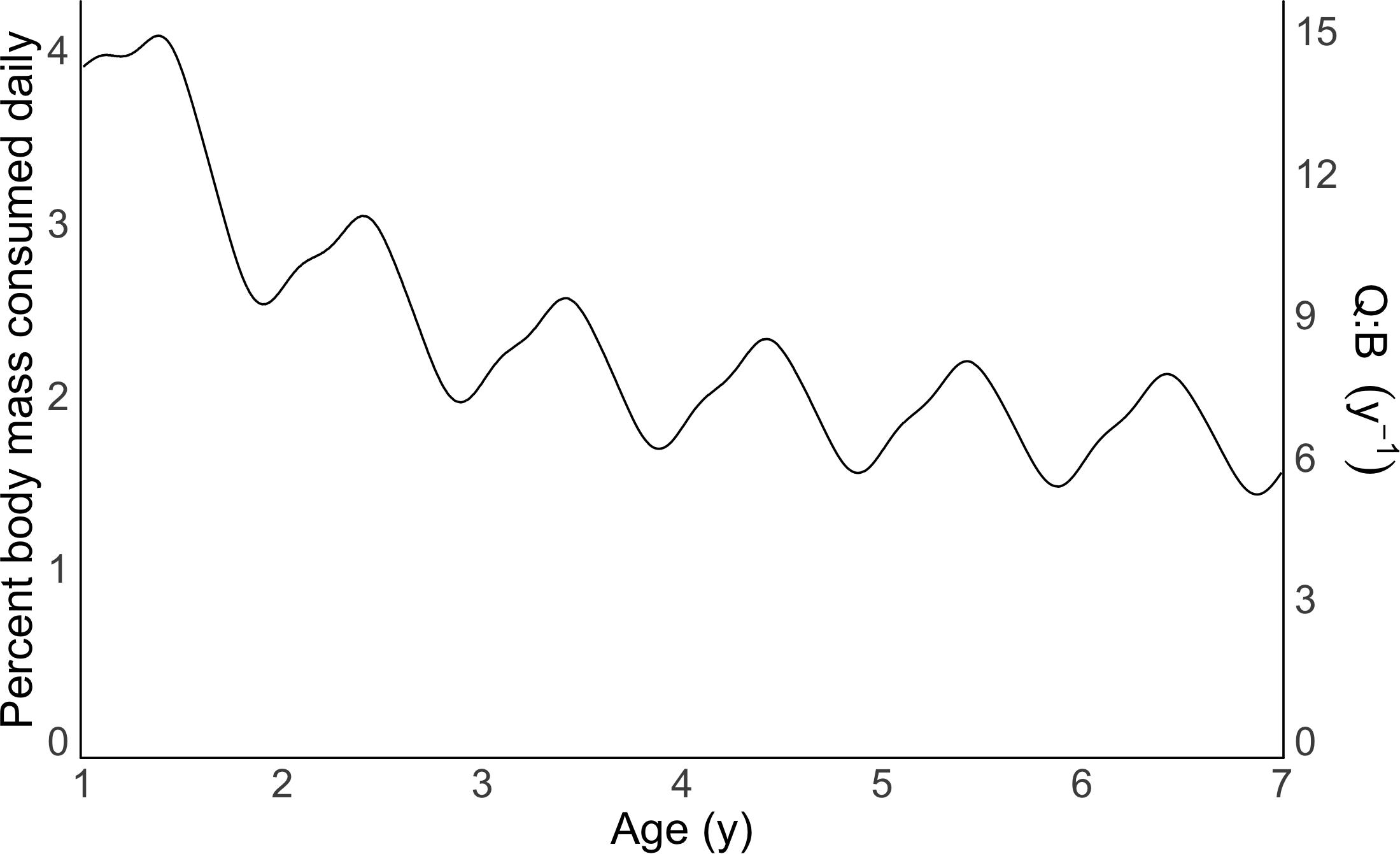
Figure 3. Body mass consumed daily (%) and consumption: biomass ratios (Q: B) of Yellowfin Bream based on the bioenergetic model and prey composition presented here. x-axis truncated to start at year 1 for clarity.

The Importance of Diet Data in Consumption Rate Estimates

The comparative scenarios that used prey compositions derived from the literature estimated lifetime consumption (g) of Bream between 24.9% lower (Morton—Autumn) and 14.7% higher (Hadwen GCA) than the primary model presented here (maximum difference 52.7%, range 11.7–17.8 kg; Table 3). The daily consumption rate (g day^–1) for the scenario with the highest consumption rate (Hadwen GCA) was up to 53% higher than the scenario with the lowest consumption rate (Morton Autumn; 7.7–11.8 g day^–1; Figure 4).

TABLE 3

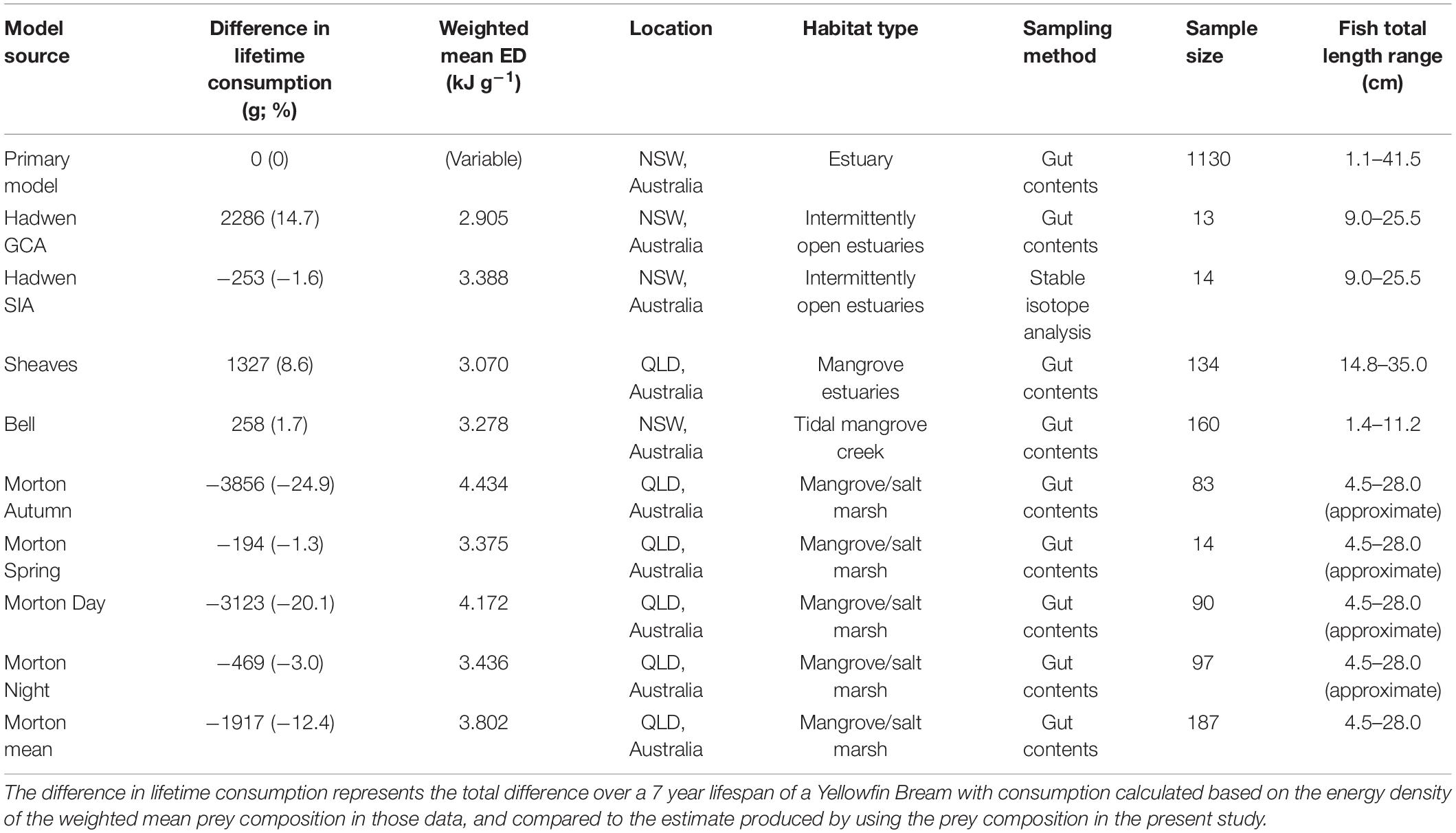
Table 3. Details of the four studies (with nine data sets in total) from which prey composition was extracted and comparative bioenergetic model scenarios constructed.

FIGURE 4

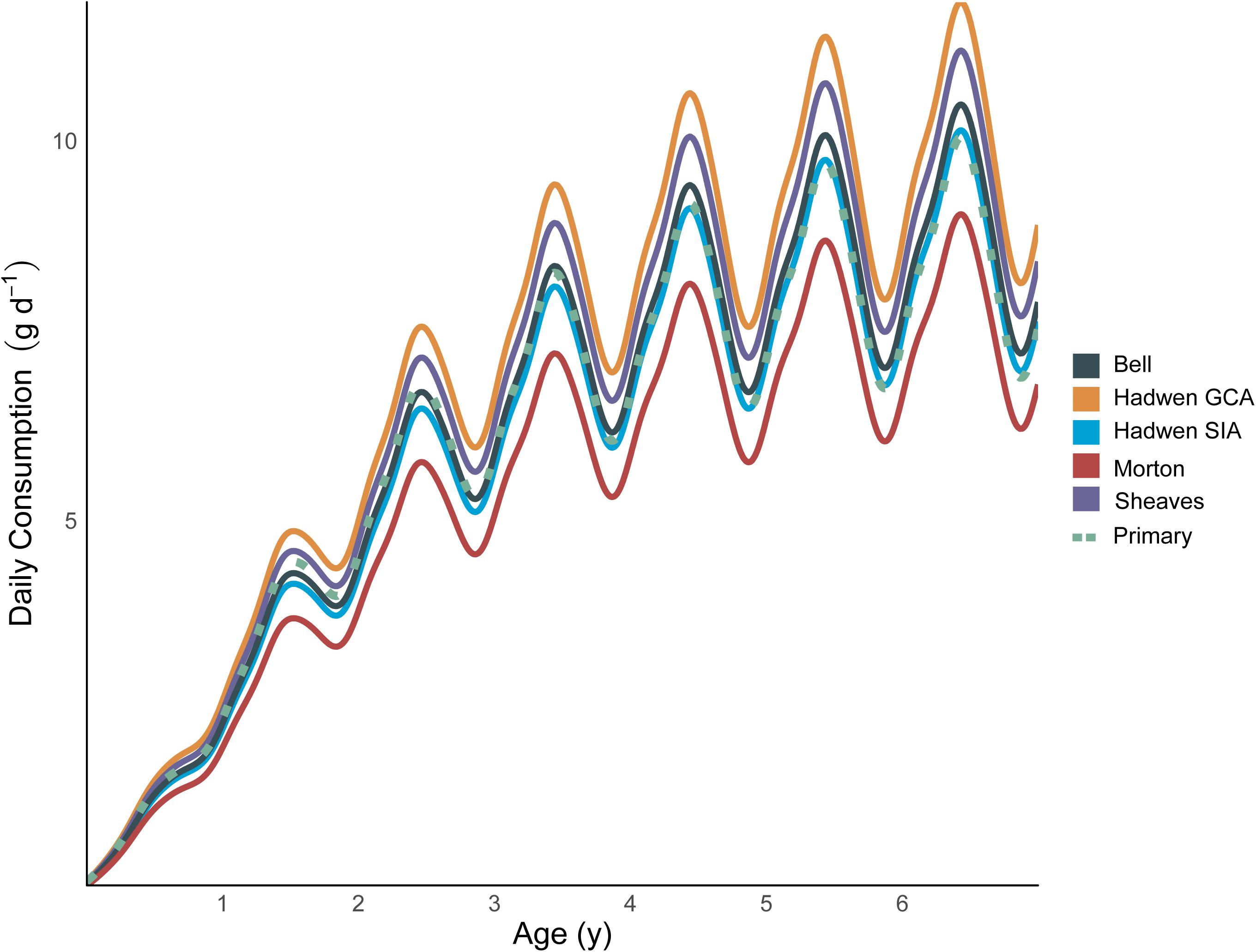
Figure 4. Daily consumption rate throughout Yellowfin Bream ontogeny calculated from bioenergetic models using different prey data. Differences in consumption arise from different energy densities of the prey observed in each study. Oscillations are caused by seasonal fluctuations in water temperature and its subsequent impact on standard metabolic rate. Each model scenario was calculated using the same bioenergetic parameters, but each using different sources of dietary data (and hence prey energy density): “Bell” used the mean of 160 gut contents samples from a tidal mangrove creek, “Hadwen GCA” used the mean of 13 gut contents from intermittently open estuaries, “Hadwen SIA” used the mean of 14 muscle stable isotope samples from intermittently open estuaries, “Morton” used the mean of 187 gut content samples from mangrove/tidal salt marsh habitat, “Sheaves” used the mean of 134 gut content samples from mangrove habitat, and “Primary” included detailed ontogenetic diet variation from 1,130 gut content samples (see main text for details). For clarity, only five of the nine comparative scenarios are plotted here. See Tables 3, 4 for results from all nine comparative scenarios.

Keeping consumption rate (in mass) constant resulted in highly variable growth rates among the model scenarios. There were consistently greater than five-fold ranges in daily growth rates among scenarios; the fastest (Moreton Autumn) and slowest growing scenario (Hadwen GCA) in the 250 g size class had a daily growth range of 0.04–1.07 g day^–1 (Table 4). The slowest growing model scenarios in the 400 g size class showed negative growth rates (Table 4), i.e., energy consumption was inadequate to meet the demands of assimilation, RMR and activity, so these individuals must either divert energy away from these processes, increase their consumption rate, or lose weight.

TABLE 4

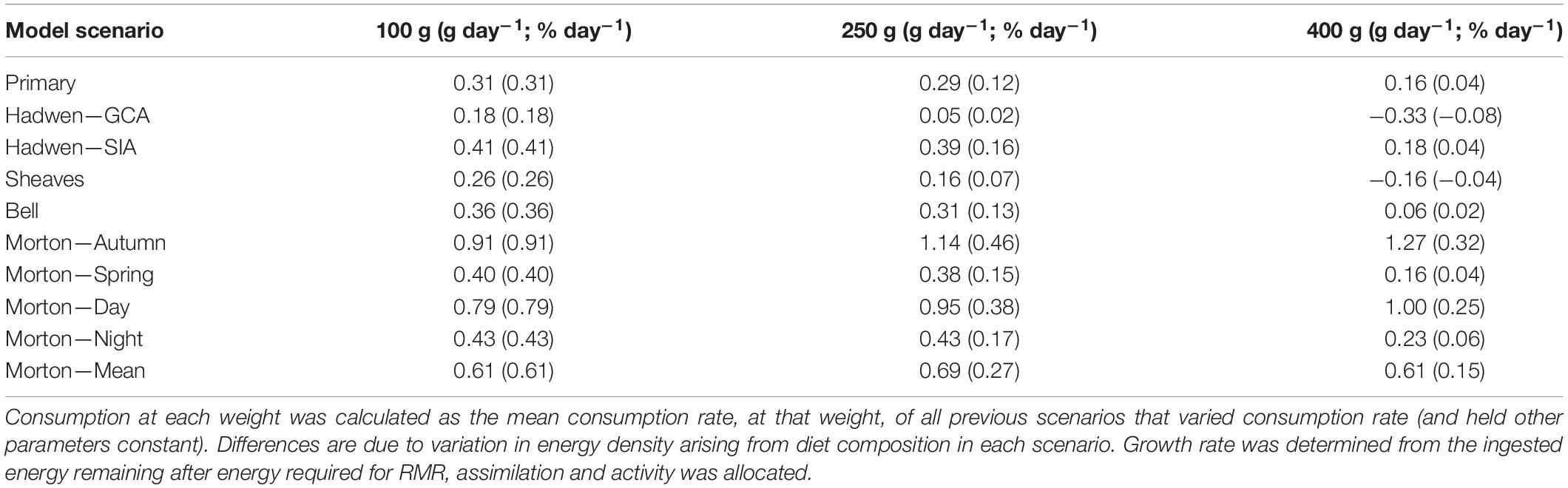
Table 4. Growth rates (g day^–1; % day^–1 in parentheses) for each model scenario when consumption (in mass) is held constant, at different size classes.

Discussion

Consumption is the primary trophic interaction in ecosystems but estimating accurate consumption rates is challenging (Lawson et al., 2019). We used a series of bioenergetic model scenarios to quantify the uncertainty in consumption rate estimates when using diet data from four published studies. We found that diet information used in bioenergetic models can strongly influence consumption rate and growth rate estimates. In reality, neither consumption or growth rate are likely to be constant, and all non-metabolic processes probably trade-off in an energy budget based on the complexities of a consumer’s environment and available prey. Our analysis quantifies, however, that observed spatial-temporal variation in prey composition for a single species, and the subsequent impact on the amount of energy available to be consumed, can result in a 53% difference in life-time consumption, and a several-fold difference in potential daily growth rate, between the least and most energy-rich diet scenarios. Our nine comparative bioenergetic model scenarios highlight that accurate estimates of consumption and growth rates of generalist predators may require detailed ontogenetic dietary information from local samples, large sample sizes, spatial and temporal variation in samples, or a combination of methods such as gut contents and SIA. This study highlights the uncertainty associated with integrating observed diet data in consumption and growth rate estimates.

The Importance of Accurate Diet Data in Consumption and Growth Rate Estimates

We show that there are substantial differences in consumption or growth rate estimates despite using seemingly detailed diet data (i.e., more detailed than simply choosing the one or two most common prey items to represent the entire diet composition; Lawson et al., 2018). The diet data described here includes ontogenetic changes in prey composition and therefore ED, but ontogenetic diet changes were not included in the comparative model scenarios because the previously published diet studies had a limited sample size or had missing/limited data for specific fish sizes. This poor ontogenetic diet resolution accounts for some of the observed differences in consumption and growth rates among model scenarios.

When consumption (in mass) was kept constant, negative growth rates were observed in two comparative scenarios, i.e., the energy consumed was less than that required for RMR, assimilation and activity costs, and so energy was taken from bodily stores. Consistent use of energy stores leads to weight loss and, if representative of actual diet composition, implies three options for individuals. First, this poor-quality diet composition is temporary and represents only a brief period when individuals rely on stored energy. Second, the individuals move to other areas or increase foraging time if prey quality declines. Third, changes in metabolic efficiency reduce the cost of standard metabolic rate to avoid weight loss (Halsey, 2018; Redman et al., 2018). Similarly, a decline in activity may also reduce total energy expenditure when experiencing a poor-quality diet, and thus prevent weight loss, but could reduce foraging intensity. So while loss of body mass is possible under certain conditions, in reality these negative growth scenarios indicate conditions under which individuals would need to either increase consumption or divert less energy to foraging or reproductive activity. This highlights the importance of accurate dietary information when using consumption and growth rate estimates to inform ecosystem models.

When diet information is lacking for a certain region, it can be common practice to instead use dietary information from a different region. Regional dietary information may be absent in terms of both prey composition and nutritional values such as ED. Here, each comparative scenario used different prey compositions that drove the discrepancies in consumption and growth estimates, likely because the original studies that informed the scenarios were conducted in multiple locations and habitats along eastern Australia. Similarly, the lower consumption rates estimated by the comparative Morton scenarios (up to 24.9% over 7 years; Table 3) arise largely from a high ED of terrestrial invertebrate prey (Supplementary Table 1). However, the ED data for terrestrial prey items were collected from different regions from the diet information of Bream, as no local data were available. The resultant high ED values of terrestrial prey used in the models may not necessarily produce erroneous consumption estimates, as terrestrial invertebrates appear to be more energy-dense in general than aquatic invertebrates. Cummins (1967) summarized ED values for 78 invertebrate species and found the mean ED of aquatic invertebrates sampled was 12.27 kJ g^–1 dry weight, compared to 22.61 kJ g^–1 for terrestrial invertebrates. Nevertheless, the actual ED values of terrestrial prey of Bream in eastern Australia, and hence associated error in consumption estimates, remain unknown. Therefore, local diet information is important for estimating consumption rates.

The Effect of Differences in Methods and Reporting of Diet Data

The method used to assess diet may also have implications for the overall diet composition and prey ED. SIA was more effective at estimating typical prey than GCA for small sample sizes, and similar trends are observed with other species (Hadwen scenarios; Table 2; Parkyn et al., 2001; Davis et al., 2012). Unlike gut contents, SIA can provide dietary information from previous weeks or months (Hyslop, 1980; Davis et al., 2012). This also accounts for individuals sampled that have empty stomachs, which can be a large portion of the total sample if species are irregular binge feeders or eject their stomach contents on capture (Hughes et al., 2014; Schilling et al., 2017). Stable isotopes may also be useful for examining diel and seasonal variation in diet that are not easily measured by GCA. For example, large differences were seen in prey composition, and hence ED, between Bream in the same location depending on season and between day and night (Table 2; Morton et al., 1987), and across these timeframes the use of stable isotopes may enable a more realistic representation of the standard diet. Hence it may be important to consider the effect that sampling method has on the resulting diet composition when estimating consumption rates. Like other methods of diet sampling, SIA requires calibration to determine the ED of prey items.

Most studies report ED as energy per dry mass, but estimating consumption requires the ED of prey as wet mass (i.e., in the form that the predator consumes the food). It may be easy to quantify how much dry prey material a consumer requires to meet a certain energy intake, but percent water content is needed to determine the amount of prey that consumer must actually forage. The difference between ED per dry mass and ED per wet mass—determined by percent water—is therefore crucial for use in bioenergetic models, but can vary substantially between prey items. For example, percent water in invertebrates ranges from 41 to 93% which, when converting from ED per dry mass to ED per wet mass, creates an eight-fold range in possible values (James et al., 2012). Most studies do not report the water content of their study species, and so ED per dry mass must be converted to ED per wet mass based on a handful of publications that state percent water content, as was performed here (Supplementary Table 3). For example, in an attempt to form a regression of prey ED vs dry-to-wet mass ratio to eliminate the need for bomb calorimetry, James et al. (2012) found just eight published studies that provided ED and percent water of any invertebrate (regardless of habitat, location, or season); just one study was found from Australia, and provides data only for coleopterans (beetles). It is therefore possible that unknown water content values contribute substantially to errors in the mean ED of prey, and hence consumption and growth rates.

Caveats and Other Sources of Error

There are sources of error in bioenergetic models other than diet quality/source that arise from uncertainty of the input parameters. This is especially true for species that lack basic bioenergetic data such as the scaling of metabolic rate with temperature or body size, which can cause several-fold ranges of energy requirement estimates (Lawson et al., 2019). Similarly to prey energy density, uncertainty in assimilation efficiency can lead to linear deviations in consumption estimates, i.e., a 10% change in assimilation efficiency can cause a 10% change in consumption estimate (Essington, 2003). However, while assimilation efficiency typically ranges from 65 to 95% (Peck et al., 2003; Fu et al., 2005; Fitzgibbon et al., 2007), prey ED may vary >10-fold (Supplementary Table 1; McCluskey et al., 2016).

While the present study focused on prey ED, it should be noted that predator ED also varies. An individual’s ED—and hence their cost of growth—can vary with ontogeny or season (Pothoven et al., 2012; Canale and Breck, 2013). For a given amount of energy allocated to growth, the growth rate (in mass) of an individual is inversely proportional to the individual’s ED (see methods). Here, a 60% linear increase in bream ED (4,000–6,400 kJ) with ontogeny results in a 1.1% reduction in lifetime consumption compared to using the mean bream ED value (Supplementary Material). This difference is likely greater at particular life stages or seasons; a variable bream ED causes up to a 30% increase in growth rate for 100-g individuals compared to a constant bream ED (Supplementary Material). However, at the same age, differences in prey ED among our model scenarios caused a 521% difference in growth rate estimates. Therefore, the effect of variable predator ED appears to be substantially smaller than the effect of variable prey ED.

Similarly, the individuals involved in the respirometry of the present study may have had altered metabolic rates or activity costs that aren’t representative of wild animals. Such differences may be associated with capture stress or a diet requiring minimal search and foraging costs. However, the objective of this study was to isolate and quantify the effect of uncertainty in one parameter—the prey source–while keeping other parameters constant. Importantly, any sources of error in such parameters will affect the early stage of the bioenergetic model, i.e., when its output remains in energy (kJ) and not mass of prey (g). As a result, the errors will be applied to all of the comparative model scenarios here equivalently, and it is unlikely that the results of the study experience substantial change. For example, if RMR of individuals was 10% lower than estimated here, the absolute amount of prey required to meet energetic demands would be altered but the relative differences among the model scenarios would be identical to those presented here.

Conclusion

Accurate estimates of species-specific consumption and growth rates are needed to model ecosystem processes, yet estimates of these rates can vary depending on the diet information used in bioenergetic models. Diet composition may be particularly variable for generalist predators and species that are found in a range of habitats. Many parameters that are lacking in specific locations, for example diet change through ontogeny, prey energy density, and Q:B, are required for ecosystem models which are used to understand trophic dynamics (Christensen et al., 2005; Leaf and Oshima, 2019). Small sample sizes may be useful for understanding general diet patterns, but large sample sizes that include ontogeny provide more realistic data for quantitative analysis and models. The magnitude of variation seen here in both consumption and growth rate show that variation attributed to diet diversity is far too large to ignore in bioenergetic models. Bioenergetics or ecosystem modeling studies can create multiple models or include uncertainty encompassing the range of diet composition a species experiences.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The animal study was reviewed and approved by The University of New South Wales Animal Care and Ethics Committee (No. 15/152B).

Author Contributions

CL, JAS, IS, and SB conceived the study. CL led the writing of the manuscript, with input from all authors. CL, SB, JMS, and NP performed fieldwork and laboratory work. MT provided diet data. CL performed model-building and data analysis, with input from JAS. All authors contributed critically to the article and approved the submitted version.

Funding

This work was funded by the Australian Research Council (Linkage Project LP150100923).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Samples for this project were collected under New South Wales Department of Primary Industries Scientific Collection Permit No. P03/0086(F)-8.1. The experiments were conducted under approval of the University of New South Wales Animal Care and Ethics Committee (No. 15/152B), and all the experiments were performed in accordance with relevant guidelines and regulations of this ethics approval. We thank all volunteers who helped with fish collection.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2021.625855/full#supplementary-material

References

Bell, J., Pollard, D., Burchmore, J., Pease, B., and Middleton, M. (1984). Structure of a fish community in a temperate tidal mangrove creek in Botany Bay, New South Wales. Mar. Freshw. Res. 35, 33–46. doi: 10.1071/mf9840033

CrossRef Full Text | Google Scholar

Brown, J. H., Gillooly, J. F., Allen, A. P., Savage, V. M., and West, G. B. (2004). Toward a metabolic theory of ecology. Ecology 85, 1771–1789. doi: 10.1890/03-9000

CrossRef Full Text | Google Scholar

Canale, R. P., and Breck, J. E. (2013). Comments on proper (and improper) solutions of bioenergetic equations for modeling fish growth. Aquaculture 404, 41–46. doi: 10.1016/j.aquaculture.2013.04.009

CrossRef Full Text | Google Scholar

Chabot, D., Steffensen, J. F., and Farrell, A. (2016). The determination of standard metabolic rate in fishes. J. Fish Biol. 88, 81–121. doi: 10.1111/jfb.12845

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, Y. J., Jeong, M. H., Min, B. H., Neill, W. H., and Fontaine, L. P. (2005). Effects of photoperiod, temperature, and fish size on oxygen consumption in the black porgy Acanthopagrus schlegeli. Fish. Aqua. Sci. 8, 142–150. doi: 10.5657/fas.2005.8.3.142

CrossRef Full Text | Google Scholar

Christensen, V., Walters, C. J., and Pauly, D. (2005). Ecopath with Ecosim: a User’s Guide. Fisheries Centre. Vancouver BC: University of British Columbia, 154.

Google Scholar

Clark, T. D., Sandblom, E., and Jutfelt, F. (2013). Aerobic scope measurements of fishes in an era of climate change: respirometry, relevance and recommendations. J. Exp. Biol. 216, 2771–2782. doi: 10.1242/jeb.084251

PubMed Abstract | CrossRef Full Text | Google Scholar

Clarke, A., and Johnston, N. M. (1999). Scaling of metabolic rate with body mass and temperature in teleost fish. J. Anim. Ecol. 68, 893–905. doi: 10.1046/j.1365-2656.1999.00337.x

CrossRef Full Text | Google Scholar

Cleveland, W. S. (1979). Robust locally weighted regression and smoothing scatterplots. J. Am. Stat. Assoc. 74, 829–836. doi: 10.1080/01621459.1979.10481038

CrossRef Full Text | Google Scholar

Cummins, K. W. (1967). Calorific Equivalents For Studies In Ecological Energetics. Pittsburgh PA: University of Pittsburgh.

Google Scholar

Daily, G. C., and Matson, P. A. (2008). Ecosystem services: from theory to implementation. PNAS 105, 9455–9456.

Google Scholar

Das, S. K., Noor, N. M., Kai, K. S., Juan, Q. Z., Mohd Iskandar, N. S., and De, M. (2018). Effects of temperature on the growth, gastric emptying time, and oxygen consumption rate of mahseer (Tor tambroides) under laboratory conditions. Aquacul. Rep. 12, 20–24. doi: 10.1016/j.aqrep.2018.08.004

CrossRef Full Text | Google Scholar

Davis, A. M., Blanchette, M. L., Pusey, B. J., Jardine, T. D., and Pearson, R. G. (2012). Gut content and stable isotope analyses provide complementary understanding of ontogenetic dietary shifts and trophic relationships among fishes in a tropical river. Freshwat. Biol. 57, 2156–2172. doi: 10.1111/j.1365-2427.2012.02858.x

CrossRef Full Text | Google Scholar

Dawson, G., Suthers, I. M., Brodie, S., and Smith, J. A. (2019). The bioenergetics of a coastal forage fish: Importance of empirical values for ecosystem models. Deep Sea Res. Pt II 175, 104700. doi: 10.1016/j.dsr2.2019.104700

CrossRef Full Text | Google Scholar

Elliott, J., and Davison, W. (1975). Energy equivalents of oxygen consumption in animal energetics. Oecologia 19, 195–201. doi: 10.1007/bf00345305

PubMed Abstract | CrossRef Full Text | Google Scholar

Essington, T. E. (2003). Development and sensitivity analysis of bioenergetics models for skipjack tuna and albacore: a comparison of alternative life histories. Trans. Am. Fish. Soc. 132, 759–770. doi: 10.1577/t02-094

CrossRef Full Text | Google Scholar

Fitzgibbon, Q., Seymour, R., Ellis, D., and Buchanan, J. (2007). The energetic consequence of specific dynamic action in southern bluefin tuna Thunnus maccoyii. J. Exp. Biol. 210, 290–298. doi: 10.1242/jeb.02641

PubMed Abstract | CrossRef Full Text | Google Scholar

Fryxell, J. M., Sinclair, A. R., and Caughley, G. (2014). Wildlife Ecology, Conservation, And Management. West Sussex: John Wiley & Sons.

Google Scholar

Fu, S. J., Xie, X. J., and Cao, Z. D. (2005). Effect of meal size on postprandial metabolic response in southern catfish (Silurus meridionalis). Comp. Biochem. Phys. A 140, 445–451. doi: 10.1016/j.cbpb.2005.02.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Fulton, E. A., Link, J. S., Kaplan, I. C., Savina-Rolland, M., Johnson, P., Ainsworth, C., et al. (2011). Lessons in modelling and management of marine ecosystems: the Atlantis experience. Fish Fish. 12, 171–188. doi: 10.1111/j.1467-2979.2011.00412.x

CrossRef Full Text | Google Scholar

Hadwen, W. L., Russell, G. L., and Arthington, A. H. (2007). Gut content-and stable isotope-derived diets of four commercially and recreationally important fish species in two intermittently open estuaries. Mar. Freshw. Res. 58, 363–375. doi: 10.1071/mf06157

CrossRef Full Text | Google Scholar

Halsey, L. G. (2018). Keeping Slim when food is abundant: what energy mechanisms could be at play? Trends Ecol. Evol. 33, 745–753. doi: 10.1016/j.tree.2018.08.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Hartman, K. J., and Brandt, S. B. (1995). Comparative energetics and the development of bioenergetics models for sympatric estuarine piscivores. Can. J. Fish. Aquat. Sci. 52, 1647–1666. doi: 10.1139/f95-759

PubMed Abstract | CrossRef Full Text | Google Scholar

Hazen, E. L., Abrahms, B., Brodie, B., Carroll, G., Jacox, M. G., Savoca, M. S., et al. (2019). Marine top predators as climate and ecosystem sentinels. Front. Ecol. Environ. 17:565–574. doi: 10.1002/fee.2125

CrossRef Full Text | Google Scholar

Heithaus, M. R., Frid, A., Wirsing, A. J., and Worm, B. (2008). Predicting ecological consequences of marine top predator declines. Trends Ecol. Evol. 23, 202–210. doi: 10.1016/j.tree.2008.01.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Hughes, J. M., Stewart, J., Lyle, J. M., and Suthers, I. M. (2014). Top-down pressure on small pelagic fish by eastern Australian salmon Arripis trutta; estimation of daily ration and annual prey consumption using multiple techniques. J. Exp. Mar. Biol. Ecol. 459, 190–198. doi: 10.1016/j.jembe.2014.05.026

CrossRef Full Text | Google Scholar

Hyslop, E. (1980). Stomach contents analysis—a review of methods and their application. J. Fish Biol. 17, 411–429. doi: 10.1111/j.1095-8649.1980.tb02775.x

CrossRef Full Text | Google Scholar

James, D. A., Csargo, I. J., Von Eschen, A., Thul, M. D., Baker, J. M., Hayer, C. A., et al. (2012). A generalized model for estimating the energy density of invertebrates. Freshw. Sci. 31, 69–77. doi: 10.1899/11-057.1

CrossRef Full Text | Google Scholar

Junhe, L., Yan, Y., Mingfu, Y., Peijian, S., Jiayang, L., and Zihua, Z. (2017). Using the loess method to describe the effect of temperature on development rate. Plant Protect. Sci. 53, 226–231. doi: 10.17221/83/2016-pps

CrossRef Full Text | Google Scholar

Kitchell, J. F., Stewart, D. J., and Weininger, D. (1977). Applications of a bioenergetics model to yellow perch (Perca flavescens) and walleye (Stizostedion vitreum vitreum). J. Fish. Res. Board Can. 34, 1922–1935. doi: 10.1139/f77-258

PubMed Abstract | CrossRef Full Text | Google Scholar

Kleiber, M. (1961). The Fire of Life. An Introduction to Animal Energetics. Malabar FL: R.E. Krieger Publishing Company.

Google Scholar

Lawson, C. L., Halsey, L. G., Hays, G. C., Dudgeon, C. L., Payne, N. L., Bennett, M. B., et al. (2019). Powering ocean giants: the energetics of shark and ray megafauna. Trends Ecol. Evol. 34, 1009–1021. doi: 10.1016/j.tree.2019.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Lawson, C. L., Suthers, I. M., Smith, J. A., Schilling, H. T., Stewart, J., Hughes, J. M., et al. (2018). The influence of ontogenetic diet variation on consumption rate estimates: a marine example. Sci. Rep. 8:10725.

Google Scholar

Lawson, J. W., Magalhães, A. M., and Miller, E. H. (1998). Important prey species of marine vertebrate predators in the northwest Atlantic: proximate composition and energy density. MEPS 164, 13–20. doi: 10.3354/meps164013

CrossRef Full Text | Google Scholar

Leaf, R. T., and Oshima, M. C. (2019). Construction and evaluation of a robust trophic network model for the northern Gulf of Mexico ecosystem. Ecol. Inform. 50, 13–23. doi: 10.1016/j.ecoinf.2018.12.005

CrossRef Full Text | Google Scholar

Lefcheck, J. S., Pfirrmann, B. W., Fodrie, F. J., Grabowski, J. H., Hughes, A. R., and Smyth, A. R. (2021). Consumption rates vary based on the presence and type of oyster structure: a seasonal and latitudinal comparison. J. Exp. Mar. Biol. Ecol. 536, 151501. doi: 10.1016/j.jembe.2020.151501

CrossRef Full Text | Google Scholar

Luecke, C., and Brandt, D. (1993). Estimating the energy density of daphnid prey for use with rainbow trout bioenergetics models. Trans. Am. Fish Soc. 122, 386–389. doi: 10.1577/1548-8659(1993)122<0386:netedo>2.3.co;2

CrossRef Full Text | Google Scholar

Mateo, I. (2007). A bioenergetics based comparison of growth conversion efficiency of Atlantic cod on Georges Bank and in the Gulf of Maine. J. Northwest Atl. Fish. Sci. 38, 23–35. doi: 10.2960/j.v38.m590

PubMed Abstract | CrossRef Full Text | Google Scholar

McCluskey, S. M., Bejder, L., and Loneragan, N. R. (2016). Dolphin prey availability and calorific value in an estuarine and coastal environment. Front. in Mar. Sci. 3:30.

Google Scholar

Morton, R., Pollock, B., and Beumer, J. (1987). The occurrence and diet of fishes in a tidal inlet to a saltmarsh in southern Moreton Bay. Queensland. Aust. J. Ecol. 12, 217–237. doi: 10.1111/j.1442-9993.1987.tb00945.x

CrossRef Full Text | Google Scholar

Parkyn, S. M., Collier, K. J., and Hicks, B. J. (2001). New Zealand stream crayfish: functional omnivores but trophic predators? Freshwat. Biol. 46, 641–652. doi: 10.1046/j.1365-2427.2001.00702.x

CrossRef Full Text | Google Scholar

Pauly, D., Christensen, V., and Sambilay, V. Jr. (1990). “Some features of fish food consumption estimates used by ecosystem modelers,” in Paper Presented at International Council for the Exploration of the Sea (ICES), (Metro Manila).

Google Scholar

Payne, N. L., Snelling, E. P., Fitzpatrick, R., Seymour, J., Courtney, R., Barnett, A., et al. (2015). A new method for resolving uncertainty of energy requirements in large water breathers: the ‘mega-flume’seagoing swim-tunnel respirometer. Methods Ecol. Evol. 6, 668–677. doi: 10.1111/2041-210x.12358

CrossRef Full Text | Google Scholar

Pease, B., Bell, J., Bunchmore, M., Middleton, M., and Pollard, D. (1981). The Ecology of Fish in Botany Bay: Biology of Commercially and Recreationally Valuable Species. In Environmental Control Study of Botany Bay Report BBS23. Sydney: State Pollution Control Commission.

Google Scholar

Peck, M. A., Buckley, L. J., and Bengtson, D. A. (2003). Energy losses due to routine and feeding metabolism in young-of-the-year juvenile Atlantic cod (Gadus morhua). Can. J. Fish. Aquat. Sci. 60, 929–937. doi: 10.1139/f03-079

PubMed Abstract | CrossRef Full Text | Google Scholar

Pereira, H. M., Leadley, P. W., Proença, V., Alkemade, R., Scharlemann, J. P., Fernandez-Manjarrés, J. F., et al. (2010). Scenarios for global biodiversity in the 21st century. Science 330, 1496–1501.

Google Scholar

Pérez-Ruzafa, A., Pérez-Marcos, M., and Marcos, C. (2018). From fish physiology to ecosystems management: Keys for moving through biological levels of organization in detecting environmental changes and anticipate their consequences. Ecol. Indic. 90, 334–345. doi: 10.1016/j.ecolind.2018.03.019

CrossRef Full Text | Google Scholar

Petersen, J. H., and Paukert, C. P. (2005). Development of a bioenergetics model for humpback chub and evaluation of water temperature changes in the grand canyon, Colorado River. Trans. Am. Fish. Soc. 134, 960–974. doi: 10.1577/t04-090.1

CrossRef Full Text | Google Scholar

Pfeiffer, D., and Anderson, P. D. (2021). Estimating sustainable fish production: effect on fish consumption rates used to develop remediation goals at contaminated sediment sites. Integr. Environ. Asses. 17, 584–596. doi: 10.1002/ieam.4372

PubMed Abstract | CrossRef Full Text | Google Scholar

Plaut, I. (2000). Resting metabolic rate, critical swimming speed, and routine activity of the euryhaline cyprinodontid, Aphanius dispar, acclimated to a wide range of salinities. Physiol. Biochem. Zool. 73, 590–596. doi: 10.1086/317746

PubMed Abstract | CrossRef Full Text | Google Scholar

Pollock, B. (1982). Spawning period and growth of yellowfin bream, Acanthopagrus australis (Günther), in Moreton Bay, Australia. J. Fish Biol. 21, 349–355. doi: 10.1111/j.1095-8649.1982.tb02840.x

CrossRef Full Text | Google Scholar

Polovina, J. J. (1984). Model of a coral reef ecosystem. Coral Reefs 3, 1–11. doi: 10.1007/bf00306135

CrossRef Full Text | Google Scholar

Pothoven, S. A., Bunnell, D. B., Madenjian, C. P., Gorman, O. T., and Roseman, E. F. (2012). Energy density of bloaters in the Upper Great Lakes. Trans. Am. Fish. Soc. 141, 772–780. doi: 10.1080/00028487.2012.675911

CrossRef Full Text | Google Scholar

R Core Development Team (2016). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.

Google Scholar

Redman, L. M., Smith, S. R., Burton, J. H., Martin, C. K., Il’yasova, D., and Ravussin, E. (2018). Metabolic slowing and reduced oxidative damage with sustained caloric restriction support the rate of living and oxidative damage theories of aging. Cell Metab. 27, 80 5–815.e4.

Google Scholar

Roell, M. J., and Orth, D. J. (1993). Trophic basis of production of stream-dwelling smallmouth bass, rock bass, and flathead catfish in relation to invertebrate bait harvest. Trans. Am. Fish. Soc. 122, 46–62. doi: 10.1577/1548-8659(1993)122<0046:tbopos>2.3.co;2

CrossRef Full Text | Google Scholar

Schilling, H. T., Hughes, J. M., Smith, J. A., Everett, J. D., Stewart, J., and Suthers, I. M. (2017). Latitudinal and ontogenetic variation in the diet of a pelagic mesopredator (Pomatomus saltatrix), assessed with a classification tree analysis. Mar. Biol. 164:75.

Google Scholar

Sheaves, M., Sheaves, J., Stegemann, K., and Molony, B. (2014). Resource partitioning and habitat-specific dietary plasticity of two estuarine sparid fishes increase food-web complexity. Mar. Freshw. Res. 65, 114–123. doi: 10.1071/mf12348

CrossRef Full Text | Google Scholar

Steffe, A. S., Murphy, J. J., Chapman, D. J., Tarlinton, B. E., and Grinberg, A. (1996). An Assessment of the Impact of Offshore Recreational Fishing in NSW Waters On The Management Of Commercial Fisheries. Fisheries Research Institute, NSW Fisheries. Sydney Olympic Park: NSW Fisheries.

Google Scholar

Surma, S., Pakhomov, E. A., and Pitcher, T. J. (2018). Energy-based ecosystem modelling illuminates the ecological role of Northeast Pacific herring. Mar. Ecol. Prog. Ser. 588, 147–161. doi: 10.3354/mes12430

CrossRef Full Text | Google Scholar