Coupled Epidemio-Hydrodynamic Modeling to Understand the Spread of a Deadly Coral Disease in Florida

For the last six years, the Florida Reef Tract (FRT) has been experiencing an outbreak of the Stony Coral Tissue Loss Disease (SCTLD). First reported off the coast of Miami-Dade County in 2014, the SCTLD has since spread throughout the entire FRT with the exception of the Dry Tortugas. However, the causative agent for this outbreak is currently unknown. Here we show how a high-resolution bio-physical model coupled with a modified patch Susceptible-Infectious-Removed epidemic model can characterize the potential causative agent(s) of the disease and its vector. In the present study, the agent is assumed to be transported within composite material (e.g., coral mucus, dying tissues, and/or resuspended sediments) driven by currents and potentially persisting in the water column for extended periods of time. In this framework, our simulations suggest that the SCTLD is likely to be propagated within neutrally buoyant material driven by mean barotropic currents. Calibration of our model parameters with field data shows that corals are diseased within a mean transmission time of 6.45 days, with a basic reproduction number slightly above 1. Furthermore, the propagation speed of the disease through the FRT is shown to occur for a well-defined range of values of a disease threshold, defined as the fraction of diseased corals that causes an exponential growth of the disease in the reef site. Our results present a new connectivity-based approach to understand the spread of the SCTLD through the FRT. Such a method can provide a valuable complement to field observations and lab experiments to support the management of the epidemic as well as the identification of its causative agent.

Introduction

Coral diseases are a major threat to coral reef ecosystems and have led to significant declines in coral cover especially within the Caribbean region (Richardson et al., 1998; Sutherland et al., 2004; Aronson and Precht, 2001; Harvell et al., 2007; Brandt and McManus, 2009; Miller et al., 2009). Indeed, the Florida Reef Tract (FRT), which was dominated by Acropora palmata and Acropora cervicornis, and often had 30% coral cover until the 1970s/80s (Dustan and Halas, 1987; Porter and Meier, 1992), is now dominated by bare substrate, octocorals, and macroalgae with only approximately 5% stony coral cover remaining (Ruzicka et al., 2013). The loss of the branching Acroporid species was attributed primarily to a disease outbreak, termed white band disease (Aronson and Precht, 2001), but several other threats such as habitat reduction, eutrophication, overfishing, hurricanes, and bleaching likely all contributed to these species decline (Acropora Biological Review Team, 2005). Subsequent losses of coral cover within the region were often linked to additional disease incidences and repeated regional coral bleaching events as a result of global climate change (Kuta and Richardson, 1996; Richardson et al., 1998; Gardner et al., 2003; Sutherland et al., 2004; Aronson and Precht, 2006; Kuffner et al., 2015; Manzello, 2015). A novel coral disease outbreak, termed Stony Coral Tissue Loss Disease (SCTLD), is now threatening the last vestiges of coral throughout the FRT.

Stony Coral Tissue Loss Disease was first documented off the coast of Miami-Dade County in the summer of 2014 by Precht et al. (2016) and has since spread throughout the entire FRT with the exception of the Dry Tortugas. To date, SCTLD has been observed affecting over 20 different stony corals species. A case definition of SCTLD has been compiled to describe the visual appearance and ecology of SCTLD (NOAA, 2018). Briefly, the gross morphology of SCTLD is described as focal or multifocal, with locally extensive to diffuse areas of acute to subacute tissue loss distributed basally, peripherally, or both. In some cases, tissues bordering areas of chronic tissue loss show indistinct bands (1–5 cm) of pallor, progressing to normal pigmentation away from the denuded skeleton. There is also a range in coral susceptibility to SCTLD, with species categorized as highly susceptible (e.g., Dendrogyra cylindrus, Dichocoenia stokesii, Meandrina meandrites), moderately susceptible (e.g., Orbicella spp., Montastraea cavernosa, Siderastrea siderea, Stephanocoenia intersepta), or tolerant (e.g., Porites spp., Acropora spp.). Unfortunately, SCTLD has not remained isolated in the FRT and has now been recorded in Mexico (Alvarez-Filip et al., 2019), the US Virgin Islands (Blondeau et al., 2020) and several other locations around the Caribbean (Kramer et al., 2019). The continued persistence of the outbreak, the high number of species affected, and the large geographical range of reports consistent with the case definition suggests that SCTLD is the largest coral disease outbreak on record.

Large-scale spatial epidemiologic analyses showed that the reefs in Florida with SCTLD are clustered, supporting a contagious mode of transmission (Muller et al., 2020). Similarly, aquaria-based experiments indicate SCTLD can be transmitted through direct contact or indirectly through the water column (Aeby et al., 2019) suggesting water can function as a SCTLD vector, at least within a controlled setting. The initial exponential increase in spread among reefs from the disease epicenter (Precht et al., 2016) and the persistent subsequent linear rate of spread of SCTLD (Muller et al., 2020), north along South Florida reefs and south into the Florida Keys, indicates that water currents may play a role in disease transmission. Furthermore, the rate of spread, estimated at 100 m per day, suggests surface currents are likely too fast to have spread SCTLD within the region. These results imply that either the middle layer or the bottom boundary layer, which are both significantly slower than surface currents, may be the vertical location in which transmission occurs (Muller et al., 2020). However, to date, there have been no attempt to link local hydrodynamic modeling efforts with the spatio-temporal dynamics of SCTLD in Florida.

Estimating the transport of the disease causative agent from reef to reef by currents cannot be performed empirically. However, experimentally calibrated numerical models that simulate currents can provide a realistic picture of the dispersal of disease agents. Nonetheless, accurately modeling water circulation at the spatial scales that affect this dispersal remains a key challenge, as small-scale flow features such as recirculation eddies around reefs and islands strongly impact exchanges between reefs (Wolanski, 1994; Burgess et al., 2007; Figueiredo et al., 2013). In this context, models that can explicitly simulate flow features down to the reef scale are needed. This represents a spatial resolution of the order of 100–1000 m in dense reef systems. As of today, most regional ocean models using traditional numerical methods cannot achieve such resolution because of the computational resources it requires. To our knowledge, the best resolution currently available among these models in the FRT is ∼900 m with the FKEYS-HYCOM model that has been developed for the Florida Keys region (Kourafalou and Kang, 2012; Sponaugle et al., 2012; Vaz et al., 2016). Unstructured-mesh ocean models offer a potential solution to this resolution issue by locally increasing the model resolution close to reefs and islands (Lambrechts et al., 2008; Thomas et al., 2014, 2015), in order to focus the computational resources where they are most needed. High resolution bio-physical dispersal models can be used to build the potential connectivity between reefs and therefore approximate exchanges between colonies in the complex topography of the coral reef systems (Frys et al., 2020).

Marine diseases differ significantly from better studied terrestrial diseases, namely due to the potential for long environmental residence times, during which pathogens may survive and disperse through the water (Harvell et al., 2007; Sokolow et al., 2009). Several recent studies have attempted to adapt traditional epidemic models (Susceptible-Infectious-Recovered, or SIR models) to coral reef systems (Sokolow et al., 2009; Bidegain et al., 2016a, b). Novel approaches have included developing pathogen pools (Bidegain et al., 2016a, b), and to model at the metapopulation scale, rather than at the scale of coral holobionts (Sokolow et al., 2009). Both of these approaches are attempting to address the same issue: disease occurs between patches of entirely sessile animals, through the dispersal of pathogen(s). Thus, there are internal within-patch disease dynamics and metapopulation-scale between-patch dynamics occurring simultaneously. The epidemic model developed in the present study utilizes the same basic architecture of previous coral reef SIR models, but rather than assume pathogen pools (e.g., Bidegain et al., 2016a, b) or ignore internal patch dynamics (e.g., Sokolow et al., 2009), we have modeled both within-patch disease dynamics and the dispersal of pathogenic agents explicitly using potential connectivity networks.

The objective of the present study is to deduce the probable propagation mechanism of the SCTLD throughout the FRT by developing an experimentally calibrated epidemio-hydrodynamic model. With a resolution of about 100 m, this model can capture potential exchanges of disease-carrying material, further denominated as “infectious” in our modeling framework, between reefs that would be ignored by coarser models. By reproducing the observed spread of disease between May 1, 2018 and April 1, 2019, we provide insight on the characteristics of the disease agent and its vector. Ultimately, our model, coupled with lab and field studies, provide novel insight into the management of the epidemic, the identification of its causative agent, and mode of transmission.

Materials and Methods

Modeling Reef Connectivity

In the present study, we focused on the exchanges of infectious material between coral reefs driven by ocean currents, which therefore have to be accurately simulated. An ocean model should provide a realistic large-scale circulation while also resolving small-scale flow features down to the scale of individual reefs. In this context, we used the unstructured-mesh depth-integrated coastal ocean model SLIM¹ to simulate ocean currents over an area that includes the FRT but also the Florida Strait and part of the Gulf of Mexico (Figure 1). By using an unstructured mesh, we increased the model resolution only over the FRT and hence concentrated computational resources where they were most needed. SLIM has already been successfully applied in complex coastal systems such as the Great Barrier Reef (Lambrechts et al., 2008; Thomas et al., 2014) and is well suited to shallow-water flows. Details of the model formulation and validation are provided in Frys et al. (2020).

FIGURE 1

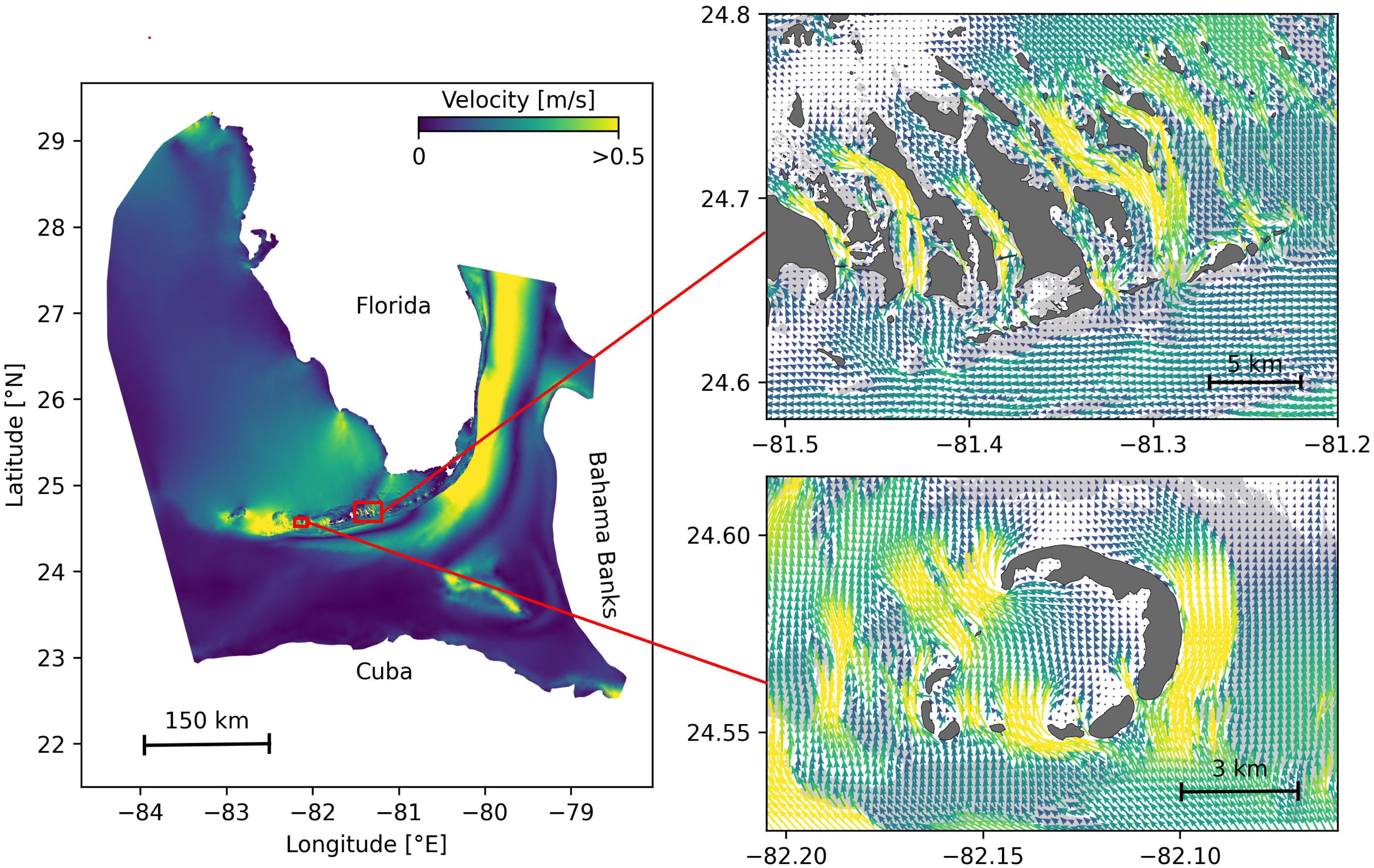
Figure 1. Model computational domain and close-up views of the mesh with snapshots of the currents on May 25, 2018 at 00:00, for the Marquesas Keys (bottom) and the Lower Keys (top). This illustrates the benefits of unstructured meshes to represent the fine-scale details of the topography and hence simulate currents down to the scale of individual reefs (shown in light gray) and islands (shown in darker gray).

The mesh resolution depended only on the distance to the coast, but we distinguished between the coastlines along the FRT where we imposed a maximum resolution of 100 m and the other coastlines along which the finest resolution was 2500 m. The mesh was generated with the open-source mesh generator GMSH (Geuzaine and Remacle, 2009) and is composed of approximately 7 × 10⁵ elements. The coarsest elements, far away from the FRT, had a characteristic length size of about 10 km. Figure 1 depicts how a 100-m spatial resolution mesh simulated fine-scale details of the ocean currents, such as recirculation eddies and currents within the dense reef system in the Lower Keys that consist of many individual reefs with narrow passages in between.

The simulated currents were then used to model dispersal of disease agents throughout the FRT. In this study, three types of potential vectors carrying the disease causative agent were considered: positively buoyant (e.g., mucus and surfactant), neutrally buoyant (e.g., fines, pelagic organisms) and negatively buoyant (e.g., sediments, composites, demersal organisms). As SLIM is a depth-averaged model, the mean currents it generates are well suited to model the dispersal of neutrally buoyant material remaining within the water column. However, these currents must be modified to correctly represent the dynamics of material evolving in the surface and bottom boundary layers. Therefore, surface current response to winds was estimated by adding 1.5% of the wind speed to SLIM currents with a stress-layer veering angle of 45° to the right for positively buoyant particles. Such parameterization is shown to be an accurate approximation of wave-induced Stokes drift and quasi-Eulerian surface currents by Ardhuin et al. (2009). For negatively buoyant material, bottom currents were obtained by taking 60% of SLIM currents velocity with a veering angle of 15° to the left. This is an approximation based on observations of bottom currents and whole water column current profiles in the shallow waters (<15 m) of Hawk Channel in the middle Florida Keys by Smith (2009), as well as observations obtained during the Atlantic Ocean Acidification Testbed project (Gramer, personal communication). This application is also consistent with the theory of current veering in the bottom Ekman layer, albeit that was previously observed in deeper (30–90 m) coastal waters, e.g., by Perlin et al. (2007) and Kundu (1976).

Using these three velocity fields, virtual particles were then released on all the reefs composing the FRT to model the dispersal of material carrying the disease causative agent. The locations of the reefs of Florida were extracted from the “coral reefs and hardbottom” layer of the Unified Florida Reef Tract Map (FWC-FWRI, 2017). The polygons of this reef map were then further divided into 500 m × 500 m squares in order to track the propagation of the disease with a finer geographical resolution, generating a total of 16,823 polygons. At the beginning of each simulated month and for each type of current, a total of about 1.5 × 10⁶ particles were released over all the reef polygons. These particles had a state composed of their polygon of origin as well as their mass, that they lose at a constant rate γ as they were moved by surface, mean or bottom currents. The value of γ was chosen so that particles had a half-life of 30 days. When the particles were brought over a reef polygon by currents, the amount of disease mass that landed on the polygon was recorded in monthly potential connectivity matrices, whose entries are denoted C_ij. The matrix rows correspond to the source reefs and the columns correspond to the destination reefs. Hence C_ij represents the mass of diseased material originating from sub-reef i that had settled on sub-reef j. This matrix was then normalized by dividing each of its rows i by the total mass of particles released on polygon i in order to obtain the normalized potential connectivity matrix $\tilde{C}$, whose entry gives the probability that disease agents produced on sub-reef i settle on sub-reef j. Connectivity matrices were computed for each type of current and for each month of the simulated period.

These connectivity matrices are more easily handled by interpreting them as large graphs whose vertices are sub-reefs and whose edges represent connectivity pathways. They were analyzed using graph theory tools. In the present study, four potential connectivity measures were used to interpret the monthly computed graphs. These indicators are described in Table 1. The first indicator is the weighted connectivity length (WCL), which gave the average dispersal distance from origin to destination for material produced on a given reef. The weighted connectivity of reef polygon i is expressed as:

TABLE 1

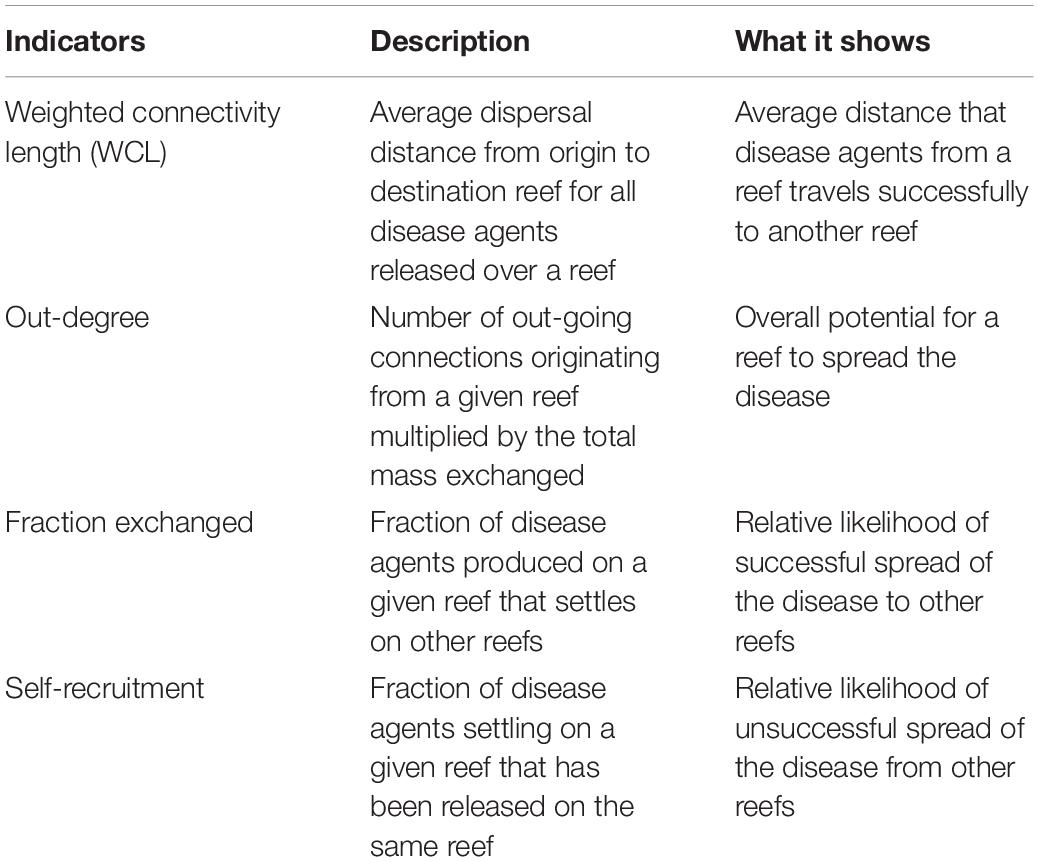
Table 1. Indicators used to analyze the modeled exchanges of infected material for each considered type of currents and for each simulated month.

$WC{L}_i=\frac{{\sum }_j\widetilde{C_{ij}}{L}_{ij}}{{\sum }_j\widetilde{C_{ij}}}(1)$

where L_ij is the distance between origin reef i and destination reef j. Another measure of the spreading potential of reef j is its out-degree, i.e., the product of the number of connections originating from reef j by the quantity of disease agents it sent to the network. This indicator was obtained by computing the number of non-zero entries of row i in the potential connectivity matrix C and multiplying it with ∑_jC_ij The information given by the out-degree was complemented by the fraction of disease agents produced on reef i that successfully settled on a reef, called the fraction exchanged of reef i. This indicator is given by ${\sum }_j{\tilde{C}}_{ij}$ Finally, the isolation of reef i in the network was given by its self-recruitment, i.e., the fraction of disease agents settling on reef i that originated from reef i, computed by $\frac{C_{ii}}{{\sum }_j{C}_{ji}}$ A large self-recruitment value indicates that little infectious material produced elsewhere settled on the reef and thus that it was isolated from the rest of the network. However, due to its relative nature, high self-recruitment could still be coupled with a large amount of exogenous diseased agents reaching the reef, although this quantity would be considered proportionally small in regard to the total mass of diseased material settling on the reef.

Epidemiological Modeling

Model Equations

The spread of the SCTLD throughout the FRT was simulated using a connectivity-based (Kermack and McKendrick, 1927) SIR model. Susceptible-Infectious-Recovered models are among the most standard epidemiological models. They divide individuals into three compartments: susceptible (S), infectious (I) and removed (R). When affected by the disease, susceptible individuals become infectious and infect other susceptible individuals until they are removed from the system, either through recovery or death. Such models usually rely on the hypothesis of an homogeneous, well-mixed population. To account for the spatial heterogeneity of the FRT, the basic SIR formulation was modified by considering the fractions of susceptible (S_j), infectious (I_j), and removed (R_j) corals of each sub-reef j. Although the pathogen of SCTLD has not been identified, studies suggest a contagious mode of transmission (Aeby et al., 2019; Muller et al., 2020). Here, we use “infectious” to denote disease agents that could be passed from individual to individual, which are responsible for causing disease signs. We note that the disease agents could be biological or non-biological in nature. In the present study’s epidemiological model, individual reefs interact through the exchange of disease agents as represented by the different connectivity matrices. For each sub-reef j and at any time, the following relations hold: 0 < S_j, I_j, R_j < 1 and S_j + I_j + R_j = 1. The evolution of these fractions through time is governed by the following equations:

$\begin{array}{c}\frac{d{S}_j}{dt}=-\text{β}{\displaystyle \sum }_i\frac{A_i}{A_j}{I}_i\widetilde{C_{ij}}{S}_j-{\text{β}}^{\prime }(I_j)S_j{I}_j\\ \frac{d{I}_j}{dt}=\text{β}{\displaystyle \sum }_i\frac{A_i}{A_j}{I}_i\widetilde{C_{ij}}{S}_j+{\text{β}}^{\prime }(I_j)S_j{I}_j-\text{σ}{I}_j(2)\\ \frac{d{R}_j}{dt}=\text{σ}{I}_j\end{array}$

where $\widetilde{C_{ij}}$ is the entry corresponding to reef pair (i, j) of the normalized potential connectivity matrix (-), A_i is the area of reef polygon i (km²), σ is the mortality rate (day^–1), and β and β′(I_j) are the inter- and intra-reef disease transmission rates (day^–1), respectively. In this model, diseased corals of sub-reef i can “infect” corals of sub-reef j if there is non-zero probability of disease agents exchange from sub-reef i to sub-reef j, given by $\widetilde{C_{ij}}$ Moreover, to account for coral resistance to the disease, the intra-reef transmission function β′ (I_j) has the shape of a smooth step function of the fraction of infectious corals I_j and is expressed as follows:

${\mathrm{\beta }}^{\prime }(I_j)=\frac{{\mathrm{\beta }}_0^{\prime }}{2}(1+\tanh [(I_j-I_0)/\mathrm{\tau }]),(3)$

where I₀ is a threshold on the infection population above which intra-reef transmission becomes significant, and τ is a measure of the interval over which the transition from low to high transmission occurs. As long as the fraction of infectious corals on sub-reef j is below I₀, the only infection mechanism taking place is connectivity-driven transmission at rate β. Once the threshold is approached, intra-reef transmission with rate ${\mathrm{\beta }}_0^{\prime }$ is activated. A larger value of threshold I₀ corresponds to a greater resistance of corals to the disease, and therefore a slower spread of the disease within reef j. Coral reproduction and natural (i.e., non-SCTLD-related) death rates are not taken into account in this model, which amounts to assume that they balance each other. For this study the same values were used for β and $\mathrm{\beta }{}_0^{\prime }$.

Calibration

Transmission and removal parameters ${\mathrm{\beta }}_0^{\prime }$ and σ were fitted to disease prevalence observations averaged over all colonies from 6 permanent monitoring sites in the Lower Keys to accurately simulate the temporal evolution of S_j, I_j, R_j on each diseased reef polygon. Three focal reef sites were established in the lower Florida Keys, one offshore (Acer 17/18), one mid-channel (Wonderland), and one nearshore reef (N. Birthday). Sites were established in May 2018, when all colonies appeared healthy. Within each site, two 10 m × 10 m quadrats were established. Quadrats were generally set up from east to west although N. Birthday was established with one quadrat further north of the other two to better capture coral cover in the site. All coral colonies >10 cm in size were mapped using self-contained underwater breathing apparatus (SCUBA). Each coral was given an (x,y) coordinate, identified to species, and maximum diameter was noted. After the initial data collection surveys, each site was visited every two to three weeks for rapid assessments to determine whether SCTLD was present. During these site visits, two divers conducted a visual assessment at each of the six quadrats. Disease was first observed in early October 2018. Detailed surveys were conducted every two to four weeks until December 2019. During the surveys, each individual coral was visually assessed for signs of SCTLD, including discoloration and tissue loss. Prevalence of diseased, apparently healthy, and dead were assessed for each time period. To relate our model framework to the compiled data, Eqs. 2 were simplified to a single-reef SIR model:

$$\begin{array}{c}\frac{dS}{dt}=-{\text{β}}_0^{\prime }SI\\ \frac{dS}{dt}=-{\text{β}}_0^{\prime }SI-\sigma I(4)\\ \frac{dR}{dt}=\text{σ}I\end{array}$$

Due to the low values of the entries in the normalized connectivity matrix $\widetilde{C_{ij}}$, intra-reef transmission, when activated, is the dominant infection mechanism of Eq. 2. Consequently, Eq. 4 gave a reasonable approximation of the evolution of the disease on sub-reefs for which I_j≤I₀. Using this approximation, the ratio ${\mathrm{\beta }}_0^{\prime }/\mathrm{\sigma }$ was estimated by matching the modeled fraction of susceptible corals remaining after the disease activity had stopped (S_∞) with observations. A standard property of a SIR model solution is such that

$S_{\mathrm{\infty }}-\frac{\mathrm{\sigma }}{{\mathrm{\beta }}_0^{\prime }}\log (S_{\mathrm{\infty }}/S(t=0))=1(5)$

where the initial fraction of susceptible corals (S(t = 0)) was taken equal to 1 = I_o (see for instance Murray, 2007). In the framework of Eq. 4, the ratio ${\mathrm{\beta }}_0^{\prime }/\mathrm{\sigma }$ gave the value of the basic reproduction number R_o, defined as the average number of secondary cases produced by one infected individual introduced into a population of susceptible individuals (Keeling and Rohani, 2007). This number is used in epidemiological models to determine whether an emerging infectious disease can spread in a population (R₀ > 1) or not (R₀ < 1). The basic reproduction number that was obtained was then used to express σ in terms of ${\mathrm{\beta }}_0^{\prime }$ and calibrate its value to reproduce, as well as possible, the temporal evolution of the colonies-averaged susceptible population shown in Figure 5.

Initialization

In order to solve Eq. 2, initial conditions were needed, i.e., fractions of susceptible, infectious and recovered corals at the beginning of the simulated period. This information was constructed from nine different field-collected datasets: (i) Coral Reef Evaluation and Monitoring Project (CREMP; 2014–2017), (ii) CREMP Presence/Absence Data (CREMP P_A; 2016–2017), (iii) Southeast Florida Coral Reef Evaluation and Monitoring Project (SECREMP; 2014–2017), (iv) Florida Reef Resilience Program Disturbance Response Monitoring (FRRP; 2014–2017), (v) Hurricane Irma Rapid Reef Assessment (IRMA; 2017; Viehman et al., 2018), (vi) the Southeast Florida Action Network citizen science program (SEAFAN; 2014–2017), (vii) the Southefrn Coral Disease Margin field effort (2017 and 2018; Neely, 2018), (viii) Mote Marine Laboratory’s Field operations data (2018–2019), and (ix) data compiled through the citizen science BleachWatch program (2018). Every dataset provided data on the presence or absence of the SCTLD (or tissue loss consistent with the SCTLD case definition) within each survey. Some also provided detailed disease metrics such as the species affected and the disease prevalence, which was subsequently compiled into presence/absence of SCTLD data by surveyed site. The locations of these observations are shown in Figure 2. Using this information, we first delineated the diseased zone by constructing the concave hull of the points where the disease was observed before May 2018. The reefs diseased prior to the beginning of our simulated period were then defined as the reefs located inside the constructed zone. The time of disease observation was then spatially interpolated on each reef of the diseased zone by kriging with a Gaussian semivariogram using Python pyKrige module (Murphy, 2014). Assuming an initial state (S, I, R) = (1−I₀,I₀,0) when the disease was observed, the fractions of susceptible, infectious and removed corals on each reef of the diseased zone on the 1st May 2018 was finally approximated using Eq. 4. Reefs outside of the diseased zone were initialized with an entirely susceptible population.

FIGURE 2

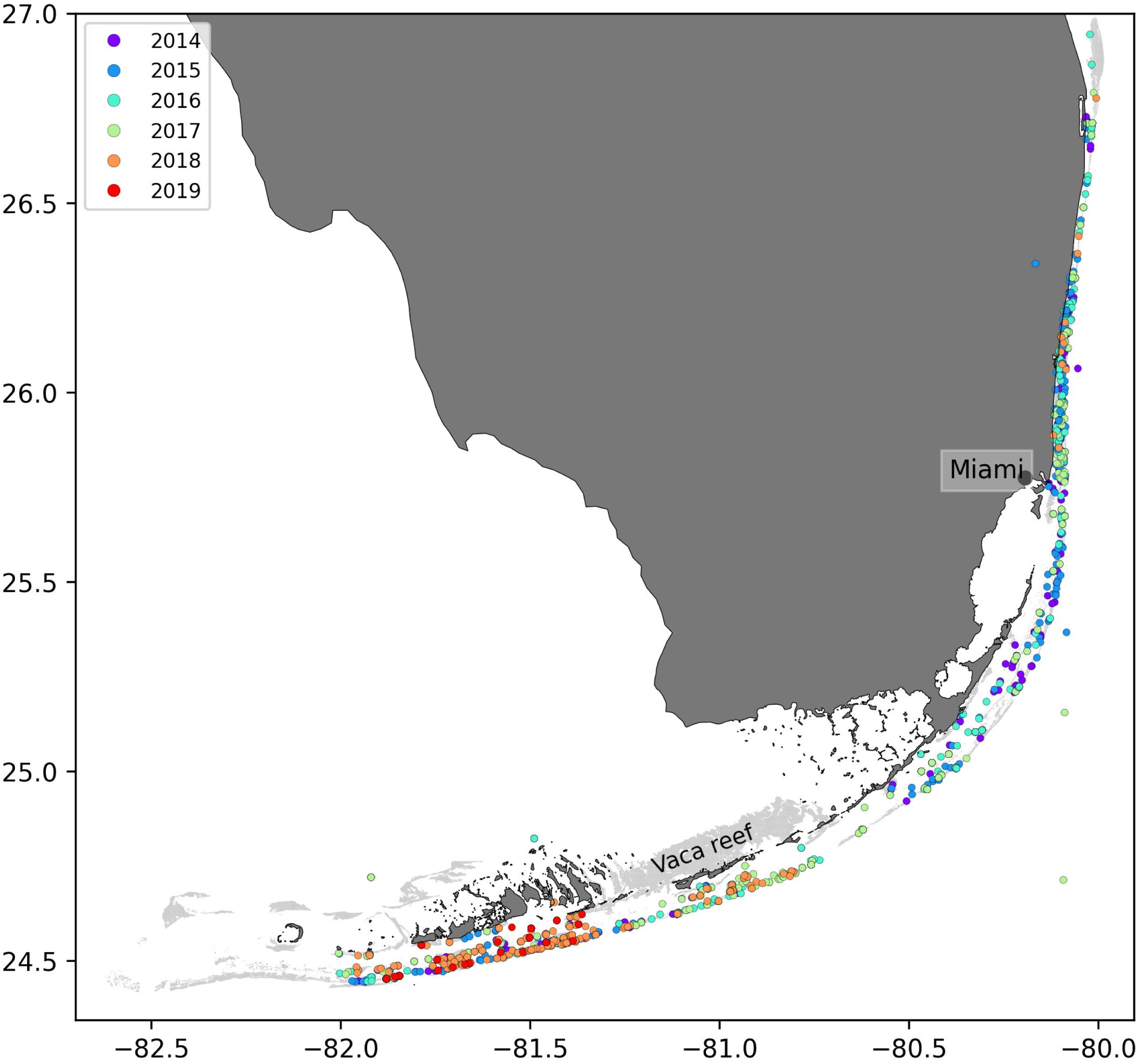
Figure 2. Locations of the disease observations between 2014 and 2019 recorded in the data sets used in this study.

Computation of Front Speed

Muller et al. (2020) estimated the speed of the spreading STCLD epidemics at around 92 m day^–1 in the southern section of the FRT. In order to assess our simulation results in regard to this value, we developed a methodology to compute the displacement of the disease front during a given time interval within our simulated period. First, the concave hull H₀ of the diseased polygons at the beginning of the time interval was delineated. Then the concave hull H₁ of the polygons diseased during the time interval was computed while the concave hull H₂ was defined as the union of H₀ and H₁. This methodology is illustrated in Figure 3. The distance traveled by the disease front was then obtained by computing the maximum distance between all pairs of points of H₀ and H₂. The epidemic’s front speed was finally obtained by dividing the resulting distance by the number of days in the simulated time interval.

FIGURE 3

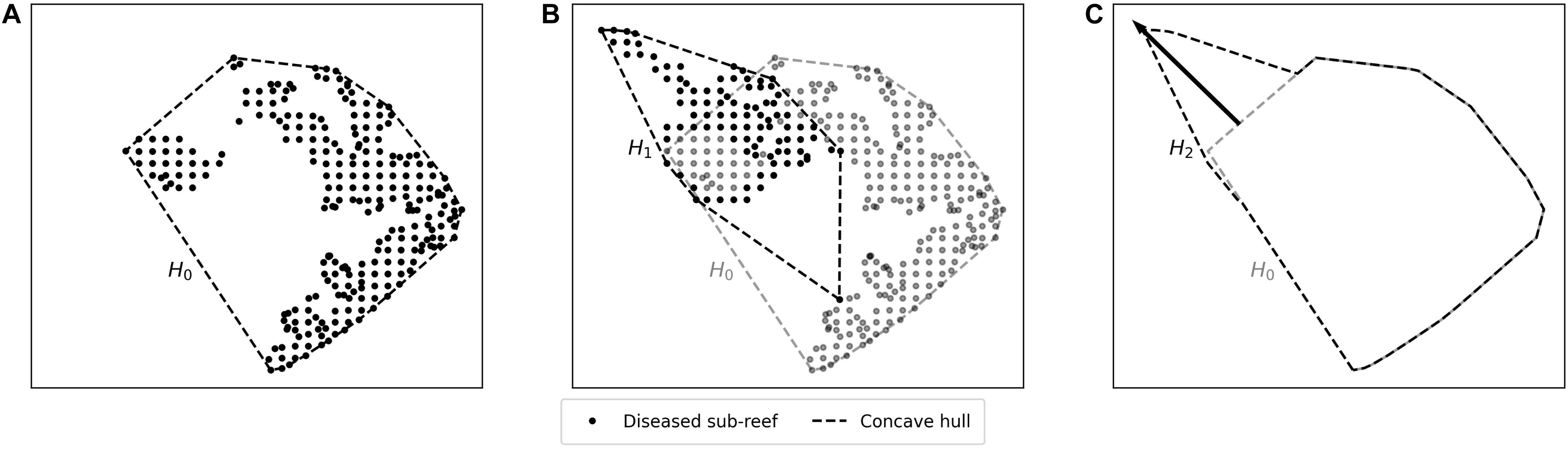
Figure 3. Method used to compute the disease front displacement during a simulated time interval. (A) Concave hull H₀ of the diseased sub-reefs at the beginning of the simulated period. (B) Concave hull H₁ of the sub-reefs diseased during the simulated time interval. (C) Arrow showing the computed front displacement during simulated time interval between H₀ and H₂, the union of H₀ and H₁.

Sensitivity Analysis

Disease agents and their vector were assumed to have a half-life of 30 days in the water column, governed by parameter γ while inter- and intra-reef infection were assumed to occur at the same rate β. Although the sensitivity of our model to these two parameters was not extensively investigated in the present study, some additional simulations were performed to estimate how variations of their value might impact our results. To assess the influence of mass loss rate y, additional connectivity matrices were computed using particles with a half-life of 15 days (γ increased with a factor 2) in our dispersal model. Connectivity indicators were then computed for these matrices and their value was compared with the ones derived from 30-day-half-life connectivity matrices. Moreover, to evaluate whether the “infectiousness” of disease agent might be reduced during its journey from reef to reef, epidemiological model simulations were performed with reduced inter-reef “infection” rate $\mathrm{\beta }=\frac{1}{2}{\mathrm{\beta }}_0^{\prime }$.

Transmission Experiments

In parallel to this modeling study, laboratory-based transmission experiments of SCTLD were conducted by several independent groups for various end points including transmission dynamics and samples for molecular and histological analysis. Requests for transmission data were sent to members of the “Transmission” sub-group of the Florida Disease Advisory Committee’s “Research” working group as well as any other additional researchers that may have been conducting transmission studies on SCTLD. Data that was requested and subsequently provided included the location, dates, and duration of the experiment, the species used as the diseased colony (donor of disease agents) and apparently healthy colony (exposed to disease agents), the number of successful transmissions as well as the “incubation” period following a contact with disease agents prior to disease signs. Additional information included the size of the colonies used in the experiment, the percent tissue loss of the diseased (donor) colony at the beginning of the experiment, and whether the apparently healthy (exposed) fragment was touching the diseased colony or not.

The average probability of successful disease transmission was determined by taking the mean of the number of colonies exposed to the disease in each study divided by the total number of coral colonies exposed to diseased colonies. The “incubation” period was identified as the average number of days after an apparently healthy coral colony was exposed to a diseased colony before visual disease signs occurred (i.e., active tissue loss). Only corals that eventually showed disease signs were integrated within the “incubation” period calculation.

Data were provided from eight different research groups representing 15 institutions and 19 total collaborators providing a total of 109 data points (see Table 2). After amalgamating the contributed data, the mean probability of transmission of SCTLD to an apparently healthy coral had a likelihood of approximately 44.8 ± 3.6%. The probability of transmission ranged from 0 to 100% depending on the experiment. Additionally, the time between exposure of an apparently healthy coral to a diseased coral and subsequently showing initial signs of tissue loss (i.e., “incubation” period) was 9.7 ± 1 days.

TABLE 2

Table 2. Data contributors to the transmission experiments described in section “Transmission Experiments,” to which the calibrated model parameters were compared.

Results

Exchanges of Infected Material

Among the three modes of transport, bottom currents exhibited the lowest propagation range as they generated the networks with the smallest weighted connectivity length (Figure 4). However, disease agents transported by bottom currents had the largest settlement success rate as these currents produced the graphs with the largest fraction exchanged. Therefore, bottom currents tend to transport more disease agents ro closer reefs compared to the two other modes of transport. Mean and surface currents, on the other hand showed similar spreading ranges with mean WCL of 20.63 and 21.39 km, respectively. However, the disease agents that surface currents transported had the lowest probability of settling successfully on reefs. Consequently, surface currents and bottom currents produced networks with similar mean out-degree, although surface currents have the potential to transport disease agents accross larger distances. Nonetheless, networks had larger median out-degree with bottom currents than with surface currents, which suggests that surface currents have a lower spreading potential than bottom currents. As a result of their large WCL and fraction exchanged, barotropic currents on the other hand exhibited the largest mean out-degree, which indicates that they have the strongest dispersal potential.

FIGURE 4

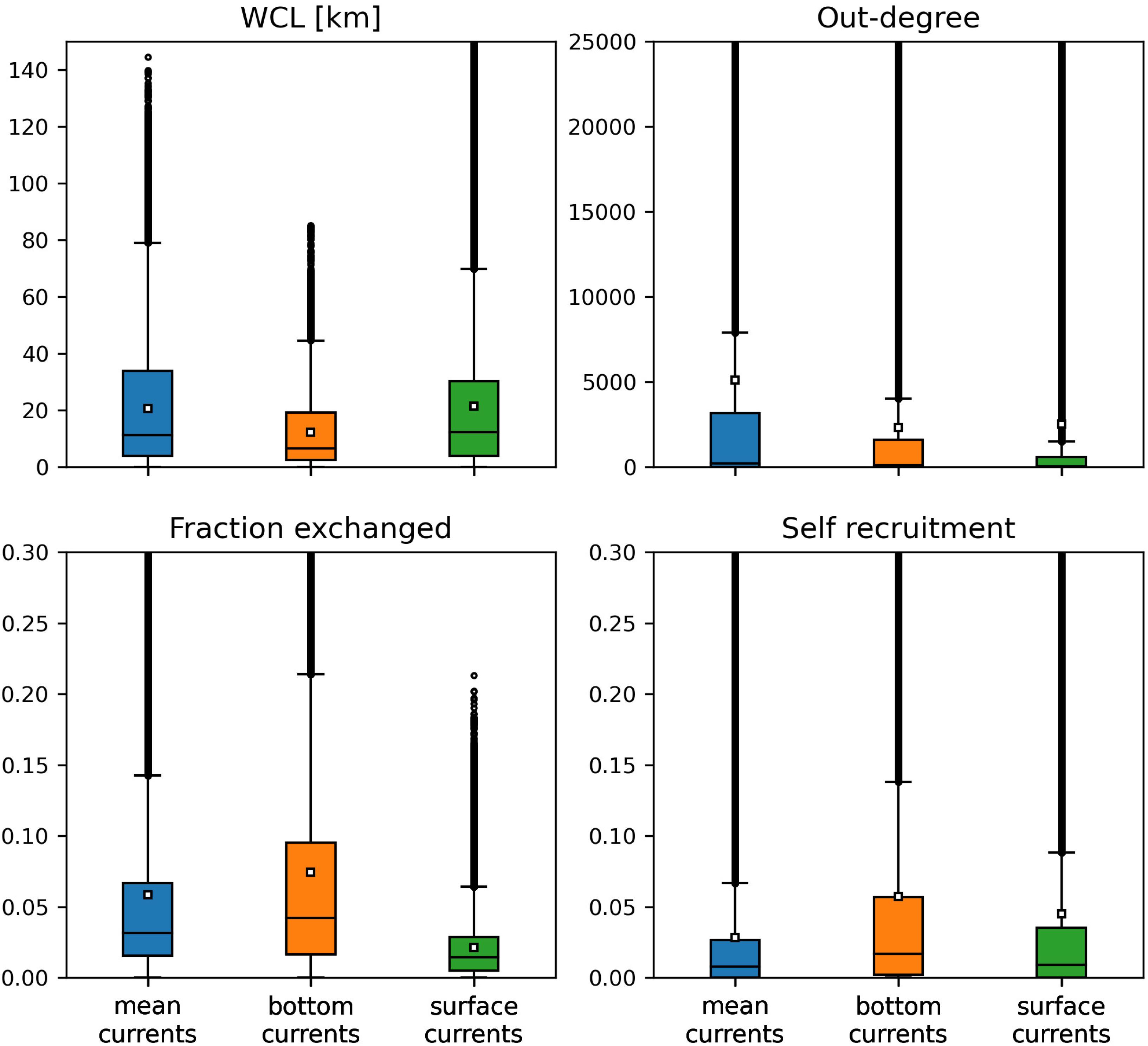
Figure 4. Distribution of the indicators derived from the monthly connectivity matrices computed for each type of current during our simulated period. Mean values are indicated by white squares.

Self-recruitment gives the fraction of disease agents settling on a reef that was produced on the same reef. The greater the self-recruitment value, the more the reef was isolated from the rest of the network. Since diseased material is less likely to settle on isolated reefs, self-recruitment informs on the potential for the disease to reach a given reef, whereas all three other indicators inform on the reef spreading potential. As mentioned before, self-recruitment is a relative measure and it might thus not give a complete picture ofthe amount of diseased material coming from upstream reefs that settles on a given reef. This is particularly true when considering reefs with different areas and coral cover. However, in the present study, we assumed a uniform coral cover and divided all the reefs into square sub-reefs with the same area. It is therefore reasonable to assume that sub-reefs with high self-recruitment act as weak sinks for diseased material. Figure 4 shows that the disease was more likely to settle on the reefs of networks generated by mean currents. This result is consistent with the values of the other connectivity measures, as reefs tended to be more strongly connected with mean currents. On the other hand, reefs were more isolated with bottom currents, as they produced the graphs with lowest WCL and out-degree. Finally, surface currents generated larger self-recruitment values than mean currents as they exhibited the lowest fraction exchanged. Therefore, although bottom currents exhibited stronger spreading potential than surface currents, reefs were more likely to become diseased with surface currents.

Although the SCTLD has not reached the Marquesas yet in 2018, a preliminary analysis of the potential for disease transmission from the Florida Keys to the Dry Tortugas (where no sign of the SCTLD has been observed to date) can be performed based on the connectivity results of the present study (see Appendix A1).

Epidemiological Model Results

As aggregated observations showed a fraction of susceptible individuals of about 85% after a year, a basic reproduction number $R_0={\mathrm{\beta }}_0^{\prime }/\mathrm{\sigma }=1.0345$ was found with Eq. 5. Using this ratio, best fit to averaged disease prevalence observations was obtained with transmission rate ${\mathrm{\beta }}_0^{\prime }=\frac{1}{6.45}$ days^–1 and mortality rate $\mathrm{\sigma }=\frac{1}{6.99}$ days^–1. Comparison of the evolution of the state described by Eqs 4 with observations is shown in Figure 5. Our model results accurately reproduced the observed fraction of susceptible individuals on colonies through time. However, the modeled fraction of removed individuals overestimated observations by about 5%. These discrepancies might be explained by the presence of “Unknown” values in our data sets as well as the simplifying assumptions of SIR models. Since “infection” and removal occur at very close rates, the instantaneous fraction of diseased individuals on the reefs remained low through the outbreak, with a maximum value of about 0.4%.

FIGURE 5

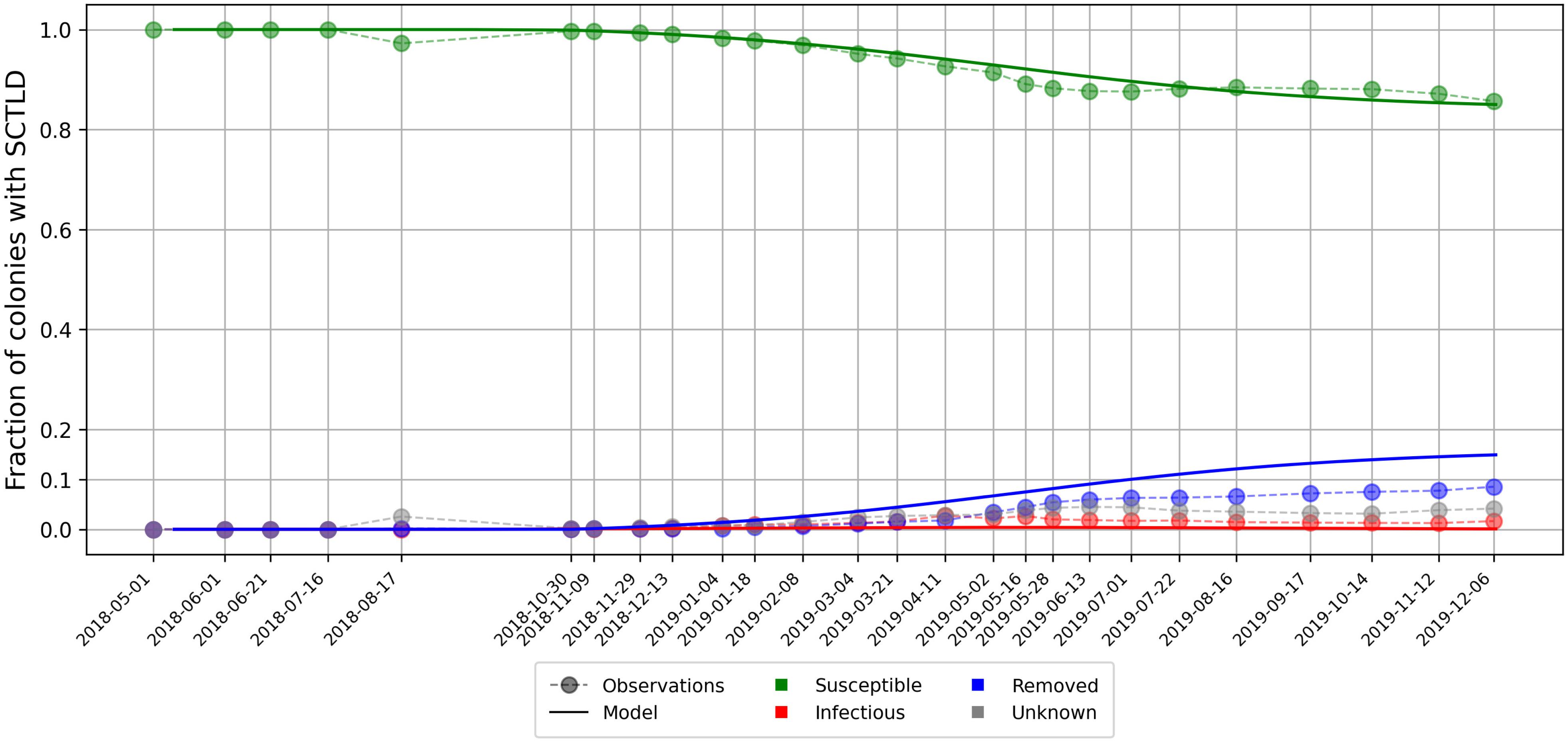
Figure 5. Disease prevalence averaged over all monitored sites over time as modeled by Eq. 4 using calibrated transmission and removal parameters ${\mathrm{\beta }}_0^{\prime }=\frac{1}{6.45}$ days^–1 and $\mathrm{\sigma }=\frac{1}{6.99}$ days^–1.

Once the model was calibrated, epidemio-hydrodynamic model simulations were performed from 1st May 2018 to 1st April 2019 for each type of current and different values of the “infection” threshold I₀. Two metrics were used to assess the accuracy of the model. First, the modeled front speed was compared to the reference rate of 92 m day^–1 derived by Muller et al. (2020). Furthermore, we computed the mean of the distances between each point where SCTLD had been observed during our simulated period (extracted from the 2018–2019 data sets described in section “Initialization”) and the centroid of the closest reef polygon predicted to be diseased by our model during the same period (Figure 6). Bottom currents produced the slowest modeled disease propagation with a maximum front speed of ∼ 20 m day^–1, while simulations performed with surface currents spread the disease at a maximum speed of about 60 m day^–1. However, surface currents tended to propagate the disease to the north, rather than westward, along the Florida Keys. This explains why bottom currents predict disease occurrence closer to field observations despite exhibiting slower front speed. Finally, mean barotropic currents outperform other types of current predictions regarding both criteria with a front speed of 107 m day^–1 and a mean geographical accuracy of ∼1.2 km. This suggests that the disease agents of SCTLD may be transported within neutrally buoyant material driven from reef to reef inside the water column by mean currents.

FIGURE 6

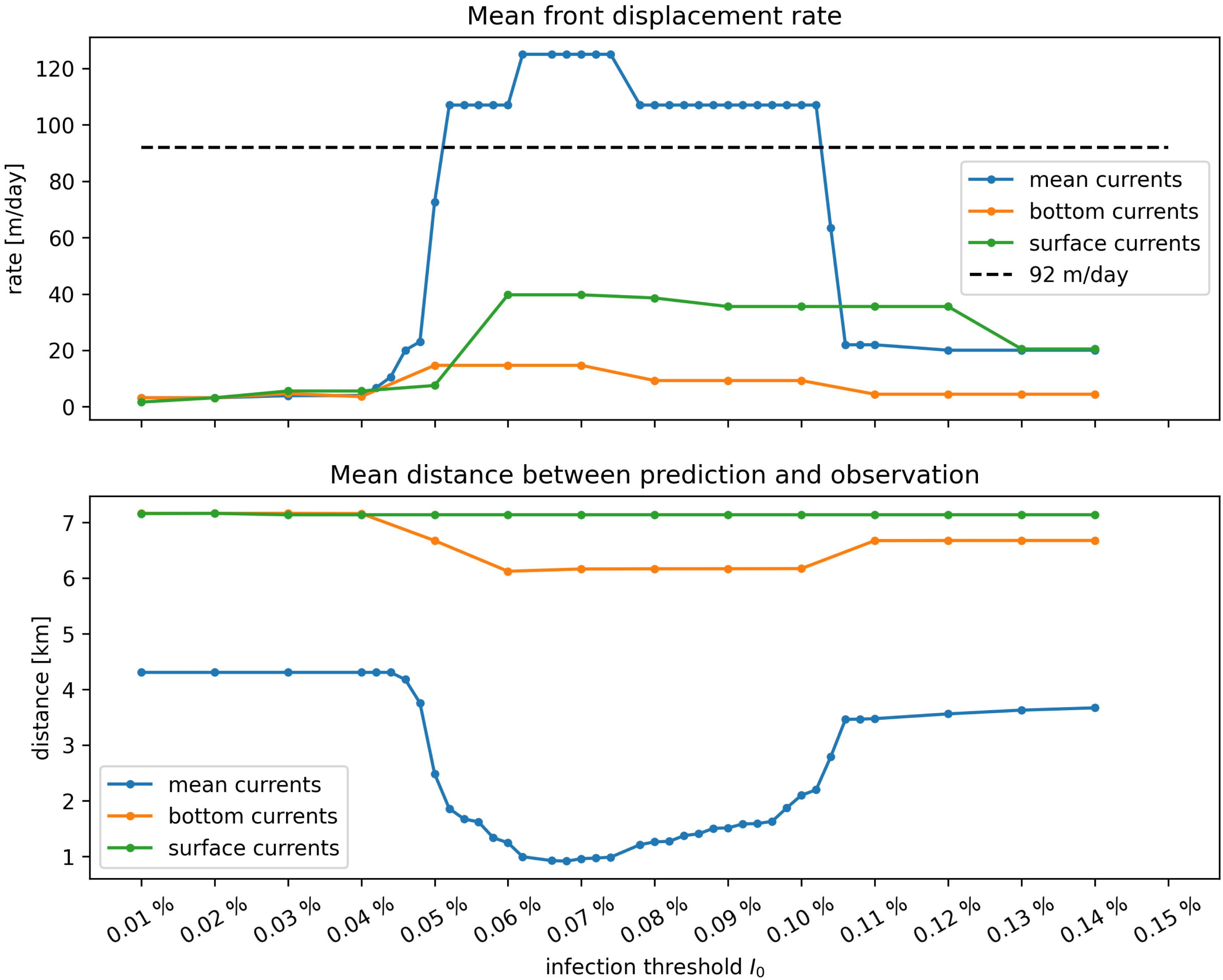
Figure 6. Summary of epidemiological model simulations with calibrated transmission parameters. (Top) Modeled disease front speed for each type of current with respect to intra-reef “infection” threshold I₀. (Bottom) Mean distance between predicted diseased reefs and observed disease points. These results show that mean barotropic currents outperformed other modes of transport at reproducing the observed spread of the disease. The appearance of a plateau suggests that the modeled spread of the disease occurs for a well-defined range of values of I₀.

Moreover, Figure 6 shows a strong dependence of the model results to “infection” threshold I₀, that gives the fraction of diseased individual that colonies can withstand before exponential disease growth is triggered on the reef. Front speeds of both mean and bottom currents reached a plateau for values of the threshold between I₀ = 0.05% and I₀ = 0.1%, while the minimal prediction error was reached around I₀≈0.078% with mean currents. For I₀ > 0.1%, intra-reef “infection” was strongly impeded and populations of “infectious” individuals on diseased reefs were not able to become sufficiently large to infect other colonies on connected reefs. For values of I₀ lower than 0.05% on the other hand, intra-reef “infection” dominated and coral populations on diseased reefs were removed too fast to efficiently spread the disease through the network. Since disease propagation throughout the FRT only occurred for fairly small values of Io in our model, corals are expected to have low resistance to the causative agent of the SCTLD.

The results shown in Figure 6 were obtained by removing the large reef located North to Vaca key, denoted Vaca reef in Frys et al. (2020), from our reef polygons. Preliminary simulations showed that this reef had close to no impact on the modeled spread of the disease to the rest of the FRT, as it sent very few disease agents to southerly and easterly neighboring reefs. Moreover, Vaca reef has a low coral coverage (0–10%), which strongly impedes disease spread on the reef. However, as coral coverage was not taken into account in our epidemiological model, propagation of the disease on the reef was overestimated. This led to unrealistically strong modeled front speed variations due to the large size of the reef. Consequently, and in the absence of SCTLD observations on Vaca reef, this area was removed from our reef polygons in order to avoid overestimating the front speed.

Sensitivity Analysis

Connectivity matrices computed using particles with a half-life of 15 days exhibited shorter range connectivity. However, the impact of increasing mass loss rate γ in our dispersal model remained limited with variations in connectivity indicator values weaker than 10%. However, reducing inter-reef “infection” rate β by a factor 2 had a significant impact on epidemiological model outputs as predicted disease front speed did not exceed 20 m day^–1, far less than the observed speed of the disease front. This strong decrease can be explained by the interplay between inter- and intra-reef disease activity. Reducing inter-reef transmission rates decreases the fraction of diseased corals on reefs attained by disease agents, which in turn reduces the amount of disease agents sent to the rest of the network.

Discussion and Conclusion

We developed an epidemio-hydrodynamic model to simulate the spread of the SCTLD throughout the entire FRT. Calibrating our model with colony-averaged prevalence observations, we estimated the species-averaged reproduction number R₀ to be slightly larger than one. Our model simulations suggest that barotropic currents best reproduce the observed spread of the disease among reefs in the lower Florida Keys. Bottom current did not spread disease agents far enough while surface currents did not allow disease agents to reside within the reefs long enough to ensure disease transmission that matched field observations. The results, therefore, suggest the causative agent of SCTLD is likely to be transported within neutrally buoyant particles in the water column. With this mode of transport, the propagation of the disease from reef to reef only occurred for a well-defined range of values of the “infection” threshold I₀. This threshold is defined as the fraction of all sub-reef colonies that were diseased which triggered a rapid spread of the disease over the entire sub-reef area. Our results suggest that this occurred once 0.05–0.1% of the colonies were diseased. These results suggest that, on average, corals appear to have a low resistance to SCTLD.

After calibration, we estimated the species-averaged basic reproduction number ${\mathrm{\beta }}_0^{\prime }/\mathrm{\sigma }$ to be equal to 1.0835. This value, being close to 1, suggests modeled diseased individuals were removed from the system almost as fast as susceptible individuals became diseased. This situation caused the fraction of infectious corals on the reefs to remain fairly low (i.e., ≤0.4%) through time. These results suggest that only a small fraction of the colonies caused the disease to spread on the reef during the outbreak. The observation-based species-averaged transmission period of 6.45 days used in the model was a reasonable estimation of the disease transmission dynamics, being of the same order of magnitude as the experimentally derived mean incubation period of 9.7 days. The difference between the two values can be explained by field measurement uncertainties as well as the inability to perfectly mimic field conditions in laboratory. In the present study, the same values were used for inter- and intra-reef “infection” rates β and ${\beta }_0^{\prime }$, i.e., disease agents “infectiousness” was assumed to remain unchanged during their journey from reef to reef. This assumption is consistent with sensitivity analysis results, which showed that reducing the value of β strongly impeded disease propagation through the network. This outcome suggests that, to reproduce the observed spread, inter- and intra-reef transmission rates must have similar magnitude, i.e., that the causative agent is not degraded while traveling from reef to reef. Given that the etiology of SCTLD is still unknown, the lack of degradation of the SCTLD causative agent over distances of tens of kilometers between reefs may help to narrow the search.

The fact that mean barotropic currents outperformed the other modes of transport can be explained by considering the trajectories of the particles used to model the transport of the disease causative agent. Due to the impact of winds on positively buoyant material, particles driven by surface currents are likely to be blown away from the reefs. Moreover, even when winds are pushing particles along the reef line, these particles spend less time over the same region than particles driven by mean and bottom currents. Smaller amounts of particle mass will therefore settle on reef polygons, leading to lower connection strengths in the potential connectivity matrix, i.e., lower exchange of infectious material between reefs. Hence, despite being able to transport the disease over greater distances, surface currents are less efficient to drive the propagation of the disease. Particles driven by bottom currents, on the other hand, remain over the same region longer, producing larger entries of the potential connectivity matrix. Due to these large exchange probabilities between reefs, bottom currents are better at propagating the disease (Figure 6). Nevertheless, because bottom currents are slower, exchanges of disease agents occur within a more limited geographical range. Mean barotropic currents that carry particles greater distances while allowing for sufficiently large amounts of diseased material to settle on reef polygons, were thus best suited to propagate the disease at a speed similar to field-collected data (Figure 6).

Since mean currents were the only mode of transport that successfully reproduced the observed propagation speed of the disease in our model, the disease causative agent is expected to be transported within neutrally buoyant material inside the water column. Current-driven propagation seems reasonable as water-borne transmission is an important spreading mechanism for multiple coral diseases, including white band disease, white plague disease, white pox disease, white syndrome disease, Porites ulcerative white spots diseases, and skeletal eroding band disease (Shore and Caldwell, 2019). These results suggest that coral mucus or sloughed off diseased coral tissue may directly transmit SCTLD if they remain suspended within mean currents. Aeby et al. (2019) showed that corals held within aquaria can transmit SCTLD to healthy colonies suggesting that these mechanisms may be occurring within reefs. Additionally, vectors such as zooplankton, phytoplankton, or even marine snow, may be transporting disease agents from reef to reef within the water column. Landsberg et al. (2018) used histology to show an association between the location of the in hospite symbiotic algae that reside within the coral gastrovascular cavity and the area of tissue necrosis occurring within SCTLD-affected corals. These results have led to the working hypothesis that SCTLD could be associated with the symbiotic algae or the process of heterotrophic feeding and ingestion. The causative agent could also be transported within fine sediments such as silt, as suggested by Rosales et al. (2020). Such sediments are easily eroded in shallow areas around coral reefs and would therefore be mostly transported inside the water column by mean barotropic currents. This hypothesis might be tested by adapting the deposition rate γ used in our experiments to be consistent with the sedimentation rate of silt. However, such modification of γ would alter the entries of our potential connectivity matrices. Nonetheless, sensitivity analysis of connectivity indicators suggest that such modifications would have a minor impact on model behavior and that the main results of this study would remain valid for larger deposition rates.

Coral resistance to SCTLD was represented by parameter I₀, defined as the maximum fraction of the colony that can become diseased without causing the disease to spread to the rest of the sub-reef site. The plateau shown in Figure 6 highlights the impact of this parameter on the modeled propagation of the disease. On the one hand, when corals were strongly susceptible to the disease, diseased individuals were removed from the system too fast to become sustainable sources of disease agents in the network. On the other hand, if corals were weakly susceptible to the disease, very few corals became diseased and the disease barely propagated. Our simulations suggest that this value of resistance must be fairly low (around 0.07%) in order to successfully spread the disease throughout the FRT. This seems to imply that susceptible coral species have very weak defense mechanisms against the causative agent of the disease.

As with any modeling study, it is important to understand the assumptions on which the model is based. Here, we have used a 2D barotropic ocean model forced by the 3D model HYCOM (Chassignet et al., 2007) in order to indirectly represent baroclinic phenomena. Such a model is well-suited to simulate the fate of neutrally buoyant material in shallow regions. However, as depth-averaged currents do not accurately approximate the motion of particles in the bottom and surface layers, they have been modified to simulate the exchanges of negatively and positively buoyant material. In order to derive bottom and surface currents from mean barotropic currents, we used parameterizations consistent with both observations and theory (Kundu, 1976; Perlin et al., 2007; Ardhuin et al., 2009; Smith, 2009). Although such parametric estimation of surface and bottom currents adds additional uncertainty to those simulations, using a 2D model as the basis for the study allowed for reef-scale resolution throughout the whole FRT with available computational resources. Such high-resolution allowed the simulation to explicitly represent recirculation eddies around islands and reefs, that significantly impact the weighted connectivity length as well as the local retention of pathogenic material on the reefs (Frys et al., 2020).

The appearance of an interval of optimal values of threshold I₀ for the propagation of the disease in our results highlights the impact of coral resistance on the spread of SCTLD through the FRT. Therefore, a next step in our modeling approach would be further dividing coral populations of our polygons into highly susceptible (e.g., D. stokesii, M. meandrites), intermediately susceptible (e.g., Orbicella faveolata, Montastrea cavernosa), and weakly susceptible (e.g., A. Palmata, A. cervicornis) sub-populations. The fractions of susceptible, infectious and removed individuals within these sub-populations would then be modeled with specific transmission (β,${\mathrm{\beta }}_0^{\prime }$) and removal (σ) rates as well as specific infection thresholds I₀. Such approach would however require a detailed knowledge of the fine-scale distribution of the different coral species throughout the FRT. This knowledge about coral coverage could also be used to avoid overestimation of the front propagation, as in the case of Vaca reef.

Despite the limitations of its current formulation, our model brings unprecedented perspectives on the propagation mechanism of SCTLD throughout the FRT. Using a reef-scale spatial resolution, we determined the most probable mode of transport for the vector of the disease agent and deduced its host-species-averaged reproduction number based on prevalence observations. In addition, our model formulation provides a framework to quantify coral resistance to the disease. This framework is a novel contribution to the study and modeling of marine diseases, as both inter- and intra-patch disease dynamics are modeled explicitly and realistically in time and space. As our model results are continuous through time, they can exhibit the variability of the propagation of SCTLD temporally and therefore bring additional insight into observation data. This study provides much-needed complementary insight into the identification of the causative agent of the SCTLD and the management of the crisis it generates. Furthermore, our modeling approach could be applied to other affected areas of the Caribbean, where there is still time to perform active management as the disease spreads throughout the region.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries should be directed to EM, emmanuel.hanert@uclouvain.be.

Author Contributions

TD developed the model, ran the simulations, and analyzed the results. EM, LG, and EH conceptualized the study and designed the modeling experiments. EM collected the biological data. DH designed the epidemiological model. All authors contributed to the writing of the manuscript.

Funding

This paper is a result of research funded by the Florida Department of Environmental Protection under award PO: B6A24 to Mote Marine Laboratory.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Computational resources were provided by the Consortium des Équipements de Calcul Intensif (CÉCI), funded by the F.R.S.-FNRS under Grant No. 2.5020.11. TD is a Ph.D. student supported by the Fund for Research Training in Industry and Agriculture (FRIA/FNRS). Field data was collected at the permanent SWG sites were collected by Sara Williams, Cory Walter, Joe Kuehl, Ray Bannister, and Érich Bartels. These sites were funded from “Florida’s State Wildlife Grant, FWC Agreement no. 16007.” Contributors listed in Table 2 provided data to the transmission study.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2020.591881/full#supplementary-material

Footnotes

1. ^ https://www.slim-ocean.be

References

Acropora Biological Review Team (2005). Atlantic Acropora Status Review Document. Seattle, WA: Report to National Marine Fisheries Service, Southeast Regional Office.

Google Scholar

Aeby, G., Ushijima, B., Campbell, J. E., Jones, S., Williams, G., Meyer, J. L., et al. (2019). Pathogenesis of a tissue loss disease affecting multiple species of corals along the Florida Reef Tract. Front. Mar. Sci. 6:678. doi: 10.3389/fmars.2019.00678

CrossRef Full Text | Google Scholar

Alvarez-Filip, L., Estrada-Saldivar, N., Perez-Cervantes, E., Molina-Hernandez, A., and Gonzalez-Barrios, F. J. (2019). A rapid spread of the stony coral tissue loss disease outbreak in the Mexican Caribbean. PeerJ 7:e8069. doi: 10.7717/peerj.8069

PubMed Abstract | CrossRef Full Text | Google Scholar

Ardhuin, F., Mariei, L., Rascle, N., Forget, P., and Roland, A. (2009). Observation and estimation of Lagrangian, Stokes, and Eulerian currents induced by wind and waves at the sea surface. J. Phys. Oceanogr. 39, 2820–2838. doi: 10.1175/2009jpo4169.1

CrossRef Full Text | Google Scholar

Aronson, R. B., and Precht, W. F. (2001). “White-band disease and the changing face of caribbean coral reefs,” in The Ecology and Etiology of Newly Emerging Marine Diseases, ed. J. W. Porter (Berlin: Springer), 25–38. doi: 10.1007/978-94-017-3284-0_2

CrossRef Full Text | Google Scholar

Aronson, R. B., and Precht, W. F. (2006). Conservation, precaution, and caribbean reefs. Coral Reefs 25, 441–450. doi: 10.1007/s00338-006-0122-9

CrossRef Full Text | Google Scholar

Bidegain, G., Powell, E., Klinck, J., Ben-Horin, T., and Hofmann, E. (2016a). Microparasitic disease dynamics in benthic suspension feeders: infective dose, non-focal hosts, and particle diffusion. Ecol. Modell. 328, 44–61. doi: 10.1016/j.ecolmodel.2016.02.008

CrossRef Full Text | Google Scholar

Bidegain, G., Powell, E. N., Klinck, J. M., Ben-Horin, T., and Hofmann, E. E. (2016b). Marine infectious disease dynamics and outbreak thresholds: contact transmission, pandemic infection, and the potential role of filter feeders. Ecosphere 7:e01286. doi: 10.1002/ecs2.1286

CrossRef Full Text | Google Scholar

Blondeau, J., Brandt, M., Donovan, C., Eakin, M., Edwards, K., Edwards, K., et al. (2020). Coral Reef Condition: A Status Report for the U.S. Virgin Islands. Available online at: https://repository.library.noaa.gov/view/noaa/24196

Google Scholar

Brandt, M. E., and McManus, J. W. (2009). Dynamics and impact of the coral disease white plague: insights from a simulation model. Dis. Aquat. Organ. 87, 117–133. doi: 10.3354/dao02137

PubMed Abstract | CrossRef Full Text | Google Scholar

Burgess, S. C., Kingsford, M. J., and Black, K. P. (2007). Influence of tidal eddies and wind on the distribution of presettlement fishes around One Tree Island. Great Barrier Reef. Mar. Ecol. Prog. Ser. 341, 233–242. doi: 10.3354/meps341233

CrossRef Full Text | Google Scholar

Chassignet, E. P., Hurlburt, H. E., Smedstad, O. M., Halliwell, G. R., Hogan, P. J., Wallcraft, A. J., et al. (2007). The HYCOM (hybrid coordinate ocean model) data assimilative system. J. Mar. Syst. 65, 60–83. doi: 10.1016/j.jmarsys.2005.09.016

CrossRef Full Text | Google Scholar

Csardi, G., and Nepusz, T. (2006). The igraph software package for complex network research. InterJ. Complex Syst. 1695, 1–9.

Google Scholar

Dustan, P., and Halas, J. C. (1987). Changes in the reef-coral community of Carysfort Reef, Key Largo, Florida: 1974 to 1982. Coral Reefs 6, 91–106. doi: 10.1007/bf00301378

CrossRef Full Text | Google Scholar

Figueiredo, J., Baird, A. H., and Connolly, S. R. (2013). Synthesizing larval competence dynamics and reef-scale retention reveals a high potential for self-recruitment in corals. Ecology 94, 650–659. doi: 10.1890/12-0767.1

CrossRef Full Text | Google Scholar

Frys, C., Saint-Amand, A., Le Henaff, M., Figueiredo, J., Kuba, A., Walker, B., et al. (2020). Fine-scale coral connectivity pathways in the Florida Reef tract: implications for conservation and restoration. Front. Mar. Sci. 7:312. doi: 10.3389/fmars.2020.00312

CrossRef Full Text | Google Scholar

FWC-FWRI (2017). Unified Reef Map v2. 0. Tallahassee, FL: Florida Fish and Wildlife Conservation Commission-Fish and Wildlife Research Institute.

Google Scholar

Gardner, T. A., Cote, I. M., Gill, J. A., Grant, A., and Watkinson, A. R. (2003). Long-term region-wide declines in Caribbean corals. Science 301, 958–960. doi: 10.1126/science.1086050

PubMed Abstract | CrossRef Full Text | Google Scholar

Geuzaine, C., and Remacle, J.-F. (2009). Gmsh: a 3-d finite element mesh generator with built-in pre-and post-processing facilities. Int. J. Numer. Methods Eng. 79, 1309–1331. doi: 10.1002/nme.2579

CrossRef Full Text | Google Scholar

Harvell, D., Jordan-Dahlgren, E., Merkel, S., Rosenberg, E., Raymundo, L., Smith, G., et al. (2007). Coral disease, environmental drivers, and the balance between coral and microbial associates. Oceanography 20, 172–195. doi: 10.5670/oceanog.2007.91

CrossRef Full Text | Google Scholar

Keeling, M. J., and Rohani, P. (2011). Modeling Infectious Diseases in Humans and Animals. Princeton University Press. ISBN: 9780691116174, 9781400841035.

Google Scholar

Kermack, W. O., and McKendrick, A. G. (1927). A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. A Math. Phys. 115, 700–721. doi: 10.1098/rspa.1927.0118

CrossRef Full Text | Google Scholar

Kourafalou, V. H., and Kang, H. (2012). Florida current meandering and evolution of cyclonic eddies along the Florida Keys Reef Tract: are they interconnected? J. Geophys. Res. 117:C05028. doi: 10.1029/2011JC007383

CrossRef Full Text | Google Scholar

Kramer, P., Roth, L., and Lang, J. (2019). Map of Stony Coral Tissue Loss Disease Outbreak in the Caribbean. Available online at: https://www.agrra.org. ArcGis Online. (accessed June 12, 2020)

Google Scholar

Kuffner, I. B., Lidz, B. H., Hudson, J. H., and Anderson, J. S. (2015). A century ofocean warming on Florida Keys coral reefs: historic in situ observations. Estuaries Coasts 38, 1085–1096. doi: 10.1007/s12237-014-9875-5

CrossRef Full Text | Google Scholar

Kundu, P. K. (1976). Ekman veering observed near the ocean bottom. J. Phys. Oceanogr. 6, 238–242. doi: 10.1175/1520-0485(1976)006<0238:evonto>2.0.co;2

CrossRef Full Text | Google Scholar

Kuta, K., and Richardson, L. (1996). Abundance and distribution of black band disease on coral reefs in the northern Florida Keys. Coral Reefs 15, 219–223. doi: 10.1007/s003380050046

CrossRef Full Text | Google Scholar

Lambrechts, J., Hanert, E., Deleersnijder, E., Bernard, P.-E., Legat, V., Remacle, J.-F., et al. (2008). A multi-scale model of the hydrodynamics of the whole Great Barrier Reef. Estuar. Coast. Shelf Sci. 79, 143–151. doi: 10.1016/j.ecss.2008.03.016

CrossRef Full Text | Google Scholar

Landsberg, J. H., Kiryu, Y., Gray, C., Wilson, P., Perry, N., and Waters, Y. (2018). MCAV Disease Lab Analyses Update. Available online at: https://floridadep.gov/sites/default/files/Copy%20of% 20FWC-FWRI_MCAV_disease_update_041118.pdf. (accessed July, 7 2020).

Google Scholar

Lane, P. V., Smith, S. L., Graber, H. C., and Hitchcock, G. L. (2003). Mesoscale circulation and the surface distribution of copepods near the south Florida Keys. Bull. Mar. Sci. 72, 1–18.

Google Scholar

Lee, T. N., Clarke, M., Williams, E., Szmant, A. F., and Berger, T. (1994). Evolution of the Tortugas Gyre and its influence on recruitment in the Florida Keys. Bull. Mar. Sci. 54, 621–646.

Google Scholar

Manzello, D. P. (2015). Rapid recent warming of coral reefs in the Florida Keys. Sci. Rep. 5:16762. doi: 10.1038/srep16762

PubMed Abstract | CrossRef Full Text | Google Scholar

Mehra, A., and Rivin, I. (2010). A real time ocean forecast system for the North Atlantic Ocean. Terr. Atmos. Ocean. Sci. 21:211. doi: 10.3319/tao.2009.04.16.01(iwnop)

CrossRef Full Text | Google Scholar

Miller, J., Muller, E., Rogers, C., Waara, R., Atkinson, A., Whelan, K., et al. (2009). Coral disease following massive bleaching in 2005 causes 60% decline in coral cover on reefs in the US Virgin Islands. Coral Reefs 28, 925–937. doi: 10.1007/s00338-009-0531-7

CrossRef Full Text | Google Scholar

Muller, E. M., Sartor, C., Alcaraz, N. I., and van Woesik, R. (2020). Spatial epidemiology of the Stony-Coral-Tissue-Loss Disease in Florida. Fron. Mar. Sci. 7:163. doi: 10.3389/fmars.2020.00163

CrossRef Full Text | Google Scholar

Murphy, B. S. (2014). Pykrige: development of a kriging toolkit for Python. AGUFM 2014, 51K–753K.

Google Scholar

Murray, J. D. (2007). Mathematical Biology: I. An Introduction. Berlin: Springer Science & Business Media.

Google Scholar

Neely, K. (2018). Surveying the Florida Keys Southern Coral Disease Boundary. Miami, FL: Florida DEP.

Google Scholar

NOAA (2018). Stony Coral Tissue Loss Disease Case Definition. Available online at: https://nmsfloridakeys.blob.core.windows.net/floridakeys-prod/media/ docs/20181002-stony-coral-tissue-loss-disease-case-definition.pdf (accessed June 4, 2020).

Google Scholar

Perlin, A., Moum, J., Klymak, J., Levine, M., Boyd, T., and Kosro, P. (2007). Organization of stratification, turbulence, and veering in bottom Ekman layers. J. Geophys. Res. 112:C05S90. doi: 10.1029/2004JC002641

CrossRef Full Text | Google Scholar

Porter, J. W., and Meier, O. W. (1992). Quantification of loss and change in floridian reef coral populations. Am. Zool. 32, 625–640. doi: 10.1093/icb/32.6.625

CrossRef Full Text | Google Scholar

Precht, W. F., Gintert, B. E., Robbart, M. L., Fura, R., and Van Woesik, R. (2016). Unprecedented disease-related coral mortality in Southeastern Florida. Sci. Rep. 6:31374. doi: 10.1038/srep31374

PubMed Abstract | CrossRef Full Text | Google Scholar

Richardson, L. L., Goldberg, W. M., Kuta, K. G., Aronson, R. B., Smith, G. W., Ritchie, K. B., et al. (1998). Florida’s mystery coral-killer identified. Nature 392, 557–558. doi: 10.1038/33302

CrossRef Full Text | Google Scholar

Rosales, S. M., Clark, A. S., Huebner, L. K., Ruzicka, R. R., and Muller, E. (2020). Rhodobacterales and Rhizobiales are associated with stony coral tissue loss disease and its suspected sources of transmission. Front. Microbiol. 11:681. doi: 10.3389/fmicb.2020.00681

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruzicka, R., Colella, M., Porter, J., Morrison, J., Kidney, J., Brinkhuis, V., et al. (2013). Temporal changes in benthic assemblages on Florida Keys reefs 11 years after the 1997/1998 El Nino. Mar. Ecol. Prog. Ser. 489, 125–141. doi: 10.3354/meps10427

CrossRef Full Text | Google Scholar

Shore, A., and Caldwell, J. M. (2019). Modes of coral disease transmission: how do diseases spread between individuals and among populations? Mar. Biol. 166:45. doi: 10.1007/s00227-019-3490-8

CrossRef Full Text | Google Scholar

Smith, N. P. (2009). The influence of wind forcing on across-shelf transport in the Florida Keys. Cont. Shelf Res. 29, 362–370. doi: 10.1016/j.csr.2007.06.013

CrossRef Full Text | Google Scholar

Sokolow, S. H., Foley, P., Foley, J. E., Hastings, A., and Richardson, L. L. (2009). Editor’s choice: disease dynamics in marine metapopulations: modelling infectious diseases on coral reefs. J. Appl. Ecol. 46, 621–631. doi: 10.1111/j.1365-2664.2009.01649.x

CrossRef Full Text | Google Scholar

Sponaugle, S., Lee, T., Kourafalou, V., and Pinkard, D. (2005). Florida current frontal eddies and the settlement ofcoral reef fishes. Limnol. Oceanogr. 50, 1033–1048. doi: 10.4319/lo.2005.50.4.1033

CrossRef Full Text | Google Scholar

Sponaugle, S., Paris, C., Walter, K., Kourafalou, V., and Alessandro, E. (2012). Observed and modeled larval settlement ofa reeffish to the Florida Keys. Mar. Ecol. Prog. Ser. 453, 201–212. doi: 10.3354/meps09641

CrossRef Full Text | Google Scholar

Sutherland, K. P., Porter, J. W., and Torres, C. (2004). Disease and immunity in caribbean and indo-pacific zooxanthellate corals. Mar. Ecol. Prog. Ser. 266, 273–302. doi: 10.3354/meps266273

CrossRef Full Text | Google Scholar

Thomas, C. J., Bridge, T. C., Figueiredo, J., Deleersnijder, E., and Hanert, E. (2015). Connectivity between submerged and near-sea-surface coral reefs: can submerged reef populations act as refuges? Divers. Distrib. 21, 1254–1266. doi: 10.1111/ddi.12360

CrossRef Full Text | Google Scholar

Thomas, C. J., Lambrechts, J., Wolanski, E., Traag, V. A., Blondel, V. D., Deleersnijder, E., et al. (2014). Numerical modelling and graph theory tools to study ecological connectivity in the Great Barrier Reef. Ecol. Modell. 272, 160–174. doi: 10.1016/j.ecolmodel.2013.10.002

CrossRef Full Text | Google Scholar

Vaz, A. C., Paris, C. B., Olascoaga, M. J., Kourafalou, V. H., Kang, H., and Reed, J. K. (2016). The perfect storm: match-mismatch of bio-physical events drives larval reef fish connectivity between pulley ridge mesophotic reef and the Florida Keys. Cont. Shelf Res. 125, 136–146. doi: 10.1016/j.csr.2016.06.012

CrossRef Full Text | Google Scholar

Viehman, S., Gittings, S., Groves, S., Moore, J., Moore, T., and Stein, J. (2018). NCCOS Assessment: Coral Disturbance Response Monitoring (DRM) Along the Florida Reef Tract Following Hurricane Irma From 2017-10-09 to 2017- 10-18 (NCEI Accession 0179071). NOAA National Centers for Environmental Information. Silver Spring, MD: National Centers for Coastal Ocean Science.

Google Scholar

Wolanski, E. (1994). Physical Oceanographic Processes of the Great Barrier Reef. Boca Raton, FL: CRCPress.

Google Scholar

Appendix

A.1 Connectivity Between the Marquesas and the Dry Tortugas

To assess the potential for disease transmission from the Marquesas to the Dry Tortugas, we computed the paths with the highest transmission probability between each possible pairing of a source reef in the Marquesas and a sink reef in the Dry Tortugas in our connectivity networks. To do so, a weight w_ij = 1 − C_ij was attributed to the edge between sub-reefs i and j, so that paths with lowest weight (i.e., shortest paths) in the network would correspond to connections with highest probability of exchange of disease agents. The shortest paths were then computed using the Python package python-igraph (Csardi and Nepusz, 2006) for each monthly matrix obtained with barotropic currents, as they drive the modeled disease propagation that best matches observations (Figure 6).

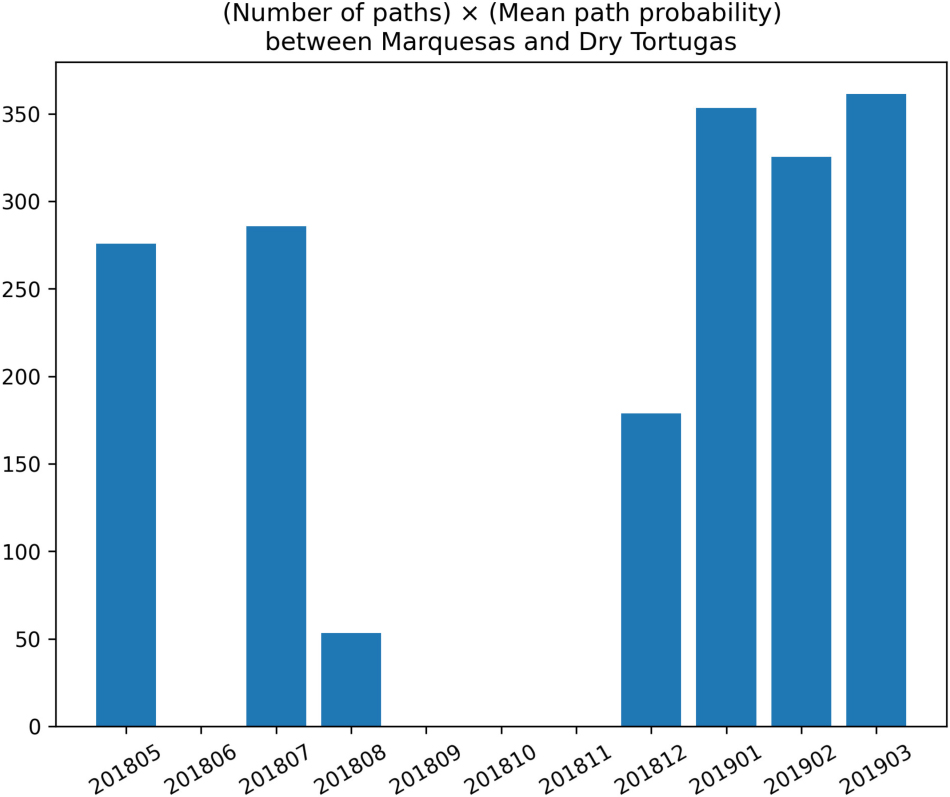
The most likely transmission pathways from the Marquesas to the Dry Tortugas are computed by taking the yearly average of the shortest paths obtained for each monthly connectivity (Figure A1). Although the SCTLD has not reached the Marquesas yet in 2018, these preliminary results bring some insight into the exchange mechanisms between the Marquesas and the Dry Tortugas. First, the existence of multiple paths from the Marquesas to the Dry Tortugas suggests a possibility for disease agents produced in the Marquesas to reach the Dry Tortugas. Moreover, disease transmission seems more likely to originate from inshore reefs as paths starting from these reefs exhibit the largest exchange probability. Furthermore, the presence of indirect transmission pathways from the Marquesas to the Dry Tortugas suggests that reefs located between these two zones act as stepping stones that facilitate the propagation of the disease. This is particularly the case for disease agents produced in reefs located more offshore. Additionally, our results suggest a seasonal variation of these exchanges as no exchange from the Marquesas to the Dry Tortugas was modeled.

FIGURE A1

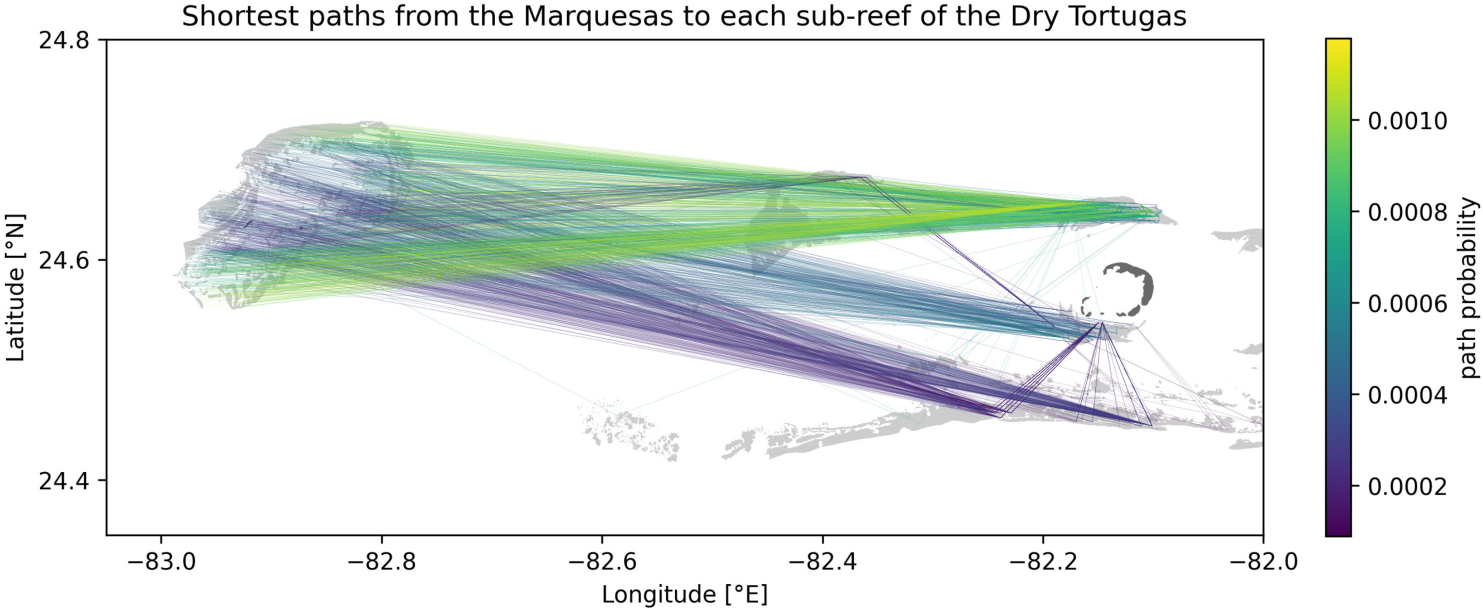
Figure A1. Shortest paths to each sub-reef of the Dry Tortugas from the Marquesas computed from the yearly averaged connectivity matrix obtained with mean barotropic currents. Reefs are highlighted in light gray while islands are shown in dark gray.

between September and November 2018 (Figure A2). This absence of connection might be explained by the seasonal variation of the wind regime on the Western Florida Shelf. A non-seasonal influence which may have played a role is the offshore circulation associated with the Florida Current. The presence or absence of an oceanic mesoscale Tortugas gyre and associated frontal eddies has been shown (Lee et al., 1994; Lane et al., 2003; Sponaugle et al., 2005) to play an important role in connectivity patterns within the lower Keys, and between this region and the Dry Tortugas. Analysis based on operational ocean models from this period in 2018 (e.g., RTOFS; Mehra and Rivin, 2010) shows that the Tortugas Gyre was absent, with the Loop Current in a strongly retracted position - essentially, flowing straight from the Yucatan Channel into the Straits of Florida in November 2018; this may have significantly reduced connectivity during this period. The most likely period during which the infection could occur seems to be winter-early spring, so the presence or absence of this larger scale setup for later years may be important in understanding both disease and larval connectivity with the Dry Tortugas.

FIGURE A2

Figure A2. Number of shortest paths from the Marquesas to the Dry Tortugas multiplied by their mean probability for each simulated month with barotropic currents.