Modeling the Distribution of Habitat-Forming, Deep-Sea Sponges in the Barents Sea: The Value of Data

Gonzalez-Mirelis, Genoveva; Ross, Rebecca E.; Albretsen, Jon; Buhl-Mortensen, Pål

doi:10.3389/fmars.2020.496688

ORIGINAL RESEARCH article

Front. Mar. Sci., 05 January 2021

Sec. Deep-Sea Environments and Ecology

Volume 7 - 2020 | https://doi.org/10.3389/fmars.2020.496688

This article is part of the Research Topic Seafloor Mapping of the Atlantic Ocean View all 13 articles

Modeling the Distribution of Habitat-Forming, Deep-Sea Sponges in the Barents Sea: The Value of Data

$\r\nGenoveva Gonzalez-Mirelis*$ Genoveva Gonzalez-Mirelis^*

Rebecca E. Ross

Jon Albretsen $Pl Buhl-Mortensen\r\n$ Pål Buhl-Mortensen

Institute of Marine Research, Bergen, Norway

The use of species occurrence as a proxy for habitat type is widespread, probably because it allows the use of species distribution modeling (SDM) to cost-effectively map the distribution of e.g., vulnerable marine ecosystems. We have modeled the distribution of epibenthic megafaunal taxa typical of soft-bottom, Deep-Sea Sponge Aggregations (DSSAs), i.e., “indicators,” to discover where in the Barents Sea region this habitat is likely to occur. The following taxa were collectively modeled: Hexadella cf. dedritifera, Geodia spp., Steletta sp., Stryphnus sp. The data were extracted from MarVid, the video database for the Marine AREAl database for NOrwegian waters (MAREANO). We ask whether modeling density data may be more beneficial than presence/absence data, and whether using this list of indicator species is enough to locate the target habitat. We use conditional inference forests to make predictions of probability of presence of any of the target sponges, and total density of all target sponges, for an area covering a large portion of the Norwegian Barents Sea and well beyond the data’s spatial range. The density models explain <31% of the variance, and the probability models have high classificatory power (AUC > 0.88), depending on the variables/samples used to train the model. The predicted surfaces were then classified on the basis of a probability threshold (0.75) and a density threshold (13 n/100 m²) to obtain polygons of “core area” and “hotspots” respectively (zones). The DSSA core area comprises two main regions: the Egga shelf break/Tromsøflaket area, and the shelf break southwest of Røst bank in the Træna trench. Four hotspots are detected within this core area. Zones are evaluated in the light of whole-community data which have been summarized as taxon richness and density of all megafauna. Total megafaunal density was significantly higher inside the hotspots relative to the background. Richness was not different between zones. Hotspots appeared different to one another in their richness and species composition although no tests were possible. We make the case that the effectiveness of the indicator species approach for conservation planning rests on the availability of density data on the target species, and data on co-occurring species.

Introduction

Classifying the variability of nature into habitat types and furthermore, projecting those habitats onto geographic space, represents a leap toward ecosystem-based management, which is now widely recognized as the best way to manage natural resources and ensure economic prosperity (Murawski, 2007). Habitat mapping has thus become a pillar of nature conservation (Hooftman and Bullock, 2012).

In the marine, benthic realm, one approach toward habitat mapping is to use species occurrence as a proxy for the realization of a habitat type (Howell et al., 2016; Buhl-Mortensen et al., 2019). Under this approach, a central requirement is a checklist of one or more (typically species-level) taxa. These are often referred to as “indicators,” albeit not in the sense of ecological indicators but rather, defined as the species/taxa of epibenthic megafauna which are typical for an ecosystem or habitat. This checklist can comprise structure-forming (i.e., habitat-forming) species, associated fauna, or simply, easy-to-identify species which are constituents of the assemblage. Given the appropriate environmental data, these benthic taxa can become the object of Species Distribution Modeling (SDM, sensu Elith and Leathwick, 2009; Franklin, 2010). The (spatial) predictions from such models are used to discern the distribution of the marine ecosystem or habitat in question. Distribution maps of vulnerable marine ecosystems (VMEs), red-listed habitats etc., are thus cost-effectively produced, even for areas that have never been sampled or observed.

Deep-sea sponge aggregations (DSSAs) are one such conservation-relevant habitat (OSPAR, 2008). Deep-sea sponges are known to be ecosystem engineers. Some DSSAs can alter the characteristics of the surrounding muddy sediment by creating dense mats of spicules. Spicule mats have been found to increase biodiversity and abundance of fauna, whether of epibenthic megafauna (Beazley et al., 2013) or macrofauna (Bett and Rice, 1992) depending on the species composition of the sponge community. DSSAs filter large quantities of water and may play a key role in nutrient recycling, benthopelagic coupling and the silicon cycle (Maldonado et al., 2005) among other ecosystem functions.

DSSAs first became a habitat of concern for marine conservation policy when they were included by the Oslo-Paris (OSPAR) Convention for the Protection of the Marine Environment of the North East Atlantic in their List of Threatened and/or Declining Species and Habitats (OSPAR, 2008). Later, OSPAR published a separate document with a more detailed definition, as well as assessment of the habitat to better support mapping efforts throughout the OSPAR region (OSPAR, 2010).

Recently, Buhl-Mortensen et al. (2020) analyzed extensive occurrence data from Arctic and subarctic waters and proposed a classification of DSSAs (among other marine ecosystems) with specific lists of indicators. One of the classes they proposed was named “soft bottom sponge aggregations” which, besides being characterized by the dominance of mud in the sediment, is further defined by the following indicators: Geodia spp., Stryphnus sp., and Steletta spp., all of which are tetractinellid sponges. These sponges are large, can be found in high densities, and modify their environment by creating mats of spicules (Maldonado et al., 2016), and they are considered habitat-forming species; they provide habitat to mobile filter-feeders and smaller mega- and macro-fauna. This habitat also corresponds with the habitat sometimes referred to as “boreal ostur” (e.g., Howell et al., 2016).

In Norway, soft-bottom sponge aggregations are known to occur in large patches across some areas of the northern Norwegian shelf from fishing by-catch observations (Klitgaard and Tendal, 2004; Mortensen, 2005). Howell et al. (2016) predict that the core distribution area of soft-bottom DSSAs at the continental scale is located largely in Norwegian waters. Fisheries and management authorities alike are therefore interested in knowing the exact locations and boundaries of these patches so that they can be sustainably managed and have requested distribution maps to support, among other things, the recent revision of the Barents Sea Management Plan. Distribution modeling of soft-bottom DSSA indicator species was quickly chosen as a basis to provide such maps. This choice of approach was also driven by the fact that Norway has an extensive database of epibenthic megafauna georeferenced records, which are collected and curated by the Marine AREAl database for NOrwegian waters (MAREANO) Programme.

The majority of benthic SDMs are built using presence-only or presence/absence data due to the cost associated with the collection of geospatial, quantitative data on benthic communities, or the issues with combining datasets from different time periods and sampling equipment (e.g., Pearce and Boyce, 2006; Howard et al., 2014; Hao et al., 2019). One of the major benefits of the MAREANO video database (MarVid) is that all records have been collected using a standardized method since 2006. Consequently, reliable abundance data (here translated into densities) are available over a large area, allowing us to make a comparison between models built using density data and those built using presence/absence data.

Also, we are interested to explore whether the presence of pre-selected species (as per a list of indicators, e.g., Burgos et al., 2020) is enough to isolate the target habitat, and we use the greater MarVid data to assess this question. Just what are these indicators indicative of, in terms of ecosystem structure and function? We start to investigate patterns of epibenthic megafaunal taxon richness (as a proxy for biodiversity), and total abundance of epibenthic megafauna (as a proxy for productivity) in relation to the predicted distribution of soft-bottom, deep-sea sponges. As, arguably, the most valuable locations would have high biodiversity and productivity, these data can act as a proxy for assessing the conservation value of model predicted hotspots.

We model the distribution of soft-bottom, deep-sea, habitat-forming species of sponges using environmental variables ranging in resolution from 800 m to 4 km. The modeling area covers a large portion of the Norwegian Barents Sea so that the results can be used to inform the revision process of the Barents Sea management plan. We compare the use of presence/absence data with abundance data to assess the benefits and weaknesses of both types of data for the purpose of informing marine management. We then provide additional context using the greater MarVid dataset to differentiate between predicted DSSA hotspots and their relative conservation value. With a view to improving the way we define and map marine ecosystems, going beyond presence of indicators, this paper addresses the two following questions: (1) Does density data (rather than presence/absence data) provide an advantage when predicting DSSA hotspots? (2) Are predictive maps which are based on lists of indicator species enough to find places of conservation interest, or are there benefits of using data from other members of the epibenthic community?

Description of Data, and Data Processing

Faunal Data

Data describing the composition of epibenthic megafauna were derived from video footage, which was in turn captured with an underwater camera under the MAREANO Programme. At each station, an underwater camera platform (Campod or Chimera) is towed along a 700 m, to 1,000 m-long, straight survey path at an approximate altitude of 1.5 m off the seabed. The platform is equipped with two video cameras, one for navigation, and a high-definition, forward-looking, color video camera (Sony HDC-X300) for visual data collection. Underwater positioning is provided by a hydroacoustic USBL (Ultra-short baseline) system (Simrad HIPAP and Eiva Navipac software) with a transponder mounted on the camera platform. This system provides positions accurate to about 2% of the water depth. A pair of laser pointers is used to estimate the width of the field of view.

Routinely, post-cruise video analysis is carried out on all video footage captured with the high-definition camera. During playback, all organisms are named (using standard taxonomic nomenclature whenever possible), counted, timestamped, and later, with the aid of cleaned navigation data, linearly georeferenced. When it is not feasible to count all individuals of a given, identifiable taxon, their abundance is estimated by percent cover. Values in percent cover units are subsequently converted to pseudo-counts by using the approximate (or average) surface area of one single individual or typical colony, derived from expert knowledge, and the area of the field of view. Species indicative of vulnerable habitats and other taxa of special interest are typically identified by their scientific name, and at a taxonomical level no higher than Family (e.g., “Paragorgia arborea,” “Axinellidae”). Most organisms are, however, identified as morphospecies (e.g., “Porifera egg-shaped”), or custom-made, morpho-taxonomical units (e.g., “Actiniaria, buried”). All of these data are collated and stored within the MarVid database. For this study, the dataset was restricted to all organisms in view which are larger than 5 cm in their longest dimension. This size filter was applied in advance of all data extractions. Henceforth, every time we use terminology like “whole-community” or “all records,” etc., we refer to this section of the community, i.e., the epibenthic megafaunal community.

The spatial domain of the dataset is the southwestern part of the Barents Sea, on Norway’s continental shelf and slope (Figure 1 and Supplementary Figure S1). The boundaries of the areas surveyed under the MAREANO Programme respond to natural features, management areas for the oil and gas industry, and other factors, not least geopolitical (e.g., the Norwegian-Russian border). Along the large transects between continental Norway and Svalbard, designed to cross the Polar Front, stations are laid out within square boxes rather than along long lines (e.g., data from 2010, Figure 1). This design responds to the ultimate purpose of the data collection, which is to make biotope maps (Buhl-Mortensen et al., 2014). Within these boundaries (henceforth, the MAREANO area) video stations are relatively evenly spaced, with a target sampling density depending on the topographic and environmental heterogeneity of each survey area. Depth spans from 40 to 2,500 m, with most stations within the 100–600 m range. The field surveys were carried out during years 2006–2017, with 61% of stations taken in the months of August, September and October but none taken in January or February.

FIGURE 1

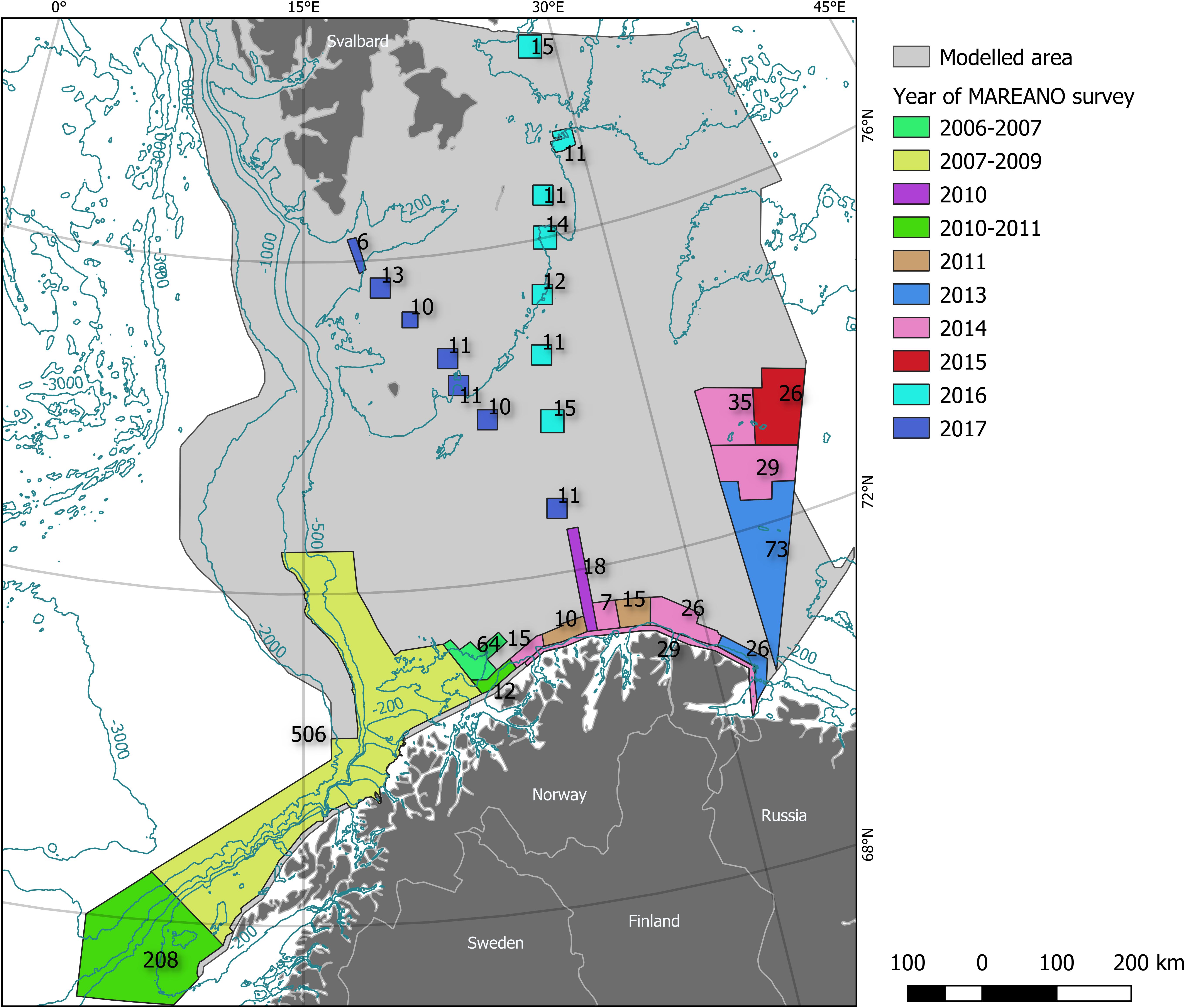
Figure 1. The faunal data used in this study were collected under the Marine AREAl database for NOrwegian waters (MAREANO) Programme. Under this government-funded, data collection programme, benthic sampling is conducted according to predefined survey areas. In this figure, we illustrate the number of video stations per survey area (labels on the map), as well as the year when the sampling was carried out (see legend for details), for the surveys that were used in this study in the Barents Sea. Also shown are bathymetric contour lines (dark blue) and land masses with political boundaries (gray). The scale on this map (scale bar) is 1:5,745,500.

In line with Burgos et al. (2020) the following species were used as indicators of soft-bottom DSSAs in the study area: Hexadella cf. dedritifera, Geodia atlantica, Geodia barretti, Geodia macandrewii, Geodia sp., Steletta sp., and Stryphnus sp. This community of sponges has also been recognized in other North Atlantic regions (Klitgaard and Tendal, 2004; Murillo et al., 2011; Beazley et al., 2013; Cárdenas et al., 2013; Maldonado et al., 2016) providing additional support to the ecological coherence of the chosen taxa. We will refer to this set of soft-bottom, deep-sea sponges as the target taxa.

From the MarVid database, we first pulled all records on any of the target taxa. Then, total abundance was pooled for the whole survey line. Total density was calculated using the average width of the field of view to calculate the total area of the surveyed strip and given in number of individuals or colonies per 100 m². Total density as well as presence/absence (derived from density) were then used as response variables.

We do not use year, or month of survey in our analyses. As far as the former is concerned, we assume we can safely ignore this information because all the target taxa are long-lived. No data points come from the winter months, where the Barents Sea may present more severe stratification. This is not necessarily a problem because neither of these organisms shows seasonal fluctuations in its distribution. Nevertheless, it is worth noting that our response data represents the mild season better than the winter season.

Subsequently, taxon richness and total abundance of all taxa were also calculated for each survey line, providing proxies for diversity and productivity to cross reference with predictions.

Environmental Data

Environmental data can be divided into four main groups: (1) bathymetric/terrain variables, (2) geological variables, (3) oceanographic variables, and (4) ocean surface (satellite-derived) variables, all of which have been found to be drivers of benthic biological composition to varying degrees (Levin et al., 2001; McArthur et al., 2010; Selkoe et al., 2010; Harris and Baker, 2019), although not necessarily of sponge distribution.

Bathymetry and Terrain Analyses

Bathymetry data for the southwest Barents Sea was downloaded from the EMODnet bathymetry portal¹ on October 2018 (i.e., after the 2018 data became available). The resolution of the Digital Terrain Model hosted by EMODnet was 1/16 × 1/16 arc minutes (circa 500 × 500 m at this latitude) (EMODnet Bathymetry Consortium, 2018). All downloaded tiles were mosaicked into one single raster layer and gridded at 800 m on a UTM projected grid (zone 33N).

We calculated: slope, terrain ruggedness index (TRI), roughness, and vector ruggedness measure (VRM, Sappington et al., 2007) in R using the raster (Hijmans, 2020), and spatialEco (for VRM, Evans, 2020) packages using default neighborhoods.

We also derived: topographic position index (TPI) using two neighborhood sizes, aspect using three analysis window sizes, and type of geomorphological feature using three analysis window sizes. TPI was also calculated in R using the raster package. Aspect and feature were calculated using GRASS 7.8 (rgrass7, Bivand, 2019) in R. See Table 1 for a summary and additional details of this part of the data processing.

TABLE 1

Table 1. Summary of multiscale analyses performed on bathymetric data.

The latter six layers, namely the three for aspect and three for geomorphology, as well as current direction (see below) were further processed before entering the model. They were put through a classification procedure and were converted to a single categorical variable, henceforth named terrain class. This classification was achieved by applying Random Forests in a supervised framework. First, 10,000 points were sampled at random. Then we used the CLARA (Clustering Large Applications) algorithm in R (available through the cluster package, Maechler et al., 2019) to classify cells into eight classes, followed by the randomForest function (and package, Liaw and Wiener, 2002) to predict class for all unsampled cells and thus generate a full coverage, categorical layer. This way we generated a new predictor variable which summarizes current direction, aspect, and feature type information. The goal was to reduce the number of (potentially correlated) predictors without losing predictive power.

Geological Data

Landscape type was also used as predictor in our SDM exercise. This spatial dataset shows a division of all Norwegian waters into different marine landscapes, defined as major features of the seabed topography (Norges geologiske undersøkelse, 2014). Examples of marine landscape types in Norwegian marine areas are fjords, marine valleys, continental slopes and deep-sea plains. The data was downloaded on 2019/08/28 as a categorical map from the Norwegian Geological Survey portal². The maximum scale of the downloaded map was 1:100,000 and it was subsequently rasterized to the appropriate resolution (800 m).

Oceanographic Data

Ocean model outputs describing the physical properties of the near-seabed environment were also included as predictors (Pearman et al., 2020). The data were derived from two separate oceanographic models known as the NorKyst-800 m (NK800) model and Barents Sea-800 m (B800) model, each covering a different part of our SDM model area (see Supplementary Figure S2). Both 800 × 800 m ocean models are based on the Regional Ocean Modeling System (ROMS, e.g., Shchepetkin and McWilliams, 2005; Haidvogel et al., 2008³, but had different external forces, and simulated different periods. The NK800 model is explained in detail in Asplin et al. (2020). The B800 model is not yet documented, but the configuration is comparable to the NK800 model and it is the best resolved regional oceanographic model available in the area. It is run and disseminated by the Institute of Marine Research, Norway but is not yet publicly available. Meanwhile, the NK800 model is well established and daily forecasts are produced by the Norwegian Meteorological Institute⁴.

From the NK800 model we were able to obtain data derived from a simulation based on years 2013–2015, and for an area which encompassed approximately the Exclusive Economic Zone around continental Norway. From the B800 model instead, the data we obtained was from a 1-year simulation (year 2010), while the area covered was more centered around the Norwegian Barents Sea. Both these simulations, although financed by MAREANO, had been ordered for purposes going beyond the objectives of this study, hence the discrepancy between the time and space coverage in relation to the video data.

Maximum, minimum, mean, and standard deviation of salinity, temperature, and current speed were obtained from each model, as well as the mean u and v component of current direction, giving a sum of fourteen fields. These fields were extracted from the bottom layer of either model, although neither model was bottom-optimized. For NK800, salinity and temperature statistics are based on daily values, while current speed and direction are based on hourly values. For B800, hourly fields of temperature, salinity and current speed and direction were used. The resulting fields were then interpolated to an 800 × 800 m regular grid defined in UTM33 coordinates using a nearest grid point-interpolation.

Fourteen pairs of raster layers were then blended with each other to yield a total of fourteen complete predictor layers covering our entire model area (Supplementary Figure S2). Blending for each combination of variable and summary statistic was generally carried out through the following steps: create intersection rasters, create points around overlapping area, calculate distances to points in overlapping area, sum distance rasters, create distance weighted rasters, and merge rasters (Wueest et al., 2012). While the seam between the two models did not fully disappear, artifacts were absent from the SDM predictions.

Sea Surface Data

The NASA Goddard Space Flight Center, Ocean Ecology Laboratory, Ocean Biology Processing Group provides ocean color data with worldwide coverage. We downloaded data on chlorophyll a, particulate organic carbon and maximum euphotic depth for use within this study from https://oceancolor.gsfc.nasa.gov/cgi/l3. They are 4 km data, resampled to 800 m. The downloaded data were pooled to a 10 years average from 2006 to 2017, in alignment with the period of MAREANO observations. All predictor layers were aligned to the bathymetry layer in terms of extent, origin, and resolution.

Modeling and Additional Analyses

Modeling Method

We used a Conditional Inference Forest (CIF, Hothorn et al., 2006b) as the modeling framework. CIF is a recursive partitioning and ensemble method for discovering patterns in multiple-predictor, complex datasets that has been found not to be biased toward variables with many values (Strobl et al., 2007). Their application in ecology remains low relative to other fields (e.g., psychology, Martin, 2015; safety, Das et al., 2009; engineering Sardá-Espinosa et al., 2017). Ecological applications include (Müller et al., 2009; Hothorn and Müller, 2010) and only a handful concern SDM (Pottier et al., 2014; Gonzalez-Mirelis and Buhl-Mortensen, 2015) despite the suitability of the method to the SDM problem, and the typically noisy ecological data.

CIFs belong to the family of Machine Learning Algorithms. The base learner of a CIF is a Conditional Inference Tree. The method for building trees is based on a well-defined theory of permutation tests, whereby splitting (i.e., partitioning) is performed based on measured correlations between predictor variables and the response. First, a global null hypothesis of independence between the response and all predictors is tested. A correlation coefficient (e.g., Pearson’s or other depending on the data), with a corresponding p-value is calculated for each variable’s association with the response. If no p-value is below the pre-selected alpha level after accounting for multiple significance tests, the global null hypothesis is not rejected, and the algorithm terminates. Otherwise, the predictor with the strongest association with the response is selected for splitting. The best split within this predictor is selected, and the training set is partitioned on this value. Finally, these steps are iteratively repeated until the global null hypothesis can no longer be rejected in all subsections (Martin, 2015).

Machine Learning algorithms have been designed to be robust in the face of correlated predictors (e.g., Nicodemus and Malley, 2009): if two of the variables provide the same child node purity the model simply selects one. This effect is controlled by the mtry parameter, which determines the number of variables tried at each split. This is one of the features that help machine learning applications excel at predicting (Shmueli, 2010).

Multicollinearity does become an issue when the goal is to interpret the patterns learned by the model. While ecological inference is not the focus of this paper, our study provides an opportunity to describe and/or validate species-habitat relationships. We therefore trained another set of models where colinear predictors (as measured by their variance inflation factors) had been eliminated so as to gain an opportunity to illustrate variable importance. Variance Inflation Factors were calculated using the usdm R library (Naimi et al., 2014).

Eight models were built in total, for all the three-way combinations of the following parameters: response variable (density, or probability of presence), number of predictors (all available, or a selected subset of non-correlated variables), and finally, number of observations (all available, or just 70% of them, reserving a set of 30% for validation purposes, see below). We conducted model training in R by means of the party package (Hothorn et al., 2006a). Additional arguments used include number of trees in the CIF (ntree = 1,000), and the number of variables tried at each split (mtry = 3).

The four density models were tested by means of the statistic developed in Li (2017): Variance Explained by Cross-Validation (VEcv). VEcv is a measure of model accuracy for continuous data that is independent of unit or scale, data mean, and data variance, and it unifies other measures of error, including the commonly used mean absolute error and root mean square error. It was calculated using the spm R package (Li, 2019).

The four probability models (effectively, binary classifiers) were assessed by means of the Area Under the Curve (AUC) statistic, which measures the area under the so-called Receiver Operating Characteristic (ROC) curve. The ROC curve is a plot of the true positive rate against the false positive rate over all possible threshold values of an automatic classifier and is commonly used in SDM applications using presence/absence data. AUC ranges from 0.5, when the model does no better than a random guess, and 1 when the model can discriminate perfectly between presence and absence. We further tested the significance of this value through the DeLong’s test for two ROC curves, where the null curve used for comparison was that obtained by randomly shuffling the response variable. For these tests we used the pROC R package (Robin et al., 2011).

Data Model

The total number of samples was n = 1,142. This set included survey lines of varying length. The mean line length was 738.16 m, with standard deviation 174.22 m. The average nearest neighbor distance was 6764.85 m. We used a prediction grid of 800 × 800 m covering an area of 614,376 km². We ignored the position of the survey lines relative to grid cells and assumed the data observed along each line to be representative of the entire cell containing the centroid of the line.

The two models used for spatial prediction were those where all variables and all observations were used for training. Henceforth these will be referred to as “the density model” and “the probability model.”

Additional Analyses

To compare the predictions between the density model and the probability model we first calculated the Pearson correlation coefficient (r) between each pair of predictions, pixel-wise, for the whole study area. We then calculated Pearson correlation between predicted density values and predicted probability values within a running window of size approximately 41 by 41 km (more precisely 51 by 51 grid cells) using the SpatialEco package (Evans, 2020). This window size captured areas big enough to display variation in the predictions within, while still showing local patterns of correlation.

Hotspots (high-density areas) and core area (high-probability areas) were defined by applying a threshold to the density and the probability predictions, respectively. Areas below the thresholds are hence forth referred to as background. The threshold for density was determined visually. The threshold for probability was conservatively derived from the True Skill Statistic (TSS), also called Youden’s J, defined as the average of the net prediction success rate for present sites and that for absent sites (Liu et al., 2009). The three obtained zones thus represent a gradient of likelihood of presence of a soft-bottom, deep-sea sponge (vulnerable) marine ecosystem.

We compared mean total taxon richness and mean total abundance of megafauna between all zones (i.e., along the gradient). There was a total of 13 observations within the hotspots, 174 observations within the core area, and 955 observations in the background zone. To achieve a balanced design, we sampled 13 observations from the core area and the background zone and used only those in the test. Furthermore, these 13 observations were stratified by the range of the variable being tested (richness, or abundance). The strata were created in each case by discretizing the variable into three classes using Jenks breaks as cut points.

We also looked at patterns of richness and abundance within the high-density zone (i.e., between hotspots). For this comparison we had very few samples available and no statistical tests were performed.

Results

Model Predictions

With this data set, spanning a vast area and collected over many years, and this set of environmental layers, most of which are themselves the outcome of other models, we were able to account for between 15 and 31% of the spatial variation in density of soft-bottom, deep-sea sponges, depending on the training data. The classificatory power of all four probability models was consistently high (Table 2). Model predictions are displayed as continuous rasters in Figure 2.

TABLE 2

Table 2. Model evaluation statistics.

FIGURE 2

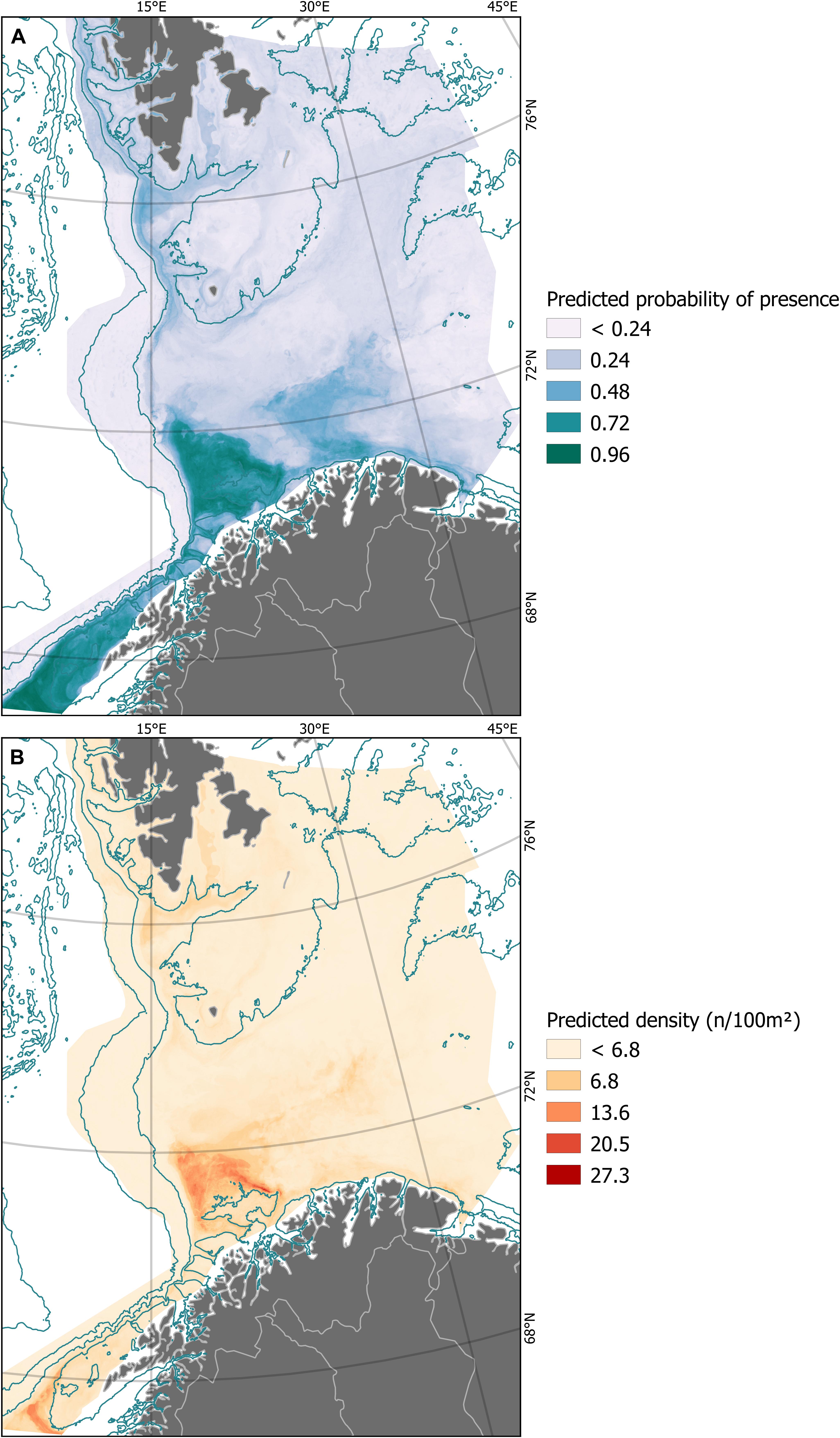
Figure 2. Model predictions of probability of presence (A) and density (B) of soft-bottom, deep-sea sponges across the Norwegian Barents Sea as modeled using conditional inference forests and multiple environmental predictors. Also shown are selected bathymetric contour lines (dark blue) and land masses with political boundaries (gray), about which more details can be found in Figure 1. For scale, refer also to Figure 1.

The following variables were eliminated from the twenty-four initial ones: slope, roughness, maximum temperature, standard deviation of current speed, standard deviation of salinity, and mean temperature. Supplementary Figure S3 ranks the remaining variables by their importance and shows that temperature (minimum), salinity (mean, minimum and maximum), and depth are the most important predictors for the target set of species. Variance Importance is reported from the density model because this is the model that had access to the most information. A look at variance importance from the probability model revealed that minimum temperature dropped by one position, ranking third instead of second; additionally, Chlorophyll a raised to position number five. The remaining top predictors were consistent. This plot can be easily generated if needed with the R Notebook provided with this paper.

The relationship between the responses and the top two predictors (namely mean salinity, and minimum temperature) can be visualized by means of partial dependence plots, in Supplementary Figure S4. When predicting abundance, the models indicate a preference of the target sponges for a mean salinity above 34.9 ppt and a temperature which does not drop below −0.5°C at any time of year. The curve for probability of presence is slightly different in the case of minimum temperature, where the probability remains low (but not zero) beyond −0.5°C and it becomes 0 at −2.0°C. The combinations of salinities and temperatures indicate that the maximum response is observed within Atlantic water.

The overall Pearson’s r between predicted densities and predicted probabilities was 0.79. Locally (at scales 10–100 km) the two models largely agreed with each other (82% of model domain with r > 0.2, blue in Figure 3), while lack of correlation, or discrepancy (16% r between −0.2 and 0.2) and disagreement (0.01% r < −0.2) between the two models also occurred. This correlation is illustrated in Figure 3 in relation to the data range, where we show the areas of disagreement in more detail than those were agreement occurred, as they provide a more useful backdrop to interpret model results. It is, however, worth mentioning that twenty-four percent of the model domain had very high (>0.7) correlation values; for a look at where those areas are located you may use the R Notebooks provided.

FIGURE 3

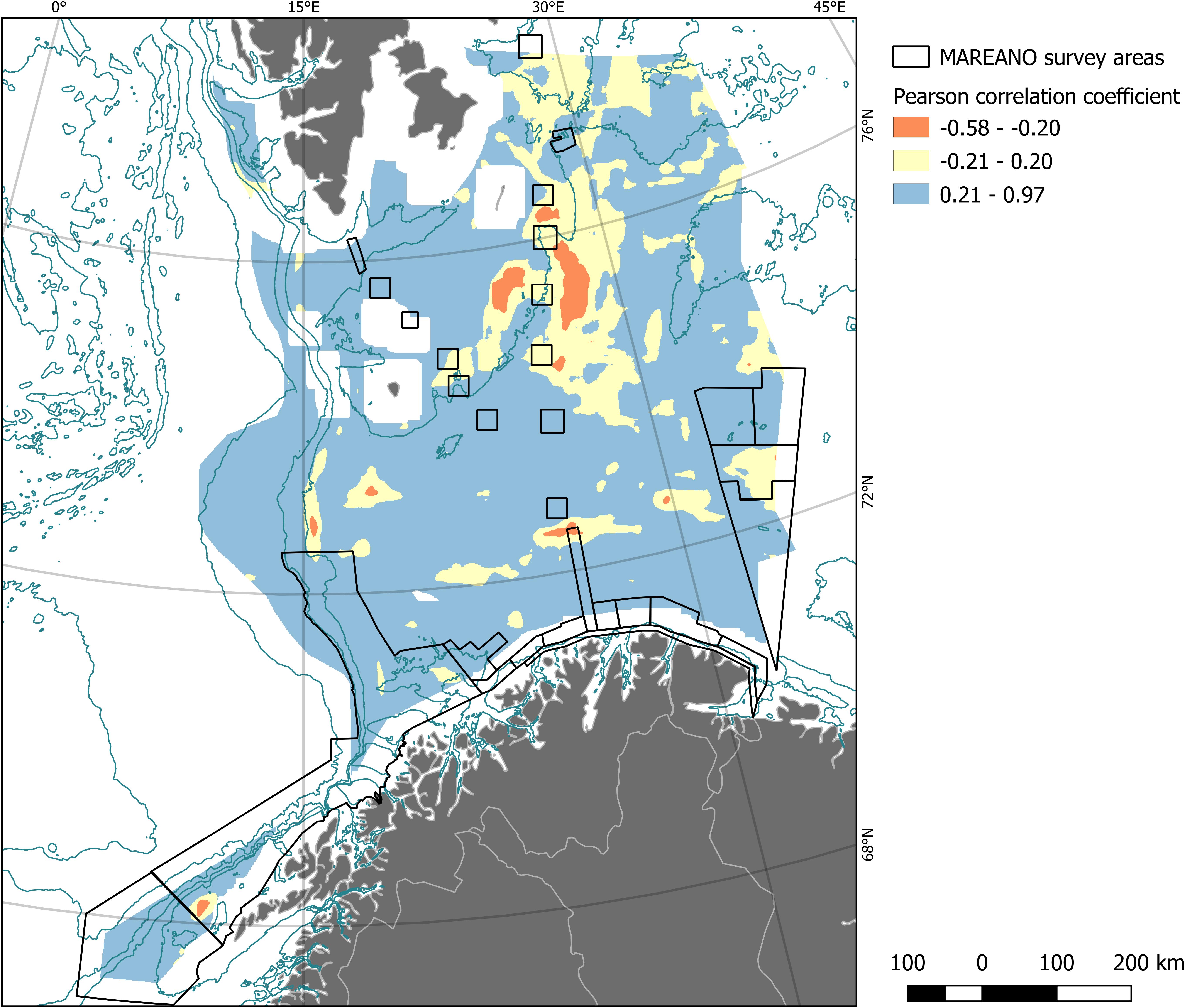
Figure 3. Pearson correlation between predicted density and predicted probability of presence of soft-bottom, deep-sea sponges for each pixel was calculated within a running window of size 41 km by 41 km. In this figure we illustrate the areas where the correlation coefficient was most negative (red, see legend for coefficient values). In yellow are shown all areas where the correlation between the two models was around zero, meaning there was no correlation between the two models. Areas of model agreement are shown in blue. The black outline overlaid is the extent of the training data coverage. Also shown are selected bathymetric contour lines (dark blue) and land masses with political boundaries (gray), about which more details can be found in Figure 1.

To decide on a threshold for the probability model we looked first at the TSS, which was 0.41. This threshold would classify as soft-bottom DSSA core area a very large region (notice the area depicted in dark green and dark blue in Figure 2A) which we deemed unpractical from the management point of view; it would also be difficult to defend a probability threshold that is below 50%, no matter the management application intended. Therefore, we raised the threshold from 0.41 to 0.75. At this level, two main regions remain: the Egga shelf break and Tromsøflaket area, as well as the area around the Røst bank and Træna Trench (see Figure 4 for reference). At 0.85 the area at Egga/Troms is reduced to a few small kernels while the size of the Træna trench area is hardly affected. Ultimately, we decided to use 0.75 as a threshold value for probability. For density, we used 13 n/100 m², which was chosen visually to mimic the main patterns in Figure 2B. We subsequently digitized the boundaries around all pixels with value above the threshold, on each layer.

FIGURE 4

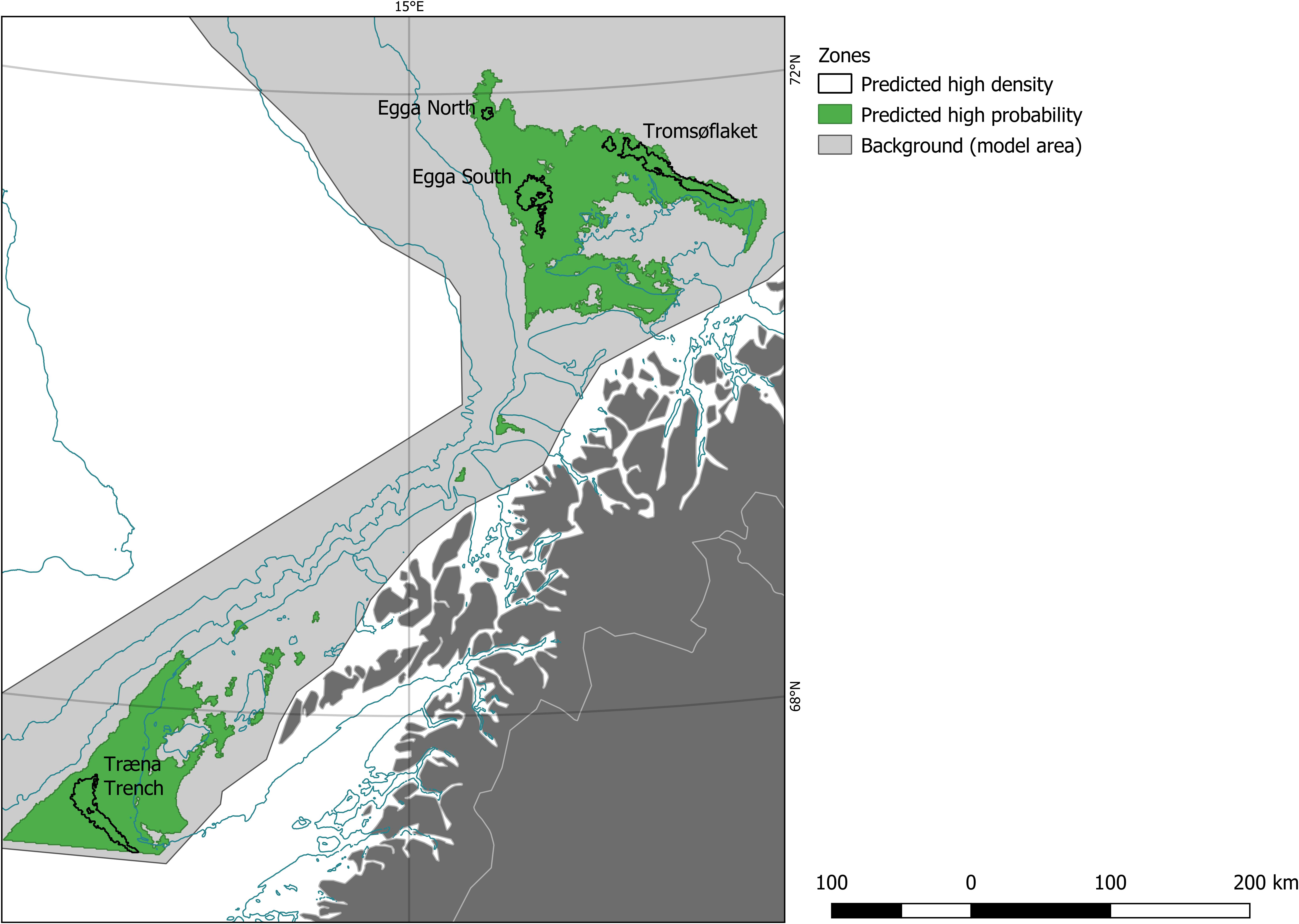
Figure 4. The areas referred to as “predicted high probability” are those where the model predicted a probability of presence of soft-bottom, deep-sea sponges larger than 0.75 (green), whereas the areas referred to as “predicted high density” enclose the pixels where the model predicted a density of the target species above 13 colonies/100 m² (outlined in black). For reference we have also plotted the extent of the model area (light gray). Also shown are selected bathymetric contour lines (dark blue) and land masses with political boundaries (gray), about which more details can be found in Figure 1. Here, we can identify four main high-density patches, or hotspots (labels).

Four hotspots can be identified if we ignore the small gaps between nearby features: one elongated patch at Tromsøflaket, two minor ones along the Egga shelf break, and a fourth one along the shelf margin west and south of Røst bank, in the Træna trench. These hotspots are all wholly contained within the identified core area (Figure 4).

Tromsøflaket had the highest observed (210 n/100 m²) and predicted densities of the whole study area. The overall (observed) mean density was 2 n/100 m².

Patterns of Richness and Abundance of All Megafauna

Figure 5 illustrates the differences in total taxon richness and total abundance of epibenthic megafauna between zones, namely, the background, the core area, and the hotspots. There was no conclusive evidence for a difference in taxon richness between zones (p = 0.08). In contrast, we found a difference in the mean total abundance of epibenthic megafauna (p = 0.008). A post hoc Tukey’s test revealed that only one two-way comparison was significant, and it was between the background and the high-density zone (extremes in the gradient).

FIGURE 5

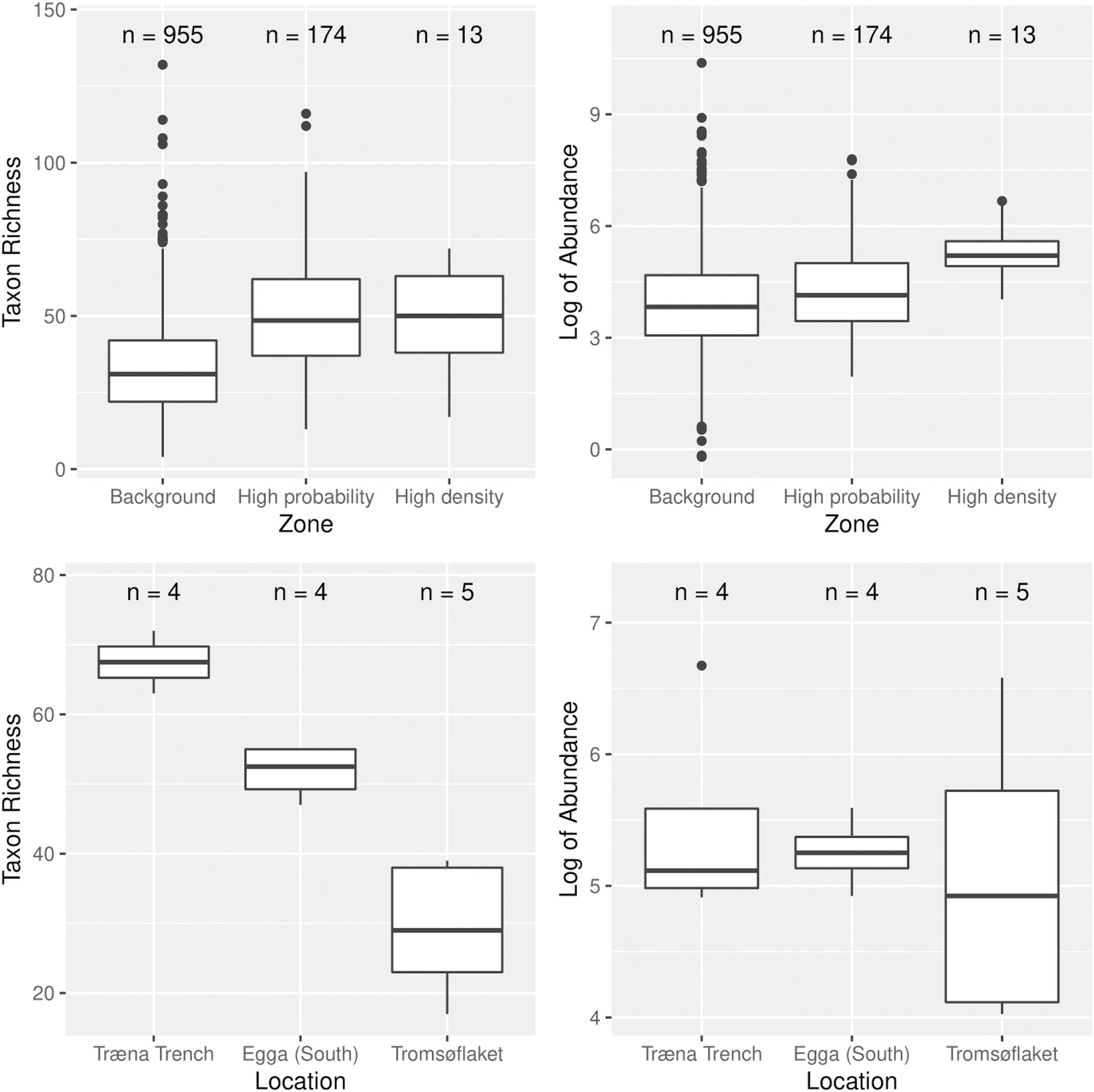
Figure 5. Boxplots illustrating patterns in epibenthic megafaunal taxon richness, and total abundance of epibenthic megafauna (which was log-transformed) in relation to the predicted distribution of soft-bottom, deep-sea sponges. On the top plots we compare these parameters (namely richness and abundance) in relation to a “gradient” toward the areas of highest predicted sponge density. The three zones compared are “background” (low probability and low density), “high probability” (probability above 0.75 and density below 13 n/100 m²) and “high density” (the four identified hotspots). On the bottom plots we compare richness and abundance among three of the four hotspots (one of them did not have any sampling stations within). Also included are the number of stations in each group. Note that the bottom plots represent the variation among the 13 samples in the high-density zone (see the plot above).

The comparison between hotspots (bottom plots in Figure 5) gave us further insight into the ecosystem structure and function of these areas in relation to each other. The hotspot at Træna had much higher taxon richness than Tromsøflaket. It is less clear whether there are real differences in total abundance between hotspots because of the large variation between samples, particularly at Træna and Tromsøflaket. There are nevertheless very few samples to draw conclusions.

The high abundance at Tromsøflaket was accounted for by the presence of brachiopods, which are in the limit of what can be considered “mega” fauna.

Discussion

This study aimed to discover the distribution of soft-bottom DSSAs in the Barents Sea region, identify the benefits of using density data over presence/absence data for this community, and explore whether the “indicator-species list” collective modeling approach is adequate to highlight conservation-relevant hotspots for this community.

In agreement with other authors (e.g., Howard et al., 2014; Dallas and Hastings, 2018) we find that predicted probability maps based on presence/absence data may be adequate to highlight regions of interest, but are insufficient to determine particular areas that may require management attention, for example because they harbor high densities of megafauna. We shall be more specific: it would be virtually impossible (for, let’s say, a fisheries manager) to delineate the boundaries of what we have termed the Tromsøflaket patch (whose existence is known from by-catch data, see Mortensen, 2005, and whose conservation value is undisputed) using the probability map alone as a supporting tool. Depending on the threshold they used, they would come up with either a huge, unmanageable area, or with a tiny, irrelevant one; no single probability threshold even approximates the boundaries the Tromsøflaket patch.

Predictive modeling of density has enabled us, in contrast, to detect specific locations of conservation interest and more importantly, of reasonable size, even if delineating their boundaries required some “visual” calibration and is admittedly, hardly reproducible. Should there be any dispute, though (let’s say between fisheries managers and conservation practitioners), this can easily be settled by looking at the stability of the boundaries in relation to thresholds. Indeed, the boundary around Tromsøflaket was very stable, while the Træna patch completely disappears raising the threshold by 1 unit! Therefore, the evidence suggests that Tromsøflaket patch should be put forward as an area where management action can help protect DSSAs.

Very few studies have looked at biological differences within the predicted range of a species or habitat of interest, although some (e.g., Hui and McGeoch, 2008; Boulangeat et al., 2012) have suggested that looking at species co-occurrence and/or biotic interactions is beneficial to model species distributions. The use of whole, epibenthic community data has enabled us to validate the indicator species approach from the point of view of total abundance of epibenthic megafauna and we provide evidence that areas of increased biomass can be detected by modeling the density of these species of soft-bottom, deep-sea sponges. But it has also called into question whether the locations detected are equivalent to one another as far as their species assemblage. We have found that there can be substantial variation between locations (keep in mind the bottom plots of Figure 5), even when they have been modeled using the same dataset and the same model. While this result is intriguing and raises interesting ecological and management-related questions (some of which will be discussed in the paragraphs that follow), it is not yet clear how dependent it is on the chosen thresholds. Further work is planned to analyze the data in a framework that is free from binning the predictions into zones but rather, are used as a continuous variable.

Modeling a collective of species rather than a single one is a good strategy from the point of view of the model because one quickly increases the number of presences in the data. But even with a list of co-occurring species, it may be that other species are in fact dominant in the result, or that mosaics are present. Indeed, the community observed at Træna consisted of many types of sponges, not only those modeled here but also taxa such as Axinellidae (including species of Phakellia and Axinella), and Antho dichotoma. It follows from our results that our knowledge on the structure and function of this marine ecosystem is still poor, and equally, that work must continue to develop indicators that point to some homogenous entity (one may even add, worthy of the name “indicator”) to ensure that detected locations are representative of each other.

On the other hand, it may be that DSSAs and probably other marine ecosystems as well, are a case of a fuzzy category, meaning that there is no list of attributes (species) that can unambiguously define the category (Levitin, 2014). From this point of view, one could only say that something is a DSSA when it looks similar to a declared DSSA, thereby doing away with the whole approach where species are used as a proxy for the presence of the habitat (the indicator species approach).

Much more work is needed to make this approach operational. For comparison, notice that an “ecological indicator” is a variable that is measured in order to derive (i.e., directly and without the need for additional data) the status of some other variable which is really the variable of interest but which itself is unfeasible to measure. Notoriously, the VME literature shows that the presence of VME indicators (or even their known density) cannot tell us whether the location should or should not be declared a VME. This is epitomized by an ongoing search for universally applicable density thresholds for VME indicators, threshold values which are proving more than a little elusive (e.g., Baco-Taylor et al., 2020). The MarVid database offers a rare opportunity to ascertain the assumptions that are implicit in using SDMs as a basis for mapping VMEs and offering conservation advice, as well as to develop new approaches more aligned with the concept of fuzzy categories which may prove easier to operationalize.

We must not forget that the (density) model accounted for less than 31% of variation in the response data. Similarly, our model may be incurring some degree of overfitting, particularly given (a) the existence of mass occurrences in the area and (b) the extent to which we have extrapolated our predictions. Therefore, model predictions should be assessed with a generous dose of skepticism.

The partial dependence plots of the top two contributing variables showed intuitive minimum values, encountered within the study region, while a maximum value was not encountered. This suggests that the model may be adequate within the survey area but should be re-trained with data from elsewhere in the Barents Sea, and particularly from the areas of model disagreement (yellow and red, in Figure 3) to increase confidence. Considering this, we would not recommend making any policy decisions based solely on the predictions that are completely outside the data range.

While additional training data would certainly improve the model, so would adjustments in the predictor variables. Let us discuss first the aspects that worked, before we move onto potential improvements.

The variables used as predictors within this study highlighted temperature and salinity, together with depth as being important for locating soft-bottom DSSAs in the Barents Sea region. All terrain and geological variables were less important. This aligns well with the findings of other studies (e.g., Beazley et al., 2015; Pearman et al., 2020) that oceanographic variables are more important than terrain variables for defining benthic species distributions. This points to a more mechanistic relationship existing between oceanographic conditions and benthic species composition (described in Young et al., 1996 for the case of sponges), which is emerging thanks to the fact that oceanographic models are becoming more accessible to researchers engaged in benthic SDM, while previous studies utilized only topographic variables and were relying upon the terrain characteristics as proxies for the oceanographic parameters (Wilson et al., 2006).

Variable importance in our model(s) reflected this very well, but not so the partial response curves, where a bell-shaped curve would have been a better diagnostic than one where a drop follows a peak. We have already discussed the degree to which model overfitting may be responsible for this, but equally, there could have been misrepresentations in the oceanographic layers. Let’s not forget that the resolution of the models is 800 m and may be missing spatial variation of temperatures and salinities occurring over the varied topography often associated with shelf break landscapes (e.g., canyons and throughs).

Similarly, our oceanographic models may not necessarily be representative of the period when the data were collected, particularly the B800 model which only ran for 1 year, and furthermore, that the Barents Sea may be experiencing broad scale climatic/oceanographic changes (Lind et al., 2018).

In addition to aligning the time period better, our ability to quantify the relationship between soft-bottom, deep-sea sponges and oceanographic descriptors may be much increased by letting the ROMS models simulate the same months where our species were observed, or in other words, exclude all the values from January and February. These factors undoubtedly limit the degree of trust we can place in the model predictions.

Among the clearly missing variables from our set of potential predictors of soft-bottom DSSAs is sediment type. The MAREANO project does routinely produce sediment maps which have coverage across the MAREANO area (Norges geologiske undersøkelse/MAREANO, 2015), but, as this study predicts beyond the range of the MAREANO area, we have strayed into areas with less reliable/non-existent sediment maps as potential model inputs. It is therefore possible that a future predictive model will be able to better refine were the soft-bottom DSSA hotspots lie, filtering out areas with non-suitable sediment types. It should be acknowledged that these soft-bottom sponges often originally settle on a small piece of gravel or stone that later becomes embedded in the adult colony’s base. Calling these species a “soft-bottom” community is therefore a slight misnomer, and indeed many of these species are found on rocks in fjord areas. However, the soft-bottom DSSA does tend to aggregate on a predominantly soft bottom, so models including sediment type may be able to improve our predictions. It is also possible that such a model may be able to identify the mosaicked hard-bottom and soft-bottom sponge community from the Træna area without a deeper examination of species lists. However, in that event we would still suggest a deeper exploration of the whole-community data to consider what other differences may be being missed by the indicator-species-only models being built.

In summary, we have produced new maps which may be useful for the identification of potential conservation-relevant hotspots for soft-bottom DSSAs in the Barents Sea. We would primarily advocate the use of probability models for identifying areas to study further. However, we would recommend using abundance or density models to try and highlight the potential conservation-relevant hotspots in a region. Lastly, we believe it is important to undertake a deeper exploration of the associated fauna, beyond only the indicator species used to build conservation-relevant models. This data can provide marine managers with more nuanced base from which to make conservation decisions, especially if there is a need to choose between hotspots when designing conservation efforts.

Data Availability Statement

The data used in this study are available for download at: https://zenodo.org/record/4302591. The source code needed to reproduce the results reported in this paper is available at this repository: https://github.com/GeOnoveva/fmars.2020.496688/releases/tag/v0.1.

Author Contributions

PB-M and GG-M proposed the concept. GG-M conducted the data analysis. GG-M and RR wrote the manuscript. JA provided access to, and information about the oceanographic data. All authors contributed to the article and approved the submitted version.

Funding

Funding for this work came in full from the MAREANO Programme (Norway).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to acknowledge the contributions by Margaret Dolan (who helped provide the satellite-derived data), Kjell Bakkeplass (who helped process some of the bathymetric data), Audun Ronesen (for technical support), and Gjertrud Jensen, Yngve Klungseth Johansen, and Anne Kari Sveistrup for their continued excellence and patience performing video analyses. Thanks are due also to Henning Wehde for a much-needed push at a critical time.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2020.496688/full#supplementary-material

Footnotes

References

Asplin, L., Albretsen, J., Johnsen, I. A., and Sandvik, A. D. (2020). The hydrodynamic foundation for salmon lice dispersion modeling along the Norwegian coast. Ocean Dyn. 70, 1151–1167. doi: 10.1007/s10236-020-01378-0