Travelling Expenses: The Energy Cost of Diel Vertical Migrations of Epipelic Microphytobenthos

The physiology of the diel movements of epipelic microphytobenthic diatoms is not fully understood. As well, the evolutionary pressures that led to migratory behavior and the ecological role of vertical migrations remain unknown. The behavioral photoprotection hypothesis, according to which the diatoms move along the vertical light gradient to find their optimal light environment, is the most generally accepted. However, the motion is associated with an energy cost that has not been fully acknowledged before. To throw light on this issue, we looked at the mechanisms of diatom locomotion and reviewed their patterns of movement. Making use of published data, we estimated an energy cost of 0.12 pJ for a typical diatom cell to move upward (or downward) in a 400 μm photic zone. This amounts to 3.93 ×10⁻¹⁸ mol of ATP, which are released by the oxidation of 1.31 ×10⁻¹⁹ mol of glucose. This represents only 0.0001% of the daily net photosynthetic production of a typical microphytobenthic diatom cell, showing that diel vertical migrations have a negligible impact on cell and ecosystem energy budget. Even though the migration energy cost of individual cells may depart almost two orders of magnitude from the central value presented for a typical diatom (depending on cell size, velocity of displacement, and viscosity of the medium), the maximum value calculated is still negligible from the metabolic and ecologic point of view. Results show that behavioral photoprotection might be an energetically cheap mechanism, offering competitive advantages when compared with structural/physiological photoprotection.

Locomotion of Diatoms

Locomotion is present among unicellular organisms (prokaryotes and eukaryotes) and eukaryotic cells of multicellular organisms. The locomotion of unicellular eukaryotes (e.g., free-living protozoa) is mainly used for feeding, whereas it plays a central role in the development of multicellular organisms. Also, in the latter type of organisms, specialized cells can move inside the body for specific reasons, such as leukocytes, which move to grant immune response, being able to travel long distances in the organs in just a few hours (Vargas et al., 2017). Eukaryotic cells and unicellular organisms evolved several mechanisms of locomotion (Chowdhury, 2013). The specific locomotion mechanism of a given organism is dependent on the characteristics of its natural habitat. If the organism lives in a liquid medium, it will swim or, in certain cases, adjust its position on the water column by changing its floatability (Villareal, 1992). If the organism lives in a thin film at the interface between a solid surface and liquid medium, or in the interior of a three-dimensional matrix, gliding will be its preferred way of locomotion (Sibley et al., 1998; Spormann, 1999). Some microorganisms may exhibit several mechanisms of locomotion. The term “amoeboid migration,” named after the protozoon Amoeba proteus, subsume several of those cellular mechanisms, ranging from blebbing motility to entirely actin-polymerization-based gliding. These apparently different mechanisms, however, might be variants of an archetypal one, showing different contributions of actin protrusion, actomyosin contraction, and substrate adhesion, where blebbing and gliding represent the extreme versions of a common “ameboid” locomotion (Lammermann and Sixt, 2009). Generally speaking, three different locomotion mechanisms have been postulated: (i) force generated by polymerization of cytoskeletal protein filaments (actin and microtubules), (ii) force generated by cytoskeletal motors by their interactions with filamentous tracks, and (iii) forces of hydrostatic (osmotic) origin (Chowdhury, 2013). In the present review we will address only the force generated by polymerization of cytoskeletal protein filaments, since it seems the only one to be involved in diatom locomotion. The motility of the colonial diatom Bacillaria paxillifera was the subject of the first research on diatoms ever published, by the Danish naturalist Otto Friedrich Müller in 1783 (Ussing et al., 2005). The synchronized movement of the individual diatom cells in the colony captured the inspiration of generations of scientists, intrigued by the mechanism of locomotion, since no mobile parts were visible. In fact, the pennate diatom Bacillaria paxillifer forms a colony where the adjacent cells smoothly and almost continuously slide, without any visible motility structure, such as cilia or flagella. Although the ecological and physiological significance of this movement is still unknown, some progress has been made on the elucidation of its mechanism. In fact, imaginative models on diatom motility have a long-standing history (Edgar, 1982). The theory of jet propulsion goes back to XIX century. In the first half of the XX century several models appeared: West (1916) and Fritsch (1935) reviewed several authors and described models as diverse as the ones based on cilia, pseudopodia, mucilaginous filaments, osmotic currents, undulating membranes, contractile protoplasm, streaming protoplasm, gas expulsion, and water jets (Hopkins and Drum, 1966). However, these models were not resounding, and another hypothesis of diatom locomotion—an actin-based motility model—was suggested by Edgar and Pickett-Heaps (1983) and Edgar and Zavortink (1983). Initially, the raphe mucilage strands (EPS, extracellular polymeric substances) adhere to the substratum during the gliding process. Additionally, transmembrane components are linked to actin bundles that lie underneath the plasmalemma at the raphe. Afterwards, a force applied to the transmembrane protein (e.g., putative myosin)/actin connectors, parallel to the actin bundle, produces movement of the transmembrane proteins through the cell, and consequent movement of the cell in the direction opposite to the force (Aumeier and Menzel, 2012). A similar mechanism has been proposed to explain the locomotion of other protists that exhibit substrate-adherence mediated gliding (Preston and King, 1996; Dobrowolski et al., 1997; Pinder et al., 1998). A variant of the Edgar model has been proposed to explain the locomotion of Navicula sp., postulating that it is done via two or more pseudopods or stalks projected out of the frustules. The adhesion can be secure due to the pull-off of one pseudopod or stalk from the substratum through EPS, and the positive pressure is produced to balance the adhesion because of the push-down of another pseudopod or stalk against the substratum. Because of the positive pressure, traction is produced, acting as a driving force of movement, and the other pseudopod or stalk can detach from the substratum, ensuing the locomotion (Wang et al., 2013). Therefore, locomotion requires two steps: temporary adhesion to the substrate, and subsequent detachment to allow displacement. Though Edgar and co-workers explained that the mucilage is detached on reaching the apical raphe ending called helictoglossa (Edgar and Pickett-Heaps, 1983), there is no empirical evidence supporting this assumption, since the expected aggregation of EPS at the helictoglossa has never been observed (Wang et al., 2013).

Cytoskeleton-disrupting drugs were used to examine the importance of actin, myosin, and microtubules in diatom gliding, providing additional evidence of their putative role. Contradictory results were found, with some drugs showing the ability to inhibit diatom gliding, where others failed to do it (Poulsen et al., 1999). Since gliding was hampered by the known actin inhibitors cytochalasin A and latrunculin A and by the myosin inhibitor 2,3-butanedione monoxime, it is thought to be driven by the actomyosin system of these diatoms (Edgar and Pickett-Heaps, 1982; Edgar and Zavortink, 1983; Poulsen et al., 1999). Latrunculin A and B inhibit actin assemblage, since they form an incompetent complex with monomeric actin, leading to F-actin depolymerization (Coué et al., 1987; Ayscough et al., 1997). In fact, in B. paxillifer, the actin bundles along the raphe disappeared after a short treatment (1 min) with latrunculin B and reappeared shortly after the removal of this drug (Yamaoka et al., 2016). However, it is not possible to exclude additional indirect effects of latrunculin in diatom motility, e.g., impairing the transport of secretion vesicles to the raphe (Poulsen et al., 1999), as postulated in the model of Edgar.

In any case, cumulative evidence points to a key role of the raphe in the mechanism of locomotion. In fact, only pennate diatoms exhibit true motility. These diatoms have bilateral symmetry and possess a long slit on the frustule (the raphe), which is required to substrate adherence and gliding (Poulsen et al., 1999). EPS, common to all motile diatoms, are excreted through or near the raphe by exocytosis, aiding to the adherence to the substrate (Edgar and Pickett-Heaps, 1982, 1983; Edgar, 1983; McConville et al., 1999). Arguably, the mucilage is cut when arrives at the end of the raphe. The cut is done by the polar fissure, a specific structure of the frustule, and the mucilage remains on the substratum leaving a trace of the gliding motion. Thus, involvement of the mucilage in gliding is also postulated (Poulsen et al., 1999). However, the previous models based exclusively in their excretion have been abandoned. This was partly due to the high energetic cost attributed to EPS synthesis, hindering locomotion. Nonetheless, the formation of certain polysaccharides, as polyuronic acids, requires little energy consumption, providing there is enough supply of glucose. Therefore, secretion of this type of polysaccharide need not to have a high energetic cost for a photosynthetic cell, when compared with more complex molecules such as acetylated glucosamines (Edgar, 1982). Since motility depends on the secreted mucilage to substrate adhesion, granting traction, it is difficult to separate adhesion from motility processes (Poulsen et al., 1999). However, recent results from Cartaxana et al. (2016) showed that the interdependence of motility and adhesion is not so tight as previously thought. In an experiment where the responses of adhesion and gliding speed to temperature were simultaneously measured, the authors found that Pinnularia viridis significantly lost substrate adhesion at temperatures above 20°C, in contrast with Nitzschia linearis, but both species increased gliding speed. The interspecific differences observed between the effects of temperature on motility and adhesion are not surprising, since myosins are strongly conserved among plant groups, whereas mucilage composition is quite diverse, even among diatoms, resulting in differential adhesion to substrates. Another remaining problem is how to explain bidirectionality. It was suggested that the presence of two actin bundles should play a key role. One hypothesis is that two actin bundles have different polarity, myosin motors changing their moving track from one to the other actin bundle during reversion of direction. Another hypothesis admit that the two actin bundles have the same polarity and that several classes of myosins are involved (Wells et al., 1999). The determination of the polarity of the actin bundles will help unravel this uncertainty.

Vertical Movements on Microphytobenthos

Benthic epipelic diatoms usually colonize substrates (intertidal mudflats) with more than 80% of silt (very fine inorganic particles, which are habitually held in suspension by minor water movements at the sediment surface) and clay (mostly colloids of hydrated aluminum silicate, together with iron and other impurities) (see e.g., Elliott et al., 1998). The photic zone of a typical sediment is 0–0.5 mm. Scalar irradiance at the surface (0–0.1 mm) may be higher (~114%) than the incident downward irradiation but it decreases exponentially to non-detectable values at 0.8 mm. This is more than the thickness of some artificial diatom biofilms (Pinularia sp.) formed in Petri dishes (150–380 μm Harbich, 2019). The dimensions of the pennate diatoms are also very variable. Wang et al. (2013) reported for Navicula sp. 10–15 μm length (longitudinal axis) and 4–5 μm wide (transversal axis). Benthic pennate diatoms inhabiting soft intertidal sediments often exhibit active motility within the substrates they inhabit (Cohn and Disparti, 1994; Serôdio et al., 1997, 2001, 2006; Du et al., 2010), in a way strongly dependent from light and other environmental conditions (Cohn and Weitzell, 1996; Cohn et al., 1999, 2015; Falciatore et al., 2000; Serôdio et al., 2006; McLashlan et al., 2012) and synchronized with daily and tidal cycles (Pinckney and Zingmark, 1993). Albeit diatoms' vertical movements were previously known, the disentanglement of its details progressed significantly with the utilization of non-invasive optical techniques such as pulse amplitude modulated fluorometry (Serôdio et al., 1997), imaging pulse amplitude modulated fluorometry (Vieira et al., 2013) and laser induced fluorescence (Utkin et al., 2013; Marques da Silva and Utkin, 2018). These diatoms accumulate at the surface of the sediment during daytime low tide and migrate downward before tidal flooding and/or sunset. Upward migration during daytime low tide allows the cells to reach the sediment photic zone, causing substantial changes on the community algal biomass engaged in photosynthesis (Vieira et al., 2011) and making these communities significant contributors to the primary production of estuarine and coastal areas (Svensson et al., 2014). It has been suggested that downward migration reduces the cells' risk of predation and facilitates the absorption of nutrients (Saburova and Polikarpov, 2003). In addition to this diel, partly endogenous, migration cycles, epipelic diatoms may also migrate downward when exposed to high irradiation (Kromkamp et al., 1998; Perkins et al., 2001; Cartaxana et al., 2011). The observation of this photophobic migration led to the formulation of the theory of “micromigration,” according to which cells continuously change their position within the light gradient, avoiding photoinhibition and increasing photosynthetic performance (Kromkamp et al., 1998; Underwood et al., 2005; Marques da Silva et al., 2017). Light quality also plays a role on diatom movement (Cohn et al., 2004; Perkins et al., 2010). Photophobic responses of pennate diatoms (Cohn et al., 1999, 2015) is based on light perception by one or more photosensitive molecules that seems to act as light sensors in diatoms (Ishikawa et al., 2009; Depaw et al., 2012; Costa et al., 2013), changing the way how mucilage filaments interact with the underlying system of actin/myosin (Edgar and Pickett-Heaps, 1983; Edgar and Zavortink, 1983; Poulsen et al., 1999). Different diatom species have specific sensibility to irradiation wavelength and intensity (Underwood et al., 2005; Serôdio et al., 2006; Cohn et al., 2015). Besides the importance of these movements to diatoms' ecological success, the species-specific EPS secretion associated with motility is involved in complex biochemical interactions and contribute to the stabilization of the algal and microbial environment (Paterson, 1989; Sutherland et al., 1998; Poulsen et al., 2014; Amin et al., 2015). Interestingly, EPS play similar stabilizing roles in very different ecosystems, such as the cyanobacteria-dominated biological soil crusts (Adessi et al., 2018), and they play a key role on the complex microorganization of paradigmatic bacterial biofilms (Marques da Silva and Casetta, 2019). The layer of EPS displays viscoelasticity, so it is neither purely viscous nor purely elastic. The viscous property of the gel adds the movement of diatoms within a biofilm (Harbich, 2019).

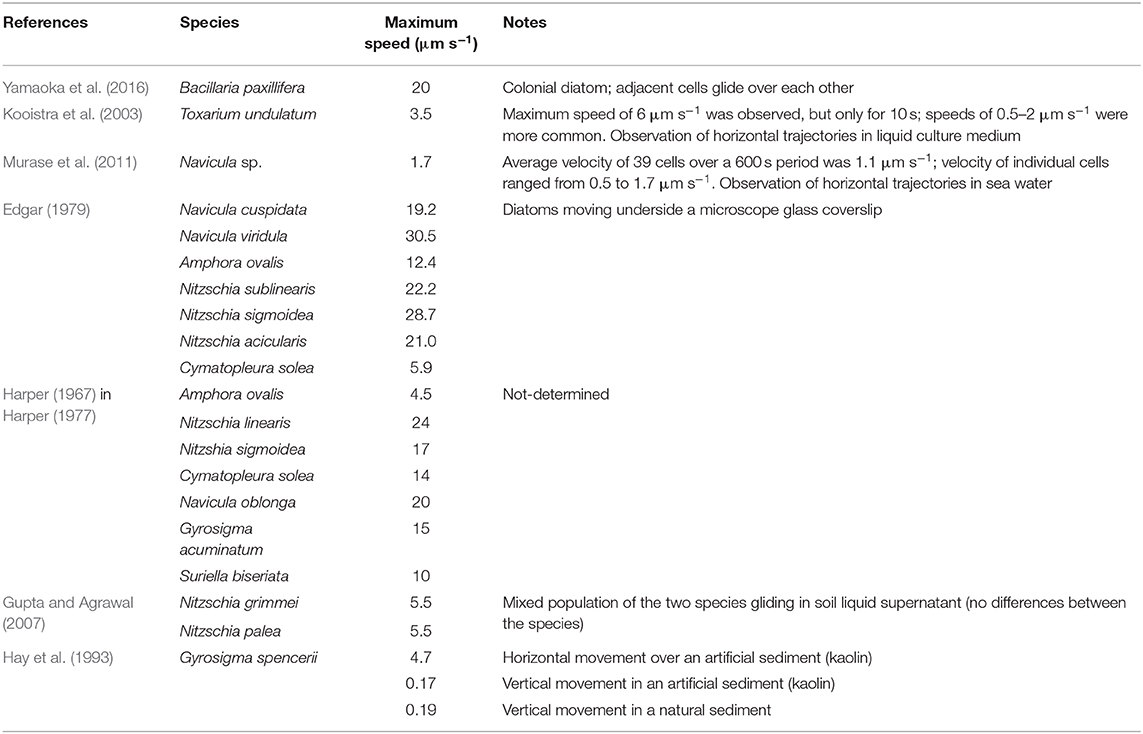
Significant fortnight and seasonal differences on the vertical migration patterns of benthic diatoms have been observed and related to the timing of the low tide, previous light history, and composition of the diatom populations (Serôdio et al., 2008). Vertical community migration movements upward and downward are typically completed in 20 min (Hopkins and Drum, 1966 and references therein) but recently Cartaxana et al. (2016) reported the beginning of downward migration almost 2 h before tidal flooding. Maximum gliding speed reported for diatoms was ~20 μm s⁻¹ (Yamaoka et al., 2016) (Table 1), but this was attained in the very specific situation of gliding in the colonial species Bacillaria paxillifera. Murase et al. (2011) refer maximum gliding speed an order of magnitude lower (1–2 μm s⁻¹) and Wang et al. (2013) cast doubts in the capacity of the current models of diatom locomotion to support even these lower speeds. Nonetheless, gliding speeds from 4 to 12 μm s⁻¹ were reported (Edgar, 1979; Kooistra et al., 2003; Gupta and Agrawal, 2007). It must be noted, however, that these results were obtained in artificial systems where diatoms moved over a plan surface. They may not entirely reflect diatoms' movement in the complex three-dimensional matrix of epipelic MPB. Furthermore, one order of magnitude lower velocities was reported for vertical movements, when compared with horizontal movements (Hay et al., 1993; Consalvey et al., 2004), see Table 1.

TABLE 1

Table 1. Maximum gliding speed of diatoms.

Both increased nutrient availability (Passy, 2007; Lange et al., 2011) and higher temperatures have been suggested to cause increased diatom motility. On one hand, it was suggested that a motile life form would be more competitive in a resource-rich environment. On the other hand, changes in the mechanism of locomotion in motile diatoms may be induced by higher temperature: the viscosity of the cytoplasm in the raphe has been shown to decrease with increased temperature, thus making the motile diatoms capable to move faster at higher temperature. Consequently, global warming may increase the competitive advantage of motile over non-motile diatoms (Svensson et al., 2014). However, when temperature exceeds a certain threshold (30–35°C) a sudden and significant (but reversible) decrease of motility is observed (Cartaxana et al., 2016). This type of temperature response (exhibiting a steady increase of speed followed to a drastic drop to near zero) strongly resembles the response of enzymatic activity to temperature, where an increase of activity is observed to the point where the enzyme undergoes denaturation (Palmer, 1991). In addition to temperature and light, diatom locomotion (and adhesion) may also be influenced by the presence of other diatoms species, since different species will compete differently for limited resources (Cartaxana et al., 2016). Different locomotion and adhesion characteristics may determine the localizations and stratification within the biofilm community. Sediment porosity (quantity of pore space) and permeability (potential water flow) may also play a role in epipelic diatoms' movements. Particle size, its mixture and compaction impact the permeability or percolation rate, with low porosity and permeability in fine grained sediment and vice versa for sands (Elliott et al., 1998). Physical characteristics impact the energy costs of diatom movements within the sediment.

Energy Costs of Vertical Migrations

Mechanical Work That Must Be Performed to Rise to the Sediment Surface

Simplified Energetic Description of the Diatom Locomotion

The minimum energy requirement for a motile diatom to elevate to the sediment surface can be estimated on the basis of the mechanical work it must do to overcome the forces affecting its body in the sediment. A diatom rising to the surface from the photic sediment depth h (Figure 1) must do the mechanical work A_m

$A_m={\displaystyle {\int }_S{F}_{\Sigma }(s)·ds}$

against the total force F_Σ acting along diatom's (in general, curved) path $\text{S}$ in the sediment parametrized in the Cartesian coordinates of Figure 1 (x, y, z) via the arc length s (see e.g., Taalman and Kohn, 2014)

$\begin{array}{l}x=x(s),y=y(s),z=z(s),d{s}^2=d{x}^2+d{y}^2+d{z}^2.\end{array}$

The dot represents the scalar product of F_Σ and local displacement ds. The total force F_Σ comprises the gravitational force F_g = m_dg = −ρ_dV_dge_z, the buoyancy force F_b = ρ_lV_dge_z and the friction force of the sediment F_f = F_f(s). Here m_d and V_d stand for the mass and volume of the diatom, ρ_d and ρ_l are the densities of the diatom and the liquid composing the sediment (water of certain degree of salinity), g = −ge_z is the gravitational acceleration (g ≈ 9.8 m s⁻²) and e_z is a unit vector associated with the vertical axis z.

FIGURE 1

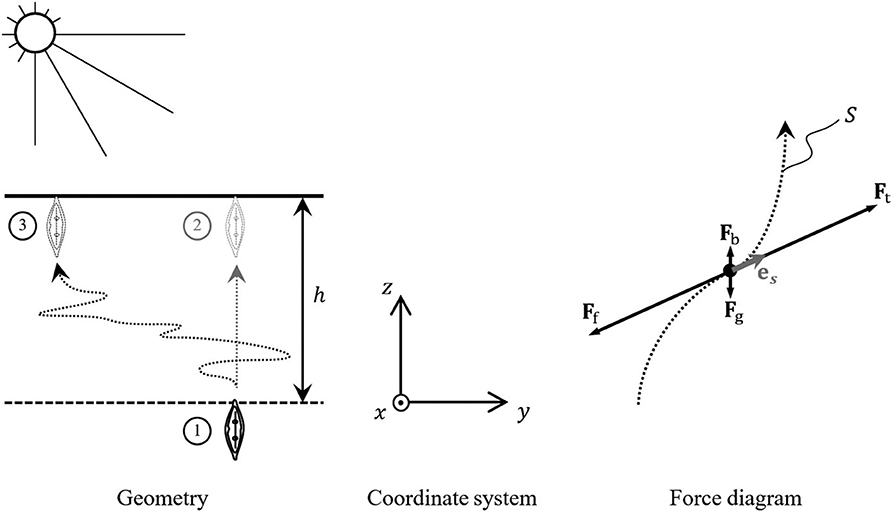
Figure 1. Vertical migratory movements of a motile diatom rising to the surface through a photic sediment layer of depth h.

Taking a conventional model diatom of the size of 10 ×10 ×100 μm³ (Edgar, 1982) and supposing that both ρ_d and ρ_l are of the same magnitude as the water density, ρ_w ≈ 1,000 kg m⁻³, one can readily assess the order of magnitude of the gravitational and buoyancy forces at the level of ρ_wV_dg ≃ 10⁻¹¹ N. Even without taking into account the fact that the two forces tend to compensate each other—producing the net effect of magnitude δρV_dg, where δρ = |ρ_d−ρ_l| ≪ ρ_w—one can exclude them from further discussion due to their smallness with respect to the friction force F_f, whose estimation will be presented below.

Within the framework of the inertialess movement approximation—conventionally used for small objects traveling the most part of its trajectory at nearly constant longitudinal velocity under the action of balanced traction and friction forces (see e.g., Dukhin et al., 1995)—we suppose

$\begin{array}{l}|{\text{F}}_t+{\text{F}}_f|=\left|m_d\frac{d{\text{v}}_d}{dt}\right|\ll \left|{\text{F}}_f\right|=F_f\end{array}$

(here v_d is the velocity of the diatom motion) and get at once F_t = −F_f. As far as the friction force is always directed against the local infinitesimal displacement (speed direction) we have

$\begin{array}{l}{\text{F}}_f=-F_f\frac{\text{d}\text{s}}{ds}=-F_f{\text{e}}_s\Rightarrow {\text{F}}_t=F_t{\text{e}}_s\end{array}$

where e_s is the unit vector tangential to the diatom trajectory, as shown in the force diagram of Figure 1.

Now the mechanical work estimation takes the form of an integral of the tractive force F_t over the diatom path S_h to the surface (z = h)

$\begin{array}{l}{A}_m=-{\displaystyle {\int }_{S_h}{F}_{\Sigma }(s)·ds}\approx -{\displaystyle {\int }_{S_h}{F}_f(s)·ds}\approx {\displaystyle {\int }_{S_h}{F}_t(s)·ds}\\ ={\displaystyle {\int }_{S_h}{F}_t(s)e_s·ds}={\displaystyle {\int }_0^{S_h}{F}_t(s)ds} \end{array}$

where s = 0 corresponds to the starting point of the diatom locomotion, S_h is the diatom path length and F_t(s) represents the module of the tractive force at the point x(s), y(s), z(s). Introducing an average tractive force $\overline{F}$ acting upon the diatom during its motion from s = 0 to s = S_h, we can reduce the mechanical work estimation to

$\begin{array}{l}{A}_m={\displaystyle {\int }_0^{S_h}}{F}_t(s)ds\approx {\displaystyle {\int }_0^{S_h}}\overline{F}ds\approx \overline{F}{\displaystyle {\int }_0^{S_h}}ds=\overline{F}{S}_h.\end{array}$

The simplest estimate of this quantity from below relates to the shortest rectilinear vertical path to the surface, ①→② in Figure 1. In this case S_h = h and

$\begin{array}{l}{A}_m=A_m^{\updownarrow }\approx \overline{F}h.\end{array}$

The value of h corresponds to the thickness of the photic sediment layer, attenuating the sunlight by a factor of 10 and for estuarine sediments can be estimated at about 400 μm (see e.g., Kühl et al., 1997; Consalvey et al., 2004). The experimental data that allow to estimate $\overline{F}$ are related to measurements by Harper and Harper (1967), yielding 8 ×10⁻¹⁰ and 1.1 ×10⁻⁸ N for Nitzschia sigmoidea and Nitzschia linearis, respectively. For the typical locomotion speed of 10 μm s⁻¹ (Edgar, 1982; Consalvey et al., 2004) and a model 10 ×10 ×100 μm³ diatom, such a resistance force was estimated by Edgar (1982) as ca. 10⁻¹⁰ N. Taking this last value as a rough estimation of the average traction force required for the locomotion, we get $A_m^{\updownarrow }\approx$ 0.04 pJ.

Assessment of the Depth-to-Surface Path Length

The actual path $\text{S}$ of the diatom traveling to the surface may be quite distinct from the straight line, representing a complicated curve like one linking positions ① and ③ in Figure 1. In the absence of complete nanoscale description of the sediment structure and the possibility of prediction of the diatom behavior, the process of its migration to the sediment surface can only be described within the framework of the stochastic approach, in which the shape of $\text{S}$ is represented by the arc-length-dependent stochastic variables x(s), y(s), z(s). For all practical purposes of the current research, the stochastic process description can be reduced to a single dimensionless chaoticity parameter

$\begin{array}{l}\sigma \begin{array}{c}\text{def}\\ =\end{array}\frac{E\left\{S_h(x(s),y(s),z(s))\right\}}{h},\end{array}$

where $\text{E}${S_h(x(s), y(s), z(s))} is the mathematical expectation of the path length S_h defined by the random process of the diatom walk along the trajectory x(s), y(s), z(s) toward the surface, starting from state ① (s = 0, z(s) = 0) and ending in state ③ (s = S_h:z(S_h) = h), when the substrate surface z = h is reached. Having σ defined, one can assess the long-run average value of the required energy expense for the mechanical work as

$\begin{array}{l}\overline{A_m}=\overline{F}E\left\{S_h(x(s),y(s),z(s))\right\}=\overline{F}\sigma h=\sigma A_m^{\updownarrow },\sigma >1,\end{array}$

where σ~1 in the case of highly directional vertical motion and σ≫1 for the case of highly chaotic or bidirectional-gliding motion (Yamaoka et al., 2016).

Concrete estimations of $\text{E}${S_h(x(s), y(s), z(s))}, as well as σ and $\overline{A_m}$, may be obtained on the basis of various stochastic models describing, to one degree or another, the real movement of different types of diatoms in accordance to their “decision making” and the sediment granularity or by analysis of recorded diatom tracks. For a very rough estimation of the path chaoticity, one can take the geometric mean of the two extreme values of 1 (rectilinear path) and 10 (highly chaotic motion), yielding an indicative value of σ = 3. For this figure, we readily have an estimation of the characteristic required energy expense of about 0.12 pJ.

Using the algorithm of the friction force estimation by Edgar (1982), we can readily provide a rough assessment of the migration energy cost for a wide range of the diatom species and locomotion conditions. Being based on the work against the viscous force in the thin film separating the raphe (active) face of the cell from the solid particles of substratum—following Edgar, the film thickness is taken to be 0.1 μm—this fully mechanistic approach does not depend on the locomotion type.

Let us introduce the specific energy expenditure per 1 μm of the displacement in the desired direction

$\begin{array}{l}\overline{a_m}=\overline{A_m}/h=\overline{F}\sigma ,\end{array}$

to be measured in femtojoule per micrometer [fJ μm⁻¹]. Acting this way, we get rid of the explicit dependence of the assessment from the thickness of the photic sediment layer h. Notably, for some, especially small path lengths, $\overline{a_m}$ may depend on h through the chaoticity parameter, which makes it desirable to provide the estimation for the entire characteristic range 1 ≤ σ ≤ 10, eventually corresponding to different sediment layer thicknesses that can be observed in real conditions. Another parameter, playing one of the key roles in Edgar's calculation of the force, is the medium viscosity, which as well is subjected to significant variation due to changes in temperature, salinity, traces of the surface-active substances, etc. Given such variety of conditions, the energy expenditure can conventionally be presented in the form of plots of $\overline{a_m}$ vs. σ, the vertical bar showing the uncertainty $\delta (\overline{a_m})$ due to possible variation of the medium viscosity, assessed in accordance with the classical data related to water (Engineeringtoolbox.com, 2020) in the temperature range from 0 to 40°C. Such plots are depicted in Figure 2 for the most illustrative results related to the species of Table 1.

FIGURE 2

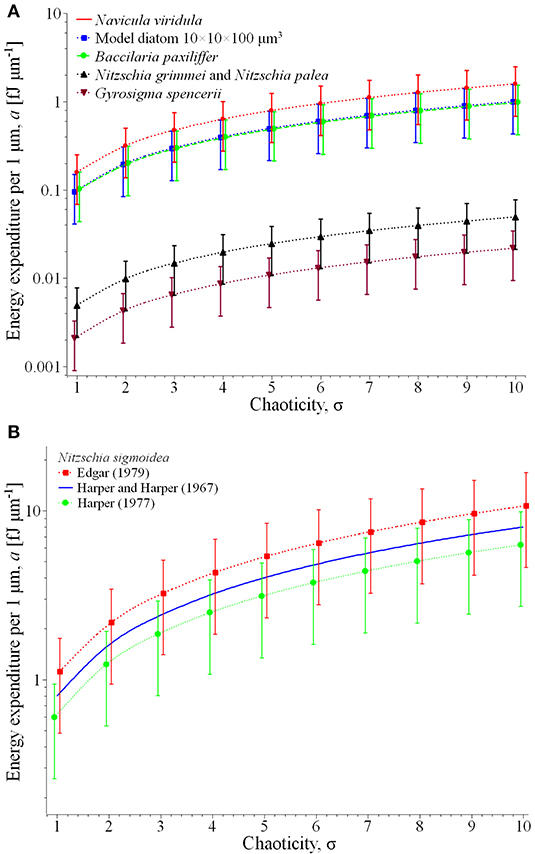
Figure 2. Energy expenditure per 1 μm of the displacement in the desired direction for the most representative species of Table 1 (A) and comparison of the specific results for Nitzschia sigmoidea (B).

Plot (A) represents $\overline{a_m}(\sigma )$ for the group of relatively fast and large diatoms: Navicula viridula, migrating with the locomotion speed v_l = 30.5 μm s⁻¹ (Edgar, 1979) and having the mean surface area of valve face of its cells $\overline{\Omega }$ = 519 μm² (Diatoms org, 2020a); Bacillaria paxillifera of v_l = 20 μm s⁻¹ (Yamaoka et al., 2016) and $\overline{\Omega }$ = 485 μm² (Diatoms org, 2020b); and the model diatom of v_l = 10 μm s⁻¹ and $\overline{\Omega }$ = 1,000 μm² (Edgar, 1982). For this group the specific energy expenditure $\overline{a_m}$ varies from ca. 0.04 (model diatom, rectilinear path in low-viscosity liquid component of the substrate) to 2.5 fJ μm⁻¹ (Navicula viridula, highly chaotic motion in high-viscosity liquid).

The same plot represents another characteristic group of slower diatoms in two extreme dimensions: Nitzschia grimmei and Nitzschia palea collected while growing almost equally in a mixed population, of v_l = 5.5 μm s⁻¹ and small $\overline{\Omega }$ = 90 μm² (Gupta and Agrawal, 2007) as well as Gyrosigma spencerii of v_l = 0.19 μm s⁻¹ (Hay et al., 1993) and large $\overline{\Omega }$ = 1,151 μm² (Phytolab, 2020). Here the energy expenditure assessment yields far lesser figures, from about 0.0009 (Gyrosigma spencerii, rectilinear path and low viscosity) to 0.075 fJ μm⁻¹ (Nitzschia grimmei and Nitzschia palea, highly chaotic motion in high-viscosity liquid).

Plot (B) illustrates a comparison of the theoretical estimate of energy expenditure for Nitzschia sigmoidea based on Edgar's calculation of the force $\overline{F}$ for two different values of the locomotion speed, 17 and 28.7 μm s⁻¹ reported respectively by Harper (1977) and Edgar (1979). As can be seen from the extension of the vertical bars of the plot, the apparently contradictory reported results may be explained by different environmental conditions of observations—in particular, unequal viscosities of the liquid phase of the substrate—in which the same traction force may result to different friction-limited velocities of locomotion. Remarkably, the results are very well-coordinated with the alternative assessment based on the experimental value $\overline{F}$ = 8 ×10⁻¹⁰ N reported by Harper and Harper (1967), represented in the plot by a solid line (no vertical bars as there is no force variation).

Metabolic Energy Requirement and Ecological Implications

The energy expended in the vertical migration of a typical diatom cell over a 400 μm photic zone−0.12 pJ—corresponds to 0.0287 pcal. Since the hydrolysis of one mol of ATP releases ~7,300 cal, the energy expended in the vertical migration of a cell amounts to 3.93 ×10⁻¹⁸ mol ATP. Albeit the theoretical yield of the full oxidation of one mol of glucose is 38 mol ATP, because of losses due to membrane leakage and the cost of transporting pyruvate and ADP into the mitochondrial matrix, more realistic estimates point to 30 mol of ATP per mol of glucose (Rich, 2003). Therefore, the vertical migration of a cell requires the respiration of 1.31 ×10⁻¹⁹ mol of glucose.

Serôdio and Catarino (2000) measured hourly net oxygen production in microphytobenthos mats in the field ranging from 1 to 15 mmol O₂ m⁻² h⁻¹ which correspond to 20–300 fmol O₂ h⁻¹ per cell. If these values are compared the data regarding Phaeodactylum tricornutum axenic cultures at 18°C (150 fmol O₂ h⁻¹ per cell; Feijão et al., 2018), we see that the observed field values are very similar to the ones measured experimentally in the lab. Taking into account that diatoms only migrate during daylight and that intertidal banks only experience one tidal cycle during the day, it is possible to assume that diatoms are only exposed to sunlight for a maximum of 4 h per day (Serôdio and Catarino, 2000). Having this value in mind, the average daily net primary productivity of a diatom cell would correspond to 640 fmol O₂ d⁻¹ per cell (considering minimum and maximum values of 80 and 1,200 fmol O₂ d⁻¹ per cell, respectively). Assuming a 1:1 stoichiometry between O₂ evolution and CO₂ fixation, and that 6 carbon atoms are needed for each glucose molecule, the average amount of glucose produced would be 106.7 fmol d⁻¹ per cell. This would mean an impact in terms of glucose expenses of 0.0001% of the daily glucose production. Even considering a two paths travel (upward and downward) these values—pertaining a typical diatom cell—remain extremely low. Even though the migration energy consumption may vary almost two orders of magnitude above and below this typical value, depending on the size of the diatom cell, the velocity, and chaocity of displacement and the viscosity of the medium (see section Assessment of the Depth-to-Surface Path Length and Figure 2), the maximum fraction of the daily energy allocated to migration would be 0.01%, still a low figure. This contrasts with the energy costs of movement determined for some prokaryotic microorganisms. It is, however, difficult to generalize this comparison, since bacteria have evolved a remarkable diversity of motility systems to adapt to different environments, including swimming in aqueous media, as well as twitching, swarming and gliding on solid and semi-solid surfaces. Albeit significant advances have been made in understanding swimming and swarming motilities powered by flagella, and twitching motility powered by Type IV pili, little is known about gliding motility (Luciano et al., 2011; Nan and Zusman, 2016), the one most directly comparable with diatom motility, where quantitative estimations of energy consumption are virtually absent. As regards swimming, Mitchell (2002) reported a universal inverse relation between the amount of energy expenditure by unit of body mass and the body mass of the organism. Taking the examples this author provides for bacteria, we calculated that these would roughly spent between 0.0004 pcal (the smaller cells) and 2 pcal (the larger cells) to move along the 400 μm of the typical photic zone in microphytobenthos, which fits in the interval between 0.0003 and 3 pcal that we calculated for diatoms. In ecological terms, the low energy cost of epipelic diatoms' vertical migration points out to a highly efficient mechanism of behavioral photoprotection, having a small impact on the ecosystem metabolism. Using this migration mechanism, a square meter of a microphytobenthos mat (considering a cell density of 5 ×10¹¹ cells per square meter; Jesus et al., 2006) releases <0.0001% of the carbon absorbed to the environment, this vertical movement having an almost neglectable effect on the diatom carbon stock. This is important considering that these organisms play a key role as ecosystem engineers and are at the basis of the mudflat trophic chain, fueling not only the sediment secondary productivity (e.g., organic matter mineralization), but also providing food for grazers, inputting significant amounts of carbon-based energy into the estuarine food webs. Moreover, this also reinforces the role of the autotrophic mats as marine carbon sinks and key players in the biological carbon pump at highly efficient rates.

Conclusion

Diatom migration costs rely on several parameters and assumptions that can vary through sediments and microphytobenthic communities. Nevertheless, and considering several average assumptions, a very rough assessment of the energy required for the mechanical diatom motion through the sediment is provided using the conventional inertialess movement approximation. It becomes clear that diatom migration energy expenses depend largely on the chaocity of the path length S_h rather than on the vertical displacement h, making chaotic curved paths highly expensive in terms of energy costs. The lack of information about the statistical properties of the (random) diatom paths in the granular sediments, which impedes reliable assessment of the mathematical expectation of the path length, constitutes a significant research gap that can potentially be bridged using contemporary approaches to the motion modeling. In particular, the asymmetric persistent random walk model (see e.g., Rossetto, 2018) can yield the desired mathematical expectation on the basis of properly assessed transport mean free paths for the upward and downward motion. Alternatively, the path length can be assessed analyzing a representative set of the diatom paths recorded during experimental research. Remarkably, both approaches are hard to implement: For the statistical models, the mean free path (along which the diatom moves quasi rectilinearly) depends on numerous parameters related to the diatom “decision making” and the sediment granularity (average grain size, its dispersion, etc.) that are hard to estimate. An equally hard task is tracking a particular diatom during its migration within highly opaque bulk of the sediment. Nevertheless, and as abovementioned, it is possible to have some average assumptions as basis in order to attain some estimations of the energetic costs associated with the diatom migrations. This was estimated linking both mechanical and biochemical features, resulting in very low energetic costs for the typical diatom cell. This reinforces the key role of vertical migration as an economic mechanism to avoid potential photoinhibition caused by excessive solar radiation on the top of the sediments and maintain the carbon fixation rates of these microphytobenthic communities elevated, and thus greatly contributing to the sediment organic matter, fuelling not only the sediment secondary productivity but also providing energy to higher trophic levels.

Author Contributions

JM conceived the idea. AU and BD did the calculations. All the authors discussed and wrote the manuscript.

Funding

The authors would like to thank Fundação para a Ciência e a Tecnologia (FCT) for funding the research via project grants PTDC/CTA-AMB/30056/2017 (OPTOX), UID/MAR/04292/2019, UID/MULTI/04046/2019 and UID/MULTI/00612/2019. B. Duarte was supported by an FCT investigation contract (CEECIND/00511/2017).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Adessi, A., Cruz de Carvalho, R., De Philippis, R., Branquinho, C., and Marques da Silva, J. (2018). Microbial extracellular polymeric substances improve water retention in dryland biological soil crusts. Soil Biol. Biochem. 116, 67–69. doi: 10.1016/j.soilbio.2017.10.002

CrossRef Full Text | Google Scholar

Amin, S. A., Hmelo, L. R., van Tol, H. M., Durham, B. P., Carlson, L. T., Heal, K. R., et al. (2015). Interaction and signalling between a cosmopolitan phytoplankton and associated bacteria. Nature 522, 98–101. doi: 10.1038/nature14488

PubMed Abstract | CrossRef Full Text | Google Scholar

Aumeier, C., and Menzel, D. (2012). “Secretion in the diatoms,” in Secretions and Exudates in Biological Systems, eds J. M. Vivanco, and F. Baluška (Berlin Heidelberg: Springer-Verlag), 221–250. doi: 10.1007/978-3-642-23047-9_10

PubMed Abstract | CrossRef Full Text | Google Scholar

Ayscough, K. R., Stryker, J., Pokala, N., Sanders, M., Crews, P., and Drubin, D. G. (1997). High rates of actin filament turnover in budding yeast and roles for actin in establishment and maintenance of cell polarity revealed using the actin inhibitor latrunculin-A. J. Cell Biol. 137, 399–416. doi: 10.1083/jcb.137.2.399

PubMed Abstract | CrossRef Full Text | Google Scholar

Cartaxana, P., Cruz, S., Gameiro, C., and Kühl, M. (2016). Regulation of intertidal microphytobenthos photosynthesis over a diel emersion period is strongly affected by diatom migration patterns. Front. Microbiol. 7:872. doi: 10.3389/fmicb.2016.00872

CrossRef Full Text | Google Scholar

Cartaxana, P., Ruivo, M., Hubas, C., Davidson, I., Serôdio, J., and Jesus, B. (2011). Physiological versus behavioral photoprotection in intertidal epipelic and epipsammic benthic diatom communities. J. Exp. Mar. Biol. Ecol. 405, 120–127. doi: 10.1016/j.jembe.2011.05.027

CrossRef Full Text | Google Scholar

Chowdhury, D. (2013). Stochastic mechano-chemical kinetics of molecular motors: A multidisciplinary enterprise from a physicist's perspective. Phys. Rep. 529, 1–197. doi: 10.1016/j.physrep.2013.03.005

CrossRef Full Text | Google Scholar

Cohn, S. A., Bahena, M., Davis, J. T., Ragland, R. L., Rauschenberg, C. D., and Smith, B. L. (2004). Characterization of the diatom photophobic response to high irradiance. Diatom Res. 19, 167–179. doi: 10.1080/0269249X.2004.9705869

CrossRef Full Text | Google Scholar

Cohn, S. A., and Disparti, N. C. (1994). Environmental factors influencing diatom cell motility. J. Phycol. 30, 818–828. doi: 10.1111/j.0022-3646.1994.00818.x

CrossRef Full Text | Google Scholar

Cohn, S. A., Halpin, D., Hawley, N., Ismail, A., Kaplan, Z., Kordes, T., et al. (2015). Comparative analysis of light-stimulated motility responses in three diatom species. Diatom Res. 30, 213–225. doi: 10.1080/0269249X.2015.1058295

CrossRef Full Text | Google Scholar

Cohn, S. A., Spurck, T. P., and Pickett-Heaps, J. D. (1999). High energy irradiation at the leading tip of moving diatoms causes a rapid change in cell direction. Diatom Res. 14, 193–206. doi: 10.1080/0269249X.1999.9705466

CrossRef Full Text | Google Scholar

Cohn, S. A., and Weitzell, R. E. Jr. (1996). Ecological considerations of diatom motility. I. characterization of motility and adhesion in four diatom species. J. Phycol. 32, 928–939. doi: 10.1111/j.0022-3646.1996.00928.x

CrossRef Full Text | Google Scholar

Consalvey, M., Paterson, D. M., and Underwood, G. J. C. (2004). The ups and downs of life in a benthic biofilm: migration of benthic diatoms. Diatom Res. 19, 181–202. doi: 10.1080/0269249X.2004.9705870

CrossRef Full Text | Google Scholar

Costa, B. S., Sachse, M., Jungandreas, A., Bartulos, C. R., Gruber, A., Jakob, T., et al. (2013). Aureochrome 1a is involved in the photoacclimation of the diatom Phaeodactylum tricornutum. PLoS ONE 8:e74451. doi: 10.1371/journal.pone.0074451

CrossRef Full Text | Google Scholar

Coué, M., Brenner, S. L., Spector, I., and Korn, E. D. (1987). Inhibition of actin polymerization by Latrunculin A. FEBS Lett. 213, 316–318. doi: 10.1016/0014-5793(87)81513-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Depaw, F. A., Rogato, A., D'alcal,á, M. R., and Falciatore, A. (2012). Exploring the molecular basis of responses to light in marine diatoms. J. Exp. Bot. 63, 1575–1591. doi: 10.1093/jxb/ers005

PubMed Abstract | CrossRef Full Text | Google Scholar

Diatoms org (2020a). Species: Navicula viridula. Available online at: https://diatoms.org/species/navicula_viridula (accessed April 21, 2020).

PubMed Abstract | Google Scholar

Diatoms org (2020b). Species: Bacillaria Paxillifera. Available online at: https://diatoms.org/species/bacillaria_paxillifera (accessed April 21, 2020).

PubMed Abstract | Google Scholar

Dobrowolski, J. M., Carruthers, V. B., and Sibley, L. D. (1997). Participation of myosin in gliding motility and host cell invasion by Toxoplasma gondii. Mol. Microbiol. 26, 163–173. doi: 10.1046/j.1365-2958.1997.5671913.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Du, G. Y., Oak, J. H., Li, H., and Chung, I. K. (2010). Effect of light and sediment grain size on the vertical migration of benthic diatoms. Algae 25, 133–140. doi: 10.4490/algae.2010.25.3.133

CrossRef Full Text | Google Scholar

Dukhin, S. S., Kretzschmar, G., and Miller, R. (1995). Dynamics of Adsorption at Liquid Interfaces: Theory, Experiment, Application. Amsterdam; New York, NY: Elsevier.

Google Scholar

Edgar, L. A. (1979). Diatom locomotion: computer assisted analysis of cine film. Br. Phycol. J. 14, 83–101. doi: 10.1080/00071617900650111

CrossRef Full Text | Google Scholar

Edgar, L. A. (1982). Diatom locomotion: a consideration of movement in a highly viscous situation. Br. Phycol. J. 17, 243–251. doi: 10.1080/00071618200650261

CrossRef Full Text | Google Scholar

Edgar, L. A. (1983). Mucilage secretions of moving diatoms. Protoplasma 118, 44–48. doi: 10.1007/BF01284745

CrossRef Full Text | Google Scholar

Edgar, L. A., and Pickett-Heaps, J. D. (1982). Ultrastructural localization of polysaccharides in the motile diatom Navicula cuspidata. Protoplasma 113, 10–22. doi: 10.1007/BF01283035

CrossRef Full Text | Google Scholar

Edgar, L. A., and Pickett-Heaps, J. D. (1983). The mechanism of diatom locomotion. I. an ultrastructural study of the motility apparatus. Proc. R. Soc. Lond. B 218, 331–343. doi: 10.1098/rspb.1983.0042

CrossRef Full Text | Google Scholar

Edgar, L. A., and Zavortink, M. (1983). The mechanism of diatom locomotion. II. Identification of actin. Proc. R. Soc. Lond. B 218, 345–348. doi: 10.1098/rspb.1983.0043

CrossRef Full Text | Google Scholar

Elliott, M., Nedwell, S., Jones, N. V., Read, S. J., Cutts, N. D., and Hemingway, K. L. (1998). Intertidal Sand and Mudflats & Subtidal Mobile Sandbanks. An Overview of Dynamic and Sensitivity Characteristics for Conservation Management of Marine SACs. Vol. 2. Oban: Scottish Association for Marine Science (UK Marine SACs Project).

Google Scholar

Engineeringtoolbox.com (2020). Water - Dynamic and Kinematic Viscosity Available online at: https://www.engineeringtoolbox.com/water-dynamic-kinematic-viscosity-d_596.html (accessed April 18, 2020).

Google Scholar

Falciatore, A., D'alcala, R., Croot, P., and Bowler, C. (2000). Perception of environmental signals by a marine diatom. Science 288, 2363–2366. doi: 10.1126/science.288.5475.2363

PubMed Abstract | CrossRef Full Text | Google Scholar

Feijão, E., Gameiro, C., Franzitta, M., Duarte, B., Caçador, I., Cabrita, M. T., et al. (2018). Heat wave impacts on the model diatom Phaeodactylum tricornutum: searching for photochemical and fatty acid biomarkers of thermal stress. Ecol. Indicators 95, 1026–1037. doi: 10.1016/j.ecolind.2017.07.058

CrossRef Full Text | Google Scholar

Fritsch, F. E. (1935). The Structure and Reproduction of the Algae. Vol. 1. Cambridge, CA: Cambridge University Press.

Google Scholar

Gupta, G., and Agrawal, S. C. (2007). Survival and motility of diatoms Navicula grimmei and Nitzschia palea affected by some physical and chemical factors. Folia Microbiol. 52, 127–134. doi: 10.1007/BF02932151

PubMed Abstract | CrossRef Full Text | Google Scholar

Harbich, T. (2019). Movement in EPS matrix: Biofilms on substrate. Available online at: https://www.diatoms.de/en/biofilms-on-substrate (accessed October 31, 2019).

Google Scholar

Harper, M. A. (1967). Locomotion of diatoms and ‘clumping' of blue-green algae (Ph.D. Thesis). University of Bristol.

Google Scholar

Harper, M. A. (1977). “Movements,” in The Biology of Diatoms. ed D. Werner (Oxford: Blackwell Scientific Publications), 224–249.

Google Scholar

Harper, M. A., and Harper, J. F. (1967). Measurements of diatom adhesion and their relationship with movement. Br. Phycol. Bull. 3, 195–207. doi: 10.1080/00071616700650051

CrossRef Full Text | Google Scholar

Hay, S. I., Maitland, T. C., and Paterson, D. M. (1993). The speed of diatom migration through natural and artificial substrata. Diatom Res. 8, 371–384. doi: 10.1080/0269249X.1993.9705268

CrossRef Full Text | Google Scholar

Hopkins, J. T., and Drum, R. W. (1966). Diatom motility: an explanation and a problem. Br. Phycol. Bull. 3, 63–67. doi: 10.1080/00071616600650081

CrossRef Full Text | Google Scholar

Ishikawa, M., Takahashi, F., Nozaki, H., Nagasato, C., Motomura, T., and Kataoka, H. (2009). Distribution and phylogeny of the blue light receptors aureochromes in eukaryotes. Planta 230, 543–552. doi: 10.1007/s00425-009-0967-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Jesus, B., Mendes, C. R., Brotas, V., and Paterson, D. M. (2006). Effect of sediment type on microphytobenthos vertical distribution: modelling the productive biomass and improving ground truth measurements. J. Exp. Mar. Biol. Ecol. 332, 60–74. doi: 10.1016/j.jembe.2005.11.005

CrossRef Full Text | Google Scholar

Kooistra, W. H. C. F., De Stefano, M., Mann, D. G., Salma, N., and Medlin, L. K. (2003). Phylogenetic position of Toxarium, a pennate-like lineage within the centric diatoms (Bacillariophyceae). J. Phycol. 39, 185–197. doi: 10.1046/j.1529-8817.2003.02083.x

CrossRef Full Text | Google Scholar

Kromkamp, J., Barranguet, C., and Peene, J. (1998). Determination of microphytobenthos PSII quantum efficiency and photosynthetic activity by means of variable chlorophyll fluorescence. Mar. Ecol. Prog. Ser. 162, 45–55. doi: 10.3354/meps162045

CrossRef Full Text | Google Scholar

Kühl, M., Lassen, C., and Revsbech, N. (1997). A simple light meter for measurements of PAR (400 to 700 nm) with fiber-optic microprobes: application for P vs E0(PAR) measurements in a microbial mat. Aquat. Microb. Ecol. 13, 197–207. doi: 10.3354/ame013197

CrossRef Full Text | Google Scholar

Lammermann, T., and Sixt, M. (2009). Mechanical modes of ‘amoeboid' cell migration. Curr. Opin. Cell Biol. 21, 636–644. doi: 10.1016/j.ceb.2009.05.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Lange, K., Liess, A., Piggott, J. J., Townsend, C. R., and Matthaei, C. D. (2011). Light, nutrients and grazing interact to determine stream diatom community composition and functional group structure. Freshw. Biol. 56, 264–278. doi: 10.1111/j.1365-2427.2010.02492.x

CrossRef Full Text | Google Scholar

Luciano, J., Agrebi, R., Le Gall, A. V., Wartel, M., Fiegna, F., Ducret, A., et al. (2011). Emergence and modular evolution of a novel motility machinery in Bacteria. PLoS Gene. 7:e1002268. doi: 10.1371/journal.pgen.1002268

PubMed Abstract | CrossRef Full Text | Google Scholar

Marques da Silva, J., and Casetta, E. (2019). “Why a species-based approach to biodiversity is not enough. lessons from multispecies biofilms,” in From Assessing to Conserving Biodiversity, eds E. Casetta, J. Marques da Silva, and D. Vecchi (Berlin: Springer), 195–217. doi: 10.1007/978-3-030-10991-2_9

CrossRef Full Text | Google Scholar

Marques da Silva, J., Cruz, S., and Cartaxana, P. (2017). Inorganic carbon availability in benthic diatom communities: photosynthesis and migration. Philos. Trans. R. Soc. Lond. B 372:20160398. doi: 10.1098/rstb.2016.0398

PubMed Abstract | CrossRef Full Text | Google Scholar

Marques da Silva, J., and Utkin, A. B. (2018). Application of laser induced fluorescence in functional studies of photosynthetic biofilms. Processes 6:227. doi: 10.3390/pr6110227

CrossRef Full Text | Google Scholar

McConville, M. J., Wetherbee, R., and Bacic, A. (1999). Subcellular location and composition of the wall and secreted extracellular sulphated polysaccharides/proteoglycans of the diatom Stauroneis amphioxys Gregoty. Protoplasma 206, 188–200. doi: 10.1007/BF01279266

CrossRef Full Text | Google Scholar

McLashlan, D. H., Underwood, G. J. C., Taylor, A. R., and Brownlee, C. (2012). Calcium release from intracellular stores is necessary for the photophobic response in the benthic diatom Navicula perminuta (Bacillariophyceae). J. Phycol. 48, 675–681. doi: 10.1111/j.1529-8817.2012.01158.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitchell, J. G. (2002). The energetics and scaling of search strategies in Bacteria. Am. Nat. 160, 727–740. doi: 10.1086/343874

PubMed Abstract | CrossRef Full Text | Google Scholar

Murase, A., Kubota, Y., Hirayama, S., Kumashiro, Y., Okano, T., Mayama, S., et al. (2011). Two-dimensional trajectory analysis of the diatom Navicula sp. using a micro chamber. J. Microbiol. Methods 87, 316–319. doi: 10.1016/j.mimet.2011.09.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Nan, B., and Zusman, D. R. (2016). Novel mechanisms power bacterial gliding motility. Mol. Microbiol. 101, 186–193. doi: 10.1111/mmi.13389

PubMed Abstract | CrossRef Full Text | Google Scholar

Palmer, T. (1991). Understanding Enzymes, 3rd Edn. Chichester: Ellis Horwood Limited.

Google Scholar

Passy, S. I. (2007). Diatom ecological guilds display distinct and predictable behavior along nutrient and disturbance gradients in running waters. Aquat. Bot. 86, 171–178. doi: 10.1016/j.aquabot.2006.09.018

CrossRef Full Text | Google Scholar

Paterson, D. M. (1989). Short-term changes in the erodibility of intertidal cohesive sediments related to the migratory behavior of epipelic diatoms. Limnol. Oceanogr. 34, 223–234. doi: 10.4319/lo.1989.34.1.0223

CrossRef Full Text | Google Scholar

Perkins, R. G., Lavaud, J., Serôdio, J., Mouget, J. L., Cartaxana, P., Rosa, P., et al. (2010). Vertical cell movement is a primary response of intertidal benthic biofilms to increasing light dose. Mar. Ecol. Prog. Ser. 416, 93–103. doi: 10.3354/meps08787

CrossRef Full Text | Google Scholar

Perkins, R. G., Underwood, G. J. C., Brotas, V., Snow, G. C., Jesus, B., and Ribeiro, L. (2001). Responses of microphytobenthos to light: primary production and carbohydrate allocation over an emersion period. Mar. Ecol. Prog. Ser. 223, 101–112. doi: 10.3354/meps223101

CrossRef Full Text | Google Scholar

Phytolab (2020). Gyrosigma spencerii. Ann Arbor: University of Michigan. reatLakesDiatomHomePage/Gyrosigma/GyrosigmaAvailable online at: http://umich.edu/~phytolab/Gspencerii/Gyrosigmaspenceriicard.html#authority (accessed April 22, 2020).

Google Scholar

Pinckney, J., and Zingmark, R. G. (1993). Photophysiological responses of intertidal benthic microalgal communities to in situ light environments: methodological considerations Limnol. Oceanogr 38, 1373–1383. doi: 10.4319/lo.1993.38.7.1373

CrossRef Full Text | Google Scholar

Pinder, J. C., Fowler, R. E., Dluzewski, A. R., Bannister, L. H., Lavin, F. M., Mitchell, G. H., et al. (1998). Actomyosin motor in the merozoite of the malaria parasite, Plasmodium falciparum: implication for red cell invasion. J. Cell Sci. 111, 1831–1839.

PubMed Abstract | Google Scholar

Poulsen, N., Kroger, N., Harrington, M. J., Brunner, E., Paasch, S., and Buhmann, M. T. (2014). Isolation and biochemical characterization of underwater adhesives from diatoms. Biofouling 30, 513–523. doi: 10.1080/08927014.2014.895895

PubMed Abstract | CrossRef Full Text | Google Scholar

Poulsen, N. C., Spector, I., Spurck, T. P., Schultz, T. F., and Wetherbee, R. (1999). Diatom gliding is the result of an actin-myosin motility system. Cell Motil. Cytoskel. 44, 23–33. doi: 10.1002/(SICI)1097-0169(199909)44:1<23::AID-CM2>3.0.CO;2-D

PubMed Abstract | CrossRef Full Text | Google Scholar

Preston, T. M., and King, C. A. (1996). Strategies for cell-substratum dependent motility among protozoa. Acta Protozool. 35, 3–12.

Google Scholar

Rich, P. R. (2003). The molecular machinery of Keilin's respiratory chain. Biochem. Soc. Trans. 31, 1095–1105. doi: 10.1042/bst0311095

PubMed Abstract | CrossRef Full Text | Google Scholar

Rossetto, V. (2018). The one-dimensional asymmetric persistent random walk. J. Stat. Mech. 2018:043204. doi: 10.1088/1742-5468/aab507

CrossRef Full Text | Google Scholar

Saburova, M. A., and Polikarpov, I. G. (2003). Diatom activity within soft sediments: behavioural and physiological processes. Mar. Ecol. Prog. Ser. 251, 115–126. doi: 10.3354/meps251115

CrossRef Full Text | Google Scholar

Serôdio, J., and Catarino, F. (2000). Modelling the primary productivity of intertidal microphytobenthos: time scales of variability and effects of migratory rhythms. Mar. Ecol. Prog. Ser. 192, 13–30. doi: 10.3354/meps192013

CrossRef Full Text | Google Scholar

Serôdio, J., Coelho, H., Vieira, S., and Cruz, S. (2006). Microphytobenthos vertical migratory photoresponse as characterised by light-response curves of surface biomass. Estuar. Coast. Shelf Sci. 68, 547–556. doi: 10.1016/j.ecss.2006.03.005

CrossRef Full Text | Google Scholar

Serôdio, J., Marques da Silva, J., and Catarino, F. (1997). Nondestructive tracing of migratory rhythms of intertidal benthic microalgae using in vivo chlorophyll a fluorescence. J. Phycol. 33, 542–553. doi: 10.1111/j.0022-3646.1997.00542.x

CrossRef Full Text | Google Scholar

Serôdio, J., Marques da Silva, J., and Catarino, F. (2001). Use of in vivo chlorophyll a fluorescence to quantify short-term variations in the productive biomass of intertidal microphytobenthos. Mar. Ecol. Prog. Ser. 218, 45–61. doi: 10.3354/meps218045

CrossRef Full Text | Google Scholar

Serôdio, J., Vieira, S., and Cruz, S. (2008). Photosynthetic activity, photoprotection and photoinhibition in intertidal microphytobenthos as studied in situ using variable chlorophyll fluorescence. Cont. Shelf Res. 28, 1363–1375. doi: 10.1016/j.csr.2008.03.019

CrossRef Full Text | Google Scholar

Sibley, L. D., Håkansson, S., and Carruthers, V. B. (1998). Gliding motility: an efficient mechanism for cell penetration. Curr. Biol. 8, R12–R14. doi: 10.1016/S0960-9822(98)70008-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Spormann, A. M. (1999). Gliding motility in bacteria: insights from studies of Myxococcus xanthus. Microbiol. Mol. Biol. Rev. 63, 621–641. doi: 10.1128/MMBR.63.3.621-641.1999

PubMed Abstract | CrossRef Full Text | Google Scholar

Sutherland, T. F., Grant, J., and Amos, C. L. (1998). The effect of carbohydrate production by the diatom Nitzschia curvilieata on the erodibility of sediment. Limnol. Oceanogr 43, 65–72. doi: 10.4319/lo.1998.43.1.0065

CrossRef Full Text | Google Scholar

Svensson, F., Norberg, J., and Snoeijs, P. (2014). Diatom cell size, coloniality and motility: Trade-offs between temperature, salinity and nutrient supply with climate change. PLoS ONE 9:e109993. doi: 10.1371/journal.pone.0109993

PubMed Abstract | CrossRef Full Text | Google Scholar

Taalman, L., and Kohn, P. (2014). Calculus. New York, NY: W.H. Freeman and Company.

Google Scholar

Underwood, G. J. C., Perkins, R. G., Consalvey, M. C., Halon, A. R. M., Oxborough, K., Baker, N. R., et al. (2005). Patterns in microphytobenthic primary productivity: species-specific variation in migratory rhythms and photosynthetic efficiency in mixed-species biofilms. Limnol. Oceanogr 50, 755–767. doi: 10.4319/lo.2005.50.3.0755

CrossRef Full Text | Google Scholar

Ussing, A. P., Gordon, R., Ector, L., Buczko, K., Desnitskiy, A. G., and Vanlandingham, S. A. (2005). The colonial diatom “Bacillaria paradoxa”: chaotic gliding motility, Lindenmeyer model of colonial morphogenesis, and bibliography, with translation of O.F. Müller (1783), about a peculiar being in the beach-water". Ruggell: Gantner Verlag.

Google Scholar

Utkin, A. B., Vieira, S., Marques da Silva, J., Lavrov, A., Leite, E., and Cartaxana, P. (2013). Compact low-cost detector for in vivo assessment of microphytobenthos using laser induced fluorescence. Opt Spectrosc. 114, 471–474. doi: 10.1134/S0030400X13030259

CrossRef Full Text | Google Scholar

Vargas, P., Barbier, L., Saéz, P. J., and Piel, M. (2017). Mechanisms for fast cell migration in complex environments. Curr. Opin. Cell Biol. 48, 72–78. doi: 10.1016/j.ceb.2017.04.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Vieira, S., Lavrov, A., Utkin, A., Santos, A., Vilar, R., Marques da Silva, J., et al. (2011). Effects of migration on intertidal microphytobenthos biomass measured by laser-induced fluorescence (LIF). Mar. Ecol. Prog. Ser. 432, 45–52. doi: 10.3354/meps09157

CrossRef Full Text | Google Scholar

Vieira, S., Ribeiro, L., Jesus, B., Cartaxana, P., and Marques da Silva, J. (2013). Photosynthesis assessment in microphytobenthos with conventional and imaging pulse amplitude modulation fluorometry. Photochem. Photobiol. 89, 97-102. doi: 10.1111/j.1751-1097.2012.01224.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Villareal, T. A. (1992). Buoyancy properties of the giant diatom Ethmodiscus. J. Plankton Res. 14, 459–463. doi: 10.1093/plankt/14.3.459

CrossRef Full Text | Google Scholar

Wang, J., Cao, S., Du, C., and Chen, D. (2013). Underwater locomotion strategy by a benthic pennate diatom Navicula sp. Protoplasma 250, 1203–1212. doi: 10.1007/s00709-013-0502-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Wells, A. L., Lin, A. W., Chen, L. Q., Safer, D., Cain, S. M., Hasson, T., et al. (1999). Myosin VI is an actin-based motor that moves backwards. Nature 401, 505–508. doi: 10.1038/46835

PubMed Abstract | CrossRef Full Text | Google Scholar

West, G. S. (1916). Algae. Vol. 1. Cambridge, CA: Cambridge University Press.

Google Scholar

Yamaoka, N., Suetomo, Y., Yoshihisa, T., and Sonobe, S. (2016). Motion analysis and ultrastructural study of a colonial diatom, Bacillaria paxillifer. Microscopy 65, 211–221. doi: 10.1093/jmicro/dfv375

PubMed Abstract | CrossRef Full Text | Google Scholar