- 1Applied Physics Laboratory and School of Oceanography, University of Washington, Seattle, WA, United States
- 2Department of Earth, Ocean, and Atmospheric Science, Florida State University, Tallahassee, FL, United States
- 3Centre for Materials and Coastal Research, Institute of Coastal Research, Helmholtz-Zentrum Geesthacht, Geesthacht, Germany
- 4Department of Atmospheric and Oceanic Sciences, University of California, Los Angeles, Los Angeles, CA, United States
- 5Rosentiel School for Marine and Atmospheric Science, University of Miami, Miami, FL, United States
- 6Department of Earth, Environmental and Planetary Science, Brown University, Providence, RI, United States
- 7Department of Mathematics, College of Staten Island, CUNY, Staten Island, NY, United States
- 8Department of Mechanical Engineering, University of Houston, Houston, TX, United States
Predicting the distribution of oil, buoyant plastics, flotsam, and marine organisms near the ocean surface remains a fundamental problem of practical importance. This manuscript synthesizes progress in this area during the time of the Gulf of Mexico Research Initiative (GoMRI; 2012–2019), with an emphasis on the accumulation of floating material into highly concentrated streaks on horizontal scales of meters to 10's of kilometers. Prior to the GoMRI period, two new paradigms emerged: the importance of submesoscale frontal dynamics on the larger scales and of surface-wave-driven Langmuir turbulence on the smaller scales, with a broad transition occurring near 100 m. Rapid progress resulted from the combination of high resolution numerical modeling tools, mostly developed before GoMRI, and new observational techniques developed during GoMRI. Massive deployments of inexpensive and biodegradable satellite-tracked surface drifters combined with aerial tracking of oil surrogates (drift cards) enabled simultaneous observations of surface ocean velocities and dispersion over scales of 10 m to 10's of kilometers. Surface current maps produced by ship-mounted radar and aerial optical remote sensing systems, combined with traditional oceanographic tools, enabled a set of coordinated measurement programs that supported and expanded the new paradigms. Submesoscale fronts caused floating material to both accumulate at fronts and to disperse as they evolved, leading to higher local concentrations, but increased overall dispersion. Analyses confirmed the distinct submesoscale dynamics of this process and the complexity of the resulting fields. Existing tools could be developed into predictive models of submesoscale statistics, but prediction of individual submesoscale features will likely remain limited by data. Away from fronts, measured rates of accumulation of material in and beneath surface windrows was found to be consistent with Langmuir turbulence, but highly dependent on the rise rate of the material and thus, for oil, on the droplet size. Models of this process were developed and tested and could be further developed into predictive tools. Both the submesoscale and Langmuir processes are sensitive to coupling with surface waves and air-sea flux processes. This sensitivity is a promising area for future studies.
1. Introduction
The Gulf of Mexico Research Initiative (GoMRI) aimed to improve society's ability to understand, respond to, and mitigate the impacts of petroleum pollution and related stressors of marine and coastal ecosystems. One focus area was the physical processes that control the spread of released oil from an oceanic spill site. Figure 1 shows satellite images of oil from the Deepwater Horizon spill on spatial scales of about 1–100 km (Figure 1A) and about 1 m–2 km (Figure 1B). These images reveal a highly heterogeneous distribution of oil on the ocean surface over a wide range of scales. The concentration of oil is patchy, with the patches of high concentration having a very wide range of scales. This review summarizes progress achieved during the GoMRI era with a particular emphasis on near-surface processes in the open ocean that create the patchiness observed in Figure 1.

Figure 1. Distribution of floating oil from the Deepwater Horizon spill. (A) On scales of 1–100 km (Image provided by NASA MODIS). (B) On scales of 1–1,500 m (Satellite Imagery Provided as a Courtesy by Maxar and Satellite Imaging Corporation).
In the mid-latitudes “mesoscale” eddies generate the most energetic variability in horizontal ocean surface currents. Mesoscale eddies have horizontal scales of roughly 100 km and they evolve and rotate on timescales of weeks to months, with high or low pressure anomalies similar to synoptic weather systems in the atmosphere. A solid understanding of the dynamics and structure of mesoscale variability emerged in the late twentieth century and serves as the basis of existing operational ocean mesoscale forecasting systems. Operational ocean models typically assimilate satellite measurements of sea surface height and surface temperature, operational weather forecasts, and robotic measurements of ocean interior temperature and salinity into ocean models to operationally define the present state of the ocean on the mesoscale. These models exhibit high skill in forecasting features larger than roughly 50 km over periods of many days (Storkey et al., 2010; Jacobs et al., 2014, 2019). The spreading of the Deepwater Horizon spill was clearly influenced by the evolving mesoscale eddy field in the northern Gulf of Mexico (Walker et al., 2011), much of which was successfully captured by an ensemble of mesoscale models (Liu et al., 2011) and some of which could be explained by analyses based on mesoscale properties (Olascoaga et al., 2013).
The image in Figure 1A shows strong variability on scales smaller than the mesoscale. These “submesoscale” motions have been the focus of intensive study in the early twenty-first century. By the time of the Deepwater Horizon spill, high-resolution modeling and theoretical studies had established that a new dynamical regime, the submesoscale, existed at horizontal spatial scales between roughly 0.1–10 km (Boccaletti et al., 2007; Capet et al., 2008; Thomas et al., 2008; Lévy et al., 2010). At the surface, submesoscale motions were predicted to take the form of numerous sharp filaments and fronts, like those seen in Figure 1A, sometimes wrapping into intense vortices with a rate of rotation many times higher than mesoscale vortices, but appearing intermittently over small areas, so amounting to less energy per unit area than the mesoscale. Unlike mesoscale motions, which have very small vertical velocities, submesoscale fronts were predicted to support significant vertical transport, so that even though submesoscale motions are less energetic than mesoscale motions, they may dominate in terms of vertical transport. Model transport occurred as surface water converged onto fronts and was injected downward into the interior ocean (Fox-Kemper et al., 2008). Importantly, these small-scale features were predicted to occur worldwide, not just in coastal waters, being continually spawned by mesoscale motions acting on the large-scale variations in temperature and density (Fox-Kemper et al., 2011). However, the role of submesoscale motions in horizontal transport, particularly the transport of floating material such as oil, had received little attention because these features are less energetic than the mesoscale motions. Observationally, although submesoscale fronts had long been known to exist (Federov and Ginsburg, 1992) and pioneering efforts had studied their properties (Flament et al., 1985; Munk et al., 2000), the task of observationally evaluating this new theoretical framework in the open ocean was just beginning (Hosegood et al., 2008; Lumpkin and Elipot, 2010; D'Asaro et al., 2011).
The image in Figure 1B shows strong variability on scales smaller than the submesoscale. The stripes of red oil a few meters across, separated by nearly oil-free regions 10's to 100's of meters wide, result from circulations within the upper ocean boundary layer. Studies of this region began in the earliest days of oceanography (Ekman, 1905), rapidly demonstrating its crucial role in ocean dynamics (Sverdrup, 1947): boundary layer “Ekman” currents translate atmospheric wind stress into ocean interior currents and its well-mixed layers mediate atmospheric heat, moisture, gas, and contaminant fluxes. These effects are controlled by the strong turbulent mixing within the boundary layer, which is its defining characteristic and differentiates it from the ocean interior. Numerous models predicting the structure and rates of this mixing as a function of atmospheric forcing were developed in the twentieth century (Kraus and Turner, 1967; Price et al., 1986; Large et al., 1994); many of these are routinely used as components within operational ocean models (Umlauf and Burchard, 2005; Li et al., 2019). However, these models only parameterize vertical processes within the boundary layer, not the horizontal processes that must play an important role in setting the structure seen in Figure 1B.
The accumulation of floating material in long streaks, as in Figure 1B, was first studied in detail by Langmuir (1938), who attributed it to the effect of counter-rotating vortices in the boundary layer, aligned roughly downwind. These are thus called “Langmuir circulations” (LC). Craik and Leibovich (1976) proposed that LC were formed by the interaction of the wind stress and surface waves, thus providing a new mechanism (CL), in addition to atmospheric fluxes, for driving turbulence in the boundary layer. Detailed testing of this idea, however, was delayed until the development of Large Eddy Simulations (LES) for the ocean boundary layer that included the CL mechanism (Skyllingstad and Denbo, 1995; McWilliams et al., 1997). LES produced detailed predictions of the boundary layer turbulence statistics, which, when compared to observations (Gargett et al., 2004; Kukulka et al., 2009, 2012; D'Asaro et al., 2014) demonstrated the importance of the CL mechanism. Only when the CL vortex force is included in model equations do LES results agree qualitatively and quantitatively with observations of the velocity and kinetic energy scales of these large-eddy LC structures. However, the task of using these new tools to develop improved parameterizations of boundary layer transport (McWilliams and Sullivan, 2000; Kantha and Clayson, 2004; Harcourt and D'Asaro, 2008; Noh and Nakada, 2010) particularly for buoyant or floating materials, was just beginning.
These theoretical and numerical approaches developed in the two decades leading up to the Deepwater Horizon spill provided the basis for the efforts during GOMRI. A series of GoMRI-funded field campaigns in the northern Gulf of Mexico specifically targeted the types of patchy features observed in Figure 1. New instruments and techniques were created and combined with existing methods to create a set of dense and overlapping data sets spanning several spatial and temporal scales. Much of the sampling focused on the structure and near-surface variability of fronts. In particular, GoMRI's Consortium for Advanced Research on Transport of Hydrocarbon in the Environment (CARTHE) carried out the Grand LAgrangian Deployment (GLAD, DeSoto Canyon, Summer 2012), the Surfzone Coastal Oil Pathways Experiment (SCOPE, Destin, Florida; inner shelf, Winter 2013–2014), the Lagrangian Submesoscale Experiment (LASER, DeSoto Canyon, Winter 2016), and the Submesoscale Processes and Lagrangian Analysis on the Shelf (SPLASH, Louisiana shelf, Spring 2017). Each field campaign used a combination of concurrent in situ Lagrangian measurements, aerial remote sensing, and shipboard sampling from multiple ships, small boats, airplanes, unoccupied aerial vehicles (UAVs), and autonomous underwater vehicles (AUVs). Two state-of-the-art, real-time models, the multiple-nested Navy Coastal Ocean Model ranging from 1 km outer nest down to 100-m horizontal resolution (Jacobs et al., 2014) and a coupled atmosphere-wave-ocean model (Curcic et al., 2016; Özgökmen et al., 2018), provided atmospheric and marine forecasts that formed a critical component of the complex planning process that was required to coordinate multiple ships and aircraft.
Here, progress in measuring, modeling and understanding submesoscale and boundary layer motions is reviewed, for the period since the Deepwater Horizon spill, the “GoMRI era,” with a particular emphasis on their effects on the transport of floating material as a surrogate for oil. GoMRI-funded research, as well as other related efforts, will be described. Readers are directed to other GoMRI synthesis articles for descriptions of work on shallow water flows, rivers, and their interactions with the ocean, on the physical, chemical and biological processes that set and modify the physical properties of oil as it is transported by the processes described here, and on resulting effects on humans and ecosystems. The remainder of this review focuses on the open ocean circulation processes and is organized around the following themes: measurement techniques (section 2), submesoscale motions (section 3), and boundary layer motions (section 4). Section 5 provides a summary and an outlook for future research directions.
2. Measurement Techniques
2.1. Challenges
A quantitative understanding of the complex patterns seen in Figure 1 requires not only a large number of measurements of the surface currents that form these patterns, but also of the patterns of surface and subsurface temperature and salinity that drive their evolution. Many thousands of pixels are required to reproduce even a small portion of either image. Traditional oceanographic tools, such as moorings attached to the ocean floor or research ship survey lines, cannot generate the time-evolving, multi-scale spatial information that is necessary to resolve ocean variability over spatial scales of 1 m to 100s of km. Similarly, high frequency radars, which revolutionized monitoring of coastal ocean currents (Roarty et al., 2019), do not have the range necessary to obtain observations in the open ocean.
2.2. Massive Deployments of Surface Drifters
CARTHE pioneered the use of massive arrays of Lagrangian instruments in an attempt to overcome this sampling challenge. On the submesoscale (e.g., Figure 1A), this was done through the development of the CARTHE drifter and the deployment of ~2,500 drifters in multiple arrays during intensive field campaigns. On boundary layer scales (e.g., Figure 1B) this was done by developing techniques to optically track numerous floating objects from UAVs (or, colloquially, “drones”), and the deployment and tracking of ~10,000 bamboo plates in multiple arrays during intensive field campaigns.
2.2.1. The CARTHE Drifter
A surface drifter floats at the ocean surface and approximately follows its motion thereby measuring ocean surface currents. Drifters have a long history (Lumpkin et al., 2017) and a large variety of designs. Modern designs combine GPS/GNSS measurements of position and satellite communications to track thousands of drifters anywhere in the world ocean in real time. Of equal importance is attention to the behavior of drifters in the complex flows at the ocean surface. A floating object moves with a velocity that combines the ocean surface drift, surface wave properties and the wind forcing. To minimize the effects of wind and waves, drifters typically minimize their surface profile, maximize underwater drag elements, and minimize irregularities in the motion of the drifter due to surface waves. Many drifters, notably the SVP (Lumpkin et al., 2016), measure currents at 15 m depth using a large drogue centered at this depth, thereby avoiding near-surface wave effects. For oil transport, however, a drifter must measure currents much closer to the surface. The CARTHE drifter (Novelli et al., 2018) was designed to be “compact and light, making it easy to transport and to store and handle…, to consist of as few parts as possible, so that it could be produced by using few suppliers and assembled quickly before deployment, … to be mass producible by machines,… to be cost effective, so that very large numbers (hundreds to thousands) could be deployed in a single experiment and … to be almost entirely biodegradable, in order to minimize long-term damage to the environment during ocean sampling” (Lumpkin et al., 2017). The drifter design (Figure 2a) consists of a floating torus housing the GPS and batteries and connected to a drogue consisting of two interlocking square pieces by a short flexible, but inextensible element. It extends ~0.6 m below the surface. The plastic elements are made of a corn-based bioplastic with a lifetime in the ocean of many months. “The drifter is mass produced by injection molding, and the two parts of the torus are spin welded together in order to avoid the use of toxic glue.” This design was based on laboratory experiments (Figure 2b) showing it to minimize wind drag while following the 0.6 m average Lagrangian water velocity accurately. Field tests (Novelli et al., 2018) found that it behaves very similarly to the CODE drifter (Davis, 1985). CARTHE drifters were deployed in arrays of several hundred often using multiple vessels to speed the deployment and usually combined with the other techniques described here. Results from these massive drifter deployments are described in sections 3.2–3.4.

Figure 2. (a) The CARTHE drifter. A surface float supports a subsurface drogue on a flexible tether. The drogue extends to 0.6 m below the surface. (b) The drifter performance was extensively tested the University of Miami wind-wave tank and (c) during oil spill exercises (from Lumpkin et al., 2017).
2.2.2. Drift Card Studies
A similar approach was taken to study motions on scales from 1 to 400 m. Currents in the upper centimeter of the ocean were measured from the motion of hundreds of bamboo dinner plates scattered on the surface from a small boat. The bamboo plates were chosen to replicate the Richardson and Stommel (1948) parsnip experiment and computer punch card experiments (e.g., Weller and Price 1988) using modern aerial imaging techniques. Cardboard pizza boxes, plywood, and bamboo plates were tested. The bamboo plates were selected as they were non-toxic, biodegradable, and easily and cheaply available for purchase in large quantities. The bamboo plates were 2 mm thick and had a draft of 1.75 cm and, unlike other materials tested, floated in the upper few cm of the water column for periods in excess of 6 h without a change in buoyancy or loss of structural integrity. Using measurements in a wave-oil tank (Figure 2C), Novelli et al. (2020) found that bamboo plates “… spread at the same rate and in the same direction as the crude oil slicks.”
Patches of bamboo plates were used to investigate dispersion during CARTHE's LASER experiment, in the northern Gulf of Mexico in January–February 2016 and during SPLASH, April–May 2017, in the Louisiana Bight (Carlson et al., 2018). During LASER, the plates were imaged from an aerostat, an aerodynamic balloon tethered to a ship; during SPLASH the imaging was done from drones. Aerostats are relatively low cost, have high persistence, high lift capacity, and stable flight characteristics even in wind speeds exceeding 10 ms−1. Federal Aviation Administration (FAA) regulations allow flights up to 150 m and operation without a license, but limit the operations region and often require advance coordination in areas, such as the northern Gulf of Mexico, with heavy helicopter usage. Mobile operations at sea required a dedicated ship and positioning of the aerostat over the plates required continual maneuvering of the ship, which was often difficult. During LASER, the FAA had not yet established the general regulations for non-recreational use of UAVs, which made the use of drones difficult. By the time of SPLASH, the FAA had greatly relaxed the rules, enabling the “drone revolution” that has since transformed low-altitude remote sensing in marine science Joyce et al. (2018). Thus, during SPLASH, the bamboo plates were imaged using multiple commercial drones, each flying for a short period before returning to the boat for new batteries. These were operated in “boat mode,” disabling features such as “return to launch” that are catastrophic during boat operations.
Carlson et al. (2018) describes the Ship-Tethered Aerostat Remote Sensing System (STARSS, Figure 3) in detail. Briefly, STARSS included a 50.6-megapixel visible wavelength camera, GPS and inertial positioning and orientation sensors and a WiFi link to transfer images to the ship every 15 s. The aerostat was flown from a chartered offshore supply vessel (M/V Masco VIII) with a nearby research vessel (R/V Walton Smith) often operating nearby to provide oceanography context, as well as X-band radar data (see section 2.3) and air-sea flux measurements. Figure 3 depicts a typical experiment, which began by deploying the aerostat to approximately 150 m. At this height, the camera's field of view (FOV) was approximately 300 × 200 m. After all onboard systems were initiated and working, the small boat crew was directed to the center of the camera's FOV and several hundred bamboo plates were released, either in a single patch or in a grid, and the high-resolution images captured by STARSS were used to quantify the dispersion of the plates over periods of up to 3 h. These STARSS imagery and position data required complex processing to yield scientific data (Carlson et al., 2018; Chang et al., 2019). Images were corrected for lens distortion and were directly georectified using position, altitude, and orientation (pitch, roll, and heading) associated with each image. Ephemeral sun glitter was detected and discarded and individual plates were detected in the images and the location of their centers determined. Higher accuracy positioning was achieved by a relative rectification process, which minimized differences between plate positions in two successive images relative to the center of mass of all plates. Trajectories of each plate were then constructed by linking individual plates between camera frames. Typically, 200–300 trajectories were computed for periods of several hours. Results from bamboo plate experiments conducted in the presence of Langmuir circulation are described in section 4.1.

Figure 3. The aerostat is launched from and tethered to a surface ship. Drift cards are released from a small boat and the ship is maneuvered to keep the aerostat over the drift card array using images transmitted from the camera on the aerostat (from Özgökmen et al., 2018).
2.3. Currents From Marine Radar Imaging
2.3.1. Methods
The use of marine radars to probe the ocean surface was developed in the decades preceding GoMRI. During the GoMRI era, these techniques were improved and used to help understand the spatial structure and evolution of the near-surface currents responsible for creating the complex patterns shown in Figure 1. Radar returns from the sea surface are dominated by scattering off surface waves with a wavelength twice the wavelength of the radar, i.e., Bragg scattering. For standard marine radars operating in X-band, the Bragg scattering waves have wavelengths of a few centimeters. Since the strength of these cm-waves is modulated by the passage of longer and larger dominant waves, the backscatter intensity is also modulated by the larger waves. Images from radar may thus show a pattern of propagating crests and troughs. This information can be used to retrieve surface wave properties such as ocean wavelength and wave propagation speed and direction (Young et al., 1985). Additional processing can be used to infer wind speed and significant wave height. These measurements can be made by specialized marine radars or by enhancing and observing “sea clutter” measured by more standard marine radar hardware.
Ocean currents can also be computed from such radar data. The propagation velocity of the wave crests and troughs, i.e., the wave phase speed, is the sum of their intrinsic velocity and the ocean current. Estimates of the ocean current can thus be computed from the difference between the observed velocity and that expected theoretically in the absence of current. This is done by computing wavenumber-frequency spectra from repeated scans and comparing the observed phase speed with the theoretical expection (Young et al., 1985; Senet et al., 2001). An estimate of the current can thus be made at each wavenumber. Longer waves are influenced by deeper currents with the effective current depth proportional to the wavelength (Stewart and Joy, 1974). In this way, profiles of near-surface current from depths of a few 10's of centimeters to about 10 m can be measured using radars repeatedly scanning the sea surface.
2.3.2. Current Mapping in Deep Water
Methods for mapping deep water currents using radar originated in the decades preceding GoMRI, but were mostly deployed on fixed platforms. The GoMRI era saw improved installations on ships. Radar measurements of current profiles from ships require precise positioning, particularly in rough conditions and/or weak mean currents. CARTHE combined precise, multi-antenna GPS measurements sampled rapidly enough to correct individual radar sweeps and calibration against hard targets to make a ship-based system (Lund et al., 2015a,b; Campana et al., 2016, 2017) with a spatial resolution of 100 m, ranges of ~4 km and temporal sampling rates of minutes. Validation of these methods in the decades preceding GoMRI saw only limited results due to the lack of appropriate calibrated surface velocity references. During GoMRI, the massive CARTHE drifter arrays provided detailed and accurate velocity standards for validation. A Helmholtz-Zentrum Geesthacht (HZG) marine radar was installed on the R/V F. G. Walton Smith during the CARTHE LASER experiment in the Northern Gulf of Mexico in January 2016. The velocities derived from this radar can clearly identify oceanic circulation features on sub-km scales. As seen in Figure 4, the marine radar was able to sample the velocities at ~100-m resolution over a sharp surface velocity gradient characteristic of a submesoscale front. Operation of the radar through the drifter arrays produced over 4,130 validation points of co-located radar and drifter observations. The radar velocities show good agreement with drifters over a large range of velocities with a highly linear relationship (R2 values of 0.94 and 0.97 for the U and V components, respectively) and biases <1 cm s−1 (Lund et al., 2018). Radar current measurements thus appear to be an excellent complement to vertical ADCP current profiles, providing horizontal current mapping of similar accuracy and time resolution, but closer to the surface. Radar observations of surface roughness were also used to identify the submesoscale front that was seeded with bamboo plates by Carlson et al. (2018), making them an excellent tool to detect interesting features that are not always visible by eye.
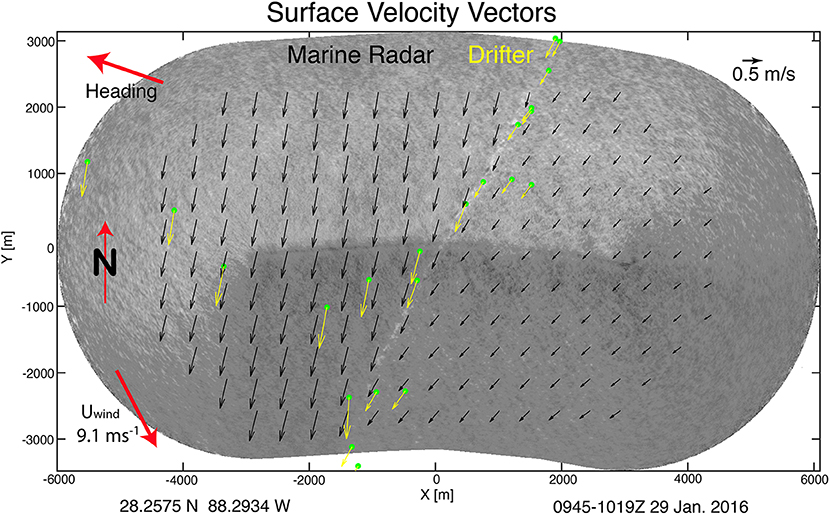
Figure 4. Ship-mounted marine radar measurements of a submesoscale front. Grayscale indicates the radar backscatter intensity. Black arrows show surface velocity measured by the radar. Green dots indicate the positions of CARTHE drifters and yellow arrows show their velocities. The LASER drifter data and radar data shown here are available at D'Asaro et al. (2017) and Lund and Haus (2018), respectively.
2.3.3. Current Mapping in Shallow Water
Current profiling in shallow water is more difficult because the wave propagation speed depends on the depth, which is often unknown. Velocity cannot then be directly estimated by the offset between the observed and expected directional wavenumber spectra. However, algorithms to measure both the current and the water depth have been developed and tested during the CARTHE SPLASH experiment. Validation tools included measurements from 500 CARTHE drifters, a shipboard acoustic Doppler current profiler and depth sounder. The error in radar-derived water depth was measured to an accuracy of 1.2 m (or ~ 7% of the mean water depth). The different between the drifter and radar-derived near-surface currents was 0.04–0.07 ms−1. About half of this difference was due to the extremely large variation of the near-surface current with depth. Removing this, the shallow water accuracy was similar to deep water accuracy, despite the greater complexity of the retrieval process.
2.4. Currents From Polarimetric Optical Imaging
CARTHE scientists spearheaded the application of optical polarimetric imaging to measure ocean surface waves and currents on scales smaller than those resolved by marine radars. The processing of optical images to obtain maps of surface wave slope fields, e.g., polarimetric slope sensing, was originally developed by Zappa et al. (2008). A single camera measures optical images of the sea surface illuminated by daylight at multiple polarizations. These are combined to create an image of sea surface slope and thus the properties of the wave field at spatial scales of millimeters and temporal scales of 10's of milliseconds. Ocean current profiles are computed from these using similar techniques to those developed for marine radars, but on much smaller scales, between 1 and 100 mm of the sea surface. During GoMRI this technique was developed, verified and used to make unique measurements of the very near surface region.
Polarimetric imaging systems were installed on the on the R/V F. G. Walton Smith during all four of the major CARTHE field programs and in the 15 m long × 1 m wide × 1 m tall wind-wave flume at the University of Miami's Surge-Structure-Atmosphere Interaction (SUSTAIN) facility (Laxague et al., 2015, 2017). In the controlled environment of SUSTAIN, the currents retrieved via polarimetric imaging agree well with particle image velocity (PIV) derived velocities as well as the drift velocity of camera-tracked dye. A field comparison made during the CARTHE SPLASH experiment in the Louisiana Bight (Figure 5) shows a velocity profile spanning a factor of 1,000 in depth below the surface measured by a variety of techniques. The polarimetric currents agree with other measurements in the upper 2 m of the water column within experimental error. The polarimetric current measurements span the range of depths important for the transport of floating oil. They also show large velocity gradients in the upper ocean important for near surface transport (see section 4.2).
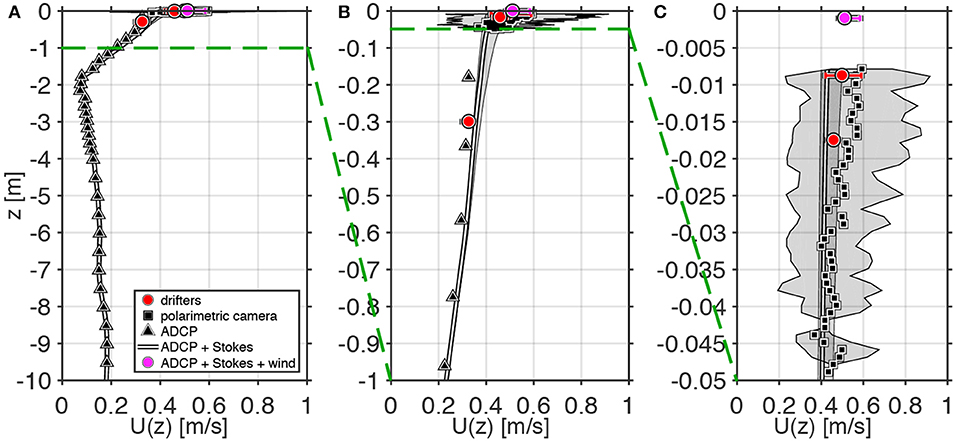
Figure 5. Profile of current speed composited from multiple instruments on 27 April 2017 in the Louisiana Bight over three different depth ranges: (A) Upper 10 m, (B) Upper 1 m, (C) Upper 0.05 m. Symbols indicate different measurement platforms: triangles-ADCP; squares-polarimetric camera; line-Stokes drift plus ADCP; magenta circle-Stokes drift plus ADCP current plus empirical 8.5 cm/s wind forcing drift; red circles-centroid speeds of bamboo plates and drifters. Shaded regions (polarimetric current, Stokes drift plus ADCP) and horizontal bars (drifting instruments) define the 5th–95th percentile range. The darker shaded region in (C) represents the 5th–95th percentile range of the Stokes drift. From Laxague et al. (2017), see paper for details.
2.5. Aircraft Thermal and Optical Imaging
Although satellite imaging of the surface (e.g., Figure 1) provides global coverage, images are often obscured by clouds, satellite passes occur only a few times per day, and the resolution of satellite images, particularly for infrared surface temperature, is usually limited to about a kilometer. Optical and thermal imaging of the sea surface from aircraft flying below the clouds can provide more detailed and consistent information particularly when combined with other sensors not available from satellites (Melville et al., 2016; Marmorino et al., 2018). An example is shown in section 3.2.
A new technique to measure fine-scale ocean current gradients from such aircraft data was developed during the GoMRI era. The propagation direction and amplitude of surface waves is modified as they propagate through variable ocean currents. The variation in wave properties can be measured by imaging sun glitter from multiple angles using a camera mounted on an aircraft. The horizontal gradients in the surface current can then be computed from the changes in wave properties (Rascle et al., 2016).
This technique was tested during the CARTHE LASER experiment using a fixed wing airplane equipped with infrared and visible cameras and operating below the cloud base (Rascle et al., 2017). The infrared system was used to locate a sharp temperature front. Sunglint images from different directions show different aspects of the roughness variations at the front (Figure 6). These were combined to estimate the strong current gradients at the front and compared to currents from the X-band radar and surface drifters. All of the methods detected a velocity change across the front of about 0.3 ms−1. Only the sun glint method, with a resolution of about 1 m, had the resolution to resolve the true width of the front, about 50 m. This technique, using optical imaging, can be applied using manned aircraft or drones. The same methods can be used on SAR images from satellites.
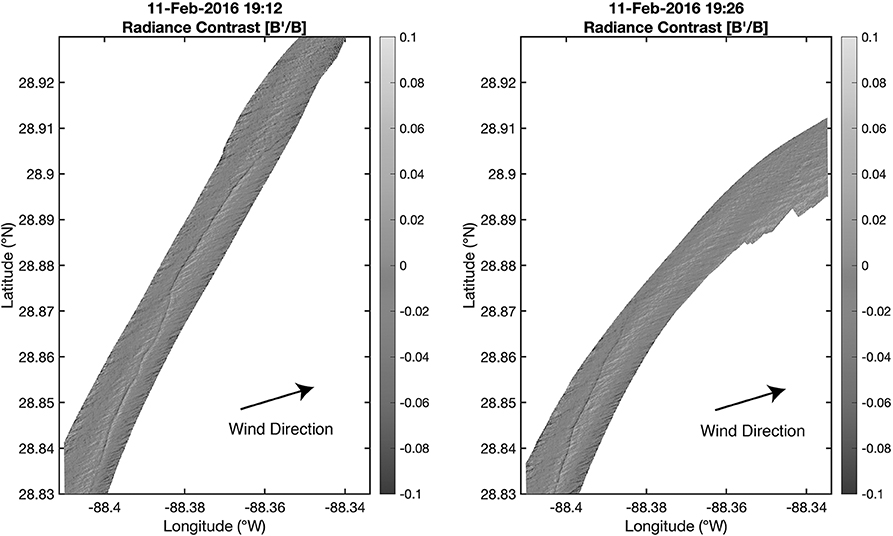
Figure 6. Variations in sunglint intensity detected for two different aircraft passes of the same front with different view angles. The current gradients at the front appear differently from the two angles. This difference can be used to compute the magnitude of the front current gradient (adapted from Rascle et al., 2017; data available at Rascle et al., 2018).
3. Submesoscale Motions
3.1. Submesoscale Simulations
The modeling tools developed before GoMRI were used during the GoMRI era to make detailed numerical predictions of the circulation and associated submesoscale structures in the northern Gulf of Mexico (Barkan et al., 2017a,b; Choi et al., 2017). Freshwater from the Mississippi-Atchafalaya River system strongly shapes the flows often spreading across the interior of the Gulf as a coherent jet, thereby enhancing lateral density gradients in a wide area. Riverine influence is thus not confined to the shelf and near shore regions (Horner-Devine et al., 2015). The structure of the submesoscale is best shown by plotting gradients of velocity or density, as in Figure 7 where the surface vorticity, the local rate of rotation of the ocean surface, is shown. The flow is organized into strongly cyclonic (red, anticlockwise rotating) linear fronts wrapping into circular cyclonic vortices, superimposed onto more weakly anticyclonic (blue, clockwise rotating) regions. These and other simulations predict that surface water converges onto these fronts and sinks. This has important implications for the distribution of surface materials (see section 3.3). These fronts also mark the boundaries of the lighter freshwater that is stirring into the heavier and saltier Gulf water. Seasonally, the intensity of the submesoscale features is controlled by the river inflow and the depth of wind mixing; stronger freshwater input and deeper mixed layers both enhance submesoscale activity. Since the maximum freshwater occurs in summer while the deepest layers occur in winter, significant submesoscale activity occurs in both seasons. These state-of-the-art model simulations, and other similar efforts, illustrate the detailed simulations of submesoscale properties that are now possible.
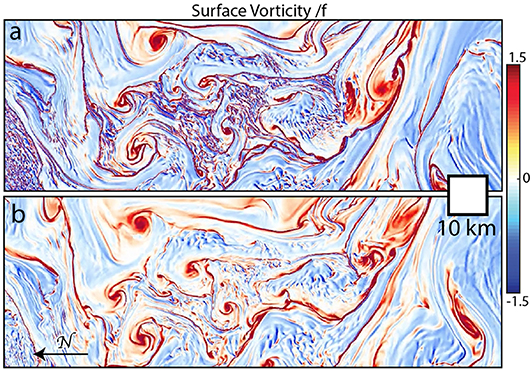
Figure 7. Simulated surface vertical vorticity divided by the Coriolis frequency from a model of the DeSoto Canyon region of the northern Gulf of Mexico (Barkan et al., 2017a) with a horizontal resolution of 150 m forced by realistic air-sea fluxes and river input, and nested within a lower resolution model of the North Atlantic. (a) Vorticity near time of maximum variance. (b) Same but near time of minimum variance a few hours later.
3.2. Experimental Verification
CARTHE conducted two experimental programs to explore the seasonal variability of the submesoscale in the DeSoto Canyon region, near the site of the Deepwater Horizon: GLAD in the summer of 2012 and LASER in the winter of 2016. As described below, both showed significant submesoscale activity consistent with the numerical predictions. LASER combined models and the new experimental tools described in section 2 to examine the submesoscale structures predicted by models (D'Asaro et al., 2018). An operational, submesoscale resolving model (Figure 8a, Jacobs et al. 2019) shows cyclonic submesoscale vortices on the gradient between the fresher, lighter water from the Mississippi and the saltier, denser water from the central Gulf. Aircraft thermal imaging (Figure 8b) shows a similar feature in a nearby location. Based on these, an array of 326 CARTHE drifters was deployed (white circles) within the vortex. Over the next few days (Figures 8c–f), about half the drifters converged to delineate a frontal line wrapping into a cyclonic vortex, as predicted. Figure 5 shows a similar front in more detail. Using the real-time drifter data as a target, the temperature, salinity, and velocity of the frontal/vortex feature was surveyed by a ship at a resolution of 1 km, showing the predicted salinity and density front at the convergence line (not shown). A water-following Lagrangian float deployed on the dense side of the front (Figure 8g) moved to the convergence zone and descended along the frontal surface, as predicted. The downward vertical velocity was measured both by the float and by the ADCP mounted on the float (Figure 8g). Taken together, these measurements confirm the presence and structure of submesoscale fronts, vortices, and vertical transport predicted by the simulations.
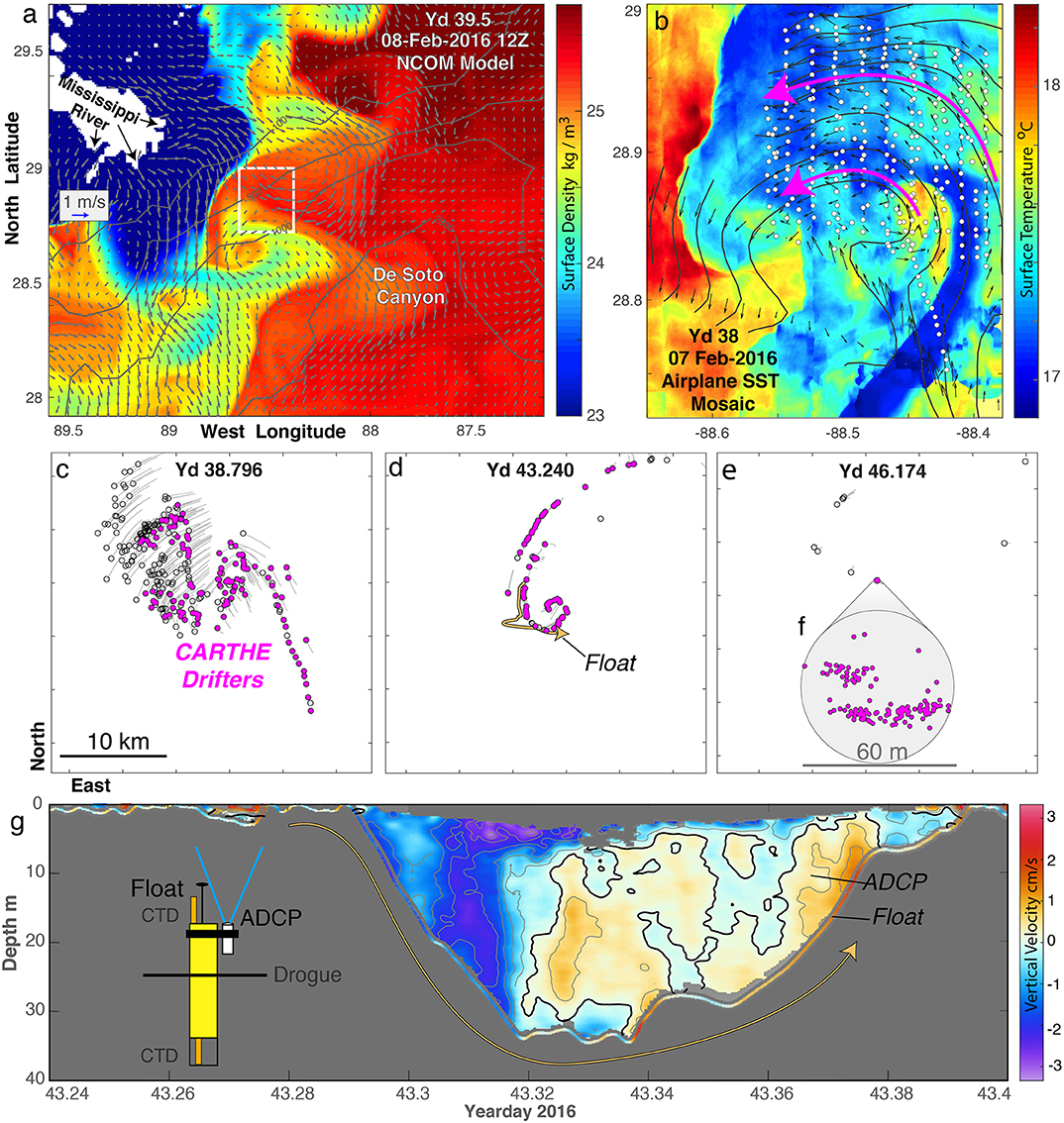
Figure 8. Clustering and vertical velocity at a submesoscale front measured during the CARTHE LASER experiment (D'Asaro et al., 2018). (a) Surface density (colors) in the experimental region as simulated by the Navy Coastal Ocean Model (NCOM). Surface velocity (vectors) and bottom depth (gray lines) are shown. (b) Aircraft survey of SST (colors) located by the white box in (a). White dots show deployment locations of surface drifters. Black vectors indicate 7 m velocity measured by the ship, black lines show streamfunction, and Magenta arrows show sense of circulation. (c–f) Evolution of the drifter array over the next 8 days with gray lines showing 7,500-s-long “tails” of drifter motion. Magenta drifters converge into a 60-m-wide cluster of 127 drifters shown in (f). (g) Vertical trajectory of a neutrally buoyant Lagrangian float (sketched in figure) carrying an upward looking acoustic Doppler velocity profiler (ADCP). The yellow line in d) shows the approximate float trajectory. Colors show vertical velocity measured by the float's motion (thin band) and by the ADCP (colored region). The float descended from the surface to about 35 m and then returned to the surface. The average descent speed measured from pressure was about 0.013±0.001ms−1; the ADCP agreed, measuring 0.013±0.001ms−1.
3.3. Dispersion and Transport
The rich set of motions predicted by submesoscale simulations imply increased dispersion of surface materials at small scales. The ~3,000 drifters deployed by CARTHE provide a strong test of this prediction. A two-point dispersion diagram (Figure 9) shows the rate of separation of particles as a function of their separation for five different drifter deployments in both winter (black) and summer (red). The scaling is chosen so that the classical Richardson diffusion (Richardson, 1926; Poje et al., 2014) results in a −2/3 slope. Although the overall scaling matches that of small-scale turbulence, a variety of more detailed statistical comparisons and comparisons between models and observations show that the submesoscale is very different by a variety of other measures (Pearson et al., 2017, 2019; Chang et al., 2019). The different deployments differ by less than a factor of 2. At a separation of 10–100 km, particles separate at 0.1–0.2 ms−1, as expected for mesoscale eddies. At the smallest measured separations, about 150 m, particles separate at 0.02–0.03 ms−1, clearly showing the existence of enhanced dispersion by the submesoscale. Between 200 m and 10 km the data show a nearly uniform slope of roughly −2/3, indicating a broad range of scales on which dispersion is “local,” i.e., dominated by eddies of the same size as the separation. These results are consistent with high resolution models of dispersion (Choi et al., 2017) in this region. These observations confirm that submesoscale motions enhance dispersion of surface materials on average.
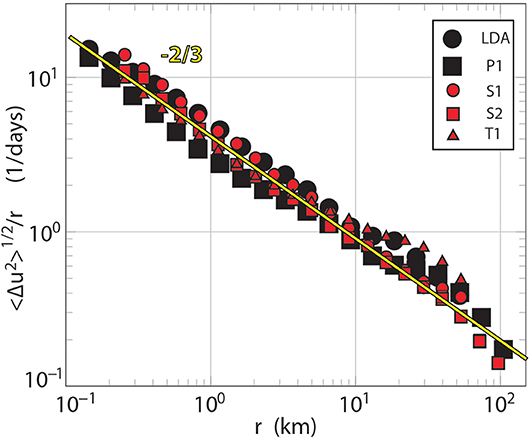
Figure 9. The scale dependent dispersion rate for five large drifter deployments in the Northern Gulf of Mexico. LDA and P1 (black) were part of LASER in winter 2016; S1, S2, and T1 were in GLAD (summer 2012). The yellow line has a slope of −2/3.
More surprising results were found by examining the trajectories in more detail (D'Asaro et al., 2018): “The classical models of dispersion build on the kinetic theory of gases to treat the spread of a patch of material as a random process governed by scale-dependent horizontal diffusion.” However, such models only predict the average concentration and, because they can only spread material not concentrate it into streaks, cannot explain much of the small-scale structure illustrated in Figure 1. Dynamically, such models usually assume the surface currents to be non-divergent, with zero vertical velocity, and with motion thus confined entirely to the horizontal plane. These assumptions are approximately valid for mesoscale oceanic motions… Submesoscale motions are predicted to have significant vertical velocities … [the] surface convergence zones that feed such downward velocities can trap and concentrate floating materials, a process not included in traditional dispersion models. Figure 8 shows a dramatic example of this effect. The initial drifter array “is about 25 km in diameter. About a week later (Figure 8f), some of the drifters (colored magenta in Figure 8) have converged into a region 60 m in diameter, a factor of 400 smaller, while the rest of the drifters have spread over a region roughly 100 km in diameter (mostly off the frame of the figure). … As the drifters disperse over a region much larger than their initial spread, they also converge into clusters much smaller than their initial separations.” This small-scale convergence is a distinguishing aspect of submesoscale motions and is largely responsible for the small-scale features apparent in Figure 1A. As surface materials converge onto fronts and the fronts wrap into eddies, the distribution of these materials marks the locations of these fronts and eddies and thus acquires a shape similar to that of the vorticity shown in Figure 7.
The experimental confirmation of strong submesoscale convergences emphasizes an important distinction between submesoscale and mesoscale eddies. The geostrophic and quasigeostrophic theories that have been developed to describe mesoscale eddies predict zero or minimal surface convergence, and are built on the assumption of lower intensity of flows (i.e., small Rossby number) than occurs at the submesoscale. It is precisely the degree to which surface convergences are important at the submesoscale that demonstrates that they cannot be described fully by such theories.
The convergence of surface material onto fronts implies that such materials move with the fronts. Figure 10 illustrates the implications for the transport within the Louisiana Bight during CARTHE's 2017 SPLASH experiment. Drifters deployed in the center of the bight are blown westward toward the Mississippi river delta (Figure 10A) but stop (Figure 10B) and spread out (Figure 10C) along a front a few kilometers offshore. As the wind direction changes, they move northward and then westward along the front (Figure 10D), remaining offshore until the front reaches the shore west of Grand Isle (Figure 10E) where they all follow the front onto the beach (Figure 10F). The front exerts a strong influence on the transport of floating material, acting as both a barrier to onshore transport and a conduit directing it to particular locations on the shore. More broadly, “Oil follows fronts.”
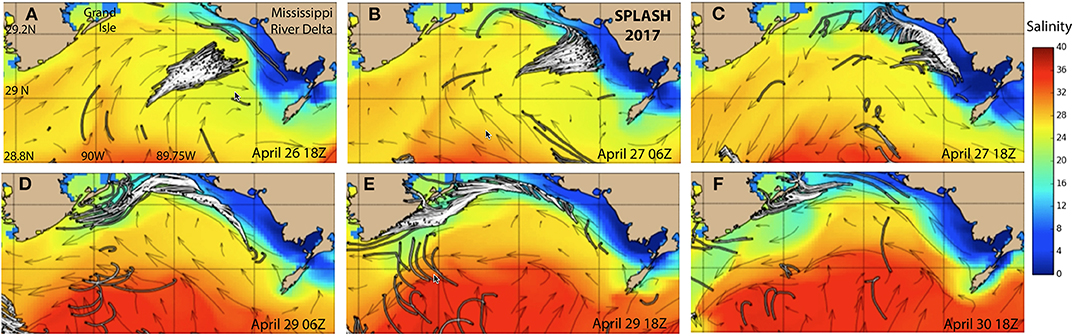
Figure 10. Motion of drifters (white lines) 26–30 April in the Louisiana Bight overlaid on velocity vectors and surface salinity from the NCOM 1 km real-time model. Drifter “tails” are 12 h long. (A) April 26 18Z. (B) April 27 06Z. (C) April 27 18Z. (D) April 29 06Z. (E) April 29 18Z. (F) April 30 18Z.
3.4. Frontal Properties and Dynamics
The properties and dynamics of very high gradient regions, e.g., fronts, appear to be crucial to understanding submesoscale dynamics and transport. An understanding of this is still evolving, but there has been much progress during the GoMRI era. Barkan et al. (2019), using data from LASER, propose a new mechanism for the intense fronts found in submesoscale flows. Traditionally, the increase in surface density gradients is driven by the nearly non-divergent mesoscale flows. The new theory shows once the gradients become sufficiently large, they will continue to increase driven by their own surface convergence independent of the mechanism that initially formed the front. This accelerates the rate of frontal formation and predicts that, without other mechanism to “arrest” this process, the front will become infinitely sharp in a finite time.
A surprising result of recent studies is the magnitude of vertical velocities in submesoscale fronts. Literature estimates of oceanic vertical velocities vary over nearly 4 orders of magnitude. Liang et al. (2017), using dynamically consistent inversions of oceanic data at 100's km scale, find values of 10−5 to 10−6 ms−1. Pallàs-Sanz et al. (2010), among many others, using Omega equation inversions at 10 km scale, find values near 10−4 ms−1. Yu et al. (2019) using a cluster of nested moorings at a few km separation, find submesoscale vertical velocities of 4 × 10−4 ms−1 below the mixed layer. Mahadevan and Tandon (2006), and many others, find values near 10−3 ms−1 in submesoscale simulations with about 1 km resolution. Figure 8 shows vertical velocities of 10−2 ms−1 measured at about 1 meter scale within a submesoscale front. Since the combination of the earth's rotation and the ocean's stratification greatly limit vertical motions at large scales, it is perhaps not surprising that vertical velocity varies so dramatically with scale. It is less clear, however, how the large velocities at small scales average to form the much smaller velocities at much larger scales. Furthermore, although models clearly indicate that these velocities reduce vertical stratification, i.e., “mix,” at small scales and increase it, i.e., “restratify,” at larger scales, the detailed mechanisms are poorly studied, particularly by observations.
A central unresolved problem is the width of fronts, or equivalently the smallest lateral scale that is still subject to submesoscale dynamics. Observationally for velocity, Figure 6 (Rascle et al., 2017) suggests a frontal width of about 50 m; Figure 8f suggests about the same for the smallest convergence scale of the drifters. For density, aircraft infrared images show a large variation in frontal width ranging from only a few meters to several kilometers (e.g., Figure 8b). Such large variability in frontal width is also found in other locations (D'Asaro et al., 2011; MacKinnon et al., 2016). Theoretically, as a front sharpens and the frontal gradients grow, a variety of shear instabilities become possible that can limit frontal width. Alternatively, since fronts coexist with the turbulent upper ocean boundary layer, this turbulence itself can limit frontal width or induce frontogenesis (McWilliams et al., 2015). Although some of these alternatives have been explored (Sullivan and McWilliams, 2018; Verma et al., 2019), “For the most part, the processes of frontal arrest are still to be discovered” (McWilliams, 2016).
3.5. Air-Sea Interactions
The initial theoretical and numerical studies of submesoscale dynamics focused on the mechanisms by which mesoscale motions created submesoscale motions. These studies mostly minimized the role of turbulence, boundary layers and air-sea interaction. However, submesoscale motions are most intense at the ocean surface (and on solid boundaries, a topic not discussed here) and thus coexist with the turbulent motions within the boundary layer. They thus modify air-sea interactions and are influenced by air-sea fluxes and boundary layer physics. An understanding of this is still evolving, but there has been some progress during the GoMRI era. Submesoscale fronts often have variations in surface temperature (e.g., Figure 8) and roughness (e.g., Figure 6), two primary parameters controlling air-sea fluxes. Direct measurements of air-sea fluxes were made across these fronts from the R/V Walton Smith during LASER (Shao et al., 2019). Marine radar, underway temperature, salinity and velocity measurements on the ship and the surrounding array of surface drifters allowed the ship to target and repeatedly cross fronts. On average, the air-sea heat flux was 1.5 × larger than the bulk value in the vicinity of the front. Wind speed also varied across the front, but in a more complex pattern. These results confirm that hydrodynamic processes near the front modify air-sea interaction, potentially influencing the overall air-sea fluxes on larger scales. The details, however, are complex and will require further study.
Air-sea forcing and boundary layer interactions can also play a large role in the evolution and structure of submesoscale motions. Several effects have been studied during the GoMRI era: First, the direction of the wind relative to the front can have a large effect on the front. A wind blowing down a front in the same direction as the frontal current, a “downfront” wind, acts to intensify the front (Thomas and Lee, 2005) through the interaction of the boundary layer Ekman transport and the frontal vorticity. This increases submesoscale variability. In contrast, the Ekman flow resulting from an “upfront” wind restratifies a front (Skyllingstad et al., 2017) thereby decreasing the submesoscale intensity. Convection also interacts with frontal circulations in complex ways (Taylor, 2018). Field studies have verified some of these effects (Thomas et al., 2016), but also revealed their complexity. Second, even without any wind the eddy viscosity in a turbulent boundary layer acts to sharpen density gradients in a manner very similar to classical frontogenesis (McWilliams, 2017). Third, variations in boundary layer turbulence, and thus viscosity, can thus modulate the intensity of the submesoscale. For example, Figure 7 shows two snapshots of simulated surface vorticity during the same day. Nearly the same fronts and vortices are present at both times although their locations have changed somewhat as they are advected by larger-scale flows. However, the features are stronger in the upper image, with the rms vorticity about 20% higher. Similar diurnal variations have been seen in the LASER drifter data (Sun et al., 2020). This variation results from the day to night variation in the intensity of the upper ocean boundary layer turbulence (Dauhajre and McWilliams, 2018). Finally, as is described in much more detail in section 4, surface waves play a large role in the dynamics of the boundary layer. Similar effects have been shown to significantly affect submesoscale motions (Suzuki et al., 2016). Furthermore, submesoscale motions modify both the waves (e.g. Figure 6), and potentially the wind generating the waves, as described above. A proper understanding of these effects may well require a coupled approach in which the ocean, the upper ocean boundary layer, the surface waves and the atmosphere interact dynamically. Many such coupled model systems exist (e.g., Chen et al. 2013), but work on extending this approach to the submesoscale is just beginning.
4. Boundary Layer Motions
Boundary layer studies in the pre-GoMRI era first built upon earlier developments for atmospheric boundary layers and then, in the late twentieth century and early twenty-first century began to more closely examine the differences that stem from the presence of surface waves in the ocean, but not in the atmosphere. The reigning theoretical model for boundary layer mixing driven by wave interaction is “Langmuir turbulence,” arising from the interaction between the waves' Stokes drift and the wind stress. This interaction appears in the equations of motion as an added body force and, most simply, acts to push downwind jets downward, thereby energizing the vertical component of the turbulence (Suzuki and Fox-Kemper, 2016). The importance of Langmuir turbulence has been persistently challenged by competing hypotheses that invoke a combination of shear stress and cooling without waves or energy input from surface wave breaking. Several studies have merged both forcings. For example, Sullivan et al. (2007) modeled the effects of breaking waves on Langmuir turbulence using LES combined with a stochastic wave breaking model, and found the creation of new Langmuir circulations by breaker-generated vortices and enhanced material entrainment due to a strong intermittent downwelling jet underneath breakers. Kukulka and Brunner (2015) found significantly enhanced near-surface mixing of buoyant particles by breaking waves for a range of wind-wave ages. Liang et al. (2018) found reduction of horizontal eddy diffusivity due to enhanced mixing by breaking waves.
The dominant tool for these studies has been LES (Large Eddy Simulation), which allows highly realistic simulations of the boundary layer in limited domains driven by the atmosphere alone and/or including Langmuir and wave breaking effects. In the GoMRI era, the focus has thus been on quantitatively testing the LES predictions against data (e.g., Chang et al. 2019), exploring effects of Langmuir turbulence on transport (see review by Chamecki et al. 2019) and improving boundary layer parameterizations based on our new understanding of these dynamics.
4.1. Langmuir Windrows
The clustering of surface materials in the convergence zones of windrows (e.g., Figure 1B) is a well-known phenomenon and the signature feature of Langmuir circulations. Quantitative measurements of this clustering using aerostat and drone observations (section 2.2.2) were directly compared to LES simulations driven by the observed stratification, air-sea fluxes, Stokes drift and parameterized wave breaking (Figure 11). Both observations (Figure 11a) and model (Figure 11b) show floating material clustering in downwind lines (Chang et al., 2019). A more detailed comparison using LES data (Figure 12) uses the first order longitudinal structure function computed by averaging the speed of (longitudinal) separation over unique drifter pairs. Since the structure functions are highly anisotropic, is computed separately for subsets of pairs with predominately downwind (dashed) and crosswind (solid) separations. Chang et al. (2019) see similar effects in structure functions from aerostat observations of bamboo plates. The observations and simulations agree well at shorter scales, as Langmuir turbulence dominates the surface expression at separations up to the length scale of large eddies, 20–30 m. In particular, the strength and scales of cross-wind convergence match closely, as do the zero-crossings and their dilation between early observations within 5 min of surface drifter deployment, and observations 15–90 min later. By comparison, simulations without Langmuir turbulence, i.e., involving only shear stress and wave breaking (not shown), are more isotropic in the early stage and then diverge at all crosswind separation scales. This comparison adds to the evidence that Langmuir turbulence provides an accurate model of transport within the boundary layer and, in particular, at the ocean surface. However, at scales larger than about 50, there are significant difference at both long and short scales, indicating additional sources of variability not explained by Langmuir turbulence and emphasizes the coupling of boundary layer and submesoscale dynamics.
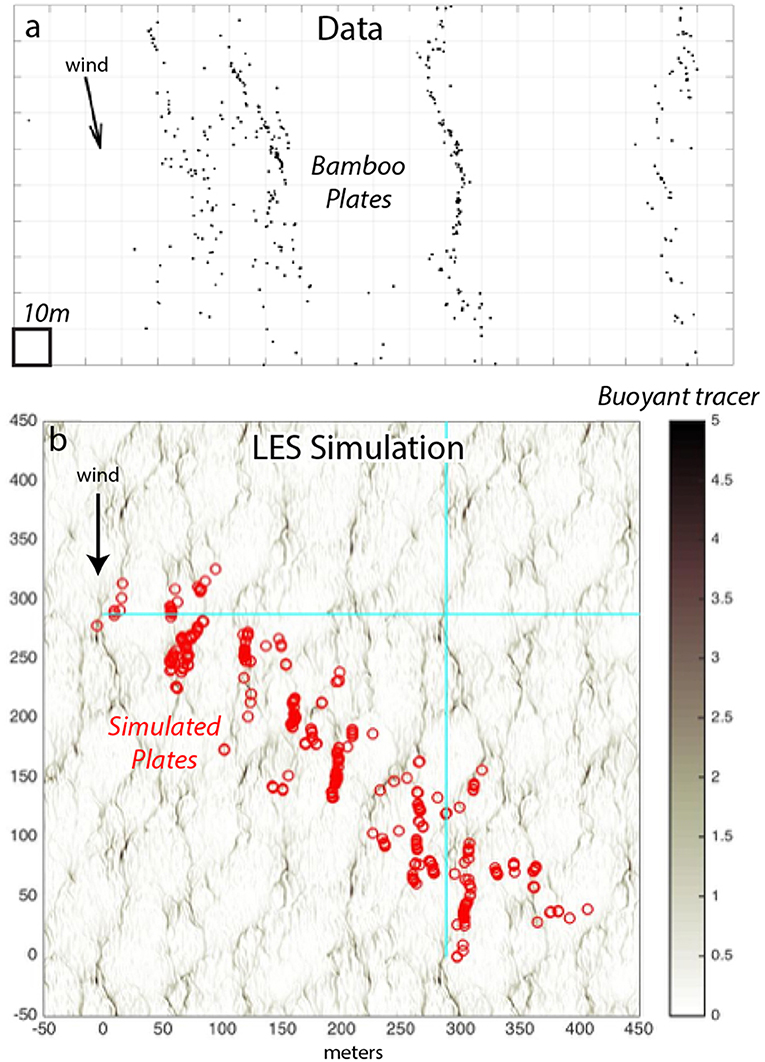
Figure 11. Clustering of surface particles in (a) Aerostat tracked bamboo plates during CARTHE LASER 125 min after deployment (from Chang et al., 2019). (b) LES simulation of these observations using observed stratification, forcing, and surface waves. Plates are shown in red; the concentration of a continuous buoyant tracer is shown in gray. Blue lines show boundaries of the spatially periodic simulation domain. Aerostat bamboo plate data are available at Carlson et al. (2017).
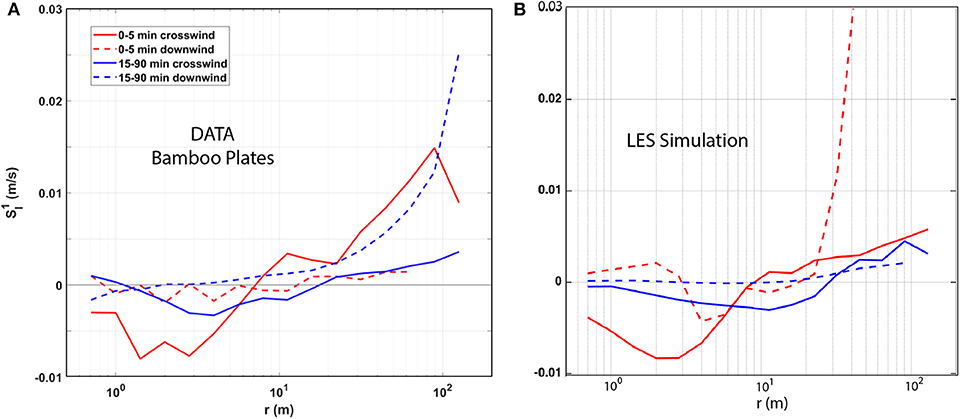
Figure 12. Longitudinal first order structure function Sl1 for crosswind (solid) and downwind (dashed) separations sampled at early (red) and late (blue) times. Times for each are given in the caption relative to the start of the measurements. (A) Data from tracked bamboo plates (from Chang et al., 2019). (B) LES simulation of observations.
4.2. Shear Dispersion of Oil
The velocity profile in Figure 5 shows a large velocity change, 0.4 ms−1, in the upper 2 m. Although such shear may not always be present, it suggests that small downward displacements of floating material could have a large effect on the lateral motion and dispersion of the material. During the GoMRI era, considerable attention has been given to studying the transport of oil droplets. These droplets have a wide range of sizes, many of which have rise velocities comparable to the vertical velocities in the ocean and thus will not remain at the surface. The three-dimensional motion in the sheared near-surface flow should be considered to accurately model the transport of these droplets. Yang et al. (2014, 2015) and Chen et al. (2016a, 2018) simulated oil transport in a LES by modeling the oil concentration field as a continuous advected scalar with a prescribed rise velocity parameterized based on the equivalent oil droplet diameter. Figures 13A,C, 14 show instantaneous surface oil distribution forming into downwind streaks, very similar to those seen in Figure 1B. The mean surface distribution (Figures 13B,D) is nearly Gaussian in shape. Both vary depending on the droplet size, due to the combined effects of finite oil droplet buoyancy, vertical transport by Langmuir turbulence, and depth-dependent mean flow direction caused by planetary rotation. Oil droplet size and levels of vertical mixing determine the vertical distribution of oil in the water column, which in turn determines the mean horizontal speed and direction of the oil plume transport. Larger, more buoyant droplets spend more time near the surface and, thus, move with the surface velocity, while smaller less buoyant droplets spend more time at depth and, thus, move with a velocity from deeper depths, potentially at a different speed or direction.
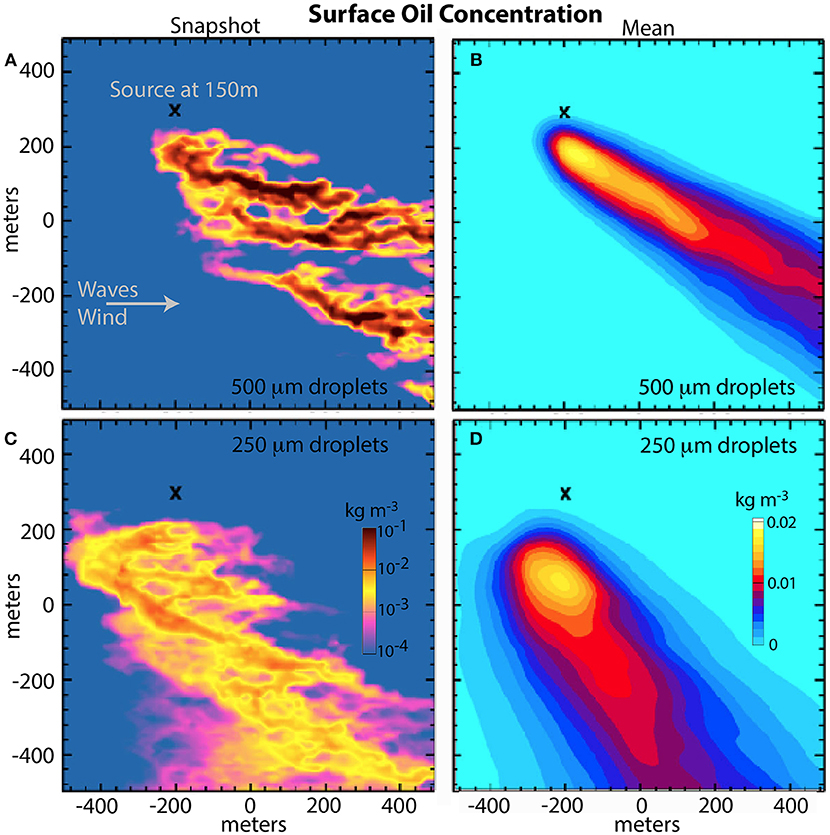
Figure 13. Simulated surface oil concentration (colors) for two different oil droplet sizes emitted from a subsurface source (“x”). Left column (A,C) shows instantaneous concentration; right column (B,D) shows average concentration. Top row (A,B) simulates droplets with 500 μm diameter rising at 22 mms−1; bottom row (C,D) 250 μm diameter rising at 5 mms−1. The instantaneous plume concentrations in (A,C) were sampled at t = 54,200 s. The averaged concentrations in (B,D) were obtained by averaging 175 instantaneous concentration fields sampled from t = 54,200 s to t = 89,000 s with a constant time interval of 200 s (from Yang et al., 2015).
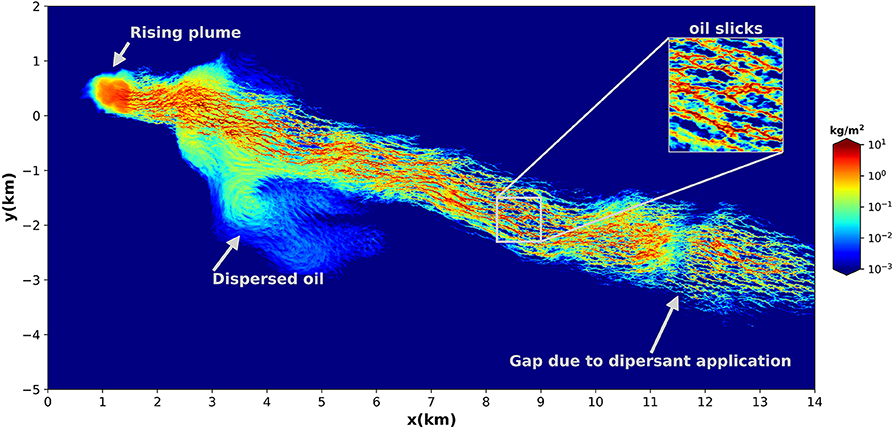
Figure 14. Patterns of total oil mass in the ocean mixed layer produced by the multiscale large-eddy simulation model 36 h after the application of dispersant in a small target area on the surface. The portion of the slick impacted by the dispersant (“dispersed oil”) disconnects from the main plume, being transported in a different direction at much lower speed (from Chen et al., 2018). Note the similarity of the patterns to those shown in Figure 1B.
Chen et al. (2016b) further extended the LES modeling capability by developing a new adaptive domain extension approach (named “ENDLESS") that overcomes the limited horizontal domain of the conventional LES, which, in combination with synthetic submesoscale eddy field, allows for modeling the oil plume evolution over a much larger domain. Using a near-field LES plume dynamics model (Yang et al., 2016) as a precursor simulator, Chen et al. (2018) applied ENDLESS to simulate the long-range near-surface oil transport and showed that dispersants, which reduce the droplet size, reduces the droplet vertical velocities resulting in a deeper penetration of oil and a change in transport direction (Figure 14).
Other investigators have found similar results from LES simulations. Mensa et al. (2015) quantified the effects of buoyancy and wind forcing on the horizontal relative diffusivity using LES of the ocean mixed layer under weak wind forcing. Chor et al. (2018a) used LES to study the transport of materials with various buoyancy levels in a pure convective ocean boundary layer, and identified two mechanisms that promote preferential concentrations of buoyant materials in convergence and vortex dominant regions on ocean surface. Liang et al. (2012, 2013) modeled the bubble distribution in the ocean surface layer and the bubble-mediated air-sea gas exchange, and developed a new parameterization of bubble-mediated gas fluxes that can be used in Earth system models. Kukulka et al. (2016) studied the influence of surface heat fluxes on the mixing of microplastic marine debris, which also provides insights for understanding the dispersion of other buoyant particles (such as oil droplets) in convective turbulence.
4.3. Modeling Vertical Transport
Despite the considerable progress achieved using LES models, their high computational cost prevents them from being used as a predictive tool to support rapid response for future subsea blowout events. Physical insights obtained from these studies need to be translated into parameterizations that can be incorporated into large-scale ocean circulation models for operational applications. The pre-GoMRI era developed parameterizations of upper-ocean turbulence into the vertical diffusivities, e.g., the K-profile parameterization (KPP) (Large et al., 1994). Given that Langmuir circulations increase vertical mixing, several studies have focused on incorporating these effects into the conventional KPP model by including additional enhancement factors (e.g., McWilliams and Sullivan 2000; Smyth et al. 2002). McWilliams et al. (2012, 2014) applied a similar wave breaking model, further investigating the effect of breaking waves on eddy momentum flux and developed a modified KPP model with breaking wave effects.
In the GoMRI era, Harcourt (2013, 2015) developed a second-moment closure model that includes the effects of Langmuir circulations, inhomogeneous pressure-strain rate and pressure-scalar gradient correlation. Based on LES results of oil plume dispersion in Langmuir turbulence, Yang et al. (2015) quantified the vertical diffusivities for momentum and oil droplet concentration, and developed a modified KPP model incorporating the effects of Langmuir circulations for a range of Langmuir circulation intensities and oil droplet sizes. Chen et al. (2016a) quantified the vertical eddy diffusivity and the nonlocal oil concentration flux under swell wave condition with various wind-swell misalignment angles. Liang et al. (2018) studied the horizontal dispersion of buoyant materials in Langmuir turbulence and developed a theoretical framework for modeling the horizontal effective diffusivity. Chor et al. (2018b) developed a theoretical framework for predicting the vertical distribution of buoyant materials and their horizontal transport based on a generalized turbulence vertical velocity scale.
4.4. Modeling Vertical Droplet Transport
Efforts to represent the vertical mixing of oil droplets and the associated impact of Langmuir turbulence on dispersal have focused on two distinct components. The first is the representation of Langmuir turbulence dynamics in upper ocean mixing schemes, and their representation in process modeling frameworks (Li et al., 2019) and in regional and global ocean models (Kumar et al., 2017). The second is representing non-local vertical fluxes for submerged buoyant tracers, e.g., oil droplets. The nonlocal fluxes are due to the large eddies, spanning most of the boundary layer depth, that separate Langmuir turbulence from shear-driven turbulence. These downwind vortices not only create the surface concentration of buoyant material within windrows (e.g., Figure 1B), but also plumes of such material streaming downward from the windrows into the interior. These plumes enhance vertical mixing within the boundary layer as can be seen by comparing their depth distributions in LES simulations with and without Langmuir forcing (Figure 15). These effects occur for conserved tracers, like heat and salt, but are more pronounced for buoyant tracers such as oil droplets or plastic particles. They cannot be modeled by local downgradient diffusive closures, but require a non-local formulation.
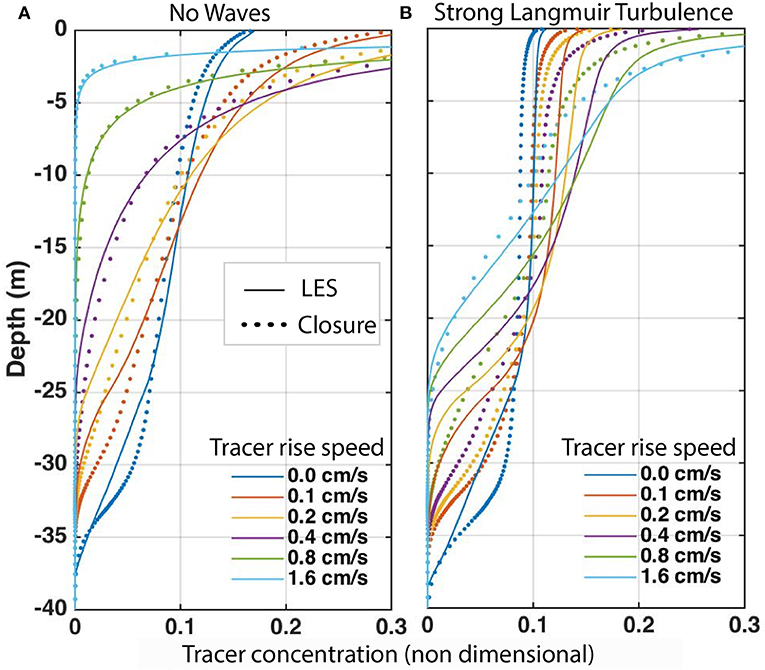
Figure 15. Profiles of concentrations of buoyant tracers with varying rise velocity in an ocean surface mixed layer (H = 33 m), driven by surface winds U10 = 10 ms−1 are shown from LES simulations (lines) with (A) and without (B) strong Langmuir turbulence wave forcing. These are compared with predictions (dots) from second moment closures (SMC) using the standard Mellor-Yamada 2.5 model (no Stokes drift; no nonlocal fluxes) and profiles of the concentrations produce by the new non-local SMC (NLSMC) accounting for both the CL forces and nonlocal vertical fluxes.
To pursue this, a nonlocal component of vertical fluxes has been implemented within a second moment closure (Harcourt, 2015) mixing parameterization, modified to account for the local effects of Langmuir turbulence. The nonlocal fluxes have been added in a dynamically consistent manner to create a non-local second moment closure scheme. While still imperfect, this shows substantial skill in improving the predicted profiles for buoyant tracers (Figure 15). Impacts on the near-surface shear are expected to be more significant for weak Langmuir forcing conditions, since the nonlocal flux contributions only become important when there is a significant local gradient within the surface layer where Stokes drift is significant. Figure 15 thus shows a parameterization of the effects shown in Figures 13, 14, allowing these to be included in regional circulation models.
5. Summary and Outlook
5.1. Measurements
5.1.1. Summary
Before GoMRI, only a few experimental programs had measured the structure of submesoscale motions in detail. During the GoMRI era, a variety of new tools were developed to measure and model submesoscale motions and to explore their implications for oil distributions. In particular, CARTHE pioneered the coordinated use of aircraft and drone remote-sensing, innovative ship measurements and operational models to guide massive deployments (i.e., hundreds to thousands) of inexpensive and biodegradable surface drifters. These techniques were effective in spanning the wide range of space and time scales, seconds and centimeters, minutes and meters, to weeks and degrees, that cover the range of surface wave, boundary layer, submesoscale, and mesoscale motions.
5.1.2. Future Directions
Most of the new techniques used in GoMRI measured near surface properties, mostly the near-surface velocity. Only a few of the drifters measured surface temperature and none measured salinity; the radar and bamboo plates only measured velocity. Aircraft remote sensing provided only occasional surface temperature maps and the limited ship surveys (e.g., Figure 8) were only sufficient to place the detailed surface velocity measurements in context; they could not match the range of scales and sampling density at the surface. Small-scale oceanic motions are important because they modify the vertical structure of the upper ocean through both mixing and vertical transport. The small scales found in the distribution of surface properties (e.g., Figure 1) are a direct result of this three-dimensional transport and cannot be understood or predicted without a three-dimensional view. Future studies thus need to develop measurement and analysis techniques that better address the subsurface and vertical transport components of upper ocean motions.
5.2. Submesoscale
5.2.1. Summary
Before GoMRI, models and theory predicted the presence of submesoscale motions distinctly different from the mesoscale motions of operational models. There was limited direct experimental confirmation and limited thought about how submesoscale motions might affect dispersion and oil distribution. The intensive, multiscale observations conducted during the GOMRI era have conclusively demonstrated the presence of motions on scales of 100 m to 20 km in a variety of different environments. They have measured the enhanced horizontal dispersion, unexpectedly strong horizontal convergence and vertical velocity, and the resulting concentration of surface materials due to submesoscale motions. These, and other data, along with improved high resolution models and theory, have established the importance of submesoscale motions in the transport and fate of buoyant material in the near-surface ocean.
5.2.2. Submesoscale Prediction
Conceivably, the location of submesoscale fronts and filaments, such as seen in Figure 8, could be directly predicted. Models that produce these rapidly-evolving features have driven submesoscale research for over a decade, and submesoscale observation capabilities continue to improve. However, direct prediction would require measuring these features at least daily as the features themselves evolve and turn over rapidly. Forecasts of where the features will go are thus only good for about a day. Even with satellites that take snapshots of submesoscale features every few days, this level of data density is currently out of reach. Yet, knowledge about fronts and their instabilities can still lead to projections or outlooks about where their effects are expected to be strong even if individual features cannot be predicted. The next paragraphs describe four approaches that can be used in this manner, in increasing order of computational cost.
First and simplest, models that resolve and forecast the evolution of mesoscale features are increasingly using parameterizations of the bulk effects of submesoscale features to improve simulation fidelity. Submesoscale features tend to enhance horizontal dispersion and vertical restratification, and parameterizations of these effects indicate the mesoscale eddy strain, surface forcing, and mesoscale frontal conditions that lead to intense submesoscale frontogenesis and filamentogenesis (Thomas and Lee, 2005; Gula et al., 2014) and submesoscale instabilities (Fox-Kemper et al., 2008, 2011; Bachman et al., 2017). Operational maps of the levels of activity of these mechanisms, generated from the parameterizations, would help to identify the “hot spots” where surface convergences are likely to be common. Note that it is not necessary to observe these features in advance of such outlooks as they are predicted by the structure of the mesoscale and forcing conditions. As mesoscale-resolving models are reasonably affordable on modern computers, basin-wide simulations can be used, alleviating the need to custom-select sub-domains where an incident is in progress.
A second class of model projections involves the stochastic simulation of the dispersive effects of such features (Carlson et al., 2010). This approach has proven useful in improving drifter dispersion (Haza et al., 2012), but also transport when built into models (Chapron et al., 2018; Cotter et al., 2019) and has been applied to oil spill modeling (Spaulding, 2017). These simulations can be used to estimate additional dispersion due to submesoscales, but better linking of the strength of stochastic variability to flow features (e.g., Resseguier et al. 2020) is needed. Furthermore, ensembles of such forecasts, or more expensive modeling approaches mapping out the probability of particular trajectories, may make this approach costlier than the scaling-based parameterizations in coarse deterministic models.
Third, submesoscale-permitting models, which are individually more expensive than mesoscale-resolving models, with realistic forcing from past years (e.g., Bracco et al. 2016; Luo et al. 2016; Gough et al. 2019) may be used to build a climatological outlook of the regions where these structures are likely to be. This approach requires a library of submesoscale simulations of past years large enough to be useful. Submesoscale observations can be assimilated to improve the fidelity of these simulations. These simulations are too expensive and their forecasts are too short to be run in real time, but they can categorize regions and conditions that may serve as useful analogs to disaster management situations. Machine learning techniques may be particularly useful in this context (e.g., Liu et al. 2016).
Finally, the most expensive, but also most direct option, would be to run a forecast ensemble of submesoscale-permitting simulations in real time. This method is familiar to us from weather forecasting (e.g., Molteni et al. 1996), particularly when a potential weather disaster is brewing. The ensemble spread can be improved to accurately represent model and observation uncertainty by making each of the ensemble members have stochastic forcing or parameterizations (e.g., Buizza et al. 1999), in this case to further improve the smaller submesoscale variability and submesoscale-boundary layer interactions that are not resolved. The forecast cone or “spaghetti plot” of a model ensemble of hurricane forecasts is becoming a familiar part of disaster preparation. Some hurricane models automatically refine the model grid in the region of the hurricane, alleviating the need for predefined domains. This approach is far beyond our present capabilities, both computational and scientific, having only arisen in weather forecasting after 50 years of gradual improvements.
5.3. Boundary Layer
5.3.1. Summary
Before GoMRI, models and theory predicted the importance of Langmuir turbulence in boundary layer mixing. Observations confirmed their presence and supported the theoretical predictions. There was only limited inclusion of this physics in boundary layer parameterizations and little thought about how this might affect lateral motion and the vertical distribution of oil. During the GoMRI era, several new parameterizations of Langmuir turbulence were developed and some incorporated into operational boundary layer model codes. In these models, upper ocean properties and the transport of buoyant materials, such as oil, has been shown to depend on their rise velocity. This suggests that improved models of oil transport should couple modules that simulate air-sea fluxes, surface waves, and the rise velocities of the constituents and size classes of the oil. Promising directions for further improvements in the predictions of vertical mixing and horizontal dispersion of oil droplets include new nonlocal flux parameterizations linked to surface convergence dynamics.
5.3.2. New Directions
Although noticeable progress has been made on incorporating Langmuir circulation effects into the KPP modeling framework, the fact that each new study (McWilliams and Sullivan, 2000; Smyth et al., 2002; Yang et al., 2015) adds another enhancement factor to obtain good agreement with their own LES simulations suggests that the community has not yet converged to a solution and in fact has generated a wider variety of model predictions (Chamecki et al., 2019; Li et al., 2019). In addition, most previous studies on KPP modeling have focused on parameterizing the effect of local fluxes, but the effects of nonlocal fluxes are equally important. Perhaps a more general framework incorporating the combined effects of shear turbulence, Langmuir circulations, breaking waves, and buoyancy on local and nonlocal fluxes is needed.
Boundary layer turbulence, such as Langmuir turbulence, tends to have large vertical velocities and narrow horizontal scales that are vertically and horizontally coherent on the 1–100 m scales that fit within the boundary layer depth. Their ratio of vertical to horizontal scale distinguishes them from Submesoscale features which are wider (kilometers) than they are tall (boundary layer depth). The submesoscale's therefore have a bigger impact on oil patches which are wider than the boundary layer is deep. Both boundary layer and submesoscales can cause intense surface convergences, associated with their vertical velocities and horizontal coherence.
The continuous growth in computer power and recent advancements on LES modeling approach have helped to push LES application toward large enough domains to study the interactions of Langmuir turbulence with submesoscale features (Hamlington et al., 2014; Sullivan and McWilliams, 2018). More efforts are desired to push from both the LES and large-scale modeling sides to further reduce this gap.
Despite progress in modeling the effects of wave breaking on boundary layer flows, our understanding of this process is still far from satisfactory. Moreover, as shown by the laboratory experiments of Li et al. (2017), plunging breakers can generate violent impact on surface oil slicks and create oil droplets of a wide range of sizes, which can be further complicated by the application of dispersants. More research efforts are needed to simple and accurate parameterizations of wave breaking into operational ocean circulation models.
In most LES studies, a constant wind stress is imposed on the averaged sea surface, while the real situation is much more complicated. The air flow in the wind field is highly turbulent and has strong coupling with the sea-surface waves, thus the wind-induced surface shear stress exhibits considerable temporal and spatial variations (Sullivan and McWilliams, 2010). These variations of wind stress may cause considerable effects on the boundary layer dynamics and transport of floating materials. With oil, additional effects of inhomogeneity arise. At low sea states. vertical mixing becomes weaker and the buoyancy of oil may cause the oil to form slicks on the surface. These slicks may interfere with the regular air-sea interaction processes, changing the wind shear stress on the water surface, the wind-induced surface wave generation, the heat and moisture fluxes and the absorption of solar radiation. For example, Xiao and Yang (2020) have shown significant absorption of sunlight by surface oil plumes with significant effects on underlying photosynthesis. This may also heat the oil, complicating the temperature structure of the boundary layer. Similar effects may persist at higher winds. As the oil forms into windrows, surface waves may be absorbed by the oil, producing a localized stress and modifying the air-sea fluxes.
5.4. Synthesis
Although this review has strongly distinguished between submesoscale and boundary layer dynamics, in reality there is significant overlap. The smaller scales of the submesoscale become increasingly turbulent, and thus more like boundary layer flows, and the larger scales of the boundary layers become rotationally influenced and stratified, and thus more like submesoscale flows. This could be viewed as “coupling” between these two distinct classes of motion, or perhaps more productively, as a different type of flow with both characteristics. Similarly, although we understand some ways that oil properties affect oil transport, there is much room here for creative and productive research. Furthermore, although GoMRI's submesoscale studies have confirmed the importance of density fronts as oil accumulation sites and conduits for oil transport, further studies including the effects of weather, oil properties, and the oceanographic environment, could allow these idea to further developed into an operational system to supplement existing transport models.
Data Availability Statement
All unpublished data are publicly available through the Gulf of Mexico Research Initiative Information and Data Cooperative (GRIIDC) at https://data.gulfresearchinitiative.org under the following DOIs: 10.7266/N7M61H9P (plate observations), 10.7266/N7W0940J (drifter data), 10.7266/N7S75DRP, 10.7266/n7-93j3-mn56 (shipboard measurements), 10.7266/n7-8h5w-nn91 (wave buoy data) and 10.7266/N7222S91 (LES model fields).
Author Contributions
ED'A, MC, RH, DC, BH, BF-K, MM, AP, and DY contributed text and/or figures. ED'A combined these and edited these with help from the other authors.
Funding
This research was made possible by multiples grants from the Gulf of Mexico Research Initiative.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Tamay Özgökmen for his wise leadership of CARTHE.
References
Bachman, S., Fox-Kemper, B., Taylor, J., and Thomas, L. (2017). Parameterization of frontal symmetric instabilities. I: Theory for resolved fronts. Ocean Model. 109, 72–95. doi: 10.1016/j.ocemod.2016.12.003
Barkan, R., McWilliams, J., Molemaker, M., Choi, J., Srinivasan, K., Shchepetkin, A., et al. (2017a). Submesoscale dynamics in the northern Gulf of Mexico. Part II: Temperature–salinity relations and cross-shelf transport processes. J. Phys. Oceanogr. 47, 2347–2360. doi: 10.1175/JPO-D-17-0040.1
Barkan, R., McWilliams, J., Shchepetkin, A., Molemaker, M., Renault, L., Bracco, A., et al. (2017b). Submesoscale dynamics in the northern Gulf of Mexico. Part I: Regional and seasonal characterization and the role of river outflow. J. Phys. Oceanogr. 47, 2325–2346. doi: 10.1175/JPO-D-17-0035.1
Barkan, R., Molemaker, M., Srinivasan, K., McWilliams, J., and D'Asaro, E. (2019). The role of horizontal divergence in submesoscale frontogenesis. J. Phys. Oceanogr. 49, 1593–1618. doi: 10.1175/JPO-D-18-0162.1
Boccaletti, G., Ferrari, R., and Fox-Kemper, B. (2007). Mixed layer instabilities and restratification. J. Phys. Oceanogr. 37, 2228–2250. doi: 10.1175/JPO3101.1
Bracco, A., Choi, J., Joshi, K., Luo, H., and McWilliams, J. (2016). Submesoscale currents in the northern Gulf of Mexico: deep phenomena and dispersion over the continental slope. Ocean Model. 101, 43–58. doi: 10.1016/j.ocemod.2016.03.002
Buizza, R., Milleer, M., and Palmer, T. (1999). Stochastic representation of model uncertainties in the ECMWF ensemble prediction system. Q. J. R. Meteorol. Soc. 125, 2887–2908. doi: 10.1002/qj.49712556006
Campana, J., Terrill, E., and de Paolo, T. (2016). The development of an inversion technique to extract vertical current profiles from X-band radar observations. J. Atmos. Ocean. Technol. 33, 2015–2028. doi: 10.1175/JTECH-D-15-0145.1
Campana, J., Terrill, E., and de Paolo, T. (2017). A new inversion method to obtain upper-ocean current-depth profiles using X-band observations of deep-water waves. J. Atmos. Ocean. Technol. 34, 957–970. doi: 10.1175/JTECH-D-16-0120.1
Capet, X., McWilliams, J., Molemaker, M., and Shchepetkin, A. (2008). Mesoscale to submesoscale transition in the California Current System. Part I: Flow structure, eddy flux, and observational tests. J. Phys. Oceanogr. 38, 29–43. doi: 10.1175/2007JPO3671.1
Carlson, D., Fredj, E., Gildor, H., and Rom-Kedar, V. (2010). Deducing an upper bound to the horizontal eddy diffusivity using a stochastic Lagrangian model. Environ. Fluid Mech. 10, 499–520. doi: 10.1007/s10652-010-9181-0
Carlson, D., Özgökmen, T., Novelli, G., Guigand, C., Chang, H., Fox-Kemper, B., et al. (2018). Surface ocean dispersion observations from the Ship-Tethered Aerostat Remote Sensing System. Front. Mar. Sci. 5:479. doi: 10.3389/fmars.2018.00479
Carlson, D., Özgökmen, T., Novelli, G., Guigand, C., Mensa, J., Rebozo, M., et al. (2017). Lagrangian Submesoscale Experiment (LASER) Aerostat Drift Cards. Gulf of Mexico, January 2016 - February 2017. Consortium for Advanced Research on Transport of Hydrocarbon in the Environment II (CARTHE II).
Chamecki, M., Chor, T., Yang, D., and Meneveau, C. (2019). Material transport in the ocean mixed layer: recent developments enabled by large eddy simulations. Rev. Geophys. 57, 1338–1371. doi: 10.1029/2019RG000655
Chang, H., Huntley, H., Kirwan, A. Jr, Carlson, D., Mensa, J., Mehta, S., et al. (2019). Small-scale dispersion in the presence of Langmuir circulation. J. Phys. Oceanogr. 49, 3069–3085. doi: 10.1175/JPO-D-19-0107.1
Chapron, B., Dérian, P., Mémin, E., and Resseguier, V. (2018). Large-scale flows under location uncertainty: a consistent stochastic framework. Q. J. R. Meteorol. Soc. 144, 251–260. doi: 10.1002/qj.3198
Chen, B., Yang, D., Meneveau, C., and Chamecki, M. (2016a). Effects of swell on transport and dispersion of oil plumes within the ocean mixed layer. J. Geophys. Res. 121, 3564–3578. doi: 10.1002/2015JC011380
Chen, B., Yang, D., Meneveau, C., and Chamecki, M. (2016b). ENDLESS: An extended nonperiodic domain large-eddy simulation approach for scalar plumes. Ocean Model. 101, 121–132. doi: 10.1016/j.ocemod.2016.04.003
Chen, B., Yang, D., Meneveau, C., and Chamecki, M. (2018). Numerical study of the effects of chemical dispersant on oil transport from an idealized underwater blowout. Physical Review Fluids, 3, 083801. doi: 10.1103/PhysRevFluids.3.083801
Chen, S., Zhao, W., Donelan, M., and Tolman, H. (2013). Directional wind-wave coupling in fully coupled atmosphere-wave-ocean models: results from CBLAST-Hurricane. J. Atmos. Sci. 70, 3198–3215. doi: 10.1175/JAS-D-12-0157.1
Choi, J., Bracco, A., Barkan, R., Shchepetkin, A., McWilliams, J., and Molemaker, M. (2017). Submesoscale dynamics in the northern Gulf of Mexico. Part III: Lagrangian implications. J. Phys. Oceanogr. 47, 2361–2376. doi: 10.1175/JPO-D-17-0036.1
Chor, T., Yang, D., Meneveau, C., and Chamecki, M. (2018a). Preferential concentration of noninertial buoyant particles in the ocean mixed layer under free convection. Phys. Rev. Fluids 3:064501. doi: 10.1103/PhysRevFluids.3.064501
Chor, T., Yang, D., Meneveau, C., and Chamecki, M. (2018b). A turbulence velocity scale for predicting the fate of buoyant materials in the oceanic mixed layer. Geophys. Res. Lett. 45, 11817–11826. doi: 10.1029/2018GL080296
Cotter, C., Crisan, D., Holm, D., Pan, W., and Shevchenko, I. (2019). Numerically modeling stochastic lie transport in fluid dynamics. Multisc. Model. Simul. 17, 192–232. doi: 10.1137/18M1167929
Craik, A., and Leibovich, S. (1976). A rational model for langmuir circulations. J. Fluid Mech. 73, 401–426. doi: 10.1017/S0022112076001420
Curcic, M., Chen, S., and Özgökmen, T. (2016). Hurricane-induced ocean waves and Stokes drift and their impacts on surface transport and dispersion in the Gulf of Mexico. Geophys. Res. Lett. 43, 2773–2781. doi: 10.1002/2015GL067619
D'Asaro, E., Guigand, C., Haza, A., Huntley, H., Novelli, G., Özgökmen, T., et al. (2017). Lagrangian Submesoscale Experiment (LASER) Surface Drifters, Interpolated to 15-minute Intervals. Consortium for Advanced Research on Transport of Hydrocarbon in the Environment II (CARTHE II).
D'Asaro, E., Lee, C., Rainville, L., Harcourt, R., and Thomas, L. (2011). Enhanced turbulence and energy dissipation at ocean fronts. Science 332:318. doi: 10.1126/science.1201515
D'Asaro, E., Shcherbina, A., Klymak, J., Molemaker, J., Novelli, G., Guigand, C., et al. (2018). Ocean convergence and the dispersion of flotsam. Proc. Natl. Acad. Sci. U.S.A. 115, 1162–1167. doi: 10.1073/pnas.1718453115
D'Asaro, E., Thomson, J., Shcherbina, A., Harcourt, R., Cronin, M., Hemer, M., et al. (2014). Quantifying upper ocean turbulence driven by surface waves. Geophys. Res. Lett. 41, 102–107. doi: 10.1002/2013GL058193
Dauhajre, D., and McWilliams, J. (2018). Diurnal evolution of submesoscale front and filament circulations. J. Phys. Oceanogr. 48, 2343–2361. doi: 10.1175/JPO-D-18-0143.1
Davis, R. (1985). Drifter observations of coastal surface currents during CODE: the statistical and dynamical views. J. Geophys. Res. 90, 4756–4772. doi: 10.1029/JC090iC03p04756
Ekman, V. (1905). On the influence of the earth's rotation on ocean currents. Arkiv Matematik Astronomi Fysik 2:52.
Federov, K., and Ginsburg, A., (eds.). (1992). The Near-Surface Layer of the Ocean. New Dehli: Thomson Press.
Flament, P., Armi, L., and Washburg, L. (1985). The evolving structure of an upwelling filament. J. Geophys. Res. 90, 11765–11778. doi: 10.1029/JC090iC06p11765
Fox-Kemper, B., Danabasoglu, G., Ferrari, R., Griffies, S., Hallberg, R., Holland, M., et al. (2011). Parameterization of mixed layer eddies. III: Implementation and impact in global ocean climate simulations. Ocean Model. 39, 61–78. doi: 10.1016/j.ocemod.2010.09.002
Fox-Kemper, B., Ferrari, R., and Hallberg, R. (2008). Parameterization of mixed layer eddies. Part I: Theory and diagnosis. J. Phys. Oceanogr. 38, 1145–1165. doi: 10.1175/2007JPO3792.1
Gargett, A., Wells, J., Tejada-Martinez, A., and Grosch, C. (2004). Langmuir supercells: a mechanism for sediment resuspension and transport in shallow seas. Science 306, 1925–1928. doi: 10.1126/science.1100849
Gough, M., Beron-Vera, F., Olascoaga, M., Sheinbaum, J., Jouanno, J., and Duran, R. (2019). Persistent Lagrangian transport patterns in the northwestern Gulf of Mexico. J. Phys. Oceanogr. 49, 353–376. doi: 10.1175/JPO-D-17-0207.1
Gula, J., Molemaker, M., and McWilliams, J. (2014). Submesoscale cold filaments in the Gulf Stream. J. Phys. Oceanogr. 44, 2617–2643. doi: 10.1175/JPO-D-14-0029.1
Hamlington, P., Van Roekel, L., Fox-Kemper, B., Julien, K., and Chini, G. (2014). Langmuir-submesoscale interactions: Descriptive analysis of multi- scale frontal spindown simulations. J. Phys. Oceanogr. 44, 2249–2272. doi: 10.1175/JPO-D-13-0139.1
Harcourt, R. (2013). A second-moment closure model of Langmuir turbulence. J. Phys. Oceanogr. 43, 673–697. doi: 10.1175/JPO-D-12-0105.1
Harcourt, R. (2015). An improved second-moment closure model of Langmuir turbulence. J. Phys. Oceanogr. 45, 84–103. doi: 10.1175/JPO-D-14-0046.1
Harcourt, R., and D'Asaro, E. (2008). Large-eddy simulation of Langmuir turbulence in pure wind seas. J. Phys. Oceanogr. 38, 1542–1562. doi: 10.1175/2007JPO3842.1
Haza, A., Özgökmen, T., Griffa, A., Garraffo, Z., and Piterbarg, L. (2012). Parameterization of particle transport at submesoscales in the Gulf Stream region using Lagrangian subgridscale models. Ocean Model. 42, 31–49. doi: 10.1016/j.ocemod.2011.11.005
Horner-Devine, A., Hetland, R., and MacDonald, D. (2015). Mixing and transport in coastal river plumes. Annu. Rev. Fluid Mech. 47, 569–594. doi: 10.1146/annurev-fluid-010313-141408
Hosegood, P., Gregg, M., and Alford, M. (2008). Restratification of the surface mixed layer with submesoscale lateral density gradients: diagnosing the importance of the horizontal dimension. J. Phys. Oceanogr. 38, 2438–2460. doi: 10.1175/2008JPO3843.1
Jacobs, G., Bartels, B., Bogucki, D. J., Beron-Vera, F. J., Chen, S. S., Coelho, E. F., et al. (2014). Data assimilation considerations for improved ocean predictability during the Gulf of Mexico Grand Lagrangian Deployment (GLAD). Ocean Model. 83, 98–117. doi: 10.1016/j.ocemod.2014.09.003
Jacobs, G., D'Addezio, J., Bartels, B., and Spence, P. (2019). Constrained scales in ocean forecasting. Adv. Space Res. doi: 10.1016/j.asr.2019.09.018. [Epub ahead of print].
Joyce, K., Duce, S., Leahy, S., Leon, J., and Maier, S. (2018). Principles and practice of acquiring drone-based image data in marine environments. Mar. Freshw. Res. 70, 952–963. doi: 10.1071/MF17380
Kantha, L., and Clayson, C. (2004). On the effect of surface gravity waves on mixing in the oceanic mixed layer. Ocean Model. 6, 101–124. doi: 10.1016/S1463-5003(02)00062-8
Kraus, E., and Turner, J. (1967). A one-dimensional model of the seasonal thermocline II. the general theory and its consequences. Tellus 19, 98–106. doi: 10.3402/tellusa.v19i1.9753
Kukulka, T., and Brunner, K. (2015). Passive buoyant tracers in the ocean surface boundary layer: 1. Influence of equilibrium wind-waves on vertical distributions. J. Geophys. Res. 120, 3837–3858. doi: 10.1002/2014JC010487
Kukulka, T., Law, K., and Proskurowski, G. (2016). Evidence for the influence of surface heat fluxes on turbulent mixing of microplastic marine debris. J. Phys. Oceanogr. 46, 809–815. doi: 10.1175/JPO-D-15-0242.1
Kukulka, T., Plueddemann, A., and Sullivan, P. (2012). Nonlocal transport due to Langmuir circulation in a coastal ocean. J. Geophys. Res. 117, 1–17. doi: 10.1029/2012JC008340
Kukulka, T., Plueddemann, A., Trowbridge, J., and Sullivan, P. (2009). Significance of Langmuir circulation in upper ocean mixing: comparison of observations and simulations. Geophys. Res. Lett. 36, 1–5. doi: 10.1029/2009GL037620
Langmuir, I. (1938). Surface motion of water induced by wind. Science 87, 119–123. doi: 10.1126/science.87.2250.119
Large, W., McWilliams, J., and Doney, S. (1994). Oceanic vertical mixing: a review and a model with a nonlocal boundary layer parameterization. Rev. Geophys. 32, 363–403. doi: 10.1029/94RG01872
Laxague, N., Haus, B., Bogucki, D., and Özgökmen, T. (2015). Spectral characterization of fine-scale wind waves using shipboard optical polarimetry. J. Geophys. Res. 120, 3140–3156. doi: 10.1002/2014JC010403
Laxague, N., Haus, B., Ortiz-Suslow, D., Smith, C., Novelli, G. H. D., et al. (2017). Passive optical sensing of the near-surface wind-driven current profile. J. Atmos. Ocean. Technol. 34, 1097–1111. doi: 10.1175/JTECH-D-16-0090.1
Lévy, M., Klein, P., Tréguier, A., Iovino, D., Madec, G., Masson, S., et al. (2010). Modifications of gyre circulation by sub-mesoscale physics. Ocean Model. 34, 1–15. doi: 10.1016/j.ocemod.2010.04.001
Li, C., Miller, J., Wang, J., Koley, S., and Katz, J. (2017). Size distribution and dispersion of droplets generated by impingement of breaking waves on oil slicks. J. Geophys. Res. 122, 7938–7957. doi: 10.1002/2017JC013193
Li, Q., Reichl, B., Fox-Kemper, B., Adcroft, A., Belcher, S., Danabasoglu, G., et al. (2019). Comparing ocean surface boundary vertical mixing schemes including Langmuir turbulence. J. Adv. Model. Earth Syst. 11, 3545–3592. doi: 10.1029/2019MS001810
Liang, J.-H., Deutsch, C., McWilliams, J., Baschek, B., Sullivan, P., and Chiba, D. (2013). Parameterizing bubble-mediated air-sea gas exchange and its effect on ocean ventilation. Glob. Biogeochem. Cycles 27, 894–905. doi: 10.1002/gbc.20080
Liang, J.-H., McWilliams, J., Sullivan, P., and Baschek, B. (2012). Large eddy simulation of the bubbly ocean: new insights on subsurface bubble distribution and bubble-mediated gas transfer. J. Geophys. Res. 117, 1–13. doi: 10.1029/2011JC007766
Liang, J.-H., Wan, X., Rose, K., Sullivan, P., and McWilliams, J. (2018). Horizontal dispersion of buoyant materials in the ocean surface boundary layer. J. Phys. Oceanogr. 48, 2103–2125. doi: 10.1175/JPO-D-18-0020.1
Liang, X., Spall, M., and Wunsch, C. (2017). Global ocean vertical velocity from a dynamically consistent ocean state estimate. J. Geophys. Res. 122, 8208–8224. doi: 10.1002/2017JC012985
Kumar, N., Cahl, D. L., Crosby, S. C., and Voulgaris, G. (2017). Bulk versus spectral wave parameters: Implications on stokes drift estimates, regional wave modeling, and HF radars applications. J. Phys. Oceanogr. 47, 1413–1431. doi: 10.1175/JPO-D-16-0203.1
Liu, Y., Weisberg, R., Hu, C., and Zheng, L. (2011). “Trajectory forecast as a rapid response to the Deepwater Horizon oil spill,” in Monitoring and Modeling the Deepwater Horizon Oil Spill: A Record-Breaking Enterprise, Volume 195 of Geophysical Monograph Series, eds Y. Liu, A. Macfadyen, Z. Ji, and R. Weisberg (Hoboken, NJ: Wiley), 153–165. doi: 10.1029/2011GM001121
Liu, Y., Weisberg, R., Vignudelli, S., and Mitchum, G. (2016). Patterns of the loop current system and regions of sea surface height variability in the eastern Gulf of Mexico revealed by the self-organizing maps. J. Geophys. Res. 121, 2347–2366. doi: 10.1002/2015JC011493
Lumpkin, R., Centurioni, L., and Perez, R. (2016). Fulfilling observing system implementation requirements with the global drifter array. J. Atmos. Ocean. Technol. 33, 685–695. doi: 10.1175/JTECH-D-15-0255.1
Lumpkin, R., and Elipot, S. (2010). Surface drifter pair spreading in the North Atlantic. J. Geophys. Res. 115:C12017. doi: 10.1029/2010JC006338
Lumpkin, R., Özgökmen, T., and Centurioni, L. (2017). Advances in the application of surface drifters. Annu. Rev. Mar. Sci. 9, 59–81. doi: 10.1146/annurev-marine-010816-060641
Lund, B., Graber, H., Hessner, K., and Williams, N. (2015a). On shipboard marine x-band radar near-surface current “calibration”. J. Atmos. Ocean. Technol. 32, 1928–1944. doi: 10.1175/JTECH-D-14-00175.1
Lund, B., Graber, H., Tamura, H., Collins, C. III., and Varlamov, S. (2015b). A new technique for the retrieval of near-surface vertical current shear from marine X-band radar images. J. Geophys. Res. 120, 8566–8486. doi: 10.1002/2015JC010961
Lund, B., and Haus, B. (2018). Radar Measurements Collected During the Lagrangian Submesoscale Experiment (LASER) Experiment Aboard R/V Walton Smith Cruise WS16015 in the Gulf of Mexico From 2016-01-20 to 2016-02-12. Consortium for Advanced Research on Transport of Hydrocarbon in the Environment II (CARTHE II).
Lund, B., Haus, B., Horstmann, J., Graber, H., Carrasco, R., Laxague, N., et al. (2018). Near-surface current mapping by shipboard marine X-band radar: a validation. J. Atmos. Ocean. Technol. 35, 1077–1090. doi: 10.1175/JTECH-D-17-0154.1
Luo, H., Bracco, A., Cardona, Y., and McWilliams, J. (2016). Submesoscale circulation in the northern Gulf of Mexico: surface processes and the impact of the freshwater river input. Ocean Model. 101, 68–82. doi: 10.1016/j.ocemod.2016.03.003
MacKinnon, J., Nash, J., Alford, M., Lucas, A., Mickett, J., Shroyer, E., et al. (2016). A tale of two spicy seas. Oceanography 29, 50–61. doi: 10.5670/oceanog.2016.38
Mahadevan, A., and Tandon, A. (2006). An analysis of mechanisms for submesoscale vertical motion at ocean fronts. Ocean Model. 14, 241–256. doi: 10.1016/j.ocemod.2006.05.006
Marmorino, G., Smith, G., North, R., and Baschek, B. (2018). Application of airborne infrared remote sensing to the study of ocean submesoscale eddies. Front. Mech. Eng. 4:10. doi: 10.3389/fmech.2018.00010
McWilliams, J. (2016). Submesoscale currents in the ocean. Proc. R. Soc. A Math. Phys. Eng. Sci. 472:20160117. doi: 10.1098/rspa.2016.0117
McWilliams, J. (2017). Submesoscale surface fronts and filaments: secondary circulation, buoyancy flux, and frontogenesis. J. Fluid Mech. 823, 391–432. doi: 10.1017/jfm.2017.294
McWilliams, J., Gula, J., Molemaker, M., Renault, L., and Shchepetkin, A. (2015). Filament frontogenesis by boundary layer turbulence. J. Phys. Oceanogr. 45, 1988–2005. doi: 10.1175/JPO-D-14-0211.1
McWilliams, J., Huckle, E., Liang, J., and Sullivan, P. (2012). The wavy Ekman layer: Langmuir circulations, breakers, and Reynolds stress. J. Phys. Oceanogr. 42, 1793–1816. doi: 10.1175/JPO-D-12-07.1
McWilliams, J., Huckle, E., Liang, J., and Sullivan, P. (2014). Langmuir turbulence in swell. J. Phys. Oceanogr. 44, 870–890. doi: 10.1175/JPO-D-13-0122.1
McWilliams, J., and Sullivan, P. (2000). Vertical mixing by Langmuir circulations. Spill Sci. Technol. Bull. 6, 225–237. doi: 10.1016/S1353-2561(01)00041-X
McWilliams, J., Sullivan, P., and Moeng, C.-H. (1997). Langmuir turbulence in the ocean. J. Fluid Mech. 334, 1–30. doi: 10.1017/S0022112096004375
Melville, W., Lenain, L., Cayan, D., Kahru, M., Kleissl, J., Linden, P., et al. (2016). The modular aerial sensing system. J. Atmos. Ocean. Technol. 33, 1169–1184. doi: 10.1175/JTECH-D-15-0067.1
Mensa, J., Özgökmen, Poje, A., and Imberger, J. (2015). Material transport in a convective surface mixed layer under weak wind forcing. Ocean Model. 96, 226–242. doi: 10.1016/j.ocemod.2015.10.006
Molteni, F., Buizza, R., Palmer, T., and Petroliagis, T. (1996). The ECMWF ensemble prediction system: methodology and validation. Q. J. R. Meteorol. Soc. 122, 73–119. doi: 10.1002/qj.49712252905
Munk, W., Armi, L., Fischer, K., and Zachariasen, F. (2000). Spirals on the sea. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 456, 1217–1280. doi: 10.1098/rspa.2000.0560
Noh, Y., and Nakada, S. (2010). Estimation of the particle flux from the convective mixed layer by large eddy simulation. J. Geophys. Res. 115, 1–7. doi: 10.1029/2009JC005669
Novelli, G., Guigand, C., Boufadel, M., and Özgökmen, T. (2020). On the transport and landfall of marine oil spills, laboratory and field observations. Mar. Pollut. Bull. 150:110805. doi: 10.1016/j.marpolbul.2019.110805
Novelli, G., Guigand, C., and Özgökmen, T. (2018). Technological advances in drifters for oil transport studies. Mar. Technol. Soc. J. 52, 53–61. doi: 10.4031/MTSJ.52.6.9
Olascoaga, M., Beron-Vera, F. J., Haller, G., Trinanes, J., Iskandarani, M., Coelho, E., et al. (2013). Drifter motion in the gulf of mexico constrained by altimetric lagrangian coherent structures. Geophys. Res. Lett. 40, 6171–6175. doi: 10.1002/2013GL058624
Özgökmen, T., Boufadel, M., Carlson, D., Cousin, C., Guigand, C., Haus, B., et al. (2018). Technological advances for ocean surface measurements by the Consortium for Advanced Research on Transport of Hydrocarbons in the Environment (CARTHE). Mar. Technol. Soc. J. 52, 71–76. doi: 10.4031/MTSJ.52.6.11
Pallás-Sanz, E., Johnston, T., and Rudnick, D. (2010). Frontal dynamics in a California Current System shallow front: 1. Frontal processes and tracer structure. J. Geophys. Res. 115, 1–14. doi: 10.1029/2009JC006032
Pearson, B., Fox-Kemper, B., Bachmann, S., and Bryan, F. (2017). Evaluation of scale-aware subgrid mesoscale eddy models in a global eddy-rich model. Ocean Model. 115, 42–58. doi: 10.1016/j.ocemod.2017.05.007
Pearson, J., Fox-Kemper, B., Barkan, R., Choi, J., Bracco, A., and McWilliams, J. (2019). Impacts of convergence on structure functions from surface drifters in the Gulf of Mexico. J. Phys. Oceanogr. 49, 675–690. doi: 10.1175/JPO-D-18-0029.1
Poje, A., Özgökmen, T., Lipphardt, B., Haus, B., Ryan, E., Haza, A., et al. (2014). Submesoscale dispersion in the vicinity of the Deepwater Horizon spill. Proc. Natl. Acad. Sci. U.S.A. 111, 12693–12698. doi: 10.1073/pnas.1402452111
Price, J., Weller, R., and Pinkel, R. (1986). Diurnal cycling: observations and models of the upper ocean response to diurnal heating, cooling, and wind mixing. J. Geophys. Res. 91, 8411–8427. doi: 10.1029/JC091iC07p08411
Rascle, N., Molemaker, J., Marie, L., and Menage, O. (2018). Airborne sea surface temperature and surface roughness images taken during the LASER drifter deployment in the Gulf of Mexico on 2016-02-11 Consortium for Advanced Research on Transport of Hydrocarbon in the Environment ii (CARTHE II).
Rascle, N., Molemaker, J., Marié, L., Nouguier, F., Chapron, B., Lund, B., et al. (2017). Intense deformation field at oceanic front inferred from directional sea surface roughness observations. Geophys. Res. Lett. 44, 5599–5608. doi: 10.1002/2017GL073473
Rascle, N., Nouguier, F., Chapron, B., Mouche, A., and Ponte, A. (2016). Surface roughness changes by finescale current gradients: properties at multiple azimuth view angles. J. Phys. Oceanogr. 46, 3681–3694. doi: 10.1175/JPO-D-15-0141.1
Resseguier, V., Pan, W., and Fox-Kemper, B. (2020). Data-driven versus self-similar parameterizations for stochastic advection by lie transport and location uncertainty. Nonlinear Proc. Geophys. 27:54. doi: 10.5194/npg-2019-54
Richardson, L. (1926). Atmospheric diffusion shown on a distance-neighbour graph. Proc. R. Soc. Lond. Ser. A 110, 709–737. doi: 10.1098/rspa.1926.0043
Richardson, L., and Stommel, H. (1948). Note on eddy diffusion in the sea. J. Meteorol. 5, 238–240. doi: 10.1175/1520-0469(1948)005<0238:NOEDIT>2.0.CO;2
Roarty, H., Cook, T., Hazard, L., George, D., Harlan, J., Cosoli, S., et al. (2019). The global high frequency radar network. Front. Mar. Sci. 6:164. doi: 10.3389/fmars.2019.00164
Senet, C., Seemann, J., and Ziemer, F. (2001). The near-surface current velocity determined from image sequences of the sea surface. IEEE Trans. Geosci. Remote Sens. 39, 492–505. doi: 10.1109/36.911108
Shao, M., Ortiz-Suslow, D., Haus, B., Lund, B., Williams, N., Özgökmen, T., et al. (2019). The variability of winds and fluxes observed near submesoscale fronts. J. Geophys. Res. 124, 7756–7780. doi: 10.1029/2019JC015236
Skyllingstad, E., and Denbo, D. (1995). An ocean large-eddy simulation of langmuir circulations and convection in the surface mixed layer. J. Geophys. Res. 100, 8501–8522. doi: 10.1029/94JC03202
Skyllingstad, E., Duncombe, J., and Samelson, R. (2017). Baroclinic frontal instabilities and turbulent mixing in the surface boundary layer. Part II: Forced simulations. J. Phys. Oceanogr. 47, 2429–2454. doi: 10.1175/JPO-D-16-0179.1
Smyth, W., Skyllingstad, E., Crawford, G., and Wijesekera, H. (2002). Nonlocal fluxes and Stokes drift effects in the K-profile parameterization. Ocean Dyn. 52, 104–115. doi: 10.1007/s10236-002-0012-9
Spaulding, M. (2017). State of the art review and future directions in oil spill modeling. Mar. Pollut. Bull. 115, 7–19. doi: 10.1016/j.marpolbul.2017.01.001
Stewart, R., and Joy, J. (1974). HF radio measurements of surface currents. Deep Sea Res. Oceanogr. Abstr. 21, 1039–1049. doi: 10.1016/0011-7471(74)90066-7
Storkey, D., Blockley, E., Furner, R., Guiavarc'h, C., Lea, D., Martin, M., et al. (2010). Forecasting the ocean state using NEMO: the new FOAM system. J. Operat. Oceanogr. 3, 3–15. doi: 10.1080/1755876X.2010.11020109
Sullivan, P., and McWilliams, J. (2010). Dynamics of winds and currents coupled to surface waves. Annu. Rev. Fluid Mech. 42, 19–42. doi: 10.1146/annurev-fluid-121108-145541
Sullivan, P., and McWilliams, J. (2018). Frontogenesis and frontal arrest of a dense filament in the oceanic surface boundary layer. J. Fluid Mech. 837, 341–380. doi: 10.1017/jfm.2017.833
Sullivan, P., McWilliams, J., and Melvill, W. (2007). Surface gravity wave effects in the oceanic boundary layer: large-eddy simulation with vortex force and stochastic breakers. J. Fluid Mech. 593, 405–452. doi: 10.1017/S002211200700897X
Sun, D., Bracco, A., Barkan, R., Berta, M., Dauhajre, D., Molemaker, M., et al. (2020). Diurnal cycling of submesoscale dynamics: Lagrangian implications in drifter observations and model simulations of the northern gulf of mexico. J. Phys. Oceanogr. 50. doi: 10.1175/JPO-D-19-0241.1
Suzuki, N., and Fox-Kemper, B. (2016). Understanding Stokes forces in the wave-averaged equations. J. Geophys. Res. 121, 3579–3596. doi: 10.1002/2015JC011566
Suzuki, N., Fox-Kemper, B., Hamlington, P., and Van Roekel, L. (2016). Surface waves affect frontogenesis. J. Geophys. Res. 121, 3597–3624. doi: 10.1002/2015JC011563
Sverdrup, H. (1947). Wind-driven currents in a baroclinic ocean; with application to the equatorial currents of the eastern Pacific. Proc. Natl. Acad. Sci. U.S.A. 33, 318–326. doi: 10.1073/pnas.33.11.318
Taylor, J. (2018). Accumulation and subduction of buoyant material at submesoscale fronts. J. Phys. Oceanogr. 48, 1233–1241. doi: 10.1175/JPO-D-17-0269.1
Thomas, L., and Lee, C. (2005). Intensification of ocean fronts by down-front winds. J. Phys. Oceanogr. 35, 1086–1102. doi: 10.1175/JPO2737.1
Thomas, L., Tandon, A., and Mahadevan, A. (2008). “Submesoscale processes and dynamics,” in Ocean Modeling in an Eddying Regime, Volume 177 of Geophysical Monograph Series, eds M. Hecht and H. Hasumi (Hoboken, NJ: Wiley), 17–38. doi: 10.1029/177GM04
Thomas, L., Taylor, J., D'Asaro, E., Lee, C., Klymak, J., and Shcherbina, A. (2016). Symmetric instability, inertial oscillations, and turbulence at the Gulf Stream front. J. Phys. Oceanogr. 46, 197–217. doi: 10.1175/JPO-D-15-0008.1
Umlauf, L., and Burchard, H. (2005). Second-order turbulence closure models for geophysical boundary layers. A review of recent work. Contin. Shelf Res. 25, 795–827. doi: 10.1016/j.csr.2004.08.004
Verma, V., Pham, H., and Sarkar, S. (2019). The submesoscale, the finescale and their interaction at a mixed layer front. Ocean Model. 140:101400. doi: 10.1016/j.ocemod.2019.05.004
Walker, N., Pilley, C., Raghunathan, V., D'Sa, E., Leben, R., Hoffmann, N., et al. (2011). “Impacts of loop current frontal cyclonic eddies and wind forcing on the 2010 gulf of mexico oil spill,” in Monitoring and Modeling the Deepwater Horizon Oil Spill: A Record-Breaking Enterprise, Volume 195 of Geophysical Monograph Series, eds Y. Liu, A. Macfadyen, Z. J. R. Weisberg (Hoboken, NJ: Wiley), 103–116. doi: 10.1029/2011GM001120
Weller, R., and Price, J. (1988). Langmuir circulation within the oceanic mixed layer. Deep-Sea Res. 35, 711–747. doi: 10.1016/0198-0149(88)90027-1
Xiao, S., and Yang, D. (2020). Effect of oil plumes on upper-ocean radiative transfer–a numerical study. Ocean Model. 145, 1–15. doi: 10.1016/j.ocemod.2019.101522
Yang, D., Chamecki, M., and Meneveau, C. (2014). Inhibition of oil plume dilution in Langmuir ocean circulation. Geophys. Res. Lett. 41, 1632–1638. doi: 10.1002/2014GL059284
Yang, D., Chen, B., Chamecki, M., and Meneveau, C. (2015). Oil plumes and dispersion in Langmuir, upper-ocean turbulence: large-eddy simulations and K-profile parameterization. J. Geophys. Res. 120, 4729–4759. doi: 10.1002/2014JC010542
Yang, D., Chen, B., Socolofsky, S., Chamecki, M., and Meneveau, C. (2016). Large-eddy simulation and parameterization of buoyant plume dynamics in stratified flow. J. Fluid Mech. 794, 798–833. doi: 10.1017/jfm.2016.191
Young, I., Rosenthal, W., and Ziemer, F. (1985). A three-dimensional analysis of marine radar images for the determination of ocean wave directionality and surface currents. J. Geophys. Res. 90, 1049–1059. doi: 10.1029/JC090iC01p01049
Yu, X., Naveira Garabato, A., Martin, A., Buckingham, C., Brannigan, L., and Su, Z. (2019). An annual cycle of submesoscale vertical flow and restratification in the upper ocean. J. Phys. Oceanogr. 49, 1439–1461. doi: 10.1175/JPO-D-18-0253.1
Keywords: submesoscale, boundary, turbulence, Langmuir, dispersion, oil, physical oceanography
Citation: D'Asaro EA, Carlson DF, Chamecki M, Harcourt RR, Haus BK, Fox-Kemper B, Molemaker MJ, Poje AC and Yang D (2020) Advances in Observing and Understanding Small-Scale Open Ocean Circulation During the Gulf of Mexico Research Initiative Era. Front. Mar. Sci. 7:349. doi: 10.3389/fmars.2020.00349
Received: 10 March 2020; Accepted: 27 April 2020;
Published: 20 May 2020.
Edited by:
Frédéric Cyr, Fisheries and Oceans Canada, CanadaReviewed by:
Shijian Hu, Institute of Oceanology, CAS, ChinaNancy Soontiens, Department of Fisheries and Oceans, Canada
Copyright © 2020 D'Asaro, Carlson, Chamecki, Harcourt, Haus, Fox-Kemper, Molemaker, Poje and Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Eric A. D'Asaro, ZGFzYXJvQGFwbC53YXNoaW5ndG9uLmVkdQ==
 Eric A. D'Asaro
Eric A. D'Asaro Daniel F. Carlson
Daniel F. Carlson Marcelo Chamecki
Marcelo Chamecki Ramsey R. Harcourt
Ramsey R. Harcourt Brian K. Haus5
Brian K. Haus5 Baylor Fox-Kemper
Baylor Fox-Kemper Andrew C. Poje
Andrew C. Poje