
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mar. Sci. , 16 June 2020
Sec. Coastal Ocean Processes
Volume 7 - 2020 | https://doi.org/10.3389/fmars.2020.00326
European coastal databases contain information on the evolution of European shorelines in the 1990s and the 1980s. We investigate if a shift toward erosion has been observed between these two periods, as it could be expected as a consequence of contemporary sea-level rise or changing coastal management practices. We select comparable European coastal sites, consider their state transitions as the parameters of a discrete-time Markov chain, and analyze their steady states in order to reveal underlying changes in shoreline evolution trends. The results suggest that European coastal wetlands and small beaches have initiated a shift toward erosion, which attenuates previous optimistic statements. Our results should be interpreted with caution due to the limited number of observations and presumed errors in the database. However, they suggest that the impact of contemporary sea-level rise along European coastlines in the 1990s may be more important than previously thought. Our results suggest that more research is needed to quantify the morphodynamics of muddy coasts and to develop data models able to represent coastal morphodynamic changes adequately.
As climate is changing, identifying its signature in current environmental observations is becoming an important societal challenge (Stone et al., 2013; Brown et al., 2014; Cramer et al., 2014; Hansen et al., 2016). This is especially relevant for the significant proportion of coastal zones that have experienced a sea-level rise close to the global average of about 15 to 20 cm since the late 19th century (Church and White, 2011; Church et al., 2013; Oppenheimer et al., 2019). Previous studies have shown that extreme and mean sea level changes display similar geographical patterns, thus raising concerns regarding current coastal flooding hazards changes (Menéndez and Woodworth, 2010; Woodworth et al., 2011). For more complex biophysical coastal systems, a key question is our ability to assess whether they are changing beyond a “baseline that characterizes its behavior in the absence of climate change,” that is, our ability to perform a “detection of impacts” (Cramer et al., 2014). This question is key in the area of shoreline changes, since impacts of sea-level rise have been hardly detected so far (Cramer et al., 2014; Le Cozannet et al., 2014; Duvat, 2019; Oppenheimer et al., 2019; Toimil et al., 2020). Coastlines may retreat due to the combined effects of climate induced sea-level rise and land subsidence (Leatherman et al., 2000; Zhang et al., 2004; Romine et al., 2013), changing wave climates and the inherited coastal morphology (Albert et al., 2016; Garcin et al., 2016; Romine et al., 2016). However, detecting impacts of sea-level rise in shoreline evolutions remains difficult for the majority of coastlines, as the signal is often hidden behind the numerous natural and anthropogenic factors affecting nearshore sediment transport (Stive et al., 2002; Stive, 2004; Cazenave and Le Cozannet, 2014; Ranasinghe, 2016). This includes human interventions, the effects of the climate variability, including the North Atlantic Oscillation (Robinet et al., 2016) and the El Nino Southern Oscillation (Barnard et al., 2015, 2017), as well as other processes affecting the sediment availability at each local coastal site, such as the influence of estuaries (Castelle et al., 2017). In the case of Europe, regional sediment shortage may be an explanation to increased beach erosion, as the large amount of sediments that reached the coast during the last deglaciation are progressively being eroded (Paskoff, 2004).
Several studies have explored shoreline changes over a large number of sites, in order to average and remove localized effects and detect broader, but more subtle shoreline evolution trends (Leatherman et al., 2000; Zhang et al., 2004, Gutierrez et al., 2011). While one of the key difficulties is the accessibility of coastal data, some unexploited opportunities exist, as large coastal databases are being collected (e.g., Thieler and Hammar-Klose, 1999; Vafeidis et al., 2008). These databases were primarily designed to assess future impacts of climate change quantitatively or by means of indicators at local to regional scale (e.g., Gornitz, 1991; Fairbank and Jakeways, 2006; Hinkel et al., 2013; Spencer et al., 2016; Ponte Lira et al., 2016). However, they are also being increasingly considered to identify changes in observed modes of shoreline changes, and, more specifically, to detect impacts of sea-level rise (see the AR5 IPCC terminology; IPCC, 2013; Cramer et al., 2014).
Previous studies have quantitatively examined the links between sea-level rise and the rates of shoreline changes (Leatherman et al., 2000; Zhang et al., 2004), but this comes with the limitation that the computation of rates can be associated with large uncertainties (Pilkey et al., 2000; Sallenger et al., 2000). Here, we explore how different groups of coastal sites may have contrasting coastal behaviors, following the clustering approach of Gutierrez et al. (2011). For example, the coastal database of the eastern United States shoreline was used to detect similarities between the spatial patterns of sea-level rise and shoreline changes, which provide insight into the role of sea-level rise in shoreline erosion (e.g., Gutierrez et al., 2011; Bulteau et al., 2015). Less attention has been given to the temporal evolution of shoreline changes. Only Morton (2008) and a few others (Singh, 1997; Ford, 2013) examined if accelerations in sea-level rise has been accompanied with increased rates of shoreline retreat, and these studies have focused on coastal sites of limited spatial extent. The European coastal database Eurosion (Eurosion, 2004) contains information regarding shoreline evolution over the 1990’s. This database has known limitations, which are further detailed in section “Data Clustering”: for example, its hydrodynamic and sea-level layers are only adapted to broad scale classifications and should not be used for local flood hazard assessments. Once corrected from geo-referencing errors, the coastal geomorphology layer contains details of less than 200 m and the boundaries between coastal geomorphic features are accurately positioned and fit for local assessments (e.g., 1:25 000), as shown in the Eurosion reports available at www.eurosion.org. Previous analysis of the whole Eurosion database showed that the regional patterns of relative sea-level rise display some consistency with the probability of shoreline evolution (erosion, accretion or stability), although the local geomorphology plays a prominent role (Yates and Le Cozannet, 2012). Here, we examine the temporal dynamics of shoreline evolution, using a complementary survey that examined the previous decade (1980’s), namely Corine Erosion Côtière survey (Quelennec et al., 1998), which is referred to as CEC hereafter. As part of the methodology for producing regional indicators, these two “snapshots” of observations, over two successive decades (1980s and 1990s), are used to assess where coastal hazards erosion might be increasing (Eurosion, 2004). Despite limitations discussed in section “Data Clustering,” this dataset is unique because of the precision of the changes it reports: for example, the database reports erosion of cliffs in Normandy or Basque country, which are approximately 20 cm/year. New global studies using satellite data to evaluate global shoreline changes may reach similar precision using the high resolution satellite images available since 2000 (e.g., Ikonos, Pleiades), but they remain limited in terms of precision over the timescales considered in the Eurosion database (1980–2000). However, to our knowledge, no systematic analysis of the temporal evolutions of shoreline changes and their causes has been performed so far based on this dataset.
We explore the Eurosion and CEC coastal databases in order to identify and interpret the causes of potential shifts, for example toward more erosion or more stability, as it could be expected as a consequence of contemporary sea-level rise and/or changing coastal management practices. By considering a large number of sites in the coastal database, we expect to average and remove localized changes, which have different signs and amplitudes depending on the coastal site considered, but are finally distributed symmetrically around a zero mean. However, although particular attention has been given to data quality control in the Eurosion project (Eurosion, 2004), some changes may actually reflect errors or inconsistencies during the process of data collection and aggregation (Le Cozannet et al., 2016), which we analyze in details below.
The article is organized as follows: in section “Data Clustering,” we present the Eurosion and CEC databases and the clustering approach used in this paper. In section “Methods,” we present a data mining approach that models transitions between shoreline states using a discrete time Markov chain, and provide an illustrative application using a virtual shoreline change dataset. Section“Application on the European coastal database” (results) presents the changes in shoreline evolution trends identified in the CEC and Eurosion database. Finally, section “Discussion” interprets the results and discusses improvements in coastal databases that would be required to support their use in studies aiming at detecting impacts of sea-level rise.
The Eurosion and CEC databases are disseminated by the European Environment Agency in the form of a spatial database. The coastal segments are described by: (1) a spatial object representing the geometry of each coastline segment and (2) tabular data, describing the physical environment (e.g., geomorphology, coastal evolution, sea-level changes), human interventions (coastal defenses) and the history of each segment wherever data has been acquired. Both databases were collected through a survey among regional and national coastal observatories, complemented with additional data and observations, including from remote sensing images (Eurosion, 2004). This section summarizes the most important features of the Eurosion and CEC databases, and how we group the information into similar clusters of coastal sites. Within such clustering approaches, there is a trade-off between two extreme situations: (1) using too many categories and get too few observations in each category to train a statistical model; (2) using too few categories and mix different modes of evolution within the same groups. Hence, the aim of section “Data Clustering” is to find an adequate balance between these two situations, considering the quality and the limitation of the dataset. More details on Eurosion are provided in public technical reports (Eurosion, 2004).
The Eurosion and CEC databases include a description of coastal geomorphology and shoreline evolution data. To produce this dataset, the Eurosion project performed a segmentation of the European shoreline allowing to associate each contiguous and homogeneous geomorphological unit with one single entry in the database. The description of geomorphology is similar in the two databases, but new information was included in Eurosion, especially where coasts have been artificially modified between the two surveys. Twenty different types of coasts are considered, including ten types of beaches, three types of cliffs as well as wetlands, artificialized coasts and virtual lines in estuaries (Eurosion, 2004). Additional information regarding the lithology is available in Eurosion. In a general case, information on the lithology is very useful to determine modes of shoreline changes (e.g., Brooks and Spencer, 2010; López et al., 2020). However, within the structure of the Eurosion database, once the coastal geomorphology is known, supplementary information regarding the lithology adds little knowledge to a prior estimation of shoreline evolution trends (Yates and Le Cozannet, 2012). Hence, we eliminate this latter information from the analysis.
We classify the shoreline evolution states of the CEC and Eurosion databases into 4 categories:
– Stable shorelines, gathering segments that remain stable at decadal timescales (36,200 km of coastline, representing 28% of European shorelines in the 1990s), and shorelines evolving around a stable position (8,000 km, representing 6% of European shorelines in the 1990s).
– Eroding shorelines, gathering segments where the available observations confirm that erosion is generalized over the whole segment (4450 km, 3% of European shorelines in the 1990s), limited to some parts of the segment (4000 km, 3% of European shorelines in the 1990s), as well as segments where erosion is considered likely despite the lack of data (6700 km, 5% of European shorelines in the 1990s).
– Accreting shorelines, including sites where accretion is confirmed by observations over the whole segment (6400 km, 5% of European shorelines in the 1990s), over a part of the segment (2500 km, 2% of European shorelines in the 1990s), as well as segments where accretion is considered likely (5200 km, 4% of European shorelines in the 1990s).
– Shorelines without data allowing characterizing the state of shorelines, and which are not considered here (55,000 km, representing 44% of European shorelines in the 1990s).
The description of shoreline evolution states has known limitations (Eurosion, 2004): as most coastline changes do not exceed ±1 m/year (Bird, 1985), the accuracy required to quantify shoreline changes is challenging for many satellite missions (Cazenave et al., 2017). For example, Luijendijk et al. (2018) report shoreline changes exceeding 0.5 m/yearr, which prevents identifying areas eroding at slower rates. However, both the Eurosion dataset and local surveys report erosion in Western France (e.g., Castelle et al., 2018), which is not observed in the global study of Luijendijk et al. (2018). In the future, the accuracy and precision of remote-sensing-based automated shoreline extraction procedures should reach the standards of local surveys (e.g., Vos et al., 2019) and offer new opportunities for studies aiming at detecting impacts of sea-level rise.
The content of the Eurosion database relies on a manual processing of remote sensing images and field observations. These observations were then made available by different national and regional coastal observatories, in order to constitute the European databases. This implies that errors can be made as coastal data from regional or national coastal observatories are harmonized and integrated into the European coastal databases (Le Cozannet et al., 2016). Furthermore, depending on the coastal data available, the first and last shoreline survey may differ slightly from site to site. Consequently, the shoreline evolution trend may actually represent observations over 5 to 10 years over the decade considered (note that for beaches evolving at shorter time periods and for which no clear shoreline evolution trend can be identified, the description that holds is “shorelines evolving around a stable position”). Finally, due to the heterogeneity of the coastal observations available, no quantitative information on the evolution rates was provided. Nevertheless, this dataset remains unique to provide statistical information on present shoreline evolution at European scales.
Figure 1 displays the available information regarding tides, waves and sea-level rise in the Eurosion database. This data results from hydrodynamic models and the interpolation of tide gauge records available at the time of the Eurosion project (Eurosion, 2004). The resolution of this information is too low to identify sheltered areas (i.e., exposed to low waves energy) or other local processes. However, it can be used to identify a few European regions affected by similar tides, waves and sea-level changes. While this information is coarse, it is sufficient for clustering coasts according to their exposure to a few typical hydrodynamic regimes along the European coastlines. In summary, the largest tidal range and wave heights are found along the Atlantic and North-Sea coasts. These coasts are also affected by sea-level rise close to the global average, as confirmed by Wahl et al. (2013) and Wöppelmann and Marcos (2016). The data show that the coasts of the Irish Sea are affected by land uplift due to the global isostatic adjustment, here mostly due to the visco-elastic response of the Earth to the melting of the north-European ice-sheets after the last glacial maximum 21,000 years ago. This results in sea level drops in Figure 1A. However, more recent studies shows that it is nearly stable (Woodworth et al., 2009; Gehrels, 2010; Shennan et al., 2012). In Scandinavia and Finland, sea level is falling or nearly stable due to the global isostatic adjustment, and the tidal range and mean significant wave heights are low. Finally, sea level changes along the Mediterranean coasts are unreliable as this region is affected by local vertical ground motions due to tectonics and groundwater or fluid extractions, as shown by geodetic data (Raucoules et al., 2008; Ferranti et al., 2010; Wöppelmann and Marcos, 2012) and sea level footmarks such as tidal notches (Lambeck et al., 2011; Evelpidou et al., 2014). Hence, the analysis of tides, waves and sea level data leads us to separate two homogeneous regions: (1) coasts of Scandinavia and Finland, where sea level is falling while waves and the tidal range are small; (2) European Atlantic and North-Sea coasts (except the Irish Sea), where sea-level rise is close to the global average while the tidal range and mean wave heights are large. However, no coastal data was collected during the 1980’s in Scandinavia and Finland. Hence, the investigations are limited to the European Atlantic and North-Sea coasts.
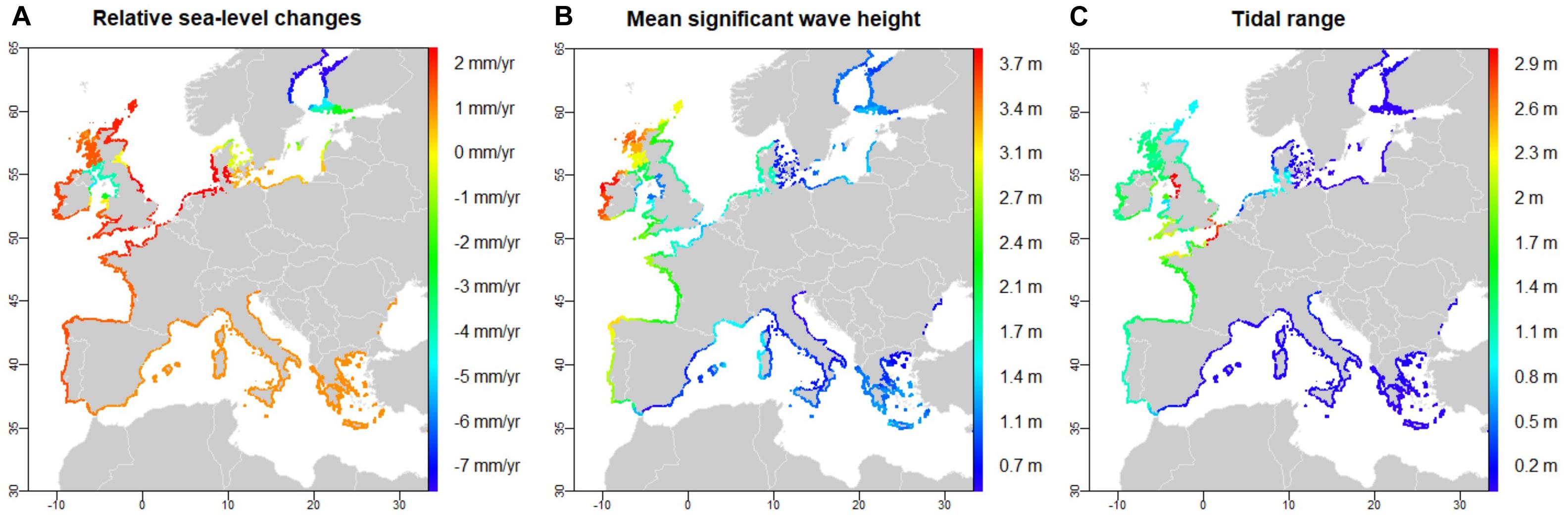
Figure 1. Relative sea level change (A), mean significant wave height (B), and tidal range (C) along the European coastlines according to the Eurosion database.
Both Eurosion and CEC coastal databases provide information regarding the location of coastal defense infrastructures. The completeness of this information has been questioned, in particular during the implementation of the European Marine Strategy Framework Directive. In France, an independent analysis of recent aerial photographs was conducted, showing that 35% of French coastlines are protected by coastal defenses (Brivois, 2016). Furthermore, the maps of protected coast is similar according to the Eurosion database and this new database. Consequently, we hypothesize that the coastal defenses with the largest impacts on coastal hydro-sedimentary processes over the 1980s and 1990s are satisfactorily referenced in the European coastal database.
This section describes our approach to characterize the temporal dynamics of coastal evolution in the CEC and Eurosion coastal databases. In this approach, we model the evolution of coastal sites from the 1980’s to the 1990’s with a discrete Markov chain. For this, we first select homogeneous groups of coastal sites, which are supposed to behave similarly, given their morphological context and exposure to waves, tides, sea level changes and human interventions (section “Selection of a Comparable Subset From the Eurosion Coastal Database”). The parameters of the Markov chain are derived from the observations in the coastal databases (section “Modeling Coastal Evolution Changes With Discrete Time Markov Chains”). Finally, as several processes driving changes in shoreline evolution are superimposed in the observations, we compute the steady state of the Markov chain derived from the observations in order to identify evolutions underpinned by the observed transitions. This last procedure is illustrated on a virtual dataset of small beaches (section “Application on a virtual dataset”). In this contribution, we use R with the “Markov chain” package to perform the simulations (Spedicato et al., 2015).
To enable comparisons, changes in coastal evolution modes from the 1980’s to the 1990’s must be considered with regards to specific types of coasts, such as beaches affected by sea level changes close to the global average and with limited human interventions. Previous studies have shown that this can be a challenge (Leatherman et al., 2000; Zhang et al., 2004), but in the case of the Eurosion database, Bayesian networks using the description of the geomorphological and hydrometeorological contexts infer the probability of coastal erosion with satisfactorily skill (Yates and Le Cozannet, 2012).
We identify homogeneous subsets of coastal sites by successively selecting:
(1) Coastal segments with updated information on coastal evolution and geomorphology in both the CEC and Eurosion databases;
(2) Coastal segments exposed to similar tides, waves and sea-level rise (see section “Tides, waves and sea-level changes”) and unaffected by direct human interventions (section “Coastal Defenses”): in fact, coastal defense infrastructures usually limit sediment transport, modify coastal shapes and hide the impacts of slower processes such as those accompanying sea-level rise (e.g., Stive, 2004); therefore, as in most previous studies aiming at investigating the causes of decadal to multidecadal shoreline changes (Zhang et al., 2004, among others), we remove coastal sites affected by large coastal defense infrastructures from our analysis;
(3) Segments with the same coastal landforms in the CEC and Eurosion database. Geomorphological changes can be due to real changes of the morphology (e.g., loss of sediments on the beach, leading to artificial coastlines or cliffs), to slightly different data models in the CEC and Eurosion databases, or the refined resolution of Eurosion data compared to the CEC survey and thus are artifacts.
Overall, these successive selections take maximum advantage of the content of the CEC and Eurosion databases, in order to finally bring together subsets of similar coastal sites.
Discrete time Markov chains are mathematical tools representing systems whose state at time t+1 only depends on the state at time t. They have been used for time series forecasting and analysis in a variety of applications. Markov chains have for instance proved relevant in econometric and financial analysis (Tsay, 2010). They serve as a basis in marketing studies such as the brand loyalty problem (Whitaker, 1978). In a completely different context, they have been proposed in hydrology to predict drought periods and their characteristics (Liu et al., 2009; Sharma and Panu, 2012), but also conversely for flood risk assessment (Beven and Hall, 2014). In biomedical research, they have been widely considered for diagnostic, prognostic and epidemiological studies (Tan, 2002). Finally, they have been used in seismology to predict patterns in volcanic activity (Wickman, 1976). Markov chains have been used for coastal evolution modeling in previous studies (Sonu and James, 1973: Ostroumov et al., 2005; Furlan, 2008; Hurst et al., 2016). The focus of most of these studies was on assessing prediction skills of a beach evolution model based on a Markov chain. However, Hurst et al. (2016) also attempted to attribute accelerated cliff erosion in South Great Britain to increased wave actions on cliff toes in a context of thinning of beach front beaches. However, to the best of our knowledge, Markov chains have not been applied yet to broad scale coastal databases for detecting changes in shoreline evolutions.
Mathematically, discrete Markov chains are defined as follows. For a finite number of states identified as i ∈ {1…n}, the sequence of random variables Xj with j ∈ {1…m} is a homogeneous discrete-time Markov chain if ∀t ∈ {1…m} and ∀ (kt ∈ {1…n}:
The first part of the equation translates the fact that the probability of being in the state kt at time step t only depends on the previous state at time step t−1. The second part of the equation expresses that the transition probabilities do not change over time.
Discrete-time homogeneous Markov chains can be represented by a graph, where the nodes indicate the possible states {1…n} of the random variable Xj, while the edges are associated with the probability of moving to state kt given that the present state is kt–1. Finally, the conditional probabilities P(Xt = p|Xt–1 = q) can be represented by a transition matrix P = [P(Xt = p|Xt−1 = q)](q,p) ∈ {1…n}2. The latter is a stochastic matrix in the sense that all its entries are positive and its rows sum to 1.
The qualitative description of the information on shoreline evolution of coastal databases (erosion, stability, and accretion) can be interpreted as a discrete state space, while the transitions between states can be learnt from the data available in the 1980’s and 1990’s. To illustrate this, we simply synthetize the states of all 6,661 coastal sites shown in Table 1, compute the parameters of the associated Markov process empirically and display its graph in Figure 2. In this graph, the observed transitions from the CEC to Eurosion database on a decadal basis are used to learn the transition probabilities, that is, the parameters of the Markov chain P(Xt = kt|Xt−1 = kt−1). The corresponding 3x3 transition matrix is represented in Table 1 and Figure 2.
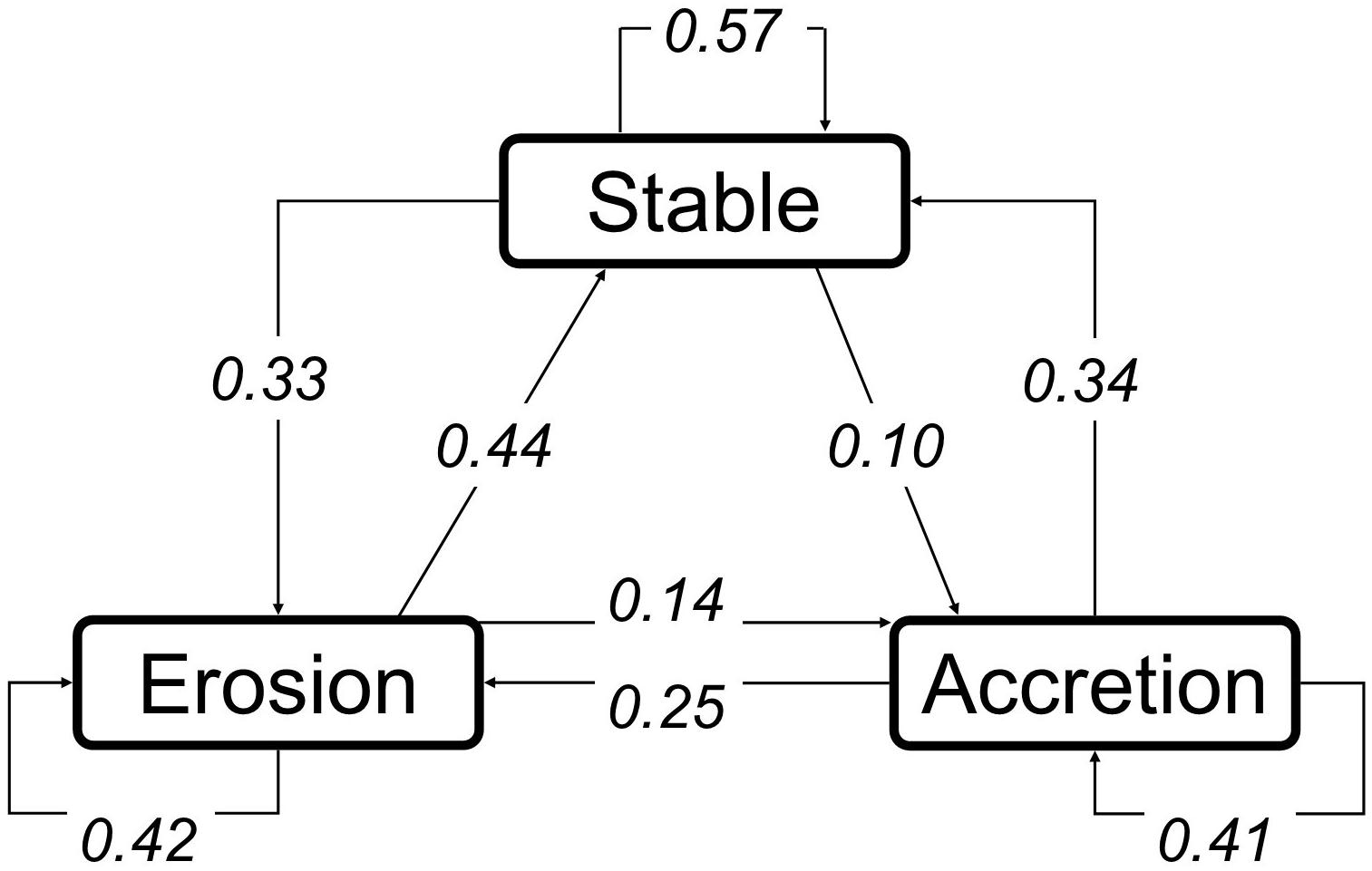
Figure 2. Example of discrete-time Markov chain representing the coastal states and their transition probabilities for the 6661 sites of Table 1. The graphic reads as follows: coastal sites in erosion in the 1980s have a probability of 0.42 to be still in erosion in the 1990s, 0.14 to be in accretion and 0.44 to be s.
Once the parameters of the Markov chain are obtained from the observations, identifying the underlying changes in shoreline evolution trends is not straightforward from the six possible transition probabilities (Figure 2 and Table 1). However, a well-known result states that:
where vt is the so-called probability vector at time t, i.e., a column vector composed of the probabilities for the Markov chain to be in the different states, and Pt is the transition matrix raised to power t. If the Markov chain has good properties, i.e., is ergodic, vt converges as t tends to infinity. Thus, a classical procedure consists in repeating the Markov process several times forward in order to identify the steady state distribution implied by the observed transitions. Provided the latter exists, it can be evaluated either by computing large powers of the transition matrix P, or, more simply, through simple operations on its eigenvector as it is implemented in the “Markov chain” package implemented in R (Spedicato et al., 2015).
In the case of the Markov chain represented in Table 1 and Figure 2, the steady state distribution is close to the observations in the 1990s: if the transition matrix shown in Table 1 is applied again to the observations in the 1990s, the resulting statistics will be very close to those of the 1990s. This suggests that there is no detectable shoreline evolution trend toward more erosion or accretion for the entire dataset. However, shoreline evolution is strongly related to the coastal geomorphology, human interventions, tides, waves and sea level changes. In the entire dataset, many sites are very different, which prevents any single interpretation. Hence, we select homogeneous subsets of coastal sites as detailed in section “Selection of a Comparable Subset From the Eurosion Coastal Database,” in order to provide information regarding the evolution of different types of coastal settings.
In the general case, shoreline evolution trends do not necessarily fulfill the requirements that for the probability of erosion, stability or accretion only depend on the state of the system over the previous decade. We assume that this requirement is fulfilled, noticing that given a coastal database with two time slices, the proposed Markov model is the simplest extension of the Bayesian networks, whose predictive skills has been demonstrated for large coastal temperate databases (e.g., United States, Europe; Gutierrez et al., 2011; Yates and Le Cozannet, 2012). The assumption that the process is ergodic is not necessarily fulfilled either. We follow López et al. (2020) by assuming that this assumptions is fulfilled, and verify it in practice through the practical computation of the limit of Pt, with large t.
In this section, we illustrate the detection approach presented above using an idealized case. To do so, we consider a virtual set of beaches, whose shoreline change rates are affected by slight changes in sea-level rise rates and other modes of variability. We compute the Markov chains and the associated steady states and discuss to which extent the approach proposed above is able to detect impacts of sea-level rise.
We consider a virtual set of beaches, whereby 33% of the segments are eroding, 50% are stable and 17% are accreting in the 1980’s. We also assume that these beaches are located in the Bay of Biscay, where a reconstruction of past sea level changes is available (Figure 3). This reconstruction is based on 15 yearly tide gauge records from the Permanent Service for Mean Sea Level corrected from vertical ground motions with collocated GPS station of the SONEL database wherever available (Santamaría-Gómez et al., 2012) and with global isostatic adjustment data from Jevrejeva et al. (2006) otherwise (see Idier et al. (2020) for details on the reconstruction method). According to this reconstruction, the rates of sea-level rise have increased from 1.2 ± 0.2 to 2.4 ± 0.2 mm/year from the 1980s to the 1990s.
According to the classical sediment balance equation (Stive, 2004), shoreline changes ΔS are the sum of two terms:
This model assumes that shorelines respond linearly to sea-level rise (SLR) and that the coefficient of proportionality is the inverse of the beach slope tan(α) (Bruun, 1962; Davidson-Arnott, 2005). In this idealized case, these assumptions induce a shift toward erosion of 0.12 m/year with beach slopes of 1% (Nicholls, 1998). The second term in the equation f represents the impacts of all the other sedimentary effects on shoreline changes (Cowell et al., 2003), which we assume to follow a Gaussian distribution with a standard deviation of 1 m, based on the review of shoreline changes of observations by Bird (1985). Under these assumptions, the increase of sea-level rise rates in the 1990s induces a shift in the distribution of shoreline change rates, as in Figure 4. If the same thresholds are used to classify beaches evolution in the 1990s and in the 1980s (dashed vertical lines at abscissa ±0.7 m/year in Figure 4), the number of eroding sites rises from 33 to 37% (Stability: 50 to 49%; Accretion: 17 to 14%) The Markov process associated with these virtual observations includes an absorbing state (erosion). Hence, if the process is repeated several times, beach evolution states will progressively be absorbed by this state (Virtual case A in Figure 5). Note that in this idealized model, repeating the same process implies that the rates of sea-level rise increase by about 1.2 mm/year each decade so that the rates of sea-level rise reach 14 mm/year by the end of this century and 0.75 m above the 2000 level (see eqn. 3). This is compliant with the median projection of the Special report on Ocean and Cryosphere in the Atlantic coast of Europe (Oppenheimer et al., 2019; see Thiéblemont et al., 2019 for regional projections in Europe).
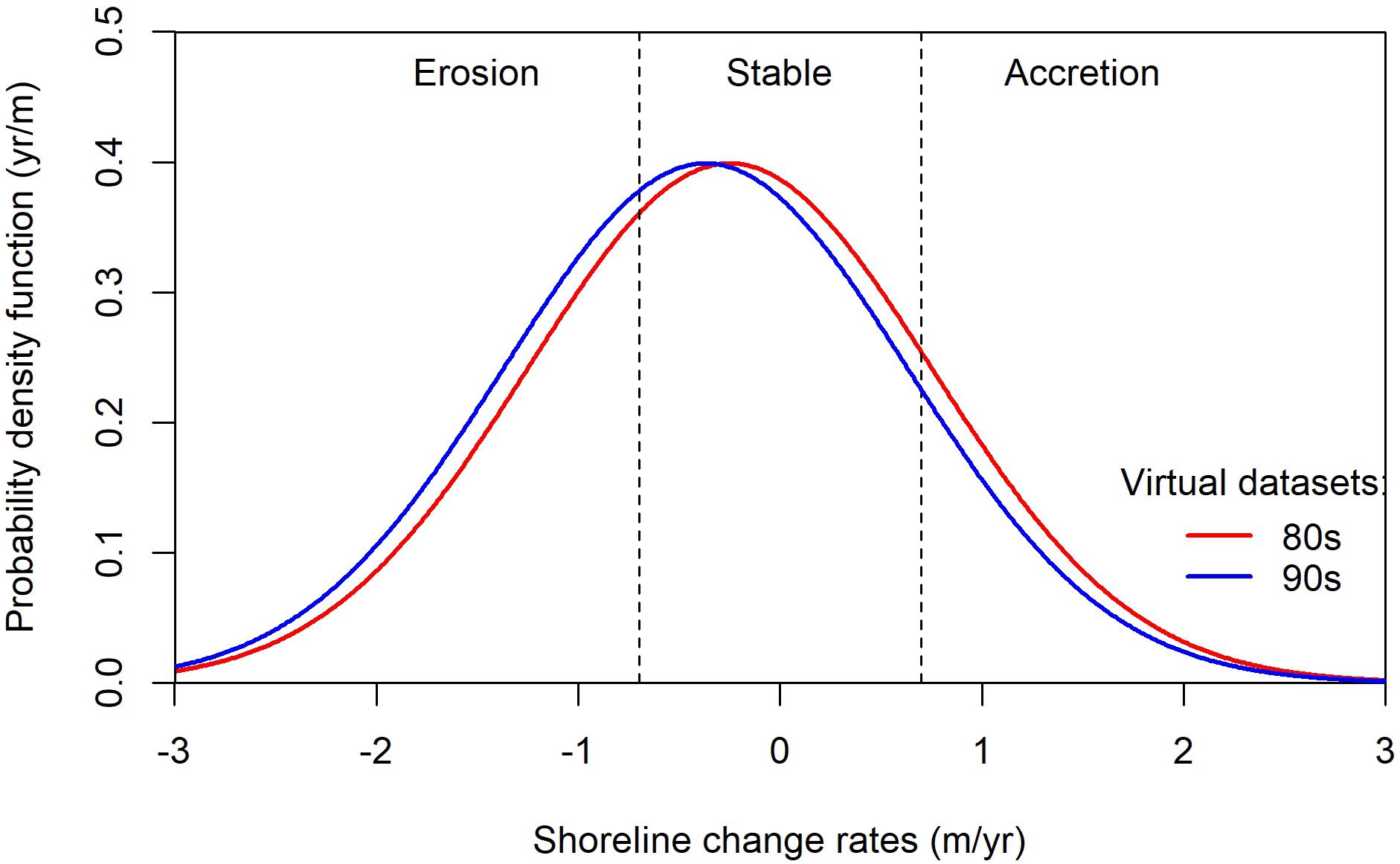
Figure 4. Shoreline change datasets used in section “Application on a Virtual Dataset” to illustrate the method used in this study. The blue probability density function refers to a virtual dataset based on small beaches in the European coastal database. The red probability function superimposes the effects of sea-level rise to the same dataset, as in eqn. 3.
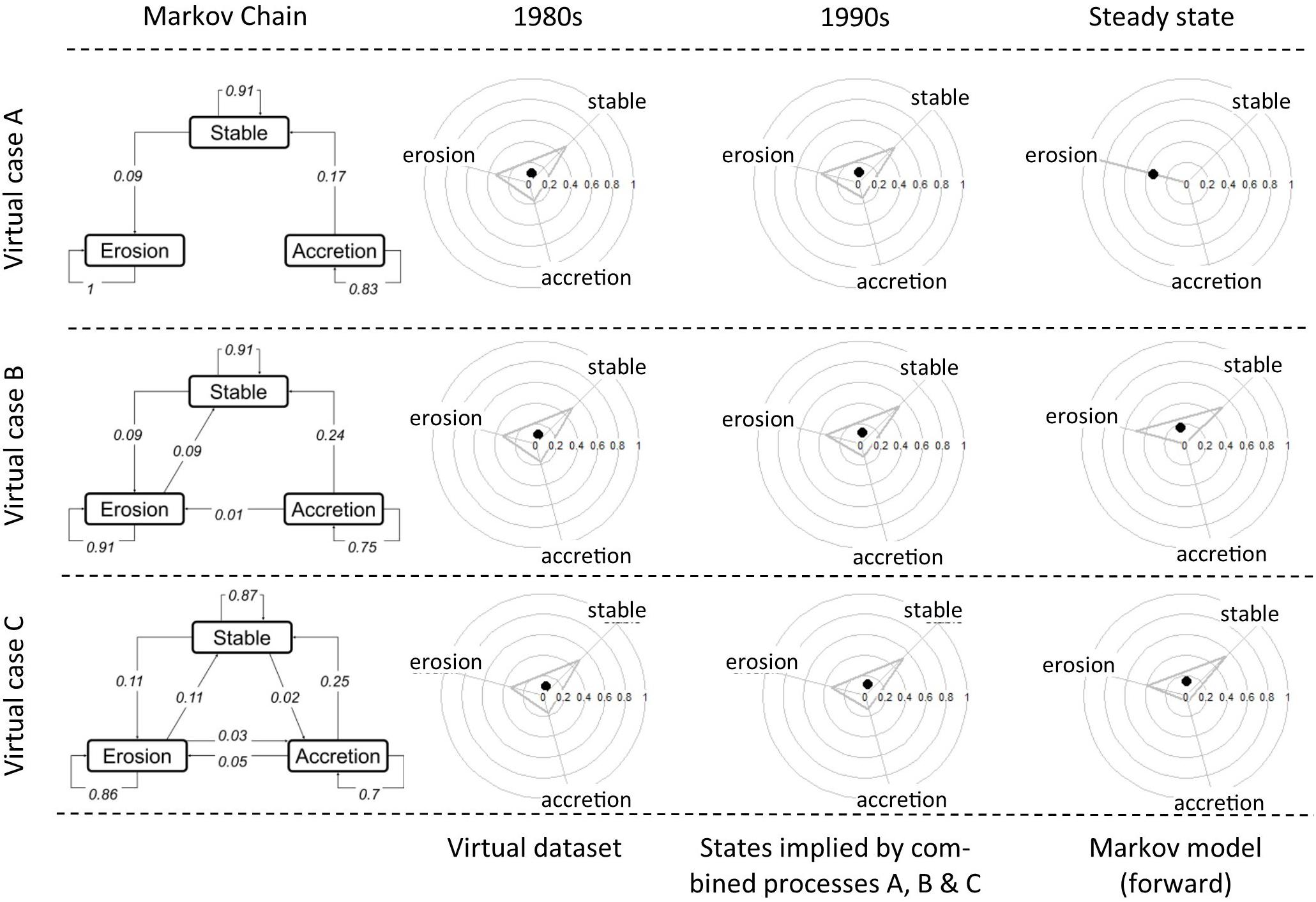
Figure 5. Illustrative virtual cases, displaying the graph associated with the Markov chain, whose parameters have been learned from the virtual dataset. The radial plots indicate the proportion of eroding, accreting and stable segments. The 1980s state assumes that 50% of coastal segments are stable, 33% are eroding and 17% accreting. The virtual case A considers sea-level rise only, as in eqn. 3. The virtual case B assumes that the effects of sea-level rise are superimposed with a process converting 10% of accreting and 10% of eroding segments to stability. The virtual case C superimposes additional random transitions with magnitudes lower than 5%. The dark plot in the radial plots indicates the barycenter (center of mass) of each triangle. The displacement of the triangle from the initial state (1980s) to the 1990s or steady states allows identification of the shoreline evolution trends underpinned by the graph (3 states, 9 parameters, among which 6 are independent parameters).
In the previous case, the detection of changes in shoreline evolution trends is straightforward. However, in the real world, other non-Gaussian effects would be superimposed on top of those of eqn. 3. These effects may either reflect modes of variability, changes in methods to collect and model the data or errors in the database. To illustrate this in a virtual case, we consider a case where the superimposed modes of variability lead to increasing the number of stable sites during the 1990s. Hence, the transition matrix of the process combining the effects of sea-level rise (as modeled in eqn. 3) and the other modes of variability are obtained by multiplying the two virtual matrices. The virtual case B in Figure 5 superimposes the effects of sea-level rise with another mode of variability shifting 10% of the eroding sites and 10% of accreting sites to stability. In this case, the changes in shoreline evolution trends are not obvious, but we identify that the steady state is more stable and erosive than the initial state. Finally, we define a virtual case C, which superimposes the virtual case B with additional random transitions lower than 5%, as shown in Figure 5. Again, the barycenter (center of mass, dark dot) of the radial plot is slightly shifted toward erosion.
To summarize, this virtual case shows that if the coastal database contains a sufficient number of observations, does not contain too many errors, and if eqn. 1 is valid, then, we expect to detect a change in shoreline evolution using the Markov chain approach presented in this paper. Furthermore, the analysis of future steady states allows identifying combined effects of an acceleration of sea-level rise or caused by other modes of variability or errors, provided that the magnitude of the effects of sea-level rise is at least comparable to those of other effects.
Figure 6 shows that the number of sites drops drastically after the successive selections of updated and comparable sites (see section “Selection of a Comparable Subset From the Eurosion Coastal Database”). In this section, we use only those coastal sites with information on coastal geomorphology and shoreline evolution for both the 1980’s and 1990’s, without geomorphology changes, exposed to sea-level rise rates larger than 1.7 mm/year, to energetic offshore waves conditions and a macrotidal regime. This reduces the analysis to 1,023 coastal sites representing 2,200 km, gathering subsets of a few tens or hundreds of homogeneous coastal sites only (Table 2). This segmentation issue originates partly from the limitations in the completeness and homogeneity of the Eurosion dataset.
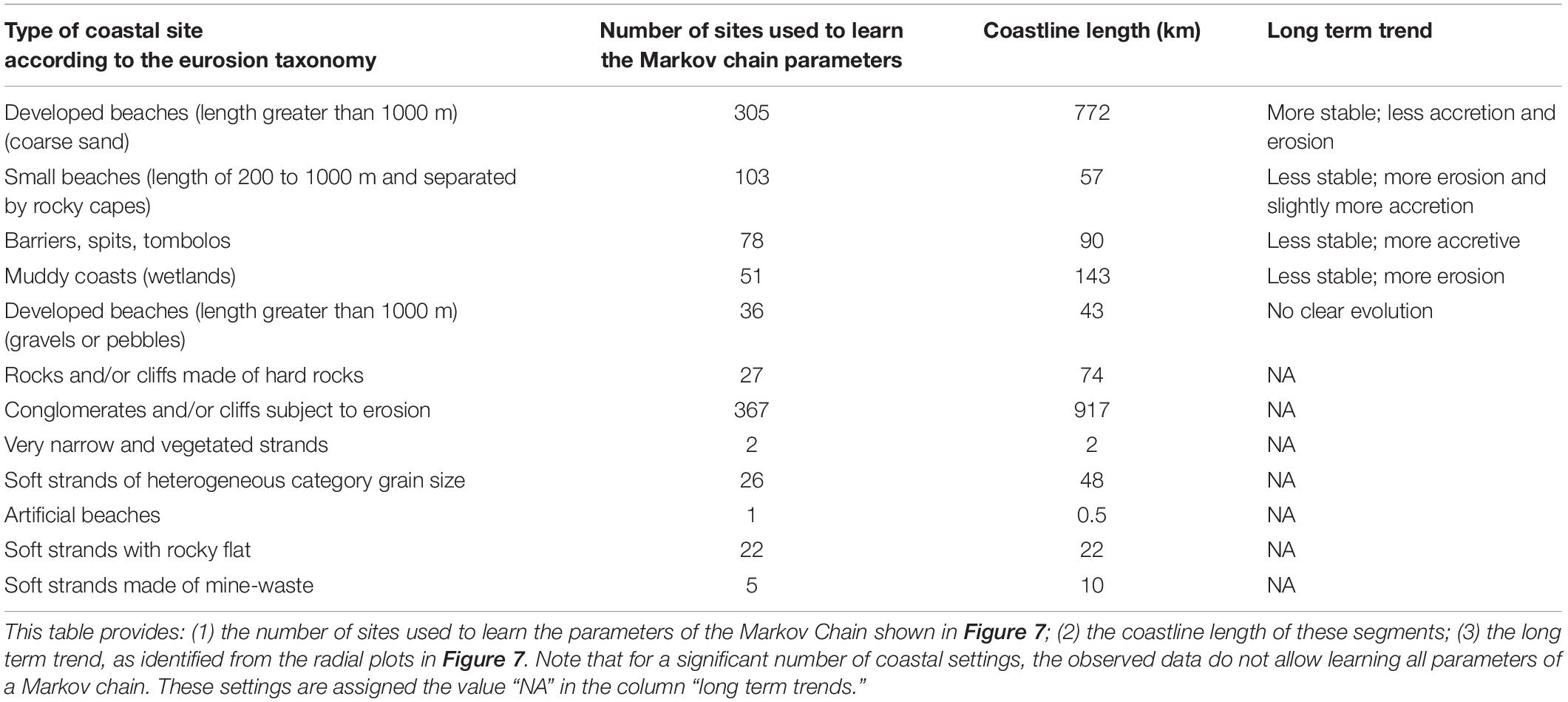
Table 2. Summary of results of the analysis of the temporal dynamics using Markov chain, for sites without coastal defense infrastructures.
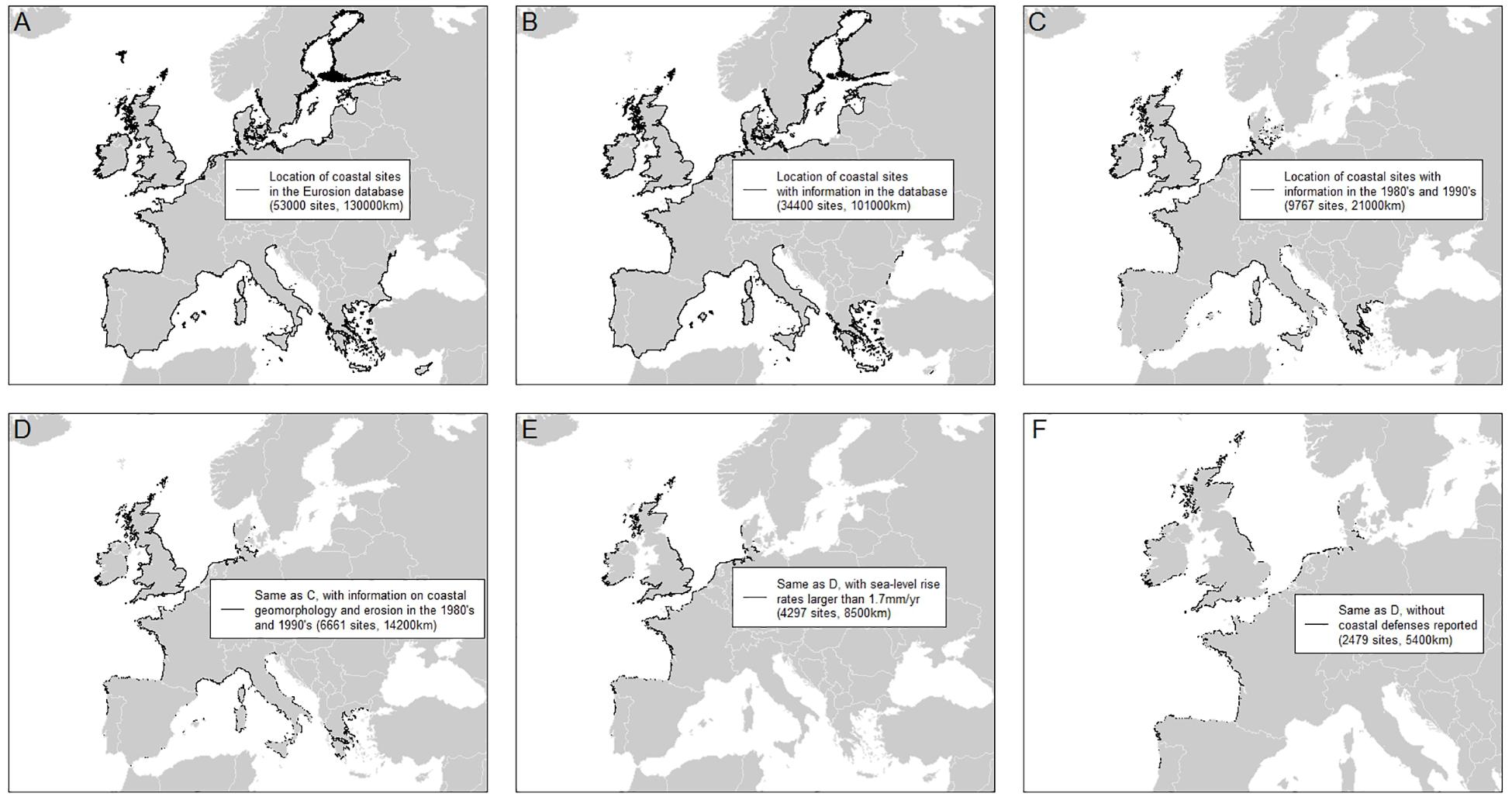
Figure 6. Location, number of coastal sites and coastline length for coasts inventoried in the European coastal databases meeting the following criteria: (A) all coastlines of the Eurosion database, including coastlines without any information; (B) as in panel A, limited to segments where observations are included in the 1980s, in the 1990s or both; (C) as in panel B, with observations in the 1980’s updated in the 1990’s (note that this does not imply that all fields are described for all these coastal sites); (D) as in panel C, with information on coastal geomorphology and evolution in both the 1980’s and 1990’s; (E): as in panel D, limited to coastal sites exposed to a sea-level rise close to the global average, to energetic offshore waves conditions and to a macrotidal regime (see section “Methods”); (F) as in panel E, without coastal defenses.
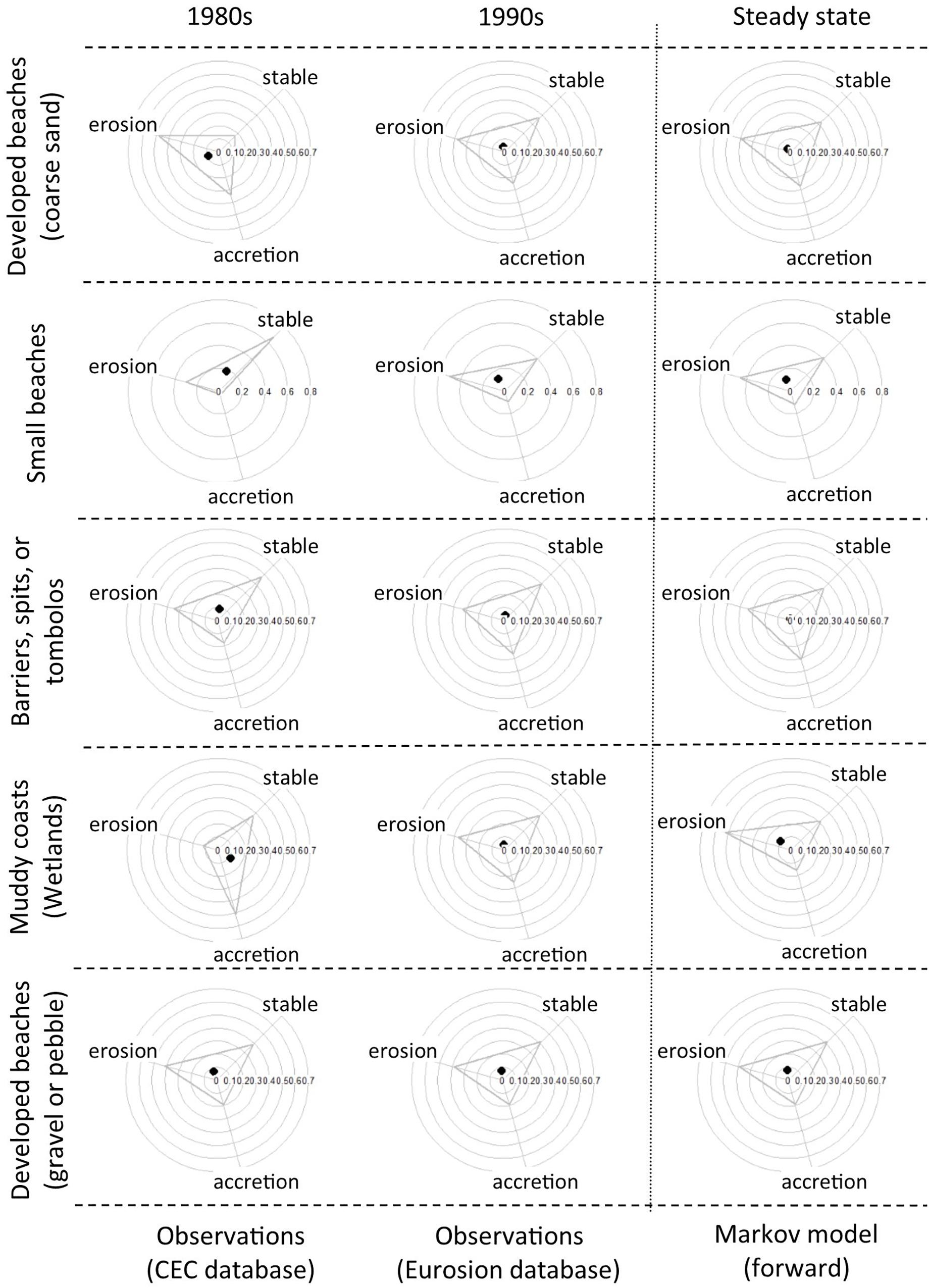
Figure 7. Observed coastal evolution states and steady states obtained using a Markov chain whose parameters have been learned from observations (see number of observations in Table 2).
Table 2 and Figure 7 present the results for coastal sites meeting criteria of section “Selection of a Comparable Subset From the Eurosion Coastal Database” with little human interventions. In Table 2, the sites are classified according to the taxonomy of the two coastal inventories (CEC and Eurosion). For each type of sites, the first column of Table 2 provides the number of segments available to derive the parameters of a Markov Chain, as shown in section “Methods.” The second column of Table 2 provides the length of these segments. These two columns help understanding the significance of the observed changes in shoreline evolution trends. For example, the confidence in the representativeness of the changes in shoreline evolution trends identified for developed sandy beaches (length greater than 1000 m) (305 segments, 772 km) would be higher than for developed beaches made of pebbles and gravels (36 segments, 43 km). The last column of Table 2 indicates the long-term trends that are identified by considering the Markov Chains (especially the steady state) in Figure 7.
For many coastal landforms referenced in the Eurosion coastal database, the observations available are not sufficient to evaluate the parameters of a Markov chain, and no long-term shoreline evolution trend can be identified for these coastal sites (last column in Table 2). For example, all conglomerates and/or cliffs subject to erosion are considered stable or eroding in the CEC, whereas Eurosion considers cases where another shoreline indicator referring to the sediments located on the beach may advance seaward. Consequently, the parameters of the Markov chain arising from the “accreting state” can not be evaluated from the observations. In this case, a change in the data model prevents drawing any conclusions regarding dynamic changes.
Finally, the results are limited to five different geomorphological types: muddy coasts (wetlands) and four different types of beaches. Wetlands experience a shift toward erosion (Figure 7 and Table 2): the proportion of eroding segments increases from 12% in the 1980s to 37% in the 1990s. At the same time, the proportion of stable segments remains approximately the same (37%). The steady state (last column in Figure 7) indicates that if the Markov model is run forward, the proportion of eroding coastal sites continues increasing (53%). At the same time, the number of accreting sites drops drastically to 16% and the number of stable segments decreases slightly to 31%. Hence, considering the steady state (third radial plot of line 4 in Figure 7) confirms the first impression that the observed evolutions (first and second radial plots of line 4 in Figure 7) corresponds to a shift toward erosion. The coastal segments driving this results seem randomly distributed spatially (Figure 8). This excludes some common issues related to the database production process, such as groups of coastal geomorphologists using different conventions to feed the databases or interpreting the data model in different ways (Le Cozannet et al., 2016). However, the main concern here is the small number of sites underlying the results, as there are only 51 segments representing 143 km.
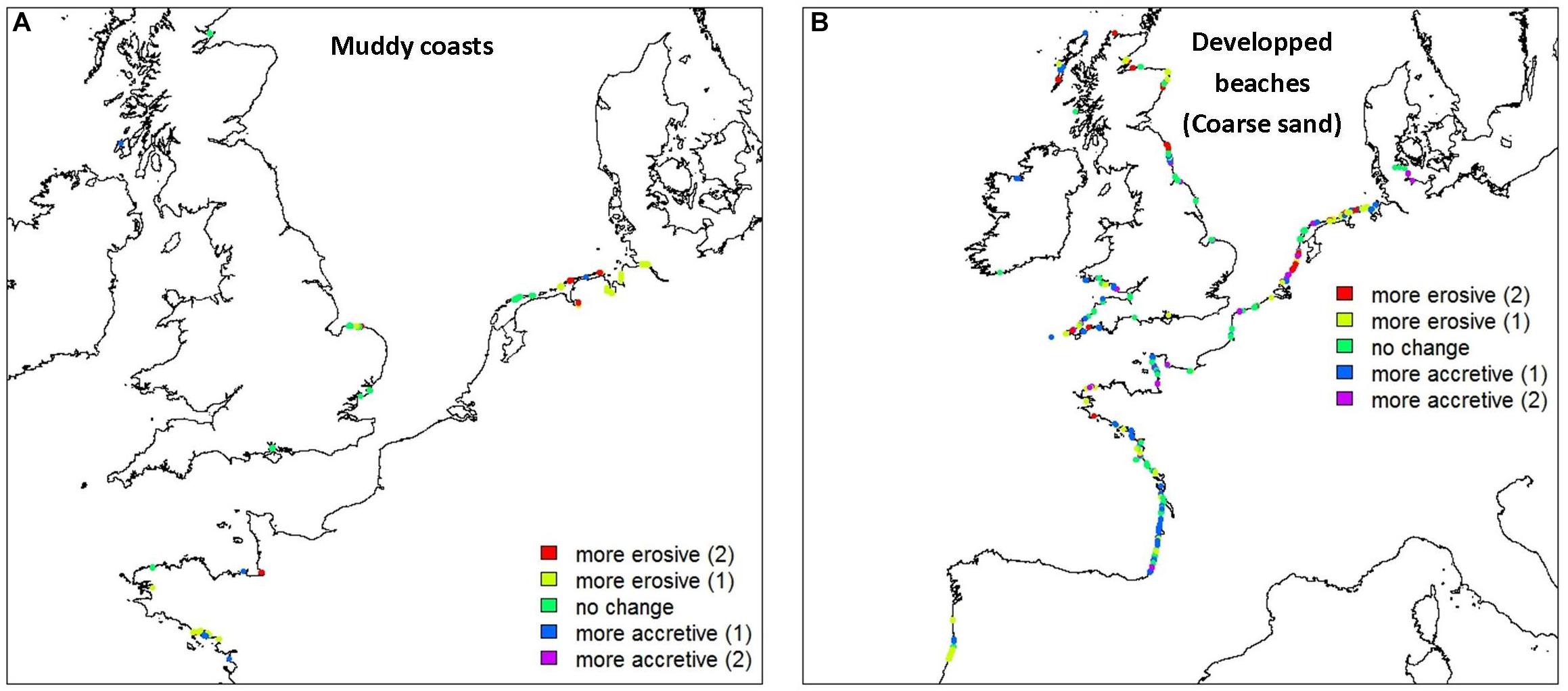
Figure 8. Transitions between shoreline evolution states, as observed when comparing the CEC and Eurosion databases, for two geomorphic types with no coastal defenses: (A) muddy coasts; (B) developed beaches made of coarse sand. Note that the legend “more erosive (2)” means that an accretive coastal site in CEC is eroding according to Eurosion, whereas “more erosive (1)” means either that an accretive coastal site has become stable, or that a site considered stable in CEC is eroding according to the Eurosion database.
The four different types of beaches experience contrasting dynamics. No clear evolution can be identified for developed beaches made of gravels and pebbles. However, due to the limited amount of data available to train the Markov model (36 sites, representing 43 km), it is doubtful that this evolution is representative of any change at large scales. Similarly, barriers, sand spits and tombolos become less accretive and more stable, but the number of sites underlying this result is limited (78 segments, representing 90 km). Again, this limits the confidence in the representativeness of these results. In the case of sandy developed beaches, a larger amount of data is available to train the parameters of the Markov model (305 sites representing 772 km). However, the results indicate that these sites are becoming more stable and less accretive and erosive. The interpretation of this change is not straightforward. Conversely, small beaches (with lengths ranging from 200 to 1000 m, and bounded by rocky capes larger than 200 m) experience the opposite trend. Interestingly, the majority of the 103 small beaches used in Figure 7 are located in the Atlantic coast of United Kingdom and France, for which the reconstruction of sea-level rise shown in Figure 3 applies. The CEC database shows that in the 1980s, approximately 30% of the sites were eroding, 67% were stable and 3% were accreting (respectively, 50, 40, and 10% in the 1990s according to Eurosion). This result could be due to the erosive effects of sea-level rise, superimposed with other local changes leading to sedimentation and therefore more accretion. It could also be due to correction of errors in the database, but the geographical distribution of sites driving the results does not display any pattern suggesting that these trends result from different practices in coastal data acquisition and interpretation depending on the country considered.
As a summary, the method is currently applicable for a limited number of coastal types only. For the five coastal types where sufficient data is available to train the parameters of the Markov model, we find contrasting evolution schemes, including a clear change in shoreline evolution trend toward erosion for coastal wetlands, a shift toward erosion superimposed with a smaller move toward accretion for small beaches, and more stability for sandy developed beaches. For barriers, spits, tombolos and developed beaches made of gravels and pebbles, the amount of data available to train the parameters of the Markov model is too small to be representative of any regional trend. In addition, the heterogeneity of the observed changes in shoreline evolution trends and the limited amount of data suggests caution with regards to the interpretation. From a methodological point of view, while a careful analysis of the transition matrix allows identification of changes in shoreline evolution trends, considering the steady states allows for a rapid screening.
The transitions shown in Figure 7 could be the result of ground truth changes, of different data models and processes used to develop the database, or they could be purely random. This section first interprets the observed changes in shoreline evolution trends (section “Can We Interpret the Observed Coastal Evolution Changes?”). Second, recognizing that the current limitations in the CEC and Eurosion databases, we examine needs for improvements and updates in coastal database design and collection, in order to support detection studies (section “Requirements For Coastal Databases”). Finally, we discuss the potential and limitation of the Markov Chain approach to detect and analyze changes in shoreline evolution (section “Potential and Limitation of the Approach”).
The results obtained in Figure 7 are consistent with previous statements that small beaches, relatively isolated from the adjacent hydro-sedimentary systems, are more vulnerable to sea-level rise and wave changes than developed beaches (Brunel and Sabatier, 2009; Dodet et al., 2010; Taborda and Ribeiro, 2015; Castelle et al., 2018). Furthermore, the results presented in section “Dynamics of Coastal Evolution” show that small beaches (with lengths ranging from 200 to 1000 m, and bounded by rocky capes) and with limited human interventions are experiencing a shift toward erosion. This result means that there is consistency between the theoretical example presented in section “Application on a Virtual Dataset” and the synthesis of observations from the European database, as revealed with the Markov chain approach. Hence, while the validity of eqn. 1 has been questioned in the literature (Cooper and Pilkey, 2004), it is not invalidated by coastal observations, so that recently developed alternative models producing a smaller response of sandy shorelines to sea-level rise can not be considered as a “better” approach yet (Ranasinghe et al., 2012; Le Cozannet et al., 2019). Our results are provided for sites with no reports of coastal defenses in the database. However, other human actions may drive the observed evolution such as beach management and nourishment. However, the latter is expected to favor stability of beach evolution and not increased erosion as identified in the database.
No obvious physical interpretation can be provided to explain the observed change in shoreline evolution trend toward more stability in the case of sandy developed beaches. We propose that this latter result is unrelated with the ground truth evolution at the scale of Western Europe: in contrast, it could be either due to difficulties encountered by coastal observatories to estimate the actual state of shorelines evolution at a regional scale, or to slight changes in the CEC and Eurosion data models and spatial resolutions. For example, some large beaches considered stable overall in CEC were sometimes divided into several segments in Eurosion, allowing isolation of some accreting sectors within an area previously considered stable as a whole.
Figure 7 suggests that wetlands are experiencing a shift toward erosion. This seems in agreement with observations suggesting that wetlands are shifting toward erosion worldwide (Cahoon, 2015). The shift toward erosion could be a consequence of sea-level rise, but also of softer coastal management approaches in non-urbanized coastal wetlands, whereby dikes are built inland while breaching is episodically accepted on the waterfront. Note that such softer management practices may result in shoreline retreat, but also in vertical accretion, which can be seen as beneficial from a biophysical point of view (Figure 8). However, due to the small number of wetlands driving the result (Table 2), there is limited confidence that the shift toward erosion suggested in Figure 7 and Table 2 is a general feature of western European coastal wetlands. Nevertheless, this result should raise awareness in the case of coastal muddy coasts. In fact, wetlands are often not considered a priority in the context of climate change, because only 13% of them are eroding in Europe according to Eurosion. We show here that the same database suggests that this situation is changing. At least, our result suggests that caution is required before communicating statistics on single European wetlands evolutions, based on a single dataset covering a limited period of time. Along with Webb et al. (2013) and others, we propose that research and observations are needed to better understand these rapidly changing coastal environments, in particular in Europe.
Large coastal databases such as CEC, Eurosion or others were not designed to analyze the causes of current shoreline changes, but rather to map coastal vulnerability (e.g., Gornitz, 1991). Unsurprisingly, the data model used in these databases describes only a small part of coastal processes, which can be observed in the field. For example, Figure 9A shows that describing shoreline evolution with three states (stability, erosion, accretion) only partly communicates what is happening on the field. This statement applies not only to wetlands displaying both horizontal retreat and vertical accretion, but also many erodible coastal cliffs (Le Cozannet et al., 2016). Furthermore, Figure 9B shows an obvious example of longshore sediment transport interrupted by coastal defense infrastructures, and shaping of the transition between artificial and natural coasts. However, neither CEC nor Eurosion provide information on the connections between different hydro-sedimentary cells. Finally, some typical coastal systems such as platform beaches are hardly identified in the European coastal database, whereas they are supposed to have specific responses to sea-level rise and human interventions (Trenhaile, 2004, 2018; de Sousa et al., 2018). These examples show the benefits of improving data models describing coastal databases, which involves transdisciplinary research based on applied mathematics, computer science and geosciences (Pshenichny and Kanzheleva, 2011).
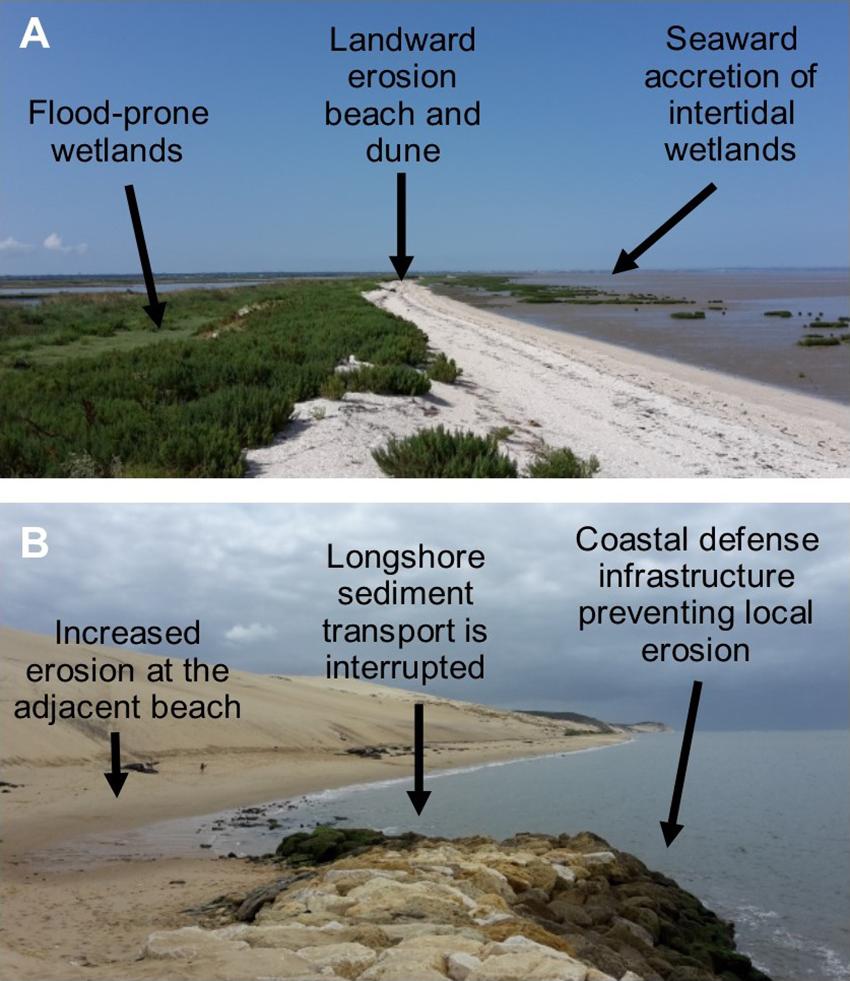
Figure 9. Examples of sites that could benefit from improvments of data models of coastal databases; (A) example of coastal wetland experiencing both a chronic retreat of the sand dune and vertical accretion of muddy landforms (Marais d’Yves, Atlantic Coast of France, Site owned by the Conservatoire du Littoral); (B) example of transition beween protected and non-protected shorelines (Dune du Pila, South-Western Aquitaine Coast).
The previous sections have shown that despite the large number of coastal sites described in the CEC and Eurosion databases, information gaps and the necessary segmentation of the dataset prevents drawing reliable conclusions regarding the ongoing evolution of European coasts and their causes. Producing more complete coastal databases has not only benefits for academic research, but also concrete benefits for adaptation. Indeed, the timescale of responding to shoreline retreat is in the order of 30 years, so that detecting early signs of sea-level rise impacts on shoreline retreat seems important to anticipate relocations or any other adaptation strategy. Hence, with limited confidence in current shoreline change modeling tools at multi-decadal timescales (Cooper and Pilkey, 2004; Ranasinghe and Stive, 2009), learning more from coastal observations seems a rational priority. Two alternative approaches can be proposed to address this need (Cazenave et al., 2017):
(1) Bottom up collection of the coastal data available: this approach was typically applied to collect the CEC and Eurosion databases; importantly, if new European surveys were undertaken now, a much more complete database could be produced because a large amount of new data has been produced since 2000, by coastal observatories or within the framework of specific regulations such as “coastal risk prevention plans” in France.
(2) Top-down approach based on semi-automated processing of satellite and aerial images (Luijendijk et al., 2018; Mentaschi et al., 2018): this approach has received attention recently, owing to cloud computing development such as “Google Earth Engine,” which are making this approach more feasible. In the future, further developments in this area could allow to meet the challenging requirements of retrieving shoreline changes in the order of O(1 m/year) or less, as expected by coastal adaptation stakeholders. However, existing coastal databases and aerial images will remain a useful dataset to analyze changes before 2000 and the era of very high-resolution satellites (see section “Geomorphology and Coastal Evolution”).
The potential of Markov chains as analytical tools to analyze shoreline change dynamics was already identified in the literature (Sonu and James, 1973: Ostroumov et al., 2005; Buscombe and Masselink, 2006; Furlan, 2008; Hurst et al., 2016). Such approaches can probably not be used easily to project future impacts of sea-level rise or other human interventions, because we are just observing the onset of erosion driven by sea-level rise, and because future human intervention could completely reshape coastlines (Oppenheimer et al., 2019). Here, we use a Markov chain-based approach to identify changes in observed shoreline change evolution. Our study therefore falls within the growing literature addressing the detection of climate change impacts (Cramer et al., 2014).
A major advantage of the approach is its ability to identify changes in observed shoreline evolution trends in large databases, which are too complex to be analyzed by a human. A key limitation is that the approach is essentially a detection approach, and does not allow attribution as defined by the AR5 WG2, because it can not quantify “the magnitude of the contribution” of sea-level rise to shoreline change (Cramer et al., 2014). In this case as well as in many other areas of climate change impacts, attribution can only be tentatively discussed, as in section “Potential and Limitation of the Approach,” based on the comparison of the observations with simplified modeling results, as shown above (Cramer et al., 2014; Le Cozannet et al., 2014). This is a significant difference with attribution in the area of climate change science, as bounded by the Working Group 1 of the IPCC, where models have demonstrated sufficient accuracy and precision to formally attribute part of the observed changes to anthropogenic climate change (IPCC, 2013).
Besides this limitation, one relevant question would be to examine whether the Markov chain approach is a best approach to detect changes in shoreline evolution trends or impacts of sea-level rise. From a methodological point of view, modeling changes in coastal databases with Markov chain appears interesting for coastal detection studies because of the limited number of free variables to be trained with observations. In this sense, the approach provides a rapid diagnostic to reveal the changes in shoreline evolution trends underpinned by current transitions, which are characterized by a 3 × 3 matrix. In future studies, more integrative data models such as dynamic Bayesian networks could be considered. In practice, such models can be seen as a dynamic extension of Bayesian networks, which have demonstrated skill in reproducing current shoreline evolution trends (see Yates and Le Cozannet, 2012, for an application in Europe): when grouping the observations of the database into homogeneous subsets, we actually implement the same procedure as during the training of the parameters of a Bayesian Network. In this sense, there is an implicit Bayesian network underpinning each Markov chain presented in this study. However, using more complex dynamic models would be premature in the case of European coastal databases, because even more information would be required to cover all possible situations and learn the parameters of such models. Therefore, we feel that given the status of the European coastal database, the Markov chain approach is simple, yet most suitable to analyze changes in shoreline evolution trends.
In this study, we explore European coastal databases, with a specific focus on the temporal dynamics of shoreline changes. While the results suggest more attention should be given to the multidecadal evolution of European coastal wetlands and small beaches, the confidence in the results is limited by gaps in the database and by an incomplete description of physical processes. In the context of detection studies, these issues become critical due to the necessity of selecting subsets of homogeneous (and therefore comparable) coastal sites.
Our results reveal changes of shoreline evolution that are present in the European coastal database, but still unidentified in previous analysis of these observations (Eurosion, 2004): European coastal wetlands and small beaches unaffected by coastal defenses may have initiated a shift toward erosion. In the case of small beaches, the result is consistent with what would be expected from the simple Bruun rule superimposed with other natural and anthropogenic processes (see section “Application on a Virtual Dataset”). In the case of European coastal wetlands, our results primarily question a previous optimistic statement, based on a statistical analysis of the database, that European coastal wetlands are still accreting today and are therefore relatively mildly vulnerable to sea-level rise.
This study identifies the need to update coastal databases and their data model. Today, the role of climate change in modifying sea-level rise is increasingly being understood. However, it remains challenging to detect early impacts to hazards such as erosion and shoreline changes due to limited access to long observations of biophysical phenomena. Meanwhile, the detection (and attribution) of climate change impacts are becoming an emerging field of research, with large implications for coastal managers concerned with anticipating adaptation or relocations in time. In Europe, coastal wetlands are often not considered to be the most threatened by contemporary sea-level rise, because a large portion of them are accreting due to active fine sedimentation processes. This study, together with other evidences, raises awareness on their case, and suggests that coastal wetlands deserve more observation and research efforts.
The Eurosion and CEC database are distributed by the European Environmental Agency. Codes are available at https://www.researchgate.net/publication/330320455_The_COas TAUD_framework_COASTAl_Uncertainties_Demystification.
GL designed the study and performed the analysis. CO participated to both CEC and Eurosion coastal databases collection, quality check and formatting, and provided information on its value and limitations (also available in the Eurosion reports, available www.eurosion.org). OB assessed the quality of the coastal defense layer. AG contextualized the Markov chain approach and helped GL setting it. MG and FL contributed to the analysis. All contributed to contextualize and wrote the manuscript.
This study was supported by the French Geological Survey (BRGM) through the “Climate Change” project as well as through project ECLISEA, which is part of ERA4CS, an ERA-NET initiated by JPI Climate, and funded by UC-IHC, HZG, BRGM, NCSRD, and CNRS with co-funding by the European Union.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We thank Conservatoire du Littoral (especially Patrick Bazin), Cyril Mallet, and Julie Mujica for useful discussions regarding coastal processes in the site they own or monitor. We thank the reviewers whose comments led to a substantially improved manuscript.
Albert, S., Leon, J. X., Grinham, A. R., Church, J. A., Gibbes, B. R., and Woodroffe, C. D. (2016). Interactions between sea-level rise and wave exposure on reef island dynamics in the Solomon Islands. Environ. Res. Lett. 11:054011. doi: 10.1088/1748-9326/11/5/054011
Barnard, P. L., Hoover, D., Hubbard, D. M., Snyder, A., Ludka, B. C., Allan, J., et al. (2017). Extreme oceanographic forcing and coastal response due to the 2015–2016 El Niño. Nat. Commun. 8:14365. doi: 10.1038/ncomms14365
Barnard, P. L., Short, A. D., Harley, M. D., Splinter, K. D., Vitousek, S., Turner, I. L., et al. (2015). Coastal vulnerability across the Pacific dominated by El Nino/Southern oscillation. Nat. Geosci. 8, 801–807. doi: 10.1038/ngeo2539
Beven, K., and Hall, J. (2014). Applied Uncertainty Analysis for Flood Risk Management. London: Imperial College Press.
Brivois, O. (2016). Avancement 2015 de l’élaboration du Programme de Surveillance de la Qualité Hydromorphologique des Masses d’eau Côtières de la Façade Manche Atlantique dans le cadre de la DCE. Rapport final. Orléans: BRGM.
Brooks, S. M., and Spencer, T. (2010). Temporal and spatial variations in recession rates and sediment release from soft rock cliffs, Suffolk coast, UK. Geomorphology 124, 26–41. doi: 10.1016/j.geomorph.2010.08.005
Brown, S., Nicholls, R. J., Hanson, S., Brundrit, G., Dearing, J. A., Dickson, M. E., et al. (2014). Shifting perspectives on coastal impacts and adaptation. Nat. Clim. Change 4, 752–755. doi: 10.1038/nclimate2344
Brunel, C., and Sabatier, F. (2009). Potential influence of sea-level rise in controlling shoreline position on the French Mediterranean Coast. Geomorphology 107, 47–57. doi: 10.1016/j.geomorph.2007.05.024
Bulteau, T., Baills, A., Petitjean, L., Garcin, M., Palanisamy, H., and Le Cozannet, G. (2015). Gaining insight into regional coastal changes on La Réunion island through a Bayesian data mining approach. Geomorphology 228, 134–146. doi: 10.1016/j.geomorph.2014.09.002
Buscombe, D., and Masselink, G. (2006). Concepts in gravel beach dynamics. Earth Sci. Rev. 79, 33–52. doi: 10.1016/j.earscirev.2006.06.003
Cahoon, D. R. (2015). Estimating relative sea-level rise and submergence potential at a coastal wetland. Estuar. Coasts 38, 1077–1084. doi: 10.1007/s12237-014-9872-8
Castelle, B., Dodet, G., Masselink, G., and Scott, T. (2018). Increased winter−mean wave height, variability, and periodicity in the Northeast Atlantic over 1949–2017. Geophys. Res. Lett. 45, 3586–3596. doi: 10.1002/2017gl076884
Castelle, B., Guillot, B., Marieu, V., Chaumillon, E., Hanquiez, V., Bujan, S., et al. (2017). Spatial and temporal patterns of shoreline change of a 280-km high-energy disrupted sandy coast from 1950 to 2014: SW France. Estuar. Coast. Shelf Sci. 200, 212–223. doi: 10.1016/j.ecss.2017.11.005
Cazenave, A., and Le Cozannet, G. (2014). sea-level rise and its coastal impacts. Earths Future 2, 15–34. doi: 10.1002/2013EF000188
Cazenave, A., Le Cozannet, G., Benveniste, J., Woodworth, P. L., and Champollion, N. (2017). Monitoring coastal zone changes from space. Eos 98, doi: 10.1029/2017EO085581
Church, J. A., Clark, P. U., Cazenave, A., Gregory, J. M., Jevrejeva, S., Levermann, A., et al. (2013). “Sea level change,” in Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, eds T. F. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S. K. Allen, J. Boschung, et al. (Cambridge: Cambridge University Press),Google Scholar
Church, J. A., and White, N. J. (2011). sea-level rise from the late 19th to the early 21st century. Surv. Geophys. 32, 585–602. doi: 10.1007/s10712-011-9119-1
Cooper, J. A. G., and Pilkey, O. H. (2004). sea-level rise and shoreline retreat: time to abandon the Bruun Rule. Glob. Planet. Change 43, 157–171. doi: 10.1016/j.gloplacha.2004.07.001
Cowell, P. J., Stive, M. J., Niedoroda, A. W., Swift, D. J., de Vriend, H. J., Buijsman, M. C., et al. (2003). The coastal-tract (part 2): applications of aggregated modeling of lower-order coastal change. J. Coast. Res. 19, 828–848.
Cramer, W., Yohe, G. W., Auffhammer, M., Huggel, C., Molau, U., Dias, M. S., et al. (2014). Detection and attribution of observed impacts. in Climate Climate Change 2014: Impacts, Adaptation, and Vulnerability, eds C. B. Field, V. R. Barros, D. J. Dokken, K. J. Mach, M. D. Mastrandrea, T. E. Bilir, et al Cambridge: Cambridge University Press, 979–1038. doi: 10.1017/cbo9781107415379.023
Davidson-Arnott, R. G. (2005). Conceptual model of the effects of sea-level rise on sandy coasts. J. Coast. Res. 21, 1166–1172. doi: 10.2112/03-0051.1
de Sousa, L. B., Loureiro, C., and Ferreira, O. (2018). Morphological and economic impacts of rising sea levels on cliff-backed platform beaches in southern Portugal. Appl. Geogr. 99, 31–43. doi: 10.1016/j.apgeog.2018.07.023
Dodet, G., Bertin, X., and Taborda, R. (2010). Wave climate variability in the North-East Atlantic Ocean over the last six decades. Ocean Model. 31, 120–131. doi: 10.1016/j.ocemod.2009.10.010
Duvat, V. K. (2019). A global assessment of atoll island planform changes over the past decades. Wiley Interdiscip. Rev. Clim. Change 10:e55.
Eurosion, (2004). Available online at: www.eurosion.org (accessed May 10, 2020).
Evelpidou, N., Melini, D., Pirazzoli, P. A., and Vassilopoulos, A. (2014). Evidence of repeated late Holocene rapid subsidence in the SE Cyclades (Greece) deduced from submerged notches. Int. J. Earth Sci. 103, 381–395. doi: 10.1007/s00531-013-0942-0
Fairbank, H., and Jakeways, J. (2006). Mapping Coastal Risk in a Changing Climate, Isle of Wight Centre for Coastal Environment, 2006. Centre for the Coastal Environment, Isle of Wight Council, p 45. doi: 10.1007/s00531-013-0942-0
Ferranti, L., Antonioli, F., Anzidei, M., Monaco, C., and Stocchi, P. (2010). The timescale and spatial extent of vertical tectonic motions in Italy: insights from relative sea level changes studies. J. Virt. Explor. 36:23. doi: 10.3809/jvirtex.2009.00255
Ford, M. (2013). Shoreline changes interpreted from multi-temporal aerial photographs and high resolution satellite images: Wotje Atoll, Marshall Islands. Rem. Sens. Environ. 135, 130–140. doi: 10.1016/j.rse.2013.03.027
Furlan, C. (2008). Hierarchical random effect models for coastal erosion of cliffs in the Holderness coast. Stat. Methods Appl. 17, 335–350. doi: 10.1007/s10260-007-0069-1
Garcin, M., Vendé-Leclerc, M., Maurizot, P., Le Cozannet, G., Robineau, B., and Nicolae-Lerma, A. (2016). Lagoon islets as indicators of recent environmental changes in the South Pacific–The New Caledonian example. Cont. Shelf Res. 122, 120–140. doi: 10.1016/j.csr.2016.03.025
Gehrels, W. R. (2010). Late Holocene land-and sea level changes in the British Isles: implications for future sea level predictions. Quat. Sci. Rev. 29, 1648–1660. doi: 10.1016/j.quascirev.2009.09.015
Gornitz, V. (1991). Global coastal hazards from future sea-level rise. Palaeogeogr. Palaeoclimatol. Palaeoecol. 89, 379–398. doi: 10.1016/0031-0182(91)90173-O
Gutierrez, B. T., Plant, N. G., and Thieler, E. R. (2011). A Bayesian network to predict coastal vulnerability to sea-level rise. J. Geophys. Res. Earth Surface 116:F02009. doi: 10.1029/2010JF001891
Hansen, G., Stone, D., Auffhammer, M., Huggel, C., and Cramer, W. (2016). Linking local impacts to changes in climate: a guide to attribution. Reg. Environ. Change 16, 527–541. doi: 10.1007/s10113-015-0760-y
Hinkel, J., Nicholls, R. J., Tol, R. S., Wang, Z. B., Hamilton, J. M., Boot, G., et al. (2013). A global analysis of erosion of sandy beaches and sea-level rise: an application of DIVA. Glob. Planet. Change 111, 150–158. doi: 10.1016/j.gloplacha.2013.09.002
Hurst, M. D., Rood, D. H., Ellis, M. A., Anderson, R. S., and Dornbusch, U. (2016). Recent acceleration in coastal cliff retreat rates on the south coast of Great Britain. Proc. Natl. Acad. Sci. 113, 13336–13341. doi: 10.1073/pnas.1613044113
Idier, D., Rohmer, J., Pedreros, R., Le Roy, S., Lambert, J., Louisor, J., et al. (2020). Coastal flood: a composite method for past events characterisation providing insights in past, present and future hazards—joining historical, statistical and modelling approaches. Nat. Hazards 101, 465–501. doi: 10.1007/s11069-020-03882-4
IPCC (2013). “Annex III: glossary [Planton, S. (ed.)],” in Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, eds T. F. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S. K. Allen, J. Boschung, et al. (Cambridge: Cambridge University Press).
Jevrejeva, S., Grinsted, A., Moore, J. C., and Holgate, S. (2006). Nonlinear trends and multiyear cycles in sea level records. J. Geophys. Res. Oceans 111:C09012.
Lambeck, K., Antonioli, F., Anzidei, M., Ferranti, L., Leoni, G., Scicchitano, G., et al. (2011). Sea level change along the Italian coast during the Holocene and projections for the future. Quat. Int. 232, 250–257. doi: 10.1016/j.quaint.2010.04.026
Le Cozannet, G., Bulteau, T., Castelle, B., Ranasinghe, R., Wöppelmann, G., Rohmer, J., et al. (2019). Quantifying uncertainties of sandy shoreline change projections as sea-level rises. Sci. Rep. 9:42. doi: 10.1038/s41598-018-37017-4
Le Cozannet, G., Bulteau, T., Garcin, M., Garnier, C., Müller, H., Hoareau, A., et al. (2016). Detecting errors in coastal databases using Bayesian Networks. J. Coast. Res. 75, 1162–1166. doi: 10.2112/SI75-233.1
Le Cozannet, G., Garcin, M., Yates, M., Idier, D., and Meyssignac, B. (2014). Approaches to evaluate the recent impacts of sea-level rise on shoreline changes. Earth Sci. Rev. 138, 47–60. doi: 10.1016/j.earscirev.2014.08.005
Leatherman, S. P., Zhang, K., and Douglas, B. C. (2000). Sea-level rise shown to drive coastal erosion. Eos 81, 55–57.
Liu, X., Ren, L., Yuan, F., and Yang, B. (2009). “Meteorological Drought Forecasting Using Markov Chain Model,” in Proceedings of the 2009 International Conference on Environmental Science and Information Application Technology (Wuhan: ESIAT 2009), doi: 10.1109/EISAT.2009.19
López, P. M., Payo, A., Ellis, M. A., Criado-Aldeanueva, F., and Jenkins, G. O. (2020). A method to extract measurable indicators of coastal cliff erosion from topographical cliff and beach profiles: application to North Norfolk and Suffolk, East England, UK. J. Mar. Sci. Eng. 8:20. doi: 10.3390/jmse8010020
Luijendijk, A., Hagenaars, G., Ranasinghe, R., Baart, F., Donchyts, G., and Aarninkhof, S. (2018). The state of the World’s Beaches. Sci. Rep. 8:6641.
Menéndez, M., and Woodworth, P. L. (2010). Changes in extreme high water levels based on a quasi−global tide−gauge data set. J. Geophys. Res. Oceans 115:C10011. doi: 10.1029/2009JC005997
Mentaschi, L., Vousdoukas, M. I., Pekel, J. F., Voukouvalas, E., and Feyen, L. (2018). Global long-term observations of coastal erosion and accretion. Sci. Rep. 8:12876. doi: 10.1038/s41598-018-30904-w
Morton, R. A. (2008). Historical changes in the Mississippi-Alabama barrier-island chain and the roles of extreme storms, sea level, and human activities. J. Coast. Res. 24, 1587–1600. doi: 10.2112/07-0953.1
Nicholls, R. J. (1998). Assessing erosion of sandy beaches due to sea-level rise. Geol. Soc. Lond. Eng. Geol. Spec. Publ. 15, 71. doi: 10.1144/gsl.eng.1998.015.01.08
Oppenheimer, M., Glavovic, B. C., Hinkel, J., van de Wal, R., Magnan, A. K., Abd-Elgawad, A., et al. (2019). “sea-level rise and implications for low-lying islands, coasts and communities,” in IPCC Special Report on the Ocean and Cryosphere in a Changing Climate, eds H.-O. Pörtner, D. C. Roberts, V. Masson-Delmotte, P. Zhai, M. Tignor, E. Poloczanska, et al. (Geneva: IPCC).
Ostroumov, V., Rachold, V., Vasiliev, A., and Sorokovikov, V. (2005). An application of a Markov-chain model of shore erosion for describing the dynamics of sediment flux. Geo Mar. Lett. 25, 196–203. doi: 10.1007/s00367-004-0201-2
Paskoff, R. P. (2004). Potential implications of sea-level rise for France. J. Coast. Res. 20, 424–434. doi: 10.1016/j.scitotenv.2014.06.111
Pilkey, O. H., Young, R. S., and Bush, D. M. (2000). Comment on sea-level rise shown to drive coastal erosion. Eos 81, 436–436.
Ponte Lira, C., Nobre Silva, A., Taborda, R., and Freire de Andrade, C. (2016). Coastline evolution of Portuguese low-lying sandy coast in the last 50 years: an integrated approach. Earth Syst. Sci. Data 8, 265–278. doi: 10.5194/essd-8-265-2016
Pshenichny, C., and Kanzheleva, O. (2011). Theoretical foundations of the event bush method. Geol. Soc. Am. Spec. Pap. 482, 139–164. doi: 10.1130/2011.2482(12)
Quelennec, R., Oliveros, C., Uhel, R., and Devos, W. (1998). CORINE Coastal Erosion. Brussels: Office for the Official Publications of the European Communities.
Ranasinghe, R. (2016). Assessing climate change impacts on open sandy coasts: a review. Earth Sci. Rev. 160, 320–332. doi: 10.1016/j.earscirev.2016.07.011
Ranasinghe, R., Callaghan, D., and Stive, M. J. (2012). Estimating coastal recession due to sea-level rise: beyond the Bruun rule. Clim. Change 110, 561–574. doi: 10.1007/s10584-011-0107-8
Ranasinghe, R., and Stive, M. J. (2009). Rising seas and retreating coastlines. Clim. Change 97, 465–468. doi: 10.1007/s10584-009-9593-3
Raucoules, D., Parcharidis, I., Feurer, D., Novalli, F., Ferretti, N., Carnec, C., et al. (2008). Ground deformation detection of the greater area of Thessaloniki (Northern Greece) using radar interferometry techniques. Nat. Hazards Earth Syst. Sci. 8, 779–788. doi: 10.5194/nhess-8-779-2008
Robinet, A., Castelle, B., Idier, D., Le Cozannet, G., Déqué, M., and Charles, E. (2016). Statistical modeling of interannual shoreline change driven by North Atlantic climate variability spanning 2000–2014 in the Bay of Biscay. Geo Mar. Lett. 36, 479–490. doi: 10.1007/s00367-016-0460-8
Romine, B. M., Fletcher, C. H., Barbee, M. M., Anderson, T. R., and Frazer, L. N. (2013). Are beach erosion rates and sea-level rise related in Hawaii? Glob. Planet. Change 108, 149–157. doi: 10.1016/j.gloplacha.2013.06.009
Romine, B. M., Fletcher, C. H., Frazer, L. N., and Anderson, T. R. (2016). Beach erosion under rising sea level modulated by coastal geomorphology and sediment availability on carbonate reef-fringed islands coasts. Sedimentology 63, 1321–1332. doi: 10.1111/sed.12264
Sallenger, A. H., Morton, R., Fletcher, C., Thieler, E. R., and Howd, P. (2000). Comment on sea-level rise shown to drive coastal erosion. Eos 81:436. doi: 10.1029/eo081i038p00436-02
Santamaría-Gómez, A., Gravelle, M., Collilieux, X., Guichard, M., Míguez, B. M., Tiphaneau, P., et al. (2012). Mitigating the effects of vertical land motion in tide gauge records using a state-of-the-art GPS velocity field. Glob. Planet. Change 98, 6–17. doi: 10.1016/j.gloplacha.2012.07.007
Sharma, T. C., and Panu, U. S. (2012). Prediction of hydrological drought durations based on Markov chains: case of the Canadian prairies. Hydrol. Sci. J. 57, 705–722. doi: 10.1080/02626667.2012.672741
Shennan, I., Milne, G., and Bradley, S. (2012). Late Holocene vertical land motion and relative sea−level changes: lessons from the British Isles. J. Quat. Sci. 27, 64–70. doi: 10.1002/jqs.1532
Singh, B. (1997). Climate-related global changes in the southern Caribbean: trinidad and tobago. Glob. Planet. Change 15, 93–111. doi: 10.1016/s0921-8181(97)00006-4
Sonu, C. J., and James, W. R. (1973). A Markov model for beach profile changes. J. Geophys. Res. 78, 1462–1471. doi: 10.1029/jc078i009p01462
Spedicato, G. A., Kang, T. S., and Yalamanchi, S. B. (2015). The markovchain Package: A Package for Easily Handling Discrete Markov Chains in R. Available online at: https://cran.r-project.org/web/packages/markovchain/vignettes/an_introduction_to_markovchain_package.pdf (accessed May 10, 2020).
Spencer, T., Schuerch, M., Nicholls, R. J., Hinkel, J., Lincke, D., Vafeidis, A. T., et al. (2016). Global coastal wetland change under sea-level rise and related stresses: the DIVA Wetland Change Model. Glob. Planet. Change 139, 15–30. doi: 10.1016/j.gloplacha.2015.12.018
Stive, M. J. (2004). How important is global warming for coastal erosion? Clim. Change 64, 27–39. doi: 10.1023/B:CLIM.0000024785.91858.1d
Stive, M. J., Aarninkhof, S. G., Hamm, L., Hanson, H., Larson, M., Wijnberg, K. M., et al. (2002). Variability of shore and shoreline evolution. Coast. Eng. 47, 211–235. doi: 10.1016/S0378-3839(02)00126-6
Stone, D., Auffhammer, M., Carey, M., Hansen, G., Huggel, C., Cramer, W., et al. (2013). The challenge to detect and attribute effects of climate change on human and natural systems. Clim. Change 121, 381–395. doi: 10.1007/s10584-013-0873-6
Taborda, R., and Ribeiro, M. A. (2015). A simple model to estimate the impact of sea-level rise on platform beaches. Geomorphology 234, 204–210. doi: 10.1016/j.geomorph.2015.01.015
Tan, W. Y. (2002). Stochastic Models with Applications to Genetics, Cancers, AIDS and Other Biomedical Systems. Series on Concrete and Applicable Mathematics. Singapore: World Scientific Publishing.
Thiéblemont, R., Le Cozannet, G., Toimil, A., Meyssignac, B., and Losada, I. J. (2019). Likely and high-end impacts of regional sea-level rise on the shoreline change of European sandy coasts under a high greenhouse gas emissions scenario. Water 11:2607. doi: 10.3390/w11122607
Thieler, E. R., and Hammar-Klose, E. S. (1999). National Assessment of Coastal Vulnerability to Sea-Level Rise; US Atlantic Coast (No. 99-593). Available online at: https://pubs.usgs.gov/of/1999/of99-593/ (accessed May 10, 2020).
Toimil, A., Camus, P., Losada, I. J., Le Cozannet, G., Nicholls, R. J., Idier, D., et al. (2020). Climate change driven coastal erosion modelling in tempreate sandy beaches: methods and uncertainty treatment. Earth Sci. Rev. 202:103110. doi: 10.1016/j.earscirev.2020.103110
Trenhaile, A. S. (2004). Modeling the accumulation and dynamics of beaches on shore platforms. Mar. Geol. 206, 55–72. doi: 10.1016/j.margeo.2004.03.013
Trenhaile, A. S. (2018). Modelling the effect of rising sea level on beaches with resistant foundations. Mar. Geol. 395, 1–13. doi: 10.1016/j.margeo.2017.09.004
Vafeidis, A. T., Nicholls, R. J., McFadden, L., Tol, R. S., Hinkel, J., Spencer, T., et al. (2008). A new global coastal database for impact and vulnerability analysis to sea-level rise. J. Coast. Res. 24, 917–924. doi: 10.2112/06-0725.1
Vos, K., Splinter, K. D., Harley, M. D., Simmons, J. A., and Turner, I. L. (2019). CoastSat: a Google Earth Engine-enabled Python toolkit to extract shorelines from publicly available satellite imagery. Environ. Model. Softw. 122:104528. doi: 10.1016/j.envsoft.2019.104528
Wahl, T., Haigh, I. D., Woodworth, P. L., Albrecht, F., Dillingh, D., Jensen, J., et al. (2013). Observed mean sea level changes around the North Sea coastline from 1800 to present. Earth Sci. Rev. 124, 51–67. doi: 10.1016/j.earscirev.2013.05.003
Webb, E. L., Friess, D. A., Krauss, K. W., Cahoon, D. R., Guntenspergen, G. R., and Phelps, J. (2013). A global standard for monitoring coastal wetland vulnerability to accelerated sea-level rise. Nat. Clim. Change 3, 458–465. doi: 10.1038/nclimate1756
Whitaker, D. (1978). The derivation of a measure of brand loyalty using a Markov brand switching model. J. Oper. Res. Soc. 29, 959–970. doi: 10.1057/jors.1978.209
Wickman, F. E. (1976). “Markov models of repose-period patterns of volcanoes,” in Random Processes in Geology, ed. D. F. Merriam (Berlin: Springer), 135–161. doi: 10.1007/978-3-642-66146-4_11
Woodworth, P. L., Menéndez, M., and Gehrels, W. R. (2011). Evidence for century-timescale acceleration in mean sea levels and for recent changes in extreme sea levels. Surv. Geophys. 32, 603–618. doi: 10.1007/s10712-011-9112-8
Woodworth, P. L., Teferle, F. N., Bingley, R. M., Shennan, I., and Williams, S. D. P. (2009). Trends in UK mean sea level revisited. Geophys. J. Int. 176, 19–30. doi: 10.1111/j.1365-246X.2008.03942.x
Wöppelmann, G., and Marcos, M. (2012). Coastal sea-level rise in southern Europe and the nonclimate contribution of vertical land motion. J. Geophys. Res. Oceans 117:C01007. doi: 10.1029/2011JC007469
Wöppelmann, G., and Marcos, M. (2016). Vertical land motion as a key to understanding sea level change and variability. Rev. Geophys. 54, 64–92. doi: 10.1002/2015RG000502
Yates, M. L., and Le Cozannet, G. (2012). Brief communication”evaluating european coastal evolution using Bayesian networks”. Nat. Hazards Earth Syst. Sci. 12, 1173–1177. doi: 10.5194/nhess-12-1173-2012
Keywords: detection, climate change impacts, shoreline changes, databases, geoinformatics
Citation: Le Cozannet G, Oliveros C, Brivois O, Giremus A, Garcin M and Lavigne F (2020) Detecting Changes in European Shoreline Evolution Trends Using Markov Chains and the Eurosion Database. Front. Mar. Sci. 7:326. doi: 10.3389/fmars.2020.00326
Received: 03 February 2020; Accepted: 21 April 2020;
Published: 16 June 2020.
Edited by:
Zhan Hu, Sun Yat-sen University, Zhuhai Campus, ChinaReviewed by:
Peng Yao, Hohai University, ChinaCopyright © 2020 Le Cozannet, Oliveros, Brivois, Giremus, Garcin and Lavigne. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gonéri Le Cozannet, Zy5sZWNvemFubmV0QGJyZ20uZnI=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.