Resource (Light and Nitrogen) and Density-Dependence of Seaweed Growth

Seaweed aquaculture is a rapidly growing component of marine food production, but the capacity to control seaweed growth lacks behind that of land agriculture. Seaweed growth requires nutrients, acquired from dissolved pools through their fronds, and light, and, as such may also be density-dependent, but general relationships between seaweed growth, nutrient concentration and incident irradiance are not yet available. We used a dataset of 1729 experimental assessments of seaweed specific growth rates and density under various nutrient and irradiance levels retrieved from the published literature to examine the relationship between seaweed growth, density, irradiance, and nutrient concentration. This analysis confirmed strong density-dependence of seaweed specific growth rates, and further confirmed that nutrient and irradiance limitation strongly impose density-dependent seaweed growth. These findings demonstrate that nutrient and irradiance limitation modulate density-dependent seaweed growth, and can help maximize growth rates in seaweed aquaculture, a rapidly growing component of global aquaculture production, by manipulating stocking density where nutrients are scarce and/or underwater light penetration poor.

Introduction

Plant stands typically show an upper, size-dependent limit to their abundance, which is expressed in the self-thinning law (Westoby, 1984). Whereas this relationship has been described across terrestrial and aquatic plants (Arenas et al., 2002; Reynolds and Ford, 2005; Li et al., 2013), the upper density for terrestrial plants is about 10-fold higher than that for aquatic photosynthetic organisms, for a given size (Agusti et al., 1987; Duarte and Kalff, 1987). This difference was interpreted as reflecting the different light environment experienced by plants growing on land and submerged (Duarte and Kalff, 1987), since the self-thinning law has been explained to derive from self-shading with increasing density.

However, in contrast to terrestrial plants, which take up nutrients from the soil, seaweed take up nutrients from dissolved nutrient pools through their fronds. Indeed, nutrient uptake by macroalgae has also been reported to be size-dependent, specifically increasing with the surface to volume ratio (or decreasing with thickness) of the plants (Hein et al., 1995). Hence, nutrient limitation may pose an additional constraint to the upper limit of seaweed density beyond which is imposed by light-limitation through self-shading. This hypothesis provides an alternative explanation for the order-of-magnitude lower density aquatic photosynthetic organisms can support compared to terrestrial plants of similar size (Duarte and Kalff, 1987). Moreover, the notion that both nutrients and light set the upper limit to the density of seaweed is supported by the observation that the highest biomass and density of seaweed is found in high-energy environments, such as kelp beds (Cheshire and Hallam, 1988), as high turbulent energy facilitates nutrient uptake (Hurd et al., 1996; Hurd, 2000; Wernberg and Connell, 2008).

Understanding the regulation of seaweed growth has now gained particular importance, as seaweed aquaculture is a rapidly growing component of marine aquaculture (Duarte et al., 2009) and relies on ambient nutrients and irradiance. The development of general relationships between seaweed growth and resource (light and nutrient) availability and density can, therefore, select sites and conditions, as well as stocking density, to maximize seaweed growth in aquaculture. Indeed, nutrients may become limited to seaweed aquaculture as this industry expands (Xiao et al., 2017), and create a demand for relationships between seaweed growth and resource availability, which, surprisingly, has not received much attention in the past.

Here we test the hypothesis that irradiance, nutrient limitation and density regulate seaweed growth. We do so through an analysis of the role of nutrients, density and irradiance in modulating the density-dependence of seaweed growth based on a comparative analysis of data on specific growth rates of seaweed across a range of densities under controlled nutrient conditions in the laboratory and aquaculture farms.

Materials and Methods

We searched the published literature for data on the density-dependence of seaweed growth under different nutrient levels. The search was based on the Web of Science^®, accessed in May 2019, using a combination of keywords including “seaweed and remediation,” “seaweed and bioremediation,” “seaweed and nitrogen removal,” and “seaweed and phosphorous removal.” These searches yielded a total of 164 papers reporting growth rates and biomass density for seaweed. We retrieved the growth rates, biomass density, concentration of the dominant forms of inorganic nutrients - ammonia, nitrate and phosphate – and incident irradiance, and recorded the taxa (chlorophyta, phaeophyta or rhodophyta). This generated a raw dataset containing a total of 1729 experimental assessments (Supplementary Table S1). For all the assessments, we further converted all growth rates to units of % day^–1 and biomass density (i.e., the seaweed biomass per unit habitat volume) to g FW L^–1. A total of 733 experimental assessments included data on specific growth rate and initial cultivation biomass density, while a total of 854 experimental assessments included data on seaweed specific growth rates and irradiance (Xiao et al., 2019).

The density-dependence of specific seaweed growth (SGR, % d^–1) was described using a power law of the form SGR = a BD^x, where BD is the biomass density (BD, g FW L^–1) and x is the power exponent describing the scaling of SGR to BD. Similarly, the irradiance-dependence of specific seaweed growth (SGR, % d^–1) was described using a power law of the form SGR = a I^x, where I is the irradiance (I, μmol photon m^–2 s^–1) and x is the power exponent describing the scaling of SGR to I. The relationship was fitted using model I linear regression on log₁₀ transformed variables. The role of nutrients in modulating the density dependence of seaweed growth rate (log₁₀ transformed) was then examined by fitting a general linear model including log₁₀ transformed density, irradiance and nutrient (N, ammonia, nitrate or phosphate, mmol L^–1) concentrations as independent variables, yielding the equation log₁₀ SGR = a + x₁ log₁₀ BD + x₂ log₁₀ I + x₃ log₁₀ N, which is equivalent, in arithmetic scale, to SGR = 10^a BD^x1 I^x2 N^x3, thereby involving interactions between density, irradiance and nutrient concentrations as covariates. All statistical analyses were conducted using JMP v. 10 software. The data supporting this study are available from the open access data repository PANGAEA (Xiao et al., 2019).

Results and Discussion

Specific growth rates ranged from below detection limit to very fast rates of 54.6% d^–1, with an average (±SE) of 6.40 ± 0.18% d^–1 (median 4.51% d^–1), and the biomass density ranged from 0.04 to 25 g FW L^–1, with an average (±SE) of 3.43 ± 0.11 g FW L^–1 (median 2.0 g FW L^–1) (Xiao et al., 2019). The mean biomass density of 2.0 g FW L^–1 for seaweed density in the data set corresponds, assuming a density of 1, to an occupation of 0.2% of the available volume by seaweed biomass. This is similar to results derived from examination of the size-dependence of the maximum abundance of aquatic organisms in culture, which indicates that they can occupy, at maximum density, 0.1% of the available volume regardless of whether they are photosynthetic organisms or animals (Duarte et al., 1987; Marquet et al., 1995).

Specific seaweed growth declined with biomass density (Figure 1) as described by the power law SGR = BD^{–1.44 (±0.18)} (Figure 1), independently of taxa (ANOVA, P > 0.05), with SGR declining from average values of 10% day^–1 at BD less than 0.2 g FW L^–1 to <1% day^–1 at BD >8 g FW L^–1. SGR increased with incident irradiance as described by the power law SGR = I ^{1.72 (±0.18)} (Figure 2), with SGR increasing from <0.1% day^–1 at I < 100 μm photon m^–2 s^–1 to average values of 100% day^–1 at I > 10,000 μm photon m^–2 s^–1.

FIGURE 1

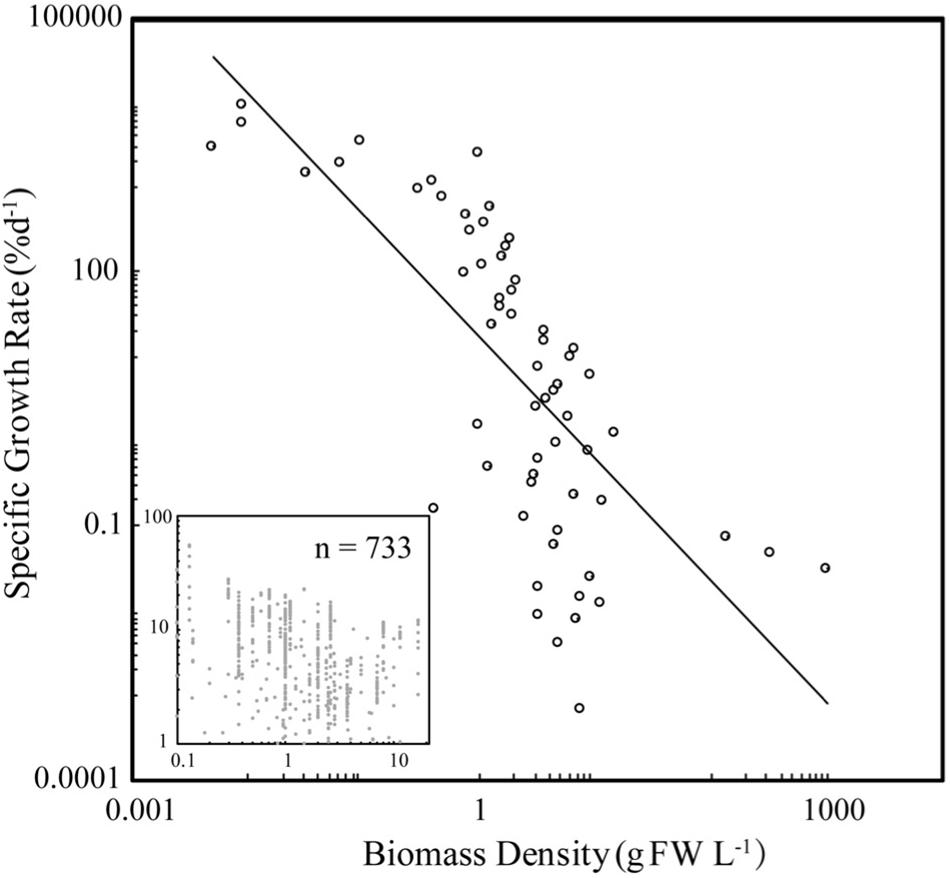
Figure 1. The relationship between specific growth rate (SGR) and biomass density (BD) for seaweed growing under experimental or culture conditions. The closed symbols show the mean values for BD bins of 0.1 g FW L^–1, for BD < 1 g FW L^–1, and intervals of 1 g FW L^–1 for greater values, and the insert shows the raw values. The fitted power law for the binned and raw data are SGR = 17.4 BD^{–1.44 ± 0.18} (R² = 0.51, F = 61.96, N = 60, P < 0.001) and SGR = 5.06 BD^{–0.21 ± 0.03} (R² = 0.06, F = 43.3, N = 733, P < 0.001).

FIGURE 2

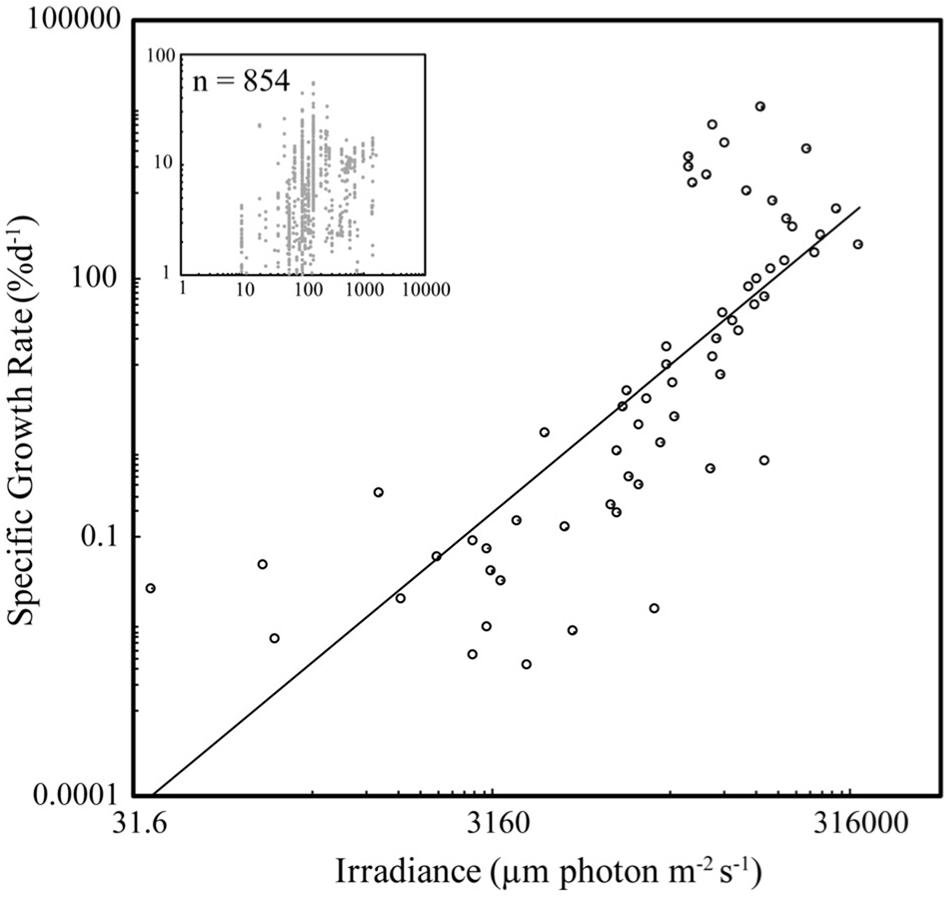
Figure 2. The relationship between SGR and irradiance (I) for seaweed growing under experimental or culture conditions. The closed symbols show the mean values for BD bins of 0.1 g FW L^–1, for BD < 1 g FW L^–1, and intervals of 1 g FW L^–1 for greater values, and the insert shows the raw values. The fitted power law for the binned and raw data are SGR = 2.0 × 10^–7 I ^{1.72 ± 0.18} (R² = 0.60, F = 90.7, N = 61, P < 0.001) and SGR = 0.58 I ^{–0.41 ± 0.03} (R² = 0.15, F = 143.8, N = 854, P < 0.001).

General linear models showed that the SGR yielded the fitted equation:

$$\text{SGR}=-0.03-0.51(\pm 0.04) \log {}_{10}\text{BD}+0.30(\pm 0.05) \log {}_{10}\text{I}+0.08(\pm 0.01) \log {}_{10}\text{NO}{}_3$$

Where nitrate has units of μmol L^–1 (R² = 0.39, N = 349, F = 74.16, P < 0.001 and t-test for all slopes have P < 0.001). While the fitted relationship for ammonia concentrations (μmol L^–1) was

$$\text{SGR}=-0.37-0.37(\pm 0.04) \log {}_{10}\text{BD}+0.30(\pm 0.05) \log {}_{10}\text{I}+0.17(\pm 0.03) \log {}_{10}\text{NH}{}_4$$

(R² = 0.33, N = 275, F = 44.4, P < 0.001 and t-test for all slopes have P < 0.001).

The general model with phosphate concentrations did not yield a significant effect for phosphate (P > 0.05).

These relationships show that seaweed growth rate for any given density increases as the ^1/3 power of irradiance and increases much faster with increasing nitrogen when this is supplied as ammonium compared to nitrate (Figure 3).

FIGURE 3

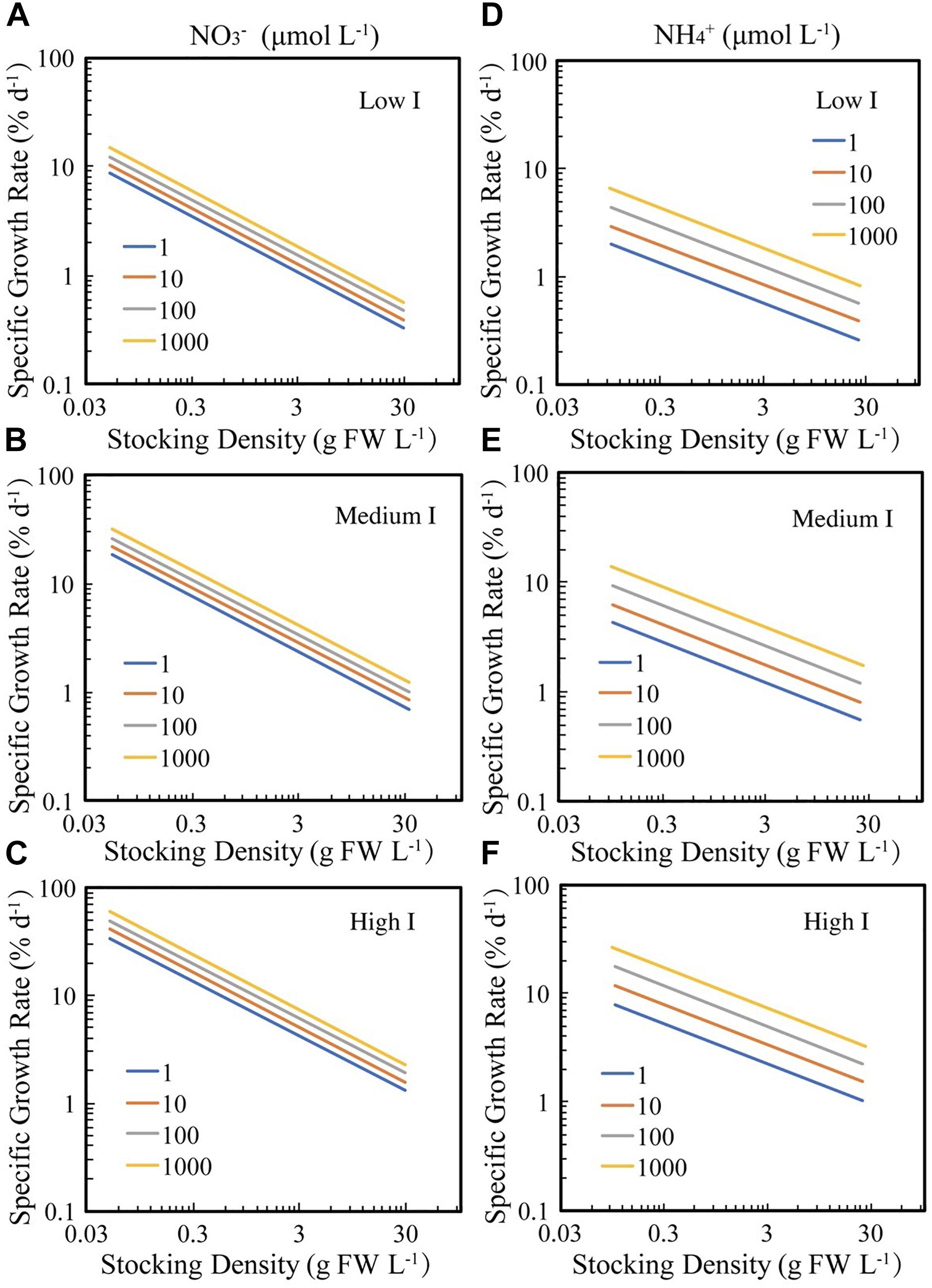
Figure 3. The fitted relationships between SGR and BD for seaweed growing under experimental or culture conditions under different irradiance (I), ammonia (NH₄⁺), and nitrate (NO₃^–) concentrations. The solid lines correspond to the fitted general linear models log₁₀ SGR = –0.03–0.51 (±0.04) log₁₀ BD + 0.08 (±0.02) log₁₀ NO₃ + 0.30 (±0.05) log₁₀ I (R² = 0.39, F = 74.16, N = 349, P < 0.0001), and log₁₀ SGR = –0.37–0.37 (±0.04) log₁₀ BD + 0.17 (±0.03) log₁₀ NH₄ + 0.30 (±0.05) log₁₀ I (R² = 0.33, F = 44.4, N = 275, P < 0.0001), respectively. Low I, medium I and high I are 10, 125, and 1000 μm photon m^–2 s^–1, respectively, which are the 2.5, 50, and 97.5% quantiles of the irradiance data. (A–C) Seaweed growth in response to nitrate (NO₃^–), under low, medium and high irradiance, respectively; (D–F) seaweed growth in response to ammonia (NH₄⁺), under low, medium and high irradiance, respectively.

These results confirm that the density-dependence of seaweed growth rate is imposed by nitrogen and light limitation, with seaweed growing under high nutrient supply and incoming irradiance able to sustain high growth rates, even when occupying 2% of the available space (Figure 2). Our results also demonstrate a contrasting role for phosphate, nitrate, and ammonia, with growth rates independent of phosphate concentrations, and increasing faster, for a given concentration, with increasing ammonia compared to nitrate (Figure 3). High irradiance and ammonia concentrations allow seaweed to achieve high growth rates, approaching 10% day^–1 even at high biomass density (3 g FW L^–1 or 3% of available space, Figure 3).

The results presented explain the high yield of seaweed in the intensive farms that have proliferated along much of the coast of China, where eutrophication leads to very high nutrient concentrations exceeding 127 μmol NH₄ and 2.21 μmol PO₄ along much of the coast of China (He et al., 2008; Huo et al., 2011; Wu et al., 2015; Xiao et al., 2017). Moreover, these findings may also help explain the occurrence of massive green tides in Chinese coastal waters in recent years, where over 1 million tons of green algae were removed from the coast during Olympic sailing events in 2008 (Wang et al., 2015; Zhou et al., 2015). The density-dependence of seaweed growth reported here is also consistent with the use of thinning to promote the growth and maturation of U. pinnatifida sporophytes in the field (Gao et al., 2014).

Whereas light limitation, resulting from self-shading, will impose an ultimate limit to seaweed growth with increasing biomass density (Westoby, 1984; Duarte and Kalff, 1987), the results presented show that the upper limits to seaweed growth in dense stands are likely imposed by nitrogen, particularly ammonium concentration, together with light, which impose an ultimate limit at biomass densities above those observed in dense seaweed stands, such as those proliferating in hypereutrophic Chinese coastal waters during green tides. Hence, nutrient and light limitation help explain the 10-fold lower density, for a given plant size, of seaweed, as well as other aquatic photosynthetic organisms, compared to terrestrial plants (Agusti et al., 1987; Duarte and Kalff, 1987).

The results presented here can help predict potential seaweed yields in aquaculture, given incident irradiance and nutrient concentrations, and also inform how density can be managed to achieve maximum growth where nutrient concentrations and or light maybe limiting. Because space is rarely a constraint in seaweed aquaculture (e.g., Oyinlola et al., 2018), reducing stocking density may allow high growth rates and yields in nutrient-poor coastal waters.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

CD, SA, JW, and XX conceived and designed the comparative analysis. XX, FL, YY, YP, and KL generated the datasets. CD and XX wrote the manuscript. All authors analyzed, interpreted the results and edited the manuscript.

Funding

This study was supported by the National Natural Science Foundation of China (Grants 21677122 and 21876148 to XX), the China’s International Science and Technology Cooperation Program (Grant 2015DFA01410 to JW and CD) from the Ministry of Science and Technology of China, King Abdullah University of Science and Technology (KAUST) through the baseline fund to CD and SA, the open fund of the Laboratory of Marine Ecosystem and Biogeochemistry, Second Institute of Oceanography, SOA (LMEB201709 to XX), and the Fundamental Research Funds for the Central Universities (to XX).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2019.00618/full#supplementary-material

References

Agusti, S., Duarte, C. M., and Kalff, J. (1987). Algal cell size and the maximum density and biomass of phytoplankton. Limnol. Oceanogr. 32, 983–986. doi: 10.4319/lo.1987.32.4.0983

CrossRef Full Text | Google Scholar

Arenas, F., Viejo, R. M., and Fernández, C. (2002). Density−dependent regulation in an invasive seaweed: responses at plant and modular levels. J. Ecol. 90, 820–829. doi: 10.1046/j.1365-2745.2002.00720.x

CrossRef Full Text | Google Scholar

Cheshire, A. C., and Hallam, N. D. (1988). Biomass and density of native stands of durvillaea potatorum(southern bull-kelp) in south eastern Australia. Mar. Ecol. Progr. Ser. Oldendorf 48, 277–283. doi: 10.3354/meps048277

CrossRef Full Text | Google Scholar

Duarte, C., Agusti, S., and Peters, H. (1987). An upper limit to the abundance of aquatic organisms. Oecologia 74, 272–276. doi: 10.1007/BF00379370

PubMed Abstract | CrossRef Full Text | Google Scholar

Duarte, C., and Kalff, J. (1987). Weight-density relationships in submerged macrophytes. Oecologia 72, 612–617. doi: 10.1007/BF00378990

PubMed Abstract | CrossRef Full Text | Google Scholar

Duarte, C. M., Holmer, M., Olsen, Y., Soto, D., Marbà, N., Guiu, K., et al. (2009). Will the oceans help feed humanity? BioScience 59, 967–976. doi: 10.1525/bio.2009.59.11.8

CrossRef Full Text | Google Scholar

Gao, X., Endo, H., Taniguchi, K., and Agatsuma, Y. (2014). Effects of experimental thinning on the growth and maturation of the brown alga Undaria pinnatifida (Laminariales; Phaeophyta) cultivated in Matsushima Bay, northern Japan. J. Appl. Phycol. 26, 529–535. doi: 10.1007/s10811-013-0071-y

CrossRef Full Text | Google Scholar

He, P., Xu, S., Zhang, H., Wen, S., Dai, Y., Lin, S., et al. (2008). Bioremediation efficiency in the removal of dissolved inorganic nutrients by the red seaweed, Porphyra yezoensis, cultivated in the open sea. Water Res. 42, 1281–1289. doi: 10.1016/j.watres.2007.09.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Hein, M., Pedersen, M. F., and Sand-Jensen, K. (1995). Size-dependent nitrogen uptake in micro-and macroalgae. Mar. Ecol. Progr. Ser. Oldendorf 118, 247–253. doi: 10.3354/meps118247

CrossRef Full Text | Google Scholar

Huo, Y. Z., Xu, S. N., Wang, Y. Y., Zhang, J. H., Zhang, Y. J., Wu, W. N., et al. (2011). Bioremediation efficiencies of Gracilaria verrucosa cultivated in an enclosed sea area of Hangzhou Bay. China. J. Appl. Phycol. 23, 173–182. doi: 10.1007/s10811-010-9584-9

CrossRef Full Text | Google Scholar

Hurd, C., Harrison, P., and Druehl, L. (1996). Effect of seawater velocity on inorganic nitrogen uptake by morphologically distinct forms of Macrocystis integrifolia from wave-sheltered and exposed sites. Mar. Biol. 126, 205–214. doi: 10.1007/bf00347445

CrossRef Full Text | Google Scholar

Hurd, C. L. (2000). Water motion, marine macroalgal physiology, and production. J. Phycol. 36, 453–472. doi: 10.1046/j.1529-8817.2000.99139.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, L., Weiner, J., Zhou, D., Huang, Y., and Sheng, L. (2013). Initial density affects biomass–density and allometric relationships in self−thinning populations of Fagopyrum esculentum. J. Ecol. 101, 475–483. doi: 10.1111/1365-2745.12039

CrossRef Full Text | Google Scholar

Marquet, P. A., Navarrete, S. A., and Castilla, J. C. (1995). Body size, population density, and the energetic equivalence rule. J. Anim. Ecol. 64, 325–332. doi: 10.2307/5894

CrossRef Full Text | Google Scholar

Oyinlola, M. A., Reygondeau, G., Wabnitz, C. C. C., Troell, M., and Cheung, W. W. L. (2018). Global estimation of areas with suitable environmental conditions for mariculture species. PLoS One 13:e0191086. doi: 10.1371/journal.pone.0191086

PubMed Abstract | CrossRef Full Text | Google Scholar

Reynolds, J. H., and Ford, E. D. (2005). Improving competition representation in theoretical models of self−thinning: a critical review. J. Ecol. 93, 362–372. doi: 10.1111/j.1365-2745.2005.00976.x

CrossRef Full Text | Google Scholar

Wang, Z., Xiao, J., Fan, S., Li, Y., Liu, X., and Liu, D. (2015). Who made the world’s largest green tide in China?—an integrated study on the initiation and early development of the green tide in Yellow Sea. Limnol. Oceanogr. 60, 1105–1117. doi: 10.1002/lno.10083

CrossRef Full Text | Google Scholar

Wernberg, T., and Connell, S. D. (2008). Physical disturbance and subtidal habitat structure on open rocky coasts: effects of wave exposure, extent and intensity. J. Sea Res. 59, 237–248. doi: 10.1016/j.seares.2008.02.005

CrossRef Full Text | Google Scholar

Westoby, M. (1984). The self-thinning rule. Adv. Ecol. Res. 14, 167–225.

Google Scholar

Wu, H., Huo, Y., Zhang, J., Liu, Y., Zhao, Y., and He, P. (2015). Bioremediation efficiency of the largest scale artificial Porphyra yezoensis cultivation in the open sea in China. Mar. Pollut. Bull. 95, 289–296. doi: 10.1016/j.marpolbul.2015.03.028

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiao, X., Agusti, S., Lin, F., Li, K., Pan, Y., Yu, Y., et al. (2017). Nutrient removal from Chinese coastal waters by large-scale seaweed aquaculture. Sci. Rep. 7:46613. doi: 10.1038/srep46613

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiao, X., Agusti, S., Lin, F., Xu, C., Yu, Y., Pan, Y., et al. (2019). Dataset on the specific growth rate of seaweed growing in experimental and aquaculture conditions at various biomass densities, irradiation and nutrient concentrations. PANGAEA. doi: 10.1594/PANGAEA.907407

CrossRef Full Text | Google Scholar

Zhou, M., Liu, D., Anderson, D. M., and Valiela, I. (2015). Introduction to the Special Issue on green tides in the Yellow Sea. Estuar. Coast. Shelf Sci. 163, 3–8. doi: 10.1016/j.ecss.2015.06.023

CrossRef Full Text | Google Scholar