Air-Sea CO2-Exchange in a Large Annular Wind-Wave Tank and the Effects of Surfactants

Ribas-Ribas, Mariana; Helleis, Frank; Rahlff, Janina; Wurl, Oliver

doi:10.3389/fmars.2018.00457

ORIGINAL RESEARCH article

Front. Mar. Sci., 30 November 2018

Sec. Marine Biogeochemistry

Volume 5 - 2018 | https://doi.org/10.3389/fmars.2018.00457

Air-Sea CO₂-Exchange in a Large Annular Wind-Wave Tank and the Effects of Surfactants

$\r\nMariana Ribas-Ribas*$ Mariana Ribas-Ribas¹^*

Frank Helleis²

Janina Rahlff¹^†

Oliver Wurl¹

¹Institute for Chemistry and Biology of the Marine Environment (ICBM), Carl-von-Ossietzky-University Oldenburg, Wilhelmshaven, Germany
²Max-Planck-Institut für Chemie (Hahn Otto -Institut), Mainz, Germany

Wind, chemical enhancement, phytoplankton activity, and surfactants are potential factors driving the air-sea gas exchange of carbon dioxide (CO₂). We investigated their effects on the gas transfer velocity of CO₂ in a large annular wind-wave tank filled with natural seawater from the North Atlantic Ocean. Experiments were run under 11 different wind speed conditions (ranging from 1.5 ms⁻¹ to 22.8 ms⁻¹), and we increased the water pCO₂ concentration twice by more than 950 μatm for two of the seven experimental days. We develop a conceptual box model that incorporated the thermodynamics of the marine CO₂ system. Surfactant concentrations in the sea surface microlayer (SML) ranged from 301 to 1015 μgL⁻¹ (as Triton X-100 equivalents) with enrichments ranged from 1.0 to 5.7 in comparison to the samples from the underlying bulk water. With wind speeds up to 8.5 ms⁻¹, surfactants in the SML can reduce the gas transfer velocity by 54%. Wind-wave tank experiments in combination with modeling are useful tools for obtaining a better understanding of the gas transfer velocities of CO₂ across the air-sea boundary. The tank allowed for measuring the gas exchange velocity under extreme low and high wind speeds; in contrast, most previous parametrizations have fallen short because measurements of gas exchange velocities in the field are challenging, especially at low wind conditions. High variability in the CO₂ transfer velocities suggests that gas exchange is a complex process not solely controlled by wind forces, especially in low wind conditions.

Introduction

The air-sea exchange of climate-relevant gases, such as carbon dioxide (CO₂) and nitrous oxide (N₂O), plays an important role in climate regulations (Liss and Duce, 2005). Air-sea exchange fluxes (F) are determined by the gas transfer velocity (k) and the difference between the gas concentrations (c) in the air and water (F = k [c_a – c_w]). Many of the gas transfer velocity parameterizations that are frequently used in oceanography are based on wind speed and temperature (Nightingale et al., 2000; Ho et al., 2006; Wanninkhof, 2014). The parameterizations describe the quadratic (Ho et al., 2006; Wanninkhof, 2014), cubic (McGillis et al., 2001, 2004), sub-linear (Krakauer et al., 2006), and multi-linear (Liss and Merlivat, 1986) relationships between wind speed and gas transfer velocity. However, wind speed alone cannot be the only gas exchange force, and according to Wanninkhof et al. (2009), “… wind by itself clearly does not control transfer across the interface but rather affects the turbulence” (p. 231). Other parametrizations have been developed on the basis of surface water turbulence (Kitaigorodskii and Donelan, 1984), friction velocity (Deacon, 1977), or wave slope (Jähne et al., 1984); however, these parameters are not easy to measure in the field, and not available as global datasets, similar to wind speed (Kalnay et al., 1996).

The sea-surface microlayer (SML) is the uppermost part of the water column that is in direct contact with the atmosphere. The thickness of the SML ranges from 1 to 1,000 μm (Wurl et al., 2017). With an experimentally measured thickness of about 60 μm (Zhang et al., 2003), the SML acts as a diffusion layer due to the enrichment of surface-active substances (Frew, 2005; Wurl et al., 2011), and the resistance to air-sea gas transfer mainly occurs over that degree of thickness (Kunz and Jähne, 2018). The SML is a distinct habitat with unique microbial communities that are likely to affect the air-sea gas exchange due to their cell metabolism (Conrad and Seiler, 1988; Upstill-Goddard et al., 2003). Chemical enhancement, bubbles, buoyancy fluxes, energy dissipation, fetch, and rain are other potential factors driving the air-sea gas exchange of climate-relevant gases (Wanninkhof et al., 2009). For example, it has already been proven that surfactants in the SML (Frew et al., 2002) and bubbles (Woolf, 1997) affect gas transfer velocities.

Another uncertainty in existing parametrizations is the lack of field in situ data at extreme low and high wind speeds. Measurements of field data at high wind speeds are challenging due to technical and safety issues, such as the deployment and operation of field equipment during storms. Recently, air-sea gas exchange measurements have been conducted in the field at wind speeds of up to 24 m s⁻¹ (Bell et al., 2017; Blomquist et al., 2017), but systematic investigations (i.e., covering a range of covariates) remains challenging under high wind conditions at sea.

Measurements at low wind speed are challenging for different reasons, e.g., the timescales for obtaining the measured signals are long and the probability of encountering low winds over the open ocean is very low. Most previous parametrizations have assumed that gas transfer velocities approach zero for low wind speeds (Nightingale et al., 2000; Ho et al., 2006; Wanninkhof, 2014). However, if differences in the air concentration (c_a) and the water concentration (c_w) occur in low wind conditions (Schneider et al., 2014b), the lack of data for the low wind regime increases the gas flux uncertainty.

The present study investigated the effects of friction velocity, wind speed, and surfactants on the gas transfer velocity of CO₂ in the Aeolotron wind-wave tank, the world's largest operational annular wind-wave facility (Mesarchaki et al., 2015). In this paper, we describe a conceptual box model to investigate the CO₂ system and fluxes in the Aeolotron under well-controlled wind speeds. We present computed gas transfer velocities in comparison to common gas transfer parametrizations and the effect of surfactants at different wind regimes. The study provides new insights about the validity of parameterizations at low and high wind speeds, at which the parameterizations are interpolated.

Materials and Methods

Aeolotron

The Small-Scale Air-Sea Interaction Facility, the Aeolotron, at the University of Heidelberg, is an annular wind-wave facility with unlimited fetch (Mesarchaki et al., 2015). For the present study, the Aeolotron was filled for the first time with ~18,000 L of natural seawater from the North Atlantic Ocean, which was collected by the R/V Poseidon in September 2014. The water was stored in the dark under ambient temperature. At the beginning of the experiment, the dissolved inorganic carbon (DIC), total alkalinity (TA), and salinity were 2128.9 μmol kg⁻¹, 2339.7 μmol kg⁻¹, and 34.6, respectively. Using the CO2SYS routine (MATLAB version) (Lewis and Wallace, 1998; Van Heuven et al., 2011), aqueous pCO₂ can be assumed to be approximately 525 μatm at the time the Aeolotron was filled. Concentration of N₂O was below the detection limit (e.g., <100 ppm).

The Aeolotron allows wave generation at controlled wind speeds (wind speeds at a height of 10 m, i.e., u₁₀) ranging from 1.5 to 22.8 m s⁻¹. A total of 40 experiments at 11 different wind speeds were performed from November 3 to November 28, 2014 over seven sampling days. Each sampling day was preceded by a lead day. The Aeolotron has two hatches on the side to allow for sampling of the SML; the hatches were opened at the end of each wind condition without turning off the axial fans. Before opening the hatches, the Aeolotron was flushed with ambient outdoor air. After sampling, the hatches were closed and the axial fans were accelerated to generate wind speeds for the next condition. Nutrients (10 μmol L⁻¹ nitrate, 10 μmol L⁻¹ silicate, and 0.6 μmol L⁻¹ phosphate) were added to the Aeolotron on September 14, 2014. To further enhance the primary productivity, 1 L of coccolithophorid algae culture (Emiliana huxleyi, 4.6 × 10⁵ cells mL⁻¹) and 6.3 L of the biogenic SML sample were added to the tank on November 22 and November 23, 2014, respectively. However, during the entire campaign, no increase was observed in chlorophyll-a (Rahlff et al., 2017). Bacterial abundance and community composition have been reported elsewhere (Rahlff et al., 2017; Engel et al., 2018).

Description of the Conceptual Box Model

Generally, the total gas transfer velocity, k_t, is calculated using Equation 1 as follows:

\begin{array}{l} \begin{matrix} k_{t} = \frac{u^{*}}{β} S c^{n} \end{matrix} & (1) \end{array}

where u* is the water-side friction velocity, β is the momentum transfer velocity, Sc is the Schmidt number (Jähne et al., 1987a), and n is the Schmidt number exponent. Friction velocity (u*) and mean square slope (mss) were measured in situ by the Small-Scale Air-Sea Interaction research group at the Institute of Environmental Physics (University Heidelberg, Germany). Wind speeds at a height of 10 m (u₁₀) were extrapolated from u* using the Dc-Parameterization for the open ocean given by Edson et al. (2013). Using the well-accepted literature limiting values of 0.67 (smooth surface) and 0.5 (rough surface) for the exponent n as a function of mss (Deacon, 1977), β was made a function of u* to explain the k_tw of N₂O as a function of wind speed. For N₂O and CO₂, we can neglect the air-side resistance because the transfer processes are controlled by the water-side. A simple box model can be formulated using two coupled differential equations, as shown in Equation 2 and Equation 3:

\begin{array}{l} ć_{a} = \frac{- A}{V_{a}} \cdot k_{t w} \cdot (c_{a} \cdot α - c_{w}) - \frac{{\overset{́}{V}}_{i}}{V_{a}} \cdot (c_{a} - c_{i n}) - \frac{{\overset{́}{V}}_{l}}{V_{a}} \\ \cdot (c_{a} - c_{l e a k}) - \frac{{\overset{́}{V}}_{f}}{V_{a}} \cdot (c_{a} - c_{f l u s h}) - \frac{{\overset{́}{V}}_{h}}{V_{a}} \cdot (c_{a} - c_{h a t c h}) & (2) \end{array}

\begin{array}{l} ć_{w} = \frac{+ A}{V_{w}} \cdot k_{t w} \cdot (c_{a} \cdot α - c_{w}) & (3) \end{array}

where, V is the volume (either of air or water), c is the inert gas concentration (in our study N₂O), and A is the surface area of the Aeolotron, i.e., the area over which the gas exchange occurs. The first term on the right-hand side of Equation 2 represents the exchange of a gas from one phase to the other due to a concentration gradient. The second term in Equation 2 represents the inputs from the Aeolotron's invasion gas handling system. The third term represents possible gas losses due to leaks in the closed tunnel originating from two sources: the flushing system and the hatches. The fourth term represents the possible gas output due to flushing; the fifth term represents the exchange between the laboratory air and air in the Aeolotron when the hatches are opened for sampling the SML. A scheme of these terms is shown in Figure 1.

FIGURE 1

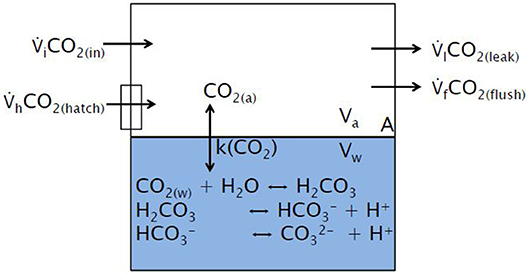
Figure 1. Conceptual model for the air-side and water-side of the system. The following naming convention was used: A: water surface area; V_a: air volume; V_w: water volume; k(CO₂): total gas transfer velocity; CO_2(a): CO₂ air concentration; CO_2(w): CO₂ water concentration; CO_2(in): CO₂ concentration in the ambient air/lab; CO_2(hatch): CO₂ concentration when the Aeolotron hatch was open; CO_2(leak) and CO_2(flush): CO₂ concentrations in the air that leaked and in the air that is being flushed in the Aeolotron. Reaction of CO₂ in the surface water is also shown; a and w stand for air and water, respectively.

In the case of CO₂, the gas exchange dynamics involve the chemistry of the marine CO₂ system, e.g., CO₂ hydration. Therefore, in Equation 3, $c_{a^{*}} α$ is replaced by pCO₂ and we can reformulate it in a form used commonly in the field of oceanography, as seen in Equation 4:

\begin{array}{l} \frac{{d (D I C)}_{w}}{d t} = \frac{+ A}{V_{w}} \cdot k_{t w} \cdot (p C O_{2, a} - p C O_{2, w}) & (4) \end{array}

In every computational step, pCO_2,w is calculated in equilibrium to the total amount of carbon in the water. In order to speed up the simulation and ensure that the model parameters were fitted, inorganic carbon system parameters were implemented in the model by interpolating data from tables generated from the CO2SYS, using the carbonate equilibria constants described by Mehrbach et al. (1973) and refitted by Dickson and Millero (1987).

The box model equations were integrated for each daily condition of an experiment with a standard Runge-Kutta 5th order routine from the Igor package (WaveMetrics, Lake Oswego, Oregon, USA). To obtain the experimental transfer velocities, the box model parameters were optimized using the standard Marquard-Levenberg algorithm, thus, integrating the box model in each iteration step to match the modeled and experimental air time series. An example of a computation combined with experimental data for the air-side concentrations is shown in Figure 2.

FIGURE 2

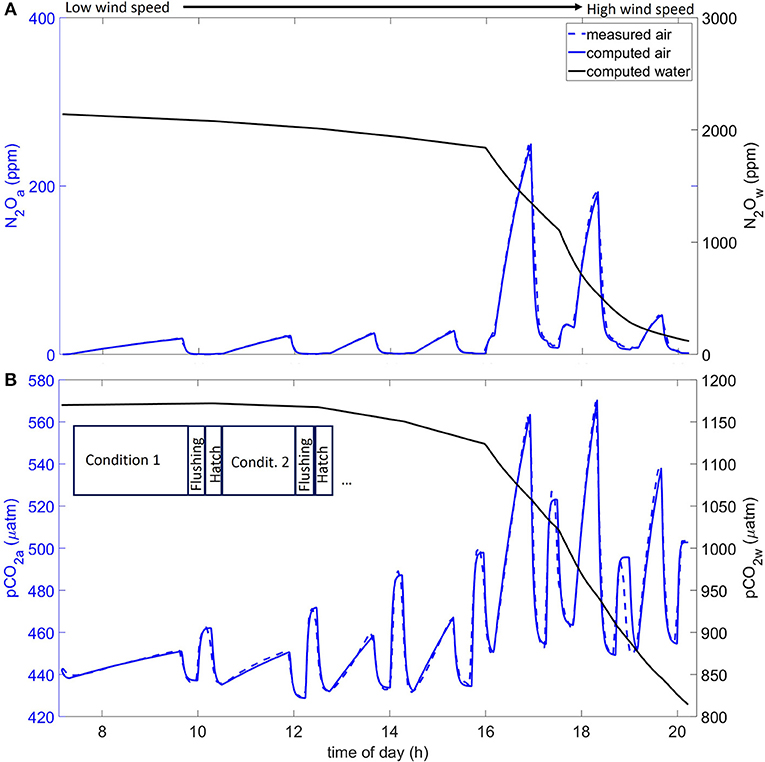
Figure 2. Example of conditions with computed water (w) and computed and measured air (a) for various times of the day on November 19, 2014. (A) N₂O; (B) pCO₂. An example of sequences with stable wind speed condition, flushing time, and sampling time (when the hatches were opened) is shown in (B). Wind speed increased from left to right, as show in the upper panel.

The output of our model shows that the air-side partial pressure of carbon dioxide (pCO_2,a) increased based on the reduction of pCO_2,w in the water-side bulk phase. We applied the described model to N₂O and CO₂, and we obtained two gas transfer velocities: k(CO₂) and k(N₂O). The ratio of k(CO₂)/k(N₂O) is interpreted as the deviation between the purely diffusive transport of an inert tracer (in this study N₂O) and additional processes, including the biogeochemical reaction of CO₂ that occurs in the SML (i.e., chemical enhancement, production, or respiration by microbial communities).

In our study, k was standardized with a Schmidt number of 660 to correct for the different temperature in the Aeolotron in comparison to the 20°C the parametrizations assumed using Equation 5:

\begin{array}{l} k_{660} = k {(\frac{660}{S c})}^{- n} & (5) \end{array}

Error/Uncertainties

Data analysis revealed that leaks cause significant systematic errors in the determination of gas transfer velocities, especially at low wind speeds. To account for leaks, the amount of tracer gas escaping the air space of the Aeolotron was monitored and corrected for. In the present study, tetrafluoromethane, a non-soluble tracer, was injected and the decrease in its concentration was monitored over time as described in Mesarchaki et al. (2015). The leak and flush rates ranged from 0.2 to 1.2 h⁻¹ and 17.6 to 20.5 h⁻¹, respectively. Due to instrument failure, no N₂O data and no flush or leak rates were obtained for November 4, 2014 and November 6, 2014. We assumed that the values obtained on November 19, 2014 and November 28, 2014 under identical wind conditions were similar, i.e., without significant variation. This method is sufficient for tracers with negligible outside concentrations.

For CO₂ with variable concentrations in the laboratory (600–1200 μatm) and in the flushing system (400–450 μatm), a differentiation between these two sources is important. From the time series of pCO_2,a and the concentrations of xylene (measured by the Max-Planck-Institute for Chemistry [Mainz, Germany]), i.e., concentrations measured while the hatches were open, we estimated the laboratory concentration and leak rates of CO₂ and xylene. Assuming that the leaks cannot contribute more than the difference between the N₂O and CO₂ transfer velocities, the contribution of leaks from the laboratory to the total leak data could not be > 4% over the entire campaign and not > 2% on most of non-enriched CO₂ days. Therefore, we ran the model with different contributions for the laboratory leak (from 0 to 4%) to evaluate the error on the CO₂ gas transfer, and we choose an upper limit when the leak was 0% and a lower limit when the leak was 2%. The uncertainties in concentrations for pCO_2,a and pCO_2,w were <4% for the typical concentrations measured in this study. The values for TA have <0.1% uncertainty, but the model output is remarkably insensitive to TA changes. The accuracy of the interpolated pCO_2,w data is better than 2 μatm. We used mean temperature for these computations; for a temperature change of ±0.5 K within an experiment, the change in the modeled water-side pCO_2,w integrated over an entire day would be ~0.5%. Furthermore, we conducted a sensitivity test showing that the temperature effect is negligible in comparison to other effects (i.e., leaks). Summarizing all the errors, we concluded that we can derive gas transfer velocities with errors due to leaks ranging from −20 to 0% for low wind speeds and from −3 to 0% for high wind speeds. Statistical errors in the fits of the gas transfer velocities for N₂O and CO₂ were typically <1%.

Partial Pressure of CO₂

The pCO₂ in the air and water were analyzed using two infrared gas analyzers (IRGA). For air, a SubCtech OceanPack™ (Kiel, Germany) with an IRGA (LI-COR LI-840x, Lincoln, Nebraska, USA) and an integrated in-line Drierite moisture trap was used. Its calibration was checked before and after the sampling campaign with an accuracy of 1.5%. The noise signal was <1 μatm; thus, the detection limit was well-below the lowest pCO_2,a level detected in the study. pCO_2,a was recorded every 30 s at a height of 80 cm above the water surface.

For the water-side measurements, the determination of pCO_2,w was based on the use of a bubble-type equilibrator that was supplied with a continuous flow of water from an Aeolotron port at a rate of 300 mL min⁻¹. CO₂ gas phase equilibrium, generated by circulating air in a closed loop through the equilibrator, was detected using infrared (IR) spectroscopy (LI-COR 6262, Lincoln, Nebraska, USA). The IR CO₂ analyzer was calibrated before the experiments were conducted using CO₂-free nitrogen and calibration gases with a CO₂ concentration of 251.74 μatm. After the campaign, the same gases were used again, and a deviation of 0.05 μatm and 0.59 μatm, respectively, was obtained. We estimate that the uncertainty of our data is <5 μatm. More details about the instrumentation and the calculation of the final pCO_2,w are given in Körtzinger et al. (1996) and Schneider et al. (2014a). The water-side pCO_2,w was recorded every 60 s. Aqueous pCO₂ (pCO_2,w) were determined only at the beginning of each experiment to provide the model with initial values. Then the model recalculated iterative the inorganic carbon system in the Aeolotron using CO2SYS.

Nitrous Oxide (N₂O)

An artificial lung (PDMSXA-1.0, PermSelect, Ann Arbor, MI, USA) was used to equilibrate a small volume of air with the water. The air was then analyzed using Fourier transform IR spectroscopy (Nicolet iS10 by Thermo Fischer Scientific, Waltham, MA, USA) with respect to the gas concentration (Krall, 2013). Lung performance was tested in the a posteriori calibration campaign at the Max-Planck-Institute for Chemistry [Mainz, Germany], and it was found to reproduce the Ostwald solubility coefficient reported in the literature within 8%, even in a non-static setup. A second Nicolet iS10 FT-IR spectrometer was used to monitor the air-side concentration of N₂O. Evasion experiments were performed to measure the transfer velocity of N₂O, meaning that the concentration of N₂O was increased in the water bulk to create a concentration gradient across the air-sea interface. On the day before each measurement sequence, N₂O (99.5% purity supplied by Air Liquide Germany GmbH, Düsseldorf, Germany) was dissolved in the water using a LiquiCel 8x20 membrane contactor (Membrana/3M, Charlotte, NC, USA). Equilibrated concentrations in the water phase were in the order of 5500–7500 ppm at the start of each measuring day. Data collection, evaluation, and calibration are described in detail in Krall (2013).

Discrete Sample Collection and Analyses

For each condition, we collected paired SML and underlying bulk water (UW) samples. Samples from the SML were collected through the open hatches of the Aeolotron using a glass plate sampler (Harvey and Burzell, 1972). The glass plate was immersed vertically, aligned with the wind, and withdrawn at a speed of 5–6 cm s⁻¹ (as consistently as conditions allowed). The SML samples adhering to the plate were scrapped off with a squeegee. The UW samples were collected from a tap in the Aeolotron at a depth of approximately 50 cm.

For the surfactants, we collected 125 mL of water samples from the SML (~25 dips) and UW in brown high-density polyethylene bottles. All the samples were stored in a refrigerator prior to analysis. The unfiltered samples were analyzed within 96 h. The surfactants were analyzed using phase-sensitive alternating current voltammetry (Metrohm VA 747, Herisau, Switzerland) with a hanging mercury drop electrode (Cosović and Vojvodić, 1998). Triton X-100 was used for standard addition methods, and data are reported in μgL⁻¹ Triton X-100 equivalents (μg Teq L⁻¹). The enrichment factors were calculated as the ratio of the surfactant concentration in the SML sample to the ratio of the concentrations in the corresponding UW sample.

We sampled TA, DIC, and salinity for three paired SML and UW samples, and for five additional UW samples. The TA and DIC samples were fixed with 100 μL of saturated mercuric chloride (HgCl₂) solution per 500 mL, and then sealed and kept in a dark environment prior to analysis. The Versatile INstrument for the Determination of Titration Alkalinity 3C (VINDTA) (Marianda, Kiel, Germany) laboratory alkalinity titration system was used to determine DIC and TA, and the Certificated Reference Materials (CRMs) were analyzed in duplicate for DIC and TA at the beginning, middle, and end of each use of a coulometric cell. The concentration of DIC was determined using coulometric analysis (Johnson et al., 1987). Analysis of TA was conducted using potentiometric titration with hydrochloric acid to the carbonic acid end point (Dickson, 1981). The accuracies of the DIC and TA measurements were 2.0 μmol kg⁻¹ and 1.5 μmol kg⁻¹, respectively, and the precisions were 1.7 μmol kg⁻¹ and 1.2 μmol kg⁻¹, respectively. Discrete salinity samples were analyzed using a salinometer (Guildline Autosal 8400B, Smiths Falls, Ontario, Canada).

Manipulation of the Carbonate Chemistry

CO₂ enrichment was carried out by adding CO₂-enriched seawater to the Aeolotron, i.e., CO₂ evasion experiments on selected days (see below). The amount of CO₂-enriched water needed to achieve the target pCO_2,w level was estimated based on the salinity, temperature, and pCO_2,w data of the seawater in the Aeolotron using the CO2SYS computer program. The addition of CO₂-enriched seawater increases DIC while TA remains constant. On November 18, 2014 and November 27, 2014, we manipulated the pCO_2,w levels in seawater to 1150 μatm and 950 μatm, respectively. The levels that were reached in the Aeolotron after the manipulation correspond to the mean and maximum values reported in the Intergovernmental Panel on Climate Change scenario RCP8.5 for 2100 (IPCC, 2013). The CO₂-enriched seawater was prepared in an air-tight 200 L tank aerated with pure CO₂ gas for approximately 6 h. Then, 115 L and 120 L of the CO₂-enriched seawater were directly transferred into the Aeolotron on November 18, 2014 and November 27, 2014, respectively. On November 27, 2014, other gases were added to the auxiliary tank for additional trace gas experiments that were run by a different group of researchers, so less saturation was reached. To achieve an even distribution of the CO₂-enriched water throughout the Aeolotron, we turned on the axial fans to produce wind against the circulation of the tank.

Statistical Analyses

Statistical analysis of the data set was performed using R version 3.4.0 (R Core Team, 2016). Normal distribution of the data was evaluated using Shapiro-Wilk and Anderson-Darling tests; variance homogeneity was tested using Bartlett's test. We used a simple linear model to compare differences in the log-transformed gas transfer velocities in relation to u₁₀ between the seven sampling days. An F-test was used to evaluate which model best fits the obtained data set. A breakpoint for k(N₂O) in relation to u* was calculated using an iterative searching method with piecewise regressions (Crawley, 2013). To assess the model's fit, we used adjusted r² and the Akaike Information Criterion (AIC). The non-parametric test (Mann-Whitney test) was performed to determine whether the k(CO₂)/k(N₂O) ratio differs significantly between the non-enriched and enriched CO₂ days. Unless otherwise indicated, the results are presented as means ± standard deviation.

Results

Box Model Performance

Figure 2 presents examples for a day of measured and computed N₂O in air and computed N₂O in water (a) and measured and computed pCO₂ in air and computed pCO₂ in water (b). We present the November 19, 2014 experiment with enriched pCO_2,w to observe enhanced fluxes. Enriched pCO₂ conditions were induced as described in section 2.6. On the course of the day, 7 wind speed conditions were performed (see Figure 2B, Condition 1 and 2 for example). After each condition, the system was flushed causing a sudden drop in N₂O and pCO₂. Then the hatches used for sampling were open causing sudden increase in pCO₂ but not in N₂O due to its absence in the ambient air. We decreased the duration of each condition with increasing wind speed due to increasing fluxes we could observe. Both computed N₂O and pCO₂ water concentrations (black lines in Figure 2) were slowly decreasing during low wind speeds and then sharply decreased during high wind conditions due to the losses via the fluxes. Figure 2A shows that the computed air N₂O values fit the measured values well (<3%). In the air-side, the agreement is good: we observed occasionally higher measured pCO_2,a than the model predicted but measured pCO_2,a was never lower than the predicted values.

N₂O Gas Transfer Velocities

In this section, the N₂O gas transfer velocities are presented; these might be interpreted as CO₂ gas transfer velocities without any chemical and biological effects. We report the relationships between k(N₂O) and water $u_{w}^{*}$ in logarithmic scale to better visualize changes at the extreme wind speeds (Figure 3). The possibility of measuring $u_{w}^{*}$ in the Aeolotron is one of the advantages of a laboratory study in comparison to field studies. Figure 3 also shows that, during evasive experiments (N₂O in Figure 3A, and enriched pCO₂ as solid points in Figure 3B), the data scatter less than during measurements at ambient pCO₂ conditions (open points in Figure 3B). This is probably because there is a larger concentration gradient across the air-sea interface and lower errors are associated with the measurements (see uncertainties section).

FIGURE 3

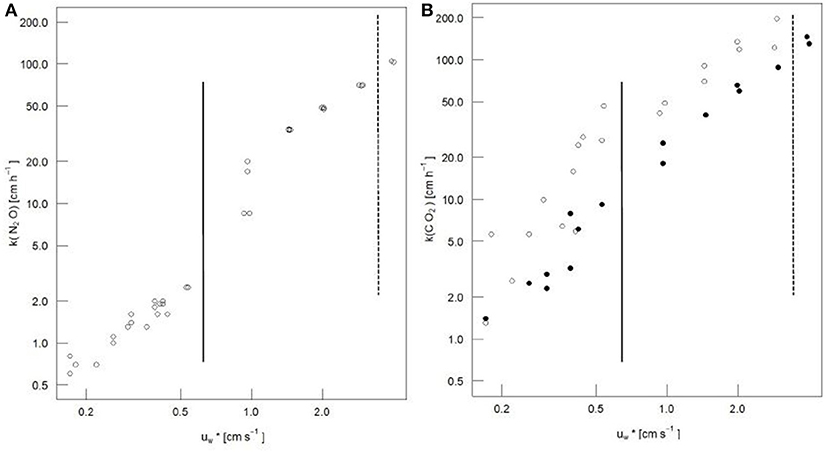
Figure 3. (A) N₂O and (B) CO₂ gas transfer velocity vs. friction velocities. The solid line represents the onset of capillary waves; the dashed line represents the onset of breaking waves. Solid circles in (B) represent enriched pCO₂ conditions.

In the present study, the N₂O gas transfer velocity had a linear segmented regression with $u_{w}^{*}$ (Figure 3). For $u_{w}^{*}$ <0.56 cm s⁻¹ (u₁₀ <5.4 m s⁻¹), the relationship was k(N₂O) = 4.45 * $u_{w}^{*}$ (r² = 0.989) no significant differences were observed from zero for the intercept (p-value = 0.105). For $u_{w}^{*}$ > 0.56 cm s⁻¹ (u₁₀ > 8.0 m s⁻¹), the relationship was k(N₂O) = 29.01 * $u_{w}^{*}$ - 11.70 (r² = 0.983). With the onset of breaking waves, no change in the regression slope was observed. Using the piecewise regression approach, the breaking wave range was defined as ranging from 5.4 to 8.0 m s⁻¹, but we did not conduct any measurements for this range (Figure 3).

CO₂ Gas Transfer Velocities

Figure 4A presents an overview of how our gas transfer velocities results compare to previous parameterizations on CO₂ gas transfer velocities (Liss and Merlivat, 1986; Nightingale et al., 2000; Ho et al., 2006; Wanninkhof, 2014). As seen, the enriched CO₂ days have good agreement with previous quadratic parametrizations, while the non-enriched days have a higher k(CO₂) than existing parametrizations (Figure 4A–C).

FIGURE 4

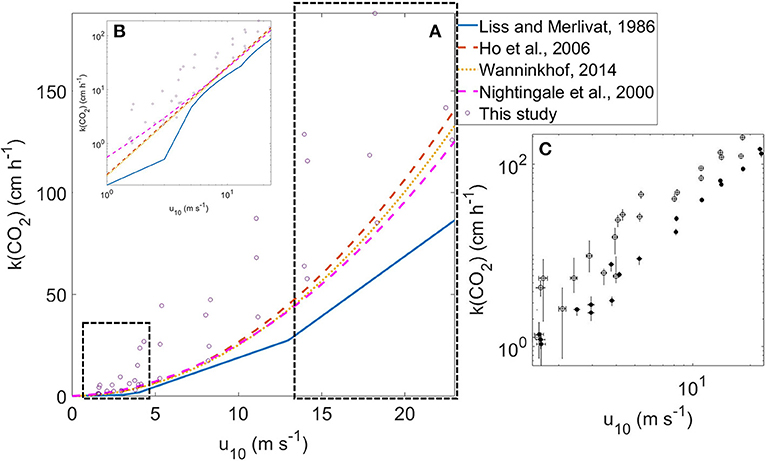
Figure 4. (A) k(CO₂) vs. wind scatterplot in linear axis in comparison to other parametrizations: Liss and Merlivat (1986), Ho et al. (2006), Wanninkhof (2014), and Nightingale et al. (2000), all scaled to a Schmidt number of 660. The data in the black box are the empirical data added in the lower and higher wind speeds where known parametrizations fall short. The insert shows the same information, but uses a double logarithmic scale (B). (C) Relationship between the gas transfer velocities for CO₂ and wind speeds for enriched pCO₂ conditions (solid circles) and non-enriched pCO₂ conditions (open data points) with asymmetric error bars in double logarithmic scale.

We found a quadratic relationship between k(CO₂) and u₁₀ (Figure 4) (r² = 0.774; p-value < 0.001; k(CO₂) = 0.32 * $u_{10}^{2}$ ) (regression lines are not shown in the figure). If we take into account the intercept, we found a quadratic relationship between k(CO₂) and u₁₀ (r² = 0.770; p-value < 0.01 for intercept and p-value < 0.001 for coefficient; k(CO₂) = 10.71 + 0.30 * $u_{10}^{2}$ ). The coefficients are within the range (with errors) by Wanninkhof (2014) as shown in Figure 4. The linear relationship between the gas transfer velocity and u₁₀ was also found to be statistically significant (r² = 0.881; p-value < 0.001; k(CO₂) = 6.26* u₁₀). The slope agrees with the slope of 5.9 for the intermediate wind regime reported by Liss and Merlivat (1986), also shown in Figures 4A,B. Broecker et al. (1978) also observed a linear relationship between k(CO₂) and u₁₀ over the entire range of wind speeds up to 16 m s⁻¹.

The fact that both the linear and quadratic relationships between k(CO₂) and u₁₀ are significant is mainly due to the existence of two groups of data (open and closed circles in Figures 3B and 4C); using a simple linear model to compare u₁₀ and log k(CO₂) for each group without interaction, the difference between them was statistically significant (F = 100.4, df = 36, p < 0.001, r² = 0.840). During experiments on November 19, 2014, November 21, 2014, and November 28, 2014, we obtained lower gas transfer velocities in comparison to observations on November 4, 6, 11, and 13 of that same year. The first group contained data from the last three days of sampling with enriched pCO_2,w (enriched days) (Table 1). The second group contained data from the first four days of sampling with non-enriched pCO_2,w and a high range of concentrations of surfactants because each sampling removed concentrated surfactants from the SML.

TABLE 1

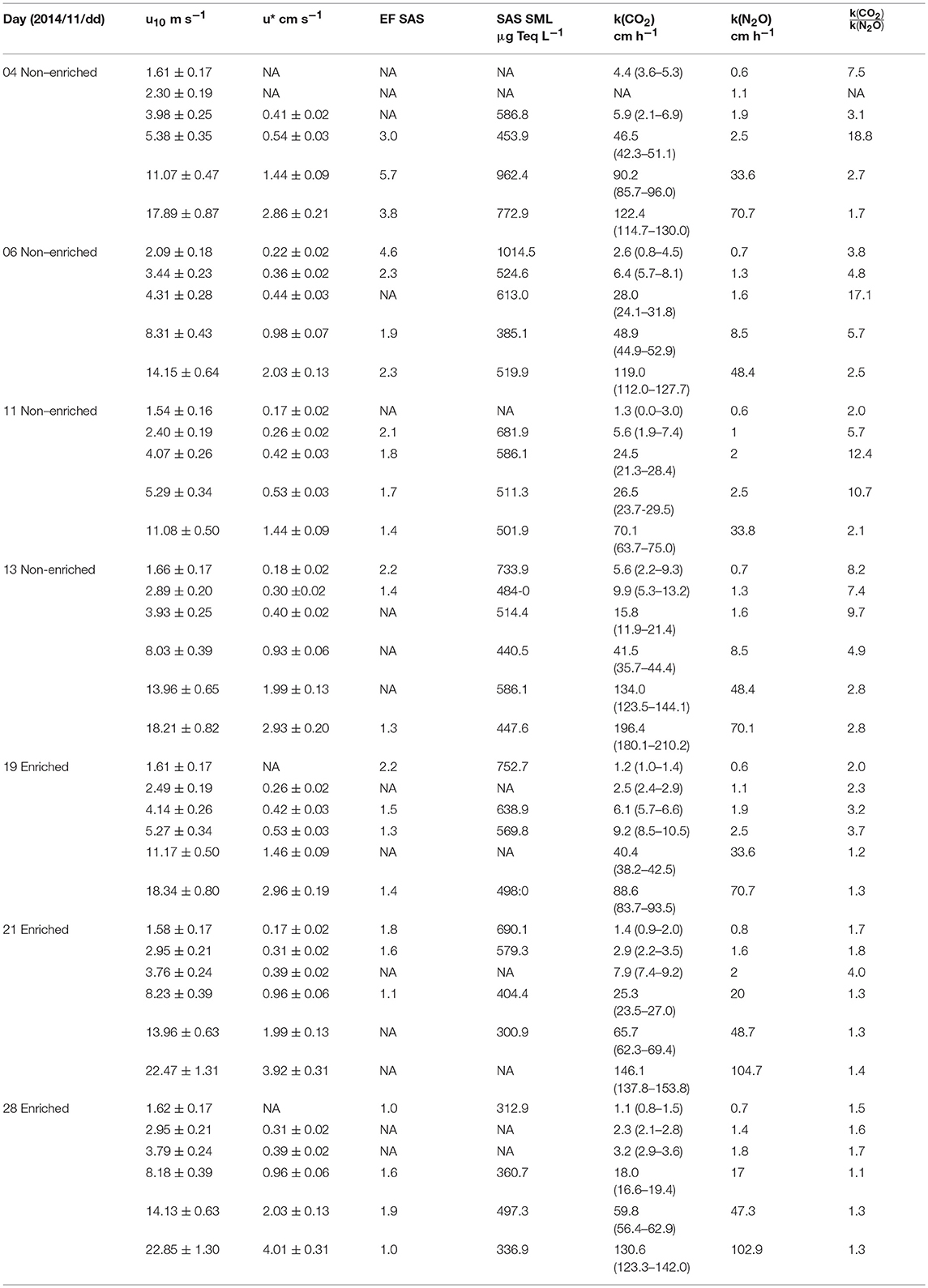
Table 1. Day of the experiment and conditions (CO₂ enriched or non-enriched), wind speed u₁₀, friction velocity (u*), enrichment factor of surfactants, surfactants in the sea surface microlayer, total water transfer velocities k measured in the Aeolotron wind-wave tank for CO₂ presented as mean (lower range–upper range), total water transfer velocities k measured in the Aeolotron wind-wave tank for N₂O and the ratio between gas transfer velocities CO₂ with the gas transfer velocities N₂O.

In our study, decrease on surfactants over the time of the study indicates that primary and bacterial production, as the source of surfactants (Ẑutić et al., 1981; Satpute et al., 2010; Engel et al., 2018), was very low (see section The Non-zero Intercept of Wind-based Parametrization of CO₂ Transfer Velocity). Also the nutrients and chlorophyll concentrations were very low (Rahlff et al., 2017). The SML is known to be dominated by heterotrophic activity (Reinthaler et al., 2008). In the Aeolotron, active bacterial communities were present (Rahlff et al., 2017). Overall, the setup in the Aeolotron represented an extremely oligotrophic system (Rahlff et al., 2017). The non-enriched pCO_2,w days might have higher systematic errors, because the pCO₂ differences were lower and the sample was more sensitive to leak rates. However, small gradients between aqueous and atmospheric concentrations are typical for oceanic conditions (Takahashi et al., 2009).

Comparison on High and Low Wind Speed

While previous parametrizations fell short in terms of the data for high and low wind speeds, our study provided data for wind speeds lower than 4 m s⁻¹ and higher than 12 m s⁻¹ (Figure 4A) We measured 18 gas transfer velocities with u₁₀ below 4 m s⁻¹, where other parametrizations have fallen short (Johnson, 2010). In the lower range of u₁₀, our model is particularly good at obeying mass balance with the assumption of chemical enhancement by a factor of two, but with higher interference from leak uncertainties. Our model does not include chemical enhancement; we obtained that by comparing k(N₂O) and k(CO₂). Importantly, CO₂ gas transfer velocities at very low u₁₀ are not equal to 0. Even if the intercept in the quadratic relationship is not statistically significant (p-value = 0.03), the AIC (362.7) for the quadratic relationship with the intercept 10.7 cm h⁻¹ was lower than the AIC (439.1) with an intercept = 0; this means that the relationship with an intercept unequal to 0 accounts for more of the variance.

Eight gas transfer velocities were measured with u₁₀ higher than 15 m s⁻¹. Therefore, we extended the measurement range from 1.5 m s⁻¹ to 22.8 m s⁻¹ [the range was 4 m s⁻¹ to 12 m s⁻¹ in parametrizations previously reported in Wanninkhof (1992); Ho et al. (2006)]. Because our model was proven to work correctly, the excess air-side CO₂ it predicted comes from either an artifact or the processes affecting the biogeochemistry of CO₂. Jähne et al. (1979) reported that their model fitted observations for a water surface covered with a surface film at low wind speeds.

Surfactants in the Sea-Surface Microlayer

Figure 5 shows scatter plots of the surfactant concentrations in the SML vs. k(CO₂) for four wind speed categories: <2.5 m s⁻¹, 2.5–5 m s⁻¹, 5–8.5 m s⁻¹, and 11–22 m s⁻¹. Excluding the highest wind category, but including both ambient and enriched pCO₂, a significant negative correlation (Spearman coefficient r = −0.5443, p = 0.0107, N = 21) was found between k(CO₂) and the surfactant concentrations in the SML. The correlation becomes stronger when excluding data measured under enriched pCO₂ conditions, i.e., if only considering ambient pCO₂ (Spearman coefficient r = −0.8226, p = 0.0006, N = 13) (Figure 5). No significant correlation was found between the enrichment of the surfactants and k(CO₂) (r = -0.3439, p = 0.2500, N = 13), and between the enrichment of the surfactants and wind speed (r = −0.2363, p = 0.4371, N = 13). However, the values for k(CO₂) were significantly different between the surfactant concentration ranges, i.e., low (360–470 μg Teq L⁻¹), moderate (470–620 μg Teq L⁻¹), and high (>620 μg Teq L⁻¹) (Figures 5B,C), based on the result of the Kruskal-Wallis test. This significant difference was observed in both data sets representing only ambient pCO₂ (p = 0.0007) and ambient+enriched pCO₂ (p = 0.0015) conditions. The three groups of ranges for the surfactant concentrations were assigned based on the observations in the Aeolotron and on a similar grouping for oligotrophic (mean 320 ± 215 μg Teq L⁻¹, N = 38), mesotrophic (mean 502 ± 532 μg Teq L⁻¹, N = 93), and eutrophic (mean 663 ± 476 μg Teq L⁻¹, N = 143) conditions in a field study (Wurl et al., 2011). The data sets include limited observations of k(CO₂) at different prevailing surfactant concentrations, but similar wind conditions. However, in general, we observed an average reduction of k(CO₂) by 54% among the three wind categories. The reduction between the three trophic ranges were similar (range: 48–63%) (Figure 5C). Figure 5A shows an irregular pattern between k(CO₂) and surfactants concentration in the SML indicating disruption of the SML at wind speed above 11 m s⁻¹. We also observed a significant negative correlation (Spearman coefficient r = −0.7802, p = 0.0017, N = 13) between the surfactant concentrations in the SML and wind speed, which becomes insignificant and weak when data from the 11–22 ms⁻¹ wind speed category are included.

FIGURE 5

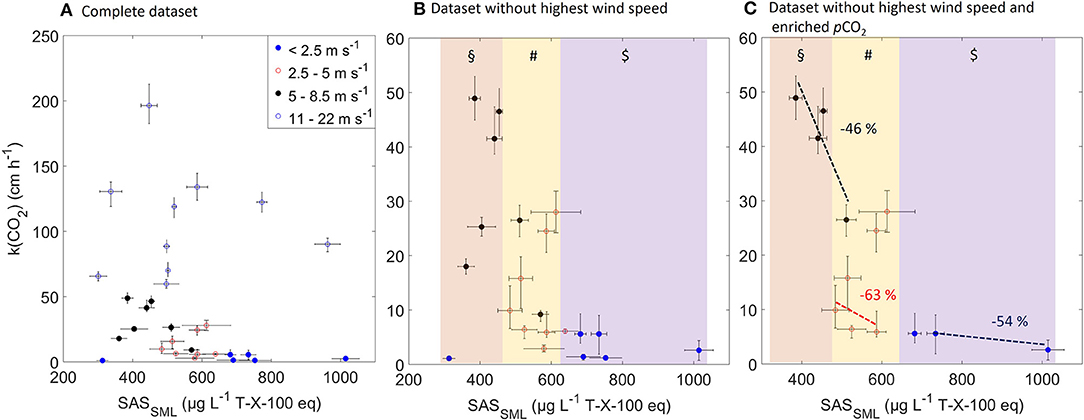
Figure 5. Scatter plots of surfactant concentrations in the SML vs. gas transfer velocity k(CO2) for (A) complete data set, (B) only for wind speeds up to 10 m s−1, and (C) only under ambient pCO2 conditions and wind speeds of up 10 m s−1. The color bands in (B) and (C) show groupings of low (§), moderate (#), and high surfactant concentrations ($). The dotted lines represent the linear trend line between the highest and lowest k within each wind category, and the numbers represent the reduction in k. For the wind speed category 2.5–5 m s−1, data points with k >20 cm h−1 were excluded when computing the trend line (see text).

Discussion

We point out that our data from the wind wave tunnel cannot be applied to fully explain complex processes in the real environment (Krall and Jähne, 2014). However, our data provides new insights into the fundamental mechanistic of gas exchange, including probable existence of a non-zero intercept of wind-based parameterization and suppressive effects of surfactants. We also considered the physico-chemical and biological impacts on CO₂ in seawater, including hydration reactions and chemical enhancement. All these controlling factors have been highly debated in the literature over the last 40 years [i.e., Broecker et al. (1978)].

Physical Factors Affecting CO₂ Gas Transfer Velocities

The onset of breaking waves in Figure 3 was already observed by Jähne et al. (1979), and it was attributed to the suppression of wind waves by surface films. The linear segments of gas transfers with wind speeds were previously reported by Liss and Merlivat (1986). They observed thresholds at 3.6 m s⁻¹ and 13.0 m s⁻¹ in linear wind wave tunnel and reported three types of regimes: a smooth surface, an undulating surface, and breaking waves. The linear relationship at low winds was originally reported by Deacon (1977), and most of the effect could be attributed to the change in the Schmidt number exponent from 0.67 to 0.5.

Wind speed may not be the best parameter for predicting k(CO₂) (Bock et al., 1999; Frew et al., 2004). In water, $u_{w}^{*}$ is a critical parameter for gas transfer (Jähne et al., 1987b); it is also a better environmental variable to estimate gas transfer than wind speed because it is intrinsically related to turbulence at the water surface (Wanninkhof et al., 2009). From a more physical perspective, it would be more correct to interpret all the results with u*. However, u₁₀ is more practical and readily available, and, traditionally, it is widely used in the field of oceanography (i.e., Wanninkhof et al. (2009)). Consequently, we interpreted our results in reference to u₁₀.

Ocampo-Torres et al. (1994) studied the gas transfer velocities of CO₂ in a linear wind-wave tunnel with wind speeds ranging from 1 to 17 m s⁻¹. Ocampo-Torres et al. (1994) found a change of regime at wind speeds ranging between 2 and 3 m s⁻¹, which means the first appearance of capillary waves. The same threshold was reported by Broecker et al. (1978) for a clean case with the first appearance of capillary waves. We did not observe a distinct change in k at 2 m s⁻¹ to 3 m s⁻¹, and neither did Broecker et al. (1978) in their examination of contaminated conditions. We did observe the capillary waves threshold from N₂O data and from a previous campaign in the same wind-wave tunnel (using fresh water). We considered the non-enriched pCO_2,w conditions to be extreme oligotrophic conditions, rather than the pure water and skimmed clean conditions that were applied in earlier wind-wave tunnel experiments (Broecker et al., 1978). In other laboratory studies, very low concentrations of surfactants have been proven to slow down gas transfer velocities (Goldman et al., 1988; Bock et al., 1999). This suggests that gas exchange in natural environments is always affected by surfactants, at least at low wind speeds.

The existence of two distinct data groups, depending on the surfactant concentrations or pCO_2,w level, highlights the need to consider more parameters than wind (as single parameter) in order to parameterize gas transfer velocity. This can also explain the different coefficients reported in previous parametrizations (Ho et al., 2006; Wanninkhof, 2014). If we had only considered enriched days, we would have obtained a quadratic relationship [k(CO₂) = 0.28 * $u_{10}^{2}$ ; r² = 0.9905] in good agreement with previously reported quadratic relationships (Ho et al., 2006; Wanninkhof et al., 2009; Wanninkhof, 2014). Broecker et al. (1978) also observed two distinct groups of data: with and without contaminating the tank water with a monolayer of oleyl alcohol (that simulated surfactant coverage). Their k(CO₂) values were also lower than those measured without the film, although in both cases they reported significant linear relationships.

Effect of the Surfactants on Gas Transfer Velocities

In the present study, higher surfactant concentrations were associated with lower gas transfer velocities, and the highest gas transfer velocities were observed during lower and moderate surfactant concentrations (Figure 5). The correlation between the concentration of the surfactants in the SML and k(CO₂) was statistically significant for wind speeds of up to 8.5 m s⁻¹. At higher wind speeds and at enriched pCO₂ conditions the correlation weakened or was insignificant. This is probably because additional processes governed the air-sea gas exchange, including more frequent surface renewal at higher wind speeds and larger concentration gradients across the air-sea interface. The enrichment factor of the surfactants ranged from 1.0 to 5.7 (mean = 2.1 ± 0.1), indicating that the concentrations of the surfactants in the SML were either equal to (single observation) or enriched in comparison to the concentrations in the UW, even at high u₁₀ (Table 1). Over all oceans, surfactants are typically enriched in the SML by up to a factor of three (Wurl et al., 2011; Sabbaghzadeh et al., 2017). We observed a reduction of k(CO₂) ranging between 46 and 63% with increasing surfactant concentration in wind speed categories up to 8.5 m s⁻¹. Two putative outliers were excluded in the calculation of the reduction in the moderate wind range (Figure 5C), and other processes may have caused an enhanced transfer velocity of up to 20 cm h⁻¹. We discuss other processes in the next section, but, due to the complexity of the air-sea gas exchange, the underlying reasons for the outliers cannot be confirmed. However, our observation that the surfactant concentrations decreased as the wind speeds increased indicates that increased turbulences caused the SML to become thinner or less pronounced; consequently, a more rapid transfer of CO₂ occurred. Indeed, surfactants have been found to slow the air-sea gas exchange (Broecker et al., 1978; Asher et al., 1997; Frew, 2005; Wanninkhof et al., 2009), and our observations confirm that the absolute concentrations of the surfactants in the SML governs the reduction of k(CO₂), and not the enrichment. Thus, surfactant films have the potential to cause significant biases in estimates of the air-sea gas exchange rates of climate-relevant gases (Wurl et al., 2011). Our observations are consistent with reductions ranging from 12 to 50% reported in field studies on artificial surface films (Salter et al., 2011), laboratory-based measurements (Pereira et al., 2016), and modeling (Tsai and Liu, 2003). Some studies have used artificial surfactants (such as Triton X-100 or oleyl alcohol) in a laboratory setting (Broecker et al., 1978; Goldman et al., 1988; Bock et al., 1999), while other studies have investigated the release of a single surfactant to create artificial films in the field (Brockmann et al., 1982; Salter et al., 2011). This reduction has been observed even at relatively high wind speeds (up to 11 m s⁻¹) (Salter et al., 2011), and it has global importance due to ubiquitous coverage of the oceans with SML (Wurl et al., 2011). We observed that surfactants in the SML decreased the CO₂ exchange velocities (Figure 5). However, with the onset of breaking waves (at u₁₀ = 15 m s⁻¹), turbulence dominated the CO₂ exchange. We could visually observe the disintegration of the surfactants film and the build-up of waves at constant wind speed, and this likely distorted the correlation we found between the surfactant concentration and k(CO₂) at the lower wind categories. It was difficult to calculate the individual physical parameters (u₁₀, u*, mss) for those conditions (Bopp, personal communication), which highlights the complexity of the processes and the fine threshold that determines the steady-state conditions. These results are in accordance with the findings reported by Asher (1997), who concluded that surfactants would actually increase the net CO₂ flux because the effects are most pronounced in regions with low wind speeds where the direction of the CO₂ flux is toward the atmosphere.

The Non-zero Intercept of Wind-Based Parametrization of CO₂ Transfer Velocity

The non-zero intercept is really important for CO₂ budgets, as for example during summer in the Baltic Sea where low aqueous pCO₂ occurs during a very low sea state (Schneider et al., 2014b). If the intercept would be assumed to be equal to 0, the sink capacity of the Baltic Sea during summer is clearly underestimated. In our study, the intercept value is 10.7 cm h⁻¹, which is similar (within error) to the asymptote of 8 cm h⁻¹ used by McGillis et al. (2004) for the equatorial Pacific, but it is higher than the intercept of 1.3 cm h⁻¹ from the Southern Ocean (Butterworth and Miller, 2016). McGillis et al. (2004) suggested that the large enhancement is due to the buoyancy fluxes associated with a strong diurnal heating cycle, which is probably less important in the Southern Ocean. Buoyancy fluxes will affect surface turbulence, and they can be parameterized with heat and momentum fluxes (Fairall et al., 2000). In our experiment, we suggest that this effect could have been significant due to the high heat fluxes and the temperature differences between the water and air and/or elevated room temperature in the facility. Overall, and in comparison with the data reported by McGillis et al. (2004); Butterworth and Miller (2016), our non-zero intercept suggests that intercepts may vary and buoyancy fluxes are important. While the intercept of k(N₂O) was 0.18 cm h⁻¹, larger concentration gradients across the air-sea interface during the N₂O evasion experiments probably makes k(N₂O) less sensitive to buoyancy fluxes.

Potential Effects of Chemical Enhancement on Observed CO₂ Transfer Velocities

We observed differences between the theoretical and fitted gas transfer velocities. k(N₂O) was lower than k(CO₂) (Table 1 and Figure 3). The ratio k(CO₂) / k(N₂O) ranged from 1.1 to 18.8. Surprisingly, ratios higher than 4 were associated with moderate u₁₀ (ranging from 1.6 m s⁻¹ to 8.3 m s⁻¹) (Table 1), and not low u₁₀, as other models predicted (Hoover and Berkshire, 1969) and as verified by other measurements (Wanninkhof and Knox, 1996; Jähne et al., 2010).

Differences between the non-enriched CO₂ days and the enriched CO₂ days were also observed for the k(CO₂)/k(N₂O) ratio. The non-enriched pCO₂ days had higher ratios (6.50 ± 4.81; N = 22) than the enriched days (1.87 ± 0.87; N = 18), and these differences were statistically significant (Mann-Whitney-U-test, p-value < 0.001). The ratios observed during the enriched days were more similar to real oceanic conditions because the mean gas transfer velocities were estimated to be higher (by a factor of 1.2 to 1.4) than the corresponding values derived for non-reactive gases (Wanninkhof and Knox, 1996). This difference is likely due to chemical enhancement (Wanninkhof and Knox, 1996), which increases with higher pH values for CO₂ transfer (Emerson, 1995).

If CO₂ reacts with water during its transport through the SML, the product can also be transported, thereby enhancing the flux (Wanninkhof and Knox, 1996). For example, carbonic anhydrase (CA) is an enzyme that can catalyze the mutual reaction from ${HCO}_{3}^{-}$ to CO₂. Membrane-bound extracellular carbonic anhydrase (eCA) enhances pCO₂ levels in close proximity to the cell for diffusion-driven carbon acquisition, which can significantly enhance the CO₂ exchange (Wanninkhof and Knox, 1996), and its enrichment in the SML of oligotrophic regions has been recently reported (Mustaffa et al., 2017). Concentrations of CA in natural SML range from 0.11 to 0.73 nM (Mustaffa et al., 2017), which is sufficient to enhance CO₂ exchange rates by 10–15% based on a conservative laminar film model described by Keller (1994). We did not measure eCA in our study, but the ubiquitous presence of eCA in microbes, as well as its proven enrichment in the oligotrophic SML and its effect on CO₂ gas exchange (Mustaffa et al., 2017), shows that, potentially, eCA may have affected the CO₂ exchange during low/intermediate wind speeds. The average chemically-enhanced CO₂ exchange velocity over the standard oceanic conditions is calculated to be 2.3 cm h⁻¹ (Wanninkhof et al., 2009). This would be one of the contributions to the non-zero intercept for a wind speed close to 0.

Potential Effects of Primary Production and Respiration on Observed CO₂ Gas Transfer Velocities

The SML is known to be dominated by heterotrophic activity (Reinthaler et al., 2008), and also in the Aeolotron active bacterial communities were present (Rahlff et al., 2017). Primary production reduces the CO₂ concentration in water and respiration by heterotrophic organisms increases it. We excluded the effects of primary production for the observed mismatch during the experiments because the nutrients and chlorophyll concentrations were very low. However, the time required for respiration to have an impact on the pCO_2,w should be shorter. Thus, we conclude that respiration processes were not likely to be the source of the excess CO₂.

Biogenic Production of Surfactants

A limitation of our study was that algal biomass was of low abundance (Rahlff et al., 2017; Engel et al., 2018), probably due to the required storage and transport of the seawater from the North Atlantic to Heidelberg. On the other site, bacteria were well and active (Rahlff et al., 2017; Engel et al., 2018). Therefore, the measured surfactant concentrations were in a typical range (300–1000 μgL⁻¹) for natural seawater (Frka et al., 2009; Wurl et al., 2011), and probably also in its composition. Nevertheless, the biological production of surfactants by phytoplankton has been known for decades (Ẑutić et al., 1981) and also by bacteria (Satpute et al., 2010) as they were more abundant in the Aeolotron. Generally, the amount of surfactants depends on cell density and, therefore, it can be assumed that during bloom conditions high amounts of surfactants are released into the surrounding seawater. Interestingly, some species are known to produce insoluble surfactants (Ẑutić et al., 1981), which play a significant role in the reduction of gas exchange rates, e.g., by slick formation (Salter et al., 2011). As the production of surfactants by phytoplankton depends on their abundance and activity, nutrients and stoichiometry affect the amount of surfactants in seawater and, therefore, the amount scavenged to the SML, e.g., by ascending bubble plumes. For example, Myklestad (1995) showed that the production of extracellular substances, potentially surface-active, increased in culture solution with an increase of N:P ratio above the classical Redfield ratio. Engel et al. (2004) reported the release of high amounts of TEP, abundant gel-particles typically enriched in the SML (Wurl and Holmes, 2008), in a mesocosm study toward the post-bloom conditions, probably due to stress conditions by nutrient limitation or sloppy feeding by zooplankton (Kujawinski et al., 2002). Our opinion is that biology have two effects; first, an indirect effect on the gas transfer velocity by being a source for surfactants, which eventually accumulates in the SML forming a diffusion layer. Second, photosynthetic and respiratory activities may drive the ΔpCO₂ gradients between the water and air side, and therefore, determine the direction and magnitude of fluxes (Wanninkhof, 2014); the latter could not be observed due to low photosynthetic biomass and limited duration of our experiment.

Conclusions

We confirmed a reduction of 46–63 % of CO₂ gas transfer velocities by natural surfactant concentrations under controlled wind speeds in seawater. Furthermore, we determined that the CO₂ gas transfer velocities in low wind speed are not equal to 0. Additionally, the present study demonstrated that the Aeolotron wind-wave tank, in combination with applied analytical techniques and modeling, provides reliable gas transfer velocities for CO₂. The gas transfer velocity of N₂O showed a segmented linear regression with friction velocities and wind speeds, with a statistical breaking point ranging between 5.5 and 8.0 m s⁻¹. The gas transfer velocities of CO₂ showed good agreement with approximate quadratic parametrization, as previously described in the literature. The present study added more empirical data on lower and higher wind speeds, where known parametrizations fall short. Our findings suggest that, in the Aeolotron, chemical enhancement had an impact on gas exchange at low and intermediate wind speeds. Future studies on the non-zero intercept are crucial because accurate intercepts of parameterizations are important for CO₂ budgets on a global scale.

Author Contributions

MR-R and OW design and conducted the experiment. MR-R, JR, and OW conducted the experiment, acquired, and analyzed the data. FH and MR-R developed the model. All authors contributed to data interpretation, writing, editing, and discussion of the manuscript.

Funding

This work was supported by the European Research Council (ERC) project PASSME [grant number GA336408]. The Aeolotron Seawater Gas Exchange Experiment was conducted within the joint project Surface Ocean Processes in the Anthropocene (SOPRAN, FKZ 03F0462F, 03F0611F, and 03F0622F) funded by the German Federal Ministry of Education and Research (BMBF).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We cordially thank Kerstin E. Krall, Bernd Jähne and all members of the Aeolotron group at Heidelberg University for providing N₂O data, feedbacks on the earlier stage of the manuscript and excellent working conditions and assistance during the preparation and measurement stages of the study. We thank A. Engel for logistics on getting the seawater to Heidelberg and B. Schneider for his instrument, DIC and TA analysis and feedbacks on the earlier stage of the manuscript. P. Hoor and his group in Mainz provided the N₂O instrument for the other follow-up measurements. We are grateful to M. Bopp for calculating and providing the u₁₀ and u* wind speed data.

References

Asher, W., Karle, L., and Higgins, B. (1997). On the differences between bubble-mediated air-water transfer in freshwater and seawater. J. Marine Res. 55, 813–845. doi: 10.1357/0022240973224210