Particle Flux Parameterizations: Quantitative and Mechanistic Similarities and Differences

The depth-attenuation of sinking particulate organic carbon (POC) is of particular importance for the ocean's role in the global carbon cycle. Numerous idealized flux-vs.-depth relationships are available to parameterize this process in Earth System Models. Here we show that these relationships are statistically indistinguishable from available POC flux profile data. Despite their quantitative similarity, we also show these relationships have very different implications for the flux leaving the upper ocean, as well as for the mechanisms governing POC flux. We discuss how this tension might be addressed both observationally and in modeling studies.

Introduction

The sinking flux of particulate organic carbon (POC) and other elements into and through the ocean's interior is a key flow in global elemental cycles (Williams and Follows, 2011). As the complex mechanisms determining this material's vertical redistribution remain poorly understood, Earth System Models parameterize particle flux as an attenuating function of depth (Gloege et al., 2017). The idealized models used for this parameterization thereby influence the characterization of global biogeochemistry. Several such models have been proposed, and have generally been argued for based on their ability to fit measurement profiles (Martin et al., 1987; Armstrong et al., 2001). Particle fluxes are however notoriously variable and challenging to measure (Buesseler, 1991), while different functions' goodness-of-fit are often strikingly similar (Figure 1). Indeed, Gloege et al. (2017) showed the power and ballast models capture observations equally, as does an exponential in the upper 1km. Such similarity is not uncommon when modeling variable environmental data, but is of particular significance here for two reasons:

• All these models have plausible and distinct (if oversimplistic) mechanistic interpretations – e.g., that some material is labile and some is refractory, that remineralization systematically declines with time/depth, or that remineralization is a second-order kinetic process. One may also argue for other mechanistic models on similar grounds (see below). Thus, these quantitatively similar models have differing implications for how particle flux works¹.

• The “export” of carbon through an upper reference depth horizon—usually the euphotic or mixed layer depth (ELD or MLD)—is of substantial interest (Buesseler and Boyd, 2009; Palevsky and Doney, 2018). However, most particle flux measurements have been made below the relevant horizon(s), necessitating depth-correction when comparing models with data and/or making global export estimates. These models diverge at shallow depths, meaning they also have widely differing implications for the magnitude of export through these depth horizon(s).

FIGURE 1

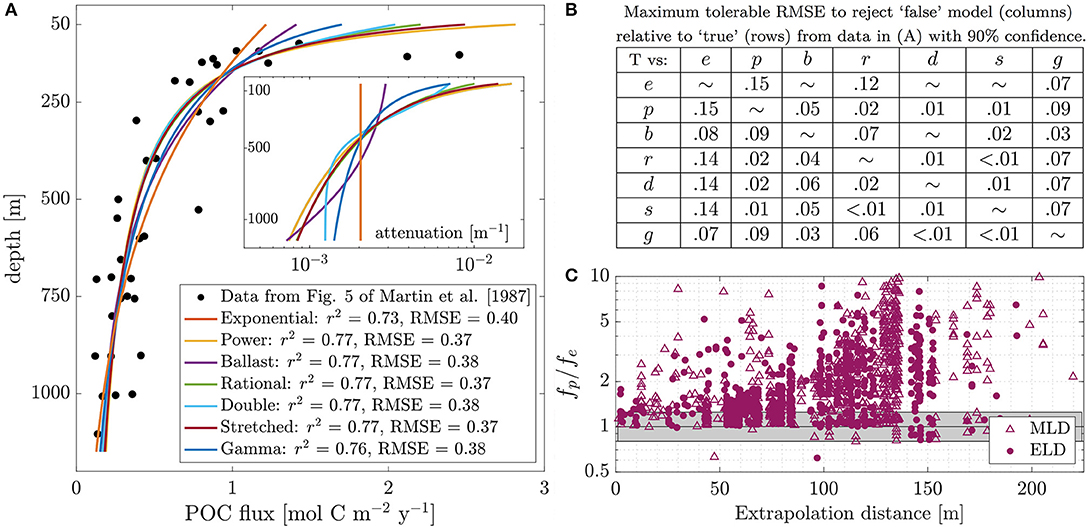
Figure 1. (A) Seven models from the text fit to mesopelagic data from Figure 5 of Martin et al. (1987; their Open Ocean Composite') and extended upwards to 50 m depth. Goodness-of-fits are very similar, but the power-law model overestimates particulate organic carbon (POC) flux at 50 m by 132% relative to the exponential model. Inset shows attenuation $(\frac{1}{f}\frac{df}{dz})$ differences are even more pronounced. Attenuation for the exponential model coincides with most others around ~400 m. (B) Maximum tolerable root-mean-square error (RMSE) to distinguish models based on data from (A) with 90% confidence, estimated using a bootstrap method (see text and Supplementary Material iii for details). Row corresponds to “true” model (from which data are assumed to be generated) and column corresponds to “false” model (to be rejected). RMSEs are small relative to those in (A), indicating differences in goodness-of-fits between the models are not statistically significant. (C) Ratio of power-law-model- and exponential-model-estimated POC flux at euphotic layer and mixed layer depths from the profiles in the data compilation as a function of extrapolation distance. Gray shading shows nominal 25% measurement uncertainty. Note the y-axis is logarithmic. The power-law model systematically and substantially overestimates relative to the exponential model (as well as the other models Supplementary Material ii.c). For 29 profiles, f_p(MLD)/f_e(MLD) > 10 (not shown).

Our purpose herein is to rigorously demonstrate the tension between these models' (i) different mechanistic interpretations and (ii) their often sizable quantitative differences at shallow depth horizons, vs. (iii) their quantitative similarity over the depths at which most particle flux measurements have been made. We derive several models mechanistically, compile a large database of measurement profiles, and perform a suite of statistical analyses. It is generally understood that these models behave similarly relative to measurement variability, and that extrapolation exaggerates differences. However, it is our opinion that the extent of these issues when modeling particle flux—the variety of plausible mechanistic models, the substantial differences that can result from even small upwards extrapolations, and the virtual impossibility of parsing between models by fitting them to measurements—is underappreciated. We discuss (i–iii) in turn, and how this tension might be addressed.

i. Several Mechanistic Particle Flux Attenuation Models

We describe seven models (Figure 1) relating POC² flux to depth, and provide mechanistic derivations for each in the Supplementary Material (i). We note that these models are neither exhaustive nor uniquely derivable, and numerous neglected processes, from particle (dis)aggregation to zooplankton behavior to ambient environmental conditions, also play important roles (Van Mooy et al., 2002; Burd and Jackson, 2009; Turner, 2015).

The basic model is an exponential (Banse, 1990):

$\begin{array}{ll}{f}_e(z):=C{e}^{-z/\ell }& (1)\end{array}$

which considers POC flux f [g m⁻² d⁻¹] as attenuating with a characteristic lengthscale ℓ: = w/k [m] determined by the settling velocity w [m/d] and remineralization rate k [1/d]. Here and below, C [g m⁻² d⁻¹] is the scale parameter for POC flux, e.g., C = f_e(0m). The most common model is a power-law or “Martin curve” (Martin et al., 1987):

$\begin{array}{ll}{f}_p(z):=C{z}^{-b}& (2)\end{array}$

which results from a systematic depth/time decrease of k (or increase of w (Supplementary Material i), e.g., due to consumption of progressively more refractory material. The other major model is a “ballast” model (Armstrong et al., 2001):

$\begin{array}{ll}{f}_b(z):=C{e}^{-z/\ell }+c& (3)\end{array}$

which augments (1) with a refractory flux c. The original depth-attenuation model is a rational (Suess, 1980):

$\begin{array}{ll}{f}_r(z):=\frac{C}{z+a}& (4)\end{array}$

which considers POC remineralization to function as a second-order kinetic process. A double exponential (Lutz et al., 2002):

$\begin{array}{ll}{f}_d(z):=C_1{e}^{-z/{\ell }_1}+C_2{e}^{-z/{\ell }_2}& (5)\end{array}$

is used to capture both rapidly- and slowly-attenuating fluxes. A stretched exponential:

$\begin{array}{ll}{f}_s(z):=C{e}^{-z^{(1-s)}/\ell }& (6)\end{array}$

where s ∈ [0, 1), results similarly to (2) from a systematic depth/time decrease of k. Lastly, what we term a gamma model

$\begin{array}{ll}{f}_g(z):=C\text{\hspace{0.22em}}\Gamma (0,z/{\ell }_{max})& (7)\end{array}$

results from labile material within particles being protected from bacteria by ballast minerals (Rothman and Forney, 2007), where Γ(·, ·) is the upper incomplete gamma function and the lengthscale ℓ_max depends partially on particles' microbial density.

Thus we have a suite of different models, each rooted in the balance between gravitational settling and bacterial remineralization, but assuming different basic characteristics for this balance. Given the enormous complexity and variability of the processes involved, all of the above are equally plausible when treated as idealized mechanistic models for particle flux attenuation.

ii. Large Differences in Export Estimates

As e.g., f_p(z → 0) = ∞ while f_e(z → 0) = C, the differences between these models becomes arbitrarily large for increasingly shallower depths. While these models are of course not applicable all the way to z → 0, they are generally used to model f below a chosen depth horizon that is often appreciably shallower than most measurements (e.g., 50 vs. 150 m). Thus the different models may imply very different exports through a depth horizon. This is evident in the figure; the functions are similar through the measurements' depth range (100−1, 100 m), but f_p(50m) exceeds f_e(50m) by 132%, with the other models yielding intermediate values. While the existence of such differences is unsurprising, these have not yet been thoroughly quantified; upon doing so, we found their magnitudes to be surprisingly large.

To investigate how model choice affected export estimates, we compiled a database of f measurement profiles. The compilation (see Supplementary Material for description (ii.a) and to access data) contains 722 profiles (n ≥ 3 depth points per profile) measured with sediment traps or the ²³⁴Th technique across the global ocean. We used profiles rather than individual measurements to derive the models' parameter values from the data being extrapolated. We then fit the above models using nonlinear least-squares regression and minimizing relative³ error, and extrapolated these fits to climatological estimates of ELD and MLD (see Supplementary Material ii.b for description and analysis).

We found f_p systematically overestimated and f_e systematically underestimated export relative to other models, and the range f_p:f_e was often substantially larger than the nominal variability between replicate measurements of 20–30% (Buesseler et al., 2000, 2007; Stanley et al., 2004). For ELD, f_p:f_e >1.25/1.5/2 for 67/45/25% of profiles, respectively. For MLD, which was typically shallower than ELD, f_p:f_e >1.25/1.5/2 for 75/62/49% of profiles, respectively. The figure shows f_p:f_e for all profiles as a function of extrapolation distance (i.e., the distance between ELD or MLD and the shallowest measurement); f_p:f_e increases with extrapolation distance as expected, but large differences are not uncommon even for small extrapolation distances. These analyses clearly indicate that the above models are often quantitatively disparate at shallow depths. As these estimates are all based on the same f(z) data from below the ELD and MLD, they imply even larger differences in attenuation $(\frac{1}{f}\frac{df}{dz}[{\text{m}}^{-1}])$ just below these depth horizons (Figure 1).

Fortunately, having consistent end-members (f_e, f_p) simplifies the situation. This suggests that when estimating export by extrapolating a measurement, one can use (f_e, f_p) as lower/upper bounds. We determined unbiased parameter values of ℓ ≈ 500 m and b ≈ 0.7 (similar to Primeau, 2006) for doing so by comparing profile fits to fixed-parameter extrapolations of only the shallowest measurement in each profile (Supplementary Material ii.c). Using these parameters, f_p still systematically overestimates with respect to f_e; f_p(ELD):f_e(ELD) ≤ 3.38 (median = 1.50), and f_p(MLD):f_e(MLD) ≤ 3.84 (median = 2.31). These parameter estimates are however influenced by spatiotemporal biases in sampling (Supplementary Material ii.a).

iii. Quantitative Indistinguishability

In contrast with (i–ii) above, these models are known to behave similarly over the depths at which most particle flux measurements have been made—in the mesopelagic and bathypelagic⁴—especially relative to these measurements' substantial variability and uncertainty (Figure 1). Are the differences in these models' ability to fit measurements sufficient to parse between them?

To address this question we applied a statistical routine to the profile database. The routine estimates for a set of measurements what level of variability is tolerable to reject one model vs. another at a chosen confidence level, or inversely the percent confidence with which those measurements can reject one model vs. another. Detailed description of the routine and examples of its application are provided in the Supplementary Material (iii). In brief, data are simulated from a “true” model, which is fit by a “false” model to be rejected. The root-mean-square error (RMSE) of the simulated data relative to each model provides a metric of goodness-of-fit. Bootstrapping yields a percent confidence in the true model vs. the false one. Repeating this process yields a true-model-vs.-false-model table either of tolerable measurement variabilities (Figure 1) or confidence levels of false model rejection (Supplementary Material iii).

Applying this routine to the data in the figure indicates these data are too variable for the differences in fit to be significant, and that the RMSE would have to be $<\frac{1}{2}$ its true value even to reject an exponential in favor of other models. The stretched and rational models are so similar that they cannot be distinguished even at 1% measurement variability from data with this sample size and depth spacing.

Assuming a conservative characteristic measurement variability of 20%, no one model can be rejected with 90% confidence in favor of any other for more than a handful of profiles in the dataset (Supplementary Material iii). Increasing depth range or sample size (either for composites of profiles (Figure 1), or for high-resolution individual profiles) tends to increase the maximum tolerable RMSE (Supplementary Material iii). However, the statistical non-significance of models' differences in fit appears extremely robust for realistic measurement variability. Thus, existing measurement profiles appear insufficient to distinguish between models. The exception to this is the exponential when bathypelagic data are included, as this is the only model for which attenuation does not change with depth. If for instance the bathypelagic data from Figure 5 of Martin et al. (1987) are included in the above analysis (11 data points from 1,400-2,000m), an exponential could be rejected with 90% confidence relative to a power-law or rational and vice versa if RMSE were ≤ 0.24 (an appreciable increase from the values seen in the table, though still below the data's true value), but the power-law and rational can still only be rejected with respect to each other when RMSE ≤ 0.04.

The root issue that complicates parsing between these models from f(z) data⁵ is that the models have multiple free parameters and therefore can take a wide range of shapes. Treating these models as mechanistic and using additional measurements to constrain their parameters may be useful in this regard. For instance, by measuring average $\bar{k}$ and $\bar{w}$ independently of f(z) data, one could fit the far-less-flexible exponential model $f_e(z)=Cexp\left[-z/(\bar{w}/\bar{k})\right]$. Being mechanistic, this approach can also provide quantitative insight about the dominant processes controlling particle flux. Of course, there are also other means by which to parse between different representations of f(z), such as suites of numerical simulations (Gloege et al., 2017), chemical composition (Armstrong et al., 2001), or mass/energy budgets (Burd et al., 2010); comprehensive understanding is likely only possible from combining multiple approaches to generate multiple constraints.

Conclusion

Several particle flux models capture observations equivalently, but carry different implications mechanistically and for magnitudes of export. Here we have attempted to illustrate this tension. When depth-correction is necessary, functional extrapolations are better used as lower (exponential) and upper (power-law) bounds. Vertically extensive high-resolution data⁶, paired with measurements of related quantities, may potentially elucidate how best to represent these processes mechanistically in Earth System Models.

Author Contributions

KB lead and BC assisted with compiling the dataset. BC lead and KB assisted with all other aspects.

Funding

The National Aeronautics and Space Administration supported this work (awards NNX16AR47G and NNX16AR49G).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We are grateful to David A. Siegel and Emmanuel Boss for their suggestions.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2018.00395/full#supplementary-material

Footnotes

1. ^To leading order and on average over large spatiotemporal scales.

2. ^These equivalently apply to other elements or total matter.

3. ^Minimizing absolute error yielded similar results (Supplementary Material ii.c).

4. ^Excepting the exponential, which performs worse in the bathypelagic (Gloege et al., 2017).

5. ^Besides the data's sparsity and variability, neither of which can be easily ameliorated.

6. ^i.e., tens of measurements spanning the full water column.

References

Armstrong, R. A., Lee, C., Hedges, J. I., Honjo, S., and Wakeham, S. G. (2001). A new, mechanistic model for organic carbon fluxes in the ocean based on the quantitative association of POC with ballast minerals. Deep Sea Res. II 49, 219–236. doi: 10.1016/S0967-0645(01)00101-1

CrossRef Full Text | Google Scholar

Banse, K. (1990). New views on the degradation and disposition of organic particles as collected by sediment traps in the open ocean. Deep Sea Res. A 37, 1177–1195. doi: 10.1016/0198-0149(90)90058-4

CrossRef Full Text | Google Scholar

Buesseler, K. O. (1991). Do upper-ocean sediment traps provide an accurate record of particle flux? Nature 353, 420. doi: 10.1038/353420a0

CrossRef Full Text | Google Scholar

Buesseler, K. O., Antia, A. N., Chen, M., Fowler, S. W., Gardner, W. D., Gustafsson, O., et al. (2007). An assessment of the use of sediment traps for estimating upper ocean particle fluxes. J. Mar. Res. 65, 345–416. doi: 10.1357/002224007781567621

CrossRef Full Text | Google Scholar

Buesseler, K. O., and Boyd, P. W. (2009). Shedding light on processes that control particle export and flux attenuation in the twilight zone of the open ocean. Limnol. Oceanogr. 54, 1210–1232. doi: 10.4319/lo.2009.54.4.1210

CrossRef Full Text | Google Scholar

Buesseler, K. O., Steinberg, D. K., Michaels, A. F., Johnson, R. J., Andrews, J. E., Valdes, J. R., et al. (2000). A comparison of the quantity and quality of material caught in a neutrally buoyant versus surface- tethered sediment trap. Deep Sea Res. I 47, 277–294. doi: 10.1016/S0967-0637(99)00056-4

CrossRef Full Text | Google Scholar

Burd, A. B., Hansell, D. A., Steinberg, D. K., Anderson, T. R., Aristegui, J., Baltar, F., et al. (2010). Assessing the apparent imbalance between geochemical and biochemical indicators of meso-and bathypelagic biological activity: What the $#! is wrong with present calculations of carbon budgets? Deep Sea Res. II 57, 1557–1571. doi: 10.1016/j.dsr2.2010.02.022

CrossRef Full Text | Google Scholar

Burd, A. B., and Jackson, G. A. (2009). Particle aggregation. Ann. Rev. Mar. Sci. 1, 65–90. doi: 10.1146/annurev.marine.010908.163904

PubMed Abstract | CrossRef Full Text | Google Scholar

Gloege, L., McKinley, G. A., Mouw, C. B., and Ciochetto, A. B. (2017). Global evaluation of particulate organic carbon flux parameterizations and implications for atmospheric pCO2. Glob. Biogeochem. Cycles 31, 1192–1215. doi: 10.1002/2016GB005535

CrossRef Full Text | Google Scholar

Lutz, M., Dunbar, R., and Caldeira, K. (2002). Regional variability in the vertical flux of particulate organic carbon in the ocean interior. Glob. Biogeochem. Cycles 16, 11-1–11-18. doi: 10.1029/2000GB001383

CrossRef Full Text | Google Scholar

Martin, J. H., Knauer, G. A., Karl, D. M., and Broenkow, W. W. (1987). VERTEX: carbon cycling in the northeast Pacific. Deep Sea Res. A 34, 267–285. doi: 10.1016/0198-0149(87)90086-0

CrossRef Full Text | Google Scholar

Palevsky, H. I., and Doney, S. C. (2018). How choice of depth horizon influences the estimated spatial patterns and global magnitude of ocean carbon export flux. Geophys. Res. Lett. 45, 4171–4179. doi: 10.1029/2017GL076498

CrossRef Full Text | Google Scholar

Primeau, F. (2006). On the variability of the exponent in the power law depth dependence of POC flux estimated from sediment traps. Deep Sea Res. I 53, 1335–1343. doi: 10.1016/j.dsr.2006.06.003

CrossRef Full Text | Google Scholar

Rothman, D. H., and Forney, D. C. (2007). Physical model for the decay and preservation of marine organic carbon. Science 316, 1325–1328. doi: 10.1126/science.1138211

PubMed Abstract | CrossRef Full Text | Google Scholar

Stanley, R. H. R., Buesseler, K. O., Manganini, S. J., Steinberg, D. K., and Valdes, J. R. (2004). A comparison of major and minor elemental fluxes collected using neutrally buoyant and surface-tethered traps. Deep Sea Res. I 51, 1387–1395. doi: 10.1016/j.dsr.2004.05.010

CrossRef Full Text | Google Scholar

Suess, E. (1980). Particulate organic carbon flux in the oceans–surface productivity and oxygen utilization. Nature 288, 260–263. doi: 10.1038/288260a0

CrossRef Full Text | Google Scholar

Turner, J. T. (2015). Zooplankton fecal pellets, marine snow, phytodetritus and the ocean's biological pump. Prog. Oceanogr. 130, 205–248. doi: 10.1016/j.pocean.2014.08.005

CrossRef Full Text | Google Scholar

Van Mooy, B. A., Keil, R. G., and Devol, A. H. (2002). Impact of suboxia on sinking particulate organic carbon: Enhanced carbon flux and preferential degradation of amino acids via denitrification. Geochim. Cosmochim. Acta 66, 457–465. doi: 10.1016/S0016-7037(01)00787-6

CrossRef Full Text | Google Scholar

Williams, R. G., and Follows, M. J. (2011). Ocean Dynamics and the Carbon Cycle: Principles and Mechanisms. Cambridge: Cambridge University Press.

Google Scholar