- 1Department of Oceanography, University of Hawai‘i at Mānoa, Honolulu, HI, United States
- 2Pacific Islands Fisheries Science Center, National Oceanic and Atmospheric Administration, Honolulu, HI, United States
- 3Department of Biology, University of Hawai‘i at Mānoa, Honolulu, HI, United States
- 4Joint Institute for Marine and Atmospheric Research, University of Hawai‘i at Mānoa, Honolulu, HI, United States
- 5Aarhus Institute of Advanced Studies (AIAS), Aarhus University, Aarhus, Denmark
Larval settlement is shaped by the interaction of biological processes (e.g., life history strategies, behavior etc.) and the environment (e.g., temperature, currents etc.). This is particularly true for many reef fishes where larval stages disperse offshore, often spending weeks to months in the pelagic realm before settling to shallow-water reefs. Our ability to predict reef fish settlement and subsequent recruitment and population dynamics depends on our ability to characterize how biological processes interact with the dynamic physical environment. Here we develop and apply an individual-based model that combines biological processes with high-resolution physical forcing to predict larval fish dispersal and settlement over time and space. Our model tracks individual larval fish from spawning to settlement and allows for the inclusion of biologically relevant stochasticity (individual variability) in modeled processes. Our model is also trait-based, which allows individuals to vary in life history characteristics, making it possible to mechanistically link the resulting variability in settlement probabilities to underlying traits such as spawning date and location, pelagic larval duration (PLD), body morphology, etc. We employ our biophysical model to examine how biology interacts with the physical environment to shape settlement predictions for reef fish off western and southern Hawai‘i Island. Linked to prevailing surface currents, we find increased probabilities of settling associated with shorter PLDs and fish spawned in southern and southwestern locations. Superimposed on this, eddies, common to leeward Hawai‘i Island, offer a second pathway to successful settlement for individuals with longer PLDs, particularly for fish spawning in summer months. Finally, we illustrate how lunar-timed spawning as well as morphological features (e.g., fin and head spines) may impact settlement success by altering the mortality landscape experienced by larvae. This work identifies life history characteristics that predict the self-recruitment pathways necessary for population persistence for the relatively isolated Hawai‘i Island. Our results can be used to develop future hypotheses regarding temporal and spatial variation in recruitment for reef fishes on Hawai‘i Island and beyond.
Introduction
A large variety of marine invertebrates and fishes begin life with a planktonic larval stage. Coral reef fishes are typical in this respect, and larvae often spend weeks to months in the pelagic realm before settling back to the reef as new recruits (Lester and Ruttenberg, 2005). Survival and dispersal during this vulnerable planktonic stage will influence population connectivity, as well as production and viability of adult populations (Houde, 2009). Self-recruitment is critical for the replenishment of reef fish populations that are not likely to receive recruits from other populations, such as the Hawaiian Islands (Toonen et al., 2011). Hawai‘i Island is located at the southern end of the Hawaiian archipelago. Major surface currents in the Hawaiian archipelago include the westward flowing North Equatorial Current that bifurcates around Hawai‘i Island to result in northward flowing currents up the archipelago (e.g., Hawaiian Lee Current, North Hawaiian Ridge Current, Lumpkin, 1998, Figure 1). The prevailing currents as well as Hawai‘i Island's position at the southernmost end of the archipelago means that this island likely relies on self-recruitment for population persistence and may act as an important source of larvae for islands downstream (Wren et al., 2016). Indeed, self-recruitment has been measured via parentage analysis for reef fish on this island (e.g., lau‘ipala or yellow tang, Zebrasoma flavescens; Christie et al., 2010).
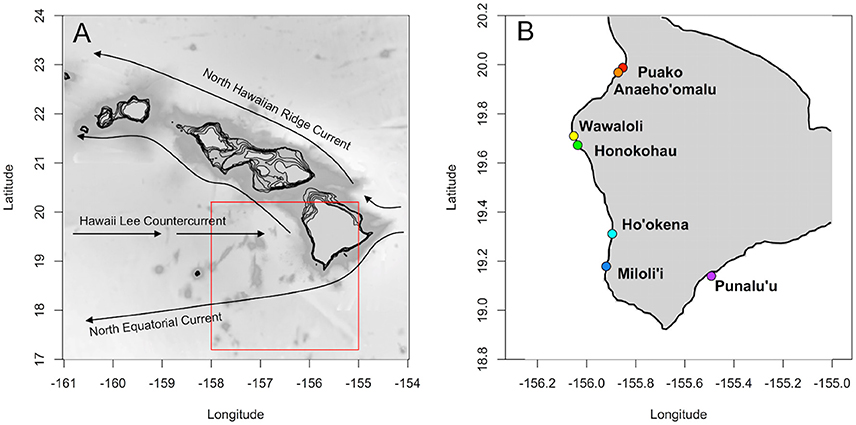
Figure 1. (A) Main Hawaiian Islands with major surface currents (after Lumpkin, 1998). Model domain denoted in red. (B) Hawai‘i Island with spawning locations (colors) as in Table S1.
The return of young fish to reefs after spending time in the plankton (i.e., “settlement” leading to “recruitment,” or the observation of a newly arrived juvenile in the adult habitat, Caley et al., 1996) can be influenced by a variety of biological and physical factors (Victor, 1983; Jones et al., 2005; Puritz et al., 2016). Interactions between a fish's life history characteristics (e.g., birth date, larval morphology, pelagic larval duration or PLD) and the physical environment such as temperature (Balch et al., 1999), food availability (e.g., phytoplankton abundance, Polovina et al., 2001; Platt et al., 2003) and currents (e.g., cyclonic eddies, Fox et al., 2012; Pusack et al., 2014) result in within- and between-species variations in production, connectivity and recruitment. For example, an individual's location and date of birth selects the state of the environment to which they are exposed during pelagic development, including their advective environment, as well as the temperature, food and mortality landscape. An individual's PLD controls the length of time they are exposed to the pelagic environment, and influences their ability to disperse and find suitable reef habitat. In addition, morphological features can influence both the costs of development as well as how larvae experience factors such as mortality during development (Sogard, 1997). For example, larval development of elongate fin and head spines found in a number of reef fish species may reduce size-selective mortality by gape-limiting predation (e.g., Moser, 1981; Price et al., 2015), thereby allowing fish with spine morphology to successfully exploit areas with higher predator densities.
These interactions between larval biology and the physical environment cause inter-annual variation in settlement and recruitment, and they ultimately influence the production and persistence of the resulting adult population (Houde, 2009). Moreover, these biophysical dynamics will shape dispersal and connectivity, as well as the potential for local adaptation (Warner, 1997). Identifying the mechanisms and outcomes regarding these biophysical interactions can help us explain production and population dynamics in coral reef ecosystems. In this contribution, we tested the hypothesis that variation in biological characteristics of birth date, birth location, PLD, and spine morphology result in variations in predicted settlement probabilities for reef fish off the western and southern coasts of Hawai‘i Island. To test this hypothesis, we developed and applied an individual-based model (IBM) that included a range in life history strategies forced by high-resolution hydrodynamic estimates of the ocean state for the region generated by the Regional Ocean Modeling System (ROMS). We followed individuals from spawning to settlement and explored the resulting trajectories and settlement success with respect to their individual life history traits. In so doing, we identified biophysical pathways influencing settlement probability and how these biophysical interactions may explain observed patterns in reef fish life histories.
Materials and Methods
We developed a stage-based model that tracks individuals from spawning, through egg and larval stages, to settlement. Our IBM links biological traits to the physical environment similar to previous IBM modeling tools (e.g., Paris et al., 2005, 2013; North et al., 2008; Banas et al., 2009; Gilbert et al., 2010; Neuheimer et al., 2010; Bidegain et al., 2013), while also allowing for individual variability in life history strategies (e.g., birth date, location, PLD, and morphology) to test the influence of life history variability on settlement probability. Moreover, our model set-up exploits the “individual” in individual-based modeling to track individuals representing all combinations of life-history traits tested. This approach allows us to quantitatively compare effects of different life history traits (e.g., spawning location vs. PLD) on settlement success, as well as consider interactions among effects (e.g., spawning date and PLD). The model followed a population matrix through time where each row was an individual and columns tracked physiological and ecological metrics as the fish moved through time and space (following Neuheimer et al., 2010). The model was initially parameterized with spawning sites and life history traits to represent a range of Hawaiian reef fishes, but at times used values specific to lau‘ipala or yellow tang (Z. flavescens), one of the better studied species in this region (e.g., Table S1 for further details).
The model was initialized with one female at each of seven known spawning locations spanning the western and southern coasts of Hawai‘i Island (Figure 1, Table S1; based on Christie et al., 2010). At each time-step (2 h), the population evolved based on stage-dependent reproduction, development, growth, transport, and mortality. A time-step of 2 h allowed for a balance between computational efficiency and the high-resolution temporal and spatial physical forcing (see also section Transport below). All modeling and data analysis was done in the programming language R (R Core Team, 2016).
Reproduction
At each time-step, individuals were spawned into the larval population. As our intention was not to investigate effects of fecundity characteristics on settlement success, individuals were added to the population based on a constant mean daily number of eggs chosen to be (i) large enough to provide a population of individuals to represent modeled life history trait variability, (ii) small enough to keep computations tractable, and (iii) realistic regarding observed variability in egg production rates among reef fishes. We used an estimate of 425 eggs female−1 day−1, which was measured for bluehead wrasse (Thalassoma bifasciatum) in the Florida Keys (Holt and Riley, 2001) and is within the range of daily egg production rates for other species and locations (e.g., between 44 and >24,000 eggs female−1 day−1 for Z. flavescens off Hawai‘i Island, Bushnell et al., 2010).
Individuals were spawned at every time-step and each of seven spawning locations (Figure 1, Table S1) to test the respective influence of birth date and spawning location on the probability of settlement. At spawning, new individuals (rows) were added to the population (matrix) representing the total number of individuals spawned. Their birth date (current time-step) and location (based on their mother) were recorded. We restricted our analyses to pelagic spawners with buoyant eggs (excluding demersal spawners), as these represent the majority of reef fish species (Thresher, 1984; Leis and Carson-Ewart, 2001; Luiz et al., 2013). Individuals were assigned an egg hatch time chosen from a uniform distribution between 24 and 48 h (Thresher, 1984). Each individual was also assigned a PLD sampled from a uniform distribution between 25 and 100 days. This PLD range represents observed PLDs for a range of pelagic spawning reef fish species (e.g., 25–90 days for Hawaiian endemics; Lester and Ruttenberg, 2005; Luiz et al., 2013), allowing us to assess the influence of PLD on settlement success. Spawned eggs are assigned a depth of 2 m to represent the positive buoyancy of eggs for the majority of reef fishes (Thresher, 1984; Colin and Clavijo, 1988) and based on field observations from Walsh (personal communication). In addition, individuals were randomly assigned spine morphology with presence or absence of elongate fin or head spines (50% probability of spine) allowing us to test the indirect influence of morphological changes on settlement probability (see also section Mortality). Eggs were assumed to be fertilized with 100% success (see section Discussion). Hereafter, “egg” refers to fertilized egg or zygote.
Development
At each time-step, egg age was compared to the individual's hatch time and eggs that were estimated to have hatched (i.e., age ≥ hatch time) were relabeled as larvae and assigned a larval depth. Larval depth was chosen from a Poisson distribution with a λ of 28 m (based on observed vertical distribution of larvae in Hawai‘i; Boehlert and Mundy, 1996; Wren et al., 2016) and was restricted to the available advection depth layers (see section Transport). For all larvae, age was compared to the individual's PLD to identify those that were expected to have settled within the time-step. Settled individuals were marked settled, recorded along with their location at settlement, and then removed from the population matrix at the beginning of the next time-step.
Growth
An estimate of individual size (total length) was needed to assess size-dependent mortality risk. Length at hatching was set at 1.5 mm (Leis and Carson-Ewart, 2001). Once hatched, individuals started growing at a constant growth rate of 0.037 mm hr−1; an estimated growth rate based on a settlement size of 50 mm (Leis and Carson-Ewart, 2001; Claisse et al., 2009) and PLD of 55 days (Christie et al., 2010) for Z. flavescens. Size at settlement ranges from 7 to 75 mm for a range of coral reef perciform fishes (Leis and Carson-Ewart, 2001).
Transport
At each time-step, all non-settled individuals were transported based on their geographic location-specific and depth-specific advection. Swimming behavior was not included in the current study but could be defined in future efforts where information on swimming speed and directionality exists (see also section Discussion). Advection estimates were obtained from a Regional Ocean Modeling System (ROMS) model developed and operated for waters around the Hawaiian Islands (Souza et al., 2015). The ROMS model assimilates daily, real-time data from satellites, autonomous gliders, Argo drifters, ship measurements, real-time high-frequency radar, and other data of opportunity. For this study, a 1 km high-resolution ROMS model was nested within the 4 km operational model described in Souza et al. (2015). We limited the larvae to the upper 100 m of the water column, which is represented by 16 depth layers: 2 m, every 5 m from 5 to 50 m, and then every 10 m from 50 m until 100 m. The ROMS model provides physical forcing estimates (current velocity and temperature) on an hourly time-step. The influence of biology on transport was included through birth date, birth location, PLD, spine morphology, and the stage-specific depth distributions described above.
At each time-step, the time-specific advection (u: m s−1: east-west or zonal component; v: m s−1 north-south or meridional component), for each individual was estimated via a 4th order Runge-Kutta method. Advection estimates on the ROMS grid were interpolated to each individual's location based on a two-dimensional barycentric interpolation. The distance traveled in the zonal direction at each time step was added to the current longitude to determine east/west movement (u · Δt). The distance traveled in the meridional direction at each time step was added to the current latitude (v · Δt) to determine the individual's new latitude. Distances were corrected for the spherical shape of the Earth. Any individual estimated to have moved onto land was placed back to its last position in the ocean. To allow for sloping coastal bathymetry, individuals moving to locations shallower than their current depth were reassigned to the depth-layer closest to the bottom depth at their new location. Individuals leaving the model domain were removed from the population.
Mortality
Individuals were removed from the population based on size-dependent and spatially varying mortality rates (and resulting survival probabilities, Figure S1). Mortality rate decreased with increasing size to represent general patterns of declines in predation with increasing size in the ocean (e.g., Landry, 1976; Bailey, 1984; Dekshenieks et al., 19971, Figure S1A). Mortality rate also decreased with bottom depth to represent the decrease in visual predators with depth in pelagic waters (e.g., following Dekshenieks et al., 1997, Figure S1B), particularly as vulnerable larvae move away from the more densely populated communities of potential predators on the reef. In both cases, mortality functions were chosen such that estimates of the integrated mortality rates did not differ significantly from that of a constant mortality rate (mconstant, see below) based on the number of recruits per female (following Dekshenieks et al., 1997; Figure S1). At each time-step (t), the survival probability of each individual (i) was estimated as:
where the mortality rate for individual i and time-step t (mi,t) was
based on the constant mortality estimate (mconstant, Table S1), Depthi,j is the bottom depth at the individual's location (m) and Lengthi,j is the individual's effective length (mm). The instantaneous mortality rate (mconstant) was obtained from the observed annual survival probability (Syear, dimensionless) of 100 individuals from 155,125 eggs female−1 (425 eggs female−1 day−1 × 365 days):
and converted to a constant mortality estimate (mconstant) with:
This approach led to a constant mortality rate of 8.4 × 10−4 hr−1 or 2.0 × 10−2 day−1; an estimate within the range of natural mortality estimates for fish egg and larval stages across species (~10−1-10−2 day−1; McGurk, 1986). Effective length was defined as egg size for egg stages (Table S1) and was defined by larval size and spine morphology for larval stages. The latter allowed us to include possible size-dependent mortality (predation) reduction for those fish exhibiting spines to make themselves effectively bigger (i.e., reducing gape-dependent predation, Fuiman and Magurran, 1994). Presence of a spine increased the effective length of individual larvae by 40%, a value within the range of relative spine length for reef fish larvae (e.g., gray triggerfish, Balistes capriscus, exhibiting spine lengths ranging from 7 to 50% of fork length during larval development; Matsuura and Katsuragawa, 1981). Each individual's fate was determined by sampling from a binomial distribution (1 = survive) based on their Si,t.
Model Simulations
The focus of this analysis was on intra-annual changes to the probability of successful settlement success. Individuals were modeled for January 2011 through December 2013, representing typical (between-ENSO) years. Three separate model runs were simulated, each for the complete time period (2011–2013), and run results were consolidated to minimize stochastic effects on model results. The population matrix was stored at each time-step with output including individual larval trajectories, as well as information on individual fish traits (e.g., birth date, year, birth location, PLD, spine morphology).
While no trade-offs in traits (e.g., spawning date, location, PLD, spine) were explicitly assigned, trade-offs due to life history strategy were implicit. For example, PLD varied among individuals. This in combination with size-dependent mortality and invariable growth rates meant shorter-PLD individuals experienced higher mortality at settlement size than those with longer PLDs.
Statistical Modeling
We used model output to test the hypothesis that variability in the settlement success of individuals back to Hawai‘i Island is explained by a suite of life history characteristics (i.e., birth date and location, PLD, and body morphology). Here, the binomial settlement result (Settled) is recorded as successful when an individual is within the 50 m depth contour of Hawai‘i Island at time of settlement (i.e., when agei,t ≥ PLDi). Reef fish are found continuously along the west Hawai‘i Island coast and, besides depth-dependence, habitat suitability is considered constant across our model domain. Future studies exploring e.g., benthic invertebrates requiring particular substrate for settling could expand on the definition of habitat suitability modeled here.
For our purposes (focus on Hawai‘i Island self-recruitment), we did not consider individuals that may settle outside the model domain (addressed in the Discussion). We assessed the hypothesis that settlement back to Hawai‘i Island (Settled) is explained by variability in life history traits: birth date (BirthDay), PLD, and morphology (i.e., presence/absence of a spine, Spine). Attempting to identify possible mechanisms behind temporal variations in settlement probability, we also included information on tidal height (Tide, m) and moon phase (Moon). The former was obtained for the Kawaihae, Hawai‘i station from the National Oceanic and Atmospheric Administration's (NOAA) Center for Operational Oceanographic Products and Services. In the latter, birth dates were labeled “New” or “Full” when they were within ±3 days of the new or full moons, respectively, or “Other” if otherwise. We also tested sensitivity of statistical results to this moon phase definition by re-assessing model results with days labeled “New” or “Full” when birth dates were ±1 or 5 days of the new or full moons (else days are labeled “Other,” as above). Finally, though the focus of this analysis is on intra-annual and island-scale changes to settlement probability, we included possible variations across years and spawning locations by including birth year (BirthYear) and spawning location (Location) as predictors.
The response (Settledi) was modeled as observations from a binomial distribution (successful vs. unsuccessful settlement back to Hawai‘i Island):
where the number of trials (binomial denominator) is ni = 1 (independent trials, i.e., a Bernoulli distribution) and the probability is πi. The probability (πi) was modeled as a function of our predictors using a generalized additive model (GAM):
including non-linear effects of continuous variables BirthDay, PLD, and Tide, in addition to interactions between BirthDay and PLD through a tensor product smoother. Effect of BirthDay was fit with a cyclic cubic spline to allow for the cyclical nature of the predictor (i.e., 31 December and 1 January are adjacent), while effects of PLD and Tide were both fit with thin plate splines. Linear effects were included for Spine (categorical with two levels as “absence” or “presence” of spine, see previous Methods), Moon (categorical with three levels as “New,” “Full,” or “Other,” see previous Methods), Location (categorical with 7 levels for locations, Figure 1, Table S1) and BirthYear (categorical with three levels as 2011, 2012, and 2013). Further interactions among predictors (e.g., Location and PLD) were not within the scope of our analysis but could be included in the future to test additional hypotheses, e.g., investigations into the spatial variability in life history characteristics of successful settlers.
The link function, g(πi) provides the relationship between the expected value of the response and the linear predictor. The canonical logit link function was originally employed:
As alternative link functions may increase model performance, we also fit our model using alternate link functions of probit:
where Φ is the standard normal distribution function, and the complementary Log-Log (cloglog) link:
and assessed model results.
The GAM was fit using the bam() function from the mgcv package in R, which eases GAM fits for very large datasets (Wood, 2011). While GAMs are somewhat robust to predictor collinearity issues, pairwise correlation among all predictor combinations was assessed prior to model fitting. Inspection of residuals and comparisons of explained deviance were used to test model validity and select among non-nested models (e.g., among link functions). In addition, the level of complexity (basis dimension) of the smoothers was assessed by examining residual variance of near neighbors compared to overall residual variance (i.e., the k index, following Wood, 2011). Model selection based on a ranking of both Akaike's Information Criterion (AIC) and Bayesian Information Criterion (BIC) was used to compare across a set of (nested) candidate models. AIC favors the predictive power of the models while BIC includes harsher penalties for complex models, making the latter useful for identifying important processes (predictors) underlying the explained deviance, particularly when sample sizes are large (Efron and Hastie, 2017). While an exhaustive model selection (including all possible predictor combinations) was not possible due to the large sample size, the candidate model set allowed us to assess the importance and likely nature (shape, interactions) of each predictor's effects (Table S2). Once the best-specified model was chosen, explained deviance was partitioned among predictors by refitting the model reduced by one predictor at a time while maintaining the estimated smoothers from the best-specified model.
Results
In total, 9,683,781 individuals were tracked over the three model runs, with a total of 56,702 fish (0.585%) successfully settling to western and southern Hawai‘i Island. Figure 2 shows examples of simulated trajectories for successful settlers.
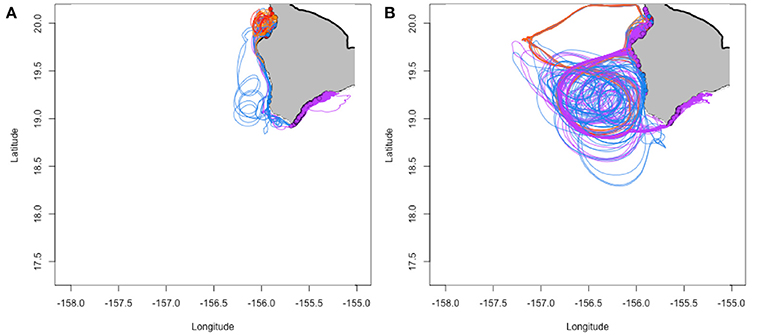
Figure 2. Example trajectories for successfully settling individuals in February (A; 962 individuals) and May (B; 215 individuals) of 2012. Colors correspond to spawning locations in Figure 1B, Table S1.
There were no significant pairwise correlations between predictor pairs, with all correlation estimates being < 0.0074; the highest pairwise correlation was expectedly between Moon and Tide at 0.0074. The starting model (with logit link, Equation 9) explained 19.2%, of the overall deviance in settlement probability. A switch of link functions to probit (Equation 10) increased explained deviance to 19.7% and resulted in slightly better-behaved residuals (though departures from normality were found, and expected given the large sample size and low probability of settling, e.g., Augustin et al., 2012). Following this, a set of candidate statistical models assembled to test model structure and predictor importance were fit using the probit link function (Table S2). Models in the candidate model set were ranked by both AIC and BIC. Two models were favored via BIC comparisons (i.e. models within ΔBIC < 2.14 of lowest):
with a BIC weight of 74.5 and 25.5% for Equations (12, 13), respectively (Table S2). These models included non-linear and interaction effects of BirthDay and PLD as well as linear effects of Spine, Location, and in one model (Equation 13) Moon. AIC ranking included these models in the top 55% of models, ranking the more complicated starting model (Equation 8) as the top model with an AIC weight of 100% (Table S2). The addition of these extra predictors in the AIC top model did not add a significant amount to the overall explained deviance (+0.006%) and we chose Equation (13) as our best-specified model, explaining 19.7% of the overall deviance in settlement probability.
Probability of settling varied significantly across birth locations, explaining the highest proportion (15%) of the total overall explained deviance (Table 1). The greatest probability of settling occurred for fish born on the south coast at Punalu‘u (4.7 × 10−2 ± 6.2 × 10−4) with all other sites associated with an order of magnitude lower probability of successfully recruiting (1.7 × 10−3-8.7 × 10−3, Table 1). Fish born in the second most southerly location (Miloli‘i) had the second highest probability of settling (8.7 × 10−3 ± 1.7 × 10−4), while individuals born at Puako and Anaeho‘omalu in the north and Ho‘okena on the southwest coast were associated with similar probabilities of settling (~2.4 × 10−3, Table 1).
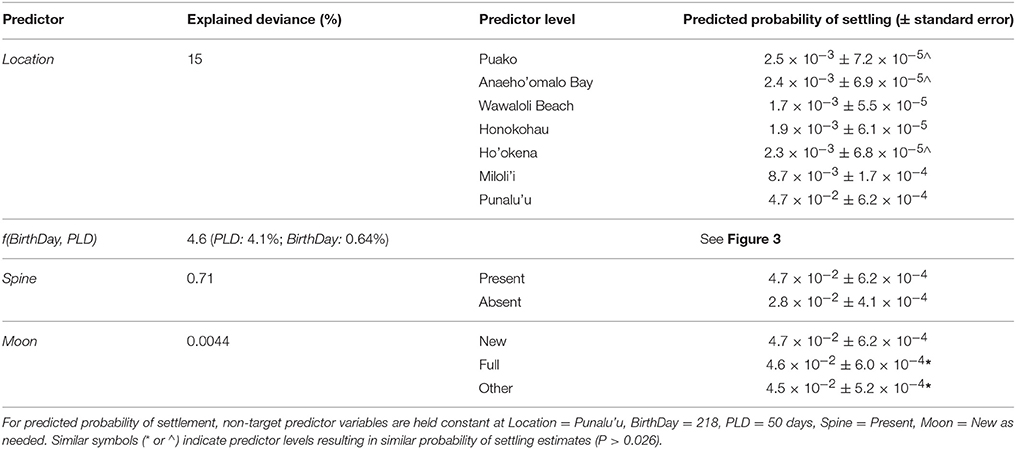
Table 1. Results of the best-specified model (Equation 13) including % explained deviance by each predictor as well as probability of settling estimates.
The non-linear and interacting effects of BirthDay and PLD explained 4.6% of the overall deviance with ~4.1% attributable to PLD and ~0.64% to BirthDay (Table 1, Figure 3). Including both non-linear and interacting effects increased model performance (Table S2). Throughout the year, those larvae with the shortest PLDs (e.g., 25 days) had the highest probability of successfully settling (Figure 3). For fish with longer PLDs (e.g., >50 days), probability of settling increased from a minimum in winter months (December–January) to a maximum in the summer (June for PLDs of 75–100 days) or fall (August/September for PLD = 50 days, Figure 3). Median PLD of individuals successfully settling was highest during typical reef fish spawning seasons (i.e., 15 January through 15 October; Walsh, 1987, see section Discussion, Figure 3, Figure S1). Due to the range of PLDs modeled, size at settlement ranged between 22 and 89 mm, similar to observed size at settlement of coral reef perciform fishes (7–75 mm, Leis and Carson-Ewart, 2001).
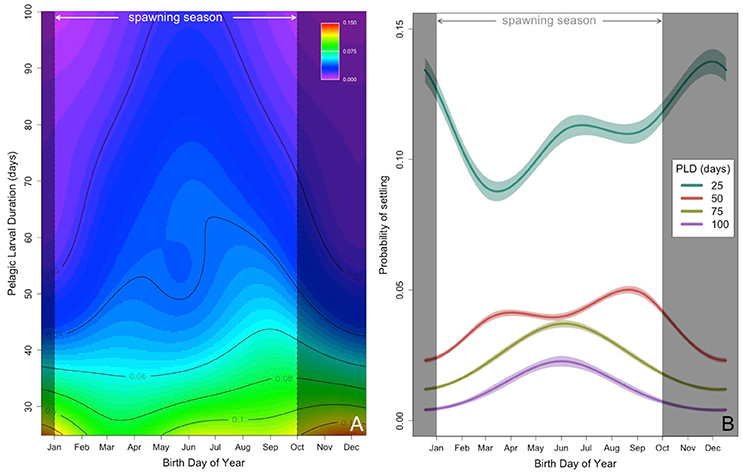
Figure 3. (A) Predicted probability of settling (contours and color scale), from high (red) to low (purple) probability, as a function of birth date (x-axis, BirthDay) and PLD (y-axis, days). (B) Predicted probability of settling (±2 standard error) as a function of birth day of year (BirthDay) and PLD (days, colors, with green = 25 days, red = 50 days, yellow = 75 days, and purple = 100 days). In both panels, times outside the common spawning season are shaded in gray (Walsh, 1987; see section Discussion). Other predictors are held constant at Location = Punalu'u, Spine = present, Moon = New.
Effects of spine morphology explained 0.7% of the overall deviance in probability of settling, with higher probability of successfully settling for fish with a spine than without (P < 0.0001). Effects of moon phase during spawning (Moon) appeared in only one of the top two models, explaining 0.0044% of overall deviance in settlement probability. Moon effects were significant only when model phase was defined ±3 days of the new or full moons; predictors estimated with definitions of ±1 day or ±5 days were not significant (based on AIC and BIC model ranking). Effects of moon phase estimated fish born under a new moon phase had a probability of settling of 0.047 (±6.2 × 10−4 standard error), which was slightly (0.001) but significantly higher than fish born under Full (P = 0.0027) or Other (P < 0.001) moon phases. There was no difference in probability of settling between fish born under Full vs. Other moon phases (P = 0.30, Table 1).
Discussion
Our results demonstrate how life history characteristics (e.g., location of birth, birth date, PLD, body morphology) can interact with the physical environment to affect the probability of reef fish settlement, using western and southern Hawai‘i Island as a case study.
Physical Challenges “Select” for Biological Characteristics
Successful settlement back to Hawai‘i Island is necessary for population persistence especially considering the remoteness of the Hawaiian archipelago. In particular, Hawai‘i Island represents the southward limit of the archipelago with surface currents generally flowing northwestward toward the rest of the main Hawaiian Islands (Figure 1). Because of this general northwestward flow, individuals born in the more southerly spawning locations (Punalu‘u and Miloli‘i) had the highest probability of settling back to the western and southern coast of Hawai‘i (e.g., 4.7 × 10−2 and 8.7 × 10−3 probability of settling, respectively, when other factors held as per Table 1), while fish born in more northerly locations had a high probability of being advected out of the model domain (e.g., 1.7 × 10−3 probability of settling when spawned at Wawaloli Beach and other factors held as per Table 1). Christie et al. (2010) provide empirical data consistent with these predictions for yellow tang (Zebrasoma flavenscens). While fish lost through this northern model boundary did not contribute to self-settlement on Hawai‘i Island, they may represent a source of larvae for other populations in the Hawaiian archipelago. Spawning location explained the most variability (deviance) in settlement success (15% of explained deviance) in our model, followed by PLD (4.1% of explained deviance; Table 1). Regarding the latter, short PLDs were associated with higher probabilities of settling—again, allowing fish to settle before they are advected out of the model domain (Figure 2A, Table 1). Short PLDs may be particularly advantageous in the southwest of Hawai‘i Island where steep bathymetry means fish do not need to go far to escape high-predation shallow waters (more on mortality in the text that follows).
Superimposed on top of this general surface current pattern, cyclonic, and anticyclonic eddies are common on the leeward side of Hawai‘i Island (Qiu et al., 1997). These eddies offer a mechanism for reef fish (particularly those with longer PLDs, Christie et al., 2010) to develop and grow away from nearshore high predation waters while at the same time provide a path back to the reef for settlement when larger (Lobel and Robinson, 1986). A similar hypothesis was offered for juvenile anchovies, which move away from higher densities of predators on the shelf where they are spawned in the Bay of Biscay to offshore waters with lower densities of predators for their development period (Irigoien et al., 2007). Reef fishes seem to be “using” these eddies: mean abundances of fish larvae were found to be 4 × higher in an eddy (34.9/1,000 m3) compared to the same waters before eddy formation (8.8/1,000 m3; Lobel and Robinson, 1986). Moreover, larval fish distribution within eddies was shown to be stage-specific, with eggs and post-hatchling larvae more abundant near the eddy core and late-stage larvae more abundant in the outer edge of the eddy (Lobel and Robinson, 1986). Off the west coast of Maui, Hawai‘i, Storlazzi et al. (2006) concluded that persistent small-scale eddies may help to retain coral larvae during the summer spawning season. Regardless of eddy size, it is possible that some larvae are able to actively respond to the eddy gradient allowing them to control the length of residence in the eddy and leave the eddy when it is time to settle (McManus and Woodson, 2012). In addition to retention mechanisms that help to maintain larvae close to original or nearby islands, eddies may also allow for faster growth by providing increased food resources or temperatures and thus likely higher survival of the larvae (Shulzitski et al., 2016, 2017).
Not all eddies are created equal: mesoscale eddies are often advected westward or northwestward, sometimes rapidly; thus resident larvae can be carried far from land before they have a chance to fully develop. The ultimate destinies of these larvae will be determined by the direction and velocity of the eddy and of the currents into which they are released when the eddy eventually dissipates. Indeed, it is the eddies that form and are positioned close to shore for extended periods of time that increase settlement probability for west Hawai‘i Island (e.g., Figure 2B) vs. eddies that quickly move offshore, away from the coast, resulting in individuals being advected far away from suitable habitat (e.g., Figure S3). During their lifetimes, mesoscale eddies may move up to 350 km in a westerly or northwesterly direction at an average of 5.2 km day−1 (Patzert, 1969). For example, cyclonic eddy Opal moved rapidly southward by ~165 km over several weeks, with an overall average displacement speed of ~8 km day−1 moving away from the islands (Maiti et al., 2008).
The seasonal timing of transport mechanisms including eddies appears to be correlated with the typical summer spawning season. Most Hawaiian reef fishes exhibit minimum spawning in winter, with spawning increasing with increasing water temperatures and day length before declining quickly as maximum water temperatures are reached in late summer/early fall (Walsh, 1984, 1987; Lobel, 1989). While the fall decline in spawning may be related to decreased larval survival or inhibition of gametogenesis because of higher summer temperatures (Walsh, 1987), our model suggests that biophysical interactions also result in declines in settlement success in the fall for those fish exhibiting longer PLDs (Figure 3). It is during the summer months (particularly April through September) when the less advective mesoscale eddies (nearshore and relatively stable) develop along the coast, allowing for longer larval development times while being retained near suitable habitat (Figure 2B). These smaller scale nearshore eddy features have been regularly and predictably observed on other islands as well (Storlazzi et al., 2006). We present evidence that dispersal and retention of larvae can be governed by the rotation and movement of eddies, and that the seasonal formation of these eddies may help explain the observed spawning season. Similarly, Donahue et al. (2015) found modeled biophysical processes predicted higher larval settlement probabilities for fish spawned during the observed spawning season for lane snapper (Lutjanus synagris) in the Florida Straits. Thus, spawning strategies that allow larval development in offshore eddies may represent a “loophole” (Bakun and Broad, 2003; Irigoien et al., 2007) that allow fish to reduce mortality, resulting in recruitment and production pulses (e.g., Munch and Conover, 2004).
Our results offer two pathways, or biophysical mechanisms, that increase self-recruitment probabilities in western and southern Hawaii Island's advective environment: (i) develop quickly (short PLD) and avoid being advected away, or (ii) catch a ride on the “right” kind of eddy (allowing for longer PLDs). These pathways appear in our predicted settlement probabilities with probability of settling maximized for individuals with short PLDs in the winter months when the environment favors less retention (e.g., lower abundance of nearshore eddies, Figures 2A, 3) and, for longer PLDs, in the summer months where nearshore eddies are more abundant (Figures 2B, 3). Moreover, this range of potential strategies that favor larval survival and recruitment is found in the PLD-trait distribution of our modeled individuals with examples of successful settlers from the entire PLD model range (25–100 days) and a median PLD of 43 ± 13 days (median ± median absolute deviance; Figure S2). These PLD estimates coincide well with many of the common species of coral reef fishes in the Hawaiian Islands, which demonstrate considerable PLD variability across species (e.g., 8–70 days for west Pacific species, and 25–90 days for Hawaiian endemics; Lester and Ruttenberg, 2005).
Influences of the Mortality Landscape
The presence of a pelagic larval phase may act to increase survival probabilities in temporally, spatially, and developmentally variable mortality environments (Johannes, 1978). Settlement success (and ultimately survival) will depend on how life history characteristics (e.g., size, stage durations, and timing) result in larvae moving through this dynamic mortality landscape. Here we incorporate both spatially (depth-dependent) and size-dependent mortality, mimicking the high nearshore and size-selective predator environment experienced by many marine animals. In this way, larval survival will change both in space (e.g., with spawning location bathymetry controlling how quickly predation pressure decreases with distance from shore) as well as time (e.g., mortality risk declines as individuals age and grow). To further illustrate how size-selective mortality landscapes may select for certain life history characteristics, we mimicked the increase in effective size that the development of elongate fin and head spines provide in some reef fish larvae (Moser, 1981). Spines potentially reduce the probability of an attack by gape-limited predators and therefore act as a mechanical deterrent to predation (Moser, 1981; Morgan, 1989; Price et al., 2015; Greer et al., 2016). The effectiveness of spines as a means of reducing predation by planktivorous fish has been experimentally demonstrated in marine crab larvae (Morgan, 1989) and is often assumed in fish larvae (Moser, 1981; Greer et al., 2016). Indeed, higher predation on fish larvae with shorter spines has been documented (Moodie, 1972), with some species increasing spine length (and other armor) when predator abundance is high (Gross, 1978; Januszkiewicz and Robinson, 2007; Weber and Brown, 2012). Small increases in effective larval size may therefore have a disproportionately large effect in reducing predation by gape-limited predators (Moser, 1981). We illustrated how the presence of a spine can increase the probability of settling by 67%, by making the individual effectively larger and thereby lowering the size-dependent mortality (Table 1). This value will vary given the predator field and strength of size-dependence on mortality. This aspect of the model could be used in the future to explore mechanisms driving the large variation of reef fish larval body plans (McCormick and Molony, 1995; Price et al., 2015), as well as estimating trade-offs between the benefit of reduced predation with the cost of spination and potential reduction in swimming speed accompanying the body-form change. Similarly, this work could be extended to explore the effects of other size-related traits on settlement success, e.g., temperature-dependent growth (Houde, 1989), size at hatching, etc.
Many species of reef fish exhibit lunar spawning periodicity with spawning around the new and/or full moons (e.g., Johannes, 1978; Walsh, 1987; Domeier and Colin, 1997; Colin, 2011). Spawning around a new or full moon may facilitate the flushing of eggs away from shallow water by using outgoing spring tides that are associated with these moon phases and quickly increasing the distance between the egg and potential predators on the reef (Johannes, 1978). Tropical reef fish have been observed spawning during an ebbing tide during which eggs are transported off the reef and away from planktivorous fish predators (James et al., 2002). Here we found that the probability of successful settlement is enhanced during new moon phases, however no significant effect of tidal height was observed. Empirically, Claisse et al. (2011) found no correlation between daily spawning movements of yellow tang and lunar cycles. Future efforts will explore other possible tidal measures (e.g., velocities) that may be underlying the higher settlement success for fish born around new moons. Note that avoiding visual predators under the cover of darkness has been hypothesized to explain settlement during new moons (Johannes, 1978). More broadly (beyond our model), the high incidence of lunar-timed spawning observed in the field may allow for reduced egg predation by spawning under low light levels and/or predator swamping (Johannes, 1978; Walsh, 1987), or may maximize fertilization success via spawning synchronization (Walsh, 1987).
Future Directions
These results motivate a number of future hypotheses that can be explored to explain biophysical forces shaping reef fish recruitment and survival. Our modeling tools can be used to examine spatial variability in life history characteristics (e.g., trait-based community structure) as well as connectivity pathways among local adult populations, both within Hawai‘i Island and beyond. Similar questions can be raised concerning the biophysical factors shaping inter-annual patterns of settlement and recruitment, particularly for longer time-series of physical forcing (e.g., exploring interactions between biology and climate oscillations including the El Niño Southern Oscillation, ENSO). In addition, model tools can be extended to include heritable trait profiles that can explore questions of life history strategy adaptations over space and time, with or without expected trade-offs in traits. Finally, our IBM can be extended to include characterizations of other biological processes (e.g., swimming behavior, Dekshenieks et al., 1996; Fiksen et al., 2007; Staaterman and Paris, 2013) as well as biophysical interactions such as patchiness, thermal and/or food controls on development (e.g., Dekshenieks et al., 1993) and light-dependent mortality (as above). In particular, our model may be extended to include characterizations of larval spatial patchiness to explore the role patchiness may play in increasing the effective mortality estimates for fish eggs and larvae (McGurk, 1986). Moreover, our tools and methods can be applied to address similar questions of biophysical controls on settlement success for benthic invertebrates also exhibiting biphasic life-histories (e.g., Gilbert et al., 2010).
Summary
We show that fundamental biophysical interactions can result in variation in settlement probability for marine species displaying a pelagic larval stage. The flexibility of our IBM along with high resolution spatial forcing allowed us to identify life history characteristics (e.g., birth date and PLD) that will result in the highest probability of successful recruitment and thus long-term persistence of reef fish populations for Hawai'i Island. We also used our model to identify possible mechanisms for the life history characteristics observed in the field (e.g., how advection may help shape spawning season and lunar-linked spawning behaviors) and demonstrated how mortality landscapes can favor morphological features (e.g., spine morphology; Morgan, 1989; Dekshenieks et al., 1997). Our modeling tool synthesizes current knowledge on reef fish ecology to test hypotheses that can direct future field and lab research to explain population dynamics and how larval fish use biophysical mechanisms in ways that minimize advective loss of larvae (e.g., Shulzitski et al., 2017). Moreover, we can use the model in future analyses to identify important knowledge gaps (e.g., environmentally dependent development rates, spatially and temporally varying mortality) needed to explore reef fish adaptive strategies and associated coral reef ecosystem dynamics.
Author Contributions
JW-A, AN, BP, and MH: Conceived of the study; JW-A, AN, and BP: Designed the study; BP: Provided high-resolution physical forcing estimates; JW-A and AN: Developed, implemented, and analyzed computational and statistical models; CC, JG, MH, MM, BP, and JW: Contributed data, theory, and interpretation; JW-A and AN: Drafted the article. All authors critically revised the article. All authors approved the final version of the article. Authorship order is by first-and-last-author-emphasis with middle authors alphabetized.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Funding to JW-A was provided by the National Science Foundation (NSF) grants OIA #0424599 and GEO #1565950 courtesy of the Center of Microbial Oceanography: Research and Education (CMORE) Scholars Program, Kamehameha Schools, Dr. Robert Toonen (NSF/OA #1416889), and the University of Hawai‘i Hsiao Endowment (courtesy of MH). This manuscript is IEA Contribution Number 2018_3.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2018.00065/full#supplementary-material
Footnotes
1. ^Prior to 2002 MA McManus published as MM Dekshenieks.
References
Augustin, N. H., Sauleau, E.-A., and Wood, S. N. (2012). On quantile plots for generalized linear models. Comput. Stat. Data Anal. 56, 2404–2409. doi: 10.1016/j.csda.2012.01.026
Bailey, K. M. (1984). Comparison of laboratory rates of predation on five species of marine larvae by three planktonic invertebrates: effects of larval size and vulnerability. Mar. Biol. 79, 303–309. doi: 10.1007/BF00393262
Bakun, A., and Broad, K. (2003). Environmental 'loopholes' and fish population dynamics: comparative pattern recognition with focus on El Nino effects in the Pacific. Fish. Oceanogr. 12, 458–473. doi: 10.1046/j.1365-2419.2003.00258.x
Balch, T., Hatcher, B. G., and Scheibling, R. E. (1999). A major settlement event associated with minor meteorologic and oceanographic fluctuations. Can. J. Zool. 77, 1657–1662. doi: 10.1139/z99-138
Banas, N. S., McDonald, P. S., and Armstrong, D. A. (2009). Green crab larval retention in Willapa Bay, Washington: an intensive Lagrangian modeling approach. Estuar. Coasts 32, 893–905. doi: 10.1007/s12237-009-9175-7
Bidegain, G., Bárcena, J. F., García, A., and Juanes, J. A. (2013). LARVAHS: predicting clam larval dispersal and recruitment using habitat suitability-based particle tracking model. Ecol. Modell. 268, 78–92. doi: 10.1016/j.ecolmodel.2013.07.020
Boehlert, G. W., and Mundy, B. C. (1996). Ichthyoplankton Vertical Distributions Near Oahu, Hawai‘i, 1985-1986: Data Report. NOAA Technical Memoir, NMFS-SWSC-235. 9 (Washington, DC: NOAA), 1148.
Bushnell, M. E., Claisse, J. T., and Laidley, C. W. (2010). Lunar and seasonal patterns in fecundity of an indeterminate, multiple-spawning surgeonfish, the yellow tang Zebrasoma flavescens. J. Fish Biol. 76, 1343–1361. doi: 10.1111/j.1095-8649.2010.02569.x
Caley, M. J., Carr, M. H., Hixon, M. A., Hughes, T. P., Jones, G. P., and Menge, B. A. (1996). Recruitment and the local dynamics of open marine populations. Annu. Rev. Ecol. Syst. 27, 477–500. doi: 10.1146/annurev.ecolsys.27.1.477
Christie, M. R., Tissot, B. N., Albins, M. A., Beets, J. P., Jia, Y., Ortiz, D. M., et al. (2010). Larval connectivity in an effective network of marine protected areas. PLoS ONE 5:e15715. doi: 10.1371/journal.pone.0015715
Claisse, J. T., Clark, T. B., Schumacher, B. D., McTee, S. A., Bushnell, M. E., Callan, C. K., et al. (2011). Conventional tagging and acoustic telemetry of a small surgeonfish, Zebrasoma flavescens, in a structurally complex coral reef environment. Environ. Biol. Fishes 91, 185–201. doi: 10.1007/s10641-011-9771-9
Claisse, J. T., McTee, S. A., and Parrish, J. D. (2009). Effects of age, size, and density on natural survival for an important coral reef fishery species, yellow tang, Zebrasoma flavescens. Coral Reefs 28, 95105 doi: 10.1007/s00338-008-0447-7
Colin, P. (2011). Timing and location of aggregation and spawning in reef fishes, in Reef Fish Spawning Aggregations: Biology, Research and Management, eds Y. Sadovy de Micheson and P. Colin (Dordrecht: Springer), 117–158.
Colin, P., and Clavijo, I. E. (1988). Spawning activity of fishes producing pelagic eggs on a shelf edge coral reef southwestern Puerto Rico. Bull. Mar. Sci. 43, 249–279.
Dekshenieks, M. M., Hofmann, E. E., Klinck, J. M., and Powell, E. N. (1996). Modeling the vertical distribution of oyster larvae in response to environmental conditions. Mar. Ecol. Prog. Ser. 136, 97–110. doi: 10.3354/meps136097
Dekshenieks, M. M., Hofmann, E. E., Klinck, J. M., and Powell, E. N. (1997). A modeling study of the effects of size-and depth-dependent predation on larval survival. J. Plankton Res. 19, 1583–1598. doi: 10.1093/plankt/19.11.1583
Dekshenieks, M. M., Hofmann, E. E., and Powell, E. N. (1993). Environmental effects on the growth and development of eastern oyster, Crassostrea virginica (Gmelin, 1791), larvae: a modeling study. J. Shellfish Res. 12, 241–254.
Domeier, M. L., and Colin, P. L. (1997). Tropical reef fish spawning aggregations: defined and reviewed. Bull. Mar. Sci. 60, 698–726.
Donahue, M. J., Karnauskas, M., Toews, C., and Paris, C. B. (2015). Location isn't everything: timing of spawning aggregations optimizes larval replenishment. PLoS ONE 10:e130694. doi: 10.1371/journal.pone.0130694
Efron, B., and Hastie, T. (2017). Computer Age Statistical Inference, Vol. 5. New York, NY: Cambridge University Press.
Fiksen, Ø., Jørgensen, C., Kristiansen, T., Vikebø, F., and Huse, G. (2007). Linking behavioural ecology and oceanography: larval behaviour determines growth, mortality and dispersal. Mar. Ecol. Prog. Ser. 347, 195–206. doi: 10.3354/meps06978
Fox, H. E., Haisfield, K. M., Brown, M. S., Stevenson, T. C., Tissot, B. N., Walsh, W. J., et al. (2012). Influences of oceanographic and meteorological features on reef fish recruitment in Hawai'i. Mar. Ecol. Prog. Ser. 463, 259–272. doi: 10.3354/meps09838
Fuiman, L. A., and Magurran, A. E. (1994). Development of predator defences in fishes. Rev. Fish Biol. Fish. 4, 145–183. doi: 10.1007/BF00044127
Gilbert, C. S., Gentleman, W. C., Johnson, C. L., DiBacco, C., Pringle, J. M., and Chen, C. (2010). Modelling dispersal of sea scallop (Placopecten magellanicus) larvae on Georges Bank: The influence of depth-distribution, planktonic duration and spawning seasonality. Prog. Oceanogr. 87, 37–48. doi: 10.1016/j.pocean.2010.09.021
Greer, A., Woodson, C., Guigand, C., and Cowen, R. (2016). Larval fishes utilize Batesian mimicry as a survival strategy in the plankton. Mar. Ecol. Prog. Ser. 551, 1–12. doi: 10.3354/meps11751
Gross, H. P. (1978). Natural selection by predators on the defensive apparatus of the three-spined stickleback, Gasterosteus aculeatus L. Can. J. Zool. 56, 398–413. doi: 10.1139/z78-058
Holt, G. J., and Riley, C. M. (2001). Laboratory spawning of Coral reef fishes: effects of temperature and photoperiod, in Proceedings of the 28th US-Japan Natural Resources Aquaculture Panel: Spawning and Maturation of Aquaculture Species. UJNR Technical Report, 33–38.
Houde, E. D. (1989). Comparative growth, mortality, and energetics of marine fish larvae: temperature and implied latitudinal effects. Fish. Bull. 87, 471–495.
Houde, E. D. (2009). Recruitment variability, in Fish Reproductive Biology: Implications for Assessment and Management,” eds T. Jakobsen, M. J. Fogarty, B. A. Megrey, and E. Moksness (Oxford, UK: Wiley-Blackwell), 91–171.
Irigoien, X., Fiksen, Ø., Cotano, U., Uriarte, A., Alvarez, P., Arrizabalaga, H., et al. (2007). Could biscay bay anchovy recruit through a spatial loophole? Prog. Oceanogr. 74, 132–148. doi: 10.1016/j.pocean.2007.04.011
James, M. K., Armsworth, P. R., Mason, L. B., and Bode, L. (2002). The structure of reef fish metapopulations: modeling larval dispersal and retention patterns. Proc. R. Soc. Lond. B Biol. Sci. 269, 2079–2086. doi: 10.1098/rspb.2002.2128
Januszkiewicz, A. J., and Robinson, B. W. (2007). Divergent walleye (Sander vitreus)-mediated inducible defenses in the centrarchid pumpkinseed sunfish (Lepomis gibbosus). Biol. J. Linn. Soc. 90, 25–36. doi: 10.1111/j.1095-8312.2007.00708.x
Johannes, R. E. (1978). Reproductive strategies of coastal marine fishes in the tropics. Environ. Biol. Fishes 3, 65–84. doi: 10.1007/BF00006309
Jones, G. P., Planes, S., and Thorrold, S. R. (2005). Coral reef fish larvae settle close to home. Curr. Biol. 15, 1314–1318. doi: 10.1016/j.cub.2005.06.061
Landry, M. R. (1976). The structure of marine ecosystems: an alternative. Mar. Biol. 35, 1–7. doi: 10.1007/BF00386669
Leis, J., and Carson-Ewart, B. (2001). Behaviour of pelagic larvae of four coral-reef fish species in the ocean and an atoll lagoon. Coral Reefs 19, 247–257. doi: 10.1007/s003380000115
Lester, S. E., and Ruttenberg, B. I. (2005). The relationship between pelagic larval duration and range size in tropical reef fishes: a synthetic analysis. Proc. R. Soc. Lond. B Biol. Sci. 272, 585–591. doi: 10.1098/rspb.2004.2985
Lobel, P. S. (1989). Ocean current variability and the spawning season of Hawaiian reef fishes. Environ. Biol. Fishes 24, 161–171. doi: 10.1007/BF00001221
Lobel, P. S., and Robinson, A. R. (1986). Transport and entrapment of fish larvae by ocean mesoscale eddies and currents in Hawaiian waters. Deep Sea Res. A. Oceanogr. Res. Pap. 33, 483–500. doi: 10.1016/0198-0149(86)90127-5
Luiz, O. J., Allen, A. P., Robertson, D. R., Floeter, S. R., Kulbicki, M., Vigliola, L., et al. (2013). Adult and larval traits as determinants of geographic range size among tropical reef fishes. Proc. Natl. Acad. Sci. U.S.A. 110, 16498–16502. doi: 10.1073/pnas.1304074110
Maiti, K., Benitez-Nelson, C., Rii, Y. M., and Bidigare, R. R. (2008). Influence of a mature cyclonic eddy on particle export in the lee of Hawaii. Deep-Sea Res. II 55, 1445–1460. doi: 10.1016/j.dsr2.2008.02.008
Matsuura, Y., and Katsuragawa, M. (1981). Larvae and juveniles of grey triggerfish, Balistes capriscus, from Southern Brazil. Jap. J. Ichthyol. 28, 267–275.
McCormick, M. I., and Molony, B. W. (1995). Influence of water temperature during the larval stage on size, age and body condition of a tropical reef fish at settlement. Mar. Ecol. Prog. Ser. 118, 59–68. doi: 10.3354/meps118059
McGurk, M. D. (1986). Natural mortality of marine pelagic fish eggs and larvae: role of spatial patchiness. Mar. Ecol. Prog. Ser. 34, 227–242. doi: 10.3354/meps034227
McManus, M. A., and Woodson, C. B. (2012). Review: Plankton distribution and oceanic dispersal. J. Exp. Biol. 215, 1008–1016. doi: 10.1242/jeb.059014
Moodie, G. E. E. (1972). Predation, natural selection and adaptation in an unusual threespine stickleback. Heredity 28, 155–167. doi: 10.1038/hdy.1972.21
Morgan, S. (1989). Adaptive significance of spination in estuarine crab zoeae. Ecology 70, 464–482. doi: 10.2307/1937551
Moser, H. G. (1981). Morphological and functional aspects of marine fish larvae, in Marine Fish Larvae. Morphology, Ecology and Relation to Fisheries, ed R. Lasker (Seattle, WA: University of Washington Press), 89–131.
Munch, S. B., and Conover, D. O. (2004). Nonlinear growth cost in Menidia menidia: theory and empirical evidence. Evolution 58, 661–664. doi: 10.1111/j.0014-3820.2004.tb01689.x
Neuheimer, A. B., Gentleman, W. C., Pepin, P., and Head, E. J. H. (2010). How to build and use individual-based models (IBMs) as hypothesis testing tools. J. Mar. Syst. 81, 122–133. doi: 10.1016/j.jmarsys.2009.12.009
North, E. W., Schlag, Z., Hood, R. R., Li, M., Zhong, L., Gross, T., et al. (2008). Vertical swimming behavior influences the dispersal of simulated oyster larvae in a coupled particle-tracking and hydrodynamic model of Chesapeake Bay. Mar. Ecol. Prog. Ser. 359, 99–115. doi: 10.3354/meps07317
Paris, C. B., Cowen, R. K., Claro, R., and Lindeman, K. C. (2005). Larval transport pathways from Cuban snapper (Lutjanidae) spawning aggregations based on biophysical modeling. Mar. Ecol. Prog. Ser. 296, 93–106. doi: 10.3354/meps296093
Paris, C. B., Helgers, J., Van Sebille, E., and Srinivasan, A. (2013). Connectivity Modeling System: a probabilistic modeling tool for the multi-scale tracking of biotic and abiotic variability in the ocean. Environ. Modell. Softw. 42, 47–54. doi: 10.1016/j.envsoft.2012.12.006
Patzert, W. C. (1969). Eddies in Hawaiian Islands. Report HIG-69-8, Hawaii Institute of Geophysics, University of Hawaii, Honolulu, HI.
Platt, T., Fuentes-Yaco, C., and Frank, K. T. (2003). Marine ecology: spring algal bloom and larval fish survival. Nature 423, 398–399. doi: 10.1038/423398b
Polovina, J. J., Howell, E., Kobayashi, D. R., and Seki, M. P. (2001). The transition zone chlorophyll front, a dynamic global feature defining migration and forage habitat for marine resources. Prog. Oceanogr. 49, 469–483. doi: 10.1016/S0079-6611(01)00036-2
Price, S. A., Friedman, S. T., and Wainwright, P. C. (2015). How predation shaped fish: the impact of fin spines on body form evolution across teleosts. Proc. R. Soc. B Biol. Sci. 282:20151428. doi: 10.1098/rspb.2015.1428
Puritz, J. B., Gold, J. R., and Portnoy, D. S. (2016). Fine-scale partitioning of genomic variation among recruits in an exploited fishery: causes and consequences. Sci. Rep. 6:36095. doi: 10.1038/srep36095
Pusack, T. J., Christie, M. R., Johnson, D. W., Stallings, C. D., and Hixon, M. A. (2014). Spatial and temporal patterns of larval dispersal in a coral-reef fish metapopulation: evidence of variable reproductive success. Mol. Ecol. 23, 3396–3408. doi: 10.1111/mec.12824
Qiu, B., Koh, D. A., Lumpkin, C., and Flament, P. (1997). Existence and formation mechanism of the North Hawaiian Ridge Current. J. Phys. Oceanogr. 27, 431–444. doi: 10.1175/1520-0485(1997)027<0431:EAFMOT>2.0.CO;2
R Core Team (2016). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. Available online at: https://www.R-project.org/
Shulzitski, K., Sponaugle, S., Hauff, M., Walter, K. D., and Cowen, R. K. (2016). Encounter with mesoscale eddies enhances survival to settlement in larval coral reef fishes. Proc. Natl. Acad. Sci. U.S.A. 113, 6928–6933. doi: 10.1073/pnas.1601606113
Shulzitski, K., Sponaugle, S., Hauff, M., Walter, K. D., D'Alessandro, E. K., and Cowen, R. K. (2017). Patterns in larval reef fish distributions and assemblages, with implications for local retention in mesoscale eddies. Can. J. Fish. Aquat. Sci. 75, 180–192. doi: 10.1139/cjfas-2016-0304
Sogard, S. M. (1997). Size-selective mortality in the juvenile stage of teleost fishes: a review. Bull. Mar. Sci. 60. 1129–1157.
Souza, J. M. A. C., Powell, B., Castillo-Trujillo, A. C., and Flament, P. (2015). The vorticity balance of the ocean surface in Hawaii from a regional reanalysis. J. Phys. Oceanogr. 45, 424–440. doi: 10.1175/JPO-D-14-0074.1
Staaterman, E., and Paris, C. B. (2013). Modelling larval fish navigation: the way forward. ICES J. Mar. Sci. 71, 918–924. doi: 10.1093/icesjms/fst103
Storlazzi, C. D., McManus, M. A., Logan, J. B., and McLaughlin, B. E. (2006). Cross-shore velocity shear, eddies and heterogeneity in water column properties over fringing coral reefs: West Maui, Hawaii. Cont. Shelf Res. 26, 401–421. doi: 10.1016/j.csr.2005.12.006
Toonen, R. J., Andrews, K. R., Baums, I. B., Bird, C. E., Concepcion, G. T., Daly-Engel, T. S., et al. (2011). Defining boundaries for ecosystem-based management: a multispecies case study of marine connectivity across the Hawaiian Archipelago. J. Mar. Biol. 2011, 1–13. doi: 10.1155/2011/460173
Victor, B. C. (1983). Recruitment and population dynamics of a coral reef fish. Science 219, 419–420. doi: 10.1126/science.219.4583.419
Walsh, W. J. (1984). Aspects of Nocturnal Shelter, Habitat Space, and Juvenile Recruitment in Hawaiian Coral reef Fishes. Dissertation/PhD thesis, University of Hawaii, Honolulu, HI.
Walsh, W. J. (1987). Patterns of recruitment and spawning in Hawaiian reef fishes. Environ. Biol. Fishes 18, 257. doi: 10.1007/BF00004879
Warner, R. R. (1997). Evolutionary ecology: how to reconcile pelagic dispersal with local adaptation. Coral Reefs 16, S115–S120. doi: 10.1007/s003380050247
Weber, M. J., and Brown, M. L. (2012). Effects of predator species, vegetation and prey assemblage on prey preferences of predators with emphasis on vulnerability of age-0 common carp. Fish. Manag. Ecol. 19, 293–300. doi: 10.1111/j.1365-2400.2011.00838.x
Wood, S. N. (2011). Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. J. R. Stat. Soc. 73:336. doi: 10.1111/j.1467-9868.2010.00749.x
Keywords: early life history, settlement, recruitment, pelagic larval duration, reef fish, individual-based model, connectivity, Hawai‘i Island
Citation: Wong-Ala JATK, Comfort CM, Gove JM, Hixon MA, McManus MA, Powell BS, Whitney JL and Neuheimer AB (2018) How Life History Characteristics and Environmental Forcing Shape Settlement Success of Coral Reef Fishes. Front. Mar. Sci. 5:65. doi: 10.3389/fmars.2018.00065
Received: 30 October 2017; Accepted: 12 February 2018;
Published: 01 March 2018.
Edited by:
Claire Beatrix Paris, University of Miami, United StatesReviewed by:
Gorka Bidegain, University of Southern Mississippi, United StatesØyvind Fiksen, University of Bergen, Norway
Copyright © 2018 Wong-Ala, Comfort, Gove, Hixon, McManus, Powell, Whitney and Neuheimer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jennifer A. T. K. Wong-Ala, amVubndvbmdhbGFAZ21haWwuY29t
†Present Address: Jennifer A. T. K. Wong-Ala, College of Earth, Ocean, and Atmospheric Sciences, Oregon State University, Corvallis, OR, United States
 Jennifer A. T. K. Wong-Ala
Jennifer A. T. K. Wong-Ala Christina M. Comfort
Christina M. Comfort Jamison M. Gove
Jamison M. Gove Mark A. Hixon
Mark A. Hixon Margaret A. McManus1
Margaret A. McManus1 Brian S. Powell
Brian S. Powell Anna B. Neuheimer
Anna B. Neuheimer